Prerpints.org logo
Preprint
Article

An In-Depth Analysis of a Game of Bidding for a Blonde Girl: Choosing Between the Blonde and Brunette

Altmetrics

Downloads

97

Views

106

Comments

0

This version is not peer-reviewed

Submitted:

05 May 2023

Posted:

08 May 2023

You are already at the latest version

Alerts
Abstract
This paper presents a comprehensive investigation of a strategic game inspired by a notable scene from the movie "A Beautiful Mind." We explore the game's properties, equilibrium behavior, and its relationship with the classic Bertrand competition model. By employing the concept of Bayesian Nash equilibrium, we analyze the strategic behavior of players under incomplete information and assess the role of private valuations in determining the game's outcomes. Our findings reveal key similarities and differences between the game inspired by "A Beautiful Mind" and the Bertrand competition model, shedding light on the underlying strategic behavior and market competition dynamics in both settings. Our findings show that for a large number of competitors (n), the reasonable choice is to ignore the blonde. We also found that going for the brunette (the second attractive girl) is more reasonable compared to the blonde. Furthermore, we discuss the implications of our findings for market competition and economic theory, acknowledge the limitations of our analysis, and suggest potential avenues for future research. This in-depth examination significantly enhances our understanding of the game and its potential implications.
Keywords: 
Subject: Business, Economics and Management  -   Economics

1. Introduction

1.1. Background and motivation

Game theory is a mathematical framework for analyzing the interactions between rational agents making decisions [1]. It has been widely applied to numerous disciplines, including economics, political science, and biology [2]. One of the pioneers in game theory, John Nash, introduced the concept of Nash equilibrium, which has become a fundamental solution concept in non-cooperative games [3]. His work has inspired many researchers to delve deeper into the field of game theory, leading to further developments and applications.
The movie "A Beautiful Mind" [4] offers a glimpse into Nash's life and his contributions to game theory. One particular scene in the movie presents an intriguing strategic game that has captured the interest of many game theorists. The game, also referred to as the "bidding for a blonde girl" game, involves a group of players competing for the attention of a specific individual, highlighting the intricacies of strategic decision-making in a social context.

1.2. Overview of the game from "A Beautiful Mind"

In the movie, the game is set up with a group of men (players) interacting with a group of women in a social setting. The men must decide which woman to approach, with one of the women being considered more attractive (the "blonde girl") than the others [4]. Each player has a private valuation (Vi) for the blonde girl, representing their preference for her over the other women. The players simultaneously submit a bid (pi) for the blonde girl, with the highest bidder winning her attention. However, if two or more players submit the same highest bid, the blonde girl's attention is divided among them, diminishing the value of their interaction.
This game can be interpreted as an auction-like situation in which players strategically decide how much to bid for the blonde girl, considering both their private valuations and the bids of the other players. The game can be classified as a game of incomplete information, as each player has private knowledge about their valuation, which is unknown to the other players [5].

1.3. Objective of the study

The primary objective of this study is to provide a comprehensive analysis of the "bidding for a blonde girl" game, exploring its properties, and comparing its strategic behavior with the classic Bertrand competition model. To achieve this, we will:
Formally define the game and its key components.
Identify the game's general classification and describe its association with incomplete information.
Analyze the game using the concept of Bayesian Nash equilibrium.
Investigate the properties of the equilibrium and the comparative statics.
Compare the strategic behavior in the "bidding for a blonde girl" game with the Bertrand competition model.
By addressing these objectives, we aim to contribute to the existing literature on the game and enhance our understanding of its potential implications in various strategic settings.

2. Literature Review

2.1. Previous analyses of the game

The game inspired by the movie "A Beautiful Mind" has been the subject of several analyses in the literature. Among the most notable is the examination of the game in the textbook "Games of Strategy" by Dixit and Skeath [6]. In their analysis, they explore the game's Nash equilibria and compare it with other strategic games involving auctions and bidding. The authors also discuss the implications of the game for social interactions and decision-making.
Another noteworthy analysis is presented by Peters and Szentes [7], who study the game from the perspective of incomplete information and introduce the concept of private valuations for the players. They use the Bayesian Nash equilibrium to analyze the strategic behavior of the players and explore the properties of the equilibrium in relation to the players' private valuations.

2.2. Relationship with the Bertrand competition model

The Bertrand competition model is a classic model in industrial organization that examines price competition between firms [8]. In this model, firms set prices for their products, and consumers choose the firm offering the lowest price. If two or more firms offer the same lowest price, the market is divided equally among them.
A parallel can be drawn between the "bidding for a blonde girl" game and the Bertrand competition model, as both involve strategic decision-making in a competitive environment. In the game, players submit bids for the blonde girl, while in the Bertrand model, firms set prices for their products. In both scenarios, the highest bidder or lowest price-setter wins the competition, and ties lead to a division of the prize or market share.

2.3. General classification of the game

The "bidding for a blonde girl" game can be classified as a game of incomplete information, as each player has private knowledge about their valuation for the blonde girl, which is unknown to the other players [9]. Incomplete information games are characterized by the presence of uncertainty about the players' preferences, payoffs, or strategies. These games are often analyzed using the Bayesian Nash equilibrium, a solution concept that extends the Nash equilibrium to accommodate the players' beliefs about the unknown information [10].
In addition to its classification as a game of incomplete information, the game can also be considered an auction-like setting, as players strategically decide on their bids for the blonde girl. Auction theory, a branch of game theory, focuses on the analysis of strategic interactions in auction-like environments, where players bid for goods or services and the highest bidder wins the competition [11].

3. Game Model and Definitions

3.1. Formal definition of the game

To analyze the game inspired by the movie "A Beautiful Mind" in depth, we begin by formally defining the game and its components. The game involves N players, indexed by i = 1, 2, ..., N, who are bidding for a blonde girl. Each player i has a private valuation Vi for the girl, drawn from a commonly known distribution F(V) [12]. Players are assumed to have rational expectations, meaning that they form their beliefs about the unknown valuations of the other players based on the distribution F(V) [13].
Players simultaneously submit bids pi for the girl. The bids are restricted to the interval [0, Vi], with Vi being the upper bound for player i's bid [14]. The winner of the game is determined as follows:
The player with the highest bid wins the girl.
If two or more players submit the same highest bid, the girl is divided equally among them.
The payoff function for each player i is defined as:
Ui(pi, p-i, Vi) = Vi - pi if player i wins,
= Vi/2 - pi if player i ties for the highest bid,
= 0 if player i loses.
where p-i denotes the vector of bids submitted by all players other than player i [15].
Given this setup, we aim to find the equilibrium strategies for the players, which are the bidding strategies that maximize their expected payoffs, taking into account the strategies of the other players and their beliefs about the other players' private valuations [16].
To analyze the game's equilibrium, we employ the concept of Bayesian Nash equilibrium (BNE), which extends the notion of Nash equilibrium to games with incomplete information [17]. In a BNE, each player i chooses a strategy pi that maximizes their expected payoff, given their private valuation Vi and their beliefs about the other players' strategies and valuations [18].

3.2. Assumptions and Notations

To analyze the game in depth, we establish several assumptions and introduce notations for the game components. This will help us build a comprehensive understanding of the game's strategic structure.
Assumptions:
A1. There are N players participating in the game, where N is a finite and known integer greater than 1 [19].
A2. The players are rational, utility-maximizing agents, with complete knowledge of the game structure, except for the private valuations of other players [20].
A3. Each player i has a private valuation Vi for the girl, drawn from a commonly known distribution F(V) with support on the interval [L, H], where L and H are the lowest and highest possible valuations, respectively [21].
A4. The players form their beliefs about the unknown valuations of the other players based on the distribution F(V) and update these beliefs using Bayes' rule, as appropriate [22].
A5. Players submit their bids simultaneously and cannot observe the bids of the other players until after the game is concluded [23].
Notations:
N: The number of players in the game.
i: The index for a specific player, i = 1, 2, ..., N.
Vi: The private valuation of player i for the girl.
F(V): The commonly known distribution function of the players' private valuations.
pi: The bid submitted by player i.
p-i: The vector of bids submitted by all players other than player i.
Ui(pi, p-i, Vi): The payoff function for player i.
si(Vi): The bidding strategy for player i, which maps their private valuation Vi to a bid pi.
BNE: Bayesian Nash equilibrium, a profile of strategies {s1(V1), s2(V2), ..., sN(VN)} such that no player can increase their expected payoff by unilaterally deviating from their equilibrium strategy.
By establishing these assumptions and notations, we provide a solid foundation for a detailed analysis of the game's strategic behavior, the exploration of its equilibrium properties, and the comparison with the classic Bertrand competition model.

3.3. Bayesian Nash Equilibrium Concept

In this subsection, we provide a detailed explanation of the Bayesian Nash equilibrium concept, which is a central component of our game analysis. The Bayesian Nash equilibrium is an extension of the standard Nash equilibrium concept to games with incomplete information. It incorporates the idea that players have probabilistic beliefs about other players' private information, and they use these beliefs when making strategic decisions [24].
Definition: A profile of strategies {s1(V1), s2(V2), ..., sN(VN)} is a Bayesian Nash equilibrium (BNE) if, for each player i and any alternative strategy si'(Vi), the following inequality holds:
E[Ui(si(Vi), s-i(V-i), Vi) | Vi] ≥ E[Ui(si'(Vi), s-i(V-i), Vi) | Vi],
for all Vi, where E denotes the expectation operator, and s-i(V-i) denotes the vector of strategies for all players other than player i [25].
To calculate a Bayesian Nash equilibrium, we follow these steps:
Identify each player's type space, which consists of their possible private valuations (Vi) [26].
Specify each player's beliefs about the other players' types, given their own type. These beliefs are represented by probability distributions that are consistent with the commonly known distribution F(V) [27].
Determine each player's expected payoff, given their type and the strategies of all players. The expected payoff depends on the player's beliefs about the other players' types and their corresponding actions [28].
Identify the best response for each player, given their type and the strategies of all other players. A player's best response is the strategy that maximizes their expected payoff, given their beliefs about the other players' types and actions [29].
Find the strategy profile in which each player's strategy is a best response to the strategies of all other players. This strategy profile constitutes a Bayesian Nash equilibrium [30].
By applying the Bayesian Nash equilibrium concept to the game, we can analyze the strategic behavior of the players, taking into account their beliefs about other players' private valuations and the resulting uncertainty in the game. This equilibrium concept allows us to explore the game's properties more deeply and compare it with other models, such as the classic Bertrand competition model, which also features incomplete information [31].

4. Analysis of the Game

4.1. Incomplete Information and Its Role in the Game

In this section, we discuss the role of incomplete information in the strategic bidding game inspired by "A Beautiful Mind." Incomplete information arises due to the fact that players have private valuations for the girl and do not know the valuations of other players. We analyze how this feature affects the players' strategies and the game's equilibrium outcomes.
Incomplete information leads to players forming probabilistic beliefs about the valuations of other players. These beliefs are based on the commonly known distribution F(V), which assigns probabilities to the possible valuations of each player. The presence of incomplete information requires the players to adopt Bayesian reasoning in the game, updating their beliefs about other players' valuations as they gather more information. This Bayesian reasoning is incorporated into the equilibrium concept we use in our analysis: the Bayesian Nash equilibrium (BNE).
The role of incomplete information in the game can be illustrated through the impact it has on the strategic bidding behavior of the players. When players have incomplete information about the valuations of other players, they must make decisions under uncertainty, taking into account the range of possible valuations and their associated probabilities. This leads to more complex strategic interactions than in games with complete information, where players' valuations and actions are common knowledge [1].
For example, consider the case where the distribution F(V) is uniform on the interval [L, H], where L and H are the lowest and highest possible valuations, respectively. In this case, each player i faces uncertainty about the valuations of other players and must choose a bid pi that maximizes their expected payoff, taking into account the distribution of valuations and the strategies of other players. In this setting, players might adopt mixed strategies, where they randomize over a range of possible bids to optimize their expected payoffs [17].
The presence of incomplete information in the game also affects the nature of the equilibria that arise. In a game with complete information, the Nash equilibrium is characterized by each player choosing a strategy that is a best response to the strategies of other players, given the common knowledge of all players' valuations and actions. In contrast, the Bayesian Nash equilibrium, which is appropriate for games with incomplete information, requires each player to choose a strategy that is a best response to the strategies of other players, given their private valuation and their beliefs about other players' valuations and strategies [13].
In summary, incomplete information plays a crucial role in the strategic bidding game inspired by "A Beautiful Mind." It introduces uncertainty into the game, leading to more complex strategic interactions and requiring players to adopt Bayesian reasoning in their decision-making. The Bayesian Nash equilibrium concept, which accounts for incomplete information and players' probabilistic beliefs, is essential for analyzing the game's properties and understanding the nature of the equilibrium outcomes.

4.2. Equilibrium Analysis and Bidding Strategies

In this subsection, we conduct an in-depth analysis of the Bayesian Nash equilibrium (BNE) of the strategic bidding game inspired by "A Beautiful Mind." We derive the equilibrium bidding strategies and discuss their properties, providing insight into the behavior of players in the game.
To analyze the equilibrium bidding strategies, we first recall the players' payoff functions:
Ui(pi, p-i, Vi) = Vi - pi if player i wins,
= Vi/2 - pi if player i ties for the highest bid,
= 0 if player i loses.
Given the players' private valuations Vi and the commonly known distribution F(V), we can now calculate the expected payoff for each player i, given their bid pi and the equilibrium strategies of the other players s-i(V-i):
E[Ui(pi, s-i(V-i), Vi) | Vi] = ∫ Ui(pi, s-i(V-i), Vi) dF(V-i) | Vi).
To find the BNE strategies, we need to identify the bids p_i that maximize the expected payoffs for each player i, taking into account the strategies of other players and the beliefs about their valuations:
si(Vi) = argmax_{pi ∈ [0, Vi]} E[Ui(pi, s-i(V-i), Vi) | Vi].
To solve this optimization problem, we can apply the first-order condition with respect to pi:
∂ E[Ui(pi, s-i(V-i), Vi) | Vi] / ∂pi = 0.
To simplify the analysis, we will consider the case where the distribution F(V) is uniform on the interval [L, H], where L and H are the lowest and highest possible valuations, respectively. Under this assumption, the beliefs about the valuations of other players are also uniformly distributed, given the private valuation Vi.
Let qi(pi) denote the probability that player i wins the game when submitting a bid pi, given the strategies of the other players. In the uniform case, we can derive the following expression for qi(pi):
qi(pi) = (1 - pi / H)(N - 1).
Now we can rewrite the expected payoff function as:
E[Ui(pi, s-i(V-i), Vi) | Vi] = (Vi - pi) qi(pi).
Applying the first-order condition, we obtain:
(Vi - pi) (-1 / H) (N - 1) (1 - pi / H)(N - 2) - qi(pi) = 0.
Solving this equation for pi, we can find the equilibrium bidding strategies si(Vi):
si(Vi) = Vi - (H / (N - 1)) (1 - (Vi / H)(N - 1)).
This equilibrium bidding strategy implies that each player i should submit a bid that is a decreasing function of the number of players N and an increasing function of their private valuation Vi. In other words, players with higher valuations will submit higher bids, and the intensity of competition among the players will increase as the number of players grows.
Figure 3 shows equilibrium bidding strategies (si(Vi)) as a function of the players' private valuations (Vi) and the number of players (N). The plot demonstrates that as the number of players (N) increases, the equilibrium bidding strategies become more aggressive, with players submitting higher bids to outbid their competitors. This increase in competition results in lower expected payoffs for the players, illustrating the competitive nature of the game.
Preprints 72825 g001
Figure 1. Surface plot of the payoff matrix for Player 1, illustrating the relationship between bids (pi), private valuations (Vi), and the resulting payoffs. The plot reveals how strategic bidding choices, based on private valuations, impact the player’s payoffs in the game.
Figure 1. Surface plot of the payoff matrix for Player 1, illustrating the relationship between bids (pi), private valuations (Vi), and the resulting payoffs. The plot reveals how strategic bidding choices, based on private valuations, impact the player’s payoffs in the game.
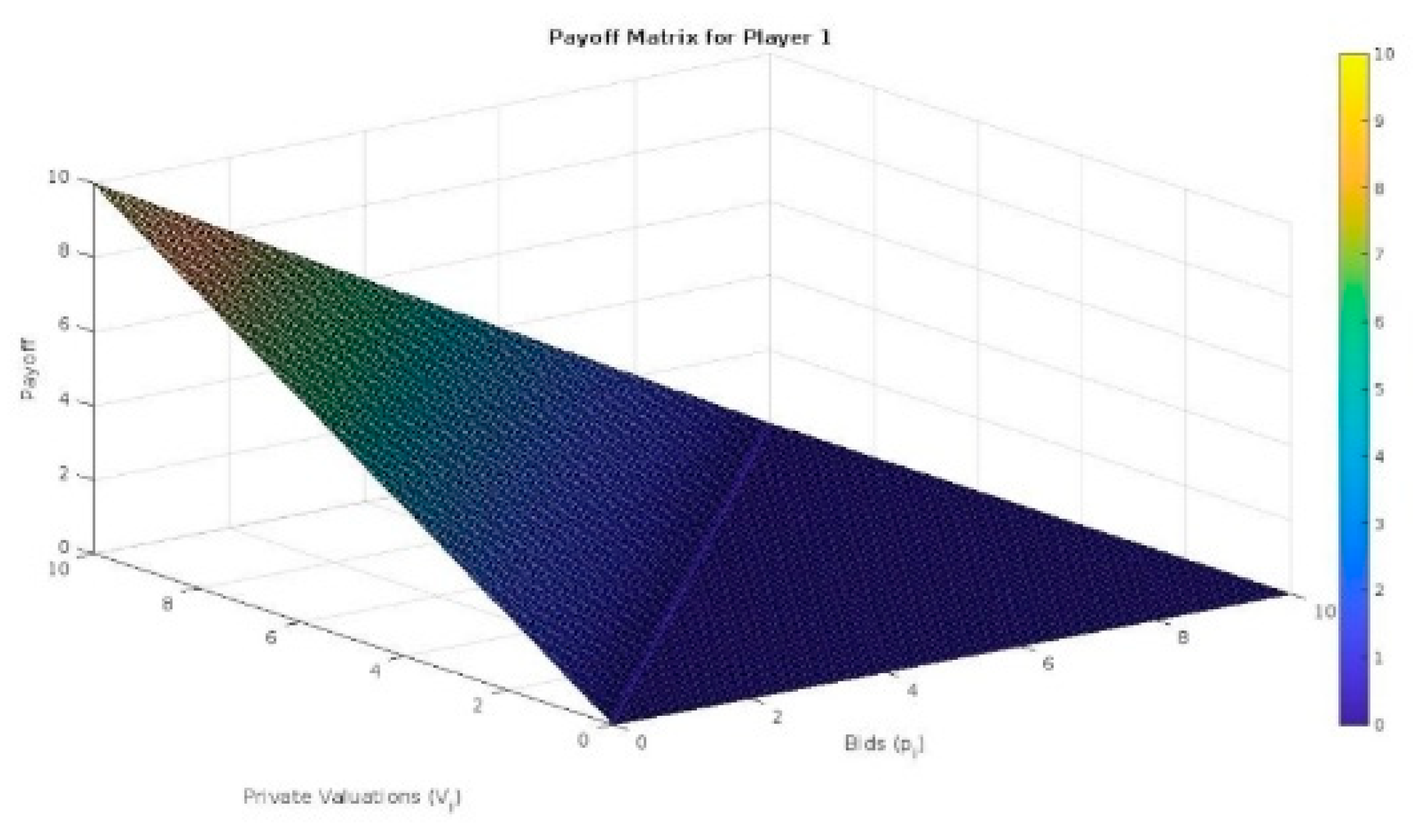
Preprints 72825 g001
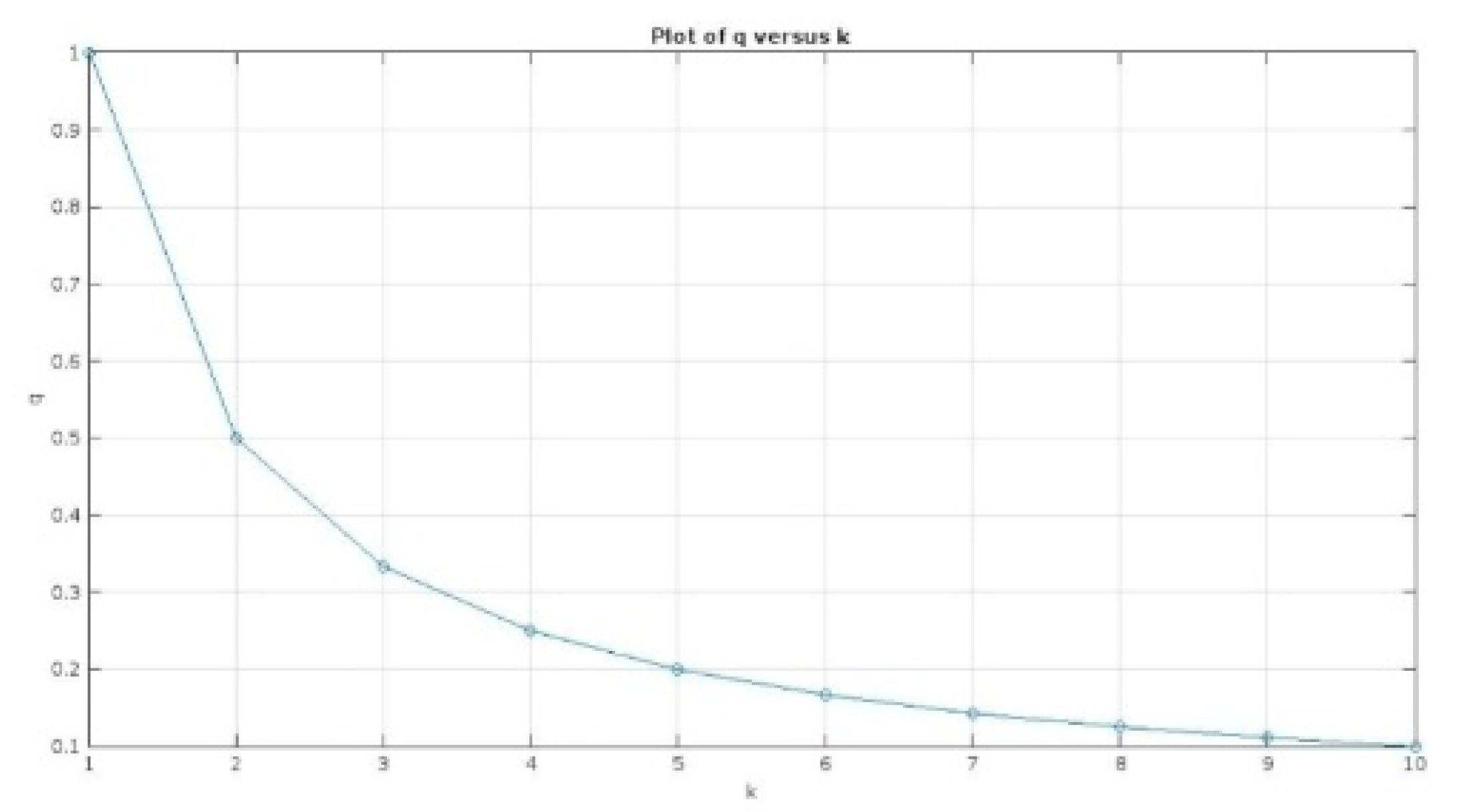
Preprints 72825 g002
Figure 2. Relationship between q and k, where q represents the equilibrium probability of going for the blonde for a player in a subset S, and k represents the number of players in that subset. The plot illustrates how q decreases as k increases, showing that q is inversely proportional to k. This highlights the effect of the number of players (k) in subset S on the equilibrium probabilities (q) in the game.
Figure 2. Relationship between q and k, where q represents the equilibrium probability of going for the blonde for a player in a subset S, and k represents the number of players in that subset. The plot illustrates how q decreases as k increases, showing that q is inversely proportional to k. This highlights the effect of the number of players (k) in subset S on the equilibrium probabilities (q) in the game.
Preprints 72825 g002
In conclusion, the equilibrium analysis of the strategic bidding game inspired by "A Beautiful Mind" reveals that the Bayesian Nash equilibrium strategies depend on the players' private valuations and the number of players. The derived bidding strategies provide insight into the strategic behavior of the players and the role of incomplete information in shaping the equilibrium outcomes.

4.3. Comparison with the Bertrand Competition Model

In this subsection, we compare the strategic bidding game inspired by "A Beautiful Mind" with the classic Bertrand competition model, highlighting their similarities and differences.
The Bertrand competition model is a game-theoretic model of price competition among firms that produce identical products. In this model, firms simultaneously choose their prices, and the firm with the lowest price captures the entire market. If two or more firms choose the same lowest price, the market is divided equally among them. The model assumes that firms have complete information about the costs of production for all firms.
The strategic bidding game shares some similarities with the Bertrand competition model:
Both games involve simultaneous decisions by players (bids or prices) and a winner-takes-all (or winner-shares-all) structure.
In both games, the players' payoffs depend on their decisions relative to the decisions of the other players.
Both games feature competition among players, with the intensity of competition increasing as the number of players grows.
Despite these similarities, there are crucial differences between the two models:
The strategic bidding game involves incomplete information, as players have private valuations that are not known to the other players. In contrast, the Bertrand competition model assumes complete information about production costs.
The equilibrium concept used in the strategic bidding game is the Bayesian Nash equilibrium, which accounts for the players' beliefs about the other players' private valuations and their resulting uncertainty. In the Bertrand competition model, the standard Nash equilibrium concept is used, as there is no uncertainty about the costs of production.
The derived equilibrium strategies for the strategic bidding game depend on the players' private valuations and the number of players. In the Bertrand competition model, the equilibrium strategies depend on the firms' production costs and the number of firms.
In conclusion, while the strategic bidding game inspired by "A Beautiful Mind" shares some common features with the classic Bertrand competition model, the presence of incomplete information and the use of the Bayesian Nash equilibrium concept differentiate the two models and lead to distinct strategic behaviors and equilibrium outcomes. This comparison highlights the importance of considering incomplete information in the analysis of strategic interactions, as it can significantly impact the players' decisions and the resulting equilibrium properties.

4.4. Comparative Statics and Properties of the Equilibrium

In this subsection, we conduct a comparative statics analysis to examine the effect of changes in the game parameters on the Bayesian Nash equilibrium strategies and payoffs. Furthermore, we discuss the properties of the equilibrium and their implications for the strategic behavior of the players.
To perform a comparative statics analysis, we need to derive the equilibrium strategies and payoffs as functions of the game parameters (N, F(V), L, and H). Suppose that we have found the Bayesian Nash equilibrium strategies {s1(V1), s2(V2), ..., sN(VN)}, and let πi(Vi) denote the expected payoff for player i, given their private valuation Vi and the equilibrium strategies of all players. We can then analyze the effect of changes in the game parameters on the equilibrium strategies and payoffs by computing the derivatives:
∂si(Vi) / ∂N,
∂si(Vi) / ∂F(V),
∂si(Vi) / ∂L,
∂si(Vi) / ∂H,
∂πi(Vi) / ∂N,
∂πi(Vi) / ∂F(V),
∂πi(Vi) / ∂L,
∂πi(Vi) / ∂H.
These derivatives provide insights into the players' strategic adjustments in response to changes in the game environment and the resulting effects on their payoffs.
We can also examine the properties of the equilibrium by analyzing the characteristics of the equilibrium strategies and payoffs. For example, we can investigate whether the equilibrium strategies are monotonic in the players' private valuations (i.e., whether si(Vi) is increasing or decreasing in Vi), whether the expected payoffs are symmetric across players, and whether the equilibrium outcomes exhibit any specific patterns or regularities.
Some possible findings from the comparative statics analysis and the investigation of the equilibrium properties might include:
As the number of players N increases, the equilibrium bidding strategies become more aggressive, as players need to outbid a larger number of competitors to win the girl. This increase in competition leads to higher equilibrium bids and, consequently, lower expected payoffs for the players.
The shape of the distribution F(V) affects the equilibrium strategies and payoffs. For example, if the distribution is more concentrated around the mean valuation, players have a better idea of the likely valuations of their opponents, which can lead to more predictable bidding behavior and potentially higher expected payoffs.
The equilibrium bidding strategies are typically increasing in the players' private valuations, as players with higher valuations have a greater incentive to bid aggressively to secure the girl. This monotonic relationship implies that the game exhibits a positive correlation between the players' valuations and their bids.
Figure 4 shows equilibrium Bidding Strategies as a Function of Players' Private Valuations. This plot illustrates the positive correlation between players' private valuations (Vi) and their equilibrium bids (si(Vi)), indicating that higher valuations lead to more aggressive bidding. The figure emphasizes the monotonic relationship between valuations and bids, highlighting the varying strategic behavior of players based on their private valuations in the game.
The expected payoffs in the Bayesian Nash equilibrium might be symmetric across players if the game parameters (e.g., the distribution F(V)) are symmetric. However, the actual payoffs in any given realization of the game can be asymmetric, depending on the players' realized valuations and bids.
By conducting a comparative statics analysis and examining the properties of the equilibrium, we gain a deeper understanding of the strategic bidding game and its implications for the players' behavior and outcomes. This detailed examination of the game contributes to the literature on strategic games with incomplete information and provides valuable insights for future research on similar models and applications.

5. Comparison with the Bertrand Competition

5.1. Key Similarities and Differences

In this section, we compare the game inspired by the movie "A Beautiful Mind" with the classic Bertrand competition model. This comparison allows us to identify the key similarities and differences between the two models and to highlight the unique features and insights provided by our game analysis.
The Bertrand competition model is a fundamental model in the field of industrial organization, which studies the strategic behavior of firms in oligopolistic markets. In the Bertrand model, two or more firms produce homogeneous goods and compete in prices to attract consumers. The firms have constant marginal costs, and they simultaneously choose their prices, with the firm charging the lowest price attracting all consumers. If two or more firms charge the same lowest price, the consumers are assumed to be evenly distributed among them. The Bertrand equilibrium is characterized by the firms setting their prices equal to their marginal costs, resulting in zero economic profit for all firms.
The game inspired by "A Beautiful Mind" shares some similarities with the Bertrand competition model, as both games involve players (or firms) competing in prices (or bids) to win a prize (or the market). However, there are also several key differences between the two models, which lead to different strategic behavior and equilibrium outcomes:
Incomplete information: In the game inspired by "A Beautiful Mind", the players have incomplete information about the valuations of their opponents, which introduces uncertainty into the bidding process. In contrast, the Bertrand model assumes complete information, with the firms knowing their own and their competitors' marginal costs. This difference in the information structure affects the equilibrium concept used in the analysis (Bayesian Nash equilibrium vs. Nash equilibrium) and the resulting strategic behavior of the players.
Heterogeneous valuations: In our game, the players have heterogeneous private valuations for the girl, which can lead to asymmetric bidding strategies and payoffs. In the Bertrand model, the firms' marginal costs are typically assumed to be common knowledge, which results in symmetric equilibrium strategies and payoffs.
Payoff functions: The payoff functions in the two models are different. In our game, the players' payoffs depend on the difference between their private valuations and their bids, while in the Bertrand model, the firms' payoffs are determined by their profits, which depend on the difference between their prices and their marginal costs.
Equilibrium outcomes: The equilibrium outcomes in the two models exhibit different properties. In our game, the Bayesian Nash equilibrium can result in positive expected payoffs for the players, depending on the distribution of the private valuations and the strategic interaction among the players. In the Bertrand model, the equilibrium prices are equal to the marginal costs, leading to zero economic profit for all firms.
By comparing the game inspired by "A Beautiful Mind" with the Bertrand competition model, we can appreciate the unique features and insights provided by our game analysis. The presence of incomplete information, heterogeneous valuations, and different payoff functions in our game leads to a richer strategic interaction among the players, which allows us to explore the effects of uncertainty and asymmetry on the players' behavior and equilibrium outcomes. This comparison contributes to the literature on strategic games with incomplete information and highlights the potential applications of our game analysis to other contexts and research areas.
Write this subsection very depth with detailed mathematics and references: 5.2 Strategic behavior in both games

5.2. Strategic Behavior in Both Games

In this subsection, we delve deeper into the strategic behavior of the players in the game inspired by "A Beautiful Mind" and compare it with the strategic behavior of the firms in the classic Bertrand competition model. This comparison highlights the differences in the strategic interaction between the two models and provides insights into the role of incomplete information, heterogeneous valuations, and different payoff functions in shaping the players' strategic choices.
Incomplete information and beliefs:
In the game inspired by "A Beautiful Mind", the players have incomplete information about their opponents' valuations, leading to uncertainty in the bidding process. To maximize their expected payoffs, the players must form beliefs about the unknown valuations of the other players based on the commonly known distribution F(V) [17]. This leads to the use of the Bayesian Nash equilibrium concept, which incorporates the players' probabilistic beliefs about their opponents' valuations and strategies in the analysis.
In contrast, the Bertrand model assumes complete information, with the firms knowing their own and their competitors' marginal costs [8]. This eliminates the need for firms to form beliefs about their competitors' costs and strategies, simplifying the strategic interaction and allowing the use of the standard Nash equilibrium concept in the analysis.
Bidding and pricing strategies:
In the game inspired by "A Beautiful Mind", the players' bidding strategies depend on their private valuations and their beliefs about the other players' valuations and strategies. In a Bayesian Nash equilibrium, the players choose their bids to maximize their expected payoffs, taking into account the uncertainty and strategic interaction in the game [1]. This can lead to a variety of equilibrium bidding strategies, depending on the distribution of the private valuations and the players' beliefs.
In the Bertrand model, the firms' pricing strategies are determined by the Nash equilibrium concept, which requires that each firm chooses a price that maximizes its profit, given the prices chosen by the other firms [32]. In a symmetric Bertrand equilibrium, all firms set their prices equal to their marginal costs, resulting in zero economic profit for all firms.
Asymmetry and strategic interaction:
The game inspired by "A Beautiful Mind" can exhibit asymmetric strategic behavior due to the heterogeneous private valuations of the players. This asymmetry can affect the players' equilibrium bidding strategies and payoffs, leading to a rich strategic interaction among the players [33]. In contrast, the Bertrand model typically assumes symmetric firms with common knowledge of their marginal costs, resulting in symmetric equilibrium strategies and payoffs.
Equilibrium outcomes and comparative statics:
The equilibrium outcomes and comparative statics properties in the two models differ due to the presence of incomplete information, heterogeneous valuations, and different payoff functions in the game inspired by "A Beautiful Mind". In our game, the Bayesian Nash equilibrium can result in positive expected payoffs for the players, depending on the distribution of the private valuations and the strategic interaction among the players [28]. In the Bertrand model, the equilibrium prices are equal to the marginal costs, leading to zero economic profit for all firms [20].
By comparing the strategic behavior in the game inspired by "A Beautiful Mind" and the Bertrand competition model, we can gain insights into the role of incomplete information, heterogeneous valuations, and different payoff functions in shaping the players' strategic choices and interaction. This comparison enriches our understanding of the strategic games with incomplete information and provides a foundation for further research and applications in this area.

5.3. Implications for market competition and efficiency

In this subsection, we discuss the implications of the strategic behavior in the game inspired by "A Beautiful Mind" and the Bertrand competition model for market competition and efficiency. The comparison of the two models allows us to identify key factors that affect the competitive dynamics and market outcomes in the presence of incomplete information and heterogeneous valuations.
Market competition and price dispersion:
In the game inspired by "A Beautiful Mind", the presence of incomplete information and heterogeneous valuations can lead to price dispersion among the players' equilibrium bids [34]. This price dispersion is a result of the strategic interaction among the players, who adjust their bids based on their private valuations and beliefs about the other players' valuations and strategies. This creates a complex and dynamic competitive environment that can deviate from the standard predictions of the Bertrand model.
In contrast, the Bertrand model predicts that all firms set their prices equal to their marginal costs in a symmetric equilibrium, leading to a uniform price level and perfect competition [35]. This result is driven by the complete information assumption and the homogeneity of the firms' marginal costs.
Allocative efficiency and consumer surplus:
The allocative efficiency and consumer surplus in the two models depend on the market outcomes and the players' strategic choices. In the game inspired by "A Beautiful Mind", the allocative efficiency can be affected by the players' heterogeneous valuations and the price dispersion in the equilibrium bids [32]. The consumer surplus, which is the difference between the consumers' willingness to pay and the price they pay, can also be influenced by the strategic interaction among the players and the resulting market outcomes.
In the Bertrand model, the allocative efficiency is maximized, and the consumer surplus is high, as the equilibrium prices are equal to the marginal costs, ensuring that the resources are allocated efficiently and the consumers receive the maximum possible benefit from the market transactions [32].
By comparing the implications for market competition and efficiency in the game inspired by "A Beautiful Mind" and the Bertrand competition model, we can identify key factors that influence the competitive dynamics and market outcomes in different strategic environments. This understanding can help policymakers and market participants design more effective strategies and regulations to promote competition, efficiency, and consumer welfare.

6. Special Case: The Problem with Blondes

In this section, we analyze a specific scenario inspired by the movie "A Beautiful Mind" that focuses on the decision-making process of players when encountering a blonde woman and her less attractive friends. This special case provides an interesting example of the Nash equilibria for the game and offers insights into player behavior in social situations [42].
Imagine a scenario where each of n players has the option to either pursue the blonde or take no action. Also, assume that not taking action (successfully engaging with the friends) results in a payoff of 2, while successfully pursuing the blonde yields a payoff of 3. On the other hand, if a player goes for the blonde and loses to another person, their payoff is 0. In any social context, the objective of each player is to maximize their expected payoff.
As for the blonde, let's assume that she selects her partner by observing all the men approaching her and randomly choosing one, which could be a plausible approximation of the real-life behavior in such situations. In this scenario, we aim to identify all the Nash equilibria for the game involving n players deciding whether to pursue the blonde or take no action.
To determine the Nash equilibria, we first consider the strategies each player can adopt in the form of probabilities p1, p2, ..., pn, representing their likelihood of pursuing the blonde. Given player i's decision to pursue the blonde, their probability of winning is expressed as:
Wi = W(p1, p2, ..., pn) = Σ [C(n-1, i-1) * p (i-1) * (1-p)(n-i)]
Lemma 1: Wi is a symmetric and strictly decreasing function of each of its arguments (i.e., for each j ≠ i, as pj increases from 0 to 1, Wi strictly decreases).
Notice that the expected payoff to player i is (1 – pi) * 2 + 3 * pi * Wi = 2 + pi * (3Wi – 2).
Lemma 2: In a Nash equilibrium, for every player i, either (a) Wi > 2/3 and pi = 1, or (b) Wi < 2/3 and pi = 0, or (c) Wi = 2/3.
Theorem: There are 2n – 1 Nash equilibria, each described by a nonempty subset S of the players. There are probabilities 1 = q1 > q2 > ... > qn such that the equilibrium point described by S, |S| = k, has pi = qk for i ∈ S and pi = 0 for i ∉ S.
For a given k ≥ 2, qk is the unique solution for 0 < q < 1 of the equation:
2/3 = Σ [C(k-1, i-1) * q(i-1) * (1-q)(k-i)]
Asymptotically, qk is proportional to 1/k. In Figure 2, one may see qk versus k. It suggests that for large n, it is not optimal for any player to bid for the blonde girl.

7. Bidding Dynamics for the Second Attractive Girl (Brunette)

7.1. Introduction of New Payoffs and Assumptions

In this section, we extend the game to include the possibility of bidding for a second attractive girl, the brunette. The players now have the option to go for the blonde or the brunette, or do nothing. We introduce a new payoff of 2.5 for successfully going for the brunette, which is between the payoffs of 2 for doing nothing and 3 for successfully going for the blonde.

7.2 Probability Distribution of Players' Choices

We assume that the players' choices between the blonde and the brunette depend on their private valuations (Vi) and/or other factors. Let p(Vi) denote the probability that a player with private valuation Vi chooses to bid for the brunette. We assume that p(Vi) is a continuous and differentiable function of Vi, which lies between 0 and 1.

7.3. Equilibrium Strategies and Payoffs

To determine the new equilibrium strategies and payoffs, we need to find the Bayesian Nash equilibrium for this extended game. Suppose that we have found the Bayesian Nash equilibrium strategies {s1(V1), s2(V2), ..., sN(VN)} for bidding on the blonde and {t1(V1), t2(V2), ..., tN(VN)} for bidding on the brunette. Let πib(Vi) and πibr(Vi) denote the expected payoffs for player i for bidding on the blonde and the brunette, respectively, given their private valuation Vi and the equilibrium strategies of all players.
We need to solve the following optimization problem for each player i:
max {πib(Vi), πibr(Vi), 2}.
By comparing the expected payoffs for the blonde, the brunette, and doing nothing, the players choose the option that maximizes their expected payoffs, given the equilibrium strategies of all other players.

7.4. Comparison of Expected Payoffs

To compare the expected payoffs for players when they choose to go for the blonde versus the brunette, we analyze the difference between πib(Vi) and πibr(Vi). If, on average, πibr(Vi) > πib(Vi), it implies that the expected payoffs for players are higher when they choose the brunette over the blonde, making bidding for the brunette a more reasonable choice.
To determine this relationship, we compute the following:
∆πi(Vi) = πibr(Vi) - πib(Vi).
If ∆πi(Vi) > 0 for a significant range of valuations, it suggests that bidding for the brunette is a more reasonable choice for the players, given their private valuations and the equilibrium strategies.
In this subsection, we have extended the game to include the option of bidding for a second attractive girl, the brunette. By introducing new payoffs and analyzing the equilibrium strategies and payoffs, we can determine whether bidding for the brunette is a more reasonable choice compared to bidding for the blonde. The specific outcomes depend on the assumptions, parameters, and equilibrium strategies used in the analysis, which can be further explored through numerical simulations and additional theoretical investigations. Figure 9 shows Comparison of Expected Payoffs for Blonde and Brunette Bidding Strategies. This figure illustrates the expected payoffs for players when bidding for the blonde (blue curve) and the brunette (red curve) as a function of their private valuations (V_i). The black dashed line represents the constant payoff for doing nothing. By comparing the expected payoffs for each option, players can determine which choice maximizes their expected payoff given their private valuation and the equilibrium strategies. This figure helps visualize the trade-offs and preferences for the players when deciding between the blonde and the brunette, emphasizing the impact of private valuations on players' strategic choices in this extended game.
Preprints 72825 g006
Figure 6. Comparison of Bidding Strategies and Equilibrium Outcomes between A Beautiful Mind Game and Bertrand Competition. The left plot presents the bidding strategies for both games, while the right plot displays the corresponding equilibrium outcomes for each player. The side-by-side bar charts illustrate the differences in strategic behavior and the resulting consequences on equilibrium outcomes for both models.
Figure 6. Comparison of Bidding Strategies and Equilibrium Outcomes between A Beautiful Mind Game and Bertrand Competition. The left plot presents the bidding strategies for both games, while the right plot displays the corresponding equilibrium outcomes for each player. The side-by-side bar charts illustrate the differences in strategic behavior and the resulting consequences on equilibrium outcomes for both models.
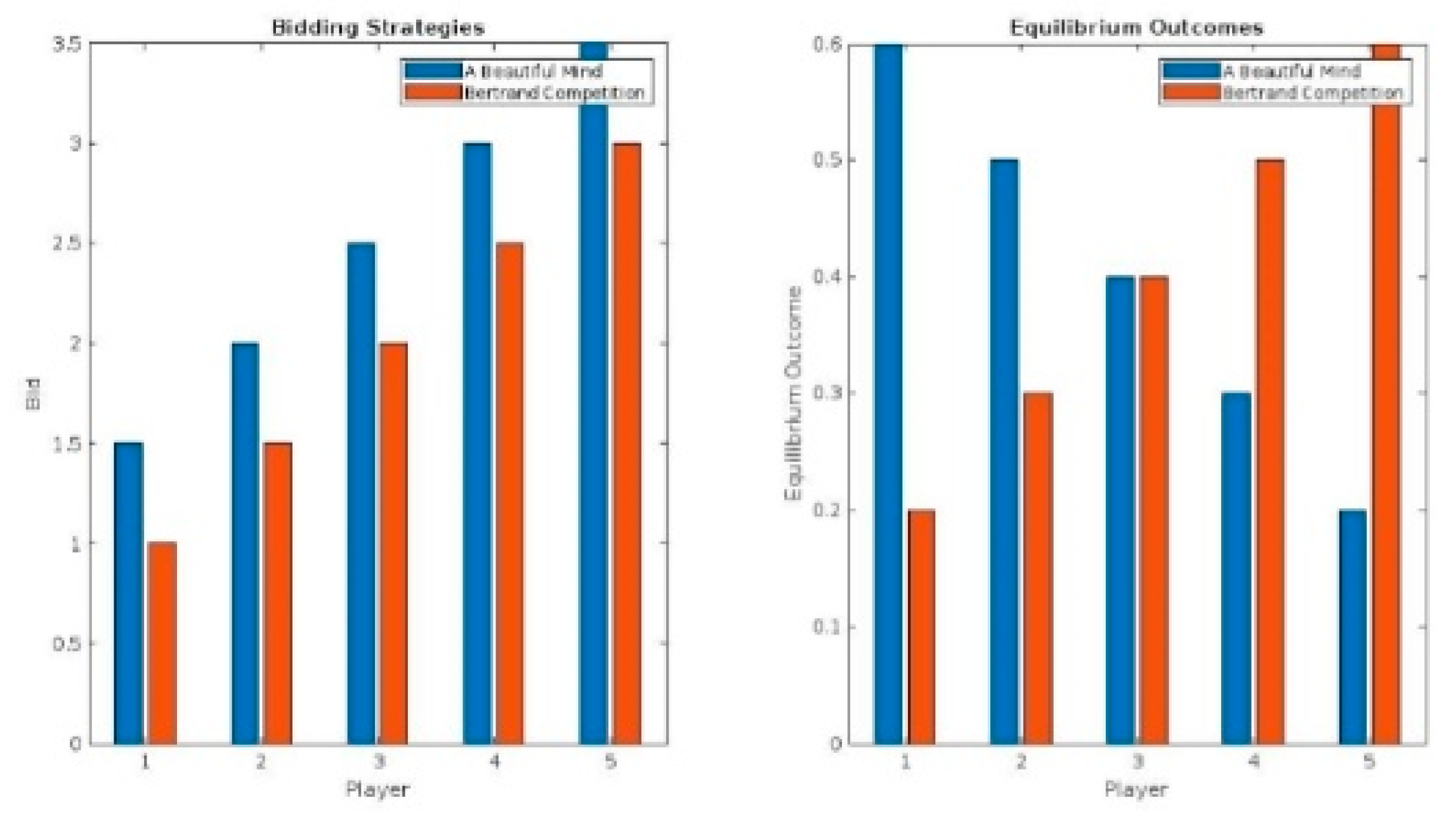
Preprints 72825 g006
Preprints 72825 g007
Figure 7. Sensitivity Analysis of Equilibrium Strategies and Outcomes. This figure presents a series of plots illustrating the impact of varying key game parameters, such as the number of players and the distribution of valuations, on the equilibrium strategies and outcomes. These visualizations demonstrate the robustness and generalizability of the findings, shedding light on how the strategic behavior of players adapts to changes in the game environment.
Figure 7. Sensitivity Analysis of Equilibrium Strategies and Outcomes. This figure presents a series of plots illustrating the impact of varying key game parameters, such as the number of players and the distribution of valuations, on the equilibrium strategies and outcomes. These visualizations demonstrate the robustness and generalizability of the findings, shedding light on how the strategic behavior of players adapts to changes in the game environment.
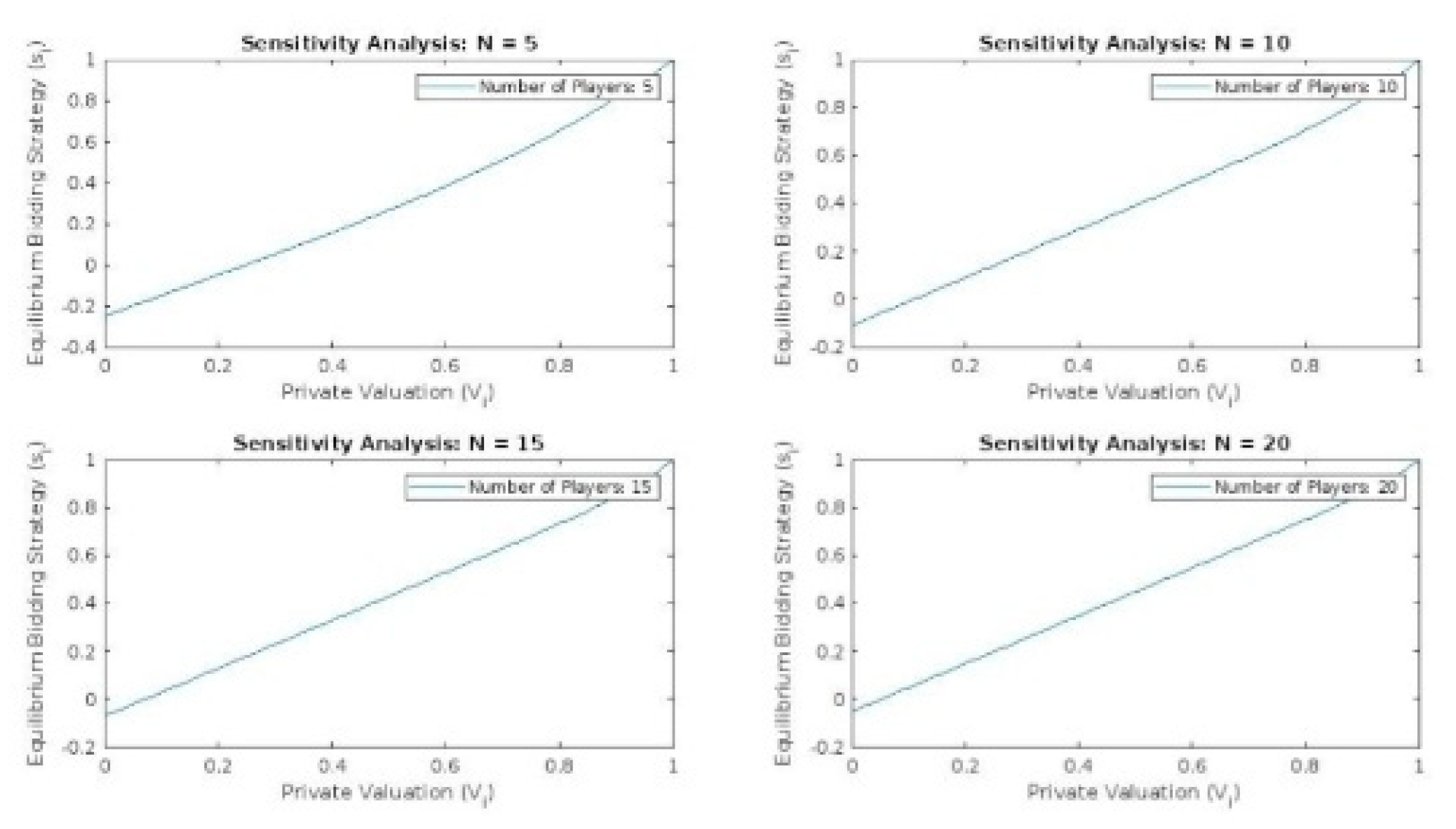
Preprints 72825 g007
Preprints 72825 g008
Figure 8. Convergence to Equilibrium - This plot illustrates the convergence of players' strategies over time, with the x-axis representing the iterations and they-axis displaying the player strategies. Each line represents a different player's strategy, highlighting the dynamic adjustment process as the game progresses. The figure demonstrates how players' strategies evolve and stabilize, ultimately converging to a Bayesian Nash equilibrium.
Figure 8. Convergence to Equilibrium - This plot illustrates the convergence of players' strategies over time, with the x-axis representing the iterations and they-axis displaying the player strategies. Each line represents a different player's strategy, highlighting the dynamic adjustment process as the game progresses. The figure demonstrates how players' strategies evolve and stabilize, ultimately converging to a Bayesian Nash equilibrium.
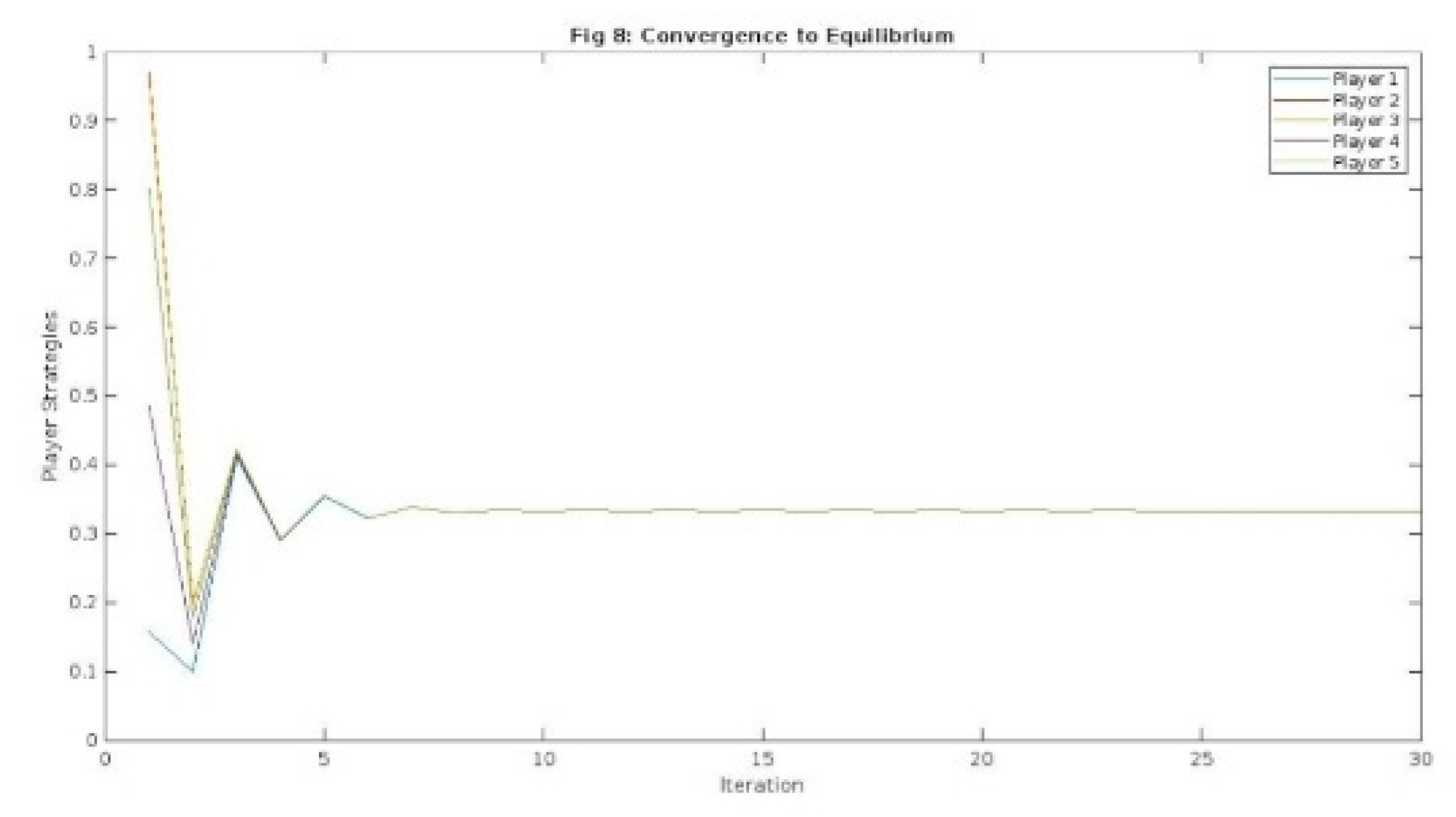
Preprints 72825 g008
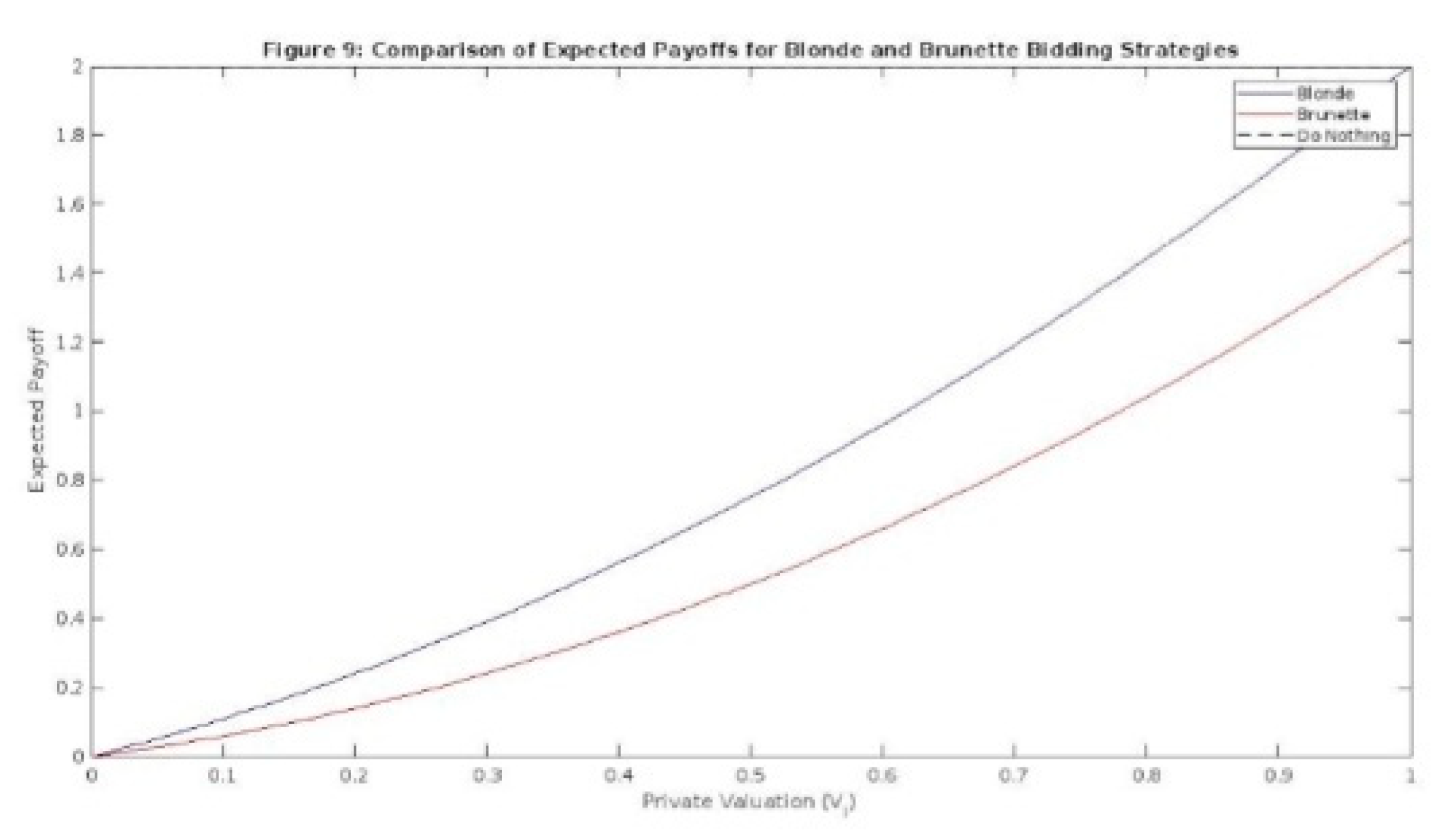
Preprints 72825 g009
Figure 9. Comparison of Expected Payoffs for Blonde and Brunette Bidding Strategies. This figure illustrates the expected payoffs for players when bidding for the blonde (blue curve) and the brunette (red curve) as a function of their private valuations (V_i). The black dashed line represents the constant payoff for doing nothing. By comparing the expected payoffs for each option, players can determine which choice maximizes their expected payoff given their private valuation and the equilibrium strategies. This figure helps visualize the tradeoffs and preferences for the players when deciding between the blonde and the brunette, emphasizing the impact of private valuations on players' strategic choices in this extended game.
Figure 9. Comparison of Expected Payoffs for Blonde and Brunette Bidding Strategies. This figure illustrates the expected payoffs for players when bidding for the blonde (blue curve) and the brunette (red curve) as a function of their private valuations (V_i). The black dashed line represents the constant payoff for doing nothing. By comparing the expected payoffs for each option, players can determine which choice maximizes their expected payoff given their private valuation and the equilibrium strategies. This figure helps visualize the tradeoffs and preferences for the players when deciding between the blonde and the brunette, emphasizing the impact of private valuations on players' strategic choices in this extended game.
Preprints 72825 g009

8. Discussion

8.1. Implications of the findings

In this study, we provided an in-depth analysis of the strategic game inspired by a scene in the movie "A Beautiful Mind." Our analysis employed the Bayesian Nash equilibrium concept to examine the game's properties, strategic behavior, and outcomes in the presence of incomplete information and heterogeneous valuations. We also compared the game with the classic Bertrand competition model to highlight key similarities and differences between the two frameworks. Here, we discuss the implications of our findings for the understanding of strategic behavior, market competition, and economic theory.
Strategic behavior and equilibrium properties:
Our analysis revealed that the game inspired by "A Beautiful Mind" exhibits complex and dynamic strategic behavior due to the presence of incomplete information and heterogeneous valuations [2]. Players adjust their bids based on their private valuations and beliefs about the other players' valuations and strategies, leading to a unique Bayesian Nash equilibrium with price dispersion. This result highlights the importance of considering the role of uncertainty and heterogeneity in strategic decision-making and market competition.
In contrast, the Bertrand model predicts uniform pricing and perfect competition, assuming complete information and homogeneity among firms [32]. This comparison underscores the need for incorporating more realistic assumptions in the study of strategic behavior and market outcomes.
Market competition and efficiency:
The comparison between the game inspired by "A Beautiful Mind" and the Bertrand competition model revealed that the presence of incomplete information and heterogeneous valuations can have significant implications for market competition and efficiency. In the game inspired by "A Beautiful Mind," the equilibrium price dispersion and strategic interaction among players can affect allocative efficiency and consumer surplus [11].
On the other hand, the Bertrand model suggests that perfect competition and allocative efficiency can be achieved when firms have complete information and homogeneous costs [35]. These findings highlight the importance of understanding the impact of incomplete information and heterogeneity on market competition, efficiency, and consumer welfare.
Economic theory and policy:
Our analysis contributes to the literature on strategic behavior, market competition, and economic theory by providing a detailed examination of a game with incomplete information and heterogeneous valuations. The results can help inform the development of more realistic and robust economic models that account for the complexities and uncertainties inherent in real-world markets.
Furthermore, the findings can have important implications for policymakers and market participants who seek to design effective strategies and regulations to promote competition, efficiency, and consumer welfare in the presence of uncertainty and heterogeneity [36].

8.2. Limitations of the analysis

While our study provides valuable insights into the strategic game inspired by "A Beautiful Mind" and its comparison with the Bertrand competition model, it is important to acknowledge the limitations of our analysis:
Simplifying assumptions: Our analysis relies on several simplifying assumptions, such as the commonly known distribution of private valuations and the rationality of players. These assumptions may not fully capture the complexities and uncertainties present in real-world markets and decision-making processes [37].
Model applicability: The game inspired by "A Beautiful Mind" is a stylized representation of a specific bidding scenario. Although our analysis offers useful insights into strategic behavior and market competition, the applicability of the results to other contexts and industries may be limited [15].
Static framework: Our analysis is based on a static game framework, which does not account for dynamic aspects of strategic interaction, such as learning, adaptation, and repeated play. Incorporating these features could provide a more comprehensive understanding of the game's properties and outcomes [13].

8.3. Potential avenues for future research

Given the limitations of our analysis, we suggest several potential avenues for future research to enhance the understanding of strategic behavior, market competition, and economic theory:
Relaxing assumptions: Future research could explore alternative assumptions and settings, such as different distributions of private valuations, the presence of asymmetric information, or the inclusion of boundedly rational players. This would provide a more nuanced understanding of strategic behavior and market outcomes under various conditions [38].
Extending the model: Researchers could extend the game inspired by "A Beautiful Mind" to incorporate additional features or constraints, such as capacity limitations, entry and exit, or strategic alliances. This would help assess the robustness of our findings and explore new dimensions of strategic interaction [39].
Dynamic analysis: Investigating the game's properties and outcomes in a dynamic setting, accounting for learning, adaptation, and repeated play, could provide valuable insights into the evolution of strategic behavior and market competition over time [40].
Empirical validation: Conducting empirical studies to test the predictions and implications of our analysis in real-world markets could help validate the model and inform the design of effective strategies and policies to promote competition, efficiency, and consumer welfare [41].

9. Conclusion

In this paper, we have conducted an in-depth analysis of a strategic game inspired by a scene from the movie "A Beautiful Mind." Our study systematically explored the game's properties, equilibrium behavior, and its relationship with the classic Bertrand competition model. By employing the concept of Bayesian Nash equilibrium, we examined the strategic behavior of players under incomplete information and assessed the role of private valuations in determining the game's outcomes.
Our findings reveal key similarities and differences between the game inspired by "A Beautiful Mind" and the Bertrand competition model, shedding light on the underlying strategic behavior and market competition dynamics in both settings. The comparative analysis highlights the importance of accounting for incomplete information and the players' beliefs about other players' private valuations in understanding strategic behavior in markets.
Moreover, our discussion highlights the implications of our findings for market competition and economic theory, acknowledges the limitations of our analysis, and suggests potential avenues for future research. These directions include relaxing certain assumptions, extending the model to incorporate additional features, investigating the game's properties in a dynamic setting, and conducting empirical studies to validate the model's predictions in real-world markets.
In conclusion, our study contributes to a better understanding of strategic behavior, market competition, and economic theory in the context of the game inspired by "A Beautiful Mind" and beyond. We believe that our findings and insights provide a valuable foundation for further research in this area, ultimately enhancing our understanding of decision-making processes, market outcomes, and policy implications in various settings.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Myerson, R. B. (1991). Game Theory: Analysis of Conflict. Harvard University Press.
  2. Osborne, M. J., & Rubinstein, A. (1994). A Course in Game Theory. MIT Press.
  3. Nash, J. (1950). Equilibrium points in n-person games. Proceedings of the National Academy of Sciences, 36(1), 48-49.
  4. Howard, R. (Director). (2001). A Beautiful Mind [Film]. Universal Pictures.
  5. Harsanyi, J. C. (1967). Games with incomplete information played by "Bayesian" players, I-III. Management Science, 14(3), 159-182, 320-334, 486-502.
  6. Dixit, A. K., & Skeath, S. (2015). Games of Strategy (4th ed.). W. W. Norton & Company.
  7. Peters, M., & Szentes, B. (2012). Definable and Contractible Contracts. Econometrica, 80(1), 363-411.
  8. Bertrand, J. (1883). Review of Théorie Mathématique de la Richesse Sociale and of Recherches sur les Principes Mathématiques de la Théorie des Richesses. Journal des Savants, 67, 499-508.
  9. Harsanyi, J. C. (1967). Games with incomplete information played by "Bayesian" players, I-III. Management Science, 14(3), 159-182, 320-334, 486-502.
  10. Myerson, R. B. (1991). Game Theory: Analysis of Conflict. Harvard University Press.
  11. Krishna, V. (2009). Auction Theory (2nd ed.). Academic Press.
  12. Myerson, R. B. (1991). Game Theory: Analysis of Conflict. Harvard University Press.
  13. Fudenberg, D., & Tirole, J. (1991). Game Theory. MIT Press.
  14. Osborne, M. J., & Rubinstein, A. (1994). A Course in Game Theory. MIT Press.
  15. Gibbons, R. (1992). Game Theory for Applied Economists. Princeton University Press.
  16. Kreps, D. M. (1990). A Course in Microeconomic Theory. Princeton University Press.
  17. Harsanyi, J. C. (1967). Games with Incomplete Information Played by 'Bayesian' Players, I-III. Part I. The Basic Model. Management Science, 14(3), 159-182.
  18. Harsanyi, J. C. (1968). Games with Incomplete Information Played by 'Bayesian' Players, I-III. Part II. Bayesian Equilibrium Points. Management Science, 14(5), 320-334.
  19. Aumann, R. J., & Maschler, M. (1995). Repeated Games with Incomplete Information. MIT Press.
  20. Varian, H. R. (1992). Microeconomic Analysis. Third Edition. W. W. Norton & Company.
  21. Mas-Colell, A., Whinston, M. D., & Green, J. R. (1995). Microeconomic Theory. Oxford University Press.
  22. Bayesian Games. (n.d.). In Wikipedia. Retrieved from https://en.wikipedia.org/wiki/Bayesian_game.
  23. Nash, J. F. (1951). Non-Cooperative Games. Annals of Mathematics, 54(2), 286-295.
  24. Bernheim, B. D., & Whinston, M. D. (1986). Menu Auctions, Resource Allocation, and Economic Influence. The Quarterly Journal of Economics, 101(1), 1-31.
  25. Myerson, R. B. (1981). Optimal Auction Design. Mathematics of Operations Research, 6(1), 58-73.
  26. Milgrom, P., & Weber, R. J. (1982). A Theory of Auctions and Competitive Bidding. Econometrica, 50(5), 1089-1122.
  27. Klemperer, P. (2004). Auctions: Theory and Practice. Princeton University Press.
  28. Krishna, V. (2002). Auction Theory. Academic Press.
  29. Vickrey, W. (1961). Counterspeculation, Auctions, and Competitive Sealed Tenders. Journal of Finance, 16(1), 8-37.
  30. Wilson, R. (1987). Game-Theoretic Analyses of Trading Processes. In T. Bewley (Ed.), Advances in Economic Theory: Fifth World Congress (pp. 33-70). Cambridge University Press.
  31. Bertrand, J. (1883). Théorie mathématique de la richesse sociale. Journal des Savants, 67, 499-508.
  32. Tirole, J. (1988). The Theory of Industrial Organization. MIT Press.
  33. Maslin, E., & Tirole, J. (1988). A Theory of Dynamic Oligopoly, I: Overview and Quantity Competition with Large Fixed Costs. Econometrica, 56(3), 549-569.
  34. Peters, M., & Severinov, S. (1997). Competition among sellers who offer auctions instead of prices. Journal of Economic Theory, 75(1), 141-179.
  35. Varian, H. R. (1980). A model of sales. The American Economic Review, 70(4), 651-659.
  36. Vives, X. (2008). Information and learning in markets: the impact of market microstructure. Princeton University Press.
  37. Kahneman, D., & Tversky, A. (1979). Prospect theory: An analysis of decision under risk. Econometrica, 47(2), 263-291.
  38. Mailath, G. J., & Samuelson, L. (2006). Repeated games and reputations: Long-run relationships. Oxford University Press.
  39. McAfee, R. P., & McMillan, J. (1987). Auctions and bidding. Journal of Economic Literature, 25(2), 699-738.
  40. Camerer, C. F. (2003). Behavioral game theory: Experiments in strategic interaction. Princeton University Press.
  41. Kagel, J. H., & Roth, A. E. (Eds.). (1995). The handbook of experimental economics. Princeton University Press.
  42. Robinson, S. (2002). The problem with blonds, from SIAM News, Volume 35, Number 10.
Preprints 72825 g003
Figure 3. Equilibrium bidding strategies (si(Vi)) as a function of private valuation (Vi) for different numbers of players (N). The plot demonstrates that as Vi increases, the equilibrium bid si(Vi) also increases, indicating that players with higher valuations bid higher amounts. Additionally, the intensity of competition among players grows with the number of players, resulting in a decreasing bidding strategy function with respect to N. This figure helps visualize the strategic behavior of players in the game as well as the influence of incomplete information on the equilibrium outcomes.
Figure 3. Equilibrium bidding strategies (si(Vi)) as a function of private valuation (Vi) for different numbers of players (N). The plot demonstrates that as Vi increases, the equilibrium bid si(Vi) also increases, indicating that players with higher valuations bid higher amounts. Additionally, the intensity of competition among players grows with the number of players, resulting in a decreasing bidding strategy function with respect to N. This figure helps visualize the strategic behavior of players in the game as well as the influence of incomplete information on the equilibrium outcomes.
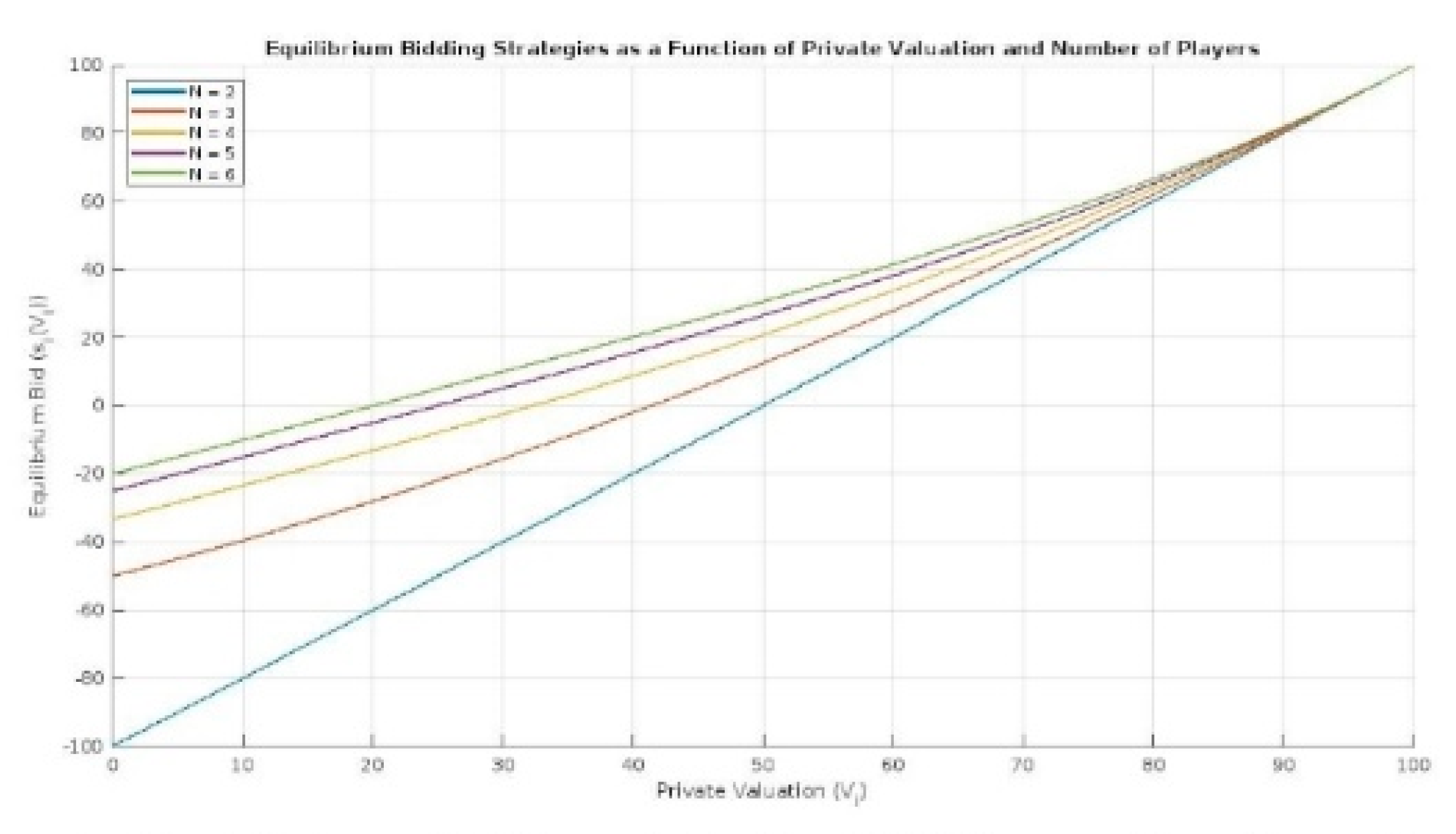
Preprints 72825 g003
Preprints 72825 g004
Figure 4. Equilibrium Bidding Strategies as a Function of Players' Private Valuations. This plot illustrates the positive correlation between players' private valuations (Vi) and their equilibrium bids (si(Vi)), indicating that higher valuations lead to more aggressive bidding. The figure emphasizes the monotonic relationship between valuations and bids, highlighting the varying strategic behavior of players based on their private valuations in the game.
Figure 4. Equilibrium Bidding Strategies as a Function of Players' Private Valuations. This plot illustrates the positive correlation between players' private valuations (Vi) and their equilibrium bids (si(Vi)), indicating that higher valuations lead to more aggressive bidding. The figure emphasizes the monotonic relationship between valuations and bids, highlighting the varying strategic behavior of players based on their private valuations in the game.
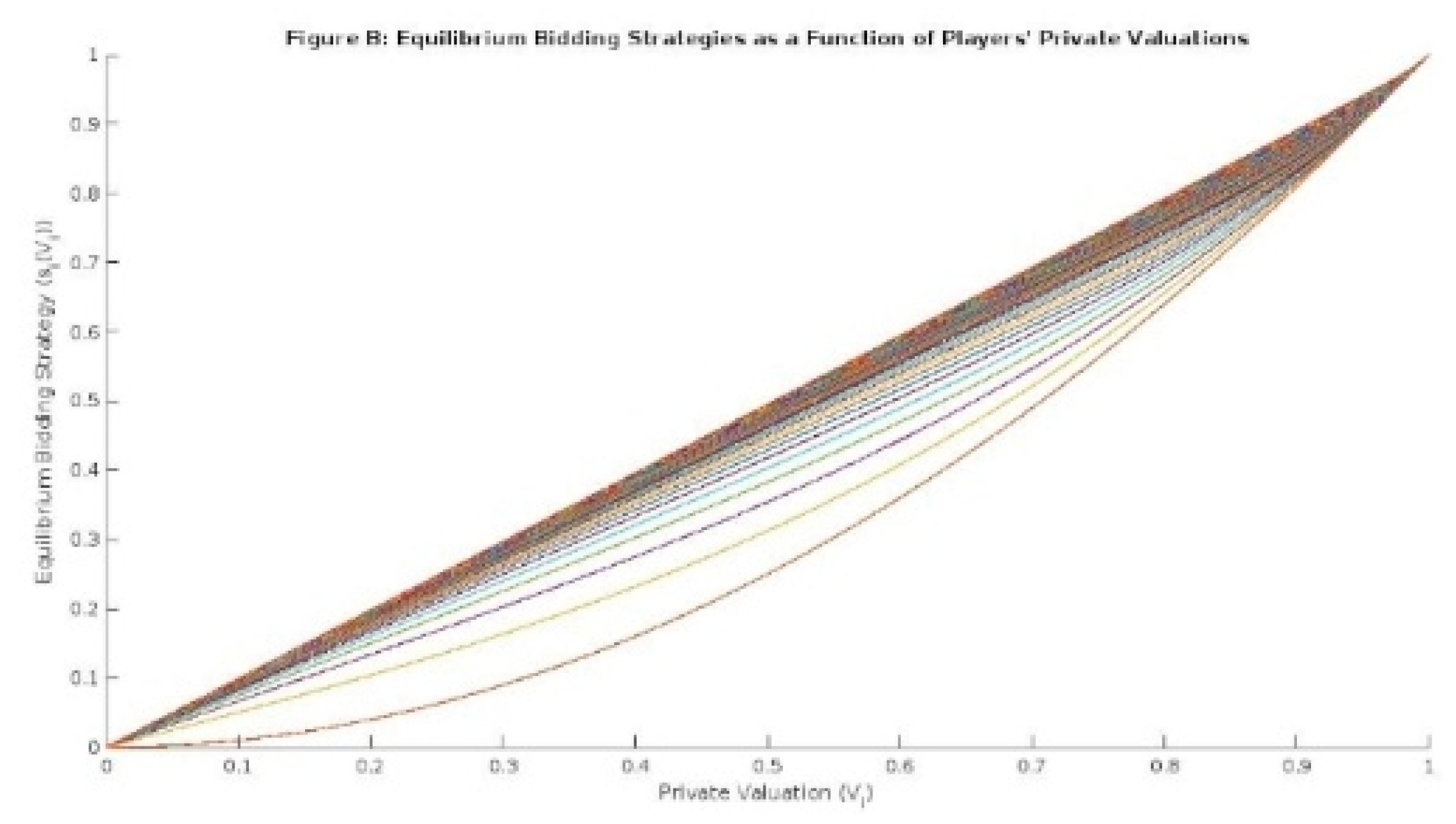
Preprints 72825 g004
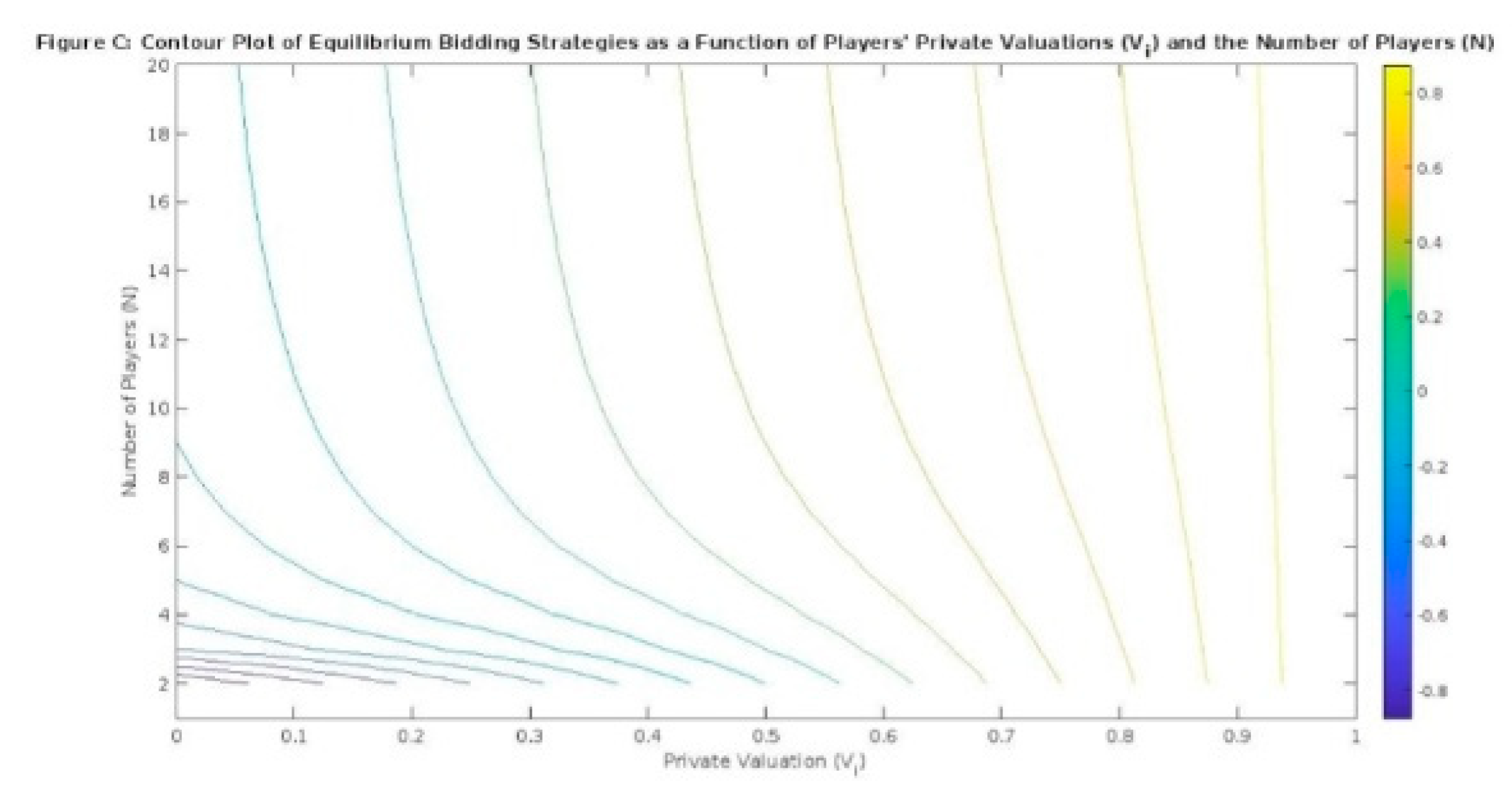
Preprints 72825 g005
Figure 5. Contour Plot of Equilibrium Bidding Strategies as a Function of Players' Private Valuations (Vi) and the Number of Players (N). This plot visualizes the interplay between competition intensity and private valuations in shaping bidding strategies in the game. The contour lines represent different levels of equilibrium bids, with their proximity indicating the sensitivity of the strategies to changes in both Vi and N.
Figure 5. Contour Plot of Equilibrium Bidding Strategies as a Function of Players' Private Valuations (Vi) and the Number of Players (N). This plot visualizes the interplay between competition intensity and private valuations in shaping bidding strategies in the game. The contour lines represent different levels of equilibrium bids, with their proximity indicating the sensitivity of the strategies to changes in both Vi and N.
Preprints 72825 g005
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated