Short–Term Memory Capacity Across Time and Language Estimated from Ancient and Modern Literary Texts

Preprint

Article

Short–Term Memory Capacity Across Time and Language Estimated from Ancient and Modern Literary Texts

Altmetrics

Downloads

121

Views

Comments

Emilio Matricciani^*

This version is not peer-reviewed

Submitted:

08 May 2023

Posted:

08 May 2023

You are already at the latest version

Alerts

Abstract

We study the short−term memory capacity of ancient readers of the original New Testament written in Greek, of its translations to Latin and modern languages. To model the short–term capacity, we have considered the number of words per interpunctions, the “word interval” , because this parameter can model how the human mind memorizes “chunks” of information. Since can be calculated for any alphabetical text, we can perform experiments − otherwise impossible − with ancient readers by studying the literary works they used to read. The “experiments” compare the of texts of a language/translation to those of another language/translation by measuring the minimum average probability of finding joint readers (those who can read both texts because of their similar short–-term memory capacity) and by defining an “overlap index”. We also define a population of universal readers who can read any the New Testament written in alphabetical language. More than 50% of the readers of specific languages overlap with the universal readers with probability . Future work is vast, with many research tracks, because alphabetical literatures are very large and allow many experiments, such as comparing authors, translations or even texts written by artificial intelligence tools.

Keywords:

Subject: Social Sciences - Language and Linguistics

1. Short−term memory and literary texts

The aim of this paper is to study the short−term memory (STM) capacity of the ancient readers of the New Testament written in Greek, in transalations to Latin and modern languages. For modelling the STM capacity, we consider the number of words per interpunctions, termed “word interval” and indicated by

I_{p}

[1,2,3,4,5,6]. This parameter can reveal, as we show, whether the population of readers of a given translation overlaps, as far as the STM capacity is concerned, with the population of readers of Greek and other languages. In other words, the study will reveal how many translations a reader – supposed to be able to understand any language equally well − could read by engaging his/her STM.

The deep–language parameter

I_{p}

varies in the same range of the STM capacity, given by Miller’s

7 \pm 2

law [7], a range that includes 95% of all cases. For words, namely data that can be restricted (i.e., “compressed”) by chunking, it seems that the average value in Miller’s range is not 7 but 5 to 6 [7].

As discussed in [1], very likely the two ranges are deeply related because interpunctions organize small portions of more complex arguments (which make a sentence) in short chunks of text, which represent the natural STM input [8,9,10,11,12,13,14,15,16,17]. Moreover,

I_{p}

, drawn against the number of words per sentence,

P_{F}

, tends to approach a horizontal asymptote as

P_{F}

increases [1,2,3,4,5,6]. The writer, unconsciously, introduces interpunctions as sentences get longer because he/she acts also as a reader, therefore limits

I_{p}

approximately in Miller’s range.

These findings can be explained, at least empirically, according to the way our mind is thought to memorize “chunks” of information in the STM. When we start reading a sentence, our mind tries to predict its full meaning from what already read, as it can be concluded from experiments. Only when an interpunction is found our mind can better understand the meaning of the text. The longer and more twisted the sentence is, the longer the ideas remain deferred until the mind can establish its meaning from all its words (i.e., from all the word intervals contained in the sentence), with the result that the text is less readable. Readability, traditionally, is therefore measured mainly according to the length of sentences by any readability formula [18,19,20,21,22,23,24,25,26,27], neglecting the STM capacity required for reading the sentence.

To overcome this shortcoming, in Reference [6] we have proposed a universal readability formula – applicable to any alphabetical language − which includes the STM capacity measured by the word interval

I_{P}

By considering

I_{P}

, we can perform experiments with ancient readers – otherwise impossible – by studying the literary works they used to read, for example the texts belonging to the Greek and Latin Literatures. These “experiments” can reveal unexpected similarity and dependence between texts, because they consider four deep−language parameters [1] – two of which are

P_{F}

and

I_{P}

, being the other two the number of characters per word,

C_{P}

, and the number on interpunctions per sentence

M_{F}

− not consciously controlled by writers.

After this introduction, Section 2 reports the statistical values of

I_{P}

for the languages/translations of the New Testament considered; Section 3 recalls and models the probability density function of

I_{P}

; Section 4 defines and discusses the probability of overlap and the overlap index; Section 5 defines the population of universal readers of the New Testament and Section 6 reports some final remarks and proposes future research work. Appendix A and Appendix B report the detailed numerical results used in the paper.

2. Translations of New Testament from Greek to Latin and modern languages

We study the statistical characteristics of

I_{P}

by considering a large selection of the New Testament (NT) books written in Greek ‒ namely the Gospels according to Matthew, Mark, Luke, John, the Book of Acts, the Epistle to the Romans, the Book of Revelation (Apocalypse), for a total of 155 chapters, according to the traditional subdivision of the original Greek texts – and their translation to Latin and 35 modern languages. A similar study could be done, of course, with other alphabetical texts.

The rationale for studying NT translations is based on its great importance for many scholars of multiple disciplines, besides the personal value for many readers. These translations, altough are very rarely verbatim, strictly respect the subdivision in chapters and verses of the Greek texts – as they are fixed today, see Reference [28] for recalling how interpunctions where introduced in the original scriptio continua − therefore they can be studied at least at these two different levels (chapters and verses), by comparing how a deep−language variable, like

I_{P},

varies from translation to translation [3,5]. Notice that in this paper “translation” is indistingushable from “language” – because we deal only with one translation per language – but notice that language plays only one of the roles in translation, being the addressed audience another one [1,2,3,4,5,6]. A “real translation” − the one we always read − is never “ideal”, i.e. it never maintains all deep–language mathematical characteristics of the original text [2].

For our analysis, as done in References [3,28], we have chosen the chapter level because the amount of text is sufficiently large to assess reliable statistics. Therefore, for each translation/language we have considered a database of

155 \times 37 = 5735

samples of

I_{P}

, sufficiently large to give reliable statistical results. The languages/translations considered are listed in Table 1 – studied also in Reference [3] for other issues − subdivided in language families, together with the mean value

m_{I_{P}}

, and standard deviation

s_{I_{P}}

I_{P}

. Notice that in all languages the list of names reported in Matthew 1.1−1.17 and in Luke 3.23−3.38 (Genealogy of Jesus of Nazareth) have been deleted for not biasing the statistics of linguistic variables [3].

Figure 1 shows the mean value and

\pm 2

−standard deviation bounds of

I_{P}

. At first glance, we can notice a large spread, however, all values are within Miller’s range

7 \pm 2

The global mean value is

6.03

, close to 6.56 found in seven centuries of Italian Literature [1] – a further confirmation that

I_{P}

is centered about the mean value predicted when memorizing words [7] − and the overall standard deviation (i.e., the square root of the sum of the mean variance and the variance of the mean [29]) is

1.56

. Therefore, by considering 2 standard deviations (which correspond to consider 95% of the samples in Miller’s range), we get

6.03 \pm 2 \times 1.56

, hence the range

2.91 ~ 9.15

, reported in Figure 1. Notice that the lower bound 2.91 is smaller than the value we should expect because − as we show in the next section − the probability density function of

I_{P}

is skewed to the right, it is not symmetrical.

For our analysis, directed to study and compare the STM capacity of ancient and modern readers of the New Testament (study case), we need to recal, in the next section, how to model the probability density function of

I_{P}

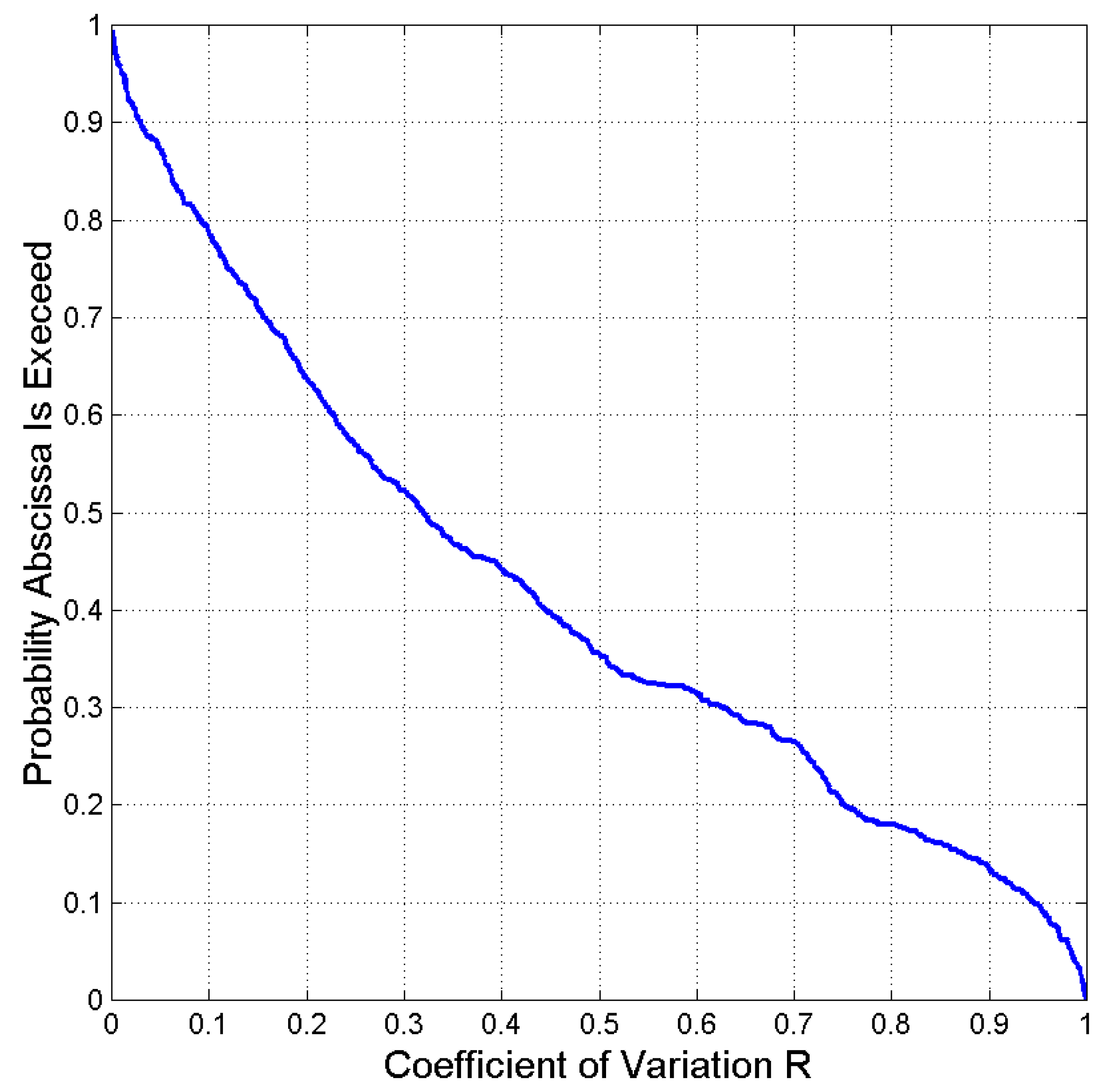
3. Probability density function of $I_{P}$

Given the experimental mean value

m_{I_{P}}

and standard deviation

s_{I_{P}}

I_{P}

, like those reported in Table 1, in Reference [1] we have shown that the experimental probability density function can be modelled with a log−normal model with three parameters:

f (I_{P}) = \frac{1}{\sqrt{2 π} σ_{I_{P}} (I_{p} - 1)} e x p \{- \frac{1}{2} {[\frac{l o g (I_{P} - 1) - μ_{I_{P}}}{σ_{I_{P}}}]}^{2}\} I_{P} \geq 1

(1)

where the constants are given by [29]:

σ_{I_{P}}^{2} = l o g [{(\frac{s_{I_{P}}}{m_{I_{P}} - 1})}^{2} + 1]

(2)

μ_{I_{P}} = l o g [(m_{I_{P}} - 1) - \frac{σ_{I_{P}}^{2}}{2}]

(3)

Figures 2−4 show, as examples,

f (I_{P})

for Ukrainian, Russian, Greek, English, Latin, Italian, Spanish, French. We can see that some densities can each other largely overlap, like Greek and English, or Italian and Spanish, while others overlap only slightly, like Ukrainian and Russian, Greek and Latin.

How can we compare the STM of the readers of a language/translation to those of another language/translation? Since

I_{P}

seems to be a reliable estimate of the STM capacity, then

f (I_{P})

represents the probability density function that defines a population of readers according to their STM capacity. This is very important because we can do some experiments even with ancient readers by considering the texts they used to read.

In the next section, we propose a way of comparing probability density functions like those shown in Figure 2, Figure 3 and Figure 4, by measuring the probability of overlap of readers (who can read both texts) and by defining an “overlap index”.

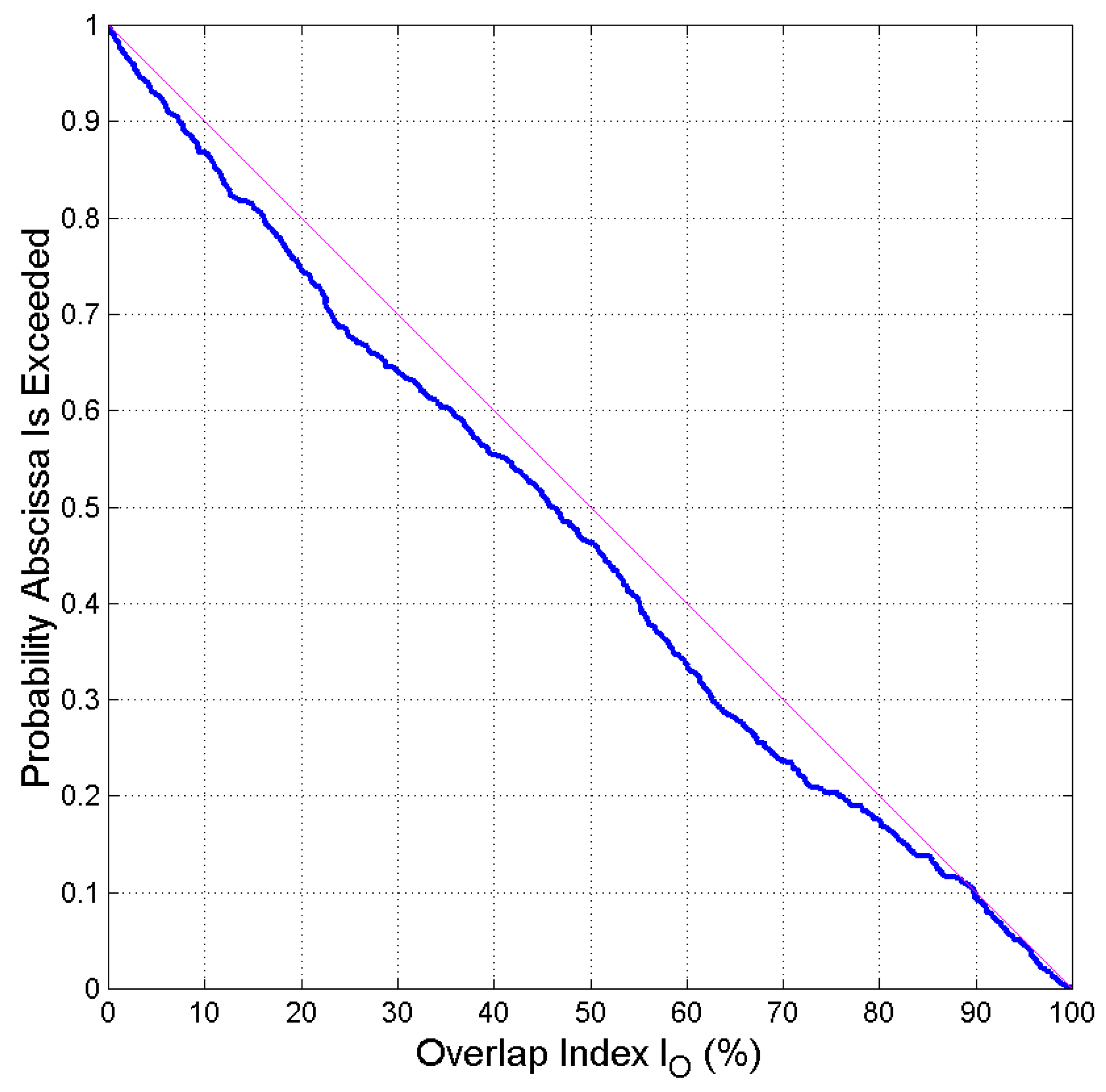
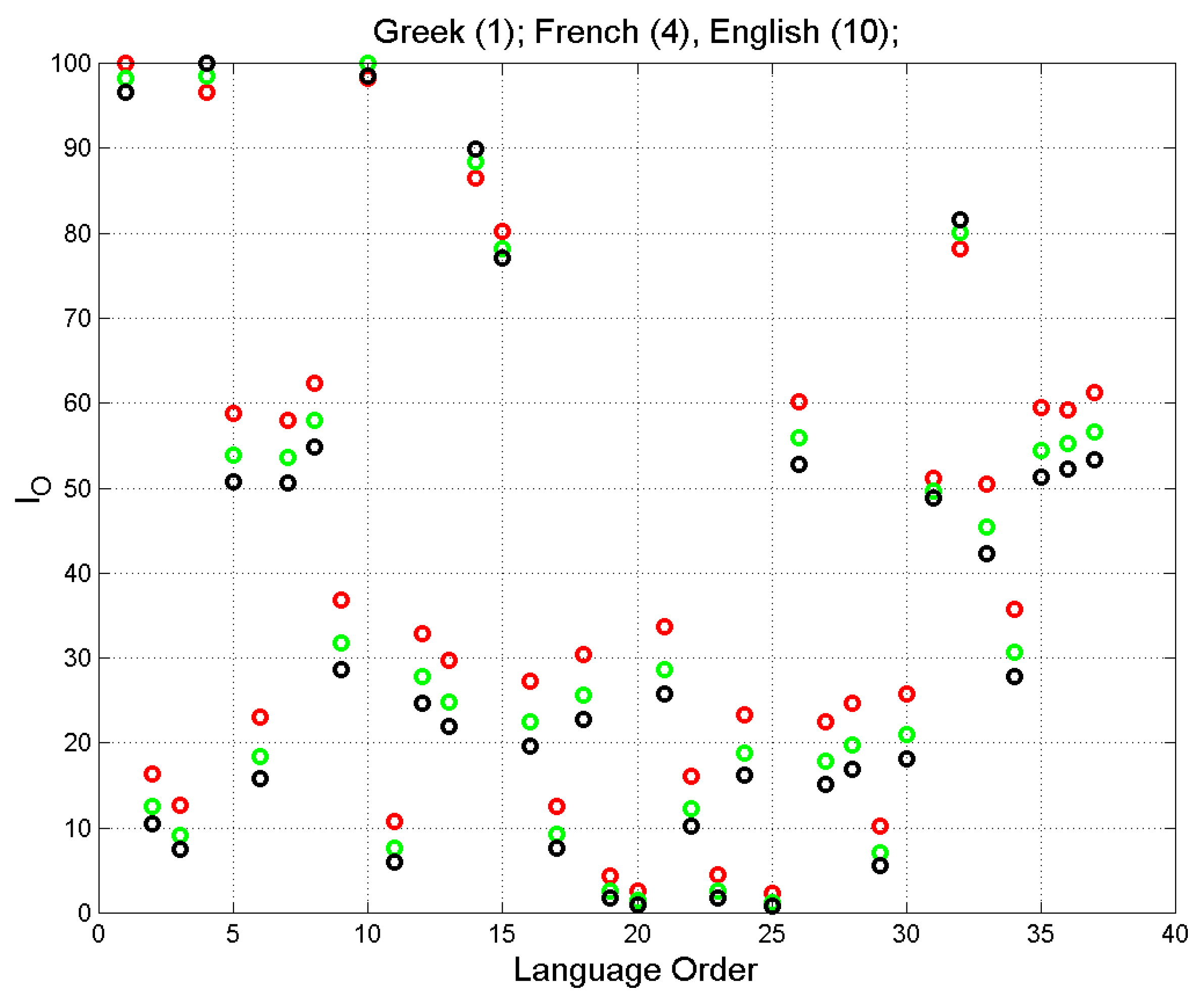
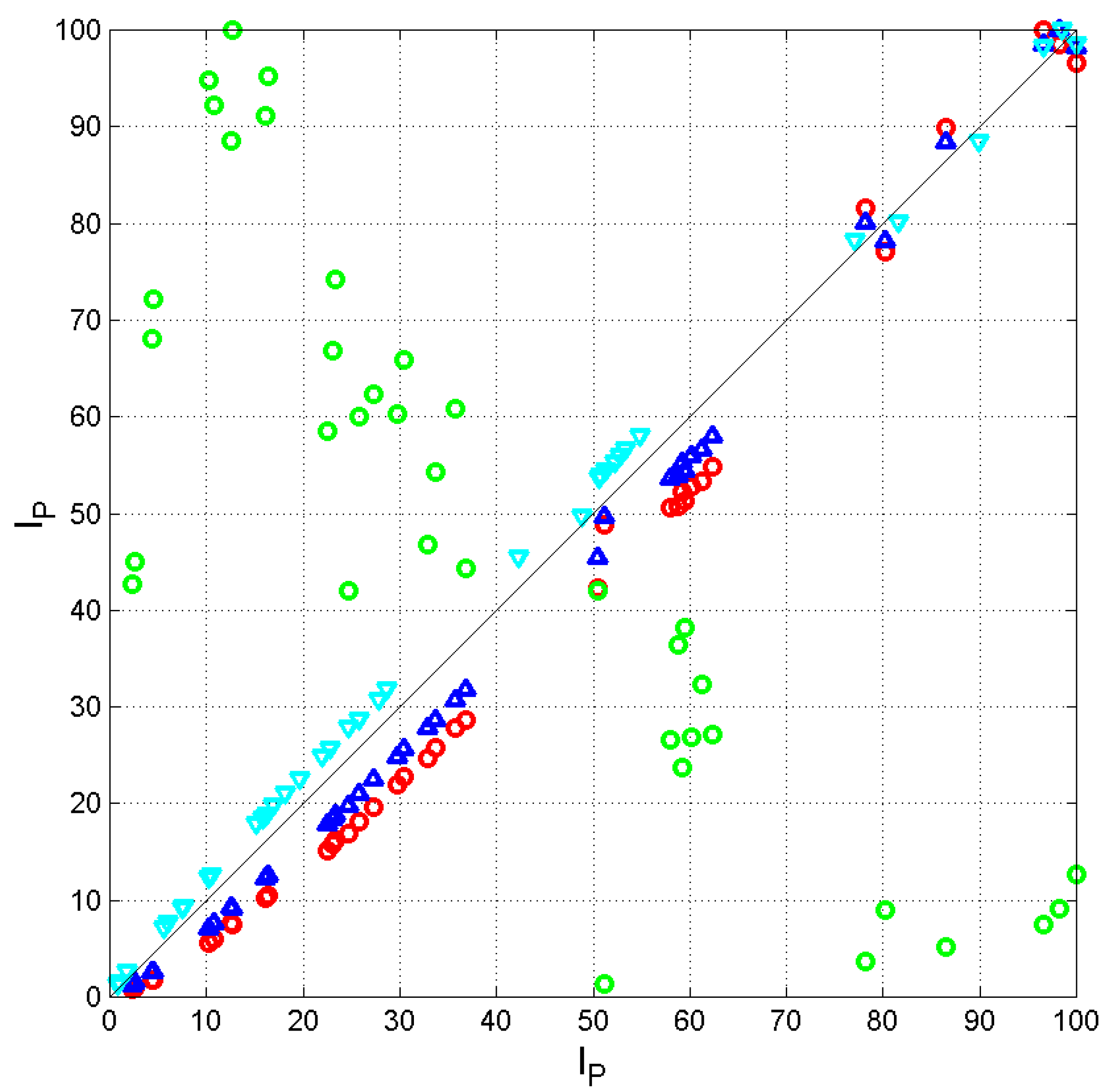
4. Probability of readers’ overlap and overlap index

Let us assume that readers can read (and understand, of course) any alphabetical language. These readers represent mankind because we study their STM capacity through the word interval

I_{P}

. Can we “measure” how many readers of text

j

can potentially read text

k

, either written in the same language or in another language? What is the minimum percentage of readers who can read both, according to the probability density function of

I_{P}

of the two texts? We study this issue by first defining the minimum average probability of overlap and then the overlap index.

A mathematical analysis of a similar problem [3] shows that the minimum average probability of overlap

p_{O} (%)

between the populations of readers of text

j

and text

k

is given by:

p_{O} (%) = 50 [\int_{I_{P, m i n}}^{\infty} g_{j} (I_{P}) d I_{P} + \int_{- \infty}^{I_{P, m i n}} g_{k} (I_{p}) d I_{P}]

(4)

This probability is interpreted as the percentage of readers who can theoretically read both texts because they share the same STM capacity.

In Equation (4)

g_{j} (I_{P}

) and

g_{k} (I_{P}

) are the log−normal probability density functions of readers of text

j

and readers of text

k

, like those shown in Figure 2, Figure 3 and Figure 4. The decision threshold

I_{P, m i n}

is given by the intersection of

g_{j} (I_{P})

and

g_{k} (I_{p})

. The integral limits in Equation (4) assume

μ_{j} < μ_{k}

, as shown in Figure 2, Figure 3 and Figure 4 with the magenta lines, therefore,

I_{P, m i n} > μ_{j}

Let us study the range of

p_{O} .

p_{O} = 0

, there is no overlap between the two densities; their mean values are centered at

- \infty

and

+ \infty

, respectively, or the two densities have collapsed to Dirac delta functions. In other words, the two populations of readers are disjoint (mutually exclusive). If

p_{O} = 50 %

, then the two densities are identical, i.e. text

j

and text

k

coincide (e.g., it almost occurs in the cases of Greek versus English, Italian versus Spanish, or English versus French, see Figure 2, Figure 3 and Figure 4). In conclusion:

0 \leq p_{O} \leq 50

, therefore, when

p_{O} = 0

the two populations of readers do not overlap; when

p_{O} = 50 = p_{O, m a x}

, the two populations fully overlap because

g_{j} (I_{P}) = g_{k} (I_{p}) .

Table A1 of Appendix A reports all values of

p_{O}

for the languages listed in Table 1. For example,

p_{O} = 60.07 %

for Ukrainian and Russia (Figure 2);

p_{O} = 98.19 %

for Greek and English (Figure 2);

p_{O} = 16.31 %

for Greek and Latin (Figure 3);

p_{O} = 91.48 %

for Italian and Spanish (Figure 3);

p_{O} = 98.54 %

for English and French (Figure 4). In other words, Greek and English readers, as well Italian and Spanish readers etc., can be confused because they share the same STM capacity.

We define the overlap index

I_{O}

as:

I_{O} = \frac{p_{O}}{p_{O, m a x}}

(5)

In Equation (5),

0 \leq I_{O} \leq 1

;

I_{O} = 0

means non−overlapping (mutually exclusive) populations,

I_{O} = 1

means totally overlapping populations.

Figure 5 shows the probability distribution of exceeding a given

I_{O}

, calculated from Table A1. It seems that a uniform probability density function fits well the data. Notice that

I_{O} > 0.9

with probability 0.1 (10% of the cases).

According to the Theory of Communication [30], if a probability distribution is defined in the finite interval [a, b] ([0 100] in our case) then the uniform distribution gives the maximum entropy supported in this interval. This seems to be the case for the overlap probability and the derived overlap index, as Figure 5 shows. In other words, the common subset of readers who can theoretically read both texts can assume any value between 0 and 100%.

An interesting parameter, linked to the correlation coefficient

r_{O}

, is the coefficient of variation [29]:

R = r_{O}^{2}

(6)

The coefficient of variation

R

gives the fraction of the total variance of the dependent variable

y

accounted for by the regression line

y = m x + q

, and

1 - R

the proportion not accounted for. In other words, if

r_{O} = \pm 1

, then

R = 1

, the regression line tells all the story linking

y

x

because there is no scattering, hence the relationship between

y

and

x

is deterministic.

Figure 8 shows the probability distribution function of exceeding a given value

R

. We can see that with probability less than 0.1 (10% of the cases

) R > 0.95

, therefore for these latter cases

95 %

of the variance of the samples of

y

is due to the regression line linking it to

x

. Table 2 lists, for example, some cases in which

R > 0.95

by reading in Table B1 (Appendix B) only the cases of positive correlation coefficients

r_{O} = \sqrt{0.9500} = 0.9747

. We can notice that belonging to a language family makes little difference, although some populations can be confused more than others, like in the cases of Italian and Spanish.

In the next section we define a “universal” reader.

5. Universal Reader of the New Testament

As mentioned in Section 2, the global mean value of the data reported in Table 1 is

6.03

and the overall standard deviation is

1.56

. Figure 9 shows the corresponding log−normal probability density function compared to that of some specific languages. This model can be considered as the probability distribution density of a population of “universal” readers who can read, as far as the STM capacity is concerned, any NT translation.

6. Final remarks and future work

We have studied the short−term memory (STM) capacity of the ancient readers of the original New Testament written in Greek, of readers of its translations to Latin and modern languages. A similar study could be done with other alphabetical texts belonging to any literature.

For modelling the STM capacity, we have considered the number of words per interpunctions, namely the “word interval”

I_{p}

, because this parameter seems to describe how the human mind memorizes “chunks” of information in the STM.

Since

I_{P}

can be calculated for any alphabetival text, we can perform experiments with ancient readers − otherwise impossible − by studying the literary works they used to read. These “experiments” can reveal unexpected similarity and dependence between texts, because they consider parameters not consciously controlled by writers, either ancient or modern.

The “experiments” done have compared the STM capacity of the readers of a language/translation to those of another language/translation, by measuring the probability of overlap of two languages/populations of readers and by defining an “overlap index”. For example, Greek and English readers, as well Italian and Spanish readers, can be confused because they practically share the same probability distribution of

I_{P}

. The detailed experimental values reported in large tables in Appendix A and Appendix B can give details on the other languages.

We have also defined a population of universal readers, namely readers who can read (and understand) any alphabetical language. We have found that more than 50% of the languages overlap with the universal reader with probability

p_{O} ≳ 70 %

Future work is vast, with many research tracks, because alphabetical Literatures are very large and many experiments such as those reported in this paper can be done, according to specific purposes, such as comparing authors, translations or even texts written by artificial intelligence tools.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

The author warmly thanks all those scholars who, with continuous great care and dedication, keep online the texts of the Bible in many languages for the benefit of everyone, specifically Bible Gateway, Perseus Digital Library and the Vatican.

Conflicts of Interest

The author declares no conflict of interest.

Appendix A. Values of the probability of overlap $p_{O}$

Table A1. Values of the probability of overlap

p_{O} (%)

for the indicated languages. The languages indicated in the first row are the reference languages, the languages indicated in the first column are the dependent languages. For example, if Greek is the reference language, the Latin overlaps for 16.31% of the readers, French overlaps for 96.56 %. Of course, symmetry is due to the definition of

p_{O}

Table A1. Values of the probability of overlap

p_{O} (%)

p_{O}

	Gr	Lt	Es	Fr	It	Pt	Rm	Sp	Dn	En
Gr	100.00	16.31	12.66	96.56	58.84	23.03	57.97	62.30	36.79	98.19
Lt	16.31	100.00	95.26	10.57	41.23	69.34	31.32	31.84	48.60	12.54
Es	12.66	95.26	100.00	7.46	36.49	66.88	26.60	27.14	44.30	9.20
Fr	96.56	10.57	7.46	100.00	50.74	15.79	50.58	54.87	28.61	98.54
It	58.84	41.23	36.49	50.74	100.00	56.64	93.84	91.48	76.75	53.94
Pt	23.03	69.34	66.88	15.79	56.64	100.00	47.04	46.59	72.49	18.38
Rm	57.97	31.32	26.60	50.58	93.84	47.04	100.00	95.67	70.40	53.68
Sp	62.30	31.84	27.14	54.87	91.48	46.59	95.67	100.00	68.50	57.99
Dn	36.79	48.60	44.30	28.61	76.75	72.49	70.40	68.50	100.00	31.73
En	98.19	12.54	9.20	98.54	53.94	18.38	53.68	57.99	31.73	100.00
Fn	10.74	89.96	92.16	6.06	32.29	59.77	22.73	23.40	38.66	7.60
Ge	32.85	50.89	46.84	24.75	71.98	76.59	65.03	63.30	94.55	27.80
Ic	29.70	63.80	60.24	21.93	65.82	89.90	56.70	55.97	82.42	24.78
Nr	86.46	7.86	5.23	89.90	43.39	11.69	42.18	46.51	22.40	88.43
Sw	80.17	12.03	9.06	77.02	45.51	16.30	42.80	46.88	26.33	78.22
Bg	27.33	65.51	62.28	19.71	62.71	93.15	53.45	52.79	79.30	22.49
Cz	12.58	89.12	88.49	7.66	34.07	58.72	24.65	25.32	39.59	9.30
Cr	30.44	69.70	65.90	22.79	64.96	91.64	55.19	54.88	78.20	25.59
Pl	4.37	67.93	68.10	1.80	18.12	37.58	10.42	11.21	20.83	2.56
Rs	2.65	47.75	44.96	1.01	11.49	22.50	5.92	6.59	11.94	1.47
Sr	33.73	58.20	54.23	25.72	71.58	82.84	63.11	62.07	89.84	28.71
Sl	16.12	92.58	91.09	10.19	42.83	75.76	32.72	33.08	52.26	12.23
Uk	4.49	70.99	72.13	1.83	19.03	40.34	11.01	11.80	22.29	2.61
Et	23.35	76.91	74.25	16.27	55.32	93.75	45.33	45.21	68.21	18.79
Hn	2.37	45.63	42.74	0.87	10.64	20.93	5.33	5.97	10.92	1.29
Al	60.19	31.60	26.89	52.79	92.60	46.83	97.77	97.89	69.46	55.90
Ar	22.57	61.19	58.47	15.19	57.57	92.95	48.59	47.74	76.32	17.85
Wl	24.69	45.83	41.96	16.86	62.64	73.75	55.66	53.81	85.25	19.75
Bs	10.27	90.71	94.85	5.62	32.28	61.76	22.59	23.22	39.37	7.14
Hb	25.77	63.11	60.05	18.19	61.35	92.45	52.33	51.52	79.35	20.95
Cb	51.11	2.58	1.41	48.80	21.27	3.48	17.75	21.16	7.72	49.60
Tg	78.23	5.95	3.73	81.52	37.57	8.78	35.64	39.92	17.80	80.11
Ch	50.47	46.73	42.03	42.28	91.01	64.59	83.05	81.77	85.73	45.47
Lg	35.72	65.10	60.84	27.83	71.44	85.19	61.72	61.38	85.35	30.76
Sm	59.43	43.00	38.26	51.26	99.53	57.83	93.25	90.95	76.82	54.46
Ht	59.27	28.38	23.70	52.23	90.15	43.32	96.57	96.64	66.54	55.25
Nh	61.29	37.06	32.33	53.38	95.95	52.11	98.80	95.99	72.93	56.58
	Fn	Ge	Ic	Nr	Sw	Bg	Cz	Cr	Pl	Rs
Gr	10.74	32.85	29.70	86.46	80.17	27.33	12.58	30.44	4.37	2.65
Lt	89.96	50.89	63.80	7.86	12.03	65.51	89.12	69.70	67.93	47.75
Es	92.16	46.84	60.24	5.23	9.06	62.28	88.49	65.90	68.10	44.96
Fr	6.06	24.75	21.93	89.90	77.02	19.71	7.66	22.79	1.80	1.01
It	32.29	71.98	65.82	43.39	45.51	62.71	34.07	64.96	18.12	11.49
Pt	59.77	76.59	89.90	11.69	16.30	93.15	58.72	91.64	37.58	22.50
Rm	22.73	65.03	56.70	42.18	42.80	53.45	24.65	55.19	10.42	5.92
Sp	23.40	63.30	55.97	46.51	46.88	52.79	25.32	54.88	11.21	6.59
Dn	38.66	94.55	82.42	22.40	26.33	79.30	39.59	78.20	20.83	11.94
En	7.60	27.80	24.78	88.43	78.22	22.49	9.30	25.59	2.56	1.47
Fn	100.00	40.86	53.80	4.19	7.70	55.60	96.26	59.68	75.91	51.31
Ge	40.86	100.00	86.50	18.99	23.24	83.25	41.51	81.86	22.17	12.55
Ic	53.80	86.50	100.00	16.95	21.49	96.70	53.76	95.69	33.23	20.33
Nr	4.19	18.99	16.95	100.00	82.31	15.01	5.55	17.98	1.08	0.60
Sw	7.70	23.24	21.49	82.31	100.00	19.61	9.28	22.54	3.08	1.95
Bg	55.60	83.25	96.70	15.01	19.61	100.00	55.26	98.64	34.47	20.90
Cz	96.26	41.51	53.76	5.55	9.28	55.26	100.00	59.75	78.77	57.34
Cr	59.68	81.86	95.69	17.98	22.54	98.64	59.75	100.00	39.16	25.38
Pl	75.91	22.17	33.23	1.08	3.08	34.47	78.77	39.16	100.00	66.82
Rs	51.31	12.55	20.33	0.60	1.95	20.90	57.34	25.38	66.82	100.00
Sr	48.17	94.54	92.92	20.19	24.51	89.69	48.62	88.76	28.71	17.40
Sl	83.62	55.08	68.76	7.39	11.60	70.96	80.78	74.16	60.00	39.35
Uk	79.92	23.81	35.44	1.08	3.13	36.85	81.57	41.42	93.08	60.07
Et	67.30	71.53	85.46	12.31	16.92	87.94	66.25	89.83	45.06	28.69
Hn	48.96	11.47	18.92	0.51	1.75	19.45	55.06	23.84	64.14	97.32
Al	23.08	64.17	56.35	44.40	44.88	53.14	25.00	55.06	10.82	6.26
Ar	51.45	81.30	91.75	10.97	15.59	94.79	50.76	99.01	29.86	16.72
Wl	35.80	90.51	86.18	11.98	16.57	81.84	36.36	80.04	17.17	8.69
Bs	96.06	41.80	55.12	3.79	7.26	57.13	92.03	60.82	71.67	46.44
Hb	53.25	83.85	95.53	13.60	18.21	99.27	52.80	97.80	32.00	18.75
Cb	1.09	6.10	5.84	55.98	71.04	4.92	1.72	6.80	0.19	0.12
Tg	2.94	14.79	13.31	91.63	85.71	11.62	4.10	14.40	0.65	0.37
Ch	37.29	80.96	74.18	35.37	38.33	70.96	38.80	72.67	21.46	13.49
Lg	55.10	89.70	93.84	22.51	26.89	91.04	55.74	93.47	35.83	23.53
Sm	34.10	72.26	66.76	44.15	46.56	63.73	35.88	66.19	19.83	12.90
Ht	20.07	61.16	52.90	43.53	43.52	49.67	22.04	51.54	8.65	4.81
Nh	28.33	67.97	61.36	45.61	47.00	58.22	30.19	60.42	15.01	9.26
	Sr	Sl	Uk	Et	Hn	Al	Ar	Wl	Bs	Hb
Gr	33.73	16.12	4.49	23.35	2.37	60.19	22.57	24.69	10.27	25.77
Lt	58.20	92.58	70.99	76.91	45.63	31.60	61.19	45.83	90.71	63.11
Es	54.23	91.09	72.13	74.25	42.74	26.89	58.47	41.96	94.85	60.05
Fr	25.72	10.19	1.83	16.27	0.87	52.79	15.19	16.86	5.62	18.19
It	71.58	42.83	19.03	55.32	10.64	92.60	57.57	62.64	32.28	61.35
Pt	82.84	75.76	40.34	93.75	20.93	46.83	92.95	73.75	61.76	92.45
Rm	63.11	32.72	11.01	45.33	5.33	97.77	48.59	55.66	22.59	52.33
Sp	62.07	33.08	11.80	45.21	5.97	97.89	47.74	53.81	23.22	51.52
Dn	89.84	52.26	22.29	68.21	10.92	69.46	76.32	85.25	39.37	79.35
En	28.71	12.23	2.61	18.79	1.29	55.90	17.85	19.75	7.14	20.95
Fn	48.17	83.62	79.92	67.30	48.96	23.08	51.45	35.80	96.06	53.25
Ge	94.54	55.08	23.81	71.53	11.47	64.17	81.30	90.51	41.80	83.85
Ic	92.92	68.76	35.44	85.46	18.92	56.35	91.75	86.18	55.12	95.53
Nr	20.19	7.39	1.08	12.31	0.51	44.40	10.97	11.98	3.79	13.60
Sw	24.51	11.60	3.13	16.92	1.75	44.88	15.59	16.57	7.26	18.21
Bg	89.69	70.96	36.85	87.94	19.45	53.14	94.79	81.84	57.13	99.27
Cz	48.62	80.78	81.57	66.25	55.06	25.00	50.76	36.36	92.03	52.80
Cr	88.76	74.16	41.42	89.83	23.84	55.06	99.01	80.04	60.82	97.80
Pl	28.71	60.00	93.08	45.06	64.14	10.82	29.86	17.17	71.67	32.00
Rs	17.40	39.35	60.07	28.69	97.32	6.26	16.72	8.69	46.44	18.75
Sr	100.00	62.48	30.60	78.74	16.14	62.62	85.45	97.05	49.18	89.10
Sl	62.48	100.00	63.59	83.03	37.29	32.92	67.33	50.44	86.00	68.82
Uk	30.60	63.59	100.00	47.90	57.43	11.42	32.33	18.72	76.30	34.38
Et	78.74	83.03	47.90	100.00	26.98	45.29	85.95	67.30	69.11	86.25
Hn	16.14	37.29	57.43	26.98	100.00	5.66	15.36	7.78	44.12	17.35
Al	62.62	32.92	11.42	45.29	5.66	100.00	48.17	54.72	22.93	51.94
Ar	85.45	67.33	32.33	85.95	15.36	48.17	100.00	81.09	53.34	96.22
Wl	97.05	50.44	18.72	67.30	7.78	54.72	81.09	100.00	36.88	82.74
Bs	49.18	86.00	76.30	69.11	44.12	22.93	53.34	36.88	100.00	54.90
Hb	89.10	68.82	34.38	86.25	17.35	51.94	96.22	82.74	54.90	100.00
Cb	7.25	2.18	0.18	4.06	0.10	19.46	2.92	2.83	0.91	4.13
Tg	16.09	5.44	0.64	9.46	0.31	37.83	8.04	8.61	2.60	10.32
Ch	80.30	48.99	22.62	62.67	12.50	82.38	65.98	71.58	37.51	69.75
Lg	95.78	68.66	37.76	83.44	22.11	61.58	85.83	90.54	55.90	89.51
Sm	72.24	44.52	20.77	56.72	12.00	92.04	58.53	63.08	34.08	62.29
Ht	59.25	29.56	9.14	41.77	4.30	98.25	44.76	51.81	19.86	48.51
Nh	67.26	38.49	15.78	50.79	8.51	97.32	53.11	58.53	28.25	56.89
	Cb	Tg	Ch	Lg	Sm	Ht	Nh
Gr	51.11	78.23	50.47	35.72	59.43	59.27	61.29
Lt	2.58	5.95	46.73	65.10	43.00	28.38	37.06
Es	1.41	3.73	42.03	60.84	38.26	23.70	32.33
Fr	48.80	81.52	42.28	27.83	51.26	52.23	53.38
It	21.27	37.57	91.01	71.44	99.53	90.15	95.95
Pt	3.48	8.78	64.59	85.19	57.83	43.32	52.11
Rm	17.75	35.64	83.05	61.72	93.25	96.57	98.80
Sp	21.16	39.92	81.77	61.38	90.95	99.93	95.99
Dn	7.72	17.80	85.73	85.35	76.82	66.54	72.93
En	49.60	80.11	45.47	30.76	54.46	55.25	56.58
Fn	1.09	2.94	37.29	55.10	34.10	20.07	28.33
Ge	6.10	14.79	80.96	89.70	72.26	61.16	67.97
Ic	5.84	13.31	74.18	93.84	66.76	52.90	61.36
Nr	55.98	91.63	35.37	22.51	44.15	43.53	45.61
Sw	71.04	85.71	38.33	26.89	46.56	43.52	47.00
Bg	4.92	11.62	70.96	91.04	63.73	49.67	58.22
Cz	1.72	4.10	38.80	55.74	35.88	22.04	30.19
Cr	6.80	14.40	72.67	93.47	66.19	51.54	60.42
Pl	0.19	0.65	21.46	35.83	19.83	8.65	15.01
Rs	0.12	0.37	13.49	23.53	12.90	4.81	9.26
Sr	7.25	16.09	80.30	95.78	72.24	59.25	67.26
Sl	2.18	5.44	48.99	68.66	44.52	29.56	38.49
Uk	0.18	0.64	22.62	37.76	20.77	9.14	15.78
Et	4.06	9.46	62.67	83.44	56.72	41.77	50.79
Hn	0.10	0.31	12.50	22.11	12.00	4.30	8.51
Al	19.46	37.83	82.38	61.58	92.04	98.25	97.32
Ar	2.92	8.04	65.98	85.83	58.53	44.76	53.11
Wl	2.83	8.61	71.58	90.54	63.08	51.81	58.53
Bs	0.91	2.60	37.51	55.90	34.08	19.86	28.25
Hb	4.13	10.32	69.75	89.51	62.29	48.51	56.89
Cb	100.00	61.90	15.98	9.30	22.49	18.00	21.96
Tg	61.90	100.00	29.99	18.49	38.50	36.74	39.45
Ch	15.98	29.99	100.00	79.19	90.97	79.16	86.92
Lg	9.30	18.49	79.19	100.00	72.60	58.06	66.91
Sm	22.49	38.50	90.97	72.60	100.00	89.54	95.46
Ht	18.00	36.74	79.16	58.06	89.54	100.00	95.32
Nh	21.96	39.45	86.92	66.91	95.46	95.32	100.00

Appendix B. Values of the correlation coefficient $r_{O}$

Table B1. Values of the correlation coefficient

r_{O}

(%) for the indicated languages. The languages indicated in the first row are the reference languages, the languages indicated in the first column are the dependent languages. For example, if Greek is the reference language, then the correlation coefficient is

r_{O} = - 0.8352

with Latin,

r_{O} = 0.9941

with French. Of course, symmetry is due to the definition of

r_{O}

Table B1. Values of the correlation coefficient

r_{O}

r_{O} = - 0.8352

with Latin,

r_{O} = 0.9941

with French. Of course, symmetry is due to the definition of

r_{O}

	Gr	Lt	Es	Fr	It	Pt	Rm	Sp	Dn	En
Gr	1	-0.8352	-0.8386	0.9941	0.4374	-0.5187	0.5240	0.5771	-0.0602	0.9978
Lt	-0.8352	1	0.9973	-0.8487	-0.2255	0.7017	-0.3402	-0.3864	0.2315	-0.8448
Es	-0.8386	0.9973	1	-0.8470	-0.2717	0.6674	-0.3831	-0.4275	0.1814	-0.8451
Fr	0.9941	-0.8487	-0.8470	1	0.3453	-0.5862	0.4386	0.4950	-0.1559	0.9991
It	0.4374	-0.2255	-0.2717	0.3453	1	0.3335	0.9862	0.9761	0.7899	0.3818
Pt	-0.5187	0.7017	0.6674	-0.5862	0.3335	1	0.1987	0.1498	0.7920	-0.5615
Rm	0.5240	-0.3402	-0.3831	0.4386	0.9862	0.1987	1	0.9970	0.6986	0.4728
Sp	0.5771	-0.3864	-0.4275	0.4950	0.9761	0.1498	0.9970	1	0.6608	0.5281
Dn	-0.0602	0.2315	0.1814	-0.1559	0.7899	0.7920	0.6986	0.6608	1	-0.1193
En	0.9978	-0.8448	-0.8451	0.9991	0.3818	-0.5615	0.4728	0.5281	-0.1193	1
Fn	-0.8592	0.9771	0.9859	-0.8556	-0.3722	0.5591	-0.4714	-0.5134	0.0561	-0.8581
Ge	-0.1579	0.3190	0.2706	-0.2498	0.7074	0.8549	0.6041	0.5628	0.9904	-0.2148
Ic	-0.3732	0.5508	0.5087	-0.4531	0.5039	0.9713	0.3776	0.3310	0.9035	-0.4233
Nr	0.9687	-0.8623	-0.8545	0.9860	0.2374	-0.6471	0.3335	0.3922	-0.2542	0.9801
Sw	0.9514	-0.8646	-0.8575	0.9606	0.2512	-0.6239	0.3415	0.3985	-0.2281	0.9575
Bg	-0.4219	0.5990	0.5594	-0.4976	0.4448	0.9863	0.3152	0.2679	0.8675	-0.4695
Cz	-0.8710	0.9692	0.9768	-0.8657	-0.3846	0.5374	-0.4809	-0.5235	0.0381	-0.8688
Cr	-0.4435	0.6297	0.5907	-0.5180	0.4283	0.9899	0.2972	0.2494	0.8523	-0.4904
Pl	-0.8577	0.8227	0.8412	-0.8247	-0.5903	0.2596	-0.6518	-0.6864	-0.2426	-0.8381
Rs	-0.7832	0.5903	0.6043	-0.7356	-0.6610	0.0261	-0.6872	-0.7162	-0.3988	-0.7540
Sr	-0.2472	0.4160	0.3696	-0.3350	0.6307	0.9086	0.5165	0.4725	0.9659	-0.3019
Sl	-0.7971	0.9848	0.9759	-0.8228	-0.1182	0.8034	-0.2435	-0.2914	0.3609	-0.8143
Uk	-0.8581	0.8563	0.8749	-0.8291	-0.5633	0.3077	-0.6315	-0.6667	-0.2018	-0.8411
Et	-0.6056	0.8036	0.7740	-0.6650	0.2335	0.9859	0.0963	0.0462	0.7075	-0.6435
Hn	-0.7709	0.5690	0.5830	-0.7224	-0.6629	0.0071	-0.6861	-0.7143	-0.4095	-0.7411
Al	0.5502	-0.3641	-0.4060	0.4665	0.9808	0.1721	0.9991	0.9992	0.6778	0.5002
Ar	-0.4282	0.5932	0.5545	-0.5023	0.4241	0.9864	0.2945	0.2475	0.8573	-0.4749
Wl	-0.2169	0.3516	0.3049	-0.3043	0.6347	0.8781	0.5256	0.4829	0.9670	-0.2713
Bs	-0.8490	0.9861	0.9941	-0.8493	-0.3409	0.5978	-0.4447	-0.4871	0.0970	-0.8504
Hb	-0.4112	0.5816	0.5418	-0.4873	0.4512	0.9831	0.3226	0.2757	0.8734	-0.4591
Cb	0.7771	-0.8187	-0.7973	0.8051	-0.0266	-0.7117	0.0639	0.1191	-0.4371	0.7943
Tg	0.9391	-0.8632	-0.8513	0.9625	0.1635	-0.6809	0.2603	0.3199	-0.3164	0.9539
Ch	0.2185	-0.0048	-0.0554	0.1197	0.9541	0.5737	0.8987	0.8746	0.9310	0.1582
Lg	-0.3202	0.5091	0.4645	-0.4047	0.5711	0.9459	0.4485	0.4026	0.9362	-0.3729
Sm	0.4301	-0.2130	-0.2593	0.3376	0.9999	0.3453	0.9838	0.9732	0.7956	0.3742
Ht	0.5704	-0.3921	-0.4329	0.4890	0.9715	0.1348	0.9966	0.9992	0.6492	0.5219
Nh	0.5142	-0.3138	-0.3573	0.4270	0.9920	0.2322	0.9988	0.9951	0.7203	0.4618
	Fn	Ge	Ic	Nr	Sw	Bg	Cz	Cr	Pl	Rs
Gr	-0.8592	-0.1579	-0.3732	0.9687	0.9514	-0.4219	-0.8710	-0.4435	-0.8577	-0.7832
Lt	0.9771	0.3190	0.5508	-0.8623	-0.8646	0.5990	0.9692	0.6297	0.8227	0.5903
Es	0.9859	0.2706	0.5087	-0.8545	-0.8575	0.5594	0.9768	0.5907	0.8412	0.6043
Fr	-0.8556	-0.2498	-0.4531	0.9860	0.9606	-0.4976	-0.8657	-0.5180	-0.8247	-0.7356
It	-0.3722	0.7074	0.5039	0.2374	0.2512	0.4448	-0.3846	0.4283	-0.5903	-0.6610
Pt	0.5591	0.8549	0.9713	-0.6471	-0.6239	0.9863	0.5374	0.9899	0.2596	0.0261
Rm	-0.4714	0.6041	0.3776	0.3335	0.3415	0.3152	-0.4809	0.2972	-0.6518	-0.6872
Sp	-0.5134	0.5628	0.3310	0.3922	0.3985	0.2679	-0.5235	0.2494	-0.6864	-0.7162
Dn	0.0561	0.9904	0.9035	-0.2542	-0.2281	0.8675	0.0381	0.8523	-0.2426	-0.3988
En	-0.8581	-0.2148	-0.4233	0.9801	0.9575	-0.4695	-0.8688	-0.4904	-0.8381	-0.7540
Fn	1	0.1451	0.3893	-0.8531	-0.8621	0.4430	0.9976	0.4770	0.9094	0.6947
Ge	0.1451	1	0.9472	-0.3410	-0.3135	0.9186	0.1262	0.9050	-0.1591	-0.3291
Ic	0.3893	0.9472	1	-0.5285	-0.5026	0.9960	0.3685	0.9919	0.0800	-0.1304
Nr	-0.8531	-0.3410	-0.5285	1	0.9809	-0.5677	-0.8635	-0.5880	-0.7989	-0.7014
Sw	-0.8621	-0.3135	-0.5026	0.9809	1	-0.5423	-0.8748	-0.5646	-0.8228	-0.7343
Bg	0.4430	0.9186	0.9960	-0.5677	-0.5423	1	0.4218	0.9983	0.1366	-0.0805
Cz	0.9976	0.1262	0.3685	-0.8635	-0.8748	0.4218	1	0.4564	0.9272	0.7316
Cr	0.4770	0.9050	0.9919	-0.5880	-0.5646	0.9983	0.4564	1	0.1726	-0.0493
Pl	0.9094	-0.1591	0.0800	-0.7989	-0.8228	0.1366	0.9272	0.1726	1	0.8799
Rs	0.6947	-0.3291	-0.1304	-0.7014	-0.7343	-0.0805	0.7316	-0.0493	0.8799	1
Sr	0.2457	0.9907	0.9786	-0.4208	-0.3940	0.9581	0.2260	0.9480	-0.0633	-0.2519
Sl	0.9312	0.4479	0.6686	-0.8456	-0.8411	0.7128	0.9171	0.7390	0.7298	0.4782
Uk	0.9354	-0.1167	0.1266	-0.8057	-0.8270	0.1837	0.9485	0.2198	0.9952	0.8417
Et	0.6784	0.7778	0.9267	-0.7192	-0.7005	0.9499	0.6582	0.9604	0.3938	0.1475
Hn	0.6747	-0.3414	-0.1468	-0.6875	-0.7209	-0.0978	0.7125	-0.0671	0.8658	0.9993
Al	-0.4928	0.5813	0.3520	0.3625	0.3695	0.2893	-0.5025	0.2710	-0.6688	-0.7008
Ar	0.4377	0.9112	0.9919	-0.5690	-0.5421	0.9979	0.4158	0.9965	0.1321	-0.0828
Wl	0.1807	0.9907	0.9619	-0.3872	-0.3571	0.9371	0.1616	0.9234	-0.1198	-0.2880
Bs	0.9974	0.1867	0.4304	-0.8492	-0.8556	0.4835	0.9911	0.5165	0.8832	0.6544
Hb	0.4242	0.9239	0.9964	-0.5573	-0.5310	0.9996	0.4028	0.9969	0.1174	-0.0964
Cb	-0.7776	-0.4984	-0.6358	0.8641	0.9126	-0.6594	-0.7894	-0.6806	-0.6845	-0.5815
Tg	-0.8436	-0.3977	-0.5731	0.9926	0.9854	-0.6084	-0.8541	-0.6286	-0.7747	-0.6726
Ch	-0.1723	0.8780	0.7228	0.0104	0.0305	0.6721	-0.1877	0.6567	-0.4406	-0.5588
Lg	0.3441	0.9703	0.9929	-0.4872	-0.4623	0.9805	0.3244	0.9755	0.0333	-0.1724
Sm	-0.3609	0.7143	0.5141	0.2295	0.2439	0.4556	-0.3737	0.4395	-0.5830	-0.6584
Ht	-0.5158	0.5500	0.3159	0.3861	0.3913	0.2527	-0.5246	0.2343	-0.6802	-0.7024
Nh	-0.4499	0.6285	0.4087	0.3215	0.3315	0.3473	-0.4610	0.3298	-0.6437	-0.6926
	Sr	Sl	Uk	Et	Hn	Al	Ar	Wl	Bs	Hb
Gr	-0.2472	-0.7971	-0.8581	-0.6056	-0.7709	0.5502	-0.4282	-0.2169	-0.8490	-0.4112
Lt	0.4160	0.9848	0.8563	0.8036	0.5690	-0.3641	0.5932	0.3516	0.9861	0.5816
Es	0.3696	0.9759	0.8749	0.7740	0.5830	-0.4060	0.5545	0.3049	0.9941	0.5418
Fr	-0.3350	-0.8228	-0.8291	-0.6650	-0.7224	0.4665	-0.5023	-0.3043	-0.8493	-0.4873
It	0.6307	-0.1182	-0.5633	0.2335	-0.6629	0.9808	0.4241	0.6347	-0.3409	0.4512
Pt	0.9086	0.8034	0.3077	0.9859	0.0071	0.1721	0.9864	0.8781	0.5978	0.9831
Rm	0.5165	-0.2435	-0.6315	0.0963	-0.6861	0.9991	0.2945	0.5256	-0.4447	0.3226
Sp	0.4725	-0.2914	-0.6667	0.0462	-0.7143	0.9992	0.2475	0.4829	-0.4871	0.2757
Dn	0.9659	0.3609	-0.2018	0.7075	-0.4095	0.6778	0.8573	0.9670	0.0970	0.8734
En	-0.3019	-0.8143	-0.8411	-0.6435	-0.7411	0.5002	-0.4749	-0.2713	-0.8504	-0.4591
Fn	0.2457	0.9312	0.9354	0.6784	0.6747	-0.4928	0.4377	0.1807	0.9974	0.4242
Ge	0.9907	0.4479	-0.1167	0.7778	-0.3414	0.5813	0.9112	0.9907	0.1867	0.9239
Ic	0.9786	0.6686	0.1266	0.9267	-0.1468	0.3520	0.9919	0.9619	0.4304	0.9964
Nr	-0.4208	-0.8456	-0.8057	-0.7192	-0.6875	0.3625	-0.5690	-0.3872	-0.8492	-0.5573
Sw	-0.3940	-0.8411	-0.8270	-0.7005	-0.7209	0.3695	-0.5421	-0.3571	-0.8556	-0.5310
Bg	0.9581	0.7128	0.1837	0.9499	-0.0978	0.2893	0.9979	0.9371	0.4835	0.9996
Cz	0.2260	0.9171	0.9485	0.6582	0.7125	-0.5025	0.4158	0.1616	0.9911	0.4028
Cr	0.9480	0.7390	0.2198	0.9604	-0.0671	0.2710	0.9965	0.9234	0.5165	0.9969
Pl	-0.0633	0.7298	0.9952	0.3938	0.8658	-0.6688	0.1321	-0.1198	0.8832	0.1174
Rs	-0.2519	0.4782	0.8417	0.1475	0.9993	-0.7008	-0.0828	-0.2880	0.6544	-0.0964
Sr	1	0.5411	-0.0187	0.8441	-0.2661	0.4922	0.9515	0.9951	0.2873	0.9615
Sl	0.5411	1	0.7703	0.8865	0.4561	-0.2686	0.7085	0.4802	0.9496	0.6976
Uk	-0.0187	0.7703	1	0.4415	0.8257	-0.6488	0.1791	-0.0780	0.9134	0.1643
Et	0.8441	0.8865	0.4415	1	0.1270	0.0693	0.9482	0.8024	0.7130	0.9428
Hn	-0.2661	0.4561	0.8257	0.1270	1	-0.6993	-0.0998	-0.3005	0.6335	-0.1133
Al	0.4922	-0.2686	-0.6488	0.0693	-0.6993	1	0.2687	0.5020	-0.4665	0.2969
Ar	0.9515	0.7085	0.1791	0.9482	-0.0998	0.2687	1	0.9327	0.4787	0.9985
Wl	0.9951	0.4802	-0.0780	0.8024	-0.3005	0.5020	0.9327	1	0.2221	0.9427
Bs	0.2873	0.9496	0.9134	0.7130	0.6335	-0.4665	0.4787	0.2221	1	0.4652
Hb	0.9615	0.6976	0.1643	0.9428	-0.1133	0.2969	0.9985	0.9427	0.4652	1
Cb	-0.5606	-0.8194	-0.6945	-0.7661	-0.5677	0.0910	-0.6501	-0.5169	-0.7775	-0.6481
Tg	-0.4732	-0.8526	-0.7830	-0.7479	-0.6585	0.2897	-0.6072	-0.4376	-0.8412	-0.5978
Ch	0.8236	0.1170	-0.4054	0.4792	-0.5653	0.8853	0.6541	0.8233	-0.1352	0.6777
Lg	0.9926	0.6273	0.0795	0.8972	-0.1882	0.4232	0.9733	0.9785	0.3847	0.9810
Sm	0.6391	-0.1050	-0.5551	0.2463	-0.6606	0.9781	0.4348	0.6421	-0.3291	0.4618
Ht	0.4586	-0.3002	-0.6623	0.0321	-0.7001	0.9989	0.2321	0.4695	-0.4909	0.2604
Nh	0.5440	-0.2134	-0.6206	0.1304	-0.6924	0.9972	0.3266	0.5512	-0.4213	0.3544
	Cb	Tg	Ch	Lg	Sm	Ht	Nh
Gr	0.7771	0.9391	0.2185	-0.3202	0.4301	0.5704	0.5142
Lt	-0.8187	-0.8632	-0.0048	0.5091	-0.2130	-0.3921	-0.3138
Es	-0.7973	-0.8513	-0.0554	0.4645	-0.2593	-0.4329	-0.3573
Fr	0.8051	0.9625	0.1197	-0.4047	0.3376	0.4890	0.4270
It	-0.0266	0.1635	0.9541	0.5711	0.9999	0.9715	0.9920
Pt	-0.7117	-0.6809	0.5737	0.9459	0.3453	0.1348	0.2322
Rm	0.0639	0.2603	0.8987	0.4485	0.9838	0.9966	0.9988
Sp	0.1191	0.3199	0.8746	0.4026	0.9732	0.9992	0.9951
Dn	-0.4371	-0.3164	0.9310	0.9362	0.7956	0.6492	0.7203
En	0.7943	0.9539	0.1582	-0.3729	0.3742	0.5219	0.4618
Fn	-0.7776	-0.8436	-0.1723	0.3441	-0.3609	-0.5158	-0.4499
Ge	-0.4984	-0.3977	0.8780	0.9703	0.7143	0.5500	0.6285
Ic	-0.6358	-0.5731	0.7228	0.9929	0.5141	0.3159	0.4087
Nr	0.8641	0.9926	0.0104	-0.4872	0.2295	0.3861	0.3215
Sw	0.9126	0.9854	0.0305	-0.4623	0.2439	0.3913	0.3315
Bg	-0.6594	-0.6084	0.6721	0.9805	0.4556	0.2527	0.3473
Cz	-0.7894	-0.8541	-0.1877	0.3244	-0.3737	-0.5246	-0.4610
Cr	-0.6806	-0.6286	0.6567	0.9755	0.4395	0.2343	0.3298
Pl	-0.6845	-0.7747	-0.4406	0.0333	-0.5830	-0.6802	-0.6437
Rs	-0.5815	-0.6726	-0.5588	-0.1724	-0.6584	-0.7024	-0.6926
Sr	-0.5606	-0.4732	0.8236	0.9926	0.6391	0.4586	0.5440
Sl	-0.8194	-0.8526	0.1170	0.6273	-0.1050	-0.3002	-0.2134
Uk	-0.6945	-0.7830	-0.4054	0.0795	-0.5551	-0.6623	-0.6206
Et	-0.7661	-0.7479	0.4792	0.8972	0.2463	0.0321	0.1304
Hn	-0.5677	-0.6585	-0.5653	-0.1882	-0.6606	-0.7001	-0.6924
Al	0.0910	0.2897	0.8853	0.4232	0.9781	0.9989	0.9972
Ar	-0.6501	-0.6072	0.6541	0.9733	0.4348	0.2321	0.3266
Wl	-0.5169	-0.4376	0.8233	0.9785	0.6421	0.4695	0.5512
Bs	-0.7775	-0.8412	-0.1352	0.3847	-0.3291	-0.4909	-0.4213
Hb	-0.6481	-0.5978	0.6777	0.9810	0.4618	0.2604	0.3544
Cb	1	0.9012	-0.2304	-0.6170	-0.0340	0.1138	0.0522
Tg	0.9012	1	-0.0621	-0.5370	0.1557	0.3137	0.2482
Ch	-0.2304	-0.0621	1	0.7778	0.9571	0.8655	0.9138
Lg	-0.6170	-0.5370	0.7778	1	0.5808	0.3879	0.4786
Sm	-0.0340	0.1557	0.9571	0.5808	1	0.9683	0.9903
Ht	0.1138	0.3137	0.8655	0.3879	0.9683	1	0.9929
Nh	0.0522	0.2482	0.9138	0.4786	0.9903	0.9929	1

References

Matricciani, E. Deep Language Statistics of Italian throughout Seven Centuries of Literature and Empirical Connections with Miller’s 7 ∓ 2 Law and Short–Term Memory. Open J. Stat. 2019, 9, 373–406. [CrossRef]
Matricciani, E. A Statistical Theory of Language Translation Based on Communication Theory. Open J. Stat. 2020, 10, 936–997. [CrossRef]
Matricciani, E. Linguistic Mathematical Relationships Saved or Lost in Translating Texts: Extension of the Statistical Theory of Translation and Its Application to the New Testament. Information 2022, 13, 20. [CrossRef]
Matricciani, E. (2022) Multiple Communication Channels in Literary Texts. Open Journal of Statistics, 12, 486–520. [CrossRef]
Matricciani, E. Capacity of Linguistic Communication Channels in Literary Texts: Application to Charles Dickens’ Novels. Information 2023, 14, 68. [CrossRef]
Matricciani, E. Readability Indices Do Not Say It All on a Text Readability. Analytics 2023, 2, 296-314. [CrossRef]
Miller, G.A. The Magical Number Seven, Plus or Minus Two. Some Limits on Our Capacity for Processing Information, 1955, Psychological Review, 343−352.
Baddeley, A.D., Thomson, N., Buchanan, M., Word Length and the Structure of Short−Term Memory, Journal of Verbal Learning and Verbal Behavior, 1975, 14, 575−589. [CrossRef]
Cowan, N., The magical number 4 in short−term memory: A reconsideration of mental storage capacity, Behavioral and Brain Sciences, 2000, 87−114. [CrossRef]
Pothos, E.M., Joula, P., Linguistic structure and short−term memory, Behavioral and Brain Sciences, 2000, 138−139.
Jones, G, Macken, B., Questioning short−term memory and its measurements: Why digit span measures long−term associative learning, Cognition, 2015, 1−13. [CrossRef]
Saaty, T.L., Ozdemir, M.S., Why the Magic Number Seven Plus or Minus Two, Mathematical and Computer Modelling, 2003, 233−244. [CrossRef]
Mathy, F., Feldman, J. What’s magic about magic numbers? Chunking and data compression in short−term memory, Cognition, 2012, 346−362. [CrossRef]
Chen, Z., Cowan, N., Chunk Limits and Length Limits in Immediate Recall: A Reconciliation, J. Exp. Psychol. Mem. Cogn., 2005, 1235−1249. [CrossRef]
Chekaf, M., Cowan, N., Mathy, F., Chunk formation in immediate memory and how it relates to data compression, Cognition, 2016, 155, 96−107. [CrossRef]
Barrouillest, P., Camos, V., As Time Goes By: Temporal Constraints in Working Memory, Current Directions in Psychological Science, 2012, 413−419. [CrossRef]
Conway, A.R.A., Cowan, N., Michael F. Bunting, M.F., Therriaulta, D.J., Minkoff, S.R.B., A latent variable analysis of working memory capacity, short−term memory capacity, processing speed, and general fluid intelligence, Intelligence, 2002, 163−183. [CrossRef]
Flesch, R., A New Readability Yardstick, Journal of Applied Psychology, 1948, 222-233. [CrossRef]
Flesch, R., The Art of Readable Writing, Harper & Row, New York, revised and enlarged edition, 1974.
Kincaid, J.P., Fishburne, R.P, Rogers, R.L., Chissom, B.S., Derivation Of New Readability Formulas (Automated Readability Index, Fog Count And Flesch Reading Ease Formula) For Navy Enlisted Personnel, 1975, Research Branch Report 8-75, Chief of Naval Technical Training. Naval Air Station, Memphis, TN, USA.
DuBay, W.H., The Principles of Readability, 2004, Impact Information, Costa Mesa, California.
Bailin, A., Graftstein, A. The linguistic assumptions underlying readability formulae: A critique, Language & Communication, 2001, 21, 285−301. [CrossRef]
DuBay (Editor), W.H. , The Classic Readability Studies, 2006, Impact Information, Costa Mesa, California.
Zamanian, M., Heydari, P., Readability of Texts: State of the Art, Theory and Practice in Language Studies, 2012, 43−53. [CrossRef]
Benjamin, R.G. Reconstructing Readability: Recent Developments and Recommendations in the Analysis of Text Difficulty, Educ Psycological Review, 2012, 63−88. [CrossRef]
Collins−Thompson, K., Computational Assessment of Text Readability: A Survey of Past, in Present and Future Research, Recent Advances in Automatic Readability Assessment and Text Simplification, ITL, International Journal of Applied Linguistics, 2014, 97−135.
Kandel, L.; Moles, A.; Application de l’indice de Flesch à la langue française. Cahiers Etudes de Radio-Télévision, 1958, 253–274.
Matricciani, E.; Caro, L.D. A Deep–Language Mathematical Analysis of Gospels, Acts and Revelation. Religions 2019, 10, 257. [CrossRef]
Papoulis, A. Probability & Statistics; Prentice Hall: Hoboken, NJ, USA, 1990.
Shannon, C.E.; A Mathematical Theory of Communication, The Bell System Technical Journal, Vol. 27, 1^st part: 379–423, 2^nd part: 623–656, 1948.

Figure 1. Mean value

m_{I_{P}}

for the indicated language in abscissa, from Table 1. The continuous cyan refers to the global mean value

6.03

, the two cyan dashed lines to a

\pm 2

−standard deviations bounds (95% of the samples in Miller’s range).

Figure 1. Mean value

m_{I_{P}}

for the indicated language in abscissa, from Table 1. The continuous cyan refers to the global mean value

6.03

, the two cyan dashed lines to a

\pm 2

−standard deviations bounds (95% of the samples in Miller’s range).

Figure 2. Probability density function

f (I_{P})

for Ukrainian (green line), Russian (black line), Greek (red line), English (blue line). The vertical magenta lines give the thresholds to be used in Equation (4) for the indicated populations. Other thresholds can be drawn such as those between English and Russian or English and Ukrainian.

Figure 2. Probability density function

f (I_{P})

Figure 3. Probability density function

f (I_{P})

for Latin (blue line), Italian (green line), Spanish (yellow line), Greek (red line). The vertical magenta lines give the thresholds to be used in Equation (4) for the indicated populations. Other thresholds can be drawn, such as those between Spanish and Latin, Spanish and Greek.

Figure 3. Probability density function

f (I_{P})

Figure 4. Probability density function

f (I_{P})

for English (green line) and French (black line). The vertical magenta line gives the threshold to be used in Equation (4).

Figure 4. Probability density function

f (I_{P})

for English (green line) and French (black line). The vertical magenta line gives the threshold to be used in Equation (4).

Figure 5. Probability distribution function of exceeding the overlap index

I_{O} (%)

in abscissa.Figure 6 shows the scatterplot of

I_{O}

calculated by comparing the population of Greek readers, assumed to be the reference population, to readers of all the other languages; or the readers of French (reference language) or English (reference language) to all the other languages.

Figure 5. Probability distribution function of exceeding the overlap index

I_{O} (%)

in abscissa.Figure 6 shows the scatterplot of

I_{O}

Figure 6. Scatterplot of the overlap index

I_{O} (%)

versus language by assuming as reference language Greek (red circles), French (black circles) and English (Green circles).In these examples, it is evident the strong correlation between the values that assume Greek as reference language (scatterplot with red circles) and those that assume French (black circles) or English (green circles) as reference languages. Figure 7 shows the scatterplots and regression lines of

I_{P}

in two languages, for several cases. For example, Greek, French and English readers can be each other confused, while this is not possible with Greek and Spanish readers. Table B1 of Appendix B reports all values of

r_{O}

Figure 6. Scatterplot of the overlap index

I_{O} (%)

I_{P}

r_{O}

Figure 7. Scatterplot of

I_{P}

and regression line of

I_{P}

in two languages, for several cases. French (

y)

versus Greek (

x)

(red circles), English versus Greek (blue upward triangles), English versus French (cyan downward triangles), Spanish versus Greek (green circles).

Figure 7. Scatterplot of

I_{P}

and regression line of

I_{P}

in two languages, for several cases. French (

y)

versus Greek (

x)

(red circles), English versus Greek (blue upward triangles), English versus French (cyan downward triangles), Spanish versus Greek (green circles).

Figure 8. Probability distribution function of exceeding the coefficient of variation

R

in abscissa.

Figure 8. Probability distribution function of exceeding the coefficient of variation

R

in abscissa.

Figure 9. Probability density function

f (I_{P})

for the Universal Reader (Un, cyan line), German (Ge, magenta line), English (En, blue line) and Greek (Gr, black line).Figure 10 shows the overlap index

I_{O}

(%) calculated by comparing the probability density function

f (I_{P})

of the universal reader with the probability density function of the language in abscissa. More than 50% of the languages overlap with the universal reader with probability

p_{O} > 69.20 %

Figure 9. Probability density function

f (I_{P})

for the Universal Reader (Un, cyan line), German (Ge, magenta line), English (En, blue line) and Greek (Gr, black line).Figure 10 shows the overlap index

I_{O}

(%) calculated by comparing the probability density function

f (I_{P})

of the universal reader with the probability density function of the language in abscissa. More than 50% of the languages overlap with the universal reader with probability

p_{O} > 69.20 %

Figure 10. Overlap index

I_{O}

(%) of the probability density function

f (I_{P})

of the languages in abscissa with the probability density function of the universal reader. The mean is 62.55%, the median is 69.20%.

Figure 10. Overlap index

I_{O}

(%) of the probability density function

f (I_{P})

of the languages in abscissa with the probability density function of the universal reader. The mean is 62.55%, the median is 69.20%.

Table 1. Mean value

m_{I_{P}}

and standard deviation

s_{I_{P}}

I_{P}

for the indicated translation and language family of the New Testament books (Matthew, Mark, Luke, John, Acts, Epistle to the Romans, Apocalypse,), calculated from 155 samples. Notice that the list of names reported in Matthew 1.1−1.17 17 and in Luke 3.23−3.38 (genealogy of Jesus of Nazareth) have been deleted for not biasing the statistics of linguistic variables [3]. The source of the texts considered is reported in Reference [3].

Table 1. Mean value

m_{I_{P}}

and standard deviation

s_{I_{P}}

I_{P}

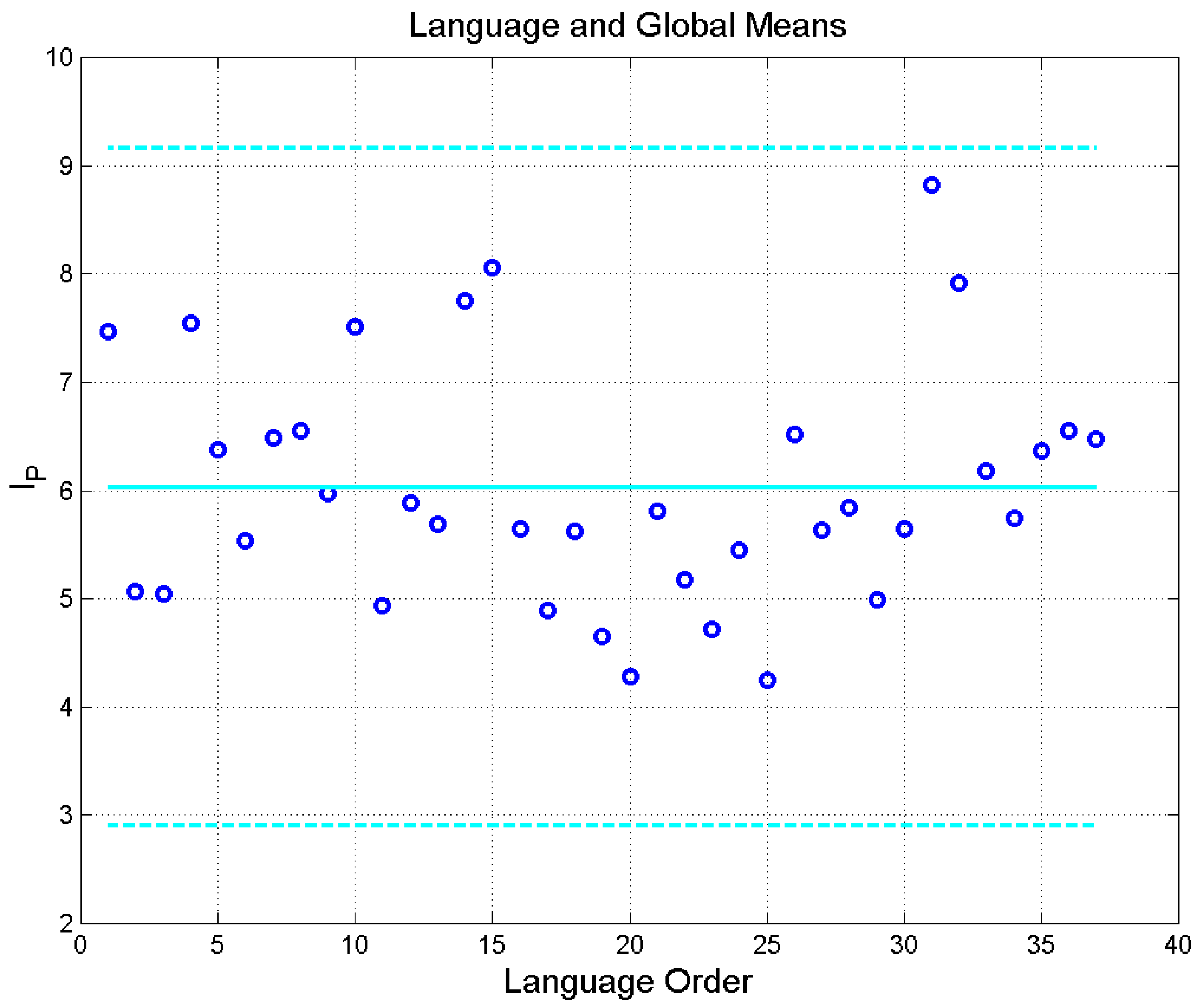
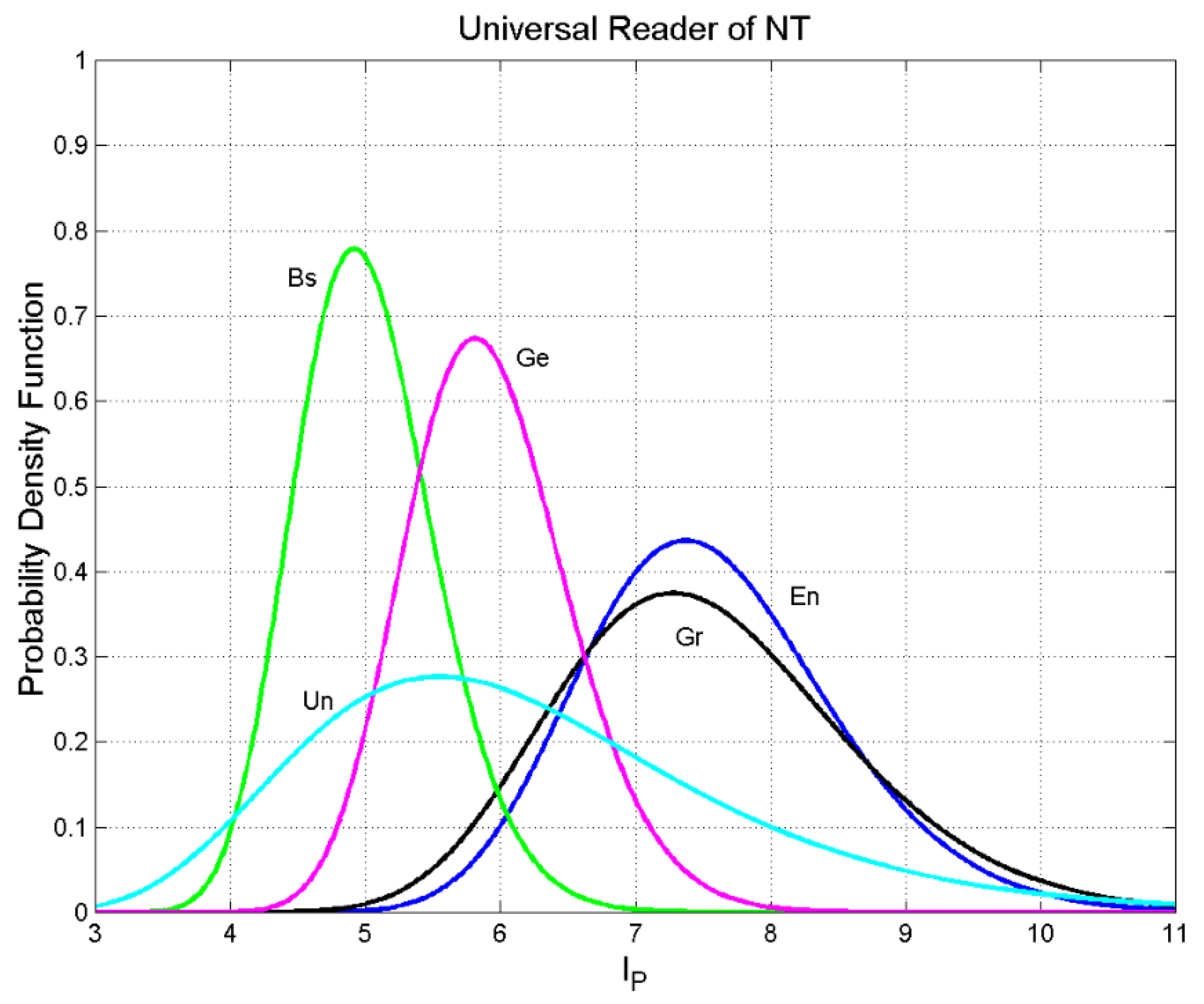
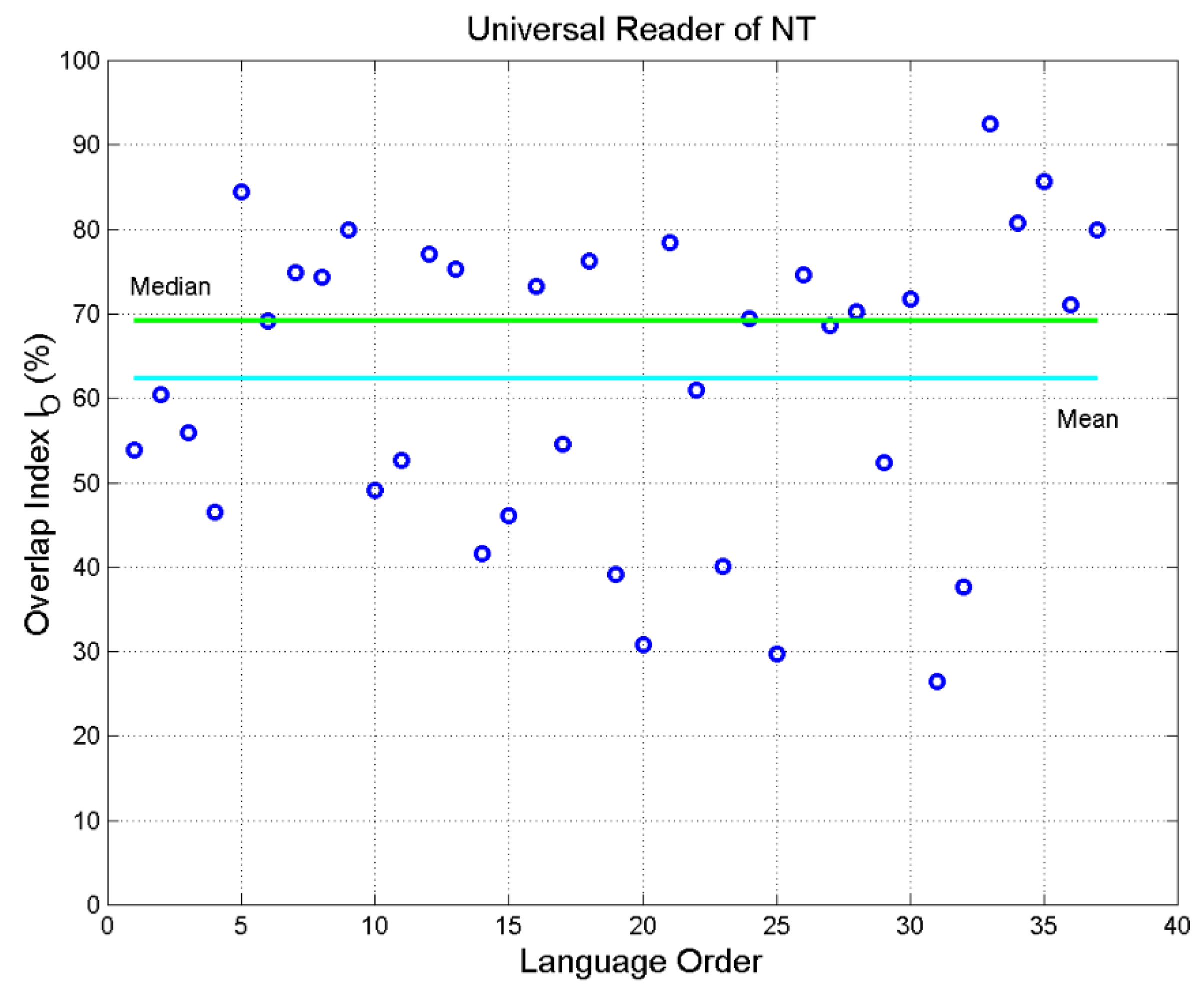
Language	Abbreviation	Order Number	Language Family	$m_{I_{P}}$	$s_{I_{P}}$
Greek	Gr	1	Hellenic	7.47	1.09
Latin	Lt	2	Italic	5.07	0.68
Esperanto	Es	3	Constructed	5.05	0.57
French	Fr	4	Romance	7.54	0.85
Italian	It	5	Romance	6.38	0.95
Portuguese	Pt	6	Romance	5.54	0.59
Romanian	Rm	7	Romance	6.49	0.74
Spanish	Sp	8	Romance	6.55	0.82
Danish	Dn	9	Germanic	5.97	0.64
English	En	10	Germanic	7.51	0.93
Finnish	Fn	11	Germanic	4.94	0.56
German	Ge	12	Germanic	5.89	0.60
Icelandic	Ic	13	Germanic	5.69	0.67
Norwegian	Nr	14	Germanic	7.75	0.84
Swedish	Sw	15	Germanic	8.06	1.35
Bulgarian	Bg	16	Balto−Slavic	5.64	0.64
Czech	Cz	17	Balto−Slavic	4.89	0.65
Croatian	Cr	18	Balto−Slavic	5.62	0.75
Polish	Pl	19	Balto−Slavic	4.65	0.43
Russian	Rs	20	Balto−Slavic	4.28	0.46
Serbian	Sr	21	Balto−Slavic	5.81	0.69
Slovak	Sl	22	Balto−Slavic	5.18	0.61
Ukrainian	Uk	23	Balto−Slavic	4.72	0.41
Estonian	Et	24	Uralic	5.45	0.66
Hungarian	Hn	25	Uralic	4.25	0.45
Albanian	Al	26	Albanian	6.52	0.78
Armenian	Ar	27	Armenian	5.63	0.52
Welsh	Wl	28	Celtic	5.84	0.44
Basque	Bs	29	Isolate	4.99	0.52
Hebrew	Hb	30	Semitic	5.65	0.59
Cebuano	Cb	31	Austronesian	8.82	1.01
Tagalog	Tg	32	Austronesian	7.92	0.82
Chichewa	Ch	33	Niger−Congo	6.18	0.87
Luganda	Lg	34	Niger−Congo	5.74	0.82
Somali	Sm	35	Afro−Asiatic	6.37	1.01
Haitian	Ht	36	French Creole	6.55	0.71
Nahuatl	Nh	37	Uto−Aztecan	6.47	0.91

Table 2. Reference language for which the coefficient of variation

R > 0.95

in the indicated languages. Data taken from Table B1 (Appendix B) only the cases of positive correlation coefficients

r_{O} = \sqrt{0.9500} = 0.9747

Table 2. Reference language for which the coefficient of variation

R > 0.95

in the indicated languages. Data taken from Table B1 (Appendix B) only the cases of positive correlation coefficients

r_{O} = \sqrt{0.9500} = 0.9747

Reference Language	$Languages with coefficient of variation R > 0.95$
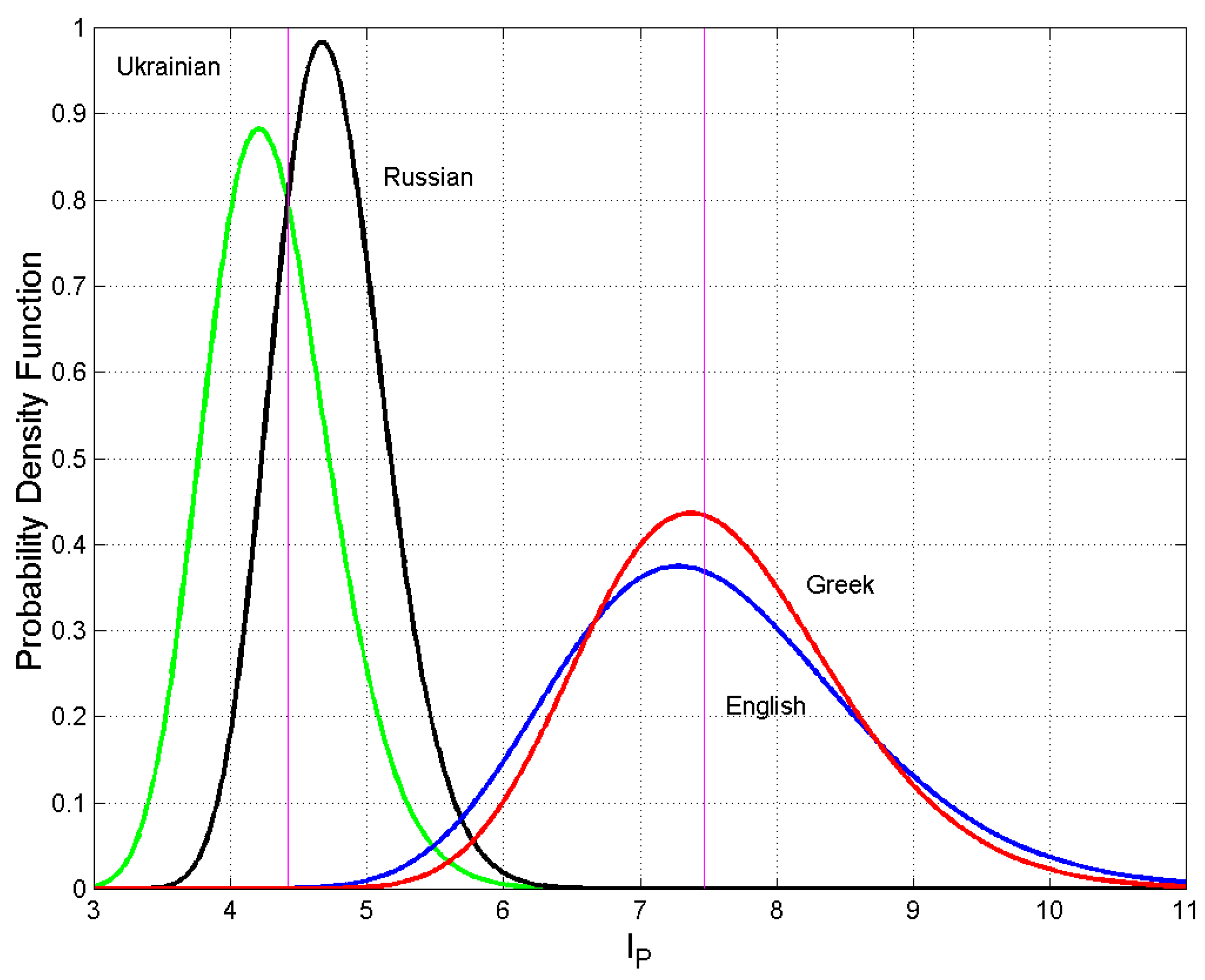
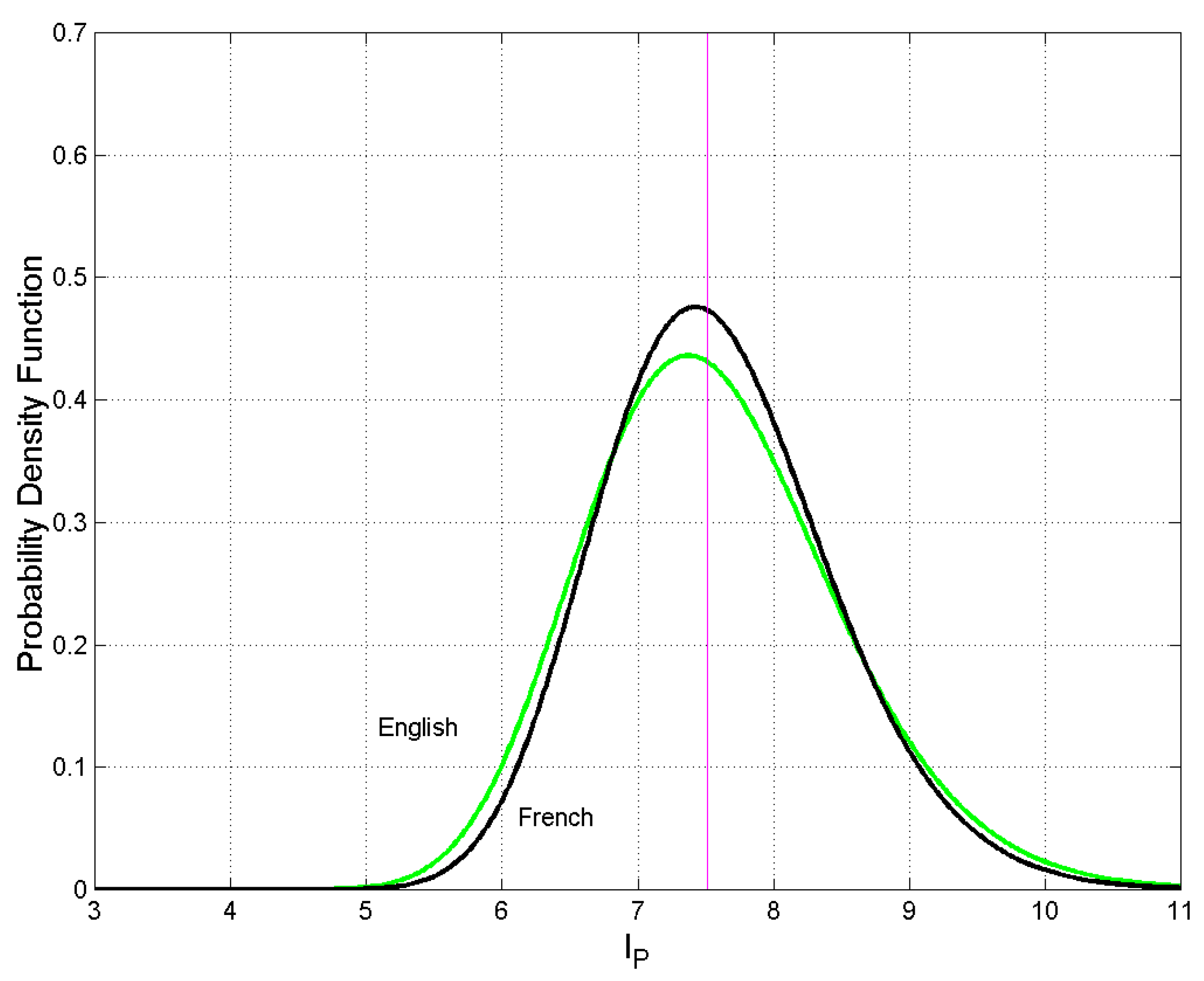
Greek	French, English
Latin	Esperanto, Finnish, Slovack
Esperanto	Latin, Finnish, Czech, Slovak, Basque
French	Greek, English, Norwegian
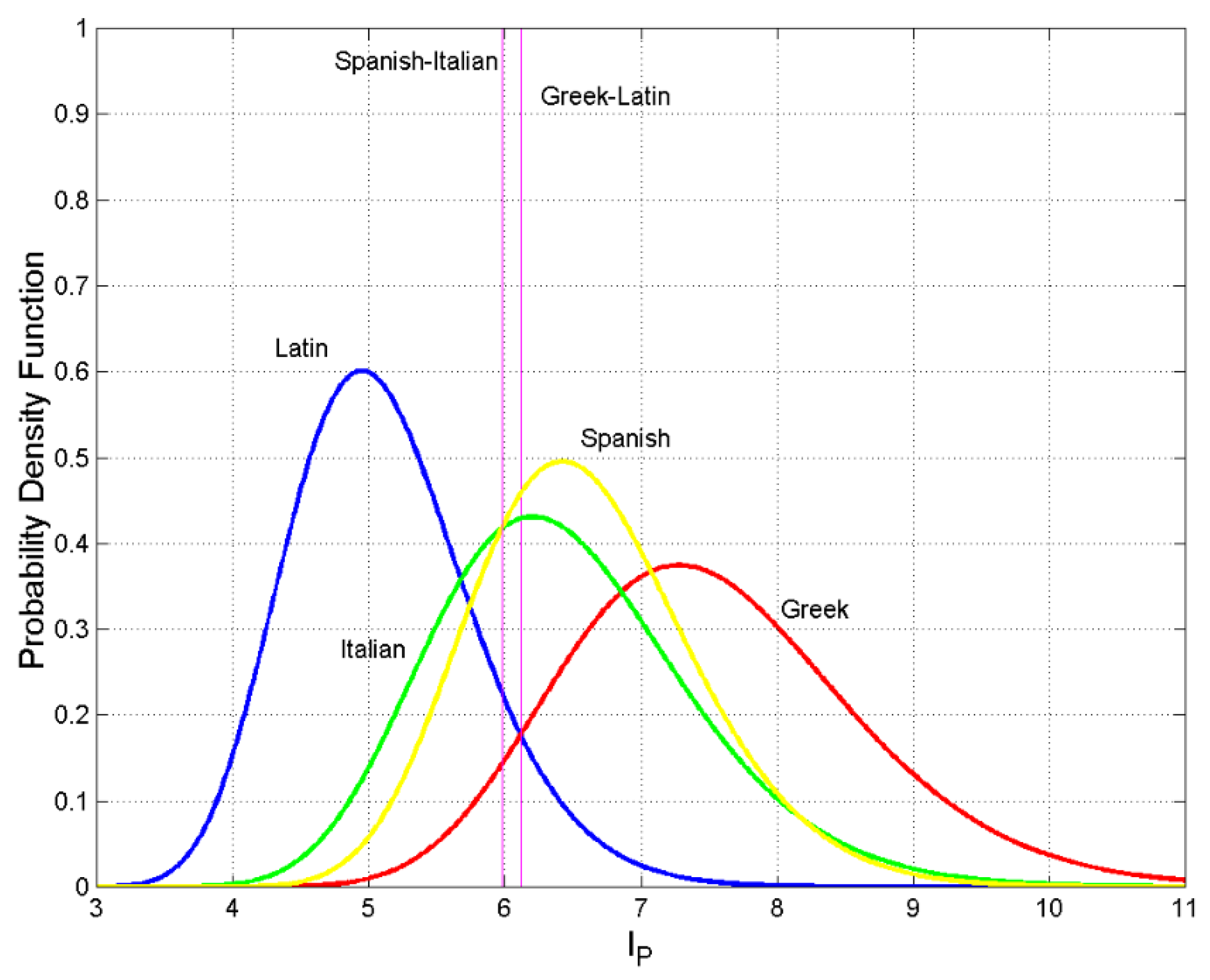
Italian	Romanian, Spanish, Albanian, Somali, Nahuatl
Spanish	Italian, Romanian, Albanian, Haitian, Nahuatl
English	Greek, French, Norwegian
German	Danish, Serbian, Welsh
Russian	Hungarian
Ukrainian	Polish

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Short–Term Memory Capacity Across Time and Language Estimated from Ancient and Modern Literary Texts

Abstract

1. Short−term memory and literary texts

2. Translations of New Testament from Greek to Latin and modern languages

3. Probability density function of I P

4. Probability of readers’ overlap and overlap index

5. Universal Reader of the New Testament

6. Final remarks and future work

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Acknowledgments

Conflicts of Interest

Appendix A. Values of the probability of overlap p O

Appendix B. Values of the correlation coefficient r O

References

MDPI Initiatives

Important Links

Subscribe

3. Probability density function of $I_{P}$

Appendix A. Values of the probability of overlap $p_{O}$

Appendix B. Values of the correlation coefficient $r_{O}$