Submitted:
08 May 2023
Posted:
09 May 2023
You are already at the latest version
Abstract
Keywords:
MSC: 41A30; 45G10; 46B45; 65R20
1. Introduction
2. Existence of a unique solution for the integral equation
- (i)
- The kernels and satisfy the conditions: where and are two constants, assume .
- (ii)
- is a constant.
- (iii)
- The function satisfies the following conditions:
- (iv)
- The function is bounded and satisfy:
3. Method of solution for the main problem
4. Convergence analysis
5. Application and numerical results
6. Conclusions and Remarks
- Under some conditions, the equation (1) has a unique solution in the space .
- After applying the proposed method, a two-dimensional integral equation of the second kind, in time and position, tends to result in an algebraic system of equations.
- A nonlinear system of algebraic equations has a solution.
- Maximum error obtained by proposed method is decreasing when number of is increasing.
- Illustrative examples are provided to evaluate and validate the effectiveness and dependability of the proposed method.
References
- Abdou, M.A.; Soliman, A.A.; Abdel–Aty, M.A. On a discussion of Volterra–Fredholm integral equation with discontinuous kernel. J. Egypt Math. Soc. 2020, 28. [Google Scholar] [CrossRef]
- Abdou, M.A.; Nasr, M.E.; Abdel-Aty, M.A. A study of normality and continuity for mixed integral equations. J. of Fixed Point Theory Appl. 2018, 20. [Google Scholar] [CrossRef]
- Al-Bugami, A.M. Numerical treating of mixed Integral equation two-dimensional in surface cracks in finite layers of materials. Advanced in math. Physics 2022, 25, 1–12. [Google Scholar] [CrossRef]
- Alipour, M.; Baleanu, D.; Babaei, F. Hybrid Bernstein block-pulse functions method for second kind integral equations with convergence analysis. Abstr. Appl. Anal. 2014, 2014, 1–8. [Google Scholar] [CrossRef]
- Bakhshayesh, S.J. , Discontinuous Galerkin approximations for Volterra integral equations of the first kind with convolution kernel. Indian Journal of Science and Technology 2015, 8, 1–4. [Google Scholar] [CrossRef]
- Brezinski, C.; Redivo-Zalglia, M. Extrapolation methods for the numerical solution of nonlinear Fredholm integral equations. J. Integral Equations Appl. 2019, 31, 29–57. [Google Scholar] [CrossRef]
- Chen, Z.; Jiang, W. An Efficient Algorithm for Solving Nonlinear Volterra-Fredholm Integral Equations. Appl. Math. Comput. 2015, 259, 614–619. [Google Scholar] [CrossRef]
- Datta, K.B.; Mohan, B.M. Orthogonal Function in Systems and Control, 9, World Scientific, 1995.
- Elzaki, T.M.; Alamri, A.S. Note on new homotopy perturbation method for solving nonlinear integral equations. J. Math. Comput. Sci. 2016, 6, 149–155. [Google Scholar]
- Golberg, M.A.; Chen, C.S. Discrete Projection Methods for Integral Equation Computational Mechanics Publications, 1997.
- Gouyandeh, Z.; Allahviranloo, T.; Armand, A. Numerical Solution of Nonlinear Volterra-Fredholm-Hammerstein Integral Equations via Tau-Collocation Method With Convergence Analysis. J. Comput. Appl. Math. 2016, 308, 435–446. [Google Scholar] [CrossRef]
- Hafez, R.M.; Youssri, Y.H. Spectral Legendre-Chebyshev treatment of 2D linear and nonlinear mixed Volterra-Fredholm integral equation. Math. Sci. Lett. 2020, 9, 37–47. [Google Scholar]
- Hashemzadeh, E.; Maleknejad, K.; Basirat, B. Hybrid functions approach for the nonlinear Volterra–Fredholm integral equations. Proc. Comput. Sci. 2011, 3, 1189–1194. [Google Scholar] [CrossRef]
- Hesameddini, E.; Riahi, M. Hybrid Legendre Block-pulse functions method for solving partial differential equations with non-local integral boundary conditions. J. Inf. Optim. Sci. 2019, 40, 1391–1403. [Google Scholar] [CrossRef]
- Katani, R. Numerical solution of the Fredholm integral equations with a quadrature method. SeMA J. 2019, 76, 449–452. [Google Scholar] [CrossRef]
- Kreyszig, E. Introductory Functional Analysis with Applications, John Wiley and Sons. Inc., New York, 1989.
- Maleknejad, K.; Ebrahimzadeh, A. An efficient hybrid pseudo-spectral method for solving optimal control of Volterra integral systems. Math. Commun. 2014, 19, 417–435. [Google Scholar]
- Maleknejad, K.; Hashemizadeh, E. Numerical solution of the dynamic model of a chemical reactor by hybrid functions. Procedia. Comput. Sci. 2011, 3, 908–912. [Google Scholar] [CrossRef]
- Maleknejad, K.; Saeedipoor, E. An efficient method based on hybrid functions for Fredholm integral equation of the first kind with convergence analysis. Appl. Math. Comput. 2017, 304, 93–102. [Google Scholar] [CrossRef]
- Mashayekhi, S.; Razzaghi, M. Numerical solution of distributed order fractional differential equations by hybrid functions. J. Comput. Phys. 2016, 315, 169–181. [Google Scholar] [CrossRef]
- Marzban, H.R.; Tabrizidooz, H.R.; Razzaghi, M. A composite collection method for the nonlinear mixed Volterra–Fredholm–Hammerstein integral equation, Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 1186–1194. [Google Scholar] [CrossRef]
- Masouri, Z. Numerical expansion-iterative method for solving second kind Volterra and Fredholm integral equations using block-pulse functions, Adv. Comput. Tech. Electromagn. 2021, 20, 7–17. [Google Scholar]
- Mirzaee, F.; Alipour, S.; Samadyar, N. Numerical solution based on hybrid of Block-pulse and parabolic functions for solving a system of nonlinear stochastic Ito-Volterra integral equations of fractional order. J. Comput. Appl. Math. 2019, 349, 157–171. [Google Scholar] [CrossRef]
- Mirzaee, F. Numerical solution of system of linear integral equations via improvement of block-pulse functions. J. Math. Model. 2016, 4, 133–159. [Google Scholar]
- Mohammadi, F.; Moradi, L.; Baleanu, D.; Jajarmi, A. A hybrid functions numerical scheme for fractional optimal control problems: Application to non analytic dynamic systems. J. Vib. Control. 2017, 24, 5030–5043. [Google Scholar] [CrossRef]
- Nasr, M.E.; Abdel-Aty, M.A. Analytical discussion for the mixed integral equations. J. of Fixed Point Theory Appl. 2018, 20. [Google Scholar] [CrossRef]
- Nasr, M.E.; Abdel-Aty, M.A. A new techniques applied to Volterra–Fredholm integral equations with discontinuous kernel. J. of Computational Analysis and Appl. 2021, 29, 11–24. [Google Scholar]
- Rafiei, Z.; Kafash, B.; Karbasi, S.M. State-control parameterization method based on using hybrid functions of Block-pulse and Legendre polynomials for optimal control of linear time delay systems. Appl. Math. Model. 2017, 45, 1008–1019. [Google Scholar] [CrossRef]
- Ray, S.S.; Singh, S. Numerical solution of stochastic Volterra-Fredholm integral equations by hybrid Legendre Block-pulse functions. Int. J. Nonlinear Sci. Numer. Simul. 2018, 19, 1–9. [Google Scholar]
- Sahu, P.K.; Ray, S.S. Hybrid Legendre Block-pulse functions for the numerical solutions of system of nonlinear Fredholm-Hammerstein integral equations. Appl. Math. Comput. 2015, 270, 871–878. [Google Scholar] [CrossRef]
- Wang, K.; Wang, Q. Taylor polynomial method and error estimation for a kind of mixed Volterra-Fredholm integral equations. Appl. Math. Comput. 2014, 229, 53–59. [Google Scholar] [CrossRef]
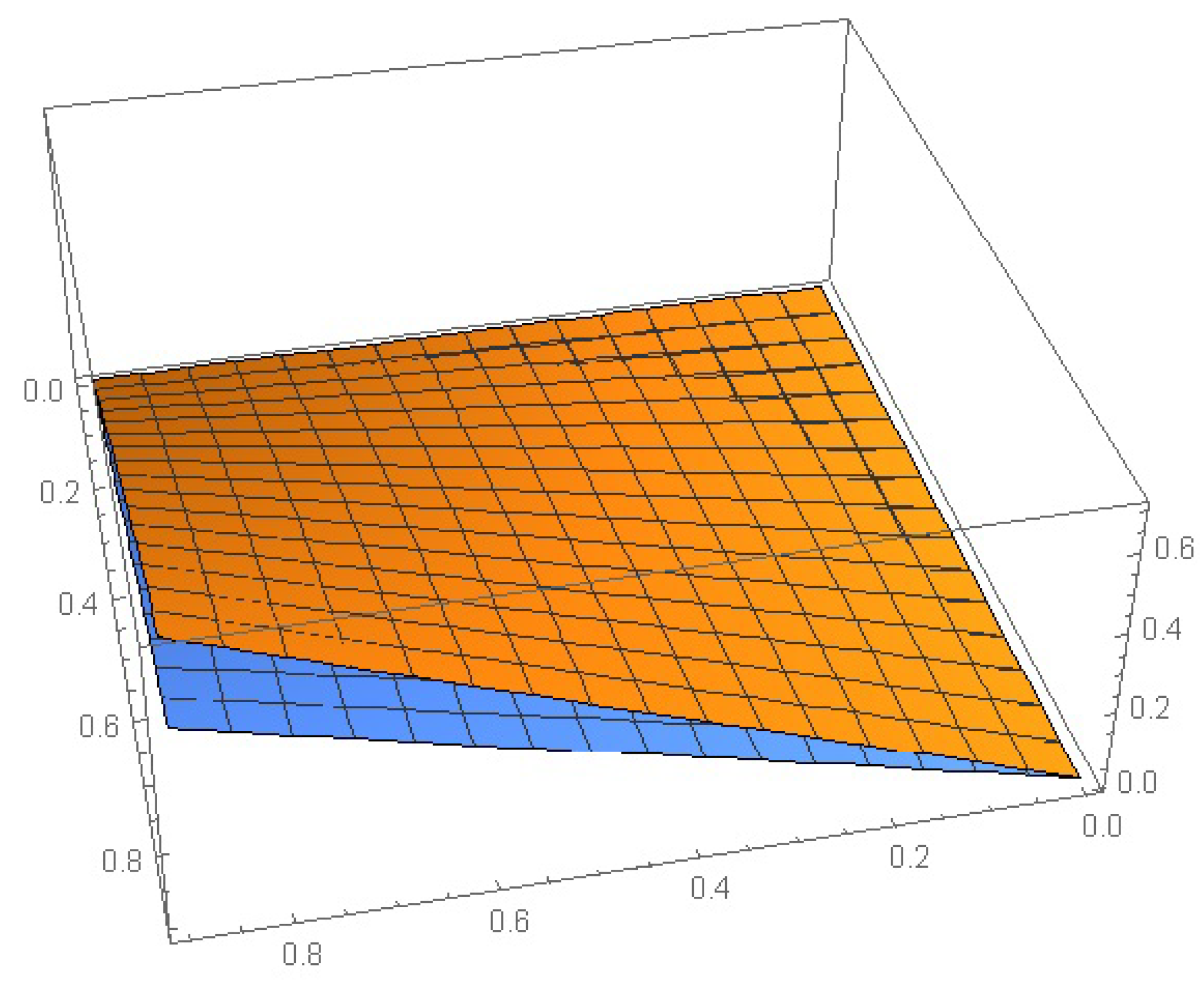
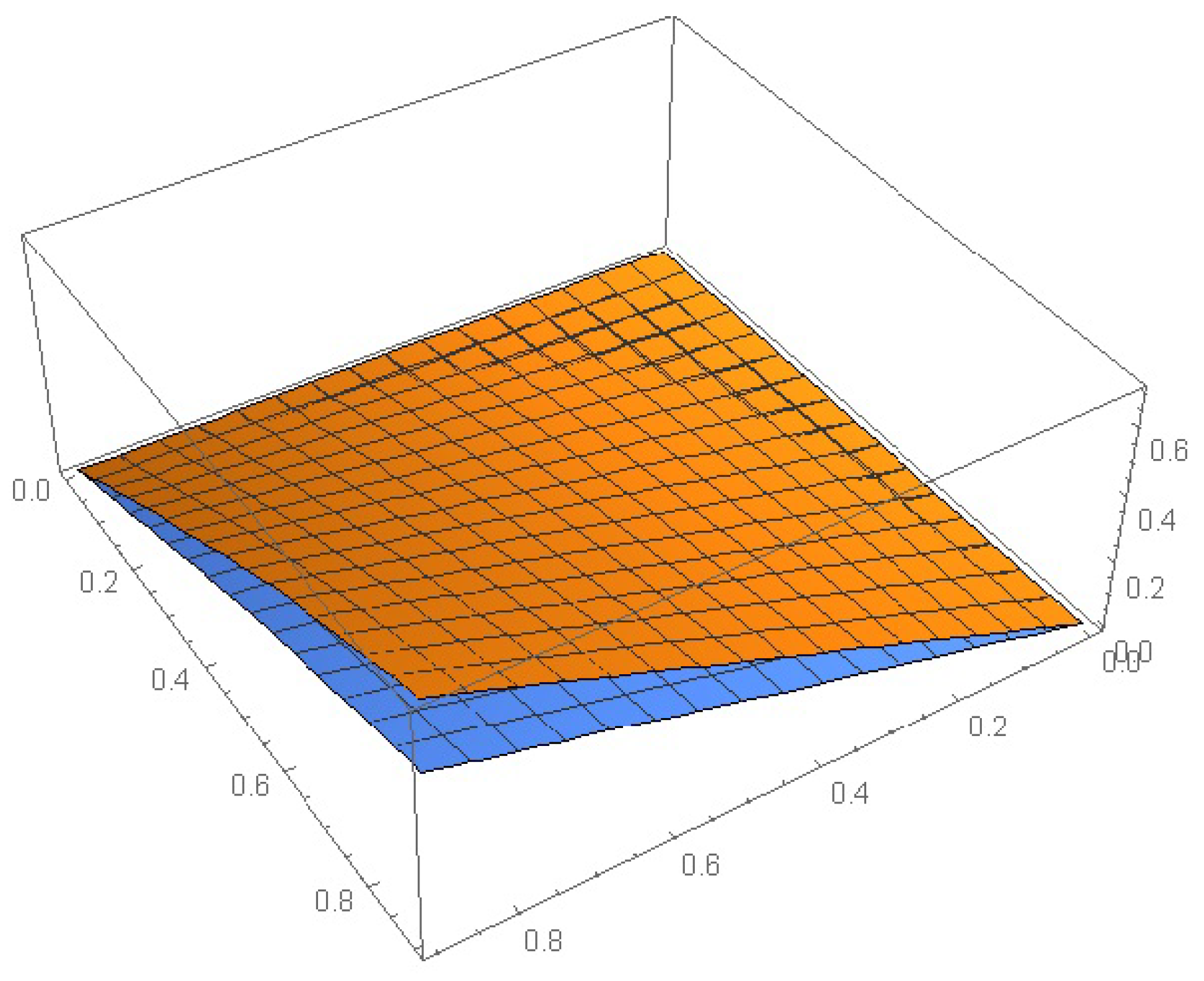
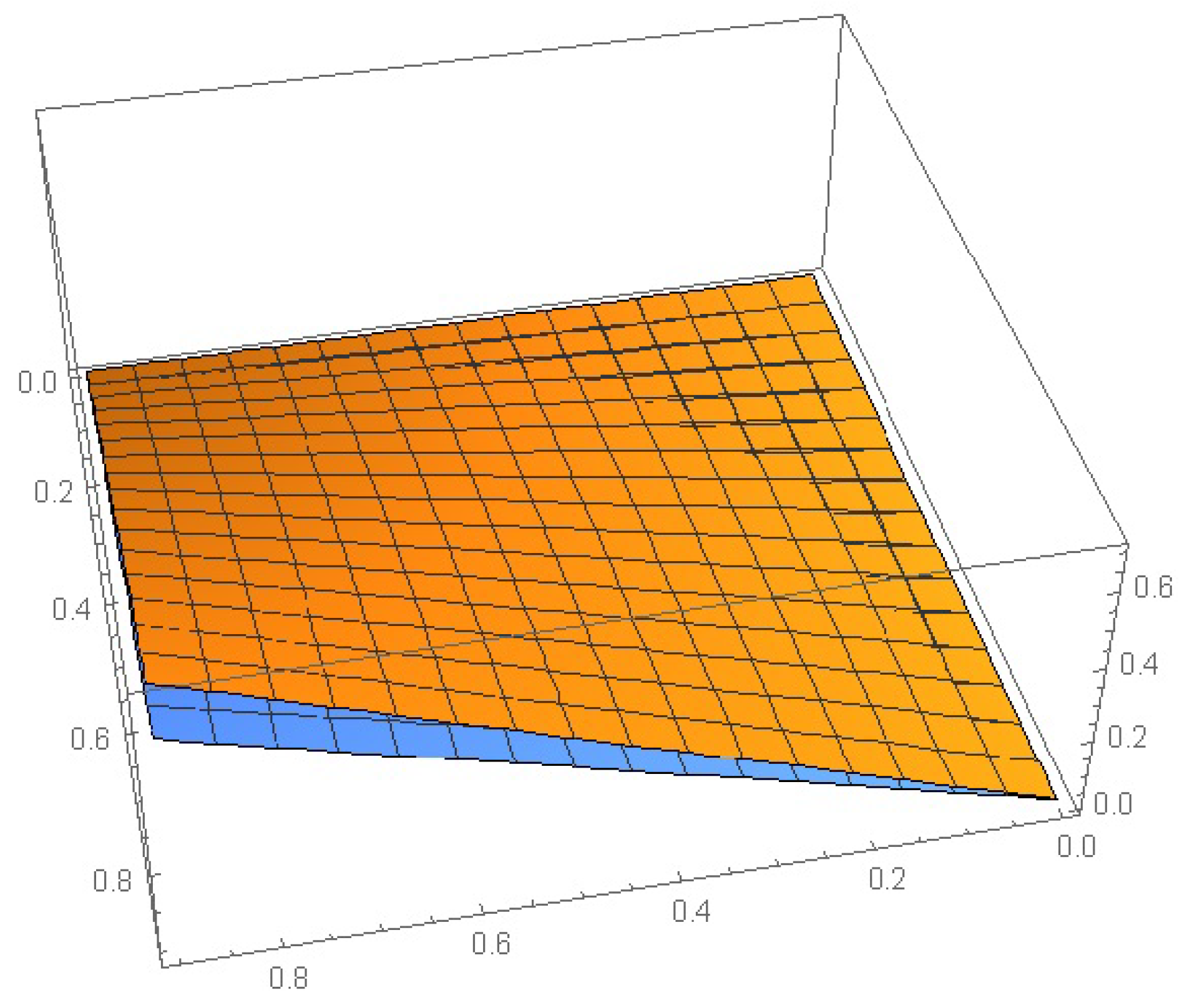
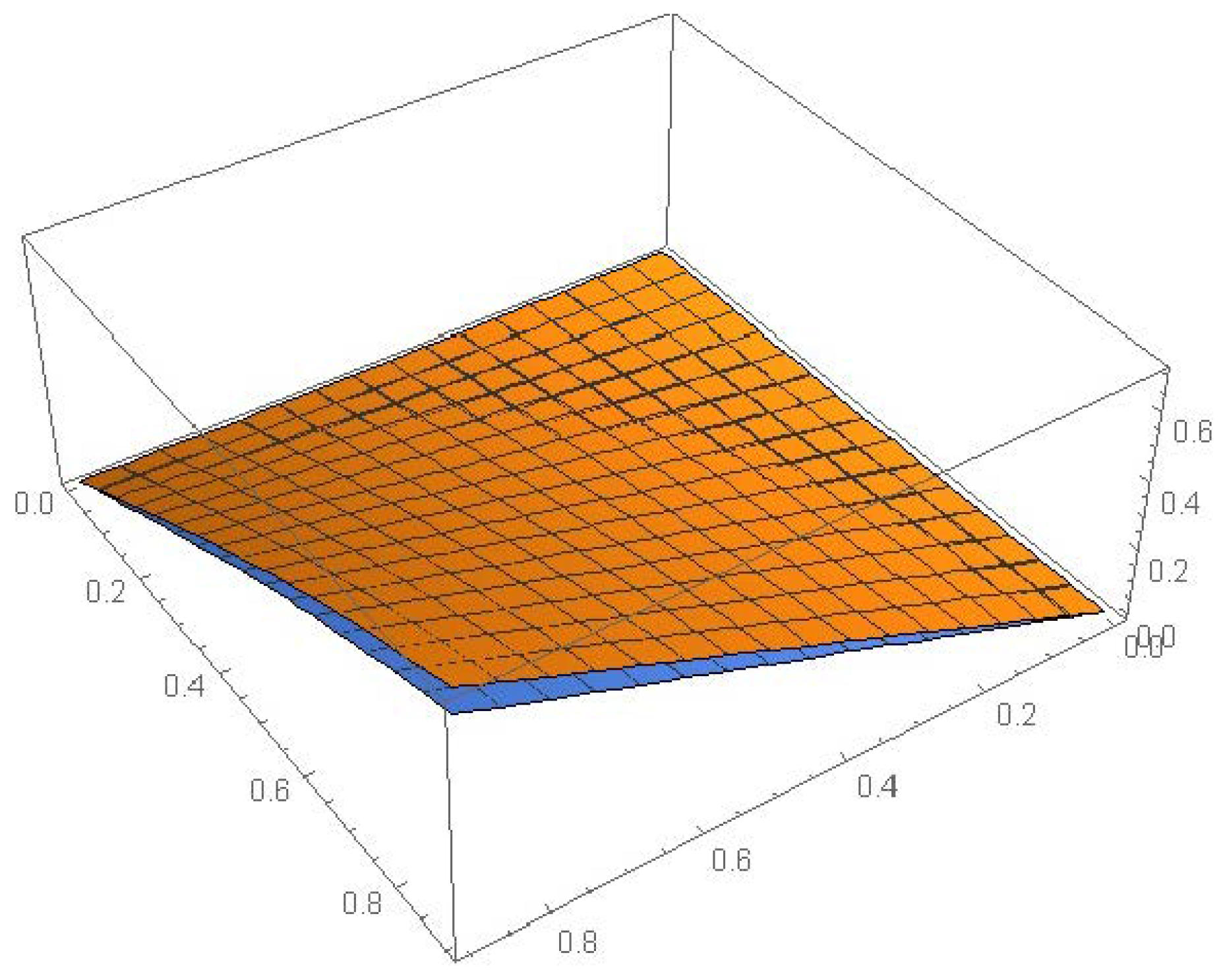
| (0,0) | 5.62845 | 3.25447 | 2.36512 | 1.32654 |
| (0.1,0.1) | 2.51405 | 2.36524 | 1.36524 | 6.32514 |
| (0.2,0.2) | 5.62103 | 2.36985 | 5.36214 | 8.22551 |
| (0.3,0.3) | 2.02154 | 3.58412 | 8.32541 | 6.32165 |
| (0.4,0.4) | 4.58721 | 3.65413 | 2.21345 | 1.32114 |
| (0.5,0.5) | 7.36212 | 2.23651 | 3.65221 | 2.36985 |
| (0.6,0.6) | 1.36521 | 1.65214 | 7.32651 | 2.92541 |
| (0.7,0.7) | 5.26512 | 1.36524 | 6.32541 | 6.32548 |
| (0.8,0.8) | 5.62514 | 4.36210 | 8.36251 | 7.32614 |
| (0.9,0.9) | 5.65214 | 6.25489 | 5.32658 | 1.36524 |
| 6.2103 | 6.53210 | 5.32658 | 1.36524 |
| (0,0) | 3.20514 | 5.32641 | 6.32141 | 2.36541 |
| (0.1,0.1) | 3.25481 | 9.32541 | 5.32187 | 3.65874 |
| (0.2,0.2) | 3.32541 | 3.21554 | 2.36414 | 7.36584 |
| (0.3,0.3) | 4.32641 | 5.32654 | 5.32684 | 3.36241 |
| (0.4,0.4) | 5.36854 | 6.36524 | 8.32546 | 6.32584 |
| (0.5,0.5) | 6.93154 | 7.1.365 | 6.32541 | 8.65241 |
| (0.6,0.6) | 1.32511 | 3.21547 | 9.99215 | 4.32516 |
| (0.7,0.7) | 4.32658 | 4.36561 | 1.32154 | 8.69854 |
| (0.8,0.8) | 5.32666 | 5.76524 | 2.34541 | 4.36215 |
| (0.9,0.9) | 6.32541 | 7.96525 | 3.25456 | 1.05214 |
| 6.32541 | 7.96525 | 3.25456 | 1.05214 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





