Prerpints.org logo
Preprint
Article

Route to Chaos in a Unidirectional Ring of Three Diffusively Coupled Erbium-Doped Fiber Lasers

Altmetrics

Downloads

102

Views

38

Comments

0

Submitted:

07 May 2023

Posted:

09 May 2023

You are already at the latest version

Alerts
Abstract
We study the synchronous dynamics of three diffusively coupled erbium-doped fiber lasers (EDLFs) in the unidirectional ring configuration without external pump modulation. The dynamical behavior of the system is analyzed using time series, Fourier spectra, Poincaré sections, bifurcation diagrams, and Lyapunov exponents for different values of the coupling strength. For weak coupling, we observe a well-known route to chaos from a stable equilibrium through a Hopf bifurcation and a series of torus bifurcations as the coupling strength is increased. An interesting result is found for large values of the coupling strength, where the phase locking is close to zero. This allows a significant increase in the peak energy of the EDFLs pulses, i.e., above the coupling strength the lasers switch to a Q-switching mode with large-amplitude short pulses. This result allows us to propose a new method for increasing the laser pulse energy based on the control of the bistability by the rotating wave in the array of three unidirectionally ring-coupled EDFLs as a function of the coupling strength. In our system, we were able to increase the peak laser power by almost 20 times more than a continuous single EDFL.
Keywords: 
Subject: Physical Sciences  -   Optics and Photonics

1. Introduction

In recent decades erbium-doped fiber lasers (EDFLs) have received revolutionary advances in research and commercialization due to an extensive use of fiber laser technology in optical communications, optical sensing, laser surgery, nonlinear optics, and optical materials [1,2,3,4,5,6]. In addition, fiber amplifier technology is currently a very practical platform for industrial applications due to its superior compactness, robustness, reliability, efficiency, including the alignment-free structure and spatial beam profile.
The EDFL active medium is an erbium-doped optical fiber where the diode-pumped laser light interacts with the active erbium ions, resulting in the high gain and a single transverse mode when the fiber parameters are suitably chosen. Among various types of fiber lasers, EDFLs have several advantages that make them very suitable for optical communications [7]. First, EDFLs can be easily integrated into optical communication networks due to the small size of their optical components. Second, the laser wavelength, especially 1550 nm, is widely used in optical communication systems because of very low losses in optical fibers [8]. Third, EDFLs exhibit very rich dynamic behavior (period doubling, chaos, multistability, etc.) [9,10], that can be controlled and used not only for chaotic communication [2,11], but also for many other applications, such as spectral interferometry [12], optical coherence tomography [13], optical sensing [14], optical metrology [15], industrial micromachining [16], LIDAR systems [17], and medicine [18].
For many applications, nonlinear effects are unwanted factors in fiber lasers, because they disturb a stable laser operation and do not allow a diffraction limit [19], i.e., they make impossible to maintain a Gaussian shape of the laser pulse. Among extensive research on nonlinear effects in EDFLs [19,20,21], there are many papers devoted to a study of multistability in these lasers [9,10,22,23,24,25]. Multistability or coexistence of several final stable states (attractors) for a given set of parameters is a fascinating phenomenon widely observed in nature and studied in almost all areas of science, including physics, engineering, chemistry, biology, and medicine (see [26] and references therein). Control of multistability allows selection of a desirable attractor or elimination of undesirable ones [27]. The coexistence of up to four periodic attractors was found in the EDFL subject to periodic modulation of the laser pump current of cavity losses. The attractors with larger periods have higher pulse energy. For example, the laser pulse amplitude in the period-5 regime is approximately 50 times higher than in the period-1 regime [28].
High pulse power fiber lasers have many applications, e.g., for cutting, welding, surgery, and especially for optical communications [7], to maintain the transmission of the optical signal over a long distance without repeated amplifiers. Recently, a selective control of multistability allowed us to obtain giant pulses in the EDFL array [29]. In addition, the mode-locking technique is considered one of the methods for generating high-energy ultrashort laser pulses, which can be either active or passive. Since 1964 [30], a variety of mode-locking resonators have been developed for a fiber laser. These resonators require a complex controllable amplitude and phase modulator. There are also several passive mode-locking techniques, such as a saturable semiconductor absorber [31,32], nonlinear polarization rotation [33,34], nonlinear optical loop mirror [35], and nonlinear amplifier loop mirror [36].
Single oscillators trace a simple path in phase space. Therefore, dynamics of complex networks of coupled oscillators is receiving a lot of attention from many researchers in different scientific fields. When two or more oscillators are coupled, the spectrum of possible behaviors becomes more complex and the equations governing their behavior become intractable. Each oscillator can be coupled with only few immediate neighbors [37]. One of the simplest network configurations is a cycle ring of coupled oscillators. The dynamics of such ring networks is extremely complex, especially when the oscillators are coupled unidirectionally, even if the uncoupled units are in a stable equilibrium. Many authors studied dynamics of ring-coupled oscillators, for example, three coupled electrical circuits, where they observed chaotic synchronization [38], chimera states in nonlocally coupled oscillators [39], generation of delays in coupled CMOS inverters [40], etc.
Among various network structures [41], the ring configuration is particularly attractive because it allows the propagation of rotating phase waves along the coupled nodes [42,43,44,45]. Such waves were first found in a ring reactor of reaction-diffusion systems [46,47]. Rotating waves arise when a homogeneous state becomes linearly unstable due to a Hopf bifurcation [48]. Later, Nekorkin and colleagues [49] discovered traveling waves propagating in a ring of coupled bistable phase oscillators with sinusoidal nonlinearity. It should be noted that unidirectional coupling is of particular interest because it means that a signal is transmitted from one subsystem to another without receiving feedback. In addition, unidirectional coupling is commonly used in electrical systems based on the Chua [50], Lorenz [51,52], and Duffing [53] models where rotating waves where discovered. Transitions from a stable equilibrium through quasiperiodicity to chaos and hyperchaos with respect to the coupling strength were observed in the rings of unidirectionally coupled Lorenz [51,54], Duffing [55], and Rulkov [56] oscillators. The mechanism leading to such transitions was studied in detail in autonomous Duffing oscillators [53,57,58,59].
Long ago, the Landau–Hopf transition to turbulence via a sequence of successive Hopf bifurcations was discovered on the route to chaos [60,61]. Later, Newhouse, Ruelle, and Takens (NRT) [62,63] proved that the 3D torus decays into a strange chaotic attractor immediately after the third successive Hopf bifurcation, due to the effect of an arbitrarily small perturbation of the so-called NRT scenario. Although several validations of this effect were verified in a large family of frameworks, little attention was paid to a study of this NRT scenario in optical systems such as lasers and especially in fiber lasers. The purpose of this work is to analyse this scenario in a cyclic ring of three diffusively coupled EDFLs. To this aim, we analyze the system behavior using time series, bifurcation diagrams, Poincaré sections, Fourier spectra, and Lyapunov exponents. We will show that although the dynamics of this ring is similar to other coupled oscillators [55], it exhibits particular features inherent to laser systems.
This paper is organized as follows. In Section 2 we describe the model of a single EDFL with pump modulation. In Section 3 we introduce the model of three ring-coupled EDFLs. In Section 4 we study dynamics of this system using time series, bifurcation diagrams, Poincaré sections, Fourier spectra, and Lyapunov exponents. Finally, main conclusions are given in Section 5.

2. Laser Model

The single-mode laser emission is determined by three differential equations, where the important state variables are the optical field, population inversion, and polarization. Depending on the laser type (A, B, or C), these variables decay on different time scales. When one of the variables is large compared to the others, that variable decays diabatically compared to other variables, and the number of equations can be reduced. Lasers in which both the population inversion and polarization decay rapidly compared to the optical field are class-A lasers. Lasers in which only polarization rapidly relaxes belong to class-B lasers. Finally, lasers in which all three variables have close relaxation rates refer to class-C lasers. Therefore, the solution of class-A laser equations is a single stable fixed point. The solution of class-B lasers is also a fixed focus point, where the phase trajectory in the space of the optical field and population inversion is attracted, making relaxation oscillations. Finally, class-C lasers produce undamped periodic or non-periodic (chaotic) pulsations. On the other hand, class-B laser emission can also exhibit periodic or chaotic oscillations under a periodic external force or delayed feedback applied to one of the laser parameters or a variable.
The EDFL considered in this paper belongs to class-B lasers along with solid-state lasers, external-discharged gas lasers (such as CO 2 and CO lasers), and semiconductor lasers [64]. The basic dynamical characteristics of the EDFL are very similar to those of other class-B lasers. In particular, polarization is adiabatically eliminated and the laser dynamics is governed by two rate equations for field and population inversion, and several routes to chaos were found [65]. However, despite the impressive amount of research on EDFL, the dynamics of networks of coupled EDFLs was investigated insufficiently.
To describe diode-pumped EDFL dynamics, the power-balance approach is applied, which takes into consideration the excited state absorption (ESA) in erbium at the 1.5- μ m wavelength and by averaging the population inversion along the pumped active fiber. Such a model addresses the evident factors (i.e., ESA at the laser wavelength and the depleting of the pump wave at propagation along the active fiber) leading to non-dumped natural oscillations in the laser, observed experimentally without external modulation [10,23,66]. The balance equations for the intracavity laser power P (i.e., a sum of the contra-propagating waves’ powers inside the cavity, in s − 1 ) and the averaged (over the active fiber length) population y of the upper ( “2" ) level (i.e., a dimensionless variable, 0 ≤ y ≤ 1 ) are derived as follows
P ˙ = 2 L T r P { r w α 0 ( y [ ξ − η ] − 1 ) − α t h } + P s p
y ˙ = − σ 12 r w P π r 0 2 ( ξ y − 1 ) − y τ + P p u m p ,
where σ 12 is the cross-section of the absorption transition from the ground state “1" to the upper state “2". We suppose that the cross-section of the return stimulated transition σ 12 is practically the same in magnitude that gives ξ = ( σ 12 + σ 21 ) / σ 12 = 2 , η = σ 23 / σ 12 being the coefficient that stands for the ratio between ESA σ 23 and ground-state absorption cross-sections at the laser wavelength. T r = 2 n 0 ( L + l 0 ) / c is the lifetime of a photon in the cavity ( l 0 being the intra-cavity tails of FBG-couplers), α 0 = N 0 σ 12 is the small-signal absorption of the erbium fiber at the laser wavelength N 0 = N 1 + N 2 is the total concentration of erbium ions in the active fiber), α t h = γ 0 + n L ( 1 / R ) / ( 2 L ) is the intra-cavity losses on the threshold ( γ 0 being the non-resonant fiber loss and R is the total reflection coefficient of the FBG-couplers), τ is the lifetime of erbium ions in the excited state “2", r 0 is the fiber core radius, w 0 is the radius of the fundamental fiber mode and r w = 1 + exp [ 2 ( r 0 / w 0 ) 2 ] is the factor addressing a match between the laser fundamental mode and erbium-doped core volumes inside the active fiber.
The population of the upper laser level “2" is given as
y = 1 n 0 L ∫ 0 L N 2 ( z ) d z ,
where N 2 is the population of the upper laser level “2", n 0 is the refractive index of a “cold” erbium-doped fiber core, and L is the active fiber length),
P s p = 10 − 3 y τ T r λ g w 0 r 0 2 α 0 L 4 π 2 σ 12
is the spontaneous emission into the fundamental laser mode, and the pump power is
P p u m p = P p 1 − exp [ − β α 0 L ( 1 − y ) ] n 0 π r 0 2 L ,
where P p is the pump power at the fiber entrance and β = α p / α 0 is the ratio of absorption coefficients of the erbium fiber at pump wavelength λ p and laser wavelength λ g . We assume that the laser spectrum width is 10 − 3 of the erbium luminescence spectral bandwidth. Note that Eqs. (1) and (2) describe the laser dynamics without external modulation.
The parameters used in our simulations correspond to the real EDFL with an active erbium-doped fiber of L = 70 cm. Other parameters are n 0 = 1.45 , l 0 = 20 cm, T r = 8.7 ns, r 0 = 1.5 cm, and w 0 = 3.5 × 10 − 4 cm. The last value was measured experimentally and it was a bit higher than 2.5 × 10 − 4 cm given by the formula for a step-index single-mode fiber w 0 = r 0 ( 0.65 + 1.619 / V 1.5 + 2.879 / V 6 ) , where the parameter V relates to numerical aperture N A and r 0 as V = 2 π r 0 N A / λ g , while the values r 0 and w 0 result in r w = 0.308 .
The coefficients characterizing resonant-absorption properties of the erbium-doped fiber at lasing and pumping wavelengths are α 0 = 0.4 cm − 1 and β = 0.5 , respectively, and correspond to direct measurements for heavily doped fiber with erbium concentration of 2300 ppm, σ 12 = σ 21 = 3 × 10 − 21 cm 2 , σ 23 = 0.6 × 10 − 21 cm 2 , ξ = 2 , η = 0.2 , τ = 10 − 2 s [10], γ 0 = 0.038 , and R = 0.8 that yields α t h = 3.92 × 10 − 2 . At last, the generation wavelength λ g = 1.56 × 10 − 4 cm ( h ν = 1.274 × 10 − 19 J) is measured experimentally, while the maximum reflection coefficients of both FBGs are centered on this wavelength. The pump parameters are the excess over the laser threshold ε defined as P p = ε P t h , where the threshold pump power
P t h = y t h τ n 0 L π w p 2 1 − exp [ − α 0 L β ( 1 − y t h ) ]
and the threshold population of the level “2"
y t h = 1 ξ 1 + α t h r w α 0
with the pump beam radius taken, for simplicity, to be the same as that for generation ( ω p = ω 0 ).

3. Normalized Equations

To simplify the laser model and generalize it in a dimensionless form, we transform Equations (1) and (2) into the simple form (see [67] and appendix [68] for more details)
d x 1 d θ = a x 1 y 1 − b x 1 + c ( y 1 + r w )
d y 1 d θ = − d x 1 y 1 − ( y 1 + r w ) + e 1 − exp − β α 0 L 1 − y 1 + r w ξ 2 r w
where x 1 is the laser intensity and y 1 is the population inversion with
a = 2 L τ s p T r ξ 1 ξ 2 α 0 = 6.6207 e + 7
b = 2 L τ s p T r α t h − α 0 ( ξ 1 − ξ 2 ) ξ 2 r w = 7.4151 e + 6
c = τ s p ξ 2 r w = 0.0163
d = τ s p ξ 2 r w σ 12 π r 0 2 γ = 4.0763 e + 3
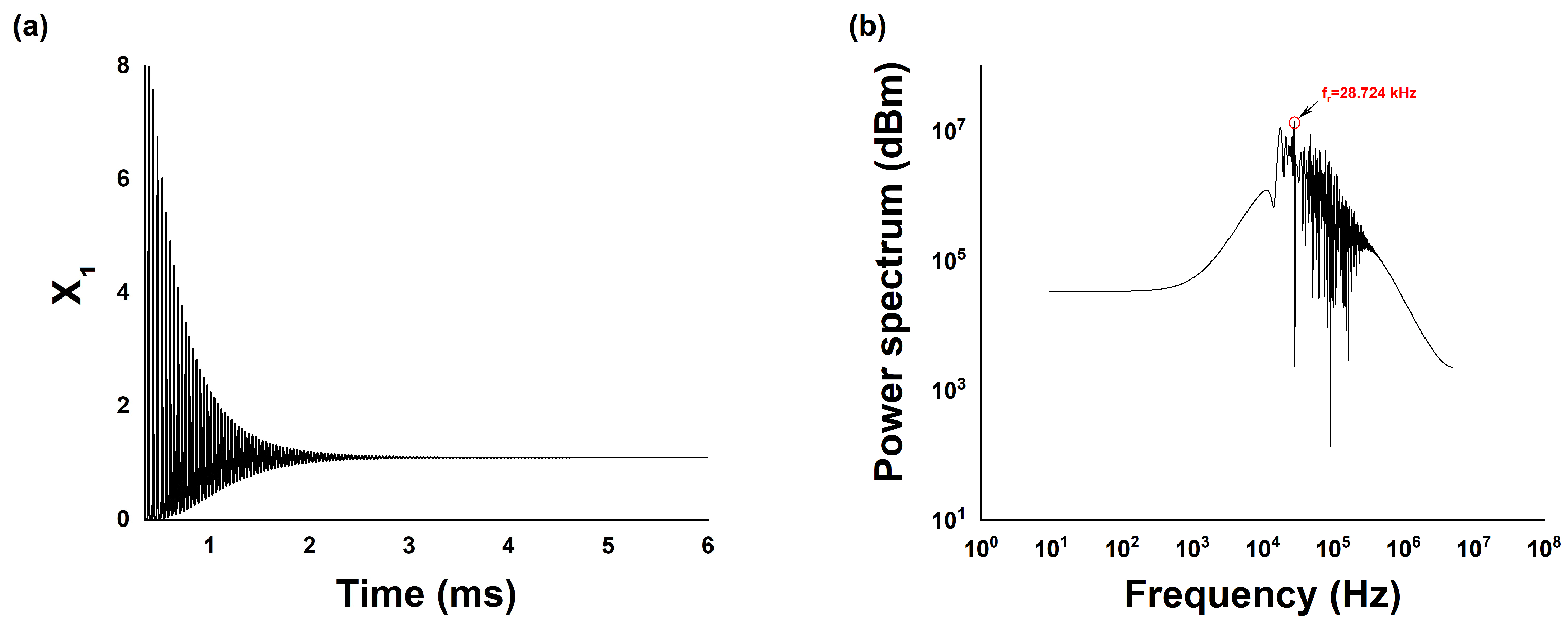
Numerical calculations using the system of equations (8) and (9) allow us to obtain time series characterizing the dynamics of the pump of the EDFL. To simulate the dynamics of the laser, we use parameters close to the experimental parameters from [22]. We chose the pump power P p 0 = 7.4 x 10 19 s − 1 to obtain a relaxation oscillation frequency of the laser of f 0 = 28.724 kHz, see time series and Fourier spectrum in Figure 1 (a) and Figure 1(b), respectively. The solution of laser Equations (8) and (9) is a stable fixed point.

4. Dynamics of the ring of three unidirectionally coupled EDFLs

Ring-coupled oscillators can be seen as a recurrent cycle of interactions [69]. Even simple network motifs formed by just three oscillators can be coupled in thirteen possible configurations [70]. The coupling can be unidirectional, bidirectional or a combination. In this paper, we are especially interested in the simplest ring of three unidirectionally coupled EDFLs, where each laser acts simultaneously as a slave and master oscillator. The dynamics of such a ring is described by two differential equations for laser intensity x j ( j = 1 , 2 , 3 ) and population inversion y j :
d x j d t = a x j y j − b x j + c ( y j + 0.3075 )
d y j d t = d x j y j − ( y j + 0.3075 ) + P p m o d j ( 1 − e − 18 ( 1 − 1 − ( y j + 0.3075 ) 0.6150 ) )
with pumping
P p m o d j = 506 ( 1 + k ( x j − 1 − x j ) )
where k is the coupling coefficient.
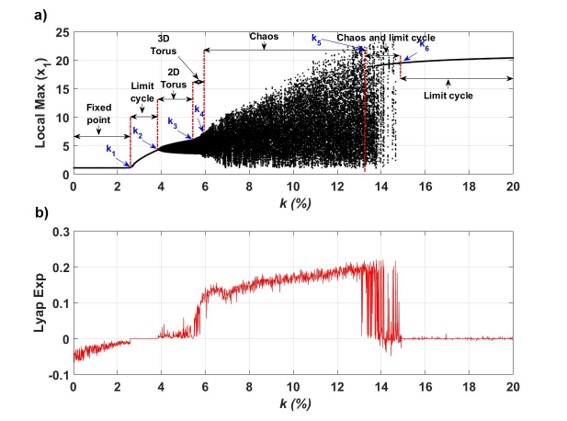
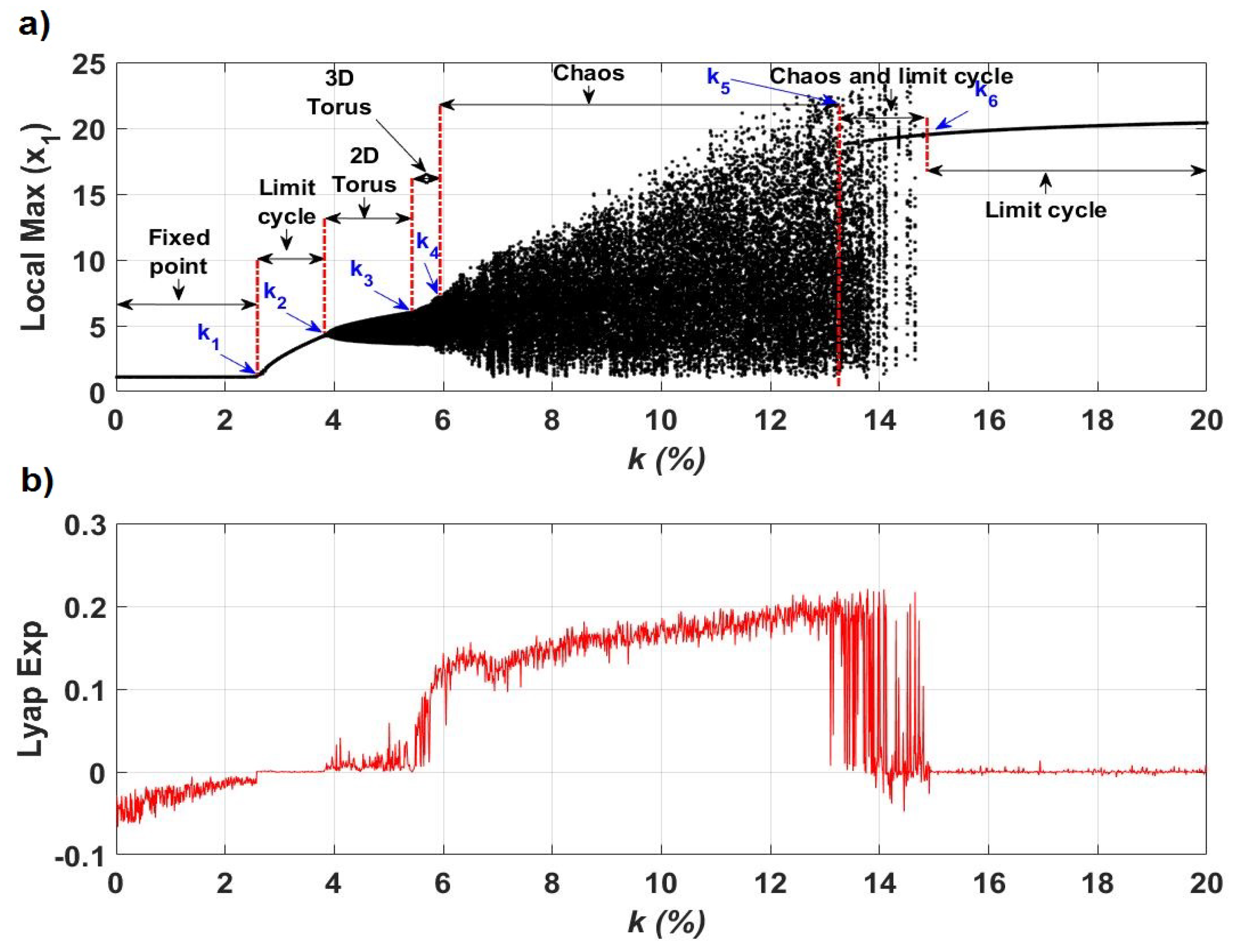
Due to the symmetry of the ring configuration, the dynamics of each laser is identical. Therefore, in Figure 2 we plot the bifurcation diagram of the peak amplitude of only one of the lasers ( x 1 ) and the largest Lyapunov exponent λ as a function of the coupling strength k. The bifurcation scenario displays the Landau route from a stable equilibrium to chaos through quasiperiodicity via subsequent Hopf bifurcations [60,61]. This scenario was described by Newhouse, Ruelle and Takens (so-called NRT scenario [62]), who found that just after the third Hopf bifurcation, a chaotic attractor appears in the form of a 3D torus. Our model Equations (10) and (11) exhibit a similar scenario to hyperchaos when the coupling strength k is changed.
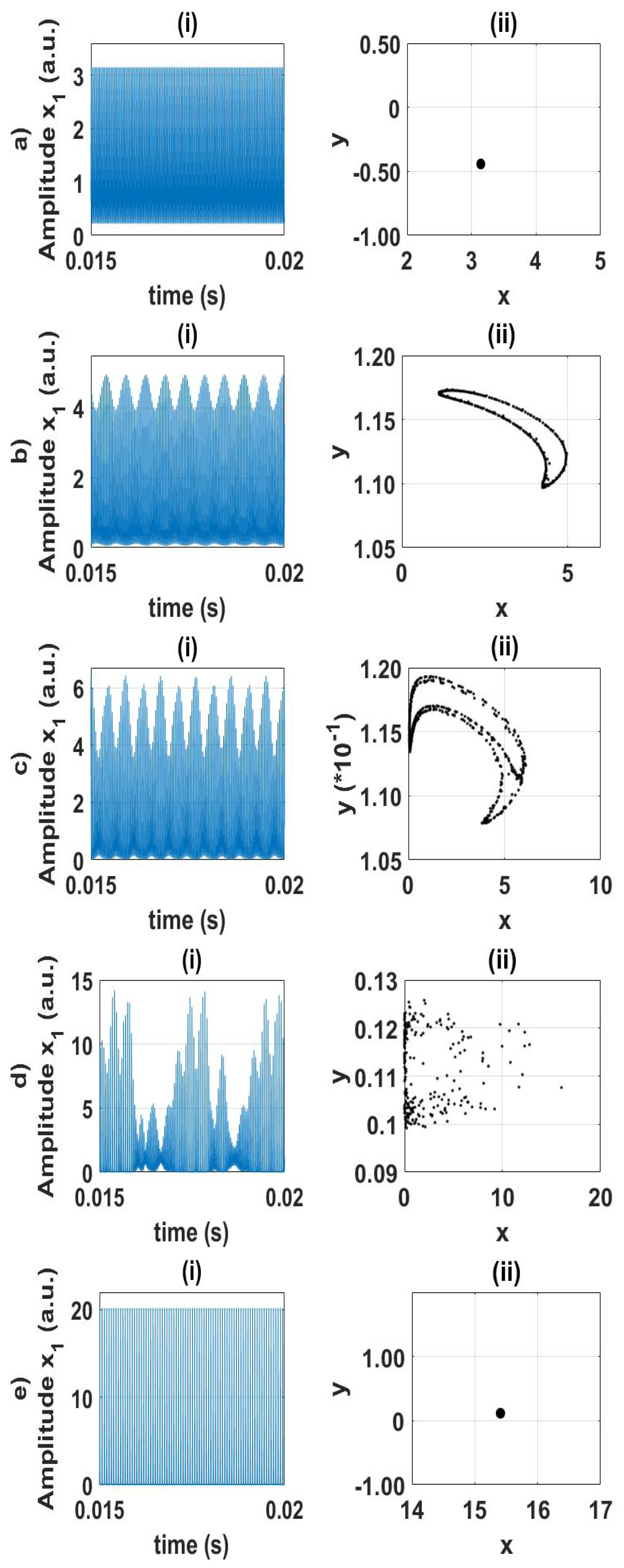
The time series and Poincaré sections in Figure 3 illustrate details of the dynamical regimes observed on the route from a stable fixed point to chaos. As the coupling strength is increased from k = 0 to k 1 ≈ 2.58 , the equilibrium (Figure 1) transforms into a limit cycle (Figure 3(a)) in the Hopf bifurcation, where the largest Lyapunov exponent approaches zero. The periodic regime is maintained within a relatively small region 2.58 < k < 3.81 . Then, at k 2 = 3.82 , the limit cycle transforms into a quasiperiodic regime (2D torus) shown in Figure 3(b). The quasiperiodicity occurs when the second largest Lyapunov exponent reaches zero. As k is further increased, a 3D torus appears at k 3 = 5.49 (Figure 3(c)), when the third largest Lyapunov exponent approaches zero. This regime is observed for 5.49 < k < 5.83 . At k 4 = 5.84 , the system becomes chaotic (Figure 3(d)) when the largest Lyapunov exponent becomes positive. A further increase in the coupling strength leads again to a stable limit cycle at k 6 = 14.81 (Figure 3(e)) when the largest Lyapunov exponent becomes zero.

4.1. Rotating wave

Consider now an interesting phenomenon known as rotating wave. As seen in Figure 3(b–d), a slow envelope (periodic, quasiperiodic, or chaotic) exists in the time series. These low-frequency oscillations result from a rotating wave (periodic, quasiperiodic, or chaotic) propagating along the ring of unidirectionally coupled oscillators due to the phase difference between high-frequency oscillations of each laser. A periodic rotating wave was first found in a ring of coupled Chua oscillators [71,72] and then in a ring of coupled Lorenz [54,73] and Duffing oscillators [53,59,74]. In fact, the rotating wave acts in a similar way as an external modulation which induces low-frequency oscillations. The interaction of the periodic rotating wave with a local limit cycle of each oscillator leads to a local 2D torus where the rotating wave becomes quasiperiodic (Figure 3(c)). For larger k, the local 2D torus interacts with the quasiperiodic rotating wave resulting in a local 3D torus (Figure 3(d)), and with increasing k the rotating wave interacts with the local 3D torus and becomes chaotic (Figure 3(e)). Finally, for very strong coupling the interaction of the rotating wave with the chaotic orbit results in a stabile limit cycle.
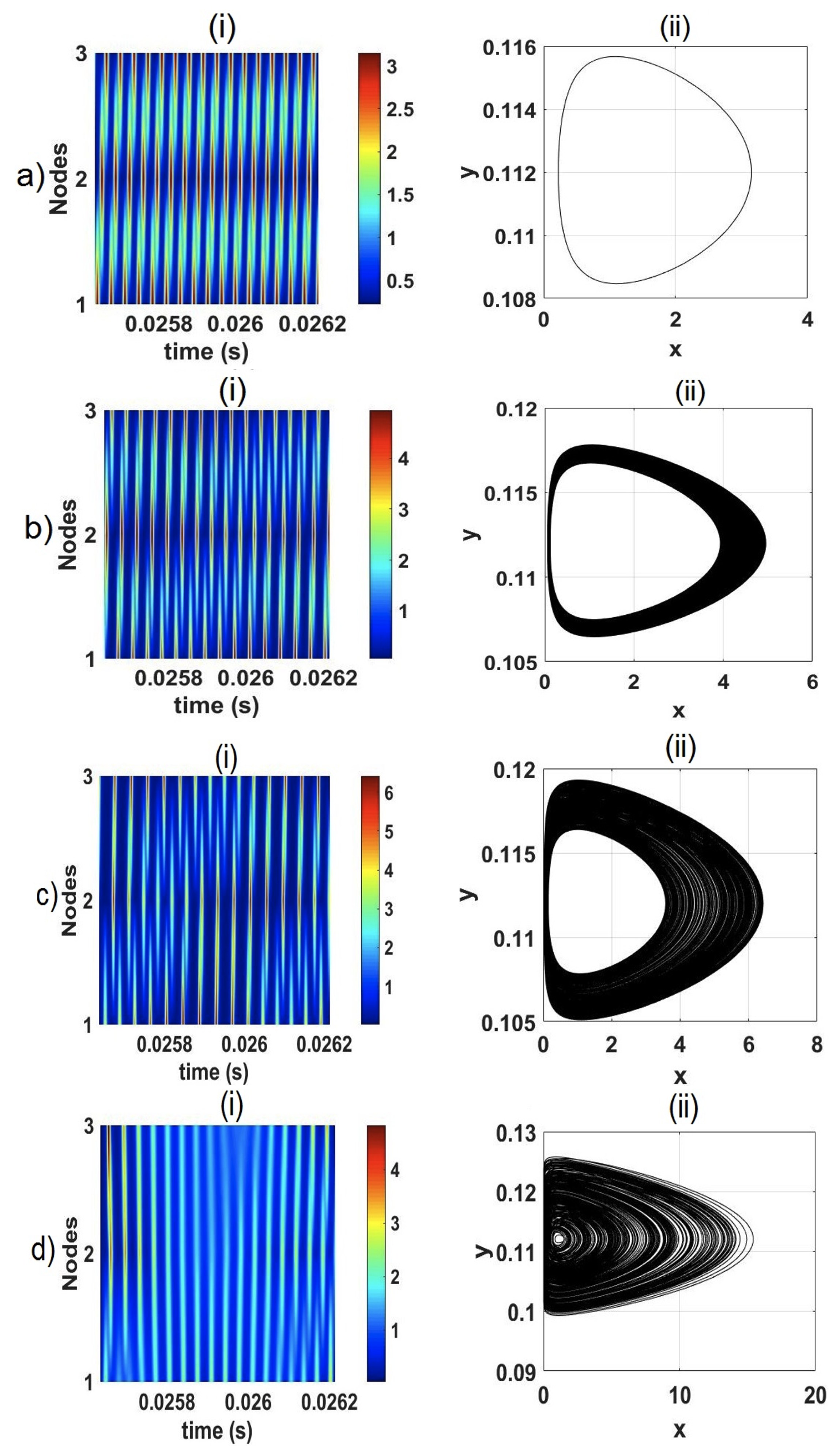
In oscillatory modes, the time series of all oscillators differ only in their phases, so that the phase shifts in each successive node, producing a phase wave that rotates in the cyclic ring. The wave dynamics in the rings of N = 3 oscillators are shown in Figure 4 for four different values of the coupling strength: k = 2.58 , k = 3.82 , k = 5.49 and k = 5.84 . In the left column, we plot the time series patterns of all oscillators, where the rotating waves show up as oblique stripes. One can clearly see the phase waves propagating along the ring of oscillators. The right column shows the phase portraits of the corresponding attractors, the same same for all oscillators since the oscillators are identical. One can see that the attractor’s size enlarges as the coupling strength is increased.

4.2. Frequency spectrum analysis on the route to chaos

The study of the fast Fourier transform (FFT) complements the classical qualitative and quantitative research tools of dynamical systems such as Poincaré maps, bifurcation diagrams of local maxima, and Lyapunov exponents. Spectral analysis of a signal using FFT is a powerful method in science and engineering for studying system dynamics [75,76].
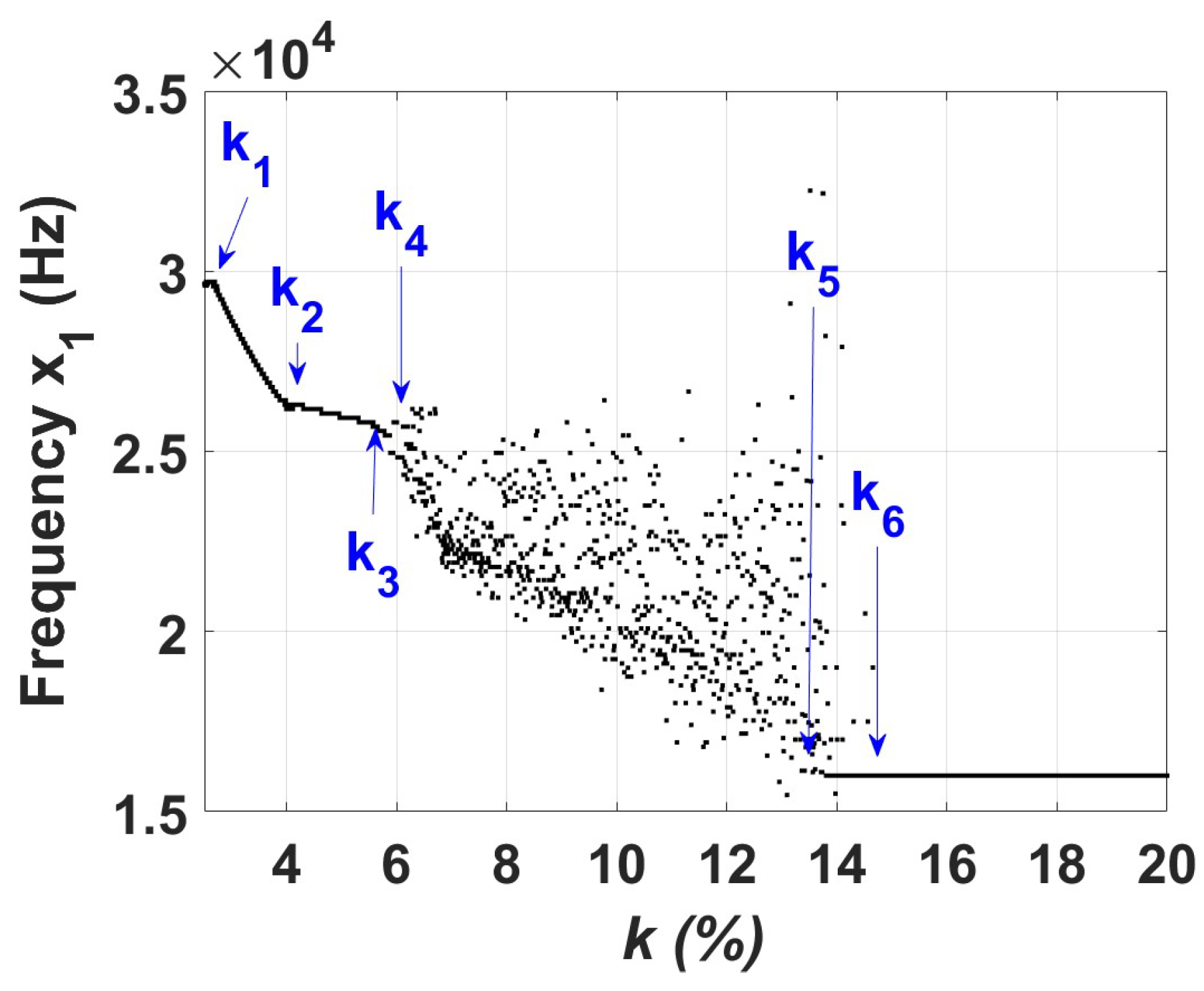
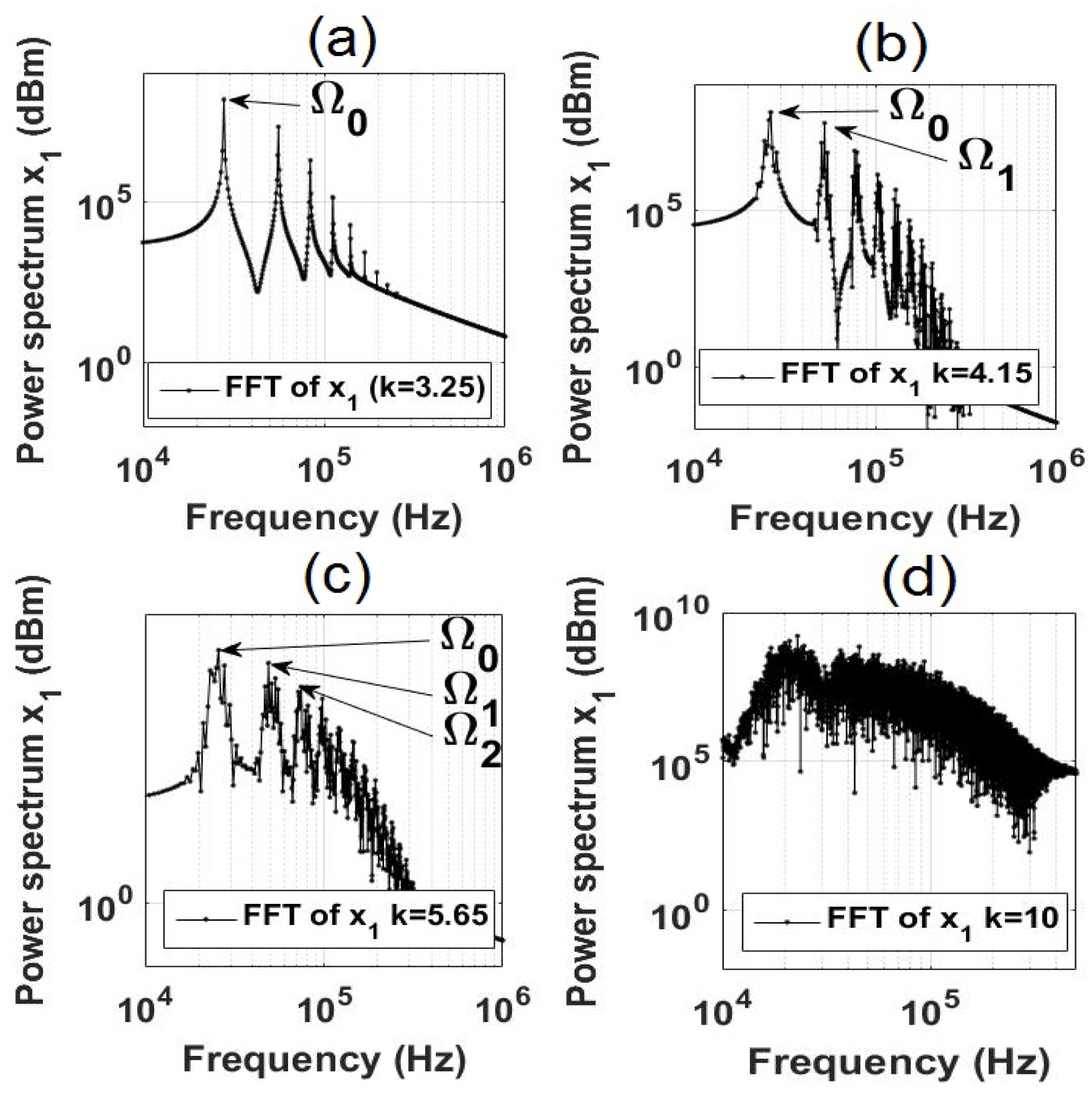
Figure 5 shows the bifurcation diagram of the dominant frequency in the power spectra of x 1 as a function of the coupling strength k. Some power spectra are illustrated in Figure 6 for fixed values of k. As seen from the bifurcation diagram in Figure 5, the first Hopf bifurcation occurs at k 1 where the system dynamics transforms from a stationary to a periodic solution and the first oscillation frequency Ω 0 appears as a single peak in Figure 6(a). A small increase in the coupling strength leads to the second Hopf bifurcation at k 2 where the limit cycle is transformed into a quasiperiodic solution characterized by two incommensurate frequencies Ω 0 and Ω 1 (see Figure 6(b)). The 2D torus exists until the next Hopf bifurcation arises at k 3 where the transition from the 2D torus to the quasiperiodic solution with three frequencies (3D torus) occurs. At the 3D torus a third independent frequency Ω 2 appears in the power spectrum (see Figure 6(d)). The 3D torus dominates within the interval k 3 < k < k 4 . A further increase in the coupling strength k leads to the destruction of the 3D torus, when the direct transition to chaos occurs for k 4 < k < k 5 . The chaotic response manifests itself in the FFT spectrum as a large number of randomly distributed frequency peaks of different amplitudes. A similar behavior was observed in other dynamical systems. For example, Sánchez et al. [54] observed a rotating wave in the ring of unidirectionally coupled Lorenz oscillators while studying the transition from a periodic rotating wave to a chaotic rotating wave via quasiperiodicity. Later, Borkowski et al. [58] reported on the observation of the rotating wave in a ring of seven unidirectionally coupled Duffing oscillators. In their study, they used the FFT bifurcation analysis.

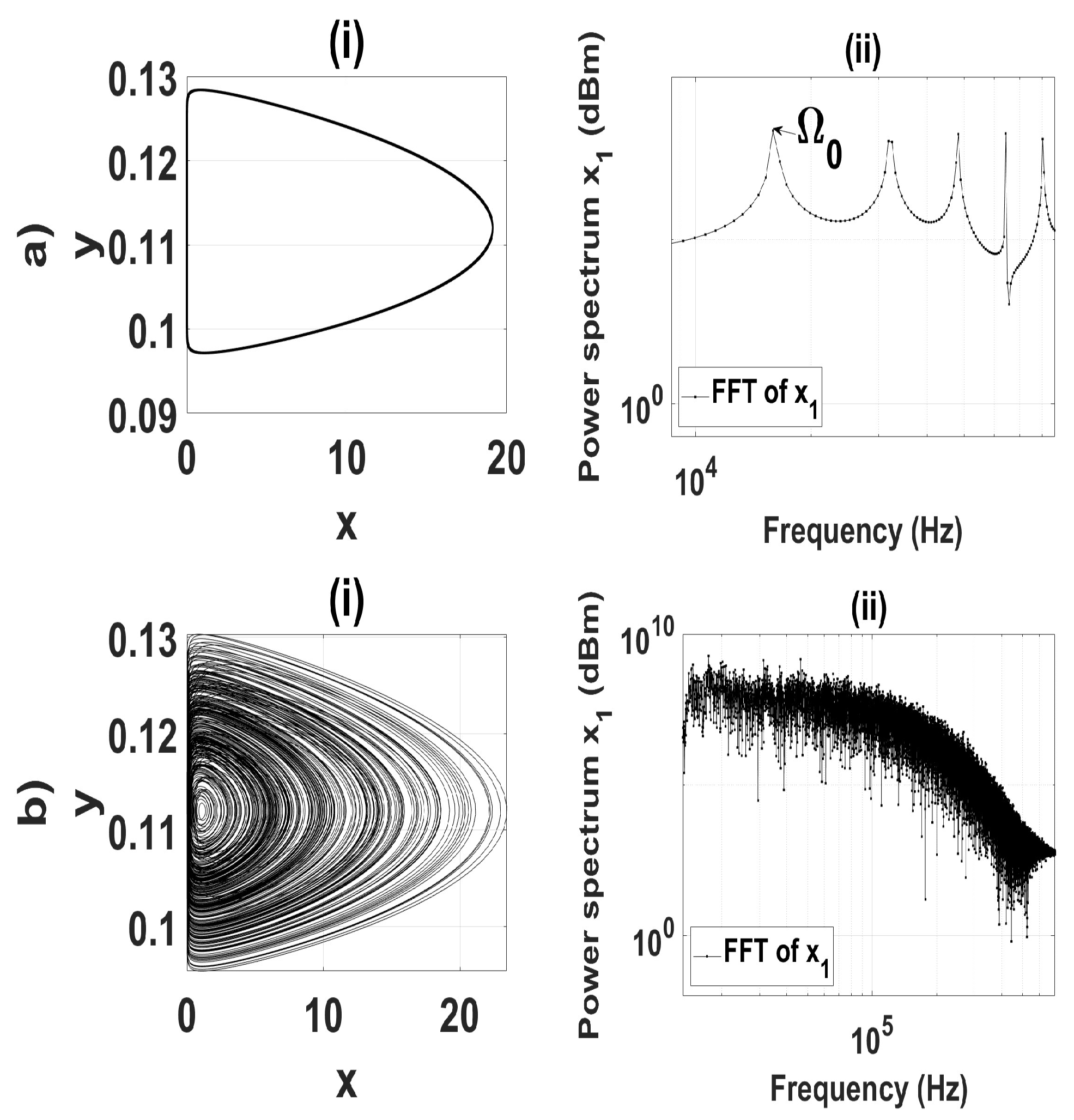
4.3. Coexistence of attractors

On the route from a stable fixed point to chaos, two different coexisting attractors appear in a narrow range of the coupling strength k 5 < k < k 6 . The phase portraits and corresponding power spectra of the coexisting periodic and chaotic regimes are shown in Figure 7 for k = 14.08 . A similar multistable behavior was also found in a ring of three fractional-order double-well Duffing oscillators [77]. In particular, by varying initial conditions, the coexistence of stable fixed points, limit cycle, 2D and 3D tori, and chaos was observed for certain values of the fractional order index and coupling strength. Here, for 13 < k 6 < 14.81 a stable limit cycle coexists with chaos (see bifurcation diagram in Figure 2). In our system, the chaotic and periodic orbits interact with the rotating wave resulting in a monostable limit cycle. A similar scenario was described in other papers (see, e.g., [78,79]), where multistability was controlled by a secondary sinusoidal perturbation. Here, the rotating wave acts as the secondary sinusoidal perturbation that significantly increases the laser pulse power, i.e., the lasers operate in a Q-switching regime by emitting very short large-amplitude pulses.

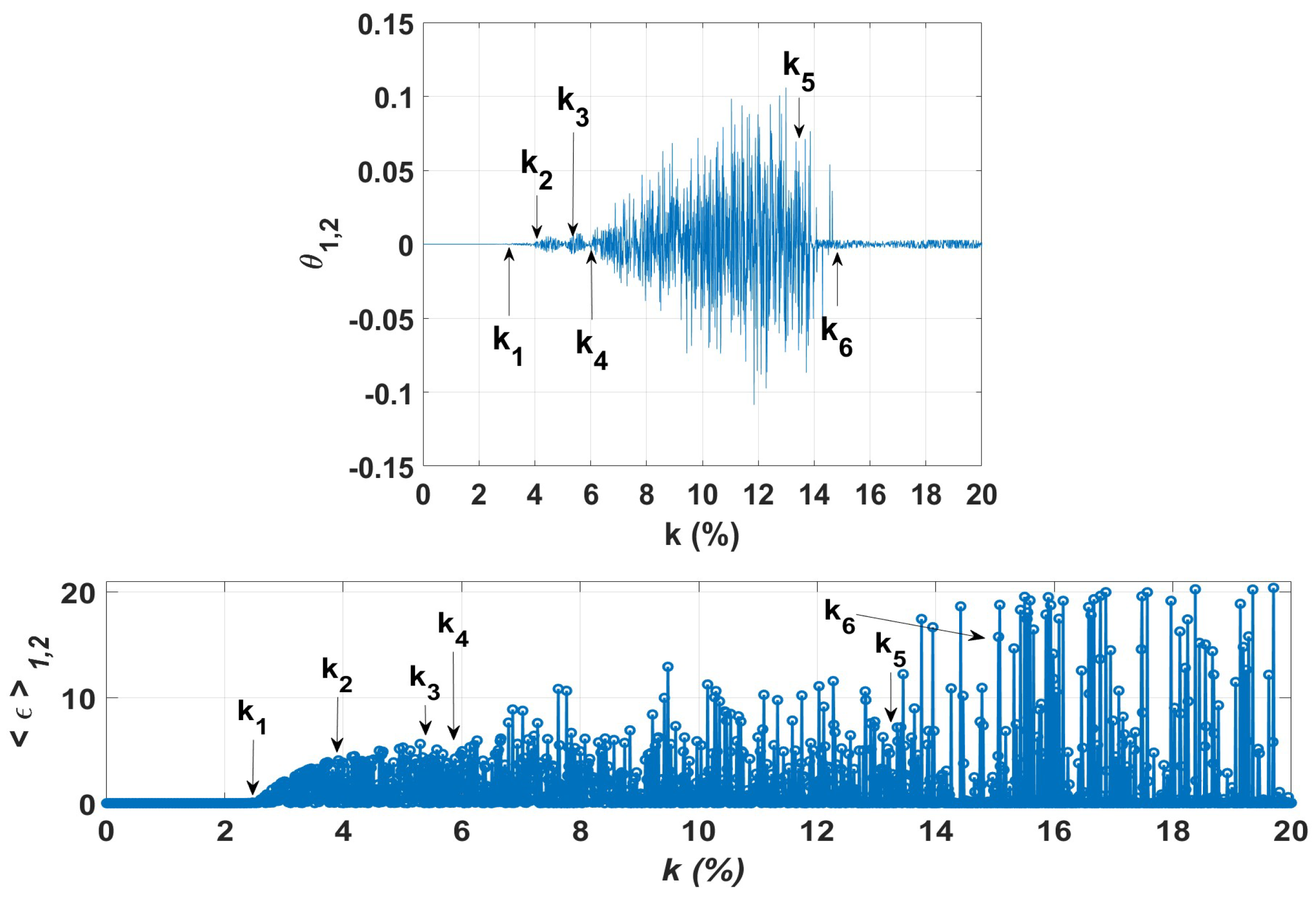
4.4. Synchronization

The rotating wave in the ring of three unidirectionally coupled EDFLs can be treated in terms of synchronization. Phase synchronization of a pair of EDFLs (i and j) can quantitatively be characterized by the difference between their instantaneous phases [70]
θ i j = ϕ i − ϕ j
ϕ i j = a r c t a n ( y i j • x i j )
whereas identical synchronization between a pair of EDFLs can be determined by the synchronization error
e i j = ( x i − x j ) 2 + ( y i − y j ) 2
Figure 8 displays the synchronization scenarios given by Equations (12) and (13). Here, we show how time-averaged phase synchronization and average synchronization error depend on the coupling strength k. One can see the synchronization scenario from a stable equilibrium to chaos. In particular, in the interval k 1 < k < k 2 , we observe a stable limit cycle due phase locking near zero or perfect phase synchronization between the θ 1 and θ 2 phases of x 1 and x 2 , respectively. In the intervals k 2 < k < k 3 and k 3 < k < k 4 , the phase locking is lost and two additional frequencies Ω 1 and Ω 2 appear leading to 2 D and 3 D tori, respectively. Similarly, in the interval k 4 < k < k 6 , phase synchronization vanishes resulting in chaos. Finally, for k > k 6 the phase locking regime appears again.
The difference of the phase of the coupled EDFLs results in the rotating wave (periodic, quasi-periodic, or chaotic) propagating along the ring. As a consequence, identical synchronization cannot be reached, i.e., the average the synchronization error Equation (14) is never zero, as seen from Figure 8(b).

5. Conclusion

In this work, we have numerically investigated the dynamics of three unidirectional ring-coupled EDFLs as a function of the coupling strength. Using a six-dimensional mathematical model with three variables for laser intensities and three variables for population inversions of all lasers, we have studied the route to chaos from a stable equilibrium in the ring. We have analyzed the system dynamics using time series, bifurcations diagrams, power spectra, Poincar’e section, and Lyapunov exponents. On the way to chaos, the system passes through a Hopf bifurcation and a series of torus bifurcations. We have paid special attention to the study of a rotating wave propagating along the ring. Depending on the coupling strength, the wave can be either periodic, quasiperiodic, or chaotic.
In addition, we have found the coexistence of periodic and chaotic orbits in a certain range of coupling strength. For strong coupling, this bistability disappears and the system becomes monostable with a single limit cycle. The mechanism of such stabilization can be understood as the interaction of the chaotic and periodic orbits with the rotating wave. In this regard, the rotating wave acts as a secondary sinusoidal perturbation which leads to the annihilation of the chaotic attractor.
An interesting result has been obtained for strong coupling when the phase locking leads to a significant increase in the peak power of laser pulses. In particular, for k > k 6 all EDFLs operate in the Q-switching mode with very short high-amplitude pulses. This regime is very promising for applications requiring giant laser pulses. In this work, we have succeeded in increasing the peak power of laser pulses by almost 20 times compared to the continuous mode, i.e., when the lasers are uncoupled. This significant achievement can be of great importance in optical communication since optical signals travel hundreds of kilometers along optical fibers and therefore are highly attenuated during propagation. Sufficiently high power of the transmitted optical signal can be achieved by using optical amplifiers based on the nonlinear properties of EDFLs. In these cases, the coexistence of Q-switching regimes with different pulse amplitudes and proper control of bistability can be useful to obtain high-power laser pulses.
On the other hand, it is worth mentioning some of the limitations of this work. First of all, in this paper, we have considered the simplest ring of only three lasers. Therefore, our results cannot be generalized to large laser networks. However, we believe that some dynamic features of our system are also inherent to larger laser networks. This is a promising topic for future research.

Author Contributions

J.O.E.T.: Writing—Original Draft, Writing—Review and Editing, Methodology, Software, Validation, Visualization. J.H.G.L.: Writing—Review and Editing, Resources, Project administration. R.J.R.: Writing—Original Draft, Supervision, Funding acquisition, Writing—Review and Editing, Resources. V.A.: Writing—Review and Editing, Resources. G.H.C.: Writing—Review and Editing, Validation, Methodology. A.N.P.: Writing—Review and Editing, Visualization, Conceptualization, Data Curation. All authors have read and agreed to the published version of the manuscript.

Funding

This project was supported by: Programa Presupuestario F003 CONACYT–MEXICO Convocatoria “Ciencia Básica y/o Ciencia de Frontera. Modalidad: Paradigmas y Controversias de la Ciencia 2022”, under project number: 320597.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

J.O.E.T. thanks CONACYT for financial support (CVU-854990). R.J.R. thanks CONACYT for financial support, project No. 320597.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Digonnet, M.J. Rare-earth-doped fiber lasers and amplifiers, revised and expanded; CRC press, 2001.
  2. Luo, L.; Chu, P. Optical secure communications with chaotic erbium-doped fiber lasers. JOSA B 1998, 15, 2524–2530. [Google Scholar] [CrossRef]
  3. Shay, T.; Duarte, F. Tunable fiber lasers. Tunable Laser Applications.
  4. Pisarchik, A.; Jaimes-Reátegui, R.; Sevilla-Escoboza, R.; García-Lopez, J.; Kazantsev, V. Optical fiber synaptic sensor. Optics and Lasers in Engineering 2011, 49, 736–742. [Google Scholar] [CrossRef]
  5. Mary, R.; Choudhury, D.; Kar, A.K. Applications of fiber lasers for the development of compact photonic devices. IEEE Journal of Selected Topics in Quantum Electronics 2014, 20, 72–84. [Google Scholar] [CrossRef]
  6. Zhao, L.; Li, D.; Li, L.; Wang, X.; Geng, Y.; Shen, D.; Su, L. Route to larger pulse energy in ultrafast fiber lasers. IEEE Journal of Selected Topics in Quantum Electronics 2017, 24, 1–9. [Google Scholar] [CrossRef]
  7. Zervas, M.N.; Codemard, C.A. High power fiber lasers: a review. IEEE Journal of selected topics in Quantum Electronics 2014, 20, 219–241. [Google Scholar] [CrossRef]
  8. Castillo-Guzmán, A.; Anzueto-Sánchez, G.; Selvas-Aguilar, R.; Estudillo-Ayala, J.; Rojas-Laguna, R.; May-Arrioja, D.; Martínez-Ríos, A. Erbium-doped tunable fiber laser. In Proceedings of the Laser Beam Shaping IX. International Society for Optics and Photonics, Vol. 7062; 2008; p. 70620. [Google Scholar]
  9. Saucedo-Solorio, J.M.; Pisarchik, A.N.; Kir’yanov, A.V.; Aboites, V. Generalized multistability in a fiber laser with modulated losses. JOSA B 2003, 20, 490–496. [Google Scholar] [CrossRef]
  10. Reategui, R.; Kir’yanov, A.; Pisarchik, A.; Barmenkov, Y.O.; Il’ichev, N. Experimental study and modeling of coexisting attractors and bifurcations in an erbium-doped fiber laser with diode-pump modulation. Laser Phys 2004, 14, 1277–1281. [Google Scholar]
  11. Ke, J.; Yi, L.; Xia, G.; Hu, W. Chaotic optical communications over 100-km fiber transmission at 30-Gb/s bit rate. Optics letters 2018, 43, 1323–1326. [Google Scholar] [CrossRef]
  12. Keren, S.; Horowitz, M. Interrogation of fiber gratings by use of low-coherence spectral interferometry of noiselike pulses. Optics Letters 2001, 26, 328–330. [Google Scholar] [CrossRef]
  13. Lim, H.; Jiang, Y.; Wang, Y.; Huang, Y.C.; Chen, Z.; Wise, F.W. Ultrahigh-resolution optical coherence tomography with a fiber laser source at 1 μm. Optics letters 2005, 30, 1171–1173. [Google Scholar] [CrossRef]
  14. Wu, Q.; Okabe, Y.; Sun, J. Investigation of dynamic properties of erbium fiber laser for ultrasonic sensing. Optics express 2014, 22, 8405–8419. [Google Scholar] [CrossRef] [PubMed]
  15. Droste, S.; Ycas, G.; Washburn, B.R.; Coddington, I.; Newbury, N.R. Optical frequency comb generation based on erbium fiber lasers. Nanophotonics 2016, 5, 196–213. [Google Scholar] [CrossRef]
  16. Kraus, M.; Ahmed, M.A.; Michalowski, A.; Voss, A.; Weber, R.; Graf, T. Microdrilling in steel using ultrashort pulsed laser beams with radial and azimuthal polarization. Optics express 2010, 18, 22305–22313. [Google Scholar] [CrossRef] [PubMed]
  17. Philippov, V.; Codemard, C.; Jeong, Y.; Alegria, C.; Sahu, J.K.; Nilsson, J.; Pearson, G.N. High-energy in-fiber pulse amplification for coherent lidar applications. Optics letters 2004, 29, 2590–2592. [Google Scholar] [CrossRef] [PubMed]
  18. Morin, F.; Druon, F.; Hanna, M.; Georges, P. Microjoule femtosecond fiber laser at 1.6 μm for corneal surgery applications. Optics letters 2009, 34, 1991–1993. [Google Scholar] [CrossRef] [PubMed]
  19. Sanchez, F.; Le Boudec, P.; François, P.L.; Stephan, G. Effects of ion pairs on the dynamics of erbium-doped fiber lasers. Physical Review A 1993, 48, 2220. [Google Scholar] [CrossRef] [PubMed]
  20. Colin, S.; Contesse, E.; Le Boudec, P.; Stephan, G.; Sanchez, F. Evidence of a saturable-absorption effect in heavily erbium-doped fibers. Optics letters 1996, 21, 1987–1989. [Google Scholar] [CrossRef] [PubMed]
  21. Rangel-Rojo, R.; Mohebi, M. Study of the onset of self-pulsing behaviour in an Er-doped fibre laser. Optics communications 1997, 137, 98–102. [Google Scholar] [CrossRef]
  22. Pisarchik, A.N.; Barmenkov, Y.O.; Kir’yanov, A.V. Experimental characterization of the bifurcation structure in an erbium-doped fiber laser with pump modulation. IEEE journal of quantum electronics 2003, 39, 1567–1571. [Google Scholar] [CrossRef]
  23. Pisarchik, A.N.; Kir’yanov, A.V.; Barmenkov, Y.O.; Jaimes-Reátegui, R. Dynamics of an erbium-doped fiber laser with pump modulation: theory and experiment. JOSA B 2005, 22, 2107–2114. [Google Scholar] [CrossRef]
  24. Pisarchik, A.; Barmenkov, Y.O. Locking of self-oscillation frequency by pump modulation in an erbium-doped fiber laser. Optics communications 2005, 254, 128–137. [Google Scholar] [CrossRef]
  25. Huerta-Cuellar, G.; Pisarchik, A.N.; Barmenkov, Y.O. Experimental characterization of hopping dynamics in a multistable fiber laser. Physical Review E 2008, 78, 035202. [Google Scholar] [CrossRef] [PubMed]
  26. Pisarchik, A.N.; Hramov, A.E. Multistability in Physical and Living Systems: Characterization and Applications; Springer Nature, 2022.
  27. Pisarchik, A.N.; Feudel, U. Control of multistability. Physics Reports 2014, 540, 167–218. [Google Scholar] [CrossRef]
  28. Huerta-Cuellar, G.; Pisarchik, A.; Kir’yanov, A.; Barmenkov, Y.O.; del Valle Hernández, J. Prebifurcation noise amplification in a fiber laser. Physical Review E 2009, 79, 036204. [Google Scholar] [CrossRef] [PubMed]
  29. Jaimes-Reátegui, R.; Esqueda de la Torre, J.O.; García-López, J.H.; Huerta-Cuellar, G.; Aboites, V.; Pisarchik, A.N. Generation of giant periodic pulses in the array of erbium-doped fiber lasers by controlling multistability. Opt. Commun. 2020, 477, 126355. [Google Scholar] [CrossRef]
  30. Hargrove, L.; Fork, R.L.; Pollack, M. Locking of He–Ne laser modes induced by synchronous intracavity modulation. Applied Physics Letters 1964, 5, 4–5. [Google Scholar] [CrossRef]
  31. Okhotnikov, O.; Grudinin, A.; Pessa, M. Ultra-fast fibre laser systems based on SESAM technology: new horizons and applications. New journal of physics 2004, 6, 177. [Google Scholar] [CrossRef]
  32. Zhang, H.; Tang, D.; Zhao, L.; Tam, H.Y. Induced solitons formed by cross-polarization coupling in a birefringent cavity fiber laser. Optics letters 2008, 33, 2317–2319. [Google Scholar] [CrossRef]
  33. Matsas, V.; Newson, T.; Richardson, D.; Payne, D.N. Self-starting, passively mode-locked fibre ring soliton laser exploiting non-linear polarisation rotation. Electronics Letters 1992, 28, 1391–1393. [Google Scholar] [CrossRef]
  34. Zhao, L.; Tang, D.; Wu, J. Gain-guided soliton in a positive group-dispersion fiber laser. Optics letters 2006, 31, 1788–1790. [Google Scholar] [CrossRef]
  35. Yun, L.; Liu, X.; Mao, D. Observation of dual-wavelength dissipative solitons in a figure-eight erbium-doped fiber laser. Optics Express 2012, 20, 20992–20997. [Google Scholar] [CrossRef] [PubMed]
  36. Richardson, D.J.; Laming, R.I.; Payne, D.N.; Matsas, V.; Phillips, M.W. Self-starting, passively mode-locked erbium fibre ring laser based on the amplifying Sagnac switch. Electronics Letters 1991, 27, 542–544. [Google Scholar] [CrossRef]
  37. Strogatz, S.H.; Stewart, I. Coupled oscillators and biological synchronization. Scientific american 1993, 269, 102–109. [Google Scholar] [CrossRef] [PubMed]
  38. Kyprianidis, I.; Stouboulos, I. Chaotic synchronization of three coupled oscillators with ring connection. Chaos, Solitons & Fractals 2003, 17, 327–336. [Google Scholar]
  39. Abrams, D.M.; Strogatz, S.H. Chimera states in a ring of nonlocally coupled oscillators. International Journal of Bifurcation and Chaos 2006, 16, 21–37. [Google Scholar] [CrossRef]
  40. Maneatis, J.G.; Horowitz, M.A. Precise delay generation using coupled oscillators. IEEE Journal of Solid-State Circuits 1993, 28, 1273–1282. [Google Scholar] [CrossRef]
  41. Boccaletti, S.; Latora, V.; Moreno, Y.; Chavez, M.; Hwang, D.U. Complex networks: Structure and dynamics. Physics reports 2006, 424, 175–308. [Google Scholar] [CrossRef]
  42. Ermentrout, G. The behavior of rings of coupled oscillators. Journal of mathematical biology 1985, 23, 55–74. [Google Scholar] [CrossRef]
  43. Keener, J.P. Propagation and its failure in coupled systems of discrete excitable cells. SIAM Journal on Applied Mathematics 1987, 47, 556–572. [Google Scholar] [CrossRef]
  44. Yamauchi, M.; Wada, M.; Nishio, Y.; Ushida, A. Wave propagation phenomena of phase states in oscillators coupled by inductors as a ladder. IEICE transactions on fundamentals of electronics, communications and computer sciences 1999, 82, 2592–2598. [Google Scholar]
  45. Van der Sande, G.; Soriano, M.C.; Fischer, I.; Mirasso, C.R. Dynamics, correlation scaling, and synchronization behavior in rings of delay-coupled oscillators. Physical Review E 2008, 77, 055202. [Google Scholar] [CrossRef] [PubMed]
  46. Cohen, D.S.; Neu, J.C.; Rosales, R.R. Rotating spiral wave solutions of reaction-diffusion equations. SIAM journal on applied mathematics 1978, 35, 536–547. [Google Scholar] [CrossRef]
  47. Noszticzius, Z.; Horsthemke, W.; McCormick, W.; Swinney, H.L.; Tam, W. Sustained chemical waves in an annular gel reactor: a chemical pinwheel. Nature 1987, 329, 619–620. [Google Scholar] [CrossRef]
  48. Alexander, J. Patterns at primary Hopf bifurcations of a plexus of identical oscillators. SIAM Journal on Applied Mathematics 1986, 46, 199–221. [Google Scholar] [CrossRef]
  49. Nekorkin, V.I.; Makarov, V.A.; Velarde, M.G. Spatial disorder and waves in a ring chain of bistable oscillators. International Journal of Bifurcation and Chaos 1996, 6, 1845–1858. [Google Scholar] [CrossRef]
  50. Matias, M.; Pérez-Muñuzuri, V.; Lorenzo, M.; Marino, I.; Pérez-Villar, V. Observation of a fast rotating wave in rings of coupled chaotic oscillators. Physical review letters 1997, 78, 219. [Google Scholar] [CrossRef]
  51. Sánchez, E.; Matías, M.A. Transition to chaotic rotating waves in arrays of coupled Lorenz oscillators. International Journal of Bifurcation and Chaos 1999, 9, 2335–2343. [Google Scholar] [CrossRef]
  52. Horikawa, Y. Metastable and chaotic transient rotating waves in a ring of unidirectionally coupled bistable Lorenz systems. Physica D: Nonlinear Phenomena 2013, 261, 8–18. [Google Scholar] [CrossRef]
  53. Perlikowski, P.; Yanchuk, S.; Wolfrum, M.; Stefanski, A.; Mosiolek, P.; Kapitaniak, T. Routes to complex dynamics in a ring of unidirectionally coupled systems. Chaos: An Interdisciplinary Journal of Nonlinear Science 2010, 20, 013111. [Google Scholar] [CrossRef]
  54. Sánchez, E.; Pazó, D.; Matías, M.A. Experimental study of the transitions between synchronous chaos and a periodic rotating wave. Chaos: An Interdisciplinary Journal of Nonlinear Science 2006, 16, 033122. [Google Scholar] [CrossRef]
  55. Barba-Franco, J.; Gallegos, A.; Jaimes-Reátegui, R.; Gerasimova, S.; Pisarchik, A. Dynamics of a ring of three unidirectionally coupled Duffing oscillators with time-dependent damping. Europhysics Letters 2021, 134, 30005. [Google Scholar] [CrossRef]
  56. Bashkirtseva, I.A.; Ryashko, L.B.; Pisarchik, A.N. Ring of map-based neural oscillators: From order to chaos and back. Chaos, Solitons & Fractals 2020, 136, 109830. [Google Scholar]
  57. Perlikowski, P.; Yanchuk, S.; Wolfrum, M.; Stefanski, A.; Kapitaniak, T. Dynamics of a Large Ring of Unidirectionally Coupled Duffing Oscillators. In Proceedings of the IUTAM Symposium on Nonlinear Dynamics for Advanced Technologies and Engineering Design: Proceedings of the IUTAM Symposium on Nonlinear Dynamics for Advanced Technologies and Engineering Design, held Aberdeen, UK, 27-30 July 2010.; pp. 201363–72.
  58. Borkowski, L.; Stefanski, A. FFT bifurcation analysis of routes to chaos via quasiperiodic solutions. Mathematical Problems in Engineering 2015, 2015. [Google Scholar] [CrossRef]
  59. Borkowski, L.; Perlikowski, P.; Kapitaniak, T.; Stefanski, A. Experimental observation of three-frequency quasiperiodic solution in a ring of unidirectionally coupled oscillators. Physical Review E 2015, 91, 062906. [Google Scholar] [CrossRef] [PubMed]
  60. Landau, L.D. On the problem of turbulence. In Proceedings of the Dokl. Akad. Nauk USSR, Vol. 44; 1944; p. 311. [Google Scholar]
  61. Hopf, E. A mathematical example displaying features of turbulence. Communications on Pure and Applied Mathematics 1948, 1, 303–322. [Google Scholar] [CrossRef]
  62. Newhouse, S.; Ruelle, D.; Takens, F. Occurrence of strange axiom A attractors near quasi periodic flows on T m, m 3. Communications in Mathematical Physics 1978, 64, 35–40. [Google Scholar] [CrossRef]
  63. Ruelle, D.; Takens, F. On the nature of turbulence. Les rencontres physiciens-mathématiciens de Strasbourg-RCP25 1971, 12, 1–44. [Google Scholar]
  64. Arecchi, F.T.; Harrison, R.G. Instabilities and chaos in quantum optics; Vol. 34, Springer Science & Business Media, 2012.
  65. Lacot, E.; Stoeckel, F.; Chenevier, M. Dynamics of an erbium-doped fiber laser. Physical Review A 1994, 49, 3997. [Google Scholar] [CrossRef]
  66. Pisarchik, A.N.; Jaimes-Reátegui, R.; Sevilla-Escoboza, R.; Huerta-Cuellar, G.; Taki, M. Rogue waves in a multistable system. Physical Review Letters 2011, 107, 274101. [Google Scholar] [CrossRef]
  67. Barba-Franco, J.; Romo-Muñoz, L.; Jaimes-Reátegui, R.; García-López, J.; Huerta-Cuellar, G.; Pisarchik, A. Electronic equivalent of a pump-modulated erbium-doped fiber laser. Integration 2023, 89, 106–113. [Google Scholar] [CrossRef]
  68. Jaimes-Reategui, R. Dynamic of complex system with parametric modulation: Duffing oscillators and a fiber laser, Ph. D. Thesis 2004. [Google Scholar]
  69. Alon, U. Network motifs: theory and experimental approaches. Nature Reviews Genetics 2007, 8, 450–461. [Google Scholar] [CrossRef] [PubMed]
  70. Boccaletti, S.; Pisarchik, A.N.; Del Genio, C.I.; Amann, A. Synchronization: from coupled systems to complex networks; Cambridge University Press, 2018.
  71. Matias, M.; Güémez, J.; Pérez-Munuzuri, V.; Marino, I.; Lorenzo, M.; Pérez-Villar, V. Size instabilities in rings of chaotic synchronized systems. Europhysics Letters 1997, 37, 379. [Google Scholar] [CrossRef]
  72. Marino, I.; Pérez-Muñuzuri, V.; Pérez-Villar, V.; Sánchez, E.; Matıas, M. Interaction of chaotic rotating waves in coupled rings of chaotic cells. Physica D: Nonlinear Phenomena 1999, 128, 224–235. [Google Scholar] [CrossRef]
  73. Matías, M.; Güémez, J. Transient periodic rotating waves and fast propagation of synchronization in linear arrays of chaotic systems. Physical review letters 1998, 81, 4124. [Google Scholar] [CrossRef]
  74. Borkowski, L.; Stefanski, A. Stability of the 3-torus solution in a ring of coupled Duffing oscillators. The European Physical Journal Special Topics 2020, 229, 2249–2259. [Google Scholar] [CrossRef]
  75. Krysko, A.; Awrejcewicz, J.; Papkova, I.; Krysko, V. Routes to chaos in continuous mechanical systems: Part 2. Modelling transitions from regular to chaotic dynamics. Chaos, Solitons & Fractals 2012, 45, 709–720. [Google Scholar]
  76. Awrejcewicz, J.; Krysko, A.; Papkova, I.; Krysko, V. Routes to chaos in continuous mechanical systems. Part 3: The Lyapunov exponents, hyper, hyper-hyper and spatial–temporal chaos. Chaos, Solitons & Fractals 2012, 45, 721–736. [Google Scholar]
  77. Barba-Franco, J.; Gallegos, A.; Jaimes-Reátegui, R.; Pisarchik, A. Dynamics of a ring of three fractional-order Duffing oscillators. Chaos, Solitons & Fractals 2022, 155, 111747. [Google Scholar]
  78. Pisarchik, A.; Jaimes-Reategui, R. Control of basins of attraction in a multistable fiber laser. Physics Letters A 2009, 374, 228–234. [Google Scholar] [CrossRef]
  79. Meucci, R.; Marc Ginoux, J.; Mehrabbeik, M.; Jafari, S.; Clinton Sprott, J. Generalized multistability and its control in a laser. Chaos: An Interdisciplinary Journal of Nonlinear Science 2022, 32, 083111. [Google Scholar] [CrossRef] [PubMed]
Preprints 72972 g001
Figure 1. (a) Time series with relaxation oscillations and (b) Fourier spectrum with relaxation oscillation frequency f r of EDFL given by Equations (8) and (9).
Figure 1. (a) Time series with relaxation oscillations and (b) Fourier spectrum with relaxation oscillation frequency f r of EDFL given by Equations (8) and (9).
Preprints 72972 g001
Preprints 72972 g002
Figure 2. (a) Bifurcation diagram of the peak intensity (in arbitrary units) and (b) largest Lyapunov exponent as a function of k.
Figure 2. (a) Bifurcation diagram of the peak intensity (in arbitrary units) and (b) largest Lyapunov exponent as a function of k.
Preprints 72972 g002
Preprints 72972 g003
Figure 3. (Left) Time series and (right) Poincaré sections at a) k = 2.58 , b) k = 3.82 , c) k = 5.49 , d) k = 5.84 , and e) k = 14.81 .
Figure 3. (Left) Time series and (right) Poincaré sections at a) k = 2.58 , b) k = 3.82 , c) k = 5.49 , d) k = 5.84 , and e) k = 14.81 .
Preprints 72972 g003
Preprints 72972 g004
Figure 4. (Left) Rotating wave and (right) phase portraits for a) k = 2.58 , b) k = 3.82 , c) k = 5.49 and d) k = 5.84 .
Figure 4. (Left) Rotating wave and (right) phase portraits for a) k = 2.58 , b) k = 3.82 , c) k = 5.49 and d) k = 5.84 .
Preprints 72972 g004
Preprints 72972 g005
Figure 5. Bifurcation diagram of the dominant frequency in the power spectra of x 1 as a function of the coupling strength k.
Figure 5. Bifurcation diagram of the dominant frequency in the power spectra of x 1 as a function of the coupling strength k.
Preprints 72972 g005
Preprints 72972 g006
Figure 6. Power spectrum at a) k = 3.25 Ω 0 = 28 kHz, b) k = 4.15 , Ω 0 = 52.32 kHz, Ω 1 = 25.83 kHz, c) k = 5.65 , Ω 0 = 25.83 kHz, Ω 1 = 49.01 kHz, Ω 2 = 74.83 kHz, and d) k = 10 .
Figure 6. Power spectrum at a) k = 3.25 Ω 0 = 28 kHz, b) k = 4.15 , Ω 0 = 52.32 kHz, Ω 1 = 25.83 kHz, c) k = 5.65 , Ω 0 = 25.83 kHz, Ω 1 = 49.01 kHz, Ω 2 = 74.83 kHz, and d) k = 10 .
Preprints 72972 g006
Preprints 72972 g007
Figure 7. (Right) Phase portraits and (left) power spectra of the coexisting (a) stable limit cycle and (b) chaos at k = 14.08 .
Figure 7. (Right) Phase portraits and (left) power spectra of the coexisting (a) stable limit cycle and (b) chaos at k = 14.08 .
Preprints 72972 g007
Preprints 72972 g008
Figure 8. Averaged (a) phase synchronization and (b) synchronization error versus coupling strength k.
Figure 8. Averaged (a) phase synchronization and (b) synchronization error versus coupling strength k.
Preprints 72972 g008
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated