Prerpints.org logo
Preprint
Article

Atmospheric Ducts and Their Electromagnetic Propagation Characteristics in the Northwestern South China Sea

Altmetrics

Downloads

113

Views

50

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

08 May 2023

Posted:

09 May 2023

You are already at the latest version

Alerts
Abstract
The propagation of electromagnetic waves beyond the line of sight can be caused by atmospheric ducts, which are a significant concerns in the fields of radar and communication. This paper utilizes data from seven automatic stations and five radio-sounding stations to statistically analyze the characteristics of the atmospheric ducts in the northwest region of the South China Sea (SCS). After verifying the practicality of numerical analysis data from NCEP CFSv2 and ERA5 in studying atmospheric ducts using measured data, we analyzed the space-time distribution characteristics of the height of the regional evaporation duct and the bottom height of the elevated duct. Using the parabolic equation model, we simulated electromagnetic propagation loss under different frequencies and radiation elevation angles in both uniform and non-uniform duct environments within a typical atmospheric duct structure. The study found that the NCEP CFSv2 data accurately captures the evaporation duct height and duct occurrence rate in the study area, and the elevated duct bottom height obtained from the inversion of ERA5 and the measured data has a good consistency. The occurrence rate and height of evaporation duct in coastal stations in the northwest of the SCS vary significantly by month, demonstrating clear monthly distribution patterns. Conversely, changes in the Xisha station are minimal, indicating good temporal uniformity. For lower atmospheric ducts, the difference in occurrence rates between 00:00 and 12:00 (UTC) is negligible. The occurrence probability of elevated ducts in the Beibu Gulf area is relatively high, mainly concentrated from January to April, and the Xisha area is dominated by surface ducts without foundation layer, mainly concentrated from June to August. The monsoon plays a critical role in the generation and evolution of atmospheric ducts in the northwest of the SCS, with the height of the evaporation duct increasing and the bottom height of the elevated duct decreasing after the onset of the summer monsoon. Electromagnetic propagation simulations demonstrate that higher frequency and lower elevation angles of radiation sources in the trapping layer of the evaporation duct make it easier to be trapped. As the evaporation duct height decreases, the amplitude of the "sinusoidal fluctuation" of the propagation loss also decreases. Frequency changes of the radiation source in the surface duct environment have minimal impact on electromagnetic propagation loss, but the elevation angle of the radiation source is a critical factor. The frequency of the "sinusoidal fluctuation" in propagation loss is higher in a hybrid duct environment compared to a uniform surface duct. Additionally, the propagation loss increases faster with distance at the height of the evaporation duct, resulting in greater electromagnetic propagation loss.
Keywords: 
Subject: Environmental and Earth Sciences  -   Remote Sensing

1. Introduction

The atmospheric layer has a significant impact on electromagnetic wave propagation, mainly through the refraction and scattering effects of the atmosphere on electromagnetic waves. Variations in temperature, humidity, and air pressure in the atmosphere can lead to changes in the refractive index of the atmosphere, which is a crucial parameter that determines the propagation characteristics of radio waves in the lower atmosphere. Atmospheric ducts are a common occurrence of super-refractive propagation conditions that greatly affect radar and communication equipment at sea [1,2,3]. Electromagnetic waves that propagate in atmospheric ducts are trapped in the duct layer, resulting in lower path loss for trapped signals and enabling beyond-line-of-sight communication [4,5,6]. Atmospheric ducts can be categorized into evaporation duct, surface duct and elevated duct (Figure 1), with surface duct and elevated duct collectively referred to as lower atmospheric ducts. The evaporation duct is formed due to the evaporation of seawater, which leads to a rapid decrease in the water content of the near-sea surface layer with increasing height, resulting in a change in the refractive index lapse rate. The evaporation duct exists almost always over the ocean, but at different heights, generally occurring at a height of 40 m in the atmosphere near the sea surface, and changes with variations in humidity, temperature, and wind speed. The formation and change of lower atmospheric ducts usually correspond to the temperature inversion process caused by atmospheric motion, such as radiation inversion, sinking inversion, advection inversion, frontal inversion, etc. [7,8,9], for some special lower atmospheric ducts can be formed by the sharp drop in humidity [10].
The evaporation duct height (EDH) is typically low, and duct height parameters can be directly measured using meteorological sounding or meteorological gradiometer techniques [11]. However, due to the unique climate environment and surface type of the ocean, there is a serious lack of meteorological observation stations, making it difficult to achieve accurate regionalization and high time resolution detection. Therefore, so the evaporation duct is diagnosed by the model developed based on the sea-air interaction similarity theory, which obtains the marine meteorological parameters and sea surface temperature through measurement or reanalysis [12,13,14]. Reanalysis data, such as the NCEP CFSv2 (National Centers for Environmental Prediction Climate Forecast System Version 2) data set, is often used for marine meteorological parameters, providing the best estimate of the state of the atmosphere and ocean from 2011 to 2022 [15]. Scholars have used this data to study the temporal and spatial distribution characteristics of offshore evaporation duct [16,17]. Commonly used models for evaporation duct diagnosis include the P-J model [18], MGB model [19], BYC model [20], and NPS model [21], with the NPS model released by the U.S. Naval Research Institute in 2000. Many scholars have used the model to study EDH in different sea areas [22,23,24,25], and the validity of the model has been verified. Lower atmospheric ducts usually occur at heights below 3 km, and their duct parameters can be obtained from meteorological sounding measurements. For lower atmospheric ducts at sea, ERA5 reanalysis (The Fifth Generation ECMWF Atmospheric Reanalysis) data is often used for analysis. Yinhe Cheng [8], Yong Zhou [26], I. Sirkoval [27], and Axel von Engeln [28] have studied the characteristics of atmospheric ducts in different regions.
When a propagating electromagnetic wave satisfies a certain trapping frequency and trapping angle, an atmospheric duct can trap part of the electromagnetic wave to form trans-horizon radio wave propagation in the duct layer. The formation of a duct propagation has a significant impact on radar detection. It can cause large errors in radar ranging, angle measurement, and speed measurement, as well as enhance radar clutter, making radar over-the-horizon detection and reception accompanied by large-area detection blind spots. With the improvement of various approximate numerical algorithms and computer calculation speed, scholars at home and abroad have been able to conduct more in-depth research on atmospheric ducts. The main models used for this research include the ray tracing model, duct model, parabolic equation model, and various hybrid methods that combine these models [29,30]. Among these models, the parabolic equation model has become the main method for simulating and analyzing the propagation characteristics of radio waves in atmospheric ducts [30,31,32,33]. Most of the literature mentioned above uses observational or numerical analysis data to statistically analyze the characteristics of atmospheric ducts in a certain area, but they seldom consider the propagation characteristics of electromagnetic waves under these characteristics. This paper, therefore, uses data from automatic and sounding stations to statistically analyze the characteristics of evaporation duct and lower atmospheric ducts at the corresponding stations and verifies the reliability of the NCEP CFSv2 and ERA5 numerical analysis data sets (see Section 2.1.2 for an introduction to the data sets) in the inversion of evaporation duct and lower atmospheric ducts. The atmospheric ducts characteristics are then obtained. By taking the statistical analysis results of atmospheric ducts at the site as prior information, the parabolic equation model is used to carry out electromagnetic propagation simulation analysis of ducting events (including hybrid ducting events) with typical ducting parameters. This analysis yields the electromagnetic propagation properties in different atmospheric ducts environments, such as uniform and non-uniform.

2. Data and Methods

Tropospheric ducts have different types and spatial structure characteristics, as shown in Figure 1, which presents the corresponding geometric features and parameters of different types of ducts. The structural characteristic quantities of each duct type mainly include the trapping layer top height ( h t ), trapping layer bottom height ( h c ), duct bottom height ( h b ), duct thickness ( h t - h b ), trapping layer thickness ( h t - h c ), and duct strength ( M 2 - M 1 ). The duct strength and trapping layer thickness are important factors that determine whether electromagnetic waves are trapped. Additionally, the occurrence rate of atmospheric ducts is a statistical feature that characterizes the probability of atmospheric ducts occurrence in a region. In this paper, we record the duct phenomenon at each time as a duct frequency, i.e., the occurrence rate of the atmospheric ducts is the percentage of the duct frequency in the statistical time frequency. For the evaporation duct, we record the duct phenomenon whose duct height is between 5∼40 m as a duct frequency.
The identification and structural characteristics of atmospheric ducts can be obtained by directly measuring the temperature, humidity, air pressure, and refractive index of the atmosphere, and other parameter profiles. The evaporation duct, in particular, uses atmospheric and sea temperature parameters at a certain height above the water surface as input for the diagnostic model to retrieve the duct height. The data obtained by direct detection has the characteristic of high precision and can generally be used as atmospheric characteristics within tens of kilometers of the observation site at sea. However, for the ocean, which seriously lacks observation stations, it is impossible to achieve regional and high-time resolution detection. Therefore, this paper studies the characteristics of atmospheric ducts and their electromagnetic characteristics in the northwest of the SCS (Figure 1) and investigates the propagation characteristics. The specific research method is shown in Figure 2. We first use the data from sounding and automatic weather station (AWS) as input for the duct model to obtain the duct characteristics of the lower atmospheric ducts and evaporation duct. Then, we compare and analyze the duct parameters obtained by the inversion of actual measurements and numerical analysis data to obtain the duct characteristics of the northwest region of the SCS. Finally, we use the typical values of evaporation and surface ducts obtained by the inversion of measured data to analyze the electromagnetic propagation characteristics of single uniform duct, hybrid duct, and non-uniform evaporation duct environments.

2.1. Data

The formation of atmospheric ducts is closely related to various factors such as weather processes of different scales and sea surface meteorological and hydrological conditions. The atmospheric temperature, humidity, air pressure, wind speed, and direction are the basic data for studying atmospheric ducts. Therefore, this paper uses measured and numerical analysis data that include the main meteorological elements such as atmospheric temperature, humidity, air pressure, wind speed, and sea surface temperature.

2.1.1. Actual observation data

Meteorological soundings can provide high-resolution data products on the vertical distribution of atmospheric temperature, humidity, pressure, and wind, while automatic stations can provide high-time-resolution meteorological elements on the ground. In this paper, we use automatic stations and sounding data from the Wyoming State Weather Network to statistically analyze the characteristics of evaporation duct and lower atmospheric ducts of the corresponding stations. There are 7 automatic stations (4 coastal stations, 1 Beibu Gulf island, and 2 Xisha islands) and 4 sounding stations (2 coastal stations, 1 Beibu Gulf island, and 1 Xisha island) used in this study. The specific locations (Figure 3), station numbers, and data information of each observation station are shown in Table 1. For automatic station data, station 48839 has more sea surface temperature (SST) observations than other stations, while station 59981 lacks observation data in 2011. Stations 48845 and 48839 of the radiosonde stations also lack observation data in some years, and there are almost no observations at 12 o’clock (UTC).

2.1.2. Numerical analysis data

ERA5 is the fifth-generation reanalysis of global climate and weather by ECMWF (European Center for Medium-Range Weather Forecasts) in the past 8 years. The current ERA5 hourly pressure layer data starts from 1940, with a total of 37 pressure layers, and the data covers the whole world scope. In this paper, the longitude and latitude are 105°E∼113°E and 15°N∼23°N, and the data from 2010 to 2022 are used to analyze the lower atmospheric ducts in the northwest of the SCS. The vertical pressure layer of the data is 400∼1000 hPa, and the meteorological elements There are temperature, specific humidity, potential and horizontal wind (U, V), see Table 2 for details.
NCEP CFSv2 is an upgraded version of CFSR (Climate Forecast System Reanalysis) [15]. This system assimilates global atmospheric data from land, surface, ships, radiosondes, aircraft and satellites, etc., and can better reproduce the true state of the atmosphere. We use the latitude and longitude of 105°E∼123°E and 15°N∼23°N, and the data from 2011 to 2022 to analyze the evaporation duct in the northwest of the SCS. The specific data information is shown in Table 3.

2.2. Atmospheric ducts model

2.2.1. Lower atmospheric ducts model

The bending characteristics of electromagnetic waves propagating in the atmospheric medium can be measured by the refractive index n, and the normal value of the atmospheric refractive index on the earth’s surface is generally between 1.00025 and 1.0004. For practical use, the atmospheric refractive index is defined N = ( n − 1 ) × 10 6 . The atmospheric ducts are a stronger super-refractive propagation condition, which is closely related to atmospheric temperature, humidity, and air pressure. Bean and Dutton [34] related the refractive index to temperature, air pressure, and water vapor pressure and derived the functional relationship as
N = 77.6 T ( P + 4810 e T )
Where N represents the atmospheric refractive index (N-units), T is the atmospheric thermodynamic temperature (K), P is the atmospheric pressure (hPa), and e is water vapor pressure (hPa). The water vapor partial pressure e can be converted from the specific humidity:
e = q P ϵ + ( 1 − ϵ ) q
Among them, q is the specific humidity (kg/kg), and ϵ is a constant (usually 0.622). When considering the curvature of the earth, the corrected atmospheric refractivity can be expressed as:
M = N + h R e × 10 6 = N + 0.157 h
Where M using M-unit, R e is the average radius of the earth (taken as 6371 km), and h is the altitude above sea level (m). The vertical gradient of modified refractivity is obtained based on Equation (3) as
d M d z = 77.6 T ∂ P ∂ z − 77.6 T 2 ( P + 9620 e T ) ∂ T ∂ z + 373256 T 2 ∂ e ∂ z + 0.157

2.2.2. Evaporation duct diagnostic model

The NPS evaporation duct model uses air temperature, relative humidity, wind speed, pressure, and sea surface temperature at a certain height or at different heights on the sea surface as input parameters and calculates EDH based on the Monin-Obukhov similarity theory. The model first obtains the temperature, humidity, and air pressure, and then obtains the atmospheric refractive index profile of the evaporation duct according to the relationship between the atmospheric refractive index, temperature, humidity, and atmospheric pressure. The EDH is then determined by correcting the position of the minimum value of M[35]. The vertical section of near-surface temperature T and specific humidity q in the model can be expressed as:
T ( z ) = T 0 + θ * κ [ ln ( z z 0 t ) − ψ h ( z L ) ] − η d z
q ( z ) = q 0 + q * κ [ ln ( z z 0 t ) − ψ h ( z L ) ]
In the formula, T ( z ) and q ( z ) are the air temperature and specific humidity at height z; T 0 , q 0 are the sea surface temperature and specific humidity, and considering the influence of seawater salinity relative humidity; q 0 =0.98 q s ( T 0 ) , q s ( T 0 ) are the sea surface saturation specific humidity calculated based on the sea surface temperature; θ * , q * respectively is the characteristic scale of potential temperature θ and specific humidity q; κ is the Karman constant; z 0 t is the temperature roughness height; ψ h is the temperature universal function; η d is the dry adiabatic lapse rate, approximately equal to 0.00976 K/m; L represents the Obukhov length; the water vapor pressure profile can be determined from the functional relationship between water vapor pressure e and specific humidity q, that is, formula (2).

2.3. Parabolic equation model

The parabolic equation (Parabolic Equation, PE) is an approximation of wave equation, which can be used to describe the propagation in a conical area concentrated in a certain direction. In the Cartesian coordinate system, the x,y,z axes represent the wave propagation direction and the horizontal and vertical directions respectively. When the atmospheric refractive index of the propagation medium is n, the two-dimensional scalar wave equation can be expressed as:
∂ 2 φ ∂ x 2 + ∂ 2 φ ∂ z 2 + k 2 n 2 φ = 0
Where k = 2 π / λ is the wave number in free space ( λ is the wavelength of the electromagnetic wave), φ represents the electric or magnetic field polarized horizontally or vertically. If the attenuation function related to x is u ( x , z ) = e − i k x φ ( x , z ) , then the wave equation becomes:
∂ 2 u ∂ x 2 + 2 i k ∂ u ∂ x + ∂ 2 u ∂ z 2 + k 2 ( n 2 − 1 ) u = 0
After factorization, the equations for the forward propagation and backward propagation about the coordinate x are obtained respectively:
∂ u ∂ x = − i k ( 1 − Q ) u
∂ u ∂ x = − i k ( 1 + Q ) u
Where Q is a pseudo-differential operator:
Q = 1 k 2 ∂ 2 ∂ 2 z + n 2 ( x , z )
At this time, the forward propagation solution can be written as
u ( x + Δ x ) = e i k Δ x ( − 1 + Q ) u ( x )
When the backpropagation is ignored, the standard parabolic equation after Taylor’s first-order expansion of the Q can be expressed as
∂ 2 u ∂ x 2 + 2 i k ∂ u ∂ x + k 2 ( n 2 − 1 ) u = 0
Due to the complexity of the atmospheric environment, formula (13) is difficult to solve analytically. In this case, a numerical solution of the electromagnetic field problem can be obtained through numerical methods. The commonly used numerical solutions of the PE model include the Split Step Fourier Transforms (SSFT) algorithm and finite difference method (FD). The SSFT solutions [36] of the narrow-angle and wide-angle parabolic equations are
u ( x + Δ x , z ) = exp [ i k ( n 2 − 1 ) Δ x 2 ] F − 1 { exp [ − i p 2 Δ x 2 k ] F { u ( x , z ) } }
u ( x + Δ x , z ) = exp [ i k ( n − 1 ) Δ x ] × F − 1 { exp [ − i p 2 Δ x k ( 1 − p 2 k 2 + 1 ) − 1 ] × F { u ( x , z ) } }
F and F − 1 represent the Fourier transform and the inverse Fourier transform respectively, p = k sin θ ( θ is the electromagnetic wave propagation angle). In radio-wave applications two parameters are of interest: propagation factor and propagation loss (usually called path loss). The path loss is the ratio between the power radiated by the transmitter antenna and the power available at a point in space, can be determined by:
PL = − 20 log u + 20 log ( 4 π ) + 10 log x − 30 log λ

3. Results and Discussion

3.1. Evaporation duct

It can be observed from Table 1 that AWS No. 48839 has sea surface temperature observations, while other stations do not have this meteorological element. Therefore, we compare and analyze the sea surface temperature data of this station with the data from NCEP CFSv2 to evaluate its accuracy. Figure 4 shows the daily average map of sea surface temperature observation errors at 00, 06, 12, and 18 o’clock (UTC) at automatic station No. 48839 and the NCEP CFSv2 sea surface temperature in 2022.
From Figure 4, it can be observed that the SST error values measured at four different times and numerical analysis show a trend of first decreasing and then increasing. The measured SST values are consistently higher than the numerical analysis throughout the year. The smallest error value is observed in April at 06:00, and the measured SST results in most months are smaller than the numerical analysis. Overall, the total average errors of SST at 00, 06, 12, and 18 are 2.5819 °C, -0.8077 °C, 3.7746 °C, and 4.3147 °C, respectively. The sea surface temperature error at 06 is mostly within the range of -3∼2 °C, while the errors at the other three time points are in the range of 0∼7 °C. Based on the analysis, it can be concluded that the NCEP CFSv2 sea surface temperature at 06:00 is relatively close to the actual observation. Therefore, for other stations that lack SST observations, the NCEP CFSv2 sea surface temperature data at 06:00 can be used as a substitute. We only analyze the characteristics of EDH at each site at 06:00, and the incidence of duct is calculated using the observation data at all four time points.

3.1.1. Characteristics of evaporating duct

As the evaporation duct in coastal areas differ significantly from those in inland seas [37,38,39], we divided the seven automatic stations into two categories: four coastal stations (48855, 48848, 59644, 59838) and three island observation stations (48839, 59981, 59985). Figure 5 illustrates the occurrence rate of evaporation duct in coastal stations (left) and the monthly average distribution of EDH at 06:00 (right). From the monthly average distribution of evaporation duct occurrence rates, it can be observed that the occurrence probability characteristics of evaporation duct in coastal stations 48855, 48848, and 59838 are relatively consistent. The occurrence rates of evaporation duct at these three sites continue to decrease from December to March/April of the following year and then begin to increase after April, with a decrease in November during the increase process. In contrast, at the 59644 site, the incidence rate continues to decrease from December to August of the following year and then continues to increase after August. Overall, the maximum occurrence probability of evaporation duct in coastal stations is in December, and all stations exhibit significant monthly non-uniformity characteristics, indicating that the occurrence probability of evaporation duct varies significantly across different months. The monthly average distribution of EDH at 06:00 indicates that the characteristics of 48855, 48848, and 59838 EDH are relatively consistent. The average height of the duct from January to December exhibits a phenomenon of first increasing and then decreasing, while the 59644 station shows a double fluctuation of increasing, decreasing, increasing, and decreasing from April to October. From the monthly average variation of EDH, the annual EDH of 48845 is relatively stable, with small monthly differences. The EDH of this station is relatively low throughout the year, with an average EDH of less than 10 m. The EDH of 59838 has significant monthly differences, and the average EDH of the station throughout the year is greater than 10 m. From the above analysis, it can be concluded that 48845 has a relatively low probability of duct occurrence and duct height, while 59838 has a relatively high probability of duct occurrence and duct height, followed by the 59644 station. Therefore, the probability of evaporation duct occurrence and duct height exhibit obvious spatial and temporal distribution characteristics. This is mainly because the formation mechanism of evaporation duct is closely related to the turbulence in the marine atmospheric boundary layer, especially at the sea-land junction. The formation mechanism and changes of evaporation duct are more complex in such areas.
Figure 6 displays the occurrence rate of evaporation duct (left) and the monthly average distribution of EDH at 06:00 (right) at automatic stations on inland sea islands. The occurrence rate of evaporation duct in 48839 is similar to that of coastal stations, decreasing from December to March/April of the following year and increasing after April. This is due to the station being surrounded by continents on three sides, which is significantly affected by land airflow. In the Xisha area, the monthly duct incidence rate of 59981 and 59985 stations remained stable, with an annual average duct incidence rate of 73.9% and 71.6%, respectively, and the monthly average incidence rate remained above 60%. However, the duct incidence rate in 48839 was relatively low, with an annual average duct incidence rate of 28.7%. Therefore, the occurrence rate of evaporation duct in the two regions exhibited notable spatial differences. Based on the monthly average distribution of duct height at 06:00, the change trend of 48839 is relatively similar to that of coastal stations, characterized by an increase from January to a peak and then a decrease towards December. The annual average duct height for 48839 is 9.47 m. In contrast, the duct height in the Xisha area fluctuates frequently but with a smaller range, and the annual duct height is relatively high (with annual average duct heights of 15.4 m and 14.0 m for 59981 and 59985, respectively), which are typically maintained at a height of over 10 m. Despite being far away from land and relatively close to each other, significant differences in the occurrence rate and height of duct between the 59981 and 59985 stations were observed in June and July. From the analysis, it can be concluded that the monthly average difference in the occurrence probability of evaporation duct is smaller in areas less affected by land airflow, and the height of the evaporation duct is higher. Furthermore, the occurrence probability and height of evaporation duct in different non-coastal areas exhibit notable differences, primarily due to the main mechanism of duct formation being the physical process of seawater evaporation, which is significantly affected by wind speed, sea surface temperature, and other factors, resulting in temporal and spatial inhomogeneity of evaporation duct.
To further demonstrate the applicability of NCEP CFSv2 data in analyzing evaporation duct, we compared the incidence of duct at station 48839 with the monthly mean distribution of duct heights at 06:00 (as shown in Figure 7). The results show that the error in duct occurrence probability is relatively large (up to 26%) in January to April, while the error in July to December is small. In terms of monthly average duct height, the difference in duct height is relatively large (up to 5 m) in March to May, while there is less variation in duct height in other months. Overall, the annual average duct probability error is 6%, and the annual average duct height difference is 0.0329 m in 06:00. This indicates that the evaporation duct characteristics obtained from NCEP CFSv2 data can reflect the actual evaporation duct phenomenon to a certain extent and have a good reference value.
The minimum trapping frequency of electromagnetic waves can be expressed by the vertical decrease rate of EDH and M as
f m i n = 12 × 10 10 · ( − d M d h ) − 0.5 · η − 1.5
where d M / d h is the vertical gradient of M , η is the EDH. That is, EDH is an important factor affecting electromagnetic wave trapping. Therefore, we used the NCEP CFSv2 data from 2011 to 2022 to calculate the monthly average distribution of EDH at 06:00 in the northwestern SCS (Figure 8). In terms of time distribution, the height of the duct gradually decreases from October to April of the following year. March/April has the smallest EDH in the whole year. However, after April, the overall EDH in the northwest of the SCS suddenly increases, and May to October is a relatively large month in the whole year, with the overall area maintaining a height above 15 m. The main reason for this phenomenon is the outbreak of the SCS summer monsoon, which leads to an increase in temperature and enhanced evaporation. This, in turn, increases EDH.
In October, the SCS winter monsoon breaks out, the temperature decreases, and seawater evaporation weakens, leading to a decrease in EDH. Regarding spatial distribution, the coastal area of Hainan, China has the highest EDH in the northwest of the SCS throughout the year. After the onset of the winter monsoon, the EDH in the southern part of the study area is greater than that in the north, and a "line" gradually appears in the area between Hainan, China and the Indochina Peninsula. The high-value area of the "strip" duct is mainly due to the prevailing northwest wind, which brings warm wind from the southeast with high-temperature and high-humidity water vapor, forming a "long strip" duct high-value area. After the summer monsoon arrives in the Beibu Gulf region, the EDH increases in May/June, and the EDH high-value area in this region begins to decrease after June. The EDH in the coastal areas of the Indochina Peninsula gradually increases after February and lasts until September. There is a high-low-high variation characteristic of EDH when extending from the coastal area to the inland sea, and Hainan, China also has this feature except for the northern coastal area. The monthly variation trend of EDH at station 48839 in Figure 8 is different from that in Figure 7 (right) due to the difference in sample size caused by the error in duct occurrence probability. The EDH calculated in Figure 7 is the result of simultaneously satisfying the automatic station and NCEP CFSv2 duct heights within the range of 5∼40 m, while in Figure 8, only the EDH of NCEP CFSv2 data is within the range of 5∼40 m.

3.1.2. Electromagnetic propagation characteristics in evaporation duct environment

In atmospheric ducts propagation, electromagnetic waves are trapped in the atmosphere, resulting in lower path loss and enabling trans-horizon propagation. However, specific conditions must be met for duct propagation to occur:
1) Atmospheric stratification junctions with d M / d z <0 must exist at a certain height near the ground layer or boundary layer.
2) The wavelength of the electromagnetic waves must be smaller than the maximum trapping wavelength λ m a x (the frequency must be higher than the lowest trapping frequency f m i n ).
3) The electromagnetic wave radiation source must be located in the atmospheric ducts layer. In the case of elevated duct, the radiation source may sometimes be located below the bottom of the duct, but in this case, the radiation source must be close to the duct bottom and the duct must be very strong.
4) The radiation elevation angle of electromagnetic waves must be less than a certain critical elevation angle.
Therefore, we considered transmission frequencies of 1 GHz, 3 GHz, 6 GHz, and 9 GHz, and used a parabolic antenna Gaussian beam for the antenna and beam type. Other radiation source parameters are shown in Table 4. Unless otherwise specified, the radiation source and receiver heights in this paper are both 8 m.
From Section 3.1.1, it can be seen that the annual average EDH around Xisha is about 15 m, so we set the EDH to 15 m, and the evaporation duct model adopts the single-parameter evaporation duct model proposed by Paulus Jeske [18]. The corresponding analytical formula is:
M ( z ) = M 0 + c 0 ( z − h d ln z + h 0 h 0 )
In the formula: M 0 is the corrected refractive index of the sea surface (380 M-unit is taken in this paper), c 0 is the neutral layered evaporation duct parameter (usually 0.13 M-units/m); h d is EDH (here is 15 m); h 0 is the roughness factor (usually 0.00015 m), at this time, the corresponding evaporation duct corrected refractive index vertical section and the propagation loss when the electromagnetic wave frequency is 9 GHz and the elevation angle is 0.5° are shown in Figure 9.
When the EDH is 15 m, the corresponding M value is 359.4998 M-units. From Figure 9 (right), it is evident that the propagation loss in the EDH layer is lower than that above the height layer, forming a "long strip" structure with low propagation loss close to the 0 m layer. This indicates that the electromagnetic wave is effectively trapped in the duct layer. As the horizontal distance increases, the propagation loss inside the trapped layer gradually increases, but the reduction is relatively small compared to the propagation loss outside the trapped layer.
Figure 10 displays the propagation loss in different elevation environments under different transmission frequencies (left) and 9 GHz (right). From the left figure, it is evident that as the frequency increases, the propagation loss decreases, with the most significant reduction in propagation loss observed when compared to 3 GHz and 6 GHz. At 6 GHz to 9 GHz, the difference in propagation loss decreases as the distance increases. From the right figure, it can be seen that in the case of a transmission frequency of 9 GHz, the propagation loss continues to increase as the elevation angle of the radiation source increases. However, the difference in propagation loss under different elevation angles does not significantly increase with the increase of horizontal distance. In summary, the higher the frequency of the radiation source and the lower the elevation angle, the easier it is to be trapped by the evaporation duct, thus forming duct propagation.
We set the duct height parameters based on the average EDH (black line in Figure 8, starting at longitude and latitude [110.2500°E, 18.5008°N], [111.4773°E, 17.2743°N]) at 06:00 in September, using a certain location in Hainan Province as the radiation source. The other duct parameters are set as shown in Figure 9 (left), and the specific duct height settings are shown in Figure 11 (a). The red dots represent the distance between each grid and the radiation source, along with its duct height. From Figure 11 (b), it is evident that electromagnetic waves are effectively trapped within the duct layer, but the difference between uniform and non-uniform evaporation duct environments is not noticeable. Therefore, we simulated the propagation losses at horizontal distances of 15 m and 17 m for EDH (Figure 11c). Within the horizontal range, the propagation losses at EDH=15 m fluctuate less with distance, while the propagation losses at EDH=17 m fluctuate more (Figure 11d). In a non-uniform duct environment, as the duct height decreases, the fluctuation of propagation loss also decreases. That is, the higher the duct height, the greater the fluctuation of propagation loss at horizontal distance.

3.2. Lower atmospheric ducts

3.2.1. Characteristics of lower atmospheric ducts

Lower atmospheric ducts can be classified into surface duct and elevated duct, with surface duct being the main cause of over-the-horizon detection for navigation radars. In contrast, evaporation duct typically only result in weak over-the-horizon detection [40]. Elevated duct have a relatively small impact on actual electromagnetic wave propagation, mainly due to their inability to meet the conditions for over-the-horizon propagation.
From the lower atmospheric ducts model, it is evident that the atmospheric stratification of is closely related to temperature, humidity, and pressure. Therefore, this study uses data from five sounding stations in the northwest of the SCS to statistically analyze the characteristics of lower atmospheric ducts. Figure 12 illustrates the monthly average distribution of lower atmospheric ducts occurrence rates at the five sounding stations. It is evident from the Figure 12 that the lower atmospheric ducts occurrence rates at stations 48839, 48845, and 48855 are relatively high. Among these stations, stations 48839 and 48845 primarily record duct events at 00:00. The monthly average occurrence rate of station 59758 is relatively low (less than 20%), mainly due to its proximity to the mainland in both the north and south, which makes it difficult to form a good sea-land breeze circulation. The average occurrence rate of 59981 exhibits a clear monthly distribution feature, with the probability first increasing and then decreasing from January to December, and reaching its maximum value in June.
To distinguish between surface duct and elevated duct, we analyzed the monthly average incidence of different types of lower atmospheric ducts at each station (Figure 13). From Figure 13 (left), it is evident that surface duct primarily occur from May to September, which is the time following the onset of the SCS summer monsoon. The probability gradually decreases after the onset of the winter monsoon. Stations 48855 and 59981 have the highest probability of surface duct occurrence among the five stations, and the monthly average distribution of occurrence probabilities with monthly variations is relatively similar for the two stations. The monthly average distribution of occurrence probabilities for the other three stations is also relatively consistent. From Figure 13 (right), it is evident that the three stations with the highest occurrence rate of elevated duct are 48839, 48855, and 48845, which exhibit distinct monthly distribution characteristics. That is, the probability of duct occurrence varies significantly with months. The other two stations have lower occurrence rates of elevated duct (less than 20%), but the probability of occurrence of elevated duct increases slightly with months and tends to stabilize.
Station 48855, 59758, and 59981 have sufficient sounding observation data at 00:00 and 12:00, allowing us to compare the monthly average occurrence probabilities of surface duct and elevated duct at these times (Figure 14). In terms of surface duct occurrence rate, the probability of duct occurrence at 48855 station at 00:00 is higher than that at 12:00. The probability of duct occurrence at 59981 station is higher before July at 00:00, but lower than that at 12:00 after July. The probability of duct occurrence at 59758 station is higher than that at 12:00 from May to August (i.e., after the onset of the SCS summer monsoon). In terms of the occurrence rate of elevated duct, the occurrence rate of ducts at stations 48855 and 59981 at 12:00 is higher than that at 00:00. However, the difference in the monthly average occurrence rate of ducts at stations 59758 and 59981 at 00:00 and 12:00 is not significant. Overall, there is little difference in the occurrence rate of lower atmospheric ducts between 00:00 and 12:00, with a higher probability of occurrence for surface duct at 00:00 and a higher probability of occurrence for elevated duct at 12:00.
Table 5 displays the percentage of surface duct without a base layer in the total surface duct. The results indicate that the 59981 site has the highest proportion of surface duct without a base layer, reaching 98.7%, followed by the 48855 site. Overall, the occurrence rate of surface duct without a base layer is higher than that of surface duct with a base layer, indicating that the surface duct observed at the statistical stations are primarily based on surface duct without a base layer.
Figure 15 presents the statistical distribution of duct strength (left) and duct thickness (right) at each station. The ducts are grouped into 0∼30 M-units intervals with a 2 M-units interval and 60∼200 m intervals with a 20 m interval. Ducts larger than 30 M-units and 200 m are grouped separately. From the duct strength distribution, it can be observed that the duct strength of 48839 and 48855 stations is primarily concentrated between 2∼8 M-units, with similar probability distributions. The duct strength of 59981 and 59758 stations is mainly concentrated between 2∼4 M-units, with similar distributions. The duct strength of 48845 station is mainly concentrated between 8∼10 M-units. Regarding duct thickness, the primary thickness at each station is below 80 m. The bottom height of the duct obtained from ERA5 data is considered to be relatively close to actual observations [8,41]. In this study, we screened the temperature, humidity, pressure, and other ERA5 data corresponding to the time of elevated duct events in the data of five sounding stations to invert the elevated duct. Subsequently, we obtained the bottom height of the elevated duct from different data sources. The comparison results between the two sources are shown in Figure 16, indicating that ERA5 data can better reflect the characteristics of the bottom height of the elevated duct.
Although ERA5 data may miss certain duct phenomena, it is known to provide a good description of the bottom height of elevated duct [41]. Figure 17 illustrates the monthly average distribution of the bottom height of the elevated duct in the northwest of the SCS. The results demonstrate that the bottom height of the duct during the onset of the summer monsoon (May to September) is the lowest month of the year, indicating that the arrival of the summer monsoon reduces the bottom height of the elevated duct. Conversely, as the winter winds arrive, the bottom height of the duct begins to increase after October, reaching its maximum value in December, and then gradually decreases until April of the following year. This suggests that the presence of winter winds lifts the height of the elevated duct. From a spatial distribution perspective, the northeast of the Beibu Gulf displays the highest height of the elevated duct from December to April of the following year. During this time period, the height of the southeast region is greater than that of the northwest region. Additionally, the area connecting the Beibu Gulf and the SCS gradually appears as a low duct with a high bottom from January to April. This phenomenon is mainly due to the prevailing southeast wind, which prevents the elevated duct from lifting well. In summary, the elevated duct exhibits obvious distribution characteristics as time and space change.

3.2.2. Electromagnetic propagation in surface duct environment

As discussed in section 3.2.1, it is evident that the surface duct without a base layer dominates at station 59981, with a high probability of duct strength of 4 M-units and duct thickness of 80 m. As a result, we set M 2 =380 M-units, M 1 =376 M-units, h t =80 m, h b =0 m and the duct structure is depicted in Figure 17 (left) when the height above 80m is increased by 120 M-units/km. Furthermore, we only considered the propagation loss in the case of radiation source elevation angles of 0°, 0.5°, 1°, 2°, and 4°. Other parameter settings are displayed in Table 5, with the radiation source frequency of 9GHz and elevation angle of 0.5°. The variation of electromagnetic propagation loss with distance and height at 5° elevation angle is demonstrated in Figure 18 (right), which clearly indicates that electromagnetic waves are trapped within the duct layer.
Figure 19 displays the electromagnetic propagation loss at a height of 8 m at different frequencies (left) and antenna elevations (right) at a frequency of 9 GHz with an elevation angle of 0.5°. The results indicate that the electromagnetic propagation loss does not decrease with an increase in horizontal distance at different radiation frequencies. However, the frequency of electromagnetic wave loss jitter increases with the increase of frequency. Moreover, at different elevation angles, it is observed that as the elevation angle increases, the propagation loss decreases. The magnitude of the propagation loss reduction also increases when increasing at 1° intervals until it cannot be trapped. In summary, the frequency variation in the surface duct environment has little effect on the electromagnetic propagation loss in the horizontal direction. However, the elevation angle of the radiation source is a critical factor in determining whether the electromagnetic wave is trapped.

3.3. Electromagnetic propagation in a homogeneously mixed duct environment

Evaporation duct are commonly observed in the lower atmospheric structure of the marine atmospheric boundary layer. For instance, in Section 3.1.1, it was found that the average annual incidence of evaporation duct in the Xisha area is over 70%. Hence, the northwest of the SCS is also susceptible to mixed atmospheric environments of evaporation duct and surface duct. Figure 20 (a) illustrates the characteristics of the hybrid duct structure employed in the simulation, with an EDH of 15 m and a surface duct height of 80 m, corresponding to the electromagnetic propagation loss at 9 GHz and an elevation of 0.5°. As shown in Figure 20 (b), compared to Figure 18 (left), the "sinusoidal wave" frequency of propagation loss in the hybrid duct environment is more frequent, and the propagation loss at a height of 15 m increases faster with distance, indicating a greater electromagnetic propagation loss. To investigate the electromagnetic propagation losses of radiation sources at an altitude of 8 m and signal reception at different altitudes, we set the signal reception heights to 4 m (below the radiation source height), 10 m (above the radiation source height), 15 m (EDH), and 20 m (above EDH). Figure 20 (c) shows that as the signal reception height increases, the propagation loss also increases, and the fluctuation at 30∼60 km also increases. For radar, areas with high propagation loss can form detection blind spots. Furthermore, when the radiation sources are at heights of 8 m, 15 m, and 20 m, the difference in vertical propagation losses is not significant (Figure 20d). The propagation losses all increase significantly above the 15 m height, indicating a phenomenon of first decreasing and then increasing from 0∼80 m height, reaching the minimum value at the 15 m height.

4. Conclusions

The presence of atmospheric duct environments has altered the path and range of electromagnetic wave propagation, resulting in unique propagation characteristics in communication, detection, navigation, and other systems. This study uses data from seven automatic stations from 2011 to 2022 and data from five sounding stations from 2010 to 2022 to statistically analyze the characteristics of evaporation and lower atmospheric ducts at corresponding stations in the northwest of the SCS. The reliability of NCEP CFSv2 and ERA5 data in the inversion of evaporation and lower atmospheric ducts is verified, and the spatiotemporal distribution characteristics of EDH and elevated duct bottom height in the study area are obtained. Moreover, based on the statistical analysis results of station atmospheric ducts as prior information, the parabolic equation model is used to simulate electromagnetic propagation in the duct environment of uniform evaporation duct, surface duct without foundation layers, non-uniform evaporation duct, and uniform mixed duct under different frequencies, elevations, and other conditions. The main conclusions obtained are as follows:
1) The maximum occurrence rate of evaporation duct at the coastal stations is in December, and all have obvious monthly non-uniform distribution characteristics. This means that the probability of evaporation duct occurring varies significantly with different months, and EDH also exhibits this feature. Furthermore, the probability and height of evaporation duct occurring in different coastal areas also have significant differences, with consistent monthly variation trends. The main reason for this is that the formation of the evaporation duct is mainly due to the physical process of seawater evaporation, which is greatly affected by wind speed, sea surface temperature, and other factors, leading to significant spatiotemporal heterogeneity of the evaporation duct. Due to the small impact of terrestrial airflow, the monthly average difference in the probability of evaporation duct occurrence at the Xisha Station is small, and the annual average value of EDH is relatively large. The monsoon has a significant impact on the evaporation duct, with an increase in EDH after the onset of the summer monsoon and a decrease in EDH due to the winter monsoon.
2) The monthly average occurrence rate of lower atmospheric ducts in the Xisha region exhibits significant monthly distribution characteristics. The probability of occurrence increases from January to June, and then decreases from July to December, reaching its maximum value in June. Surface duct mainly consist of non-base layer surface duct. The occurrence rate of lower atmospheric ducts at other stations does not show significant changes with months. In terms of time, there is not much difference in the occurrence rate of lower atmospheric ducts between 00:00 and 12:00, but the probability of occurrence of surface duct is relatively high at 00:00, while the occurrence rate of elevated duct is mainly at 12:00. The monsoon plays a crucial role in the generation and evolution of elevated duct in the northwest of the SCS. After the onset of the summer monsoon, the bottom height of the elevated duct decreases, while the presence of the winter monsoon lifts the elevated duct, resulting in an increase in their bottom height.
3) Comparing observation and numerical analysis data of sea surface temperature, evaporation duct occurrence rate and height, and elevated duct bottom height, it is evident that the NCEP CFSv2 sea surface temperature at 06:00 is relatively close to the actual observation, with a total average error of -0.8077 °C, while significant errors were observed at other times. The annual average evaporation duct occurrence rate error obtained from NCEP CFSv2 inversion is 6%, and the annual average duct height difference in 06:00 was 0.0329 m. Additionally, ERA5 data can effectively reflect the characteristics of duct bottom height. Hence, NCEP CFSv2 and ERA5 data can be used to analyze the characteristics of evaporation duct and lower atmospheric ducts in the SCS region, respectively.
4) In a uniform evaporation duct environment, a "long strip" structure with low propagation loss is easily formed within the duct layer. The higher the frequency of the radiation source and the lower the elevation angle, the easier it is to be trapped by the evaporation duct. In a non-uniform evaporation duct environment, as the duct height decreases, the fluctuation of propagation loss decreases. Therefore, the higher the duct height, the greater the fluctuation of propagation loss in horizontal distance. In a uniform surface duct environment, frequency variation has a relatively small impact on electromagnetic propagation loss in the horizontal direction. However, the elevation angle of the radiation source is an important factor determining whether electromagnetic waves are trapped in this environment. In the hybrid duct environment combining evaporation duct and surface duct, the "sine wave" frequency of propagation loss is more similar to that in the uniform surface duct. The propagation loss in the EDH within the hybrid duct increases faster with distance, indicating that electromagnetic propagation loss is greater.

Author Contributions

Conceptualization, N.Y. and T.W.; methodology, N.Y. and T.W.; validation, N.Y. and T.W.; formal analysis, N.Y. and T.W.; investigation, N.Y.; resources, N.Y.; data curation, T.W. and N.Y.; writing—original draft preparation, N.Y.; writing—review and editing, D.S.; visualization, N.Y.; supervision, T.W.; project administration, T.W.; funding acquisition, T.W. All authors have read and agreed to the published version of the manuscript

Funding

This research received no external funding.

Data Availability Statement

The study used the dataset from the ECMWF team (https://cds.climate.copernicus.eu/, accessed on 20 February 2023) and University of Wyoming (http://weather.uwyo.edu/, accessed on 25 February 2023).

Acknowledgments

We acknowledge the use of data from the ECMWF team (https://cds.climate.copernicus.eu/, accessed on 26 September 2021) and University of Wyoming (http://weather.uwyo.edu/, accessed on 25 February 2023)

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Kulessa, A.S.; Barrios, A.; Claverie, J.; et al. The Tropical Air-Sea Propagation Study (TAPS). Bulletin of the American Meteorological Society 2017, 98, 517–537. [Google Scholar] [CrossRef]
  2. Gunashekar, S.D.; Warrington, E.M.; Siddle, D.R. Long-term statistics related to evaporation duct propagation of 2 GHz radio waves in the English Channel. Radio Science 2010, 45, 1–14. [Google Scholar] [CrossRef]
  3. Thompson, W.T.; Haack, T. An Investigation of Sea Surface Temperature Influence on Microwave Refractivity: The Wallops-2000 Experiment. J APPL METEOROL CLIM 2011, 50, 2319–2337. [Google Scholar] [CrossRef]
  4. Huang, L.-F.; Liu, C.-G.; Wang, H.-G.; Zhu, Q.-L.; Zhang, L.-J.; Han, J.; Zhang, Y.-S.; Wang, Q.-N. Experimental Analysis of Atmospheric Ducts and Navigation Radar Over-the-Horizon Detection. Remote Sens, 2022, 14, 2588. [Google Scholar] [CrossRef]
  5. Kaissassou, S.; Lenouo, A.; Tchawoua, C.; et al. Climatology of radar anomalous propagation over West Africa. Journal of Atmospheric and Solar-Terrestrial Physics, 2015, 123, 1–12. [Google Scholar] [CrossRef]
  6. Li, X.; Sheng, L.; Wa, N.W. Elevated Ducts and Low Clouds over the Central Western Pacific Ocean in Winter Based on GPS Soundings and Satellite Observation. Journal of Ocean University of China 2021, 20, 244–256. [Google Scholar] [CrossRef]
  7. Alappattu, D.P.; Wang, Q.; Kalogiros, J. Anomalous propagation conditions over eastern Pacific Ocean derived from MAGIC data. Radio Science 2016, 51, 1142–1156. [Google Scholar] [CrossRef]
  8. Cheng, Y.; Zha, M.; You, Z.; et al. Duct climatology over the South China Sea based on European Center for Medium Range Weather Forecast reanalysis data. Journal of Atmospheric and Solar-Terrestrial Physics 2021, 222, 105720. [Google Scholar] [CrossRef]
  9. Liang, Z.; Ding, J.; Fei, J.; et al. Maintenance and Sudden Change of a Strong Elevated Ducting Event Associated with High Pressure and Marine Low-Level Jet. Journal of Meteorological Research 2020, 34, 1287. [Google Scholar] [CrossRef]
  10. Zhu, J.; Zou, H.; Kong, L.; et al. Surface atmospheric duct over Svalbard, Arctic, related to atmospheric and ocean conditions in winter. Arctic Antarctic and Alpine Research 2022, 54, 264–273. [Google Scholar] [CrossRef]
  11. Guo, X.; Zhao, D.; Zhang, L.; Wang, H.; Kang, S.; Lin, L. C band transhorizon signal characterisations in evaporation duct propagation environment over Bohai Sea of China. IET Microw. Antennas Propag. 2019, 13, 407–413. [Google Scholar] [CrossRef]
  12. Zhao, X.; Yang, P.; Zhou, F.; Zhou, Z. Comparison of evaporation duct height statistics based on surface bulk measurements over Yongxing Island. IEEE Antennas and Wireless Propagation Letters 2023. [Google Scholar] [CrossRef]
  13. Wang, B. Evaporation Duct Height Nowcasting in China’s Yellow Sea Based on Deep Learning. Remote Sensing 2021, 13, 1557. [Google Scholar]
  14. Pozderac, J.; Johnson, J.; Yardim, C.; et al. X-Band Beacon-Receiver Array Evaporation Duct Height Estimation[J]. IEEE Transactions on Antennas and Propagation 2015, 916–917. [Google Scholar]
  15. Saha, Suranjana and Coauthors. The NCEP Climate Forecast System Version 2. Journal of Climate J. Climate, 2014, 27, 2185–2208. [Google Scholar] [CrossRef]
  16. Shi, Y.; Yang, K.; Yang, Y.; et al. A New Evaporation Duct Climatology over the SCS. Journal of Meteorological Research 2015, 29, 764–778. [Google Scholar] [CrossRef]
  17. Shi, Y.; Wang, S.; Yang, F.; et al. Statistical Analysis of Hybrid Atmospheric Ducts over the Northern South China Sea and Their Influence on Over-the-Horizon Electromagnetic Wave Propagation. Journal of Marine Science and Engineering, 2023, 11, 669. [Google Scholar] [CrossRef]
  18. Paulus, R.A. Practical application of an evaporation duct model. Radio Science 1985, 20, 887–896. [Google Scholar] [CrossRef]
  19. Musson-Genon, L.; Gauthier, S.; Bruth, E. A simple method to determine evaporation duct height in the sea surface boundary layer. Radio Sci. 1992, 27, 635–644. [Google Scholar] [CrossRef]
  20. Babin, S.M.; Young, G.S.; Carton, J.A. A New Model of the Oceanic Evaporation Duct. J. Appl. Meteor. Climatol. 1997, 36, 193–204. [Google Scholar] [CrossRef]
  21. Babin, S.M.; Dockery, G.D. LKB-based evaporation duce model comparison with buoy data. J Appl Meteor 2002, 41, 434–446. [Google Scholar] [CrossRef]
  22. Yang, S.; Li, X.; Chao, W.; et al. Application of the PJ and NPS evaporation duct models over the South China Sea (SCS) in winter. PLoS ONE 2017, 12, e0172284. [Google Scholar] [CrossRef] [PubMed]
  23. Guo, X.; Zhao, D.; Zhang, L.; et al. A Comparison Study of Sensitivity on PJ and NPS Models in China Seas. Journal of Ocean University of China 2019, 18, 22–30. [Google Scholar] [CrossRef]
  24. Ding, J.; Fei, J.; Huang, X.; et al. Development and validation of an evaporation duct model. Part I: Model establishment and sensitivity experiments. Journal of Meteorological Research 2015, 29, 467–481. [Google Scholar] [CrossRef]
  25. Zhao, W.; et al. An Evaporation Duct Height Prediction Model Based on a Long Short-Term Memory Neural Network. IEEE Transactions on Antennas and Propagation 2021, 69, 7795–7804. [Google Scholar] [CrossRef]
  26. Zhou, Y.; Liu, Y.; Qiao, J.; Li, J.; Zhou, C. Statistical Analysis of the Spatiotemporal Distribution of Lower Atmospheric Ducts over the Seas Adjacent to China, Based on the ECMWF Reanalysis Dataset. Remote Sensing. 2022, 14, 4864. [Google Scholar] [CrossRef]
  27. Sirkova, I. Duct occurrence and characteristics for Bulgarian Black sea shore derived from ECMWF data - ScienceDirect. Journal of Atmospheric and Solar-Terrestrial Physics 2015, 135, 107–117. [Google Scholar] [CrossRef]
  28. von Engeln, A.; Teixeira, J. A ducting climatology derived from the European Centre for Medium-Range Weather Forecasts global analysis fields. J. Geophys. Res. 2004, 109, D18104. [Google Scholar] [CrossRef]
  29. FENG, G.; HUANG, J.; SU, H. A New Ray Tracing Method Based on Piecewise Conformal Transformations. IEEE Transactions on Microwave Theory and Techniques, Microwave Theory and Techniques, IEEE Transactions on, IEEE Trans. Microwave Theory Techn, 2022, 70, 2040–2052. [Google Scholar] [CrossRef]
  30. Akan, Ozgur B, Dinc, et al. Channel Model for the Surface Ducts: Large-Scale Path-Loss, Delay Spread, and AOA. IEEE Transactions on Antennas and Propagation, 2015, 63, 2728–2738. [Google Scholar] [CrossRef]
  31. Zhao X F, Huang S X, Wang D X. Using particle filter to track horizontal variations of atmospheric duct structure from radar sea clutter. Atmospheric Measurement Techniques, 2012, 5, 2859–2866. [Google Scholar] [CrossRef]
  32. Zhao X and Sixun Huang. Estimation of Atmospheric Duct Structure Using Radar Sea Clutter. J. Atmos. Sci., 2012, 69, 2808–2818. [Google Scholar] [CrossRef]
  33. Ozgun, O.; Sahin, V.; Erguden, M.E.; Apaydin, G.; Yilmaz, A.E.; Kuzuoglu, M.; Sevgi, L. PETOOL v2.0: Parabolic Equation Toolbox with Evaporation Duct Models and Real Environment Data. Comput. Phys. Commun. 2020, 256, 107454. [Google Scholar] [CrossRef]
  34. Engeln, A. V., Nedoluha, G., Teixeira, J. An analysis of the frequency and distribution of ducting events in simulated radio occultation measurements based on ECMWF fields. J. Geophys. Res. 2003, 108, 4669. [Google Scholar]
  35. Shifeng Kang, Yusheng Zhag, Hongguang Wang. Atmospheric Duct in Troposphere Environment, 1rd ed.; Science Press: BeiJing, China, 2014; pp. 85–86. [Google Scholar]
  36. Ozgun O, Apaydin G, Kuzuoglu M, et al. PETOOL: MATLAB-based one-way and two-way split-step parabolic equation tool for radiowave propagation over variable terrain. Computer Physics Communications, 2011, 182, 2638–2654. [Google Scholar] [CrossRef]
  37. HAUS, B. K. et al. CLASI: Coordinating Innovative Observations and Modeling to Improve Coastal Environmental Prediction Systems. Bulletin of the American Meteorological Society, 2022, 103, 889–898. [Google Scholar] [CrossRef]
  38. Thompson W T, Haack T. An Investigation of Sea Surface Temperature Influence on Microwave Refractivity: The Wallops-2000 Experiment. Journal of Applied Meteorology and Climatology, 2011, 50, 2319–2337. [Google Scholar] [CrossRef]
  39. SHI Yang, YANG Kunde, YANG Yixin, MA Yuanliang. A New Evaporation Duct Climatology over the South China Sea. J. Meteor. Res., 2015, 29, 764–778. [Google Scholar] [CrossRef]
  40. Huang, L.-F.; Liu, C.-G.; Wang, H.-G.; Zhu, Q.-L.; Zhang, L.-J.; Han, J.; Zhang, Y.-S.; Wang, Q.-N. Experimental Analysis of Atmospheric Ducts and Navigation Radar Over-the-Horizon Detection. Remote Sens. 2022, 14, 2588. [Google Scholar] [CrossRef]
  41. von Engeln, A.; Nedoluha, G.; Teixeira, J. An analysis of the frequency and distribution of ducting events in simulated radio occultation measurements based on ECMWF fields. J. Geophys. Res. 2003, 108, 4669. [Google Scholar] [CrossRef]
Preprints 73070 g001
Figure 1. Geometric characteristics and parameters of atmospheric ducts: (a) evaporation duct. (b) surface duct without base layer. (c) surface duct with base layer. (d) elevated duct. (e) hybrid duct. h t is trapping layer top height, h c is trapping layer bottom height, h b is duct bottom height.
Figure 1. Geometric characteristics and parameters of atmospheric ducts: (a) evaporation duct. (b) surface duct without base layer. (c) surface duct with base layer. (d) elevated duct. (e) hybrid duct. h t is trapping layer top height, h c is trapping layer bottom height, h b is duct bottom height.
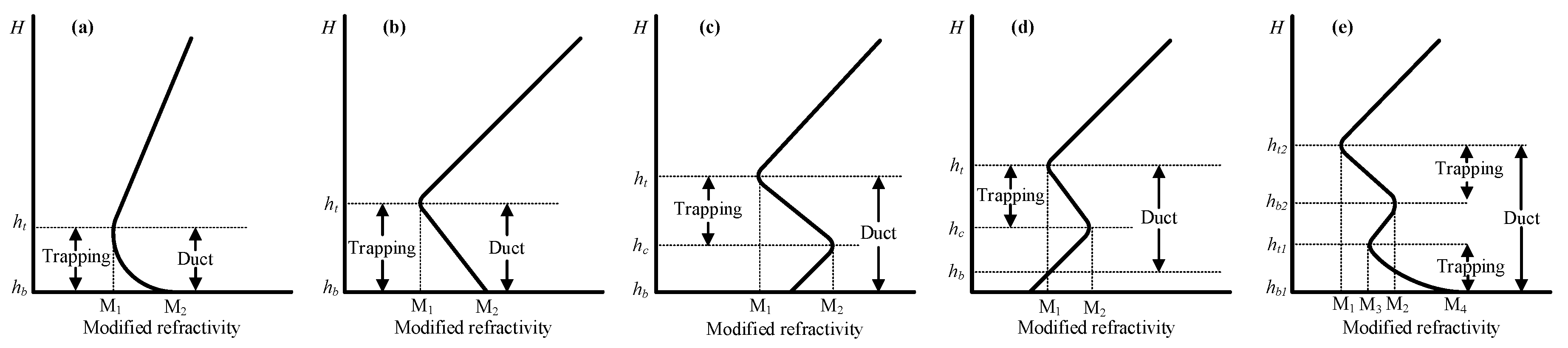
Preprints 73070 g001
Preprints 73070 g002
Figure 2. The research flow chart of this paper.
Figure 2. The research flow chart of this paper.
Preprints 73070 g002
Preprints 73070 g003
Figure 3. The research flow chart of this paper.
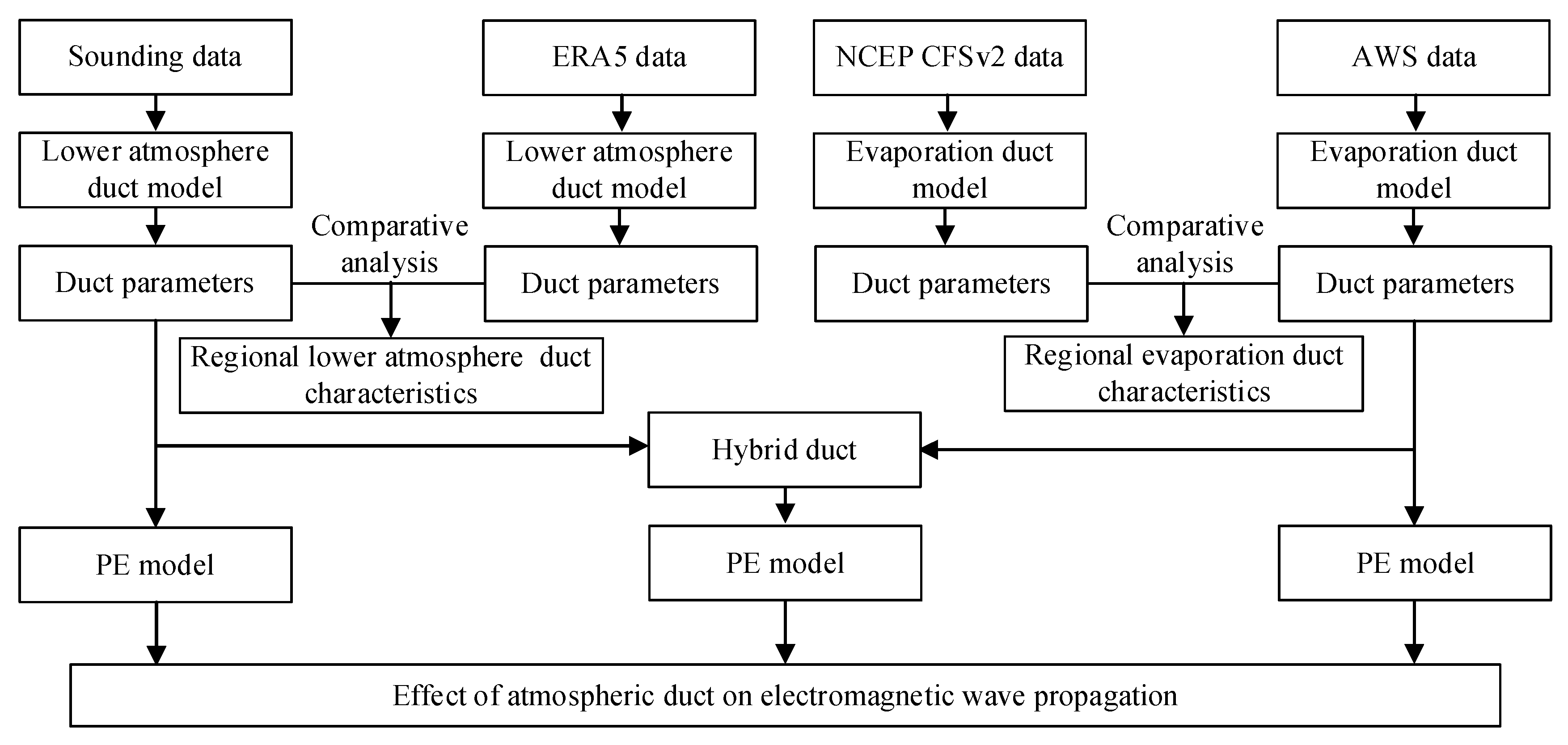
Figure 3. The research flow chart of this paper.
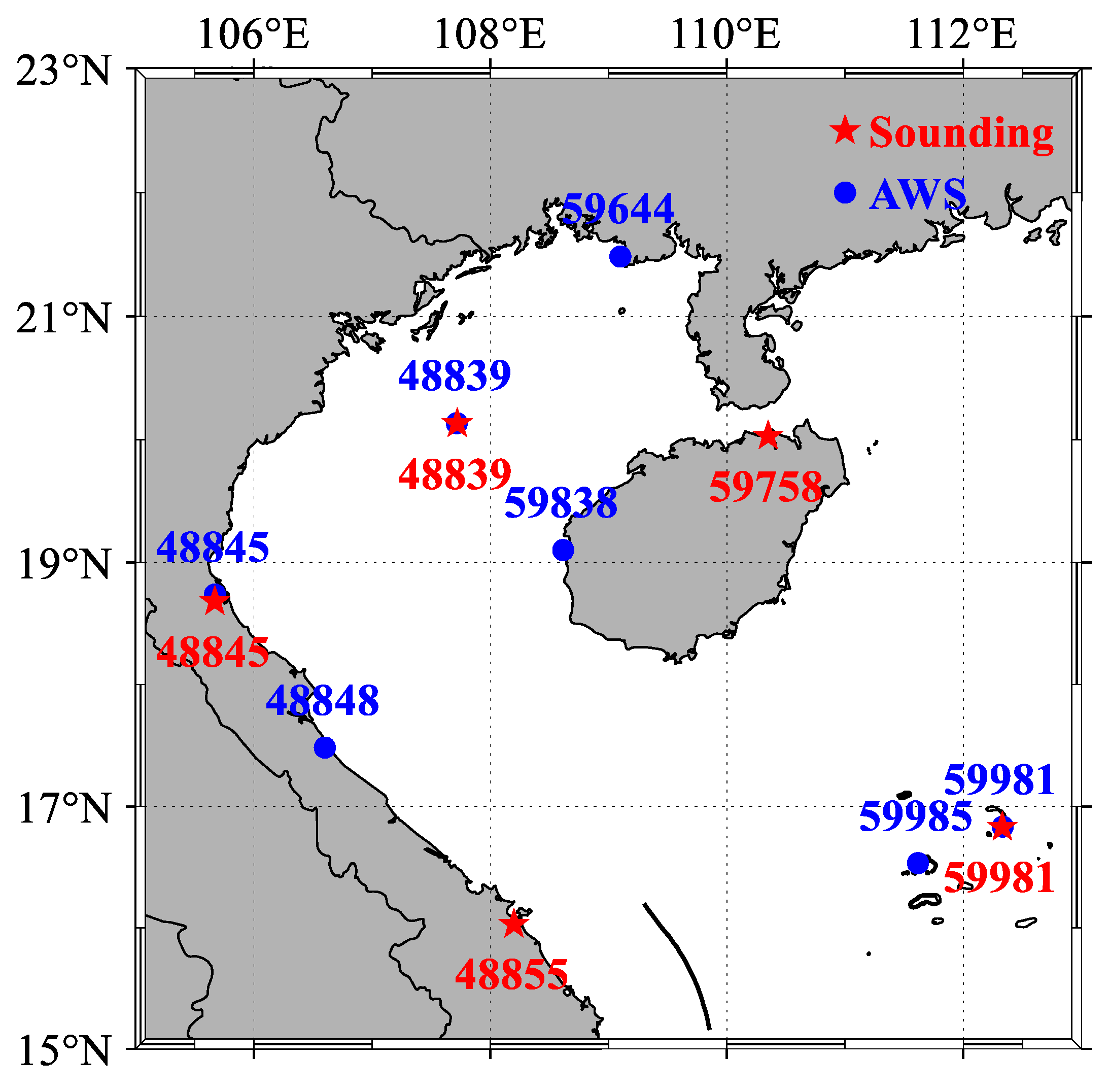
Preprints 73070 g003
Preprints 73070 g004
Figure 4. The daily average map of observation error between 48839 and NCEP CFSv2 sea surface temperature at 00, 06, 12, and 18 hours (UTC).
Figure 4. The daily average map of observation error between 48839 and NCEP CFSv2 sea surface temperature at 00, 06, 12, and 18 hours (UTC).
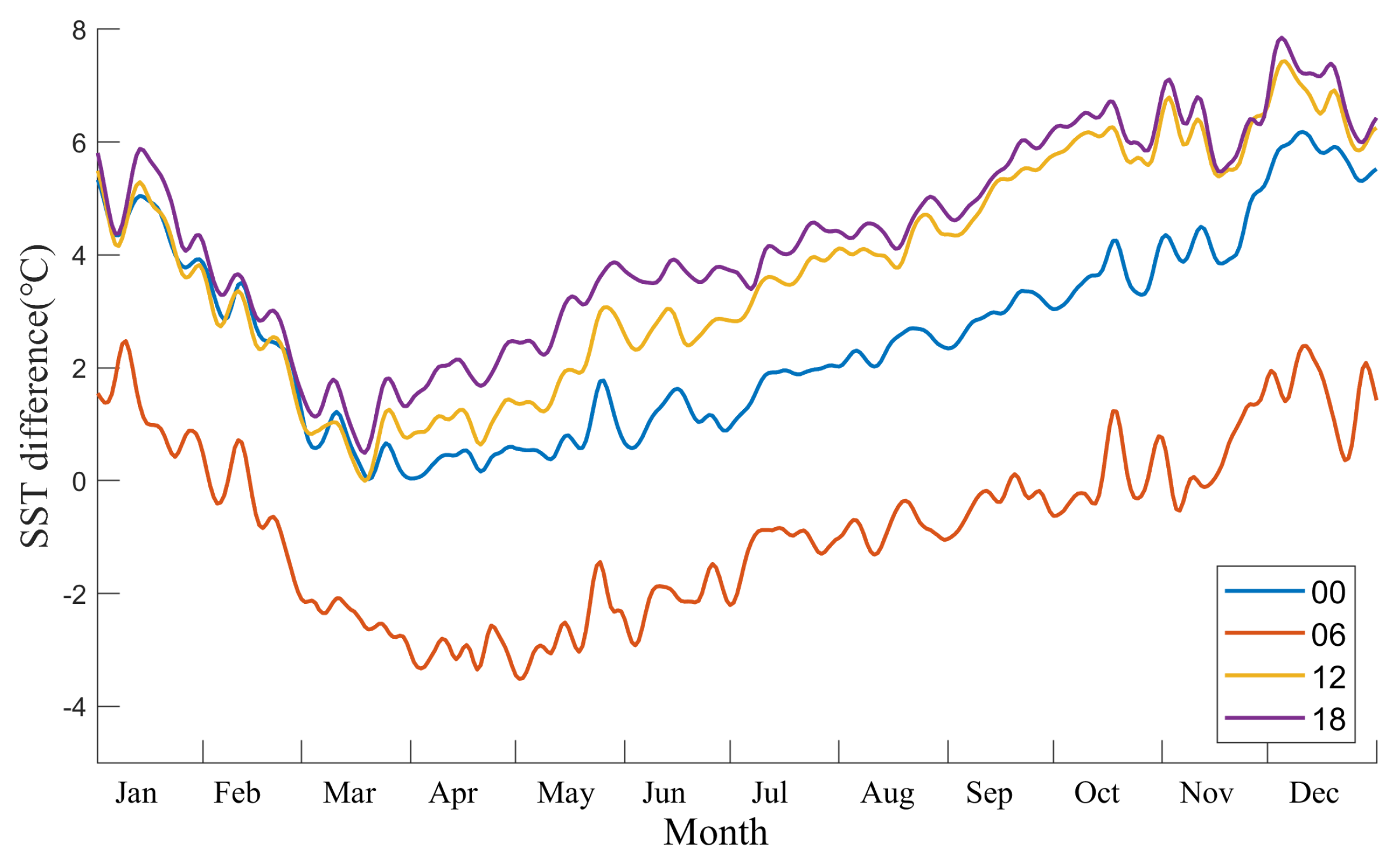
Preprints 73070 g004
Preprints 73070 g005
Figure 5. The incidence of evaporation duct in coastal stations (left) and the monthly average distribution of EDH at 06:00 (right)
Figure 5. The incidence of evaporation duct in coastal stations (left) and the monthly average distribution of EDH at 06:00 (right)
Preprints 73070 g005
Preprints 73070 g006
Figure 6. Incidence of evaporation duct (left) and monthly average distribution of EDH at 06:00 (right) at automatic stations in inland sea islands
Figure 6. Incidence of evaporation duct (left) and monthly average distribution of EDH at 06:00 (right) at automatic stations in inland sea islands
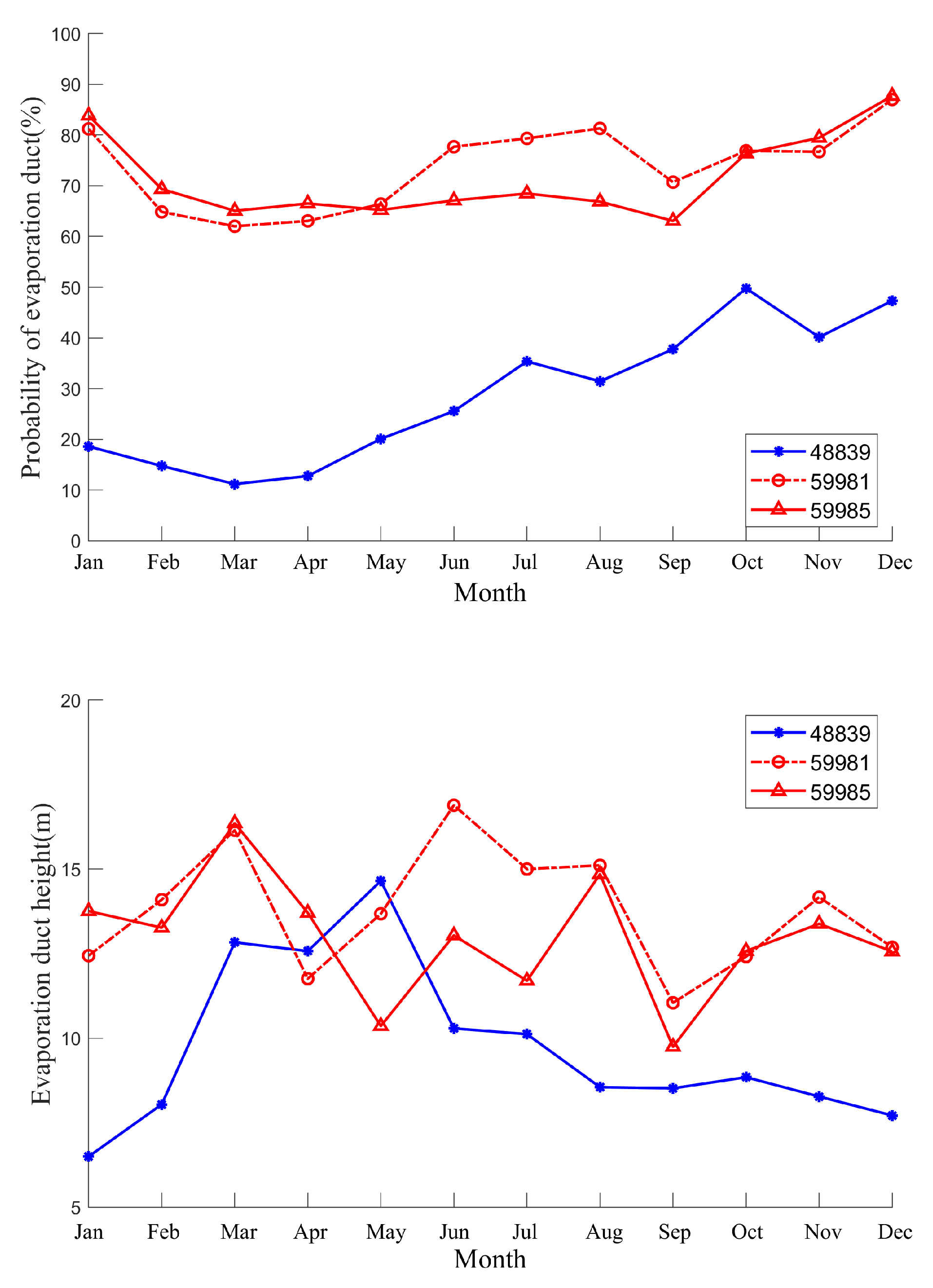
Preprints 73070 g006
Preprints 73070 g007
Figure 7. The duct occurrence rate of station 48839 (left) and the monthly average distribution of EDH at time 06 (right)
Figure 7. The duct occurrence rate of station 48839 (left) and the monthly average distribution of EDH at time 06 (right)
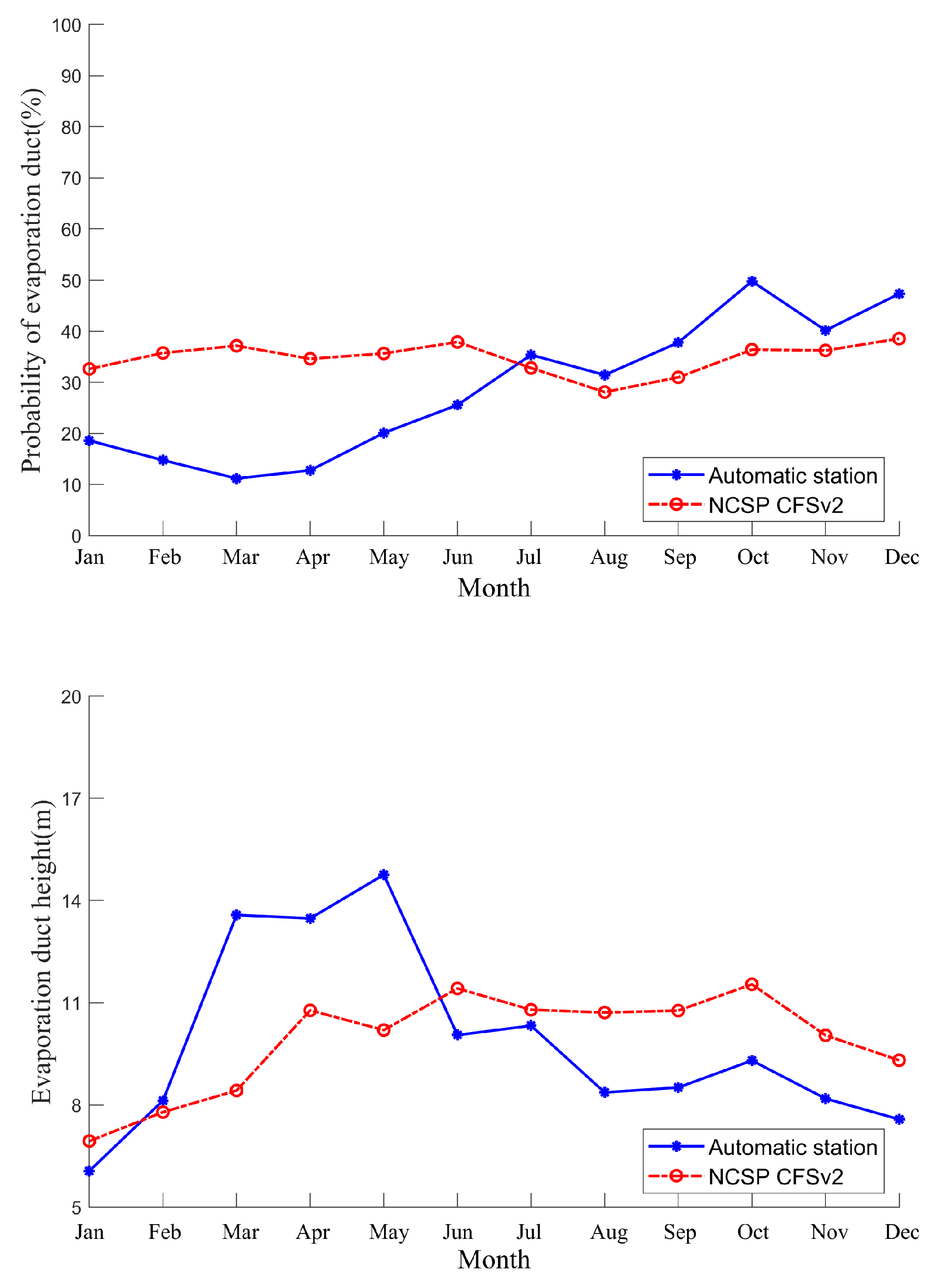
Preprints 73070 g007
Preprints 73070 g008
Figure 8. The monthly average distribution of EDH at 06:00 in the northwest of the SCS, where the black dots in September indicate the position of the radiation source, and the lines indicate the path of electromagnetic wave radiation.
Figure 8. The monthly average distribution of EDH at 06:00 in the northwest of the SCS, where the black dots in September indicate the position of the radiation source, and the lines indicate the path of electromagnetic wave radiation.
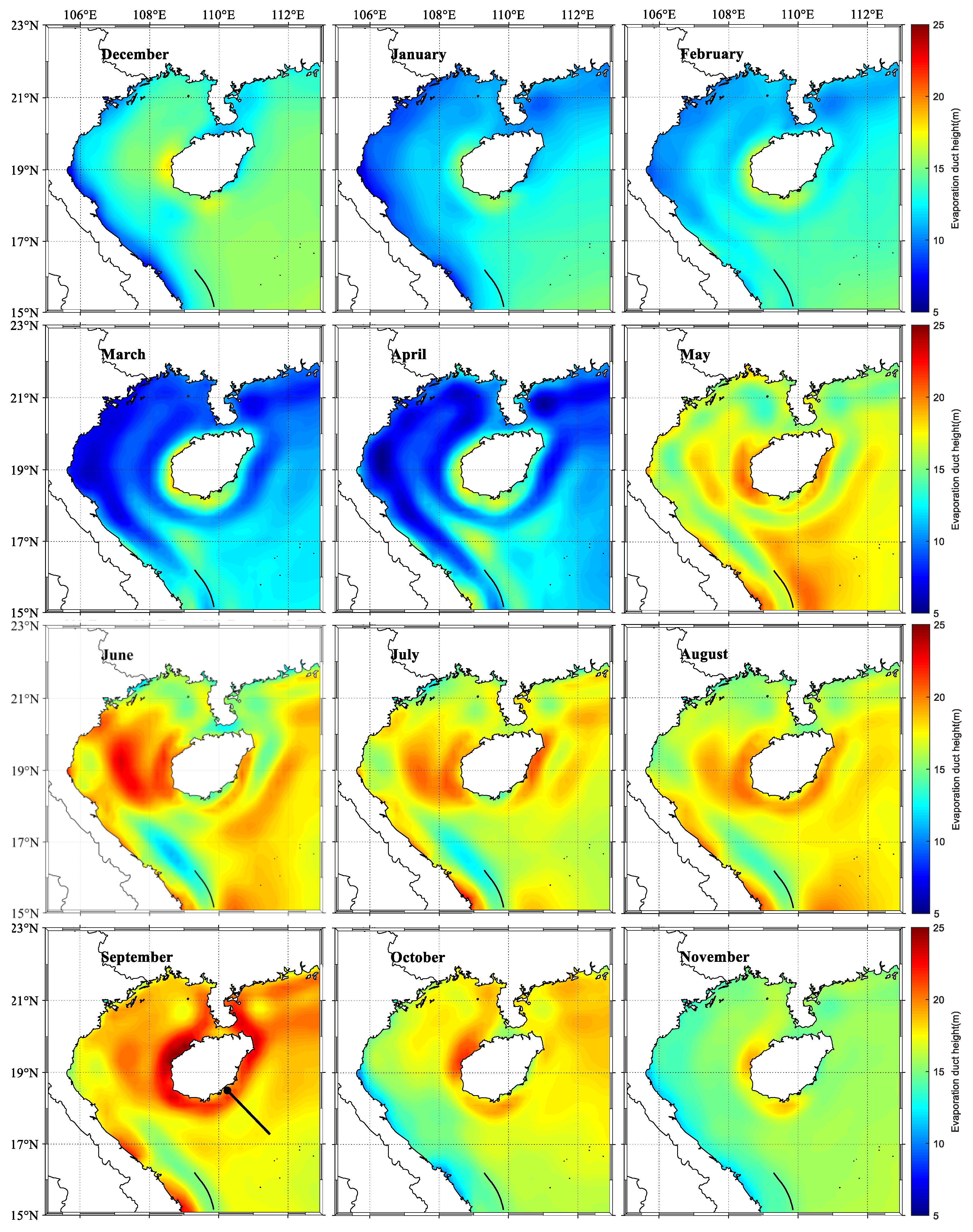
Preprints 73070 g008
Preprints 73070 g009
Figure 9. The vertical profile of the evaporation duct with corrected refractive index (left) and the propagation loss when the height of the electromagnetic wave radiation source is 8 m, the frequency is 9 GHz, and the elevation angle is 0.5° (right)
Figure 9. The vertical profile of the evaporation duct with corrected refractive index (left) and the propagation loss when the height of the electromagnetic wave radiation source is 8 m, the frequency is 9 GHz, and the elevation angle is 0.5° (right)
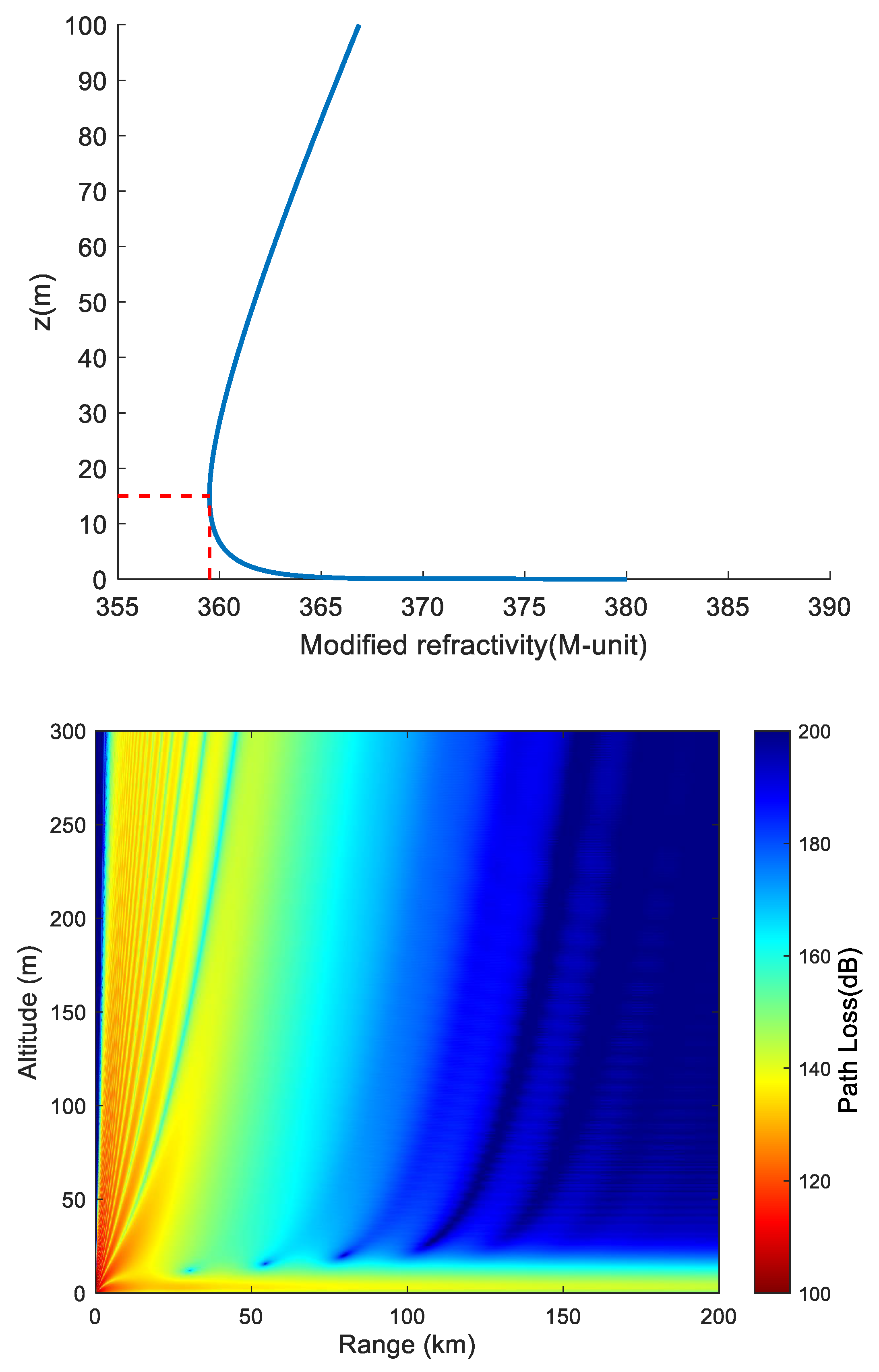
Preprints 73070 g009
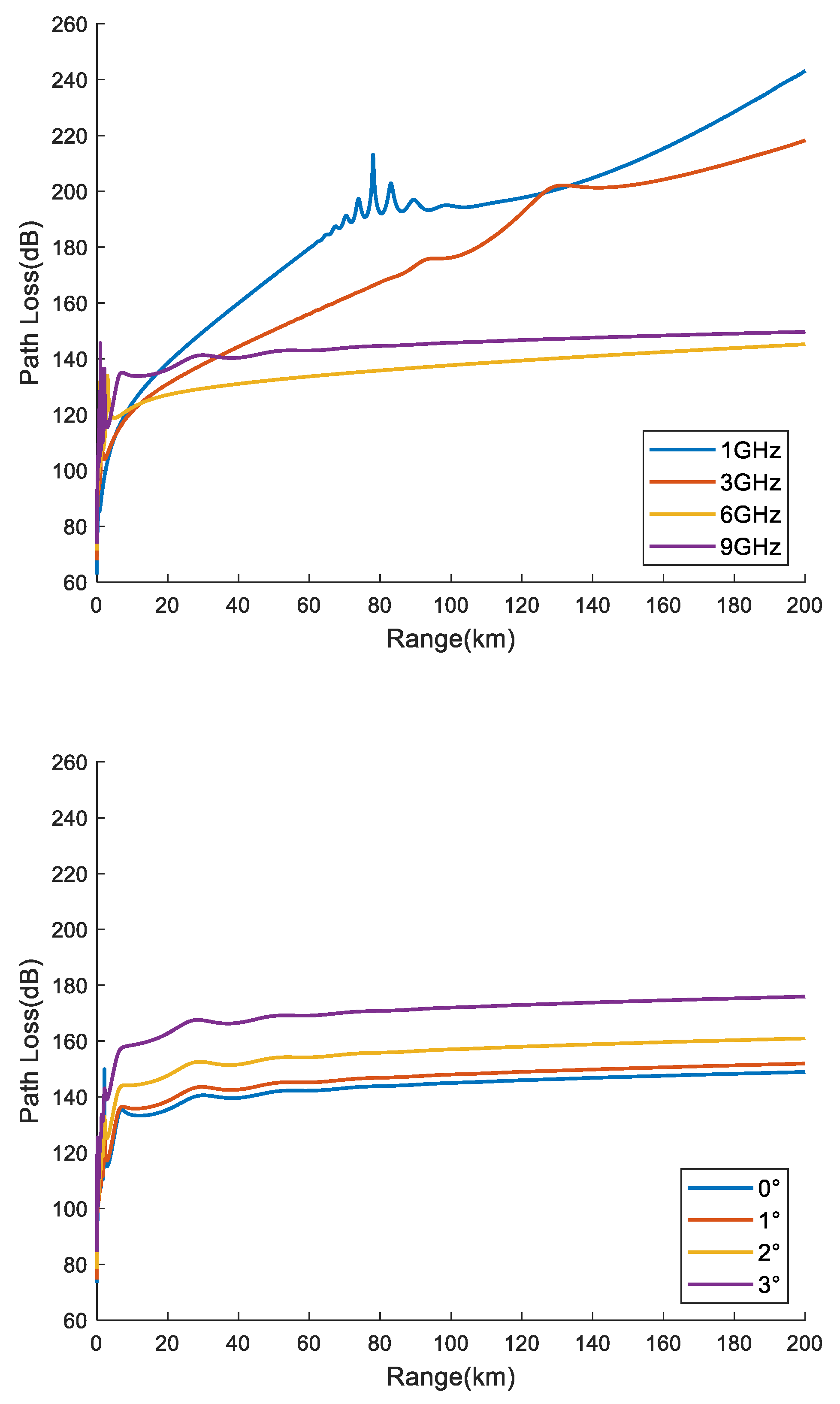
Preprints 73070 g010
Figure 10. Propagation loss at 8 m height of radiation source at different radiation frequencies (left) and different elevation angles (right) at 9 GHz frequency
Figure 10. Propagation loss at 8 m height of radiation source at different radiation frequencies (left) and different elevation angles (right) at 9 GHz frequency
Preprints 73070 g010
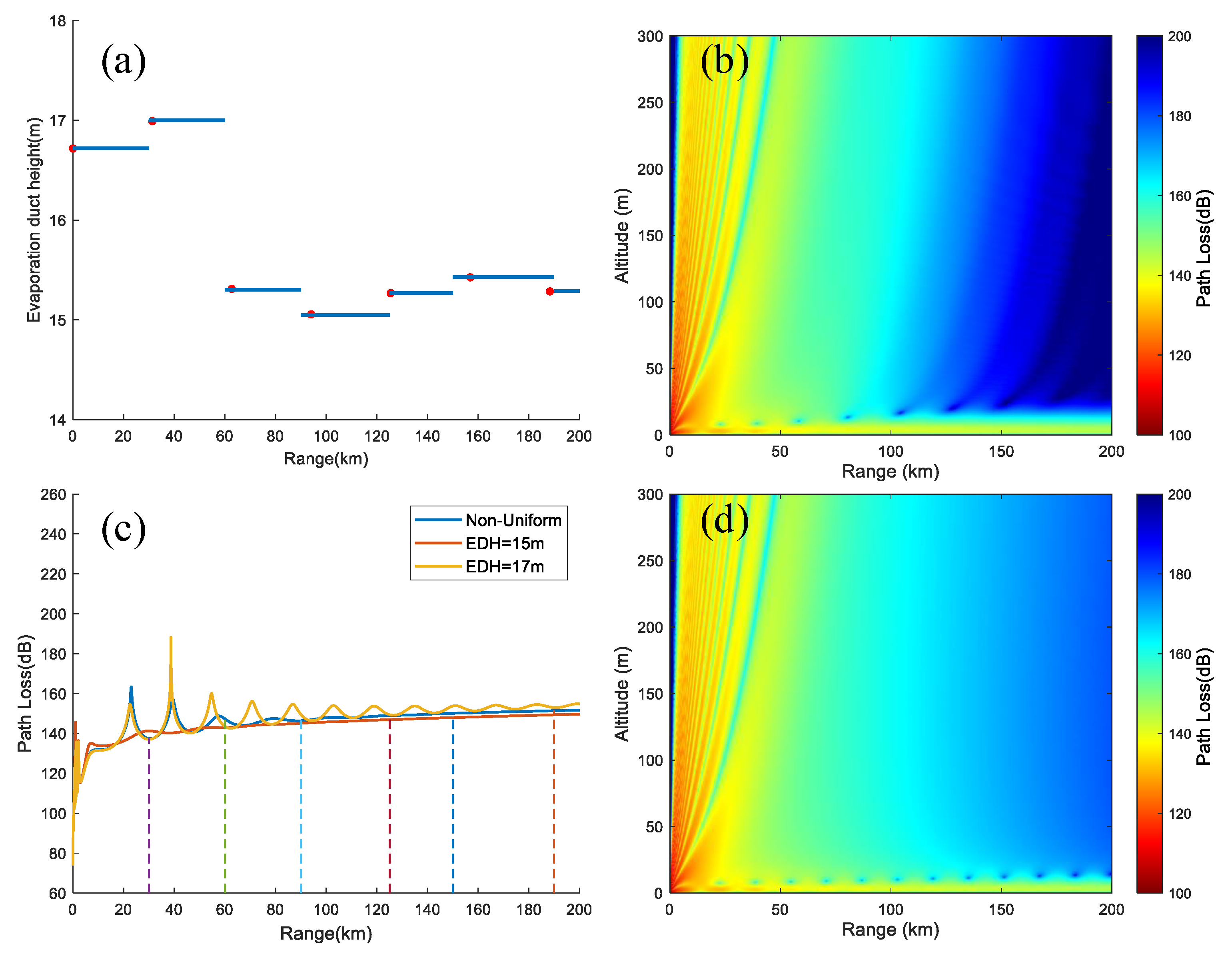
Preprints 73070 g011
Figure 11. Electromagnetic propagation losses in uniform and non-uniform evaporation duct environments.(a) Non-uniform EDH setting, with red dots indicating the distance between each grid and the radiation source and its EDH;(b) Electromagnetic propagation loss in non-uniform duct environment;(c) The propagation loss in uniform and non-uniform duct environments with an elevation of 0.5°, a frequency of 9 GHz, and a radiation source. The dashed line represents the horizontal distance boundary between different EDH; (d) Propagation loss at an elevation of 0.5°, a frequency of 9 GHz, and a duct height of 17 m.
Figure 11. Electromagnetic propagation losses in uniform and non-uniform evaporation duct environments.(a) Non-uniform EDH setting, with red dots indicating the distance between each grid and the radiation source and its EDH;(b) Electromagnetic propagation loss in non-uniform duct environment;(c) The propagation loss in uniform and non-uniform duct environments with an elevation of 0.5°, a frequency of 9 GHz, and a radiation source. The dashed line represents the horizontal distance boundary between different EDH; (d) Propagation loss at an elevation of 0.5°, a frequency of 9 GHz, and a duct height of 17 m.
Preprints 73070 g011
Preprints 73070 g012
Figure 12. Monthly average distribution of lower atmospheric ducts incidence in sounding stations.
Figure 12. Monthly average distribution of lower atmospheric ducts incidence in sounding stations.
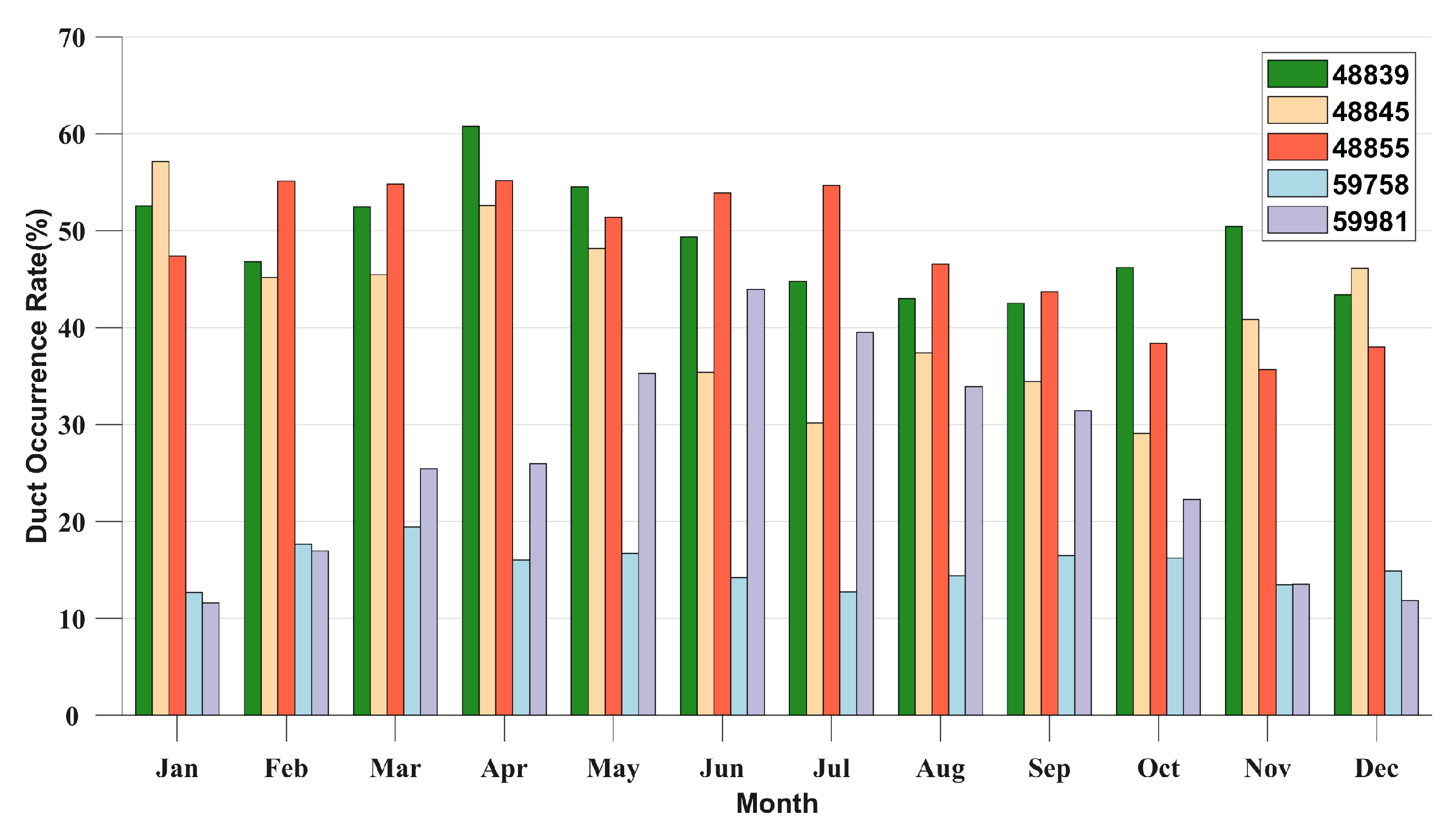
Preprints 73070 g012
Preprints 73070 g013
Figure 13. The occurrence rate of the surface duct (left) and elevated duct (right) of the sounding station
Figure 13. The occurrence rate of the surface duct (left) and elevated duct (right) of the sounding station
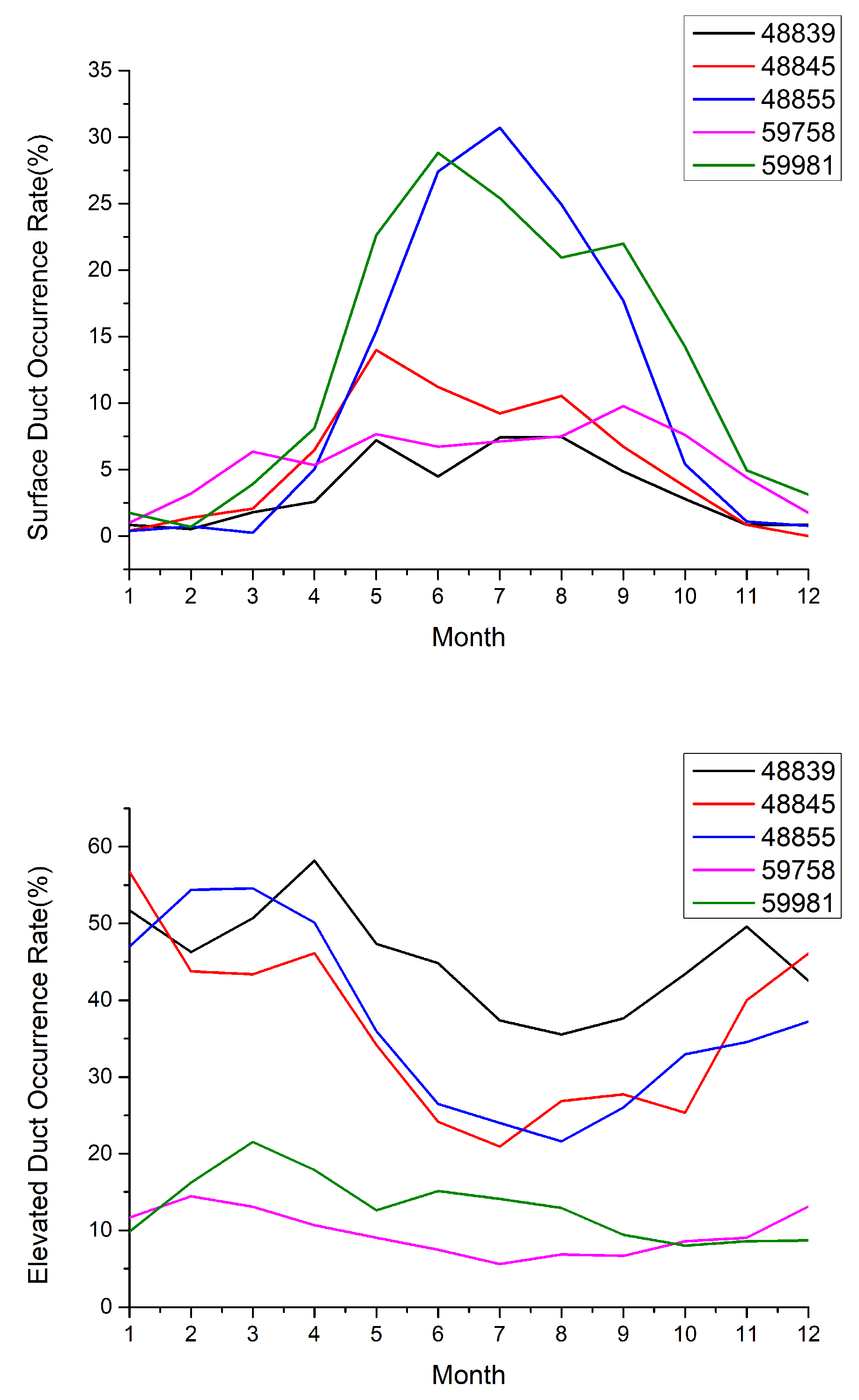
Preprints 73070 g013
Preprints 73070 g014
Figure 14. Incidence rates of surface duct (left) and elevated duct (right) at 00:00 and 12:00
Figure 14. Incidence rates of surface duct (left) and elevated duct (right) at 00:00 and 12:00
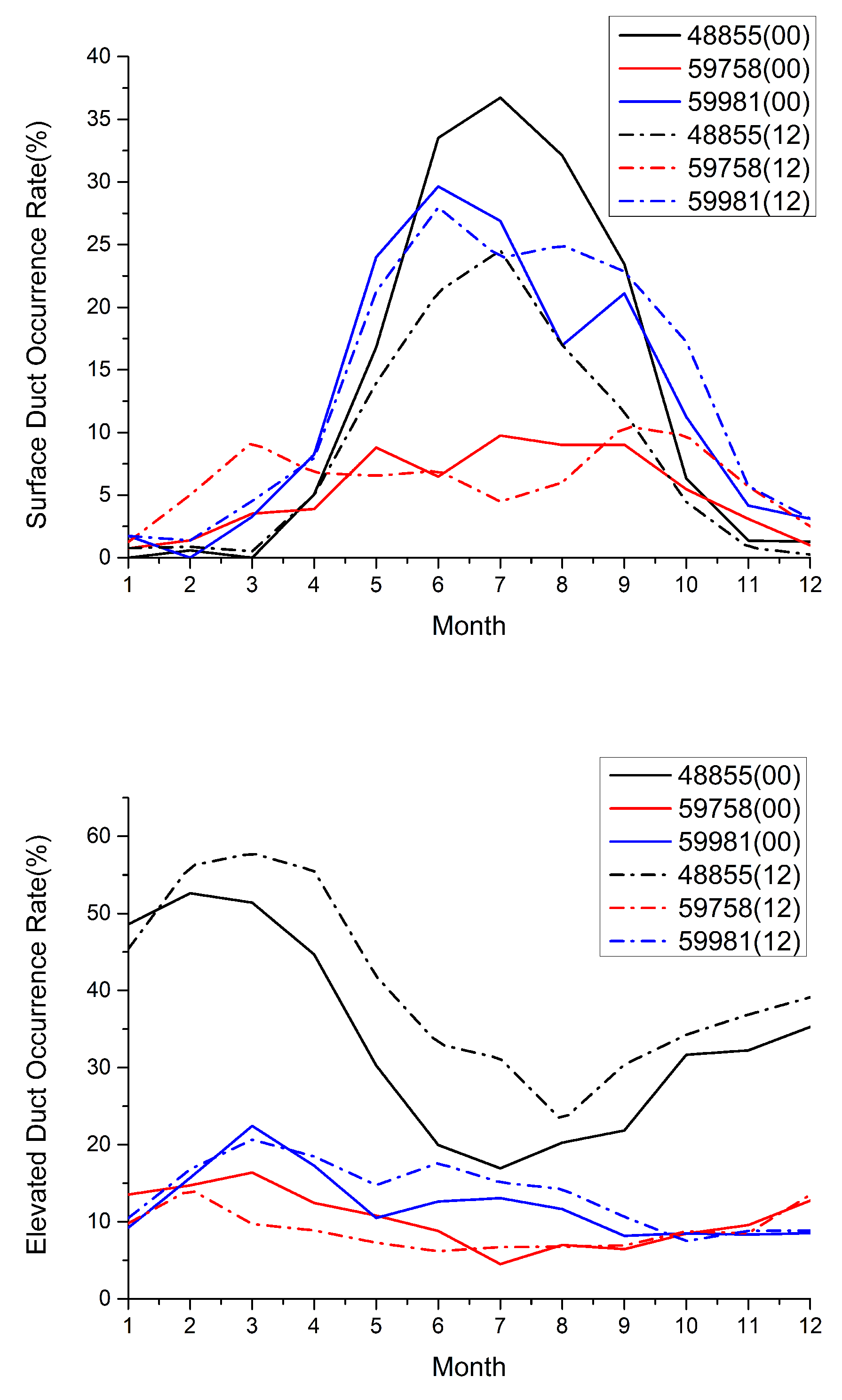
Preprints 73070 g014
Preprints 73070 g015
Figure 15. Statistical distribution of surface duct strength (left) and duct thickness (right)
Figure 15. Statistical distribution of surface duct strength (left) and duct thickness (right)
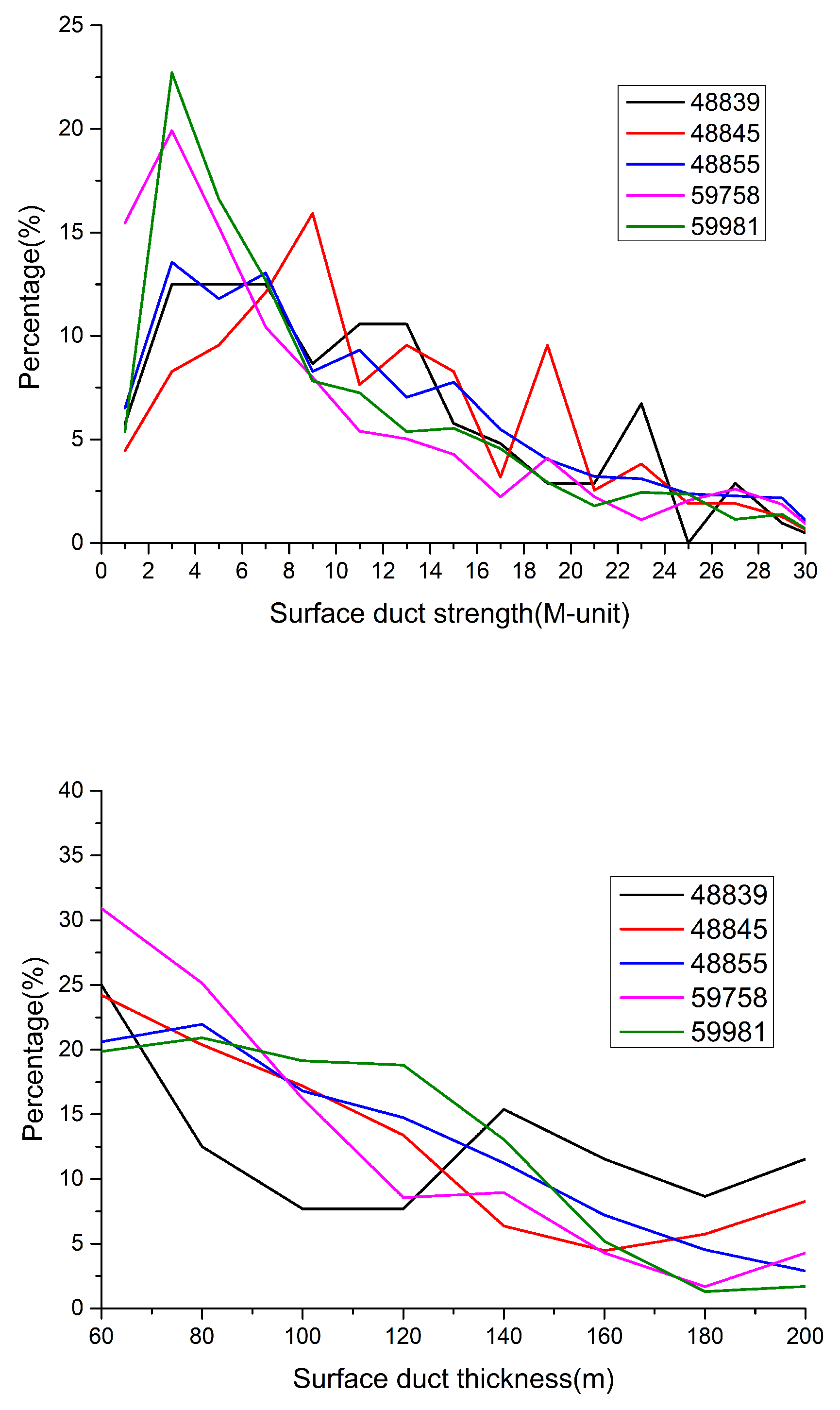
Preprints 73070 g015
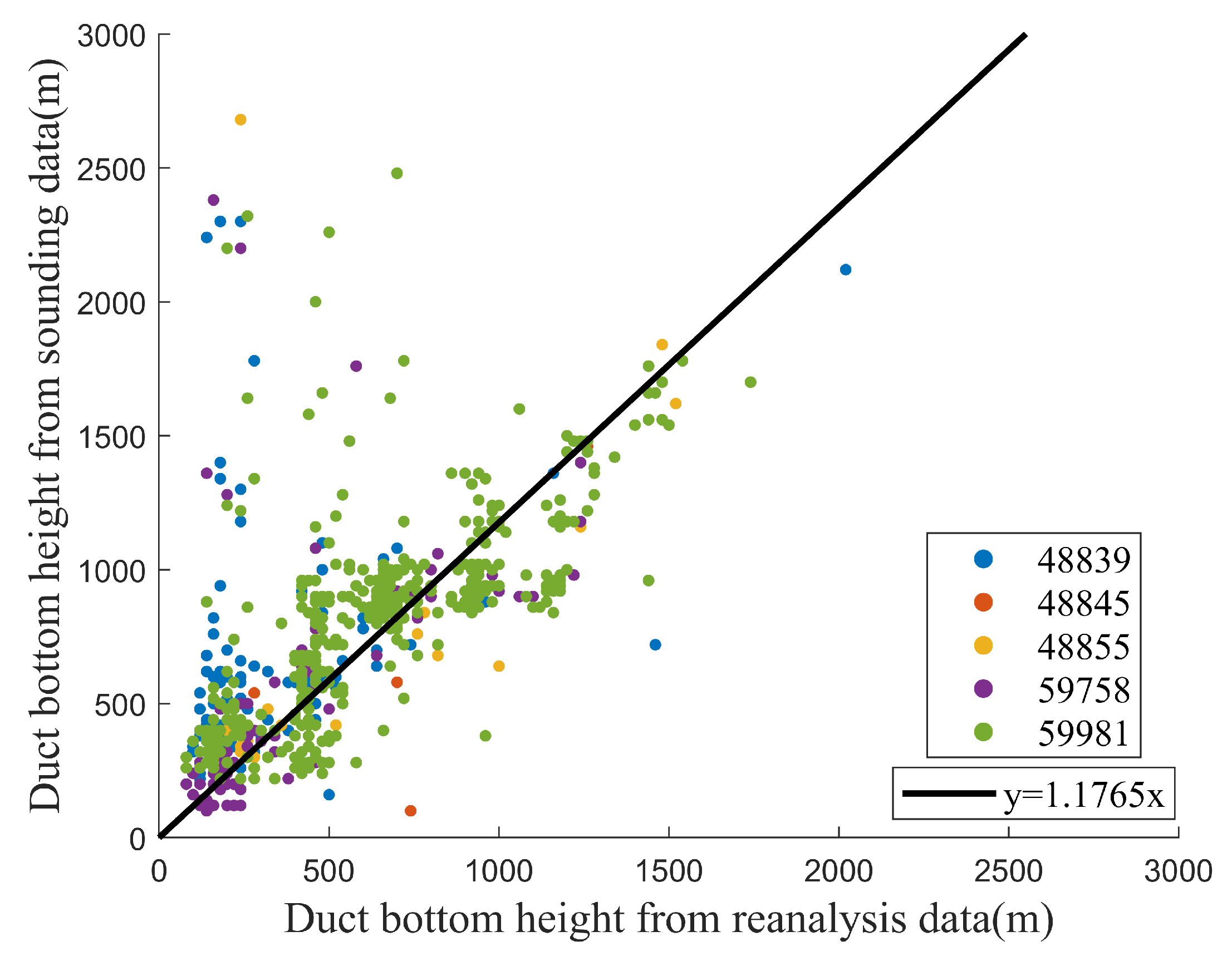
Preprints 73070 g016
Figure 16. Scatter diagram of bottom height of elevated duct retrieved from sounding data and ERA5 data.
Figure 16. Scatter diagram of bottom height of elevated duct retrieved from sounding data and ERA5 data.
Preprints 73070 g016
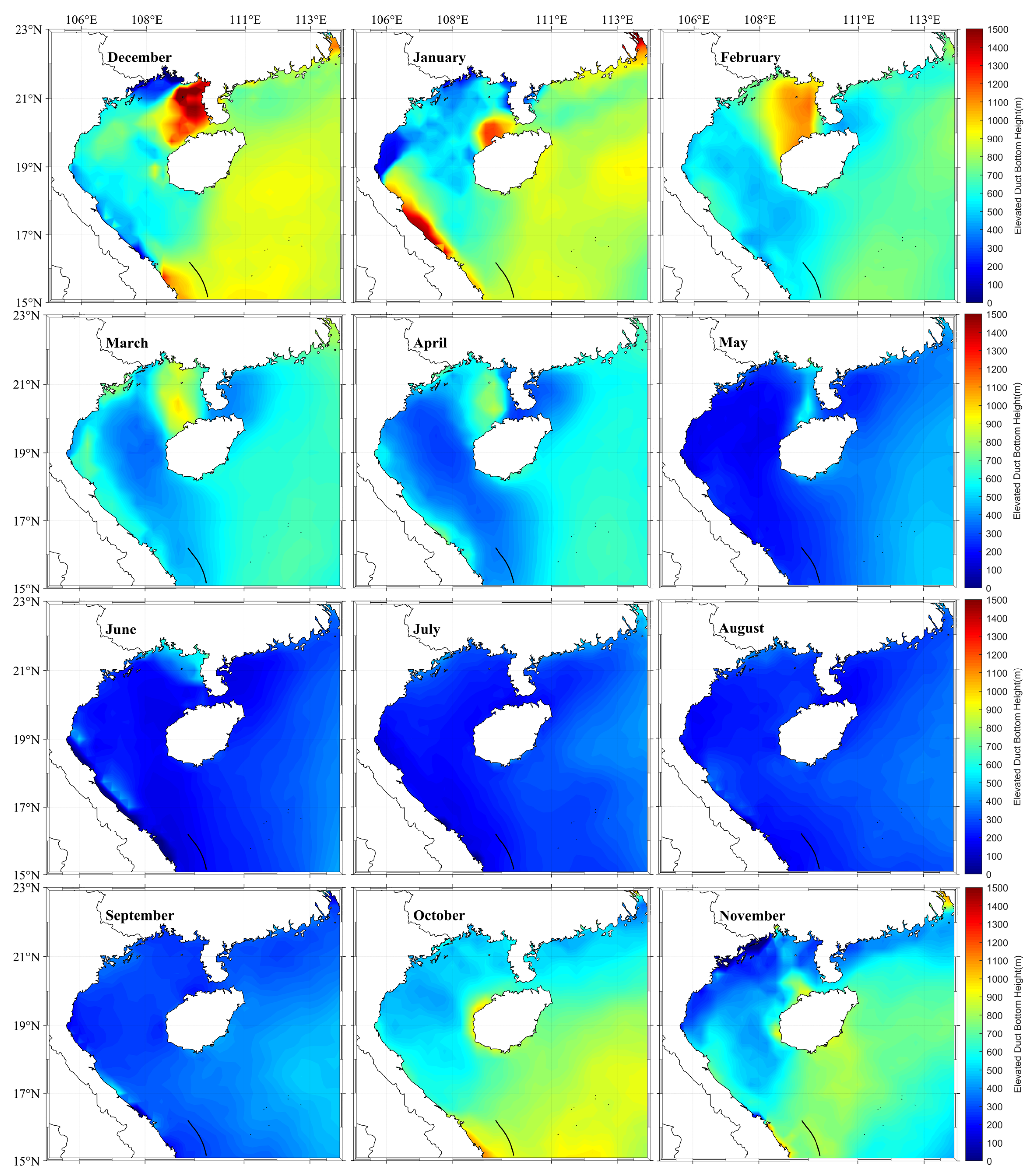
Preprints 73070 g017
Figure 17. Monthly average distribution of the bottom height of the elevated duct in the northwest of the SCS.
Figure 17. Monthly average distribution of the bottom height of the elevated duct in the northwest of the SCS.
Preprints 73070 g017
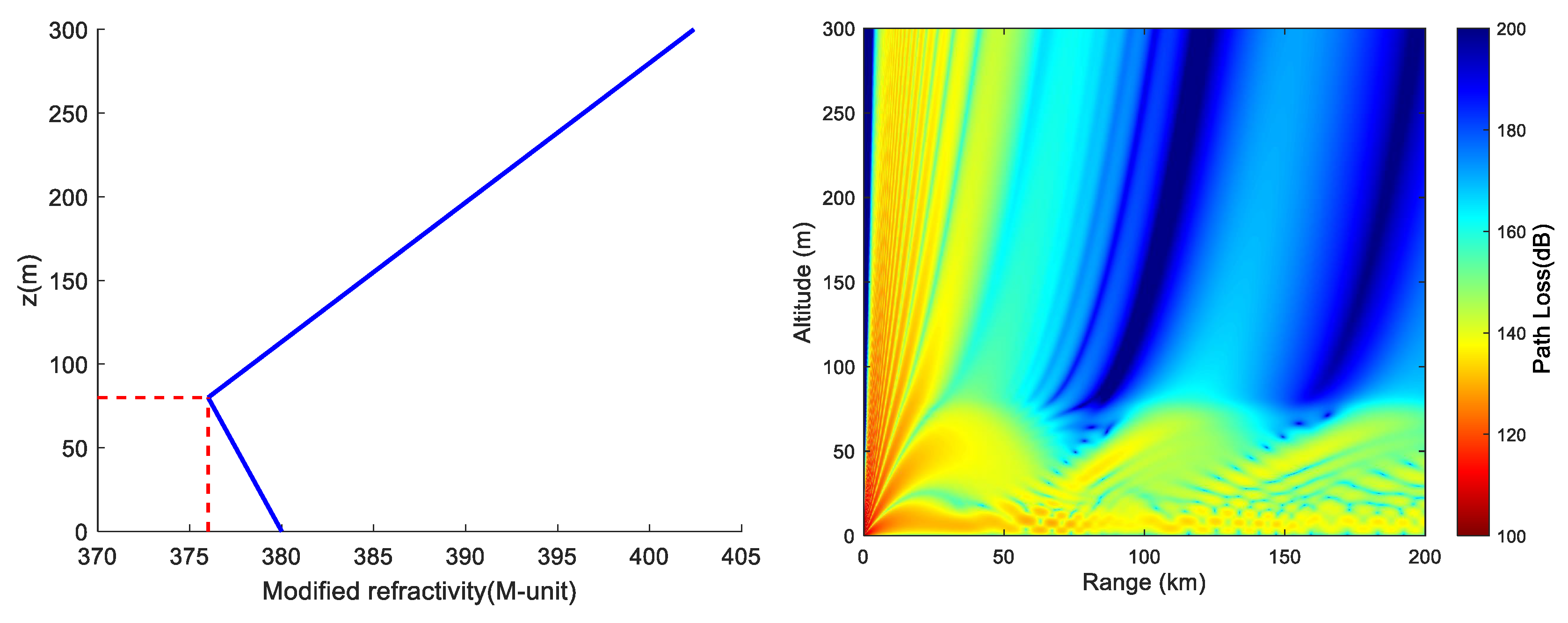
Preprints 73070 g018
Figure 18. The surface duct structure used in the simulation (left) and the electromagnetic propagation loss at a radiation source frequency of 9 GHz and an elevation angle of 0.5° (right)
Figure 18. The surface duct structure used in the simulation (left) and the electromagnetic propagation loss at a radiation source frequency of 9 GHz and an elevation angle of 0.5° (right)
Preprints 73070 g018
Preprints 73070 g019
Figure 19. Propagation loss at different frequency (0.5° elevation angle, left) and antenna elevation angle (9 GHz frequency, right)
Figure 19. Propagation loss at different frequency (0.5° elevation angle, left) and antenna elevation angle (9 GHz frequency, right)
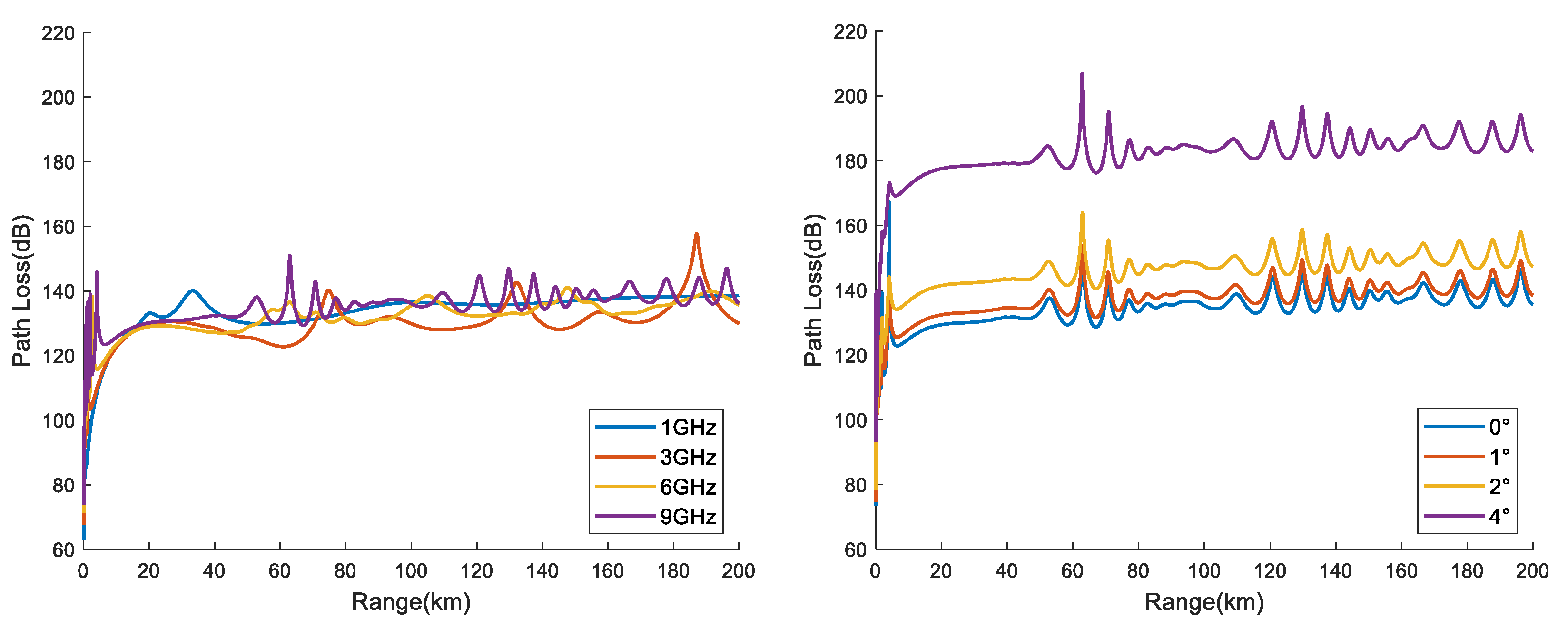
Preprints 73070 g019
Preprints 73070 g020
Figure 20. Electromagnetic propagation loss in a hybrid duct environment.(a) Hybrid duct structure;(b) Propagation loss at 9 GHz and 0.5° elevation angle; (c) Propagation loss at different heights (The frequency is 9 GHz, elevation angle is 0.5°); (d) Radiation source at different heights and horizontal distances is the vertical propagation loss at 100 km
Figure 20. Electromagnetic propagation loss in a hybrid duct environment.(a) Hybrid duct structure;(b) Propagation loss at 9 GHz and 0.5° elevation angle; (c) Propagation loss at different heights (The frequency is 9 GHz, elevation angle is 0.5°); (d) Radiation source at different heights and horizontal distances is the vertical propagation loss at 100 km
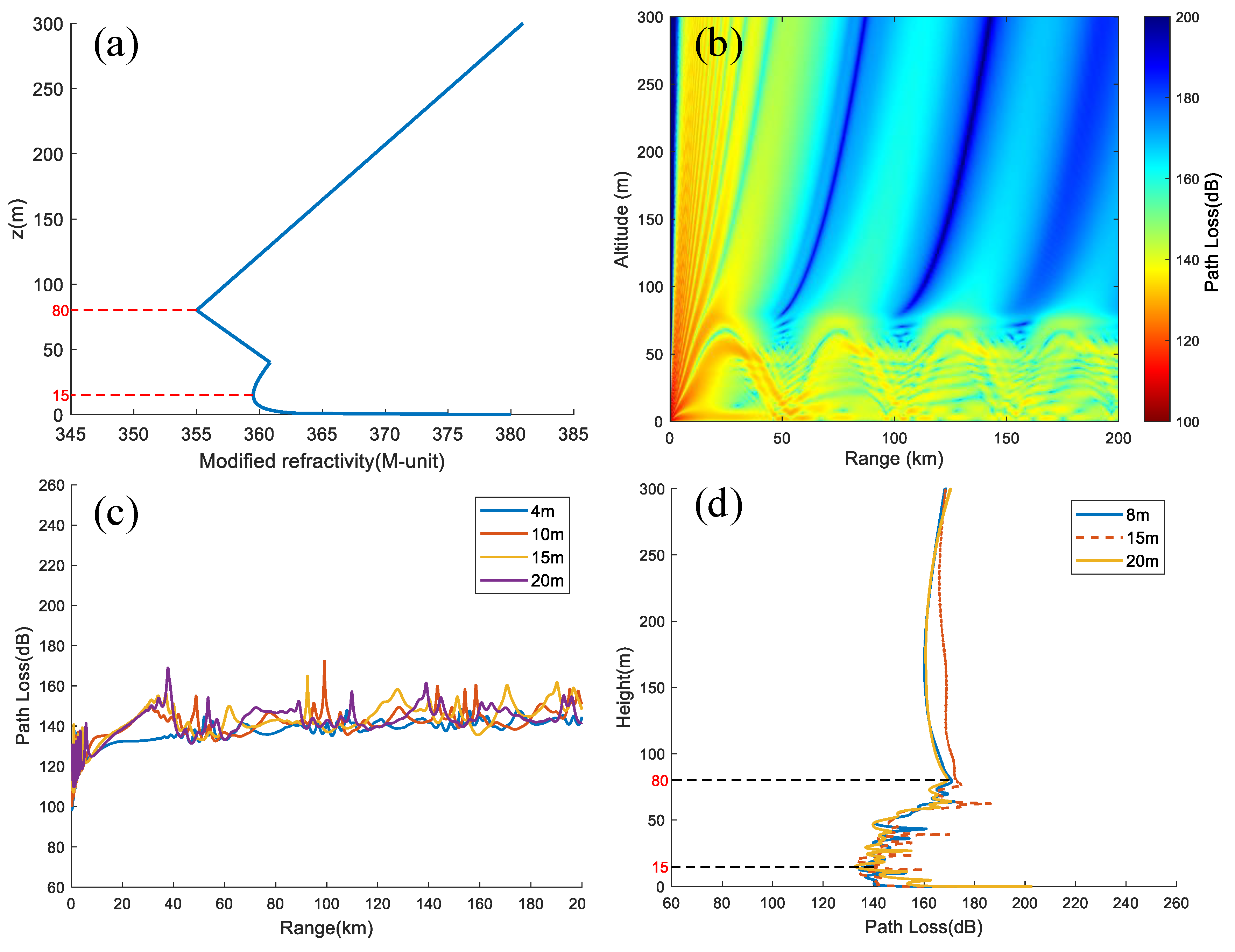
Preprints 73070 g020
Table 1. Data information of AWS and sounding stations.
Table 1. Data information of AWS and sounding stations.
Data Source Station No Longitude Latitude Meteorological Elements Data Years Span
59981 112.333°E 16.833°N sea level pressure, station pressure,
wind speed, temperature, dew point		 2012-2022
48839 107.717°E 20.133°N sea level pressure, station pressure, wind speed,
temperature, dew point, SST		 2011-2022
AWS 59985 111.617°E 16.533°N
59838 108.617°E 19.100°N sea level pressure,
48848 106.600°E 17.483°N station pressure,wind speed, 2011-2022
59644 109.100°E 21.483°N temperature, dew point
48845 105.671°E 18.737°N
59981 112.333°E 16.833°N 2010-2022
48855 108.200°E 16.030°N 2010-2022
Sounding stations 48845 105.671°E 18.737°N pressure, altitude, temperature, dew point 2014-2022
48839 107.717°E 20.133°N 2013-2022
59758 110.350°E 20.030°N 2010-2022
Table 2. ERA5 data information used in this article.
Table 2. ERA5 data information used in this article.
Item Content
Data Type Conventional longitude and latitude grid data
Time Span 2010∼2022
Horizontal Resolution 0.25°×0.25°
Vertical Pressure Layer (hPa) 400, 450, 500, 550, 600, 650, 700, 750, 775, 800, 825, 850,875,
900, 925, 950, 975, 1000
Time Resolution 1 hour
Spatial Range 105°E∼113°E, 15°N∼23°N
Meteorological Elements Temperature, Specific humidity, Geopotential, UV Wind
Table 3. NCEP CFSv2 data information used in this paper.
Table 3. NCEP CFSv2 data information used in this paper.
Item Content
Data Type Conventional longitude and latitude grid data
Time Span 2011∼2022
Horizontal Resolution 0.205°×0.205°
Spatial Range 105°E∼113°E, 15°N∼23°N
Meteorological Elements Surface press, Specific humidity of 2 meters, Temperature of 2 meters,
Surface temperature, U of 10 meters, V of 10 meters
Table 4. Atmospheric Refraction Types.
Table 4. Atmospheric Refraction Types.
Radiation Source Parameters Specific Settings
Frequency 1 GHz, 3 GHz, 6 GHz, 9 GHz
Antenna and receiving height 8 m, 8 m
Antenna elevation angle 0°, 0.5°, 1°, 2°, 3°
Polarization mode Horizontal polarization
Horizontal and vertical range 0∼200 km, 0∼300 m
Antenna and beam type Parabolic antenna Gaussian beam
Table 5. Percentage of surface duct without base layer in total surface duct.
Table 5. Percentage of surface duct without base layer in total surface duct.
Station No 48845 48839 48855 59758 59981
Percentage(Total number of surface duct) 58.0%(157) 62.5%(104) 73.6%(966) 63.7%(537) 98.7%(1228)
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated