Prerpints.org logo
Preprint
Article

Bearing Behavior of Cold-Formed Thick-Walled Steel Plates with Single Bolt

Altmetrics

Downloads

85

Views

15

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

03 May 2023

Posted:

09 May 2023

You are already at the latest version

Alerts
Abstract
This paper presents the results of an experimental and analytical study on the behavior of cold-formed thick-walled steel plates connected by a single bolt under double shear. Experimental studies were conducted on a total of 54 bolted connections fabricated from two thickness of cold-formed thick-walled steel plates with the nominal thickness of 6 mm and 10 mm. The effects of end distance, edge distance and steel plate thickness were investigated on the bolt bearing behavior. Codes of (modified) ANSI/AISC 360-16 and EN1993-1-8 were applied to predict failure modes and bearing resistance of connections and the predictions were compared with that of measurements. A method was proposed to calculate the elongation of bolt hole at ultimate load. The studies show that fractures occurred on shear planes of specimens failed by shear out due to reduced ductility caused by cold forming process. The modified ANSI/AISC gives the most accurate predictions of failure modes and bearing resistance. However, the bearing resistance will be overestimated if the reduction in area of shear planes caused by occurrence of fracture is ignored for specimens with end distance being higher than 2.0d0 and a reduction factor is needed for calculating bearing resistance of connections. The method proposed in our paper can predict the elongation of bolt hole very well.
Keywords: 
Subject: Engineering  -   Civil Engineering

1. Introduction

Cold-formed steel sections are widely used in civil engineering. In early stage, only thin-walled steel could be manufactured. With the improved technology of cold forming, more and more cold-formed steel members were applied in practice with thickness beyond traditional limitations specified in codes of thin-walled steel members [1,2,3]. In the new version of AISI standard (2016 edition) [4] and Chinese GB standard (GB 50018-draft standard for discussion) [5], the thickness of cold-formed steel members was increased to 25.4mm. However, design criteria based on the study results of hot rolled steel was adopted in these codes when the thickness of steel plate in bolted connections is beyond a certain limitation. For example, the standard of AISI S100 [4] specifies that for bolted connections in which the thickness of the thinnest connected part is greater than 4.76 mm, ANSI/AISC 360 [6] shall apply. Similarly, EN 1993-1-3 [2] specifies that for thickness larger than or equal to 3 mm the rules for bolts in EN 1993-1-8 [7] should be used.
Thick-walled steel is usually used in tubular members. The ductility of steel is expected to decrease with the increase of strength during the process of cold work. According to the research of Guo [8] and Hu [9], the ratios of tensile strength and elongation at fracture between flat element and virgin material are in the range of 1.03-1.20 and 0.81-0.90 respectively and these ratios are in the range of 1.44-1.64 and 0.32-0.44 for corner elements. In the design of bearing-type bolted connections, strain hardening properties of the plate material are utilized and the design is based on ultimate tensile strength of the steel. Besides, bearing resistance is developed accompanied with significant plastic deformation around the bolt hole due to high stress concentration [10]. For hot rolled steel which has a favorable ductility, a fully developed bearing resistance can be ensured and the ductility requirement of steel is implicitly included in the design criteria. Therefore, it is necessary to check whether the current calculation formulae which are derived on the basis of behavior of hot rolled steel are still applicable for bolted connections of thick-walled steel.
For connection design using component-based method, bolt in shear is a basic component and is treated as a spring with specified load-deflection behavior. However, many studies [11,12,13,14,15,16] have been focused on the bearing resistance of bolted connections and there are only a few research [17,18] concentrated on the deflection of bolted connection.
This paper reports the results of an experimental and analytical study on the behavior of cold-formed and thick-walled plates connected by a single bolt under double shear. Effects of end/edge distance were investigated on the bolt bearing behavior. Bearing resistance predicted by the (modified) ANSI/AISC 360 [6] and the EN1993-1-8 [7] were compared with that of measurements. A method was proposed to calculate the elongation of bolt hole at ultimate load.

2. Experimental investigation

2.1. Subsection Specimen preparation

Single bolt connections in double shear were investigated in the tests. In total, 54 tests were conducted and Table 1 lists the main parameters of test specimens. The tests were designed to investigate the effects of different end/edge distance combinations on failure modes of connections. These tests used 24 mm bolts with 26 mm bolt holes. Grades 8.8 and 10.9 bolts were applied to connect the test specimens with 6 mm and 10 mm thick steel plates respectively.
Steel plates used in the connections were taken from the middle of flat parts of hollow tubes which were cold formed by structural steel sheets with a nominal yield strength of 235 MPa. The nominal dimensions of hollow tubes were 200×200×10 mm and 150×150×6 mm and the inside radii of rounded corners were 8 mm and 6 mm respectively. The plates were all cut from the longitudinal direction.

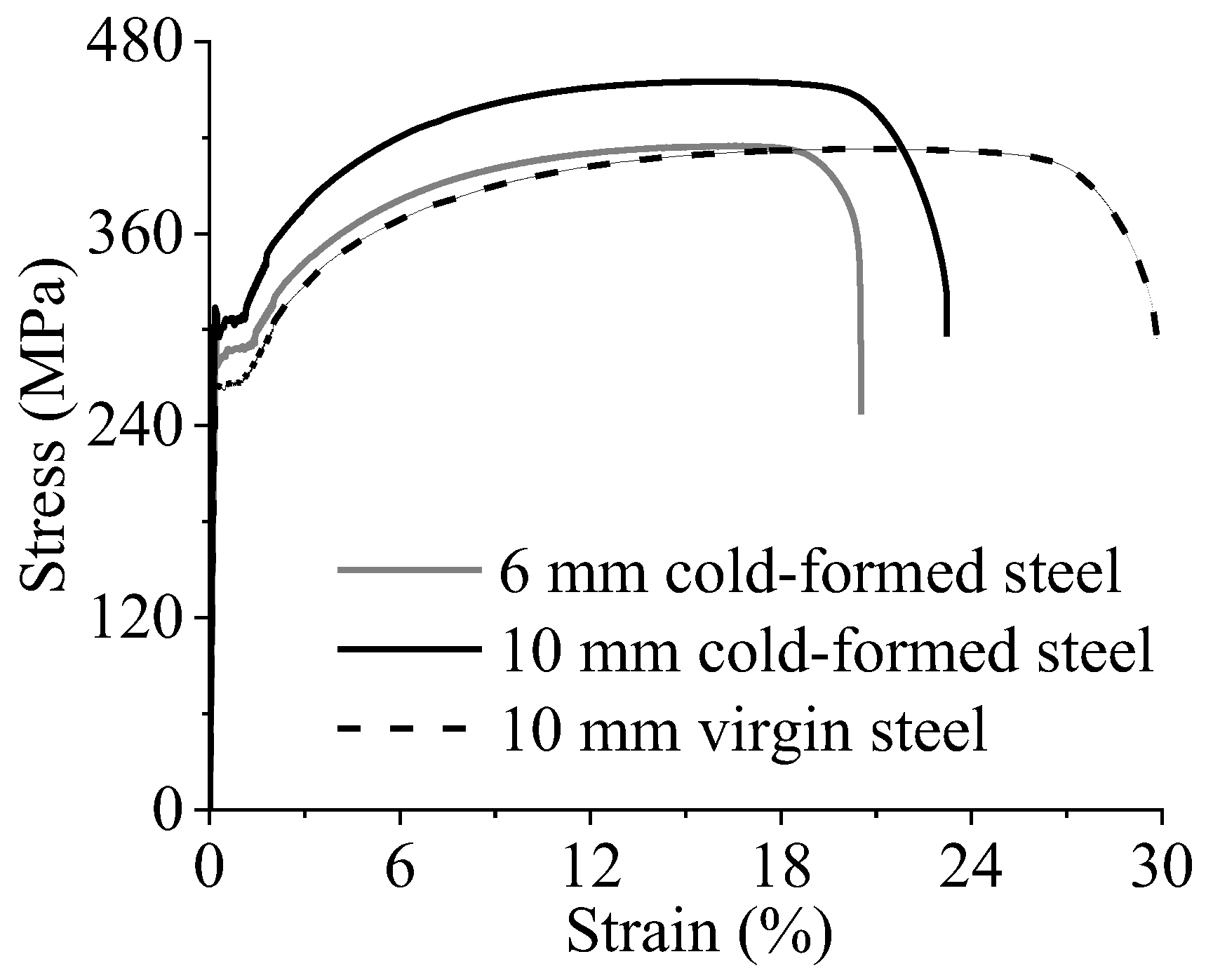
2.2. Mechanical properties of cold-formed thick-walled steel

Steel plates used in tensile coupon test were taken from the same batch and same location as that of lap shear test. For each thickness of cold-formed thick-walled steel plates, three tensile coupon tests were conducted in accordance with GB/T 228.1-2010 [19]. Mechanical properties were also tested for 10 mm virgin steel plates. Stress-strain relationships of all steel plates were presented in Figure 1 and the measured material properties were summarized in Table 2, in which E is the elasticity modulus, fy is the yield strength, fu is the tensile strength, εu is the strain corresponding to the tensile strength and ∆ is the elongation ratio at fracture.
Being different from cold-formed thin-walled steels which are generally characterized by a rounded stress-strain response with no yield plateau, curves of stress-strain relationship of cold-formed thick-walled steel are similar to that of hot-rolled steels which can be characterized by four ranges, being linearly elastic, yielding, hardening and necking. However, cold-formed thick-walled steels have higher strength and smaller ductility than that of hot-rolled steels. For example, the tensile strength of 10 mm cold-formed steel increased by 9.6% and the elongation ratio at fracture decreased by 19% compared to the corresponding value of 10 mm virgin steel.

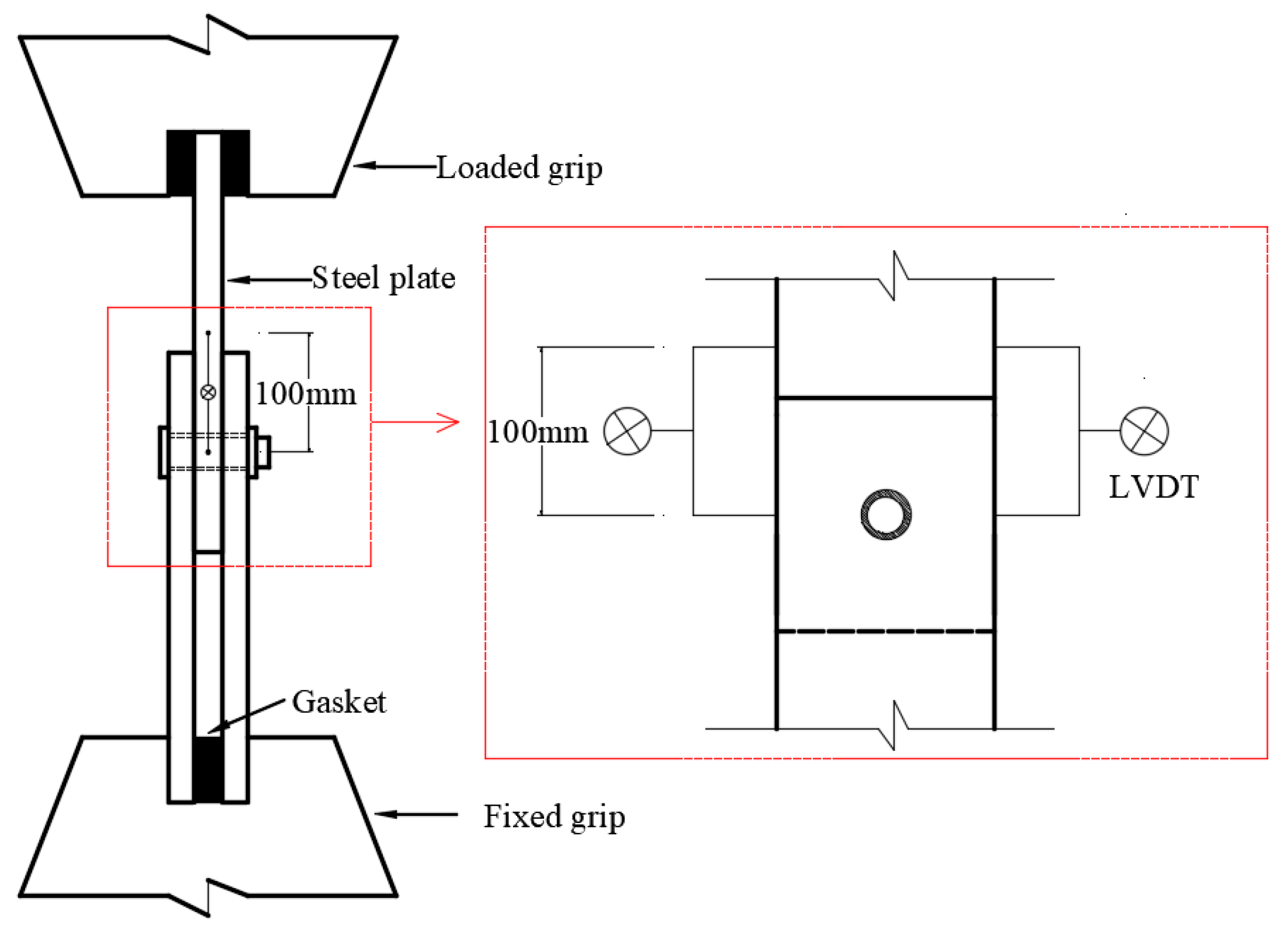
2.3. Test method

Lap shear tests were conducted on a servo-controlled hydraulic machine with the loading capacity of 1000kN. The bolts were tightened in a way that firm contact of steel plates can be achieved but no pretension was generated in the bolts so that load was transferred primarily by bearing instead of friction. The specimens were loaded at a prescribed displacement rate of 1.5mm/min until failure of specimens. The applied load was recorded by the sensor of hydraulic loading machine. Bolt hole elongation was measured by two linearly variable displacement transducers (LVDT), as shown in Figure 2.

3. Experimental observations and test results

3.1. Failure modes

Similar failure modes were observed for specimens with 6 mm and 10 mm thick steel plates. Therefore, only 10 mm thick specimens were presented to show the effect of different end/edge distance combinations on failure modes. Figure 3 shows failure modes of specimens under different end distance and the edge distance is fixed at 3.0d0. Figure 4 presents Failure modes of specimens under different edge distance and a constant end distance of 1.5d0.
Specimens in Figure 3 were all failed due to excessive bearing stress in front of bolt hole and the failure of these specimens was accompanied with fracture at the edge of the elongated bolt hole at two symmetrical locations oriented at approximately 45℃ and 135℃ to the axis of loading. The elongation of bolt hole and fracture length were increased with the increasing of end distance. The elongation of bolt hole was composed of two components of deformation, being protrusion of the bolt from the plate material and embedding of the bolt into the plate material. The largest bolt protrusion was observed in specimen D10-1.0-3.0. With the increased end distance, the proportion of bolt protrusion is reduced and the proportion of bolt embedding grow. Both large shear fracture and significant bearing deformation were observed in specimen D10-2.5-3.0.
For specimens in Figure 4, failure modes and deformation of bolt hole were governed by the value of edge distance. With the increasing of edge distance from 1.0d0 to 2.0d0, failure modes of specimens were from net section fracture to shear out and the deformed zone was from longitudinal side of the bolt hole to the front side.
Two typical failure modes were observed in our tests, being shear out and net section fracture. Shear out occurs when the end distance is relatively small. The material in front of the bolt yields and is pushed out from the plate, creating two shear planes. The connection fails when material in the shear planes reaches its ultimate strength. The shear out failure can be very ductile for hot rolled specimens and no fracture occurred [14]. Lower ductility is expected for cold formed specimens due to the less development of local plastic deformation of cold formed steel plates. Meanwhile, fracture was observed along the shear planes of cold formed connecting plates.
Net section fracture occurs when the edge distance is relatively small, as shown in Figure 4(a) and 4(b). The fracture appeared after necking of the net section, during which bolt hole elongation developed. The bolt hole elongation of specimens failed by net section fracture depends not only on the ductility of steel plates, but also on the geometrical arrangement of specimens. For example, the edge distance of specimen D10-1.5-1.0 is small because the plastic strain is limited to the middle of net cross section at which the net area is the smallest. Structural response of such failure has a relatively low ductility. The bolt hole elongation of specimen D10-1.5-1.2 is larger than that of specimen D10-1.5-1.0 because the plastic deformation of net cross section is not merely confined to the middle point. With the further increasing of edge distance, net section strength of steel plate was approaching to shear out strength and a mixed deformation was observed along both longitudinal side and front side of bolt hole, as shown in Figure 4(c).

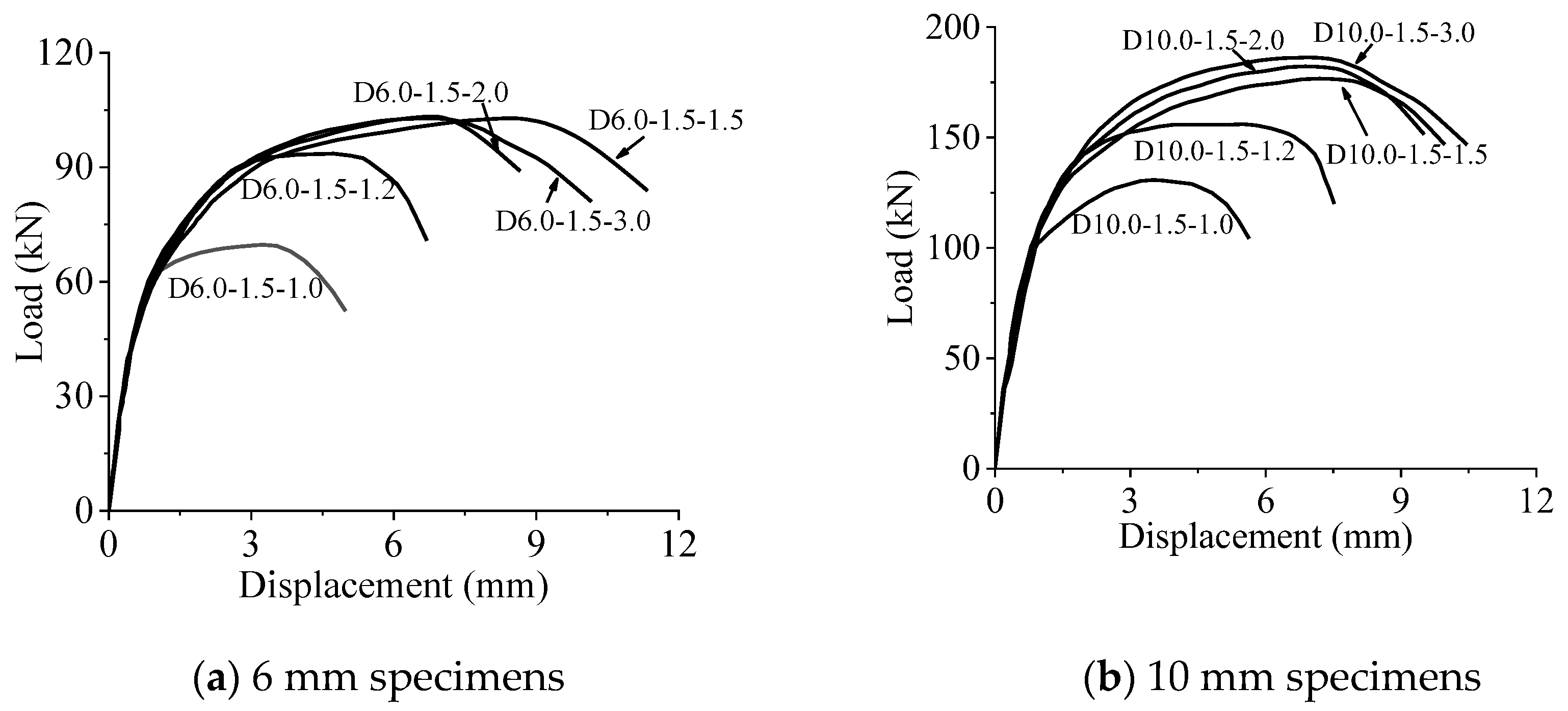
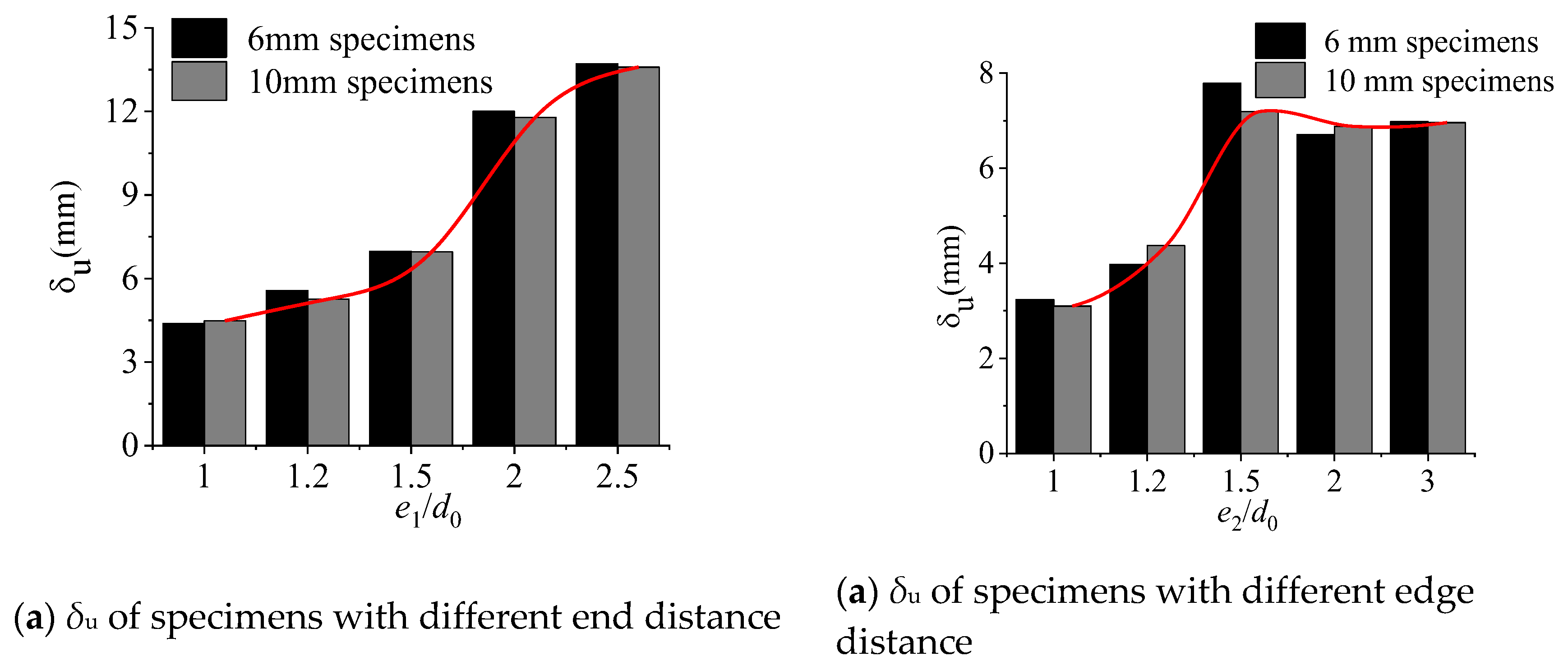
3.2. Bearing resistance and deformation

Figure 5 and Figure 6 show the load-displacement curves of specimens with varying end distance and edge distance respectively. Curves of load-displacement relationship in Figure 5 and Figure 6 omit any possible slip phase and assume that the bolt bears directly against the back of the hole from the start of loading.
Load-displacement curves in Figure 5 and Figure 6 have an initial elastic region followed by a nonlinear hardening region. For curves in Figure 5, peak point of each curve was reached when the stress on shear planes attained the ultimate strength of steel material. The bearing resistance of each specimen is termed as Fu and δu is the deformation corresponding to Fu. Both Fu and δu were increased with the increasing of end distance. For curves in Figure 6, both Fu and δu were increased with the increasing of edge distance when the edge distance is not more than 1.5d0. Beyond 1.5d0, the increasing of edge distance had little effect on bearing resistance of specimens. The measured Fu and δu were summarized in Table 3 and Table 4.
Figure 7 and Figure 8 present relationships of ultimate load versus end distance and ultimate load versus edge distance respectively. Figure 7 shows that, with adequate edge distance, the bearing resistance is linearly proportional to the end distance when the end distance is in the range of 1.0d0-2.0d0. The scale factor between bearing resistance and end distance goes down when the end distance is increased to 2.5d0. This may be caused by the decreased area of shear planes after fracture. Figure 8 shows that the bearing resistance of specimens goes up when the edge distance is increased from 1.0d0 to 1.5d0. Beyond 1.5d0, the bearing resistance of specimens stays constant. Given the same end distance of 1.5d0, failure modes of net section fracture and shear out were observed for specimens with edge distance of 1.2d0 and edge distance of 1.5d0 respectively, and the bearing resistance was increased by 15% when the edge distance was varied from 1.2d0 to 1.5d0.
Figure 9 presents the effect of end and edge distance on displacement of specimens. Given a constant edge distance of 3.0d0, the displacement of specimens shows an exponential relationship with end distance, as can be seen in Figure 9(a). Under the fixed end distance of 1.5d0, the largest displacement appeared for specimen with edge distance of 1.5d0. In this case, edge distance was adequate to avoid net section fracture but not wide enough to prevent plastic deformation of the net cross section, and at the same time, deformation in front of bolt hole also contributed to the displacement of specimens.

4. Discussion

According to the scope of application specified in design codes of AISI S100-16 [4] and EN 1993-1-3 [2], ANSI/AISC 360-16 [6] and EN 1993-1-8 [7] were applied to predict bearing resistance of specimens in our tests. Measured material properties were used in the calculation and all partial factors were set as 1.0. Before predicting bearing resistance of specimens, failure modes need to be identified.

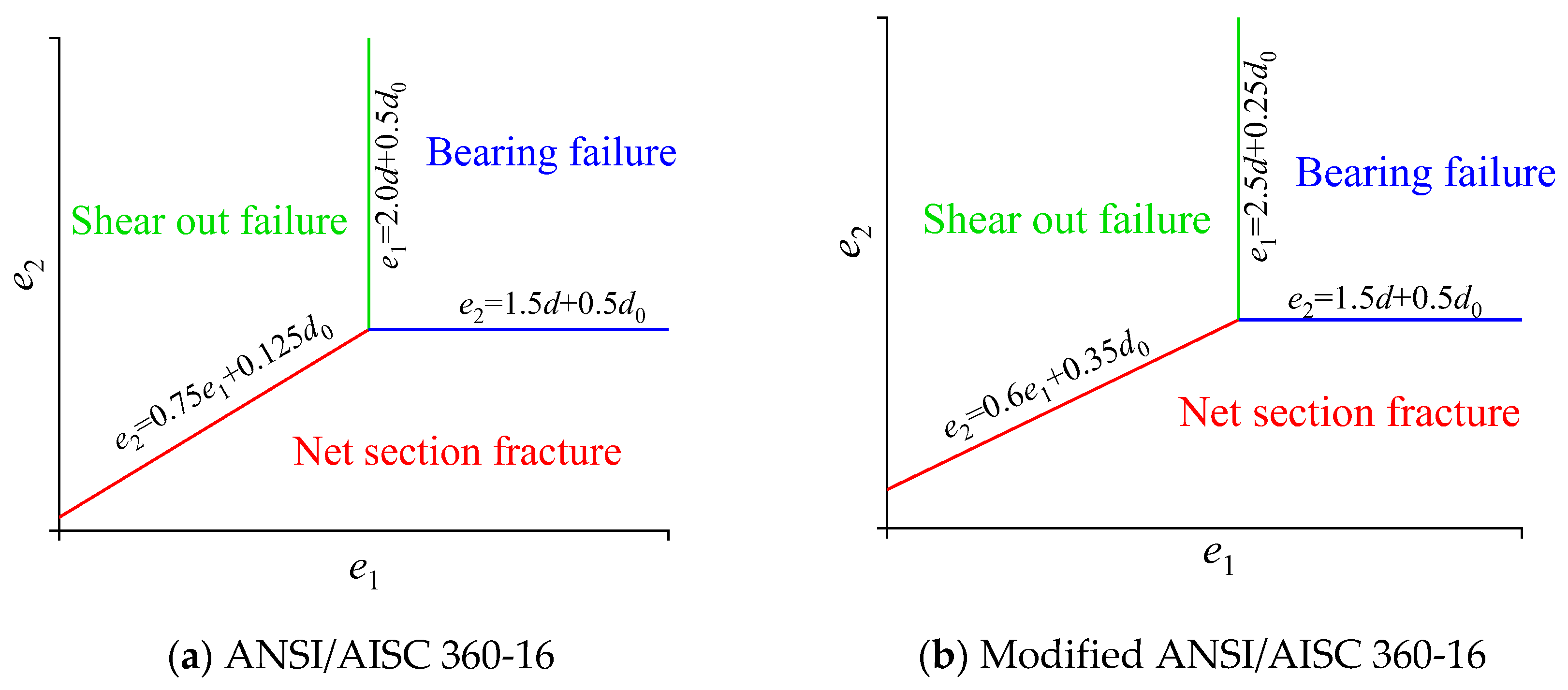
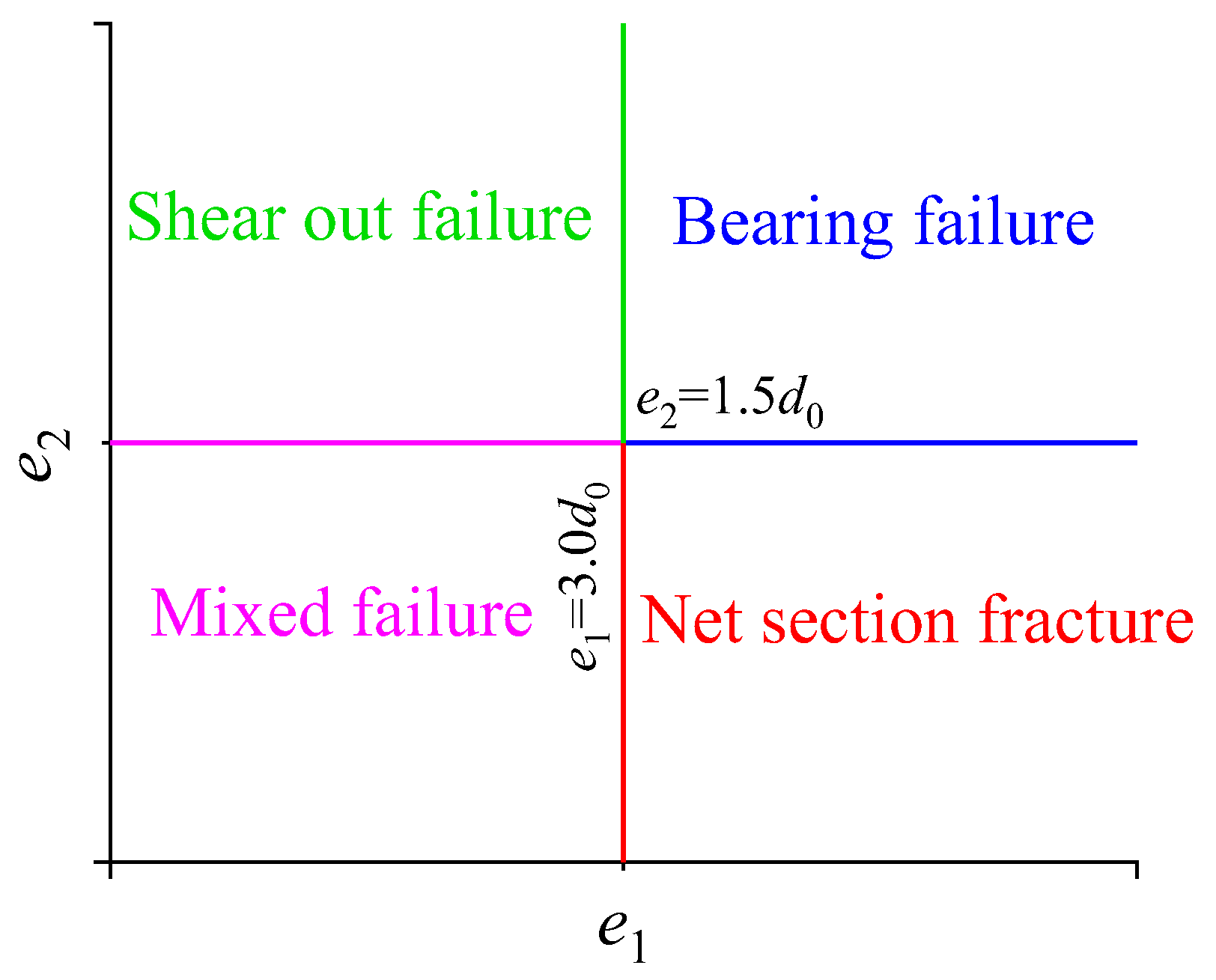
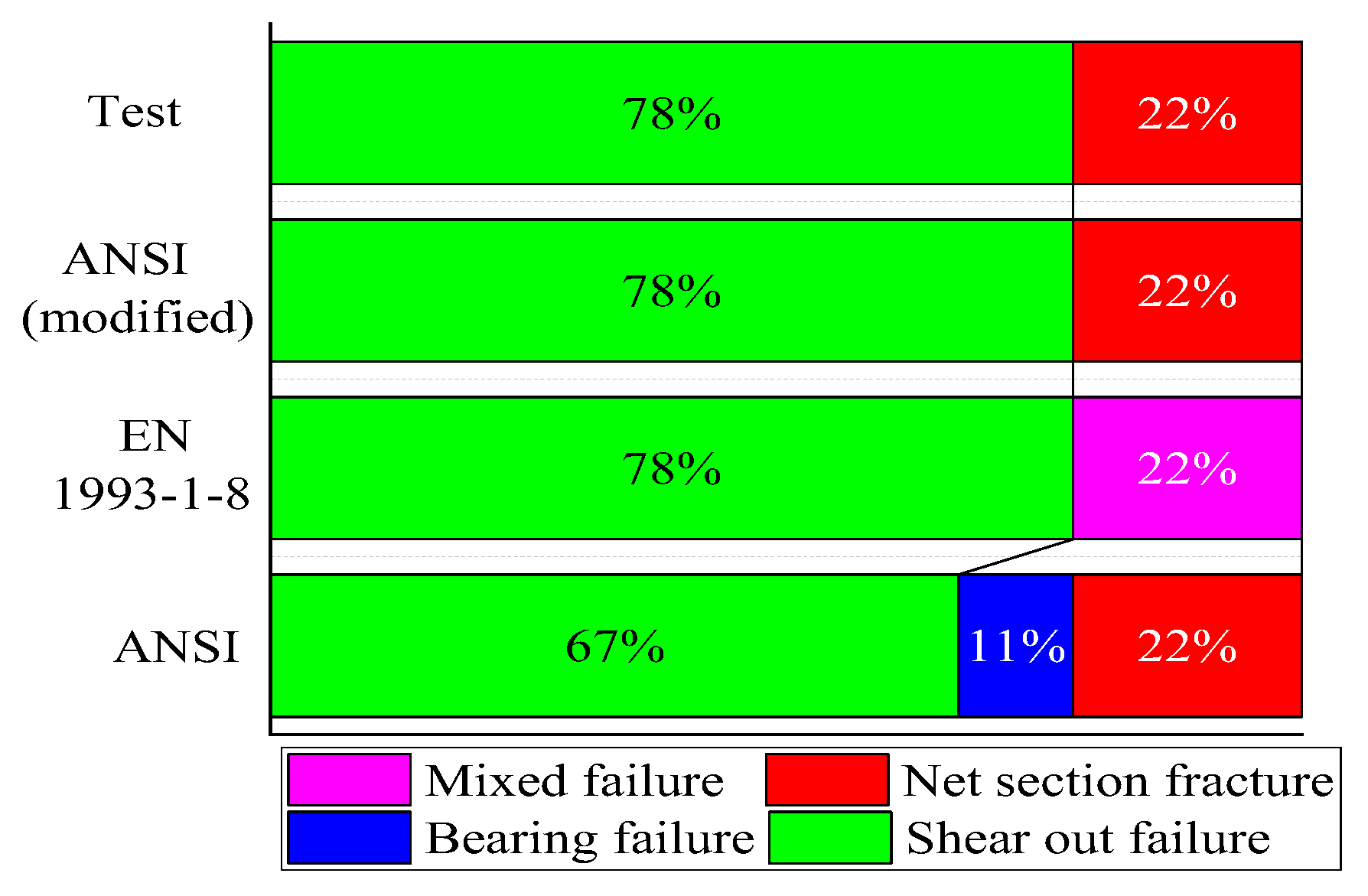
4.1. Comparison of failure modes

In the standard of ANSI/AISC 360-16 [6], ultimate capacities can be calculated by equations (1), (2) and (3) for specimens with failure modes of net section rupture, bearing and shear out.
R n = f u A e = ( 2 e 2 − d 0 ) f u t ,
R b = 3.0 d t f u
R s = 1.5 l c t f u = 1.5 ( e 1 − 0.5 d 0 ) t f u
where fu is tensile strength of connected plates, Ae is net area subject to tension, t is base steel thickness of section, d is bolt diameter, lc is clear distance in the direction of the force.
Bearing failure happens when Rb< Rs and Rb< Rn. From equations (1)-(3), it can be obtained that bearing failure occurs when e1>2d+0.5d0 and e2>1.5d+0.5d0. Similarly, shear out failure occurs when e1<2d+0.5d0 and e2>0.75e1+0.125d0 and net section fracture occurs when e2<min [1.5d+0.5d0, 0.75e1+0.125d0]. Figure 10(a) presents conditions of end/edge distance combinations for different failure modes specified in design code of ANSI/AISC 360-16 [6].
When equation (3) is used to calculate the ultimate capacity of shear out failure, assumptions are made that steel plates fail along centerlines of the bolt holes in the loading direction and the limiting stress along the shear failure planes is 0.75fu. However, it is impossible that the shear failure plane coincides with the centerline of bolt holes in the loading direction because shear stress on this plane is zero when the bearing stress in front of bolt is symmetrically distributed. This has been confirmed by the results of finite element analysis of [20] and experimental observations of [21] and our tests. Therefore, Teh [22] proposed a definition of effective shear planes which were the midways between net and gross shear planes and they were assumed to be the shear failure planes. Also, the maximum stress was assumed to be 0.60fu on effective shear planes. Based on studies of Teh [22], the ultimate capacity of shear out failure can be calculated by the following equation:
R s , m = 1.2 l e t f u = 1.2 ( e 1 − 0.25 d 0 ) t f u
where le is the effective shear length, being mean value of the net shear length (e1-0.5d0) and gross shear length (e1).
According to equations (1), (2) and (4), conditions of end/edge distance combinations can be obtained for specimens failed by bearing, shear out and net section fracture, as shown in Figure 10(b).
In the standard of EN1993-1-8 [7], bearing resistance for individual fastener is defined as follows:
R = α b k 1 f u d t
where αb and k1 are parameters relating to end and edge distances respectively.
α b = min { e 1 3 d 0 , f u b f u , 1.0 }
k 1 = min { 2.8 e 2 d 0 − 1.7 , 2.5 }
According to different magnitude of end and edge distance, equation (5) can be split into the following four equations:
when e1≥3d0 and e2≥1.5d0,
R = R b = 2.5 f u d t
when e1≥3d0 and e2<1.5d0,
R = R n = ( 2.8 e 2 / d 0 − 1.7 ) f u d t
when e1<3d0 and e2≥1.5d0,
R = R s = 2.5 ( e 1 / 3 d 0 ) f u d t
when e1<3d0 and e2<1.5d0,
R = R m = ( 2.8 e 2 / d 0 − 1.7 ) ( e 1 / 3 d 0 ) f u d t
Equations (5-1) - (5-4) correspond to calculation formula of ultimate capacities for specimens failed by bearing, net section fracture, shear out and mixed failure respectively. Figure 11 shows conditions of end/edge distance combinations for different failure modes.
Failure modes can be predicted based on the analysis above and the predicted failure modes were compared with that observed in our test. Table 5 lists the comparison results. On the basis of results in Table 5, percentage of specimens with different failure modes were presented in Figure 12.
Failure modes predicted by the modified ANSI/AISC 360-16 are identical to that of test results. Given adequate edge distance, bearing failure occurs when end distance satisfies conditions of e1>3.0d0 and e1>2.0d+0.5d0 according to the EN1993-1-8 [7] and the ANSI/AISC 360-16 [6] respectively. Therefore, specimens with end distance of 2.5d0 are predicted to be failed by shear out and bearing respectively. Mixed failure mode was predicted to occur for specimens with edge distance of 1.0d0 and 1.2d0 in accordance with the EN1993-1-8 [7]. However, net section fracture was observed for these specimens, as predicted by the ANSI/AISC 360-16 [6] and the modified ANSI/AISC 360-16. Correct decision of failure modes is the basis of accurate prediction of bearing resistance. From the comparison above it can be seen that the failure modes of connections predicted by the modified ANSI/AISC 360-16 agrees best with that of our test.

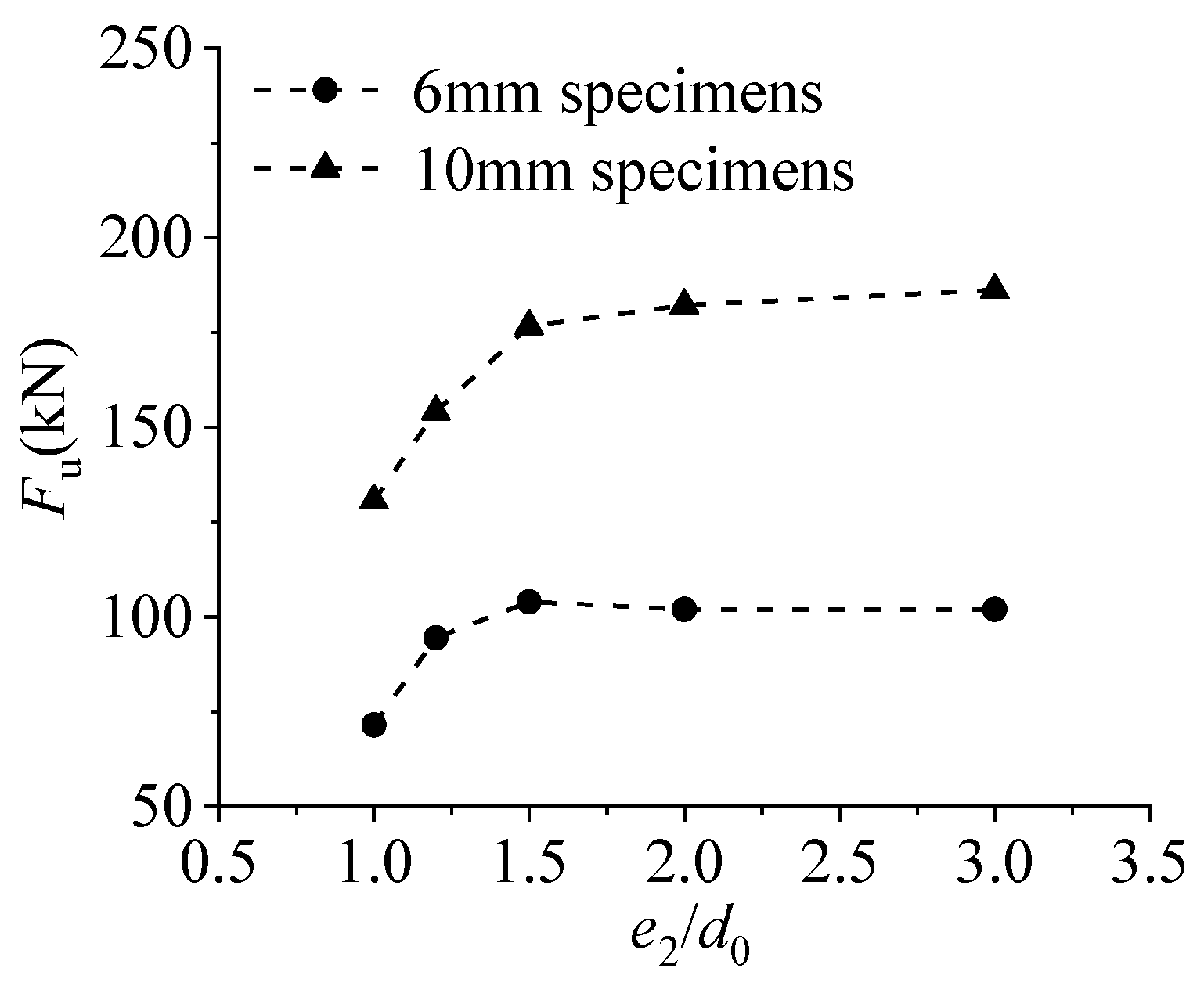
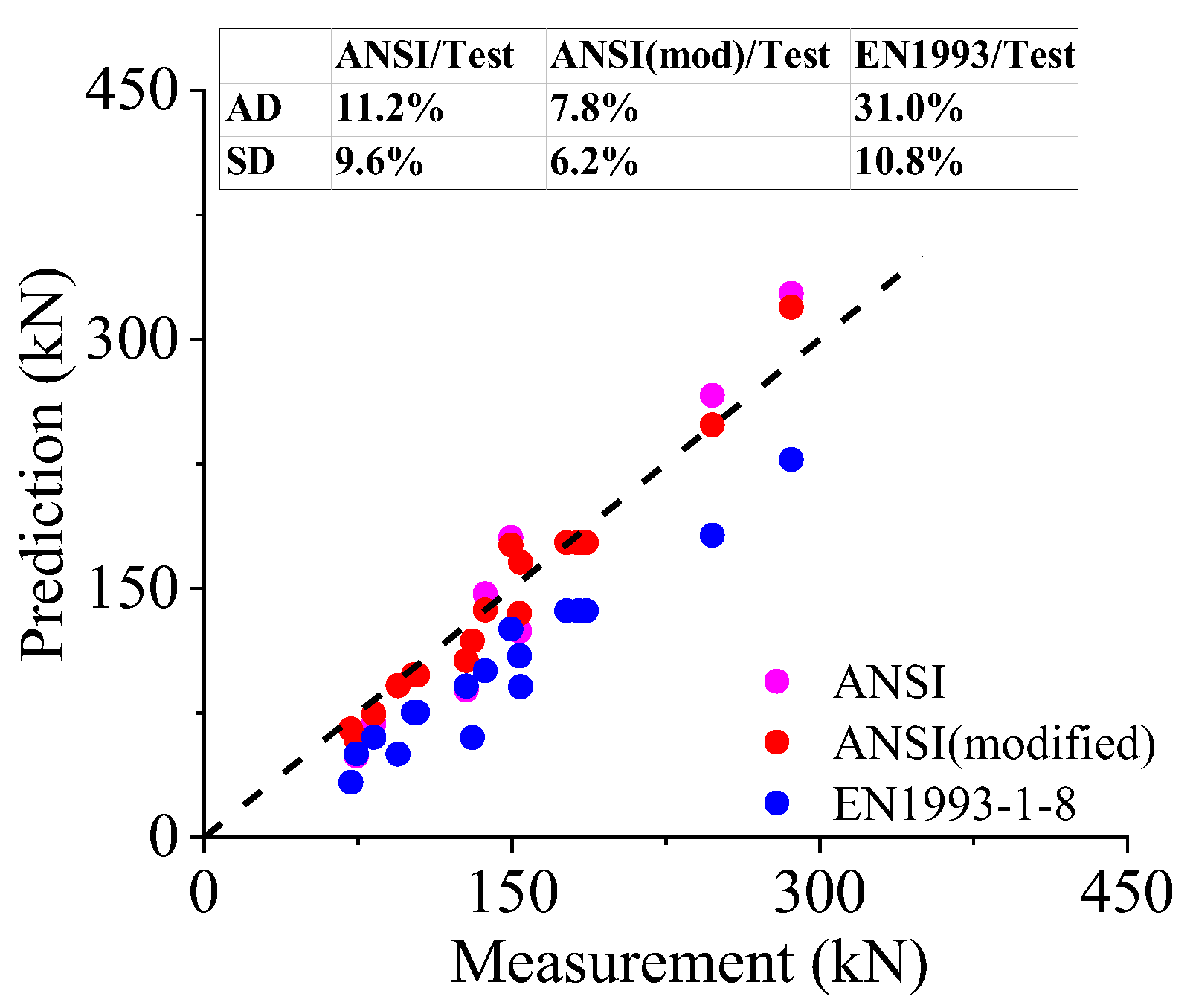
4.2. Comparison of bearing resistance

Table 6 lists measured and predicted bearing resistance of all specimens. Comparisons of bearing resistance between measurements and predictions were presented in Figure 13.
It can be seen that the bearing resistance predicted by the modified ANSI/AISC 360-16 agrees best with that of test results, with average difference and standard deviation of 7.8% and 6.2% respectively. Predictions of the EN1993-1-8 [7] is excessively conservative compared to the measurements and the average difference and standard deviation are 31.0% and 10.8% respectively.
For specimens failed by shear out, the measured bearing resistance are generally lower than the predictions when the end distance of specimens is less than 2.5d0. The ANSI/AISC 360-16 [6] and the modified ANSI/AISC 360-16 overestimate the bearing resistance by 17.6% and 14.7% respectively when the end distance of specimens is equal to 2.5d0. This can be explained by the reduced area of shear planes due to fracture occurred, as have been mentioned in section 3.2. In this case, a reduction factor of 0.85 is recommended based on our test results.
From the comparison above, attention should be drawn that the calculation formula proposed on the basis of test results of hot-rolled steel specimens with shear out failure may overestimate the bearing resistance of cold-formed steel connections because of the reduced area of shear planes caused by fracture. The existing test data are very limited and further investigation is needed to confirm the proposed reduction coefficient.

5. Conclusions

This paper has presented the results of a comprehensive experimental and analytical study to investigate the bearing behavior of cold-formed thick-walled steel plates connected with a sing bolt. The effects of end distance, edge distance and plate thickness were investigated on failure modes and bearing resistance. The measured bearing resistance was compared with that of calculated by (modified) ANSI/AISC 360-16 and EN1993-1-8. A method was proposed for calculating the elongation of bolt hole at ultimate load. The main conclusions are as follows:
(1) Bearing behavior of specimens with 6 mm steel plates is similar to that with 10 mm steel plates. Shear out and net section fracture were the main failure modes in our test. Being different from observations of hot rolled steel specimens, fracture occurred on shear planes of thick-walled steel specimens because of the reduced ductility caused by cold forming process.
(2) The bearing resistance of the specimens with shear out failure is linearly proportional to end distance when the end distance is no more than 2.0d0. The scale factor between bearing resistance and end distance goes down when the end distance is beyond 2.0d0 because of the reduced area of shear planes cause by fracture. In this case, bearing resistance of connections will be overestimated if the fracture caused reducing in shear area is ignored and a reduction factor of 0.85 is recommended based on our test results.
(3) The measured failure mode is shear out for specimens with end distance of 2.5d0 and they are predicted to be failed by bearing according to ANSI/AISC 360-16. The measured failure mode is net section fracture for specimens with edge distance of 1.0d0 and 1.2d0 and they are predicted to be failed by mixed failure according to the EN1993-1-8. The measured failure modes are exactly the same as that of predicted by the modified ANSI/AISC 360-16. Meanwhile, the modified ANSI/AISC code gives the most accurate predictions of bearing resistance, with average difference of 3.7% and standard deviation of 9.5%. Bearing resistances predicted by the Eurocode are excessively conservative compared to the measurements, with average difference of 31.1% and standard deviation of 10.8%.

References

  1. American Iron and Steel Institute. North American Specification for the Design of Cold-Formed Steel Structural Members. AISI S100-12, Washington DC, 2012.
  2. CEN. Eurocode 3: Design of Steel Structures. Part 1-3: General Rules-Supplementary Rules for Cold-Formed Members and Sheeting. EN 1993-1-3, European Committee for Standardization, Brussels, 2006.
  3. GB 50018-2002; Technical Code of Cold-Formed Thin-Walled Steel Structures. Standardization Administration of the People’s Republic of China: Beijing, 2002. (In Chinese)
  4. American Iron and Steel Institute. North American Specification for the Design of Cold-Formed Steel Structural Members. AISI S100-16, Washington DC, 2016.
  5. GB 50018-201X (draft standard for discussion); Technical Code of Cold-Formed Steel Structures. (In Chinese)
  6. American Institute of Steel Construction. Specification for Structural Steel Buildings. ANSI/AISC 360-16, Chicago, 2016.
  7. CEN. Eurocode 3: Design of Steel Structures. Part 1-8: Design of Joints. EN 1993-1-8, European Committee for Standardization, Brussels, 2005.
  8. Guo, Y. J.; Zhu, A. Z.; Pi, Y. L.; Tin-Loi, F. Experimental study on compressive strengths of thick-walled cold-formed sections. Journal of Constructional Steel Research. 2007, 63, 718–723. [Google Scholar] [CrossRef]
  9. Hu, S. D.; Ye, B.; Li, L. X. Material properties of thick-wall cold-rolled welded tube with a rectangular or square hollow section. Construction and Building Materials. 2011, 25, 2683–2689. [Google Scholar] [CrossRef]
  10. Wang, Y. B.; Lyu, Y. F.; Li, G. Q.; Liew, J. R. Behavior of single bolt bearing on high strength steel plate. Journal of Constructional Steel Research. 2017, 137, 19–30. [Google Scholar] [CrossRef]
  11. Kim, T. S.; Kuwamura, H.; Kim, S. H.; <monospace> </monospace>Lee, Y.; Cho, T. Investigation on ultimate strength of thin-walled steel single shear bolted connections with tow bolts using finite element analysis. Thin-Walled Structures. 2009, 47, 1191–1202. [Google Scholar] [CrossRef]
  12. Može ,P.; Beg, D. High strength steel tension splices with one or two bolts. Journal of Constructional Steel Research. 2010, 66, 1000–1010. [CrossRef]
  13. Salih, E. L.; Gardner, L.; Nethercot, D. A. Bearing failure in stainless steel bolted connections. Engineering Structures. 2011, 33, 549–562. [Google Scholar] [CrossRef]
  14. Može, P.; Beg, D. A complete study of bearing stress in single bolt connections. Journal of Constructional Steel Research. 2014, 95, 126–140. [Google Scholar] [CrossRef]
  15. The, L. H.; Uz, M. E. Ultimate shear-out capacities of structural-steel bolted connections. Journal of Structural Engineering. 2015, 141, 04014152-1-04014152-9. [Google Scholar]
  16. Xing, H. Y.; Teh, L. H.; Jiang, Z. Y.; <monospace> </monospace>Ahmed, A. Shear-out capacity of bolted connections in cold-reduced steel sheets. Journal of Structural Engineering. 2020, 146, 04020018-1-04020018-10. [Google Scholar] [CrossRef]
  17. He, Y. C.; Wang, Y. C. Load-deflection behaviour of thin-walled plates with a single bolt in shearing. Thin-Walled Structures. 2011, 49, 1261–1276. [Google Scholar] [CrossRef]
  18. He, Y. C.; Wang, Y. C. Load-deflection behaviour of thin-walled plates with multiple bolts in shearing. Thin-Walled Structures. 2012, 55, 51–63. [Google Scholar] [CrossRef]
  19. GB/T 228.1-2010; Metallic Materials-Tensile Testing-Part 1: Method of Test at Room Temperature. Standardization Administration of the People’s Republic of China: Beijing, 2010. (In Chinese).
  20. Clements, D. D. A.; Teh, L. H. Active shear planes of bolted connections failing in block shear. Journal of Structural Engineering. 2013, 139, 320–327. [Google Scholar] [CrossRef]
  21. Cai, Q.; Driver, R. G. Prediction of bolted connection capacity for block shear failures along atypical paths. Engineering Journal. AISC. 2010, 47, 213–221. [Google Scholar]
  22. Teh, L. H.; Deierlein, G. G. Effective shear plane model for tearout and block shear failure of bolted connections. Engineering Journal. AISC. 2017, 54, 181–194. [Google Scholar]
Preprints 72572 g001
Figure 1. Stress-strain relationships of cold-formed and virgin steel materials
Figure 1. Stress-strain relationships of cold-formed and virgin steel materials
Preprints 72572 g001
Preprints 72572 g002
Figure 2. Set-up of lap shear test
Figure 2. Set-up of lap shear test
Preprints 72572 g002
Preprints 72572 g003
Figure 3. Failure modes of 10 mm thick specimens with varying end distance
Figure 3. Failure modes of 10 mm thick specimens with varying end distance
Preprints 72572 g003
Preprints 72572 g004
Figure 4. Failure modes of 10 mm thick specimens with different edge distance
Figure 4. Failure modes of 10 mm thick specimens with different edge distance
Preprints 72572 g004
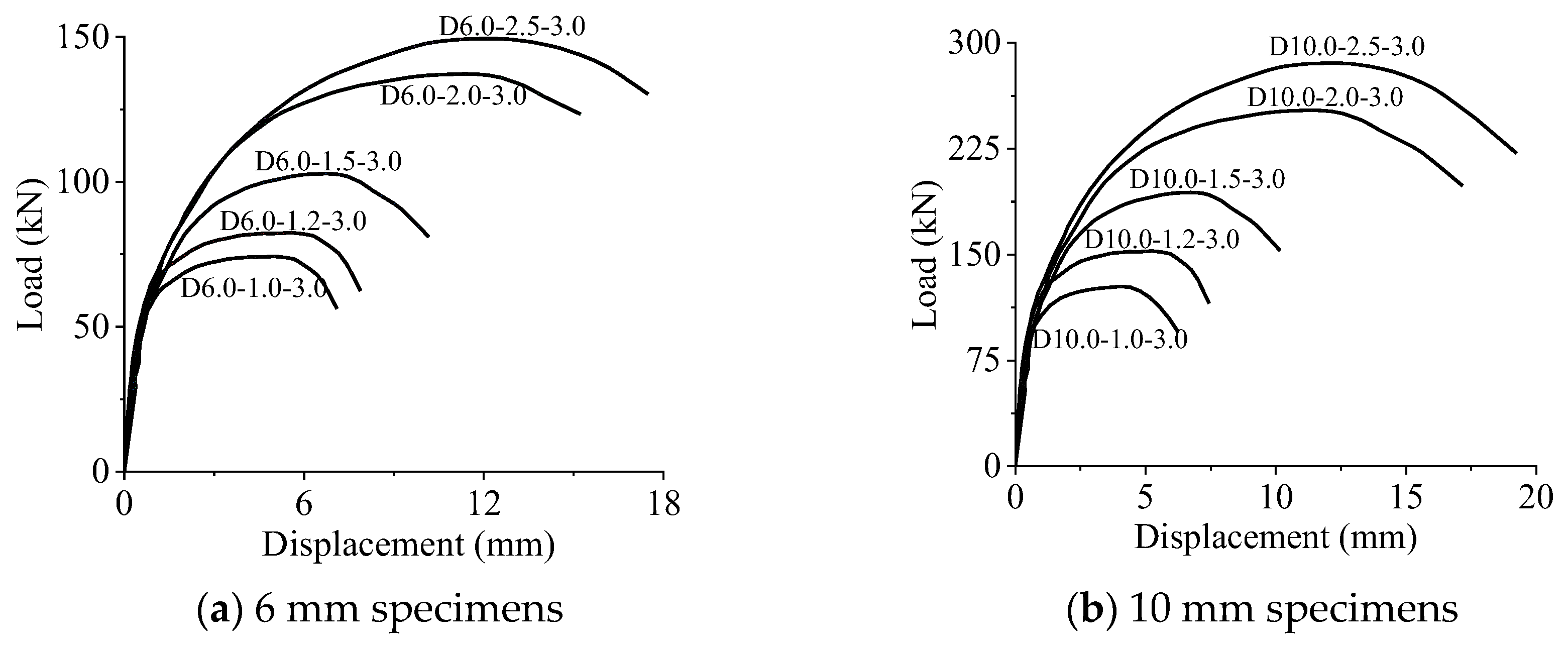
Preprints 72572 g005
Figure 5. Load-displacement curves of specimens with varying end distance
Figure 5. Load-displacement curves of specimens with varying end distance
Preprints 72572 g005
Preprints 72572 g006
Figure 6. Load-displacement curves of specimens with varying edge distance
Figure 6. Load-displacement curves of specimens with varying edge distance
Preprints 72572 g006
Preprints 72572 g007
Figure 7. Curves of relationship between (normalized) ultimate strength and normalized end distance.
Figure 7. Curves of relationship between (normalized) ultimate strength and normalized end distance.
Preprints 72572 g007
Preprints 72572 g008
Figure 8. Curves of relationship between ultimate strength and normalized edge distance
Figure 8. Curves of relationship between ultimate strength and normalized edge distance
Preprints 72572 g008
Preprints 72572 g009
Figure 9. Displacement of specimens with varying end and edge distance
Figure 9. Displacement of specimens with varying end and edge distance
Preprints 72572 g009
Preprints 72572 g010
Figure 10. Conditions of end/edge distance combinations of different failure modes according to (modified) ANSI/AISC 360-163.1.1. Subsubsection
Figure 10. Conditions of end/edge distance combinations of different failure modes according to (modified) ANSI/AISC 360-163.1.1. Subsubsection
Preprints 72572 g010
Preprints 72572 g011
Figure 11. Conditions of end/edge distance combinations of different failure modes according to EN1993-1-8
Figure 11. Conditions of end/edge distance combinations of different failure modes according to EN1993-1-8
Preprints 72572 g011
Preprints 72572 g012
Figure 12. Proportion of specimens with different failure modes
Figure 12. Proportion of specimens with different failure modes
Preprints 72572 g012
Preprints 72572 g013
Figure 13. Comparison between measured and predicted bearing resistance
Figure 13. Comparison between measured and predicted bearing resistance
Preprints 72572 g013
Table 1. Main parameters of test specimens
Table 1. Main parameters of test specimens
Specimen ID t (mm) e1/d0 e2/d0 d0 (mm)
D6.0-1.0-3.0 6.0 1.0 3.0 26.0
D6.0-1.2-3.0 6.0 1.2 3.0 26.0
D6.0-1.5-3.0 6.0 1.5 3.0 26.0
D6.0-2.0-3.0 6.0 2.0 3.0 26.0
D6.0-2.5-3.0 6.0 2.5 3.0 26.0
D6.0-1.5-1.0 6.0 1.5 1.0 26.0
D6.0-1.5-1.2 6.0 1.5 1.2 26.0
D6.0-1.5-1.5 6.0 1.5 1.5 26.0
D6.0-1.5-2.0 6.0 1.5 2.0 26.0
D10.0-1.0-3.0 10.0 1.0 3.0 26.0
D10.0-1.2-3.0 10.0 1.2 3.0 26.0
D10.0-1.5-3.0 10.0 1.5 3.0 26.0
D10.0-2.0-3.0 10.0 2.0 3.0 26.0
D10.0-2.5-3.0 10.0 2.5 3.0 26.0
D10.0-1.5-1.0 10.0 1.5 1.0 26.0
D10.0-1.5-1.2 10.0 1.5 1.2 26.0
D10.0-1.5-1.5 10.0 1.5 1.5 26.0
D10.0-1.5-2.0 10.0 1.5 2.0 26.0
Table 2. Mechanical properties of cold-formed and virgin steels
Table 2. Mechanical properties of cold-formed and virgin steels
Steel plate E(Gpa) fy(Mpa) fu(Mpa) εu(%) ∆(%)
6 mm cold-formed 201.0 287.0 418.3 16.8% 20.5%
10 mm cold-formed 204.0 295.0 455.0 17.0% 23.5%
10 mm virgin 193.0 269.4 415.3 21.6% 29.0%
Table 3. Test results for specimens with varying end distance
Table 3. Test results for specimens with varying end distance
Specimen Failure mode Fu(kN) Fu /fudt δu (mm)
D6.0-1.0-3.0 Shear out 74.2 1.23 4.38
D6.0-1.2-3.0 Shear out 82.7 1.37 5.57
D6.0-1.5-3.0 Shear out 102.0 1.69 6.98
D6.0-2.0-3.0 Shear out 137.0 2.28 12.00
D6.0-2.5-3.0 Shear out 149.5 2.48 13.71
D10.0-1.0-3.0 Shear out 127.7 1.17 4.48
D10.0-1.2-3.0 Shear out 153.7 1.41 5.26
D10.0-1.5-3.0 Shear out 186.2 1.71 6.96
D10.0-2.0-3.0 Shear out 247.7 2.27 11.78
D10.0-2.5-3.0 Shear out 286.2 2.62 13.59
Table 4. Test results for specimens with varying edge distance
Table 4. Test results for specimens with varying edge distance
Specimen Failure mode Fu(kN) Fu /fudt Fu /fuAnet δu (mm)
D6.0-1.5-1.0 Net section fracture 71.5 − 0.95 3.24
D6.0-1.5-1.2 Net section fracture 94.5 − 1.05 3.98
D6.0-1.5-1.5 Shear out 104.0 1.73 − 7.79
D6.0-1.5-2.0 Shear out 102.0 1.69 − 6.71
D6.0-1.5-3.0 Shear out 102.0 1.69 − 6.98
D10.0-1.5-1.0 Net section fracture 130.7 − 0.96 3.10
D10.0-1.5-1.2 Net section fracture 154.2 − 0.94 4.37
D10.0-1.5-1.5 Shear out 176.7 1.62 − 7.19
D10.0-1.5-2.0 Shear out 182.2 1.67 − 6.88
D10.0-1.5-3.0 Shear out 186.2 1.71 − 6.96
Table 5. Comparison of failure modes between test results and predictions
Table 5. Comparison of failure modes between test results and predictions
specimen e1/d0 e2/d0 failure modes
test prediction
ANSI ANSI-modified EC
D6.0(10.0)-1.0-3.0 1.0 3.0 S S S S
D6.0(10.0)-1.2-3.0 1.2 3.0 S S S S
D6.0(10.0)-1.5-3.0 1.5 3.0 S S S S
D6.0(10.0)-2.0-3.0 2.0 3.0 S S S S
D6.0(10.0)-2.5-3.0 2.5 3.0 S B S S
D6.0(10.0)-1.5-1.0 1.5 1.0 N N N M
D6.0(10.0)-1.5-1.2 1.5 1.2 N N N M
D6.0(10.0)-1.5-1.5 1.5 1.5 S S S S
D6.0(10.0)-1.5-2.0 1.5 2.0 S S S S
S: shear out failure; N: net section fracture; M: mixed failure
Table 6. Comparison of failure modes between test results and predictions
Table 6. Comparison of failure modes between test results and predictions
specimen e1/d0 e2/d0 Bearing resistance (kN)
test prediction
ANSI ANSI-modified EC
D6.0-1.0-3.0 1.0 3.0 74.2 48.9 58.7 50.2
D6.0-1.2-3.0 1.2 3.0 82.7 68.5 74.3 60.2
D6.0-1.5-3.0 1.5 3.0 102.0 97.8 97.8 75.2
D6.0-2.0-3.0 2.0 3.0 137.0 146.7 136.9 100.3
D6.0-2.5-3.0 2.5 3.0 149.5 180.6 176.1 125.4
D6.0-1.5-1.0 1.5 1.0 71.5 65.2 65.2 33.1
D6.0-1.5-1.2 1.5 1.2 94.5 91.3 91.3 50.0
D6.0-1.5-1.5 1.5 1.5 104.0 97.8 97.8 75.2
D6.0-1.5-2.0 1.5 2.0 102.0 97.8 97.8 75.2
D10.0-1.0-3.0 1.0 3.0 127.7 88.7 106.5 91.0
D10.0-1.2-3.0 1.2 3.0 153.7 124.2 134.9 109.2
D10.0-1.5-3.0 1.5 3.0 186.2 177.5 177.5 136.5
D10.0-2.0-3.0 2.0 3.0 247.7 266.2 248.4 182.0
D10.0-2.5-3.0 2.5 3.0 286.2 327.6 319.4 227.5
D10.0-1.5-1.0 1.5 1.0 130.7 118.3 118.3 60.1
D10.0-1.5-1.2 1.5 1.2 154.2 165.6 165.6 90.6
D10.0-1.5-1.5 1.5 1.5 176.7 177.5 177.5 136.5
D10.0-1.5-2.0 1.5 2.0 182.2 177.5 177.5 136.5
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated