Prerpints.org logo
Preprint
Article

Thrust Vectoring Control for Heavy UAVs, Employing a Redundant Communication System

Altmetrics

Downloads

114

Views

42

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

08 May 2023

Posted:

09 May 2023

You are already at the latest version

Alerts
Abstract
Recently, various research has been developed addressing communication sensors for Unmanned Aerial Systems (UASs); especially when pondering control difficulties, communication is a crucial component. To this end, strengthening a control algorithm with redundant linking sensors ensures the overall system works accurately even if some components fail. This paper proposes a novel approach to integrate several sensors and actuators for a heavy Unmanned Aerial Vehicle (UAV). Additionally, a cutting-edge Robust Thrust Vectoring Control (RTVC) technique is designed to control various communicative modules during a flying mission and converge the attitude system to stability. The results of the study demonstrate that even though RTVC is not frequently utilized, it works as well as cascade PID controllers, particularly for multi-rotors with mounted flaps, and could be perfectly functional in UAVs powered by thermal engines to increase the autonomy since the propellers cannot be used as controller surfaces.
Keywords: 
Subject: Engineering  -   Control and Systems Engineering

1. Introduction

If you are far away from your enemy make him believe that you are near, written by Sun Tzu, about 2500 years ago [1]. It seems that the mentioned phrase was an old edition of Unmanned areal vehicles (UAV) subject; a technical system combined from several layers to make a flying platform, from communication to control and structural systems. UAVs are almost known as aircraft without a pilot onboard, which have been increasingly dominant due to their wide usage as remote-controlled vehicles in different fields, such as; military, firefighting, logistics, and agriculture. The abbreviation has been changed to become unmanned aerial system (UAS), to show that such a system does not only depends upon the aircraft itself, but it depends upon several important issues such as; the ground control station (GCS), Communication systems with its complexity, and the computing system. UAVs have several classifications, based on flight endurance, weight, flying application, altitude, flight range, and the structural type [2], which amongst, the weight and endurance are sub-objectives of this research. According to European Union aviation safety agency (EASA) regulations for civil UASs open category, four general types are considered regarding the weight classification; Class A1 (less than 900 g ), Class A2 (less than 4 k g ), Class A3 (less than 25 k g ), and for more than 25 k g other categories are observed that based on each one some operational restrictions, piloting requirements, and flying zones are considered [3]. In counterpart, according to the AP-3.3.7 mission qualifications of the global NATO-STANAG 4670 UAS category, they are divided into nano-scale (less than 250 g ), micro-scale (less than 2 k g ), small-scale (less than 25 k g ), medium-scale (less than 150 k g ), and large-scales (more than 150 k g ) [2,3]. Among the latter classification, the heavier the UAV, the more cargo payload benefits from a longer range in a single load. The medium scales are limited to a lower flight endurance and payload carriage. Therefore, many recent contexts are concentrated on heavy-lifter UAVs to improve the control and communication system for such platforms. Likewise, this research investigates a large-scale UAV of 200 k g weight, which contains several communication and control layers to maintain the safety of the flight meanwhile the payload system is a releasable low-dense liquid that complicates the system’s dynamic.
Heavy UAVs consist of many components, in which, the most crucial ones function as the communication system that is not only in charge of internal commands transmission but also external UAVs, which can be seen as ad-hoc nodes, concatenating in a subcategory of the ad-hoc network called Flying ad-hoc network (FANET) [3]. Several novel technologies are proposed, infrastructure-based network (IBN), wireless sensor network (WSN), wireless mesh network (WMN), and Flying ad-hoc network (FANET) [4,5]. Amongst, cellular assistant UAV communication is a novel technology handled by multi-aerial nodes [2,6,7]. The objective of this technology is to utilize the maximum 5G and beyond network quality supported by air-to-air and ground-to-air access points to maintain robustness in the presence of disturbance. Behjati et al. [8], represented several machine learning-based visual line of sight (VLoS) models to estimate the reference signal power and quality by various mathematical methods. They found that the quality depends heavily upon the distance of the UAV and the GCS, and the flight altitude which leads to elevation angle. The nonlinear models conquer the linear ones due to their highly accurate prediction. Whereas, authors in [9] proposed a novel MANET protocol called UAV-to-UAV (U2U) plus UAV-to-Infrastructure (U2I) communication and outlined its benefits equipped with WSN and linear sensor network (LSN) as data collectors, regarding the latency. They implemented a dynamic system to change the communication layers by relays, considering various radios based on the strength of every node to be exchanged; then resulting versus average delay, service time, and delivery ratio compared several topologies, they claimed the LSNs links to each other with minimum delay when the packets are transmitted in a queue, ordering by a lesser generation time; however, their work did not include any piratical scenarios.
Whilst, in this research, a newly released U2I communication system is integrated into a WSN topology and is easily installed but responds with a way lesser latency even when transmitting high-quality videos to the ground control station (GCS). In this submission, the UAV’s weight and payload type impact saliently on the communications utilized; so that in a mini UAV, the communication links are way limited; while, the danger is also negligible, in contrast, in a large case, the communication is way critical and if the payload material is of liquid, even more, special sensors, such as thermal, chemical pressure sensors, will be needed.
On the other hand, the control system brings several challenges to stabilizing heavy UAVs, especially when conventional solutions are not effective; i.e., nowadays, electrical UAVs mostly work accurately and have been improved a dozen times, however, they all suffer from low flight time, and if electrical motors be substituted by thermal engines, the controller surfaces would be changed due the limits of a thermal system, which previously, the authors have discussed the limitations and solutions proposed in [10,11]. In this paper, a novel approach is put forth that, despite its rarity in the history of aeronautics, if constructed properly, may stabilize an unmanned aerial vehicle (UAV) for a long period of time, even in the presence of wind disturbances. Also, more literature reviews could be found in authors’ previous works [10,11,12,13,14].
This paper is organized into six sections as follows; section two discusses UAV communication subsystems, section three denotes the dynamic model and control, section four compares results, and finally, section six concludes the paper.

2. UAV Communication Subsystems

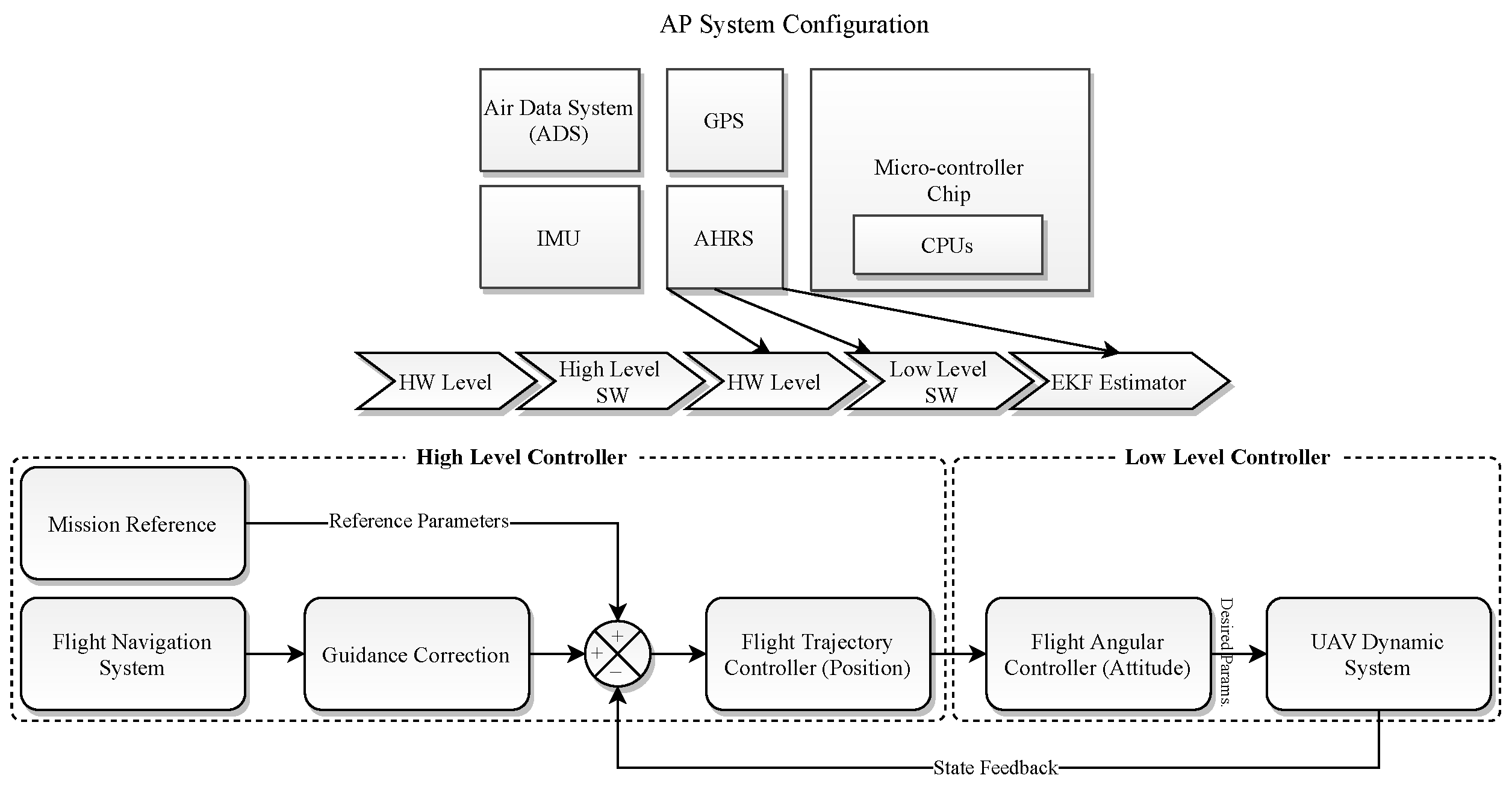
In particular, this paper represents a complete UAV system, consisting of various components that are all controlled by the autopilot (AP); the majority of connections are direct and in minor sub-components like the cameras and lasers, an onboard computer processes the images data and collaborate with the AP in a lower level, as shown in Figure 1, and is elaborated in Figure 2, meanwhile, the positioning data are enhanced by the global navigation satellite system (GNSS). Moreover, the power management Unit (PMU) supplies the energy for all subsystems, which not only regulates the thermal energy to two main outputs of 12 V and 24 V but also, aliments the power system that includes the engine control unit (ECU), three internal combustion motors and an engine monitor to demonstrate and regulate the power system in case of danger, as shown in Figure 1. Furthermore, the UAV is empowered with a redundant radio system, which principally, the command and control radio leads all the communication levels regarding internal subsystems and outperforms the U2I communication, which is further described in Figure 3. While, in case of no functionality, the backup radio compensates the essential subsystems to follow up the last waypoints stored in the buffer to return to land in safe mode. Especially, the safety package consists of a flight termination system (FTS) to manage the whole UAV in an emergency case. This system is simplified to an electric board that receives every moment the last flight modes and important logs, stores them, and automatically activates when the PMU output power decreases suddenly, which means a fatal fail. To continue, the system is detailed in several subsections, the AP and digital system, the power system, the safety system, and the communication package.

2.0.1. Autopilot (AP) and Digital Systems

The AP configuration system is made up of several layers that receive the actual state traumas of each component equipped with a real-time operating system (RTOS), which analyzes the data in hierarchical series and prohibits the non-critical processes to interfere with the principal functions and performing adequate safety. Moreover, the powerful NXP-based microcontroller board is equipped with a double CPU configuration to parallelize the data logging and calculation process. Meanwhile, the high-level reference data are outputted by the guidance loop that includes a flight navigation system corrected by several references, then, the low-level orientations and estimations are provided by the attitude and heading reference system (AHRS), which Imports the position desired values and desired attitude angles, and generates the necessary moments for the dynamics system of the UAV, which are later saturated for the actuators. While the controller SW loops are divided into two modes, the guidance corrections are constantly impacting the input reference values in a closed-loop system to regulate the desired outputs. In addition, the digital system contains a Jetson Xavier onboard flight computer to control and analyze the camera output and stream the video in the multi-cast mode for ground observers. Meanwhile, the flight computer is connected directly to the AP, and some of the less important commands, such as navigation enhancement by processing an Extended Kalman Filter (EKF) algorithm, utilizing an additional IMU to compare the data with the AP IMU and recording auxiliary telemetry.
Preprints 73069 g002
Figure 2. The AP infrastructure and its sub-components.
Figure 2. The AP infrastructure and its sub-components.
Preprints 73069 g002

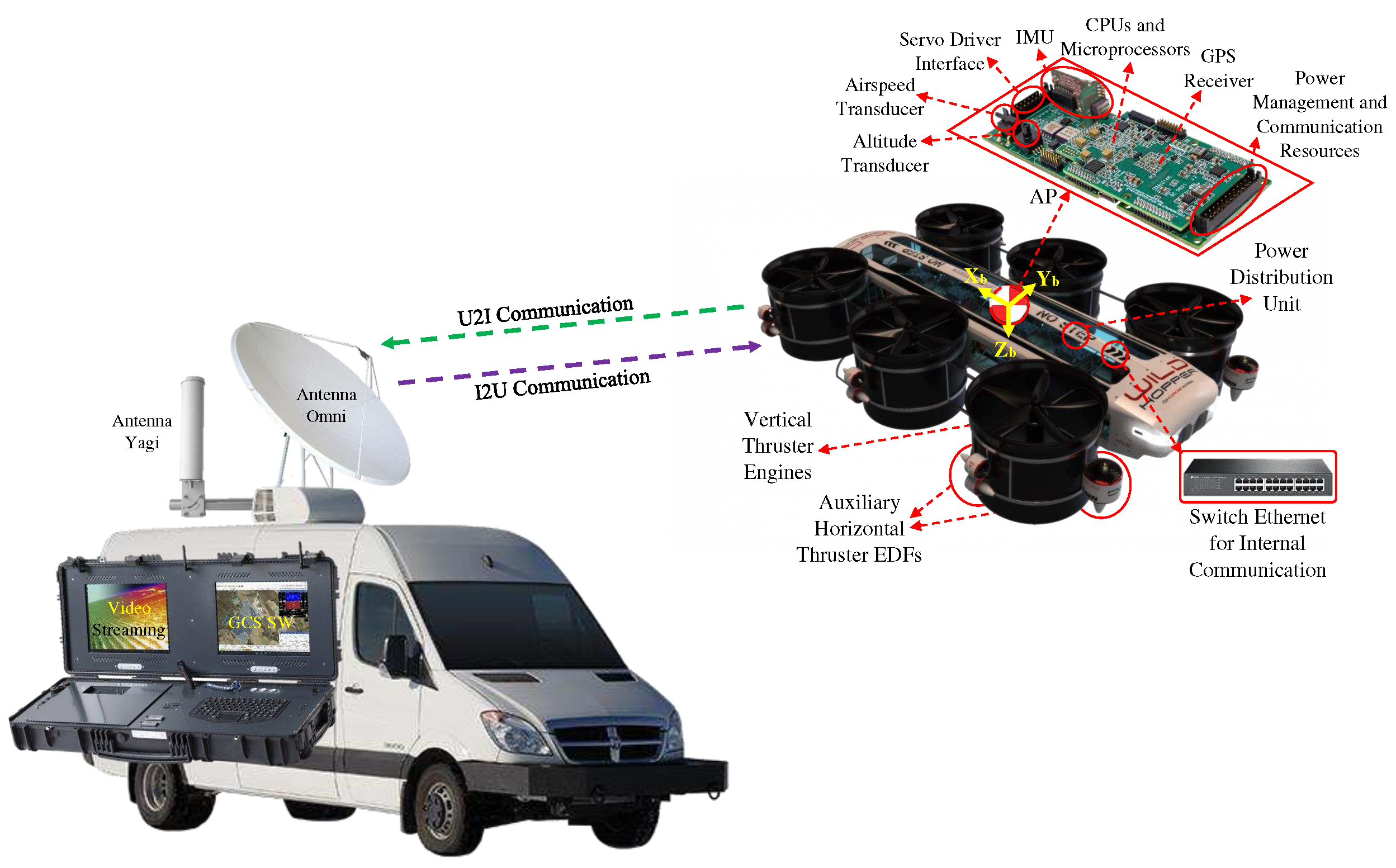
2.0.2. Communication System

As mentioned in the introduction, the UAV is empowered by a duplicate communication system, in which, the principal command and control radio leads the critical commands between the autopilot and other subsystems. Explicitly, two types of communication are considered, internal communication system and external communication with the GCS (U2I). The internal commands are transmitted by a standard RS-485 serial interface facilitated through an internal switch to receive/send the data with the least latency (less than 5 m s ) and to secure the communication system. All the auxiliary connections, namely, video streaming, the onboard computer commands, and the lights are transmitted through a separate line. Regarding the U2I communication, two antennas are installed on the UAS, as shown in Figure 3, once an omnidirectional antenna plate is utilized for distances lesser than 10 k m , which is highly powerful for flights bounded in small areas, but with a lack of performance to handle all the data for longer distances. Then, a yagi antenna is installed for distances longer than 10 k m .
Preprints 73069 g003
Figure 3. The UAS infrastructure and the communication system.
Figure 3. The UAS infrastructure and the communication system.
Preprints 73069 g003

3. Dynamic System and Control

In order to ensure successful missions for heavy UAVs, the performance of various components and dynamic systems necessitates optimization of the overall reaction to commands, in which, minimizing error time is one of the most crucial optimization criteria, i.e., reaching zero error in the higher controller loop and all of its derivatives as quickly as possible. Among possibilities, the vertical thermal thrusters regulate the altitude with the least error, benefiting a long flight; however, regarding the horizontal flight, the system suffers the efficiency due to the latent response of motors when the speed controller unit (ECU) commands distinct spin rates in small time intervals. Therefore, one of the most efficient solutions presented is the thrust vectoring control (TVC) [15], which aims for both the optimal time and the least error. Typically, TVC works with consists of sensors and actuators. The sensors provide information on the UAV’s attitude and motion, while the actuators adjust the flaps’ deflection angle in response to the control signals generated by the autopilot. Particularly in the case of a multi-rotor, the system could be thought of as a multi-ducted fan (MDF), in which each duct contains a set of lateral and longitudinal flaps corresponding to a servo (the number of flap vanes could vary depending on the design, but the fewer servos control employed, the less functional issues and AP limitations). In this section, two studies are conducted, aerodynamic analysis and dynamic stability.

3.1. Aerodynamics Analysis

Optimizing the structure according to aerodynamics principles, TVC performance mostly depends on duct design and outlet duct section; the larger diameter of the outlet section, the more lift production and lesser energy consumption [15], as shown in the form of continuity in Equation (1).
ρ A r v r = ρ A e v e → v e = A r v r A e S r , e = 0.25 π ( D r , e 2 − D s 2 ) → β d = S e S r
Where, { } r , e is about the rotor and exhaust prefixes, respectively, A is the section area, S is the air inlet area, which is extracted from the central spinner area, D is the section diameter, v is the airflow velocity, and β d is duct sectional efficiency. This is experimented with by expanding the exhaust duct area up to 1.7 times, the efficiency is advanced up to 1.3 times [15]. This phenomenon is also observable with flap presence, while, the thruster flap vanes intrigue a product drag force that decreases the total thrust.
In addition, the blade profile leads the inlet air impacts directly on the thrust and the power consumption [16], the higher the pitch angle at the blade tip, the more thrust is produced and more power is consumed, as shown in Figure 4. Likewise, the pressure drop cowling is doubled a tip angle is implied, also the nozzle outlet pressure is increased, as shown in the right side table of Figure 4(a) and (b), which states an overall better performance with the tip angle, which is also observable in the diagram of duct exit pressure. Both tests are conducted with a rotational rate of 5000 R P M .
Furthermore, to have a better thrust, the number of blades has an outstanding effect. To investigate the importance and find a suitable blade number, four different types are studied, with 5, 8, 16, and 32 blades. As shown in Figure 5, four models are analyzed up to 6500 R P M , the more blades installed, the more thrust and power consumption are obtained. Also, as is shown in Figure 5, right tables, the nozzle exhaust and duct outlet pressures are varying significantly in the transient mode, during the first 5 s , but mostly converged to a steady value after 5 . 5 s , which the best one is with 8 blades. Therefore, comparing all increments of thrust, power consumption, and pressure drop, in which the first one is desirable and two letters are unwanted, a configuration with 8 blades is the best option to have also a continuous stream down the duct, as shown in Figure 5.
According to several experiments [17,18,19], to take more benefits of flap vanes and less production drag, the CoM of the UAV is considered above the rotor section, i.e., the more distance between flap vanes, the more lift forces generated. Therefore, the aerodynamic forces generated by the vanes are described as follows,
L i f t f = 0.5 ρ v 2 C l A f D r a g f = 0.5 ρ v 2 C d A f

3.2. Control Strategy

A brief equation set of a robust sliding mode TVC is presented in this section for UAV multirotor systems. Generally, hexagonal cases are equipped with more motors and propellers that provide more redundancy and improve control in the case of a motor failure. Thus, hexacopters are thus a well-liked option for heavy-lift applications [20,21,22]. Then, as mentioned in the introduction, the solution provided in this paper is about installing flap vanes at the engine exhaust, which leads to employing a ducted fan application. Considering mentioned clues, and the position reference objective for the system, the system’s primary state matrix contains x , y , z , ϕ , θ , ψ , and their derivatives. Addressing the servos connected to the flap vanes, the whole attitude controller is upon their movements, so if every duct has four flaps at the exit, then, four deflection angles per duct will be added to the system’s states which complicates the process. Simplifying the problem, all the desired movements and turns could be summarized into the combination of all ducts, therefore, two flap vanes per duct will be sufficient for easiness in both mechanical and computational processes, which concludes two extra angles per duct and overall yields 12 deflection angles as additional states, δ 11 , δ 12 , δ 21 , δ 22 , δ 31 , δ 32 , δ 41 , δ 42 , δ 51 , δ 61 , δ 61 , δ 62 that in δ i j , i represents the duct number and j ∈ 1 , 2 demonstrates the latitudinal or longitudinal mode of the vanes, respectively. Thus, knowing the actual and desired states of the drone, two principal modes are considered: vertical and attitude controller, which leads to the planar controller. Among several sliding modes (SMs) design approaches: pole placement, Lyapunov-based, optimal control-based, and model predictive methods, we chose a Lyapunov candidate that converges to zero and in a finite time and maintains there. To this end, a suitable sliding surface is defined, containing all attitude variables, which yield;
S = s i n ( ψ d − ψ ) c o s ( θ d − θ ) c o s ( ϕ d − ϕ ) − c o s ( ψ d − ψ ) s i n ( θ d − θ ) c o s ( δ f , d − δ f )
Where, ϕ , θ , ψ are roll, pitch, and yaw angles, respectively, δ f is the flap vane’s deflection angle, and the { } d is the desired value. Conditioning the Lyapunov candidate to be positive-definite, radially bounded, and decreasing along the sliding surface, the function and its derivative of V ( s ) with respect to time are as follows,
V ( s ) = 0.5 S 2 P S → d V ( s ) / d t = 0.5 P ( 2 S d S / d t S + S 2 d S / d t )
Where P is a positive-definite matrix, and d V ( s ) / d t must be always negative to ensure that during the sliding mode, the system is always in a neighborhood of the sliding surface and will converge to the desired state despite any disturbances or uncertainties in the system. Defining SMC law as, d S / d t = u = − k 1 S i g n ( S ) + k 2 tanh ( k 3 S ) , in which k i , i ∈ 1 , 2 , 3 are constants that determine the rate of convergence to the sliding surface and are obtained through the controller design process. Thus,
d V ( s ) / d t = 0.5 P ( 2 S ( − k 1 S i g n ( S ) + k 2 tanh ( k 3 S ) ) S + S 2 ( − k 1 S i g n ( S ) + k 2 tanh ( k 3 S ) ) ) → d V ( s ) / s t = P S 2 ( k 2 tanh ( k 3 S ) − k 1 | S | )
Since tanh ( k 3 S ) is bounded between − 1 and 1, d V ( s ) / d t will be negative whenever k 2 tanh ( k 3 S ) < k 1 | S | (since P and the constants k 1 , k 2 , k 3 are all positive). This means that d V ( s ) / d t is negative for all non-zero values of S when k 1 > k 2 and k 3 < 1 . Therefore, it is proven that d V ( s ) / d t is always negative and the system converges to a stable equilibrium point, and the control law given by u = − k 1 S i g n ( S ) − k 2 tanh ( k 3 S ) guarantees the stability of the closed-loop system. Finally, substituting the earlier expression of S,
d V ( s ) / d t = [ ( S ( e ψ ) C ( e θ ) C ( e ϕ ) − C ( e ψ ) S ( e θ ) ) / C ( e δ f ) ] 2 ∗ P [ C ( δ f , d ) C ( ϕ d ) C ( δ f ) C ( ϕ ) + S ( δ f , d ) S ( ϕ d ) S ( δ f ) S ( ϕ ) + C ( δ f , d ) S ( θ d ) C ( δ f ) S ( θ ) + S ( δ f , d ) C ( θ d ) S ( δ f ) C ( θ ) ] S ( e ψ ) C ( e θ ) C ( e ϕ ) C ( δ f , d ) C ( δ f ) C ( ϕ ) + S ( δ f , d ) S ( ϕ d ) S ( δ f ) S ( ϕ ) + C ( δ f , d ) S ( θ d ) C ( δ f ) S ( θ )
Where, S ( ) ≅ s i n ( ) , C ( ) ≅ cos ( ) , and e refers to the difference between the desired and actual value. Hence, considering the control law, the attitude controller with respect to the flaps vanes’ deflection angle could be rewritten as,
U r o l l = I x ( δ ¨ f , d − k 1 e ˙ ϕ ) − k 1 tanh ( k 3 S ) U p i t c h = I y ( δ ¨ f , d − k 2 e ˙ θ ) − k 1 tanh ( k 3 S ) U y a w = I z ( δ ¨ f , d − k 3 e ˙ ψ ) − k 2 tanh ( k 1 S )
Where, the constants k i , i ∈ 1 , 2 , 3 will be obtained by trial and error during the implementation, and I demonstrate the inertial moment.

4. Results

Affirming the TVC algorithm proposed through the control design section, a complete platform is implemented to observe the results, in which, several platforms and trajectories were tested to optimize and tune the controller gains. Meanwhile, since the control objective in this research is to stabilize a smooth movement without harsh maneuvers, the best trajectories were ones with a few sharp turns, but still long to observe the thermal engines’ performance. Hereupon, two routes are suggested in a 300 × 300 m 2 area, once a circular route and then a rectangular one to be compared thereafter, where both plans are smoothed in corners.
As shown in Figure 6, a semicircular route is projected in the horizontal plane, where the desired values are highlighted with the red line, and the actual UAV movement is in blue. The flight plan constantly follows a 5 m altitude so that the vertical Z axis is not considered. Starting from ( 0 , 0 ) , the heavy UAV moves with a constant velocity of 5 m / s flowing smoothly along the reference trajectory, containing a random noise applied to the controller to examine the performance in the long run as a steady state mode.
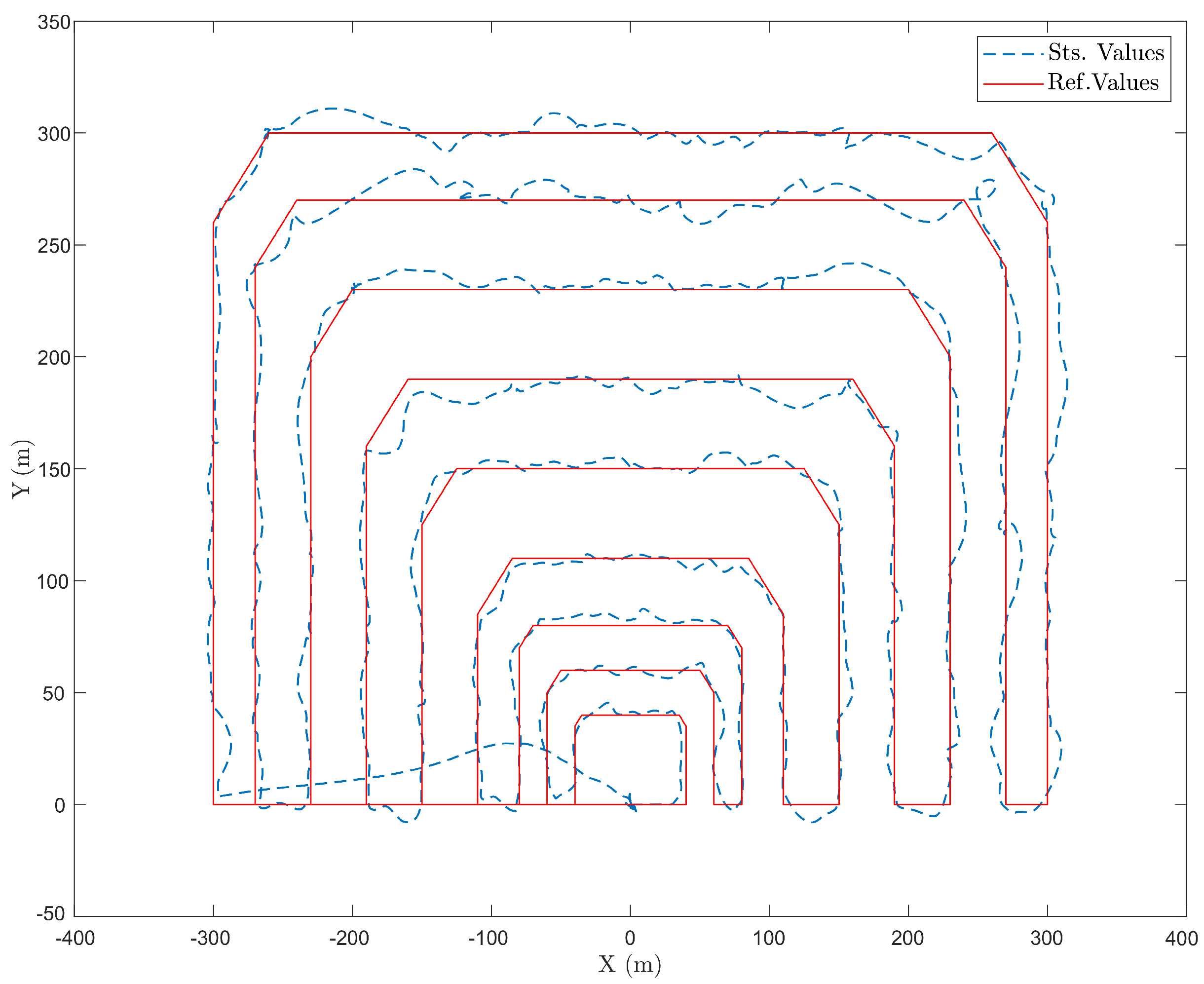
Likewise, as shown in Figure 7 a rectangular trajectory with more direct and longer routes was planned in the presence of a random wind disturbance, and the controller performed better, because of lesser radial lines through the trajectory. In both cases, the steady state error was less than 2 % , which proves the efficiency of the SMC presented.

5. Conclusions and Future Work

This research addresses theoretical and practical controller platforms, offering novel solutions to the key control issues that arise when combined with communication problems in the case of multi-UAVs for remote sensing operations. Utilizing the aerodynamics results, a suitable duct geometry concentrating on the exhaust area is exploited, and an optimized number of rotors was considered to have a better performance. Also, In order to enhance functionality when thermal engines are used, a novel sliding mode controller based on thrust vectoring control principles is presented. The results demonstrate acceptable performance for long-range flights, but improving the TVC’s theory and practical application is required to design industrial platforms Meanwhile, a double simultaneous communication is carried out to support both medium and long distances between the UAV and the ground control sustain. Future work will include the analysis of the sensors and the useful outcomes of the enhanced system.

Author Contributions

Conceptualization, M.S.A.I., A.R.R., M.A.L., M.M.A.E.K., and P.C.; Formal analysis, M.S.A.I., A.R.R., M.A.L., M.M.A.E.K., and P.C.; Funding acquisition, P.F.P., and A.R.R.; Investigation, M.S.A.I., A.R.R., M.A.L., M.M.A.E.K., and P.C.; Methodology, M.S.A.I., A.R.R., M.A.L., M.M.A.E.K., and P.C.; Project administration, A.R.R., and P.C.; Software, M.S.A.I., M.A.L., and M.M.A.E.K.; Supervision, A.R.R., and P.C.; Writing—original draft, M.S.A.I.; Writing—review and editing, M.S.A.I., and A.R.R. All authors have read and agreed to the published version of the manuscript.

Acknowledgments

We would thank the University of Carlos III, campus Leganes, Madrid, for performing laboratories and hangers through our research. Also, we thank our colleagues at Drone Hopper for their support during the project. This work is conducted to complete the doctoral project of Mohammad Sadeq Ale Isaac, with the support of Professor Pascual Campoy and Dr. Ahmed Refaat Ragab.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:
UAV Unmanned Aerial Vehicle
UAS Unmanned Aerial System
H2020 Horizon 2020
GCS Ground Control Station
SMC Sliding Mode Controller
TVC Thrust Vectoring Control
FANET Flying ad hoc Network
IBN Infrastructure-Based Network
WSN Wireless Sensor Network
WMN Wireless Mesh Network

References

  1. Tzu, S. The art of war. In Strategic Studies; Routledge, 2008; pp. 63–91.
  2. Zeng, Y.; Zhang, R.; Lim, T.J. Throughput maximization for UAV-enabled mobile relaying systems. IEEE Transactions on communications 2016, 64, 4983–4996. [CrossRef]
  3. Castrillo, V.U.; Manco, A.; Pascarella, D.; Gigante, G. A Review of Counter-UAS Technologies for Cooperative Defensive Teams of Drones. Drones 2022, 6, 65. [CrossRef]
  4. Nawaz, H.; Ali, H.M.; Laghari, A.A. UAV communication networks issues: a review. Archives of Computational Methods in Engineering 2021, 28, 1349–1369. [CrossRef]
  5. Li, B.; Fei, Z.; Zhang, Y. UAV communications for 5G and beyond: Recent advances and future trends. IEEE Internet of Things Journal 2018, 6, 2241–2263. [CrossRef]
  6. Mozaffari, M. Wireless Communications and Networking with Unmanned Aerial Vehicles: Fundamentals, Deployment, and Optimization. PhD thesis, Virginia Tech, 2018.
  7. Li, B.; Fei, Z.; Dai, Y.; Zhang, Y. Secrecy-optimized resource allocation for UAV-assisted relaying networks. 2018 IEEE Global Communications Conference (GLOBECOM). IEEE, 2018, pp. 1–6. [CrossRef]
  8. Behjati, M.; Zulkifley, M.A.; Alobaidy, H.A.; Nordin, R.; Abdullah, N.F. Reliable aerial mobile communications with RSRP & RSRQ prediction models for the Internet of Drones: A machine learning approach. Sensors 2022, 22, 5522. [CrossRef]
  9. Jawhar, I.; Mohamed, N.; Al-Jaroodi, J.; Agrawal, D.P.; Zhang, S. Communication and networking of UAV-based systems: Classification and associated architectures. Journal of Network and Computer Applications 2017, 84, 93–108. [CrossRef]
  10. Isaac, M.S.A.; Ragab, A.R.; Garcés, E.C.; Luna, M.A.; Peña, P.F.; Cervera, P.C. Mathematical Modeling and Designing a Heavy Hybrid-Electric Quadcopter, Controlled by Flaps. Unmanned Systems 2022, 10, 241–253. [CrossRef]
  11. Ale Isaac, M.S.; Luna, M.A.; Ragab, A.R.; Ale Eshagh Khoeini, M.M.; Kalra, R.; Campoy, P.; Flores Peña, P.; Molina, M. Medium-Scale UAVs: A Practical Control System Considering Aerodynamics Analysis. Drones 2022, 6, 244. [CrossRef]
  12. Luna, M.A.; Ale Isaac, M.S.; Ragab, A.R.; Campoy, P.; Flores Peña, P.; Molina, M. Fast Multi-UAV Path Planning for Optimal Area Coverage in Aerial Sensing Applications. Sensors 2022, 22, 2297. [CrossRef]
  13. Ragab, A.R.; Isaac, M.S.A.; Luna, M.A.; Flores Peña, P. WILD HOPPER Prototype for Forest Firefighting. International Journal of Online & Biomedical Engineering 2021, 17. [CrossRef]
  14. Isaac, M.; Naghash, A.; Mirtajedini, S. Control and guidance of an autonomous quadrotor landing phase on a moving platform. Proceedings of the IMAV Annual Conference of Autonomous Vehicles, Madrid, Spain, 2019, Vol. 29.
  15. Urban, D.; Kusmirek, S.; Socha, V.; Hanakova, L.; Hylmar, K.; Kraus, J. Effect of Electric Ducted Fans Structural Arrangement on Their Performance Characteristics. Applied Sciences 2023, 13, 2787. [CrossRef]
  16. Eltayesh, A.; Castellani, F.; Burlando, M.; Hanna, M.B.; Huzayyin, A.; El-Batsh, H.M.; Becchetti, M. Experimental and numerical investigation of the effect of blade number on the aerodynamic performance of a small-scale horizontal axis wind turbine. Alexandria Engineering Journal 2021, 60, 3931–3944. [CrossRef]
  17. Jacobsen, E.B. Modelling and Control of Thrust Vectoring Mono-copter 2021. p. 89.
  18. Abrego, A.I.; Bulaga, R.W.; Rutkowski, M. Performance study of a ducted fan system. American Helicopter Society Aerodynamics, Acoustics and Test and Evaluation Technical Specialists Meeting, 2002.
  19. Muehlebach, M.; D’Andrea, R. The flying platform–a testbed for ducted fan actuation and control design. Mechatronics 2017, 42, 52–68. [CrossRef]
  20. Karpinska, F.; Pachtrachai, J. Comparison of hexacopter and quadcopter performance for aerial photography. 2015 10th International Conference on Electrical and Electronics Engineering (ELECO). IEEE, 2015, pp. 867–871. doi:10.1109/ELECO.2015.7394554. [CrossRef]
  21. Reddy, R.S.; Dash, S.K. Design and Analysis of a Hexacopter for Heavy Lift Applications. International Journal of Engineering Research & Technology (IJERT) 2014, 3, 1352–1357.
  22. Tovar, D. Quadcopter vs Hexacopter: Pros and Cons. UAV Coach, 2018.
Preprints 73069 g001
Figure 1. The overall schematic of the UAV system.
Figure 1. The overall schematic of the UAV system.
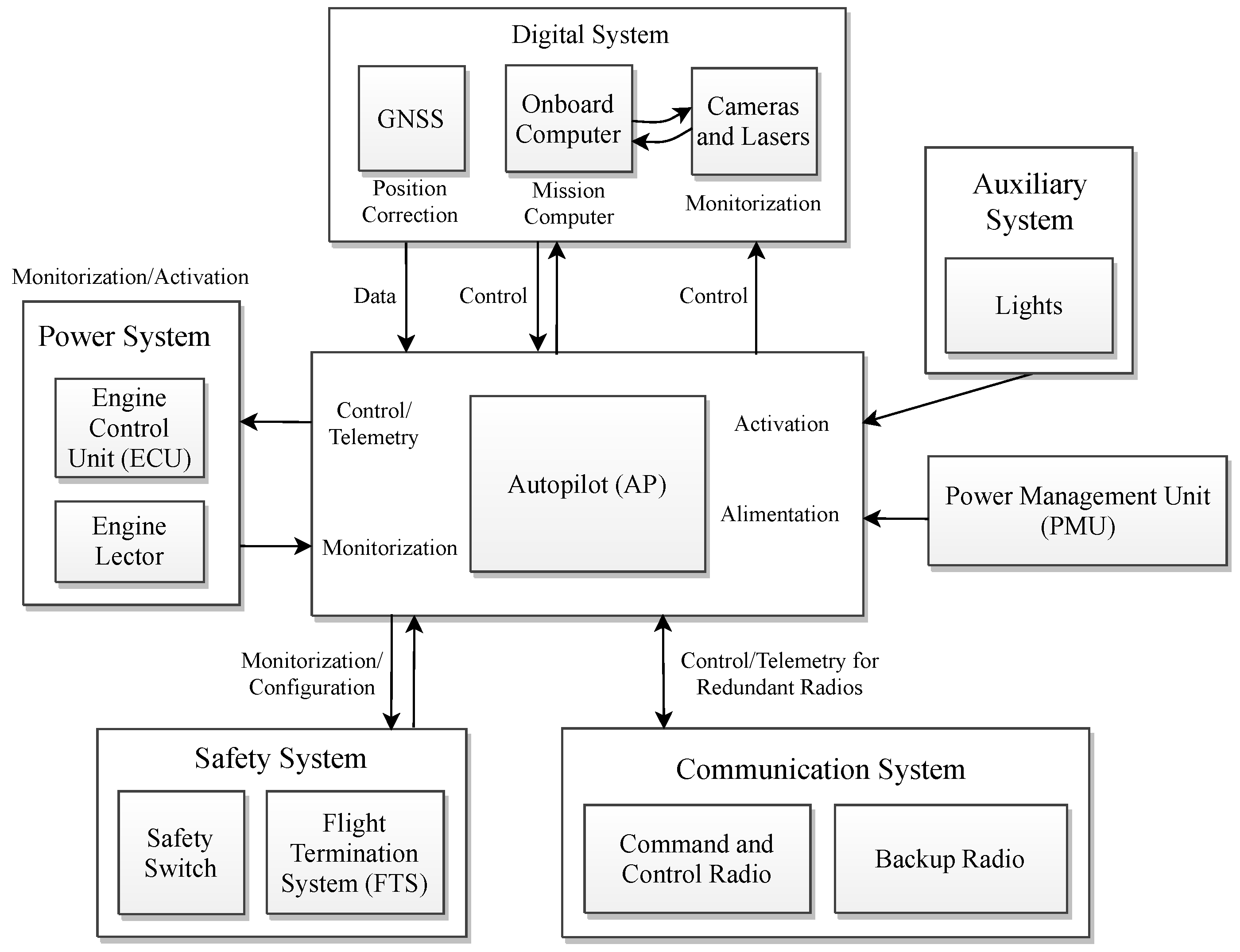
Preprints 73069 g001
Preprints 73069 g004
Figure 4. Effect of the blade tip angle on the thrust generation and power consumption.
Figure 4. Effect of the blade tip angle on the thrust generation and power consumption.
Preprints 73069 g004
Preprints 73069 g005
Figure 5. Effect of the blade numbers on the thrust generation and power consumption.
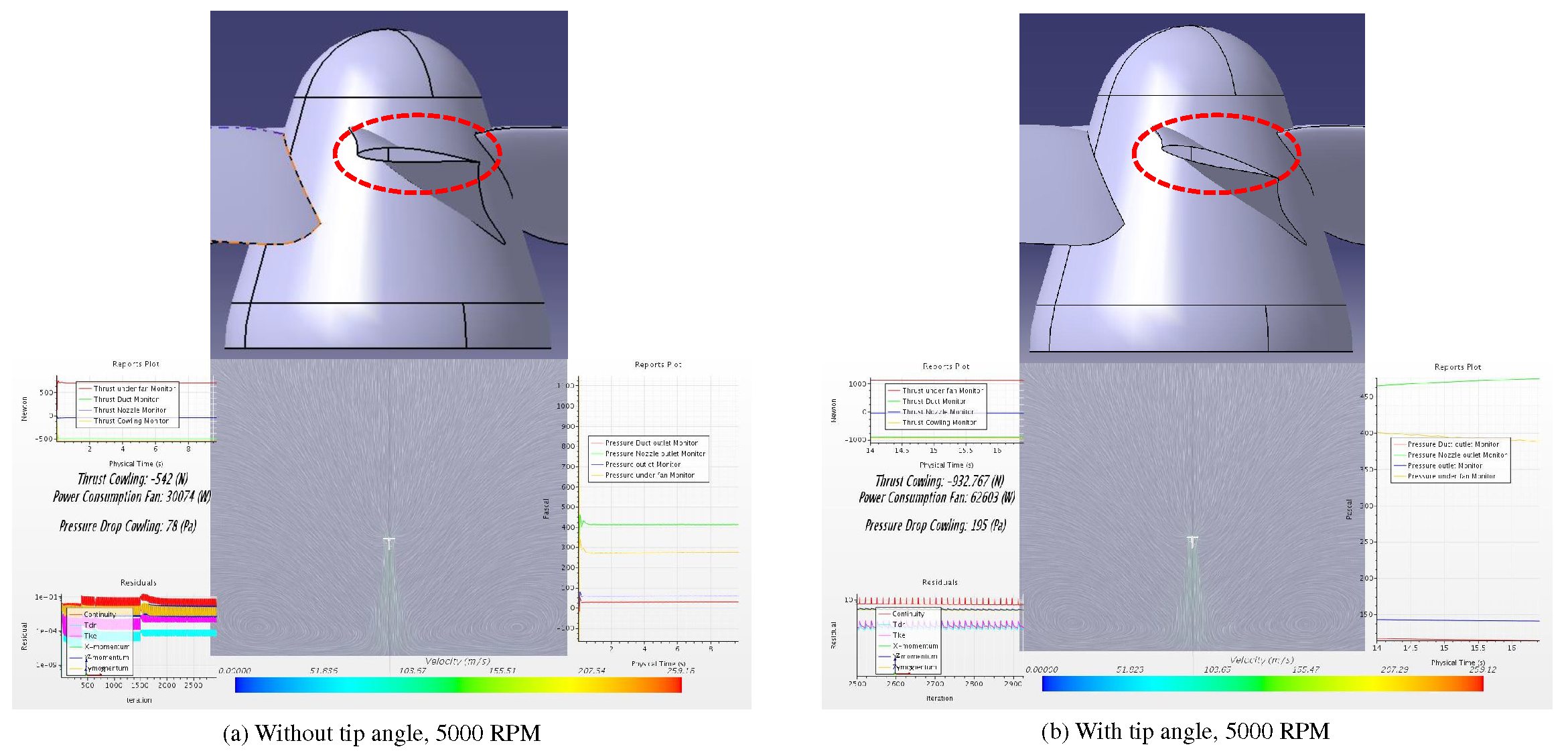
Figure 5. Effect of the blade numbers on the thrust generation and power consumption.
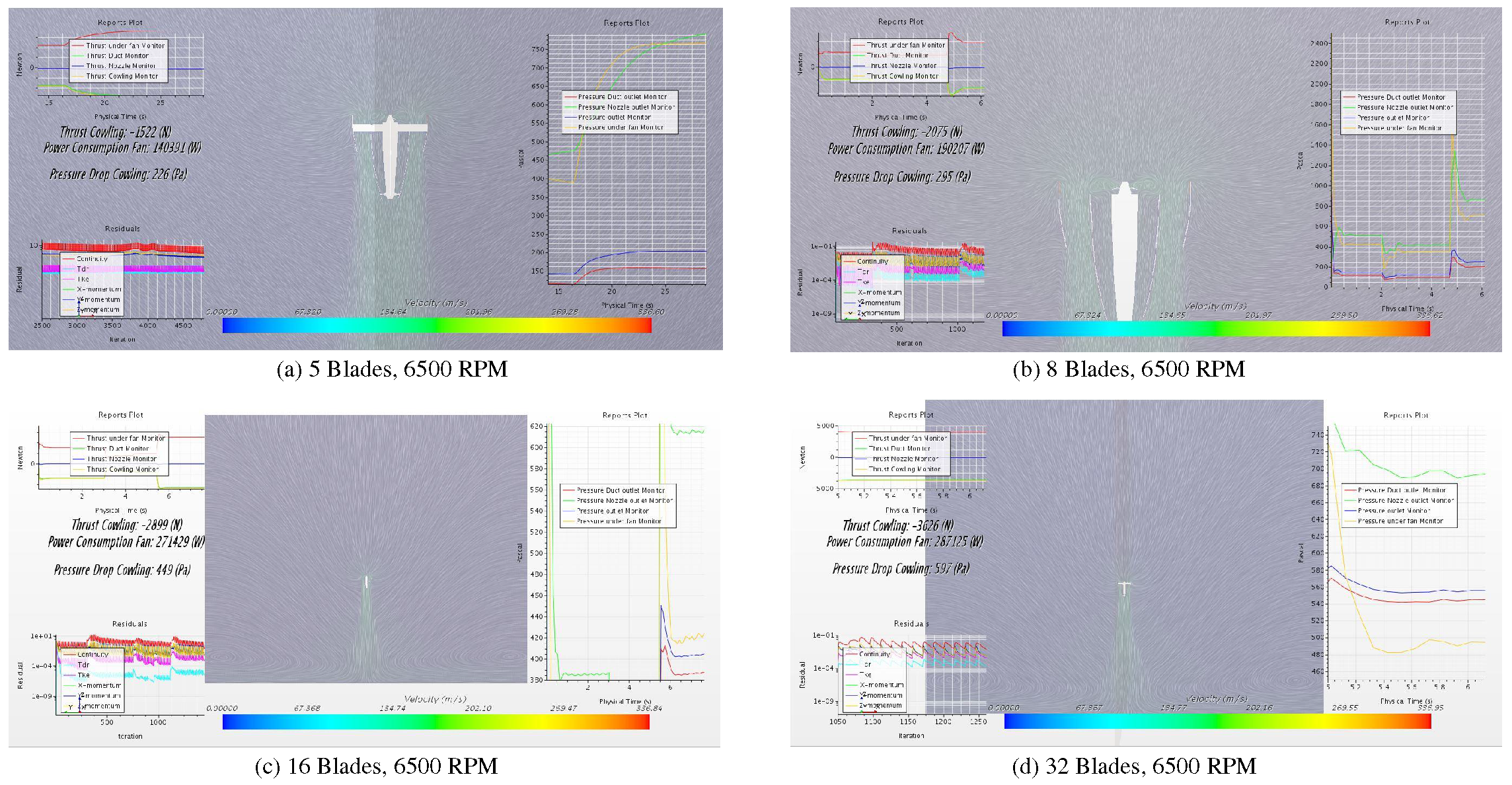
Preprints 73069 g005
Preprints 73069 g006
Figure 6. The horizontal projection of the reference and actual trajectory, in the presence of a random wind disturbance and a semi-circular area.
Figure 6. The horizontal projection of the reference and actual trajectory, in the presence of a random wind disturbance and a semi-circular area.
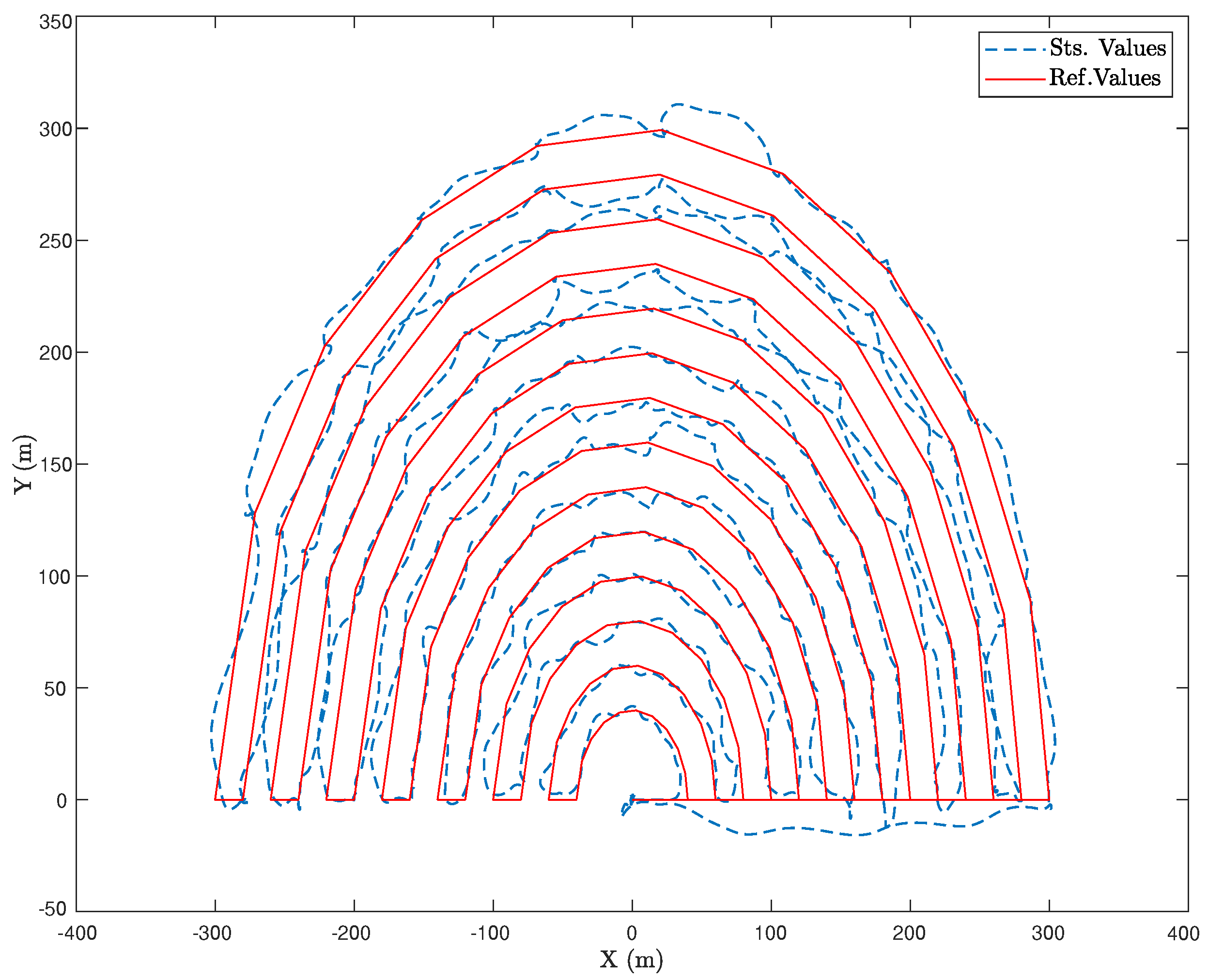
Preprints 73069 g006
Preprints 73069 g007
Figure 7. The horizontal projection of the reference and actual trajectory, in the presence of a random wind disturbance and a rectangular area.
Figure 7. The horizontal projection of the reference and actual trajectory, in the presence of a random wind disturbance and a rectangular area.
Preprints 73069 g007
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated