Prerpints.org logo
Preprint
Article

New Probabilistic Seismic Hazard Model for Nepal Himalayas Integrating Distributed Seismicity and Major Thrust Faults

Altmetrics

Downloads

235

Views

126

Comments

0

A peer-reviewed article of this preprint also exists.

supplementary.pdf (642.34KB )

Submitted:

09 May 2023

Posted:

09 May 2023

You are already at the latest version

Alerts
Abstract
Nepal is one of the most seismically active regions in the world, as highlighted by the recent devastating 2015, Mw7.8 Gorkha earthquake and a robust assessment of seismic hazard is paramount for the design of earthquake-resistant structures. In this study we present a new probabilistic seismic hazard assessment (PSHA) model for Nepal. We considered data and findings from recent scientific publications, which allowed us to develop a unified homogenized seismicity catalogue, propose alternative Seismic Source Characterization (SSC) models including up-to-date parameters of major thrust faults like Main Frontal Thrust – MFT and Main Boundary Thrust – MBT, while also considering existing SSC models and various hazard modelling strategies within a logic tree framework. The sensitivity analyses show the hazard levels are generally higher for SSC models integrating the major thrust faults, followed by homogenous volume sources and smoothed seismicity approach. The hazard maps covering entire Nepal is presented as well as the Uniform Hazard Spectra (UHS) for 5 selected locations (Kathmandu, Pokhara, Biratnagar, Nepalganj and Dipayal) at return periods of 475- and 2,475-years considering Vs,30=760 m/s. The results obtained are generally consistent with most recent studies. However, a notable variability in hazard levels and several discrepancies with respect to the Nepal Building Code NBC105: 2020 [1] and Global Hazard Model, GEM [2] are noted and possible causes are discussed.
Keywords: 
Subject: Environmental and Earth Sciences  -   Geophysics and Geology

1. Introduction

Nepal is one of the most tectonically active regions of the world characterized by a rapid crustal deformation mainly due to rather rapid convergence between India and Eurasia plates, with shortening rates of 18-21 mm/yr [3,4,5]. This active convergence region has recorded some of the largest magnitude earthquakes in an inter-plate continental context (e.g., recently the 2015 Mw~7.8 Gorkha earthquake, 1934 Mw~8.0 Bihar earthquake). In addition, it is believed that the Himalayan region has potential to initiate megathrust earthquakes like the historical event that occurred on June 6, 1505, with an estimated moment magnitude up to 8.5 [4,6]. One of the particularities of earthquakes in the Himalayan region, unlike other subduction-like domains, is their shallow focal depths (< 20-40 kms), which usually initiate within the Main Himalayan Thrust (MHT) and propagate southward to the large faults of the Main Frontal Thrust (MFT) or the Main Boundary Thrust (MBT). These relatively shallow depth and high magnitude events pose a very high seismic risk issue for Nepal.
Assessing credible seismic hazard estimations for Nepal is a critical step to prepare, prevent and minimize the damages due to earthquakes. The need of credible seismic hazard assessment was highlighted through several recent seismic hazard studies ([8,9,10,11,13]) and the recent revision of national seismic building code of Nepal NBC105: 2020 [1]. These recent studies improved the seismic hazard assessment for Nepal. However, several key elements for state-of-the-art practice to conduct probabilistic seismic hazard assessment are yet to be explored, challenged, and reviewed to attain a comprehensive and up-to-date seismic hazard assessment for Nepal.
Among the recent PSHA models, the seismic source model integrated in Global Hazard Model (GEM)[2] is adapted from a study conducted at the scale of the Indian sub-continent by [7] and based on large scale area source zones which also includes deep seismogenic sources (up to 25-70 km) seems to be clearly not appropriate given the seismotectonic context of Nepal based on recent findings (for e.g., [71]). Most of seismic hazard studies previously performed relied on one single area-based source hazard model (e.g.: [8,9]) without sufficient consideration of uncertainties in terms of geometry, depth, and other seismic parameters.
The recent PSHA study [10] conducted specially for the new national building code of Nepal (in the seismic building code improvement efforts after 2015 Gorkha Earthquake) is a step toward a new seismic hazard model for Nepal. However, one of the main limitations of the study [10] is that the integrated model considers the MHT as the main controlling seismic source, without considering for alternative seismic source models. The recent works by [11,12] in the context of Nepal also mark important improvement in terms of consideration of alternative source models albeit limitations notably in consideration of seismic catalogue and propagation of uncertainties.
PSHA calculation involves considering the occurrence of multiple earthquake rupture scenarios and their uncertainties in a probabilistic manner to evaluate the probability of exceeding several ground motion levels over a certain time for a given site. Although, original methodology of PSHA calculation from Cornell [14] is well established, it continues to be improved with several recent advances notably in terms of propagation of both aleatory and epistemic uncertainties through input seismic parameters, methods of seismic rate computations (for e.g., homogenous, heterogenous or characteristic approaches), recent ground motion models and availability on more robust empirical data (e.g., instrumental catalogue, faults studies, seismic campaigns). Thus, this study attempts to consider these latest advancements in terms of PSHA methods to improve PSHA for Nepal Himalayas. Moreover, through this study we try to valorize recent data and findings for Nepal Himalayas to offer improvement notably through incorporation of an up-to-date earthquake catalogue, consideration of major fault sources, existing and alternative source models, and ground-motion models.
The adaptation and enforcement of credible seismic hazard estimations through the building codes provisions is paramount to prevent or minimize the damages of buildings and catastrophic losses due to earthquakes. In this study, we attempt to propose new alternative PSHA source models with the objective to contribute towards comprehensive seismic hazard studies for Nepal and potentially for the rational evolutions in seismic provisions within the future version of Nepalese building code (NBC). Hence, we perform a comparative evaluation of the uniform hazard spectra (UHS) obtained in this study with the design spectra proposed in the recent national building code NBC105:2020 [1] to assess the potential causes for differences.

2. Geodynamics and seismotectonic context

The Himalayan chain in Nepal is characterized by a complex fault system of predominantly ~1000km-long sub-parallel major thrusts from the south to the north: the Main Frontal Thrust (MFT), Main Boundary Thrust (MBT) and Main central Thrust (MCT)(Figure 1a). Minor crustal lateral and normal faults distributed overall the Himalayan chain accommodate part of the convergence at smaller scale. The MFT corresponds to surface active fault and is exposed along the southern edge of the Sub-Himalayan foothills with a roughly WNW-ESE strike. At depth, the MFT merges with a “decollement” that dips gently to the north beneath the Lesser Himalaya forming together the well-known Main Himalayan Thrust (MHT). The MHT results from the subduction between Indian and Asian plates and acts as a subduction interface even though the idea of a continental subduction (through under thrusting?) is still debated [15,16,17,18,19,20]. The MBT lies on the same “decollement” with steeper dip angle nearby surface whereas the MCT corresponds to an old thrusts zone underlying the green-schist facies rocks at the base of the Greater Himalayan Sequence. Geological reconstruction and micro seismicity models on the MHT agreed about the presence of two or three sub horizontal surface (or flat) bounded on several sides by more steeply dipping ramps. The presence or not of a duplex structure at depth is still debated [21,22] regarding to the lateral variation of the seismicity distribution. In any case, according to along-strike variation of the distance between the mid-crustal ramp and the surface trace of the MFT, it is clear that the geometry of the MHT system at depth is complex and varies from east to west [23](Figure 1b).
Geodetic studies shows a convergence perpendicular to the arc varying from 20.2±1.1 mm/yr in western Nepal to 21.2±2 mm/yr in eastern Nepal consistent with the long-term geomorphic shortening rates of 18-21 mm/yr [3,4,5]. Recent studies refined the total convergence rate between India and Asia at ~36 mm/yr from continuous GPS stations [24](Figure 1a) estimating that half of the convergence (reduced to ~14-19 mm/yr) is accommodated across Himalaya [25]. How this geodetic strain (i.e., stress accumulation) is distributed over the active structures of the Himalaya remains poorly documented because of gaps in GPS measurements. However, GPS observations allow to estimate that during the interseismic period the shortening rate rise from 0 mm/yr at the MFT to ~3mm/yr at the Himalaya piedmont (bounded by the MBT) to ~13-17 mm/yr north of the High Himalaya (bounded by the MCT)[26]. Furthermore, the authors deduced from geodetic data that the MHT is actually locked ~100-150km downdip from the MFT, that corresponds to a maximum depth of >20km [3,25], and this locked portion of fault can ruptures all the way to the surface during large earthquakes (Mw>8) as confirmed by geomorphic studies [22,27,28,29]. In terms of interseismic coupling, the MHT seems to be largely coupled along its complete length suggesting that there is no aseismic creep close to the MFT [30]. Yet, recent studies show that the MHT displays lateral variations of its coupling ratio suggesting regional heterogeneities with local low coupling ranging from 0.2 to 0.8 [31,32]. Hence, it is unclear which part of the interseismic shortening is involved in elastic/anelastic deformation which is critical to determine seismic potential of faults. In our models, we take a large range of fault coupling to overcome this issue.
Whereas the MBT formed earlier than the MFT, as suggested by parallel lithological contact with the Proterozoic stratigraphy level (named Lesser Himalaya domain) exposed in its hanging wall, recent activity along one of its reactivated segment has been observed through geological and geomorphic studies [6,33]. Even if no clear fault scarps have been documented along the MBT, geomorphic studies allowed to describe the occurrence of at least two large earthquakes over the last 2000 years (Figure 1b). The MFT and the MBT are located at the southern part of Nepal, spaced 20-50km apart, and bounded the Sub-Himalaya domain built out of Siwaliks sedimentary foreland basin. The MCT, located further north, formed at ~22-18 Ma and seems to have accommodated a total shortening of 140-500km [34,35]. At present-day, the MCT is considered as inactive by many authors [36,37] but might have actually remained episodically active as suggested by [15,38]. To the north of the MBT, the deformation is distributed over moderate active faults with right-lateral strike-slip component (i.e. Western Nepal Fault System, Karakoram fault…, [39]) then gradually displaying both lateral and normal components toward the Tibetan plateau.
Regarding the instrumental and historical seismicity, the region is characterized by dense and localized seismicity in the West and East-Southeast Nepal, with much less activity in the central part of the country (Figure 1b). Large (Mw>7) and great (Mw>8) earthquakes follow the same geographic distribution such as the two historical Mw>8 earthquakes, Mw ~ 8.5 in 1505 and Mw ~ 8.1 in 1833 and were situated more than 70km northward the MFT. The regional focal mechanisms reflect the surface fault style with mostly thrusting in the south, strike-slip in the central part and normal in the northern part [13]. The seismically active section of the MHT, because of its sub-horizontal dip (mean dip of ~8-10°), underlies most of Nepal and concentrates along the northern, down-dip edge of the coupled zone (interpreted as the brittle-ductile transition zone at depth and located ~100-150km from the MFT) suggesting that the well-known 1505 earthquake (and so the 1505 magnitude-like events) have been initiated on the MHT [6,40]. It appears that most of the seismicity in Nepal (>70%) is shallow seismicity (<25km) so are in the hanging-wall of the MHT or probably on the MHT itself, with a small chance of being on secondary splay faults (or/and duplex?). The up to 30km-depth part of the seismicity is randomly distributed over the whole country while the earthquakes up to 40km-depth seems to underline a roughly ~W-E-oriented wide band.

3. Seismicity database

3.1. Compilation of Seismicity Database

In Nepal, National seismic monitoring through localized seismic networks began in early 1980s. Since then, the catalogue completeness in the region has changed significantly over time due to the increase in the seismic station’s coverage. The historical events were compiled through various relevant studies [9,41] and Global Historical Earthquake Archives (GHEA)[42]. The instrumental earthquake catalogs for the Nepal and surrounding regions are mainly available from the National Seismological Centre, Nepal (DMN) and National Centre for Seismology – India (NDI). The global catalogues which provide revised estimation for magnitude (CMT), for location (EHB) and ISC-GEM catalogue [43,44,45] were also considered based on a broad region between 75°E and 93°E in longitude and 24°N and 34°N in latitude, to be able to work with a robust seismic sample to establish the correlations between the different magnitude scales and the moment magnitude Mw.
The data available from various agencies/institutes (see Table 2) were used for compilation of unified catalogue. Duplicate events were identified and removed in the final earthquake catalogue. Time, distance, and magnitude intervals were chosen by trial-and-error tests. The potential duplicate events were flagged and then manually reviewed to check that duplicates were correctly identified. We adopted the scheme (difference in distance, time, magnitude) presented in Table 1 as a final choice.
After identification of duplicates, the location of the events was retained according to the following source priority criteria defined based on the relative degree of reliability on the epicentral locations: ISC_GEM, EHB, ISC, NDI, USGS, REF, GHEA and GCMT. Figure S1 represents the repartition of source epicentral locations as a function magnitude and time for final compiled catalogue for this study. The final homogenized raw catalogue contains 12,584 events above Mw* ≥ 1.0, among which 145 are Mw* ≥ 6.0 and 39 are Mw* ≥ 7.0 and 8 are Mw* ≥ 8.0.

3.2. Magnitude Homogenization

Magnitude homogenization into moment magnitude Mw, was carried out adopting a priority scheme based on magnitude types: direct moment magnitude (Mwd), proxy moment magnitude (Mwp), local magnitudes (mL), surface wave magnitude (Ms), body wave magnitude (mb), duration magnitude (md), coda wave (Mc) and Non-specified magnitude (M).
We compared the magnitude pairs and different magnitude conversions available in the recent bibliography along with two general and ordinary orthogonal regressions (GOR and OOR) evaluated based on the magnitude pairs obtained in this study (Figure 2, Table 3). The Mw, NDI show the systematic shift with respect to GCMT, a possible underestimation specifically for magnitude lower than 5.5. Thus, GOR established through the pairs (which considers uncertainty in two directions), was used to adjust direct moment magnitudes Mw, NDI. And proxy moment magnitude (Mwp) was adopted as equivalent to Mw as it mostly concerns events from ISC_GEM catalogue which are reviewed.
Similarly for other magnitude types, the analysis of magnitude pairs led to choose of relationship proposed by [44] for Ms, [52] for Mb and [51] for mL, DMN .
GOR relationship established through magnitude pairs evaluated in this study (Figure 2, Table 3) was adopted for mL, NDI, and mL, BJI. Regarding the events that contains only md, Mc or M, considering lack of enough magnitude pairs with reference Mw for specific evaluation, we adopted 1:1 equivalent relationship to convert to Mw. The homogenized magnitude is noted as Mw* with an uncertainty equal to recombined variance of the original magnitude estimate and of the variance associated with the conversion models.

3.3. Declustering of the Seismicity Catalogue

The spatio-temporal windows proposed by Gardener and Knopoff (GK74) [53] was adopted to obtain statistically independent declustered catalogue. The histogram (Figure 3) shows that for both raw and declustered catalogue, the number of events below magnitude 4.0 marks an inflection point which indicates that the catalogue is mostly not complete below the magnitude of 4.0. The declustering process identified about half of the events (53.7%) as mainshocks and rest of the events are identified as either foreshocks (9.4%) or aftershocks (36.9%). The other algorithms available for declustering like the one from Uhrhammer [54] were not considered in this study. They will be considered for the tests of their applicability in future updates.

3.4. Completeness Periods

The catalogue of seismicity was analyzed to define the completeness periods (after which the annual rate of earthquakes become approximately constant i.e., stationary) per range of magnitudes based on the evaluation of cumulative number of events and inter-event variance [55] (Figure 4, Figure S1 and Figure S2). For each magnitude bin, we evaluated the range of completeness year to consider uncertainties (Table 4). This uncertainty range increases for higher magnitude bins for which the completeness period is longer and data are scarce. The mean completeness period established is 21 years for lowest magnitude range of Mw3.0-3.5 and 821 years for the highest magnitude range of Mw8.0-9.0. We considered 2021 as end year to avoid possible biases since seismicity data for the recent years is usually not complete or are subject to revisions.

4. Seismic Source Characterization

The seismic source models (SSM) are made of seismic source zones that represent volumes of the earth crust and linear individual faults exhibiting the same seismotectonic regime and seismicity occurrence features. They are modeled assuming that the seismicity is either homogenously or heterogeneously distributed over their extent and the occurrence parameters are calculated by processing the subset of events that occurred within the polygon describing the seismic source. Seismic hazard studies previously performed in Nepal [8,9,11,13,56], provides significantly variable PSHA results since the SSC models and hypothesis used are not consistent from one study to other. Thus, the intent of the current study was to consider the existing model proposed by [9], which is mostly based on seismicity patterns, and to also develop independent and more accurate SSM applicable to the Nepalese Himalayas including in turn three types of seismic sources at regional scale: the crustal volume sources, the major Himalayan crustal fault sources and the subduction-like interface domain.
From the previous models [8,9,11,56] it was evidenced that the seismic hazard was controlled by crustal zones and fault sources. However, there is a deep thrust decollement layer (the Main Himalayan thrust, MHT) acting as a wide plate interface with an important seismogenic potential that must be considered into the models. [13] previously included the MHT also the Karakoram fault as single fault sources in their probabilistic hazard models associated to sparse areal sources centered on active faulting region. However, the models do not consider the others main structures connecting on the MHT at depth as alternative source of hazard for Nepal despite their recent activity [6,15,33,38]. In contrast to [13] and based on the MHT fault coupling values from [31,32], we decided to consider in our models the two major seismogenic structures of Nepal accommodating most of the regional shortening rate, that is to say mainly the Main Frontal Thrust (MFT) and the Main Boundary Thrust (MBT), and also a minor part on the Main Central Thrust (MCT) and active strike-slip/normal faults located in northern Nepal.
Therefore, the models developed in this study incorporate alternative source model geometries, based on the geometrical complexity of the seismogenic structures at depth (i.e. ramp and flat on the MHT) and include the tectonic lateral variations observed in the region [3,4,5,6,13,25,33,57,58,59,60,61,62,63]. This approach of modelling implies that although specific active faults are not introduced in the hazard model, they are modelled through generation of fictious rupture planes anywhere in the volume however not able to generate earthquakes stronger than the adopted magnitude threshold.
The intention is also to adopt two alternative methods for the determination of the activity rates. In the first one, the activity rates are assumed to be homogenously distributed in each seismotectonic volume. In the other, the spatial variability of the activity rates is accounted for by a smoothed seismicity approach in which alternative kernel functions are considered.

4.1. Homogenous Volume Sources

4.1.1. Source model based on Thapa and Wang (2013) – SM1

The seismic source model named SM1 is inspired from [9] and is composed of initially 23 zones to which a zone was added in the foreland basin of the Himalaya chain, allowing to consider the seismicity at the southernmost Nepal (Figure 5). These 24 zones encompass the major seismotectonic domains to cover the active regions to the West (India), the East (Bhutan) and to the North (Tibet plateau, China). The SM1 zonation encompasses the Nepalese Himalayan mountains, from South to North: (i) the ~W-E to WNW-ESE active thrusts (MFT, MBT) in the Outer Himalaya, (ii) the mainly ~W-E reverse to ~N-S lateral faulting in the Lesser Himalaya and (iii) the mainly ~ N-S normal to ~SE-NW lateral faulting of the extensional Tethys Himalaya at southern Tibet. In terms of seismicity magnitude and distribution, most of the instrumental and historical seismicity is distributed along an arc-parallel band in the Lesser Himalaya. In detail, the seismicity is concentrated into two clusters with the highest magnitude earthquakes localized in the East, in the vicinity of Kathmandu city, and in the Far Western region. While [9] set a hypocenter depth for active crustal seismicity comprised between 0-10km for the whole region, we applied maximum depth of rupture up to 20km for the zones Z1 to Z8 and Z24, 30 km for the zones Z9 to Z18, 40 km for the zones Z19 to Z23, according to the northward low-dipping geometry of the thrust beneath the whole Nepal [64,65] and considering that the majority of the earthquakes in Nepal occurred along and above the MHT. In addition, we consider a subduction-like interface domain with maximum magnitude up to Mw~9.0 for the zones Z9 to Z18, where the greatest magnitude historical seismicity is assumed to be localized. Whereas the zones Z1 to Z8 and Z19 to Z24 are referenced as a domain of active crustal deformation that corresponds to an intraplate tectonic regime where the magnitude of earthquakes never exceeds Mw~7 (Table 5). As such, according to the maximum magnitude at each zone provided by the seismicity catalog, we attributed maximum magnitude of Mw~7.5 for the region Z1 to Z8 and Z24, and Mw~7 for the area Z19 to Z23. In both cases, we cautiously add 0.5 to the maximum magnitude observed at each zone before integration into the model (see appendix A, Table for detailed parameters).
In terms of faults characterization parameters, we used the comprehensive AFEAD fault catalog (http://neotec.ginras.ru/index/mapbox/database_map.html) to draw the active faults traces overall the region and to collect fault attributes. We also compiled the focal mechanism from the literature [3,57,59,61,62,66,67] and the CMT catalog (https://www.globalcmt.org) in order to better assess the kinematics of faulting in each area. Thus, we assign a major, medium, and minor percentage coefficient for the three categories of fault kinematics (strike-slip, reverse, normal) corresponding to what have been observed or inferred within each zone. Finally, for each category, we determine the fault attributes values associated to their uncertainties (strike, dip, and rakes) based on the AFEAD fault database and the references therein.

4.1.2. Source model including the MHT geometry – SM2

The seismic source model named SM2 developed for this study is composed of 19 zones that cover the major seismotectonic domain of Himalayan Mountain i.e., western Nepal, North and East India and South of Tibet (Figure 6). The SM2 area source model varies from the SM1 model in the sense that we consider the kinematics but also the geometry of the faults, the seismicity magnitude and distribution and we mimic the geometry of the ramp-and-flat pattern of the decollement layer (MHT) at depth to define the boundary of the areas. The geometry and size of the polygons areas are consistent with the surface faults traces encompassing : (i) the sparse strike-slip faults within the foreland basin (S1) (ii) the ~1000km long ~W-E to WNW-ESE active thrusts (MFT, MBT) in the Outer Himalaya (S2-S5), (iii) the mainly ~W-E reverse to ~N-S lateral faulting in the Lesser Himalaya (S6-S10), (iv) the MCT and MCT sub-parallel ~E-W reverse faults to ~N-S and NW-SE strike-slip and normal faults (S11-S16), (v) the mainly ~ N-S normal to ~E-W lateral faulting of the extensional Tethys Himalaya at southern Tibet (S17-S19). For SM2 model, we assigned the same depth distribution than in the SM1 model, with a maximum depth of rupture up to 20km for the zones S1 to S5, 30 km for the zones S6 to S10, 40 km for the zones S11 to S19. In addition, the SM2 source model extends further north and west than the SM1 model since we consider here the ramp-and-flat basal decollement layer extending over more than ~150km beneath the Nepal with a surface extent of ~1000 km (maximum rupture length of the MHT) encompassing the seismicity clustering to the west [13,23,60](Figure 6). Therefore, this implies that the subduction-like interface domain with maximum magnitude up to Mw~9.0 encompasses the zones S6 to S10 and S14 to S16, where the greatest magnitude seismicity is localized. Whereas the zones S1 to S5, S11 to S13 and S17 to S19 are referenced as active crustal deformation that corresponds to an intraplate tectonic regime where the magnitude of earthquakes never exceeds Mw~7. As such, according to the maximum magnitude at each zone provided by the seismicity catalog, we attributed maximum magnitude of Mw~9 for the zones S14 to S16 located around the epicenter of 1505 AD earthquake. We attributed maximum magnitude of Mw~8.5 for the zone S6 in the East (Kathmandu vicinity), ~Mw8 for the zones S7 to S10, Mw~7.5 for the zones S1 to S2, S11 to S13, S17 to S19 and Mw~7 for the zones S3 to S5. In both cases, we cautiously add 0.5 to the maximum magnitude observed at each zone before the integration to the model (see appendix A, Table for detailed parameters). In terms of crustal structure, we delimitate the polygons boundaries reflecting the geometry of the MHT proposed by [13] with a simplified ramp-flat-ramp symmetrical structure emerging at the MFT and rooting at 20-40 km depth. This is consistent with the fact that the surface fault traces as well as the seismicity distribution are related to the geometry of the basal thrust at depth according to [3] and as it has been highlighted during the 2015, Gorkha earthquake [68].
As for the previous source model, we used the comprehensive AFEAD fault catalog (http://neotec.ginras.ru/index/mapbox/database_map.html), the focal mechanism from the literature [3,57,59,61,62,66,67] and CMT catalog (https://www.globalcmt.org) in order to better assess the kinematics of faulting in each area.

4.1.3. Macrozone/Fault source model – SM3F

To consider the major thrust faults of Nepal region capable to accommodate the entire convergence rate and thus, to produce large to great earthquakes (Mw>8) we defined two simplified homogenous seismic zones model at regional scale (called SM3F). Unlike the two previous models, we consider the faults in the north area as 3D planes that allow to reflect accurately the geometry and kinematics of the major faults at depth, associated (or not) to the basal decollement layer (MHT). In order to prioritize the effect of the major fault in the seismic hazard models, we simplify the seismicity source volumes to two areas with homogenous seismicity (Figure 7) and in turn, we consider that the great magnitude earthquakes (Mw≥8) initiate on the MHT at defined depth and can rupture the main structures such as the MFT and the MBT. Furthermore, according to recent published studies [68,69,70] that highlight a slip rate deficit over the Himalaya chain, we propose, as a new approach, that part of the convergence rate can also be distributed among known (or unknown) individuals crustal faults, with or without surface expression, located northward between the MBT and the Tibetan plateau (e.g. the MCT) that can also produce large magnitude earthquakes. Each of these structures are weighted, depending on their probability of occurrence (given their recurrence rate of earthquakes, whether it is known), before to be introduced into the models. In addition, three fault recurrence models are applied based either on geological data (i.e., slip rate) or on the seismicity catalog distribution to account for the epistemic uncertainties.
Hence, the simplified two seismic source zones (NPL_NORTH, NPL_SOUTH) are located either side of the frontal thrust (MFT) that circumscribe the seismically active zone at North and the less active foreland basin at South as suggested by the distribution of the seismicity. The external boundaries encompass the most active part of Himalaya eastward and westward Nepal (i.e., India at South, East and West and Tibetan Plateau at North). In addition, the north area (NPL_NORTH) is considering as a subduction-like interface domain capable of Mw≥8, according to the historical records of M>8.5 events (e.g. the 1505 earthquake)[4,28] with major reverse and minor lateral and normal faulting components and includes 3D faults geometry with a depth of rupture varying from 15km to 40km (see Appendix A, Table for detailed parameters). Unlike Northern zone, the Southern zone (NPL_SOUTH) is considered as a domain of active shallow crustal deformation (that corresponds to an intraplate tectonic regime) where the magnitude of earthquakes never exceeds Mw~7.5 with maximum depth of 20km and with a major strike-slip component.
The internal boundary between the two polygons follows the sharp geometry of the very frontal thrust (MFT) that reflects the complex geometry of the flat-and-ramp fault plane at depth.

4.1.4. Homogenous Activity Parameters

The observed activity rates of the seismotectonic zones of the crustal and subduction interface sources are determined from the catalogues compiled for this study. In each zone, the seismicity is homogeneous, and the Gutenberg-Richter relationship [72] is assessed. The Gutenberg–Richter model has been adopted to calculate the seismic activity rates in its truncated form. The EPRI [73] method is adopted to determine the a and b value which is an updated and improved version of the Weichert method [74] which takes into account the magnitude uncertainty of each event. Figure 8 is an example of the Gutenberg Richter model evaluation made for a zone (Z17) volume source included in SM1 which represents one of the most active regions of Nepal. The parameters (a and b values) obtained are consistent with expectation for the active regions. We merged the zones of similar tectonic features to compute GR to make the seismicity sample more statistically robust (for example we merged Z1, Z2 and Z3 in Southwest of Nepal). The Gutenberg-Richter models derived for all the sources SM1, SM2 and SM3 (see Appendix A, Table to Table for further details) are reasonably well constrained. The a-value parameters are scaled to area of million square kilometers for inter-comparability purpose. It should be underlined that b-values obtained for the sources are close to the adopted prior value 1.0.
The comparison of activity rates in terms of annual rate of occurrence (λ) (scaled to million km² considering Mw≥6.0) derived from the GR adjustments (Figure 9) shows the variation of effective seismicity rates. In general, we can observe the progression of higher rates from zones in south to the zones in north consistently with the historical seismicity patterns. The highest rate is obtained for zone Z17 in SM1 and zone S8 in SM2. For the case of SM3, the highest seismicity rate is obtained for NPL_NORTH. These differences between SM1, SM2 and SM3 demonstrates the part of epistemic uncertainties for final PSHA calculations.

4.2. Major Himalayan Thrust Fault Sources

The MHT is the main seismic source in Nepal and has potential for mega earthquakes. The MHT is thought to extend as a succession of flat and ramp decollement beneath the Lesser Himalaya and to form a steeper ramp at the front of the High Himalaya (Figure 7b). Most of the crustal deformation in the Himalaya occurs on the Main Himalayan Thrust fault (MHT) [5,58], where the Indian lithosphere underthrusts beneath the chain. The MHT absorbs about 20 mm/yr of the India-Eurasia convergence [76] which accounts for about half of the total convergence rate. The MHT reaches the surface at the Main Frontal Thrust fault (MFT) [36], where the secular slip rate has been estimated from the study of uplift of Holocene terraces to be ~20 mm/yr [4,5,61,70]. Whereas the MBT formed earlier than the MFT, as suggested by parallel lithological contact with the Proterozoic stratigraphy level (named Lesser Himalaya domain) exposed in its hanging wall, recent activity along one of its reactivated segment has been observed through geological and geomorphic studies allowing to describe the occurrence of at least two large earthquakes over the last 2000 years [6,33]. The MCT, located further north, formed at ~22-18 Ma and seems to have accommodated a total shortening of 140-500km [34,35]. At present-day, the MCT is considered as inactive by many authors [36,37] but might have actually remained episodically active as suggested by [15,38]. To the north of the MBT, the deformation is distributed over moderate active faults with right-lateral strike-slip component (i.e. the Western Nepal Fault System, the Karakoram fault, … [39]) then gradually displaying both lateral and normal components toward the Tibetan plateau
Previous geodetic and modelling studies [23,76,77,78] assumed the MHT to be locked from the surface to a certain depth and found a satisfying fit to the data with a mean fault dipping about 8-10° to the north and a downdip end of the locked part of the fault about 100-150 km from its surface trace. The observation of meter-scale displacements on some regions of the MFT indicates that during large (Mw > 8) earthquakes, the locked portion of the fault sometimes ruptures all the way to the surface [28,36]. The width of the fault surface that corresponds to the locked-to-creeping transition has been estimated around >20km depth [25,79]. In our models, we consider that the Mw>8 great earthquakes initiate on the MHT and either propagate onto the MFT (MHT+MFT) accommodating 60% of the slip rate or onto the MBT (MHT+MBT) accommodating 20% of the slip rate or onto various individual crustal faults scattered between the MBT and the normal-faulting Tibetan plateau (including the MCT) accommodating the last 20% of the slip rate [23,76].
Furthermore, according to paleo seismological studies, Himalaya may have produced earthquakes with magnitudes as high as Mw 8.8. Along the Himalayan foothills in Nepal, there is evidence for a ~17m slip event on the MFT (dated to 1100 C.E) at locations separated by 240 km along strike [28,36]. Evidence for a similar event with an age loosely constrained to ca. 1413 C.E. was also found in the Kumaon and Garhwal Himalaya [40]. In fact, there is a possibility that these paleo ruptures may relate to the 1505 historical earthquake, which would then be inferred to have ruptured the Himalayan front from western Nepal to Garwhal over a distance possibly as large as 800km [80]. Hence, regarding the maximum magnitude (Mw ≤ 9) and depth of rupture (≤ 40 km), we assume than the fault surface rupture does not exceed an average length of 1000 km that can rupture at once. In addition, to be consistent with the geological data from the literature we consider in our model a mean slip rate of 16 mm/yr overall Nepal [23], a MHT mean dip of ~8° [3], a wide range of fault seismic coupling comprised between 20% and 80% [27,31] as predicted from its lateral geometry variation [31,32].
Three alternative recurrence seismicity models were considered for the faults which includes a characteristic model [81] CHAR_YC85 and exponential model [81] GR_YC85 for which the fault activity is characterized by documented geologic, geomorphic, or geodesic data. In characteristic (CHAR_YC85) model, the annual rate takes a uniform distribution above a certain threshold of magnitude while in the exponential (GR_YC85) approach, the distribution of the seismic annual rates with magnitude takes a truncated exponential form: the activity rate is constrained by the upper bound magnitude, the b-value for the region and the fault slip rate. The third model is Poissonian, GR_ab model based on GR parameters calculated from the seismic catalogue.
The limit of background Mmax 8.0 is chosen since we model the major thrusts able to generate the megathrusts earthquakes. Below this magnitude threshold, the seismicity is uniformly distributed in the volume of the background zone on fictitious faults and constrained by the GR parameters of the zone. The sensitivity analysis due to alternative recurrence models is conducted and subsequently weights are assigned which is discussed in details section 6.

4.3. Heterogenous or Smoothed Models – SM4

As an alternative to the homogenous seismicity rate model, a smoothing approach was used which avoid the use of any seismotectonic zonation. This method assumes that future earthquakes are considered more likely to occur near past earthquakes than in areas where no earthquakes have been observed.
Two types of algorithms were used for the definition of the kernel: firstly a fixed kernel [82] whose width is proportional to the magnitude of the earthquake only and a second algorithm called adaptative kernel that defines the kernel adaptively [83] based on number of neighboring events. The smoothing width corresponds to the distance to the nth nearest earthquake whose magnitude is greater than or equal to the minimum magnitude threshold. A magnitude threshold of 4.5 was chosen assuming that catalogue is relatively well constrained only above this threshold and the rates were computed for each grid points at 10 x 10 kms. The computed smoothed seismicity rates were implemented considering the seismicity limits and parameters defined for SM2, and thus introduced into the final SSC logic tree (Figure 13) as SM4. Similarly, the major thrust faults were introduced while considering the smoothed seismicity rates for the background seismicity and seismicity limits and parameters defined for SM3F and thus into the final SSC logic tree (Figure 13) as SM4F.
In the region characterized by a relatively high concentration of earthquakes like Nepal, the short smoothing width is deemed most appropriate. Two alternative kernels SA5 and SF10 (Figure 10) were finally selected as enough and non-redundant within a logic tree framework of SSC to better account for the epistemic uncertainties in the activity rate estimates. No spatial limits are applied for what concern the region of interest to compute the rates to take into consideration the uncertainty linked to the limits between high activity in North-Northeast and relatively stable South-Southwest to consider the uncertainty in location of major thrust faults.

5. Ground Motion Models

Selection of appropriate ground motion models (GMMs) applicable to Nepal is clearly one of the main challenges since currently, no fully local GMM based on locally observed seismic data has been developed suitable for PSHA purpose [84]. Some efforts have been made in recent years to develop GMM adapted for Himalayan context (e.g.[85,86,87]), however, for this study, we exclude the application of such GMMs due to several limitations such as model developed for estimation of PGA only or/and use of very limited local data from Nepal for development of GMM. Hence, for this project, we made the simple choice to adopt a multiple GMM approach using GMMs developed based on global or Japanese datasets.
Hence, we carefully analyzed GMMs recently published and also the ones used in recent PSHAs carried out in Nepal [2,84] and selected several GMMs developed based on data from similar seismotectonic settings to account for epistemic uncertainties. The suitability of the set of GMMs were verified according to the criteria (e.g., tectonic regime, functional form, regression coefficients, frequency range of the model, datasets, etc.) based on [88]. The final selected GMMs, combines five GMMs to model the ground motion in Active Shallow Crustal (ACR) sources and six GMMs developed for the subduction interface-like sources.
Among the six GMMs selected for the subduction interface-like sources, we selected three GMMs of ACR type and three GMMs of subduction interface type consistently with the strategy adopted in some recent studies e.g. [12]. However, we considered interface type GMMs with lower weight, because although subduction like ground motion is not fully ruled out for applicability in Himalayan region, several studies ([8,9,10,11,13]) have suggested ACR type GMMs are most likely more appropriate for Nepal, albeit they are based on the evaluation made from limited empirical data available.
The sensitivity analysis (Figure 11), shows that the variability due to GMMs are essentially controlled by subduction type sources and the ACR type GMMs indicates very limited variability. It is simply because the contribution of ACR type sources to the hazard remains very limited for the considered site (in this case Kathmandu). In general, among the GMMs applied to subduction like sources, the AB03 [89] leads to lowest hazard levels while ZH16 leads to the highest. All other GMMs [90,91,92] leads to hazard levels fluctuating close to median. Finally, among GMMs grouped into the subduction interface type, we weighted all the crustal type GMMs (2/3) while giving relatively lower weight (1/3) to the subduction type GMMs. Furthermore, all the ACR type GMMs considered for subduction interface sources were equally weighted among each other, while among the subduction interface type GMMs i.e., ZH16 [93] was given slightly lower weight since it leads to the highest relative differences among GMMs used for subduction type sources.
Preprints 73215 g011
Figure 11. Relative differences in response spectra calculated for each GMMs, return period of 475 years, site of Kathmandu, Vs30=760 m/s (a) GMPEs applied to interface type sources and (b) ACR type sources. Note the difference of y-scale between two figures.
Figure 11. Relative differences in response spectra calculated for each GMMs, return period of 475 years, site of Kathmandu, Vs30=760 m/s (a) GMPEs applied to interface type sources and (b) ACR type sources. Note the difference of y-scale between two figures.
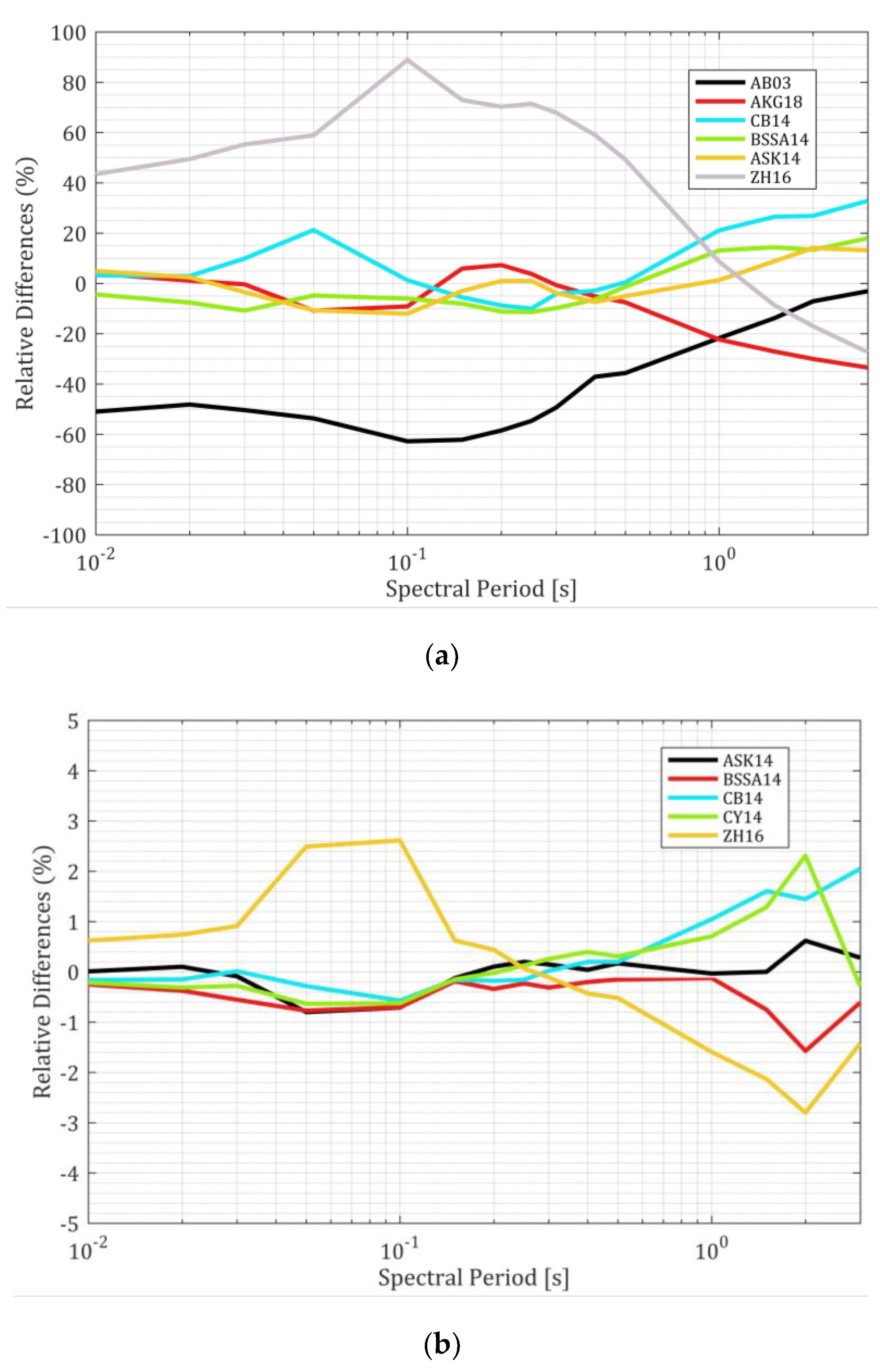
Preprints 73215 g011
Table 5. Selected GMPEs for crustal and Himalayan collision domain.
Table 5. Selected GMPEs for crustal and Himalayan collision domain.
Target
Source 		GMM GMM
Type		 Weight
Active shallow crustal sources CB14 [92] Crustal 0.2
BSSA14 [91] Crustal 0.2
CY14 [94] Crustal 0.2
ASK14 [90] Crustal 0.2
ZH16 [95] Crustal 0.2
Himalayan Collision Zones
(Subduction interface like sources)		 AB03 [89] Subduction 0.13
ZH16 [93] Subduction 0.08
AKG18 [96] Subduction 0.13
BSSA14 [91] Crustal 0.22
CB14 [92] Crustal 0.22
ASK14 [90] Crustal 0.22

6. SSC Sensitivity Analysis and Logic Tree

The sensitivity analysis was carried out to better identify the components of the SSC models that affect the most the hazard estimates. The seismotectonic models presented in Section 4 are integrated into a sensitivity test to determine the impact on the hazard calculation of each of the hypotheses considered (Figure 13). An aleatory uncertainty related to distribution for magnitude, hypocentral depth and fault orientations were also explored. A right trapezoidal distribution was used for hypocentral depth, left trapezoidal distribution for maximum magnitude between two bounds (see Appendix A, Table to Table for further details). For each seismic sources, the style of fault mechanisms can be normal, reverse or strike-slip for which a probability was assigned based mainly on evaluation of fault parameters in fault database and focal mechanisms of past events.
The results of the sensitivity test are shown for the return periods of 475 years (Figure 12). We chose to make sensitivity analyses based on tornado plot which allows to visualize sensitivity of all SSC branches introduced and for different sites in same figure. The different seismicity models introduce significant variability, of about ± 25% to ± 50% depending on the site. In general, regardless of site and spectral periods, the models integrating the major fault sources (SM3F and SM4F in logic tree) lead to the higher results compared to the average of the models. The homogenous volume models without individual faults (SM1 and SM2) are either close to the center of the distribution or lower compared to the models integrating the thrust faults. Similarly, the smoothing models without individual faults (SA5 and SF10) lead to lower results compared to the average of all the models.
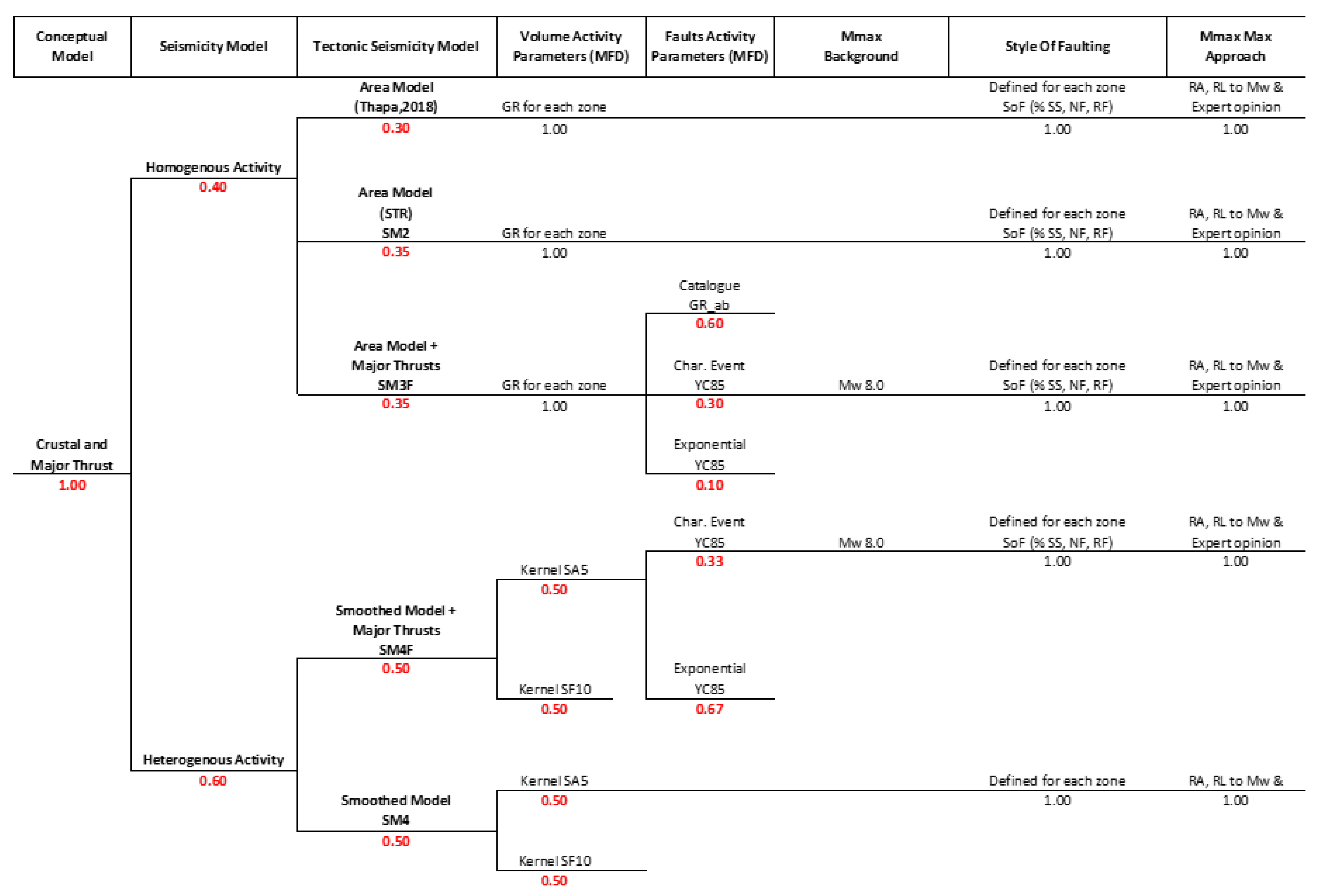
The application of a logic tree allows the capturing of epistemic uncertainties in different input models [97,98] by deploying alternative models in the hazard estimation. The SSC logic tree (Figure 13) was built by selecting and weighting the conceptual models (models in volume source zones, models by fault and smoothed models), then by selecting and weighting the models within each of the conceptual models.
In the study area, seismicity catalogue seems to better capture the local variability of seismicity. We therefore attribute a slightly higher weight of 60% to the heterogenous or smoothed models compared to the 40% for homogenous models.
The sub-branches concerning the homogenous models, a higher weight of 35% each is adopted for models developed within the framework of this study (SM2 and SM3F) since it relies on both seismicity distribution and division of the seismotectonic units by large active structures among which the SM3F introduces a clearer distinction based on the seismicity distribution of the background and major thrusts. The zones in SM1 model were developed mostly based on seismicity patterns only. For this reason, it was decided to assign a lower weight (30%) to SM1 compared to the SM2 and SM3F (35% each one).
The sub-branches concerning the recurrence activity of the faults in SM3F, constitutes three alternative models. The recurrence model derived from the exponential Gutenberg Richter parameter of the background zone, SM3F_GR_ab model is given highest weight (60%) among others because we believe that the seismicity sample is relatively more representative of the actual seismicity compared to the other two models namely characteristic (SM3F_CHAR_YC85) and exponential model (SM3F_GR_YC85) based on [81] which are based on slip rates that remain highly uncertain. The YC85 exponential model (SM3F_GR_YC85) is assigned the lowest weight of 10% since, in the sensitivity analysis, it follows closely the hazard levels attained by SM3F_GR_ab for which we assigned highest weight.
Regarding the smoothed models, the two kernels (SA5 and SF10) are introduced with equal weighting. An equal weight is assigned between the smoothed models with (SM4F) or without (SM4) individual thrust faults. Similarly, the sub-branches concerning the recurrence activity of the faults in SM4F (for which the background seismicity adopted is from gridded approach), constitutes two models namely characteristic (SM4F_CHAR_YC85) and exponential model (SM4F_GR_YC85) based on [81]. We give higher weight (2/3) to the exponential model (SM4F_GR_YC85) mainly because the exponential model seems to be more consistent with the bulk of results obtained from all other SSC models considered.
Preprints 73215 g013
Figure 13. Logic tree adopted for the seismotectonic model in hazard calculation and treatment of uncertainties.
Figure 13. Logic tree adopted for the seismotectonic model in hazard calculation and treatment of uncertainties.
Preprints 73215 g013

7. Results and discussion

Results of the probabilistic seismic hazard assessment are presented in the form of Uniform Hazard Spectra (UHS) for horizontal components after post processing the seismic hazard curves obtained for a series of combinations of the SSC and GMC interpretations and 200 samples of Monte-Carlo exploration in seismic parameters (GR parameters, magnitude, hypocentral depth, style of faulting, etc.). The PSHA hazard calculations were carried out with a minimum magnitude of integration of 5.0, considering the high seismic activity of the target region. The PSHA calculation was performed using SEISTER inhouse SHA toolbox.

7.1. UHS at Five Selected Locations

The uniform hazard spectra (UHS) (Figure 14 and Figure 16) obtained at both return periods considered (475 and 2,475 years) show that the highest hazard among the five locations considered is obtained for the Northwestern town of Dipayal while the lowest is obtained for the Southern city of Biratnagar.
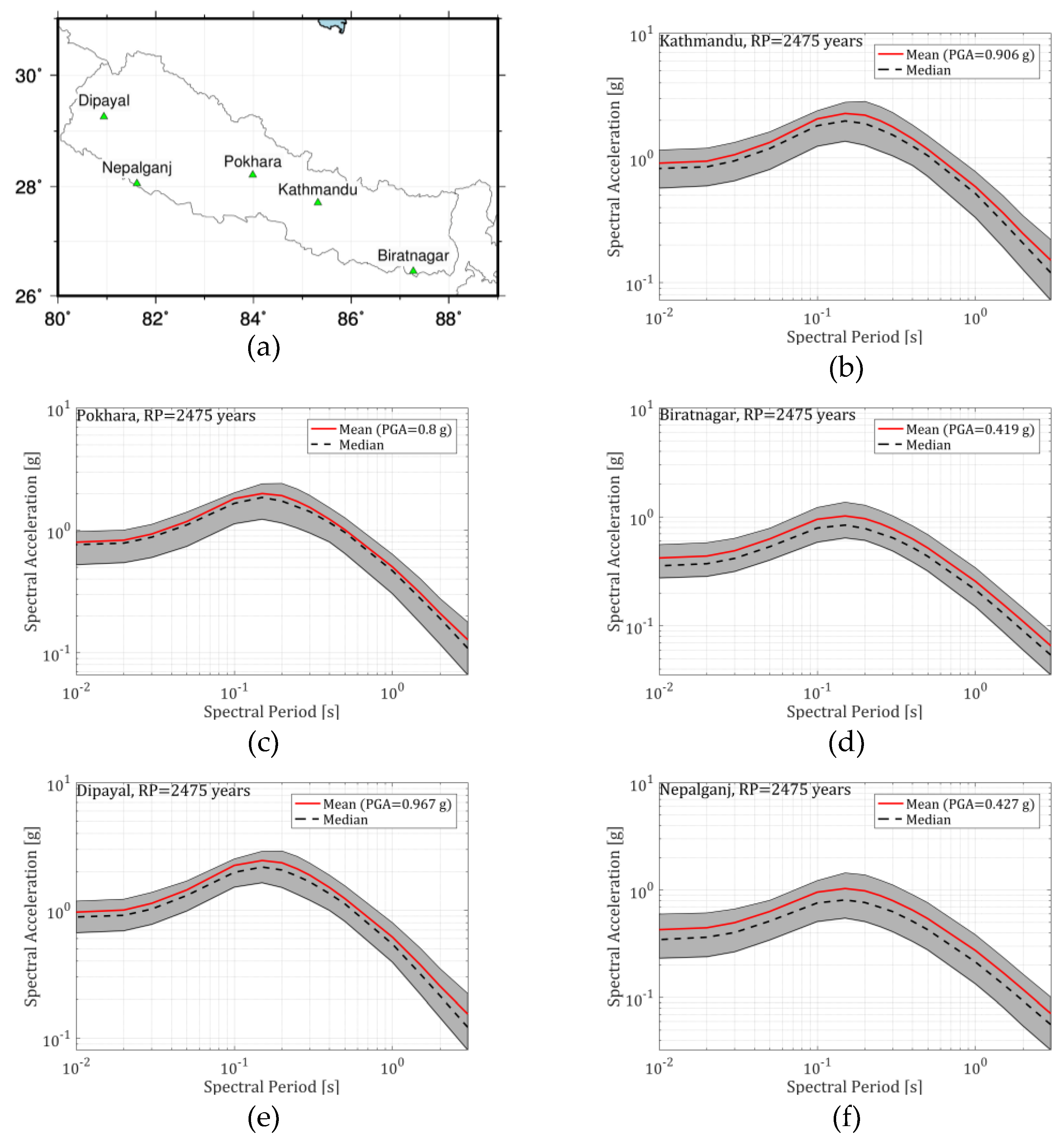
At 475-year return period and considering Vs,30 of 760 m/s, the mean PGA obtained among the studied sites varies from 0.186g at Biratnagar to 0.488g at Dipayal. The mean PGA obtained at Kathmandu, Pokhara and Nepalganj are 0.424g, 0.381g and 0.190g respectively. Similarly, at 2,475-year return period, the mean PGA obtained among the studied sites varies from 0.419g at Biratnagar to 0.967g at Dipayal. The mean PGA obtained at Kathmandu, Pokhara and Nepalganj are 0.906g, 0.8g and 0.427g respectively. At both return periods and all sites, the consistency of the mean and median (the mean lies slightly above the median) demonstrates the well-balanced logic tree adopted. We note that these hazard levels are closely coherent with the hazard levels obtained in some of the previous studies e.g. [12].
The uncertainty coefficients computed based on equation [99] which considers the centiles 16 and 84% for UHS obtained at Kathmandu are at 52.6 and 63.1 % for 475- and 2475-year return periods respectively. This relatively large uncertainty coefficient reflects the large degree of uncertainty integrated through SSC and GMM models. Moreover, it also reflects the uncertainties propagated in various seismic parameters like maximum magnitude, depth, style of faulting, etc.
The evaluation of the relative impact of the SSC logic tree scheme (Figure 15) demonstrates that regardless of the site considered, the SSC models integrating the major faults lead to a higher mean compared to the obtained weighted mean. On the other hand, the smoothed models and homogenous volume models lie relatively below the weighted average. Thus, the weighting scheme seems to balance the possible underestimation or overestimation due to various SSC models. Moreover, we observe that the cities located in the foreland areas (i.e., the less active region of Nepal) display larger variability compared to that region with higher seismic hazard.
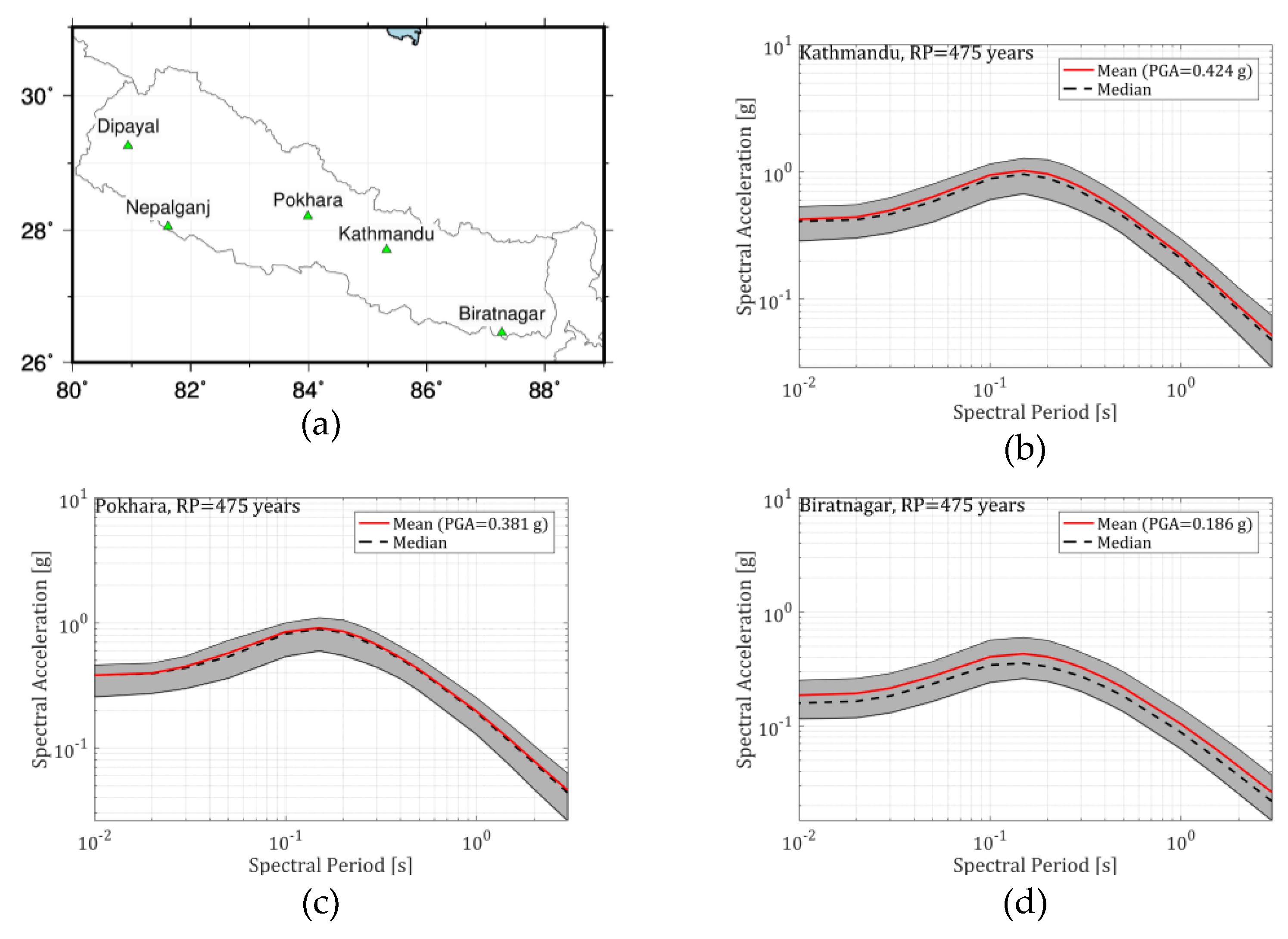
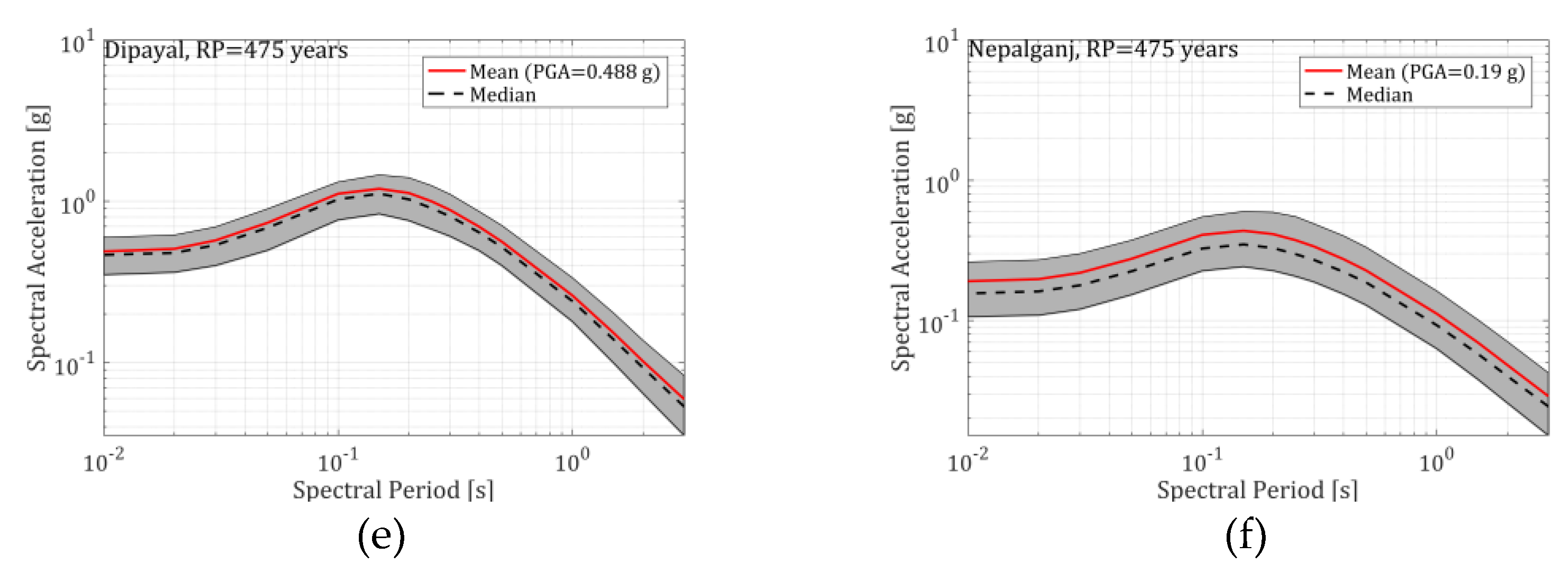
Preprints 73215 g014aPreprints 73215 g014b
Figure 14. (a) Map showing considered 5 locations and UHS and the centiles of the 5 selected cities of Nepal at return period of 10% exceedance probability in 50 years (return period of 475 years) considering the site condition of (Vs,30=760 m/s) for (b) Kathmandu; (c) Pokhara; (d) Biratnagar; (e) Dipayal and (f) Nepalganj. Note that the graph is in log-log scale. The grey shaded area represents the range of UHS between centile 16 and 84%.
Figure 14. (a) Map showing considered 5 locations and UHS and the centiles of the 5 selected cities of Nepal at return period of 10% exceedance probability in 50 years (return period of 475 years) considering the site condition of (Vs,30=760 m/s) for (b) Kathmandu; (c) Pokhara; (d) Biratnagar; (e) Dipayal and (f) Nepalganj. Note that the graph is in log-log scale. The grey shaded area represents the range of UHS between centile 16 and 84%.
Preprints 73215 g014aPreprints 73215 g014b
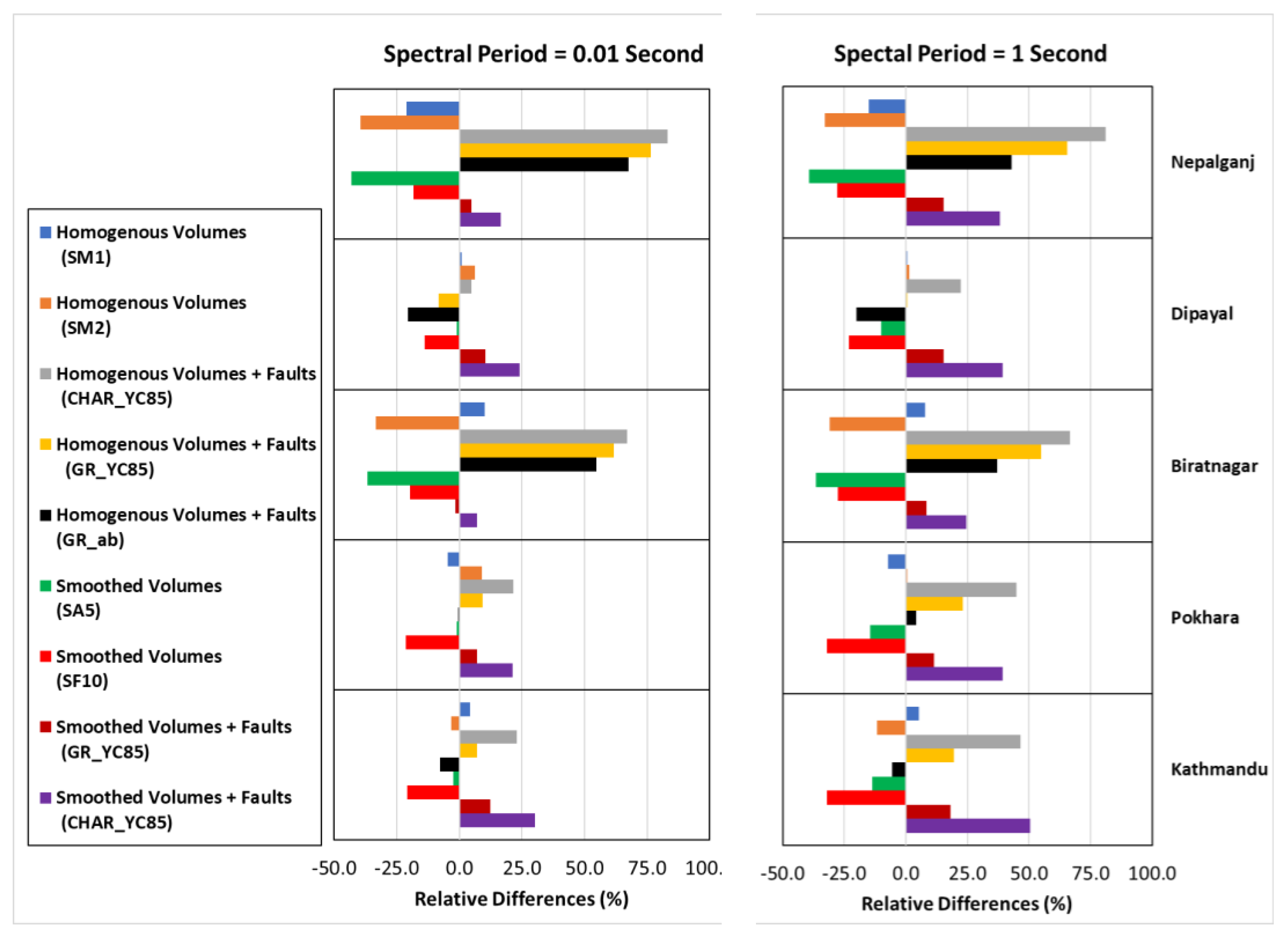
Preprints 73215 g015
Figure 15. Relative difference of each mean of SSCs to the weighted average based on the final logic tree at return period of 475 years and for five locations considered, (a) Spectral period of 0.01 second; (b) Spectral period of 1 second.
Figure 15. Relative difference of each mean of SSCs to the weighted average based on the final logic tree at return period of 475 years and for five locations considered, (a) Spectral period of 0.01 second; (b) Spectral period of 1 second.
Preprints 73215 g015
Preprints 73215 g016
Figure 16. (a) Map showing considered 5 locations and UHS and the centiles of the 5 selected cities of Nepal at return period of 2% exceedance probability in 50 years (return period of 2,475 years) considering the site condition of (Vs,30=760 m/s) for (b) Kathmandu; (c) Pokhara; (d) Biratnagar; (e) Dipayal and (f) Nepalganj. Note that the graph is in log-log scale. The grey shaded area represents between centile 16 and 84%.
Figure 16. (a) Map showing considered 5 locations and UHS and the centiles of the 5 selected cities of Nepal at return period of 2% exceedance probability in 50 years (return period of 2,475 years) considering the site condition of (Vs,30=760 m/s) for (b) Kathmandu; (c) Pokhara; (d) Biratnagar; (e) Dipayal and (f) Nepalganj. Note that the graph is in log-log scale. The grey shaded area represents between centile 16 and 84%.
Preprints 73215 g016

7.2. Comparison of PSHA results

The mean UHS results obtained in this PSHA study considering standard rock condition with Vs,30 of 760 m/s are compared with the design response proposed in NBC105: 2020 for Soil class A sites. The comparison shows notable discrepancies and differences in terms of hazard levels and shape of spectra.
Firstly, at 475-year return period considering standard soil condition with Vs,30 of 760 m/s (Figure 17, Figure 18 and Figure 19), the comparison of mean UHS shows that the levels recommended in NBC105: 2020 Soil A are quite different for all the sites considered. In the case of the city of Kathmandu, Bhaktapur and Dipayal (sites which lie effectively north of MFT), this difference is more pronounced at the plateau (notably at spectral periods between 0.1 and 0.3 second). Hazard levels in this study are up to 37% higher at spectral period of 0.15s for the city of Dipayal. While for the longer spectral period (0.3 to 2 second) the hazard levels obtained are lower for all sites (up to 65% for site Biratnagar at spectral period of 1 second). Furthermore, the mean UHS, obtained in this study for the site locations which lie south of the MFT and MBT (Biratnagar and Nepalganj), is significantly below or completely enveloped by design spectra recommended by NBC105:2020 for the whole range of spectral periods.
In other words, the results obtained in this study highlight the possibility that NBC105: 2020 design spectrum could have underestimated the hazard levels in high seismicity region and overestimated them in the relatively lower seismic hazard region, for both return periods considered in this study. The differences in results obtained in this study with respect to that of NBC105:2020 could be most likely related to differences in SSC and GMM models considered in these studies. The singular SSC model used without alternative SSC models might have led to systematic bias in hazard estimates obtained in study by [10] which was eventually adopted to derive design spectra for NBC105:2020.
The comparison of hazard levels obtained at 475-year return period, Vs,30 of 760 m/s (Figure 19), to recent studies shows that regardless of the locations considered, hazard levels from GEM [2] are above the results obtained in this study and the difference is more significant for the sites which lies north of the MFT (for example Kathmandu, Pokhara, Dipayal). The possible reason for these discrepancies of the results obtained in this study with respect to results in GEM [2] could be associated to use of very different seismic source models and method used to take in to account the uncertainties in the SSC model, which could have led to possible bias in the estimates. Moreover, the strategy for use of ground motion models (ACR or subduction type) could also have led to significant differences. For the same return period, at Kathmandu, the mean hazard levels obtained in [12] are very close to the one obtained in this study. Similarly, the comparison with [9,11] shows that the hazard levels are in the same order of magnitude but slightly above the hazard levels obtained in this study.

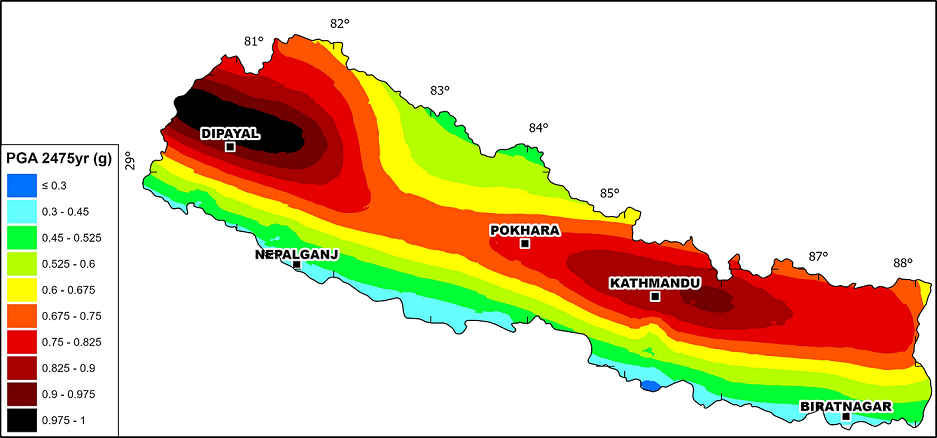
7.3. Hazard Maps

The PGA values have been calculated using a grid of 20km x 20km, for soil A condition (Vs,30=760m/s) at 475- and 2475 years return periods (Figure 20a). At 475- year return period (10 % probability of exceedance in 50 years), the value of PGA varies from ~0.1 g in the south to 0.5 g in the northern part of Nepal. As expected, the highest values of ground motions are found in the far northwest of Nepal where they exceed 0.45 g and in the north-eastern edge where they range from 0.45 to 0.50 g. Conversely, a medium to low hazard is observed in the central region of Nepal with PGA values ranging from 0.25 g to 0.35 g. The PGA value is relatively lower (< 0.25 g) in southern and far north Nepal than in any region of the country. The PGA distribution for 2,475 years return period (2% probability of exceedance in 50 years) is shown in Figure 20b. The pattern of the distribution is relatively the same as for the 475-year return period and the PGA values range from 0.3 g to ~1 g. The northwestern area concentrates the highest hazard with ground motion exceeding 0.9 g while the eastern region has slightly lower values of 0.7 g to 0.9 g. These hazard levels are coherent and in the same order of magnitude with some recent studies [11,12].
These results are consistent with the structural and geological fabrics observed in Nepal and show a spatial distribution strongly controlled by the MFT and the MBT that concentrate the highest hazard along an ~WNW-ESE thrust-parallel axis. At depth, the MHT geometry varies from west to east with a slightly structural change at the 83°E longitude (see the MHT geometry and depth contour in Figure 1) that coincides with the medium to low PGA values of the central part. In addition, the highest hazard areas seem to correspond to abrupt changes in the dip of the ramp as in the west where the patch of high hazard coincides to the transition zone between the deeper ramp of the decollement and the mid-slope flat. At the northern tip of Nepal, the decrease of the PGA values for both return period coincides with the supposed transitional coupling/decoupling zone of the MHT [23,32,60].

8. Conclusions and perspectives

An updated probabilistic seismic hazard model covering the entire Nepal is presented. The PSHA methodology and its components adopted in this study represent an improvement with respect to previous PSHA for Nepal. The hazard model is the result of recent advances in research and development of geological and seismological data for Nepal, in particular concerning seismicity catalogue, geometry, and seismicity parameters for the MHT and MBT. We considered the available data and methods systematically, and we propose alternative source models while also considering previous models in a logic-tree framework. This allowed to consider the range of epistemic uncertainty prevailing in the identification and characterization of the seismic sources.
The seismicity catalogue and the strategy adopted to merge the different source catalogues in this study are an improvement in the context of seismic hazard studies conducted for Nepal. The compilation and construction of the catalogue was elaborated in the perspective to continue the efforts towards a comprehensive and homogenized catalogue utilizable for seismic hazard studies in the region.
This study shows that consideration of alternative source models can lead to very different hazard assessments. Sensitivity analyses demonstrate that the SSC models integrating faults lead to higher hazard levels followed by homogenous volumes and smoothed volumes models. The logic-tree scheme was constructed based on evaluation of sensitivity analysis establishing a rationale of weighting schemes for the models and considering the epistemic uncertainties. The PSHA maps obtained in this study are quite similar (in same order of magnitude) to the results obtained in other studies [11,12]. In line with these studies [11,12], our results confirm that the foreland basin at the southern belt of Nepal (including e.g. Biratnagar and Nepalganj cities) is a low seismic hazard region as well as the northern boundary at the vicinity of Tibetan Plateau. This latter likely reflects the decrease of the fault coupling of the MHT interface related to the downdip brittle/ductile transition. Besides, the central part of Nepal, north of the MFT, is one of the most active regions including important cities like Katmandu and Pokhara. Indeed, the seismic hazard is concentrated along an WNW-ESE elongated band, sub-parallel to the main thrust axis, with highest PGA values laterally distributed in the southeastern- and northwesternmost regions with a relatively lower hazard area between them. The seismic hazard spatial distribution in this study may reflect the E-W variation of the MHT geometry consistently with geologic reconstruction and geodetic observations [15,23,68] such as (i) the 83°E structural change of orientation observed along the MFT and MBT fault traces leading to low hazard area, (ii) the changes in the dip of the decollement at depth with high hazard associated to mid-crustal ramp allowing highest fault coupling [60] and/or (iii) the presence of duplex structure and basement rocks stacked precluding slip on the MHT [15]. Since the seismicity sample presents relatively small completeness periods and the paleo seismological context is only barely known, it is not excluded that the low hazard area may reflect a long-term moment deficit [3,23,25]. In any case, the geometrical and rheological variation along the MHT interface seems to have a strong influence on the seismic hazard distribution in Nepal (with respect to standard rock condition) and confirms the need of integrating geological structures and physical factors (e.g., fault coupling, stress rate, rheological transition) to PSHA studies in tectonically active regions.
The comparison of mean UHS obtained in this study with the design spectra NBC105: 2020 adopted based on the study by [10] shows critical differences and discrepancies. This comparative evaluation shows that the hazard levels recommended in NBC105: 2020 for the locations situated south of MFT/MBT surface traces (like Biratnagar, Nepalganj) are possibly overestimated while the hazard levels recommended for many other major cities (like Kathmandu and Pokhara which lies North of the MFT/MBT) might have been significantly underestimated, especially at spectral periods of interest which concerns majority of building typology prevalent in Nepal i.e. small to mid-size buildings. The possible reason for this discrepancy could be related fact that PSHA study [10] conducted for purpose of NBC105:2020 relies on singular source model, limited GMMs and the method (for example in recurrence models for fault sources) might have led to bias in hazard estimates.
In this study, several limitations have been identified and might be considered for future seismic hazard assessment. Indeed, limited effort was devoted at this stage to the construction of the GMM, for which a simple multi-GMMs approach has been adopted as in previous studies. Further studies should be devoted to a more comprehensive assessment of the uncertainties in ground motion estimates for Nepal. In addition, the inclusion of the individual crustal faults once the fault databases are further consolidated would help to better constrain the hazard estimates. Future research should also focus on making critical evaluation of the empirical site amplification factors using locally recorded strong motion data to consolidate the most applicable factors. The contradiction in the hazard levels recommended by NBC105: 2020 with the ones obtained in this study and in several recent studies [11,12] should be addressed through a future comprehensive research. Indeed, the hazard levels recommended through a building code guideline must be well scrutinized and consolidated to ensure the safe design of new buildings or reinforcements of existing ones. The consideration of locally developed ground motion models, individual crustal faults, and consolidation of the MHT fault system parameters could be a way forward to consider for the future hazard studies in the region.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org. Figure S1: Distribution of epicentral location sources through different time periods of history; Figure S2. Completeness analysis, cumulative number of earthquakes as a function of time (red circles), inter-event variance (black dashed line), best-estimate is shown as green dashed line, gray shade represents the lower to upper estimates; Table S1: Seismicity parameters for seismic source zones of SM1; Table S2: Seismicity parameters for seismic source zones of SM2; Table S3: Seismicity parameters for seismic source zones of SM3F.

Author Contributions

Conceptualization, S.M. and A.P.; methodology, S.M. and A.P.; software, D.B. and G.A.; validation, D.B., G.A., S.M., A.P. and C.M.; formal analysis, S.M., A.P. and C.M.; investigation, A.P. and S.M.; resources, S.M., A.P. and C.M.; data curation, S.M. and A.P.;writing—original draft preparation, S.M. and A.P.; writing—review and editing, S.M., A.P., C.M., Y.B., G.A., K.H. and H.S.; visualization, S.M., A.P. and D.B.; supervision, C.M., D.B. and G.A.; project administration, C.M.; funding acquisition, C.M., D.B. and G.A. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

We ensure that data shared are in accordance with consent provided by participants on the use of confidential data. The data presented in this study are available in the supplementary materials (see below) and are available on request from the corresponding author.

Acknowledgments

We would like to be thankful to Francois Vaysse and Romain Leroux-Mallouf from the TEGG team (Électricité de France - EDF) for allowing us to publish these data.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. NBC105: 2020 Nepal National Building Code, Seismic Design of Buildings in Nepal 2020.
  2. Pagani, M.; Garcia-Pelaez, J.; Gee, R.; Johnson, K.; Poggi, V.; Silva, V.; Simionato, M.; Styron, R.; Viganò, D.; Danciu, L.; et al. The 2018 Version of the Global Earthquake Model: Hazard Component. Earthquake Spectra 2020, 36, 226–251. [Google Scholar] [CrossRef]
  3. Ader, T.; Avouac, J.-P.; Liu-Zeng, J.; Lyon-Caen, H.; Bollinger, L.; Galetzka, J.; Genrich, J.; Thomas, M.; Chanard, K.; Sapkota, S.N. Convergence Rate across the Nepal Himalaya and Interseismic Coupling on the Main Himalayan Thrust: Implications for Seismic Hazard. Journal of Geophysical Research: Solid Earth 2012, 117. [Google Scholar] [CrossRef]
  4. Bollinger, L.; Sapkota, S.N.; Tapponnier, P.; Klinger, Y.; Rizza, M.; Van der Woerd, J.; Tiwari, D.R.; Pandey, R.; Bitri, A.; Bes de Berc, S. Estimating the Return Times of Great Himalayan Earthquakes in Eastern Nepal: Evidence from the Patu and Bardibas Strands of the Main Frontal Thrust. Journal of Geophysical Research: Solid Earth 2014, 119, 7123–7163. [Google Scholar] [CrossRef]
  5. Lavé, J.; Avouac, J.P. Active Folding of Fluvial Terraces across the Siwaliks Hills, Himalayas of Central Nepal. Journal of Geophysical Research: Solid Earth 2000, 105, 5735–5770. [Google Scholar] [CrossRef]
  6. Hossler, T.; Bollinger, L.; Sapkota, S.N.; Lavé, J.; Gupta, R.M.; Kandel, T.P. Surface Ruptures of Large Himalayan Earthquakes in Western Nepal: Evidence along a Reactivated Strand of the Main Boundary Thrust. Earth and Planetary Science Letters 2016, 434, 187–196. [Google Scholar] [CrossRef]
  7. Nath, S.K.; Thingbaijam, K.K.S. Probabilistic Seismic Hazard Assessment of India. Seismological Research Letters 2012, 83, 135–149. [Google Scholar] [CrossRef]
  8. Pradhan, P.M.; Timalsina, S.P.; Bhatt, M.R. Probabilistic Seismic Hazard Analysis for Nepal. Lowland Technology International 2020, 22, 75–80. [Google Scholar]
  9. Thapa, D.; Wang, G. Probabilistic Seismic Hazard Analysis in Nepal. Earthquake Engineering and Engineering Vibration 2013, 12, 577–586. [Google Scholar] [CrossRef]
  10. Chamlagain, D.; Tamrakar, M.R.; Bista, M.; Ojha, S.; Gautam, B.; Acharya, I.; Maskey, P.; Dhakal, R. NBC105: 2019 Seismic Design of Buildings in Nepal: New Provisions in the Code. 2020.
  11. Rahman, M.M.; Bai, L. Probabilistic Seismic Hazard Assessment of Nepal Using Multiple Seismic Source Models. Earth and Planetary Physics 2018, 2, 327–341. [Google Scholar] [CrossRef]
  12. Parajuli, H.R.; Bhusal, B.; Paudel, S. Seismic Zonation of Nepal Using Probabilistic Seismic Hazard Analysis. Arab J Geosci 2021, 14, 2090. [Google Scholar] [CrossRef]
  13. Stevens, V.L.; Shrestha, S.N.; Maharjan, D.K. Probabilistic Seismic Hazard Assessment of Nepal. Bulletin of the Seismological Society of America 2018, 108, 3488–3510. [Google Scholar] [CrossRef]
  14. Cornell, C.A. Engineering Seismic Risk Analysis. Seism. Soc. 1968. [Google Scholar] [CrossRef]
  15. Dal Zilio, L.; Hetényi, G.; Hubbard, J.; Bollinger, L. Building the Himalaya from Tectonic to Earthquake Scales. Nat Rev Earth Environ 2021, 2, 251–268. [Google Scholar] [CrossRef]
  16. Klootwijk, C.T.; Conaghan, P.J.; Powell, C. McA. The Himalayan Arc: Large-Scale Continental Subduction, Oroclinal Bending and Back-Arc Spreading. Earth and Planetary Science Letters 1985, 75, 167–183. [Google Scholar] [CrossRef]
  17. Liou, J.G.; Tsujimori, T.; Zhang, R.Y.; Katayama, I.; Maruyama, S. Global UHP Metamorphism and Continental Subduction/Collision: The Himalayan Model. International Geology Review 2004, 46, 1–27. [Google Scholar] [CrossRef]
  18. O’Brien, P.J. Eclogites and Other High-Pressure Rocks in the Himalaya: A Review. Geological Society, London, Special Publications 2019, 483, 183–213. [Google Scholar] [CrossRef]
  19. Soret, M.; Larson, K.P.; Cottle, J.; Ali, A. How Himalayan Collision Stems from Subduction. Geology 2021, 49, 894–898. [Google Scholar] [CrossRef]
  20. Zheng, T.; He, Y.; Ding, L.; Jiang, M.; Ai, Y.; Mon, C.T.; Hou, G.; Sein, K.; Thant, M. Direct Structural Evidence of Indian Continental Subduction beneath Myanmar. Nat Commun 2020, 11, 1944. [Google Scholar] [CrossRef]
  21. DeCelles, P.G.; Gehrels, G.E.; Quade, J.; Ojha, T.P.; Kapp, P.A.; Upreti, B.N. Neogene Foreland Basin Deposits, Erosional Unroofing, and the Kinematic History of the Himalayan Fold-Thrust Belt, Western Nepal. Geological Society of America Bulletin 1998, 110, 2–21. [Google Scholar] [CrossRef]
  22. Harvey, J.E.; Burbank, D.W.; Bookhagen, B. Along-Strike Changes in Himalayan Thrust Geometry: Topographic and Tectonic Discontinuities in Western Nepal. Lithosphere 2015, 7, 511–518. [Google Scholar] [CrossRef]
  23. Lindsey, E.O.; Almeida, R.; Mallick, R.; Hubbard, J.; Bradley, K.; Tsang, L.L.H.; Liu, Y.; Burgmann, R.; Hill, E.M. Structural Control on Downdip Locking Extent of the Himalayan Megathrust. Journal of Geophysical Research: Solid Earth 2018, 123, 5265–5278. [Google Scholar] [CrossRef]
  24. Wang, M.; Shen, Z.-K. Present-Day Crustal Deformation of Continental China Derived from GPS and Its Tectonic Implications. Journal of Geophysical Research: Solid Earth 2020, 125, e2019JB018774. [Google Scholar] [CrossRef]
  25. Stevens, V.L.; Avouac, J.P. Interseismic Coupling on the Main Himalayan Thrust. Geophysical Research Letters 2015, 42, 5828–5837. [Google Scholar] [CrossRef]
  26. Li, S.; Wang, Q.; Yang, S.; Qiao, X.; Nie, Z.; Zou, R.; Ding, K.; He, P.; Chen, G. Geodetic Imaging Mega-Thrust Coupling beneath the Himalaya. Tectonophysics 2018, 747–748, 225–238. [Google Scholar] [CrossRef]
  27. Avouac, J.-P. Mountain Building, Erosion, and the Seismic Cycle in the Nepal Himalaya. Advances in geophysics 2003, 46, 1–80. [Google Scholar]
  28. Lavé, J.; Yule, D.; Sapkota, S.; Basant, K.; Madden, C.; Attal, M.; Pandey, R. Evidence for a Great Medieval Earthquake (∼ 1100 AD) in the Central Himalayas, Nepal. Science 2005, 307, 1302–1305. [Google Scholar] [PubMed]
  29. Sapkota, S.N.; Bollinger, L.; Klinger, Y.; Tapponnier, P.; Gaudemer, Y.; Tiwari, D. Primary Surface Ruptures of the Great Himalayan Earthquakes in 1934 and 1255. Nature Geoscience 2013, 6, 71–76. [Google Scholar] [CrossRef]
  30. Bilham, R.; Mencin, D.; Bendick, R.; Bürgmann, R. Implications for Elastic Energy Storage in the Himalaya from the Gorkha 2015 Earthquake and Other Incomplete Ruptures of the Main Himalayan Thrust. Quaternary International 2017, 462, 3–21. [Google Scholar] [CrossRef]
  31. Dal Zilio, L.; Jolivet, R.; van Dinther, Y. Segmentation of the Main Himalayan Thrust Illuminated by Bayesian Inference of Interseismic Coupling. Geophysical Research Letters 2020, 47, e2019GL086424. [Google Scholar] [CrossRef]
  32. Michel, S.; Jolivet, R.; Rollins, C.; Jara, J.; Dal Zilio, L. Seismogenic Potential of the Main Himalayan Thrust Constrained by Coupling Segmentation and Earthquake Scaling. Geophysical Research Letters 2021, 48, e2021GL093106. [Google Scholar] [CrossRef]
  33. Bollinger, L.; Tapponnier, P.; Sapkota, S.N.; Klinger, Y. Slip Deficit in Central Nepal: Omen for a Repeat of the 1344 AD Earthquake? Earth, Planets and Space 2016, 68, 1–12. [Google Scholar] [CrossRef]
  34. Gansser, A. The Geodynamic History of the Himalaya. Zagros Hindu Kush Himalaya Geodynamic Evolution 1981, 3, 111–121. [Google Scholar]
  35. Robinson, D.M.; DeCelles, P.G.; Garzione, C.N.; Pearson, O.N.; Harrison, T.M.; Catlos, E.J. Kinematic Model for the Main Central Thrust in Nepal. Geology 2003, 31, 359–362. [Google Scholar] [CrossRef]
  36. Nakata, T. Active Faults of the Himalaya of India and Nepal. Geological Society of America Special Paper 1989, 232, 243–264. [Google Scholar]
  37. Searle, M.P.; Law, R.D.; Godin, L.; Larson, K.P.; Streule, M.J.; Cottle, J.M.; Jessup, M.J. Defining the Himalayan Main Central Thrust in Nepal. Journal of the Geological Society 2008, 165, 523–534. [Google Scholar] [CrossRef]
  38. Hodges, K.V.; Hurtado, J.M.; Whipple, K.X. Southward Extrusion of Tibetan Crust and Its Effect on Himalayan Tectonics. Tectonics 2001, 20, 799–809. [Google Scholar] [CrossRef]
  39. Murphy, M.A.; Taylor, M.H.; Gosse, J.; Silver, C.R.P.; Whipp, D.M.; Beaumont, C. Limit of Strain Partitioning in the Himalaya Marked by Large Earthquakes in Western Nepal. Nature Geosci 2014, 7, 38–42. [Google Scholar] [CrossRef]
  40. Kumar, S.; Wesnousky, S.G.; Rockwell, T.K.; Briggs, R.W.; Thakur, V.C.; Jayangondaperumal, R. Paleoseismic Evidence of Great Surface Rupture Earthquakes along the Indian Himalaya. Journal of Geophysical Research: Solid Earth 2006, 111. [Google Scholar] [CrossRef]
  41. Bilham, R. Himalayan Earthquakes: A Review of Historical Seismicity and Early 21st Century Slip Potential. Geological Society, London, Special Publications 2019, 483, 423–482. [Google Scholar] [CrossRef]
  42. Albini, M.; Musson, R.M.W.; Capera, A.A.G.; Locati, M.; Rovida, A.; Stucchi, M.; Vigano, D. Global Historical Earthquake Archive and Catalogue (1000-1903). In Global Historical Earthquake Archive and Catalogue (1000-1903); GEM Technical Report 2013-01, 2013.
  43. Di Giacomo, D.; Engdahl, E.R.; Storchak, D.A. The ISC-GEM Earthquake Catalogue (1904–2014): Status after the Extension Project. Earth Syst. Sci. Data 2018, 10, 1877–1899. [Google Scholar] [CrossRef]
  44. Storchak, et. al ISC-GEM, Global Instrumental Earthquake Catalogue (1900–2009) Final Scientific Report. 2013.
  45. Storchak, D.A.; Di Giacomo, D.; Engdahl, E.R.; Harris, J.; Bondár, I.; Lee, W.H.K.; Bormann, P.; Villaseñor, A. The ISC-GEM Global Instrumental Earthquake Catalogue (1900–2009): Introduction. Physics of the Earth and Planetary Interiors 2015, 239, 48–63. [Google Scholar] [CrossRef]
  46. Engdahl, E.R.; van der Hilst, R.; Buland, R. Global Teleseismic Earthquake Relocation with Improved Travel Times and Procedures for Depth Determination. Bulletin of the Seismological Society of America 1998, 88, 722–743. [Google Scholar] [CrossRef]
  47. Ekström, G.; Nettlesa, M.; DZIEWOŃSKIB, A.M. The Global CMT Project 2004–2010: Centroid-Moment Tensors for 13,017 Earthquakes (2012). Physics of the Earth and Planetary Interiors 2012. [Google Scholar] [CrossRef]
  48. ISC International Seismological Center. Available online: http://www.isc.ac.uk.
  49. National Earthquake Monitoring & Research Center. Available online: http://www.seismonepal.gov.np/ (accessed on 24 March 2023).
  50. USGS United States Geological Survey, Global Earthquake Catalogues Covering the Period 1979- 2019.
  51. Official Website of National Center of Seismology. Available online: https://riseq.seismo.gov.in/riseq/earthquake (accessed on 22 March 2023).
  52. Scordilis, E.M. Empirical Global Relations Converting MS and Mb to Moment Magnitude. Journal of seismology 2006, 10, 225–236. [Google Scholar] [CrossRef]
  53. Gardner, J.K.; Knopoff, L. Is the Sequence of Earthquakes in Southern California, with Aftershocks Removed, Poissonian? Bulletin of the seismological society of America 1974, 64, 1363–1367. [Google Scholar] [CrossRef]
  54. Uhrhammer, R. Characteristics of Northern and Central California Seismicity. Earthquake Notes 1986. [Google Scholar]
  55. Hakimhashemi, A.H.; Grünthal, G. A Statistical Method for Estimating Catalog Completeness Applicable to Long-Term Nonstationary Seismicity Data. Bulletin of the Seismological Society of America 2012, 102, 2530–2546. [Google Scholar] [CrossRef]
  56. Thapa, D.R. Seismicity of Nepal and the Surrounding Region. Bulletin of the Department of Geology 2018, 83–86. [Google Scholar] [CrossRef]
  57. Baillard, C.; Lyon-Caen, H.; Bollinger, L.; Rietbrock, A.; Letort, J.; Adhikari, L.B. Automatic Analysis of the Gorkha Earthquake Aftershock Sequence: Evidences of Structurally Segmented Seismicity. Geophysical Journal International 2017, 209, 1111–1125. [Google Scholar] [CrossRef]
  58. Cattin, R.; Avouac, J.P. Modeling Mountain Building and the Seismic Cycle in the Himalaya of Nepal. Journal of Geophysical Research: Solid Earth 2000, 105, 13389–13407. [Google Scholar] [CrossRef]
  59. Duvall, M.J.; Waldron, J.W.; Godin, L.; Najman, Y. Active Strike-Slip Faults and an Outer Frontal Thrust in the Himalayan Foreland Basin. Proceedings of the National Academy of Sciences 2020, 117, 17615–17621. [Google Scholar] [CrossRef] [PubMed]
  60. Hubbard, J.; Almeida, R.; Foster, A.; Sapkota, S.N.; Bürgi, P.; Tapponnier, P. Structural Segmentation Controlled the 2015 Mw 7.8 Gorkha Earthquake Rupture in Nepal. Geology 2016, 44, 639–642. [Google Scholar] [CrossRef]
  61. Laporte, M.; Bollinger, L.; Lyon-Caen, H.; Hoste-Colomer, R.; Duverger, C.; Letort, J.; Riesner, M.; Koirala, B.P.; Bhattarai, M.; Kandel, T. Seismicity in Far Western Nepal Reveals Flats and Ramps along the Main Himalayan Thrust. Geophysical Journal International 2021, 226, 1747–1763. [Google Scholar] [CrossRef]
  62. Sheehan, A.F.; de la Torre, T.; Monsalve, G.; Schulte-Pelkum, V.; Bilham, R.; Blume, F.; Bendick, R.; Wu, F.; Pandey, M.R.; Sapkota, S. Earthquakes and Crustal Structure of Himalaya from Himalayan Nepal-Tibet Seismic Experiment (HIMNT). Journal of Nepal Geological Society 2008, 38, 1–8. [Google Scholar] [CrossRef]
  63. Stöcklin, J. Geology of Nepal and Its Regional Frame: Thirty-Third William Smith Lecture. Journal of the Geological Society 1980, 137, 1–34. [Google Scholar] [CrossRef]
  64. Berger, A.; Jouanne, F.; Hassani, R.; Mugnier, J.L. Modelling the Spatial Distribution of Present-Day Deformation in Nepal: How Cylindrical Is the Main Himalayan Thrust in Nepal? Geophysical Journal International 2004, 156, 94–114. [Google Scholar] [CrossRef]
  65. Cotton, F.; Campillo, M.; Deschamps, A.; Rastogi, B.K. Rupture History and Seismotectonics of the 1991 Uttarkashi, Himalaya Earthquake. Tectonophysics 1996, 258, 35–51. [Google Scholar] [CrossRef]
  66. Bai, L.; Klemperer, S.L.; Mori, J.; Karplus, M.S.; Ding, L.; Liu, H.; Li, G.; Song, B.; Dhakal, S. Lateral Variation of the Main Himalayan Thrust Controls the Rupture Length of the 2015 Gorkha Earthquake in Nepal. Science Advances 2019, 5, eaav0723. [Google Scholar] [CrossRef]
  67. Hazarika, P.; Kumar, M.R.; Srijayanthi, G.; Raju, P.S.; Rao, N.P.; Srinagesh, D. Transverse Tectonics in the Sikkim Himalaya: Evidence from Seismicity and Focal-Mechanism Data. Bulletin of the Seismological Society of America 2010, 100, 1816–1822. [Google Scholar] [CrossRef]
  68. Elliott, J.R.; Jolivet, R.; González, P.J.; Avouac, J.-P.; Hollingsworth, J.; Searle, M.P.; Stevens, V.L. Himalayan Megathrust Geometry and Relation to Topography Revealed by the Gorkha Earthquake. Nature Geoscience 2016, 9, 174–180. [Google Scholar] [CrossRef]
  69. Meade, B.J. The Signature of an Unbalanced Earthquake Cycle in Himalayan Topography? Geology 2010, 38, 987–990. [Google Scholar] [CrossRef]
  70. Mugnier, J.-L.; Gajurel, A.; Huyghe, P.; Jayangondaperumal, R.; Jouanne, F.; Upreti, B. Structural Interpretation of the Great Earthquakes of the Last Millennium in the Central Himalaya. Earth-Science Reviews 2013, 127, 30–47. [Google Scholar] [CrossRef]
  71. Hoste-Colomer, R.; Bollinger, L.; Lyon-Caen, H.; Adhikari, L.B.; Baillard, C.; Benoit, A.; Bhattarai, M.; Gupta, R.M.; Jacques, E.; Kandel, T. Lateral Variations of the Midcrustal Seismicity in Western Nepal: Seismotectonic Implications. Earth and Planetary Science Letters 2018, 504, 115–125. [Google Scholar] [CrossRef]
  72. Gutenberg, B.; Richter, C.F. Magnitude and Energy of Earthquakes. Annals of Geophysics 1956, 9, 1–15. [Google Scholar]
  73. EPRI Technical Report: Central and Eastern United States Seismic Source Characterization for Nuclear Facilities; EPRI, Palo Alto, CA, U.S. DOE, and U.S. NRC: 2012, 2012.
  74. Weichert, D.H. Estimation of the Earthquake Recurrence Parameters for Unequal Observation Periods for Different Magnitudes. Bulletin of the Seismological Society of America 1980, 70, 1337–1346. [Google Scholar] [CrossRef]
  75. Johnston, A.C.; COPPERSMITH, L.R.; KANTER; CORNELL, C.A. The Earthquakes of Stable Continental Regions – Assessment of Large Earthquake Potential. Electric Power Research Institute (EPRI) 1994.
  76. Bilham, R.; Larson, K.; Freymueller, J. GPS Measurements of Present-Day Convergence across the Nepal Himalaya. Nature 1997, 386, 61–64. [Google Scholar] [CrossRef]
  77. Jouanne, F.; Mugnier, J.L.; Sapkota, S.N.; Bascou, P.; Pecher, A. Estimation of Coupling along the Main Himalayan Thrust in the Central Himalaya. Journal of Asian Earth Sciences 2017, 133, 62–71. [Google Scholar] [CrossRef]
  78. Jouanne, F.; Mugnier, J.L.; Pandey, M.R.; Gamond, J.F.; Le Fort, P.; Serrurier, L.; Vigny, C.; Avouac, J.P. Oblique Convergence in the Himalayas of Western Nepal Deduced from Preliminary Results of GPS Measurements. Geophysical Research Letters 1999, 26, 1933–1936. [Google Scholar] [CrossRef]
  79. Bollinger, L.; Avouac, J.P.; Beyssac, O.; Catlos, E.J.; Harrison, T.M.; Grove, M.; Goffé, B.; Sapkota, S. Thermal Structure and Exhumation History of the Lesser Himalaya in Central Nepal: THERMAL STRUCTURE OF THE LESSER HIMALAYA. Tectonics 2004, 23. [Google Scholar] [CrossRef]
  80. Mishra, R.L.; Singh, I.; Pandey, A.; Rao, P.S.; Sahoo, H.K.; Jayangondaperumal, R. Paleoseismic Evidence of a Giant Medieval Earthquake in the Eastern Himalaya. Geophysical Research Letters 2016, 43, 5707–5715. [Google Scholar] [CrossRef]
  81. Youngs, R.R.; Coppersmith, K.J. Implications of Fault Slip Rates and Earthquake Recurrence Models to Probabilistic Seismic Hazard Estimates. Bulletin of the Seismological Society of America 1985, 75, 939–964. [Google Scholar] [CrossRef]
  82. Woo, G. Kernel Estimation Methods for Seismic Hazard Area Source Modeling. Bulletin of the Seismological Society of America 1996, 86, 353–362. [Google Scholar] [CrossRef]
  83. Helmstetter, A.; Kagan, Y.Y.; Jackson, D.D. High-Resolution Time-Independent Grid-Based Forecast for M >= 5 Earthquakes in California. Seismological Research Letters 2007, 78, 78–86. [Google Scholar] [CrossRef]
  84. Douglas, J. Ground Motion Predication Equations 1964-2021. Department of Civil and Environmental Engineering, University of Strathclyde, Glasgow, United Kingdom. 2022.
  85. Singh, S.K.; Srinagesh, D.; Srinivas, D.; Arroyo, D.; Pérez-Campos, X.; Chadha, R.K.; Suresh, G.; Suresh, G. Strong Ground Motion in the Indo-Gangetic Plains during the 2015 Gorkha, Nepal, Earthquake Sequence and Its Prediction during Future Earthquakes. Bulletin of the Seismological Society of America 2017, 107, 1293–1306. [Google Scholar] [CrossRef]
  86. Basu, J.; Podili, B.; Raghukanth, S.T.G.; Srinagesh, D. Ground Motion Parameters for the 2015 Nepal Earthquake and Its Aftershocks. Nat Hazards 2023, 116, 2091–2134. [Google Scholar] [CrossRef]
  87. Bajaj, K.; Anbazhagan, P. Determination of GMPE Functional Form for an Active Region with Limited Strong Motion Data: Application to the Himalayan Region. J Seismol 2018, 22, 161–185. [Google Scholar] [CrossRef]
  88. Cotton, F.; Scherbaum, F.; Bommer, J.J.; Bungum, H. Criteria for Selecting and Adjusting Ground-Motion Models for Specific Target Regions. Journal of Seismology 2006, 10. [Google Scholar] [CrossRef]
  89. Atkinson, G.M. Empirical Ground-Motion Relations for Subduction-Zone Earthquakes and Their Application to Cascadia and Other Regions. Bulletin of the Seismological Society of America 2003, 93, 1703–1729. [Google Scholar] [CrossRef]
  90. Abrahamson, N.A.; Silva, W.J.; Kamai, R. Summary of the ASK14 Ground Motion Relation for Active Crustal Regions. Earthquake Spectra 2014, 30. [Google Scholar] [CrossRef]
  91. Boore, D.; Stewart, J.; Seyhan, E.; Atkinson, G.M. NGA-West2 Equations for Predicting PGA, PGV, and 5% Damped PSA for Shallow Crustal Earthquakes. Earthquake Spectra 2014. [Google Scholar] [CrossRef]
  92. Campbell, K.W.; Bozorgnia, Y. NGA-West2 Ground Motion Model for the Average Horizontal Components of PGA, PGV, and 5%-Damped Linear Acceleration Response Spectra. Earthquake Spectra 2014, 30, 1087–1115. [Google Scholar] [CrossRef]
  93. Zhao, J.X.; Liang, X.; Jiang, F.; Xing, H.; Zhu, M.; Hou, R.; Zhang, Y.; Lan, X.; Rhoades, D.A.; Irikura, K.; et al. Ground-Motion Prediction Equations for Subduction Interface Earthquakes in Japan Using Site Class and Simple Geometric Attenuation FunctionsGMPEs for Subduction Interface Earthquakes in Japan. Bulletin of the Seismological Society of America 2016, 106, 1518–1534. [Google Scholar] [CrossRef]
  94. Chiou, B.; Youngs, R.R. Update of the Chiou and Youngs NGA Model for the Average Horizontal Component of Peak Ground Motion and Response Spectra. Earthquake Spectra 2014. [Google Scholar] [CrossRef]
  95. Zhao, J.X.; Zhou, S.; Zhou, J.; Zhao, C.; Zhang, H.; Zhang, Y.; Gao, P.; Lan, X.; Rhoades, D.; Fukushima, Y.; et al. Ground-Motion Prediction Equations for Shallow Crustal and Upper-Mantle Earthquakes in Japan Using Site Class and Simple Geometric Attenuation FunctionsGMPEs for Shallow Crustal and Upper-Mantle Earthquakes in Japan. Bulletin of the Seismological Society of America 2016, 106, 1552–1569. [Google Scholar] [CrossRef]
  96. Abrahamson, N.; Gregor, N.; Addo, K. BC Hydro Ground Motion Prediction Equations for Subduction Earthquakes. Earthquake Spectra 2016, 32, 23–44. [Google Scholar] [CrossRef]
  97. Bommer, J.J.; Abrahamson, N.A. Why Do Modern Probabilistic Seismic-Hazard Analyses Often Lead to Increased Hazard Estimates? Bulletin of the Seismological Society of America 2006, 96, 1967–1977. [Google Scholar] [CrossRef]
  98. Sabetta, F.; Lucantoni, A.; Bungum, H.; Bommer, J.J. Sensitivity of PSHA Results to Ground Motion Prediction Relations and Logic-Tree Weights. Soil Dynamics and Earthquake Engineering 2005, 25, 317–329. [Google Scholar] [CrossRef]
  99. Douglas, J.; Ulrich, T.; Bertil, D.; Rey, J. Comparison of the Ranges of Uncertainty Captured in Different Seismic-Hazard Studies. Seismological Research Letters 2014, 85, 977–985. [Google Scholar] [CrossRef]
Preprints 73215 g001
Figure 1. (a) Structural map of Nepal and Himalayan mountains showing the major thrusts, strike-slip and normal faults. Black and white arrows indicate India plate motion relative to Eurasia in ITRF 2005. Cities with highest population are labelled. MCT: Main Central Thrust, MBT: Main Boundary Thrust, MFT: Main Frontal Thrust. (b) Seismicity map (raw catalogue) of Nepal and Himalayan mountains (see section 3.1 for further details about the seismicity catalogue used in this study). The depth contours of the MHT decollement layer is from [23] with depth values in bold. Magnitude>8 earthquakes are labeled (in italic for historical event with higher uncertainty on their epicentral location).
Figure 1. (a) Structural map of Nepal and Himalayan mountains showing the major thrusts, strike-slip and normal faults. Black and white arrows indicate India plate motion relative to Eurasia in ITRF 2005. Cities with highest population are labelled. MCT: Main Central Thrust, MBT: Main Boundary Thrust, MFT: Main Frontal Thrust. (b) Seismicity map (raw catalogue) of Nepal and Himalayan mountains (see section 3.1 for further details about the seismicity catalogue used in this study). The depth contours of the MHT decollement layer is from [23] with depth values in bold. Magnitude>8 earthquakes are labeled (in italic for historical event with higher uncertainty on their epicentral location).
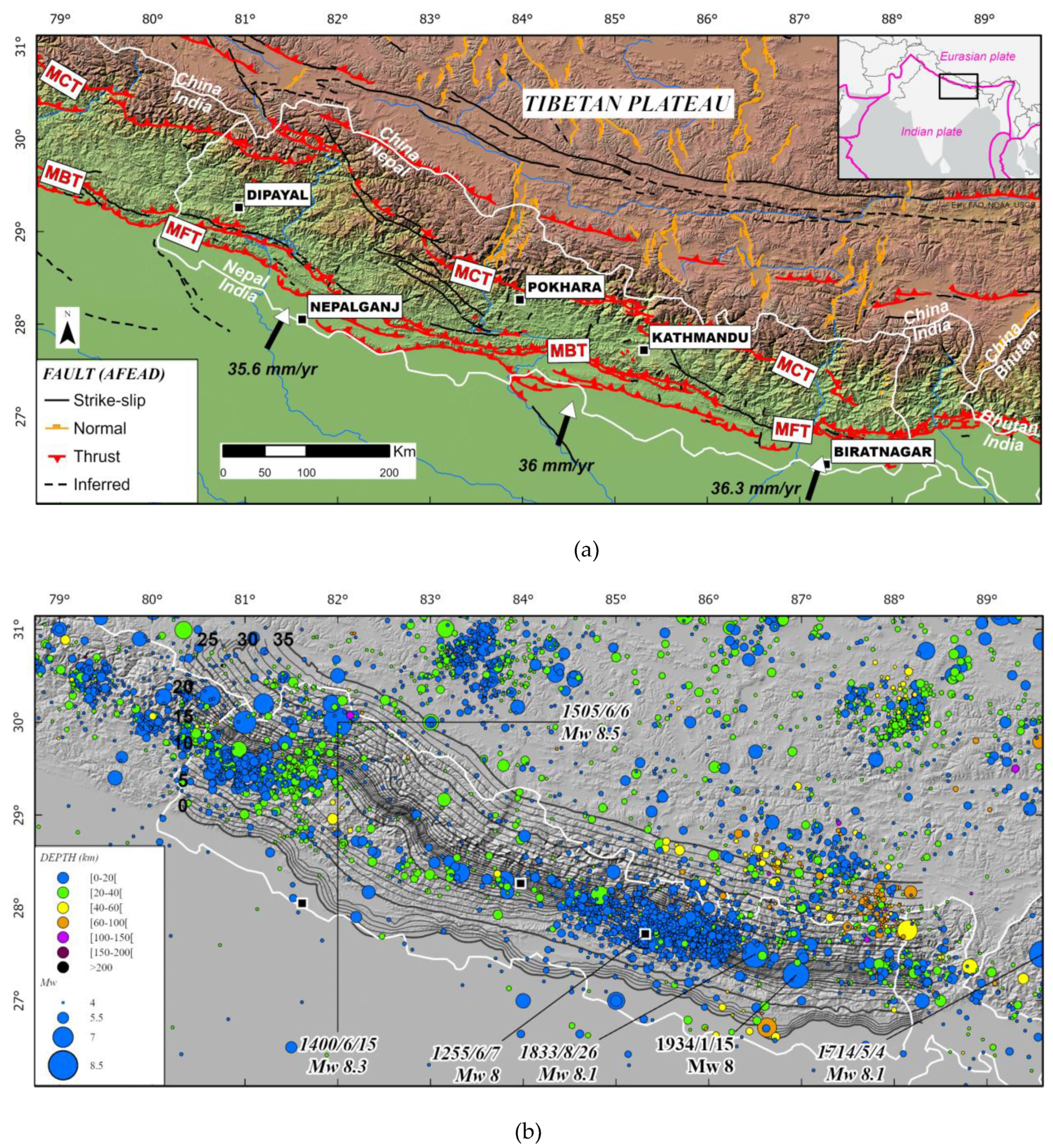
Preprints 73215 g001
Preprints 73215 g002aPreprints 73215 g002b
Figure 2. Magnitude pairs and magnitude regression relationships for homogenization of the earthquake catalogue in Mw*. (a) Mw, NDI – Mw, GCMT; (b) Ms, ALL – Mw, GCMT; (c) Mb, ALL – Mw, GCMT; (d) mL, DMN – Mw, GCMT, NEIC; (e) mL, NDI – Mw, GCMT, NEIC (f) mL, BJI – Mw, GCMT, NEIC.
Figure 2. Magnitude pairs and magnitude regression relationships for homogenization of the earthquake catalogue in Mw*. (a) Mw, NDI – Mw, GCMT; (b) Ms, ALL – Mw, GCMT; (c) Mb, ALL – Mw, GCMT; (d) mL, DMN – Mw, GCMT, NEIC; (e) mL, NDI – Mw, GCMT, NEIC (f) mL, BJI – Mw, GCMT, NEIC.
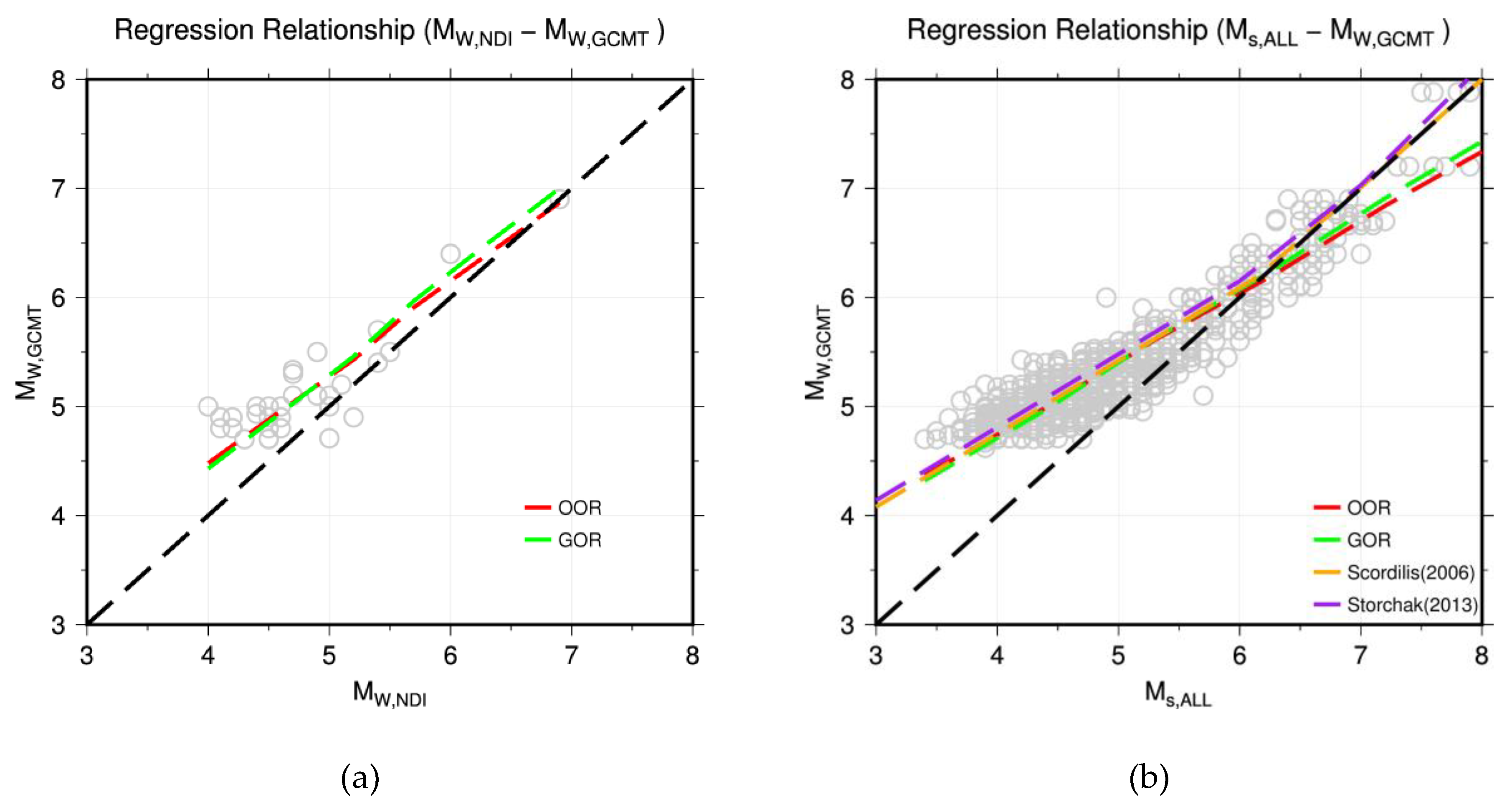
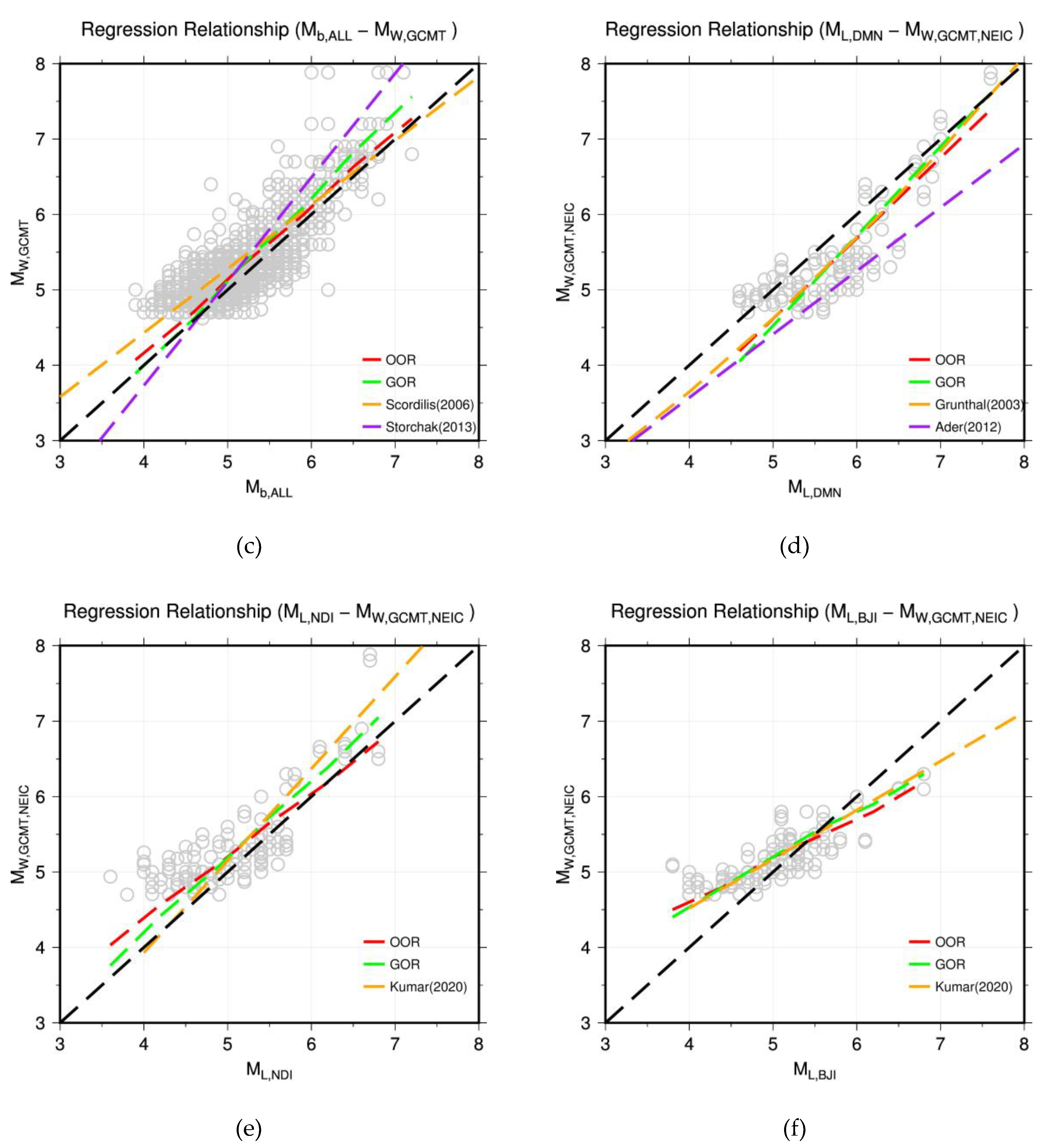
Preprints 73215 g002aPreprints 73215 g002b
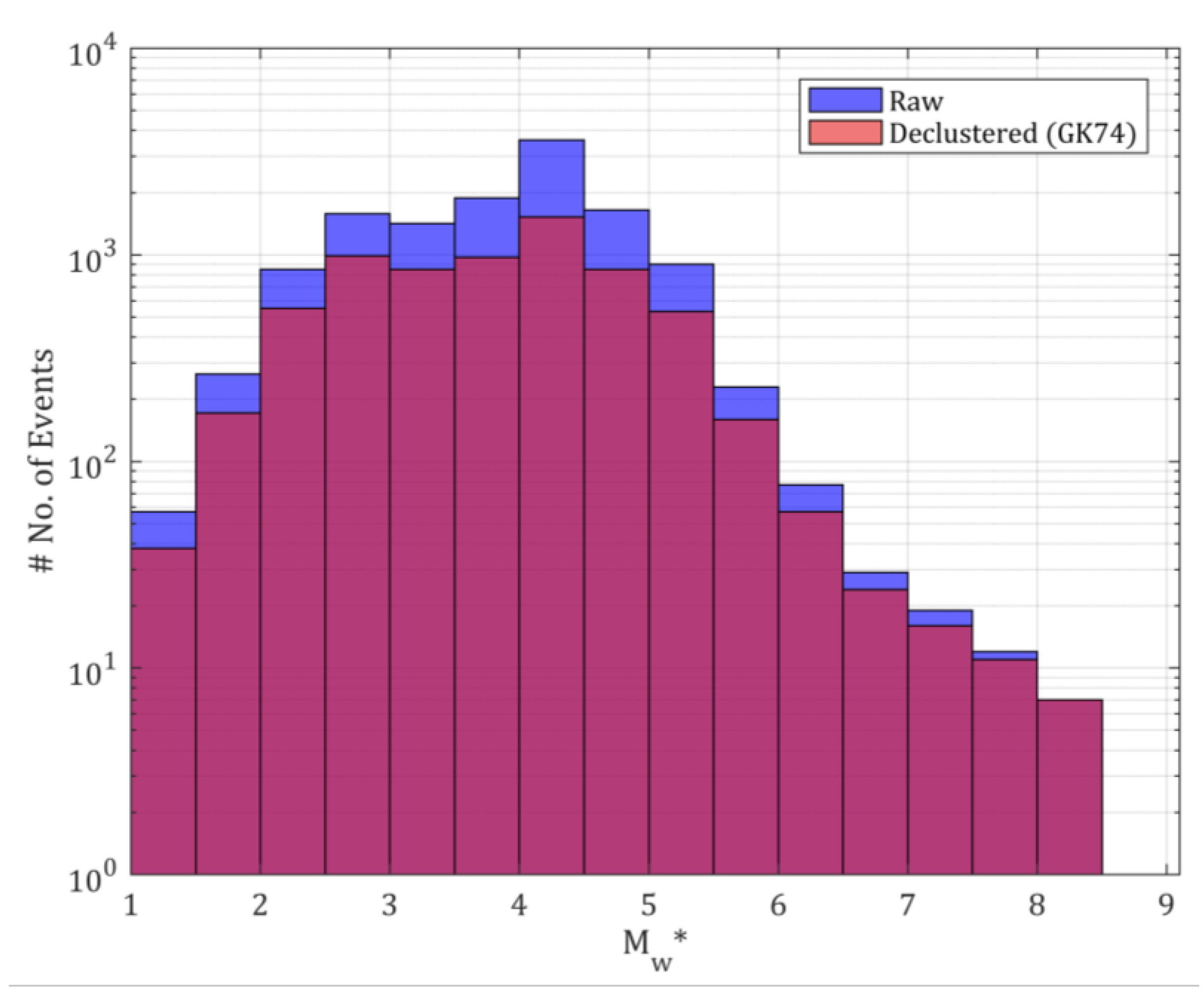
Preprints 73215 g003
Figure 3. Magnitude histogram of raw and declustered catalogue developed in this study.
Figure 3. Magnitude histogram of raw and declustered catalogue developed in this study.
Preprints 73215 g003
Preprints 73215 g004
Figure 4. Examples of completeness analysis performed for magnitude bin of (a) Mw5.0 - 5.5 and (b) Mw5.5 - 6.0. Cumulative number of earthquakes as a function of time (red circles). Inter-event variance (black dashed line). Best-estimate is shown as green dashed line. Gray shade represents the lower to upper estimates.
Figure 4. Examples of completeness analysis performed for magnitude bin of (a) Mw5.0 - 5.5 and (b) Mw5.5 - 6.0. Cumulative number of earthquakes as a function of time (red circles). Inter-event variance (black dashed line). Best-estimate is shown as green dashed line. Gray shade represents the lower to upper estimates.
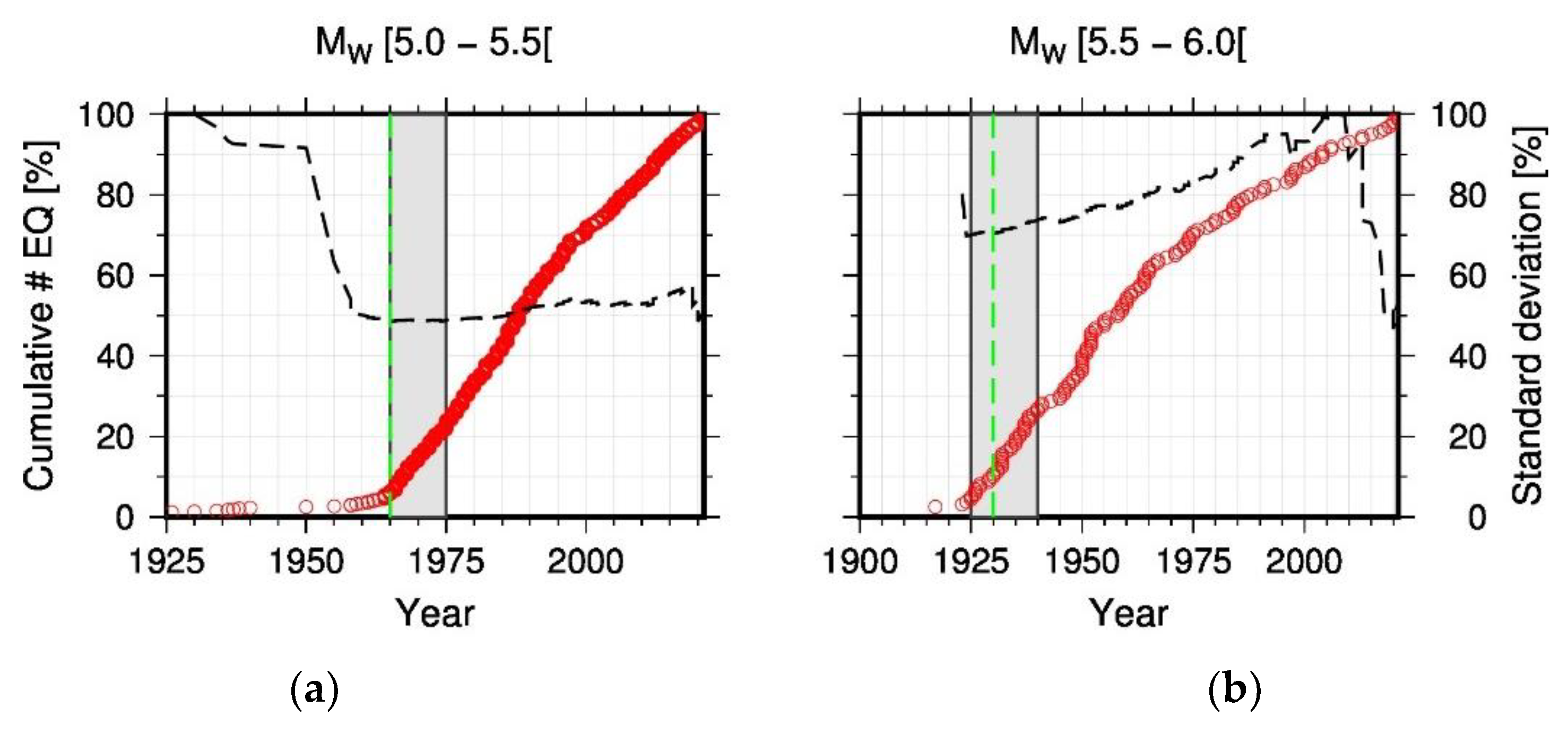
Preprints 73215 g004
Preprints 73215 g005
Figure 5. SM1 model zonation overlapped on the seismotectonic map of Nepal displaying main active faults (from AFEAD database, http://neotec.ginras.ru/index/mapbox/database_map.html), seismicity and focal mechanisms mainly from the CMT catalog (https://www.globalcmt.org) where red pattern is for normal, green for strike-slip and blue for thrust faulting events.
Figure 5. SM1 model zonation overlapped on the seismotectonic map of Nepal displaying main active faults (from AFEAD database, http://neotec.ginras.ru/index/mapbox/database_map.html), seismicity and focal mechanisms mainly from the CMT catalog (https://www.globalcmt.org) where red pattern is for normal, green for strike-slip and blue for thrust faulting events.
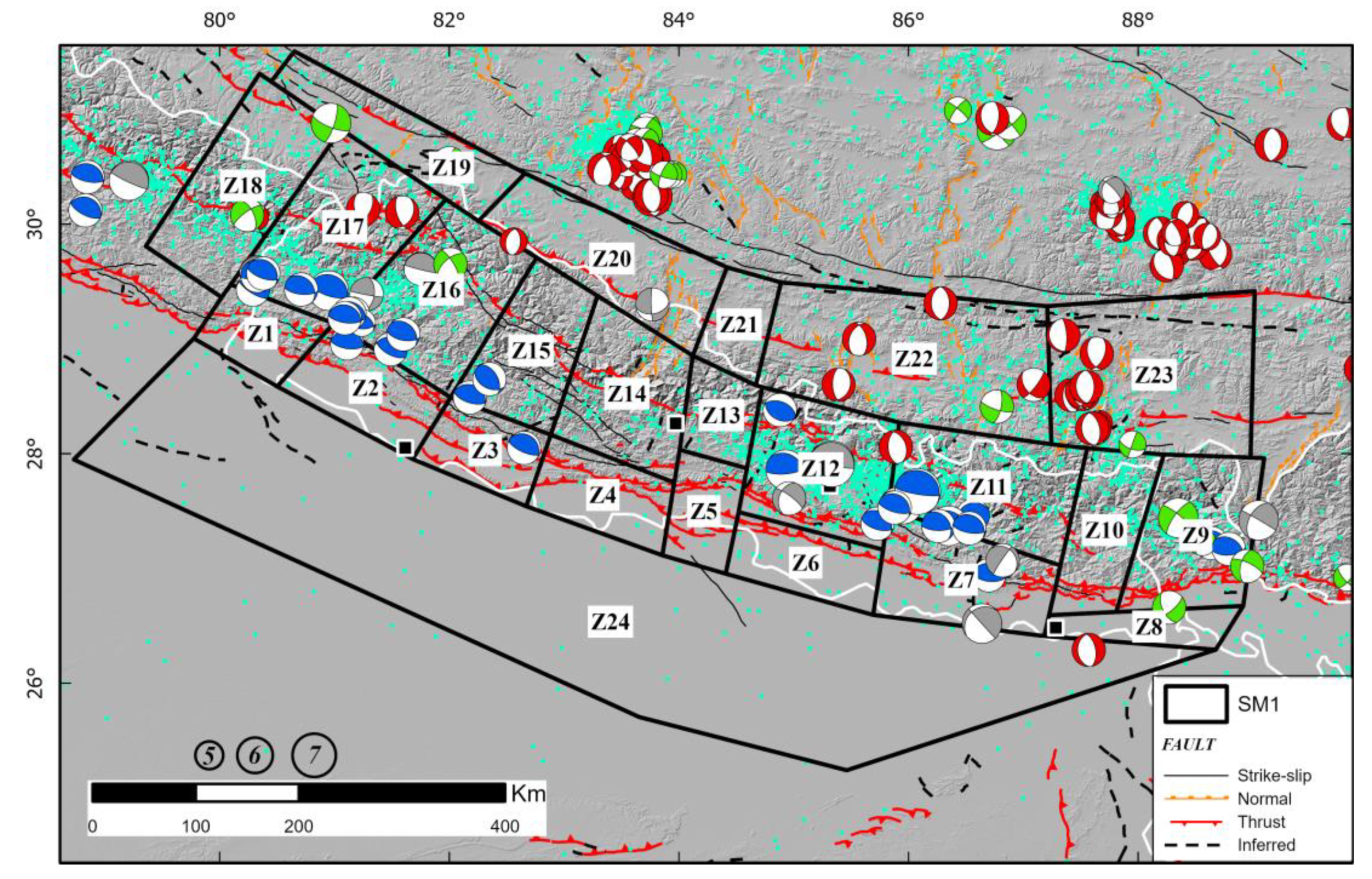
Preprints 73215 g005
Preprints 73215 g006
Figure 6. SM2 model zonation overlapped on the seismotectonic map of Nepal displaying main active faults (from AFEAD database, http://neotec.ginras.ru/index/mapbox/database_map.html), seismicity and focal mechanisms mainly from the CMT catalog (https://www.globalcmt.org) where red pattern is for normal, green for strike-slip and blue for thrust faulting events. Grey patterns are for undefined faulting events due to either stress heterogeneity or spatial variations of stress.
Figure 6. SM2 model zonation overlapped on the seismotectonic map of Nepal displaying main active faults (from AFEAD database, http://neotec.ginras.ru/index/mapbox/database_map.html), seismicity and focal mechanisms mainly from the CMT catalog (https://www.globalcmt.org) where red pattern is for normal, green for strike-slip and blue for thrust faulting events. Grey patterns are for undefined faulting events due to either stress heterogeneity or spatial variations of stress.
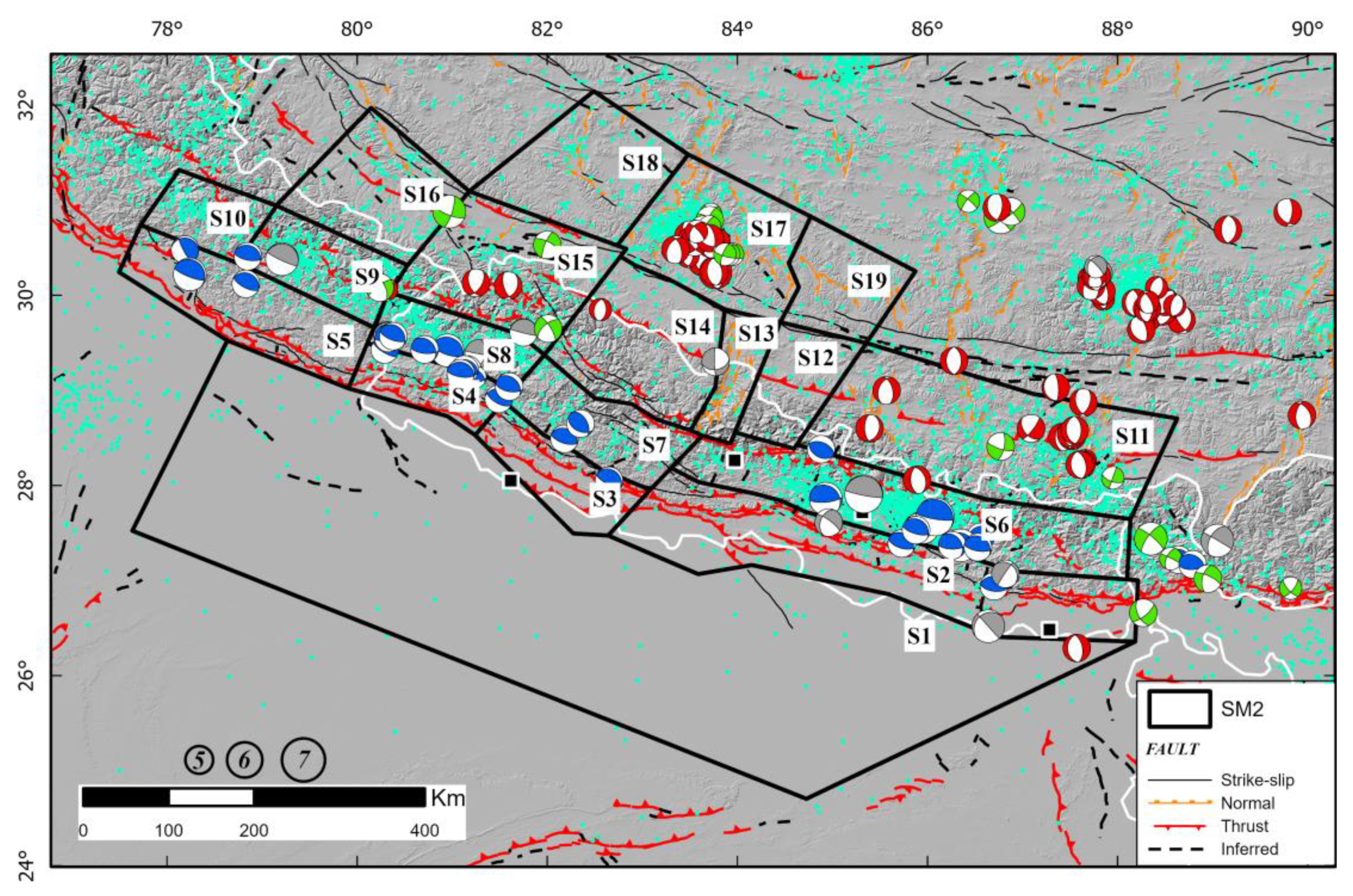
Preprints 73215 g006
Preprints 73215 g007aPreprints 73215 g007b
Figure 7. (a) Macrozone/Fault SM3F model zonation with the surface traces for simplified main thrust faults considered into the model. (b) Simplified and not to scale cross section of the MHT with the main related thrusts considered into the SM3F model modified after [71].
Figure 7. (a) Macrozone/Fault SM3F model zonation with the surface traces for simplified main thrust faults considered into the model. (b) Simplified and not to scale cross section of the MHT with the main related thrusts considered into the SM3F model modified after [71].
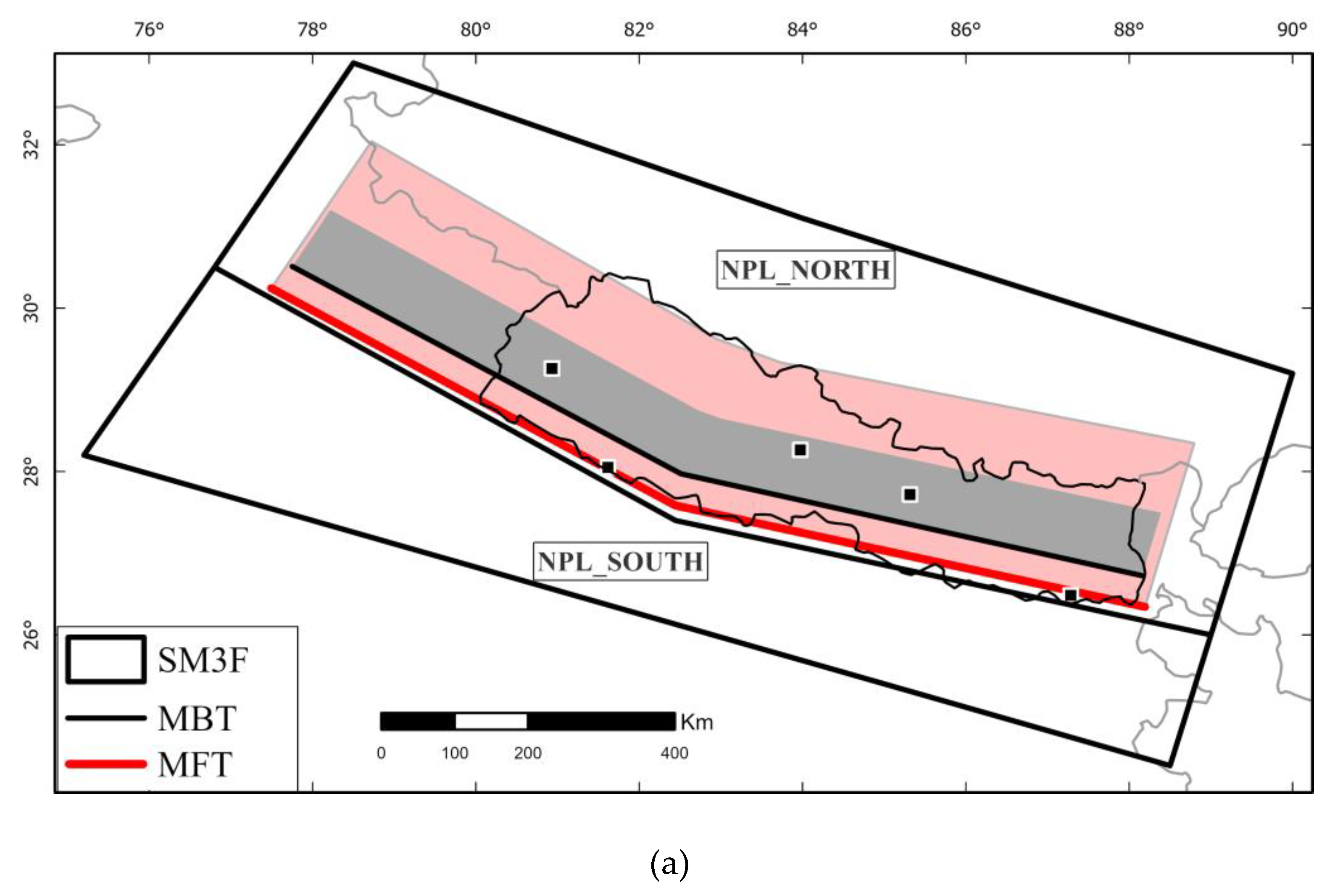
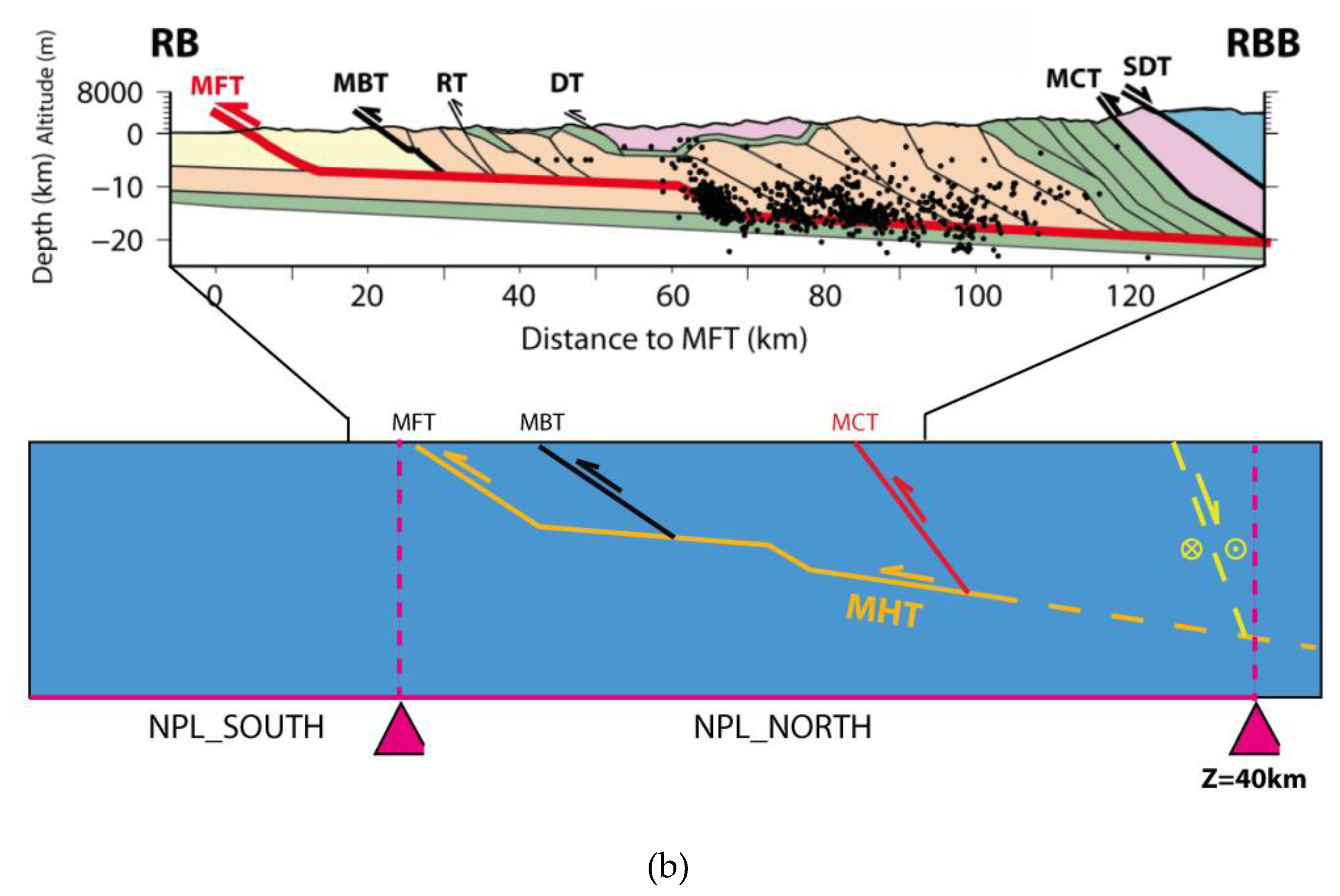
Preprints 73215 g007aPreprints 73215 g007b
Preprints 73215 g008
Figure 8. Example of GR evaluation performed for the zone Z17 for SM1 evaluated based on catalogue developed in this study. (Top-left) Observed seismicity rates (blue circles for individual solutions) compared to modeled G-R curves (gray lines for individual solutions). The mean G-R curve is shown in black and compared to the SCR G-R defined by [75] shown in purple. The red color refers to the solution obtained with the original catalogue. (Top-right) Map of the seismicity considered in the analysis. Only the epicenter shown as red circles are selected for the calculation after applying the completeness criteria (Bottom-left) Statistics of the a-values (per 1 million km2) and b-values obtained through the Monte-Carlo sampling (gray circles). The percentiles 2, 16, 50, 84, 98th are shown as squares. (Bottom-right) Analysis of the correlation of the individual G-R solutions (gray circles).
Figure 8. Example of GR evaluation performed for the zone Z17 for SM1 evaluated based on catalogue developed in this study. (Top-left) Observed seismicity rates (blue circles for individual solutions) compared to modeled G-R curves (gray lines for individual solutions). The mean G-R curve is shown in black and compared to the SCR G-R defined by [75] shown in purple. The red color refers to the solution obtained with the original catalogue. (Top-right) Map of the seismicity considered in the analysis. Only the epicenter shown as red circles are selected for the calculation after applying the completeness criteria (Bottom-left) Statistics of the a-values (per 1 million km2) and b-values obtained through the Monte-Carlo sampling (gray circles). The percentiles 2, 16, 50, 84, 98th are shown as squares. (Bottom-right) Analysis of the correlation of the individual G-R solutions (gray circles).
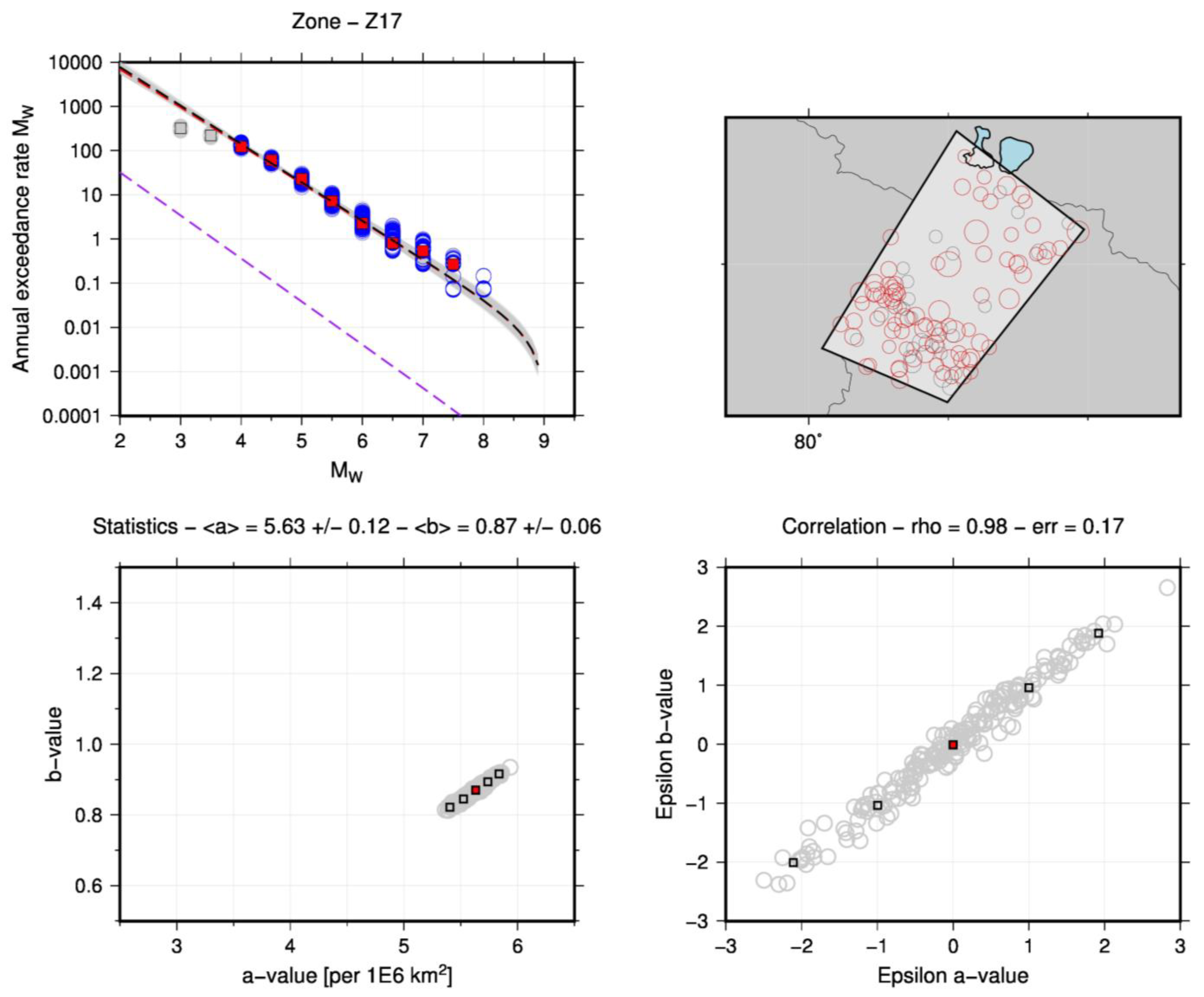
Preprints 73215 g008
Preprints 73215 g009aPreprints 73215 g009b
Figure 9. Cumulated annual activity rates scaled to million km² considering Mw≥6.0 for the three models (a) SM1; (b) SM2 and (c) SM3F. The color scale prevails for the three models.
Figure 9. Cumulated annual activity rates scaled to million km² considering Mw≥6.0 for the three models (a) SM1; (b) SM2 and (c) SM3F. The color scale prevails for the three models.
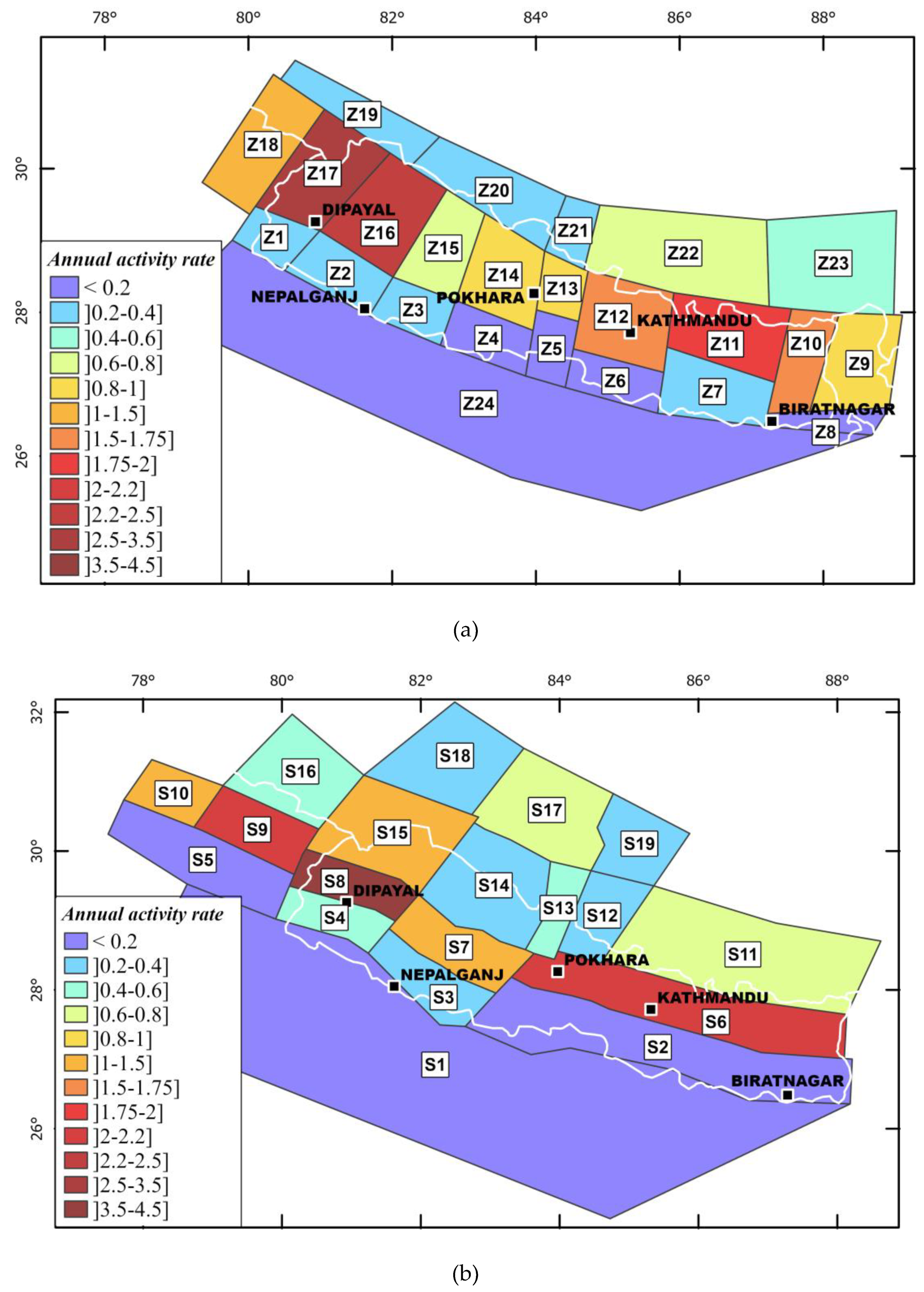
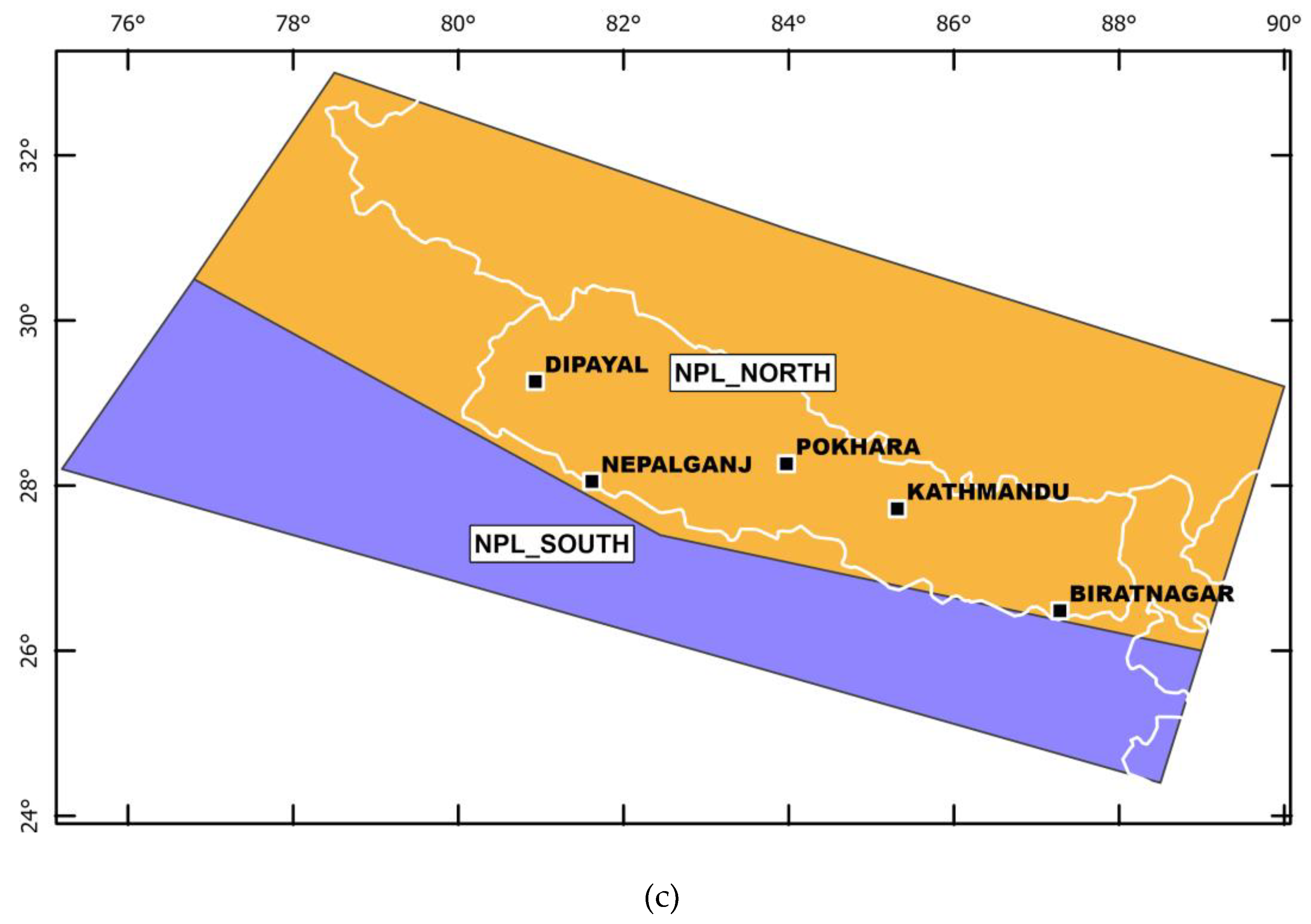
Preprints 73215 g009aPreprints 73215 g009b
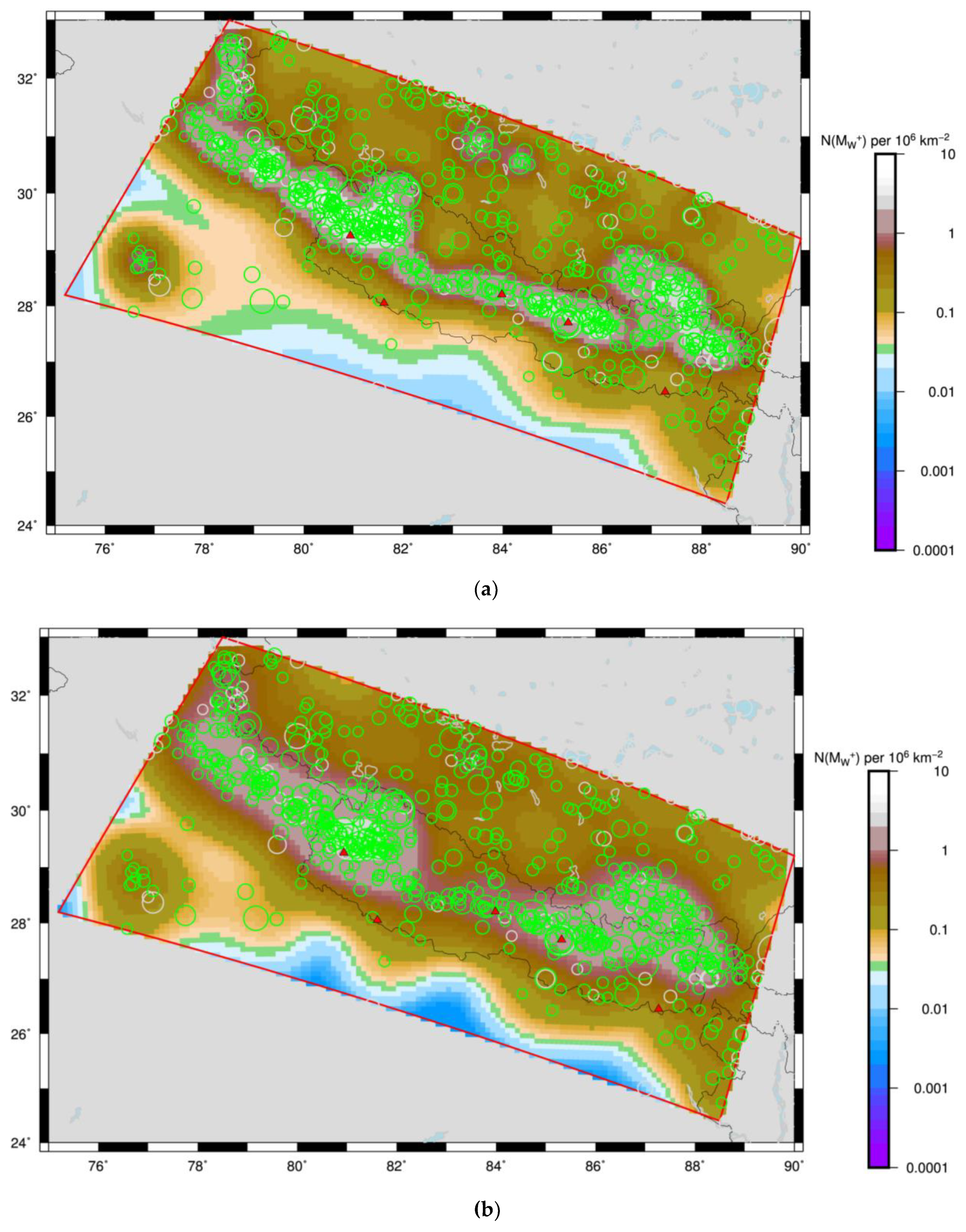
Preprints 73215 g010
Figure 10. N-value (Number of events greater than Mw* ≥ 6) per million km2 computed for the target region using kernel functions (a) Adaptative kernel using 5 neighboring events (SA5) and (b) Fixed kernel using 10 neighboring events (SF10). The green circles are epicentral locations of the events within the completeness period of consideration and grey ones are outside completeness period and are not considered for assessment of activity parameters. The sites considered for the UHS results comparison in red triangles.
Figure 10. N-value (Number of events greater than Mw* ≥ 6) per million km2 computed for the target region using kernel functions (a) Adaptative kernel using 5 neighboring events (SA5) and (b) Fixed kernel using 10 neighboring events (SF10). The green circles are epicentral locations of the events within the completeness period of consideration and grey ones are outside completeness period and are not considered for assessment of activity parameters. The sites considered for the UHS results comparison in red triangles.
Preprints 73215 g010
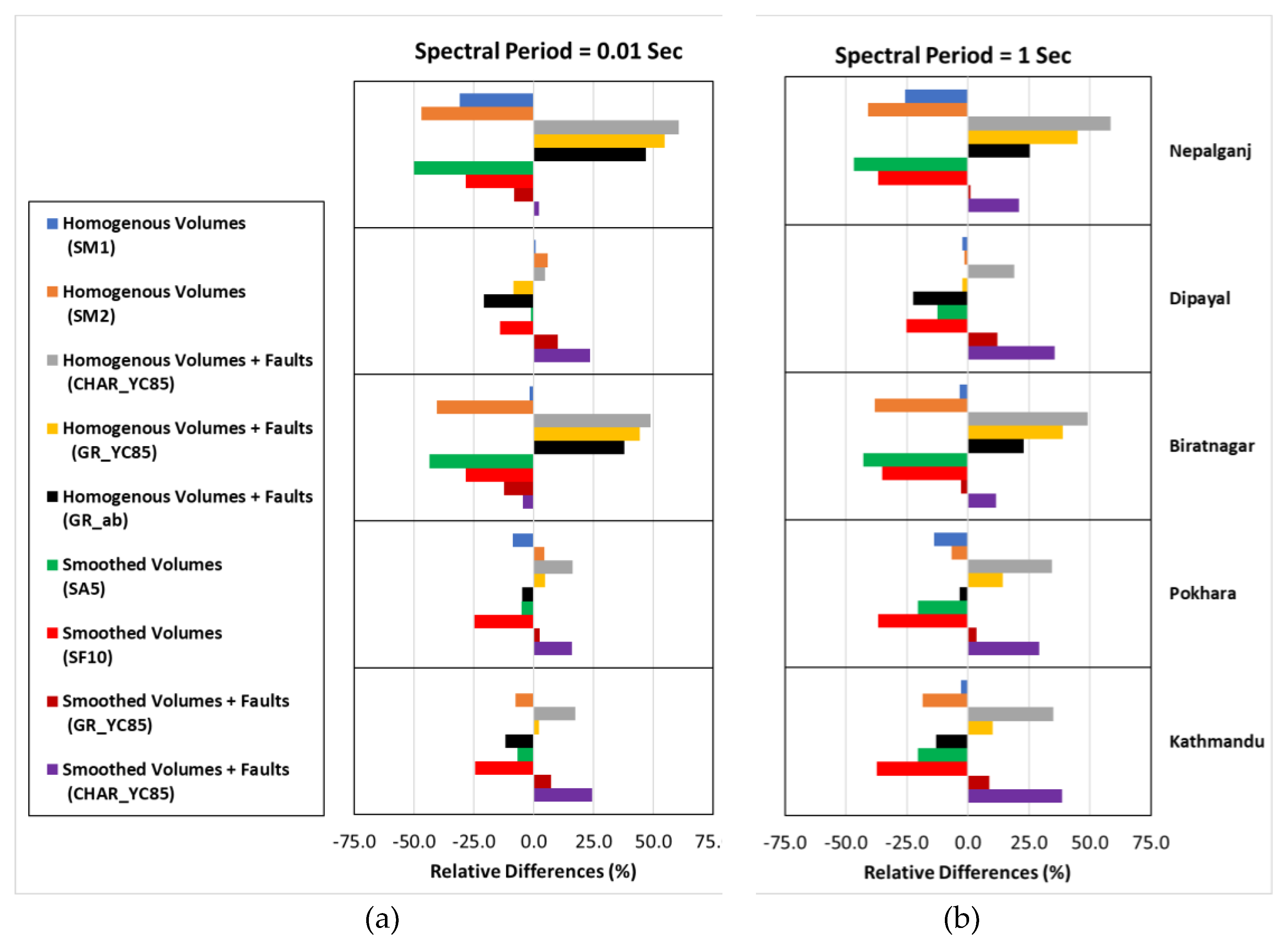
Preprints 73215 g012
Figure 12. Sensitivity analysis of the spectral accelerations from the SSC models. Relative difference of each mean UHS to the unweighted average of all SSCs considered at return period of 475 years and for five sites considered. (a) Spectral period of 0.01 second; (b) Spectral period of 1 second.
Figure 12. Sensitivity analysis of the spectral accelerations from the SSC models. Relative difference of each mean UHS to the unweighted average of all SSCs considered at return period of 475 years and for five sites considered. (a) Spectral period of 0.01 second; (b) Spectral period of 1 second.
Preprints 73215 g012
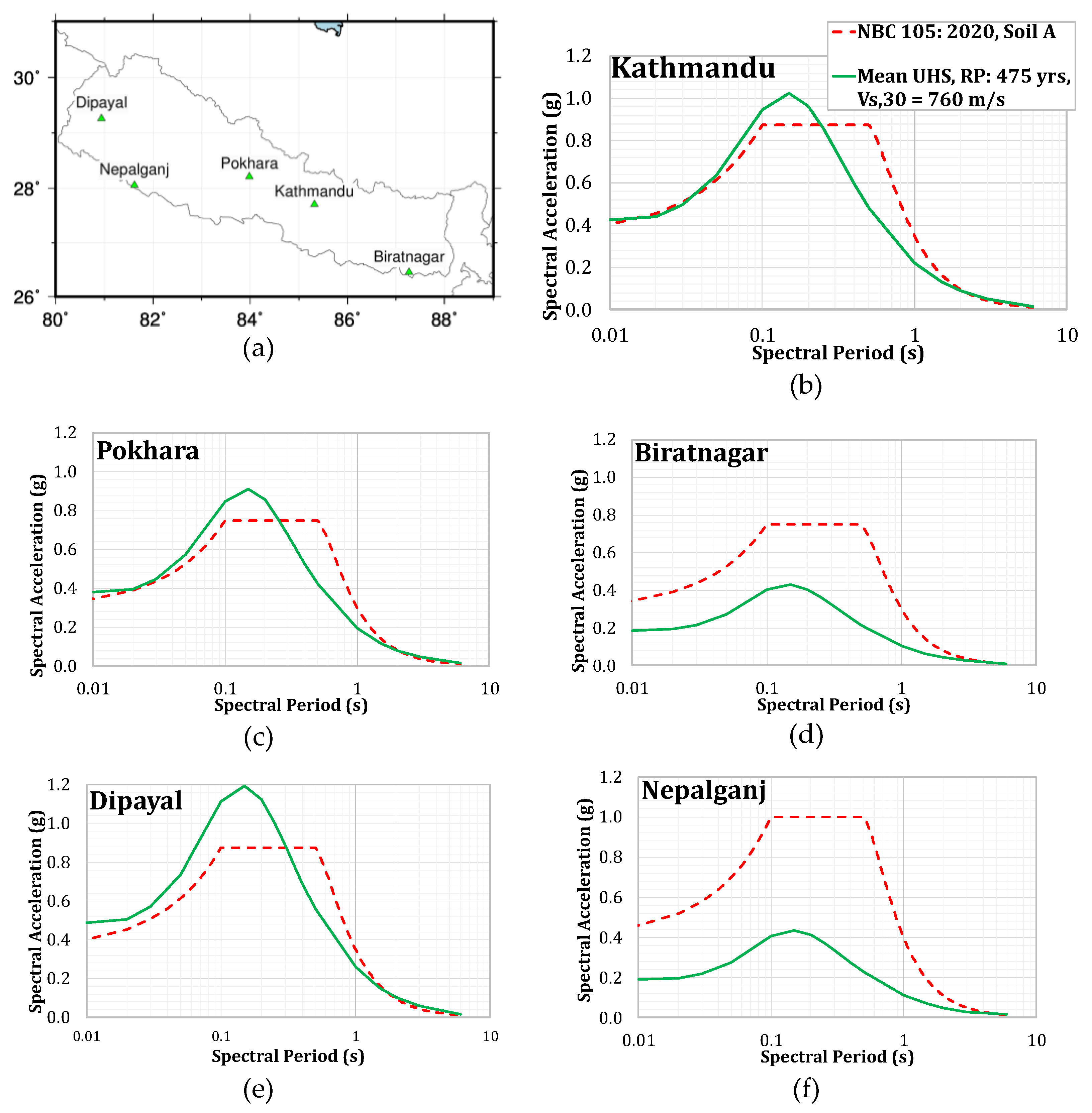
Preprints 73215 g017
Figure 17. (a) Map showing considered 5 location and mean UHS at return period of 475 years for five selected locations obtained in this study considering the site condition of (Vs,30=760 m/s) obtained in this study compared with NBC105: 2020 design spectrum for Soil A (b) Kathmandu; (c) Pokhara; (d) Biratnagar; (e) Dipayal; (f) Nepalganj. Note that the x-axis is in log scale.
Figure 17. (a) Map showing considered 5 location and mean UHS at return period of 475 years for five selected locations obtained in this study considering the site condition of (Vs,30=760 m/s) obtained in this study compared with NBC105: 2020 design spectrum for Soil A (b) Kathmandu; (c) Pokhara; (d) Biratnagar; (e) Dipayal; (f) Nepalganj. Note that the x-axis is in log scale.
Preprints 73215 g017
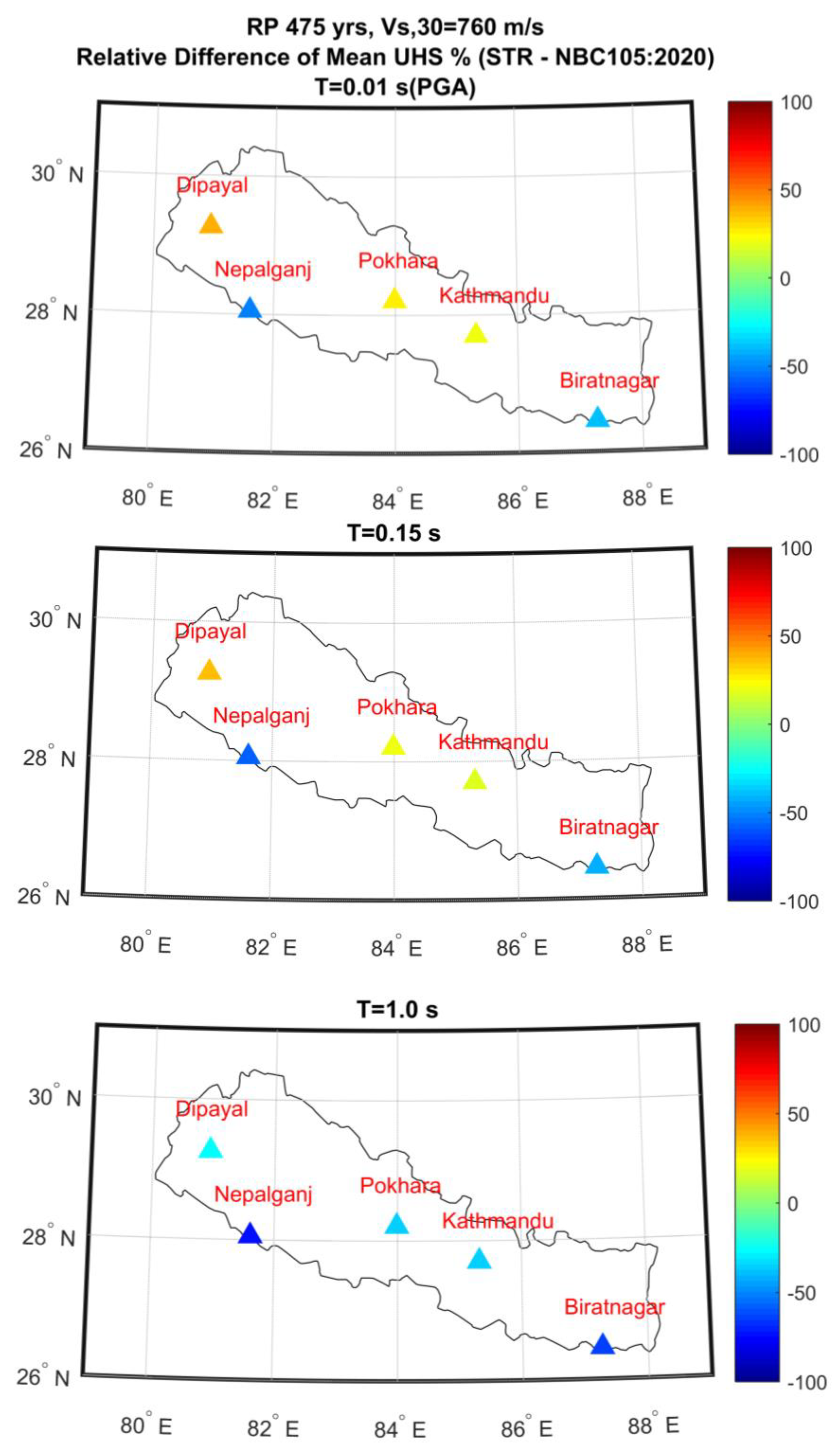
Preprints 73215 g018
Figure 18. Relative difference (%) in terms of mean spectral acceleration parameters between the current study (STR) and the levels recommended in Nepal Building Code, NBC105: 2020.Return periods of 475 considering Vs,30 of 760 m/s or soil A for NBC105:2020 for five sites selected for comparison. for spectral periods PGA (0.01s), 0.15s; and 1.0s.
Figure 18. Relative difference (%) in terms of mean spectral acceleration parameters between the current study (STR) and the levels recommended in Nepal Building Code, NBC105: 2020.Return periods of 475 considering Vs,30 of 760 m/s or soil A for NBC105:2020 for five sites selected for comparison. for spectral periods PGA (0.01s), 0.15s; and 1.0s.
Preprints 73215 g018
Preprints 73215 g019
Figure 19. Comparison of mean PGA at 475-year return period, considering standard rock condition (Vs,30=760 m/s) compared with previous studies including NBC105:2020.
Figure 19. Comparison of mean PGA at 475-year return period, considering standard rock condition (Vs,30=760 m/s) compared with previous studies including NBC105:2020.
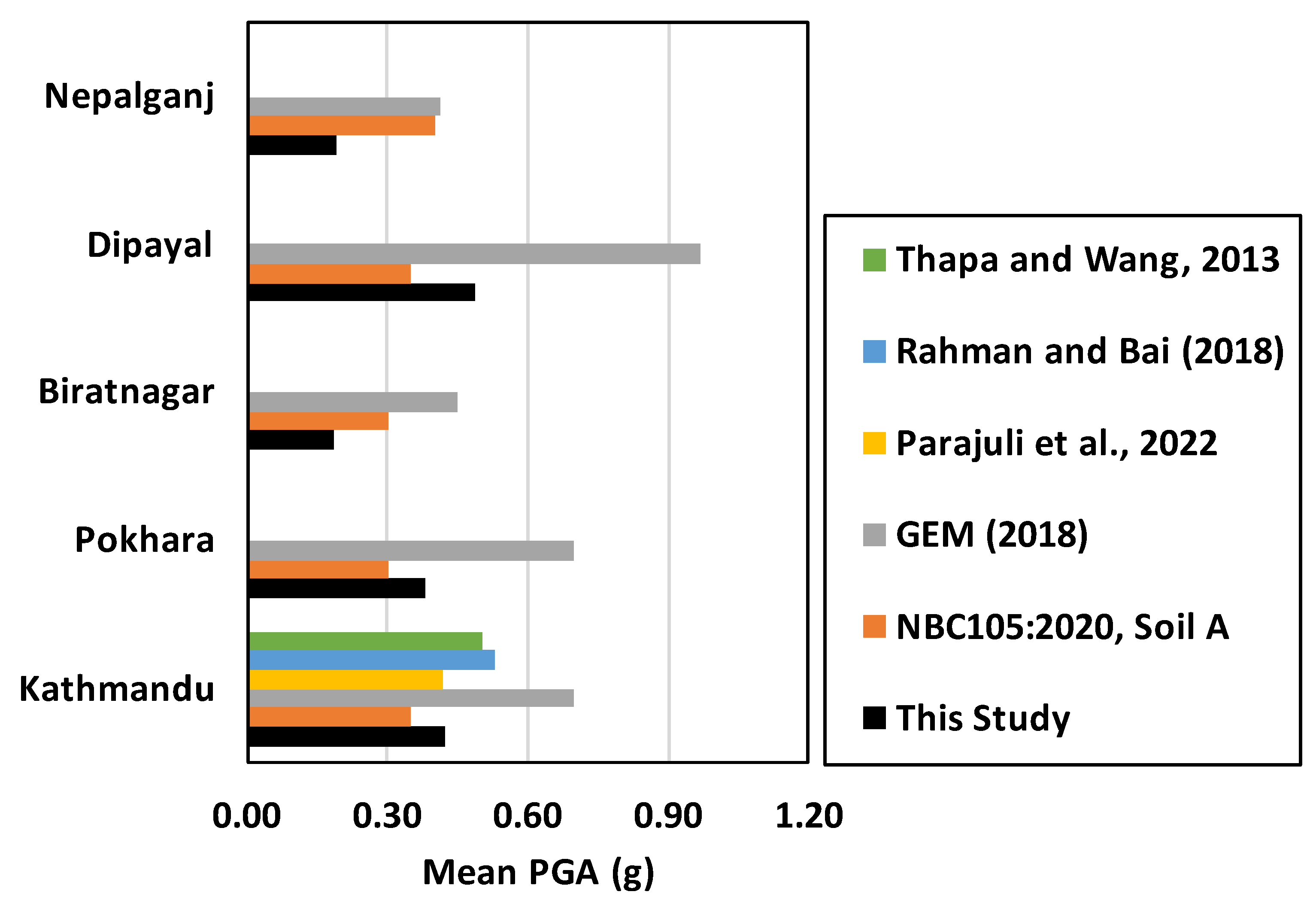
Preprints 73215 g019
Preprints 73215 g020
Figure 20. Seismic hazard maps of Nepal showing the peak ground acceleration (PGA) distribution at standard bedrock (i.e., Vs30 = 760 m/s) level. (a) PGA with 10 % probability of exceedance in 50 years. (b) PGA with 2 % probability of exceedance in 50 years. Note that the color scales are different between (a) and (b).
Figure 20. Seismic hazard maps of Nepal showing the peak ground acceleration (PGA) distribution at standard bedrock (i.e., Vs30 = 760 m/s) level. (a) PGA with 10 % probability of exceedance in 50 years. (b) PGA with 2 % probability of exceedance in 50 years. Note that the color scales are different between (a) and (b).
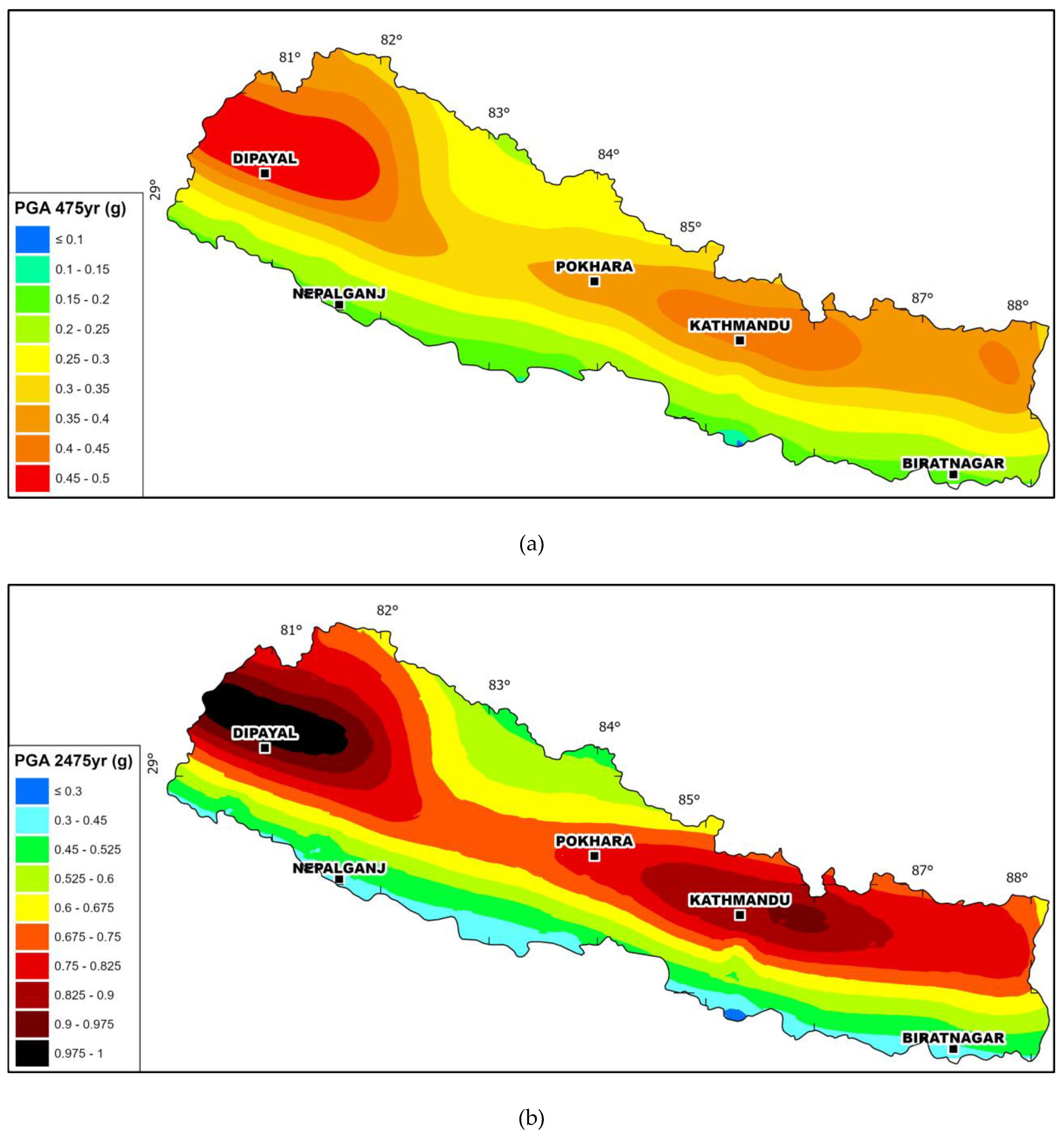
Preprints 73215 g020
Table 1. Scheme use to identify the duplicate events among different source catalogues.
Table 1. Scheme use to identify the duplicate events among different source catalogues.
Time period Distance [km] Time Magnitude
≤ 1900 500 2.5 hours 3.0
1901-1979 500 120 s 2.0
1980 - 1999 250 60 s 2.0
≥ 2000 100 30 s 1.0
Table 2. The main sources of information used to develop the new catalog for this study.
Table 2. The main sources of information used to develop the new catalog for this study.
Source Databases (Acronym, References) Period Covered Description
REF
[9,41]		 1223 - 1900 The lists of historical seismicity for Himalayan region provided in various scientific publications.
GHEA
[42]		 1411 - 1900 The Global Historical Earthquake Achieves (GHEA) is the worldwide database of historical seismic events.
ISC-GEM
[43,44,45]		 1904 - 2016 ISC-GEM V9.1, Global instrumental earthquake catalogue compiled, reviewed and magnitude homogenized mostly for larger earthquakes (M≥5.0).
EHB
[46]		 1964 - 2017 Revision of hypocenter location for the larger events (generally M≥4.0) for ISC catalogue.
GCMT
[47]		 1976 - 2021 The Global Centroid Moment Tensor (GCMT) catalogue comprises the revision of magnitude based on [47]. This catalog provides events of magnitude mostly greater than 5, revised in magnitude, since 1976. The main interest in CMT catalogue is Mw magnitude estimates information, which is often taken as a reference magnitude.
ISC
[48]		 1900 - 2022 International Seismological Center (ISC) is the most complete source for pre-instrumental and instrumental events. Note that, the data for National Seismological Centre, Nepal (DMN)[49] was recovered through ISC bulletins for use in this study.
USGS
[50]		 1985 - 2022 United States Geological Survey (USGS) is the earthquake catalogue compiled and distributed by the United States Geological Survey (USGS).
NDI
[51]		 1720 - 2022 National Centre of Seismology (NDI) is an Indian national database of seismological data which covers both historical and instrumental period.
Table 3. Regression relationships derived from the Generalized Orthogonal Regression (GOR) method utilized in this study.
Table 3. Regression relationships derived from the Generalized Orthogonal Regression (GOR) method utilized in this study.
Conversion Intercept Gradient σ N Magnitude Range
Mw, NDI – Mw* 0.8754 (± 0.40) 0.8878 (± 0.08) 0.20 41 4.0 - 6.9
mL, NDI – Mw* 0.0629 (± 0.37) 1.0273 (± 0.07) 0.28 270 3.6 – 6.8
mL, BJI – Mw* 1.9015 (± 0.27) 0.6524 (± 0.05) 0.19 182 3.8 – 6.8
*N represents the number pairs used to develop relation and σ represents the sigma of the relationship.
Table 4. Estimates of the year of completeness.
Table 4. Estimates of the year of completeness.
Mw
range		 Best estimate completeness year Minimum completeness year Maximum completeness year End
year		 Mean
completeness (years)
3.0 - 3.5 2000 1995 2005 2021 21
3.5 - 4.0 2000 1995 2005 2021 21
4.0 - 4.5 1995 1995 2000 2021 26
4.5 - 5.0 1980 1975 1985 2021 41
5.0 - 5.5 1965 1965 1975 2021 56
5.5 - 6.0 1930 1925 1940 2021 91
6.0 - 6.5 1910 1900 1920 2021 111
6.5 - 7.0 1910 1900 1920 2021 111
7.0 - 8.0 1800 1800 1850 2021 221
8.0 - 9.0 1200 1180 1250 2021 821
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated