Framework for Representing, Building and Reusing Novel State-of-the-art 3D Object Detection Models in Point Clouds Targeting Self-Driving Applications

Preprint

Article

Framework for Representing, Building and Reusing Novel State-of-the-art 3D Object Detection Models in Point Clouds Targeting Self-Driving Applications

Altmetrics

Downloads

128

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

09 May 2023

Posted:

10 May 2023

You are already at the latest version

Alerts

Abstract

The rapid development of Deep Learning brought novel methodologies for 3D Object Detection using LiDAR sensing technology. These improvements in precision and inference speed performances lead to notable high performance and real-time inference, which is especially important for self-driving purposes. However, the developments carried by these approaches overwhelm the research process in this area since new methods, new technologies, and software versions lead to different project necessities, specifications and requirements. Moreover, the improvements brought by the new methods may be due to improvements in newer versions of deep learning frameworks and not just the novelty and innovation of the model architecture. Thus, it became crucial to create a framework with the same software versions, specifications and requirements that accommodate all these methodologies and allow the easy introduction of new methods and models. A framework is proposed that abstracts the implementation, reusing and building of novel methods and models. The main idea is to facilitate the representation of state-of-the-art (SoA) approaches and simultaneously encourage the implementation of new approaches by reusing, improving and innovating modules in the proposed framework, which has the same software specifications to allow a fair comparison. This makes it possible to determine if the key innovation approach outperforms the current SoA by comparing models in a framework with the same software specifications and requirements.

Keywords:

Subject: Computer Science and Mathematics - Artificial Intelligence and Machine Learning

1. Introduction

The field of computer vision has seen significant advancements in recent years, particularly in the area of 3D object detection from point cloud data. However, there is still a need for a general representation framework that can be applied to a wide range of 3D object detection tasks, regardless of the specific sensor or application domain. The development verified in recent years of the computational power offered by cutting-edge GPUs allowed the application of deep learning algorithms to detect objects in several domains. One such domain is autonomous driving using Light Detection And Ranging (LiDAR) data, representing a considerable gain in detection efficiency, precision, and inference speed [1].

In recent years, there has been significant progress in 3D object detection models based on LIDAR data for self-driving applications. A multitude of frameworks and projects have been proposed, each with its own unique approach to addressing the challenges of detecting and tracking objects in a 3D environment. However, this diversity also poses a challenge when it comes to deploying these models for onboard inference in a self-driving vehicle [4,17].

One major issue is the enormous variation in software versions, libraries, and supported platforms, making it difficult to assemble and deploy these models correctly. Additionally, self-driving requirements must be taken into consideration, such as the need for operationalisation with different modules and the limited computational resources available in onboard systems.

Regardless, the 3D object detection models discussed in the literature take point clouds as input and are known to be more complex. These models have a deeper pipeline and process a more significant amount of data. For example, a point cloud usually comprises between 100k-120k [4], where each point holds data related to the Euclidean distance and signal reflection, that is, 128 bits to translate each information of each point.

The literature includes recent research such as [1,2,3,4], it has been suggested that the minimum operating requirements for self-driving applications should include an overall class classification of at least 60 mAP and an inference time of less than 100 ms.

In this context, the need for a standardized and optimized framework for 3D object detection based on LIDAR data becomes even more important. Such a framework could simplify the deployment process, enable better interoperability across different systems, and facilitate the development of more efficient and effective self-driving systems.

1.1. Our Contribution

This paper aims to propose a general SoA representation framework for 3D object detection from the point cloud. It supports multiple SoA 3D object detection methods with highly refactored codes for both one-stage and two-stage methods. Also, it enables the implementation and reusing of different approaches with less manual engineering efforts by proposing an abstract way of building object detectors. At the same time, it facilitates the implementation of new methods in each module of the framework. By implementing different SoA we are trying to facilitate a new approach for the scientific community. In this way, it will be possible to offer a framework for real-time testing inference and measure the trade-off between metrics (mAPvs inference time) in one single framework 3D model objects applying for self-driving applications. Therefore, the contributions proposed in this paper are as follows:

An abstract framework for the implementation/representation of edge for 3D object detection models using LIDAR data.
Less engineer effort to implement new methods in different framework models.
A simpler way to change hyperparameters and retrain models using YML files.
An easily represented model using these YML files automatically.

The organisation of this paper is as follows: In the next Section 2, some of the state-of-the-art works related to 3D object detection systems and hardware platforms for their implementation are presented. Section 3 shows a four-step methods used to select, train, and tune a deep learning model for deployment on a hardware device. The following section, Section 4, presents the selected 3D object detection model, as well as its deep learning components, specifying the details about the architecture of the target hardware device and the implementation of the hardware components and software. The presentation of performance evaluation results, comparison of results and discussion of these results occur in Section 7. Finally, Section 8 presents the main results achieved in this paper and future work.

2. Related Work

In recent years, object detection models in point cloud presented in the literature have been highly improved, and more and more detection performance has been achieved. Based on the literature, the most discussed models are divided into two broad categories: approaches based on CNN 3D and approaches based on CNN 2D, where different data representations, backbone networks and multiscale resource learning techniques can be adopted [4].

When it comes to 3D object detection approaches, they can be classified into three types. The first category is based on volumetric representation. The second is based on Pillars. Finally, the third is based on raw points. Furthermore, they are novel models recognised by the scientific community that provide innovation in the diverse architecture pipeline, high accuracy and performance in 3D object detection.

The first category, which can be divided into one-stage or two-stage, is usually based on the volumetric representation to discretize the point cloud. The one-stage representation only has a single stage, and SECOND [8] is an example. This 3D convolution-based technique produces item class prediction, bounding box regression, and orientation classification. The two-stage representation got the same results as the single stage but fine-tuned the bounding box. Examples of two-stage are P-RCNN [9], VoxelRCNN [7] and

P o i n t A^{2}

[10]. Usually, these methods require more resources in terms of computing power because they either use the costly volumetric representation of the point cloud or rely on computationally intensive 3D convolutions.

The second category of models fall under one-stage methods and use 2D convolutions in place of the computationally intensive 3D convolutions. PointPillar [18] is an example of this approach. To decrease the high computational cost of handling 3D LiDAR data, these models usually compress the data into a 2D projection or organize it into Pillars [18]. While these methods are quicker and suitable for real-time applications, they sacrifice detection capabilities by losing some information. This highlights the trade-off between inference time and accuracy.

The third category of methods, such as Point RCNN [12], utilizes a two-stage approach based on raw point data and voxel representation to take advantage of their respective benefits. In the first stage, the network uses voxel representation as input and performs light convolutional operations, which results in a small number of high-quality initial predictions. An attention mechanism effectively combines coordinate and indexed convolutional features of each point in the initial forecast, maintaining both accurate localization and contextual information. The second stage uses the fused feature of interior points to refine the prediction [13].

3. Methodology

To implement/represent the 3D Object Detection models based on Deep Learning in the framework, we employed a three-step methodology, which is depicted in Figure 1. (1) Firstly, a set of model architecture and hyper-parameter specifications are defined in different configuration files. These files define the specifications of the components of each module in the framework (described in Section 4) as well as the training and test specifications that are then used to build, train and test the object detectors. We chose the models for 3D Object Detection based on a review of existing literature, which is outlined in Section 2 and elaborated further in [4]. The framework, described in the Section 4 section, was developed to facilitate the representation of any Object Detection model.

Once the object detector is built, it is subjected to a training and evaluation pipeline (2), where various optimizations can be performed to enhance the accuracy metrics and fulfill the inference time requirements. In our project, since different components need to operate simultaneously, such as the SLAM algorithm and object detector, we define an overall mAP of 60% and an inference time of less than 100ms (metrics are always subject to trade-offs). The training and evaluation step can be done by changing the training specification in the respective model configuration. The concept behind defining the training and testing parameters in these configuration files is to make it easier to modify them and subsequently submit the object detector to the same training and evaluation pipeline. The pipeline was executed on a server-side node with an Intel Core i9 processor, 64GB of RAM, and a Quadro RTX 8000 GPU. Therefore, the proposed workflow follows an iterative process, where the model is fine-tuned. The training and evaluation steps are repeated whenever necessary until it meets the requirements and satisfies the application requirements. The evaluation and comparison process is carried out using KITTI benchmarks using the validation set on the aforementioned server node. In conclusion, this workflow guarantees that the models meet the application requirements and attain the highest possible accuracy. This procedure identifies a group of potential Object Detection models for the subsequent step.

After completing step (2) workflow, a comparison phase of the resulting models (step 3) is conducted to select the model that can ensure a better balance between precision and inference time. The subsequent section presents information on the architecture of the framework, the chosen Deep Learning models, and the parameters used in the fine-tuning process.

4. Framework for Representing 3D Object Detection Models

Our framework’s key innovation is that it facilitates the representation of any object detector through YML configuration files that define their module specifications in each framework component. Moreover, this framework, shown in Figure 2, aims to facilitate the implementation and integration of new modules in each framework component to allow the comprehensive representation of the different state-of-the-art 3D object detectors.

The first component, (1) Data Representation, receives the set of points and discretises them in a set o data structures, such as Pillars or Voxels or only passes the set of points to be used by the Middle Extractor module (3). (2) The local feature encoder receives as input these data structures, more specifically, the set of Pillars or Voxels and encodes and concatenates their features. Then, in the Middle Extractor (3), 3D and/or 2D Backbones extract features from local encoded features, which are used by the (4) Detection Head to predict object class, bounding box offsets and direction (5). (4.1) This Detection Head based on RPN can be assisted by two modules, a (4.2) Point Head module and (4.3) Region of Interest (RoI) Head module, which refines the predicted bounding box offsets and orientation. (4.2) Point Head module is composed of three networks: a Point Intra Part Offset Head [10], a point-based segmentation head for keypoint segmentation [14], and another point-based segmentation head based on [12]. The (4.3) RoiHead module is defined for each state-of-the-art model based on their specificities, but typically it is composed of a Proposal Layer, which proposes a set of RoIs, a RoI Feature Extraction that pooled the RoI features and a RoI Head that predicts RoI class and bounding box offsets.

4.1. Point Cloud Data Representation

We receive an unordered set of points

P C = {p_{1}, p_{2}, p_{3} \dots p_{n}}

, where

n > 0

and each point p is represented as

(p^{x}, p^{y}, p^{z}, p^{r})

, where

p^{x}, p^{y}

and

p^{z}

correspond to coordinates in the three-dimension cartesian axis and

p^{r}

is the reflectance value provided by the LiDAR sensor. A point cloud range

P C_{R}

is a tuple

(L, H, W)

, where L consists of

(x_{m i n}, x_{m a x})

, H consists of

(y_{m i n}, y_{m a x})

, and W consists of

(z_{m i n}, z_{m a x})

. We denote a point cloud subset with respect to

P C_{R}

P C_{R} = {p_{i} : p_{i} \in P C, x_{m i n} \leq p_{i}^{x} \leq x_{m a x}, y_{m i n} \leq p_{i}^{y} \leq y_{m a x}, z_{m i n} \leq p_{i}^{z} \leq z_{m a x}}

4.1.1. Pillar Representation

The framework receives the points in

P C_{R}

and discretises them in the X-Y axis thus creating a set of pillars

P L_{p} = {p l_{1}, p l_{2}, p l_{3}, \dots, P L_{p}}

, where

p = m p

m p

is the max number of Pillars and

m p \in N^{+}

. Each

P L_{p}

has a fixed size in

P C_{R}

, and it is represented by a tuple

S_{P L_{p}} = (w, h)

, where w is the width of the Pillar along the x axis, and h is the height of the Pillar along the y axis. The points are grouped accordingly with the Pillar that resides.

To deal with the sparsity problem and save computation, a max number of points per pillar

N P

is defined. The points are randomly sampled if the number of points in each pillar is higher than

N P

. On the other hand, zero padding is added in case of less than

N P

points.

4.1.2. Voxel-based Representation

The voxelisation process assumes a similar way as proposed in Pillar discretisation; however, the received points are discretised in the X-Y-Z axis. It allows the creation of a set of voxels

V L_{j} = {v l_{1}, v l_{2}, v l_{3} \dots v l_{j}}

, where

j = m v

m v

means the max number of Voxels and

m v \in N^{+}

and each

V L_{j}

assumes a fixed size in

P C_{R}

, and a tuple represents it

S_{V L_{j}} = (w, h, d)

. w is the width of the voxel along the x axis, h is the height of the voxel along the y axis, and d is the depth of the voxel along the z axis.

A Random Sampling strategy is also applied to save computation, and a max number of points per voxel

N V

is also used. The strategy to sample points or apply zero padding is the same as the Pillar Representation.

4.1.3. Point-based

The idea in the point-based strategy is to pass the cropped point cloud, herein denoted as

P C_{R}

, to the Middle Feature Encoder.

4.2. Local Feature Encoder

The Local Feature Encoder receives the data representation structures

D S

, such as Pillars denoted as

P L

, Voxels

V L

or just the set of points of cropped area

P C_{R}

. Then, a set of methods are applied to obtain features and produce dense tensors in the case of Pillar Feature Network (PFN) and Voxel Feature Encoder (VFE) or calculate these features by simply calculating the mean values of point coordinates within each voxel using Mean VFE method.

4.2.1. Pillar Feature Network

The features of each Pillar,

P L

, are augmented in a tensor

D = (x, y, z, r, x_{c}, y_{c}, z_{c}, x_{p l c},

y_{p l c})

, where c describes the distance to the arithmetic mean of all points in

P L

, and

p l c

is the offset distance from the

P l_{x, y}

center.

For this purpose, (1) Pillar Feature Network (PFN) receives the Pillar augmented features as input and applies linear transformations to each point, herein described as

l i n e a r (P l_{i n}) = P l_{o u t}

, where

P l_{i n}

corresponds to the initial tensor

P l_{i n} = (P, N, D_{i n})

, and

P l_{o u t}

to the output tensor. In

P l_{o u t}

, all but the last dimension are the same shape as the input. Dimension

D_{o u t}

results from the linear transformation of

D_{i n}

, thus producing

P l_{i n} = (P, N, D_{o u t})

. Then, Batch-Norm and ReLU are applied to this tensor. Afterwards, all resulting features are aggregated. This process allows generating a dense tensor to represent the Pillar as a tuple

(D, P, N)

, where D is the above-mentioned augmented point, P is the number of non-empty pillars per batch, and N is the number of points per Pillar. Next, max pooling operations over the channels are used to generate a tensor of size

(D_{o u t}, P)

4.2.2. Voxel Feature Encoder

Similar to PFN, the points in each Voxel,

V L_{j} = {p t_{i} = (x_{i}, y_{i}, z_{i}, r_{i}) \in R^{4}}, i = {1, 2, . . ., N V}

, are augmented by calculating offset distance of the point to the

V L_{x, y, z}

center herein denoted as

v l c

, which generates the tensor

V L_{j} = {p t_{i} = (x_{i}, y_{i}, z_{i}, r_{i}, x_{v l c}, y_{v l c}, z_{v l c}) \in R^{7}}, i = {1, 2, . . ., N V}

, where

N V

as mentioned before is the max number of points per Voxel. Afterwards, each

p t_{i}

is subject VFE Layers

V F E L_{l}

, where

l \geq 1

. Each

V F E L_{l}

is composed by a set of transformations, where linear transformation, Batch-Norm, and ReLU are applied. Then, all points features of

V L_{j}

, resulting from the above-mentioned transformations, herein described as

p f_{j}

, are aggregated. Each

p f_{j}

can be described as

p f_{j} \in R^{o u t}

, where

o u t

is the output dimension that results from the linear transformation of all points

p t_{i}

. The output size

o u t

resulting from the linear transformation can be described as

o u t_{l} = F_{o} / 2

, where

F_{o} = {f_{1}, f_{2}, . . ., f_{o}}, F_{o} \in N^{+}

means the output features of a specific

V F E L

index l. After, all point features

P F, p f_{j} \in P F

are subject to a max pooling operation over the channels. The output tensor is described as

p f r_{m} \in R^{o u t}

where

m = 1

. Afterwards, a repeat process of the above tensor is performed

r e p e a t (p f r, k)

V L_{j}

, which means the repeat point feature resulted from max pooling k times, where

k = {1, 2, 3, . . ., N V}

. Each

p f r_{k}

is augmented with

p f_{j}

to generate

p f o_{j} = (p f r_{k}, p f_{j}) \in R^{2 o u t}, k = {1, 2, . . ., N V}

and

j = {1, 2, . . ., N V}

. The set of features for each voxel can be described by the tuple

V L_{o u t} = {V L_{j} = s t a c k (p f o_{j})}

, where

j = {1, 2, 3, . . ., N V}

s t a c k = (p f o_{1} \times p f o_{2} \times . . . p f o_{j})

, and applies linear, Batch-Norm, ReLU and max pooling to each

V L_{j}

. Thus,

V L_{j} \in R^{F}

, means that

V L_{j}

has output dimension F, the output feature of the last VFE layer.

Finally, it generates a list of obtained voxel features

V L A_{o u t}

V L A_{o u t} = {V L_{j} = {v l_{1}, v l_{2}, \dots, v l_{j}}, V L_{j} \in R^{F}, F = f_{o}

, where

V L A_{j}

is the above-mentioned augmented features of all voxels.

4.2.3. Mean Voxel Feature Encoder

Mean VFE receives a set of Voxels

V L

, sums all points residing in each Voxel in a specific axis, and divides by the number of points of each one. This operation can be described as

V L M_{o u t} ≜ {m e a n {(v l_{j})}_{k = 0}^{m v} = {p t f_{i} = (\sum {(p t x)}_{i = 1}^{n v} ∣ c o u n t (p t x), \sum {(p t y_{i})}_{i = 1}^{n v} ∣ c o u n t (p t y), \sum {(p t z_{i})}_{i = 1}^{n v} ∣ c o u n t (p t z), \sum {(p t r_{i})}_{i = 1}^{n v} ∣ c o u n t (p t r)) \in R^{4}}}, k = [0, N V [,

c o u n t (p t x) \to p t x \in v l_{j}, c o u n t (p t y) \to p t y \in v l_{j}, c o u n t (p t z) \to p t z \in v l_{j}, c o u n t (p t r) \to p t r \in v l_{j}

n v

corresponds to the total number of points of the Voxel

v l_{j} \in V L

in a given axis,

m v

the max number of Voxels and

p t f_{i} \in V L P F

corresponds to a resulting point. This strategy considers the voxel-wise features a new Voxel center

V L_{x, y, z, r}

and approximately equivalent to raw point cloud data. The idea herein is to process the voxel-wise features in Middle Feature Encoder more efficiently, especially by the 3D sparse convolutions since it generates

m v

(max number of voxels as described in Section 4.1) number of non-empty Voxels.

4.3. Middle Feature Extractor

The (3) Middle Feature Extractor is responsible for extracting more features from the (2) Local Feature Encoders to provide more context for the shape description of objects for the networks of the Detection Head module. Various methods are used; herein, we separated into 3D Backbones and 2D Backbones, which will be described in more detail above.

4.3.1. Backbone 3D

A variety of methods resort to 3D backbones based on sparse convolutions (sparse CNN), such as SECOND (Figure 4), PV-RCNN (Figure 6), PartA² (Figure 7) and Voxel-RCNN (Figure 8). In particular, PV-RCNN uses a Voxel Set Abstraction 3D backbone, which is used to encode the multiscale semantic features obtained by sparse CNN to keypoints. PointRCNN (Figure 5) uses PointNet++ [9] with multiscale grouping for feature extraction and gets more context to the shape of objects and then passes these features to (4) Detection Head module.

3D Sparse Convolution

The 3D Sparse Convolution method receives the voxel-wise features of VFE,

V L A_{o u t}

or Mean VFE,

V L M_{o u t}

This backbone is represented as a set of blocks

B L C

, in the form

{b l c_{1}, b l c_{2}, \dots b l c_{m}}

, where

m = 6

. Each block

b l c_{j} \in B L C, j = m

can be defined by a set of Sparse Sequential operations denoted as

S S Q_{s} = {s s q_{1}, s s q_{2}, s s q_{3}, \dots s s q_{s}}, s \geq 1

. Each

S S Q_{s}

is described by

((S u M \to \neg S p C) \lor (S p C \to \neg S u M)), B n, R L)

, where

S u M

means Submanifold Sparse Convolution 3D [12],

S p C

Spatially-sparse Convolution 3D [16],

B n

1D Batch Normalisation operation, and

R L

represents ReLU method. The last method assumes the standard procedure as mentioned in [17].

In our framework, the set of blocks assumes the following configurations:

The input block $b l c_{1}$ can be described by $b l c_{1} = {s q_{1} = (S u M, B N, R L)}$ ;
The next block is represented in the form $b l c_{2} = {s q_{1} = (S u M, B N, R L)}$ ;
The block 3 is represent as $b l c_{3} = {s q_{1} = (S p C, B N, R L), s q_{2} = (S u M, B N, R L), s q_{3} = (S u M, B N, R L)}$ ;
The block 4 is denoted as $b l c_{4} = {s q_{1} = (S p C, B N, R L), s q_{2} = (S u M, B N, R L), s q_{3} = (S u M, B N, R L)}$ ;
The block 5 is denoted as $b l c_{4} = {s q_{1} = (S p C, B N, R L), s q_{2} = (S u M, B N, R L), s q_{3} = (S u M, B N, R L)}$ ;
The last block is defined by $b l c_{6} = {s q_{1} = (S p C, B N, R L)}$ .

The Batch Normalisation

B n

element is defined by

(I n B, e p, m n)

, which represents the formula in [18].

I n B

represents the input features, which are the output features of Submanifold Sparse or Spatially-sparse Convolutions 3D, so that

(O u t S \to \neg O u t M \lor O u t M \to \neg O u t S)

e p

represents the eps, and

m n

the momentum values. These values are defined in the following Table 1.

The element

S p C

can be represented as

(I n S, O u t S, K s S, S t S, P d S, D l S, O p S)

I n S

represents the input features of

S p C

and it is denoted as

S p C \in N +, I n S = O u t M

where

O u t M

represents the output features of Submanifold Sparse Conv3D. The element

O u t S

represents the output features resulting from applying

S p C

K s S

means kernel size of a Spatially-sparse Convolution 3D and it is denoted as

K s S_{s} = {K s S_{1}, K s S_{2}, K s S_{s}}

where

s = {1, . . ., 3}

K s S_{s} \in N +

and

k s S_{s} = k s S_{s + 1}

. The stride

S t S

can be described as a set

S t S_{r} = {s t s_{1}, s t s_{2}, s t s_{r}}, r = {1, . . ., 3}, S t S_{r} \in N +

and

s t s_{r} = s t s_{r + 1}

P d S

designates padding, and a set can define it

P d S_{v} = {p d s_{1}, p d s_{2}, p d s_{v}}, v = {1, . . ., 3}, P d_{v} \in N +, p d s_{v} = p d s_{v + 1}

D l S

means dilation and can be defined as a set

D l S_{l} = {d l s_{1}, d l s_{2}, d l s_{l}}, l = {1, . . ., 3}, D l S_{l} \in N +, d l s_{l} = d l s_{l + 1}

. The output padding

O p S

is represented as a in the form

O p S_{a} = {o p s_{1}, o p s_{2}, o p s_{a}}, a = {1, . . ., 3}, O p S_{a} \in N +

and

o p s_{a} = o p_{a + 1}

. The configurations used in our framework are represented in Table 2.

S u M

is represented by

(I n M, O u t M, k s M, S t M, P d M, D l M, O p M)

[12].

I n M

represents the input features passed by (2) Local Feature Encoder or by the last Sparse Sequential block

S q_{s}

, and

O u t M

the output features of

S u M

. Thus,

I n M \in N +, I n M = 4

in the case of the Local Encoder be Mean VFE, otherwise

I n = F

, where F are the output features of the VFE network. Also,

I n S

can be represented by

I n M = O u t M

and

I n M = O u t S

, where

O u t S

represents the output features of a

S p C

. The element

K s

represents the kernel size that can be defined as

K s_{t} = {k s_{1}, k s_{2}, k s_{t}}

where

t = {1, . . ., 3}

K s_{t} \in N +

and

k s_{t} = k s_{t + 1}

S t M

means stride and can be defined as a set

S t_{r} = {s t_{1}, s t_{2}, s t_{r}}, r = {1, . . ., 3}, S t_{r} \in N +

and

s t_{r} = s t_{r + 1}

P d M

represents padding, and a set can describe it in the form

P d_{p} = {p d_{1}, p d_{2}, p d_{p}}, p = {1, . . ., 3}, P d_{p} \in N +, p d_{p} = p d_{p + 1}

D l

means dilation and can be described as a set

D l_{d} = {d l_{1}, d l_{2}, d l_{d}}, d = {1, . . ., 3}, D l_{d} \in N +, d l_{d} = d l_{d + 1}

O p

represents the output padding, and a set describes it in the form

O p_{u} = {o p_{1}, o p_{2}, o p_{p}}, u = {1, . . ., 3}, O p_{u} \in N +

and

o p_{u} = o p_{u + 1}

. The configurations used in our framework are represented in Table 3.

The hyperparameters used in each

b l c_{j}

are defined in Table 7.

Finally, the output spatial features

S P

is defined by

S P \in R

, where SP is defined by a tuple (B, C, D, H, W). B represents the batch size, C the output features of

b l c_{5}

represented in

S p C

O u t S

, D depth, H height and W width.

PointNet++

We use a modified version of PointNet++ [9] based on [12] to learn undiscretised raw point cloud data (herein denoted as

P C_{R}

) features in multi-scale grouping fashion. The objective is to learn to segment the foreground points and contextual information about them. For this purpose, a Set Abstraction module herein denoted as

S A_{M}

is used to sub-sampling points at a continuing increase rate, and a Feature Proposal module, described as

F P_{M}

, is used to capture feature map per point with the objective of point segmentation and proposal generation. A

S A_{M}

is composed by

S A_{M} = {p t n_{1}, p t n_{2}, \dots, p t n_{g}}, g \in N^{+}, g = {1, 2, \dots, 4}

, where

p t n

means PointNet Set Abstraction module operations. Each

p t n_{g} \in P T N

is represented by

(Q G L, M L)

, where

Q G L

corresponds to Query and Grouping operations to learn multi-scale patterns from points, and

M L

are the set of specifications of the PointNet before the global pooling for each scale.

Q G L

means ball query operation

Q L

followed by a grouping operation

G L

. It can be defined by the set

{q g l_{1}, q g l_{2}}

where

q g l_{1}

and

q g l_{2}

correspond to two query and group operations. A ball query

Q L

is represented as

(R, N S, P, C P)

, where R means the radius within all points will be searched from the query point with an upper limit

N S, N S \in N^{+}

, in a process called ball query, P means the coordinates of the point features in the form

P F = {p f_{n} = (x_{n}, y_{n}, z_{n},) \in R^{3}}, n \in N

that are used to gather the point features,

C P

represents the coordinates of the centers of the ball query in the form

C P = {c p_{p} = (x c_{p}, y c_{p}, z c_{p}) \in R^{3}}, p \in N^{+}, p \leq n, p = {1, 2, \dots, 4}

, where

x c

y c

, and

z c

are center coordinates of a ball query. Thus, this ball query algorithm search for point features P in a radius R with an upper limit of

N S

query points from the centroids (or ball query centers)

C P

. This operation generates a list of indices

I D

in the form

{i d_{1}, i d_{2}, \dots, i d_{x}}, x \geq 1, i d_{x} \in I D, i d_{x} \in N^{N C P \times N S}

, where

N C P

corresponds to the number of

C P

I D

represents the indices of point features that form the query balls. After, a grouping operation

G L

is performed to group point features and can be described by

(P F, I D)

, in which

P F

and

I D

correspond to point features and indices of the features to group with, respectively. In each

Q G L

of a

p t n

, the number of centroids

N C P

will decrease, so that

N C P_{p} > N C P_{p + 1}, p = {1, 2, \dots, 4}, N C P \in N^{+}

, and due to the relation of the centroids in ball query search, the number of indices

N I D

and corresponding point features will also decrease. Thus, in each

p t n

the number of points features is defined by

N P_{n} > N P_{n + 1}, N P_{n + 1} = N C P_{p}, p > 1

. The number of centroids defined in QGL during

p t n

operations is defined in Table 4.

Afterwards, a

M L

is performed, defined by a set of specifications of the PointNet before the

Q G L

operations. The idea herein is to capture point-to-point relations of the point features in each

C P

local region. The point features coordinates translation to the local region relative to the centroid point is performed by the operation

L R = {f r_{f} = (p x_{f} - x c_{f}, p y_{f} - y c_{f}, p z_{f} - z c_{f}) \in R^{3}}, f = {1, 2, \dots, N S}

p x

p y

, and

p z

are coordinates of point features

P F

as mentioned before, and

x c

y c

, and

z c

are coordinates of the centroid center.

M L

can be defined by a set

S Q = {s q_{1}, s q_{2}}

that represent two sequential methods. Each

S Q

is represented by the set of operations

O P = {o p_{s} = (C 2 D, B n 2 D, R L)}, s = {0, 1, \dots, 3}

, where

C 2 D

means Convolution 2D,

B n 2 D

2D Batch Normalisation, and

R L

represents the ReLU method.

C 2 D

is defined by

(I n C 2 D, O u t C 2 D, K s C 2 D, S C 2 D)

I n C 2 D

, where

I n C 2 D \in N^{+}

, represents the input features that can be received by

Q G L

or by the output features

O u t C 2 D, O u t C 2 D \in N^{+}

of the

o p_{s - 1}

K s C 2 D

the kernel size, and

S C 2 D

the stride of the Convolution 2D. The kernel size

K s C 2 D

is defined by the set

{k s c 2 d_{1}, k s c 2 d_{2}}, k s c 2 d_{1} = k s c 2 d_{2}

and

\forall o p_{s} \in S Q, S Q \in M L, M L \in P T N, k s c 2 d_{1} = 1

. Also, the stride

S C 2 D

is represented by a set

{s c 2 d_{1}, s c 2 d_{2}}, s c 2 d_{1} = s c 2 d_{2}

, and

s c 2 d_{1} = 1,

with

\forall o p_{s} \in S Q, S Q \in M L, M L \in P T N

. The set of specifications used in our models regarding

O P

are summarised in Table 5.

p t n_{i} \in P T N

can be defined as:

\begin{matrix} P T N ≜ {p t n_{i} = m a x (M L (S G (p f_{i})))} \end{matrix}

(1)

, where

m a x

denotes max pooling,

S G

denotes random sampling of

p f_{i}

features,

M L

multi-layer perceptron network to encode features and relative locations.

Finally, a Feature Proposal

F P_{M}

is applied employing a set of feature proposal modules

{f p_{1}, f p_{2}, \dots, f p_{m}}, m = {1, 2, \dots, 4}, m \in N^{+}

. Each

f p_{m} \in F P_{M}

is defined by the element

S Q

as defined above. Also, the element

S Q

assumes a set

{s q_{1}, s q_{2}}

and each

S Q

has the same operations with the only difference in the element s that describes the number of operations, assuming

s = {1, 2}

instead of

s = {1, 2, 3}

. The configurations used in our models are summarised in Table 6.

Voxel Set Abstraction

This method aims to generate a set of keypoints from given point cloud

P C_{R}

and use a keypoint sampling strategy based on Farthest Point Sampling. This method generates a small number of keypoints that can be represented by

K ≜ {p_{j} = (x_{j}, y_{j}, z_{j}) \in R^{B * 3}}, j = [1, N K]

, where

N K

is the number of points features that have the largest minimum distance, and B the batch size. The Farthest Point Sampling method is defined according to a given subset

P A ≜ {p a_{j} = (x a_{j}, y a_{j}, z a_{j})}, j = {1, 2, \dots, M}, P A \subset P F

, where M is the maximum number of features to sample, and subset

P B ≜ {p b_{k} (x b_{k}, y b_{k}, z b_{k})}, k = {0, 1, 2, . . ., N}, P B \subseteq P F

, where N is the total number of points features of

P F

, the point distance metric is calculated based on

D ≜ {d_{i} = {{(x b_{k} - x a_{j})}^{2} + {(y b_{k} - y a_{j})}^{2} + {(z b_{k} - z a_{j})}^{2})}}, i \leq M

. Based on D a operation

S M ≜ {s m_{k} = {m i n (d_{i}, s m_{i - 1})}}, k \leq M, i \leq N

is performed, which calculates the smallest value distance between

d_{i}

and

s m_{i - 1}

s m_{k} \in S M, k < N

and

S M

represents the list of the last known largest minimum distance of point features. Assuming

s m_{k} = s m_{i - 1} ∣ d_{i} < s m_{i - 1}

, it returns the index

I D X = {i d x_{k} = (i - 1)},

. Based on

s m_{k} = {d_{i} ∣ d_{i} > s m_{i - 1}}

, thus

I D X = {i d x_{k} = (i)}

. Finally, this operation generates a set of indexes in the form

I D X ≜ {i d x_{0}, i d x_{1}, . . ., i d x_{m}}, i d x_{m} \in I D X, m \leq M

, and

I D X \in R^{B * M}

, where B corresponds to the batch size and M the maximum number of features to sample. The keypoints K are given by

K ≜ {p f_{i d x_{0}}, p f_{i d x_{1}}, \dots, p f_{i d x_{m}}}

These keypoints K are subject to an interpolation process utilising the semantic features encoded by the 3D Sparse Convolution as

S P

. In this interpolation process, these semantic features are mapped with the keypoints to the voxel features

V L

that reside. Firstly, this process defines the local relative coordinates of keypoints with Voxels

V L

by means

V L I ≜ {v l i_{i} = (\frac{(k x_{i} - P C_{R x_{m i n}})}{v l x_{k}}, \frac{(k y_{i} - P C_{R y_{m i n}})}{v l y_{k}}) \in R^{2}}, k = [0, NK [, i = [0, NV [

. Then, a bilinear interpolation is carried out to map the point features

S P

from 3D Sparse Convolution in a radius R with the

V L B

, the local relative coordinates of keypoints. This is perform

PR ≜ {\forall sp \leq R, s p \in SP ∣ R = (xr, yr) \in R^{2}, {sp}_{i} = ({pfx}_{i}, {pfy}_{i})}, i = [0, NK [

. Afterwards, indexes of points are defined according to

v l i a \in V L I ∣ v l i a_{i} = {vli}_{i}

in the form

(x a, y a)

and another

v l i b ≜ (x b = (x a + 1), y b = (y a + 1))

. The expression that gives the features

s p_{i}

from the BEV perspective based on

v l i a

and

v l i b

is the following:

$S B E V A ≜ (s p_{v l i a x}, s p_{v l i a y})$
$S B E V B ≜ (s p_{v l i b x}, s p_{v l i a y})$
$S B E V C ≜ (s p_{v l i a x}, s p_{v l i b y})$
$S B E V D ≜ (s p_{v l i b x}, s p_{v l i b y})$

Thus, the weights between these indexes

v l i a_{i}

v l i b_{i}

and

v l i_{i}

are calculated, as follows:

$W A ≜ {(v l i x_{i} - p r x_{i}) \times (v l i y_{i} - v l i y_{i})}$ ;
$W B ≜ {(v l i x_{i} - p r x_{i}) \times (v l i y_{i} - v l i y a_{i}))}$
$W C ≜ {(v l i x_{i} - p r a x_{i}) \times (v l i b y_{i} - v l i y_{i}))}$
$W D ≜ {(v l i x_{i} - p r a x_{i}) \times (v l i y_{i} - v l i a y_{i}))}$

Finally, the bilinear expression that gives the features

s p_{i}

from the BEV perspective is

P F B E V ≜ (s b e v a_{i} * w a_{i}) + (s b e v b_{i} * w b_{i}) + (s b e v c_{i} * w c_{i}) + (s b e v d_{i} * w d_{i})

, where

s b e v a_{i} \in S B E V A

s b e v b_{i} \in S B E V B

s b e v c_{i} \in S B E V C

s b e v d_{i} \in S B E V D

. Also,

w a_{i} \in W A

w b_{i} \in W B

w c_{i} \in W C

w d_{i} \in W D

, and

i = [0, NV [

The local features of

p f b e v_{j} \in P F B E V

is indicated by

v l b_{i} = ∣ v l_{k} - s p_{i} ∣, k = [0, NK [, i = [0, NV [

and aggregated using PointNet++ according with their specification defined above. It will generate

P T N

that are voxel-wise features within the neighbouring voxel set

v l i_{i}

s p_{i}

, transforming using PointNet++ specifications. This generates

p t n_{i} \in P T N

according

P T N ≜ p t n_{i} = p t n_{0}, \cdot, p t n_{N K}

and each

p t n_{i}

are aggregate features of 3D Sparse Convolution

s p_{i}

with

p f b_{i}

from different levels according to Table 4.

Backbone 2D

PointPillars (Figure 3) uses only a 2D Backbone since they require fewer computational resources when compared to 3D Backbones. However, they introduce information loss that can be mitigated by readjusting the objects back to LiDAR’s Cartesian 3D system with minimal information loss. For this purpose, the features resulting from the PFN are used by the Backbone Scatter component, which scatters them back into a 2D pseudo-image. The next component, the Detection Head, then uses this 2D pseudo-image.

Other models, such as SECOND (Figure 4), PV-RCNN (Figure 6), PartA² (Figure 7) and Voxel-RCNN (Figure 8) compress the information into Bird’s-eye view (BEV) after using a 3D Backbone for feature extraction. After, they perform feature encoding and concatenation using an Encoder Conv2D. After this process, the resulting features are passed to the Detection Head module.

Backbone Scatter

The features resulting from the PFN are used by the PointPillars Scatter component, which scatters them back to a 2D pseudo-image of size

(D_{o u t}, H, W)

, where H and W denote height and width, respectively.

BEV Backbone

BEV Backbone module receives 3D feature maps from 3D Sparse Convolution and reshapes them to BEV feature map. Admitting the given sparse features

S P ≜ (B, C, D, H, W)

, the new sparse features are

(B, C \times D, H, W)

. The BEV Backbone is represented as a set of blocks

B L C

, in the form

b l c_{1}, b l c_{2}, \dots b l c_{m}

, where

m \geq 1

. Each block

b l c_{j} \in B L C, j \leq m

, is represented by

(n, F, U, S)

. The element n represents the number of convolutional layers in

B L C_{j}

. The set of convolutional layers C in

B L C_{j}

is described as a set

{c_{1}, c_{2}, c_{3} \dots c_{n}}

, where

n \geq 1

. F represents the number of filters of each

c_{i} \in C, i \leq n

, U is the number of upsample filters of

c_{i}

. Each of the upsample filters has the same characteristics, and their outputs are combined through concatenation. S denotes the stride in

c_{1}

. If

S > 1

, we have a downsampled convolutional layer (

c_{1}

). There are a certain convolutional layers (

c_{i}

, such that

i > 1

) that follow this layer. BatchNorm and ReLU layers are applied after each convolutional layer.

The input for this set of blocks

B L C

is spatial features extracted by 3D Sparse Convolution or Voxel Set Abstraction modules and reshaped to BEV feature map.

Table 7. The different block configuration (

b l c_{j} \in B L C

) used. N.A. - Not Applicable.

Table 7. The different block configuration (

b l c_{j} \in B L C

) used. N.A. - Not Applicable.

Models	${blc}_{1}$	${blc}_{2}$	${blc}_{3}$
PointPillars	(3, 64, 128, 2)	(5, 128, 128, 2)	(5, 128, 128, 2)
SECOND	(5, 64, 128, 1)	(5, 128, 256, 2)	N.A.
PV-RCNN	(5, 64, 128, 1)	(5, 128, 256, 2)	N.A.
PointRCNN	N.A.	N.A.	N.A.
PartA²	(5, 128, 256, 2)	(5, 128, 256, 2)	N.A.
VoxelRCNN	(5, 128, 256, 2)	(5, 128, 256, 2)	N.A

Encoder Conv2D

Based on features extract in each block

b l c_{j}

and after upsampled based on

U = 2 D

, where D means downsample factor of the convolution layer C, upsample features

u_{j} \in U, j = [0, m [

are concatenate, such that

U F ≜ cat (u_{j})

, where cat means

u_{j} + u_{j + 1}, j = [0, m [

4.4. Detection Head

After that, the (4) Detection Head component receives the 2D encoded features as input and performs operations based on three modules: RPN Head, Point Head, and RoI Head.

4.4.1. RPN Head

Based on 2D encoded features, a set of convolutions to predict class labels, regression offsets, and direction are performed. Thus, a set of 1x1 convolutions

C 1 x = {c 1 x_{1}, c 1 x_{2}, \dots, c 1 x_{k}}

, where

k = 3

, is applied. Each

c 1 x_{k}

can be represented by

C 2 D ≜ (I C, O C, K S)

, where

C 2 D

mean Convolution 2D,

I C

input channels,

O C

output channels and

K S

kernel size.

c 1 x_{1}

is the class prediction convolution and can be described by

(U F, N A \times N C, 1)

, where

N A

means number of anchor per location and

N C

number of target classes to predict.

c 1 x_{2}

is the convolution for bounding box offset regression and can be defined by

(U F, N A \times N C \times 7, K S)

where it generates 2 anchors

N A

for each class

N C

and 7 are the number of bounding box offsets. Finally,

c 1 x_{3}

is performed based on

(U F, N A \times N B, K S)

where

N A

represent the same number of anchor per location as previously mentioned,

N B

the number of bins per anchor location and

K S

kernel size.

The figure representing our baseline network for each block can be seen in Figure 2. We use three blocks with a BEV backbone for PointPillars, while for the other models, we use two blocks. Each block is represented as described in Table 7. Table 8 describes the configuration of the RPN Head.

4.4.2. Point Head

Different implementations of Point Head have been proposed to refine RPN predictions or generate class labels, bounding box regression offsets, and direction. It can be composed of a class layer regression

C R

in the form

C R ≜ l i n e a r (I N, O T)

and bounding box layer

B B R

described as

P R ≜ l i n e a r (I N, O T)

. The point class layer

C R

provides the segmentation score of foreground points, and

P R

gives the relative location of foreground points as

P R ≜ {p r_{p} = (x_{f}, y_{f}, z_{f})}

and calculated based on a foreground point

f p_{p} = (x_{p}, y_{p}, z_{p})

using

{(x_{t} = \frac{(x_{p} - x_{c})}{w} + 0.5, \frac{y_{t} = (y_{p} - x_{c})}{l} + 0.5, z_{t} = {\frac{(z_{p} - z_{c})}{h} + 0.5}, (c o s {(θ)}_{p} - c o s {(θ)}_{c}, s i n {(θ)}_{p} - s i n {(θ)}_{c}))}

, where

x_{c}

y_{c}

z_{c}

are center coordinates of the bounding box, h, w, and l means height, width, length of bounding box respectively, and

θ

is the box orientation in bird-view.

Firstly, bounding box targets are normalised in a canonical coordinate system by first checking if the given points

P T ≜ p_{i} = (x_{i}, y_{i}, z_{i}), P T \in b b_{k}

are within the Bounding box

b b_{k} ≜ (x c_{i}, y c_{i}, z c_{i}, d x_{i}, d y_{i}, d z_{i}, θ_{i})

by performing

((\frac{∣ x_{i} - x c_{k} ∣}{2} + 0.00001 | ∣ x_{i} - x c_{k} ∣ < d x_{i} & \frac{∣ y_{i} - y c_{k} ∣}{2} + 0.00001 | ∣ y_{i} - y c_{k} ∣ < d y_{i}),

where if the given statement is true the local

l x n_{i}

and

l y n_{i}

are calculated. The operation is

l x n_{i} = ((x_{i} - x c_{k}) \times (c o s (- θ_{i}))) + ((y_{i} - y c_{k}) \times (- s i n (- θ_{i})))

and

l n y_{i} = ((x_{i} - x c_{k}) \times (s i n (- θ_{i}))) + ((y_{i} - y c_{k}) \times (c o s (- θ_{i})))

. After, we determine the local relative coordinate of

p_{i}

concerning bounding box

b b_{k}

in X-Y by means

l r_{i} = ((x_{i} - x c_{k}) \times (c o s (- θ_{i}))) + ((y_{i} - y c_{k}) \times (- s i n (- θ_{i}))), l y n_{i} = ((x_{i} - x c_{k}) \times (s i n (- θ_{i}))) + ((y_{i} - y c_{k}) \times (c o s (- θ_{i})))

and then determine if a point belongs and returning respective index to bounding box by

(□ (l n x_{i} < \frac{d x_{i}}{2} + 0.00001 \lor \frac{l n y_{i}}{2} + 0.00001 < d y_{i}) \to i d = i,

. After getting the points indexes within the bounding Boxes, all inside points are aggregated with PointNet++.

Point Intra Part Offset

It is both

C R

and

P R

to predicted point class labels and point bounding box offsets.

Point Head Simple

It is only composed of

C R

. However, it has modifications to its architecture

C R ≜ {c r_{1}, c r_{2}, c r_{3}}

where each

c r

is represented by a tuple

(L R, B N, R L)

where

L R

means linear regression,

B N

batch normalisation, and

R L

ReLU method.

B N

can be defined by

(N F)

where

N B

means the number of features and typically assumes the same value as

O T

Point Head Box

It is composed of

C R

and

P R

with architecture modifications.

C R {c r_{1}, c r_{2}}

where

C R ≜ (L R, B N, R L)

where

L R

means linear regression,

B N

batch normalisation, and

R L

ReLU method.

P R

is composed of

P R ≜ {p r_{1}, p r_{2}}

, where each

p r

is defined by the same tuple

(L R, B N, R L)

4.4.3. RoI Head

The Regions of Interest (RoI) Head is responsible for taking the RoI features of each box proposal of the RPN Head and then optimising the imperfect bounding box proposals by predicting and fixing the size and location (centre and orientation) residuals relative to the input bounding box predictions. Besides each model’s specificities, any RoI Head is composed of a proposal layer that generates/refines a set of RoIs based on RPN RoIs, denoted as

P L

, an RoI feature extraction method

R F

, and Head module

H M

that can be composed but not restricted to Shared Fully Connected Layer

S F C

, up-down layer

U L

and

D L

, class layer

C L

, regression layer

R L

, RoI Point Pool 3D layer (

R o I P L

), RoI Grid Pool layer (

R o I G L

), RoI-aware Pool 3D layer (

R o i A P 3 D

), and a convolution part (

C n v P

) and convolution RPN (

C n v R P N

S F C

are responsible for feature extraction and can be defined by a set

{s f c_{0}, \dots s f c_{f}}

f = [0, 2 [

, and

s f c_{f} \in S F C

and

s f c_{f}

is represented by a tuple

(C 1 D, B N 1 D, R L, D R O)

, where

C 1 D

means convolution 1D,

B N 1 D

means batch normalisation 1D,

R L

ReLU, and

D R O

means dropout.

C L

can be defined by the set

{c l_{0}, \dots, c l_{c}}, c = [0, 2 [

and each

c l_{c}

(C 1 D, B N 1 D, R L, D R O)

R L

produces box predictions and is composed by the set

{r l_{0}, \dots, r l_{r}}, r = [0, 2 [

, where each

r l_{r}

is defined by

(C 1 D, B N 1 D, R L, D R O)

D L

and

U L

mean bottom-up box generation proposal layers from foreground points. A sequence of Convolution 2D and ReLU methods can define the

D L

. A

U L

is represented as

u l_{1}, u l_{2}

and each

u l

by the same sequence of Convolution 2D and ReLU methods.

R o I P L

specifically pool 3D points and their corresponding point features according to the location of each 3D proposal of

P L

. Admitting the given output of bounding boxes

B B

and a specific bounding box

b b_{n} \in B B

, where

B B ≜ {b b_{n} = (x_{n}, y_{n}, z_{n}, h_{n}, w_{n}, l_{n}, θ_{n})}

, where x, y, z are center coordinates of the predicted bounding box, h, w, and l denotes the height, width, and length of the bounding box, and

θ

the orientation of bounding box. Herein the

R O I P L

produces an enlarged set of

b b e_{n} \in B B E

that can be defined by

(x_{n}, y_{n}, z_{n}, h_{n} + η, w_{n} + η, l_{n} + η, θ_{n})

, where

η

represents a constant value to resize the bounding box. The depth information loss for each bounding box proposal is compensated by including the distance information to the LiDAR sensor to the

u f_{p} \in U F

that are BEV spatial features. Each

u f_{p}

is augmented with

d_{b} ≜ \sqrt{{(x_{p} - x_{c})}^{2} + {(y_{p} - y_{c})}^{2} + {(z_{p} - z_{c})}^{2}}, d_{b} \in D

, where

x_{p}

y_{p}

, and

z_{p}

correspond to coordinates of point features of Local Encoder module and

x_{c}

y_{c}

, and

z_{c}

center coordinates of LiDAR sensor. Thus, it generates a tensor in the form

(V L M_{o u t}, D)

that is fed to PointNet++ as described in Section 4.3.1 to encode the augmented tensor with local features with global semantic BEV features

U F

. This generates a feature vector for confidence classification and box refinement.

The idea of

R o I G L

is to aggregate the keypoint features to the RoI-grid points with multiple receptive fields. Grid points are uniform sampling and can be described by

G P ≜ {g p_{1}, g p_{2}, \dots, g p_{s}}, s = 216

, which means that a grid

6 \times 6 \times 6

are usually adopted. Firstly, the identification of neighbouring keypoints to grid

g p_{i}

in a radius R is performed by means

G F ≜ {\forall p \leq r, p \in K ∣ R = (x r, y r, z r) \in R^{3}, p_{j} = (p x_{j}, p y_{j}, p z_{j}) \in R^{3} | g p_{s} = (g p x_{j}, g p y_{j}, g p z_{j}) \in R^{3} | ‖ p_{j} - g p_{s} ‖^{2}}, i = [0, NK [

. After all, a PointNet block is used to aggregate neighbouring keypoint set

G F

in the same way of Equation 2:

\begin{matrix} P T N ≜ {p t n_{i} = m a x (M L (S G (g f_{i})))} \end{matrix}

(2)

Then, the two MLP layers,

S F C (P T N)

and

S C (P T N)

, are performed.

R o I A P 3 D

aims to provide bounding box score confidence and refinement by aggregating the local feature information (

V L M_{o u t}

) with global semantic BEV features (

U F

) within the proposals. Two operations are performed within the point features

p f_{i}

of bounding boxes

B B

, such that

B B ≜ {b b_{k} = {p f_{i} \in R^{C}}}, i = [0, m [, p f_{i} \in P F

and scattered to the voxel data structures

V L B ≜ {v l b_{k} = (x_{j}, y_{j}, z_{j}), i = [0, m [}

where

x_{j}

y_{j}

z_{j}

are encoded in canonical coordinates using Point Head module, m are the number of inside points within bounding box

b b_{k}

. The objective is to solve the problem of different proposals generating the same pooled points. For this purpose, average pooling for pooled part features operation denoted as

P P F

, and max pooling for pooled RPN features defined as

P R P N

are adopted and can be described as

P P F ≜ R o I M a x (V L B, P F, B B), P P F \in R^{S_{x} \times S_{y} \times S_{z} \times C}

and

P R P N ≜ R o I A v g (V L B, P F, B B), P P F \in R^{S_{x} \times S_{y} \times S_{z} \times C}

where

S_{x}

S_{y}

S_{z}

are the resolution of Voxels spatial shape. The operations RoIMax and RoIAvg can be described more specifically:

R o I M a x = \{\begin{matrix} m a x ({p f_{i} \in v l b_{k}}), & if c o u n t (P P F) > 0 \\ 0, & otherwise \end{matrix}

R o I A v g = \{\begin{matrix} \frac{\sum_{i = 0}^{c o u n t (P P F)} p f_{i}}{c o u n t (P P F)}, p f_{i} \in v l b_{k} ({p f_{i} \in v l b_{k}}), & if c o u n t (P P F) > 0 \\ 0, & otherwise \end{matrix}

5. 3D Object Detection Model Specifications

Herein, we will specify each model in the different module frameworks. These models were selected based on the requirements established and defined in Section 1, since they are the models that best guarantee the trade-off between metrics (mAP and inference time). The set of models and their specificities concerning the developed framework is illustrated in Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8. The modules of each model are represented in the figures as green boxes, and the flow of the tensors occurs in the direction of the orange arrows.

Figure 3. Structure of the PointPillars model represented in the developed framework.

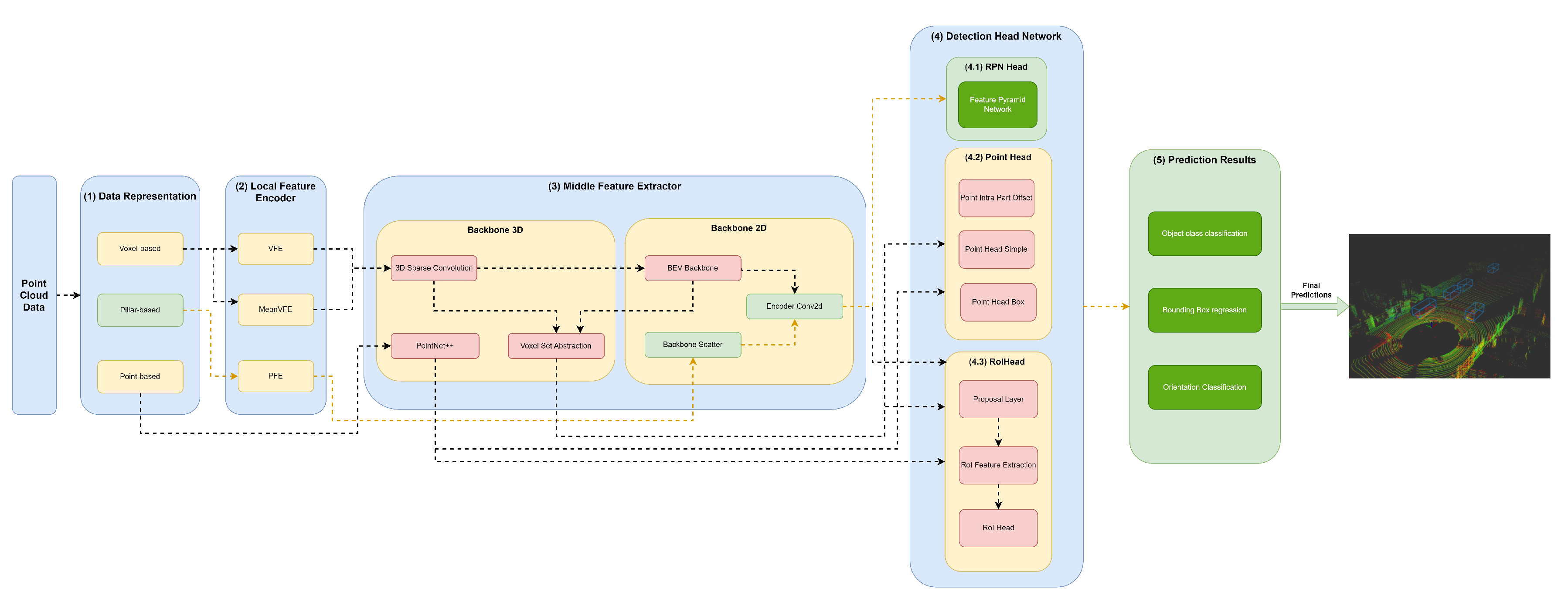
Figure 4. Structure of the SECOND model represented in the developed framework.

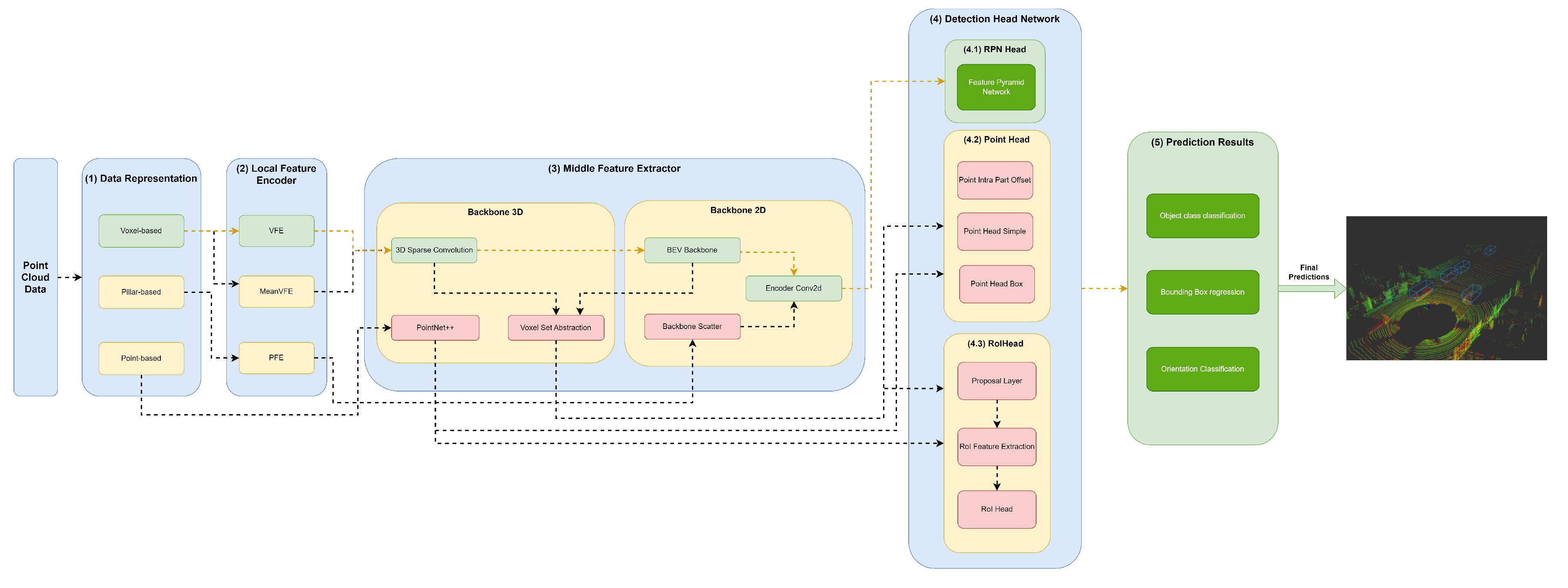
Figure 5. Structure of the PointRCNN model represented in the developed framework..

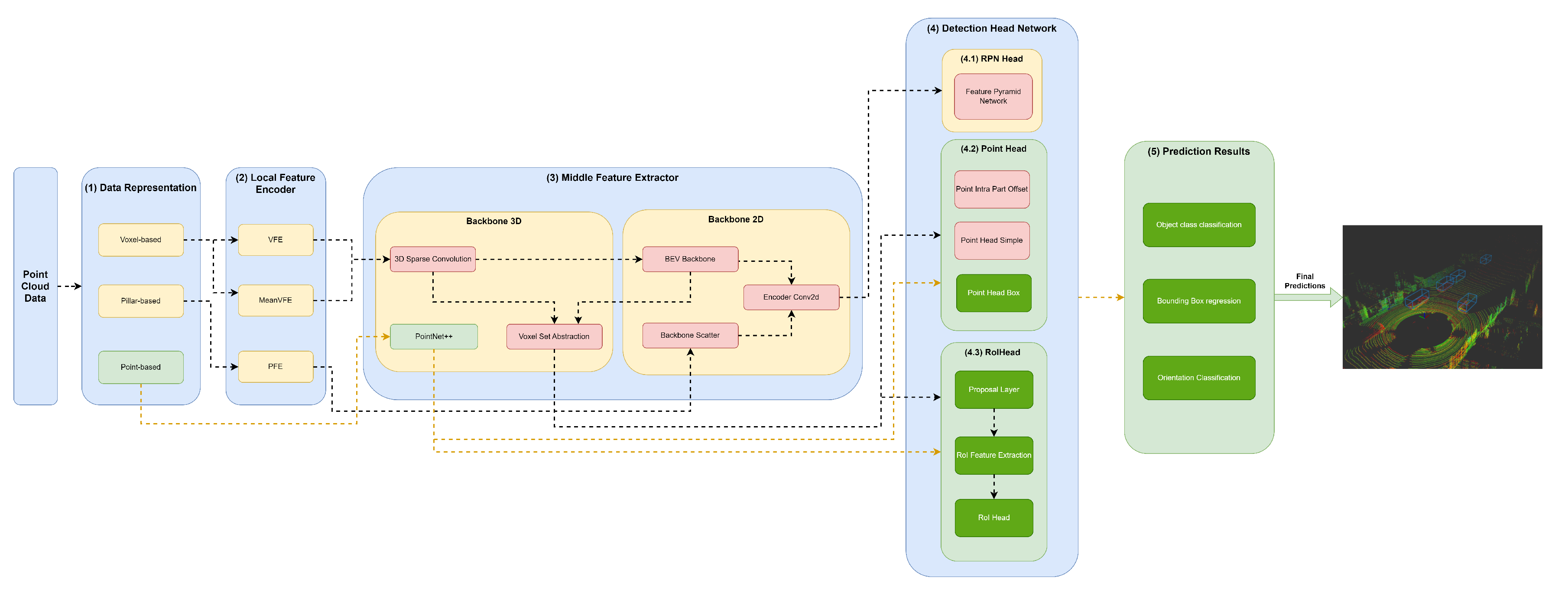
Figure 6. Structure of the PV RCNN model represented in the developed framework.

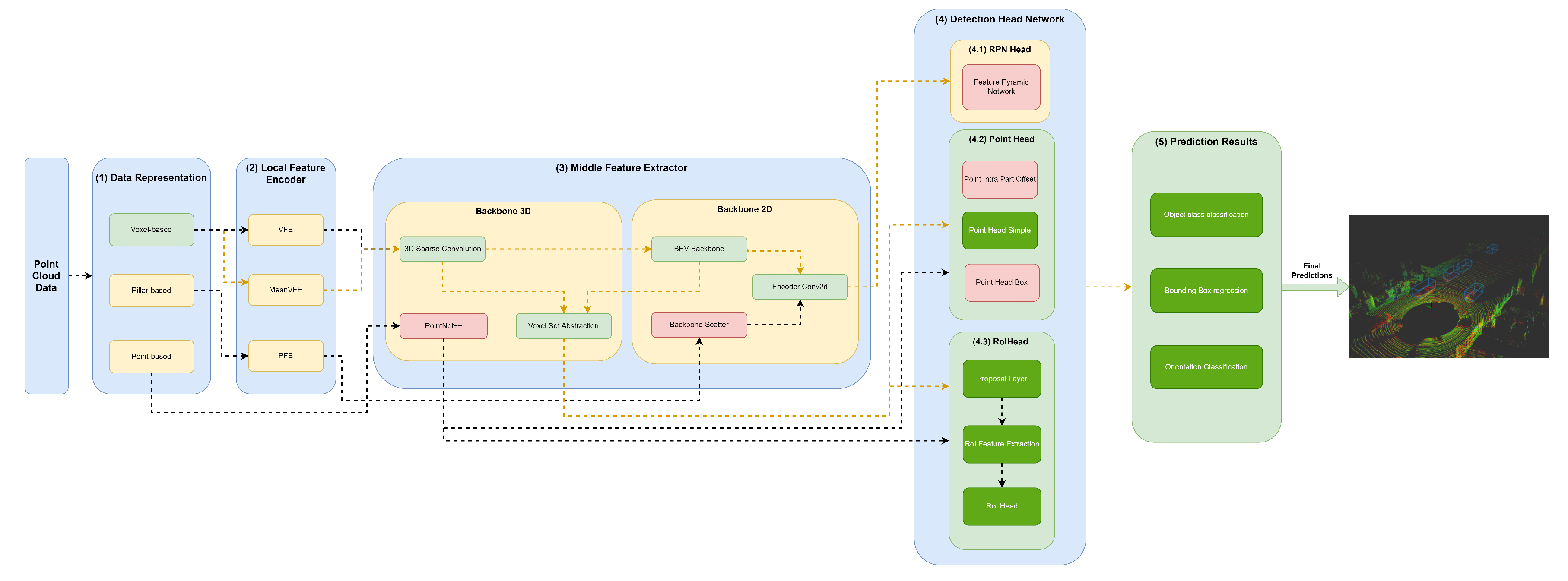
Figure 7. Structure of the

{PartA}^{2}

model represented in the developed framework.

Figure 7. Structure of the

{PartA}^{2}

model represented in the developed framework.

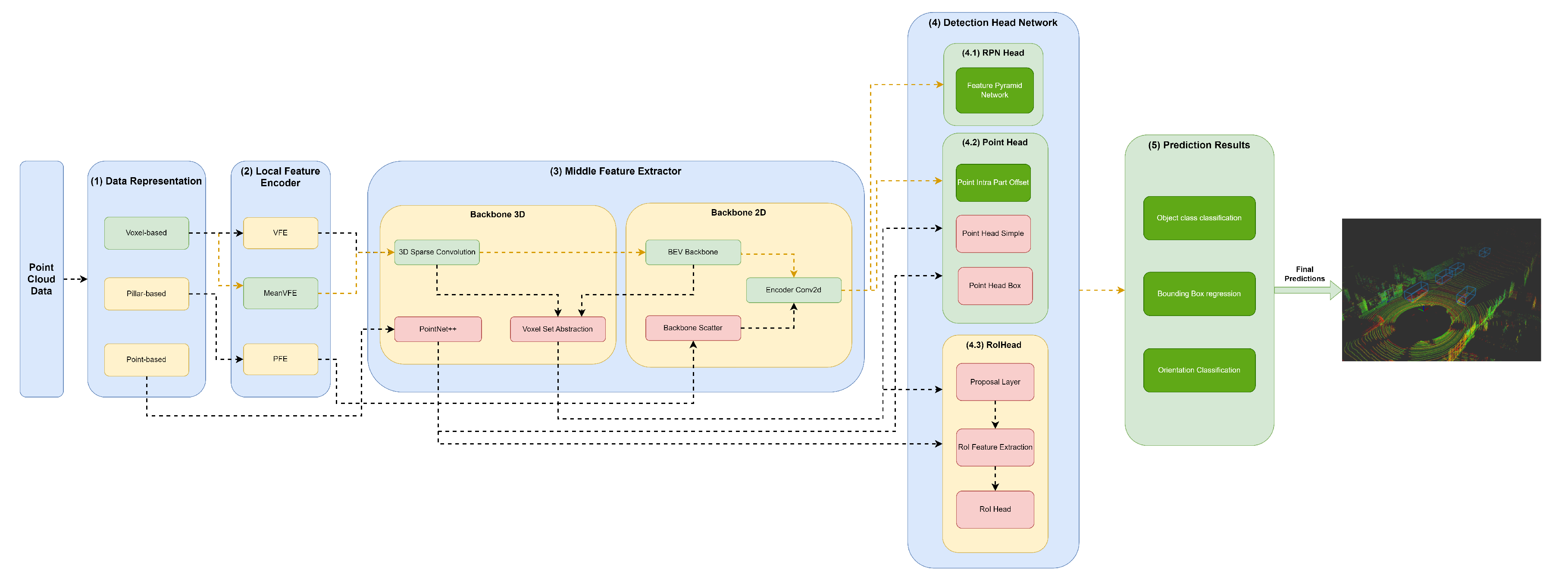
Figure 8. Structure of the VoxelRCNN model represented in the developed framework.

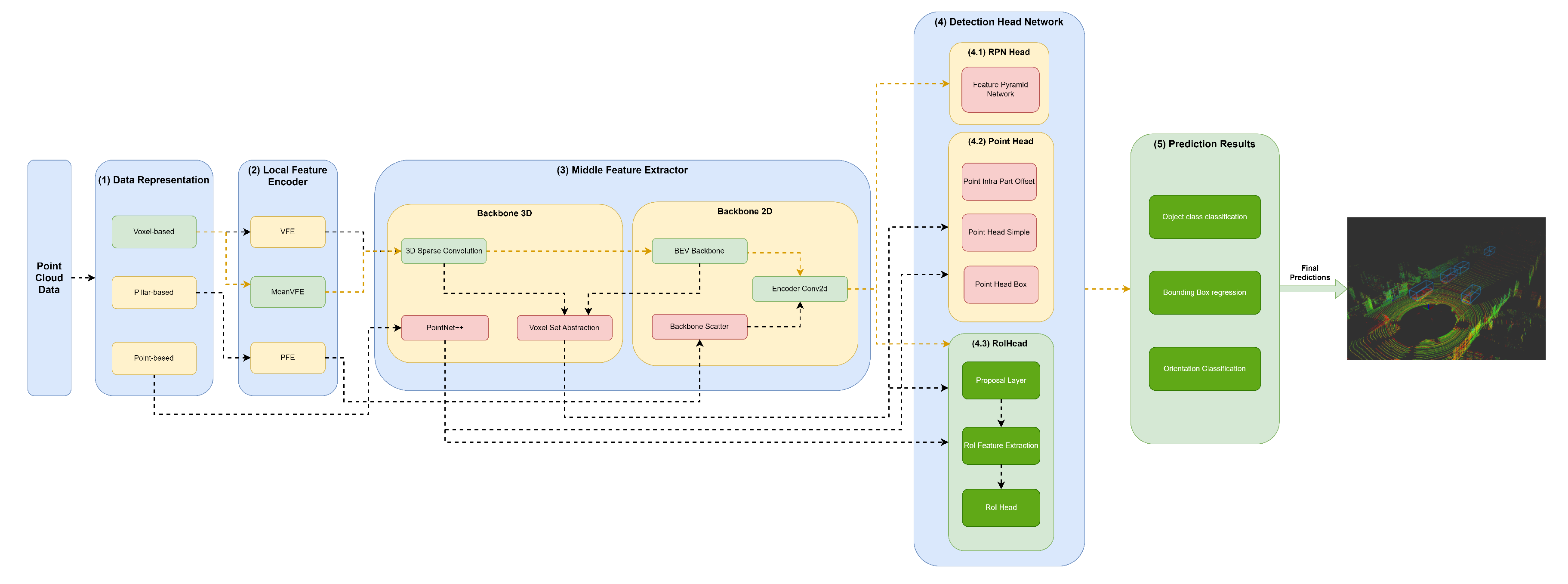
5.1. Data Representation

Typically the models of Figure 4, Figure 6, Figure 7 and Figure 8 choose to represent the point cloud in Voxels. In this data structure, the point cloud is delimited (using the cropping technique), and a grid is produced where the data is discretised along the X-Y-Z axis.

Only PointPillars, illustrated in Figure 3, discretises this delimited space of the point cloud on the X-Y axis, creating a set of Pillars.

In the case of the PointRCNN model (Figure 5), it provides the delimited point cloud without any data discretisation and structuring process for the Middle Feature Encoder.

5.2. Local Feature Encoders

As illustrated in the Figures, three strategies are used by the models to improve the efficiency of the object detectors in the feature extraction of the data structures. Typically, these modules are responsible for the local feature extraction and then, via concatenation, aggregate these features. Three networks are used: VFE for SECOND (Figure 4), PFE for PointPillars (Figure 3) and Mean VFE for PV RCNN (Figure 6),

{PartA}^{2}

(Figure 7), and VoxelRCNN (Figure 8).

5.3. Middle Feature Extractor

A variety of methods use 3D Backbones based on sparse and sub-manifold convolutions, such as SECOND (Figure 4), PV-RCNN (Figure 6),

{PartA}^{2}

(Figure 7 ) and Voxel-RCNN (Figure 8). In the case of PV-RCNN, the 3D Voxel Set Abstraction backbone encodes the multiscale semantic features obtained by the 3D sparse CNN for keypoints. PointRCNN (Figure 5) uses PointNet++ [9] with multiscale clustering for feature extraction and get more context to the shape of objects and then passes these features to the Detection Head module.

Only PointPillars (Figure 3) uses 2D Backbones since they require fewer computational resources when compared to 3D Backbones. However, they introduce a loss in the information that is easily mitigated since it is possible to readjust the objects again to the Cartesian 3D system of LiDAR with fewer loss of information. For this purpose, the resulting PFE features are used by the Backbone Scatter component, which scatters them back into a 2D pseudo-image. The next Detection Head component then uses this 2D pseudo-image.

Other models, such as SECOND (Figure 4), PV RCNN (Figure 6),

{PartA}^{2}

(Figure 7) and Voxel-RCNN (Figure 8) compress the information in Bird’s-eye view (BEV) using the BEV Backbone for feature extraction then encode and concatenate the features using the Encoder Conv2D component. After this process, the resulting features are passed to the Detection Head.

5.4. Detection Head

As mentioned earlier, this module comprises three networks: RPN Head, Point Head and RoI Head.

All models except PointRCNN use the RPN Head to generate RoIs using a low-level algorithm called Selective Search [19] to produce proposed regions per frame of the point cloud. Selective Search generates sub-segments to generate many candidate regions and, following bottom-up grouping, recursively combines similar regions into larger regions to provide more accurate final candidate proposals. Each of these regions is submitted independently to the CNN module. The output feature map is then fed to an SVM classifier to predict the object class within the candidate RoI. Along with object class prediction, the algorithm also predicts four Bounding Box offset values.

The Point Head is used to assist the RPN Head, as illustrated in Figure 6 and Figure 7, or generate predictions of object classes and predict four values that are the Bounding Box offsets, as shown in Figure 5 and Figure 8. Point Head generates various masks of objects or parts of objects in a multiscale way, followed by a simple bounding box inference to generate proposals, also called point proposals, using each point to contribute to the reconstruction of the 3D geometry of the object.

The RoI Head used by the PointRCNN (Figure 5), PV-RCNN (Figure 6),

{PartA}^{2}

(Figure 7) and Voxel-RCNN ( Figure 8), naturally uses the RoI features of each bounding box proposed in the RPN, and then optimises the imperfect bounding boxes from previous stages, predicting and correcting the size and location (center and orientation) in relation to the predictions of the input bounding boxes.

6. Network Training and Fine-Tuning

The models described in this document were trained using the KITTI data sets. In addition, the models were evaluated based on the KITTY benchmarks, namely for detecting 3D objects and BEV, considering a validation set. Regarding the number of epochs used in the training phase, a methodology spread by the literature was considered. Thus we use 200 epochs, considering the data described in Table 13. Considering training hyperparameters, We define the initial learning rate of 0.01, learning rate decay of 0.1, decay epoch methodology, weight decay of 0.01, gradient clipping normalisation with a max value of 10, beta1 of 0.95 and beta2 of 0.85. We use learning rate decay, weight decay, and gradient clipping normalisation as regularisation procedures to prevent overfitting. The evaluation metrics in the results were based on the official KITTY evaluation detection metrics. Hence, the metrics used were mAP for a BEV and 3D Object Detection. The partition of the training data used in this work consisted of a division discussed in [17]. This approach divides the 7481 training examples that are provided, into a training set of 3712 samples, with the remaining 3769 samples belonging to the evaluation set. Moreover, the benchmarks presented in this article are based on the evaluation set only.

We select three target classes in all experiments: car, pedestrian and cyclist. Typically, all the models described herein generate two separate networks. One network is optimised for predicting cars and another for pedestrians and cyclists. However, this approach can be improper in self-driving car applications since low-edge devices with few resources must cope with two parallel models. For this reason, we trained all classes in a one-single model for all 3D Object Detectors.

For the fine-tuning process, we save the results of the mAP for each epoch to understand when models converge. Herein, we provide a study with the consequences of the number of samplings and min points per class sampling compared with the study made in [20]. In [20], we used different class sampling strategies but without changing the number of min points for class sampling.

Sampling Instance Strategy. We focus on optimising the number of sampling instances and min points per class sampling. The main objective of the sampling strategy is to soften the KITTI dataset imbalance issue. During training, the point cloud is randomly fed with these instances, which means they are placed into the current point cloud. Although this is true, the min points affect whether or not a certain instance can be used for sampling. If we increase the min number of points in the training process, instances such as pedestrians and cyclists are less sample because few points exist to describe their shape. On the other hand, if we decrease too many min points, the model suffers in distinguishing between the foreground and the background points. In our experiments, we use the configurations described in Table 9. The min point for class sampling was fixed per class as 5 instead of 10 points for pedestrian and cyclist classes and 5 points for the car.

Point Cloud Range. The point cloud range affects any Object Detector’s detection range, limiting its detection range. Our research uses the original point cloud range for all models to represent the location of ground truth objects for all frames in the KITTI dataset frame. For example, in cars, it is possible to verify in terms of depth information that most ground truth instances are between the 0 and 70 meters. After 70 meters from the LiDAR sensor centre, the number of instances drastically decreases. This can be explained by the fact that after this range, the number of points to describe an object’s shape is very few, making detecting objects difficult. Thus, this experiment compares the point cloud range of PointPillars and the other models where the detection range is not compromised. The point cloud ranges are depicted in Table 10. Also, we analyse the number of data structures (max number of Pillars or Voxels) compared with the study in [20].

Data structure sizes. The object detection model receives the points in

P C_{R}

and discretises them in the X-Y axis, thus creating a set of pillars, or discretises in X-Y-Z and creates a set of Voxels. Each data structure

D S

has a fixed size in

P C_{R}

. The data structure size directly impacts model accuracy and inference time. Increasing the data structure size can result in too much data being encoded and consequently randomly sampled, leading to information loss (the maximum number of points per data structure is set for computational saving purposes). On the other hand, reducing the data structure size can increase the number of non-empty data structures, increasing memory usage and inference time. Two

D S

configurations were used in our fine-tuning process, as shown in Table 11.

Number of Data Structures. Max number of data structures is defined to explore the KITTI dataset sparsity problem since most data structures will be empty. Using a large number of Data Structures can result in most of them being filled with zeros (to create a dense tensor), making it inefficient for inference time purposes. Based on the distribution of the number of points per data structure in the KITTI dataset, a max number of points is also defined, as shown in Table 12.

7. Performance Evaluation, Comparison, and Discussion

This section reports the set of experiments, which results from the random search methodology, used to achieve a better trade-off between accuracy and inference time performance metrics. Table 13 depicts the experiments and corresponding network configurations and models. PointPillars settings and their results are also provided to understand the impact of producing a model optimised to produce three-class output rather than separating into two distinct networks (one for cars and another for pedestrians and cyclists).

Table 13. The set of experiments conducted and respective network configurations.

Experiment	Model	${PC}_{R}$ Config.	SI Config.	No. Output	$S_{PL}$ Config.	P Config.
	Config.			Classes
1	PointPillars	$P C_{R 1}$	$S I_{1}$	3	$S_{D S 16}$	$P_{12 K}$
2	SECOND	$P C_{R 2}$	$S I_{1}$	3	$S_{D S 5}$	$P_{16 K}$
3	PV-RCNN	$P C_{R 2}$	$S I_{1}$	3	$S_{D S 5}$	$P_{16 K}$
4	PointRCNN	$P C_{R 2}$	$S I_{1}$	3	$S_{D S 5}$	$P_{16 K}$
5	Part A²	$P C_{R 2}$	$S I_{1}$	3	$S_{D S 5}$	$P_{16 K}$
6	VoxelRCNN	$P C_{R 2}$	$S I_{1}$	3	$S_{D S 5}$	$P_{16 K}$
7	PointPillars	$P C_{R 1}$	$S I_{2}$	3	$S_{D S 16}$	$P_{12 K}$
8	SECOND	$P C_{R 2}$	$S I_{2}$	3	$S_{D S 5}$	$P_{16 K}$
9	PV-RCNN	$P C_{R 2}$	$S I_{2}$	3	$S_{D S 5}$	$P_{16 K}$
10	PointRCNN	$P C_{R 2}$	$S I_{2}$	3	$S_{D S 5}$	$P_{16 K}$
11	Part A²	$P C_{R 2}$	$S I_{2}$	3	$S_{D S 5}$	$P_{16 K}$
12	VoxelRCNN	$P C_{R 2}$	$S I_{2}$	3	$S_{D S 5}$	$P_{16 K}$

The following Table 14, Table 15, Table 16, and Table 17 provide the results of experiments of Table 13 in terms of AP for three difficulty levels (Easy, Moderate and Hard) and different Intersection over Union (IOU) thresholds, according to KITTI benchmarks. For cars, IOU is 70%, while for pedestrians and cyclists, it is required IOU of 50%. Table 18 presents the comparative results of the experiments carried out in this study with the original results in the literature. The comparison considers the overall three identified classes, both for 3D and BEV. The results presented for the developed experiments consider the overall values per class for the best detection metric.

As demonstrated in the before-mentioned results, the improvements introduced for three-class trained models produced better mAP and very close inference time results (Table 19 and Table 20). However, it is clear that there is always a cost in terms of mAP for producing three-class inference models and our results are for the KITTI validation set, and the original results are for the KITTI test set. Regarding the point cloud range in our networks, we reproduced original configurations for all models, with fewer

D S

when compared with the study in [20] since most

D S

will be empty. This improvement drastically decreases the inference time when comparing PointPillars with the same research. Although the original model inference times are better when compared with our results (Table 19 and Table 20), this can be explained by the fact that original models obtained their results by training separated networks, one for cars and another for pedestrians and cyclist (a standard literature practice on KITTI benchmarks). By training three-class models, gradients are affected by all those instances, which leads our models to lose the specialisation for prediction. However, as mentioned in [20], producing separate networks is impractical for self-driving applications.

Reducing the minimum points to consider a sample instance brought gains in terms of mAP and for the same model architecture since more instances can be used for data augmentation. This allows for expanding the diversity of the training data and our models to learn more patterns from data.

8. Conclusions

The research about deep learning methods for 3D Object Detection on LiDAR data has increased tremendously in recent years, with many models, repositories, and different technologies being developed. Although this benefits scientific development in this area, the various technologies, software, repositories and models are a bottleneck for testing and improving the current methods.

To cope with this limitation, we develop a framework for representing multiple SoA 3D object detectors with highly refactored codes for both one-stage and two-stage methods. The main idea of this framework is to facilitate the implementation, reusing and implementation of new techniques in each framework module with less manual engineering effort. In conclusion, it enables the abstract implementation, reusing and building of any object detector in one single 3D object detector framework.

Nonetheless, it is evident that creating three-class inference models comes with a trade-off in terms of mAP. Our study’s results are based on the KITTI validation set, while the original findings were obtained using the KITTI test set. We replicated the original network configurations for all models concerning the point cloud range, but with fewer DS and than the research mentioned in previous section. The improvement mentioned earlier leads to a considerable reduction in the inference time when PointPillars is compared to the same research.

Author Contributions

Conceptualization, A.S., P.O., and D.D.; methodology, A.S., P.O., and D.D.; software, A.S., and P.O; validation, P.M.P., J.Mac., P.N., A.S, P.O., D.D., D.F. R.N., and J.M.; formal analysis, A.S., P.O., D.D., J.Mac., P.N., D.F., R.N., P.M.P, J.M.; investigation, A.S., P.O., and D.D.; resources, J.Mac, P.N., P.M.P., and J.M.; data curation, A.S., P.O. and R.N.; writing—original draft preparation, A.S., P.O., and D.D.; writing—review and editing, A.S., P.O., D.D, R.N., D.F., J.Mac., P.N., J.M. and P.M.P.; visualization, A.S., P.O., D.D., D.F., J.Mac., P.N., P.M.P. and J.M.; supervision, J.Mac., P.N., P.M.P., and J.M.; project administration, J.Mac., P.N., J.M., and P.M.P.; funding acquisition, J.Mac., P.N., J.M. and P.M.P. All authors have read and agreed to the published version of the manuscript.

Funding

This work has been supported by FCT—Fundação para a Ciência e Tecnologia within the R&D Units Project Scope: UIDB/00319/2020 and the project “Integrated and Innovative Solutions for the well-being of people in complex urban centers” within the Project Scope NORTE-01-0145-FEDER-000086. The work of Pedro Oliveira was supported by the doctoral Grant PRT/BD/154311/2022 financed by the Portuguese Foundation for Science and Technology (FCT), and with funds from European Union, under MIT Portugal Program.

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Conflicts of Interest

The authors declare no conflicts of interest.

References

Cosmas, K.; Kenichi, A. Utilization of FPGA for onboard inference of landmark localization in CNN-Based spacecraft pose estimation. Aerospace 2020, 7, 159. [Google Scholar] [CrossRef]
Ngadiuba, J.; Loncar, V.; Pierini, M.; Summers, S.; Di Guglielmo, G.; Duarte, J.; Harris, P.; Rankin, D.; Jindariani, S.; Liu, M.; et al. Compressing deep neural networks on FPGAs to binary and ternary precision with hls4ml. Mach. Learn. Sci. Technol. 2020, 2, 015001. [Google Scholar] [CrossRef]
Sharma, H.; Park, J.; Amaro, E.; Thwaites, B.; Kotha, P.; Gupta, A.; Kim, J.K.; Mishra, A.; Esmaeilzadeh, H. Dnnweaver: From high-level deep network models to fpga acceleration. In Proceedings of the Workshop on Cognitive Architectures; 2016. [Google Scholar]
Fernandes, D.; Silva, A.; Névoa, R.; Simões, C.; Gonzalez, D.; Guevara, M.; Novais, P.; Monteiro, J.; Melo-Pinto, P. Point-cloud based 3D object detection and classification methods for self-driving applications: A survey and taxonomy. Inf. Fusion 2021, 68, 161–191. [Google Scholar] [CrossRef]
Alzubaidi, L.; Zhang, J.; Humaidi, A.J.; Al-Dujaili, A.; Duan, Y.; Al-Shamma, O.; Santamaría, J.; Fadhel, M.A.; Al-Amidie, M.; Farhan, L. Review of deep learning: Concepts, CNN architectures, challenges, applications, future directions. J. Big Data 2021, 8, 53. [Google Scholar] [CrossRef] [PubMed]
Xu, L.; Zhou, X.; Tao, Y.; Liu, L.; Yu, X.; Kumar, N. Intelligent Security Performance Prediction for IoT-Enabled Healthcare Networks Using Improved CNN. IEEE Trans. Ind. Inform. 2021, 1. [Google Scholar] [CrossRef]
Zhou, Y.; Tuzel, O. VoxelNet: End-to-End Learning for Point Cloud Based 3D Object Detection. arXiv 2017, arXiv:cs.CV/1711.06396. [Google Scholar]
Yan, Y.; Mao, Y.; Li, B. Second: Sparsely embedded convolutional detection. Sensors 2018, 18, 3337. [Google Scholar] [CrossRef] [PubMed]
Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. Pointnet++: Deep hierarchical feature learning on point sets in a metric space. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 5099–5108. [Google Scholar]
Shi, S.; Wang, Z.; Shi, J.; Wang, X.; Li, H. From points to parts: 3d object detection from point cloud with part-aware and part-aggregation network. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 43, 2647–2664. [Google Scholar] [CrossRef] [PubMed]
Ye, M.; Xu, S.; Cao, T. Hvnet: Hybrid voxel network for lidar based 3d object detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 1631–1640. [Google Scholar]
Graham, B.; van der Maaten, L. Submanifold Sparse Convolutional Networks. [1706.01307].
Graham, B. Sparse 3D convolutional neural networks. [1505.02890].
Qi, C.R.; Liu, W.; Wu, C.; Su, H.; Guibas, L.J. Frustum pointnets for 3d object detection from rgb-d data. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 918–927. [Google Scholar]
Meyer, G.P.; Laddha, A.; Kee, E.; Vallespi-Gonzalez, C.; Wellington, C.K. Lasernet: An efficient probabilistic 3d object detector for autonomous driving. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–17 June 2019; pp. 12677–12686. [Google Scholar]
Li, B.; Zhang, T.; Xia, T. Vehicle detection from 3d lidar using fully convolutional network. arXiv 2016, arXiv:1608.07916. [Google Scholar]
Chen, X.; Ma, H.; Wan, J.; Li, B.; Xia, T. Multi-view 3d object detection network for autonomous driving. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1907–1915. [Google Scholar]
Lang, A.H.; Vora, S.; Caesar, H.; Zhou, L.; Yang, J.; Beijbom, O. Pointpillars: Fast encoders for object detection from point clouds. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–17 June 2019; pp. 12697–12705. [Google Scholar]
Jo, J.; Kim, S.; Park, I.C. Energy-Efficient Convolution Architecture Based on Rescheduled Dataflow. IEEE Trans. Circuits Syst. I Regul. Pap. 2018, 65, 4196–4207. [Google Scholar] [CrossRef]
George, A.D.; Wilson, C.M. Onboard Processing With Hybrid and Reconfigurable Computing on Small Satellites. Proc. IEEE 2018, 106, 458–470. [Google Scholar] [CrossRef]
Qiu, J.; Wang, J.; Yao, S.; Guo, K.; Li, B.; Zhou, E.; Yu, J.; Tang, T.; Xu, N.; Song, S.; Wang, Y.; Yang, H. Going Deeper with Embedded FPGA Platform for Convolutional Neural Network. In Proceedings of the 2016 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays, Monterey, CA, USA, 21–23 February 2016; pp. 26–35. [Google Scholar] [CrossRef]
Yang, Z.; Yan, L.; Yuan, J. Design and Implementation of Driverless Perceptual System Based on CPU + FPGA. In Proceedings of the 2020 5th International Conference on Control, Robotics and Cybernetics (CRC), Wuhan, China, 16–18 October 2020; pp. 261–265. [Google Scholar] [CrossRef]
Chen, Y., Liu, S., Shen, X., Jia, J. . Fast point r-cnn. In Proceedings of the IEEE/CVF international conference on computer vision (pp. 9775-9784).
Abdelouahab, K.; Pelcat, M.; Serot, J.; Bourrasset, C.; Berry, F. Tactics to directly map CNN graphs on embedded FPGAs. IEEE Embed. Syst. Lett. 2017, 9, 113–116. [Google Scholar] [CrossRef]
Kathail, V. Xilinx Vitis unified software platform. In Proceedings of the 2020 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays, Seaside, CA, USA, 23–25 February 2020; pp. 173–174. [Google Scholar]
Duarte, J.; Han, S.; Harris, P.; Jindariani, S.; Kreinar, E.; Kreis, B.; Ngadiuba, J.; Pierini, M.; Rivera, R.; Tran, N.; et al. Fast inference of deep neural networks in FPGAs for particle physics. J. Instrum. 2018, 13, P07027. [Google Scholar] [CrossRef]
Xilinx. DPUCZDX8G for Zynq UltraScale+ MPSoCs. Product Guide. Xilinx. 2021. Available online: http://aiweb.techfak.uni-bielefeld.de/content/bworld-robot-control-software/ (accessed on).
Afonso, T.; Girão, P.; Simões, Cláudia Fernandes, D.; Silva, A.; Névoa, R.; Gonzalez, D.; Guevara, M.; Novais, P.; Monteiro, J.; Melo-Pinto, P. Real-time object detection and SLAM in a Low-Cost LiDAR Test Vehicle Setup. Sensors submitted.
Krishnamoorthi, R. Quantizing deep Convolutional Networks for Efficient Inference: A Whitepaper. arXiv 2018, arXiv:cs.LG/1806.08342. [Google Scholar]
Nagel, M.; van Baalen, M.; Blankevoort, T.; Welling, M. Data-Free Quantization Through Weight Equalization and Bias Correction. arXiv 2019, arXiv:cs.LG/1906.04721. [Google Scholar]

Figure 1. Methodology for object detection model fine-tuning.

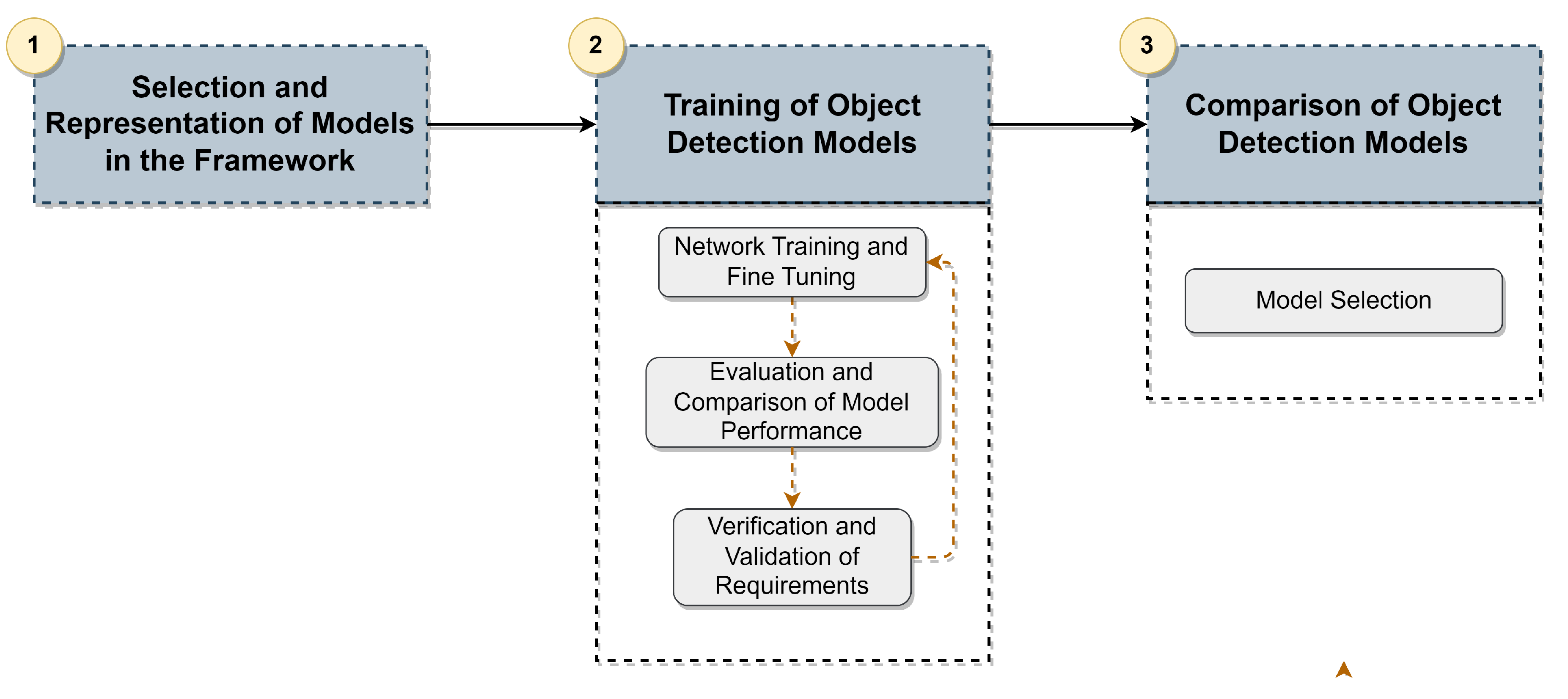
Figure 2. Framework used for the implementation/representation of Object Detection models.

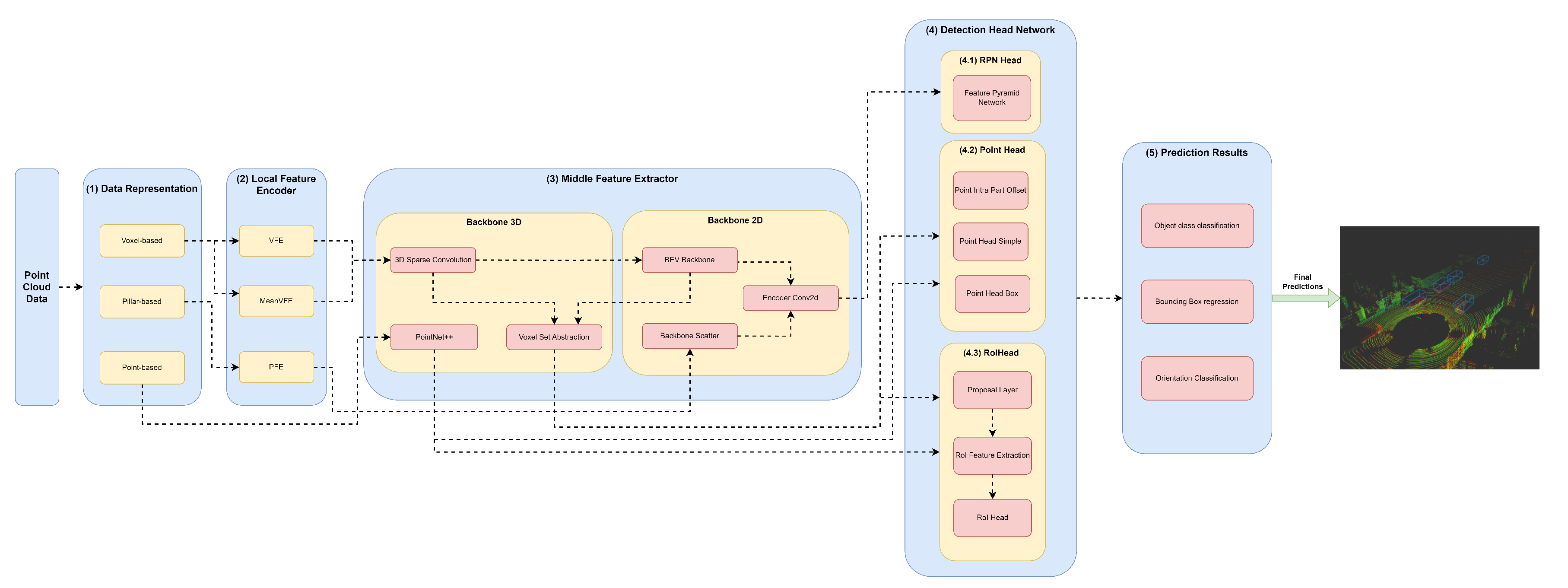
Table 1. Values used in

B n

Table 1. Values used in

B n

Bn Element	Value
$e p$	0.001
$m n$	0.01

Table 2. Configurations used in

S p C

for each element.

Table 2. Configurations used in

S p C

for each element.

SpC Element	Value
$K s S_{t}$	3
$S t S_{r}$	1
$P d S_{v}$	1
$D l S_{l}$	1
$O p S_{a}$	0

Table 3. Configurations used in

S u M

and

S p C

for each block. N.A. - Not applicable.

Table 3. Configurations used in

S u M

and

S p C

for each block. N.A. - Not applicable.

SuM Element	InS	OutS	InM	OutM	Ks	St	Pd	Dl
$b l c_{1} \land s q 1 \to S u M$	N.A	N.A	4	16	3	1	1	1
$b l c_{2} \land s q 1 \to S u M$	N.A.	N.A.	16	16	3	1	0	1
$b l c_{3} \land s q 1 \to S p C$	16	32	N.A.	N.A.	3	2	1	1
$b l c_{3} \land s q 2 \to S u M$	N.A.	N.A.	32	32	3	1	0	1
$b l c_{3} \land s q 3 \to S u M$	N.A.	N.A.	32	32	3	1	0	1
$b l c_{4} \land s q 1 \to S p C$	32	64	N.A.	N.A.	3	2	1	1
$b l c_{4} \land s q 2 \to S u M$	N.A.	N.A	64	64	3	1	0	1
$b l c_{4} \land s q 3 \to S u M$	N.the A.	N.A.	64	64	3	1	0	1
$b l c_{5} \land s q 1 \to S p C$	64	64	N.A.	N.A.	3	2	0	1
$b l c_{5} \land s q 2 \to S u M$	N.A.	N.A.	64	64	3	1	0	1
$b l c_{5} \land s q 3 \to S u M$	N.A.	N.A.	64	64	3	1	0	1
$b l c_{6} \land s q 1 \to S p C$	64	128	N.A.	N.A.	3	2	0	1

Table 4. Configurations used in

N C P

for each element.

Table 4. Configurations used in

N C P

for each element.

NCP Element	Value
$n c p_{1}$	4096
$n c p_{2}$	1024
$n c p_{3}$	256
$n c p_{4}$	64

Table 5. Set of configurations used in

O P

of a specific

S Q

of the

M L

element in a specific

P T N

Table 5. Set of configurations used in

O P

of a specific

S Q

of the

M L

element in a specific

P T N

NCP Element	InC2D	OutC2D
$o p_{1} \land s q_{1} \land p t n_{1}$	4	16
$o p_{2} \land s q_{1} \land p t n_{1}$	16	16
$o p_{3} \land s q_{1} \land p t n_{1}$	16	32
$o p_{1} \land s q_{2} \land p t n_{1}$	4	32
$o p_{2} \land s q_{2} \land p t n_{1}$	32	32
$o p_{3} \land s q_{2} \land p t n_{1}$	32	64
$o p_{1} \land s q_{1} \land p t n_{2}$	99	64
$o p_{2} \land s q_{1} \land p t n_{2}$	64	64
$o p_{3} \land s q_{1} \land p t n_{2}$	64	128
$o p_{1} \land s q_{2} \land p t n_{2}$	99	64
$o p_{2} \land s q_{2} \land p t n_{2}$	64	96
$o p_{3} \land s q_{2} \land p t n_{2}$	96	128
$o p_{1} \land s q_{1} \land p t n_{3}$	259	128
$o p_{2} \land s q_{1} \land p t n_{3}$	128	196
$o p_{3} \land s q_{1} \land p t n_{3}$	196	256
$o p_{1} \land s q_{2} \land p t n_{3}$	259	128
$o p_{2} \land s q_{2} \land p t n_{3}$	128	196
$o p_{3} \land s q_{2} \land p t n_{3}$	196	256
$o p_{1} \land s q_{1} \land p t n_{4}$	515	256
$o p_{2} \land s q_{1} \land p t n_{4}$	256	256
$o p_{3} \land s q_{1} \land p t n_{4}$	256	512
$o p_{1} \land s q_{2} \land p t n_{4}$	515	256
$o p_{2} \land s q_{2} \land p t n_{4}$	256	384
$o p_{3} \land s q_{2} \land p t n_{4}$	384	512

Table 6. Set of configurations used in

O P

of a specific

S Q

in a specific

F P_{M}

Table 6. Set of configurations used in

O P

of a specific

S Q

in a specific

F P_{M}

NCP Element	InC2D	OutC2D
$o p_{1} \land s q_{1} \land f p_{1}$	257	128
$o p_{2} \land s q_{2} \land f p_{1}$	128	128
$o p_{1} \land s q_{1} \land f p_{2}$	608	256
$o p_{2} \land s q_{2} \land f p_{2}$	256	256
$o p_{1} \land s q_{1} \land f p_{3}$	768	512
$o p_{2} \land s q_{2} \land f p_{3}$	512	512
$o p_{1} \land s q_{2} \land f p_{4}$	1536	512
$o p_{2} \land s q_{2} \land f p_{4}$	512	512

Table 8. The different RPN configurations (

c 1 x_{k} \in C 1 x

) used. N.A. - Not Applicable.

Table 8. The different RPN configurations (

c 1 x_{k} \in C 1 x

) used. N.A. - Not Applicable.

Models	$c 1 x_{1}$	$c 1 x_{2}$	$c 1 x_{3}$
PointPillars	(512, 18, 1)	(5, 128, 128, 2)	(5, 128, 128, 2)
SECOND	(512, 18, 1)	(512, 42, 1)	N.A.
PV-RCNN	(512, 18, 1)	(512, 42, 1)	N.A.
PartA²	(512, 18, 1)	(512, 42, 1)	N.A.
VoxelRCNN	(5, 128, 256, 2)	(5, 128, 256, 2)	N.A

Table 9. Number of sampling instances (SI) per class.

SI Configuration	Car	Pedestrian	Cyclist
$S I_{1}$	15	10	10
$S I_{2}$	25	20	20

Table 10. The different point cloud ranges (

P C_{R}

) configurations used in fine-tuning.

Table 10. The different point cloud ranges (

P C_{R}

) configurations used in fine-tuning.

${PC}_{R}$ Configuration	$X_{\min}$	$X_{\max}$	$Y_{\min}$	$Y_{\max}$	$Z_{\min}$	$Z_{\max}$
$P C_{R 1}$	0	69.12	-39.68	39.68	-3	1
$P C_{R 2}$	0	70	-40	40	-3	1

Table 11. Pillar size (

S_{D S}

) configurations used in fine-tuning.

Table 11. Pillar size (

S_{D S}

) configurations used in fine-tuning.

$S_{DS}$ Configuration	$S_{DS} length$	$S_{DS} height$	$S_{DS} depth$
$S_{D S 16}$	0.16	0.16	1
$S_{D S 5}$	0.05	0.05	0.1

Table 12. Total number of data structures used in fine-tuning.

P Configuration	Total Number of $DS$	Max Number of Points Per $DS$
$P_{12 K}$	12K	100
$P_{16 K}$	16K	5

Table 14. Results in validation set for BEV detection metric for experiment 1-6.

Model	Epoch	Experiment	Car			Cyclist			Pedestrian			Overall
Model	Epoch	Experiment	Easy	Mod.	Hard	Easy	Mod.	Hard	Easy	Mod.	Hard	Overall
Voxel R-CNN	197	6	96.9	94.89	95.08	73.03	77.68	80.3	85.03	85.54	85.97	87.12
Part A²	187	5	97.64	96.72	96.6	81.37	83.02	83.38	90.21	90.81	90.95	90.31
PointPillars	160	1	76.29	79.05	80.80	57.52	58.01	58.10	77.75	72.52	73.62	70.84
PointRCNN	24	4	92.83	88.64	88.55	80.71	79.85	80.9	89.35	89.03	88.67	86.04
PV-RCNN	92	3	94.52	93.91	93.58	78.65	79.46	80.65	80.83	80.32	80.59	84.94
SECOND	154	2	87.97	83.75	84.43	71.29	76.0	78.23	77.99	78.96	79.55	80.74

Table 15. Results in validation set for 3D detection metric for experiment 1-6.

Model	Epoch	Experiment	Car			Cyclist			Pedestrian			Overall
Model	Epoch	Experiment	Easy	Mod.	Hard	Easy	Mod.	Hard	Easy	Mod.	Hard	Overall
Voxel R-CNN	140	6	89.55	83.37	82.63	69.72	72.7	73.53	72.16	71.38	72.71	76.29
Part A²	182	5	79.15	77.31	77.25	73.6	74.84	76.11	72.63	74.94	76.01	76.46
PointPillars	179	1	63.49	58.98	59.27	52.27	60.16	63.0	41.06	40.38	38.99	53.75
PointRCNN	89	4	84.87	79.86	79.37	68.96	71.11	71.35	76.55	75.01	74.36	75.03
PV-RCNN	139	3	88.86	83.57	82.89	71.52	73.21	74.39	64.34	64.53	64.28	73.86
SECOND	147	2	75.55	72.19	72.43	55.23	62.36	65.06	61.77	62.05	61.34	66.28

Table 16. Results in validation set for BEV detection metric for experiment 7-12.

Model	Epoch	Experiment	Car			Cyclist			Pedestrian			Overall
Model	Epoch	Experiment	Easy	Mod.	Hard	Easy	Mod.	Hard	Easy	Mod.	Hard	Overall
Voxel R-CNN	199	12	97.19	96.11	96.32	74.43	77.55	79.92	88.53	88.29	88.42	88.22
Part A²	195	11	97.75	96.71	96.61	78.23	80.9	82.74	89.99	90.41	90.76	90.04
PointPillars	21	7	85.76	81.04	82.87	67.04	73.04	75.8	55.39	57.19	58.58	72.42
PointRCNN	16	10	96.3	90.84	90.83	78.31	78.51	79.01	85.88	85.24	85.32	85.05
PV-RCNN	190	9	96.4	93.45	94.08	69.05	72.34	74.74	78.77	80.17	80.7	83.17
SECOND	162	8	90.61	86.51	86.05	78.66	79.76	79.91	66.27	73.66	76.79	80.92

Table 17. Results in validation set for 3D detection metric for experiment 7-12.

Model	Epoch	Experiment	Car			Cyclist			Pedestrian			Overall
Model	Epoch	Experiment	Easy	Mod.	Hard	Easy	Mod.	Hard	Easy	Mod.	Hard	Overall
Voxel R-CNN	186	12	83.72	81.21	81.33	68.44	71.01	73.69	67.62	69.28	70.42	75.15
Part A²	187	11	83.29	82.53	82.87	74.13	75.38	76.2	69.46	70.95	70.82	76.63
PointPillars	21	7	69.49	66.31	66.94	47.58	52.72	56.98	37.4	36.91	39.48	54.57
PointRCNN	39	10	89.96	83.36	81.59	68.66	71.26	71.32	73.52	74.04	72.66	75.19
PV-RCNN	44	9	83.42	80.46	80.61	63.75	67.41	70.22	63.18	63.38	63.45	71.42
SECOND	162	8	76.02	70.24	72.77	56.1	63.59	65.77	56.2	58.87	58.14	65.56

Table 18. Our results in KITTI validation set vs Original results in KITTI test set for 3D and BEV detection metrics.

Model	Our results (Overall per Class)						Original results (Overall per Class)
	3D			BEV			3D			BEV
	Car	Cyc.	Ped.	Car	Cyc.	Ped.	Car	Cyc.	Ped.	Car	Cyc.	Ped.
Voxel R-CNN	85.18	71.98	72.08	96.54	77.3	88.41	83.19	-	-	89.94	-	-
Part A²	82.9	75.24	70.41	96.99	82.59	90.66	79.94	66.54	45.50	88.03	71.34	34.92
PointPillars	67.58	52.43	37.93	83.22	71.96	57.05	75.29	62.56	44.09	86.48	66.07	50.67
PointRCNN	84.97	70.41	73.41	90.01	80.49	89.02	77.77	62.10	41.12	87.41	70.03	47.91
PV-RCNN	85.11	73.04	64.38	94.0	79.59	80.58	82.83	66.65	45.25	90.59	71.26	52.39
SECOND	73.39	60.88	61.72	87.72	79.44	72.24	79.20	62.56	44.09	88.4	68.36	47.63

Table 19. Our inference time metric results.

Model	Total (ms) ~	Speed (Hz) ~
PointPillars	17.25	57.97
SECOND	34.1	29.33
PV-RCNN	118.03	8.47
PointRCNN	97.83	10.22
Part A²	82.66	12.10
VoxelRCNN	59	16.95

Table 20. Original model inference time metric results.

Model	Total (ms) ~	Speed (Hz) ~
PointPillars	16	62.5
SECOND	110	9.09
PV-RCNN	80	12.5
PointRCNN	100	10
Part A²	80	12.5
VoxelRCNN	40	25

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Framework for Representing, Building and Reusing Novel State-of-the-art 3D Object Detection Models in Point Clouds Targeting Self-Driving Applications

Abstract

1. Introduction

1.1. Our Contribution

2. Related Work

3. Methodology

4. Framework for Representing 3D Object Detection Models

4.1. Point Cloud Data Representation

4.1.1. Pillar Representation

4.1.2. Voxel-based Representation

4.1.3. Point-based

4.2. Local Feature Encoder

4.2.1. Pillar Feature Network

4.2.2. Voxel Feature Encoder

4.2.3. Mean Voxel Feature Encoder

4.3. Middle Feature Extractor

4.3.1. Backbone 3D

4.4. Detection Head

4.4.1. RPN Head

4.4.2. Point Head

4.4.3. RoI Head

5. 3D Object Detection Model Specifications

5.1. Data Representation

5.2. Local Feature Encoders

5.3. Middle Feature Extractor

5.4. Detection Head

6. Network Training and Fine-Tuning

7. Performance Evaluation, Comparison, and Discussion

8. Conclusions

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe