Preprint
Article
The Effects of Individuals’ Opinion and Non-opinion Characteristics on the Organization of Influence Networks in the Online Domain
This version is not peer-reviewed.
Submitted:
09 May 2023
Posted:
10 May 2023
You are already at the latest version
A peer-reviewed article of this preprint also exists.
Abstract
The opinion dynamics literature argues that the way people perceive social influence depends not only on the opinions of interacting individuals, but also on the individuals’ non-opinion characteristics, such as age, education, gender, or place of residence. The current paper advances this line of research by studying longitudinal data that describe the opinion dynamics of a large sample (~30,000) of online social network users, all citizens of one city. Using these data, we systematically investigate the effects of users’ demographic (age, gender) and structural (degree centrality, the number of common friends) properties on opinion formation processes. We revealed that females are less easily influenced than males. Next, we found that individuals that are characterized by similar ages have more chances to reach a consensus. Besides, we report that individuals who have many common peers find an agreement more often. We also demonstrated that the impacts of these effects are virtually the same, and despite being statistically significant, are far less strong than that of opinion-related features: knowing the current opinion of an individual and, what is even more important, the distance in opinions between this individual and the person that attempts to influence the individual is much more valuable. Next, after conducting a series of simulations with an agent-based model, we revealed that accounting for non-opinion characteristics may lead to not very sound but statistically significant changes in the macroscopic predictions of the populations of opinion camps, primarily among the agents with radical opinions (≈ 3% of all votes). In turn, predictions for the populations of neutral individuals are virtually the same. Besides, we demonstrated that the accumulative effect of non-opinion features on opinion dynamics is seriously moderated by whether the underlying social network correlates with the agents’ characteristics. After applying the procedure of random shuffling (in which the agents and their characteristics were randomly scattered over the network), the macroscopic predictions have changed by ≈ 9% of all votes. What is interesting, the population of neutral agents was again not affected by this intervention.
Keywords:
Subject:
Social Sciences - Behavior Sciences1. Introduction
Social influence is perhaps one of the most intriguing and fascinating phenomena that affects our daily lives. In so-called opinion formation models (aka social influence models), the social influence effects are captured by specific mathematical rules that outline how agents’ opinions (operationalized as discrete or continuous quantities standing for agents’ choices or subjective attitudes toward predefined controversial issues) are changed after being exposed to peers’ opinions (Flache et al., 2017; Proskurnikov & Tempo, 2017). For example, in the classical DeGroot model, agents’ opinions are represented on a continuous scale, and an agent’s opinion at the next time model is defined as a convex combination of their current opinion and the opinions of the agent’ peers at the previous time moment (DeGroot, 1974):
In (1), is the list of ’s peers, and represents how strong is the influence directed from to . In turn, outlines how stubborn (self-confident) agent is. The quantities are usually called the influence weights; the weight is sometimes referred to as the self-weight. The set of all influence weights defines the influence network—directed weighted graph whose edges represent how individuals influence each other and how individuals’ trusts are distributed among their peers. Despite this terminology being usually applied within the framework of the DeGroot model (and other models that are extensions of the DeGroot model (Friedkin et al., 2016)), we will use the term “influence network” in a broader context—to describe how open individuals are to the influences from their peers and how strong are their attachments to their own opinions (without assuming that opinions evolve in accordance with the DeGroot model).
The influence network is a key ingredient without which we cannot predict the evolution of opinions in society. A large line of studies is dedicated to the extraction of the influence network from repeated measurements of individuals’ opinions (Ravazzi et al., 2021). A different line of research investigates how influence weights are linked to the intrinsic characteristics of people. At the moment, we already know a lot about how individuals perceive their peers’ opinions in information exchanges. For example, we know that individuals with radical opinions tend to be more stubborn (Kozitsin, 2023). In contrast, younger individuals are considered to be more vulnerable to social influence (Sears, 1986). Next, according to Refs. (Peshkovskaya et al., 2017, 2018, 2019) females cooperate better than males, and thus we should hypothesize that females are more easily influenced. However, such differences may stem from status inequalities (Eagly, 1983)—for example, according to empirical studies, males tend to have more friends and thus may perceive themselves as more valuable (Kozitsin et al., 2023). Further, we know that the perception of a message depends on how distant the message is from the focal individual in terms of the opinion space—too distant opinions may be less attractive (Moussaïd et al., 2013), a phenomenon referred to as bounded confidence (Deffuant et al., 2000; Hegselmann & Krause, 2002; Kurahashi-Nakamura et al., 2016). Next, empirical studies indicate that individuals that have common non-opinion features (such as age, place of residence, or culture) display more trust toward each other even if their opinions differ significantly (Balietti et al., 2021). Beside this, structural similarity, measured, for example, as the number of common friends, fosters the propagation of opinions and ideas (Aral & Walker, 2014).
Further, an individual’s perception of external information and openness to influence may depend on how influential the individual’s opinions were in previous discussions, even if these discussions were dedicated to completely different topics (the theory of reflected appraisals) (Friedkin, 2011). According to this theory, individuals whose opinions contributed most to previous conversations will reinforce their self-confidences in the next conversation and so on.
Despite our advantages in understanding the structure of trust in social networks, we still lack a systematic investigation and comparison of various factors affecting influence weights. In this paper, we attempt to challenge this problem by studying empirical longitudinal data derived from an online social network. In these data, detailed information on users’ opinions, structural (social ties), and demographic (age and gender) attributes is provided. This gives us an opportunity to rigorously investigate and compare the effects of various, both opinion and non-opinion, factors on the organization of influence networks. To paraphrase, we will study how the influence weights depend on the nodal and structural characteristics of the networked social system.
The rest of the paper is organized as follows. Section 2 describes the empirical data. Section 3 outlines our notations and terminology. In Section 4, we apply regression analysis to the data. Section 5 conducts a series of simulation experiments to test the results of the empirical analysis from Section 4. Section 6 discusses the results and makes concluding remarks. In the Appendix, auxiliary information is provided.
2. Data
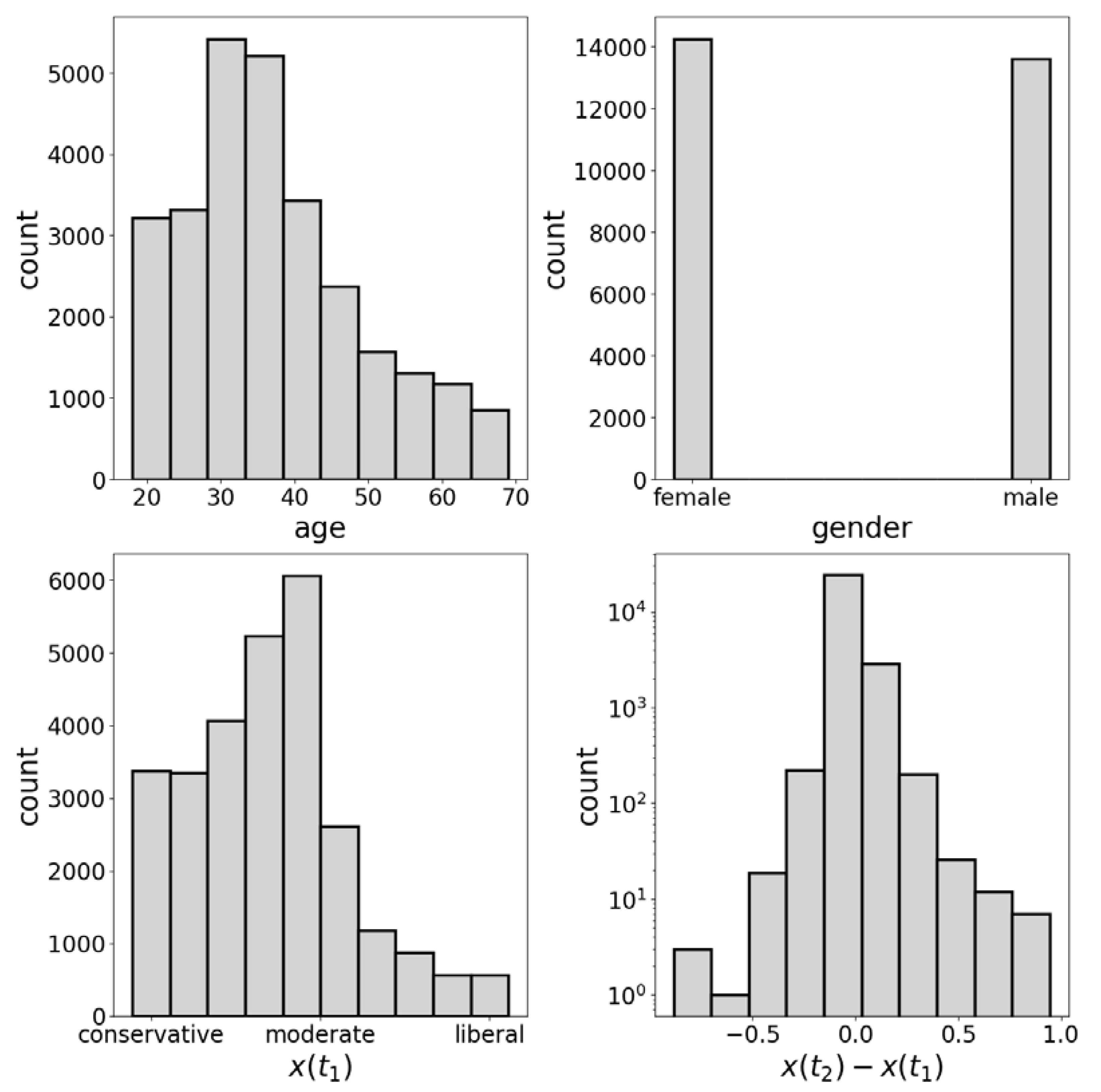
We investigate the dataset introduced for the first time in (Kozitsin et al., 2023). That dataset includes two snapshots of the online network VKontakte (VK), describing friendship-type connections and the opinions of a sample of VK users, all citizens of the same city. The snapshots were made in March and September 2019. The information regarding users’ ages and genders is also available. Users’ opinions (on a political issue) were measured on the scale using the information regarding users’ subscriptions to information sources (public pages and bloggers) with help of the methodology from (Kozitsin et al., 2020). It is worth noting that the sample was cleaned of any accounts that were employed in the opinion estimation procedure (to facilitate the independence of estimated opinions). The sample comprises adults (age > 17) with open VK accounts that were active no less than one time per month during the observation period. One more filter restricts users to having no less than 10 and no more than 200 followees (this ensures the highest accuracy of the opinion estimations). However, similarly to (Kozitsin et al., 2023), we focus on the giant connected component that includes ~95% of all vertices. As a result, we end up with a sample of users. For more information regarding the dataset, we refer the reader to Ref. (Kozitsin et al., 2023) (Sections 4, 5, and Appendix B). Further, Figure C1 (Appendix C in the current manuscript) presents some histograms that help to understand the organization of the data.
3. Notations and Terminology
We denote the network snapshots by and , where represents the sample users and stand for edges between them at times (March 2019) and (September 2019). Correspondingly, the vectors and outline estimated users’ opinions. For a user , their opinion is denoted by , their age and gender are signified as and (1—females, 2—males), respectively. Throughout the paper, the set of natural numbers from 1 to is denoted by . To denote the cardinal number of a set, we use the notation . The number of the user ’s friends at time is . The number of peers users and have in common at time is presented by .
Following Ref. (Takács et al., 2016), we will say that a positive opinion shift is undertaken if it is directed toward the opinion of the influence source. If an opinion shift is directed oppositely, then it is negative.
If an individual influences an individual , then we will say that is an influence object (focal individual) and is an influence source.
4. Analysis of Opinion Dynamics
4.1. Map of Opinion Shifts
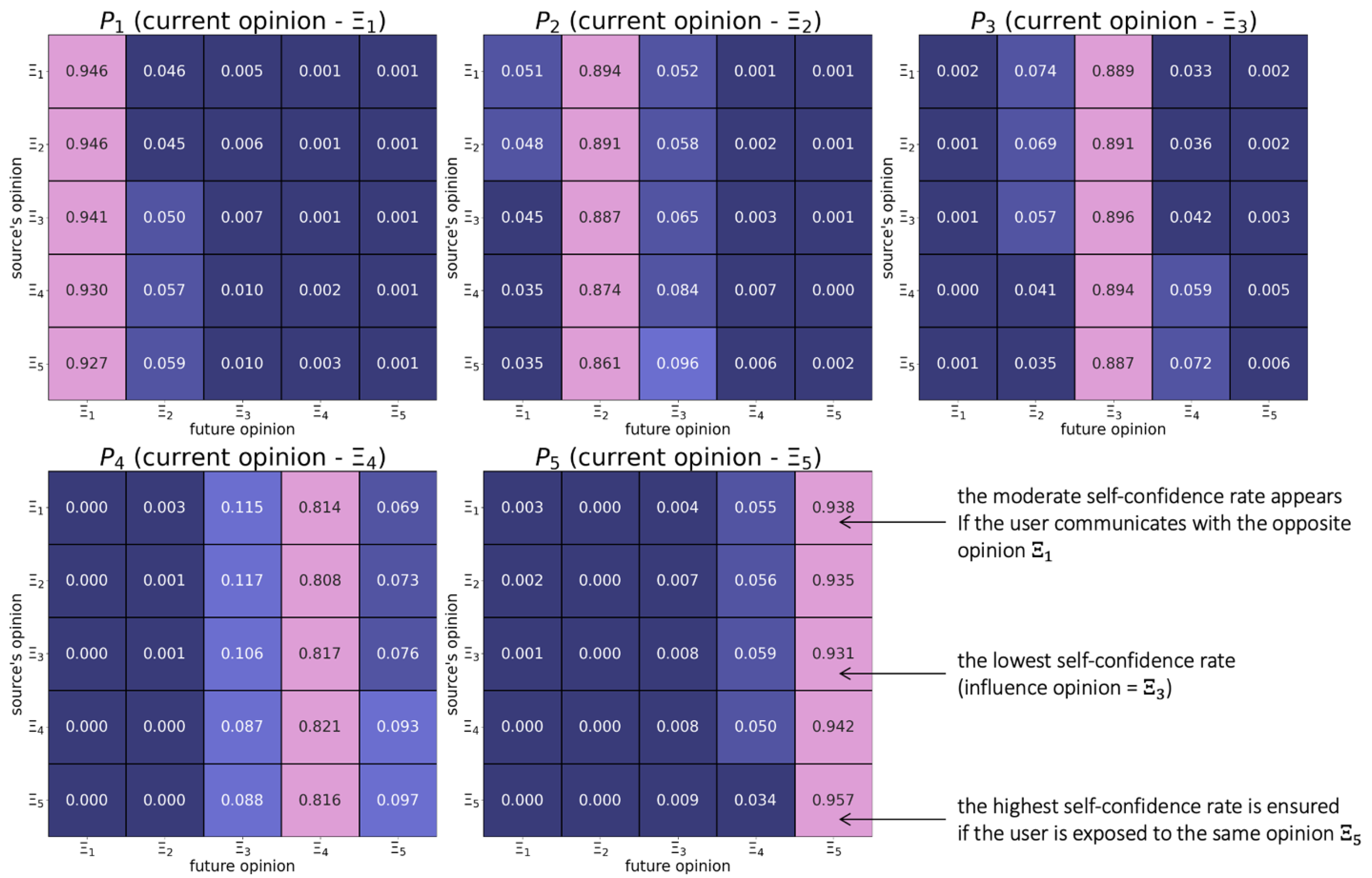
We first need to answer the following question: given the opinions of two befriended users at time , can their opinions at time be predicted? To answer this question, we discretize the opinion scale into aggregated opinion values , and then the probabilities of all possible opinion changes (including static ones ) are computed across all possible influencing opinions . The resulting quantities (see Appendix A for details on their computation), where the low indices are synchronized with the indices of the fixed opinions , and , can be grouped into square row-stochastic matrices , where the matrix showcases how users with opinion respond to peers’ opinions (see Figure 1). Within such an encoding strategy, in matrix , the -th column contains the self-confidence rates of users with opinion across different values of the influence source opinion. From Figure 1 we conclude that:
- -
- Individuals change their positions relatively rarely.
- -
- Users with radical positions are more stubborn.
- -
- Both positive and negative opinion shifts can happen, but positive shifts occur more often.
- -
- Positive shifts tend to feature the assimilative influence mechanism, whereby more distant opinions induce positive responses with larger probabilities.
- -
- Individuals with the right radical opinion (see the matrix in Figure 1) display a tendency to distrust too distant opinions (aka moderated bounded confidence).
It is worth noting that all these observations are in line with the previous empirical studies on opinion dynamics (Carpentras et al., 2022; Friedkin et al., 2021; Kozitsin, 2022b, 2023; Moussaïd et al., 2013; Takács et al., 2016).
Figure 1.
These heatmaps show how the probability of opinion shift depends on the opinions of the interacting agents. For this purpose, we discretize the opinion scale into five subintervals . The values are presented to three decimal places.
Figure 1.
These heatmaps show how the probability of opinion shift depends on the opinions of the interacting agents. For this purpose, we discretize the opinion scale into five subintervals . The values are presented to three decimal places.
4.2. Effects of Non-Opinion Characteristics on Opinion Shifts
In the previous analysis, we completely ignored the possible effects of non-opinion characteristics on opinion changes. As we said in Introduction, the way individuals perceive information could largely depend on the non-opinion characteristics of the interacting agents, such as age, gender, or the common number of friends. Let us now shed light on this issue. For this purpose, we employ the quantity
as a dependent variable. It measures the magnitude of an opinion shift subject to its direction: if the shift is pointing towards the source’s opinion , then the dependent variable is positive. Otherwise, is negative. By doing so, we want to find out what conditions facilitate the likelihood that the opinion stimuli will receive a positive response (will induce a positive opinion shift).
The list of independent variables is presented in Table 1. At the same place, we provide our intuition regarding the effects of these covariates on the dependent variable. Apart from the covariates that measure different sorts of similarity (structural one—as in the case of the common number of friends,—or demographic one—as in the case of the differences in age or gender), we also control for various characteristics of the focal node (influence object). This allows us to discern any specific nodal-level effects.
To develop a corpus of observations, we take each edge and then calculate the quantities introduced above by considering first as an influence object and as an influence source and then reverse. As a result, each user may potentially appear in observations (due to the filters specified below, not all observations will participate in the further analysis). The weakness of such an approach is that each edge is considered (twice) in isolation, thus ignoring potential influence from the rest of the peers of and . However, the influences of these peers are also added to the corpus as independent observations (we will return to this confounding factor in Section 6). As in the case of the computation of the probabilities of opinion changes presented in Figure 1, this approach silently assumes that during the observation period, each user was influenced by each of their friends strictly one time, with all these influences being independent from each other. In fact, such sort of interactions (aka one-to-one) is widely adopted in opinion formation models—see Refs. Deffuant et al., 2000; Mäs & Flache, 2013). However, the assumption that each pairwise interaction has happened is quite strict. We will return to this point in Section 6.
To facilitate the comparability of the covariates’ effects, we standardize the data by making a zero mean and unit variance for each factor. Further, we exclude from our analysis those observations that violate the following restrictions:
- -
- (the tie should remain unchanged).
- -
- (the number of common friends should be constant as it could have an effect on opinion dynamics).
- -
- (the influence source’s opinion should not undergo significant changes during the observation period—otherwise, we cannot precisely locate its value)1.
As a result of such filtering, we end up with a corpus of 390,149 observations.
However, preliminary analysis (see Table 2) revealed that age is highly correlated with other covariates. On this basis, we decided to exclude it from the list of independent variables. Table 3 shows the results of OLS regression, and Figure 2 depicts the estimated values of the regression coefficients. We see that all the covariates, excepting the absolute difference in gender and the nodal degree appear to have significant effects on the dependent variable. Further, the effects of those covariates that were estimated to be significant (at the level of 0.05) coincide with our prior intuition (see Table 1). A surprising exception is that females appeared to be less easily influenced than males, other things being equal. From Figure 2, we conclude that the opinion-related covariates ( and ) have the highest effects on the opinion formation processes (the highest effect is provided by ). The contributions of other covariates are far less strong and, besides, roughly similar. The small values of the estimated coefficients stem largely from the fact that for most observations, the dependent variable is zero or small (see Figure C1 in Appendix C).
5. Simulations
The results presented in the previous section indicate that despite some non-opinion features having significant effects on the way opinions change at the microscopic level, their impacts are not very sound. As such, the question arises if accounting for these features will change the macro-level behavior of the social system at stake. To answer this question, we perform auxiliary simulations with an agent-based opinion dynamics model using the empirical data from the dataset (see Section 2) to calibrate the model’s parameters.
As a workhorse model, we employ the one from Ref. (Kozitsin, 2022a). That model was specially designed to investigate and simulate the patterns of opinion dynamics of empirical systems. In this model, agents connected by a social network are initially endowed with opinions from an abstract opinion alphabet . At each moment, a randomly chosen agent communicates with one of their neighbors (which is also chosen by chance). Let assume that the opinions of and are and respectively. As a result of the communication, the agent ’s opinion stochastically updates according to the distribution , in which the quantity stands for the probability that the opinion shift will occur (the low indices are synchronized with the indices of the underlying opinions , and ). The quantities form a 3D mathematical object that is called the transition matrix. In some cases, it is convenient to represent the transition matrix as a list of 2D row-stochastic matrices , where . In fact, previously, we have already worked with this kind of objects—see Figure 1. However, on that occasion, we used such a construction to investigate the already existing opinion dynamics. For now, we employ the transition matrix to develop our own opinion dynamics with the aim of predicting the further evolution of the empirical system at stake.
The macroscopic behavior of the model can be captured by the variables that describe the populations of opinion camps at time . Further, we will employ the normalized versions of these quantities: .
Below, the model introduced above will be referred to as the Basic Model.
However, in its current form, the Basic Model assumes that the outcome of an interaction depends on the interacting agents’ opinions only, thus ignoring the effects of non-opinion covariates, which, as reported in Subsection 4.2, have some impact on opinion dynamics. To account for this issue, instead of applying a single transition matrix, we will use several ones, with each transition matrix dedicated to the description of its own specific combination of non-opinion characteristics of the interacting agents.
To be more specific, motivated by the results obtained in Subsection 4.2, we introduce two new features of agents (we use the same notations as in Subsection 2): (i) and (ii) (1—females, 2—males). Let us consider two interacting agents (influence object) and (influence source). For now, we assume that the outcome of this interaction depends on (i) how different the agents are in terms of age (), (ii) the number of friends and have in common (denoted by ), and, finally, (iii) the gender of . Depending on the values of these variables, each pair of interacting agents is assigned to one of the 8 possible types (see Table 4). For each type , a specific transition matrix is recruited (which has the same properties as the transition matrix in the Basic Model). The resulting model is called the Advanced Model.
Now we compare the macroscopic predictions (captured by variables ) of the Basic and Advanced Models. We use the empirical data from the dataset to calibrate the models’ parameters: (i) initial characteristics of agents, (ii) the social network, and (iii) the transition matrices. To project the opinion scale (on which the empirical opinions were estimated) to the opinion alphabet , we discretize the range into three subintervals standing for a three-element opinion alphabet (). Next, we use the dataset snapshots to calibrate the transition matrices by replicating the algorithm presented in Appendix A. In the case of the Basic Model, non-opinion covariates are not accounted for, and we end up with one transition matrix (see Appendix B, Figure B1). For the Advanced Model, 8 transition matrices are constructed (see Appendix B, Figure B2, Figure B3, Figure B4, Figure B5, Figure B6, Figure B7, Figure B8 and Figure B9).
For each model, we conduct 20 independent simulations. Each simulation starts from the same state defined by the first snapshot of the dataset. The network structure and the agents’ characteristics are delicately inherited from the empirical data. To isolate the effect of the correlations between the network and agents’ features (Kozitsin et al. (2023) revealed that the underlying networked system is assortative with respect to the opinion, age, and gender covariates), we also randomly shuffle the nodes of the network (keeping the nodes’ characteristics fixed) so that all the correlations between the nodal characteristics and the network disappear3. As a result, we end up with four possible Scenarios (see Table 5). Each simulation lasts 4,000,000 iterations: pilots revealed that this time ensures that the system reaches equilibrium in terms of the populations of the opinion camps4. Figure 3 compares the aggregated results of simulations across Scenarios 1–4. We see that if ignoring the non-opinion covariates, then the shuffle procedure does not affect the macroscopic behavior of the model – in both cases, the system finds itself in the equilibrium state . However, simulations with the Advanced Model revealed two important observations. First, we report that if not applying random shuffling (Scenario 3), then the Advanced Model stabilizes around the distribution , which differs from the prediction of the Basic model by 1,000 agents (3% of all votes). However, topologies with suppressed assortativity lead to even larger deviations: simulations within Scenario 4 tend to end up in the state —the advantage of the leftists has increased by of all votes, if compared to Scenario 3. In all Scenarios, the population of the neutral opinion camp at the equilibrium remains virtually the same (). Of course, one should keep in mind that all these differences in opinion distributions appear in the long run.
6. Discussion and Conclusion
In this paper, using longitudinal data from an online social network, we systematically analyzed how individuals’ opinion and non-opinion characteristics affect opinion dynamics. We revealed that females are harder to convince than males. Next, we found that individuals that are characterized by similar ages have more chances to reach a consensus. Finally, we report that individuals who have many common peers find agreement more often.
In general, these results align with the literature (perhaps, the effect of gender is somewhat novel). We believe that our contribution here is that we demonstrated that the impacts of these effects are virtually the same. Further, our analysis indicates that the effects of non-opinion characteristics, despite being statistically significant, are far less strong than those of opinion characteristics: knowing the current opinion of an individual and, what is even more important, the distance in opinions between this individual and the person that attempts to influence the individual is much more valuable than the information regarding their ages, genders, and the number of peers they have in common.
To gain a better understanding of this issue, we conducted a series of agent-based experiments using the underlying empirical data to calibrate the agents’ characteristics and the way they interact with each other. We revealed that accounting for non-opinion characteristics lead to not very sound but statistically significant changes in the macroscopic predictions of the populations of opinion camps in the long run, primarily among the agents with radical opinions ( of all votes). In turn, predictions for the populations of neutral individuals are virtually the same. Besides, we demonstrated that the effect of non-opinion features is seriously moderated by whether the underlying social network correlates with the agents’ characteristics. After applying the procedure of random shuffling (in which the agents and their characteristics were randomly scattered over the network), the macroscopic predictions have changed by of all votes. What is interesting, the population of neutral agents was not affected by this intervention.
The main disadvantage of our analysis is that it draws upon the data from the natural experiment, so we have no opportunity to control for many confounding factors, for example we completely dismiss external effects (Petrov et al., 2023). In fact, we do not know the history of users’ interactions during the observational period. Likely not all users were active in promoting their views to their friends. Usually, individuals with radical opinions are those who translate their opinions more often (Preoţiuc-Pietro et al., 2017). In turn, our assumption was that each user influenced each of their friends. Further, we considered each pair of befriended users and as two independent observations, sequentially changing the roles of the agents (influence object and influence source). This approach is weakened by the following confounding factors: it ignores the possibility that the dynamics of the opinions of and may be subject to some external effects, such as opinions of the ’s and ’s peers (external stimuli). Despite this possibility being partially suppressed by the fact that we also considered the influences of ’s and ’s peers as independent observations, the assumption of independent observations is likely violated on this occasion, so our regression analysis, as well as our algorithm for the calibration of the transition matrices may lead to inaccurate estimations. In Refs. (Kozitsin, 2022b, 2023), this issue was controlled for to some extent because the influence directed on a user was estimated as the mean of the opinions of the user ’s friends. However, in our case, this approach is questionable because apart from opinions, we attempt to consider other users’ characteristics. For a given user, the joint distribution of these characteristics among the user’s friends may be quite complex and nontrivial, and simple averaging may suppress some important information.
At the end, we would like to highlight that in our analysis, we concentrated on the role of observable and easily recoverable user characteristics in opinion formation processes. Indeed, ages, genders, and the numbers of users’ peers can be promptly retrieved from the Web using API facilities with a relatively small investment in resources. Of course, using more detailed information can lead to more precise predictions. For example, Bond et al. (2012) reported that the allocation of a user’s trust is highly correlated with how intensively the user likes their peers, with more likes indicating more trust. However, this sort of information requires employing API facilities that was unavailable to us on this occasion. Nevertheless, it would be a promising direction for further research.
Funding
The research was supported by a grant of the Russian Science Foundation (project no. 22-71-00075).
Data availability
All of the data and codes can be obtained upon a reasonable request.
Appendix A
The quantities were computed via the following formula:
It is worth noting that in the above formula, each edge appears two times: (i) when is an influence object and is an influence source; (ii) when is an influence source and is an influence object5. Next, to control for the confounding factors conditioned by the dynamics of ties and possible changes in the opinion of the influence source, we discard those observations from our analysis that violate the following restrictions:
- -
- (the focal tie should remain unchanged).
- -
- (the number of common friends should be constant as it could have an effect on opinion dynamics).
- -
- (the influence source’s opinion should not undergo significant changes during the observation period—otherwise, we cannot precisely locate its value).
The transition matrix for the Basic Model (see Figure B1 in Appendix B) is constructed using the same approach. The transition matrices for the Advanced Model are calculated in a similar fashion. For example, the components of the transition matrix that describe interactions of type 1 (see Figure B2 in Appendix B) are defined as follows:
Appendix B
Figure B1.
This transition matrix was estimated based on the empirical data (non-opinion covariates are ignored).
Figure B1.
This transition matrix was estimated based on the empirical data (non-opinion covariates are ignored).
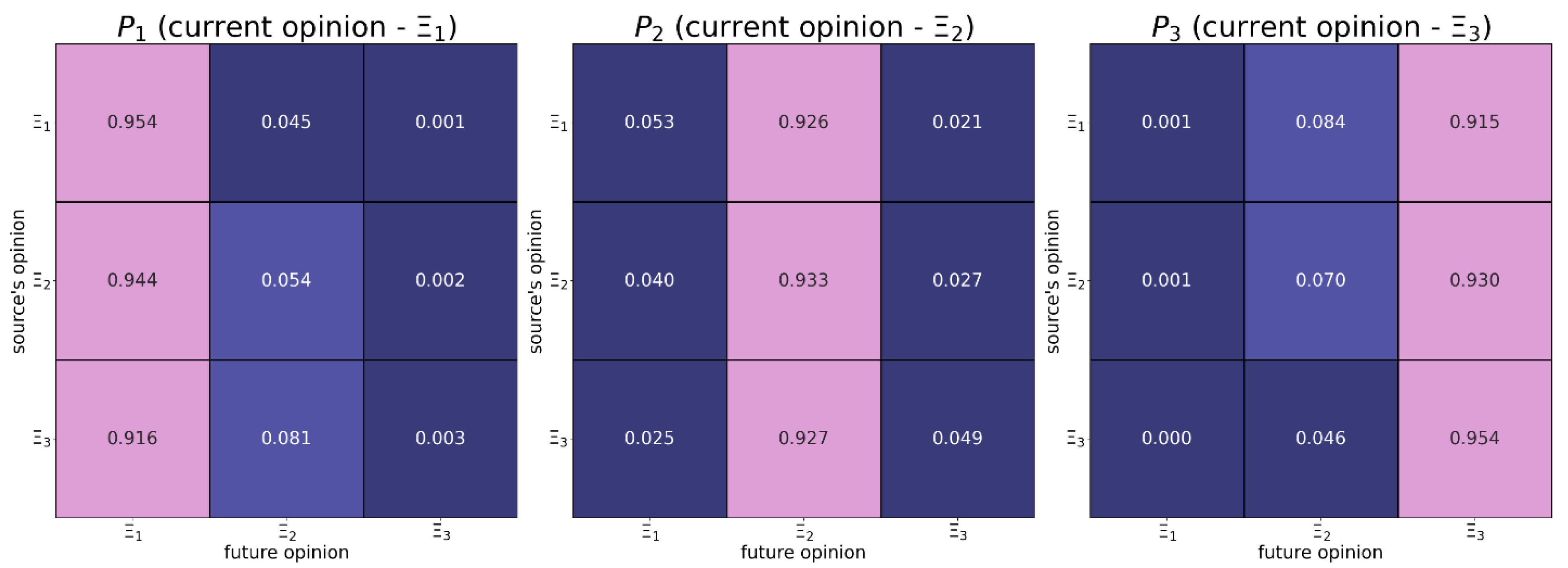
Figure B2.
This transition matrix was estimated based on the empirical data (type 1 – see Table 4).
Figure B2.
This transition matrix was estimated based on the empirical data (type 1 – see Table 4).
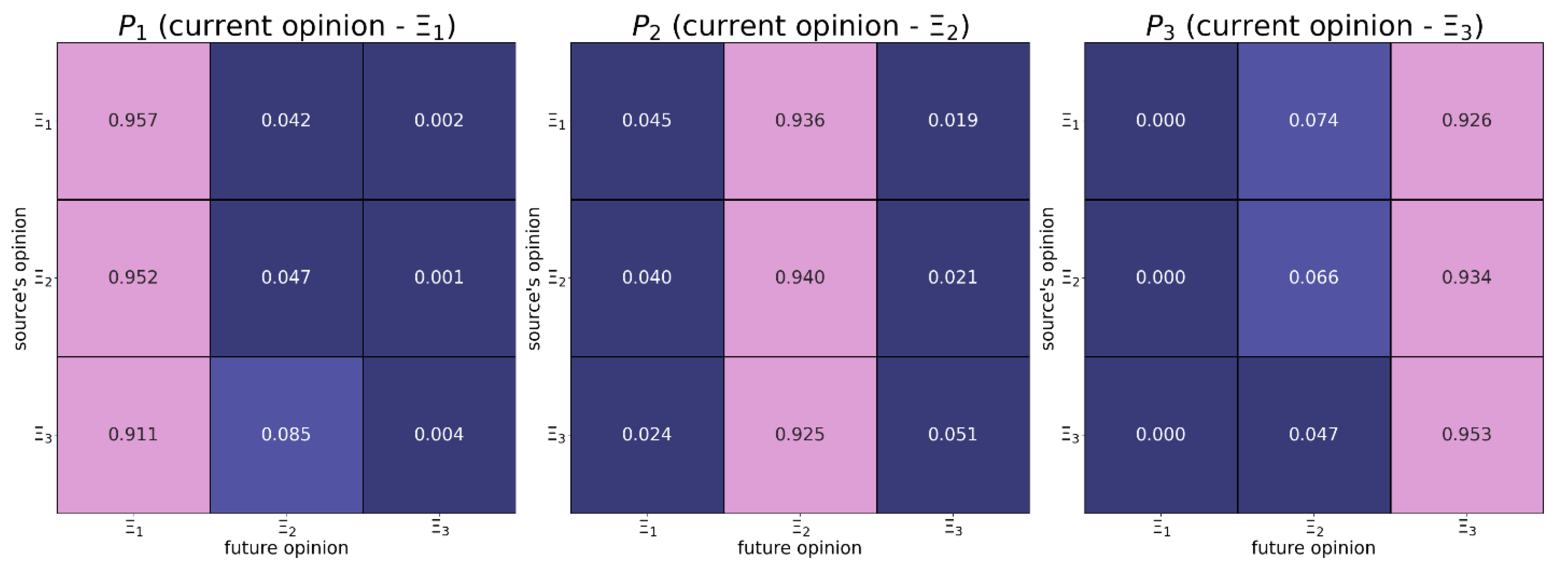
Figure B3.
This transition matrix was estimated based on the empirical data (type 2 – see Table 4).
Figure B3.
This transition matrix was estimated based on the empirical data (type 2 – see Table 4).
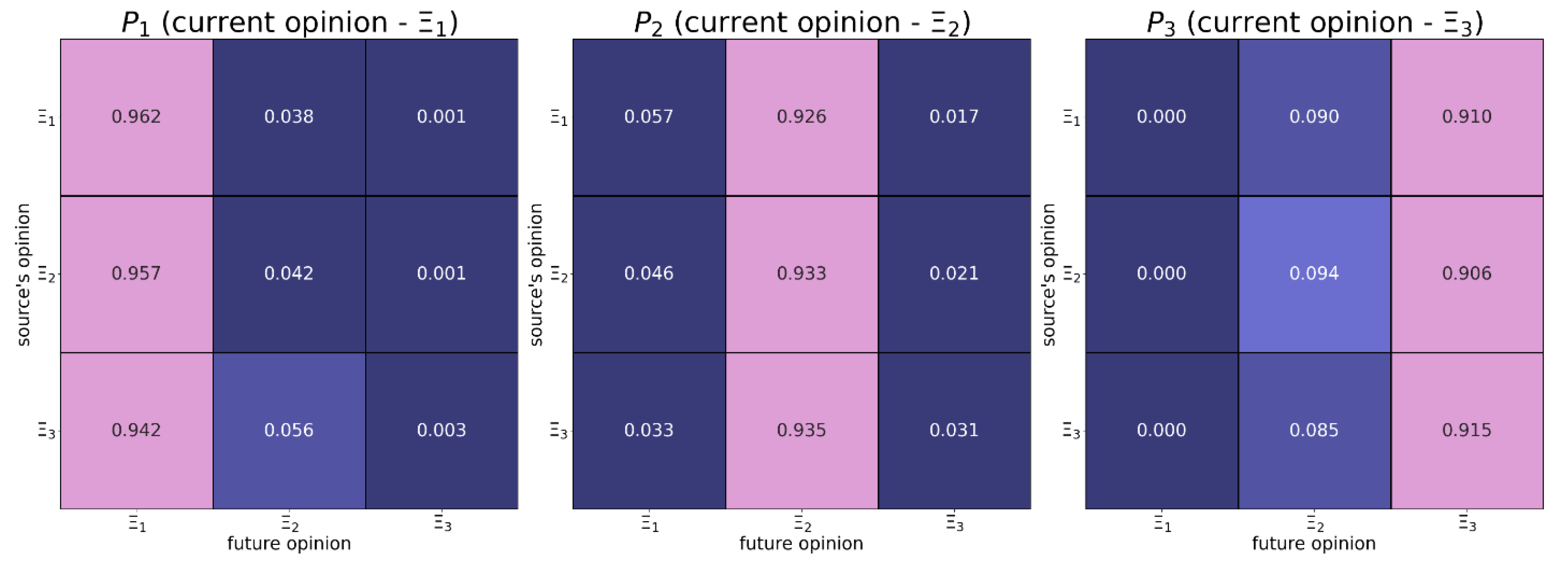
Figure B4.
This transition matrix was estimated based on the empirical data (type 3 – see Table 4).
Figure B4.
This transition matrix was estimated based on the empirical data (type 3 – see Table 4).
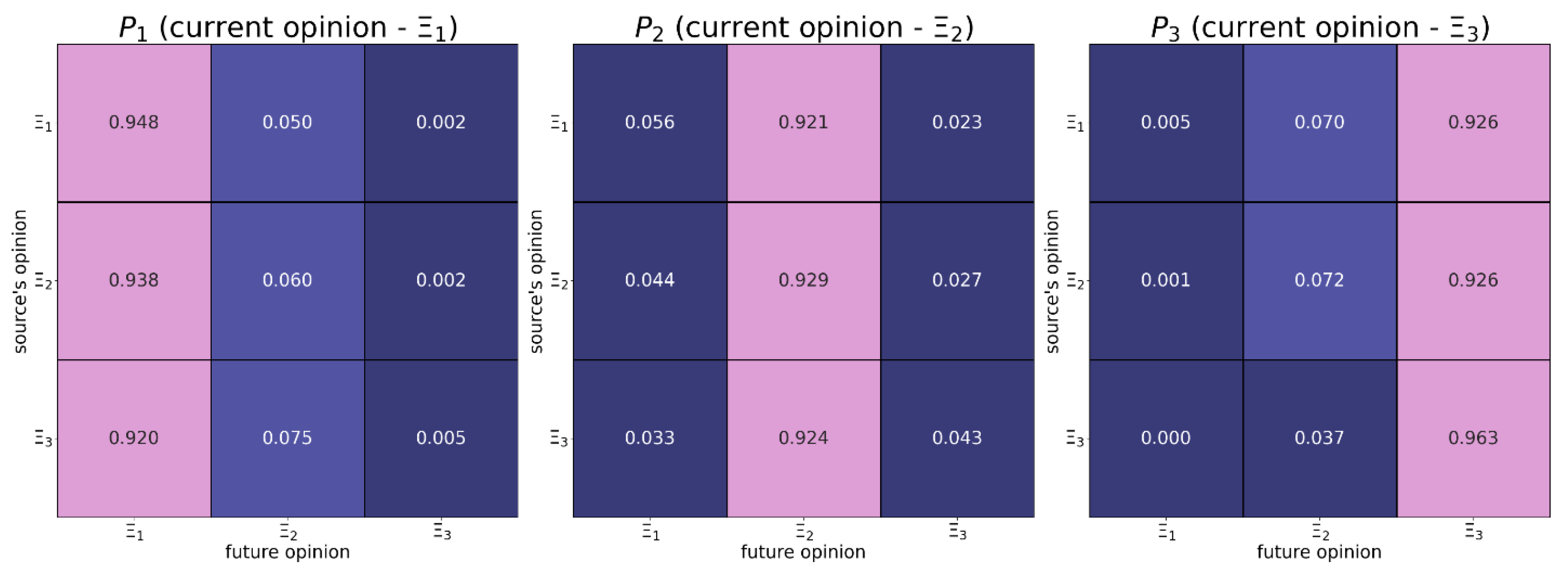
Figure B5.
This transition matrix was estimated based on the empirical data (type 4 – see Table 4).
Figure B5.
This transition matrix was estimated based on the empirical data (type 4 – see Table 4).
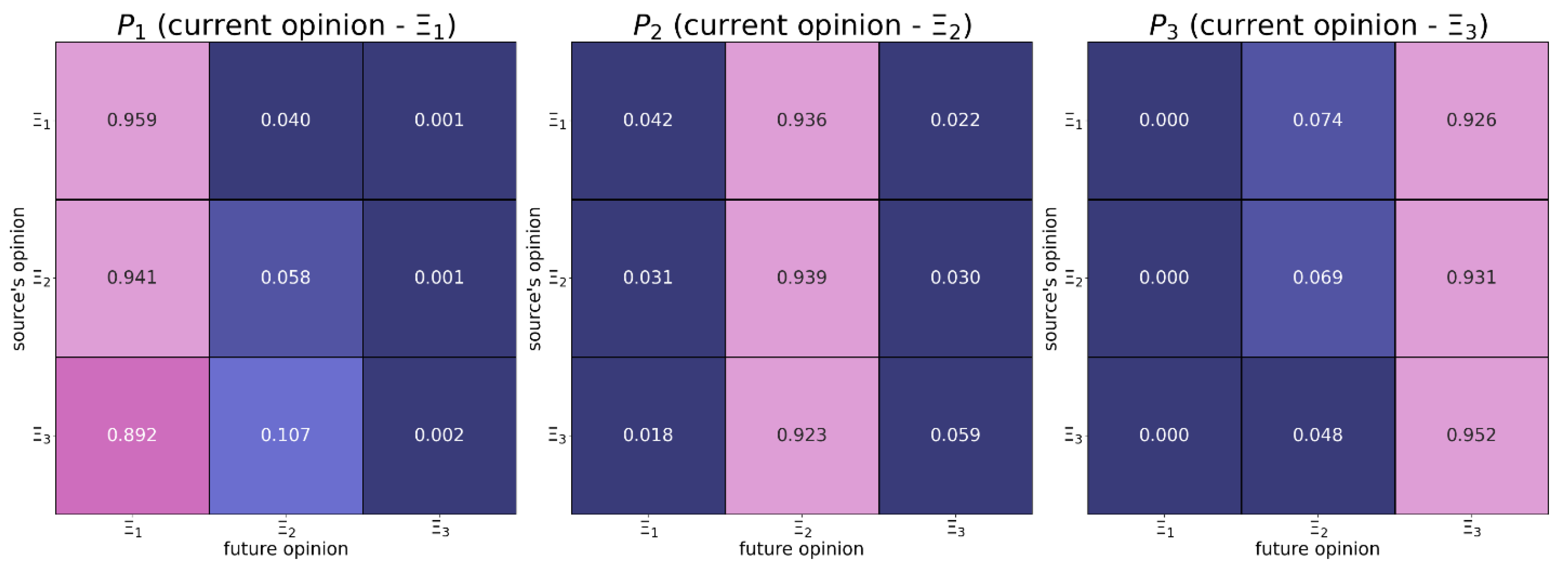
Figure B6.
This transition matrix was estimated based on the empirical data (type 5 – see Table 4).
Figure B6.
This transition matrix was estimated based on the empirical data (type 5 – see Table 4).
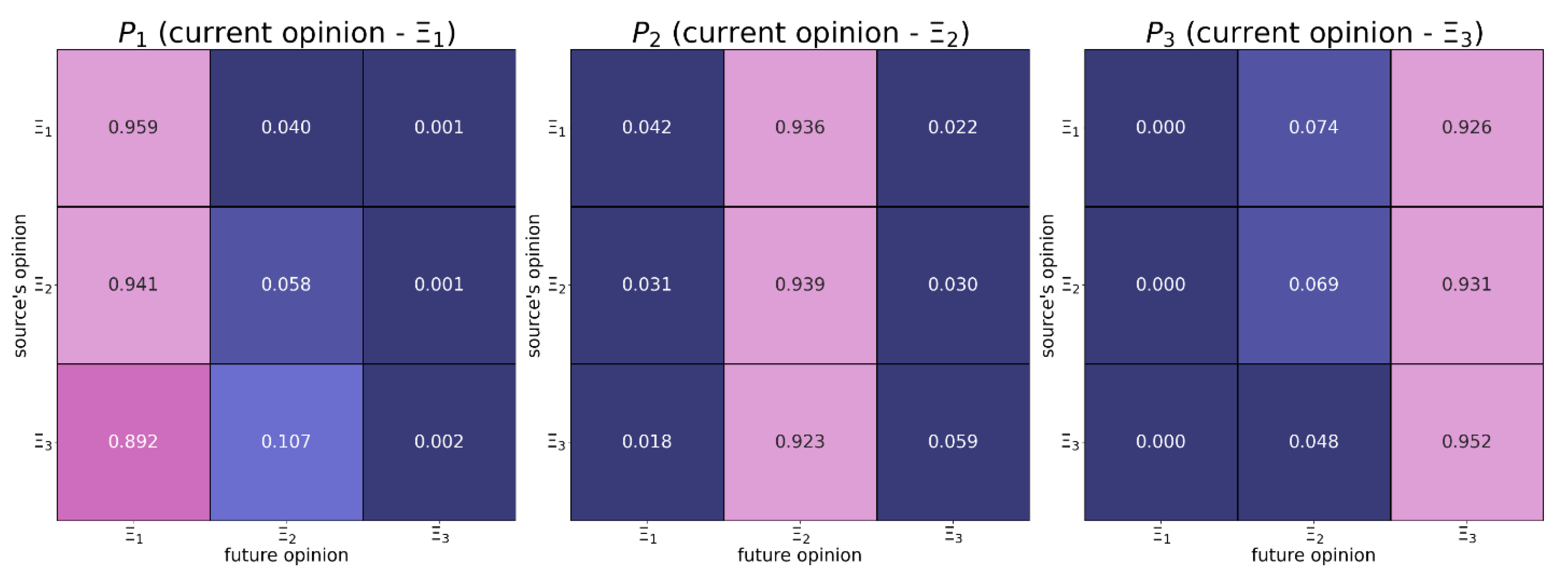
Figure B7.
This transition matrix was estimated based on the empirical data (type 6 – see Table 4).
Figure B7.
This transition matrix was estimated based on the empirical data (type 6 – see Table 4).
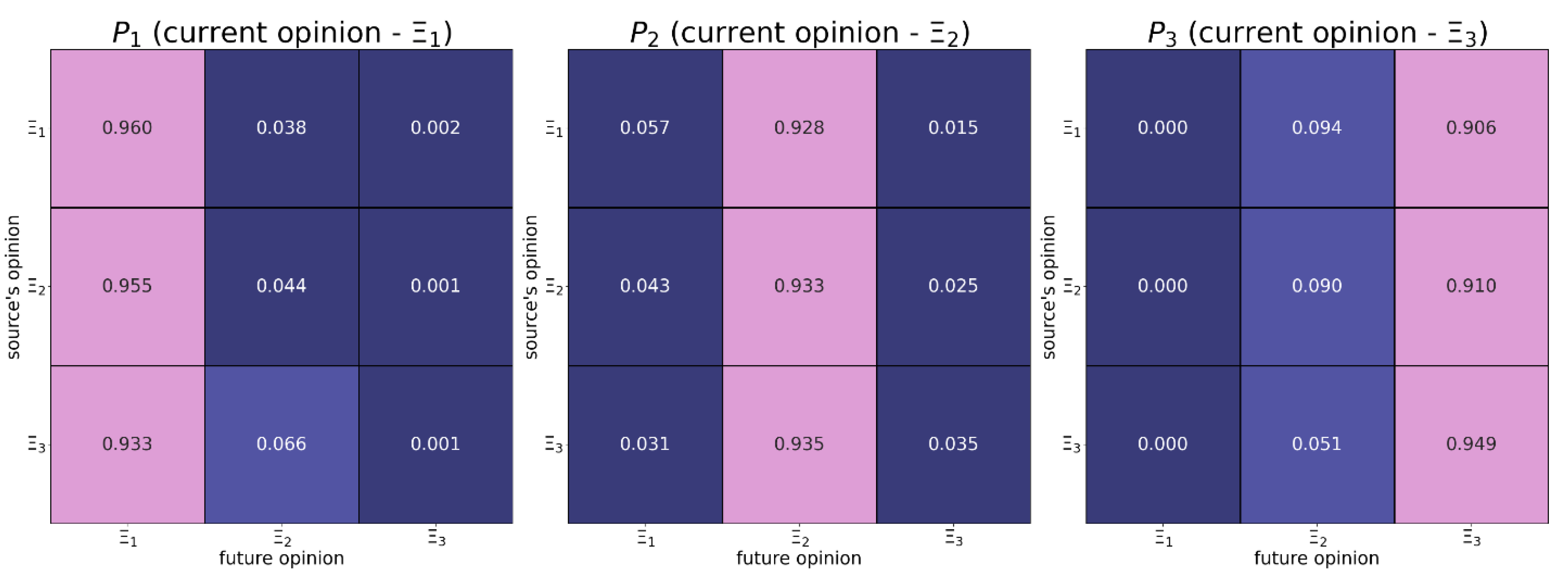
Figure B8.
This transition matrix was estimated based on the empirical data (type 7 – see Table 4).
Figure B8.
This transition matrix was estimated based on the empirical data (type 7 – see Table 4).
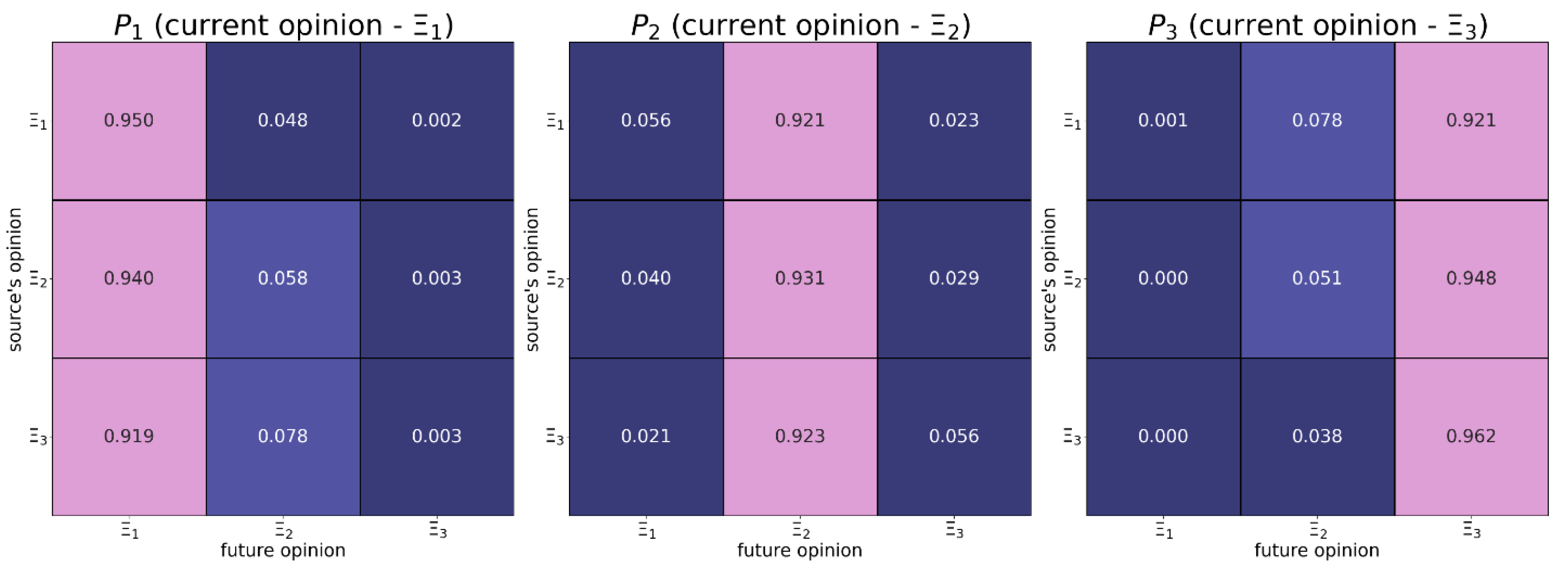
Figure B9.
This transition matrix was estimated based on the empirical data (type 8 – see Table 4).
Figure B9.
This transition matrix was estimated based on the empirical data (type 8 – see Table 4).
Appendix C
Figure C1.
These histograms show the structure of the dataset. The histograms that represent the age, gender, and opinion distributions are borrowed from the Ref. (Kozitsin et al., 2023).
Figure C1.
These histograms show the structure of the dataset. The histograms that represent the age, gender, and opinion distributions are borrowed from the Ref. (Kozitsin et al., 2023).
| 1 | In fact, if in a pair of connected vertices , one vertex (say, ) has changed its opinion for more than 0.05, then the inverse pair will not appear in the corpus of observations. Further, if both the vertices have substantially modified their opinions, then the tie is completely ignored. |
| 2 | Initially, we wanted to use the median value 3 to discretize the range of , but we decided that this threshold is too small for being used as a separator between ages. However, the results remain virtually the same if using the threshold of 3. |
| 3 | It is worth noting that this procedure does not suppress the correlations at the nodal level—for example, even after applying the shuffling, younger agents will be biased towards the right opinion . |
| 4 | To be more specific, equilibrium is reached at . To understand what this time span stands for, one should recall that in our case, one Monte-Carlo step (30,000 iterations) corresponds to the observational period (6 months). From this perspective, according to the model, the empirical social system should reach an equilibrium in years. Of course, such estimations are unlikely applicable to the description of real-life processes because the underlying empirical system is not closed and is subject to external affairs that affect its development. |
| 5 | This approach silently assumes that during the observation period, each user was influenced by each of their friends strictly one time, with all these influences being independent from each other. In fact, such sort of interactions (aka one-to-one) is widely adopted in opinion formation models – see Refs. Deffuant et al., 2000; Mäs & Flache, 2013). However, the assumption that each pairwise interaction has happened is quite strict. |
References
- Aral, S.; Walker, D. Tie Strength, Embeddedness, and Social Influence: A Large-Scale Networked Experiment. Management Science 2014, 60, 1352–1370. [Google Scholar] [CrossRef]
- Balietti, S.; Getoor, L.; Goldstein, D.G.; Watts, D.J. Reducing opinion polarization: Effects of exposure to similar people with differing political views. Proceedings of the National Academy of Sciences 2021, 118. [Google Scholar] [CrossRef] [PubMed]
- Bond, R.M.; Fariss, C.J.; Jones, J.J.; Kramer, A.D.; Marlow, C.; Settle, J.E.; Fowler, J.H. A 61-million-person experiment in social influence and political mobilization. Nature 2012, 489, 295. [Google Scholar] [CrossRef]
- Carpentras, D.; Maher, P.J.; O’Reilly, C.; Quayle, M. Deriving an Opinion Dynamics Model from Experimental Data. Journal of Artificial Societies and Social Simulation 2022, 25, 4. [Google Scholar] [CrossRef]
- Clifford, P.; Sudbury, A. A model for spatial conflict. Biometrika 1973, 60, 581–588. [Google Scholar] [CrossRef]
- Deffuant, G.; Neau, D.; Amblard, F.; Weisbuch, G. Mixing beliefs among interacting agents. Advances in Complex Systems 2000, 3, 87–98. [Google Scholar] [CrossRef]
- DeGroot, M.H. Reaching a consensus. Journal of the American Statistical Association 1974, 69, 118–121. [Google Scholar] [CrossRef]
- Eagly, A.H. Gender and social influence: A social psychological analysis. American Psychologist 1983, 38, 971–981. [Google Scholar] [CrossRef]
- Flache, A.; Mäs, M.; Feliciani, T.; Chattoe-Brown, E.; Deffuant, G.; Huet, S.; Lorenz, J. Models of Social Influence: Towards the Next Frontiers. Journal of Artificial Societies & Social Simulation 2017, 20. [Google Scholar]
- Friedkin, N. E. A formal theory of reflected appraisals in the evolution of power. Administrative Science Quarterly 2011, 56, 501–529. [Google Scholar] [CrossRef]
- Friedkin, N.E.; Proskurnikov, A.V.; Bullo, F. Group dynamics on multidimensional object threat appraisals. Social Networks 2021, 65, 157–167. [Google Scholar] [CrossRef]
- Friedkin, N.E.; Proskurnikov, A.V.; Tempo, R.; Parsegov, S.E. Network science on belief system dynamics under logic constraints. Science 2016, 354, 321–326. [Google Scholar] [CrossRef]
- Hegselmann, R.; Krause, U. Opinion dynamics and bounded confidence models, analysis, and simulation. Journal of Artificial Societies and Social Simulation 2002, 5. [Google Scholar]
- Kozitsin, I.V. A general framework to link theory and empirics in opinion formation models. Scientific Reports 2022, 12, 1. [Google Scholar] [CrossRef]
- Kozitsin, I.V. Formal models of opinion formation and their application to real data: Evidence from online social networks. The Journal of Mathematical Sociology 2022, 46, 120–147. [Google Scholar] [CrossRef]
- Kozitsin, I.V. Opinion dynamics of online social network users: A micro-level analysis. The Journal of Mathematical Sociology 2023, 47, 1–41. [Google Scholar] [CrossRef]
- Kozitsin, I.V.; Chkhartishvili, A.G.; Marchenko, A.M.; Norkin, D.O.; Osipov, S.D.; Uteshev, I.A.; Goiko, V.L.; Palkin, R.V.; Myagkov, M.G. Modeling Political Preferences of Russian Users Exemplified by the Social Network Vkontakte. Mathematical Models and Computer Simulations 2020, 12, 185–194. [Google Scholar] [CrossRef]
- Kozitsin, I.V.; Gubanov, A.V.; Sayfulin, E.R.; Goiko, V.L. A nontrivial interplay between triadic closure, preferential, and anti-preferential attachment: New insights from online data. Online Social Networks and Media 2023, 34–35, 100248. [Google Scholar] [CrossRef]
- Kurahashi-Nakamura, T.; Mäs, M.; Lorenz, J. Robust clustering in generalized bounded confidence models. Journal of Artificial Societies and Social Simulation 2016, 19. [Google Scholar] [CrossRef]
- Mäs, M.; Flache, A. Differentiation without distancing. Explaining bi-polarization of opinions without negative influence. PloS One 2013, 8, e74516. [Google Scholar] [CrossRef]
- Moussaïd, M.; Kämmer, J.E.; Analytis, P.P.; Neth, H. Social Influence and the Collective Dynamics of Opinion Formation. PLOS ONE 2013, 8, e78433. [Google Scholar] [CrossRef] [PubMed]
- Peshkovskaya, A.; Babkina, T.; Myagkov, M. Social context reveals gender differences in cooperative behavior. Journal of Bioeconomics 2018, 1–13. [Google Scholar] [CrossRef]
- Peshkovskaya, A.; Babkina, T.; Myagkov, M. In-Group Cooperation and Gender: Evidence from an Interdisciplinary Study. In Global Economics and Management: Transition to Economy 4.0; Kaz, M., Ilina, T., Medvedev, G.A., Eds.; Springer International Publishing, 2019; pp. 193–200. [Google Scholar] [CrossRef]
- Peshkovskaya, A.; Myagkov, M.; Babkina, T.; Lukinova, E. Do women socialize better? Evidence from a study on sociality effects on gender differences in cooperative behavior. 2017.
- Petrov, A.; Akhremenko, A.; Zheglov, S. Dual Identity in Repressive Contexts: An Agent-Based Model of Protest Dynamics. Social Science Computer Review 2023, 08944393231159953. [Google Scholar] [CrossRef]
- Preoţiuc-Pietro, D.; Liu, Y.; Hopkins, D.; Ungar, L. Beyond binary labels: Political ideology prediction of twitter users; 2017; Volume 1, pp. 729–740. [Google Scholar]
- Proskurnikov, A.V.; Tempo, R. A tutorial on modeling and analysis of dynamic social networks. Part I. Annual Reviews in Control 2017, 43, 65–79. [Google Scholar] [CrossRef]
- Ravazzi, C.; Dabbene, F.; Lagoa, C.; Proskurnikov, A.V. Learning Hidden Influences in Large-Scale Dynamical Social Networks: A Data-Driven Sparsity-Based Approach, in Memory of Roberto Tempo. IEEE Control Systems Magazine 2021, 41, 61–103. [Google Scholar] [CrossRef]
- Sears, D.O. College sophomores in the laboratory: Influences of a narrow data base on social psychology’s view of human nature. Journal of Personality and Social Psychology 1986, 51, 515–530. [Google Scholar] [CrossRef]
- Takács, K.; Flache, A.; Mäs, M. Discrepancy and Disliking Do Not Induce Negative Opinion Shifts. PLOS ONE 2016, 11, e0157948. [Google Scholar] [CrossRef]
Figure 2.
The values of the estimated OLS regression coefficients plotted with the corresponding confidence intervals.
Figure 2.
The values of the estimated OLS regression coefficients plotted with the corresponding confidence intervals.
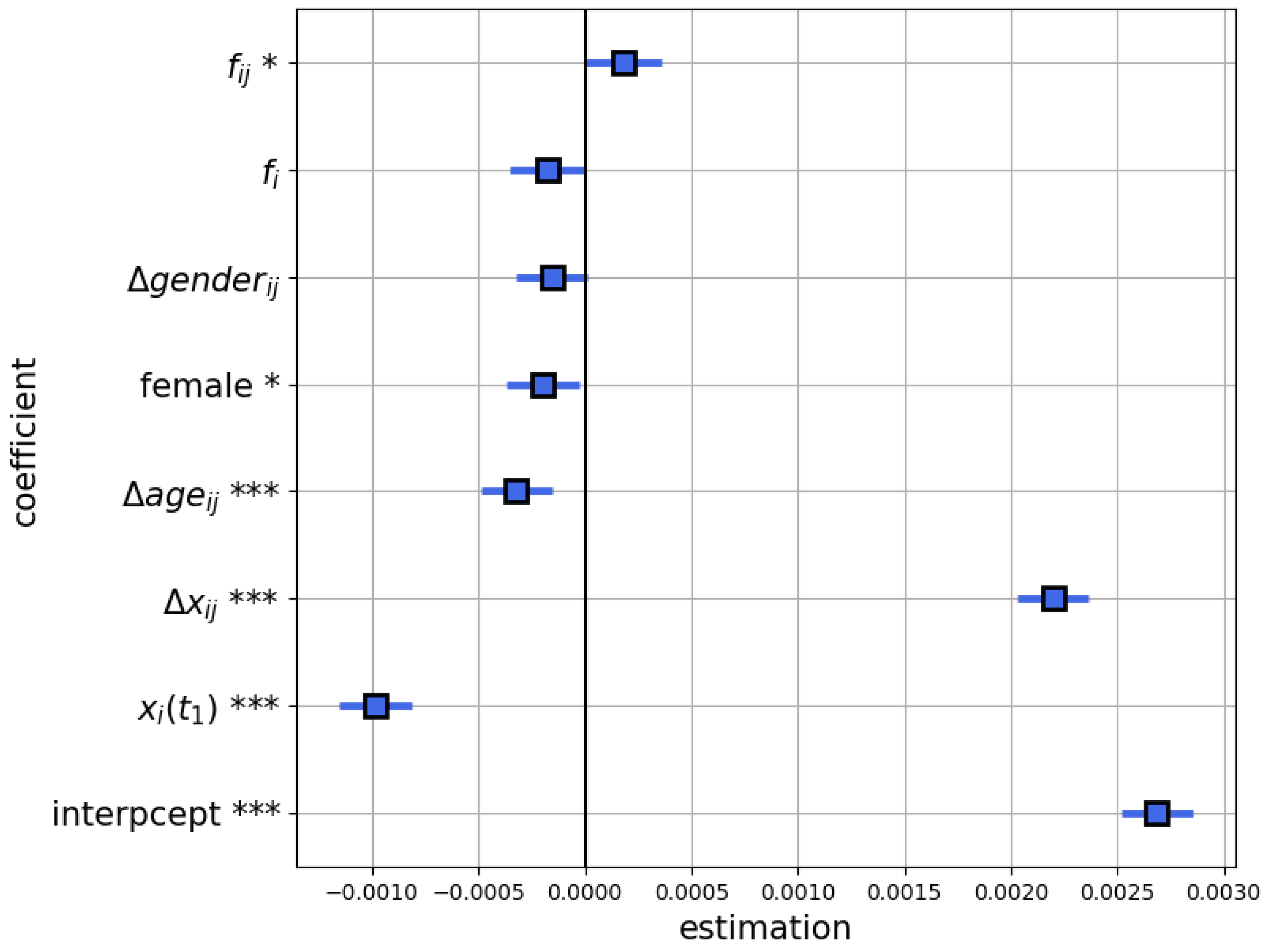
Figure 3.
The figure demonstrates the averaged dynamics of the populations of leftists (upper panels) and rightists (bottom panels) across Scenarios 1–4. For each Scenario, the colored area is formed by the upper and lower contours of the corresponding simulations, and the curve represents the averaged trajectory. The left panels depict the time span , the right panels investigate the range .
Figure 3.
The figure demonstrates the averaged dynamics of the populations of leftists (upper panels) and rightists (bottom panels) across Scenarios 1–4. For each Scenario, the colored area is formed by the upper and lower contours of the corresponding simulations, and the curve represents the averaged trajectory. The left panels depict the time span , the right panels investigate the range .
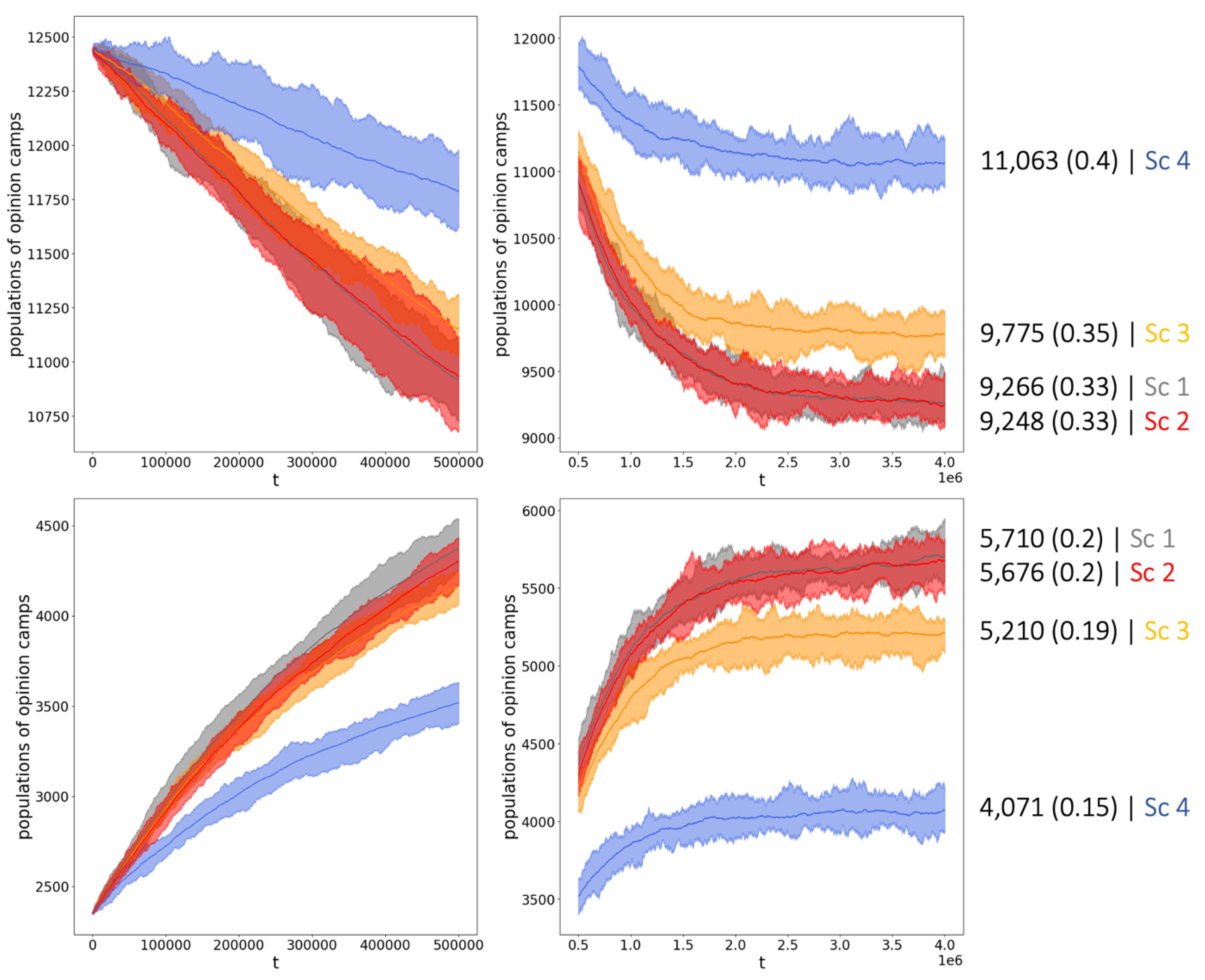
Table 1.
Independent variables (—influence object, —influence source).
| Independent variable | Definition | Hypothesis |
| The absolute difference in opinions | should have a positive effect on the dependent variable—from Figure 1 it follows that more distant opinions tend to be more attractive. | |
| The absolute difference in age | should have a negative effect on the dependent variable—a non-opinion similarity stimulates the decrease in opinion discrepancies (Balietti et al., 2021). | |
| This variable demonstrates if two users have different genders () or not () | should have a negative effect on the dependent variable—a non-opinion similarity stimulates the decrease in opinion discrepancies (Balietti et al., 2021). | |
| The nodal degree of the influence object | may have a negative effect on the dependent variable—we hypothesize that individuals that have many friends should perceive themselves as more valuable and having a higher social status and thus should be more attached to their own views (Eagly, 1983). | |
| The number of common friends | should have a positive effect on the dependent variable—strong ties are more effective in conducting social influence (Aral & Walker, 2014). | |
| The opinion of the influence object | should have a negative effect on the dependent variable—from Figure 1 it follows that users whose opinions are close to the right endpoint of the opinion spectrum are more stubborn. | |
| This dummy variable shows if the gender of is female | should have a positive effect on the dependent variable—according to Refs. (Peshkovskaya et al., 2017, 2018) females cooperate better than males. | |
| The age of | This covariate should have a negative effect on the dependent variable—younger individuals tend to be more sensitive to influence (Sears, 1986). |
Table 2.
VIF computed for the covariates in two cases: (1) the age covariate is accounted for (the upper row); (2) the age covariate is omitted (the bottom row).
Table 2.
VIF computed for the covariates in two cases: (1) the age covariate is accounted for (the upper row); (2) the age covariate is omitted (the bottom row).
| 2.508 | 1.857 | 1.448 | 1.874 | 1.483 | 3.432 | 1.901 | 5.346 |
| 2.247 | 1.556 | 1.422 | 1.853 | 1.45 | 2.948 | 1.701 | – |
Table 3.
The results of OLS regression.
| Coefficient | Std error | t | P > |t| | |
| Intercept | 0.0027 | 8.53e-05 | 31.467 | 0.000*** |
| 0.0022 | 8.63e-05 | 25.451 | 0.000*** | |
| -0.0003 | 8.6e-05 | -3.724 | 0.000*** | |
| -0.0002 | 8.57e-05 | -1.826 | 0.068 | |
| -0.0002 | 9.06e-05 | -1.911 | 0.056 | |
| 0.0002 | 9.01e-05 | 2.018 | 0.044* | |
| -0.001 | 8.71e-05 | -11.329 | 0.000*** | |
| -0.0002 | 8.67e-05 | -2.276 | 0.023* |
Note. Significance codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘ ’ 1.
Table 4.
Definition of the types of agent pairs.
| Types of pairs | The values of the variable | ||
| Type 1 | |||
| Type 2 | |||
| Type 3 | |||
| Type 4 | |||
| Type 5 | |||
| Type 6 | |||
| Type 7 | |||
| Type 8 | |||
Note: the value of 5 that discretizes the range of was chosen as the mean of this variable (the 60th percentile)2. The threshold value 1 that separates the range of is the median.
Table 5.
Design of simulation scenarios.
| Agents’ characteristics used in simulations | Random shuffle of nodes | ||
| Opinion | Non-opinion characteristics | ||
| Scenario 1 | + | - | - |
| Scenario 2 | + | - | + |
| Scenario 3 | + | + | - |
| Scenario 4 | + | + | + |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
MDPI Initiatives
Important Links
© 2025 MDPI (Basel, Switzerland) unless otherwise stated






