Prerpints.org logo
Preprint
Article

Anomaly Detection in Endemic Disease Surveillance Data Using Machine Learning Techniques

Altmetrics

Downloads

169

Views

69

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

09 May 2023

Posted:

10 May 2023

You are already at the latest version

Alerts
Abstract
Disease surveillance is critical to monitor ongoing control activities, detect early outbreaks and to inform intervention priorities and policies. Unfortunately, most data from disease surveillance remain under-utilised to support decision-making in real-time. Using the Brazilian Amazon malaria surveillance data as a case study, we explore unsupervised anomaly detection machine learning techniques to analyse and discover potential anomalies. We found that our models are able to detect early outbreaks, peak of outbreaks as well as change points in the proportion of positive malaria cases. Specifically, the sustained rise in malaria in the Brazilian Amazon in 2016 was flagged by several models. We also found that no single model detects all the anomalies across all health regions. The approaches using Clustering-based local outlier algorithm ranked first before Principal component analysis and Stochastic outlier selection in maximising the number of anomalies detected in local health regions. Because of this, we also provide the minimum number of machine learning models (top-k models) to maximise the number of anomalies detected across different health regions. We discovered that the top-3 models that maximise the coverage of the number and types of anomalies detected across the 13 health regions are: Principal component analysis, Stochastic outlier selection and Multi-covariance determinant. Anomaly detection approaches provide interesting solutions to discover patterns of epidemiological importance when confronted with a large volume of data across space and time. Our exploratory approach can be replicated for other diseases and locations to inform timely interventions and actions toward endemic disease control.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

Disease surveillance programs established by local, state and national governments collect health data of potential epidemiological importance [1]. The volume and velocity of data collected through these systems are increasing over time in both formal and informal methods of collecting data [2]. Despite the availability of large quantities of disease surveillance data, most of them are not adequately or optimally [2] utilised to support real-time public health decisions. The reasons for this under-utilisation of epidemiological data include limited availability of data analysts, data quality issues such as delayed and missing data, and competing priorities for health system resources [3,4,5]. As a consequence, more data are collected than can be analysed, missing an opportunity to inform timely decisions. Here, using a malaria case study, we explore the benefits of using anomaly detection approaches to inform timely decisions about appropriate disease interventions and increase the chance of controlling disease transmission within the population [6].
Different methods of generating evidence from surveillance data are useful to support public health decisions, depending on the type of disease outbreak. For pandemics where daily growth estimates, peak size and timing are reported and frequently analysed by humans, a simple dashboard of a statistical summary of case numbers and corresponding locations might be sufficient to re-target available interventions. However, for endemic diseases where frequent analysis of case reports by humans is not frequently performed but regular insights are still required, methods that enable automated generation of evidence from surveillance data are required. In this paper, we focus on malaria, which is an endemic tropical disease.
Among the evidence required for endemic disease management, we found the following important: identifying the acceptable disease burden within a population; when, why and how rapid growth (flareup) in case numbers would occur beyond the acceptable threshold; the spatiotemporal variation in progress towards disease elimination, and the effectiveness of interventions [7]. Most of the evidence required for endemic disease management is detected as deviations from the known characteristics of the endemic disease recorded in the surveillance data during outbreak monitoring. The departure from normal behaviour and the process of detecting such departures by mining the collected data is termed anomaly or outlier detection [8,9,10].
An anomaly is an observation that deviates so much from other observations as to arouse suspicion that it was generated by a different mechanism [10] or as an error in the current mechanism. Anomaly detection is the process of mining the patterns in data that do not tally with the expected behaviour of the system that generates the data [9]. Anomalies may occur as a result of reporting error, variability in measurement, change in natural processes, human-induced errors, fault in machines, fraudulent activities, response to intervention measures, among other reasons. Anomaly detection is a part of Artificial intelligence (AI) methods. AI is generally concerned with building smart machines (powered by algorithms) capable of performing tasks that typically require human intelligence [11] and are able to discover patterns based on several experiences presented to them [12].
In this paper, we focus on applying AI-based anomaly detection methods to detect anomalies in endemic disease surveillance data, with the purpose of assisting public health managers to make better decisions. In doing this work, we intend to achieve the following objective: (i) designing an anomaly detection framework that enables the repeatable integration of methods, data and generated insights into the decision support system of different regions to assist in the control and eventual elimination of endemic diseases; (ii) evaluating the potential epidemiological significance of the spatio-temporal anomalous patterns detected by the machine learning models, and (iii) assessing the consistency and variation in anomalous patterns detected by models in order to select the best models to be deployed into production for anomaly detection in surveillance data streams.
With the above objectives in mind, we answer the following research questions: (1) What are the relevant epidemiological anomalies that can be detected in routine disease surveillance data? (2) What are the minimum number of models (top-k models) that can be deployed to maximise the number of detected anomalies across different health regions? How consistent and variable are the performance of these models across the data from different health regions?
The case study for this research is the state of Para in Brazilian Amazon region (see Figure 1) where malaria has remained endemic especially in the northern region. The surveillance data for this case study is a de-identified and public version of the Brazilian epidemiological surveillance system of malaria (SIVEP-Malaria) database recorded from 2009 to 2019 [13]. This data set contains daily positive and negative test results (but aggregated into months in this work as the days and dates have been removed) malaria diagnosis outcome for each patient. The state of Para is divided into 13 health regions for health administration purposes.
In the remainder of this paper, we first introduce the framework for exploring anomaly detection in surveillance data and then explain the data set we used to validate this framework. We then describe the various unsupervised machine learning algorithms that we employed for exploring the anomalies in the data. Further, we present results and then discuss the aspects of the framework and anomaly detection methods and results that are most relevant to the control and management of endemic disease outbreaks.

2. Methods

In this section, we first introduce our design of a framework to enable automated and repeatable surveillance data analysis anomaly detection irrespective of space and time. We then leverage the components of the framework to describe how we processed the data and applied different unsupervised anomaly detection algorithms to the data to detect patterns and anomalies of different types.

2.1. Anomaly Detection Framework

A major consideration in designing modern data analysis framework or pipeline is taking concept drift and data drift into consideration [14,15]. These concepts refer to the change in data distribution over time and as you move from one hospital or health region to another. Continuously integrating new data and retraining the detection algorithm are important for updating the performance of the deployed model.
Figure 2 presents a decision support framework that is based on anomaly detection using endemic disease surveillance data. As an endemic disease, we assume that case numbers and situation reports are not analysed on daily basis by humans. This assumption is in contrast with on-going pandemics like COVID-19 [16] in which daily case analysis is carried out. Hence, only a monthly review triggered by alerts would lead to conscious analysis and investigation by humans. Daily reports take an average of one month to be collated and aggregated into the health regions that make up a state government. The entire surveillance data per health region is used as a training set for the anomaly detection models.
To understand the framework in Figure 2, Table 1 provides the description of each of the steps. The framework can be used to consistently apply anomaly detection models to surveillance data collected over time in different regions and for different endemic diseases.
The remaining subsections will give further details on the data transformation, feature extraction, machine learning algorithms used for anomaly detection models training and the major parameters used by the training algorithms.

2.2. Epidemiological Feature Selection and Pre-Processing

Although there are 42 fields recorded in the SIVEP time series surveillance data for malaria, for the purpose of this study we used four fields: Date (in Months), total number of tests, number of negative results and number of positive results. These last three features were converted into a single feature: the proportion of positive tests, I P , which is the proportion of tests that were conducted that returned a positive result for malaria, for each state and health region. I P is mathematically defined as:
I P = N P N T
where N P is the total number of positive cases per month and N T is the number of tests carried out per month. As I P is a proportion, we can compare values across time and space even if the testing capacity is changing over the months and across the geographical health regions. However, we assume a uniform distribution of cases across a health region such that we have equal chance of detecting an infected person within a health region.
With the assumed uniform distribution of positive cases per health region, an increase in I P would then truly represent the situation where more people in the health region are becoming affected. The reason for the rise will then be investigated. Given the same testing capacity ( N T ), a decline in I P would then represent either a naturally dying epidemic or the outcome of a deployed intervention.
In Figure 3, we show the state level aggregated data from the Para state of Brazil which we used to demonstrate the original epidemiological features of interest that we used to derive I P .
Similar data to Figure 3 was extracted for the 13 health regions by separating the Para state into its health regions. The extracted data were then transformed to I P for each of the health regions. An example outcome of the data transformation is shown in Figure 4. To reduce noise, we applied the moving average transformation to the derived feature, I P using a window size of six months. Moving average is used to remove some noise and irregularity ( e ( t ) in Equation (2)) to enhance the prediction accuracy of the machine learning algorithms.
A time series data, y ( t ) can be generalised using an additive model as:
y ( t ) = g ( t ) + s ( t ) + h ( t ) + e ( t )
where:
g ( t ) is the trend (changes over a long period of time)
s ( t ) is seasonality (periodic or short term changes)
h ( t ) is the effects of holidays to the forecast
e ( t ) is the error term or irregularities (the unconditional changes specific to a circumstance).
Different learning algorithms can model time series data well depending on what components of time series are present in the data. The unsupervised approach to anomaly detection is exploratory in nature and the evaluation are subjectively performed by humans.
Although unsupervised anomaly detection algorithms are given certain inputs by humans that enable them set a metric threshold for objectively and automatically detecting anomalies, the detected anomalies will need to be certified by experts. Table 2 shows the unsupervised models which are integrated in the Pycaret framework [17] and uses a specific distance measure to estimate the point anomalies in a time series data.
Clustering-based local outlier (cluster or CBL), Local outlier factor (lof) and Connectivity-based local outlier (cof) are based on local outlier concepts. CBL uses a distance measure that considers both the distance of an object to its nearest cluster and also the size of the cluster. So, small clusters are not simply discarded as outliers as a whole. The lof algorithm uses k-nearest neighbour to define the density of objects whose distances from one another would be considered in defining the density of the locality. The reachability distance, which is a non-symmetric measure of distance, is used to determine an outlier. Each data point may have a different reachability distance and this distance is used to define the degree of anomaly. The larger the value, the more anomalous the point from its local neighbours [18].
Connectivity-based local outliercof is an improved version of lof. The density-based lof algorithm has a shortcoming in that it completely depends on the density of the neighbouring points. It performs poorly when the density of the outlier is similar to its nearby data points. Hence, cof recognises that anomalies must not be of a lower density than the data it deviates from [19].
Isolation Forest (iforest) algorithm is an unsupervised version of decision tree. It is a binary decision tree. The iforest algorithm is based on the assumption that anomalies are few and unique and that they belong to the shallow branches where they easily isolate themselves from the rest of the tree branches. A random set of features are selected and used to build the tree using the data points. The sample that travels deep into the tree is unlikely to be anomalies. The Isolation Forest algorithm is computationally efficient and it is very effective in anomaly detection. However, the final anomaly score depends on the contamination parameter provided while training the model - meaning that we should have an idea of what percentage of the data is anomalous so as to get a better prediction [20].
Histogram-based anomaly detection (histogram) assumes feature independence and builds the histogram of each feature. The anomaly score is based on histogram-based outlier score (HBOS). HBOS can be constructed from either univariate or multivariate features of each data point. For multivariate problems, the anomaly score of all variables is added up to rank the data. Given d variables with p data points, the HBOS is calculated as: [21]
H B O S ( p ) = ∑ i = 0 d l o g 1 h i s t i ( p )
Histogram outlier detector first constructs a histogram for a variable by choosing a bin. The computed score for each variable is normalised to 1.0 and summed up across the d variables to compute the global outlier score. A data point may be anomalous in one variable but not in others. Hence, a data point that is an outlier in almost all the variables is almost definitely an anomaly in the data set.
K-Nearest Neighbors (KNN) is popularly used as a supervised learning algorithm. However, it can also be used as an unsupervised learning algorithm and can be used to detect outliers or anomalies in data. The assumption in this implementation for anomaly detection is that outliers are not in close proximity with other neighbours. A threshold is defined for proximity and used to determine data points that do not belong to a neighbourhood. A key parameter that determines the number of neighbours that will be used in calculating the proximity measure is the n _ n e i g h b o r s parameter.
One-class SVM detector (svm) is an unsupervised version of a traditional SVM regressor or classifier. It uses either a min-volume hyper-sphere [23] or a max-margin hyperplane metric to separate anomalous data from the normal ones. The major purpose of one-class SVM is to detect novelty in data. It helps to detect rare events. Novelty and weak signals are special aspects of anomaly detection. In one-class SVM, data points that lie outside the hyper-shere or below the hyper-plane are considered anomalies.
Principal Component Analysis (PCA) is a method that decomposes a signal into its major components. The first component is usually the most important. This is followed by the second, third and so on. The idea of using PCA for outlier detection is that the data point with high reconstruction error from its principal components are outliers from the dataset [24]. For different PCA algorithms, the way the anomaly score is calculated may differ. The use of residuals, leverage and influence of a data point may all be put into consideration. However, these metrics are better utilised in a visualisation than in an automated outlier detection system. Hence, some human evaluation and domain knowledge may need to apply in setting the threshold for outlier threshold using the appropriate metrics for the problem domain.
Minimum Covariance Determinant (MCD) is an anomaly detection method that uses the fact that tightly distributed data will have a smaller covariance determinant value. So, instead of using the entire data set to calculate distribution parameters (such as mean and standard deviation), it divides the data into sub-samples and then computes the covariance determinant of each sub-group. The number of sub-samples h is such that n 2 < h < n , where n is the total number of data points [25]. The group with minimum determinant would be used as the central group for distance calculation. It is best suited for determining outliers in multivariate data [25]. MCD uses robust distance measures that are not amenable to the unrealistic distributional assumptions that underlie the use of Mahalanobis distance measures for outlier detection in most other classical methods. Mahalanobis distance computation is sensitive to the presence of outliers in data as the outliers tend to draw the distributional statistics towards themselves. Hence, the robust distance is a robust calculation of the Mahalanobis distance such that the effect of outliers is minimised.
Stochastic oultier selection (SOS) [26] method is a statistical modeling method for anomaly detection. This method assumes that the data follows a stochastic model with a form of probability density function (pdf). Normal data exists in areas of higher density while anomalies exist in areas of lower density. Hence, the measure of distance used to determine anomaly is probability density. For parametric stochastic models, a pdf is assumed apriori, with some values assumed for the model parameters. However, for non-parametric modelling, little or no assumption is made about the value of these parameters and the algorithm has to learn the model parameters directly from the data. We have followed largely non-parametric modelling in this work. We focus on discovering the model that best models the data based on the type of anomaly that is of interest to epidemiologists. In this research, we are interested in outbreak anomalies.
A major parameter and assumption that underlie the algorithms and methods employed in this work, which is based on unlabelled data, is the use of Proportion of anomaly or Contamination rate, η. Contamination rate is the fraction of the total data that we assume to be anomalous. Our default value is 0.1 (10%) fraction of the data. In our standard experiments, we have set η = 0.1 . We also conducted a sensitivity analysis for this parameter, using values of η = [ 0.1 , 0.2 , 0.3 , 0.4 ] .

2.3. Selecting Top-k Models for Maximum Coverage

The problem of selecting models that optimise both anomaly detection coverage and reduced inference time (Top-k model) is a version of the classical set cover and maximum coverage problems [27]. The set cover problem is described thus: given a universe U and a family S of subsets of U , a cover is a subfamily K ⊆ S of sets whose union is U . In simple terms and in this research, the set cover problem is finding the least number of models that can detect the same number of anomalies detected by the 10 models. In situations where the top k models cannot detect all the possible anomalies, the maximum coverage problem wants to ensure that no other k models set can detect more anomalies than the selected top k models. Hence, we want to select the top k models to maximise anomaly detection.
In this work, we gradually increased coverage until k models were selected or 100% coverage was achieved. At each stage, we chose a model with a detected anomaly set K i , which contained the largest number of uncovered elements. We repeated this process until 100% coverage was achieved, up to a maximum of k times. We then recorded the model set that achieved 100% coverage or the t o p − k models and the percentage coverage they achieved. We performed this analysis for each health region and also for health regions combined into a single unit.

3. Results

We present the major results relating to algorithms and discovered anomalies of interest.

3.1. Anomalies by Contamination Rate

The number of anomalies detected by each algorithm is linearly proportional to the contamination rate, η . This observation is consistent across the 13 health regions. The anomalous data points were subjected to evaluation by epidemiological experts to interpret their significance. As the contamination rate increases, more data points are flagged as anomalies. The contamination rate that identifies all the anomalies that are of interest to epidemiologists is retained and deployed for anomaly detection within that health region. In the next subsection, we see the nature and location of the detected anomalies.

3.2. Detected Anomalies and Epidemiological Significance

For the purpose of this study, we define epidemiological events of interest as the onset of an outbreak, the peaks and troughs of an outbreak, and change points in the proportion of positive cases. Models that distinctly flagged these events are considered to perform better than others.
Figure 5 shows the anomalies detected from ARAGUAIA and XINGU. Figure 5a shows that the early rising or decline of cases can be detected from the data. So, the change points in the data sets are detected as anomalies. This is appropriate for either early detection of outbreaks or early signs of effectiveness of an intervention as indicated by declining incidence.
On the other hand, Figure 5b detected continuous rising points, peak points and continuous falling points as anomaly. These anomaly clusters show a strong change in curve direction. This latter anomaly detector is suitable for reducing false alarms. An alarm for anomalous points is only triggered when a change in direction of data have been strongly established.
The models that produced the results in Figure 5a,b are Stochastic outlier selection (SoS) and cluster-based models, respectively. Therefore, health regions with low-risk tolerance can implement the SoS model while more risk-tolerant health regions can implement cluster-based anomaly detectors.
It is worth understanding how early an outbreak can be detected. The outbreak detection time is the time between the first report of a rising epidemic to the time that the models flag a report as anomalous. Another important time to note is the time between the first rising outbreak detection to the peak of the outbreak. This later time determines how effective a deployed intervention could be when an anomaly is detected. Figure 6 shows results from the ARAGUAIA health region illustrating how early the two major outbreaks over the ten years could have been detected. In this figure, we have zoomed into the relevant portions of Figure 5a to illustrate an early flagging of outbreaks. We have chosen ARAGUAIA as it has numerous number of outbreaks throughout the decade of 2009 to 2019.
In Figure 6a, the first instance of increasing proportion of positive cases ( I P ) was reported in January 2012. As the next report in February 2012 arrived, the data was reported as being anomalous. So, only one time step delay was allowed before anomaly detection. This outbreak peaked in July 2012, 5 months after it was detected. There were no further alarms between February and July 2012, meaning that the flareup trend continued.
In Figure 6b, we had a larger outbreak. In April 2015, the first occurrence of high case prevalence was flagged immediately as anomalous. Hence, there was zero delay in flagging that very early phase of an outbreak as being anomalous. No further alarm was triggered until September 2015 and then January 2016 until the outbreak peaked in May 2016. Whereas the alert in September 2015 can be explained as possible slow down in the outbreak, that of January 2016 indicates a continued rising in proportion of positives. These are strategic anomalous alerts that should be very useful for planning intervention or investigating why existing interventions are not successful.
In both examples shown in Figure 6a, it is clear that we can detect outbreaks very early (with zero or 1-lag time step) using the appropriate anomaly detection algorithm that is suitable for modeling early detection using in a given health region.

3.3. Consistency and Variation in Anomaly Detected by Models

For the dates whose proportion of positive cases were detected as anomalous, we checked how many of the models jointly detected such dates as anomalous. We plotted a heat map of the number of anomalous dates jointly detected by model pairs. Certain patterns can be seen to emerge within and cross health regions as shown in Figure 7. We highlight which models mostly agreed and which models rarely agreed with other models.
The pattern shows that majority of the models found the same points as anomalous. Specifically, cluster, cof, forest, histogram, knn, lof, svm and mcd agreed on at least 85% of their detected anomalous data points. In contrast, pca and sos disagreed with all other models and with each other on the data points marked as anomalous. Models that are jointly consistent their prediction or detection may be used as ensemble to cross-validate anomalous data points and increase the confidence of decision makers. Other models that vary considerably in their prediction or disagree with other models may not be discarded. These later types of models are important in detecting novelty, rare events, early changes or weak signals.
In other health regions, some new patterns and changes to previously described patterns were observed as shown in Figure 8. Most models detected different types of anomalies and did not agree in most cases like previously.
Most of the jointly consistent models continued to detect the same type and number of anomalies but to lesser extent. One can observe that , svm and mcd disagreed with other models that they were previously consistent with and strongly agreed with each other by detecting the same number of anomalies. In CARAJAS, all the data points flagged as anomalous by svm were also flagged as anomalous by mcd. In LAGO DE TUCURI, both models had 13 out of 14 anomalous points they detected as being the same. In LAGO DE TUCURI, however, it is difficult to establish strong consistency among models. It seems all models are detecting largely disjoint anomalous points. As inconsistencies continues to wane across models, sos even showed stronger disagreement(see MARAJO II) with other models in the type of anomalies jointly detected.
It can be inferred that even though different models detect similar anomalies, the distribution of each dataset coming from different region will likely change the behaviour of each model, resulting in different type and number of anomalies detected in each region.
Without detailed reference to the mathematical details about these models, we can identify similar models irrespective of data distribution. Next, we examine the temporal variation in the detected anomalies.

3.4. Temporal Location of Detected Anomalies

We observed that the temporal location of the flagged anomalies by models were significantly different, despite most of the models flagging almost equal number of anomalies per contamination rate. Figure 9 exemplifies the location of detected anomalies by some algorithms as distributed across different months and years.
Figure 9 clearly shows the variation in the temporal location of detected anomalies by two algorithms. The One-Class SVM (Figure 9a) and the PCA (Figure 9b) provided interesting but contrasting anomalies. Whereas the first detected the peaks of the outbreaks, the other detected the troughs of the dying epidemic. Hence, the attention of human experts may be required to validate the output of each model and then select the best model for each region based on the anomaly event relevant to the region.
To compare the location of detected anomalies across models, time and space, we defined a parameter called Proportion of anomaly per year. This is the ratio of anomaly detected by a model in a year to the total number of anomalies detected over a decade. Hence, the values lie between 0 and 1. Figure 10 shows two major variations in the temporal location of the detected anomalies across regions.
In Figure 10 (Araguaia), 8 out of 10 models detected 77% or more anomalies in 2016 alone. This is a very strong agreement among the models irrespective of the type of anomaly detected by each model. This provides a strong evidence for supporting further investigation about what happened in 2016 in the epidemiology of malaria that region in 2016 in comparison with other years. Hence, we can say that the anomalies in this health region clustered in 2016. We observed similar situation is Carajas (2011), Metropolitana I (2010), Metropolitana III (2010) and Rio Caetes (2010).
The dispersed temporal location of anomalies was observed in some regions as no single year had large number of anomalies detected. However, some models co-detected anomalies in certain year. For eample, in Baixo Amazonas, a significant number of models (at least 6 out of 10) detected more than 20% of anomalies in each of 2010, 2013 and 2016. Again, 2016 has strong outlier content. This is because knn, lof and mcd detected more than 40% anomalies in 2016 alone when compared to 9 other years under consideration.
The importance of anomalies detected by models may be seen from the perspective of more models detecting the same anomaly within certain temporal domain or few models detecting few anomalies within a temporal domain. Each of these behaviour may prove either that a known anomalous even occurred within a temporal location or that a novelty is being detected by a few models.

3.5. Model Selection for Inclusion in Endemic Disease Surveillance System

For practical purposes, not up to ten models will be deployed and maintained in each of the 13 health regions under study. It could be financially and technically demanding for the state government to maintain 10 models across 13 health regions. Also, some of the models detected redundant anomalies such that up to eight models jointly detected one anomaly. Although this redundant detection helps to increase our confidence in the detected anomaly, it will increase inference time in production. Hence, after establishing consistency in detected anomalies across models, we propose to select the top k models that either gives us 100% coverage of all the anomalies or a pre-determined high (75 - 95) percentage of all anomalies.
To solve the above problem, we applied the classical set cover and maximum coverage greedy heuristic algorithm [27]. The results showing the progression of percentage coverage as more models are added to the k-subsets is shown in Figure 11.
Across the 13 regions between four to eight models are required to achieve 100% coverage per region. This is known as the local coverage as only the anomalies detected in each region are fed as input to the set cover algorithm. For global coverage analysis, Figure 11b shows that all models are required to achieve 100% coverage. However, first few models have high percentage of anomaly coverage. Only two models (pca and sos) are required to cover 50% of all the anomalies in the 13 health regions. Three models achieved 73.53% while six models achieved 94.81% coverage. With 95% coverage, there is a good coverage of all possible anomalies without implementing the last four models, but without considering which models are locally relevant to a health region.
With reference to individual health regions, Figure 12 shows the coverage progression as more models are added to a health region. We have used Araguaia (Figure 12a) and Tocantins (Figure 12b) to illustrate regions that required the smallest number of models to achieve 100% coverage and the largest number of models to achieve 100% coverage, respectively.
It is interesting to see how the local ranking of models differs from global ranking of models. The top-ranked models locally differ a bit from the global ranking. For example, the top-3 global models (Figure 11b) are pca,sos and mcd - covering 73.53% of all anomalies. In contrast, the top-3 local models (in Araguaia) are cluster, sos and pca covering about 97%. In Tocantins, the top-3 models are cluster, pca and cof, covering only 72.2% of anomalies detected in the region. Only pca consistently ranked among the top-3 models in the global and local coverage problem. The cluster algorithm only ranked 6th in the global coverage problem while it ranked 1st in the two local coverage problems. This result shows that whereas cluster may have detected most anomalies in Araguaia and Tocantins, the reverse is the case for most of the other 11 regions under consideration.

4. Discussion

The availability of large public health data is not currently matched by their use to support real-time public health decision-making [4]. Methods and frameworks are needed that can use historic data to discover patterns and provide insights to support decision-making. In this work, we have explored ten unsupervised machine-learning models to and assessed their potential to discover anomalies in malaria surveillance data. In addition, we have designed a framework that enables continuous integration of new data to update our decisions in near real-time.
The three major anomalous patterns detected by the models we explored models that are relevant to epidemiology are: rapid growth (flareup), drastic decline in case number, and change in trend direction of the proportion of positive cases. These events and patterns were chosen on the basis of having been deemed epidemically important in previous work [28,29]. The one-class svm model was the model best able to detect the peaks of outbreak flareups while pca was best able to detect the valley of decline in the proportion of positive cases. The change in direction of positive case trends was helpful in early detection of outbreaks through the sos model. The findings for each health region differ in some ways and therefore, a standard framework was adopted so that data from new region or disease can be analysed in a reproducible way using all models available.
We found that no single method or model performed well in detecting all pre-defined anomalies across all health regions. When all the 13 health regions in Para state were combined, pca, sos and mcd were found to be the top-3 models that maximised the number and types of anomalies detected. However, in some individual health regions, cluster algorithm ranked first before pca and sos in terms of maximising the number of anomalies detected when used alone. Overall, pca and sos performed well on average across individual health regions and for the combined health regions.
These results can provide guidance about model selection when we are focusing either on a specific type of anomaly or on maximising the broad range of anomalies detected, and when we are focusing on either a specific health region or on the combination of regions at the state level. The choice of which combination of models to use is likely to be driven by the risk appetite of a health region and the type of epidemiological anomaly they are most interested in detecting and mitigating. For risk-averse regions, models that detect rare events should be included, even though not many other models confirm this rare event. Health regions with higher risk appetite would focus on models that confirm well known anomalies. For example, model ensembles ( s v m , m c d , c l u s t e r ) that confirm that an outbreak has actually taken-off will be deployed regions with higher risk appetite while models that detect early outbreaks such as s o s would be deployed in risk-averse regions even when no other model confirms an alert for early warning against a potential outbreak.
There are two methods of controlling alarm fatigue from both true positive and false alarms considered in this work. The first is reducing the contamination rate parameter for each anomaly detector. The second approach is through the confirmation of an alarm event by all top-k models before a warning alarm is sent out. In this second case, k would be the set of models that determine the same type of anomalies more often than not. Hence, model selection will depend on their consistency in detecting the anomaly of concern over time. The limit in the number of models that will be selected and deployed will also be affected by the space and time complexity [30]. The number of alarms sent out per unit time and the critical nature of an alarm will determine how fatigued a human recipient will become.
The pipeline in Figure 2 can be replicated in different settings with different surveillance data to select the best model for anomalies of different kinds ranging from flareups, a decline in cases, and change in epidemic curve directions. Further, it serves as a simple framework experimental framework but compliant with continuous integration and Continuous deployment (CI/CD) paradigm [15], which is relevant in dynamic software engineering environments. With the dynamic nature of disease outbreaks, a CI/CD - compliant framework will take care of both data drift and concept drift [31,32] and continually select the best model as new data arrive. Concept and data drift will be experienced within a health region over time and will also be encountered as model trained using data from one region is deployed into another region or for different disease surveillance data. With concept drift, the statistical properties of data change over time and across regions. Hence, the idea of adapting the CI/CD paradigm into an anomaly detection framework as depicted in Figure 2 helps to handle data and concept drifts that would be associated with epidemiological data collected over time and in different regions.
This work has several limitations and possibilities for future extension. As unsupervised anomaly detection methods do not use labelled event classification, they will require some time to be validated by many domain experts. New patterns are first identified from the data and plausible interpretations are given afterwards. Hence, the epidemiological significance assigned to different anomalies detected in this endemic data are still subject to further expert evaluations. Again, although we assumed that the distribution of data will change over time, we did not quantify the magnitude of the drift in order to formally and dynamically determine when model swap or retraining should be triggered. Future work will focus on performing drift analysis and formalising the drift threshold [14,31] for warning alerts and automatic model selection, retraining or replacement.
In conclusion, this paper has demonstrated that anomaly detection models can be successfully applied to epidemiological surveillance data to discover unknown patterns that are relevant for intervention design and formulation of disease elimination strategy. However, only the top-k models that maximises the detection of the anomaly of concern should be deployed and maintained in production. This approach strikes a balance between the detection of all anomalies and the cost of resources required to run multiple models to maximise the type of anomalies detected.
The volume and variety of some public health data have rendered most statistical methods inadequate for extracting evidence for robust decision-making. For example, other sources of public health information such as patients’ health records and other digital traces such as social media, blogs, internet documents, phone logs and recorded voice logs cannot be adequately analysed using statistical methods [33]. Artificial Intelligence and unsupervised machine learning methods such as anomaly detection methods can utilise a larger volume of surveillance data to provide deeper insights better to support decision-making for the elimination of endemic diseases.

Author Contributions

Conceptualization, I.V., P.E., N.G., and I.C.; Data curation, P.E.; Formal analysis, N.G., I.V. and I.C.; Funding acquisition, N.G.; Investigation, I.V., P.E., N.G., and I.C.; Methodology, P.E., N.G., and I.C.; Software, P.E.; Supervision, N.G., and I.C.; Visualization, P.E.; Writing – original draft, P.E.; Writing – review and editing, I.V., N.G., and I.C.

Funding

This research was funded by NHMRC Centre of Research Excellence grant number APP1170960, under the scheme Supporting Participatory Evidence generation to Control Transmissible diseases in our Region Using Modelling (SPECTRUM). This work was also supported by the Department of Foreign Affairs and Trade Australia, ASEAN Pacific Infectious Disease Detection and Response Program 2019 through the project: Strengthening Preparedness in the Asia-Pacific Region through Knowledge (SPARK).

Institutional Review Board Statement

Not Applicable.

Informed Consent Statement

Not Applicable.

Data Availability Statement

De-identified and derived datasets analyzed or generated during the study, including code, can be found at https://github.com/KingPeter2014/Anomaly_in_malaria_surveillance_data.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:
AI Artificial Intelligence
PCA Principal Component Analysis
pdf Probability density function
SVM Support Vector Machine

References

  1. Health, A. Surveillance systems reported in Communicable Diseases Intelligence, 2016. Available online: https://www1.health.gov.au/internet/main/publish (accessed on 4 June 2021).
  2. Dash, S. , Shakyawar S.K. and Sharma M. Big data in healthcare: Management, analysis and future prospects. J. Big Data 2019, 6, 1–25. [Google Scholar] [CrossRef]
  3. CDC. Principles of Epidemiology in Public Health Practice, Third Edition An Introduction to Applied Epidemiology and Biostatistics. Int. J. Syst. Evol. Microbiol. 2012, ss1978. [Google Scholar]
  4. Felicity T., C. , Matt H. Seroepidemiology: An underused tool for designing and monitoring vaccination programmes in low- and middle-income countries. Trop. Med. Int. Health 2016, 21, 1086–1090. [Google Scholar] [CrossRef]
  5. Jayatilleke, K. Challenges in Implementing Surveillance Tools of High-Income Countries (HICs) in Low Middle Income Countries (LMICs). Curr. Treat. Options Infect. Dis. 2020, 1–11. [Google Scholar] [CrossRef] [PubMed]
  6. Nekorchuk, D.M. , Gebrehiwot T., Awoke W., Mihretie A., Wimberly M. C. Lake M. Comparing malaria early detection methods in a declining transmission setting in northwestern Ethiopia. BMC Public Health 2021, 21, 1–15. [Google Scholar] [CrossRef]
  7. Charumilind S., Craven M., Lamb M., Lamb J., Singhal S., Wilson M. Pandemic to endemic: How the world can learn to live with COVID-19; Mckinsey and Company 2021; pp. 1–8. Available online: https://www.mckinsey.com/industries/healthcare-systems-and-services/our-insights/pandemic-to-endemic-how-the-world-can-learn-to-live-with-covid-19.
  8. Clark J., Liu Z., Japkowicz N. Adaptive Threshold for Outlier Detection on Data Streams. In Proceedings of the 2018 IEEE 5th International Conference on Data Science and Advanced Analytics (DSAA) 2018; pp. 41–49. [CrossRef]
  9. hao M., Chen J.,Li Y. A Review of Anomaly Detection Techniques Based on Nearest Neighbor. In Proceedings of the 2018 International Conference on Computer Modeling, Simulation and Algorithm (CMSA 2018); 2018; 151, pp. 290–292. [CrossRef]
  10. Hagemann T., Katsarou K. A Systematic Review on Anomaly Detection for Cloud Computing Environments. In Proceedings of the 2020 ACM 3rd Artificial Intelligence and Cloud Computing Conference; 2021; pp. 83–96. [CrossRef]
  11. Turing, A.M. Computing Machinery and Intelligence. Mind 1950, 49, 433–460. [Google Scholar] [CrossRef]
  12. Bitterman D.S, Miller T.A, Mak R.H, Savova G.K. Clinical Natural Language Processing for Radiation Oncology: A Review and Practical Primer. Int. J. Radiat. Oncol. Biol. Phys. 2021, 110, 641–655. [CrossRef]
  13. Baroni, L. et al. An integrated dataset of malaria notifications in the Legal Amazon. BMC Res. Notes 2020, 13, 1–3. [CrossRef]
  14. Baena-garcia M., Campo-avila J.D, Fidalgo R., Bifet A., Gavalda R., Morales-Bueno R. Early drift detection method. In Proceedings of the Fourth International Workshop on Knowledge Discovery from Data Streams 2006; pp. 1–10. Available online: https://www.cs.upc.edu/ abifet/EDDM.pdf.
  15. Weaveworks. Building Continuous Delivery Pipelines Deliver better features, faster. Weaveworks Inc. 2018; pp. 1–26. Available online: https://www.weave.works/assets/images/blta8084030436bce24/CICD_eBook_Web.pdf.
  16. Shereen M.A., Khan S., Kazmi A., Bashir N., Siddique R. COVID-19 infection: Origin, transmission, and characteristics of human coronaviruses. J. Adv. Res. 2020, 24, 91–98. [CrossRef]
  17. Ali, M. PyCaret: An open source, low-code machine learning library in Python. PyCaret version 1.0.0 2020, 24. [Google Scholar]
  18. Schubert E, Wojdanowski R., Kriegel H.P. On Evaluation of Outlier Rankings and Outlier Scores. In Proceedings of the 2012 SIAM International Conference on Data Mining 2012; pp. 1047–1058. [CrossRef]
  19. Tang J., Chen Z., Fu A.W., Cheung D.W. Enhancing Effectiveness of Outlier Detections for Low Density Patterns In: Chen MS., Yu P.S., Liu B. (eds) Advances in Knowledge Discovery and Data Mining. Lecture Notes in Computer Science 2002, 2336, 535–548. [CrossRef]
  20. Akshara. Anomaly detection using Isolation Forest – A Complete Guide. Analytics Vidya 2021, 2336, 1–10. [Google Scholar]
  21. Goldstein M. and Dengel A. Histogram-based Outlier Score (HBOS): A fast Unsupervised Anomaly Detection Algorithm. Conference paper 2012, 1–6. Available online: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.401.5686&rep=rep1&type=pdf.
  22. Gu X., Akogluand L., Fu A.W, and Rinaldo A. Statistical Analysis of Nearest Neighbor Methods for Anomaly Detection. 33rd Conference on Neural Information Processing Systems (NeurIPS 2019), Vancouver, Canada. 2019, 1 – 11. Available online: https://proceedings.neurips.cc/paper/2019/file/805163a0f0f128e473726ccda5f91bac-Paper.pdf.
  23. Tax, D.M. J and Duin R.P.W. Support Vector Data Description. Machine Learning 2004, 54, 45–66. [Google Scholar] [CrossRef]
  24. McCaffrey J. Anomaly Detection Using Principal Component Analysis (PCA). The Data Science Lab,The Visual Studio Magazine 2021, 582–588. Available online: https://visualstudiomagazine.com/articles/2021/10/20/anomaly-detection-pca.aspx. /.
  25. Fauconnier C., Haesbroeck G. Outliers detection with the minimum covariance determinant estimator in practice. Statistical Methodology 2009, 6, 363–379. [CrossRef]
  26. Janssens J.H.M. Outlier selection and One-class classification. Ph.D thesis, Tilburg Universityy, Netherlands 2013, 59–95. Available online: https://github.com/jeroenjanssens/phd-thesis/blob/master/jeroenjanssens-thesis.pdf.
  27. Chandu, D.P. Big Step Greedy Heuristic for Maximum Coverage Problem. International Journal of Computer Applications (0975 – 8887) 2015, 125, 19–24. [Google Scholar]
  28. Jaramillo-Valbuena S.,Londono-Pelaz J.O., Cardona S.A. Performance evaluation of concept drift detection techniques in the presence of noise. Revista 2017, 38, 1–10.
  29. Geyshis D. 8 Concept Drift Detection Methods. Aporia 2021, 1–5. Available online: https://www.aporia.com/blog/concept-drift-detection-methods/.
  30. Farrington C.P., Andrews N.J, Beale A.J., Catchpole D. A statistical algorithm for the early detection of outbreaks of infectious disease. Journal of the Royal Statistical Society Series, Rockefeller University Press 1996, 159, 547–563.
  31. Noufaily A., Enki D.G., Farrington P., Garthwaite P., Andrews N. and Charlett A. An improved algorithm for outbreak detection in multiple surveillance systems. Stat. Med. 2012, 32, 1206–1222. [CrossRef]
  32. Abdiansah A; Wardoyo R. Time Complexity Analysis of Support Vector Machines(SVM) in LibSVM. Int. Comput. Appl. 2018, 128, 28–34.
  33. Shweta, B.; Gerardo, C.; Lone, S.; Alessandro, V.; Cécile, V.; Lake, M. Big Data for Infectious Disease Surveillance and Modeling. J. Infect. Dis. 2016, 214, s375–s379. [Google Scholar] [CrossRef]
  34. Kovacs, G.; Sebestyen, G.; Hangan, G. Evaluation metrics for anomaly detection algorithms in time-series. Acta Univ. Sapientiae Inform. 2019, 11, 113–130. [Google Scholar] [CrossRef]
  35. Antoniou, T.; Mamdani, M. Evaluation of machine learning solutions in medicine. Analysis CPD 2021, 193, 41–49. [Google Scholar] [CrossRef] [PubMed]
Preprints 73201 g001
Figure 1. Map of Brazil showing the northern states in the Amazon area that accounts for 99% of malaria cases in Brazil. The state of Para can be seen in the north-central region.
Figure 1. Map of Brazil showing the northern states in the Amazon area that accounts for 99% of malaria cases in Brazil. The state of Para can be seen in the north-central region.
Preprints 73201 g001
Preprints 73201 g002
Figure 2. An anomaly detection framework showing process and surveillance data flow. M 1 to M n refer to ensembles of anomaly detection models. The appropriate definition of an anomaly for each health region is used to select the best anomaly detector ( M b e s t ) for that health region. The models are retrained and tuned over time as novel data becomes available.
Figure 2. An anomaly detection framework showing process and surveillance data flow. M 1 to M n refer to ensembles of anomaly detection models. The appropriate definition of an anomaly for each health region is used to select the best anomaly detector ( M b e s t ) for that health region. The models are retrained and tuned over time as novel data becomes available.
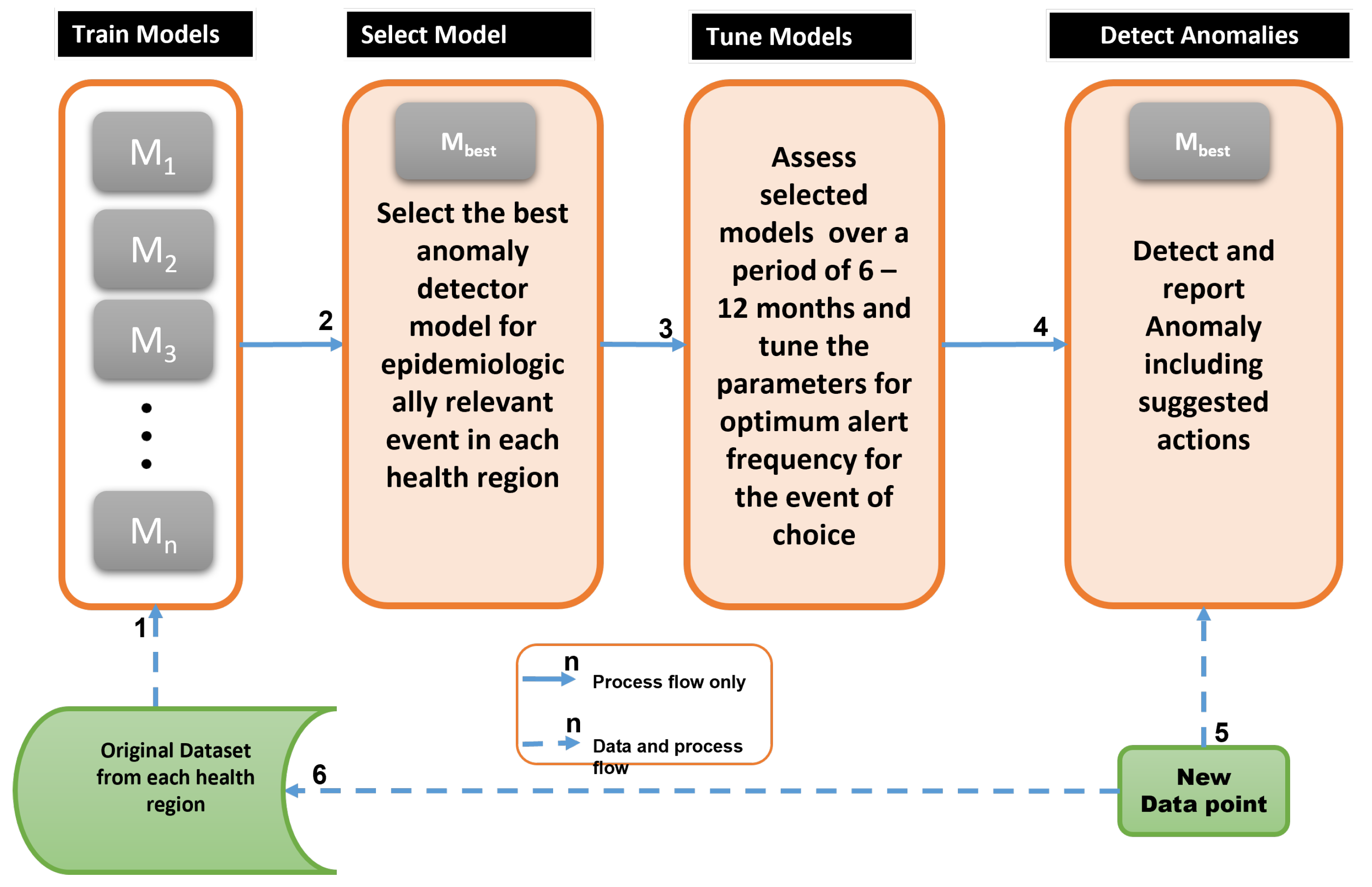
Preprints 73201 g002
Preprints 73201 g003
Figure 3. Original recorded surveillance data from Para state in Brazil. This shows the monthly total tests (blue), number of negatives (green) and number of positives (red).
Figure 3. Original recorded surveillance data from Para state in Brazil. This shows the monthly total tests (blue), number of negatives (green) and number of positives (red).
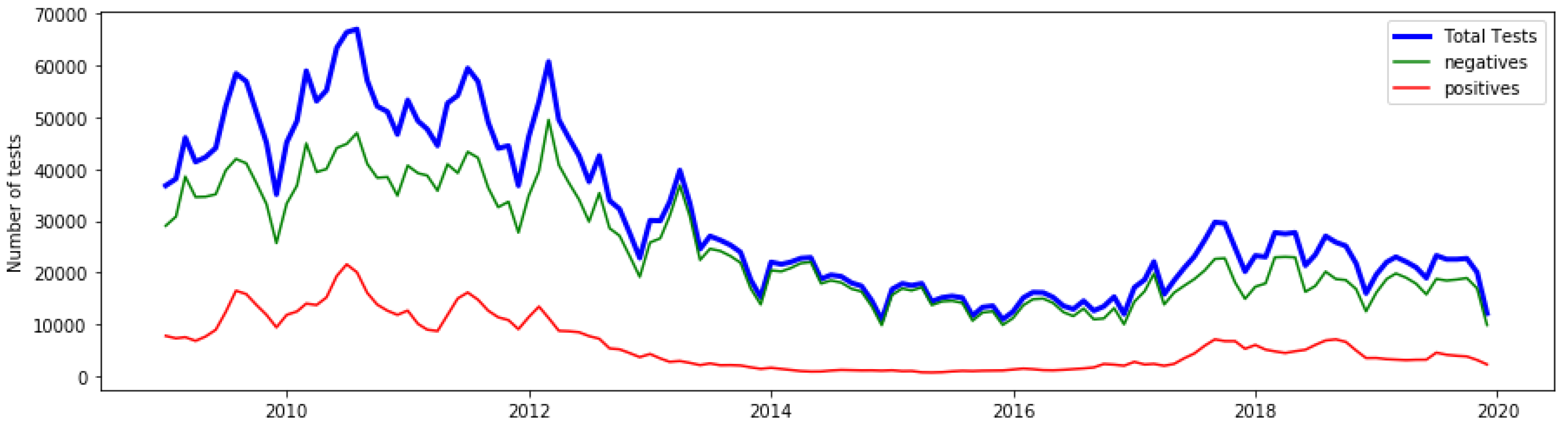
Preprints 73201 g003
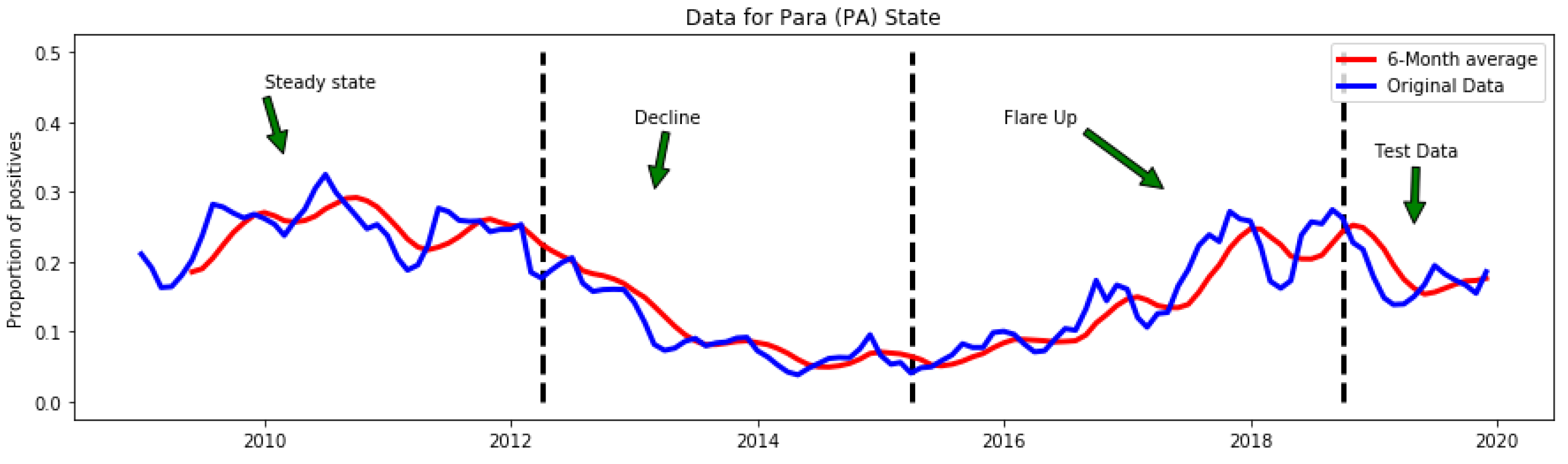
Preprints 73201 g004
Figure 4. Feature engineering and time series data transformation. Endemic outbreaks could move from a Steady state to periods of either a rapid growth (flareup) or Decline in I P .
Figure 4. Feature engineering and time series data transformation. Endemic outbreaks could move from a Steady state to periods of either a rapid growth (flareup) or Decline in I P .
Preprints 73201 g004
Preprints 73201 g005
Figure 5. Early change-point anomalies vs collocated anomalies.
Figure 5. Early change-point anomalies vs collocated anomalies.
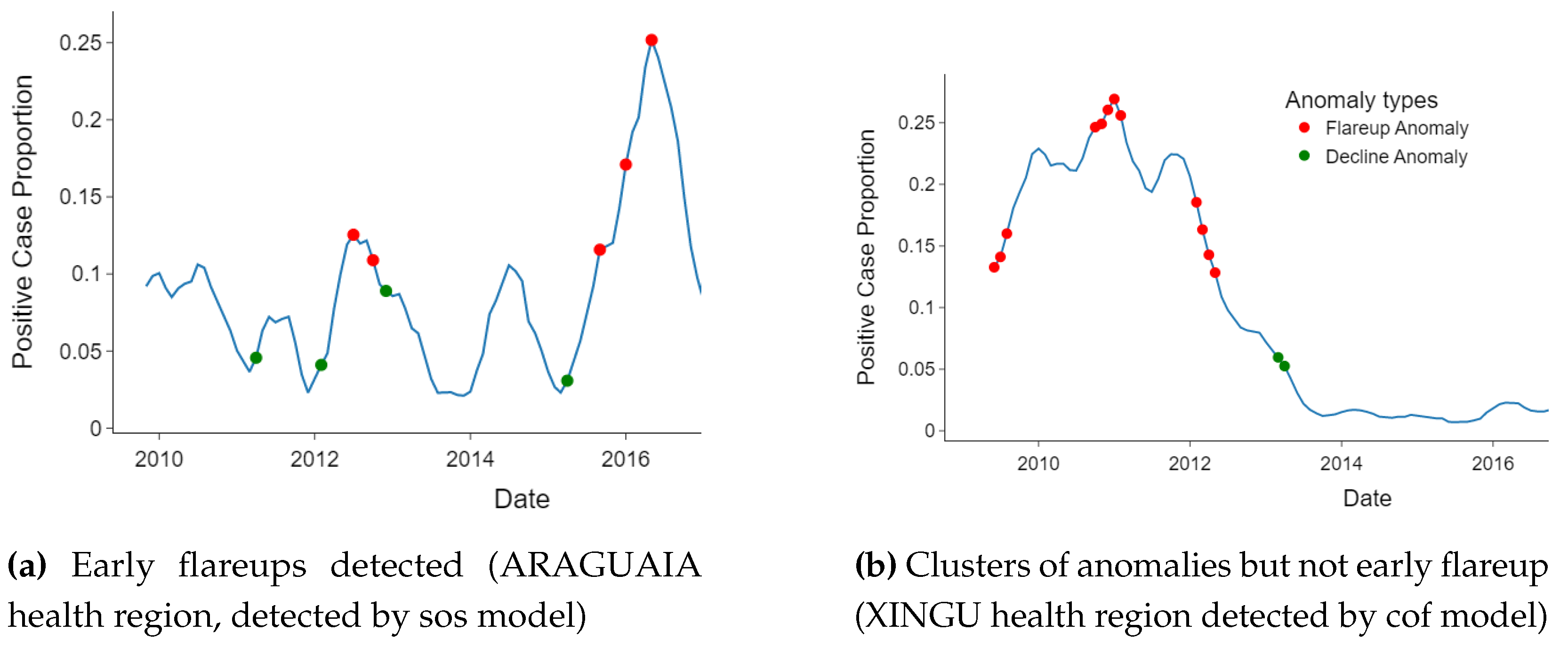
Preprints 73201 g005
Preprints 73201 g006
Figure 6. For early detection of endemic disease transitions, the sos algorithm is more appropriate. The yellow dashed line represents the threshold for separating anomalies that occur within outbreaks (when the positivity rate is more than or equal to the 10% of the sampled population) and endemic situations (when the positivity rate is less than 10% of the sampled population).
Figure 6. For early detection of endemic disease transitions, the sos algorithm is more appropriate. The yellow dashed line represents the threshold for separating anomalies that occur within outbreaks (when the positivity rate is more than or equal to the 10% of the sampled population) and endemic situations (when the positivity rate is less than 10% of the sampled population).
Preprints 73201 g006
Preprints 73201 g007
Figure 7. Each cell in the heat map shows the anomalies detected jointly by two models.The models, pca and sos, have strong disagreement with each other and other models on the dates flagged as anomalous
Figure 7. Each cell in the heat map shows the anomalies detected jointly by two models.The models, pca and sos, have strong disagreement with each other and other models on the dates flagged as anomalous
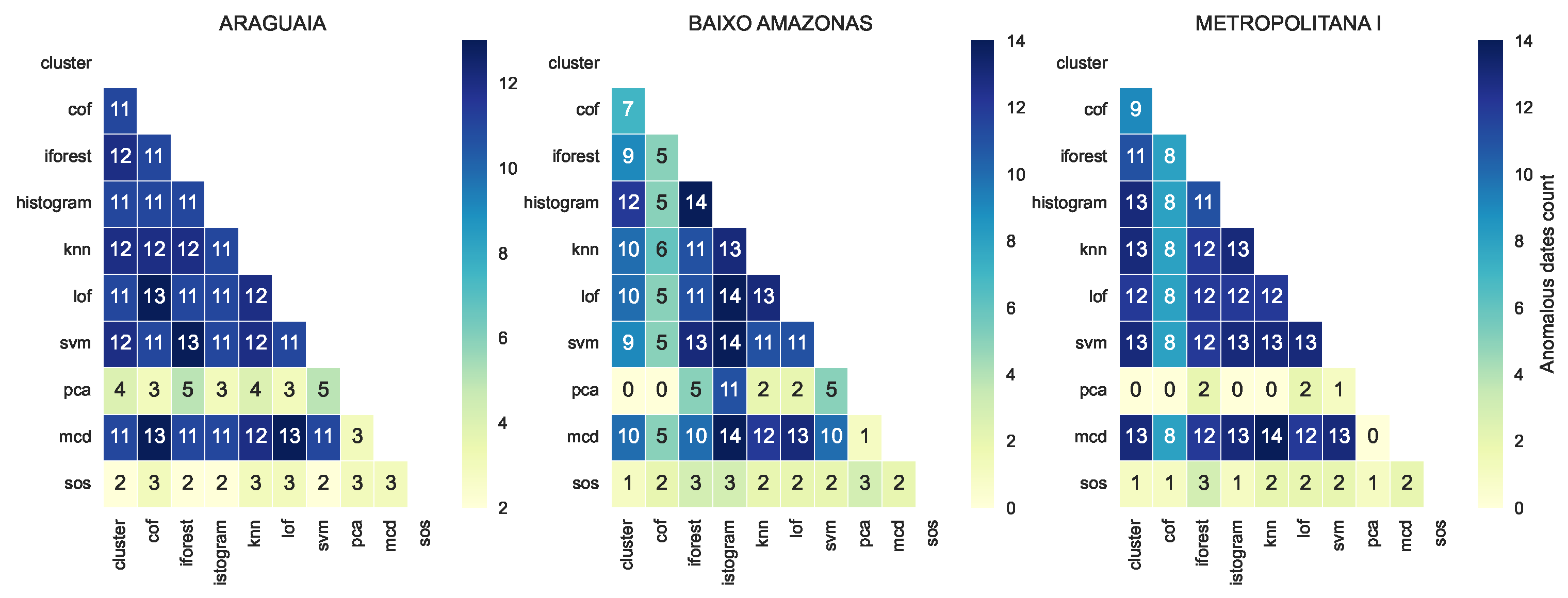
Preprints 73201 g007
Preprints 73201 g008
Figure 8. Increasing variation in jointly detected anomalies in some health regions.
Figure 8. Increasing variation in jointly detected anomalies in some health regions.
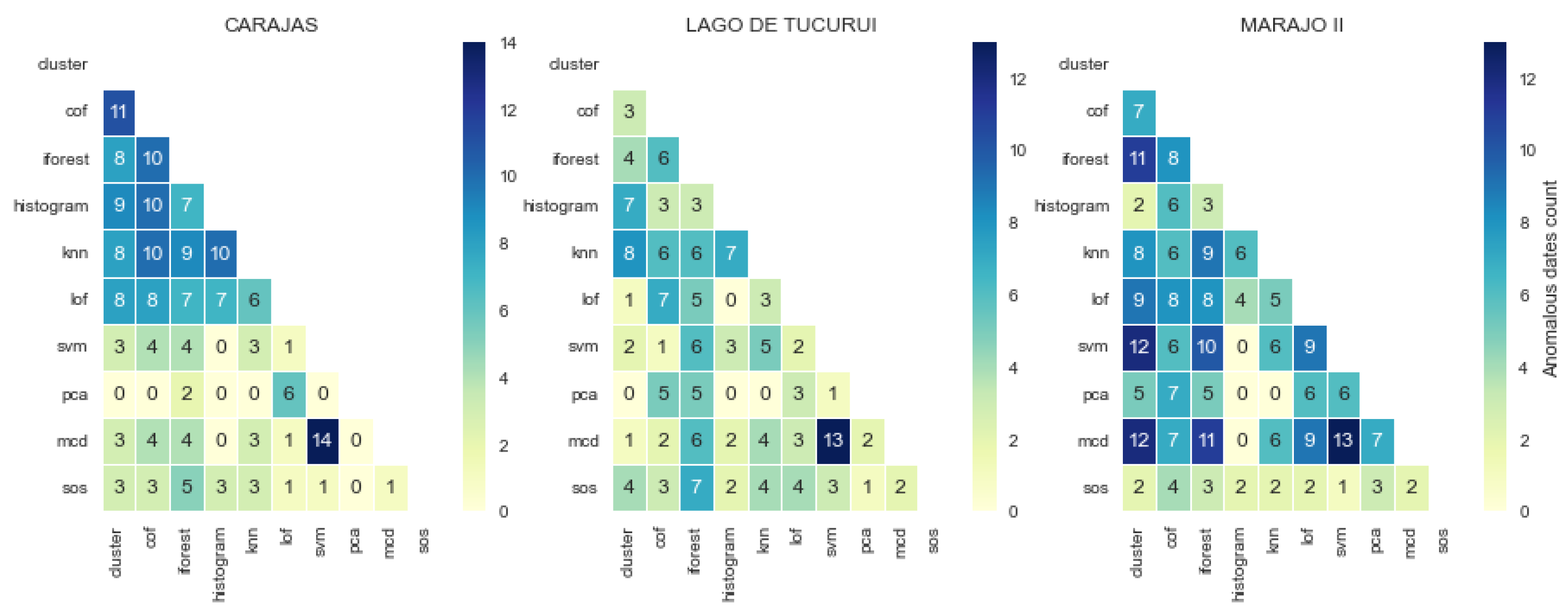
Preprints 73201 g008
Preprints 73201 g009
Figure 9. The location of anomalies detected by different algorithms varied in years in which they were detected. Event occurring in these years in a given health region may help to interpret the significance of the detected anomaly in that region.
Figure 9. The location of anomalies detected by different algorithms varied in years in which they were detected. Event occurring in these years in a given health region may help to interpret the significance of the detected anomaly in that region.
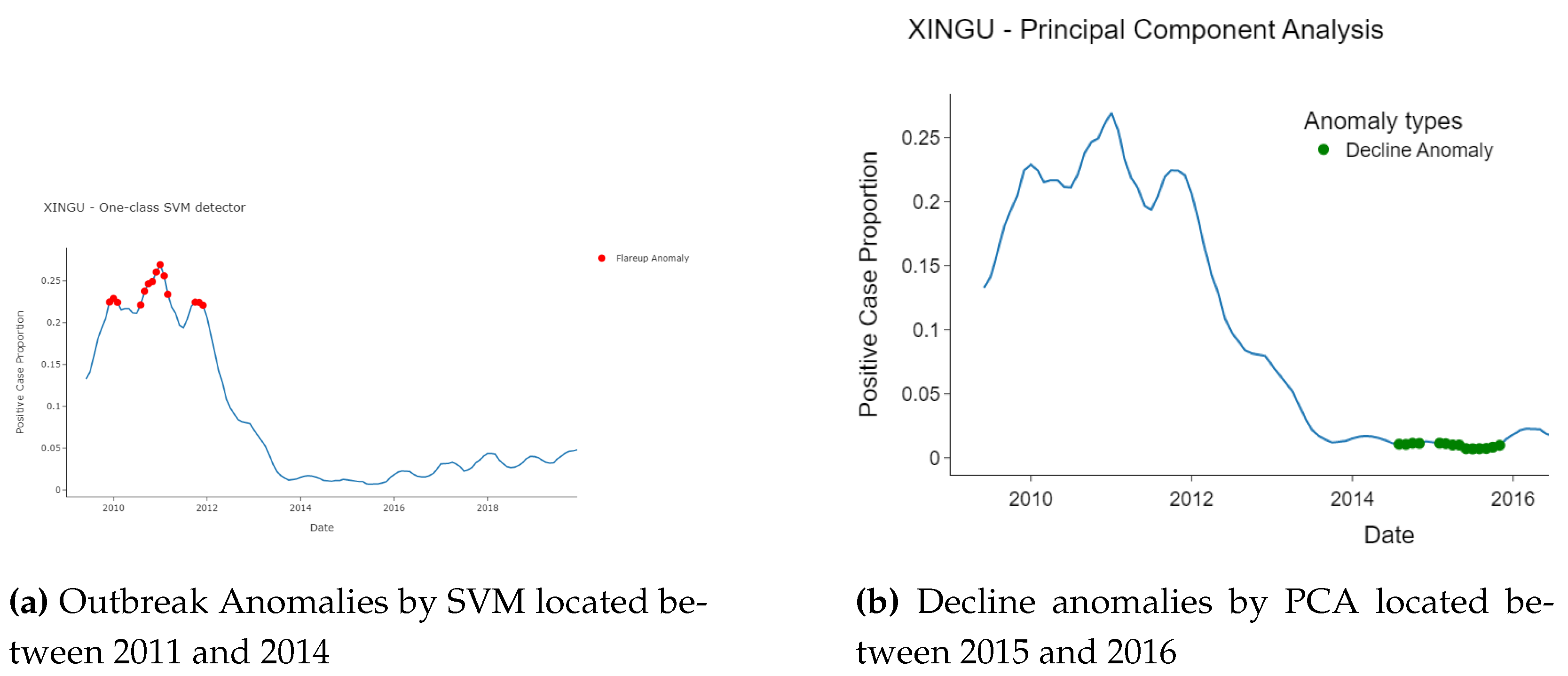
Preprints 73201 g009
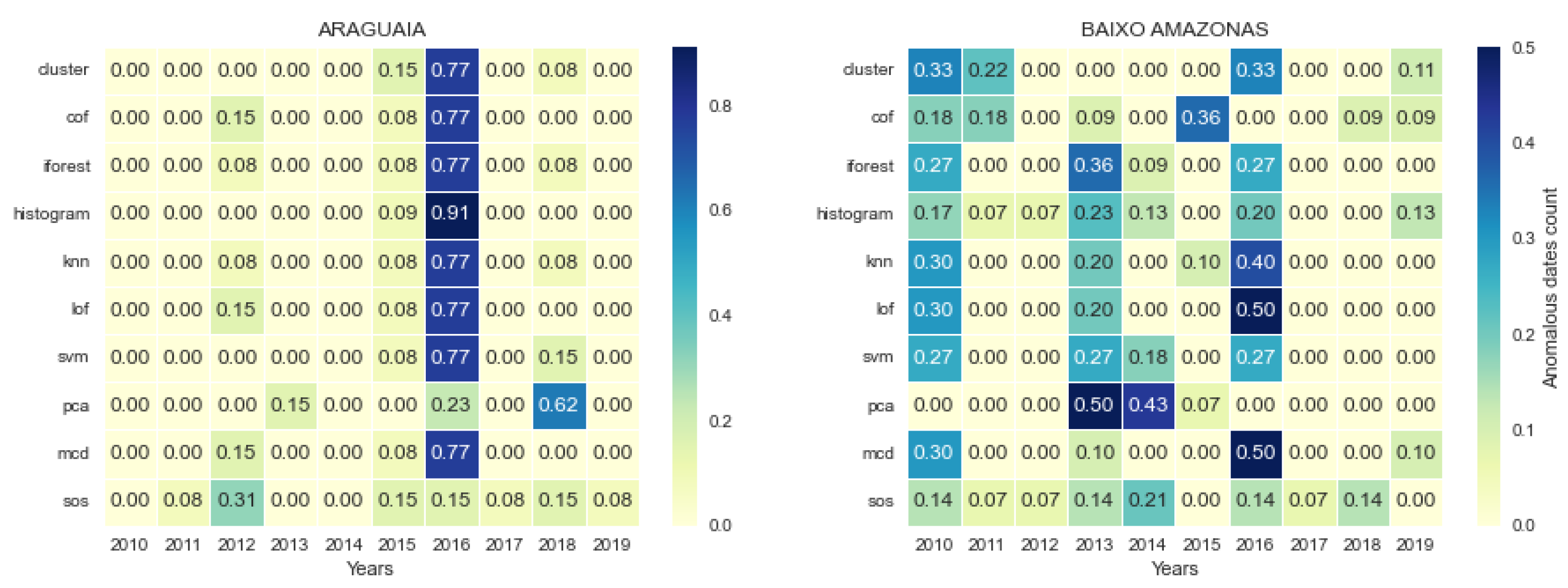
Preprints 73201 g010
Figure 10. Proportion of anomaly per model per year. There is a clustered temporal location( ARAGUAIA) and a dispersion temporal location (BAIXO) of anomalies.
Figure 10. Proportion of anomaly per model per year. There is a clustered temporal location( ARAGUAIA) and a dispersion temporal location (BAIXO) of anomalies.
Preprints 73201 g010
Preprints 73201 g011
Figure 11. Local and global coverage by t o p − k models: (a) Between 4 – 8 models are required to achieve 100% coverage per health region. (b) Anomaly coverage of top-k when anomalies from the 13 health regions are combined. Six models achieved 95% coverage across the 13 health regions
Figure 11. Local and global coverage by t o p − k models: (a) Between 4 – 8 models are required to achieve 100% coverage per health region. (b) Anomaly coverage of top-k when anomalies from the 13 health regions are combined. Six models achieved 95% coverage across the 13 health regions
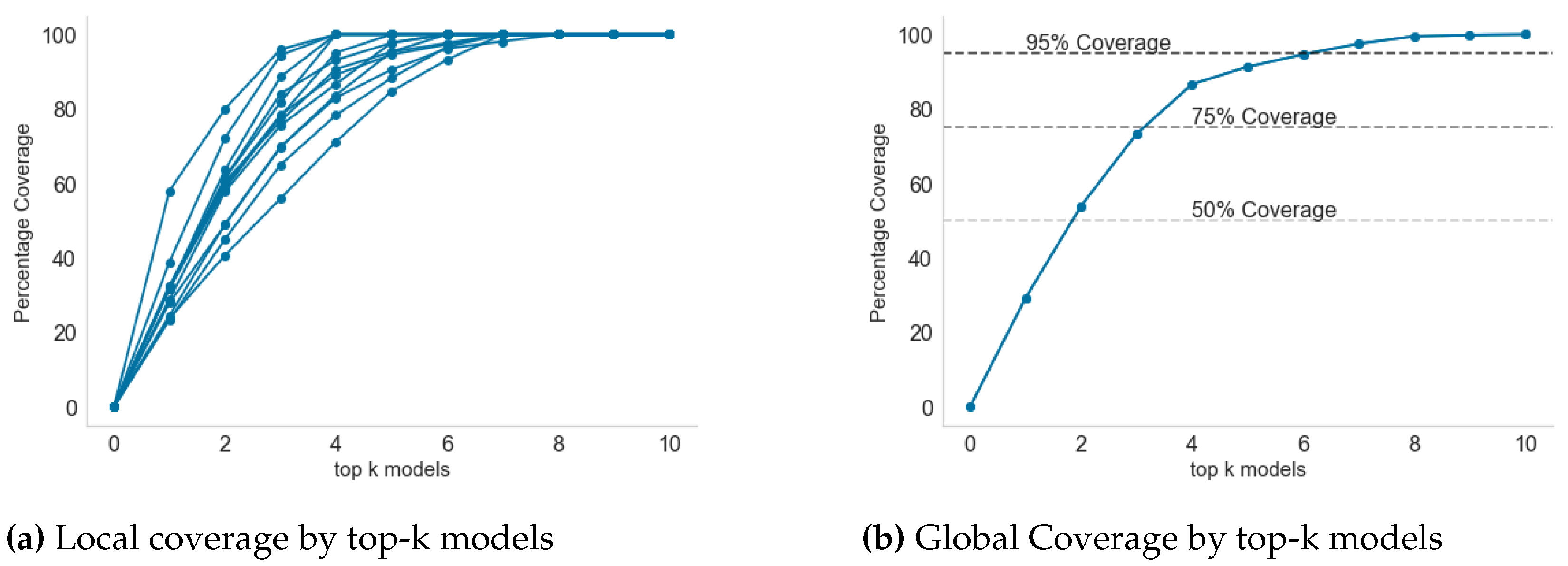
Preprints 73201 g011
Preprints 73201 g012
Figure 12. Progression of coverage in selected health regions with minimum (four) and maximum (eight) model sets to achieve 100% anomaly coverage
Figure 12. Progression of coverage in selected health regions with minimum (four) and maximum (eight) model sets to achieve 100% anomaly coverage
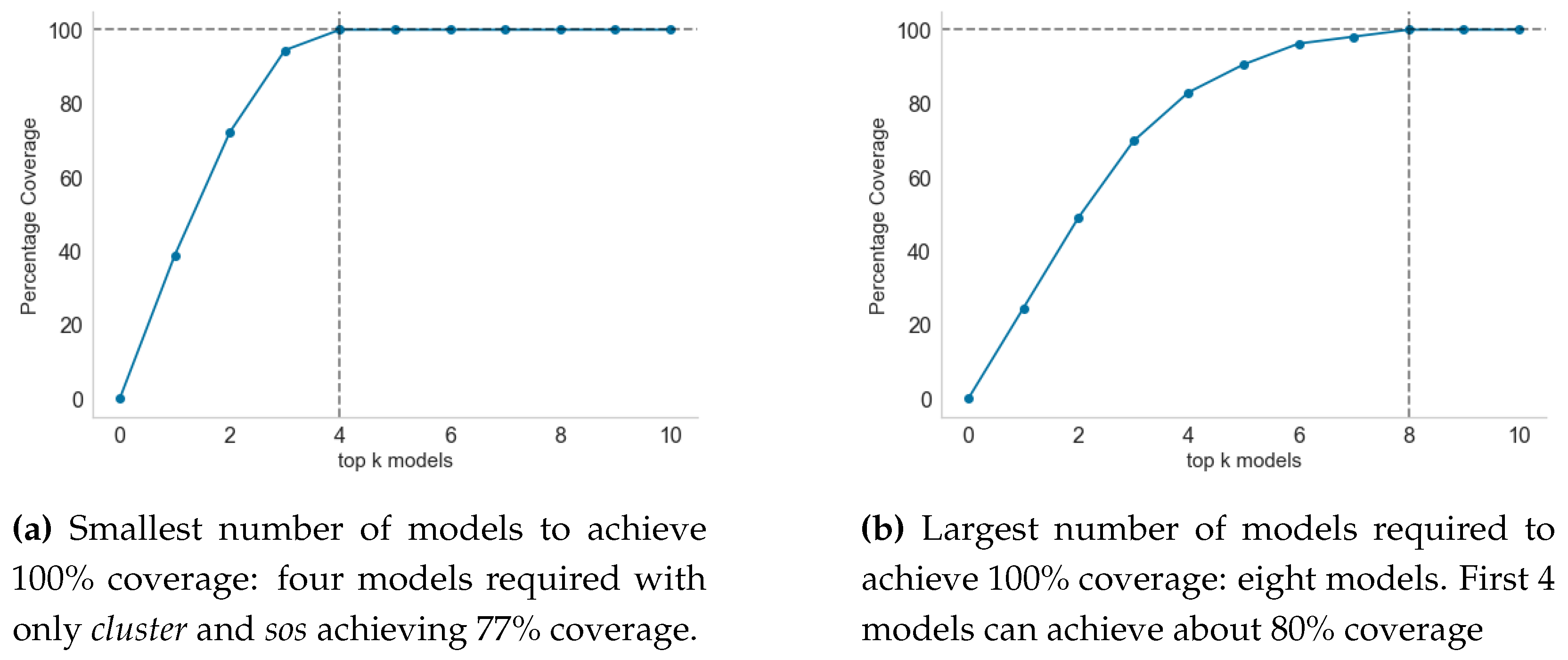
Preprints 73201 g012
Table 1. Summary of the pipeline methods and steps for online anomaly detection using surveillance data
Table 1. Summary of the pipeline methods and steps for online anomaly detection using surveillance data
Step No. Major activities
1 Train candidate anomaly detectors per health region using train set
2 Based on local epidemic demands, select best anomaly detector, M b e s t
3 Tune model parameters after using for 6 - 12 months to evaluate performance
4 As new data arrives, use the best detector, M b e s t A to detect and interpret anomaly
5 New data for evaluation and model re-training
6 Update the models with the new data and repeat from Step 1
Table 2. Unsupervised anomaly detection algorithms. The distance measures used by each algorithm differ. A single anomaly score will be computed for each data point. Based on a contamination rate (10% by default) a threshold on anomaly score is used to flag anomalous data points.
Table 2. Unsupervised anomaly detection algorithms. The distance measures used by each algorithm differ. A single anomaly score will be computed for each data point. Based on a contamination rate (10% by default) a threshold on anomaly score is used to flag anomalous data points.
No. Model ID. Model Name Core Distance measure
1 cluster Clustering-Based Local Outlier [18] Local outlier factor
2 cof Connectivity-Based Local Outlier [19] average chaining distance
3 iforest Isolation Forest [20] Depth of leaf branch
4 histogram Histogram-based Outlier Detection [21] HBOS
5 knn K-Nearest Neighbors Detector [22] Distance Proximity
6 lof Local Outlier Factor [18] Reacheability distance
7 svm One-class SVM detector [23] hyper-sphere volume
8 pca Principal Component Analysis [24] Magnitude of reconstruction error
9 mcd Minimum Covariance Determinant [25] Robust distance from MCD
10 sos Stochastic Outlier Selection [26] Affinity probability density
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated