A Study of Roots of a Certain Class of Counting Polynomials

Preprint

Article

A Study of Roots of a Certain Class of Counting Polynomials

Altmetrics

Downloads

128

Views

Comments

A peer-reviewed article of this preprint also exists.

Modjtaba Ghorbani^*,

Razie AliDehi Ravandi,

Matthias Dehmer,

Frank Emmert-Streib

Modjtaba Ghorbani^*,

Razie AliDehi Ravandi,

Matthias Dehmer,

Frank Emmert-Streib

This version is not peer-reviewed

Submitted:

10 May 2023

Posted:

10 May 2023

You are already at the latest version

Alerts

Abstract

Suppose G is a graph with vertex-orbits O1,1 O2, . . . ,Ot, and jOi j denotes the cardinallity of Oi. Then OG (x) = åt 2 i=1 xjOi j is called as orbit polynomial. It is well-known that this polynomial 3 has a unique positive zero d in the interval [0, 1]. The aim of this paper is to study the specific 4 properties of this polynomial and then we determine the location of this root for several classes of 5 complex networks to compare with other graphical measures. Besides, we compare the unique 6 positive zero measure with several well-known centrality graph measures.

Keywords:

Subject: Computer Science and Mathematics - Discrete Mathematics and Combinatorics

1. Introduction

The orbit polynomial of a graph is a polynomial that encodes information about the orbits of its automorphism group. Its roots and their properties have become an important tool for studying the symmetry structure and other structural features of networks in many different fields, including graph theory, physics, chemistry, and computer science.

The unique positive root of the orbit polynomial, denoted

δ

, has gained particular attention due to its ability to serve as a structural descriptor for networks.

δ

has been shown to provide insight into the symmetry structure of a graph, with its value being closely related to the size and complexity of its automorphism group. This line of research has given rise to a range of applications of

δ

in network analysis, including the classification and comparison of different types of networks.

Overall, the study of the roots of the orbit polynomial of networks has opened up new avenues for research into the structural properties of networks, with many potential applications in various fields. Ongoing efforts are addressing open questions related to the computation, properties, and applications of the orbit polynomial and its roots, with the aim of furthering our understanding of the structure of networks and their applications in many different areas of science.

Recently, the concept of orbit polynomial [13] for a connected network

N

was defined as follows:

O_{G} (x) = \sum_{i = 1}^{t} x^{| O_{i} |},

where

O_{1}, O_{2}, \dots, O_{t}

are all vertex-orbits of

N

and the cardinallity of an orbit is denoted by

| O_{i} |

. Moreover, the modified version of this polynomial or M-orbit polynomial is defined as

O_{N}^{★} (x) = 1 - \sum_{i = 1}^{t} x^{| O_{i} |} .

(1)

The difinition of this polynomial is based on two concepts: the automorphism group and the vertex-orbits. It is well-known that the orbit polynomial has a unique positive zero

δ

in the interval

[0, 1]

, see [13]

Ghorbani et al. in [20] generalized the concept of orbit polynomial as follows: Consider the action of permutation group

Γ

acting on the set X. Then the generalized orbit polynomial is

O_{Γ} (x) = \sum_{i = 1}^{t} c_{i} x^{| O_{i} |}

, where

O_{1}, \dots, O_{t}

are all orbits of

Γ

. It is clear that for a graph

N

with automorphism group

Γ = A u t (N)

O_{Γ}

equals with the ordinary orbit polynomial.

It should be noted that in computing the orbit polynomial of a network, not only the group

Γ

is important but also the orbit-set

X

has a vital role in computing the orbit polynomial. In other words, for two isomorphic but not permutationaly isomorphic permutation groups

Γ_{1}

and

Γ_{2}

, we may obtain distinct orbit polynomials. This means that the cycle-type of all permutations or at least the cycle-type of the generators of the automorphism group has a significant role in the structure of orbit polynomial.

We proceed as follows. Section 2 outlines the concepts and definitions that will be used in this paper. In Section 3, we compute the several bounds for the roots of M-orbit polynomial. Finally, in Section 4, we compute some topological indices for certain networks like Human B Cell, BioGRID Drosophila, US Airports and Email with QuACN-package [28].

2. Preliminaries

Our notation is standard and mainly taken from standard books of graph theory such as [25]. The vertex and edge sets of a network

N

are denoted by

V (N)

and

E (N)

, respectively. All networks considered in this paper are simple, connected, and finite. For a network

N

with automorphism group

A_{N} = A u t (N)

and an arbitrary vertex

v \in V (N)

, the vertex-orbit of v(or orbit of v) is the set of all

α (v)

’ s, where

α

is an automorphism of

N

. Finding the automorphism group of a network could take exponential time, since, for example, the complete graph

K_{n}

has

S_{n}

as its automorphism group. Let

A (N)

be the adjacency matrix of network

N

and

P_{σ}

be a permutation matrix, corresponding to the permutation

σ \in S_{n}

. Then,

σ

is an automorphism of network

N

if and only if

P_{σ}^{t} A P_{σ} = A

. Here, computing the automorphism group, as well as the orbits of considered networks was done with the aid of the i-graph package [12].

3. Location of Roots

In [18,21,22,23,24] several bounds for the positive root

δ

are given and some properties of the orbit polynomial are investigated. In this section, we obtain several results concerning the location of zeros of the modified orbit polynomial. The following proposition sharpens previous results along with some of the other known results which were based on Walsh classical theorem. Moreover, an R-code is developed to construct polynomials, and compare the bounds obtained by our result with these known results.

Proposition 1.

Let

f (z) = \sum_{k = 0}^{n} a_{k} z^{k}

(a_{k} \neq 0)

be a non-constant polynomial with complex coefficients. Then all its zeros lie in disc

C = {z \in C : | z | \leq r}

, where

i): [9] $r <$ $1 + {max}_{0 \leq k \leq n - 1} {|a_{k}|},$
ii): [31] (Walsh) $r = \sum_{k = 0}^{n - 1} {|a_{k}|}^{1 / (n - k)},$
iii): [10] (Carmichael et. al.) $r = \sqrt{1 + \sum_{k = 0}^{n - 1} {|a_{k}|}^{2}}$ .

It is not difficult to see that, if G is a vertex-transitive graph, then

O_{G} (x) = x^{n}

O_{G}^{★} (x) = 1 - x^{n}

and thus its positive root is one. Also, if

A_{G} ≅ i d

(namely, G is asymmetric graph with identity automorphism group), then

O_{G} (x) = n x

O_{G}^{★} (x) = 1 - n x

and its positive root is

\frac{1}{n}

. This yields that for a given graph G on n vertices, which is neither vertex-transitive nor identitiy graph, then

δ \in (\frac{1}{n}, 1)

. In the case that G is not vertex-transitive and

A_{G} \neq i d

, then clearly we have

0 \leq a_{i} \leq n - 2

and according to Theorem 1(i), it can be verified that

r < n - 1

and

0 < |z| < n - 1

. By Theorem 1(ii), we obtain

r = a_{0}^{1 / n} + a_{1}^{1 / n - 1} + \dots + a_{n - 2}^{1 / 2} + a_{n - 1} .

(2)

For

i > [n / 2]

, it is clear that

a_{i} \in {0, 1}

and only one of

a_{i}

’s is 1. On the other hand, if the order of orbits is smaller than

[n / 2]

, the number of terms in the Eq.(2) will be increased and thus the value of r. The maximum number of terms holds if all

a_{i}

’s are one. Since

\sum_{i = 1}^{n} i a_{i} = n

, a graph in which

n = 1 + 2 + 3 + \dots + m

(for some integer m), has the largest value of r. Hence,

m = \frac{- 1 + \sqrt{8 n}}{2}

and so

r \leq 1 + m = \frac{1 + \sqrt{8 n}}{2},

or equivalently

|z| < \frac{1 + \sqrt{8 n}}{2} .

If the number of terms in the Eq.(2) decreases, the value of r will be decreased and if the orders of the orbits of graph are equal, then Eq.(2) will be a monomial. It is not difficult to see that by Theorem 1 (ii), the minimum value of r is

r \geq 1 + 2^{2 / n} > 2,

in which

O_{G}^{★} (x) = 1 - 2 x^{n / 2} .

By Theorem 2.1 (iii), we yield

r = \sqrt{1 + \sum_{k = 0}^{n - 1} {|a_{k}|}^{2}} = \sqrt{1 + (1^{2} + a_{1}^{2} + a_{2}^{2} + \dots + a_{n - 1}^{2})} .

Knowing that the graph is not vertex-transitive and

A_{G} \neq i d

, it can be inferred that

2 \leq \sum a_{i} \leq n - 1

and thus

\sum a_{i}^{2} < {(\sum a_{i})}^{2} \leq {(n - 1)}^{2},

or equivalently,

r < \sqrt{2 + {(n - 1)}^{2}} = (n - 1) \sqrt{1 + \frac{2}{{(n - 1)}^{2}}} .

Thus, if

n \geq 3

, we may conclude that

r < (n - 1) \sqrt{\frac{3}{2}} .

The lower bound for r using Theorem 1 (iii) is (G is not vertex-transitive and

A_{G} \neg ≅ i d

)

r \geq \sqrt{1 + (1^{2} + 1^{2} + 1^{2})} = 2 (a_{n - 1}, a_{1} = 1) .

Hence, we proved the following theorem.

Theorem 1.

Suppose G is a graph on n vertices, then all zeros of modified orbit polynomial

O_{G}^{★}

lie in disc

C = {z \in C : |z| < \frac{1 + \sqrt{8 n}}{2}}

Corollary 1.

For the star graph

S_{n}

with n vertices,

O_{S_{n}} (x) = x + x^{n - 1}

and all the zeros of

O_{S_{n}}^{★} (x) = 1 - (x + x^{n - 1})

lie in

[- 2, 2]

Theorem 2.

[10] Let

f (z) = a_{n} z^{n} + a_{n - 1} z^{n - 1} + \dots + a_{0}, a_{n} a_{n - 1} \neq 0,

be a complex polynomial. All zeros of

f (z)

lie in

|z| \leq \frac{1 + ϕ}{2} + \frac{\sqrt{{(ϕ - 1)}^{2} + 4 M_{2}}}{2},

where

ϕ : = |\frac{a_{n - 1}}{a_{n}}|,

and

M_{2} : = max_{0 \leq j \leq n - 2} |\frac{a_{j}}{a_{n}}| .

Theorem 3.

Let

N

be a network on

n \geq 3

vertices that is not vertex-transitive and

A_{N} \neq i d

, with the orbit polynomial

O_{N} (x) = \sum_{i = 1}^{t} a_{i} x^{i}

. Then all zeros lie in

(\frac{- 1}{n - 2}, n - 2]

Proof.

We know that

a_{i} \leq n - 2

, therefore Theorem 2 implies that

M a x ϕ = \frac{n - 2}{1} = n - 2 .

Hence, the orbit polynomial is of form

x^{2} + (n - 2) x

and so

M_{2} = 0

. Consequently,

z \leq \frac{1 + (n - 2)}{2} + \frac{\sqrt{{(n - 3)}^{2}}}{2} = n - 2 .

Also

M i n ϕ = \frac{1}{n - 2} .

Thus, the orbit polynomial is

(n - 2) x^{2} + x

. Since

M_{2} = 0

and

\sum_{i = 1}^{t} i a_{i} = n

, we conclude that n=3. This means that if n>3 there is no graph with

M i n ϕ = \frac{1}{n - 2} .

□

Theorem 4.

Let

N

be a network on

n \geq 3

vertices and

(n - 1)

orbits. Then

O_{N} (x) = x^{2} + (n - 2) x

and

A_{N} ≅ Z_{2}

Proof.

Since

N

has

(n - 1)

orbits, one can easily conclude that there are

(n - 2)

singleton orbits and an orbit of order 2. This completes the proof. □

Example 1.

We utilized the Sage software [30] to analyze all networks up to the order of 10 and made an observation about the structure of graphs with orbit polynomial

O_{N} (x) = x^{2} + (n - 2) x

. Our finding revealed that the structure of such graphs falls under one of the categories illustrated in Figure 6.

3.1. The Location of Positive Root $δ$

In last section, we showed that

δ \in [\frac{1}{n}, 1]

. In addition, in [3], it has been shown that as

δ

increases towards one, the graph becomes more symmetric, and as

δ

tends to zero, the graph will be less symmetric, especially for sufficiently large values of n.

Based on the above discussions, this section aims to develop a framework to discuss the behavior of the positive root of the modified orbit polynomial, which can capture meaningful structural information.

Theorem 5.

Let

N

be a network on

n \geq 3

vertices with the orbit polynomial

O_{N} (x) = \sum_{i = 1}^{t} a_{i} x^{i}

and

O^{★}_{N} (x) = 1 - \sum_{i = 1}^{t} a_{i} x^{i}

. If for

i \in {1, 2, \dots, n}

m \leq \sqrt[i]{a_{i}}

, then

δ \in (0, \frac{1}{m}]

Proof.

O_{N}^{★} (\frac{1}{m}) = 1 - (\frac{1}{m} a_{1} + \frac{1}{m^{2}} a_{2} + \dots + \frac{1}{m^{i}} a_{i} + \dots + \frac{1}{m^{t}} a_{t}) \leq 0,

Considering that

O_{N}^{★} (0) > 0

and

O_{N}^{★} (1) < 0

it can be concluded

δ \in (0, \frac{1}{m}]

. □

Example 2.

Let

N

be a network with the orbit polynomial

O_{N} (x) = 4 x + 7 x^{2} + 25 x^{3}

and

O^{★}_{N} (x) = 1 - (4 x + 7 x^{2} + 25 x^{3})

. Since

a_{1} = 4

we may conclude that

m \leq 4

and

a_{2} = 7

gives

m^{2} \leq 7

. Also

a_{3} = 25

yields

m^{3} \leq 25

and thus

max (m) = 4

and

δ \in (0, \frac{1}{4}]

Corollary 2.

The value

δ = \frac{1}{2}

holds for a network with orbit polynomial

O_{N} (x) = 2^{i} x^{i}

and if the network

N

has k singleton orbits, then the positive root

O^{★}_{N} (x)

lies in

(0, \frac{1}{k}]

Theorem 6.

For any rational number α in the interval

(- \infty, 0]

there is a network

N

such that

O_{N} (α) = 0

. Moregenerally, the set of all roots of

O_{N}

is dense.

Proof.

Let

a, b \in N

. There is a network of order

n = a + 2 b

such that

O_{N} (x) = a x + b x^{2}

. An example of such networks is shown in Figure 7. It is enough to have a network with a vertices and putting two pendants vertices in the position of the b vertices, such that no pair of vertices on the path

P_{b}

can be permuted to each other. □

Theorem 7.

If the network

N

has an orbit of order

n - i

(i \leq \frac{n}{2})

, then

δ \in (\frac{1}{i + 1}, 1)

Proof.

It is clear that

a_{n - i} = 1

and i vertices lie in orbits by order smaller than

\frac{n}{2}

. So the orbit polynomial as follows:

O_{N} (x) = a_{1} x^{1} + a_{2} x^{2} + \dots + a_{k} x^{k} + x^{n - i} (k < \frac{n}{2}) .

The maximum value of

O_{N} (δ)

holds if

O_{N} (x) = i x (a_{1} = i)

and

O_{N}^{★} (\frac{1}{i + 1}) = i (\frac{1}{i + 1}) < 1

. This means that

δ \in (\frac{1}{i + 1}, 1) .

The maximum value of

O_{N} (δ)

holds if

O_{N} (x) = i x + x^{n - i} (a_{1} = i)

and

O_{N}^{★} (\frac{1}{i + 1}) = 1 - (i (\frac{1}{i + 1}) + {(\frac{1}{i + 1})}^{n - i}) > 0

. This means that

δ \in (\frac{1}{i + 1}, 1) .

□

Theorem 8.

Suppose the tree T has an orbit of order 2

(|O_{i}| = 2)

and the other orbits are singleton, then

〈O_{i}〉 ≅ P_{3}

Proof.

O_{i} = {y, z}

it is clear that there is an automorphism like

φ

so that

φ (y) = z

. Now if y and z lie in different branches of T such as

B_{1}

and

B_{2}

, then it follows from

φ (y) = z

that

φ (B_{1}) = B_{2}

which is contradiction. Therefore y and z are in the same branch like B. Let’s assume that the root of the branch B is x, , and the paths from y and z to x are denoted by

p_{1}

and

p_{2}

, respectively. So

φ (p_{1}) = p_{2}

and if t is a vertex on

p_{1}

, then there is a vertex like

t^{'}

p_{2}

which

φ (t) = t^{'}

that is contradiction. Hence,

d (x, y) = d (x, z) = 1

and the issue is confirmed. □

Corollary 3.

Let T be a tree on

n \geq 3

vertices and

O_{T} (x) = x^{2} + (n - 2) x

, then

δ = \frac{2}{\sqrt{{(n - 2)}^{2} + 4} + (n - 2)} .

Proof.

Suupose

O_{T}^{★} (x) = 1 - (x^{2} + (n - 2) x)

, then clearly the roots are

x_{1, 2} = \frac{- (n - 2) \pm \sqrt{{(n - 2)}^{2} + 4}}{2}

and thus

δ = \frac{2}{\sqrt{{(n - 2)}^{2} + 4} + (n - 2)} .

This completes the proof. □

Corollary 4.

Let T be a tree on n vertices:

1) If

A_{T} ≅ i d

, then

δ = \frac{1}{n}

2) If

A_{T} \neq i d

, then

δ \in [α, 1]

so that

α = \frac{\sqrt{{(n - 2)}^{2} + 4} - (n - 2)}{2} .

4. The Role of $δ$ in the Study of Real Network Structures

Complex networks have been extensively studied in various fields in recent years. The concept of entropies has been used to characterize and quantify the structure of networks, and has been investigated in many studies [1,2,4,5,6,7,8,11]. As a specific definition for graph entropies, we use the definition proposed by Dehmer [15,16,17,29], which involves a probability vector

p = (p_{1}, \dots, p_{n})

that satisfies two conditions:

0 \leq p_{i} \leq 1

and

\sum {i - 1}^{n} p i = 1

. The Shannon’s entropy is then defined as

I (p) = \sum_{i - 1}^{n} p i l o g (p_{i}) .

Mowshowitz and Dehmer [27] introduced the symmetry index

S (G)

, which is defined as

\begin{matrix} S (G) & = & (l o g n - I_{a} (G)) + l o g | A G | \\ = & \frac{1}{n} (\sum_{i = 1}^{t} | O i | l o g | O i |) + l o g | A_{G} | . \end{matrix}

I (G)

and

I (H)

are two graph invariants of graphs G and H, respectively, the graph distance measure between

I (G)

and

I (H)

is defined as

d_{I} (G, H) = 1 - e^{- {(\frac{I (G) - I (H)}{σ})}^{2}}

, according to [14]. The values of orbit entropy

I_{a}

, size of the automorphism group, symmetric index

S (G)

, unique positive root

δ

, distance measure between

δ

and

I_{a}

, and distance measure between

δ

and

S (G)

of biological and technological networks are reported in Table 1.

Table 1.

	n	$\|A\|$	$δ$	$I_{a}$	$S$	$d (δ, I_{a})$	$d (δ, S)$
Human B Cell Genetic	5930	5.94 × 10 $^{13}$	1710× 10 $^{- 7}$	3.77	13.8	14.20	189.83
Caenorhabditis elegans Genetic	2060	6.99 × 10 $^{161}$	6258× 10 $^{- 7}$	3.20	161.96	10.22	26.23× 10 $^{3}$
BioGRID Human	7013	1.26 × 10 $^{485}$	1764× 10 $^{- 7}$	3.73	485.2	13.93	23.54× 10 $^{4}$
BioGRID Saccharomyccscerevisiae	5295	6.86 × 10 $^{64}$	1958× 10 $^{- 7}$	3.70	64.86	13.71	4206.4
BioGRID Drosophila	7371	3.07 × 10 $^{493}$	1690× 10 $^{- 7}$	3.76	493.6	14.10	24.36× 10 $^{4}$
BioGRID Mus musculus	209	5.35 × 10 $^{125}$	221440× 10 $^{- 7}$	1.46	126.59	2.06	16.02× 10 $^{3}$
Yeast Protein Interactions	1458	1.07 × 10 $^{254}$	11599× 10 $^{- 7}$	2.88	254.30	8.31	64.67× 10 $^{3}$
c. elegans metabolic	453	1.93 × 10 $^{10}$	25702× 10 $^{- 7}$	2.60	10.33	6.78	106.79
Internet	22332	1.28 × 10 $^{11, 298}$	1035× 10 $^{- 7}$	3.67	11.3× 10 $^{3}$	13.44	12.77× 10 $^{7}$
US Power Grid	4941	5.18 × 10 $^{152}$	2380× 10 $^{- 7}$	3.63	152.77	13.20	23.34× 10 $^{3}$
US Airports	332	2.59 × 10 $^{24}$	40472× 10 $^{- 7}$	2.39	24.54	5.71	602.07
www California searchsubnet	5925	1.24 × 10 $^{1, 298}$	2820× 10 $^{- 7}$	3.45	1298.4	11.93	16.86× 10 $^{5}$
www EPA.gov subnet	4253	1.28 × 10 $^{2, 321}$	4992× 10 $^{- 7}$	2.91	2321.8	8.47	53.91 × 10 $^{5}$
www Political Blogs	1222	2.40 × 10 $^{35}$	8741× 10 $^{- 7}$	3.04	35.43	9.25	1254.9
Email	1133	1.53 × 10 $^{9}$	9216× 10 $^{- 7}$	3.04	9.20	9.23	84.62
Media ownership	4475	3.36 × 10 $^{4, 818}$	13278× 10 $^{- 7}$	2.16	4820.01	4.68	23.23× 10 $^{6}$
Geometry Co-authorship	3621	1.90 × 10 $^{320}$	4419× 10 $^{- 7}$	3.38	320.45	11.45	10.27× 10 $^{4}$
Erdös Collaboration	6927	3.46 × 10 $^{4, 222}$	5491× 10 $^{- 7}$	2.956	4223.4	8.73	17.84× 10 $^{6}$
PhD network	1025	2.98 × 10 $^{292}$	25245× 10 $^{- 7}$	2.55	292.93	6.49	85.81× 10 $^{3}$

Table 2 shows that the correlation values of

δ

and

I_{a}

in biological and technological networks are very close. However, it appears that there may be differences in the effective variables that contribute to the structure of social networks compared to other types of networks. This suggests that further research should be conducted to investigate these differences.

Table 3 presents a collection of well-known real-world networks with distinct topologies. Analysis of the reported data shows that the symmetry measure

δ

is strongly correlated with the orbit entropy

I_{a}

(with a correlation coefficient

R = - 0.73

), but does not appear to be correlated with

S (G)

(with a correlation coefficient

R = - 0.15

For the networks listed in Table 3, various topological indices, including the first Zagreb index (

M_{1}

), second Zagreb index (

M_{2}

), spectral radius

(ρ)

, Randic index

(R)

, Laplacian Estrada index

(L E E)

, Laplacian energy

(L E)

, Harary index

(H)

, Estrada index

(E E)

, energy

(E)

, Balaban ID

(B I)

, and atom-bond connectivity

(A B C)

, were calculated, as reported in [28]. The results indicate that among all the above indices, Laplacian energy has the strongest correlation with

δ

, with a coefficient of greater than 0.91.

(\begin{matrix} M_{1} & M_{2} & ρ & R & L E E & L E & H & E E & E & B I & A B C \\ δ & - 0.07 & 0.47 & - 0.19 & - 0.17 & - 0.02 & 0.91 & - 0.17 & - 0.16 & - 0.20 & - 0.23 & - 0.20 \end{matrix})

For this study, all graphs of orders 4-7, all trees of orders 7-20, together with 470 randomly generated trees of order 21 and 1248 randomly generated trees of order 25 were considered, and two measures based on the automorphism group and Laplacian eigenvalues of a graph were established. The computed correlation values between the unique positive root

δ

and Laplacian energy of a graph, denoted by

L E (G)

, are reported in Table 4. For trees of order 21 and 25, the correlation values were 0.556 and 0.589, respectively, while for other classes they were less than 0.5.

Although the correlation between

δ

and

L E (G)

in real networks is meaningful, it appears that in the class of trees, the correlation value between

δ

and

L E (G)

increases as the order of the tree increases. In other words, an appropriate analogy is the case of two functions that have very different functional forms on the same set of variables.

5. Small-World Graphs

A social network is called a small-world network, if most nodes are not neighbors of one another, but most nodes can be reached from every other by a small number of hops. The clustering coefficient of a graph is a measure to find which vertices in the graph tend to form a clique. There are two types of clustering coefficient, namely local and global. The local clustering coefficient

C (v)

of vertex v is defined as

\frac{2 e (v)}{d_{v} (d_{v} - 1)}

, where

e (v)

is the number of edges

〈 N_{G} (v) 〉

. The global clustering coefficient of graph G is

C^{Δ} = \frac{3 t}{l_{2}}

, where t is the number of triangles and

l_{2}

is the number of paths of length two [32]. Assume that

C_{r a n d}^{Δ}

is the clustering coefficient of an equivalent ER random graph with the same order and size. In [32], it is proved that

L_{r a n d} = \frac{ln (n)}{ln (2 k)}

and

C_{r a n d}^{Δ} = \frac{2 k}{n}

. Additionally, the small-worldness of a graph is expressed by

S^{Δ} = \frac{C_{g}^{Δ} L_{r a n d}}{C_{r a n d}^{Δ} L_{g}} .

Example 3.

Consider three graphs Karate Club

K

, Dolfin graph

D

, and the network

G

, as depicted in Figure 8. The following R programs determine their small-worldness which are respectively 1.48, 2. 10, and 4.58.

The aim of continuing this paper is to determine whether removing a vertex or an edge can decreases or increases the small-worldness of a graph. In the second step, our goal is to detrmine the small-worldness of two smallworld graphs linked by a new edge. To do this, we consider 1000 random small-world networks of the same order. Our results show that by removing a random edge, the resuting graph is again a small-world graph with small-worldness greater tan one. We repeated this way by removing a random vertex to conclude a similar result. We applied the following program written by R to obtain our results.

An R program for computing smallworldness of networks:

library(NetworkToolbox)

library(igraph)

library(Matrix)

count<-0

repeat{

a<-sample(50:60,1)

b<-sample(3:8,1)

g<-sample_smallworld(1,a,b,0.05)

H<-as_adj(g)

L<-matrix(H,nrow=a,ncol=a)

x<-smallworldness(L,method="rand")

p<-sample(V(g),1)

g1<-delete_vertices(g,p)

A<-as_adjacency_matrix(g1)

B<-matrix(A,nrow=a-1,ncol=a-1)

y<-smallworldness(B,method="rand")

t<-cbind(x$swm,y$swm)

write.table(t,file="G-v.csv",append=T,sep=",",col.names=F,row.names=F)

count<-count+1

if(count==1000){break}

}

For the second step, we also generate 1000 random small-world graphs joined by a new edge and the resulted graph is again small-world by almost the same small-worldness. The following program do this.

Algorithm 2:

library(igraph)

library(Matrix)

library(NetworkToolbox)

library(rgl)

count<-0

repeat{

a<-sample(50:100,1)

b<-sample(3:8,1)

g1<-sample_smallworld(1,a,b,0.05)

H<-as_adj(g1)

L<-matrix(H,nrow=a,ncol=a)

x<-smallworldness(L,method="rand")

d<-sample(50:100,1)

e<-sample(3:8,1)

g2<-sample_smallworld(1,d,e,0.05)

K<-as_adj(g2)

M<-matrix(K,nrow=d,ncol=d)

y<-smallworldness(M,method=”rand”)

g3<-(g1+g2)%<% add_edegs(c(1,a+d))

A<-as_adjacency_matrix(g3)

B<-matrix(A,nrow=a+d,ncol=a+d)

z<-smallworldness(B,method=”rand”)

write.table(c(x,y,z),file=”new.csv”,append=T,sep=”,”,col.names=F ,row.names=F)

count<-count+1

if(count==1000){break}

}

To summarize, the results of the investigation indicate that the

δ

metric is not redundant, and offers unique information about the symmetry structure of graphs that cannot be obtained from standard measures such as small-worldness. Additionally, the successful use of

δ

as a structural descriptor for chemical structures highlights its potential applications in diverse fields beyond network analysis.

However, further research is necessary to determine the full range of structural properties that can be captured by the orbit polynomial, and to better understand the relationship between

δ

and other graph metrics. Overall, the results suggest that

δ

is a valuable and versatile tool for analyzing complex systems and may have important implications for a variety of fields.

6. Conclusion

Dehmer et al. proposed a novel approach to compare graphs based on their symmetry structure using the modified orbit polynomial and the unique positive root,

δ

. The characteristics of

δ

have been demonstrated and it has been applied successfully to several network classes to investigate correlations with other graph indices.

Furthermore, the successful application of

δ

as a structural descriptor for chemical structures is significant because it opens up new possibilities for studying the symmetry structure of various complex systems beyond networks, such as molecules and crystals. This demonstrates the versatility and potential of

δ

in a range of fields beyond network analysis.

In conclusion, the orbit polynomial and its associated metric,

δ (G)

, provide a novel approach to comparing graphs based on their symmetry structure.

However, further research is needed to fully understand the range of structural properties captured by the orbit polynomial and to investigate the relationship between

S (G)

and

I_{a}

, as both are defined based on the number and sizes of orbits belonging to a graph’s automorphism group. This would provide a more comprehensive understanding of the relationship between symmetry and other graph metrics, and could potentially lead to new insights and applications for

δ

and related metrics.

References

Anand, K.; Bianconi, G. Entropy measures for networks: Toward an information theory of complex topologies. Phys. Rev. E. 2009, 80, 045102. [Google Scholar] [CrossRef]
Basak, S. C.; Balaban, A. T.; Grunwald, G. D.; Gute, B. D. Topological indices: Their nature and mutual relatedness. J. Chem. Inf. Comput. Sci. 2000, 40, 891–898. [Google Scholar] [CrossRef]
Bollobás, B. Random Graphs, 2nd ed.; Cambridge Studies in Advanced Mathematics; Cambridge University Press, Cambridge, UK, 2001.
Bonchev, D. Information Theoretic Indices for Characterization of Chemical Structures; Research Studies Press: Chichester, UK, 1983. [Google Scholar]
Bonchev, D. Kolmogorov’s information, Shannon’s entropy, and topological complexity of molecules. Bulg. Chem. Commun. 1995, 28, 567–582. [Google Scholar]
Bonchev, D.; Rouvray, D.H. Eds., Complexity in Chemistry, Biology, and Ecology; Mathematical and Computational Chemistry, Springer, New York, NY, USA, 2005.
Bonchev, D.; Trinajstić, N. Information theory, distance matrix and molecular branching, J. Chem. Phys. 1977, 67, 4517–4533. [Google Scholar] [CrossRef]
Butts, C. T. The complexity of social networks: Theoretical and empirical findings. Soc. Netw. 2001, 23, 31–71. [Google Scholar] [CrossRef]
Cauchy, A. L. Exercices de mathématique, in: Oeuvres. 1829, 9, p. 122.
Carmichael, D. R.; Mason, T.E. Note on roots of algebraic equations. Bull. Amer. Math. Soc. 1914, 21, 14–22. [Google Scholar] [CrossRef]
Constantine, G. Graph complexity and the Laplacian matrix in blocked experiments. Linear Multilinear Algebra. 1990, 28, 49–56. [Google Scholar] [CrossRef]
Csardi, G.; Nepusz, T. The igraph software package for complex network research. InterJournal, Complex Systems. 2006, 1695. https://igraph.org.
Dehmer, M.; Chen, Z.; Emmert-Streib, F.; Mowshowitz, A.; Varmuzag, K.; Jodlbauer, H.; Shih, Y.; Tripathi, S.; Tao, J. The orbit-polynomial: A novel measure of symmetry in graphs. IEEE Access. 2020, 8, 36100–36112. [Google Scholar] [CrossRef]
Dehmer, M.; Emmert-Streib, F.; Shi, Y. Interrelations of graph distance measures based on topological indices. PLoS One. 2014, 9, e94985. [Google Scholar] [CrossRef] [PubMed]
Dehmer, M.; Barbarini, N.; Varmuza, K.; Graber, A. Novel topological descriptors for analyzing biological networks. BMC Struct. Biol. 2010, 10, 10–18. [Google Scholar] [CrossRef] [PubMed]
Dehmer, M.; Mehler, A. A new method of measuring similarity for a special class of directed graphs. Tatra Mt. Math. Publ. 2007, 36, 39–59. [Google Scholar]
Dehmer, M.; Mowshowitz, A. A history of graph entropy measures. Inform. Sci. 2011, 1, 57–78. [Google Scholar] [CrossRef]
Dehmer, M.; Emmert-Streib, F.; Mowshowitz, A.; Ilić, A.; Chen, Z.; Yu, G.; Feng, L.; Ghorbani, M.; Varmuza, K.; Tao, J. Relations and bounds for the zeros of graph polynomials using vertex orbits. Appl. Math. Comput. 2020, 380, 125–239. [Google Scholar] [CrossRef]
Ghorbani, M.; Dehmer, M.; Rajabi-Parsa, M.; Emmert-Streib, F.; Mowshowitz, A. Hosoya entropy of fullerene graphs. Appl. Math. Comput. 2019, 352, 88–98. [Google Scholar] [CrossRef]
Ghorbani, M.; Alidehi-Ravandi, R.; Dehmer, M. Fullerenes via their Counting Polynomials. submitted.
Ghorbani, M.; Dehmer, M. On the roots of the modified orbit polynomial of a graph. Symmetry 2021, 13, 972. [Google Scholar] [CrossRef]
Ghorbani, M.; Dehmer, M. Network Analyzing by the aid of orbit polynomial. Symmetry 2021, 13, 801. [Google Scholar] [CrossRef]
Ghorbani, M.; Jalali-Rad, M.; Dehmer, M. Orbit polynomial of graphs versus polynomial with integer coefficients. Symmetry 2021, 13, 710. [Google Scholar] [CrossRef]
Ghorbani, M.; Dehmer, M.; Emmert-Streib, F. On the degeneracy of the orbit polynomial and related graph polynomials. Symmetry 2020, 12, 1643. [Google Scholar] [CrossRef]
Harary, F. Graph Theory; Addison-Wesley Publishing Company, Boston, MA, USA, 1969.
MacArthur, B.D.; Sánchez-García, R.J.; Anderson, J.W. Symmetry in complex networks. Discrete Applied Mathematics. 2008, 156, 3525–3531. [Google Scholar] [CrossRef]
Mowshowitz, A.; Dehmer, M. A symmetry index for graphs. Symmetry Cult. Sci. 2010, 21, 321–327. [Google Scholar]
Mueller, L.A.; Kugler, K.G.; Dander, A.; Graber, A.; Dehmer, M. QuACN: An R package for analyzing complex biological networks quantitatively. Bioinformatics. 2011, 27, 140–141. [Google Scholar] [CrossRef] [PubMed]
Shannon, C.E.; Weaver, W. The Mathematical Theory of Communication; University of Illinois Press, Urbana, IL, USA, 1949.
SageMath, https://sagecell.sagemath.org/.
Walsh, J.L. An inequality for the roots of an algebraic equation. Ann. Math. 1924, 2, 285–286. [Google Scholar] [CrossRef]
Watts, D. J. Strogatz, S. H. Collective dynamics of ’small-world’ networks. Nature. 1998, 393, 440–442. [CrossRef]

Figure 6. All structures of graphs with

O_{N} (x) = x^{2} + (n - 2) x

Figure 6. All structures of graphs with

O_{N} (x) = x^{2} + (n - 2) x

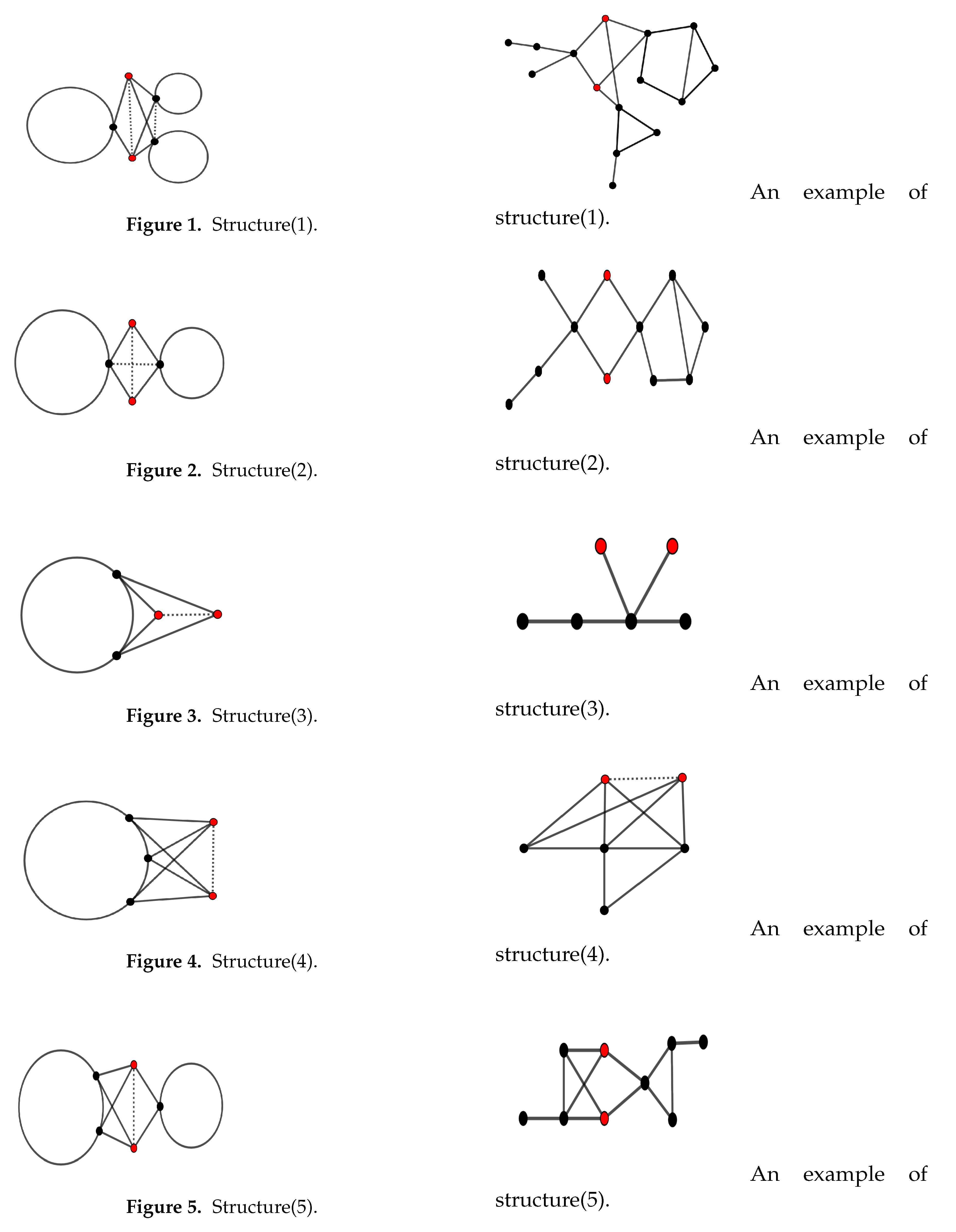
Figure 7. An example of a graph with orbit polynomial

O_{N} (x) = a x + b x^{2} .

Figure 7. An example of a graph with orbit polynomial

O_{N} (x) = a x + b x^{2} .

Figure 8. Three small-world graphs (a) Karate Club

K

, (b) Dolfin graph

D

, and (c) the network

G

Figure 8. Three small-world graphs (a) Karate Club

K

, (b) Dolfin graph

D

, and (c) the network

G

Table 2. The correlation values.

Biological Networks	Technological Networks	Social Networks
$(\begin{matrix} δ & I_{a} & S \\ δ & 1 & - 0.88 & - 0.20 \\ I_{a} & - 0.88 & 1 & 0.33 \\ S & - 0.20 & 0.33 & 1 \end{matrix})$	$(\begin{matrix} δ & I_{a} & S \\ δ & 1 & - 0.86 & - 0.37 \\ I_{a} & - 0.86 & 1 & 0.48 \\ S & - 0.37 & 0.48 & 1 \end{matrix})$	$(\begin{matrix} δ & I_{a} & S \\ δ & 1 & - 0.64 & - 0.19 \\ I_{a} & - 0.64 & 1 & - 0.55 \\ S & - 0.19 & - 0.55 & 1 \end{matrix})$

Table 3. A set of well-known real-world networks with distinct topologies and their graph invariants.

Table 4. The correlation values between randomly graphs.

#Graphs	Graph Order	$R (δ, L E$ )
9	2 to 4	-0.414
21	5	-0.009
121	6	0.065
853	7	0.029
33	unicycle graph of order 7	0.031
11	Tree of order 7	0.290
3159	Tree of order 14	0.381
7741	Tree of order 15	0.441
19320	Tree of order 16	0.429
48629	Tree of order 17	0.466
123867	Tree of order 18	0.466
317955	Tree of order 19	0.493
823065	Tree of order 20	0.499

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

A Study of Roots of a Certain Class of Counting Polynomials

Abstract

1. Introduction

2. Preliminaries

3. Location of Roots

3.1. The Location of Positive Root δ

4. The Role of δ in the Study of Real Network Structures

5. Small-World Graphs

6. Conclusion

References

MDPI Initiatives

Important Links

Subscribe

3.1. The Location of Positive Root $δ$

4. The Role of $δ$ in the Study of Real Network Structures