Preprint
Article
UFO-Net: A Linear Attention-Based Network for Point Cloud Classification
Altmetrics
Downloads
137
Views
55
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
09 May 2023
Posted:
10 May 2023
You are already at the latest version
Alerts
Abstract
3D point cloud classification tasks have been a hot topic in recent years. Most existing point cloud processing frameworks lack context-aware features due to the deficiency of sufficient local feature extraction information. Therefore, we design an augmented sampling and grouping (ASG) module to efficiently obtain fine-grained features from the original point cloud. In particular, this method strengthens the domain near each centroid and makes reasonable use of the local mean and global standard deviation to mine point cloud’s local and global features. In addition to this, inspired by the transformer structure UFO-ViT in 2D vision tasks, we first try to use a linearly-normalized attention mechanism in point cloud processing tasks, investigating a novel transformer-based point cloud classification architecture UFO-Net. An effective local feature learning module is adopted as a bridging technique to connect different feature extraction modules. Importantly, UFO-Net employs multiple stacked blocks to better capture feature representation of the point cloud. Extensive ablation experiments on public datasets show that our method outperforms other state-of-the-art methods. For instance, our network performed with 93.7% overall accuracy on the ModelNet40 dataset, which was 0.5% higher than PCT. Our network also archived 83.8% overall accuracy on the ScanObjectNN dataset, which is 3.8% better than PCT.
Keywords:
Subject: Engineering - Electrical and Electronic Engineering
1. Introduction
As sensors become more prevalent in capturing geometric information in 3D scenes, point cloud classification has become increasingly significant for various graphic and vision tasks. Point clouds, as physical 3D world data or an electronic signal, are widely used in mapping, autonomous driving, remote sensing, robotics, and metadata [1,2,3,4,5]. Point cloud data is usually generated by optical sensors, acoustic sensors, LiDAR, and other direct or indirect contact scanners [3,6]. Specifically, researchers can obtain feature information through convolutional neural networks (CNNs) [7,8], which can then be used in subsequent processing tasks. Unlike 2D images, 3D point cloud data are nonuniform and unstructured. Point cloud processing can yield rich spatial location features and texture geometry information by designing different algorithms [9,10,11,12] to complete some 3D tasks. Point cloud classification plays an important role in many fields, such as object recognition in machines. The focus of this paper is on the shape classification of the point cloud, which is a significant task for point cloud processing.
Aimed at the existing works on classification tasks, several properties can be summarized as the following aspects. Applicability. On the one hand, 3D applications in reality are extensive and extremely dependent on mature technical research. In order to accurately identify the ground objects, researchers design a large number of networks to improve the score of point cloud tasks from the underlying theory. Complexity. When it comes to designing a brand-new method to solve hard-core tasks, simple point networks can` t complete the complex demands. Almost all models with hierarchical structures require complex array operations. Point cloud classification still requires researchers’ efforts to continue to promote theoretical analysis and model building.
Different from convolutional neural networks that process natural language and image data, CNNs can`t be applied to unordered 3D point cloud data directly. Therefore, training neural networks on point sets is a challenging task. The success of CNNs in point cloud analysis has attracted a lot of attention. The rapid development of deep learning facilitates the diversification of methods for point cloud processing tasks. After recent years of research, point cloud processing methods have been derived based on a grid format, or converting them to multi-view images. All these point cloud processing methods give good results in point cloud classification tasks. However, numerous experiments have shown that these transformations lead to large computational demands and even loss of much geometric information. The point-based approaches effectively alleviate this aspect of deficiency. PointNet [10] is a pioneering point-based approach. It obtains the features of the input point cloud by directly processing each point using shared MLPs and a max-pooling symmetry function. This method learns the relative relationships between points by designing models to resolve the irregularities of the point cloud. However, PointNet [10] ignores the correlation features of points in local areas due to the direct processing of points to obtain shape-level features, which leads to an imbalance between local domain and global features. PointNet++ [11] proposes a hierarchical approach to extract local features, and the results showed the importance of local features in point cloud analysis. To further investigate the extraction of local features, DGCNN [12] is a new scheme to explore local features. DGCNN not only refers to the previous work but proposes a unified operator to obtain local features. Although PointNet++ and DGCNN consider mining local region features, almost all of them use a max-pooling strategy to aggregate features. This single operation considers only focuses on the most prominent feature, ignoring the other relevant geometric information. Consequently, the local information of the point cloud is not fully exploited. Therefore, to further ameliorate the performance and generalization capability, we introduce a lightweight local geometric affine module. This approach addresses point sparsity and irregular geometric structures in the local threshold.
Recently, with the strong expressiveness of the transformer structure in the field of natural language processing and image recognition, attention mechanisms have also been widely used in point cloud learning tasks. Since transformers are permutation invariant, they are well suited for point cloud learning [13,14,15,16]. The original structural components of the Transformer are mainly composed of input encoding, position encoding, and self-attention (SA) mechanism [33]. The attention mechanism is the core structure of the transformer. In detail, the attention mechanism takes the sum of the input encoding and the position encoding as input. Attention weights are obtained by dot-producting queries and keys. Therefore, the attention feature is a weighted sum of all values with attention weights. It is the nature of this obtained correlation between features that the extraction of point location features seems to be very effective. Naturally, the output of attention represents the features of the input sequence, which can be learned by the subsequent multi-layer perceptrons to complete the point cloud analysis. In summary, inspired by UFO-ViT [17], we propose a new framework, UFO-Net, adopting the idea of a unified force operation (UFO) layer that uses the -norm to normalize the feature map in the attention mechanism. UFO decomposes the transformation layer into a product of multiple heads and feature dimensions. The point cloud features are then obtained by matrix multiplication.
The main contributions of the proposed model are at three aspects:
- 1)
- We propose a novel network UFO-Net conforming to the point cloud input, which leverages the advantages of UFO mechanism to replace the original self-attention mechanism in PCT [16]. UFO incorporates a softmax-like scheme CNorm, which is a novel constraint scheme. The essence of CNorm is a common -norm CNorm learns point-to-point relational features by generating a unit hypersphere [17]. Furthmore, the offset matrices introduced in UFO attention are effective in reducing the impact of noise and ensuring that this method provides sufficient characteristic information for downstream tasks.
- 2)
- We observe that the input coordinates of the point cloud are less correlated with the features, and while the attention mechanism learns global features effectively, it tends to overlook some local features. Thus, we introduce an augmented sampling and grouping (ASG) module that rethinks the sampling and grouping of the point cloud to improve association between points, which ultimately improves network performance.
- 3)
- We perform extensive experiments and analyses on two publicly available benchmark datasets, ModelNet40 and ScanObjectNN. Results verify the effectiveness of our framework, which can achieve competitive scores compared with the state-of-the-art (SOTA) methods. Our proposed framework provides a promising approach for point cloud tasks, and we believe it has the potential to drive further research in this field.
2. Related Works
Traditional 3D data algorithms are commonly used in the fields of robot vision navigation, artificial verification, and 3D reconstruction [1,2,8]. Recently, convolutional neural networks (CNNs) have facilitated the development of image recognition due to their robustness advantage in feature extraction [5]. Gradually, these approaches have been applied to the 3D domain, deriving intelligent point cloud processing schemes. These methods provide some practical neural networks to process point cloud data directly or indirectly, and successfully mine the potential features of point cloud data. To some extent, the ability to extract features can determine the accuracy of point cloud classification tasks. To address these challenges, many researchers have designed different neural networks to implement point cloud tasks by modifying the input form of point clouds. In this section, we broadly review the existing approaches, which are generally subdivided into four aspects overall.
2.1. Voxel-Based Methods
Truc Le et al. [18] first adopted a volumetric grid structure to voxelize the unsorted 3D point clouds into a regular 3D grid structure. This approach is a 3D convolutional mesh dealing with a constant number of points and allows better learning of local geometric features by using approximation functions. For example, VoxNet [19] pioneers the implementation of 3D learning. However, these methods are difficult to acquire high-dimensional features due to the rasterization process, causing a large amount of memory consumption and complex computational efforts. Clearly, these methods also have difficulty capturing high-resolution or fine-grained features due to sparsity. Furthermore, in order to alleviate the problem of large memory consumption and storage difficulties, methods based on Octree-based [20], and Kd-tree-based [21] refine the model performance. Vv-Net [22] proposes a variational autoencoder (VAE) and radial basis function (RBF) to represent voxels, which further learns local features. Park et al. [13] proposed a lightweight self-attention module to encode the voxel hash architecture for efficiency. Then, the voxel-based methods provide a new strategy to calculate the unstructured 3D point cloud.
2.2. Graph-Based Methods
Graph-based neural networks are gradually being studied and applied to irregular point cloud data, and this innovation increases the diversity of point cloud learning tasks. Graph convolutional neural networks (GNNs) are often used to learn local geometric features between multiple points. For example, the pioneered Edge-conditional convolution (ECC) [23] converts the disordered point cloud data into graphs. Jing et al. [24] proposed a novel feature extraction module based on attention pooling strategy called attention graph module (AGM), which constructs a topology structure in the local region and aggregates the important features by the novel and effective attention pooling operation. 3DGCN [25] introduces a learnable 3D kernel structure to guarantee scale invariance, and a 3D graph max-pooling operator to obtain more features. In addition, to make spectral convolution kernels applicable to different graph topologies, Lin et al. [26] proposed SPH3D-GCN a separable spherical convolutional layer for effective graph neural networks. DeepGCNs [27] adopts a deep graph convolutional network that can capture local and global features of point clouds by transferring concepts such as residual/dense connections and dilated convolutions from CNNs to GCNs. Ulteriorly, The GAPNet [28] designing graph attention point layer (GAP layer) learns point features by assigning different attention weights to the neighborhoods, which enhanced the robustness of the network. The graph-based methods are flexible to process irregular date, achieving competitive performance on point cloud learning.
2.3. Point-Based Methods
The PointNet [10] network is a well-known point-based approach that learned point-wise features using multilayer perceptrons (MLPs) without data preprocessing. After that, a channel-wise symmetric function (max-pooling) is used to obtain global feature information. However, PointNet lacks the ability to extract more fine-grained structures and local features. PointNet++ [11] fills this deficiency by designing two hierarchical schemes for local feature extraction. The hierarchical structure consisted of set abstraction modules. Each set abstraction module consists of a sampling layer, a grouping layer, and a mini-PointNet layer. The set abstract scheme improves feature aggregation and enhances the performance of PointNet. Experiments with PointNet and PointNet++ show that the point-based approaches can learn point features more effectively in point cloud learning. In addition, Xu et al. [29] proposed GS-Net to effectively learn point descriptors with holistic context to enhance the robustness to geometric transformations. Li et al. [30] proposed an X-conv operator that combined geometric and color features of nearby points to compute convolutional filters. Overall, point-based approaches offer solutions for many scholars to study point clouds.
2.4. Attention-Based Methods
The attention mechanism originates from natural language processing [31,32,33]. Tao et al. [34] improved the attention mechanism by proposing multi-head attention and solely relying on attention itself. Compared with the limited receptive fields of CNNs, transformer characterized by the attention mechanism shows its capabilities in feature capturing [13,16]. Several attention-based methods for point cloud classification have been proposed recently. For example, Zhao et al. [15] considered the self-attention operator and position encoding to act on the neighborhood near each point, leading to a network purely based on self-attention and point-wise manipulations. The point cloud transformer (PCT) network proposed by Guo et al. [16] enhances the input embedding with the support of farthest point sampling and nearest neighbor search. PCT also modifies the self-attention mechanism and proposed offset-attention to better complete the point cloud tasks. On top of that, SA-Net [35] proposes the skip-attention mechanism to fuse local region features from encoder to the point features of decoder, which selectively conveys geometric information at different resolutions. Han et al. [36] proposed an end-to-end architecture, dubbing a Cross-Level Cross-Scale Cross-Attention Network (3CROSSNet) to extract features from different scales or resolutions. To better get features of different scales, CSANet [37] proposes a cross self-attention network and a multi-scale fusion module to adaptively consider the information of different scales and establishes a fast descent branch to bring richer gradient information. Additionally, Qiu et al. [38] adopted the idea of error correction feedback structure to fully capture the local features of point clouds, leading a geometric back-projection network for point cloud classification.
3. Materials and Methods
In this section, we illustrate how our UFO-Net can be used for point cloud classification tasks. The designed details of UFO-Net are also systematically presented as follows.
The overall architecture of UFO-Net is depicted in Figure 1. It consists of four main components: 1) Backbone: a backbone for mining features from point clouds; 2) Augmented sampling and grouping (ASG) modules: two ASG modules designed to extract features from different dimensions; 3) Stacked UFO attention layers: four stacked UFO attention layers to extract more detailed information and form global feature; 4) Prediction heads: global feature classified by two cascaded feed-forward neural networks LBRs (combing Linear, BatchNorm (BN) and LeakyRelu layers) each with a dropout probability of 0.5, finished by a Linear layer to predict the final scores. In detail, UFO-Net aims to transform the input points into a new higher dimensional feature space, which can describe the affinities between points as a basis for various point cloud processing tasks. Mapping points to high-dimensional space simplifies the extraction of local and global features of the point cloud. The encoder of UFO-Net starts by embedding the input coordinates into a new feature space. The embedded features are later fed into 2 cascaded ASGs to obtain more local detailed information. The detailed features are then fed into 4 stacked UFO layers to learn a semantically rich and discriminative representation for each point, followed by a linear layer to generate the output feature. Overall, the encoder of UFO-Net shares almost the same philosophy of design as PCT. We refer the reader to [16] for details of the original Point Cloud Transformer.
3.1. Augmented Sampling and Grouping Module
In the field of optical images, the local area of a pixel can usually be represented as a pixel in the vicinity of a fixed image element size. In 3D point cloud operations, the neighborhood of a single point is defined by the metric distance in the 3D coordinate system. Due to the sparse local regions and irregular geometric structure of the point cloud, the sampling and grouping (SG) [16] operation cannot capture well the different 3D geometric structure features among different regions. This indirectly leads to a learning bottleneck in the subsequent nonlinear mapping layer, and a different extractor is required.
Formally, given a set of unordered point clouds with , where N is the number of points and d is the feature dimension. When each point is represented by 3D coordinates , then d = 3. For any pi ∈ P, there are k-nearest points pj ∈ P, where j ∈ N. This paper uses the k-nearest neighbor (KNN) search scheme based on comparative experiments. But the existing local shape model with KNN is vulnerable to the local density of the point cloud. In other words, points near the centroid are feature-rich, while points far from the centroid are easily ignored. Therefore, we seek an optimized feature extractor. We draw upon the ideas of PCT [16] and PointNorm [39] to design an augmented local neighbor aggregation strategy ASG. The ASG module optimizes the point embedding and augments UFO-Net’s ability of local feature extraction. Therefore, ASG module is the important component of our UFO-Net framework.
The ASG module introduces a geometric affine operator to local feature extraction. First, the input coordinates are projected using two MLPs to increase the dimension to . In this paper, is taken as 64. Then, the specific implementation of the ASG module is divided into three steps: (i) selecting local centroids by using farthest point sampling (FPS); (ii) obtaining grouped local neighbors (GLNs) using the KNN algorithm based on Euclidean distance; (iii) normalizing the GLNs by using the affine function. To obtain features from different local regions, the GLNs are passed through a lightweight geometric affine function. This operation can help overcome the disadvantage of uneven sampling.
The feature process of ASG can be simply described as follows:
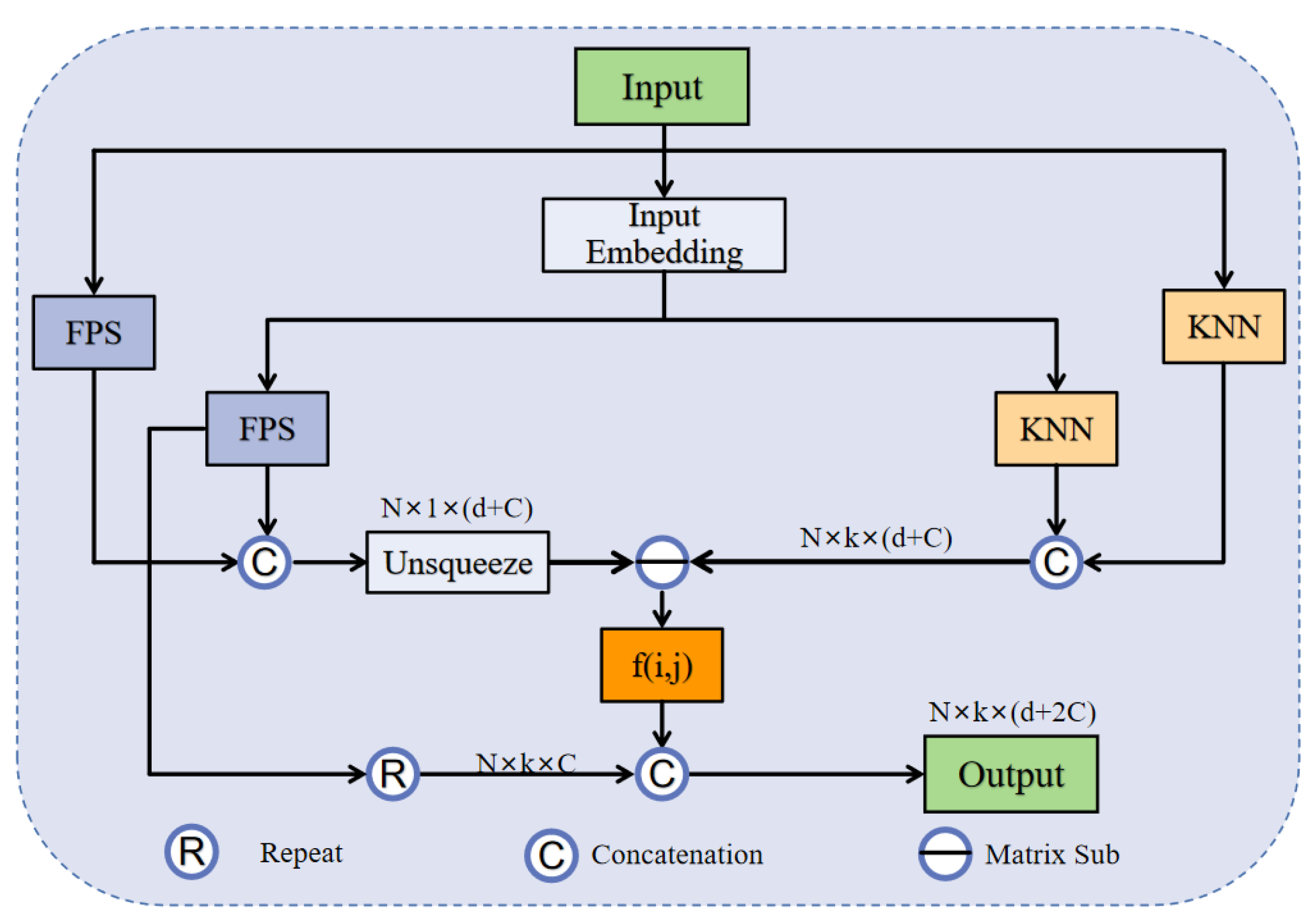
The ASG process is shown in Figure 2, where is the k neighbor features found by KNN from the projection coordinates, is the k neighbor features found by FPS from the original coordinates, is the k neighbor points found by KNN from the original coordinates, and is the centroid computed by the FPS algorithm from the original coordinates. In addition, and are learnable affine transformation parameters, denotes the Hadamard production of element directions, is a number that keeps the value stable, and I is the unsqueeze operation. Very importantly, is a scalar describing the deviation of features between all local groups and channels, obtained from the variance. This helps to obtain more useful features. And f (i, j) is denoted as the lightweight geometric affine function . It is the ASG that transforms the local features into a normally distributed process that maintains the geometric properties of the original points. Specifically, this method enhances the identification of domain features in the vicinity of each centroid. The sizes of the point cloud are decreased to 512 and 256 points within the two ASG layers.
Herein, different from the sampling and grouping method, ASG continues to consider the projection features sampled at the farthest point. The input feature is a matrix with subsampling points, d-dim coordinates and two -dim projection features. The output is a feature matrix , where k is the number of points in the nearest domain of the centroid.
Figure 2.
The illustration of the proposed augmented sampling and grouping (ASG) module. FPS represents Farthest Point Sampling algorithm. KNN represents k-nearest neighbor algorithm and f (i, j) means a lightweight function.
Figure 2.
The illustration of the proposed augmented sampling and grouping (ASG) module. FPS represents Farthest Point Sampling algorithm. KNN represents k-nearest neighbor algorithm and f (i, j) means a lightweight function.
3.2. Effective Local Feature Learning Module
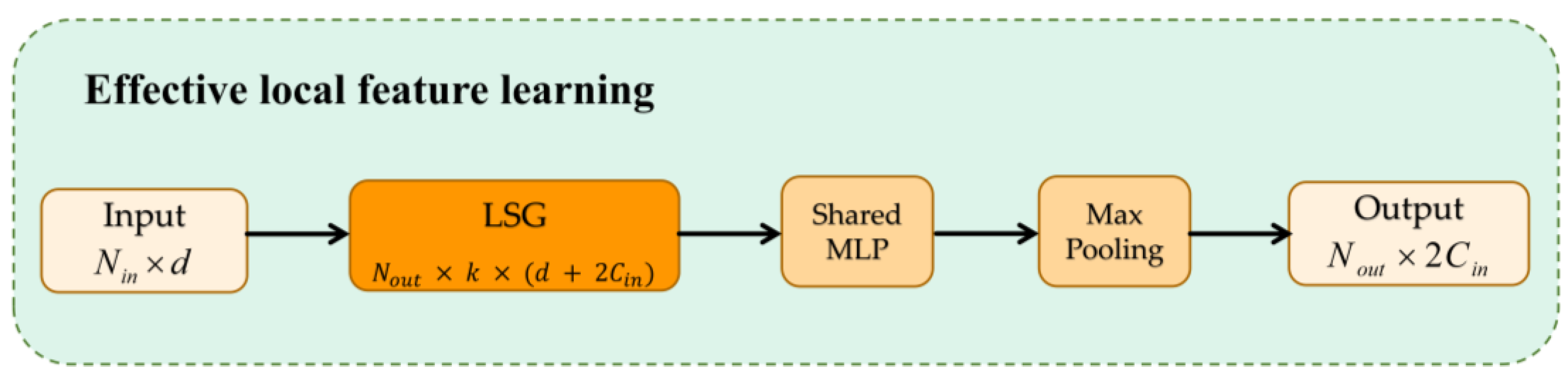
The existing works [10,40,41] usually use symmetric functions such as max/mean/sum pooling to downscale and preserve the main features to solve the disorder of point clouds. The features obtained from the original point clouds processed by the ASG module lack global properties. To solve this problem, we design an effective local feature learning (EFL) module. In order to utilize the feature information collected from ASG, it is necessary to find a reasonable bridging technique between the two feature processing methods, the ASG module and the following UFO layers. Usually, the max-pooling function is applied to k neighbors of each elaborated local graph to obtain feature representations that aggregate local contexts as the center. Here, we denote the EFL module as:
For local sampling and grouping regions , we use a shared neural network comprising two cascaded LBRs A and a max-pooling operator M as symmetric functions to aggregate features. The alignment invariance of the point cloud can be fully guaranteed by ELF. By this learning, the output size of ELF changes from the input matrix to the feature size .
Figure 3.
The architecture of Effective local feature learning (EFL). After ASG’s learning, EFL gets a high-level feature by a shared neural network comprising two cascaded LBRs and a max-pooing operator.
Figure 3.
The architecture of Effective local feature learning (EFL). After ASG’s learning, EFL gets a high-level feature by a shared neural network comprising two cascaded LBRs and a max-pooing operator.
3.3. Stacked UFO Attention Layers
To develop the exposition of the single UFO attention layer, we first revisit the principle of the self-attention (SA) mechanism. The key to SA mechanism is made up of query, key, and value matrices, which are denoted by Q, K, and V, respectively. The Q, K, and V matrices are generated from encoded local features using linear transformations [33]. Here, is the dimension of the key vectors, and the softmax function is applied to the dot product of the query and key matrices. Formally, the traditional SA mechanism is expressed as:
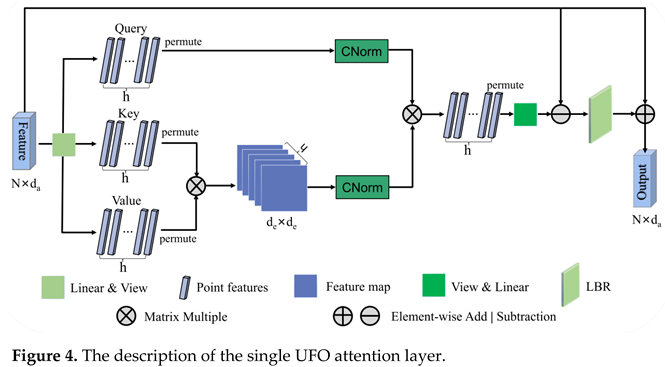

The UFO attention mechanism is explained in the forthcoming note. The architecture of the single UFO attention layer is depicted in Figure 4. We use linear transformation and view operation to convert the input features into three new representations, query, key, and value matrices, respectively. Given an input feature mapping , where N is the number of point clouds and is the feature dimension. Formally, the feature dimension, , is given that h is the number of head and de is the dimension of each head.
Then the single UFO attention layer is expressed as:
where ψ, Φ, γ are linear transformation and view operation. After permutation, , , , note that h = 4 selected by the ablation experiment. We compute the product of KUT and VU to obtain the spatial correlation matrix KV_Attenion for all points. Next, we use CN to normalize KV_Attenion to get KV_Norm. At the same time, we use CN to normalize QU to obtain Q_Norm. It is a common L2-norm, but it is applied along two dimensions: the spatial dimension of KUTVU and the channel dimension of QU. Thus, it is called CrossNorm. Then, permutation and view operation are also adopted.
CrossNorm (CN) is computed as follows:
where λ is a learnable parameter initialized as a random matrix and x is the transformed feature. It generates h clusters through linear kernel method. The operation process can be described as:
Let , th-en U(x) can be represented as:
x is replaced by .
The computational nature of CN shows that this is a l2-normalization, acting successively on the feature channel and the feature channel of KUTVU and QU, respectively. Similarly, based on the analysis of the graph convolutional network [42] for the Laplace matrix L = D - E in place of the adjacency matrix E, the offset matrix can diminish the effect of noise [16]. This method provides sufficient discriminative feature information. Therefore, we design offset method to efficiently learn the representation of the distinction of the embedded features. Additionally, the output feature is further obtained through a LBR network and an element-wise addition operation with the input feature.
As the output dimension of each layer is kept the same as the input features, the output of the single UFO attention layer is concatenated four times through the feature dimension, followed by a linear transformation, and more features are obtained. This process can be denoted as:
We then concatenate the input features and the output of stacked UFO attention layers to fully obtain contextual features.
4. Experiments and Results
In this section, we first introduced the experimental settings, as well as some general parameters and experimental data. Then, we showed how to train UFO-Net to perform the shape classification tasks. Immediately, we compared our model with other existing methods quantitatively and qualitatively. We evaluated the performance of the network on two public classification datasets. We implemented the project with Pytorch [43] and Python. This paper involved experiments using a single Tesla T4 GPU card under CUDA 10.0.
The input point cloud contained only 1024 points with three-dimensional space coordinate information (x, y, z). The model derived 64 size vectors from the embedding module, subsequently fed to the transformer block. To examine the performance of our network, we replaced the two SG modules in PCT with two ASG and EFL modules, and replaced the original attention mechanism with stacked UFO attention layers as the backbone. In particular, the number of nearest neighbors k for ASG was set as 32, derived from subsequent ablation experiments. To classify the input point cloud data into categories, the output processed by a max-pooling (MP) operator and an average-pooling (AP) operator were concatenated on the learned point-wise feature to get the global feature sufficiently. The decoder consisted two cascaded feed-forward neural network LBRDs layers (including Linear, BatchNorm (BN), and LeakyRelu layers each with probability 0.2 and dropout rate with each probability 0.5). The final classification score was predicted by a linear layer.
During training, to prevent overfitting, we performed a random input dropout, a random panning, and a random anisotropic scaling operations to augment the input point clouds. The same soft cross-entropy loss function as [16] was adopted. The stochastic gradient descent (SGD) optimizer with a momentum of 0.9 and weight decay 0.0001 were used for training. During the testing period, a post-processing voting strategy was used. For 300 training phases, the batch size was set to 32 and the initial learning rate was 0.01, with a cosine annealing schedule to adjust the learning rate at each epoch. We chose the mean classification accuracy (mAcc) and the overall accuracy (OA) as evaluation metrics for the experiment.
4.1. Experiments on ModelNet40 Dataset
The ModelNet40 dataset is a widely used benchmark for point cloud shape classification proposed by Princeton University [43], containing 12,311 CAD models of 40 classes of man-made objects in the 3D world. For a fair comparison, we divided the dataset into a training/testing ratio of 8:2 following the convention, with 9843 universally divided objects for training and 2468 objects for testing. Using a common sampling strategy, each object was sampled uniformly to 1024 points and normalized to the unit length.
As shown in Table 1, we compare our proposed UFO-Net with a series of previous representative methods. The results of the classification experiments indicate that UFO-Net can effectively aggregate the global features of the point cloud. In Table 1, the mAcc and OA on ModelNet40 dataset are 90.8% and 93.7% respectively. As shown in Table 3, we can observe that (1) Compared with the classical point-based PointNet, mAcc of our UFO-Net is increased by 4.6%, and OA is improved by 4.5%. (2) Compared with the convolution-based DGCNN, mAcc of our UFO-Net is increased by 0.6%, and OA is increased by 0.8%. (3) Compared with the transformer-based LFT-Net, mAcc of our UFO-Net is increased by 1.1%, and OA is increased by 0.5%. We can also observe from Table 1 that almost the voxel-based methods perform worse than the point-based methods, which is due to the limitation of less local information. Therefore, our method can effectively learn the spatial invariance of point clouds, and the network has obvious advantages over other methods in 3D object classification. This is because our UFO-Net extracts local features of point clouds by the ASG module and the stacked UFO layers, which allows for obtaining more information.
To further explore the neighbor feature extraction capability of our UFO-Net, we evaluate the accuracy of each class. The classification accuracy calculation results are shown in Table 2. When the model is tested, the data is classified according to the label. Models with the same label are grouped into the same category to get 40 model categories. The number in parentheses after each category indicates the number of models. Under a given number of test models, the classification accuracy of 10 objects such as airplane, bed, bowl, guitar, laptop, person, sofa, stairs, stool, toilet reaches 100%. Although there are also some categories that have a low classification accuracy, it can be seen that the classification accuracy rate of most categories is high. Therefore, it can be concluded that our model has good feature extraction ability for some objects that are important for edge articulation features.
4.2. Experiments on ScanObjectNN Dataset
Due to the rapid development of point cloud research, it can no longer fully meet some practical needs. For this reason, we also conducted experiments on the Scanned Object Neural Network dataset (ScanObjectNN) [53], a real-world point cloud dataset based on LiDAR scanning. ScanObjectNN is a more cumbersome set of point cloud category benchmark, dividing about 15k objects in 700 specific scenarios into 15 classes and 2902 different object instances in the real world. The ScanObjectNN dataset has some variables, of which we are considering the most troublesome variable in the evaluation (PB_T50_RS). Each perturbation variable (prefix PB) in this dataset randomly shifts from the box centroid of the bounding box to 50% of the original size along a specific axis. Suffix R and S represents rotation and scaling [53]. PB_T50_RS contains 13,698 real-world point cloud objects from 15 categories. In particular, 11416 objects are used for training and 2282 objects are used for testing. This dataset is especially a huge challenge for existing point cloud classification techniques. In this experiment, each point cloud object sampled 1024 points, and model was trained using only the local (x, y, z) coordinates.
Table 3.
Classifification results on ScanObjectNN dataset.
| Method | mAcc (%) | OA (%) |
| 3DmFV [9] PointNet [10] PointNet++ [11] SpiderCNN [54] DGCNN [12] PointCNN [30] BGA-DGCNN [53] PCT [16] DRNet [50] GBNet [38] RPNet++ [55] UFO-Net (ours) |
58.1 63.4 75.4 69.8 73.6 75.1 75.7 77.3 78.0 77.8 79.9 82.3 |
63.0 68.2 77.9 73.7 78.1 78.5 79.7 80.0 80.3 80.5 82.0 83.8 |
For real-world point cloud classification, we use the same network, training strategy, and 1k of 3D coordinates as input. We quantitatively compared our UFO-Net with other state-of-the-art methods on the hardest ScanObjectNN benchmark dataset. In Table 3, we show the results of competing methods for scanning objective network datasets. Our network has an overall accuracy of 83.8% and an average class accuracy of 82.3%, which is a significant improvement on this benchmark. The results show that mAcc is improved by 5%, and OA is increased by 3.8%, compared with the classical PCT. Furthermore, even when measured using the dynamic local geometry capture network RPNet++, we still have a fairly good lifting in mAcc and OA, with increments of 2.4% and 1.8% respectively, which seems to be tailor-made for this dataset. On top of that, we observe that our UFO-Net creates the smallest gap between mAcc and OA. This phenomenon shows that our method has good robustness.
Since the ScanObjectNN dataset has some difficult cases to classify, the presence of feature-independent background points in ScanObjectNN can pose a challenge to the network. To obtain a global representation of the point cloud, we use the ASG module to learn a local fine-grained feature representation. This is because the design of ASG enhances the relationships between points and enriches the information of geometric features distributed on long edges. Furthermore, our approach provides an efficient solution with stacked UFO attention layers aiming to minimize the impact of these points by equally weighting them according to their channel affinity.
4.3. Model Complexity
We now compute the complexity of UFO-Net with previous state-of-the-art methods on ModelNet40 dataset [43], as shown in Table 4. We compared the number of model parameters to different creative algorithms. PointNet and PointNet++ have less parameters as they only use MLPs to extract features. Besides, DGCNN and PCT also have a small number of parameters, while KPConv and Point Transformer have larger parameters due to their complex network design. Despite this, our UFO-Net achieves a higher accuracy of 93.7%. Notably, our method achieves a similar parameter count to PointNet, yet realizes a state-of-the-art (SOTA) performance on ModelNet40. This result reveals that our UFO-Net improves attention-based methods effectively.
5. Ablation Studies
To further investigate the effectiveness of our proposed method, we also conducted alternative comparative experiments on the ModelNet40 dataset. In order to ensure the fairness of the experiment, the details of experiments remained unchanged. We experienced a comprehensive empirical analysis of the ASG module and stacked UFO attention layers. A series of ablation experiments were reported to verify the effectiveness of the proposed module. In detail, we explored the impact of some important hyper-parameters such as impact of different point sampling densities, the number of nearest neighbors in ASG, and h parameter in stacked UFO attention layers.
5.1. Impact of Point Density
Robustness of point cloud density. Sampling density has an influence on point clouds as shown in Figure 4. Therefore, we conducted experiments to evaluate the ability of UFO-Net to extract features.
Figure 4.
Examples with different point sampling densities on chair and airplane.
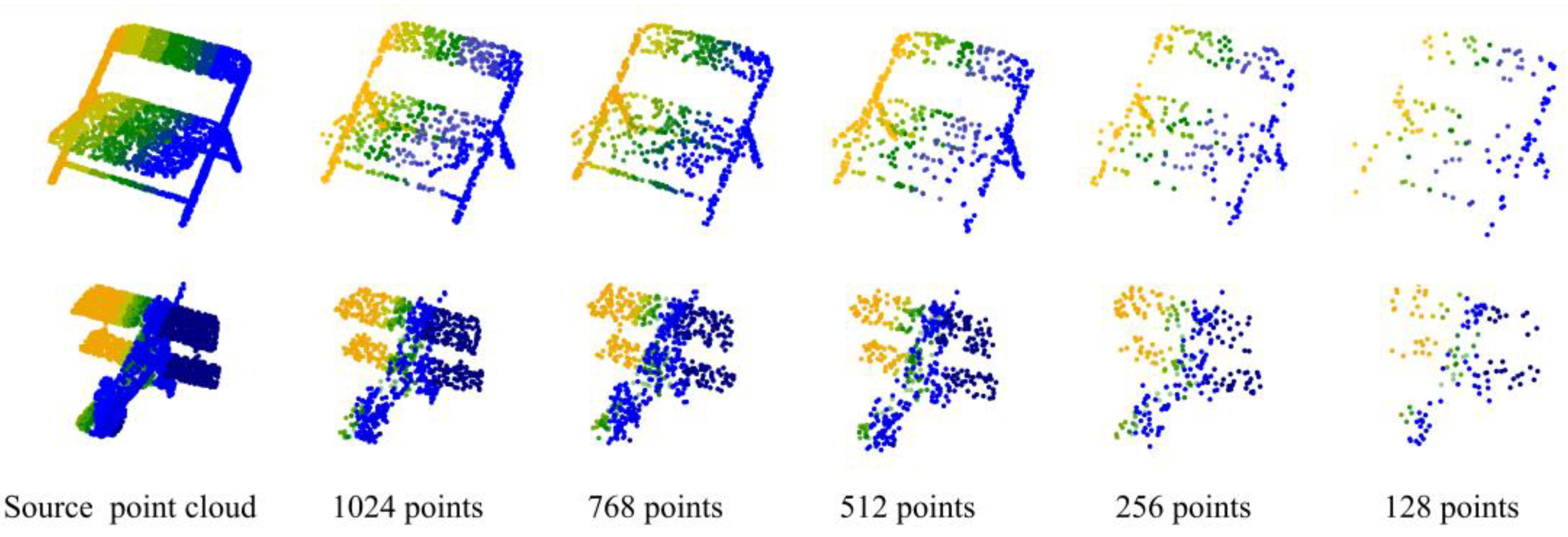
The accuracy of experimental curves for different point densities is shown in Figure 5. From Figure 5, it can be seen that the use of 1024 points to train the model to extract features is effective for the designed network. In real-world scenarios, however, point clouds are always fragmented and not completely cover the surface of the target object. So, in this section, we also conduct experiments at different point densities to evaluate the performance of our network. Figure 5 shows the overall accuracy at different input points on the ModelNet40 dataset. We trained our network using a random sample of 1024, 768, 512, 256, and 128 input points. The curves in the figure expose the accuracy trend of the classification model test. Compared with other methods, our model has good robustness to point cloud density. Even at low point densities, our network maintains good accuracy. For example, 91.1% can be reached at 128 input points. The results show that this model can be widely used in different point densities. For relatively sparse scenes, the model can still work with contextual features efficiently.
5.2. Impact of h Parameter
To further explore the parameter setting details of the stacked UFO attention layers, we evaluated the effect of h on the model performance. For the ModelNet40 dataset, we fairly built a set of experiments corresponding to the value h in each single UFO attention layer. The experimental settings remain unchanged. The experimental results for different h value are shown in Table 5.
We sequentially evaluated the results at 2, 4, 8 and 16 h values respectively. In our original network, h is set to 4. We trained and tested all h parameters using the same dataset to perform fair quantitative evaluations. It can be seen from Table 5 that if h is 2, the final overall accuracy is reduced by 1.3%; if h is 8, the final overall accuracy is reduced by 0.8%; if h is 16, the final overall accuracy is reduced by 0.5%. Therefore, it can be concluded that the network performs best when the h parameter is set to 4. Last but not least, there is no doubt that we can achieve comparable results regardless of the number of h. The result further indicates good stability of our approach on the ModelNet40 dataset.
Immediately after, we evaluate the testing OA curves for h values of 2, 4, 8 and 16 on the ModelNet40 dataset. The results are demonstrated in Figure 6. It can be seen from the figure that the model training climbs slowly when h = 2 or 16. When h is 4 or 8, the model can reach high accuracy rate quickly, and the former reach the fitness peak more quickly. Overall, it seems that all of our models have fast convergence ability.
5.3. Impact of Querying Methods and Number of Neighbors
Our approach relies heavily on ASG module. In addition to the above large number of experiments, we also studied the adaptability of the neighbor point selection method to the network. The mainstream range search methods for obtaining local features today are ball query and k-nearest neighbor (KNN) search. The former ball method usually returns all points in the radius range class of a point [11], while the latter KNN returns a fixed number of points near a point [12]. We tested the impact of the two methods on UFO-Net separately. Here, to keep the experiment fair, we guaranteed that the number of neighbors was the same. The testing results on the ModelNet40 dataset are shown in Table 6. The results show that our proposed ASG method prefers the k-nearest neighbor selection method for the local feature aggregation. Therefore, we believe that KNN discards ambiguous feature information when acquiring features.
Besides, we also evaluated the effect of the number of points in each neighborhood, which was the effect of the number k. In order to ensure the fairness of the experiment, we still adopted 4 stacked UFO attention layers in this experimental stage. Table 7 shows the results of the number k on accuracy. In this experiment, we just sampled some representative numbers of nearest neighbors to test UFO-Net. We reported results of 8, 16, 24, 32, 40, and 48, with k = 32 achieving the best results. From Table 7, we can see that if the value of k is small, the neighborhood characteristics cannot be fully expressed. This may be because strong feature correlation cannot be achieved between attention layers. Certainly, when the value of k is large, the Euclidean distance cannot estimate its geometry, which will produce a large noise deviation during feature extraction. Our network achieves the highest mAcc of 90.8% and OA of 93.7%, when k is 32.
6. Conclusions
In this paper, we have designed a new point cloud classification network called UFO-Net. A novel transformer method suitable for learning irregular domain point cloud is proposed. For the first time, we employ the linearly-normalized attention mechanism in point cloud processing tasks, as it can help to mitigate the effects of differences in scale between different features. In order to solve the problem of uneven sampling of points in the local feature extraction module, we introduce a novel augmented sampling and grouping (ASG) module. This module reconsiders a local feature aggregation module and a more comprehensive method of feature processing. Our model also employs an effective feature learning (EFL) pipeline connecting ASG and stacked UFO attention layers for processing geometric features. Among them, our module generates rich contextual information and is able to fully capture spatial features with significant local feature variations through tacked UFO attention layers. Based on these strategies above, we have designed an end-to-end deep convolutional neural network for point cloud classification. This method achieved state-of-the-art results in the task of classifying point clouds using only 3D coordinates as input. Moreover, we have proven the superiority of our modules through various ablation experiments. Experiments show that our method achieves a better performance than other current frameworks. What’s more, we hope that our work will provide further research into the characteristics of transformer in point cloud processing tasks. And we plan to investigate the idea of our new network architecture in part segmentation tasks and semantic segmentation tasks.
Author Contributions
Conceptualization, S.H. and H.Y.; methodology, S.H.; resources, S.H. and H.Y.; writing—original draft preparation, S.H.; writing—review and editing, S.H., P.G., Z.T., D.G., L.W. and H.Y.; visualization, S.H. and P.G.; supervision, H.Y.; project administration, S.H.; funding acquisition, H.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported and funded by The National Key R&D Project from Ministry of Science and Technology (2021YFA1201603).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
We used two publicly available datasets in this study, ModelNet40 and ScanObjectNN. ModelNet40 can be found here: https://modelnet.cs.princeton.edu/. ScanObjectNN can be found here: https://hkust-vgd.github.io/scanobjectnn/.
Acknowledgments
The authors want to thank the computing resources supported by the high-performance Computing Platform of Guangxi University.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rahman, M.M.; Tan, Y.; Xue, J.; Lu, K. Recent advances in 3d object detection in the era of deep neural networks: A survey. IEEE Trans. Image Process. 2020, 29, 2947–2962. [Google Scholar] [CrossRef] [PubMed]
- Schwarz, B. Lidar: Mapping the world in 3d. Nat. Photonics 2010, 4, 429–430. [Google Scholar] [CrossRef]
- Zhang, R.; Candra, S.A.; Vetter, K.; Zakhor, A. Sensor Fusion for Semantic Segmentation of Urban Scenes. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 1850–1857. [Google Scholar]
- Dewi, C.; Chen, R.C.; Yu, H.; Jiang, X. Robust detection method for improving small traffic sign recognition based on spatial pyramid pooling. J. Ambient. Intell. Humaniz. Comput. 2021, 1–18. [Google Scholar] [CrossRef]
- Biswas, J.; Veloso, M. Depth Camera Based Indoor Mobile Robot Localization and Navigation. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Saint Paul, MN, USA, 14-18 May 2012; pp. 1697–1702. [Google Scholar]
- Zermas, D.; Izzat, I.; Papanikolopoulos, N. Fast Segmentation of 3d Point Clouds: A Paradigm on Lidar Data for Autonomous Vehicle Applications. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May-3 June 2017; pp. 5067–5073. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; IEEE: Piscataway Township, NJ, USA, 2016. [Google Scholar]
- Zhao, H.; Jia, J.; Koltun, V. Exploring self-attention for image recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 10076–10085. [Google Scholar]
- Ben-Shabat, Y.; Lindenbaum, M.; Fischer, A. , 3DmFV: Three-dimensional point cloud classification in real-time using convolutional neural networks. IEEE Robot. Autom. Lett. 2018, 3, 3145–3152. [Google Scholar] [CrossRef]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. PointNet: Deep Learning on Point Sets for 3d Classification and Segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 652–660. [Google Scholar]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. PointNet++: Deep Hierarchical Feature Learning on Point Sets in A Metric Space. In Proceedings of the 31st International Conference on Neural Information Processing Systems (NIPS), Long Beach, CA, USA, 4–7 December 2017; pp. 5099–5108. [Google Scholar]
- Wang, Y.; Sun, Y.; Liu, Z.; Sarma, S.E.; Bronstein, M.M.; Solomon, J.M. Dynamic graph cnn for learning on point clouds. ACM Trans. Graph. (Tog) 2019, 38, 1–12. [Google Scholar] [CrossRef]
- Park, C.; Jeong, Y.; Cho, M.; Park, J. Fast point transformer. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 19–24 June 2022; pp. 16949–16958. [Google Scholar]
- Han, X.F.; Jin, Y.F.; Cheng, H.X.; Xiao, G.Q. Dual transformer for point cloud analysis. IEEE Trans. Multimed. 2022, 1–10. [Google Scholar] [CrossRef]
- Zhao, H.; Jiang, L.; Jia, J.; Torr, P.H.; Koltun, V. Point transformer. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Nashville, TN, USA, 20–25 June 2021; pp. 16259–16268. [Google Scholar]
- Guo, M. H.; Cai, J.; Liu, Z. N.; Mu, T. J.; Martin, R. R.; Hu, S. , Pct: Point cloud transformer. Comput. Vis. Media 2020, 7, 187–199. [Google Scholar] [CrossRef]
- Song, J.g. , UFO-ViT: High Performance Linear Vision Transformer without Softmax. ArXiv 2021, abs/2205.13805.
- Le, T.; Duan, Y. Pointgrid: A deep network for 3d shape understanding. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 9204–9214. [Google Scholar]
- Maturana, D.; Scherer, S. VoxNet: A 3D Convolutional Neural Network for real-time object recognition. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 922–928. [Google Scholar]
- Vo, A.V.; Truong-Hong, L.; Laefer, D.F.; Bertolotto, M. Octree-based region growing for point cloud segmentation. ISPRS J. Ph- Otogramm. Remote Sens. 2015, 104, 88–100. [Google Scholar] [CrossRef]
- Klokov, R.; Lempitsky, V. Escape from cells: Deep kd-networks for the recognition of 3d point cloud models. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 863–872. [Google Scholar]
- Meng, H.Y.; Gao, L.; Lai, Y.K.; Manocha, D. Vv-net: Voxel vae net with group convolutions for point cloud segmentation. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27–28 October 2019; pp. 8500–8508. [Google Scholar]
- Simonovsky, M.; Komodakis, N. Dynamic edge-conditioned filters in convolutional neural networks on graphs. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 3693–3702. [Google Scholar]
- Jing, W.; Zhang, W.; Li, L.; Di, D.; Chen, G.; Wang, J. , AGNet: An attention-based graph network for point cloud classification and segmentation. Remote Sens. 2022, (4), 1036. [Google Scholar] [CrossRef]
- Lin, Z.H.; Huang, S.Y.; Wang, Y.C.F. Convolution in the cloud: Learning Deformable Kernels in 3D Graph Convolution Networks for Point Cloud Analysis. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 1800–1809. [Google Scholar]
- Lei, H.; Akhtar, N.; Mian, A. S. , Spherical kernel for efficient graph convolution on 3d point clouds. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 43, 3664–3680. [Google Scholar] [CrossRef]
- Li, G.; Müller, M.; Qian, G.; Perez, I. C. D.; Abualshour, A.; Thabet, A. K.; Ghanem, B. , DeepGCNs: Making gcns go as deep as cnns. IEEE Transactions on Pattern Analysis and Machine Intelligence 2021. [CrossRef] [PubMed]
- Chen, C.; Fragonara, L.Z.; Tsourdos, A. GAPNet: Graph attention based point neural network for exploiting local feature of point cloud. Neurocomputing 2021, 438, 122–132. [Google Scholar] [CrossRef]
- Xu, M.; Zhou, Z.; Qiao, Y. , Geometry Sharing Network for 3D Point Cloud Classification and Segmentation. In Proceedings of the AAAI Conference on Artificial Intelligence (AAAI), New York, USA, 7-12 February 2020; pp. 12500–12507. [Google Scholar]
- Li, Y.; Bu, R.; Sun, M.; Wu, W.; Di, X.; Chen, B. Pointcnn: Convolution on x-transformed points. Adv. Neural Inf. Process. Syst. 2018, 31, 820–830. [Google Scholar]
- Luong, T.; Pham, H.; Manning, C. D. , Effective Approaches to Attention-based Neural Machine Translation. ArXiv 2015, abs/1508.04025.
- Bahdanau, D.; Cho, K.; Bengio, Y. , Neural Machine Translation by Jointly Learning to Align and Translate. CoRR 2014, abs/1409.0473.
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS), Los Angeles, CA, USA, 4–9 December 2017; pp. 5998–6008. [Google Scholar]
- Tao, Z.; Zhu, Y.; Wei, T.; Lin, S. Multi-head attentional point cloud classification and segmentation using strictly rotation invariant representations. IEEE Access 2021, 9, 71133–71144. [Google Scholar] [CrossRef]
- Wen, X.; Li, T.; Han, Z.; Liu, Y. S. , Point cloud completion by skip-attention network with hierarchical folding. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13-19 June 2020; pp. 1936–1945. [Google Scholar]
- Han, X. F.; He, Z. Y.; Chen, J.; Xiao, G. Q. , 3CROSSNet: Cross-level cross-scale cross-attention network for point cloud representation. IEEE Robot. Autom. Lett. 2022, 7, 3718–3725. [Google Scholar] [CrossRef]
- Wang, G.; Zhai, Q.; Liu, H. Cross self-attention network for 3d point cloud. Knowl. Based Syst. 2022, 247, 108769. [Google Scholar] [CrossRef]
- Qiu, S.; Anwar, S.; Barnes, N. Geometric back-projection network for point cloud classification. IEEE Trans. Multimed. 2021, 24, 1943–1955. [Google Scholar] [CrossRef]
- Zheng, S.; Pan, J.; Lu, C.-T.; Gupta, G. , PointNorm: Normalization is All You Need for Point Cloud Analysis. ArXiv 2022, abs/2207.06324.
- Liu, Y.; Fan, B.; Xiang, S.; Pan, C. Relation-shape convolutional neural network for point cloud analysis. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 8895–8904. [Google Scholar]
- Yu, T.; Meng, J.; Yuan, J., Multi-view Harmonized Bilinear Network for 3D Object Recognition. 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18-23 June 2018; pp. 186–194. 23 June.
- Bruna, J.; Zaremba, W.; Szlam, A.; LeCun, Y. Spectral networks and deep locally connected networks on graphs. In Proceedings of the International Conference on Learning Representations, Munich, Germany, 14–16 April 2014. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. Pytorch: An imperative style, high-performance deep learning library. Adv. Neural Inf. Process. Syst. 2019, 32. Available online: https://proceedings.neurips.cc/paper/2019/hash/bdbca288fee7f92f2bfa9f7012727740-Abstract.html (accessed on 24 October 2022).
- Wu, Z.; Song, S.; Khosla, A.; Yu, F.; Zhang, L.; Tang, X.; Xiao, J. 3d shapenets: A deep representation for volumetric shapes. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1912–1920. [Google Scholar]
- Su, H.; Maji, S.; Kalogerakis, E.; Learned-Miller, E. Multi-view convolutional neural networks for 3d shape recognition. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 945–953. [Google Scholar]
- Feng, Y.; Zhang, Z.; Zhao, X.; Ji, R.; Gao, Y. GVCNN: Group-view convolutional neural networks for 3D shape recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; IEEE Computer Society Press: Los Alamitos, CA, USA, 2018; pp. 264–272. [Google Scholar]
- Ravanbakhsh, S.; Schneider, J. G.; Póczos, B. , Deep Learning with Sets and Point Clouds. ArXiv 2016, abs/1611.04500.
- Thomas, H.; Qi, C.R.; Deschaud, J.E.; Marcotegui, B.; Goulette, F.; Guibas, L.J. Kpconv: Flexible and deformable convolution for point clouds. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea, 27–28 October 2019; pp. 6411–6420. [Google Scholar]
- Gao, Y.; Liu, X.; Li, J.; Fang, Z.; Jiang, X.; Huq, K. M. S. , LFT-Net: Local feature transformer network for point clouds analysis. IEEE Transactions on Intelligent Transportation Systems 2023, 24, 2158–2168. [Google Scholar] [CrossRef]
- Qiu, S.; Anwar, S.; Barnes, N. Dense-resolution network for point cloud classification and segmentation. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision (WACV), Waikoloa, HI, USA, 3–8 January 2021; pp. 3813–3822. [Google Scholar]
- Atzmon, M.; Maron, H.; Lipman, Y. , Point convolutional neural networks by extension operators. ACM Trans. Graph. (TOG) 2018, 37, 1–12. [Google Scholar] [CrossRef]
- Li, Y.; Lin, Q.; Zhang, Z.; Zhang, L.; Chen, D.; Shuang, F. MFNet: Multi-level feature extraction and fusion network for large scale point cloud classification. Remote. Sens. 2022, 14, 5707. [Google Scholar] [CrossRef]
- Uy, M.A.; Pham, Q.H.; Hua, B.; Nguyen, D.; Yeung, S. Revisiting Point Cloud Classification: A new benchmark dataset and classification model on real-world data. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019; pp. 1588–1597. [Google Scholar]
- Xu, Y.; Fan, T.; Xu, M.; Zeng, L.; Qiao, Y. Spidercnn: Deep learning on point sets with parameterized convolutional filters. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 87–102. [Google Scholar]
- Sheshappanavar, S. V.; Kambhamettu, C. , Dynamic Local Geometry Capture in 3D Point Cloud Classification. In Proceedings of the IEEE 4th International Conference on Multimedia Information Processing and Retrieval (MIPR). Tokyo, Japan, 8-10 Septemper 2021; pp. 158–164. [Google Scholar]
- Mao, J.; Wang, X.; Li, H. Interpolated Convolutional Networks for 3d Point Cloud Understanding. In Proceedings of the IEEE/C- VF International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019; pp. 1578–1587. [Google Scholar]
- Lu, D.; Xie, Q.; Gao, K.; Xu, L.; Li, J. , 3DCTN: 3D convolution-transformer network for point cloud classification. IEEE Trans. Intell. Transp. Syst. 2022, 23, 24854–24865. [Google Scholar] [CrossRef]
Figure 1.
The architecture of UFO-Net. The input point cloud is processed into embedding module. Then, two cascaded ASG and EFL modules are used to mine features. Next, we connect output with stacked UFO layers to obtain high-level features by a concatenation operation. Both Max-pooling and average-pooling are adopted to aggregate features, as well as fully connected layers to obtain the class scores.
Figure 1.
The architecture of UFO-Net. The input point cloud is processed into embedding module. Then, two cascaded ASG and EFL modules are used to mine features. Next, we connect output with stacked UFO layers to obtain high-level features by a concatenation operation. Both Max-pooling and average-pooling are adopted to aggregate features, as well as fully connected layers to obtain the class scores.
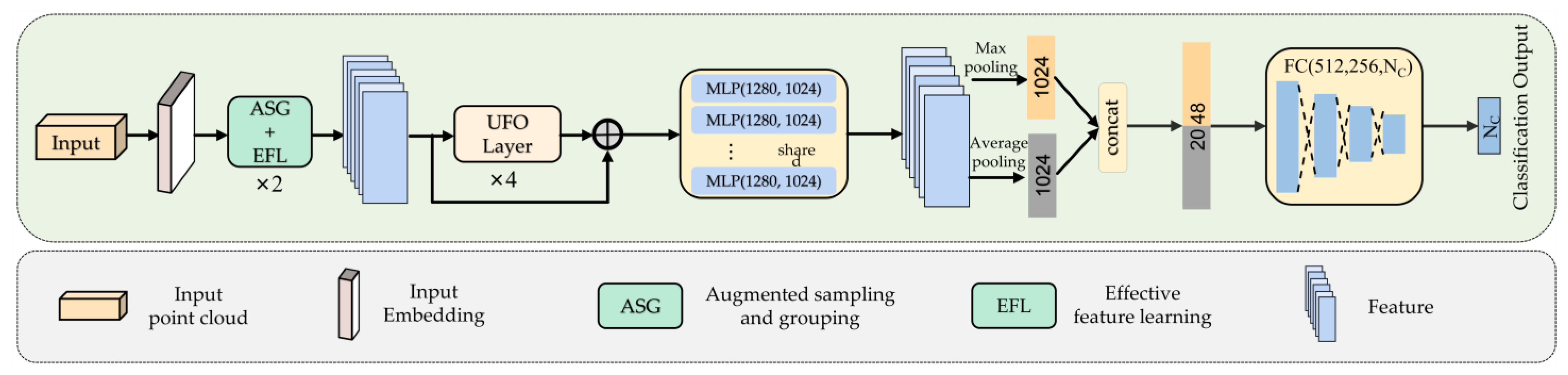
Figure 5.
Classification results for different input points on the ModelNet40 dataset.
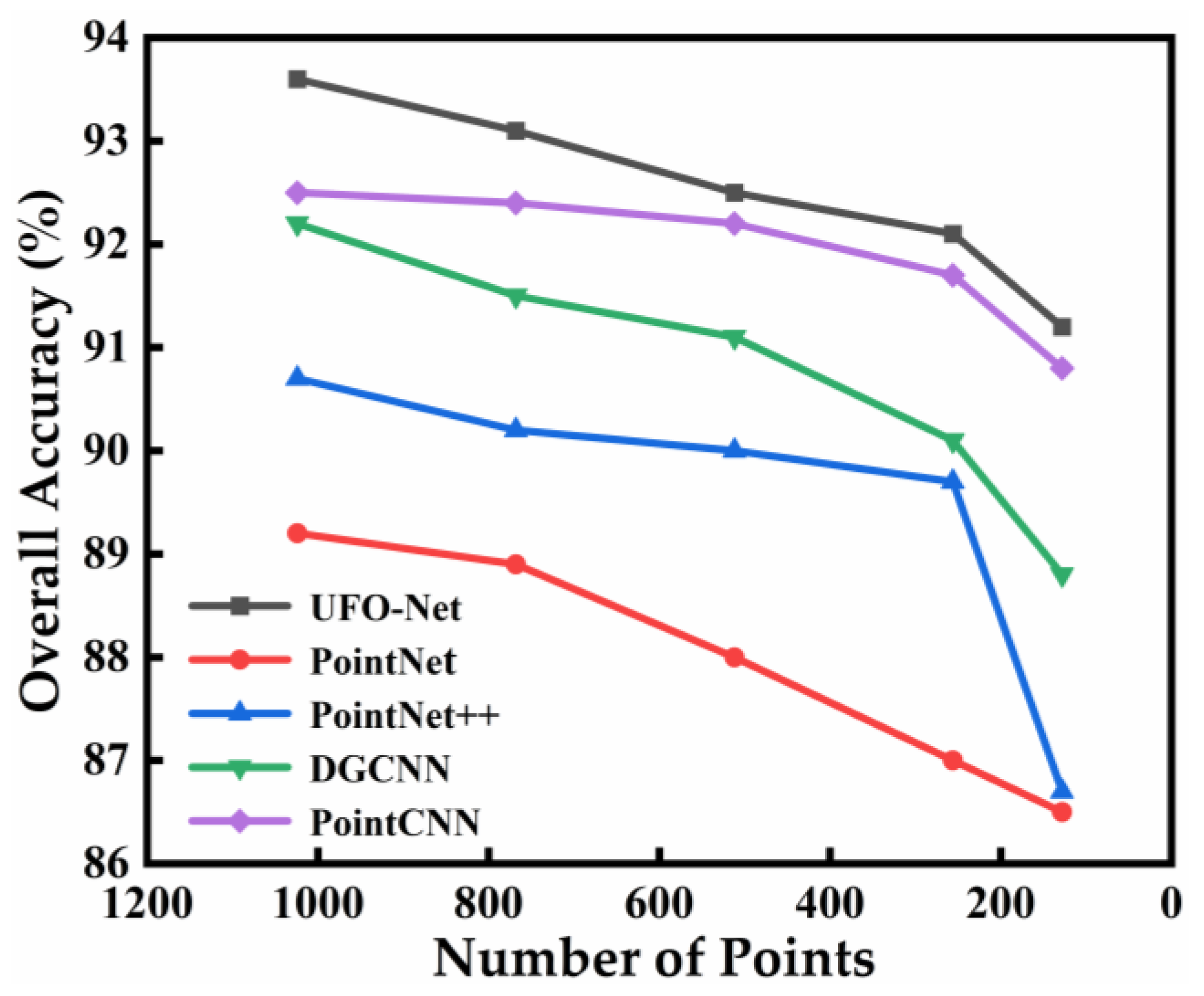
Figure 6.
Four run results (OA) of UFO-Net with different h values on ModelNet40 test dataset. We use h to represent the value of UFO`s head.
Figure 6.
Four run results (OA) of UFO-Net with different h values on ModelNet40 test dataset. We use h to represent the value of UFO`s head.
Table 1.
Comparison with state-of-the-art approaches on ModelNet40 dataset.
| Method | Representation | Input size | mAcc (%) | OA (%) |
| VoxNet [19] 3DShapeNets [44] MVCNN [45] GVCNN [46] DeepNet [47] ECC [23] PointNet [10] PointNet++ [11] DGCNN [12] KPConv [48] RS-CNN [40] LFT-Net [49] GAPNet [28] PointCNN [30] DRNet [50] PCNN [51] MFNet [52] PCT [16] AGNet [24] Point Transformer [15] UFO-Net (ours) |
voxel voxel multi-view multi-view point point point point+normal point point point point+normal point point point point point point point point point |
323 303 12×2242 8× 5000×3 1024×3 1024×3 1024×3 1024×3 7000×3 1024×3 1024×3 1024×3 1024×3 1024×3 1024×3 1024×3 1024×3 1024×3 1024×3 1024×3 |
83.0 77.3 - - - 83.2 86.2 - 90.2 - - 89.7 89.7 88.1 - - 91.4 - 90.7 90.6 90.8 |
85.9 84.7 90.1 93.1 90.0 87.4 89.2 91.9 92.9 92.9 92.9 93.2 92.4 92.2 93.1 92.3 93.1 93.2 93.4 93.7 93.7 |
Table 2.
Classification accuracy under different categories on ModelNet40.
| Categories | Accuracy | Categories | Accuracy | Categories | Accuracy | Categories | Accuracy |
| airplane (100) bathtub (20) bed (100) bench (20) bookshelf (100) bottle (100) bowl (20) car (100) chair (100) cone (20) |
1.00 0.98 1.00 0.81 0.98 0.97 1.00 0.99 0.97 0.96 |
cup (20) curtain (20) desk (86) door (20) dresser (86) flower pot (20) glass box (20) guitar (100) keyboard (20) lamp (20) |
0.65 0.96 0.93 0.95 0.89 0.34 0.90 1.00 0.95 0.92 |
laptop (20) mantel (100) monitor (100) night stand (86) person (20) piano (20) plant (100) radio (20) range hood (100) sink (20) |
1.00 0.95 0.98 0.62 1.00 0.95 0.86 0.75 0.95 0.96 |
sofa (100) stairs (20) stool (20) table (100) tent (20) toilet (100) tv stand (100) vase (100) wardrobe (20) xbox (20) |
1.00 1.00 1.00 0.91 0.97 1.00 0.87 0.86 0.81 0.91 |
Table 4.
Comparisons of UFO-Net’s complexity on ModelNet40 dataset.
| Method | Input | Parameters | OA (%) |
| PointNet [10] PointNet++ [11] KPConv [48] InterpCNN [56] DGCNN [12] Point Transformer [15] PCT [16] 3DCTN [57] UFO-Net (ours) |
1024 1024 1024 1024 1024 1024 1024 1024 1024 |
3.47M 1.48M 15.2M 12.5M 1.81M 4.34M 2.88M 4.22M 3.46M |
89.2 91.9 92.9 93.0 92.9 93.7 93.2 93.3 93.7 |
Table 5.
Experimental results of h parameter setting on the ModelNet40 dataset.
| value of h | mAcc (%) | OA (%) |
| 2 4 8 16 |
89.4 90.8 89.6 90.2 |
92.4 93.7 92.9 93.2 |
Table 6.
Experimental results of different querying methods.
| Grouping Method | Neighbors | OA (%) |
| ball query KNN |
32 32 |
93.1 93.7 |
Table 7.
Experimental results of UFO-Net on ModelNet40 test set with k neighbors in the definition of LSG module.
Table 7.
Experimental results of UFO-Net on ModelNet40 test set with k neighbors in the definition of LSG module.
| Number of Neighbors(k) | mAcc(%) | OA (%) |
| 8 16 24 32 40 48 |
86.4 87.6 89.6 90.8 89.9 88.6 |
89.4 91.2 92.1 93.7 92.5 91.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






