Orders Between Channels and Some Implications for Partial Information Decomposition

Preprint

Article

Orders Between Channels and Some Implications for Partial Information Decomposition

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

André Gomes^*,

Mário A.T. Figueiredo

André Gomes^*,

Mário A.T. Figueiredo

This version is not peer-reviewed

Submitted:

09 May 2023

Posted:

10 May 2023

You are already at the latest version

Alerts

Abstract

The partial information decomposition (PID) framework is concerned with decomposing the information that a set of random variables has with respect to a target variable into three types of components: redundant, synergistic, and unique. Classical information theory alone does not provide a unique way to decompose information in this manner and additional assumptions have to be made. Inspired by Kolchinsky's recent proposal for measures of intersection information, we introduce three new measures based on well-known partial orders between communication channels and study some of their properties.

Keywords:

Subject: Computer Science and Mathematics - Other

1. Introduction

Williams and Beer [1] proposed the partial information decomposition (PID) framework as a way to characterize, or analyze, the information that a set of random variables (often called sources) has about another variable (referred to as the target). PID is a useful tool for gathering insights and analyzing the way information is stored, modified, and transmitted within complex systems [2,3]. It has found applications in areas such as cryptography [4] and neuroscience [5,6], with many other potential use cases, such as in understanding how information flows in gene regulatory networks [7], neural coding [8], financial markets [9], and network design [10].

Consider the simplest case: a three-variable joint distribution

p (y_{1}, y_{2}, t)

describing three random variables: two sources,

Y_{1}

and

Y_{2}

, and a target T. Notice that, despite what the names sources and target might suggest, there is no directionality (causal or otherwise) assumption. The goal of PID is to decompose the information that

Y = (Y_{1}, Y_{2})

has about T into the sum of 4 non-negative quantities: the information that is present in both

Y_{1}

and

Y_{2}

, known as redundant information R; the information that only

Y_{1}

(respectively

Y_{2}

) has about T, known as unique information

U_{1}

(respectively

U_{2}

); the synergistic information S that is present in the pair

(Y_{1}, Y_{2})

but not in

Y_{1}

Y_{2}

alone. That is, in this case with two variables, the goal is to write

I (T; Y) = R + U_{1} + U_{2} + S,

(1)

where

I (T; Y)

is the mutual information between T and Y [11]. Because unique information and redundancy satisfy the relationship

U_{i} = I (T; Y_{i}) - R

(for

i \in {1, 2}

), it turns out that defining how to compute one of these quantities (R,

U_{i}

, or S) is enough to fully determine the others [1,12]. As the number of variables grows, the number of terms appearing in the PID of

I (T; Y)

grows super exponentially [13]. Williams and Beer [1] suggested a set of axioms that a measure of redundancy should satisfy, and proposed a measure of their own. Those axioms became known as the Williams-Beer axioms and the measure they proposed has subsequently been criticized for not capturing informational content, but only information size [14].

Spawned by that initial work, other measures and axioms for information decomposition have been introduced; see, for example, the work by Bertschinger et al. [15], Griffith and Koch [16], and James et al. [17]. There is no consensus about what axioms any measure should satisfy or whether a given measure is capturing the information that it should capture, except for the Williams-Beer axioms. Today, there is still debate about what axioms a measure of redundant information should satisfy and there is no general agreement on what is an appropriate PID [17,18,19,20,21].

Recently, Kolchinsky [12] suggested a new general approach to define measures of redundant information, also known as intersection information (II), the designation that we adopt hereinafter. At the core of that approach is the choice of an order relation between information sources (random variables), which allows comparing two sources in terms of how informative they are with respect to the target variable. Every order relation that satisfies a set of axioms introduced by Kolchinsky [12] yields a valid II measure.

In this work, we take previously studied partial orders between communication channels, which correspond to partial orders between the corresponding output variables in terms of information content with respect to the input. Following Kolchinsky’s approach, we show that those orders thus lead to the definition of new II measures. The rest of the paper is organized as follows. In Section 2 and Section 3, we review Kolchinsky’s definition of an II measure and the degradation order. In Section 4, we describe some partial orders between channels, based on the work by Korner and Marton [22], derive the resulting II measures, and study some of their properties. Section 5 presents and comments on the optimization problems involved in the computation of the proposed measures. In Section 6, we explore the relationships between the new II measures and previous PID approaches, and we apply the proposed II measures to some famous PID problems. Section 7 concludes the paper by pointing out some suggestions for future work.

2. Kolchinsky’s Axioms and Intersection Information

Consider a set of n discrete random variables,

Y_{1} \in Y_{1}, . . ., Y_{n} \in Y_{n}

, called the source variables, and let

T \in T

be the (also discrete) target variable, with joint distribution (probability mass function)

p (y_{1}, . . ., y_{n}, t)

. Let ⪯ denote some partial order between random variables that satisfies the following axioms, herein referred to as Kolchinsky’s axioms [12]:

Monotonicity of mutual information1 w.r.t. T: $Y_{i} ⪯ Y_{j} \Rightarrow I (Y_{i}; T) \leq I (Y_{j}; T)$ .
Reflexivity: $Y_{i} ⪯ Y_{i}$ for all $Y_{i}$ .
For any $Y_{i}$ , $C ⪯ Y_{i} ⪯ (Y_{1}, . . ., Y_{n})$ , where $C \in C$ is any variable taking a constant value with probability one, i.e.,, with a distribution that is a delta function or such that $C$ is a singleton.

Kolchinsky [12] showed that such an order can be used to define an II measure via

I_{\cap} (Y_{1}, . . ., Y_{n} \to T) : = sup_{Q : Q ⪯ Y_{i}, i \in {1, . ., n}} I (Q; T),

(2)

and that this II measure satisfies the William-Beer axioms. In the following, we will omit “

\to T

” from the notation (unless we need to explicitly refer to it), with the understanding that the target variable is always some arbitrary, discrete random variable T.

3. Channels and the Degradation/Blackwell Order

Given two discrete random variables

X \in X

and

Z \in Z

, the corresponding conditional distribution

p (z | x)

corresponds, in an information-theoretical perspective, to a discrete memoryless channel with a channel matrix K, i.e.,, such that

K [x, z] = p (z | x)

[11]. This matrix is row-stochastic:

K [x, z] \geq 0

, for any

x \in X

and

z \in Z

, and

\sum_{z \in Z} K [x, z] = 1

The comparison of different channels (equivalently, different stochastic matrices) is an object of study with many applications in different fields [23]. That study addresses order relations between channels and their properties. One such order, named degradation order (or Blackwell order) and defined next, was used by Kolchinsky to obtain a particular II measure [12].

Consider the distribution

p (y_{1}, . . ., y_{n}, t)

and the channels

K^{(i)}

between T and each

Y_{i}

, that is,

K^{(i)}

is a

| T | \times | Y_{i} |

row-stochastic matrix with the conditional distribution

p (y_{i} | t)

Definition 1.

We say that channel

K^{(i)}

is a degradation of channel

K^{(j)}

, and write

K^{(i)} ⪯_{d} K^{(j)}

Y_{i} ⪯_{d} Y_{j}

, if there exists a channel

K^{U}

from

Y_{j}

Y_{i}

, i.e.,, a

| Y_{j} | \times | Y_{i} |

row-stochastic matrix, such that

K^{(i)} = K^{(j)} K^{U}

Intuitively, consider 2 agents, one with access to

Y_{i}

and the other with access to

Y_{j}

. The agent with access to

Y_{j}

has at least as much information about T as the one with access to

Y_{i}

, because it has access to channel

K^{U}

, which allows sampling from

Y_{i}

, conditionally on

Y_{j}

[20]. Blackwell [24] showed that this is equivalent to saying that, for whatever decision game where the goal is to predict T and for whatever utility function, the agent with access to

Y_{i}

cannot do better, on average, than the agent with access to

Y_{j}

Based on the degradation/Blackwell order, Kolchinsky [12] introduced the degradation II measure, by plugging the “

⪯_{d}

” order in (2):

I_{\cap}^{d} (Y_{1}, . . ., Y_{n}) : = sup_{Q : Q ⪯_{d} Y_{i}, i \in {1, . ., n}} I (Q; T) .

(3)

As noted by Kolchinsky [12], this II measure has the following operational interpretation. Suppose

n = 2

and consider agents 1 and 2, with access to variables

Y_{1}

and

Y_{2}

, respectively. Then

I_{\cap}^{d} (Y_{1}, Y_{2})

is the maximum information that agent 1 (resp. 2) can have w.r.t. T without being able to do better than agent 2 (resp. 1) on any decision problem that involves guessing T. That is, the degradation II measure quantifies the existence of a dominating strategy for any guessing game.

4. Other Orders and Corresponding II Measures

4.1. The “Less Noisy” Order

Korner and Marton [22] introduced and studied partial orders between channels with the same input. We follow most of their definitions and change others when appropriate. We interchangeably write

Y_{1} ⪯ Y_{2}

to mean

K^{(1)} ⪯ K^{(2)}

, where

K^{(1)}

and

K^{(2)}

are the channel matrices as defined above.

Before introducing the next channel order, we need to review the notion of Markov chain [11]. We say that three random variables

X_{1}

X_{2}

X_{3}

form a Markov chain, and write

X_{1} \to X_{2} \to X_{3}

, if the following equality holds:

p (x_{1}, x_{3} | x_{2}) = p (x_{1} | x_{2}) p (x_{3} | x_{2})

, i.e.,, if

X_{1}

and

X_{3}

are conditionally independent, given

X_{2}

. Of course,

X_{1} \to X_{2} \to X_{3}

if and only if

X_{3} \to X_{2} \to X_{1}

Definition 2.

We say that channel

K^{(2)}

is less noisy than channel

K^{(1)}

, and write

K^{(1)} ⪯_{l n} K^{(2)}

, if for any discrete random variable U with finite support, such that both

U \to T \to Y_{1}

and

U \to T \to Y_{2}

hold, we have that

I (U; Y_{1}) \leq I (U; Y_{2})

The less noisy order has been primarily used in network information theory to study the capacity regions of broadcast channels [25]. It has been shown that

K^{(1)} ⪯_{l n} K^{(2)}

if and only if

C_{S} = 0

, where

C_{S}

is the secrecy capacity of the Wyner wiretap channel with

K^{(2)}

as the main channel and

K^{(1)}

as the eavesdropper channel [26] (Corollary 17.11). Secrecy capacity is the maximum rate at which information can be transmitted over a communication channel while keeping the communication secure from eavesdroppers [27].

Plugging the less noisy order

⪯_{l n}

in (2) yields a new II measure

I_{\cap}^{l n} (Y_{1}, . . ., Y_{n}) : = sup_{Q : Q ⪯_{l n} Y_{i}, i \in {1, . ., n}} I (Q; T) .

(4)

Intuitively,

I_{\cap}^{l n} (Y_{1}, . . ., Y_{n})

is the information that the random variable Q that is most informative about T, but such that every

Y_{i}

is less noisy than Q, has about T. In the

n = 2

case and if

Y_{1} ⪯_{l n} Y_{2}

, then

I_{\cap}^{l n} (Y_{1}, Y_{2}) = I (Y_{1}; T)

, and consequently

C_{S} = 0

. On the other hand, if there is no less noisy relation between

Y_{1}

and

Y_{2}

, then the secrecy capacity is not null and

0 \leq I_{\cap}^{l n} (Y_{1}, Y_{2}) < min {I (Y_{1}; T), I (Y_{2}; T)}

4.2. The “More Capable” Order

The next order we consider, termed “more capable”, was used in calculating the capacity region of broadcast channels [28] or in deciding whether a system is more secure than another [29]. See the book by Cohen et al. [23], for more applications of the degradation, less noisy, and more capable orders.

Definition 3.

We say that channel

K^{(2)}

is more capable than

K^{(1)}

, and write

K^{(1)} ⪯_{m c} K^{(2)}

, if for any distribution

p (t)

we have

I (T; Y_{1}) \leq I (T; Y_{2})

Inserting the “more capable” order into (2) leads to

I_{\cap}^{m c} (Y_{1}, . . ., Y_{n}) : = sup_{Q : Q ⪯_{m c} Y_{i}, i \in {1, . ., n}} I (Q; T),

(5)

that is,

I_{\cap}^{m c} (Y_{1}, . . ., Y_{n})

is the information that the ‘largest’ (in the more capable sense), but no larger than any

Y_{i}

, random variable Q has w.r.t. T. Whereas under the degradation order, it is guaranteed that if

Y_{1} ⪯_{d} Y_{2}

, then agent 2 will make better decisions, for whatever decision game, on average, under the “more capable” order such guarantee is not available. We do, however, have the guarantee that if

Y_{1} ⪯_{m c} Y_{2}

, then for whatever distribution

p (t)

we know that agent 2 will always have more information about T than agent 1. That is,

I_{\cap}^{m c} (Y_{1}, . . ., Y_{n})

is characterized by a random variable Q that ‘always’ has, at most, the lowest information any

Y_{i}

has about T (‘always’ in the sense that it holds for any

p (t)

). It provides an informational lower bound for a system of variables characterized by

p (Y_{1}, . . ., Y_{n}, T)

For the sake of completeness, we could also study the II measure that would result from the capacity order. Recall that the capacity of the channel from a variable X to another variable Z, which is only a function of the conditional distribution

p (z | x)

, is defined as [11]

C = max_{p (x)} I (X; Z) .

(6)

Definition 4.

Write

W ⪯_{c} V

if the capacity of V is at least as large as the capacity of W.

Even though it is clear that

W ⪯_{m c} V \Rightarrow W ⪯_{c} V

, the

⪯_{c}

order does not comply with the first of Kolchinsky’s axioms (since the definition of capacity involves the choice of a particular marginal that achieves the maximum in (6), which may not coincide with the marginal corresponding to

p (y_{1}, . . ., y_{n}, t)

), which is why we don’t define an II measure based on it.

4.3. The “Degradation/Supermodularity” Order

In order to introduce the last II measure, we follow the work and notation of Américo et al. [30]. Given two real vectors r and s with dimension n, let

r \lor s : = (max (r_{1}, s_{1}), . . ., max (r_{n}, s_{n}))

and

r \land s : = (min (r_{1}, s_{1}), . . ., min (r_{n}, s_{n}))

. Consider an arbitrary channel K and let

K_{i}

be its ith column. From K, we may define a new channel, which we construct column by column using the JoinMeet operator

⋄_{i, j}

. Column l of the new channel is defined, for

i \neq j

, as

{(⋄_{i, j} K)}_{l} = \{\begin{matrix} K_{i} \lor K_{j}, & i f l = i \\ K_{i} \land K_{j}, & i f l = j \\ K_{l}, & o t h e r w i s e \end{matrix} .

Américo et al. [30] used this operator to define the following two new orders. Intuitively, the operator

⋄_{i, j}

makes the rows of the channel matrix more similar to each other, by putting in column i all the maxima and in column j the minima, between every pair of elements in columns i and j of every row. In the following definitions, the s stands for supermodularity, a concept we need not introduce in this work.

Definition 5.

We write

W ⪯_{s} V

if there exists a finite collection of tuples

(i_{k}, j_{k})

such that

W = ⋄_{i_{1}, j_{1}} (⋄_{i_{2}, j_{2}} (. . . (⋄_{i_{m}, j_{m}} V))

Definition 6.

Write

W ⪯_{d s} V

if there are m channels

U^{(1)}, . . ., U^{(m)}

such that

W ⪯_{0} U^{(1)} ⪯_{1} U^{(2)} ⪯_{2} . . . ⪯_{m - 1} U^{(m)} ⪯_{m} V

, where each

⪯_{i}

stands for

⪯_{d}

⪯_{s}

. We call this the degradation/supermodularity order.

Using the “degradation/supermodularity” (ds) order, we define the ds II measure as:

I_{\cap}^{d s} (Y_{1}, . . ., Y_{n}) : = sup_{Q : Q ⪯_{d s} Y_{i}, i \in {1, . ., n}} I (Q; T) .

(7)

The ds order was recently introduced in the context of core-concave entropies [30]. Given a core-concave entropy H, the leakage about T through

Y_{1}

is defined as

I_{H} (T; Y_{1}) = H (T) - H (T | Y_{1})

. In this work, we are mainly concerned with Shannon’s entropy H, but as we will elaborate in the future work section below, one may apply PID to other core-concave entropies. Although the operational interpretation of the ds order is not yet clear, it has found applications in privacy/security contexts and in finding the most secure deterministic channel (under some constraints) [30].

4.4. Relations Between Orders

Korner and Marton [22] proved that

W ⪯_{d} V \Rightarrow W ⪯_{l n} V \Rightarrow W ⪯_{m c} V

and gave examples to show that the reverse implications do not hold in general. As Américo et al. [30] note, the degradation (

⪯_{d}

), supermodularity (

⪯_{s}

), and degradation/supermodularity (

⪯_{d s}

) orders are structural orders, in the sense that they only depend on the conditional probabilities that are defined by each channel. On the other hand, the less noisy and more capable orders are concerned with information measures resulting from different distributions. It is trivial to see (directly from the definition) that the degradation order implies the degradation/supermodular order. Américo et al. [30] showed that the degradation/supermodular order implies the more capable order. The set of implications we have seen is schematically depicted in Figure 1.

These relations between the orders, for any set of variables

Y_{1}, . . ., Y_{n}, T

, imply via the corresponding definitions that

\begin{matrix} I_{\cap}^{d} (Y_{1}, . . ., Y_{n}) \leq I_{\cap}^{l n} (Y_{1}, . . ., Y_{n}) \leq I_{\cap}^{m c} (Y_{1}, . . ., Y_{n}) \end{matrix}

(8)

and

\begin{matrix} I_{\cap}^{d} (Y_{1}, . . ., Y_{n}) \leq I_{\cap}^{d s} (Y_{1}, . . ., Y_{n}) \leq I_{\cap}^{m c} (Y_{1}, . . ., Y_{n}) . \end{matrix}

(9)

These inequalities, in turn, imply the following result.

Theorem 1.

The partial orders

⪯_{l n}

⪯_{m c}

, and

⪯_{d s}

, satisfy Kolchinsky’s axioms.

Proof.

Let

i \in {1, . . ., n}

. Since any of the introduced orders implies the more capable order, it follows that they all satisfy the axiom of monotonicity of mutual information. Axiom 2 is trivially true since every partial order implies reflexivity by definition. As for axiom 3, the rows of a channel corresponding to a variable C taking a constant value must all be the same (and yield zero mutual information with any target variable T). From this, it is clear that any

Y_{i}

satisfies

C ⪯ Y_{i}

for any of the introduced orders, by definition of each order. To see that

Y_{i} ⪯ Y = (Y_{1}, . . ., Y_{n})

for the less noisy and the more capable, recall that for any U such that

U \to T \to Y_{i}

and

U \to T \to Y

, it is trivial that

I (U; Y_{i}) \leq I (U; Y)

, hence

Y_{i} ⪯_{l n} Y

. A similar argument may be used to show that

Y_{i} ⪯_{m c} Y

, since

I (T; Y_{i}) \leq I (T; Y)

. Finally, to see that

Y_{i} ⪯_{d s} (Y_{1}, . . ., Y_{n})

, note that

Y_{i} ⪯_{d} (Y_{1}, . . ., Y_{n})

[12], hence

Y_{i} ⪯_{d s} (Y_{1}, . . ., Y_{n})

. □

5. Optimization Problems

We now focus on some observations about the optimization problems of the introduced II measures. All problems seek to maximize

I (Q; T)

(under different constraints) as a function of the conditional distribution

p (q | t)

, equivalently with respect to the channel from T to Q, which we will denote as

K^{Q} : = K^{Q | T}

. For fixed

p (t)

– as is the case in PID –

I (Q; T)

is a convex function of

K^{Q}

[11, Theorem 2.7.4]. As we will see, the admissible region of all problems is a compact set and, since

I (Q; T)

is a continuous function of the parameters of

K^{Q}

, the supremum will be achieved, thus we replace sup with max.

As noted by Kolchinsky [12], the computation of (3) involves only linear constraints, and since the objective function is convex, its maximum is attained at one of the vertices of the admissible region. The computation of the other measures is not as simple. To solve (4), we may use one of the necessary and sufficient conditions presented by Makur and Polyanskiy [25, Theorem 1]. For instance, let V and W be two channels with input T, and

Δ^{T - 1}

be the probability simplex of the target T. Then,

V ⪯_{l n} W

if and only if, for any pair of distributions

p (t), q (t) \in Δ^{T - 1}

, the inequality

χ^{2} (p (t) W | | q (t) W) \geq χ^{2} (p (t) V | | q (t) V)

(10)

holds, where

χ^{2}

denotes the

χ^{2}

-distance2 between two vectors. Notice that

p (t) W

is the distribution of the output of channel W for input distribution

p (t)

; thus, intuitively, the condition in (10) means that the two output distributions of the less noisy channel are more different from each other than those of the other channel. Hence, computing

I_{\cap}^{l n} (Y_{1}, . . ., Y_{n})

can be formulated as solving the problem

\begin{matrix} max_{K^{Q}} & I (Q; T) \\ s . t . & K^{Q} i s a s t o c h a s t i c m a t r i x, \\ \forall p (t), q (t) \in Δ^{T - 1}, \forall i \in {1, . . ., n}, χ^{2} (p (t) K^{(i)} | | q (t) K^{(i)}) \geq χ^{2} (p (t) K^{Q} | | q (t) K^{Q}) . \end{matrix}

Although the restriction set is convex since the

χ^{2}

-divergence is an f-divergence, with f convex [26], the problem is intractable because we have an infinite (uncountable) number of restrictions. One may construct a set

S

by taking an arbitrary number of samples S of

p (t) \in Δ^{T - 1}

to define the problem

\begin{matrix} max_{K^{Q}} & I (Q; T), \\ s . t . & K^{Q} i s a s t o c h a s t i c m a t r i x, \\ \forall p (t), q (t) \in S, \forall i \in {1, . . ., n}, χ^{2} (p (t) K^{(i)} | | q (t) K^{(i)}) \geq χ^{2} (p (t) K^{Q} | | q (t) K^{Q}) . \end{matrix}

(11)

The above problem yields an upper bound on

I_{\cap}^{l n} (Y_{1}, . . ., Y_{n})

. To compute

I_{\cap}^{m c} (Y_{1}, . . ., Y_{n})

, we define the problem

\begin{matrix} max_{K^{Q}} & I (Q; T) \\ s . t . & K^{Q} i s a s t o c h a s t i c m a t r i x, \\ \forall p (t) \in Δ^{T - 1}, \forall i \in {1, . . ., n}, I (Y_{i}; T) \geq I (Q; T), \end{matrix}

(12)

which also leads to a convex restriction set, because

I (Q; T)

is a convex function of

K^{Q}

. We discretize the problem in the same manner to obtain a tractable version

\begin{matrix} max_{K^{Q}} & I (Q; T) \\ s . t . & K^{Q} i s a s t o c h a s t i c m a t r i x, \\ \forall p (t) \in S, \forall i \in {1, . . ., n}, I (Y_{i}; T) \geq I (Q; T), \end{matrix}

(13)

which also yields an upper bound on

I_{\cap}^{m c} (Y_{1}, . . ., Y_{n})

. The final introduced measure,

I_{\cap}^{d s} (Y_{1}, . . ., Y_{n})

, is given by

\begin{matrix} max_{K^{Q}} & I (Q; T) \\ s . t . & K^{Q} i s a s t o c h a s t i c m a t r i x, \\ \forall i, K^{Q} ⪯_{d s} K^{(i)} . \end{matrix}

(14)

The proponents of the

⪯_{d s}

partial order have not yet found a condition to check if

K^{Q} ⪯_{d s} K^{(i)}

(private communication with one of the authors) and neither have we.

6. Relation with Existing PID Measures

Griffith et al. [31] introduced a measure of II as

\begin{matrix} I_{\cap}^{◃} (Y_{1}, . . ., Y_{n}) : = max_{Q} I (Q; T), such that \forall i Q ◃ Y_{i}, \end{matrix}

(15)

with the order relation ◃ defined by

A ◃ B

A = f (B)

for some deterministic function f. That is,

I_{\cap}^{◃}

quantifies redundancy as the presence of deterministic relations between input and target. If Q is a solution of (15), then there exist functions

f_{1}, . . ., f_{n}

, such that

Q = f_{i} (Y_{i}), i = 1, . . ., n

, which implies that, for all

i, T \to Y_{i} \to Q

is a Markov chain. Therefore, Q is an admissible point of the optimization problem that defines

I_{\cap}^{d} (Y_{1}, . . ., Y_{n})

, thus we have that

I_{\cap}^{◃} (Y_{1}, . . ., Y_{n}) \leq I_{\cap}^{d} (Y_{1}, . . ., Y_{n})

Barrett [32] introduced the so-called minimum mutual information (MMI) measure of bivariate redundancy as

I_{\cap}^{MMI} (Y_{1}, Y_{2}) : = min {I (T; Y_{1}), I (T; Y_{2})} .

It turns out that, if

(Y_{1}, Y_{2}, T)

are jointly Gaussian, then most of the introduced PIDs in the literature are equivalent to this measure [32]. As noted by Kolchinsky [12], it may be generalized to more than two sources,

I_{\cap}^{MMI} (Y_{1}, . . ., Y_{n}) : = sup_{Q} I (Q; T), such that \forall i I (Q; T) \leq I (Y_{i}; T),

which allows us to trivially conclude that, for any set of variables

Y_{1}, . . ., Y_{n}, T

I_{\cap}^{◃} (Y_{1}, . . ., Y_{n}) \leq I_{\cap}^{d} (Y_{1}, . . ., Y_{n}) \leq I_{\cap}^{m c} (Y_{1}, . . ., Y_{n}) \leq I_{\cap}^{MMI} (Y_{1}, . . ., Y_{n}) .

One of the appeals of measures of II, as defined by Kolchinsky [12], is that it is the underlying partial order that determines what is intersection - or redundant - information. For example, take the degradation II measure, in the

n = 2

case. Its solution, Q, satisfies

T ⊥ Q | Y_{1}

and

T ⊥ Q | Y_{2}

, that is, if either

Y_{1}

Y_{2}

are known, Q has no additional information about T. Such is not necessarily the case for the less noisy or the more capable II measures, that is, the solution Q may have additional information about T even when a source is known. However, the three proposed measures satisfy the following property: the solution Q of the optimization problem that defines each of them satisfies

\forall i \in {1, . . ., n}, \forall t \in S_{T}, I (Y_{i}; T = t) \geq I (Q; T = t),

where

I (T = t; Y_{i})

refers to the so-called specific information [1,33]. That is, independently of the outcome of T, Q has less specific information about

T = t

than any source variable

Y_{i}

. This can be seen by noting that any of the introduced orders imply the more capable order. Such is not the case, for example, for

I_{\cap}^{MMI}

, which is arguably one of the reasons why it has been criticized for depending only on the amount of information, and not on its content [12]. As mentioned, there is not much consensus as to what properties a measure of II should satisfy. The three proposed measures for partial information decomposition do not satisfy the so-called Blackwell property [15,34]:

Definition 7.

An intersection information measure

I_{\cap} (Y_{1}, Y_{2})

is said to satisfy the Blackwell property if the equivalence

Y_{1} ⪯_{d} Y_{2} \Leftrightarrow I_{\cap} (Y_{1}, Y_{2}) = I (T; Y_{1})

holds.

This definition is equivalent to demanding that

Y_{1} ⪯_{d} Y_{2}

, if and only if

Y_{1}

has no unique information about T. Although the

(\Rightarrow)

implication holds for the three proposed measures, the reverse implication does not, as shown by specific examples presented by Korner and Marton [22], which we will mention below. If one defines the “more capable property” by replacing the degradation order with the more capable order in the original definition of the Blackwell property, then it is clear that measure k satisfies the k property, with k referring to any of the three introduced intersection information measures.

Also often studied in PID is the identity property (IP) [14]. Let the target T be a copy of the source variables, that is,

T = (Y_{1}, Y_{2})

. An II measure

I_{\cap}

is said to satisfy the IP if

I_{\cap} (Y_{1}, Y_{2}) = I (Y_{1}; Y_{2}) .

Criticism was levied against this proposal for being too restrictive [17,35]. A less strict property was introduced by [21], under the name independent identity property (IIP). If the target T is a copy of the input, an II measure is said to satisfy the IIP if

I (Y_{1}; Y_{2}) = 0 \Rightarrow I_{\cap} (Y_{1}, Y_{2}) = 0 .

Note that the IIP is implied by the IP, but the reverse does not hold. It turns out that all the introduced measures, just like the degradation II measure, satisfy the IIP, but not the IP, as we will show. This can be seen from (8), (9), and the fact that

I_{\cap}^{m c} (Y_{1}, Y_{2} \to (Y_{1}, Y_{2}))

equals 0 if

I (Y_{1}; Y_{2}) = 0

, as we argue now. Consider the distribution where T is a copy of

(Y_{1}, Y_{2})

, presented in Table 1.

We assume that each of the 4 events has non-zero probability. In this case, channels

K^{(1)}

and

K^{(2)}

are given by

K^{(1)} = [\begin{matrix} 1 & 0 \\ 1 & 0 \\ 0 & 1 \\ 0 & 1 \end{matrix}], K^{(2)} = [\begin{matrix} 1 & 0 \\ 0 & 1 \\ 1 & 0 \\ 0 & 1 \end{matrix}] .

Note that for any distribution

p (t) = [p (0, 0), p (0, 1), p (1, 0), p (1, 1)]

, if

p (1, 0) = p (1, 1) = 0

, then

I (T; Y_{1}) = 0

, which implies that, for any of such distributions, the solution Q of (12) must satisfy

I (Q; T) = 0

, thus the first and second rows of

K^{Q}

must be the same. The same goes for any distribution

p (t)

with

p (0, 0) = p (0, 1) = 0

. On the other hand, if

p (0, 0) = p (1, 0) = 0

p (1, 1) = p (0, 1) = 0

, then

I (T; Y_{2}) = 0

, implying that

I (Q; T) = 0

for such distributions. Hence,

K^{Q}

must be an arbitrary channel (that is, a channel that satisfies

Q ⊥ T

), yielding

I_{\cap}^{m c} (Y_{1}, Y_{2}) = 0

Now recall the Gács-Korner common information [36] defined as

\begin{matrix} C (Y_{1} \land Y_{2}) : = & sup_{Q} & H (Q) \\ s . t . & Q ◃ Y_{1} \\ Q ◃ Y_{2} \end{matrix}

(16)

We will use a similar argument and slightly change the notation to show the following result.

Theorem 2.

Let

T = (X, Y)

be a copy of the source variables. Then

I_{\cap}^{l n} (X, Y) = I_{\cap}^{d s} (X, Y) = I_{\cap}^{m c} (X, Y) = C (X \land Y)

Proof.

As shown by Kolchinsky [12],

I_{\cap}^{d} (X, Y) = C (X \land Y)

. Thus, (8) implies that

I_{\cap}^{m c} (X, Y) \geq C (X \land Y)

. The proof will be complete by showing that

I_{\cap}^{m c} (X, Y) \leq C (X \land Y)

. Construct the bipartite graph with vertex set

X \cup Y

and edges

(x, y)

p (x, y) > 0

. Consider the set of maximally connected components

M C C = {C C_{1}, . . ., C C_{l}}

, for some

l \geq 1

, where each

C C_{i}

refers to a maximal set of connected edges. Let

C C_{i}, i \leq l

, be an arbitrary set in

M C C

. Suppose the edges

(x_{1}, y_{1})

and

(x_{1}, y_{2})

, with

y_{1} \neq y_{2}

are in

C C_{i}

. This means that the channels

K^{X} : = K^{X | T}

and

K^{Y} : = K^{Y | T}

have rows corresponding to the outcomes

T = (x_{1}, y_{1})

and

T = (x_{1}, y_{2})

of the form

K^{X} = [\begin{matrix} ⋮ \\ 0 & \dots & 0 & 1 & 0 & \dots & 0 \\ 0 & \dots & 0 & 1 & 0 & \dots & 0 \\ ⋮ \end{matrix}], K^{Y} = [\begin{matrix} ⋮ \\ 0 & \dots & 0 & 1 & 0 & 0 & \dots & 0 \\ 0 & \dots & 0 & 0 & 1 & 0 & \dots & 0 \\ ⋮ \end{matrix}] .

Choosing

p (t) = [0, . . ., 0, a, 1 - a, 0, . . ., 0]

, that is,

p (T = (x_{1}, y_{1})) = a

and

p (T = (x_{1}, y_{2})) = 1 - a

, we have that,

\forall a \in [0, 1], I (X; T) = 0

, which implies that the solution Q must be such that,

\forall a \in [0, 1], I (Q; T) = 0

(from the definition of the more capable order), which in turn implies that the rows of

K^{Q}

corresponding to these outcomes must be the same, so that they yield

I (Q; T) = 0

under this set of distributions. We may choose the values of those rows to be the same as those rows from

K^{X}

- that is, a row that is composed of zeros except for one of the positions whenever

T = (x_{1}, y_{1})

T = (x_{1}, y_{2})

. On the other hand, if the edges

(x_{1}, y_{1})

and

(x_{2}, y_{1})

, with

x_{1} \neq x_{2}

, are also in

C C_{i}

, the same argument leads to the conclusion that the rows of

K^{Q}

corresponding to the outcomes

T = (x_{1}, y_{1})

T = (x_{1}, y_{2})

, and

T = (x_{2}, y_{1})

must be the same. Applying this argument to every edge in

C C_{i}

, we conclude that the rows of

K^{Q}

corresponding to outcomes

(x, y) \in C C_{i}

must all be the same. Using this argument for every set

C C_{1}, . . ., C C_{l}

implies that if two edges are in the same CC, the corresponding rows of

K^{Q}

must be the same. These corresponding rows of

K^{Q}

may vary between different CCs, but for the same CC, they must be the same.

We are left with the choice of appropriate rows of

K^{Q}

for each corresponding

C C_{i}

. Since

I (Q; T)

is maximized by a deterministic relation between Q and T, and as suggested before, we choose a row that is composed of zeros except for one of the positions, for each

C C_{i}

, so that Q is a deterministic function of T. This admissible point Q implies that

Q = f_{1} (X)

and

Q = f_{2} (Y)

, since X and Y are also functions of T, under the channel perspective. For this choice of rows, we have

\begin{matrix} I_{\cap}^{m c} (X, Y) = & sup_{Q} I (Q; T) \leq & sup_{Q} H (Q) & = C (X \land Y) \\ s . t . Q ⪯_{m c} X & s . t . Q = f_{1} (X) \\ Q ⪯_{m c} Y & Q = f_{2} (Y) \end{matrix}

where we have used the fact that

I (Q; T) \leq min {H (Q), H (T)}

to conclude that

I_{\cap}^{m c} (X, Y) \leq C (X \land Y)

. Hence

I_{\cap}^{l n} (X, Y) = I_{\cap}^{d s} (X, Y) = I_{\cap}^{m c} (X, Y) = C (X \land Y)

if T is a copy of the input. □

Bertschinger et al. [15] suggested what later became known as the (*) assumption, which states that, in the bivariate source case, any sensible measure of unique information should only depend on

K^{(1)}, K^{(2)}

, and

p (t)

. It is not clear that this assumption should hold for every PID. It is trivial to see that all the introduced II measures satisfy the (*) assumption.

We conclude with some applications of the proposed measures to famous (bivariate) PID problems, with results shown in Table 2. Due to channel design in these problems, the computation of the proposed measures is fairly trivial. We assume the input variables are binary (taking values in

{0, 1}

), independent, and equiprobable.

We note that in these fairly simple toy distributions, all the introduced measures yield the same value. This is not surprising when the distribution

p (t, y_{1}, y_{2})

yields

K^{(1)} = K^{(2)}

, which implies that

I (T; Y_{1}) = I (T; Y_{2}) = I_{\cap}^{k} (Y_{1}, Y_{2})

, where k refers to any of the introduced partial orders, as is the case in the

T = Y_{1} AND Y_{2}

and

T = Y_{1} + Y_{2}

examples. Less trivial examples lead to different values over the introduced measures. We present distributions that show that our three introduced measures lead to novel information decompositions by comparing them to the following existing measures:

I_{\cap}^{◃}

from Griffith et al. [31],

I_{\cap}^{MMI}

from Barrett [32],

I_{\cap}^{WB}

from Williams and Beer [1],

I_{\cap}^{GH}

from Griffith and Ho [37],

I_{\cap}^{Ince}

from Ince [21],

I_{\cap}^{FL}

from Finn and Lizier [38],

I_{\cap}^{BROJA}

from Bertschinger et al. [15],

I_{\cap}^{Harder}

from Harder et al. [14] and

I_{\cap}^{dep}

from [17]. We use the dit package [39] to compute them as well as the code provided in [12]. Consider counterexample 1 by [22] with

p = 0.25, ϵ = 0.2, δ = 0.1

, given by

K^{(1)} = [\begin{matrix} 0.25 & 0.75 \\ 0.35 & 0.65 \end{matrix}], K^{(2)} = [\begin{matrix} 0.675 & 0.325 \\ 0.745 & 0.255 \end{matrix}] .

These channels satisfy

K^{(2)} ⪯_{l n} K^{(1)}

(it is easy to numerically confirm this using (10), whenever T only takes two values) but

K^{(2)} ⪯_{d} K^{(1)}

. This is an example that satisfies, for whatever distribution

p (t)

I_{\cap}^{l n} (Y_{1}, Y_{2}) = I (T; Y_{2})

. It is interesting to note that even though there is no degradation order between the two channels, we have that

I_{\cap}^{d} (Y_{1}, Y_{2}) > 0

because there is a nontrivial channel

K^{Q}

that satisfies

K^{Q} ⪯_{d} K^{(1)}

and

K^{Q} ⪯_{d} K^{(2)}

. We present various PID under different measures, after choosing

p (t) = [0.4, 0.6]

(which yields

I (T; Y_{2}) \approx 0.004

) and assuming

p (t, y_{1}, y_{2}) = p (t) p (y_{1} | t) p (y_{2} | t)

Table 3. Different decompositions of

p (t, y_{1}, y_{2})

Table 3. Different decompositions of

p (t, y_{1}, y_{2})

$I_{\cap}^{◃}$	$I_{\cap}^{d}$	$I_{\cap}^{l n}$	$I_{\cap}^{d s}$	$I_{\cap}^{m c}$	$I_{\cap}^{MMI}$	$I_{\cap}^{WB}$	$I_{\cap}^{GH}$	$I_{\cap}^{Ince}$	$I_{\cap}^{FL}$	$I_{\cap}^{BROJA}$	$I_{\cap}^{Harder}$	$I_{\cap}^{dep}$
0	0.002	0.004	*	0.004	0.004	0.004	0.002	0.003	0.047	0.003	0.004	0

We write

I_{\cap}^{d s} =

* because we don’t yet have a way to find the ‘largest’ Q, such that

Q ⪯_{d s} K^{(1)}

and

Q ⪯_{d s} K^{(2)}

. See counterexample 2 by [22] for an example of channels

K^{(1)}, K^{(2)}

that satisfy

K^{(2)} ⪯_{m c} K^{(1)}

but

K^{(2)} ⪯_{l n} K^{(1)}

, leading to different values of the proposed II measures. An example of

K^{(3)}, K^{(4)}

that satisfy

K^{(4)} ⪯_{d s} K^{(3)}

but

K^{(4)} ⪯_{d} K^{(3)}

is presented by Américo et al. [30, page 10], given by

K^{(3)} = [\begin{matrix} 1 & 0 \\ 0 & 1 \\ 0.5 & 0.5 \end{matrix}], K^{(4)} = [\begin{matrix} 1 & 0 \\ 1 & 0 \\ 0.5 & 0.5 \end{matrix}] .

There is no stochastic matrix

K^{U}

, such that

K^{(4)} = K^{(3)} K^{U}

, but

K^{(4)} ⪯_{d s} K^{(3)}

because

K^{(4)} = ⋄_{1, 2} K^{(3)}

. Using (10) one may check that there is no less noisy relation between the two channels. We present the decomposition of

p (t, y_{3}, y_{4}) = p (t) p (y_{3} | t) p (y_{4} | t)

for the choice of

p (t) = [0.3, 0.3, 0.4]

(which yields

I (T; Y_{4}) \approx 0.322

) in Table 4.

We write

I_{\cap}^{l n} = 0^{*}

because we conjecture, after some numerical experiments, that the ‘largest’ channel that is less noisy than both

K^{(3)}

and

K^{(4)}

is a channel that satisfies

I (Q; T) = 0

7. Conclusions and Future Work

We introduced three new measures of intersection information for the partial information decomposition (PID) framework, studied some of their properties, and formulated optimization problems that provide upper bounds for two of these measures.

Finally, we point at several directions for future research.

Investigating conditions to check if two channels $K^{(1)}$ and $K^{(2)}$ satisfy $K^{(1)} ⪯_{d s} K^{(2)}$ .
Kolchinsky [12] showed that when computing $I_{\cap}^{d} (Y_{1}, . . ., Y_{n})$ , it is sufficient to consider variables Q with support size, at most, $\sum_{i} | S_{Y_{i}} | - n + 1$ , as a consequence of the admissible region of $I_{\cap}^{d} (Y_{1}, . . ., Y_{n})$ being a polytope. Such is not the case with the less noisy or the more capable II measures, hence it is not clear if it suffices to consider Q with the same support size. This is a direction of future research.
Studying under which conditions the different II measures are continuous.
Implementing the different introduced measures.
Considering the usual PID framework, but instead of decomposing $I (T; Y) = H (Y) - H (Y | T)$ , one can decompose different H-mutual informations, induced by different entropy measures, such as the guessing entropy [40] or the Tsallis entropy [41]. See the work by [30] for other core-concave entropies that may be decomposed under the introduced partial orders, as these entropies are consistent with the introduced orders.
Another line for future work is to define measures of union information with the introduced partial orders, as suggested in Kolchinsky [12], and study their properties.

Funding

This research was partially funded by FCT –Fundação para a Ciência e a Tecnologia, under grants number SFRH/BD/145472/2019 and UIDB/50008/2020, and by Instituto de Telecomunicações.

Conflicts of Interest

The authors declare no conflict of interest.

References

Williams, P.; Beer, R. Nonnegative decomposition of multivariate information. arXiv 2010, arXiv:1004.2515. [Google Scholar] [CrossRef]
Lizier, J.; Flecker, B.; Williams, P. Towards a synergy-based approach to measuring information modification. 2013 IEEE Symposium on Artificial Life (ALIFE). IEEE, 2013, pp. 43–51. [CrossRef]
Wibral, M.; Finn, C.; Wollstadt, P.; Lizier, J.; Priesemann, V. Quantifying information modification in developing neural networks via partial information decomposition. Entropy 2017, 19, 494. [Google Scholar] [CrossRef]
Rauh, J. Secret sharing and shared information. Entropy 2017, 19, 601. [Google Scholar] [CrossRef]
Vicente, R.; Wibral, M.; Lindner, M.; Pipa, G. Transfer entropy—a model-free measure of effective connectivity for the neurosciences. J. Comput. Neurosci. 2011, 30, 45–67. [Google Scholar] [CrossRef] [PubMed]
Ince, R.; Van Rijsbergen, N.; Thut, G.; Rousselet, G.; Gross, J.; Panzeri, S.; Schyns, P. Tracing the flow of perceptual features in an algorithmic brain network. Sci. Rep. 2015, 5, 1–17. [Google Scholar] [CrossRef] [PubMed]
Gates, A.; Rocha, L. Control of complex networks requires both structure and dynamics. Sci. Rep. 2016, 6, 1–11. [Google Scholar] [CrossRef] [PubMed]
Faber, S.; Timme, N.; Beggs, J.; Newman, E. Computation is concentrated in rich clubs of local cortical networks. Netw. Neurosci. 2019, 3, 384–404. [Google Scholar] [CrossRef] [PubMed]
James, R.; Ayala, B.; Zakirov, B.; Crutchfield, J. Modes of information flow. arXiv 2018, arXiv:1808.06723. [Google Scholar] [CrossRef]
Arellano-Valle, R.; Contreras-Reyes, J.; Genton, M. Shannon Entropy and Mutual Information for Multivariate Skew-Elliptical Distributions. Scand. J. Stat. 2013, 40, 42–62. [Google Scholar] [CrossRef]
Cover, T. Elements of information theory; John Wiley & Sons, 1999. [Google Scholar]
Kolchinsky, A. A Novel Approach to the Partial Information Decomposition. Entropy 2022, 24, 403. [Google Scholar] [CrossRef]
Gutknecht, A.; Wibral, M.; Makkeh, A. Bits and pieces: Understanding information decomposition from part-whole relationships and formal logic. Proc. R. Soc. A 2021, 477, 20210110. [Google Scholar] [CrossRef] [PubMed]
Harder, M.; Salge, C.; Polani, D. Bivariate measure of redundant information. Phys. Rev. E 2013, 87, 012130. [Google Scholar] [CrossRef] [PubMed]
Bertschinger, N.; Rauh, J.; Olbrich, E.; Jost, J.; Ay, N. Quantifying unique information. Entropy 2014, 16, 2161–2183. [Google Scholar] [CrossRef]
Griffith, V.; Koch, C. Quantifying synergistic mutual information. In Guided self-organization: Inception; Springer, 2014; pp. 159–190. [Google Scholar]
James, R.; Emenheiser, J.; Crutchfield, J. Unique information via dependency constraints. J. Phys. Math. Theor. 2018, 52, 014002. [Google Scholar] [CrossRef]
Chicharro, D.; Panzeri, S. Synergy and redundancy in dual decompositions of mutual information gain and information loss. Entropy 2017, 19, 71. [Google Scholar] [CrossRef]
Bertschinger, N.; Rauh, J.; Olbrich, E.; Jost, J. Shared information—New insights and problems in decomposing information in complex systems. Proceedings of the European conference on complex systems 2012. Springer, 2013, pp. 251–269. [CrossRef]
Rauh, J.; Banerjee, P.; Olbrich, E.; Jost, J.; Bertschinger, N.; Wolpert, D. Coarse-graining and the Blackwell order. Entropy 2017, 19, 527. [Google Scholar] [CrossRef]
Ince, R. Measuring multivariate redundant information with pointwise common change in surprisal. Entropy 2017, 19, 318. [Google Scholar] [CrossRef]
Korner, J.; Marton, K. Comparison of two noisy channels. Topics in Information Theory, I. Csiszr and P. Elias, Eds., Amsterdam, The Netherlans 1977, pp. 411–423. [Google Scholar]
Cohen, J.; Kempermann, J.; Zbaganu, G. Comparisons of stochastic matrices with applications in information theory, statistics, economics and population; Springer Science & Business Media,, 1998. [Google Scholar]
Blackwell, D. Equivalent comparisons of experiments. The annals of mathematical statistics 1953, pp. 265–272.
Makur, A.; Polyanskiy, Y. Less noisy domination by symmetric channels. 2017 IEEE International Symposium on Information Theory (ISIT). IEEE, 2017, pp. 2463–2467. [CrossRef]
Csiszár, I.; Körner, J. Information theory: Coding theorems for discrete memoryless systems; Cambridge University Press, 2011. [Google Scholar]
Wyner, A. The wire-tap channel. Bell Syst. Tech. J. 1975, 54, 1355–1387. [Google Scholar] [CrossRef]
Gamal, A. The capacity of a class of broadcast channels. IEEE Trans. Inf. Theory 1979, 25, 166–169. [Google Scholar] [CrossRef]
Clark, D.; Hunt, S.; Malacaria, P. Quantitative information flow, relations and polymorphic types. J. Log. Comput. 2005, 15, 181–199. [Google Scholar] [CrossRef]
Américo, A.; Khouzani, A.; Malacaria, P. Channel-Supermodular Entropies: Order Theory and an Application to Query Anonymization. Entropy 2021, 24, 39. [Google Scholar] [CrossRef] [PubMed]
Griffith, V.; Chong, E.; James, R.; Ellison, C.; Crutchfield, J. Intersection information based on common randomness. Entropy 2014, 16, 1985–2000. [Google Scholar] [CrossRef]
Barrett, A. Exploration of synergistic and redundant information sharing in static and dynamical Gaussian systems. Phys. Rev. E 2015, 91, 052802. [Google Scholar] [CrossRef] [PubMed]
DeWeese, M.; Meister, M. How to measure the information gained from one symbol. Network Comput. Neural Syst. 1999, 10, 325. [Google Scholar] [CrossRef]
Rauh, J.; Banerjee, P.; Olbrich, E.; Jost, J.; Bertschinger, N. On extractable shared information. Entropy 2017, 19, 328. [Google Scholar] [CrossRef]
Rauh, J.; Bertschinger, N.; Olbrich, E.; Jost, J. Reconsidering unique information: Towards a multivariate information decomposition. 2014 IEEE International Symposium on Information Theory. IEEE, 2014, pp. 2232–2236. [CrossRef]
Gács, P.; Körner, J. Common information is far less than mutual information. Probl. Control. Inf. Theory 1973, 2, 149–162. [Google Scholar]
Griffith, V.; Ho, T. Quantifying redundant information in predicting a target random variable. Entropy 2015, 17, 4644–4653. [Google Scholar] [CrossRef]
Finn, C.; Lizier, J. Pointwise Partial Information Decomposition Using the Specificity and Ambiguity Lattices. Entropy 2018, 20. [Google Scholar] [CrossRef]
James, R.; Ellison, C.; Crutchfield, J. “dit“: A Python package for discrete information theory. J. Open Source Softw. 2018, 3, 738. [Google Scholar] [CrossRef]
Massey, J. Guessing and entropy. Proceedings of 1994 IEEE International Symposium on Information Theory. IEEE, 1994, p. 204. [CrossRef]
Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]

In this paper, mutual information is always assumed as referring to Shannon’s mutual information, which, for two discrete variables

X \in X

and

Z \in Z

, is given by

I (X; Z) = \sum_{x \in X} \sum_{z \in Z} p (x, z) log \frac{p (x, z)}{p (x) p (z)},

and satisfies the following well-known fundamental properties:

I (X; Z) \geq 0

and

I (X; Z) = 0 \Leftrightarrow X ⊥ Z

(X and Z are independent) [11].

The

χ^{2}

distance between two vectors u and v of dimension n is given by

χ^{2} (u | | v) = \sum_{i = 1}^{n} {(u_{i} - v_{i})}^{2} / v_{i}

Figure 1. Implications satisfied by the orders. The reverse implications do not hold in general.

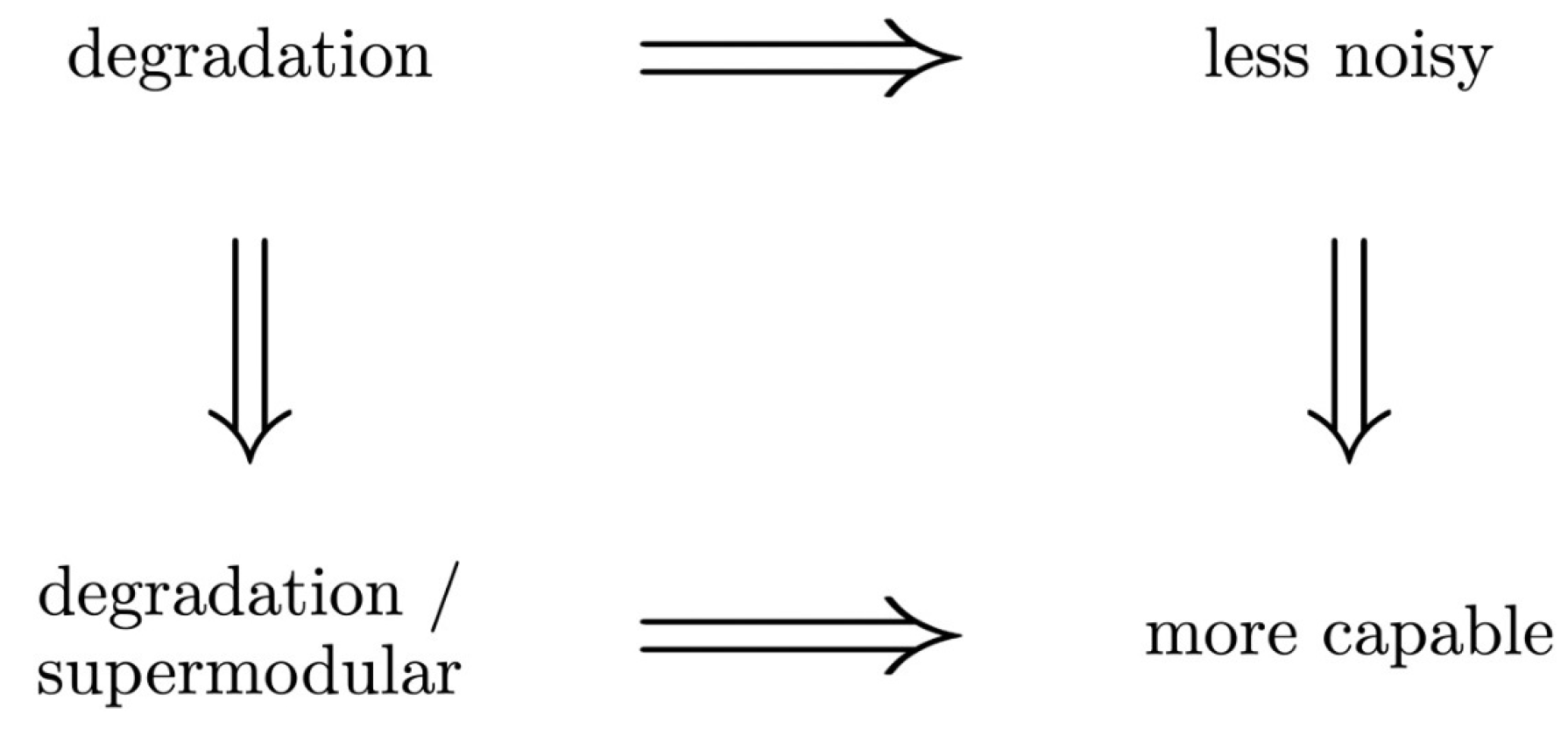
Table 1. Copy distribution.

T	$Y_{1}$	$Y_{2}$	$p (t, y_{1}, y_{2})$
(0,0)	0	0	$p (0, 0)$
(0,1)	0	1	$p (0, 1)$
(1,0)	1	0	$p (1, 0)$
(1,1)	1	1	$p (1, 1)$

Table 2. Application of the measures to famous PID problems.

Target	$I_{\cap}^{◃}$	$I_{\cap}^{d}$	$I_{\cap}^{l n}$	$I_{\cap}^{d s}$	$I_{\cap}^{m c}$	$I_{\cap}^{M M I}$
$T = Y_{1} AND Y_{2}$	0	0.311	0.311	0.311	0.311	0.311
$T = Y_{1} + Y_{2}$	0	0.5	0.5	0.5	0.5	0.5
$T = Y_{1}$	0	0	0	0	0	0
$T = (Y_{1}, Y_{2})$	0	0	0	0	0	1

Table 4. Different decompositions of

p (t, y_{3}, y_{4})

Table 4. Different decompositions of

p (t, y_{3}, y_{4})

$I_{\cap}^{◃}$	$I_{\cap}^{d}$	$I_{\cap}^{l n}$	$I_{\cap}^{d s}$	$I_{\cap}^{m c}$	$I_{\cap}^{MMI}$	$I_{\cap}^{WB}$	$I_{\cap}^{GH}$	$I_{\cap}^{Ince}$	$I_{\cap}^{FL}$	$I_{\cap}^{BROJA}$	$I_{\cap}^{Harder}$	$I_{\cap}^{dep}$
0	0	$0^{*}$	0.322	0.322	0.322	0.193	0	0	0.058	0	0	0

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Orders Between Channels and Some Implications for Partial Information Decomposition

Abstract

1. Introduction

2. Kolchinsky’s Axioms and Intersection Information

3. Channels and the Degradation/Blackwell Order

4. Other Orders and Corresponding II Measures

4.1. The “Less Noisy” Order

4.2. The “More Capable” Order

4.3. The “Degradation/Supermodularity” Order

4.4. Relations Between Orders

5. Optimization Problems

6. Relation with Existing PID Measures

7. Conclusions and Future Work

Funding

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe