Preprint
Article
NUVO Model for the Grand Unified Theory Initial Formalization Part I: Cosmic Scale
Altmetrics
Downloads
65
Views
1263
Comments
0
This version is not peer-reviewed
Submitted:
09 May 2023
Posted:
10 May 2023
You are already at the latest version
Alerts
Abstract
n this article a first attempt at formalizing a new approach to the grand unified theory is introduced. This theory named NUVO is based primarily on considering two aspects of inertia. The first aspect is how a mass couples to space, introducing definitions to distinguish massive particles from massless particles. The second aspect is space’s availability to couple to massive particles. In essence these are the two contributions of inertia; mass and space. Postulates, clarifications, and a mathematical structure are introduced. Part 1 covers the physics of the very large (cos- mic), laying ground work for part two which applies the structure to the very small (quantum). The cosmic application of the theory will show a strong correlation to empirical data and correspondence to General Rela- tivity, including; time dilation, length contraction, and orbital advances. Departing from the canonical findings of General Relativity by predicting a quantization of physical units under the effect of acceleration and or gravity.
Keywords:
Subject: Physical Sciences - Astronomy and Astrophysics
1. NUVO Introduction
NUVO, which has no acronym meaning, is based on a concept developed in the author’s undergraduate study and continued into graduate studies. Intertwined with the concept is how divergent General Relativity and Quantum Mechanics became within a relatively short window of history. At that time in history two mathematical concepts were being introduced and worked into the sciences; Differential Geometry and Linear Algebra. A simple question the author wrestled with was do these two events in history have any relationship? This leads one to imagine if history did not introduce Differential Geometry or Linear Algebra into physics, how would these concepts maturated? In applying this imaginative approach a mathematical mapping of space to model time dilation is derived and consequences of the mapping investigated.
This investigation lead to part of my doctoral thesis and several published articles. With this being the first attempt at formalizing a framework for a theory.
2. Definitions, Clarifications, and Concepts
Introduced here are definitions needed for a better understanding of the theory. Some of the definitions are purely for decoupling a concept (inertia), which has two parts, the mass’s coupling to space and the space’s coupling to the mass. The desire in distinguishing these parts is remove ambiguity when only the term inertia is used.
2.1. Terminology
-
InertiaMass’s coupling to space, the inverse is space’s coupling to mass.
-
PinertiaThe magnitude of a mass’s coupling to space (the inverse of space’s coupling to mass). This definition is in the spirit of inertia but created due to the subtle differences and removal of ambiguity from inertial mass, inertial frames, and other areas of established inertia definitions used in calculations.
-
SinertiaThe magnitude of space’s ability to couple with mass (the inverse of mass’s coupling to space). This definition is to distinguish the attribute of space’s ability to couple with mass from mass’s attribute to couple with space.
-
Massless ParticleAny particle with zero magnitude pinertia is termed massless, by a priori all massless particles move at the speed of light in a vacuum.
-
Exemplar SpaceA volume of space where the magnitude of sinertia’s availability is at its maximum natural allowed value.
-
Privo SpaceA volume of space where the magnitude of sinertia’s availability is less than its maximum natural allowed value.
-
Kenos SpaceA volume of space where the magnitude of sinertia’s availability is zero
2.2. Postulates
- (1)
- Space has a finite magnitude of sinertia available.
- (2)
- Mass reduces the magnitude of space’s available sinertia.
- (3)
- Mass’s pinertia is dependent upon sinertia magnitude at the mass’s location in space (Mass’s inertia is dependent upon the space it is located in, thus momentum is dependent upon the space the mass is located in).
- (4)
- Mass’s pinertia to sinertia ratio is invariant for all space as measured by an observer at the location of the mass (Inertial mass is invariant between observers).
- (5)
- Space attempts to maintain equilibrium of sinertia across all space (sinertia forms a flux in a volume of space).
2.3. Clarifications
Application of SR will only be considered applicable in inertial frames. Thus, SR is not applicable for any space (frame) under the influence of acceleration or a massive particle accelerating. Included in this list of accelerated influence is a gravitational field, rotations, and orbital paths. This paper holds the time dilation in SR is an illusion, in the same manner as an object moves farther away it appears to the stationary observer to shrink, the shrinkage is only an illusion of the observation and not an actual shrinkage of the object and the space about it. Another distinguishing prediction of SR is in a standard configuration both observers observe the other frame’s clock ticking faster [1] (at the same boost). This prediction eliminates SR from being used to calculate time dilation of an object in orbit. For instance, the use of GPS satellite’s clock rate to "verify" SR is in violation of SR predictions, as the observers at both locations do not observe the other’s clock rate as moving faster than the clock in their frame. Therefore SR will be excluded from any calculation of time dilation in accelerating frames. Even if the equation appears to be the same, it is decoupled from SR by residing in an accelerated frame, thus, disqualifying the applicability of its postulates and derivatives.
Within SR the concept of rest mass energy was developed. Such as, the invariance of the rest mass energy is limited to inertial frames and the author of this paper feels it is an improper assumption to transfer this invariance to non-inertial frames without formal proof. One aspect of inertial frames is all experiments carried out within them transfer to other inertial frames regardless of their relative constant velocity [2]. The author contends this effect will only hold true if the ratios of natures interactions are constant between frames when an experiment is conducted in any inertial (non-accelerated) frame. This can be demonstrated with a simple thought experiment carried out in two locations (A and B) within a gravitational field at different radial distances from the generating massive object (Lab A is deeper in the gravity well than lab B). According to GR (and empirical data) there is a blueshift in an electromagnetic wave as it travels into the gravity well and a redshift as it travels out of the well [3]. GR also considers an infinitesimal space as inertial (Minkowski space) allowing for experiments to be carried out that behave as if they were in an inertial frame. When the event in the lab covers multiple infinitesimal spaces they are stitched together with differential geometry, yet each infinitesimal location is considered inertial [4].
Now considering the two labs in the thought experiment. Lab A prepares two forms of energy, a massive particle and a massless particle (a photon) of equal energy and delivers them to Lab B. Lab B receives the two particles and observes the massive particle arrived with no change in energy as measured in their lab. But the massless particle does have a change in energy as measured in their lab. Since this is a thought experiment a device is introduce in lab B that transforms energy from one state to another with no loss of energy. Thus, at lab B the massless particle received is converted to a massive particle and each mass returned to Lab A. Upon arrival at Lab A the two massive particle are in agreement with the measurements made in Lab B. Another finding from Lab A measurements is the energy transferred originally (the electromagnetic energy and the massive particle energy) does not equal the returned energy from the round trip. The final energy is less than the initial energy. Lab A then takes the smaller mass (the one converted from massless to mass at Lab B) and converts it back to massless energy and returns it to Lab B, along with the original mass that has not undergone any transformation at either lab. Upon many round trips the energy that has undergone transformation will eventually approach zero. A correlation of this through experiment is when the transport starts with Lab B instead of Lab A, the energy would approach infinity after many rounds. One interpretation is massive particles have an invariant energy exchange rate while massless particles energy exchange rate depends upon an attribute of space in which the exchange takes place.
This though experiment highlights the author’s concept as to why rest energy’s invariance is an SR derived invariance and not a GR derived invariance and GR needs a formal proof of the global invariance before claiming it exist.
Another clarification from SR is constant velocity does not change the rate of a clock, only the illusion of changing the rate as previously mentioned. In contrast acceleration does cause a physical change in the clock rate between a relative stationary observer and an accelerated observer. For example, there are two observers (). During ’s observation of there are five time intervals . During the velocity is constant between the observers, with the velocity equal zero for , they are at rest relative to each other. During interval there is a positive constant acceleration of as observed by . During there is a constant velocity between the observers. During interval there is a constant negative acceleration of as observed by . The magnitude of velocity relative to and are equal for time interval and . In this scenario the observers share each other’s coordinate origin at the start of . During time interval the instantaneous measured boost is changing and at the start of time interval a new boost of is measured that remains constant for the interval. During each observer notices the other’s clock run faster than their clock (an outcome of SR). Again during time interval the instantaneous measured boost is changing and at the start of time interval a new boost of is measured that remains constant for the interval. observes the constant velocity between them for is the same as measured in , thus the boost in , is equal to .
In this scenario the author contends the only time a physical change in the rate of ’s and ’s clock is during time interval and (during acceleration). If the accelerations in and are equal in magnitude but opposite in direction and and , the observers will again have their coordinate origins cross at the end of interval . When they compare their clocks at the origin, they will no longer be in sync, clock will have slowed. The physical dilation between the clocks occur only during acceleration and is not a shared observation (like seeing each other’s clock run faster, as in SR), instead only the accelerated clock is observed to run slower. This is a physical example of the difference between an illusion of time dilation (as in SR) and a physical time dilation due to acceleration. The author contends within SR there is no physical time dilation, only the illusion (artifact of observation) of time dilation.
2.4. Conceptual Hypothesis
Conceptually the model is based on a very simple hypothesis. Massive particles in space reduce the amount of available sinertia at its location in space. Since space has a finite availability of sinertia within a volume of space, the coupling (inertia) of mass and space is reduced around the massive object generating the reduction in sinertia. This reduction will cause a flux in the sinertia of space to flow (creating a flux) toward the massive object in an effort to maintain equilibrium of sinertia throughout space. As the sinertia flows there will be an imbalance in inertia of the space around a test particle near the massive particle generating the reduction in sinertia. This imbalance will cause a change in momentum of the test particle, thus via Newtonian principles causing a force to act upon the test particle. The force will appear to be applied in the direction of the flow of sinertia, thus making the test particle appear attracted to the massive particle.
This hypothesis will be shown to cause time dilation, length dilation, and observational effects as quanta of various entities such as length, time, energy, etc.. This hypothesis will lead to a minimum first order equivalence of General Relativity and provide a path for modeling quantum mechanics. In addition:
- Model predicts photons (electromagnetic waves) are not coupled to space as massive particles are. Photons have no pinertia.
- Model predicts time and length dilate equally
- (Part 2) Model the creation and absorption of photons as being proportional to the action of space’s change in curvature. In other words, the interaction of photons with massive particles causes a curvature change in space. Leading to a speculation and possible hypothesis that photons are encapsulated space.
- Model will predict acceleration and gravitational affects time differently, one will be shown to be a global effect, the other a local effect. One triggers a propagation through space, the other does not. This leads to a possible scenario for an experiment to measure the difference between acceleration due to gravity and acceleration due a force applied to it.
3. Mapping Change in Inertia
Presented here is a scalar field map about the space of a massive object. Working with postulates 1, 2 and 5 a conceptual map is derived to obtain the value for postulate 3’s sinertia at every location in space about a massive object. In considering the map the empirical data of a clock running slower within a gravitational potential field than a clock outside a gravitational field is used. One observation of the data is a clock runs at its maximum relative rate when there is no gravitational potential field, thus a static, non-rotating, non-accelerating clock’s maximum rate is within empty space. Therefore it is assumed space void of a gravitational potential is where sinertia’s finite magnitude from postulate 1 is found. This space by definition is termed exemplar space . Once a gravitational potential is introduced into space, sinertia is reduced from its finite maximum, then by definition becomes privo space. The sinertia of space appears to have a gradient from exemplar space to the massive object generating the gravitational field, decreasing from exemplar to the massive object. Thus, any mapping must show this gradient. Secondly, the gradient has a dependency on the magnitude of the mass generating the field. As such a ratio of the gravitational potential energy and the rest mass energy of the generating mass is considered.
Where is a scalar map dependent on the radial distance r from the center of the generating mass M, G is the Newtonian gravitational constant, m the mass in the gravitational field, c the speed of light in a vacuum. A value for m is needed to map the field. Here the potential is measured by applying a virtual point mass at every point in space with the same magnitude as M generating the field. Therefore
Allowing the ratio in equation 1 to become:
Continuing to develop the map, the postulates as previously discussed, show the maximum sinertia when r goes to infinity. This value will be considered normalized to one. Then any gravitational potential (the presence of mass) reduces the sinertia by a gradient from equation 3. Therefore the initial candidate mapping for space about a massive object is:
What does this mapping represent? By this model it represents the reduction in sinertia at a location in space due to the generating mass’s reduction of sinertia. (Postulates 1, 2, 5). A consequence of postulate 3 is pinertia (the coupling of mass to space) is reduced proportionally to sinertia’s reduction. Consider a Coulomb force acting on an electron about an atomic nucleus. If the electron’s coupling to space is reduced it requires less force to change its momentum, thus allowing it to relax to an orbital distance farther away (into a weaker Coulomb field area). In the same manner if the electron’s coupling to space is increased it requires more force to change its momentum and contracts into a orbital distance closer (into a stronger Coulomb field area). This change of sinertia would be observed as a clock rate changing if the clock rate is based on the cycle of a massive object. For the model the question arises as to what is the ratio of sinertia change to pinertia change? The model chooses a ratio of one, thus time dilates in a gravitational field via:
Where subscripts represent privo and exemplar space respectively. As a clock moves closer to the generating mass the interval in a clock’s rate grows larger in magnitude relative to a clock not under the influence of a generating mass. How does this compare to GR? Consider the Schwartzschild metric, a solution to Einstein’s field equations. With a change in radial distance only () the time component at a location is dilated (as compared to a time component at infinity) by:
Where is the time as measured in the gravitational field and is measured outside a gravitational field. Equation 6 series expanded to first order is
Which is exactly equation 5 when one considers . Thus, the model at this point in construction aligns to a minimum first order equivalence of GR for mapping time dilation in a gravitational potential field. This mapping represents the model’s scalar field map about a massive object, it is the reduction in sinertia at a location in space. This is a static effect only. Meaning time dilation due to motion in the field has not been constructed or applied to the field at this point in introducing the model.
3.1. Simple Coordinate Transformation
For continuity of the conceptual development a static coordinate transformation from exemplar space to privo space (and vice-versa) is minimally introduced at this stage. Impact of movement in the scalar field has not been defined for the model at this point, therefore the simple transformation does not include an effect of velocity, acceleration, or other types of movement through the field to affect the observations as they are transformed. To endow the field with a coordinate system a method of measurement is needed. Einstein’s postulate that all observers view the speed of light the same has been empirically tested for over a century with no contradictory findings. As such the method of measurement is performed locally (proper time in SR and GR) using a local clock. Any unit of time may be used as long as it is a standard physical method (spring, Cesium, laser interaction) for measuring the cycle (a tick of time). Since the speed of light is universally observed, the length (distance) a ray of light travels in time is the unit of length equal to . Thus in a coordinate system of three dimensions of space and one time, the distance from any point to any point locally uses the Euclidean distance formula:
Where are coordinate base units each normalized to equal 1 and physically measured having a magnitude of . Utilizing equation 5, the distance measure at a location in will be observed by an observer in as follows:
Where returns a scalar. For ease of use, the scalar value is at times represented by A. Thus, the transformation of distance from to is a simple scaling.
And time transforms in the same manner as:
3.2. Transformation of Units
Before continuing the development of the model the concept of units and how they transform is discussed. Local observers are observers who make a measurement at a time and location as if they were located at that location and time. In forming their measurements they use units that are both natural and derived. For example, the unit time is derived from a natural oscillation in nature. Then length is derived from the universal speed of light. Derived units come from a combination of base units. A generic list of often used measurements are in Table 1:
The * marked values are derived values, made up of a combination of base measurements.
Equipped with length, time, mass and derived values one may transform from to or vice-versa using the inverse of A (the . Of note, some derived values transform one to one (in other words they are observed locally the same in both to ). For example, velocity is a derived unit from length and time as follows:
Both observers view each others velocity the same or more precisely the ratio is invariant in the transformation. Yet acceleration transforms as:
Thus, the ratios of units making up acceleration are not invariant under transformation. Table 2 shows many familiar derived units and how they transform from to .
This collection of measurement units can be formed into a group that all observers use in making their observations. This group can then be divided into two subgroups. One group whose transformation scalar value is 1 and the other group whose transformation scalar value is not equal to one. Subgroup is shown in Table 3 and subgroup shown in Table 4. These groups play a role in what the model predicts as invariant to all observers, and what is invariant under special circumstances (like in Special Relativity).
If over the course of a trajectory an observer sees no change at any point in the path of the ratios (units) then the path is termed to have a fixed state of ratios. If however there is a change in the ratios at any point in the path, then the trajectory is termed to have a mixed state of ratios. It will be shown this mixed state occurs when there is a change in A from equations 10 and 11.
3.3. Groupings and Consequences
Reflecting back on the groups of units (natural and derived) here in is introduced a function that is a type of commutator for a function utilizing elements from the group by an observer at one location and how they "commute" to an observer at another location. Consider the function of multiplication . In the subgroup the product of any element with another element of the subgroup commutes with value zero with the defined commutation. Let be an element of then
When is an element of then
Members of the group with multiplication are invariant as measured locally to all observers. Members of group must be handled carefully when making observations and comparing results with observations from other locations. For example, velocity is a member of the group but length and time are not a member. Thus, when working with velocity (like the speed of light), the value c is equal to:
While c, as a member of the group is invariant, the elements that make up c may or may not be invariant. As the value is a length and not a member of , thus the value of energy as derived by:
is not invariant. But energy is a member of ! Therefore the definition of what makes up subgroup must be made more precise. To be a member of the commutation from equation 15 must equal zero for the measurement. This definition allows some derived measurements such as energy to be excluded from the group because their local measurement is not always invariant. Other measurements of energy do commute with zero value, for instant:
Commutes to a value of zero and is invariant by all local measurements. But the setting equal of two equations and solving for an answer does not guarantee the value of the equation is invariant, thus it doesn’t guarantee the equation is a member of . Consider:
The LHS of is not a member of while the RHS is a member of . Another consequence of units of measure not being a part of is when an observer in GR tries to reduce a local space (using GR terms) down to the level of an infinitesimal patch so that Minkowski space can be applied and the laws of physics be the same for all observers, it is impossible to locally measure an acceleration of an observed particle accurately. At the infinitesimal level the particle observed accelerating is in a different location on the manifold (the value of has changed) due to it’s acceleration and will have a local effect (the part of the transformation in equation 24). The commutation between the units as measured by the particle accelerating and the units measured by the observer at rest relative to the accelerating particle is not zero. Thus the observation will have an uncertainty proportional to the value of the commutation. The system will be considered in a mixed state.
3.4. Motion in a Static Gravitational Field
Here the concept of global and local affects of sinertia are introduced to the model. Motion must account for two components acting upon the particle in motion, one is the field due to the reduction in sinertia, the other is the affect the motion of the particle has on the available sinertia. The first is consider a global effect, the second is considered a local effect. This section only considers the global effect, then in the following sections both global and local effects are defined, discussed, and shown how they affect a coordinate transformation. Postulate 5 states an attribute of space is to maintain an equilibrium of sinertia, meaning if a change in sinertia takes place at a location the surrounding space will (via flowing sinertia into or away from the location) attempt to bring the difference between the two locations sinertia to zero.
This flow (or flux) of sinertia implies mathematically space is a source of sinertia and mass acts as a sink to sinertia. Postulate 1 was introduced using the word available for sinertia to reflect space intrinsically maintains the coupling to mass, this maintaining implies a force continues to act upon a mass to "hold" it to space. When mass is introduced to space it reduces the sinertia at its location and this reduction induces a flux of available sinertia from surrounding space to flow toward the mass generating the reduction in sinertia. This reaction by space to maintain equilibrium generates a field in space, thus a mass at one location will have an effect on a mass’s pinertia at different location as the reaction to equalize the field propagates through space (for this model the reaction propagates at the velocity of the speed of light). As the field’s gradient is propagated, the sinertia at a location is changed from equilibrium at a location to being out of equilibrium. In other words sinertia has a higher magnitude in one direction and a lower magnitude in another direction. This in-equilibrium causes a mass to be unequally coupled to space. This model holds that the unequal coupling to space causes a change in inertia (Newtonian) and thus acceleration for the mass. This scenario models Newtonian gravity as a force. The difference with the model is the propagation of effect (as sinertia changes it must propagate through the field, not instantaneously), and the change in sinertia changes the time as measured by observers in the field. This effect of mass reducing sinertia is a global effect, it changes the field about it as it propagates through the field.
Another affect to sinertia is when a mass travels through a field. There is the global effect aforementioned of the change in the field due to the moving reduction in sinertia, this is propagated through the field. The movement of the mass through the field also affects locally the available sinertia to the mass in motion. The flux will increase as it moves through space, thus changing its pinertia and time observations.
3.5. Local vs Global Effect
At this point in the development of the model it is necessary to distinguish between a global (field) effect and a local (location based) effect. Consider along a trajectory where (the radial distance from the central mass) and , the ratios remain constant. Unit time and unit length remain the same for the entire trajectory. If and or along the path then ratios are in a mixed state as shown in Table 2 over the path. The motion of a test particle along the path that causes a change in r induces a mixing of ratios from a global gravitational field that all test particles at that location will experience.
The motion of a test particle that causes a change in v ( for entire path) also causes a mixed state of ratios (over the path). But, unlike the effect, the is a local effect, dependent upon the instantaneous velocity of the test particle. The does not affect the global field. In other words, the local effect depends only on local conditions (the instantaneous velocity of the test particle).
Well established is Einstein’s SR which showed velocity is relative. So by SR the effect of velocity can only be measured relative to another particle (or frame). So this local effect is relative to observations that are transformed between two frames and based on their differential in velocity. But these local effects do not globally affect a field. They are dependent upon differentials in observed velocity. Where as dr in gravitational field affects all locations regardless of their relative velocity.
Putting the local effect in terms of the model, a global effect causes a change in a space’s sinertia, which triggers a propagation in the field that changes available sinertia at all locations. A local effect does not trigger a change in space’s sinertia triggering a propagation in the field. The test mass moving through the field will experience a higher availability of sinertia in the direction of velocity when compared to a particle with relative zero velocity elsewhere in the field. But no effect is triggered in space changing available sinertia at a location. Note: At this point in the development of the model, charge particles have not been considered.
The higher availability of sinertia in the direction of the velocity (relative to another observer) increase the pinertia of the test particle. This in effect adds to its coupling to space as observed by a different observer. If between observers over the path than the ratios do not change (the transformation scalar value is constant). This local affect on pinertia provides a path (should one wish to pursue it) for corresponding the model to SR.
GLOBAL vs LOCAL
-
GlobalCauses a change in space’s available sinertia and triggers a propagation throughout space.
-
LocalDoes not cause a change in sinertia, causes a change in pinertia of the particle at the location. There is no triggering of propagation throughout space.
3.6. Local Effect of Movement in the Field
A massive particle moving through space has both a global and local effect. The global effect is a reduction in sinertia of space. When in motion it creates a wave (propagation) of reduction in sinertia as a result of space working to maintain an equilibrium (as previously discussed). The local effect is the flux of sinertia available for pinertia increases in the direction of motion. In developing a model to represent the local effect, the same type of approach is used as in the sinertia reduction in a field used previously (equation 1), a ratio of energies. In the local case the mass is moving with a velocity that is a relative (depends on configuration of observers), and as discussed in a previous section, constant velocity does not affect the physical system (i.e. time dilation), both observers observe the same time dilation, their clock runs slower than the other’s clock. The local case only has an effect on the available sinertia for pinertia when accelerating. Thus this effect cannot use SR construct or equations. Armed with knowledge the model requires acceleration for there to be a change in sinertia and pinertia, instantaneous velocity when is used for calculating the local effect. One form of energy based on velocity of an object is kinetic energy. Classically (Newtonian) the kinetic energy of a particle is [5]:
To apply this energy in the same manner gravitational potential energy was applied in equation 1 caution must taken. First, the velocity must be modified to only be instantaneous velocity when , this velocity will be term to represent the constraint. Secondly, the rest energy to be considered must be local (since it a local effect), this requires the rest energy used for the ratio of energies must be the particle’s rest energy. Putting this together in one ratio, a candidate local effect of motion on time is:
When not moving in a gravitational field the total time dilation between an object in acceleration (t) and an object not in acceleration () is
Adding this effect to equation 5 with the constraint that any observer in is not under acceleration, equation 5 becomes:
In this initial candidate for a transformation between spaces the acceleration’s instantaneous velocity through the field contributes half the time dilation effect the accelerated field does. If this holds, there appears to be a difference between the field acceleration (gravitational induced) and acceleration in the field. Note in the model the traditional gravitational field and the acceleration both slow the time compared to an observer who is not experiencing acceleration or in a gravitational field. This is in contrast to many examples of using both GR and SR to describe time dilation as in the Global Positioning Satellite system (GPS) [6]. Within the model acceleration always causes a "slow down" in the clock rate.
The transformation in equation 24 will be given a more formal treatment in the next few sections. There are obvious weaknesses in the way it is prepared. Einstein’s equivalence principal is at play in understanding if it is possible to tell if one is accelerating or in a gravitational field. Secondly, the acceleration is relative to what? For instance an orbiting satellite may be compared to the massive object it is orbiting and easily recognize the acceleration, but if another orbiting satellite was beside it, could it tell it was in an accelerated field by observing only the other satellite? These types of scenarios need to be strengthened in the formalization that follows.
4. Does a Manifold Model Apply?
With the derivation of the transformation in equation 24 the next logical step mathematically is to configure a Riemannian manifold and mimic the methodology of General Relativity [4]. As it will be shown this method has inconsistencies that make it at best usable in special circumstances or with special rules.
4.1. Initial Manifold
The math of General Relativity is based on differential geometry, specifically that of a Riemannian Manifold [4]. Therefore it would be idea to start with this mathematical structure as an initial formalization. Einstein, in the beauty of his theory give a very simple looking equation (though in the opinion of many, including the author, not simple in evaluation):
The simplicity of the concept is elegant. Stress energy warps space and the warping of space decides how a free particle moves. Arguably the most popular solution to Einstein’s field equations is the Schwartzschild metric [7]. With this solution one may solve for many of the predictions of GR, including perihelion advance of Mercury (and other gravitational orbits), time dilation, light bending around massive objects, and so forth. Since the Schwartzschild metric is based on a static configuration (field does not change over time) it does not directly support the calculations of gravitational waves, as they require the field to change over time as the wave propagates. But none-the-less the Schwartzschild solution is elegant in the same manner Einstein’s theory is.
Although the transformation from equation 5 was shown to be equivalent to a first order series of Schwartzschild’s metric for time dilation, it does not translate to a solution for Einstein’s field equations when one sets the stress energy tensor equal to zero (empty vacuum). Though this is not a solution to Einstein’s equations it doesn’t exclude equation 5 from using the math structure of a manifold or possibly a Riemannian manifold.
The model at this stage of development considers two events that dilate time in a field; the presence of a mass (globally affects the field), and the acceleration of mass (locally affects the field). Mass and energy at this stage are not considered interchangeable on a global level, only between inertial frames as in SR. Each of these will need to be treated separately and independent of each other. Looking at equation 24, local and global effects are decoupled as:
The local part is contributed by the kinetic energy due to acceleration of the particle moving in the field and therefore has a relative value to the frame it is observed from. To standardize the observation, all measurements for the local part will be made locally with instantaneous velocity measured with respect to a stationary (in SR terms at rest) observer in space. In a configuration like the Schwartzschild metric the central mass is at rest with an observer in space (at infinite distance from the central mass), but caution should be used to not treat this as a default unless specified. In cases where an orbiting body’s mass is not much much less than the center mass a measurable effect may be loss by holding the the assumption the central mass is at rest in relation to an observer at rest in .
Armed with how to take measurements, the next step is to setup a manifold. The manifold is smooth with dimensions with three spatial components and one temporal. The metric tensor is:
Where I is the identity matrix and is from equation 24. In a Euclidean coordinate system the metric reduces to a scalar ratio connection between local coordinate systems. Thus a distance all observers agree to is:
Where the infinitesimal are measured locally. The time unit scales in the same manner as length.
Where unit time is measure locally.
One observation from this configuration is one can form parallel tangent planes along the radial. On a spherical surface with radius equal to the parallel planes tangent to the surface, all tangent spaces on the spherical surface will share the same scalar value for the metric. This is visualized in Figure 1.
Further observation is as the spherical surface asymptotically approaches the tangent surface. At an infinite distance away from the massive object generating the field, the tangent surface and the radial surface are the same. These tangent planes and radial surface correspond to and have a value of 1, allowing the entire space to be treated as Euclidean. As the rate at which the radial surface separates from the tangent plane (the curvature) increases. For now, dealing with the point at is delayed to later in the formalization for reasons that will become apparent.
A foliation of manifolds formed by concentric spheres where can be formed. Each manifold well have the same scalar valued metric for the whole surface. Transforming coordinate values from one leaf of the foliation to another amounts to a scalar multiple of the coordinates. In this transformation consider the following calculation. Pick any r value greater than zero and not in and draw out a great circle path on the surface of sphere with radius r. Align a plane such that it contains the great circle path. On the plane it will form a circle of radius as measured locally. Project this circle onto a parallel plane in and it will form a circle with a radius less than . This can be shown with the transformation from equation 24 by transferring the length of radius to . The reverse process can be performed by using the inverse of , in which case the image of the circle in will be projected onto a leaf in space.
Next consider a test particle moving along this path and how its trajectory is transferred to the plane in . This requires the local effect of equation 26 to be considered in addition to the global effect since the trajectory must have a velocity about the path to traverse the path. Here the dimensions of 3+1 comes into play. Unlike GR this is 3 dimensions with time separate, thus the distance does not include time within its calculation. None-the-less time is being swept out as the test particle transverse the path and as such its transformation scalar from should be considered. To visualize see Figure 2, as space is transverses so is time, therefore the value of should be squared when moving through both time and space (unlike a static transformation where time is not considered).
Thus, a particle undergoing acceleration will traverse an arc length greater than the arc length predicted by the calculation using only the global effects of the field. Both predict a greater arc length than if there is no field effect (global or local). The local effect is predicted for both a gravitation field generated by a mass and in an empty vacuum. Consider only the gravitational field (global):
And when only the local effect due to acceleration is considered:
In both cases the value of is greater than 1, thus the arc length traversed is greater than . Note: This is for a circular path projected from to .
Experiments performed in one lab will transfer to another lab by:
Consider an orbit in , since there is no gravitational effect the objects orbital velocity will be measured by , but without the global field effect, only the local accelerated effect takes place. The local effect is:
Locally at a leaf foliation of r radius, the arc length is:
Note, this is NOT saying two observers see two different arc lengths of the same event. Instead it is predicting the same experiment (an orbiting particle) performed in two labs, one in and the other in at radius r from the generating mass, will transform accordingly. Equation 33 for the lab in and equation 34 for the lab in . All experiments in with the same r under the influence of a single non-rotating massive object will transform the same (1 to 1).
At this juncture in the development the setup looks very much like GR, and it should as GR is a well backed theory by empirical data when dealing with the very large. There are several major differences, this model has not placed a strong constraint on the curvature of space being determined by the stress energy tensor or even energy, this model has not introduced geodesic’s as a free particle’s motion. Some corresponding calculations have been derived, but that is the extent of similarity at this juncture.
The model’s manifold that is built on the metric in equation 27 has an inherent issue. Consider the static transformation of distance d in a gravitational field from to
When the transformation is
When distance , distance . This causes a shift in what is observed at infinity to what is physically happening. Zero is observed when there is still a magnitude or r greater than zero. This makes a type of discreteness/discontinuity at zero, a type of shift as shown in Figure 3. When working with discrete spaces calculus is not an option, nor are Riemannian manifolds. Thus, the ability to transfer between spherical surfaces needs a solution that is not continuous. A method to approximate with the ability to scale to a high level of precision is sought. For clarity and completeness, the transformation does not create a pure numerical discreteness. Instead it creates a shifted zero quantity (), thus every number on a number line is shifted by observation, but the underlying forces must be calculated using the un-shifted values. Consider a transformation of a radial distance:
Where k is a constant. When , is not zero. Thus any between spherical radial lengths is:
To an observer the k value is not measured since they started at zero with no gaps (it was considered smooth when they measured the difference), but the physical laws behave with the k value included. Contemplate a center potential energy calculated as
as measured by an observer, but hidden to the observer is the shift in zero as in Figure 3, thus what is measured is
When a is calculated it is not
but
When the difference is not measurable, but as r approaches k in magnitude the measurements will show a considerable difference. Secondly, if there is a summation over spherical surfaces of differing r magnitudes the k value may become a multiplied effect. In the models transformation a radial orbit could be observed as zero magnitude, yet the observed center based force would not be zero.
The model at this juncture predicts when observing the large () there is a negligible (possibly not even measurable) effect when considering a smooth manifold. But as there may be conflicting observations to physical laws like a based force, where a zero radius produces a force. When gravitational forces are involved, the values below show a residual radial magnitude when radius is zero in .
Free Fall*
Orbital
Static (No Particle Acceleration)
The static only has the global field effect, free fall and orbital have both global and local effects.
*The free fall affect will be closer analyzed later as its motion (acceleration) is in the same direction as the field. It should be noted in Schwartzschild’s solution to Einstein’s equation the metric
is used when transforming the length as observed from infinity [7] to a local position within the gravity well the metric reduces to:
By performing a series expansion about
and observing when a constant in the series emerges.
This is the same as the model’s static zero value from equation 45. It appears GR has the same number line shift built into it. As the r in cancels leaving the constant value from equation 49. It should be noted the value has been termed the characteristic value for a gravitational system [4].
It is here the author contends the model’s transformation corresponds to GR when and only the static field is considered (no motion in the field) as shown in equation 7. At values of r where the model’s number line shift has less and less impact allowing the treatment of a smooth manifold in these areas to produce small effects (possibly immeasurable errors compared to empirical data). But unlike GR, this model does reflect the constant from the series and exploits to form a possible seamless path to a unified theory.
Observing Figure 3 it is not a large jump to understand how a type of gravitational wave might propagate throughout space as the mass or the center of mass changes over time.
Having shown a manifold approach does not work for the model, one possible starting place is to consider transformation from one frame (coordinate system) to another. This is not straightforward as there are a minimal two types of transformations; static and dynamic.
4.2. Static Transformation
The static transformation is the transformation of coordinates and time representing a test particle in space that is stationary (static). Since Einstein’s SR introduces the concept of relative velocity, the definition of static as used for a transformation is the transformation of coordinates and time for a test particle that is stationary relative to a non-moving observer in space. As a consequence of a stationary test particle, the local effect due to acceleration is zero. Therefore the transformation is reduced to only the potential part.
Thus, a vector in space transforms to space via:
Time transforms in the same manner:
The time interval (for example a second) increases as . One unit of time in space is observed as "longer" than one unit of time in space. Another observation is when the distance r is transformed from to , an invariant length independent of of r arises.
One immediate consequence of this is when equals zero, does not equal zero. Instead it is observed from as . A second observance is an invariant length observed as added to all sphere’s radial distance r. This invariant length added to all radial distances as observed from (or any other space) is the reason a Lorentzian manifold is not an appropriate description for the concentric spheres and tangent spaces. The Lorentzian manifold is constructed over a minimum twice differentiable () space. As a consequence of the added length the space is no longer differentiable between spherical surfaces or tangential spaces. For convenience the characteristic length will be termed . Although this value was discussed in the book Gravitation and derived from GR it is not applied in the same manner it is here.
Consider a central potential force that varies as , the change in the potential in a continuous space (like Lorentzian) will take the form of:
But in this model’s transformation there is a difference between the observed and the actual radial distance (as previously discussed). The observed change in potential energy is:
Which is different than equation 54. There is a shift in the observance. The in the transformation has the same effect when transforming a static circle.
There is an additional arc length observed to the circle. In theory this is not observable in a circle because the circle’s extra arc length overlaps the same arc of the circle, thus making it un-observable. Consider the trivial Figure 4, one transformation has an advance, the other doesn’t. Yes, it is laughable, silly and thus trivial, but the point is an observer cannot distinguish between a circle transformed with an advance and one transformed without an advance. In an ellipse this is not the case, an advance can be observed.
The length in a static transformation corresponds to the shifted value visualized in Figure 3.
4.3. Dynamic Transformation
A dynamic transformation, unlike a static transformation, contains movement. The test particle is not stationary, but moving through space and time. If the particle (against Einstein’s SR postulate) could move instantly with no time passage, then it would move through space without velocity, but that is not possible with any know experiment. Therefore it is moving through space and time. Since the test particle is moving through space and time, a type of area (space X time) is being swept out as the particle moves. To properly transform this type of dynamic, a transformation of space (length) and temporal (time) must be performed on the particles trajectory. Thus a motion about a circular path would have the following arc path transformation
Note the A is squared to properly transform both spatial and temporal transformation.
5. Classical Orbital Mechanics (Large Scale)
5.1. Orbit
A particle in a gravitational circular orbit will have a velocity of
and an advance of
Thus there is an invariant advance for all circular orbits in the system of
In an orbit that is elliptical one can place a dependency of r to . In this scenario there is a constant advance for all orbits. Consider r defined as
Then the value of A (the scalar transformation) is
The second part of equation 63 has a dependency on , when integrating from to the value goes to zero (that of an orbit), leaving only
Equation 64 integrated over 0 to is
This is the arc distance greater than , to obtain the advance in radians, divide by the semi-major axis a
This is exactly what General Relativity predicts as the advance of an orbiting planet, such as mercury [4].
5.2. Light Path
The logic behind the choice of a hyperbolic trajectory is space contracts (length) as a trajectory travels from Exemplar to Privo. Thus when at a distance r from a massive object, the radius R appears larger than it is locally (at the massive object’s location). Thus the contraction is based on the characteristic length (a constant in the system). In a dynamic (non-static) system the value must be squared as previously shown. Since photons do not couple to space in the same manner as massive particles, they do not experience a local effect, only a global. The amount of contraction in this trajectory is equivalent to the semi-major axis for a hyperbolic trajectory. The foci is the sum of the semi-major axis (the amount of contraction) and the radius of the massive body. An observer at distance r will set a light ray path aimed at the edge of the massive body (Thus distance R). But as the light ray travels toward the massive object, the space around it will contract by the amount of the semi-major axis. This will cause the light to appear to bend around a massive object. A photon is a massless particle and by definition of the model it has zero pinertia. Therefore there is no local effect of sinertia, only the global effect of the field’s gradient. Thus, the transformation for the photon trajectory is:
The photon follows a path of a hyperbolic path as shown in Figure 5. The angle between the two lines with slope is the angle a photon path bends around an object. Using the terms in the list Section 5.2 with M equal to the mass of the sun and R equal to the radius of the sun, the model predicts a curvature of for a photon travel closest to the surface of the sun. This is in good agreement with empirical data and GR’s prediction [8]. The model implies a photon can never orbit a massive object, it will either follow the path of a hyperbola or interact with the massive object.
Hyperbolic Path
- R = The radius of the massive body (c - a) in Figure 5
- a = Semi-major axis a, with value
- f = foci c = R + a
- e = eccentricity =
- b = Semi-minor axis =
- =
- =
- =
5.3. Curvature due to Energy
This section is a quick overview of how the basic form of the transformation relates to Einstein’s General Relativity. In General Relativity, Einstein’s equation relates the curvature of space-time to the energy about the space-time. As previously discussed, the characteristic length is the amount of curvature (contraction by the NUVO model) caused by mass’s interaction with space. is:
If one takes the rest energy of the mass and calculates as a function of energy they will arrive at
This form is General Relativity’s form if the LHS of is converted to a Ricci tensor and Ricci scalar while the RHS’s E is converted to a stress energy tensor. The NUVO model, though a different approach, aligns in many places with the form of General Relativity. And it should as General Relativity is a well established and experimentally confirmed theory. Any theoretical approach to join General Relativity and Quantum mechanics must correspond to General Relativity in the physics of the very large, only departing from the theory as it approaches the physics of the very small.
5.4. GPS Time Dilation Real World Example
The GPS system is often used as a "proof" of General Relativity and Special Relativity [6]. As previously discussed this author strongly disagrees with any use of SR for calculating values in a non-inertial frame, it is a gross miss-use and miss-understanding of SR to do so. Any valid theory should be able to account for all time dilation due to acceleration (gravitational field or acceleration through the field) of a system. To calculate the time dilation of the GPS system (as compared to a clock on Earth) using NUVO one simply calculates the the value of for each location (the Earth and the Satellite). For this calculation the rotation of the earth will not be added to the equations as it adds no real contribution as the Earth’s surface rotates at about 19 meters per second compared to lights 299,792,458 meters per second. The value for the Earth is:
for the satellite is:
Where the middle term of the RHS is due to the instantaneous velocity experienced by the satellite. A static transformation from the satellites position (accounting for all accelerations, both global - GR, and local - orbital acceleration) to the Earth’s surface position one needs to transform both to Exemplar space and take the difference. To tranform to Exemplar space the inverse of is used.
When the dilation is multiplied by the number of nano-seconds in a day () the dilation is nano-seconds per day. This corresponds to known measured effects, and to calculations when both GR and SR are used to calculate the dilation [6].
6. Observations
In working with the model, one occasionally comes across an interesting (or at least interesting to the author) correlation. Consider a photon of wavelength and the curvature of space’s characteristic length from equation 68. Using Compton’s wavelength (involving mass), set the photon wavelength equal to the characteristic length and solve for mass.
This value is Planck’s Natural number for mass (Planck’s units not divided by ), this is shown in Figure 6 The product of the wavelength and the curvature of space due to the energy is a constant.
7. Summary
In this article a first attempt at formalizing NUVO as a theory is presented. The cosmic level predictions and calculations agree well with empirical data and General Relativity. In the next article the second part of the formalization will introduce how NUVO relates to and predicts aspects of Quantum mechanics.
References
- Stephen, T. Thornton, A.R. Modern Physics For Scientists and Engineers, 2002. [Google Scholar]
- Nolting, W. Theoretical Physics 4, first ed.; Springer, 2016.
- Wald, R.M. General Relativity; Chicago Univ. Pr.: Chicago, USA, 1984. [Google Scholar] [CrossRef]
- Misner, Thorne, W. Gravitation, 1970.
- Marion, J.B. Classical Dynamics of Particles and Systems, second ed.; Academic Press, 1970.
- Ashby, N. Relativity and the Global Positioning System. Physics Today 2002. [Google Scholar] [CrossRef]
- Schwarzschild, K. 1999; Schwarzschild, K. On the gravitational field of a mass point according to Einstein’s theory, 1999, [arXiv:physics.hist-ph/physics/9905030]. [Google Scholar] [CrossRef]
- Mikhailov, A.A. The deflection of light by the gravitational field of the Sun (George Darwin Lecture). Monthly Notices of the Royal Astronomical Society 1959, 119, 593. [Google Scholar] [CrossRef]
Figure 1.
Parallel Planes
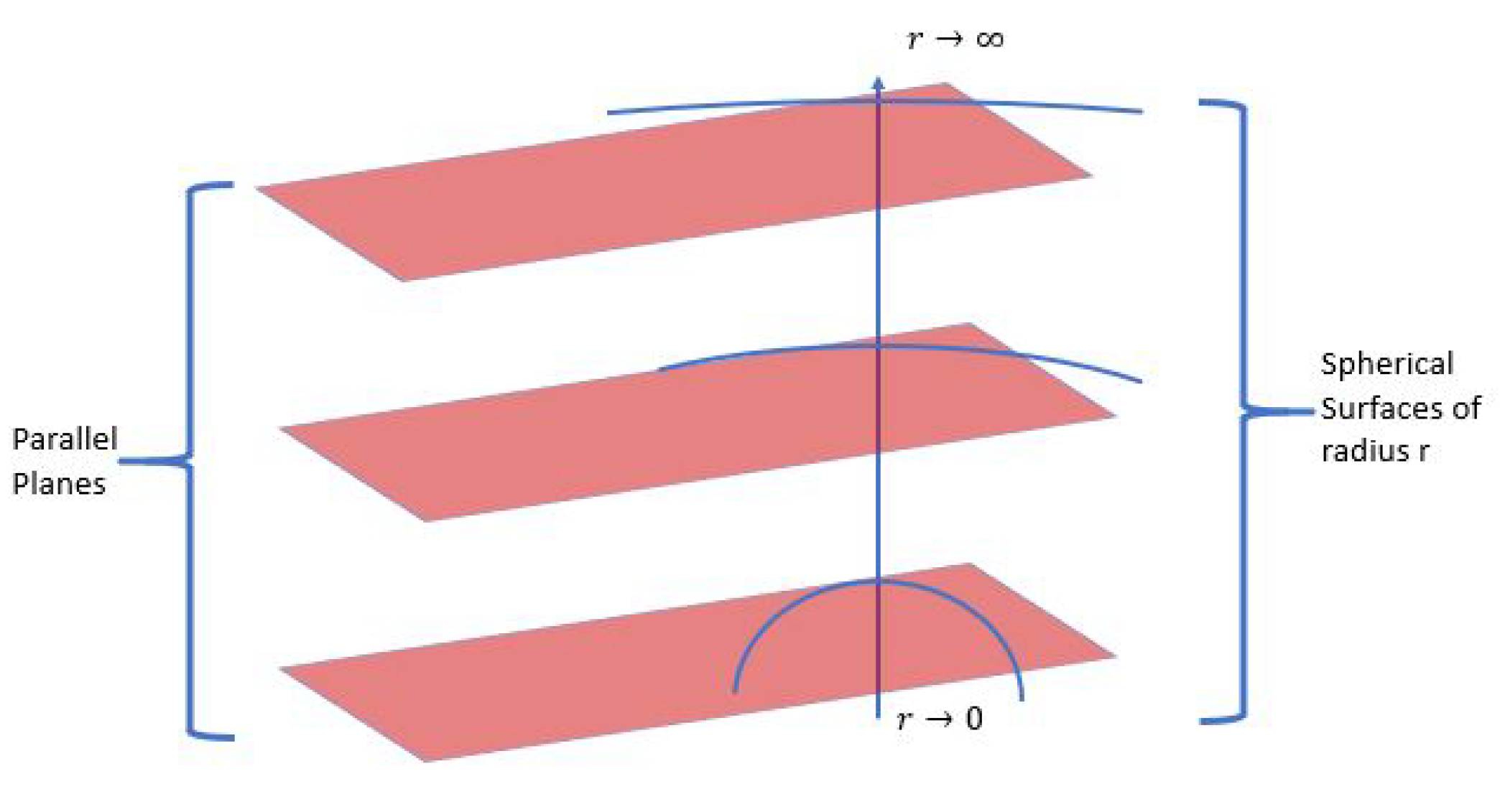
Figure 2.
Parallel Planes
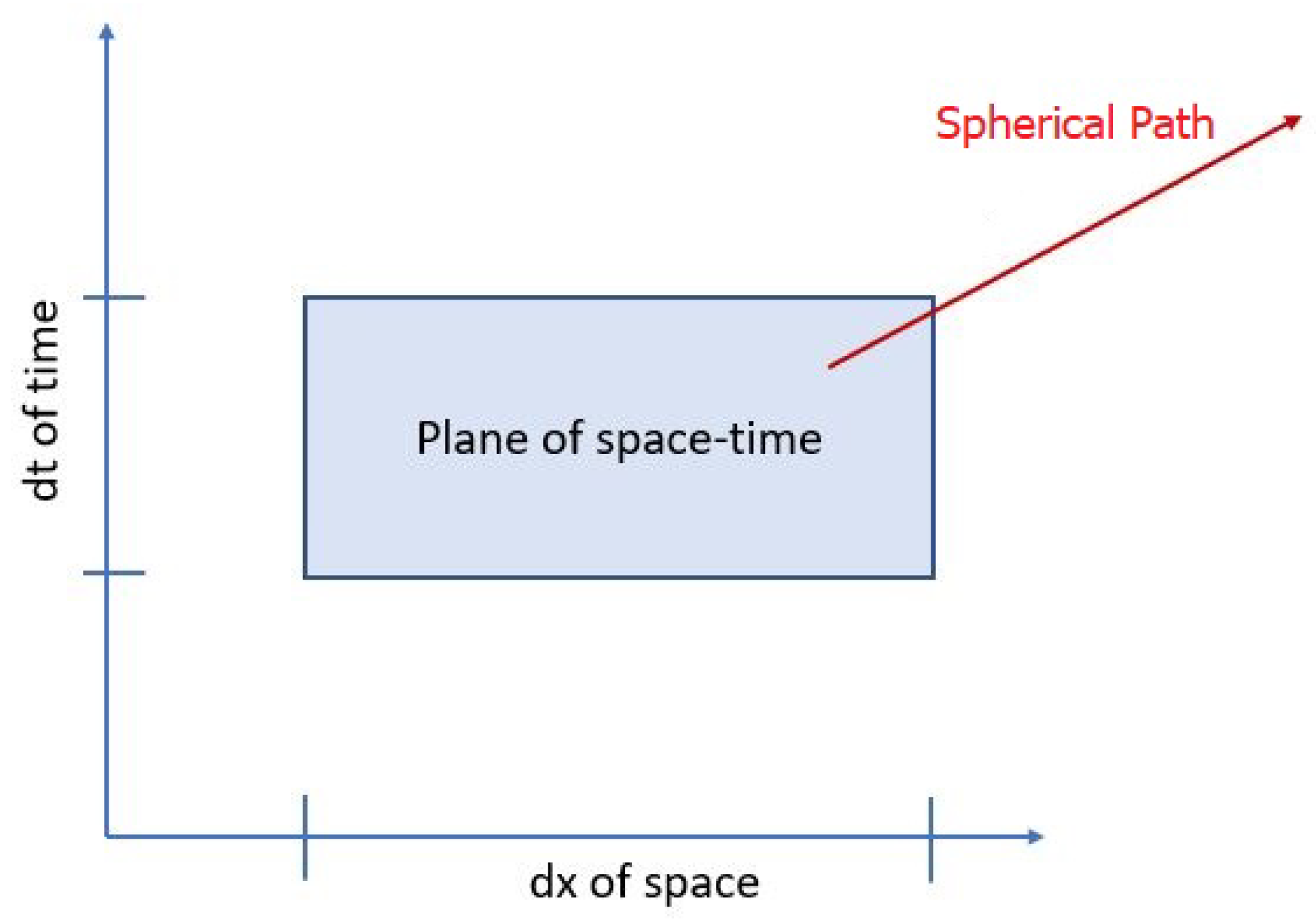
Figure 3.
Shifted Zero Axis
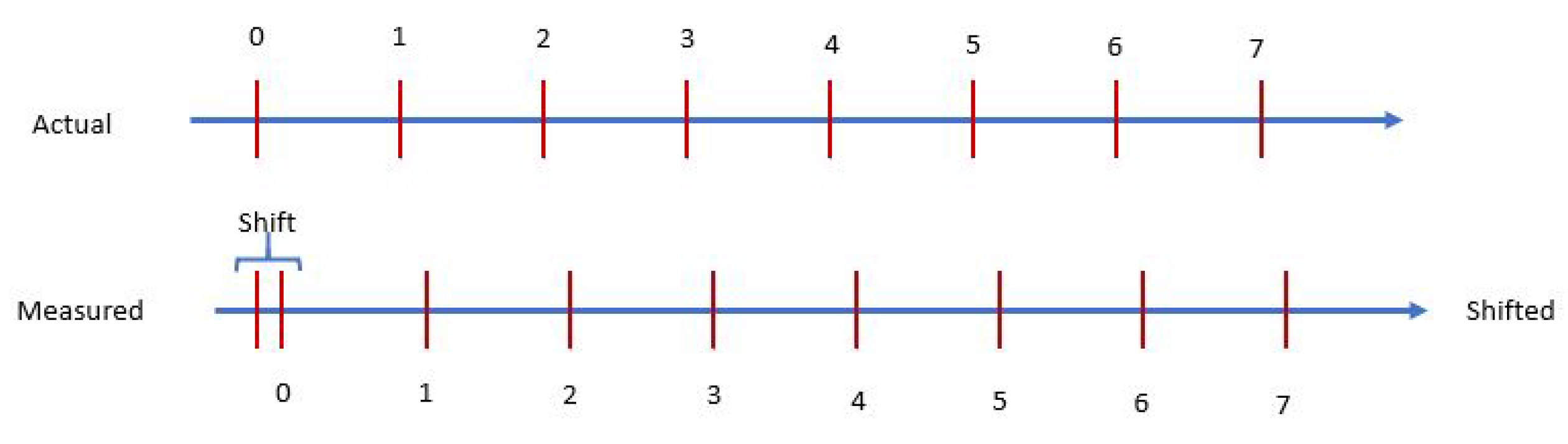
Figure 4.
Circle Advance Inspection
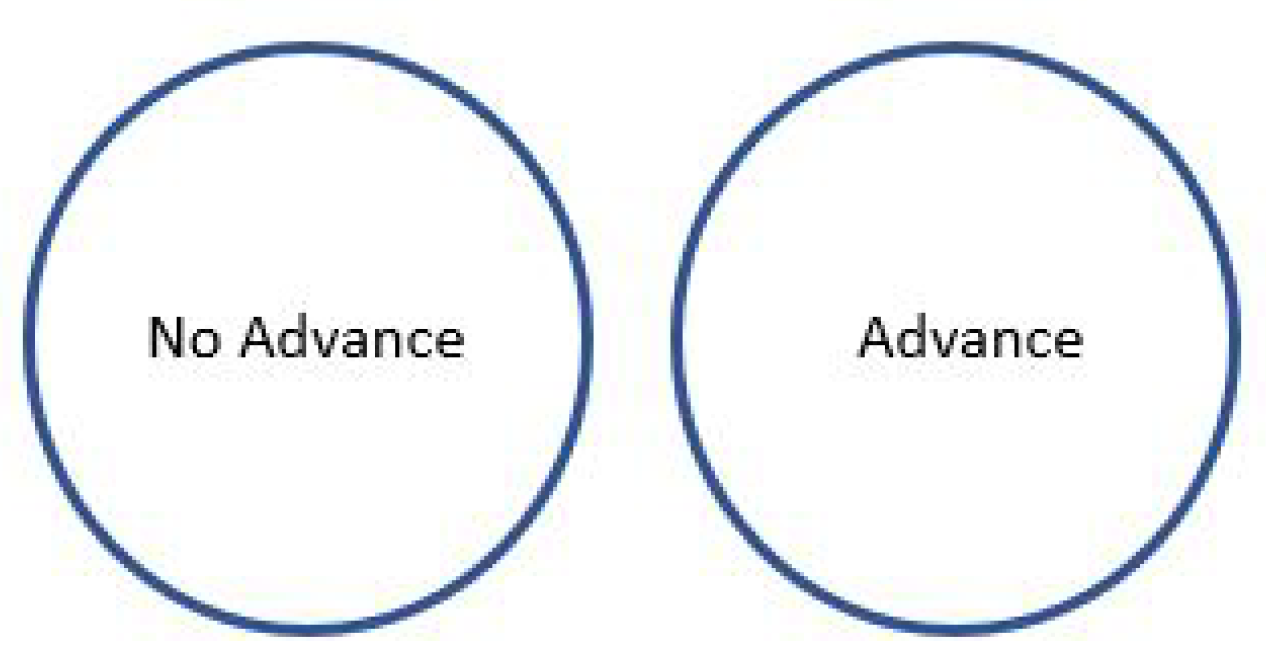
Figure 5.
Hyperbolic Path
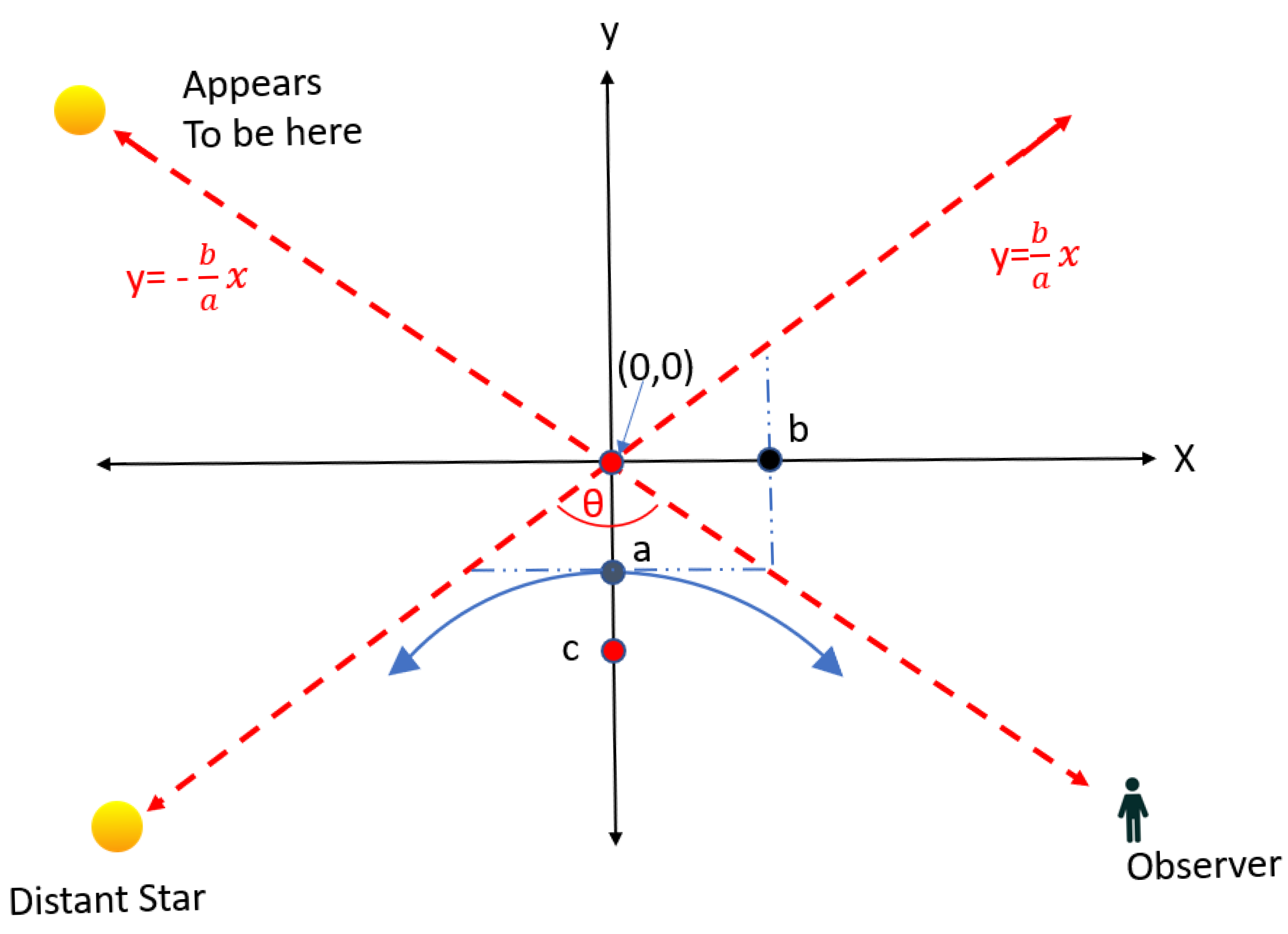
Figure 6.
Mass Lambda Comparison
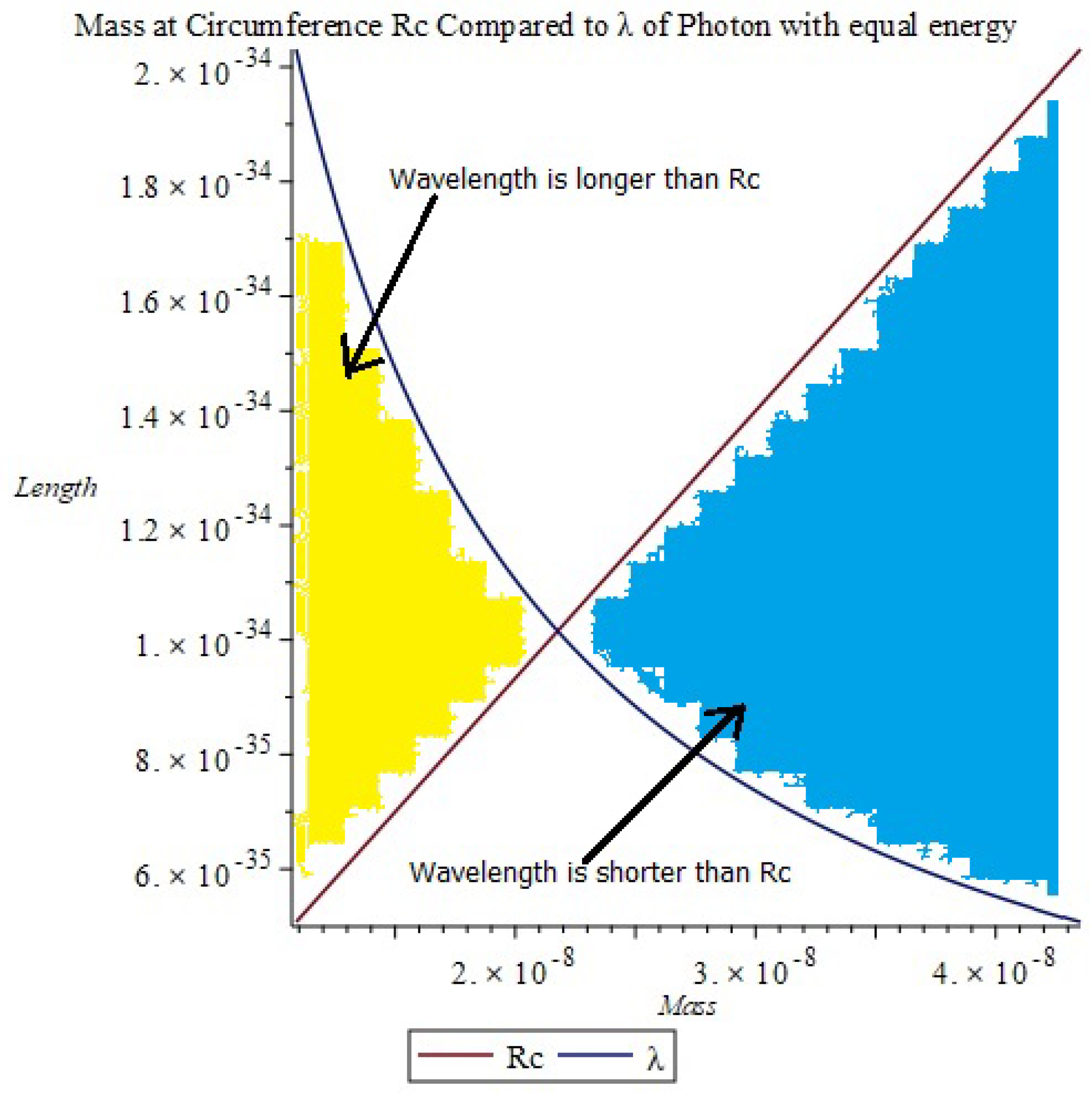
Table 1.
Measurement Group.
| Dimension | Abbreviation | Base Dimension(s) |
|---|---|---|
| Time | T | T |
| Length | L | L |
| Velocity* | v | L T |
| Mass | M | M |
| Momentum* | p | M v |
| Acceleration* | a | L T |
| Force* | F | ML T |
| Area* | A | L |
| Volume* | V | L |
| Pressure* | P | MLT |
| Energy* | E | MLT |
| Power* | P | MLT |
| Angular Momentum* | LMv |
Table 2.
Transformation of Physical Dimensions.
| Dimension | Abbreviation | Base Dimension(s) | Transformation Scalar |
|---|---|---|---|
| Time | T | T | A |
| Length | L | L | A |
| Velocity | v | L T | 1 |
| Mass | M | M | 1 |
| Momentum | p | M v | 1 |
| Acceleration | a | L T | A |
| Force | F | ML T | A |
| Area | A | L | A |
| Volume | V | L | A |
| Pressure | P | MLT | A |
| Energy | E | MLT | 1 |
| Power | P | MLT | A |
| Pressure · Volume | PV | ML2T | 1 |
| Angular Momentum | LMv | A |
Table 3.
Exemplar Measurement Subgroup
| Dimension | Abbreviation | Base Dimension(s) | Transformation Scalar |
|---|---|---|---|
| Velocity | v | L T | 1 |
| Mass | M | M | 1 |
| Momentum | p | M v | 1 |
| Energy | E | MLT | 1 |
Table 4.
Privo Measurement Subgroup
| Dimension | Abbreviation | Base Dimension(s) | Transformation Scalar |
|---|---|---|---|
| Time | T | T | A |
| Length | L | L | A |
| Acceleration | a | L T | A |
| Force | F | ML T | A |
| Area | A | L | A |
| Volume | V | L | A |
| Pressure | P | MLT | A |
| Power | P | MLT | A |
| Angular Momentum | LMv | A |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






