1. Introduction
The properties of the final product depend on the composition of the steel and the heat treatment process. The microstructure determines the overall mechanical behaviour of the steel and heat treatment provides an efficient way of manipulating the properties of the steel by controlling the cooling rate. When heat treating steels, it is necessary to achieve the required cooling rate and final product temperature to obtain the required mechanical properties. The cooling strategy is determined by the size and shape of the product. Especially in the steel industry, large products with different sizes (shape and thickness) are heat treated with the same cooling unit, so proper regulation of the cooling rate by changing the coolant pressure and flow rate is necessary to achieve good material properties for different product sizes. For these reasons, spray cooling is one of the most common cooling methods used for heat treatment in the steel industry. The design of spray cooling sections is complicated by the existence of different types of nozzles, their proper positioning, sizing, and other parameters affecting the spray cooling of hot surfaces (presence of boiling) [
1,
2].
The parameters affecting spray cooling of hot steel surfaces can be divided into two groups [
3,
4]. The first group relates to spray parameters such as water mass flux (amount of water sprayed onto the surface), water temperature, water additives and droplet size [
4]. The second group relates to the cooled surface: temperature, velocity, roughness, and the presence of oxide scale [
4]. The key factors are the water mass flux and the cooled surface temperature [
5]. The influence of each factor on the heat transfer coefficient and/or Leidenfrost temperature is briefly described below to illustrate the complexity of the spray cooling problem in the presence of boiling.
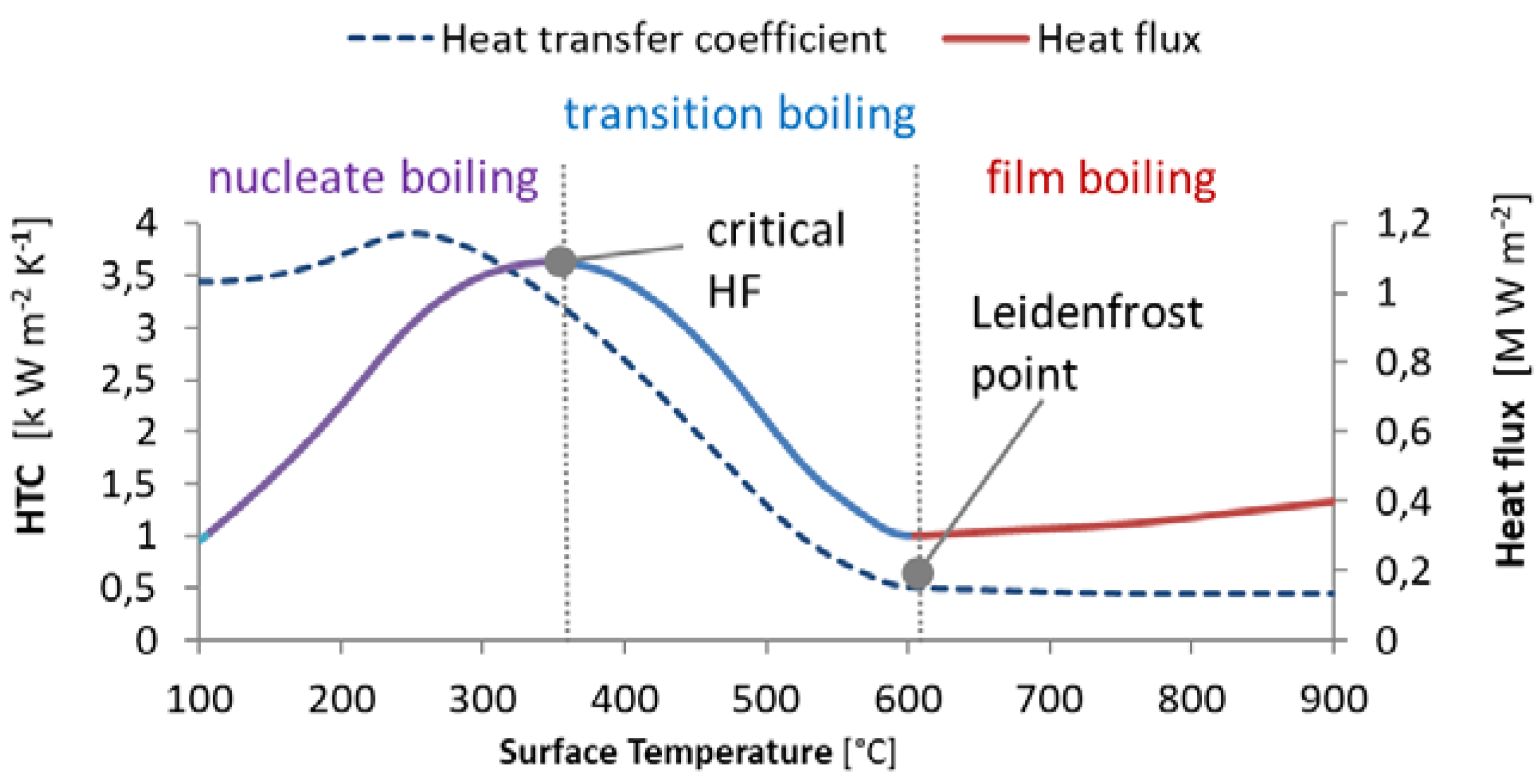
The influence of surface temperature on spray cooling is significant and relates to different boiling regimes. As described in many heat transfer textbooks [
6,
7] when a liquid is in close contact with a surface that is significantly hotter than the boiling point of the liquid, the heat transfer boiling phenomena can be characterised by four different regimes: a) free convection (single phase), b) nucleate boiling, c) transition boiling and d) film boiling (
Figure 1). Based on the boiling curve, at the onset of film boiling (between the transition boiling and film boiling regimes) the heat flux is minimal, and the corresponding temperature is known as the Leidenfrost temperature (TL) or point. The critical heat flux (CHF) occurs when the heat flux reaches the maximum on the boiling curve. The CHF point is the transition point between the transition boiling regime and the nucleate boiling regime. The heat transfer coefficient (HTC) is significantly lower in the film boiling regime than in the nucleate boiling regime. The Leidenfrost temperature is sensitive to the surface condition (scale, roughness) as will be shown later.
The amount of water sprayed onto the cooled surface is commonly expressed as the water mass flux (𝑚̇ [kg m
-2 s
-1]), which is commonly referred to as the impingement density [
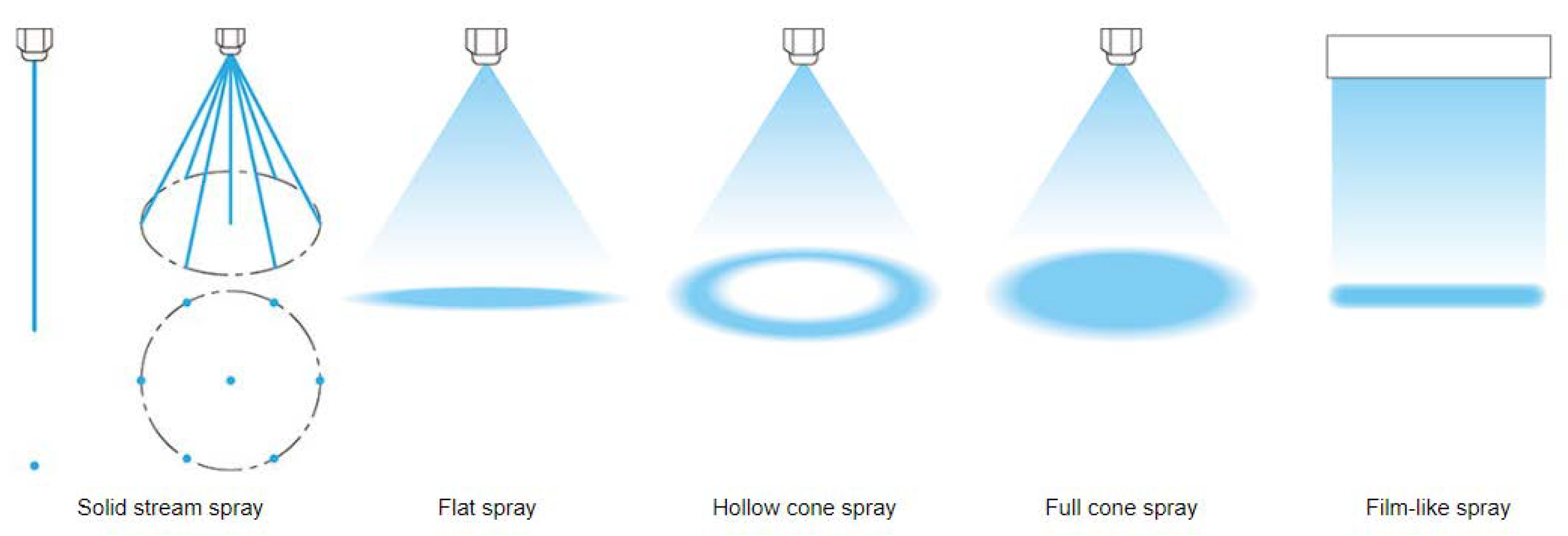
5]. Increasing the water mass flux increases the heat transfer coefficient for all surface temperatures [
5,
8,
9]. There are different types of nozzles with different spray footprints (
Figure 2). The water mass flux is influenced by the size of the nozzle (which determines the water flow rate) and the spray area (which is influenced by the distance between the nozzle and the cooled surface and by the shape of the jet). The use of nozzles allows a wide range of cooling rates to be achieved by changing the process water pressure. Increasing the water pressure increases the amount of water sprayed, which in turn increases the cooling rate. Increasing the water mass flow also increases the Leidenfrost temperature and the temperature at which the critical heat flux occurs [
10].
It is common in the steel industry, that the temperature of the cooling water varies during seasons. The water temperature influences the heat transfer coefficient and has a significant effect on the Leidenfrost temperature [
12]. A 30 K increase in water temperature (typical in the industry due to seasonal effects) causes a 10 % decrease in the film boiling heat transfer coefficient and a 17 % decrease in the Leidenfrost temperature [
13].
Water additives mainly affect the duration of the film boiling regime [
14]. Additives can be divided into two groups according to their influence on the duration of the film boiling regime (prolonging and shortening) [
14]. The first group (prolonging) consists of solid particles (ceramic particles, carbon black, nanoparticles [
15]), gases (N
2, O
2 and CO
2) and liquids (oil and fat) that are insoluble or poorly soluble in water. The second group (shortening) consists of salts, acids and alkalis that are soluble in water. NaCl is the most common inorganic salt, sometimes used in immersion quenching, but its use in spray cooling is unusual.
The type and size of the nozzle and the water pressure influence the droplet size and velocity. In general, droplet diameter and droplet velocity influence cooling [
16]. The higher the droplet velocity, the higher the heat transfer coefficient [
9].
Surface roughness and the presence of scales (oxides) on the surface influence spray cooling. Higher surface roughness results in a higher heat transfer coefficient [
17]. Oxide scales mainly affect the Leidenfrost temperature [
18,
19] and can increase cooling [
20].
Differences in the spray cooling of static and moving plates (typical industrial situation) were reported in [
21].
The surface temperature dependent heat transfer coefficient is a necessary input for numerical simulations of the cooling process. At present, some empirical correlations exist for predicting the heat transfer coefficient or Leidenfrost temperature [
3,
5,
9,
10,
13], but they are mainly a function of the water mass flux. Due to the many parameters that influence the spray cooling of a hot surface, it is impossible to accurately estimate the heat transfer coefficient by some analytical or empirical equation that takes all these parameters into account. Laboratory measurement provides a fast and accurate method of obtaining the heat transfer coefficient for spray cooling of hot surfaces.
The process of designing cooling sections for heat treatment is an iterative research process involving several important steps. First, the cooling regime (cooling rate and cooling time) that will give the desired mechanical properties must be found. Then the appropriate nozzle types and positions are determined. The cooling section is designed, and the heat transfer coefficient of the designed cooling is measured under different conditions. The next step is to perform numerical simulations showing the optimum cooling settings (water pressure, cooling length and product speeds) for different product sizes (thicknesses). The final step is to validate the designed cooling in a full-scale laboratory or pilot plant test.
2. Finding the optimal cooling regime
The first step is to determine the appropriate cooling regime that will give the required mechanical properties. This can be done by the metallurgist using a Continuous Cooling Transformation (CCT) diagram and numerical simulation of cooling, and/or by quenching tests using small samples and a nozzle [
2,
22]. These tests are carried out on steel specimens with embedded sheathed thermocouples (typically type K with a diameter of 1.5 mm or less). The thermocouples are positioned at different depths to monitor the temperature across the thickness of the specimen.
The test procedure is as follows. The sample with embedded thermocouples is heated to a specified temperature and held at that temperature for a specified time. The required water pressure is then set, the sample is removed from the furnace and placed under the nozzle. The deflector is opened for a specified time and the sample is cooled. After the test, the sample is cut, and the hardness and microstructure are measured. These tests are repeated with different settings (nozzle type, water pressure, cooling time) until the required mechanical properties are found. Examples of measured data (temperature record, hardness and microstructure obtained) are shown in
Figure 3,
Figure 4,
Figure 5 and
Figure 6. Once the best solution is found, the cooling section can be designed and tested.
3. Cooling section design: nozzles selection and positioning
It is necessary to know the heat transfer coefficient of different nozzle configurations (type, size, and position) in order to design long cooling sections formed by hundreds of nozzles. Nozzle positions are limited by space constraints, which are influenced by conveyor design, presence of piping and other technology. The first step (finding the cooling regime) and existing empirical correlations provide rough information on the required water mass flux. This can be used as initial information for nozzle selection. If very intensive cooling is required, it is better to use large flat jet nozzles. In the case of soft cooling, the small full cone nozzles can provide an efficient cooling method. The positions of the nozzles should be chosen according to the space limitations and taking into account the estimated water mass flux. Examples of design are shown in
Figure 7 and
Figure 8.
The preliminary designed cooling sections/zones are manufactured in a small, economical version and then tested in the laboratory. The heat transfer coefficients for different nozzle configurations are obtained from these tests. These are used in numerical simulations of the cooling process to validate the required cooling intensity for different products. The preliminary designed cooling section can be modified (optimised) until sufficient cooling homogeneity and the required cooling rate (heat transfer coefficient) are achieved.
4. Description of laboratory measurement of heat transfer coefficient
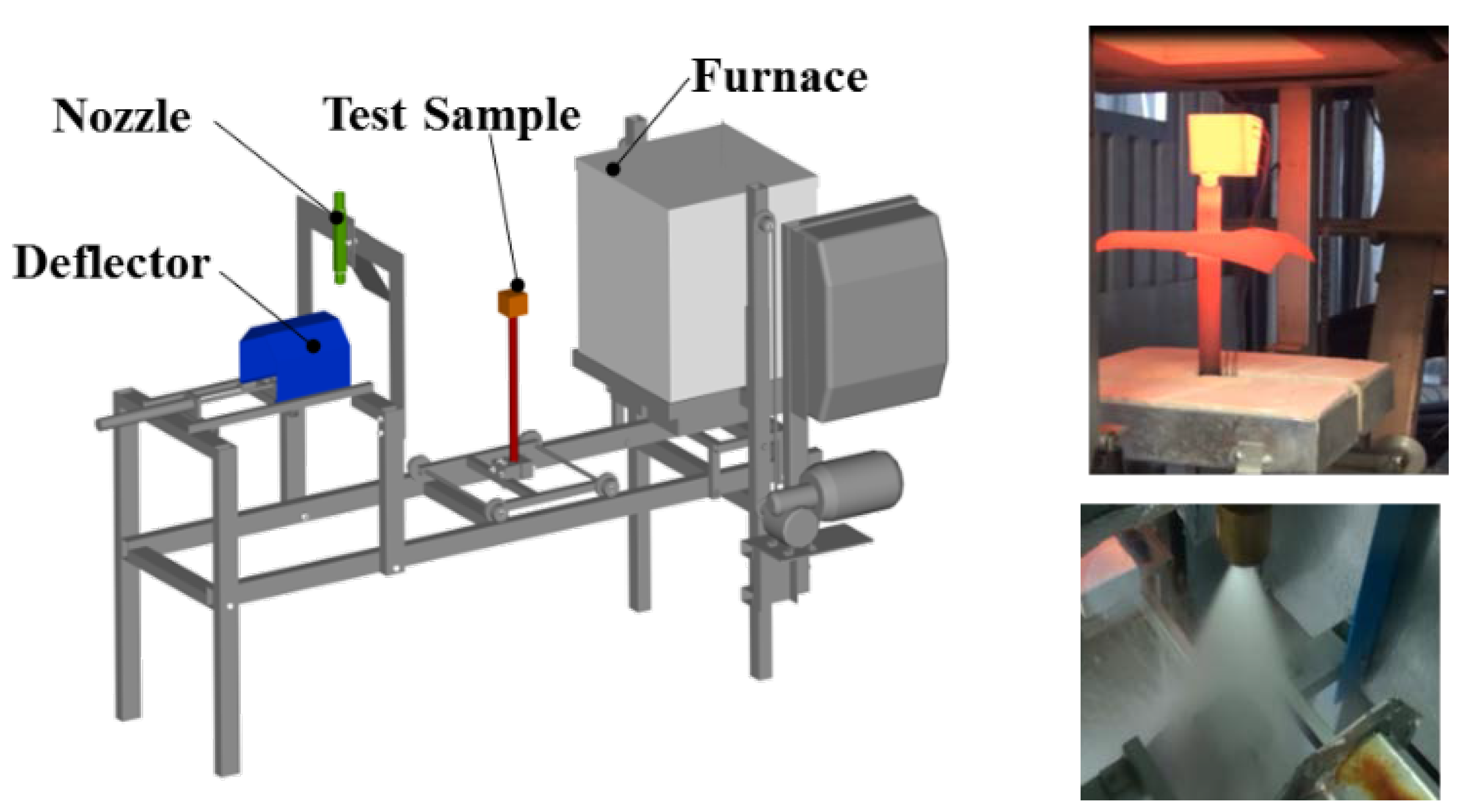
Laboratory measurements of the heat transfer coefficient are performed with a moving sample. This allows the heat transfer coefficient to be mapped along the length of the cooling. The schematic is shown in
Figure 9 and photos of tests with different products (plate, tube, and rail) are shown in
Figure 10.
The test procedure starts with the production of a test sample of the original shape (plate, tube, rail, etc.) and the embedding of thermocouples in the test sample. The embedded sensors are calibrated to provide reliable and repeatable heat transfer coefficient values. The sample is connected to the test bench and heated to the desired temperature (typically 900 °C). Once the cooling conditions are set, the data logger begins recording temperatures and sample position. The sample is moved reversibly through a cooling zone until it has cooled to room temperature. The maximum speed of movement on the test bench is 10 m s-1. The recorded data is then transferred to a computer for analysis.
Cooling uniformity is critical to design. During testing, cooling uniformity can be measured using thermocouples in different positions or by using line scanners or infrared cameras. A typical output from a line scanner measurement is shown in
Figure 11. The tests on flat products are carried out for top and bottom cooling and the optimum setting of the bottom cooling should be found to provide the same top and bottom cooling.
After the measurement, the inverse heat conduction problem is solved to calculate the time-dependent boundary conditions: HTC, heat flux and surface temperature. Beck's sequential approach is used [
23,
24,
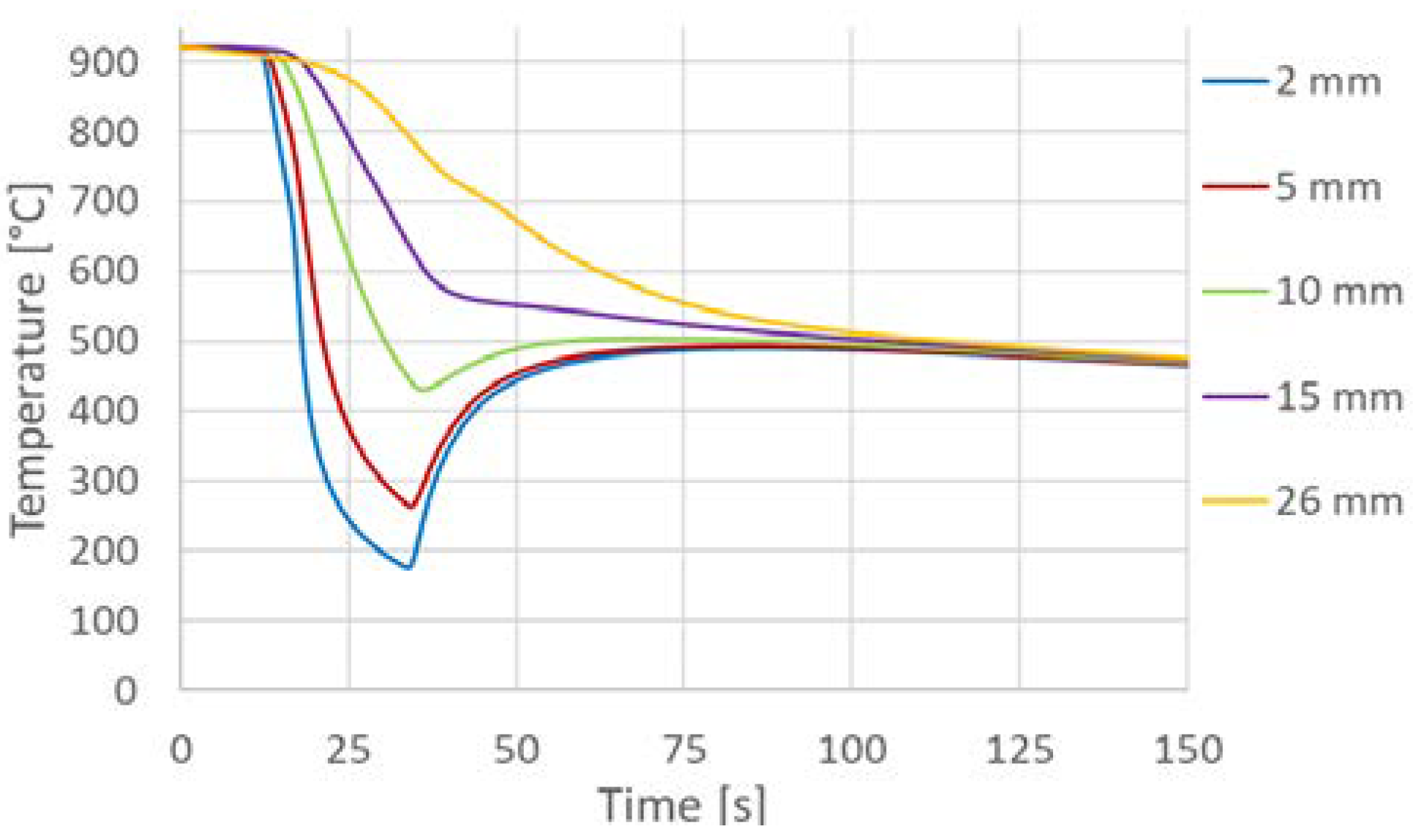
25]. This method uses a sequential estimation of the time-varying boundary conditions and future time steps. The example of the calculated time-dependent surface temperature and heat transfer coefficient is shown in
Figure 12. The dependence of the HTC on the surface temperature and the position in the cooling section is obtained by interpolation (
Figure 13). This boundary condition can be simplified to the dependence of the HTC on the surface temperature by averaging along the position (
Figure 14 - left). This boundary condition can be easily applied in commercial FEM software. The dependence of HTC on position (
Figure 14 - right), obtained by averaging along the surface temperature axis, can be useful for optimising nozzle positions. A large distance between the nozzles can cause a rapid decrease in the heat transfer coefficient between the nozzles.
5. Simulation of the real cooling process
The cooling process can be numerically simulated using the boundary conditions known from the previous step. The simple 1D finite element method (FEM) simulation can be used for thin flat products. Otherwise (shaped profiles, rails, ...) the 2D FEM model should be used to simulate the cooling process. The ideal boundary condition is the heat transfer coefficient as a function of surface temperature and position in the cooling section. The laboratory boundary conditions obtained with the short cooling section can be combined to form a boundary condition for the long cooling section (
Figure 15).
The results of numerical simulations with different settings are the cooling curves for different conditions (product size, product speed, cooling water pressure, ...). These cooling curves are then compared, and the optimum cooling settings are selected for different product sizes.
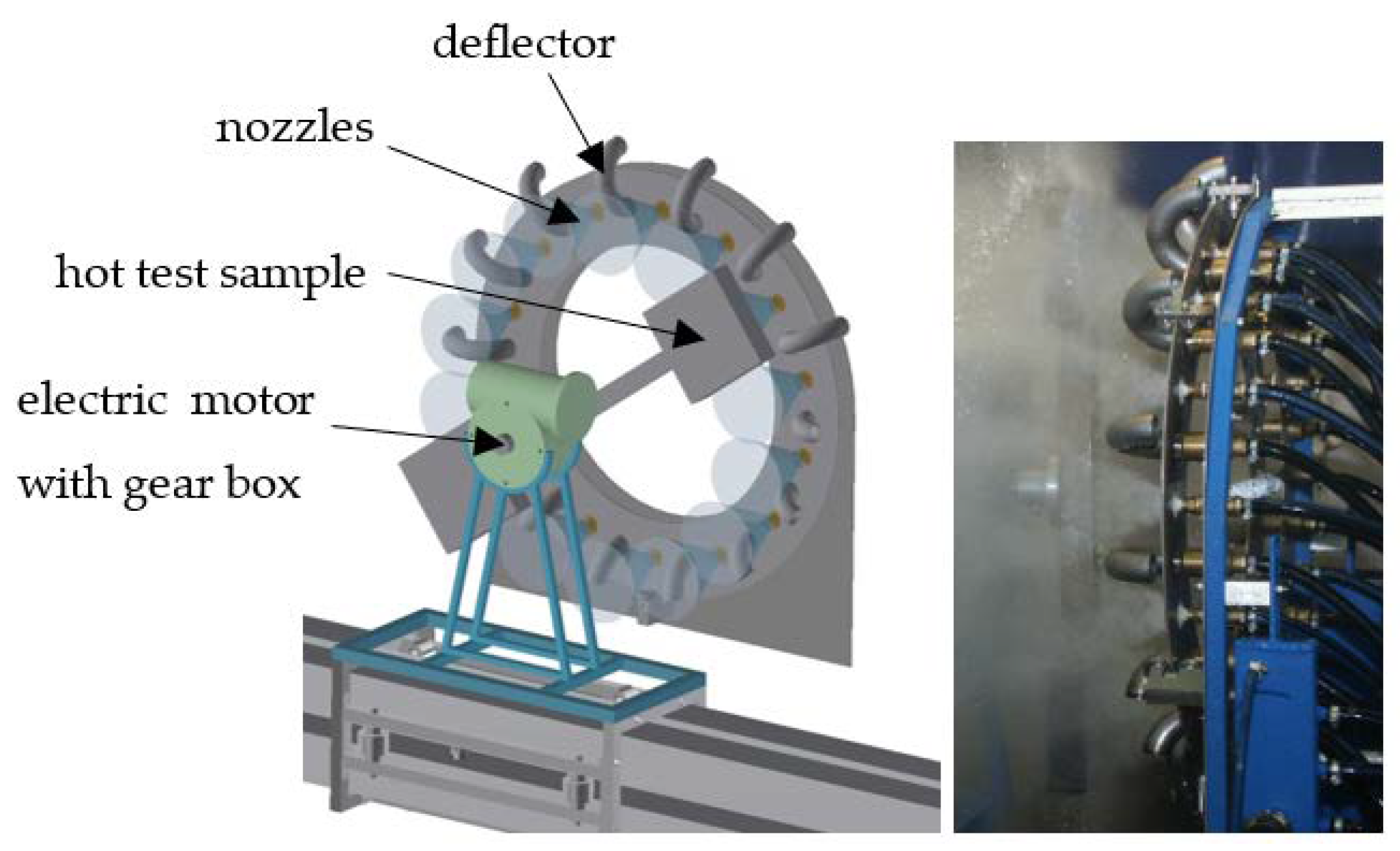
The final step is to validate the mechanical properties of the heat-treated material. The best way to do this is to carry out expensive pilot tests in the plant/rolling mill. Laboratory tests with rotating samples can be an inexpensive way to simulate continuous cooling under plant conditions with high product speed and long cooling section. Straight motion is converted into rotation. A schematic diagram and photo of a laboratory test bench is shown in
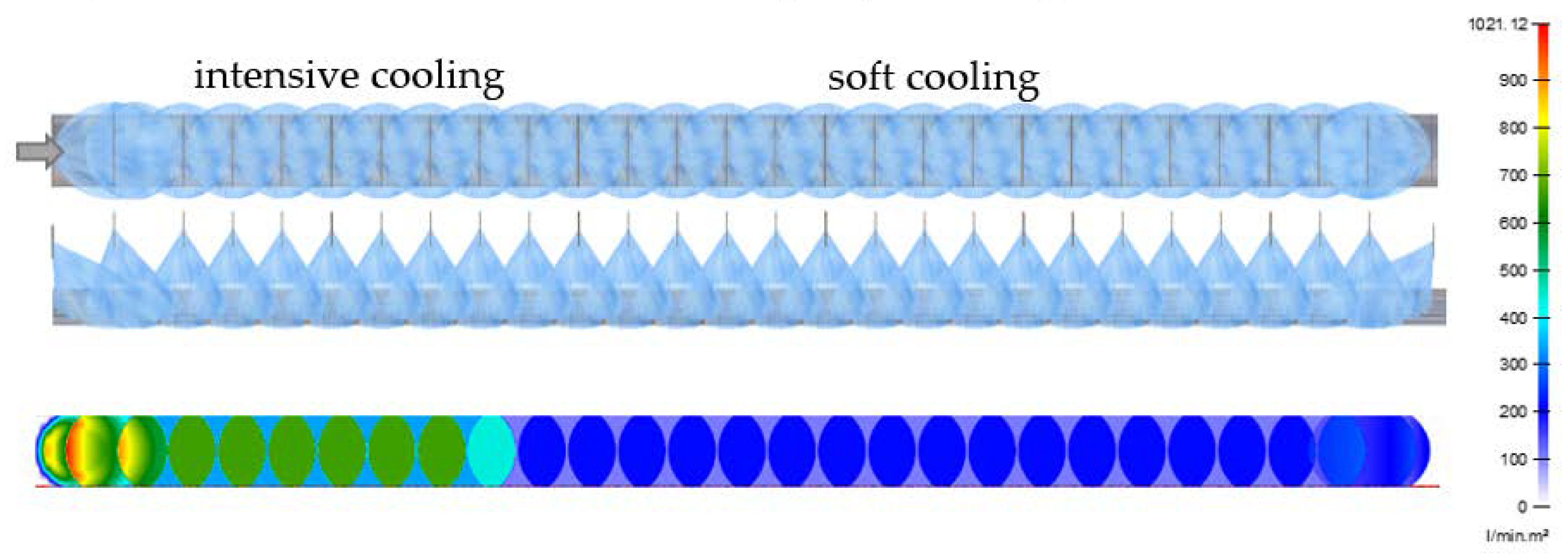
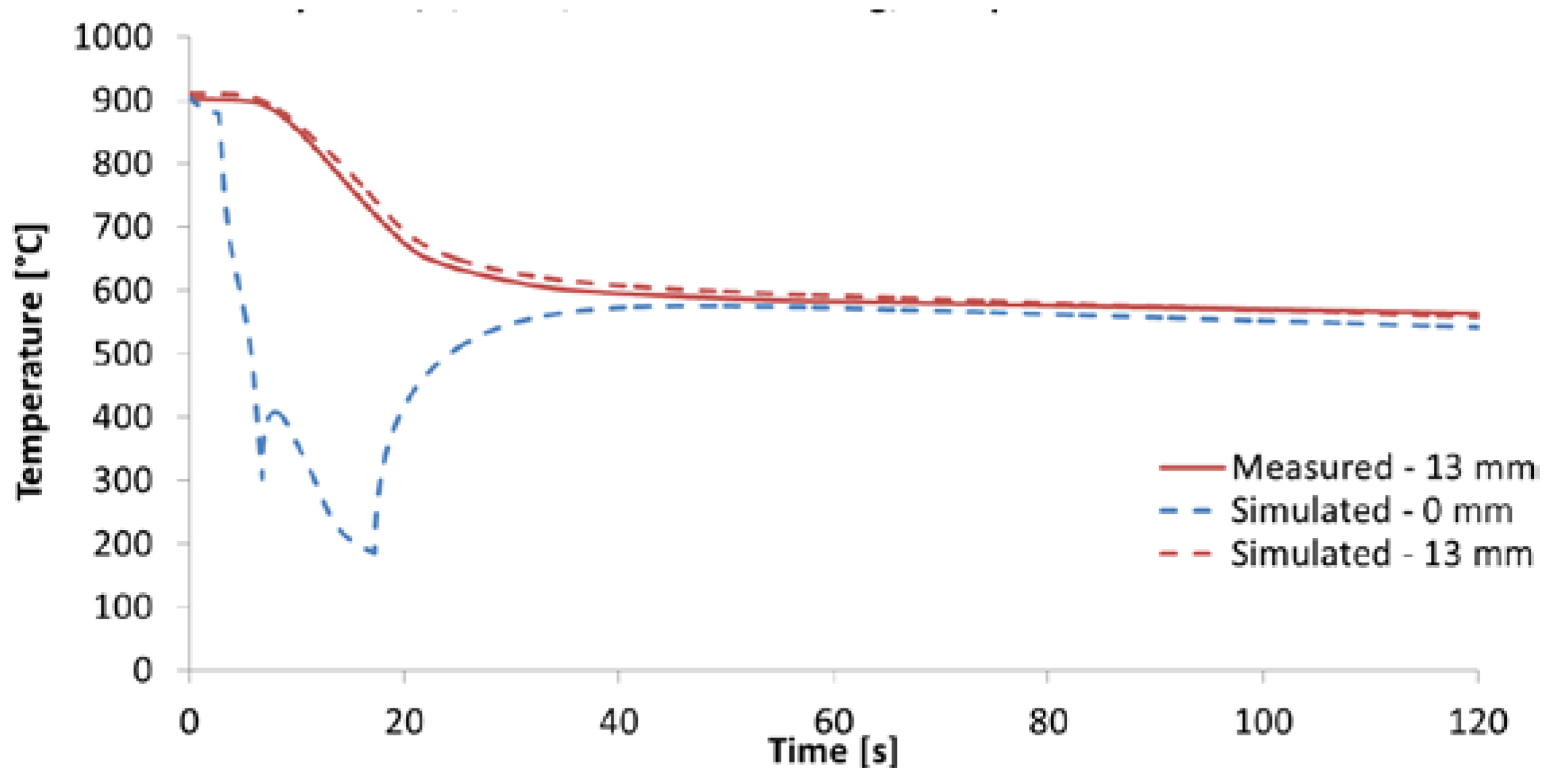
Figure 16. It consists of nozzles, deflector, and rotating arm with hot test sample. This test bench allows switching between two types of nozzles to simulate an initial intensive cooling followed by a soft cooling. An example of the temperatures measured on this test bench for one-sided cooling of a 20 mm thick plate (simulation of two-sided cooling 40 mm) is shown in
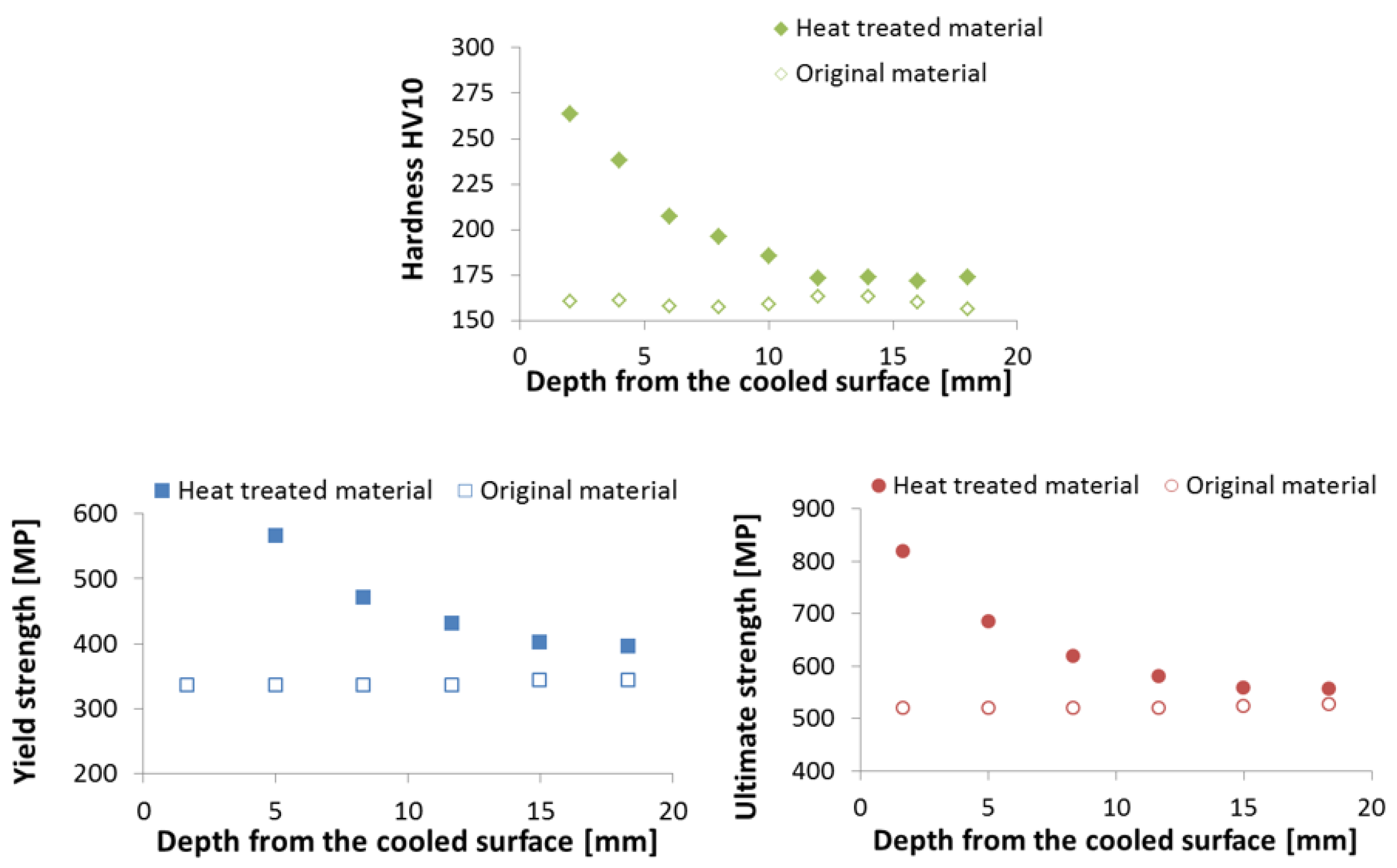
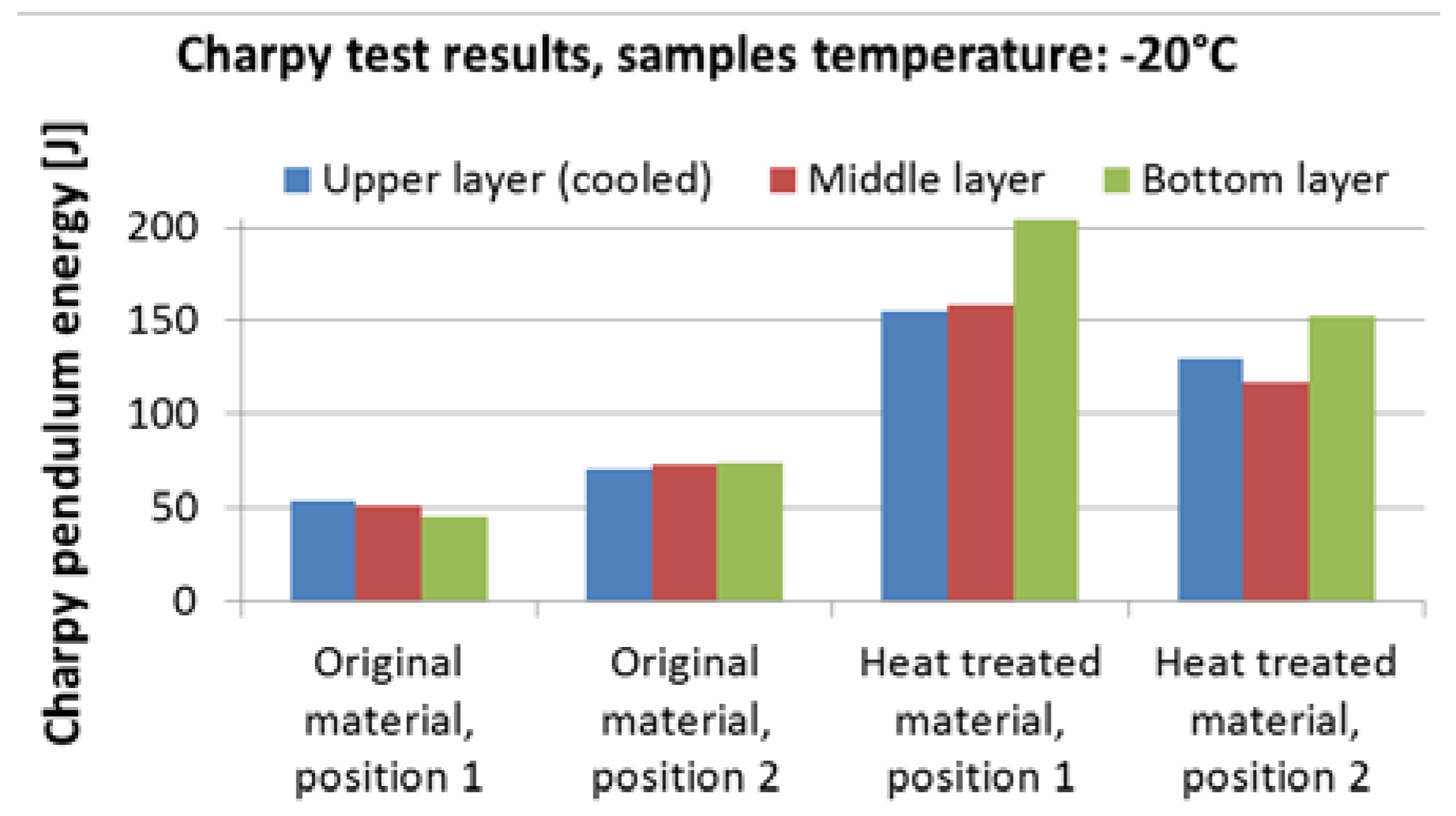
Figure 17. The result of the numerical simulation for this cooling regime (simulation was carried out before this measurement) is added to this graph and it shows good agreement with the measurement. The results of measured hardness, tensile and Charpy pendulum tests of this heat-treated material (real cooling conditions) are shown in
Figure 18 and
Figure 19.
6. Conclusions
The design technique presented combines numerical simulations, laboratory measurements and, in the final stage, testing under production conditions. Such a technique minimises the number of expensive pilot trials and avoids potential design errors. Optimum design is achieved by accurately measuring the heat transfer coefficient of the designed cooling system. This allows accurate numerical modelling of the cooling process. This method can be used to design new cooling sections as well as to optimise existing cooling. An optimised design based on laboratory measurements of the heat transfer coefficients allows the required mechanical properties to be achieved without the need for complex on-site testing, and the new cooling section can be commissioned more quickly and without the need for additional cooling modifications. The optimised design saves water, pumping energy, and manufacturing costs by optimising the length of the cooling section and the number of nozzles.
Author Contributions
Methodology, P.K.; writing—original draft preparation, M.C. and P.K.; writing—review and editing, O.R.; performing experiments, O.R. and M.C.; visualization, date evaluation, J.K and T.L.; supervision, P.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the internal grant of the Brno University of Technology focused on specific research and development No. FSI-S-23-8254.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hnizdil, M.; Kotrbacek, P. Heat treatment of rails. Materiali in Tehnologije, 2017, vol. 51, no. 2, pp. 329-332.
- Pohanka, M.; Kotrbacek, P. Design of cooling units for heat treatmen. In Heat treatment conventional and applications; Czerwinski, F.; InTech: Rijeka, Croatia, 2012; ISBN: 978-953-51-0768- 2.
- Liang, G.; Mudawar, I. Review of spray cooling – Part 2: High temperature boiling regimes and quenching applications. International Journal of Heat and Mass Transfer, 2017, vol. 115, pp. 1206-1222. [CrossRef]
- Chabicovsky, M.; Horsky, J. Factors influencing spray cooling of hot steel surfaces. In METAL 2017 - 26th International Conference on Metallurgy and Material, Brno, Czech Republic, 2017, Tanger, Ostrava, ISBN: 978-80-87294-79-6.
- Wendelstorf, J.; Spitzer, K.-H.; Wendelstorf, R. Spray water cooling heat transfer at high temperatures and liquid mass fluxes. International Journal of Heat and Mass Transfer, 2008, vol. 51, pp. 4902–4910. [CrossRef]
- Incropera, F.P. Fundamentals of Heat and Mass Transfer, 6th ed.; John Wiley & Sons: Hoboken, US, 2007.
- Holman, J.P. Heat Transfer, 10th ed.; McGraw-Hill, New York, NY, 2010.
- Yao, S.; Cox, T.L. A general heat transfer correlation for impacting water sprays on high-temperature surfaces. Experimental Heat Transfer, 2002, vol. 15, no. 4, pp. 207–219. [CrossRef]
- Chabicovsky, M.; Kotrbacek, P.; Bellerova, H.; Kominek, J.; Raudensky, M. Spray cooling heat transfer above leidenfrost temperature. Metals, 2020, vol. 10, no. 9, pp. 1270. [CrossRef]
- Hnizdil, M.; Kominek, J.; Lee, T.; Raudensky, M.; Carnogurska, M.; Chabicovsky, M. Prediction of Leidenfrost Temperature in Spray Cooling for Continuous Casting and Heat Treatment Processes. Metals, 2020, vol. 10, no. 11, pp. 1551. [CrossRef]
- Spray Pattern, Spray Angle & Spray Distribution. Available online: https://www.ikeuchi.id/technology/19/ (accessed on 28.4.2023).
- Raudensky, M.; Hnizdil, M.; Hwang, J. Y.; Lee, S.H.; Kim S. Y. Influence of the Water Temperature on the Cooling Intensity of Mist Nozzles in Continuous Casting. Materiali in Tehnologije, 2012, vol. 46, pp. 311-315.
- Kotrbáček, P., Chabičovský, M., Kominek, J., Resl, O. & Bellerova, H. Influence of water temperature on spray cooling at high surface temperatures. Applied Thermal Engineering, 2022, vol. 216. [CrossRef]
- Luty, W. Cooling Media and Their Propertie. In Quenching theory and technology. 2nd ed.; Liscic, B.; Tensi, H. M..; CRC Press Taylor & Francis Group: Boca Raton, US, 2010; ISBN: 978-0849392795.
- Bellerova, H.; Tseng, A.A.; Pohanka, M. Heat transfer of spray cooling using alumina/water nanofluids with full cone nozzles. Heat and Mass Transfer/Waerme- und Stoffuebertragung, 2012, vol. 48, no. 11, pp. 1971-1983. [CrossRef]
- Kotrbacek, P.; Bellerova, H.; Luks, T.; Raudensky, M. Heat Transfer Correlations for Secondary Cooling in Continuous Casting. Steel Research International, 2021, vol. 92, no. 3. [CrossRef]
- Sinha, J.; Hochreiter, L.; Cheung, F.-B. Effects of surface roughness, oxidation level, and liquid subcooling on the minimum film boiling temperature, Experimental Heat Transfer, 2003, vol. 16, pp. 45-60. [CrossRef]
- Wendelstorf, R.; Spitzer, K.-H.; Wendelstorf, J. Effect of oxide layer on spray water cooling heat transfer at high surface temperatures. Int. Journal of Heat and Mass Transfer, 2008, vol. 51, pp. 4892-4901. [CrossRef]
- Chabicovsky, M.; Hnizdil, M.; Tseng, A.A; Raudensky, M. Effects of oxide layer on Leidenfrost temperature during spray cooling of steel at high temperatures. International Journal of Heat and Mass Transfer, 2015, vol. 88, pp. 236-246. [CrossRef]
- Raudensky, M.; Chabicovsky, M.; Hrabovsky, J. Impact of oxide scale on heat treatment of steels. In METAL 2014 – 23rd International Conference on Metallurgy and Material, Brno, Czech Republic, 2014, Tanger, Ostrava, ISBN: 978-80-87294-54- 3.
- Raudensky, M.; Horsky, J. Secondary cooling in continuous casting and Leidenfrost temperature effects. Ironmaking and Steelmaking, 2005, vol. 32, no. 2, pp. 159-164. [CrossRef]
- Heat Treatment. Available online: https://www.heatlab.cz/research/heat-treatment/ (accessed on 28.4.2023).
- Raudensky, M. Heat Transfer Coefficient Estimation by Inverse Conduction Algorithm. Int. J. Num. Meth. Heat Fluid Flow, 1993, vol. 3 pp. 257-266. [CrossRef]
- Pohanka, M.; Woodbury, K. A. A Downhill Simplex method for computation of interfacial heat transfer coefficients in alloy casting. Inverse Problems in Engineering, 2003, vol.11, pp. 409-424. [CrossRef]
- Kominek, J.; Pohanka, M. Estimation of the number of forward time steps for the sequential Beck approach used for solving inverse heat-conduction problems. Materiali in Tehnologije, 2016, vol. 50, pp. 207-210. [CrossRef]
Figure 1.
Dependences of the heat transfer coefficient (blue) and heat flux (red) on the surface temperature [
4].
Figure 1.
Dependences of the heat transfer coefficient (blue) and heat flux (red) on the surface temperature [
4].
Figure 2.
Different jet shapes and their footprints [
11].
Figure 2.
Different jet shapes and their footprints [
11].
Figure 3.
Laboratory heat treatment test bench - stationary spray quenching tests [
22].
Figure 3.
Laboratory heat treatment test bench - stationary spray quenching tests [
22].
Figure 4.
Example of measured results for sample thickness 30 mm and steel grade S355: cooling curves in different positions from the cooled surface.
Figure 4.
Example of measured results for sample thickness 30 mm and steel grade S355: cooling curves in different positions from the cooled surface.
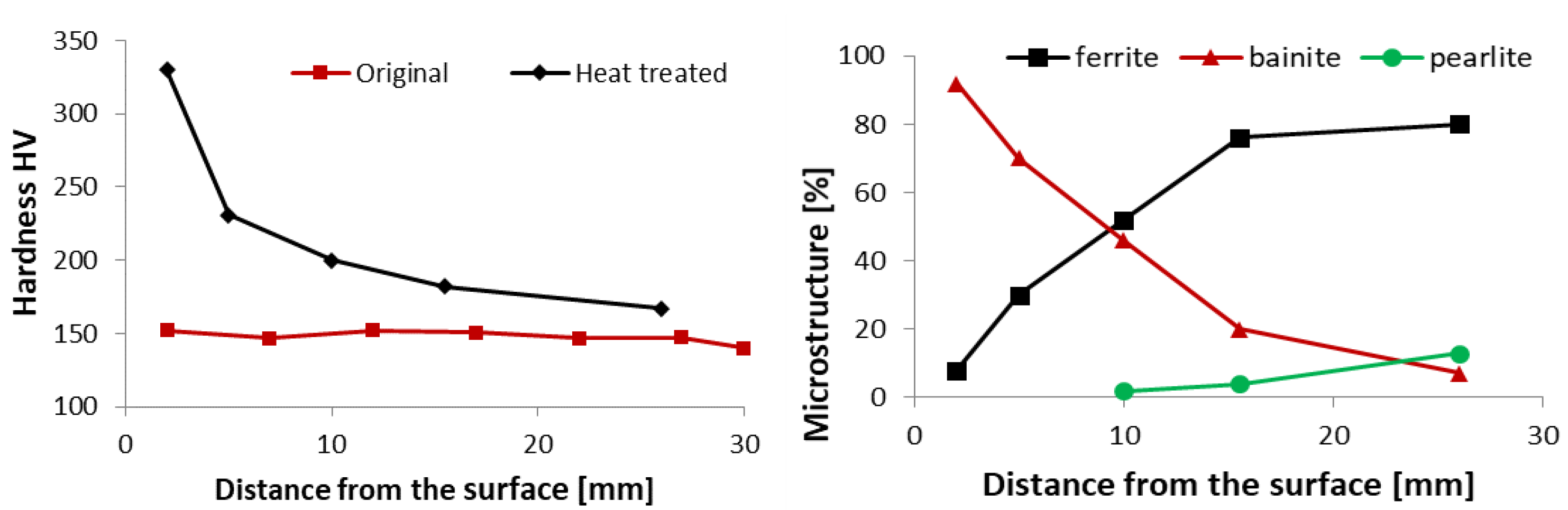
Figure 5.
Example of measured results for sample thickness 30 mm and steel grade S355: measured hardness (left), microstructure composition (right).
Figure 5.
Example of measured results for sample thickness 30 mm and steel grade S355: measured hardness (left), microstructure composition (right).
Figure 6.
Example of measured results for sample thickness 30 mm and steel grade S355: microstructure analysis.
Figure 6.
Example of measured results for sample thickness 30 mm and steel grade S355: microstructure analysis.
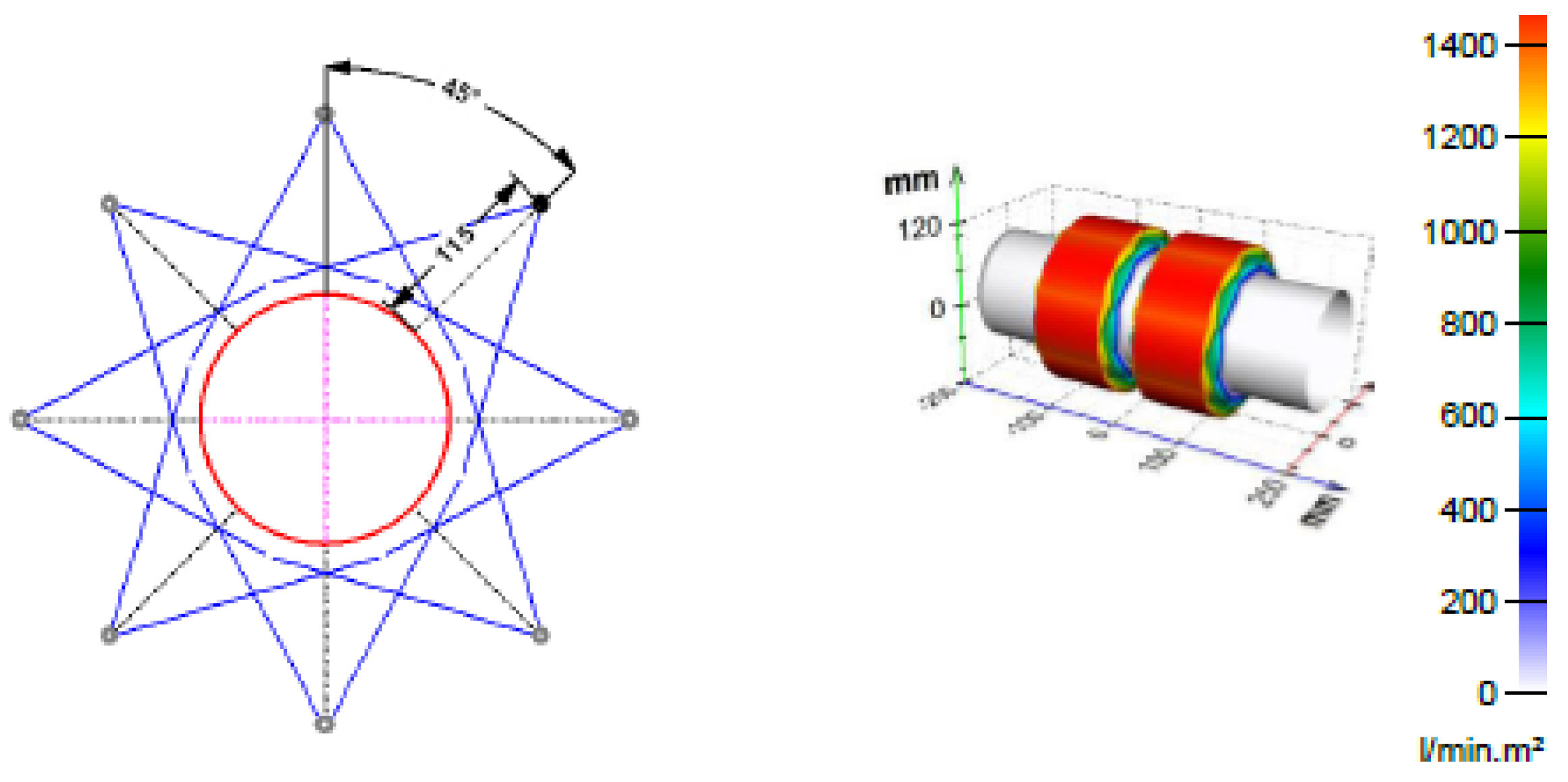
Figure 7.
Example of preliminary design for steel flat strip: top - nozzles positions (top and side view), bottom - water distribution.
Figure 7.
Example of preliminary design for steel flat strip: top - nozzles positions (top and side view), bottom - water distribution.
Figure 8.
Example of preliminary design for steel tubes: left - nozzles positions, right - water distribution.
Figure 8.
Example of preliminary design for steel tubes: left - nozzles positions, right - water distribution.
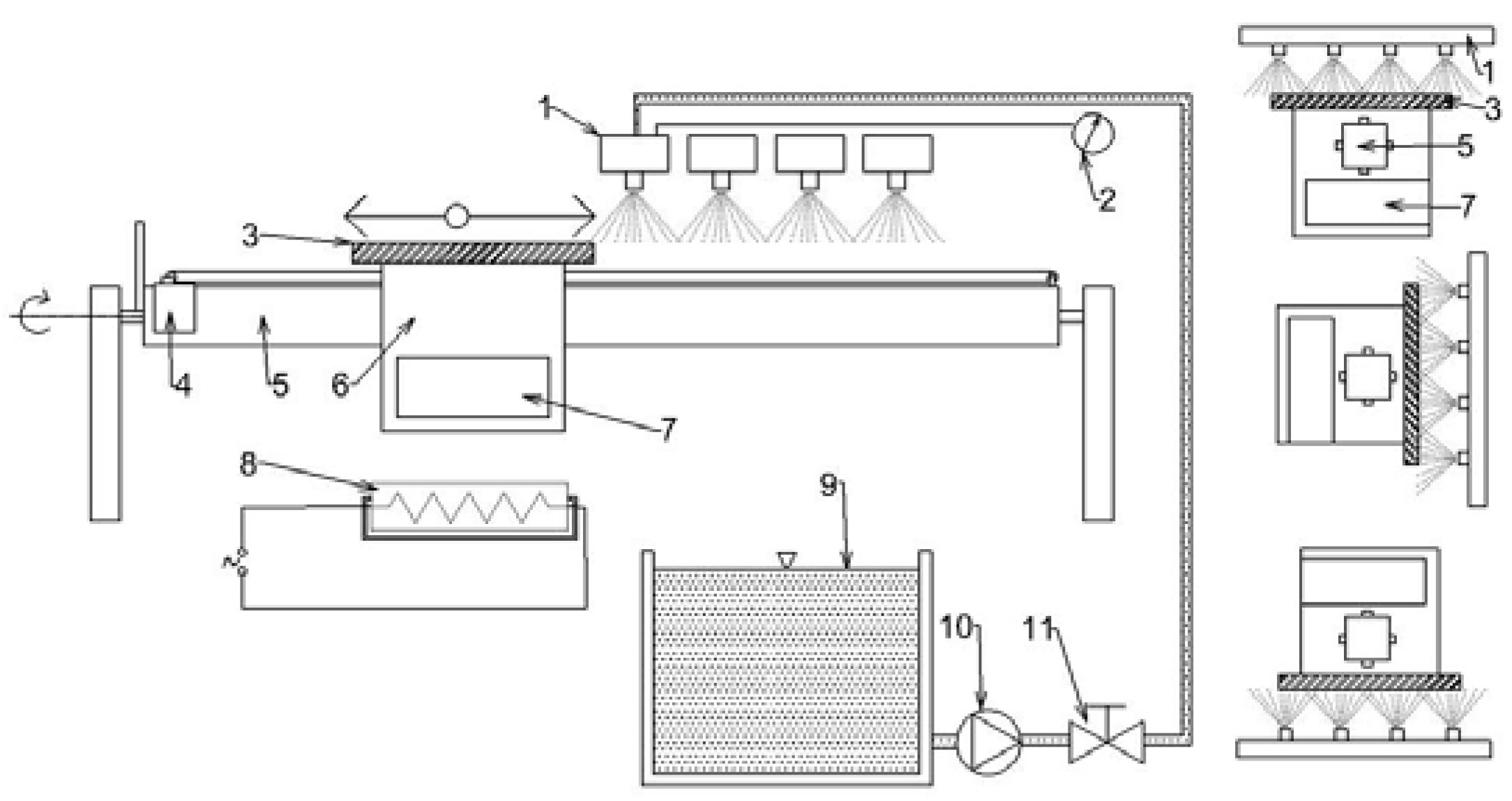
Figure 9.
Schematic of the laboratory test bench for measuring the heat transfer coefficient: 1 – headers with nozzles, 2 – pressure gauge, 3 – test plate, 4 – motor moving trolley, 5 – girder carrying trolley, 6 – movable trolley, 7 – data logger, 8 – heater, 9 – water tank, 10 – pump, 11 – control valve.
Figure 9.
Schematic of the laboratory test bench for measuring the heat transfer coefficient: 1 – headers with nozzles, 2 – pressure gauge, 3 – test plate, 4 – motor moving trolley, 5 – girder carrying trolley, 6 – movable trolley, 7 – data logger, 8 – heater, 9 – water tank, 10 – pump, 11 – control valve.
Figure 10.
Photos of laboratory stand with tested cooling for plate, tube, and rail.
Figure 10.
Photos of laboratory stand with tested cooling for plate, tube, and rail.
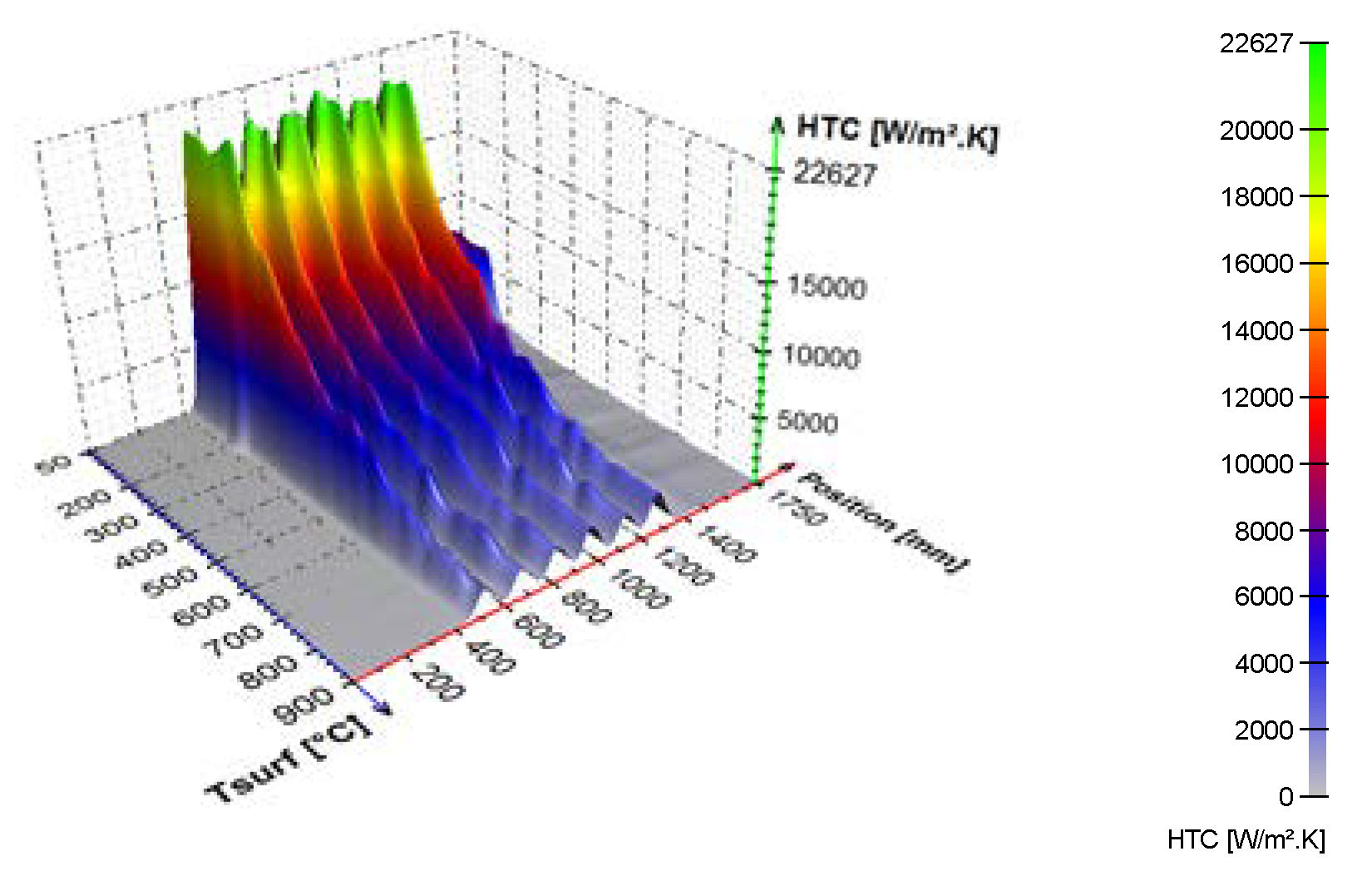
Figure 11.
Example of typical results obtained with the line scanner.
Figure 11.
Example of typical results obtained with the line scanner.
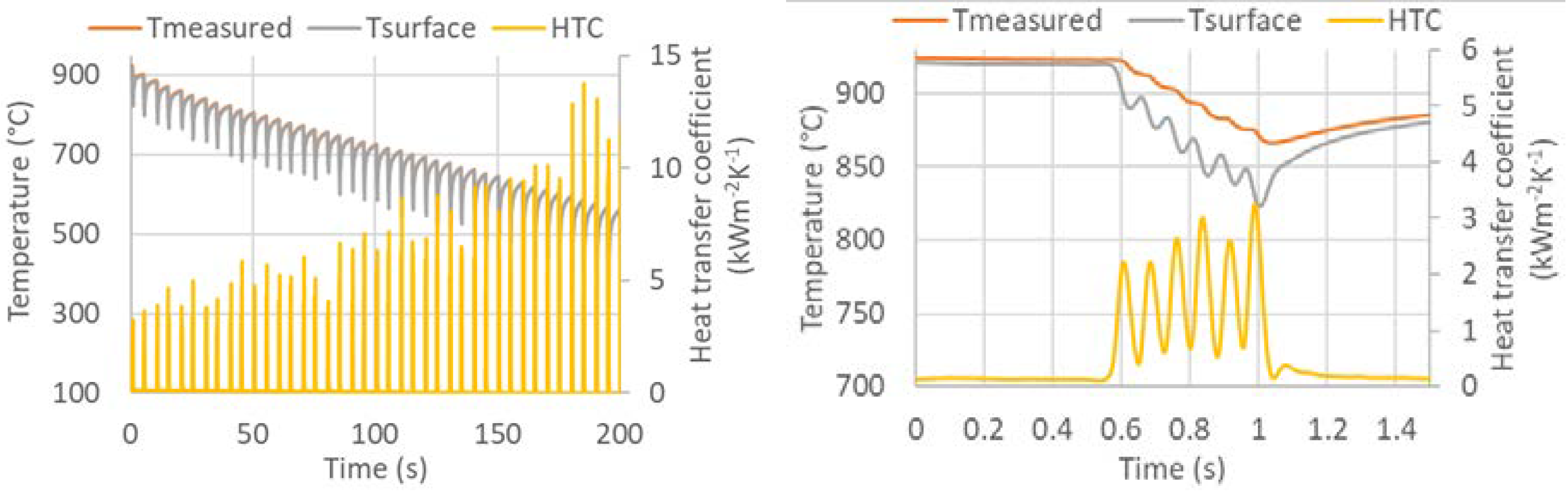
Figure 12.
Measured temperature, computed surface temperature and computed heat transfer coefficient (left: all experiment, right: detail of the first pass through the cooling section).
Figure 12.
Measured temperature, computed surface temperature and computed heat transfer coefficient (left: all experiment, right: detail of the first pass through the cooling section).
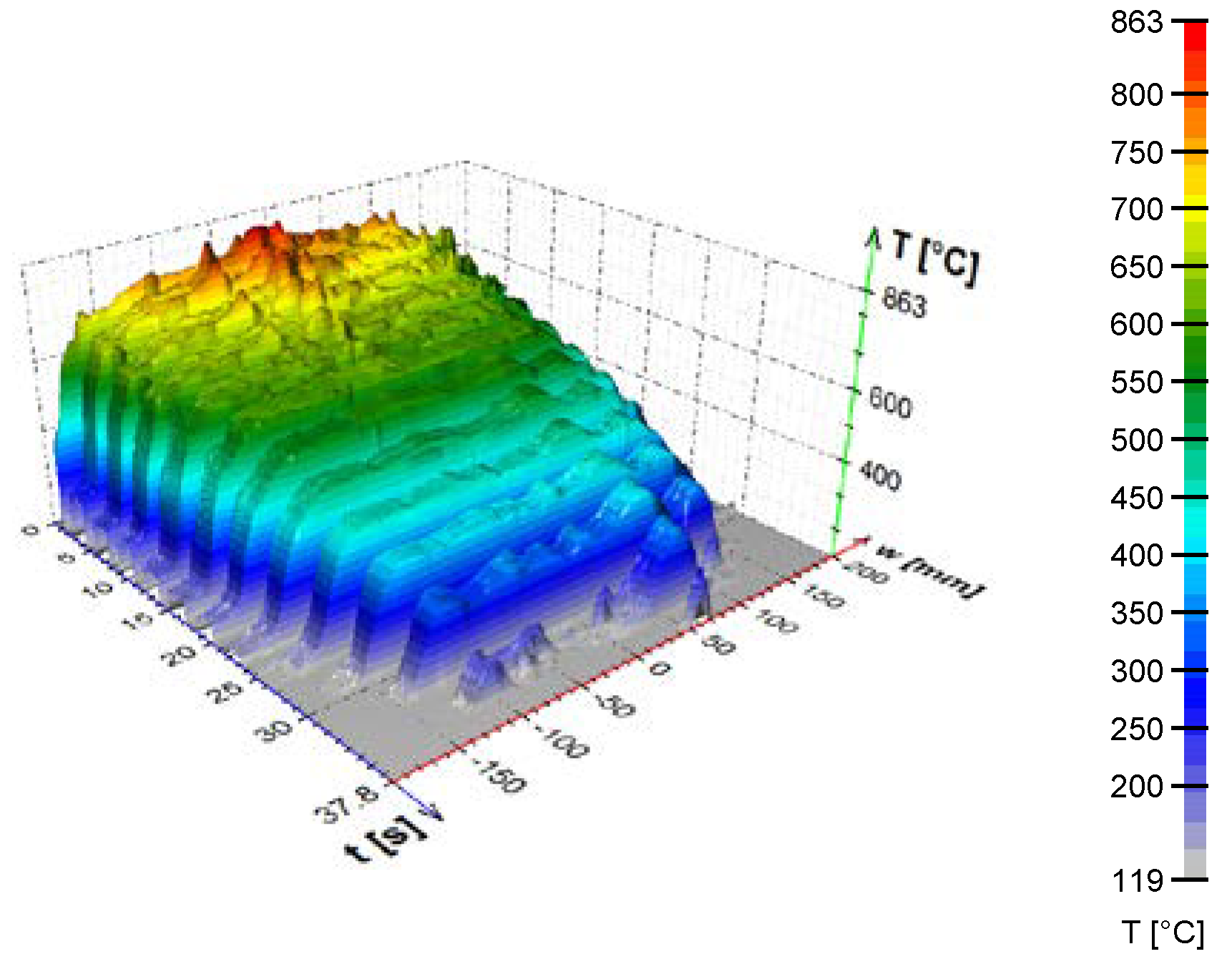
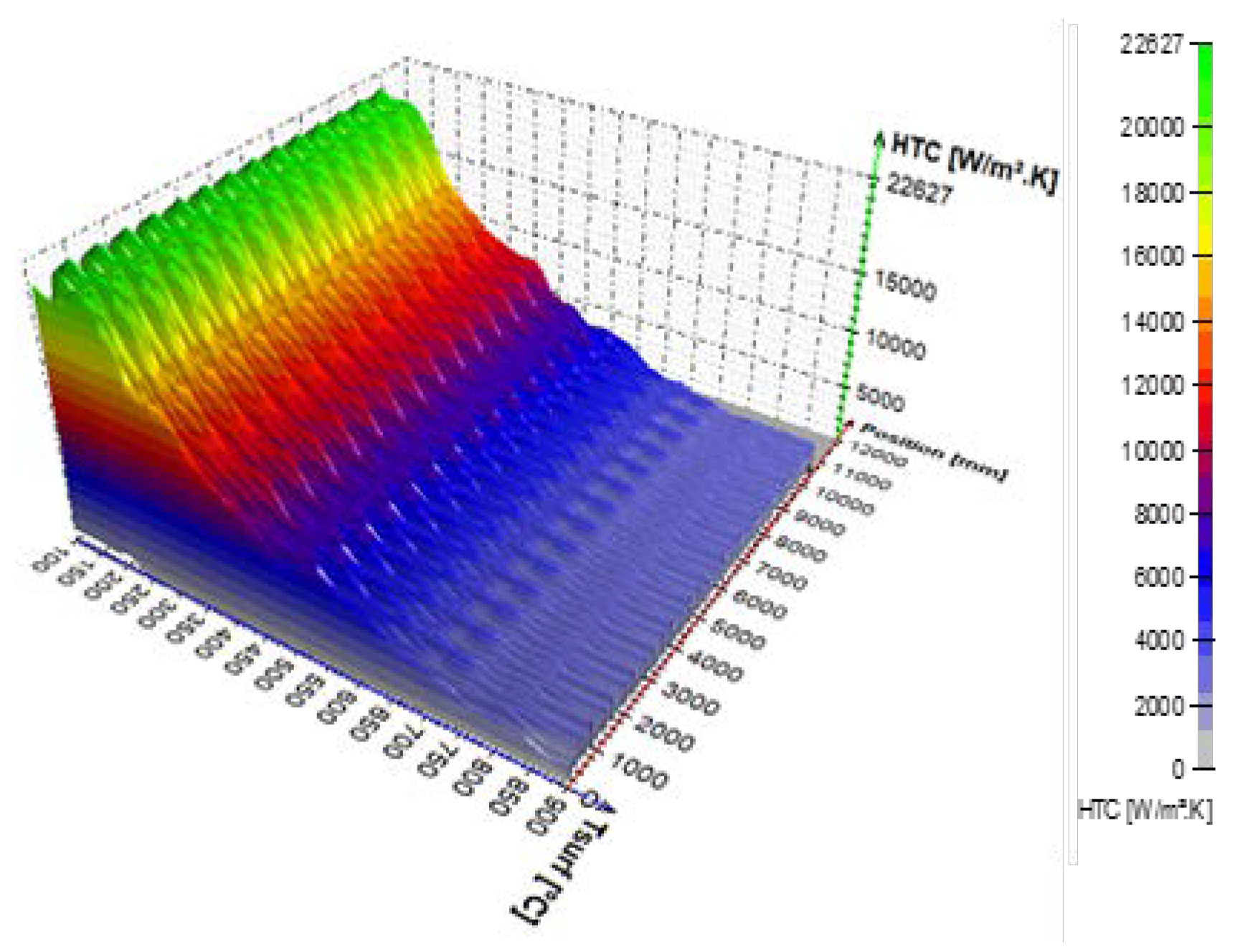
Figure 13.
HTC as a function of position and surface temperature.
Figure 13.
HTC as a function of position and surface temperature.
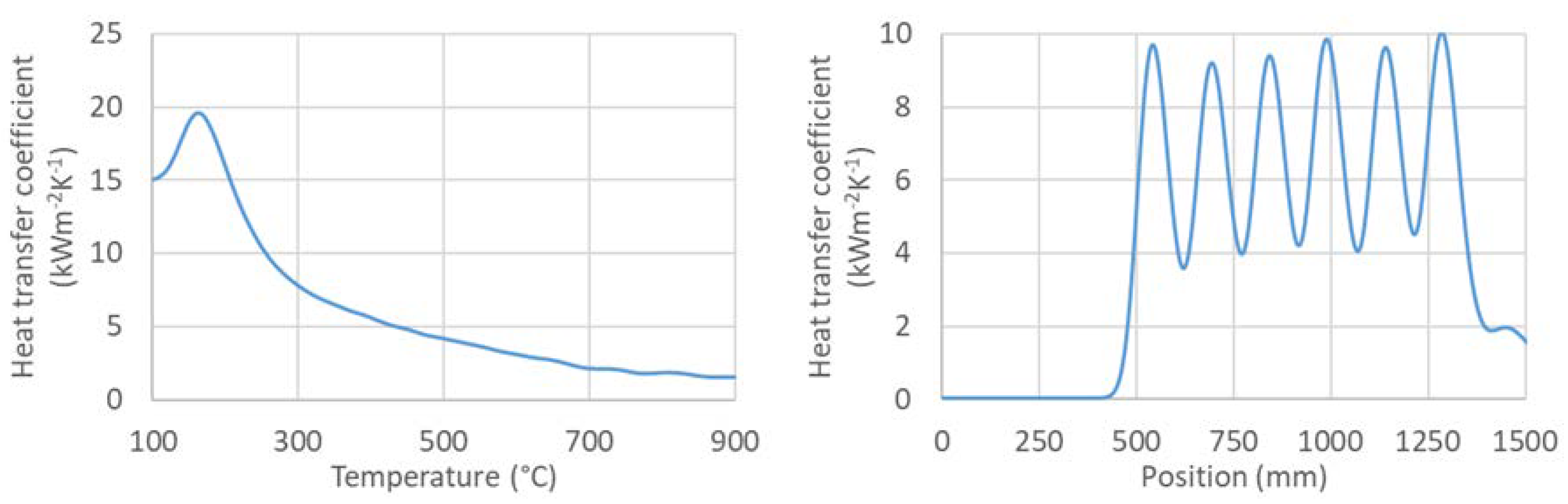
Figure 14.
Left: HTC as a function of surface temperature, right: HTC as a function of position (50 - 900 °C).
Figure 14.
Left: HTC as a function of surface temperature, right: HTC as a function of position (50 - 900 °C).
Figure 15.
Combined boundary condition (12 m).
Figure 15.
Combined boundary condition (12 m).
Figure 16.
Laboratory test bench with rotating sample.
Figure 16.
Laboratory test bench with rotating sample.
Figure 17.
Example of measured temperatures (test bench with rotating sample) for one-sided cooling of a 20 mm thick plate of S355 steel (simulation of two-sided cooling of a 40 mm thick plate). Cooling regime: Intensive cooling - 8 bar, length 16 m (4 s) and then soft cooling - 4 bar, length 42 m (10.5 s), product speed 4 m s-1. Total length of cooling section - 58 m (14.5 s).
Figure 17.
Example of measured temperatures (test bench with rotating sample) for one-sided cooling of a 20 mm thick plate of S355 steel (simulation of two-sided cooling of a 40 mm thick plate). Cooling regime: Intensive cooling - 8 bar, length 16 m (4 s) and then soft cooling - 4 bar, length 42 m (10.5 s), product speed 4 m s-1. Total length of cooling section - 58 m (14.5 s).
Figure 18.
Measured Vickers hardness for material S355: original material and heat treated (regime shown in
Figure 17).
Figure 18.
Measured Vickers hardness for material S355: original material and heat treated (regime shown in
Figure 17).
Figure 19.
Results of Charpy pendulum tests for material S355: original material and heat treated (regime shown in
Figure 17).
Figure 19.
Results of Charpy pendulum tests for material S355: original material and heat treated (regime shown in
Figure 17).
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).