Detecting and Evaluating Displacement of Paving Blocks Adjacent to Deep Excavation Sites Using Terrestrial Photogrammetry

In urban areas, deep excavation-induced ground deformation may damage adjacent existing structures and is conventionally evaluated by levelling at installed settlement points. However, a small number of measurements cannot represent the total change in ground deformation adjacent to excavation sites. Furthermore, significant local subsidence may occur in places where settlement points have not been installed and only noticed after an accident. For deep excavation sites located in urban areas, paved pedestrian sidewalks are often located adjacent to sites, and construction activity can cause these paving blocks to displace. This study introduces a method to detect paving block displacement adjacent to deep excavation sites using terrestrial photogrammetry. A digital camera creating point cloud data (PCD) and an acquisition method satisfying the frontal and side overlap requirements were demonstrated. To investigate the displacement detection and measurement capabilities by PCD analysis, an experimental program was conducted, including a PCD comparison containing the uplift, settlement, and horizontal paving block displacement and reference data. The cloud-to-cloud distance computation algorithm was adopted for PCD comparison. Paving block displacement was detected for displacements of 5, 7.5, and 10 mm in the uplift, settlement, and horizontal directions; however, the horizontal displacements were less clear. PCD analysis enabled satisfactory measurements between 0.024 and 0.881 mm for the vertical-displacement cases, but a significant error was observed for the horizontal-displacement cases owing to the cloud-comparison algorithm. The measurement blind spot of limited settlement points was overcome by the proposed method that detected and measured paving block displacement adjacent to excavation sites.

Keywords:

Subject: Engineering - Civil Engineering

1. Introduction

Recent emphasis on serviceability control in geotechnical engineering projects demands accurate measurement of the displacement of structures and the ground surface. Routine measurements of ground settlements adjacent to a deep excavation project are legally mandated, although only a minimum number of monitoring points are controlled in most projects with tight budgets. Unfortunately, such legal efforts have not successfully prevented a catastrophic collapse, mainly because the location initiating the collapse is often out of the range controlled by the measurement of the monitoring points. The adaptive management technique for ground deformation control including the inverse analysis is also limited because it relies on those monitoring points [1,2]. Consequently, a technique for measuring the displacements induced by excavation work in the entire range or full field is crucial for ensuring construction safety [3].

Recent developments in computer performance and the increased use of digital photographs have stimulated advances in photogrammetric software. Photogrammetry is a technique for determining the three-dimensional geometry of physical objects by measuring and analyzing their two-dimensional photographs. Terrestrial photography provides detailed dimensional information about an object using images near or on the surface of the earth. In close-range terrestrial photography, the size of the object and the camera-to-object distance are both less than 100 m [4]. Several papers related to close-range photogrammetry have been dedicated to various application fields such as industrial engineering [5], cultural heritage documentation [6,7,8,9,10], and geomorphology [11,12,13,14,15]. Close-range terrestrial digital photogrammetry is widely applied in rock mass discontinuity characterization [16]. In civil engineering, close-range photogrammetry plays a vital role in engineering surveys, including as-built documentation of existing facilities and building information modeling. The bridge deformation and health monitoring was measured with photogrammetry technique [4,17,18,19,20,21]. The deformation of concrete tanks and retaining walls under working conditions can be measured using high-precision photogrammetry with high-resolution cameras [22,23].

Various applications of the close-range terrestrial photogrammetry technique also reveal the possibility of full-field measurement of displacements induced by deep excavation work in urban areas. Pedestrian sidewalks paved with concrete pavement blocks are frequently located adjacent to deep excavation sites. Measuring the displacements of these pavement or paving blocks via close-range photogrammetry can resolve the practical difficulties in investigating the ground deformation induced by deep excavation works in urban areas. To the best of our knowledge, the monitoring technique of measuring the displacement of paving blocks via close-range photogrammetry has not been systemically presented. Figure 1 displays the paving block adjacent to the excavation site. In the Figure 1, the construction site is located behind the wall; moreover, various displacements of paving blocks can be observed.

This study introduces a workflow for detecting the displacement of paving blocks adjacent to deep excavation sites. This workflow mainly relies on close-range terrestrial photogrammetry and structure-from-motion (SfM) photogrammetric techniques. The requirements for establishing reliable point cloud data (PCD) for paving blocks including ground sampling distance, image network geometry, and parameters of the camera mounted on an unmanned ground vehicle (UGV) are presented. The applicability of the cloud-to-cloud (C2C) distance computation algorithm is discussed to trace temporal changes in the uplift, settlement, and horizontal movement of paving blocks.

2. Materials and Methods

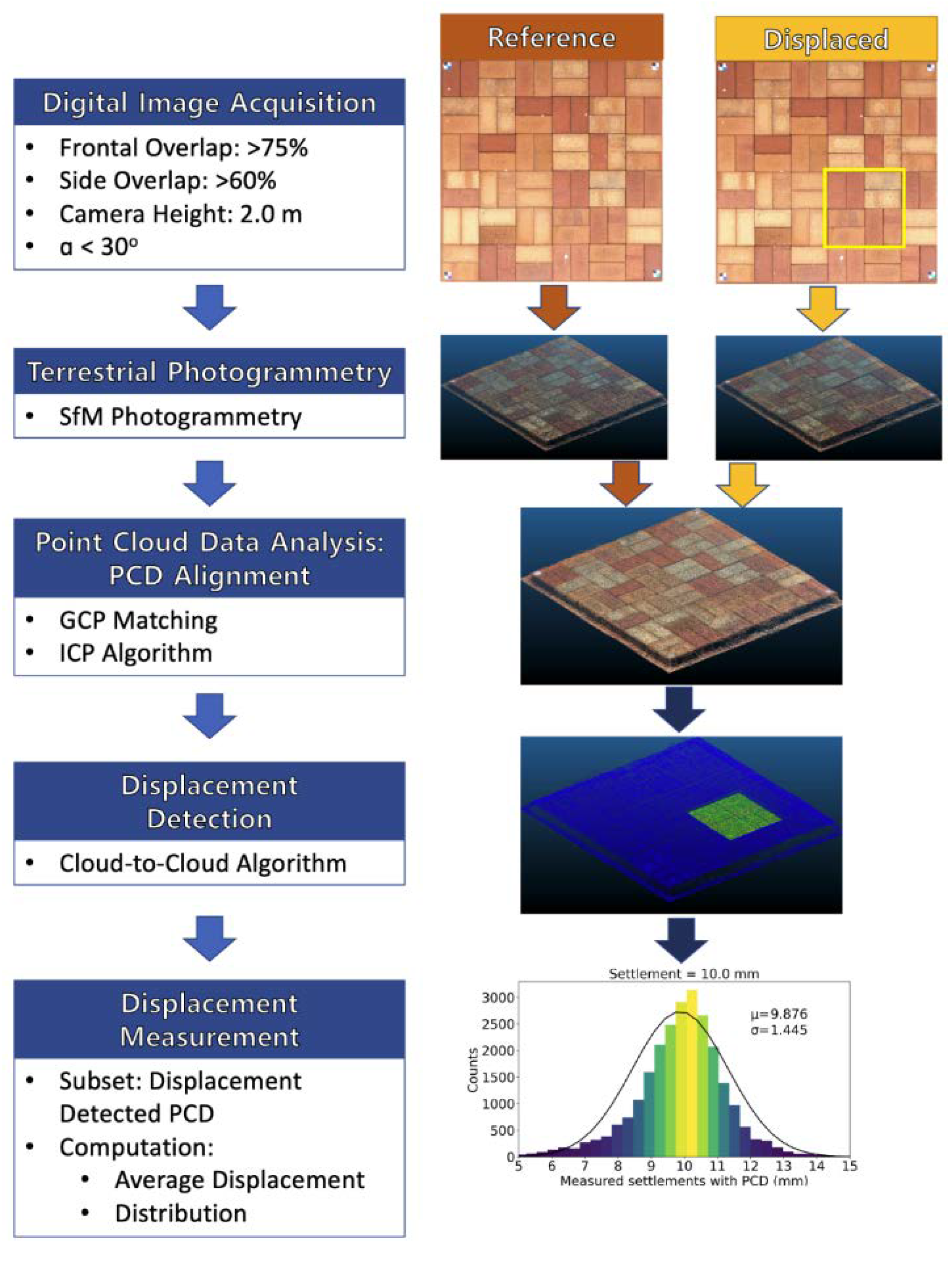
Figure 2 shows a flowchart of the proposed methodology. It shows the flow of the digital-image-acquisition method, PCD creation using digital images, and displacement detection and measurement through PCD comparison. The details of each item in the flowchart are presented in the following sections.

2.1. Digital Image Acquision

A camera was selected to move the UGV in a paving block adjacent to the excavation site. The camera must be lightweight, capable of continuous shooting for photogrammetry, and able to obtain stable images without shaking. An action camera (GoPro HERO7 Black) was used to obtain digital images for terrestrial photogrammetry. Action cameras specialize in recording smooth videos while moving. It may not need a gimbal, but using a gimbal makes it easy to adjust the angle of viewing and can also provide auxiliary stabilization. The GoPro HERO 7 Black weighs 116 g, and the Feiyu WG2X gimbal used weighs 238 g. If a digital single-lens reflex camera was employed for image acquisition, the total weight would be greater than 3 kg. This is approximately ten times heavier than that of the action camera system, and therefore, the UGV would be inefficient as more energy is used to move.

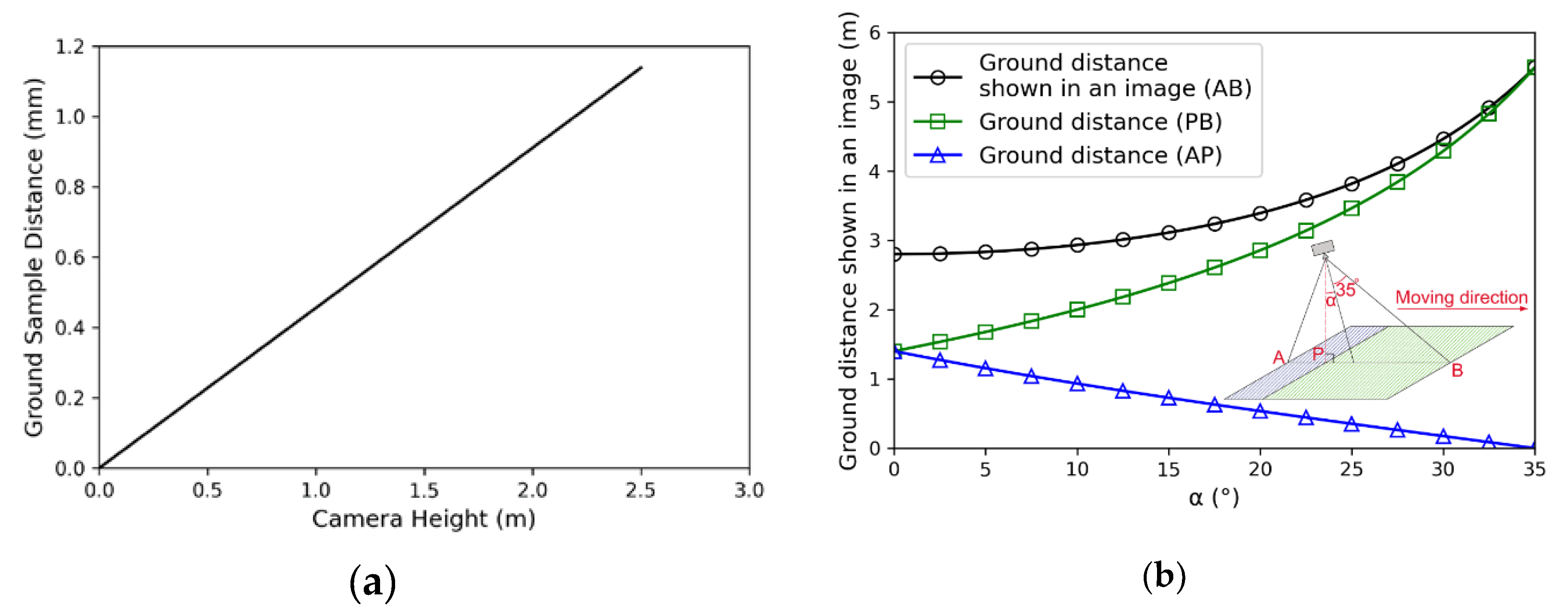
To obtain digital images for terrestrial photogrammetry, it is necessary to evaluate the ground sample distance (GSD), which is the distance between pixel centers measured on the ground and the field of view (FOV) according to the camera shooting height. For the employed camera, the width of the charge-coupled device was 6.17 mm with 4096 pixels, and the horizontal FOV was 86°. As shown in Figure 3(a), the GSD increased with the camera shooting height, and was less than 0.911 mm when the shooting height was lower than 2.0 m. The GSD value appeared to be sufficient to evaluate the paving block displacement adjacent to the excavation sites. The maximum shooting height was set to be 2.0 m.

Figure 3(b) shows the ground distance shown in an image with α at the camera height of 2.0 m, where α is defined as the pitch, assuming that the camera is mounted such that the camera looks down and the top of the image points to the front. Half of the vertical FOV of the camera was 35°. When α is greater than 0°, the image becomes oblique, so it shows more of the ground in the travel direction. The ground distance PB shown in Figure 3(b) increases rapidly with increasing α, increasing the ground distance AB. However, the distance AP decreases. As a result, information far from the camera's position can be included in the image with a large α, making it difficult to properly create PCD. Consequently, a low-oblique image closer to a vertical image or vertical image was adopted to create PCD, rather than the high-oblique images. This is consistent with the recommendations of the SfM software manual that the camera should be kept as constant as possible over the terrain to ensure the desired GSD. The Pix4D mapper was used for the SfM software in this study.

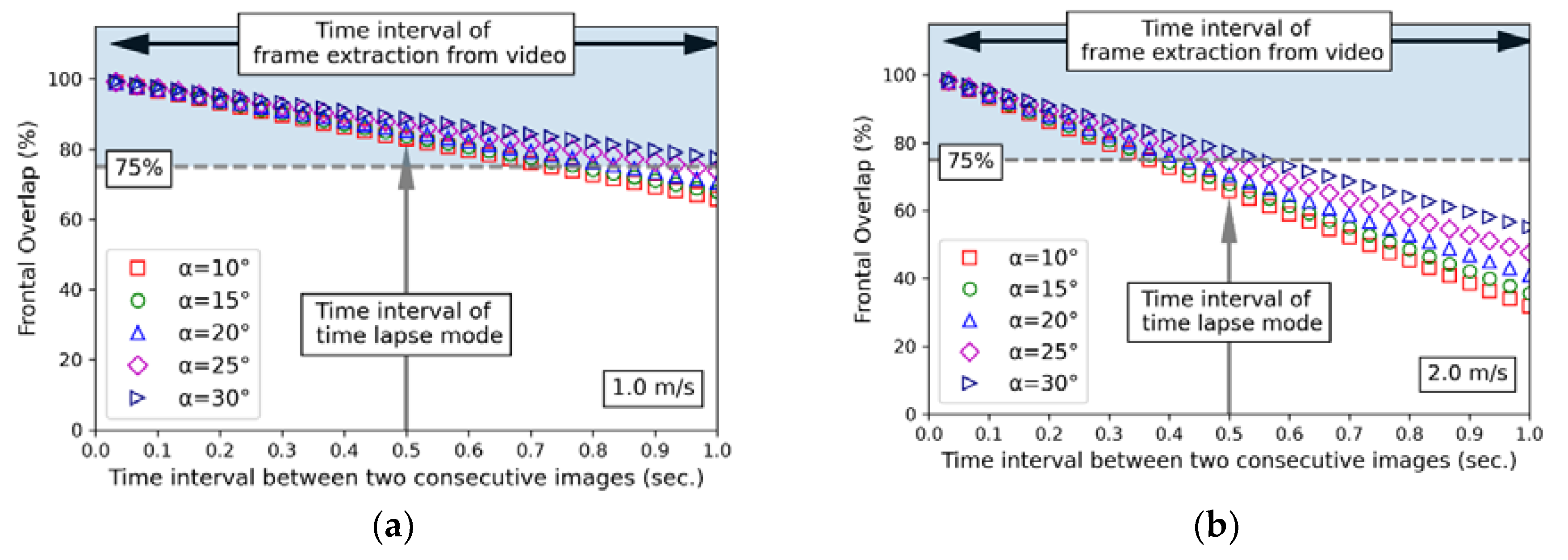
To create a PCD, the recommended frontal overlap between the images should be at least 75%. The camera employs two methods to obtain digital images: capturing a snapshot with time lapse and extracting a frame from a video. The minimum interval between images is 0.5 s for time lapse. For frame extraction from a video at 30 fps, 30 images can be obtained in 1 s; therefore, the time interval between two consecutive images is 0.033 to 1 s. Note that digital images are obtained while moving on the sidewalk; therefore, moving at a high speed is dangerous for pedestrians. Accordingly, the practical moving speed range for image acquisition is 2.0 m/s or less, which is a typical jogging speed. As shown in Figure 4, the frontal overlap is affected by the movement speeds and α. If the moving speed is fast, it may not be possible to obtain a sufficient number of images that satisfy the 75% minimum frontal overlap recommended for photogrammetry [24]. When the moving speed was 1.0 m/s, frontal overlap could be satisfied with both image acquisition methods, as shown in Figure 4(a). However, when the moving speed was 2.0 m/s, as shown in Figure 4(b), only the frame extraction whose interval was shorter than 0.33 s could satisfy the required frontal overlap, regardless of α The method of capturing a snapshot with time lapse cannot satisfy the requirement when α is smaller than or equal to 25°; only the case of α = 30° can satisfy the requirement. Consequently, a method of extracting frames from videos was selected to obtain sufficient images for PCD creation.

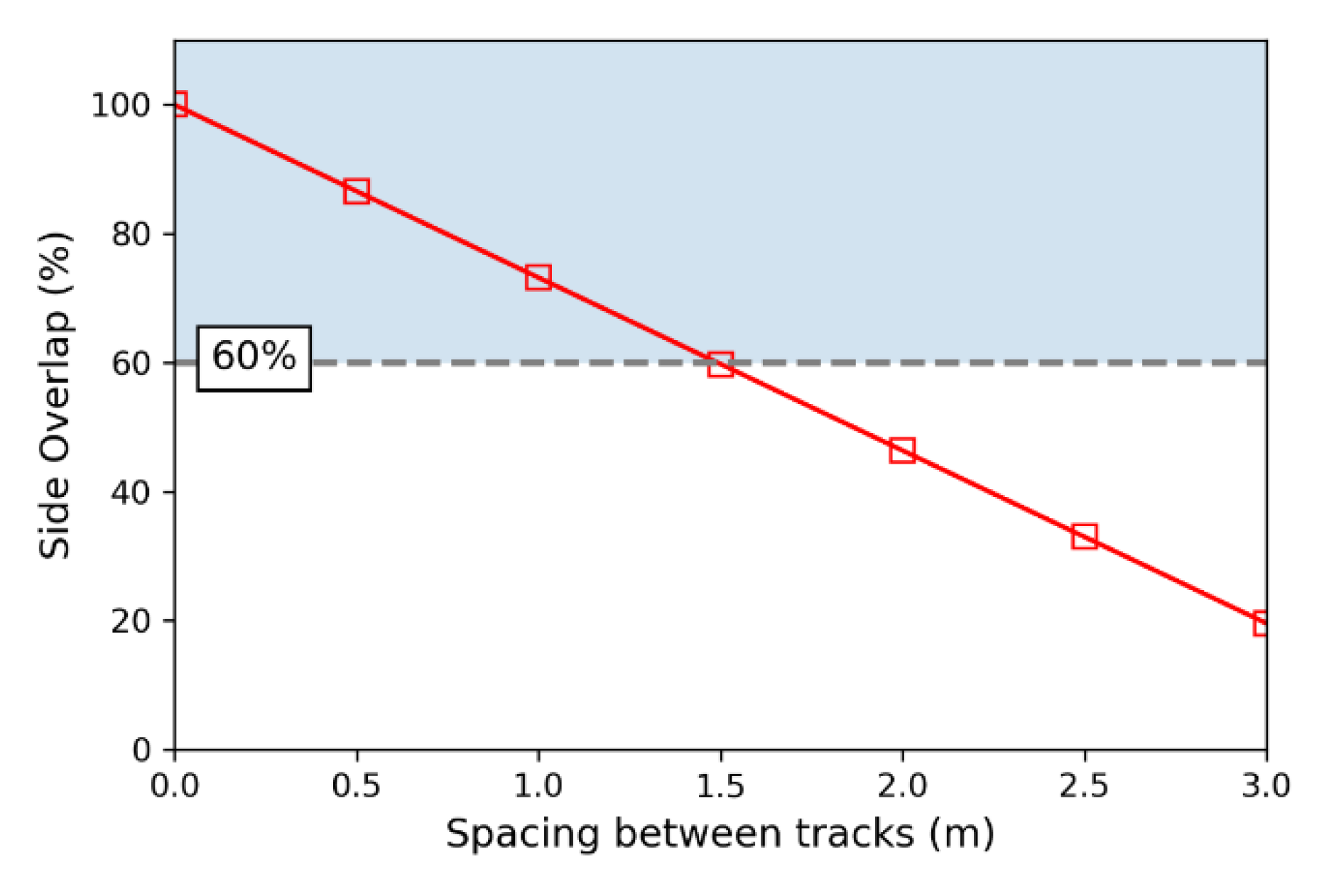
For a side overlap, the spacing between moving tracks is important to satisfy the requirement of at least 60% [24]. As shown in Figure 5, when the spacing was shorter than approximately 1.5 m, the required overlap was satisfied. Accordingly, the spacing was set shorter than 1.5 m when obtaining the images. Note that the camera shooting height of 2.0 m was maintained constant.

2.2. Testing program

In urban areas, existing buildings are often demolished and new buildings are constructed. In this case, the sidewalk adjacent to the excavation site used before construction continues to be used. Accordingly, ground movement adjacent to the excavation site causes displacement of the paving blocks. In this study, three cases of paving block movements that can be found in Figure 1 were evaluated: uplift, settlement, and horizontal displacement. Evaluations were performed at 5 mm, 7.5 mm, and 10 mm in each case.

Figure 6 shows the reference without displacement setup to detect and measure the movement of the paving blocks measuring 1380 cm × 1380 cm. Seventy-two paving blocks of dimension 230 mm × 115 mm × 60 mm were used. The four corner markers were ground control points (GCPs), where the coordinates were measured using a global navigation satellite system rover, Trimble R10. These GCPs were utilized for georeferencing of the PCD. By adding geographic information to the image, it is easy to detect and calculate changes in the PCD. The uplift and horizontal displacement of the paving block were induced by installing spacers in the reference paving block setup. Settlement was created by lowering the level of the floor where the paving block was placed.

For each test setup, two round-trip videos were recorded using GoPro 7 Hero Black, and the frames extracted from the video were used for PCD creation. In a single round trip, videos were recorded along the same track at a height of 2 m. The distance between the tracks was within 1.5 m to satisfy the side-overlap requirement. The PCD was created using a Pix4D mapper.

2.3. Data Interpretation

PCD with various displacements, PCDd, were compared with the reference PCD, PCDr. The open-source software CloudCompare was used for point cloud processing. Since identical GCPs were used for the creation of the PCD, the PCD were well aligned during the comparison. For better results, PCDd was slightly rotated and translated to fit PCDr using the iterative closest point (ICP) algorithm. Note that the ICP algorithm can minimize the difference between two PCD and is often used to construct a single PCD from different scans in several engineering fields. The displaced paving blocks were excluded while the ICP algorithm optimized the transformation matrix to determine the best fit, because the displaced paving blocks would influence matrix optimization. After obtaining the optimized transformation matrix, it was applied to the paving blocks with displacements. By conducting this process, it was possible to precisely align the PCD.

The C2C algorithm was used to compare PCDd with PCDr. It calculates the distance between two PCD by simply determining the nearest neighbor distance between points. After calculation using the C2C algorithm, the points in the zones where the displacement occurrence was detected were subset. For this subset, the mean and standard deviation of the displacements were calculated, and the distribution was analyzed using a histogram.

3. Results and Discussion

3.1. Vertical displacements

For the investigation of uplift cases, eight paving blocks were lifted by 5, 7.5, and 10 mm. As shown in Figure 7, Figure 8 and Figure 9, it was possible to detect every tested uplift case. Note that blue indicates no displacement and green indicates displacement. The number of subset points where displacement occurred was approximately between 25,000 and 30,000. 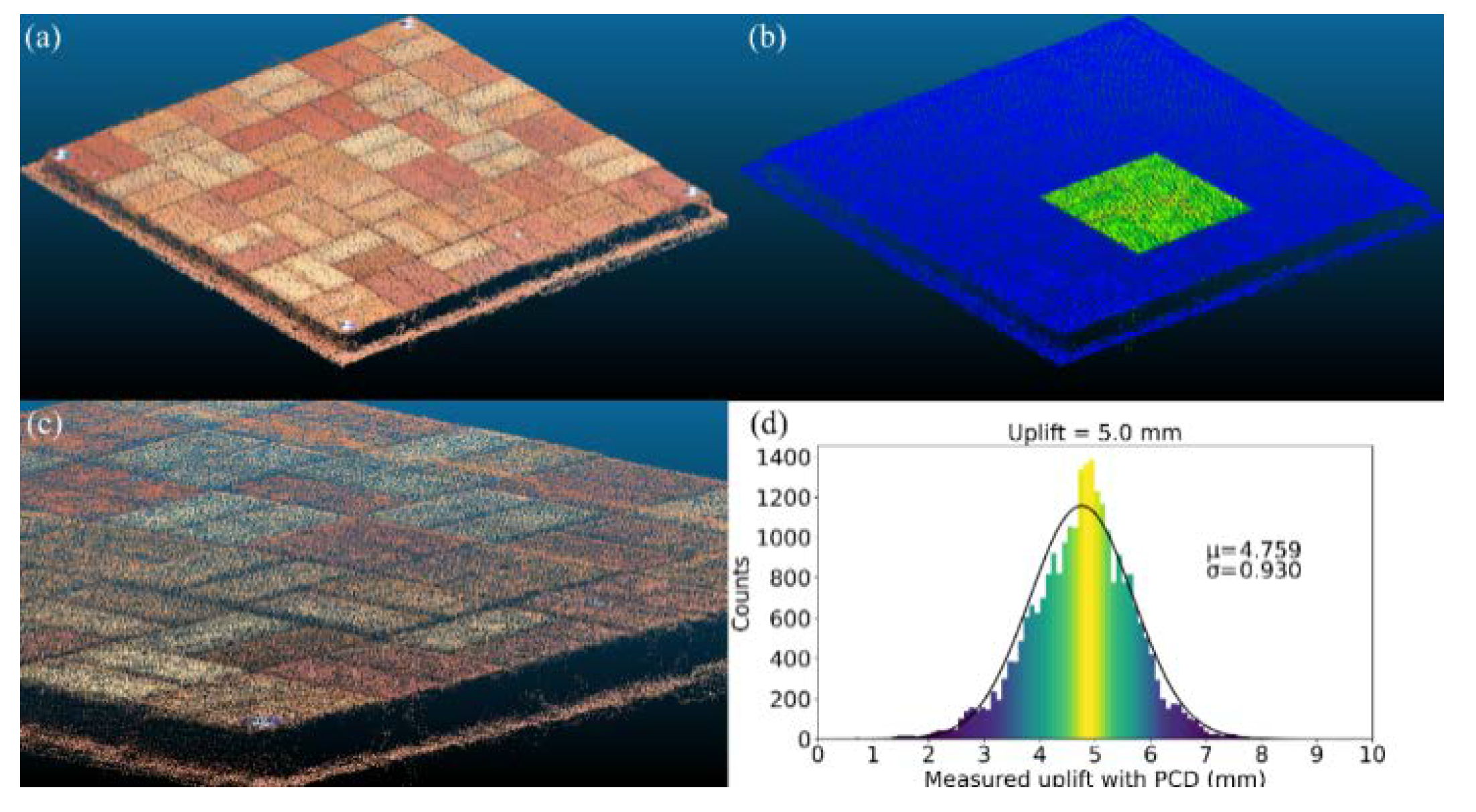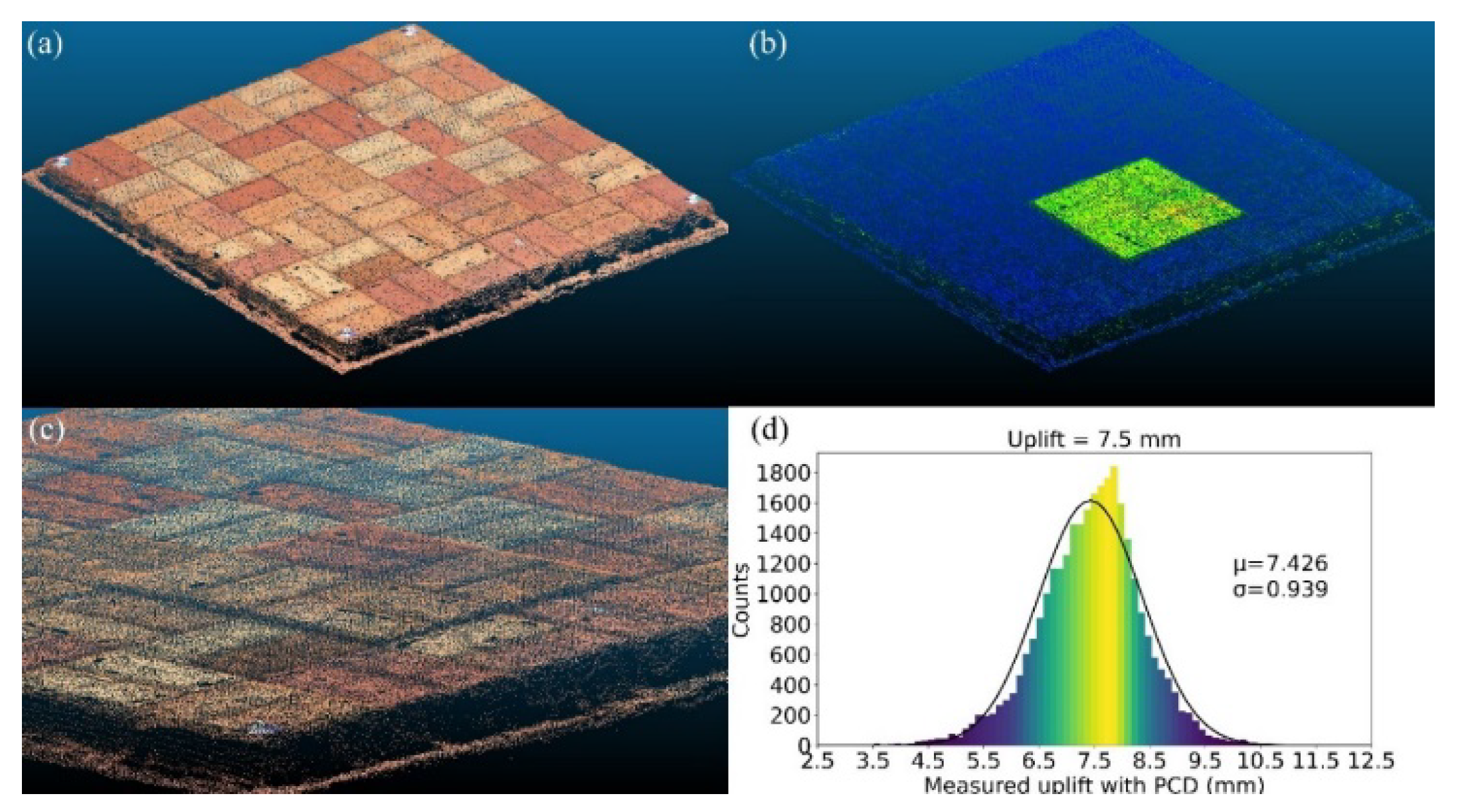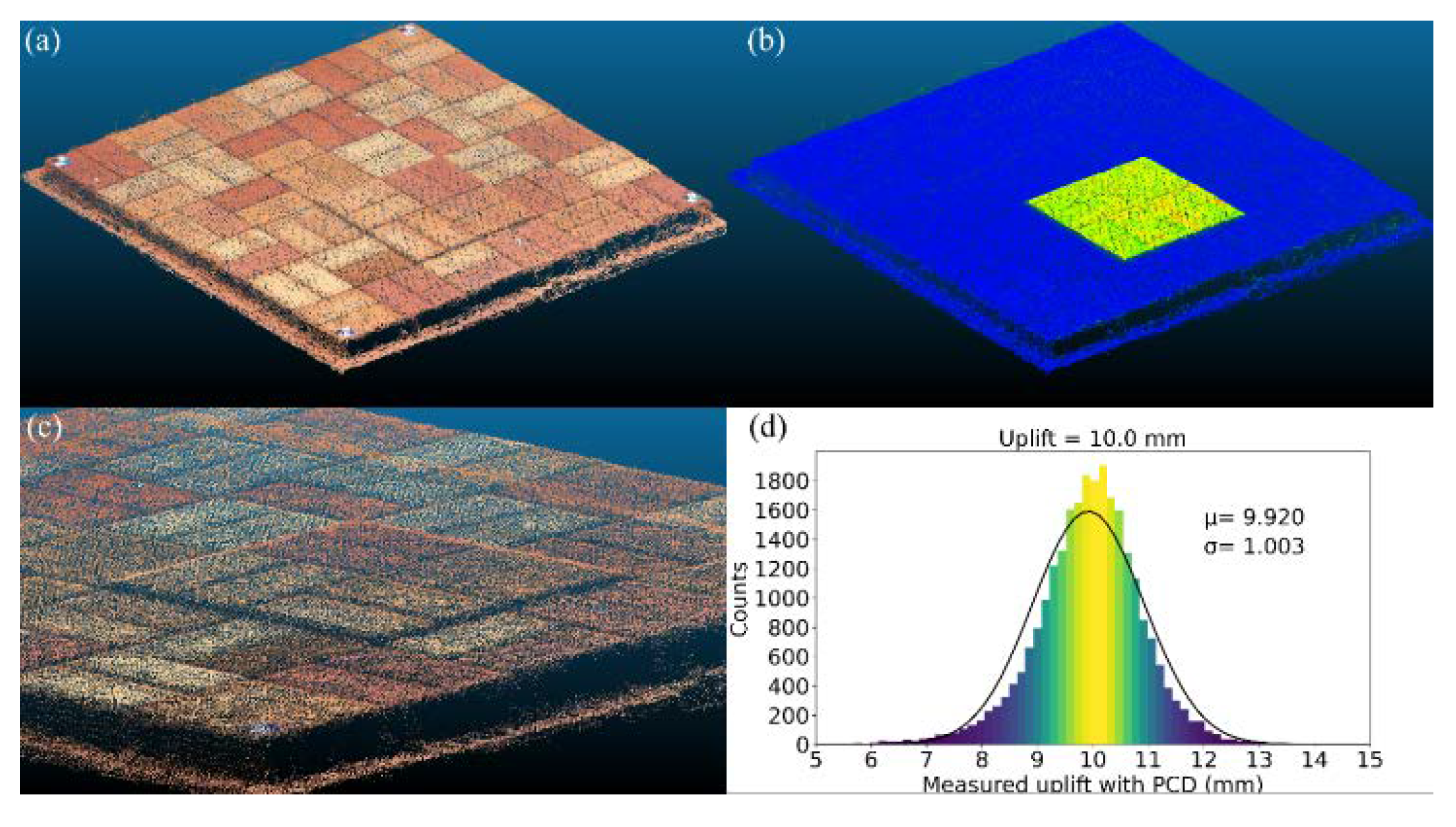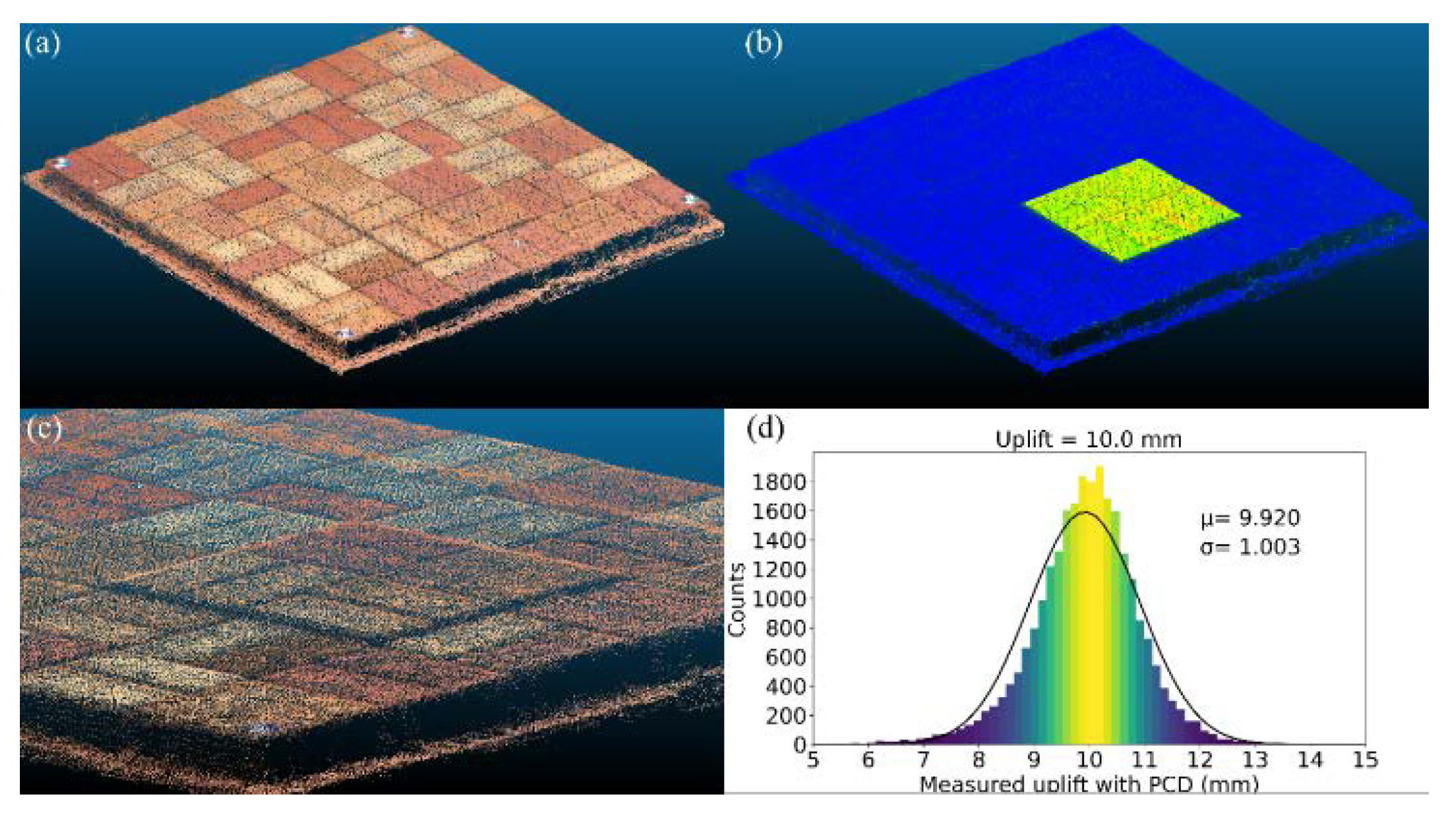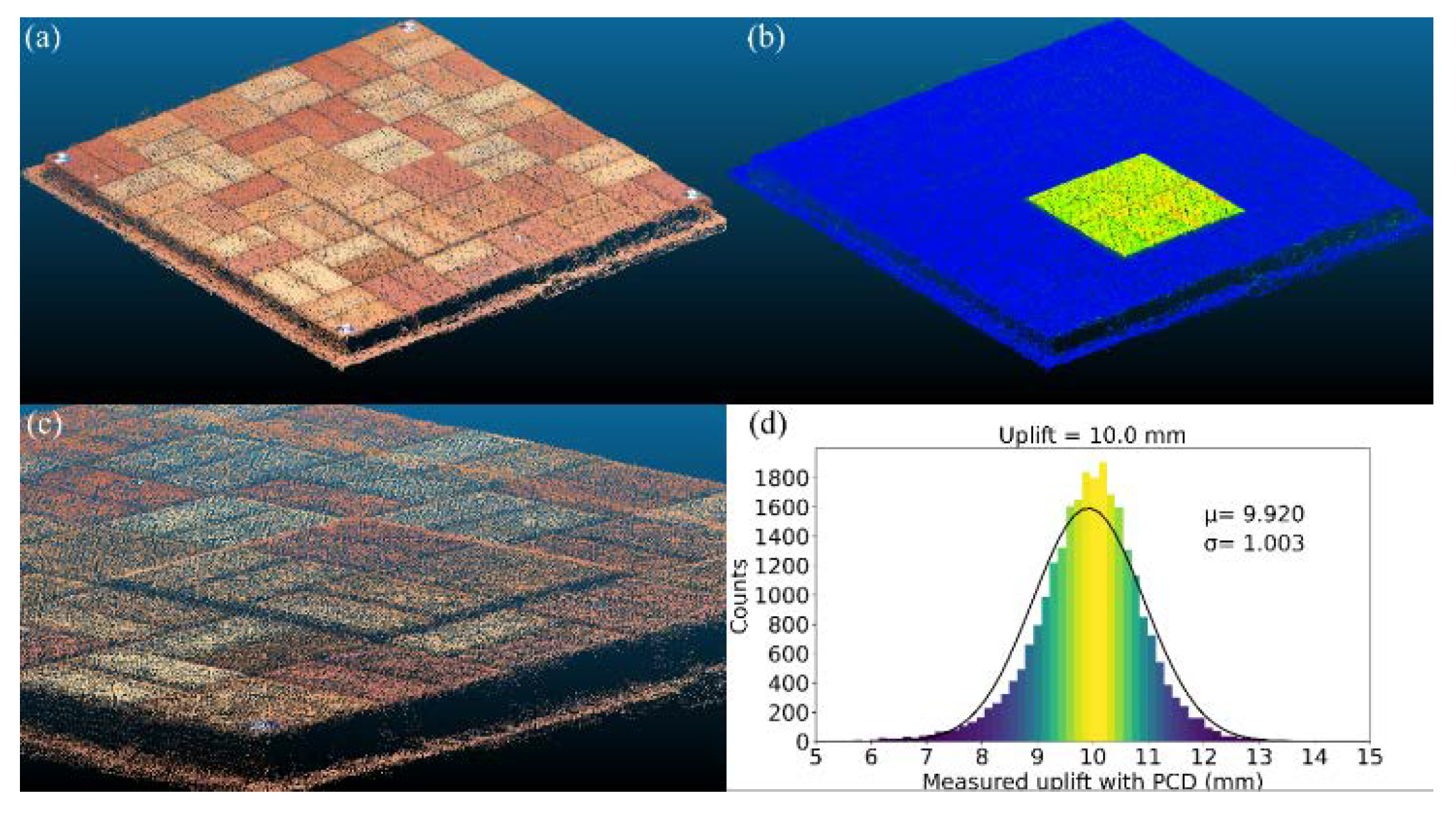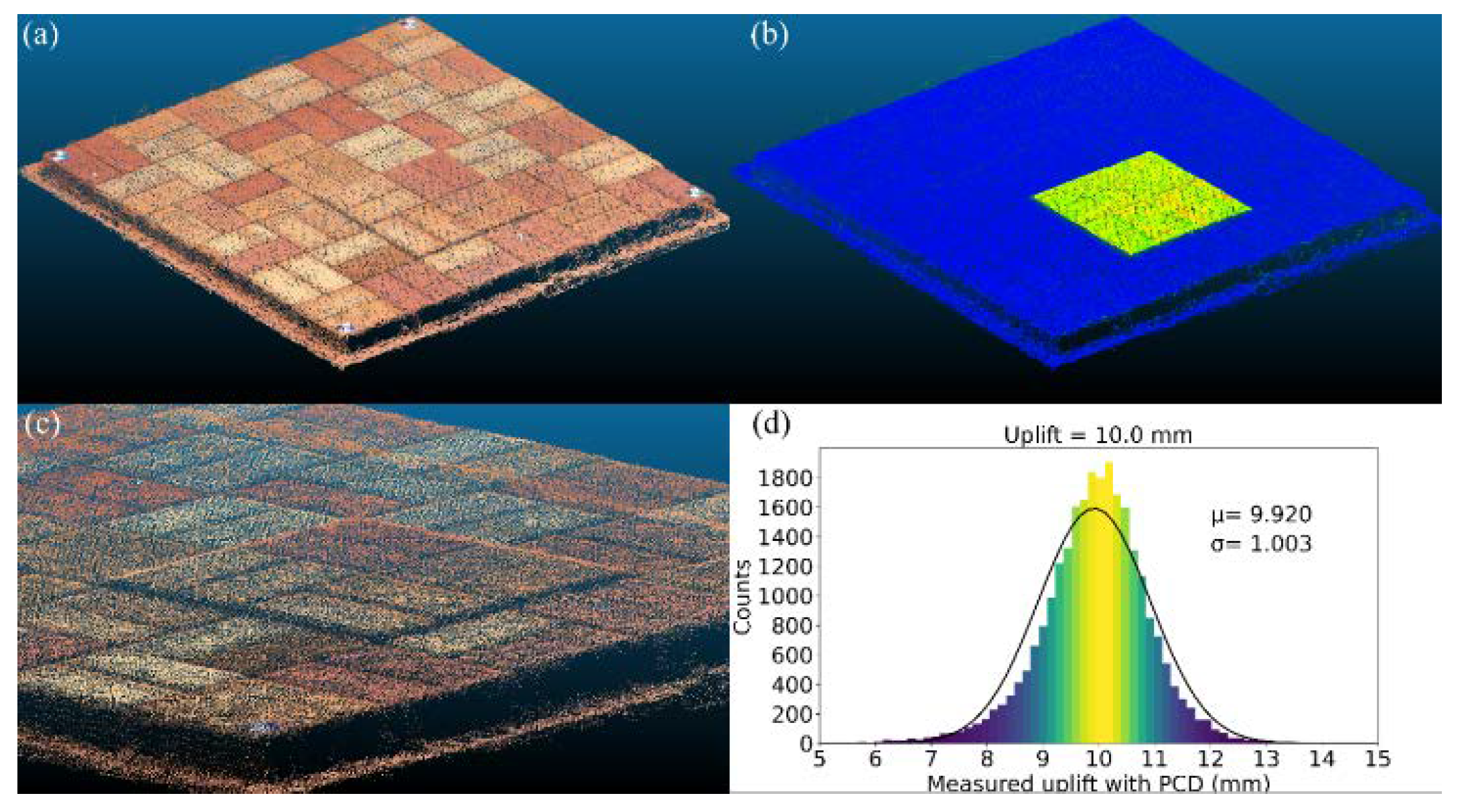As shown in the subfigure (d) of Figure 7, Figure 8 and Figure 9, it can be seen that the distribution of displacements appears close to the normal distribution. When the accuracy was evaluated by subtracting the actual uplift value from the mean value (μ) measured by the PCD, the tested cases of 5, 7.5, and 10 mm were 0.241, 0.074, and 0.080 mm, respectively. Herein, the standard deviation (σ) of the PCD measurements was regarded as precision. The precisions for the tested cases of 5, 7.5, and 10 mm were 0.930, 0.939, and 1.003 mm, respectively.

To investigate the settlement of the paving blocks, eight paving blocks were set to 5, 7.5, and 10 mm. As shown in Figure 10, Figure 11 and Figure 12, it is possible to detect every tested case. Since the C2C algorithm calculates the distance to the nearest point between PCD, information about directionality, such as settlement and uplift, is unknown. Similar to the investigated uplift cases, blue indicates no displacement, and green indicates displacement. The number of subset points where displacement occurred was approximately between 25,000 and 30,000. As shown in the histogram of each case, the distribution was close to the normal distribution like the uplift cases. The mean values of the PCD measurements for the three cases were 5.881, 7.468, and 9.876 mm, respectively. When the accuracy was evaluated as in the uplift cases, the accuracies of the 5-, 7.5-, and 10-mm cases were 0.881, 0.032, and 0.024 mm, respectively. In addition, the standard deviation of each case was 1.672, 1.231, and 1.445 mm for cases of 5, 7.5, and 10 mm, respectively.

Conventionally, the vertical displacement is evaluated by the level instrument at the installed settlement point; therefore, information about only that point can be obtained. However, the advantage of the level instrument is that it can measure a vertical displacement of 5 mm or less, which has not been tested here. Note that the standard deviation for the 1 km double-run levelling of these instruments is approximately 1 or 2 mm, as evaluated by ISO 17123-2 [25]. Based on the cases investigated using terrestrial photogrammetry, it can be inferred that it was possible to detect a vertical displacement of more than 5 mm. Vertical displacement evaluation using PCD is a measurement of a surface, and not a single point. Accordingly, it has the advantage of being able to determine displacements that would not have been known if there were no settlement points for the level instrument. From this point of view, PCD measurements seem to be sufficiently valuable for evaluating the vertical displacement adjacent to a deep excavation site. If the vertical displacement of the ground adjacent to the construction site is measured at the levelling error level, it is also possible to perform displacement detection using PCD and apply the level measurement to the area where displacement occurs.

3.2. Horizontal displacements

To investigate the horizontal displacement of the paving blocks, six blocks were horizontally displaced by 5, 7.5, and 10 mm, respectively. As shown in Figure 13, it was possible to detect all the investigated cases, but the horizontal displacement of 5 mm was not clear, compared with the other cases. Overall, the horizontal displacement cases were not clearly visible compared with the vertical displacement. Note that blue indicates no displacement and green indicates displacement. Since the displacement zone is narrow, the number of subset points is approximately 1,000, which is only 4% of that of the vertical cases. If the number of detected displaced points is small, the visibility may be poor.

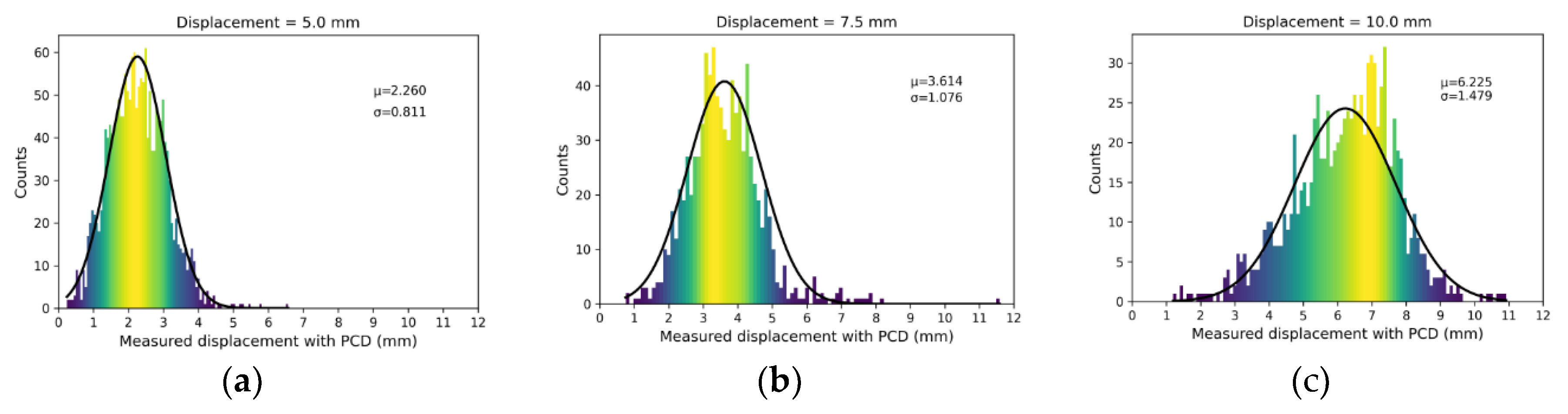
As shown in Figure 14, the histogram of each case was close to the normal distribution, but the histogram bars were jagged compared with the vertical cases. The mean values of the PCD measurements for the 5-, 7.5-, and 10-mm displacement cases were 2.260, 3.614, and 6.225 mm, respectively. Clearly, the difference between the actual displacement value and mean was large, and the counts were very small at the actual displacement. Although horizontal displacement can be detected, the measurement error is significant.

To determine why the measurement errors in the horizontal displacement were large compared with the vertical cases, further investigation was performed on the horizontal displacement cases. Figure 15 shows the PCD of the reference and investigated cases of a 10-mm horizontal displacement. Note that only a portion was extracted from the PCD for better presentation. The small dent shown in Figure 15(a) represents the chamfers of two closely adjoining paving blocks. Figure 15(b) shows the PCD when one of the two adjacent paving blocks is horizontally separated by 10 mm, and the two PCD are plotted together in Figure 15(c). In Figure 15(d), the color of PCDd is expressed using the calculated distance from PCDr instead of actual color information obtained from the digital image, and the distance scale is shown in the color bar. As previously noted, the algorithm used to compare PCDd with PCDr was C2C, which calculates the distance between two PCD. Since the algorithm simply computes the distance between the nearest neighbor points, the calculated distance does not represent the horizontal displacement; rather, it is closer to the vertical distance. Thus, it only provides scalar information and not vectors. Also, it cannot be concluded whether the vertical displacement is a rise or subsidence based on the computation results alone. When a displacement is detected, it is necessary to compare the PCD in the corresponding area.

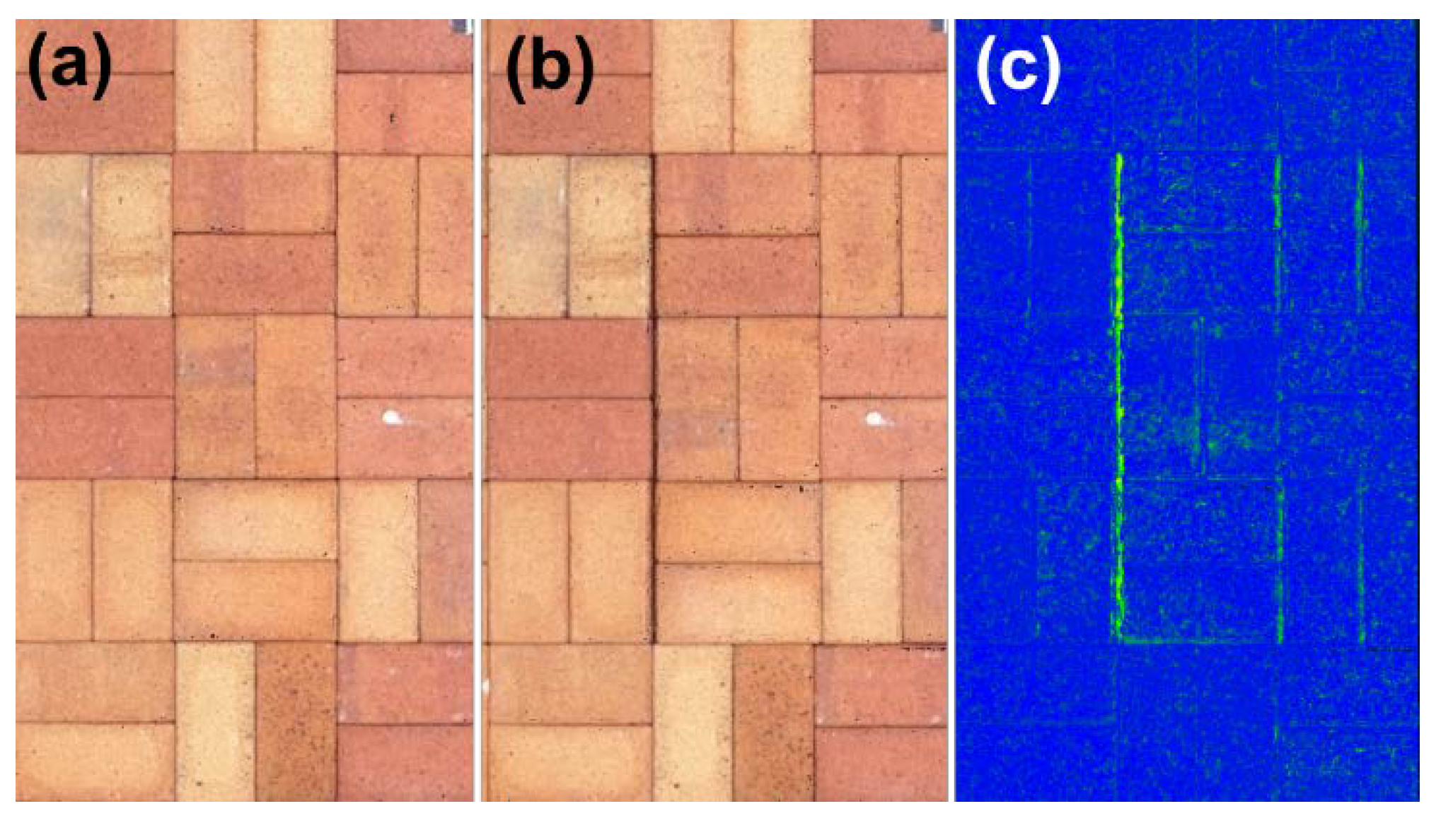
Figure 16 shows an enlarged view of the area where the 10 mm horizontal displacement occurred. As can be seen in Figure 16, a 10-mm displacement could be found from the PCDd with the actual color. In addition, it was not easy to determine the difference from Figure 16(b). However, it was shown that the green lines parallel to the slit were found to the right of the 10-mm displacement in Figure 16(c), and the PCD was expressed using the calculated distance from PCDr. This is because the paving blocks on the right side of the slit moved to the right when the spacing was 10 mm. When paving blocks are horizontally displaced, this pattern is expected to be found in the field.

4. Conclusions

The close-range terrestrial photogrammetry technique was applied to measure the displacements of paving blocks, indicating the ground movement caused by deep excavation works. Sequential sets of PCD were generated using Pix4D software with SfM photogrammetry. The workflow for measuring temporal changes in the displacement of the paving blocks by computing the PCD sets is provided. The requirements of the photogrammetric technique, such as ground sampling distance, image network geometry, and camera parameters, were presented to obtain reliable point-cloud data.

Vertical displacements of the paving blocks exceeding 5 mm could be detected through the workflow using the C2C algorithm. However, the detection of the horizontal displacements was less successful than that of the vertical displacements, possibly because of the theoretical limit of the adopted C2C algorithm. The measurement accuracy of the proposed workflow can be improved by introducing a vector-based algorithm to compare PCD sets.

Author Contributions

Conceptualization, T.K. and Y.-H.J.; Methodology, T.K.; Software, J.J.; Validation, H.C., J.J. and H.M.; Formal Analysis, H.C. and H.M.; Investigation, H.C.; Resources, H.M.; Data Curation, J.J.; Writing—Original Draft Preparation, T.K. and H.C.; Writing—Review & Editing, Y.-H.J. and J.J.; Visualization, T.K. and H.C.; Supervision, Y.-H.J. and H.M.; Project Administration, Y.-H.J. and H.M.; Funding Acquisition, Y.-H.J. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by a grant (code: 22SCIP-C151582-04) from the Construction Technologies Program funded by the Ministry of Land, Infrastructure and Transport of the Korean government and the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (No. 2019R1A2C1089155).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

Kim, S.; Finno, R.J. Inverse Analysis of a Supported Excavation in Chicago. J. Geotech. Geoenviron. Eng. 2019, 145, 04019050. [Google Scholar] [CrossRef]
Kim, T.; Jung, Y.-H. Optimizing Material Parameters to Best Capture Deformation Responses in Supported Bottom-up Excavation: Field Monitoring and Inverse Analysis. KSCE J Civ Eng 2022, 26, 3384–3401. [Google Scholar] [CrossRef]
Kim, T.; Jung, J.; Min, H.; Jung, Y.-H. An Entropy Analysis-Based Window Size Optimization Scheme for Merging LiDAR Data Frames. Sensors 2022, 22, 9293. [Google Scholar] [CrossRef] [PubMed]
Jiang, R.; Jáuregui, D.V.; White, K.R. Close-Range Photogrammetry Applications in Bridge Measurement: Literature Review. Measurement 2008, 41, 823–834. [Google Scholar] [CrossRef]
Luhmann, T. Close Range Photogrammetry for Industrial Applications. ISPRS Journal of Photogrammetry and Remote Sensing 2010, 65, 558–569. [Google Scholar] [CrossRef]
Yilmaz, H.M.; Yakar, M.; Gulec, S.A.; Dulgerler, O.N. Importance of Digital Close-Range Photogrammetry in Documentation of Cultural Heritage. Journal of Cultural Heritage 2007, 8, 428–433. [Google Scholar] [CrossRef]
Remondino, F. Heritage Recording and 3D Modeling with Photogrammetry and 3D Scanning. Remote Sensing 2011, 3, 1104–1138. [Google Scholar] [CrossRef]
Fiorillo, F.; Limongiello, M.; Jiménez Fernández-Palacios, B. Testing GoPro for 3D Model Reconstruction in Narrow Spaces. ACTA IMEKO 2016, 5, 64. [Google Scholar] [CrossRef]
Altuntas, C.; Hezer, S.; Kırlı, S. Image Based Methods For Surveying Heritage Of Masonry Arch Bridge With The Example Of Dokuzunhan In Konya, Turkey. 2017. [Google Scholar] [CrossRef]
Angelini, A.; Cozzolino, M.; Gabrielli, R.; Gentile, V.; Mauriello, P. Three-Dimensional Modeling and Non-Invasive Diagnosis of a Huge and Complex Heritage Building: The Patriarchal Basilica of Santa Maria Assunta in Aquileia (Udine, Italy). Remote Sensing 2023, 15, 2386. [Google Scholar] [CrossRef]
Eltner, A.; Sofia, G. Structure from Motion Photogrammetric Technique. In Developments in Earth Surface Processes; Elsevier, 2020; Vol. 23, pp. 1–24. ISBN 9780444641779. [Google Scholar]
Dabove; Grasso; Piras Smartphone-Based Photogrammetry for the 3D Modeling of a Geomorphological Structure. Applied Sciences 2019, 9, 3884. [CrossRef]
Stumpf, A.; Malet, J.-P.; Allemand, P.; Pierrot-Deseilligny, M.; Skupinski, G. Ground-Based Multi-View Photogrammetry for the Monitoring of Landslide Deformation and Erosion. Geomorphology 2015, 231, 130–145. [Google Scholar] [CrossRef]
Gance, J.; Malet, J.-P.; Dewez, T.; Travelletti, J. Target Detection and Tracking of Moving Objects for Characterizing Landslide Displacements from Time-Lapse Terrestrial Optical Images. Engineering Geology 2014, 172, 26–40. [Google Scholar] [CrossRef]
Demmler, C.; Adams, M.; Hormes, A. From UAV-Photogrammetry to Displacement Rates-Monitoring Slope Deformations in Alpine Terrain. In Proceedings of the EGU General Assembly 2020, Online, May 4 2020. [Google Scholar]
Sturzenegger, M.; Stead, D. Close-Range Terrestrial Digital Photogrammetry and Terrestrial Laser Scanning for Discontinuity Characterization on Rock Cuts. Engineering Geology 2009, 106, 163–182. [Google Scholar] [CrossRef]
Bales, F.B. Close-Range Photogrammetry for Bridge Measurement. In Proceedings of the Transportation Research Record; Washington, DC, USA; 1984; pp. 39–44. [Google Scholar]
Leitch, K.R. Close-Range Photogrammetry Measurement of Bridge Deformation: A Non-Contact Analysis Method. Ph.D Thesis, New Mexico State University, 2002. [Google Scholar]
Lee, H.; Han, D. Deformation Measurement of a Railroad Bridge Using a Photogrammetric Board without Control Point Survey. Journal of Sensors 2018, 2018, 1–10. [Google Scholar] [CrossRef]
Ahn, Y.; Peterson, S.; Nazari, M. Bridge Monitoring Using a Digital Camera: Photogrammetry-Based Bridge Dynamics Monitoring; Mineta Transporation Institute: San Jose, CA, USA, 2019. [Google Scholar]
Lee, H.; Oh, J. 3D Displacement Measurement of Railway Bridge According to Cyclic Loads of Different Types of Railcars with Sequential Photogrammetry. Applied Sciences 2023, 13, 1359. [Google Scholar] [CrossRef]
Luhmann, T.; Robson, S.; Kyle, S.; Boehm, J. Close-Range Photogrammetry and 3D Imaging; De Gruyter, 2019; ISBN 9783110607253. [Google Scholar]
McGuire, M.P.; Yust, M.B.S.; Shippee, B.J. Application of Terrestrial Lidar and Photogrammetry to the As-Built Verification and Displacement Monitoring of a Segmental Retaining Wall. In Proceedings of the Geotechnical Frontiers 2017; American Society of Civil Engineers: Orlando, Florida, 2017; pp. 461–471. [Google Scholar]
Professional Photogrammetry and Drone Mapping Software Available online:. Available online: https://www.pix4d.com/ (accessed on 5 May 2023).
ISO 17123-2:2001. Available online: https://www.iso.org/standard/30199.html (accessed on 5 May 2023).

Figure 1. Displacement of paving blocks adjacent to the deep excavation site: (a) settlement and non-uniform block pavements; (b) uplift; and (c) settlement and horizontal displacement.

Figure 2. Flowchart of the proposed methodology.

Figure 3. (a) Ground sample distance with camera height. (b) Ground distance shown in an image with α.

Figure 4. Frontal overlap depending on the time interval between two consecutive images: moving speed (a) 1.0 m/s; (b) 2.0 m/s.

Figure 5. Side overlap versus distance between tracks.

Figure 6. Reference set up for paving block for the detection and measurement of block displacement.

Figure 7. PCD of 5.0 mm uplift: (a) PCD; (b) visualization of uplifted zone; (c) zoomed in 5.0 mm uplifted zone; (d) histogram of uplifted zone.

Figure 8. PCD of 7.5 mm uplift: (a) PCD; (b) visualization of uplifted zone; (c) zoomed in 7.5 mm uplifted zone; (d) histogram of uplifted zone.

Figure 9. PCD of 10.0 mm uplift: (a) PCD; (b) visualization of uplifted zone; (c) zoomed in 10 mm uplifted zone; (d) histogram of uplifted zone.

Figure 10. PCD of 5.0 mm settlement: (a) PCD; (b) settled zone visualization; (c) zoomed in 5.0 mm settled zone; (d) histogram of settled zone.

Figure 11. PCD of 7.5 mm settlement: (a) PCD; (b) settled zone visualization; (c) zoomed in 7.5 mm settled zone; (d) histogram of settled zone.

Figure 12. PCD of 10.0 mm settlement: (a) PCD; (b) settled zone visualization; (c) zoomed in 10.0 mm settled zone; (d) histogram of settled zone.

Figure 13. PCD analysis results of horizontal displacement cases of 5 mm, 7.5 mm, and 10 mm.

Figure 14. Histogram of investigated horizontal displacement cases: (a) 5 mm; (b) 7.5 mm; (c) 10 mm.

Figure 15. PCD of reference and investigated cases for 10 mm horizontal displacement: (a) reference; (b) 10 mm horizontal displacement; (c) reference with 10 mm horizontal displacement; and (d) C2C distance.

Figure 16. Enlarged view of the area with 10 mm horizontal displacement: (a) before displacement occurred; (b) after 10 mm displacement; (c) differences between PCD.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer