Preprint
Review
A Taxonomic Survey of Physics-Informed Machine Learning
Altmetrics
Downloads
468
Views
223
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
10 May 2023
Posted:
11 May 2023
You are already at the latest version
Alerts
Abstract
Physics-informed machine learning (PIML) refers to the emerging area of extracting physically relevant solutions to complex multiscale modeling problems and has enjoyed significant interest from the research community. This paper discusses the recent critical advancements in the PIML domain. Novel methods and applications of domain decomposition in physics-informed neural networks (PINN) in particular are highlighted. Additionally, we explore recent Works toward utilizing neural operator learning to intuit relationships in physics systems traditionally modeled by sets of complex governing equations and solved with expensive differentiation techniques. Finally, expansive applications of traditional physics-informed machine learning and potential limitations are discussed. In addition to summarizing recent work, we propose a novel taxonomic structure to catalog physics-informed machine learning based on how the physics-information is derived and injected into the machine learning process. The taxonomy assumes the explicit objectives of facilitating interdisciplinary collaboration in methodology, thereby promoting a wider characterization of what types of physics-problems are served by the physics-informed learning machines, and assisting in identifying apt targets for future work. To summarize, the major twofold goal of this work is to summarize recent advancements and introduce a taxonomic catalog for applications of physics-informed machine learning.
Keywords:
Subject: Computer Science and Mathematics - Computer Science
1. Introduction
Building reliable multiphysics models is an essential operation in nearly any given area of scientific research. However, solving and interpreting the said models is an essential limitation for many. Traditional methods towards differentiation can be prohibitively expensive, while theoretical derivations and experimental observation can also limit the applicability of certain models. Furthermore, traditional learning machines fail to learn relationships in many complex physical systems due to the typical imbalance of data on the one hand, and the lack of physically relevant knowledge on the other. Problems lacking trustworthy observational data are typically modeled by precise systems of complex equations with initial conditions and tuned coefficients.
This work details recent advancements in physics-informed machine learning. Physics-informed machine learning is a tool by which researchers can extract physically relevant solutions to multiscale modeling problems. Crucially, physics-informed learning machines have been shown to accurately learn general solutions to complex physical processes having sparse, multifidelity, and/or otherwise incomplete data by leveraging the knowledge of the underlying physical features. What differentiates physics-informed learning from traditional statistical model is the somehow tangible inclusion of physically relevant prior knowledge. The constitutional need for qualitatively defined, physically relevant learning interventions further increases the need for a qualitative taxonomy.
Most notably among the recent advancements, we focus on the increasing parallelism of the physics-informed neural network algorithm, and the introduction of neural operators for learning systems of differential equations. In 2021, Karniadakis et al. provide a comprehensive review of the methods leveraged in physics-informed learning and provide an outline of biases catalyzed by prior physical knowledge [1]. Karniadakis et al. assert as a key point, “Physics-informed machine learning integrates seamlessly data and mathematical physics models, even in partially understood, uncertain and high-dimensional contexts” [1]. This comprehensive review primarily details physics-informed neural learning machines for applicability to a diverse set of difficulty ill-posed and inverse problems. Karniadakis et al. continue to discuss domain decomposition for scalability and operator learning as future areas of research. Toward recent expansion in a wide rang of application, the use of physics-informed learning machines has seen the method’s application in diverse fields from fluids [2], heat transfer [3] to COVID-19 spread [4,5], and cardiac modeling [6,7,8]. Cai et al. [2] offer a review of physics-informed machine learning implementations for three-dimensional wake flows, supersonic flows, and biomedical flows. High-dimensional and noisy data from fluid flows is prohibitively difficult to train with traditional learning algorithms; this review highlights the applicability of physics-informed neural networks tackling this problem in fluid flow modeling. For heat transfer problems, Cai et al. [3] discuss a variety of physics-informed machine learning in convection heat transfer problems with unknown boundary conditions, including several forced convection and mixed convection problems. Again, Cai et al. showcase diverse applications of physics-informed nerual networks to apply neural learning machines in traditionally impractical settings where injecting physically relevant prior information makes neural network modeling viable. In 2022, Nguyen et al. [4] provide an SEIRP-informed neural with architecture and training routine changes defined by governing compartmental infection model equations. Additionally, Cai et al. [5] propose the fractional PINN (fPINN), a physics-informed neural network created for the rapidly mutable COVID-19 variants trained on Caputo-Hadamard derivatives in the loss propagation of the training process. Cuomo et al. [9] provide a summary of several physics-informed machine learning use-cases . The wide range of apt applications for physics-informed machine learning further perpetuates the need for qualitative discussion and sub-classification.
The need for computational methods, especially where problems are modeled by complex and/or multiscale systems of nonlinear equations, is growing expeditiously. An exhaustive amount of scholarly thought has recently been afforded toward methods advancing data-driven learning of partial differential equations. Raissi et al. [10] infer lift and drag from velocity measurements and flow visualizations. Here, Navier-Stokes are estimated using automatic differentiation to obtain the required derivatives and compute residuals which compose loss step augmentations. A similar process is common for learning process augmentations in physics-informed learning. Raissi et al. [11] introduce a hidden physics model for learning nonlinear partial differential equations (PDEs) from noisy and limited experimental data by leveraging the underpinning physical laws. This approach uses the Gaussian process to balance model complexity and data fitting. The hidden physics model was applied to the data-driven discovery of PDEs such as Navier–Stokes, Schrödinger, Kuramoto–Sivashinsky equations. Later, in another article, two neural networks are employed for similar problems [12]. The first neural network models the prior of the unknown solution, and the second neural network models the nonlinear dynamics of the system. In another work, the same group used deep neural networks combined with a multi-step time-stepping scheme to identify nonlinear dynamics from noisy data [13]. The effectiveness of this approach was shown for nonlinear and chaotic dynamics, Lorenz system, fluid flow, and Hopf bifurcation. In 2019, Raissi et al. [14] also proposed two types of algorithms: continuous time and discrete time models. The so-titled physics-informed neural network (PINN) is tailored to two classes of problems as follows: a) data-driven solution of PDEs and b) data-driven discovery of PDEs. The approach’s effectiveness was demonstrated for several problems, including Navier-Stokes, Burgers’ equation, and Schrödinger equations. Consequently, the PINN has been adapted to intuit governing equations or solution spaces for many types of physical systems. For Reynolds-averaged Navier Stokes problems, Wang et. al [15] propose a physics-informed random forest model for assisting data driven flow modeling. Other research introduce physics-constraints, consequently biasing the learning process driven by prior relevant knowledge. Sirignano et al. [16] accurately solve highly dimensional free boundary partial differential equations and prove the approximation utility of neural networks for quasilinear partial differential equations. Han et al. [17] propose a deep learning method for high dimensional partial differential equations with backward stochastic differential equation reformulations. Rudy et al. propose a method for estimating governing equations of numerically derived flow data using automatic model selection. Long et al. [18] propose another data-driven approach for governing equation discovery, and Leake et al. [19] introduce the combination of the Deep Theory of Functional Connections with neural networks to estimate solutions to partial differential equations. The preceding selection includes examples of the transition from solving partial differential equations with expensive techniques toward learning solutions with high-throughput learning machines, and we cover some works on the latter topic next. Figure 1 show how physics-informed machine learning is used in the learning process to accelerate training and allow applicability of models to problems whose data inconsistencies posed obstacles to traditional learning.
In neural networks, Figure 1 shows: (1) learning bias in the form of physically relevant modeling equations used directly in training propagation (2) inductive bias through neural model architecture augmentation to introduce previously understood physical structures (3) observational bias in the form of data gathering techniques introducing physical bias via informed data structures of simulation or observation. Here, i are input features. display an arbitrary number of hidden layers, of arbitrary size. and C are physically relevant structures. For example, in compartmental epidemiology the population bins and their underplying governing equations being differentiated in process (1). Biases are explored further in Section 2.2.
This survey aims to summarize recent advances in physics-informed machine learning, including improved parallelism and the introduction of the neural operator, while also discussing the broadening scope to which physics-informed machine learning is applied. Most crucially, we introduce a taxonomic system for classifying the source and effect of physics-based information augmentations on learning machines to categorize existing work and promote the wide applicability of PIML by highlighting problems well-posed for the informed learning machine paradigm.
The body of work surveyed herein was obtained by Google Scholar searches with the keywords “physics-informed machine learning” or “physics-informed neural networks”. We restricted the search results to only recent articles appearing since 2021. Both queries return greater than 17,000 publications as of January 2023. Further filtering by keywords appearing in the title is hence needed. Publications chosen for this survey are meant to be representative of recent trends and are chosen for usefulness in discussing the proposed taxonomic structure. Hence, the individual paper impact is considered less important than its utility for taxonomic discussion - for all intents and purposes of this work. Moreover, some additional papers predating our search, which are foundational to the selected works have been added for clarity of the narrative. Given the acute popularity of these methods, an exhaustive survey is intangible. Thus, a representative group of research has been selected to cover recent trends and to adequately inform our taxonomic structure, which in itself is necessitated by the wide range of new work.
2. Taxonomy
Machine learning techniques toward learning initial-intermediate state relationships in systems traditionally modeled by complex collections of differential equations solved with conventional numerical methods are experiencing a growing popularity and vitally increasing applicability. So too must our understanding of how information gathered from the physical understanding of systems is employed to facilitate the learning processes and how physically-derived information is injected into the machine learning pipeline. To this end, a taxonomy to classify physics-informed machine learning applications is proposed. In summary, physics-information is implicitly driven by numerically derived data or explicitly driven by well-understood relationships in the physical system; where both drivers are often generated with, or informed by traditionally studied governing differential equations. There are several typical sources for such prior physical knowledge. Data can enforce physics information in several ways: physical symmetries could be introduced or implicit relationships from high-fidelity simulations can implicitly affect model convergence. Additionally, physically relevant information in the form of high-fidelity models can be imposed on the learning process. Governing equations can be incorporated directly into the optimization process, or learning machine architectures can be tweaked to reflect physically important model qualities.
Toward increasing explainability in physics-informed machine learning, the taxonomic system affords a researcher the framework to answer two fundamental questions. First, where is the physics-information which is applied to the learning process originating from - or, how is the information driven? In other words, what is the driver of physically relevant priors. Two general answers are proposed: physics-model and physics-data drivers. Second, in what way is physics-derived information utilized in the learning process? Or, in which way is physical bias introduced to the learning process. Three biases, outlined by Karniadakis et al. [1], are proposed as solution to question two: observational, inductive, and learning biases. The proposed taxonomic structure promotes collaborations toward future work in physics-informed machine learning by offering a structure where researchers utilizing scientific machine learning may discern strategies by which physics-derived information can bolster the learning processes. Furthermore, the taxonomic structure illuminates how model-driven analyses of physical systems can be supplemented by cost-mitigating methods of machine learning. We next identify the basic components of physics-informed machine learning models to motivate the design of the proposed taxonomy.
2.1. Driver
How can we categorize the origin of prior physics-based knowledge?
The pipeline of physics-informed machine learning is given in Figure 2. The primary consideration when confronting the explainability of PIML modeling is, how was physics-based information obtained for use in the machine learning process? This question crucially differentiates the qualifications for physics-based learning while further broadening scope and promoting the introduction of physics-informed machine learning. The proposed taxonomy draws two distinctions: first, physics-information is enforced on the learning process through governing equations or physical structural patterns, and second, physics-information is encoded implicitly into the data through simulation or observation. The data may be structured in a physically relevant way, or physics-information is derived from traditional multiphysics models directly, as typically expressed by the governing equations. Figure 2 adopts the images of heat transfer problems, fluid flow problems, neural networks, or generic datasets as stand-ins for any physics-based model, learning machine, or physically structured dataset, respectively. Additionally, Figure 2 depicts the desire for researchers to create model-driven predictions for physical problems. Traditionally, expensive differentiation is employed to realize the predictive power of the physics-based model. However, Figure 2 displays the alternative PIML pipeline in the context of the two possible drivers of prior physics-information.
Physics-model driven. First - and most tangibly - physics-information can be derived from preexisting physical models of a given problem. Commonly, governing equations are directly infused into the learning process. The learning machine might also realize these augmentations in the form of architectural augmentations which reflect physical symmetries. The features of the machine learning model are explicitly constrained by the problem’s underlying physics.
Physics-data driven. Second - and expressed broadly - physics-information can be derived implicitly from numerically data-driven methods. It is not to say that all data-driven machine learning is “physics-informed”. Yet if data has a physical structure informed by high fidelity, numerically-derived training data or by empirical data quantifiable by a trustworthy physical model - such a model is at least indirectly, constrained by the well understood underlying physical priors. After all, it is the same relationships traditionally modeled by complex systems of differential equations that researchers are attempting to learn, in lieu of differentiating expensively.
2.2. Bias
In what discernible way is physics-information injected into learning machines?
Karniadakis et al. in their 2021 review of physics-informed machine learning [1] provided a categorization of bias in the machine learning process. An interpretation of those processes are given in Figure 3 - which adopts the same general abstractions as Figure 2 and includes the generic representation of a physics-model’s governing equations by and . The wide variety of drivers and biases are given in Table 1.
Observational bias. Physics-information can be incorporated into the learning process through data. Models learning from numerically derived data-driven methods intuit physically relevant relationships in the structure of the data which has been produced ipso facto by the researcher’s understanding of the underlying physics. The abundance of various sensors makes physically relevant observational data for multiphysics modeling problems equally abundant. Much work has incorporated the need to gain maximum generalizability from sparse simulated data and other sources of multi-fidelity data.
Inductive bias. Physics-information is directly injected into the learning process through architecture-level decisions of the model. Various partitions of the model can be trained in a multitask fashion to implicitly satisfy the underlying physics. Architecture level changes induce bias on the training process by influencing modeling choices with intrinsic physical principles.
Learning bias. Physics-information is given as an informed biasing of the optimization step in the machine learning model. Often, loss functions are directly informed by calculating residuals of underlying physics-equations. Rather than implicitly influencing the training process, learning bias forces constraints on the model in a multi-task learning process where the model is trained with constraints informed by the underlying physical features.
2.3. Taxonomy Tableau
The works surveyed in this paper include taxonomically distinguishable implementations of the physics-informed machine learning paradigm and are grouped by the classifying drivers and biases as explained above. Articles that share multiple methods or otherwise cannot be categorized are excluded for the sake of readability.
It becomes abundantly obvious that the extremely popular physics-informed neural network paradigm dominates our space of surveyed methods. In fact, physics-informed neural networks, which train on some numerical data, train with loss estimates derived from the governing equations, and augment the model architecture to fit physically relevant parameters typically check each box of the proposed taxonomic catalog. This fact however does not diminish the utility of the taxonomy, instead it highlights how the minutiae differentiating applications of physics-informed learning machines can be discussed rather precisely within the confines of the taxonomy framework. In other words, the differences between two methods which appear the same in terms of name and taxonomic qualities can be discussed in the context of how each of its drivers or biases are individually implemented. Additionally, many applications of physics-informed neural networks include implementations of several problems. For this reason, if a taxonomic quality is found in any of the individual examples, it is included in the Table 1.
The proposed taxonomic structure facilitates tangible description and discussion about the qualities by which physics-informed learning machines and their applications might be differentiated. For example, two models might both include learning biases where one model calculates Caputo-Hadamard fractional representations of governing equations and another calculates algebraic differential equation solutions.
3. Discussion
We next discuss the advances in physics-information driven machine learning. One major consideration in recent physics-informed machine learning work has been the increasing potential parallelism. Spearheading advancements in the parallelism of PIML are techniques for domain decomposition in physics-informed neural networks. Implementations of the extended physics-informed neural network algorithm employ domain decomposition traditionally accomplished by expensive meshed differentiation. Progression in physics-data driven machine learning has an important feedback relationship with physics-model-driven machine learning. Select methods by which physics-data driven machine learning is performed also discussed next. Namely, we revisit the methods for approximating solutions to largely nonlinear differential equations with neural operators. This feedback relationship has led to the introduction of the physics-informed neural operator and other methods for learning functionals with physics-based constraints.
Domain decomposition
One important applicability of physics-informed neural networks are in the regime of problems traditionally resolved with expensive meshing methods like finite element, for example. In several applications, PINNs reduce the cost with substantial accuracy, while training time and residual calculations can still be concerning. Toward the end of mitigating cost, much work has improved the parallelization of the PINN architecture. Jagtap et al. [22] introduce XPINN, a generally applicable space-time decomposition for easily parallelized subdomains governed by individually, interconnected sub-PINNs. XPINN’s wide applicability to forward and inverse modeling problems were displayed. Impressively complex subdomains can be solved reliably with XPINN due to the formulation of relatively simple interfacing conditions. XPINN employs model driven inductive and learning biases by augmenting network shape and loss functions based upon physical priors. XPINN is a broad example which encompasses each of the branches of the taxonomy. Jagtap et al. employ XPINN on complex subdomains. Observational bias is introduced through simulated training data produced with a Hopf-Cole transformation provided analytical solutions to one-dimensional viscous Burgers equations , , . Like the PINN, XPINN includes physical structures in the architecture and loss calculations for physics-model driven inductive and learning biases. Hu et al. [23] further display the applicability of domain decomposition in PINNs toward parallel speedup. A general framework of discerning applicability of the extended PINN paradigm in various modeling problems is presented. Their study provides computational examples on KdV, heat, advection, Poisson, and compressible Euler equations. The Poisson solution employs the De Ryck regularization method [49] - a regularization technique proposed particularly for PINNs. This study trains on high-fidelity simulations, tweaks model architecture, and incorporates governing equations into optimization, thus exemplifying observational, inductive, and learning biases in one or all of the examples presented.
Shukla et al. [24] provide a parallel implementation of the previously proposed cPINN [25] and XPINN on two-dimensional steady-state incompressible Navier–Stokes equations, viscous Burgers equation, and a steady-state heat conduction with variable conductivity inverse problem. This work shows the advantages and disadvantages of each method and their use in tandem. Further, optimization of the distributed computing process are given. Each implementation further exemplifies the applicability of domain decomposition methods for physics informed neural networks toward arbitrarily shaped and complex subdomains. As fundamentally similar to XPINN, Shukla et al. [24] and Jagtap el al. [25] display physics-model driven inductive and learning biases. Physics-data drivers are available depending upon modeling choices. Jagtap et al. [26] display XPINN’s effectiveness toward inverse problems in supersonic flows. Enforced physics-information includes governing equations as well as entropy conditions - displaying the utility of additional physics-information beyond the model governing system. In this study, the conservative form Euler PDE equations are given by: . Here, both conservation laws: and entropy conditions: are applied as learning biases. Papadopoulos et al. [27] provides an XPINN implementation for steady-state heat transfer in composite materials with interface interaction.
The general adaptability of domain decomposition in physics-informed neural networks is further exemplified by APINNs [28], proposed by Hu et al.; they provide a variable decomposition technique for fine-tuning subdomain boundaries. APINN utilizes a gating network to mimic XPINN and provide soft domain decomposition. hp-VPINN gives an additional method for domain decomposition [50], which is a variational method for neural network approximation via high-order polynomial projections toward efficient domain decomposition in physics-informed neural networks. Finally, Xu et al. [29] provides an MPI implementation for physics-constrained learning (PCL) [30,31] employing the halo domain decomposition method. PCL carefully couples artificial neural networks and finite element models. The constitutive law in the finite element model is approximated using the neural learning machine.
Neural operator learning
One example of advancement in physic-data driven machine learning worth highlighting for its consequent physics-model driven adaptation is the neural operator. The ubiquity of the operator approach toward learning solutions to complex physical problems has led to incorporating physics-model based information into the operator learning process. The neural operator approximates latent operators which govern a mapping between input parameters and solutions. As notated by Lu et al. [51] any point y in the domain of , the output is a real number. Hence, the network receives two component inputs: u and y, and outputs . For operator learning, sufficiently many discrete underlying function sensor values are utilized for training. The neural operator abstracts complex multiphysics modeling problems as control function maps. Importantly, the introduction of the neural operator and the functional learning paradigm change drastically how model driven inductive biases can be used in physics-informed machine learning. Li et al. [32] presents a framework for the use of Fourier transform layers in neural operator networks, applying the method to many examples, including Navier-Stokes, Burgers’, and Darcy Flow problems. The Fourier neural operator performs zero-shot super-resolution. Kovachki et al. [33] provide a study on the general applicability of Fourier neural operators to inverse problems governed by highly nonlinear differential equations. Another neural operator learning machine, the DeepONet, has received recent attention. Deng et al. [34] study the convergence of operator learning by branch and trunk networks in the context of Burgers’ equation and advection-diffusion problems. Several important theorems regarding the convergence of functional learning machines are also included. Most importantly, the neural operator learning paradigm exemplifies a predisposition to the introduction of learning, inductive, or observational biases with model and data drivers.
Physics-informed neural operators
Neural operators are included in our discussion of physics-informed machine learning for their obvious potential toward physics-model driven learning machines - whether or not methods discussed previously are distinctly have implemented drivers of physics-informed machine learning. Regardless, advancements in neural operators have already led to the use of physics-informed neural operators (PINOs). Li et al. [35] employ Fourier neural operator layers, alongside physics-informed learning with observational biases. Learning bias is introduced via physics-informed residuals computed by automatic differentiation via autograd, function-wise differentiation, or Fourier continuation. The physics-informed neural operator is applied to a wide range of examples including Burgers, Darcy, and Kolmogorov flow problems. Wang et al. [36] provide the framework for physics-informed DeepONets, applying to a Burgers’ transport problem and a 2-dimensional eikonel equation, among other PDE models. A physics-model informed learning bias is introduced by augmenting loss calculations by merging latent representations of solutions. Toward its general applicability, the DeepONet dos not specify the architecture of its constituent branch and trunk networks, affording the use of many learning architectures.
Regularization mechanisms can also force functional learning toward desired partial differential equation formulation. Goswami et al. [37] have given a variational physics-informed DeepONet applied toward quasi-brittle materials modeling. Two well-studied fracture models are used to benchmark variation. By extension of the underlying models, learning bias is introduced into the functional learning framework in the loss calculations. Additionally, Schiassi et al. [38] propose an extreme learning machine (X-TFC) approach for learning functionals, employing physics-model informed learning bias toward several optimal control problems by initial and boundary constraints in the Extreme Learning Machine algorithm with constrained expressions.
Physics-informed neural networks have become widely applied in research areas where physics-model and physics-data driven information is available. Consequently, an all-encompassing discussion of applications is difficult. Instead, the remaining discussion’s focus will be on work which has advanced theory of machine learning via physics-informed neural networks or discussions on the limitations facing physics-informed machine learning.
Learning processes
Some work has been done on advancing the specific mechanisms of physics informed learning machines. As mentioned previously, De Ryck et al. [49], have formulated error estimates for PINNs approximating the Navier Stokes equations. Wu et al. [52] have proposed an adaptive method for the formulation and calculation of residuals, reducing the number of residual points required. Jagtap et al. [39] give an adaptive activation function method for improving accuracy and reducing expense, applying a PINN to the Burgers’ equation, and deep neural networks to MNIST and CIFAR-10, among other examples. In another work, Jagtap et al. provide a technique for locally adaptive activation functions. Work has also been done in improving the scope of model types for which PINNs are applicable. Several complexity reduction methods have been proposed to deal with particularly stiff underlying equations which model chemical kinetics [40,41]. Additionally, PINNs have been adapted to serve fractional expressions of differential equations with a Caputo-Hadamard augmentation [5,42]. Jagtap et al. [43] have also proposed models which train multi-fidelity data from observation and simulation applied to Serre-Green-Naghdi equations. Finally, novel types of learning machines have been introduced to the physics-informed paradigm. McClenny et al. [44] and Rodriguez et al. [45] propose attention based mechanisms for physics-informed learning. Finally, in multiple articles, Schiassi et al. have employed the Theory of Functional Connections to ease the computational expense in working with complex, constrained PDEs [38,46,47,48].
Limitations
Like other multiphysics and multiscale modeling, traditional physics-informed learning machines are often plagued by high-dimensionality and model complexity. Models demanding high order differentiation present high computational expense and make optimization difficult. Spectral biases on solution frequencies can force the model toward inaccurate equilibria. In complex models, residual calculations for training can still present prohibitive cost. The addition of Fourier features and other mathematical innovations have begun to address frequency bias issues.
Wang et al. [53] studied the limitation of physics informed neural networks using the Neural Tangent Kernel (NTK) theory and showed the PINNs learning function is biased toward the dominant Eigen directions of the data. They proposed a new architecture with coordinate embedding layers, which leads to a robust and accurate estimation of the target function. This architecture showed excellent performance for wave propagation and reaction–diffusion dynamics where the regular PINNs often fail. In another paper, Wang et al. [54] study PINN training failures, and propose a neural tangent kernel guided optimization method for addressing convergence rate issues.
Another important limitation on physics-informed machine learning is data acquisition and benchmarking. In many problems where the physics-informed machine learning architecture is applicable, the right data is simply not available. Much work has generated models capable of learning general solutions from sparse and incomplete data. In general, benchmarking for physics-informed machine learning is difficult, but the comparison to traditional methods and development of baseline tools is addressing the benchmarking concerns. Mishra et al. [55] provide robust justification for the use of physics-informed neural networks in data assimilation or unique continuation inverse problems. Estimates on the PINNs generalization error are given via conditional stability estimates. Finally, Aditi et al. [57] explore possible failure modes of physics-informed neural networks. The authors conclude that the generic formulation of physics-informed neural networks utilizing soft regularization methods are susceptible to the burden of ill-posed problems. It is noted that the loss landscape in complex PINNs can be difficult to optimize, while introducing regularizaton techniques to ease training.
4. Conclusions
A well-defined taxonomy can provide a guide for first-time researchers entering the field of physics-informed machine learning, and serve as a tool for seasoned researchers to sift through large volumes of new work while providing insight into novel use cases of the physics-informed learning paradigm. Recent advancements in techniques toward domain decomposition and methods toward addressing particularly ill-posed models that are difficult to study traditionally or with learning machines are important to the development of physics-informed machine learning. Work in improving the training regimen of physics-informed learning machines must continue while its application broadens. Decreasing the burden of complex loss calculations and creating tailored optimization algorithms will continue to be of paramount importance moving forward.
Future work in this field can surely benefit from a taxonomic structure: whether assisting in building physics-informed models or allowing a framework by which they can be studied. The applicability of physics-informed machine learning is limited only by systems with some well-understood prior physical knowledge - which is not much of a limiting factor. Most crucially, future explorations of physics-informed machine learning is primarily limited by the number of researchers and students who understand its robust applicability. This is the primary motivation for providing a framework for taxonomic surveys of physics-informed machine learning.
Author Contributions
Conceptualization, J.P., P.R. and P.G.; methodology, J.P., P.R. and P.G.; investigation, J.P., P.R. and P.G.; resources, P.G.; writing—original draft preparation, J.P., P.R. and P.G.; writing—review and editing, J.P., P.R. and P.G.; visualization, J.P.; funding acquisition, P.G. All authors have read and agreed to the published version of the manuscript.
This work was partially supported by NSF CBET 1802588.
The authors declare no conflict of interest.
Funding
This work was partially supported by NSF CBET 1802588.
References
- Karniadakis, G.E.; Kevrekidis, I.G.; Lu, L.; Perdikaris, P.; Wang, S.; Yang, L. Physics-informed machine learning. Nat. Rev. Phys. 2021, 3, 442–440. [Google Scholar] [CrossRef]
- Cai, S.; Mao, Z.; Wang, Z.; Yin, M.; Karniadakis, G.E. Physics-informed neural networks (PINNs) for fluid mechanics: A review. Acta Mech. Sin. 2021, 37, 1727–1738. [Google Scholar] [CrossRef]
- Cai, S.; Wang, Z.; Wang, S.; Perdikaris, P.; Karniadakis, G.E. Physics-Informed Neural Networks (PINNs) for Heat Transfer Problems. J. Heat Transf. 2021. [Google Scholar] [CrossRef]
- Nguyen, L.; Raissi, M.; Seshaiyer, P. Modeling, Analysis and physics-Informed Neural Network approaches for studying the dynamics of COVID-19 involving human-human and human-pathogen interaction. Comput. Math. Biophys. 2022, 1, 1–17. [Google Scholar] [CrossRef]
- Cai, M.; Karniadakis, G.E.; Li, C. Fractional SEIR model and data-driven predictions of COVID-19 dynamics of Omicron variant. Chaos: Interdiscip. J. Nonlinear Sci. 2022, 32, 071101. [Google Scholar] [CrossRef]
- Costabal, F.S.; Yang, Y.; Perdikaris, P.; Hurtado, D.E.; Kuhl, E. Physics-Informed Neural Networks for Cardiac Activation Mapping. Front. Phys. 2020, 8. [Google Scholar] [CrossRef]
- Kissas, G.; Yang, Y.; Hwuang, E.; Witschey, W.R.; Detre, J.A.; Perdikaris, P. Machine learning in cardiovascular flows modeling: Predicting arterial blood pressure from non-invasive 4D flow MRI data using physics-informed neural networks. Comput. Methods Appl. Mech. Eng. 2020, 258, 112623. [Google Scholar] [CrossRef]
- Grandits, T.; et al. Learning Atrial Fiber Orientations and Conductivity Tensors from Intracardiac Maps Using Physics-Informed Neural Networks. Funct. Imaging Model. Heart. [CrossRef]
- Cuomo, S.; Cola, V.S.D.; Giampaolo, F.; Rozza, G.; Raissi, M.; Piccialli, F. Scientific Machine Learning through Physics-Informed Neural Networks: Where we are and What’s next.” (arXiv.org) June, 2022. Available online: https://arxiv.org/abs/2201.05624 (accessed on 7 January 2023).
- Raissi, M.; Wang, Z.; Triantafyllou, M.S.; Karniadakis, G.E. Deep learning of vortex-induced vibrations. J. Fluid Mech. 2018, 861, 119–137. [Google Scholar] [CrossRef]
- Raissi, M.; Karniadakis, G.E. Hidden physics-models: Machine learning of nonlinear partial differential equations. J. Comput. Phys. 2018, 357, 125–141. [Google Scholar] [CrossRef]
- Raissi, M. Deep Hidden physics-Models: Deep Learning of Nonlinear Partial Differential Equations. J. Mach. Learn. Res. 2018, 19, 1–24. Available online: https://www.jmlr.org/papers/volume19/18-046/18-046.pdf?ref=https://githubhelp.com (accessed on 9 January 2023).
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E.; Multistep Neural Networks for Data-driven Discovery of Nonlinear Dynamical Systems. arXiv:1801.01236 [nlin, physics:physics, stat], Jan. 2018. Available online: https://arxiv.org/abs/1801.01236 (accessed on 9 January 2023).
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Wang, J.X.; Wu, J.L.; Xiao, H. Physics-informed machine learning approach for reconstructing Reynolds stress modeling discrepancies based on DNS data. Phys. Rev. Fluids 2017, 2, 034603. [Google Scholar] [CrossRef]
- Sirignano, J.; Spiliopoulos, K. DGM: A deep learning algorithm for solving partial differential equations. J. Comput. Phys. 2018, 375, 1339–1364. [Google Scholar] [CrossRef]
- Han, J.A.; Jentzen, W.E. Solving high-dimensional partial differential equations using deep learning. Proc. Natl. Acad. Sci. USA 2018, 115, 8505–8510. [Google Scholar] [CrossRef]
- Long, Z.; Lu, Y.; Ma, X.; Dong, B. PDE-Net: Learning PDEs from Data. proceedings.mlr.press, Jul. 03, 2018. Available online: http://proceedings.mlr.press/v80/long18a.html?ref=https://githubhelp.
- Leake, C.; Mortari, D. Deep Theory of Functional Connections: A New Method for Estimating the Solutions of Partial Differential Equations. Mach. Learn. Knowl. Extr. 2020, 2, 37–55. [Google Scholar] [CrossRef] [PubMed]
- Rudy, S.H.; Brunton, S.L.; Proctor, J.L.; Kutz, J.N. Data-driven discovery of partial differential equations. Sci. Adv. 2017, 3, e1602614. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.L.; Xiao, H.; Paterson, E. Physics-informed machine learning approach for augmenting turbulence models: A comprehensive framework. Phys. Rev. Fluids 2018, 3, 074602. [Google Scholar] [CrossRef]
- Jagtap, A.D.; Karniadakis, G.E. Extended Physics-Informed Neural Networks (XPINNs): A Generalized Space-Time Domain Decomposition Based Deep Learning Framework for Nonlinear Partial Differential Equations. Commun. Comput. Phys. 2020, 28, 2002–2041. [Google Scholar] [CrossRef]
- Hu, Z.; Jagtap, A.D.; Karniadakis, G.E.; Kawaguchi, K. When Do Extended Physics-Informed Neural Networks (XPINNs) Improve Generalization? SIAM J. Sci. Comput. 2022, 44, A3158–A31822. [Google Scholar] [CrossRef]
- Shukla, K.; Jagtap, A.D.; Karniadakis, G.E. Parallel physics-informed neural networks via domain decomposition. J. Comput. Phys. 2021, 447, 110683. [Google Scholar] [CrossRef]
- Jagtap, A.D.; Kharazmi, E., G. E.K. Conservative physics-informed neural networks on discrete domains for conservation laws: Applications to forward and inverse problems. Comput. Methods Appl. Mech. Eng. 2020, 365, 113028. [Google Scholar] [CrossRef]
- Jagtap, A.D.; Mao, Z.; Adams, N.; Karniadakis, G.E. Physics-informed neural networks for inverse problems in supersonic flows. J. Comput. Phys. 2022, 466, 111402. [Google Scholar] [CrossRef]
- Papadopoulos, L.; Bakalakos, S.; Nikolopoulos, S.; Kalogeris, I.; Papadopoulos, V. A computational framework for the indirect estimation of interface thermal resistance of composite materials using XPINNs. Int. J. Heat Mass Transf. 2023, 200, 123420. [Google Scholar] [CrossRef]
- Hu, Z.; Jagtap, A.D.; Karniadakis, G.E.; Kawaguchi, K.; Augmented Physics-Informed Neural Networks (APINNs): A gating network-based soft domain decomposition methodology. arXiv:2211.08939. Available online: https://arxiv.org/abs/2211.08939 (accessed on 12 January 2023).
- Xu, K.; Zhu, W.; Darve, E.; Distributed Machine Learning for Computational Engineering using MPI. arXiv:2011.01349. Available online: https://arxiv.org/abs/2011.01349 (accessed on 12 January 2023).
- Liu, X.; Tao, F.; Du, H.; Yu, W.; Xu, K. Learning Nonlinear Constitutive Laws Using Neural Network Models Based on Indirectly Measurable Data. J. Appl. Mech. 2020, 87, 2020. [Google Scholar] [CrossRef]
- Xu, K.; Darve, E. Physics constrained learning for data-driven inverse modeling from sparse observations. J. Comput. Phys. 2022, 453, 110938. [Google Scholar] [CrossRef]
- Li, Z.; et al. Fourier Neural Operator for Parametric Partial Differential Equations. 0 arXiv:2010.08895. 2020. Available online: https://arxiv.org/abs/2010, 8895.
- Kovachki, N.; Lanthaler, S.; Mishra, S. On Universal Approximation and Error Bounds for Fourier Neural Operators. J. Mach. Learn. Res. 2021, 22, 1–76. Available online: https://www.jmlr.org/papers/volume22/21-0806/21-0806.pdf (accessed on 12 January 2023).
- Deng, B.; Shin, Y.; Lu, L.; Zhang, Z.; Karniadakis, G.E.; Convergence rate of DeepONets for learning operators arising from advection-diffusion equations. arXiv:2102.10621. 2021. Available online: https://arxiv.org/abs/2102.10621 (accessed on 12 January 2023).
- Li, Z.; et al.; Physics-Informed Neural Operator for Learning Partial Differential Equations arXiv:2111.03794. 2022. Available online: https://arxiv.org/abs/2111.03794 (accessed on 12 January 2023).
- Wang, S.; Wang, H.; Perdikaris, P. Learning the solution operator of parametric partial differential equations with physics-informed DeepONets. Sci. Adv. 2021, 7. [Google Scholar] [CrossRef]
- Goswami, S.; Bora, A.; Yu, Y.; Karniadakis, G.E.; Physics-Informed Deep Neural Operator Networks. arXiv:2207.05748. 2022. Available online: https://arxiv.org/abs/2207.05748 (accessed on 12 January 2023).
- Schiassi, E.; Furfaro, R.; Leake, C.; Florio, M.D.; Johnston, H.; Mortari, D. Extreme theory of functional connections: A fast physics-informed neural network method for solving ordinary and partial differential equations. Neurocomputing 2021, 457, 334–356. [Google Scholar] [CrossRef]
- Jagtap, A.D.; Kawaguchi, K.; Karniadakis, G.E. Adaptive activation functions accelerate convergence in deep and physics-informed neural networks. J. Comput. Phys. 2020, 404, 109136. [Google Scholar] [CrossRef]
- Ji, W.; Qiu, W.; Shi, Z.; Pan, S.; Deng, S. Stiff-PINN: Physics-Informed Neural Network for Stiff Chemical Kinetics. J. Phys. Chem. A 2021, 125, 8098–8106. [Google Scholar] [CrossRef] [PubMed]
- Weng, Y.; Zhou, D. Multiscale Physics-Informed Neural Networks for Stiff Chemical Kinetics. J. Phys. Chem. A 2022, 126, 8534–8543. [Google Scholar] [CrossRef] [PubMed]
- Pang, G.; Lu, L.; Karniadakis, G.E. fPINNs: Fractional Physics-Informed Neural Networks. SIAM J. Sci. Comput. 2019, 41, A2603–A2626. [Google Scholar] [CrossRef]
- Jagtap, A.D.; Mitsotakis, D.; Karniadakis, G.E. Deep learning of inverse water waves problems using multi-fidelity data: Application to Serre–Green–Naghdi equations. Ocean. Eng. 2022, 248, 110775. [Google Scholar] [CrossRef]
- McClenny, L.; Braga-Neto, U. Self-Adaptive Physics-Informed Neural Networks using a Soft Attention Mechanism. 0 arXiv:2009.04544. 2022. Available online: https://arxiv.org/abs/2009, 4544.
- Rodriguez-Torrado, R.; et al. Physics-informed attention-based neural network for hyperbolic partial differential equations: Application to the Buckley–Leverett problem. Sci. Rep. 2022, 12. [Google Scholar] [CrossRef] [PubMed]
- Schiassi, E.; Florio, M.D.; Ganapol, B.D.; Picca, P.; Furfaro, R. Physics-informed neural networks for the point kinetics equations for nuclear reactor dynamics. Ann. Nucl. Energy 2022, 167, 108833. [Google Scholar] [CrossRef]
- Schiassi, E.; D’Ambrosio, A.; Drozd, K.; Curti, F.; Furfaro, R. Physics-Informed Neural Networks for Optimal Planar Orbit Transfers. J. Spacecr. Rocket. 2022, 59, 834–849. [Google Scholar] [CrossRef]
- de Florio, M.E.; Schiassi, E.; Ganapol, B.D.; Furfaro, R. Physics-informed neural networks for rarefied-gas dynamics: Thermal creep flow in the Bhatnagar–Gross–Krook approximation. Phys. Fluids 2021, 33, 047110. [Google Scholar] [CrossRef]
- Ryck, T.D.; Jagtap, A.D.; Mishra, S. Error estimates for physics informed neural networks approximating the Navier-Stokes equations. 0 arXiv:2203.09346. Available online: https://arxiv.org/abs/2203, 9346.
- Kharazmi, E.; Zhang, Z.; Karniadakis, G.E. hp-VPINNs: Variational physics-informed neural networks with domain decomposition. Comput. Methods Appl. Mech. Eng. 2021, 374, 113547. [Google Scholar] [CrossRef]
- Lu, L.; Jin, P.; Karniadakis, G.E. Deeponet: Learning nonlinear operators for identifying differential equations based on the universal approximation theorem of operators. arXiv 2019, arXiv:1910.03193. [Google Scholar]
- Wu, C.; Zhu, M.; Tan, Q.; Kartha, Y.; Lu, L. A comprehensive study of non-adaptive and residual-based adaptive sampling for physics-informed neural networks. Comput. Methods Appl. Mech. Eng. 2023, 403, 115671. [Google Scholar] [CrossRef]
- Wang, S.; Wang, H.; Perdikaris, P. On the eigenvector bias of Fourier feature networks: From regression to solving multi-scale PDEs with physics-informed neural networks. Comput. Methods Appl. Mech. Eng. 2021, 384, 113938. [Google Scholar] [CrossRef]
- Wang, S.; Yu, X.; Perdikaris, P. When and why PINNs fail to train: A neural tangent kernel perspective. J. Comput. Phys. 2022, 449, 110768. [Google Scholar] [CrossRef]
- Mishra, S.; Molinaro, R. Estimates on the generalization error of physics-informed neural networks for approximating a class of inverse problems for PDEs. IMA J. Numer. Anal. [CrossRef]
- Goswami; Yin, M. ; Yu, Y.; Karniadakis, G.E. A physics-informed variational DeepONet for predicting crack path in quasi-brittle materials. Comput. Methods Appl. Mech. Eng. 2022, 391, 114587. [Google Scholar] [CrossRef]
- Aditi, K.; Amir, G.; Shandian, Z.; Robert, K.; Michael, M.W. Characterizing possible failure modes in physics-informed neural networks. Adv. Neural Inf. Process. Syst. 2021, 34, https://proceedings.neurips.cc/paper/2021/hash/df438e5206f31600e6ae4af72f2725f1–Abstracthtml. Available online: https://proceedings.neurips.cc/paper/2021/hash/df438e5206f31600e6ae4af72f2725f1-Abstract.html (accessed on 13 January 2023).
- Jagtap, A.D.; Kawaguchi, K.; Karniadakis, G.E. Locally adaptive activation functions with slope recovery for deep and physics-informed neural networks. Proc. R. Soc. A Math. Phys. Eng. Sci. 2020, 476, 20200334. [Google Scholar] [CrossRef]
Figure 1.
The popular PINN architecture aptly exemplifies the three biases informing learning processes (1) learning bias (2) inductive bias (3) observational bias.
Figure 1.
The popular PINN architecture aptly exemplifies the three biases informing learning processes (1) learning bias (2) inductive bias (3) observational bias.
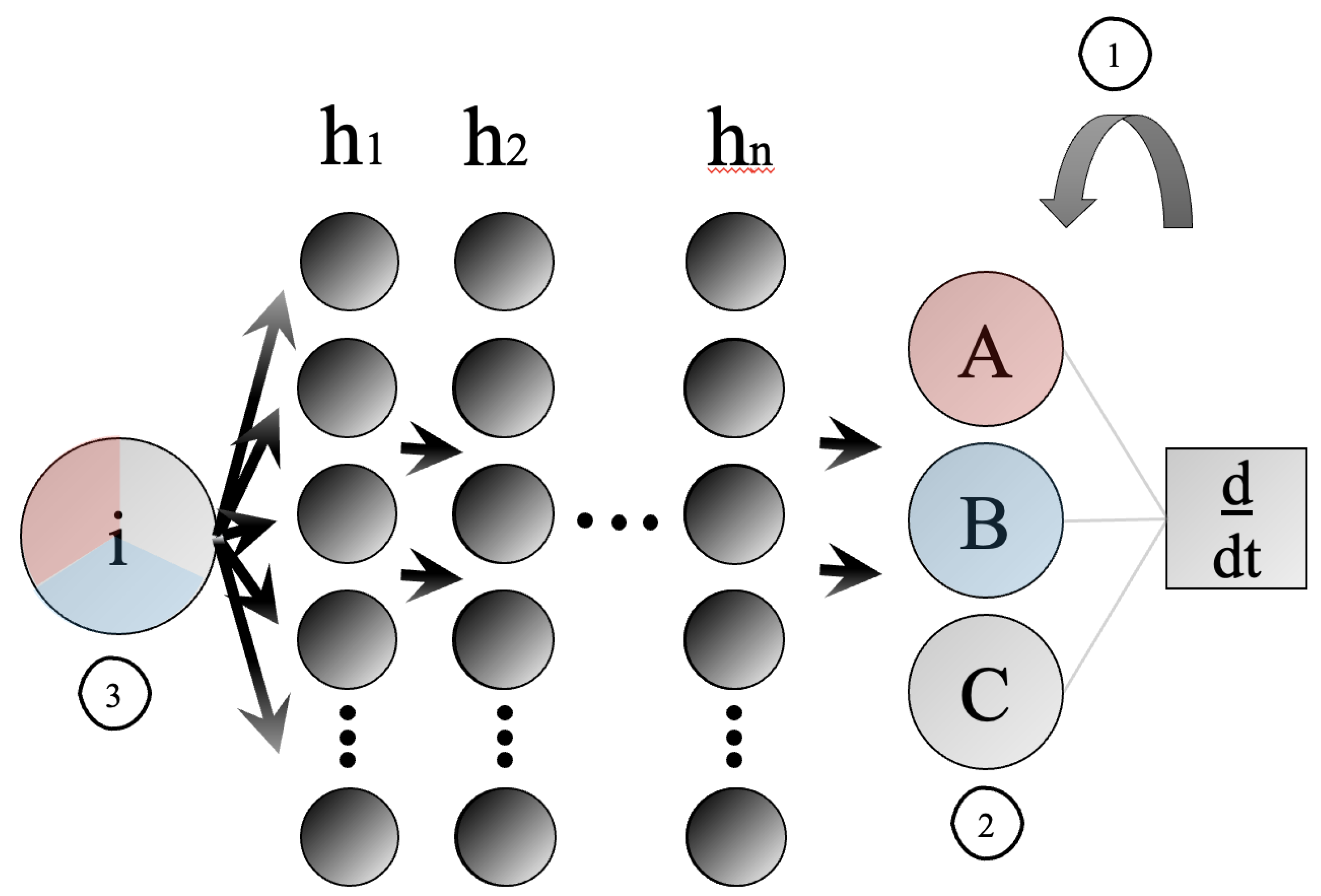
Figure 2.
Flow chart of the physics-informed machine learning pipeline, as a parallel to traditional multiphysics modeling.
Figure 2.
Flow chart of the physics-informed machine learning pipeline, as a parallel to traditional multiphysics modeling.
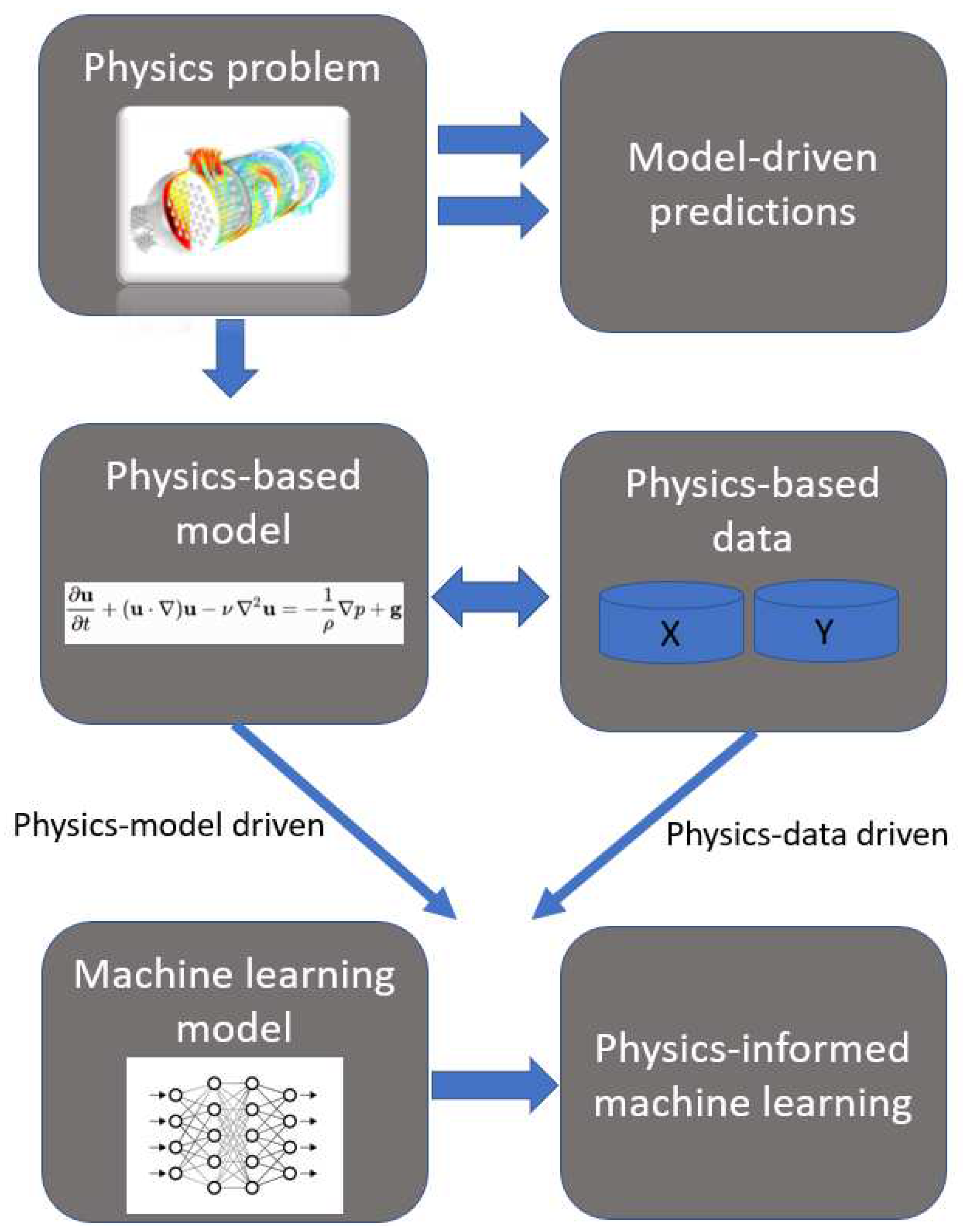
Figure 3.
Example schematics of observational, inductive, learning biases. These categories can be interpreted with broad applicability and have only been represented by singular examples.
Figure 3.
Example schematics of observational, inductive, learning biases. These categories can be interpreted with broad applicability and have only been represented by singular examples.
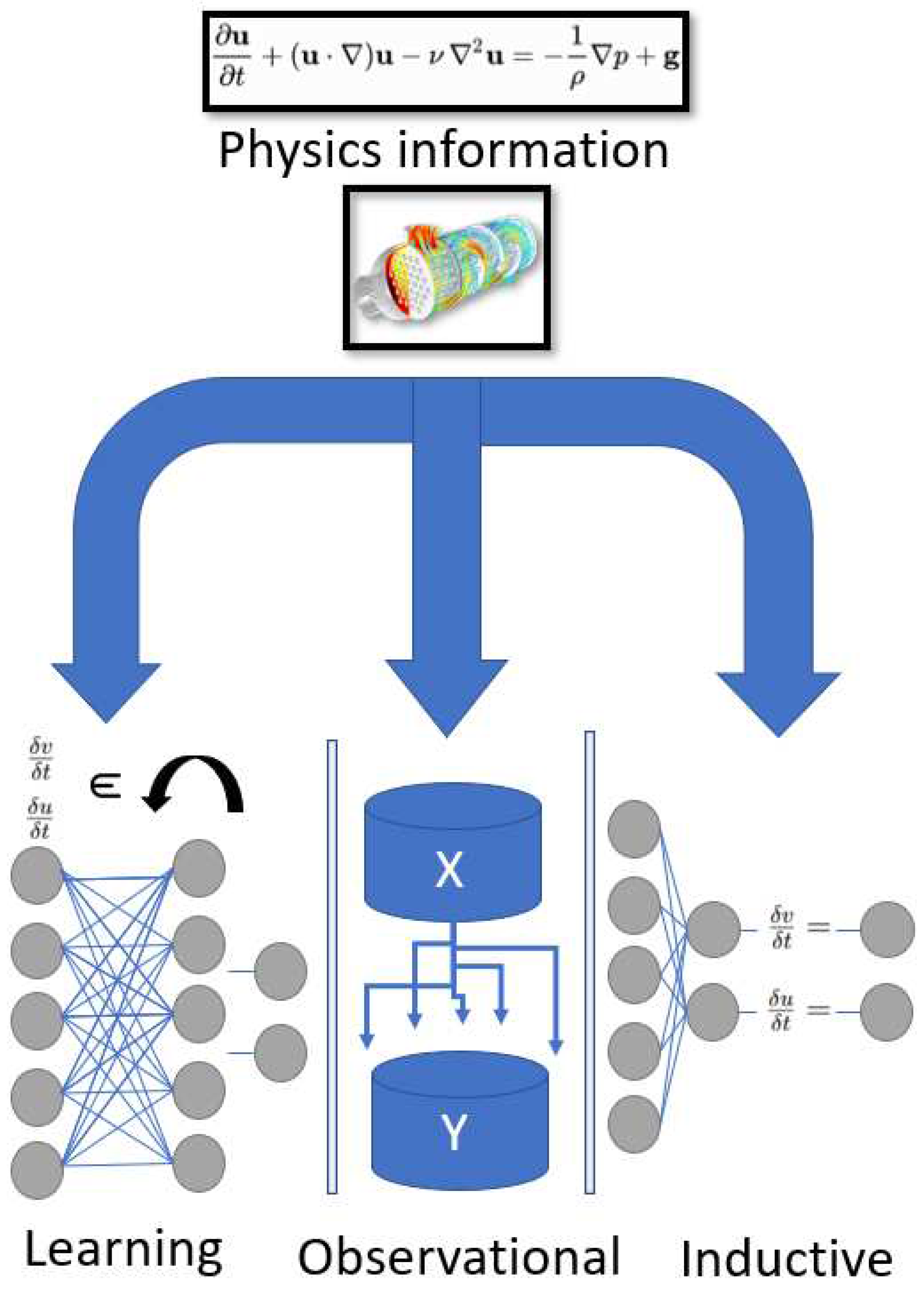
Table 1.
Taxonomic survey of recent applications of physics-informed machine learning
| Physics-model driven | Physics-data driven | Observ. bias | Inductive bias | Learning bias | |
|---|---|---|---|---|---|
| [4] | X | X | X | ||
| [5] | X | X | X | ||
| [6] | X | X | |||
| [7] | X | X | X | ||
| [8] | X | X | |||
| [10] | X | X | X | ||
| [16] | X | X | X | X | |
| [17] | X | X | X | X | |
| [20] | X | X | X | ||
| [18] | X | X | X | ||
| [19] | X | X | |||
| [11] | X | X | |||
| [12] | X | X | X | X | X |
| [13] | X | X | X | X | X |
| [14] | X | X | X | X | X |
| [15] | X | X | X | ||
| [21] | X | X | X | ||
| [22] | X | X | X | X | X |
| [23] | X | X | X | X | X |
| [24] | X | X | X | X | X |
| [25] | X | X | X | X | X |
| [26] | X | X | X | X | X |
| [27] | X | X | X | X | X |
| [28] | X | X | X | X | X |
| [29] | X | X | X | X | |
| [30] | X | X | X | X | |
| [31] | X | X | X | X | |
| [32] | X | X | X | ||
| [33] | X | X | X | ||
| [34] | X | X | X | ||
| [35] | X | X | X | X | X |
| [36] | X | X | X | X | X |
| [37] | X | X | X | X | X |
| [38] | X | X | |||
| [39] | X | X | X | X | X |
| [40] | X | X | X | X | X |
| [41] | X | X | X | X | X |
| [42] | X | X | X | X | X |
| [43] | X | X | X | X | X |
| [44] | X | X | X | X | X |
| [45] | X | X | X | X | X |
| [38] | X | X | X | X | X |
| [46] | X | X | X | X | X |
| [47] | X | X | X | X | X |
| [48] | X | X | X | X | X |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






