Preprint
Article
Systematic Sampling of Large-Scale LiDAR Point Clouds for Semantic Segmentation in Forestry Robotics
Altmetrics
Downloads
196
Views
76
Comments
0
This version is not peer-reviewed
Submitted:
11 May 2023
Posted:
12 May 2023
You are already at the latest version
Alerts
Abstract
Recently, new semantic segmentation and object detection methods have been proposed for direct processing of three-dimensional (3D) LiDAR sensor point clouds. LiDAR can produce
highly accurate and detailed 3D maps of natural and man-made environments and is used for sensing
in many contexts due to its ability to capture more information and its robustness to dynamic changes
in the environment. In addition, the cost of LiDAR sensors has decreased in recent years, which is
an important factor for many application scenarios. The challenge with 3D LiDAR sensors like the
Velodyne HDL-64E S2 is that they can output large 3D data at up to 1,300,000 points per second,
which is difficult to process in real time when applying complex algorithms and models for efficient
semantic segmentation. Most existing approaches are either only suitable for relatively small point
clouds or rely on computationally intensive sampling techniques to reduce their size. As a result,
most of these methods do not work in real-time in realistic field robotics application scenarios, making
them unsuitable for practical applications. Systematic point selection is a possible solution to reduce
the amount of data to be processed, but although it is memory and computationally efficient, it selects
only a small subset of points, which may result in important features being missed. To address this problem, we propose a new approach to semantic segmentation in forestry that uses a systematic sampling method in which the local neighbors of each point are retained to preserve geometric details. Our approach has been shown to process up to 1 million points in a single pass. It outperforms the state of the art in efficient semantic segmentation in large datasets such as Semantic3D. We also present a preliminary study on the performance of LiDAR-only data, i.e., intensity values from LiDAR sensors without RGB values for semi-autonomous robot perception.
Keywords:
Subject: Engineering - Electrical and Electronic Engineering
1. Introduction
Wildfires have recently caused major natural disasters in countries such as the United States and in Mediterranean countries such as Portugal, Spain, Italy, and Greece [1]. Over the past 25 years, there have been about 65,000 fires per year in Europe and about 18,000 fires per year in Portugal alone, with more than 100 victims since 2017 [2,3]. One of the measures to prevent wildfires is to encourage landscaping by actively reducing the accumulation of combustible material and identifying which plants and forest debris catch fire more easily than others. However, these and other adopted measures have not yet solved the problem, as they lead to huge investments and focus heavily on the required human resources, for which it is difficult to find employees willing to work in landscaping due to the harsh and dangerous conditions.
Semi-autonomous robots have become a promising solution in forestry providing significant cost savings in the maintenance of forests [2,4,5]. They also can be particularly useful in performing tasks that are difficult to find humans willing to do or that are dangerous for humans, such as tasks that pose a high risk of accidents and tasks that can lead to injuries, including back injuries, cuts, numbness, lacerations, and falls, without fully replacing humans. However, a semi-autonomous robot needs a perception system that allows it to navigate the forest, and for example perform landscaping for fire prevention with the intention of actively reducing the accumulation of combustible material. An important module of a perception system is efficient semantic segmentation, as it enables the identification of objects of interest in the robot’s environment.
As average selling prices for LiDARs have declined and they are less affected by adverse weather conditions, they are increasingly being used for robotic perception, and they can capture more information than an RGB camera therefore they are increasingly being used for robot perception. A semi-autonomous vehicle with a 3D LiDAR sensor can detect whether the region is traversable or not to gain a better understanding of the real environment. Therefore, this work aims to address two problems: a) developing state-of-the-art semantic segmentation techniques to support forest monitoring by semi-autonomous robot navigation as an application of deep learning techniques for semantic segmentation to semi-automatically manage forest fuels in areas with complex terrain using data from a LiDAR sensor and b) investigating the performance of LiDAR-only data, i.e., intensity values from LiDAR sensors without RGB values for semi-autonomous robot perception. It can also be used in other applications of field robots, such as in agriculture and relay information to a human controller. In addition, efficient semantic segmentation can be used to enable intelligent real-time systems such as augmented reality.
Deep convolutional networks have recently become state of the art in 2D structured computer vision tasks such as classification, object detection, and semantic segmentation. However, it is challenging to use them directly for classification and semantic segmentation of unstructured point clouds [6]. Raw point cloud data are typically unstructured, they are not arranged in a regular grid (Unlike 2D images (Figure 1) where for every pixel there is a neighboring pixel on all four sides), the density is variable, i.e., objects closer to the sensor receive more points than those farther away, and they are unordered (i.e., permutation invariant), which can be challenging for deep convolutional networks.
Another challenge is almost all of existing 3D point clouds semantic segmentation algorithms can process only small scale 3D data (e.g., 4k points or 1×1 meter blocks) but can not scale to larger datasets (e.g., millions of points and up to 200×200 meters) [7]. Therefore, it is only logical to sample these 3D points and select a subset of them. However, selecting a small subset of 3D points from a larger 3D point cloud may not capture the geometric structure of the point clouds and may miss relevant information that 3D LiDAR sensors capture.
There is also a lack of training and testing datasets that meet two requirements for semantic segmentation using 3D LiDAR data in forests. First, they should be acquired from outdoor woodland environments. Second, they should be annotated per point. For example, the TartanAir dataset [8] meets one of the two requirements, namely: It is annotated per point, but very little outdoor woodland environments data, and the QuintaReiFMD dataset [9] has outdoor woodland areas, but no annotations. To our knowledge, there are no known research reports on the use of 3D LiDAR data points acquired from outdoor woodland environment and no publicly available labelled 3D LiDAR data for semantic segmentation tasks that meet both requirements. Furthermore, due to the complex and unstructured nature of outdoor woodland environments, labelling this data can be an arduous task and requires expertise.
2. Literature Review
Several strategies have been proposed in the literature to address the unique challenges presented by large 3D point clouds.
Figure 2 shows a taxonomy of the different approaches that exist in the literature to address this type of problem. We will be briefly reviewing these approaches in the following text, however an in-depth discussion can be found in the survey paper by Bello et al. [10].
2.1. Non-Deep Learning Based Approaches
Traditional machine learning algorithms, unlike deep learning methods that learn to select features on their own, require more human intervention to correctly learn selection of features. The basic idea in feature selection is to select those that maximise the discriminative power of each class. However, depending on the application, this can be difficult to achieve. For example, Aubry et al. [11] carefully define features from a point cloud using statistical properties of the points. However, it is not a trivial task to find optimal feature combinations that are specifically chosen to be invariant to certain transformations [12]. In the following list, we describe the two main approaches proposed in the literature for manual feature definition and selection for 3D data points and depth images as inputs to traditional machine learning algorithms:
- 3D Keypoint Detection: Lo and Siebert [13] use an improved version of the Scale Invariant Feature Transform (SIFT) algorithm [14], namely 2.5D SIFT, to detect keypoints in a depth image. They create a discrete scale space representation of the depth image using Gaussian smoothing and Difference Of Gaussian (DOG). The signal maxima and minima are detected within the DOG scale space. Key points are then validated and located by comparing the ratio of principal curvatures to a predefined threshold. The 2.5D SIFT achieved better fitting performance than the 2D SIFT [15]. Knopp et al. [16] first voxelize a mesh into a 3D voxel image. They then compute the second-order derivatives at each voxel using box filters with increasing standard deviation and define a saliency measure for each voxel and a scale based on the Hessian matrix. Local extrema are then determined and used to identify 3D SURF keypoints and their corresponding scales. Our own analysis has shown that both SIFT and SURF [17] for 3D data points have a computational complexity of for 3D data points, which is not suitable for point cloud preprocessing. After keypoint detection, geometric information of the local surface around the keypoint can be extracted and encoded in a feature descriptor, which is another additional computational step;
- Novel statistical feature definition [18]: This approach is based on manual feature definition from 2D images. Features are defined by calculating the mean, median, standard deviation, coefficient of variance, skewness, covariance, kurtosis, correlation, and entropy of neighbouring 3D points. These calculations result in a set of feature vectors for a 3D point cloud. This set of features is then input to a feature optimization step before being passed to a machine learning model. Like the other manual feature definition approaches, this one is computationally intensive and dependent on human supervision.
The best known algorithms for non-deep learning are Gradient Boosted Random Forest [19,20], Support Vector Machines [21] and K-nearest Neighbours [22]. In addition to manual feature definition, a post-processing step such as clustering [23] is required to improve the classification results of traditional machine learning methods, which also increases the computational cost.
2.2. Deep Learning Based Approaches
Traditional machine learning algorithms are not well suited for large amounts of data because they perform simple, mostly linear inference. In particular, for 3D point clouds, it can be difficult to learn complex features [24]. deep convolutional networks have recently been shown to be effective when applied to structured 2D computer vision data. Therefore, researchers have turned to deep learning to process 3D point data [25]. The research can be mainly divided into two categories: those that require the 3D data points to be converted into a more compact intermediate representation before being input into a deep learning model, and the others where the raw 3D points are directly input into a deep learning model.
2.2.1. 3D Data Into An Intermediate Representation
One of the two categories of approaches to input 3D point data into a deep learning model is to convert the 3D data points into a more compact intermediate representation before inputting them into a deep learning model. Some of the proposed approaches are described in this section.
3D Data As 2D Images or Voxels
This method proposes the projection of 3D data points onto 2D images or 3D voxels to avoid irregularities in the 3D data. Moreover, processing 3D data points as images is computationally efficient because much research is being done on 2D data in the field of computer vision and deep learning using convolutional neural networks. Although this method has produced impressive results over the years, it makes the data unnecessarily voluminous, and much of the useful information contained in the 3D data points is lost. In addition, converting 3D data points into 2D images, as described by Li et al. [26], and into 3D voxels, as described by Graham et al. [27] leads to poor results because the 3D data are too sparse. Furthermore, these approaches are computationally intensive and may not be well suited for real-time systems [6].
3D Data As 2D images From Multiple Views
The Multiview Convolutional Neural Networks (MVCNN) method developed by Qi et al. [28] is reported to provide better performance for object detection task than the methods that represent 3D data as voxels or images. The idea is to represent a 3D data object as images obtained from multiple viewpoints. The authors use 12 viewpoints on an object and train convolutional neural networks (CNNs) on the data as images. Each of the 12 viewpoints is used as input to an independent CNN, and the outputs of these 12 CNNs are then used as input to another CNN for segmentation. It’s nontrivial to extend this method to 3D tasks such as point classification and shape completion.
3D Data As Grids
Ben-Shabat et al. [29], who proposed 3DmFV (three-dimensional points as Fisher vectors), have found that converting 3D data to a grid does not have to work directly with raw 3D data as input to a deep learning model. Nor does the data need to be projected onto 2D images. Also, this method has the advantage of being reversible to restore the original raw 3D data points, unlike the method of rasterizing 3D data onto images. 3DmFV transforms 3D data to a grid using Fisher vectors and can revert from grid to 3D data points. This method performs similarly to the methods that use projection 3D data to 2D images or voxels. However, it cannot work in real time.
3D Data To Hough Space
Other researchers working on classification of 3D objects from point clouds, such as Song et al. [12], propose transforming LiDAR data points into the Hough Space. First, they project the 3D data onto the x-z plane. Second, they map the x-z plane onto the Hough space. Finally, they use the accumulator count of the individual curves in Hough space as input to a deep learning model. However, this method cannot distinguish between trees and walls because these objects produce similar outcomes in Hough space.
2.2.2. Raw 3D Data as Input
Recent research suggests that it is possible to use 3D data points directly as input to a deep neural network. The problem of data irregularity has been studied and solved by modelling a symmetric function and designing a transformer network. The authors of PointNet [6] paper, which is a pioneer work in the field of using raw 3D data points as input to artificial neural networks (ANNs), have developed a promising approach that directly processes raw 3D point clouds. The authors propose using a function that models a symmetric function using shared multilayer perceptrons (MLPs). A symmetric function is used to account for the permutation invariance of 3D points, and a spatial transformer network is used to correct for affine transformations that may occur in 3D data points. The PointNet approach, while computationally efficient, does not capture the geometric context for each point because the symmetric function only captures the maximum features and discards the fine local features [7,30]. In Pointnet++ [30], which is an extension of Pointnet, each local region is passed independently to a symmetric function. Both Pointnet and Pointnet++ suffer from the problem that they can only be trained and work on small-scale point clouds.
To overcome the challenge that the geometric context is not captured for each point, many subsequent ANNs have been introduced [30,31,32,33,34]. All of them achieve promising results in semantic segmentation, but they are limited to small 3D point clouds (e.g. processing times range from 10 to 200 seconds for these ANNs to process points on an NVIDIA RTX2080Ti) and cannot be easily scaled to larger point clouds [7] which makes them not feasible for an UAV or semi-autonomous robot applications. The main reason for this is that almost all of them use computationally intensive or memory inefficient sampling techniques to select points and add them to the subset of points used as input to the deep ANNs. The following are some of the methods proposed in the literature for sampling 3D data points:
- Farthest Point Sampling (FPS): To select a subset of K points from the N original points, the algorithm returns a reordering of points , such that each is the farthest point from the points already selected. FPS has been widely used in the literature, including Pointnet++ [30] and Pointcnn [25] for semantic segmentation tasks. Despite the good coverage of an entire point cloud and the good representation of the data, the computational complexity is . RandLA-Net authors report for a large point cloud (), this sampling algorithm takes up to 200 seconds to process on a single NVIDIA RTX2080Ti GPU. Therefore, it cannot be used for sampling large point clouds in real-time;
- Policy Gradient based Sampling: To select a subset it formulates the sampling operation as a Markov decision process. It sequentially learns a probability distribution to sample the points. The RandLA-Net authors report that for a sample of 10% of points, the exploration space is , which is difficult for a neural network to converge to;
- Inverse Importance Sampling: to select a subset of K points from all N points, the algorithm orders all N points by their distance to a given reference point. The distance of each point becomes its density. All points are reordered according to their density. Then the top K points are selected [35]. The computational complexity is on the order of . RandLA-Net authors found through experiments that this algorithm takes 10 seconds to process points. Compared to Farthest point Sampling and Policy Gradient based Sampling, this algorithm is computationally efficient. However, it is sensitive to outliers and also not suitable for use in a real-time system;
- Random Sampling: It randomly selects K points from N original points. The method runs in O(1), constant time, and is independent of the number of points, so it can be scaled to any number of points. Compared to other sampling algorithms in the literature, it is the most computationally efficient method. According to RandLA-Net, it takes only 0.004s to process points.
Landrieu et al. [36], who introduced large-scale point cloud semantic segmentation with superpoint graphs (SPG), propose a technique to deal with large scale raw 3D points using superpoints, similar to superpixels in 2D images, as inputs to a deep convolutional neural network. The creation of superpoints is very computationally intensive due to a pre-processing step that partitions the points by geometric positions [7]. Moreover, it can be difficult to detect a whiteboard on a white wall using superpoint partitioning [30].
The authors of RandLA-Net, who use randomly selection of raw 3D points to be able to run in real time, have found a solution to this problem that has been shown to work better than previous methods. The authors use a random selection of points and drop the unselected points before inputting them into a deep neural network. These methods have better accuracy than the best performing state-of-the-art methods for semantic segmentation of 3D data points, including rasterization of 3D data in image methods using only 3D point data as input.
In our work, we input raw 3D data into our deep learning network. As mentioned in the introduction (see Section 1), we use a systematic sampling of points that can scale and process even larger 3D data in real time for efficient semantic segmentation.
2.3. Dataset
As we saw in Section 1, there is a lack of 3D datasets of outdoor woodland environments annotated per point. Therefore, we will first use known datasets from the autonomous driving research community to test our proposed method and compare it to existing 3D deep learning algorithms. Furthermore, self-driving car datasets contain objects such as vegetation, trees, people, and roads that may also be present in outdoor woodland environments.
We plan to evaluate our proposed work against a large public dataset, Semantic3D [37], to be fair in comparison to RandLA-Net. The Semantic3D dataset consists of 15 point clouds for training and 15 for online testing. Each point cloud contains up to 100 million points covering up to 160×240×30 metres in real 3D space. The raw 3D points belong to 8 classes and contain 3D coordinates, RGB information and intensity. For simplicity, state-of-the-art method authors use only the 3D coordinates and colour information to train and test their networks. The Mean Intersection-over-Union (mIoU) and Overall Accuracy (OA) of all classes are used as standard metrics. Table 1 describes the classes of the Semantic3D dataset.
2.4. Comparative Evaluation of State of the Art Approaches
Some of the works in literature on 3D data are summarized in Table 2 which summarizes deep learning based strategies on the SemanticKitti dataset and Table 3 summarizes different deep learning based strategies on Modelnet40 dataset [38]. Table 4 presents a summary of different deep learning based solutions in the literature. It presents a comparative analysis of design features of deep learning based strategies.
3. Systematic Selection of 3D Points
As mentioned earlier, it is difficult to process larger 3D data points and make inference in real time. Therefore, we propose a 3D point selection approach to select a subset of points, which is a better method for point selection than the random point selection proposed in RandLA-Net and has the advantage of being able to scale to larger point clouds by saving training time and significantly reduce the number of parameters. We also ensure that the order of input of 3D data points does not affect the performance of the segmentation algorithm since the geometric features of the data points are preserved.
Our proposed sampling algorithm is based on the graph colouring algorithm [40] to perform point selection, since we want to ensure that we obtain a subset of points that are representative of the 3D points in the scene. This algorithm ensures that the points we get are part of the skeleton of every object in the scene, which Pointnet calls critical points. According to Pointnet, only part of the skeletons of objects is sufficient to detect objects in the scene, since the critical points are not affected by density variations in the point cloud. In addition, it has been shown that not all points are necessary for the correct detection of an object. Pointnet has shown that up to 40% of points can be omitted or occluded without affecting performance, and that up to 60% can be omitted without significantly reducing object detection performance. These results were obtained without considering the encoding of local geometric features as we propose in our approach.
A graph is a nonlinear data structure with at least one node. In a graph, there may be nodes that are connected to each other; this connection is called an edge. A node is sometimes called a vertex. Formally, a graph consists of a set of vertices and edges. A graph is denoted as G(E,V). Two nodes are considered adjacent if they have an edge between them. The adjacent nodes are also called neighbours. The number of edges a node has is called the degree. A tree is a special type of graph that has no cyclic connections between nodes. A k-dimensional tree or kd-tree [41] is a binary tree of points with more than one dimension. Since 3D LiDAR points are three-dimensional data, a kd-tree is a very effective way to construct the 3D data point graph using the nearest neighbour algorithm.
The process of constructing a kd-tree on three-dimensional data has a complexity of , as can be seen in Figure 3, where N is the number of nodes. After creating a graph, we use K-nearest neighbours to find nearest neighbours for each point (to save calculations, we use the square distance instead of the square root to find the Euclidean distance). RandLa-Net randomly selects points for each point cloud therefore we choose varying number of neighbours (i.e. from k = 14 to k = 81 depending on the total number of points in the point cloud) for each point cloud to sample ≈ 100k points. The systematically sampled points are then used as inputs to a shared MLP. Our algorithm ensures that the selected points are not adjacent, which can be essentially compared to the FPS algorithm, with the difference that our method is faster. To take advantage of the ensemble learning method proposed by Yang et al. [42], we pass a different subset of nodes for each epoch. This leverages a new technique called auto-ensemble, where ensemble learning is created as a collection of different learning models in one, rather than tuning different hyperparameters individually during training and validation.
4. Local and Global Information Aggregation
In addition to systematically selecting points, we preserve local geometric structures using Local Spatial Encoding (LocSE) and attentive pooling to automatically preserve useful local features. We also stack multiple LocSE units and attentive pooling into an extended residual block, significantly increasing the effective receptive field for each point. Each point sampled in the systematic selection of points is considered as a reference point. We refer to each reference point as point and each of its neighbours as . In our work, the step of finding the nearest neighbours does not take any additional computation time since the nearest neighbours are already computed during the systematic sampling, unlike RandLA-Net which performs the computations in this step.
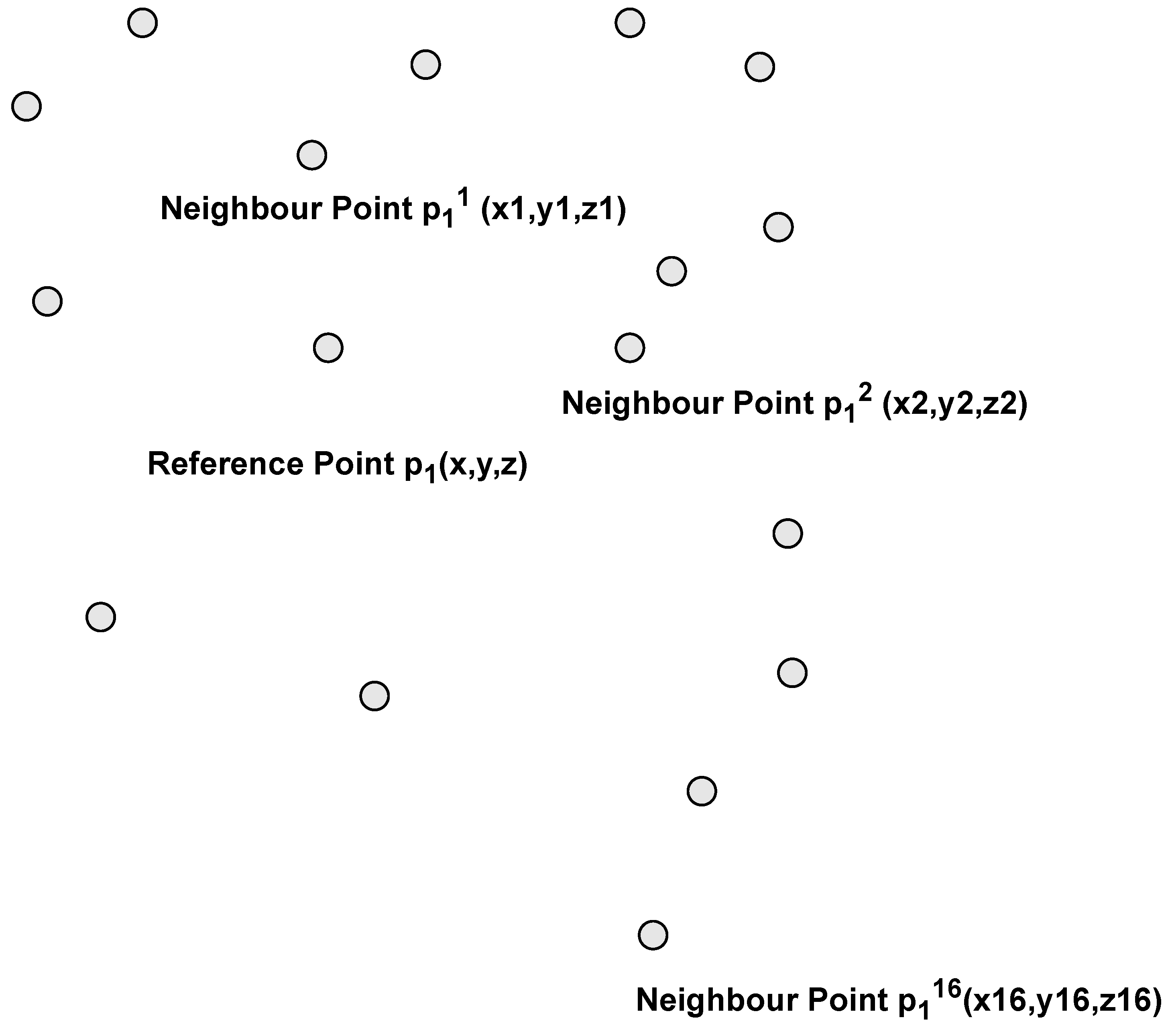
In order for the deep neural network to learn the relative position of each point and its geometric features, we need to preserve the sampled points and their considered neighbours because during the selection of a subset of points, many points are discarded. To get relative positions, the x, y, and z positions of the 16 neighbours are concatenated as features in the feature map along with the x, y, and z positions of the reference point. After we performed a heuristic hyperparameter search we found 16 neighbours is the number of neighbours that provide best results. In addition, the Euclidean and Manhattan distances of the selected point relative to each of the reference point’s nearest neighbours are encoded into the feature to complete the feature map.
Figure 4.
A reference point with its nearest neighbours. The neighbours’ x,y,z respective position are encoded as shown in the Equation (1).
Figure 4.
A reference point with its nearest neighbours. The neighbours’ x,y,z respective position are encoded as shown in the Equation (1).
Relative point position encoding:
where ⊕ is the concatenation operation, is the Euclidean distance, is the difference between centre and neighbouring point k, is the selected point, is each of the k = 16 neighbours. MLP() = input for MultiLayer Percepton and is the encoding of the relative point position. This encoding is concatenated with the other features such as the RGB colours of each point and its intensity value as shown in Figure 5.
The following equation introduces the concatenation process,
where are the RGB values and intensity value for each point and is the point feature augmentation.
is the attention score from the softmax outputs of a shared MLP given by
where g is the function estimated from a shared MLP with input features , and w are the learned weights after training the shared MLP.
Instead of selecting only the maximum features and ignoring the rest, we give each feature a weight according to its importance by concatenating the attention scores of each feature with its corresponding feature (see Figure 5).
5. Deep Learning Architecture
Instead of max-pooling to approximate the underlying symmetric function in the data, we use attentive pooling Inspired by Engelmann et al. [43]. The reason for this is that max-pooling tends to drop features that did not respond the most. Therefore, it is difficult to integrate the neighbouring features, which results in losing much of the information. Since we only use a subset of points, we need all the neighbouring information we collect. This technique is inspired by the work of Yang et al. [44]. Attentive pooling uses an attention mechanism to automatically learn important local features.
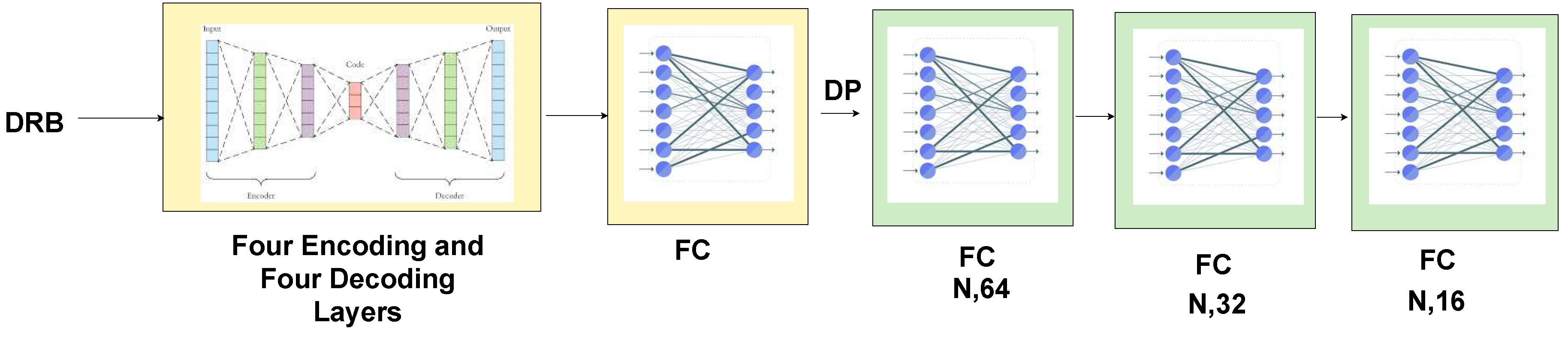
We need to encode the geometric information of many more neighbours as we select only a subset of points from an entire scene. The Dilated Residual Block is a repeat of the Local Feature Aggregation module and an attentive pooling (see Figure 6). The subsequent Local Feature Aggregation module receives input from the output of the previous attentive pooling. Therefore, the number of neighbours collected as features after repetition increases from n neighbours to neighbours.
There are four encoding layers and four decoding layers. Selected subsets of points and the Dilated Residual Block are input to each encoding layer. In the encoding layers, the filter size (feature map) is gradually increased from 8 to 32 to 128 to 256 to 512, and the number of points is downsampled using strided convolution from N to N/4 to N/16 to N/256. The four decoding layers are the mirror image of the encoding layers. The number of points is gradually up-sampled from N/256 to N/16 to N/8 and back to N to perform semantic segmentation. The output of the last decoding layers is connected to a fully-conneted layer, which is connected to three other fully-connected layers that precede each other to predict the class for each point. This combination of decoder/encoder and four fully-connected layers produced the best performance in the Semantic3D dataset after an extensive search for hyperparameters.
Figure 7.
Encoder and decoder for downsampling and upsampling the features of the input points for the semantic segmentation task. (N, D) stands for the number of points and the feature dimension, respectively. FC stands for Fully Connected Layer. DP stands for Dropout Layer. DRB stands for Dilated Residual Block. N is the number of 3D points. Green boxes represent proprietary work and yellow boxes represent work adapted from RandLA-Net.
Figure 7.
Encoder and decoder for downsampling and upsampling the features of the input points for the semantic segmentation task. (N, D) stands for the number of points and the feature dimension, respectively. FC stands for Fully Connected Layer. DP stands for Dropout Layer. DRB stands for Dilated Residual Block. N is the number of 3D points. Green boxes represent proprietary work and yellow boxes represent work adapted from RandLA-Net.
6. Experimental Evaluations
In Table 5 we summarize the evaluation of the computational complexity of our network on real, large-scale 3D point clouds for semantic segmentation. Specifically, we evaluate our network on the SemanticKITTI dataset [45] taking as a reference the complexity reported by RandLA-Net for a fair comparison. The SemanticKITTI dataset includes 43,552 scans divided into 21 sequences. Each scan has about 100,000 points distributed over a volume of 160 by 160 by 20 metres. The sequences are divided into a training set with sequences 00 to 07, 09 and 10 (19,130 scans), a validation set with sequence 08 (4,071 scans) and sequences 11 to 21 for testing (20,351 scans). The dataset includes 19 classes, including cars, road signs, vegetation, people, terrain, cyclists, roads, sidewalks, etc. Our algorithm has higher computational complexity than Inverse Density Importance Sampling and Random Selection. However, Inverse Density Importance Sampling is sensitive to outliers and Random Selection is not a systematic approach to point selection. Our algorithm is not sensitive to outliers, has reasonable complexity, and works like Random Selection in real time.
We used a GeForce RTX 3090 Nvidia GPU with 24 GB of memory for both training and testing the Semantic3D dataset. We conducted four experiments. In the first experiment we use the 3D coordinates and the color information of each point were used to train and test our network as did other researchers. The Mean Intersection-over-Union (mIoU) and Overall Accuracy (OA) of all classes were used as standard metrics.
In Table 6, we summarize the results of mIOU of our network on real, large-scale 3D point clouds for semantic segmentation. Specifically, we evaluate our network on the Semantic3D dataset [37] against the mIOU reported by RandLA-Net for a fair comparison. It can be seen that our network outperforms the RandLA-Net, which represents the state of the art in all eight classes. Further improvements are needed for the low vegetation class. Like the RandLA-Net, our network performs poorly because of the limited data available for training this class.
For the second experiment, only the 3D coordinates of each point were used to train and test our network, since most 3D datasets do not contain color information. The Mean Intersection-over-Union (mIoU) and Overall Accuracy (OA) of all classes were used again as standard metrics.
In Table 7, we summarize the results of mIOU. The mIOU decreased by about ten percentage points to 62.25, as did the accuracies of each individual class.
For the third experiment, the 3D coordinates of each point and the intensity values were used to train and test our network as LiDAR-only data. The Mean Intersection-over-Union (mIoU) and Overall Accuracy (OA) of all classes were used once again as standard metrics.
In Table 8, we summarise the results of mIOU. The mIOU decreased only about three percentage points to 68.15 compared to 72.23 for 3D coordinates with colour information. This shows that intensity values can perform almost as well as 3D coordinates with colour information even without colour information.
For the fourth experiment, we used input fusion with 3D coordinates, colour information, and intensity values to train and test our network. Mean Intersection-over-Union (mIoU) and Overall Accuracy (OA) of all classes were used here as well as standard metrics.
In Table 9, we summarise the results of mIOU. The mIOU is lower than that of 3D coordinates with colour information and that of 3D coordinates with intensity values. Notably, our network also achieves superior performance on six of the eight classes, except Man-made and Natural classes.
Table 10 summarises the benchmarking of our network with the state-of-the-art RandLA-Net on Semantic3D (reduced-8) data with RBG features as baseline with the four experiments we performed. Our first experiment provides the best mIOU, the best overall accuracy, the best accuracy of Man-made class, Natural class, High Vegetation class, Low Vegetation class, Scanning Artefacts class, and Cars class. The second experiment provides the best accuracy for Hard Scape class. The fourth experiment provides the best accuracy for Buildings class. It can also be observed that our network without RGB or intensity performs better than our first experiment for objects with classes with blocks such as Buildings and Hard Scape.
Figure 8 and Figure 9 enable a qualitative evaluation of the performance of our network on the test set of the Semantic3D dataset of the first experiment. In general, our network seems to produce good quality results, but can mistake things like hills as buildings. This could be due to the RGB channel features in the Semantic3D dataset that make hills look like old buildings. In some rare cases, our network may also mistake bushes for grass.
7. Conclusions and Future Work
In this paper, we have shown that systematic sampling of 3D data points outperfoms a simple random selection of points and has the advantage that large point clouds can be used as input and processed in real time. It strongly supports the key tasks of navigation, situational perception such as identification of flammable materials, coordination of robotic teams and decision-making by providing fine information of local environment. It also provides, efficient semantic segmentation that can be used to provide decision-making modules with task-oriented context to inform the actions that the robot should enact.
The baseline of state of the art for efficient semantic segmentation shows further improvements are needed for the low vegetation class. Like the RandLA-Net, our network performs poorly because of the limited data available for training this class. The mIOU for intensity only from the third experiment decreased only about four percentage points to 68 compared to 72 for 3D coordinates with colour information from the first experiment. This shows that points with x, y, a and intensity values without colour information (LiDAR-only data) can perform almost as well as 3D coordinates with colour information. In future work we will analyze the impact of the stacking ensemble technique on our two models, namely: the model trained on Semantic3D with RGB without intensity and the model trained on Semantic3D without RGB values but with intensity values.
Author Contributions
Conceptualization, H.M., P.P. and J.F.F; investigation, H.M; methodology, H.M.; validation, H.M.; writing - original draft, H.M.; supervision, P.P. and J.F.F.; writing - review & editing, P.P. and J.F.F. All authors have read and agreed to the published version of the manuscript.
Funding
Project co-financed by Programa Operacional Regional do Centro, Portugal 2020, European Union FEDER Fund, Project: CENTRO-01-0247-FEDER-045931.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Appendix A
We provide a video to show qualitative results of our work on Semantic3D dataset with x,y,z and RGB values, which can be viewed at https://youtu.be/VuBYh4MHdbc.
References
- San-Miguel-Ayanz, J.; Schulte, E.; Schmuck, G.; Camia, A.; Strobl, P.; Libertà, G.; Giovando, C.; Boca, R.; Sedano, F.; Kempeneers, P.; et al. Comprehensive Monitoring of Wildfires in Europe: The European Forest Fire Information System (EFFIS); 2012. [CrossRef]
- Couceiro, M.S.; Portugal, D.; Ferreira, J.F.; Rocha, R.P. SEMFIRE: Towards a new generation of forestry maintenance multi-robot systems. 2019 IEEE/SICE International Symposium on System Integration (SII). IEEE, 2019, pp. 270–276.
- Dennis, F.C. ; others. Fire-resistant landscaping, 1999. [Google Scholar]
- Ben Abdallah, F.; Bouali, A.; Meausoone, P.J. Autonomous Navigation of a Forestry Robot Equipped with a Scanning Laser. AgriEngineering 2022, 5, 1–11. [Google Scholar] [CrossRef]
- Idrissi, M.; Hussain, A.; Barua, B.; Osman, A.; Abozariba, R.; Aneiba, A.; Asyhari, T. Evaluating the Forest Ecosystem through a Semi-Autonomous Quadruped Robot and a Hexacopter UAV. Sensors 2022, 22, 5497. [Google Scholar] [CrossRef] [PubMed]
- Charles, R.; Su, H.; Kaichun, M.; Guibas, L.J. PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation. 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR); IEEE Computer Society: Los Alamitos, CA, USA, 2017; pp. 77–85. [Google Scholar] [CrossRef]
- Hu, Q.; Yang, B.; Xie, L.; Rosa, S.; Guo, Y.; Wang, Z.; Trigoni, N.; Markham, A. RandLA-Net: Efficient Semantic Segmentation of Large-Scale Point Clouds. 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2020, pp. 11105–11114. [CrossRef]
- Wang, W.; Zhu, D.; Wang, X.; Hu, Y.; Qiu, Y.; Wang, C.; Hu, Y.; Kapoor, A.; Scherer, S. TartanAir: A Dataset to Push the Limits of Visual SLAM. 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), 2020, pp. 4909–4916. [CrossRef]
- da Silva, D.Q.; dos Santos, F.N.; Sousa, A.J.; Filipe, V.; Boaventura-Cunha, J. Unimodal and Multimodal Perception for Forest Management: Review and Dataset. Computation 2021, 9, 127. [Google Scholar] [CrossRef]
- Bello, S.A.; Yu, S.; Wang, C.; Adam, J.M.; Li, J. Review: Deep Learning on 3D Point Clouds. Remote Sensing 2020, 12, 1729. [Google Scholar] [CrossRef]
- Aubry, M.; Schlickewei, U.; Cremers, D. The wave kernel signature: A quantum mechanical approach to shape analysis. 2011 IEEE International Conference on Computer Vision Workshops (ICCV Workshops); IEEE Computer Society: Los Alamitos, CA, USA, 2011; pp. 1626–1633. [Google Scholar] [CrossRef]
- Song, W.; Zhang, L.; Tian, Y.; Fong, S.; Liu, J.; Gozho, A. CNN-based 3D Object Classification Using Hough Space of LiDAR Point Clouds. Hum.-Centric Comput. Inf. Sci. 2020, 10, 1–14. [Google Scholar] [CrossRef]
- Lo, T.W.; Siebert, J. Local feature extraction and matching on range images: 2.5D SIFT. Comput. Vis. Image Underst. 2009, 113, 1235–1250. [Google Scholar] [CrossRef]
- Lowe, D. Distinctive Image Features from Scale-Invariant Keypoints. Int. J. Comput. Vis. 2004, 60, 91. [Google Scholar] [CrossRef]
- Guo, Y.; Bennamoun, M.; Sohel, F.; Lu, M.; Wan, J. 3D Object Recognition in Cluttered Scenes with Local Surface Features: A Survey. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 36, 2270–2287. [Google Scholar] [CrossRef]
- Knopp, J.; Prasad, M.; Willems, G.; Timofte, R.; Van Gool, L. Hough Transform and 3D SURF for Robust Three Dimensional Classification. 2010, Vol. 6316, pp. 589–602. [CrossRef]
- Bay, H.; Ess, A.; Tuytelaars, T.; Van Gool, L. Speeded-Up Robust Features (SURF). Comput. Vis. Image Underst. 2008, 110, 346–359. [Google Scholar] [CrossRef]
- Ghrabat, M.; Ma, G.; Maolood, I.; Alresheedi, S.; Abduljabbar, Z. An effective image retrieval based on optimized genetic algorithm utilized a novel SVM-based convolutional neural network classifier. Hum.-Centric Comput. Inf. Sci. 2019, 9. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Xu, Z.; Huang, G.; Weinberger, K.Q.; Zheng, A.X. Gradient Boosted Feature Selection. Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining; Association for Computing Machinery: New York, NY, USA, 2014. [Google Scholar] [CrossRef]
- Hearst, M.; Dumais, S.; Osuna, E.; Platt, J.; Scholkopf, B. Support vector machines. IEEE Intell. Syst. Their Appl. 1998, 13, 18–28. [Google Scholar] [CrossRef]
- Guo, G.; Wang, H.; Bell, D.; Bi, Y.; Greer, K. KNN Model-Based Approach in Classification. On The Move to Meaningful Internet Systems 2003: CoopIS, DOA, and ODBASE; Meersman, R., Tari, Z., Schmidt, D.C., Eds.; Springer Berlin Heidelberg: Berlin, Heidelberg, 2003; pp. 986–996. [Google Scholar] [CrossRef]
- Weinmann, M.; Weinmann, M.; Mallet, C.; Brédif, M. A Classification-Segmentation Framework for the Detection of Individual Trees in Dense MMS Point Cloud Data Acquired in Urban Areas. Remote Sens. 2017, 9, 277. [Google Scholar] [CrossRef]
- Liu, J.; Yang, Y.; Lv, S.; Wang, J.; Chen, H. Attention-based BiGRU-CNN for Chinese question classification. J. Ambient. Intell. Humaniz. Comput. 2019. [Google Scholar] [CrossRef]
- Li, Y.; Bu, R.; Sun, M.; Wu, W.; Di, X.; Chen, B. PointCNN: Convolution on X-Transformed Points. Proceedings of the 32nd International Conference on Neural Information Processing Systems; Curran Associates Inc.: Red Hook, NY, USA, 2018. [Google Scholar] [CrossRef]
- Li, B.; Zhang, T.; Xia, T. Vehicle Detection from 3D Lidar Using Fully Convolutional Network. Robotics: Science and Systems XII, University of Michigan, Ann Arbor, Michigan, USA, - June 22, 2016; Hsu, D.; Amato, N.M.; Berman, S.; Jacobs, S.A., Eds., 2016. 18 June. [CrossRef]
- Graham, B.; Engelcke, M.; Maaten, L.v.d. 3D Semantic Segmentation with Submanifold Sparse Convolutional Networks. 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2018, pp. 9224–9232. [CrossRef]
- Qi, C.R.; Su, H.; NieBner, M.; Dai, A.; Yan, M.; Guibas, L.J. Volumetric and Multi-view CNNs for Object Classification on 3D Data. 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR); IEEE Computer Society: Los Alamitos, CA, USA, 2016; pp. 5648–5656. [Google Scholar] [CrossRef]
- Ben-Shabat, Y.; Lindenbaum, M.; Fischer, A. 3DmFV: Three-Dimensional Point Cloud Classification in Real-Time Using Convolutional Neural Networks. IEEE Robot. Autom. Lett. 2018, 3, 3145–3152. [Google Scholar] [CrossRef]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. PointNet++: Deep Hierarchical Feature Learning on Point Sets in a Metric Space. Proceedings of the 31st International Conference on Neural Information Processing Systems; Curran Associates Inc.: Red Hook, NY, USA, 2017. [Google Scholar] [CrossRef]
- Li, J.; Chen, B.M.; Lee, G.H. SO-Net: Self-Organizing Network for Point Cloud Analysis. 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2018, pp. 9397–9406. [CrossRef]
- Huang, Q.; Wang, W.; Neumann, U. Recurrent Slice Networks for 3D Segmentation of Point Clouds. 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2018, pp. 2626–2635. [CrossRef]
- Zhang, Z.; Hua, B.; Yeung, S. ShellNet: Efficient Point Cloud Convolutional Neural Networks Using Concentric Shells Statistics. 2019 IEEE/CVF International Conference on Computer Vision (ICCV); IEEE Computer Society: Los Alamitos, CA, USA, 2019; pp. 1607–1616. [Google Scholar] [CrossRef]
- Zhao, H.; Jiang, L.; Fu, C.W.; Jia, J. PointWeb: Enhancing Local Neighborhood Features for Point Cloud Processing. 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2019, pp. 5560–5568. [CrossRef]
- Groh, F.; Wieschollek, P.; Lensch, H.P.A. Flex-Convolution (million-scale point-cloud learning beyond grid-worlds). Computer Vision - ACCV 2018; Jawahar, C.V., Li, H., Mori, G., Schindler, K., Eds.; Springer International Publishing: Cham, 2019; pp. 105–122. [Google Scholar] [CrossRef]
- Landrieu, L.; Simonovsky, M. Large-Scale Point Cloud Semantic Segmentation with Superpoint Graphs. 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2018, pp. 4558–4567. [CrossRef]
- Hackel, T.; Savinov, N.; Ladicky, L.; Wegner, J.; Schindler, K.; Pollefeys, M. Semantic3D.net: A new Large-scale Point Cloud Classification Benchmark. Isprs Ann. Photogramm. Remote Sens. Spat. Inf. Sci. [CrossRef]
- Wu, Z.; Song, S.; Khosla, A.; Yu, F.; Zhang, L.; Tang, X.; Xiao, J. 3D ShapeNets: A deep representation for volumetric shapes. 2015, pp. 1912–1920. [CrossRef]
- Milioto, A.; Vizzo, I.; Behley, J.; Stachniss, C. RangeNet ++: Fast and Accurate LiDAR Semantic Segmentation. 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), 2019, pp. 4213–4220. [CrossRef]
- Dutton, R.D.; Brigham, R.C. A new graph colouring algorithm. Comput. J. 1981, 24, 85–86. [Google Scholar] [CrossRef]
- Bentley, J. Multidimensional Binary Search Trees in Database Applications. IEEE Trans. Softw. Eng. -5. [CrossRef]
- Yang, J.; Wang, F. Auto-Ensemble: An Adaptive Learning Rate Scheduling Based Deep Learning Model Ensembling. IEEE Access 2020, 8, 217499–217509. [Google Scholar] [CrossRef]
- Engelmann, F.; Kontogianni, T.; Leibe, B. Dilated Point Convolutions: On the Receptive Field Size of Point Convolutions on 3D Point Clouds. 2020 IEEE International Conference on Robotics and Automation (ICRA), 2020, pp. 9463–9469. [CrossRef]
- Yang, B.; Wang, S.; Markham, A.; Trigoni, N. Robust Attentional Aggregation of Deep Feature Sets for Multi-view 3D Reconstruction. Int. J. Comput. Vis. 2019, 128, 53–73. [Google Scholar] [CrossRef]
- Behley, J.; Garbade, M.; Milioto, A.; Quenzel, J.; Behnke, S.; Gall, J.; Stachniss, C. Towards 3D LiDAR-based semantic scene understanding of 3D point cloud sequences: The SemanticKITTI Dataset. Int. J. Robot. Res. 2021, 40, 959–967. [Google Scholar] [CrossRef]
- Xu, K.; Ba, J.; Kiros, R.; Cho, K.; Courville, A.; Salakhudinov, R.; Zemel, R.; Bengio, Y. Show, attend and tell: Neural image caption generation with visual attention. International conference on machine learning. PMLR, 2015, pp. 2048–2057.
- Eldar, Y. Irregular image sampling using the voronoi diagram. PhD thesis, M. Sc. thesis.
- Eldar, Y.; Lindenbaum, M.; Porat, M.; Zeevi, Y.Y. The farthest point strategy for progressive image sampling. IEEE Trans. Image Process. 1997, 6, 1305–1315. [Google Scholar] [CrossRef]
- Kahn, H.; Marshall, A.W. Methods of reducing sample size in Monte Carlo computations. J. Oper. Res. Soc. Am. 1953, 1, 263–278. [Google Scholar] [CrossRef]
Figure 1.
Typical example of 3D LiDAR data (i.e. point cloud) corresponding to a woodland environment. As can be seen, the 3D points are unstructured, sparse, and it is difficult to identify objects.
Figure 1.
Typical example of 3D LiDAR data (i.e. point cloud) corresponding to a woodland environment. As can be seen, the 3D points are unstructured, sparse, and it is difficult to identify objects.

Figure 2.
Taxonomy of classification, semantic segmentation, and object detection research with 3D LiDAR Point Clouds. C stands for classification, SS for semantic segmentation, OD for object detection, DL for deep learning, NDL for non-deep learning, SVM for Support Vector Machines, RF for Random Forest, KNN for K-nearest Neighbours, and HS for Hough Space.
Figure 2.
Taxonomy of classification, semantic segmentation, and object detection research with 3D LiDAR Point Clouds. C stands for classification, SS for semantic segmentation, OD for object detection, DL for deep learning, NDL for non-deep learning, SVM for Support Vector Machines, RF for Random Forest, KNN for K-nearest Neighbours, and HS for Hough Space.
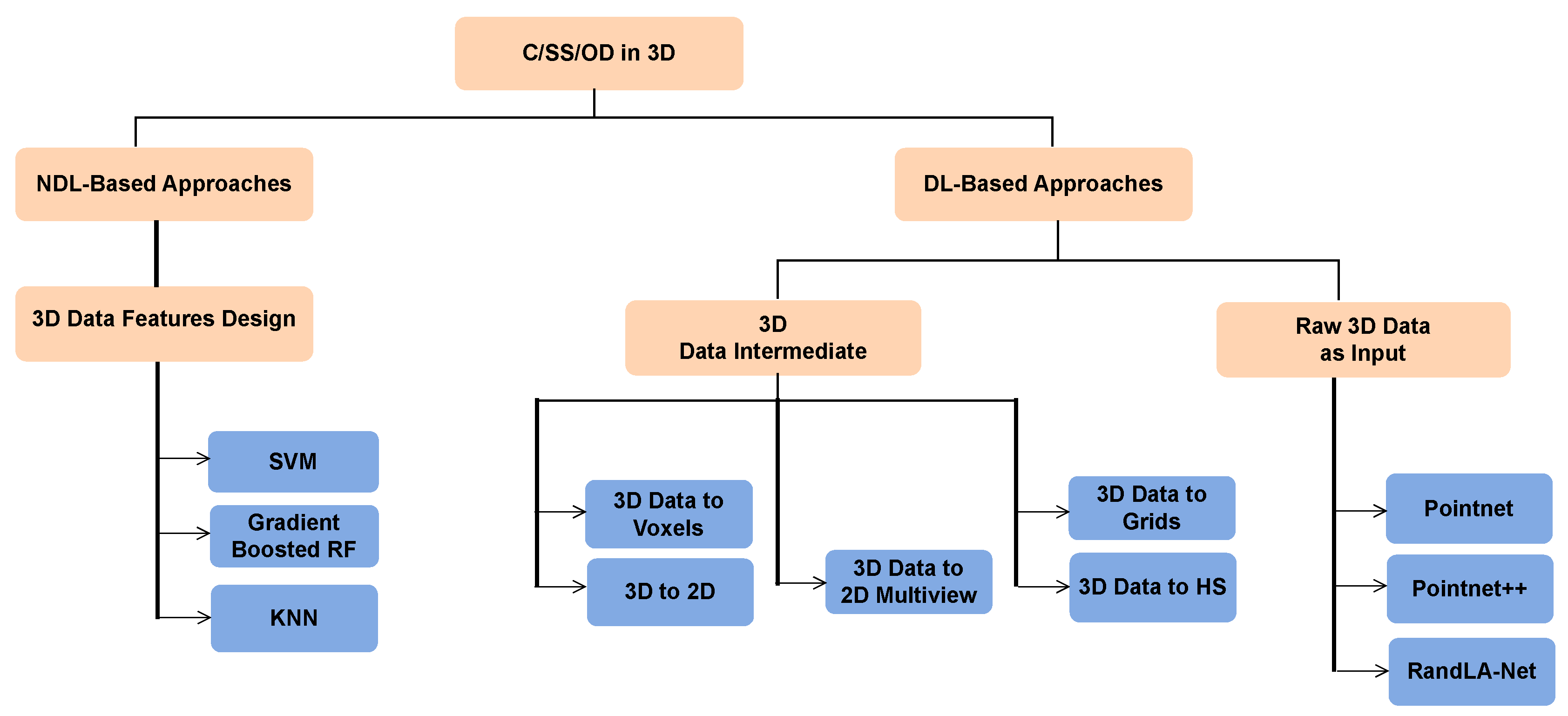
Figure 3.
kd-tree on 3-dimensional data. When inserting the 3D points, the first node becomes the root node at level 0 and the next node goes to the left if its x-coordinate is smaller than the x-coordinate of the root, and goes to the right if its x is larger than the x of the root. At level 1, a node’s y-coordinate is compared with the y-coordinates of the node at the level, if they are smaller we go to the left, if they are larger we go to the right. On level 2 the z coordinates are compared. On level 3 is the x coordinates that are compared as done on level 0. So the process repeats. Note that, this algorithm makes precedence of placing a node closer to its nearest neighbour over the process described above as it can be seen with node 9,4,0.
Figure 3.
kd-tree on 3-dimensional data. When inserting the 3D points, the first node becomes the root node at level 0 and the next node goes to the left if its x-coordinate is smaller than the x-coordinate of the root, and goes to the right if its x is larger than the x of the root. At level 1, a node’s y-coordinate is compared with the y-coordinates of the node at the level, if they are smaller we go to the left, if they are larger we go to the right. On level 2 the z coordinates are compared. On level 3 is the x coordinates that are compared as done on level 0. So the process repeats. Note that, this algorithm makes precedence of placing a node closer to its nearest neighbour over the process described above as it can be seen with node 9,4,0.
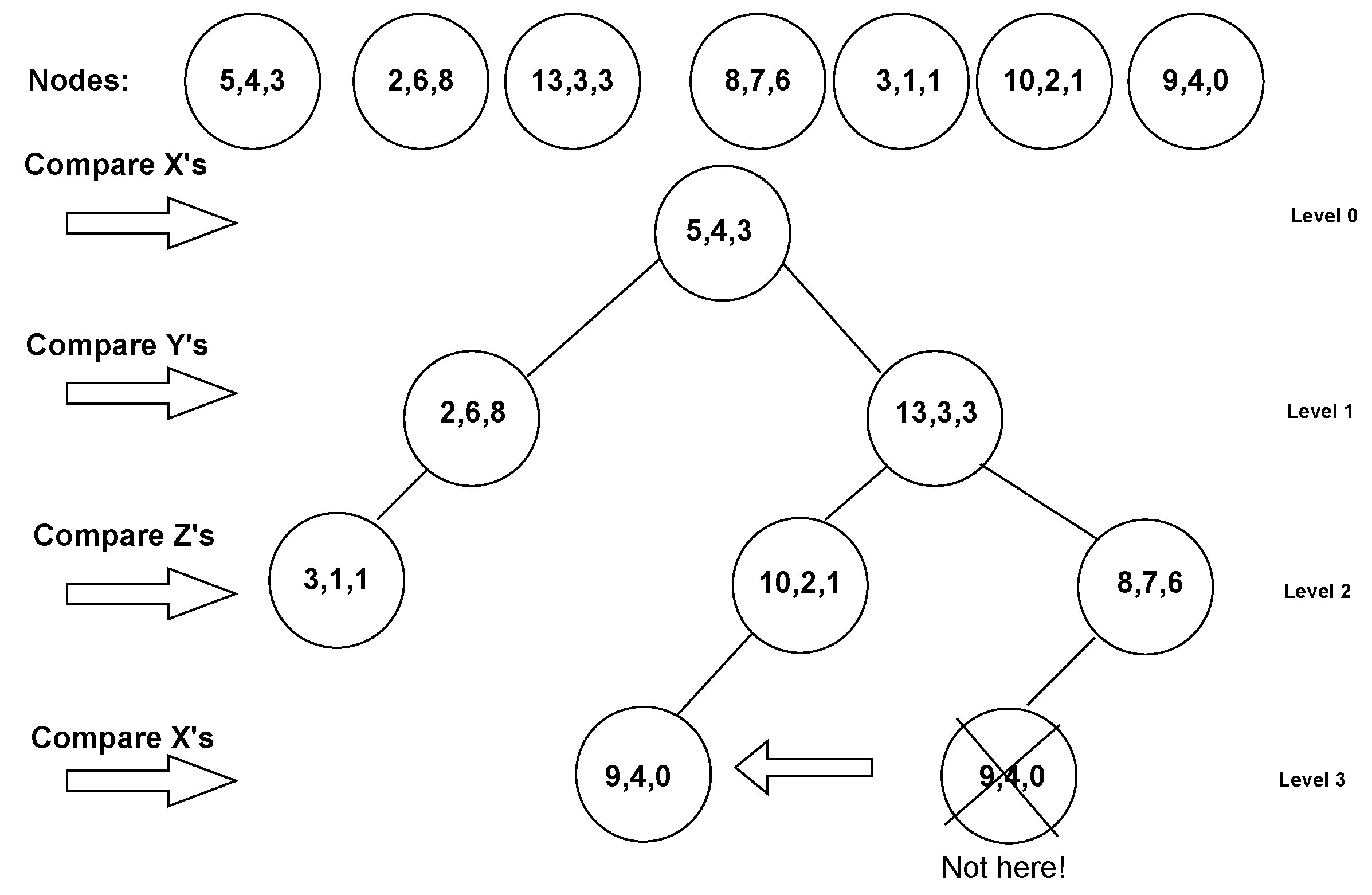
Figure 5.
Attentive pooling to produce attentive features instead of using maxpooling. ⊕ is the concatenation operation, ⊙ is the dot product operation and ⓢ is the Softmax layer.
Figure 5.
Attentive pooling to produce attentive features instead of using maxpooling. ⊕ is the concatenation operation, ⊙ is the dot product operation and ⓢ is the Softmax layer.

Figure 6.
Dilated Residual Block containing module for Local Feature Aggregation and attentive pooling repeated twice to increase geometric feature encoding. To avoid overfitting, we avoid repeating more than twice. Green boxes represent proprietary work, blue boxes represent work adapted from Yang et al., and yellow boxes represent work adapted from Engelmann et al.
Figure 6.
Dilated Residual Block containing module for Local Feature Aggregation and attentive pooling repeated twice to increase geometric feature encoding. To avoid overfitting, we avoid repeating more than twice. Green boxes represent proprietary work, blue boxes represent work adapted from Yang et al., and yellow boxes represent work adapted from Engelmann et al.
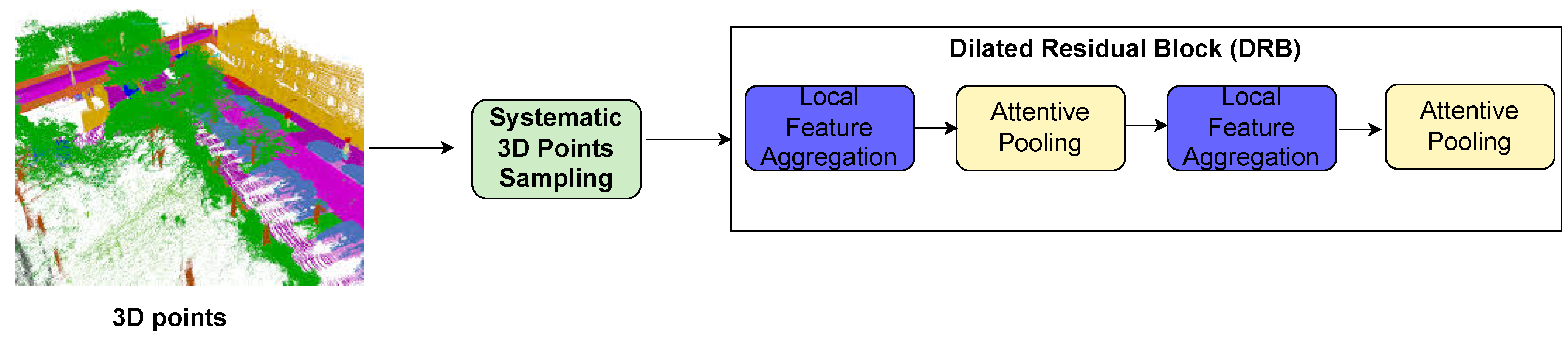
Figure 8.
Qualitative analysis of our network from one view in the scene showing bush, buildings, trees, grasses, hardscape, artefacts, and road.
Figure 8.
Qualitative analysis of our network from one view in the scene showing bush, buildings, trees, grasses, hardscape, artefacts, and road.

Figure 9.
Qualitative analysis of our network from another view in the scene showing bush, trees, grasses, artefacts, road, and a car. It can also being seen that a rock on a hill is being classified as a building, since the rock resembles some buildings in the dataset.
Figure 9.
Qualitative analysis of our network from another view in the scene showing bush, trees, grasses, artefacts, road, and a car. It can also being seen that a rock on a hill is being classified as a building, since the rock resembles some buildings in the dataset.

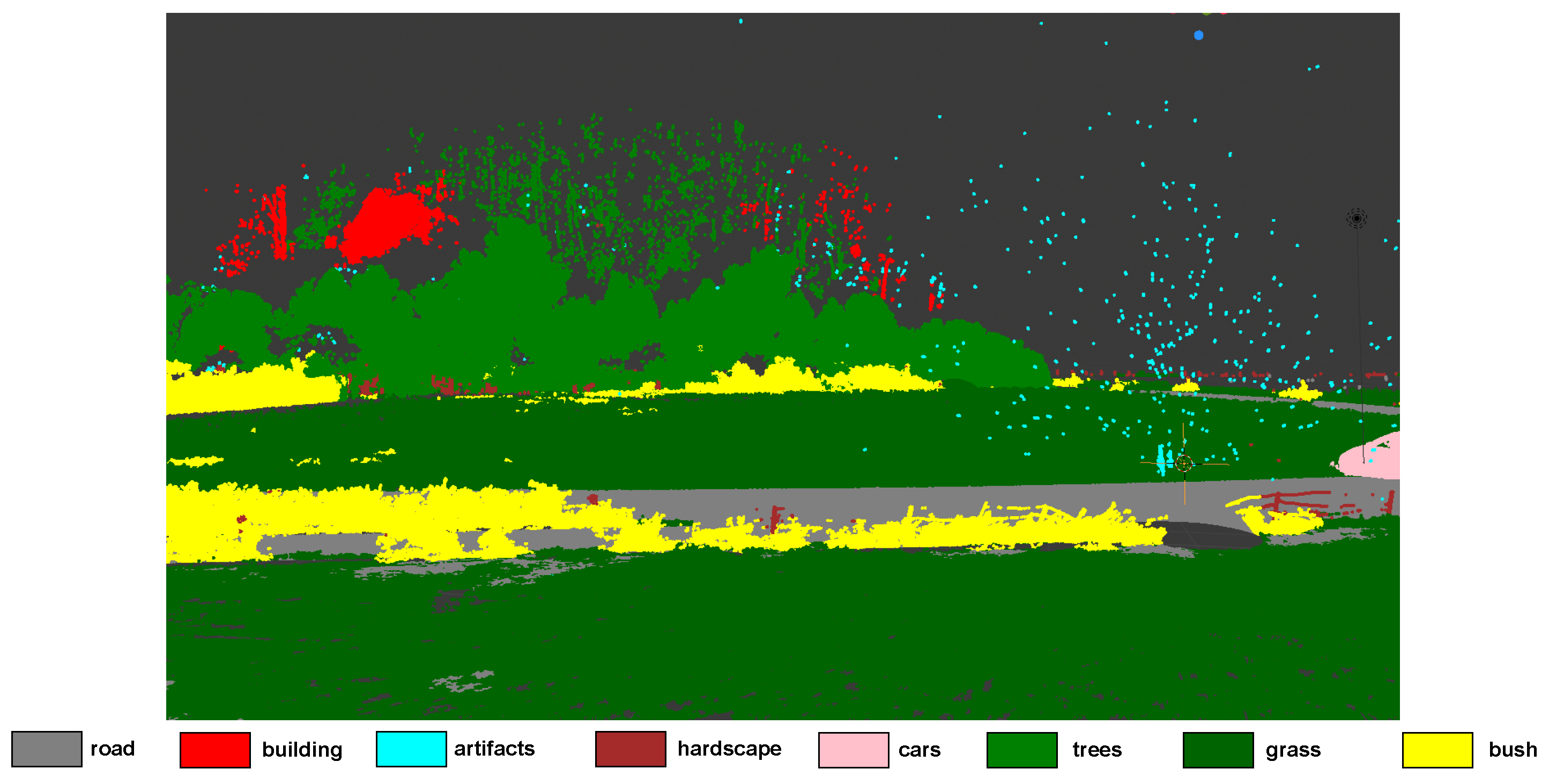
Table 1.
A description of Semantic3D (reduced-8) dataset classes.
| Class | Description |
|---|---|
| man-made | man-made terrain which is mostly pavement. |
| natural | natural terrain which is mostly grass. |
| high vegetation | high vegetation which is trees and large bushes. |
| low vegetation | low vegetation which is flowers or small bushes which are smaller than 2m of height. |
| building | houses, city halls, churches, stations, tenements and so on. |
| hard scape | a clutter class with garden walls, fountains, and banks. |
| scanning arts | artefacts caused by dynamically moving objects during static scan acquisition (this class may overlap with other classes, such as cars, if the cars are moving). |
| cars | cars and trucks. |
Table 2.
Comparative evaluation of the performance of different deep learning based strategies on the Semantic Kitti dataset using the Mean Intersection Over Union (mIOU) metric. Larger values imply better performance.
Table 2.
Comparative evaluation of the performance of different deep learning based strategies on the Semantic Kitti dataset using the Mean Intersection Over Union (mIOU) metric. Larger values imply better performance.
| Work | Description | Input | Type | mIOU |
|---|---|---|---|---|
| PointNet [6] | Takes into account the irregularity of point clouds and transformation invariant | 3D points | Raw data | 14.60 |
| PointNet++ [30] | An extension of pointnet where each local location is passed independently to a symmetric function | 3D points | Raw data | 20.10 |
| RangeNet++ [39] | Rasterize the data points as range images | 2.5D Data | Range images | 52.20 |
| RandLANet [7] | Subset of data points is randomly selected to be able to run in real time | 3D points | Raw data | 53.90 |
Table 3.
Comparative evaluation of the performances of different deep learning based strategies on the Modelnet40 dataset [38] using the Mean Intersection Over Union (mIOU) metric. Larger values imply better performance.
Table 3.
Comparative evaluation of the performances of different deep learning based strategies on the Modelnet40 dataset [38] using the Mean Intersection Over Union (mIOU) metric. Larger values imply better performance.
| Work | Description | Input | Type | mIOU |
|---|---|---|---|---|
| Volumetric [27] | Convert data points as voxels | Voxels | Transformed 3D points | 83.00 |
| MVCNN [28] | Obtains 12 views images of an object | 2D images | Transformed 3D points | 90.10 |
| 3dmfv [29] | Convert data into Fisher vectors | Grid | Transformed 3D points | 91.40 |
Table 4.
Summary of the desired features of the solutions proposed in the literature compared to our proposed approach. A large scale of points refers to hundreds of thousands of points or more.
Table 4.
Summary of the desired features of the solutions proposed in the literature compared to our proposed approach. A large scale of points refers to hundreds of thousands of points or more.
| Solution | Runs in Real Time | Raw 3D data as input | LiDAR only | Scale of points | Sampling approach |
|---|---|---|---|---|---|
| Volumetric [27] | ✓ | unknown | N/A | ||
| MVCNN [28] | ✓ | ✓ | unknown | N/A | |
| RangeNet++ [39] | ✓ | ✓ | unknown | N/A | |
| PointNet [6] | ✓ | ✓ | small | FPS | |
| 3dmfv [29] | ✓ | small | N/A | ||
| PointNet++ [30] | ✓ | ✓ | small | FPS | |
| RandLANet [7] | ✓ | ✓ | ✓ | large | random |
| Ours | ✓ | ✓ | ✓ | large | systematic |
Table 5.
Benchmarking our systematic sampling algorithm with other 3D point selection algorithms as reported by RandLA-Net. Smaller values imply better performance.
Table 5.
Benchmarking our systematic sampling algorithm with other 3D point selection algorithms as reported by RandLA-Net. Smaller values imply better performance.
| Algorithm | Complexity |
|---|---|
| Policy Gradient based Sampling [46] | does not converge for large data |
| Farthest Point Sampling [47,48] | |
| Inverse Density Importance Sampling [49] | |
| Random Sampling [7] | |
| Ours |
Table 6.
Benchmarking our network with the state-of-the-art RandLA-Net on Semantic3D (reduced-8) dataset with x, y, z and RGB values and no intensity. Larger values imply better performance.
Table 6.
Benchmarking our network with the state-of-the-art RandLA-Net on Semantic3D (reduced-8) dataset with x, y, z and RGB values and no intensity. Larger values imply better performance.
| RandLA-Net | Ours | |
|---|---|---|
| mIOU (%) | 69.31 | 72.23 |
| Overall Accuracy (%) | 89.50 | 91.30 |
| man-made (%) | 94.09 | 94.74 |
| natural (%) | 81.87 | 85.72 |
| high veg. (%) | 85.39 | 89.52 |
| low veg. (%) | 37.09 | 39.49 |
| building (%) | 82.18 | 85.77 |
| hard scape (%) | 25.71 | 28.85 |
| scanning arts (%) | 61.36 | 62.95 |
| cars (%) | 86.80 | 90.77 |
Table 7.
Benchmarking our network with state-of-the-art RandLA-Net on Semantic3D (reduced-8) data, omitting RBG features. Larger values imply better performance.
Table 7.
Benchmarking our network with state-of-the-art RandLA-Net on Semantic3D (reduced-8) data, omitting RBG features. Larger values imply better performance.
| RandLA-Net | Ours | |
|---|---|---|
| mIOU (%) | 53.79 | 62.25 |
| Overall Accuracy (%) | 81.00 | 85.60 |
| man-made (%) | 77.39 | 81.74 |
| natural (%) | 31.44 | 41.07 |
| high veg. (%) | 70.54 | 83.33 |
| low veg. (%) | 23.53 | 34.38 |
| building (%) | 89.95 | 89.92 |
| hard scape (%) | 17.36 | 31.80 |
| scanning arts (%) | 55.25 | 59.66 |
| cars (%) | 64.91 | 76.09 |
Table 8.
Benchmarking our network with state-of-the-art RandLA-Net on Semantic3D (reduced-8) data, omitting RBG features but adding intensity information. Larger values imply better performance.
Table 8.
Benchmarking our network with state-of-the-art RandLA-Net on Semantic3D (reduced-8) data, omitting RBG features but adding intensity information. Larger values imply better performance.
| RandLA-Net | Ours | |
|---|---|---|
| mIOU (%) | 47.01 | 68.15 |
| Overall Accuracy (%) | 75.80 | 89.23 |
| man-made (%) | 76.22 | 91.99 |
| natural (%) | 17.51 | 76.16 |
| high veg. (%) | 47.28 | 84.06 |
| low veg. (%) | 13.72 | 38.63 |
| building (%) | 87.12 | 85.18 |
| hard scape (%) | 17.85 | 24.50 |
| scanning arts (%) | 54.22 | 62.89 |
| cars (%) | 62.17 | 81.79 |
Table 9.
Benchmarking our network with state-of-the-art RandLA-Net on Semantic3D (reduced-8) data, with RBG features and intensity information. Larger values imply better performance.
Table 9.
Benchmarking our network with state-of-the-art RandLA-Net on Semantic3D (reduced-8) data, with RBG features and intensity information. Larger values imply better performance.
| RandLA-Net | Ours | |
|---|---|---|
| mIOU (%) | 61.07 | 67.93 |
| Overall Accuracy (%) | 85.20 | 89.07 |
| man-made (%) | 93.14 | 92.10 |
| natural (%) | 82.72 | 77.30 |
| high veg. (%) | 64.89 | 74.85 |
| low veg. (%) | 23.32 | 37.65 |
| building (%) | 78.22 | 91.46 |
| hard scape (%) | 21.31 | 26.93 |
| scanning arts (%) | 53.71 | 59.17 |
| cars (%) | 71.26 | 83.95 |
Table 10.
Benchmarking our network with state-of-the-art RandLA-Net on Semantic3D (reduced-8) data with RBG features as baseline with our four experiments we conducted. Larger values imply better performance.
Table 10.
Benchmarking our network with state-of-the-art RandLA-Net on Semantic3D (reduced-8) data with RBG features as baseline with our four experiments we conducted. Larger values imply better performance.
| RandLA-Net | x,y,z + RGB | x,y,z only | x,y,z + intensity | x,y,z + RGB + intensity | |
|---|---|---|---|---|---|
| mIOU (%) | 69.31 | 72.23 | 62.25 | 68.15 | 67.93 |
| Overall Acc. (%) | 89.50 | 91.30 | 85.60 | 89.23 | 89.07 |
| man-made (%) | 94.09 | 94.74 | 81.74 | 91.99 | 92.10 |
| natural (%) | 81.87 | 85.72 | 41.07 | 76.16 | 77.30 |
| high veg. (%) | 85.39 | 89.52 | 83.33 | 84.06 | 74.85 |
| low veg. (%) | 37.09 | 39.49 | 34.38 | 38.63 | 37.65 |
| building (%) | 82.18 | 85.77 | 89.92 | 85.18 | 91.46 |
| hard scape (%) | 25.71 | 28.85 | 31.80 | 24.50 | 26.93 |
| scanning arts (%) | 61.36 | 62.95 | 59.66 | 62.89 | 59.17 |
| cars (%) | 86.80 | 90.77 | 76.09 | 81.79 | 83.95 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





