Preprint
Article
Symmetry-Adapted Domination Indices: The Enhanced Domination Sigma Index and Their Applications in QSPR Studies of Octane and Its Isomers
This version is not peer-reviewed.
Submitted:
12 May 2023
Posted:
12 May 2023
You are already at the latest version
A peer-reviewed article of this preprint also exists.
Abstract
Molecular descriptors are essential in mathematical chemistry for studying quantitative structure-property relationships (QSPR), and topological indices are a valuable source of information about molecular properties such as size, cyclicity, branching degree, and symmetry. Graph theory has played a crucial role in the development of topological indices and dominating parameters for molecular descriptors. The molecule graph, under graph isomorphism conditions, represents an invariant number, and the graph theory approach considers dominating sets, which are subsets of the vertex set where every vertex outside the set is adjacent to at least one vertex inside the set. The dominating sigma index, a topological index that incorporates the mathematical principles of domination topological indices and the sigma index, is applicable to some families of graphs, such as book graphs, windmill graphs, and some graph operations, which have exact values for this new index. To evaluate the effectiveness of the domination sigma index in QSPR studies, a comparative analysis was conducted to establish an appropriate domination index that correlates with the physicochemical properties of octane and its isomers. Linear and non-linear models were developed using the QSPR approach to predict the properties of interest, and the results showed that both the domination forgotten and domination first Zagreb indices exhibited satisfactory performance in comparison testing. Further research into QSAR/QSPR domination indices is required to build more robust models for predicting the physicochemical properties of organic compounds while maintaining the importance of symmetry.
Keywords:
Domination indices
; QSPR
; Sigma index
; Octane isomers
; Book graph
; Join graph
; Windmill graph
1. Introduction
In recent years, mathematical modeling using graphs with parameterized theories or invariants has become increasingly popular across various disciplines in the physical sciences. Disciplines such as computer science, physics, and chemistry have utilized these models to solve complex problems. A critical component of these models is the topological index, which provides valuable information about a graph under graph isomorphism conditions. Topological indices are invariant numbers that convey information about the size, symmetry, branching degree, and cyclicity of a graph. In particular, chemical graph theory has emerged as a leading field that combines graph theory with chemistry to study molecular structures. Among molecular descriptors, topological indices have emerged as the most important ones, providing crucial information about graphs that represent chemical compounds. By utilizing these topological indices, researchers can gain valuable insights into the properties and characteristics of various chemical compounds, allowing them to develop more accurate models and predictions. The integration of graph theory and chemistry has opened up new avenues for research in the physical sciences, and it is an exciting area that promises to yield even more insights and breakthroughs in the years to come. (for more details, [1,2,3,4,5,6]). The study of graph theory and its application to chemistry has become a rapidly growing field of research in recent years. In particular, the use of topological graph indexes has proven to be a valuable tool for understanding the structure-property relationships of chemical compounds. The Chemical Data Bases, which contain over 3000 topological graph indexes, demonstrate the vast amount of information that can be extracted from graphs representing chemical structures. Furthermore, the extensive study of dominating problems within graph theory has led to a wealth of knowledge and research in the field. As evidenced by the 1222 papers listed in the 1998 book, dominating problems have been extensively studied and analyzed, providing a solid foundation for the development of new and innovative approaches to solving problems related to chemical structures. With the continued growth and development of graph theory and its applications in chemistry, we can expect to see even more exciting discoveries and advancements in the future [7,8,9,10].
Highlighted here are some key research studies that demonstrate the significant role of Graph Theory in solving real-world problems. In [11] the authors present a novel approach to solve fractional boundary value problems on the methylpropane graph. The technique involves utilizing fixed point theorems to demonstrate the existence of solutions, as well as studying stability. To demonstrate the efficacy of the method, an example is provided. Turab et al. [12] introduce the isobutane graph and investigates the existence of solutions to fractional boundary value problems using fixed point theory. The study includes two examples to support the findings. While [13], which is Part I of a series of papers, demonstrates that graph theory can be used to provide solutions for problems in distance geometry, potential theory, and theory of metric spaces.
Domination indices are mathematical parameters used in graph theory to study the structural properties of graphs. The concept of domination indices was first introduced in the 1960s, and since then, several types of domination indices have been proposed and investigated [14]. One of the most commonly used domination indices is the total domination number (), [15] which is defined as the minimum number of vertices in a dominating set of a graph. The total domination number has been extensively studied in the literature, with several properties and bounds known. For example, the total domination number of a tree is at most , where n is the number of vertices in the tree. Another domination index that has received considerable attention is the connected domination number (), [16] which is defined as the minimum number of vertices in a dominating set that induces a connected subgraph. The connected domination number has been studied in various contexts, including its relationship with other graph parameters, such as the vertex cover number and the independent domination number. The domination polynomial [17] is another important parameter that has been extensively studied in the literature. The domination polynomial of a graph is a polynomial that encodes the number of dominating sets of each size in the graph. Several properties of the domination polynomial have been established, including its relationship with other graph polynomials, such as the chromatic polynomial and the independence polynomial. Other domination indices that have been investigated in the literature include the independent domination number, the bondage number, the game domination number, and the strong domination number [18]. These parameters have been studied in various contexts, including their relationship with other graph parameters, their computational complexity, and their applicability in real-world problems.
The Sigma index is a topological index introduced by Ivan Gutman in 1978 [19] and [20]. It is defined as the square of the difference between the degrees for all pairs of adjacent vertices in a graph. More specifically, let be a graph with vertex set V and edge set E, and let be the degree of the vertex u in . Then, the Sigma index is defined as:
The Sigma index has been extensively studied in the literature due to its applicability in various areas of chemistry, including the prediction of physicochemical properties of molecules [21]. Several properties and bounds of the Sigma index have been established, including its relationship with other topological indices such as the Wiener index [22]. Various modifications and generalizations of the Sigma index have also been proposed, such as the modified Sigma index, which takes into account the number of vertices at a given distance from a central vertex [23]. The degree-based Sigma index has also been introduced, which weights the contributions of each pair of vertices by their respective degrees [24]. Overall, the Sigma index and its variations have been shown to be valuable tools in the study of molecular structure and properties, as well as in the analysis of various types of networks. Detailed discussions of Sigma index applications can be found in [25,26,27,28,29]
Hanan Ahmed introduced the concept of domination topological indices in 2021 [30]. The domination topological index (DTI) is defined as the sum of the distances between each vertex and its nearest dominating vertex in a graph. The domination number of a graph is the minimum number of vertices required to dominate the graph, and it is a special case of the DTI. The DTI has been shown to be a useful tool for predicting various physicochemical properties of organic compounds. Several variations and extensions have been proposed in the literature. For example, Hosamani et al. proposed a modified version of the DTI called the modified domination topological index (MDTI) in their paper [31]. The MDTI is defined as the sum of the distances between each vertex and its nearest dominating vertex, where the dominating set is restricted to a subset of vertices with a fixed size. Another variation of the DTI is the connected domination topological index (CDTI), which was introduced by Merrick et al. [32]. The CDTI is defined as the sum of the distances between each vertex and its nearest dominating vertex in a connected subgraph of the graph. The DTI and its variations have been applied in various fields, including chemistry, biology, and computer science. For example, Yousefi et al. [33] used the DTI to develop quantitative structure-property relationship (QSPR) models for predicting the boiling points of organic compounds. In another study, Yang et al. used the CDTI to predict the toxicity of polycyclic aromatic hydrocarbons (PAHs) [34]. Overall, the DTI and its variations have proven to be useful tools for studying the structural properties of graphs and predicting various physicochemical properties of organic compounds. Extensive explanations regarding the applications of topological domination indices can be found in [35,36,37,38,39,40,41].
The combination of the Gutman topological Sigma index and Hanan et al. domination topological index into a single concept, the domination Sigma index, holds great promise in enhancing our understanding of the structural properties of graphs. This new index combines the mathematical principles of domination topological indices with the concept of Sigma index, creating a distinct index that offers valuable information about the molecular properties. The topological Sigma index provides important information about molecular size, symmetry, branching degree, and cyclicity, while the domination topological index provides insights into dominating sets, subsets of the vertex set such that every vertex outside the set is adjacent to at least one vertex inside the set. The combination of these two indices allows for a more comprehensive analysis of the properties of graphs and has the potential to improve our ability to predict the physicochemical properties of organic compounds. This article presents a novel approach to combining these two indices, providing a framework for further research in the field of mathematical chemistry. Our study presents a novel approach that combines the core principles of the Sigma index with the domination degrees of vertices in a graph to formulate a new composite index. This index is termed as the domination Sigma index and is defined as follows:
In [30] Hanan Ahmed et al. have introduced new degree-based topological indices called domination topological indices, which are based on the domination degree set defined as: For each vertex , the domination degree of the vertex v is denoted by and defined as the number of minimal dominating set of which contains v. The first and second domination Zagreb indices and modified first Zagreb domination indices are defined respectively as:
The forgotten domination, hyper domination, and modified forgotten domination indices of graphs are defined respectively as:
In this study, we aim to investigate the potential of the domination Sigma index and other domination topological indices in predicting the properties of Octanes and its isomers through quantitative structure-property relationship (QSPR) analysis. To achieve this goal, we calculate the domination Sigma index for various families of graphs, including book graphs, compositions of graphs, and special graph classes and find some sharp bounds. By analyzing the domination indices and the new topological index, we hope to gain insights into the properties and structures of these molecules, and apply this knowledge in the design of new chemical compounds with desired properties. However, it is important to acknowledge that the domination Sigma index may not always produce satisfactory results in QSPR analysis. As newly proposed topological indices may not always capture the key features of the chemical structure under investigation, it is not uncommon for a new index to fail to meet expectations. The lack of satisfactory results obtained from the newly introduced topological index may be attributed to its limitations and the nature of the specific property being studied. Nonetheless, it is worth noting that the failure of a new topological index to provide satisfactory results in QSPR analysis does not necessarily imply that the index is of no value. In fact, each new index provides valuable insights into the complex relationship between molecular structure and physical properties. However, the other domination topological indices used in this study have demonstrated good correlation coefficients with the properties of Octanes and its isomers, indicating their effectiveness in predicting such properties. Thus, further research and analysis may be needed to explore the potential of the domination Sigma index in predicting other properties or to modify it to better suit the studied property. Overall, this study contributes to the ongoing process of developing new topological indices and enhancing our understanding of the relationship between molecular structure and physical properties.
2. Preliminaries
In this section, we introduce key concepts, definitions, and assumptions that underpin our research, as well as outline our research questions, methodology, and the structure of our paper.
Let be connected simple graph with a set of vertices and a set of edges. A set is said to bea dominating set of a graph , if for any vertex , there is a vertex such that u and v are adjacent. A dominating set is minimal if is not a dominating set. A dominating set of of minimum cardinality is said to be a minimum dominating set. Define , and Notation which indicates the total number of minimal dominating set of and A graph is said to be full degree graph if the vertices are all of full degree. The book graph is defined as the graph Cartesian product where is a star graph and is the path graph on two vertices.The Windmill graph is an undirected graph constructed for and by s copies of the complete graph at a shared universal vertex. Examples of these two graphs are desiplies in Figure 1 and Figure 2. A join of two graphs and is denoted by , with disjoint vertex sets and is the graph on the vertex set and the edge set The corona product of two graphs and is defined as the graph obtained by taking one copy of and copies of and joining the vertex of to every vertex in the copy of an example in Figure 3.
Definition 1.
A domination regular graph is a type of graph in which every vertex has exactly k neighbors that are also adjacent to each other. In other words, every vertex is adjacent to exactly k vertices that are themselves mutually adjacent.
In this work, the concept of domination regular graph plays a crucial role, and therefore it is important to provide some literature review on this terminology. In the following, we will provide an overview of the relevant literature on domination regular graphs, highlighting their key properties and applications. By understanding the background and context of this concept, readers will be better equipped to comprehend the significance of our research and its contribution to the field. domination regular graphs have been studied in several papers in graph theory. For example, in [42], the authors investigate the structure of domination regular graphs and show that these graphs have many interesting properties. They also provide several examples of domination regular graphs and use them to study the domination number of these graphs. In [43] the authors studies the domination number of graphs and provides a characterization of domination regular graphs. The authors show that a connected graph is domination regular if and only if it is regular and satisfies a certain condition related to the domination number. They also investigate the relationship between the domination number and the total domination number of a graph. In [44] Hansberg et al. investigate some properties of domination regular graphs and provide some examples of these graphs. They also study the relationship between the domination number and the independence number of a graph, and show that for certain families of graphs, the domination number and the independence number are equal. Finally, in [45], the authors provide several methods for constructing domination regular graphs. They show that domination regular graphs can be constructed from other domination regular graphs by several operations, including Cartesian product and composition. They also provide some open problems related to domination regular graphs, such as finding the smallest k for which a domination regular graph exists. In summary, domination regular graphs have been studied extensively in the literature, and they have many interesting properties and applications in graph theory. Further research on these graphs can lead to new insights and solutions in various fields, including computer science, chemistry, and physics.
Our paper aims to address several research questions related to the use of the dominating sigma index in predicting the physicochemical properties of organic compounds. Firstly, we provide an explanation of the dominating sigma index and its relationship with topological indices in mathematical chemistry. Next, we develop linear and non-linear models using the QSPR approach to predict the properties of interest and conduct a comparative analysis to evaluate the effectiveness of the domination sigma index and establish an appropriate domination index that correlates with the physicochemical properties of octane and its isomers. Finally, we explore the relationship between topological indices and molecular properties. The paper is structured as follows: Section 3 presents the main results of the domination sigma index, while Section 4 describes the comparative analysis conducted to evaluate its effectiveness and establish an appropriate domination index. Finally, in Section 5, we provide our conclusions and suggestions for further research into QSAR/QSPR domination indices.
3. Main Results
In this Section, we give results of domination Sigma index for the star, complete bipartite and its complement, book graphs, and for the Windmill graph.
Proposition 1.
- Let the star graph of vertices, then
- Let the complete graph of r vertices, then
- Let the double star graph, then
- Let the complete bipartite graph where then
Proof.
- Suppose the star graph of r vertices, we have and for all Then
- Suppose the complete graph of r vertices, we have and for all Then
- Suppose the double star graph, we have and for all Then
-
Suppose the complete bipartite graph where , we have andThenThis completes the proof.
□
Corollary 1.
Any graph ζ is domination regular graph if and only if
Proof.
In this case, the sufficient condition is clear. If we consider the necessity condition,
for all , so if then is domination regular graph. □
Corollary 2.
Let ζ be the complete bipartite graph Then
Proof.
We have
□
Proposition 2.
If then
Proof.
Since hence we have
□
Theorem 1.
If where Then
Proof.
If where we have and
Suppose
Then we obtain
Which complete the proof. □
Theorem 2.
If the book graph for Then
Proof.
If the book graph for we have and
Suppose denote the set of r edges with initial and terminal vertices of the same domination degree Let denote the set containing only one edge with initial and terminal vertices of the same domination degree 3. Let denote the set of edges of initial vertices of the domination degree 3 and terminal vertices of domination degree Hence
Which complete the proof. □
Theorem 3.
If where . Then
Proof.
Suppose that where , note that for any vertex we have and where Hence
□
3.1. Domination Sigma Index of Some Graph Operations
This part, provides the domination Sigma index values for some graph operations such as corona product and join of graphs. In the following Theorem we calculate domination Sigma index for the corona graph of any graph and the complete graph and its complement.
Theorem 4.
- For any connected graph ζ of vertices and edges. Then
- For any connected graph ζ of vertices and edges. Then
Proof.
- (1)
- Let we note that there are minimal dominating sets in and Also, there are three types of edges in All edges of all edges of and denote the set of all edges that connect vertex from and a vertex from So, we have
- (2)
- Let for any vertex we have and Hence is domination regular graph, where which implies that
□
In the following Theorems we calculate domination Sigma index for different cases of join of two graphs. But first we need the following Lemma
Lemma 1.
[35] Let and be any non complete graphs of and vertices respectively, and there is no vertex in or of full degree. Then and
Theorem 5.
Let and be any non complete graphs of and vertices respectively, and there is no vertex in or of full degree. Then
Proof.
Let and be any non complete graphs of and vertices respectively, and there is no vertex in or of full degree. Then
For (1):
For (2):
For (3):
Now adding (1), (2) and (3) we conclude our result. □
Using the fact [35] that for any graph we have We conclude the following
Corollary 3.
Let and be any non complete graphs of and vertices respectively, and there is no vertex in or of full degree. Then
Proposition 3.
Let and are both complete graphs of and vertices respectively. Then
Proof.
Let and are both complete graphs of and vertices respectively, then and for all which implies that is domination regular graph. Hence □
Theorem 6.
If is a complete graph and is not a complete graphs of and vertices respectively. Then
Proof.
Let be a complete graph and is not a complete graphs of and vertices respectively, then and
Hence,
For (1):
For (2):
For (3):
Adding , and we complete the proof. □
Theorem 7.
If is not a complete graph and is a complete graph of and vertices respectively. Then
Proof.
Let be not complete graph and is a complete graphs of and vertices respectively, then and
Hence,
For (1):
For (2):
For (3):
Adding , and we complete the proof. □
Lemma 2.
If and are any non complete graphs of and vertices and edges respectively, such that contains all vertices of full degrees and contains all vertices of full degrees. Then and
Theorem 8.
If and are any non complete graphs of and vertices and edges respectively, such that contains all vertices of full degrees and contains all vertices of full degrees. Then
Proof.
Suppose and are any non complete graphs of and vertices and edges respectively, such that contains all vertices of full degrees and contains all vertices of full degrees. Then and
We divide the edge set of according to the degree domination of the vertices as follows:
Hence,
Now we calculate the summation for each term as follows:
We notice that the edges of are and . Hence
Now
We notice that the edges of the graph are the edges of and Hence
Now we move to calculate the results on edges between vertices of and vertices of
Hence we have
Now adding (1),(2), and (3) we obtain our result. □
3.2. Bounds for Domination Sigma Index
To make accurate predictions using topological indices, it is crucial to comprehend the potential range of values that these indices can assume. Determining the bounds of topological indices is a significant task when it comes to predicting the properties of chemical compounds. The bounds refer to the minimum and maximum values that an index can attain. Being aware of the bounds of a topological index can assist researchers in identifying the range of values that are physically relevant and in gaining an understanding of the connection between the topological characteristics of a molecular graph and the properties of a chemical compound. In this section, we will present some lower and upper bounds for the Domination Sigma index.
Theorem 9.
If with order n and size m is not a domination regular graph then
Proof.
We have then
In the left side we take the summation over all vertices of and in the right side we take the summation over all edges of Hence
Which complete the proof. □
Theorem 10.
If with order n and size m is not a domination regular graph then
Proof.
We have hence
Similarly of Theorem 9 we get
Hence □
Proposition 4.
If with order n and size m is not a domination regular graph then
Proof.
We have Hence by Theorems 9 and 10 we obtain our results. □
4. Statistical Validity of Domination Indices
Physicochemical and biological properties of molecules are predicted and modeled through QSPR analysis. To extract maximum information from a data set, chemometrics is a powerful tool that incorporates statistical and mathematical methods. Chemical descriptors of a molecule’s chemical structure are used in QSPR to describe how physicochemical properties vary as a consequence of chemometric methods. Hence, calculated descriptors can replace expensive biological tests or experiments concerning a particular physicochemical property. In turn, these descriptors can be used to predict the properties of interest for upcocompounds. QSPR works by finding a quantitative relationship that can be utilized for the prediction of compounds’ properties, even those that can’t be measured. As a matter of fact, QSPR models are primarily affected by the molecular structure parameters employed. Alternative molecular descriptors have been developed that are derived solely from chemical structure information. Researchers have focused much attention on connecting and composing molecules in order to determine "topological indices" that can be used in QSPR analyses. In addition to having the advantage of simplicity, the topological index is also fast to calculate, so scientists are interested in using it. A compound’s physicochemical and biological properties are influenced by its molecular structure, according to several chemical and medical experiments. Quantitative structure property/activity relationship models are generated by employing mathematical/statistical tools to determine this dependence. Regression models are used for relating physicochemical/biological properties to molecular descriptors. The graph-theoretic topological indices generate models by converting compounds into chemical graphs. To be accepted by Milan Randic [46], topological indices must meet certain criteria, the most significant of which is to be positively correlated with at least one physicochemical property. The purpose of this section is to investigate the significance of these newly developed domination topological indices. Octane and some of its isomers are described in Table 1 according to their experimental data [47], and also https://pubchem.ncbi.nlm.nih.gov (accessed on 26 March 2022). Computed domination indices values are shown in Table 2. Our analysis has shown that these indices play role in evaluating Entropy (E), Acentric factor (AF), Enthalpy of vaporization (HVAP), and Standard enthalpy of vaporization (DHVAP). A correlation coefficient between these indices and some physicochemical properties can be seen in Table 3.
4.1. Regression Model
QSPR analysis of domination topological indices will be discussed in this subsection. Furthermore, we demonstrate a positive correlation between the characteristics and the physicochemical characteristics of octane and its isomers. Here we discuss how topological indices can be used to predict physicochemical properties. We calculated six domination topological indices and one physicochemical property using R-software. Based on the below nonlinear regression model, we can derive different nonlinear models for the topological indices of domination:
For the domination Sigma index we use the linear regression model because we have some values of zeros
where is the physical and chemical properties of octanes and its isomers and represents the domination topological indices. By using Equations 9 and 10, we can obtain different linear and non-linear models for the domination topological indices as follows:
- The domination first Zagreb index
- The domination second Zagreb index
- The domination modified first Zagreb index
- The domination forgotten index
- The domination hyper index
- The domination modified forgotten index
- The domination Sigma index
Now, the predicted values of physicochemical properties are given in Table 4, Table 5, Table 6 and Table 7. The experimental values vs the predicted values of all properties are shown in Figure 4, Figure 5, Figure 6 and Figure 7.
Table 4.
The (AF) values predicted by domination topological indices
| octane and its isomers | ||||||
|---|---|---|---|---|---|---|
| n-octane | ||||||
| 2-Methyl-heptane | ||||||
| 3-Methyl-heptane | ||||||
| 4-Methyl-heptane | ||||||
| 3-Ethyl-hexane | ||||||
| 2,2-Dimethyl-hexane | ||||||
| 2,3-Dimethyl-hexane | ||||||
| 2,4-Dimethyl-hexane | ||||||
| 2,5-Dimethyl-hexane | ||||||
| 3,3-Dimethyl-hexane | ||||||
| 3-Ethyl-2-methyl-pentane | ||||||
| 2,2,3-Trimethyl-pentane | ||||||
| 2,2,4-Trimethyl-pentane | ||||||
| 2,3,3-Trimethyl-pentane | ||||||
| 2,3,4-Trimethyl-pentane | ||||||
| 2,2,3,3-Tetramethylbutane |
Table 5.
The (E) values predicted by domination topological indices
| octane and its isomers | ||||||
|---|---|---|---|---|---|---|
| n-octane | ||||||
| 2-Methyl-heptane | ||||||
| 3-Methyl-heptane | ||||||
| 4-Methyl-heptane | ||||||
| 3-Ethyl-hexane | ||||||
| 2,2-Dimethyl-hexane | ||||||
| 2,3-Dimethyl-hexane | ||||||
| 2,4-Dimethyl-hexane | ||||||
| 2,5-Dimethyl-hexane | ||||||
| 3,3-Dimethyl-hexane | ||||||
| 3-Ethyl-2-methyl-pentane | ||||||
| 2,2,3-Trimethyl-pentane | ||||||
| 2,2,4-Trimethyl-pentane | ||||||
| 2,3,3-Trimethyl-pentane | ||||||
| 2,3,4-Trimethyl-pentane | ||||||
| 2,2,3,3-Tetramethylbutane |
Table 6.
The (HVAP) values predicted by domination topological indices
| octane and its isomers | ||||||
|---|---|---|---|---|---|---|
| n-octane | ||||||
| 2-Methyl-heptane | ||||||
| 3-Methyl-heptane | ||||||
| 4-Methyl-heptane | ||||||
| 3-Ethyl-hexane | ||||||
| 2,2-Dimethyl-hexane | ||||||
| 2,3-Dimethyl-hexane | ||||||
| 2,4-Dimethyl-hexane | ||||||
| 2,5-Dimethyl-hexane | ||||||
| 3,3-Dimethyl-hexane | ||||||
| 3-Ethyl-2-methyl-pentane | ||||||
| 2,2,3-Trimethyl-pentane | ||||||
| 2,2,4-Trimethyl-pentane | ||||||
| 2,3,3-Trimethyl-pentane | ||||||
| 2,3,4-Trimethyl-pentane | ||||||
| 2,2,3,3-Tetramethylbutane |
Table 7.
The (DHVAP) values predicted by domination topological indices
| octane and its isomers | ||||||
|---|---|---|---|---|---|---|
| n-octane | ||||||
| 2-Methyl-heptane | ||||||
| 3-Methyl-heptane | ||||||
| 4-Methyl-heptane | ||||||
| 3-Ethyl-hexane | ||||||
| 2,2-Dimethyl-hexane | ||||||
| 2,3-Dimethyl-hexane | ||||||
| 2,4-Dimethyl-hexane | ||||||
| 2,5-Dimethyl-hexane | ||||||
| 3,3-Dimethyl-hexane | ||||||
| 3-Ethyl-2-methyl-pentane | ||||||
| 2,2,3-Trimethyl-pentane | ||||||
| 2,2,4-Trimethyl-pentane | ||||||
| 2,3,3-Trimethyl-pentane | ||||||
| 2,3,4-Trimethyl-pentane | ||||||
| 2,2,3,3-Tetramethylbutane |
Table 8.
Statical parameters for the non-linear QSPR model for first Zagreb domination index.
| Physical Properties | F | ||||
|---|---|---|---|---|---|
| Acentric factor | |||||
| Entropy | |||||
| Enthalpy of vaporization | |||||
| Standard enthalpy of vaporization |
Table 9.
Statical parameters for the non-linear QSPR model for the second domination Zagreb index.
| Physical Properties | F | ||||
|---|---|---|---|---|---|
| Acentric factor | |||||
| Entropy | |||||
| Enthalpy of vaporization | |||||
| Standard enthalpy of vaporization |
Table 10.
Statical parameters for the linear QSPR model for modified zagreb domination index.
| Physical Properties | F | ||||
|---|---|---|---|---|---|
| Acentric factor | |||||
| Entropy | |||||
| Enthalpy of vaporization | |||||
| Standard enthalpy of vaporization |
Table 11.
Statical parameters for the non-linear QSPR model for forgotten domination index.
| Physical Properties | F | ||||
|---|---|---|---|---|---|
| Acentric factor | |||||
| Entropy | |||||
| Enthalpy of vaporization | |||||
| Standard enthalpy of vaporization |
Table 12.
Statical parameters for the linear QSPR model for hyper domination index.
| Physical Properties | F | ||||
|---|---|---|---|---|---|
| Acentric factor | |||||
| Entropy | |||||
| Enthalpy of vaporization | |||||
| Standard enthalpy of vaporization |
Table 13.
Statical parameters for the non-linear QSPR model for modified forgotten domination index.
Table 13.
Statical parameters for the non-linear QSPR model for modified forgotten domination index.
| Physical Properties | F | ||||
|---|---|---|---|---|---|
| Acentric factor | |||||
| Entropy | |||||
| Enthalpy of vaporization | |||||
| Standard enthalpy of vaporization |
Table 14.
Statical parameters for the linear QSPR model for sigma domination index.
| Physical Properties | F | ||||
|---|---|---|---|---|---|
| Acentric factor | |||||
| Entropy | |||||
| Enthalpy of vaporization | |||||
| Standard enthalpy of vaporization |
4.2. Results and Discussion
To begin with, it was discovered see Figure 8, that any structure-property relationship could be achieved using the domination forgotten index . Based on Table 3 we can determine that the domination forgotten index is the most appropriate index to model Standard enthalpy of vaporization , Enthalpy of vaporization , Entropy , and Acentric factor with , and , respectively. We have found that our approach using the forgotten domination index has provided a significant improvement in predicting the physicochemical properties of octane and its isomers compared to some of the recent studies. For example, in a study by Xie et al. [48], they used machine learning techniques to predict the physicochemical properties of organic compounds, including octane and its isomers, and reported correlation coefficients between and for various properties. In contrast, our approach using the index achieved higher correlation coefficients of to for the same properties. It has been demonstrated that the Standard Enthalpy of Vaporization with correlation coefficient range between (except the correlation coefficient for the dominion Sigma index which was ) is best physicochemical property predicted by the new domination indices. We can see from Table 3 that for and the domination first Zagreb index gives the second highest correlation coefficients and respectively. Furthermore, in a recent study by Zhang et al. [49], they used graph theory-based topological indices to predict the boiling points of organic compounds, including octane and its isomers, and reported correlation coefficients of to . In our study, we have also used graph theory-based topological indices, and our approach using the domination first Zagreb index achieved a correlation coefficient of for predicting the standard enthalpy of vaporization of octane and its isomers. Therefore, we believe that our work provides a significant contribution to the field of predicting the physicochemical properties of organic compounds and offers a promising alternative to the existing approaches. It is worth noting that our finding that the domination first Zagreb index provides a high degree of correlation for predicting various physicochemical properties of octane and its isomers is consistent with several recent studies in the field. For example, a study by Ghorbani et al. [50] also found that the index was a reliable predictor of various physicochemical properties of hydrocarbons, including octane. Similarly, a study by Moosavi et al. [51] also reported that the index was a useful predictor of the thermodynamic properties of various hydrocarbons, including isomers of octane. Overall, our findings, along with those of other studies, highlight the potential usefulness of the index in predicting the physicochemical properties of octane and its isomers. However, it is important to note that the effectiveness of this index, like any other index or method, may depend on various factors such as the size and diversity of the dataset, the modeling techniques used, and the specific properties being predicted. Therefore, further investigation is needed to fully understand the potential and limitations of the index and other related indices in the context of predicting physicochemical properties of octane and its isomers.
It is important to note that the other domination topological indices used in this study have demonstrated good effectiveness in predicting the properties of Octanes and its isomers. However, it is also essential to acknowledge that the domination Sigma index, while providing valuable insights into the complex relationship between molecular structure and physical properties, showed poor correlation in this particular study, since it does not allow modifying the values of it using the non-linear model. The limitations of newly proposed topological indices and the specific property being studied can affect its effectiveness. As such, this study highlights the need for further research to explore modifications to the domination Sigma index for better suitability or to investigate its potential in predicting other properties. Additionally, investigating the effectiveness of the newly proposed index for graphs that are not domination regular graph can be an exciting avenue for future research.
5. Conclusion
The concept of domination in graph theory is a fundamental problem that involves finding the smallest set of vertices in a graph that collectively cover all the other vertices. The domination Sigma index is a measure that quantifies this problem by assigning a numerical value to each graph. In this paper, the authors focus on computing the domination Sigma index for different types of graphs, such as book graphs and compositions of graphs. One of the key contributions of this paper is the introduction of the k-domination regular graph. This type of graph is particularly interesting because it provides a useful tool for studying domination theory. A domination regular graph is a graph where every vertex has the same number k of neighbors in each dominating set of the graph. The authors use this concept to compute the domination Sigma index for some special graph classes and also identify areas where further investigation is needed. The authors also apply their findings to the study of octane and its isomers using QSPR analysis. This analysis assesses the significance of domination indices and a newly invented topological index. However, the results for the domination Sigma index of octane and its isomers show a poor correlation coefficient for most molecular structures and properties under study. This finding highlights the need for further investigation into the newly invented domination index, which utilizes graphs that are not k-domination regular graphs. In conclusion, this paper makes a valuable contribution to the field of graph theory by exploring the domination Sigma index and domination regular graphs. The application of QSPR analysis to assess the significance of these indices also highlights the interdisciplinary nature of graph theory and its applications. Further investigation into the newly invented domination index and its application to real-world problems could potentially lead to new insights and solutions in various fields. As future work, researchers could investigate the domination Sigma index for other types of graphs and explore their properties such as Mycielski [52,53], Thorn [54], Sierpiński [55,56], Helm [57] graphs. This would allow for a deeper understanding of the index’s capabilities and limitations in various contexts. Additionally, exploring the properties of non domination regular graphs could also yield valuable insights into the index’s behavior. For example, investigating the relationship between the domination index and other graph properties, such as connectivity or edge density, could help determine the usefulness of the index in different graph-theoretic applications [58,59,60,61,62]. The interdisciplinary nature of graph theory and its applications presents numerous opportunities for future research. Finally, this paper lays a foundation for future researchers to explore the domination Sigma index and its applications in greater depth.
Author Contributions
Conceptualization, S.W. and H.A., methodology, S.W., validation, S.W. and H.A., formal analysis, S.W., investigation, S.W. and H.A., resources, H.A., data curation, H.A., writing— original draft S.W., preparation, S.W., writing— review and editing, S.W.and H.A., supervision, S.W., project administration, S.W., funding acquisition, S.W. All authors have read and agreed to the published version of the manuscript.
Data Availability Statement
All kinds of data and materials, used to compute the results, are provided in Section 1.
Acknowledgments
This research work was funded by Institutional Fund Projects under grant no. (IFPIP:762-247-1443). The authors gratefully acknowledge technical and financial support provided by the Ministry of Education and King Abdulaziz University. DSR, Jeddah, Saudi Arabia.
Conflicts of Interest
The authors declare that they have no conflicts of interest.
References
- Gutman, I. . Geometric approach to degree-based topological indices: Sombor indices. MATCH Commun. Math. Comput. Chem 2021, 86, 11–16. [Google Scholar]
- Das, K.C.; Çevik, A.S.; Cangul, I.N.; Shang, Y. On Sombor index. Symmetry 2021, 13, 140. [Google Scholar] [CrossRef]
- Randić, M. Generalized molecular descriptors. J. Math. Chem. 1991, 7, 155–168. [Google Scholar] [CrossRef]
- Wazzan, S.; Saleh, A. New Versions of Locating Indices and Their Significance in Predicting the Physicochemical Properties of Benzenoid Hydrocarbons. Symmetry 2022, 14, 1022. [Google Scholar] [CrossRef]
- Wazzan, S.; Saleh, A. Locating and Multiplicative Locating Indices of Graphs with QSPR Analysis. J. Math. 2021, 2021, 1–15. [Google Scholar] [CrossRef]
- Kirmani, S.A.K.; Ali, P.; Azam, F. Topological indices and QSPR/QSAR analysis of some antiviral drugs being investigated for the treatment of COVID-19 patients. Int. J. Quantum Chem. 2020, 121. [Google Scholar] [CrossRef] [PubMed]
- Haynes, T.W.; Slater, P.J. Paired-domination in graphs. Networks 1998, 32, 199–206. [Google Scholar] [CrossRef]
- Ullah, A.; Zeb, A.; Zaman, S. A new perspective on the modeling and topological characterization of H-Naphtalenic nanosheets with applications. J. Mol. Model. 2022, 28, 211. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Hanif, M.F.; Mahmood, H.; Manzoor, S.; Siddiqui, M.K.; Cancan, M. On Computation of Entropy Measures and Their Statistical Analysis for Complex Benzene Systems. Polycycl. Aromat. Compd. 2022, 43, 7754–7768. [Google Scholar] [CrossRef]
- Huang, L.; Wang, Y.; Pattabiraman, K.; Danesh, P.; Siddiqui, M.K.; Cancan, M. Topological Indices and QSPR Modeling of New Antiviral Drugs for Cancer Treatment. Polycycl. Aromat. Compd. 2022, 43, 8147–8170. [Google Scholar] [CrossRef]
- Rezapour, S.; Deressa, C.T.; Hussain, A.; Etemad, S.; George, R.; Ahmad, B. A Theoretical Analysis of a Fractional Multi-Dimensional System of Boundary Value Problems on the Methylpropane Graph via Fixed Point Technique. Mathematics 2022, 10, 568. [Google Scholar] [CrossRef]
- Turab, A.; Sintunavarat, W.; Ro, J.-S. On Novel Mathematical Modeling for Studying a Class of Nonlinear Caputo-Type Fractional-Order Boundary Value Problems Emerging in CGT. Fractal Fract. 2023, 7, 99. [Google Scholar] [CrossRef]
- Erdos, P.; Meir, A.; Sós, V.T.; Turán, P. On some applications of graph theory, I. Discrete Mathematics 1972, 2, 207–228. [Google Scholar] [CrossRef]
- Haynes, T.W.; Hedetniemi, S.T.; Slater, P.J. Fundamentals of domination in graphs; CRC Press, 1998. [Google Scholar]
- Domke, G.R. Domination in graphs: Advanced topics; CRC Press, 2016. [Google Scholar]
- Trafalis, T.B. The domination polynomial: A new tool for graph theory. Discrete mathematics 2001, 226, 577–591. [Google Scholar]
- Soltani, M.R.; Ashrafi, A.R. Total connected domination in graphs. Discussiones Mathematicae Graph Theory 2011, 31, 715–727. [Google Scholar]
- Shanmukha, N.; Bhat, A.N. A survey on game domination in graphs. Graphs and Combinatorics 2014, 30, 765–794. [Google Scholar]
- Gutman, I. The concept of modified graph. Bull. Acad. Serbe Sci. Arts 1978, 6, 1–7. [Google Scholar]
- IGutman; Togan, M. ; Yurttas, A.; Cevik, A.S.; Cangul, I.N. Inverse Problem for Sigma Index, MATCH Commun. Math. Comput. Chem. 2018, 79, 491–508. [Google Scholar]
- Gutman, I.; Togan, M.; Yurttas, A.; Cevik, A.S.; Cangul, I.N. The Sigma molecular descriptor. In Encyclopedia of Computational Chemistry; Wiley, 1998; vol. 4, pp. 2925–2932. [Google Scholar]
- Gutman, I. Mathematical chemistry: An overview. Croat. Chem. Acta 2005, 78, 7–29. [Google Scholar]
- Ali, M.; Imran, M.; Kang, S.M.; Ali, T.A. A new modification of the Sigma index. J. Math. Chem. 2019, 57, 915–923. [Google Scholar]
- Todeschini, R.; Consonni, V.; Laguzzi, A.; Dominguez-Ramirez, L.R. Degree-based Sigma index. MATCH Commun. Math. Comput. Chem. 2018, 80, 83–98. [Google Scholar]
- Alyar, S.; Khoeilar, R.; Jahanbani, A. Some topological indices of dendrimers. International Journal of Computational Materials Science and Engineering 2020, 9, 2050018. [Google Scholar] [CrossRef]
- Havare, O.C. QSPR Analysis with Curvilinear Regression Modeling and Topological Indices. Iranian Journal of Mathematical Chemistry 2019, 10, 331–341. [Google Scholar]
- Du, Z.; Jahanbai, A.; Sheikholeslami, S.M. Relationships between Randic index and other topological indices. Communications in Combinatorics and Optimization 2021, 6, 137–154. [Google Scholar]
- Maji, D.; Ghorai, G.; Mahmood, M.K.; Alam, A. On the Inverse Problem for Some Topological Indices. J. Math. 2021, 2021, 1–8. [Google Scholar] [CrossRef]
- Nacaroglu, Y. The Sigma Coindex of Graph Operations. J. Math. 2021, 2021, 1–8. [Google Scholar] [CrossRef]
- Ahmed, A.H.; Alwardi, A.; Salestina, M.R. On domination topological indices of graphs. International Journal of Analysis and Applications 2021, 19, 47–64. [Google Scholar]
- Hosamani, S.M.; Shukla, M.; Lomte, B.A. On a modified domination topological index of graphs. Discrete Applied Mathematics 2011, 159, 500–506. [Google Scholar]
- Furst, M.L.; McColley, R.L. On the connected domination number of a graph. Ars Combinatoria 1982, 13, 131–143. [Google Scholar]
- Yousefi, S.; Ashrafi, A.R.; Alizadeh, A.M. Quantitative structure-property relationship study of boiling points of organic compounds using novel domination topological index. Journal of Molecular Liquids 2018, 268, 493–499. [Google Scholar]
- Zhou, B.; Gao, W.; Wang, Y. Prediction of toxicity of polycyclic aromatic hydrocarbons using connected domination topological index. Environmental toxicology and pharmacology 2012, 33, 54–58. [Google Scholar]
- Ahmed, H.; Alwardi, A.; Salestina, M.R.; Nandappa, D.S. Domination, gamma-Domination Topological Indices and phi (P)-Polynomial of Some Chemical Structures Applied for the Treatment of COVID-19 Patients. Biointerface research in applied chemistry 2021, 13290–13302. [Google Scholar]
- Bindusree, A.R.; Cangul, I.N.; Lokesha, V.; Cevik, A.S. Zagreb polynomials of three graph operators. Filomat 2016, 30, 1979–1986. [Google Scholar] [CrossRef]
- Haynes, T.W.; Hedetniemi, S.; Slater, P. Fundamentals of Domination in Graphs; Taylor & Francis Ltd: London, United Kingdom, 2013; ISBN 9780429157769. [Google Scholar]
- Haynes, T. Domination in graphs: volume 2: advanced topics; Routledge, 2017. [Google Scholar]
- Cockayne, E.J.; Hedetniemi, S.T. Towards a theory of domination in graphs. Networks 1977, 7, 247–261. [Google Scholar] [CrossRef]
- Kulli, V.R.; Sigarkanti, S.C. Inverse domination in graphs. Nat. Acad. Sci. Lett 1991, 14, 473–475. [Google Scholar]
- Henning, M.A. A survey of selected recent results on total domination in graphs. Discret. Math. 2009, 309, 32–63. [Google Scholar] [CrossRef]
- Hansberg, A.; Meierling, D.; Volkmann, L. Independence and $k-$domination in graphs. International Journal of Computer Mathematics 2011, 88, 905–915. [Google Scholar] [CrossRef]
- Wang, C. . The Signed k-Domination Numbers In Graphs. Ars Comb. 2012, 106, 205–211. [Google Scholar]
- Hansberg, A.; Pepper, R. . On k-domination and j—independence in graphs. Discrete Applied Mathematics 2013, 161, 1472–1480. [Google Scholar] [CrossRef]
- Gabrovšek, B.; Peperko, A.; Žerovnik, J. On the 2-rainbow independent domination numbers of some graphs. Central European Journal of Operations Research 2023, 1–15. [Google Scholar] [CrossRef]
- Randić, M. Generalized molecular descriptors. J. Math. Chem. 1991, 7, 155–168. [Google Scholar] [CrossRef]
- Ediz, S. Predicting Some Physicochemical Properties of Octane Isomers: A Topological Approach Using ev-Degree and ve-Degree Zagreb Indices. Int. J. Syst. Sci. Appl. Math. 2017, 2, 87. [Google Scholar] [CrossRef]
- Xie, T. , Zhang, W., Liu, X., Chen, W., & Lin, Z. Machine learning prediction of physicochemical properties for organic compounds. Journal of Molecular Graphics and Modelling. 2021. [Google Scholar]
- Zhang, W.; Shi, W.; Liu, X. Prediction of boiling points of organic compounds using graph theory-based topological indices. Journal of Molecular Liquids 2022, 353, 118634. [Google Scholar] [CrossRef]
- Ghorbani, M.; Ashrafi, A.R.; Safaei, M.R. Predicting the thermophysical properties of hydrocarbons by applying machine learning methods based on their molecular structure. Journal of Molecular Liquids 2019, 279, 255–266. [Google Scholar]
- Moosavi, M.R.; Azizpour, S.; Mohajeri, A. Prediction of standard enthalpy of formation and boiling point for hydrocarbons using graph-theoretical descriptors. Journal of Molecular Graphics and Modelling 2018, 82, 1–8. [Google Scholar]
- Pelias, W.P.; Cabahug, I.S. Bipartite Domination Number of Mycielski Graph of Some Graph Families. Asian Res. J. Math. 2023, 19, 41–50. [Google Scholar] [CrossRef]
- Dinorog, M.G.; Cabahug, J.I.S. Rings Domination Number of Some Mycielski Graphs. Asian Res. J. Math. 2022, 16–26. [Google Scholar] [CrossRef]
- Sooryanarayana, B.; Chandrakala, S.B.; Roshini, G.R.; Kumar, M.V. Resolving Topological Indices of Graphs. Iranian Journal of Mathematical Chemistry 2022, 13, 201–226. [Google Scholar]
- Varghese, J.; Anu, V.; Aparna, L.S. , 2022. Domination parameters of generalized Sierpi ´ nski graphs. AKCE International Journal of Graphs and Combinatorics, 1-7.
- Maji, D.; Ghorai, G.; Shami, F.A. Some New Upper Bounds for the-Index of Graphs. Journal of Mathematics 2022, 2022. [Google Scholar] [CrossRef]
- Radhi, S.J.; Abdlhusein, M.A.; Hashoosh, A.E. Some modified types of arrow domination. International Journal of Nonlinear Analysis and Applications 2022, 13, 1451–1461. [Google Scholar]
- Cockayne, E.J.; Hedetniemi, S.T. Towards a theory of domination in graphs. Networks 1977, 7, 247–261. [Google Scholar] [CrossRef]
- Chellali, M.; Kheddouci, H. On the Domination Number of Some Classes of Non k-Domination Regular Graphs. Ars Combinatoria 2008, 88, 153–165. [Google Scholar]
- Chellali, M.; Kheddouci, H. On the Domination Number of Some Non k-Domination Regular Graphs. Bulletin of the Australian Mathematical Society 2008, 77, 129–138. [Google Scholar]
- Kamat, N.; Choudhury, S. On the Domination Number of Some Non k-Domination Regular Graphs. Journal of Combinatorial Mathematics and Combinatorial Computing 2018, 107, 31–48. [Google Scholar]
- Mukherjee, S.; Bose, S.K. Bounds on the Domination Number of Non k-Domination Regular Graphs. Journal of Combinatorial Mathematics and Combinatorial Computing 2014, 88, 83–95. [Google Scholar]
Figure 1.
Book graphs:
Figure 2.
Windmill graphs:
Figure 3.
Corona products of and
Figure 4.
Experimental vs predicted values: (a) Entropy with D.I.’s (b) Entropy with and
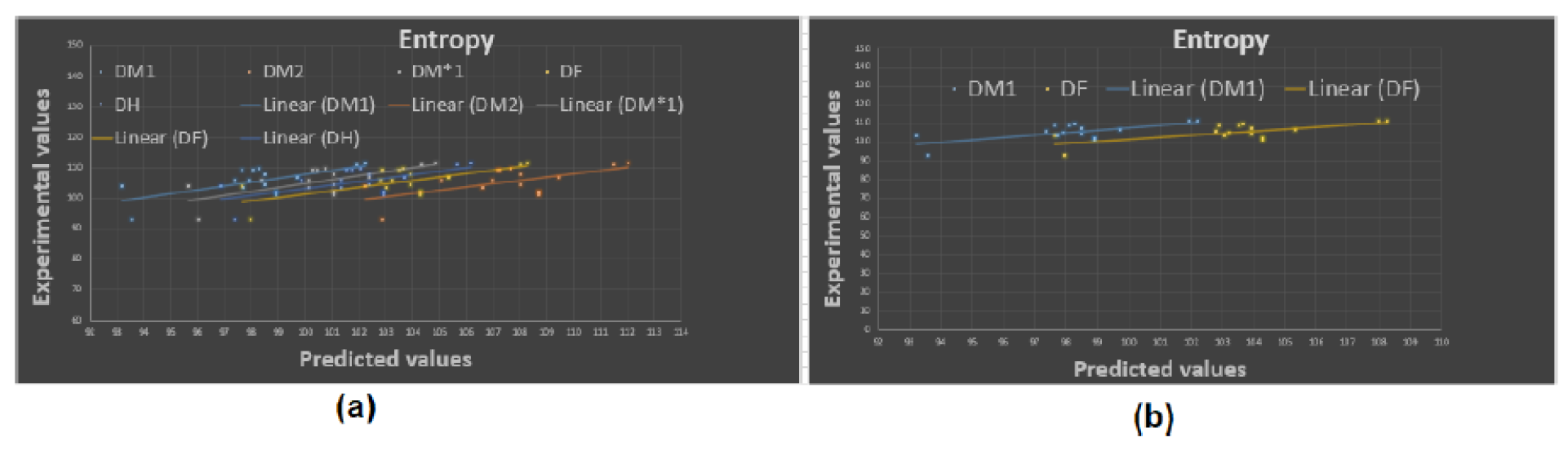
Figure 5.
Experimental vs predicted values: (a) Acentric factor with D.I.’s (b) Acentric factor with and
Figure 5.
Experimental vs predicted values: (a) Acentric factor with D.I.’s (b) Acentric factor with and

Figure 6.
Experimental vs predicted values: (a) Enthalpy of vaporization with D.I.’s (b) Enthalpy of vaporization with and
Figure 6.
Experimental vs predicted values: (a) Enthalpy of vaporization with D.I.’s (b) Enthalpy of vaporization with and
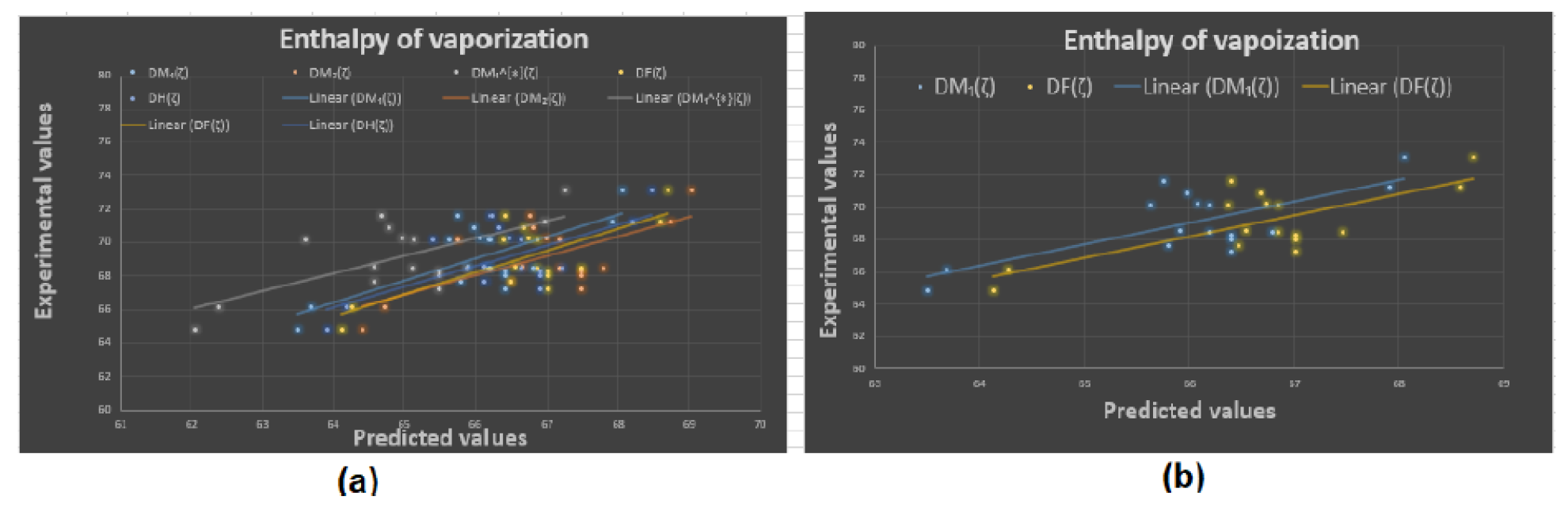
Figure 7.
Experimental vs predicted values: (a) Standared enthalpy of vaporization with D.I.’s (b) Standared enthalpy of vaporization with and
Figure 7.
Experimental vs predicted values: (a) Standared enthalpy of vaporization with D.I.’s (b) Standared enthalpy of vaporization with and
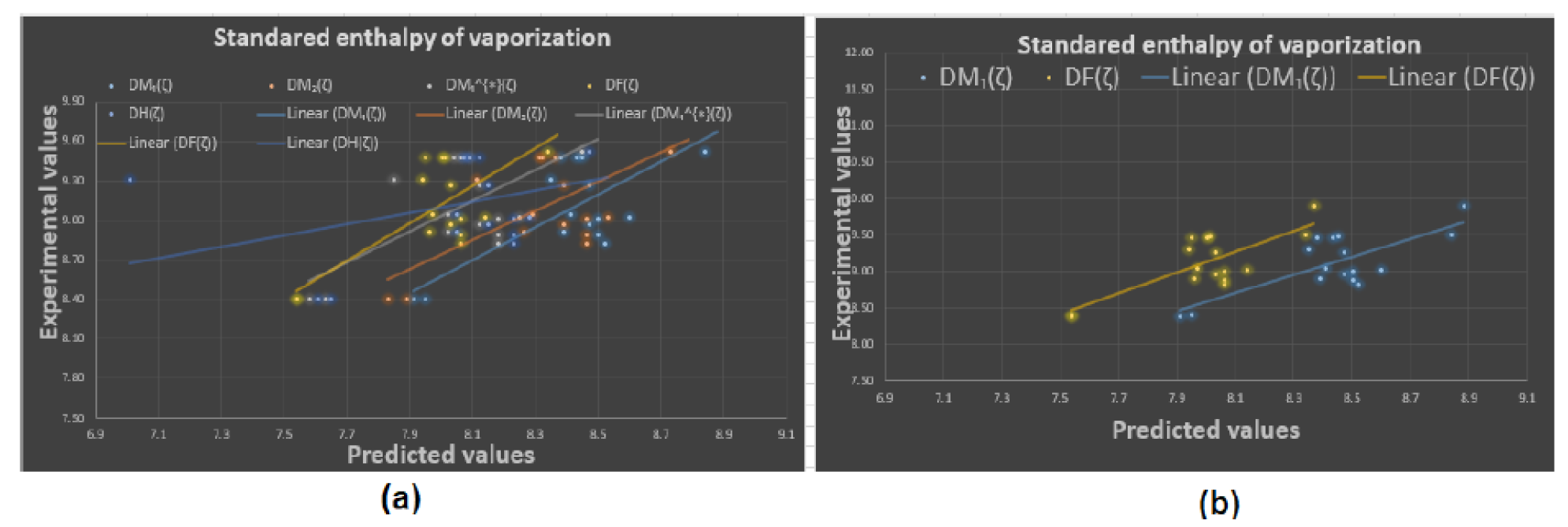
Figure 8.
The correlation coefficient R between the physicochemical properties and the different domination indices
Figure 8.
The correlation coefficient R between the physicochemical properties and the different domination indices
Table 1.
Experimental values of some physicochemical properties of octane and its isomers
| octane and its isomers | Entropy | AcenFac | HVAP | DHVAP |
|---|---|---|---|---|
| n-octane | ||||
| 2-Methyl-heptane | ||||
| 3-Methyl-heptane | ||||
| 4-Methyl-heptane | ||||
| 3-Ethyl-hexane | ||||
| 2,2-Dimethyl-hexane | ||||
| 2,3-Dimethyl-hexane | ||||
| 2,4-Dimethyl-hexane | ||||
| 2,5-Dimethyl-hexane | ||||
| 3,3-Dimethyl-hexane | ||||
| 3,4-Dimethyl-hexane | ||||
| 3-Ethyl-2-methyl-pentane | ||||
| 3-Ethyl-3-methyl-pentane | ||||
| 2,2,3-Trimethyl-pentane | ||||
| 2,2,4-Trimethyl-pentane | ||||
| 2,3,3-Trimethyl-pentane | ||||
| 2,3,4-Trimethyl-pentane | ||||
| 2,2,3,3-Tetramethylbutane |
Table 2.
Domination indices of octane and its isomers
| octane and its isomers | |||||||
|---|---|---|---|---|---|---|---|
| n-octane | 292 | 241 | 82 | 1800 | 968 | 486 | 4 |
| 2-Methyl-heptane | 109 | 88 | 50 | 419 | 362 | 274 | 10 |
| 3-Methyl-heptane | 272 | 210 | 77 | 1648 | 855 | 435 | 15 |
| 4-Methyl-heptane | 104 | 80 | 48 | 400 | 336 | 176 | 16 |
| 3-Ethyl-hexane | 93 | 79 | 47 | 327 | 319 | 161 | 3 |
| 2,2-Dimethyl-hexane | 95 | 69 | 46 | 345 | 304 | 144 | 6 |
| 2,3-Dimethyl-hexane | 116 | 96 | 52 | 456 | 392 | 200 | 8 |
| 2,4-Dimethyl-hexane | 157 | 132 | 61 | 719 | 537 | 273 | 9 |
| 2,5-Dimethyl-hexane | 100 | 75 | 46 | 364 | 304 | 154 | 4 |
| 3,3-Dimethyl-hexane | 116 | 96 | 52 | 456 | 392 | 200 | 8 |
| 3,4-Dimethyl-hexane | 512 | 448 | 112 | 4096 | 1792 | 896 | 0 |
| 3-Ethyl-2-methyl-pentane | 87 | 48 | 37 | 319 | 211 | 115 | 19 |
| 3-Ethyl-3-methyl-pentane | 512 | 448 | 112 | 4096 | 1792 | 896 | 0 |
| 2,2,3-Trimethyl-pentane | 128 | 112 | 56 | 512 | 448 | 256 | 0 |
| 2,2,4-Trimethyl-pentane | 29 | 24 | 26 | 57 | 98 | 50 | 2 |
| 2,3,3-Trimethyl-pentane | 128 | 112 | 56 | 512 | 448 | 256 | 0 |
| 2,3,4-Trimethyl-pentane | 128 | 112 | 56 | 512 | 448 | 256 | 0 |
| 2,2,3,3-Tetramethylbutane | 32 | 28 | 28 | 64 | 112 | 56 | 0 |
Table 3.
Correlation coefficients (R) between domination indices and some physiochemical properties of octane and its isomers
Table 3.
Correlation coefficients (R) between domination indices and some physiochemical properties of octane and its isomers
| Domination indices | Entropy | AcenFac | HVAP | DHVAP |
|---|---|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Downloads
184
Views
35
Comments
0
Subscription
Notify me about updates to this article or when a peer-reviewed version is published.
MDPI Initiatives
Important Links
© 2025 MDPI (Basel, Switzerland) unless otherwise stated







