Preprint
Article
Time Evolution of Energy States
Altmetrics
Downloads
440
Views
254
Comments
0
This version is not peer-reviewed
Submitted:
02 April 2024
Posted:
05 April 2024
You are already at the latest version
Alerts
Abstract
In our investigation of the time evolution of energy states Einstein’s interpretation from more than a century ago is found to have greater internal consistency than that of non-relativistic quantum mechanics. We choose to align more closely with his methods by abandoning the non-relativistic Hamiltonian method, which has been the standard for nearly a century, in favor of a relativistically correct Lagrangian method. Integral equations of motion for the absorption and emission of radiation are derived that underlie and anticipate the differentially motivated Schrödinger equation. This new interpretation applies to a large volume of experimental evidence of both classical and quantum mechanical origin. Among the examples discussed in support are Planck’s law describing black body radiation, matrix mechanics, the function of the simplest quantum mechanical system an electron cyclotron, chaos theory, and evolutionary biology.
Keywords:
Subject: Physical Sciences - Theoretical Physics
1.0. Introduction
There are two distinct approaches for obtaining the equations of motion of a material system.
The more common method is to derive equations that correctly predict the value of physical variables.
We evaluate the correctness of the equation by how well predictions coincide with measurements.
This is how the Hamiltonian formulation of quantum mechanics originated and was manifested
formally in matrix mechanics, wave mechanics, and the path integral formulation. There is an
alternate, more fundamental method we can use if we are not sure which equation is the correct one.
This method allows one to collect together all the equations and express them as the stationary
property of a certain action function, the time-integral of the Lagrangian [1,2]. The Lagrangian
method has the advantage that it can easily be expressed relativistically, on account of the action
function being a relativistic invariant. It calls for minimizing a single physical quantity, the action, in
order to obtain the path actually taken
2. Theory
The Schrödinger equation is a linear partial differential equation that determines how the wave function evolves over time. A probability distribution of all possible particle paths is obtained by taking the square of the wave function. Only one of the paths is realized, the path that results in a particle measurement. However, there is an alternate method that describes the quantum system by taking the time integral of a Lagrangian. It expresses the meaning of the entire set of differential equations describing the paths, irrespective of whether a path is confirmed by measurement. The path realized is the path for which the action is minimized. This second method allows the differential equations of motion for any physical system to be reformulated as an equivalent integral equation.
To describe the time evolution of a quantum state with the Lagrangian method we use symmetry arguments and define the electron shells as surfaces specified by the generalized coordinates R1 and R2. Because quantization consists of two distinct electron paths to complete one cycle, excitation and decay, two equations of motion are required. The first equation describes the electron’s path from R1 to R2 as the action minimum of a Lagrangian. Upon arrival the fields are localized and assume the experimentally determined orbital angular momentum (T-V) = 2πE.
The action functional, S[r(t)], describes the absorption process four-dimensionally as a continuous path that proceeds from the ground state to that of the excited state. It has as its argument an infinite number of functions, the possible electron trajectories r(t). If the initial time t1 of the excitation is arbitrarily set at zero, then the action integral for one sinusoidal cycle of fields is evaluated as follows:
Simplifying, field quantization is described as E τ = ћ.
Emission follows absorption and consists of a four-dimensional localization of fields, the Lagrangian density of the fields and their first derivatives £(ϕi, ϕi,μ), in the region of space-time between the excited and ground states R2 and R1. This allows for a complete accounting of the energy interactions, where ϕi is the current density due to a transitioning electron and ϕi,μ is the localized electromagnetic field strength that results in the creation of a photon.
Solving 2) we obtain an expression for the localized fields of a photon Eτ=ћ. The action S[ϕi(t)] is a functional, a function of the values of generalized coordinates on the discrete boundaries of the space-time surfaces R2 and R1 which are in turn functions of the continuous space-time variables of the fields within the surface. The photon is described therefore as a four-dimensional localization of fields contained within the volume ∫d3x and the time interval t2-t1 . Thus discrete and continuous properties of the energy transformation process are described in a single equation.
We will use the time evolution of quantum states given by 1) and 2) to introduce new perspectives for deriving the laws of nature. Rather than formulating classical laws separately from quantum mechanical laws we seek equations of motion that include classical and quantum concepts together. Thus the time evolution of a quantum state consists of a continuous energy increase of classical origin, a discrete quantum mechanical transformation, followed by the emission of a four-dimensional localization of energy. We will show in the following that this physical model, as described by 1) and 2), has heuristic value and leads to further insights into the behavior of natural phenomena.
3.0. Applications
3.1. Absorption and Emission of Radiation
Einstein made significant contributions towards the formulation of a quantum theory of radiation [4]. He was the first to describe the properties of photons in detail, assigning a momentum +E/c to an absorption and momentum -E/c to an emission. He anticipated the invention of lasers with the concept of stimulated emission and his analysis of momentum transfer in a thermal radiation field is a good preliminary description of laser cooling. Despite making substantial progress towards formulating the foundations, he disagreed in the end with the final form that quantum mechanics took. Many have questioned why he chose a solitary path, but he never explained the precise reasons, saying only [5] “I cannot base this conviction on logical reasons, but can only produce my little finger as witness, that is, I offer no authority which would be able to command any kind of respect outside of my own hand." In the following pages we will uncover his reasons for diverging from orthodox quantum theory by examining his unfinished work.
The first sentence of Einstein’s seminal paper ”On the quantum theory of radiation” summarizes the content of the entire paper [4]. “The formal similarity between the chromatic distribution curve for thermal radiation and the Maxwell velocity-distribution law is too striking to have remained hidden for long.” By drawing attention to the formal similarity between the Planck radiation curve and the Maxwell-Boltzmann curve he emphasizes their close physical relationship. The only possible meaning it could have is that the radiation energy of quantum mechanical origin emitted by a black body is directly proportional to the kinetic energy of classical origin that is absorbed. He continues, “By postulating some hypotheses on the emission and absorption of radiation by molecules, which suggested themselves from quantum theory, I was able to show that molecules with a quantum-theoretical distribution of states in thermal equilibrium, were in dynamical equilibrium with the Planck radiation.” If, as Einstein asserts, molecules radiate while in thermal equilibrium, then a molecule’s kinetic energy, as specified by temperature, determines to close approximation the energy of the photon that it emits.
Building on the presumed proportionality between absorption and emission energy he makes use of momentum conservation to analyze more closely the relationship between the classically defined thermal energy and quantum mechanical emissions [4].
“We now turn to the investigation of the motion which our molecules execute under the influence of radiation. In doing this we use a method which is well known from the theory of Brownian movement, and which I have used repeatedly for calculations of movements in a domain of radiation. In order to simplify the calculation, we carry it out only for the case where movement occurs just in one direction, i.e., in the X- direction of the coordinate system. The molecule can then be treated with ordinary mechanics. . . Let a molecule of given kind be in uniform motion with speed v along the X-axis of the coordinate system K. We inquire about the momentum transferred on the average from the radiation to the molecule per unit time. To calculate this we must consider the radiation from a coordinate system K′ that is at rest with respect to the given molecule. For we have formulated our hypotheses about emission and absorption only for molecules at rest.”
The coordinate system K is classical, while K′ is quantum mechanical. Heat is absorbed by molecules continuously in K and is then emitted discretely in K′. Einstein uses the conservation of momentum to justify a causal relationship with energy exchange and hypothesize the existence of the A and B coefficients. For an atom with energy states |1> and |2> the coefficient B12 refers to induced energy and momentum “transferred on average from the radiation to the molecule” in the coordinate system K. The coefficient A21 refers to spontaneous emission and B21 refers to induced emission, both measured relative to a coordinate system K' at rest relative to a given molecule. A more complete description of the influence of the conservation laws on the absorption and emission of radiation appears elsewhere [6].
Although Einstein did not complete a quantum theory of radiation he did show that its initial conditions require two equations of motion to describe absorption and emission, a classical equation to describe molecular impulses in K(r,t) that satisfies Maxwell-Boltzmann statistics, and a quantum mechanical equation in K'(r,t) that satisfies photon emission according to Planck statistics. The wave function ψ(r,t) is an equation of motion that uses three spatial dimensions and time to describe the emission and absorption of radiation. It has sufficient degrees of freedom to describe a quantum system’s energy exchanges in K', but not for exchanges of momentum in K that use continuous physical variables to describe kinetic energy. By associating the equations K and K' with the equations 1) and 2) we interpret non-relativistic theory in a way that is more fundamental because it is relativistically correct.
3.2. Matrix Mechanics
Heisenberg discovered sets of complex mathematical rules that reconcile the continuity of radiation fields with the discrete energy states of an atom by expressing electron transitions in the form of matrices [6].
The diagonal elements n=m represent the observable properties of energy, the transition probabilities and frequencies, which are emissions formulated relative to the internal coordinates of an atom. Non-diagonal matrix elements n≠m refer to net zero exchanges of absorption and emission energy, E23 – E32 = 0, but overall positive exchanges of absorption energy are induced causing increases in the kinetic energy of molecules and temperature of the gas. However, because impulses due to molecular impact cannot be observed individually Heisenberg did not take them into account believing that quantum mechanics should be “founded exclusively upon relationships between quantities which in principle are observable”.
Although he eliminated exchanges of momentum, from consideration due to an inability to measure them Heisenberg soon realized that something was missing, lamenting to Pauli in a letter [7], “But the worst thing is that I am quite unable to clarify the transition [of matrix mechanics] to the classical theory.” If he had properly considered Einstein’s findings, that momentum and energy are causally related, he would have realized that he had violated the conservation of energy by disregarding classical theory and going directly to quantum theory. Because quantum emissions cannot occur without the absorption of heat energy, matrix mechanics is an incomplete formulation of quantum mechanics so that a formal link between the classical and quantum theories could not be established. A complete matrix would add positive, though indeterminate kinetic energy values to all matrix elements, diagonal and non-diagonal, due to exchanges of momentum, where the non-diagonal elements are described in K and diagonal elements in K'. A comparison of Einstein’s system with that of matrix mechanics is more completely described elsewhere [3].
3.3. The Geonium Atom
We have discussed the time evolution of energy states in abstract terms by using the theoretically derived equations 1) and 2) and Einstein’s A and B coefficients. We wish now to compare theory and practice with a fascinating series of experiments that could not possibly have been imagined by the founders of quantum mechanics in 1926. The experiments are superior in precision and simplicity to the single-electron hydrogen atom used to derive non-relativistic quantum mechanics. In fact the “geonium atom” is the simplest possible quantum system since it replaces the nucleus with an external apparatus bound to the earth [8]. It is possible to trap single electrons in a “bottle” made of intersecting electric and magnetic fields and cool them to near absolute zero. The fields may then be used to manipulate the motion of an electron as it transitions between energy levels at rates many magnitudes slower than the electrons in an atom. The trapped electron constitutes an artificial atom or “quantum cyclotron”. The measurements are so sensitive that the influence of the earth’s gravitational field must be taken into account in order to calculate the equations of motion.
Applying a relatively large constant magnetic field to the trap causes the electron to execute two different types of motion simultaneously; circular orbits perpendicular to the field and axial drifts parallel to it. The experiments are used to precisely observe the absorption and emission of energy by a quantum oscillator. As they describe it, “There is a small alternating magnetic field in the particle’s rest frame, which is perpendicular to the large constant magnetic field. This alternating magnetic field has a frequency component and so a spin-flipping resonance occurs when the drive frequency equals the anomaly frequency.” In other words, the electron is stimulated by a small classically defined magnetic field in K with varying frequency. The drive frequency gradually shifts upwards with increasing energy until it causes a discrete “spin-flip” to occur in K'.
According to the standard model electromagnetic field energy is quantized before it is absorbed. Experiments performed with geonium, the simplest possible quantum system, clearly indicate otherwise. As Einstein anticipated, energy is absorbed continuously due to classical magnetic resonance and emitted discretely in the form of a spin-flip. Belief that pure quantum states exhibit time reversal symmetry is denied here by experimental proof. Spin flips cannot be manipulated to reproduce or counteract the continuously variable potential of magnetic fields. Thus experimental techniques have outstripped theoretical principles derived a century ago when relatively simple spectroscopic measurements were all that was available. The change in state of an electron that is isolated physically and subjected to an electromagnetic potential is correctly interpreted by applying equations 1) and 2).
3.4. The Time Parameter
Quantum mechanics as presently formulated does not distinguish clearly between the determination of states and the time evolution of states. The energy of a state is measured at single points in time whereas the time evolution of energy states occurs continuously over a period of time. To illustrate the difference consider Planck’s radiation law Bν(ν, T) for black body radiation which gives the distribution of energy states, or frequencies, for oscillators at a given temperature.
Each point on the curve describing Planck’s law represents emission frequency due to the decay of an oscillator from an excited state to a lower energy state at a given temperature. Einstein introduced the idea that quantized packets of energy are required to account for the electron decays [9]. The measurements are manifestly non-relativistic since temperature cannot be transformed relativistically [10].
Equation 3) successfully describes the observed distribution of quantum states in terms of their frequencies, but it does not describe how the quantum states themselves evolve. Einstein was not satisfied with his non-relativistic interpretation of Planck’s law so he continued studying the question. Four years later he was finally able to obtain a detailed balance equation describing the mean square fluctuation in energy due to photon numbers combined with the superposition of electromagnetic fields [11].
As Einstein describes it, “According to the current theory, the expression would be reduced to the second term (fluctuation due to interference). If the first term alone were present, the fluctuations of the radiation pressure could be completely explained by the assumption that the radiation consists of independently moving, not too extended complexes of energy hν. In this case, too, the formula says that in accordance with Planck's formula the effects of the two causes of fluctuation mentioned act like fluctuations (errors) arising from mutually independent causes.” The first term is given discretely in K' and the second term continuously in K.
There are very noticeable differences in the equations 3) and 4), both of which describe Planck’s radiation law, for the simple reason that each one is designed for a particular purpose. By accurately describing the spectral density of black body radiation Planck’s derivation of 3) succeeds in predicting what is observed (see 1.0). It is a non-relativistic equation because it is only valid in inertial systems relative to absolute time; that is, in the absence of the influence of gravitational fields. On the other hand, Einstein’s equation 4) is formulated in continuous time as a statistical balance between the incoming energy resulting from the wave properties of electromagnetic radiation in K and the outgoing energy due to photon emission in K'. The total energy, discrete and continuous, emitted by the time evolution of states is obtained by integrating, which occurs physically by means of the averaging effects of a detector. As a balance equation formulated continuously in time it holds irrespective of the intensity of gravitational fields. Because it corrects naturally for time dilation we say it is formulated relativistically.
3.5. Liquid Helium in a Box
Quantum mechanics is believed to be restricted to applications at the microscopic level. There are, however, many classical experiments which look suspiciously like the quantum jump. Consider the flow of heat through a quantity of liquid helium confined in a box [12]. When a very small temperature difference of a mere 0.001°C is applied to the upper and lower sides of the box, heat energy flows continuously causing cylindrical rolls of fluid to be created by the thermal currents. The rolls conduct a continuous flow of energy from high temperature to low. We can associate the equations of motion of helium molecules with paths whose action minima are described by equation 1).
A slight increase of heat causes a wobble to appear and then the period doubles, or "bifurcates" as a second oscillation is added. The bifurcation, which increases energy flow by adding a second dissipation center, may be described as a four-dimensional localization of energy as in equation 2). The flows do not interfere with each other so the superposition is continuous. However, the appearance of the new dissipation center occurs discontinuously. Continuous increases of energy are followed by discrete transitions to a new center of flow and a heightened flow level overall. It supports the hypothesis that the time evolution of energy states described in 2.0 has universal value since it can be applied to both microscopic and macroscopic phenomena.
3.6. Pendulum Connected to an External Drive
We can also observe bifurcations graphically by tracing a pendulum’s motion with respect to equally spaced points in time [13]. In the Figure 1 and Figure 2) we see the time-asymptotic phase-space orbit of a pendulum as it transitions from period one motion to period two motion in response to an external drive. In period one motion the pendulum repeats the same motion over and over. In period two motion the cycles are distinguishable from each other and are repeated on alternate periods of the external drive. The transition from period one to period two occurs unpredictably at a single moment in time.
The diagrams describe the time evolution between classical energy states. The symmetry of the experiment calls for generalized coordinates in the plane of the orbits just as generalized coordinates on electron shells is called for by the atomic transitions described in equations 1) and 2). Rather than deriving differential equations of motion by calculating the positions and velocities of the pendulum as in Newtonian mechanics; we apply Hamilton’s principle, which states that the path actually taken is the path for which the action is minimized, where the action S[q(t)] is given by the time integral of a Lagrangian.
We describe the energy state of period one motion in 6) relativistically by integrating the action over the period of an orbit t2 – t1. The energy state of period 2 motion (two oscillations) is slightly higher than twice the energy of period 1 motion. The transition between period one and period two motion, referred to as a “bifurcation”, occurs discretely. As in the case of quantum states, it is impossible to describe the change in path of the transition deterministically by means of a differential equation of motion.
A non-relativistic description of pendulum motion would seek to predict the energy difference between period 1 motion and period 2 motion. This is because the Schrödinger equation describes transitions between energy states (the eigenvalues) as time-independent values measured at single points in time. It would disregard the continuous motion of the pendulum and instead attempt to measure the difference between the period one and period two energy states, the transition energy. As noted in 3.4 transition energy is non-relativistic if it is measured discretely at a single point in time, and relativistic if a continuous increase of energy is followed by a discrete transition to a higher energy state.
4.0. Conclusion
An improved description of the time evolution of energy states is obtained by using a Lagrangian formulation for it includes both classical and quantum mechanical concepts: continuous absorption, discrete four-dimensional localization, and the release of energy. The differences between a non-relativistic Hamiltonian formulation and the more fundamental Lagrangian formulation become especially apparent when macroscopic phenomena are considered. In macroscopic, classically defined experiments such as period doubling (Figure 3) absorptions are continuous, easily measured, and evolve in regular intervals determined by the Feigenbaum constants [14]. Thus changes of state are more accurately interpreted by means of Lagrangian methods which describe continuous energy absorption with 1) and discrete energy emission with 2).
This new physical model describing the time evolution of energy states has heuristic value in the search for a more complete understanding of nature. The gradually increasing energy of a material system followed by discrete changes in structure is a pattern that is repeated countless times. We find it in the extremely small, the emission of a photon by an atom; the extremely complex, period doubling phenomena in chaos theory; and the extremely large, the gravitational collapse of a star that results in the formation of a black hole. The same energy transformation pattern is even found in a theory of evolutionary biology. Periods of uniformity in the fossil record are often followed by sudden structural change in a process referred to as “punctuated equilibrium” [15]. By establishing the correct mathematical foundations as in 2.0 it is possible to appreciate that quantum mechanics is a truly universal theory of nature touching every aspect of the world around us, both microscopic and macroscopic.
Although the Hamiltonian formulation of quantum mechanics provides an accurate description of what is observed, the emission energy, it gives an incomplete description of what cannot be observed, the absorption energy. Absorption energy must precede emission energy in order to satisfy energy conservation. Thus the wave function represents two events, and due to the conservation of energy the first (absorption) must be carried out to completion before the second one (emission) can begin. Each one is governed by the uncertainty principle since each one follows a path determined by the action minimum ћ. Because the wave function includes twice the action minimum it does not describe paths or particles, rather it represents one cycle of a quantum oscillator.
References
- Lanczos, C. The Variational Principles of Mechanics 4th edn. (Dover, 1970).
- Dirac, P.A.M., “The Lagrangian in quantum mechanics” Phys Zeit Sow 3, 1933, p.1. https://www.informationphilosopher.com/solutions/scientists/dirac/Lagrangian_1933.pdf.
- Oldani R. (2024). Foundations of Quantum Mechanics Revealed by the Conservation Laws. https://www.qeios.com/read/ROFQKG.7.
- Einstein, A. “On the quantum theory of radiation” Phys Z 18, 121 1917, p. 63. https://www.informationphilosopher.com/solutions/scientists/einstein/1917_Radiation.pdf.
- Born-Einstein letters, 1916-1955.
- W. Heisenberg Z Phys 33 (1) (1925), in B.L. van der Waerden (ed.), Sources of Quantum Mechanics (Amsterdam, 1967). http://www.mat.unimi.it/users/galgani/arch/heis25ajp.pdf.
- Pauli, W. Wissenschaftlicher Briefwechsel mit Bohr, Einstein, Heisenberg. Vol 1 Hermann, A., von Meyenn, K., & Weisskopf, V. Eds. (NY: Springer, 1979), p. 251.
- Brown, L.S.; Gabrielse, G. (1986). “Geonium theory: physics of a single electron or ion in a Penning trap”Reviews of Modern Physics. 58 (1): 233–311. [CrossRef]
- Einstein, A. “On a heuristic point of view about the creation and conversion of light” Annalen der Physik 17 (1905). [CrossRef]
- Landsberg, P. and Matsas, G. “The impossibility of a universal relativistic temperature transformation” Physica A 340 (1-3) (2004), 92-94. [CrossRef]
- Einstein, A. “On the present status of the radiation problem” Phys Z 10 (1909) 185-93. https://einsteinpapers.press.princeton.edu/vol2-trans/.
- Libchaber in Nonlinear Phenomena at Phase Transitions and Instabilities, ed. T. Riste (NY: Plenum, 1982), p. 259.
- Fitzpatrick, R. Introduction to Computational Physics (University of Texas), p. 155, 164.
- Feigenbaum, M. J. (1978). "Quantitative universality for a class of nonlinear transformations". Journal of Statistical Physics. 19 (1): 25–52. [CrossRef]
- Eldredge, N.; Niles, S.J. (1972). “Punctuated equilibria: An alternative to phyletic gradualism” In Schopf, T.J.M. (ed.). Models in Paleobiology. San Francisco, CA: Freeman Cooper. p. 82.
Figure 1.
Period one motion.
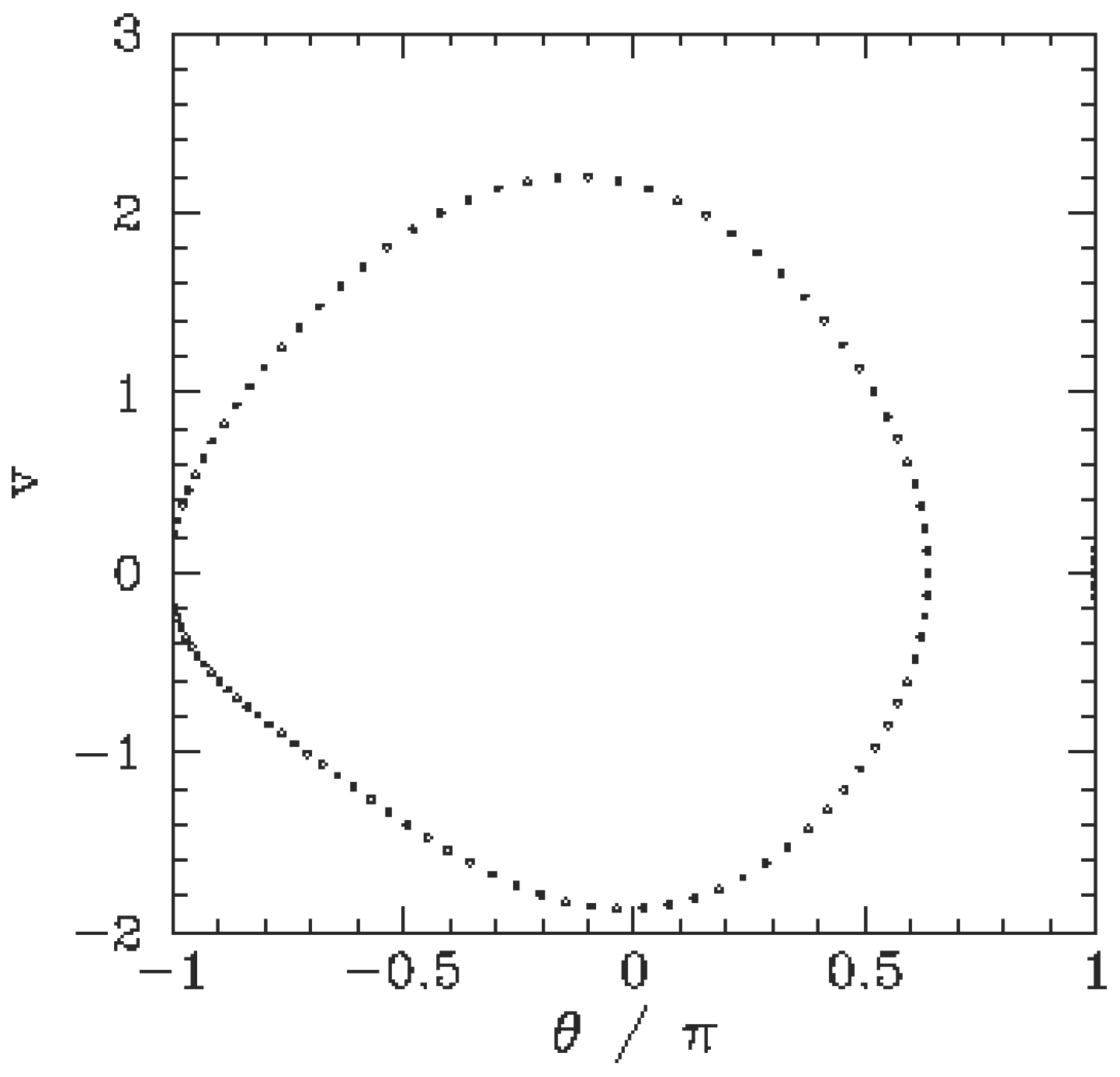
Figure 2.
Period two motion.
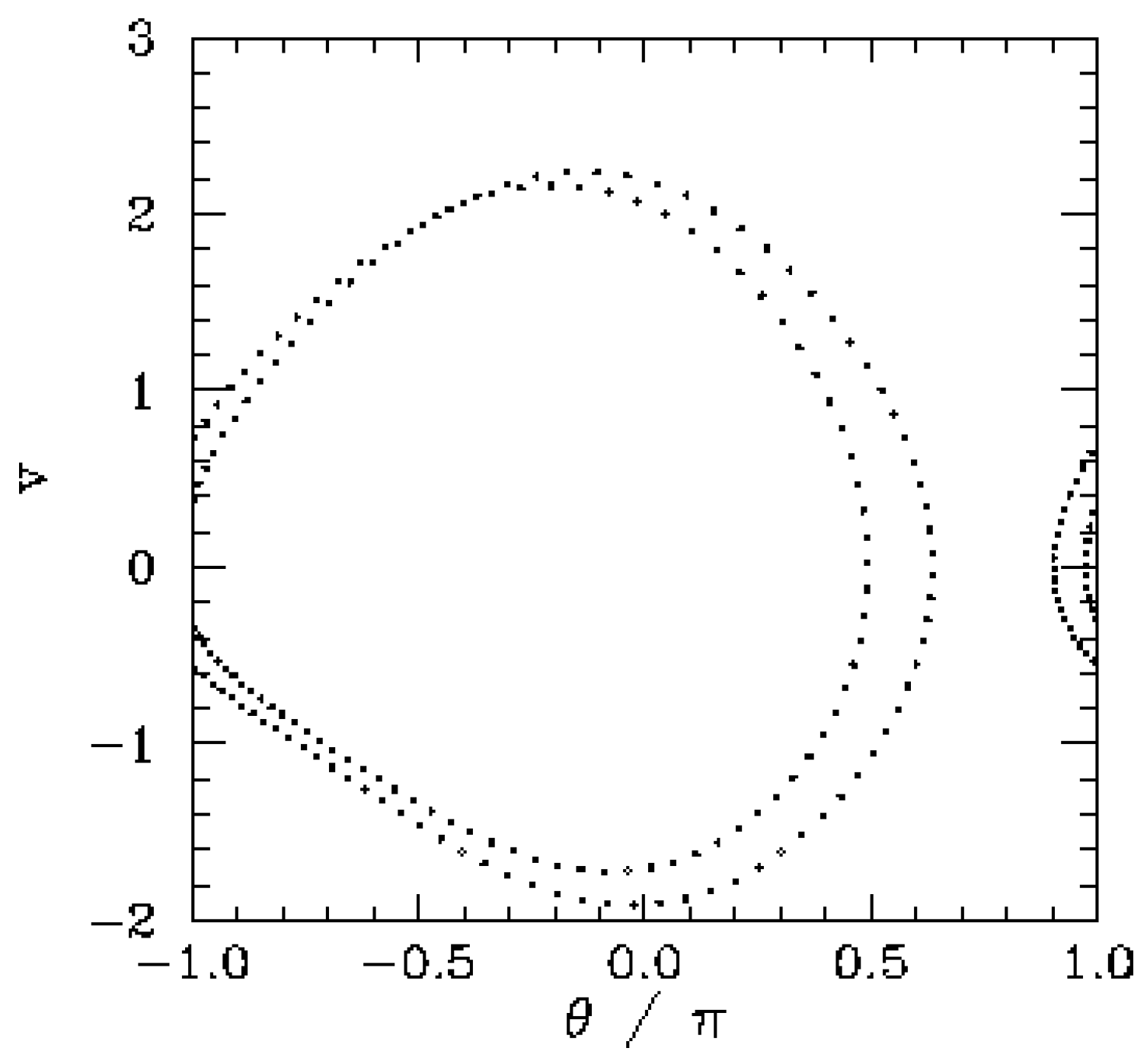
Figure 3.
Period doubling on the way to chaos.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





