Prerpints.org logo
Preprint
Article

Enhanced Automated Deep Learning Application for Short Term Load Forecasting

Altmetrics

Downloads

186

Views

59

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

12 May 2023

Posted:

15 May 2023

You are already at the latest version

Alerts
Abstract
Nowadays, power sector is an area that gather great scientific interest, due to events such as the increase in electricity prices in the wholesale energy market and new investments due to technological development in various sectors. These new challenges have in turn created new needs, such as the accurate prediction of the electrical load of the end users. On the occasion of the new challenges, Artificial Neural Networks approaches have become increasingly popular due to their ability to adopt efficiently to time-series predictions. In this paper, it is presented the development of a model which, through an automated process, will provide an accurate prediction of electrical load for the island of Thira in Greece. Through an automated application, deep learning load forecasting models have been created, such as Multilayer Perceptron, Long Short-Term Memory (LSTM), Convolutional Neural Network One Dimensional (CNN-1D), CNN-LSTM, Temporal Convolutional Network (TCN) and a proposed hybrid model called Convolutional LSTM Encoder-Decoder. The results in terms of prediction accuracy show satisfactory performances for all models, with the proposed hybrid model achieving the best accuracy.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

The power energy sector is perhaps gathering the most interest from scientists and stakeholders in recent years, due to the rapid development and changes that have occurred. New investments, which create needs for new equipment, but also the establishment of new rules and legislation aimed at protecting the environment and eliminating the greenhouse effect, make this sector more critical and create necessary conditions for its control. At the same time, a wide and extensive energy crisis has been created on a global scale, mainly due to the recent phenomenon of the war that has broken out in Northern Europe. Large industrial units and businesses are suspending their operations due to increased operating costs. With the global increase in electricity demand, the uncertainties and energy risks have also increased. Electrical load forecasting is extremely important for all energy parts to ensure the performance and effective of the power network. This sector is generally classified as very short-term load forecasting (VSLTF) forecasts load for few minutes, short-term load forecasting (SLTF) ranges from one hour to one week ahead, mid-term load forecasting (MLTF) forecasts load more than one week to few months and long-term load forecasting (LTLF) could forecast load longer than one year [1]. In this work, STLF is used to predict future electrical demand. In terms of electrical load forecasting, several methodologies have been introduced and can be classified into two main groups the traditional and the modern methods. In traditional techniques, statistical methods are mostly applied. These include models like autoregression (AR), moving average (MA), autoregressive moving average (ARMA), autoregressive integrated moving average (ARIMA), ARMA and ARIMA with exogenous inputs (ARMAX and ARIMAX respectively), grey (GM) and exponential smoothing (ES) [2,3].
On the other hand, modern load forecasting methods take advantage of neural networks, which are more suitable for processing complex associations within the data and for developing robust forecasting models that are tolerant to noise. The simplest Artificial Neural Network (ANN) is the Multi-Layer Perceptron (MLP) which can model non-linear trends, is able to manage missing values in the datasets, but also provide fast predictions after training [4], such as Kontogiannis et al. were observed at trials with household electrical power consumption data. The proposed MLP model in comparison with LSTM models with several configurations and 1D CNN model presents lower loss function score (mean absolute error) and faster average converge time [5]. Arvanitidis et al. use MLP models to suggest novel train data pre-processing approaches [6] and clustering techniques [7] for SLTF. Furthermore, MLP architecture is extended to conduct a day-ahead electricity price forecasting [8].
Moreover, another type of ANNs are the long short-term memory (LSTM) networks, which are capable to identify the long-term dependencies between data points. In 2017, Zheng et al. [9] presented a hybrid algorithm that combines similar days (SD) selection, Empirical Mode Decomposition (EMD), and LSTM neural networks to construct a prediction model for STLF of ISO New England. This hybrid model compared to other forecasting models shows a good effectiveness on SDs clustering and accurate forecasting on complex non-linear electric load time series. Additionally, Kwon et al. in 2020 [10], proposed a LSTM model combined with fully-connected (FC) layers, which predicts Korea’s total electrical load. Specifically, the LSTM layer is used to extract the variability and dynamics from historical data, while FC layers are used to project prediction data and shape the relationship with the output of the layer. The proposed model demonstrated lower load forecasting error (mean absolute percentage error) compared with the STLF method which Korea’s power operator have been using. Another hybrid model was presented from Jin et al. [11] for the real power prediction in three Australian major states, which accomplishes high prediction accuracy. Authors to strengthen the prediction performance were focused on the importance of the data pre-processing with variational mode decomposition (VMD) method and conducted an advanced optimization technique with the binary encoding genetic algorithm (BEGA) to optimize the length of the input data sample unit of the LSTM and the number of the cell units.
Furthermore, a few studies have found that the LSTM models can be combined with the Convolutional Neural Networks (CNNs) which can extract the features of the input data. In 2018, Tian et al.[12] firstly introduced a new STLF model which combines CNN and LSTM modules to improve the forecasting accuracy. After several conducted detailed experiments on real world load data from the Italy-North area, authors were concluded that the proposed model improve performance at least 12% and 14% compared the individual CNN and LSTM prediction models, respectively. Similarly, Rafi et al. [13] found that the developed CNN-LSTM network provides the lowest values of evaluation metrics compared to LSTM, radial basis functional network and extreme gradient boosting models for the short-term load forecasting in the Bangladeshi power system. In [14], the authors studied the forecasting performance of an attention-based CNN combined with LSTM and bidirectional LSTM model with a time sequenced, non-linear, and complex electrical load data from an integrated energy system park in North China. The examined model and other attention-based LSTM models prediction performances were better than the traditional machine learning models like backpropagation neural network (BPNN), random forests regression (RFR) and support vector regressor (SVR). Even though the previous mentioned ANN models present exceptional forecast performance, researchers [15] mentioned that extracted features of the CNN module influences the training of LSTM. So, they were also suggested a combined CNN and LSTM model but the CNN module and LSTM module work in two parallel paths, the processed data then enters a fully connected layer, which includes dense and dropout layers, and leads to the final prediction. The suggested framework named PLCNet, was tested in two case studies for different time horizons and manifest that this approach has advantages in accuracy and model convergence speed.
In addition to the previous mentioned ANNs topologies, recent studies have examined the use of the Temporal Convolutional Network (TCN) model for short-term load forecasting due to the superiority in long-term feature extraction in time series. Peng and Liu [16] suggests a TCN prediction model for residential short term load forecasting based on the AMPds2 smart energy meter dataset. The important consumption elements are determined as auxiliary inputs to the prediction model, after a correlation analysis among total load and appliance loads of the household. In terms of prediction performance, the proposed model obtains the lower evaluation metrics than the compared models. In [17], researchers examined a hybrid TCN – LightBGM model opposed to statistical, deep learning, tree and hybrid models for a range of industrial consumers. This hybrid model utilizes the benefits of TCN in feature extraction and LightGBM in load prediction which yields to improved forecast accuracy in comparison with the contrast models. Other researchers were proposed [18] a novel STLF model based on TCN and Attention Mechanism (AM), which examines the effect of weather fluctuations on the load forecast and reveals the non-linear association between weather and load data. Additionally, a combination of fuzzy c-means (FCM) clustering algorithm and dynamic time wrapping (DTM) was applied to classify in clusters similar power data. Despite the proposed framework presented slower training time per epoch than the compared models, due to the requirement of more weight parameters to be trained. But also presented a more accurate prediction in terms of evaluation metrics.
Lastly, the ANN topology we propose in this work for STLF is a hybrid model named Convolutional LSTM Encoder-Decoder which was used by other researchers to forecast global total electron content [19] and to predict the El Niño-related Oceanic Niño Index (ONI) and El Niño events [20]. Generally, our research contributions can be summarized as follows:
  • Proposal of a hybrid model called Convolutional LSTM Encoder-Decoder for power production time series.
  • Presentation of an automated STLF algorithm which incorporates data pre-processing techniques, training, and optimization several AI models, testing and prediction of the results.
The remaining part of the paper is organized as follows: Section 2 presents several short-term load forecasting approaches. Section 3 analyses the dataset, the essential procedures related to the pre-processing of the data used for forecasting, the architecture of the artificial intelligence models and the automated STLF algorithm. In Section 4, the experiments of the case study are illustrated and the results of experiments are discussed. Finally, Section 5 contains the conclusions of this work and suggests some directions for future work.

2. Materials and Methods

This section provides a brief and concise description of the fundamental concepts of each of the Deep Learning models that are used in this paper. More specifically, the following descriptions for each model are presented.

2.1. Forecasting Approaches

2.1.1. Long Short-Term Memory Networks

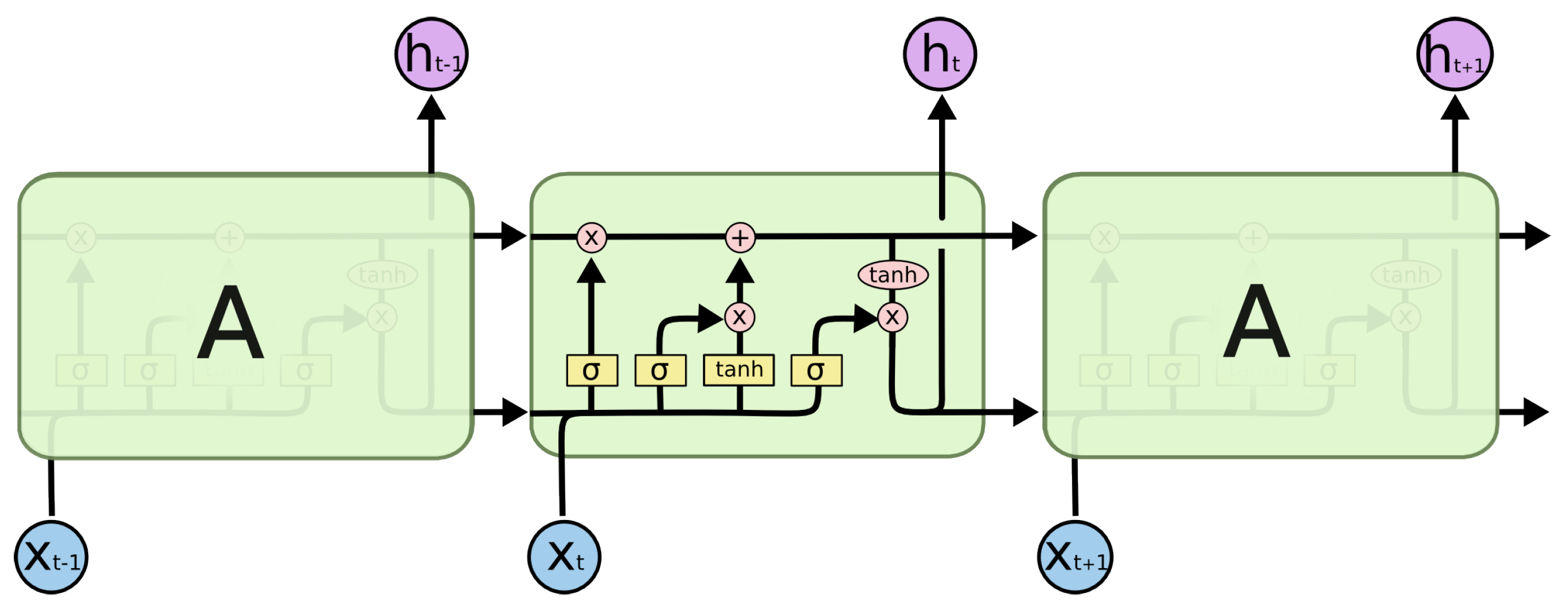
Long Short-Term Memory models are a variant kind of RNNs networks that overcomes the vanishing or explosion of gradients of the latter when processing the long-term dependencies of load series. They were proposed firstly in 1970 in order to handle efficiently the long-term dependencies may exist in time series. Through adding the input, output, and forget gates to the RNN, the LSTM has been widely used in natural language processing (NLP), machine translation, load forecasting and at the health sector.
About the architecture and working principle about the core idea behind the LSTM (Figure 1), the key operating point is the cell state, which is the horizontal black line at the top of the middle module and is connecting link between the modules [21].
The working mechanism of the LSTM structure, from left to right, is described below:
  • Forget Gate: It is decided which bits of the cell state (long term memory of the network) are useful given both the previous hidden state and new input data. At bottom, the forget gate controls which part of the long- term memory must be forgotten.
    f t = σ ( W f h t − 1 , x t + b f )
  • Input Gate: The main operation of the input gate is to update the cell state of the LSTM unit. Firstly, a sigmoid layer decides which values it is going to be updated. Next, a tanh layer creates a vector of all possible values that can be added to the cell state and finally these two are combined to update the cell state.
    i t = σ W i h t − 1 , x t + b f
    C t ˜ = t a n h ( W C h t − 1 , x t + b C )
  • Cell State: The Cell State multiplies the old state by f t and then adds i t * C t ˜ .
    C t = f t * C t − 1 + i t * C t ˜
  • Output Gate: The output gate decides what information it is going to output. Using a sigmoid and a tanh function to multiply the two outputs they create, it is decided what information the hidden state must carry.
    o t = σ W o h t − 1 , x t + b o
    h t = o t * t a n h ( C t )

2.1.2. Multi-Layer Perceptron

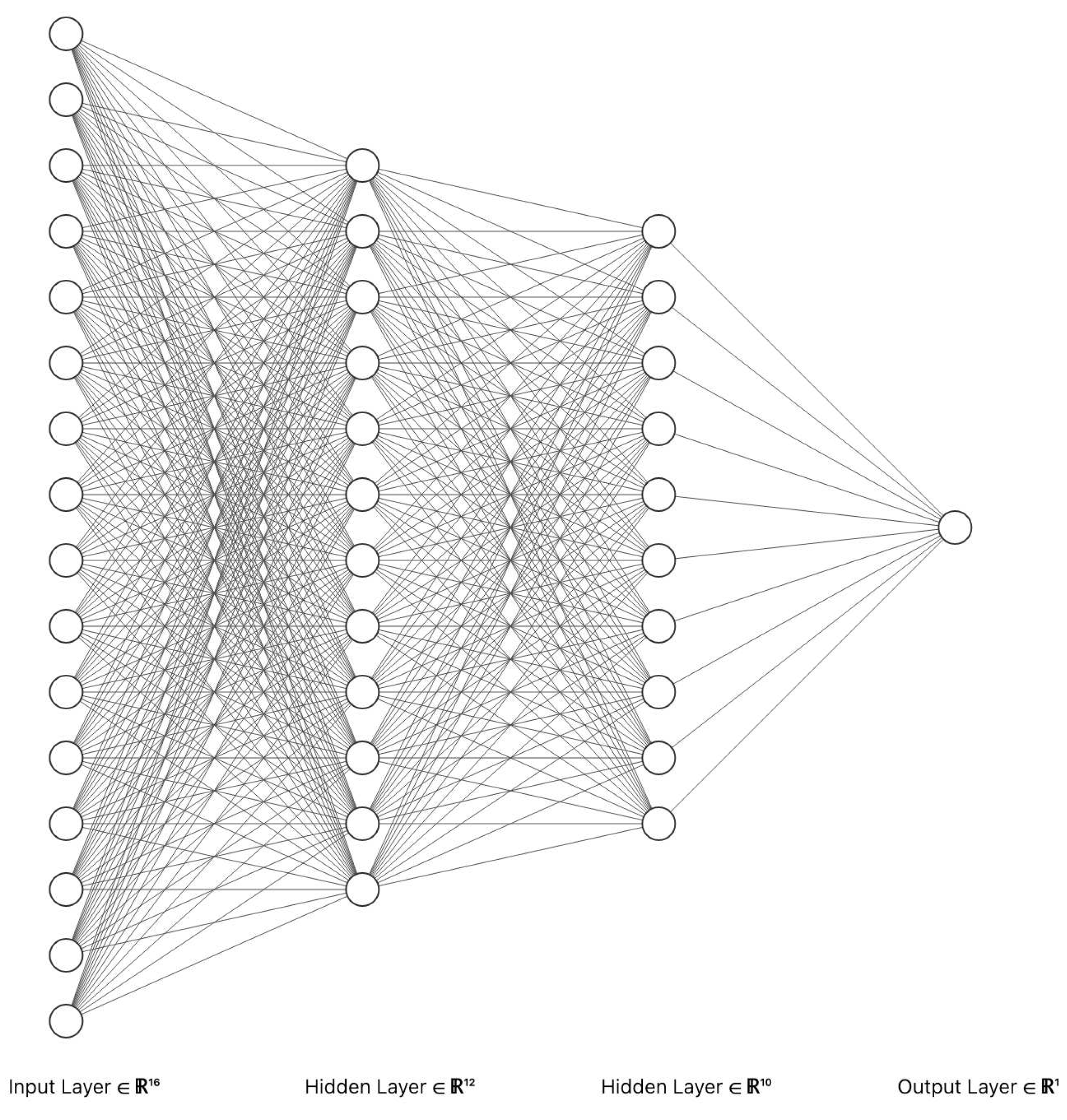
Multilayer Perceptron (MLP) is a type of Deep Learning Feed-forward Neural Network that consists of a fully connection of hidden layers and has one input and one output layer. The MLP’s architecture is illustrated in Figure 2.
The process by which MLP algorithms are trained to be able to predict future data is as follows:
  • Firstly, MLP algorithms use a Forward Propagation Process to calculate their parameters at the training period, as they propagate data from the input to the output layer.
  • Secondly, the network calculates the value of loss function, which contains the difference between actual and forecasting data and tries to find the optimal solution, minimizing the error [23].
  • Then, using backpropagation algorithms, they calculate the gradient of loss function and updated the values of the synaptic weights between neurons [24].
This process is repeated until the model finds its optimal hyperparameters.

2.1.3. Convolutional Neural Networks

Convolutional Neural Networks (CNN/ ConvNet) is a type of deep learning feedforward algorithm, which was originally used for pattern recognition. They are quite similar to conventional neural networks, as MLPs, since they consist of neurons that contain synaptic weights and biases (learnable weights and biases).
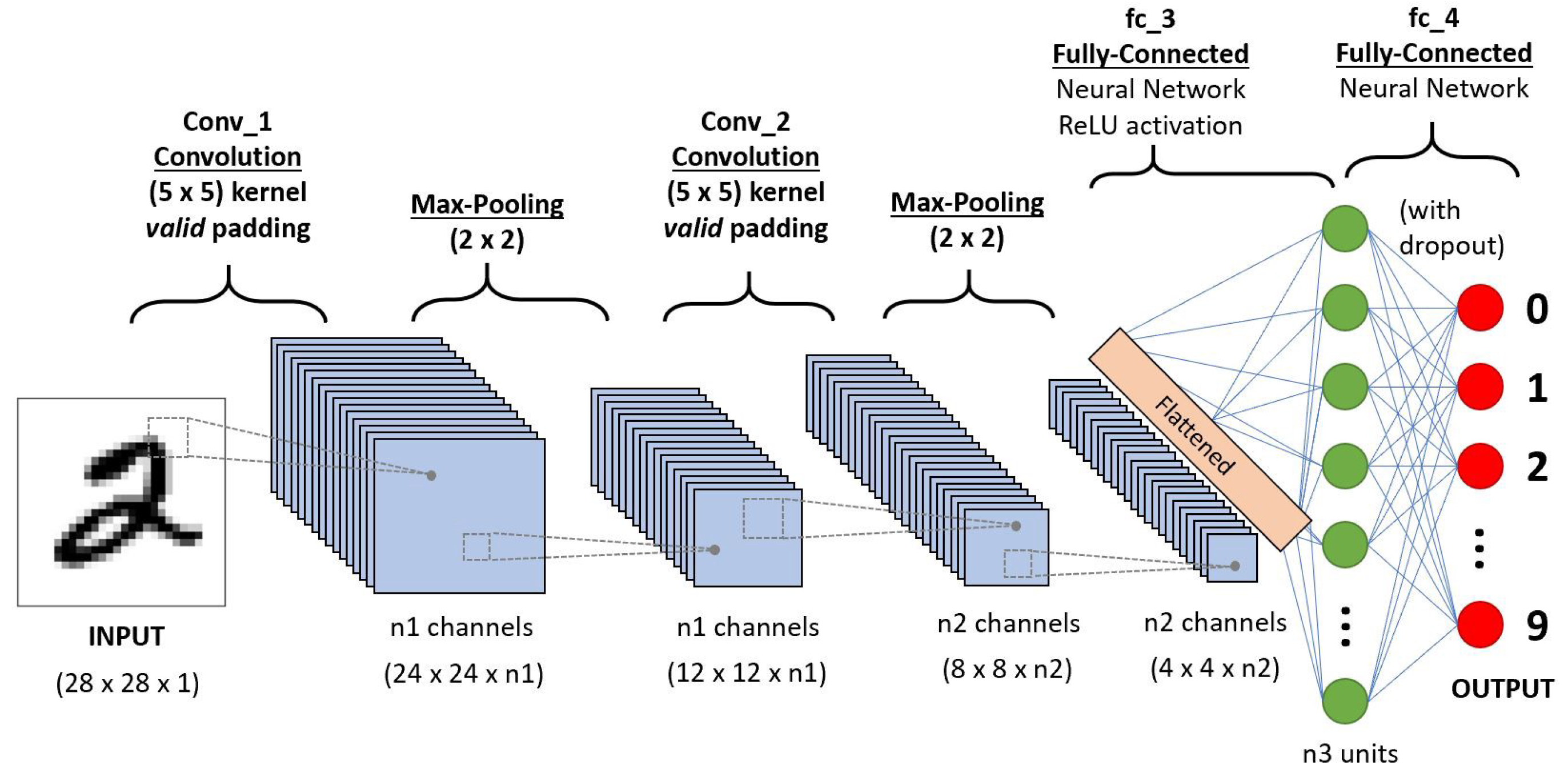
A CNN Model is a sequence of layers. Each CNN neuron receives some inputs and performs a vector operation (dot product). The basic architecture consists of three main types of layers, a Convolutional Layer, a Pooling Layer and a Fully Connected Layer. Each Layer accepts an input a 3D vector and converts it to an output 3D vector through a differentiable function [25]. The main working principle of each of the three main layers are explained below and presented in Figure 3:
  • Convolutional Layer: The Convolutional layer is the core building block of a Convolutional Network that does most of the computational heavy lifting.
  • Pooling Layer: The objective of the Pooling Layer is the progressively reduction of the spatial size of the representation in order to reduce computation volume of the system and as a result to reduce the overfitting at the training process.
  • Fully-Connected Layer: Neurons in a fully connected layer have full connections to all activations in the previous layer, as seen in regular Neural Networks. Their activations can hence be computed with a matrix multiplication followed by a bias offset.

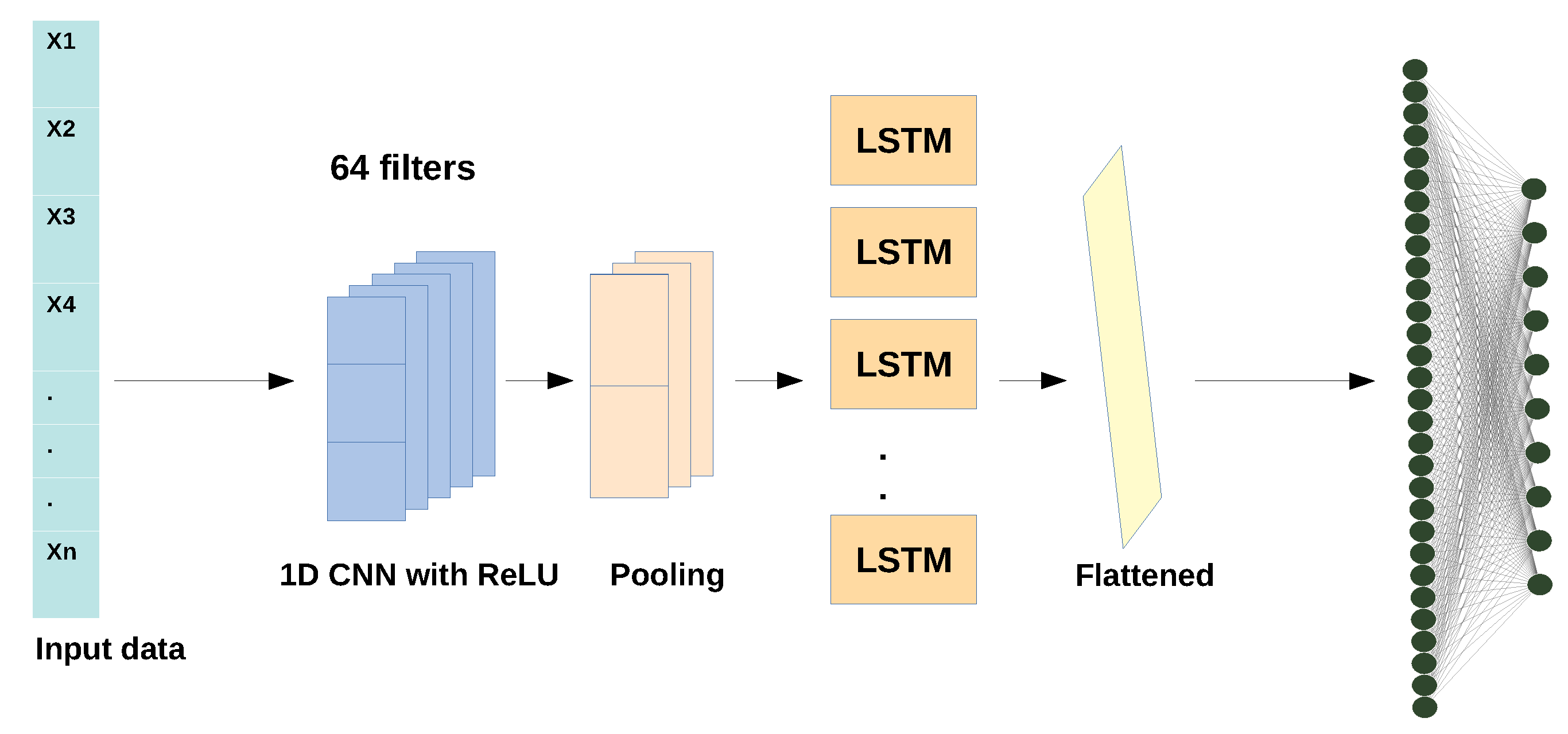
2.1.4. Hybrid CNN-LSTM Model

The CNN-LSTM model is a hybrid deep learning algorithm that uses the CNN layers for feature extraction of the input dataset and the LSTM model for sequence prediction, like multistep ahead forecasting of timeseries. Although the process of this model is divided into two parts, the operation of each of the two components-models separately is the same as described in subSection 2.1.1 and Section 2.1.3 for LSTM and CNN algorithms, respectively. Figure 4 shows the CNN – LSTM’s architecture.

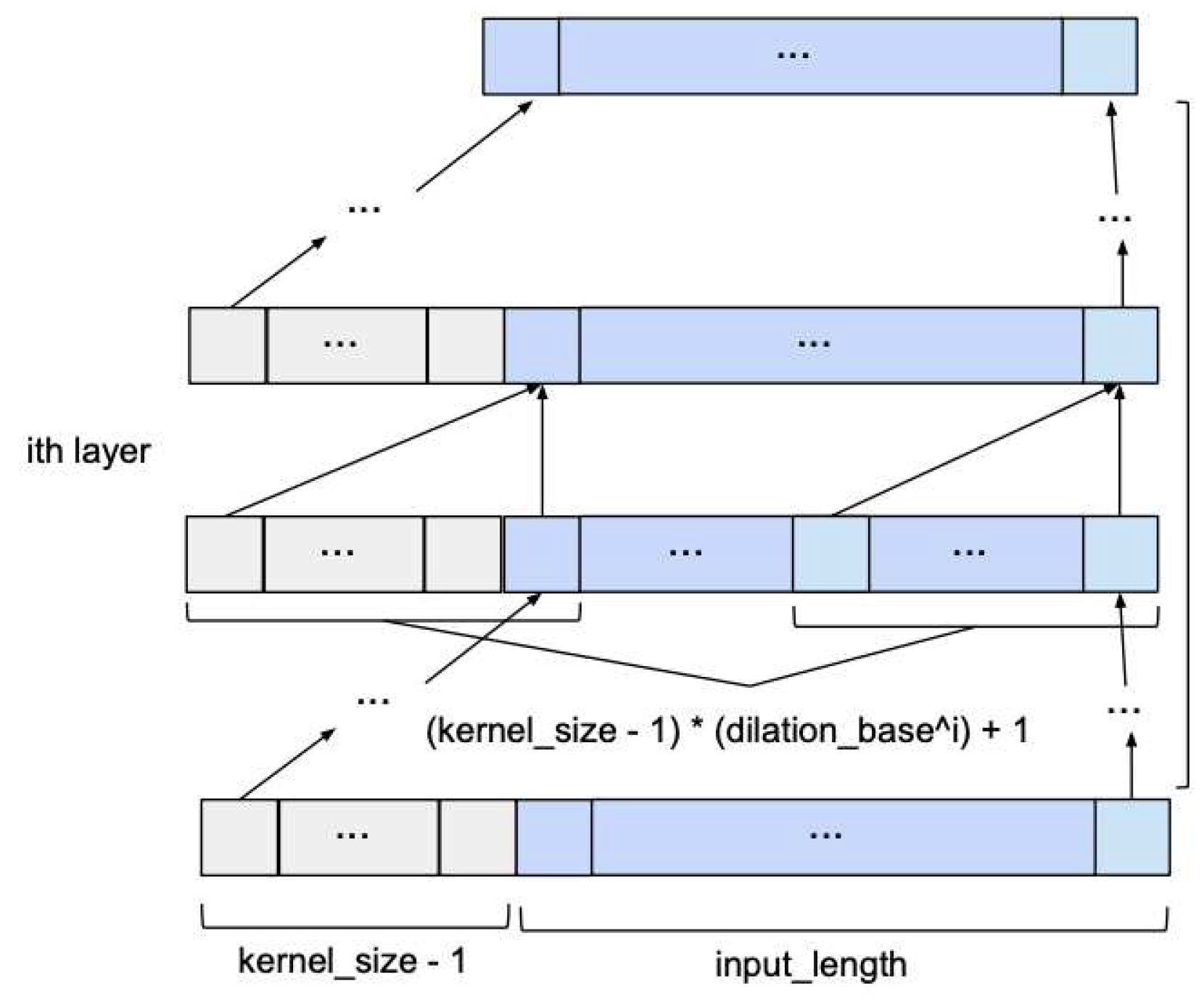
2.1.5. Temporal Convolutional Networks

Temporal Convolutional Network (TCN) is a relatively new type of deep learning model that has a dilation of CNN- 1D layers with the same input and output length. The working principle of TCNs is the following [28]:
  • At first, the model computes the low-level features using the CNN-1D modules encoding the spatial - temporal information,
  • Secondly, the model feeds this information and classifies them using Recurrent Neural Networks.
Recent studies have proven that TCNs have great performance in predicting time series with multiple seasonalities and trends. Figure 5 presents the basic architecture of a TCN.

2.2. Proposed Approach: Convolutional LSTM Encoder-Decoder Model

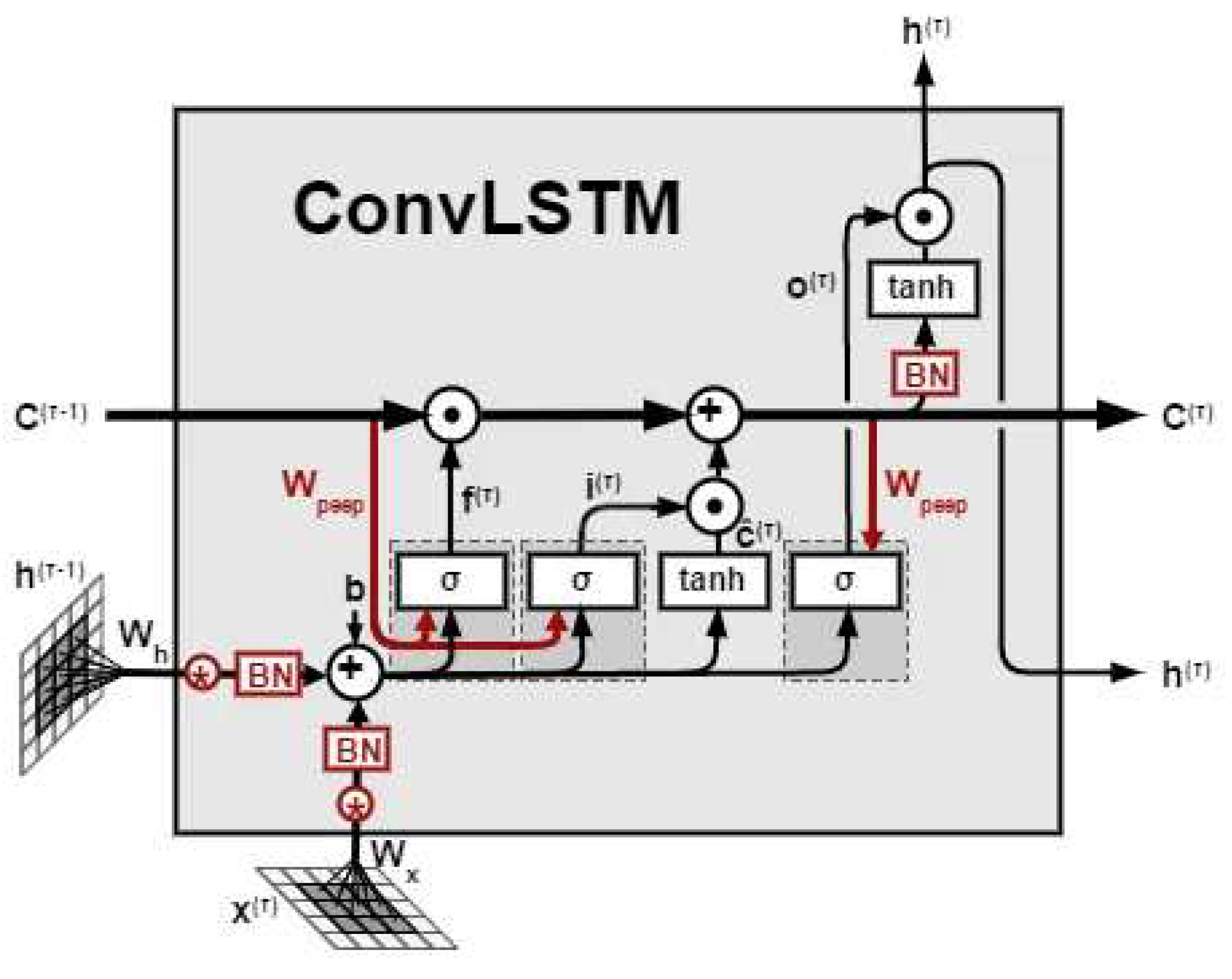
For the proposed model, at the beginning, a description of Convolutional LSTM Network (ConvLSTM) is made and then the basic operation of Encoder-Decoder Mechanism is analysed.
ConvLSTM model uses Recurrent Layers, such as simple RNN and LSTM Networks but, in contrast with these type of models, the internal matrix multiplications are exchanged with convolution operations, as this model has convolutional structures in both the input-to-state and state-to-state transitions. As a result, the data that flows through the ConvLSTM cells keeps the input dimension (3D in our case) instead of being just a 1D vector with features [30]. The basic architecture of ConvLSTM model is presented in Figure 6.
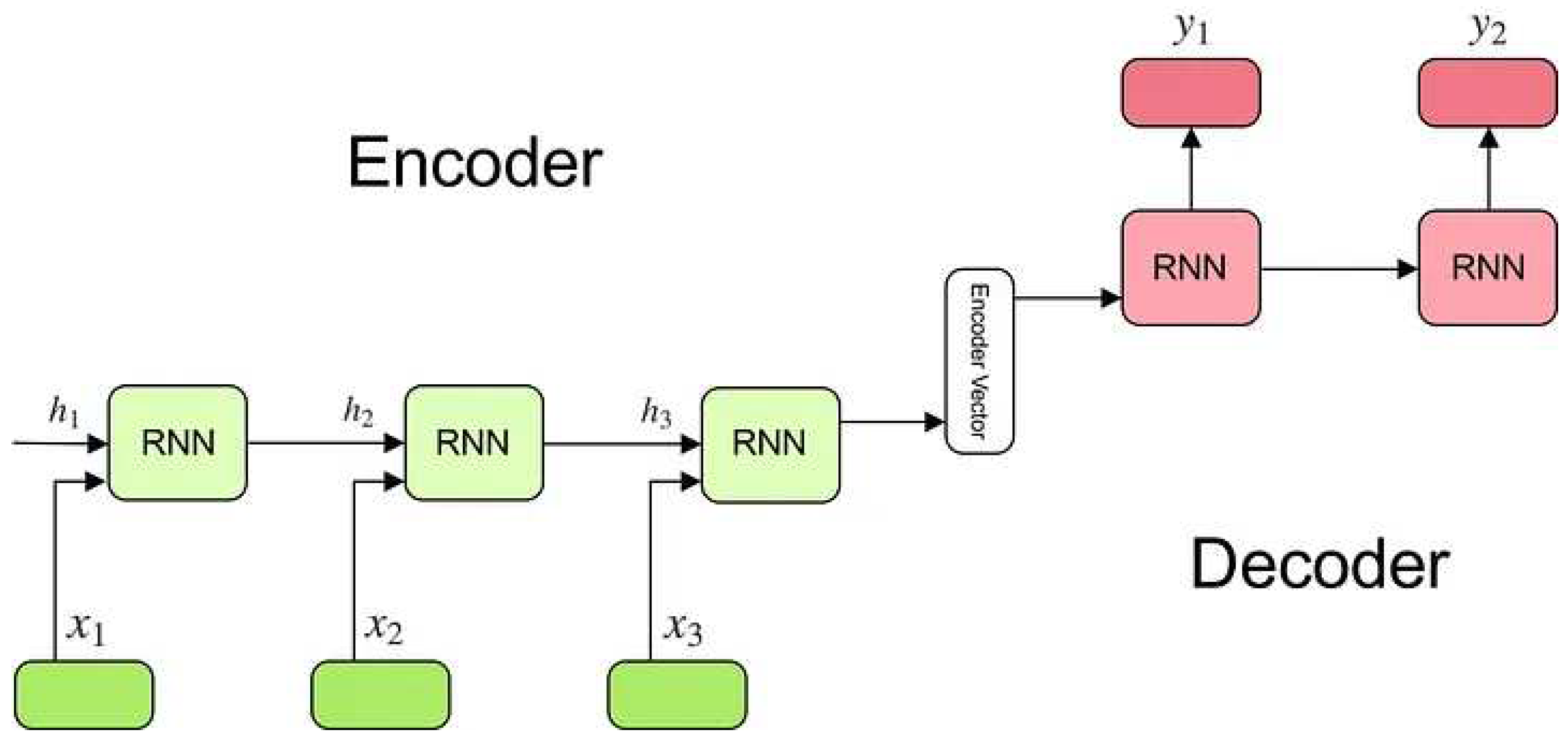
Additionally, the proposed model is a hybrid method that uses an Encoder-Decoder mechanism for the hourly prediction of electricity demand. The Encoder-Decoder mechanism provides efficient techniques for Sequence-to-Sequence (Seq2Seq) forecasting, such as Natural Language Processing (NLP) and time series forecasting, as well as Image Recognition and Sentiment Analysis. An Encoder-Decoder model (Figure 7) consists of three main parts [32]:
  • The Encoder Component: It is the first component of the Network and its main function the feature extraction of the input dataset and this is the reason that is called ‘encoder’. It receives an input the sequence and it passes the information values into the internal state vectors or Encoder Vectors, creating in this way a hidden state.
  • The Encoder Vector: The encoder vector is the last hidden state of the Network which converts the 2D output of the RNN (ConvLSTM in our case) model to a high length 3D vector, in order to help the Decoder Component to make better predictions.
  • The Decoder Component: The Decoder Component consists of one or a stack of several recurrent units, each one of them predicting an output y at a timestep t.
One of the main advantages that makes this model stands out from others is that the input and output vector length may be different, allowing this model to have effective performance in big Seq2Seq problems and video captioning.

2.3. Automated STLF Algorithm

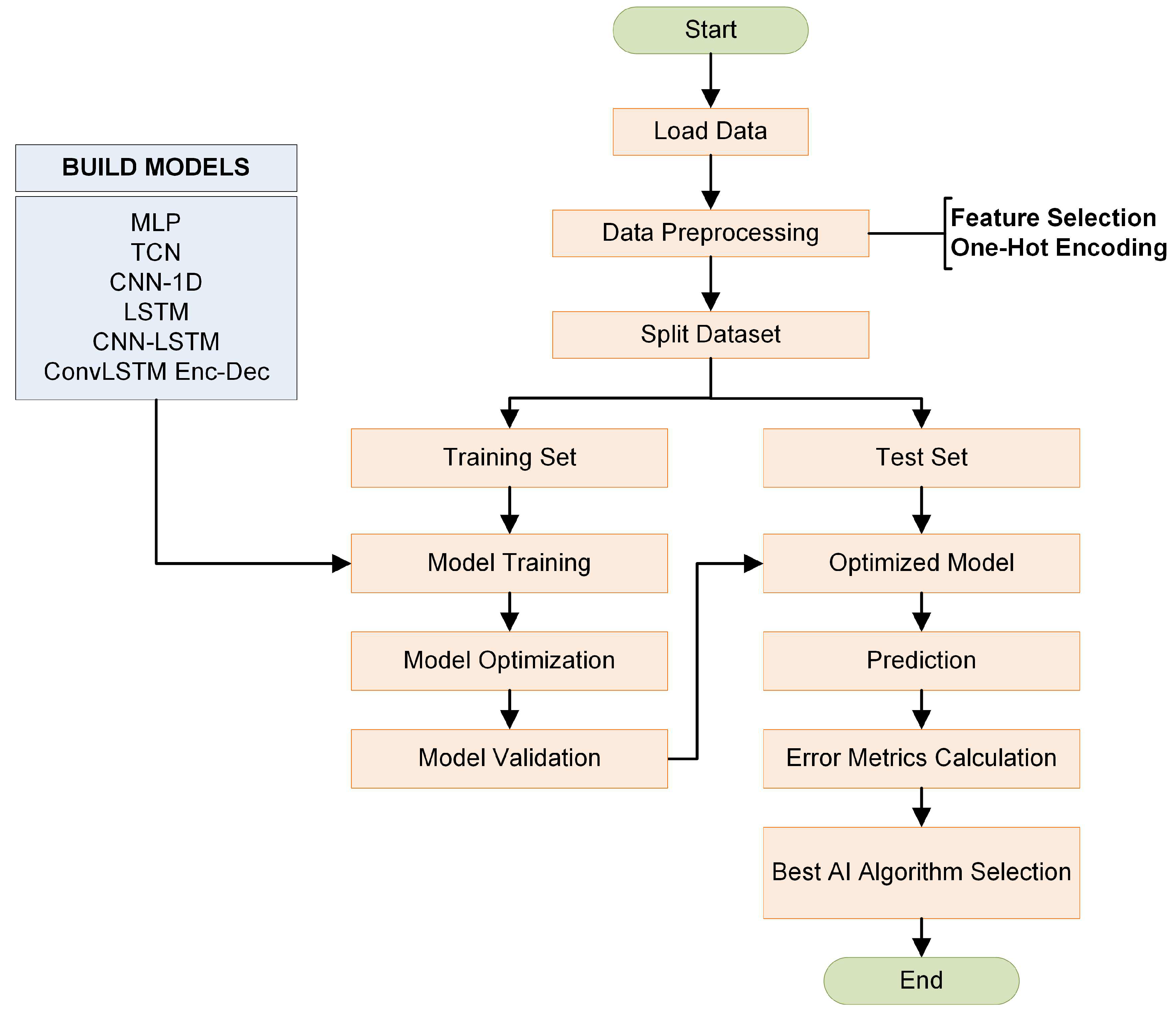
Using Deep Learning techniques, a DL Based forecasting algorithm was implemented, in order to easily and efficiently find the best forecasting model for every kind of timeseries datasets. The function of the algorithm includes the following steps:
  • The algorithm loads the dataset.
  • The algorithm proceeds to Preprocessing Step, in which the dataset is normalized using Min-Max Scaling algorithm and the Cyclical Time Features are created using One-Hot Encoding.
  • The dataset is splitted to Train, Validation and Test sets.
  • Every Deep Learning Model is trained and evaluated using Bayesian Optimization Algorithm.
  • Selection of the best model in terms of higher prediction accuracy to be used from the algorithm for future predictions.
The algorithmic process is described in the Figure 8.

3. Case Study

In this section, we present the case study used to test the proposed approach. The final dataset used for our experiments incorporates weather conditions and power demand from the Greek Cycladic Island, in Aegean Sea, Thira also known as Santorini. Thira island is a non-interconnected island to the Greek electrical bulk network and the power production is solely based on fossil fuel generators. The dataset period is three years from January 2017 to December 2019.

3.1. Climate Dataset

The climate data was collected from Santorini’s airport Meteorological Aerodrome Reports (METAR) [34,35]. The airport’s International Civil Aviation Organization (ICAO) code is LGSR. A typical report usually is generated every hour or half-hour and contains data for the temperature, dew point, wind direction and speed, precipitation, cloud cover and heights, visibility, and barometric pressure. For the current work we retrieve hourly values for temperature in oC, dewpoint in oC, wind speed in m/s and degrees of wind direction. Interpolation was applied to infill climate data missing values.

3.2. Electrical Power Dataset and Exploratory Analysis

Power production dataset contains hourly power production data of island’s electrical thermal station [36]. Table 1 presents a descriptive analysis of the of the power consumption data set. Based on the above table, it is observed that the dataset contains a total of 25944 values. Also, its mean value and standard deviation are 23.31 MW and 9.95 MW, respectively. The minimum value is 8.50 MW and the maximum 51.52 MW. Finally, regarding the intermediate values, it turns out that 25% of the dataset values are smaller than 14.70 MW, 50% smaller than 21.15 MW and 75% smaller than 31 MW, respectively.
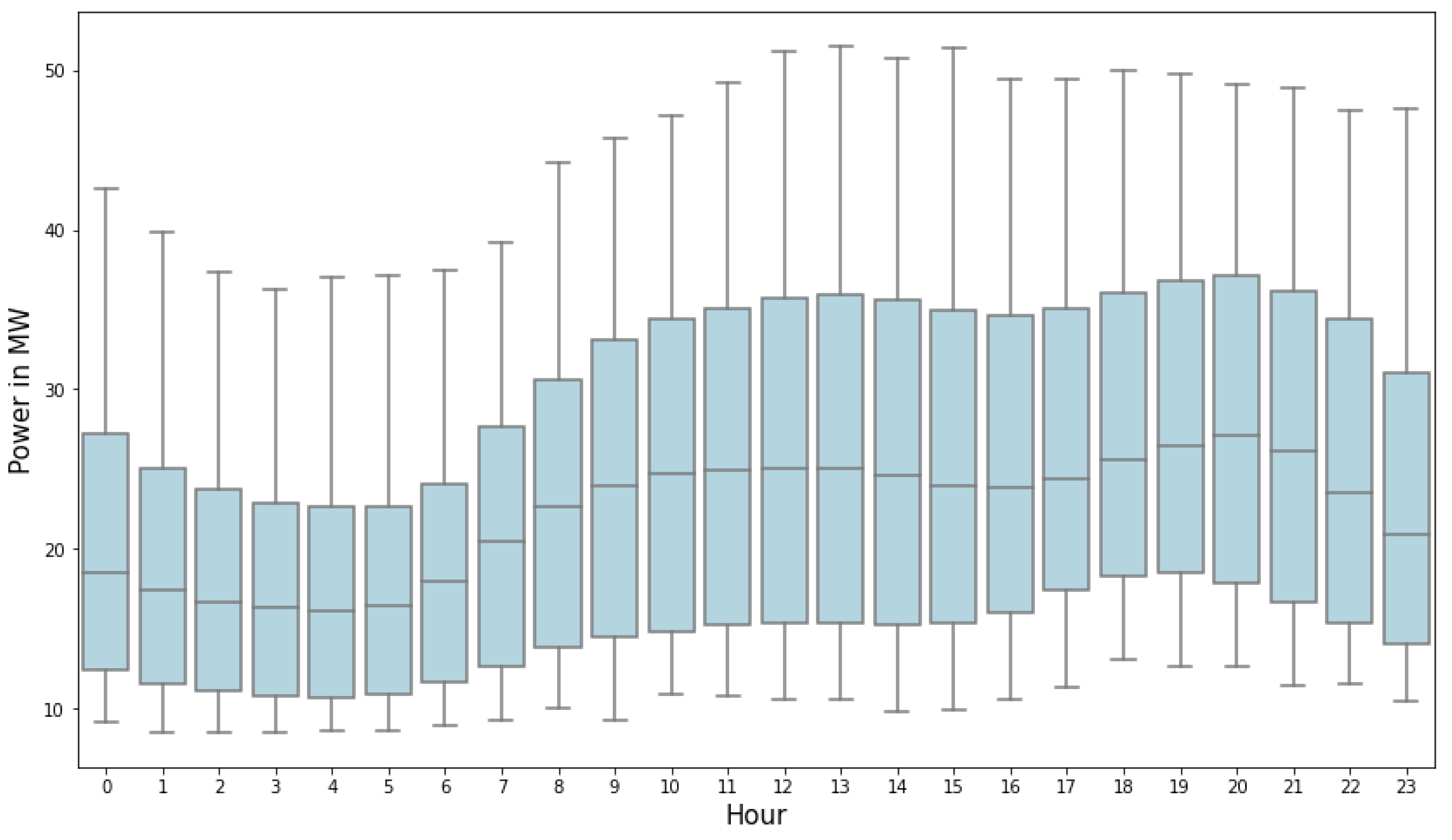
In order to have a better observation of the daily distribution of power consumption, a boxplot was created. Figure 9 presents the variation of average hourly power per day. It is worth noting that the peak demand is at 01:00 pm and 08:00 pm every day. The event is more intense on summer days, due to the increased number of tourists on the island.

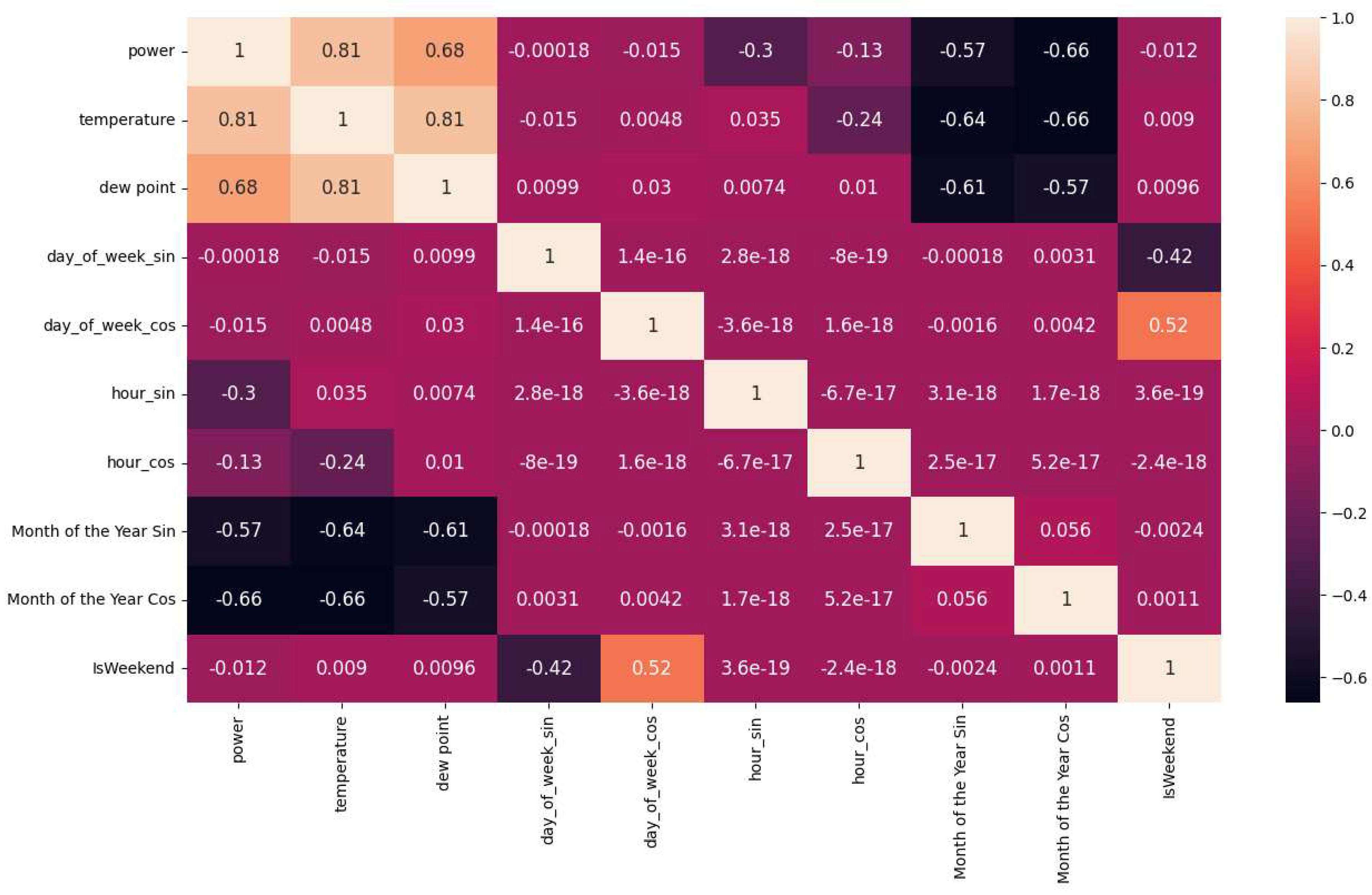
3.2.1. Correlation Heatmap

Figure 10 presents the Correlation Heatmap which visualizes the strength of relationships between all the numerical variables that have been created. For instance, it is clear that “temperature” variable has a very strong relationship with “power” variable, which is equal to 0.81 with maximum possible value of 1.

3.3. Feature Selection

Several input features were studied and evaluated for this study to understand the most significant for predicting electricity demand. A total of ten input features were studied for predicting electricity demand one hour ahead. The data were used as input variables are the same for all the Deep Learning Models and are shown in Table 2:

3.4. Data Prepossessing

3.4.1. Min-Max Scaling

The prepossessing technique for all the dataset that used in this paper is Min-Max Scaling, which scales all the data points between 0 - 1. For this reason, two different scalers were used, one for input and one for output datasets. The mathematical formulation is given by the follow equation:
X s c a l e d = X a c t u a l − X m i n X m a x − X m i n
Where X a c t u a l is the real value of a data, and X m i n and X m a x is the minimum and maximum value of the dataset, accordingly. The main reason Min-Max Scaling is used is that it helps the deep learning models to be trained more efficiently at the training period and converge faster to the optimal solution of the loss function.

3.4.2. One-Hot Encoding

One-Hot encoding is a mathematical methodology that converts categorical to numerical vectors and transforms the numerical data to cyclical, using trigonometric transformation. Using this technique, day of the week, hour of the day and also month of the year were converted to Sin and Cosine type.

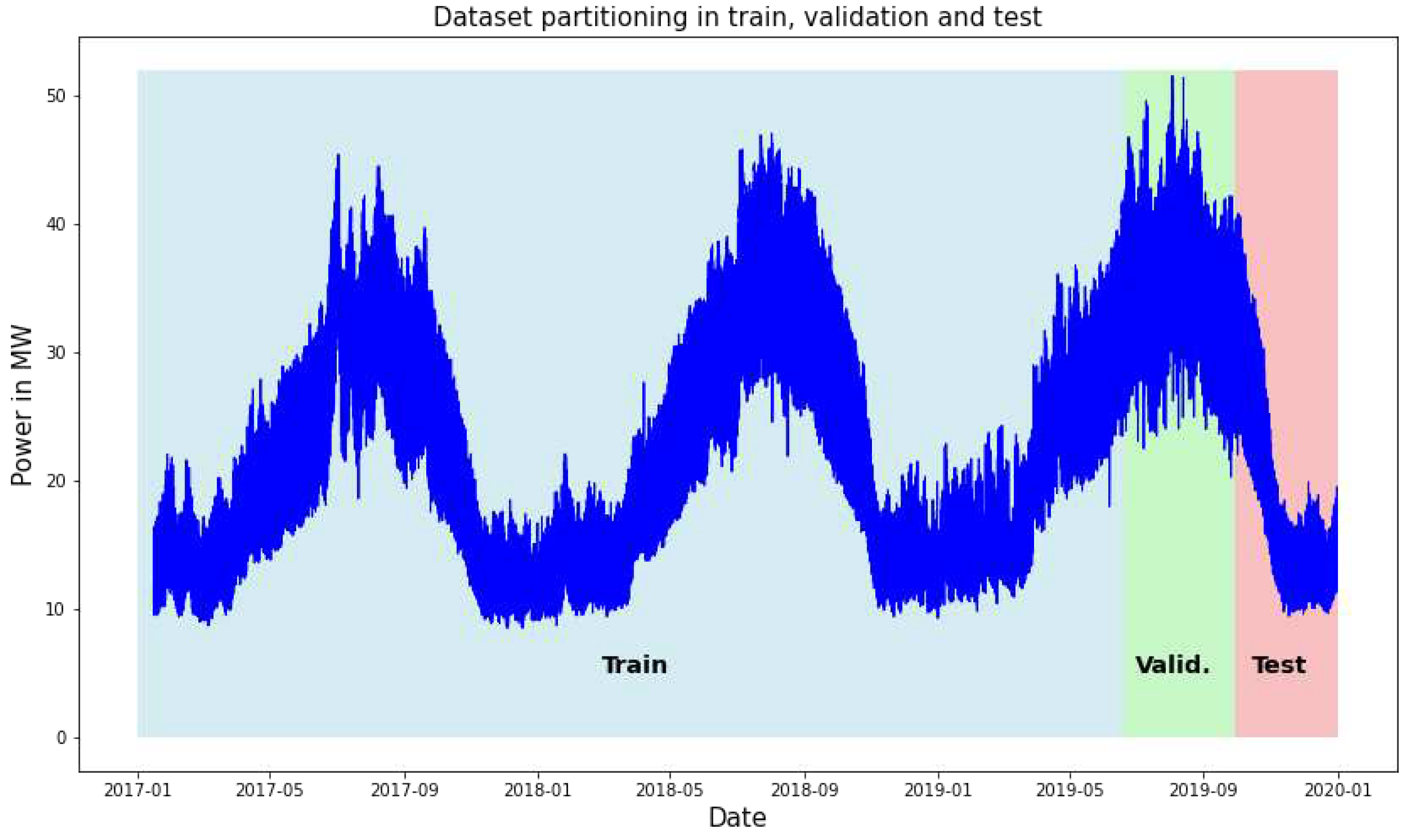
3.5. Data Partitioning

The data was split into a training and test set while maintaining the temporal order of the data. The data from 1 January 2017 to 30 September 2019, were used as the training set and the last 10% of this were used for the validation of the models. The data from 1 October 2019 to 31 December 2019, were used as the test set. The specific interval is not random but was chosen because throughout its range it has both an interval with a trend and an interval which is stationary. Thus, the deep learning models are tested in the most difficult case that could be extracted from our dataset. Figure 11 presents the visualization plot of the power consumption for all the dataset and the individual partitioning sections.

3.6. Model Architecture

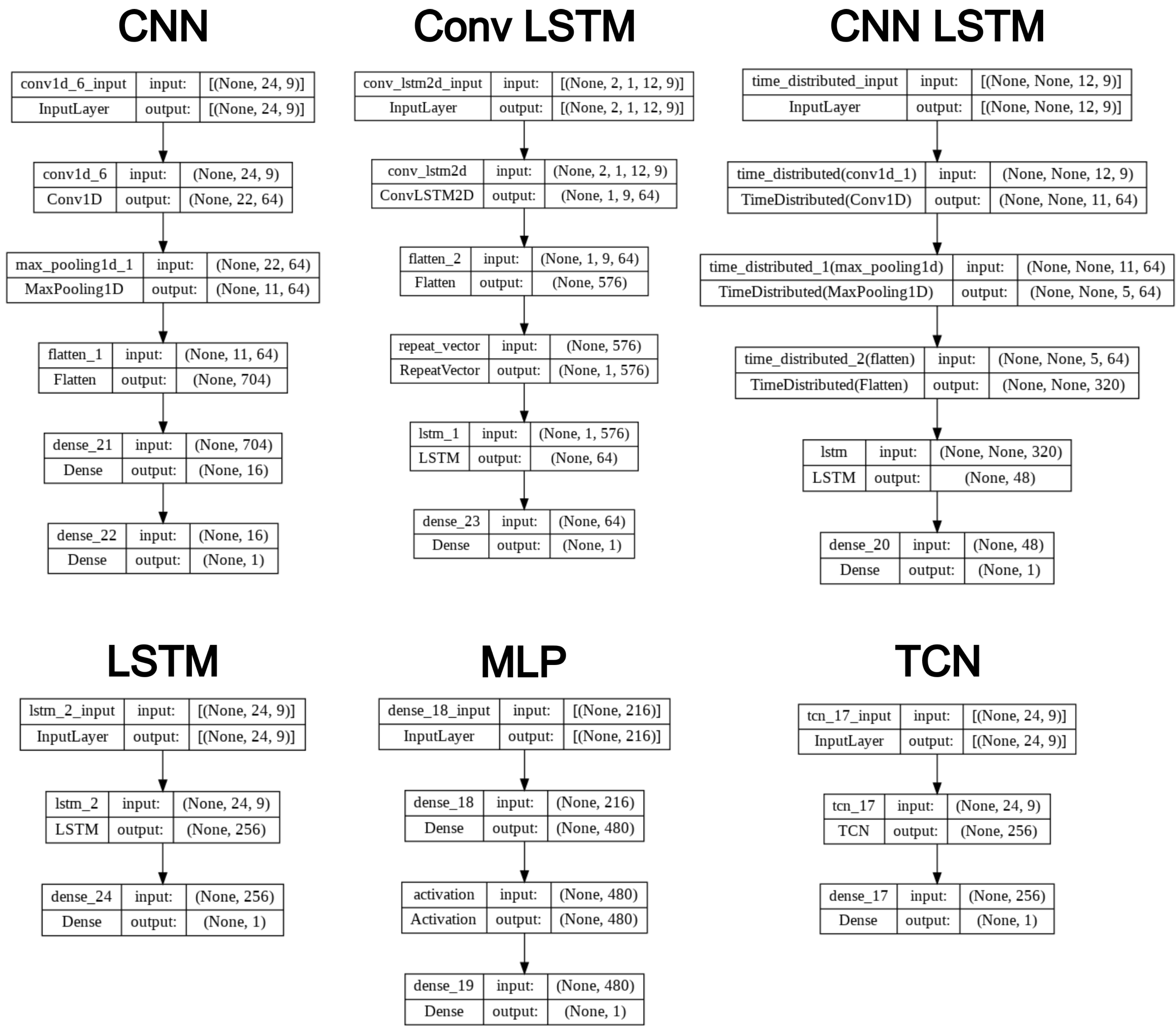
This subsection details the architectures of each model used in this paper, in order to have a clear understanding of the optimal parameters that were extracted. The hyperparameters of all models were chosen after applying Bayesian Hyperparameter Optimization Algorithm with maximum 60 iterations trials in every search. More specifically, these parameters are presented below:

3.6.1. LSTM Model

The LSTM model that performs the best accuracy at optimization process has the following hyperparameters:
  • Units of lstm network = 256
  • Batch size = 128
  • ReLU activation function for the LSTM Module, as well as the output Dense Layer
  • Optimizer = Adam
  • Learning rate = 0.0010
  • Epochs = 100

3.6.2. CNN-LSTM Model

The hyperparameters of the hybrid CNN-LSTM model have been resulted are presented below:
  • filters=64
  • kernel size=2
  • ReLU activation function for the both the CNN and LSTM Module
  • 48 units for the LSTM Module
  • MaxPooling1D with pool size=2
  • Batch size 128
  • Optimizer = Adam
  • Learning rate 0.0010
  • Epochs = 100

3.6.3. Multilayer Perceptron Model

After converging to the optimal forecasting accuracy, the hyperparameters for the MLP model are formulated as follow:
  • 480 Neurons for the Input Layer
  • Batch size = 128
  • ReLU activation function for the Input Layer, as well as the output Dense Layer
  • Optimizer = Adam
  • Learning rate 0.0011
  • Epochs = 500

3.6.4. Temporal Convolution Network

  • Filters = 256
  • Dilations = [1, 2, 4, 8, 16, 32]
  • Batch size = 128
  • Optimizer = Adam
  • Epochs = 100

3.6.5. CNN–1D Model

  • Filters = 64
  • Kernel size = 3
  • MaxPooling1D (pool size=2)
  • Neurons of Dense Layer = 16
  • ReLU activation function for the CNN Module, as well as the output Dense Layer
  • Optimizer = Adam
  • Epochs = 100

3.6.6. ConvLSTM Encoder- Decoder Model

This is the hybrid proposed model of this paper that outperforms the other deep learning models. The hyperparameters that compose the architecture of this model are the followings:
  • Filters = 64
  • Kernel size = (1,4)
  • ReLU activation function for the ConvLSTM2D Module, for the LSTM Layer, as well as the output Dense Layer
  • Encoder Vector with size = 1
  • 64 Units for the LSTM module
  • Optimizer = Adam
  • Learning rate = 0.0068
  • Epochs = 100
A visualization of each model is presented in Figure 12.

3.7. Software Environment

The experiments presented in this study were implemented in Python Language, using the Open-Source software library Tensorflow 2 and the high-level API, Keras. Pandas and Numpy libraries were used for data analysis and visualization of the problem. The project was executed on Google Colab Pro platform, using a GPU with the following characteristics: NVIDIA- SMI 460.32.03, Driver Version: 460.32.03, CUDA Version: 11.2, RAM: 25.45 GB and Disk: 166.77 GB.

3.8. Performance Metrics (Evaluation Metrics)

In this section, we present the performance metrics used in the evaluation of the hourly power prediction models. Mean Absolute Error (MAE) [37] is a commonly used metric with regression models, comparing actual and predicted values, which gives a measure of average error. MAE is calculated by the following formula where y i is the predicted value and x i is the actual value in a set of n samples:
M A E = ∑ i = 1 n | y i − x i | n
Moreover, Mean Absolute Percentage Error (MAPE) [38] is used as a measure of quality for regression and time series models because it is explains intuitively the relative error. MAPE is computed by the following formula which uses the same parameters as the MAE calculation:
M A P E = 100 n ∑ i = 1 n | y i − x i x i |
Furthermore, Mean Squared Error (MSE) [37] and Root Mean Squared Error (RMSE) [39] error metrics are included in the performance evaluation of this study. The MSE metric measures the average squared difference between the predicted and the true values. In this study, we used MSE as the loss function for the training of the neural network prediction models due to the characteristic that gives a higher weight on extreme error values. Additionally, RMSE metric is the square root of the MSE, use the same parameters as the previously mention evaluation metrics and the computation formulas are the following:
M S E = 1 n ∑ i = 1 n ( y i − x i ) 2
R M S E = ∑ i = 1 n ( y i − x i ) 2 n
Additionally, the coefficient of determination or R squared is used as a performance metric on this study, which represents the proportion of variance (of y) that has been explained by the independent variables in the model. It indicates a proper model fit and measures how unobserved samples are possible to be forecasted by the model, through the proportion of explained variance. R squared can be more informative than the former mention metrics in regression analysis evaluation [39]. R squared is calculated by the following formula where y i is the predicted value, x i is the actual value and x ¯ is the mean of the actual values in a set of n samples:
R 2 = 1 − sum squared regression ( SSR ) total sum of squares ( TSS ) , = 1 − ∑ i = 1 n ( y i − x i ) 2 ∑ i = 1 n ( x ¯ − x i ) 2

4. Results Analysis and Discussion

In the presented work, an automated application was implemented in order to find the optimal forecasting model for hourly electricity data in MWs. For this purpose, six artificial deep learning models were created and optimized as shown in the tables above. Essentially, an application was implemented which will be able to run not only on electric power data but will be used in any kind of timeseries forecasting problems.
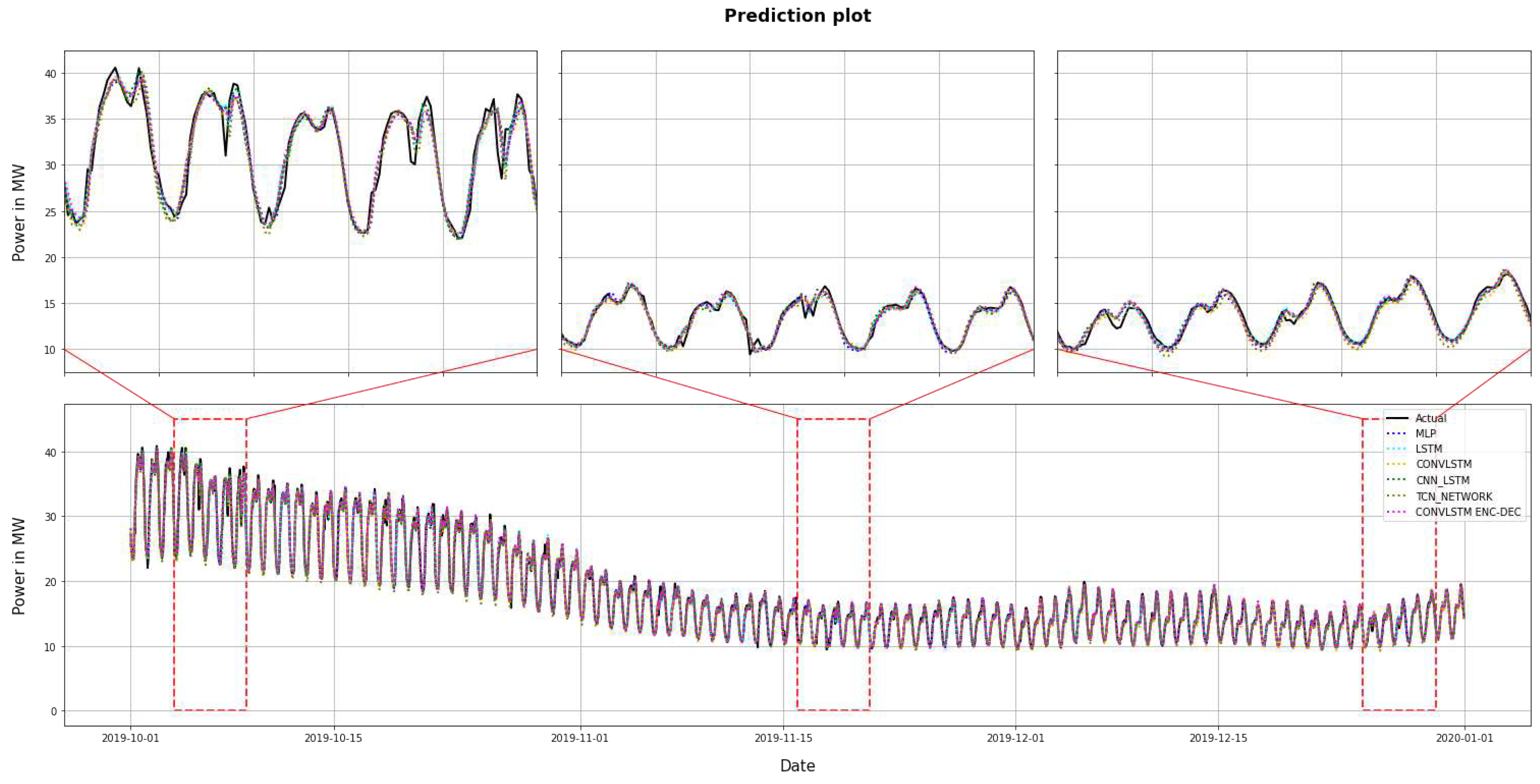
The results obtained from the algorithmic experiments are presented and an analysis of their results is made. In Figure the daily hourly demand prediction in MWs for the three-month period, from 1/10/2019 to 31/12/2019 is presented.
Preprints 73495 g013
Figure 13. The prediction results. Lower subfigure represents the whole testing dataset. Upper subfigures describe different five – day predictions plot from the same training dataset.
Figure 13. The prediction results. Lower subfigure represents the whole testing dataset. Upper subfigures describe different five – day predictions plot from the same training dataset.
Preprints 73495 g013
More specifically, Table 3 presents the values of R2, MAE, MSE, RMSE and MAPE for each model.
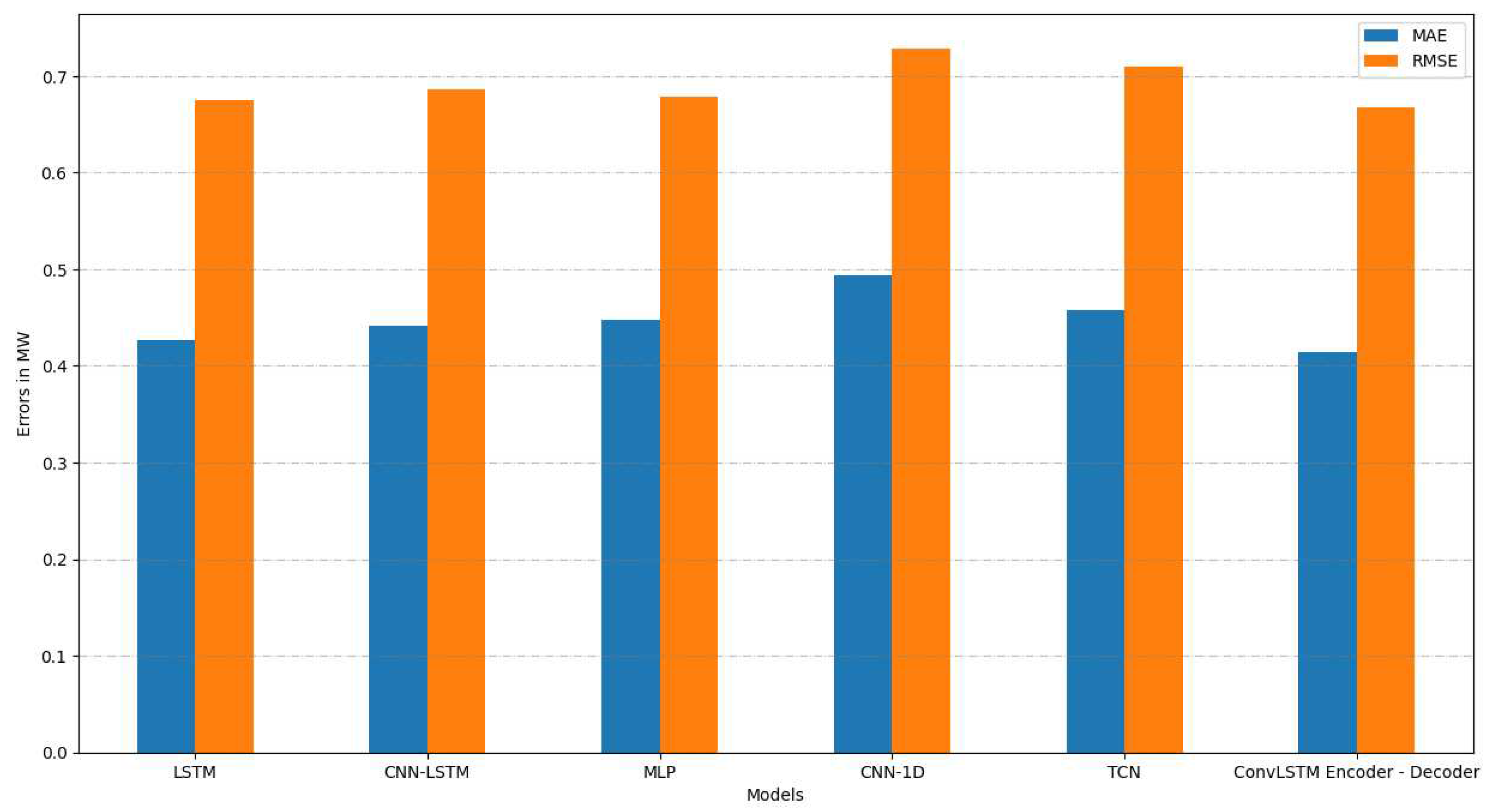
Based on the experiments carried out, it is easy to see that the worst models are the TCN and MLP networks and it seems that Recurrent Networks, such as LSTM and the two hybrid models implemented, show the best accuracy. More specifically, simple LSTM model performs a MAE 0.4272 and RMSE 0.6747, while hybrid CNN-LSTM network has MAE 0.4412 and RMSE 0.6866. MLP and TCN models have MAE 0.4477 and 0.4936 and RMSE 0.6784 and 0.7096, accordingly.
The proposed model, which has not been used extensively in electricity forecasting datasets is a hybrid model, called Convolutional LSTM Encoder-Decoder. The advantage of this model compared to the other implemented models and mainly to the hybrid CNN-LSTM model is the use of a ConvLSTM Network, which offers better feature extraction and accuracy. Thus, the profile of a timeseries with multiple seasonalities such as the one studied in our case is recognized in a more efficient way, making this model capable of performing MAE and RMSE 0.4142 and 0.6674, respectively. Figure 14 presents the comparative values of MAE and RMSE for each of the six models proposed and illustrated.

5. Conclusions and Future Work

In recent years, the energy sector has undergone significant changes, due to events such as the rapid increase in demand and the energy crisis. In these circumstances, new needs have been created, with the aim of dealing with new phenomena and ensuring the proper functioning of the network. For this reason, in this study an innovative and automated forecasting model for power usage was implemented, in order to create a capable model for predicting future electricity situations.
Regarding the contribution of the paper, we can highlight the following. Firstly, an automated system with which we can find for any type of time series the optimal model that is suitable for predicting future data was implemented. Beyond the electricity data that was studied in this paper, the specific application could be applied both to financial data and meteorological phenomena as wind power forecasting [40]. Additionally, this application could be utilized in the aviation industry with a combination of a scientific tool which incorporates building and electrical system simulation, climate data, flights, and passengers’ flow [41].
Secondly, through the application a new and innovative deep learning model is proposed with the aim of the highest possible forecast accuracy. The specific model consists of a ConvLSTM network, which is used to encode the information contained in the input time series vectors. Then, the information through an Encoder Vector is distributed in an LSTM model, whose goal is to predict future data.
About future studies that could arise based on this paper, this automated model could be enriched with more and efficient models, such as Exponential Smoothing LSTM (ESLSTM) model and Transformers. Another challenge for the models created is to apply them to medium and long-term predictions tasks, in order to test their stability in long sequences. Also, testing the specific application and simultaneously series of other types of data is in itself a significant challenge. Furthermore, another task that could be tested in a future study would be the application of the above models used in this paper with models with Custom Activation Functions, in order to compare their prediction accuracy in time-series tasks. Finally, the use of the above algorithms in Demand Side Management problems could be a challenge, due to the fast that these type o programs require high accuracy forecasting techniques at high short-term level [42].

Author Contributions

Conceptualization, V.L. and G.V.; methodology, V.L.; software, V.L. and G.V.; validation, V.L., G.V., D.B., A.D. and L.H.T.; formal analysis, V.L. and G.V.; investigation, V.L. and G.V.; resources, V.L. and G.V.; data curation, V.L. and G.V.; writing—original draft preparation, V.L. and G.V.; writing—review and editing, V.L., G.V., D.B., A.D. and L.H.T.; visualization, V.L. and G.V.; supervision, D.B., A.D. and L.H.T.; project administration, D.B. and A.D. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data are available in a publicly accessible repository. The load data used in this study are available from the HEDNO portal in [36]. The weather dataset was retrieved from ogimet portal in [35]. These datasets were processed as the input for the design and performance assessment of the forecasting models described in this article.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

AM Attention Mechanism
BO Bayesian Optimization
BEGA Binary Encoding Genetic Algorithm
BPNN Backpropagation Neural Network
CNN-1d Convolutional Neural Network One Dimensional
CNN-LSTM Convolutional Neural Network - Long Short-Term Memory
ConvLSTM Convolutional Long Short Term Memory
DTM Dynamic Time Wrapping
FC Fully-Connected
LSTM Long Short-Term Memory
MAE Mean Absolute Error
MAPE Mean Absolute Percentage Error
MLP Multilayer Perceptron
NLP Natural language processing
R2 R-Squared
RFR Random Forests Regression
RMSE Root Mean Squared Error
RNN Recurrent Neural Network
STLF Short Term Load Forecasting
SVR Support Vector Regressor
TCN Temporal Convolutional Network

References

  1. Mamun, A.A.; Sohel, M.; Mohammad, N.; Haque Sunny, M.S.; Dipta, D.R.; Hossain, E. A Comprehensive Review of the Load Forecasting Techniques Using Single and Hybrid Predictive Models. IEEE Access 2020, 8, 134911–134939. [Google Scholar] [CrossRef]
  2. Hammad, M.A.; Jereb, B.; Rosi, B.; Dragan, D. Methods and models for electric load forecasting: a comprehensive review. Logist. Supply Chain. Sustain. Glob. Challenges 2020, 11, 51–76. [Google Scholar] [CrossRef]
  3. Hong, T.; Fan, S. Probabilistic electric load forecasting: A tutorial review. Int. J. Forecast. 2016, 32, 914–938. [Google Scholar] [CrossRef]
  4. Deep Learning Tutorial for Beginners: Neural Network Basics. https://www.guru99.com/deep-learning-tutorial.html#5. (accessed on 18 November 2022).
  5. Kontogiannis, D.; Bargiotas, D.; Daskalopulu, A. Minutely active power forecasting models using Neural Networks. Sustainability 2020, 12, 3177. [Google Scholar] [CrossRef]
  6. Arvanitidis, A.I.; Bargiotas, D.; Daskalopulu, A.; Laitsos, V.M.; Tsoukalas, L.H. Enhanced Short-Term Load Forecasting Using Artificial Neural Networks. Energies 2021, 14, 7788. [Google Scholar] [CrossRef]
  7. Arvanitidis, A.I.; Bargiotas, D.; Daskalopulu, A.; Kontogiannis, D.; Panapakidis, I.P.; Tsoukalas, L.H. Clustering Informed MLP Models for Fast and Accurate Short-Term Load Forecasting. Energies 2022, 15, 1295. [Google Scholar] [CrossRef]
  8. Kontogiannis, D.; Bargiotas, D.; Daskalopulu, A.; Arvanitidis, A.I.; Tsoukalas, L.H. Error compensation enhanced day-ahead electricity price forecasting. Energies 2022, 15, 1466. [Google Scholar] [CrossRef]
  9. Zheng, H.; Yuan, J.; Chen, L. Short-term load forecasting using EMD-LSTM neural networks with a Xgboost algorithm for feature importance evaluation. Energies 2017, 10, 1168. [Google Scholar] [CrossRef]
  10. Kwon, B.S.; Park, R.J.; Song, K.B. Short-term load forecasting based on deep neural networks using LSTM layer. J. Electr. Eng. Technol. 2020, 15, 1501–1509. [Google Scholar] [CrossRef]
  11. Jin, Y.; Guo, H.; Wang, J.; Song, A. A hybrid system based on LSTM for short-term power load forecasting. Energies 2020, 13, 6241. [Google Scholar] [CrossRef]
  12. Tian, C.; Ma, J.; Zhang, C.; Zhan, P. A deep neural network model for short-term load forecast based on long short-term memory network and convolutional neural network. Energies 2018, 11, 3493. [Google Scholar] [CrossRef]
  13. Rafi, S.H.; Nahid-Al-Masood. ; Deeba, S.R.; Hossain, E. A Short-Term Load Forecasting Method Using Integrated CNN and LSTM Network. IEEE Access 2021, 9, 32436–32448. [Google Scholar] [CrossRef]
  14. Wu, K.; Wu, J.; Feng, L.; Yang, B.; Liang, R.; Yang, S.; Zhao, R. An attention-based CNN-LSTM-BiLSTM model for short-term electric load forecasting in integrated energy system. Int. Trans. Electr. Energy Syst. 2021, 31, e12637. [Google Scholar] [CrossRef]
  15. Farsi, B.; Amayri, M.; Bouguila, N.; Eicker, U. On Short-Term Load Forecasting Using Machine Learning Techniques and a Novel Parallel Deep LSTM-CNN Approach. IEEE Access 2021, 9, 31191–31212. [Google Scholar] [CrossRef]
  16. Peng, Q.; Liu, Z.W. Short-Term Residential Load Forecasting Based on Smart Meter Data Using Temporal Convolutional Networks. 2020 39th Chinese Control Conference (CCC). IEEE, 2020, pp. 5423–5428. [CrossRef]
  17. Wang, Y.; Chen, J.; Chen, X.; Zeng, X.; Kong, Y.; Sun, S.; Guo, Y.; Liu, Y. Short-Term Load Forecasting for Industrial Customers Based on TCN-LightGBM. IEEE Trans. Power Syst. 2021, 36, 1984–1997. [Google Scholar] [CrossRef]
  18. Tang, X.; Chen, H.; Xiang, W.; Yang, J.; Zou, M. Short-term load forecasting using channel and temporal attention based temporal convolutional network. Electr. Power Syst. Res. 2022, 205, 107761. [Google Scholar] [CrossRef]
  19. Xia, G.; Zhang, F.; Wang, C.; Zhou, C. ED-ConvLSTM: A Novel Global Ionospheric Total Electron Content Medium-Term Forecast Model. Space Weather. 2022, 20, e2021SW002959. [Google Scholar] [CrossRef]
  20. Wang, S.; Mu, L.; Liu, D. A hybrid approach for El Niño prediction based on Empirical Mode Decomposition and convolutional LSTM Encoder-Decoder. Comput. Geosci. 2021, 149, 104695. [Google Scholar] [CrossRef]
  21. Olah, C. Understanding LSTM Networks. Available online: https://colah.github.io/posts/2015-08-Understanding-LSTMs/ (accessed on 12 Jauary 2023).
  22. Loukas, S. How to classify handwritten digits using a multilayer perceptron classifier-Towards AI. Available online: https://towardsai.net/p/l/how-to-classify-handwritten-digits-using-a-multilayer-perceptron-classifier (accessed on 7 Jauary 2023).
  23. Banoula, M. An Overview on Multilayer Perceptron (MLP). Available online: https://www.simplilearn.com/tutorials/deep-learning-tutorial/multilayer-perceptron#forward_propagation (accessed on 7 Jauary 2023).
  24. Andrew Zola, J.V. What is a backpropagation algorithm? Available online:. Available online: https://www.techtarget.com/searchenterpriseai/definition/backpropagation-algorithm (accessed on 7 Jauary 2023).
  25. CS231n Convolutional Neural Networks for Visual Recognition. Available online: https://cs231n.github.io/convolutional-networks/#fc (accessed on 7 Jauary 2023).
  26. Ratan, P. What is the Convolutional Neural Network Architecture? Available online:. Available online: https://www.analyticsvidhya.com/blog/2020/10/what-is-the-convolutional-neural-network-architecture/ (accessed on 7 Jauary 2023).
  27. Hamad, R.A.; Yang, L.; Woo, W.L.; Wei, B. Joint learning of temporal models to handle imbalanced data for human activity recognition. Appl. Sci. 2020, 10, 5293. [Google Scholar] [CrossRef]
  28. Lara-Benítez, P.; Carranza-García, M.; Luna-Romera, J.M.; Riquelme, J.C. Temporal convolutional networks applied to energy-related time series forecasting. Appl. Sci. 2020, 10, 2322. [Google Scholar] [CrossRef]
  29. Lässig, F. Temporal Convolutional Networks and Forecasting – Unit8. https://unit8.com/resources/temporal-convolutional-networks-and-forecasting/, accessed on 2023-01-12.
  30. Tian, H.; Chen, J. Deep Learning with Spatial Attention-Based CONV-LSTM for SOC Estimation of Lithium-Ion Batteries. Processes 2022, 10, 2185. [Google Scholar] [CrossRef]
  31. Xavier, A. An introduction to ConvLSTM – Medium. Available online: https://medium.com/neuronio/an-introduction-to-convlstm-55c9025563a7 (accessed on 12 Jauary 2023).
  32. Brownlee, J. How Does Attention Work in Encoder-Decoder Recurrent Neural Networks. Available online: https://machinelearningmastery.com/how-does-attention-work-in-encoder-decoder-recurrent-neural-networks/ (accessed on 12 Jauary 2023).
  33. Kostadinov, S. Understanding Encoder-Decoder Sequence to Sequence Model – Towards Data Science. Available online: https://towardsdatascience.com/understanding-encoder-decoder-sequence-to-sequence-model-679e04af4346 (accessed on 12 Jauary 2023).
  34. METAR - Wikipedia. Available online: https://en.wikipedia.org/wiki/METAR (accessed on 12 Jauary 2023).
  35. Ogimet. Available online: https://www.ogimet.com/home.phtml.en (accessed on 12 Jauary 2023).
  36. Thira ES - HEDNO. Available online: https://deddie.gr/en/themata-tou-diaxeiristi-mi-diasundedemenwn-nisiwn/leitourgia-mdn/dimosieusi-imerisiou-energeiakou-programmatismou/thira-es/ (accessed on 10 Jauary 2022).
  37. Sammut, C.; Webb, G.I. (Eds.) , C.; Webb, G.I., Eds.; Springer: Boston, MA, USA, 2010; pp. 652–653. doi:10.1007/978-0-387-30164-8.Learning. In Encycl. Mach. Learn.; Sammut, C.; Webb, G.I. (Eds.) Springer: Boston, MA, USA, 2010; Springer: Boston, MA, USA, 2010; pp. 652–653. [Google Scholar] [CrossRef]
  38. de Myttenaere, A.; Golden, B.; Le Grand, B.; Rossi, F. Mean Absolute Percentage Error for regression models. Neurocomputing 2016, 192, 38–48. [Google Scholar] [CrossRef]
  39. Chicco, D.; Warrens, M.J.; Jurman, G. The coefficient of determination R-squared is more informative than SMAPE, MAE, MAPE, MSE and RMSE in regression analysis evaluation. PeerJ Comput. Sci. 2021, 7, e623. [Google Scholar] [CrossRef] [PubMed]
  40. Arvanitidis, A.I.; Kontogiannis, D.; Vontzos, G.; Laitsos, V.; Bargiotas, D. Stochastic Heuristic Optimization of Machine Learning Estimators for Short-Term Wind Power Forecasting. 2022 57th International Universities Power Engineering Conference (UPEC). IEEE, 2022, pp. 1–6. [CrossRef]
  41. Vontzos, G.; Bargiotas, D. A Regional Civilian Airport Model at Remote Island for Smart Grid Simulation. Smart Energy for Smart Transport: Proceedings of the 6th Conference on Sustainable Urban Mobility, CSUM2022, 31 August–, Springer: Skiathos Island, Greece, 2023; pp. 183–192. 2 September. [CrossRef]
  42. Laitsos, V.M.; Bargiotas, D.; Daskalopulu, A.; Arvanitidis, A.I.; Tsoukalas, L.H. An incentive-based implementation of demand side management in power systems. Energies 2021, 14, 7994. [Google Scholar] [CrossRef]
Preprints 73495 g001
Figure 1. Basic Structure of LSTM model [21].
Figure 1. Basic Structure of LSTM model [21].
Preprints 73495 g001
Preprints 73495 g002
Figure 2. Multilayer Perceptron Architecture [22].
Figure 2. Multilayer Perceptron Architecture [22].
Preprints 73495 g002
Preprints 73495 g003
Figure 3. Main ConvNet Architecture [26].
Figure 3. Main ConvNet Architecture [26].
Preprints 73495 g003
Preprints 73495 g004
Figure 4. CNN-LSTM Model Architecture [27].
Figure 4. CNN-LSTM Model Architecture [27].
Preprints 73495 g004
Preprints 73495 g005
Figure 5. Temporal Convolutional Network [29].
Figure 5. Temporal Convolutional Network [29].
Preprints 73495 g005
Preprints 73495 g006
Figure 6. A ConvLSTM cell [31].
Figure 6. A ConvLSTM cell [31].
Preprints 73495 g006
Preprints 73495 g007
Figure 7. Encoder Decoder Mechanism [33]
Figure 7. Encoder Decoder Mechanism [33]
Preprints 73495 g007
Preprints 73495 g008
Figure 8. STLF automated algorithm structure.
Figure 8. STLF automated algorithm structure.
Preprints 73495 g008
Preprints 73495 g009
Figure 9. Daily average hourly consumption.
Figure 9. Daily average hourly consumption.
Preprints 73495 g009
Preprints 73495 g010
Figure 10. Feature Correlation Heatmap.
Figure 10. Feature Correlation Heatmap.
Preprints 73495 g010
Preprints 73495 g011
Figure 11. Dataset partitioning in train, validation and test sets.
Figure 11. Dataset partitioning in train, validation and test sets.
Preprints 73495 g011
Preprints 73495 g012
Figure 12. Models visualization.
Figure 12. Models visualization.
Preprints 73495 g012
Preprints 73495 g014
Figure 14. Comparison of the models in terms of MAE and RMSE error metrics.
Figure 14. Comparison of the models in terms of MAE and RMSE error metrics.
Preprints 73495 g014
Table 1. Power consumption descriptive analysis.
Table 1. Power consumption descriptive analysis.
Power consumption descriptive analysis
Number of samples 25944
Mean value 23.31 MW
Standard deviation 9.95 MW
Minimum value 8.50 MW
Percentile 25% 14.70 MW
Percentile 50% 21.15 MW
Percentile 75% 31.00 MW
Maximum value 51.52 MW
Table 2. Deep learning models input variables.
Table 2. Deep learning models input variables.
Input Variable Description
Power The sequence of 24 hours of load values for 1 day.
Temperature The sequence of 24 hours of temperature values for 1 day.
Dew Point The sequence of 24 hours of dew point values for 1 day.
Cos of Day of Week/ Sin of Day of Week The Day of the Week converted by One-Hot Encoding to
sin and cosine type.
Cos of Hour of Day/ Sin of Hour of Day The Hour of Day 1-24, converted by One-Hot Encoding to
sin and cosine type.
Cos of Month of Year/ Sin of Month of Year The Month of the Year converted by One-Hot Encoding to
sin and cosine type.
IsWeekend A dummy variable “Is Weekend”, the takes 0 for
working days and 1 for weekends.
Table 3. Evaluation metrics.
Table 3. Evaluation metrics.
Method R2 (MW) MAE (MW) MSE (MW) RMSE (MW) MAPE (%)
LSTM 0.9920 0.4275 0.4552 0.6747 2.25%
CNN-LSTM 0.9917 0.4412 0.4714 0.6866 2.31%
CNN-1D 0.9906 0.4936 0.5302 0.7282 2.66%
MLP 0.9919 0.4477 0.4602 0.6784 2.38%
TCN 0.9910 0.4576 0.5036 0.7096 2.40%
ConvLSTM Encoder Decoder 0.9921 0.4142 0.4454 0.6674 2.15%
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated