Prerpints.org logo
Preprint
Article

Absence of Weak Localization Effects in Strontium Ferromolybdate

Altmetrics

Downloads

107

Views

22

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

15 May 2023

Posted:

16 May 2023

You are already at the latest version

Alerts
Abstract
Sr2FeMoO6-δ (SFMO) double perovskite is a promising candidate for room-temperature spintronic applications since it possesses a half-metallic character (with theoretically 100% spin polarization), a high Curie temperature of about 415 K, and a low-field magnetoresistance (LFMR). However, due to different synthesis conditions of ceramics as well as thin films, different mechanisms of electrical conductivity and magnetoresistance prevail. In this work, we consider the weak localization effect in SFMO occurring in disordered metallic or semiconducting systems at very low temperatures due to quantum interference of back-scattered electrons. We calculate the quantum corrections to conductivity and the contribution of electron scattering to the resistivity of SFMO. We attribute the temperature dependence of SFMO ceramics resistivity in the absence of a magnetic field to the fluctuation induced tunneling model. Also, we attribute the decreasing resistivity in the temperature range from 409 K up to 590 K to adiabatic small polaron hopping and not to localization effects. Both fluctuation induced tunneling and adiabatic small polaron hopping do not favor quantum interference. Additionally, we demonstrate that the resistivity upturn behavior of SFMO cannot be explained by weak localization. Consequently, to the best of our knowledge, there is still no convincing evidence for the presence of weak localization in SFMO.
Keywords: 
Subject: Physical Sciences  -   Applied Physics

1. Introduction

In a disordered electronic system, the electron motion is diffusive due to scattering at non-uniformities. Weak localization is a physical effect which occurs in disordered electronic systems at very low temperatures. The effect manifests itself as a correction Ds to the conductivity (or correspondingly the resistivity) of a metal or semiconductor arising in the case that the mean free path l is in the order of the wavelength λF = 2π/kF of the carrier wavefunctions, i.e. kFl~1, with kF denoting the Fermi wave vector. The weak localization correction comes from quantum interference of back-scattered electrons. Labeling all the trajectories by the time t it takes for a classical particle to go around a loop, the classical probability dP that the diffusing particle returns into the phase volume dV at a given time t is given by [1] (p. 153)
d P = d V ( 4 π D t ) d / 2
where P is the probability for a quantum mechanical particle to return to the starting point (the wave function of both time-reversed paths will constructively interfere with each other), D= vF2t/d is the diffusion constant, t is the elastic scattering time and d is the dimension. The relevant phase volume can be estimated as vF dt (δρδφ)d−1[2,3], where vF= (2EF/me)1/2 is the Fermi velocity, EF the Fermi energy, me the electron mass, δρ and δφ characterize the transverse distance between the electron trajectories 1 and 2 at the intersection point and δφ is the intersection angle between the both trajectories. For the interference between paths 1 and 2 to be effective, the uncertainty relation should hold
p F δ ρ δ ϕ = ℏ k F δ ρ δ ϕ = h
where pF = mevF is the Fermi momentum and h the Planck constant. This leads to a relative change in conductivity of two and three dimensional systems yielding [1] (p. 183):
δ σ 2 D σ 0 = − 2 π k F l e ln l Φ l e , Δ σ 3 D σ 0 = − 3 2 ( k F l e ) 2
where s0 is the residual low temperature conductivity taken as the Drude conductivity, i.e. sD = e2nete/me, determined by relaxation time t of the dominating charge scattering mechanism, the electron charge e, the electron density ne, the elastic scattering time τe and the electron mass me. In eq. (3), the negative sign is due to the fact that the returning trajectory should arrive at the intersection point with the momentum almost opposite to the initial one. This means that interference lowers the conductivity. Note that for small sizes b the volume (Dt)d/2 should be replaced by (Dt)d/2b3-d since the charge carrier has a chance to diffuse repeatedly from one wall to the other and the probability of finding it at any point across films or wires limited in size will be the same [4]. However, we are considering macroscopic sizes rather than sizes of the order of atomic distances. The lower cutoff τe is justified with the fact that within a time τe no elastic scattering occurs, and therefore there will be no closed trajectories. The upper limit is given by [5]:
τ Φ − 1 ∼ ( T D d / 2 N 0 a 3 − d ) 2 / ( 4 − d ) ,
where D = (vF2te/d) is the diffusion constant, N0 is the one-spin density of states, d the characteristic sample dimension. The phase coherence time tϕ defines the phase coherence length lϕ = (Dtϕ)1/2. This yields conductivity corrections for two and three dimensional systems amounting in terms of quantum conductance e2/h to [1] (p. 282):
Δ σ 2 D = − 2 e 2 π h ln l φ l e = − e 2 π h ln ( l φ l e ) 2 , Δ σ 3 D = − e 2 π h ( 1 l e − 1 l φ ) ,
with le the mean free path of the electron.
Temperature modifies the phase coherence length lϕ and, therefore, modifies the weak localization correction. The temperature dependence of lφ can be described as [6,7]
1 l ϕ 2 ( T ) = 1 l ϕ 2 ( 0 ) + A e e T p 1 + A e p T p 2 ,
where lφ(0) is the zero-temperature phase coherence length and AeeTp1 and AepTp2 represent the contributions from two different dephasing mechanisms, e.g. electron-electron (ee) and electron-phonon (ep) interactions, respectively. Note that the temperature exponents p1 and p2 changes fundamentally with the system dimensionality [8]. If electron-electron interaction is the dominant dephasing mechanism (also denoted as Nyquist dephasing mechanism), this gives rise to τee ∝ T-p with values of p equal to 0.66, and 1 for d = 1 and d = 2, respectively [1] (chapter 13.6.4), [5]. For d = 3 eq. (4) yields p = 2 while the result in [1] (p. 509) is p = 1.5. The electron-phonon interaction decoherence mechanism would provide a temperature dependence of the dephasing time tϕ ∝T-3 [9]. Typically, one finds τφ ≈ τep ∝ T-p with the exponent of temperature p ≈ 2–4.
In metals and semiconductors at low temperatures, quasielastic (small energy transfer) electron-electron scattering is the dominant dephasing process. Assuming only one dephasing process and accounting that lφ(0) is in the order of 50 nm to several micrometers, that is, usually lφ(0) >> lφ(T) [6,7,10,11,12], a simplified approximation formula is given by [11]:
1 l ϕ 2 ( T ) ≈ A ´ T p 1 ,
with p1 = 1 for quasielastic electron-electron scattering in agreement with experimental results in Bi2Te3 thin films [13], 50 nm-thick Cd3As2 films [11], Bi2Te3 single crystals [7], MoxW1-xTe2+d ultrathin films [14]. As a result, we obtain for quasi-elastic electron-electron scattering:
l φ 2 = l φ 2 ( T 0 ) ⋅ T 0 T ,
Consequently, eq. (5) transforms to
Δ σ 2 D , W L = − e 2 π h ln ( l ϕ 2 ( T 0 ) l e 2 ⋅ T 0 T ) = e 2 π h ln ( l e 2 l ϕ 2 ( T 0 ) ⋅ T T 0 ) = = e 2 π h [ ln ( l e 2 l ϕ 2 ( T 0 ) ) + ln ( T T 0 ) ] , δ σ 3 D , W L = − e 2 π ( 1 l e − 1 l ϕ ) = − e 2 π ⋅ l e + e 2 π ⋅ l ϕ ( T 0 ) ( T T 0 ) 1 / 2
Finally, the total conductivity consisting of 2D at high magnetic fields and 3D contributions is written as:
σ ( T ) = σ 0 + A ⋅ ln ( T T 0 ) + B ⋅ ( T T 0 ) 1 / 2 ,
with
σ 0 = σ D − e 2 π h b ⋅ ln ( l ϕ 2 ( T 0 ) l e 2 ) − e 2 π h ⋅ l e ,
and the coefficients:
A = e 2 π h b ,   B = e 2 π h ⋅ l ϕ ( T 0 ) ,
where b is the effective thickness of the 2D layer introduced to convert a 2D conductivity to a 3D one. A minimum of conductivity appears only when the second right-side term in Equation (10) changes sign, i.e.:
B = − 2 A ( T max / T 0 ) 1 / 2 = T 0 = T max − 2 A ,
With regard to Equation (10), quantum correction to residual conductivity may be written as [15]:
Δ σ ( T ) = A ′ ln T + B ′ T 1 / 2 ,
Assuming that Mathiessen’s rule holds, and representing resistivity as a sum of elastic and inelastic contributions where the latter increase with increasing temperature due to a power law (e.g. a term CTn), the resistivity data can be be fitted to [16,17]:
ρ ( T ) = 1 σ 0 + A ′ ⋅ ln T + B ′ ⋅ T 1 / 2 + C n T n ,
with n equal to 3/2, 2, 3, depending on the dominant scattering mechanism [18].
Separate conductivity quantum correction terms in the form A´lnT and B´T1/2 were introduced for La0.7Ca0.3MnO3 by Kumar et al [19]. Here, the first term A´lnT was attributed also to the Kondo effect [20]. In order to account for higher order scattering mechanisms and to extend the analytical description to higher temperatures, an additional term CTn was included. The electron-electron interaction term B´T1/2 was applied also to La0.7−xYxSr0.3MnO3 (0 ≤ x ≤ 0.2) ceramics of 1 mm thickness [21], to La0.7A0.3MnO3 (A=Ca,Sr,Ba) ceramics [22], to La0.6Re0.1Ca0.3MnO3 (Re = Pr, Sm, Gd, Dy) ceramics of 1 mm thickness all three prepared by conventional solid state reaction [23], to SrRuO3 thin films with a thickness of 6 to 8 nm deposited by pulsed laser deposition onto (100)SrTiO3 substrates [16], to ultrathin La0.7Sr0.3MnO3 films (3.5 to 40 nm), deposited by molecular beam epitaxy [17], and to metallic SrRuO3 and LaNiO3 thin films deposited by pulsed laser deposition with a thickness of 6 and 240 nm, respectively [24].
In the La0.7Sr0.3MnO3 ultrathin film case, a crossover from T1/2 to a lnT behavior in the low-temperature resistivity dependence with decreasing thicknesses was related to a change in the dimensionality of the system, going from 3D for samples thicker than 20 nm to 2D in the limit of ultrathin samples. The origin of this effect is that in the case of a film thickness larger than the Landau orbit length LH = (ħ/2eB)1/2 the system behaves essentially as 3D while in the opposite electron confinement results in a 2D behavior of the system. In the 3D case of metallic and ferromagnetic SrRuO3 and of metallic and paramagnetic LaNiO3 epitaxial thin films the term B´T1/2 was spitted into two terms where in the 3D case first term b1Tp/2 accounts for the weak localization and the b2T1/2 term stands for the renormalized electron-electron interaction quantum corrections [25]. In the 2D case, both these quantum corrections to conductivity have a similar temperature dependence. Here, only a lnT term remains. The quantum correction of conductivity in metallic LaNi1-xCoxO3 (0 ≤ x ≤ 0.75) below 2 K follows a power law BTm where away from the metal-insulator transition (x ≤ 0.4) m takes a value of m = 0.3…0.4. Such power-law conductivities are seen at the metallic side of the metal-insulator transition also for other ABO3 oxides [26].
In this work, we attribute the temperature dependence of the SFMO ceramic resistivity in the absence of a magnetic field to the fluctuation induced tunneling model and the decrease of resistivity in the temperature range from 409 K up to 590 K not to localization effects but to adiabatic small polaron hopping. Both fluctuation induced tunneling and adiabatic small polaron hopping do not favor quantum interference. Also, we demonstrate that the resistivity upturn behavior of SFMO cannot be explained by the weak localization effect.

2. Methods

First we estimate the coefficient A´ in Equation (15). Taking lF < 0.46 nm at room temperature [27] and b = 20 nm [17], the ratio of the coefficients A´/B´ will be in the order of 10-2. Since for arguments larger than one the natural logarithm function will be smaller than the root function, the logarithmic term can be neglected. A further indication of small A´ coefficients arises from the depth of the conductance minimum, i.e. the difference r(0)-r(Tmin), which changes with increasing magnetic flux [19]. Values of above 35 mW⋅cm in the absence of a magnetic field down to 2.4 mW⋅cm at 7 T [28] yield coefficients A´ = 10-2 ⋅(r(0)-r(Tmin)) [20,29]. In La0.7Sr0.3MnO3 ultrathin films (3.5 to 40 nm), deposited by molecular beam epitaxy [17], the agreement of fits of conductivity data to equation (15) with only the A´lnT term (B`= 0) was much worse than in the case with only the B´T1/2 term (A´= 0). Therefore, we neglect in the following the term A´lnT. This corresponds to the common practice of describing similar materials like La0.7−xYxSr0.3MnO3 (0 ≤ x ≤ 0.2) ceramics of 1 mm thickness prepared by conventional solid state reaction [21], La0.7A0.3MnO3 (A=Ca,Sr,Ba) ceramics prepared by conventional solid state reaction [22], and SrRuO3 thin films with a thickness of 6 to 8 nm deposited by pulsed laser deposition onto (100)SrTiO3 substrates [16].
The coefficient B´ is given by [15]:
B ´ = 0.0309 e 2 ℏ ⋅ k ℏ D = 2.72149 ⋅ Ω − 1 K − 1 / 2 s − 1 / 2 D [ m 2 / s ] .
with ħ = h/2p the Planck constant expressed in J s radian-1. For a mean free path le of 0.46 nm at room temperature [27] and a carrier relaxation time t of 1.6×10-14s [30], the carrier diffusion constant will be 1.32×10-5 m2 s-1 yielding a coefficient B´≈ 748 W-1 m-1 K-1/2 in satisfactory agreement with values of B´≈ 360…500 W-1 m-1 K-1/2 in in (Ni0.5Zr0.5)1-xAlx metallic glasses [31] and with a universal value of B´≈ 600 W-1 m-1 K-1/2 of amorphous and disordered metals [32]
The coefficient Cn was calculated as follows: We start with Drude conductivity:
ρ D = ℏ k F n e e 2 l e ,
where ne the electron density and e the electron charge. Taking ne= 1.1×1028 m-3 [33] we obtain ħkF = 4.8⋅10-25 Jsm-1 and
ρ D = 1.87 ⋅ 10 − 15 Ω m l e [ m ] ,
We assume electron mean free paths le = 0.46 nm and 1.11 nm at room temperature and 4 K, respectively, calculated from the ordinary Hall coefficient [27]. This yields rD = 4.07 µWm at room temperature and rD = 1.68 µWm at 4 K in satisfactory agreement with experimental data of single crystal SFMO in [34]. Now we assume that in a ferromagnetic state below room temperature magnetic scattering controls electrical transport in SFMO at low temperatures [27]. The mean free path of electron scattered by a spin wave with energy Es travelling through the bcc I4/mmm lattice in thermal equilibrium at a temperature T, is given by [35]:
l e = S 2 V 1 / 3 θ − 7 / 2 π ζ ( 3 / 2 ) ( E σ / k T ) ≈ 0.38 ⋅ S 9 / 2 a ⋅ ( J k T ) 5 / 2 ,
where S is the effective spin Seff =(SFeSMo)1/2 = (1/2⋅5/2)1/2=1.118, V the unit cell volume, q a dimensionless temperature, z the Rieman Zeta function, a the lattice constant, and J the exchange constant of the 180° Fe-O-Fe interaction amounting to -25 K [36,37]. Finally, we arrive at:
ρ D = 2.413 ⋅ 10 − 9 ⋅ T 5 / 2 Ω m ,
Compared to the experimental value of R2.5=1.4×10-11 WmK-5/2 in a relation r = r0+R2.5T2.5 the calculated value of R2.5 is overestimated by almost two orders of magnitude in part due to the approximation of the Fermi surface as a sphere and the disregard of additional s-d transitions in transition metals which reduce the mean free path [38]. Also, the value of R2.5 may be lowered by assuming a higher effective spin.

3. Results and discussion

Strontium ferromolybdate Sr2FeMo6-d (SFMO) is a half-metallic, ferrimagnetic compound with a saturation magnetization of 4 µB/f.u [28]. However, SFMO does not exhibit a general metallic conductivity mechanism. In the absence of a magnetic field, the temperature dependence of conductivity of SFMO ceramics [28] is well described by the fluctuation-induced tunneling (FIT) model [39], e.g., by the presence of conducting grains separated by nanosized energy barriers where large thermal voltage fluctuations occur when the capacitance of an intergrain junction is in the order of 0.1 fF. Here, tunneling occurs between large metallic grains via the intergrain junctions with a width w and area A. The FIT model is specified by three parameters [39]: (i) The temperature T1 characterizing the electrostatic energy of a parabolic potential barrier,
k T 1 = A ⋅ w ⋅ ε o E 0 2 2 ,
where k is the Boltzmann constant and the characteristic field E0 is determined by:
E 0 = 4 V 0 e ⋅ w ,
(ii) the temperature T0 representing T1 divided by the tunneling constant,
T 0 = T 1 ⋅ ( π χ w 2 ) − 1 ,
with the reciprocal localization length of the wave function
χ = 2 m * V 0 ℏ 2 ,
where m*e is the effective electron mass, and (iii) the residual resistivity r0. The resulting resistivity of this model is then given by [39]:
ρ ( T ) = ρ 0 exp ( T 1 T 0 + T ) ,
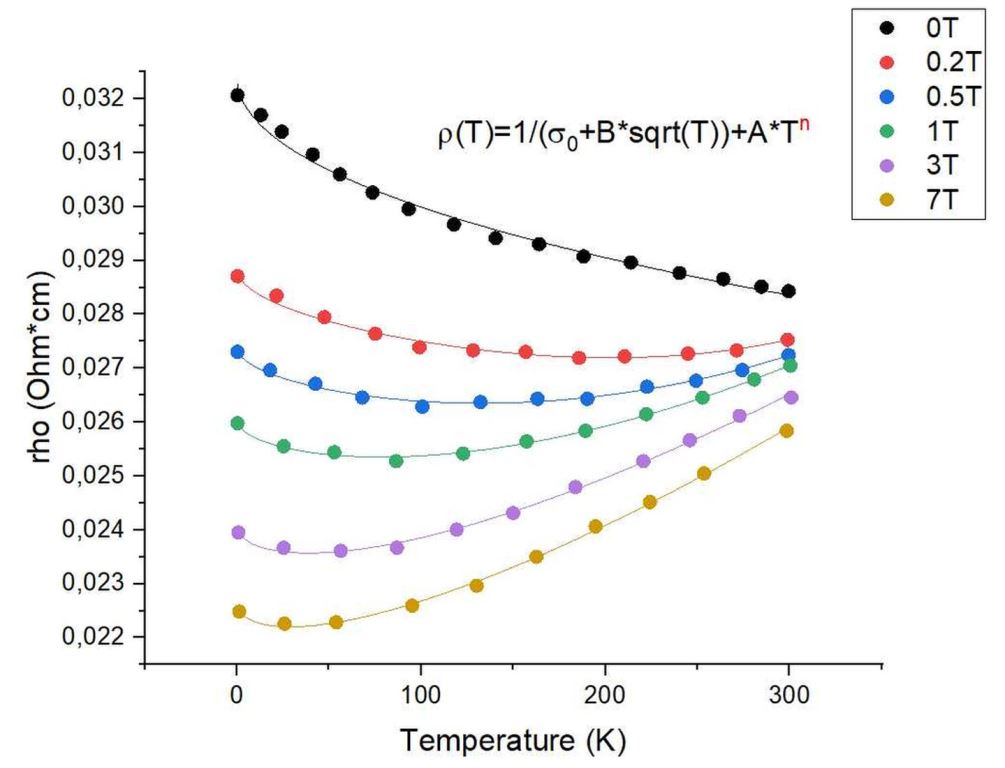
In our case, the model parameters amount to T0 = 141.1 K, T1 = 25.6 K and s0 = 1/r0 =37.16 S/cm (cf. Figure 1). The FIT model was recently applied to intergrain tunneling in polycrystalline Sr2CrMoO6 and Sr2FeMoO6 ceramics [40], in half-metallic double-perovskite Sr2BB’O6 (BB’– FeMo, FeRe, CrMo, CrW, CrRe) ceramics [41] and in Ba2FeMoO6 thin films [42].
One feature attributed to weak localization in SFMO ceramics is the decrease of resistivity in the temperature range between 405 K and 590 K [43]. In the following this resistivity behavior should be considered more in detail. According to [43], the resistivity behavior of vacuum-annealed SFMO ceramics above room temperature is separated into three regions: (i) From 300 K up to the Curie temperature of about 405 K the electrical resistivity increases with temperature and shows metallic behavior, (ii) Above 405 K up to approximately 590 K the resistivity decreases with temperature, (iii) Finally, from 590 K up to 900 K the resistivity increases since the material becomes metallic again [43].
Another report on the electrical resistivity of SFMO indicates metallic behavior up to 420 K, a decrease of resistivity in the temperature range 420–820 K, and the reversion to metallic behavior between 820 and 1120 K [44]. A similar resistivity behavior with a resistivity maximum at about 450 K, far above the Curie temperature of ~330 K [45], was obtained for Ba2FeMoO6-d while Ca2FeMoO6-d shows solely metallic behavior in the whole temperature range 320-1120 K [44].
A more detailed consideration of the reported resistivity behavior of Sr2FeMoO6-d and Ba2FeMoO6-d above TC [43,44], reveals a convincing fit to the adiabatic small polaron hopping model [46] (Figure 2). In the small polaron model, electrical conduction of perovskites at higher temperature, i.e., above a certain transition temperature, occurs by small polarons moving through the lattice by thermally activated jumps between neighboring sites. The transition temperature from small polaron motion in a conduction band to small polaron hopping was estimated to be in the order of θD/2 with θD the Debye temperature which amounts to 338 K for SFMO [47]. The adiabatic small polaron hopping model yields a resistivity of [46]:
ρ = ρ 0 T exp ( E a k T )
where Ea is the thermal activation energy. The obtained Ea values are 0.045-0.08 eV for Sr2FeMoO6-δ and about 0.13 eV for Ba2FeMoO6-δ and are in the order of the values of other perovskites and double perovskites: La1-xSrxCo1-yFeyO3 [48], Sr1.6Sm0.4MgMoO6-δ, Sr1.4Sm0.6MgMoO6-δ, and Sr1.2Sm0.8MgMoO6-δ [49], as well as Sr2Fe1.5Mo0.5O6-d and Sr2Fe1.5Mo0.5-xNbxO6-d [50].
Weak localization effects were taken into account in order to explain the presence of minima in the ρ–T curves of perovskite oxides exhibiting metallic conductivity [17,19,25,51,52]. It has been suggested [20,21] that the resistivity minimum and, consequently, the resistivity upturn at lower temperature arises from the competition of two contributions—one, usual, increasing and the other, decreasing with the increase of the temperature. In eq. (15), the corresponding terms are (B´lnT)-1 and CnTn, respectively. The resistivity versus temperature plots of SFMO ceramics in a magnetic field [28] are very similar to the ones of La0.7Ca0.3MnO3and La0.7Sr0.3MnO3 thin films [17,19]. Also here, a resistivity minimum appears in polycrystalline SFMO ceramics at low temperature [28] which was explained by weak localization [52]. In this case, a quantum correction terms AWTp/2 [17,52] was added to the residual resistivity s0 and an electron interaction term ApTn to the resistivity. A similar approach was applied to perovskite ceramics (LaNixCo1-xO3 and NaxTayW1-yO3 [53], La0.5Pb0.5MnO3 and La0.5Pb0.5MnO3 ceramics containing 10 at.% Ag in a dispersed form [15].
To evaluate the origin of the low temperature resistivity minimum in SFMO, we fitted the experimental data [28] to eq. (15) assuming A´= 0 (Figure 3, Table 1). The increase of the s0(B) values correspond to a negative magnetoresistance obtained in ferrimagnetic SFMO ceramics which arises due to the suppression of spin disorder by the magnetic field [27,28,43]. The fitted s0 values describe a power law magnetic flux dependence of the magnetoresistance, -MR ∝ Bm, with a power of m = 0.284. This value lies in-between the values of m = 0.5 for metallic behavior and electron-electron interaction in the temperature range between the temperature of minimum resistivity and the Curie temperature and m = 0.1 for semiconducting conductivity behavior, both at high magnetic fluxes [54]. The fitted B´ values are three orders of magnitude lower than the ones calculated above. Consequently, the elastic scattering time should be reduced by six orders of magnitude. This is physically nonsense. Also, the CnTn term does not correspond to physically meaningful quantities. The values of the exponent n cannot be attributed to a certain electron scattering mechanism. On the other hand, electron scattering should sufficiently change in dependence on the magnetic flux. When assuming n = 2 for electron-electron scattering, and taking the value Cn = 2.16×10-11 WmK-2 from [33], the fit becomes of much worse quality (Figure 4). Here, a satisfactory fit occurs only for B = 0. Assuming n = 2.5 and taking the value Cn of eq. (20), the fit is even worse with a no satisfactory fit even for B = 0.
Thus, the only possible conclusion is that the resistivity upturn at low temperatures in Sr2FeMoO6 ceramics cannot be modeled by the weak localization correction due to quantum interference. Note that neither fluctuation induced tunneling nor adiabatic small polaron hopping provide favored conditions for quantum interference of back-scattered electrons.

4. Conclusions

We have related the temperature dependence of the SFMO resistivity in the absence of a magnetic field to the fluctuation induced tunneling model. The decrease in resistivity above the resistivity maximum around Curie temperature was attribute to adiabatic small polaron hopping instead to localization effects. Both fluctuation induced tunneling and adiabatic small polaron hopping do not favor quantum interference. This is evidenced by the observation that the resistivity upturn behavior of SFMO cannot be explained by weak localization. Consequently, to the best of our knowledge, there is still no convincing evidence for the presence of weak localization in SFMO.

Author Contributions

Conceptualization, G.S.; methodology, G.S; software, E.A; validation, G.S. and E.A.; formal analysis, G.S.; investigation, G.S. and E.A..; resources, G.S.; data curation, E.A.; writing—original draft preparation, G.S.; writing—review and editing, E.A..; visualization, E.A..; supervision, G.S.; project administration, G.S.; funding acquisition, G.S. All authors have read and agreed to the published version of the manuscript.

Funding

This work was funded by the EU project H2020-MSCA-RISE-2017-778308- SPINMULTIFILM.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Acknowledgments

The authors thank Prof. N. Sobolev (University Aveiro) for valuable discussions on the topic of this work.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Akkermans. A., G. Montambaux, G. Mesoscopic Physics of Electrons and Photons. Cambridge University Press, Great Britain, 2007).
  2. Aleiner, I.L.; Altshuler, B.L.; Gershenson, M.E. Interaction effects and phase relaxation in disordered systems. Waves Random Media 1999, 9, 201–239. [Google Scholar] [CrossRef]
  3. Senz,. V., Quantum transport in interacting two-dimensional systems, PhD thesis, ETH, Zürich (Switzerland), 02, p.25. 20 March. [CrossRef]
  4. Abrikosov, A. Fundamentals of the theory of metals, Elsevier, Amsterdam, Netherlands, 1988, p.213.
  5. Altshuler, B.L.; Aronov, A.G.; Khmelnitzky, D.E. Effects of electron-electron collisions with small energy transfers on quantum localization. J. Phys. C: Solid State Phys. 1982, 15, 7367–7386. [Google Scholar] [CrossRef]
  6. Xu, G.; Wang, W.; Zhang, X.; Du, Y.; Liu, E.; Wang, S.; Wu, G.; Liu, Z.; and Zhang, X.X. Weak Antilocalization Effect and Noncentrosymmetric Superconductivity in a Topologically Nontrivial Semimetal LuPdBi. Sci Rep. 2014, 4, 5709. [Google Scholar] [CrossRef] [PubMed]
  7. Shrestha, K.; Chou, M.; Graf, D.; Yang, H.D.; Lorenz, B. Chu, C.W. Extremely large nonsaturating magnetoresistance and ultrahigh mobility due to topological surface states in the metallic Bi2Te3 topological insulator. Phys. Rev. B - Condens. Matter Mater. Phys 2017, 95, 195113. [Google Scholar] [CrossRef]
  8. Lin, J.J.: Bird, J.P. Recent experimental studies of electron dephasing in metal and semiconductor mesoscopic structures. J. Phys.: Condens. Matter 2002, 14, R501–R596. [CrossRef]
  9. Rammer, J.; Schmid, A. Destruction of phase coherence by electron-phonon interactions in disordered conductors, Phys. Rev. B - Condens. Matter Mater. Phys. 1986, 34, 1352–1355. [Google Scholar] [CrossRef]
  10. Sahnoune, A.; Strom-Olsen, J.O. Weak localization and enhanced electron-electron interaction in amorphous Ca70(Mg,Al)30, Phys. Rev. B - Condens. Matter Mater. Phys., 1989, 39, 7561–7566. [Google Scholar] [CrossRef] [PubMed]
  11. Zhao, B.; Cheng, P.; Pan, H.; Zhang, S.; Wang, B.; Wang, G.; Xiu, F.; Song, F. , Weak antilocalization in Cd3As2 thin films. Sci. Rep. 2016, 6, 22377. [Google Scholar] [CrossRef]
  12. Islam, S.; Bhattacharyya, S.; Nhalil, H.; Banerjee, M.; Richardella, A.; Kandala, A.; Sen, D.; Samarth, N.; Elizabeth, S.; Ghosh, A. , Low-temperature saturation of phase coherence length in topological insulators, Phys. Rev. B - Condens. Matter Mater. Phys. 2019, 99, 245407. [Google Scholar] [CrossRef]
  13. Dey, R.; Pramanik, T.; Roy, A.; Rai, A.; Guchhait, S.; Sonde, S.; Movva, H.C.P.; Colombo, L.; Register, L.F.; Banerjee, S.K. Strong spin-orbit coupling and Zeeman spin splitting in angle dependent magnetoresistance of Bi2Te3, Appl. Phys. Lett. 2014, 104, 223111. [Google Scholar] [CrossRef]
  14. Mathew, R.J.; Inbaraj, C.R.P.; Sankar, R.; Hudie, S.M.; Nikam, R.D.; Tseng, C.-A.; Lee, C.-H.; Chen, Y.-T. High unsaturated room-temperature magnetoresistance in phase-engineered MoxW1-xTe2+d ultrathin films, J. Mater. Chem. C 2019, 7, 10996. [Google Scholar] [CrossRef]
  15. Rozenberg, E.; Auslender, M.; Felner, I.; Gorodetsky, G. Low-temperature resistivity minimum in ceramic manganites. J. Appl. Phys. 2000, 88, 2578–2582. [Google Scholar] [CrossRef]
  16. Herranz, G.; Martínez, B.; Fontcuberta, J.; . Sánchez, F.; Ferrater, C.; García-Cuenca, M.V.; Varela, M. Enhanced electron-electron correlations in nanometric SrRuO3 epitaxial films. Phys. Rev. B - Condens. Matter Mater. Phys. 2003, 67, 174423. [Google Scholar] [CrossRef]
  17. Maritato, L.; Adamo, C.; Barone, C.; . De Luca, G.M; Galdi, A.; Orgiani, P.; Petrov, A.Yu. Low-temperature resistivity of La0.7Sr0.3MnO3 ultra thin films: Role of quantum interference effects. Phys. Rev. B - Condens. Matter Mater. Phys. 2006, 73, 094456. [Google Scholar] [CrossRef]
  18. Lee, P.A.; Ramakrishnan, T.V. Disordered electronic systems, Rev. Mod. Phys. 1985, 57, 287–337. [Google Scholar] [CrossRef]
  19. Kumar, D.; Sankar, J.; Narayan, J.; Singh, R.K.; Majumdar, A.K. , Low-temperature resistivity minima in colossal magnetoresistive La0.7Ca0.3MnO3 thin films. Phys. Rev. B - Condens. Matter Mater. Phys. 2002, 65, 094407. [Google Scholar] [CrossRef]
  20. Kondo, J. Resistance minimum in dilute magnetic alloys, Prog. Theor. Phys. 1964, 32, 37–49. [Google Scholar] [CrossRef]
  21. Barman, A.; Ghosh, M.; Biswas, S.; De, S.K. ; Chatterjee, S. Electrical and magnetic properties of La0.7-xYxSr0.3MnO3 (0 ≤ x ≤ 0:2) perovskite at low temperature, J. Phys.: Condens. Matter 1998, 10, 9799–9811. [Google Scholar] [CrossRef]
  22. Tiwari, A.; Rajeev, K.P. Low-temperature electrical transport in La0.7A0.3MnO3, (A: Ca, Sr, Ba). Solid State Commun. 1999, 111, 33–37. [Google Scholar] [CrossRef]
  23. Barman, A., Ghosh, M., Biswas, S.,. De, S.K:, Chatterjee, S. Electrical properties of La0.6Re0.1Ca0.3MnO3 (Re=Pr, Sm, Gd, Dy) at low temperature. Solid State Commun. 1998, 106, 691–694. [CrossRef]
  24. Herranz, G.; Sánchez, F.; Martínez, B.; Fontcuberta, J.; García-Cuenca, M. V.; Ferrater, C.; Varela, M.; Levy, P. Weak localization effects in some metallic perovskites. Eur. Phys. J. B 2004, 40, 439–444. [Google Scholar] [CrossRef]
  25. Herranz, G.; Sánchez, F.; Fontcuberta, J.; Laukhin, V.; Galibert, J.; García-Cuenca, M.V.; Ferrater, C.; Varela, M. Magnetic field effect on quantum corrections to the low-temperature conductivity in metallic perovskite oxides Phys. Rev. B - Condens. Matter Mater. Phys., 2005, 72, 014457. [Google Scholar] [CrossRef]
  26. Raychaudhuri, A.K.; Rajeev, K.P.; Srikanth, H.; Mahendiran, R. Low temperature studies on normal perovskite oxides: role of correlation and disorder. Physica B: CondensMat. 1994, 197, 124–132. [Google Scholar] [CrossRef]
  27. Westerburg, W. Spinpolarisierter Transport in epitaktischen Manganoxid und Doppelperowskitschichten, Ph.D. Thesis, Universität Mainz, October 6th, 2000. [Google Scholar]
  28. Kobayashi, K.I.; Kimura, T.; Sawada, H.; Terakura, K.; Tokura, Y. Room-Temperature Magnetoresistance in an Oxide Material with an Ordered Double-Perovskite Structure. Nature 1998, 395, 677–680. [Google Scholar] [CrossRef]
  29. 29. B. Knook, De anomale electrische Weerstand van een aantal Cu-, Ag-, en Au-Legeringen, PhD Thesis, University of Leiden, Netherlands, April 4th, 1962.
  30. Mazur, D.; Gray, K. E.; Zasadzinski, J.F.; Ozyuzer, L.; Beloborodov, I.S.; Zheng, H.; Mitchell, J.F. Redistribution of the density of states due to Coulomb interactions in La2−2xSr1+2xMn2O7. Phys. Rev. B - Condens. Matter Mater. Phys. 2007, 76, 193102. [Google Scholar] [CrossRef]
  31. Nath, T. K.; Majumdar A., K. Quantum interference effects in (Ni0. 5Zr0.5)1-xAlx metallic glasses, Phys. Rev. B - Condens. Matter Mater. Phys., 2007, 55, 5554–5557. [Google Scholar] [CrossRef]
  32. Cochrane, R.W.; Strom-Olsen, J.O. Scaling behavior in amorphous and disordered metals, Phys. Rev. B - Condens. Matter Mater. Phys. 1984, 29, 1088–1090. [Google Scholar] [CrossRef]
  33. Tomioka, Y.; Okuda, T.; Okimoto, Y.; Kumai, R.; Kobayashi, K.; Tokura, Y. Magnetic and Electronic Properties of a Single Crystal of Ordered Double Perovskite. Phys. Rev. B - Condens. Matter Mater. Phys. 2000, 61, 422–427. [Google Scholar] [CrossRef]
  34. Yanagihara, H.; Salamon, M.B.; Lyanda-Geller, Y.; Xu, S.; Moritomo, Y. Magnetotransport in double perovskite Sr2FeMoO6: Role of magnetic and nonmagnetic disorder. Phys. Rev. B - Condens. Matter Mater. Phys. 2001, 64, 214407. [Google Scholar] [CrossRef]
  35. Dyson, F.J. , General Theory of Spin-Wave Interactions, Phys. Rev. 1956, 102, 1217–1230. [Google Scholar] [CrossRef]
  36. Motida, K.; Miyahara, S. On the 90° exchange interaction between cathions (Cr3+, Mn2+, Fe3+ and Ni2+) in oxides, J. Phys. Soc. Jpn. 1970, 28, 1188–1196. [Google Scholar] [CrossRef]
  37. Voogt, F.C.; Palstra, T.T.M.; Niesen, L.; Rogojanu, O.C.; James, M. A.; Hibma, T. Superparamagnetic behavior of structural domains in epitaxial ultrathin magnetite films Phys. Rev. B - Condens. Matter Mater. Phys. 1998, 57, R8107–R8110. [Google Scholar] [CrossRef]
  38. Suchaneck, G.; Artiukh, E.; Gerlach, G. Resistivity and tunnel magnetoresistance in double-perovskite strontium ferromolybdate ceramics. Physica Status Solidi B 2022, 259, 2200012. [Google Scholar] [CrossRef]
  39. Sheng, P.; Sichel, E.K.; Gittleman, J.I. Fluctuation-induced tunneling conduction in carbon-polyvinylchloride composites, Phys. Rev. Lett. 1978, 40, 1197–2000. [Google Scholar] [CrossRef]
  40. Fisher, B.; Genossar, J.; . Chashka, K.B; Patlagan, L.; Reisner, G.M. Remarkable power-law temperature dependencies of inter-grain conductivity. Solid State Commun. 2006, 137, 641–644. [Google Scholar] [CrossRef]
  41. Fisher, B.; Genossar, J.; Chashka, K.B.; Patlagan, L.; Reisner, G.M. Inter-grain tunneling in the half-metallic double-perovskites Sr2BB'O6(BB'= FeMo, FeRe,CrMo, CrW, CrRe). Proceedings of the EPJ Web of Conferences 2014, 75, 01001. [Google Scholar] [CrossRef]
  42. S. Granville, I.L. Farrell, A.R. Hyndman, D.M. McCann, R.J. Reeves, G.V.M. Williams, Indications of spin polarized transport in Ba2FeMoO6 thin films, (2017). Available online: http://arxiv.org/abs/1707.01208, accessed on April 14th, 2023.
  43. Niebieskikwiat, D.; Sánchez, R.; Caneiro, A.; Morales, L.; Vásquez-Mansilla, M.; Rivadulla, F.; Hueso, L. High-Temperature Properties of the Double Perovskite: Electrical Resistivity, Magnetic Susceptibility, and ESR. Phys. Rev. B - Condens. Matter Mater. Phys 2000, 62, 3340–3345. [Google Scholar] [CrossRef]
  44. Zhang, L.; Zhou, Q.; He, Q.; He, T. Double-Perovskites A2FeMoO6-δ (A = Ca, Sr, Ba) as Anodes for Solid Oxide Fuel Cells. J. Power Sources 2010, 195, 6356–6366. [Google Scholar] [CrossRef]
  45. Maignan, A.; Raveau, B.; Martin, C.; Hervieu, M. Large Intragrain Magnetoresistance above Room Temperature in the Double Perovskite Ba2FeMoO6. J. Solid State Chem. 1999, 144, 224–227. [Google Scholar] [CrossRef]
  46. Emin, D.; Holstein, T. Studies of Small-Polaron Motion IV. Adiabatic Theory of the Hall Effect. Ann. Phys. 1969, 53, 439–520. [Google Scholar] [CrossRef]
  47. Okuda, T.; Kobayashi, K.-I.; Tomioka, Y.; Tokura, Y. Anomalous low-temperature specific heat around the metal-insulator transition in ordered double-perovskite alloys Sr2Fe(Mo1-yWy)O6 (0 ≤ y ≤ 1). Phys. Rev. B - Condens. Matter Mater. Phys 2003, 68, 144407. [Google Scholar] [CrossRef]
  48. Tai, L.W.; Nasrallah, M.M.; Anderson, H.U.; Sparlin, D.M.; Sehlin, S.R. Structure and Electrical Properties of La1-xSrxCo1-yFeyO3. Part 2. The System La1-xSrxCo0.2Fe0.8O3. Solid State Ionics 1995, 76, 273–283. [Google Scholar] [CrossRef]
  49. Zhang, L.; He, T. Performance of Double-Perovskite Sr2-xSmxMgMoO6-δ as Solid-Oxide Fuel-Cell Anodes. J. Power Sources 2011, 196, 8352–8359. [Google Scholar] [CrossRef]
  50. Hou, M.; Sun, W.; Li, P.; Feng, J.; Yang, G.; Qiao, J.; Wang, Z.; Rooney, D.; Feng, J.; Sun, K. Investigation into the Effect of Molybdenum-Site Substitution on the Performance of Sr2Fe1.5Mo0.5O6-δ for Intermediate Temperature Solid Oxide Fuel Cells. J. Power Sources 2014, 272, 759–765. [Google Scholar] [CrossRef]
  51. Auslender, M.; Kar’kin, A.E.; Rozenberg, E. Low-temperature resistivity minima in single-crystalline and ceramic La0.8Sr0.2MnO3: Mesoscopic transport and intergranular tunneling. J. Appl. Phys. 2001, 89, 6639–6641. [Google Scholar] [CrossRef]
  52. Kalanda, N.; Demyanov, S.; Yarmolich, M.; Petrov, A.; Sobolev, N.; Electric transport characteristics of Sr2FeMoO6–δ ceramics with structurally inhomogeneous surfaces, In: Workshop book, 2nd International Workshop on Advanced Magnetic Oxides (IWAMO), -25, Aveiro, Portugal, 2021, p.24. 24 November.
  53. Raychaudhuri, A.K.; Rajeev, K.F.; Srikanth, H.; Gayathri, N. Metal-insulator transition in perovskite oxides: Tunneling experiments. Phys. Rev. B - Condens. Matter Mater. Phys. 1995, 51, 7421–7428. [Google Scholar] [CrossRef]
  54. Saloaro, M.; Majumdar, S.; Huhtinen, H.; Paturi, P. Absence of traditional magnetoresistivity mechanisms in Sr2FeMoO6 thin films grown on SrTiO3, MgO and NdGaO3 substrates. J. Phys.: Condens. Matter 2012, 24, 366003. [Google Scholar] [CrossRef]
Preprints 73679 g001
Figure 1. Fitting of the conductivity data of SFMO ceramics at zero magnetic flux [28] to the fluctuation induced tunneling model [39]. Fitting parameters are: T0 = 141.1 K, T1 = 25.6 K and s0 = 37.16 S/cm.
Figure 1. Fitting of the conductivity data of SFMO ceramics at zero magnetic flux [28] to the fluctuation induced tunneling model [39]. Fitting parameters are: T0 = 141.1 K, T1 = 25.6 K and s0 = 37.16 S/cm.
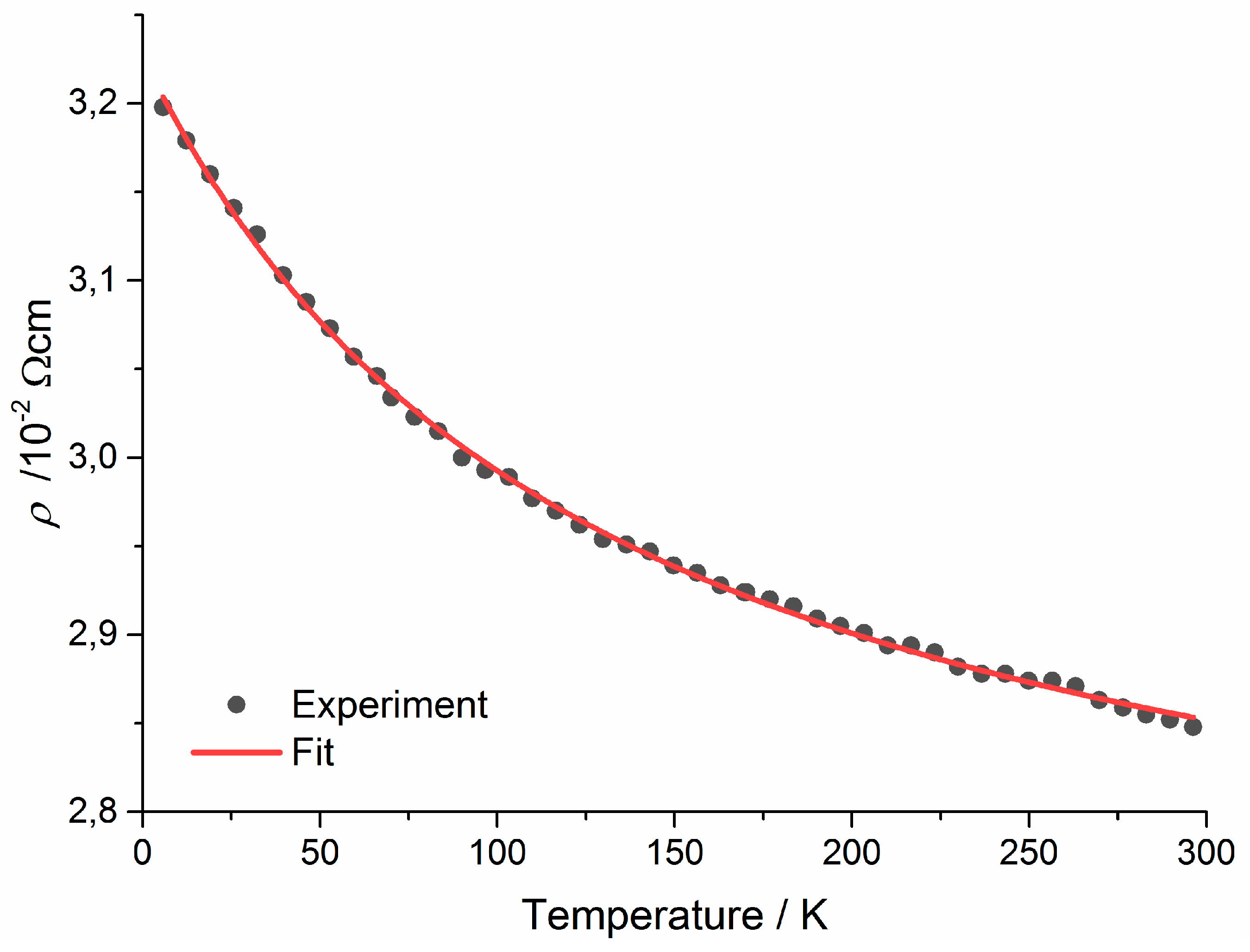
Preprints 73679 g001
Preprints 73679 g002
Figure 2. Fitting of the conductivity data of Sr2FeMoO6 ceramics between 405 K and 590 K [43] as well as of Sr2FeMoO6 ceramics between 420 and 870 K and Ba2FeMoO6 ceramics between 520 and 1120 K [44] to the adiabatic small polaron hopping model [46].
Figure 2. Fitting of the conductivity data of Sr2FeMoO6 ceramics between 405 K and 590 K [43] as well as of Sr2FeMoO6 ceramics between 420 and 870 K and Ba2FeMoO6 ceramics between 520 and 1120 K [44] to the adiabatic small polaron hopping model [46].
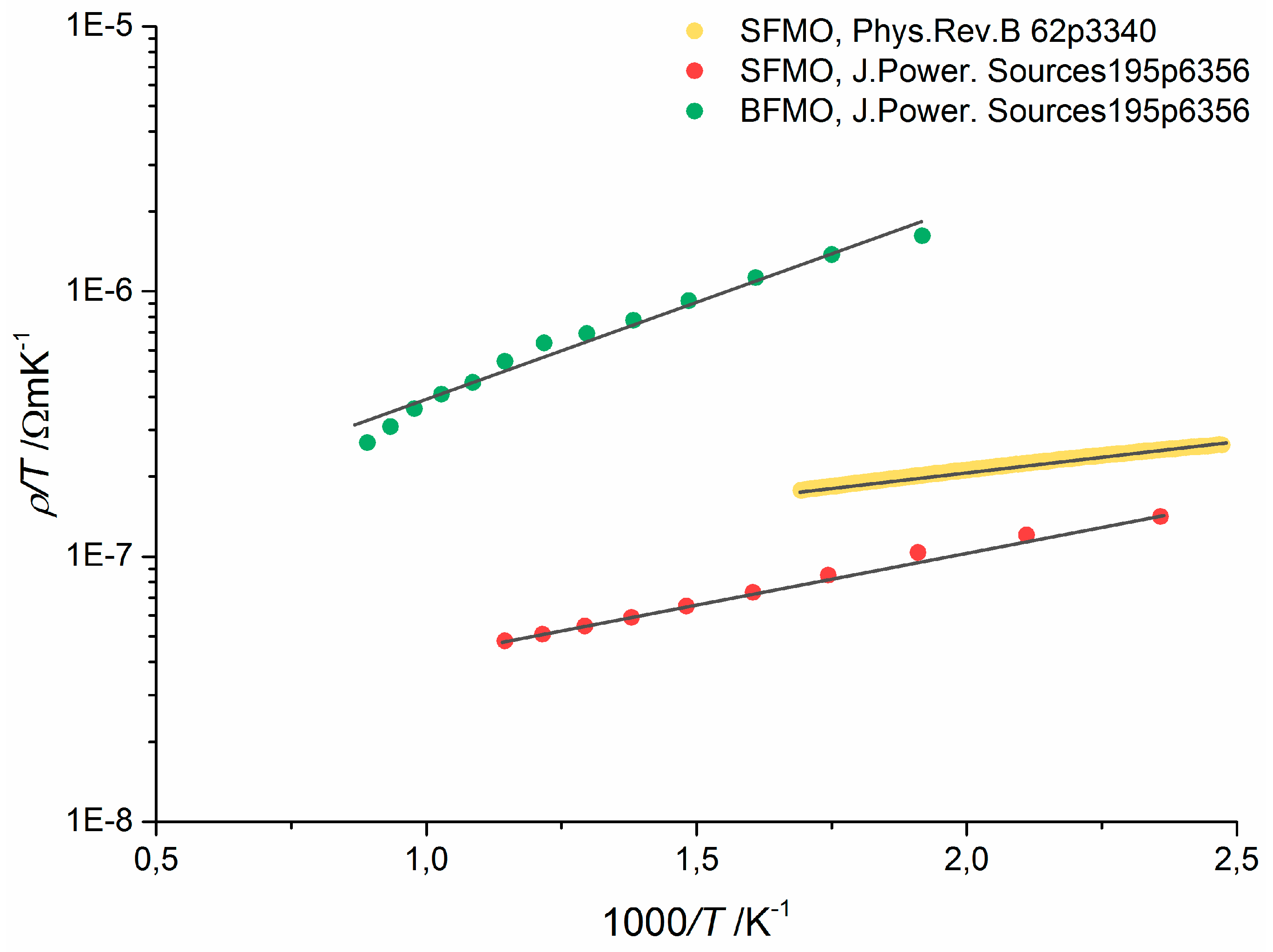
Preprints 73679 g002
Preprints 73679 g003
Figure 3. Fit of the conductivity data of Sr2FeMoO6 [28] to eq. (15) assuming A´= 0.
Figure 3. Fit of the conductivity data of Sr2FeMoO6 [28] to eq. (15) assuming A´= 0.
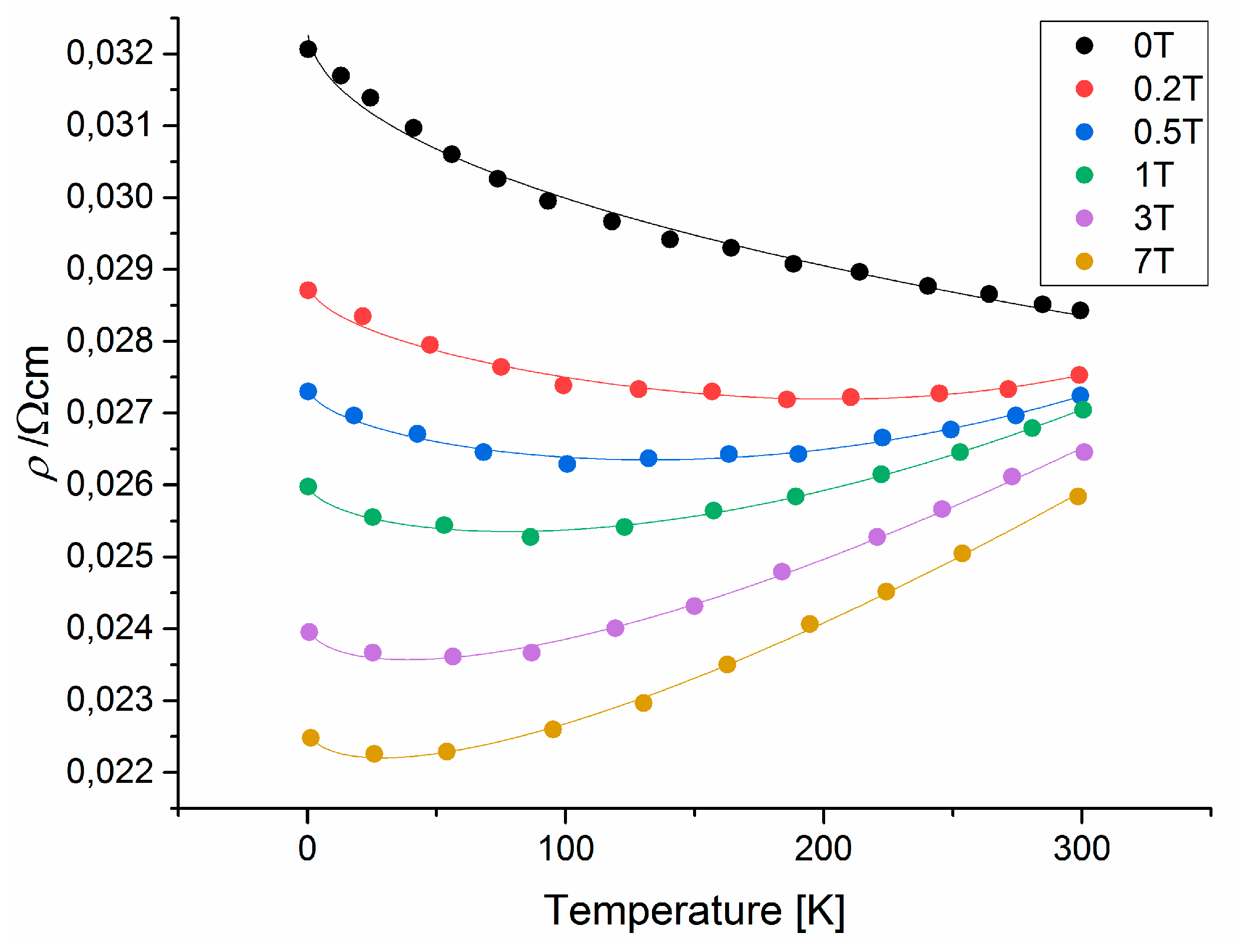
Preprints 73679 g003
Preprints 73679 g004
Figure 4. Fit of the conductivity data of Sr2FeMoO6 [28] to eq. (15) assuming A´ = 0, Cn = 2.16×10-11, n = 2.
Figure 4. Fit of the conductivity data of Sr2FeMoO6 [28] to eq. (15) assuming A´ = 0, Cn = 2.16×10-11, n = 2.
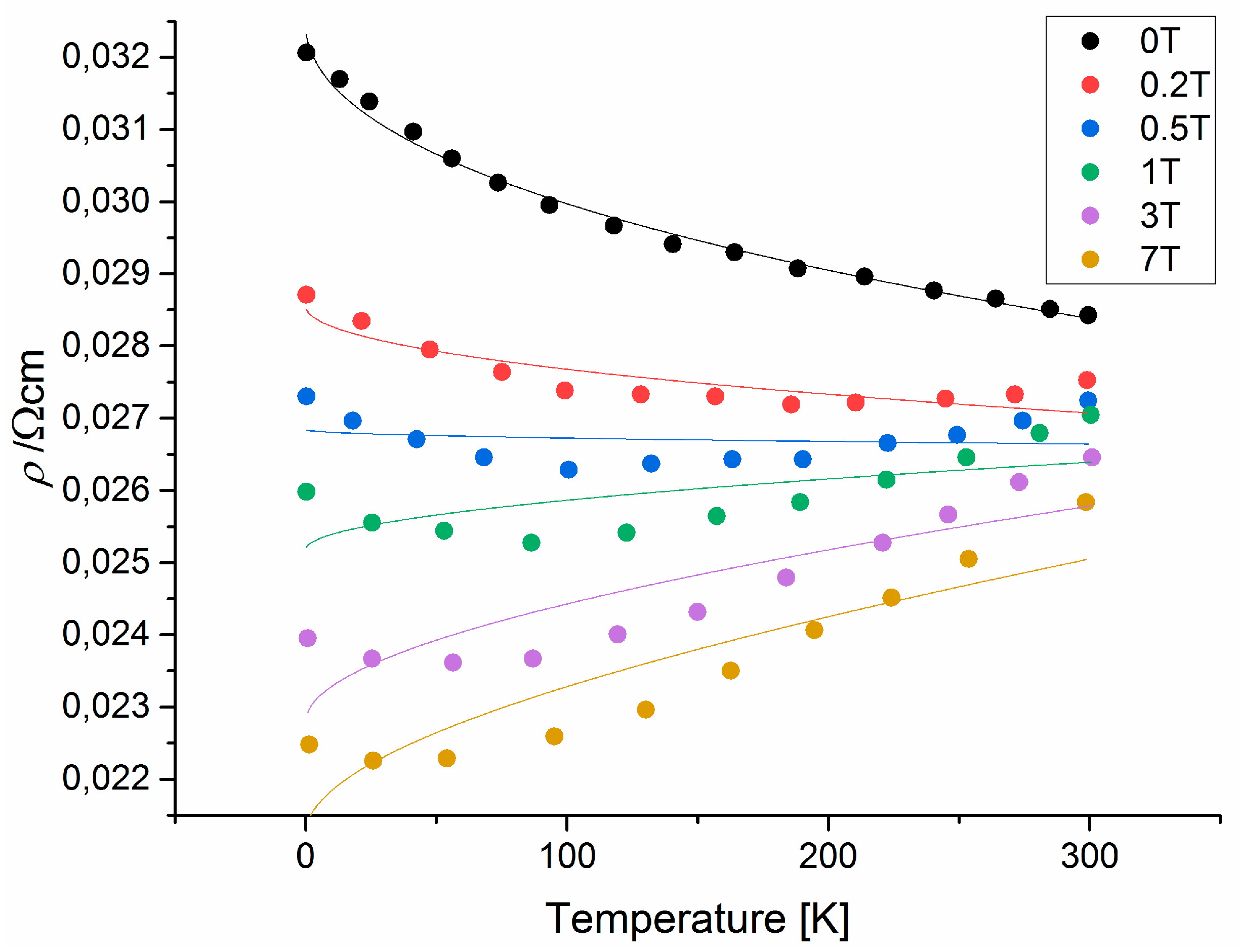
Preprints 73679 g004
Table 1. Fit of the parameters of eq. (15) assuming A´=0 to experimental data in [28].
Table 1. Fit of the parameters of eq. (15) assuming A´=0 to experimental data in [28].
B, T s0, Sm-1 B´, Sm-1K-1/2 Cn, WmK-n n
0 3087 0.222 -1.37×10-5 0.61
0.2 3464 0.174 6.09×10-12 3.31
0.5 3649 0.161 3.75×10-9 2.29
1 3839 0.166 1.15×10-7 1.77
3 4150 0.235 2.21×10-6 1.34
7 4414 0.270 3.73×10-6 1.22
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated