Preprint
Article
Mathematical Decomposition of Fault Signature using Multinomial Identity and Differentiating for Detection of Broken Rotor Bar in Induction Motor
Altmetrics
Downloads
206
Views
254
Comments
0
This version is not peer-reviewed
Submitted:
15 May 2023
Posted:
16 May 2023
You are already at the latest version
Alerts
Abstract
Fault detection at the early stage of development is of great importance in the maintenance of electric motors. In this regard, Motor Current Signature Analysis (MCSA) is cited in many articles to detect rotor bar fracture. The popularity of MCSA is due to its non-invasive and non-destructive nature, simplicity, and, compatibility with several signal processing tools. The vast variety of the signal processing tools which are commonly used for detecting the broken rotor bar fault is based on the Fast Fourier Transform (FFT) of the stator current signal and analysis of the produced Fourier spectrum; however, because of the small amplitude at the fault frequency relative to the main frequency amplitude, the former cannot be easily discriminated from the latter. Therefore, the peak at the fault frequency is hidden in the shadow of the main frequency component, hence the fault will not be detectable. As a solution to vanish the base frequency component, a method based on the Algebraic Identity of trinomial expansion is proposed in this paper which enables us to display the difference between the frequency of the fault signature and the base frequency. In this article, the fault of the broken rotor bars of the squirrel cage induction motor is revealed by the proposed method. In addition, a frequency weighting technique is presented to magnify the component at the fault related frequency compared to the lower frequencies. To validate the proposed methods, they are examined on the laboratory data obtained from three different operating conditions including the direct online start, the direct torque control, and the scalar control and the results show the ability of the proposed methods in fault detection of an induction motor.
Keywords:
Subject: Engineering - Electrical and Electronic Engineering
1. Introduction
Squirrel cage induction motors (SQIM) are widely used in various industries [1,2]. In industries, where uninterrupted motor operation is necessary, timely detection of rotor faults is important, as these faults account for approximately 10% of all motor faults. This issue is especially critical in harsh environments, such as oil and gas environments, traction, and mines, where motor failures can result in heavy process losses [3,4].
Over the past few years, the use of induction motors in the electric vehicle (EV) industry has become increasingly widespread. The electric motor is a crucial component of an EV as it converts electric energy to mechanical energy [5]. Therefore, any failure in any of its components can directly impact the reliability of the powertrain and the safety of passengers [6,7]. As a result, it is crucial to develop an electric motor that enhances the efficiency and performance of EVs [8,9]. Among the various types of electric motors used in EVs, the induction motor (IM) is more effective and economical than others due to its reliability, simple mechanical design, and effective field-weakening characteristics [8].
To increase the reliability of IMs used in EVs, researchers have focused on different fault diagnosis methods in the past decade, in line with the growth of the EV industry. These methods are aimed at identifying and diagnosing faults in IMs before they lead to motor failure, and include techniques such as vibration analysis, Motor Current Signal Analysis (MCSA), and motor current signature analysis [8,10,11,12,13,14,15,16,17]. By implementing these fault diagnosis methods, the reliability of IMs can be enhanced, thereby improving the overall performance and safety of EVs.
A broken rotor bar (BRB) is a type of rotor fault that can cause damage to other parts of the motor, including the winding, bearings, and mechanical parts. In addition, BRBs can lead to torque and speed pulsation and create harmonics in the current, air-gap flux, and induced voltage of stray flux [3,18,19]. Therefore, given that the BRB of SQIM is a common type of rotor defect, this article will focus on the diagnosis of BRBs.
Model-based approaches require a precise and accurate mathematical model of the motor, and knowledge-based approaches have low accuracy in transient conditions and require different and high-volume data for diagnosing different motors [25]. Therefore, signal-based methods are of great interest for fault detection in electric motors.
Any type of faults affects the general signals of the motor, such as current, torque, speed, and voltage, in a specific way and creates special harmonics in them. Most of the existing electrical condition monitoring and fault detection methods are based on the analysis of the measured output signals [3,26,27]. To detect the fault based on the signal, three steps are usually taken:
- acquiring a suitable signal to detect the fault,
- using the proper method to analyze the signal,
- determining the index to make the decision about the faulty or healthy condition.
According to articles analyzing various types of motor output signals, research on fault diagnosis includes MCSA, methods based on terminal voltage analysis, air gap torque analysis, impedance sequence component analysis, leakage flux measurement, infrared detection, stray flux detection, vibration analysis, thermal analysis, acoustic analysis, electromagnetic field interference, and more [28,29]. Among these methods, MCSA is utilized in this paper due to its non-destructive nature, compatibility with several signal processing tools, and being a spectral analysis method that is commonly used for online and remote monitoring of induction motors in industrial environments [18,30,31]. The following are some MCSA methods: frequency spectral analysis, current envelope analysis method, components of negative, positive, and zero current sequences, and Park’s vector representation of three-phase current and Clark transformation [4,27,32].
Although positive, negative, and zero sequence components of current or Park and Clark vector transformations can be used for MCSA, they require sampling of three-phase current [33], which increases the cost compared to single-phase current sampling, and there is no indicator to recognize the fault type in many cases. In the current envelope analysis method, there is a challenge to produce a suitable envelope without auxiliary processing tools, and it does not show clear results for fault detection. A common and simple frequency-domain method for detecting BRB is applying the FFT on the stator current and then analyzing the produced spectrum [3,25]. However, the sampled current is almost always accompanied by noise, and for motors that operate at small slips, the fault frequency is hidden in the shadow of the base frequency. This means that base frequency leakage can mask fault frequencies, making rotor fault detection difficult, and motor damage may progress to severe damage [34]. Therefore, direct application of frequency spectral analysis and FFT method on the stator current will not have a useful and usable result and requires initiatives and auxiliary processing tools.
In order to increase the slip and distinguish between the fault frequency and the base frequency, a rotor breakage detection test has been performed in [35], which is not in the steady state motor operation mode. In [36], a normalized energy operator in the frequency domain (FDEO) is proposed for BRB fault detection, and energy operators have also been used to diagnose the broken rotor bar in some other papers [37]. Among the different methods, those that can be practical in the condition of high current noise are preferred, and in order to reduce the cost, sampling the current of one phase is preferable. Therefore, in this paper, we sample the current of one phase of the stator and use the sum square identity along with methods to remove unnecessary frequency components from the current signal.
Different signal processing tools have been utilized in various studies. Typically, these tools can be categorized into three groups: time domain, frequency domain, and time-frequency domain [38]. Time domain indicators such as mean, median, peak, kurtosis, and skewness are less commonly used to detect BRB faults. Instead, some research studies have utilized time-frequency decomposition tools to identify fault components and harmonics [39,40]. For example, the Hilbert-Huang transform (HHT) is often used for analyzing non-linear and non-stationary signals, but identifying the signal with the fault frequency can be challenging [41]. Another commonly used time-frequency domain transform is the wavelet transform. In some applications, wavelet transform is used as a filter, and simple filters can also be effective. In some articles, wavelet transform has been used for time-frequency analysis of non-stationary signals [42]. In other cases, the short-time Fourier transform (STFT) has also been used [35], but it has lower ability compared to the wavelet transform.
Other methods belonging to the time-frequency signal processing tools include the adaptive slope transform (AST), the Multiple Signal Classification (MUSIC) algorithm, the Wigner-Ville distribution (WVD), and the Choi-William distribution [43,44]. While fault detection and evaluation in the time-frequency domain may require a skilled user with powerful pattern recognition techniques, it also takes more time for investigation and a relatively long start-up time.
In this paper, FFT is used for BRB fault detection due to its high speed and ease of analyzing the FFT spectrum results to identify the dominant frequency of the BRB. Furthermore, FFT is widely applied in other articles [45,46] and provides the possibility to define an index for the detection of the severity of the fault and its type.
The rest of the paper is structured as follows: In Section 2, the methodology used in this study is explained. Section 3 presents the benchmark and experimental results. Section 4 and Section 5 are dedicated to techniques for elevating the peak at the fault frequency, using derivation and convolution, respectively. The paper concludes with a summary in Section 6.
2. Methodology
The fault-related component obtained through direct FFT analysis of the current signal is often characterized by a much lower amplitude when compared to the fundamental frequency component (as illustrated in Figure 1). Furthermore, given that the fault frequency is usually very close to the fundamental frequency, the latter can mask the former, particularly during low-slip operations. In other words, within the FFT spectrum, the fault frequency spectrum can be concealed within the shadow of the fundamental frequency spectrum, thus rendering the fault undetectable [47]. To overcome this issue, it is crucial to attenuate the fundamental frequency component while magnifying the fault frequency component to distinguish the fault frequency in the spectrum. To this end, one possible solution is to calculate the difference between the fault frequency and the base frequency. In this context, we propose a mathematical method that is based on a particular identity, which we present in the following.
where is the fault frequency of broken rotor bar, ., s is slip and is the fundamental frequency. A fault detection method is proposed in which the fault signature concealed by the fundamental frequency component is detected using the trinomial expansion. To facilitate understanding of this approach, the identity of the trinomial expansion is presented in equation (2).
where are either numbers or variables. In cases of squirrel-cage induction motor (SQIM) with rotor bar breakage, two sideband frequencies related to the rotor bar breakage will appear in the stator current signal spectrum, around the fundamental frequency (). Specifically, referring to equation (1) with , these frequencies are denoted by and , and they are both situated in proximity to . Let us consider a signal comprising three sinusoidal terms :
Here . It is known that and . Using the trigonometric relations and neglecting the term of yields:
Thus, (4) has one component at DC and six terms with frequencies twice or nearly twice the base frequency () and one component at the difference of the base frequency and the fault frequency or at . Six components among them are filtered out, and only the component at the frequency of is used in the proposed fault detection method. Table 1 shows all of these components and indicates that which of them are going to be used in the proposed fault detection technique. Therefore, what remains is the following signal, which is used to diagnose the faulty motor:
A pseudo code of the proposed technique is shown in Figure 2. By applying the trinomial expansion identity to the stator current signal and subsequently obtaining its corresponding Hilbert transform while removing unwanted frequencies, a resulting signal can be obtained that contains expression (5). The differential frequency of this expression can be obtained by using FFT transformation.
3. Benchmark and experimental results
The characteristics of the motor under examination are presented in Table 2. The experimental setup comprises a 3 kW AC generator, a 1.5 kW induction motor with broken rotor bars, and the corresponding load, a LA55-P/SP1 Hall effect current sensor and a DSP, TMS320F28379D and a control drive and a computer. The resolution level of the DSP analog to digital converter is 12 bits. A photo of the setup is illustrated in Figure 3.
The proposed methods were tested under three different operating conditions, including direct online start (DOL), direct torque control (DTC), and scalar control. Each operating condition was evaluated under three load levels: light, medium, and heavy (full) loads. The light load mode represented the condition where no electric load was connected to the generator. In the medium and full load modes, 600 watts and 1200 watts of electric loads were respectively connected to the generator. Accounting for the 80% efficiency of the generator, the load on the motor was 750 watts and 1500 watts for medium and full load modes respectively. The sampling frequency used was 10 kHz. The experimental setup was illustrated in Figure 4.
For instance, in direct online start (DOL) operation mode under the light load condition, the signal to be analyzed is shown in Figure 5. After removing the DC component and the component at frequencies around twice the base frequency (), the resulting signal is used for analysis. The rotor speed in this case is 1493 RPM, and the corresponding slip is . The results for three scenarios, including the healthy state, one broken rotor bar, and two broken rotor bars, are depicted in Figure 6.
Figure 7 illustrates the analysis results for the case of direct torque control (DTC) under the light load operation mode, where the rotor speed is 1490 RPM. The analysis was conducted for three scenarios, including the healthy rotor, one broken rotor bar, and two broken rotor bars, and the results are presented in Figure 7.
Figure 8 shows the results for the case of scalar control under the light load mode of operation. In this case the rotor speed is 1492 RPM and the situation of healthy motor, one broken rotor bar and two broken rotor bars are studied.
4. Elevating the peak at the fault frequency using derivation
After differentiating Equation (5), the following equation is obtained, in which the amplitude is weighted by the difference between the fault frequency and the base frequency:
This technique elevates the peak at the fault frequency in comparison to the neighboring peaks at lower frequencies, making the fault signature more prominent and facilitating fault detection. The results for the DOL operating condition under full load, with one broken rotor bar, without frequency weighting and with frequency weighting through derivation, are depicted in Figure 10. Comparison of Figure 10 (fig9a) and (fig9b) reveals that the differentiating technique increases the ratio of the peak value at the fault frequency relative to the lower frequency region.
5. Elevating the peak at the fault frequency using convolution
Based on the convolution theorem, convolution in the time domain corresponds to multiplication in the frequency domain [45,47,50].
Therefore, by performing the convolution of the and its derivative in the time domain while strengthening the fault component amplitude with frequency weighting in the time domain, the fault frequency amplitude is magnified in the frequency domain. Consequently, in the FFT spectrum, the amplitude of the fault frequency is amplified, while the amplitude of the frequency components around the fault frequency is weakened. The block diagram of the proposed method is shown in Figure 11.
By using this technique, the peak at the fault frequency in the FFT spectrum is more pronounced compared to neighboring peaks. This means that the fault signature becomes more visible in the spectrum with high resolution. To illustrate, Figure 12 depicts the fault frequency spectrum using the proposed method during Direct-On-Line (DOL) operation under full load conditions with a single Broken Rotor Bar (BRB). Figure 13 illustrates the fault frequency spectrum under light load mode and during Direct Torque Control (DTC) operation.
Figure 14 shows the scalar operation mode and light load condition to distinguish the severity of faults with one or two broken rotor bars from the healthy state. The figure illustrates that the proposed method accurately detects the state and severity of faults compared to the healthy state.
6. Conclusion
This article presents a diagnostic approach to identify and detect the broken rotor bar defect in squirrel cage induction motors using the identity of the square of sum, and the results are compared and analyzed. To validate the proposed methods, laboratory data obtained from three different operating conditions, including Direct-On-Line (DOL) start, Direct Torque Control (DTC), and scalar control, are examined, and the results demonstrate the effectiveness of the proposed methods in fault detection of induction motors.
Through the analysis of results and formulas, it is evident that the proposed method accurately identifies the broken rotor bar defect in squirrel cage induction motors. As the severity of the rotor bar breakage increases, the amplitude of the spectrum at the fault frequency also increases. Additionally, a frequency weighting tool is presented to enhance the clarity of observing the fault frequency in the resulting spectrum. The accuracy of the proposed method is shown to be higher with the frequency weighting method, which involves deriving the signal under spectrometry to obtain a frequency weighting factor.
In conclusion, this article presents a high-resolution broken rotor bar fault detection method, which has the potential to improve the performance of induction motors in various applications.
References
- Ojaghi, M.; Sabouri, M.; Faiz, J. Performance Analysis of Squirrel-Cage Induction Motors Under Broken Rotor Bar and Stator Inter-Turn Fault Conditions Using Analytical Modeling. IEEE Transactions on Magnetics 2018, 54, 1–5. [CrossRef]
- Gyftakis, K.N.; Spyropoulos, D.V.; Kappatou, J.C.; Mitronikas, E.D. A Novel Approach for Broken Bar Fault Diagnosis in Induction Motors Through Torque Monitoring. IEEE Transactions on Energy Conversion 2013, 28, 267–277. [CrossRef]
- Mirzaeva, G.; Saad, K.I. Advanced Diagnosis of Rotor Faults and Eccentricity in Induction Motors Based on Internal Flux Measurement. IEEE Transactions on Industry Applications 2018, 54, 2981–2991. [CrossRef]
- Gyftakis, K.N.; Spyropoulos, D.V.; Mitronikas, E.D. Advanced Detection of Rotor Electrical Faults in Induction Motors at Start-Up. IEEE Transactions on Energy Conversion 2021, 36, 1101–1109. [CrossRef]
- Haghgooei, P.; Jamshidpour, E.; Corne, A.; Takorabet, N.; Khaburi, D.A.; Baghli, L.; Nahid-Mobarakeh, B. A Parameter-Free Method for Estimating the Stator Resistance of a Wound Rotor Synchronous Machine. World Electric Vehicle Journal 2023, 14. [CrossRef]
- Eldeeb, H.H.; Zhao, H.; Mohammed, O.A. Detection of TTF in Induction Motor Vector Drives for EV Applications via Ostu’s-Based DDWE. IEEE Transactions on Transportation Electrification 2021, 7, 114–132. [CrossRef]
- Kral, C.; Haumer, A.; Kapeller, H.; Pirker, F. Design and Thermal Simulation of Induction Machines for Traction in Electric and Hybrid Electric Vehicles. World Electric Vehicle Journal 2007, 1, 190–196. [CrossRef]
- Aishwarya, M.; Brisilla, R.M. Design and Fault Diagnosis of Induction Motor Using ML-Based Algorithms for EV Application. IEEE Access 2023, 11, 34186–34197. [CrossRef]
- Zechmair, D.; Steidl, K. Why the Induction Motor Could be the Better Choice for Your Electric Vehicle Program. World Electric Vehicle Journal 2012, 5, 546–549. [CrossRef]
- Gor, C.; Shah, V. Modelling, Analysis And Control of Five Phase Induction Motor Drive under Open Circuit Fault for Electric Vehicle. 2019 IEEE 1st International Conference on Energy, Systems and Information Processing (ICESIP), 2019, pp. 1–6. [CrossRef]
- Praneeth, A.; Williamson, S.S. Algorithm for prediction and control of induction motor stator interturn faults in electric vehicles. 2017 IEEE Transportation Electrification Conference and Expo (ITEC), 2017, pp. 130–134. [CrossRef]
- Yepes, A.G.; Shawier, A.; Abdel-Azim, W.E.; Abdel-Khalik, A.S.; Ahmed, S.; Doval-Gandoy, J. General Online Current-Harmonic Generation for Increased Torque Capability With Minimum Stator Copper Loss in Fault-Tolerant Multiphase Induction Motor Drives. IEEE Transactions on Transportation Electrification 2023, pp. 1–1. [CrossRef]
- Choudhary, A.; Mian, T.; Fatima, S.; Panigrahi, B.K. Fault Diagnosis of Electric Two-Wheeler Under Pragmatic Operating Conditions Using Wavelet Synchrosqueezing Transform and CNN. IEEE Sensors Journal 2023, 23, 6254–6263. [CrossRef]
- Chikondra, B.; Muduli, U.R.; Behera, R.K. An Improved Open-Phase Fault-Tolerant DTC Technique for Five-Phase Induction Motor Drive Based on Virtual Vectors Assessment. IEEE Transactions on Industrial Electronics 2021, 68, 4598–4609. [CrossRef]
- Berzoy, A.; Eldeeb, H.H.; Mohammed, O.A. On-Line Detection of Stator Faults in DTC-Driven IM Using SC Impedance Matrix Off-Diagonal Term. IEEE Transactions on Industry Applications 2019, 55, 5906–5915. [CrossRef]
- Kral, C.; Kapeller, H.; Pirker, F. A Stator and Rotor Fault Detection Technique for Induction Machines in Traction Applications for Electric or Hybrid Electric Vehicles. World Electric Vehicle Journal 2007, 1, 184–189. [CrossRef]
- Zhang, X.; Han, K.; Cao, H.; Wang, Z.; Huo, K. Fault Injection Model of Induction Motor for Stator Interturn Fault Diagnosis Research Based on HILS. World Electric Vehicle Journal 2021, 12. [CrossRef]
- Shin, J.; Park, Y.; Lee, S.B. Flux-Based Detection and Classification of Induction Motor Eccentricity, Rotor Cage, and Load Defects. IEEE Transactions on Industry Applications 2021, 57, 2471–2480. [CrossRef]
- Hosseinpoor, Z.; Arefi, M.M.; Razavi-Far, R.; Mozafari, N.; Hazbavi, S. Virtual Sensors for Fault Diagnosis: A Case of Induction Motor Broken Rotor Bar. IEEE Sensors Journal 2021, 21, 5044–5051. [CrossRef]
- Ali, M.Z.; Shabbir, M.N.S.K.; Liang, X.; Zhang, Y.; Hu, T. Machine Learning-Based Fault Diagnosis for Single- and Multi-Faults in Induction Motors Using Measured Stator Currents and Vibration Signals. IEEE Transactions on Industry Applications 2019, 55, 2378–2391. [CrossRef]
- Gao, Z.; Cecati, C.; Ding, S.X. A Survey of Fault Diagnosis and Fault-Tolerant Techniques—Part I: Fault Diagnosis With Model-Based and Signal-Based Approaches. IEEE Transactions on Industrial Electronics 2015, 62, 3757–3767. [CrossRef]
- Gao, Z.; Cecati, C.; Ding, S.X. A Survey of Fault Diagnosis and Fault-Tolerant Techniques—Part II: Fault Diagnosis With Knowledge-Based and Hybrid/Active Approaches. IEEE Transactions on Industrial Electronics 2015, 62, 3768–3774. [CrossRef]
- Ying, X. Characteristic Performance Analysis of Squirrel Cage Induction Motor With Broken Bars. IEEE Transactions on Magnetics 2009, 45, 759–766. [CrossRef]
- Chang, L.; Xu, X.; Liu, Z.g.; Qian, B.; Xu, X.; Chen, Y.W. BRB Prediction With Customized Attributes Weights and Tradeoff Analysis for Concurrent Fault Diagnosis. IEEE Systems Journal 2021, 15, 1179–1190. [CrossRef]
- Shao, S.; Yan, R.; Lu, Y.; Wang, P.; Gao, R.X. DCNN-Based Multi-Signal Induction Motor Fault Diagnosis. IEEE Transactions on Instrumentation and Measurement 2020, 69, 2658–2669. [CrossRef]
- Naha, A.; Samanta, A.K.; Routray, A.; Deb, A.K. A Method for Detecting Half-Broken Rotor Bar in Lightly Loaded Induction Motors Using Current. IEEE Transactions on Instrumentation and Measurement 2016, 65, 1614–1625. [CrossRef]
- de la Barrera, P.M.; Otero, M.; Schallschmidt, T.; Bossio, G.R.; Leidhold, R. Active Broken Rotor Bar Diagnosis in Induction Motor Drives. IEEE Transactions on Industrial Electronics 2021, 68, 7556–7566. [CrossRef]
- Nandi, S.; Toliyat, H.; Li, X. Condition Monitoring and Fault Diagnosis of Electrical Motors—A Review. IEEE Transactions on Energy Conversion 2005, 20, 719–729. [CrossRef]
- Morales-Perez, C.; Rangel-Magdaleno, J.; Peregrina-Barreto, H.; Amezquita-Sanchez, J.P.; Valtierra-Rodriguez, M. Incipient Broken Rotor Bar Detection in Induction Motors Using Vibration Signals and the Orthogonal Matching Pursuit Algorithm. IEEE Transactions on Instrumentation and Measurement 2018, 67, 2058–2068. [CrossRef]
- Puche-Panadero, R.; Martinez-Roman, J.; Sapena-Bano, A.; Burriel-Valencia, J. Diagnosis of Rotor Asymmetries Faults in Induction Machines Using the Rectified Stator Current. IEEE Transactions on Energy Conversion 2020, 35, 213–221. [CrossRef]
- Spyropoulos, D.V.; Panagiotou, P.A.; Arvanitakis, I.; Mitronikas, E.D.; Gyftakis, K.N. Extraction of Frequency Information for the Reliable Screening of Rotor Electrical Faults Via Torque Monitoring in Induction Motors. IEEE Transactions on Industry Applications 2021, 57, 5949–5958. [CrossRef]
- Mazzoletti, M.A.; Donolo, P.D.; Pezzani, C.M.; Oliveira, M.O.; Bossio, G.R.; De Angelo, C.H. Stator Faults Detection on Induction Motors Using Harmonic Sequence Current Components Analysis. IEEE Latin America Transactions 2021, 19, 726–734. [CrossRef]
- St-Onge, X.F.; Cameron, J.; Saleh, S.; Scheme, E.J. A Symmetrical Component Feature Extraction Method for Fault Detection in Induction Machines. IEEE Transactions on Industrial Electronics 2019, 66, 7281–7289. [CrossRef]
- Agah, G.R.; Rahideh, A.; Khodadadzadeh, H.; Khoshnazar, S.M.; Hedayatikia, S. Broken Rotor Bar and Rotor Eccentricity Fault Detection in Induction Motors Using a Combination of Discrete Wavelet Transform and Teager–Kaiser Energy Operator. IEEE Transactions on Energy Conversion 2022, 37, 2199–2206. [CrossRef]
- Jerkan, D.G.; Reljić, D.D.; Marčetić, D.P. Broken Rotor Bar Fault Detection of IM Based on the Counter-Current Braking Method. IEEE Transactions on Energy Conversion 2017, 32, 1356–1366. [CrossRef]
- Li, H.; Feng, G.; Zhen, D.; Gu, F.; Ball, A.D. A Normalized Frequency-Domain Energy Operator for Broken Rotor Bar Fault Diagnosis. IEEE Transactions on Instrumentation and Measurement 2021, 70, 1–10. [CrossRef]
- Wang, W.; Song, X.; Liu, G.; Chen, Q.; Zhao, W.; Zhu, H. Induction Motor Broken Rotor Bar Fault Diagnosis Based on Third-Order Energy Operator Demodulated Current Signal. IEEE Transactions on Energy Conversion 2022, 37, 1052–1059. [CrossRef]
- Sangeetha B., P.; S., H. Rational-Dilation Wavelet Transform Based Torque Estimation from Acoustic Signals for Fault Diagnosis in a Three-Phase Induction Motor. IEEE Transactions on Industrial Informatics 2019, 15, 3492–3501. [CrossRef]
- Esam El-Dine Atta, M.; Ibrahim, D.K.; Gilany, M.I. Broken Bar Faults Detection Under Induction Motor Starting Conditions Using the Optimized Stockwell Transform and Adaptive Time–Frequency Filter. IEEE Transactions on Instrumentation and Measurement 2021, 70, 1–10. [CrossRef]
- Mahmud, M.; Wang, W. A Smart Sensor-Based cEMD Technique for Rotor Bar Fault Detection in Induction Motors. IEEE Transactions on Instrumentation and Measurement 2021, 70, 1–11. [CrossRef]
- Fernandez-Cavero, V.; Pons-Llinares, J.; Duque-Perez, O.; Morinigo-Sotelo, D. Detection of Broken Rotor Bars in Nonlinear Startups of Inverter-Fed Induction Motors. IEEE Transactions on Industry Applications 2021, 57, 2559–2568. [CrossRef]
- CusidÓCusido, J.; Romeral, L.; Ortega, J.A.; Rosero, J.A.; GarcÍaGarcia Espinosa, A. Fault Detection in Induction Machines Using Power Spectral Density in Wavelet Decomposition. IEEE Transactions on Industrial Electronics 2008, 55, 633–643. [CrossRef]
- Morinigo-Sotelo, D.; de J. Romero-Troncoso, R.; Panagiotou, P.A.; Antonino-Daviu, J.A.; Gyftakis, K.N. Reliable Detection of Rotor Bars Breakage in Induction Motors via MUSIC and ZSC. IEEE Transactions on Industry Applications 2018, 54, 1224–1234. [CrossRef]
- Sapena-Bano, A.; Burriel-Valencia, J.; Pineda-Sanchez, M.; Puche-Panadero, R.; Riera-Guasp, M. The Harmonic Order Tracking Analysis Method for the Fault Diagnosis in Induction Motors Under Time-Varying Conditions. IEEE Transactions on Energy Conversion 2017, 32, 244–256. [CrossRef]
- Sapena-Bañó, A.; Pineda-Sanchez, M.; Puche-Panadero, R.; Martinez-Roman, J.; Matić, D. Fault Diagnosis of Rotating Electrical Machines in Transient Regime Using a Single Stator Current’s FFT. IEEE Transactions on Instrumentation and Measurement 2015, 64, 3137–3146. [CrossRef]
- Bezerra de Deus, D.B.; Sobrinho, C.A.N.; Belo, F.A.; Brito, A.V.; de Souza Ramos, J.G.G.; Lima-Filho, A.C. Density of Maxima Approach for Broken Bar Fault Diagnosis in Low Slip and Variable Load Conditions of Induction Motors. IEEE Transactions on Instrumentation and Measurement 2020, 69, 9797–9804. [CrossRef]
- Puche-Panadero, R.; Martinez-Roman, J.; Sapena-Bano, A.; Burriel-Valencia, J.; Pineda-Sanchez, M.; Perez-Cruz, J.; Riera-Guasp, M. New Method for Spectral Leakage Reduction in the FFT of Stator Currents: Application to the Diagnosis of Bar Breakages in Cage Motors Working at Very Low Slip. IEEE Transactions on Instrumentation and Measurement 2021, 70, 1–11. [CrossRef]
- Park, Y.; Choi, H.; Lee, S.B.; Gyftakis, K.N. Search Coil-Based Detection of Nonadjacent Rotor Bar Damage in Squirrel Cage Induction Motors. IEEE Transactions on Industry Applications 2020, 56, 4748–4757. [CrossRef]
- Puche-Panadero, R.; Pineda-Sanchez, M.; Riera-Guasp, M.; Roger-Folch, J.; Hurtado-Perez, E.; Perez-Cruz, J. Improved Resolution of the MCSA Method Via Hilbert Transform, Enabling the Diagnosis of Rotor Asymmetries at Very Low Slip. IEEE Transactions on Energy Conversion 2009, 24, 52–59. [CrossRef]
- Pezzani, C.; Donolo, P.; Bossio, G.; Donolo, M.; Guzmán, A.; Zocholl, S.E. Detecting Broken Rotor Bars With Zero-Setting Protection. IEEE Transactions on Industry Applications 2014, 50, 1373–1384. [CrossRef]
Figure 1.
Direct application of FFT on stator current and comparison of the healthy rotor and one broken bar in DTC operating condition and low load.
Figure 1.
Direct application of FFT on stator current and comparison of the healthy rotor and one broken bar in DTC operating condition and low load.
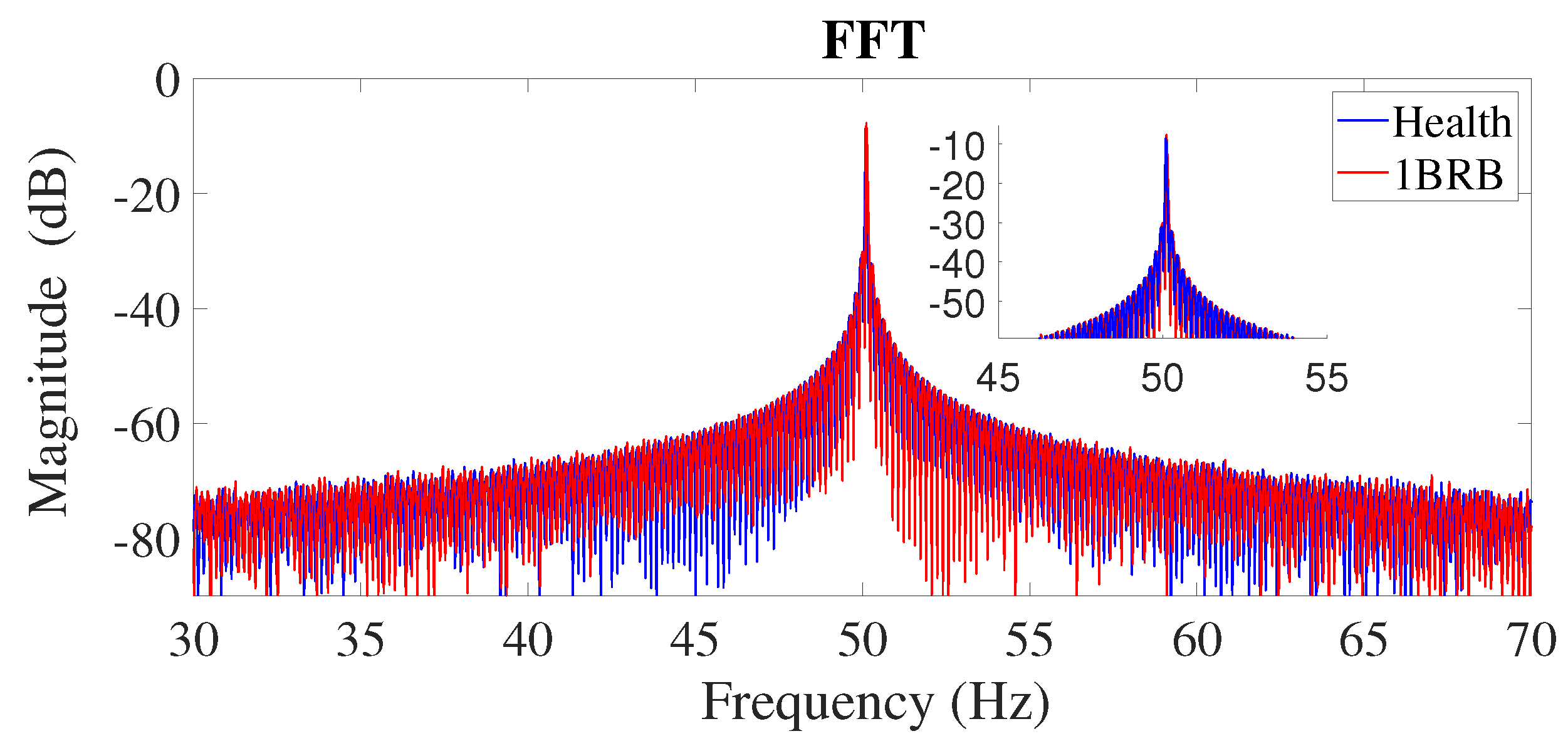
Figure 2.
The proposed technique.

Figure 3.
The experimental setup and the rotor with two broken bars.

Figure 4.
Schematic diagram of the test.
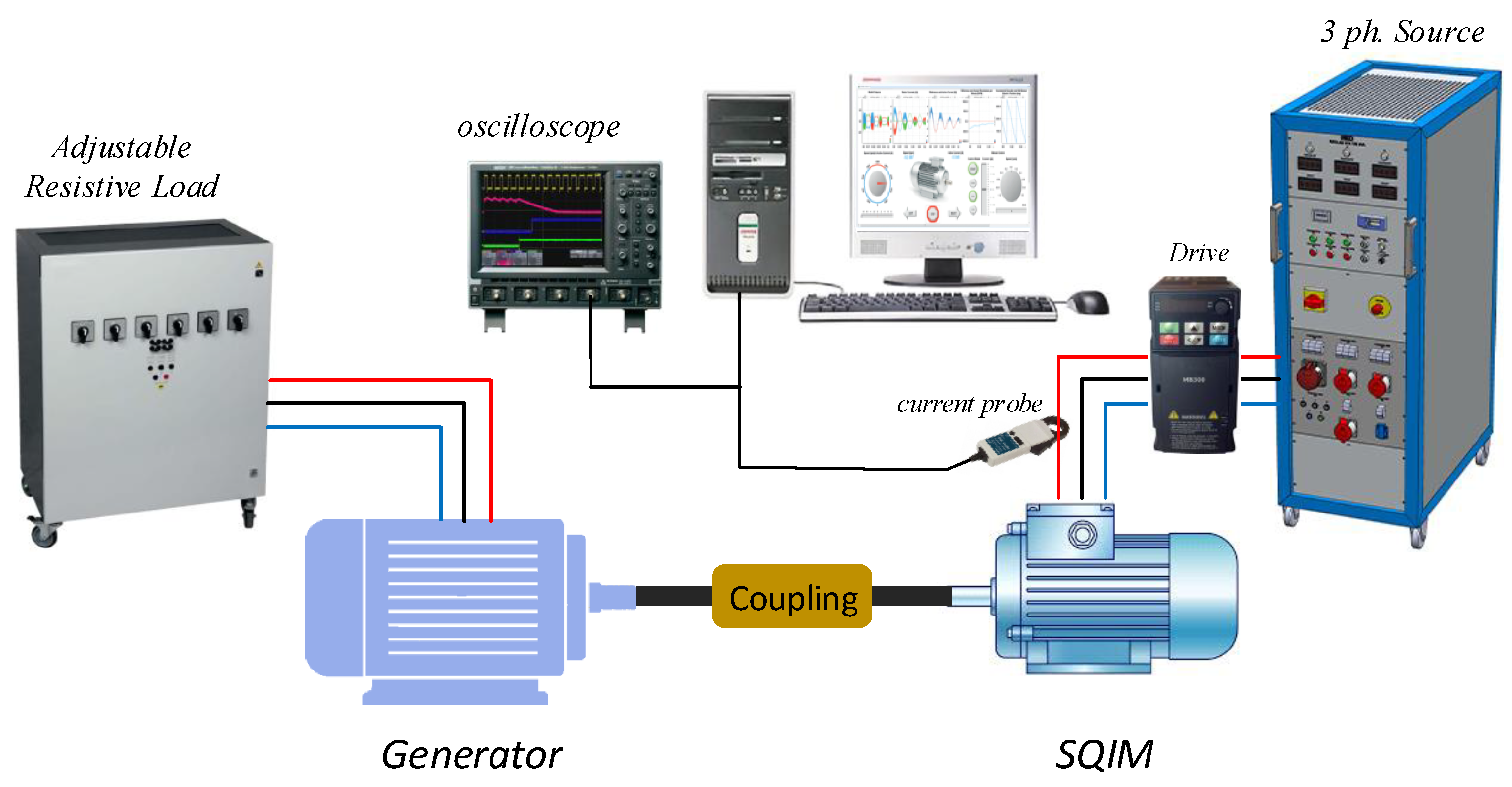
Figure 5.
Sample output signal containing equation (5) in DOL operating mode under the light load.
Figure 5.
Sample output signal containing equation (5) in DOL operating mode under the light load.
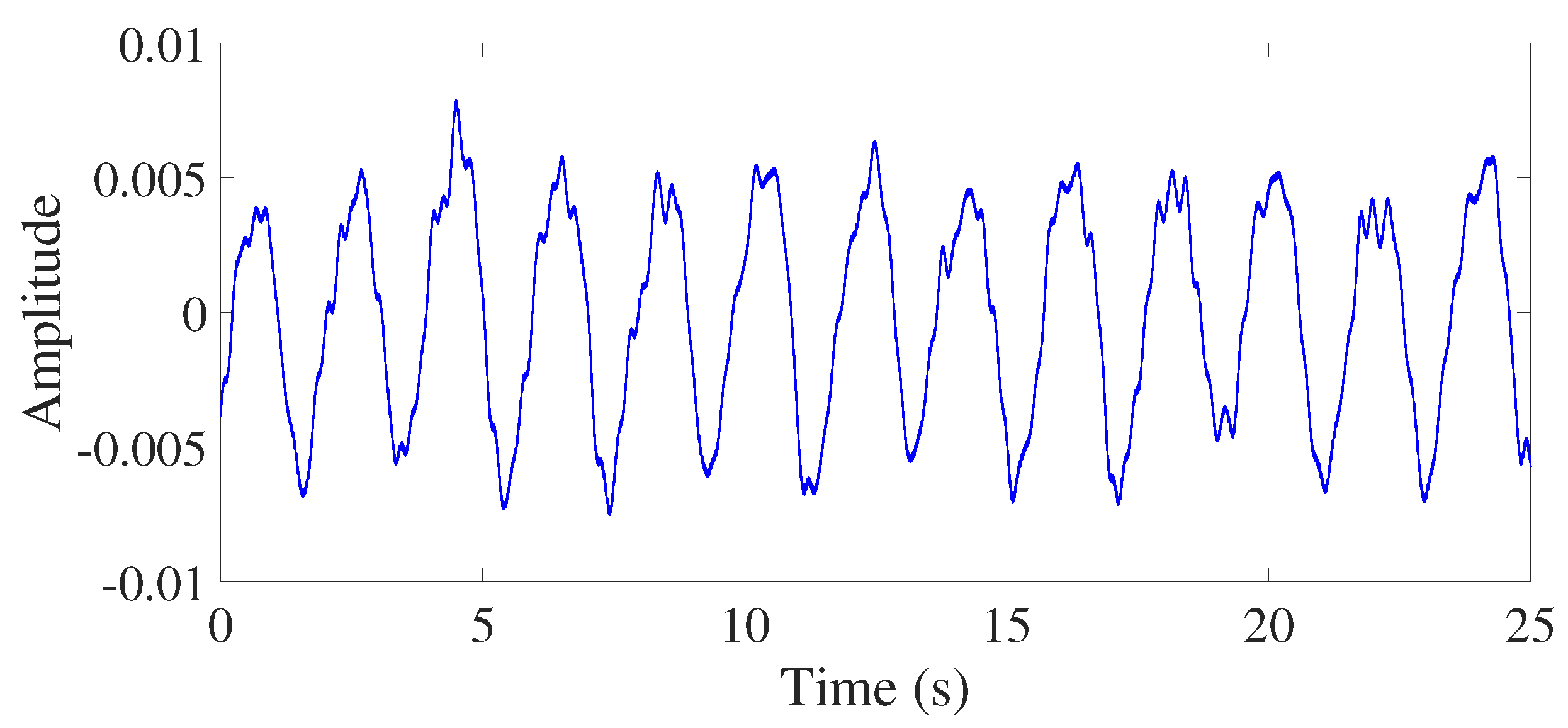
Figure 6.
Produced spectrum, under the light load mode in the case of DOL operating conditions, with (a) healthy rotor, (b) one broken bar, and (c) two broken bars.
Figure 6.
Produced spectrum, under the light load mode in the case of DOL operating conditions, with (a) healthy rotor, (b) one broken bar, and (c) two broken bars.
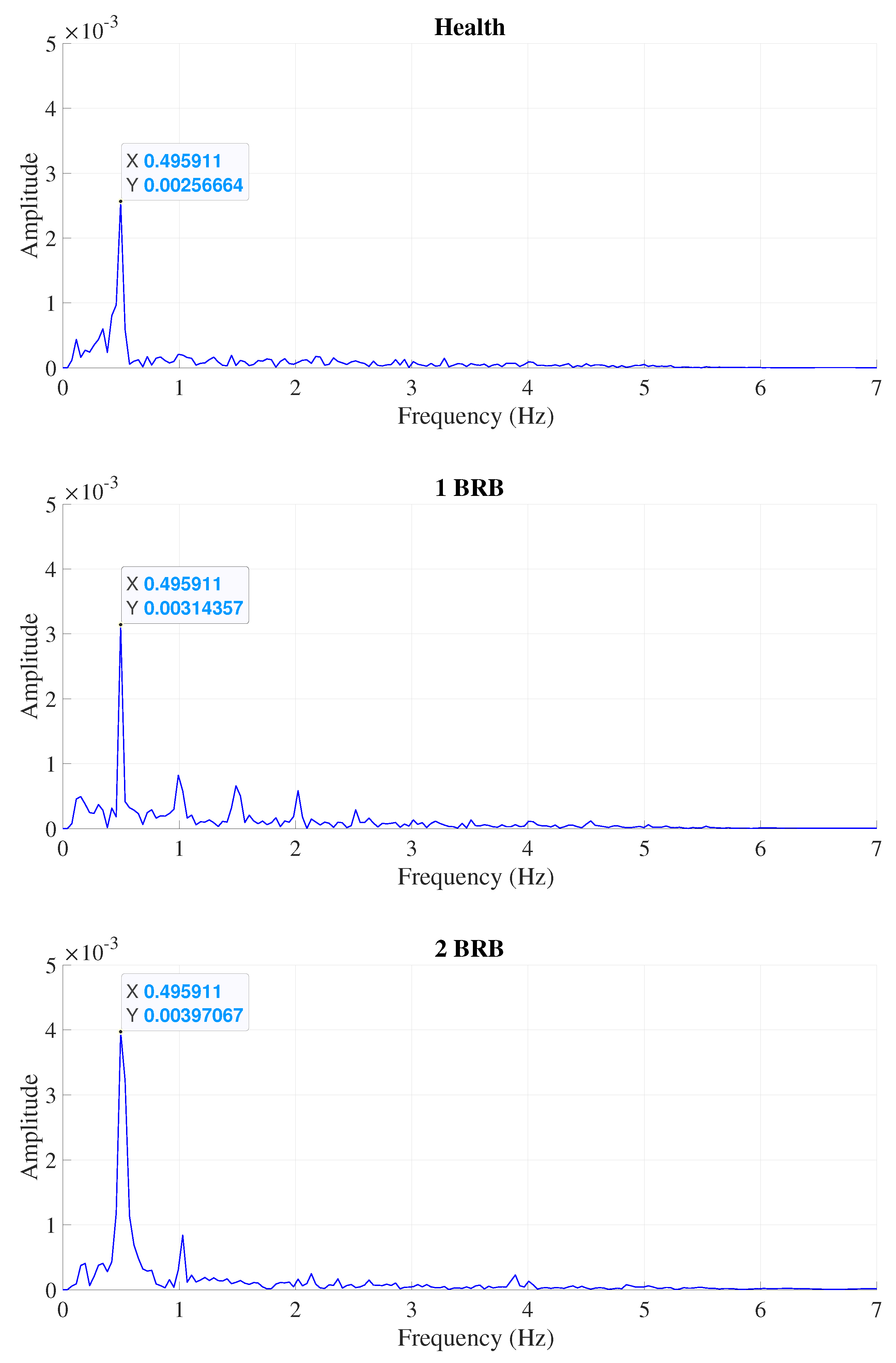
Figure 7.
Produced spectrum, under the light load mode in the case of DTC operating conditions, with (a) healthy rotor, (b) one broken bar, and (c) two broken bars.
Figure 7.
Produced spectrum, under the light load mode in the case of DTC operating conditions, with (a) healthy rotor, (b) one broken bar, and (c) two broken bars.
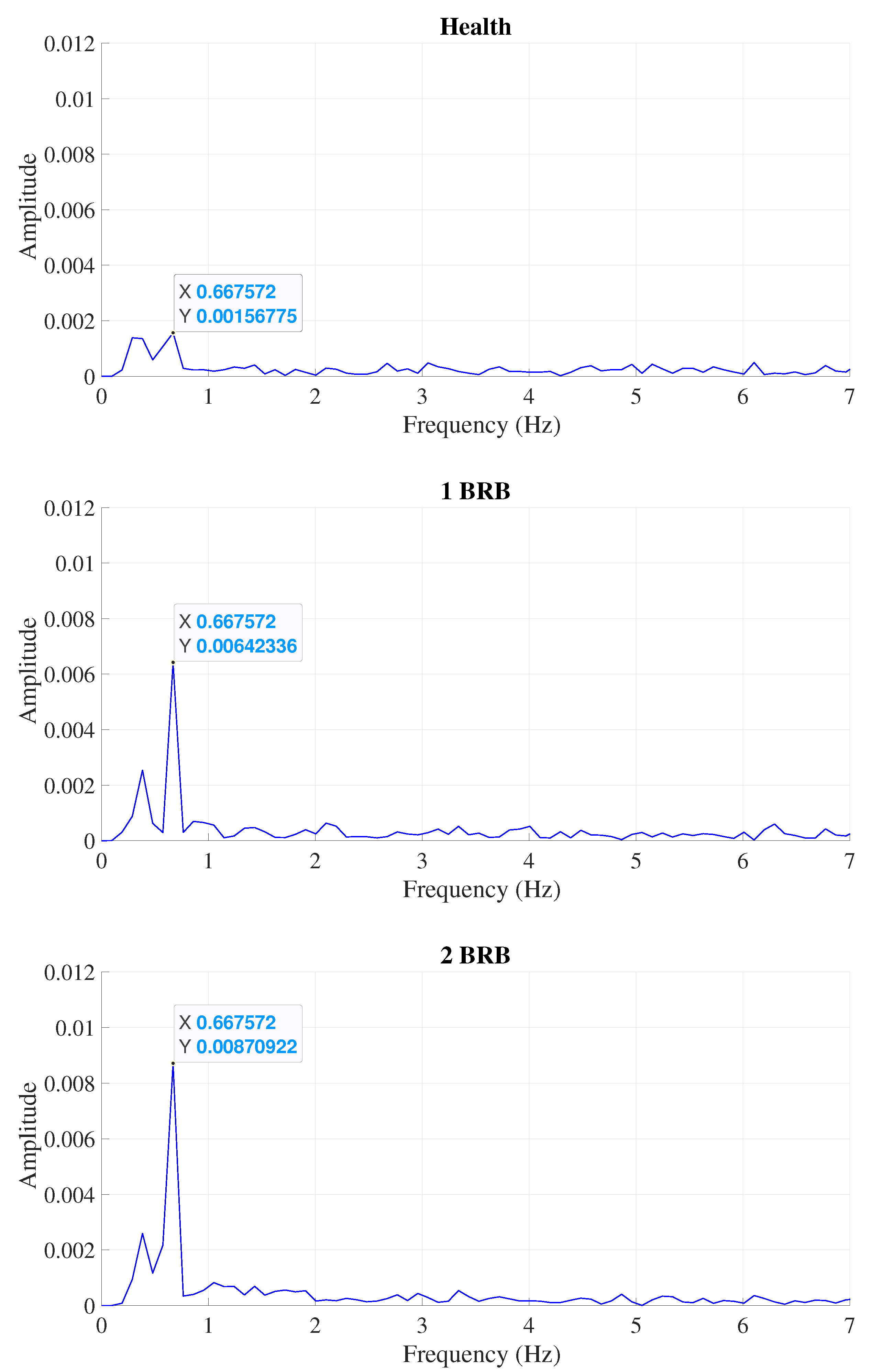
Figure 8.
Produced spectrum, under the light load mode in the case of scalar control, with (a) healthy rotor, (b) one broken bar, and (c) two broken bars.
Figure 8.
Produced spectrum, under the light load mode in the case of scalar control, with (a) healthy rotor, (b) one broken bar, and (c) two broken bars.
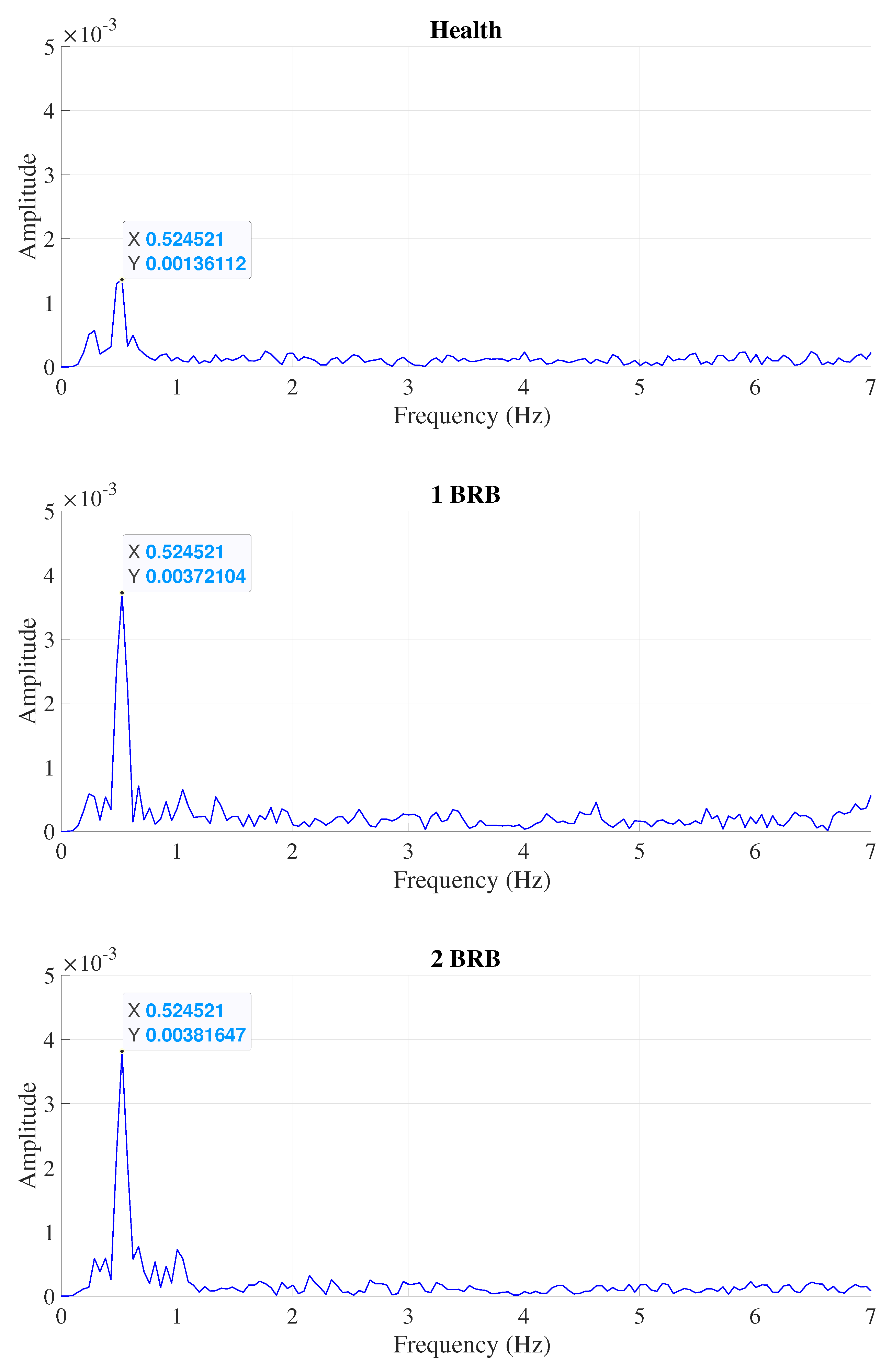
Figure 9.
Summarizing the frequency results obtained by the proposed method.
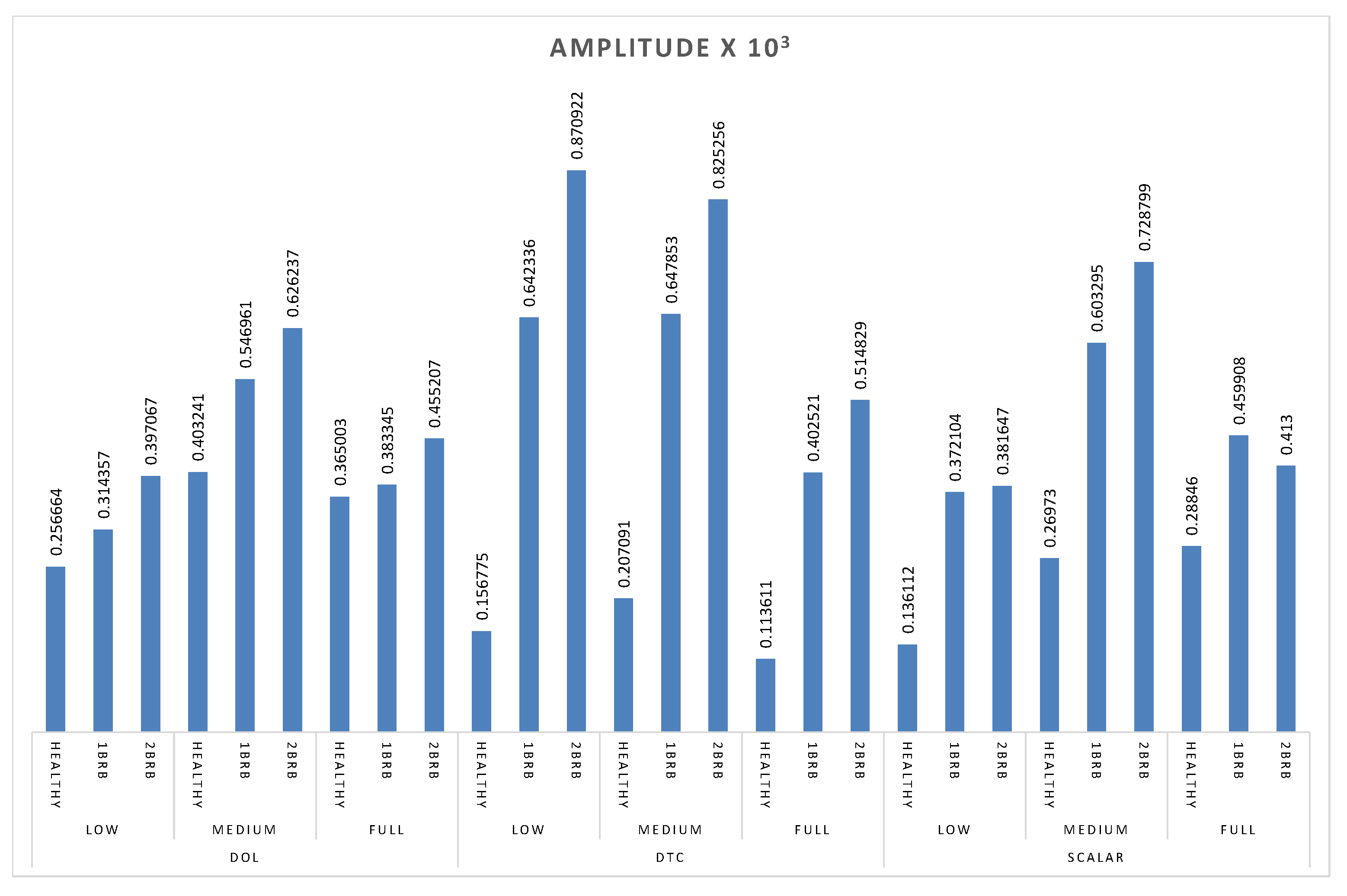
Figure 10.
Comparison of fault frequency detection (a) without frequency weighting and (b) with frequency weighting through derivation.
Figure 10.
Comparison of fault frequency detection (a) without frequency weighting and (b) with frequency weighting through derivation.
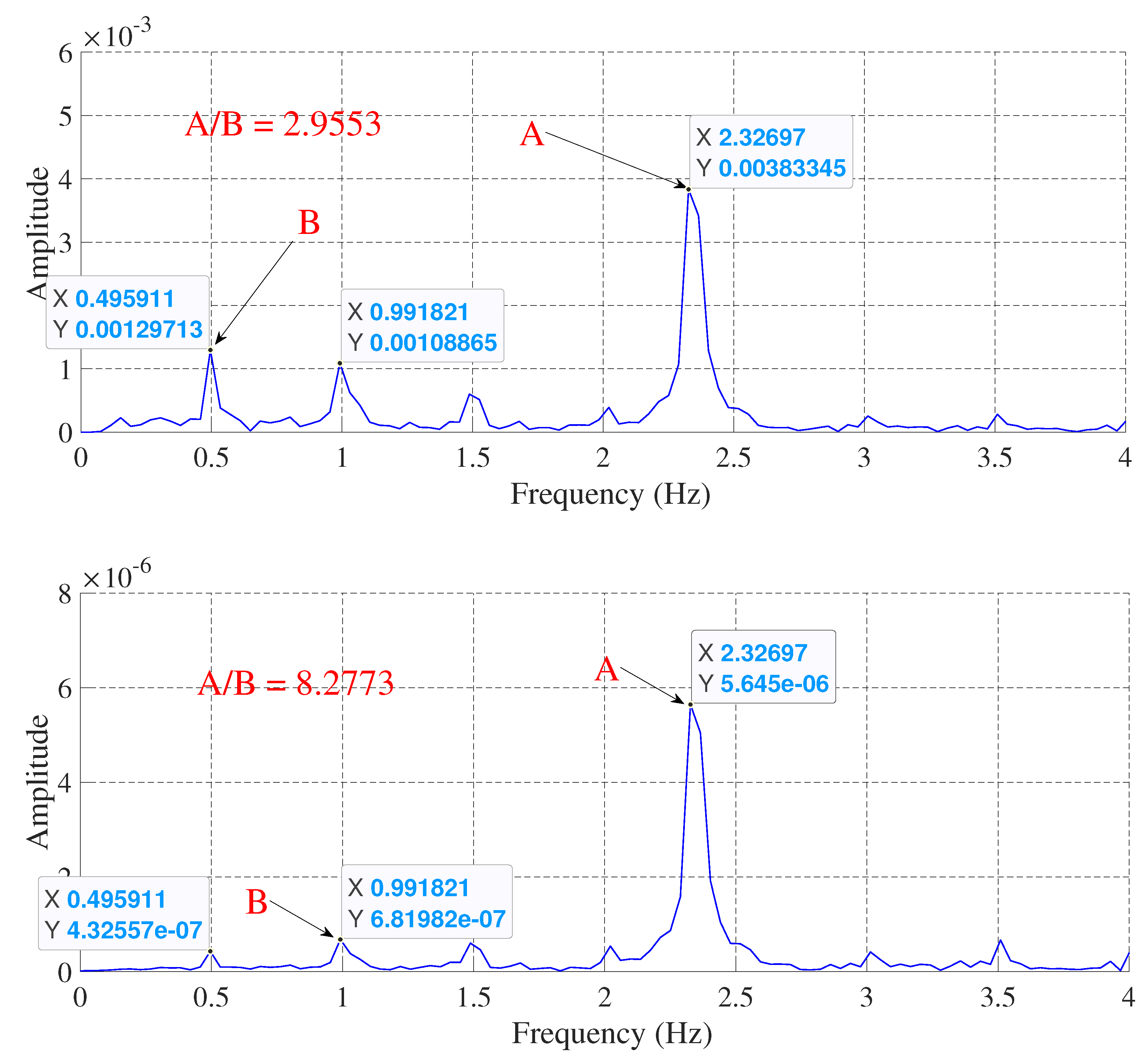
Figure 11.
Proposed method for high resolution FFT.
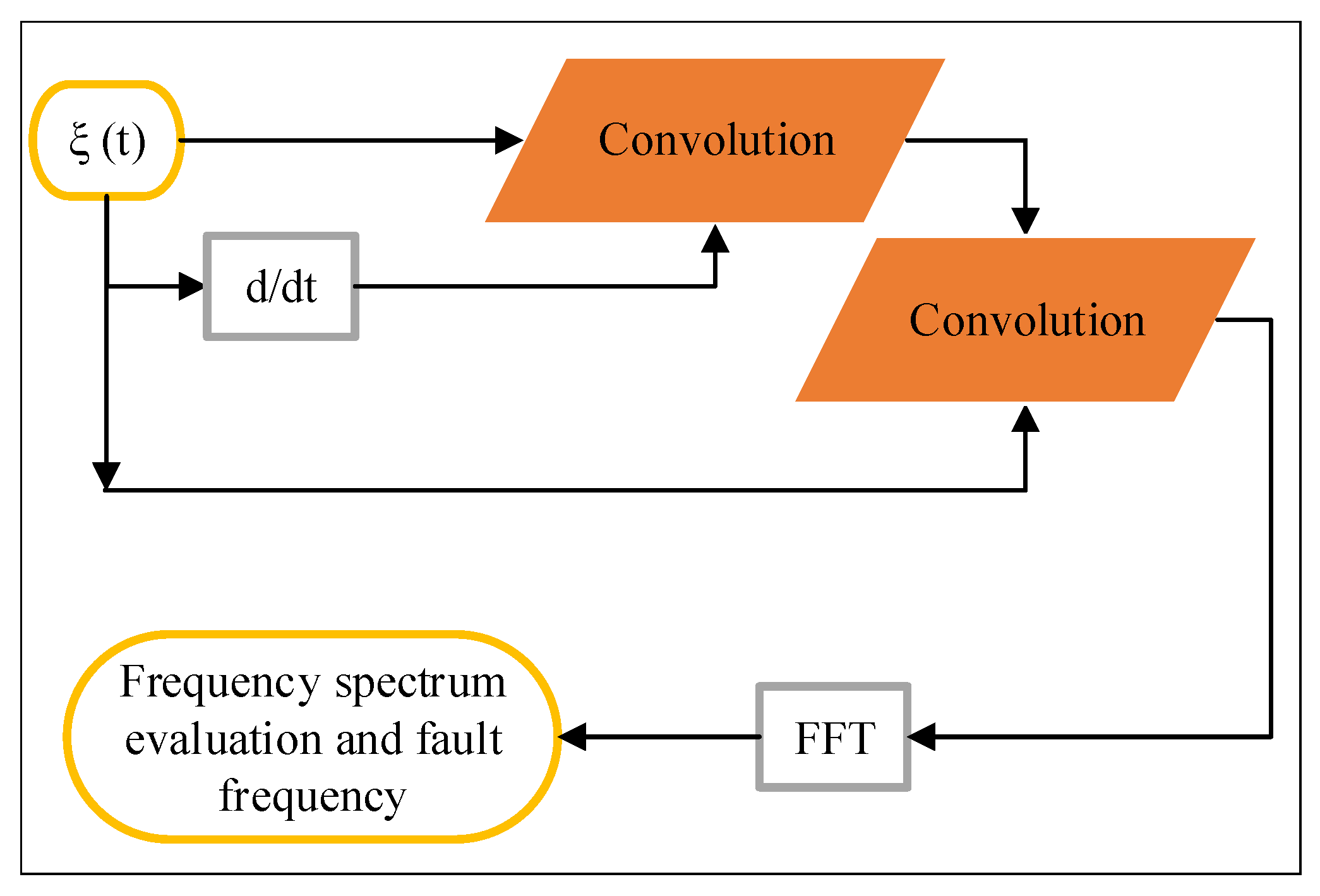
Figure 12.
Fault frequency spectrum with proposed method in DOL operation at full load state and one BRB.
Figure 12.
Fault frequency spectrum with proposed method in DOL operation at full load state and one BRB.
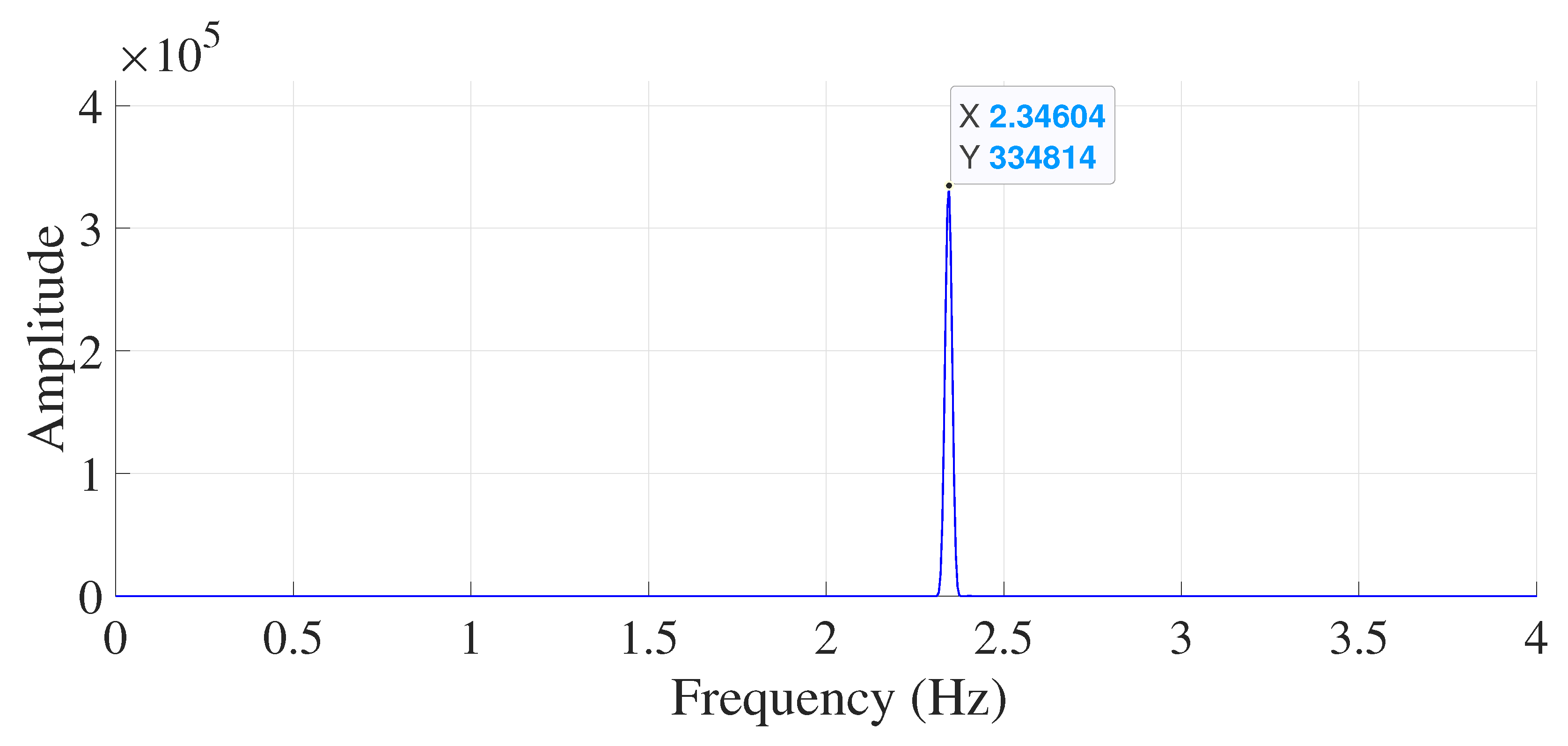
Figure 13.
Fault frequency spectrum with proposed method in DTC operation at light load state and one BRB.
Figure 13.
Fault frequency spectrum with proposed method in DTC operation at light load state and one BRB.
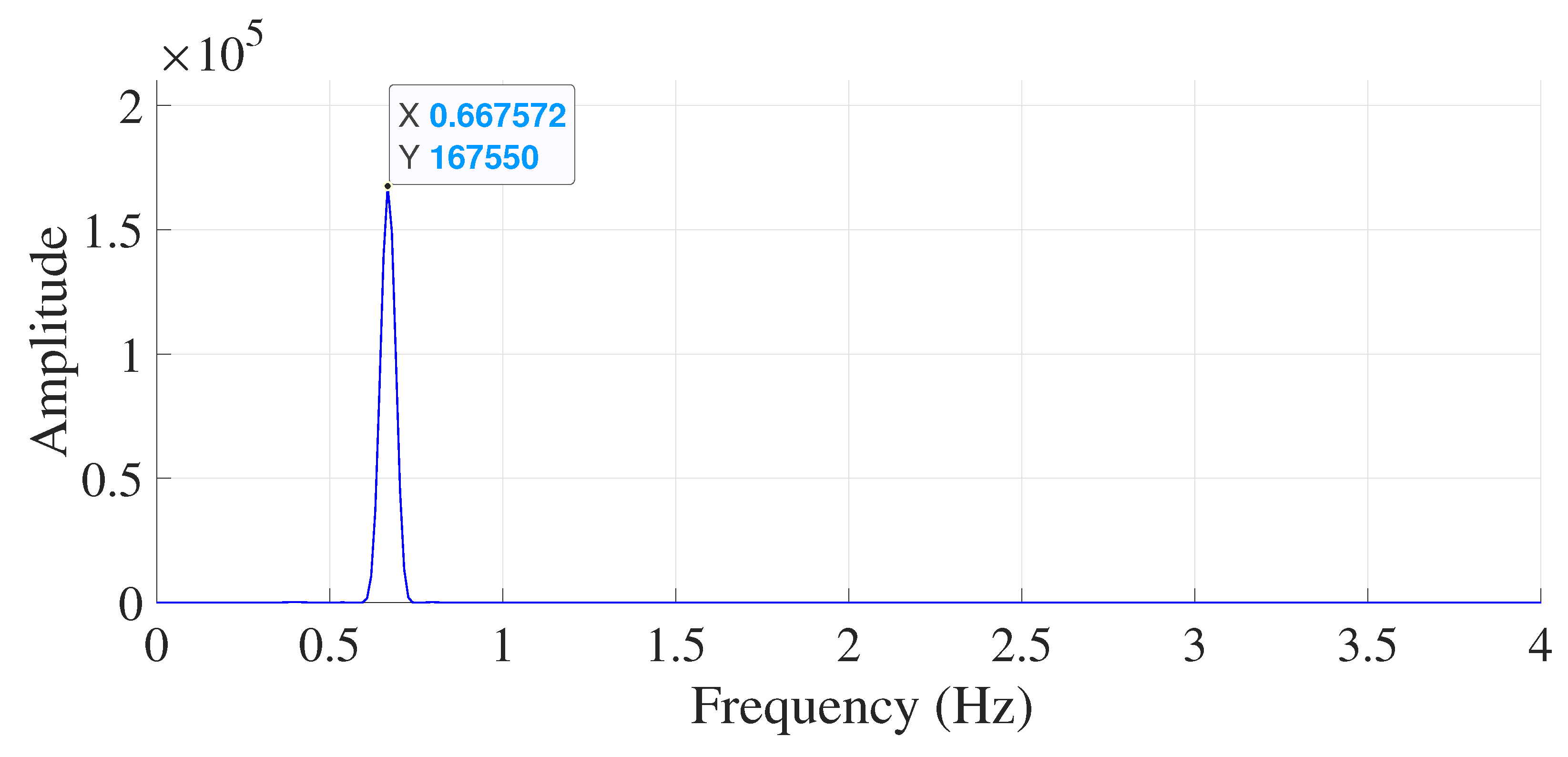
Figure 14.
Comparing healthy, one and two broken bars condition in the scalar operation mode and light load.
Figure 14.
Comparing healthy, one and two broken bars condition in the scalar operation mode and light load.
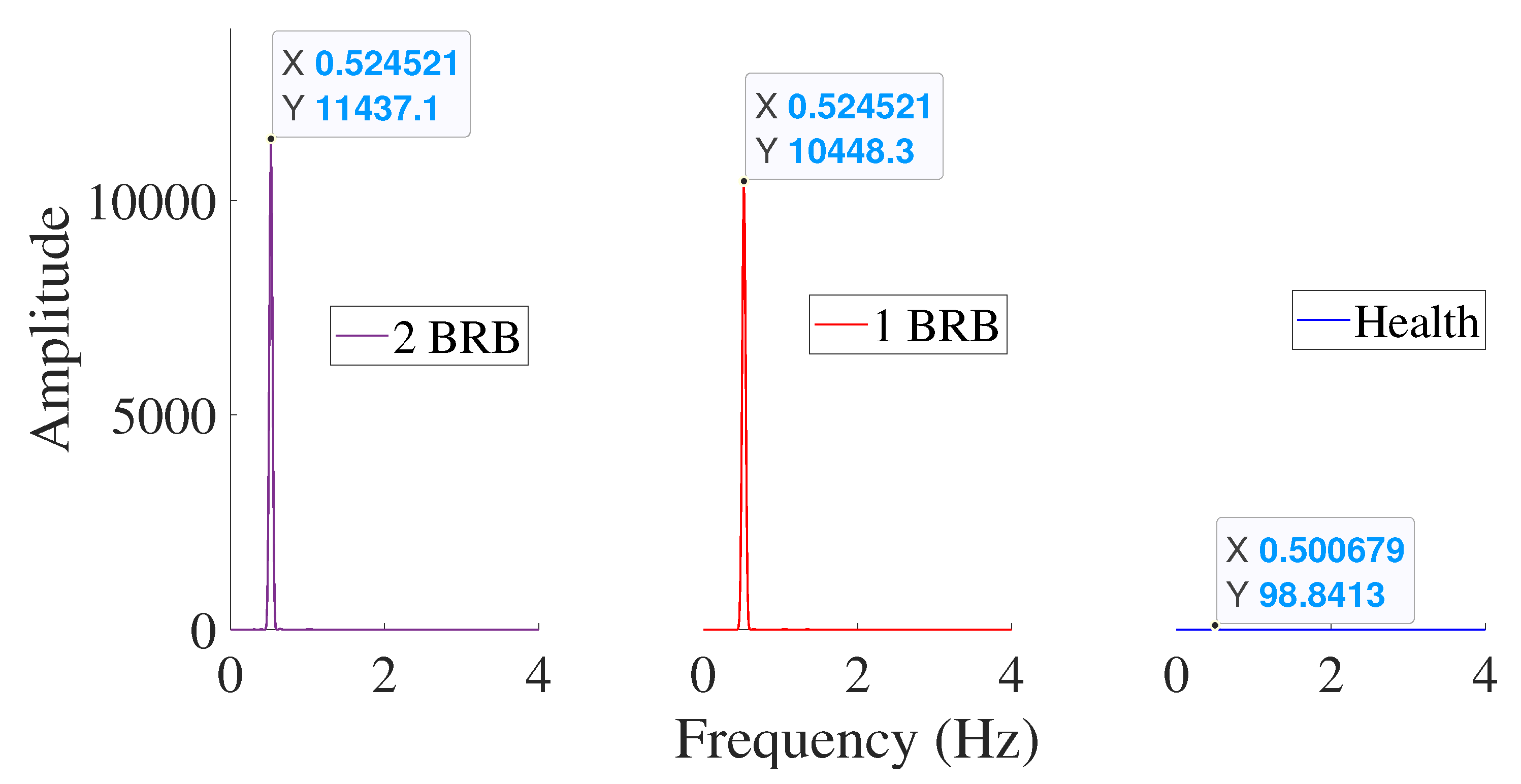
Table 1.
Analysis of terms and frequency components of relation (4)
Table 1.
Analysis of terms and frequency components of relation (4)
| Term | Frequency | Used for FD | Frequency elimination method |
|---|---|---|---|
| DC and | no | DC part by removing the average value and by low pass filter | |
| DC and | no | DC part by removing the average value and by low pass filter | |
| DC and | no | DC part by removing the average value and by low pass filter | |
| Difference of base and fault frequencies | yes | needed for fault diagnosis | |
| nearly | no | by low pass filter | |
| nearly | no | by low pass filter |
Table 2.
The specifications of the experimented motor.
| Rated Power | 1.5 kW | Rated Voltage () | 220/380 V |
| Rated Frequency | 50 Hz | Rated Current () | 5.7/3.3 A |
| Rated Speed | 1500 RPM | Power Factor | 0.81 |
| Efficiency | 85.3% | Pole no. | 4 |
| Rotor Bar no. | 28 | Air Gap Length | 0.25 mm |
Table 3.
Summarizing the frequency results obtained by the method
| Starting Method | Load Amount | Motor Status | Amplitude | Measured Frequency |
|---|---|---|---|---|
| DOL | Low | Healthy | 0.00256664 | 0.495911 |
| 1BRB | 0.00314357 | 0.495911 | ||
| 2BRB | 0.00397067 | 0.495911 | ||
| Medium | Healthy | 0.00403241 | 1.15256 | |
| 1BRB | 0.00546961 | 1.22071 | ||
| 2BRB | 0.00626237 | 1.2207 | ||
| Full | Healthy | 0.00365003 | 2.32697 | |
| 1BRB | 0.00383345 | 2.32697 | ||
| 2BRB | 0.00455207 | 2.36511 | ||
| DTC | Low | Healthy | 0.00156775 | 0.667572 |
| 1BRB | 0.00642336 | 0.667572 | ||
| 2BRB | 0.00870922 | 0.667572 | ||
| Medium | Healthy | 0.00207091 | 1.4782 | |
| 1BRB | 0.00647853 | 1.4782 | ||
| 2BRB | 0.00825256 | 1.52588 | ||
| Full | Healthy | 0.00113611 | 2.81334 | |
| 1BRB | 0.00402521 | 2.81334 | ||
| 2BRB | 0.00514829 | 2.86102 | ||
| Scalar | Low | Healthy | 0.00136112 | 0.524521 |
| 1BRB | 0.00372104 | 0.524521 | ||
| 2BRB | 0.00381647 | 0.524521 | ||
| Medium | Healthy | 0.0026973 | 1.19209 | |
| 1BRB | 0.00603295 | 1.23978 | ||
| 2BRB | 0.00728799 | 1.28746 | ||
| Full | Healthy | 0.0028846 | 2.38419 | |
| 1BRB | 0.00459908 | 2.43187 | ||
| 2BRB | 0.00413 | 2.47955 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Mathematical Decomposition of Fault Signature using Multinomial Identity and Differentiating for Detection of Broken Rotor Bar in Induction Motor
Habib Behnamnia
et al.
,
2023
Introducing a New Comprehensive Model for Fault Detection and Condition Monitoring of Rotor Bars of Large Induction Motors Based on MCSA and ZCT Methods
Abolfazl Attar
,
2021
Incipient Inter Turn Short Circuit Fault Detection on Induction Motors Through Data Fusion and Statistical Machine Learning Strategy
Arturo Yosimar Jaen-Cuellar
et al.
,
2023
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated









