Prerpints.org logo
Preprint
Article

Dynamic Reconfiguration to Optimize Energy Production on Moving Photovoltaic Panels

Altmetrics

Downloads

112

Views

56

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

16 May 2023

Posted:

17 May 2023

You are already at the latest version

Alerts
Abstract
In recent years, intensive work has been carried out to achieve maximum energy production in photovoltaic power plants. Today, this challenge has to be solved for arrays of solar panels that move with the object on which they are installed (vehicles, trucks, ships, etc.). The present work tries to find the best solution for both constant voltage systems and for cases of maximum intensity. Once found, these solutions will be applied in real time for the dynamic recharging of battery packs, trying to achieve energetically autonomous vehicles.To solve these situations, a new computational method of voltage and amperage calculation has been developed in this paper, based on Dijkstra’s minimum path finding algorithm on graph theory, adapted to electrical circuits. For this purpose, panel performance analysis sensors, developed at the University of Malaga, have been combined with different electronic solutions (wifi relay devices using esp8266 or similar chips) achieving an accurate and sufficiently fast solution at very low cost. With this, series or parallel configurations can be carried out depending on the type of energy generation sought. The theoretical solutions using Minkowski paths, achieved in the past, have been simulated and subsequently constructed in this article, indicating the diagrams necessary for their realisation.
Keywords: 
Subject: Computer Science and Mathematics  -   Applied Mathematics

1. Introduction

Today’s societies are increasingly dependent on their transport methods. But both the environmental impact of these methods and the energy restrictions that are taking place today (reduction in the use of gas or limitation of dependence on foreign markets) are forcing a change in the technological paradigm in their design and manufacture [1].
In order to solve this situation, it is necessary to find the most efficient renewable energy source for vehicles on the move or, at least, those that increase their autonomy of movement. Hence, it is solar energy that, at present, is sufficiently developed and can meet some of these requirements.
Because solar-based electricity production sources have lower charging speeds, systems with higher amperage or higher voltage or both are needed. Obviously this energy will at least cover the needs both for additional services and to support their autonomy [2].
The possibility of incorporating photovoltaic panels in moving locations is well known and widely used. Since its use on motorhomes and boats at the beginning of the 21st century for supplementary power while parked, it has evolved to the present day, where it also provides electricity supply for battery charging, back-up services and supplementary energy sources. New hybrid and electric vehicles are being developed that already feature solar technologies in their design: from the Lightyear One in 2020 to today’s Mercedes-Benz Vision EQXX, all have photovoltaic panels integrated into their surfaces. In the future, recent research into new materials (such as graphene, TMD semiconductors or perovksite) applied to flexible [3] panels will also see the electrical output generated by the solar panels being incorporated into real-time motion.
It should be noted that the paper [4], led by the Director of the Research Center for Smart Energy Technology, Toyota Technological Institute (Nagoya-Japan), already shows as an experimental result that, for panels with an efficiency of more than 30%, energy can be supplied daily to cover 30 km in a family car, without any fuel supplement. This study also predicts that the global development of cars powered by photovoltaic panels will take place between 2030 and 2040.
Hence, our research aims to complement this development by making battery charging and power supply processes more efficient. Both from the point of view of centralised systems (which we will call the low-cost model) and the simplified autonomous response system (which we will call the minimum model), the proposed solutions are aimed at favouring these processes.
The current price decrease of rigid photovoltaic panels (PV) and, from this, the commercial development of flexible panels (Figure 1) have opened up a wider range of applications for photovoltaic technology. They are being incorporated into the design of experimental prototypes, and in the coming years will be used in commercial vehicles1, requires a much more comprehensive real-time monitoring and optimisation process of energy production [5].
Static panels are much less likely to lose capacity due to cloud cover, tree shade or dirt on the panel than when they are incorporated into the structure of a moving vehicle (Figure 2). Hence, we need to increase the speed and accuracy of decisions when it comes to adding or discarding any of the solar cells that make them up [6].
With these principles in mind, we have decided to analyse flexible panel configurations that can be fitted to current vehicle designs. Most of these panels have a resistant Teflon layer, which gives them elasticity and less weight, and can be installed on any surface by means of clips or screws and without the need for adhesion, being easily repairable or interchangeable. On the other hand, they have transparent coatings that protect them from inclement weather, increasing their resistance and durability.
Once the type of panel has been chosen, the configurations are distributed in matrix form (Figure 3), by means of intercommunicating rows and columns. A priori, the basic configuration is columns interconnected in series up to the first row, and in this last row all the columns are connected in parallel.
The article is structured as follows: Section 2 outlines the foundations on which the problem has been built in previous research. Section 3 develops a new method for calculating voltage and current in electrical circuits based on Dijkstra’s algorithm for graph theory. Section 4 introduces the concept of dynamic configuration and the basis of artificial intelligence learning. Finally, Section 5 specifies the electronic solutions that enable the reconfiguration of moving solar panels in its two variants, one centralised and the other fully autonomous.

2. Genesis

This article aims to provide the technical solutions necessary to develop the theoretical models presented in 2018 by S.Merino, F.Sánchez, M.Sidrach de Cardona et al [7]. The concepts summarised below were presented and concluded by proposing the work presented in this article as future work.
A solar PV array is defined in a matrix by columns of panels connected in series and linked together by parallel connections (Figure 4). The array will try to produce the highest energy intensity under a constant voltage, whatever the prevailing weather conditions. The various factors affecting this output (dust, bird droppings or shading) can significantly unbalance the output and decrease it considerably.
This unbalance causes some panels to work at different maximum power points on their corresponding current-voltage curves (I-V curve). The worst conditioned panel will decrease the performance of the whole column by modifying the overall maximum power point (MPP) to a lower value [8,9]. In Figure 5 it can be seen how the string current at the MPP (solid line) is limited by the MPP current of the third PV.
By summing the voltages of each PV in series on a column, the column voltage is calculated. However, the final current depends on the number of parallel columns (Figure 10). A generalisation of this phenomenon for PVs can be found in [10]. In order to calculate the voltages and currents in real time, the following adaptation of Dijkstra’s algorithm is developed.

3. Dijkstra algorithm and electrical conversion

We start from the basic rules of voltage and current calculation:
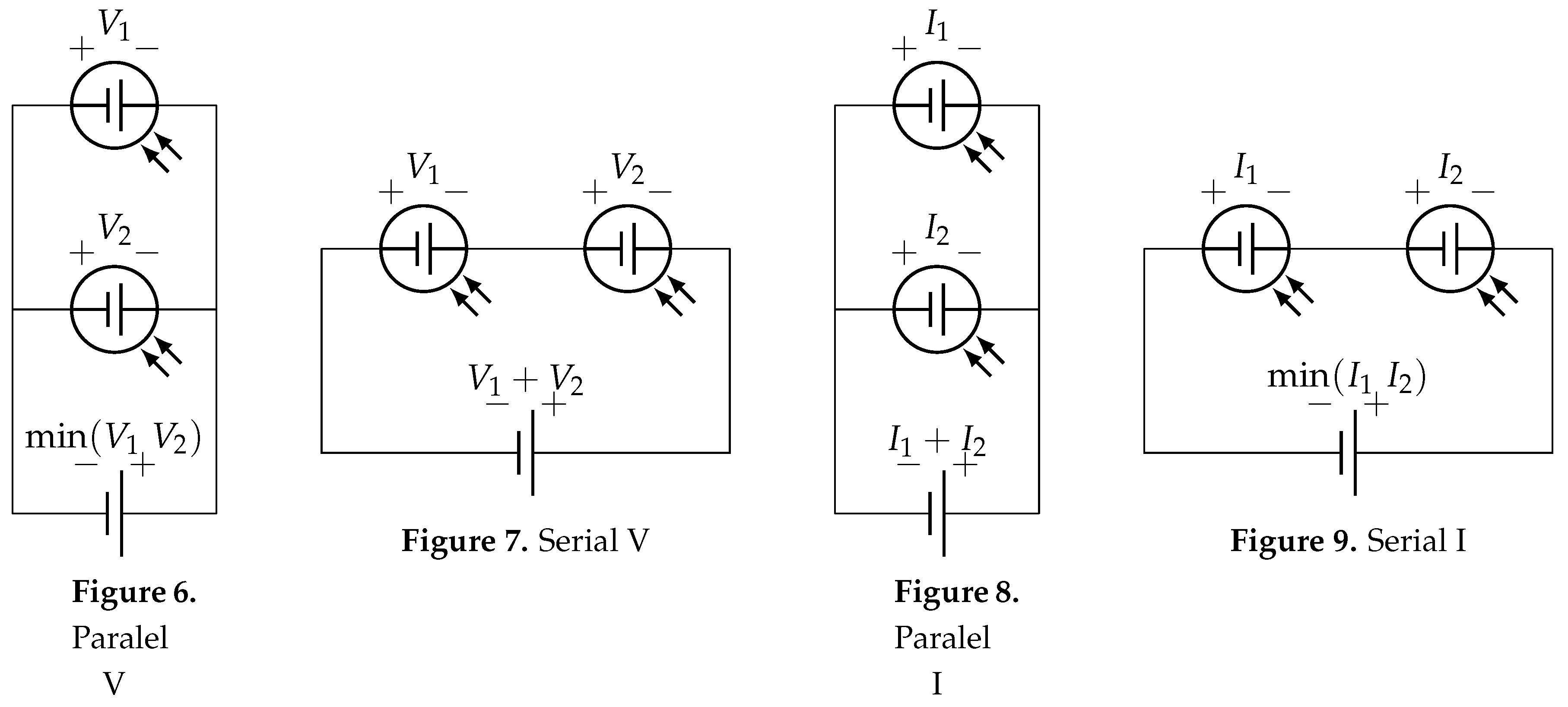
Preprints 73821 g006
Figure 10. Voltage and Intensity, Paralel and Serial.
Figure 10. Voltage and Intensity, Paralel and Serial.
Preprints 73821 g006
Dijkstra’s algorithm has usually been used in its original version, i.e. to calculate the minimum path between two points [11,12]. However, in this case we are going to reprogram the algorithm itself to calculate voltages and intensities between points in a novel way. Let us first establish a notational parallelism to pass these circuits to graphs, considering in each vertex the value to be studied (voltage or current) and in the edges the operation carried out (minimum=m and sum=+). For example:
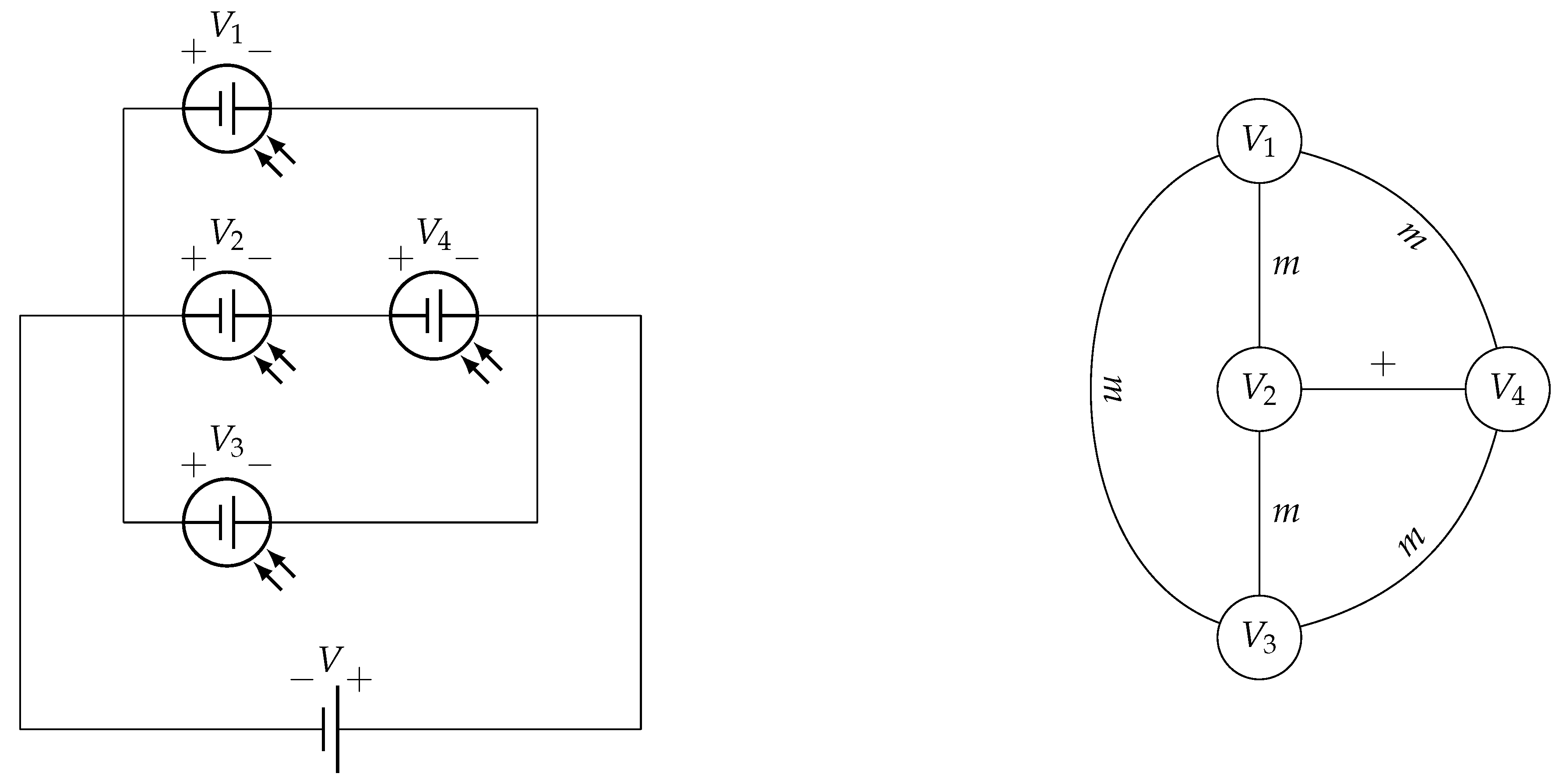
Preprints 73821 g007
Figure 11. First example of transition from electrical circuit to mathematical graph.
Figure 11. First example of transition from electrical circuit to mathematical graph.
Preprints 73821 g007
To solve it, we reformulate Dijkstra’s method, applying values to the vertices together with operations on the edges. This method will allow us to calculate both voltages and currents by simply interchanging the operations on the edges. We will call the new method ”Electrical Dijkstra Algorithm”.

3.1. Electrical Dijkstra Algorithm

1.
We start from the first vertex and we have to get to the last one passing through all of them.
2.
We cancel the column of the chosen vertex and we proceed to calculate the operations indicated in each edge with the values of the combined vertices.
3.
If we find "+" we make the sum of the values and we mark them both with a superscript sum accompanied by the value of the vertex.
4.
If we find "m" we calculate the minimum of the values and we mark them both with a subscript m accompanied by the calculated minimum.
5.
In each step we look for the minimum of the row results to choose that vertex as a new starting point, circling the chosen value and using that value to be summed in the next step.
6.
If, when using a vertex, it has a superscript or a subscript, the value that accompanies it must be subtracted in the calculations (if it is a sum, the value of the superscript is removed, and if it is a minimum, the value of the subscript is removed).
7.
If two vertices are not related, the value they had is left, and if they had no value, it is set to infinity.
8.
In each step, if the value in the previous row is less than the one currently calculated, the lesser value is left.
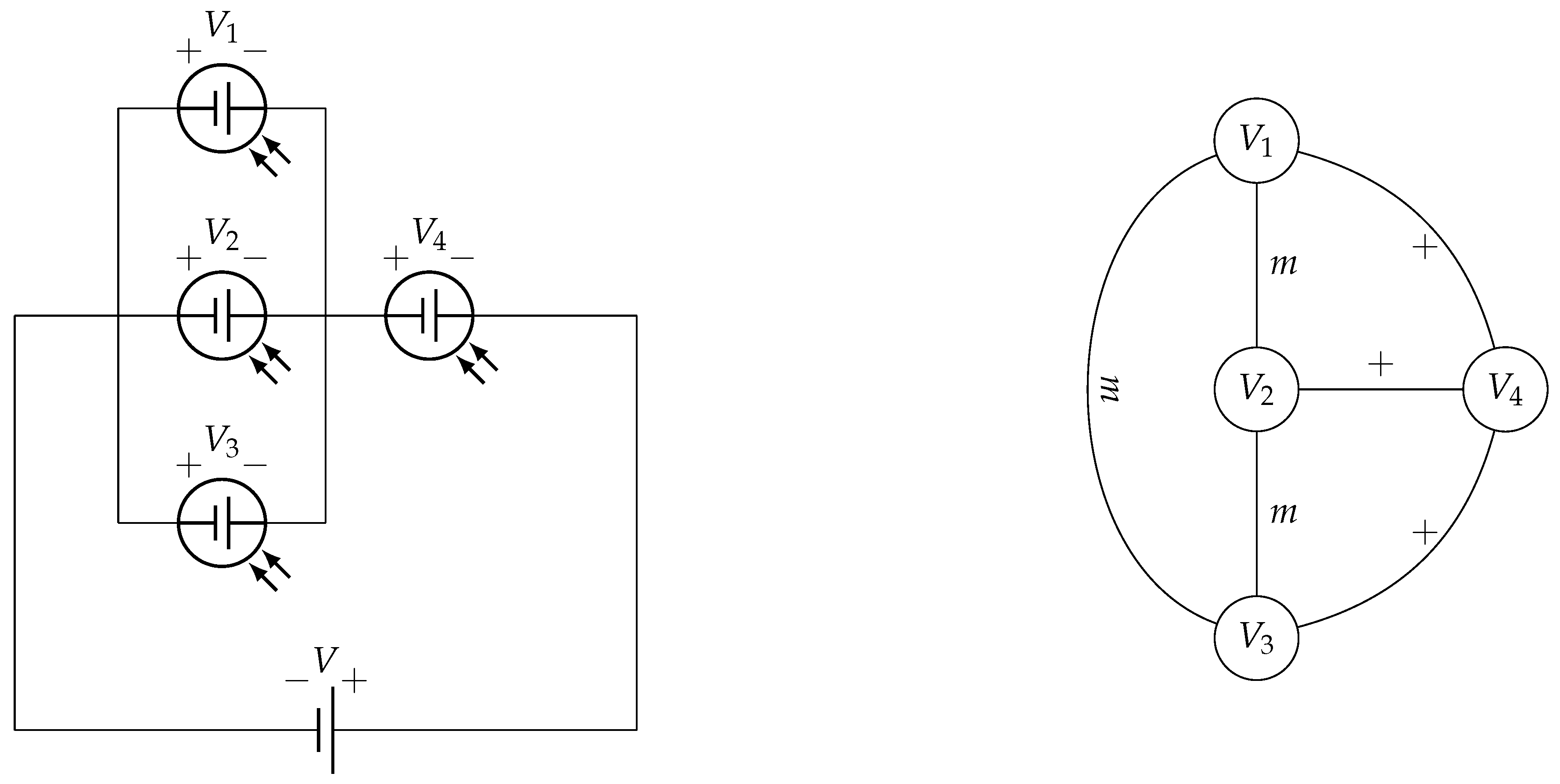
Preprints 73821 g008
Figure 12. Second example of transition from electrical circuit to mathematical graph.
Figure 12. Second example of transition from electrical circuit to mathematical graph.
Preprints 73821 g008
Example to be solved: calculate V
Preprints 73821 g009
Figure 13. Circuit to solve.
Figure 13. Circuit to solve.
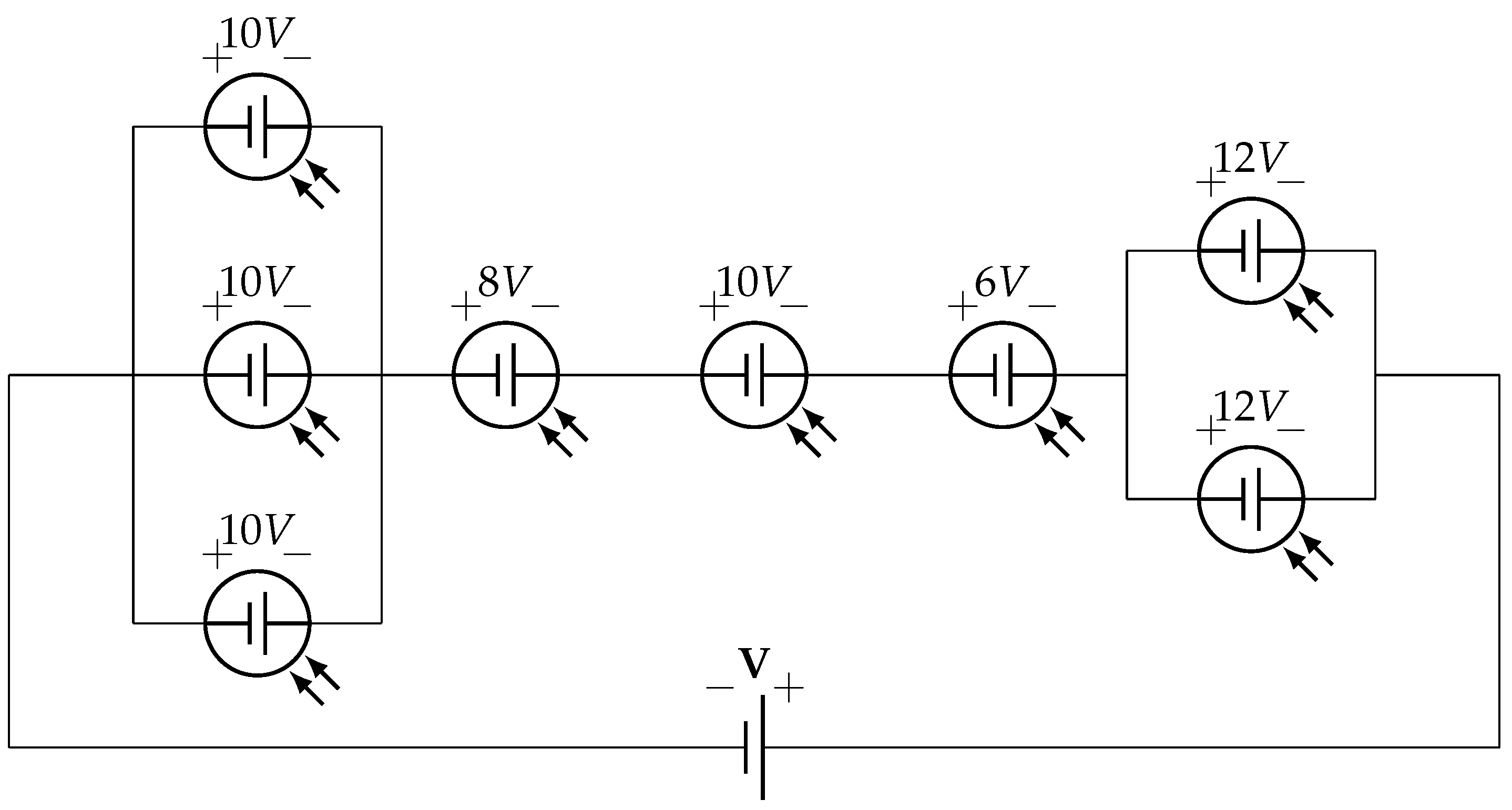
Preprints 73821 g009
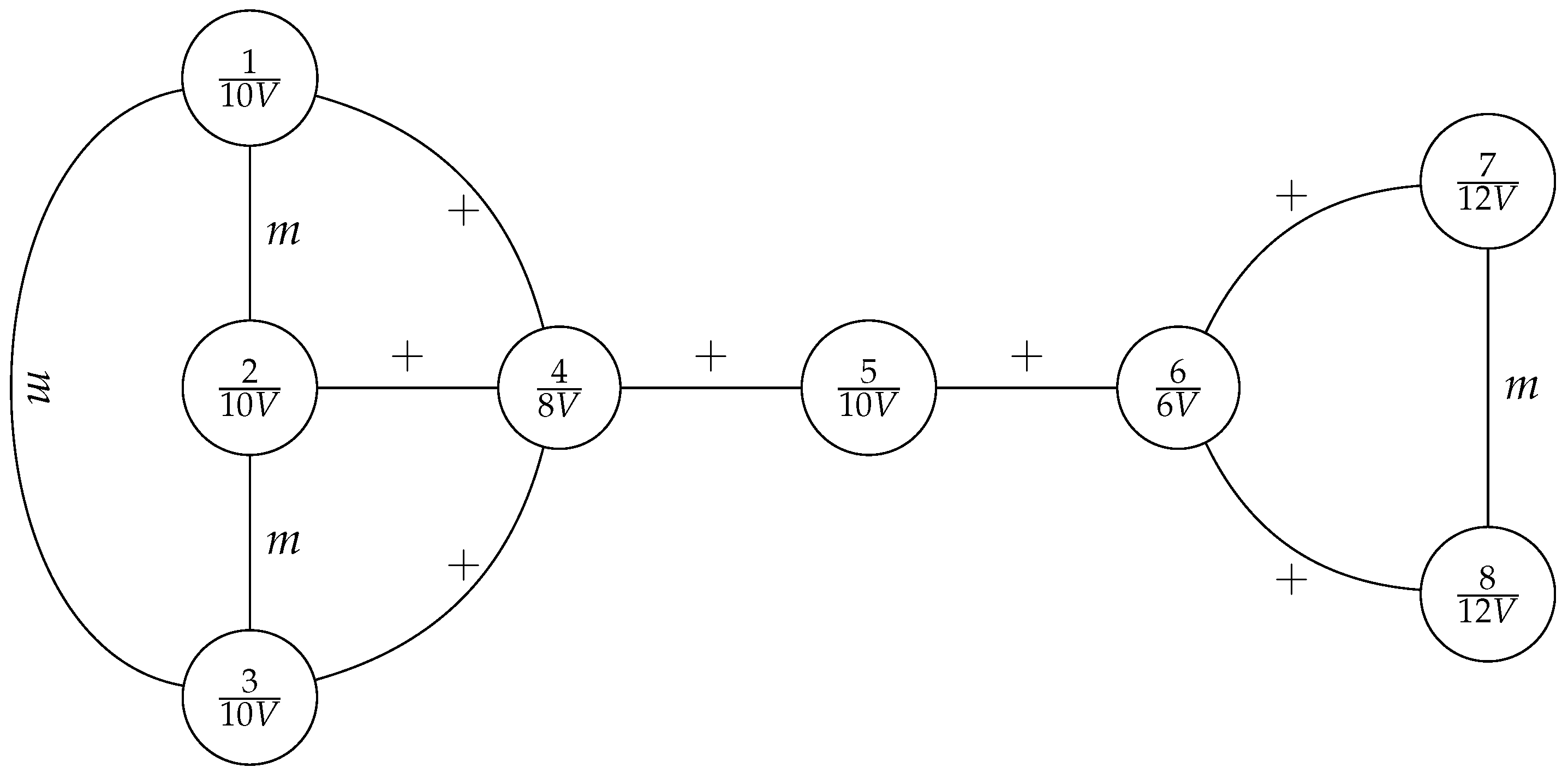
Preprints 73821 g010
Figure 14. Translation to graph.
Figure 14. Translation to graph.
Preprints 73821 g010
Matrix application of algorithm
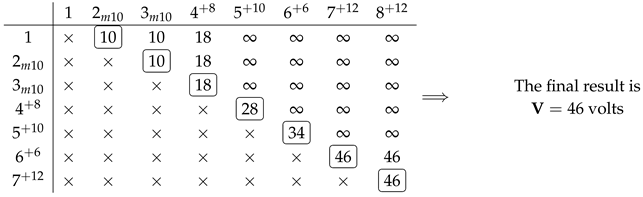
Preprints 73821 i001
Computational resolution
The adjacency matrix is generated under the assumptions:
  • -1 is a parallel connection (minimum)
  • 0 is a serial connection (sum)
  • 1 is no relation edge
In the above case (Figure 14) it would be:
A = 10 − 1 − 1 0 1 1 1 1 − 1 10 − 1 0 1 1 1 1 − 1 − 1 10 0 1 1 1 1 0 0 0 8 0 1 1 1 1 1 1 0 10 0 1 1 1 1 1 1 0 6 0 0 1 1 1 1 1 0 12 − 1 1 1 1 1 1 0 − 1 12
The algorithm in MatLab (version R2020a) is executed in three phases
1.
Sorting (in increasing order of types of connections exposed in the matrix A)
col=zeros(1,size(A,1));
for i=1:size(A,1)
    for j=i+1:size(A,1)-1
        for k=j+1:size(A,1)
            if A(i,j)>A(i,k) && col(j)==0
                pivot=A(j,:);A(j,:)=A(k,:); A(k,:)=pivot;
                pivot=A(:,j);A(:,j)=A(:,k); A(:,k)=pivot;
                col(j)=1;
                if j==size(A,1)-1
                    col(k)=1;
                end
            end
        end
    end
end
Obtaining, in this case, the same matrix A as above.
2.
Weights
A temporary weight matrix is created where
  • the weights are negative if it is a parallel join
  • the weights are positive if it is a series connection
B=[];
for i=1:size(A,1)
    for j=i+1:size(A,1)
        if A(i,j)==-1
            B(i,j)=-A(i,i);
        elseif A(i,j)==0
            B(i,j)=A(j,j);
        else
            B(i,j)=0;
        end
    end
end
Obtaining:
B = 0 − 10 − 10 8 0 0 0 0 0 0 − 10 8 0 0 0 0 0 0 0 8 0 0 0 0 0 0 0 0 10 0 0 0 0 0 0 0 0 6 0 0 0 0 0 0 0 0 12 12 0 0 0 0 0 0 0 − 12
3.
Electrical Dijkstra (with the accumulated increment at the last column)
increment=0;C=[]; C(1,size(A,1)+1)=0;
for i=1:size(A,1)
 
    if i>1 && B(i-1,i)>0
        increment=C(i-1,i)-A(i,i)
    end
 
    if i>1
        increment=max(increment,C(i-1,size(A,1)+1));
        C(i-1,size(A,1)+1)=increment;
    end
 
    for j=i+1:size(A,1)
        if B(i,j)<0
            C(i,j)=increment+min(-B(i,j),A(i,i));
        elseif B(i,j)>0
            C(i,j)=increment+A(i,i)+B(i,j);
        else
            if i>1
               if C(i-1,j)>0
                  C(i,j)=C(i-1,j);
               else
                  C(i,j)=inf;
               end
            else
               C(i,j)=inf;
            end
        end
    end
end
Remaining:
C = 0 10 10 18 I n f I n f I n f I n f 0 0 0 10 18 I n f I n f I n f I n f 0 0 0 0 18 I n f I n f I n f I n f 10 0 0 0 0 28 I n f I n f I n f 18 0 0 0 0 0 34 I n f I n f 28 0 0 0 0 0 0 46 46 34 0 0 0 0 0 0 0 46 34

4. Dynamic reconfiguration

Based on the reconfiguration of PVs, an algorithm was established to solve it by maintaining the voltage and maximising the overall intensity. This improves the efficiency of the array through appropriate series or parallel connections of the panels. The system obtains the maximum energy intensity in DC until it reaches the inverter, which transforms it into AC and feeds it into the grid. This reconfiguration procedure is called Totally Cross Tied (TCT), and uses serial or parallel connections of each panel to its adjacent panels, using the switching matrix.

4.1. Maximum efficiency topology

The theoretical data acquisition device was proposed by F.Sánchez, M.Sidrach de Cardona et al [9]. From this real time measurement via PLC it is possible to create topologies or reconfigurations with maximum efficiency. An important fact will be to reduce the downtime of the assembly, hence the electronic devices and configurations that will be presented below.
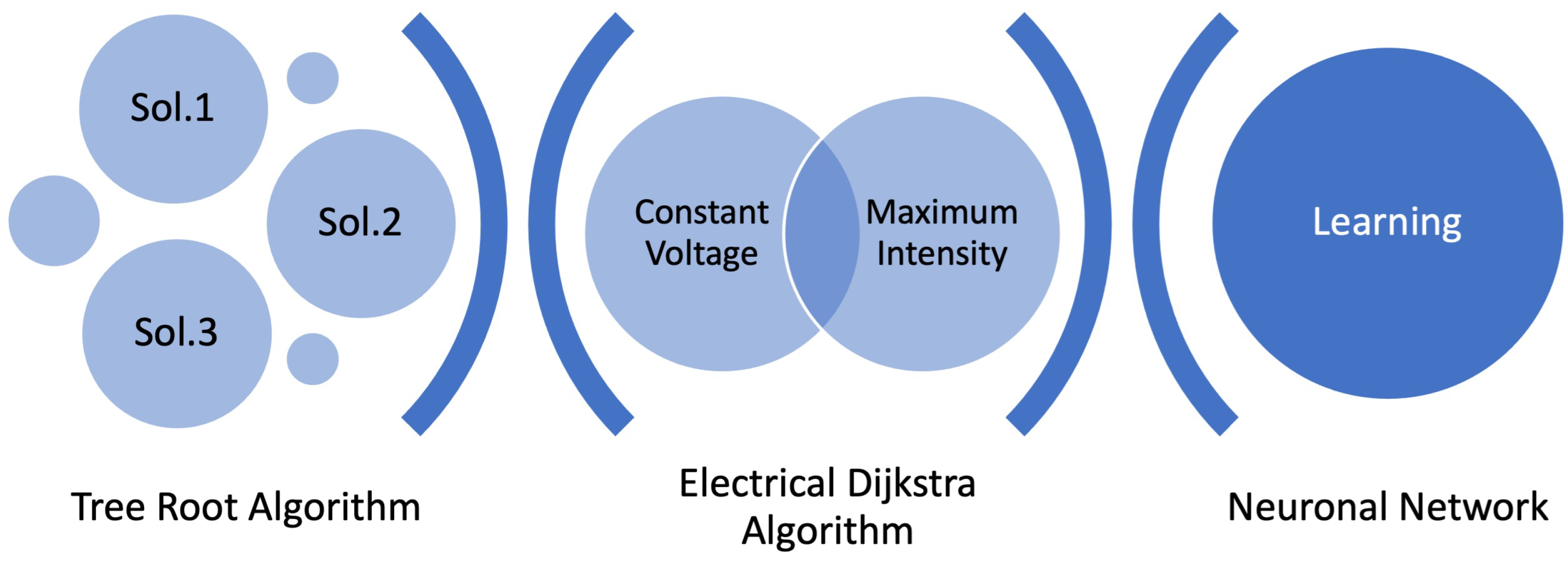
The resolution algorithms will be based on the Minkowsky path theory and are developed using MatLab. They allow the affected panels to be isolated or replaced without modifying the optimal output of the rest of the installation. The final procedure was defined as tree root algorithm.
Once the possible solutions (solution space) have been chosen, their measurement by means of the electric Dijkstra algorithm will give us the objective function with which to achieve the optimal solution. This solution can be registered, by means of artificial intelligence, as the solution of a neural network. The inputs will be the different production states of the solar panels and the output will be the solution found, which will be implemented (Figure 15). This system will provide the permanent knowledge and learning to the system of choice of solutions.

5. Electronic solutions

Once the theoretical model has been developed, we must establish a procedure to arrive at the most efficient technical solution. Therefore we will create the following models:
1.
Low cost model: development based on the Esp8266 chip with 4 relays. These devices will accompany each of the panels and will allow independent solutions, depending on their configuration, of maximum voltage and maximum amperage.
2.
Minimum model: simplification on the previous model based on the voltage drop on a relay. It offers constant voltage and is especially recommended for linear configurations (buses, trams, motorhomes, etc.).

5.1. Low cost model

This model consists of two items. On the one hand it makes use of the tree root algorithm and on the other hand it electronically develops the circuit diagram for real application.

5.1.1. Tree root algorithm

The algorithm on which this physical model has been built was exposed in the article developed in 2018 by S. Merino, F. Sánchez, M. Sidrach de Cardona et al [7]. It is based on the Minkowsky paths and after its application (Figure 16) we would obtain:
δ = 1 1 1 1 1 1 1 − 1 1 1 1 1 − 1 1 − 1 1 1 1 1 1 1 1 1 1 D 0 = 1 1 1 1 1 1 2 − 1 2 2 2 2 − 1 0 − 1 3 3 3 0 0 0 4 4 4
D 1 = 1 1 1 1 1 1 2 − 1 2 2 2 2 − 1 0 − 1 3 3 3 0 0 5 4 4 4 ⇒ D 2 = 1 1 1 1 1 1 2 − 1 2 2 2 2 − 1 0 − 1 3 3 3 0 6 5 4 4 4 ⇒
D = 1 1 1 1 1 1 2 − 1 2 2 2 2 − 1 7 − 1 3 3 3 7 6 5 4 4 4

5.1.2. Electronic development

The following low-cost devices are used for their application:
Preprints 73821 g013
Figure 17. Control device via esp8266 for 4 relays.
Figure 17. Control device via esp8266 for 4 relays.
Preprints 73821 g013
Below we provide the new solutions that resolve the two possible situations: search for maximum voltage or establishment of maximum amperage.
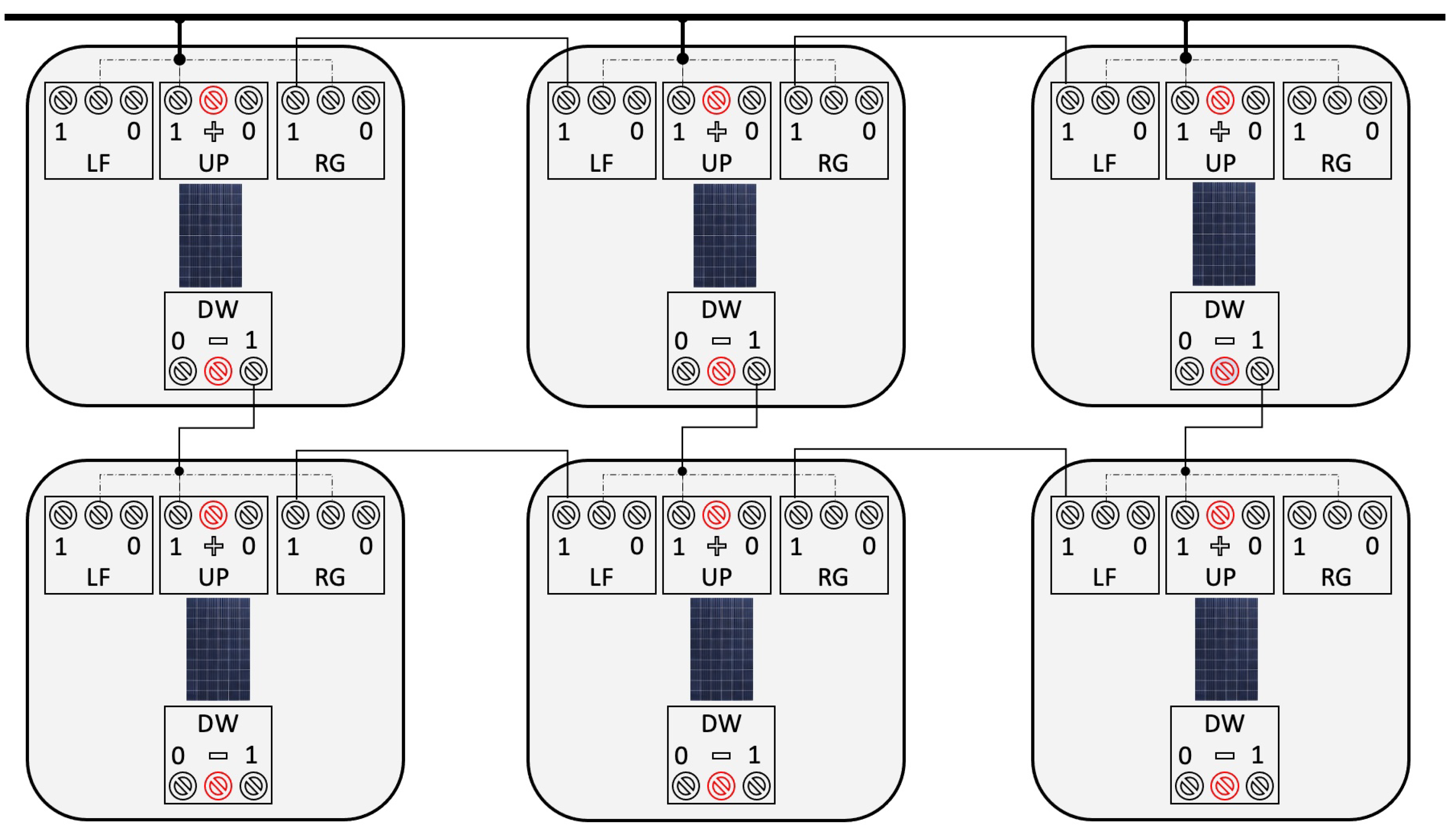
Preprints 73821 g014
Figure 18. Maximum voltage (parallel connection).
Figure 18. Maximum voltage (parallel connection).
Preprints 73821 g014
Reconfiguration systems using quad relays managed by esp8266 devices (both figures)
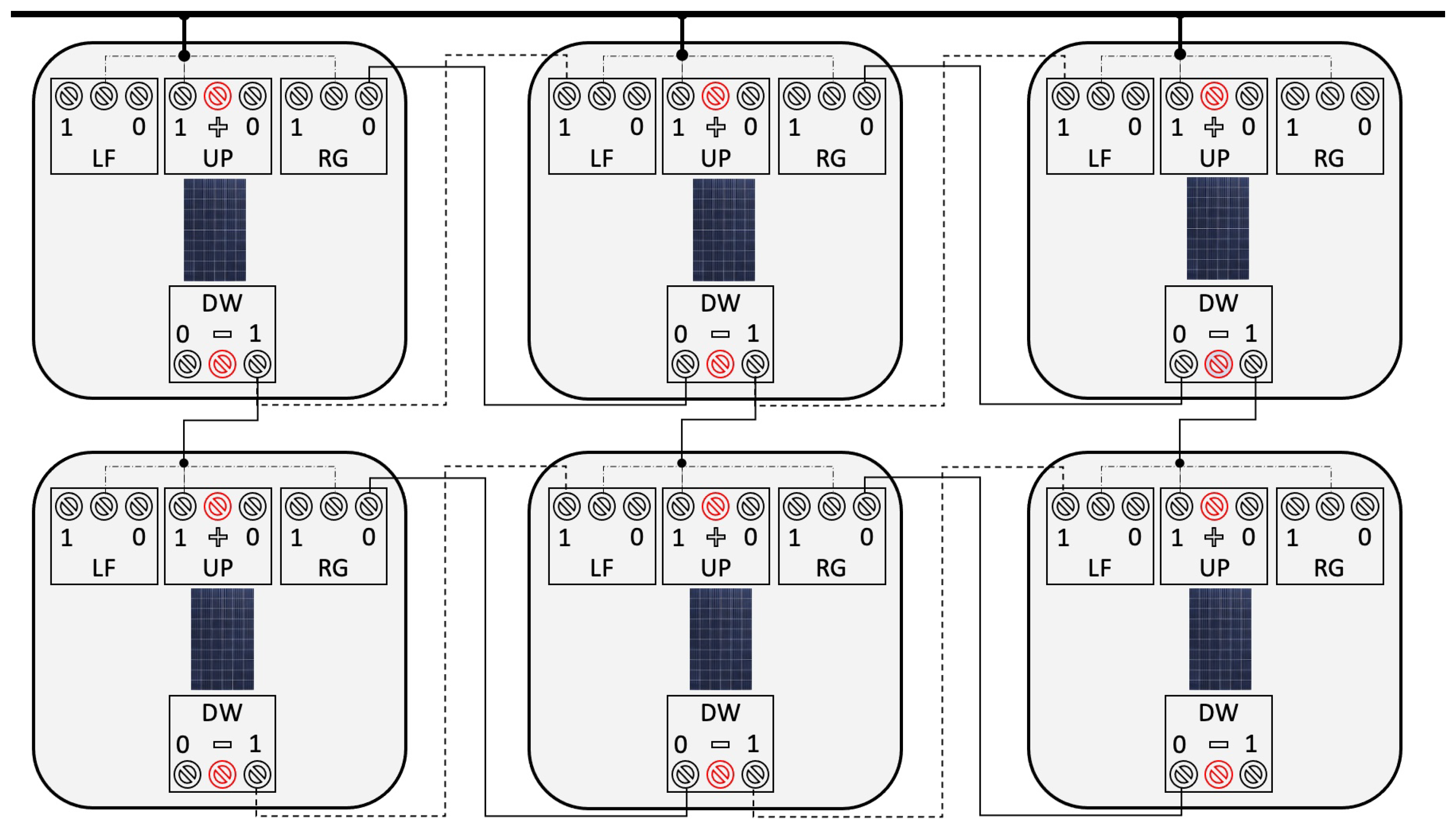
Preprints 73821 g015
Figure 19. Maximum amperage (serial connection).
Figure 19. Maximum amperage (serial connection).
Preprints 73821 g015

5.2. Minimum model

As mentioned above, one of the problems with the connection of the panels in photovoltaic parks today is that, in a first assembly, they are connected in parallel, in order to enable the maximum current contribution to the inverters. The main problem with this assembly lies in the fact that, when one of them reduces its performance due to shadows or dirt on its surface, the voltage of the set is reduced and, consequently, the energy supplied to the injector is minimised.
The solution found proposes to use basic relays as a tool to establish a connection or to suppress it. Electrically, what is proposed is to use the energy generated in each of the sets of photovoltaic cells that make up the panel as a power supply to activate the switching of the panel’s own relay that will control the connection of the panel to the set of panels in parallel, adding its intensity to that generated by the other panels, or disconnecting that panel from the set (in the event of a decrease in the voltage or intensity generated).
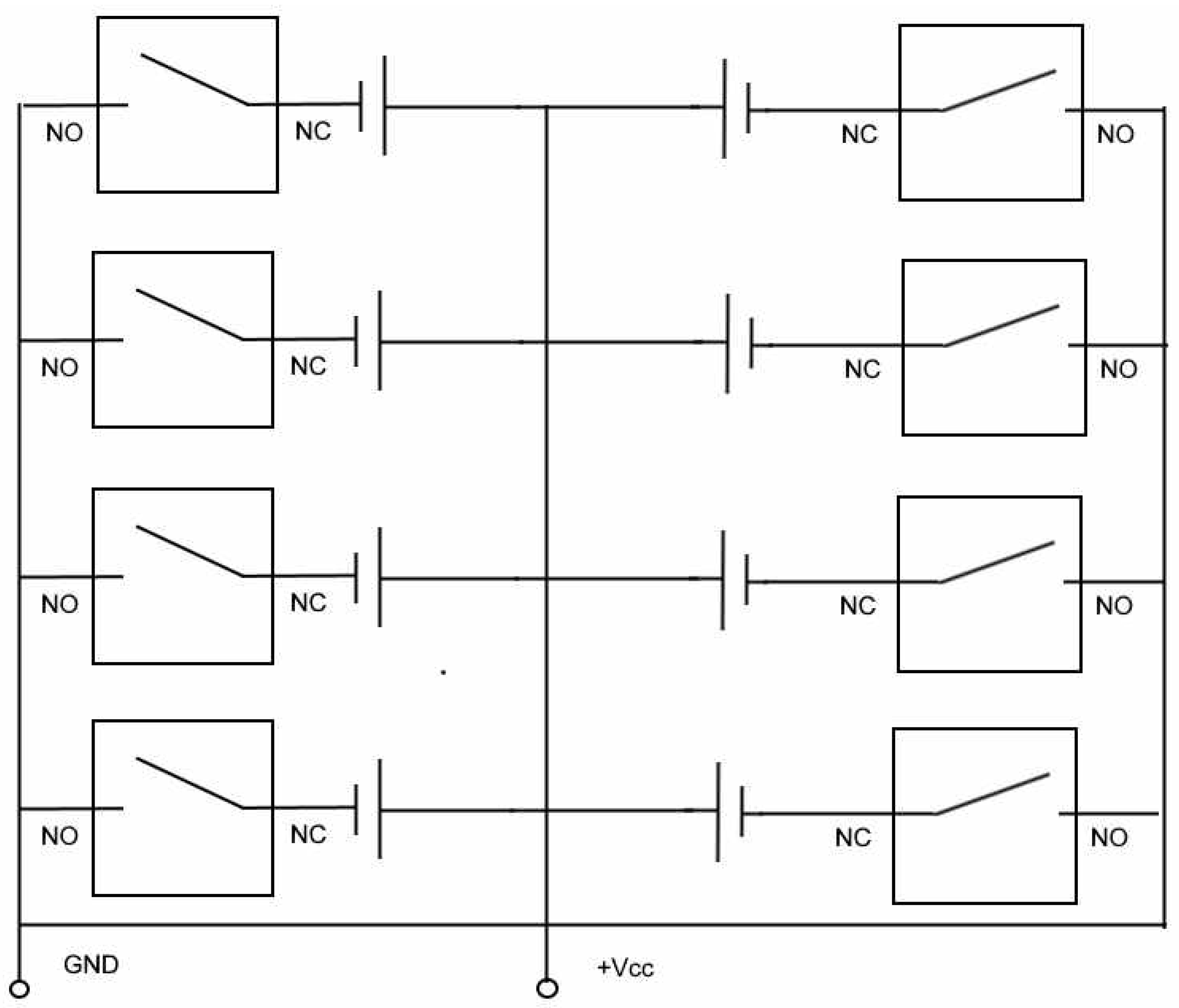
Preprints 73821 g016
Figure 20. Minimal model in linear distribution (two columns of panels).
Figure 20. Minimal model in linear distribution (two columns of panels).
Preprints 73821 g016
As long as the array of cells allows, in its connection terminals, the potential difference that allows the parallel connection of the different arrays and their injection into the inverters, the relays will be activated and the current generated will be added, maintaining the voltage at the terminals of all the connections, individually, to the operating voltage of the inverters.
When, due to shadows or dirt on the cells, the voltage of the set does not reach the service voltage of the inverters, which is the same as the activation voltage of the relays, the relay in charge of managing the connection of that set will return to its idle state and that panel will be disconnected from the set. In this way, the operating voltage will be maintained, even if the current supplied by the panel is reduced, but the total power generated by the streamer will still be produced, even if a panel stops producing.
Once the problem has been rectified, the relay will automatically activate and reconnect the panel in parallel with the others.
This setup will allow the power generated by an array of PV panels to be optimised automatically and without the need for a microcontroller or management system.
The design would be optimised to the maximum if the panel could be fitted with multiple connections that would allow it to work with the minimum set of cells that make it up, and whose terminal voltage would be that of the injector’s service voltage. In this case, a relay would be placed in each of these connections, proceeding in the same way as described for the case of working with the whole panel, but improving the system by not eliminating the whole panel, but only the set in which some of the cells have been left in shadow.
The main novelties of this system are highlighted below:
  • By working directly using the energy generated by the different panels as a source of energy for the activation of the switching relay, its operation is independent of any external system (either control or power supply) so that any environmental alteration or decrease in the supply of solar energy that affects the panel will lead to the switching of the relay.
  • The need for wiring is simplified to the maximum to control the switching and achieve the change of connection of the panels, going from series to parallel connection and vice versa when established by the conditions of energy production of the same at an individual level.
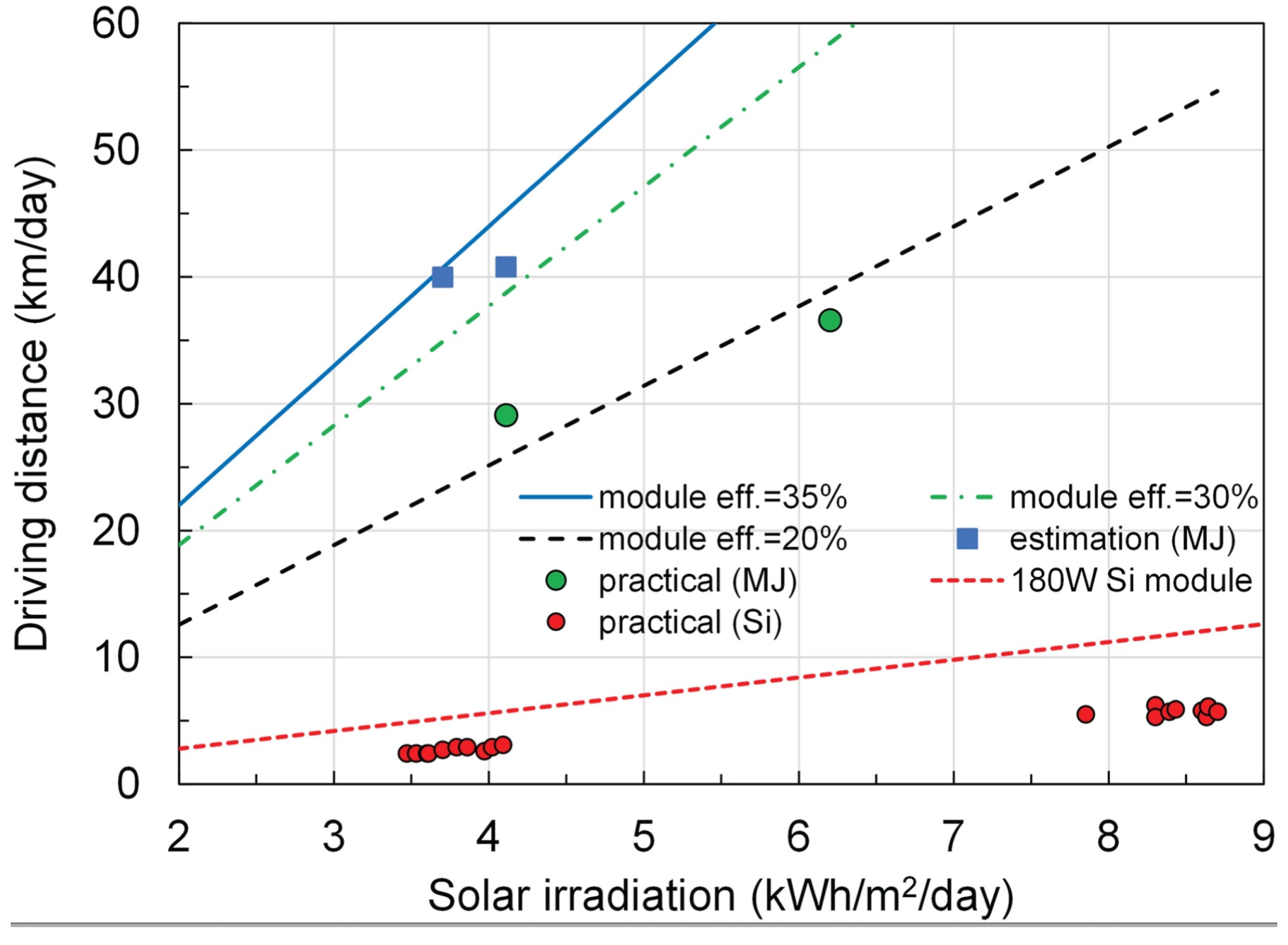
  • The system has been initially designed as a supplementary contribution to an energy supply system powered by batteries but, given that its application ensures the stability of the voltage supplied by the set of panels, it could be used as a primary energy system (provided that the number of panels installed supplies sufficient current to power the loads to be connected) and, if so desired, the surplus generated could be used to charge them during periods of inactivity (case for flexible panels of Multijunction-MJ and Silicon-Si types studied by Masafumi Yamaguchi team: Figure 21).
  • As it is a decentralised control system and autonomous operation, it does not require the intervention of microcontrollers and energy measurement systems that record the intensity supplied by each of the panels to establish the way in which it will be connected to the set.
The experiments carried out with the proposed system have shown that there is a significant unbalance between the voltage required to activate the relays and the value that causes them to deactivate. Moreover, this unbalance is particular to each relay model and even to each range within the model. For this reason, it has become essential to incorporate a pull up and pull down resistor [14] that allows us to minimise the margin in which we can consider the value of the potential difference that conditions the connection in series or in parallel of the panel to the installation as a whole to be adequate.
Preprints 73821 g017
Figure 21. Distance travelled on the basis of solar irradiation [4].
Figure 21. Distance travelled on the basis of solar irradiation [4].
Preprints 73821 g017

6. Conclusions and future work

Having developed and tested the models for determining the optimum connection of the panels, evaluated in this article, with the aim of ensuring the potential difference at the terminals of the power supply circuits and also the maximum current that the system can supply under these conditions, it has been found that:
  • Complexity: From the point of view of computational complexity, for the application of control algorithms based on software logic, using a microcontroller with its appropriate programming to send orders to the sp8266 and this, in turn, organises the serial or parallel connection of the adjacent panels, it is more appropriate to program it on the so-called "low-cost" model using MatLab [15].
  • Non-linear distribution: In panels with non-linear or non-geometric distribution (for example in solar farms), management must be carried out by means of low-cost models using linear programming techniques. For this purpose, an objective function (Adjacency Matrix) will be established and the possible solutions will be evaluated through the electric Dijkstra algorithm presented in this work.
  • Minimum model: Considering the simplicity of the installation, for systems that interact automatically by potential drop, the minimum model optimises the cost of the total installation and the number of devices and, therefore, reduces the complexity of the system. The relays responsible for establishing the electrical connection mode will be located on the panels themselves.
  • Artificial intelligence: As an application of artificial intelligence, when establishing the resolution mechanism for our problem, the result is optimised if we start from the search of the solution space using the tree root algorithm. Finally, after finding the most efficient solution, the underlying neural network will be reprogrammed, providing new knowledge and learning to the system.
Preprints 73821 g018
Figure 22. Artificial intelligence process.
Figure 22. Artificial intelligence process.
Preprints 73821 g018
In the future both models will be applied depending on the expected panel distribution [16]. We foresee two cases:
1.
Non-linear distribution (Figure 23): Applied to boats and cars.
Given the complexity of their possible PV surfaces, flexible panels would be used and solved by the low-cost model.
2.
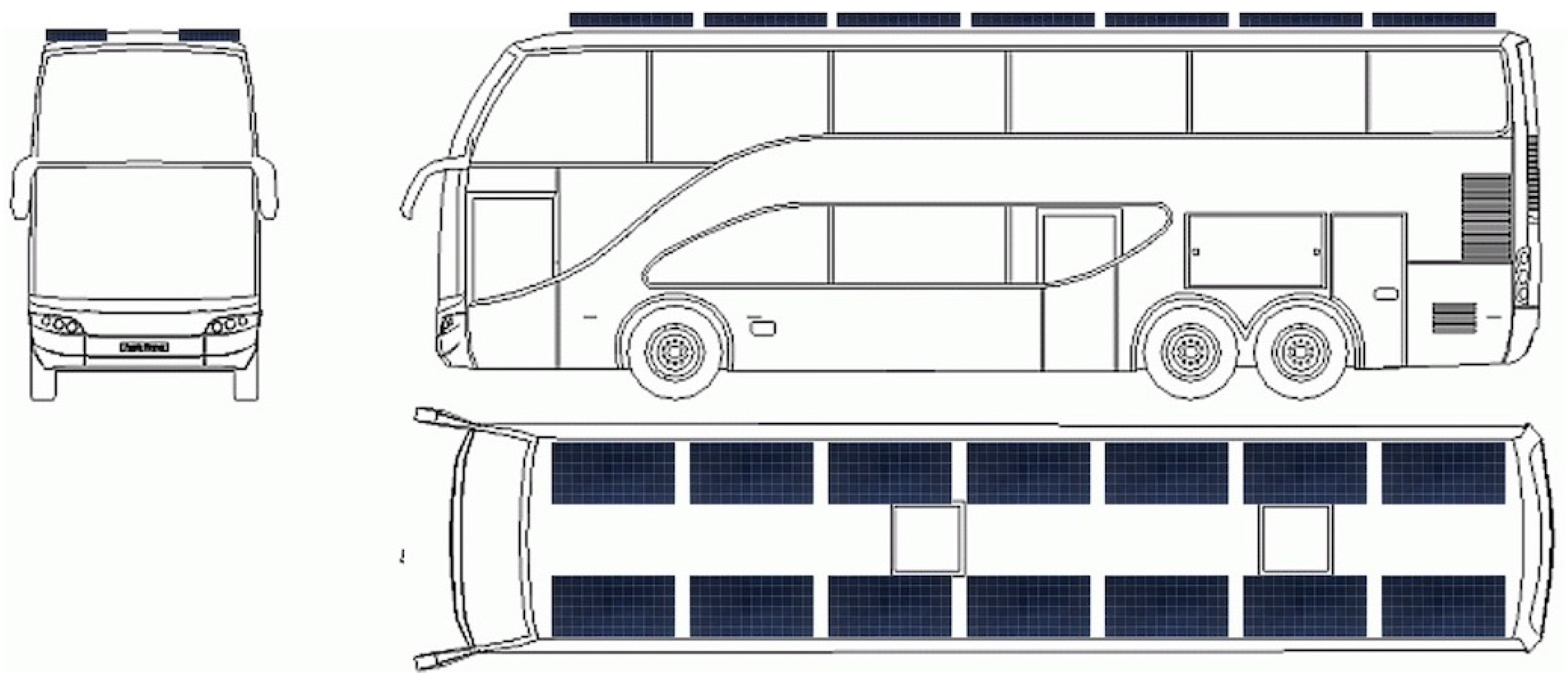
Linear distribution (Figure 24): Applied to buses and trams.
Due to their rectangular and elongated roofs, they offer a suitable layout for linear configurations, being solvable under the minimum model.
The fact that we work with high volumen transport means that are exposed to the open air allows us to incorporate a large energy storage capacity. In these cases, the combination of optimised load in motion or at standstill increases the stored energy [17] and thus the autonomy of these means of transport. We will therefore focus our future work on the applicability of the techniques and devices presented here on the one hand, and on battery designs based on different materials [5] and with higher charging capacity [18] on the other.

Acknowledgements

We thank the support of this paper from University of Malaga and CBUA (funding for open access charge: Universidad de Málaga / CBUA). This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

References

  1. Muttana, S.; Dey, R.; Sardar, A. Prospects of Electric Bus Integrated with Solar Photovoltaic Cells. In SAE Technical Paper. 2017. [CrossRef]
  2. Myeongchan, O.; Sung-Min K.; Hyeong-Dong P. Estimation of photovoltaic potential of solar bus in an urban area: Case study in Gwanak, Seoul, Korea. Renew. Energy. Vol.160, 2020, 160, 1335–1348. [CrossRef]
  3. Nassiri Nazif, K.; Daus, A.; Hong, J. et al. High-specific-power flexible transition metal dichalcogenide solar cells. Nat Commun. Vol 12, 2021. [CrossRef]
  4. Yamaguchi, M.; Masuda, T.; Araki, K. et al. Development of high-efficiency and low-cost solar cells for PV-powered vehicles application. Prog Photovolt Res Appl.. Vol.29, 2021, 684–693. [CrossRef]
  5. Wartak, M.S.; Tsakmakidis, K.L.; Hess, O. Introduction to metamaterials. In La physique au Canada. 2011, 67, No. 1.
  6. Merino, S.; Guzmán, F.; Martínez, J. Metadomotic optimization using genetic algorithms, Appl. Math. Comput. 2015, 267, 170–178. [CrossRef]
  7. Merino, S.; Sánchez, F.J.; Sidrach-de-Cardona, M.; Guzmán, F.; Guzmán, R.; Martínez, J.; Sotorrío, P.J. Optimization of energy distribution in solar panel array configurations by graphs and Minkowski’s paths, Appl. Math. Comput. 2018, 319, 48–58. [CrossRef]
  8. Petrone, G.; Spagnuolo, G.; Zhao, Y.; Lehman, B.; Ramos-Paja, C.A.; Orozco, M.L. Control of Photovoltaic Arrays, Dynamical Reconfiguration for Fighting Mismatched Conditions and Meeting Load Requests, IEEE Ind. Electron. Mag. 2015, 9, 62–76.
  9. Sánchez, F.J.; Sotorrío, P.J.; Heredia, J.R.; Pérez, F.; Sidrach-de-Cardona, M. PLC-Based PV Plants Smart Monitoring System: Field Measurements and Uncertainty Estimation, IEEE Trans. Instrum. Meas., 2014, 63, 2215–2222. [CrossRef]
  10. Dallago, E.; Liberale, A.; Miotti, D.; Venchi, G. Direct MPPT algorithm for PV sources with only voltage measurements, IEEE Trans. Power Electron., 2015, 30, 6742–6750. [CrossRef]
  11. Ustun, T.S.; Ozansoy, C.; Zayegh, A. Implementation of Dijkstra’s algorithm in a dynamic microgrid for relay hierarchy detection. In 2011 IEEE International Conference on Smart Grid Communications (SmartGridComm 2011)2011. [CrossRef]
  12. Mohan, P. Determining the Shortest Current Flow Path Using Dijkstra’s Algorithm in Mess Circuit. International Journal of Innovative Technology and Exploring Engineering (IJITEE), 2019, 8, 1635–1638. ISSN: 2278-3075.
  13. Amaresh, K.; Sankar, V. Modeling of Photovoltaic System Interconnected with Radial Distribution System using MATLAB/SIMULINK. International Journal of Engineering and Innovative Technology (IJEIT), 2013, 3, 251–257.
  14. Glaser, C.; Solar Panel MPPT for Pulsed-load Applications. In Solar Technology by Texas Instruments, 2022.
  15. Grama, A.; Dan, M.; Lázár, E. Photovoltaic panel model using Matlab. 39th International Spring Seminar on Electronics Technology (ISSE), 2016, 322–327. [CrossRef]
  16. Möller, M.C.; Krauter, S. Hybrid Energy System Model in Matlab/Simulink Based on Solar Energy, Lithium-Ion Battery and Hydrogen, Energies, 2022, 15, 1–23. [CrossRef]
  17. Yan, H.W.; Narang,A.; Tafti, H.D.; Farivar, G.G.; Ceballos, S.; Pou, J. Minimizing Energy Storage Utilization in a Stand-Alone DC Microgrid Using Photovoltaic Flexible Power Control, IEEE Trans. Smart Grid, 2021, 12, 3755–3764. [CrossRef]
  18. Chacón, J.; Soler, P.R. Electrically rechargeable Aluminum-air batteries to power Smart Cities,2013 International Conference on New Concepts in Smart Cities: Fostering Public and Private Alliances (SmartMILE), 2013, 1–4. [CrossRef]
1
The following launches are foreseen: Lightyear One, Sono Sion, Hyundai Sonata Hybrid, Mercedes Vision EQXX and Toyota Prius PHV
Preprints 73821 g001
Figure 1. Different models of flexible PV
Figure 1. Different models of flexible PV
Preprints 73821 g001
Preprints 73821 g002
Figure 2. Solar tram carriages
Figure 2. Solar tram carriages
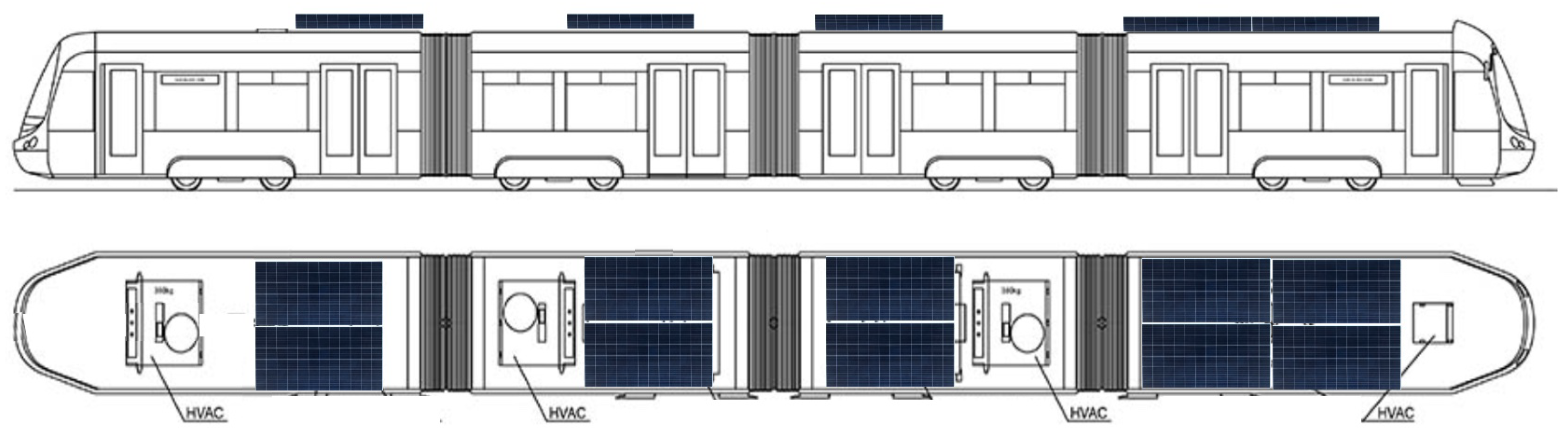
Preprints 73821 g002
Preprints 73821 g003
Figure 3. Matrix configuration
Figure 3. Matrix configuration
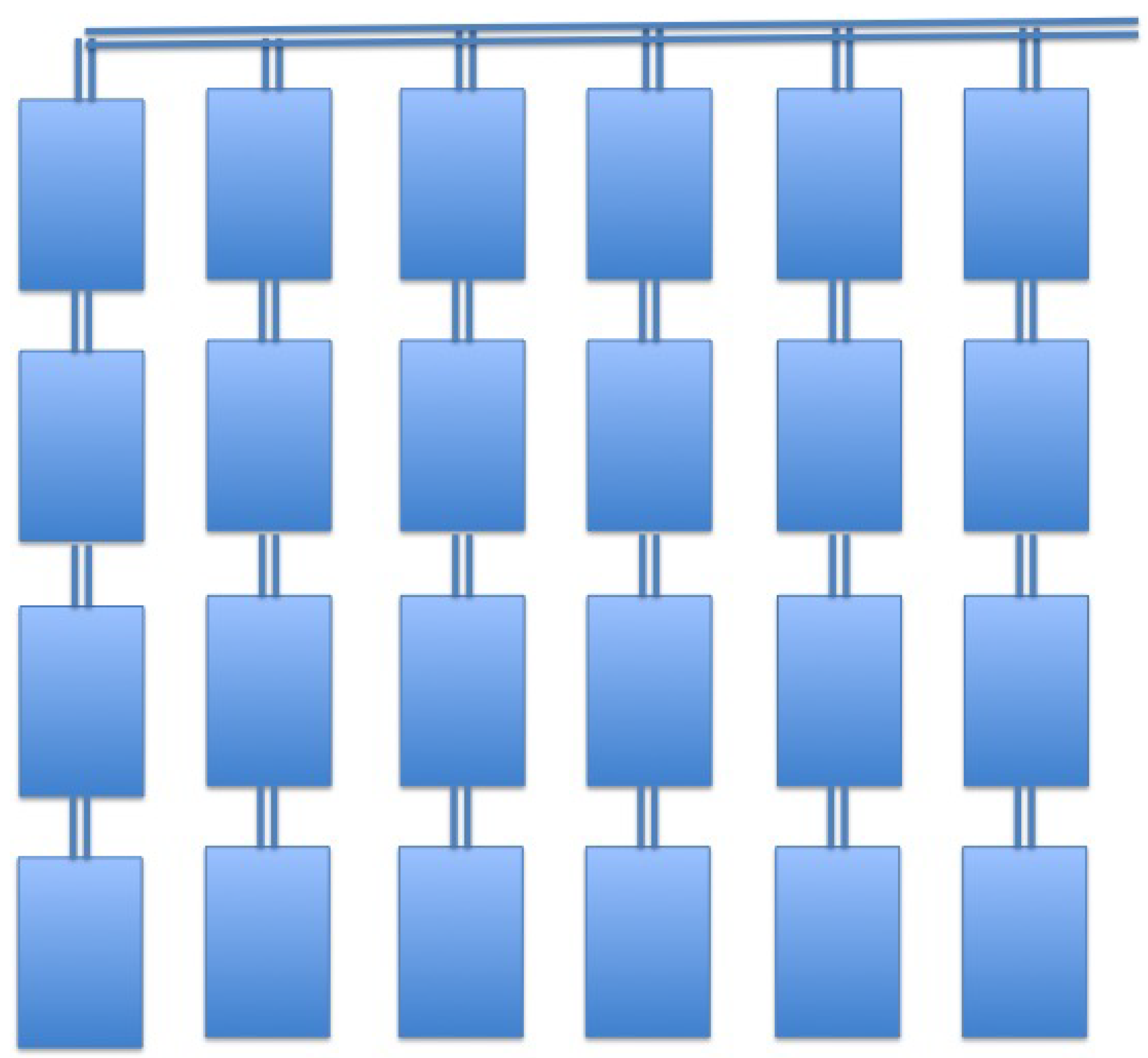
Preprints 73821 g003
Preprints 73821 g004
Figure 4. Parallel connection matrix of strings made of PVs connected in series
Figure 4. Parallel connection matrix of strings made of PVs connected in series
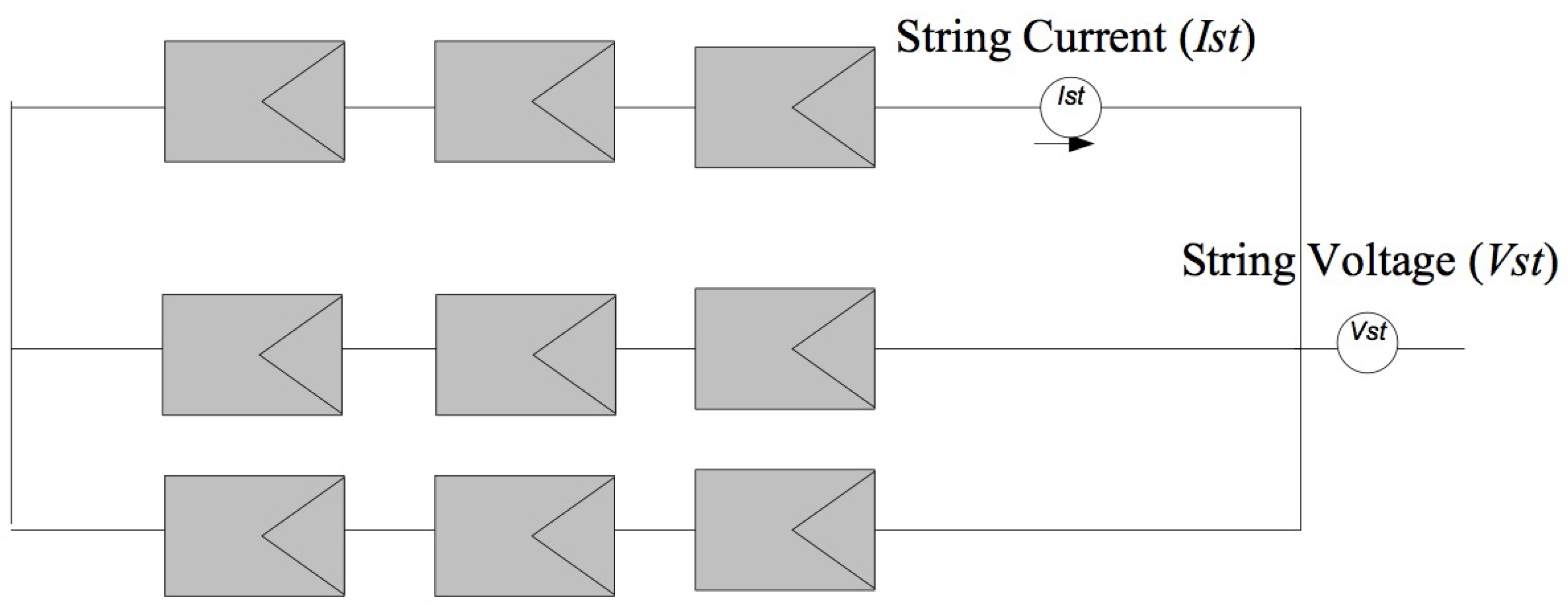
Preprints 73821 g004
Preprints 73821 g005
Figure 5. PV panels I-V characteristic curves under applying climatic conditions: PVP 1 (dotted line), PVP 2 (small dashes line), PVP 3 (big dashes line) and String (solid line).
Figure 5. PV panels I-V characteristic curves under applying climatic conditions: PVP 1 (dotted line), PVP 2 (small dashes line), PVP 3 (big dashes line) and String (solid line).
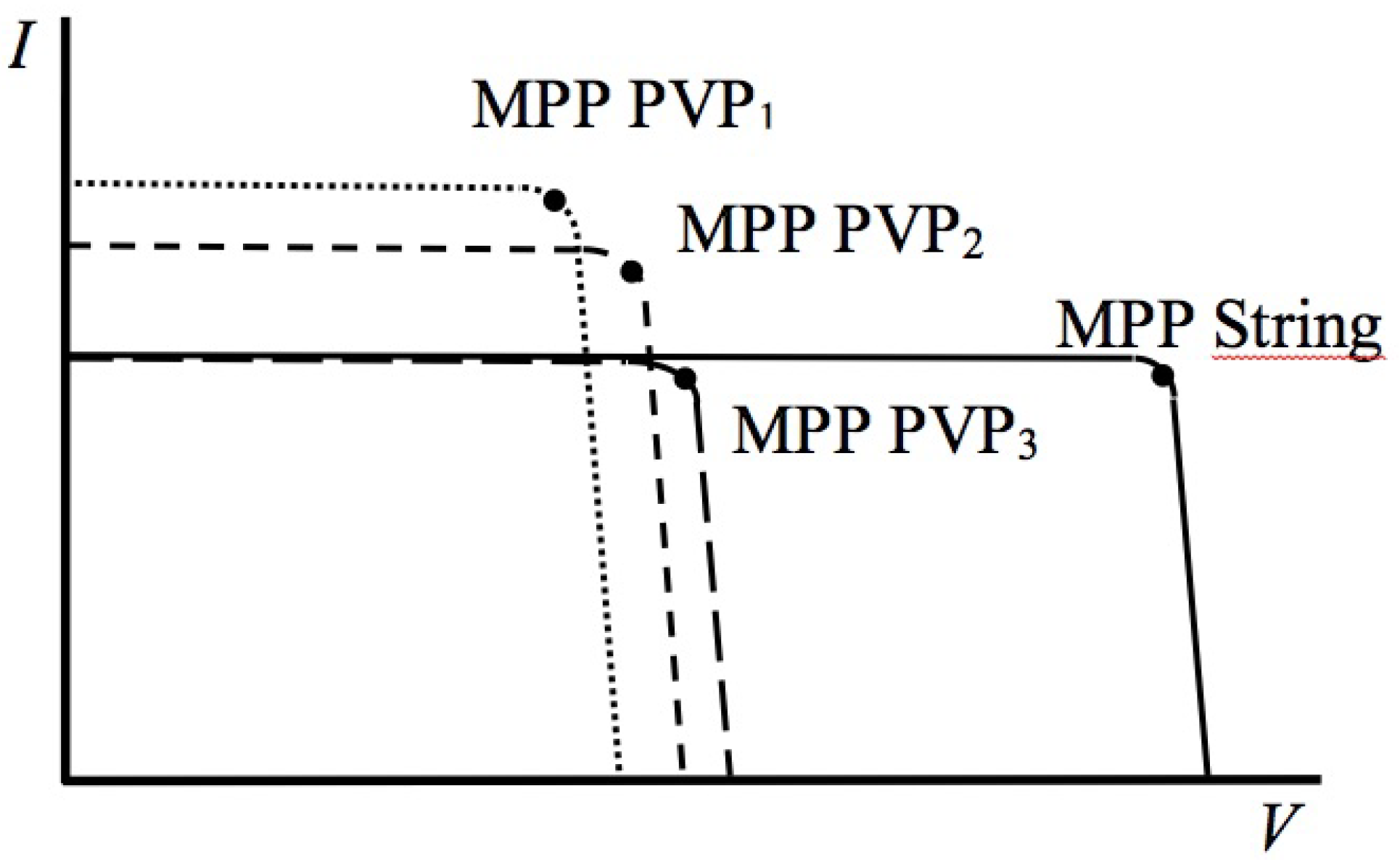
Preprints 73821 g005
Preprints 73821 g011
Figure 15. Neural network on PV states
Figure 15. Neural network on PV states
Preprints 73821 g011
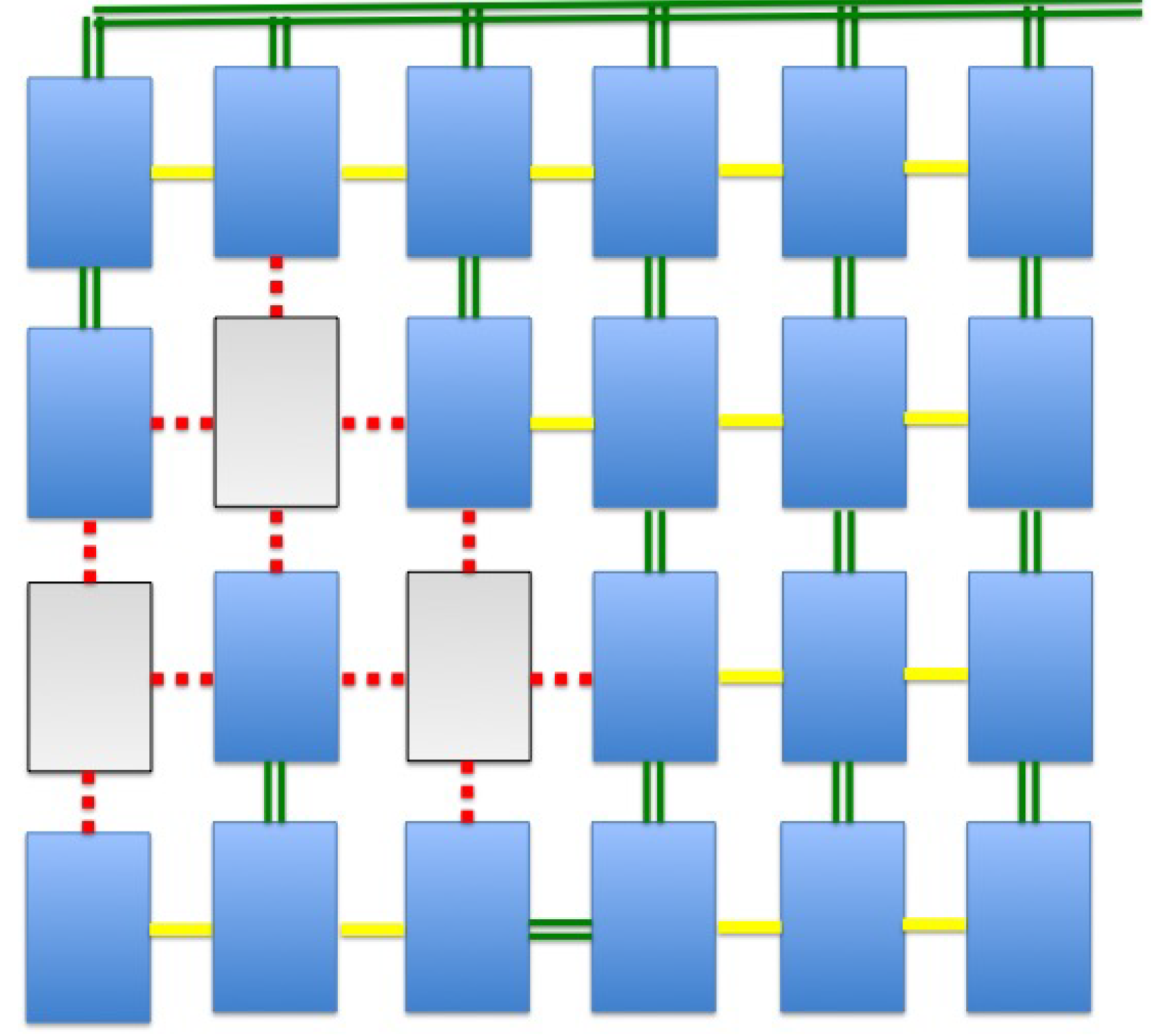
Preprints 73821 g012
Figure 16. Example to solve (non-linear distribution).
Figure 16. Example to solve (non-linear distribution).
Preprints 73821 g012
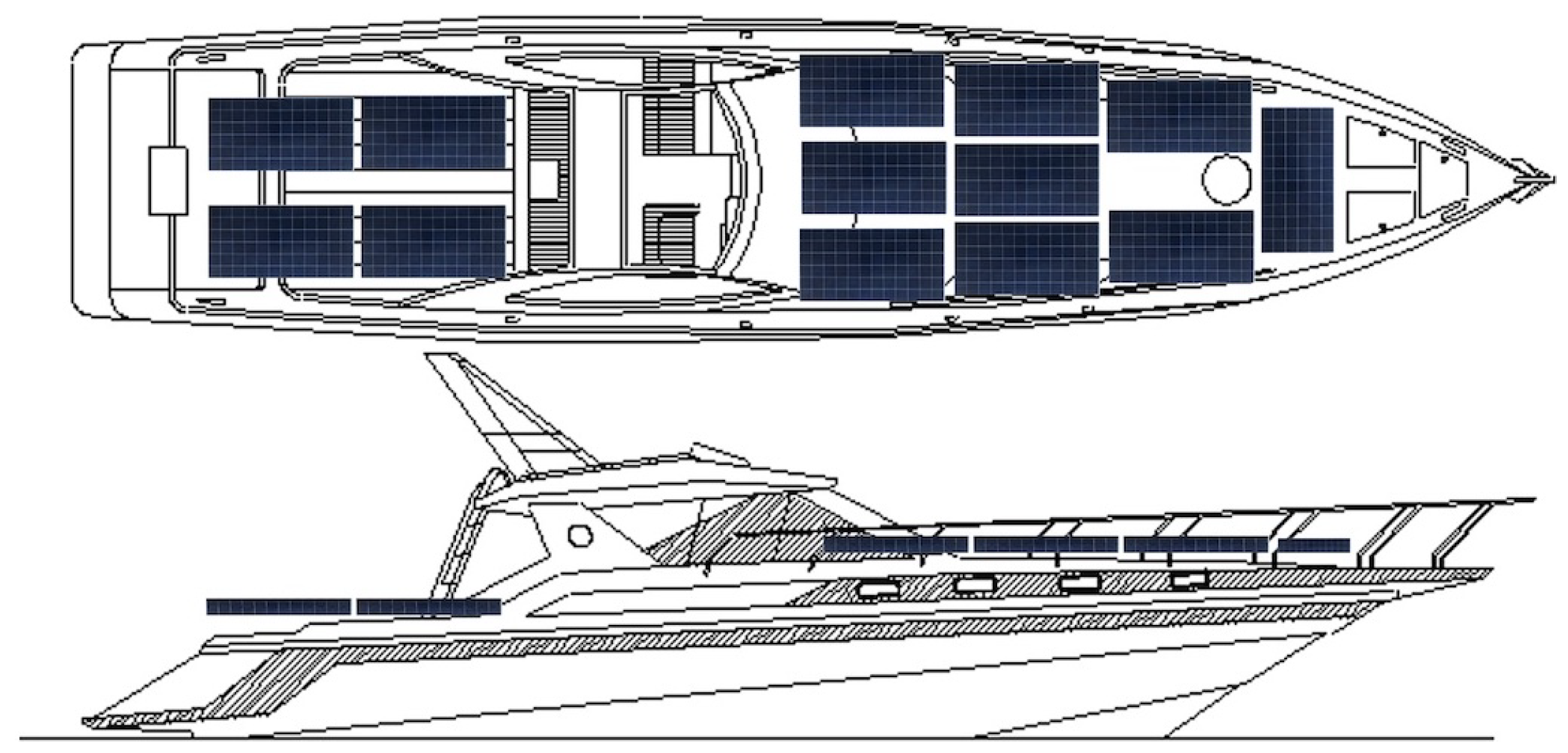
Preprints 73821 g019
Figure 23. Non-linear distribution
Figure 23. Non-linear distribution
Preprints 73821 g019
Preprints 73821 g020
Figure 24. Linear distribution
Figure 24. Linear distribution
Preprints 73821 g020
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated