Prerpints.org logo
Preprint
Article

Low-Noise Amplifier and Neurostimulator in submicron CMOS for Closed-Loop Deep-Brain Stimulation (CLDBS)

Altmetrics

Downloads

228

Views

129

Comments

0

Submitted:

16 May 2023

Posted:

17 May 2023

You are already at the latest version

Alerts
Abstract
Deep-Brain Stimulation (DBS) is a a highly effective and safe medical treatment that improves the lives of patients with a wide range of neurological and psychiatric deceases, and has been consolidated as a first-line tool in the treatment of these conditionsin the last two decades. Closed Loop Deep-Brain Stimulation (CLDBS) pushes this tool further by automatically adjusting the stimulation parameters to the brain response in real time. In this context, this paper presents a Low-Noise Amplifier (LNA) and a Neurostimulator circuits fabricated in the low-power/low-voltage 65 nm CMOS process from the TSMC, which were designed targeting implantable applications. To achieve the best trade-off between input-referred noise and power consuption, metaheuristic algorithms were employed to determine and optimizes the dimentions of the LNA devices during the design phase. The measurement results showed that the LNA had a gain of 40.6 dB, a 3 dB bandwidth spanning over three decades from 10 Hz to 8.6 kHz, and a power consumption of 6.19 uW. Simulations results indicated an input-referred noise of 4.86 uVrms for the LNA. The circuit of the Neurostimulator is a programmable Howland Current-Pump, whose measurements showed its ability to generate currents with arbitrary shapes ranging from between 325 uA to +318 uA. The simulations showed a quiescent power consumption of 0.13 W with a zero neurostimulation current. The LNA and the Neurostimulator circuits are supplied with 1.2 V voltage and occupy a microdevice area of 145 um x 311 um and 88 um x 89 um, respectively, making them suitable for implantation in applications involving Closed Loop Deep-Brain Stimulation.
Keywords: 
Subject: Medicine and Pharmacology  -   Neuroscience and Neurology

1. Introduction

Deep Brain Stimulation (DBS) is a surgical procedure that involves the implantation of a medical device called a neurostimulator (often called a brain pacemaker) that sends mild impulses to specific areas of the brain through implanted electrodes [1,2,3]. The electrical current used is very low in the range of μA and is injected into strategic points in the brain, which are mostly located deep within the brain tissue. This type of procedure involves inserting implantable tips, with electrodes rings at the ends, into specific points in the thalamus, subthalamic region, globus pallidus, among others. The electrodes are then connected to the neurostimulator itself by means of extension cables containing metallic wires [4]. The neurostimulator is a device with dimensions no larger than a matchbox and includes an attached battery to provide power and be able to operate [5,6,7].
The first current use of the DBS technique dates back to 1997, when authorization was granted by the American FDA (Food and Drug Administration) for the treatment of Parkinson's disease [8]. Since then, and thanks to proven success, DBS has become first-line therapy option for relieving symptoms associated with neurological and movement disorders that are unresposible to other therapies [9], namely chronic pain [10,11], Parkinson's disease [12,13], tremor [14,15], dystonia [16,17], morbid obesity [18], Tourette's syndrome [19], essential tremor [20], and obsessive-compulsive disorder [21].
There are two paradigms for classifying DBS, namely open-loop DBS (also known as conventional DBS) and closed-loop DBS (also known as adaptive DBS or CLDBS) [22]. In the case of open-loop DBS, a neurologist manually adjusts the stimulation parameters every 3-12 months after implantation. On the other hand, in the case of closed-loop DBS, programming of stimulation parameters is performed automatically based on some measured biomarkers [22]. Biomarkers are acquired signals and they can have different natures, namely bioelectrical, psychological, biochemical, among others [22]. Biomarkers are essential indicators in closed-loop DBS because, based on the disease to be treated, they help to adaptively reconfigure the signals used in neurostimulation [22].
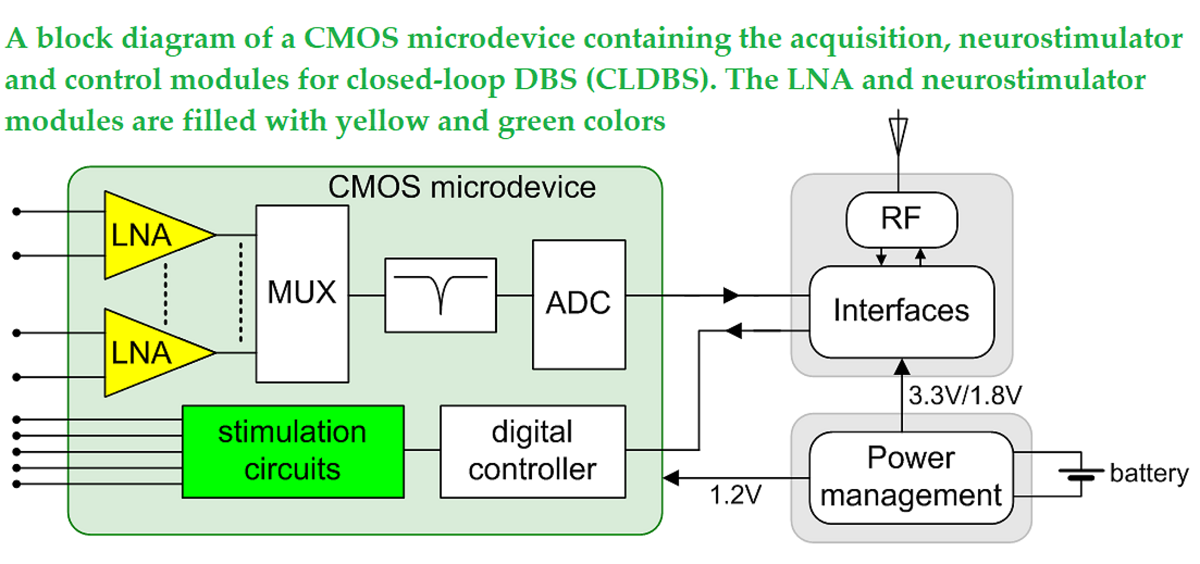
It is interesting to note that advances in the microelectronics are paving the way for the simultaneous acquisition of several types of biopotentials with the same microdevice resulting in the closed loop DBS. It was precisely this that motivated the development of the CMOS microdevice presented in this paper. Figure 1 illustrates the block diagram containing the acquisition, neurostimulator and control modules of a CMOS microdevice for application on CLDBS. The Low-Noise Amplifier (LNA) and the Neurostimulator modules presented in this paper are shown in yellow and green colors in the block diagram, respectively.

2. Design

The signals at the input of an LNA present a variety of challenges, such as low amplitudes, on the order of microvolts, low frequencies, very close to 0 Hz, or both. The amplifiers for neural recordings found in the literature typically exibit a mid-band gain of 40 dB, with bandwidths ranging from sub-Hz to a few kHz or even a few dozens of kHz [23,24,25,26,27,28,29,30,31,32].
Figure 2a shows the schematic of the LNA presented in this paper [32]. This amplifier is composed by an operational amplifier (OpAmp), two pairs of capacitors C1 and C2, and a pair of resistors R2. The internal schematic of the OpAmp, in turn, is presented in Figure 2b. The OpAmp has a basic configuration with two stages and comprises six PMOS and four NMOS transistors. The PMOS transistors M1 and M2 form a differential pair, working as the input stage. The NMOS transistors M3 and M4 form an active pair load. The PMOS transistors M5 and M7 form the biasing circuit for the input and output stages, respectively. These two PMOS mirror the current Isd9 of M9, multiplying it to form Isd5 and Isd7. The NMOS M6 forms a common source amplifier and provides additional gain to the input stage, thereby increasing the total gain of the OpAmp. The PMOS M8p and the NMOS M8n act as a resistance in series with the capacitor CC, creating a dominant pole fp and ensuring that the OpAmp is unconditional stable.
The calculation of the LNA gain requires the knowledge of the input and feedback impedances Z1 and Z2, respectively. These impedances are given by:
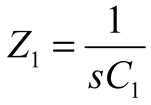
Preprints 73853 i001
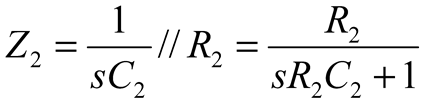
Preprints 73853 i002
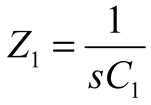
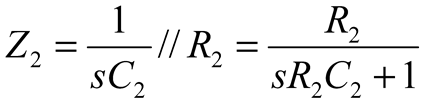
The relation of the impedances Z1 with (Z1+Z2), named feedback factor, is given by:
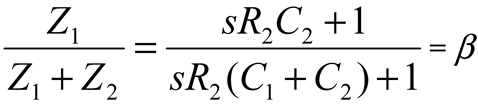
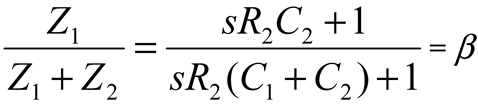
Preprints 73853 i003
The gain of the LNA can be easily deduced if we consider VIM= -VIP = Vin/2 (Figure 2) Since the complete LNA forms a difference amplifier, the voltage Vout at the output of LNA, is given by:
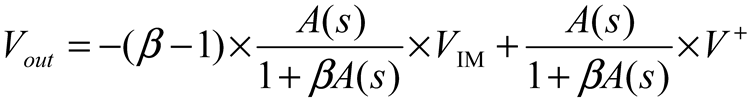
Preprints 73853 i004
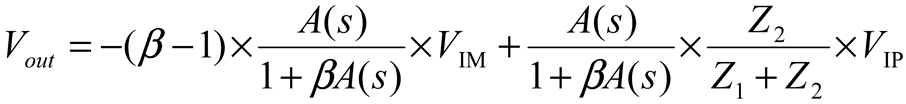
Preprints 73853 i005
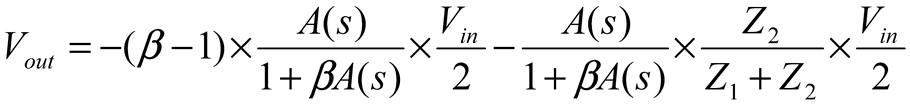Preprints 73853 i006
where A(s) is the transfer function of the OpAmp. Therefore, the gain of the LNA, i.e., the feedback gain, Af(s) is given by:
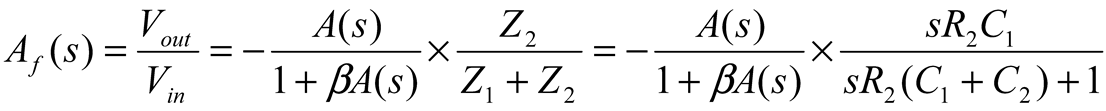
Preprints 73853 i007
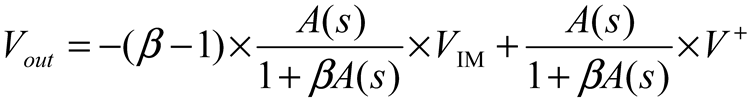
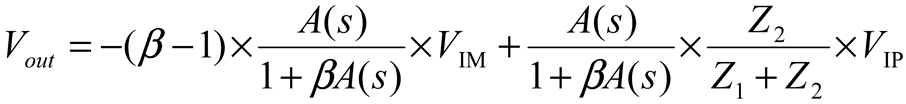
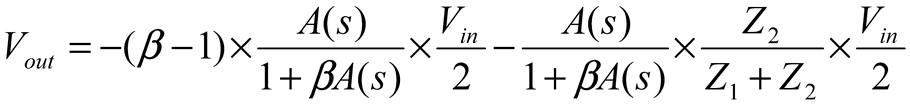
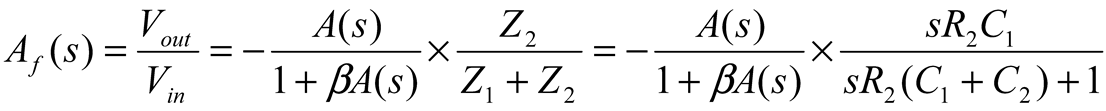
Normally, A(s) can be expressed with a single pole, or at least with a dominant pole close to the origin. However, additional poles must be considered if they exists and are located near the pass-band of the LNA. The one-pole appoximation is a useful and general model, employed here for deducing the feedback gain and to understanding the frequency behavior of the LNA. Taking the example of the existence of only one pole, the OpAmp transfer function A(s) is given by:
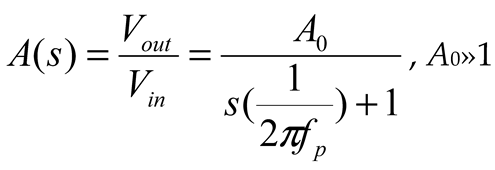
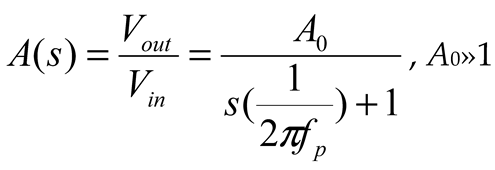
Preprints 73853 i008
Now, by substituting A(s) into equation (5), a new expression for the LNA is found:
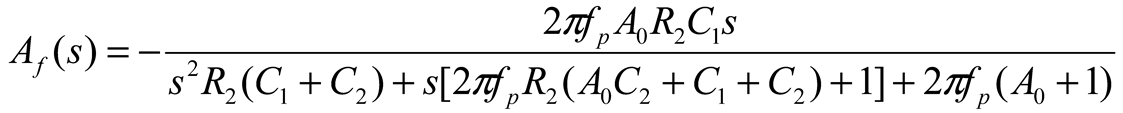
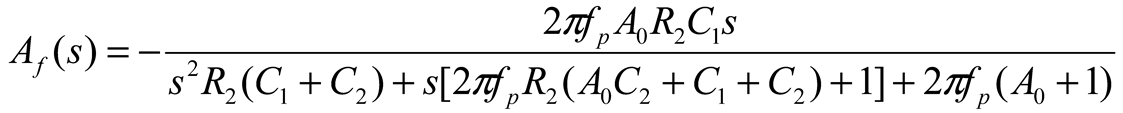
Preprints 73853 i009
It must be noted that the transfer function of the LNA has a zero at 0 Hz and two negative poles, which are called pL = -1/(2πfL) and pH = -1/(2πfH) (fL and fH are postive real numbers). If A0 is such that A0 >> 1, then, 2πfpA0 >> 1/(R2C2), i.e., the gain × bandwidth product (GBW) of the OpAmp is such that GBW>>1/(R2C2), the expression for Af(s) can be approximated as:
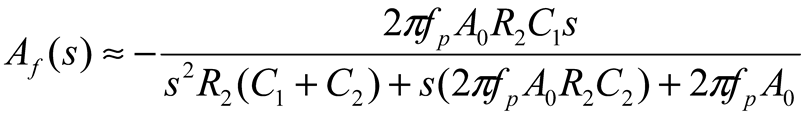
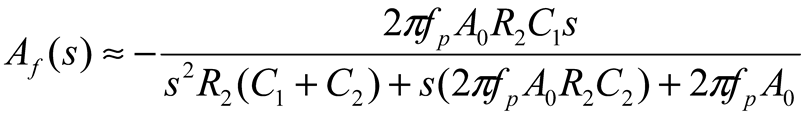
Preprints 73853 i010
Additionaly, if the two poles pL and pH are well spaced between one to each other and assuming that pL << pH, then, the approximated values for fL and fH can be found as follows:
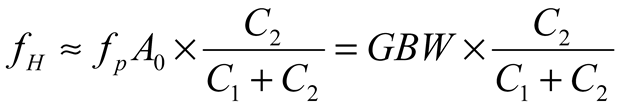
Preprints 73853 i011
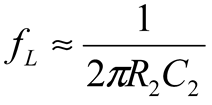
Preprints 73853 i012
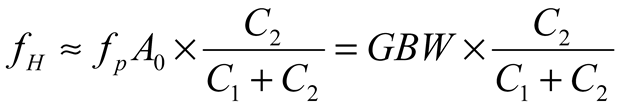
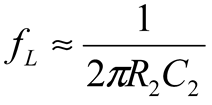
and relation (8) can be rewritten as:
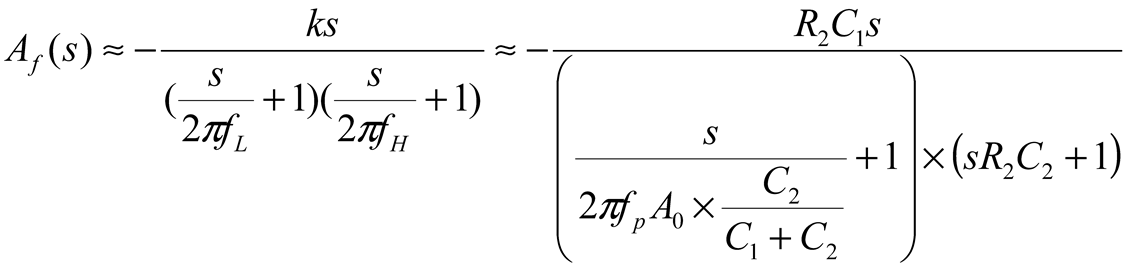
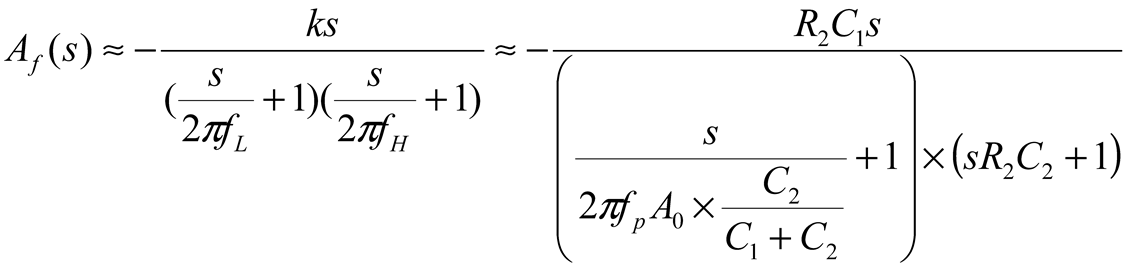
Preprints 73853 i013
For medium frequencies operation, i.e., fL << frequency << fH, the LNA gain is then:
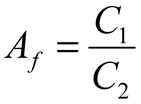Preprints 73853 i014
which is in accordance with what is stated in literature [32].
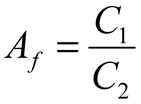
The capacitances C1 and C2 are in the order of pF, therefore, the resistor R2 must be in the order of TΩ, to ensure that the first pole fL=1/(2πR2C2) of Af(s), equation (8), has a value near or lower than 1.0 Hz.
High-value resistors, like R2, can not be implemented in a conventional form in an integrated circuit due to the large area they would occupy.
Pseudo-resistors are a widely recognized method for implementing high-value resistors, as described in references [33]. Figure 2a also illustrates the implementation of resistors R2 with pseudo-resistors. Each of these pseudo-resistors employs a series of two PMOS transistors, as detailed in the zoomed section of the figure. It has been found that these pseudo-resistors can reach values in the order of TΩ and occupy an area many orders of magnitude smaller than that of a conventional resistor implementation. These implementations are called "pseudo" because they mimic the behavior of a real resistor when small voltages are applied at their terminals. The red dots at terminal A of the pseudo-resistors R2 serve to show how these pseudo-resistors connect to the LNA.
To achieve low noise and low power, even using an OpAmp with a simple configuration, the LNA design in this work was done through the use of metaheuristic algorithms, specifically particle swarm and simulated annealing [34,35]. To accomplish this task, a framework for transistor sizing and circuit optimization, based on metaheuristics, was applied. The framework requires for its operation a rating score for each design, obtained through electrical simulations. To acquire the design score, an aggregated objective function must be developed that generates a simulation file containing the circuit netlist, device sizes, and simulation commands. The function also triggers an electrical simulation, reads the results, and calculates the score. To carry out this calculation, the relevant circuit attributes are measured and predefined shaping functions. Figure 3, which reflect desired goals, are applied to the measured values. Finally, the fuction outputs are combined to build the score. Users can choose which shaping function to apply for each attribute result, enabling them to tailor the sizing and optimization to their specific needs. For example, if an attribute must be kept below a certain limit, the function < d1 d2( ) can be used; if the attribute should be minimized, the function / d1 d2( ) is applied.
Objective functions are tailored to specific classes of circuits, such as Voltage Reference Sources, OpAmps, Oscillators, Prescalesr, and neuronal LNAs. Once the objective function of a class is available, the framework will make possible the sizing/optimization of any circuit topology for which a SPICE like parameterized netlist, describing this particular topology, is provided. In Figure 4 is shown part of the parameterized SPICE netlist of the LNA (Figure 2 presents the circuit described in the netlist). For the netlist, X1, .., X12 are the circuit parameters that provide the device dimensions, and their values will be adjusted in the sizing/optimization process. The level of detail included in the netlist, such as the areas and perimeters of the transistor drain/source, parasitic elements, etc., as well as the knowledge embedded in it, such as the fact that dimensios of M5 and M7 shoud be related to avoid a systematic offset, directly affects the quality of the optimization.
M1 1 in 4 4 pch L='X1*1u' W='X5*1u' AD='X5*1u*Wpadrao/2' PD ='X5*1u Wpadrao'
+AS= 'X5*1u*Wpadrao/2' PS = 'X5*1u + Wpadrao'
M2 3 ip 4 4 pch L='X1*1u' W = 'X5*1u' AD='X5*1u*Wpadrao/2' PD='X5*1u + Wpadrao'
+AS = 'X5*1u*Wpadrao/2' PS = 'X5*1u + Wpadrao'
M3 1 1 vs vs nch L ='X2*1u' W='X6*1u' AD='X6*1u*Wpadrao/2' PD ='X6*1u + Wpadrao'
+M = 'nint(X12)'
M4 3 1 vs vs nch L='X2*1u' W= X6*1u' AD='X6*1u*Wpadrao/2' PD ='X6*1u + Wpadrao'
+M = 'nint(X12)'
M5 4 bias vd vd pch L='X3*1u' W='X7*1u' AD='X7*1u*Wpadrao/2' PD='X7*1u + Wpadrao'
+M = '2*nint(X12)*nint(X8)'
M6 out 3 vs vs nch L='X2*1u' W='X6*1u' AD ='X6*1u*Wpadrao/2' PD ='X6*1u
+Wpadrao'
M7 out bias vd vd pch L = 'X3*1u' W='X7*1u' AD='X7*1u*Wpadrao/2' PD='X7*1u + Wpadrao'
+M= 'nint(X8)'
*** compensation
M8n 3 vd 5 vs nch L ='X4*1u' W ='X9*1u' AD ='X9*1u*Wpadrao/2' PD = 'X9*1u + Wpadrao'
+As = 'X9*1u*Wpadrao/2' Ps ='X9*1u + Wpadrao'
M8p 3 vs 5 vd pch L = 'X4*1u' W = '2*X9*1u' AD = '2*X9*1u*Wpadrao' PD = '2*X9*1u
+Wpadrao' +AS = '2*X9*1u*Wpadrao' Ps = '2*X9*1u + Wpadrao'
Cc 5 out 'X10*1p'
** Bias
M9 bias bias vd vd pch L = 'X3*1u' W = 'X7*1u' AD = 'X7*1u*Wpadrao/2' PD = 'X7*1u
+Wpadrao'
* external bias current
Ibb bias 0 DC '(10^X11)*1u'
Figure 1 Parameterized SPICE netlist for AmOp of Figure 2. X1, .. X12 are the wanted parameters of the sizing/optmization process.
The framework has already been employed for design of Reference Voltage Sources [36], OpAmps, LNAs, VCOs, Prescalers [37], etc. The metaheuristics available in it are genetic algorithms (GA), simulated annealing (SA), particle swarm (PSO), quatum QPSO (QPSO) among others.
In Figure 5 the operation flux of the framework is detailed. The sizing/optimization process starts with the selection of a circuit class for which an objective function is available. Next, a topology of the specified class is chosen, along with some parameter values (power supply, operation frequency), the goals of the sizing/optimization (power consuption, noise, gain, etc.), the shaping functions applied to each goal, and the search space (minimum and maximum allowed values for circuit parameters to be sized). Finally, a metaheuristic, along with execution conditions (initial solutions, stop condition, etc.) is selected, and the sizing/optimizing process begins. The process will continue until the stop condition is met, and the duration of the process can vary from a few minutes to several hours, depending on factors such as the size and operation of the circuit, the performed simulations, and the stop condition employed. In this work, the number of evaluated circuits was used as the stop condition.
For the design of a circuit, one or more sizing/optimization processes were performed. When multiple processes are applied, they may or may not be independent. In the latter case, the results of the optimization are used as initial conditions for the next.
For the calculation of the design score in the neuronal LNA class, the following attributes are taken in consideration: the Differential gain, Common Mode gain, CMRR (Commum Mode Rejection Rate), PSRR (Power Supply Rajection Rate), common mode volatage range, slew rate, and phase margin of the AmpOp; the gain, power consuption, input noise, low and high cut off frequency, and area of the LNA. The evaluations of the area do not require simulations and are estimated based on the width and length of the transistors and of capacitors.
Table 1 presents the simulated characteristics of the final version of the sized/optmized LNA.
Note that during the design otimization, an input noise of 4.0 μVrms was initially specified. However, achieving this level of noise requires a significant amount of power consuption in the technology applied, due to various factors, including the large gate capacitance of the diferential pair transistors, M1 and M2. Technologies with larger minimum dimensions, like 180 nm technology, can be advantageously used in the design of low noise LNAs.
Several neural amplifiers aim for noise floors as low as 1-3 μVrms, which is significantly below the cortical recording noise [23,26]. For this reason, in our design, we increased the input noise while maintaining a low power consuption.
Table 2 lists the dimensions of the MOSFETs of the OpAmp and of the pseudo-resistors and the value of the capacitor Cc generated by the sizing/optimization algorithms. The listed Total (W/L) refers to the total value ratio and the other columns refere to the numer of paralel transistors and number of fingers applied. For example, the transistors M1 and M2 with Total (W/L)1,2=(59 μm/0.52 μm) are composed of two parallel transistors, each with dimensions of (24.5 μm/0.52 μm) and, at the same time, containing ten fingers measuring (2.45 μm/0.52 μm). In another example, the transistor M5 with Total (W/L)5=(48 μm/2.22 μm) is composed by twenty four parallel transistors, each with dimensions of (2 μm/2.22 μm) containing only one finger for each of the twenty-four parallel transistors. The capacitor CC was composed by 36 sub-capacitors of MIMcap type, which are connected in parallel and form a 6 × 6 array arrangement. Each sub-capacitor cell measures 10 μm × 10 μm.

2.2. Neurostimulator

The neurostimulators must preferably provide current pulses with biphasic shape due to electrical safety reasons, such as avoiding the accumulation of charges at the interfaces between the electrodes and the ionic species within the neuronal tissue [39]. Figure 6a,b illustrate two examples of pulse shaping, where the durations (or stimulation times), frequency, amplitudes, and interpulses delay of the pulses can be settled according medical requirements. The mean value of the signals is zero on both examples in Figure 6a,b, thanks for the arbitrary pulse shaping. The neurostimulator presented in this paper can generate other types of pulses with arbitrary shapes, gradients, amplitudes and mean values.
To maintain electrical safety, as previously mentioned, the neurostimulator circuit was designed to offer the capability of generating current with a biphasic waveform, which can invert the direction of charge injection in the neuronal tissue. The phenomenon to nullify charge accumulation is called charge balance [39]. Traditionally, the inversion of the current direction requires a bridge with H-topology [40], with the disadvantage of requiring four transistors for current inversion, increasing the number of necessary components and the programming complexity. However, the biggest disadvantage of the H-topology is that it requires access to two different contact points on the electrodes, which are normally unipolar. For these reasons, the circuit responsible for injecting the current into the electrodes is based on the Howland Current-Pump [41]. This circuit is easy to integrate because it uses low resistance values, that is, below 20 kΩ.
Figure 7a shows the schematic of the Current-Pump that implements the neurostimulator, which is a Howland Current-Pump circuit. The neurostimulator is composed by an OpAmp and four resistors {R1, R2, R3, R4}, all fully implemented using the mask layers of the TSMC 65 nm CMOS process.
Figure 7b presents the schematic of the OpAmp used by the Current-Pump. The PMOS M8 also works as resistance Rc in series with the capacitor Cc. The series combination of Rc/Cc is placed in parallel with the capacitor Cx to form a struture that ensures unconditional stability of the OpAmp.
Table 3 lists the dimensions of the MOSFETs of the OpAmp and the internal capacitance Cx generated by the sizing/optimization algorithm. The relations (W/L) listed in the table follows the same logic of the relations in the Table 2. The same applies to the capacitors Cc and Cx.

3. Experimental Results

3.1. LNA

Figure 8a illustrates a photograph of the laboratory setup used during the experimental tests. Figure 9b illustrates how the common-mode voltage VCM is produced. The circuit to produce the VCM voltage uses a commercial Operational Amplifier TL081 with a symmetrical voltage supply of ±9 V, which is powered by two 9V batteries to ensure low noise at the output. The voltage supply of 1.2 V for the CMOS microdevice is obtained with the AMS1117 voltage regulator. In addition, each battery is connected in series with two potentiometers working as soft starters to prevent potential high gradients of charge currents of the MOSFET parasitic capacitances, particularly those used in the inputs of the LNA. The gate areas of the MOSFETs in the inputs of the LNA present high values, such as 59 μm × 0.52 μm, and, in consequence, a high gate capacitance.
Figure 8c shows the measured gain for several common-mode voltages VCM and input signals with amplitude of 2 mVpp. Figure 8d also shows the measured gain for several common-mode voltages VCM and input signals with amplitude of 10 mVpp. In both sets of plots, the simulation results are also shown (solid blue) to allow comparisons.
Table 4 lists the measured common-mode voltage VCM,out at the output of LNA and its maximum gain Gmax in terms of the input voltage Vin and the common-mode voltage VCM.
The measurements, in general, agree well with the simulations. An increase in the common-mode voltage (VCM), as depicted in Figure 8c, results in an improvement of the gain at low frequencies, but a corresponding degradation at high frequencies gains. On the other hand, the variations in VCM within the range of [0.46, 0.54] V did not result in significantly different gains, thus demonstrating the robustness of this LNA with respect to VCM, and amplifying the range of interest for acquiring neuronal signals with practically unchanged gain, resulting in a low potential for linear distortion of the signals during amplification.
The biasing voltage applied in the tests was VBIAS = 0.68 mV, obtained using a bias resistence RBIAS = 810 kΩ connected to the Vbias node, Figure 2b. This resulted in a biasing current IBIAS = 770 nA, higher than the designed value. Even in such conditions, the LNA behavior is satisfactory, except by the total power consuption of 27.7 μW,
This LNA was also tested with a saline solution to emulate an ex-vivo situation and evaluate its performance in real in-vivo applications. Figure 9a illustrates a photograph of the experimental setup used in these measurements, while Figure 9b presents the measured gain for signals injected into the saline solution with an amplitude of 20 mVpp. It should be noted that this was not the amplitude at the input of the amplifier, which was measured simultaneously with the amplitude at the output of LNA to calculate the LNA gain.
During the tests with saline solution, it was not possible to completely compensate for the effects of 60 Hz interference for input signals with frequencies less than 20 Hz. As a result, it was impossible to accurately characterize the LNA at these low frequencies. However, above 20 Hz, the gains, red points on the plot of measured gain, were easily and accurately measured. As seen in Figure 9b, the gain did not show any appreciable reduction in the frequency range between 20 Hz and 10 kHz. In fact, it is possible to observe that the gain remained high, with its maximum value of 40.1 dB at 30 Hz.

3.2. Neurostimualtor Circuit

The tests of this electronic module can be divided in static and dynamic tests. In static tests, the signals applied to the circuit do not change over time. On the other hand, in the dynamic tests, the different signals vary over time. The experimental setups used for both types of tests are essentially the same, except for the way in which the test signals were generated.
Figure 10a illustrates the schematic of the experimental setup for the static characterization of the neurostimulator circuit. This setup comprise a voltage follower, implemented with the operational amplifier TL084, to generate the common-mode voltage VCM,electrode applied in the reference terminal of the electrode. The implantable electrode is represented by the load resistor RLOAD.
Although it is possible to apply a resistor between the gate of M9 node and Vdd, Figure 7b, to bias the OpAmp, it is more convenient to apply a voltage VBIAS directly to this node, since an external voltage can be easily ajusted, making the testing process simpler. A circuit similar to the one used to generate VCM,electrode was also used to generate and trim the bias voltage VBIAS, which was settled to 315 mV.
The circuits used for generating the common mode voltages are similar to the one presented in Figure 8b, where the VCM adjustment was done manually. The manual adjustament is not a real problem in our setup because only a few common-mode voltages were needed. Specifically, the common-mode voltage VCM in the reference electrode was set between 0 V and 1.2 V in coarse steps of 0.3 V.
Two breakout boards based on the MCP4725 digital-to-analogue converter (DAC) with an I2C interface were used to provide fine tuning adjustments to the inputs V+ and V- and, thus, precise adjustments of the currents injected into the load resistor RLOAD. An Arduino board was selected to control the DACs.
Figure 10b shows a photograph of the experimental setup used in the static characterization of the Current-Pump. Figure 10c illustrates the currents for the various combinations of control and common mode voltages {V+, V-, VCM,electrode} in “raw” form to allow a clear and immediate visualization of the wide and quasi-symmetrical range of currents that are possible to generate with this Current-Pump. In contrast, Figure 10d illustrates the currents parameterized in terms of the reference voltage of the electrode VCM,electrode and the inverting input voltage V-. The output current was determined by the following expression:
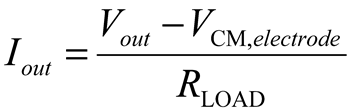Preprints 73853 i015
where Vout is the output voltage of Current-Pump (node X in Figure 8a)
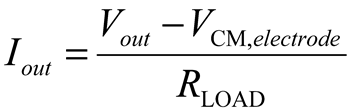
A load resistance of RLOAD = 986.5 Ω was used for these tests. The output voltage Vout can range from 0 V to 1.2 V, therefore, the output current Iout can either be positive or negative, simply making the voltage of the reference electrode VCM,electrode either equal to 0 V or 1.2 V, respectively. As it is possible to observe in Figure 12c,d, other intermediate currents are possible to be generated. The inversion of current direction is mandatory in Deep Brain Stimulation applications.
The Current-Pump was able to generate stimulation currents from -325 μA to +318 μA. The path marked with the dashed yellow lines in Figure 12d illustrates how continuous current signals can be generated from -325 μA to +318 μA.
Figure 12a illustrates the schematic of the experimental setup for the dynamic characterization. Figure 12b shows the photograph of the experimental setup.
The frequency of the signal at V- is ten times higher than the frequency of the signal applied at V+. The amplitude of both signals varies between 0 V and 1.2 V. These settings result in a wave, product of the two input waves, with a sliced sine shape . In this setup, the reference voltage VCM,electrode of the electrode was manually adjusted between 0 V and 1.2 V.
Figure 12c shows the experimental results of the dynamic characterization. A set of sine waves with common-mode voltage of 0.6 V and different amplitudes were applied in the non-inverting input V+ with V- and VCM,electrode settled to one of the voltages {0, 0.6, 1.2} V. The voltage ΔV+ in the plot is the difference between the maximum and the minimum values of the voltage V+. The voltage ΔV+ is equal to 2A+ for a non-inverting input V+ of V+ = 0.6+A+.cos(2πft). The amplitude ΔV+ was swept from 0.2 V to 1.2 V in steps of 0.2 V. The non-inverting input V+ voltage variation is rail-to-rail for A+ = 0.6 V. Figure 12d shows the results for seven combinations of {V-, VCM,electrode} in the set {0, 0.6, 1.2} V. Each combination defines the admissible range of the output current, whose plane domains are bounded above and below by two straight lines. The upper line occurs for V+ = 0.6+ΔV+, while the bottom line occurs for V+ = 0.6-ΔV+. It is possible to observe in Figure 12d the abillity to dynamically sweep the complete current limit, ranging from Imax = +375 μA to Imin = -218 μA, simply selecting the most suitable voltage combination of {V+, V-, VCM,electrode}.
It is also possible to observe in Figure 12c that a limited set of voltage combination of {V+, V-, VCM,electrode} must be avoided, under the penalty of not being able to generate very specific values of electric current. These voltage combinations are associated with the “no-man's land” regions marked with gray shading. The “no-man's land” regions are the combinations that are not contained in the set of the seven plane domains for the different voltage combinations {V+, V-, VCM,electrode}.
The measurements showed that these results are valid with all voltage combinations {V+, V-, VCM,electrode} for a frequency up to f-3dB = 1.5 MHz. This frequency is the one that narrows the current range Imax-Imin to -3 dB. For example, the measurements showed that Imax = +297 μA and Imin = +248.4 μA for V+ = 0.6+0.1cos(2πft) or ΔV+ = 0.2 V with f<f-3dB/10, and V- = 0 V and VCM,electrode = 0 V. This results on ΔIout = Imax-Imin = +49 μA. The measurements also showed ΔIout = (+49)×(2)-1/2×(10-6) = +34.6 μA for f = f-3dB = 1.5 MHz.

4. Conclusions

This paper presented a low-noise amplifier (LNA) and a neurostimulator circuit, which were optimized for application on Closed-Loop Deep-Brain Stimulation (CLDBS). The LNA and neurostimulator were designed and fabricated in the CMOS 65 nm from TSMC. Table 5 compares this LNA with a few related key works found in the literature [12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32]. It was calculated the figure-of-merit (FOM) to better rank and compare this work with the others with respect to the internal noise-power consuption trade off. The noise efficiency factor (NEF) was introduced in 1987 by Steyaert et al. [38], and since then, it has been widely used. It is given by:
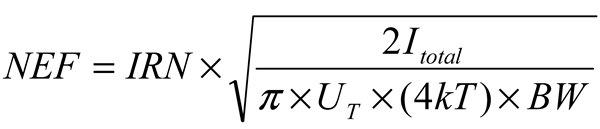
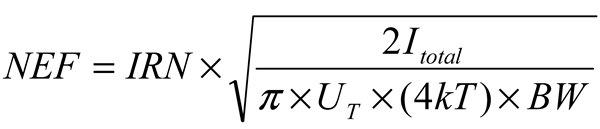
Preprints 73853 i016
where Itotal is the total current absorbed by the amplifier stage (this current excludes the amount absorbed by the bias stage), UT is the thermal voltage given by kT/q (≈ 26 mV at the room temperature of 300 K), k is the Boltzmann constant, T is the room temperature expressed in Kelvin, IRN [Vrms] is the total input-referred noise, and BW is the LNA bandwidth.
It must be noted that this FOM compares the noise-power trade-off with that of a single ideal bipolar transistor. The lowest the FOM, the better will be the LNA with relation to the global noise performance.
Two important observations must be made regarding the results presented in Table 5: the two circuits with the lowest NEF, [24,28], use a single-input CMOS inverter as the first gain stage. The invert has half the number of transistors compared to the inpu stage of an OpAmp, and therefore introduces approximately half the amount of power noise. Consequently, the NEF is reduced by (2)½ ; implementations with technologies with higher minimum length, [29,30,31,32], have a better NEF.
The LNA presented in this work exhibits an NEF that is comparable to the best ones found in the literature. This result is partly due to the sizing/optimization process performed through the application of metaheuristics.
Table 6 compares the features of this neurostimulator circuit with few related key works found in the literature [42,43,44,45,46,47,48]. All works listed in Table 6 were implemented using CMOS components. The neurostimulator presented in this paper and the neurostimulator presented by Adams et al [46] are the only ones that simultaneously allows the generation of current signals with non-standard waveforms and are suitable for delayed feedback.
To conclude, Figure 12 shows a photograph of the fabricated CMOS microdevice, which occupies 1.8 mm × 1.8 mm of area. Moreover, this figure also makes an emphasis to the LNA and neurostimulator presented in this paper.
Preprints 73853 g011
Figure 12. Photograph of the fabricated CMOS microdevice (1.8 mm × 1.8 mm), with emphasis to the LNA presented in this paper and to one of the ESD protections.
Figure 12. Photograph of the fabricated CMOS microdevice (1.8 mm × 1.8 mm), with emphasis to the LNA presented in this paper and to one of the ESD protections.
Preprints 73853 g011

Author Contributions

Conceptualization, T.M.N., R.H.G., and J.P.C.; Methodology, T.M.N., R.H.G. and J.P.C.; Validation, T.M.N., G.A.J., M.L.M.A. and R.H.G.; Writing—original draft preparation, T.M.N., R.H.G., J.N. and J.P.C.; Supervision, E.T.F. and E.C.; Project administration, M.L., J.N., J.P.C. and M.A.R.; Funding acquisition, M.L., J.N., J.P.C. and M.A.R.

Funding

This work was partially supported by the FAPESP agency (Fundação de Amparo à Pesquisa do Estado de São Paulo) through the project with the reference 2019/05248-7. Professor João Paulo Carmo was support by a PQ scholarship with the reference CNPq 304312/2020-7.

Acknowledgments

Tiago Mateus Nordi was sponsored by Federal University of São Carlos (USFCar).

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Appleby, B.S.; Duggan, P.S.; Regenberg, A., and P. V. Rabins. Psychiatric and Neuropsychiatric Adverse Events Associated With Deep Brain Stimulation: A Meta-analysis of Ten Years’ Experience. Movement Disorders 2007, 22, 1722–1728. [CrossRef] [PubMed]
  2. Sui; Y; Tian; Y.; Ko; W.K.D.; Wang; Z.; Jia; F.; Horn; A.; de Ridder; D.; Choi; K.S.; Bari; A.A.; Wang, S.; et al. Deep brain stimulation initiative: Toward innovative technology, new disease indications, and approaches to current and future clinical challenges in neuromodulation therapy. Front. Neurol. 2021, 11, 59745.
  3. Medtronic DBS Therapy for Parkinson’s Disease, Medtronic Inc., Catalog UC201607188bEE. 2020. Available online: https://asiapac.medtronic.com/content/dam/medtronic-com/uk-en/patients/documents/parkinsons-disease/pd-brochure-uc201607188ee.pdf?bypassIM=truelead (accessed on 5 March 2022).
  4. Hickey; P; Stacy, M. Deep Brain Stimulation: A Paradigm Shifting Approach to Treat Parkinson’s Disease. Front. Neurosci. 2016, 10, 173.
  5. VerciseTM DVBS Leads: Directions for Use, Boston Scientific Corporation, Catalog 91172963-02 REV A 2017-02. 2017. Available online: https://www.bostonscientific.com/content/dam/Manuals/eu/current-rev-da/91172963-02_Vercise%E2%84%A2_DBS_Leads_DFU_multi-OUS_s.pdf (accessed on 1 Dec. 2021).
  6. Hoang; K.B.; Cassar; I.R.; Grill; W.M.; Turner, D.A. Biomarkers and Stimulation Algorithms for Adaptive Brain Stimulation. Front. Neurosci. 2017, 11, 1–15.
  7. VerciseTM Deep Brain Stimulator System. Available online: https://www.bostonscientific.com/en-IN/products/deep-brain-stimulation-systems/vercise-deep-brain-stimulation-system.html (accessed on 17 January 2023).
  8. Fins, J.J., Chapter 9: Deep Brain Stimulation: Ethical Issues in Clinical Practice and Neurosurgical Research, pp. 81–91, Neuromodulation. Academic Press. 2009.
  9. Kringelbach, M.L.; Jenkinson, N.; Owen, S.L.F.; Aziz, T.Z. Translational principles of deep brain stimulation. Nature Reviews Neuroscience 2007, 8, 623–635. [Google Scholar] [CrossRef] [PubMed]
  10. Owen, S.L.; Green, A.L.; Stein, J.F., and T. Z. Aziz. Deep brain stimulation for the alleviation of poststroke neuropathic pain. Pain 2006, 120, 202–206. [CrossRef] [PubMed]
  11. Marchand, S.; Kupers, R.C.; Bushnell, M.C., and G. H. Duncan. Analgesic and placebo effects of thalamic stimulation. Pain 2003, 105, 481–488. [CrossRef] [PubMed]
  12. Bittar, R.G.; et al. . Deep brain stimulation for movement disorders and pain. Journal of Clinical Neuroscience 2005, 12, 457–463. [Google Scholar] [CrossRef]
  13. Cury, R.G.; Galhardoni, R.; Fonoff, E.T.; Lloret, S.P.; Ghilardi, M.G.S.; Barbosa, E.R.; Teixeira, M.J., and D. C. de Andrade. Sensory abnormalities and pain in Parkinson disease and its modulation by treatment of motor symptoms. European Journal of Pain 2016, 20, 151–165. [CrossRef]
  14. Rehncrona, S.; et al. . Long-term efficacy of thalamic deep brain stimulation for tremor: Double blind assessments. Movement Disorders 2003, 18, 163–170. [Google Scholar] [CrossRef]
  15. Ghilardi, M.G.S.; Ibarra, M.; Alho, E.J.L.; Reis, P.R.; Contreras, W.O.L.; Hamani, C., and E. T. Fonoff. Double-target DBS for essential tremor: 8-contact lead for cZI and Vim aligned in the same trajectory. Neurology 2018, 90, 476–478. [CrossRef] [PubMed]
  16. Fonoff, E.T.; Ghilardi, M.G.S.; Cury, R.G., Neurocirurgia funcional para o Clínico: Estimulação Cerebral Profunda em Doença de Parkinson, Distonia e Outros Distúrbios do movimento, pp. 53 67, Capítulo de livro, Condutas em Neurologia: 11ª edição. Ricardo Nitrini (Ed.). Manole Editora. 2016. In Portuguese.
  17. Vidailhet, M.; et al. . Bilateral deep-brain stimulation of the globus pallidus in primary generalized dystonia. The New England Journal of Medicine 2005, 352, 459–467. [Google Scholar] [CrossRef] [PubMed]
  18. R. Franco, E. T. Fonoff, P. Alvarenga, A. C. Lopes, E. C. Miguel, M. J. Teixeira, D. Damiani, and C. Hamani, “DBS for Obesity”, Brain Sciences, Vol. 6, No. 3, pp. 1–23, 2016.
  19. Almeida, L.; Ramirez, D.M.; Rossi, P.J.; Peng, Z.; Gunduz, A., and M. S. Okun. Chasing tics in the human brain: Development of open, scheduled and closed loop responsive approaches to deep brain stimulation for tourette syndrome. Journal of Clinical Neurology 2015, 11, 122–131. [CrossRef] [PubMed]
  20. Herron, J.A.; Thompson, M.C.; Brown, T.; Chizeck, H.J.; Ojemann, J.G., and A. L. Ko. Chronic electrocorticography for sensing movement intention and closed-loop deep brain stimulation with wearable sensors in an essential tremor patient. Journal of Neurosurgery 2017, 127, 580–587. [CrossRef] [PubMed]
  21. Gadot, R.; Najera, R.; Hiran, S.; Anand, A.; Storch, E.; Goodman, W.K.; Shofty, B., and Sameer A Sheth. Efficacy of deep brain stimulation for treatment-resistant obsessive-compulsive disorder: Systematic review and meta-analysis. Journal of Neurology, Neurosurgery & Psychiatry 2022, 93, 1166–1173.
  22. Hoang, K.B.; Cassar, I.R.; Grill, W.M., and D. A. Turner. Biomarkers and Stimulation Algorithms for Adaptive Brain Stimulation. Frontiers in Neuroscience 2017, 11, 564. [CrossRef]
  23. Chandrakumar, H.; Marković, D. An 80-mVpp linear-input range, 1.6-G􀀁 input impedance, low-power chopper amplifier for closed-loop neural recording that is tolerant to 650-mVpp common-mode interference. IEEE J. Solid-State Circuits 2017, 52, 1–18. [Google Scholar] [CrossRef]
  24. K.A.; Xu, Y.P. A multi-channel neural-recording amplififier system with 90 dB CMRR employing CMOS-inverter-based OTAs with CMFB through supply rails in 65 nm CMOS. In Proceedings of the 2015 IEEE International Solid-State Circuits Conference (ISSCC) Digest of Technical Papers, San Francisco, CA, USA, 22–26 Feb. 2015; pp. 1–3.
  25. Biederman, W.; Yeager; D.J.; Narevsky; N.; Koralek; A.C.; Carmena; J.M.; Alon; E.; Rabaey, J.M.A.; Fully-Integrated, Miniaturized (0.125 mm2) 10.5 μW Wireless Neural Sensor. IEEE J. Solid-State Circuits 2013, 48, 960–970. [CrossRef]
  26. Muller, R.; Le, H.-P.; Li, W.; Ledochowitsch, P.; Gambini, S.; Bjorninen, T.; Koralek, A.; Carmena, J.M.; Maharbiz, M.M.; Alon, E.; Rabaey, J.M. ‘‘A minimally invasive 64-channel wireless µECoG implant,’’ IEEE J. Solid-State Circuits 2015, 50, 344–359. [Google Scholar] [CrossRef]
  27. Yang, T.; Holleman, J. ‘‘An ultralow-power low-noise CMOS biopotential amplififier for neural recording,’’ IEEE Trans. Circuits Syst. II, Exp. Briefs 2015, 62, 927–931. [Google Scholar]
  28. Zhang, F.; Holleman; J.; Otis, B.P. Design of Ultra-Low Power Biopotential Amplifier for Biossignal Acquisition Application. IEEE Trans. Biomed. Circuits Syst. 2012, 6, 244–355.
  29. Kim, H.-J.; Park, Y.; Eom, K.; Park, S.-Y. An Area- and Energy-Efficient 16-Channel, AC-Coupled Neural Recording Analog Frontend for High-Density Multichannel Neural Recordings. Electronics 2021, 10, 1972. [CrossRef]
  30. Kwak, J.Y.; Park, S.-Y. Compact Continuous Time Common-Mode Feedback Circuit for Low-Power, Area-Constrained Neural Recording Amplifiers. Electronics 2021, 10, 145. [CrossRef]
  31. Tasneem, N.T.; Mahbub, I. A 2.53 NEF 8-bit 10 kS/s 0.5 μm CMOS Neural Recording Read-Out Circuit with High Linearity for Neuromodulation Implants. Electronics 2021, 10, 590. [CrossRef]
  32. Harrison, R.R.; Charles, C. A low-power low-noise cmos for amplifier neural recording applications. IEEE J. Solid-State Circuits 2003, 38, 958–965. [CrossRef]
  33. Kassiri, H.; Abdelhalim, K.; Genov, R. "Low-distortion super-GOhm subthreshold-MOS resistors for CMOS neural amplifiers," 2013 IEEE Biomedical Circuits and Systems Conference (BioCAS), Rotterdam, Netherlands, 2013, pp. 270–273.
  34. M. Clerc and J. Kennedy. The particle swarm – explosion, stability, and convergence ia a multimensional complex space,” Trans. Evolutionary Compution 2002, 6.
  35. T.O. Weber and W.A.M.V. Noije. Design of analog circuits using simulated annealing/quenching with crossovers and particle swarm optimization,” in Simulating Annealing – Advances, Apllications and Hybridizations, M.S.G. Tuzuki Ed., IntechOpen, 2012. pp 219-244.
  36. E.I. Ishibe and J.N. Soares. A CMOS bandgap reference circuit with a temperature coefficient adjustment block,” in Proccedings of the 26th Symposium on Integrated Circuits and Systems Design (SBCCI), Sept. 2013, pp. 1–6.
  37. Navarro, J.; Luppe, M. "Performance Comparison of High-Speed Dual Modulus Prescalers Using Metaheuristic Sizing/Optimization," 2020 33rd Symposium on Integrated Circuits and Systems Design (SBCCI), Campinas, Brazil, 2020, pp. 1–6.
  38. Steyaert, M.S.; Sansen, W.M. A micropower low-noise monolithic instrumentation amplifier for medical purposes. IEEE J. Solid-State Circuits 1987, 22, 1163–1168. [CrossRef]
  39. Kölbl, F.; N’Kaoua, G.; Naudet, F.; Berthier, F.; Faggiani, E.; Renaud, S.; Benazzouz, A., and N. Lewis. An Embedded Deep Brain Stimulator for Biphasic Chronic Experiments in Freely Moving Rodents. IEEE Transactions on Biomedical Circuits and Systems 2016, 10, 72–84. [CrossRef]
  40. Kölbl, F.; et al. . An Embedded Deep Brain Stimulator for Biphasic Chronic Experiments in Freely Moving Rodents. IEEE Trans. on Biomedical Circuits and Systems 2016, 10, 72–78. [Google Scholar] [CrossRef]
  41. AN-1515, A Comprehensive Study of the Howland Current Pump, 26 Apr 2013, Texas Instruments.
  42. Pinnell, R.C.; de Vasconcelos, A.P.; Cassel, J.C.; and U., G. Hofmann. A miniaturized programmable deep-brain stimulator for group-housing and water maze use. Frontiers in Neuroscience 2018, 12, 231. [CrossRef]
  43. Ewing, S.G.; Lipski, W.J.; Grace, A.A., and C. Winter. An inexpensive charge-balanced rodent deep brain stimulation device a step-by-step guide to its procurement and construction. Journal of Neuroscience Methods. 2013, 219, 1–17. [CrossRef]
  44. Kouzani, A.Z.; Abulseoud, O.A.; Tye, S.J.; Hosain, M.D.K., and M. Berk. A low power micro deep brain stimulation device for murine preclinical research. IEEE Journal of Translacional Engineering Health Medicine 2013, 1, 1500109. [CrossRef] [PubMed]
  45. Pinnell, R.C.; Dempster, J., and J. Pratt. Miniature wireless recording and stimulation system for rodent behavioural testing. Journal of Neural Engineering 2015, 12, 066015. [CrossRef] [PubMed]
  46. Adams, S.D.; Bennet, K.E.; Tye, S.J.; Berk, M., and A. Z. Kouzani. Development of a miniature device for emerging deep brain stimulation paradigms. PLoS ONE 2019, 14, e0212554. [CrossRef]
  47. Tibara, H.; Naudeta, F.; Kölblc, F.; Ribota, B.; Faggiania, E.; N’Kaouac, G.; Renaudc, S.; Lewisc, N.; Benazzouza, A. ,“ In vivo validation of a new portable stimulator for chronic deep brain stimulation in freely moving rats. Journal of Neuroscience Methods 2020, 333, 108577. [Google Scholar] [CrossRef]
  48. Fluri, F.; Mützel, T.; Schuhmann, M.K.; Krstić, M.; Endres, H., and J. Volkmann. Development of a head-mounted wireless microstimulator for deep brain stimulation in rats. Journal of Neuroscience Methods 2017, 291, 249–256. [CrossRef]
Preprints 73853 g001
Figure 1. A block diagram of a CMOS microdevice containing the acquisition, neurostimulator and control modules for closed-loop DBS (CLDBS). The Low Noise Amplifier (LNA) and the Neurostimulator modules presented in this paper are filled with the yellow and green colors.
Figure 1. A block diagram of a CMOS microdevice containing the acquisition, neurostimulator and control modules for closed-loop DBS (CLDBS). The Low Noise Amplifier (LNA) and the Neurostimulator modules presented in this paper are filled with the yellow and green colors.
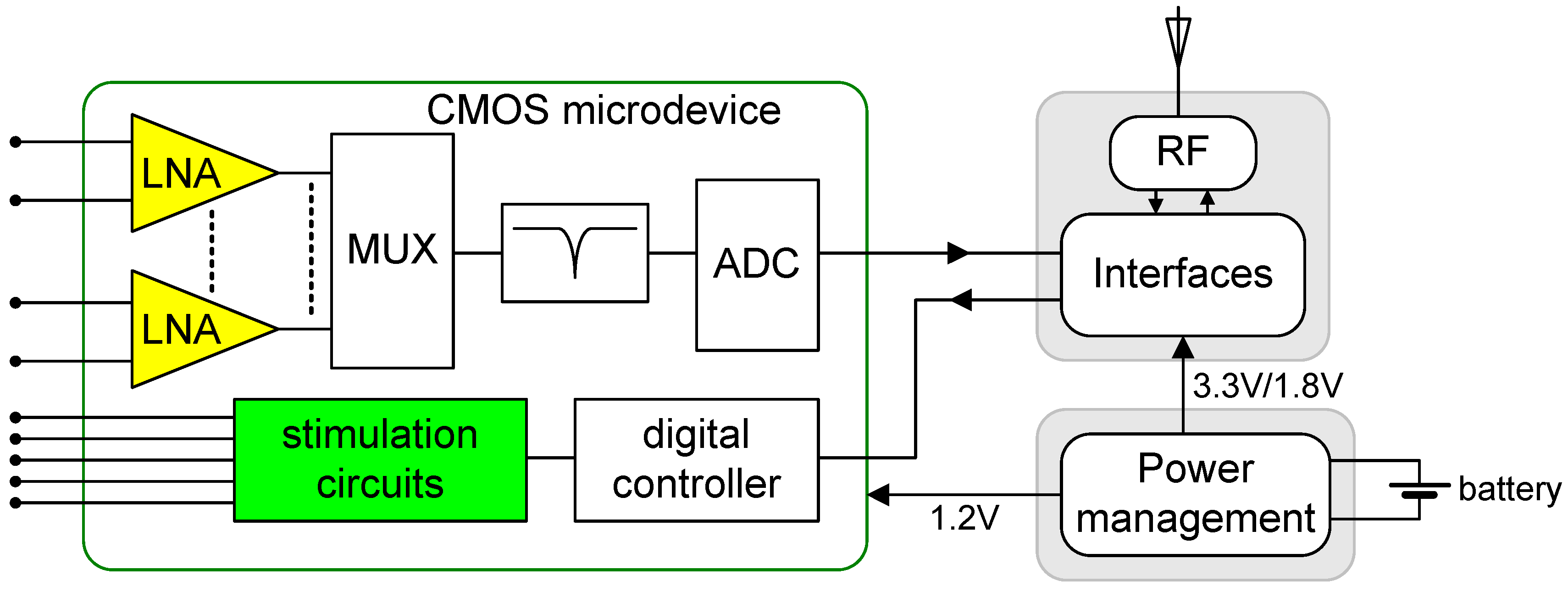
Preprints 73853 g001
Preprints 73853 g002
Figure 2. Schematics (a) of the Low-Noise Amplifier, and (b) of the OpAmp.
Figure 2. Schematics (a) of the Low-Noise Amplifier, and (b) of the OpAmp.
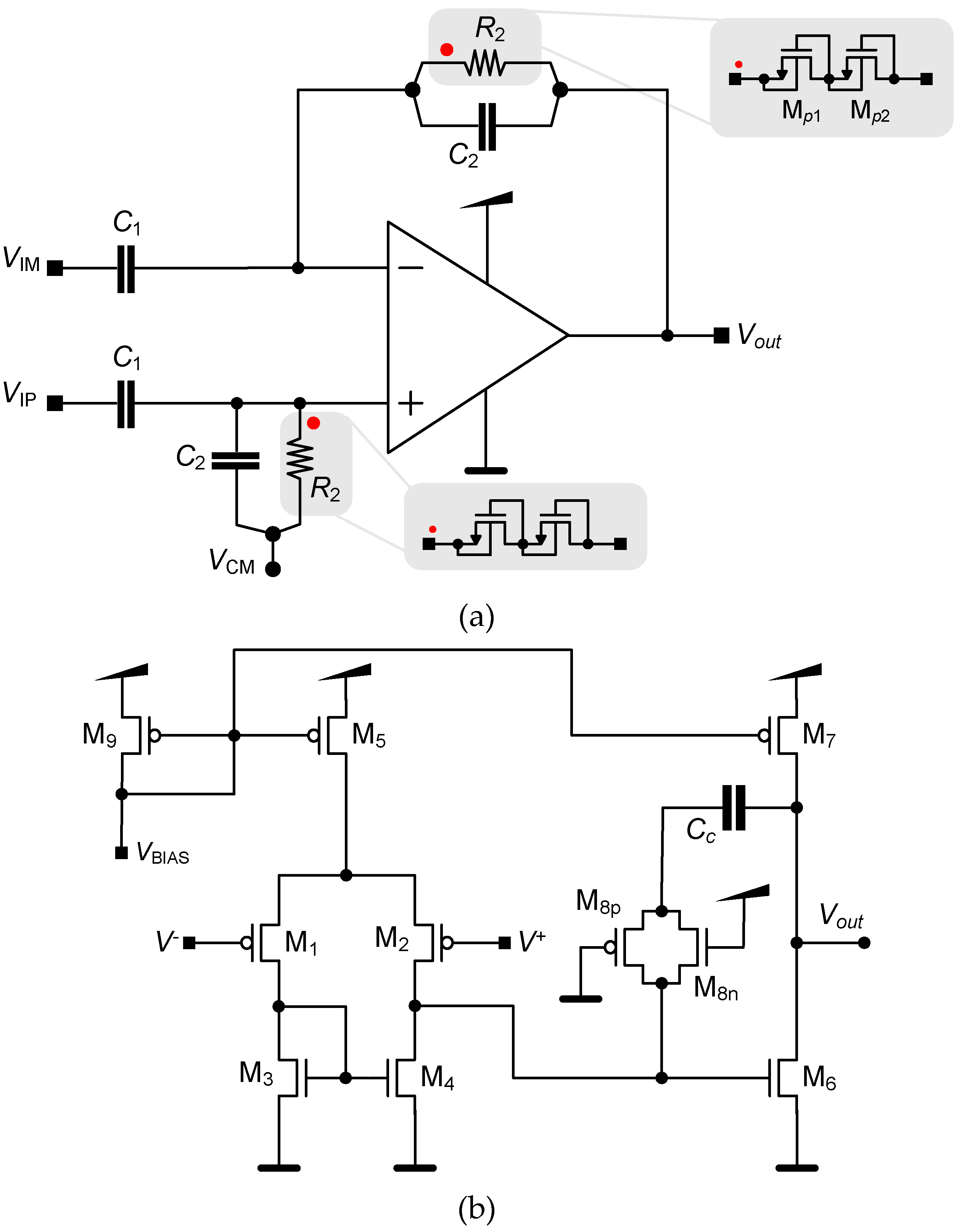
Preprints 73853 g002
Preprints 73853 g003aPreprints 73853 g003b
Figure 3. Shaping function examples (Output Score × Input Value).
Figure 3. Shaping function examples (Output Score × Input Value).
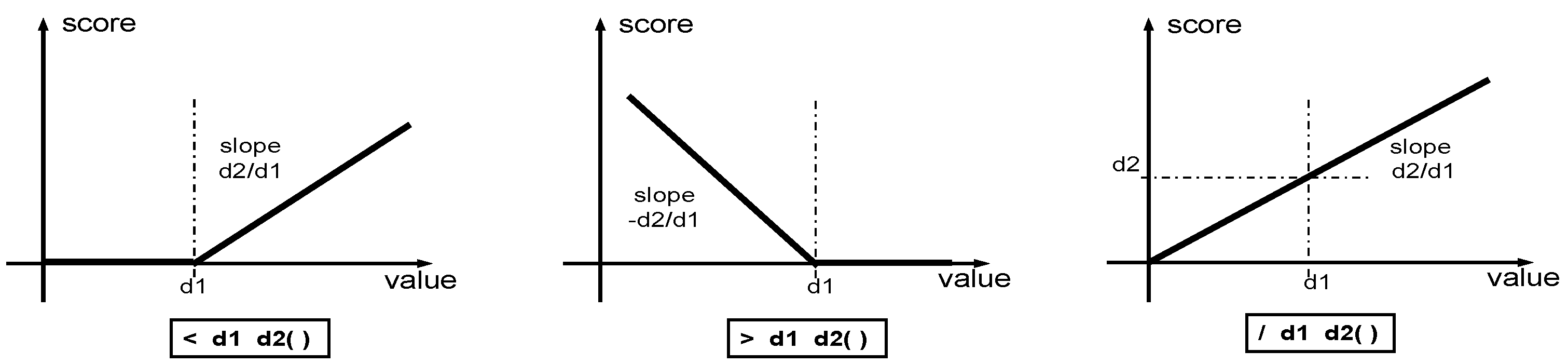
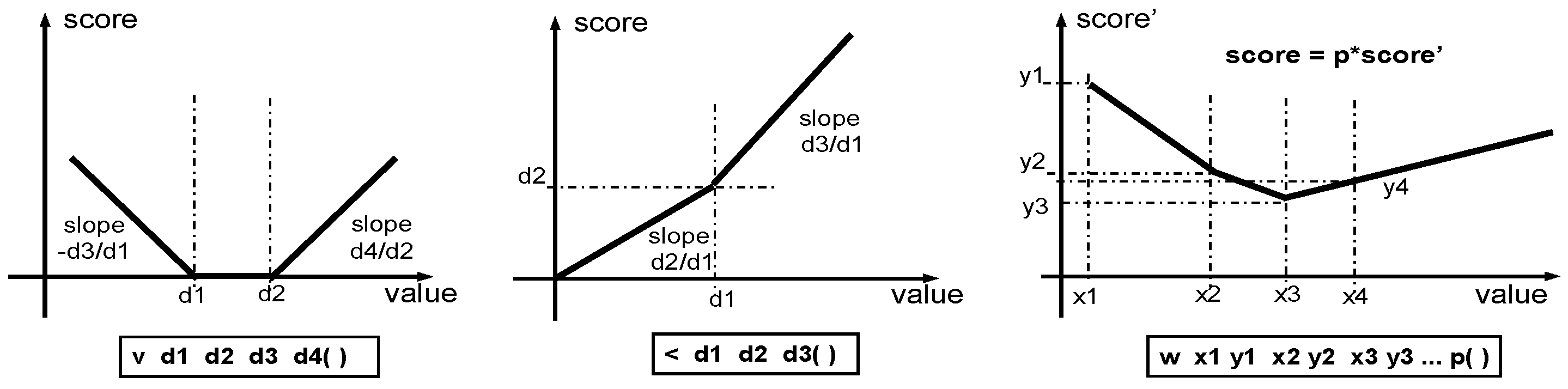
Preprints 73853 g003aPreprints 73853 g003b
Preprints 73853 g004
Figure 5. Sizing/optimization framework flowchart.
Figure 5. Sizing/optimization framework flowchart.
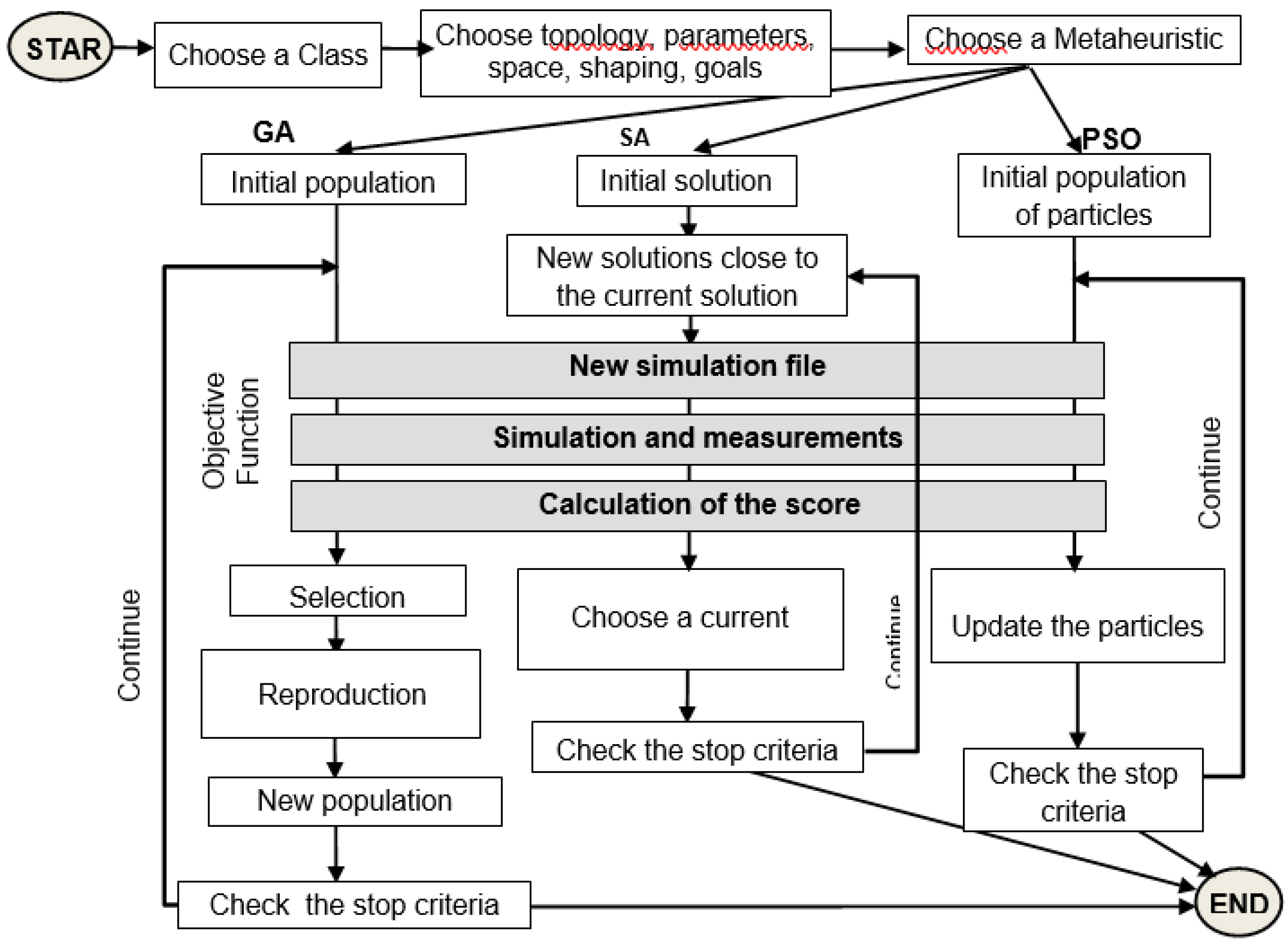
Preprints 73853 g004
Preprints 73853 g005
Figure 6. (a) Example of symmetric biphasic pulse shape without interpulses delay and mean value of zero, and (b) two examples of asymmetric biphasic pulse shape, with zero (on left) non-zero (on right) interpulses delay and also with mean value of zero.
Figure 6. (a) Example of symmetric biphasic pulse shape without interpulses delay and mean value of zero, and (b) two examples of asymmetric biphasic pulse shape, with zero (on left) non-zero (on right) interpulses delay and also with mean value of zero.
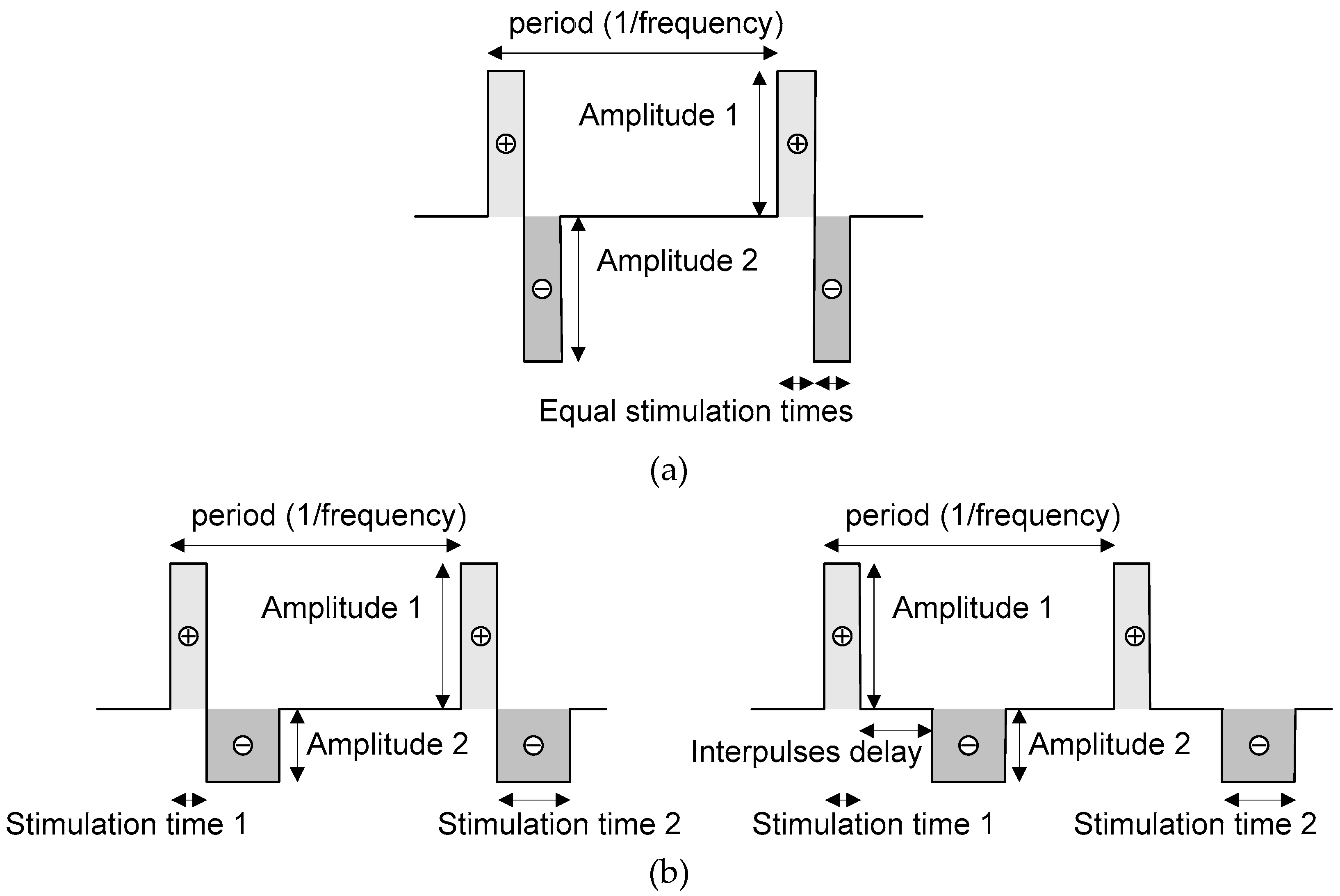
Preprints 73853 g005
Preprints 73853 g006
Figure 7. Schematics (a) of the Current-Pump that implements the neurostimulator, and (b) of the OpAmp used by the Current-Pump.
Figure 7. Schematics (a) of the Current-Pump that implements the neurostimulator, and (b) of the OpAmp used by the Current-Pump.
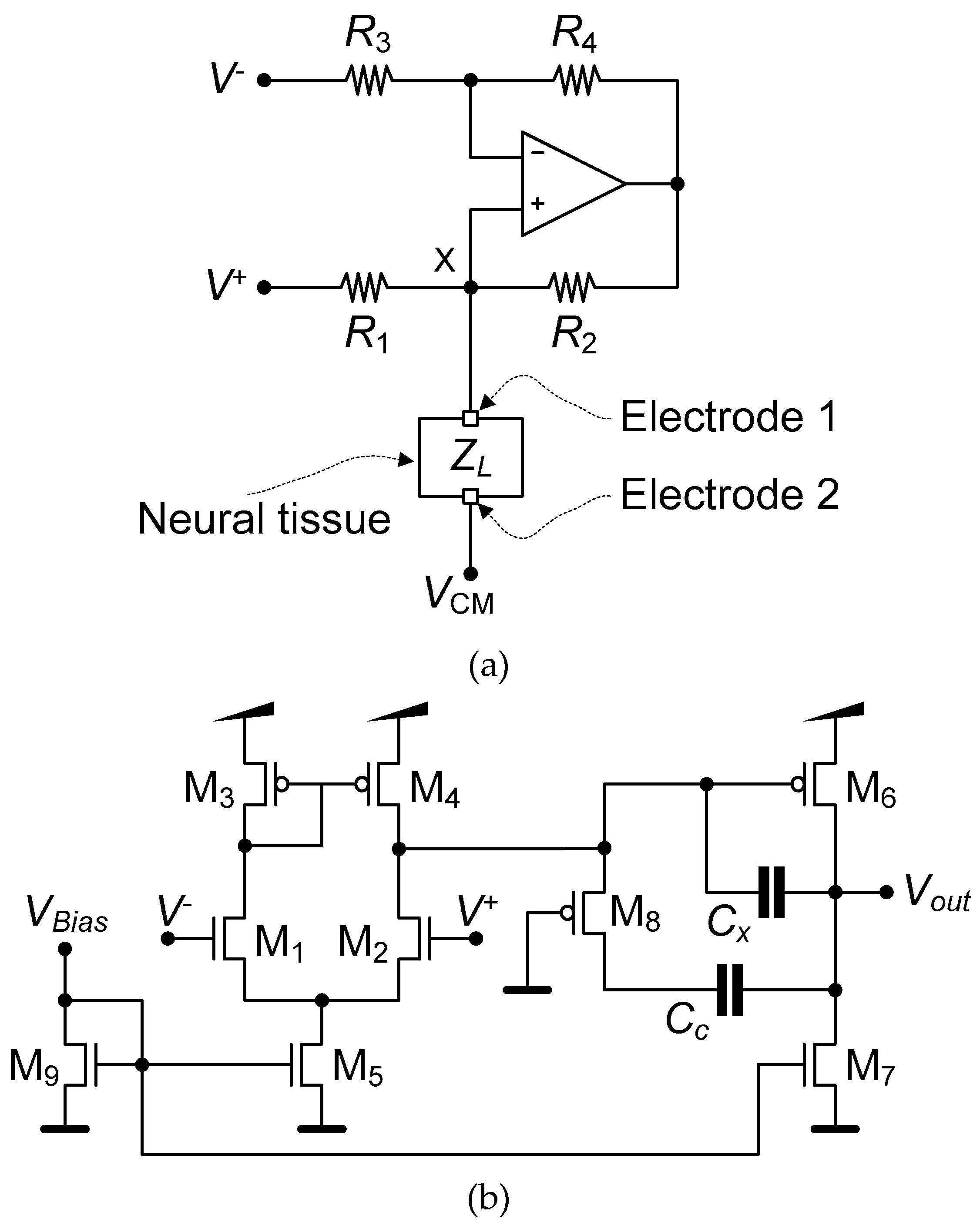
Preprints 73853 g006
Preprints 73853 g007aPreprints 73853 g007b
Figure 8. (a) Photograph of the experimental setup used to obtain the gain and bandwidth characteristics of the LNA. (b) The electronic circuit used to adjust the various common-mode voltages VCM of the LNA. (c Plots of the measured gain with the input signals with an amplitude of 2mVpp that was measured for several values of VCM. (d) Plots of the measured gain with the input signals with an amplitude of 10mVpp that was measured for several values of VCM. Both sets of plots in (c) and (d) are compared with the simulations (line in solid blue).
Figure 8. (a) Photograph of the experimental setup used to obtain the gain and bandwidth characteristics of the LNA. (b) The electronic circuit used to adjust the various common-mode voltages VCM of the LNA. (c Plots of the measured gain with the input signals with an amplitude of 2mVpp that was measured for several values of VCM. (d) Plots of the measured gain with the input signals with an amplitude of 10mVpp that was measured for several values of VCM. Both sets of plots in (c) and (d) are compared with the simulations (line in solid blue).
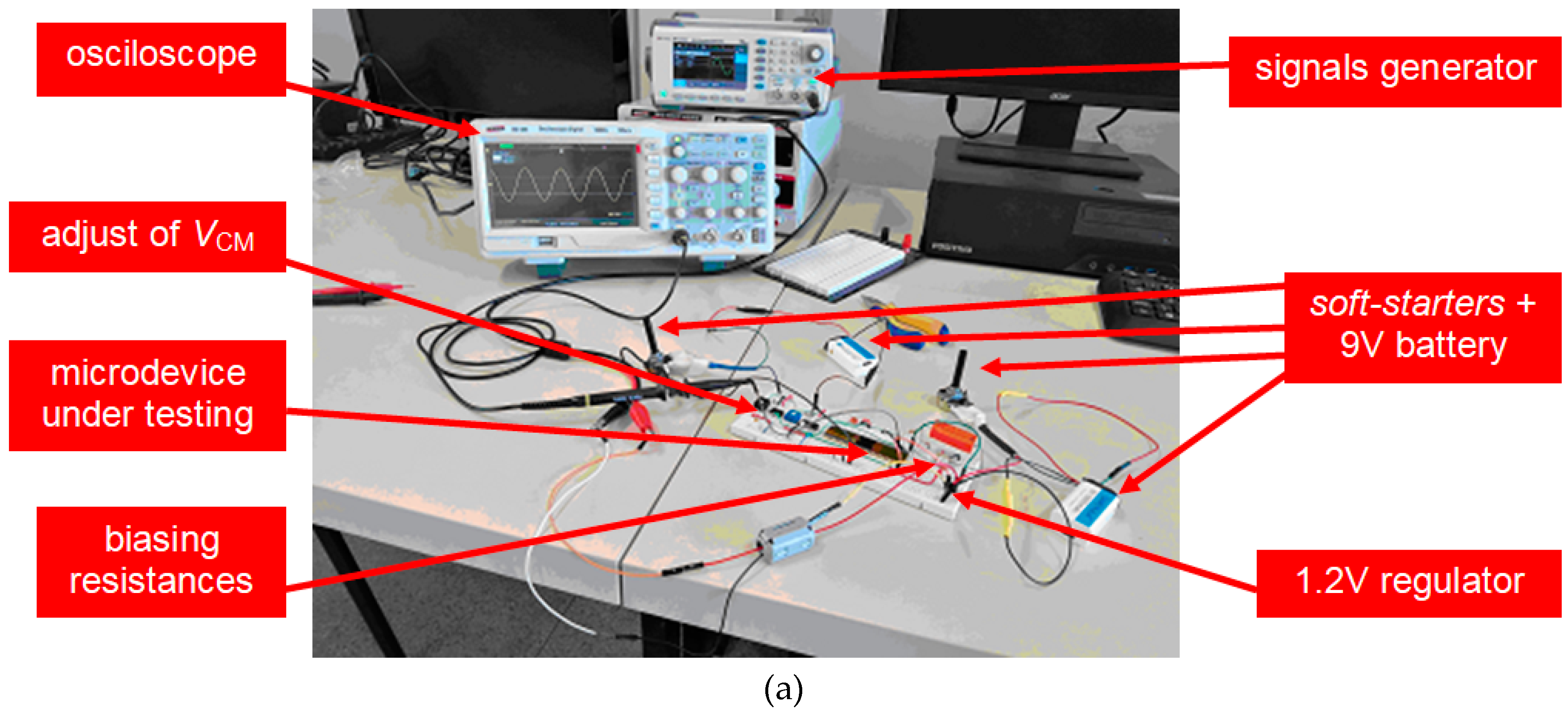
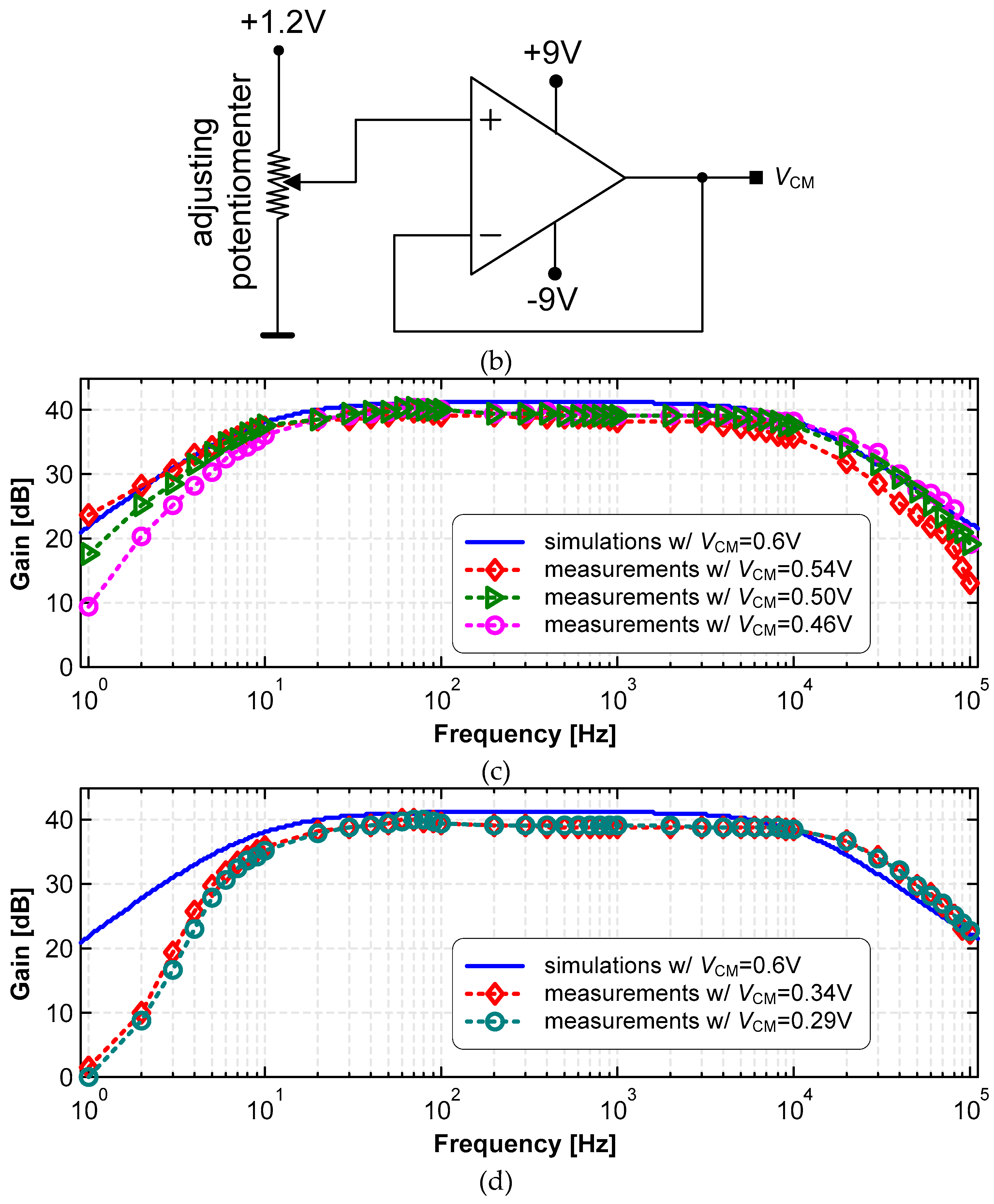
Preprints 73853 g007aPreprints 73853 g007b
Preprints 73853 g008aPreprints 73853 g008b
Figure 9. (a) Photograph of the experimental setup used in the characteristics of the LNA in saline solution. (b) Plot of the measured gain for signals injected into the solution with amplitude of 20mVpp.
Figure 9. (a) Photograph of the experimental setup used in the characteristics of the LNA in saline solution. (b) Plot of the measured gain for signals injected into the solution with amplitude of 20mVpp.
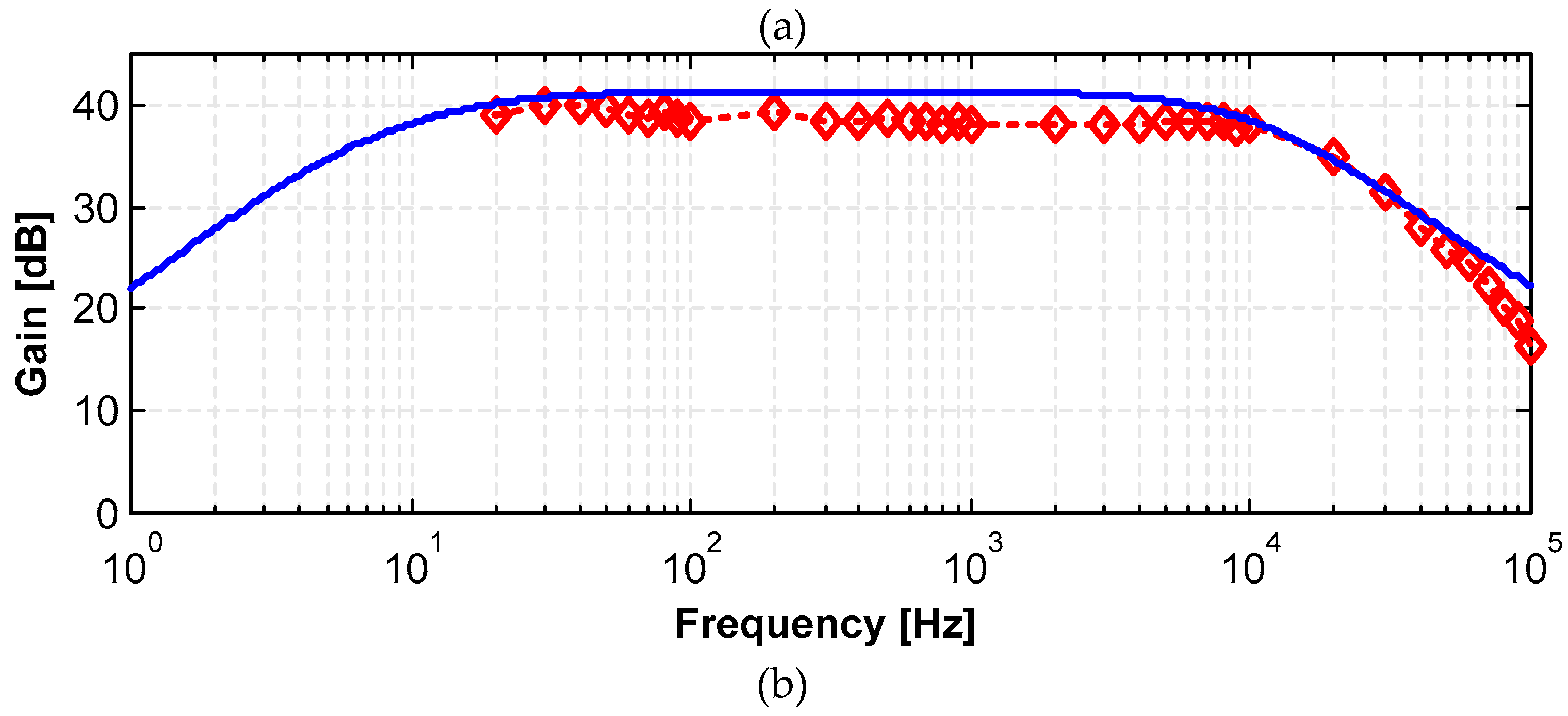
Preprints 73853 g008aPreprints 73853 g008b
Preprints 73853 g009aPreprints 73853 g009b
Figure 10. (a) Schematic of the experimental setup used on the static characterization of the neurostimulator circuit. (b) Photograph of the experimental setup used in the static characterization of the Current-Pump. (c) Stimulation currents for the various combinations of voltages {V+,V-,VCM,electrode} in “raw” form to allow a clear and immediate visualization of the wide and quasi-symmetrical range of currents. (d) Stimulation currents doubly parameterized in terms of the reference voltage of the electrode VCM,electrode and the inverting input V-.
Figure 10. (a) Schematic of the experimental setup used on the static characterization of the neurostimulator circuit. (b) Photograph of the experimental setup used in the static characterization of the Current-Pump. (c) Stimulation currents for the various combinations of voltages {V+,V-,VCM,electrode} in “raw” form to allow a clear and immediate visualization of the wide and quasi-symmetrical range of currents. (d) Stimulation currents doubly parameterized in terms of the reference voltage of the electrode VCM,electrode and the inverting input V-.
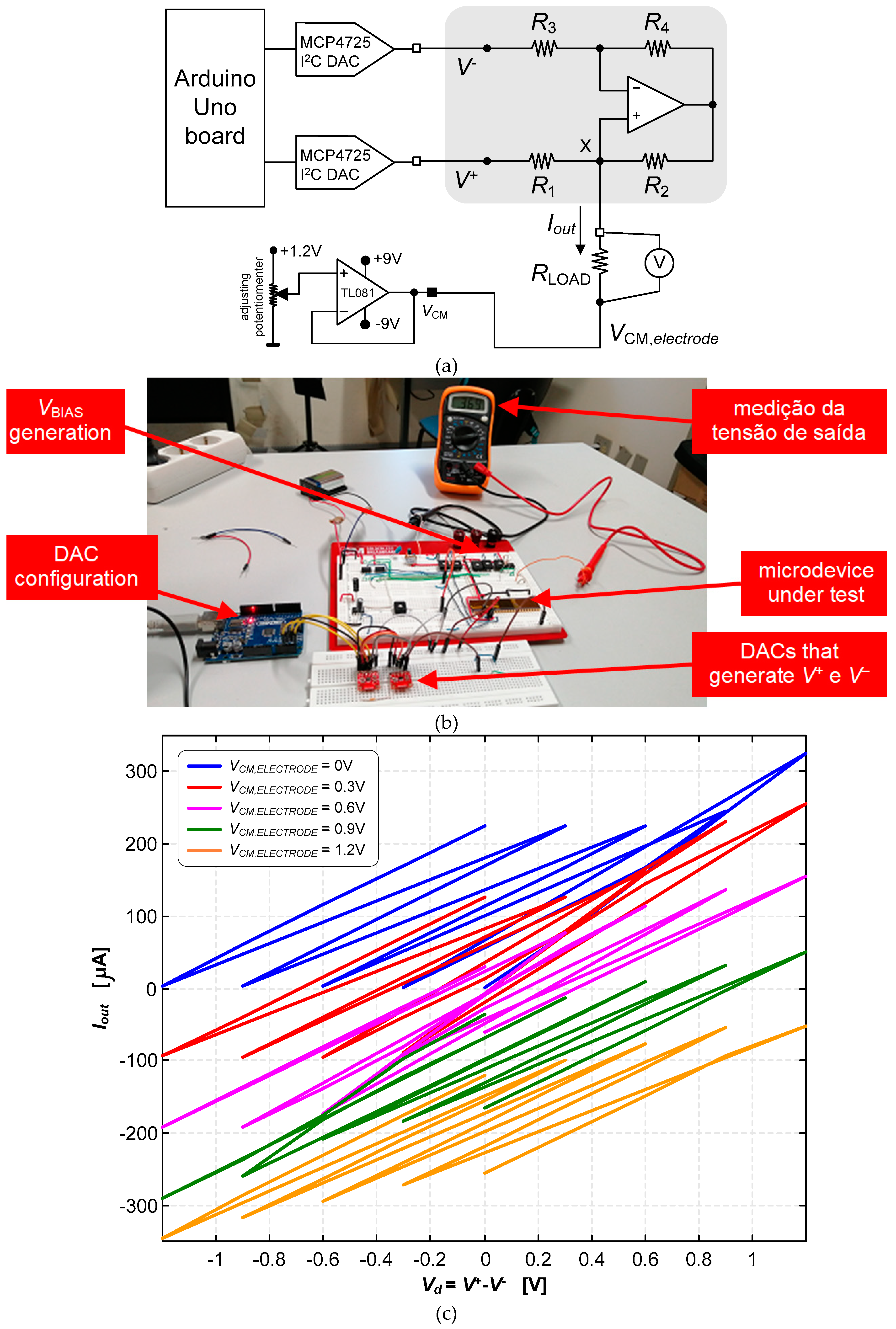
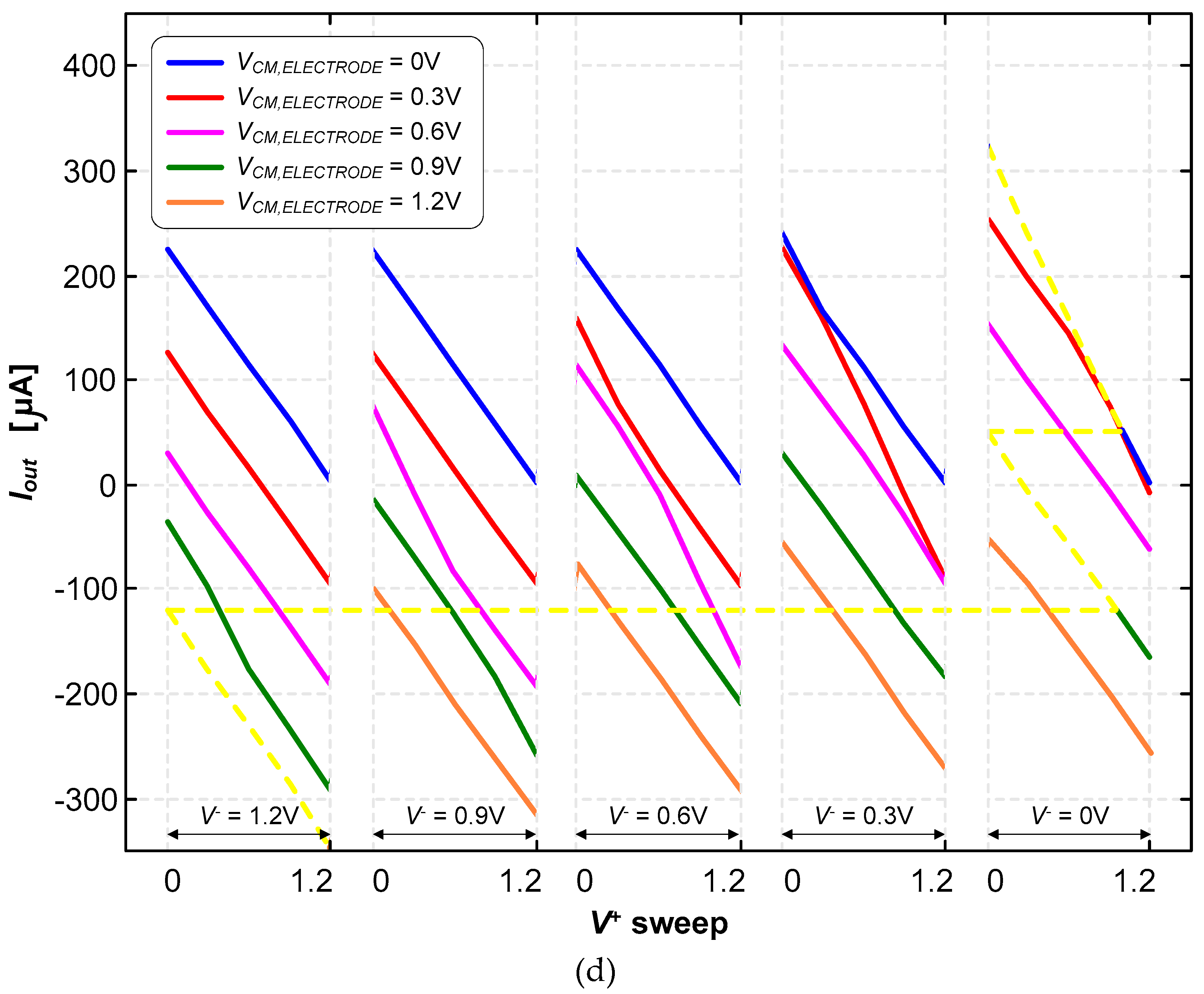
Preprints 73853 g009aPreprints 73853 g009b
Preprints 73853 g010aPreprints 73853 g010b
Figure 12. (a) Schematics of the experimental setup used on dynamic characterization of the neurostimulator circuit. (b) Photograph of the experimental setup used in the static characterization of the Current-Pump. (c) Dynamic characterization using sine waves with rail-to-rail amplitude.
Figure 12. (a) Schematics of the experimental setup used on dynamic characterization of the neurostimulator circuit. (b) Photograph of the experimental setup used in the static characterization of the Current-Pump. (c) Dynamic characterization using sine waves with rail-to-rail amplitude.
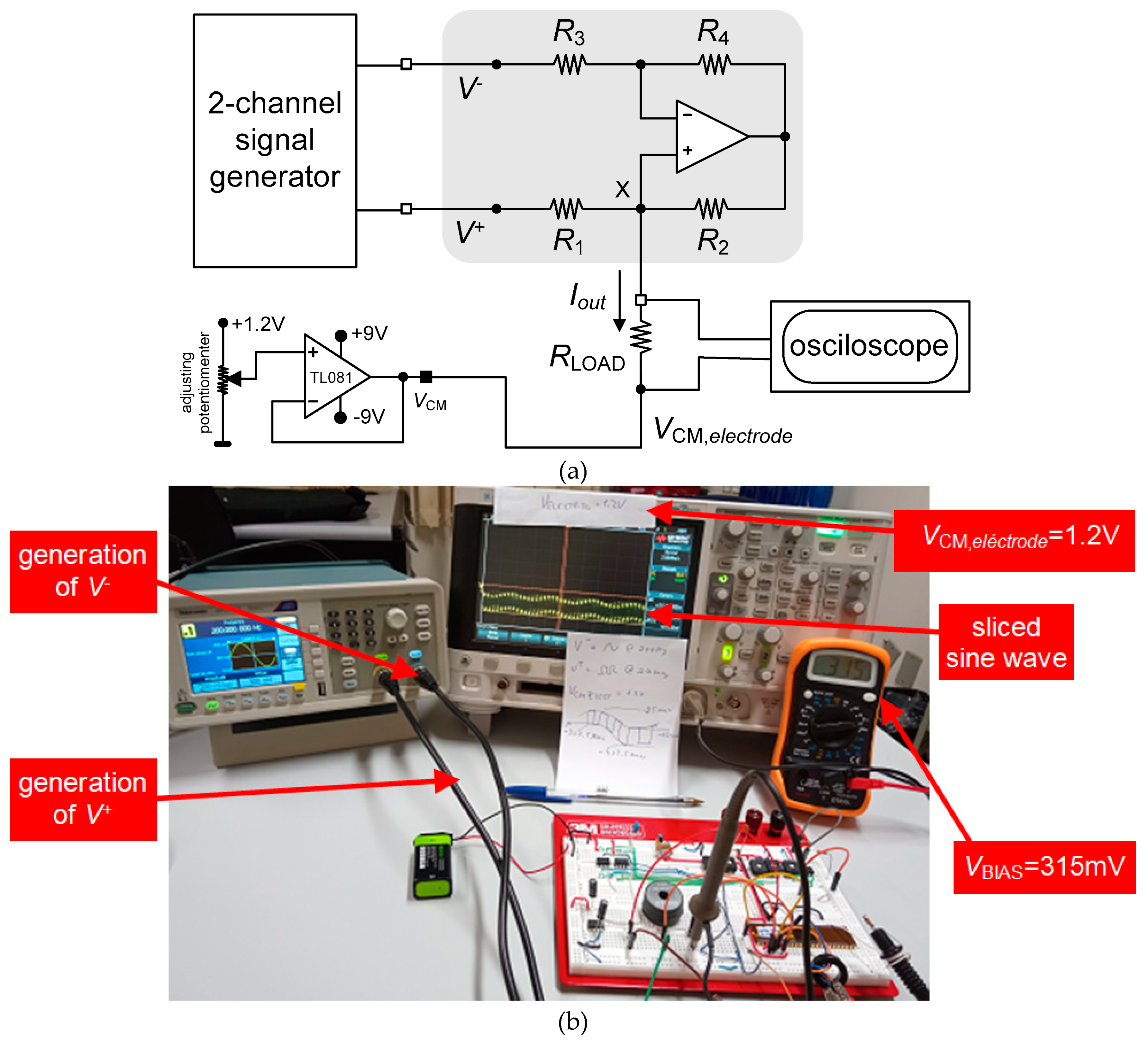
Preprints 73853 g010aPreprints 73853 g010b
Table 1. LNA characteristics for the corner models (power supply equal to 1.2 V). The biasing of the circuit is achieved by connecting a bias resistor of 4.4 MΩ between the VBIAS node (Figure 2b) and ground.
Table 1. LNA characteristics for the corner models (power supply equal to 1.2 V). The biasing of the circuit is achieved by connecting a bias resistor of 4.4 MΩ between the VBIAS node (Figure 2b) and ground.
Characteristics Value
tt		 Value
ss		 Value
ff		 Value
sf		 Value
fs
OpAmp
Differential gain [dB] 76.6 76.7 75.1 76.2 76.9
Common Mode Rejection Rate [dB] (CMRR) 72.8 71.1 70.4 74.7 70.9
Power Supply Rejection Rate [dB] (PSRR) 71.7 69 74 72.8 70.4
Phase Margin [º] 48 40 37 41 42
Slew Rate [V/μs] 0.138 0.132 0.145 0.142 0.134
LNA
Gain [dB] 40.43 40.66 40.1 40.19 40.78
Low cut off frequency (-3 dB) [Hz] 19 13.3 32.6 24.5 16.3
High cut off frequency (-3 dB) [kHz] 9.0 8.1 10.1 9.8 8.1
Power consumption [μW] 6.19 5.85 6.5 6.4 5.97
Input noise [μVrms] 4.86 4.85 4.84 4.72 5.03
Table 2. Dimensions of the MOSFETs that comprises the OpAmp and the pseudo-resistors, and the value of the capacitor Cc, obtained with the optimizer.
Table 2. Dimensions of the MOSFETs that comprises the OpAmp and the pseudo-resistors, and the value of the capacitor Cc, obtained with the optimizer.
MOSFET Total
(W/L)		 Multiplier
(parallel MOSFETs)		 Fingers/multiplier
M1, M2 59 μm/0.52 μm 2 10
M3, M4 25 μm/14.9 μm 2 1
M5 48 μm/2.22 μm 24 1
M6 12.5 μm/14.9 μm 1 1
M7 12 μm/2.22 μm 6 1
M8n 1.55 μm/12 μm 1 1
M8p 3.1 μm/12 μm 1 1
M9 2 μm/2.22 μm 1 1
Pseudo-resistors 12 μm/0.6 μm 1 1
Capacitor Total value Type Sub-capacitor size Nr. of sub-capacitors
Cc 7.5 pF MIMcap 10 μm × 10 μm 36 (6 × 6 array)
Table 3. Dimensions of the MOSFETs that comprises the OpAmp, the value of the capacitor Cx, and the resistors used by the Howland Current-Pump.
Table 3. Dimensions of the MOSFETs that comprises the OpAmp, the value of the capacitor Cx, and the resistors used by the Howland Current-Pump.
MOSFET Total
(W/L)		 Multiplier
(parallel MOSFETs)		 Fingers/multiplier
M1, M2 14.8 μm/0.24 μm 2 1
M3, M4 4.68 μm/0.18 μm 2 2
M5 14.4 μm/0.36 μm 1 10
M6 18.72 μm/0.18 μm 2 6
M7 28.8 μm/0.36 μm 2 10
M9 0.80 μm/0.36 μm 1 1
MOSFET Total
(W/L) 		Number of MOSFETs in series with common gate connections Fingers/each series multiplier
M8 0.51 μm/7.2 μm 4 1
Capacitor Total value Type Sub-capacitor size Nr. of sub-capacitors
Cc 2.5 pF MIMcap 10 μm × 10 μm 12 (4 × 3 parallel array)
Cx 417.2 fF MIMcap 10 μm × 10 μm 2 (2 × 1 parallel array)
Resistor Total value Type Nr. of sub-resistors
R1, R2 ≈3.52 kΩ P+ poly resistor without salicide (rppolyw0), R?≈690 Ω Parallel of 2 series, each series composed by 2 subresistors of ≈3.52 kΩ
R3, R4 ≈24.61 kΩ Parallel of 2 series, each series composed by 2 subresistors of ≈24.61 kΩ
Table 4. Measured common-mode voltage VCM,out and the maximum gain Gmax at the output of LNA.
Table 4. Measured common-mode voltage VCM,out and the maximum gain Gmax at the output of LNA.
Vin [mVpp] VCM [V] VCM,out [V] Gmax [dB]
2 0.54 0.92 40.0
0.50 0.6 40.6
0.46 0.53 40.6
10 0.34 0.6 40.1
0.29 0.63 40.2
Table 5. Comparison of this LNA with the state-of-the art.
Table 5. Comparison of this LNA with the state-of-the art.
Ref. CMOS process Mid-Band Gain [dB] Bandwidth [Hz] Power Supply
[V]		 Power
Consup.
[μW]		 Area [mm2] IRN [μVrms] FOM [kHz/(μVrms.μW)]
this work+ 65nm 40.4 19 － 9k 1.2 6.19 0.046 4.86 4.34
[23] 40nm 25.7 200 － 5.0k 1.2 2.8 N/A 5.3 4.40
[24] 65nm 52.1 1.0 － 8.2k 1.0 2.8 0.042 4.13 2.93
[25] 65nm 46 1.0 － 10k 0.5 1.5 0.0039 6.5 4.34
[25] 65nm 30 300 － 10k 0.5 2.3 0.025 5.8 4.76
[27] 90nm 58.7 0.49 － 10.5k 1.0 2.85 0.137 3.04 1.93
[28] 0.13μm 40 0.05 － 10.5k 1.0 12.1 0.072 2.2 2.90
[29] 0.18μm 40 0.1 － 7.4k 1.0 3.44 0.012 4.27 3.07
[30] 0.18μm 40 0.05 － 7.5k 1.2 4.8 0.022 3.87 3.44
[31] 0.5μm 49.26 － 60.63 0.5 － 300
0.27－12.9k		 3.3 4.12 0.0144 3.16 2.53
[32] 0.5μm 39.5 0.025 －7.2k ±2.5 80 μW 0.16 2.2 4.0
+ simulation results.
Table 6. Comparison of this neurostimulator with the state-of-the art.
Table 6. Comparison of this neurostimulator with the state-of-the art.
Ref. Current
[μA]		 Voltage [V] Maximum pulse frequency/
Bandwidth [Hz] 		Minimum pulse duration/
Bandwidth-1 [μs]		 Charge balance Active charge
balancing method
This work -325 to +318 1.2 1.5×106 (BW) 25 Active Continuous (Howland
Current-Pump)
[42] 20 to 2000 12 500 10 Active Switched (H-bridge)
[43] -200 to +200 3.6 (bat) 185 90 Active Switched
[44] 0 to 200 3.2 (bat) 130 90 Passive Switched
[45] 30 to 1000 3.7 (bat) 5000 10 Active Switched
[46] -375 to +250 10 5000 20 Active Continuous (Howland
Current-Pump)
[47] 20 to 2000 4.8 (bat) 300 40 Active Switched (H-bridge)
[48] 10 to 500 3.1 (bat) 200 60 Passive Switched
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated