Prerpints.org logo
Preprint
Article

Tiny Deep Learning Architectures Enabling Sensor-near Acoustic Data Processing and Defect Localization

Altmetrics

Downloads

136

Views

35

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

16 May 2023

Posted:

17 May 2023

You are already at the latest version

Alerts
Abstract
The timely diagnosis of defects at their incipient stage of formation is crucial to extend the life-cycle of technical appliances. This is the case of mechanical-related stress, either due to long aging degradation processes (e.g., corrosion) or in-operation forces (e.g., impact events), which might provoke detrimental damages, such as cracks, disbonding or delaminations, most commonly followed by the release of acoustic energy. The localization of these sources can be successfully fulfilled via adoption of Acoustic Emission (AE)-based inspection techniques through the computation of the Time of Arrival (ToA), namely the time at which the induced mechanical wave released at the occurrence of the acoustic event arrives to the acquisition unit. However, the accurate estimation of the ToA may be hampered by poor Signal-to-Noise ratios (SNRs). In these conditions, standard statistical methods typically fail. In this work, two alternative Deep Learning methods are proposed for ToA retrieval, namely a Dilated Convolutional Neural Network (DilCNN) and a Capsule Neural Network for ToA (CapsToA). These methods have the additional benefit of being portable on resource-constrained microprocessors. Their performance has been extensively studied on both synthetic and experimental data, focusing on the problem of ToA identification for the case of a metallic plate. Results show that the two novel methods can achieve localization errors which are up to 70% more precise than those yielded by conventional strategies, even when the SNR is severely compromised (i.e., down to 2 dB). Moreover, DilCNN and CapsNet have been implemented in a tiny machine learning environment and then deployed on microcontroller units, showing a negligible loss of performance with respect to offline realizations.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

Acoustic Emission (AE)–based monitoring represents one of the most effective Non Destructive Evaluation (NDE) approaches for the Structural Health Monitoring (SHM) of structures or materials subject to stress [1,2]. The underpinning principle behind AE is that the occurrence of acoustic events (such as cracks, delaminations, disbonding, etc.) is intrinsically related to the structural status of integrity: the higher the frequency and the intensity of the recorded acoustic activity, the higher the level of potential structural degradation. A general AE-based SHM system comprises a distributed network of passive sensors, which can localize such sources by analysing the acoustic response of the structure. In particular, the estimation of the Time of Arrival (ToA), also known as onset time, namely the instant at which the induced mechanical wave arrives at the acquisition unit [3], deserves primary importance.
The taxonomy of the strategies proposed for the task of ToA estimation is very broad and spans from statistical methods to artificial intelligence (AI) solutions [4], the latter being an emerging trend of research in recent years thanks to their superior ability in learning very complicated patterns hidden within data. Indeed, machine learning methods are superior in that they can be applicable even when the Signal–to–Noise ratio (SNR) is poor: this might happen either as a consequence of electromagnetic noise and rubbing disturbances in the surrounding of the monitored environment, or due to the electronic noise affecting the employed instrumentation [5]. Conversely, standard methods comprise the Akaike Information Criterion (AIC) [6], which is based on the analysis of second order statistics, and the Short-Time Average on Long-Time Average (STA/LTA) [7] method, that computes the ToA from the ratio between the mean amplitude of two moving time windows of different size.
To attain sufficient estimation accuracy, most of these AI methodologies are very onerous in terms of computational power and model size; thus, they are typically deployed in remote servers. However, this framework requires the periodic transmission of long time series to a central aggregating unit, a condition which might cause severe problems in terms of network congestion, especially in presence of battery-operated systems. A viable solution to bypass this bottleneck is offered by the edge/extreme edge computing perspective. Indeed, in this novel framework, data are processed in a sensor-near manner by exploiting the native Digital Signal Processing (DSP) functionalities of embedded microprocessors to extract semantic information from raw data. The advantage is that, in this scenario, the entire waveform can be collapsed into a batch of representative parameters (such as the ones related to the ToA), which are the only quantities to be transmitted over the monitoring network; this solution minimizes the network payload and, in turn, reduces the overall system latency.
Nevertheless, the deployment of AI models in resource–constrained devices [8] represents a pivotal challenge for the development of the next generation of AE–driven and DL-empowered AE architectures. A tangible response to this need is offered by the novel and pioneering approaches driven by the Tiny Machine Learning (TinyML) ecosystem: the latter is defined as the capability of running AI at the boundary between the physical and the digital world1, i.e., by means of edge or extreme edge devices, in a low–power and computationally–efficient manner. Notwithstanding these promising opportunities, which are expected to revolutionize the standard approach to on-condition maintenance, there is still a lack of effective AI methodologies and experimental evidence about TinyML solutions for AE data processing.
This work aims at bridging the gap above by demonstrating the actual embodiment of different AI models for ToA estimation on a general-purposes embedded system equipped with a low–power and low–cost microcontroller unit (MCU), which is actually in charge of running NN models for ToA computation in a self–contained manner. The validity of the proposed AE workflow is showcased for the condition assessment of a representative metallic plate.
The content of the work is organized as follows. In Section 2, the proposed Neural Network (NN) architectures are firstly presented; then, the different quantization schemes necessary for their TinyML porting are discussed. The experimental validation Section is extensively treated in Section 3 in terms of materials and methods, while performance metrics are shown in Section 4. Conclusions and future outlooks end the paper.

1.1. Related works

AE characterization via ToA is analogous to the identification of wave arrivals in seismology, a field of research in which several Deep Learning (DL) solutions have initially started to emerge to address this goal. Just to name a few examples, in [9] Ross et al. proposed a template–based artificial neural network for earthquake phase detection, while an unsupervised fuzzy clustering logic has been explored in [10]. A variant of the well-known U-Net [11] was also investigated in [12] for seismic arrival–time picking, on the premise of the outstanding results obtained for segmentation in biomedical applications. Different studies exploited the capabilities of Recurrent Neural Networks (RNNs) in learning time dependencies across the input sequences for the accurate detection of the onset of target events. For example, the Long Short-Term Memory (LSTM) is adopted in [13], while in [14] the authors combined dilated convolutional layers with Gated Recurrent Units (GRU) to enlarge the temporal receptive field at the input of the recurrent layer. The drawback of this kind of architectures is that they are less parallelizable than feedforward solutions, requiring long training time when the original sequence is composed by hundreds of timestamps, even in the case of tiny models. Furthermore, it is worth mentioning the works of Saad et al. ([15] and [16]), who trained Capsule Neural Networks (CapsNet) [17] to classify seismic data in combination with a sliding window logic: wave onset picking was achieved, in their case, by means of non-trainable post processing techniques. A comprehensive list of some recent developments in such direction is presented in [18].

1.2. Contribution

Inspired by previous studies, alternative DL solutions are proposed in this work for ToA extraction from AE time series. More specifically, we advance the results obtained in [4] and [19] introducing the following novelties:
  • We propose two DL architectures for the purpose of ToA identification, one based on a Dilated Convolutional Neural Network (DilCNN) and the latter being an improvement of the Capsule Neural Network (CapsNet) described in [4];
  • We extensively validate the performances of the two novel models against various noise levels, proving their superiority in addressing two different tasks: i) accuracy in the pure ToA estimation while working on synthetic data, ii) precision in acoustic source localization for the experimental use case of a metallic aluminum plate; in particular, we will show that DilCNN and CapsNet can achieve a localization error which is up to 70% more accurate than STA/LTA and AIC even when the SNR is considerably below 4 dB;
  • We implemented the devised NN models in a tiny machine learning environment and eventually deployed on a general-purpose and resource-constrained microprocessor, namely the STM32L4 microcontroller unit based on the ARM ®Cortex-M4®core: we demonstrate that these tiny variants score negligible loss of performances with respect to the cloud-running alternatives.

2. Neural Network Architectures for ToA Extraction

In this section, the designed architectures are described in detail, along with the adopted methodologies and tools for their coding. To this end, all the NN models have been implemented and trained using Keras2, an high level deep learning API built on top of the open source platform TensorFlow3 (TF).

2.1. Dilated Convolutional Neural Networks

Convolutional Neural Networks (CNNs) are extremely popular DL models which have achieved impressive performance in a wide variety of applications, including images and time signal classification. Their functioning is inspired by the visual perception mechanism of animals [20]. CNNs extract relevant information from training data, preserving them in form of linear filters (i.e., weights) and bias, which are applied to new inputs to obtain maps related to the spatial occurrences of informative features. In this way, weights are shared between different positions and the output of a convolutional layer is equivariant with respect to shift operations [21].
For problems involving the extraction of global information from data, such as image classification, a progressive undersampling of the input dimensions is performed by means of pooling layers of non-unitary stride: these aim at suppressing noisy or irrelevant features, while offering high level representations [21] and preserving computational resources. However, strides are associated with some undesirable drawbacks, such as the loss of temporal dependencies and the aliasing phenomenon, which might be particularly important for time series analysis. Hence, the solutions presented in [4] and [19], although being based on deep regression models with extremely low algorithmic burden, could not offer the optimal choice: the reason is that, for regression problems like event picking tackled in this work, all the information related to the instant of occurrence of a specific feature might be lost due to the pooling layers and because of strides.
Consequently, to maximize the ToA prediction accuracy, it is mandatory to preserve temporal resolution whilst also considering a sufficiently long observation window, necessary to make each prediction aware of the full signal history. This means that the receptive field of a single output neuron associated to an input instant, defined as the patch of the input that affects its activation, should be wide enough. Considering a single path processed via a fully convolutional 1-dimensional neural network, the receptive field R f L associated to a generic neuron at layer L is expressed by:
R f L = ∑ l = 1 L ( k l − 1 ) ∏ i = 1 l − 1 d t i + 1
where k l is the kernel size of the l-layer while d t i is the stride factor at layer i. Another possibility to increase the network prediction capability if offered by the increment in the dimension of the kernel and/or in the number of hidden layers. However, for hardware-oriented applications in which spatial information must be preserved across the network and the neural models must be run on edge sensors with limited computational capabilities, this solution is not viable.
To overcome this issue, a more fruitful alternative is proposed in this work, which is based on the exploitation of dilated convolutional operators in place of the standard convolutional layers. The key point behind dilated convolution (schematically depicted in Figure 1) is that certain weights are fixed to zero, hence introducing a sort of holes in the kernels. The spacing between non-zero coefficients is constant along each dimension, and the associated dilation rate d is defined as the spacing plus one. It follows that, when d = 1 , conventional convolution is performed. Consequently, Equation (1) can be rewritten by replacing, in all layers, the kernel size k with a novel formulation, reading as:
k ˜ = d ( k − 1 ) + 1
By looking at Figure 1, it is notable that NN architectures based on dilated convolution can support exponential expansion of the receptive field without loss of resolution or coverage [22]. When the stride factor is fixed at 1 and the appropriate padding is applied, the dimension of the output is the same as the one of the input.
The resulting model proposed in this study is presented in Figure 2a, while the structure of the constitutive building blocks is illustrated in Figure 2b; in the following, this network will be referred to as DilCNN. First, local features are extracted using convolutional blocks with unitary dilation rate. At the end of each block, a MaxPooling operator is introduced to suppress noisy information and reduce the computational complexity of the subsequent layers. Although such operation implies a loss of temporal resolution, its effect become negligible when the number MaxPooling layers is limited, in favor of a better compatibility with the tight constraints of low-end microprocessors. Then, local features are combined with a stack of non causal dilated convolutions, to exploit both the past and the future trends of the signal which might be equally informative for our purposes. The dilation rate is increased exponentially after each layer, with an exponential basis equal to 2. Finally, the probability of the presence of an acoustic ToA in each timestamp is computed by means of a 1 × 1 convolution activated by a sigmoid function.
The network is trained end-to-end using binary cross-entropy as loss function, after converting each time label into a single hot vector of proper dimension. Nevertheless, this strategy might suffer from the same problems proper of unbalanced segmentation, i.e., the networks might tend to assign a score denoting the dominant class (the absence of an acoustic onset) to each timestamp: hence, a weight W p ≥ 1 has been applied to the false negative term, leading to the loss function L c e in Equation (3):
L c e = − 1 N ∑ i = 1 N W p y i l o g ( y ˜ i ) + ( 1 − y i ) l o g ( 1 − y ˜ i )
with N being the number of samples, while y i and y ˜ i are the label and the prediction associated to instant i, respectively. Residual connections between different blocks are also added to avoid potential gradient losses, that may be a typical problem of deep NNs [24].

2.2. Capsule Neural Networks

CapsNets have been introduced in [17] to solve some of the intrinsic limitations of CNNs when solving image classification tasks. The latter can be summarized as follows: i) CNNs have difficulties in generalizing to novel viewpoints [17]: the ability to deal with translation is built-in, but in the case of other affine transformations, we have to enlarge the training data with additional data samples that can provide knowledge about such new viewpoints; ii) conventional CNNs classification architectures relies on gradual undersampling of the input space, which can lead to the loss of significant information and spatial relationship between features [4,16], e.g., the classifier can be tricked and infer a false positive if an object in the scene has the same sub-components of the target but in different positions, thus belonging to a different class.
CapsNets overcome these issues by: i) using transformation matrices that learn how to encode the intrinsic spatial relationship between a part and a whole, ensuring better generalization capabilities, ii) substituting scalar activations by vectors which are equivariant with respect to the transformations to be applied to the input [17,25]. Another non negligible benefit of CapsNets is their ability to learn from comparatively smaller datasets, preserving salient data information such as position and location [16].
A CapsNet architecture is typically stacked on top of a convolutional network, which is in charge of local feature extraction, and consists of the following two layers:
  • Primary Capsule Layer: the first component of this layer is a convolutional operator with a number of channels M P C × D P C , where M P C indicates the number of primary capsules per spatial - or temporal - position. Thus, the output of this operator is reshaped, starting from the channel dimension, into a set of N P C = K × M P C vectors s i with D P C coordinates, which are the so called primary capsules u i , with K being the number of temporal positions. These primary capsules are activated by means of a non-linear squash function and finally mapped into a probability value, according with [17]:
    u i = | | s i | | 2 1 + | | s i | | 2 s i | | s i | | 2
  • Capsule Layer: each primary capsule u i with i ∈ { 1 . . . N P C } generates a prediction u i | j for every j − t h class - with j ∈ { 1 . . . N c l a s s } - by means of a weight opinion matrix W i j :
    u ^ i | j = W i j u i
    Such opinion matrices are learned during training and encode the relationship between local low-level features and the high-level entities associated to classes; hence, they are invariant to transformations applied to the input. In this way, capsules provide a simple way to detect global features by recognizing the individual contributions of the parts [25]. A global prediction p j for each class is, indeed, computed as a linear combination of the vectors obtained via Equation (5), yielding to:
    p j = ∑ i = 1 N P C c i j u ^ i | j
    Individual p j are then activated by the squash function in Equation 4. Coefficients c i j are determined following the dynamic routing protocol [17]. It consists in an iterative process, summarized in Algorithm 1, which combines together the output of single capsules with the appropriate parent belonging to the layer above. The pairing procedure works as follows: if u ^ i | j has a large scalar product with the global output of a possible parent class, there is a top-down feedback which increases the coupling coefficient for that parent while decreasing it for the other ones. It follows that, the higher the norm of an output vector, i.e., the higher the level of agreement between low-level capsules which are associated to its parts, the higher the likelihood that the corresponding feature class describes the input data.
The margin loss has been used as cost function during training, since it can sum together the components related to individual classes:
L m a r g i n = ∑ k = 1 N c l a s s T k m a x ( 0 , m + − | | v k | | ) 2 + λ ( 1 − T k ) m a x ( 0 , | | v k | | − m − ) 2
where T a = 1 if class a (a being 1 or 0) is present, while m + = 0.9 , m − = 0.1 and λ = 0.5 are tunable hyperparameters.
Algorithm 1 Dynamic Rounting
  • for all capsule i in layer l and capsule j (i.e., class) in layer ( l + 1 ) : b i j ← 0
  • forr iterations do
  •     for all capsule i in layer l: c i j ← softmax ( b i j ) = e x p ( b i j ) ∑ k e x p ( b i k )
  •     for all capsule j in layer ( l + 1 ) : p j ← ∑ i c i j u ^ i | j
  •     for all capsule j in layer ( l + 1 ) : v j ← squash ( p j )
  •     for all capsule i in layer l and capsule j in layer ( l + 1 ) : b i j ← b i j + u ^ i | j · v j
  • end for
  • return v j for all capsule j in layer ( l + 1 )
In this work, r = 3 has been imposed after an appropriate tuning of this parameter. CapsNets based on dynamic routing can solve classification problems where it is reasonable to assume that, at most, only one instance per class is present in the input scene [17]. Accordingly, in our scenario, only one wave arrival is supposed to be present in each processed time series, which are thus split into overlapped windows of length N w = 400 : label 1, corresponding to class A E , is assigned only when a data point has no samples preceding ToA, i.e., it is fully contained into the time slot corresponding to the target acoustic event and not into its pre–onset temporal sequence; otherwise, class N o i s e (label 0) is attributed, indicating noisy windows. The task solved by the designed CapsNet is, thus, to perform a binary classification distinguishing between these two classes, i.e., AE event or noise. Hence, a dedicated post-processing logic has to be applied to extract the sought ToA.
Similar to the solutions adopted in [4,15,16,26], predictions are formulated by computing the probability curve related to the A E class, i.e., sliding a window with a constant stride and calculating the norm of the output vector corresponding to such class for each shift. The stride factor has been selected equal to the pooling factor of the feature extraction layers in the DilCNN model (i.e., 8), in order to obtain a fair comparison between the two networks using the same temporal resolution. To this end, a dilated CNN, similar to the one presented in Section 2.1 but without the first three d = 1 convolutional layers followed by MaxPooling and different number of channels (i.e., 16, 32 and 64), has been considered: in this way, it is possible to detect the window containing the onset of the signal without relying on less generalizable and prone to noise methods such as simple thresholding schemes. The overall CapsNet model, henceforth denoted as CapsToA, is illustrated in Figure 3: in particular, Figure 3a shows the capsule neural network adopted for the classification of windows, while the post–processing dilated CNN is reported in Figure 3b. The two model are trained separately and the input of the latter is constituted by the time sequence obtained by concatenating A E class predictions related to adjacent windows. Since no padding is applied and input signals consist of 5000 samples, such curve is composed by ( 5000 − N w ) / s t r i d e + 1 = ( 5000 − 400 ) / 8 + 1 = 576 timestamp.

2.3. Quantization Schemes

Models have to be converted into MCU-compliant and low-depth format (i.e., 8-bit) to be portable on edge devices. This procedure, referred to as quantization, is crucial to provide a significant reduction in both the memory footprint and computational complexity, especially considering the critical resource constrains which characterize tiny embedded devices with low-power consumption. Another fundamental reason supporting the necessity of quantization is that a great number of hardware platforms widely used in DSP applications is equipped with instruction sets (ISA) which are optimized for sub-word operands [27]: this means that a single instruction can be applied simultaneously to multiple operands with a bit resolution smaller than the parallelism of the data bus. However, the conversion of weights and activations into int8 type could lead to a performance degradation due to the lower representation capability provided by the NN models. Techniques have been developed to minimize the effect of this unavoidable operation.
In general terms, a quantization scheme can be defined as the mapping between the bit-representation of values (denoted q in the following) and their interpretation as real mathematical numbers (r) [28]. Quantization procedures are typically implemented using integer-only arithmetic during inference and floating-point arithmetic at training time. We refer to post-training quantization (PTQ) when the model is converted into a lower precision representation after a training process consisting in a stochastic gradient descent implemented in floating point via a backpropagation algorithm. An alternative to this approach is the so called quantization-aware training (QAT), in which trainable parameters, i.e., weights and biases, are updated in floating point arithmetic as usual, while the forward propagation necessary to the computation of the loss for each batch relies on fake-quantization layers. The latter are used to emulate non-linear noise introduced by the desired compression of weights and activations by means of a rounding mechanism [28,29]. QAT has the advantage of totally preserving the accuracy of the model after conversion, but typically leads to longer training time [29,30] and could imply a worst overall performance with respect to PTQ. For such reasons, only PTQ will be adopted in this work: it has been implemented in a static fashion, meaning that activation ranges are calculated during model conversion from a reduced batch of sample data, allowing to calibrate quantization parameters without introducing any overhead at runtime.
To accomplish this, public open source libraries have been used. More in detail, DilCNN models were quantized by means of TensorFlow Lite4 (TFLite), a framework for deploying TF models on mobile and other edge devices, also providing a specific library for the execution on MCUs (the TensorFlow Lite for Microcontroller framework5 or TFLite-Micro) including 8-bits kernel implementations of the majority of the Keras layers and TF built-in operators. TFLite-based quantization uses integer-only arithmetic without relying on a fixed-point format for the purpose of value conversion: it applies an affine mapping of integers q to real numbers r [28] according with:
r = S ( q − Z )
where S is a floating point number denoted as scale factor while Z is the integer zero-point. This quantization scheme uses the same quantization parameters for all values within each activation or weight array. Hence, separate arrays use different quantization parameters. Weights of dilated convolutional layers have been mapped as pair or values ( S , Z ) (corresponding to per-axis or per-channel conversion), since this can reduce the impact of quantization [31].
Such parameters (S and Z) depend both on the number of bits adopted in the quantized layer and on the numerical range covered by a tensor. For this reason, while the ones associated with weights can be derived directly from the trained model, a representative set of input data is required in order to calibrate the ones related to activations for the case of static PTQ. For further details, the reader is referred to [28] and to the TFLite documentation for 8-bit quantization6.
Contrariwise, for the 8-bit implementation of the CapsNet architecture, we rely on the framework proposed in [31]7, which provides a ready-to-use library for the edge execution of capsule Layers on Arm®Cortex®-M and RISC-V MCUs, along with a quantization tool in Python environment compatible with models developed in Keras. This library developed for Cortex-M is an extension of CMSIS-NN [32] and implements 8-bit optimized kernels for matrix multiplication which uses the Single Instruction - Multiple Data (SIMD) features of Armv7E-M and Armv8-M architectures for Multiply-and-Accumulate (MACC) operations. Since the related ISA do not feature 4x8-bit operands MACC, they rely on 2x16-bit MACC performed after a sign extension.
Unlike the TFLite framework, a fixed point notation with power-of-two scaling is used in this case for the quantization of trainable parameters and activations, i.e., each tensor is associated to a Q m . n format where m is number of integer bits while the remaining n are considered for the fractional part. It is important to note that m + n = 7 since the last bit is used for the sign. The framework proposed in [31] enhances the precision in layers with very small weights by virtually increasing the number of fractional bits: every weight still fits in 8 bits, but the quantization format can, virtually, surpass this barrier. Once the right fixed-point formats are defined, weights and biases are appropriately scaled and clipped into the range [-128, 127]. Then, the amount of bit-wise shifts which should be applied after each fixed point matrix operations is calculated. Nevertheless, the output probability related to the AE class is retained into a 32-bit format in order to avoid the saturation of the curve, which would complicate the extraction of the ToA, then rescaled into an 8-bit representation via Equation (8) before passing through the subsequent DilCNN model. The final DilCNN-based ToA logic has been quantized analogously to the previously described DilCNN by means of the TFLite framework, since the two models of CapsToA are trained separately and then stacked together.

3. Model deployment process, training and testing

3.1. Materials

The STM32L496ZGT-P Nucleo board [33] equipped with an ARM ®-Cortex®M4 core and maximum clock frequency of 80 MHz has been employed for prototyping purposes. It features 1 MB of FLASH memory and 320 KB of SRAM, which are compatible with the typical characteristics of edge nodes to be deployed for long–lasting SHM monitoring. The X–CUBE–AI expansion package 8 has been used as development environment for the embodiment of the sought models.

3.2. Dataset generation

The dataset for the training phase has been built via numerical simulations. This procedure based on synthetic AE signals has been preferred over a purely experimental approach for two main reasons: the former is that it allows to speed up the data collection phase, since a relatively short amount of time is necessary to generate a representative pool of data; secondly, and more importantly, it permits the fast creation of ground truth labels for supervised learning (as it is the case of the adopted solutions), a condition which is not applicable in passive AE monitoring scenarios where the true AE triggering time is always unknown to the sensing system.
When an AE event occurs in a waveguide as a consequence of crack, corrosion or delamination, the corresponding release of energy can travel along the structure in the form of ultrasonic guided waves (GWs). The propagation characteristics of GWs can be numerically modeled when the geometrical and mechanical parameters of the monitored structure are known. To this end, an ad–hoc ray–tracing algorithm has been exploited in this work, which simulates the peculiar propagation behavior of GWs between different combinations of points on a thick aluminum plate while taking into consideration also the effects of multiple reflections due to the mechanical boundaries.
The entire number of combinations between the selected points for AE actuation and reception has been chosen randomly, while also changing the SNR into the set { 1 , 2 , 4 , 6 , 8 , 10 , 12 , 15 , 18 , 20 , 25 , ∞ } for a total amount of 60 000 time series: 80% of this data was used for training and validation and the remaining 20% was allocated to testing. In Figure 4, exemplary signals are showed with the assigned labels.

3.3. Validation process

The performance of the different models has firstly been assessed on the synthetic testing dataset (12 000 time series) introduced in Section 3.2. Mean Absolute Error (MAE) and Root Mean Square Error (RMSE) are used in this first validation step as performance metrics. Then, the ToA prediction algorithms have also been tested for localization purposes in an experimental setting involving a thin aluminum plate ( 1000 × 1000 × 3 mm ) instrumented with three custom sensor nodes (installed on three corners of the structure) developed within the Intelligent Sensor Systems lab of the University of Bologna and located at as many corners of the structure (see Figure 5). Thanks to the compact design including all the circuitry and electronics necessary to collect, pre-process and characterize signals, each device works as a miniaturized oscilloscope capable of acquiring, at the same time, signals on three different input channels with a capacity of 4 MS/s. All the details about the sensor node characteristics can be found in [34,35]. This plate has been selected since it presents identical mechanical and geometrical properties to the one adopted for numerical simulations; thus, it allows the exploitation of the same NN models trained on the simulated time series.
Nine different positions have been considered for excitation: each test has been repeated three times, for a total amount of 27 tests. The adopted sensor installation plan is compatible with the triangulation method in [36], whose complete mathematical formulation can be found in [4]: the algorithm is advantageous in that, thanks to simple geometrical considerations, it allows the retrieval of a source position simply by knowing the difference in ToA of three sensing units placed at known position. Such testing procedure has been necessary since, as anticipated, it is not possible to get an educated guess about the true label in case of real–field scenario due to the passive nature of AE monitoring. In these terms, localization offers an indirect means for quantifying the performances in ToA estimation by computing the spatial error between the true impact position and the estimated one.
Furthermore, since the primary advantage of AI approaches is that they can efficiently learn patterns even in very noisy data, the impact of progressively increasing noise levels on the predicted ToA has been specifically evaluated. To this end, gathered data have been corrupted with an additive white Gaussian noise (AWGN) such that the corresponding SNR moves from 20 dB to 2 dB at integer steps of 4 dB. Despite the fact that the nature of the background noise of real AE signals can differ [5], additive white stationary noise (such as the one generated by electronic components) can be assumed to be the main source of SNR degradation and, consequently, was used to simulate noisy AE scenarios in this study.

4. Results

4.1. Preliminary validation on synthetic signals

Results on synthetic waveforms are summarized in Table 1, for different intervals of SNR. The performances attained by AIC and the STA/LTA–based thresholding algorithm are also reported. In the latter case, the ratio between the two moving average is computed on the absolute value of Hilbert–transformed signals: ToA has been retrieved as that time index for which threshold is exceeded first. Such threshold has been fixed at 10 while the two window lengths (5 and 250, respectively) have been empirically tuned on a subset of training data.
As can be observed from Table 1, all the DL models widely outperforms other statistical or threshold-based methods, especially in presence of high noise levels. More in detail, DilCNN is quite insensitive to noise, obtaining very similar MAE and RMSE for all the considered SNRs. Moreover, it is paramount to emphasize that its quantized version (DilCNN int8) scores the same accuracy levels, with a negligible loss of performances. CapsToA behaves comparatively better than AIC and STA/LTA, even if proving to be more sensitive to noise disturbances. A slight degration is noticeable for its MCU implementation (CapsToA int8), but still reaching significantly better metrics (both for MAE and RMSE) than the alternative DL-free solutions, as demonstrated by average gain of 30x for the whole set of noise ranges.
Additionally, the computational complexity, intended as the number of MACC operations, has also been estimated, together with the overall execution time (expressed both in clock cycles T c k and m s ) and the RAM and flash footprint of the generated models when run on the STM32L4 MCU. All these values are summarized in Table 2 and are provided only for the int8 quantized models, since they are the only DL architectures running on the target embedded platforms, hence being these defining parameters of crucial interest.
By looking at Table 2, it is possible to observe how differences in kernel implementations affects the computational efficiency of our networks. In fact, TFLite micro kernels used for the implementation of DilCNNs models performs much faster in case of conventional convolution if compared to dilated convolution, as demonstrated by the difference in the Tck/MACC ratio between the first model and the DilCNN-based post–processing logic adopted in the CapsToA architectures: the reason is that the former distributes its complexity mainly on d = 1 convolution operations, unlike the latter.

4.2. Real–field validation for AE localization

In this Section, the results in terms of localization accuracy when dealing with real-field data are presented, by sweeping the SNR. Figure 6 reports some examples of collected signals, along with the predictions obtained by using the different identification, which are better magnified in the second row in which a zoomed interval is depicted.
Results for source localization are statistically analysed in Figure 7 in terms of boxplots for the noise-free configuration, while Figure 8 summarizes the outcomes when testing on signals corrupted by increasing levels of artificial AWGN added via software elaboration. Boxes are limited between the 25th and 75th percentiles of the sample data, while the horizontal line stands for the statistical median. Data points marked with a black cross are outliers, which are identified as those values greater than q 3 + 1.5 ( q 3 − q 1 ) or less than q 1 − 1.5 ( q 3 − q 1 ) , where q 1 and q 3 are respectively the 25th and 75th percentiles. The dashed vertical extrema of each box represent the whiskers.
Moreover, it is important to mention that large errors in ToA identification may lead to non-physical configuration in which a possible source location does not exist analytically or it is located out of the geometrical boundaries of the plate: when this applies, the corresponding tests has been denoted as failed. The different failure rates, expressed as the ratio between the total number of failed tests over the total amount of performed experiments, are summarized in Table 3, for each algorithm and SNRs; median values in localization accuracy have also been displayed.
Above results confirm again the superiority of DL models in dealing with critically noisy scenarios with respect to traditional methods. Indeed, these charts validates that, for all the considered noise configurations, both the failure rate and source position estimation are significantly improved when AI models solutions are considered, being AIC and STA/LTA affected by i) a remarkable statistical dispersion (larger boxplots) and ii) much lower success rate. For example, when the SNR is equal or below 4 dB, median error values reached by the less performing quantized neural model, i.e., CapsToA int8, decrease more than 66% and 62% at 4 dB and 2 dB, respectively, when compared to AIC-related scores (which is the most accurate amidst the two conventional algorithms). Proof is the fact that, opposite to its quantization-free version, CapsToA int8 undergoes a penalty on median value of about 17.9% at 4 dB and 22.7% at 2 dB after quantization.
DilCNN presents a moderate performance degradation as the noise level increase, as opposite to behavior observed in case of synthetic AE signals. This might be due to the slight difference between the simulated and the actually measured data, as evident by comparing the waveforms in Figure 4 and Figure 6. However, between the two DL networks, DilCNN is the one which shows the best accuracy at low SNRs after conversion to 8-bit precision, with a maximum degradation in the median value below the 21% and a 48% for the worst case situation of SNR = 4 dB. All these experimental observations further corroborate the quality of the previously quantified results obtained in case of analytical frameworks, disclosing novel opportunities for sensor-near AE signal characterization and defect localization.

5. Conclusions and Future Works

In this work, NN models suited for the estimation of the ToA in acoustic signals have been presented and deployed on a general-purpose MCU, showing their aptness for sensor-near AE data mining even in presence of significant noise levels. A prototyping board equipped with an STM32L4 MCU has been used to attain this goal: the performances of the devised solutions, called as DilCNN and CapsToA, have been thoroughly validated on both synthetic signals and real–field data under different noisy conditions. The obtained outcome shows that, when working on simulated waveforms, the devised models can predict ToA with a MAE which is up to 16x and 36x lower than the one scored by the standard AIC and STA/LTA algorithm, respectively. More importantly, it has been shown that the same models can be run on the target low-end microcontroller without affecting the resulting performances. Similar metrics were confirmed also when processing real data in a framework involving the localization of AE sources on a metallic plate: in this case, the adoption of AI solutions can reduce the median error from 25 cm (AIC) down to 5 cm (DilCNN) when the SNR is as low as 4 dB.
These evidences unlock new potential for the edge or extreme–edge inference of AE data and, by extension, propose novel approaches to AE-based SHM: the designed networks are superior in that they can alleviate the burdensome requirement of transmitting long time series to central processing units while preserving the accuracy of the integrity evaluation process. Future works will explore data augmentation techniques, necessary for the sake of data representation and increased generalization capabilities. From a TinyML perspective, parallel ultra-low-power edge microprocessors will be exploited as target boards in order to shrink further the computation time.

Author Contributions

Conceptualization, G.D. and F.Z.; methodology, G.D. and F.Z.; software, G.D.; validation, G.D. and F.Z.; formal analysis, G.D. and F.Z.; investigation, G.D. and F.Z.; resources, F.Z. and L.D.M.; data curation, G.D. and F.Z.; writing—original draft preparation, G.D. and F.Z.; writing—review and editing, G.D., F.Z. and L.D.M.; visualization, G.D. and F.Z.; supervision, F.Z. and L.D.M.; project administration, L.D.M.; funding acquisition, F.Z. and L.D.M. All authors have read and agreed to the published version of the manuscript.

Funding

This research was partly funded by PNRR – M4C2 – Investimento 1.3, Partenariato Esteso PE00000013 – “FAIR – Future Artificial Intelligence Research” – Spoke 8 “Pervasive AI”, funded by the European Commission under the NextGeneration EU programme.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data for this work are not available.

Acknowledgments

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:
AE Acoustic Emission
AI Artificial Intelligence
AIC Akaike Information Criterion
CapsNet Capsule Neural Network
CapsToA CapsNet for ToA estimation
CNN Convolutional Neural Network
DilCNN Dilated Convolutional Neural Network
DL Deep Learning
DSP Digital Signal Processing
ISA Instruction Set
MACC Multiply and Accumulate
MAE Mean Absolute Error
MCU Microcontroller Unit
RMSE Root Mean Square Error
SHM Structural Health Monitoring
SLA/STA Short-Time Average on Long-Time Average
SNR Signal-to-noise Ratio
TinyML Tiny Machine Learning
TF Tensorflow
TF Lite Tensorlflow Lite
ToA Time of Arrival

Notes

1
https://www.tinyml.org/, accessed on Tuesday, 2 May 2023
2
https://keras.io/, accessed on Friday, 28 April 2023
3
https://www.tensorflow.org/, accessed on Friday, 28 April 2023
4
https://www.tensorflow.org/lite, accessed on Thursday, 27 April 2023
5
https://github.com/tensorflow/tflite-micro, accessed on Thursday, 27 April 2023
6
https://www.tensorflow.org/lite/performance/quantization_spec, accessed on Thursday, 27 April 2023
7
https://gitlab.com/ESRGv3/q7-capsnets, accessed on Thursday, 27 April 2023
8
https://www.st.com/en/development-tools/stm32cubemx.html, accessed on Tuesday, 2 May 2023

References

  1. Nair, A.; Cai, C. Acoustic emission monitoring of bridges: Review and case studies. Engineering structures 2010, 32, 1704–1714. [Google Scholar] [CrossRef]
  2. Pedersen, J.F.; Schlanbusch, R.; Meyer, T.J.; Caspers, L.W.; Shanbhag, V.V. Acoustic Emission-Based Condition Monitoring and Remaining Useful Life Prediction of Hydraulic Cylinder Rod Seals. Sensors 2021, 21, 6012. [Google Scholar] [CrossRef] [PubMed]
  3. Madarshahian, R.; Ziehl, P.; Todd, M.D. Bayesian Estimation of Acoustic Emission Arrival Times for Source Localization. In Model Validation and Uncertainty Quantification, Volume 3; Springer, 2020; pp. 127–133.
  4. Zonzini, F.; Bogomolov, D.; Dhamija, T.; Testoni, N.; De Marchi, L.; Marzani, A. Deep Learning Approaches for Robust Time of Arrival Estimation in Acoustic Emission Monitoring. Sensors 2022, 22, 1091. [Google Scholar] [CrossRef] [PubMed]
  5. Barat, V.; Borodin, Y.; Kuzmin, A. Intelligent AE signal filtering methods. Journal of Acoustic Emission 2010, 28, 109–119. [Google Scholar]
  6. St-Onge, A. Akaike information criterion applied to detecting first arrival times on microseismic data. In SEG technical program expanded abstracts 2011; Society of Exploration Geophysicists, 2011; pp. 1658–1662.
  7. Trnkoczy, A. Understanding and parameter setting of STA/LTA trigger algorithm. In New manual of seismological observatory practice (NMSOP); Deutsches GeoForschungsZentrum GFZ, 2009; pp. 1–20.
  8. Gopinath, S.; Ghanathe, N.; Seshadri, V.; Sharma, R. Compiling KB-sized machine learning models to tiny IoT devices. In Proceedings of the Proceedings of the 40th ACM SIGPLAN Conference on Programming Language Design and Implementation, 2019, pp. 79–95. 79–95.
  9. Ross, Z.E.; Rollins, C.; Cochran, E.S.; Hauksson, E.; Avouac, J.P.; Ben-Zion, Y. Aftershocks driven by afterslip and fluid pressure sweeping through a fault-fracture mesh. Geophysical Research Letters 2017, 44, 8260–8267. [Google Scholar] [CrossRef]
  10. Chen, Y. Automatic microseismic event picking via unsupervised machine learning. Geophysical Journal International 2020, 222, 1750–1764. [Google Scholar] [CrossRef]
  11. Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015: 18th International Conference, Munich, Germany, October 5-9, 2015, Proceedings, Part III 18. Springer, 2015, pp. 234–241.
  12. Zhu, W.; Beroza, G.C. PhaseNet: a deep-neural-network-based seismic arrival-time picking method. Geophysical Journal International 2019, 216, 261–273. [Google Scholar] [CrossRef]
  13. Zheng, J.; Lu, J.; Peng, S.; Jiang, T. An automatic microseismic or acoustic emission arrival identification scheme with deep recurrent neural networks. Geophysical Journal International 2018, 212, 1389–1397. [Google Scholar] [CrossRef]
  14. Han, Z.; Li, Y.; Guo, K.; Li, G.; Zheng, W.; Liu, H. A Seismic Phase Recognition Algorithm Based on Time Convolution Networks. Applied Sciences 2022, 12, 9547. [Google Scholar] [CrossRef]
  15. Saad, O.M.; Chen, Y. Earthquake detection and P-wave arrival time picking using capsule neural network. IEEE Transactions on Geoscience and Remote Sensing 2020, 59, 6234–6243. [Google Scholar] [CrossRef]
  16. Saad, O.M.; Chen, Y. CapsPhase: Capsule neural network for seismic phase classification and picking. IEEE Transactions on Geoscience and Remote Sensing 2021, 60, 1–11. [Google Scholar] [CrossRef]
  17. Sabour, S.; Frosst, N.; Hinton, G.E. Dynamic routing between capsules. Advances in neural information processing systems 2017, 30. [Google Scholar]
  18. Rojas, O.; Otero, B.; Alvarado, L.; Mus, S.; Tous, R. Artificial neural networks as emerging tools for earthquake detection. Computación y Sistemas 2019, 23, 335–350. [Google Scholar] [CrossRef]
  19. Zonzini, F.; Donati, G.; De Marchi, L. A Tiny Machine Learning Approach to the Edge Localization of Acoustic Sources via Convolutional Neural Networks. In Proceedings of the Advances in System-Integrated Intelligence: Proceedings of the 6th International Conference on System-Integrated Intelligence (SysInt 2022), September 7-9, 2022, Genova, Italy. Springer, 2022, pp. 340–349.
  20. Tabian, I.; Fu, H.; Sharif Khodaei, Z. A convolutional neural network for impact detection and characterization of complex composite structures. Sensors 2019, 19, 4933. [Google Scholar] [CrossRef] [PubMed]
  21. Zeiler, M.D.; Fergus, R. Visualizing and understanding convolutional networks. In Proceedings of the Computer Vision–ECCV 2014: 13th European Conference, Zurich, Switzerland, September 6-12, 2014, Proceedings, Part I 13. Springer, 2014, pp. 818–833.
  22. Yu, F.; Koltun, V. Multi-scale context aggregation by dilated convolutions. arXiv preprint 2015, arXiv:1511.07122. [Google Scholar]
  23. Zhang, Z. Improved adam optimizer for deep neural networks. In Proceedings of the 2018 IEEE/ACM 26th international symposium on quality of service (IWQoS). Ieee, 2018, pp. 1–2.
  24. He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the Proceedings of the IEEE conference on computer vision and pattern recognition, 2016, pp. 770–778.
  25. Hinton, G.E.; Krizhevsky, A.; Wang, S.D. Transforming auto-encoders. In Proceedings of the Artificial Neural Networks and Machine Learning–ICANN 2011: 21st International Conference on Artificial Neural Networks, Espoo, Finland, June 14-17, 2011, Proceedings, Part I 21. Springer, 2011, pp. 44–51.
  26. He, Z.; Peng, P.; Wang, L.; Jiang, Y. PickCapsNet: Capsule network for automatic P-wave arrival picking. IEEE Geoscience and Remote Sensing Letters 2020, 18, 617–621. [Google Scholar] [CrossRef]
  27. ARM Holdings. The DSP capabilities of ARM® Cortex®-M4 and Cortex-M7 Processors, 2016.
  28. Jacob, B.; Kligys, S.; Chen, B.; Zhu, M.; Tang, M.; Howard, A.; Adam, H.; Kalenichenko, D. Quantization and training of neural networks for efficient integer-arithmetic-only inference. In Proceedings of the Proceedings of the IEEE conference on computer vision and pattern recognition, 2018, pp. 2704–2713.
  29. Gholami, A.; Kim, S.; Dong, Z.; Yao, Z.; Mahoney, M.W.; Keutzer, K. A survey of quantization methods for efficient neural network inference. arXiv preprint 2021, arXiv:2103.13630. [Google Scholar]
  30. Rusci, M.; Fariselli, M.; Croome, M.; Paci, F.; Flamand, E. Accelerating RNN-Based Speech Enhancement on a Multi-core MCU with Mixed FP16-INT8 Post-training Quantization. In Proceedings of the Machine Learning and Principles and Practice of Knowledge Discovery in Databases: International Workshops of ECML PKDD 2022, Grenoble, France, September 19–23, 2022, Proceedings, Part I. Springer, 2023, pp. 606–617.
  31. Costa, M.; Costa, D.; Gomes, T.; Pinto, S. Shifting capsule networks from the cloud to the deep edge. ACM Transactions on Intelligent Systems and Technology (TIST) 2022, 13, 1–25. [Google Scholar] [CrossRef]
  32. Lai, L.; Suda, N.; Chandra, V. Cmsis-nn: Efficient neural network kernels for arm cortex-m cpus. arXiv preprint 2018, arXiv:1801.06601. [Google Scholar]
  33. ST Microelectronics. UM2179 User Manual STM32 Nucleo-144 boards (MB1312), 2019.
  34. Bogomolov, D.; Testoni, N.; Zonzini, F.; Malatesta, M.; de Marchi, L.; Marzani, A. Acoustic emission structural monitoring through low-cost sensor nodes. In Proceedings of the 10th International Conference on Structural Health Monitoring of Intelligent Infrastructure, 2021.
  35. Zonzini, F.; Malatesta, M.M.; Bogomolov, D.; Testoni, N.; Marzani, A.; De Marchi, L. Vibration-based SHM with upscalable and low-cost sensor networks. IEEE Transactions on Instrumentation and Measurement 2020, 69, 7990–7998. [Google Scholar]
  36. Jiang, Y.; Xu, F. Research on source location from acoustic emission tomography. In Proceedings of the 30th European Conference on Acoustic Emission Testing & 7th International Conference on Acoustic Emission, Granada, Spain; 2012. [Google Scholar]
Preprints 73817 g001
Figure 1. Working principle behind dilated convolutions.
Figure 1. Working principle behind dilated convolutions.
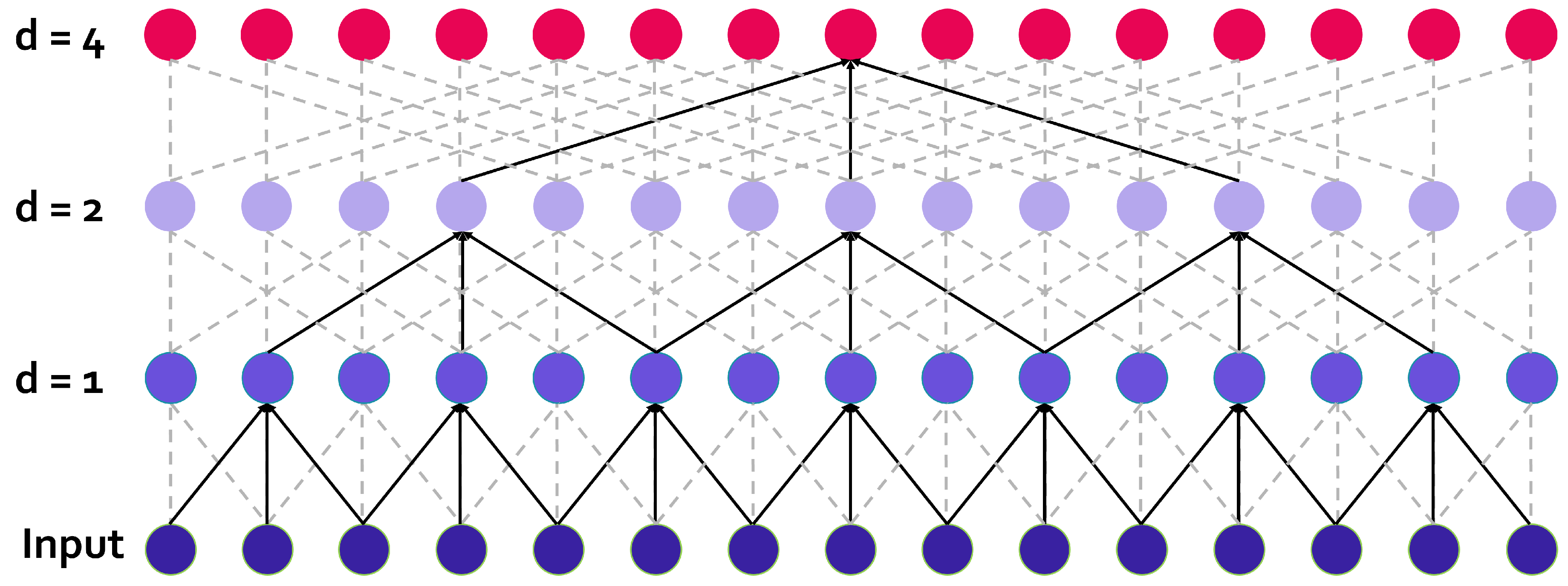
Preprints 73817 g001
Preprints 73817 g002
Figure 2. The DilCNN architecture proposed for ToA estimation: (a) full architecture, (b) constitutive building blocks. The model has been trained with Adam optimizer [23] for 10 epochs, using a learning rate equal to 0.001 and a batch size of 32. The parameter W p has been tuned at the value of 10. The total number of parameters is 86,153, of which 85,273 are trainable, while the network implies 117.89 millions of floating point operations. The number of timestamp at each layer is also reported in parentheses.
Figure 2. The DilCNN architecture proposed for ToA estimation: (a) full architecture, (b) constitutive building blocks. The model has been trained with Adam optimizer [23] for 10 epochs, using a learning rate equal to 0.001 and a batch size of 32. The parameter W p has been tuned at the value of 10. The total number of parameters is 86,153, of which 85,273 are trainable, while the network implies 117.89 millions of floating point operations. The number of timestamp at each layer is also reported in parentheses.
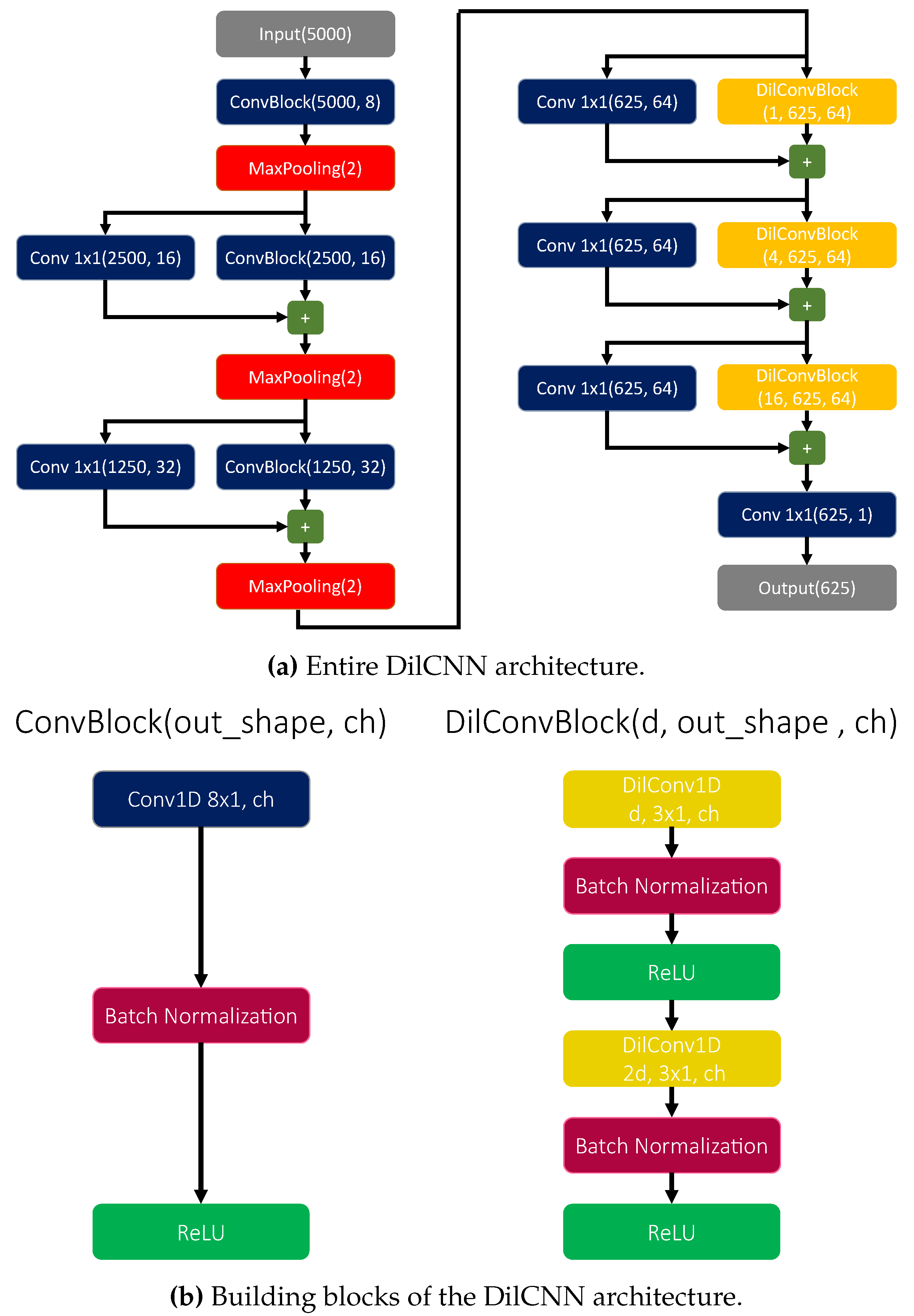
Preprints 73817 g002
Preprints 73817 g003
Figure 3. Implemented CapsToA: (a) CapsNet used as classifier: the model has been trained with Adam optimizer for 10 epochs using a learning rate equal to 0.001 and a batch size of 32; it relies on 54,136 trainable parameters and a single inference requires 0.567 millions of floating point operations; (b) post–processing dilated CNN: while training hyperparameters and optimizator are the same, in this case, the number of parameters is 27,697, of which 27,249 are trainable, and an inference requires 31.005 millions of floating point operations. Hence, the total number of parameters is 81,833: an amount which is comparable to the one related to the network described in Section 2.1.
Figure 3. Implemented CapsToA: (a) CapsNet used as classifier: the model has been trained with Adam optimizer for 10 epochs using a learning rate equal to 0.001 and a batch size of 32; it relies on 54,136 trainable parameters and a single inference requires 0.567 millions of floating point operations; (b) post–processing dilated CNN: while training hyperparameters and optimizator are the same, in this case, the number of parameters is 27,697, of which 27,249 are trainable, and an inference requires 31.005 millions of floating point operations. Hence, the total number of parameters is 81,833: an amount which is comparable to the one related to the network described in Section 2.1.
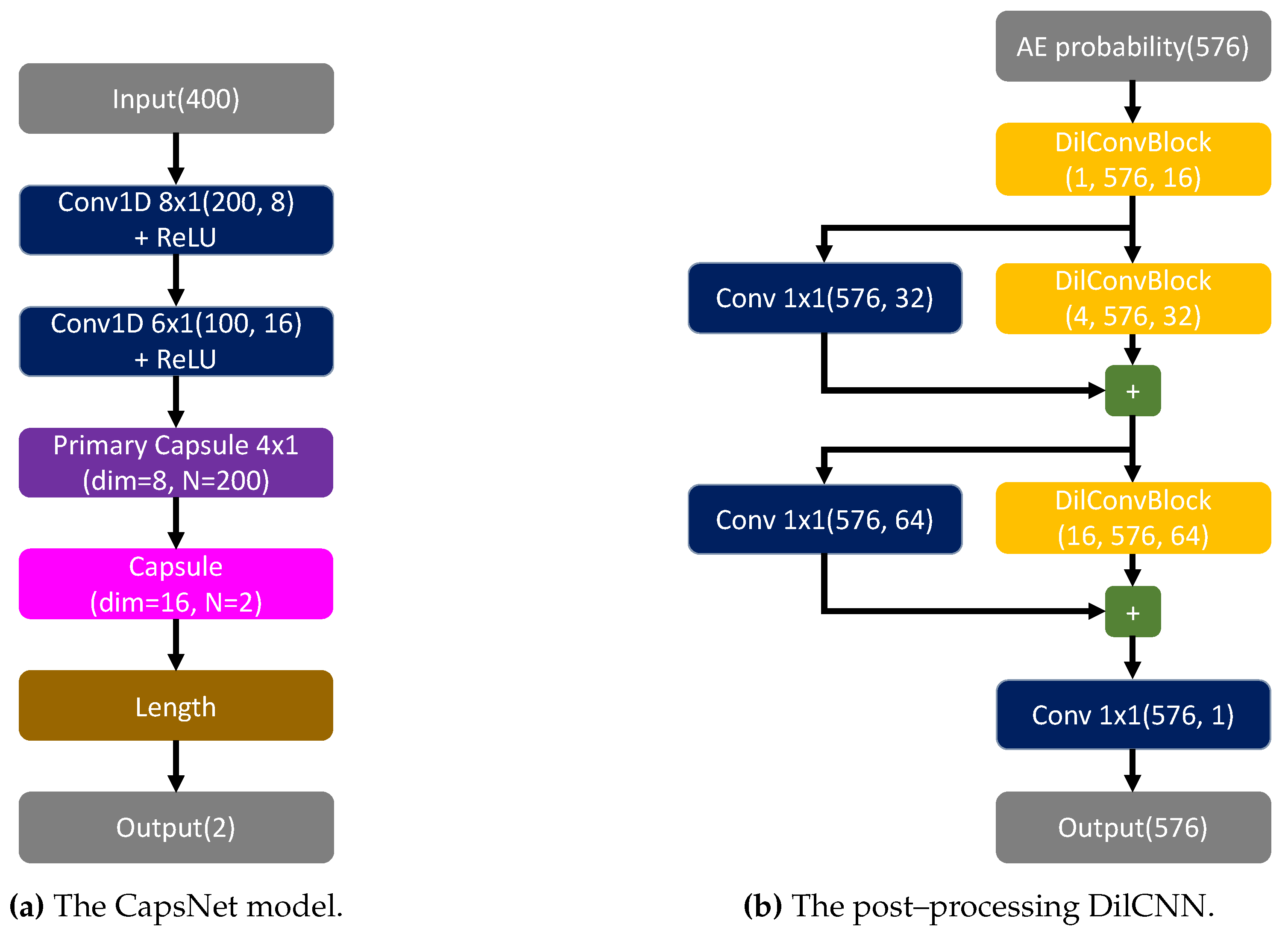
Preprints 73817 g003
Preprints 73817 g004
Figure 4. Example of signals generated by the numerical simulation at different SNRs. Ground truth labels are indicated with a red cross.
Figure 4. Example of signals generated by the numerical simulation at different SNRs. Ground truth labels are indicated with a red cross.
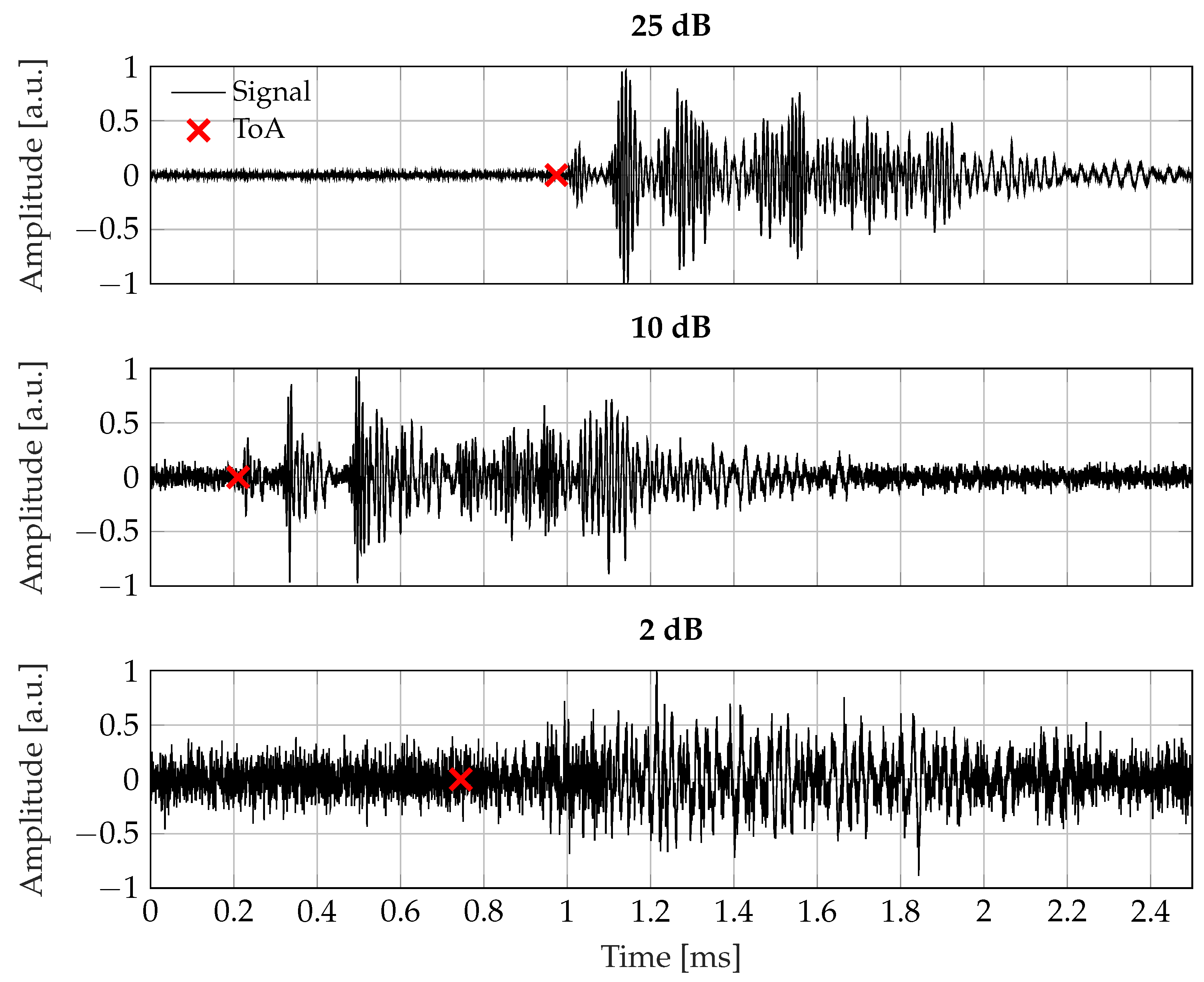
Preprints 73817 g004
Preprints 73817 g005
Figure 5. Experimental setup employed for AE source localization: three sensors (S1, S2, S3) are installed on three corners of the plate, while 9 different points equally spaced are considered for AE actuation.
Figure 5. Experimental setup employed for AE source localization: three sensors (S1, S2, S3) are installed on three corners of the plate, while 9 different points equally spaced are considered for AE actuation.
Preprints 73817 g005
Preprints 73817 g006
Figure 6. Examples of real signals acquired using the setup described in Section 3.3, along with the different predictions: 20 dB on the left, 4 dB of SNR on the right.
Figure 6. Examples of real signals acquired using the setup described in Section 3.3, along with the different predictions: 20 dB on the left, 4 dB of SNR on the right.
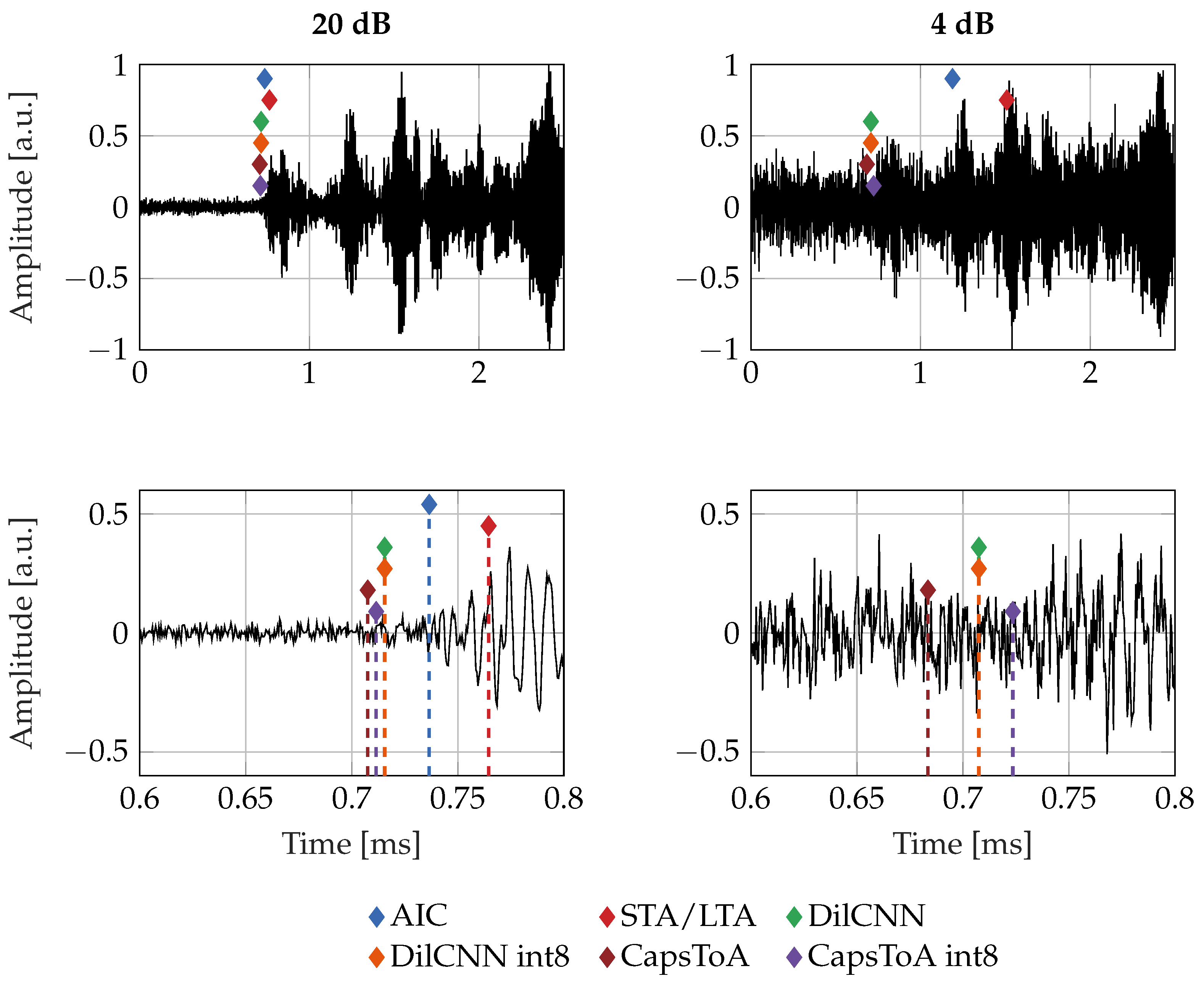
Preprints 73817 g006
Preprints 73817 g007
Figure 7. Boxplots related to localization performance achieved by the different ToA identification strategies when dealing with real–field AE signals: from SNR 20 dB down to 2 dB.
Figure 7. Boxplots related to localization performance achieved by the different ToA identification strategies when dealing with real–field AE signals: from SNR 20 dB down to 2 dB.
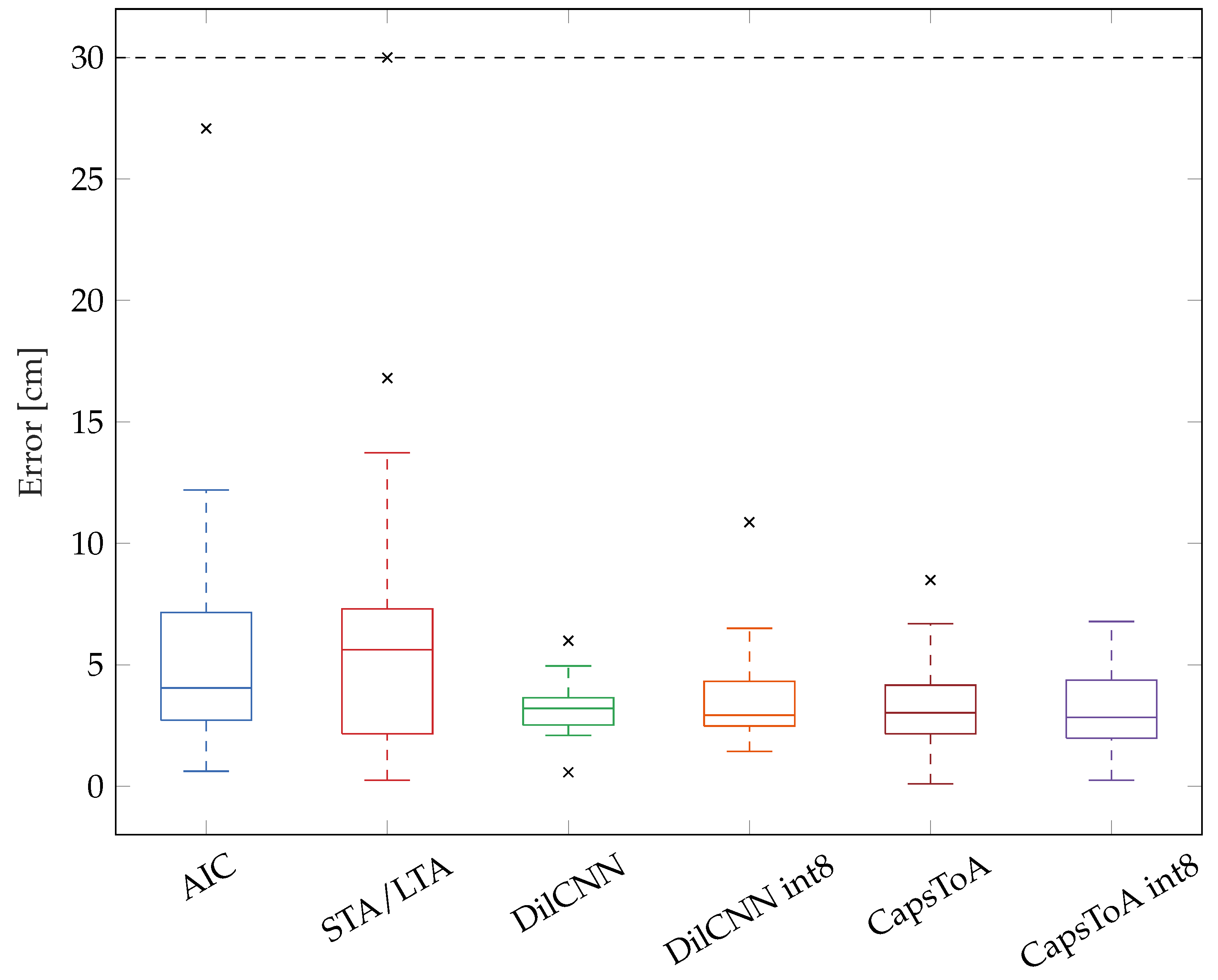
Preprints 73817 g007
Preprints 73817 g008
Figure 8. Boxplots related to the localization precision achieved by the different algorithms and models in the real–field validation test with superimposed AWGN.
Figure 8. Boxplots related to the localization precision achieved by the different algorithms and models in the real–field validation test with superimposed AWGN.
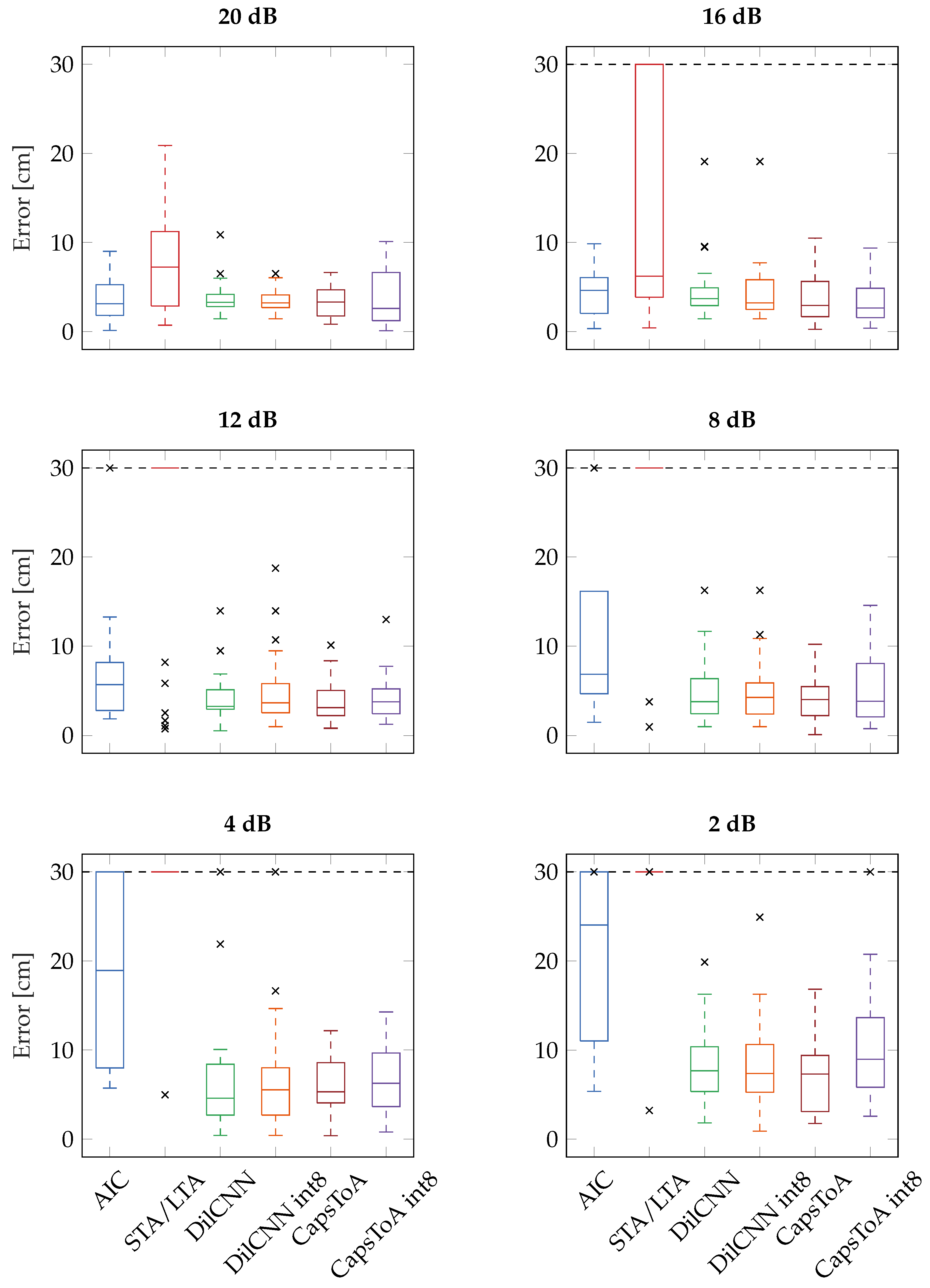
Preprints 73817 g008
Table 1. MAE and RMSE in ToA identification (expressed in µs) for different SNR intervals. NNs performances are reported both for floating point Keras models and for the int8-quantized versions.
Table 1. MAE and RMSE in ToA identification (expressed in µs) for different SNR intervals. NNs performances are reported both for floating point Keras models and for the int8-quantized versions.
Method SNR [dB] MAE [ µ s ] RMSE [ µ s ]
AIC ≥ 20 29.47 40.10
12 - 20 68.96 89.02
6 - 12 115.47 133.79
< 6 132.74 151.74
STA/LTA ≥ 20 59.56 106.23
12 - 20 150.38 213.31
6 - 12 229.00 321.83
< 6 301.88 401.31
DilCNN ≥ 20 8.29 29.98
12 - 20 8.25 29.89
6 - 12 8.23 29.81
< 6 8.24 29.78
DilCNN int8 ≥ 20 8.27 29.93
12 - 20 8.24 29.85
6 - 12 8.22 29.77
< 6 8.26 29.79
CapsToA ≥ 20 7.63 11.4
12 - 20 10.15 14.41
6 - 12 14.54 28.51
< 6 25.56 55.72
CapsToA int8 ≥ 20 16.39 23.68
12 - 20 19.81 50.29
6 - 12 22.46 32.05
< 6 43.79 71.08
Table 2. System performance of the analyzed models with 8-bit numerical precision while running on the target STM32L4 MCU at 80 MHz of clock frequency.
Table 2. System performance of the analyzed models with 8-bit numerical precision while running on the target STM32L4 MCU at 80 MHz of clock frequency.
Model SRAM Flash MACC Tck Tck/MACC Exec Time
[KB] [KB] [ms]
DilCNN int8 171.50 120.27 59,120,625 332,758,980 5.628 4159.359
CapsToA int8 CapsNet 16.18 54.14 280,032 2,076,305 7.415 25.954
DilCNN 136.00 49.50 15,750,720 147,491,915 9.364 1843.551
Overall 152.18 103.64 177,049,152 1,343,443,595 7.588 16793.044
Table 3. Median values and percentage of failed tests obtained with the different methods by varying the signal-to-noise ratio.
Table 3. Median values and percentage of failed tests obtained with the different methods by varying the signal-to-noise ratio.
Model Metric ∞ 20 dB 16 dB 12 dB 8 dB 4 dB 2 dB
AIC Median [cm] 4.05 3.12 4.62 5.68 6.85 18.93 24.03
Failure Rate 0% 0% 0% 7.7% 23.1% 34.6% 23.1%
STA/LTA Median [cm] 5.62 7.23 6.21 Failed Failed Failed Failed
Failure Rate 3.8% 0% 34.6% 76.9% 92.3% 96.2% 88.5%
DilCNN Median [cm] 3.21 3.3 3.69 3.24 3.76 4.58 7.67
Failure Rate 0% 0% 0% 0% 0% 0% 0%
DilCNN int8 Median [cm] 2.92 3.22 3.23 3.64 4.24 5.54 7.36
Failure Rate 0% 0% 0% 0% 0% 0% 0%
CapsToA Median [cm] 3.02 3.32 2.92 3.09 4.01 5.32 7.31
Failure Rate 0% 0% 0% 0% 0% 0% 0%
CapsToA int8 Median [cm] 2.84 2.6 2.64 3.75 3.81 6.27 8.97
Failure Rate 0% 0% 0% 0% 0% 0% 7.7%
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated