Prerpints.org logo
Preprint
Article

Experimental and Numerical Analysis of Crack Propagation of the Tensile Composite Plate with the Hole

Altmetrics

Downloads

198

Views

34

Comments

0

This version is not peer-reviewed

Submitted:

16 May 2023

Posted:

17 May 2023

You are already at the latest version

Alerts
Abstract
The analysis concerned a thin-walled plate with a circular central hole made of CFRP (Carbon Fiber Reinforced Polymer) material. The test object was subjected to a tensile test to investigate the cracking mechanism of the composite structure. The tests were performed using two independent test methods experimentally and numerically. In the experiment, the force was recorded as a function of elongation of the tensile plate and the elongation of the plate was investigated using an Aramis non-contact optical measurement system. As part of the numerical analysis, an FEM model adequate to the experimental conditions was performed in the Abaqus system. The fracture process was modeled using the extended finite element method XFEM. This approach enabled the structure of the composite to be investigated over the full range of tensile loading. The behaviour of the circular hole plate before the damage symptoms was investigated, the damage initiation force was determined, then the initial cracking and delamination of the layers were analysed, as well as the crack propagation process leading to the complete failure of the composite structure (cracking of all laminate layers).
Keywords: 
Subject: Engineering  -   Mechanical Engineering

1. Introduction

The use of modern material technologies and advanced manufacturing methods in the design process of thin-walled structures results in such structures having more beneficial operational and strength properties. Such structures are used in a wide range of industries, including aerospace, automotive and the currently expanding yacht industry [1,2]. Significant increases in the stiffness and strength properties of structural elements are achieved by replacing previously used classical construction materials with modern composite materials. This group of composites mainly includes polymeric laminates reinforced with continuous fibres, most commonly carbon fibre reinforced polymer (CFRP) and glass fibre reinforced polymer (GFRP). This is especially true for thin-walled stiffening elements for the covering of structures, usually designed as open and closed profiles with complex cross-sectional shapes. The scientifically proven beneficial mechanical properties of these materials, combined with their low mass, make it possible to use them in the manufacture of load-bearing elements for structures that are subjected to complicated loading conditions during exploitation [3,4,5,6,7]. Laminates make it possible to create the mechanical properties of designed components in terms of their ability to carry the appropriate type of load [8,9,10,11]. This feature makes it possible to achieve highly advantageous structural designs; however, this requires the use of modern testing methods that enable the performance of the structure to be analysed over the full load range. Studies of composite structures known from the literature mostly concern analytical and numerical analyses of structures with typical cross-sections, subjected to simple load cases. Only to a limited extent are these considerations verified by experimental studies of actual structural components [6,12,13,14,15,16,17].
In fibre laminates, the stress state depends on the fibre configuration and changes from layer to layer making it a complex problem. For this reason, the stress concentrations induced by a hole in the laminate vary from layer to layer and the general stress concentration factor specified for isotropic materials cannot be used in such cases (the classic Kirsch problem [18]). In the author's opinion, such a condition is possible to describe numerically, since, as is known from scientific publications, the occurrence of holes in thin-walled structures is unavoidable, if only for technological requirements [3,19,20,21,22,23]. The complexity of the above issue, resulting from the possibility of shaping the material properties of laminated composites, makes the subject still current and researched by researchers. In the literature, one could find works [24,25,26,27,28], which present proposed solutions to the problem of the occurrence of holes in composite materials.
The extended finite element method (XFEM) eliminates the need for a conformal finite element mesh [29]. The extended finite element method was first introduced by renowned scientists Belytschko and Black [30]. It is an extension of the conventional finite element method based on the concept of partition of unity Melenka and Babuski [31], which allows local enrichment functions to be easily integrated into the finite element approximation. The presence of discontinuities is provided by special functions enriched in combination with additional degrees of freedom. However, the finite element structure and its properties, such as sparsity and symmetry are retained. The use of the XFEM method does not dispense with the need for adequate mesh densification near the crack tip. The use of the XFEM method also ensures that crack initiation and propagation along the path is studied without the need to re-discretise the numerical model [29,32]. Enrichment functions consisting of asymptotic near tip functions are used for such crack analyses. Asymptotic singularity functions are only considered when modelling stationary cracks in Abaqus/Standard [33]. Moving cracks are modeled using one of two alternative approaches: cohesive segment approach or linear elastic fracture mechanics (LEFM) approach [29,32,34]. Using these technics, crack initiation is defined up to the onset of cohesive degradation on the enriched component, and the degradation stage is reached when the stresses or strains meet the specified crack initiation criteria.
This paper is concerned with the qualitative and quantitative determination of the fracture behaviour of a thin-walled composite plate weakened by a central circular hole during a tensile test. The work is focused on a detailed description of the cracking mechanics of the CFRP composite structure [35,36,37,38,39,40,41,42,43,44,45]. The failure process is described with independent test methods in the full range from damage initiation through crack propagation to full failure of the composite structure [37,46,47,48,49]. The tensile plate with a hole was investigated experimentally and numerically using the finite element method. This approach made it possible to develop numerical models that were adequate to the real structures [46,50,51,52,53,54,55,56]. It is worth mentioning that the work uses the now very popular FEM method, which is widely used in many fields of science [57,58,59,60,61,62,63,64,65].

2. Object of the Study

The test object was a thin-walled plate weakened by an oval hole made of a laminate composite. The hole cut into the specimens served to weaken the structure and cause the composite to fracture in a specific area during the tensile test. The plate was made from a unidirectional HeXPly prepreg strip (from Hexcel) of carbon fibre-reinforced composite in an epoxy matrix. The polymerisation process took place in an autoclave, the curing process curve was characterised by a package vacuum of 0.08 MPa, overpressure and autoclave temperature: 0.4 MPa and 135°C for 2 hours. The analysed laminate structure was characterised by a symmetrical fibre lay-up configuration on the composite layers [0/90/0/902 /0/90/0].
Figure 1a shows the test object, which included 3 plates measuring 20mm (width) x 160mm (length) x 1,084mm (overall thickness). Each specimen had a 10mm diameter oval hole made centrally in the centre of the plate. In addition, a contrast patterning was applied to the specimens to enable the use of a non-contact optical measurement method during experimental testing as shown in Figure 1b.
Table 1 shows the mechanical properties of a single layer of CFRP laminate in the three orthotropic directions: E - tensile modulus, G - shear modulus, ν - Poisson's number, FT - tensile strength, FS - shear strength and FC - compressive strength. The properties of the carbon-epoxy composite were determined experimentally based on the ISO standard. This allowed the actual mechanical properties of the produced material to be obtained, which may differ from the ideal properties stated by the manufacturer. The determined properties were used to define the material model as part of a numerical analysis based on the Abaqus finite element method.

3. Methodology of the Experimental Study

The manufactured plates with a central oval hole were subjected to an axial tensile test. For the experimental tests, a Cometech QC-505 M2F universal testing machine was selected, equipped with a load cell with a range up to 50kN and an accuracy class of 0.5%. Dedicated wedge grips with facings for flat specimens with a thickness range of 0.2÷11mm were attached to the pins of the testing machine. These were used to clamp the test specimen, which was inserted axially 20mm into each of the upper and lower wedge grips. This made it possible to obtain a test area of a 20x120mm plate. During the experimental tensile test, the force and elongation of the hole plate were recorded at a constant crosshead speed of 1mm/min. In addition, the displacement of the composite structure in the frontal plane of the plate over time was recorded using an Aramis non-contact optical measurement system. This system is equipped with a 20M resolution camera (5472 x 3648 px) and has a working area of 20 x 15 mm2 to 5000 x 4000 mm2 allowing the sample to be observed with images taken at up to 17 Hz. The use of such a system made it possible to completely observe the behaviour of a specimen with a hole in it during the stretching process that causes it to crack and fail.
Figure 2 shows the complete experimental test stand. Figure 2b shows the testing machine used, with the force measuring device mounted on the upper crosshead and the wedge grips in which the test specimen is fixed. In front of the machine, the measuring camera of the Aramis non-contact optical system used was installed, which is oriented perpendicular to the face of the specimen painted with the corresponding patterns. Before each experimental test, the camera was calibrated to obtain measurement images taken at 17Hz of the highest possible quality. Figure 2a shows the experimental test recording rig equipped with dedicated software running the testing machine and the Aramis non-contact optical measurement system.

4. Numerical Analysis

The numerical analysis was performed using the finite element method in the commercial version of the Abaqus system [66]. As part of this, an adequate FEM model corresponding to the experimental sample was prepared. For this, a CAD model was made of a 20x120 object with a thickness of 0.84mm with an oval hole made in the centre point of the plate. The mechanical properties of the material of the numerical model were assumed according to Table 1. The structure of the laminate was made by modeling the layers as separate solids. The FEM model consisted of 8 solids of 20mm (width) x 120mm (length) x 0.131mm (thickness) stacked. For each solid, the fibre stacking orientation was assigned according to the laminate configuration [0/90/0/90/90/0/90/0]. Figure 3 presents the FEM model of the composite with the fibre arrangement displayed in each layer.
In order to speed up the FEM calculation time, the numerical model was limited to the test area of the specimen during the experimental test (20mmx120mmx1.048mm plate). Therefore, boundary conditions were defined for the cross-sectional surfaces of the FEM model. The lower surface was given all degrees of freedom Ux=Uy=Uz=URx= URy=URz=0, while the upper surface was given two translational degrees of freedom Ux=Uz=0 and three rotational degrees of freedom URx= URy=URz=0. In order to realise a tensile force applied at the puncta, a reference point RP lying at the midpoint of the upper surface was made and linked by a Kinematic Coupling relation to the upper surface giving all degrees of freedom. A force of 10 kN was defined at the reference point according to the Y-vector expression, as shown in Figure 4a. In order to guarantee the consistency of the FEM model, the individual layers of the modelled composite were tied together. When configuring the XFEM analysis, a contact interaction property was selected for each layer of the laminate, which defines the behaviour of the compression fracture surfaces. The interactions of the FEM model are presented in symbolic form in Figure 4b. The numerical model was discretised with C3D8R hex solid elements having linear interpolation with 8 nodes and reduced-integration. For the structural mesh, partitions of the FEM model were made and the density of the finite element mesh was increased around the circumference of the circular hole. The discretised model had 20480 elements and 43840 nodes as shown in Figure 4c. The finite element size was adopted based on a preliminary numerical analysis, which proved that decreasing the finite element size does not affect the quality of the numerical results.
The use of the extended finite element method (XFEM) allows the study of crack initiation and propagation without the need to re-mesh the model [29]. For crack analysis, enrichment functions typically consist of asymptotic near tip functions that capture the singularity around the crack tip, and a discontinuous function that represents the displacement jump on the crack surfaces. Nodal displacement vector enrichment function u [67,68]:
u = ∑ I = 1 N N I X u I + H X A I + ∑ α = 1 4 F α X B I α
Where: N I X – nodal shape function, u I – nodal displacement vector of the continuous part of the finite element solution, H X – discontinuous jump function across the crack surface; A I – nodal vector of degrees of freedom; F α X – elastic asymptotic function of the crack tip; B I α – nodal vector of degrees of freedom. Whereby the first term of the formula applies to all nodes in the model, the second term applies to nodes whose shape function support is intersected by the crack interior, and the third term is used only for nodes whose shape function support is intersected by the crack tip - Figure 5.
Discontinuous jump function across the fracture surface H X could be presented as follows [68]:
H X = 1         i f X − X * · n ≥ 0 − 1         o t h e r w i s e
Where: X – is the sample point (Gaussian), X * – is the point on the crack closest to X , n – the unit outward normal to the crack at X * .
The asymptotic crack tip function for an elastic material is described by the following relation [29]:
F α X = r   sin θ 2 ,   r   cos θ 2 ,   r   sin θ s i n θ 2 ,       r   sin θ c o s θ 2      
Where: r i θ are a polar coordinate system whose origin is at the crack apex and θ = 0 is finally tangent to the crack.
Asymptotics crack tip functions are only considered when modelling stationary cracks in Abaqus/Standard. Moving cracks are modelled using one of two alternative approaches: cohesive segment approach or linear elastic fracture mechanics (LEFM) approach [29]. Crack initiation is defined up to the onset of cohesive degradation on the enriched component. In contrast, the degradation stage occurs when the stresses or strains meet certain crack initiation criteria. One such criterion is the maximum principal stress (MAXPS) criterion, which is as follows [33]:
F =   〈 σ M A X 〉 σ M A X 0
Where: σ M A X 0 is the maximum permissible principal stress.
The maximum principal stress ratio 〈 σ M A X 〉 shown in parentheses Macaulay assumes that damage begins when a value equal to 1 is reached [33]:
〈 σ M A X 〉 = 0       if       σ M A X < 0 〈 σ M A X 〉 = σ M A X       if       σ M A X ≥ 0

5. Results of the Study

In order to describe the damage initiation process, crack propagation and failure of the composite material, the plate weakened by a central circular hole made of CFRP material was subjected to tension. The study was carried out in parallel using two independent experimental and numerical methods using the finite element method. The initial result obtained from the FEM analysis in the form of the maximum stress field in the longitudinal direction of the plate is presented in Figure 6. The numerical analysis at this stage showed that the highest tensile stresses in the longitudinal direction of the specimen occur symmetrically on both sides of the circular hole. The maximum tensile laminate layers were all layers with a 0˚ fibre configuration coinciding with the longitudinal direction of the specimen. The results shown in Figure 6 are presented for non-failure stresses in the composite σt,S11=1828.8 MPa, i.e. not exceeding the limiting tensile stress in the longitudinal direction σt,S11 ≤ FT1=1867.2 MPa (Table 1).
The initiation of damage to the composite structure was observed once the FT1 longitudinal strength limit was exceeded. This was followed by crack propagation of the individual laminate layers. Figure 7 presents a bitmap showing the beginning of the fracture process of the laminate structure of the circular hole plate. The cracking process was determined numerically using the extended XFEM finite element method. Cracking started when a value of 1 was reached according to the maximum principal stress ratio criterion. The damage process of the composite structure started with the symmetric cracking of the outermost layers of the laminate with 0˚ fibre configuration in the area of the circular hole, as presented in Figure 7. It should be added that the damage criterion started to initiate the cracking of the other layers of the laminate with 0˚ fibre configuration (layers 3 and 6).
As part of the complete experimental observation of the tensile test of the composite plate with hole, the non-contact optical measurement system Aramis was used. Within which it was possible to measure the displacements of the specimen. The measurement system used enables the generation of a graphical displacement map superimposed on the real plate. Figure 8 shows a comparison of all tests for the analysis of elongation of plates with a hole in the tensile test. The proposed experimental method allowed the elongation of the specimens to be measured before complete failure. The elongation for the experimental samples was in the range <0.691mm÷0.809mm> and represented the percentage elongation of the plate containing in the range <0.61%÷0.69%>, as presented in Figure 8a-c. In addition, the elongation of the real plates in the hole area was measured, which was in the range <0.364mm(3.8%)÷0.428mm(4%)> (Figure 8a-c). The experimental tests obtained were compared with the results of the numerical analysis. The deformations for both test methods used were found to be consistent. The maximum elongation of the numerical sample before failure was 0.701mm (Figure 8d) and coincided with the experimental measurements. Based on the results obtained, there was qualitative and quantitative agreement between the experiment and the numerical analysis result. The results obtained confirmed the agreement of the proposed FEM model with the experimental sample.
Experimental and numerical tests were carried out in the full range of tensile loading leading to complete failure of the composite. Figure 9a-c shows the experimental forms of failure of a plate with a circular hole. In all cases, the actual specimen cracked in the assumed area where it had previously been weakened by the hole. The fracture path passed across the plate midway along its length. Parallel numerical analysis showed a consistent failure mode, as presented in Figure 9d. The onset of crack propagation of the FEM model (Figure 7) was initiated in the area corresponding to the experiment (Figure 9a-c) and progressed in the transverse direction. The strength of the panel depended on the strength of the layers with 0˚ fibre configuration, which were the most stressed in the tensile test. The destruction of the composite structure progressed horizontally and consisted of cracking and subsequent delamination of areas of the individual layers.
The tensile force as a function of specimen elongation was recorded experimentally. This made it possible to determine the working paths of the tensile plates over the full load range leading to failure - figure 10a-c. Adequate characteristics were determined for the numerical model, as presented in Figure 10d. This approach allowed the damage force corresponding to the initiation of laminate fracture and the failure force causing complete failure of the composite structure to be determined graphically. Damage force Pd corresponded to the first sudden increase in elongation recorded along the working path, while failure force Pf for the experimental study was determined at the point of radical decrease in tensile force (Figure 10a-c). Within the numerical characterisation, Pd was determined as for the experiment, while Pf was determined at the point characterising the highest tensile load.
Table 2 presents all the designated experimental and numerical damage force and failure force values. The determined experimental values of the laminate damage initiation force Pd(EXP) were in the range <4099.2N÷4443.9N>, while the numerical Pd(FEM)=5153.3N. Failure forces corresponding to complete failure of the composite due to fracture were Pf(EXP)= <7735.1N÷8264.5N> and Pf(FEM)=9298.7N. Based on the results obtained, the percentage increase in the failure force of the composite structure Pf from the failure initiation force Pd was determined. The tensile real structure after reaching the damage force could still carry the load increased by <85%÷90%>.
Figure 11 presents a comparison of the working paths determined for all experimental tests and the numerical analysis. The experimental working paths show the expected agreement of the experimental tests carried out. The numerical working path of the plate is characterised by a higher stiffness. The maximum increase in stiffness of the FEM model compared to experiment is 11%. The difference in stiffness between the numerical and experimental paths may be evidenced by material imperfections, the occurrence of which is unavoidable in real structures. Based on the results obtained, there was qualitative and quantitative agreement between the experiment and the numerical analysis. The results obtained also confirm the adequacy of the developed FEM/XFEM numerical model to the experiment.
In future research, it is planned to investigate the effect of circular hole size on the tensile strength of a plate made in a carbon-epoxy composite. As part of this, an experiment will be performed, which will be validated numerically using the currently popular FEM finite element method [69,70,71,72,73,74,75,76,77,78]. The research methodology and conclusions presented in this manuscript will be used for this study.

6. Conclusions

The study investigated a circular central hole plate made of a carbon-epoxy composite in tensile test. As a result, the cracking mechanism of the laminate structure was described. The research was performed in two ways, experimentally and numerically. The experiment made it possible to analyse the deformation of the plate using an Aramis non-contact optical measurement system, and to develop work paths for the tensile central hole plate. The numerical analysis allowed an FEM model to be made including the XFEM cracking effect. This approach enabled the structure of the composite to be investigated over the full range of tensile loading. The behaviour of the hole plate before the damage symptoms, the initiation of damage and the initial cracking and delamination of the layers, as well as the crack propagation process leading to the complete failure of the composite structure (cracking of all laminate layers) were analysed.
Initial numerical analysis showed that the highest tensile stresses in the longitudinal direction of the specimen occurred symmetrically on both sides of the circular hole. The maximum stressed laminate layers were all layers with a 0˚ fibre configuration, consistent with the longitudinal direction of the specimen. The initiation of damage to the composite structure was observed when the FT1 longitudinal direction was exceeded. This was followed by crack propagation of the individual laminate layers. Cracking started when the value 1 was reached according to the maximum principal stress ratio criterion. The damage process of the composite structure started with symmetrical cracking of the outer layers of the laminate with 0˚ fibre configuration in the circular hole area. It should be added that the cracking of the first layers started to initiate the cracking of the remaining layers of the laminate with 0˚ fibre configuration.
The proposed experimental method allowed the elongation of the specimens to be measured before complete failure. The elongation for the experimental specimens was in the range <0.691mm÷0.809mm> and represented the percentage elongation of the slab containing in the range <0.61%÷0.69%>. In addition, the extension of the actual plates in the bore area was measured, which was in the range <0.364mm(3.8%)÷0.428mm(4%)>. The experimental tests obtained were compared with the results of the numerical analysis. The deformations for both test methods used were found to be consistent. The maximum elongation of the numerical specimen before failure was 0.701mm and coincided with the experimental measurements.
Experimental and numerical tests were carried out in the full range of tensile loading leading to complete failure of the composite. In all cases, the real specimen cracked in the circular hole region. The fracture path passed across the plate midway along its length. Parallel numerical analysis showed a consistent failure mode, the crack propagation onset of the FEM model was initiated in the area coinciding with the experiment and progressed in the transverse direction. The strength of the plate depended on the strength of the layers with 0˚ fibre configuration, which were the most stressed in the tensile test. The destruction of the composite structure progressed horizontally and consisted of cracking and subsequent delamination of areas of the individual layers.
The determined working paths of the tensile plates allowed the graphical determination of the damage force corresponding to the initiation of laminate fracture and the failure force causing the complete failure of the composite structure. Damage force Pd corresponded to the first sudden increase in elongation recorded along the working path, while failure force Pf at the point characterising the highest tensile load. The determined experimental values of the laminate failure initiation force Pd(EXP) are in the range <4099N÷4444N>, while the numerical Pd(FEM)=5153N. The failure force corresponding to complete failure of the composite due to fracture is Pf(EXP)= <7735N÷8264N> and Pf(FEM)= 9299N. From the results obtained, the percentage increase in the failure force of the composite structure Pf from the failure initiation force Pd was determined. The tensile real structure, after reaching the damage force, could still carry a load increased by <85%÷90%>.
The experimental working paths show the expected agreement of the experimental tests carried out. The numerical working path of the plate is characterised by a higher stiffness. The maximum increase in stiffness of the FEM model compared to experiment is 11%. This is due to the fact that the numerical model is an ideal structure free of defects. Defects contributing to the lower stiffness of the real plates could have been material imperfections such as uneven fibre alignment or matrix porosity. Based on the results obtained, there was qualitative and quantitative agreement between the experiment and the result of the numerical analysis. The results obtained confirmed the agreement of the proposed FEM model with the experimental test.

References

  1. Campbell, F.C. Manufacturing Technology for Aerospace Structural Materials; 1st ed.; Elsevier: Amsterdam ; Boston, 2006; ISBN 978-1-85617-495-4.
  2. Kassapoglou, C. Design and Analysis of Composite Structures: With Applications to Aerospace Structures; AIAA education series; 1st ed.; American Institute of Aeronautics and Astronautics: Reston, Va. : United Kingdom : b John Wiley & Sons, 2010; ISBN 978-0-470-97263-2.
  3. Jain, P.; Kumar, A. Postbuckling Response of Square Laminates with a Central Circular/Elliptical Cutout. Composite Structures 2004, 65, 179–185. [CrossRef]
  4. Parlapalli, M.R.; Soh, K.C.; Shu, D.W.; Ma, G. Experimental Investigation of Delamination Buckling of Stitched Composite Laminates. Composites Part A: Applied Science and Manufacturing 2007, 38, 2024–2033. [CrossRef]
  5. Turvey, G.J.; Zhang, Y. A Computational and Experimental Analysis of the Buckling, Postbuckling and Initial Failure of Pultruded GRP Columns. Computers & Structures 2006, 84, 1527–1537. [CrossRef]
  6. Singer, J.; Arbocz, J.; Weller, T. Buckling Experiments: Experimental Methods in Buckling of Thin-Walled Structures; Wiley: Chichester ; New York, 1998; ISBN 978-0-471-95661-7.
  7. Teter, A.; Kolakowski, Z. Coupled Dynamic Buckling of Thin-Walled Composite Columns with Open Cross-Sections. Composite Structures 2013, 95, 28–34. [CrossRef]
  8. Kubiak, T.; Mania, R.J. Hybrid versus FR Laminate Channel Section Columns – Buckling and Postbuckling Behaviour. Composite Structures 2016, 154, 142–149. [CrossRef]
  9. Gliszczynski, A.; Kubiak, T.; Wawer, K. Barely Visible Impact Damages of GFRP Laminate Profiles – An Experimental Study. Composites Part B: Engineering 2019, 158, 10–17. [CrossRef]
  10. Gliszczynski, A.; Wiącek, N. Experimental and Numerical Benchmark Study of Mode II Interlaminar Fracture Toughness of Unidirectional GFRP Laminates under Shear Loading Using the End-Notched Flexure (ENF) Test. Composite Structures 2021, 258, 113190. [CrossRef]
  11. Kolakowski, Z.; Kubiak, T. Interactive Dynamic Buckling of Orthotropic Thin-Walled Channels Subjected to in-Plane Pulse Loading. Composite Structures 2007, 81, 222–232. [CrossRef]
  12. Debski, H.; Kubiak, T.; Teter, A. Experimental Investigation of Channel-Section Composite Profiles’ Behavior with Various Sequences of Plies Subjected to Static Compression. Thin-Walled Structures 2013, 71, 147–154. [CrossRef]
  13. Wong, P.M.H.; Wang, Y.C. An Experimental Study of Pultruded Glass Fibre Reinforced Plastics Channel Columns at Elevated Temperatures. Composite Structures 2007, 81, 84–95. [CrossRef]
  14. Orifici, A.C.; Thomson, R.S.; Degenhardt, R.; Kling, A.; Rohwer, K.; Bayandor, J. Degradation Investigation in a Postbuckling Composite Stiffened Fuselage Panel. Composite Structures 2008, 82, 217–224. [CrossRef]
  15. Kim, S.-C.; Kim, J.S.; Yoon, H.-J. Experimental and Numerical Investigations of Mode I Delamination Behaviors of Woven Fabric Composites with Carbon, Kevlar and Their Hybrid Fibers. Int. J. Precis. Eng. Manuf. 2011, 12, 321–329. [CrossRef]
  16. Carlsson, L.A.; Adams, D.F.; Pipes, R.B. Experimental Characterization of Advanced Composite Materials; 4. ed.; CRC Press: Boca Raton, Fla., 2014; ISBN 978-1-4398-4858-6.
  17. Fascetti, A.; Feo, L.; Nisticò, N.; Penna, R. Web-Flange Behavior of Pultruded GFRP I-Beams: A Lattice Model for the Interpretation of Experimental Results. Composites Part B: Engineering 2016, 100, 257–269. https://doi.org/10.1016/j.compositesb.2016.06.058.
  18. Timoshenko, S.; Gere, J.M. Theory of Elastic Stability; 2nd ed., Dover ed.; Dover Publications: Mineola, N.Y, 2009; ISBN 978-0-486-47207-2.
  19. Cheng, B.; Zhao, J. Strengthening of Perforated Plates under Uniaxial Compression: Buckling Analysis. Thin-Walled Structures 2010, 48, 905–914. [CrossRef]
  20. B. S. Jayashankarbabu; Karisiddappa Stability Of Square Plate With Concentric Cutout. 2014. [CrossRef]
  21. Ghannadpour, S.A.M.; Najafi, A.; Mohammadi, B. On the Buckling Behavior of Cross-Ply Laminated Composite Plates Due to Circular/Elliptical Cutouts. Composite Structures 2006, 75, 3–6. [CrossRef]
  22. Lorenzini, G.; Helbig, D.; Silva, C.; Real, M.; Santos, E.; Rocha, L. Numerical Evaluation of the Effect of Type and Shape of Perforations on the Buckling of Thin Steel Plates by Means of the Constructal Design Method. IJHT 2016, 34, S9–S20. [CrossRef]
  23. El-Sawy, K.M.; Ikbal Martini, M. Elastic Stability of Bi-Axially Loaded Rectangular Plates with a Single Circular Hole. Thin-Walled Structures 2007, 45, 122–133. [CrossRef]
  24. Kaltakci, M.Y. Stress Concentrations and Failure Criteria in Anisotropic Plates with Circular Holes Subjected to Tension or Compression. Computers & Structures 1996, 61, 67–78. [CrossRef]
  25. Durão, L.M.P.; Matos, J.E.; Loureiro, N.C.; Esteves, J.L.; Fernandes, S.C.F. Damage Propagation by Cyclic Loading in Drilled Carbon/Epoxy Plates. Materials 2023, 16, 2688. [CrossRef]
  26. Joy Mathavan, J.; Hassan, M.H.; Xu, J.; Franz, G. Hole Quality Observation in Single-Shot Drilling of CFRP/Al7075-T6 Composite Metal Stacks Using Customized Twist Drill Design. J. Compos. Sci. 2022, 6, 378. [CrossRef]
  27. Wang, H.; Wu, Y.; Zhang, Y.; Zhang, X. Influence of the Temperature-Dependent Characteristics of CFRP Mechanical Properties on the Critical Axial Force of Drilling Delamination. Polymers 2023, 15, 680. [CrossRef]
  28. Reeder, J.; Song, K.; Chunchu, P.; Ambur, D. Postbuckling and Growth of Delaminations in Composite Plates Subjected to Axial Compression. In Proceedings of the 43rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference; American Institute of Aeronautics and Astronautics: Denver, Colorado, April 22 2002.
  29. Elguedj, T.; Gravouil, A.; Combescure, A. Appropriate Extended Functions for X-FEM Simulation of Plastic Fracture Mechanics. Computer Methods in Applied Mechanics and Engineering 2006, 195, 501–515. [CrossRef]
  30. Belytschko, T.; Black, T. Elastic Crack Growth in Finite Elements with Minimal Remeshing. Int. J. Numer. Meth. Engng. 1999, 45, 601–620. [CrossRef]
  31. Melenk, J.M.; Babuška, I. The Partition of Unity Finite Element Method: Basic Theory and Applications. Computer Methods in Applied Mechanics and Engineering 1996, 139, 289–314. [CrossRef]
  32. Nagashima, T.; Suemasu, H. X-FEM Analyses of a Thin-Walled Composite Shell Structure with a Delamination. Computers & Structures 2010, 88, 549–557. [CrossRef]
  33. 2016; 33. Abaqus HTML Documentation; 2016;
  34. Liu, P.F.; Gu, Z.P.; Peng, X.Q.; Zheng, J.Y. Finite Element Analysis of the Influence of Cohesive Law Parameters on the Multiple Delamination Behaviors of Composites under Compression. Composite Structures 2015, 131, 975–986. [CrossRef]
  35. Sohn, M.S.; Hu, X.Z.; Kim, J.K.; Walker, L. Impact Damage Characterisation of Carbon Fibre/Epoxy Composites with Multi-Layer Reinforcement. Composites Part B: Engineering 2000, 31, 681–691. [CrossRef]
  36. Duarte, A.P.C.; Díaz Sáez, A.; Silvestre, N. Comparative Study between XFEM and Hashin Damage Criterion Applied to Failure of Composites. Thin-Walled Structures 2017, 115, 277–288. [CrossRef]
  37. Rozylo, P.; Wysmulski, P. Failure Analysis of Thin-Walled Composite Profiles Subjected to Axial Compression Using Progressive Failure Analysis (PFA) and Cohesive Zone Model (CZM). Composite Structures 2021, 262, 113597. [CrossRef]
  38. Falkowicz, K.; Ferdynus, M.; Rozylo, P. Experimental and Numerical Analysis of Stability and Failure of Compressed Composite Plates. Composite Structures 2021, 263, 113657. [CrossRef]
  39. Batra, R.C.; Gopinath, G.; Zheng, J.Q. Damage and Failure in Low Energy Impact of Fiber-Reinforced Polymeric Composite Laminates. Composite Structures 2012, 94, 540–547. [CrossRef]
  40. Kubiak, T.; Samborski, S.; Teter, A. Experimental Investigation of Failure Process in Compressed Channel-Section GFRP Laminate Columns Assisted with the Acoustic Emission Method. Composite Structures 2015, 133, 921–929. [CrossRef]
  41. Lapczyk, I.; Hurtado, J.A. Progressive Damage Modeling in Fiber-Reinforced Materials. Composites Part A: Applied Science and Manufacturing 2007, 38, 2333–2341. [CrossRef]
  42. Camanho, P.P.; Davila, C.G.; de Moura, M.F. Numerical Simulation of Mixed-Mode Progressive Delamination in Composite Materials. Journal of Composite Materials 2003, 37, 1415–1438. [CrossRef]
  43. Li, W.; Cai, H.; Li, C.; Wang, K.; Fang, L. Progressive Failure of Laminated Composites with a Hole under Compressive Loading Based on Micro-Mechanics. Advanced Composite Materials 2014, 23, 477–490. [CrossRef]
  44. Banat, D.; Mania, R.J. Failure Assessment of Thin-Walled FML Profiles during Buckling and Postbuckling Response. Composites Part B: Engineering 2017, 112, 278–289. [CrossRef]
  45. Barbero, E.J.; Cosso, F.A. Determination of Material Parameters for Discrete Damage Mechanics Analysis of Carbon-Epoxy Laminates. Composites Part B: Engineering 2014, 56, 638–646. [CrossRef]
  46. Rozylo, P.; Falkowicz, K. Stability and Failure Analysis of Compressed Thin-Walled Composite Structures with Central Cut-out, Using Three Advanced Independent Damage Models. Composite Structures 2021, 273, 114298. [CrossRef]
  47. Rozylo, P. Comparison of Failure for Thin-Walled Composite Columns. Materials 2021, 15, 167. [CrossRef]
  48. Rozylo, P. Failure Phenomenon of Compressed Thin-Walled Composite Columns with Top-Hat Cross-Section for Three Laminate Lay-Ups. Composite Structures 2023, 304, 116381. [CrossRef]
  49. Falkowicz, K. Experimental and Numerical Failure Analysis of Thin-Walled Composite Plates Using Progressive Failure Analysis. Composite Structures 2023, 305, 116474. [CrossRef]
  50. Kurşun, A.; Şenel, M.; Enginsoy, H.M. Experimental and Numerical Analysis of Low Velocity Impact on a Preloaded Composite Plate. Advances in Engineering Software 2015, 90, 41–52. [CrossRef]
  51. Debski, H.; Samborski, S.; Rozylo, P.; Wysmulski, P. Stability and Load-Carrying Capacity of Thin-Walled FRP Composite Z-Profiles under Eccentric Compression. Materials 2020, 13, 2956. [CrossRef]
  52. Wysmulski, P. The Effect of Load Eccentricity on the Compressed CFRP Z-Shaped Columns in the Weak Post-Critical State. Composite Structures 2022, 301, 116184. [CrossRef]
  53. Wu, M.Q.; Zhang, W.; Niu, Y. Experimental and Numerical Studies on Nonlinear Vibrations and Dynamic Snap-through Phenomena of Bistable Asymmetric Composite Laminated Shallow Shell under Center Foundation Excitation. European Journal of Mechanics - A/Solids 2021, 89, 104303. [CrossRef]
  54. Wysmulski, P.; Falkowicz, K.; Filipek, P. Buckling State Analysis of Compressed Composite Plates with Cut-Out. Composite Structures 2021, 274, 114345. [CrossRef]
  55. Wysmulski, P. Non-Linear Analysis of the Postbuckling Behaviour of Eccentrically Compressed Composite Channel-Section Columns. Composite Structures 2023, 305, 116446. [CrossRef]
  56. Falkowicz, K.; Valvo, P. Influence of Composite Lay-Up on the Stability of Channel-Section Profiles Weakened by Cut-Outs – A Numerical Investigation. Adv. Sci. Technol. Res. J. 2023, 17, 108–115. [CrossRef]
  57. Samborski, S.; Gliszczynski, A.; Rzeczkowski, J.; Wiacek, N. Mode I Interlaminar Fracture of Glass/Epoxy Unidirectional Laminates. Part I: Experimental Studies. Materials 2019, 12, 1607. [CrossRef]
  58. Rogala, M.; Gajewski, J. Numerical Analysis of Porous Materials Subjected to Oblique Crushing Force. J. Phys.: Conf. Ser. 2021, 1736, 012025. [CrossRef]
  59. Grzejda, R.; Warzecha, M.; Urbanowicz, K. Determination of the Preload of Bolts for Structural Health Monitoring of a Multi-Bolted Joint: FEM Approach. Lubricants 2022, 10, 75. [CrossRef]
  60. Gliszczynski, A.; Samborski, S.; Wiacek, N.; Rzeczkowski, J. Mode I Interlaminar Fracture of Glass/Epoxy Unidirectional Laminates. Part II: Numerical Analysis. Materials 2019, 12, 1604. [CrossRef]
  61. Jonak, J.; Karpiński, R.; Wójcik, A.; Siegmund, M.; Kalita, M. Determining the Effect of Rock Strength Parameters on the Breakout Area Utilizing the New Design of the Undercut/Breakout Anchor. Materials 2022, 15, 851. [CrossRef]
  62. Jonak, J.; Karpiński, R.; Wójcik, A. Influence of the Undercut Anchor Head Angle on the Propagation of the Failure Zone of the Rock Medium—Part II. Materials 2021, 14, 3880. [CrossRef]
  63. Nozdrzykowski, K.; Grządziel, Z.; Grzejda, R.; Warzecha, M.; Stępień, M. An Analysis of Reaction Forces in Crankshaft Support Systems. Lubricants 2022, 10, 151. [CrossRef]
  64. Rzeczkowski, J.; Paśnik, J.; Samborski, S. Mode III Numerical Analysis of Composite Laminates with Elastic Couplings in Split Cantilever Beam Configuration. Composite Structures 2021, 265, 113751. [CrossRef]
  65. Grzejda, R. Thermal Strength Analysis of a Steel Bolted Connection under Bolt Loss Conditions. EiN 2022, 24, 269–274. [CrossRef]
  66. Jonak, J.; Karpinski, R.; Wojcik, A.; Siegmund, M. The Effect of Undercut Anchor Diameter on the Rock Failure Cone Area in Pullout Tests. ASTRJ 2022, 16.
  67. Remmers, J.; Deborst, R.; Needleman, A. The Simulation of Dynamic Crack Propagation Using the Cohesive Segments Method. Journal of the Mechanics and Physics of Solids 2008, 56, 70–92. [CrossRef]
  68. Ventura, G.; Benvenuti, E. Equivalent Polynomials for Quadrature in Heaviside Function Enriched Elements: EQUIVALENT POLYNOMIALS FOR HEAVISIDE FUNCTION ENRICHED ELEMENTS. Int. J. Numer. Meth. Engng 2015, 102, 688–710. [CrossRef]
  69. Rogala, M.; Gajewski, J.; Ferdynus, M. The Effect of Geometrical Non-Linearity on the Crashworthiness of Thin-Walled Conical Energy-Absorbers. Materials 2020, 13, 4857. [CrossRef]
  70. Jonak, J.; Karpiński, R.; Wójcik, A. Influence of the Undercut Anchor Head Angle on the Propagation of the Failure Zone of the Rock Medium. Materials 2021, 14, 2371. [CrossRef]
  71. Jonak, J.; Karpiński, R.; Wójcik, A. Numerical Analysis of Undercut Anchor Effect on Rock. J. Phys.: Conf. Ser. 2021, 2130, 012011. [CrossRef]
  72. Jonak, J.; Karpiński, R.; Wójcik, A. Numerical Analysis of the Effect of Embedment Depth on the Geometry of the Cone Failure. J. Phys.: Conf. Ser. 2021, 2130, 012012. [CrossRef]
  73. Jaszak, P.; Skrzypacz, J.; Borawski, A.; Grzejda, R. Methodology of Leakage Prediction in Gasketed Flange Joints at Pipeline Deformations. Materials 2022, 15, 4354. [CrossRef]
  74. Rogala, M.; Gajewski, J.; Gawdzińska, K. Crashworthiness Analysis of Thin-Walled Aluminum Columns Filled with Aluminum–Silicon Carbide Composite Foam. Composite Structures 2022, 299, 116102. [CrossRef]
  75. Samborski, S.; Rzeczkowski, J. Numerical Modeling and Experimental Testing of the DCB Laminated Composite Beams with Mechanical Couplings.; Lublin, Poland, 2018; p. 080010.
  76. Różyło, P.; Smagowski, W.; Paśnik, J. Experimental Research in the Aspect of Determining the Mechanical and Strength Properties of the Composite Material Made of Carbon-Epoxy Composite. Adv. Sci. Technol. Res. J. 2023, 17, 232–246. [CrossRef]
  77. Rzeczkowski, J.; Paśnik, J.; Samborski, S. Corrigendum to “Mode III Numerical Analysis of Composite Laminates with Elastic Couplings in Split Cantilever Beam Configuration.” Composite Structures 2021, 266, 113920. [CrossRef]
  78. Paśnik, J.; Samborski, S.; Rzeczkowski, J. Application of the CZM Technique to Delamination Analysis of Coupled Laminate Beams. IOP Conf. Ser.: Mater. Sci. Eng. 2018, 416, 012075. [CrossRef]
Preprints 73860 g001
Figure 1. Test object: a) real composite panels with the hole, b) specimen with contrast plating.
Figure 1. Test object: a) real composite panels with the hole, b) specimen with contrast plating.
Preprints 73860 g001
Preprints 73860 g002
Figure 2. Test stand: a) recording software, b) testing machine with test specimen fixed.
Figure 2. Test stand: a) recording software, b) testing machine with test specimen fixed.
Preprints 73860 g002
Preprints 73860 g003
Figure 3. Numerical model of the laminate.
Figure 3. Numerical model of the laminate.
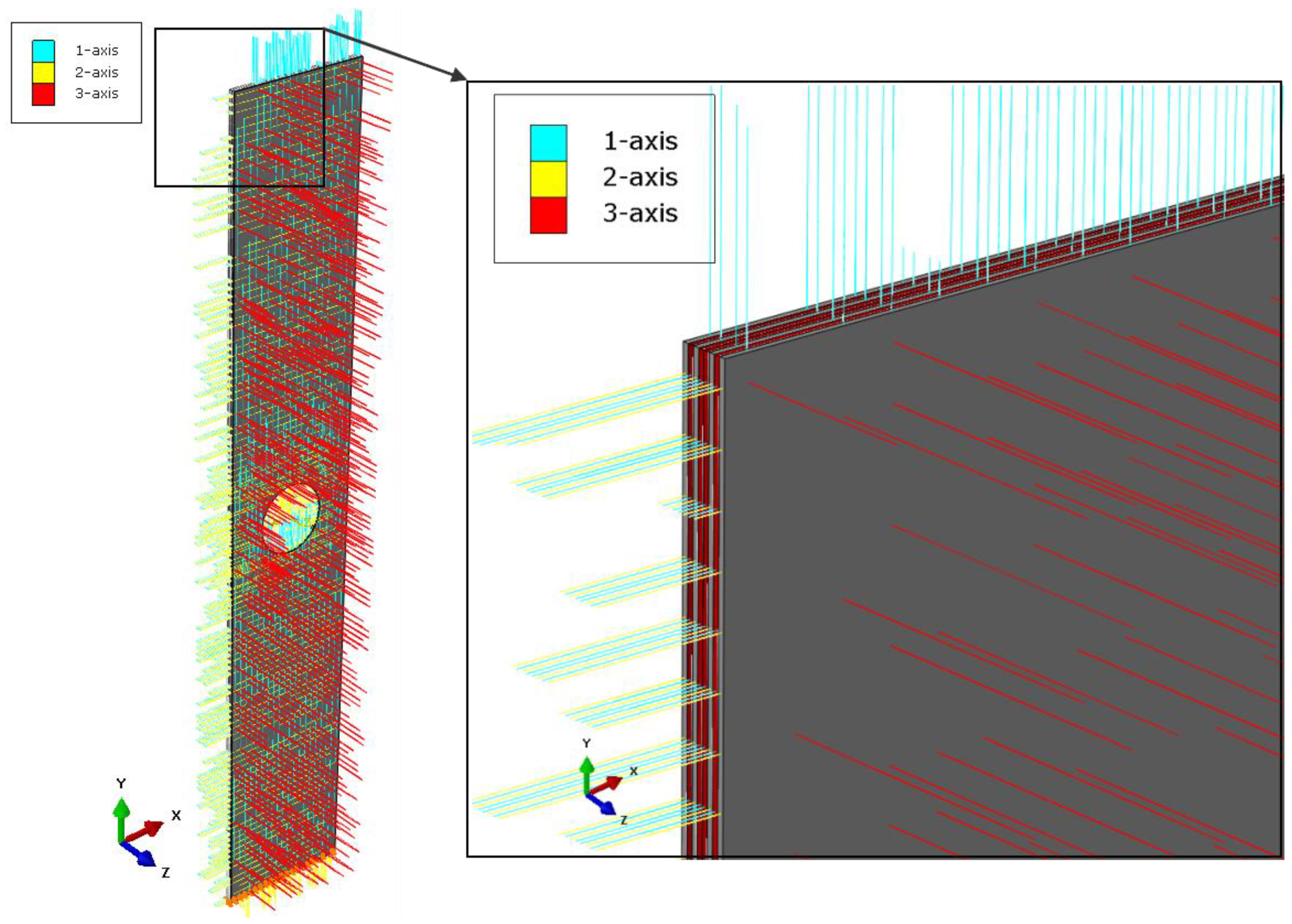
Preprints 73860 g003
Preprints 73860 g004
Figure 4. Numerical model: a) implementation of boundary conditions, b) layer-by-layer interactions, c) model discretisation.
Figure 4. Numerical model: a) implementation of boundary conditions, b) layer-by-layer interactions, c) model discretisation.
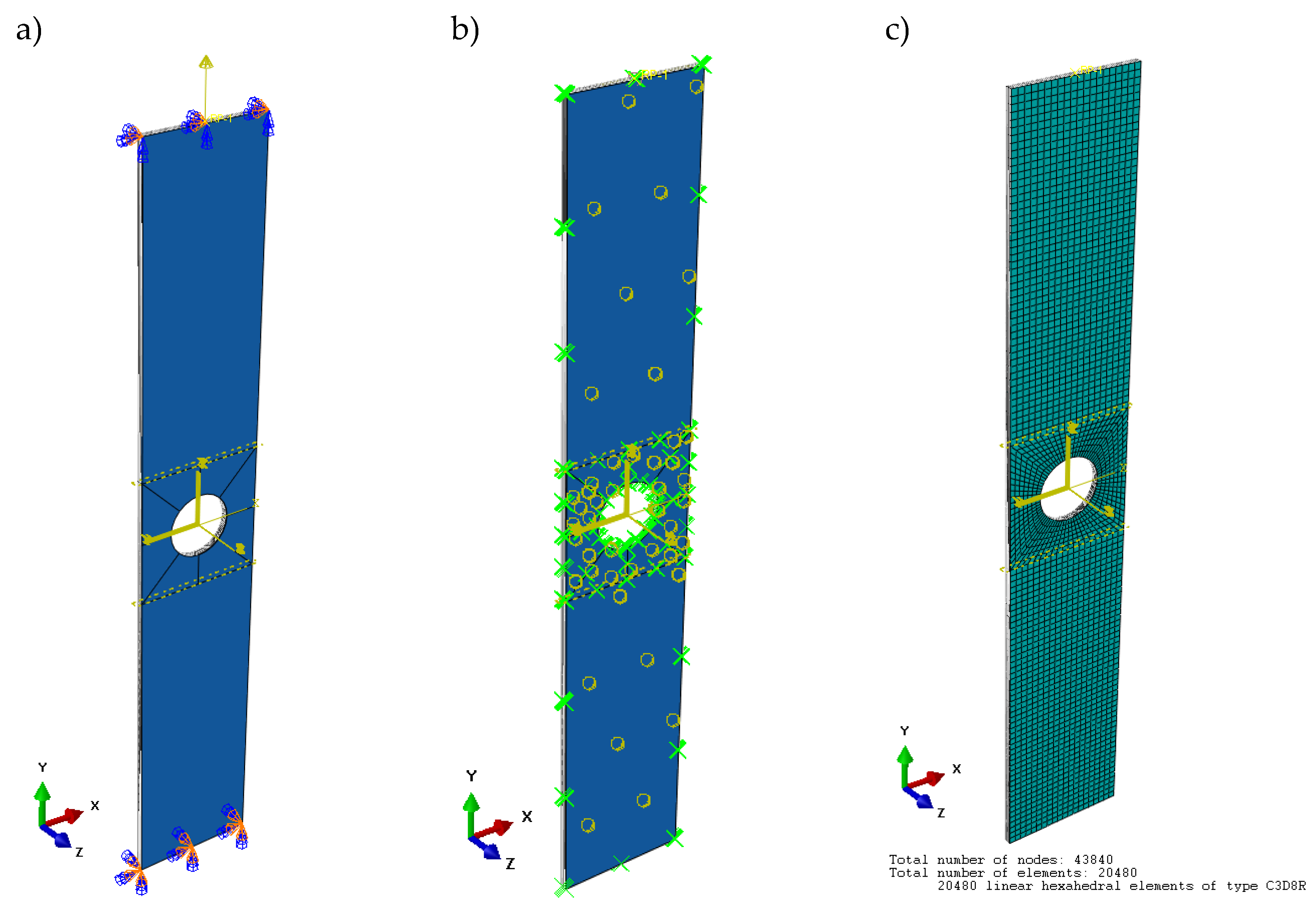
Preprints 73860 g004
Preprints 73860 g005
Figure 5. Normal and tangential vectors for a smooth fracture.
Figure 5. Normal and tangential vectors for a smooth fracture.
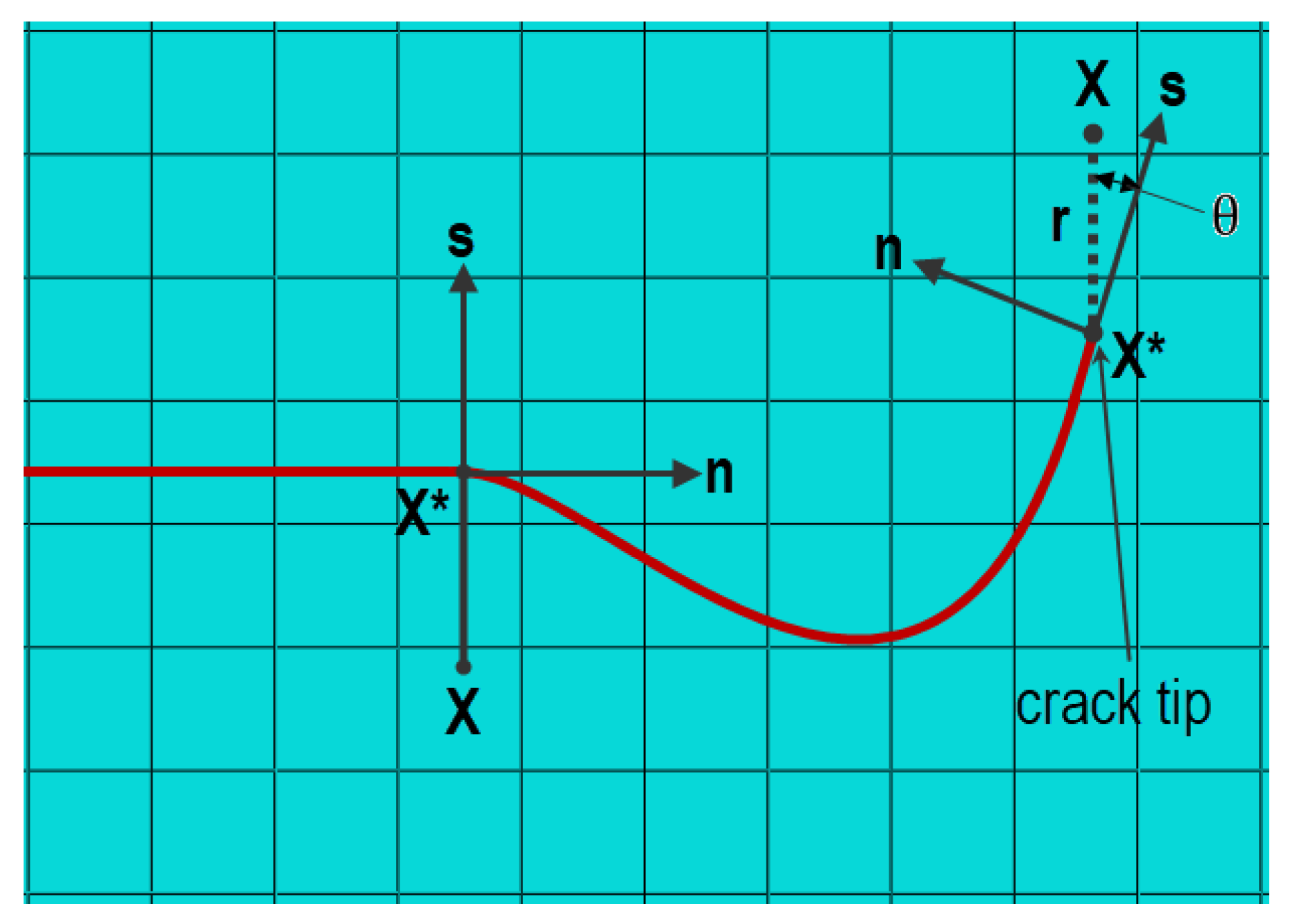
Preprints 73860 g005
Preprints 73860 g006
Figure 6. Stress analysis of the composite material before damage.
Figure 6. Stress analysis of the composite material before damage.
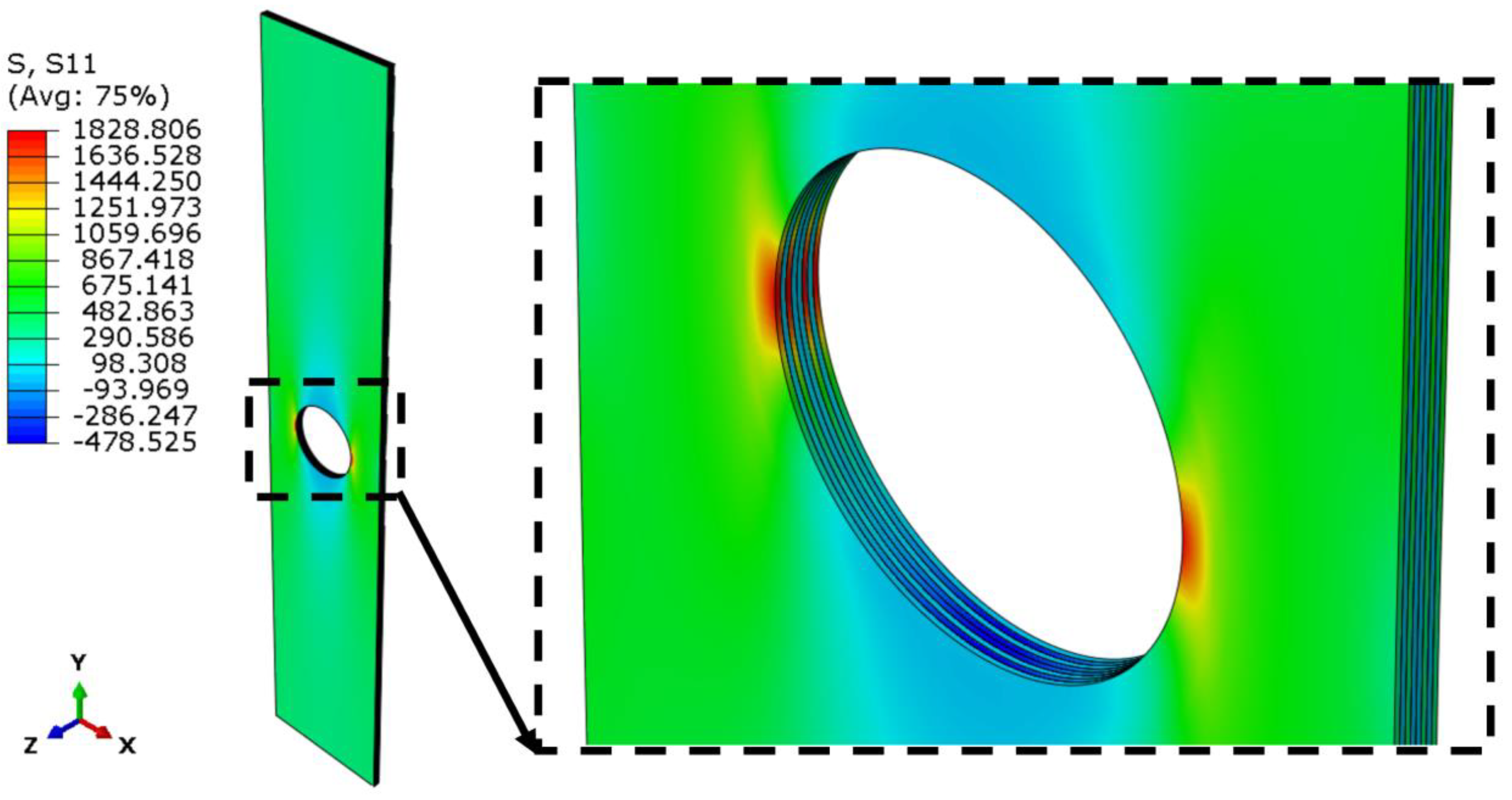
Preprints 73860 g006
Preprints 73860 g007
Figure 7. Damage and crack propagation of the composite structure.
Figure 7. Damage and crack propagation of the composite structure.
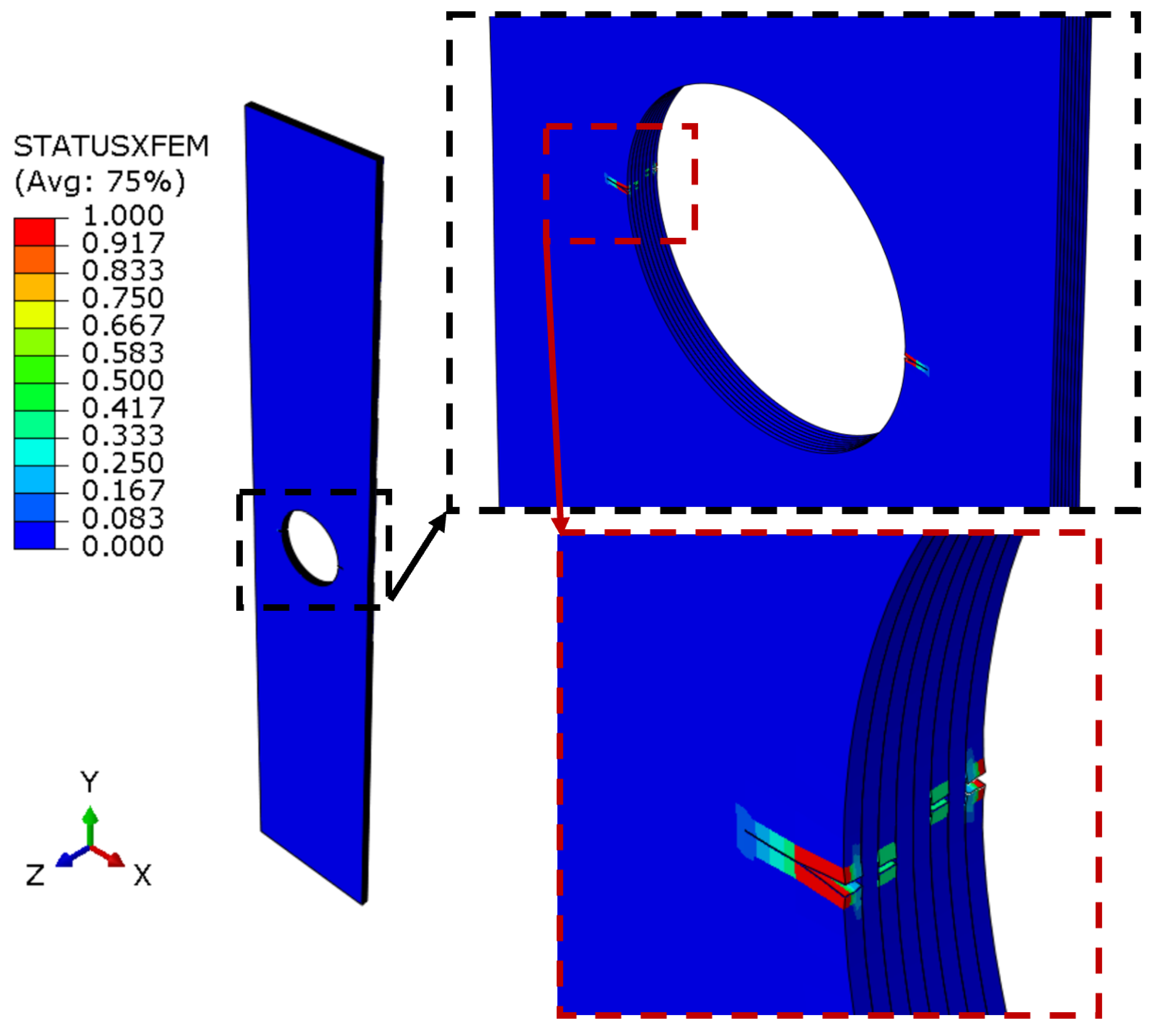
Preprints 73860 g007
Preprints 73860 g008
Figure 8. Longitudinal elongation maps of a plate with a hole: a) real sample 1, b) real sample 2, c) real sample 3, d) FEM model.
Figure 8. Longitudinal elongation maps of a plate with a hole: a) real sample 1, b) real sample 2, c) real sample 3, d) FEM model.
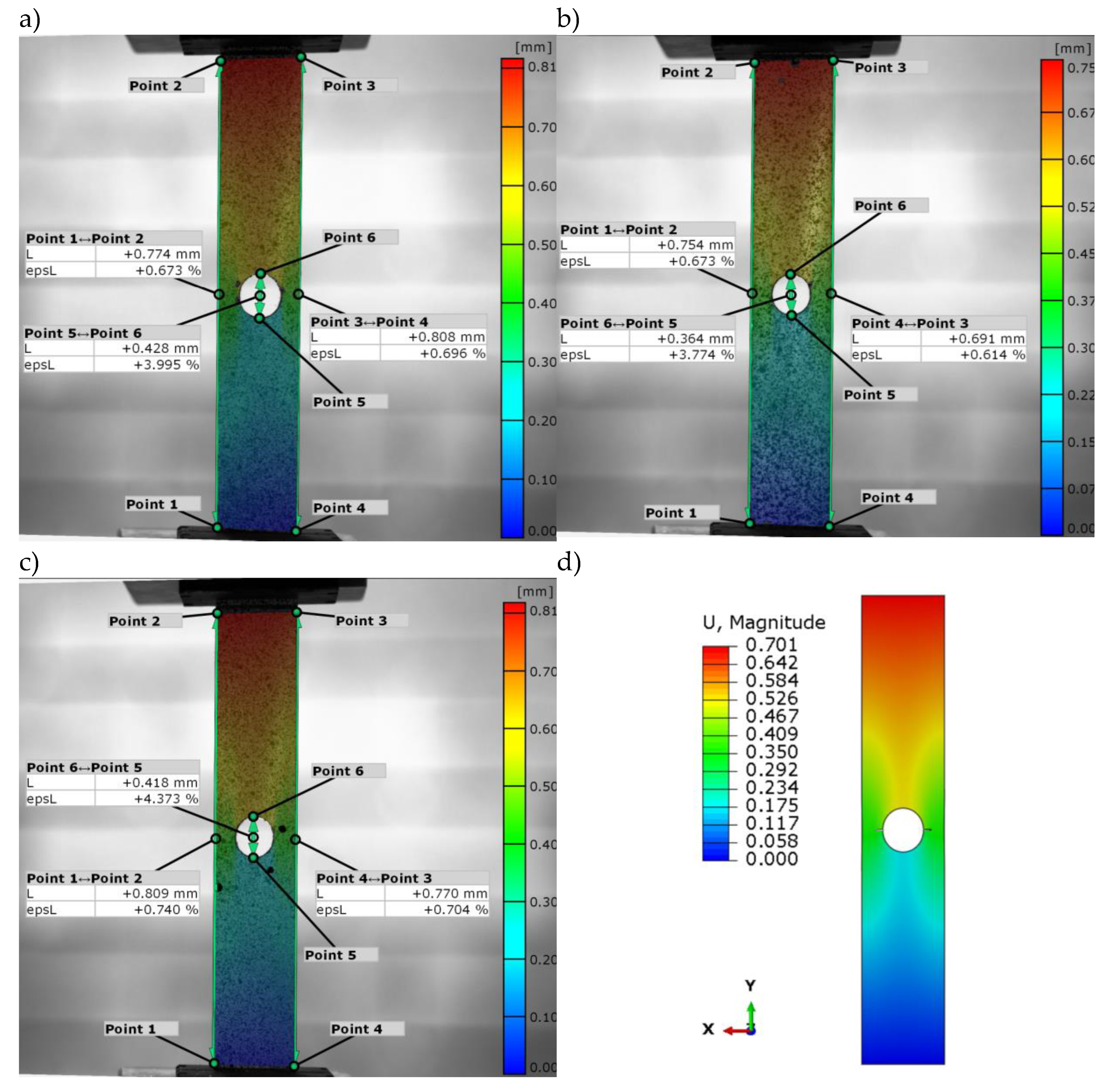
Preprints 73860 g008
Preprints 73860 g009
Figure 9. Complete failure of laminate structure: a) real sample 1, b) real sample 2, c) real sample 3, d) FEM model.
Figure 9. Complete failure of laminate structure: a) real sample 1, b) real sample 2, c) real sample 3, d) FEM model.
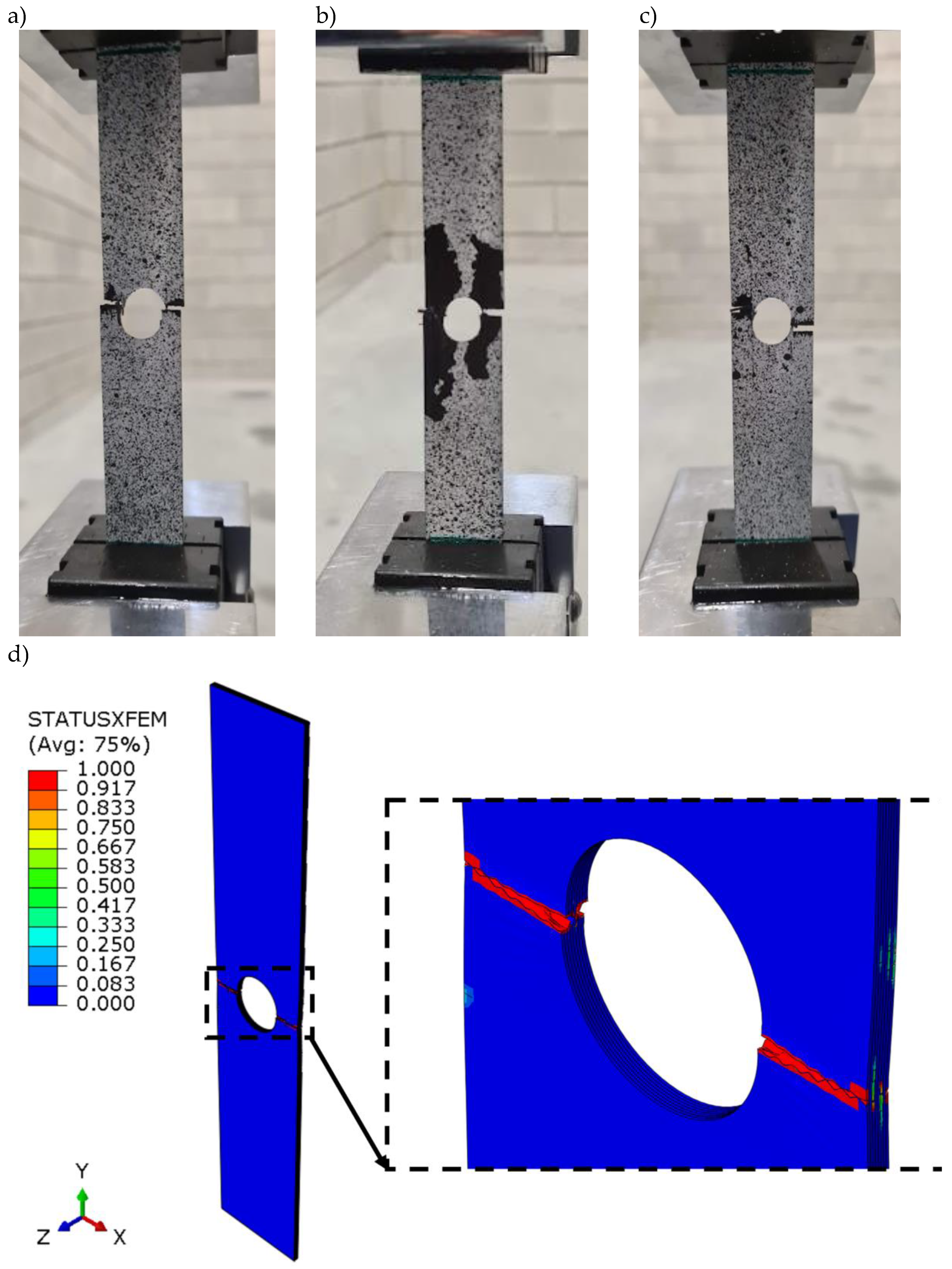
Preprints 73860 g009
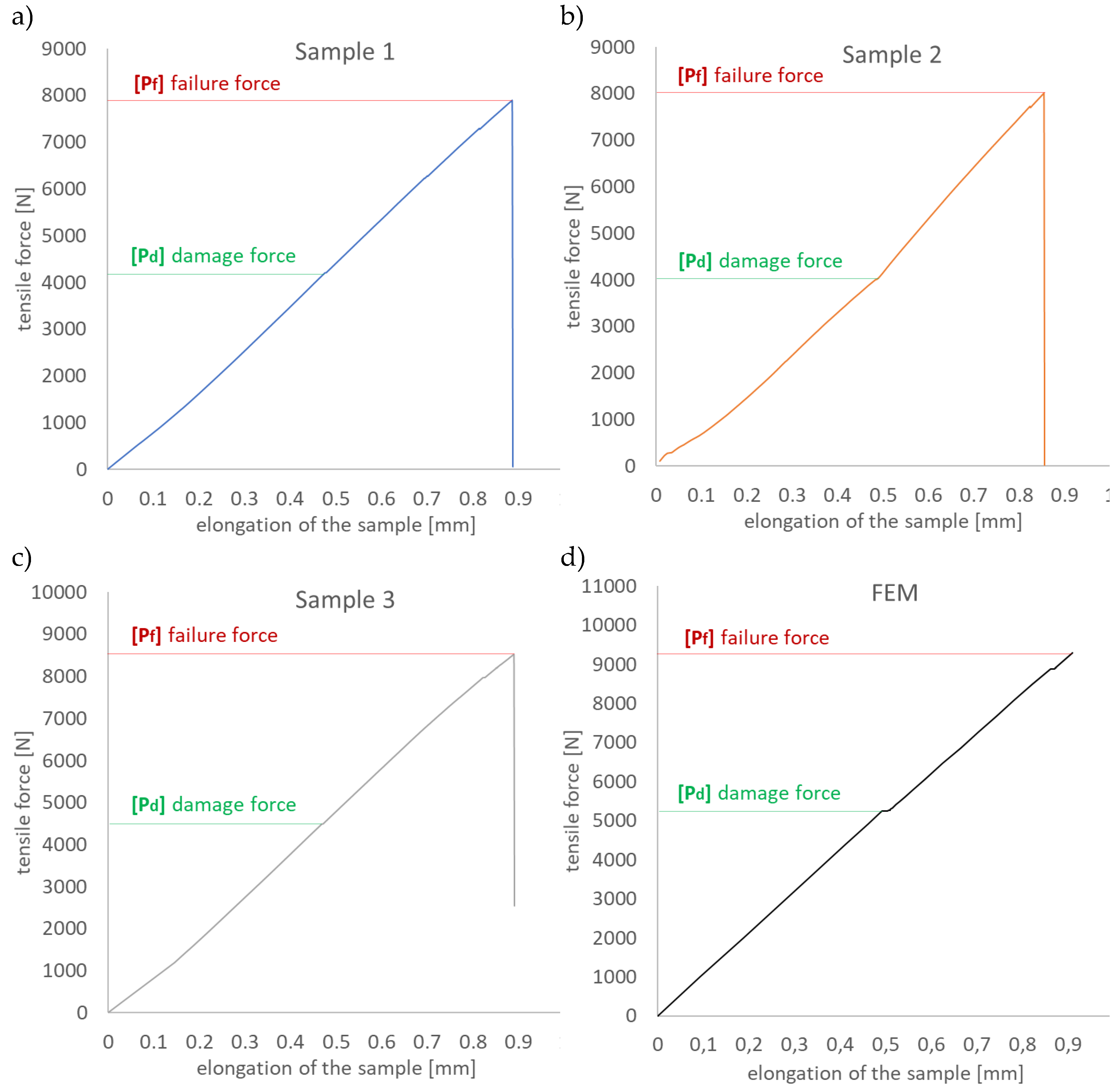
Preprints 73860 g010
Figure 10. Structure working paths: a) real sample 1, b) real sample 2, c) real sample 3, d) FEM model.
Figure 10. Structure working paths: a) real sample 1, b) real sample 2, c) real sample 3, d) FEM model.
Preprints 73860 g010
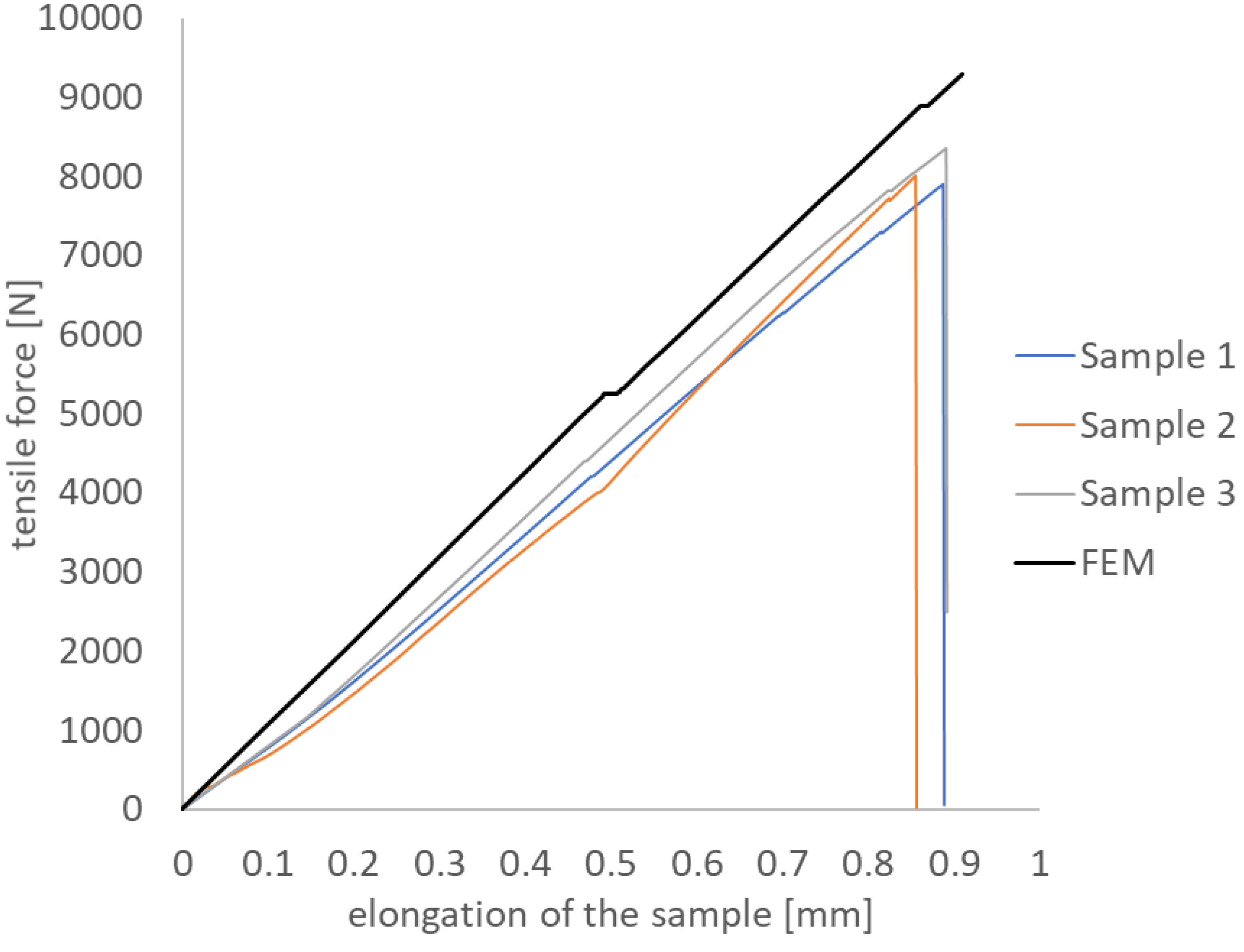
Preprints 73860 g011
Figure 11. Comparison of the experimental and numerical work paths of the plate.
Figure 11. Comparison of the experimental and numerical work paths of the plate.
Preprints 73860 g011
Table 1. Mechanical properties of CFRP.
Table 1. Mechanical properties of CFRP.
E1 E2,3 G12,13,23 ν12,13,23 FT1 FT2 FS FC1 FC2
GPa MPa MPa – MPa MPa MPa MPa MPa
130.71 6360 4180 0.32 1867.2 25.97 100.15 1531 214
Table 2. Damage force and failure force composite structure.
Table 2. Damage force and failure force composite structure.
FEM Sample 1 Sample 2 Sample 3
Pd [N] 5153.3 4185.9 4099.2 4443.9
Pf [N] 9298.7 7735.1 7801.5 8264.5
80% 85% 90% 86%
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated