Influence of Body Heat Loss on Temperature and Velocity Fields in a Whole-Body Cryotherapy Chamber

This study aims to investigate the impact of body heat loss on the thermal and aerodynamic conditions in a whole-body cryotherapy chamber. The underlying hypothesis is that the heat generated by the human body alters the thermal and aerodynamic environment inside the cabin. A numerical study was conducted to test this hypothesis to analyze the thermodynamic exchanges between the human body and the cabin during a 3-minute whole-body cryotherapy session. The computational fluid dynamics (CFD) approach was used to study the unsteady heat transfer between the human body and the interior of the cryotherapy cabin. A thermal boundary condition, based on a mathematical model developed from experimental data, was applied to simulate skin cooling kinetics over time. The post-processing of the 3D results, including temperature, velocity fields, and thermal flux maps at the body surface, provided insight into the thermo-convective mechanisms involved in a whole-body cryotherapy session. The study found that body heat loss significantly affects the temperature fields inside the cabin, leading to global modifications of the aeraulic and thermal conditions. These findings suggest that cryotherapy protocols may need to be adjusted or the cabin set temperature optimized to enhance the therapeutic benefits.

Keywords:

Subject: Engineering - Mechanical Engineering

1. Introduction

Whole body cryotherapy (WBC) is a method that involves exposing one or more subjects to extremely cold dry air for a period of one to four minutes [1]. Studies have shown that cryotherapy provides physiological, psychological, and physical benefits [2,3,4]. Cryotherapy methods have been developed to improve recovery from exercise, relieve pain, depression, and anxiety symptoms in patients with rheumatism and inflammatory diseases [5,6,7]. To achieve analgesic and anti-inflammatory effects, the patient must undergo a thermal shock following a sudden drop in skin temperature [8,9,10]. The intensity of the thermal shock will therefore depend on the temperature difference between the inside of the cryotherapy chamber (from -110 to -195 °C depending on the manufacturer) and the patient’s skin temperature [11,12]. When discussing thermal shock, it is necessary to consider the aerodynamic aspect. The basic principle of cryotherapy is that exposure to cold activates thermosensitive skin receptors, which is believed to be the main cause of the effectiveness of cryostimulation as it triggers regulatory mechanisms aimed at maintaining a constant core temperature. The resulting changes in skin temperature then become the key parameter on which the cryostimulation process relies. The thermal and metabolic response as it appears after cryostimulation is at least partially linked to what happened during the cryostimulation session, especially the speed of skin cooling.

The physiological response to extreme cold exposure is inherently linked to the thermal and airflow conditions within the cryotherapy chamber [13,14]. To achieve the expected therapeutic and analgesic effects, the temperature gradient between the human body and its environment must be significant [15]. Therefore, knowledge of the airflow and thermal conditions within the chamber throughout the cryotherapy session is fundamental [16].

In this context, it is necessary to take into account all parameters that could affect the temperature within the chamber, especially the heat generated by the patient’s body. Indeed, thermal transfers between the body and its environment can locally or on a larger scale modify temperatures inside the cryotherapy chamber. Depending on the size of the cryotherapy chamber, 1 to 3 patients can be accommodated, and it is difficult to precisely determine the impact of these heat sources on the actual temperature inside the chamber. It may be necessary to adjust the protocol duration or adjust the set temperature based on the number of patients present in the cryotherapy chamber. The first step in this reflection would be to estimate the impact of a single patient on the temperature inside a whole-body cryotherapy chamber. Currently, thermal measurements inside cryotherapy chambers are difficult due to the extreme temperatures that can damage the electronic circuits of measuring devices. Another alternative is to use numerical means such as CFD (Computational Fluid Dynamics), which allows for a precise approach to the airflow and thermal conditions within a cryotherapy chamber. CFD also provides access to flow variables that are difficult to obtain experimentally under extreme conditions. In a recent study, we used CFD to perform thermodynamic modeling aimed at optimizing the circulation of cold air flows in a partial-body cryotherapy chamber using an electric cooling system that produces air at -30°C [17]. The numerical results were compared to experimental results, which demonstrated the potential of the method we developed

In this study, we model the thermodynamic transfers between the human body and its environment during a 3-minute whole-body cryotherapy session. The ultimate goal is to determine the influence of the heat input from the human body on the temperature fields inside the cryotherapy chamber. A CFD calculation code based on the finite volume method is used to study the unsteady evolution of heat transfers. The results, presented in the form of temperature fields, velocity, and thermal flux maps on the body surface, provide a better understanding of the thermo-convective mechanisms involved during a whole-body cryotherapy session. This study is the first step in the process of adapting cryotherapy protocol duration and/or cryotherapy chamber set temperature according to the number of patients inside the chamber.

2. Materials and Methods

2.1. Geometry and Computational Domain

This section describes the first step of the numerical process used in the study, which involves defining the geometry of the whole-body cryotherapy (WBC) cabin and the human body inside it. The geometry of the cabin was created using computer-aided design (CAD) software ANSYS Workbench© Design Modeler (ANSYS 2020 R2, ANSYS, Inc., Canonsburg, PA, USA), based on the main dimensional characteristics of the cryotherapy cabin. The geometry of the human body was obtained using 3D scanning of a person wearing cryotherapy-specific protective clothing and was modeled as a heat transfer surface without considering the internal physical properties of the body. The simulations focus on air circulation and heat transfer between the human body and its environment, without taking into account the complex biological mechanisms of the human body. The resulting numerical model allows for the analysis of the thermo-convective mechanisms involved in a WBC session and provides a better understanding of the impact of the heat generated by the human body on the temperature fields inside the cryotherapy cabin.

2.2. Boundary Conditions

The boundary conditions of the problem are presented in Figure 1. Cold air is injected at the ceiling of the WBC cabin at a temperature of -92°C and a constant velocity of 0.177 m/s, which corresponds to the incoming air flow rate given by the manufacturer of the equipment (Mecotec, Germany). An outflow condition is applied at the ventilation grilles located at the bottom of the chamber. For simplification, the walls of the chamber are considered adiabatic. To model the evolution of skin temperature during a whole-body cryotherapy session, a thermal boundary condition is applied to the surface of the body. Equation (1) describes the evolution of skin temperature during a WBC session. This mathematical model of skin cooling kinetics was developed based on experimental data [12]. The skin temperature as a function of time can be expressed as follows:

T_{S K} (t) = {[K e^{{- (a t)}^{n}}]}_{0 \to 30} + {[A t + B]}_{30 \to β}

(1)

Where K, a, A and B are constants to be analytically determined using both thermal boundary conditions and a C¹- continuous junction between these two functions. The resulting analytical expression of the skin temperature is

T_{S K} (t) = {[T_{s k 0} {(\frac{T_{s k 0}}{{T s k}_{1} + C_{0} (30 - β)})}^{{- (\frac{t}{30})}^{n}}]}_{0 \to 30} + {[C_{0} t + (T_{s k 1} - C_{0} β)]}_{30 \to β}

(2)

With

n = (\frac{{- 30 C}_{0}}{[T_{s k 1} + C_{0} (30 - β)] l n (\frac{T_{s k 0}}{{T s k}_{1} + C_{0} (30 - β)})})

(3)

Tsk₀, Tsk_1, and C₀ are respectively the baseline skin temperature, the skin temperature at the end of the session, and the rate of cooling, and β corresponds to the end of the session.

In this calculation, the system was initialized at a temperature of -76°C which corresponds to the average temperature measured experimentally in the cryotherapy chamber. The iterative calculation was performed over a duration of 3 minutes with a time step of 0.02 s. We chose two different planes to analyze the kinetics of temperature and velocity evolution and to study the dissipation of heat from the human body into the ambient air. The two planes that intersect the body along its symmetry axes are shown in Figure 1.

2.3. Computational Grid

A surface mesh is first created on the body, followed by a Cartesian volumetric mesh for the fluid domain. The cell size in the computational domain is less than or equal to 0.023 m. The cell size applied to the body ensures good resolution of the boundary layer and sufficient accuracy for thermal transfer and convection calculations in the air. The structured Cartesian mesh improves the convergence of results and limits the number of mesh cells. In total, the mesh consists of over 3.5 million cells. Figure 2 illustrates the mesh structure on the body walls as well as in its vicinity.

2.4. Numerical Methods

This study used the commercial calculation code ANSYS Fluent® 2020 R2. This CFD calculation code based on the finite volume method allows the solution of the system of equations governing fluid flow. The numerical study is both three-dimensional, time-dependent and non-isothermal. The SIMPLE algorithm was preferred to solve the pressure-velocity coupling, using a first-order discretization scheme [17]. The standard k-ε turbulence model was chosen for closure of the Reynolds-averaged Navier-Stokes equations. Heat transfer as well as mass transfer by convection are described by the following equations:

The continuity equation:

\frac{{\partial w}_{x}}{\partial x} + \frac{{\partial w}_{y}}{\partial y} + \frac{{\partial w}_{z}}{\partial z} = 0

(4)

The Navier-Stokes equations:

\frac{{\partial w}_{x}}{\partial τ} + w_{x} \frac{{\partial w}_{x}}{\partial x} + w_{y} \frac{{\partial w}_{x}}{\partial y} + w_{z} \frac{{\partial w}_{x}}{\partial z} = - \frac{1}{ρ} \frac{\partial P}{\partial x} + ν (\frac{{\partial^{2} w}_{x}}{\partial x^{2}} + \frac{{\partial^{2} w}_{x}}{\partial y^{2}} + \frac{{\partial^{2} w}_{x}}{\partial z^{2}}) + g_{x}

(5)

\frac{{\partial w}_{y}}{\partial τ} + w_{x} \frac{{\partial w}_{y}}{\partial x} + w_{y} \frac{{\partial w}_{y}}{\partial y} + w_{z} \frac{{\partial w}_{y}}{\partial z} = - \frac{1}{ρ} \frac{\partial P}{\partial y} + ν (\frac{{\partial^{2} w}_{y}}{\partial x^{2}} + \frac{{\partial^{2} w}_{y}}{\partial y^{2}} + \frac{{\partial^{2} w}_{y}}{\partial z^{2}}) + g_{y}

(6)

\frac{{\partial w}_{z}}{\partial τ} + w_{x} \frac{{\partial w}_{z}}{\partial x} + w_{y} \frac{{\partial w}_{z}}{\partial y} + w_{z} \frac{{\partial w}_{z}}{\partial z} = - \frac{1}{ρ} \frac{\partial P}{\partial z} + ν (\frac{{\partial^{2} w}_{z}}{\partial x^{2}} + \frac{{\partial^{2} w}_{z}}{\partial y^{2}} + \frac{{\partial^{2} w}_{z}}{\partial z^{2}}) + g_{z}

(7)

The energy equation:

ρ_{f} C_{p, f} (\frac{{\partial T}_{f}}{\partial τ} + w_{x} \frac{{\partial T}_{f}}{\partial x} + w_{y} \frac{{\partial T}_{f}}{\partial y} + w_{z} \frac{{\partial T}_{f}}{\partial z}) = \frac{\partial}{\partial x} (λ_{f} \frac{{\partial T}_{f}}{\partial x}) + \frac{\partial}{\partial y} (λ_{f} \frac{{\partial T}_{f}}{\partial y}) + \frac{\partial}{\partial z} (λ_{f} \frac{{\partial T}_{f}}{\partial z})

(8)

With

w

being the fluid velocity (m/s);

ν

the dynamic viscosity (kg/m.s);

x

y

z

the spatial coordinates (m);

P

the Pressure (Pa);

ρ

the density (kg/m³);

T

the temperature (K);

C_{p}

the specific heat (J/Kg.K);

λ

the thermal conductivity (W/m/K).

To account for the evolution of the thermo-physical properties of air with temperature, polynomial laws were implemented in the computational code. They allow for the calculation of the density, dynamic viscosity, thermal conductivity, and specific heat at each time step within the temperature range of interest (-110°C to 33°C).

3. Results

Figure 3 displays the distribution of air flow velocities (a) and temperatures (b) for plane P1 at t=1, 2, and 3 minutes, respectively, while Figure 4 illustrates the distribution of air flow velocities (a) and temperatures (b) for plane P2 at t=1, 2, and 3 minutes, respectively. Note that we have limited the temperature range between -92°C and -72°C and the velocity range between 0 and 1.5 m/s to highlight even small gradients of velocity or temperature.

The results confirm a strong heterogeneity of temperatures in the chamber, with one of the main reasons being the presence of the human body, which behaves both as an obstacle and as a source of heat. The results also indicate that the highest temperatures are located near the body, while the coldest temperatures are located in the areas far from the body.

We can observe that the highest velocities are located around the body and above the head, due to the development of a thermal plume around the body. This thermal plume, which accelerates the airflow in the boundary layer and the heat transfers within the chamber, has a maximum velocity estimated at 1.3 m/s. To complement the results, Figure 4 illustrates the trajectory of the streamline in the WBC chamber at t=60 s.

The streamlines are colored by the vertical velocity, with a range limited to the interval of -0.5 to 0.5 m/s to better illustrate the smallest gradient of velocity. The streamlines allow to highlight the three-dimensional structure of the flow in the cryotherapy chamber at t = 60 s. The 3D streamlines (Figure 5a) show that the flow is composed of multiple vortex structures that interact with each other. The streamlines represented in a plane (Figure 5b) indicate that the human body acts as an obstacle for the flow of air coming from the ceiling of the chamber. The presence of large vortex structures indicates an interaction between the upward flows in the vicinity of the body and the downward flows resulting from the injection of cold air into the chamber. The air warmed by contact with the body, with a lower density, tends to rise while the cold air, with a higher density, descends to the floor.

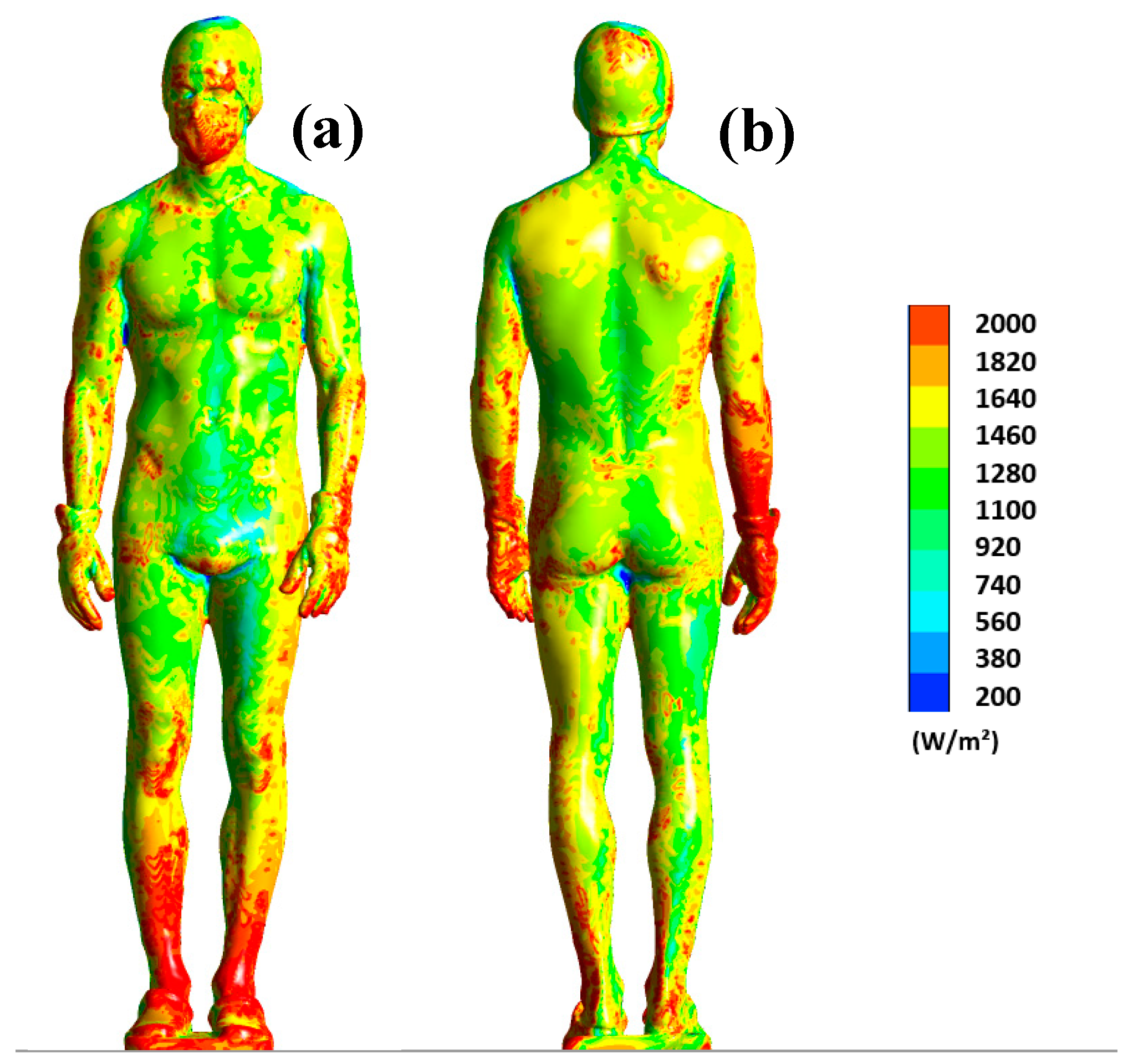
To complete, Figure 6 shows the distribution of surface flux on the human body at t = 180 s. Note that the range has been limited to the interval of 200 to 2000 W/m² to better visualize the differences.

The results show us that the distribution of heat flux on the body is uneven. For example, the legs dissipate much more heat, especially at the ankles where the dissipated flux exceeds 2000 W/m². The same observation can be made for the back of the wrists. This Figure highlights the areas that are more likely to cool down, such as the legs or forearms, because a high heat flux indicates significant heat dissipation. Note also that the distribution of heat flux on the surface of the human body is inherently dependent on the aerodynamic conditions inside the chamber. Thus, the higher the air velocity, the more heat is dissipated.

4. Discussion

The results confirm the hypothesis that the heat input from the human body significantly increases the temperatures within the WBC chamber, as the human body transfers heat to its close environment [18]. During exposure to cold, the layer of air, i.e. the boundary layer, developing at the surface of the human body limits the transfer of heat from the body to the air inside the chamber [19]. The development of this boundary layer is visible in Figure 3 and Figure 4 in the form of a thermal plume that rises upward and induces thermal stratification in the chamber. Several articles in the literature have highlighted the formation of a thermal plume during WBC sessions [20] or PBC (Partial Body Cryotherapy) sessions [17,21].

Heat exchange between the human body and its environment in indoor spaces has also been the subject of scientific studies [22]. A study conducted by Settles and Craven [23] examined the development of the thermal plume created by the presence of an individual in an indoor environment. The researchers studied the interaction between a standing (clothed) man and his environment (a closed and unventilated room at ambient temperature). The experimental and numerical results revealed that the flow velocity could reach 0.24 m/s above the subject’s head [23]. The difference in temperature gradient between the skin temperature of the human body (around 33°C on average) and the air temperature in the cryotherapy chamber (-90 to -110°C) is considerably greater in our study.

Therefore, the convection flow velocity is naturally higher. The results obtained in our study are consistent with those of Marreiro et al. [20] who estimated the velocity of the thermal plume dissipating above a subject during a whole-body cryotherapy session at -110°C. In their study, the velocity measured in the thermal plume was about 1.5 m/s [20], while it is estimated to be around 1.3 m/s in the present study.

Concretely, the thermal plume that develops around the body accelerates the air flow in the boundary layer as well as the heat transfer within the chamber. These results confirm the hypothesis that the heat generated by the human body modifies the aerodynamic and thermal conditions within the chamber. This results in an overall increase in temperature within the chamber, which leads to a decrease in the value of the surface flux that is particularly notable for certain parts of the body such as the abdomen (Figure 6). The distribution of the thermal flux suggests a more pronounced cooling in the lower part of the body, where the thermal plume develops. Moreover, the air flow tends to accelerate the heat transfer between the human body and its environment through a forced convection phenomenon [16].

On the one hand, the resulting flow displaces warm air around the body, but on the other hand, it accelerates the heat transfer between the human body and the air inside the cryotherapy chamber. This leads to a progressive increase in temperatures within the treatment space (Figure 3 and Figure 4), which in turn will modify the distribution of heat flux at the surface of the human body. What is also interesting is that the flows associated with the thermal plume are counter-current to the flows of air injected to cool the cryotherapy chamber. This process will generate a series of vortical structures allowing a mixing of the flow within the chamber while limiting the phenomena of thermal stratification that could occur if there were no heat source. Finally, our results demonstrate that the heat generated by the human body is capable of significantly increasing the temperature of its immediate surroundings, even under extreme conditions such as cryotherapy. Given that multiple patients can participate in a cryotherapy session simultaneously, further studies are needed to evaluate the impact of these heat sources on the temperature inside the cryotherapy chamber. Indeed, a significant increase in temperature within the chamber could reduce the therapeutic effectiveness of cryotherapy.

Limitations

The results of this study need to be interpreted in light of several limitations. First, the numerical model does not take into account the physiological behavior of the human body. Indeed, the interaction between the human body and the cabin occurs mainly at the skin level, and the skin temperature can reflect the balance between heat loss to the environment and heat produced by metabolically active tissues. Furthermore, the thermal boundary condition imposed on the human body assumes that at time t=0, the surface temperature is uniformly distributed over the body surface, whereas in reality the thermal response differs depending on the body segment. Finally, the patient is static, while in reality, patients are asked to move, which generates disturbances in the flow field and local modification of heat transfers.

5. Conclusions

The objective of this study was to investigate the impact of the heat generated by the human body on the thermal and aerodynamic conditions inside a whole-body cryotherapy chamber (WBC). To achieve this, a 3-minutes cryotherapy session was modeled using a computational fluid dynamics (CFD) method. A thermal boundary condition was applied to the body based on a mathematical model developed from experimental data, enabling simulation of the skin cooling kinetics over time. Post-processing of the 3D results revealed the development of a complex flow consisting of multiple vortical cells that continuously modify the thermal and aerodynamic conditions inside the chamber. The thermal plume generated around the human body interacts with the cold air supplied from the ceiling to cool the chamber, resulting in counter-rotating vortical cells. The distribution of heat flux on the body surface suggests a close link between the temperature distribution on the body surface and the unsteady flow dynamics within the chamber. Further experimental measurements and calculations are required to quantify the impact of one or more patients on the temperature fields within a cryotherapy chamber. These preliminary results also suggest the need to adapt cryotherapy protocols or adjust the set temperature to account for the heat input from the human body.

Author Contributions

Conceptualization, R.E. and G.P.; methodology, F.B.; software, R.E.; validation, B.A., G.P. and B.B.; formal analysis, F.B.; investigation, G.P.; resources, B.B.; data curation, B.A.; writing—original draft preparation, F.B.; writing—review and editing, R.E.; visualization, G.P.; supervision, B.A.; project administration, B.B. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

The datasets generated during the current study are available from the first author on reasonable request.

Conflicts of Interest

The authors declare no conflict of interest.

References

Polidori, G.; Taiar, R.; Legrand, F.; Beaumont, F.; Murer, S.; Bogard, F.; Boyer, F.C. Infrared thermography for assessing skin temperature differences between Partial Body Cryotherapy and Whole Body Cryotherapy devices at −140 °C. Infrared Phys. Technol. 2018, 93, 158–161. [Google Scholar] [CrossRef]
Hausswirth, C.; Schaal, K.; Le Meur, Y.; Bieuzen, F.; Filliard, J.-R.; Volondat, M.; Louis, J. Parasympathetic activity and blood catecholamine responses following a single partial-body cryostimulation and a whole-body cryostimulation. PLoS ONE 2013, 8, e72658. [Google Scholar] [CrossRef] [PubMed]
Banfi, G.; Melegati, G.; Barassi, A.; Dogliotti, G.; Melzi d’Eril, G.; Dugué, B.; Corsi, M.M. Effects of whole-body cryo-therapy on serum mediators of inflammation and serum muscle enzymes in athletes. J. Therm. Biol. 2009, 34, 55–59. [Google Scholar] [CrossRef]
Straburzyńska-Lupa, A.; Kasprzak, M.P.; Romanowski, M.W.; Kwaśniewska, A.; Romanowski, W.; Iskra, M.; Rutkowski, R. The Effect of Whole-Body Cryotherapy at Different Temperatures on Proinflammatory Cytokines, Ox-idative Stress Parameters, and Disease Activity in Patients with Ankylosing Spondylitis. Oxid. Med. Cell Longev. 2018, 2018, 2157496. [Google Scholar] [CrossRef] [PubMed]
Algafly, A.A.; George, K.P. The effect of cryotherapy on nerve conduction velocity, pain threshold and pain tolerance. Br. J. Sports Med. 2007, 41, 365–369. [Google Scholar] [CrossRef] [PubMed]
Rymaszewska, J.; Ramsey, D.; Chładzińska-Kiejna, S. Whole-body cryotherapy as adjunct treatment of depressive and anxiety disorders. Arch. Immunol. Ther. Exp. 2008, 56, 63–68. [Google Scholar] [CrossRef] [PubMed]
Vitenet, M.; Tubez, F.; Marreiro, A.; Polidori, G.; Taiar, R.; Legrand, F.; Boyer, F.C. Effect of whole body cryotherapy interventions on health-related quality of life in fibromyalgia patients: A randomized controlled trial. Complement. Ther. Med. 2018, 36, 6–8. [Google Scholar] [CrossRef]
Cholewka, A.; Stanek, A.; Sieroń, A.; Drzazga, Z. Thermography study of skin response due to whole-body cryotherapy. Ski. Res. Technol. 2012, 18, 180–187. [Google Scholar] [CrossRef]
Fonda, B.; De Nardi, M.; Sarabon, N. Effects of whole-body cryotherapy duration on thermal and cardio-vascular response. J. Therm. Biol. 2014, 42, 52–55. [Google Scholar] [CrossRef]
Costello, J.T.; McInerney, C.D.; Bleakley, C.M.; Selfe, J.; Donnelly, A.E. The use of thermal imaging in assessing skin temperature following cryotherapy: A review. J. Therm. Biol. 2012, 37, 103–110. [Google Scholar] [CrossRef]
Bleakley, C.; Hopkins, J. Is it possible to achieve optimal levels of tissue cooling in cryotherapy? Phys. Ther. Rev. 2010, 15, 344–350. [Google Scholar] [CrossRef]
Polidori, G.; Elfahem, R.; Abbes, B.; Bogard, F.; Legrand, F.; Bouchet, B.; Beaumont, F. Preliminary study on the effect of sex on skin cooling response during whole body cryostimulation (−110 °C): Modeling and prediction of exposure durations. Cryobiology 2020, 97, 12–19. [Google Scholar] [CrossRef] [PubMed]
Stocks, J.M.; Taylor, N.A.S.; Tipton, M.J.; Greenleaf, J.E. Human physiological responses to cold exposure. Aviat. Space Environ. Med. 2004, 75, 444–457. [Google Scholar] [PubMed]
Castellani, J.W.; Young, A.J. Human physiological responses to cold exposure: Acute responses and acclimatization to prolonged exposure. Auton. Neurosci. Thermoregul. 2016, 196, 63–74. [Google Scholar] [CrossRef] [PubMed]
Huizenga, C.; Zhang, H.; Arens, E.; Wang, D. Skin and core temperature response to partial-and whole-body heating and cooling. J. Therm. Biol. 2004, 29, 549–558. [Google Scholar] [CrossRef]
Bouzigon, R.; Arfaoui, A.; Grappe, F.; Ravier, G.; Jarlot, B.; Dugue, B. Validation of a new whole-body cryotherapy chamber based on forced convection. J. Therm. Biol. 2017, 65, 138–144. [Google Scholar] [CrossRef] [PubMed]
Beaumont, F.; Bogard, F.; Hakim, H.; Murer, S.; Bouchet, B.; Polidori, G. Modeling of an Innovative Nitrogen-Free Cryotherapy Device. Dynamics 2021, 1, 204–216. [Google Scholar] [CrossRef]
Savic, M.; Fonda, B.; Sarabon, N. Actual temperature during and thermal response after whole-body cryotherapy in cryo-cabin. J. Therm. Biol. 2013, 38, 186–191. [Google Scholar] [CrossRef]
Schlichting, H.; Gersten, K. Boundary-Layer Theory. Springer: 2016.
Marreiro, A.; Beaumont, F.; Taiar, R. , Polidori. Application des techniques d’imagerie thermique infrarouge et de mécanique des fluides numérique à la cryothérapie corps entier (CCE). Instrum. Mes. Métrologie 2017, 16, 11–32. [Google Scholar]
Beaumont, F.; Bogard, F.; Murer, S.; Anger, D.; Bouchet, B.; Polidori, G. Partial body cryotherapy in confined cryosaunas: Effects of inherent thermal stratification. Ser. Biomech. 2018, 32, 12–17. [Google Scholar]
Liu, Y.; Liu, Z.; Luo, J. Numerical Investigation of the Unsteady Thermal Plume around Human Body in Closed Space. Procedia Eng. 2015, 131, 1919–1926. [Google Scholar] [CrossRef]
Craven, B.A.; Settles, G.S. A computational and experimental investigation of the human thermal plume. ASME. J. Fluids Eng. 2006, 128, 1251–1258. [Google Scholar] [CrossRef]

Figure 1. Boundary conditions.

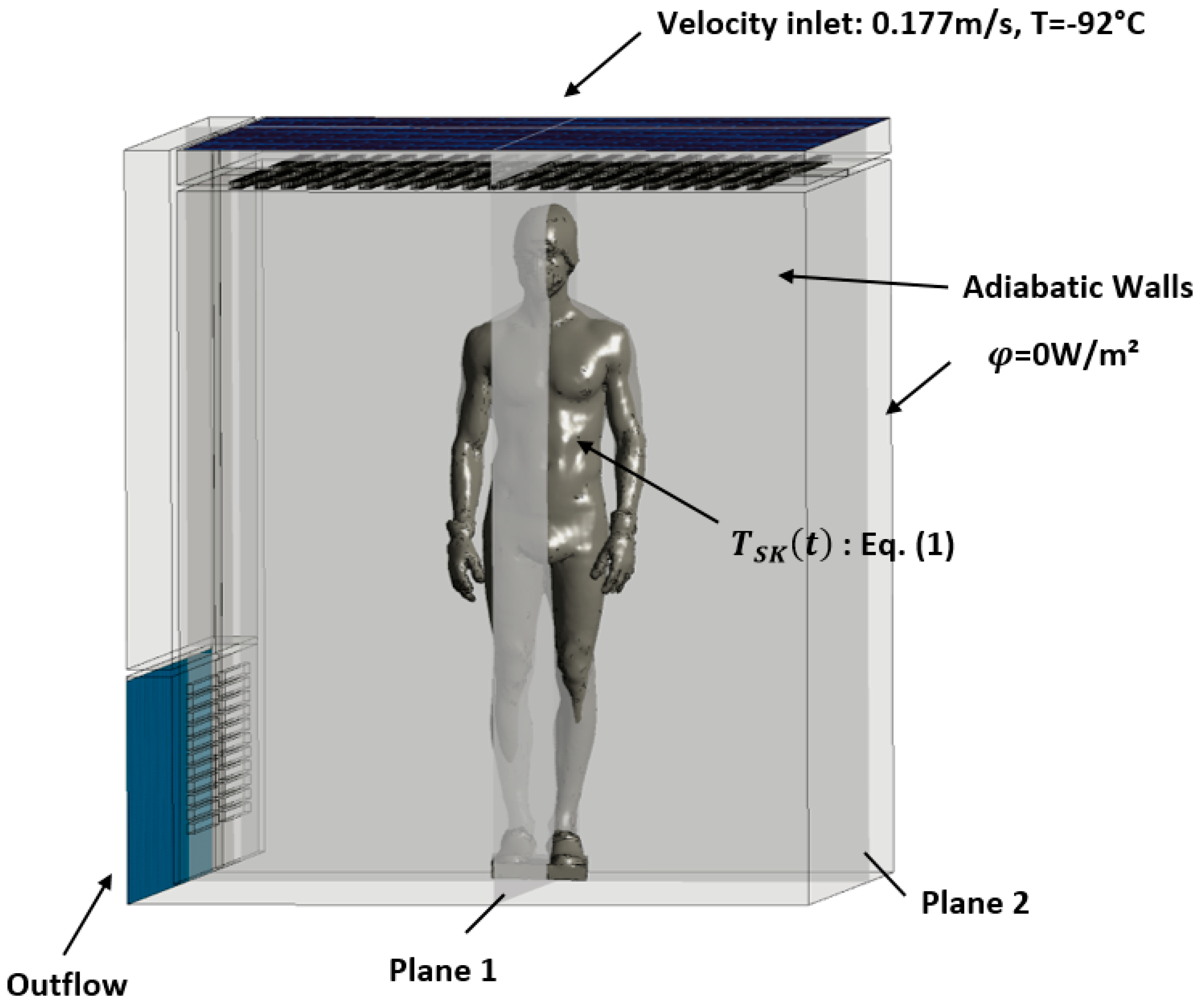
Figure 2. (a) Surface mesh on the body; (b) detailed view of the inflation mesh around the body displayed in a 2D vertical plane intersecting the body.

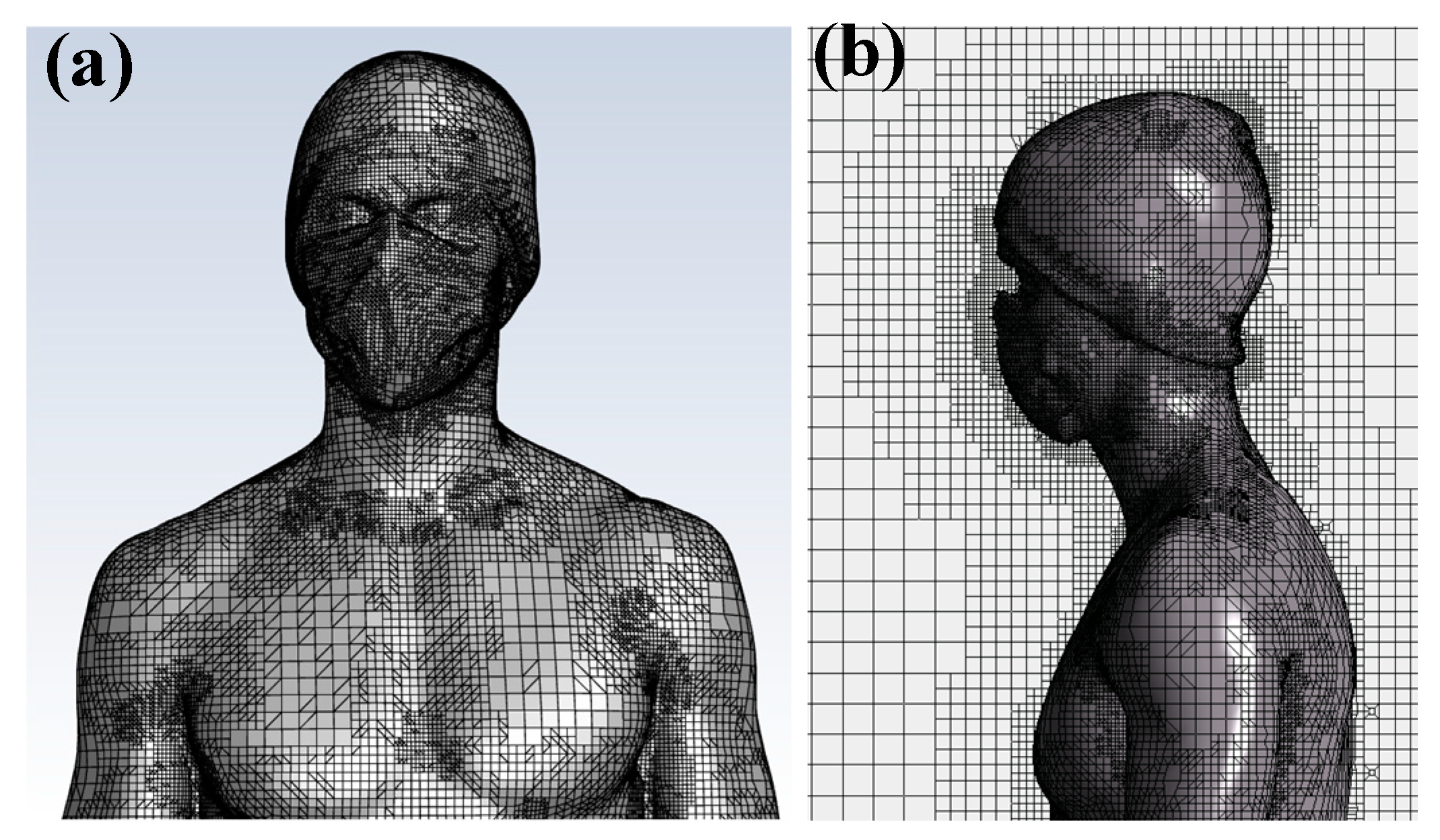
Figure 3. Velocity (a) and temperature (b) fields for plane P1 at t=1 min, t=2 min, and t=3 min.

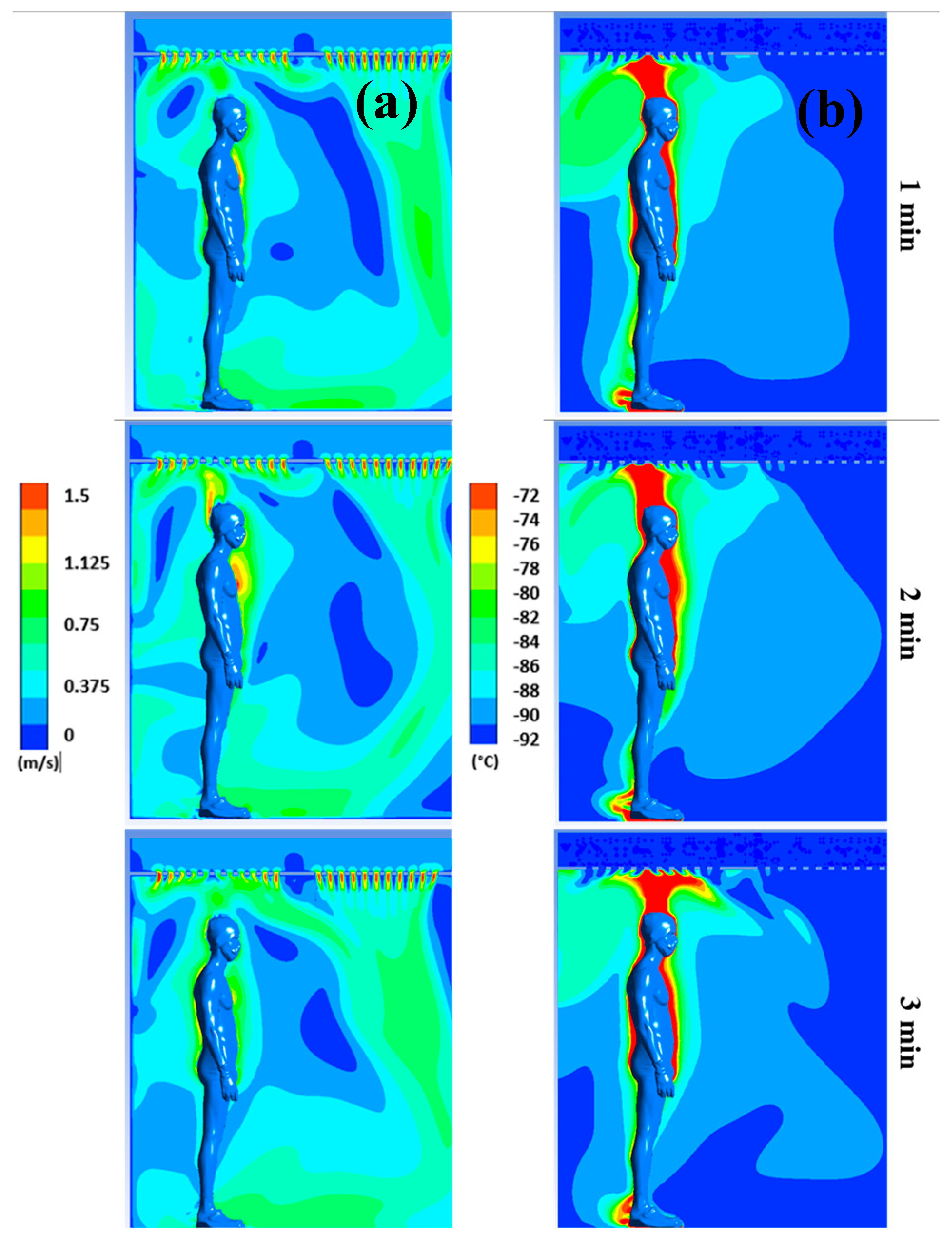
Figure 4. Velocity (a) and temperature (b) fields for plane P2 at t=1 min, t=2 min, and t=3 min.

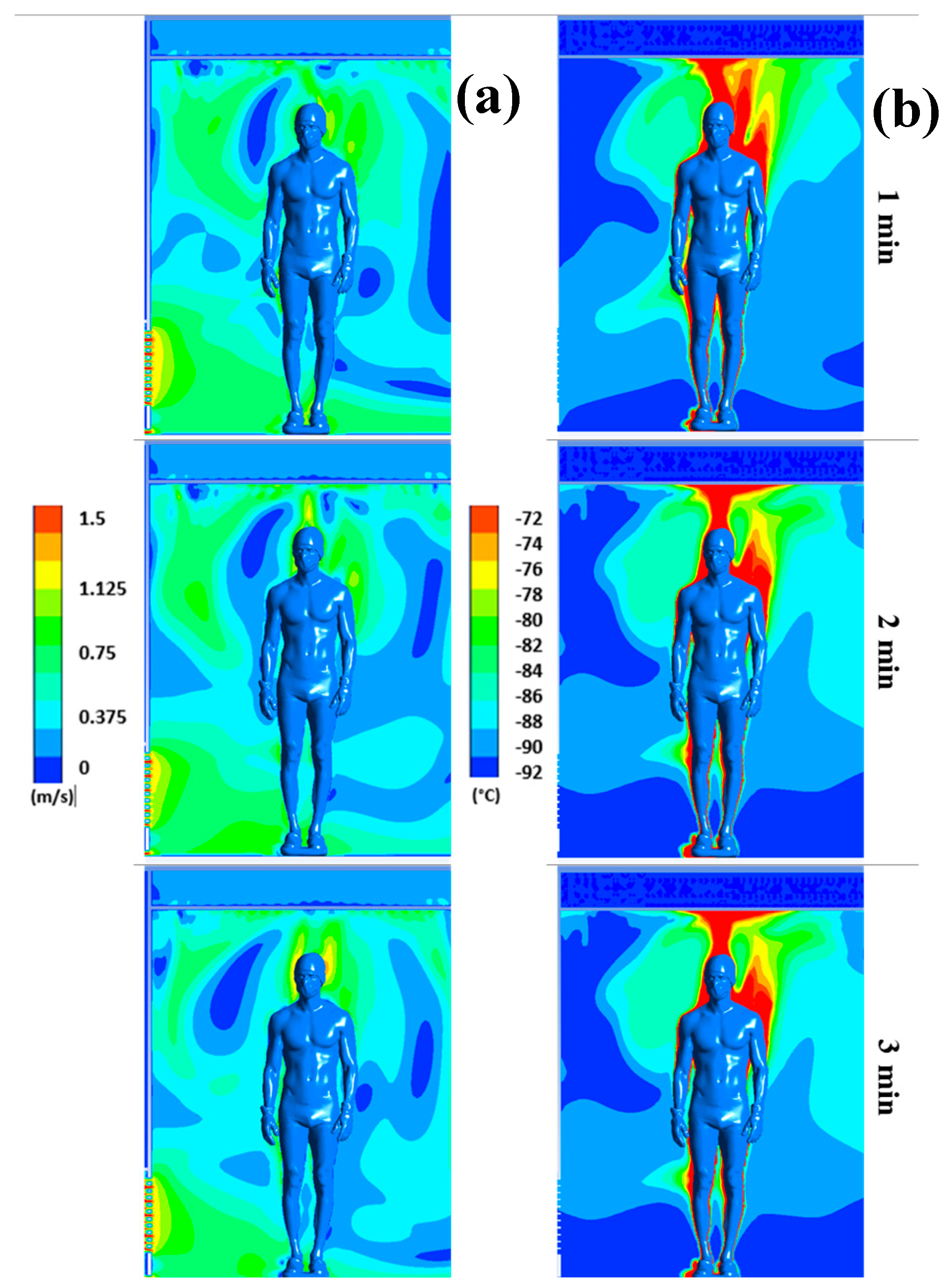
Figure 5. Streamlines colored by the vertical velocity component at t=60s in 3D (a); 2D streamlines plotted in a vertical plane passing through the body and colored by the vertical velocity component.

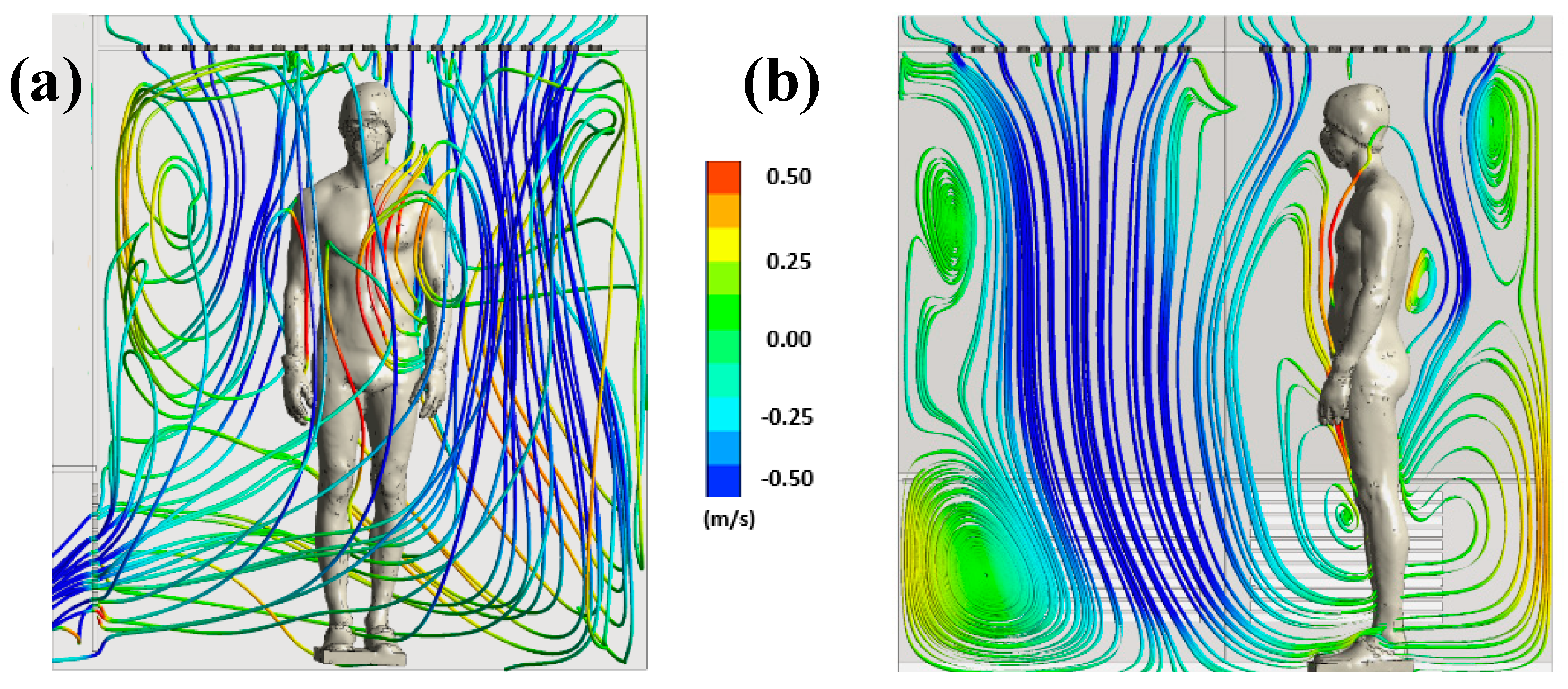
Figure 6. Surface heat flux dissipated by the human body at t = 180 s for the front side (a) and the back side (b).

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer