Prerpints.org logo
Preprint
Review

Investigation on Perceptual-Aware Optimization for Single Image Super Resolution on Embedded Systems

Altmetrics

Downloads

121

Views

47

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

17 May 2023

Posted:

18 May 2023

You are already at the latest version

Alerts
Abstract
Deep learning has been introduced to single-image super-resolution (SISR) in the last decade. These techniques have taken over the benchmarks of SISR tasks. Nevertheless, most architectural designs necessitate substantial computational resources, leading to a prolonged inference time on embedded systems or rendering them infeasible for deployment. This paper presents a comprehensive survey of plausible solutions and optimization methods to address this problem. Then, we propose a pipeline that aggregates the latter in order to enhance the inference time without significantly compromising the perceptual quality. We investigate the effectiveness of the proposed method on a lightweight GAN-based perceptual-oriented model as a case study. The experimental results show that our proposed method leads to significant improvement in the inference time on both Desktop and Jetson Xavier NX, especially for higher resolution input sizes on the latter, thereby making it deployable in practice.
Keywords: 
Subject: Computer Science and Mathematics  -   Computer Vision and Graphics

1. Introduction

Super-resolution is a low-level vision task that estimates a high-resolution image (HR) from an input image with less information called a low-resolution image (LR). If we have a high-resolution image, it is easy to create a low-resolution image by using degradation operations such as noise and blur. But the reverse problem is challenging because we have too little information in low-resolution images to make a rich-information image. Moreover, many natural images can downsample precisely to a given low-resolution input, which leads to not being able to find an explicit interpolation function that converts a low-resolution image to a high-resolution one. Granted, super-resolution (SR) is a tough problem, but it is a crucial demand since it brings some applications needed to solve this problem, including medical imaging [1,2,3], satellite imaging [4,5], and multimedia streaming [6,7].
  • In medical imaging, intrinsic and extrinsic factors cause an image’s resolution loss. The intrinsic limitation mainly originates from the physical limitations of imaging systems such as X-rays, MRIs, CTs, and ultrasounds. An imaging system’s spatial resolution is limited by factors such as the size of the detector or sensor, the wavelength of the imaging radiation, and the optics used to focus the radiation onto the detector. Extrinsic resolution limitations result from various factors during the image acquisition process, such as motion artifacts, patient movement, and image noise. SR technique can overcome extrinsic drawbacks.
  • In the satellite field, the image captured can be affected by some natural conditions, such as haze, fog, and cloud cover. This impacts the quality and resolution of satellite images. These conditions can cause distortion, blurring, or loss of contrast in the images, affecting interpretation and analysis accuracy. Moreover, the system itself considerably contributes to the quality of the image. The size and design of the imaging sensor, the satellite’s altitude, and the imaging sensor’s angle are some factors that limit the ability to detect and identify small objects or features. SR helps recover important information, which can be used for image classification or image recognition of an area or geographical location.
  • In the field of information transmission, because high-resolution images require more data to represent, transmitting or storing high-resolution images requires more bandwidth and storage space than lower-resolution ones. This can lead to network congestion and high latency, which negatively affect the user experience with phenomena like video lag or prolonged loading. SR can address this issue. Firstly, the image will be degraded in quality before being sent to the gateway. Secondly, the low-resolution image is processed into a high-quality image before being sent to the end-user device.
Meanwhile, deep learning-based approaches have significantly improved the image’s reconstruction quality in recent years. However, most methods stack deeper layers or introduce the complex architecture, which results in enormous execution time and computational requirements even on desktops, let alone low-end devices such as mobiles or embedded systems. The main contributions of our work in this paper can be summarized as follows:
  • Conduct a comprehensive survey of feasible solutions and optimization methods for SISR problems.
  • Revisit the optimization methods to fit with our previous work F2SRGAN, a lightweight GAN-based perceptual-oriented SISR model [8] to reduce the inference time without significantly compromising the perceptual quality as a case study.
  • Conduct in-depth experiments to prove the effectiveness of the proposed optimization pipeline.
The rest of the paper is constructed as follows. Section 2 comprehensively presents a survey of existing approaches for SISR. Meanwhile, Section 3 presents three optimization techniques for the above-mentioned problems in SISR. Then, we propose a method to reduce the inference time of our previous work as a case study in Section 4. The implementation and experiments to demonstrate effectiveness of the proposed method are presented in Section 5. Finally, Section 6 provides the final concluding remarks and future works.

2. Existing Approaches for Single-Image Super-Resolution (SISR)

In this section, we present a comprehensive survey of existing approaches to SISR. We characterize these methods into seven categories as summarized in Table 1.

2.1. Convolutional Neural Network (CNN) based methods

The most primitive and pioneering method using CNN is the SRCNN proposed by Dong et al. [9], which has proven to be superior to traditional non-deep learning methods in terms of reconstructed image quality. This study also shows that the normal sparse-coding-based image recovery model can be viewed as a depth model. However, the three-layer network is unsuitable for recovering compressed images, especially when dealing with blocking artifacts and smooth regions. When different artifacts are concatenated together, the features extracted by the first layer will be noisy, which causes unexpected noise patterns during the reconstruction.
Because of the real-time advantage of the SRCNN model and to overcome the computational disadvantage, Ahn et al. [10] proposed a model that can be implemented directly on the FPGA named Optimal-FSRCNN. This model has used the TDC method to convert the deconvolution layer to the equivalent convolution layer to overcome the inherent overlapping sum problem, which causes increased latency, consumes a lot of power and other hardware resources, and maximizes real-time super-resolution image parallelization using lightweight deep learning.
Inheriting the improvement of the above disadvantages, another model was formed to contribute to their improvement, which is the LAPSRN model proposed by Lai et al. [11]. Deep supervision with the Charbonnier loss function improves performance through better handling of outliers. Therefore, the model has a great ability to learn complex mappings and is effective in minimizing undesirable visualizations. Furthermore, learning upsampling filters not only minimizes the generation of reconstruction artifacts produced by bicubic interpolation but also contributes to minimizing computational complexity. Experimental results show that this model is capable of solving the story of time. However, the model size is still relatively large. To reduce the number of parameters, one can replace the deep convolution layers at each level with recursive layers. In terms of image quality, not only LAPSRN but most other parametric SR methods fail to recover fine structure.

2.2. Distillation method

Although the CNN-based models achieve outstanding performance, the proposed networks still have disadvantages. To achieve better performance, one tends to design a deeper network. But as a result, these methods are computationally expensive and consume large amounts of hardware resources, which are rarely applied in mobile and embedded applications.
To solve that problem, some researchers have proposed some models to meet the needs. First, Hui et al. [12] proposed the IDN model, which extracts more helpful information with fewer convolutional layers. Although IDN has reduced parameters compared to the previous method, this reduction is achieved at the cost of significant performance sacrifice. Then, they proposed an alternative model, IDMN [13], based on their previous work IDN with a more lightweight structure and faster running. The IMDN model uses an information multi-distillation block (IMDB) to further improve performance in both PSNR and inference time and takes first place in the AIM 2019 constrained image super-resolution challenge [37]. However, the number of parameters in the IMDN model is greater than most lightweight SR models, such as VDSR [38] and IDN. However, the IMDN model still has room for improvement to be more lightweight.
The main component of both IDN and IMDN is an Information Distillation Mechanism (IDM) that explicitly divides previously extracted features into two parts: Retained and refined. On the other hand, IDM is not efficient enough and brings inflexibility to network design. It isn’t easy to combine identity connections with IDM. However, models using this approach can be geared towards real-time systems because such models are often very flexible in making the trade-off between PSNR and inference time via a parameter called Channel Modulation Coefficient.

2.3. Attention-based method

The authors in [14] introduced SENet that uses channel attention to exploit interdependencies between channels of a model, improving feature map efficiency. This CNN-based squeeze-and-excitation network enhances classification networks and is now widely used in neural network design for down-streaming computer vision tasks [39].
Channel attention mechanisms have been introduced to improve the performance of neural networks in the image super-resolution domain. Zhang et al. [15] developed a CNN model called RCAN that utilizes channel attention to address SISR problems. RCAN combines residual in residual (RIR) and channel attention (CA), in which RIR is used to propagate low-frequency information [40] from the input to the output, allowing the network to learn residual information at a coarse level. The deep architecture of RCAN, with over 400 layers, enables the network to learn deeply and achieve high performance.
Super-resolution algorithms aim to restore mid-level and high-level frequencies because the low-level frequencies can be obtained from the input low-resolution image without the need for highly complex computations. The RCAN model modeled the features equally or on a limited scale, ignoring the abundantly rich frequency representation at other scales. As such, these lack discriminative learning capability and capacity across channels, limiting convolutional neural network capabilities. To overcome this limitation, Anwar et al. [16] proposed the DRLN network, which uses dense connections between RBs to utilize previously computed features. The model also uses the Laplacian pyramid attention to weigh the features at multiple scales and according to their importance. The DRLN network has fewer convolutional layers than the RCAN model but more parameters. Nevertheless, it is computationally efficient due to the multiplexing of the channels, unlike RCAN, which uses a more expensive operation that involves more channels.
Channel attention-based approaches in image super-resolution have limitations in preserving texture and natural details due to the processing of feature maps at different layers, which can result in the loss of details in the reconstructed image. To address this issue, Niu et al. [17] proposed the HAN network, which can discover correlations between hierarchical layers, channels within each layer, and the positions of each channel, thereby activating the representative power of CNN. The HAN model also proposes a LAM model to demonstrate the relationship between features at hierarchical levels to promote CNN’s performance. Additionally, the CSAM module improves the discriminative learning of the network. However, LAM only assigns a single importance weight to all features in the same class and does not consider the difference in the spatial position of these features. While discovering relationships between features at different layers can benefit representational learning in neural networks, it is computationally expensive due to the quadratic complexity of dot-product attention, increasing the complexity from ( H W ) 2 L to ( H W L ) 2 , where H and W are the sizes of the feature mapping and L is the number of layers.

2.4. Feedback network-based methods

The feedback mechanism differs from conventional input-to-target mapping, incorporating a self-correcting phase during the model’s learning process. In computer vision, feedback mechanisms have become increasingly popular in recent years. In particular, feedback mechanisms are commonly used in SR models because they can transfer in-depth information to the front end of the network to help process shallow information more effectively. This aids in the reconstruction of HR images from LR images.
Haris et al. [18] proposed a method called DBPN to capture the interdependencies between LR and HR image pairs. The method uses iterative back projection to calculate reconstruction error and extract high-frequency features, which are then merged to improve the accuracy of the HR image. DBPN alternates between the upsampling and downsampling layers and improves the performance through dense connections, especially for magnification by a factor of eight. However, this method is computationally expensive and increases network complexity and inference time.
Zhen et al. [19] developed the SRFBN network, which employs the negative feedback mechanism of human vision to enhance low-level representations with high-level information. The intermediate states in a constrained RNN are used to implement this feedback mode. The feedback blocks are designed to handle the feedback wiring system and generate high-level information more efficiently. The SRFBN network improves the reconstruction performance with few parameters to reduce the likelihood of over-fitting due to the feedback mechanism. Still, this approach leads to an increase in computational costs. However, networks like DBPN and SRFBN cannot learn feature mapping at multiple context scales.
The feedback mechanism used in SRFBN only propagates the highest-level feature to a shallow layer, leaving out other high-level information captured in different receptive fields. As a result, SRFBN does not make full use of high-level features or adequately refine low-level features. To address these drawbacks, Li et al. [20] introduced the GMFN network, which transfers refined features to the shallow layers. They assume that enough contextual information can refine the basic layers. The feature maps extracted at different layers contain complementary information for image reconstruction and are captured in different receptive fields. Then, the feedback connection optimizes the basic information with the help of the advanced counterpart.
Liu et al. [21] developed the HBPN network, taking inspiration from the DBPN model. It employs residual hourglass modules in a hierarchical structure to improve error estimation and achieve superior results. However, the ability of these models to generalize is restricted by the kernel set k and scaling factors s. Furthermore, the HBPN model requires both RGB and YUV images as input, resulting in considerable computational overhead.
The authors in [22] also introduced an ABPN network that follows the concept of the HBPN model and utilizes RBPB blocks to expand the receptive field of back-projection blocks. By leveraging the original information in the LR input, RBPB can enhance the SR performance by exploiting the interdependencies between the LR input and the SR output. However, ABPN has some limitations. Firstly, it fails to merge high-frequency features. Secondly, the standard convolutional layers and self-attention modules do not distinguish between different degrees of feedback errors, resulting in back-projection blocks being unable to focus on areas with significant errors and reducing the correction effect.

2.5. Recursive learning-based methods

The feedback-based model utilizes self-correcting parameters, distinguishing it from the recursive learning-based model, where the parameters are shared among the modules.
The CARN network proposed by Ahn et al. [23] uses a lightweight model that replaces the standard RB block with an efficient RB version, which has fewer parameters and computational costs than RB but similar learning capabilities. The CARN network achieved super-resolution benchmark results among lightweight models with a parameter count of less than 1.5 million. Still, the performance is limited by the number of parameters, and the PSNR and SSIM metrics are reduced.
To reduce computational complexity and cost, Choi et al. [24] proposed the BSRN network, which includes an initial feature extractor, a recursive RB, and an upscaling part. The SRRFN model, on the other hand, was proposed by Li et al. [25] and achieved superior results with fewer parameters and less execution time than the RCAN model. SRRFN introduced a new fractal module (FM), which can create multiple topological structures based on a simple component to detect rich image features and increase the fault tolerance of the model.
The LP-KPN network proposed by Cai et al. [26] is based on the Laplacian pyramid to learn kernels per pixel for the decomposed image pyramid to achieve high computational efficiency with large kernel sizes. The LP-KPN model outperformed the CRAN models trained on simulation data while having fewer convolutional layers. However, the LP-KPN model only reconstructs the LR image by collaborating with different pixel-local reconstructions, which does not fully use hierarchical features across different frequencies.

2.6. GAN-based methods

GANs [41] use a game theory approach that includes the generator and the discriminator trying to fool each other. The generator generates SR images that the discriminator cannot distinguish as real or artificial HR images. In this way, HR images with better perceptual quality are produced. The corresponding PSNR values are often attenuated, highlighting the problem that the quantitative measures common in the SR literature do not encapsulate the perceptual accuracy of the generated HR outputs.
GAN models overcome the weakness when using the loss function MSE as the criterion. Although minimizing MSE also maximizes PSNR and is a common metric used to evaluate and compare SR algorithms, the ability of MSE (and PSNR) to capture relevant differences in terms of perceptions, such as high texture details, is very limited because they are determined based on differences in the image in pixels. The higher PSNR does not necessarily reflect a better perceptual outcome. Realizing the above, Ledig et al. [27] proposed the generative model related to GAN in the super-resolved problem as SRGAN. The SRGAN model uses a deep residual network (ResNet) with skip connections and diverges from the MSE as the sole optimization objective. The model also identifies a new perceptual loss function using VGG network high-level feature mappings combined with a discriminator that encourages solutions that are difficult to distinguish from HR images. Although SRGAN significantly improves the overall image quality of the reconstruction, its disadvantage is that the model is difficult to train, often producing artifacts in SR images.
To avoid the generation of SR images with artifacts, Xintao Wang et al. [28] proposed the ESRGAN network to make the reconstructed image more realistic. Firstly, this model removes the BN layer, reducing computational costs and memory. Moreover, it also contributes to reducing the artifacts in the SR image. Second, the use of pre-activation features results in a more accurate brightness distribution closer to the actual brightness, producing sharper edges and richer textures. Third, the deep learning model shows outstanding performance in easy training thanks to the RRDB block without the BN layer. Even so, the model has difficulty recreating the high-frequency edges. Furthermore, the regeneration effect will greatly deteriorate when the ESRGAN model is applied to multiple degradations. One form of the SRGAN model with a slight variation that can give the most satisfactory results in terms of inference time and applies to low-end devices such as embedded systems is the SwiftSRGAN model proposed by Koushik Sivarama Krishnan et al. [29] so that the model can run on a time-constrained system; the model changed the convolution block to a DSC block.
The generator structure of the SRGAN model uses a deep residual network called SRResNet. This type of architecture gives good results in terms of structural similarity and detail. However, in experiments, it was found to perform poorly in maintaining global information and high-level structure, sometimes distorting the overall characteristics of the image. Therefore, Mirchandani et al. [30] proposed the DPRSGAN model. To avoid the above problem, the model uses dilated convolution to capture global structures and fewer parameters. On the other hand, changing the discriminator to a Markovian discriminator (PatchGAN) speeds up model training and produces sharper details.
Besides, in order to deal with the degraded images in the real world in general, Real-ESRGAN was formed with the proposal of Wang et al. [42]. Compared to ESRGAN models, Real-ESRGAN is trained entirely on synthetic data, which helps it to recover complex real-world images with better image performance. Another model used for the real-world image super-resolution problem is BSRGAN, proposed by Zhang et al. [31]. It has been proposed as a real-world degradation model to remove the disadvantages of synthetic data generation and build a robust model for different combinations of downsampling kernels, blur kernels, and noise. The method demonstrates outstanding results when dealing with real-world datasets where the degradation model is unknown. Nevertheless, since the models are trained using pairs of images generated by such real-world degradation models and considered for the general scenario, it can be confirmed that the denoising has surpassed the required level. Hence, the real-world degradation model is not appropriate for specific visual inspection tasks that require fixed high-resolution and low-resolution noise levels for noise reduction.
In addition, F2SRGAN [8] enhances the receptive field of the convolution operator by employing Fast Fourier Convolution. This technique enables the model to capture low-frequency characteristics in the frequency domain, resulting in quicker coverage of high-frequency features compared to the traditional spatial domain of standard convolution.

2.7. Transformer-based methods

Methods using CNN or GAN can generally only use local information about the image, and they ignore the global interaction between parts of the image, resulting in low-quality recovery. Transformer is a new deep learning model that applies a self-attention mechanism with the principle of placing different weights on the importance of each part of the input data. Since very early on, it has been a state-of-the-art method in natural language processing (NLP). Due to its ability to solve long-term dependency problems, Transformer has become increasingly popular in computer vision tasks, such as object detection, segmentation, classification, and ISR. It can exploit local and global information in the input image, which will add a more detailed effect to the output image. This breakthrough attracted many researchers and introduced a new network structure for ISR.
A typical model for applying Transformer to this super-resolution problem is the ESRT proposed by Zhisheng et al. [32]. The model consists of an LCB block, which uses HPB blocks to automatically adjust the feature map size to extract intensive feature mappings with low computational cost. The model also has an LTB block to capture long-term dependencies between similar patches in an image with the help of specially designed Efficient Transformer (ET) and Efficient Multi-Head Attention (EMHA) mechanisms. This model is proposed to effectively enhance the feature representation and long-term dependence of similar patches in an image, to achieve better performance with low computational cost. Although Transformer is a powerful model, there is still the problem that Transformer-based models are heavy models, i.e., the number of parameters and the amount of data to train are still large.

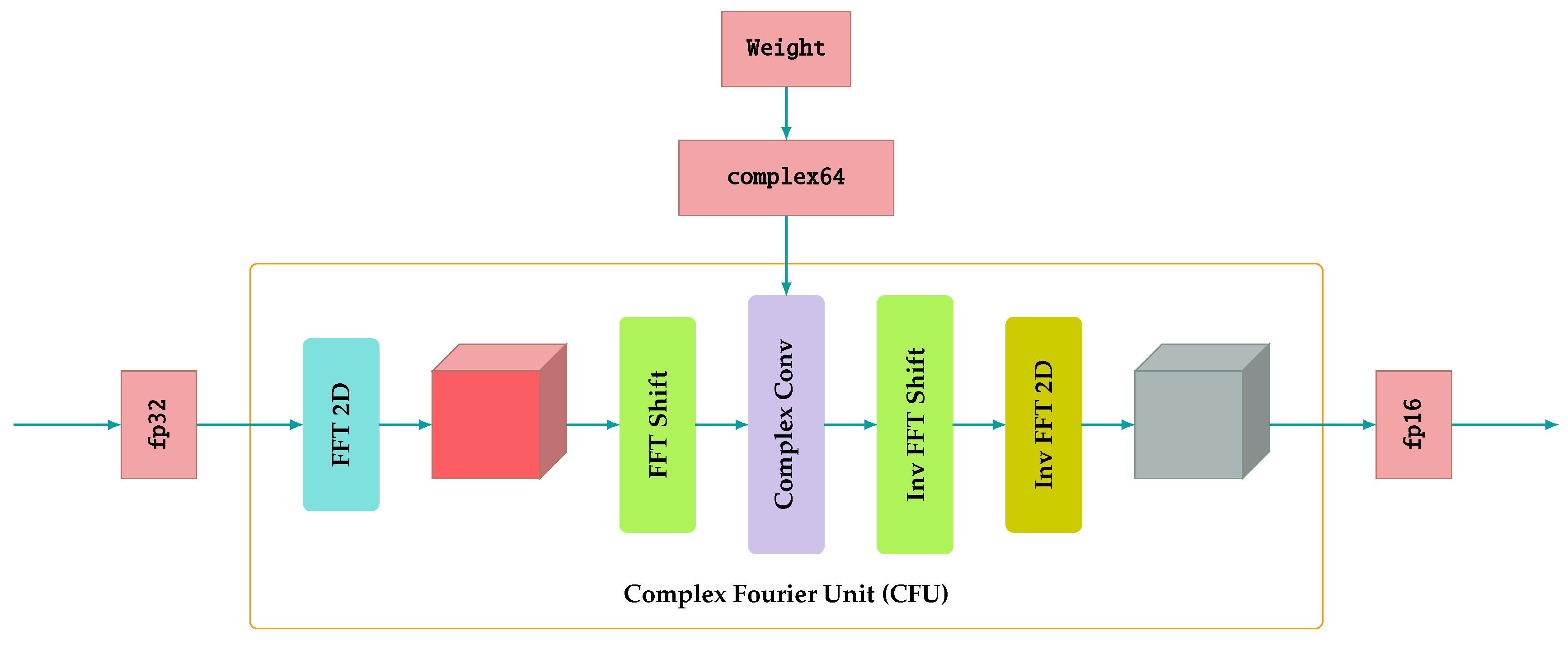
2.8. Frequency-domain based methods

SR algorithms that use a frequency domain-based method transform LR input images into the frequency domain to estimate an HR image. The reconstructed HR image is then transformed back into the spatial domain. Two groups of algorithms that depend on the transformation used for transforming the images to the frequency domain are Fourier transform-based and Wavelet transform-based methods. In [35], the authors converted LR satellite images to the discrete Fourier transform (DFT) domain and combined them using the relation between the aliased DFT coefficients of the LR images and those of the unknown HR image. The advantages of frequency-domain-based SR approaches include enhancing the high-frequency information of images and having low computational complexity. However, these methods have some drawbacks, including being insufficient to handle real-world applications and having difficulty expressing prior knowledge used to regularize the SR problem. Many frequency-domain approaches rely on Fourier transform properties such as the shifting and sampling theorems, making them easy to understand and apply. Some frequency-domain methods make assumptions that enable the use of efficient procedures for computing restoration, such as the Fast Fourier Transform (FFT).
Implicit neural functions, parameterized by multilayer perceptrons (MLP), have shown great success in representing continuous-domain signals such as images, shapes, and signals. However, one drawback of using a standalone MLP is that it tends to focus on low-frequency components [43] and may not capture fine details [44]. To address this limitation, Lee et al. [36] introduced a dominant frequency estimator called the LTE tool, which improves the input features of the MLP. The LTE model includes three additional trainable layers that process the encoder output and correspond to sine and cosine waves’ amplitude, frequency, and phase. This output is then used as input for an MLP that has four fully connected layers. To further enhance the results, a global skip connection with a bilinear upscaled version of the input is added to the entire model, allowing the deep model to focus on the residual between the closed-form approximation and the final result. While LTE has achieved high-quality arbitrary-scale rectangular super-resolution with high-frequency details, its spatially varying nature prevents it from evaluating a frequency response for image warping.
Zhang et al. [33] developed a model called SwinFIR that combines the SwinIR model proposed by Liang et al. [34] with the FFC block [45]. This model uses a frequency-domain approach to capture global information better and restore high-frequency details in images. The SwinFIR model performs well in restoring images with periodic transformations and challenging samples. However, one limitation of this model is that it is slow for large-scale images, as measuring importance at a global spatial scale requires vector multiplications along rows and columns. Recently, Nguyen et al . [8] proposed an enhanced model F2SRGAN that further improves the FFC block by performing the convolution operator directly in the frequency domain rather than splitting the real and imaginary part and implementing it separately.

3. Optimization Techniques for SISR Problems

3.1. Quantization

Quantization reduces the bit-width of computations and tensor storage compared to floating-point precision. This leads to more compact model representation, faster operations, and lower computational costs during runtime while maintaining reasonable accuracy.
Quantization involves two main operators: Quantize (Q) and Dequantize (DQ). For x ∈ [ β , α ] as the range of real values and b as the bit-width of the lower precision format. β and α are the smallest and largest values of the range of real floating-point values. A b-bit signed integer precision format can represent 2 b possible integer values, with its value range between [ − 2 b − 1 , 2 b − 1 − 1 ] . In this super-resolution problem, we consider the real value range as a single-precision floating-point value range, which is a floating-point number with 32-bit precision. The quantization operation maps a real value x ∈ [ β , α ] to a value within the value range of b bits with low precision [ − 2 b − 1 , 2 b − 1 − 1 ] .
The quantization operator includes two processes: real-value transformation and clipping process. The process of transforming a real value x into a quantized value x q can be defined as Eq. (1).
x q = x s − z ,
where z is an immutable parameter (zero point) of the same type as the quantized value. It represents the quantization value x q corresponding to the real value of zero ( x = 0 ) . s is a scaling factor that divides the real value range into a number of parts. In asymmetric quantization − α ≠ β , we can calculate the scaling factor s and zero point as Eq. (2).
s = α − β 2 b − 1 z = β ( 2 b − 1 ) α − β + 2 b − 1
However, if the output x q falls outside the precision range of b bits, meaning it falls outside the interval [ − 2 b − 1 , 2 b − 1 − 1 ] , then we clip the range so that it does not fall outside that range. This means that if x q < − 2 b − 1 , we adjust x q = − 2 b − 1 , and if x q > 2 b − 1 − 1 , we adjust x q = 2 b − 1 − 1 . Mathematically, we can define the quantized value Q ( x , b ) with x as the real value and b as the low-precision bit width using Eq. (3).
Q ( x , b ) = min max x q , − 2 b − 1 , 2 b − 1 − 1
The approximate quantization of a real value by a quantized operation is defined as Eq. (4).
D ( q ) = s ( q + z )
In general, the coefficients s and z depend heavily on the real interval [ β , α ] . This is called clipping range learning. There are two approaches to determine this clipping range: determining the range without re-training model and determining the range through re-training model. Two typical methods that reflect these approaches are Post-Training Quantization (PTQ) and Quantization-Aware Training (QAT), respectively.
The approach that determines the clipping range without re-training model (such as PTQ) forms the clipping range by feeding representative samples into the model. Then, the model is quantized based on the results obtained after having some representative samples. This method is fast but produces lower output accuracy compared to learning the clipping range through re-training model.
The approach of clipping range through re-training model (such as QAT) involves more steps and takes longer to tune the model but provides better output accuracy than the PTQ approach. Regarding the QAT method, the quantization nodes (Q Nodes) and de-quantization nodes (DQ Nodes) are inserted into the network according to a specific set of rules [46]. Then, the network is trained again in several batches in a process called fine-tuning. The Q/DQ nodes simulate quantization loss and add it to the training loss during fine-tuning, making the network more flexible in terms of quantization. However, a problem arises during the back-propagation stage of model tuning, where there exists a rounding function that is non-differentiable at some points and equal to 0 at almost all points.
d d x x = Undefined if x ∈ N 0 if x ∉ N
One way to overcome this problem is to use STE [47]. STE is a way of estimating gradients for thresholding in neural networks. The concept of STE is to set the input gradients to a thresholding function equal to its output gradients, ignoring the derivative of the thresholding function. Specifically, STE allows us to approximate the derivative of the floor function as 1.
d d x x ≈ 1
This means that we are allowed to "skip" the backpropagation calculation when passing through Q and DQ blocks during network training. Figure 1 shows an example of a simple forward and backward computation used in QAT. The QAT quantization process consists of the following four stages:
  • Stage 1: Train the network with floating-point operations.
  • Stage 2: Insert Fake quantization layers Q fake into the trained network. The Q fake layer is used to simulate the process of integer quantization using floating-point computations. It is usually performed by a quantization step (Q) followed by a dequantization step (DQ).
  • Stage 3: Perform fine-tuning of the model. Note that in this process, the gradient is still used in floating-point.
  • Stage 4: Perform execution by removing Q fake and loading the quantized weights.

3.2. Network pruning

Network pruning is an important technique for both memory size and bandwidth reduction. This allows neural networks to be deployed in constrained environments such as embedded systems.
To effectively prune a pre-trained model, two aspects need exploration: pruned architecture and candidate selection. Pruned architecture can be divided into two types: human-defined and algorithmic. Human-defined pruning involves determining a fixed ratio of pruned channels in each layer, while automatic pruning determines the target architecture through algorithms based on global comparisons of structure importance across layers. Unstructured pruning is a form of automatic pruning, where the positions of pruned weights are determined during training and the positions of zeros cannot be predetermined.
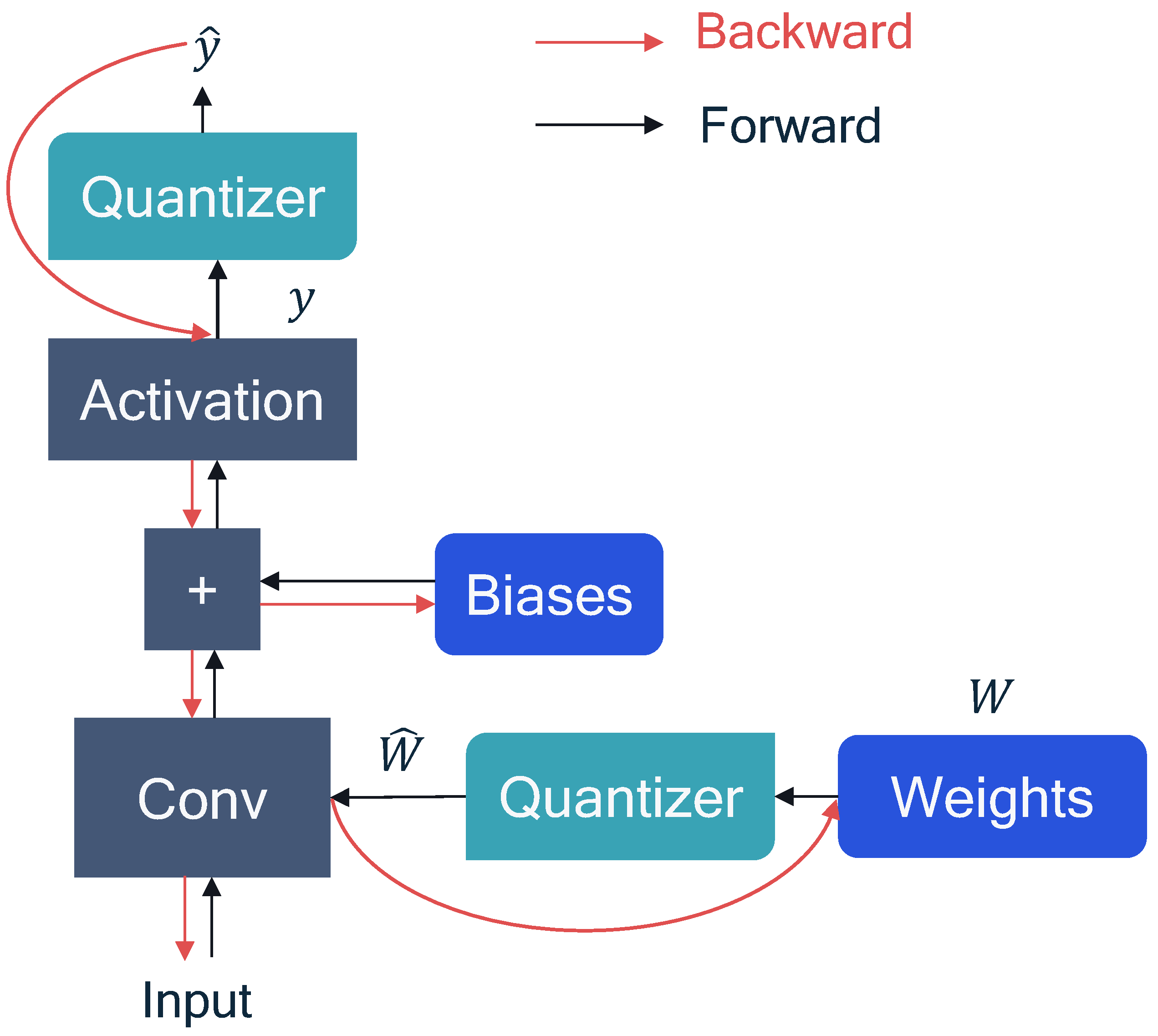
Preprints 73943 g001
Figure 1. Forward and backward-propagation for QAT with the assumption of using STE. [48]
Figure 1. Forward and backward-propagation for QAT with the assumption of using STE. [48]
Preprints 73943 g001
For automatic network pruning, the most commonly used approach is to remove redundant weights that provide little information to the pre-trained model. The brute-force method was the earliest approach used, which involves setting each weight to 0 and checking the loss function’s change. However, due to the large search space, this method is not efficient. Therefore, other methods have been developed, broadly categorized into two types: Magnitude-based pruning and Penalty-based pruning. Both approaches generate values close to 0 for weights, effectively overcoming the drawback of the brute-force method.
Magnitude-based pruning method prunes weights based on the idea that those trained with larger values are more important. The most basic methods are to prune weights with a value of 0 or all weights within a given threshold. One method based on the Hessian matrix is LeCun et al.’s Optimal Brain Damage (OBD) [49], which uses a second-order Taylor expansion approximation to minimize the difference between the loss value of the pruned model weights and the loss value of the model weights before pruning. This method achieves high accuracy but requires significant computation, particularly for the inverse matrix in the optimization solution.
The Penalty-based pruning method aims to reduce the overfitting of the model using regularization. This involves adding an extra term to the loss function to evaluate the complexity of the model. This new loss function is called the regularization loss function, which is usually defined as Eq. (7).
L reg ( w ) = L ( w ) + λ R ( w ) ,
where L ( w ) is the original loss function of the model, and R ( w ) is the regularization term depending only on the weights of the model. The constant λ is usually a small positive number, also known as the regularization parameter. The regularization parameter is often chosen to be small to ensure that the solution of the optimization problem for L reg ( w ) is not far from the solution of the optimization problem for L ( w ) . The regularization term often used in the regularization technique is the use of the L p regularization function, which is defined as Eq. (8).
w p = ∑ i = 1 n w i p 1 p
where n is the number of elements in the vector w . For p = 1 , it is called LASSO pruning, and for p = 2 , it is called weight decay pruning. The use of LASSO pruning has been shown to be more effective in weight selection than using weight decay pruning because the use of the L 2 regularization function (also known as the ridge loss function) only generates weights that approach 0 rather than being equal to 0, while using the L 1 regularization function generates better 0 weights. However, using the L 1 regularization function raises a trade-off problem between the sparsity and performance of the model [50].
The mentioned pruning algorithms only prune at the weight-level, but higher-level pruning requires pruning methods based on structures like groups or networks. The regularization technique can be extended to grouped regularization, expressed as the grouped regularization loss function:
L reg ( W ) = L ( W ) + λ ∑ k = 1 K R ( W k ) ,
where L ( W ) is the original loss function of the model, W is the set of weights that can be trained for all K layers in the model, and R ( W k ) is the regularization operator in layer k to prune the set of weights, W k . The parameter λ is the regularization parameter, which is used to balance the loss function and the pruning criterion. Yuan and Lin [51] proposed the grouped LASSO regularization. To reduce subsets of weights such as filters or channels, the subsets need to be considered as groups in the regularization criterion. The grouped LASSO restricts subsets of unnecessary parameters to simultaneously equal 0. The regularization term of the grouped LASSO is defined as Eq. (10).
R G L ( W k ) = ∑ g ∈ G W g k 2
where g ∈ G is a group in the set of groups G, W g k is the weight matrix or weight vector of group g is a submatrix or subvector in W k . However, estimating the sum of regularization terms across different layers may not be cumulative and therefore meaningless due to differences in distribution and intensity. Realizing this, Gongfan Fang et al. [52] proposed a regularization term in which the importance level of regularization terms is normalized for each layer by adding a constant for each different layer, to ensure that removing groups becomes safer. Specifically, the regularization term that Gongfan Fang et al. [52] defined is represented as Eq. (11).
R D G ( W k ) = ∑ g ∈ G γ k W g k 2
where R D G ( W k ) represents the regularization term of layer k and γ k is the regularization parameter for layer k.

3.3. Knowledge distillation

Knowledge Distillation (KD) refers to the process of transferring knowledge from one or a set of large, complex models to a smaller, deployable model under real-world constraints. It was first demonstrated by Buciluǎ et al. [53] to compress a model and transfer information to train a smaller model without sacrificing accuracy. A knowledge distillation system consists of three main components: knowledge, distillation schemes, and distillation algorithms.
In a neural network, knowledge typically refers to the learned weights and biases. There are three main types of knowledge that can be distilled from a teacher model to a student model. The first is response-based knowledge, where the student model mimics the output of the teacher model. This is the most common type of knowledge system. The loss of information in such cases is related to the computation of the divergence between the logits of the teacher and student models. Kullback-Leibler divergence (KL divergence) is commonly used in feedback-based knowledge distillation methods [54,55]. In feature-based knowledge systems, the teacher model learns to recognize features in its intermediate layers, which can be used to train the student model. The loss function for knowledge distillation achieves this by minimizing the difference between the feature activations of the teacher and student models. Finally, in relation-based knowledge systems, the relationships between feature mappings are used to train the student model. These relationships can be modeled as correlations between feature maps, graphs, similarity matrices, feature embeddings, or probability distributions based on feature representations.
In terms of distillation schemes, there are three major techniques that are commonly used: Offline Distillation, Online Distillation, and Self-Distillation. Offline Distillation is the most popular method, where a pre-trained teacher model is used to guide the student model. In the Offline Distillation process, the pre-trained teacher model is usually a large deep neural network. In some use cases, the pre-trained model may not be available for Offline Distillation. To address this limitation, Online Distillation can be used where both teacher and student models are updated simultaneously in an end-to-end training process. Online Distillation can be operated using parallel computing, making it a highly efficient method. Knowledge Distillation has two issues. The first issue is that the selection of the teacher model significantly impacts the accuracy of the student model. The second issue is that student models cannot always achieve the same high accuracy as teacher models [56], which may lead to unacceptable accuracy degradation during deployment. Self-Distillation addresses these issues by using the same network as both teacher and student. First, Self-Distillation attaches some shallow attention-based classifiers after the intermediate layers of the network at different depths. Then, during training, the deeper classifiers are regarded as teacher models. They are used to guide the training of the student models using a divergence-based loss function on the outputs and an L 2 loss function [57] on the feature maps. In the deployment stage, all the additional shallow classifiers are removed.
Meanwhile, in terms of distillation algorithm, there are currently nine commonly used algorithms. The first type is adversarial learning, which enhances existing training sets to improve model performance or allow teacher-student models to learn better data distributions [58]. The second type is multi-teacher distillation, which uses different teacher structures that can provide different types of knowledge. When distilled into a student model, it can produce better predictions than individual models. The third type is cross-modal distillation, which transfers knowledge between different modalities. This situation arises when data or labels are not available for specific modalities during training or testing [59], so knowledge must be transferred between modalities. The fourth type is graph-based distillation, which captures internal data relationships using a graph. The graph is used in two ways - as a means of transferring knowledge and to control the transfer of teacher knowledge. The fifth type is attention-based distillation, which transfers knowledge using attention mappings. The sixth type is a data-free distillation process, which synthesizes data from a pre-trained teacher model. The seventh type is quantization distillation, which transfers knowledge from a high-precision teacher network (e.g., 32-bit floating point) to a low-precision student network (e.g., 8 bits). The eighth type is lifelong distillation based on the continuous learning mechanisms of lifelong learning, continual learning, and meta-learning, where previously learned knowledge is accumulated and transferred to future learning. The ninth type is NAS-based distillation, which is also used to determine suitable student model architectures for optimizing learning from teacher models.

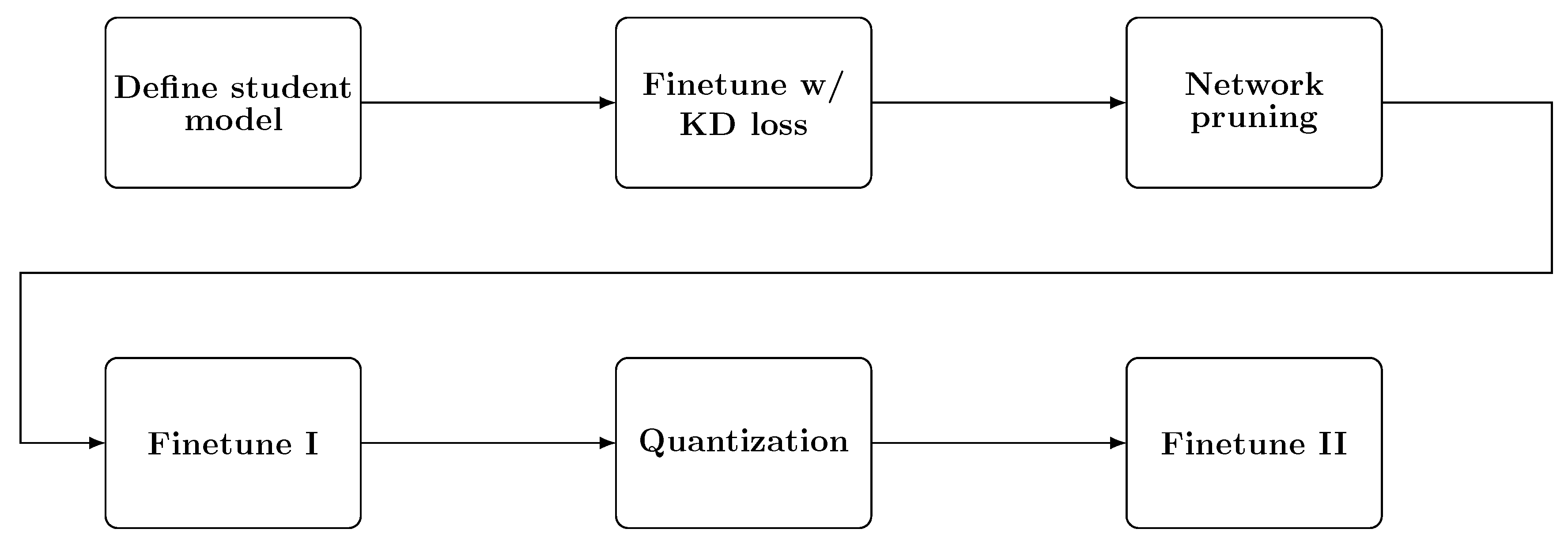
4. A Case Study

In this section, we have opted to employ three optimization methodologies in order to illustrate their influence on the inference time of a specific SISR model, namely F2SRGAN [8]. The optimization techniques employed include quantization, network pruning, and knowledge distillation; each is then revisited to fit the F2SRGAN model. The reason why we choose F2SRGAN is that: first, it is a lightweight GAN-based model which feasible to deploy on embedded systems; second, F2SRGAN is a perceptual-oriented model producing SR images that look more natural in comparison to the common PSNR-oriented model; third, F2SRGAN learns features in the frequency domain to extract global information, and the Fast Fourier Transform (FFT) may pose a bottleneck to the model, so optimization is needed to address this problem. Finally, we propose a pipeline to combine three methods. The result is a new model called Light F2SRGAN.

4.1. Quantization

Calculating a two-dimensional fast Fourier transform (2D-FFT) in F2SRGAN model when using only a 16-bit floating-point range is a drawback. Consider a 2D matrix f with all elements in the range ( 0 , 1 ) . We use the Fourier transform of the matrix f have size N × M to get the matrix F with the element at the position ( u , v ) of the matrix F defined by the equation (12):
F ( u , v ) = ∑ x = 0 N − 1 ∑ y = 0 M − 1 f ( x , y ) e − j 2 π u x N + v y M
Put u = 0 and v = 0 into the equation (12), we have:
F ( 0 , 0 ) = ∑ x = 0 N − 1 ∑ y = 0 M − 1 f ( x , y ) e − j 2 π 0 × x N + 0 × y M = ∑ x = 0 N − 1 ∑ y = 0 M − 1 f ( x , y )
Equation (13) proves that the value of the element at position ( 0 , 0 ) of the Fourier matrix F is equal to the sum of all elements of the input matrix f . If we consider the case of an 8K image, i.e. with a resolution of 1080 × 1080 and whose elements are all equal to 0.5, the value of F ( 0 , 0 ) is:
1080 × 1080 × 0.5 = 583200
The number 583200 is not in the 16-bit floating-point range (from − 65504 to 65504) but is in the 32-bit floating-point range (from − 3.4 × 10 38 to 3.4 × 10 38 ). This is enough to prove that it is impossible to calculate the FFT2D of all matrices using only a 16-bit floating-point range with image resolutions up to 1080 × 1080 .
Through the analysis of the above drawback, we decided to use mixed precision. We use a 16-bit floating point to reduce the calculation time and a 32-bit floating point to make it possible to calculate FFT and avoid unexpected results due to being outside the range of the 16-bit floating point. The F2SRGAN model is quantized to ensure that the accuracy reduction is not significant, but the execution time is shortened using the QAT method. Specifically, the discriminator model is preserved here, and we perform quantization at the generator. Specifically, we insert fake quantization, including Q (quantization) and DQ (dequantization) layers, into basic convolution-related layers like DSC and activation layers like ReLU and PreLU.
During inference, the input to the model is a matrix of elements with a precision of 16-bit floating-point instead of 32-bit floating-point. For the CFU block, we compute it entirely with 32-bit floating-point precision. Details of the 32-bit floating-point calculation of the CFU block are shown in Figure 2. More specifically, during inference, a 16-bit floating-point number input will be expanded to a 32-bit floating-point. Moreover, the weight to calculate the Complex Convolution is extended from the real and complex parts of the weight to a 32-bit floating point so that the weight of the complex number has the precision of a 64-bit floating point so that the CFU block can be calculated within a 32-bit floating-point without problems related to output values that do not fall within the range allowed by a 16-bit floating-point. After computing in the CFU block with 32-bit floating-point precision, the output will be converted to a value with 16-bit floating-point precision.

4.2. Network pruning

In network pruning, we apply the newest method presented in [52], where the authors proposed the automatic pruning process via a dependency graph to represent the dependency between layers. Moreover, the proposed method doesn’t rely on a specific problem or architecture. Therefore, even with simple pruning criteria, it gives better results compared to previous ones.
Firstly, we load the pre-trained model to optimize the weight of the particular model. This step varies depending on a specific task or problem. Secondly, we build the dependency graph on that model. The dependency graph represents the dependency between layers via a symmetric boolean matrix. The author defines two types of dependency: inter-layer dependency and intra-layer dependency. The former is known when the structure of the network is pre-defined. We only have to check whether a connection exists from one layer’s output to another’s input. While the latter inspects if they have the same pruning schemes. The Batch Norm layer does share pruning schemes, whereas Convolution doesn’t work in most cases. Let F be the network with L layers on which we want to build the dependency graph. Dependency graph G has the size of 2 L × 2 L as there are L layers overall. For layer i, we have F i − and F i + as the input and output, respectively. If i = j , it is an intra-layer dependency, and they share the same pruning schemes, denoted as s c h ( F i − ) = s c h ( F i + ) . While i ≠ j , it is an inter-layer dependency. Overall, it can be formulated by Eq. (14).
G F i − , F j + = i ≠ j ∧ C O N N E C T F i − , F j + ∨ i = j ∧ s c h ( F i − ) = s c h ( F j + ) ,
where ∧ and ∨ is logic operator AND and OR respectively and function C O N N E C T F i − , F j + represent the whether there is a connection between F i − and F j + . After that, layers relate to each other through the dependency graph are grouped together, which created a set of grouped layers.
The next step is to prune the network based on the grouped layers and their importance score. To simplify the process, we choose to experiment on three different importance scores as follows:
  • Random: Randomize the importance score of parameters within each group.
  • Mean Absolute Error ( L 1 ): Li et al. [60] propose to prune a proportion of filter that has the least sum of its absolute kernel weight. Let filter j is W j , i ∈ R k × k and m is the number of filters, the importance score of filter j is defined by Eq. (15).
    s j = ∑ i = 1 m W j , i 1 .
  • LAMP: Conceptually, LAMP measures the importance of a connection with the unpruned ones. LAMP considers network layers as operators, following the logic of lookahead pruning [61]. Based on minimizing model-level L 2 distortion, Lee et al. [62] propose a score function. First, the author sorts the weight tensor W 1 , . . . , W L in ascending order so that for any pair of u and v with u < v , the connected weights maintain at least the same inequality W [ u ] ≤ W [ v ] . The LAMP score is calculated using Eq. (16).
    L A M P ( u , W ) = W [ u ] 2 ∑ u ≥ v W [ v ] 2 ,
    where W is weight tensor and u the index of calculated weight. The score function guarantees that only one weight in each layer has a score of 1, which is the highest magnitude.
In addition, the authors in [52] proposed a different way to calculate the importance score on a whole set of groups. Finally, the model is much lighter after pruning all components with low importance scores. However, the accuracy decreases as a result. Therefore, we have to finetune the model at the end to address this issue.

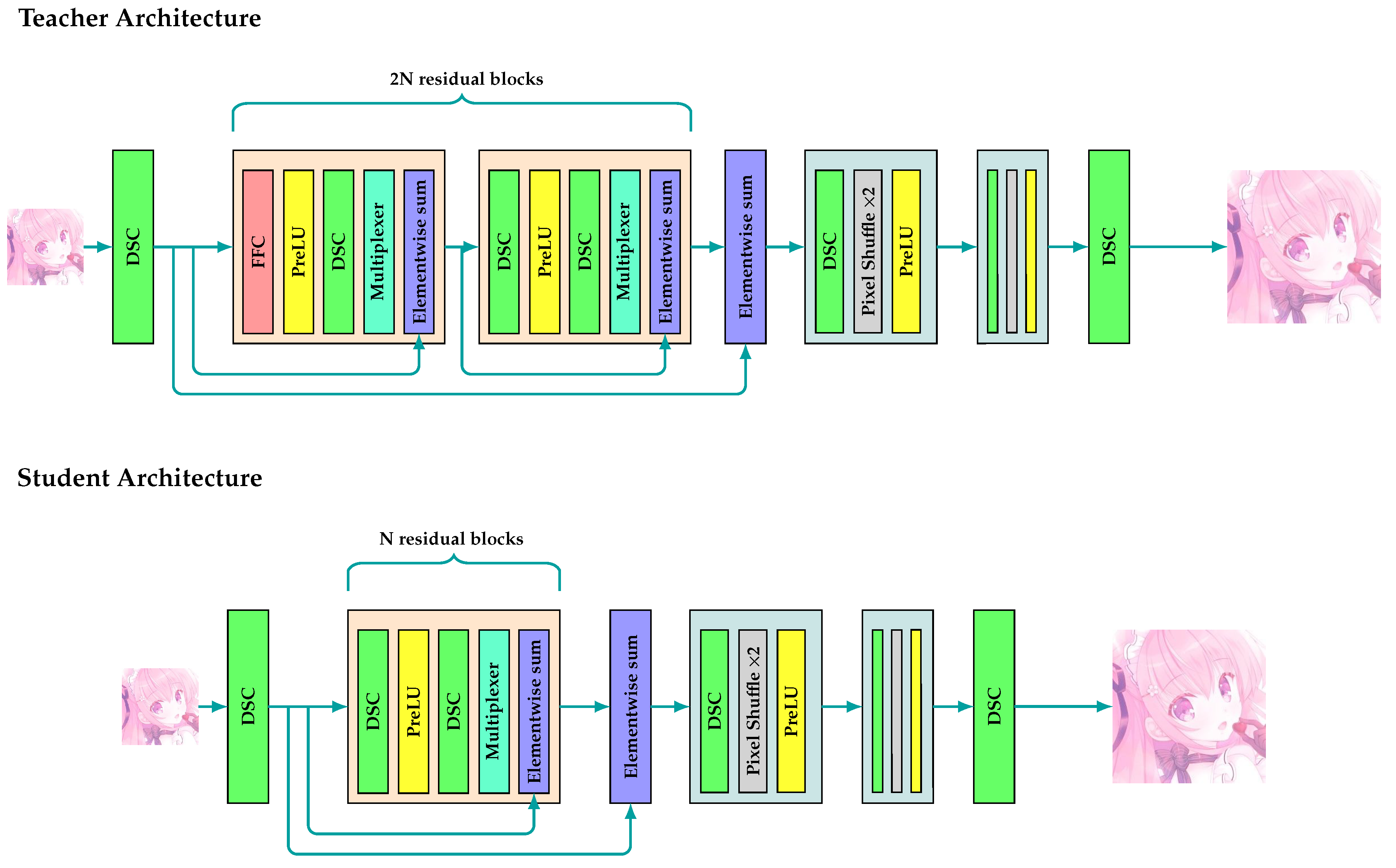
4.3. Knowledge distillation

In the F2SRGAN model, the transfer process between the frequency domain and the spatial domain may prolong the overall inference time of the model. To address this problem, we design a Student network without the Fourier Residual Block, which means that it now has 8 Residual Block without BN instead of 16 in the Teacher model. The overall Teacher and Student network architecture is represented in Figure 3.
As F2SRGAN prioritizes learning low-frequency features to cover faster high-frequency ones, we want the Student network to behave similarly via feature-based knowledge distillation. Specifically, let h T = { h 1 T , . . . , h T T } and h S = { h 1 S , . . . , h S S } is a feature candidate from Teacher and Student with S, and T is the number of feature candidate of Teacher and Student. We respectively include two loss components as follows:
  • Activation-based and Gradient-based Attention Transfer: Attention Transfer (AT) distillation is proposed by Sergey Zagoruyko et al. [63] with the use of attention maps, which can be formulated by (17):
    L AT = 1 2 ∑ j ∈ J ϕ ˜ C ( h j T ) − ϕ ˜ C ( h j S ) p
    where J is the indices of all Student-Teacher attention maps pair, ϕ ˜ C represents the aggregated feature map in space with L 2 normalization, which means that we replace each vectorized attention map Q with Q Q 2 .
  • Attention-based Feature Distillation: Attention-based Feature Distillation is proposed by Mingi Ji et al. [64] to define hint position and weights for hints. The author evaluates the pair of features between Student and Teacher through attention values α t , s . The loss component can be presented by (18):
    L AFD = 1 2 ∑ t ∑ s α t , s ϕ ˜ C ( h t T ) − ϕ ˜ C ( h ^ s S ) p
    where p = 2 according to the author, ϕ ˜ C represents the normalized channel-wise average pooling function with L 2 normalization. h ^ s S is the up-sampled or down-sampled version of h s S to match the feature map size of the Teacher model.
In addition, the authors in [63] and [64] used the Kullback-Leibler loss in their studies. Let a probability vector soften with a hyper-parameter τ for network f is p f ( τ ) . The value k of the soften probability vector p f ( τ ) is calculated as Eq. (19).
p k f ( τ ) = exp z k f τ ∑ j = 1 K exp z j f τ ,
where z k f is the k value of vector logit z f , K is the number of classes and exp ( x ) = e x is the natural exponential. The Kullback-Leibler loss is defined as Eq. (20).
L KL p s ( τ ) , p t ( τ ) = τ 2 ∑ j p j t ( τ ) log p j t ( τ ) p j s ( τ ) .
The overall loss function for Student is defined as Eq. (21).
L Student = L G + γ L KD + δ L KL ,
where L KD is the knowledge distillation loss, which is L AT or L AFD in this case, γ và δ is the hyper-parameter, and L G is the loss function proposed for F2SRGAN Generator. However, including the L KL increases the overall PI and hurts the perceptual quality.

4.4. Light F2SRGAN

Figure 4 represents step-by-step to produce a Light F2SRGAN model. Firstly, we define a student model based on F2SRGAN, in which we exclude all Fourier Residual blocks and only keep the Residual block since the Fourier operator may pose a bottleneck in the model. Then we re-train the student model with the knowledge distillation scheme. Secondly, we apply network pruning for the result and finetune it due to the accuracy loss during the pruning process. Finally, we apply quantization to the pruned model, then finetuning it. This pipeline is genetic and can be applied to the F2SRGAN model and any solution. In addition, it can be used for other problems rather than limited to SISR problems.

5. Experiments

5.1. Datasets

Following the settings on F2SRGAN [8], we train the model on the high-resolution image dataset of DIV2K [65] (800 train images + 100 test images), Flicker2K [66] (2650 images). Specifically, we randomly crop the patch image with the size of 48 and then downscale it to produce the low-resolution training image. In addition, horizontal flip, vertical flip, and rotation are included. The validation dataset is the DIV2K test images. Finally, we evaluate the result on Image Super-Resolution benchmark datasets Set5, Set14, BSD100, and Urban100.

5.2. Implementation Details

We use the AdamW [67] with the default setting of β 1 = 0.9 and β 2 = 0.999 and weight decay 0. In F2SRGAN [8], the author presents the training process consisting of two phases. However, the implementation details vary among our methods. In quantization and network pruning, we load the pre-trained F2SRGAN model, and after performing quantization or pruning, we finetune the model following the second phase. Regarding the knowledge distillation method, we first train the student teacher with the first phase of the process, and then we load the pre-trained F2SRGAN model as the Teacher model to aim for the second phase. Our implementation is based on PyTorch and runs on an Intel Xeon CPU and Tesla P100 GPU.

5.3. Evaluation Metrics

The most common metric in super-resolution tasks is image reconstruction accuracy, like PSNR. Besides, we also evaluate the model with Perceptual Index (PI) [68] due to the limitation of PSNR. The best results are selected based on the latter, as better PI demonstrates better perceptual quality.
Regarding the inference time, we evaluate the model on both Desktop and Jetson Xavier NX. The Desktop setting includes CPU Intel Xeon and GPU Tesla P100. We average out 50 inference times on various sizes of square images to get the best result.

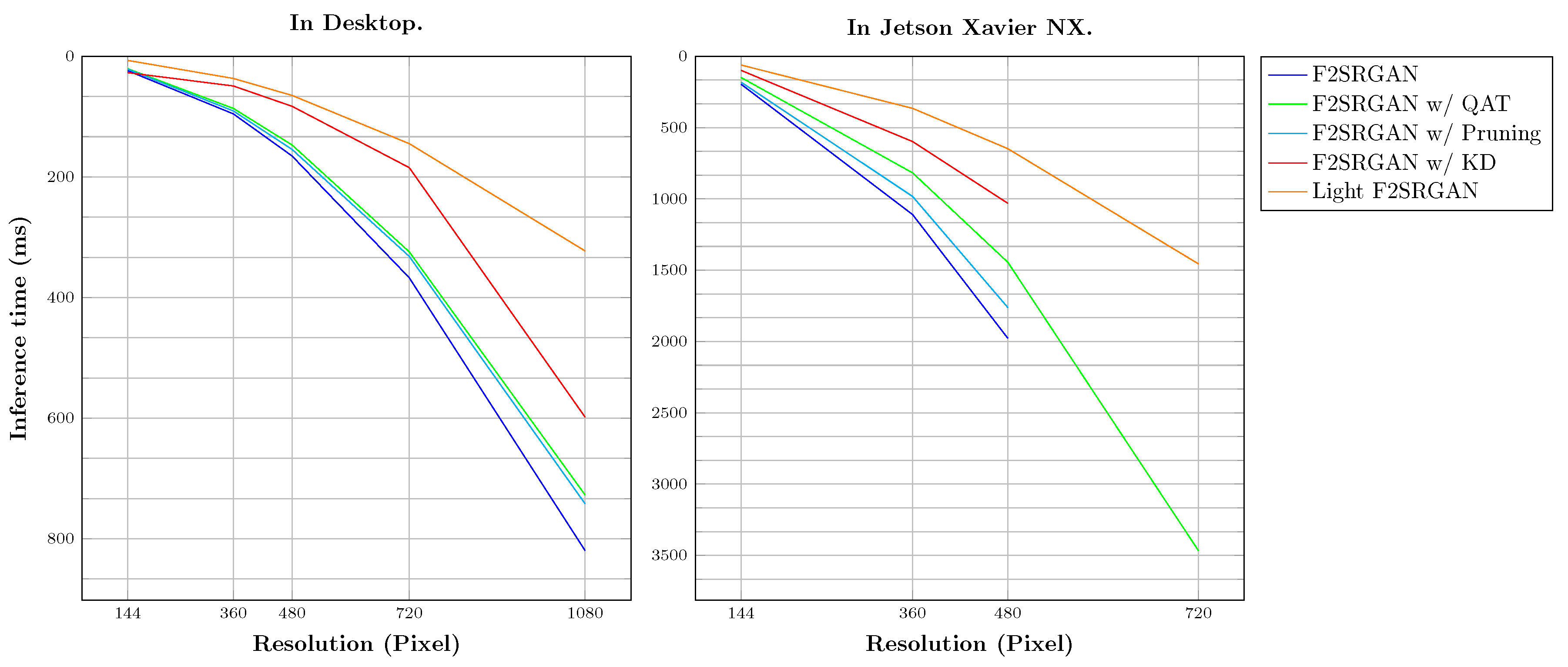
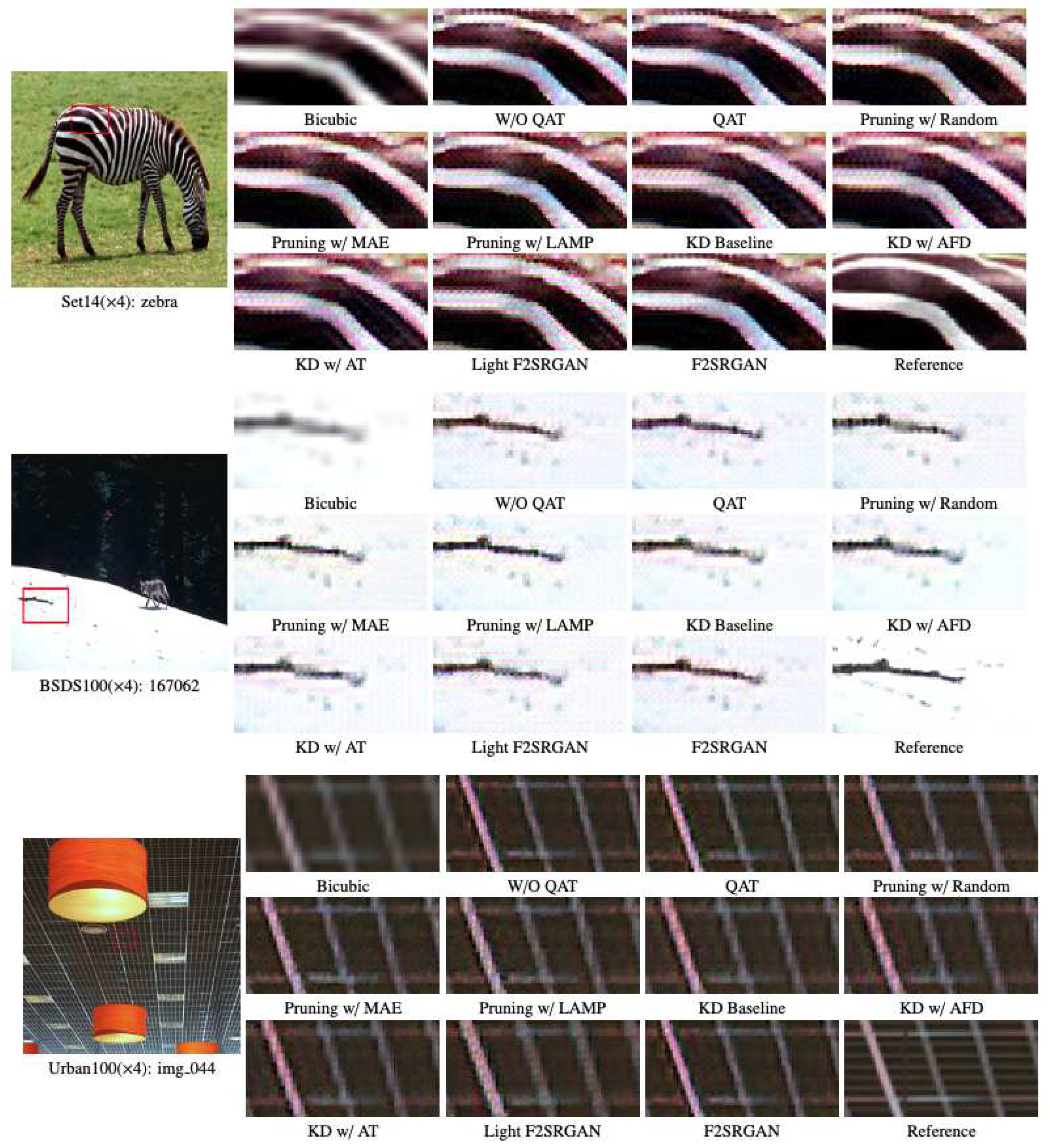
5.4. Experimental Results

Table 2 summarizes the quantitative perceptual of different methods. Specifically, applying quantization for F2SRGAN further improves the PI, which is even better than the F2SRGAN baseline’s quantitative result, while reducing the average inference time. Regarding the network pruning method, calculating the importance score using LAMP yields the best PI among the three investigated scores. The AT loss component in the knowledge distillation method significantly improves the PI compared to the baseline, which excludes the teacher model and trains on a normal scheme. While the AFD loss component slightly enhances the PI metric.
Table 2. Quantitative perceptual (average PI/PSNR) comparison between optimization methods on benchmark datasets on the Y channel from the YCbCr space. Each line separates each method.
Table 2. Quantitative perceptual (average PI/PSNR) comparison between optimization methods on benchmark datasets on the Y channel from the YCbCr space. Each line separates each method.
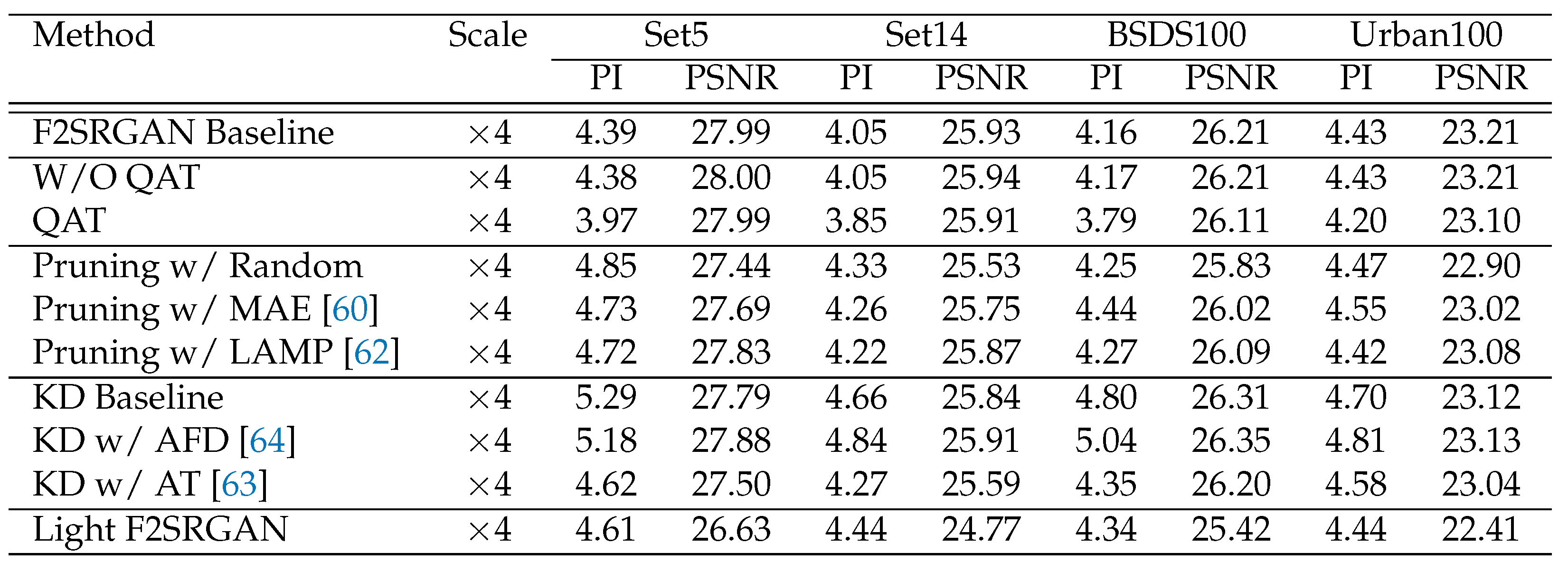Preprints 73943 i001
Figure 5 depicts the average inference time of optimization methods on both Desktop and Jetson Xavier NX. The left chart shows the improvement in inference time of all forms, especially our proposed Light F2SRGAN reduces the inference time from over 800ms to about 300ms on 1080 squared input image. At the same time, the right chart illustrates the run time on Jetson Xavier NX. Due to the limited computation strength, we can only run models with a resolution from 144 to 480 squared input images. However, the quantization method makes it possible to deploy with 720-pixel resolution. In addition, our proposed Light F2SRGAN continues to show large advancement in model inference time on Jetson Xavier NX.
In general, the network pruning, knowledge distillation, and Light F2SRGAN focus more on inference time so that they may introduce artifacts and distortion in the visual results. However, the quantization method gains better enhancement in color intensity and light effect, especially in the visual result of image 167062 in the BSDS100 dataset, the second visual result in Figure 6.

6. Conclusions

In this paper, we conduct an in-depth survey of possible solutions and optimizations for SISR problems on common embedded systems. Then, we propose a pipeline that can be applied to any solution for inference time optimization. The experimental results on F2SRGAN with SISR problem show that our proposal achieved significant improvement in inference time on both Desktop and Jetson Xavier NX, especially the quantization method makes our solution deployable on 720-pixel squared input images.

Author Contributions

Conceptualization, K.H.V., D.P.N. and H.-A.P.; methodology, K.H.V., D.P.N. and D.D.N.; validation, K.H.V., D.P.N., D.D.N. and H.-A.P.; investigation, K.H.V. and D.P.N.; writing—original draft preparation, K.H.V. and D.P.N.; writing—review and editing, D.D.N. and H.-A.P.; supervision, D.D.N. and H.-A.P.; All authors have read and agreed to the published version of the manuscript.

Funding

This research is funded by the Vietnam National University Ho Chi Minh City (VNU-HCM) under grant number NCM2021-20-02.

Acknowledgments

We acknowledge Ho Chi Minh City University of Technology (HCMUT), VNU-HCM for supporting this study.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Park, J.; Hwang, D.; Kim, K.Y.; Kang, S.K.; Kim, Y.K.; Lee, J.S. Computed tomography super-resolution using deep convolutional neural network. Physics in Medicine & Biology 2018, 63, 145011. [CrossRef]
  2. You, C.; Li, G.; Zhang, Y.; Zhang, X.; Shan, H.; Li, M.; Ju, S.; Zhao, Z.; Zhang, Z.; Cong, W.; others. CT Super-resolution GAN Constrained by the Identical, Residual, and Cycle Learning Ensemble (GAN-CIRCLE). IEEE Transactions on Medical Imaging 2019, 39, 188–203. [CrossRef]
  3. Chen, Y.; Xie, Y.; Zhou, Z.; Shi, F.; Christodoulou, A.G.; Li, D. Brain MRI super resolution using 3D deep densely connected neural networks. 15th International Symposium on Biomedical Imaging (ISBI 2018). IEEE, 2018, pp. 739–742. [CrossRef]
  4. Müller, M.U.; Ekhtiari, N.; Almeida, R.M.; Rieke, C. Super-resolution of multispectral satellite images using convolutional neural networks. arXiv preprint arXiv:2002.00580 2020.
  5. Shermeyer, J.; Van Etten, A. The Effects of Super-Resolution on Object Detection Performance in Satellite Imagery. IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), 2019, pp. 1432–1441. [CrossRef]
  6. Kwon, I.; Li, J.; Prasad, M. Lightweight Video Super-Resolution for Compressed Video. Electronics 2023, 12, 660. [CrossRef]
  7. Khani, M.; Sivaraman, V.; Alizadeh, M. Efficient Video Compression via Content-Adaptive Super-Resolution. IEEE/CVF International Conference on Computer Vision (ICCV), 2021, pp. 4521–4530. [CrossRef]
  8. Nguyen, D.P.; Vu, K.H.; Nguyen, D.D.; Pham, H.A. F2SRGAN: A Lightweight Approach Boosting Perceptual Quality in Single Image Super-Resolution via a Revised Fast Fourier Convolution. IEEE Access 2023, 11, 29062–29073. [CrossRef]
  9. Dong, C.; Loy, C.C.; He, K.; Tang, X. Image Super-Resolution Using Deep Convolutional Networks. CoRR 2015, abs/1501.00092. [CrossRef]
  10. Ahn, S.; Kang, S.J. Deep Learning-based Real-Time Super-Resolution Architecture Design. Journal of Broadcast Engineering 2021, 26, 167–174. [CrossRef]
  11. Lai, W.; Huang, J.; Ahuja, N.; Yang, M. Deep Laplacian Pyramid Networks for Fast and Accurate Super-Resolution. CoRR 2017, abs/1704.03915. [CrossRef]
  12. Hui, Z.; Wang, X.; Gao, X. Fast and Accurate Single Image Super-Resolution via Information Distillation Network. CoRR 2018, abs/1803.09454. [CrossRef]
  13. Hui, Z.; Gao, X.; Yang, Y.; Wang, X. Lightweight Image Super-Resolution with Information Multi-distillation Network. 27th ACM International Conference on Multimedia. ACM, 2019, p. 2024–2032. [CrossRef]
  14. Hu, J.; Shen, L.; Sun, G. Squeeze-and-Excitation Networks. 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2018, pp. 7132–7141. [CrossRef]
  15. Zhang, Y.; Li, K.; Li, K.; Wang, L.; Zhong, B.; Fu, Y. Image Super-Resolution Using Very Deep Residual Channel Attention Networks. CoRR 2018, abs/1807.02758. [CrossRef]
  16. Anwar, S.; Barnes, N. Densely Residual Laplacian Super-Resolution, 2019. [CrossRef]
  17. Niu, B.; Wen, W.; Ren, W.; Zhang, X.; Yang, L.; Wang, S.; Zhang, K.; Cao, X.; Shen, H. Single Image Super-Resolution via a Holistic Attention Network, 2020. [CrossRef]
  18. Haris, M.; Shakhnarovich, G.; Ukita, N. Deep Back-Projection Networks For Super-Resolution, 2018. [CrossRef]
  19. Li, Z.; Yang, J.; Liu, Z.; Yang, X.; Jeon, G.; Wu, W. Feedback Network for Image Super-Resolution, 2019. [CrossRef]
  20. Li, Q.; Li, Z.; Lu, L.; Jeon, G.; Liu, K.; Yang, X. Gated Multiple Feedback Network for Image Super-Resolution, 2019. [CrossRef]
  21. Liu, Z.S.; Wang, L.W.; Li, C.T.; Siu, W.C. Hierarchical Back Projection Network for Image Super-Resolution. 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), 2019, pp. 2041–2050. [CrossRef]
  22. Liu, Z.S.; Wang, L.W.; Li, C.T.; Siu, W.C.; Chan, Y.L. Image Super-Resolution via Attention based Back Projection Networks, 2019, [arXiv:eess.IV/1910.04476].
  23. Ahn, N.; Kang, B.; Sohn, K. Fast, Accurate, and, Lightweight Super-Resolution with Cascading Residual Network. CoRR 2018, abs/1803.08664. [CrossRef]
  24. Choi, J.; Kim, J.; Cheon, M.; Lee, J. Lightweight and Efficient Image Super-Resolution with Block State-based Recursive Network. CoRR 2018, abs/1811.12546. [CrossRef]
  25. Li, J.; Yuan, Y.; Mei, K.; Fang, F. Lightweight and Accurate Recursive Fractal Network for Image Super-Resolution. 2019 IEEE/CVF International Conference on Computer Vision Workshop (ICCVW), 2019, pp. 3814–3823. [CrossRef]
  26. Cai, J.; Zeng, H.; Yong, H.; Cao, Z.; Zhang, L. Toward Real-World Single Image Super-Resolution: A New Benchmark and A New Model. CoRR 2019, abs/1904.00523. [CrossRef]
  27. Ledig, C.; Theis, L.; Huszar, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.; Tejani, A.; Totz, J.; Wang, Z.; Shi, W. Photo-Realistic Single Image Super-Resolution Using a Generative Adversarial Network. IEEE Conference on Computer Vision and Pattern Recognition (CVPR). IEEE Computer Society, 2017, pp. 105–114. [CrossRef]
  28. Wang, X.; Yu, K.; Wu, S.; Gu, J.; Liu, Y.; Dong, C.; Qiao, Y.; Loy, C.C. ESRGAN: Enhanced Super-Resolution Generative Adversarial Networks. European Conference on Computer Vision (ECCV) Workshop. Springer International Publishing, 2019, pp. 63–79. [CrossRef]
  29. Krishnan, K.S.; Krishnan, K.S. SwiftSRGAN - Rethinking Super-Resolution for Efficient and Real-time Inference. 2021 International Conference on Intelligent Cybernetics Technology & Applications (ICICyTA), 2021, pp. 46–51. [CrossRef]
  30. Mirchandani, K.; Chordiya, K. DPSRGAN: Dilation Patch Super-Resolution Generative Adversarial Networks. 6th International Conference for Convergence in Technology (I2CT), 2021, pp. 1–7. [CrossRef]
  31. Zhang, K.; Liang, J.; Van Gool, L.; Timofte, R. Designing a Practical Degradation Model for Deep Blind Image Super-Resolution, 2021. [CrossRef]
  32. Lu, Z.; Liu, H.; Li, J.; Zhang, L. Efficient Transformer for Single Image Super-Resolution. CoRR 2021, abs/2108.11084. [CrossRef]
  33. Zhang, D.; Huang, F.; Liu, S.; Wang, X.; Jin, Z. SwinFIR: Revisiting the SwinIR with Fast Fourier Convolution and Improved Training for Image Super-Resolution, 2022. [CrossRef]
  34. Liang, J.; Cao, J.; Sun, G.; Zhang, K.; Van Gool, L.; Timofte, R. SwinIR: Image Restoration Using Swin Transformer. 2021 IEEE/CVF International Conference on Computer Vision Workshops (ICCVW), 2021, pp. 1833–1844. [CrossRef]
  35. Tsai, R. Multiframe Image Restoration and Registration. Advance Computer Visual and Image Processing 1984, 1, 317–339.
  36. Lee, J.; Jin, K.H. Local Texture Estimator for Implicit Representation Function. 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2022, pp. 1919–1928. [CrossRef]
  37. Zhang, K.; Gu, S.; Timofte, R.; Hui, Z.; Wang, X.; Gao, X.; Xiong, D.; Liu, S.; Gang, R.; Nan, N.; Li, C.; Zou, X.; Kang, N.; Wang, Z.; Xu, H.; Wang, C.; Li, Z.; Wang, L.; Shi, J.; Sun, W.; Lang, Z.; Nie, J.; Wei, W.; Zhang, L.; Niu, Y.; Zhuo, P.; Kong, X.; Sun, L.; Wang, W. AIM 2019 Challenge on Constrained Super-Resolution: Methods and Results, 2019. [CrossRef]
  38. Kim, J.; Lee, J.K.; Lee, K.M. Accurate Image Super-Resolution Using Very Deep Convolutional Networks. CoRR 2015, abs/1511.04587, [1511.04587].
  39. Xie, C.; Zeng, W.; Jiang, S.; Lu, X. Bidirectionally aligned sparse representation for single image super-resolution. Multimedia Tools and Applications 2018, 77, 7883–7907.
  40. Yang, C.; Lu, G. Deeply Recursive Low- and High-Frequency Fusing Networks for Single Image Super-Resolution. Sensors 2020, 20. [CrossRef]
  41. Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Networks. Commun. ACM 2020, 63, 139–144. [CrossRef]
  42. Wang, X.; Xie, L.; Dong, C.; Shan, Y. Real-ESRGAN: Training Real-World Blind Super-Resolution with Pure Synthetic Data. IEEE/CVF International Conference on Computer Vision Workshops (ICCVW), 2021, pp. 1905–1914. [CrossRef]
  43. Rahaman, N.; Baratin, A.; Arpit, D.; Draxler, F.; Lin, M.; Hamprecht, F.; Bengio, Y.; Courville, A. On the Spectral Bias of Neural Networks. 36th International Conference on Machine Learning. PMLR, 2019, pp. 5301–5310.
  44. Tancik, M.; Srinivasan, P.P.; Mildenhall, B.; Fridovich-Keil, S.; Raghavan, N.; Singhal, U.; Ramamoorthi, R.; Barron, J.T.; Ng, R. Fourier Features Let Networks Learn High Frequency Functions in Low Dimensional Domains. 34th International Conference on Neural Information Processing Systems. Curran Associates Inc., 2020, NIPS’20, pp. 7537––7547.
  45. Chi, L.; Jiang, B.; Mu, Y. Fast Fourier Convolution. Advances in Neural Information Processing Systems; Larochelle, H.; Ranzato, M.; Hadsell, R.; Balcan, M.; Lin, H., Eds. Curran Associates, Inc., 2020, Vol. 33, pp. 4479–4488.
  46. Jacob, B.; Kligys, S.; Chen, B.; Zhu, M.; Tang, M.; Howard, A.; Adam, H.; Kalenichenko, D. Quantization and Training of Neural Networks for Efficient Integer-Arithmetic-Only Inference. IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2018, pp. 2704–2713. [CrossRef]
  47. Bengio, Y.; Léonard, N.; Courville, A.C. Estimating or Propagating Gradients Through Stochastic Neurons for Conditional Computation. CoRR 2013, abs/1308.3432. [CrossRef]
  48. Siddegowda, S.; Fournarakis, M.; Nagel, M.; Blankevoort, T.; Patel, C.; Khobare, A. Neural Network Quantization with AI Model Efficiency Toolkit (AIMET). CoRR 2022, abs/2201.08442. [CrossRef]
  49. LeCun, Y.; Denker, J.; Solla, S. Optimal Brain Damage. Advances in Neural Information Processing Systems, 1989, Vol. 2.
  50. Zhang, Y.; Wang, H.; Qin, C.; Fu, Y. Learning Efficient Image Super-Resolution Networks via Structure-Regularized Pruning. International Conference on Learning Representations (ICLR), 2022.
  51. Yuan, M.; Lin, Y. Model Selection and Estimation in Regression with Grouped Variables. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 2006, 68, 49–67. [CrossRef]
  52. Fang, G.; Ma, X.; Song, M.; Mi, M.B.; Wang, X. Depgraph: Towards Any Structural Pruning. arXiv:2301.12900 2023. [CrossRef]
  53. Buciluundefined, C.; Caruana, R.; Niculescu-Mizil, A. Model Compression. 12th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. ACM, 2006, p. 535–541. [CrossRef]
  54. Kim, T.; Oh, J.; Kim, N.Y.; Cho, S.; Yun, S.Y. Comparing Kullback-Leibler Divergence and Mean Squared Error Loss in Knowledge Distillation. Thirtieth International Joint Conference on Artificial Intelligence, (IJCAI), 2021, pp. 2628–2635. [CrossRef]
  55. Hinton, G.; Vinyals, O.; Dean, J. Distilling the Knowledge in a Neural Network. arXiv:1503.02531 2015. [CrossRef]
  56. Mirzadeh, S.; Farajtabar, M.; Li, A.; Ghasemzadeh, H. Improved Knowledge Distillation via Teacher Assistant: Bridging the Gap Between Student and Teacher. CoRR 2019, abs/1902.03393, [1902.03393].
  57. Pham, M.; Cho, M.; Joshi, A.; Hegde, C. Revisiting Self-Distillation. ArXiv 2022, abs/2206.08491. [CrossRef]
  58. Wang, X.; Zhang, R.; Sun, Y.; Qi, J. KDGAN: Knowledge Distillation with Generative Adversarial Networks. Advances in Neural Information Processing Systems; Bengio, S.; Wallach, H.; Larochelle, H.; Grauman, K.; Cesa-Bianchi, N.; Garnett, R., Eds. Curran Associates, Inc., 2018, Vol. 31.
  59. Gupta, S.; Hoffman, J.; Malik, J. Cross Modal Distillation for Supervision Transfer. IEEE Conference on Computer Vision and Pattern Recognition (CVPR). IEEE Computer Society, 2016, pp. 2827–2836. [CrossRef]
  60. Li, H.; Kadav, A.; Durdanovic, I.; Samet, H.; Graf, H.P. Pruning Filters for Efficient ConvNets. CoRR 2016, abs/1608.08710. [CrossRef]
  61. Park, S.; Lee, J.; Mo, S.; Shin, J. Lookahead: a Far-Sighted Alternative of Magnitude-based Pruning. CoRR 2020, abs/2002.04809. [CrossRef]
  62. Lee, J.; Park, S.; Mo, S.; Ahn, S.; Shin, J. A Deeper Look at the Layerwise Sparsity of Magnitude-based Pruning. CoRR 2020, abs/2010.07611. [CrossRef]
  63. Zagoruyko, S.; Komodakis, N. Paying More Attention to Attention: Improving the Performance of Convolutional Neural Networks via Attention Transfer. CoRR 2016, abs/1612.03928. [CrossRef]
  64. Ji, M.; Heo, B.; Park, S. Show, attend and distill: Knowledge distillation via attention-based feature matching. AAAI Conference on Artificial Intelligence, 2021, Vol. 35, pp. 7945–7952.
  65. Agustsson, E.; Timofte, R. NTIRE 2017 Challenge on Single Image Super-Resolution: Dataset and Study. IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), 2017, pp. 1122–1131. [CrossRef]
  66. Lim, B.; Son, S.; Kim, H.; Nah, S.; Lee, K.M. Enhanced Deep Residual Networks for Single Image Super-Resolution. IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), 2017, pp. 1132–1140. [CrossRef]
  67. Loshchilov, I.; Hutter, F. Fixing Weight Decay Regularization in Adam. CoRR 2017, abs/1711.05101. [CrossRef]
  68. Blau, Y.; Mechrez, R.; Timofte, R.; Michaeli, T.; Zelnik-Manor, L. The 2018 PIRM Challenge on Perceptual Image Super-Resolution. European Conference on Computer Vision (ECCV) Workshops; Leal-Taixé, L.; Roth, S., Eds. Springer International Publishing, 2019, pp. 334–355. [CrossRef]
Preprints 73943 g002
Figure 2. Implement the calculation on the 32-bit floating-point precision of the CFU block, where fp32 is a floating-point number with 32-bit precision and complex64 is a 64-bit floating-point complex number (the real part has 32-bit floating-point precision, and the imaginary part also has 32-bit floating-point precision).
Figure 2. Implement the calculation on the 32-bit floating-point precision of the CFU block, where fp32 is a floating-point number with 32-bit precision and complex64 is a 64-bit floating-point complex number (the real part has 32-bit floating-point precision, and the imaginary part also has 32-bit floating-point precision).
Preprints 73943 g002
Preprints 73943 g003
Figure 3. F2SRGAN Teacher and Student architecture.
Figure 3. F2SRGAN Teacher and Student architecture.
Preprints 73943 g003
Preprints 73943 g004
Figure 4. Light F2SRGAN construction pipeline.
Figure 4. Light F2SRGAN construction pipeline.
Preprints 73943 g004
Preprints 73943 g005
Figure 5. Average inference time of optimization methods for × 4 scale with different resolution. The left chart demonstrates Desktop inference time, while the right chart is Jetson Xavier NX inference time.
Figure 5. Average inference time of optimization methods for × 4 scale with different resolution. The left chart demonstrates Desktop inference time, while the right chart is Jetson Xavier NX inference time.
Preprints 73943 g005
Preprints 73943 g006
Figure 6. Visual results ( × 4 ) of optimization methods on benchmark datasets.
Figure 6. Visual results ( × 4 ) of optimization methods on benchmark datasets.
Preprints 73943 g006
Table 1. Existing Approaches for Single-Image Super-Resolution (SISR)
Table 1. Existing Approaches for Single-Image Super-Resolution (SISR)
Categories Related Works
Convolutional Neural Network (CNN) based methods  [9], [10], [11]
Distillation methods  [12], [13]
Attention-based methods  [14], [15], [16], [17]
Feedback network-based methods  [18], [19], [20], [21], [22]
Recursive learning-based methods  [23], [24], [25], [26]
GAN-based methods  [8], [27], [28], [29], [30], [31]
Transformer-based methods  [32], [33], [34]
Frequency-domain based methods  [8], [35], [36], [33], [34]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated