Background

Methods

• Data pre-processing: the data was cleaned and prepared to manage missing values, encoding categorical variables, and standardizing or normalizing continuous variables.
• Synthetic data generation: the synthetic data records were generated for each centre using a widely used synthetic Data Vault's Gaussian Copula model, based on the data characteristics from patients' records.
• Model development: trained and implemented three standard classification models - Logistic Regression (LR), Support Vector Machine (SVM), and Random Forest (RF) - on both real-world and synthetic data. These models were used to predict multimorbidity among women with endometriosis.
• Model evaluation: models were assessed the performance of the models by comparing their average accuracies on real-world and synthetic data. Multiple metrics’ of accuracy, precision, recall, and F1-score were used to evaluate the models' performances.
• Comparison and analysis: the results of the models trained on real-world data and synthetic data to determine if synthetic data could serve as a viable alternative for real-world data in predicting multimorbidity among women with endometriosis.

Ethics approval

Anonymous data used in this study was approved by the North of Scotland Research Ethics Committee 2 (LREC: 17/NS/0070) for the RLS study conducted at the University of Liverpool.

The model used age, height, symptoms, commodities and weight in a mathematical formulation. Let $x_i$ be the vector containing these recordings for the $i^{\mathrm{t}\mathrm{h}}$ person and let $x=(x_1,\dots ,x_n)$ be the matrix containing the data about all $n$ people. As part of developing methodological rigour, we considered a working example to predict whether each person in the sample develops depression. Let $y=(y_1,\dots ,y_n)$ be the vector of response variables where:

$$y_i=\left\{\begin{array}{c}1\mathrm{if}\mathrm{patient}i\mathrm{develops}\mathrm{a}\mathrm{depression}\\ 0\mathrm{if}\mathrm{patient}i\mathrm{does}\mathrm{not}\mathrm{developp}\mathrm{depression}.\end{array}\right.$$

In this example, s we collect data for $n=3$ people and have $p=3$ recordings for each person $i$, (i.e., age, height and weight). These are represented by $x_{i1},x_{i2}$ and $x_{i3}$ respectively. The data can be summarised in Table 1 as follows:

Table 1. Example Dataset for Predicting Depression.

Table 1. Example Dataset for Predicting Depression.

PERSON #	AGE	HEIGHT (M)	WEIGHT (KG)	DEPRESSION
1	67	1.9	65	1
2	43	1.2	75	0
3	23	1.5	43	0

We created a function, $f_{\beta }$ with parameters $\beta$, that takes the age, height, and weight ($x_{i1},x_{i2},x_{i3}$) of the person $i$, as input and outputs a prediction of whether they will develop depression. Let $y_i^{*}$ be the prediction of whether person $i$ develops depression, then we say that

$$y_i^{*}=f_{\beta }\left(x_i\right).$$

The performance of parameters $\beta$ can be tested through a loss function, defined as $\mathcal{L}\left(\beta \right)$ which measures the difference between the true values of $y$ and the predictions, $y^{*}=(y_1^{*},\dots ,y_n^{*})$. The loss function imposes a penalty when incorrect predictions are made. Hence, to find the best $\beta$, we solve the optimisation problem:

$${\beta }^{*}=\underset{\beta }{\mathrm{argmin}}\mathcal{L}(\beta ,y,y^{*}).$$

The function $f_{{\beta }^{*}}$ can then be used to make predictions for patients who haven’t been tested for depression.

An initial observation was that our prediction function could become over-fitted to the data. This meant that the function captured the specific distribution between $x$ and $y$ very well, but if this data was not in a structured format representing the true distribution between symptoms and comorbidities, the prediction function would not be generalisable to other types of data.

The performance of the prediction function on unseen data can be estimated by separating the data into a training set, $(x^{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}},y^{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}})$ and test set, ($x^{\mathrm{t}\mathrm{e}\mathrm{s}\mathrm{t}},y^{\mathrm{t}\mathrm{e}\mathrm{s}\mathrm{t}})$. The optimal parameters are found using the training set and then the model’s accuracy is tested on the test set. This accuracy is measured by the proportion of correctly classified data. This is measured by a confusion matrix, which records the frequencies of each possible outcome. Let $C$ be the confusion matrix defined as:

$$C=\left(\begin{array}{cc}{C}_{00}& C_{01}\\ C_{10}& C_{11}\end{array}\right)$$

(1)

where $C_{ij}$ is the number of times $y^{\mathrm{t}\mathrm{e}\mathrm{s}\mathrm{t}}=i$ while $y^{{\mathrm{t}\mathrm{e}\mathrm{s}\mathrm{t}}^{*}}=j$. The accuracy of our model is then

$$\mathrm{A}\mathrm{c}\mathrm{c}\mathrm{u}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{y}\left(\%\right)=\frac{C_{00}+C_{11}}{C_{00}+C_{01}+C_{10}+C_{11}}.$$

(2)

To summarise, the approach is broken down into the following three steps,

1)

Solve optimisation problem

$${\beta }^{*}=\underset{\beta }{\mathrm{argmin}}\mathcal{L}\left(\beta ,y^{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}},y^{{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}}^{*}}\right)$$

on the training set, where the set of prediction values, $y^{{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}}^{*}}$, is found by

$$y^{{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}}^{*}}=f_{\beta }\left(x^{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}}\right).$$

2)

Make predictions on the test set using optimal weights ${\beta }^{*}$

$$y^{{\mathrm{t}\mathrm{e}\mathrm{s}\mathrm{t}}^{*}}=f_{{\beta }^{*}}\left(x^{\mathrm{t}\mathrm{e}\mathrm{s}\mathrm{t}}\right).$$

3)

Construct confusion matrix, $C$ as is defined in (1) and find the accuracy of the model on unseen data by equation (2).

Data preparation – Manchester

In the Manchester dataset, for each patient, the presence of various symptoms and multiple diagnoses among women with Endometriosis are recorded. These are summarised, with descriptions in Table 2. A total of $p=15$ recordings are made for each person, and so we define $x_i=(x_{i1},\dots ,x_{ip})$ to be the vector containing the recordings for person $i$.

Table 2. Manchester Data Feature Variables.

Table 2. Manchester Data Feature Variables.

Feature	Data Type	Description
Age	Integer	Age of the Patient
Menorrhagia	Binary	Whether or not the patient has been diagnosed with menorrhagia
Dysmenorrhea	Binary	Whether or not the patient has been diagnosed with dysmenorrhea
Non menstrual Pelvic pain	Binary	Whether or not the patient experiences non-menstrual pelvic pain
Dysphasia	Binary	Whether or not the patient experiences dysphasia
Dyspareunia	Binary	Whether or not the patient experiences dyspareunia
other symptoms	Binary	Whether or not the patient has any other symptoms besides the ones recorded in other features
Infertility	Binary	Whether or not the patient is infertile
No of Endo symptoms	Binary	Whether or not the patient has more than 1 symptom
Year of diagnosis	Date	The year of the patient’s diagnosis of endometriosis
Other surgery – Not related to endometriosis	Binary	Whether or not the patient received any surgeries not related to endometriosis
Discharged	Binary	Whether or not the patient was discharged
follow up	Binary	Follow up clinical appointments
Hormonal treatment Currently	Binary	Whether or not the patient is taking any hormonal treatment
No of hormonal treatment tried	Integer	The number of hormonal treatments the patient is taking

Additionally, for each individual , three response variables are documented, which are summarised, along with their descriptions, in Table 3. These variables are defined as follows:

$$y_i^M=\left\{\begin{array}{c}1\mathrm{if}\mathrm{patient}i\mathrm{develops}\mathrm{a}\mathrm{mental}\mathrm{health}\mathrm{condition}\\ 0\mathrm{if}\mathrm{patient}i\mathrm{does}\mathrm{not}\mathrm{develop}\mathrm{any}\mathrm{mental}\mathrm{health}\mathrm{condition}\end{array},\right.$$

$$y_i^I=\left\{\begin{array}{c}1\mathrm{if}\mathrm{patient}i\mathrm{develops}\mathrm{irritable}\mathrm{bowel}\mathrm{syndrome}\\ 0\mathrm{if}\mathrm{patient}i\mathrm{does}\mathrm{not}\mathrm{develop}\mathrm{irritable}\mathrm{bowel}\mathrm{syndrome}\end{array},\right.$$

$$y_i^C=\left\{\begin{array}{c}1\mathrm{if}\mathrm{patient}i\mathrm{develops}\mathrm{at}\mathrm{least}\mathrm{one}\mathrm{of}\mathrm{various}\mathrm{other}\mathrm{comorbidities}\\ 0\mathrm{if}\mathrm{patient}i\mathrm{does}\mathrm{not}\mathrm{develop}\mathrm{at}\mathrm{least}\mathrm{one}\mathrm{of}\mathrm{various}\mathrm{other}\mathrm{comorbidities}\end{array}\right..$$

Table 3. Manchester Data Response Variables.

Table 3. Manchester Data Response Variables.

Variable	Name	Description
${\mathit{y}}^{\mathit{M}}$	Mental Health	The presence of at least one of various mental health conditions
${\mathit{y}}^{\mathit{I}}$	IBS	The presence of irritable bowel syndrome (IBS)
${\mathit{y}}^{\mathit{C}}$	Comorbidities (Other)	The presence of at least one other disease (Perhaps we have a list of these?).
${\mathit{y}}^{\mathbf{C}\mathbf{o}\mathbf{m}\mathbf{b}}$	Combined	The presence of at least one of the above conditions.

We examined three models of fit, one for each response variable. We defined a fourth response variable, “Combined”, as shown in the final row of table 3, which indicates the presence of at least one of the other three conditions. Formally, $y^{\mathrm{C}\mathrm{o}\mathrm{m}\mathrm{b}}$ is defined as:

$$y_i^{\mathrm{C}\mathrm{o}\mathrm{m}\mathrm{b}}=\left\{\begin{array}{c}1\mathrm{if}\mathrm{patient}i\mathrm{develops}\mathrm{at}\mathrm{least}\mathrm{one}\mathrm{of}\mathrm{any}\mathrm{of}\mathrm{the}\mathrm{conditions}\\ 0\mathrm{if}\mathrm{patient}i\mathrm{does}\mathrm{not}\mathrm{develop}\mathrm{at}\mathrm{least}\mathrm{one}\mathrm{of}\mathrm{any}\mathrm{of}\mathrm{the}\mathrm{conditions}\end{array}\right..$$

We fitted a fourth model for this response variable.

We converted the binary variables, including our response variables of “Yes” and “No” to 1 and 0, respectively. There was no missing data in the Manchester dataset, and as such, we make use of all $n=99$ observations.

Data preparation – Liverpool

The data from Liverpool had a sample size of $913$ patients. The raw data defined 68 possible different symptoms which was considered as feature variables. A significant rate of missing data was identified. The complete list of features along with their percentage missing values can be found in Table 4.

To prepare the data, we first filtered by “Endometriosis = TRUE” which included patients with a diagnosis of endometriosis leaving a sample of$339$ patients. Then we removed features with more than 1% of missing values with 29 final features. The feature “Endometriosis” is a binary identifier, which, after filtering, is always true, so we dropped this feature too. The final$27$ features are summarised, with descriptions, in Table 5.

Table 4. Liverpool Data Percentage Missing Data.

Table 4. Liverpool Data Percentage Missing Data.

Feature	NaN (%)	Feature	NaN (%)	Feature	NaN (%)	Feature	NaN (%)
Sample ID	0.0	Age at diagnosis	98.5	Pain interferes with daily activities	0.0	Hormones	0.0
Age	0.1	Endometriosis symptoms	97.8	Dysmenorrhoea score	97.5	Other information	28.6
Ethnicity	96.7	Endometriosis stage	70.2	Non-menstrual pelvic pain	0.0	Previous ablation	0.0
Postcode	94.4	VAS	91.5	Analgesia for pain	0.0	Medications	85.9
Sample type	2.8	FH ENDO	98.1	Pain prevents daily activities	0.0	Endometrial cancer	0.0
Hair colour	96.7	Adenomyosis	0.0	Pelvic pain score	97.4	Metastatic lesion	0.0
Eye colour	96.7	Menorrhagia	0.0	Miscarriages	44.5	Metastatic lesion location	100.0
Height (m)	0.1	Fibroids	0.0	Polycystic ovary syndrome	0.0	Type of cancer	99.8
Weight (kg)	0.4	Reseason for surgery	18.7	Irregular cycles	0.0	Cancer comments	98.7
BMI	0.0	Previous history	84.7	Cu coil	0.0	Grade	100.0
Smoker	0.0	Gravidity	97.3	Menarche	97.2	Stage	99.8
Pack years	99.1	Parity	8.3	LMP	15.7	Pathology findings	99.8
Exercise	97.4	Deliveries	96.8	Menopause	100.0	Cancer staging	0.0
Alcohol	0.0	Infertility	0.0	Post-menopause	0.0	Dating by histology	64.3
Drinks per week	98.5	Dyspareunia	0.0	Cycle length	17.4	Hormonal dating	99.8
Endometriosis	0.0	Dysmenorrhoea	0.0	Days of bleeding	18.4	Agreement of date	0.0
Age first symptoms	98.6	Analgesia	0.0	Contraceptive/hormone treatment	59.9	Comments	70.1

Table 5. Liverpool Data Features with Less than 1% Missing Data.

Table 5. Liverpool Data Features with Less than 1% Missing Data.

Feature	Data Type	Description
Age	Integer	Age of patient
Height (m)	Real	Height of patient in meters
Weight (kg)	Real	Weight of patient in kilograms
BMI	Real	BMI of patient
Smoker	Binary	Whether of not the patient smokes
Alcohol	Binary	Whether or not the patient consumes alcohol
Adenomyosis	Binary	Whether or not the patient has been diagnosed with Adenomyosis
Menorrhagia	Binary	Whether or not the patient has been diagnosed with Menorrhagia
Fibroids	Binary	Whether or not the patient has been diagnosed with Fibroids
Infertility	Binary	Whether or not the patient is infertile
Dyspareunia	Binary	Whether or not the patient has been diagnosed with Dyspareunia
Dysmenorrhoea	Binary	Whether or not the patient has been diagnosed with Dysmenorrhoea
Analgesia	Binary	Whether or not the patient takes analgesia
Pain interferes with daily activities	Binary	Whether or not the patient experiences pain with daily activities
Non-menstrual pelvic pain	Binary	Whether or not the patient experiences non-menstrual pelvic pain
Analgesia for pain	Binary	Whether or not the patient takes analgesia to relieve pain
Pain prevents daily activities	Binary	Whether or not the patient says that pain prevents them from performing daily activities
PCOS	Binary	Whether or not the patient has polycystic ovary syndrome
Irregular cycles	Binary	Whether or not the patient experiences irregular menstrual cycles
Cu coil	Binary	Whether the patient has ever had a CU coil
Post-menopausal	Binary	Whether or not the patient has had menopause
Hormones	Binary	Whether or not the patient is taking any hormonal replacement treatments
Previous ablation	Binary	Whether the patient has had a previous ablation
Endometrial cancer	Binary	Whether or the patient have or had endometrial cancer
Metastatic lesion	Binary	Whether or not the patient had any cancerous lesions
Cancer staging agreement with Pathology	Binary	Whether or not the patient had an existing involvement within the cancer pathway
Agreement of staging	Binary	Whether or not the patient had a staging agreement

A total of 4 patients were identified with missing values and subsequently removed them from the dataset, resulting in a final sample size of $n=310$ patients. We selected two diseases as our response variables for prediction (Table 6). Given our ultimate objective of predicting multimorbidity in patients, we constructed a final response variable, “Combined”, as a binary variable representing the presence of at least one of the other two response variables, akin to the data from Manchester. Their formal definitions of these response variables are as follows:

$$y_i^A=\left\{\begin{array}{c}1\mathrm{if}\mathrm{patient}i\mathrm{develops}\mathrm{Adenomyosis}\\ 0\mathrm{if}\mathrm{patient}i\mathrm{does}\mathrm{not}\mathrm{develop}\mathrm{Adenomyosis}\end{array},\right.$$

$$y_i^I=\left\{\begin{array}{c}1\mathrm{if}\mathrm{patient}i\mathrm{develops}\mathrm{Menorrhagia}\\ 0\mathrm{if}\mathrm{patient}i\mathrm{does}\mathrm{not}\mathrm{develop}\mathrm{Menorrhagia}\end{array},\right.$$

$$y_i^C{y}_i^C=\left\{\begin{array}{c}1\mathrm{if}\mathrm{patient}i\mathrm{develops}\mathrm{at}\mathrm{least}\mathrm{one}\mathrm{of}\mathrm{any}\mathrm{of}\mathrm{the}\mathrm{conditions}\\ 0\mathrm{if}\mathrm{patient}i\mathrm{does}\mathrm{not}\mathrm{develop}\mathrm{at}\mathrm{least}\mathrm{one}\mathrm{of}\mathrm{any}\mathrm{of}\mathrm{the}\mathrm{conditions}\end{array}\right..$$

Table 6. Liverpool Data – Response Variables.

Table 6. Liverpool Data – Response Variables.

Variable	Name	Description
${\mathit{y}}^{\mathit{A}}$	Adenomyosis	Whether the patient has been diagnosed with Adenomyosis
${\mathit{y}}^{\mathit{M}}$	Menorrhagia	Whether the patient has been diagnosed with Menorrhagia
${\mathit{y}}^{\mathbf{C}\mathbf{o}\mathbf{m}\mathbf{b}}$	Combined	The presence of at least one of the above conditions.

Manchester Data

We initiated our analysis with the Manchester data, and after fitting the Gaussian Copula to our 99 samples, we generated an additional 1000 samples.

By employing SDV’s SD Metrics library, we were able to evaluate the similarity between the real and synthetic data. We examined how closely the synthetic data relates to the real data in order to determine whether we have adequately captured the true distribution. This assessment involved comparing the distribution similarities across each feature, and we adopted two approaches for this evaluation.

Initially, we measured the similarities across each feature by comparing the shapes of their frequency plots, as illustrated in Figure 1. This comparison was conducted based on the “age” distribution for both the real and synthetic data.

Figure 1. Age distribution shape comparison.

Figure 1. Age distribution shape comparison.

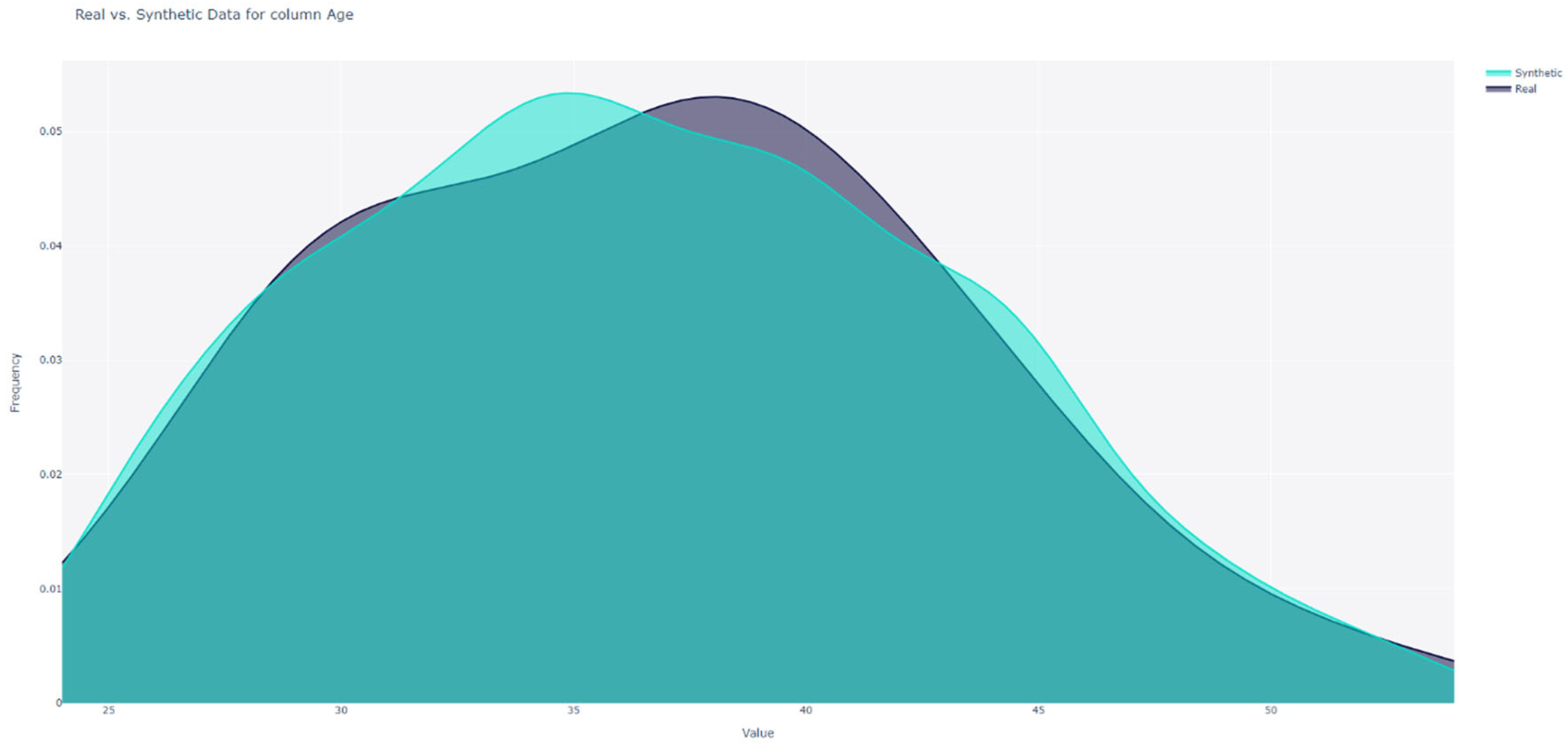
For numerical data, SDV computed the Kolmogorov-Smirnov (KS) statistic, which represents the maximum difference between the cumulative distribution functions. The value of this distance ranges between 0 and 1, with SDV converting it to a score by:

$$\mathrm{S}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}=1-\mathrm{KS-statistic}.$$

For Boolean data, SDV calculates the Total Variation Distance (TVD) between the real and synthetic data. We determined the frequency of each category value and represented it as a probability. The TVD statistic compares the differences in probabilities, as given by:

$$\delta \left(R,S\right)=\frac{1}{2}\sum _{\omega \in \mathsf{\Omega }}|R_{\omega }-S_{\omega }|$$

where $\mathsf{\Omega }$ represents the set of possible categories, and $R_{\omega }$ and $S_{\omega }$ are the frequencies of category $\omega$ in the real and synthetic datasets respectively. The similarity score is then given by:

$$\mathrm{s}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}=1-\delta \left(R,S\right).$$

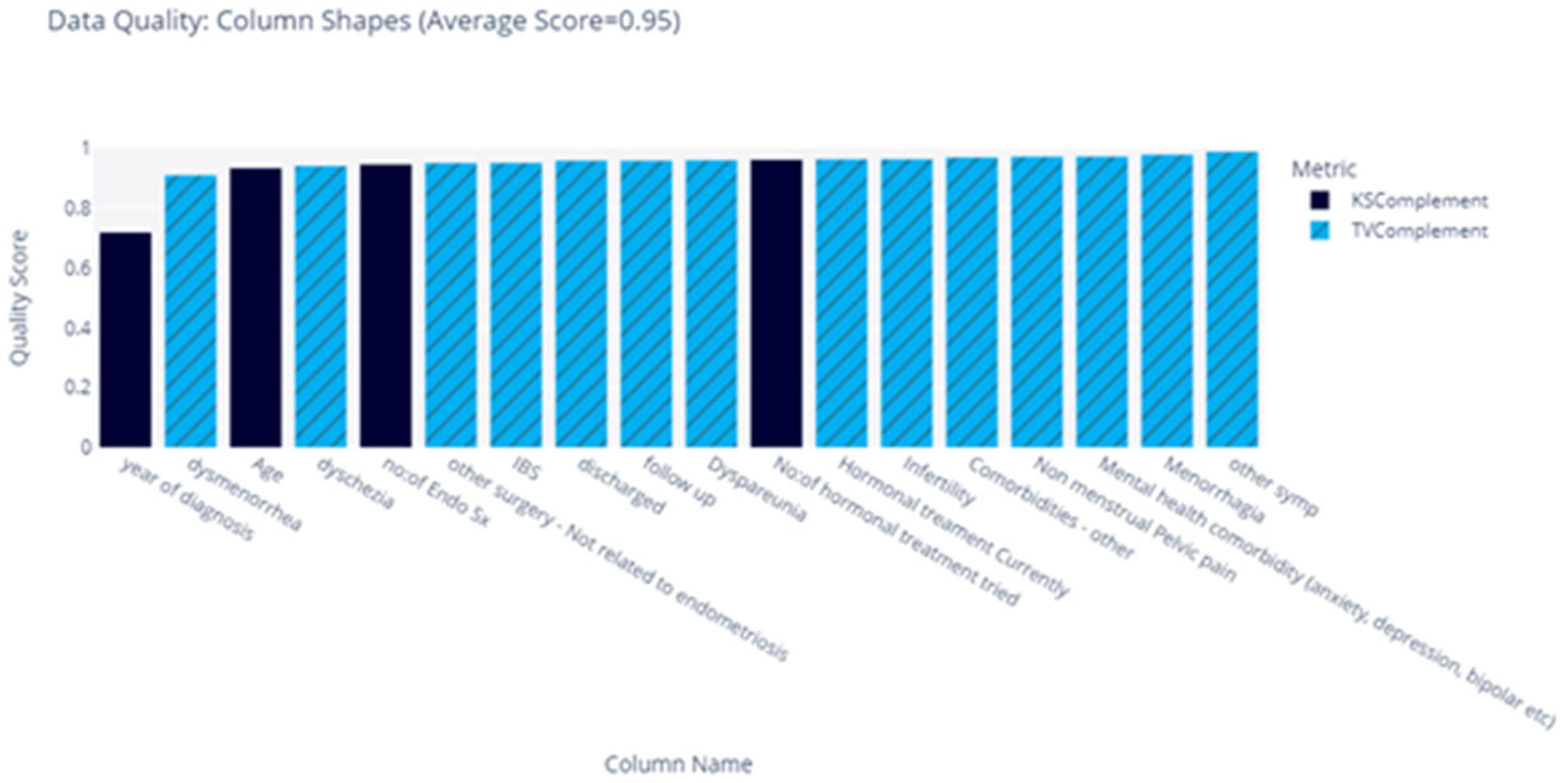
The score for each feature is summarised in Figure 2, and we obtained an average similarity score of 0.92.

For the second measure of similarity, we constructed a heatmap to compare the distribution across all possible combinations of categorical data. This was accomplished by calculating a score for each combination of categories. To initiate this process, two normalised contingency tables were constructed; one for the real-world data and one for the synthetic data. Let $\alpha$ and $\beta$ be two features, the contingency tables describe the proportion of rows that have each combination of categories in $\alpha$ and $\beta$, thereby illustrating the joint distributions of these categories across the two datasets.

Figure 2. Feature Distribution Shape Comparison.

Figure 2. Feature Distribution Shape Comparison.

To compare the distributions, SDV computes the difference between the contingency tables using Total Variation Distance. This distance is subsequently subtracted from 1, implying that a higher score denotes greater similarity. Let $A$ and $B$ represent the set of categories in features $\alpha$ and $\beta$ respectively; the score between features $\alpha$ and $\beta$ are calculated as follows:

$$score=1-\frac{1}{2}{\sum }_{a\in A}{\sum }_{b\in B}|S_{a,b}-R_{a,b}|,$$

(3)

where $S_{a,b}$ and $R_{a,b}$ represent the proportions of categories $a$ and $b$ occurring simultaneously, as derived from the contingency tables for the synthetic and real data, respectively. It is important to note that we did not employ a measure of association between features, such as Cramer’s V, since it does not measure the direction of the bias and may consequently yield misleading results.

A score of 1 indicates that the contingency table was identical between the two datasets, while a score of 0 indicates that the two datasets were as dissimilar as possible. These scores for all combinations of features are depicted as a heatmap (Figure 3). It is worth noting that continuous features, such as “Age”, were discretized in utilise Equation (3) in determining a score.

Figure 3. Distribution Comparison Heatmap.

Figure 3. Distribution Comparison Heatmap.

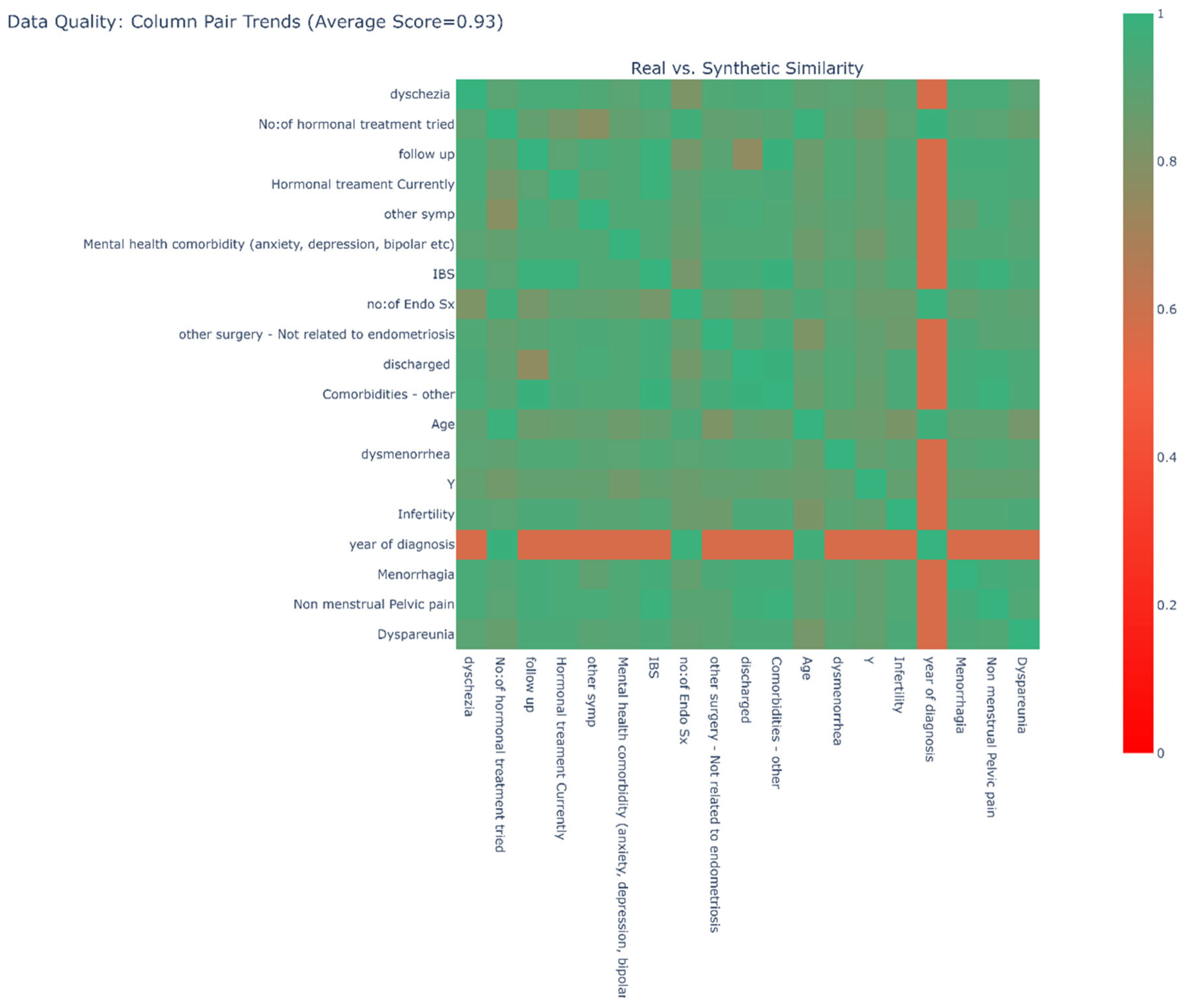
The heatmap suggests that most features exhibit a strikingly similar distribution across the two datasets, with the exception for “Year of Diagnosis”. This discrepancy could potentially be attributed to the feature’s inherent nature as a date, despite being treated as an integer in the model. This issue merits further investigation.

Based on these metrics, we confidently concluded, that the new data closely adhered to the distribution of the original data.

Liverpool Data

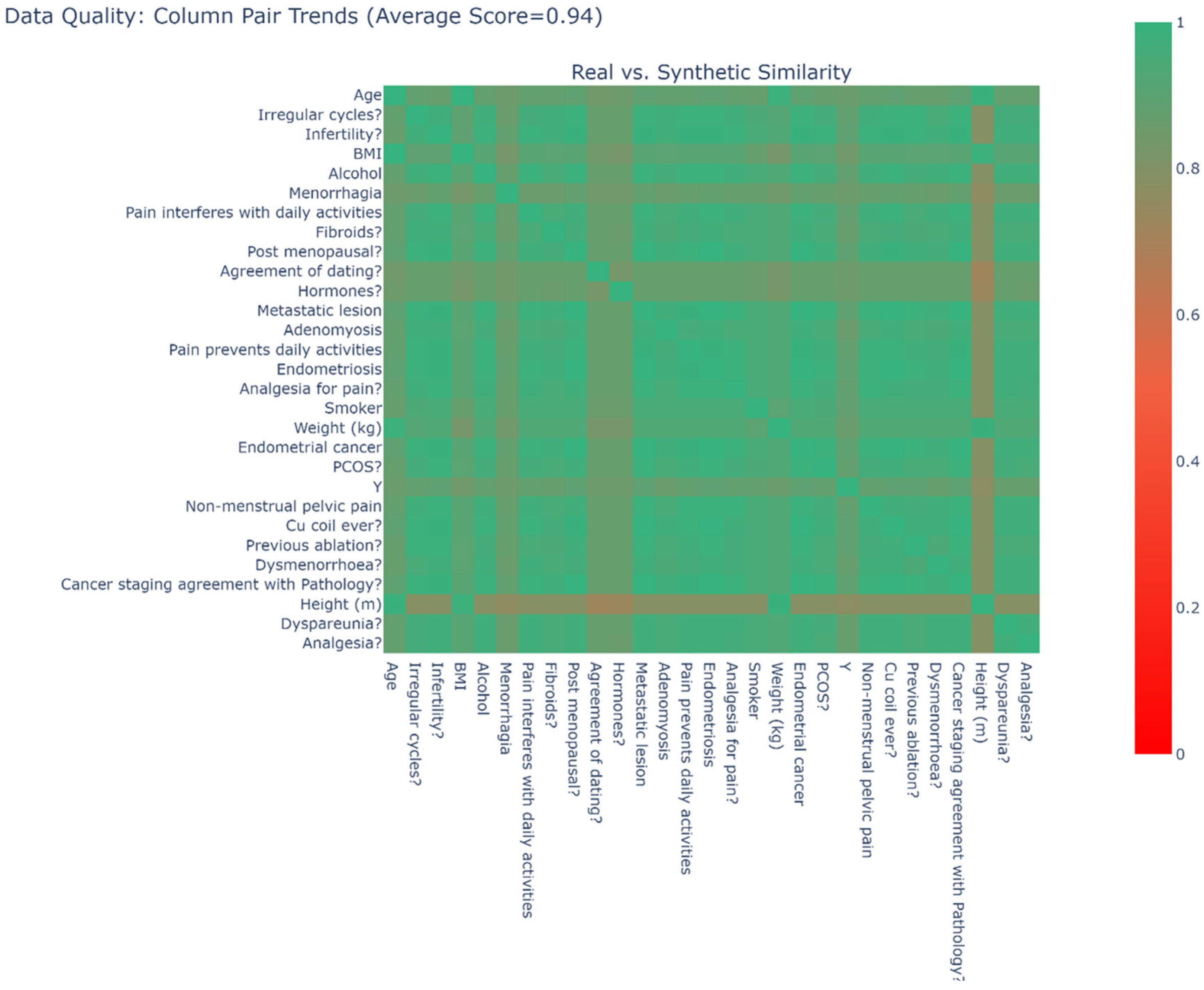
To generate synthetic data, we adhered to the same procedure as with the Manchester data. We produced 1000 additional samples from a Gaussian copula fitted to the 311 real samples and combined them with the real data to create a new dataset. Using contingency tables, we developed a heatmap by applying the formula in Equation (3) to generate scores; this heatmap is displayed in Figure 4. A score of 1 implies that the contingency table was identical between the two datasets, whereas a score of 0 indicates that the two datasets were as distinct as possible. Our analysis revealed an average similarity of 0.94.

Figure 4. Real Vs Synthetic Data Distribution Heatmap (Liverpool Data).

Figure 4. Real Vs Synthetic Data Distribution Heatmap (Liverpool Data).

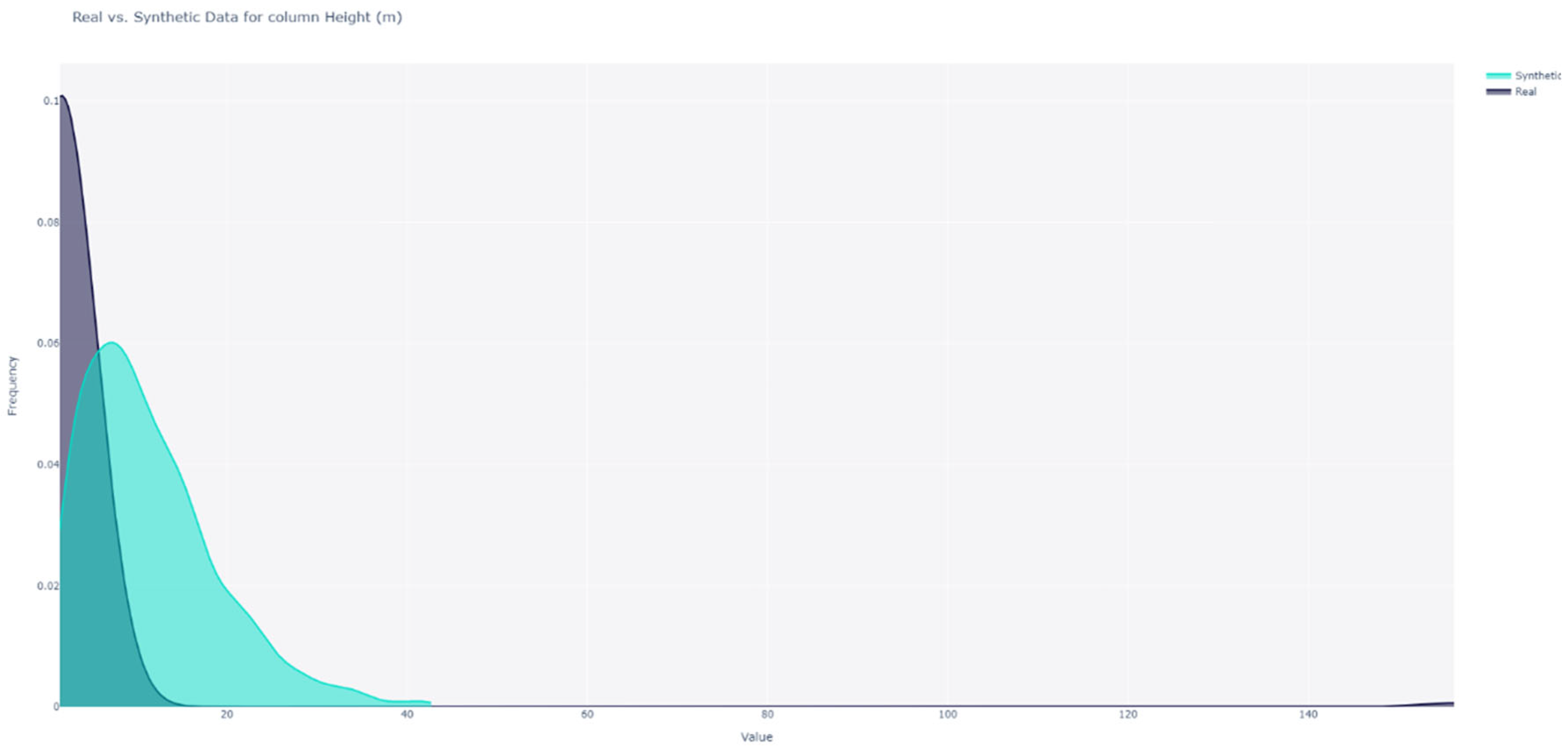
We compared the shape of the distributions for each feature; for instance, the distributions for the “Height” feature are illustrated in Figure 5. We observed that the distributions were dissimilar. To calculate similarity scores, we employed the KS statistic for numerical features and Total Variation Distance for Boolean features. These scores are summarised in Figure 6. We found that the distributions of “Height” and “Weight” were not similar; however, the distributions of the remaining features exhibited similarity. With an average similarity of 0.75, we concluded that the data distributions were, on average similar. The distributions of all categorical features were accurately captured, but two of the continuous features were not.

Figure 5. Height Distribution Shape Comparison (Liverpool).

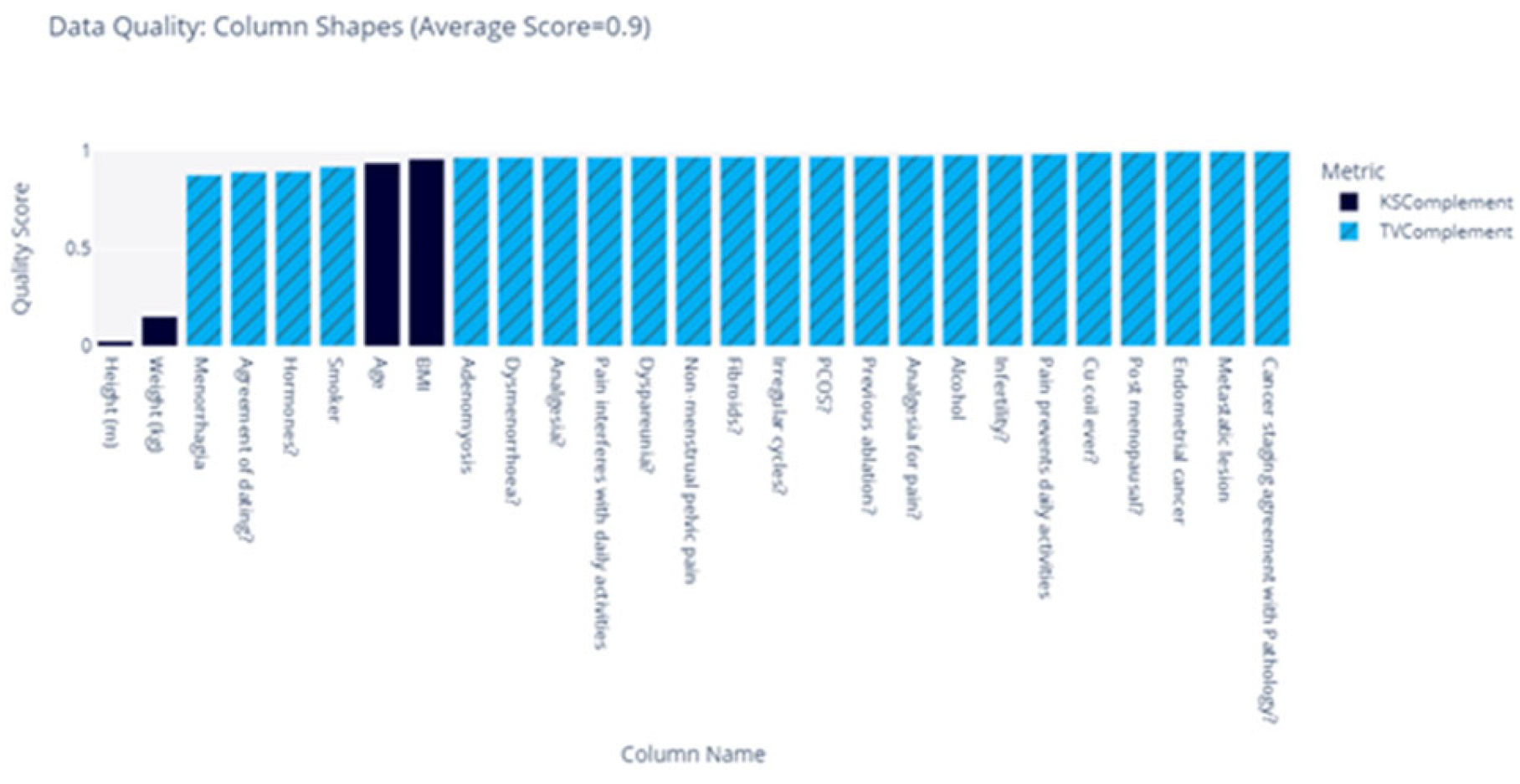
Figure 5. Height Distribution Shape Comparison (Liverpool).

Figure 6. Feature Distribution Shape Comparison Between Real and Synthetic Data (Liverpool).

Figure 6. Feature Distribution Shape Comparison Between Real and Synthetic Data (Liverpool).

Logistic Regression

We used scikit-learn to fit logistic regression models of the form in equation (4). We performed a grid search using 5-fold cross-validation (CV) to investigate the optimal value of $\lambda .$ The CV accuracies for each response variable can be found in Figure 7. For each response variable, the $\lambda$ that yielded the highest CV accuracy was chosen, refitted to the entire training set, and tested on the test set. The accuracies on the test set and summarised in Table 7.

Table 7. Logistic Regression Model Comparison Across Real and Synthetic Data.

Table 7. Logistic Regression Model Comparison Across Real and Synthetic Data.

	Real		Synthetic
	$\mathit{\lambda }$	Accuracy	$\mathit{\lambda }$	Accuracy
IBS	${10}^{-5}$	$59.18\%$	$1$	$95.45\%$
Mental Health	${10}^{-2}$	$77.55\%$	${10}^{-2}$	$60.39\%$
Comorbidities (Other)	$1$	$48.98\%$	${10}^3$	$61.04\%$
Combined	${10}^{-5}$	$71.43\%$	${10}^2$	$71.43\%$
Average		64.29%		69.90%

Figure 7. Logistic Regression Cross-Validation.

Figure 7. Logistic Regression Cross-Validation.

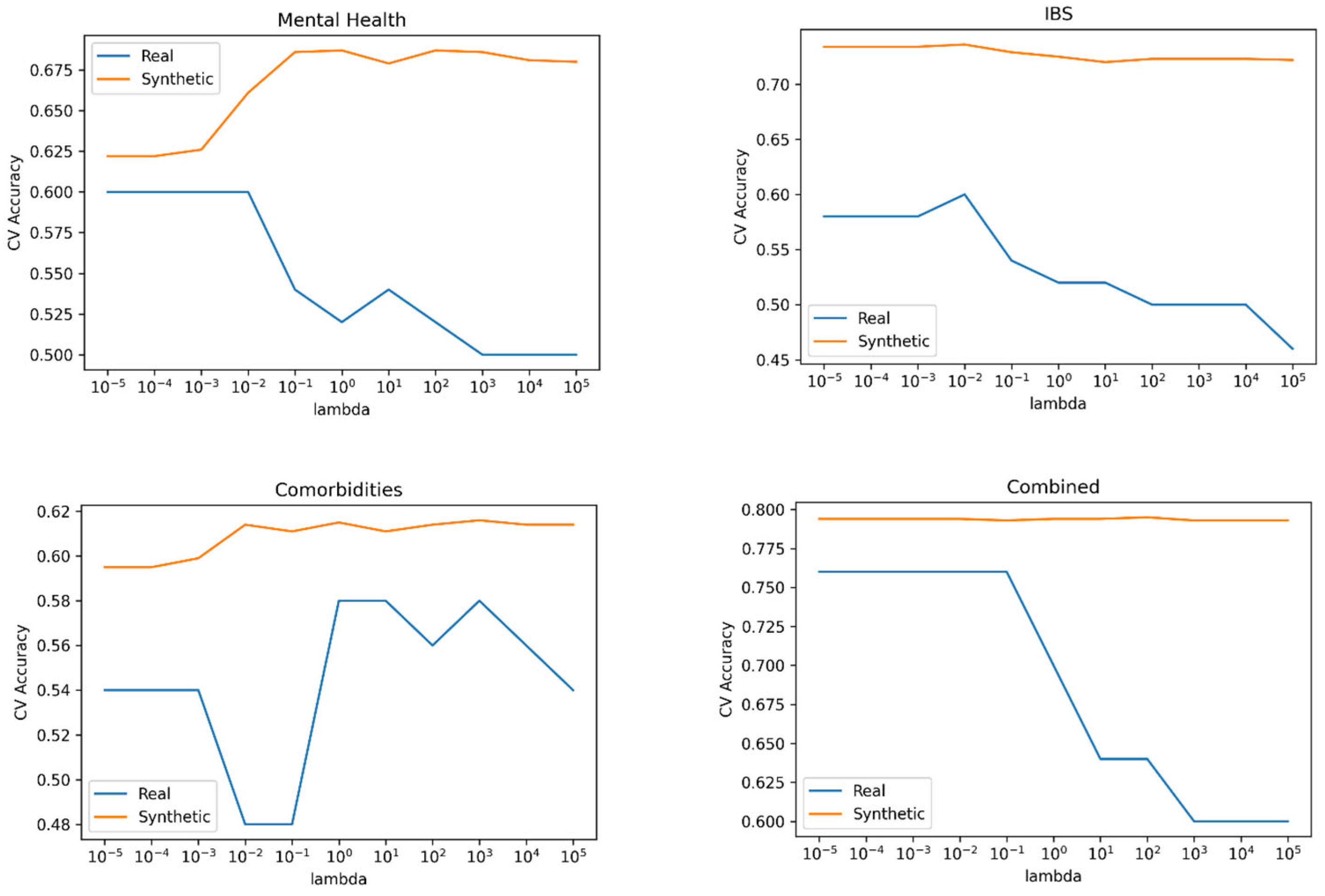
We can see that for all response variables, the models performed slightly better when trained on synthetic data.

SVM

We used Scikit-learn’s svm.SVC to train and test SVMs of the form in equation (5) on our data., Scikit-learn is a popular and well-tested choice for SVMs that has shown high performance on a variety of types of datasets. We performed a grid search using 5-fold cross-validation to find the optimal value of $\lambda$; these are summarised in Figure 8. For each response variable, the $\lambda$ that yielded the highest CV accuracy was chosen, refitted to the entire training set, and tested on the test set. The accuracies on the test set are summarised in Table 8. We can see that the models trained on synthetic data performed the same as the models trained on real data for all response variables except “Comorbidities (other),” where the model trained on synthetic data performed better, giving the models trained on synthetic data a better performance on average.

Table 8. SVM comparison with synthetic data.

Table 8. SVM comparison with synthetic data.

	Real		Synthetic
	$\mathit{\lambda }$	Accuracy	$\mathit{\lambda }$	Accuracy
IBS	${10}^4$	$59.18\%$	${10}^5$	$59.18\%$
Mental Health	${10}^{-5}$	$79.59\%$	${10}^{-5}$	$79.59\%$
Comorbidities (other)	${10}^{-5}$	$59.18\%$	${10}^5$	$67.35\%$
Combined	${10}^{-5}$	$71.43\%$	${10}^{-5}$	$71.43\%$
Average		67.35%		69.39%

Figure 8. SVM Cross-Validation.

Figure 8. SVM Cross-Validation.

Random Forest

Finally, we fitted random forest models to the data. For each response variable, we used $\mathrm{1,5},10,\dots ,500$ trees, and performed a grid search using 5-fold cross-validation to find the best number of trees (Figure 9). The CV accuracies are summarised in Table 9. For each response variable, the number of trees that gave the highest CV accuracy was chosen, refitted to the whole training set, and tested on the test set. The accuracies on the test set and summarised in Table 9.

Table 9. Random Forest Comparison with Synthetic Data.

Table 9. Random Forest Comparison with Synthetic Data.

	Random Forest accuracy
	Real		Synthetic
	No. Trees	Accuracy	No. Trees	Accuracy
IBS	$55$	$55.10\%$	$175$	$59.18\%$
Mental Health	$210$	$61.22\%$	$455$	$87.76\%$
Comorbidities (other)	$1$	$51.02\%$	$20$	$57.14\%$
Combined	$5$	$67.35\%$	$480$	$71.43\%$
Average		$58.67\%$		$68.88\%$

Figure 9. SVM Comparison with Synthetic Data.

Figure 9. SVM Comparison with Synthetic Data.

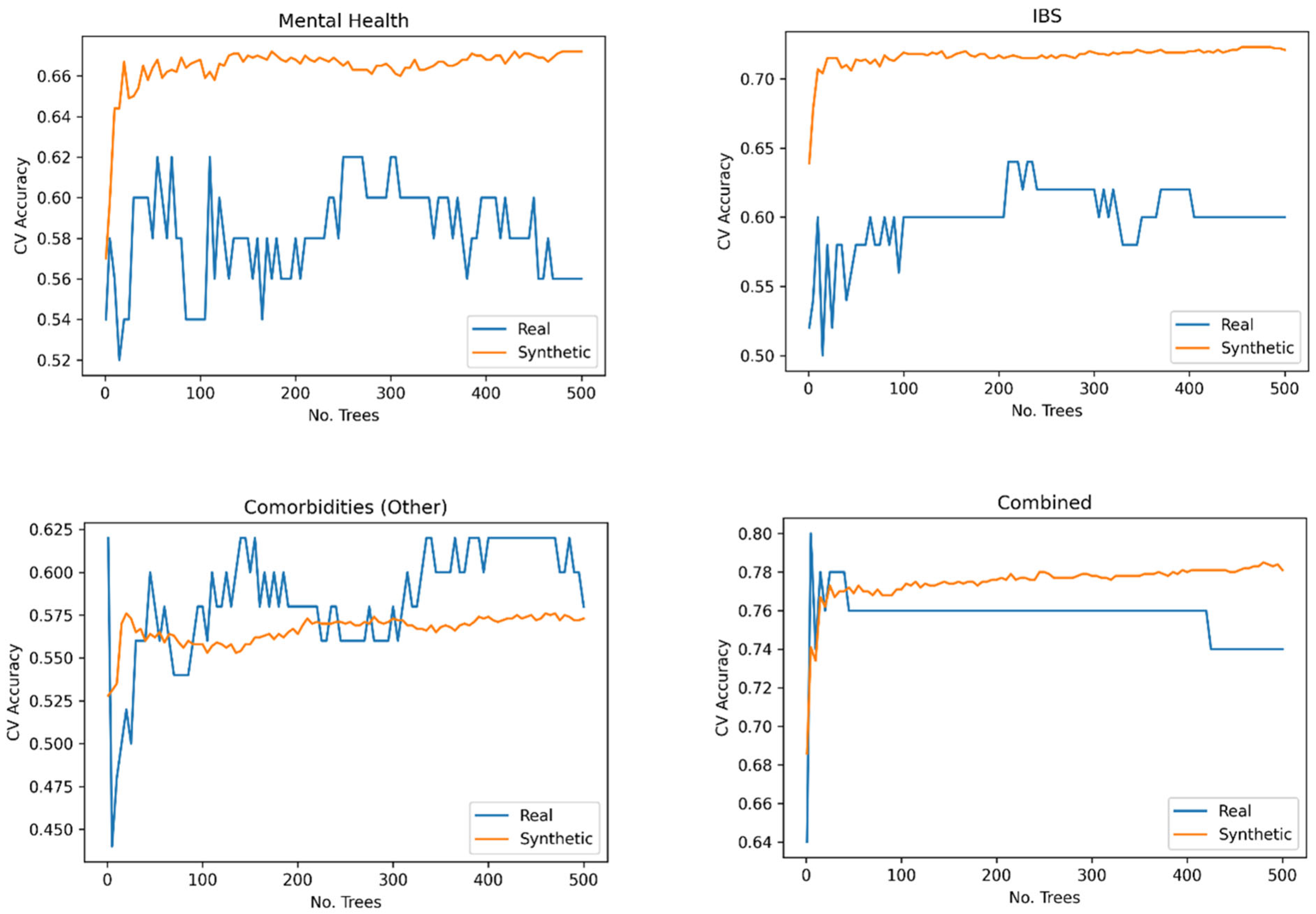
Upon examining the average accuracies of all our models in Table 10, we can draw some conclusions about the performance of the models trained on synthetic data compared to those trained on real data. It is evident that on average, models trained on synthetic data performed better than those trained on real data across all response variables. This result suggests that synthetic data can effectively replace real data in training machine learning models without sacrificing performance. In some cases, it may even lead to improved performance, as demonstrated by the results.

Solver comparison

In conclusion, the use of synthetic data proves to be a promising approach to training machine learning models when real data is limited or unavailable. The models trained on synthetic data in this study were not only able to perform at a comparable level to those trained on real data, but they often outperformed them. This finding supports the adoption of synthetic data generation methods as a viable alternative or complement to real data in machine learning applications.

Table 10. Sensitivity Analysis on Manchester Data.

Table 10. Sensitivity Analysis on Manchester Data.

Data	Logistic Regression	SVM	Random Forest
Real	$64.29\%$	$67.35\%$	$58.67\%$
Synthetic	$69.90\%$	$69.39\%$	$68.88\%$

Sensitivity Analysis

Table 11. Comparison of all Models.

Liverpool Results

Logistic Regression

We employed Scikit Learn to fit logistic regression models, as described in Equation (45),and performed a grid search using 5-fold cross-validation to investigate the optimal value of $\lambda .$ The CV accuracies for each response variable can be found in figure 10. For each response variable, the $\lambda$ that gave the highest CV accuracy is chosen, refitted to the whole training set and tested on the test set. The accuracies on the test set are summarised in table 12.

Table 12. Logisitc Regression Model Comparison (Liverpool).

Table 12. Logisitc Regression Model Comparison (Liverpool).

	Real		Synthetic
	$\mathit{\lambda }$	Accuracy	$\mathit{\lambda }$	Accuracy
Adenomyosis	${10}^{-5}$	$95.45\%$	${10}^{-5}$	$95.45\%$
Menorrhagia	${10}^{-5}$	$56.49\%$	${10}^3$	$60.39\%$
Combined	${10}^{-5}$	$55.19\%$	${10}^{-1}$	$61.04\%$
Average		$69.04\%$		$72.29\%$

Figure 10. Logistic Regression Cross-Validation.

Figure 10. Logistic Regression Cross-Validation.

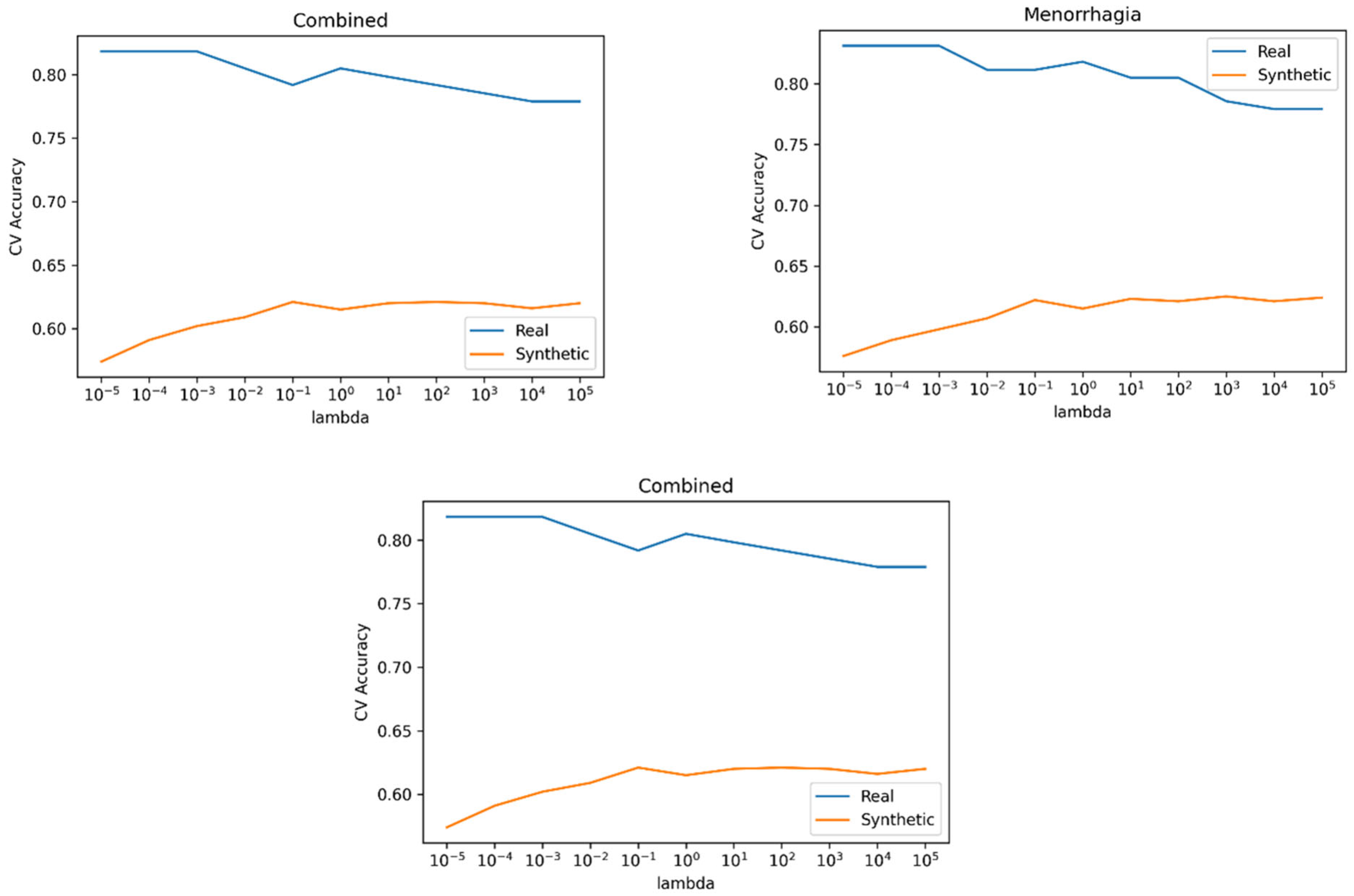
The models in Table 12, trained on synthetic data, exhibited similar performance in predicting adenomyosis and demonstrated improved performance for the remaining response variables

SVM

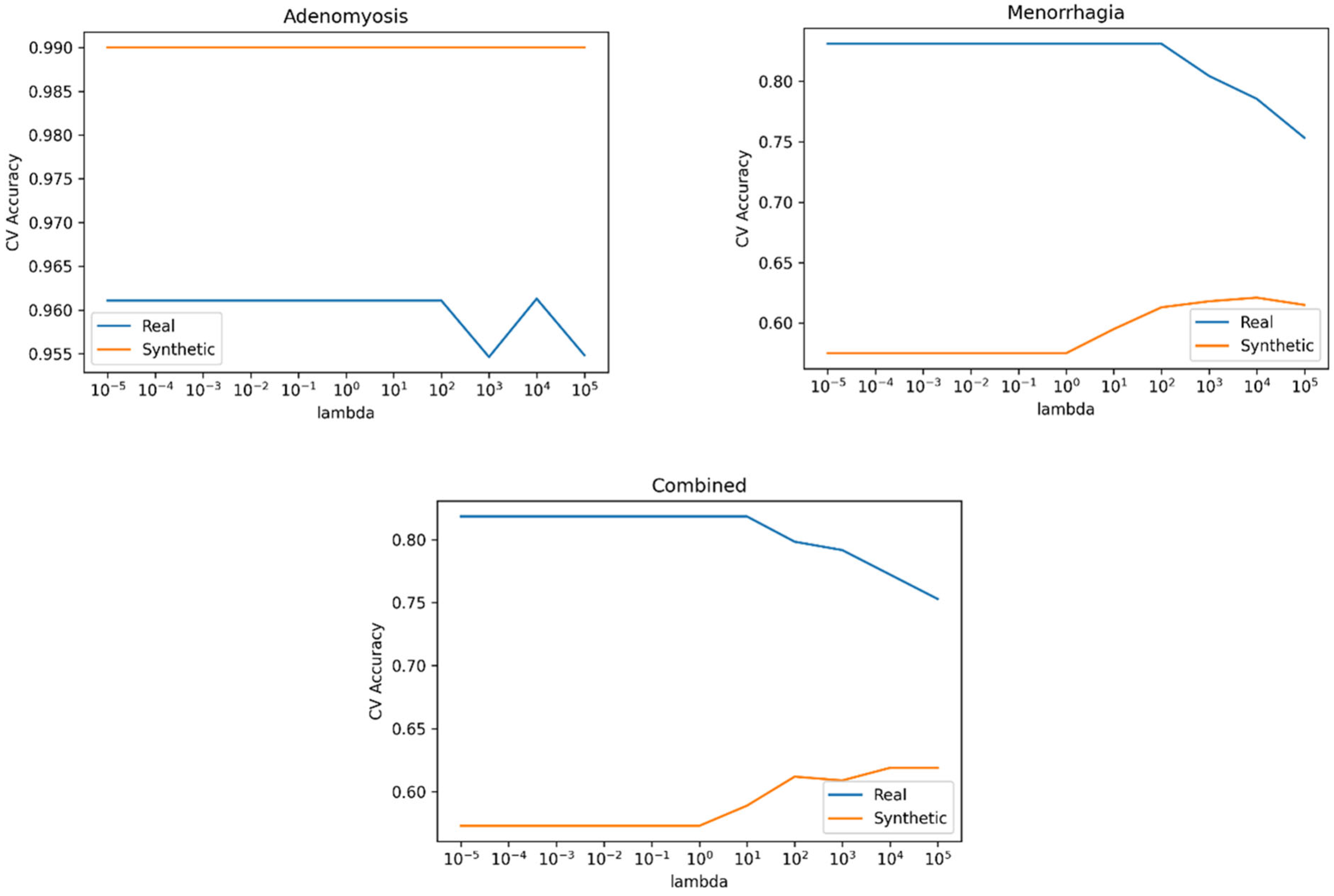
We trained and tested SMVs, as defined in Equation (5), using Scikit Learn’s svm.SVC on our data. We employed a 5-fold cross-validation grid to find the optimal value of $\lambda$, summarised in figure 11. For each response variable, we selected the $\lambda$ yielding the highest CV accuracy, refitted it to the entire training set, and evaluated it on the test set. Test set accuracies are provided in table 13.

Table 13. SVM Model Comparison.

Table 13. SVM Model Comparison.

	Real		Synthetic
	$\mathit{\lambda }$	Accuracy	$\mathit{\lambda }$	Accuracy
Adenomyosis	${10}^4$	$94.16\%$	${10}^{-5}$	$95.45\%$
Menorrhagia	${10}^{-5}$	$56.49\%$	${10}^4$	$57.79\%$
Combined	${10}^{-5}$	$55.19\%$	${10}^4$	$57.14\%$
Average		$68.61\mathrm{\%}$		$70.13\%$

The models trained on synthetic data demonstrated improved performance for all response variables (Table 13).

Figure 11. SVM Cross-Validation.

Figure 11. SVM Cross-Validation.

Random Forest

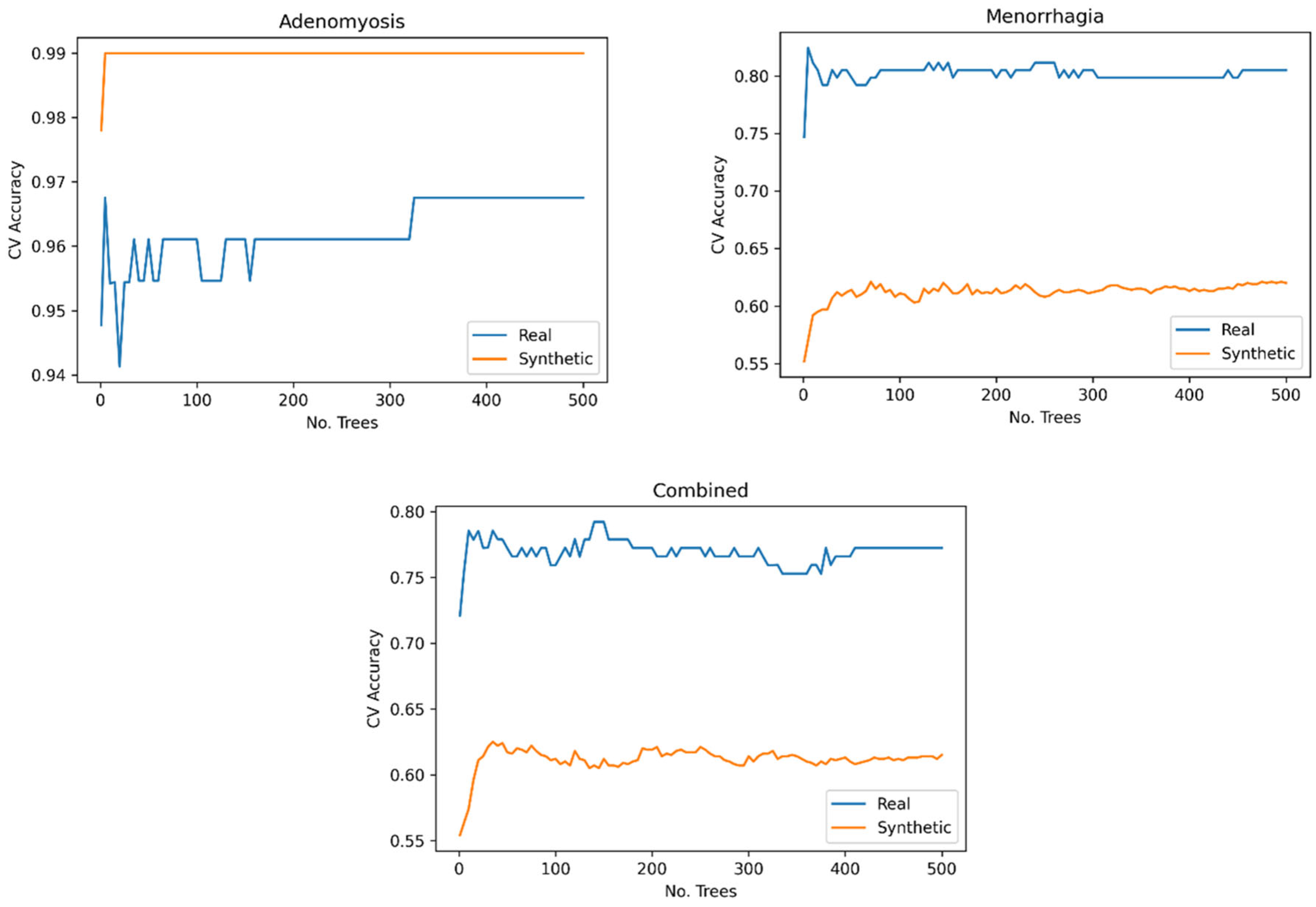
We fitted random forest and performed a grid search using 5-fold cross-validation to test $\mathrm{1,5},10,\dots ,500$ trees, which displayed a higher degree of CV accuracy (Figure 12). For each response variable, we chose the number of trees with the highest CV accuracy, , refitted them to the entire training set, and evaluated them on the test set. Test set accuracies are summarised in Table 14.

Table 14. Random Forest Model Comparison.

Table 14. Random Forest Model Comparison.

	Random Forest accuracy
	Real		Synthetic
	No. Trees	Accuracy	No. Trees	Accuracy
Adenomyosis	$5$	$95.45\%$	$5$	$95.45\%$
Menorrhagia	$5$	$55.84\%$	$495$	$59.09\%$
Combined	$140$	$52.60\%$	$35$	$55.19\%$
Average		73.76%		74.62%

The model trained on synthetic data performed comparably to the model trained on real data for adenomyosis and better for the remaining response variables. Consequently, the models trained on synthetic data performed better on avarage.

Figure 12. Random Forest Cross-Validation.

Figure 12. Random Forest Cross-Validation.

Solver Comparison

To summarise, the average accuracies of all models are presented in Table 15. The best over-all performing model is the random forest, trained on the synthetic data. We also observed that, on average, the models trained on synthetic data outperformed those trained on real data. These results support the use of synthetic data in place of the real data.

Table 15. Comparison of all Models.

Table 15. Comparison of all Models.

Data	Logistic regression	SVM	Random Forest
Real	$69.04\%$	$68.61\%$	$73.76\%$
Synthetic	$72.29\%$	$70.13\%$	$74.62\%$

Sensitivity Analysis

Table 16. Sensitivity Analysis on Liverpool Data.

Comparison Across Datasets

Table 17. Comparison of all Models.

Discussion

Limitations

Conclusions

References

1. Delanerolle G, Ramakrishnan R, Hapangama D, Zeng Y, Shetty A, Elneil S, Chong S, Hirsch M, Oyewole M, Phiri P, Elliot K, Kothari T, Rogers B, Sandle N, Haque N, Pluchino N, Silem M, O'Hara R, Hull ML, Majumder K, Shi JQ, Raymont V. A systematic review and meta-analysis of the Endometriosis and Mental-Health Sequelae; The ELEMI Project. Womens Health (Lond). 2021 Jan-Dec;17:17455065211019717. doi: 10.1177/17455065211019717. [CrossRef]
2. Alimohammadian M, Majidi A, Yaseri M, Ahmadi B, Islami F, Derakhshan M, Delavari A, Amani M, Feyz-Sani A, Poustchi H, Pourshams A. Multimorbidity as an important issue among women: results of a gender difference investigation in a large population-based cross-sectional study in West Asia. BMJ open. 2017 May 1;7(5):e013548.
3. Tripp-Reimer T, Williams JK, Gardner SE, Rakel B, Herr K, McCarthy AM, Hand LL, Gilbertson-White S, Cherwin C. An integrated model of multimorbidity and symptom science. Nursing outlook. 2020 Jul 1;68(4):430-9.. doi:10.1016/j.outlook.2020.03.003. [CrossRef]
4. Oni T, McGrath N, BeLue R, Roderick P, Colagiuri S, May CR, Levitt NS. Chronic diseases and multi-morbidity-a conceptual modification to the WHO ICCC model for countries in health transition. BMC public health. 2014 Dec;14(1):1-7. https://doi.org/10.1186/1471-2458-14-575. [CrossRef]
5. Delanerolle GK, Shetty S, Raymont V. A perspective: use of machine learning models to predict the risk of multimorbidity. LOJ Medical Sciences. 2021 Sep 14;5(5).
6. Hassaine A, Salimi-Khorshidi G, Canoy D, Rahimi K. Untangling the complexity of multimorbidity with machine learning. Mechanisms of ageing and development. 2020 Sep 1;190:111325.
7. Jensen AB, Moseley PL, Oprea TI, Ellesøe SG, Eriksson R, Schmock H, Jensen PB, Jensen LJ, Brunak S. Temporal disease trajectories condensed from population-wide registry data covering 6.2 million patients. Nature communications. 2014 Jun 24;5(1):4022.
8. Giannoula A, Gutierrez-Sacristán A, Bravo Á, Sanz F, Furlong LI. Identifying temporal patterns in patient disease trajectories using dynamic time warping: A population-based study. Scientific reports. 2018 Mar 9;8(1):1-4.