A Dynamic Model of Profit Maximization for a Carsharing Services: Astana, Republic of Kazakhstan

Preprint

Article

A Dynamic Model of Profit Maximization for a Carsharing Services: Astana, Republic of Kazakhstan

Altmetrics

Downloads

117

Views

Comments

A peer-reviewed article of this preprint also exists.

Beibut Amirgaliyev

Oleksandr Kuchanskyi,

Yurii Andrashko^*

Didar Yedilkhan

Beibut Amirgaliyev

Oleksandr Kuchanskyi,

Yurii Andrashko^*

Didar Yedilkhan

This version is not peer-reviewed

Submitted:

17 May 2023

Posted:

18 May 2023

You are already at the latest version

Alerts

Abstract

The study considers building a dynamic model of profit maximization for the car-sharing system and its verification on the example of implementing such a system in Astana (Republic of Kazakhstan). The region, bounded by the administrative boundaries of Astana, was divided into subregions by covering the region with regular hexagons placed side by side. A dataset was built with information on 1168 trips to Astana from January to March 2023. The Kepler visualization service constructed maps of the beginning and end of trips in the region and a map of trips binding to the hexagonal grid cells. Each cell of the grid corresponds to a specific sub-region, for which the quantitative parameters necessary for solving the profit maximization problem in the car-sharing system are calculated. Stations with cars will be placed in the cells of the grid, which will be available to car-sharing service customers. Based on the collected data, a dynamic (four periods per day) and static profit maximization model in the car-sharing system was built. Modeling was carried out based on the built models in the example of Astana. It was established that using a dynamic model of profit maximization in the car-sharing system increases the profit by 3.7%.

Keywords:

Subject: Computer Science and Mathematics - Applied Mathematics

1. Introduction

The sharing market has been growing dynamically, especially in the last decade. In 2019, the sharing market was valued at nearly $400 billion. Moreover, in 2024, according to some estimates, the global market value of the sharing economy may reach more than 1.5 trillion dollars. The annual growth rate is more than 30% [1]. According to some estimates, the sharing market will add 160 to 572 million euros to the economy of the European Union in the next few years [2]. Some analytical calculations regarding the growth of the sharing market are described in [3]. The changes associated with the rapid development of the sharing market are a crucial aspect of the evolution and transformation of transport systems. The paper [4] investigated how the sharing market potentially leads to reduced emissions, congestion, etc. This has a positive effect on the development of cities, which leads to an increase in the quality of life of the residents of these cities.

One of the essential components of the sharing market is car sharing. The basis of the car-sharing system is the client's short-term use of the car for a fixed fee. The client can travel by car without being tied to the movement of public transport for sufficiently long distances. An essential advantage of using the car-sharing service is that the client pays only for the time using the car and does not pay for its maintenance, insurance, parking, etc. The cost of using car sharing is generally lower compared to using taxi services. In addition to car sharing, micro-sharing systems are being considered. However, such systems are designed for different sectors of customers and have their characteristics, which are not considered in this work.

In order to make a profit, the owner of the car-sharing system must calculate the total costs of car maintenance, the costs of transporting cars to different parts of the city, etc. That is, many components of the system must be calculated, which determine the price policy of the owner and the system of restrictions for the user. The task of managing a car-sharing system is complex. The influence of various factors can quickly lead to an imbalance of the system, inevitably leading to its possible unprofitability. Management should occur in real-time and in different regions of the city network in different ways. When building a car-sharing system, several problems arise at the same time. The first of them is the division of regions into subregions according to specific criteria, which would simplify the management of system parameters. Next, you need to calculate the characteristics that determine the balance of the system and ensure their calculation in dynamics. The second task is to build a model for maximizing the profits of the car-sharing system, taking into account the specified characteristics and distribution into subregions.

The study aims to build a dynamic optimization model for maximizing the profit of the car-sharing service. For this, you need to solve two problems:

- build the optimal division of the region into subregions following the features of the location of the city infrastructure and the needs of system users;

- define and adjust the parameters that will be integrated into the dynamic profit maximization model for each subregion.

2. Literature Review

Building an effective car-sharing system and organizing an excellent car-sharing service is an urgent task for both the user and the owner. From the owner's point of view, such a system can be profitable, given the dynamics of market development in this direction in recent years. Also, the potential profitability of the system is determined by the peculiarities of the region in which it is implemented and the client's needs in the work of the car-sharing service. From the customer's point of view, such a system is an excellent alternative to own transport, taxi services, and public transport. The functioning of the car-sharing system within a specific region has a positive effect on reducing traffic jams, reducing air pollution, increasing revenues to the regional budget, etc. [5]. This obviously has a positive effect on improving the comfort of the region's residents.

Building an optimization model of profit maximization for car-sharing services must be completed and requires a separate study. The creation of such a model is closely related to the requests of the system owner. Therefore, parameters that affect the owner's profit should be reflected in the model, considering regional characteristics, demand, and customer needs. Also, the maximization model depends on the type of car sharing, which exerts influence and profitability of the system in different regional and geographical conditions. In particular, work [6] describes the system of car sharing using electric cars. This study found that such a system still needs to be fixed since electric cars need a long time to charge. This leads to a decrease in the profitability of such a system over time compared to a traditional car-sharing system. The paper [7] describes the model of the use of electric car sharing and micro-mobility, as well as the potential impacts that these types of car sharing exert. However, the problem of maximizing the profitability of such systems needs to be described. The positive impact on the development of city infrastructure and the improvement of the quality of life of city residents is determined by the effective functioning of such a car-sharing system, which is beneficial for the system's owner. Otherwise, there is no point in investing in developing this type of service.

For the effective functioning of the car-sharing system, operational decisions must be made constantly. Some of them require solving relevant optimization problems. In particular, the work [4] describes the profit maximization model of the car-sharing system and the mathematical programming method for finding its solution. In this model, cars do not move without the participation of customers. In [8], a simulation model for evaluating options for such movements was developed. However, the specified model is static and does not consider the change in demand for cars in different parts of the region and the time of day. This is important for a rational calculation of the potential profit of the system, taking into account the built-in restrictions. The paper [9] describes a mixed integer programming model for establishing the sequence of actions for moving cars in a car-sharing system. In works [10, 11], a system for optimizing the movement of vehicles is considered.

The work [12] describes the problem of maximizing the profit of the car-sharing system, which considers car maintenance costs. Integer programming was used to solve the problem. The problem of linear programming for maximizing the profits of the car-sharing system is described in [13]. An overview of scientific studies on modeling and optimization for the car-sharing system is described in [14]. In [14], the authors classify the literature into three categories: strategic, tactical, and operational, according to the level of decisions made in optimization tasks. Optimization models and solution methods proposed in existing studies are considered for each category. In particular, in the category of studies on state strategic planning, the critical publications that aim to maximize profits are works [15,16,17]. It is described in works in the category of making operational decisions on managing the car-sharing system to optimize profits [18,19,20]. The problem of profit maximization related to the relocation of cars is described in works [21,22,23]. Related problems must also be solved, such as user verification [24,25,26] and the problem of managing a complex transport system [27].

This study considers building a profit maximization model for a car-sharing service for the capital of the Republic of Kazakhstan, Astana. Regional aspects and needs of customers in this region determine the need to develop this kind of service. Moreover, it is about the development of car-sharing services. Microservices in this region may be less popular due to the significant distances that city residents travel daily. This is related to the vastness of the city and the peculiarity of the location of urban infrastructure facilities.

3. Methods and Data

3.1. Basic Concepts

Ensuring the effective functioning of the car-sharing system depends on many internal and external factors, including geographical features of the region, economic parameters, restrictions, and conditions under which the system is implemented. The theory of sets was used to formalize the parameters that can influence the maximization of profits of the car-sharing system. The hexagonal tessellation method was used to cover the area of the region. The theory of discrete optimization was used to create a profit maximization model. This study continues the authors' study published in the paper [5].

This study builds a profit maximization model of the car-sharing system for Astana, Republic of Kazakhstan. There is no accessible information about trips within the city of Astana. A separate task in the study was the collection of data on trips within the city of Astana at different times of the day. This is necessary to implement a dynamic model of profit maximization of the car-sharing system.

3.2. The Method of Selecting Subregions using Hexagonal Tessellation

The first task for building a dynamic model of profit maximization of car-sharing services is to build an optimal division of the region into sub-regions following the features of the location of city infrastructure and the needs of system users. Also, this task is related to presenting and storing geo-informational data.

Methods of presenting and storing geo-informational data were investigated in [5]. This is necessary for selecting sub-regions in the region where the car-sharing system is implemented. For each subregion, it is fashionable to calculate the parameters, highlight the restrictions, and place the stations. This has a qualitative effect on the support of operational decisions on the management of this system. It was established that a rational way of presenting data is to cover the region with a grid. Moreover, the properties of the objects will be stored in the grid cell that covers them.

An urgent task is to choose a method of covering the region with a grid. A simple method is administrative, when streets, district boundaries, geographic objects, etc, determine cell boundaries. This method accurately reflects the data about the region, but the disadvantage is the complex shape of the cell boundaries. Keeping the region's boundary as broken requires significant amounts of data, and the variety of cell boundaries significantly complicates algorithms for their processing. Methods of tessellation with uniform grids allow for solving this problem. The basis of tessellation methods is covering the region with a grid, each cell of which has the shape of a regular n-gon, particularly a triangle, square, or hexagon [28].

The frameworks H3 from Uber [29] and S2 from Google [30] were analyzed to cover the region with geometric shapes of different areas. As a result of the comparison, it was established that both frameworks could be used to cover any region and provide an opportunity to choose a grid scale within vast limits. A significant difference between the H3 and S2 frameworks is the shape of the grid. The main advantage of covering with a hexagonal grid is that the distance between the centers of neighboring cells is constant. This property significantly simplifies algorithms for finding the shortest paths between cells. First, you need to specify the region's borders to cover the map with hexagons using the H3 framework. The data on the boundaries of the regions provided by the GADM service [31] were used. The Kepler service [32] was used to visualize the coverage.

3.3. Mathematical Model of the Profitability of the Car Sharing System

Let us consider the parameters that must be determined for the effective functioning of the car-sharing system. Since the car-sharing system functions cyclically, that is, every day in the system, depending on the type of system, cars may be relocated to those areas that are in demand by users at the appropriate time. Let T be the number of periods into which one iteration of the cycle of the car-sharing system is divided. We will assume that after the completion of the iteration, the system returns to the initial state. The system's initial state can be determined by relocating a certain number of cars to certain areas. As the demand for car-sharing services in these areas changes, the system's initial state changes in a new cycle. We will assume that one cycle iteration is divided evenly into T periods

(t_{i}, t_{i + 1})

i = \bar{0, T - 1}

, that is, we will determine the state of the car-sharing system at moments in time

〈 t_{0}, t_{1}, \dots, t_{T} 〉

Let the car-sharing system be implemented in region R. Let us divide region R into subregions

(r_{0}, r_{2}, \dots, r_{n - 1})

. The distribution can be performed by the hexagonal tessellation method. For each subregion

r_{j}

j = \bar{0, n - 1}

for the corresponding period

(t_{i}, t_{i + 1})

i = \bar{0, T - 1}

, we calculate the following parameters:

–

K_{j} (t_{i + 1})

– the number of occupied cars in the subregion

r_{j}

j = \bar{0, n - 1}

;

–

k_{j} (t_{i + 1})

– the number of free cars in the subregion

r_{j}

j = \bar{0, n - 1}

;

–

C_{j q} (t_{i + 1})

– the number of cars that traveled from the subregion

r_{j}

to the subregion

r_{q}

j = \bar{0, n - 1}

q = \bar{0, n - 1}

j \neq q

;

–

p_{j q} (t_{i + 1})

– the probability of a car trip from the subregion

r_{j}

to the subregion

r_{q}

j = \bar{0, n - 1}

q = \bar{0, n - 1}

j \neq q

;

–

g_{j} (t_{i + 1})

– maintenance costs (repair, washing, etc.) of cars in the subregion

r_{j}

j = \bar{0, n - 1}

;

–

P_{j q} (t_{i + 1})

– the cost of a car trip from the subregion

r_{j}

to the subregion

r_{q}

j = \bar{0, n - 1}

q = \bar{0, n - 1}

j \neq q

;

L_{j q} (t_{i + 1})

– expenses for a car trip from the subregion

r_{j}

to the subregion

r_{q}

j = \bar{0, n - 1}

q = \bar{0, n - 1}

j \neq q

The cost of a car trip from the subregion

r_{j}

to the subregion

r_{q}

for the relevant period

(t_{i}, t_{i + 1})

i = \bar{0, T - 1}

can be calculated using the formula:

P_{j q} (t_{i + 1}) = τ (t_{i + 1}) \cdot u_{j q},

where

u_{j q}

is the length of the route when traveling from the subregion

r_{j}

to the subregion

r_{q}

τ (t_{i + 1})

is the fare for travel to the neighboring subregion for the relevant period

(t_{i}, t_{i + 1})

i = \bar{0, T - 1}

. When using the hexagonal tessellation method, the adjacent subregion is defined by a hexagon whose side is directly adjacent to the hexagon that defines the current subregion.

Expenses for a car trip from the subregion

r_{j}

to the subregion

r_{q}

for the relevant period

(t_{i}, t_{i + 1})

i = \bar{0, T - 1}

can be calculated using the formula:

L_{j q} (t_{i + 1}) = β \cdot C_{j q} (t_{i + 1}) \cdot u_{j q},

where

β

is the coefficient considers the fuel cost for travel to the neighboring subregion.

After calculating the system of parameters, it is possible to determine the objective function that will determine the maximization of the car-sharing system implemented in the specified region:

\sum_{j = 0}^{n - 1} \sum_{q = 0}^{n - 1} \sum_{i = 0}^{T - 1} P_{j q} (t_{i + 1}) - \sum_{j = 0}^{n - 1} \sum_{q = 0}^{n - 1} \sum_{i = 0}^{T - 1} L_{j q} (t_{i + 1}) - \sum_{j = 0}^{n - 1} \sum_{i = 0}^{T - 1} g_{j} (t_{i + 1}) \to \max,

(1)

where

\sum_{j = 0}^{n - 1} \sum_{q = 0}^{n - 1} \sum_{i = 0}^{T - 1} P_{j q} (t_{i + 1})

is the income received from all trips from each sub-region

r_{j}

to the subregion

r_{q}

for the complete cycle of the car-sharing system, i.e., for the period

(t_{0}, t_{T - 1})

;

\sum_{j = 0}^{n - 1} \sum_{q = 0}^{n - 1} \sum_{i = 0}^{T - 1} L_{j q} (t_{i + 1})

is the costs from all trips from each sub-region

r_{j}

to the subregion

r_{q}

for the complete cycle of the car-sharing system, i.e., for the period

(t_{0}, t_{T - 1})

;

\sum_{j = 0}^{n - 1} \sum_{i = 0}^{T - 1} g_{j} (t_{i + 1})

is the car maintenance costs in each subregion

r_{j}

for the complete cycle of the car-sharing system, i.e., for the period

(t_{0}, t_{T - 1})

The task is to find the optimal distribution of cars in all subregions at the initial moment. Such distribution can be determined based on statistical data on customers' trips in these subregions at specific points in time. For example, you can cover a region with hexagons, and for each hexagon corresponding to the corresponding subregion, determine the number of taxi orders in the morning period. Next, you can distribute the cars available in the car-sharing system proportionally across these subregions. That is, at the initial moment, the distribution of cars takes place according to the following formulas:

\sum_{j = 0}^{n - 1} k_{j} (t_{0}) = γ,

(2)

\sum_{j = 0}^{n - 1} k_{j} (t_{i + 1}) \leq γ, i = \bar{0, T - 1},

(3)

where is the total number of cars that are available,

k_{j} (t_{0})

is the number of free cars at the initial time point in the subregion

r_{j}

j = \bar{0, n - 1}

k_{j} (t_{i + 1})

is the number of free cars at the initial time point in the subregion

r_{j}

j = \bar{0, n - 1}

for the period

(t_{i}, t_{i + 1})

At the following points in time, the distribution of cars will be determined according to the formulas that determine the restrictions on the use of free cars in the subregions. In particular, the number of cars that customers can use for trips from a subregion

r_{j}

to other subregions cannot exceed the number of free cars in this subregion:

\sum_{q = 0}^{n - 1} C_{s q} (t_{i + 1}) = k_{s} (t_{i}) + \sum_{q = 0}^{n - 1} C_{q j} (t_{i}) - \sum_{q = 0}^{n - 1} C_{s q} (t_{i}), i = \bar{0, T - 1}, s = \bar{0, n - 1},

(4)

C_{q j} (t_{i}) = 0, q = \bar{0, n - 1}, j = \bar{0, n - 1},

(5)

where

C_{q j} (t_{i}) = 0

is the condition that determines that at the initial moment, cars do not make trips;

k_{s} (t_{i})

is the number of free cars in the subregion

r_{s}

for the period

(t_{i}, t_{i + 1})

i = \bar{0, T - 1}

s = \bar{0, n - 1}

;

C_{s q} (t_{i + 1})

is the number of cars that left the subregion

r_{s}

to the subregion

r_{q}

for the period

(t_{i}, t_{i + 1})

;

C_{q j} (t_{i})

is the number of cars that left the subregion

r_{q}

to the subregion

r_{j}

for the period

(t_{i - 1}, t_{i})

;

C_{s q} (t_{i})

is the number of cars that left the

r_{s}

to the subregion

r_{q}

for the period

(t_{i - 1}, t_{i})

The relationship between the a priori probability of a car trip from the subregion

r_{s}

to the subregion

r_{q}

and the number of free cars in the subregion

r_{s}

is defined by the function

C_{s q} (t_{i + 1}) = f (p_{s q} (t_{i + 1}), k_{s} (t_{i}))

. Analytically, such a function is difficult to describe, so it is fashionable to use simulation modeling to find it. The trips of each free vehicle from each subregion over period

(t_{i - 2}, t_{i - 1})

are simulated. We generate

k_{s} (t_{i})

times a pseudorandom number from the interval

[0, 1)

. If the number falls into a gap

[0, p_{s 1} (t_{i + 1}))

, then we simulate a car trip to the subregion

r_{1}

, if the number falls into a gap

[p_{s 1} (t_{i + 1}), p_{s 1} (t_{i + 1}) + p_{s 2} (t_{i + 1}))

, then we simulate a car trip to the subregion

r_{2}

, etc., if the number falls into a gap

[\sum_{u = 1}^{q - 1} p_{s u} (t_{i + 1}), \sum_{u = 1}^{q} p_{s u} (t_{i + 1}))

, then we simulate a car trip to the subregion

r_{q}

, etc., if the number falls into a gap

[\sum_{u = 1}^{n - 1} p_{s u} (t_{i + 1}), 1)

, then we simulate a car trip to the subregion

r_{n}

. After carrying out the simulation modeling procedure, we get the integer linear programming problem (1)–(5). To find a solution to this problem, you can use the CPLEX application [33].

4. Results

4.1. Collection of Data

Car-sharing systems are developed in the EU, USA, Canada, and Japan. At the same time, there is a sufficient amount of data to analyze and improve these systems considering the changes that are taking place. This research was focused on building a model of profit maximization in the region, for which there needs to be more information on passenger transportation in free access. Therefore, data collection was a separate task.

As part of the project based on which this study was carried out, cars were purchased with the appropriate equipment for recording the number of transportation, the route of transportation of passengers, and other necessary parameters. These cars were used on a test basis to transport passengers in Astana in the mode of taxi service from January 30, 2023 to March 11, 2023. Data were collected on 1,168 transportation within the administrative boundaries of Astana. Settlements that are satellites of the city of Astana should have been considered. For each transportation, several parameters were fixed:

−: the time and coordinates of the start of the trip;
−: the time and coordinates of the end of the trip;
−: the cost of the trip;
−: the number of passengers.

This mode of transportation allows you to obtain essential indicators since transportation is not fixed by specific routes, as in public transport. Passengers with average wealth also use this mode of transportation. This category of city residents is considered in the car-sharing system for which the model is being built in this study. The obtained results make it possible to identify the subregions of the city in which the most calls for cars are made, the subregions of the city where the transportation service users move the most, and at what time of day. Other recorded parameters are essential for building a dynamic model of profit maximization of the car-sharing system considering regional characteristics.

4.1. The Results of Building a Dynamic Model of Profit Maximization of the Car-Sharing System in the City of Astana

Collected data on trips within the city of Astana in the taxi service mode from January 30, 2023 to March 11, 2023 were processed. Figure 1 shows a city map in administrative boundaries, visualized using Google maps. In total, information on 1168 trips was processed. All trips were divided into four groups, depending on the start time of the trip:

−: A (trip start recorded from 5:00 am to 11:00 am);
−: B (trip start recorded from 11:00 am to 5:00 pm);
−: C ( the start of the trip is fixed from 5:00 pm to 11:00 pm);
−: D (the start of the trip is fixed from 11:00 pm to 5:00 am).

The number of trips in each group is shown in Table 1. Most trips were recorded between 11:00 am and 5:00 pm (group B). The fewest trips were recorded between 11:00 pm and 5:00 am (group D).

The coordinates of the start and stop of trips in these groups are visualized using the python language's mathplotlib library and shown in Figure 2 and Figure 3.

As can be seen from the visualization, the distribution of boarding and disembarking points differs significantly at different periods of the day. The coordinates of the start and end of the trips were tied to the corresponding cells of the hexagonal grid. The probability of a trip is calculated as the ratio of the number of trips from subregion to subregion

r_{q}

to the total number of trips in the region in one day. Using the Kepler visualization service [32], a hexagonal tessellation of the selected region (the city of Astana, Republic of Kazakhstan) was constructed and visualized based on the collected dataset for the period from January 30, 2023 to March 11, 2023 (Fig. 4). The number of trips related to the corresponding cell is displayed in colors. The lighter the color of the cell, the greater the number of trips. Accordingly, the probability of ordering a car in this subregion will be greater. This information is essential for placing stations with cars in the appropriate sub-regions and determining the number of cars in each subregion at a particular time.

As can be seen from the visualization, the hexagonal grid evenly covers almost all of Astana. The number of trips for each cell varies from 1 to 10. It can also be established that the number of trips to cells located in the city center exceeds the number of trips to cells located on the outskirts.

The average fare in Astana taxi services is about $1.2 per passenger boarding and about $0.1 per kilometer of travel. The mass tab of grid cell eight was chosen during the hexagonal tessellation of the Astana region using the H3 framework. At this scale, the hexagon's side size is 461 meters. As a result, we get that the value of the tariff 0,15≤τ(t)≤0,3. The β coefficient in the profit maximization model can be estimated between 0.05 and 0.07. When building a dynamic profit maximization model, it was assumed that β=0.06.

5. Discussion

5.1. Findings

The dynamic profit maximization model for the car-sharing system was built. Data on passenger trips in the taxi service mode were also collected to adjust this model to the region where the system is being implemented (Astana). The region bounded by the administrative borders of the city of Astana was covered by a hexagonal grid, each cell of which defines a separate subregion. For this, the H3 framework [29] was used to choose different scales for the required number of subregions. Several parameters reflecting changes in customer behavior in dynamics were calculated for each subregion. A visualization of the movement of taxi service customers in the city at different times of the day was carried out. The dynamic model of profit maximization of the car-sharing system is built based on calculated parameters. The model built in this way considers the change in the demand for trips of customers of the car-sharing system during the day.

The two cases were considered to verify the results of developing a dynamic model of profit maximization of the car-sharing system. The first case concerns finding the maximum profit of the car sharing system for the city of Astana if the data on the time of the customers' trips are not taken into account, but the coordinates of the start and end of the trips are taken into account. To find the maximum profit of the car-sharing system, the model (1)-(5) with the value of the parameter T=1 was applied. In this case, the system ceases to be dynamic and becomes static. The second case concerns finding the maximum profit of the car-sharing system for the city of Astana if the data on the start and end times of the trip, as well as the coordinates of the trips, are taken into account. For this, model (1)-(5) is used. All trips are grouped into four periods: A (the start of the trip is fixed from 5:00 am to 11:00 am), B (the start of the trip is fixed from 11:00 am to 5:00 pm), C (the start of the trip is fixed from 5:00 pm to 11:00 pm), D (the start of the trip is fixed from 11:00 pm to 5:00 am). That is the value of the parameter T=4. Each case was considered for a different number of cars available in the car-sharing system (

γ = 1, \dots, 20

). The initial allocation of cars was carried out based on collected data on customer trips to Astana (Fig. 3). The results of calculating the profit of the car-sharing system in the city of Astana based on static (T=1) and dynamic (T=4) models are shown in Table 2.

As a result, it was established that using a dynamic profit maximization model increases it by an average of 3.7%.

5.2. Limitations and Future Research Lines

The built dynamic model is unidirectional. That is, costs for the distribution of cars by subregions after the completion of the trip cycle are not taken into account in the model. These costs, as shown in [8], will be non-zero. The limitations of the built dynamic model are that the number of periods and subregions should be small. This is explained by the complexity of calculations, which will grow exponentially for discrete optimization. The work did not focus on selecting the optimal method for solving problems (1)–(5), which is the subject of further research.

6. Conclusions

The method of covering the region with geometric shapes, which divides the region into subregions, is described. For this problem, the rational choice was to cover the region with regular hexagons, which are placed side by side. A dataset with information about trips to the village was built. Astana. Constructed maps of the start and end of trips in the region and a map of trips bound to the hexagonal grid cells using the Kepler visualization service. Each cell of the grid corresponds to a specific sub-region, for which quantitative parameters are calculated: the number of free cars in the sub-regions, the probability of a car trip from one sub-region to another, the costs of car maintenance and operation, the income from the trip.

The objective function of profit maximization in the dynamic model was determined, and the restrictions were established considering the peculiarities of passenger transportation in Astana. The simulation was carried out based on the constructed profit maximization model for the car-sharing system using the example of Astana. For this, 2 cases were considered. The first case corresponds to the static model (T=1), and the second corresponds to the dynamic model (T=4). It was established that using a dynamic model of profit maximization in the car-sharing system increases the profit by 3.7%.

Author Contributions

Conceptualization and methodology, O.K. and Y.A.; software, Y.A.; analysis, O.K., Y.A., A.B. and D.Y.; coding, Y.A.; writing – original draft preparation, O.K. and Y.A.; writing–review and editing, A.B., O.K. and. Y.A.; visualization O.K. and Y.A.; project administration, A.B. and D.Y. All authors have read and agreed to the published version of the manuscript.

Funding

This paper was written in the framework of the state order to implement the science program for budget program 217 "Development of Science", IRN No. BR10965311 with the topic: " Development of the intelligent information and telecommunication systems for municipal infrastructure: transport, environment, energy and data analytics in the concept of Smart City ".

Data Availability Statement

All data is available in this publication.

Acknowledgments

The authors thank the reviewers and editors for their generous and constructive comments that have improved this paper.

Conflicts of Interest

The authors declare no conflicts of interest.

References

Shared Economy: WeWork, Uber, Airbnb and Lyft. (2020). bbcResearch. Retrieved from: https://www.bccresearch.com/market-research/finance/shared-economy-wework-uber-airbandb-lyft-market.html. Accessed April 01, 2023.
A European agenda for the collaborative economy. (2016). European Commission. Retrieved from: <https://www.eumonitor.eu/9353000/1/j9vvik7m1c3gyxp/vkbkcwzb2szn>. Accessed , 2023. 01 April.
Shaheen, S.A.; Cohen, A.P. Growth in Worldwide Carsharing: An International Comparison. Transp. Res. Rec. J. Transp. Res. Board 2007, 1992, 81–89. [Google Scholar] [CrossRef]
Rycerski, P. , Koutra, S., Genikomsakis, K. N., & Ioakimidis, C. S. (2016). A university survey with a comparative study of an E-bikes sharing system. EVS 2016 - 29th Int. Electr. Veh. Symp, Montreal, 1–11.
Amirgaliyev, B.; Andrashko, Y.; Kuchansky, A. Building a dynamic model of profit maximization for a carsharing system accounting for the region’s geographical and economic features. Eastern-European J. Enterp. Technol. 2022, 2, 22–29. [Google Scholar] [CrossRef]
Perboli, G.; Ferrero, F.; Musso, S.; Vesco, A. Business models and tariff simulation in car-sharing services. Transp. Res. Part A: Policy Pr. 2018, 115, 32–48. [Google Scholar] [CrossRef]
Liao, F.; Correia, G. Electric carsharing and micromobility: A literature review on their usage pattern, demand, and potential impacts. Int. J. Sustain. Transp. 2022, 16, 269–286. [Google Scholar] [CrossRef]
Jorge, D.; Molnar, G.; Correia, G.H.d.A. Trip pricing of one-way station-based carsharing networks with zone and time of day price variations. Transp. Res. Part B: Methodol. 2015, 81, 461–482. [Google Scholar] [CrossRef]
Bruglieri, M.; Colorni, A.; Luè, A. The Vehicle Relocation Problem for the One-way Electric Vehicle Sharing: An Application to the Milan Case. Procedia - Soc. Behav. Sci. 2014, 111, 18–27. [Google Scholar] [CrossRef]
Nourinejad, M.; Roorda, M.J. A dynamic carsharing decision support system. Transp. Res. Part E: Logist. Transp. Rev. 2014, 66, 36–50. [Google Scholar] [CrossRef]
Correia, G.H.D.A.; Jorge, D.R.; Antunes, D.M. The Added Value of Accounting For Users’ Flexibility and Information on the Potential of a Station-Based One-Way Car-Sharing System: An Application in Lisbon, Portugal. J. Intell. Transp. Syst. 2014, 18, 299–308. [Google Scholar] [CrossRef]
Boyacı, B.; Zografos, K.G.; Geroliminis, N. An integrated optimization-simulation framework for vehicle and personnel relocations of electric carsharing systems with reservations. Transp. Res. Part B: Methodol. 2016, 95, 214–237. [Google Scholar] [CrossRef]
Monteiro C., M. , Machado C. A. S., Lage M. de O., Berssaneti F. T., Davis Jr. C. A., & Quintanilha J. A. (2019). Maximizing carsharing profits: an optimization model to support the carsharing planning. Procedia Manufacturing, 39, 1968–1976.
Wu, T.; Xu, M. Modeling and optimization for carsharing services: A literature review. Multimodal Transp. 2022, 1. [Google Scholar] [CrossRef]
Correia, G.H.A.; Antunes, A.P. Optimization approach to depot location and trip selection in one-way carsharing systems. Transp. Res. Part E: Logist. Transp. Rev. 2012, 48, 233–247. [Google Scholar] [CrossRef]
Hu, L.; Liu, Y. Joint design of parking capacities and fleet size for one-way station-based carsharing systems with road congestion constraints. Transp. Res. Part B: Methodol. 2016, 93, 268–299. [Google Scholar] [CrossRef]
Huang, K.; Correia, G.H.d.A.; An, K. Solving the station-based one-way carsharing network planning problem with relocations and non-linear demand. Transp. Res. Part C: Emerg. Technol. 2018, 90, 1–17. [Google Scholar] [CrossRef]
Fan, W. (. Optimizing Strategic Allocation of Vehicles for One-Way Car-sharing Systems Under Demand Uncertainty. J. Transp. Res. Forum, 2014; 55, 7–20. [Google Scholar] [CrossRef]
Boyacı, B.; Zografos, K.G. Investigating the effect of temporal and spatial flexibility on the performance of one-way electric carsharing systems. Transp. Res. Part B: Methodol. 2019, 129, 244–272. [Google Scholar] [CrossRef]
Zhou, T. , Osorio, C., & Fields, E. (2017). A data-driven discrete simulation-based optimization algorithm for large-scale two-way car-sharing network design. Massachusetts Inst. Technol., Boston, MA, USA, Tech. Report. Retrieved from: <http://web.mit.edu/osorioc/www/papers/zhoOsoFieCarSharing.pdf >. Accessed , 2023. 01 April.
Huo, X.; Wu, X.; Li, M.; Zheng, N.; Yu, G. The allocation problem of electric car-sharing system: A data-driven approach. Transp. Res. Part D: Transp. Environ. 2020, 78, 102192. [Google Scholar] [CrossRef]
Huang, K.; An, K.; Correia, G.H.d.A.; Rich, J.; Ma, W. An innovative approach to solve the carsharing demand-supply imbalance problem under demand uncertainty. Transp. Res. Part C: Emerg. Technol. 2021, 132, 103369. [Google Scholar] [CrossRef]
Jian, S.; Rey, D.; Dixit, V. An Integrated Supply-Demand Approach to Solving Optimal Relocations in Station-Based Carsharing Systems. Networks Spat. Econ. 2018, 19, 611–632. [Google Scholar] [CrossRef]
Amirgaliyev, B.; Yegemberdiyeva, G.; Kuchansky, A.; Andrashko, Y.; Korol, I. Automating the customer verification process in a car sharing system based on machine learning methods. Eastern-European J. Enterp. Technol. 2022, 4, 59–66. [Google Scholar] [CrossRef]
Darapaneni, N.; Evoori, A.K.; Vemuri, V.B.; Arichandrapandian, T.; Karthikeyan, G.; Paduri, A.R.; Babu, D.; Madhavan, J. Automatic Face Detection and Recognition for Attendance Maintenance. 2020 IEEE 15th International Conference on Industrial and Information Systems (ICIIS). LOCATION OF CONFERENCE, IndiaDATE OF CONFERENCE; pp. 236–241.
Sun, X.; Wu, P.; Hoi, S.C. Face detection using deep learning: An improved faster RCNN approach. Neurocomputing 2018, 299, 42–50. [Google Scholar] [CrossRef]
Boyko, R. , Shumyhai, D., & Gladka, M. (2017). Concept, definition and use of an agentin the multi-agent information managementsystems at the objects of various nature. Advances in Intelligent Systems and Computing, 543, 59–63.
Uber H3 for Data Analysis with Python. Retrieved from: <https://towardsdatascience.com/uber-h3-for-data-analysis-with-python-1e54acdcc908>. Accessed , 2023. 01 April.
H3. Retrieved from: <https://h3geo.org/docs/>. Accessed April 01, 2023.
S2 Geometry. Retrieved from: https://s2geometry.io/. Accessed April 01, 2023.
GADM maps and data. Retrieved from: https://kepler.gl/. Accessed April 01, 2023.
kepler.gl. Make an impact with your location data. Retrieved from: https://www.ibm.com/analytics/cplex-optimizer. Accessed , 2023. 01 April.
IBM ILOG CPLEX Optimizer. (2022). IBM. Retrieved from:. Accessed , 2023. 01 April.

Figure 1. Map of the city of Astana in administrative boundaries (visualized using the Google maps service).

Figure 2. Coordinates of the start of trips in groups A,B,C,D.

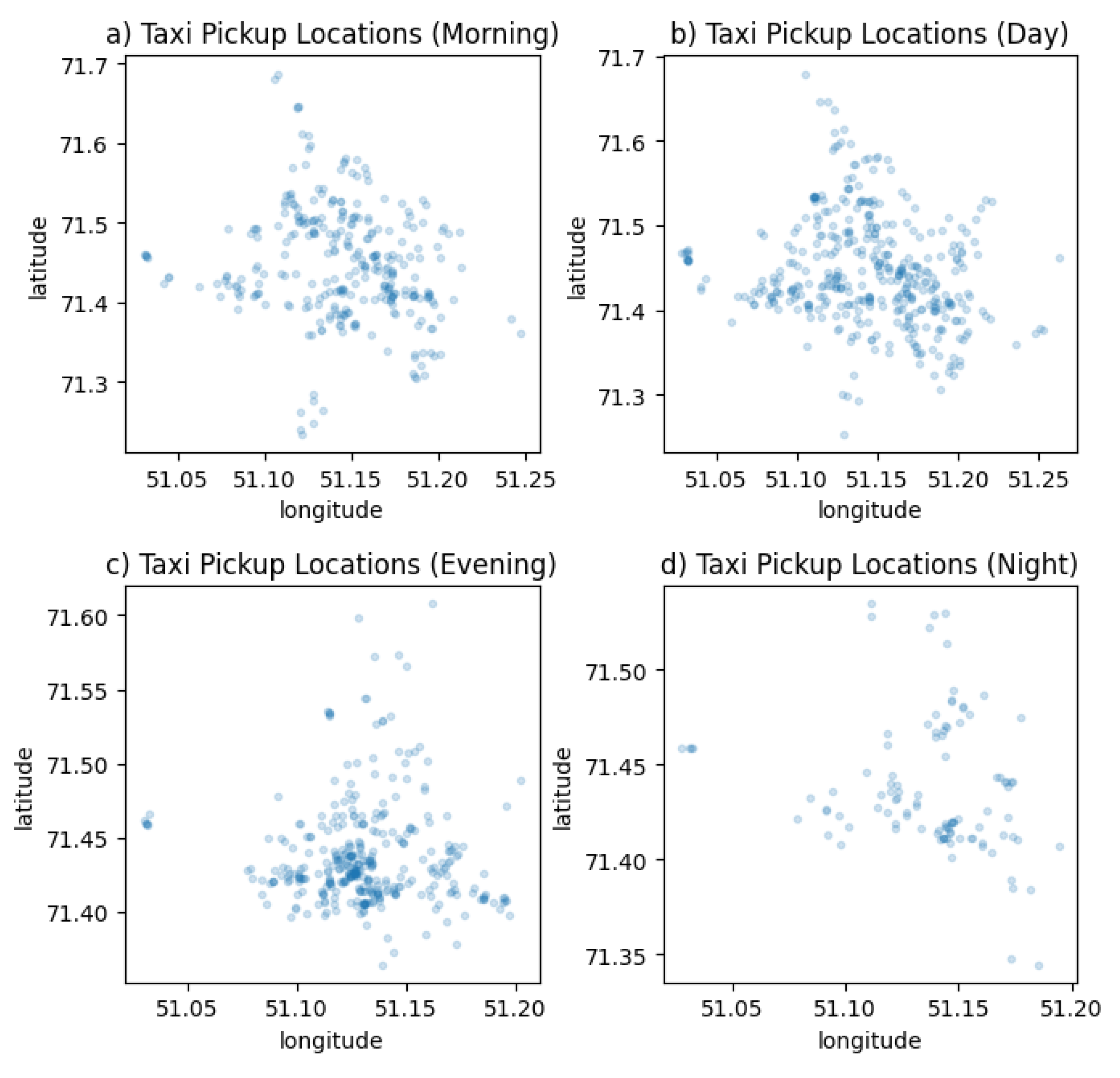
Figure 3. Coordinates of the end of trips in groups A,B,C,D.

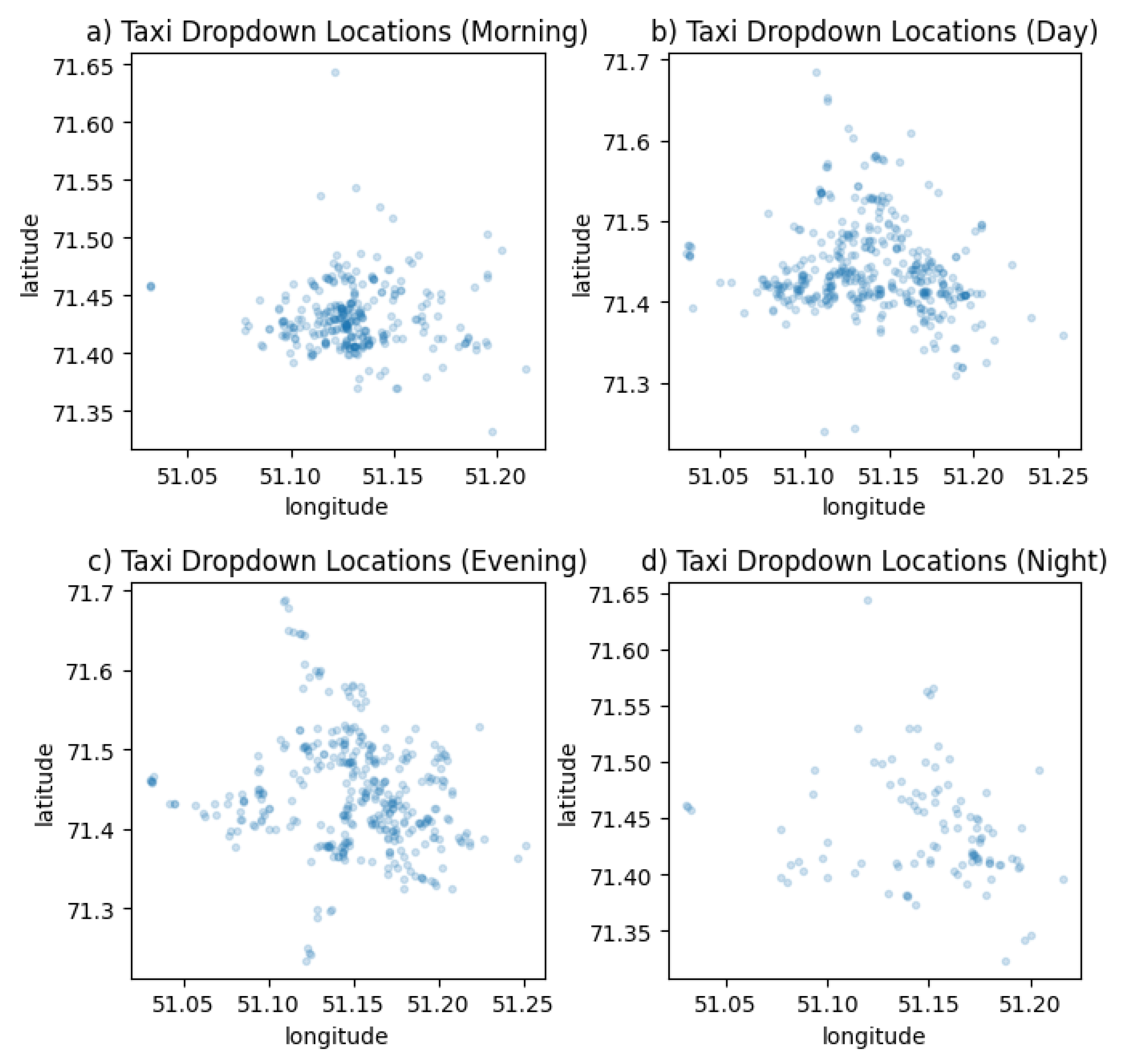
Figure 4. Map of car trips concerning the cells of the hexagonal grid in the city of Astana, built based on a dataset collected using the Kepler visualization service.

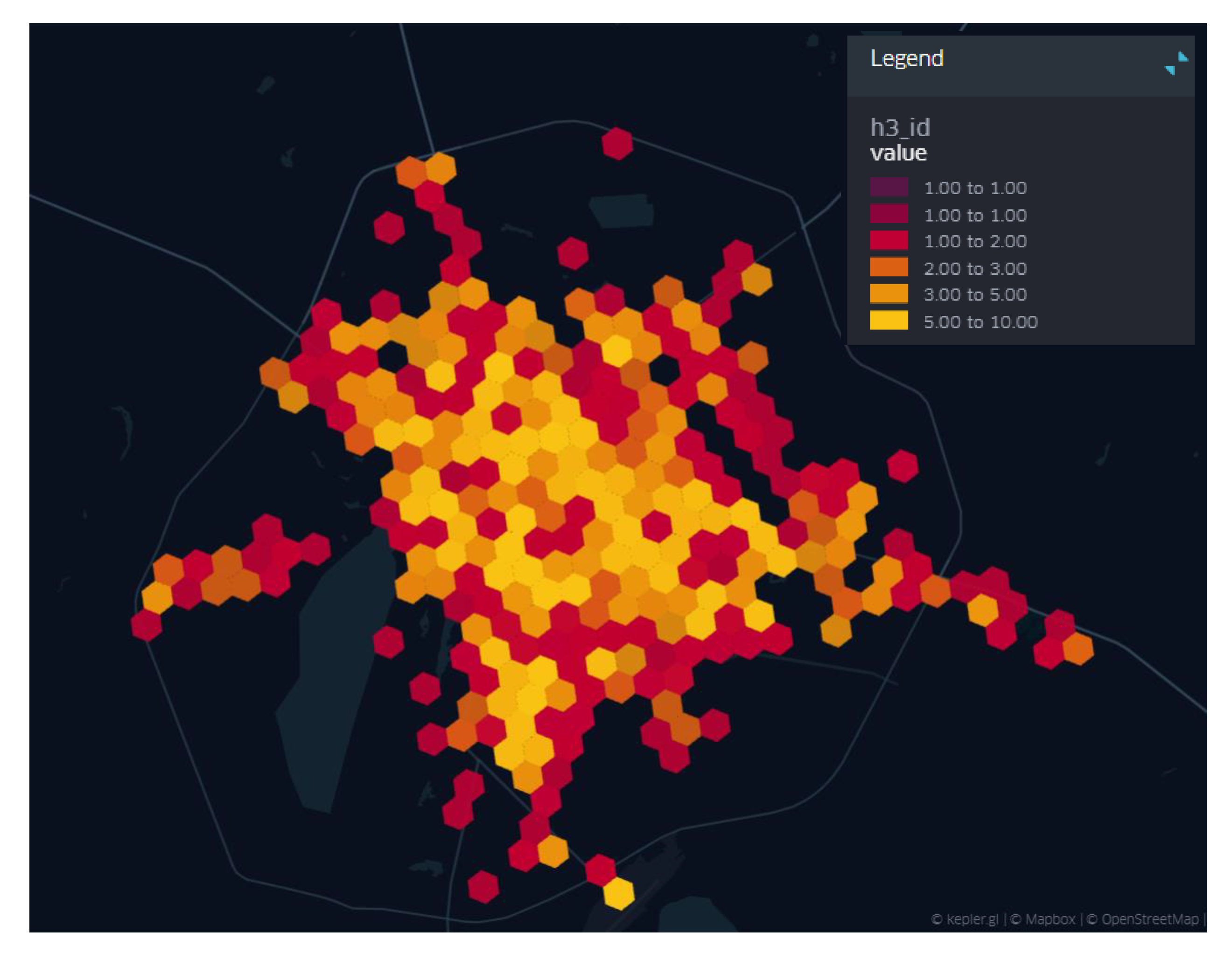
Table 1. Number of trips in each group A,B,C,D.

Groups	Number of trips
А	300
В	403
С	362
D	103
All	1168

Table 2. Calculation of the profit of the car-sharing system based on static and dynamic models of maximization in the city of Astana.

	T=1	T=4	Difference
1	1207	1291	6,5%
5	4824	4954	2,6
10	8227	8427	2,4%
20	15665	16201	3,3%

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

A Dynamic Model of Profit Maximization for a Carsharing Services: Astana, Republic of Kazakhstan

Abstract

1. Introduction

2. Literature Review

3. Methods and Data

3.1. Basic Concepts

3.2. The Method of Selecting Subregions using Hexagonal Tessellation

3.3. Mathematical Model of the Profitability of the Car Sharing System

4. Results

4.1. Collection of Data

4.1. The Results of Building a Dynamic Model of Profit Maximization of the Car-Sharing System in the City of Astana

5. Discussion

5.1. Findings

5.2. Limitations and Future Research Lines

6. Conclusions

Author Contributions

Funding

Data Availability Statement

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe