Submitted:
18 May 2023
Posted:
19 May 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
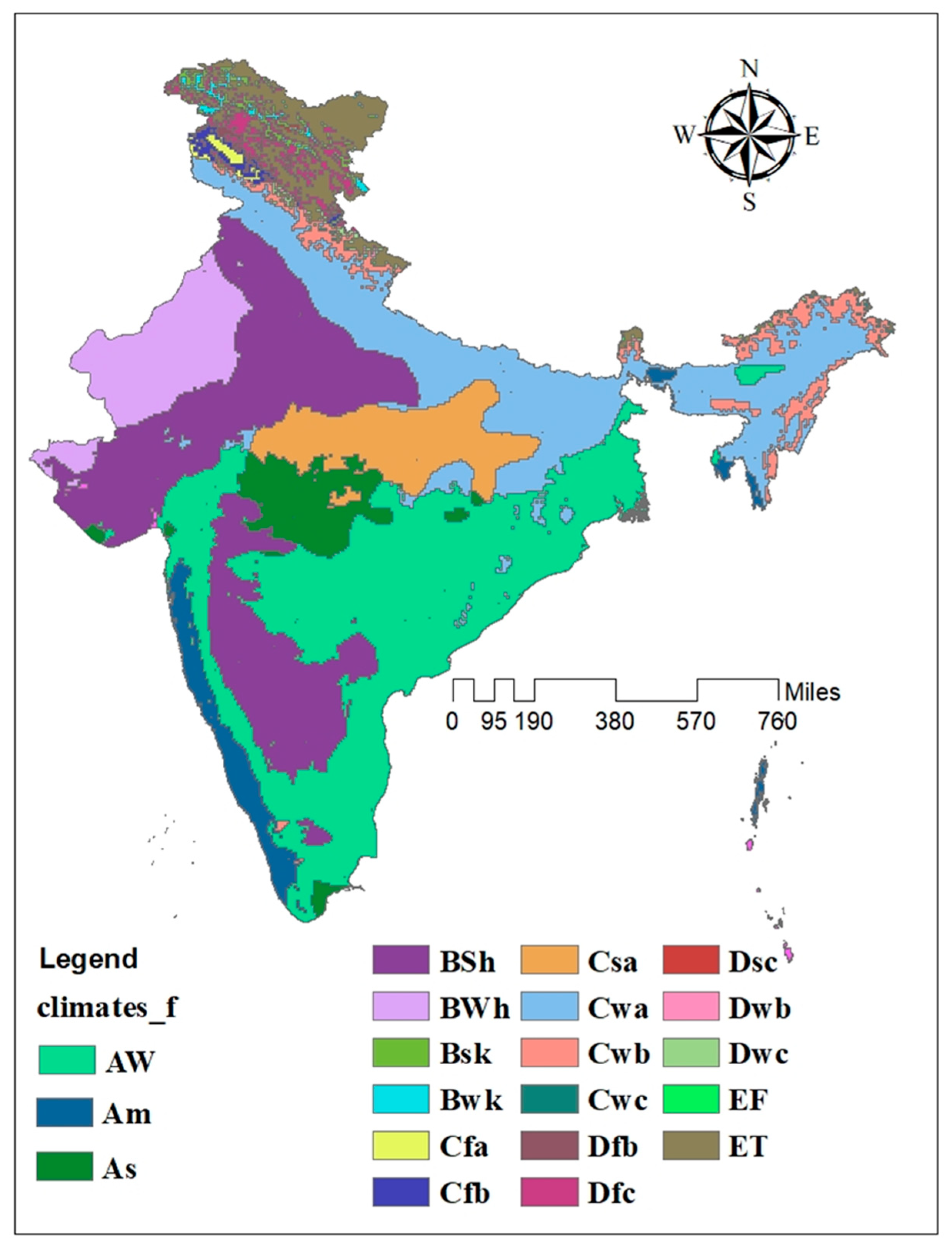
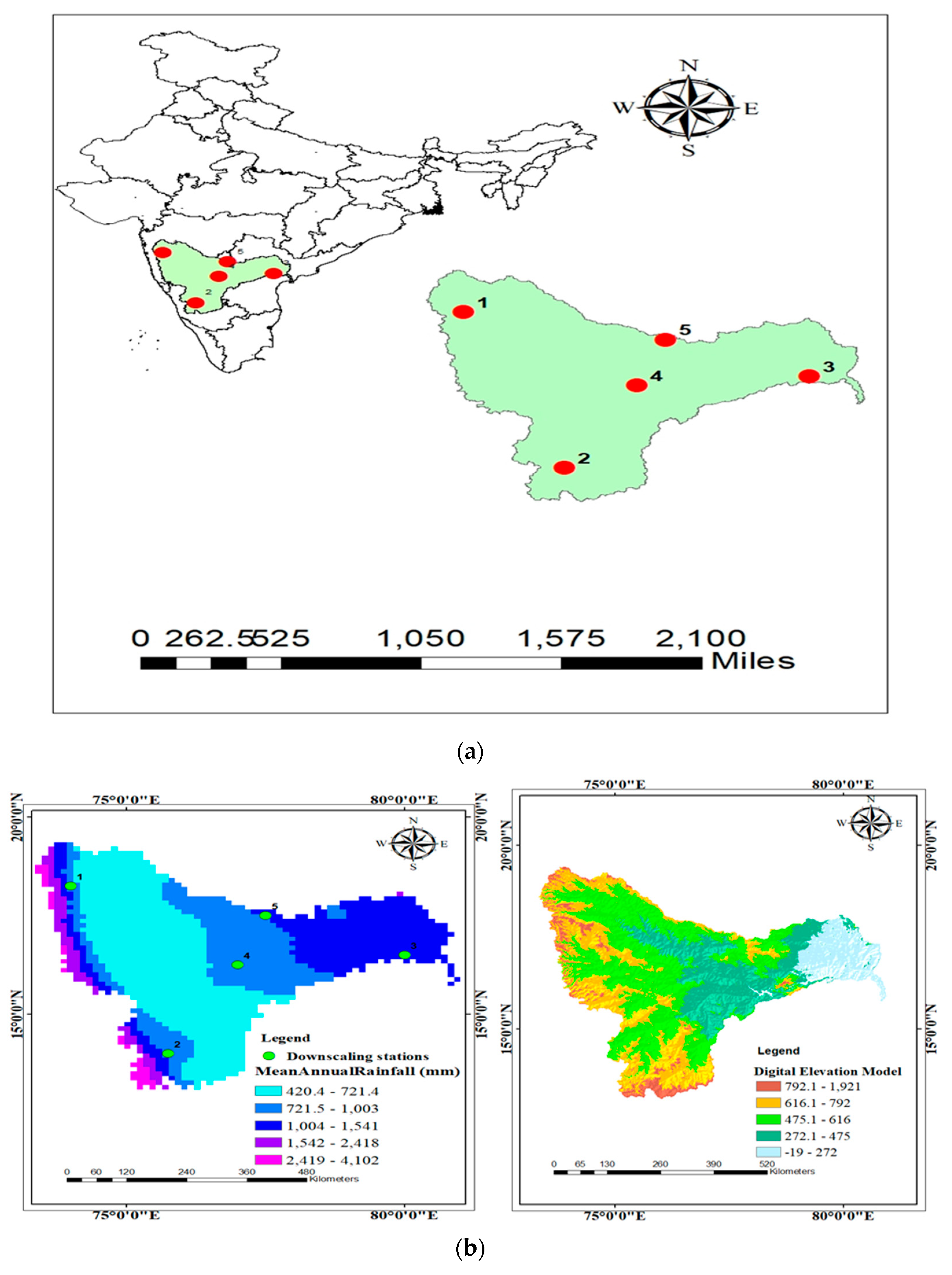
2. Study Area and Data Used
- (i.)
- Indian Ocean Dipole (IOD), also called Indian Nino, is an irregular oscillation of sea surface temperature in the western Indian Ocean and affects rainfall variability in East Africa, India, Indonesia, and Southern Australia[22]. IOD is one of the major climate drivers for rainfall in India and is also referred to as the difference in sea surface temperature (SST) anomalies in the region in IOD West at 50 E to 70 E and also IOD East at 10 S to 10 N. Data is downloaded from https://www.esrl.noaa.gov/psd/gcos_wgsp/Timeseries/Data/dmi.long.data and is available at monthly scale from the period of 1870 to 2018.
- (ii.)
- North Atlantic Oscillation (NAO) is a weather phenomenon that occurs in the North Atlantic Ocean, and its fluctuations are calculated based on the difference between subpolar low and subtropical high. Monthly data for these climatic indices can be obtained from the NOAA climate prediction Centre (CPC). The data is available for each month from 1948 to 2018.
- (iii.)
- Nino 3.4 index: El Nino and La Nina events are most commonly defined by Nino 3.4 index. The anomalies of Nino 3.4 are thought to represent east-central Tropical Pacific SSTs. The data is available from 1870 to 2019 on a monthly scale.
- (iv.)
- Pacific Decadal Oscillation (PDO) is often referred to as El Nino but acts at a larger scale, with a pattern mostly observed in North Pacific [23]. Extreme phases of the PDO index have been classified as warm or cool based on the ocean temperature anomalies in the tropical and northeast Pacific Ocean, and the length of the data available is from 1948 to 2018. The NAO, NINO 3.4, and PDO data are downloaded from https://www.esrl.noaa.gov/psd/data/climateindices/list/.
3. Methods
3.1. Wavelet Transform (WT)
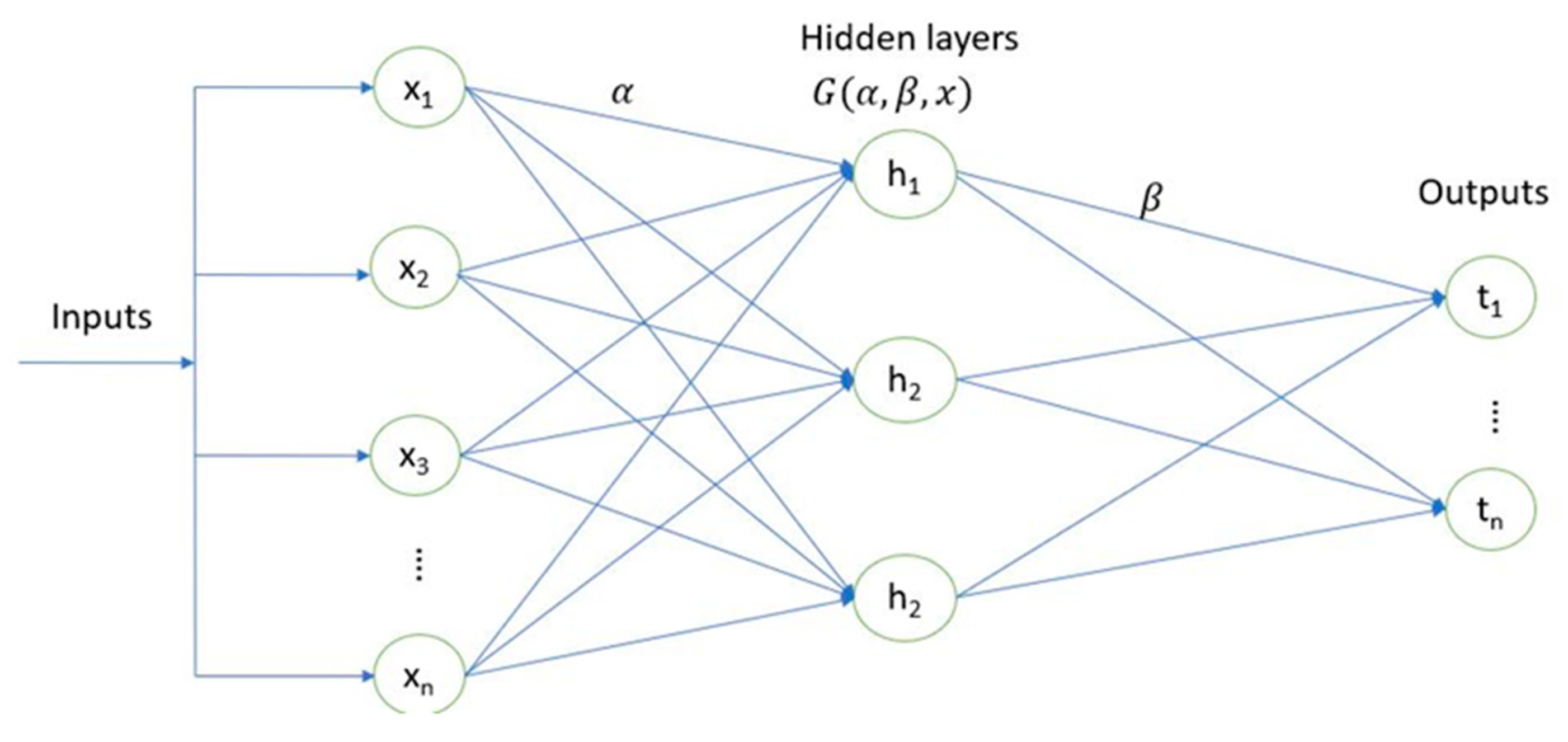
3.2. Extreme Learning Machines (ELM)
3.3. Wavelet Hybrid Models
4. Methodology
- (a)
- Single scale models (MLR, FFBP-NN, ELM)
- (b)
- Wavelet Hybrid models (WT-FFBP-NN and WT-ELM)
- (c)
- Performance Measures
- i.
- Root Mean Square Error (RMSE)
- ii.
- Correlation (R2)
- iii.
- Nash Sutcliffe Efficiency (NSE)
- iv.
- Most Absolute Error (MAE)
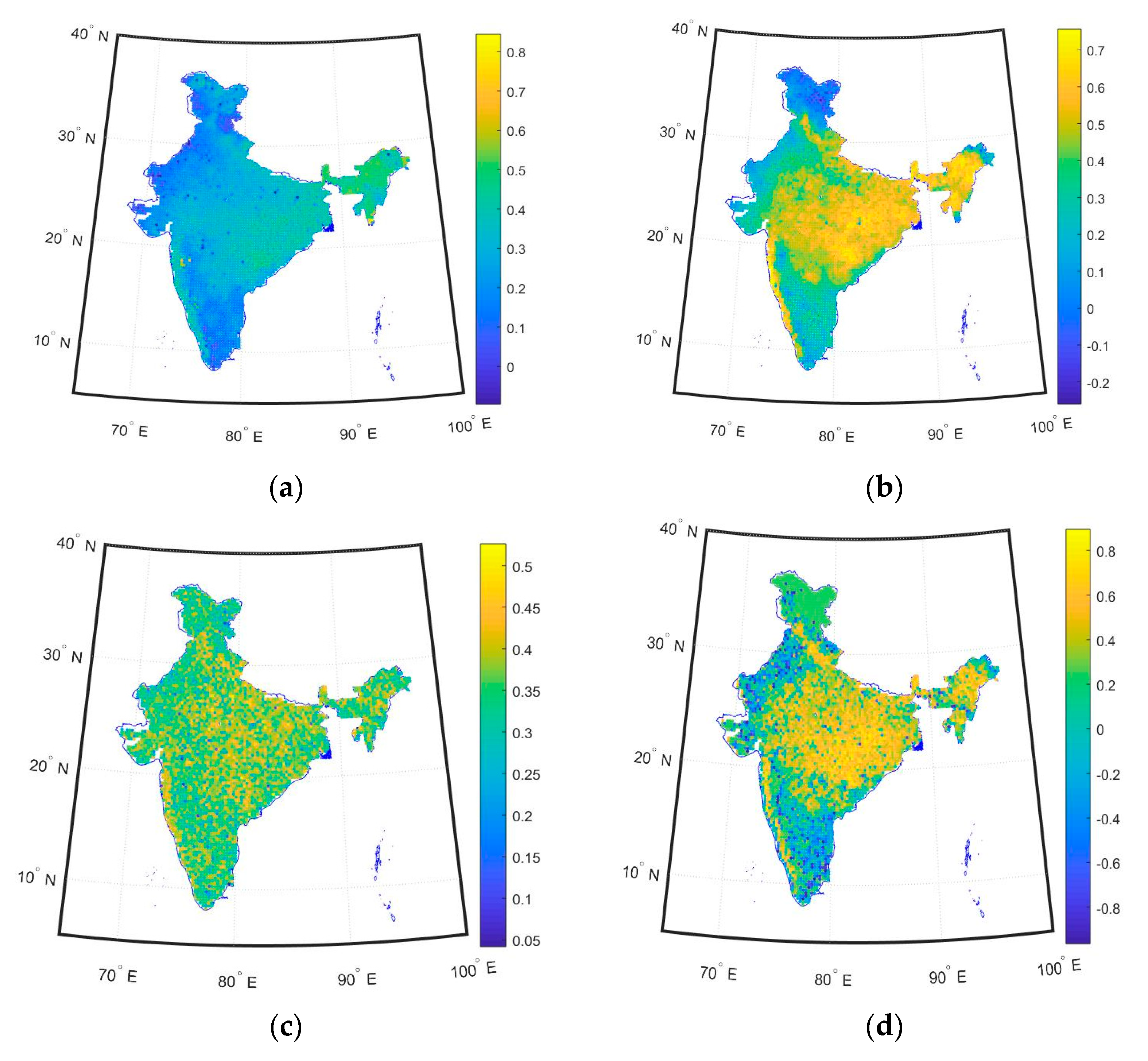
5. Results and Discussions
5.1. Forecasting using Single Scale Models
- (a)
- Results of the models using only local climate variables as predictors
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- K. E. Trenberth, L. Smith, T. Qian, A. Dai, and J. Fasullo, “Estimates of the global water budget and its annual cycle using observational and model Data,” Journal of Hydrometeorology, vol. 8, no. 4. pp. 758–769, Aug. 2007. [CrossRef]
- R. Abdi and T. Endreny, “A river temperature model to assist managers in identifying thermal pollution causes and solutions,” Water (Switzerland), vol. 11, no. 5, May 2019. [CrossRef]
- R. Maheswaran and R. Khosa, “A Wavelet-Based Second Order Nonlinear Model for Forecasting Monthly Rainfall,” Water Resources Management, vol. 28, no. 15, pp. 5411–5431, Dec. 2014. [CrossRef]
- L. Xu, N. Chen, X. Zhang, and Z. Chen, “A data-driven multi-model ensemble for deterministic and probabilistic precipitation forecasting at seasonal scale,” Clim Dyn, vol. 54, no. 7–8, pp. 3355–3374, Apr. 2020. [CrossRef]
- A. G. Yilmaz and N. Muttil, “Runoff Estimation by Machine Learning Methods and Application to the Euphrates Basin in Turkey,” J Hydrol Eng, vol. 19, no. 5, pp. 1015–1025, May 2014. [CrossRef]
- G. L. Feng et al., “Improved prediction model for flood-season rainfall based on a nonlinear dynamics-statistic combined method,” Chaos, Solitons and Fractals, vol. 140. Elsevier Ltd, Nov. 01, 2020. [CrossRef]
- L. Cuo, T. C. Pagano, and Q. J. Wang, “A review of quantitative precipitation forecasts and their use in short- to medium-range streamflow forecasting,” Journal of Hydrometeorology, vol. 12, no. 5. pp. 713–728, Oct. 2011. [CrossRef]
- Z. Hao, V. P. Singh, and Y. Xia, “Seasonal Drought Prediction: Advances, Challenges, and Future Prospects,” Reviews of Geophysics, vol. 56, no. 1, pp. 108–141, Mar. 2018. [CrossRef]
- H. S. Bauer et al., “Quantitative precipitation estimation based on highresolution numerical weather prediction and data assimilation with WRF - a performance test,” Tellus, Series A: Dynamic Meteorology and Oceanography, vol. 67, no. 1, 2015. [CrossRef]
- D. J. Stensrud et al., “Convective-scale warn-on-forecast system: A vision for 2020,” Bull Am Meteorol Soc, vol. 90, no. 10, pp. 1487–1499, 2009. [CrossRef]
- S. K. Saha et al., “Improved simulation of Indian summer monsoon in latest NCEP climate forecast system free run,” International Journal of Climatology, vol. 34, no. 5, pp. 1628–1641, 2014. [CrossRef]
- F. Molteni, R. Buizza, T. N. Palmer, and T. Petroliagis, “The ECMWF Ensemble Prediction System: Methodology and validation,” 1996.
- B. Choubin, S. Khalighi-Sigaroodi, A. Malekian, and Ö. Kişi, “Multiple linear regression, multi-layer perceptron network and adaptive neuro-fuzzy inference system for forecasting precipitation based on large-scale climate signals,” Hydrological Sciences Journal, vol. 61, no. 6, pp. 1001–1009, Apr. 2016. [CrossRef]
- L. Xu, N. Chen, X. Zhang, and Z. Chen, “An evaluation of statistical, NMME and hybrid models for drought prediction in China,” J Hydrol (Amst), vol. 566, pp. 235–249, Nov. 2018. [CrossRef]
- M. Ghamariadyan and M. A. Imteaz, “A wavelet artificial neural network method for medium-term rainfall prediction in Queensland (Australia) and the comparisons with conventional methods,” International Journal of Climatology, vol. 41, no. S1, pp. E1396–E1416, Jan. 2021. [CrossRef]
- R. K. Chowdhury and S. Beecham, “Australian rainfall trends and their relation to the southern oscillation index,” Hydrol Process, vol. 24, no. 4, pp. 504–514, Feb. 2010. [CrossRef]
- J. Abbot and J. Marohasy, “Application of artificial neural networks to rainfall forecasting in Queensland, Australia,” Adv Atmos Sci, vol. 29, no. 4, pp. 717–730, Jul. 2012. [CrossRef]
- D. Rivera, M. Lillo, C. B. Uvo, M. Billib, and J. L. Arumí, “Forecasting monthly precipitation in Central Chile: A self-organizing map approach using filtered sea surface temperature,” Theor Appl Climatol, vol. 107, no. 1–2, pp. 1–13, 2012. [CrossRef]
- R. Barzegar, A. Asghari Moghaddam, J. Adamowski, and B. Ozga-Zielinski, “Multi-step water quality forecasting using a boosting ensemble multi-wavelet extreme learning machine model,” Stochastic Environmental Research and Risk Assessment, vol. 32, no. 3, pp. 799–813, Mar. 2018. [CrossRef]
- M. Alizamir, O. Kisi, and M. Zounemat-Kermani, “Modelling long-term groundwater fluctuations by extreme learning machine using hydro-climatic data,” Hydrological Sciences Journal, vol. 63, no. 1, pp. 63–73, Jan. 2018. [CrossRef]
- B. J. Li and C. T. Cheng, “Monthly discharge forecasting using wavelet neural networks with extreme learning machine,” Sci China Technol Sci, vol. 57, no. 12, pp. 2441–2452, Dec. 2014. [CrossRef]
- C. C. Ummenhofer, A. Sen Gupta, M. H. England, and C. J. C. Reason, “Contributions of Indian Ocean sea surface temperatures to enhanced East African rainfall,” J Clim, vol. 22, no. 4, pp. 993–1013, Feb. 2009. [CrossRef]
- M. Rathinasamy, A. Agarwal, B. Sivakumar, N. Marwan, and J. Kurths, “Wavelet analysis of precipitation extremes over India and teleconnections to climate indices,” Stochastic Environmental Research and Risk Assessment, vol. 33, no. 11–12, pp. 2053–2069, Dec. 2019. [CrossRef]
- I. Daubechies, “The Wavelet Transform, Time-Frequency Localization and Signal Analysis,” IEEE Trans Inf Theory, vol. 36, no. 5, pp. 961–1005, 1990. [CrossRef]
- M. Küçük, E. Tigli, and N. Ağiralioğlu, “Wavelet Transform Analysis For Nonstationary Rainfall-Runoff-Temperature Processes,” 2004. [Online]. Available: http://www.r-project.org.
- J. Park and M. E. Mann, “Paper No. 1 • Page 1 Copyright,” 2000. [Online]. Available: http://EarthInteractions.org.
- A. Grossmann and J. Morlet, “DECOMPOSITION OF HARDY FUNCTIONS INTO SQUARE INTEGRABLE WAVELETS OF CONSTANT SHAPE*,” 1984. [Online]. Available: https://epubs.siam.org/terms-privacy.
- O. Renaud, J. L. Starck, and F. Murtagh, “Wavelet-based combined signal filtering and prediction,” IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics, vol. 35, no. 6, pp. 1241–1251, Dec. 2005. [CrossRef]
- J. Adamowski and K. Sun, “Development of a coupled wavelet transform and neural network method for flow forecasting of non-perennial rivers in semi-arid watersheds,” J Hydrol (Amst), vol. 390, no. 1–2, pp. 85–91, Aug. 2010. [CrossRef]
- R. Maheswaran and R. Khosa, “Comparative study of different wavelets for hydrologic forecasting,” Comput Geosci, vol. 46, pp. 284–295, Sep. 2012. [CrossRef]
- G. Bin Huang, Q. Y. Zhu, and C. K. Siew, “Extreme learning machine: Theory and applications,” Neurocomputing, vol. 70, no. 1–3, pp. 489–501, Dec. 2006. [CrossRef]
- G. Bin Huang, “What are Extreme Learning Machines? Filling the Gap Between Frank Rosenblatt’s Dream and John von Neumann’s Puzzle,” Cognit Comput, vol. 7, no. 3, pp. 263–278, Jun. 2015. [CrossRef]
- Z. M. Yaseen et al., “Stream-flow forecasting using extreme learning machines: A case study in a semi-arid region in Iraq,” J Hydrol (Amst), vol. 542, pp. 603–614, Nov. 2016. [CrossRef]
- R. C. Deo and M. Şahin, “An extreme learning machine model for the simulation of monthly mean streamflow water level in eastern Queensland,” Environ Monit Assess, vol. 188, no. 2, pp. 1–24, Feb. 2016. [CrossRef]
- R. C. Deo and M. Şahin, “Application of the Artificial Neural Network model for prediction of monthly Standardized Precipitation and Evapotranspiration Index using hydrometeorological parameters and climate indices in eastern Australia,” Atmos Res, vol. 161–162, pp. 65–81, Jul. 2015. [CrossRef]
- P. Swapna et al., “The IITM earth system model : Transformation of a seasonal prediction model to a long-term climate model,” Bull Am Meteorol Soc, vol. 96, no. 8, pp. 1351–1368, Aug. 2015. [CrossRef]
- H. L. Ren, B. Lu, J. Wan, B. Tian, and P. Zhang, “Identification Standard for ENSO Events and Its Application to Climate Monitoring and Prediction in China,” Journal of Meteorological Research, vol. 32, no. 6, pp. 923–936, Dec. 2018. [CrossRef]
- V. Sehgal, A. Lakhanpal, R. Maheswaran, R. Khosa, and V. Sridhar, “Application of multi-scale wavelet entropy and multi-resolution Volterra models for climatic downscaling,” J Hydrol (Amst), vol. 556, pp. 1078–1095, Jan. 2018. [CrossRef]
- S. Kannan and S. Ghosh, “Prediction of daily rainfall state in a river basin using statistical downscaling from GCM output,” Stochastic Environmental Research and Risk Assessment, vol. 25, no. 4, pp. 457–474, May 2011. [CrossRef]
- A. Lakhanpal, V. Sehgal, R. Maheswaran, R. Khosa, and V. Sridhar, “A non-linear and non-stationary perspective for downscaling mean monthly temperature: a wavelet coupled second order Volterra model,” Stochastic Environmental Research and Risk Assessment, vol. 31, no. 9, pp. 2159–2181, Nov. 2017. [CrossRef]
- Y. P. Kumar, R. Maheswaran, A. Agarwal, and B. Sivakumar, “Intercomparison of downscaling methods for daily precipitation with emphasis on wavelet-based hybrid models,” J Hydrol (Amst), vol. 599, Aug. 2021. [CrossRef]
- R. Maheswaran and R. Khosa, “Wavelet Volterra Coupled Models for forecasting of nonlinear and non-stationary time series,” Neurocomputing, vol. 149, no. PB, pp. 1074–1084, Feb. 2015. [CrossRef]
- D. J. Olive, “Prediction Intervals for Regression Models,” 2006.
- M. J. Alizadeh, M. R. Kavianpour, O. Kisi, and V. Nourani, “A new approach for simulating and forecasting the rainfall-runoff process within the next two months,” J Hydrol (Amst), vol. 548, pp. 588–597, 2017. [CrossRef]
- Ö. Kişi, “Neural Networks and Wavelet Conjunction Model for Intermittent Streamflow Forecasting,” J Hydrol Eng, vol. 14, no. 8, pp. 773–782, 2009. [CrossRef]
- V. Nourani, M. Komasi, and A. Mano, “A multivariate ANN-wavelet approach for rainfall-runoff modeling,” Water Resources Management, vol. 23, no. 14, pp. 2877–2894, 2009. [CrossRef]
- U. Okkan and O. Fistikoglu, “Evaluating climate change effects on runoff by statistical downscaling and hydrological model GR2M,” Theor Appl Climatol, vol. 117, no. 1, pp. 343–361, Sep. 2014. [CrossRef]
- B. Ahmed and M. A. Al Noman, “Land cover classification for satellite images based on normalization technique and Artificial Neural Network,” in 1st International Conference on Computer and Information Engineering, ICCIE 2015, Institute of Electrical and Electronics Engineers Inc., Feb. 2016, pp. 138–141. [CrossRef]
- M. T. Vu, T. Aribarg, S. Supratid, S. V. Raghavan, and S. Y. Liong, “Statistical downscaling rainfall using artificial neural network: significantly wetter Bangkok?,” Theor Appl Climatol, vol. 126, no. 3–4, pp. 453–467, Nov. 2016. [CrossRef]
- D. E. Rumelhart, B. Widrow, and M. A. Lehr, “The Basic Ideas in Neural Networks,” Commun ACM, vol. 37, no. 3, pp. 87–92, 1994. [CrossRef]
- R. J. Kuligowski and A. P. Barros, “Localized Precipitation Forecasts from a Numerical Weather Prediction Model Using Artificial Neural Networks,” 1998.
- A. S. Tokar and M. Markus, “Precipitation-Runoff Modeling Using Artificial Neural Networks and Conceptual Models,” J Hydrol Eng, vol. 5, no. 2, pp. 156–161, Apr. 2000. [CrossRef]
- R. Maheswaran and R. Khosa, “Wavelet Volterra Coupled Models for forecasting of nonlinear and non-stationary time series,” Neurocomputing, vol. 149, no. PB, pp. 1074–1084, 2015. [CrossRef]
- S. Haykin, Neural Networks and Learning Machines, vol. 3. 2008. ISBN 978-0131471399.
- S. Shanmuganathan, Studies in Computational Intelligence 628 Artificial Neural Network Modelling, vol. 628. 2016. [Online]. Available: http://www.springer.com/series/7092.
- C. A. G. Santos, O. Kisi, R. M. da Silva, and M. Zounemat-Kermani, “Wavelet-based variability on streamflow at 40-year timescale in the Black Sea region of Turkey,” Arabian Journal of Geosciences, vol. 11, no. 8, Apr. 2018. [CrossRef]
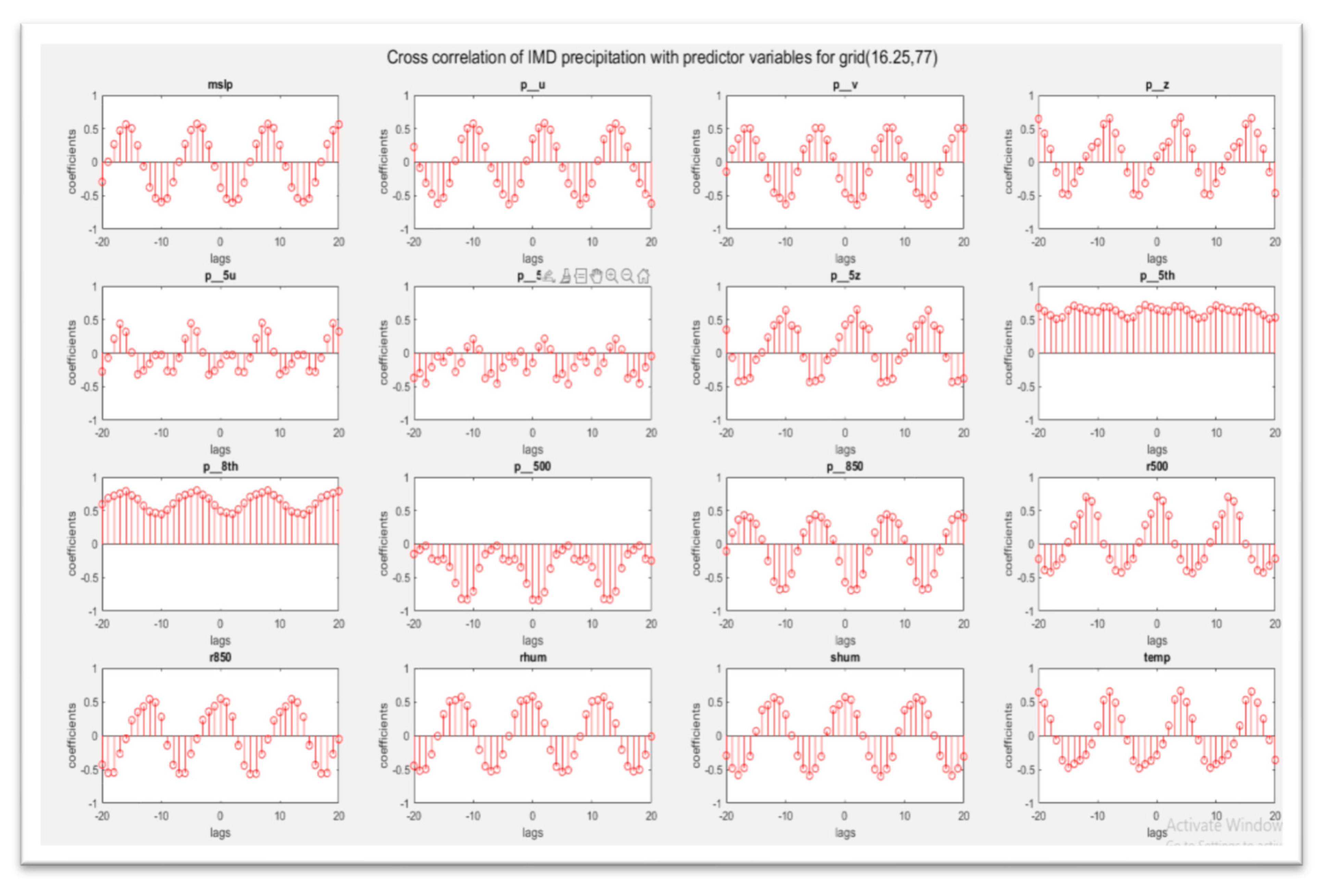
| Level | Predictands |
|---|---|
| Global | Indian Oceanic Dipole (IOD) North Atlantic Oscillation (NAO) NINO Pacific Decadal Oscillation (PDO) |
| Local | Mean Sea level pressure (mslp) Zonal velocity component (p_u) Meridional velocity component (p_v) Vorticity (p_z) Specific humidity (shum) Relative humidity (rhum) Surface air temperature (temp) Zonal velocity component (p5_u) Meridional velocity component (p5_v) Vorticity (p5 _z) Wind direction (p5th) Geopotential height (p500) Relative humidity (r500) Wind direction (p8th) Geopotential height (p850) Relative humidity (r850) |
| Station | MLR | |||
| RMSE(mm) | Correlation | NSE | MAE(mm) | |
| 1 | 0.096 | 0.355 | 0.164 | 0.099 |
| 2 | 0.160 | 0.332 | 0.124 | 0.100 |
| 3 | 0.162 | 0.376 | 0.137 | 0.105 |
| 4 | 0.144 | 0.309 | 0.157 | 0.092 |
| 5 | 0.048 | 0.309 | 0.119 | 0.055 |
| FFBP-NN | ||||
| 1 | 0.090 | 0.694 | 0.481 | 0.058 |
| 2 | 0.091 | 0.680 | 0.458 | 0.063 |
| 3 | 0.092 | 0.669 | 0.446 | 0.065 |
| 4 | 0.063 | 0.730 | 0.529 | 0.032 |
| 5 | 0.052 | 0.713 | 0.504 | 0.036 |
| ELM | ||||
| 1 | 0.070 | 0.407 | 0.407 | 0.053 |
| 2 | 0.101 | 0.489 | 0.403 | 0.067 |
| 3 | 0.157 | 0.343 | 0.343 | 0.117 |
| 4 | 0.122 | 0.419 | 0.419 | 0.096 |
| 5 | 0.052 | 0.561 | 0.515 | 0.037 |
| WT FFBP-NN | ||||
| 1 | 0.111 | 0.598 | 0.385 | 0.077 |
| 2 | 0.106 | 0.644 | 0.403 | 0.075 |
| 3 | 0.113 | 0.572 | 0.385 | 0.078 |
| 4 | 0.113 | 0.567 | 0.391 | 0.078 |
| 5 | 0.108 | 0.636 | 0.383 | 0.080 |
| WT ELM | ||||
| 1 | 0.093 | 0.785 | 0.494 | 0.064 |
| 2 | 0.088 | 0.803 | 0.452 | 0.063 |
| 3 | 0.125 | 0.812 | 0.418 | 0.088 |
| 4 | 0.096 | 0.798 | 0.465 | 0.063 |
| 5 | 0.113 | 0.848 | 0.434 | 0.076 |
| Station | MLR | |||
| RMSE(mm) | Correlation | NSE | MAE(mm) | |
| 1 | 0.053 | 0.573 | 0.573 | 0.037 |
| 2 | 0.091 | 0.536 | 0.536 | 0.057 |
| 3 | 0.123 | 0.597 | 0.597 | 0.084 |
| 4 | 0.096 | 0.646 | 0.646 | 0.063 |
| 5 | 0.058 | 0.442 | 0.442 | 0.033 |
| FFBP-NN | ||||
| 1 | 0.055 | 0.545 | 0.545 | 0.038 |
| 2 | 0.086 | 0.576 | 0.576 | 0.054 |
| 3 | 0.012 | 0.600 | 0.600 | 0.078 |
| 4 | 0.092 | 0.678 | 0.678 | 0.058 |
| 5 | 0.062 | 0.713 | 0.362 | 0.031 |
| ELM | ||||
| 1 | 0.066 | 0.473 | 0.473 | 0.039 |
| 2 | 0.094 | 0.496 | 0.496 | 0.060 |
| 3 | 0.127 | 0.565 | 0.565 | 0.089 |
| 4 | 0.094 | 0.653 | 0.653 | 0.062 |
| 5 | 0.057 | 0.423 | 0.423 | 0.032 |
| WT FFBP-NN | ||||
| 1 | 0.109 | 0.771 | 0.556 | 0.069 |
| 2 | 0.082 | 0.779 | 0.549 | 0.057 |
| 3 | 0.084 | 0.753 | 0.505 | 0.063 |
| 4 | 0.061 | 0.787 | 0.563 | 0.041 |
| 5 | 0.070 | 0.765 | 0.520 | 0.052 |
| WT ELM | ||||
| 1 | 0.118 | 0.779 | 0.575 | 0.087 |
| 2 | 0.086 | 0.765 | 0.557 | 0.065 |
| 3 | 0.078 | 0.817 | 0.579 | 0.054 |
| 4 | 0.075 | 0.738 | 0.518 | 0.056 |
| 5 | 0.084 | 0.742 | 0.518 | 0.063 |
| station | MLR | |||
| RMSE(mm) | Correlation | NSE | MAE(mm) | |
| 1 | 0.053 | 0.578 | 0.578 | 0.037 |
| 2 | 0.090 | 0.533 | 0.533 | 0.057 |
| 3 | 0.122 | 0.602 | 0.602 | 0.084 |
| 4 | 0.096 | 0.653 | 0.653 | 0.063 |
| 5 | 0.059 | 0.439 | 0.439 | 0.034 |
| FFBP-NN | ||||
| 1 | 0.050 | 0.616 | 0.616 | 0.035 |
| 2 | 0.083 | 0.604 | 0.604 | 0.049 |
| 3 | 0.108 | 0.691 | 0.691 | 0.069 |
| 4 | 0.087 | 0.714 | 0.714 | 0.053 |
| 5 | 0.052 | 0.5600 | 0.5600 | 0.032 |
| ELM | ||||
| 1 | 0.051 | 0.680 | 0.680 | 0.034 |
| 2 | 0.065 | 0.757 | 0.757 | 0.042 |
| 3 | 0.090 | 0.784 | 0.784 | 0.064 |
| 4 | 0.075 | 0.782 | 0.782 | 0.047 |
| 5 | 0.037 | 0.754 | 0.754 | 0.026 |
| WT FFBP-NN | ||||
| 1 | 0.083 | 0.892 | 0.741 | 0.055 |
| 2 | 0.072 | 0.849 | 0.648 | 0.052 |
| 3 | 0.077 | 0.784 | 0.595 | 0.056 |
| 4 | 0.061 | 0.802 | 0.636 | 0.036 |
| 5 | 0.064 | 0.820 | 0.591 | 0.042 |
| WT ELM | ||||
| 1 | 0.070 | 0.925 | 0.852 | 0.052 |
| 2 | 0.069 | 0.843 | 0.697 | 0.053 |
| 3 | 0.075 | 0.813 | 0.625 | 0.058 |
| 4 | 0.053 | 0.847 | 0.700 | 0.035 |
| 5 | 0.073 | 0.779 | 0.625 | 0.053 |
| Station | Central India | |||
| RMSE(mm) | Correlation | NSE | MAE(mm) | |
| 1 | 0.0718 | 0.9084 | 0.8152 | 0.0059 |
| 2 | 0.0680 | 0.8751 | 0.7200 | 0.0491 |
| 3 | 0.0757 | 0.9260 | 0.8538 | 0.0584 |
| 4 | 0.0755 | 0.8775 | 0.7574 | 0.0567 |
| North India | ||||
| 1 | 0.0733 | 0.8437 | 0.7012 | 0.0537 |
| 2 | 0.0610 | 0.8864 | 0.7733 | 0.0447 |
| 3 | 0.0800 | 0.8286 | 0.6816 | 0.0581 |
| 4 | 0.0728 | 0.7804 | 0.5477 | 0.0554 |
| Peninsular | ||||
| 1 | 0.0927 | 0.8406 | 0.6619 | 0.0686 |
| 2 | 0.1009 | 0.7936 | 0.6112 | 0.0780 |
| 3 | 0.0419 | 0.9324 | 0.8580 | 0.0325 |
| 4 | 0.1030 | 0.8728 | 0.7602 | 0.0781 |
| Northwest | ||||
| 1 | 0.0784 | 0.9178 | 0.8401 | 0.0603 |
| 2 | 0.0628 | 0.8873 | 0.7437 | 0.0448 |
| 3 | 0.0802 | 0.7611 | 0.5025 | 0.0578 |
| 4 | 0.0696 | 0.8356 | 0.6765 | 0.0532 |
| Climatic variable | Original scale | D1 | D2 | D3 | D4 | D5 | D6 | D7 | D8 | D9 | D10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| p5zas | 0.011 | 0.011 | 0.051 | 0.061 | 0.061 | 0.081 | 0.161 | 0.361 | 0.421 | 0.271 | 0.121 |
| p5th | 0.131 | 0.001 | -0.009 | -0.019 | -0.059 | -0.069 | -0.079 | 0.001 | 0.361 | 0.141 | 0.081 |
| p8th | -0.019 | 0.001 | 0.001 | 0.011 | 0.001 | -0.029 | -0.159 | -0.369 | -0.409 | -0.329 | -0.109 |
| rhum | 0.111 | 0.021 | 0.031 | 0.061 | 0.121 | 0.201 | 0.331 | 0.401 | 0.361 | 0.331 | 0.171 |
| shum | 0.141 | 0.011 | 0.031 | 0.051 | 0.101 | 0.171 | 0.321 | 0.421 | 0.411 | 0.371 | 0.161 |
| temp | 0.071 | -0.009 | -0.019 | -0.049 | -0.099 | -0.159 | -0.199 | -0.129 | 0.051 | 0.011 | 0.021 |
| mslp | -0.079 | -0.039 | -0.079 | -0.139 | -0.169 | -0.149 | -0.239 | -0.349 | -0.389 | -0.349 | -0.099 |
| uas | 0.021 | 0.021 | 0.041 | 0.081 | 0.151 | 0.191 | 0.291 | 0.431 | 0.401 | 0.371 | 0.091 |
| vas | -0.029 | 0.021 | 0.041 | 0.061 | 0.071 | 0.081 | 0.031 | -0.269 | -0.399 | -0.319 | -0.139 |
| zas | 0.171 | 0.011 | 0.221 | 0.021 | 0.021 | 0.021 | 0.001 | 0.021 | 0.071 | 0.041 | 0.031 |
| p5 uas | -0.159 | 0.011 | 0.021 | 0.031 | 0.061 | 0.081 | 0.061 | -0.029 | -0.379 | -0.179 | -0.089 |
| p5 vas | 0.021 | 0.021 | 0.031 | 0.021 | 0.001 | -0.019 | -0.019 | -0.109 | -0.269 | -0.089 | -0.009 |
| p500 | 0.091 | -0.029 | -0.069 | -0.119 | -0.149 | -0.159 | -0.209 | -0.289 | -0.369 | -0.119 | -0.009 |
| p850 | -0.059 | -0.039 | -0.089 | -0.159 | -0.199 | -0.209 | -0.359 | -0.469 | -0.439 | -0.379 | -0.089 |
| r500 | 0.101 | 0.011 | 0.041 | 0.071 | 0.111 | 0.181 | 0.311 | 0.431 | 0.421 | 0.371 | 0.121 |
| r850 | 0.051 | 0.021 | 0.041 | 0.071 | 0.141 | 0.211 | 0.321 | 0.411 | 0.351 | 0.301 | 0.141 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





