Prerpints.org logo
Preprint
Article

Analysis of Tool Wear in GH4169 Material Milling Process

Altmetrics

Downloads

90

Views

26

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

18 May 2023

Posted:

19 May 2023

You are already at the latest version

Alerts
Abstract
Nickel base superalloy GH4169 is a material with strong mechanical properties and is difficult to process. In order to reduce tool wear during material processing and improve workpiece surface processing quality, based on the finite element simulation software DEFORM, the influence of n, ap, and fz parameters on tool wear during carbide tool milling GH4169 was studied, and a simulation orthogonal experimental model was established, The prediction model of tool wear is obtained; The ultrasonic vibration milling is compared with ordinary milling, and the improvement degree of different coating materials on carbide tool wear is explored. The results show that the ultrasonic vibration signal is helpful to reduce tool wear, improve the surface quality of the workpiece, and improve the stability of the milling process. TIALN/TIN (WC) composite coated tools have good cutting performance, help to reduce tool temperature, reduce tool wear, and improve tool life.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

1. Introduction

The main elements of the matrix material of high temperature nickel base alloy GH4169 (Inconel 718 alloy in the United States) [1,2] are iron, nickel and cobalt, and then some titanium and aluminum are added to strengthen its structure, with good fatigue performance, fracture performance, thermal stability, corrosion resistance, hot working performance and welding performance. After years of development, the service temperature of this alloy has increased from 500 ℃ to about 1000 ℃ [3,4], More and more widely used in aerospace engine blades, ships, power, chemical, nuclear reactor and other industries; As one of the difficult to machine materials, GH4169 high temperature nickel base alloy has many problems, such as poor thermal conductivity, high cutting temperature, large cutting force, large tool wear and serious work hardening. At present, the demand for GH4169 high-temperature alloy in the manufacturing market is increasing, and the processing requirements are also increasing. This requires the continuous advancement of nickel based high-temperature alloy processing technology. In recent years, domestic and foreign experts and scholars have mainly studied the mechanical properties, processing methods, and other aspects of GH4169 high-temperature nickel based alloy materials, fully combining simulation and experiments, and have achieved fruitful results.
Ma Jianwei and others found that the tool geometric parameters seriously affected tool wear and tool life when high-speed milling Inconel 718 surfaces. Specifically, for tools with a helix angle greater than 30 °, a small rake angle has greater strength and superiority. An increase in the rake angle can improve the tool life, and the tool life decreases with an increase in the helix angle. This study provides a theoretical basis for the tool wear mechanism and tool geometric parameter selection of high-speed milling Inconel 718 surface, to ensure the machining efficiency of high-speed milling Inconel 718 surface [5]. Fan Yihang et al., based on the characteristics of cutting Inconel 718 alloy and the microstructure of carbide tools, revealed the wear characteristics and mechanism of carbide tools in the process of cutting Inconel 718 alloy by means of multi scale analysis. The main wear forms of debris peeled off from the tool matrix are given, and the evolution mechanism of tool wear caused by cracks in the cutting process is deeply studied [6]. Qiao Yang [7,8] et al. conducted experiments on the life of carbide cutting nickel base superalloy tools, and studied the mechanism of tool wear by using scanning electron microscope and energy spectrum analysis. It was found that the main forms of tool wear were bond and abrasive wear. Liu Yali et al. [9] found through experiments that the machining of inconel 718 tools mainly involves wear on the back face, while wear on the front face is characterized by crescent pit wear, flaky peeling, etc.
C. Leone et al. used regression analysis (RA) and artificial neural network (ANN) paradigms to process tool wear measurement data of turning Inconel 718 aircraft engine parts, and achieved the goal of online prediction of tool wear trend. A four constant empirical model of tool wear is derived to predict the tool flank wear with the function of cutting time and cutting speed [10]. J. Zhou et al. conducted high-speed cutting GH4169 experiment, and found that the tool wear of high-speed cutting GH4169 is different from that of ordinary cutting. First, the edge wear is serious. In the process of tool wear, VN>VC>VBmax. First to achieve VN blunting standard; Secondly, the tool wear wear on the rake face is serious, and in a very short time, the wear extends to the tool edge [11]. A. R.F. Oliveira et al. conducted research on milling force, milling temperature, and residual stress in the Inconel718 end milling experiment. The results showed that the greater the lateral wear of the tool, the higher the processing temperature and cutting force. The lateral wear of the cutting tool reduces the microhardness of the machined surface of the workpiece, resulting in tensile residual stress due to the high heat generated [12]. D. M. D'Addona et al. analyzed the influence of different speeds from low to high (60 m/min, 90 m/min, 190 m/min, 255 m/min) on tool wear and surface roughness through turning tests [13]. In 2007, Attanasio et al. used DEFORM-3D 3D cutting simulation to obtain the tool wear amount. In 2013, Martynov, a Russian scientist, made significant progress by using extreme standard analysis methods to predict tool wear results [15]. D.G. Thakur, L. Vijayaghavan and others in the UK found that in the process of cutting Inconel718, tool wear increased because the tool material softened [16]. Yun Chang Yen [17] simulated tool wear using DEFORM-2D finite element software based on the Usui adhesive wear rate equation. L. J.Xie [18] used Abaqus finite element software to simulate tool wear based on the Usui wear rate equation. Foreign scholars such as D. Umbrello and A. Atanasio [19,20] combined simulation with experiments to establish a diffusion wear model and abrasive wear model based on reverse engineering verification, and studied the wear mechanism of uncoated hard alloy tools.
In recent years, experts and scholars' research on difficult to machine material GH4169 has not only focused on cutting process parameters, but also explored the impact of different auxiliary milling methods and different coating materials on the milling surface integrity and tool wear of GH4169.
Zheng Minli [21] and others analyzed the wear mechanism of carbide tools, ceramic tools and superhard tools when cutting nickel base superalloys. Research shows that 50% and 25% immersion ratios can better balance tool life and production efficiency. Yu He [22] analyzed the influence of ultrasonic vibration assisted machining on the surface quality, chip shape and tool wear of Inconel 718 workpiece. The relationship between processing parameters and the performance of ultrasonic vibration assisted machining was also explored. By analyzing the relationship between tool trajectory and workpiece surface motion, the reason why ultrasonic vibration assisted machining improves the surface quality of the workpiece is explained. Wenping Mou [23] studied the mechanism of vibration, tool wear and surface roughness of ceramic inserts during machining Inconel 718 alloy under dry machining and LN2 machining conditions. The experimental results indicate that LN2 machining has better machinability and longer tool life. The vibration acceleration is reduced by 14-32%. It was observed that the surface roughness of the workpiece decreased by 17-34%. Side wear and notches are the main forms of wear in LN2 machining and dry machining, with a reduction of 16-34% in side wear during LN2 machining. Sharman. Al et al. conducted a ball head tool cutting of Inconel 718, and found that the TiAIN coating had the greatest impact on tool life, followed by cutting speed, and finally the working angle. GH4169 has excellent performance. In the process of machining, it will also produce such phenomena as poor cutting stability, high cutting temperature, severe work hardening, and large tool wear. Therefore, it is very necessary to explore the milling mechanism and tool wear of GH4169 by combining simulation and experiment.
In this paper, the empirical formula of tool wear prediction is established by means of multiple linear regression, and the accuracy of the prediction model is verified by range analysis. The mechanism of tool wear in the milling process of Inconel 718 nickel base superalloy is studied; The chip shape, milling area temperature, equivalent stress of workpiece surface, tool temperature and tool wear in the process of vibration milling and ordinary milling are compared and analyzed, and the advantages of ultrasonic vibration milling are obtained; The influence of coating materials TIALN, TIN and their composite coating materials on tool wear is explored, which provides a theoretical basis for predicting tool wear and reducing tool wear.

2. Establishment of GH4169 Simulation Model for Hard Alloy Milling

In the actual machining process of nickel base superalloy, the machining surface precision of the workpiece is low, the tool is easy to collapse, and the tool wear wear is serious. In the process of machining, the tool needs to be changed many times, the machining efficiency is low, and the cost of capital is large. With the rapid development of computer-aided technology, the finite element simulation technology is widely used in the field of metal cutting. Through the finite element simulation technology, not only the test cost can be reduced, but also the test cycle can be shortened, Revealing the essence of the actual cutting process and predicting potential problems that may arise during the actual cutting process, the application of finite element simulation technology has good guiding significance for actual production and processing. In this paper, the finite element software DEFORM is used to establish the simulation model of carbide tool milling GH4169, and analyze the influence of three cutting elements on carbide tool wear.

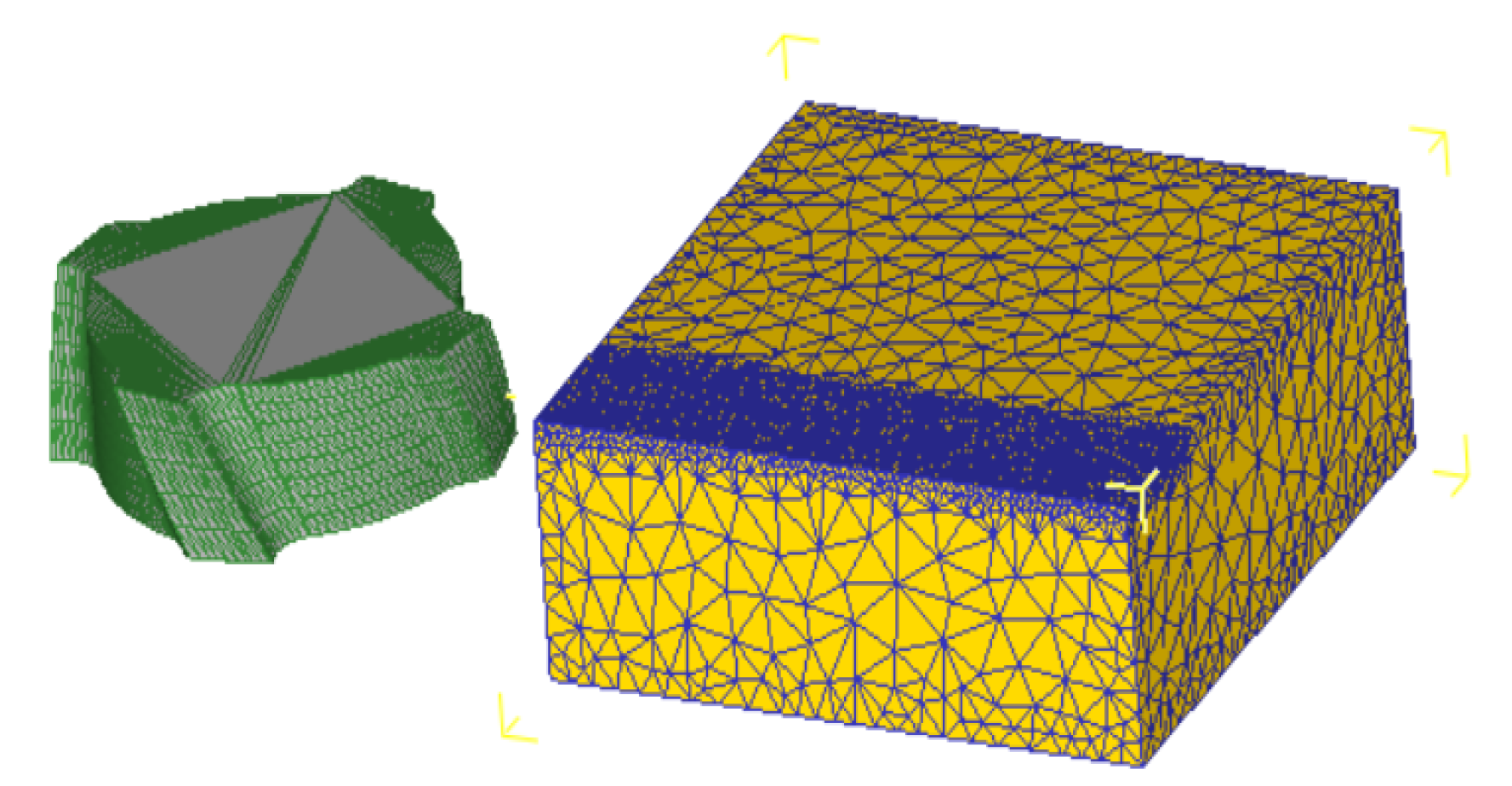
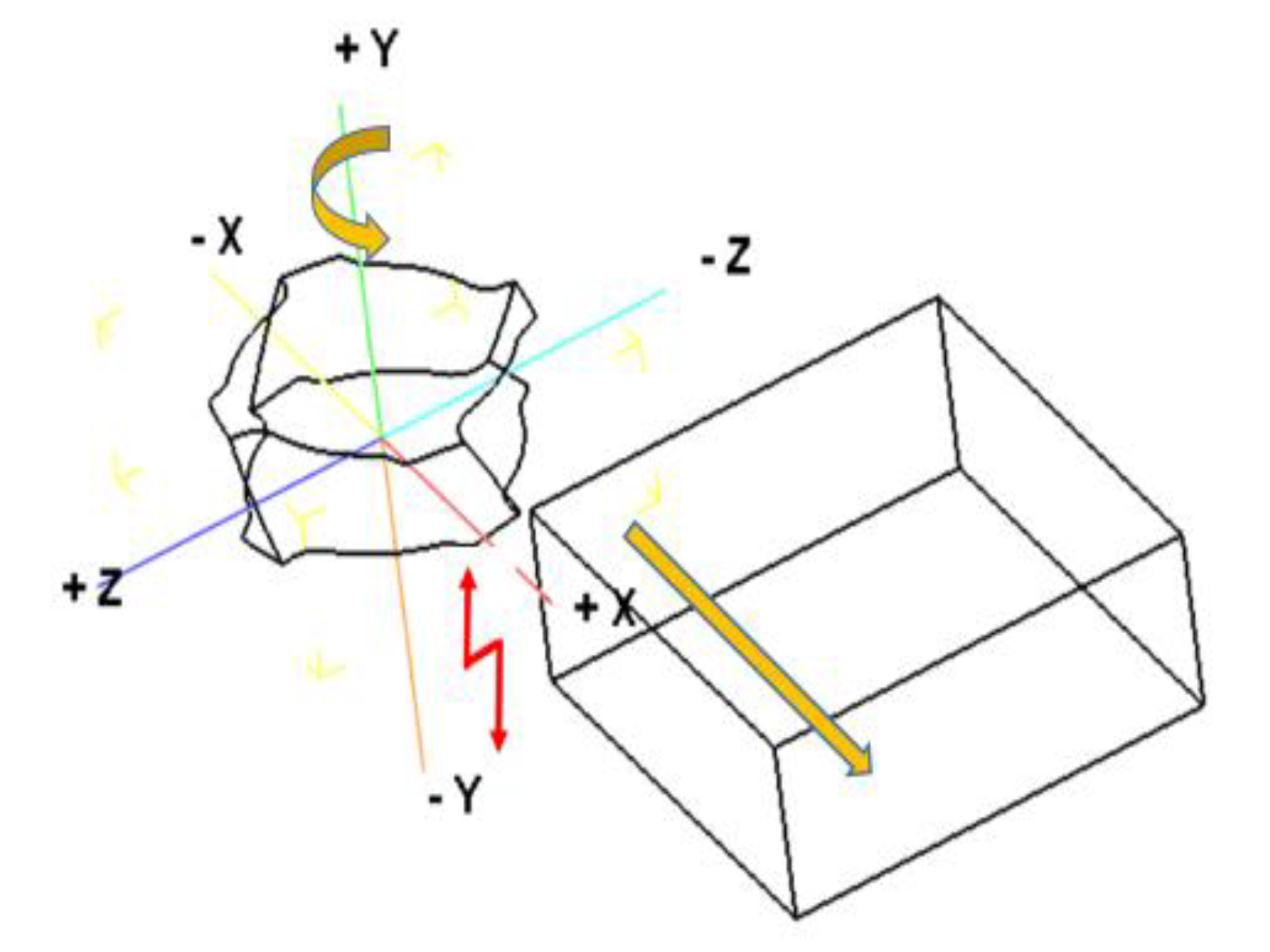
2.1. Establish Geometric Modeling of Tool and Workpiece

In order to be closer to actual machining, this simulation will make the model of the end milling cutter as close as possible to the actual situation. The model is shown in Figure 1, and the specific parameters are shown in Table 1:

2.2. Setting up Workpiece and Tool Materials and Grid Division

Set the tool as a rigid body and the workpiece as a plastic body. The material of the tool selected in the experimental section of this article is WC, and nickel based high-temperature alloy GH4169 (Inconel 718) is used as the material of the workpiece. The constitutive relationship curve of GH4169 in the material library of DEFORM software is shown in Figure 2. In this model, the tool set grid is 32000, the workpiece set grid is 30000, the minimum grid size of the tool is 0.131mm, and the minimum grid size of the workpiece is 0.121mm. The parts in the contact area between the tool and the workpiece were divided into local grids, with the refinement ratios of 0.1 and 0.0001, as shown in Figure 1.

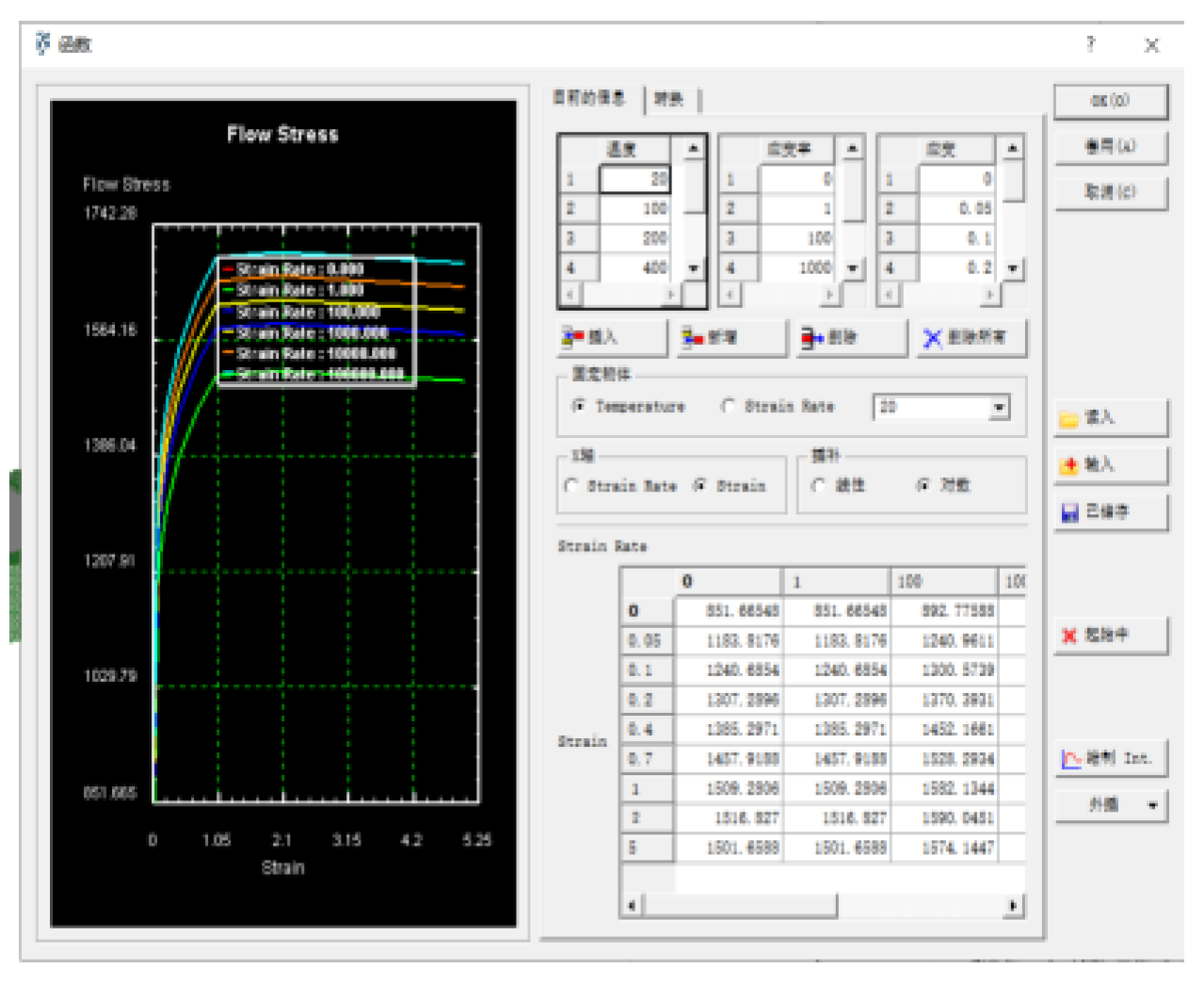
2.3. Tool and Workpiece Simulation Working Condition Settings

Set the milling width to 3mm, the ambient temperature to 20 ° C, the convective heat transfer coefficient to 0.02N/sec/mm/C, the friction coefficient to 0.6, and the thermal conductivity coefficient to 45N/sec/mm/C. This article uses the Usui wear model in DEFORM, which is more suitable for continuous machining processes, such as metal cutting, and its main form of wear is adhesive wear.
Tool wear Usui's model:
w = ∫ ap v e − b / T d t
This formula is generally used for continuous processes such as metal cutting (adhesive wear).
Where p - contact surface pressure; V - sliding speed; T - Contact surface temperature; Dt - Time increment; The classic values for cutting are: a=0.00001, b=855, and a and b are characteristic constants (mainly determined by cutting parameters and materials).

2.4. Establishment of Tool Wear Prediction Model for Ordinary Milling

In order to accurately calculate the empirical formula of the prediction model for maximum tool wear, this chapter adopts the orthogonal experimental method. The effects of spindle speed, feed rate per tooth and cutting depth on tool wear are mainly studied; Compared with multi tooth continuous cutting, the tool wear of this intermittent cutting simulation is smaller, and the wear difference between teeth is larger;
The selection of orthogonal experimental factors and levels needs to follow certain principles. There are different orthogonal experimental tables for different factors and levels. Choosing a suitable orthogonal experimental plan can generally be divided into the following steps:
(1) Determine the number of columns, which is the number of influencing factors;
(2) Determine the number of levels, which means that each factor has several different values;
(3) Select an orthogonal table, mainly based on the number of columns and levels determined in the first two steps;
(4) The order of column numbers, prioritizing the factors that need to be examined for interaction, and placing other factors without interaction in the following columns;
(5) Implement the plan according to the orthogonal experimental table.
This chapter designs 16 sets of orthogonal experiments with 3 factors, 4 levels, and the experimental factors are axial cutting depth ap, spindle speed n, and feed rate fz per tooth. From the actual situation, the values of each factor level are within the operating range of the machine tool. The experimental parameter range is as follows:
(1) Spindle speed n: 3000-4500r/min;
(2) Axial cutting depth ap: 0.2-0.5mm;
(3) The feed rate per tooth fz: 0.1-0.4mm/r.
The orthogonal experiment and simulation data are shown in Table 2:
Establish an M file using MATLAB software, and input the cutting force values and milling parameters in the equation into the program for multiple linear regression [25-26] calculation. Input:
y=[-0.2541 ,-0.3019 ,-0.4647 ,-0.4547 ,-0.4123 ,-0.1090 ,-0.4572 ,-0.3526 ,-0.6819 ,-0.4908 ,0.0043 ,-0.1904 ,-0.5100 ,-0.4401 ,-0.1439 ,-0.0467];
x1=[3.4771 ,3.4771 ,3.4771 ,3.4771 ,3.5441 ,3.5441 ,3.5441 ,3.5441 ,3.6021 ,3.6021 ,3.6021 ,3.6021 ,3.6532 ,3.6532 ,3.6532 ,3.6532];
x2=[-0.6990 ,-0.5229 ,-0.3979 ,-0.3010 ,-0.6990 ,-0.5229 ,-0.3979 ,-0.3010 ,-0.6990 ,-0.5229 ,-0.3979 ,-0.3010 ,-0.6990 ,-0.5229 ,-0.3979 ,-0.3010];
x3=[-1.0000 ,-0.6990 ,-0.5229 ,-0.3979 ,-0.6990 ,-1.0000 ,-0.3979 ,-0.5229 ,-0.5229 ,-0.3979 ,-1.0000 ,-0.6990 ,-0.3979 ,-0.5229 ,-0.6990 ,-1.0000];
X=[ones(length(y),1),x1',x2' x3'];
Y=y';
[b,bint,r,rint,stats]=regress(Y,X);
b,bint,stats
According to the results obtained from MATLAB, a0=-1.9922, a1=0.4112, a2=0.5345, a3=-0.6866. Therefore, the multiple regression model is: y=-1.9922+0.4112x1+0.5345x2-0.6866x3.
The empirical formula for predicting the maximum wear of cutting tools can be obtained from the above: H=0.01•n0.4112•ap0.5345•fz-0.6866.

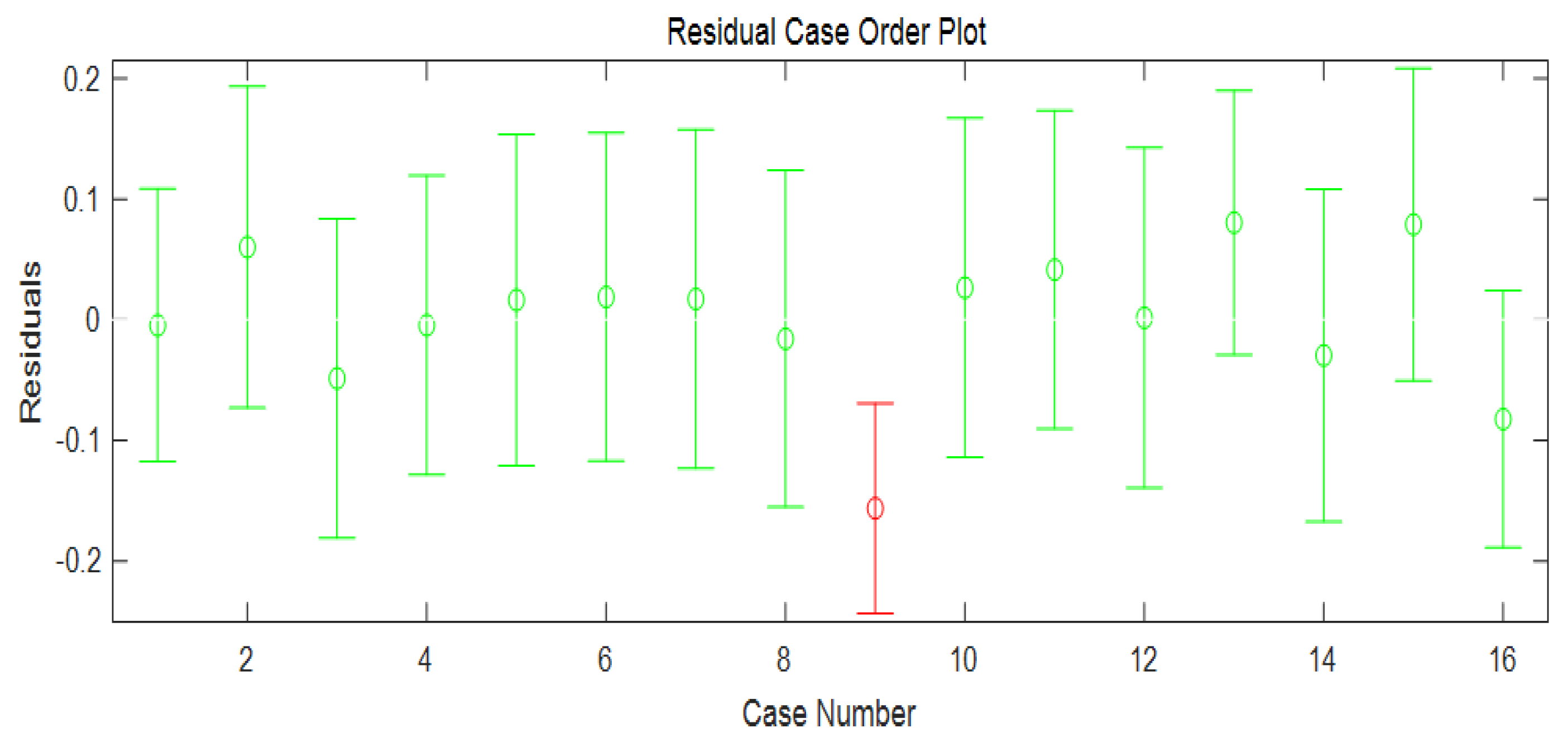
2.5. Linear Regression Significance Test

According to the results obtained from MATLAB, it can be concluded that:
(1) Tool wear regression system array:
a0=-1.9922, confidence interval of a0 (-3.9917, 0.0072),
a1=0.4112, confidence interval of a1 (-0.1472, 0.9695),
a2=0.5345, confidence interval of a2 (0.2881, 0.7808),
a3=-0.6866, confidence interval of a3 (-0.8487, -0.5244);
The statistical variable stats obtained: r2=0.9016, F=36.6678, p=0.0000, indicating a significant difference in p<α= 0.05.
Perform residual analysis on this coefficient and input: rcoplot (r, rint) in the MATLAB window to obtain the residual plot as shown in Figure 3:
From the residual analysis chart, it can be seen that except for the 9th data, the residuals of all other data are close to zero, and the confidence intervals of the residuals all include zero, indicating that the regression model can better match the original data. The 9th data can be regarded as an outlier, and it is believed that the regression model is reliable [27].
From the above, it can be concluded that the regression model y=-1.9922+0.4112x1+0.5345x2-0.6866x3 is valid. Therefore, the empirical formula for maximum tool wear H=0.01•n0.4112•ap0.5345•fz-0.6866 has significant significance.

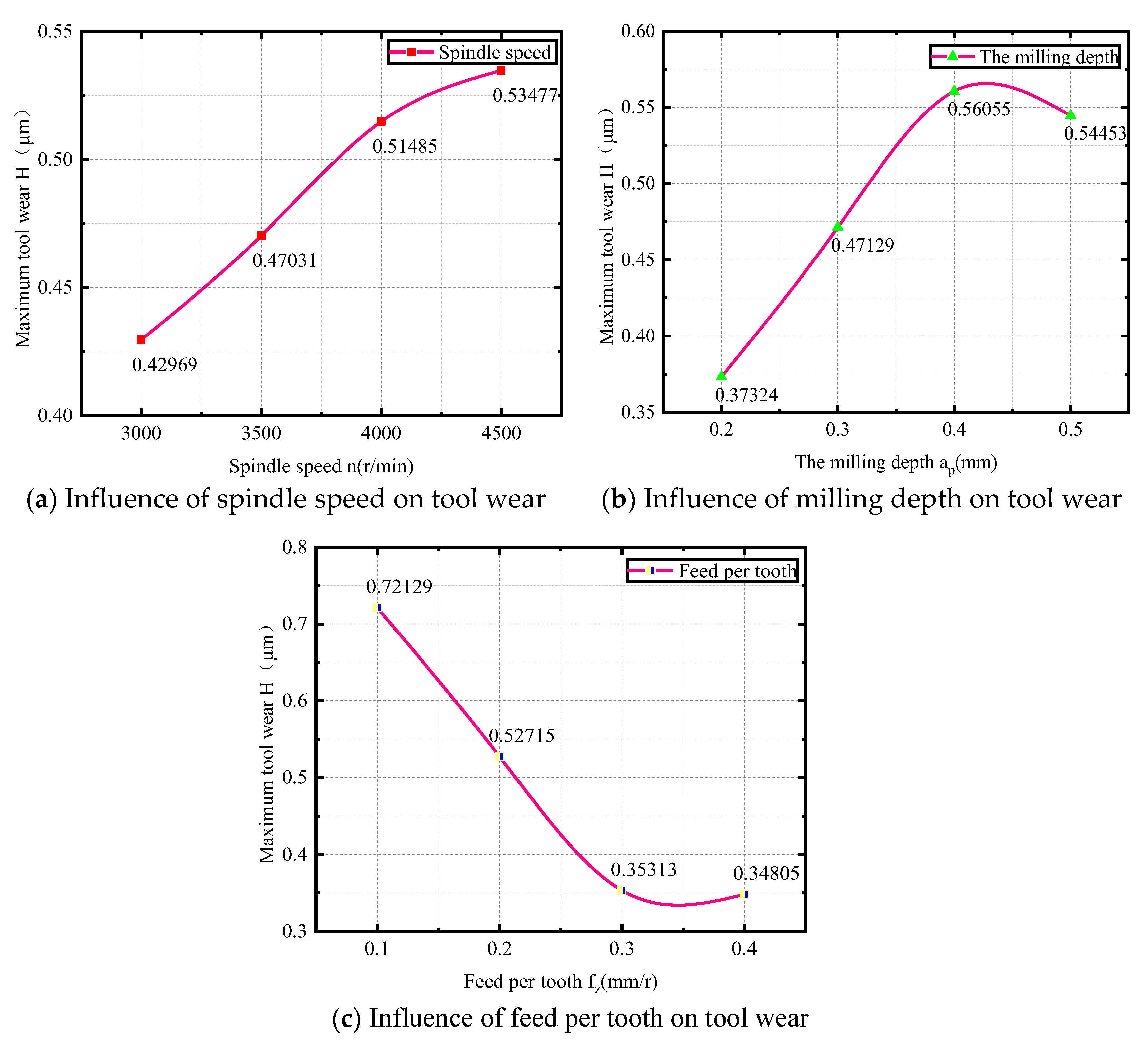
2.6. Analysis of Impact Patterns

The range analysis method can be used in the analysis of orthogonal experimental results to obtain the primary and secondary order of the influence of various factors on the target parameters, the optimal combination scheme, and the influence law of the influencing factors on the target parameters. Therefore, it has a wide range of applications [28]. To obtain the order of the influence of the three cutting elements on the maximum tool wear, the range analysis method was used to analyze the simulation results, as shown in Table 3:
Figure 4 shows the trend of the influence of spindle speed n, axial cutting depth ap, and feed rate fz per tooth on the maximum wear of the tool. Based on this graph, the variation of the maximum wear of the tool when each parameter changes can be intuitively seen. By analyzing the range table and indicator factor trend chart, it can be concluded that:
(1) The degree of influence of each milling parameter on the maximum tool wear H is in descending order of fz, ap, and n. Among them, fz has a greater impact, ap has a moderate impact on the maximum tool wear, and n has a smaller impact on the maximum tool wear. From the perspective of reducing tool wear, the optimal combination of milling parameters is n=3000 r/min, ap=0.2 mm, fz=0.4 mm/r.
(2) It can be seen from Figure a that the tool wear increases with the increase of the spindle speed. When the speed is between 3000-4000 r/min, the increment of the maximum tool wear is relatively large. When the speed is between 4000-5000 r/min, the increment of tool wear decreases. As the rotational speed increases, the thickness of the workpiece material in contact with the tool per unit time also increases, and the impact force received is relatively large. The cutting force also increases, resulting in a sharp increase in tool wear. As the spindle speed increases to a certain extent, the chip is generated faster, which will take away most of the heat, the tool temperature decreases, and the tool wear speed is eased.
(3) It can be seen from Figure b that with the increase of axial cutting depth, the tool wear is gradually increasing. When the axial cutting depth increases from 0.2mm-0.4mm, the removal of material by the tool increases, resulting in an increase in work done, resulting in an increase in cutting force and temperature in the milling area, leading to an increase in tool wear; It should be noted that when the cutting depth is small or micro, it can cause scraping or only cut to the hardened layer on the surface of the workpiece, resulting in significant wear of the tool and a decrease in tool life. Especially when rough machining the workpiece, the cutting depth should be increased as much as possible within the allowable range of machine power and technology. When the axial cutting depth is 0.4-0.5mm, the tool wear is relatively reduced. In the cutting process, more heat is taken away due to the chip falling, and the tool temperature is also reduced, which alleviates the tool wear. In general, the tool wear increases with the increase of the axial cutting depth.
(4) The quantitative analysis of Figure (c) shows that when the feed per tooth increases, the tool wear gradually decreases, and when fz=0.4mm/rad, the tool wear reaches the minimum, 0.34805 μ m.

3. Comparative Analysis of Ultrasonic Vibration Milling and Ordinary Milling

At present, ultrasonic vibration assisted machining is more and more widely used in the field of difficult to machine materials. Ultrasonic vibration milling is conducive to chip fracture, greatly reducing the temperature of the tool and workpiece area, reducing the vibration of sudden contact between the tool and workpiece, reducing tool wear, reducing the milling force, improving system stability, and is conducive to obtaining high-precision surface quality and lower surface roughness. In this paper, the GH4169 model of carbide tool vibration milling is established, and the ultrasonic vibration is compared with ordinary milling in order to reduce tool wear and improve the workpiece surface processing quality.

3.1. Establishment of GH4169 Model for Cemented Carbide Vibration Milling

According to the principle of axial ultrasonic vibration, a low-frequency and periodic vibration is added to the milling cutter along the axial direction of the tool, as shown in Figure 5. The tool movement path is planned. The motion of the tool relative to the workpiece consists of three parts, as shown in the figure: (1) the milling cutter rotates along its own axis; (2) the milling cutter moves uniformly along the feed direction of the workpiece in a straight line; and (3) the milling cutter oscillates low-frequency along its own axis.
The motion equation of the milling cutter center is [29]:
X 1 = V f · t Z 1 = 0 y 1 = A s i n ( 2 π f t + φ 0 )
The parameters used in this simulation are: f=20HZ,A=10μm, N=6000rad/min, fz=0.1mm/rad, ap=0.2mm,φ0=0.
Then the above formula is transformed into:
X 1 = 40 · t Z 1 = 0 y 1 = 0.01 s i n ( 40 π t )
Use Matlab to generate a vibration displacement map in the y-direction, then export the data and import it into the DEFORM path chart. The generated tool path is shown in Figure 6.

3.2. Comparison of Results between Axial Ultrasonic Vibration Milling and Ordinary Milling

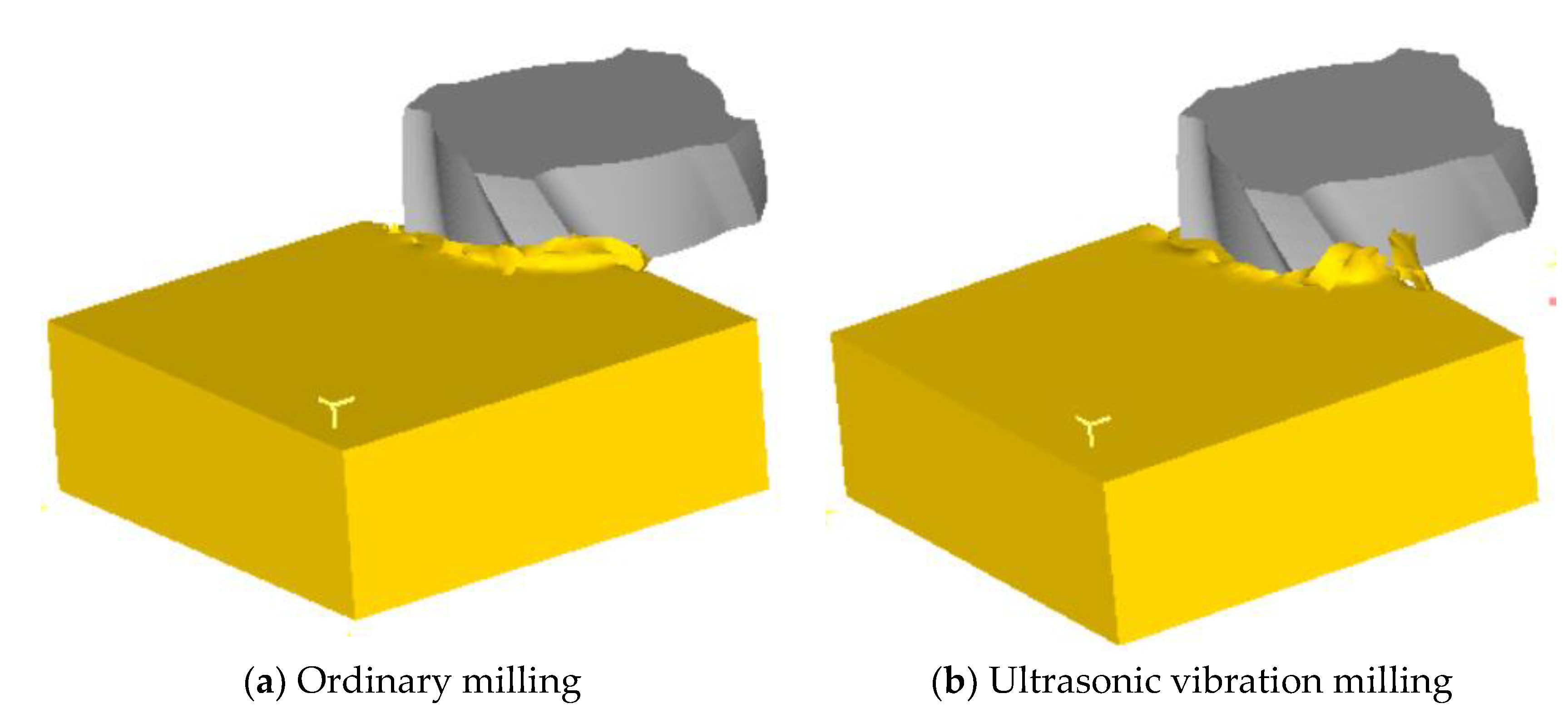
3.2.1. Comparison of Chip Shapes

When cutting GH4169 stably with hard alloy, a tool stroke of 8.5mm is selected, as shown in Figure 8. The chips from ordinary milling appear as ribbons, while the chips from vibration milling have already broken. Under low-frequency vibration, the difference in chip shape is not significant, and the chips from vibration milling are more prone to fracture. In terms of chip breakage, ordinary milling is a physical chip, and the chips are squeezed by the tool and the workpiece. Chip fracture depends on the material's inherent performance, Uncontrollable chip length and chip breakage; Vibration milling belongs to geometric chip breaking, and low-frequency vibration will accelerate chip fracture, with controllable chip length and chip breaking. The fracture of chips not only helps to release heat, but also helps to transmit stress, prevent stress concentration, and avoid chips sticking to the tool, replacing the tool for cutting, thereby affecting the quality and roughness of the machining surface. At the same time, it also reduces the adhesive wear caused by the detachment of chips bonded to the tool.

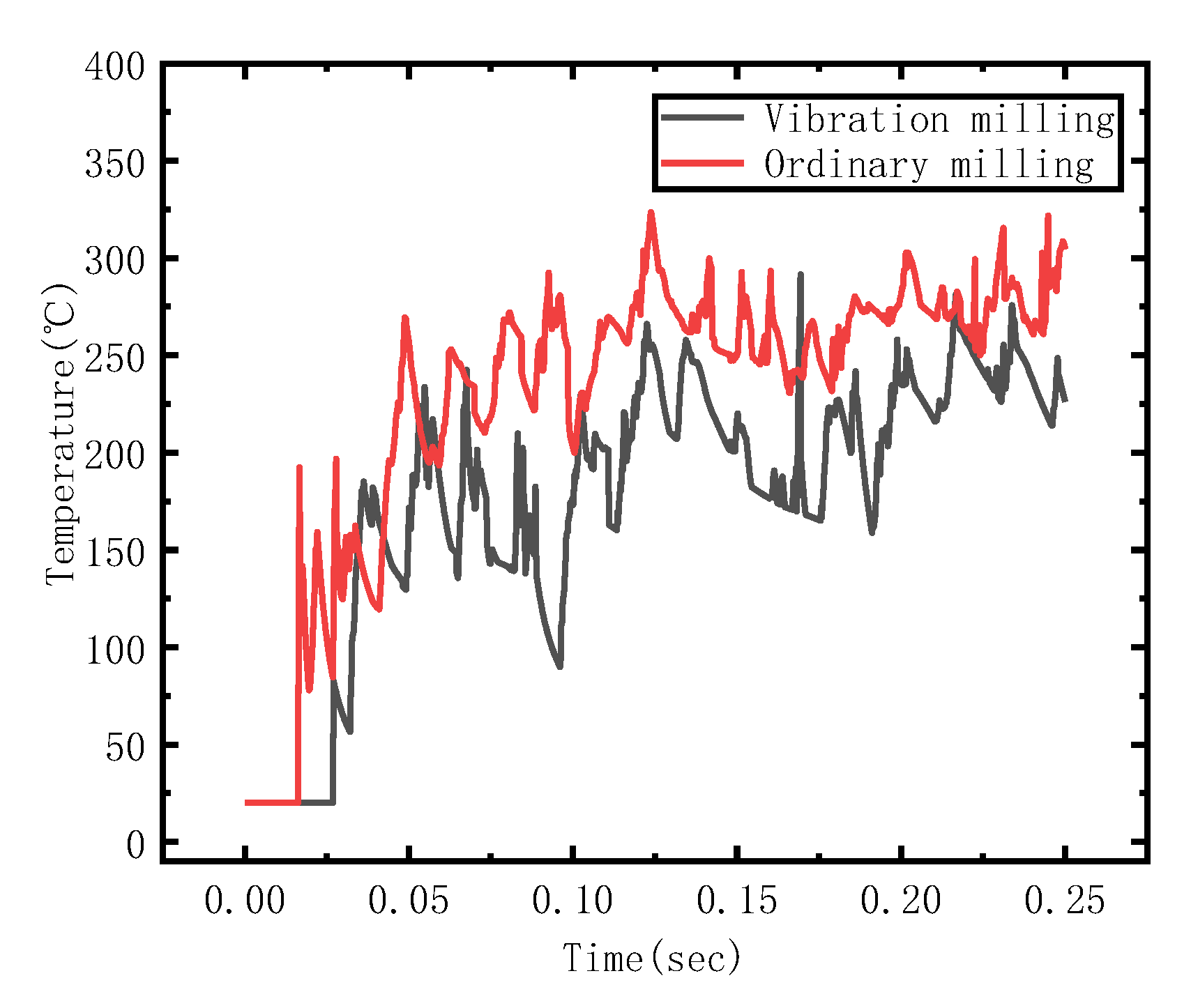
3.2.2. Temperature Comparison in Milling Area

According to Figure 9, it can be clearly seen that when the tool first comes into contact with the workpiece, there is a significant sudden change in the temperature of ordinary milling, while the temperature of vibration milling increases relatively slowly. The range of temperature changes in the ordinary milling area is large, indicating that vibration milling alleviates the impact force of the tool on the workpiece, reduces cutting force, and the temperature of the cutting area also decreases. When the cemented carbide is stably milling GH4169, the temperature of ordinary milling area is between 200-300 ℃, and the temperature of vibration milling is lower than that of ordinary milling. This is because in the process of vibration milling, the chip is more likely to break, and the chip takes away a lot of heat. At the same time, the Contact process between the tool and the workpiece is in a state of fluctuation, making the heat easier to transfer out.

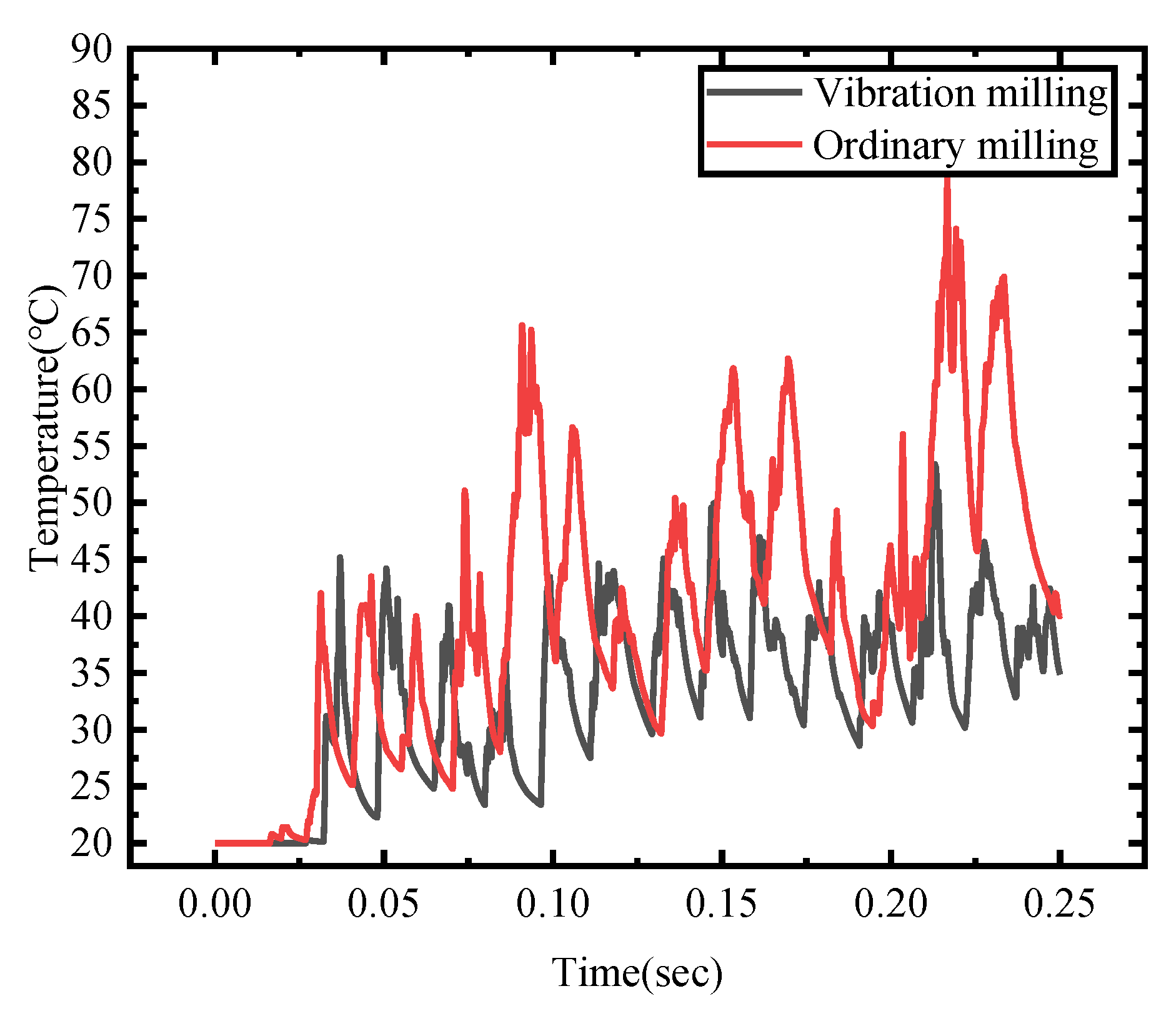
3.2.3. Tool Temperature Comparison

According to Figure 10, it can be seen that when the tool first comes into contact with the workpiece, the temperature in the ordinary milling area rises first. There is a heat conduction phenomenon between the tool and the workpiece, which causes the tool temperature to rise first. However, during vibration milling, the tool temperature rises slowly and the fluctuation range is small. The temperature of the cutting tool is closely related to the temperature of the milling area. During intermittent milling, every contact between the cutting tooth and the workpiece causes a drastic fluctuation in temperature, leading to an increase in milling force, increased work, and an increase in the temperature of the milling area. As a result, the temperature of the cutting tool increases. Vibration milling alleviates the impact force during contact, making it easier to release pressure and heat. The heat transmitted to the cutting tool is less, and the temperature of the cutting tool is relatively stable. Overall, the tool temperature fluctuates within the range of 20-60 ℃.

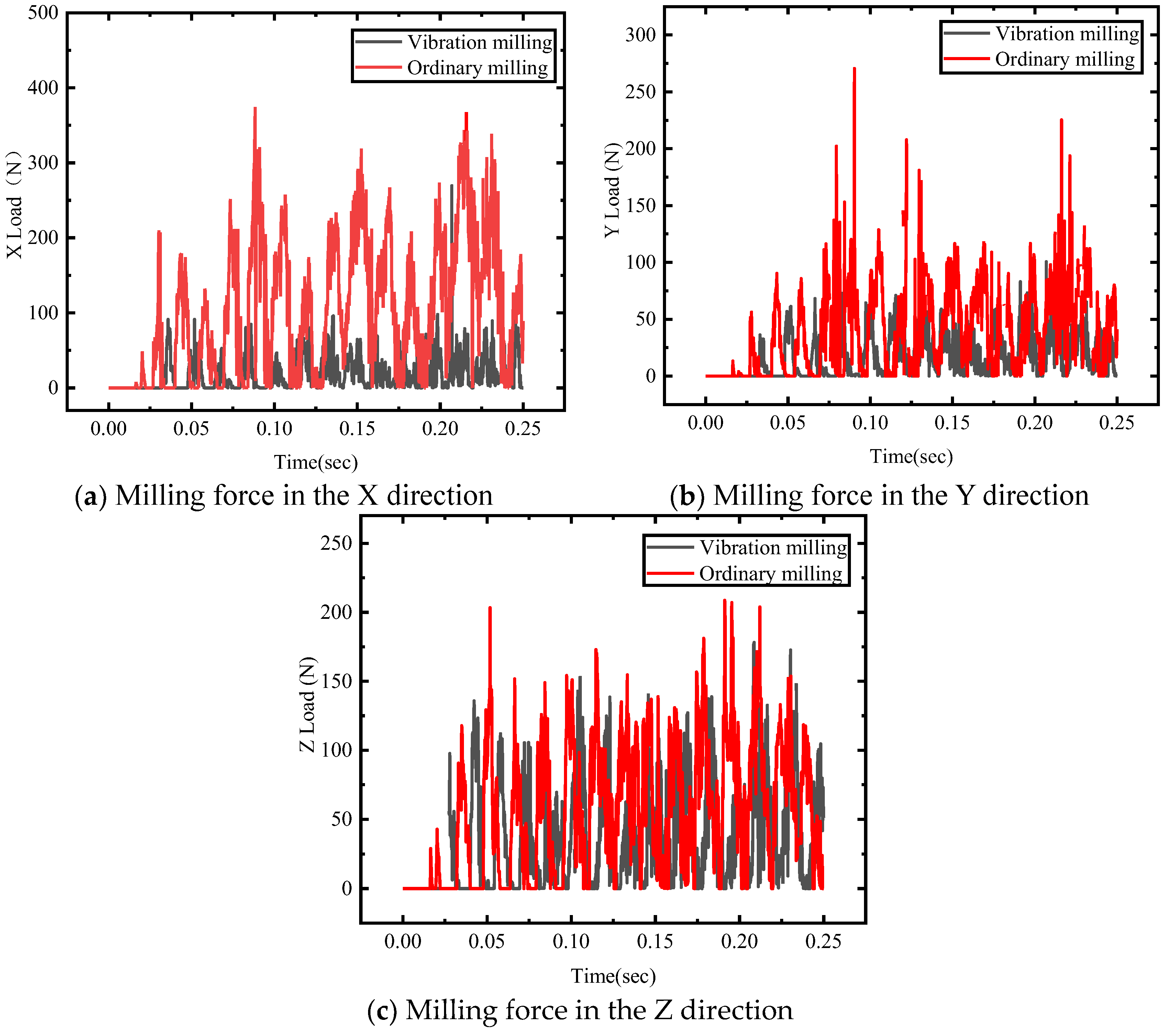
3.2.4. Comparison of Three Way Milling Forces

Figure 11 shows the comparison of three-dimensional milling forces between vibration milling and ordinary milling. Overall, the milling force of ordinary milling is greater than that of vibration milling, and the milling process is intermittent. Therefore, during the ordinary milling process, the tool and workpiece suddenly come into contact multiple times, resulting in significant fluctuations in milling force. During vibration milling, chips are prone to detachment, reducing the resistance of chips to the tool. At the same time, the temperature in the milling area decreases, and the tool always maintains good hardness, which is beneficial for reducing milling force. The overall milling force is: FX>FZ>FY. The vibration signal has a greater impact on the feed force and axial force, and a smaller impact on the radial force. In this experiment, the overall milling width and depth are relatively small, so the milling force is also relatively small.

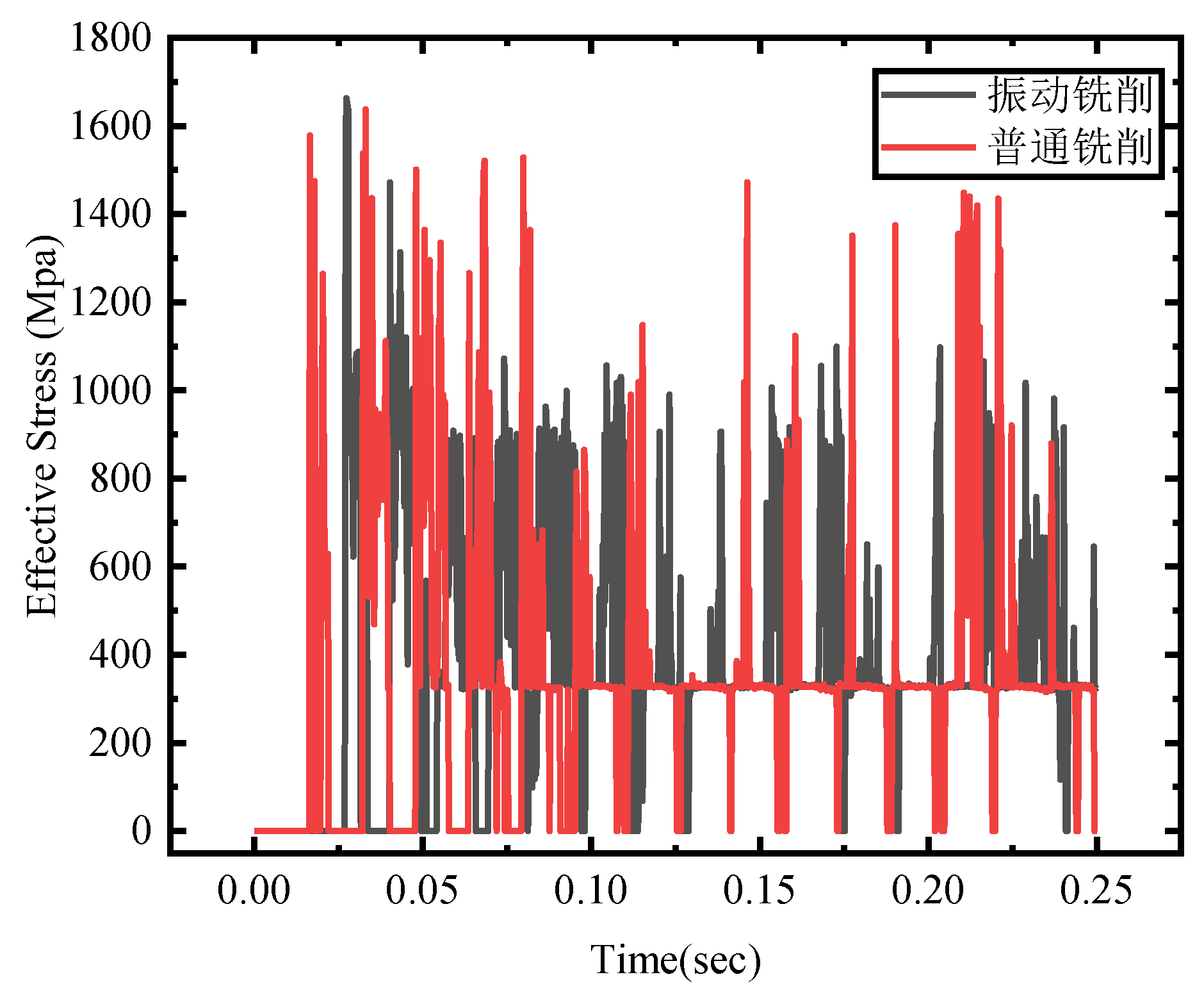
3.2.5. Comparison of Surface Stress of Workpieces

From Figure 12, it can be seen that the equivalent stress of the workpiece in ordinary milling is greater than that in vibration milling, and ordinary milling is more prone to severe mutations due to sudden contact and separation between the workpiece and the tool; The stress in vibration milling is relatively dense, and low-frequency vibration signals cause frequent stress fluctuations. Ultrasonic vibration milling reduces the equivalent stress on the surface of the workpiece, prevents stress concentration on the surface of the workpiece and reduces the performance of the part, which is beneficial for enhancing the surface quality of the workpiece.

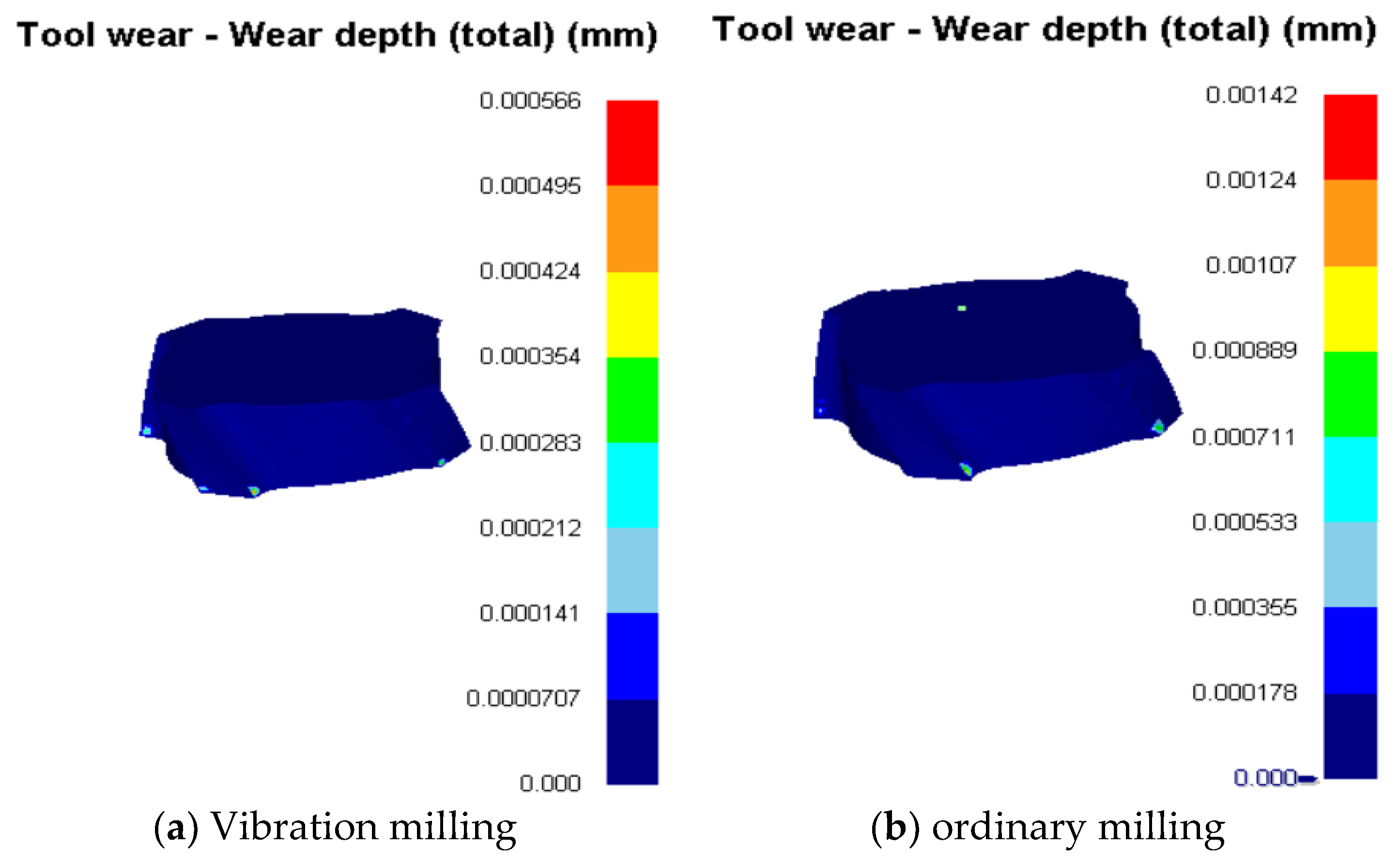
3.2.6. Comparison of Tool Wear

As can be seen from Figure 13, when the tool travel is 10mm, the wear amount of vibration milling is about 1/2 of that of ordinary milling. Because the chips produced by vibration milling are more likely to break, the chips are more regular, the milling process is more stable, and the tool temperature and cutting force in the cutting process are greatly reduced, which reduces the tool wear. In contrast, the temperature of ordinary milling area is too high, and the impact force of intermittent cutting is relatively large, The internal stress of the workpiece is concentrated, and the deformation is more serious. The cutting force will increase and produce larger fluctuations, which will increase the tool wear.

4. Effect of Coating Materials on Tool Wear in GH4169 Milling

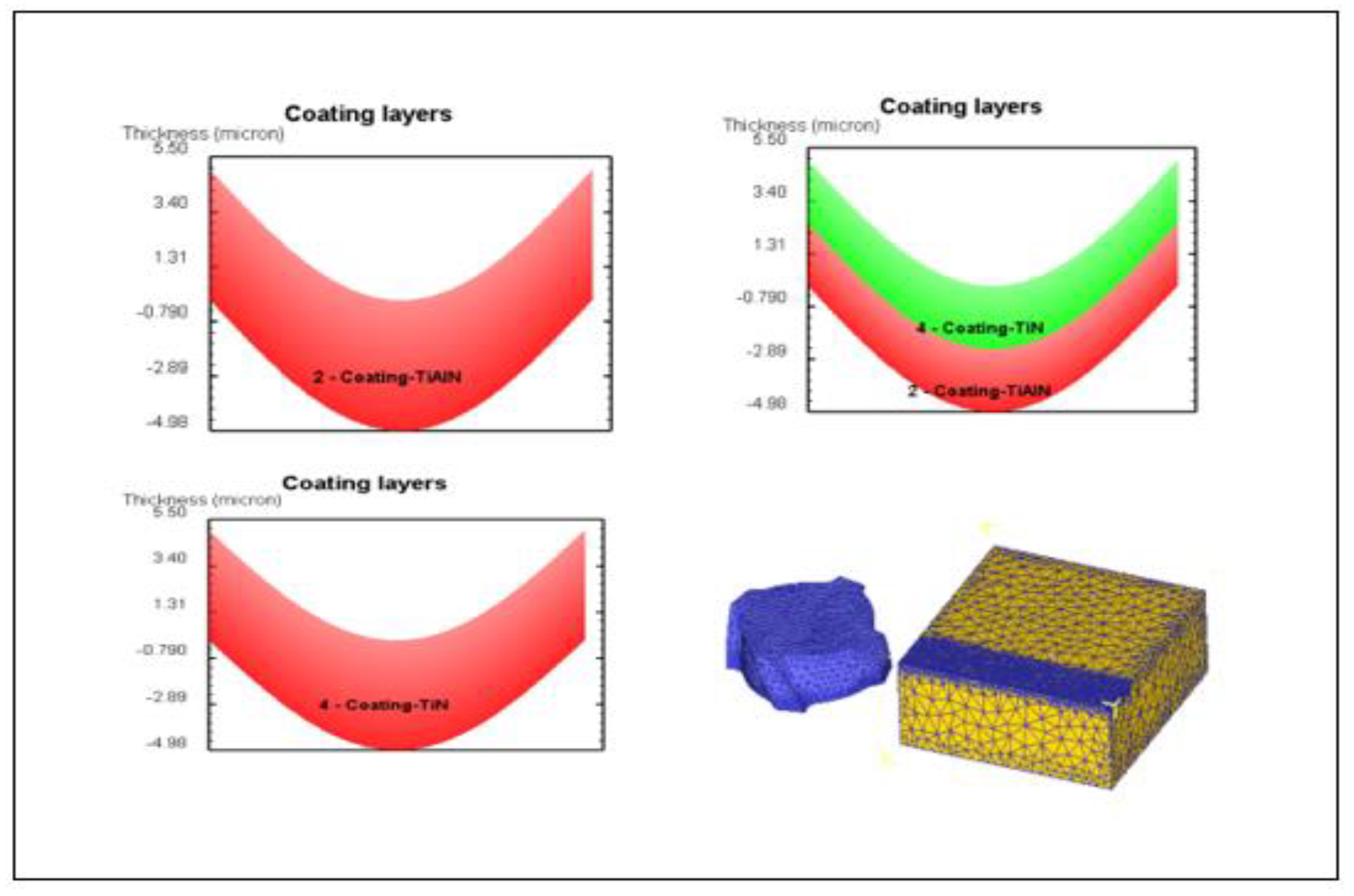
4.1. Establishment of Simulation Model for GH4169 Milling with Coated Tools

Coated tools have high hardness, high wear resistance, high oxidation resistance and strong film substrate bonding strength, which meet the requirements of today's high-precision and high-efficiency machining. Coated tools can improve the surface machining quality of the workpiece, reduce the milling force, reduce the surface temperature of the tool, and reduce tool wear; The physical properties of various common coatings have been encapsulated in the material library of DEFORM, and only need to be selected. Special structural coatings or newly developed coatings can be added to the material library based on their physical properties. The default bonding between coatings and between coatings and substrate in the model is good.
The following main study focuses on the influence of TIALN and TIN coatings on the milling process of hard alloy GH4169. This article sets the tool substrate material as WC, the axial milling depth of the tool is 2mm, the spindle speed is 6000r/min, and the feed rate per tooth is 0.1mm/rad. The distribution of coatings is shown in Figure 14:
The performance of TIN and TIALN coatings is shown in Table 4 [30],

4.2. Analysis of Simulation Results

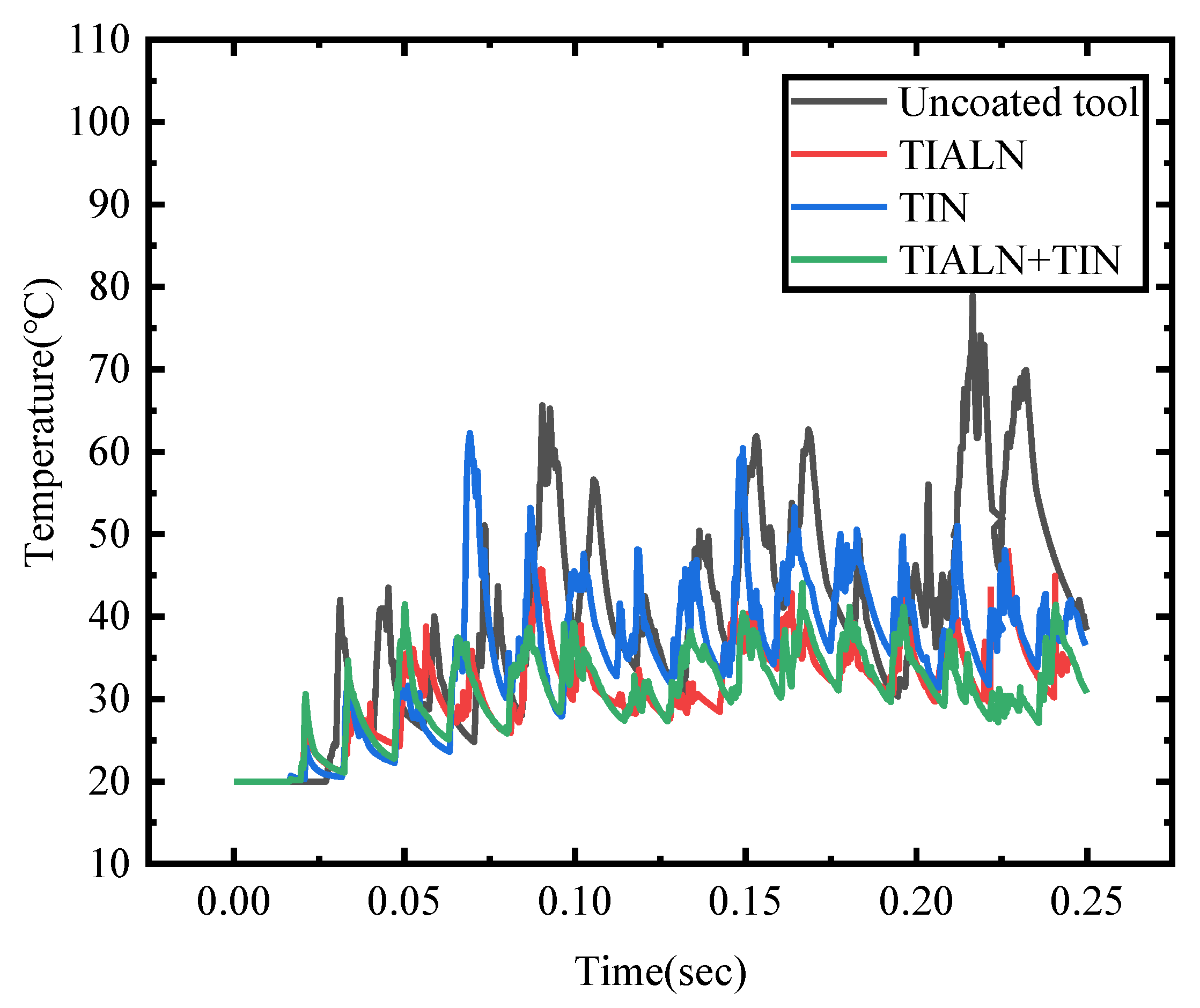
4.2.1. Temperature Changes of Cutting Tools with Different Coating Types

From Figure 15, it can be seen that when the tool first comes into contact with the workpiece, the temperature difference between different types of coated and uncoated tools is not significant. At the beginning of cutting, the tool has less cutting material, less cutting force, and the temperature transmitted to the tool is relatively low. As cutting progresses, the contact area between the tool and the workpiece increases, the cutting force also increases, the temperature of the cutting area increases, and the heat transmitted to the tool also increases. The tool temperature undergoes periodic changes as chips are generated and shed. The temperature of uncoated tools is maximum. Due to the maximum thermal conductivity, a large amount of heat generated in the milling area is transmitted to the tool, causing a rapid increase in tool temperature. Secondly, the temperature of TIN coated tools is the highest, with TIALN coated tools having the lowest temperature, and TIN/TIALN composite coated tools having the lowest temperature. This coating has a soft and hard structure, greatly alleviating the stress on the tool. The composite coating can better prevent the temperature in the milling area from spreading inside the tool, It has a great protective effect on cutting tools and greatly reduces tool wear.

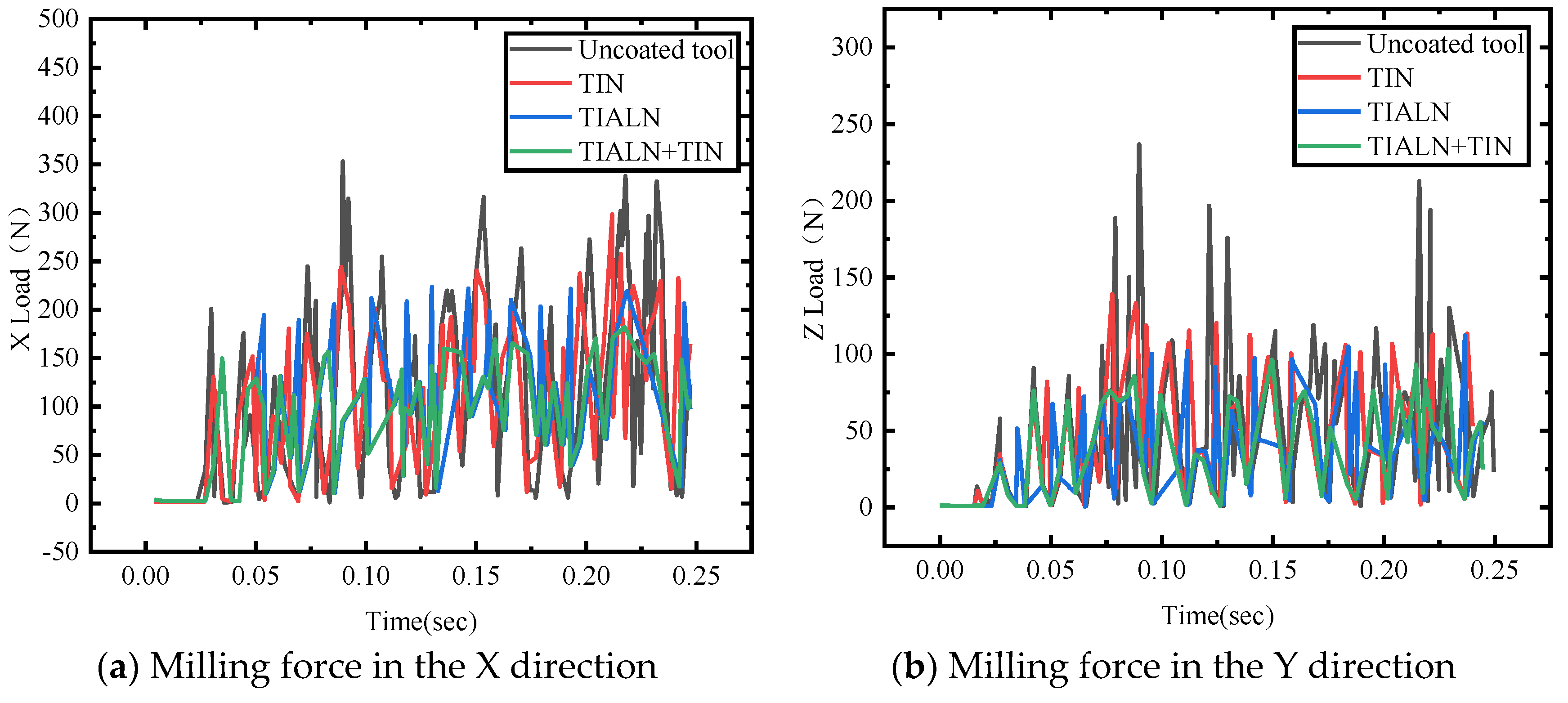
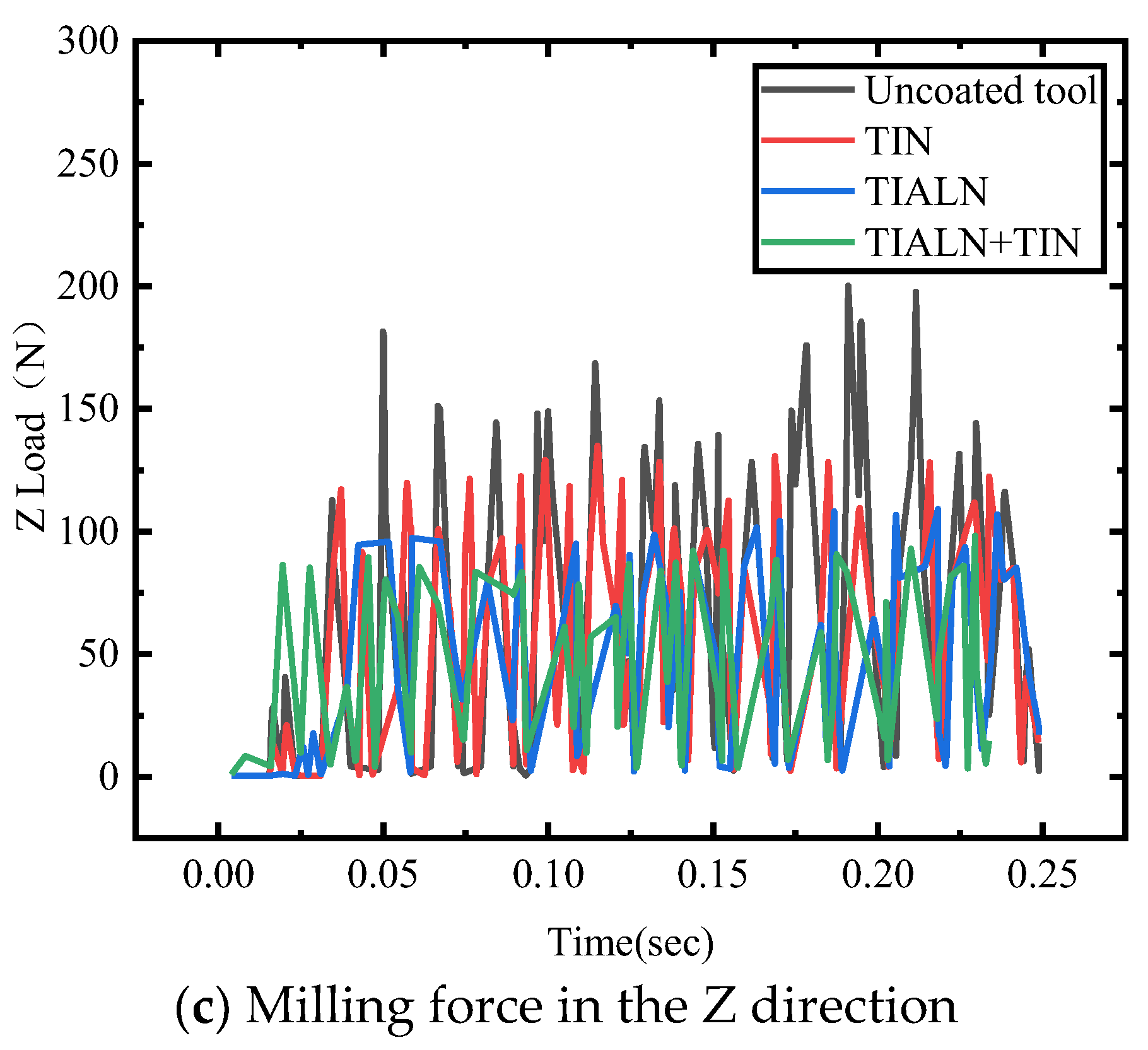
4.2.2. Changes in Milling Force of Different Coating Types of Cutting Tools

From Figure 16, it can be seen that in the early stage of milling, the tool and workpiece just come into contact, the cutting distance is short, the temperature in the milling area is low, the milling force is also small, and the coating material has not yet been effective. With the progress of cutting, the temperature in the milling area increases, and the thermal conductivity of the coating material is small, resulting in less heat entering the tool. The high temperature in the milling area causes the workpiece material to soften, resulting in a decrease in milling force. The material cut by the uncoated tool has a higher hardness, and the tool itself has a lower hardness than the coated material, so the milling force is relatively large. The difference in friction coefficient between TIALN and TIN coatings is not significant, and the main factor affecting milling force is the thermal conductivity coefficient. During the milling process, it can be roughly seen that FTIALN+TIN<FTIALN<FTIN<FUncoated, and the thermal conductivity of the composite coating is low. The soft and hard structure can serve as a good thermal barrier, with a greater degree of material softening and less milling force. Secondly, the milling force of TIALN coated tools is smaller than that of TIN coated tools, with uncoated tools having the highest milling force. At the same time, it can be seen that the fluctuation range of milling force for TIN+TIALN coated tools is relatively small, indicating that the composite coating can reduce the impact force during the milling process and increase the stability of the milling process.

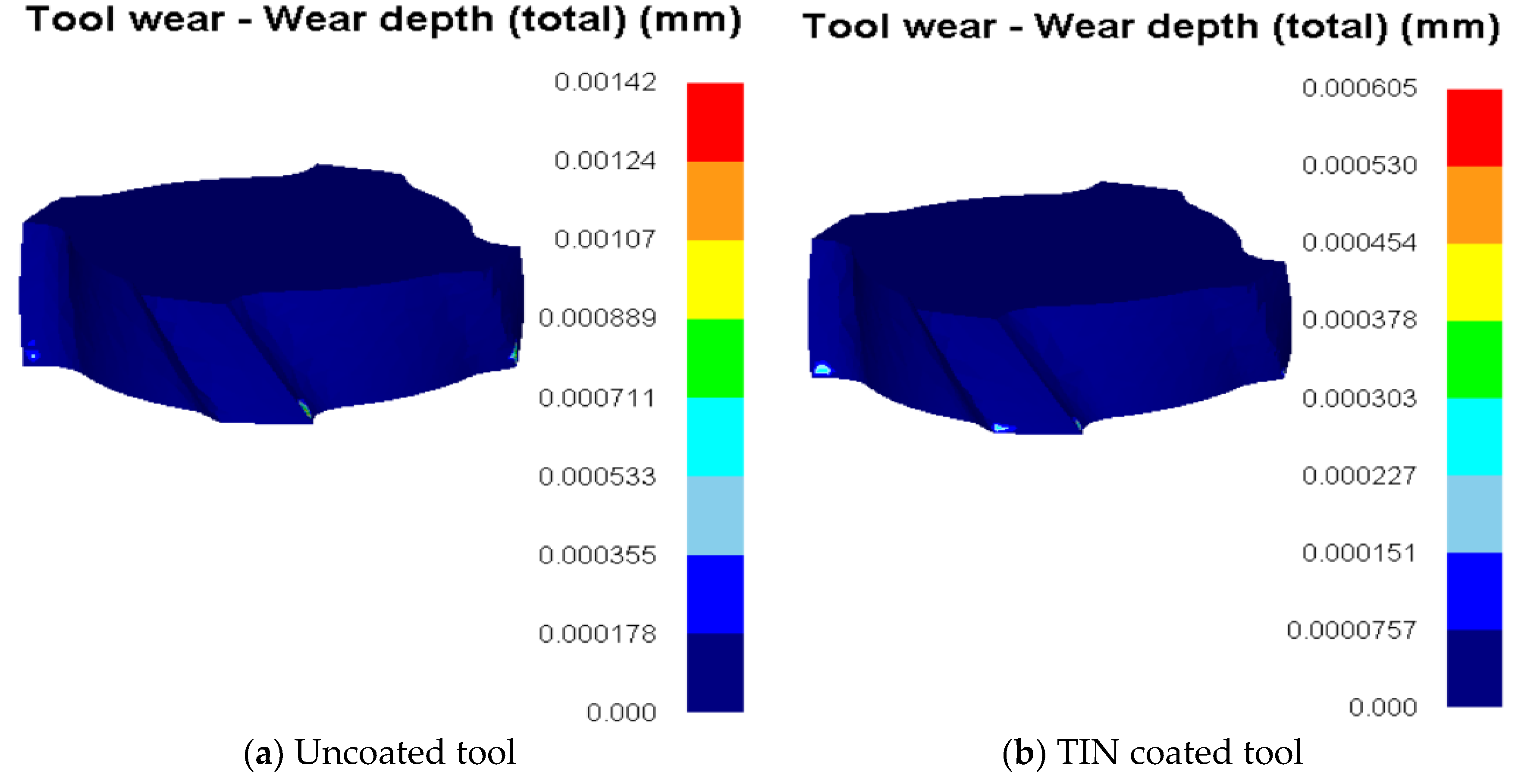
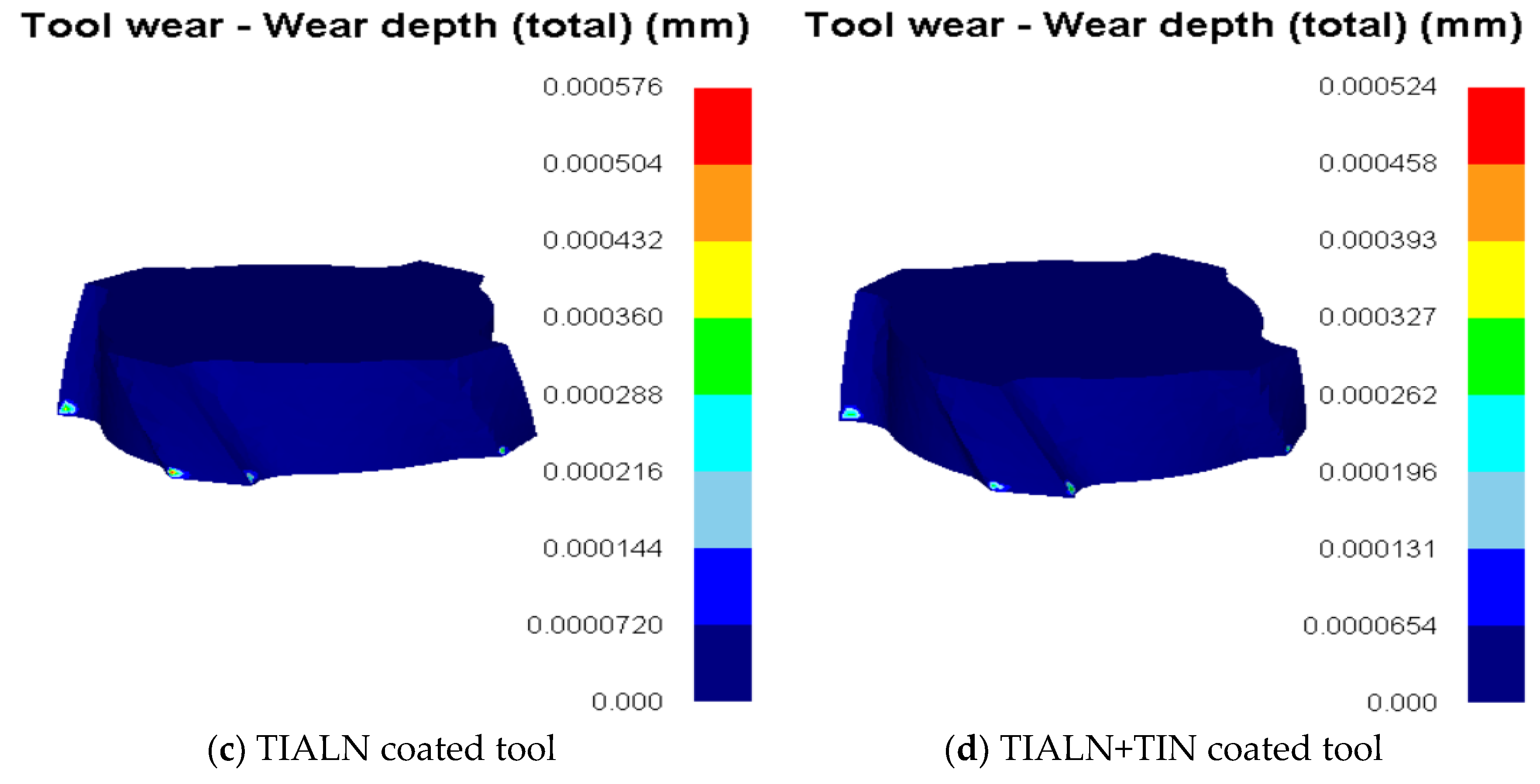
4.2.3. Comparison of Tool Wear of Different Coating Types

From Figure 17, it can be seen that when the milling stroke of the tool is 10mm, the minimum wear of the TIN+TIALN coated tool is 0.524 μ m. Secondly, TIALN coating tool wear is 0.576 μ m. The wear amount of TIN coated tools is 0.605 μ m. Maximum uncoated tool wear, 1.42 μ m. This simulation uses the Usui wear calculation formula. The tool wear is related to the temperature and pressure of the contact surface. TIN+TIALN coated tools have good impact resistance and thermal insulation, and the milling force and tool temperature are relatively low, so the tool wear is relatively small. TIALN and TIN also reduce tool wear, which is due to the low thermal conductivity of the coating material, which keeps the tools with good hardness, and the tool temperature and cutting force are small. The impact of uncoated tools and workpiece materials is large, the workpiece surface hardens seriously, and the tool milling force and temperature are large, so the tool wear is large.

5. Conclusion

(1) Using the finite element simulation software DEFORM, the GH4169 model for carbide milling was established. The orthogonal experiments of tool wear simulation on n, ap, and fz parameters were carried out, and the regression prediction model of tool wear was established. The range analysis of the model was conducted, and the simulation effect was good. The empirical formula of tool wear was H=0.01 • n0.4112 • ap0.5345 • fz-0.6866.
(2) In the process of milling GH4169, the order of the influence of n, ap, and fz on tool wear is: fz>ap>n. n. The larger the ap, the greater the tool wear. When fZ increases, the tool wear will decrease. Taking the minimum tool wear as the target, the optimal milling parameters were obtained as n=3000 r/min, ap=0.2 mm, fz=0.4 mm/r.
(3) Based on the path planning method, a simulation model of ultrasonic vibration milling GH4169 is established. Compared with ordinary milling, it is found that ultrasonic vibration assisted milling is beneficial to chip breaking, reducing the temperature of milling area, milling force, workpiece surface stress, and cutting tool temperature, which is of great significance to reduce tool wear and optimize the quality of machined surface.
(4) The GH4169 simulation model of coated tool milling is established. By analyzing the milling conditions of cemented carbide tools, TIALN coated tools, TIN coated tools, TIALN coated tools, and TIALN/TIN composite coated tools, the influence of coating materials on tool temperature, milling force, and tool wear is obtained. The results show that coating materials greatly reduce tool surface temperature, three-way milling force, and tool wear. The TIALN/TIN composite coating has the best cutting performance and is more suitable for milling difficult to machine material GH4169.

Funding

This work was financially supported by National Natural Science Foundation of Jilin Province,China (Grant No. 20200201065JC).

Availability of Data and Materials

Available.

Acknowledgments

This work was financially supported by National Natural Science Foundation of Jilin Province, China (Grant No. 20200201065JC). The authors would also like to thank the anonymous reviewers for their helpful comments.

Conflicts of Interest

The authors declare that they have no conflict of interest.

Ethics Declarations

Compliance with ethical standards.

References

  1. Paulonis, D.F.; Oblak, J.M.; Duvall, D.S. Precipitation in Nickel-BaseAlloy718. Transactions of the ASM 1969, 62, 611–622. [Google Scholar]
  2. Lingenfelter, A. Welding of Inconel Alloy 718: A Historical Overview. Superalloy 1989, 718, 673–683. [Google Scholar]
  3. De Bartolomeis, A.; Newman, S.T.; Jawahir, I.S.; et al. Future research directions in the machining of Inconel 718. Journal of Materials Processing Technology 2021, 297, 117260. [Google Scholar] [CrossRef]
  4. ASM Specialty Handbook: Nickel, Cobalt, and Their Alloys; ASM International, 2000.
  5. Ma, J.; Jia, Z.; He, G.; et al. Influence of cutting tool geometrical parameters on tool wear in high-speed milling of Inconel 718 curved surface. Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture 2019, 233, 18–30. [Google Scholar] [CrossRef]
  6. Fan, Y.H.; Wang, T.; Hao, Z.P.; et al. Research on tool wear based on multi-scale simulation in high speed cutting Inconel718. Archives of Civil and Mechanical Engineering 2018, 18, 928–940. [Google Scholar] [CrossRef]
  7. Qiao, Y.; Ai, x.; Liu, Z.; Zhao, J. Experimental Investigation into Milling of Nickel-Based Powder Metallurgy Superalloy with Coated Tools. Journal of South China University of Technology (Natural Science Edition) 2010, 38, 83–88. [Google Scholar] [CrossRef]
  8. Qiao, Y.; Ai, x.; Zhao, J.; Liu, Z. Failure Mechanism of Coated Carbide Tools in Milling of Nickel-base Powder Metallurgy Superalloy. Journal of Beijing University of Technology 2011, 37, 1–6. [Google Scholar]
  9. Liu, Y.; Liu, G. Analysis of milling tool for Nickel-based superalloy. China Water Transport 2008, 8, 170–171. [Google Scholar] [CrossRef]
  10. Leone, C.; D’Addona, D.; Teti, R. Tool wear modelling through regression analysis and intelligent methods for nickel base alloy machining. CIRP Journal of Manufacturing Science and Technology 2011, 4, 327–331. [Google Scholar] [CrossRef]
  11. Zhou, J.; Han, R.D. The Investigation of Tool Wear in High Speed Cutting INCONEL718. Applied Mechanics and Materials 2010, 33, 347–350. [Google Scholar] [CrossRef]
  12. Oliveira, A.R.F.; Da Silva, L.R.R.; Baldin, V.; et al. Effect of tool wear on the surface integrity of Inconel 718 in face milling with cemented carbide tools. Wear 2021, 476, 203752. [Google Scholar] [CrossRef]
  13. D’addona, D.M.; Raykar, S.J.; Narke, M.M. High speed machining of Inconel 718: tool wear and surface roughness analysis. Procedia CIRP 2017, 62, 269–274. [Google Scholar] [CrossRef]
  14. Attanasio, A.; Ceretti, E.; Rizzuti, S. 3D finite element analysis of tool wear in machining. CIRP Annals - Manufacturing Technology 2008, 57, 61–64. [Google Scholar] [CrossRef]
  15. Martynov, V.V.; Martynov, P.V. Automation and Modern Technologies. 2013, 4, 7–18. [Google Scholar]
  16. Thakur, D.G.; Ramamoorthy, B.; Vijayaraghavan, L. Some investigations on high speed machining of aerospace material Inconel 718 using multicoated carbide inserts. Materials and Manufacturing Processes 2012, 27, 1066–1072. [Google Scholar] [CrossRef]
  17. Yen, Y.C.; Altan, T. Estimation of Tool Wear in Orthogonal Cutting Using the Finite Element Analysis. Journal of Materials Processing Technology 2004, 82–91. [Google Scholar] [CrossRef]
  18. Xie, L.J. 2D FEM Estimate of Tool Wear in Turning Operation. Wear 2005, 1479–1490. [Google Scholar] [CrossRef]
  19. Umbrello, D.; Filice, L.; Micari, F. Prediction of Tool Wear Progress in Machining of Carbon Steel using different Tool Wear Mechanisms. Int JMater Form 2008, 1, 571–574. [Google Scholar] [CrossRef]
  20. Attanasio, A.; Umbrello, D. Abrasive and diffusive tool wear FEM simulation. Int J Mater Form 2009, 2, 543–46. [Google Scholar] [CrossRef]
  21. Zheng, M.; Fan, Y. An Overview of Tool Friction and Wear Behavior in High-speed Machining-typical Difficult-to-cut Material. Journal of Harbin University of Science and Technology 2011, 16, 22–30. [Google Scholar] [CrossRef]
  22. He, Y.; Zhou, Z.; Zou, P.; et al. Study of ultrasonic vibration–assisted thread turning of Inconel 718 superalloy. Advances in Mechanical Engineering 2019, 11, 1687814019883772. [Google Scholar] [CrossRef]
  23. Mou, W.; Zhu, S. Vibration, tool wear and surface roughness characteristics in turning of Inconel 718 alloy with ceramic insert under LN2 machining. Journal of the Brazilian Society of Mechanical Sciences and Engineering 2020, 42, 1–12. [Google Scholar] [CrossRef]
  24. Sharman, A.; Dewes, R.C.; Aspinwall, D.K. Too1 life when high speed bal1 nose end milling Inconel 718. Journal of Materials Processing Technology 2001, 118, 29–35. [Google Scholar] [CrossRef]
  25. Wang, Q. Research and application of functional principal component analysis and functional linear regression model. Dissertation, Chongqing Technology and Business University, 2020. [Google Scholar]
  26. Ma, Y.; Yue, Y. Research on Surface Roughness Prediction Model of T-itanium Alloy TC25 Milling. Manufacturing Technology & Machine Tool 2020, 141–145. [Google Scholar] [CrossRef]
  27. Liu, A. SPSS basic analysis tutorial; Peking University Press: Beijing, 2014. [Google Scholar]
  28. Peng, D. Prediction of Milling Process and Analysis of Surface Quality for TC4. Dissertation, Tianjin University, 2012. [Google Scholar]
  29. Yang, Y. Numerical Simulation and Experimental Study on Axial Ultrasonic Vibration Assisted Milling of Titanium Alloy. Dissertation, Nanjing University of Science and Technology, 2021. [Google Scholar]
  30. Liu, Z.; Zhang, C.; Ren, J. Dry cutting technology and its application; China Machine Press: Beijing, China, 2005. [Google Scholar]
Preprints 74054 g001
Figure 1. Milling Model.
Figure 1. Milling Model.
Preprints 74054 g001
Preprints 74054 g002
Figure 2. GH4169 Constitutive Material Model.
Figure 2. GH4169 Constitutive Material Model.
Preprints 74054 g002
Preprints 74054 g003
Figure 3. Residual Analysis of tool wear.
Figure 3. Residual Analysis of tool wear.
Preprints 74054 g003
Preprints 74054 g004
Figure 4. Influence distribution of n, ap and fz on tool wear.
Figure 4. Influence distribution of n, ap and fz on tool wear.
Preprints 74054 g004
Preprints 74054 g005
Figure 5. Schematic diagram of axial vibration milling.
Figure 5. Schematic diagram of axial vibration milling.
Preprints 74054 g005
Preprints 74054 g006
Figure 6. Axial vibration path planning.
Figure 6. Axial vibration path planning.
Preprints 74054 g006
Preprints 74054 g007
Figure 8. Comparison of chip cutting between ordinary milling and vibration milling.
Figure 8. Comparison of chip cutting between ordinary milling and vibration milling.
Preprints 74054 g007
Preprints 74054 g008
Figure 9. Temperature distribution diagram of vibration milling and ordinary milling area.
Figure 9. Temperature distribution diagram of vibration milling and ordinary milling area.
Preprints 74054 g008
Preprints 74054 g009
Figure 10. Temperature Distribution Diagram of Vibration Milling and Common Milling Cutters.
Figure 10. Temperature Distribution Diagram of Vibration Milling and Common Milling Cutters.
Preprints 74054 g009
Preprints 74054 g010
Figure 11. Trend of milling force between vibration milling and ordinary milling.
Figure 11. Trend of milling force between vibration milling and ordinary milling.
Preprints 74054 g010
Preprints 74054 g011
Figure 12. Equivalent Stress Trend of Vibration Milling and Ordinary Milling Workpieces.
Figure 12. Equivalent Stress Trend of Vibration Milling and Ordinary Milling Workpieces.
Preprints 74054 g011
Preprints 74054 g012
Figure 13. Analysis of tool wear in Vibration Milling and Ordinary Milling.
Figure 13. Analysis of tool wear in Vibration Milling and Ordinary Milling.
Preprints 74054 g012
Preprints 74054 g013
Figure 14. TIALN and TIN coating distribution diagram.
Figure 14. TIALN and TIN coating distribution diagram.
Preprints 74054 g013
Preprints 74054 g014
Figure 15. Temperature variation trend of cutting tools with different coating types.
Figure 15. Temperature variation trend of cutting tools with different coating types.
Preprints 74054 g014
Preprints 74054 g015aPreprints 74054 g015b
Figure 16.  
Figure 16.  
Preprints 74054 g015aPreprints 74054 g015b
Preprints 74054 g016aPreprints 74054 g016b
Figure 17. Distribution of maximum wear of different types of coated tools.
Figure 17. Distribution of maximum wear of different types of coated tools.
Preprints 74054 g016aPreprints 74054 g016b
Table 1. Milling cutter model parameters.
Table 1. Milling cutter model parameters.
Diameter Tooth number Front Angle back Angle helix Angle radius of the tool
10mm 4 8° 12° 30° 1mm
Workpiece parameters: 14mm*14mm*5mm.
Table 2. Orthogonal Simulation Experimental Data.
Table 2. Orthogonal Simulation Experimental Data.
Spindle speed n（r/min） Cutting depth ap（mm） Feed per tooth fz（mm/r） Tool wear amountH（μm）
1 3000 0.2 0.1 0.557
2 3000 0.3 0.2 0.499
3 3000 0.4 0.3 0.343
4 3000 0.5 0.4 0.351
5 3500 0.2 0.2 0.387
6 3500 0.3 0.1 0.778
7 3500 0.4 0.4 0.349
8 3500 0.5 0.3 0.444
9 4000 0.2 0.3 0.208
10 4000 0.3 0.4 0.323
11 4000 0.4 0.1 1.01
12 4000 0.5 0.2 0.645
13 4500 0.2 0.4 0.309
14 4500 0.3 0.3 0.363
15 4500 0.4 0.2 0.718
16 4500 0.5 0.1 0.898
Table 3. Analysis of Maximum Tool Wear (H) Range.
Table 3. Analysis of Maximum Tool Wear (H) Range.
A（Speed） B（The millin depth） C（Feed per tooth）
K1 1.7500 1.4610 3.2430
K2 1.9580 1.9630 2.2490
K3 2.1860 2.4200 1.3580
K4 2.2880 2.3380 1.3320
k1 0.4375 0.3653 0.8108
k2 0.4895 0.4908 0.5623
k3 0.5465 0.6050 0.3395
k4 0.5720 0.5845 0.3330
RF 0.1345 0.2398 0.4778
主次顺序 fz>ap>n
Table 4. Performance Table of TIALN and TIN Coatings.
Table 4. Performance Table of TIALN and TIN Coatings.
Coating types TIALN TIN
Hardness value（HV） 3300 2300
The coefficient of friction（N/sec/mm/C） 0.4 0.49
Coefficient of heat conduction 10 23
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated