Prerpints.org logo
Preprint
Article

Dual-function meta-grating based on tunable Fano resonance for reflective filter and sensor applications

Altmetrics

Downloads

138

Views

51

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

18 May 2023

Posted:

19 May 2023

You are already at the latest version

Alerts
Abstract
Localized surface plasmon resonance (LSPR) based sensors exhibit enormous potential in the areas of medical diagnosis, food safety regulation and environmental monitoring. While, the broadband spectral lineshape of LSPR hampers the observation of wavelength shifts in sensing processes, thus preventing their widespread applications in sensors. Here, we describe an improved plasmonic sensor based on Fano resonances between LSPR and Rayleigh anomaly (RA) in a metal-insulator-metal (MIM) meta-grating, which is constructed by silver nanoshells array, an isolation grating mask and a continuous gold film. The MIM configuration offers more freedoms to control the optical properties of LSPR, RA and the Fano resonance between them. Strong couplings between LSPR and RA form a series of narrowband reflection peaks (with a linewidth of ~20 nm in full width at half maximum (FWHM) and a reflectivity closing to 100%) within a LSPR based broadband extinction window in experiment, making the meta-grating promising for applications of high-efficiency reflective filters. While, a well-optimized Fano resonance between LSPR and RA by carefully adjusting the angles of incident light can switch such nano-device to an improved biological/chemical sensor with the figure of merit (FOM) large than 60 and capability for detecting the local refractive index changes caused by the bonding of target molecules on surface of the nano-devices. The figure of merit of hybrid sensor in detection of target molecules is 6 and 15 times higher than the simple RA and LSPR based sensors, respectively.
Keywords: 
Subject: Physical Sciences  -   Optics and Photonics

1. Introduction

Localized surface plasmon resonances, as a result of collective oscillation of free electrons in noble metals, show great potential in chemical/biological sensors, owing to their capability of manipulating electromagnetic wave in nanoscale and inherent sensitivity to changes in refractive index (RI) of local environment[1,2,3,4]. However, the figure of merit (FOM) values which is defined as the value of RI sensitivities divided by resonance linewidths in FWHM of LSPR sensors[5], are generally small due to the broadband spectral lineshape of LSPR (FOM<15)[6,7,8,9,10], thus preventing the widespread application of LSPR sensors. To solve this problem, an effective method is to introduce one more resonance mode with high quality factor (Q), such as waveguide mode[11,12], optical microcavity resonance mode[13,14], high-order plasmonic resonance [15,16,17] or Rayleigh anomaly diffraction mode[18,19,20], to the system, and then utilize the newly generated Fano resonance between LSPR and the high-Q modes for sensor applications. The hybridization between LSPR and high-Q resonance modes not only reduces the linewidths of LSPR based sensors, but also modulates the enhanced electric-intensity distribution near the nanostructure, making it more access and sensitive to molecular species. Therefore, the FOM value of LSPR sensor can be effectively increased by such modes coupling processes[21].
In above mentioned works, the hybrid sensors based on Fano resonance between LSPR and RA is worthy of attention. Rayleigh anomaly, corresponding to a diffraction tangential to the grating surface, is well known for its sharply asymmetric lineshape[22] and high sensitivity to changes in RI of environment (with the sensitivity proportional to the period of grating, i. e., S R A = P ( 1 + s i n ⁡ ( θ ) ) with P and 𝜃 denoting the grating period and incident angle, respectively)[23,24,25]. Those exotic characteristics make the RA related hybrid sensor more suitable for the detection of low-concentration biological/chemical molecule or explosive molecules [10,18]. Unfortunately, in the rarely reported works, due to lack of suitable platforms to carefully regulate the coupling relationship between LSPR and RA to modulate the enhanced electric-intensity distribution near the nanostructure, the abilities of such kind of Fano resonance in measuring local RI changes caused by the adsorption of target molecules on surface of the nano-devices are not yet fully exploited.
In this work, we investigate a tunable Fano resonance between LSPR and RA in a MIM meta-grating constructed by silver nanoshells array, an isolation grating mask and a continuous gold film. MIM configuration offers more degrees of freedom to control the optical properties of LSPR, RA and the Fano resoance between them. Both experimental and simulated results show that the coupling behavior between LSPR and RA including coupling strength and spectral contrast can be modulated effectively by the angles of incident light in an optimized meta-grating. Strong couplings between LSPR and RA worked at large incident angles form a series of narrowband and high-contrast reflective peaks (with a linewidth of ~20 nm in FWHM and a reflectivity of closing to 100%) in a LSPR based dark background, which are capable for the applications of high-efficiency reflective filters. While, a well-optimized Fano resonance to modulate the enhanced electric-intensity distribution near the nanostructure by carefully adjusting the angles of incident light can enhance effectively the light-matter interaction in nanoscales, and thus switch such nano-device to a high-performance biological/chemical sensors with FOM large than 60, and capability to detect the binding of small (organic) molecules to the nanodevices surface. The FOM of the hybrid sensor in detection of local RI changes is 6 and 15 times higher than the simple RA and LSPR based sensor, respectively.

2. Results

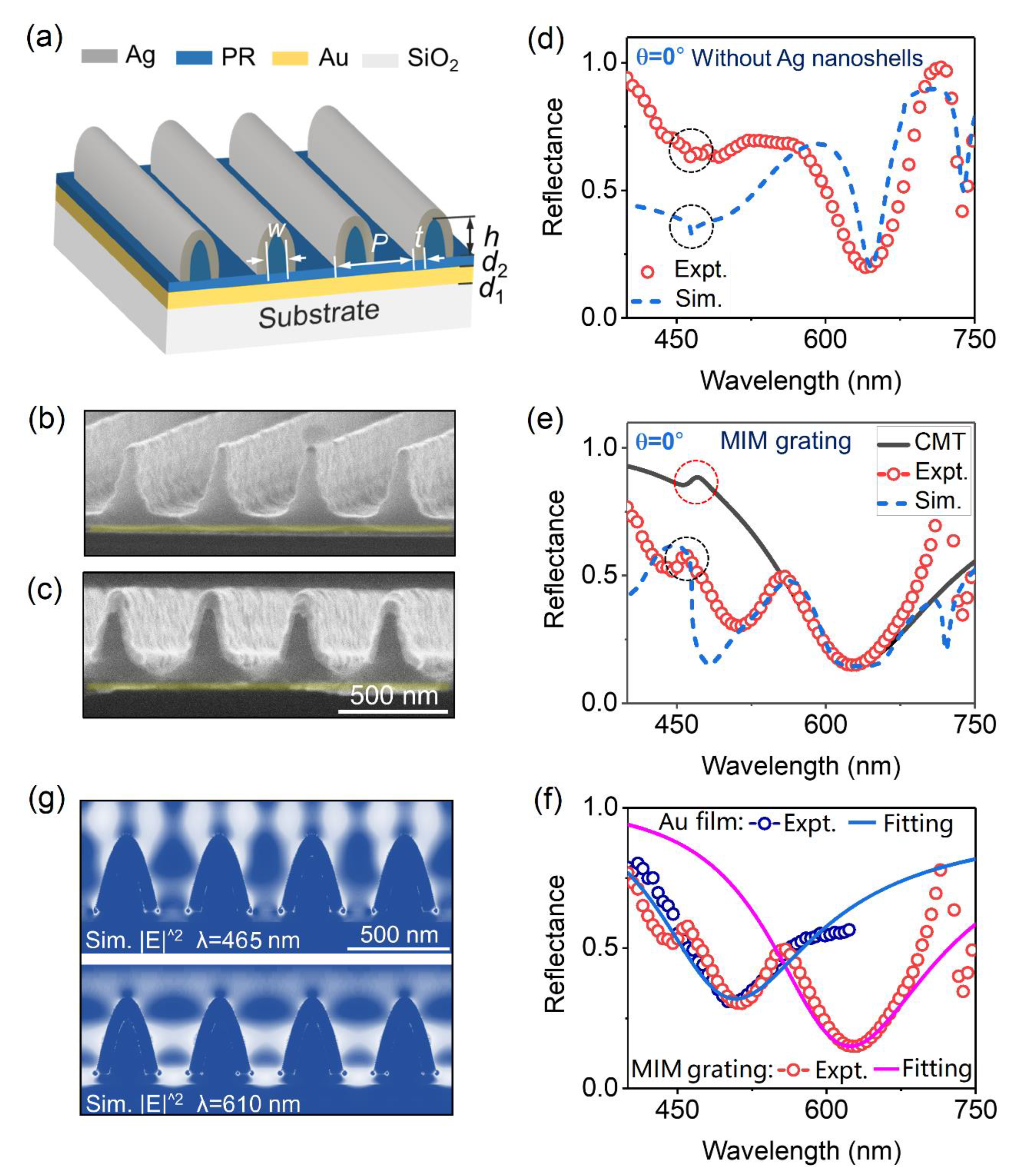
2.1. Design and Characterization of the Meta-Grating

Figure 1(a) schematically depicts the geometry of the meta-grating we designed, which is composed of an array of silver nanoshells and a continuous gold film separated by a photoresist (PR) grating mask that is not developed to the end. The gold film prohibits any transmission through the system so that only the reflection of the device needs to be considered, laying the basis for generating high-contrast RA diffraction [26]. Near-filed coupling between two metallic layers (i.e. Ag nanoshells and the gold film) forms a series of LSPR[27,28] in different wavelengths with their features dictated by geometrical details as defined in Figure 1(a). The structural parameters of the MIM meta-grating are defined as follow: the thickness of the Au film d1; the thickness of the photoresist spacer d2; the modulation depth of the PR grating h; the full width at half maximum of the PR grating lines W; the period of the nanocavity array P. Figure 1(b) and 1(c) depict, respectively, the scanning-electron-microscopic (SEM) pictures of part of the fabricated sample before and after the deposition of Ag nanoshells on surface of the PR grating. Refer to [15,29] for the detailed fabrication process of such MIM meta-grating. Through parameter sweeps on the geometrical parameters, such as the full width at half maximum of the PR grating lines, the thickness of photoresist spacer and Ag nanoshells, using finite-difference time-domain (FDTD) simulations, we optimized the geometric parameters of the MIM mete-grating in the experiments as follow: P≈465 nm, d1=70 nm, d2= 50 nm, h=260 nm, W=165 nm.
We experimentally characterize the optical properties of the fabricated samples depicted in Figures 1(b) and 1(c) for the sake of comparison. Red circles in Figures 1(d) and 1(e) represent the measured reflectance spectra of the samples under the illuminations of normally incident lights for TM polarization (perpendicular to the extending direction of grating lines), which are in nice agreement with corresponding FDTD simulations as plotted by blue dotted curves in Figures 1(d) and 1(e), respectively. In our simulations, geometric parameters of the simulated nanostructures are derived from the experiments. Meanwhile, the intrinsic absorptions of metallic materials are also considered in the simulation. For the dielectric grating without Ag nanoshells, the RA resonances in two spectra (i. e. the measured and simulated reflectance spectra of the grating) as marked by black dotted circular rings in Figure 1(d) are observed as two extremely shallow dips at 463 nm for their natural sub-radiation properties. The linewidth of RA mode in FWHM is about 8 nm. The other two dips appear at 645 nm and 740 nm in two spectra, respectively, corresponding to SPP modes bound to different interfaces (i.e., the interface between Au film and PR spacer layer, and the interface between Au film and the SiO2 substrate) (see Figure S1 in the supplementary information for the corresponding electric-intensity distribution). Those spectral features can also be confirmed by the corresponding angle-resolved reflectance spectrum in below.
As to the MIM meta-grating, the RA resonances in two spectra as highlighted by the black and red dotted circular ring, respectively in Figure 1(e) turn to weak peaks due to the relatively weak Fano couplings between RA and the broadband plasmonic modes with their central wavelength at λ ≈ 610 n m . Near-field interaction between Ag nanoshells and gold film forms such broadband plasmonic modes with stronger absorption and electric-field enhancement (~150 nm in FWHM and a reflectivity below 20% at central wavelength), which lays the basis for the realization of wide range tunable Fano resonances. Compared to the simple RA mode mentioned in Figure 1(e), the linewidth of the hybrid RA modes in FWHM is increased to 12 nm in this case. To quantitatively evaluate the optical properties of RA, the plasmonic modes and the coupling behavers between them, we applied the coupled-mode theory (CMT) mentioned in [15,30] to help us precisely extract the basic parameters of the resonance modes, including the intrinsic damping, the radiation damping, and the coupling strength between such two resonance modes, where the system is simplified as a one-port (reflection geometry) two-mode (considering only the RA and LSPR modes in this work) model. The black solid curve in Figure 1(e) shows the CMT fitting spectrum with parameters as follow: radiation damping of RA and the broadband LSPR: ΓRAe=5, ΓLSPRe=25; intrinsic damping of such two modes: ΓRAi=0.5, ΓLSPRi=55; coupling strength between such two resonance modes: t=5. Good agreement is observed between the measurement and the CMT fitting. In this case (i.e. θ = 0 ° ), the radiation ability to far field and the linewidth of the hybrid RA mode are slightly influenced by the relatively weak coupling process.
While, it’s worth noting that the relatively low reflectance of the MIM meta-grating in the wavelength range of 400-550 nm actually results from the intrinsic absorption of the gold film, which can be verified by the measured reflectance spectra of gold film as depicted in Figures 1(f) and plotted by blue circles. Therefore, the spectral superposition of the intrinsic absorption of gold film and the broadband LSPR at λ ≈ 610 n m can perfectly reproduce the relatively complex spectral lineshape of MIM meta-grating in Figure 1(e), which can be seen from the corresponding CMT fitting results as depicted in Figures 1(f) and plotted by blue (the intrinsic absorption of gold film) and red (the broadband LSPR) solid curves, respectively. Meanwhile, the reflectance peaks appear at 720 nm, corresponding to the Fano resonances between the broadband LSPR and the SPP mode (see Figure S2 in the supplementary information for the corresponding electric-intensity distribution), which can also be demonstrated by the following angle-resolved reflectance spectra. Figure 2(g) shows the electric-intensity distribution of the MIM meta-grating at λ ≈ 465 n m and 610 n m , corresponding to the RA and LSPR modes, respectively, where the enhanced electric fields are mainly distributed on surface of the MIM grating and the interspace between two Ag nanoshells, respectively. Own to the weak Fano coupling between LSPR and RA, the near-field distribution of RA is slightly modulated by the LSPR, inducing relatively weak electric field localized in the interspace between two Ag nanoshells.
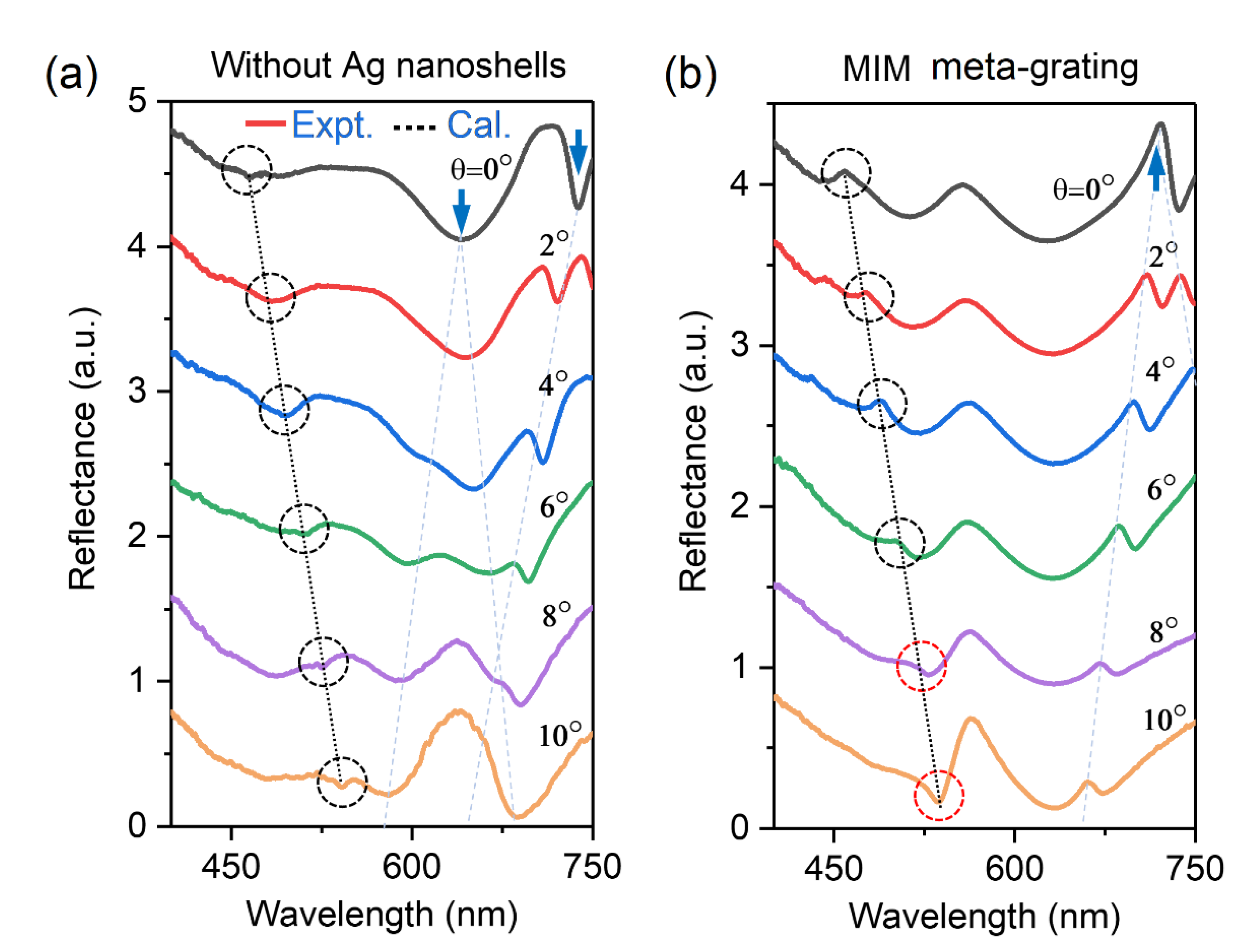
Figures 2(a) and 2(b) show the angle-resolved reflectance spectra of the fabricated samples depicted in Figures 1(b) and 1(c), respectively, with the incident angles turned from 0° to 10°, where the spectral shift of RA resonances are highlighted by series of dotted circular rings. Three obvious features near the RA diffracted wavelengths can be observed: (1) The diffracted wavelengths of RA in experiments are basically consistent with the theoretical calculations as plotted by black dotted lines in Figures 2(a) and 2(b). The central wavelength of RA is determined by the diffraction formula of n P ( s i n θ + 1 ) = λ [24], where n is the refractive index of the environment and n equals 1 when the grating is located in air, P is the grating period, and λ is the diffracted wavelength of RA. Such an angle-resolved behaver further verify their identities of RA diffractions; (2) The RA resonances in dielectric grating are indeed reflectance dips (see Figure 2(a)), while they are reflectance peaks in MIM meta-grating (see Figure 2(b)), except for the resonances as marked by red dotted circular rings where the Fano resonances between RA modes and the broadband plasmonic resonances are disturbed to a certain extent by the intrinsic absorption of gold film; (3) The coupling strengths between RA and the broadband plasmonic mode can be tuned by the incident angles (see Figure 2(b)). Disturbed by the intrinsic absorption of gold film, the coupling strengths have no evident changes at small incident angles (i. e. θ = 0 ° ~ 8 ° ), indicated by weak radiation ability to far field of RA resonances. While, as the incident angle increased to 10 ° , an enhanced reflectance peak near RA mode can be recognized from the spectrum, implying the enhancement of the coupling strengths between such two modes. Meanwhile, we also note other angle-resolved features in Figures 2(a) and 2(b) at the wavelength range of 600-750 nm, which are marked by blue arrows and shallow-blue dotted lines. The angle-resolved features for those resonance modes are basically consistent with that of SPPs, thus, further verify their identities.

2.2. High-Contrast Fano Resonance and Its Application in Reflective Filters

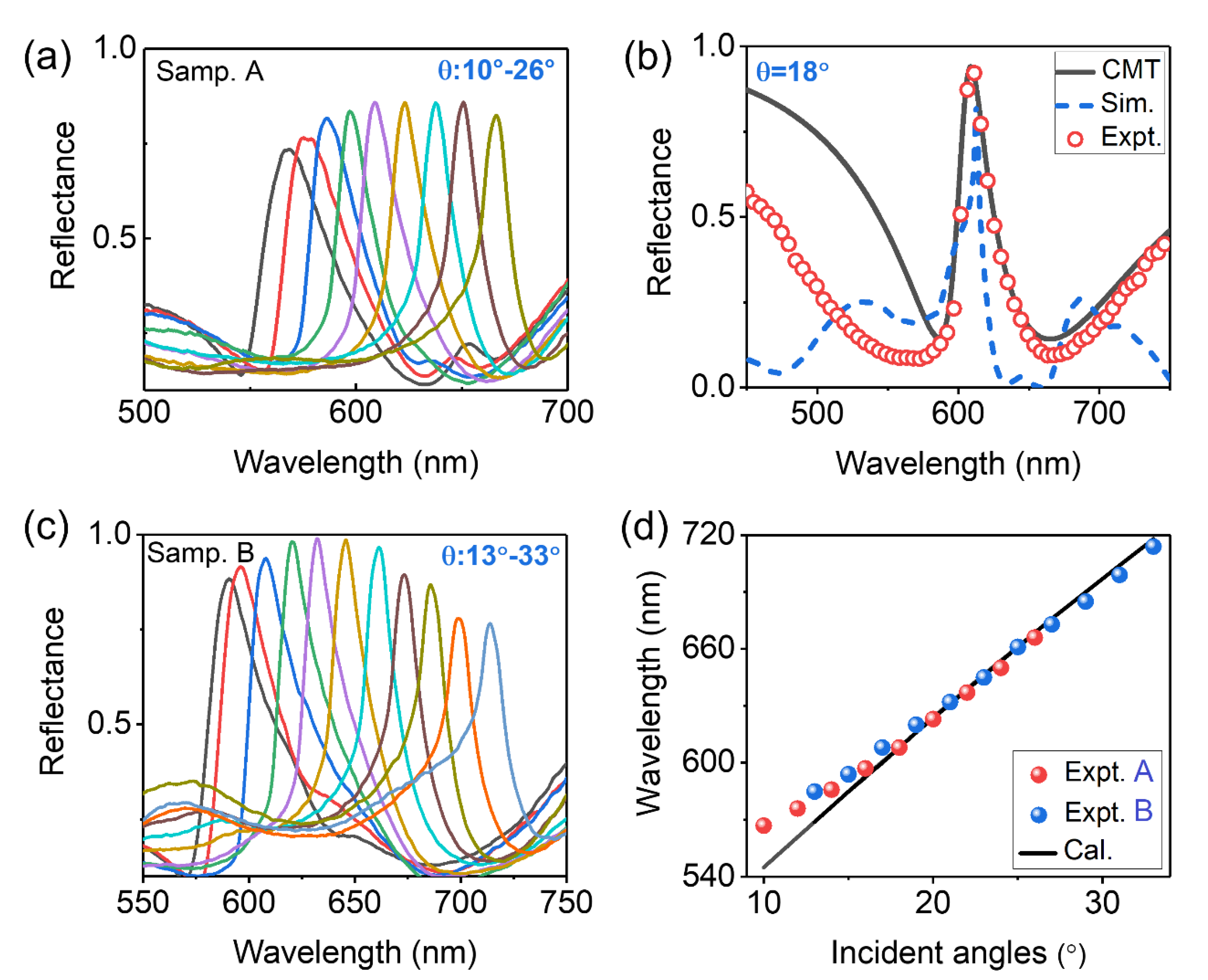
Continuing to increase the angles of incident light, we observe gradually enhanced Fano couplings between RA and the broadband LSPR. Figure 3(a) shows the corresponding angle-resolved reflectance spectra of the MIM meta-grating depicted in Figure 1 (c) with the incident angles turned from 10° to 26°, where the meta-grating is labeled as “Samp. A”. In the angle-resolved spectra, we observe a series of narrowband and high-contrast reflection peaks turned from 567 nm to 667 nm, and with relatively high reflectance changed from 75% to 88%, which imply the gradually enhanced coupling strength between RA and the broadband LSPR. The reflectance reaches to the peak as the RA mode shift to the central wavelength of LSPR (i.e. λ=610 nm ) at the incident angle of θ = 18 ° .
Figure 3(b) shows the corresponding measured and simulated reflectance spectra of Samp. A at θ = 18 ° , which are plotted by red circles and blue dotted curves, respectively. The reflectance of the hybrid RA mode is up to 88%. While, as to strong Fano coupling between RA and the broadband LSPR, the linewidth of the hybrid RA mode in FWHM is increased to about 20 nm. The black solid curve in Figure 3(a) shows the CMT fitting spectrum with parameters as follow: radiation damping of RA and broadband LSPR: ΓRAe=10, ΓLSPRe=25; intrinsic damping of such two modes: ΓRAi=0.5, ΓLSPRi=55; coupling strength between such two resonance modes: t=28. Good agreement can be observed between the measurement and the CMT fitting except for the region of intrinsic absorption of gold film. Obviously, stronger coupling between such two modes enhances the radiation ability of RA mode to a certain degree (ΓRAe turn from 5 to10 as the incident angles increased from 0 ° to 18 ° ), while, it also increases the linewidth of the hybrid mode correspondingly, which is actually not appreciated in biological/chemical sensing applications.
The peak reflectance location of the hybrid RA can be turned by changing the central wavelength of LSPR, which can be verified by the angle-resolved reflectance spectra of the MIM meta-grating labeled as “Samp. B” as shown in Figure 3(c). The central wavelength of LSPR in “Samp. B” is about 630 nm. Therefore, the reflectance reaches to about 100% near the central wavelength of LSPR at the incident angles of 19 ° , 21 ° and 23 ° . Obviously, the hybrid RA in “Samp. B” exhibit higher reflectance (i.e., 76%-100% as the incident angles turned from 13° to 33°). Compared to “Samp. A”, the thickness of the photoresist spacer d2 and the modulation depth of the PR grating h of “Samp. B” are turned to 55 nm and 300 nm, respectively, while, other geometric parameters keep unchanged. Such superior spectral performances of such MIM meta-grating make it promising for the application of high-efficiency and narrowband reflective filters. The diffracted wavelengths of the hybrid RA mode in Figures 3(a) and 3(c) are basically consistent with the theoretical calculation, which are demonstrated in Figure 3(d) and plotted by red (Samp. A) or blue (Samp. B) circles (measurement results) and black solid line (theoretical calculation), respectively.

2.3. Sensor Performances of the MIM Meta-Grating

Benefit both from extremely high RI sensitivity and sharply asymmetric lineshape of RA diffraction, the FOM of such hybrid sensor based on Fano resonance between RA and the broadband LSPR can be described specifically as:
F O M = S R A / ∆ λ R A = P ( 1 + s i n ⁡ ( θ ) ) / ∆ λ R A
where the subscript “RA” denotes the hybrid RA mode. Based on above results, we know that for the MIM metagrating with defined period   P , larger incident angle would introduce two inverse effects. On the one hand, it can effectively increases the sensitivity S R A of the hybrid sensors, on the other hand, it broadens the linewidth of the RA mode due to the strong coupling between RA and the broadband LSPR, and thereby worsening the sensors performances. As for such contradiction, we should find a balance between the sensitivity and linewidth of the resonance mode in such hybrid sensor by carefully controlling the angles of incident light.
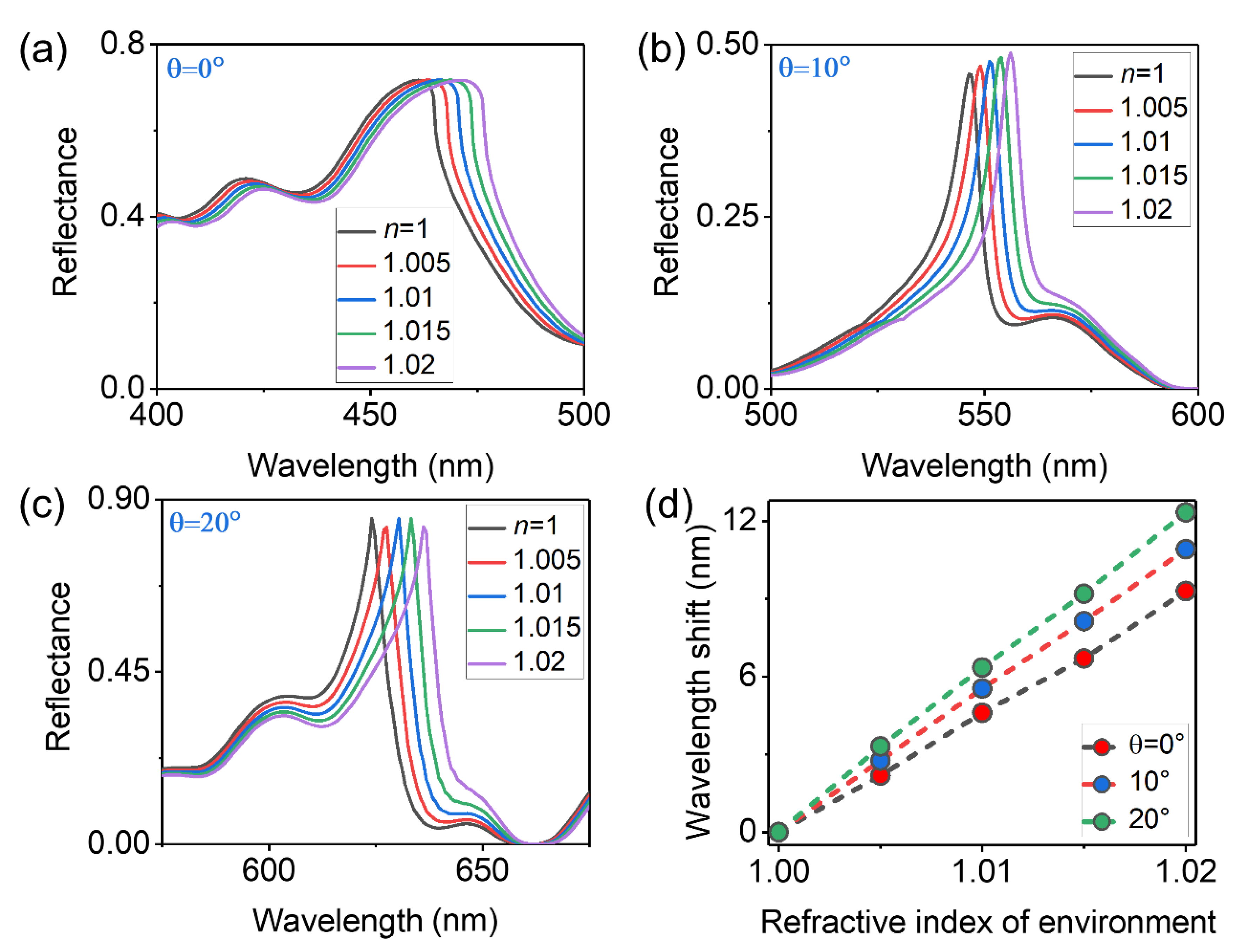
To demonstrate above analysis, we simulate the reflectance spectra of the hybrid sensor immersing in different RI environments for incident angles of θ = 0 ° , 10 ° and 20 ° , and depict them in Figures 4(a)-(c), respectively. The environmental RI are changed from 1 to 1.02 with a small step size of 0.005. It should be mentioned that “Samp. A” is applied in this section, while, the intrinsic absorption of gold is ignored to avoid its influence on sensor performances. As the incident angle is 0 ° , relatively broadband hybrid RA mode due to the degeneracy of ± 1 order RA modes appears at about 465 n m in Figure 4(a) [18]. The sensitivity of the hybrid sensor is about S 0 ° ≈ 474.3 − 465 / 0.02 ≈ 465 n m / R I U , which shows good agreement with the theoretical expectation. As the incident angles increase to 10 ° and 20 ° , the sensitivities of the hybrid sensor increase to about S 10 ° ≈ 556.5 − 545.7 / 0.02 ≈ 540 n m / R I U and S 20 ° ≈ 624 − 636.4 / 0.02 ≈ 620 n m / R I U , respectively. The slight deviation between simulation results and theoretical calculations (i. e., S 10 ° = 545.7     n m / R I U   and S 20 ° = 624     n m / R I U , respectively.) may be due to angular dispersion of the reflectance spectra at large incident angles with relatively broadband source in FDTD simulations. Figure 4(d) summarizes the simulated results and re-plots the wavelength shifts of sensor signal as a function of the environmental RI at incident angles of 𝜃= 0 ° , 10 ° and 20 ° with different colour dotted lines and decorated with different colour circles. It is obvious that the sensitivity of the hybrid sensors at 𝜃= 20 ° is the highest. While, affected by the relatively broad linewidths of the hybrid RA, the FOM of the sensor at 𝜃= 20 ° is not the highest. The simulated linewidths of the hybrid RA at the incident angles of 0 ° , 10 ° and 20 ° are 22 nm, 9 nm, 14 nm, respectively. Correspondingly, the FOM of those sensors are 22, 60 and 44.5. Therefore, the hybrid sensor performs better overall or has higher sensory quality when working at incidence angles of around 10 ° , which can also be demonstrated in the following sensor performances.
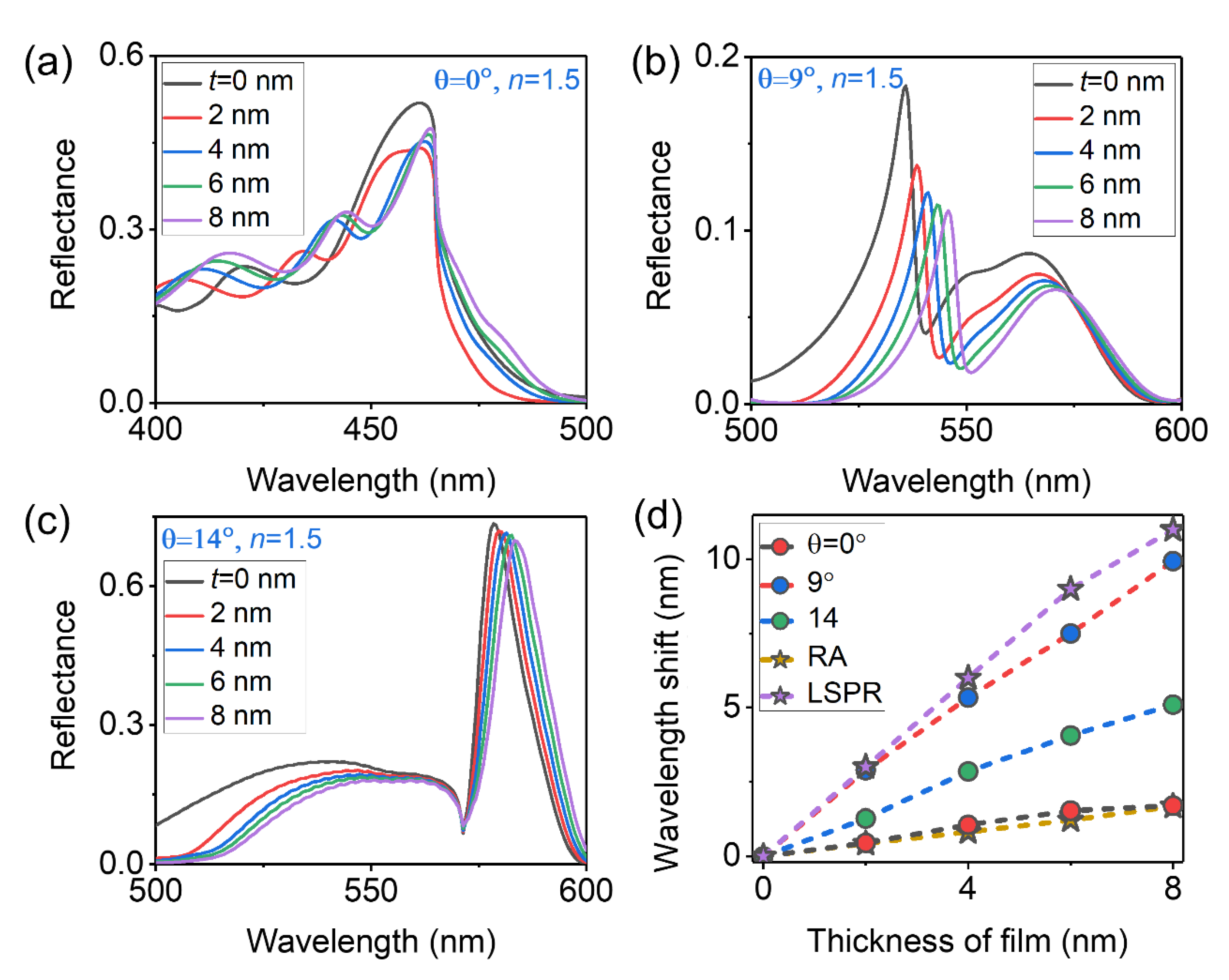
Figure 5(a)-5(c) show the reflectance spectra of the hybrid sensor which is covered uniformly by different thickness of thin film with RI n=1.5 for incident angles of 𝜃= 0 ° , 9 ° and 14 ° , where the thickness of the coating layer are changed from 0 to 8 nm with a step size of 2 nm. Such a scheme is applied to mimic the local RI changes caused by the binding of target molecules on surface of the nano-devices. Through parameter sweeping on the incident angles, we ultimately choose such three typical sensor spectra at 𝜃= 0 ° , 9 ° and 14 ° . Obviously, the hybrid sensor worked at 𝜃= 9 ° is really the best. Figure 5(d) summarizes the simulated results and re-plots the wavelength shifts of sensor signal as a function of the thickness of coating film at incident angles of 𝜃= 0 ° , 9 ° and 14 ° with different colour dotted lines and decorated with different colour circles. Meanwhile, we compare the performance of the hybrid sensor with the simple RA based sensor worked at 𝜃= 9 ° and the broadband plasmonic sensor worked at 𝜃= 0 ° for the sake of fairnessas, which are plotted in Figure 5(d) by different colour dotted line and decorated with yellow and purple pentagonal shapes, respectively. According to the figure of merit for thin layer detecting (i.e. F O M l a y e r * = d λ / ( d l * ∆ λ R A ) with d l denoting the thickness of the coating film) introduced by J. Becker et al.[5], the average F O M l a y e r * of the hybrid sensor worked at 𝜃= 9 ° , the simple RA worked at 𝜃= 9 ° and the LSPR based sensor are about 0.139, 0.024 and 0.0092, respectively. Obviously, the hybrid sensor worked at 𝜃= 9 ° does really perform the best.
Furthermore, simulated results in Figure 5(d) help us understand some more intriguing and important phenomenon. First, the spectral shift now depends on the relative thickness of the molecules to the volume of the resonance modes field penetrates into the medium. Due to strong electric-field enhancement of the LSPR and hybrid RA mode in nanoscale, the sensitivity of those sensors decreases slightly with the increase of film thickness. Therefore, the spectral shift of those sensors as a function of the thickness of thin film are non-linear distributions. Second, LSPR based sensor is the most sensitive to the local RI changes caused by the bonding of thin film, while, affected by the broadband lineshape, the F O M l a y e r * of the LSPR sensor is the lowest. Simple RA based sensor has narrowband linshape, while, it is not sensitive to local RI changes due to RA relatively large mode volume and weak photon state density. Finally, own to both the relatively narrowband lineshape of hybrid RA and its ability to modulate the enhanced electric-intensity distribution near the nanostructure, the FOM of hybrid sensor in detection of local RI changes is enhanced to 6 and 15 times than the simple RA and LSPR based sensors, respectively.

3. Conclusions

We report a dual-function nano-devices based on the tunable Fano resonances between localized surface plasmon resonances and Rayleigh anomaly in a MIM meta-grating. The meta-grating is constructed by silver nanoshells array, an isolation grating mask and a continuous gold film. Both experimental and simulated results show that the coupling behavior between such two modes can be modulated by the angles of incident light in an optimized meta-grating. Strong couplings between LSPR and RA worked at large incident angles form a series of narrowband and high-contrast reflective peaks in a LSPR based dark background, making the meta-grating promising for the application of high-efficiency reflective filter. While, a well-optimized Fano resonance by carefully adjusting the angles of incident light can switch such nano-device to a high-sensitivity sensor with the FOM large than 60 and capability for the detection of bonding molecules by the nanostructures. Simulated results show that the figure of merit of hybrid sensor in detection of local RI changes is 6 and 15 times higher than the simple RA and LSPR based sensor, respectively.

Acknowledgments

This works was supported by the National Natural Science Foundation of China (62005197); Ph.D. startup foundation of Tianjin Normal University (52XB2001) and the scientific research projects of the Inner Mongolian higher educational system (NJZY21290).

References

  1. Anker, J.N.; Hall, W.P.; Lyandres, O.; Shah, N.C.; Zhao, J.; van Duyne, R.P. Biosensing with plasmonic nanosensors. Nat. Mater. 2008, 7, 442–453. [Google Scholar] [CrossRef] [PubMed]
  2. V. Kabashin, P. Evans, S. Pastkovsky, W. Hendren, G. A. Wurtz,et al., Plasmonic nanorod metamaterials for biosensing. Nat. Mater., 2009, 8, 867–871.
  3. K. M. Mayer and J. H. Hafner, Localized surface plasmon resonance sensors. Chem. Rev. 2011, 111, 3828–3857.
  4. Ciracì, C.; Hill, R.T.; Mock, J.J.; Urzhumov, Y.; Fernández-Domínguez, A.I.; Maier, S.A.; Pendry, J.B.; Chilkoti, A.; Smith, D.R.; Ciracì, C.; et al. Probing the Ultimate Limits of Plasmonic Enhancement. Science 2012, 337, 1072–1074. [Google Scholar] [CrossRef] [PubMed]
  5. Becker, J.; Trügler, A.; Jakab, A.; Hohenester, U.; Sönnichsen, C. The Optimal Aspect Ratio of Gold Nanorods for Plasmonic Bio-sensing. Plasmonics 2010, 5, 161–167. [Google Scholar] [CrossRef]
  6. Chen, H.; Kou, X.; Yang, Z.; Ni, W.; Wang, J. Shape- and Size-Dependent Refractive Index Sensitivity of Gold Nanoparticles. Langmuir 2008, 24, 5233–5237. [Google Scholar] [CrossRef] [PubMed]
  7. Tam, F.; Moran, C.; Halas, N. Geometrical Parameters Controlling Sensitivity of Nanoshell Plasmon Resonances to Changes in Dielectric Environment. J. Phys. Chem. B 2004, 108, 17290–17294. [Google Scholar] [CrossRef]
  8. Colombelli, A.; Lospinoso, D.; Rella, R.; Manera, M.G. Tunable Nanoplasmonic Transducers: Performance Analysis and Potential Application. Chemosensors 2023, 11, 109. [Google Scholar] [CrossRef]
  9. Scroccarello, F. D. Pelle, M. D. Carlo, D. Compagnone, Optical plasmonic sensing based on nanomaterials integrated in solid supports. A critical review, Anal. Chim. Acta. 2023, 1237, 340594–1. [Google Scholar]
  10. Shen, Y.; Zhou, J.; Liu, T.; Tao, Y.; Jiang, R.; Liu, M.; Xiao, G.; Zhu, J.; Zhou, Z.-K.; Wang, X.; et al. Plasmonic gold mushroom arrays with refractive index sensing figures of merit approaching the theoretical limit. Nat. Commun. 2013, 4, 2381. [Google Scholar] [CrossRef]
  11. Christ, A.; Tikhodeev, S.G.; Gippius, N.A.; Kuhl, J.; Giessen, H. Waveguide-Plasmon Polaritons: Strong Coupling of Photonic and Electronic Resonances in a Metallic Photonic Crystal Slab. Phys. Rev. Lett. 2003, 91, 183901–183901. [Google Scholar] [CrossRef]
  12. Zhang, X.; Ma, X.; Dou, F.; Zhao, P.; Liu, H. A Biosensor Based on Metallic Photonic Crystals for the Detection of Specific Bioreactions. Adv. Funct. Mater. 2011, 21, 4219–4227. [Google Scholar] [CrossRef]
  13. Ameling, R.; Langguth, L.; Hentschel, M.; Mesch, M.; Braun, P.V.; Giessen, H. Cavity-enhanced localized plasmon resonance sensing. Appl. Phys. Lett. 2010, 97, 253116. [Google Scholar] [CrossRef]
  14. Bahramipanah, M.; Dutta-Gupta, S.; Abasahl, B.; Martin, O.J.F. Cavity-Coupled Plasmonic Device with Enhanced Sensitivity and Figure-of-Merit. ACS Nano 2015, 9, 7621–7633. [Google Scholar] [CrossRef]
  15. Liu, F.; Zhang, X.; Mu, Y.; Lin, J.; Wang, M.; Ma, H. Complementary Dark and Bright Plasmonic Nanocavities with Controllable Energy Exchange for SERS Sensing. Adv. Opt. Mater. 2020, 8. [Google Scholar] [CrossRef]
  16. Hao, F.; Sonnefraud, Y.; Dorpe, P.V.; Maier, S.A.; Halas, N.J.; Nordlander, P. Symmetry Breaking in Plasmonic Nanocavities: Subradiant LSPR Sensing and a Tunable Fano Resonance. Nano Lett. 2008, 8, 3983–3988. [Google Scholar] [CrossRef]
  17. Sonnefraud, Y.; Verellen, N.; Sobhani, H.; Vandenbosch, G.A.; Moshchalkov, V.V.; Van Dorpe, P.; Nordlander, P.; Maier, S.A. Experimental Realization of Subradiant, Superradiant, and Fano Resonances in Ring/Disk Plasmonic Nanocavities. ACS Nano 2010, 4, 1664–1670. [Google Scholar] [CrossRef]
  18. Liu, F.; Zhang, X. Fano coupling between Rayleigh anomaly and localized surface plasmon resonance for sensor applications. Biosens. Bioelectron. 2015, 68, 719–725. [Google Scholar] [CrossRef]
  19. Jia, S.; Li, Z.; Chen, J. High-sensitivity plasmonic sensor by narrowing Fano resonances in a tilted metallic nano-groove array. Opt. Express 2021, 29, 21358–21368. [Google Scholar] [CrossRef]
  20. Choi, B.B.; Kim, B.; Bice, J.; Taylor, C.; Jiang, P. Inverse DVD-R grating structured SPR sensor platform with high sensitivity and figure of merit. J. Ind. Eng. Chem. 2022, 116, 321–330. [Google Scholar] [CrossRef]
  21. Luk'Yanchuk, B.; Zheludev, N.I.; Maier, S.A.; Halas, N.J.; Nordlander, P.; Giessen, H.; Chong, C.T. The Fano resonance in plasmonic nanostructures and metamaterials. Nat. Mater. 2010, 9, 707–715. [Google Scholar] [CrossRef]
  22. Hessel and A., A. Oliner, A new theory of wood's anomalies on pptical gratings, Appl. Opt. 1965, 4, 1275–1297. [Google Scholar]
  23. Eitan, M.; Iluz, Z.; Yifat, Y.; Boag, A.; Hanein, Y.; Scheuer, J. Degeneracy Breaking of Wood’s Anomaly for Enhanced Refractive Index Sensing. ACS Photon- 2015, 2, 615–621. [Google Scholar] [CrossRef]
  24. Feng, S.; Darmawi, S.; Henning, T.; Klar, P.J.; Zhang, X. A Miniaturized Sensor Consisting of Concentric Metallic Nanorings on the End Facet of an Optical Fiber. Small 2012, 8, 1937–1944. [Google Scholar] [CrossRef]
  25. Zhang, X.; Feng, S.; Zhai, T. Energy transfer channels at the diffraction-anomaly in transparent gratings and applications in sensors. Photon- Nanostructures - Fundam. Appl. 2013, 11, 109–114. [Google Scholar] [CrossRef]
  26. Liu, F.; Zhang, X. Contrast- and intensity-enhancement of sensor signals based on Rayleigh anomaly in metal-coated gratings. Opt. Mater. Express 2016, 6. [Google Scholar] [CrossRef]
  27. Qu, C.; Ma, S.; Hao, J.; Qiu, M.; Li, X.; Xiao, S.; Miao, Z.; Dai, N.; He, Q.; Sun, S.; et al. Tailor the Functionalities of Metasurfaces Based on a Complete Phase Diagram. Phys. Rev. Lett. 2015, 115, 235503. [Google Scholar] [CrossRef]
  28. Liu, N.; Mesch, M.; Weiss, T.; Hentschel, M.; Giessen, H. Infrared Perfect Absorber and Its Application As Plasmonic Sensor. Nano Lett. 2010, 10, 2342–2348. [Google Scholar] [CrossRef]
  29. Liu, F.; Zhang, X.; Fang, X. Plasmonic plano-semi-cylindrical nanocavities with high-efficiency local-field confinement. Sci. Rep. 2017, 7, 40071. [Google Scholar] [CrossRef]
  30. Fan, S.; Suh, W.; Joannopoulos, J.D. Temporal coupled-mode theory for the Fano resonance in optical resonators. J. Opt. Soc. Am. A 2003, 20, 569–572. [Google Scholar] [CrossRef]
Preprints 74065 g001
Figure 1. (a) Design scheme of MIM meta-grating constructed by an array of silver nanoshells and a continuous gold film separated by a PR grating mask without developing to the end; (b) and (c): SEM pictures of part of the fabricated sample before and after the deposition of Ag nanoshells on surface of the PR grating; (d) and (e): Measured (red circles) and simulated (blue dotted curve) reflectance spectra of the samples depicted in (b) and (c), respectively, at 𝜃= 0 ° . The black solid curve in (d) denotes the CMT fitting result of the MIM meta-grating; (f): Spectral decomposition of MIM meta-grating, where the red circles denotes the original measurement spectrum of MIM meta-grating. The pink solid curve denotes the CMT fitting result of the plasmonic mode. The blue circles and blue solid curve represent the measured and CMT fitting spectra of intrinsic absorption of gold, respectively; (g) Electric-intensity distribution of the MIM meta-grating at λ≈465 nm and 610 nm, corresponding to the RA and LSPR modes, respectively.
Figure 1. (a) Design scheme of MIM meta-grating constructed by an array of silver nanoshells and a continuous gold film separated by a PR grating mask without developing to the end; (b) and (c): SEM pictures of part of the fabricated sample before and after the deposition of Ag nanoshells on surface of the PR grating; (d) and (e): Measured (red circles) and simulated (blue dotted curve) reflectance spectra of the samples depicted in (b) and (c), respectively, at 𝜃= 0 ° . The black solid curve in (d) denotes the CMT fitting result of the MIM meta-grating; (f): Spectral decomposition of MIM meta-grating, where the red circles denotes the original measurement spectrum of MIM meta-grating. The pink solid curve denotes the CMT fitting result of the plasmonic mode. The blue circles and blue solid curve represent the measured and CMT fitting spectra of intrinsic absorption of gold, respectively; (g) Electric-intensity distribution of the MIM meta-grating at λ≈465 nm and 610 nm, corresponding to the RA and LSPR modes, respectively.
Preprints 74065 g001
Preprints 74065 g002
Figure 2. (a) and (b): Angle-resolved reflectance spectra of the fabricated samples depicted in Figures 1(b) and 1(c), respectively, with the incident angles turned from 0° to 10°. The black dotted line denotes the theoretical calculation of RA diffraction wavelengths.
Figure 2. (a) and (b): Angle-resolved reflectance spectra of the fabricated samples depicted in Figures 1(b) and 1(c), respectively, with the incident angles turned from 0° to 10°. The black dotted line denotes the theoretical calculation of RA diffraction wavelengths.
Preprints 74065 g002
Preprints 74065 g003
Figure 3. (a) Angle-resolved reflectance spectra of the samples depicted in Figure 1(c) and labeled as “Samp. A” with the incident angles turned from 10° to 26°; (b) Measured (red circles), simulated (blue dotted curve) and CMT fitting (black solid curve) reflectance spectra of the samples depicted in Figure 1(c) at 𝜃= 18 ° ; (c) Angle-resolved reflectance spectra of “Samp. B” with the incident angles turned from 13° to 33°, where other geometric parameters of “Samp. B” are same with “Samp. A” except for d2 =55 nm and h=300 nm; (d) RA diffraction wavelength as function of incident angles. The red and blue circles correspond to the measurement results of “Samp. A” and “Samp. B”, respectively. The black solid lines represents the theoretical calculations.
Figure 3. (a) Angle-resolved reflectance spectra of the samples depicted in Figure 1(c) and labeled as “Samp. A” with the incident angles turned from 10° to 26°; (b) Measured (red circles), simulated (blue dotted curve) and CMT fitting (black solid curve) reflectance spectra of the samples depicted in Figure 1(c) at 𝜃= 18 ° ; (c) Angle-resolved reflectance spectra of “Samp. B” with the incident angles turned from 13° to 33°, where other geometric parameters of “Samp. B” are same with “Samp. A” except for d2 =55 nm and h=300 nm; (d) RA diffraction wavelength as function of incident angles. The red and blue circles correspond to the measurement results of “Samp. A” and “Samp. B”, respectively. The black solid lines represents the theoretical calculations.
Preprints 74065 g003
Preprints 74065 g004
Figure 4. (a)-(c): Simulated reflectance spectra of the hybrid sensor immersing in different RI environments turned from 1 to 1.02 for incident angles of 𝜃= 0 ° , 10 ° and 20 ° , respectively. (d) Wavelength shift of the hybrid sensor signal as a function of the environmental RI at incident angles of 𝜃= 0 ° , 10 ° and 20 ° .
Figure 4. (a)-(c): Simulated reflectance spectra of the hybrid sensor immersing in different RI environments turned from 1 to 1.02 for incident angles of 𝜃= 0 ° , 10 ° and 20 ° , respectively. (d) Wavelength shift of the hybrid sensor signal as a function of the environmental RI at incident angles of 𝜃= 0 ° , 10 ° and 20 ° .
Preprints 74065 g004
Preprints 74065 g005
Figure 5. (a)-(c): Simulated reflectance spectra of the hybrid sensor covered uniformly by different thickness of thin film with RI n=1.5 for incident angles of 𝜃= 0 ° , 9 ° and 14 ° , respectively. (d) Wavelength shift of hybrid sensor signal as a function of the thickness of the coating film at incident angles of 𝜃= 0 ° , 9 ° and 14 ° plotted by different colour dotted lines and decorated with different colour circles. The yellow dotted line decorated with yellow pentagonal shapes and the purple dotted line decorated with purple pentagonal shapes represent the performances of simple RA (worked at 𝜃= 9 ° ) and LSPR (at 𝜃= 0 ° ) based sensor, respectively.
Figure 5. (a)-(c): Simulated reflectance spectra of the hybrid sensor covered uniformly by different thickness of thin film with RI n=1.5 for incident angles of 𝜃= 0 ° , 9 ° and 14 ° , respectively. (d) Wavelength shift of hybrid sensor signal as a function of the thickness of the coating film at incident angles of 𝜃= 0 ° , 9 ° and 14 ° plotted by different colour dotted lines and decorated with different colour circles. The yellow dotted line decorated with yellow pentagonal shapes and the purple dotted line decorated with purple pentagonal shapes represent the performances of simple RA (worked at 𝜃= 9 ° ) and LSPR (at 𝜃= 0 ° ) based sensor, respectively.
Preprints 74065 g005
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated