Weak Spatial Target Extraction Based on Small-Field Optical System

Compared to wide-field telescopes, small-field detection systems have higher spatial resolution, resulting in stronger detection capabilities and higher positioning accuracy. When detecting by small-field in synchronous orbit, both space debris and fixed stars are imaged as point targets, making it difficult to distinguish them. In addition, with the improvement of detection capabilities, the number of stars in the background rapidly increases, which puts higher requirements on recognition algorithms. Therefore, star detection is indispensable for identifying and locating space debris in complex backgrounds. To address these difficulties, this paper proposes a real-time star extraction method based on adaptive filtering and multi frame projection. We use bad point repair and background suppression algorithms to preprocess star image. Afterwards, we analyze and enhance the target signal-to-noise ratio(SNR). Then, we use multi frame projection to fuse information. Subsequently, adaptive filtering, adaptive morphology, and adaptive median filtering algorithms are proposed to detect trajectories. Finally, the projection is released to locate the target. Our recognition algorithm has been verified by real star images, and the images were captured using small-field telescope. The experimental results demonstrate the effectiveness of the algorithm proposed in this paper. We successfully extracted hip-27066 star, which has magnitudes about 12 and SNR about 1.5. Compared with existing methods, our algorithm has advantages in both recognition rate and false-alarm rate, and can be used as real time target recognition algorithm for space-based synchronous orbit detection payload.

Keywords:

Subject: Engineering - Aerospace Engineering

1. Introduction

Space targets include celestial bodies, in-orbit satellites, and space debris. As humans continue to launch aerospace equipment into space, more and more space debris is generated by space activities. Due to the long natural decay cycle, various orbital spaces outside the earth are becoming increasingly crowded. The US space surveillance network has catalogued over 40000 space targets, but there are still many smaller space debris that are difficult to observe[1]. These space debris are usually small and very dim. If normally operating spacecraft collides with space debris, space traffic accidents will occur and cause damage or derailment of space equipment[2]. Identifying and locating weak space debris is of great significance for ensuring the safety of space environment and spacecraft.

Space target monitoring methods mainly include radar technology and optoelectronic echnology. Radar technology belongs to active detection, which has the advantage of uninterrupted operation throughout the day. But the limited detection distance and accuracy make it difficult to identify small space debris in high orbit for radar. The advantages of optoelectronic technology are long detection distance and high detection accuracy, which can be used for synchronous orbit debris detection[3]. But it‘s easily affected by weather due to its passive detection mode. Space target detection modes can be divided into ground-based and space-based detection. Usually, different detection methods are combined to form a space surveillance network. The relatively mature technology is the advantage of ground-based detection systems, but they are susceptible to geographical limitations and atmospheric interference[4]. The space-based detection system operates outside the atmosphere, so it can directly receive target radiation energy without passing through clouds, and can detect a wider spatial range [5]. Space-based detection systems have significant advantages over ground-based systems, and therefore will be the main development direction in the future.The algorithm proposed in this article can be applied to the optoelectronic detection of space-based synchronous orbits.

Due to inherent detector noise, cosmic radiation noise and stray light noise generated by interference source, weak targets usually have very low SNR in the image. In addition, due to the weak targets are often small and far away from the camera, they only occupy few pixels and don’t have obvious geometric texture features. In cosmic space, with the increase of stellar magnitude, the number of stars increases exponentially. Therefore, weak spatial targets have extremely complex background. Real time extraction of spatial targets in complex backgrounds with low SNR is currently a research difficulty.

The best method for detecting small targets in sequence images is three-dimensional matching filter, which can maximize the target SNR when the motion information is known[6]. However, when the target prior information is unknown, it requires traversing all paths in all images, which requires a huge computational load and cannot achieve real-time processing. To balance the real-time and reliability of detection, many algorithms have emerged in recent years, attempting to identify small targets as accurately as possible while reducing computational complexity.

Reference[7] proposes a star suppression method based on multi frame maximum projection and median projection, but there will be residual stars after processing, which are difficult to distinguish with weak targets. Reference[8] proposes a star detection method of multiplying adjacent frames after registration, but it‘s difficult to detect weak stars when registration is inaccurate. Reference[9] proposes a star suppression method based on enhanced dilation difference, which solves the problem of edge residue caused by inaccurate registration and star brightness changes, but it may lose weak targets near the star. The above methods are essentially single frame target extraction after fusing several frames of images. Due to the inevitable information loss during the fusion process, the reliability of target recognition is limited.

Reference[10] proposes a spatial object detection algorithm based on robust features, but it's not suitable for weak targets with only a few pixels.Reference[11,12] uses guided filtering to remove stars and identify target motion fringes, but it's difficult to directly generate stable and continuous target fringes in high orbit small-field spatial object detection. References[13,14] use deep learning algorithms to classify targets, but currently the model can only distinguish target motion stripes and point noise under different SNR.Reference[15] proposes a spatial object detection method based on parallax, but this method requires two imaging devices and can only distinguish between targets and stars in synchronous orbits. The multi-level hypothesis testing method proposed in references[16,17] predicts the conversion region through inter frame motion, which can be used to detect continuous or discontinuous target trajectories. However, it's inaccurate and slow in multi target detection. References[12,18] use hough transform to detect target trajectories, but it requires to detect and remove stars in advance. References[19,20] use two-dimensional matched filtering to detect targets, but this method requires traversing paths in different directions, lengths, and shapes in image. Although the computational complexity is smaller than that of three-dimensional matched filtering, it still takes a long time.

Most existing algorithms recognize space targets with wide-view telescopes, but to improve the weak targets detection ability, small-field telescopes need to be used to improve spatial resolution. This article proposes a weak targets extraction method from small-field starry background based on spatiotemporal domain adaptive directional filtering, which achieves low SNR multi-spatial target recognition in small-field ground-based optical system. Due to the complex starry background, identifying stars is a necessary operation before recognizing space debris when both them are imaged as dots. Therefore, this article analyzes the extraction of weak stars in the image, providing necessary technical guarantees for space debris recognition. The overall idea of the article is as follows. Firstly, repair the bad points and suppress the non-uniform background in the image. Secondly, enhancement algorithms are used to improve the SNR of weak stars. Thirdly, compress and extract key information from the sequence images with multi-frame projection algorithm, and iterative thresholding algorithm is used for thresholding processing. Then, use the registration results to construct directional filter operators, which retain trajectory features while filtering out noise. Afterwards, use different morphological operators to perform morphological closure operations to connect the target trajectories. Next, adaptive median filter operators are used to eliminate false trajectories and obtain the final results of star trajectories. Finally, the trajectories obtained from multi-frame projections are deconjected to obtain star detection results for single image.

The method proposed in this article can effectively detect weak stars in images.The maximum detectable magnitude is greater than 11 when using ground-based telescopes. If space-based synchronous orbit detection is used, the relative speed between stars and camera is same as that of ground-based detection. In addition, space-based detection is significantly less affected by noise interference compared to ground-based detection, and weaker spatial targets can be detected under the same conditions. Therefore, the method proposed in this article has important reference significance for weak targets real-time detection in space-based synchronous orbits, spacecraft navigation and space debris identification and cataloging. The structure of this article is as follows. The first section introduces the research background and current situation. The second section introduces weak star recognition methods. The third section introduces the experimental results. The fourth section summarizes the entire text.

2. Target Recognition

The small-field large aperture telescope can improve the angular resolution of the imaging system and fully collect photons. To improve the target imaging SNR while avoiding electron overflow caused by bright stars, we set the camera integration time to 1 second. The motion speed of high orbit space debris and background stars in the image are both slow, so they are imaged as point targets.

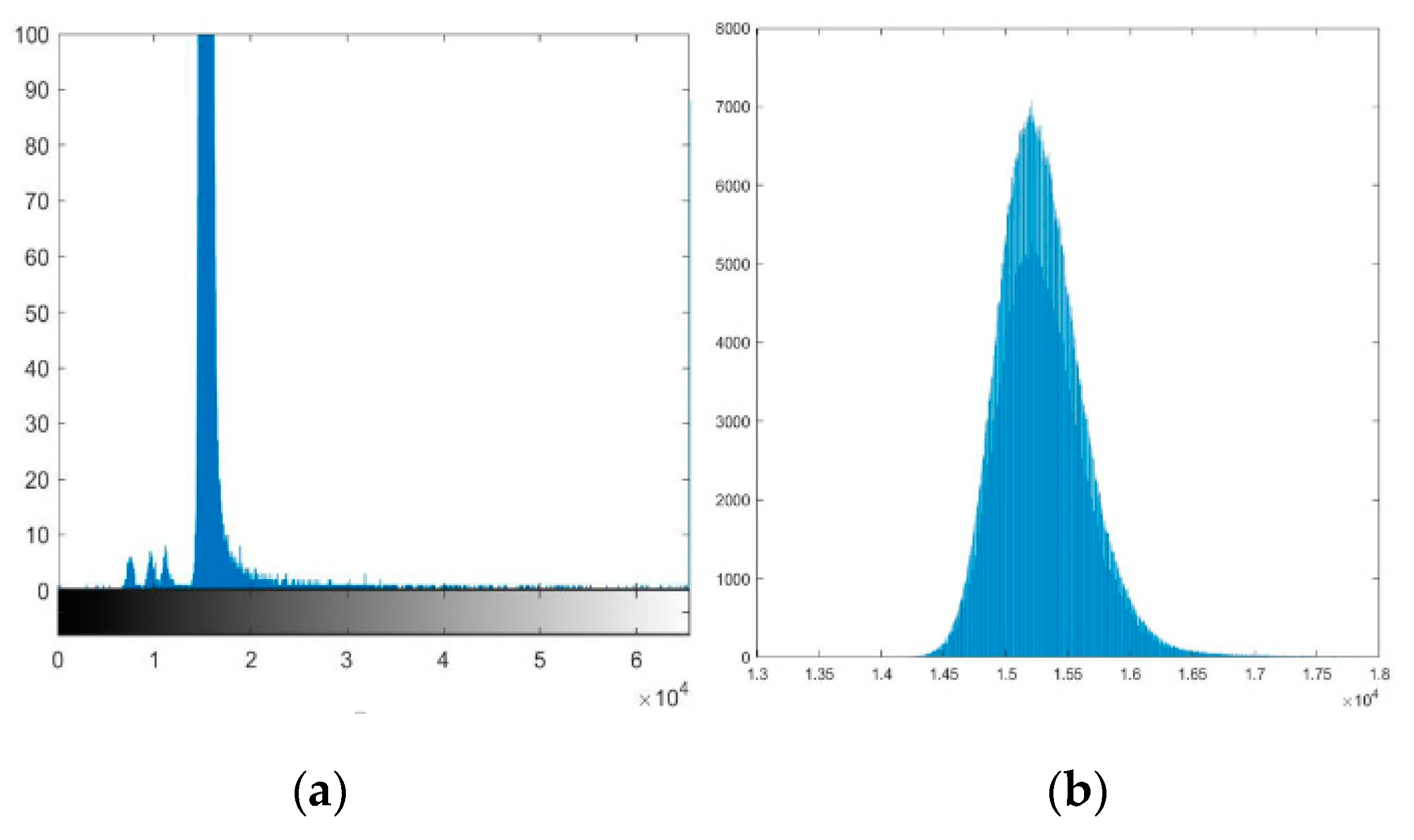
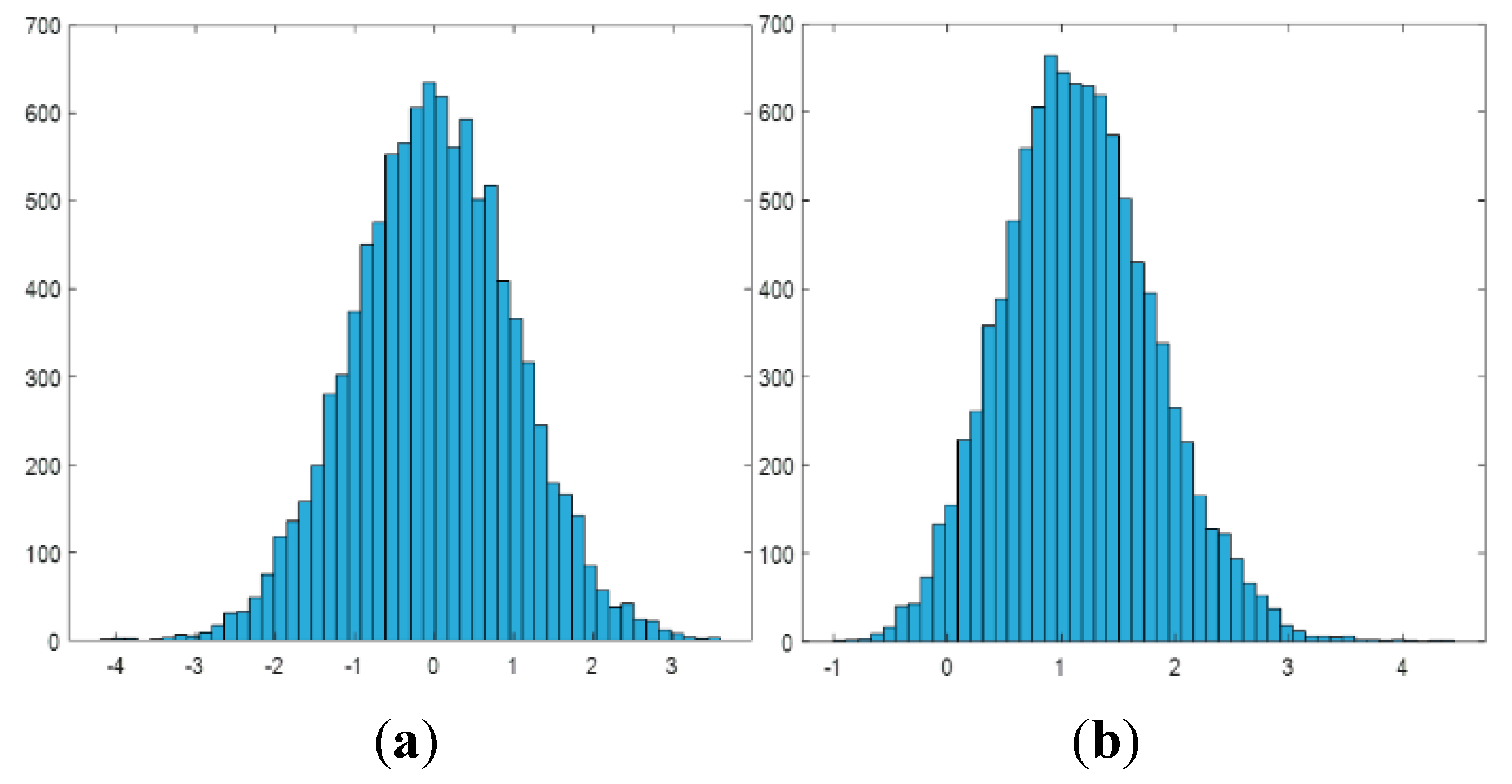
After analyzing the global histogram Figure 1(a) and local histogram Figure 1(b) of the taken image, it‘s found that most pixels are distributed between 14000 and 17000 and roughly obey the Gaussian distribution. According to the local grayscale histogram, it can be seen that the pixels number on right side of the peak is more than that on left side, because there are weak spatial targets submerged in Gaussian noise. If threshold segmentation is directly used, it’s easy to eliminate weak targets and mistakenly identify some noise as targets. Identifying these weak targets that are difficult to distinguish from noise is the significance of this article.

2.1. Bad point repair

The detector inherent bad points are usually caused by defects in the photoelectric conversion array. In order to clearly observe bad points, this article uses large-size morphological operators for corrosion operations. Then it can be seen that there are several black points in the image. Black spots are local pixel anomalies caused by detector defects, which are amplified after morphological corrosion operations. Figure 2 (a) and (b) respectively show the original image and the morphological corrosion image. It can be seen that the grayscale of different bad points are not same. Some points are completely damaged, causing the pixel grayscale to be zero, while others have small grayscale due to low photoelectric conversion efficiency.

The idea of the bad point repair algorithm used in this article is as follows. If the grayscale at same position in multiple consecutive frames are significantly abnormal compared to the neighborhood, then the position is determined as a detector bad point, and the grayscale is set to the mean of it's neighborhood. Figure 2 (c) and (d) respectively show local enlarged images before and after bad points repairment.

2.2. Background correction

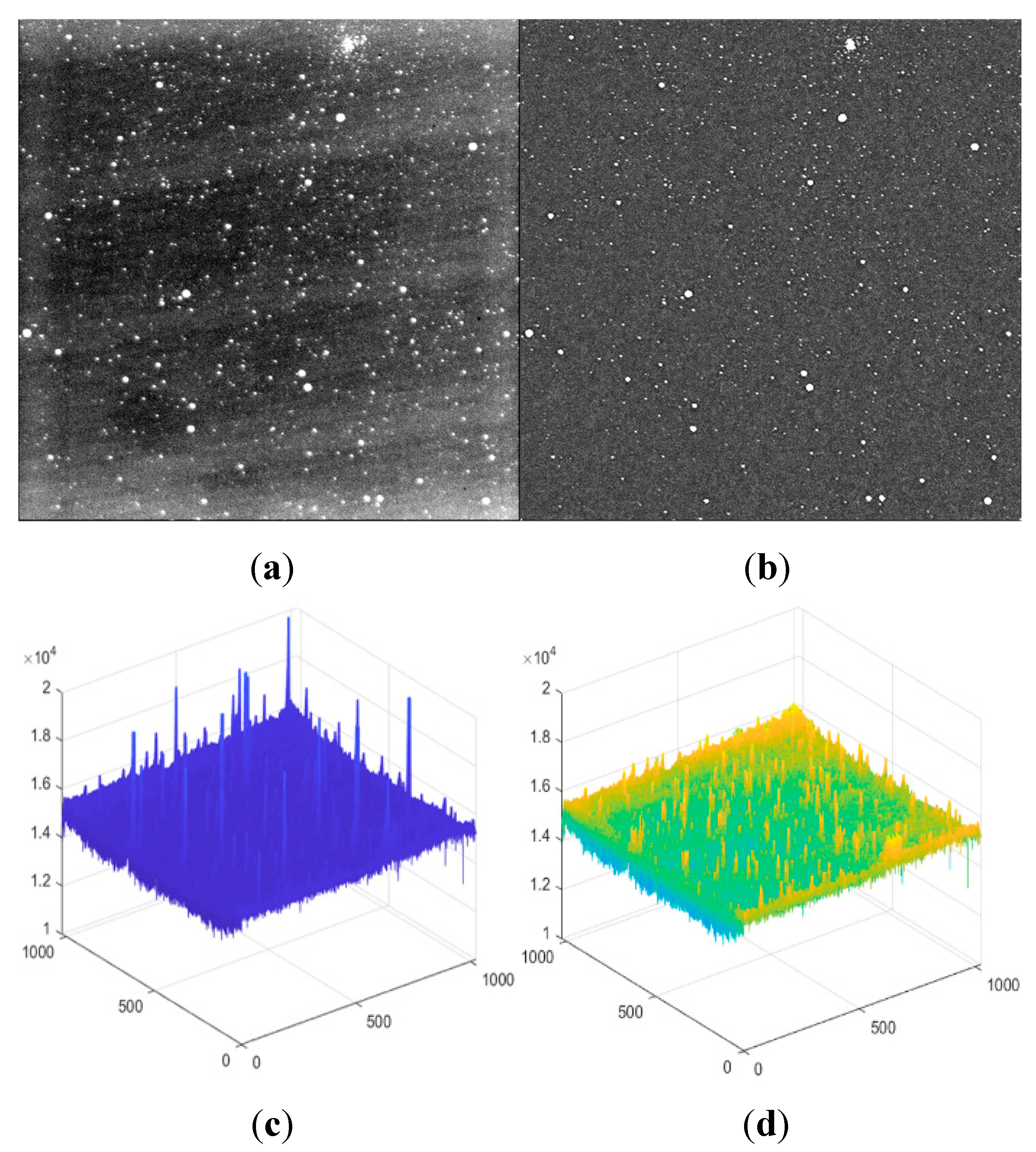
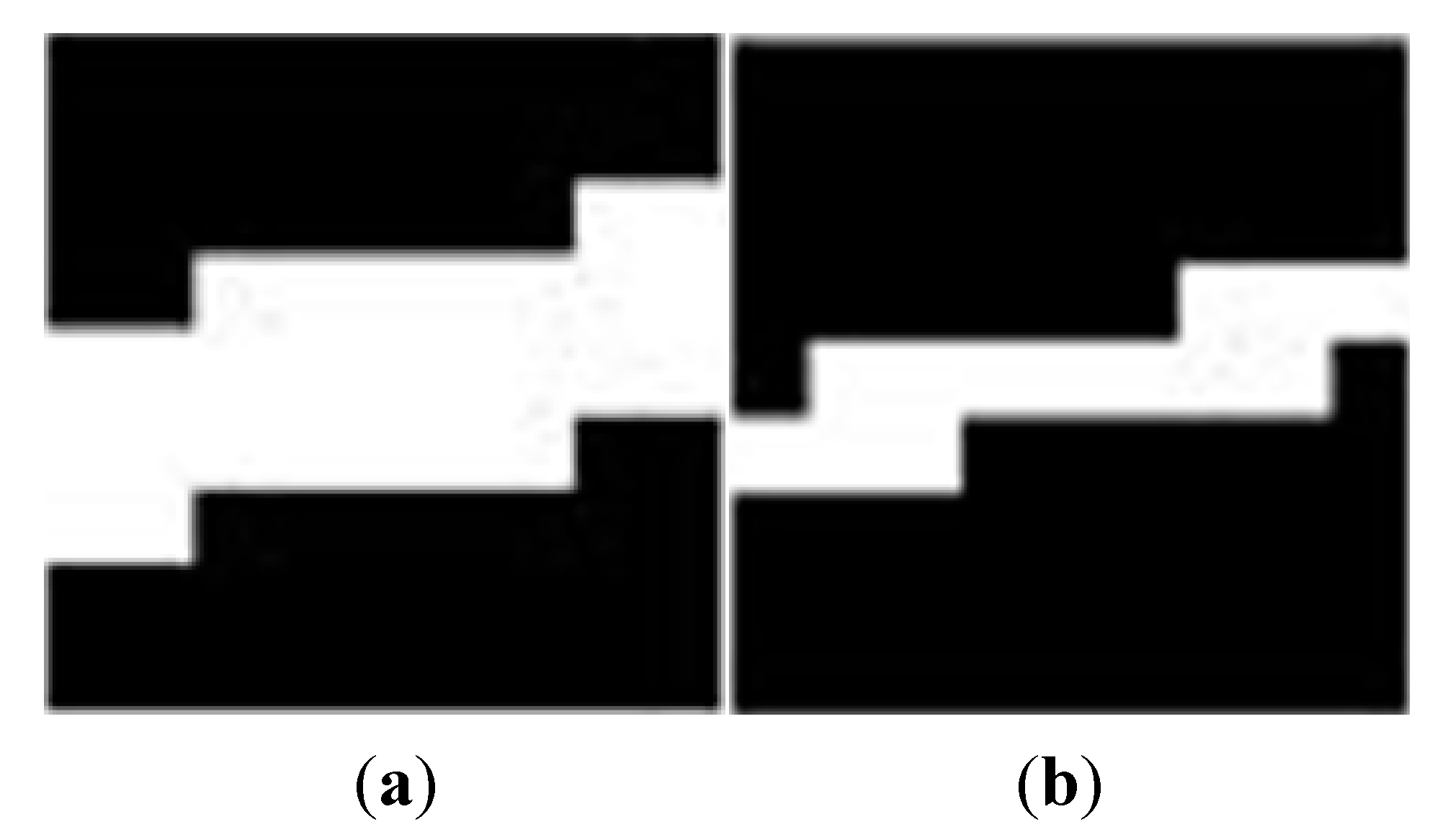
Due to the weak stray light in cosmic environment and non-uniform response of the detector, the starry image background is not uniform. Although it‘s difficult for the human to directly observe non-uniformity with their eyes, its impact on weak target recognition is significant. To observe the non-uniform background more intuitively, Figure 3 (a) display the image in a partial grayscale range. It can be seen that the image edges are severely affected by stray light, and there are also stripe backgrounds formed by non-uniform response.

Morphological operation is a commonly used method for detecting background[21]. But when the operator size is small, some larger stars will be mistaken for the background. If the size of operator is increased, although the above phenomenon will decrease, the background estimation will be inaccurate, which is unacceptable in small target detection. To improve the performance of small-size operators, this paper proposes an improved morphological background estimation algorithm. After obtaining the preliminary background through morphological operation, determine the threshold based on its mean and variance. Then replace the grayscale which greater than the threshold with mean of its neighborhood. After correcting the background through the above operation, subtract it to eliminate non-uniformity. Figure 3 (b) shows the image after non-uniformity correction, (c) shows the three-dimensional image of preliminary estimated background, and (d) shows the three-dimensional image of final estimated background.

2.3. Image Enhancement

In low-orbit target detection, due to the fast motion speed of targets, camera can usually obtain the target motion fringes within the integration time. Currently, many works use the motion information contained in fringes to identify the target. However, in high-orbit target detection, the target movement is slower and usually can only obtain point targets within a limited integration time.

When detecting weak targets, there is a significant difference in energy between bright and dark stars. When the exposure time is long, CCD will easily occur electron overflow around bright stars, leading to overexposure. This will create bright stripes on the image and cause significant interference with target recognition. Figure 4 shows the overexposed image after extending the integration time. Therefore, it‘s difficult for cameras to increase the integration time too much to detect weak targets. The image used in this article has an integration time of one second.

Within a certain time range, the longer camera exposure time, the higher weak target SNR in the image. But when there are target dragging or streaks in the image, the target SNR will no longer increase and gradually decrease. Because at that time, the noise energy accumulates but the signal energy remains unchanged.

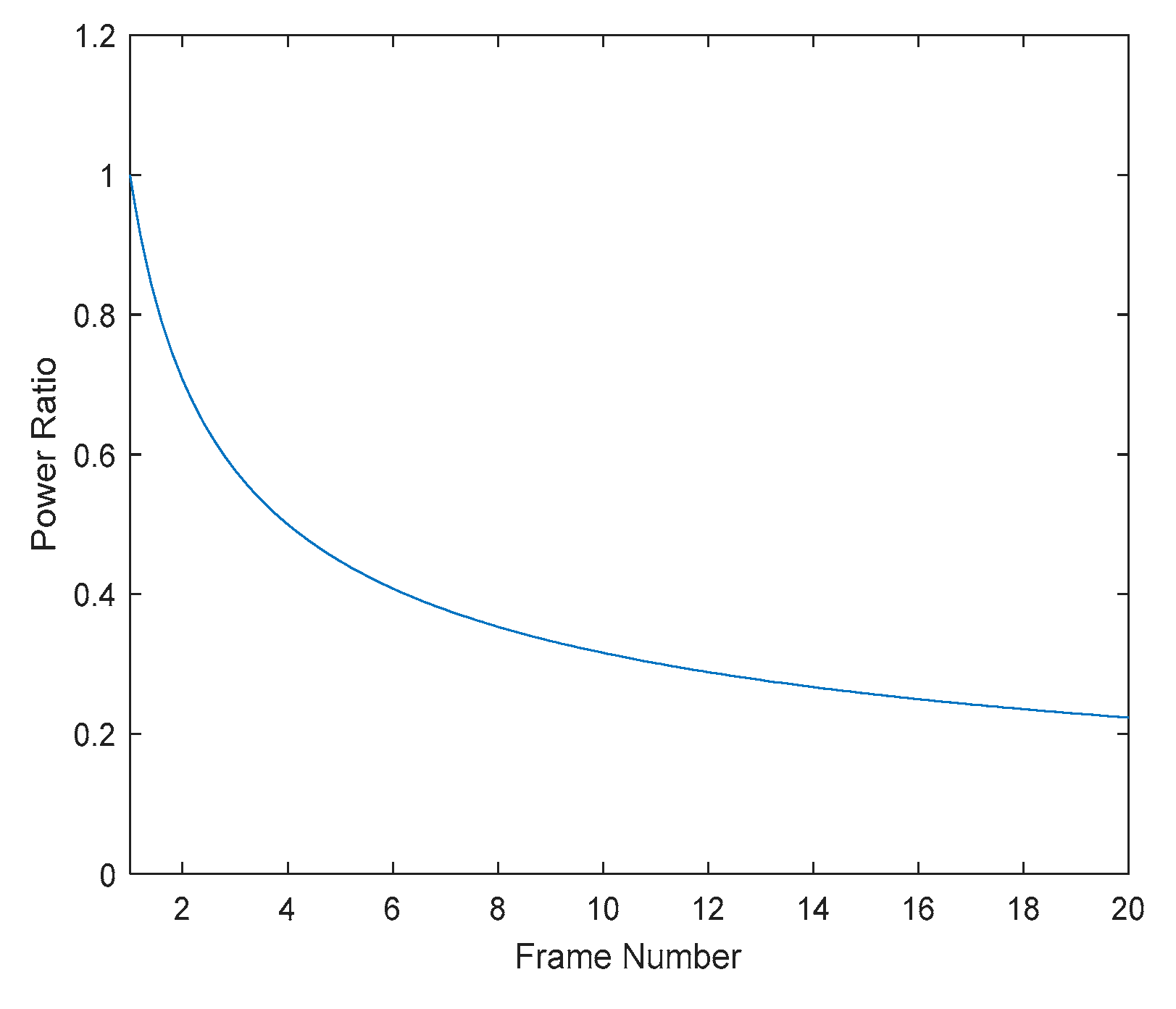
To improve the SNR of weak targets, this article uses a multi-frame image enhancement algorithm. Utilizing the principle of correlated target signals but uncorrelated noise signals after registration, multiple frames of images are accumulated. After accumulating N frames, the target signal is increased by N times, and the noise variance is increased by N times. According to the SNR calculation formula(1), the total SNR is increased by

\sqrt{N}

times[22]. Figure 5 shows the ratio curve of noise power between N-frame enhance image and the original image.

{S N R}_{N} = \frac{N \cdot {S N R}_{0} \cdot σ_{0}}{\sqrt{N \cdot {σ_{0}}^{2}}} = \sqrt{N} \cdot {S N R}_{0}

(1)

If the target motion speed is v(pixel/s), the target SNR reaches maximum when the camera integration time is 1/v. Assuming the optimal signal noise ratio is SNR, and the noise variance is

σ_{0}

. If the camera integration time is t which is larger than 1/v, the signal noise ratio of the stripe target is calculated as equation (2). If t is smaller than 1/v, the signal noise ratio of the point target is calculated as equation (3).

{S N R}_{0} = \frac{S N R \cdot σ_{0}}{\sqrt{t \cdot v \cdot {σ_{0}}^{2}}} = \frac{S N R}{\sqrt{t \cdot v}}

(2)

{S N R}_{1} = \frac{t \cdot v \cdot S N R \cdot σ_{0}}{\sqrt{t \cdot v \cdot {σ_{0}}^{2}}} = \sqrt{t \cdot v} \cdot S N R

(3)

When using (

1 / t \cdot v

) frames to enhance point target, the SNR increased by

1 / \sqrt{t \cdot v}

times compared to the original image, which can achieve the optimal SNR. When the number of frames used for enhancement is more than (

1 / t \cdot v

), the enhanced target SNR will be better than the optimal target SNR of single frame. From this, it can be seen that the target SNR after enhancement of multi frame short exposure image may be better than the target stripe SNR obtained by long exposure time.

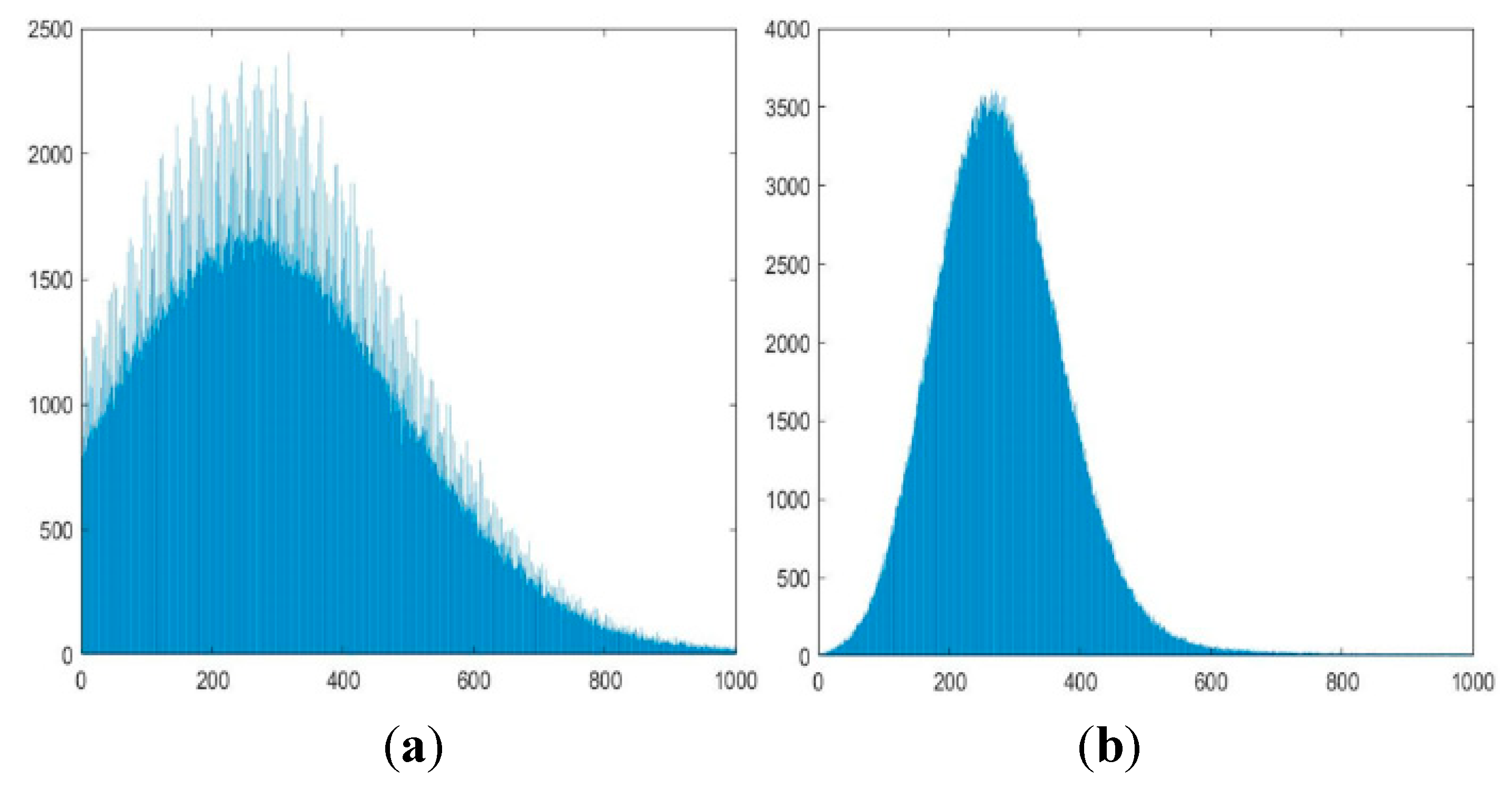
Considering that the more images used for enhancement, the smaller their common sub images will be, also balancing real-time and reliability, this article selects consecutive 5 frames for enhancement. Add the five registered images to get the target enhancement image. Due to the small variance variation, the intuitive changes in the image are difficult to observe. From the grayscale histogram shown in Figure 6, it can be seen that the noise variance of enhanced image is significantly reduced compared to before, and more small targets are no longer submerged in the noise.

2.4. Multi frame projection

Through the analysis in section 2.4, it can be concluded that short exposure point targets may have a better SNR than long exposure stripe targets after multiple frame enhancement. However, point targets don’t have the motion information contained in striped targets, which makes it difficult to accurately extract them from noisy images even with high SNR. In order to quickly extract target motion information, this article uses multi-frame projection to fuse information from several images, so that the target forms stripes in the image, which is conducive to extracting weak targets from noise.

Reference[23] derives the optimal projection operator, the operator expression(4) is as follows. Where

z_{0}

is the pixel value after projection, N is the number of projected frames,

r (i, j, t)

is the grayscale value of a certain frame at position

(i, j)

, and S is the SNR of this point. Due to the need to estimate the SNR of each point, a significant amount of computation is required during projection.

z_{0} (i, j) = l n [\sum_{t = 1}^{N} e^{S \cdot r (i, j, t)}]

(4)

Reference[24] points out that when the length of the signal trajectory is M and the signal noise ratio of the target signal is SNR, if the number of projected frames is N, then the output signal noise ratio of full dimensional matched filter is

\sqrt{M} \cdot

SNR, the output signal noise ratio of two-dimensional matched filter after summation projection is

\sqrt{M} \cdot

SNR/

\sqrt{N}

. It's difficult to obtain an analytical solution for the output signal noise ratio after optimal projection and maximum projection. The output SNR after projection are all lower than that of full dimensional matched filtering, which is an inevitable result of partial information loss after multi-frame information fusion. When the SNR of original image is low, the output SNR of optimal projection and summation projection are similar, and the loss are both large. When the SNR of original image is large, the output SNR of optimal projection and maximum projection are similar, and the loss are both small. Equation(5) is the mean projection expression, Equation(6) is the maximum projection expression, where K is the number of projection frames.

z_{1} (i, j) = m e a n [r (i, j, k)], (1 \leq k \leq K)

(5)

z_{2} (i, j) = m a x [r (i, j, k)], (1 \leq k \leq K)

(6)

Due to we use five consecutive images in target enhancement module, the output SNR of maximum projection and average projection of five frames are quantitatively analyzed. Because of the high computational complexity, the optimal projection is discarded. Using five unrelated noise images that follow the normal distribution

(μ, σ)

, we statistically analyze the noise distribution after maximum projection. The experiment shows that it roughly follows a normal distribution (

μ

+1.16

σ

,0.66

σ

). Figure 7 shows the grayscale histogram of the noisy image before and after projection.

Assuming the target grayscale is x, then equation(7) is the expression for the target SNR before projection, equation (8) is that after maximum projecting. According to the formula, when x > (

μ + 3.4 σ

), the target SNR is improved compared to the original image. So when using the maximum projection algorithm, if the target SNR is large, it can be further improved. If using the mean projection, then equation(9) is the expression for processed target SNR. According to the formula, the image SNR after processing is always smaller than that of original image. After comparing the two projection methods, it can be concluded that when x>

(μ + 2.37 σ)

, the target SNR after maximum projection is higher.

{S N R}_{2} = \frac{x - u}{σ}

(7)

{S N R}_{3} = \frac{x - (μ + 1.16 σ)}{0.66 \cdot σ}

(8)

{S N R}_{4} = \frac{(x - u) / 5}{σ / \sqrt{5}}

(9)

The appropriate projection method can be selected based on the target SNR. The remaining part of this article selects the maximum projection method, which also has the advantage for conveniently releasing projection, which will play a significant role in target localization. Figure 8 (a) and (b) respectively show the results of mean and maximum projection by five frames.

2.5. Threshold processing

The threshold segmentation algorithm is used to eliminate unwanted background grayscale and residual noise. The commonly used threshold algorithms include the maximum inter class variance method, iterative threshold method, and adaptive threshold method[25]. But these methods only work well when there are two peaks in the histogram. In the grayscale histogram of starry image, there are usually single peaks composed of noise, and the target is scattered irregularly on larger grayscale values without forming peaks. This article improves on the traditional adaptive threshold method and proposes an iterative adaptive threshold algorithm.

First, calculate mean

(μ)

and variance

(σ)

of the starry image, and use

(μ + 3 σ)

as the threshold for preliminary threshold processing. Then, the mean

(u_{1})

and variance

(σ_{1})

of grayscale exceeding the threshold are counted, and the threshold is processed again using

(u_{1} + 3 σ_{1})

. After, iteratively calculating the threshold in this way. According to

3 σ

-Criterion, stop iteration when the difference between new and previous threshold is less than 0.15%.

Using the iterative threshold method to process starry image, the results are shown in Figure 9. The threshold remains basically unchanged after approximately three iterations. After successfully estimating the background variance

(σ_{0})

of the original image, the image is processed with

(u_{0} + n σ_{0})

as the threshold, where

u_{0}

is the mean of the projected image. The value of n determines the SNR of detectable targets in the original image. If n is too large, it‘s not conducive to weak target recognition. If n is too small, it increases the false alarm rate and computational burden.

2.6. Directional filtering

To reduce the computational burden, the camera's image acquisition rate is set to 2s/frame, which makes some trajectories discontinuous. In addition, noise interference also makes it difficult to extract trajectories. In response to the above difficulties, this article proposes an adaptive directional filtering method. The specific steps are as follows. Firstly, use adaptive filtering operator for neighborhood submaximum filtering to preliminarily reduce noise. Then, use the adaptive morphological operator to connect trajectories. Finally, the adaptive median filtering is used to eliminate false trajectories and residual noise.

According to the method described in section 2.5, we use 1.2 as the value of n to threshold the projected image. After threshold processing, continuous or discrete target motion trajectories are formed, while false target and noise appear as points. Median filtering belongs to nonlinear filters and is a commonly used noise removal algorithm. However, when processing multi-frame projection images, the median filtering algorithm is prone to destroying trajectories. Reference[12] proposes an improved median filtering algorithm, while reference[13] proposes a local threshold filtering method. These methods have improved compared to traditional median filtering in processing starry image, but there are still some shortcomings.

In this paper, an adaptive filter operator is proposed. Based on the results of image registration and the distance from points to ideal straight line, the best operator can be found. The specific implementation method is as follows. Taking the filtering operator center as fixed point, calculating the slope based on the registration result, an ideal straight line is made within the filtering operator. Then, calculate the distance from all pixels to the ideal line in the filtering operator, and select m pixels with shorter distances to form the filtering operator. Figure 10 (a) shows the construction principle of 5×5 filter operator, and the size and effective pixel number(m) of operator can be set as needed.

In this article, C is defined as the maximum translation parameter of adjacent frames. Taken (6C+1) as the adaptive filtering operator size, which can ensure when there are discontinuous breakpoints, the trajectory will not be damaged. The effective pixels number within the filtering operator is set to 2 (6C+1). The filtering value is taken as the second largest value in the neighborhood, which increases the filtering stability. Figure 10(b) is the filtering operator used in this article. Perform logic and operation on the images before and after adaptive filtering to obtain the filtering results. Repeat the above filtering process until the image grayscale no longer changes. If the original projection graph is M and the filtering operator is

F

, then equation(10) is the calculation expression for the directional filtering graph(DF), where

*

is the filtering operation.

D F = M, D F = l o o p ((D F * F) & D F

u n t i l (D F = l o o p ((D F * F) & D F))

(10)

Figure 11(a) and Figure 11(b) show the local enlarged images before and after filtering. After using the method proposed in this paper, the trajectory features were successfully preserved while filtering out isolated noise. To demonstrate the superiority of our method, we compare it with improved median filtering algorithms and local threshold filtering methods. Figure 11(c) shows the image obtained after improved median filtering, with a small amount of target trajectories being damaged. Figure 11(d) shows the image obtained after local threshold filtering. Although it can retain most trajectories information while filtering out noise, it still has a significant impact on discontinuous trajectories. Our algorithm has significant advantages.

2.7. Trajectory detection

After filtering out isolated noise points, the trajectory is connected using large expansion operator and small corrosion operator. All morphological operators are constructed using the adaptive method described in section 2.6. The size of expansion and corrosion operators are both (2C+1), which can connect the broken line and ensure the line length before and after processing are same. The effective pixel number of dilation operator is set to 3 (2C+1), and the effective pixel number of corrosion operator is set to (3C+1). Thinner corrosion operator can avoid line breakage. Equation(11) is the calculation expression for the trajectory connection image (CT), where A is the expansion operator and B is the corrosion operator,

\oplus

is the expansion operation and

⊝

is the corrosion operation. Figure 12(a) and Figure 12(b) respectively show the morphological dilation operator and corrosion operator used in this paper.

C T = D F \oplus A ⊝ B

(11)

Figure 13(a) and Figure 13(b) respectively show the enlarged images using adaptive morphological operators of expansion and post expansion corrosion. All trajectories in Figure 13(b) are connected after morphological closure operations.

After connecting trajectories through morphological closed operations, iterative adaptive median filtering is used to remove false trajectories and residual noise, resulting in continuous trajectory detection results. The median filtering operator size is (4C+1), which can filter out false trajectories that are too short. The effective pixels number within the operator is 2 (4C+1). Median filtering used in this article don't take the median value, because the best effect is achieved when taking the value at 2/3 positions sorted from smallest to largest. Perform logic and operation on the images before and after adaptive median filtering to obtain the filtering results. Repeat the above filtering process until the image no longer changes. Equation(12) is the calculation expression for the median filtering image MF, where

*

is the median filtering operation and

C

is the median filtering operator. Equation(13) perform logic and operation between the median filtering image MF and directional filtering image DF to obtain the final trajectory image FT.

M F = C T, M F = l o o p ((M F * C) & M F)

u n t i l (M F = l o o p ((M F * C) & M F))

(12)

F T = M F & D F

(13)

2.8. Target positioning

This article applies deprjection operation for the maximum projection image to extract stars from single frame. Given the maximum projection image

z_{2} (i, j)

, the release projection image(

R_{i}

) of each frame can be calculated. Equation(14) is the calculation method for the release projection image of fifth frame. By performing dot product operation on the trajectory image FT and the fifth frame release projection image(

R_{5}

), the star positioning image of fifth frame can be obtained. Equation(15) is the calculation expression of positioning image(

L_{5}

). Figure 15 shows the star positioning image and its partially enlarged image.

R_{5} (i, j) = \{\begin{matrix} z_{2} (i, j), r (i, j, 5) = z_{2} (i, j) \\ 0, r (i, j, 5) \neq z_{2} (i, j) \end{matrix}

(14)

L_{5} (i, j) = R_{5} (i, j) \cdot F T (i, j)

(15)

3. Experimental Result

In this section, we analyze the recognition rate, false alarm rate and limit detection performance of the proposed method through experiments. The self-developed optical system used in the experiment has the field of 3.17 °×3.17 °, 240mm focal length and 150mm aperture. The detector using e2v CCD47-20, which has 1024×1024 pixels, 13.3mm×13.3mm focal plane, 13um pixel size, 11.18'' pixel resolution, and 16 bit AD quantization during image readout. Image processing is carried out in MATLAB R2017b, the computer processor is Intel(R) Core(TM) i5-7300HQ CPU(4-core, 2.5GHz) with 8GB memory. On the existing experimental platform, the algorithm can complete the operation within 4 seconds.

We use the Hipparcos catalog to test the recognition rate and ultimate magnitude recognition ability of our algorithm. Although the catalog contains stars that has magnitude up to 12, it can‘t be used to calculate false alarm rates, because it only has complete stars for 9 magnitude. We use the triangle matching algorithm[26] to match starry image without prior information. If the matching fails, reselect the points. 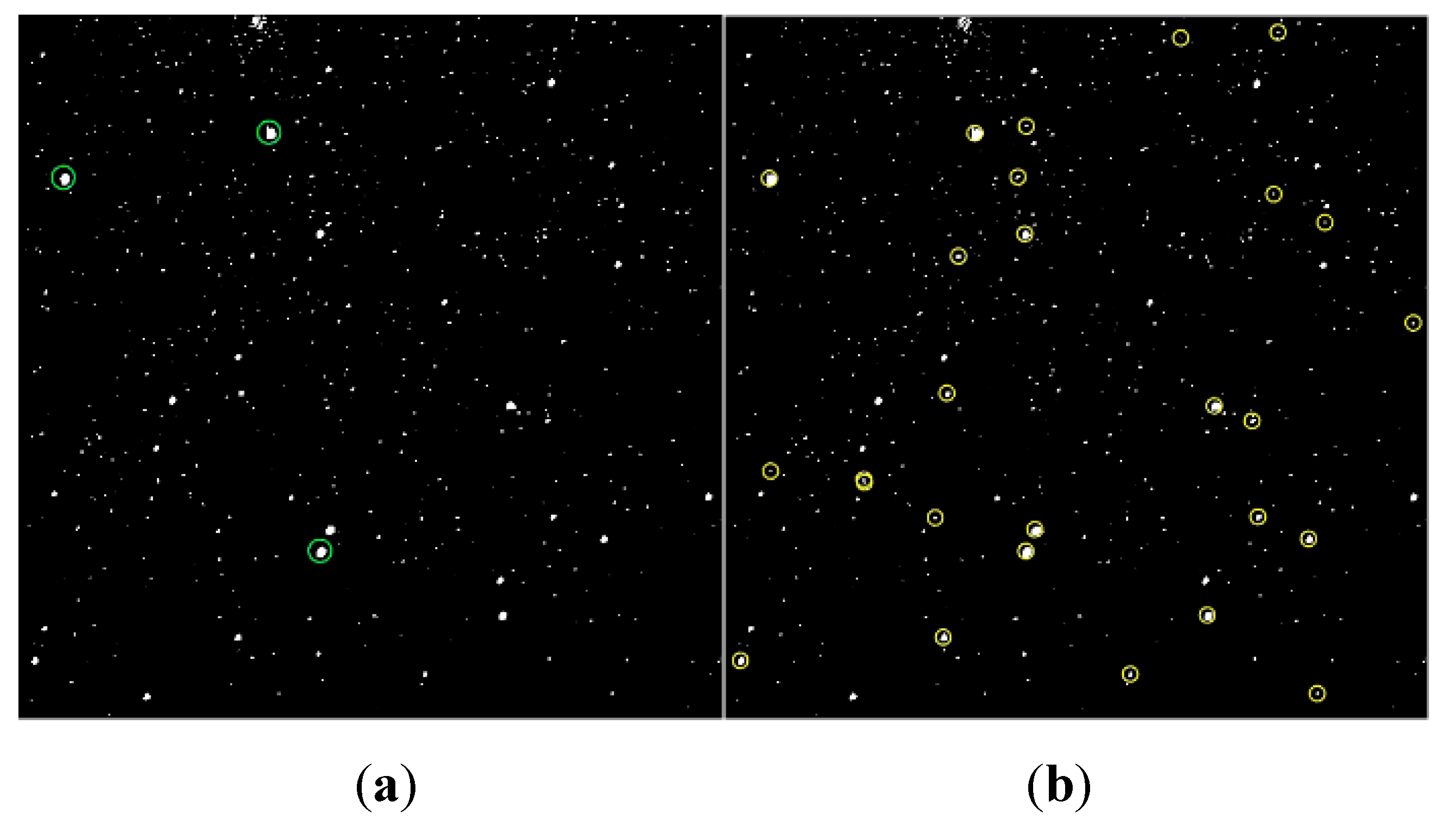When the matching results are not unique, select fourth point and use the pyramid matching algorithm[27]. If the matching is successful, the attitude matrix is calculated based on the matching results, the right ascension and declination of all the stars in image are located. Then, all the stars are identified by matching with Hipparcos catalog. The stars used for matching are marked in Figure 16(a). The successfully identified stars are marked in Figure 16(b) with a recognition accuracy of 0.01°. Due to the flipped imaging of camera, Figure 16 has been corrected compared to the original taken image.

Based on the camera pointing, camera FOV and the star catalog, we create the ideal image Figure 17(a) which only contains stars. The image rotation is calculated by using the image registration algorithm, and Figure 17(b) is obtained after correcting the ideal image. Because the image rotation difference between ideal and actual image, the two images differ slightly at the edge. Except for the M37 nebula in the upper part of image, which is difficult to identify due to centroid positioning errors, other stars in Hipparcos catalog are successfully identified. The success rate of single frame recognition reaches 96.3%.

In Figure 18(a), two stars with magnitudes higher than 11 are marked. They are numbered as hip-27066 and hip-27825 in Hipparcos catalog. They approximately have 16000 grayscale and 1.5 SNR in the image. These two are the weakest stars in Hipparcos catalog within this sky region, occupying less than 10 pixels, and both have been successfully identified. Figure 18(b) is the partially enlarged image of Figure 18(a).

Due to the lack of the complete star catalog, it's difficult to use star matching method to verify the false alarm rate of our algorithm. In this section, we associate the star extraction results from adjacent frames. After removing new stars entered and exited, if a certain star doesn't have a mapping relationship between adjacent frames, the detection result is regarded as false alarm. The mapping criteria between two stars are designed as follows. Their centroid error less than 1 pixel, size error less than 20% and brightness error less than 20%.The statistical method for false alarm rate is not entirely reliable and is only for reference. Table.1 shows the detection results of stars with different SNR. To demonstrate the superiority of the proposed method, we used median projection method(MP) and inter frame multiplication method(IFM) to detect stars within the same region. The detection results of stars with different SNR are recorded in Table 2 and Table 3.

Our method not only has a lower false alarm rate and higher recognition rate compared to existing algorithms, but also has advantages in star brightness extraction and size extraction. The stars detected by MP have different brightness from the actual stars, which can‘t effectively remove stars from the original image. When the star brightness changes, the stars detected by IFM are prone to deformation, which will cause significant errors in centroid positioning.

4. Conclusion

In this article, we propose a star detection algorithm based on small-field telescope, which can achieve real-time detection of stars with SNR of 1.5 or higher, and its performance meets the requirements of space surveillance systems. With the improvement of optical system detection ability, the number of background stars in the image increases exponentially. When space debris and stars are both imaged as point targets, it’s difficult to distinguish between them. Therefore, high-precision star detection is a prerequisite for space debris recognition. Our proposed background correction algorithm can maintain target energy while removing stray light. The multi-frame enhancement algorithm can increase the target SNR to no less than that obtained from long exposure imaging. Multi-frame projection algorithm can compress multi-frame information and extract motion trajectories. The iterative adaptive threshold algorithm can accurately estimate background parameters. The adaptive filtering algorithm we proposed can remove noise while preserving the target trajectory, and has high robustness to trajectory breakage and overlap. After the adaptive morphological algorithm connects trajectories, the adaptive median filtering algorithm can filter out false trajectories. Finally, releasing projection operation can accurately locate stars in the single image.

The actual starry image processing result shows that the proposed method overcomes the difficulties of star extraction in complex backgrounds with small-field, has high detection rate and low false alarm rate. Compared to wide-field length exposure imaging, it has the advantages of high real-time performance and strong detection ability. The method proposed in this article has important reference significance for weak stars real-time detection in space-based synchronous orbits, spacecraft navigation ,high precision cataloging of space debris and so on.

Author Contributions

methodology, Xuguang Zhang; software, Xuguang Zhang; investigation, Huixian Duan; data curation, Yunmeng Liu; supervision, E Zhang; project administration, Yunmeng Liu. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

Not applicable.

Acknowledgments

The authors are grateful to the anonymous reviewers for their critical review, insightful comments, and valuable suggestions.

Conflicts of Interest

The authors declare no conflict of interest.

References

Yunpeng H U, Kebo L I, Liang Y, et al. Review on strategies of space-based optical space situational awareness[J]. Systems Engineering and Electronics: English version, 2021, 32(5): 15.
Maclay T, Mcknight D. Space environment management: Framing the objective and setting priorities for controlling orbital debris risk[J]. Journal of Space Safety Engineering, 2020. [CrossRef]
T, Schildknecht, and, et al. Optical observations of space debris in GEO and in highly-eccentric orbits[J]. Advances in Space Research, 2004. [CrossRef]
Kurosaki, H, Oda, et al. Ground-based optical observation system for LEO objects[J]. Advances in Space Research the Official Journal of the Committee on Space Research, 2015, 56(3): 414-420.
Liu MY, Wang H, Yi WH, et al. Space Debris Detection and Positioning Technology Based on Multiple Star Trackers[J]. Applied Sciences-Basel, 2022, 12(7): 3593. [CrossRef]
Reed, I. S , Gagliardi, et al. Application of Three-Dimensional Filtering to Moving Target Detection[J]. Aerospace and Electronic Systems, IEEE Transactions on, 1983, AES-19(6):898-905. [CrossRef]
Sun Q, Niu Z, Wang W, et al. An Adaptive Real-Time Detection Algorithm for Dim and Small Photoelectric GSO Debris[J]. Sensors, 2019, 19(18):4026-. [CrossRef]
Liu, Wang, Li, et al. Space target detection in optical image sequences for wide-field surveillance[J]. International Journal of Remote Sensing, 2020.
Sun Q, Niu Z D, Yao C. Implementation of Real-time Detection Algorithm for Space Debris Based on Multi-core DSP[J]. Journal of Physics Conference Series, 2019, 1335:012003. [CrossRef]
Lin B, Yang X, Wang J , et al. A Robust Space Target Detection Algorithm Based on Target Characteristics[J]. IEEE geoscience and remote sensing letters, 2022(19-). [CrossRef]
Jiang P, Liu C, Yang W, et al. Automatic extraction channel of space debris based on wide-field surveillance system[J]. npj Microgravity. [CrossRef]
Jiang P, Liu C, Yang W, et al. Space Debris Automation Detection and Extraction Based on a Wide-field Surveillance System[J]. The Astrophysical Journal Supplement Series, 2022, 259(1):4 (13pp). [CrossRef]
Xi J, Xiang Y, Ersoy O K, et al. Space Debris Detection Using Feature Learning of Candidate Regions in Optical Image Sequences[J]. IEEE Access, 2020, PP(99):1-1. [CrossRef]
Jia P, Liu Q, Sun Y. Detection and Classification of Astronomical Targets with Deep Neural Networks in Wide Field Small Aperture Telescopes[J]. The Astronomical Journal, 2020, 159(5). [CrossRef]
Joseph, Tompkins, Stephen, et al. Near earth space object detection using parallax as multi-hypothesis test criterion[J]. Optics Express, 2019, 27(4):5403-5419.
Liu D, Wang X, Xu Z, et al. Space target extraction and detection for wide-field surveillance[J]. Astronomy and ComputingElsevier, 2020(32-):32. [CrossRef]
Li M, Yan C, Hu C, et al. Space Target Detection in Complicated Situations for Wide-Field Surveillance[J]. IEEE Access, 2019. [CrossRef]
Virtanen J, Poikonen J, Saentti T, et al. Streak detection and analysis pipeline for space-debris optical images[J]. Advances in Space Research, 2016, 57(8):1607-1623. [CrossRef]
Levesque M P. Image Processing Technique for automatic detection of satellite streaks[J]. Technical Report. Defence R&D Canada, 2007.
Vananti A, Schild K, Schildknecht T. Improved detection of faint streaks based on a streak-like spatial filter[J]. Advances in Space Research, 2020, 65(1):364-378. [CrossRef]
Wei M S, Xing F, You Z. A real-time detection and positioning method for small and weak targets using a 1D morphology-based approach in 2D images[J]. LIGHT-SCIENCE & APPLICATIONS, 2018, 7(1):9.
Pan H B, Song G H, Xie L J, et al. Detection method for small and dim targets from a time series of images observed by a space-based optical detection system[J]. Optical Review, 2014, 21(3):292-297.
Chu, P. L. Optimal projection for multidimensional signal detection[J]. Acoustics, Speech and Signal Processing, IEEE Transactions on, 1988. [CrossRef]
Chu P L. Efficient detection of small moving objects [R]. Lexington, Massachusetts Institute of Technology, Lincoln Laboratory, 1992: 1－70.
Xu W, Li Q, Feng H J, et al. A novel star image thresholding method for effective segmentation and centroid statistics[J]. Optik - International Journal for Light and Electron Optics, 2013, 124(20):4673-4677. [CrossRef]
Wang Z, Quan W. An all-sky autonomous star map identification algorithm[J]. IEEE Aerospace & Electronic Systems Magazine, 2004, 19(3):10-14.
Mortari D, Samaan M A, Bruccoleri C, et al. The Pyramid Star Identification Technique[J]. Navigation, 2004, 51(3):171–183. [CrossRef]

Figure 1. Image grayscale histogram. Panel (a) is the enlarged global histogram of the original image. Panel (b) is the local histogram of the original image.

Figure 2. Panel (a) is the original image. Panel (b) is the result of morphological erosion by a large operator on the original image. Panel (c) is a local enlarged image of a bad point in the original image. Panel (d) is the processed local enlarged image of bad point.

Figure 3. Panel (a) is the original image after adjusting the grayscale display range. Panel (b) represents the image obtained from background correction. Panel (c) represents the first estimated background Panel (d) is the final estimated background.

Figure 4. Excessive stellar energy leads to electron overflow after extending the integration time.

Figure 5. The ratio of noise power between the original image and the enhanced image using N frames.

Figure 6. panel (a) represents the local grayscale histogram of the preprocessed image. Panel (b) represents the local grayscale histogram of the enhanced image.

Figure 7. Panel (a) is the statistical histogram of standard normal distribution, and panel (b) is the statistical histogram after the projection of the maximum value of five frames.

Figure 8. Panel (a) represents the mean projected image using five frames. Panel (b) represents the maximum projected image using five frames.

Figure 9. The variation of segmentation threshold with number of iterations.

Figure 10. Panel (a) is schematic diagram of constructing an adaptive filter operator with size of 5×5. Panel (b) is an adaptive directional filtering operator.

Figure 11. Enlarged local results of different filtering methods. Panel (a) represents the image before filter. Panel (b) represents the adaptive filtering result. Panel (c) represents the improved median filtering result. Panel (d) represents the local threshold filtering result.

Figure 12. Panel (a) is morphological dilation operator. Panel (b) is morphological corrosion operator.

Figure 13. Panel (a) shows the local results of morphological expansion. Panel (b) shows the local corrosion results after morphological expansion.

Figure 14. Panel (a) shows the local adaptive median filtering graph. Panel (b) shows the local final trajectory detection graph.

Figure 15. Panel (a) shows the fifth frame star positioning image. Panel (b) shows a partially enlarged view of panel (a).

Figure 16. The successfully matched stars are marked in panel (a). The successfully identified stars are marked in panel (b).

Figure 17. Panel (a) represents the ideal imaging of the camera. Panel (b) represents the ideal imaging after image rotation correction.

Figure 18. The two weakest stars are marked in Panel (a). Panel (b) is a locally enlarged image of panel (a).

Table 1. The results of star detection using our method.

SNR	average number	recognition rate	false alarm rate
1.5	853	97.8%	5.09%
2	655	97.2%	4.66%
3	445	96.5%	3.97%
4	329	94.2%	3.14%

Table 2. The results of star detection using MP

SNR	average number	recognition rate	false alarm rate
1.5	5010	98.1%	74.3%
2	1476	96.8%	50.1%
3	714	92.6%	44.2%
4	496	88.5%	36.7%

Table 3. The results of star detection using IFM

SNR	average number	recognition rate	false alarm rate
1.5	2673	97.9%	74.8%
2	854	97.2%	51.4%
3	538	87.8%	42.5%
4	378	37.0%	39.9%

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer