Prerpints.org logo
Preprint
Article

Formulating Equations for Estimating Forest Stand Carbon Stock for Various Tree Species Groups at the Ngao Demonstration Forest, Northern Thailand

Altmetrics

Downloads

166

Views

81

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

19 May 2023

Posted:

19 May 2023

You are already at the latest version

Alerts
Abstract
Through this study, we established equations for estimating the standing tree carbon stock, based on 24 tree species in multiple size classes in a case study at the Ngao Demonstration Forest (NDF) in northern Thailand. Four hundred thirty-nine wood samples from trees in mixed deciduous forest (MDF), dry dipterocarp forest (DDF), and dry evergreen forest (DEF), were collected using non-destructive methods to estimate above-ground carbon equations through statistical regression. The equations were established based on four criteria: 1) the coefficient of determination (R2), 2) Standard error of estimate (SE), 3) F-value, and 4) Significant value (p-value, α ≤ 0.05). The above-ground carbon stock (C) equations for standing trees in the MDF was C = 0.0199DBH2.1887H0.5825, for DDF was C = 0.0145DBH2.1435 H0.748, for DEF was C = 0.0167DBH2.1423H0.7070, and the general equation for all species/wood density groups was C = 0.017543DBH2.1625H0.6614, where DBH is tree diameter at breast height and H is tree total height. The above-ground carbon stock in the DDF, MDF, and DEF was 142, 53.02, and, 12 tons/ha, respectively, and the estimated above-ground carbon stock in the Mae Huad sector at the NDF was 61 tons/ha.
Keywords: 
Subject: Biology and Life Sciences  -   Forestry

1. Introduction

Climate change and global warming is a serious environmental issue worldwide [1,2,3,4]. Global warming is caused by inordinate emissions of greenhouse gasses [5], with the ensuing climate change and natural disasters affecting human activities and the availability of natural resources. Climate change can result in environmental and financial losses, which can be detrimental for the survival of humans and other species. Carbon dioxide (CO2) is an important greenhouse gas, which is stored in the ecosystems and specifically in trees, for a long period of time [6]. It has been estimated that forests contain 77% of the carbon stored in land vegetation, out of which approximately 60% of carbon is stored in the tropical forests, 17% in temperate forests, and 23% in boreal forests [7]. Plants or trees can potentially trap atmospheric carbon through the photosynthesis process[8], which involves the conversion of carbon from CO2 to carbohydrates, glucose, and starch that are stored in the leaves, stems, branches, and roots, and contribute to a plant’s growth [9]. As such, plants store carbon as living biomass, which becomes a part of the food chain and enters the soil as soil carbon [10].
Normally, the carbon stored in trees is estimated as the product of the volume of biomass and the carbon fraction (generally assumed as 0.47 [11]), based on field data collection methods and estimations of different complexity levels [12,13,14]. Tree biomass can be estimated using either direct or indirect methods. The direct method involves felling of trees and weighing various tree components [15], while the indirect method involves the use of allometric equations for estimating the tree sample biomass [16].
The biomass or tree volume equations to estimate the tree carbon storage specific to Thailand are inaccurate as the commonly used allometric equations are biased (i.e., they tend to over- or under-estimate the tree volume)[17]. Additionally, the existing equations do not cover the major tree species frequently found in forests such as Tectona grandis, teak[18], or various dipterocarp species [19]. This is primarily due to the fact that the estimations are based on equations constructed using the destructive sampling of a relatively small number of trees. Some volume equations use only the diameter at breast height (DBH) as the independent variable and do not include tree height[20,21]. Also, some equations were constructed only to estimate the traded logged volume and did not include the smaller trees [21]. Therefore, a novel approach is proposed to estimate the standing tree carbon content as a function of tree attributes in a natural forest with different tree size classes. This approach would avoid the felling of trees and would use combustion methods to estimate the real carbon fraction.
This study aims to formulate the standing tree carbon equations to estimate the carbon stocks in three forest types: a mixed deciduous forest (MDF), dry dipterocarp forest (DDF), and a dry evergreen forest (DEF) at the Mae Huad sector, Ngao Demonstration Forest (NDF) in northern Thailand. The Mae Huad sector has a vast forest cover in the NDF, with several tree species and is one of the five most important biosphere reserves area in Thailand [22]. The equations determined in this research to estimate the carbon stock were constructed using specific carbon fraction of tree species, without the need to calculate the biomass to estimate the tree carbon stock. The non-destructive method used to establish the equations for many tree species sampled from the MDF, DDF, and DEF can also be used to estimate the carbon stored in other sites of Thailand.

2. Materials and Methods

2.1. Study area

The Mae Huad Sector was chosen as the study site (Figure 1) and is one of of the four designated sectors in the NDF. The NDF consists of four sectors, Mae Heang, Mae Huat, Mae Ngao, and Mae Teeb and covers an area of approximately 43.431.75 hectares, including several forest types. It is located in the north-western part of the Lampang Province in northern Thailand between 18º 30' and 18º 54' north latitude, and 99º 50' and 100º east. The NDF was established in 1961 and is the only demonstration forest in Thailand, and has a long history of functioning as a base for the introduction, testing, and adaption of new forest management techniques [21]. Most of the land in Mae Huad sector is under forest cover, i.e., 38,557.50 hectares or 84.246 % of the total area. Most of the tree cover is part of the Ngao Demonstration Forest, while a total of 6,526.80 hectares is classified as agricultural land or 14.261 % and is located in the national reserve forest by law. It is expected that the agricultural area will increase over time if the enforcement of the law is weak. Additionally, the area has a porcelain mine which covers an area of 11.00 hectares or 0.24 % of the total area. There are two types of infrastructure in the site, i.e., power lines and paved road (ASEAN highway or the Phaholyothin road). The power lines go underneath the forest, but the roads cover an area of 1.136 square kilometers or 0.248 % of the total area. Ancient settlements, namely Ban (or village) Pong, Ban Tak, Ban Huad, Ban Suan Sak, Ban Pang Lah, and Ban Prow, are also located in this study area, covering an area of 545.90 hectares. This study focuses only on the natural forest of MDF, DEF and DDF. The equations developed in these forest types can be applied to estimate the carbon storage in forest trees in the tropical rain forest.

2.2. Forest inventory and sample collection

Trees from plotless inventory data are used for the collection of tree samples, wood samples, and calculated stand carbon stock. The distribution of trees in Mae Huad sector NDF, Northern Thailand, was determined using stratified sampling [23,24] and a uniform fixed grid of 3 x 3-kilometer systematic arrangement that covered the whole of the Mae Huad sector. The point sampling technique [25,26,27] was used to collect tree data which included diameter at breast height (DBH), total height (H), trees species, and forest type at each sample point. This grid and point sampling were part of the APFNET project [21]. The point sampling data were used to calculate the importance value index ( IVI), which is the quantitative value for measured dominance of trees species [28], that was used to select the sample trees by diameter classes. The suitable sample size (i.e., the number of sampling points) was calculated using equation 1 [29]
n = t 2 ( cv ) 2 AE 2
where, n is the target number of sample points, t is the t-value at the 95% probability level, cv is coefficient of variation in DBH, AE is allowable sampling error in DBH at point sampling (this research used 10%)
In each forest type, all the selected tree species were grouped into 10 groups based on their wood density. The species with the highest IVI in each group was selected as a representative of the group for tree data and wood sample collection. Each selected species was further classified into one of three diameter classes (small, medium, and large) (15 trees sample in each species, total was 450 sample trees).
The bole of each sample tree was measured for the stem diameter by 2-meter sections from the base to the first major branch, to calculate the tree bole volume. Wood samples were collected from the selected sample trees in the north and east directions using an increment borer or a handsaw at 1.3-meter height (2 wood sample in each tree, The total was 900 wood sample) to determine the carbon fraction.

2.3. Sample preparation and carbon fraction analysis

Wood sample preparation: this process was for estimated the wood carbon fraction in sample trees. The wood wet volume of the collected sample wood was calculated using Newton's formula (Equation 2) [27,30]:
V t = ∑ i = 1 n L 6 ( Ab i + 4 Am i + Au i )
where, Vt is tree wet volume, Abi is cross-sectional area at base of stem segment i, Am i is cross-sectional area at middle of stem segment i, Aui is cross-sectional area at upper of stem segment i, L is length of stem segment i (m).
The wet volumes of the wood samples were calculated. The wood samples were weighed and were dried in an air-dry oven at 80 °C for 24 - 48 hours, until their weights became constant, to determine the final dry weights. Two dry samples from the same tree were then pulverized together using a crushing machine to obtain a 100-gram dry weight sample.
Carbon fraction analysis: A 100-gram pulverized sample was analyzed carbon fraction using combustion methods via a carbon analyzer (e.g., PerkinElmer 2400 series II CHNS/O Elemental Analyzer). recommended by Kraenzel et al. and Wulzler et al. [31,32]

2.4. Data analysis

1) Carbon storage in wood samples: This process was calculated by using the relationships between carbon fraction and wood sample dry weight
The carbon proportion (carbon fraction) was obtained as a percentage of dry weight using the method described by Duangsathaporn et al. [20]and Khantawan et al. [33] to convert the carbon fraction to carbon weight in a wood sample (Equation 3):
C c = C w   ×   W d
where, Cc is weight of carbon in a wood sample core (kg), Wd is dry weight of a wood sample core (kg), Cw is carbon fraction in a sample core (%).
Furthermore, the carbon wood sample and carbon fraction in each species was used to estimate the carbon stored in the standing tree using Equation 4:
C t = C c V w   ×   V t
where, Ct is weight of carbon in a standing sample tree bole (kg), Cc is weight of carbon in a wood sample core (kg), Vw is wet volume of wood sample core, and Vt is wet volume of standing tree bole.
2) The calculation of standing tree carbon stock: this process calculated the standing trees carbon storage in tree samples to estimate the carbon equation. The above-ground standing tree carbon was determined through three steps.
In the first step, a piece of sample tree in tree bole was used to estimate the bole volume and carbon. The wet bole volume (V) of every sample from a total of 362 sample trees was calculated using the Smalian’s formula (equation 5) [27,30] and the carbon stock in each wood sample core was then estimated using the dry weight carbon in the wood sample core multiplied by the carbon fraction in each wood sample core [20]. The whole-bole carbon stock of each sample tree was then calculated using the proportion of dry weight carbon in a wood sample core and the wet volume of wood sample core multiplied by the wet volume of standing tree bole (Equation 4).
V t = ∑ i = 1 n L 2 ( Ab i + Au i )
where, Ab i is cross-sectional area at base of stem segment i, Au i is cross-sectional area at upper of stem segment i, and L is length of stem segment i (m)
In the second step, the branch and leaf carbon stock were estimated using leaf and branch biomass of the tree estimated using the standard equation multiplied by the carbon fraction. The equation recommended in Tsutsumi et al. as used to estimate the branch and leaf biomass for trees from the DEF [34], and the equation recommended in Ogawa et al. as used to estimate the branch and leaf biomass for trees from the MDF and DDF [35]. These equations for estimating carbon stock in leaves and branches in each tree are shown in Table 1
In the third step, the above-ground carbon stock in each sample tree was obtained by combining stem, branch, and leaf carbon stock. This was then used to develop the tree carbon storage equations.
Remark: Ws is biomass of stem (kg/tree), Wb is biomass of branches (kg/tree),Wl biomass of leaves (kg/tree), Wsb is biomass of stem + biomass of branches (kg/tree), DBH is diameter at breath height and H is height of tree
3) The construction of standing tree carbon equations: The equations to estimate the above- ground standing tree carbon were constructed using the model C=aDBHbHc, where C is standing tree carbon stock, DBH is diameter at breast height, H is total height, and a, b and c are model parameters to be estimated. The model parameters were estimated using log transformation and linear multiple regression.
The equations) were fitted for each forest type. In order to select the optimal tree carbon equations, statistics which included the coefficient of determination (R2), standard error of estimate (SE), F-value, and significance value (p-value, α ≤ 0.05) were evaluated. The normality of the model residuals was also examined using basic program of statistics. The equations of the three forest types were compared with the general equation for all species/wood density groups. This was done by calculating the relative differences and statistics between the mean of the equations of the three forest types and the optimal forest type equations. Data from 30 randomly selected sample trees were used to test the differences between the optimal equation and forest type equations.
4) Estimated stand carbon stock: All trees in point sampling inventory from 2.1 used for calculating stand carbon storage. The carbon stock per hectare (ha) at each sampling point was estimated by summing the estimated carbon content of the sample tree and expressing it on a per unit area basis for the major forest types in the study area, using the Equations 6-9 adapted from van Laar and Akça [26].
C p = BAF   × ∑ i = 1 n C i B A i
where; C p is carbon stock at sampling point (kg/ha), BAF is basal area factor, C i   is the carbon storage in tree i of point sampling, and B A i is basal area in tree i of point sampling.
C a = A t   ×   C -
where, Ca is mean carbon stock in forest area, A t is forest area in the study, and C ¯ is the average carbon stock in all sampling points.
C t = C a   ±   t   ×   SE C a
and
SE C a = A t   ×   SE c -
where, C𝑡 is carbon stock of forest area, SEca is standard error in stand carbon stock of forest area, and SEc̅ is the standard error of the mean carbon stock in forest area.

3. Results

3.1. Forest inventory for building a species list, sample trees selection, and wood sample extraction.

A 54-sample fixed grid of size 3 x 3 kilometers was established in the the Mae Huad sector. Forty-four sampling points fell in the forested area and classified under either of the three forest types, while the remaining 10 sampling points were in the agriculture field. Seventy-six tree species were found in the Mae Huad sector, with 46 tree species in the MDF, 18 in the DDF, and 31 in the DEF. The IVI was calculated and used to classify and select the sample trees. The highest species IVI in the MDF were Xylia xlocarpa, Tectona grandis, and Prerocapus macrocapus, in the DDF were Shorea siamensis, Shorea obtusa, and P. macrocarpus, and in the DEF were Mallorus macrostachyus, Hopea odorata, and Duabanga grandiflora. The X. xylocarpa, Dalbergia oliveri, P. macrocarpus, Terminalia corticosa, Terminalia. alata, and Quercus kerri were found in all the three forest types. Within the three forest types and 10 species groups for each forest type, the sample trees were grouped into wood density classes, for a total of 30 groups. In each group, the selected species had the highest value of IVI for the sample tree species. The 10 sample trees species per forest type were classified into three DBH classes (small, medium, and large) from inventory data covering a DBH range of 4.50 to 147.00 cm. The wood density range and representative tree species are shown in Table 2.

3.2. Wood carbon fraction analysis

The carbon fraction of tree in NDF analyzed using combustion techniques from PerkinElmer 2400 series II CHNS/O Elemental Analyzer in the laboratory was between 45.75% and 49.66%, with an average of 47.43%. Carbon fraction of MDF for 10 species and 155 sample ranged from 45.75% to 49.66 % with an average 47.61%. The 3rd highest of carbon fraction in each MDF sample species was Tectona grandis, 49.66%, T. corticosa, 48.55%, and (3) Lannea coromandelica, 45.75%, respectively. Carbon fraction of DDF for 9 species and 134 sample ranged from 46.06% to 48.55% with an average 47.50% and each 3rd highest species carbon fraction was T. corticosa ,48.55%, P. macrocarpus, 48.41% and Haldina cordifolia, 48.26%, respectively. Carbon fraction of DEF for 10 species and 150 sample ranged from 45.43% to 48.41% with an average 47.17%, and each 3rd highest species carbon fraction was P. macrocarpus,48.41%, Artocarpus lakoocha,48.31%, X. xylocarpa, 48.03% respectively.. Carbon fraction of sample trees in the Mae Huad sector, NDF are listed in Table 2.

3.3. Carbon storage

The standing trees carbon stock in each species was calculated using Equations (3) - (5), and branch and leaf carbon was calculated using the equations in Table 1. Above-ground carbon stock in sample trees of NDF ranged between 6.12 - 8,673.15 kilogram (kg). In MDF, above-ground cabon stock from 155 sample trees ranged from 8.18 to 2,006.99 kg., above-ground carbon stock in DDF from134 sample trees ranged from 6.12 – 2,006.99 kg, and above-ground carbon stock in DEF from 150 sample trees ranged from 8.45 – 8,673.15 kg. Carbon stock by tree component and the above-ground carbon stock per cubic meter are shown in Table 2. All above-ground carbon stock sample tree data were used to develop stading tree carbon stock equations using regression analysis (Section 3.4).

3.4. Standing tree above-ground carbon equations

The above-ground carbon stock sample data were used to establish standing tree carbon equations for MDF, DDF, and DEF, and a general equation for all the species/wood density groups. Multiple regression analysis was used, where the dependent vairable was carbon stock (C), and the independent variables included DBH and H. The two variable, DBH and H, both showed a high relationships to C more than only DBH or only H (Table 3).
The equations for the MDF, DDF, and DEF were estimated from 10, 9, and 10 species, resectively, and the the general equation was estimated from 24 species. The DBH range of trees used in the construction of equations for MDF, DDF, DEF, as well as the general equation, was between 8.70 -71.00 cm, 10.00 - 66.80 cm, 9.70 - 147.00 cm, and 8.70 - 147.00 cm, respectively. The suitable equations are shown in Table 4.
Remark CNDF, CMDF, CDDF, and CDEF indicate the above-ground standing tree carbon stock in the general equation for all species/wood density groups in the NDF, MDF, DDF, and DEF, respectively (kg/tree), while DBH is diameter at breast height of tree (cm), H is total height of tree (m).
The coefficient of determination (R2), standard error of estimate (SE), F-value, and significant value (p-value, α ≤ 0.05) ), to determine the best fit equations were determined for each forest type. The R2 values for the equations constructed for MDF, DDF, DEF, and NDF were 0.9678, 0.9412, 0.9770, and 0.9642, while the SE was 0.101, 0.139, 0.100, and 0.114, respectively.The F-value was 2281.89, 1048.28, 2127.52, and 5870.00, respectively, while the p-value for all the equations was less than 0.01, which was highly significant. All the related statistical values for each forest type are shown Table 4.
The residuals between the actual and estimated carbon stock for the various values of carbon stock are shown in Figure 2. Residuals for the overall model can be seen to be unbiased as were for all species in the MDF, DDF, DEF, and all species in the NDF. In other words, the errors are distributed uniformly with no apparent dependence on any of the potential predictors.
Sample trees were used to estimate the tree carbon stock for each forest type. using tree DBH and H.. The carbon storage of tree samples were estimated using the equations constructed for the MDF, DDF, DEF and the optimal equation of this project. The equations to estimate the carbon content in the MDF, DDF, and DEF were similar to the optimal equation. The relative difference of the two carbon equations was between 0.088 - 2.416%, 0.050 – 2.545%, and 1.076 – 2.191%, respectively. The comparison of the mean between the equations of three forest types and the optimal equation was not significant difference.

3.5. Forest stand carbon stock in the NDF

The standing tree carbon stockwas used to calculate the carbon stock in the NDF forest stand using the equation from van Laar and Akça, (20). The carbon stock of the 44 sampling points ranged from 6.15 to 175.64 ton/ha, with an average per point of 61,837.96 kg/ha (Table 5). Carbon stock per hectare by forest type in the DDF, MDF, and DEF was 142 ton/ha , 53.02 tons/ha and 12 tons/ha, respectively. The carbon stock in the MDF was approximately between 0.932 and 1.4 million tons (1.20 mean million tons), that in the DDF was approximately between 0.289 and 0.454 million tons (0.371 mean million tons), and that in the DEF was approximately between 0.049 and 0.078 million tons (0.063 mean million tons). The carbon storage in the Mae Huad sector forest was approximately between 1.27 and 1.99 million tons (average 1.632 million tons).

4. Discussion

4.1. Carbon fraction

Normally, the carbon fraction is assumed to be 50% of a tree's total biomass [2,12,38]. The carbon fraction in this study ranged from 45.75% to 49.66%, with an average of 47.43%. This is less than the normally assumed value but more than the Intergovernmental Panel on Climate Change (IPCC) carbon fraction value of 47% of tree biomass [11]. However, much research explained the variations in carbon fraction estimates might result from the methods used for different species, the components of a tree or a stand used (stem, roots, and leaves), and the age of the stand [12,39]. For example, the study by Thomas and Martin report the difference of carbon fraction in part of trees, was shown 37%, 76%, 48%, 81% and 63%, respectively, of the variation in bark, branch, twig, coarse root and fine root carbon fraction value[12]. The difference of carbon fractions was confirmed by IPCC reports. The amounts of components of wood tissues such as cellulose, hemicellulose, lignin, and variety of nonstructural chemicals resulted in different amounts of carbon by mass [40]. The carbon fraction of trees growing in plantations of Thailand was reported by Diloksumpun and Staporn who estimated the carbon stock through combustion techniques. They found carbon fraction for eucalyptus spp. was 48.36 %[41], while Duangsathaporn et al., who estimated the sequestered carbon in standing teak trees in the Thong Phaphum teak plantation through combustion techniques, reported a carbon fraction of 46.58%[20].
We investigated the relationship between average carbon per cubic meter and wood density; higher density wood had a higher carbon content per cubic meter (Table 6). The relationship between average carbon weight per wood volume (kg/m3) and wood density class was analyzed using a linear relationship. This linear relationship was not significant (Figure 3), but there was a trend showing variation in the wood samples due to different wood elements (e.g., lignin, cellulose, and hemicellulose) in a unit of tree sample volume. Thus, the carbon stock per volume will be different, similar to the study of Campbell and Sederoff who found the differences of lignin in different tree species in sample trees [42]. A study by Navarro, et al. also found that indirect indicators of wood density and carbon fraction affected carbon storage, as high wood density in some species of tropical forests was shown high carbon content [43]. Other studies have also not found such a relationship between carbon storage and wood density. For example, Weber et al. studied the variations between tree growth, density, and carbon concentration and did not find any significant relation between wood density and carbon concentration [44].

4.2. Above-ground carbon equation

Generally, equations for estimating carbon storage use indirect methods, such as the product of tree biomass and carbon fraction, to evaluate the carbon stored in a standing tree. In Thailand, to estimate carbon storage, Viriyabuncha used an aggregate of six equations in a mixed species forest [18], Yuan et al. used 11 equations in a mixed species forest [45], and the Department of Environmental Quality Promotion used six equations from trees in a mixed deciduous, dry dipterocarp, dry evergreen, pine, and mangrove forest which included mixed species [46]. All of these studies conducted in Thailand used destructive sampling methods [45]. Destructive methods involve the cutting down of all the trees in the sampling area and measuring the weight of the different components such as the tree trunk, leaves, and branches and measuring the oven-dried weight of these components [47,48].
In this research, the equations for estimating carbon storage were constructed by combining the non-destructive method of Montès et al.[49] and the collection of the wood samples as proposed by Duongsathaporn, et al.[20] and Khantawan, et al.[33]. The regression technique was used to estimate the tree carbon storage in only the mixed deciduous, dry dipterocarp, and dry evergreen forest types. In addition, these equations can only be used for estimating the carbon stored in the standing trees with a DBH 8.70 to 147.00 cm, in the three forest types of a tropical forest. Thus, similar studies need to be done in other forest types in Thailand and trees of a wider range of DBH. The advantage of the non-destructive sampling method is that, at present in Thailand, the destructive sampling method cannot be used as there is an ongoing logging ban since 1989 [50].
The most frequently used equations for estimating trees biomass in Thailand are those proposed by Ogawa et al.; these equations were based on 90 standing sample trees in MDF and DDF (the coefficient of determination (R2) = 0.9326) [35]. Another equation widely used is that of Tsutsumi et al., which used six standing sample trees in a DEF (R2 = 0.97)[34]. All these equations are suitable for estimating tree biomass in the respective forest types, but the estimation of standing tree carbon is arduous as it still requires the estimation of the carbon fraction. Thus, the equations developed in this study are more suitable for directly estimating the carbon stored in standing trees in the MDF, DDF and DEF forest types.

5. Conclusions

The optimal above-ground carbon equations were formulated from a large sample of trees (155, 134, and 150 trees samples in MDF, DDF and DEF, respectively), of various sizes, and trees species (24 tree species in 3 forest types). We conclude that such equations can be used to estimate the carbon stocks in Thailand, and in the assessment of carbon stock. However, the present carbon estimation did not cover other species in other forest types, such as mangrove forests, and would be the endeavor of a future study.

6. Patents

This research was supported by Scholarships for International Publication of The Graduate School, Kasetsart University: 2015-2016 and Asia-Pacific Network for Sustainable Forest Management (APFNet).

References

  1. Hassan, M. Heshmati. "Impact of Climate Change on Life." In Environmental Issues and Sustainable Development, edited by Sarvajayakesavalu Suriyanarayanan and Charoensudjai Pisit, Ch. 12. Rijeka: IntechOpen, 2020.
  2. Mbah, Marcellus F., Ayesha Shingruf, and Petra Molthan-Hill. "Policies and Practices of Climate Change Education in South Asia: Towards a Support Framework for an Impactful Climate Change Adaptation." Climate Action 1, no. 1 (2022): 28. [CrossRef]
  3. Singh, Raj Bharat. Global Warming Impact and Future [Erspexctive. Janeza Trdind 9, 5100 Rijeka, Croatia: InTech, 2012.
  4. Basuki, TM, PE Van Laake, AK Skidmore, and YA Hussin. "Allometric Equations for Estimating the above-Ground Biomass in Tropical Lowland Dipterocarp Forests." Forest Ecology and Management 257, no. 8 (2009): 1684-94. [CrossRef]
  5. Lorenz, Klaus, and Rattan Lal. Carbon Sequestration in Forest Ecosystems. Dordrecht Heidelberg London New York: Springer, 2010.
  6. Srivastav, Asheem. The Science and Impact of Climate Change. Springer Nature Singapore Ltd.: Springer, 2019.
  7. Griffiths, Howard, and G Paul Javis. The Carbon Balance of Forest Biomes. Oxon, UK: Taylor & Francis, 2005.
  8. Lukac, Martin, Carlo Calfapietra, Alessandra Lagomarsino, and Francesco Loreto. "Global Climate Change and Tree Nutrition: Effects of Elevated Co2 and Temperature." Tree Physiology 30(9) (2010): 1202-20. [CrossRef]
  9. Duca, Maria. Plant Physiology. Heielberg, New York: Spriger, 2015.
  10. Gao, Yang, Jimin Cheng, Zhengrui Ma, Yu Zhao, and Jishuai Su. "Carbon Storage in Biomass, Litter, and Soil of Different Plantations in a Semiarid Temperate Region of Northwest China." Annals of Forest Science 71, no. 4 (2014): 427-35. [CrossRef]
  11. IPCC. "Guidelines for National Greenhouse Gas Inventories—Volume 4: Agriculture, Land Use and Forestry (Gl-Afolu)." http://www.ipcc-nggip.iges.or.jp/public/2006gl/vol4.htm (accessed 15 December 2023).
  12. Thomas, C Seen, and R Adam Martin. "Carbon Content of Tree Tissues: A Synthesis." Forests 3 (2012): 332-52.
  13. Sylvanus, Mensah, Veldtman Ruan, du Toit Ben, Glèlè Kakaï Romain, and Seifert Thomas. "Aboveground Biomass and Carbon in a South African Mistbelt Forest and the Relationships with Tree Species Diversity and Forest Structures." Forests 7 (2016): 79.
  14. Bartholomée, Océane, Karl Grigulis, Marie-Pascale Colace, Cindy Arnoldi, and Sandra Lavorel. "Methodological Uncertainties in Estimating Carbon Storage in Temperate Forests and Grasslands." Ecological Indicators 95 (2018): 331-42. [CrossRef]
  15. West, P W. Tree and Forest Measurement. 2 ed. Berlin Heidelberg: Springer, 2009.
  16. Njana, Marco A. "Indirect Methods of Tree Biomass Estimation and Their Uncertainties." Southern Forests: a Journal of Forest Science 79, no. 1 (2017): 41-49. [CrossRef]
  17. Losi, J Christopher, G Thomas Siccama, Richard Condit, and E Juan Morales. "Analysis of Alternative Methods for Estimating Carbon Stock in Young Tropical Plantations." Forest Ecology and Management 184 (2003): 355-68.
  18. Viriyabuncha, Chingchai, P. Chittachumnonk, Chudchawan Sutthisrisinn, S. Samran, and Kantinan Peawsa-ad. "Adjusting Equation to Estimate the above-Ground Biomass of Teak Plantation in Thailand." 2002.
  19. Wongsing, Yoawwaluk, Sasitorn Poungparn, and Pipat Patanaponpaiboon. "Allometric Relationship for Estimating above- and Below-Ground Biomass of Dipterocarpaceous Seedlings." THAI JOURNAL OF BOTANY 4, no. Special Issue (2012): 37-46.
  20. Duangsathaporn, Khwanchai, Prasong Sagunthum, and patsi Prasomsin. Carbon Sequestration of Timber Product in Teak Plantation. Kasetsart University, Bankok 2011.
  21. Kasetsart University, and Asia-Pacific Network for Sustainable Forest Management and Rehabilitation. "Technical Report No.1: Development of Standing – Tree Carbon Equation in to Demonstrate the Development and Application of Standing-Tree Carbon Equations to Improve the Accuracy of Forest-Cover Carbon Stock Estimates in Thailand." Kasetsart university, Bangkok, 2018.
  22. UNESCO. "Biosphere Reserves in Asia and Pacific." http://en.unesco.org/biosphere/aspac. (accessed 3 May 2023).
  23. Tongco, Maria Dolores C. "Purposive Sampling as a Tool for Informant Selection." Ethnobotany Research and Applications 5 (2007): 147-58.
  24. Palinkas, Lawrence A., Sarah M. Horwitz, Carla A. Green, Jennifer P. Wisdom, Naihua Duan, and Kimberly Hoagwood. "Purposeful Sampling for Qualitative Data Collection and Analysis in Mixed Method Implementation Research." Administration and Policy in Mental Health and Mental Health Services Research 42, no. 5 (2015): 533-44. [CrossRef]
  25. Pieter, G Vries. Sampling Theory for Forest Inventory. 1 ed. Springer Berlin, Heidelberg: Springer, 1986.
  26. van Laar, Anthonie, and Alparslan Akça. Forest Mensuration, Managing Forest Ecosystems. Dordrecht, The Netherlands.: Springer Netherlands, 2007.
  27. Kershaw, J. A., M. J. Ducey, T. W. Beers, and B. Husch. Forest Mensuration. 5 ed. Chichester, UK: John Wiley & Sons, 2017.
  28. Ismail, MOHD HASMADI, PAKHRIAZAD HASSAN Zaki, MOHD FADLI AHMAD Fuad, and NOOR JANATUN NAIM Jemali. "Analysis of Importance Value Index of Unlogged and Logged Peat Swamp Forest in Nenasi Forest Reserve, Peninsular Malaysia." International Journal of Bonorowo Wetlands 7, no. 2 (2017): 74-78. [CrossRef]
  29. Shiver, B. D. , and B. E. Borders. Sampling Techniques for Forest Resource Inventory. 1 ed: Wiley, 1996.
  30. Prasomsin, patsi. Handbook of Field Forest Mensuration I. Forest Management Department, Faculty of Forestry: Kasetsart University, 1991.
  31. Kraenzel, Margaret, Alvaro Castillo, Tim Moore, and Catherine Potvin. "Carbon Storage of Harvest-Age Teak (Tectona Grandis) Plantations, Panama." Forest Ecology and Management 173, no. 1 (2003): 213-25. [CrossRef]
  32. Wutzler, Thomas, Barbara Köstner, and Christian Bernhofer. "Spatially Explicit Assessment of Carbon Stocks of a Managed Forest Area in Eastern Germany." European Journal of Forest Research 126, no. 3 (2007): 371-83. [CrossRef]
  33. Khantawan, Chokdee, Khwanchai Duangsathaporn, and patsi Prasomsin. "Relationship between Carbon Content and Growth of Teak in Natural Forest and Plantation, Lampang Province, Thailand." Agriculture and Natural Resources 53, no. S1 (2019): 267–73.
  34. Tsutsumi, T, K Yoda, P Shahunalu, P Dhamamnoda, and B Prachaiyo. "Chapter 3 : Forest: Felling, Burning and Regeneration." In Shifting Cultivation: An Experiment at NamPhrom, Northeast ThailBnd, and its Implications for Upland Farming in the Monsoon Tropics, edited by K Kyuma and C Pairintra, 13-62. KyotoUniversity. Japan, 1983.
  35. Ogawa, Husato, Kyoji Yoda, Kazuhiko Ogino, and Tatuo Kira. "Comparative Ecological Studies on Three Main Types of Forest Vegetation in Thailand. Ii. Plant Biomass." Nature and Life in South East Asia 4 (1965): 49-80.
  36. Forest_Research_and_Development_Bureau. The Thai Hardwoods. Bangkok: Royal Forest Department., 2007.
  37. ———. General Characteristics of Thai Timbers. Bangkok: Royal Forest Department, 2010.
  38. Martin, Adam R, Grant M Domke, Mahendra Doraisami, and Sean C Thomas. "Carbon Fractions in the World’s Dead Wood." Nature communications 12, no. 1 (2021): 889.
  39. IPCC. Good Practice Guidance for Land Use, Land-Use Change and Forestry. Edited by Jim Penman, Michael Gytarsky, Taka Hiraishi, Thelma Krug, Dina Kruger, Ritta Pipatti, Leandro Buendia, Kyoko Miwa, Todd Ngara, Kiyoto Tanabe and Fabian Wagner. Hayama, Kanagawa: IGES, 2003.
  40. Lamlom, Sabah H, and Rodney A Savidge. "Carbon Content Variation in Boles of Mature Sugar Maple and Giant Sequoia." Tree physiology 26, no. 4 (2006): 459-68. [CrossRef]
  41. Diloksumpun, Sapit, and Duriya Staporn. "Carbon Storage of Eucalypts Planted on Paddy Bunds in Chachoengsao Province." Thai Journal of Forestry 28, no. 3 (2009): 72-84.
  42. Campbell, Malcolm M, and Ronald R Sederoff. "Variation in Lignin Content and Composition (Mechanisms of Control and Implications for the Genetic Improvement of Plants)." Plant physiology 110, no. 1 (1996): 3. [CrossRef]
  43. Navarro, Marcela, Róger Moya, Robin Chazdon, Edgar Ortiz, and Braulio Vilchez. "Successional Variation in Carbon Content and Wood Specific Gravity of Four Tropical Tree Species." Bosque 34, no. 1 (2013): 33-43. [CrossRef]
  44. Weber, John C., Carmen Sotelo Montes, Tougiani Abasse, Carlos R. Sanquetta, Dimas A. Silva, Sandra Mayer, Graciela I. B. Muñiz, and Rosilei A. Garcia. "Variation in Growth, Wood Density and Carbon Concentration in Five Tree and Shrub Species in Niger." New Forests 49, no. 1 (2018): 35-51. [CrossRef]
  45. Yuen, Jia Qi, Tak Fung, and Alan D. Ziegler. "Review of Allometric Equations for Major Land Covers in Se Asia: Uncertainty and Implications for above- and Below-Ground Carbon Estimates." Forest Ecology and Management 360 (2016): 323-40. [CrossRef]
  46. Department of environmental quality promotion. The Developing Method for Assessing Carbon Sequestration and Carbon Exchange Processes of Trees and Forest under the Tool / Methods Development of Carbon Sequestration Assessments.. Bangkok: Environmental research and training center. Department of environmental quality promotion, 2018.
  47. Ravindranath, N. H. , and Madelene Ostwald. "Methods for Estimating above-Ground Biomass." In Carbon Inventory Methods Handbook for Greenhouse Gas Inventory, Carbon Mitigation and Roundwood Production Projects, edited by N. H. Ravindranath and Madelene Ostwald, 113-47. Dordrecht: Springer Netherlands, 2008.
  48. Supriya Devi, L. , and P. S. Yadava. "Aboveground Biomass and Net Primary Production of Semi-Evergreen Tropical Forest of Manipur, North-Eastern India." Journal of Forestry Research 20, no. 2 (2009): 151-55.
  49. Montès, N., T. Gauquelin, W. Badri, V. Bertaudière, and El H. Zaoui. "A Non-Destructive Method for Estimating above-Ground Forest Biomass in Threatened Woodlands." Forest Ecology and Management 130, no. 1 (2000): 37-46. [CrossRef]
  50. Subcommittee for Drafting National Forest Policy and Draft National Forest Development Master Plan. National Forest Policy. The National Forest Policy Committee.. Royal Forest Department. Bangkok.: Royal Forest Department., 2019.
Preprints 74126 g001
Figure 1. The study area in the Mae Huad sector, NDF in northern Thailand.
Figure 1. The study area in the Mae Huad sector, NDF in northern Thailand.
Preprints 74126 g001
Preprints 74126 g002
Figure 2. Residuals or the difference between observed and predicted above-ground carbon content in of the selected trees: MDF, DDF, DEF, and Mae Huad sector NDF.
Figure 2. Residuals or the difference between observed and predicted above-ground carbon content in of the selected trees: MDF, DDF, DEF, and Mae Huad sector NDF.
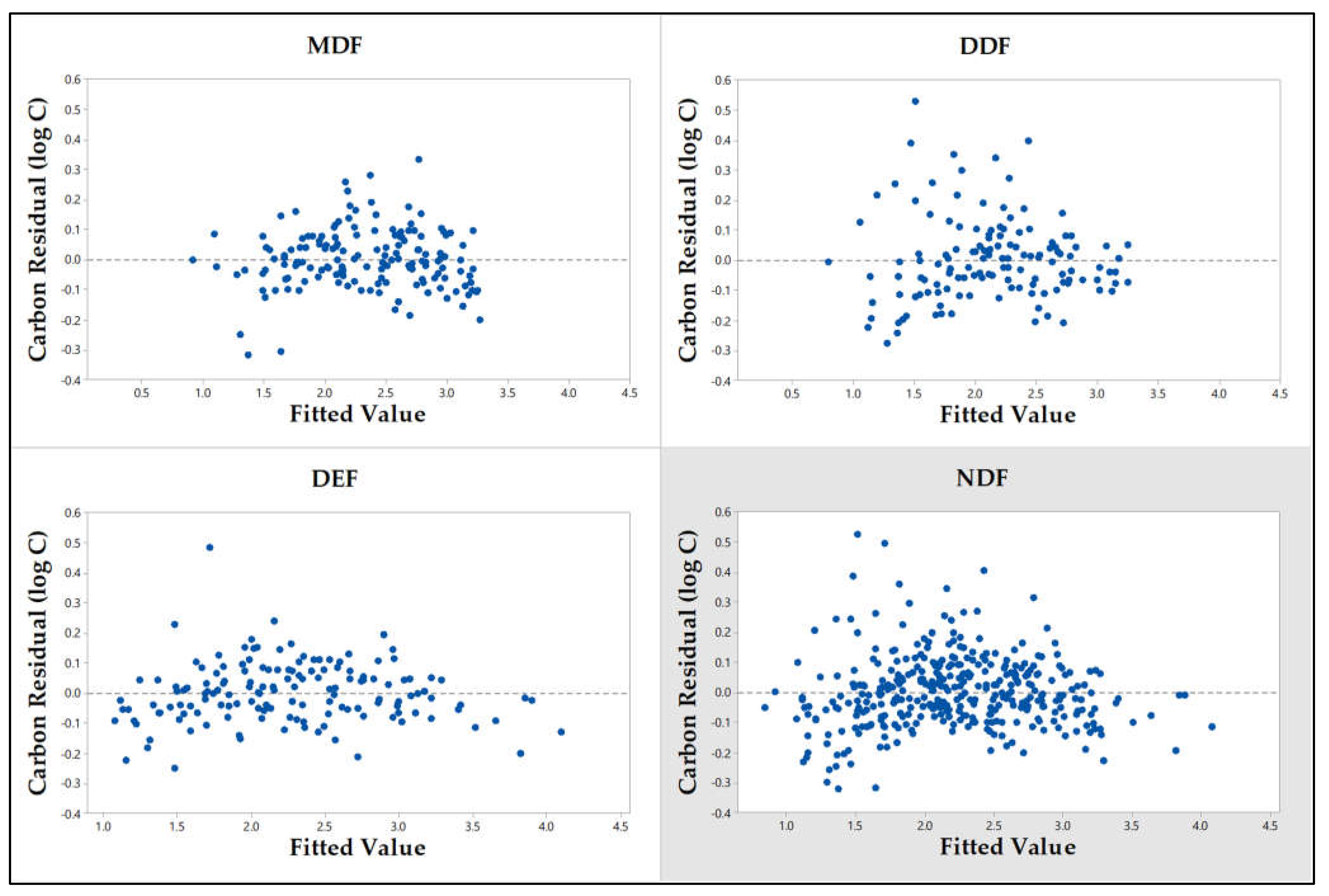
Preprints 74126 g002
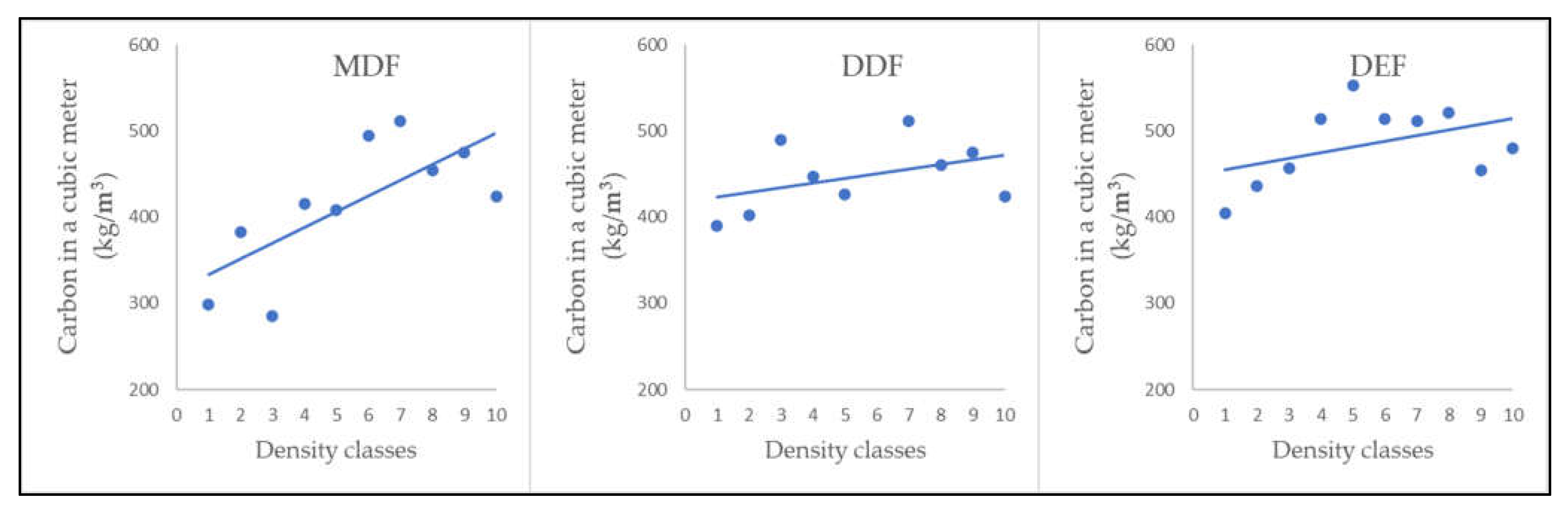
Preprints 74126 g003
Figure 3. The relationships shown between stored carbon per cubic meter and wood density class.
Figure 3. The relationships shown between stored carbon per cubic meter and wood density class.
Preprints 74126 g003
Table 1. The equation for estimating carbon storage in leaves and branches in individual trees.
Table 1. The equation for estimating carbon storage in leaves and branches in individual trees.
Forest type Equation location Source
Dry evergreen forest Wb = 0.00893DBH2H0.977 Namphom Pitsanulok Thailand Tsutsumi et al., 1983
Wl = 0.0140DBH2H0.669
Dry deciduous forest Ws = 0.0396 DBH2H 0.9326 Nakon-ratchasema Thailand Ogawa et al,1965
Wb = 0.003487DBH2H 1.0270
Wl = (25.0/Wsb+0.025)–1
Mixed deciduous forest Ws = 0.02903 DBH2H 0.9813 Nakon-ratchasema Thailand Ogawa et al,1965
Wb = 0.003487DBH2H 1.0270
Wl = (28.0/Wsb+0.025)–1
Table 2. Number of sample trees, carbon content, and carbon stock in sample trees.
Table 2. Number of sample trees, carbon content, and carbon stock in sample trees.
Forest Type Density class Wood density range*(kg/m3) Representative species (Scientific name) DBH range (cm) No. sample trees %Carbon Carbon stock in sample trees (stem+Branch+Leaf) (kg)
min max Average
Mixed deciduous forest 1 283-385 Cananga latifolia. 4.50-43.00 15 47.75 23.90 454.29 163.37
2 386-488 Litsea glutinosa 4.50-62.40 15 46.86 38.65 1,297.63 505.81
3 489-591 Lannea coromandelica 4.50-58.00 16 45.75 11.19 1,252.27 407.75
4 592-694 Tectona grandis 4.50-71.00 16 49.66 8.18 1,385.72 589.75
5 695-797 Albizia odoratissima 4.50-42.50 15 46.84 12.17 502.36 186.04
6 798-900 Terminalia nigrovenulosa 4.50-61.29 16 47.13 38.10 1,161.93 402.95
7 901-1,003 Pterocarpus macrocarpus 4.50-61.50 15 48.41 20.22 1,489.53 445.37
8 1,004-1,106 Xylia xylocarpa 4.50-66.80 15 48.03 29.40 1,340.78 489.37
9 1,107-1,209 Dalbergia oliveri 4.50-42.80 17 47.13 14.89 724.67 264.32
10 1,210-1,312 Terminalia corticosa 4.50-66.30 15 48.55 22.87 2,006.99 590.11
Dry dipterocarp forest 1 401-485 Mitragyna brunonis 4.50-41.00 15 47.57 16.05 496.35 189.90
2 486-570 Bridelia pierrei 4.50-25.80 12 47.16 6.12 186.67 70.35
3 571-655 Gardenia sootepensis 4.50-32.40 15 46.06 23.53 680.13 175.37
4 656-740 Haldina cordifolia 4.50-41.9 15 48.26 8.86 604.76 177.12
5 741-825 Dipterocarpus obtusifolius 4.50-42.50 15 47.62 9.77 505.84 145.02
6 826-910 NA
7 911-995 Pterocarpus macrocarpus 4.50-61.50 15 48.41 20.22 1,489.53 445.37
8 996-1,080 Shorea siamensis 4.50-58.20 15 46.76 11.99 1,148.05 438.29
9 1,081-1,165 Dalbergia oliveri 4.50-42.80 17 47.13 14.89 724.67 264.33
10 1,166-1,250 Terminalia corticosa 4.50-66.30 15 48.55 23.87 2,006.99 590.11
Dry evergreen forest 1 388-474 Duabanga grandiflora 4.50-147.00 15 46.92 59.58 8,673.15 2,572.99
2 475-561 Croton roxburghii 4.50-42.00 15 47.77 16.81 353.85 130.37
3 562-648 Careya sphaerica 4.50-38.30 15 47.47 12.97 256.03 117.36
4 649-735 Artocarpus lakoocha 4.50-47.30 15 48.31 13.12 915.60 269.66
5 736-822 Cratoxylum formosum 4.50-22.60 15 46.83 8.45 119.54 42.31
6 823-909 Anogeissus acuminata 4.50-71.70 15 46.81 56.61 2,365.23 761.73
7 910-996 Pterocarpus macrocarpus 4.50-61.50 15 48.41 20.22 1,489.53 445.37
8 997-1,083 Terminalia alata 4.50-50.00 15 45.75 25.75 1,271.14 410.04
9 1,084-1,170 Xylia xylocarpa 4.50-66.80 15 48.03 29.40 1,340.78 489.37
10 1,171-1,257 Quercus kerrii 4.50-43.7 15 45.43 11.78 499.12 181.19
Source: * Forest Research and Development Bureau (2007; 2010) [36,37].
Table 3. The regression equations tested to etimate standing tree carbon stock..
Table 3. The regression equations tested to etimate standing tree carbon stock..
Forest type Variables Statistic criterion value Remark
R2(%) SE F-value p-value
MDF DBH 0.9604 0.11 3,708.54 <0.001
H 0.7361 0.29 426.8 <0.001
DBH, H 0.9678 0.10 2,281.89 <0.001 *Best variables
DDF DBH 0.9259 0.16 1,649.54 <0.001
TH 0.7303 0.30 357.5 <0.001
DBH, H 0.9412 0.14 1,048.28 <0.001 *Best variables
DEF DBH 0.9633 0.13 3,888.38 <0.001
TH 0.7039 0.36 351.89 <0.001
DBH, H 0.9770 0.10 3,127.52 <0.001 *Best variables
NDF DBH 0.9526 0.13 8,779.48 <0.001
TH 0.7171 0.32 1,107.98 <0.001
DBH, H 0.9642 0.11 5,870.73 <0.001 *Best variables
Table 4. Carbon stock equations, DBH range, and statistical goodness of fit values of the constructed general equation.
Table 4. Carbon stock equations, DBH range, and statistical goodness of fit values of the constructed general equation.
Forest Type Equation DBH Range (cm) R2 (%) SE F-Value p-value
MDF CMDF = 0.0199 DBH2.1887 H0.5825 8.70 -71.00 0.9678 0.10 2,281.89 <0.01
DDF CDDF = 0.0145 DBH2.1435 H0.7480 10.00 – 66.80 0.9412 0.14 1,048.28 < 0.01
DEF CDEF = 0.0167 DBH2.1423 H0.7070 9.70 – 147.00 0.9770 0.10 3,127.52 < 0.01
NDF CNDF = 0.017543 DBH2.1625 H 0.6614 8.70-147.00 0.9642 0.11 5,870 < 0.01
Table 5. Carbon stock (CS) per sample point in the Mae Huad sector.
Table 5. Carbon stock (CS) per sample point in the Mae Huad sector.
Point NO. CS Forest Type Point NO. CS Forest Type Point NO. CS Forest Type
(kg/ha) (kg/ha) (kg/ha)
1 88,287.97 MDF 16 126,052.64 DDF 31 9,129.03 DEF
2 17,097.92 DEF 17 20,736.35 MDF 32 23,084.19 MDF
3 69,643.47 MDF 18 42,646.39 MDF 33 64,055.07 MDF
4 7,201.58 DEF 19 47,857.28 MDF 34 22,489.32 DEF
5 128,574.47 DDF 20 165,600.93 DDF 35 106,388.19 MDF
6 100,360.65 DDF 21 38,493.44 MDF 36 67,442.07 MDF
7 58,061.08 MDF 22 11,156.50 MDF 37 148,058.31 DDF
8 6,152.98 DEF 23 59,036.21 MDF 38 43,768.32 MDF
9 27,286.41 MDF 24 162,671.46 DDF 39 79,015.26 MDF
10 63,391.82 MDF 25 38,514.85 MDF 40 70,904.44 MDF
11 59,217.74 MDF 26 42,606.07 MDF 41 133,507.34 DDF
12 46,099.49 MDF 27 63,438.04 MDF 42 57,309.07 MDF
13 28,610.93 MDF 28 63,581.88 MDF 43 46,216.42 MDF
14 8,623.92 DEF 29 9,828.38 DEF 44 11,595.44 DEF
15 61,435.68 MDF 30 175,641.25 DDF Average 61,837.96 kg/ha
Table 6. The average carbon per cubic meter in a sample trees and wood density.
Table 6. The average carbon per cubic meter in a sample trees and wood density.
Density class Carbon in a cubic meter (kg) in MDF Carbon in a cubic meter (kg) in DDF Carbon in a cubic meter (kg) in DEF
Stem Branch leaf Total Stem Branch leaf Total Stem Branch leaf Total
1 220.34 60.06 17.76 298.15 289.33 73.00 27.95 390.27 227.50 167.51 9.03 404.03
2 281.49 78.52 22.89 382.90 284.83 84.54 33.00 402.37 260.01 164.63 10.81 435.45
3 221.62 48.75 14.48 284.85 365.20 89.50 34.70 489.40 257.70 187.24 12.10 457.04
4 293.32 94.68 27.66 415.66 301.62 105.00 39.93 446.55 314.15 187.81 11.52 513.47
5 319.23 68.76 20.35 408.33 317.04 79.18 30.63 426.85 314.15 223.06 15.37 552.57
6 354.41 108.68 31.72 494.81 NA 307.47 195.46 10.48 513.40
7 385.07 98.06 28.83 511.96 385.07 98.06 28.83 511.96 385.07 98.06 28.83 511.96
8 345.14 84.59 24.77 454.51 350.46 79.55 29.77 459.77 348.71 162.78 9.69 521.17
9 386.94 68.10 20.10 475.13 386.94 68.10 20.10 475.13 345.14 84.59 24.77 454.51
10 314.15 84.83 24.92 423.91 314.15 84.83 24.92 423.91 342.86 128.51 9.03 480.40
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated