Preprint
Article
Energy and Probability Density Computation for Muonic Hydrogen
Altmetrics
Downloads
188
Views
50
Comments
0
This version is not peer-reviewed
Submitted:
19 May 2023
Posted:
22 May 2023
You are already at the latest version
Alerts
Abstract
This paper discusses about the quantum energy levels of muonic hydrogen considering only Coulomb interaction. The computational analysis in this paper will help the reader get a good understanding of how different a muonic hydrogen is from its electronic counterparts. Energy eigenvalues are calculated by numerical method and the probability density distribution of muon around the nucleus is plotted for different quantum states using special functions. The code is written in python. A comparative study of emission spectra between the muonic hydrogen and hydrogen has also been discussed.
Keywords:
Subject: Physical Sciences - Atomic and Molecular Physics
1. Introduction
Interaction of muons with matter has been extensively studied since the discovery of muon in the year 1936 [1]. Muon is found to behave as a heavy electron or positron in matter. When stopped by a target, muons are captured by the nuclei. On interaction with matter, muonic atoms are formed. In 1947, John Wheeler suggested that particles other than electrons could form a bound system with a nucleus, particularly the negative muon having a mass of 1.883 × 10−28 kg and mean lifetime of 2.2 × 10−6 s with a charge of [2]. A muonic atom is an atom where an electron is replaced by a muon, which also belongs to the lepton family. Importance of muonic atom lies in the fact that the wave function of muon in all states, especially in the lowest state, overlaps with the nucleus more strongly than the normal electronic wave functions.
1.1. Discovery
Muons are constantly being produced in the upper atmosphere by the interaction of cosmic rays with the atmospheric air. Due to their high energy, a large fraction of them reaches the ground and even penetrate deep into rocks [3]. Pions decay into muons. Pions are created in the following interactions:
In 1953, using a NaI synchrocyclotron, two American scientists Fitch and Rainwater observed radiation from muonic atoms [4]. This work indicated that the size of atomic nuclei was smaller than what had been supposed. In 1964, the NaI scintillation spectrometer was replaced by Ge(Li) detector because of its high resolution to investigate the muonic X-ray spectra that made great advances in accuracy and precision. The production of muon atoms in laboratory is carried out with a particle accelerator. Protons are incident on atomic nuclei like lithium or carbon after being accelerated to high energies. This collision creates a whole bunch of particles including pions. They decay into a muon and a neutrino.
These muons are then selectively channeled into beam lines and transported to the spectrometer where the sample lies. The muon is slowed down and captured by an atom into an orbit forming muonic atom.
Muonic atoms are nuclear probes and are used to test principles from quantum electrodynamics to chemical physics. Prior to 1980, most research was in negative muonic atoms. During the last few years positive muonic atoms are also being studied. In hadronic atoms, due to strong interaction between the hadron and the nucleus, the energy levels are shifted and broadened as compared to muonic atoms with strong dependence on the nuclear charge. The proton and neutron distribution insidethe nucleus can be separately analyzed by means of combined muonic and hadronic atom data, as the muon interacts mainly with the protons and the hadrons with both types of nucleons.
2. Hydrogen Atom
2.1. Bohr’s Model of an Atom
In this section, we apply Bohr’s model of hydrogen atom [5] to muonic hydrogen and calculate the orbit size for various principal quantum number n.
The radius of the nth orbit is given by
where symbols have their usual meaning.
The reduced mass of muonic hydrogen is
where and are rest masses of proton and muon respectively. Using 1.8835 × 10−28kg, the reduced mass for muonic hydrogen is . Table 1 lists the orbit sizes for various values of n for electronic and muonic hydrogen atoms.
The radius of the nth orbit of muonic hydrogen atom (H) is 186 times less than the electronic hydrogen atom (H). This is shown in Table 1. The energy of muon in nth orbit is
The relation between the energy levels of H and H is
i.e., the corresponding energy levels of H is 186 times greater than H.
2.2. Quantum Mechanical Model of Hydrogen Atom
The hydrogen atom problem in quantum mechanics is a two-body problem for which Schrödinger’s equation should be solved. We present below a brief derivation of the stationary states of the hydrogen atom for Coulomb potential [6]. The Schrödinger equation is
The Hamiltonian is
where is the kinetic energy operator, and is the potential energy term. If represents spatial part of the wave function , then for stationary states, we can write
where E represents the energy eigenvalue of the system. General solution is of the form
The Laplacian operator can be expressed in spherical polar coordinates as
One can write as
where is the radial part and is the angular part of . Using Equation (1) in the Schrödinger’s equation, we get the radial equation as
The angular part of the Schrödinger’s equation is
where is the separation constant. Equation (2) can be further simplified by setting Thus
Equation (3) has two variables and which can be separated as
where is the separation constant. Equation (5) can be solved to get
Equation (4) can be solved as
where is the associated Legendre polynomial. If , then . Therefore, we must have for solution to exist; l is a non-negative integer; . Now, which represents spherical harmonics. Normalizing, we get
where for and for . It can be shown that the stationary part of the wave function is
where L is associated Laguerre polynomial, and
The allowed energies of the hydrogen atom are
Equation (7) is identical to the energy expression derived using Bohr’s model. Hence quantum mechanically, the energy eigenvalues are the same.
We define
For and state of H, A is of the order of and respectively. For and state of H, A is of the order of and respectively. These normalization constants do not have any physical significance.
For H, 5.290 × 10−11 m and for H, = 2.846 × 10−13 m from Equation (6). Clearly . The most probable value of r in the ground state and for the first excited state for both H and H are calculated and compared. The most probable value of r means that the probability of finding an electron or muon is highest for a given stationary state .
For state,
The probability of finding electron or muon within an elemental volume is
Using (8),
where
By definition, the slope of the curve is zero where the probability is a maximum [5].
Therefore, the most probable value of r in state is the Bohr’s radius a. For electronic hydrogen, electron is more likely to be found at m. For muonic hydrogen, muon is more likely to be found at m. Thus one sees that the muon is closer to the nucleus than the electron in state by a couple of orders.
3. Numerical Method
In this section we explain the method to solve the Schrödinger’s equation numerically for a given potential, in particular, for Coulomb potential in the case of hydrogen atom.
3.1. Finite Difference Method
Finite difference methods are a class of numerical techniques for solving differential equations by approximating derivatives with finite differences [7]. Suppose , its first derivative is
By definition
where is the change in the variable x. Therefore, one can write
provided h is reasonably small. One can replace the derivative by a difference in the differential equation and solve it. Using index notation, one can write
For 2nd order derivative, we have
Approximating using finite difference method we write,
Using index notation, we write
3.2. Numerical Method for Schrödinger’s Equation
While solving the Schrödinger’s equation analytically, we get an expression for radial part of the stationary state as
where . We will be using Equation (9) to determine the energy eigenvalues for the hydrogen atom. Equation (9) can be written as
Equation (10) is an eigenvalue equation. We need to express different terms on left hand side in matrix form. As previously mentioned, term can be replaced by a finite difference
where the index i is iterated up to N. This can be written as a square matrix of order N as
can be written in a square matrix of order N as
can be written as a square matrix of order N as
The sum of all the above matrices will be the square matrix of the eigenvalue equation for which eigenvalues and eigenvectors will be determined.
4. Computation
4.1. Program 1
The +python+ program for energy computation is the following:

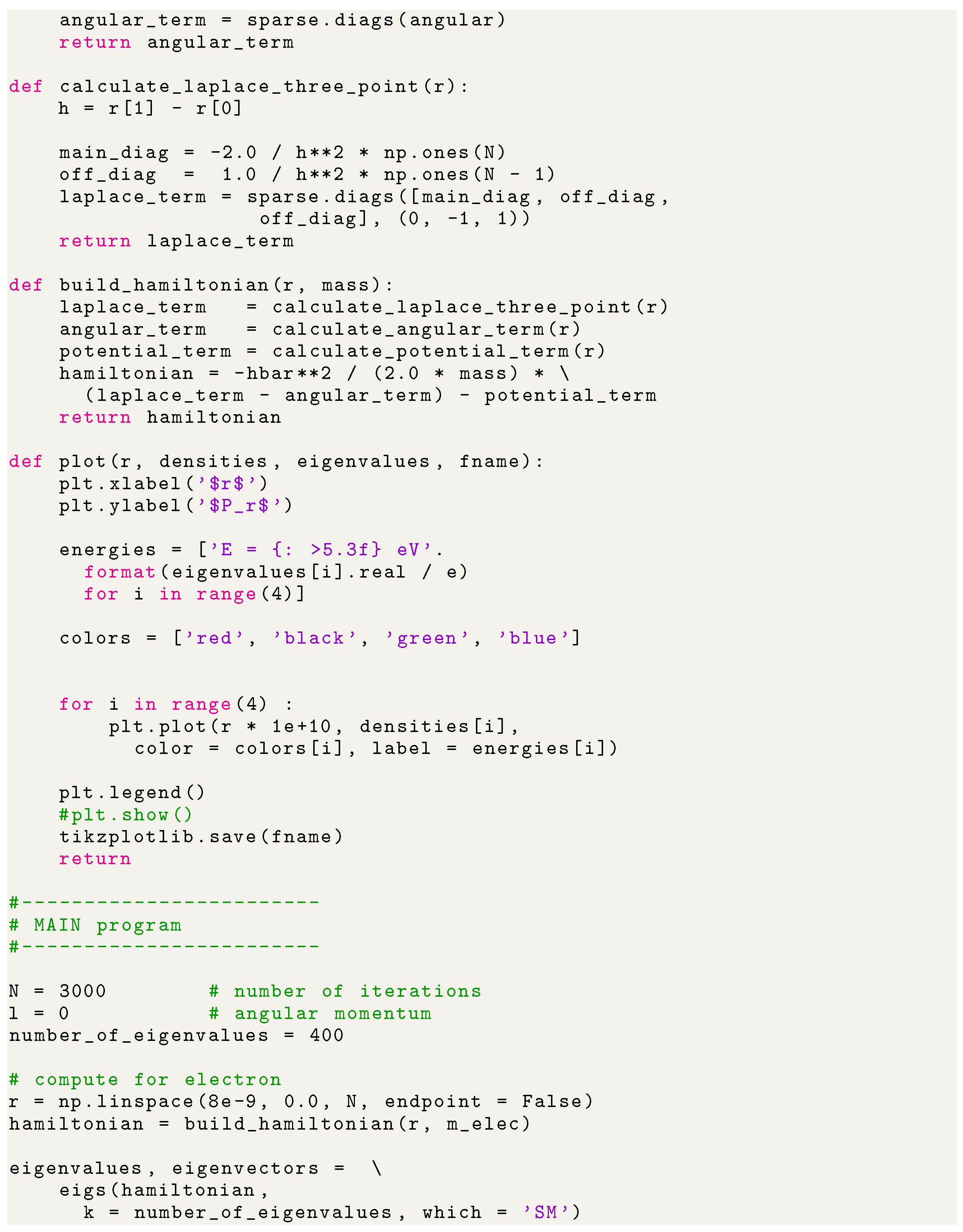

The +python+ program for radial density distribution computation is the following:
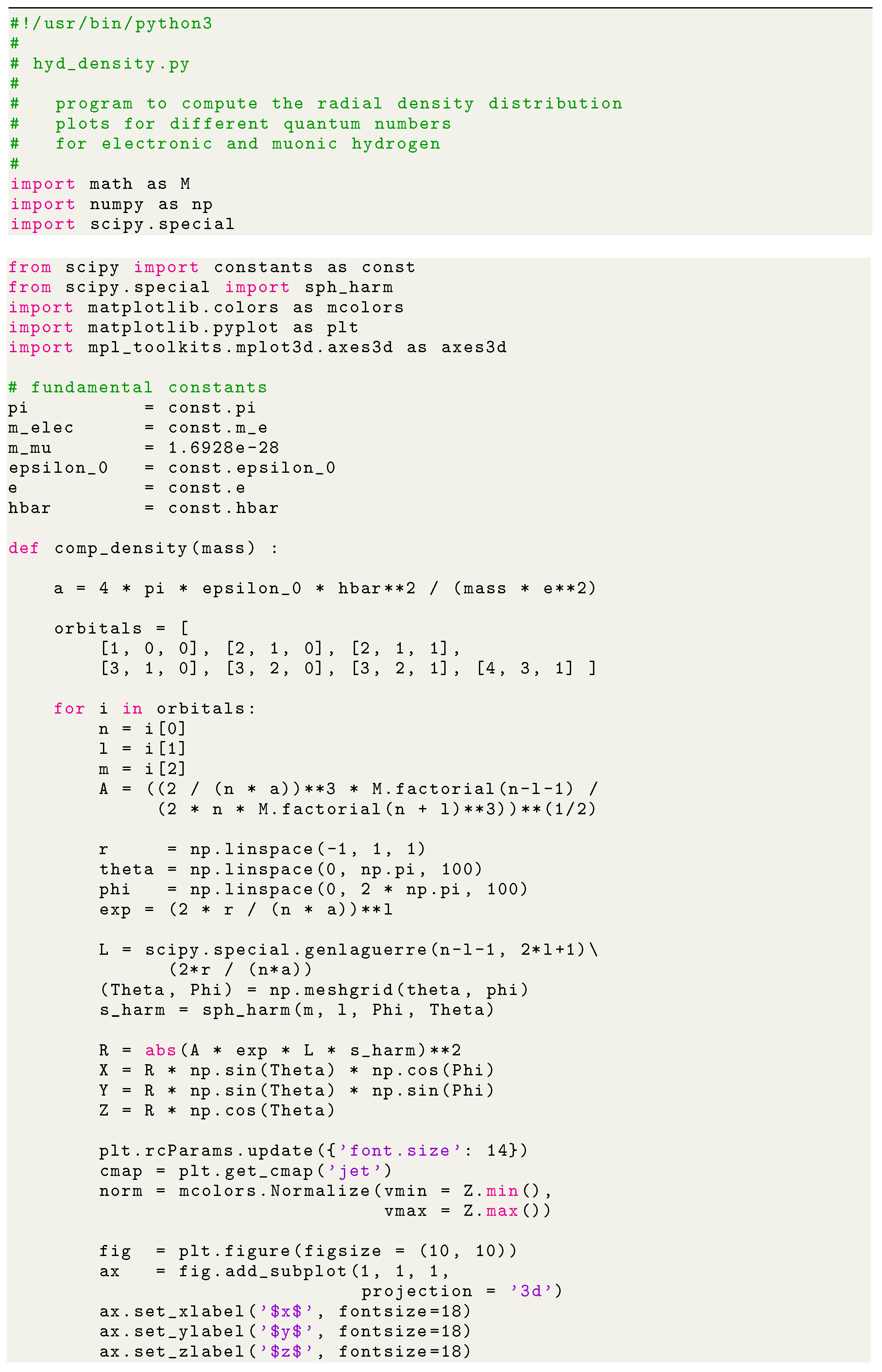
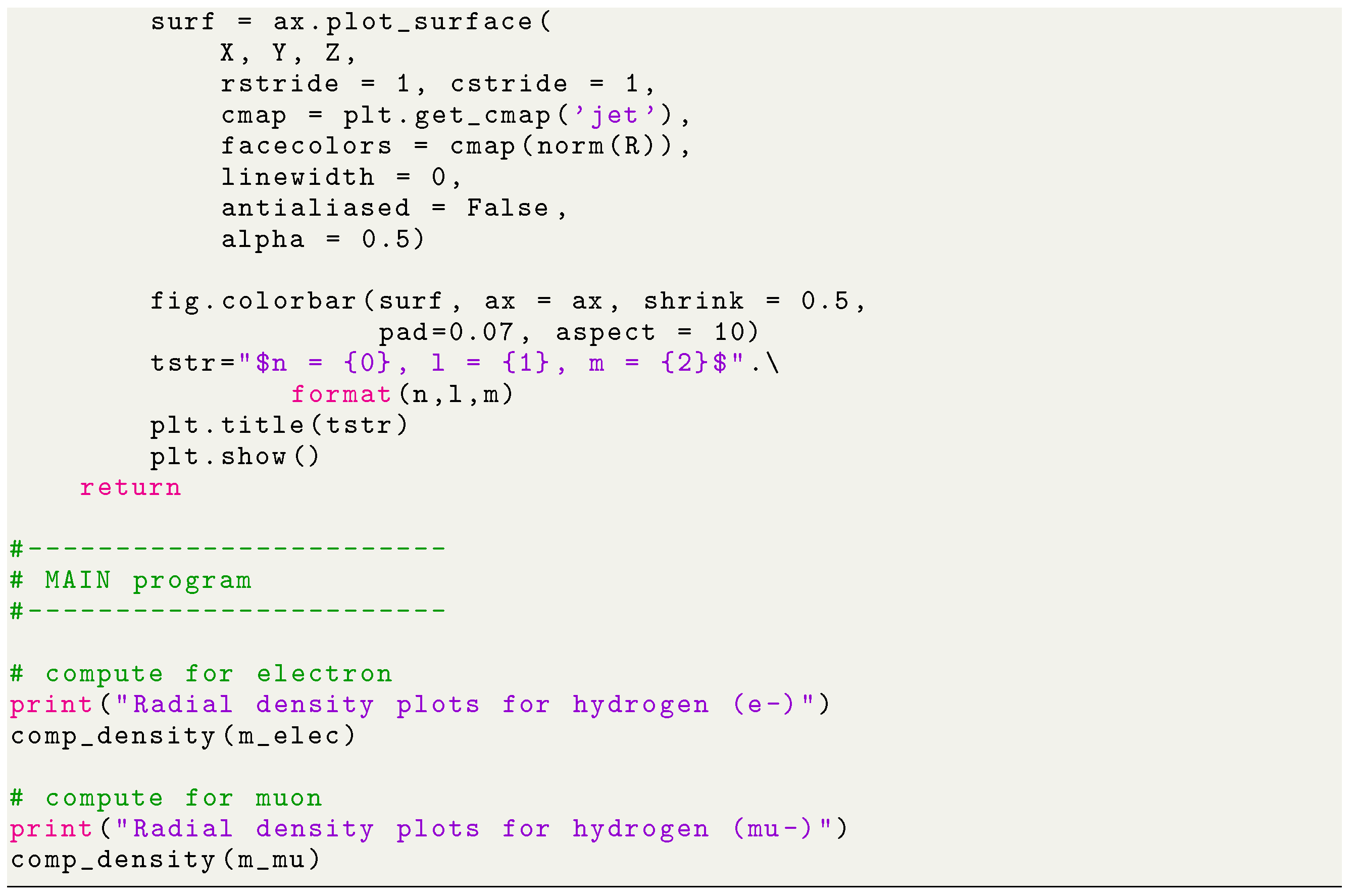
5. Results and Discussion
5.1. Energy Computation
The equation used for energy computation is
For the case of H, the electronic mass is replaced by the reduced mass of H, and the range of r for calculating energy is taken from 4 ×10 −11 m to the point at nucleus, excluding it.
The number of iteration points is taken as to get more accurate energies. Increasing N will increase the time to compute. Since the order of the square matrix is 3000, there will be 3000 eigenvalues. There are n stationary states for the hydrogen atom, where n is the principal quantum number. While solving numerically, a given eigenvector will have a corresponding energy eigenvalue. Therefore, while constructing the solution, many points will correspond to the same energy. Once, a stationary state is determined, the next stationary state will be found which has a different eigenvalue. In this way all eigenvectors and eigenvalues are determined.
The computed first ten eigenenergies of H and H are shown in Table 2. We observe that the eigenvalues nearly match the experimentally observed energies for H.
5.2. Probability Density Computation
The program also plots the probability density () as a function of r for the first four eigenstates of H and H. Here by probability we mean . Figure 1 and Figure 2 show the plots for H and H respectively for different energy eigenstates.
Table 2.
Computed energy eigenvalues of H and H atoms.
| H | H | |
| n | () | () |
| 1 | -13.597 | -2526.967 |
| 2 | -3.401 | -632.001 |
| 3 | -1.512 | -280.911 |
| 4 | -0.850 | -158.017 |
| 5 | -0.544 | -101.132 |
| 6 | -0.378 | -70.231 |
| 7 | -0.278 | -51.580 |
| 8 | -0.211 | -38.648 |
| 9 | -0.150 | -25.259 |
| 10 | -0.075 | -8.307 |
5.2.1. Observations
- The probability density curves for H and H are similar except for the magnitude. It can be seen that the muon is closer to the nucleus in H than an electron in H by two orders of magnitude.
- It can be observed that , , and states have one, two, three and four most probable values for r respectively for both H and H.
The python program to compute the energy eigenvalues and probability density as a function of r is given in Section 4.1.
5.3. Radial Probability Density Computation
A python program has been written to compute the spatial distribution of electron and muon in hydrogen for different values of n, l, and m quantum numbers.
Density distribution plots for ; , and for H and H are shown in Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16.
The probability of finding the particle decreases from red to blue in the density plots.
5.3.1. Observations
- The state for H and H is spherically symmetric as expected.
-
When the electron has non-zero angular momentum, the density distributions are no longer spherical. This is the case for p, d and f orbitals. The electron distributions for these orbitals assume a characteristic shape.
- −
- −
- In H, the scale is much higher than in H. It is noted that the density is again zero at the nucleus.
- −
- −
- −
- It is evident that all the orbitals with the same value of n and l are similar, but differ in their spatial orientations.
5.4. Hydrogenic Spectrum
Here, we will interpret the physical meaning of the values obtained. A comparative study of the energy levels of H and H is done, followed by a discussion about their spectra.
In the absence of magnetic and electric field, the hydrogen atom will be in a stationary state. Until and unless energy is absorbed or emitted, the atom’s energy will be the same. In quantum mechanics, a particle or a system cannot have any arbitrary energy. Only certain discrete energies are allowed. These are referred to as the Bohr energies. Bohr energy levels depend only on the principal quantum number n, and independent of other quantum numbers such as l, , and . Further, the Bohr energy comprises several closely spaced levels called the fine structure, and hyperfine structure. We restrict ourselves to only Bohr energy levels here.
Table 2 shows the computed Bohr energies for H and H atoms. The negative sign means that the particle is in a bound state; here it is bound to the nucleus. The particle in its lowest energy state (ground state) has energy in the case of electron and energy for muon. The muonic energy levels have more energy than the corresponding electronic energy levels. One can say that the muons are in a deeper energy well than the electrons.
To excite a H it requires more energy than to excite an H. The energy levels of H correspond to ultra-violet, visible and infrared region in electromagnetic spectrum, whereas those of H correspond to the X-ray region of the electromagnetic spectrum. The atom will make a transition from one energy level to a higher energy level when energy of the incident radiation is equal to the difference. H atoms can be excited by UV, visible, and infrared photons; muonic hydrogen atoms can be excited only by X-ray photons. During de-excitation, photons in the corresponding regions are emitted.
Let represent the energy of one stationary state and represent the energy of another stationary state. When a photon of frequency is absorbed by the atom, transition happens from . When the atom transitions from then a photon of same frequency is emitted. From the calculated energy levels of H and H we can calculate the emission and/or absorption spectrum using the above formula. In literature, different series in the hydrogen spectrum are given different names. When an atom makes a transition from any higher level to first, second, third, fourth and fifth energy levels, the spectral series corresponding to these are called Lyman, Balmer, Paschen, Brackett, and Pfund series respectively (see Table 2).
Experimentally, when measuring the wavelengths of emission spectrum of muonic atoms, they have to be measured quickly because the mean lifetime of a muon is about . Experimentalists have measured X-ray spectra of various muonic atoms to study the nuclear structure as the muonic probability density is higher in the vicinity of the nucleus.
6. Conclusions
The computational studies of muonic hydrogen atom imply that the muon orbits are closer to the nucleus as compared to their electronic counterparts.
It is found that the energies of the muonic hydrogen in different states is significantly larger than those of the electronic hydrogen by a few orders of magnitude.
The spectrum of electronic hydrogen is in the UV, visible, and infrared regions of the electromagnetic spectrum whereas for the muonic hydrogen it lies in X-ray region.
Acknowledgments
The work in this article was prepared for M.Sc. project conducted in the year 2021. We express our sincere respect and gratitude to our guide, Prof. Sridhar M. A., Department of Studies in Physics, Manasagangotri, Mysuru, for his valuable guidance. We also thank Ms. Akhileshwari P., Research Scholar, Department of Studies in Physics, Manasagangotri, Mysuru, for her constant help and support.
References
- C. S. Wu and L. Wilets. “Muonic Atoms and Nuclear Structure”. In: Annual Review of Nuclear Science 19.1 (1969), pp. 527–606. [CrossRef]
- B. H. Bransden and C. J. Joachain. Introduction to Quantum Mechanics. 1989. 1989.
- A. Knecht, A. Skawran, and S. M. Vogiatzi. “Study of Nuclear Properties with Muonic Atoms”. In: The European Physical Journal Plus 135.10 (2020), pp. 1–18. [CrossRef]
- V. L. Fitch and J. Rainwater. “Studies of X-Rays from Mu- Mesonic Atoms”. In: Phys. Rev. 92 (3 1953), pp. 789–800. [CrossRef]
- D. Halliday, R. Resnick, and J.Walker. Fundamentals of Physics. John Wiley and Sons, New York, 2000. 2000.
- D. J. Griffiths and D. F. Schroeter. Introduction to Quantum Mechanics. Cambridge University Press, 2018. 2018.
- R. J. LeVeque. Finite Difference Methods for Ordinary and Partial Differential Equations: Steady-State and Time-Dependent Problems. SIAM, 2007.
Figure 1.
Probability density as a function of the distance (r) for different energy eigenvalues of electronic hydrogen.
Figure 1.
Probability density as a function of the distance (r) for different energy eigenvalues of electronic hydrogen.
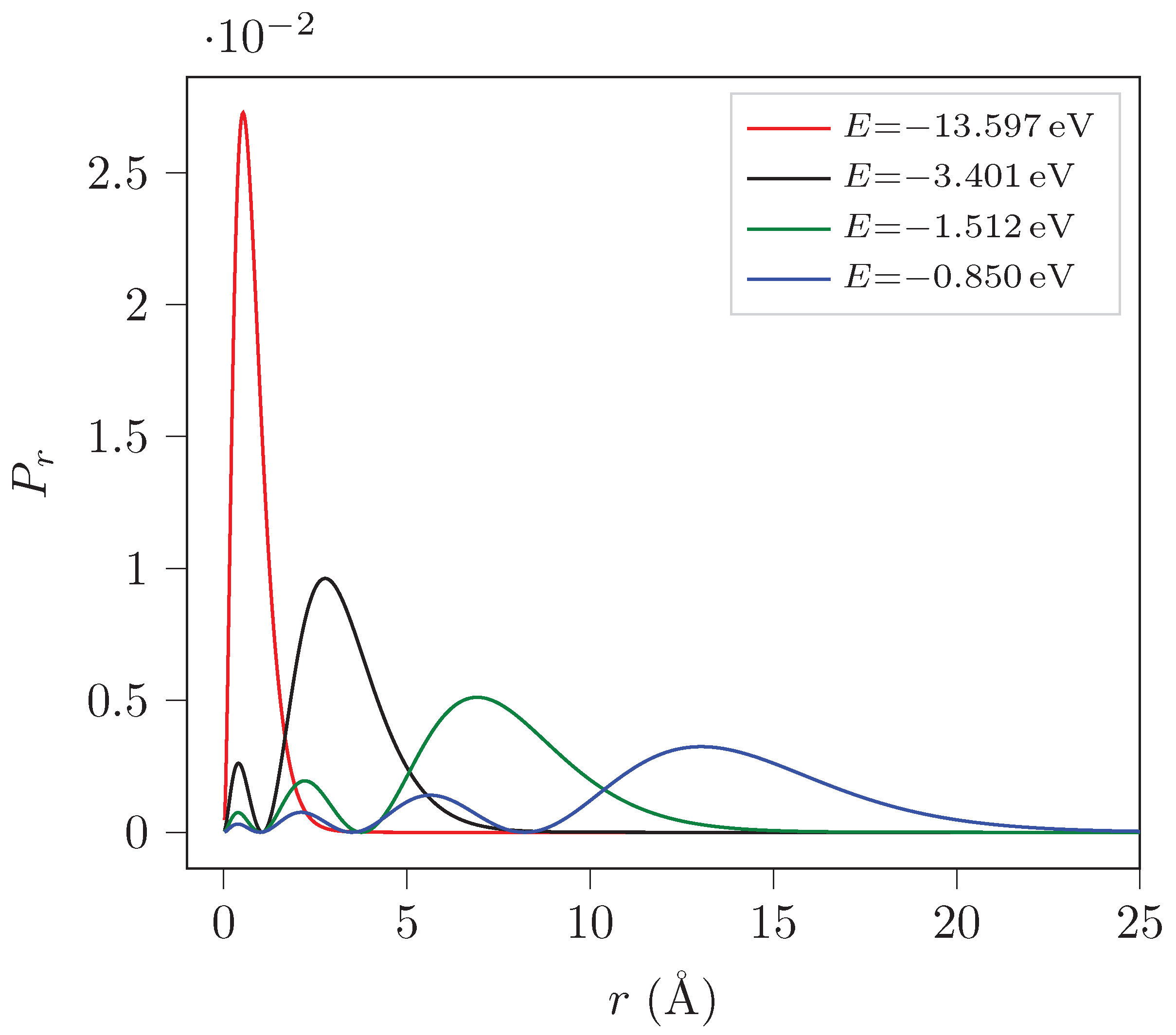
Figure 2.
Probability density as a function of the distance (r) for different energy eigenvalues of muonic hydrogen.
Figure 2.
Probability density as a function of the distance (r) for different energy eigenvalues of muonic hydrogen.
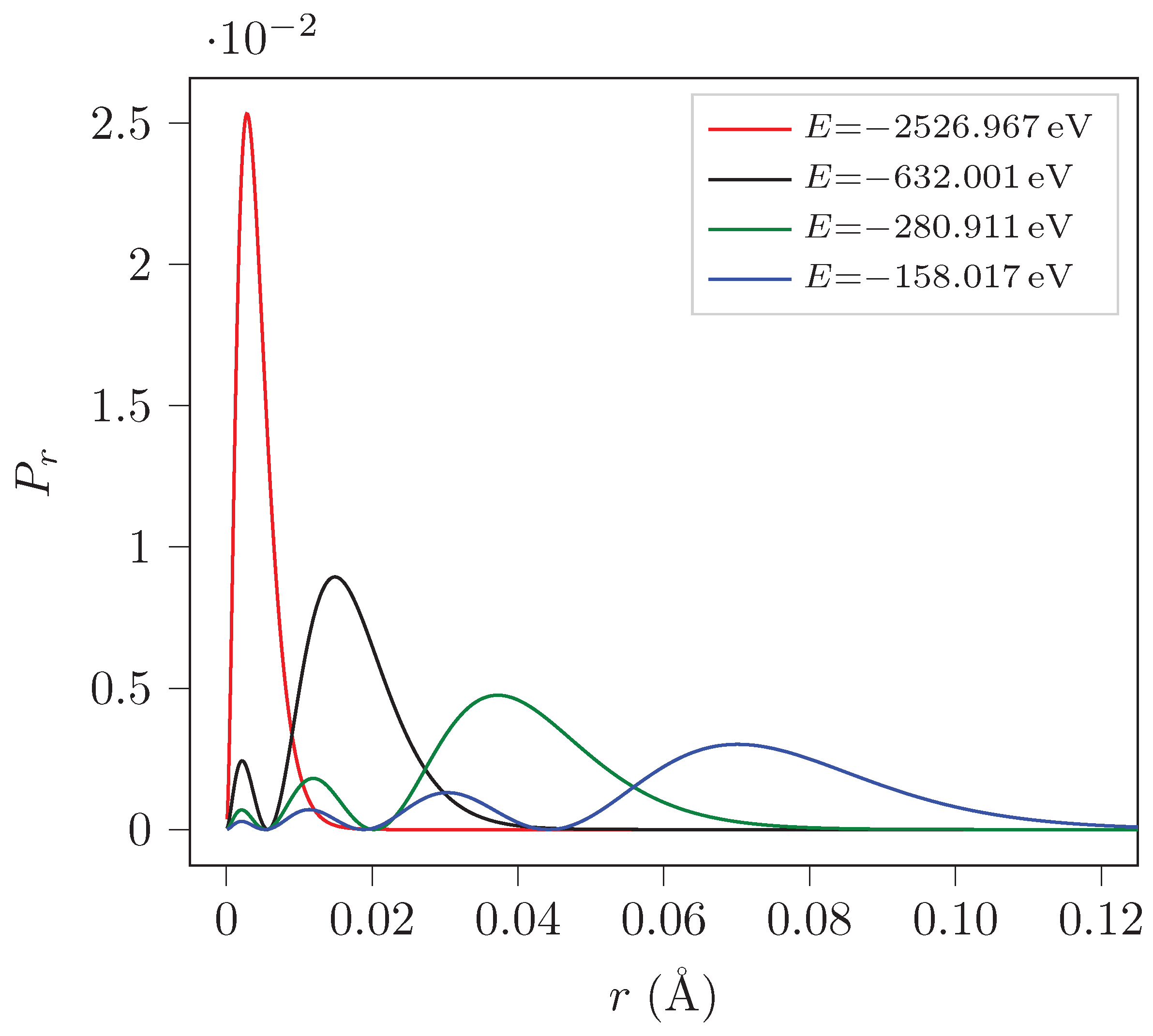
Figure 3.
Plot of for H.
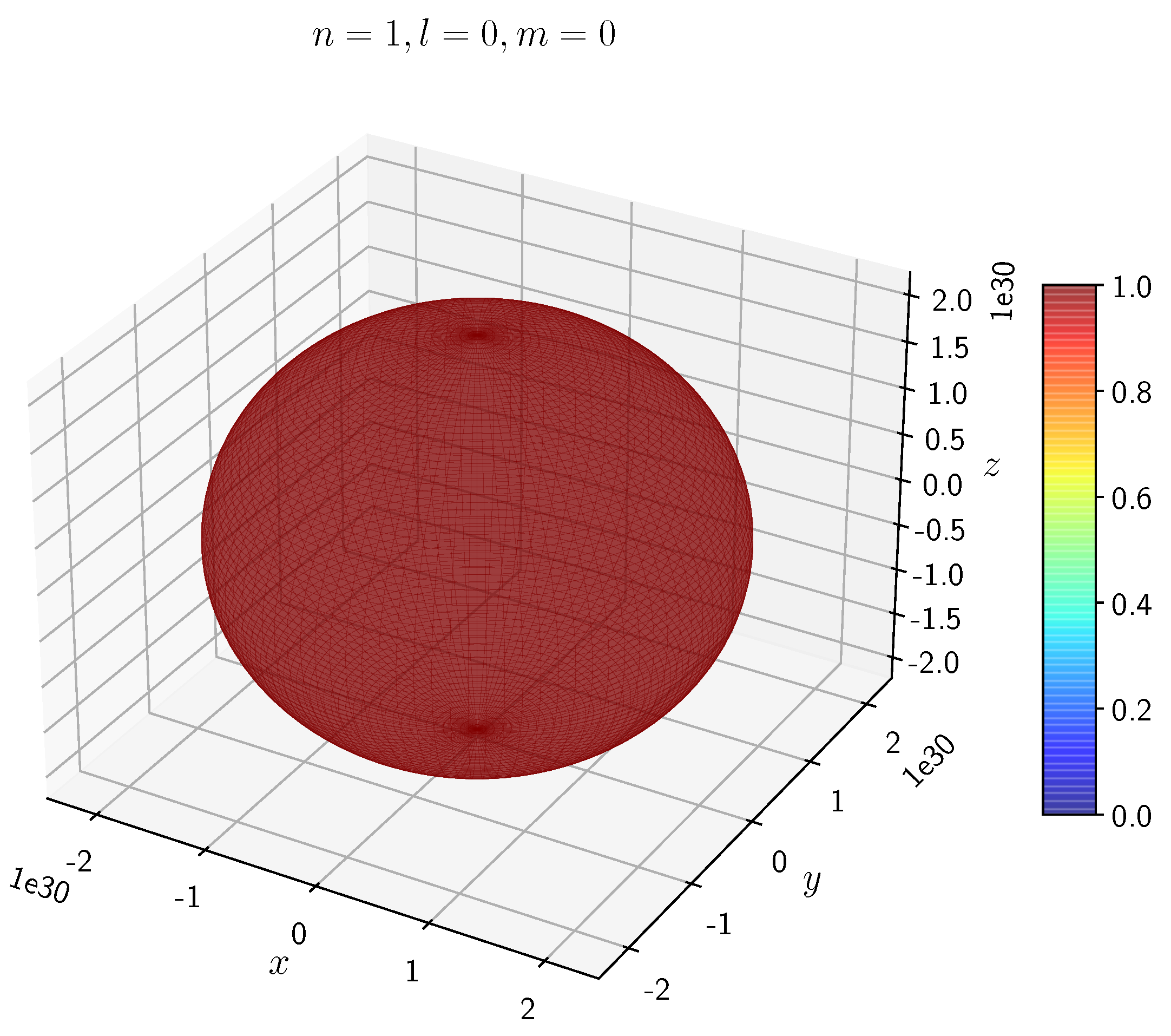
Figure 4.
Plot of for H.
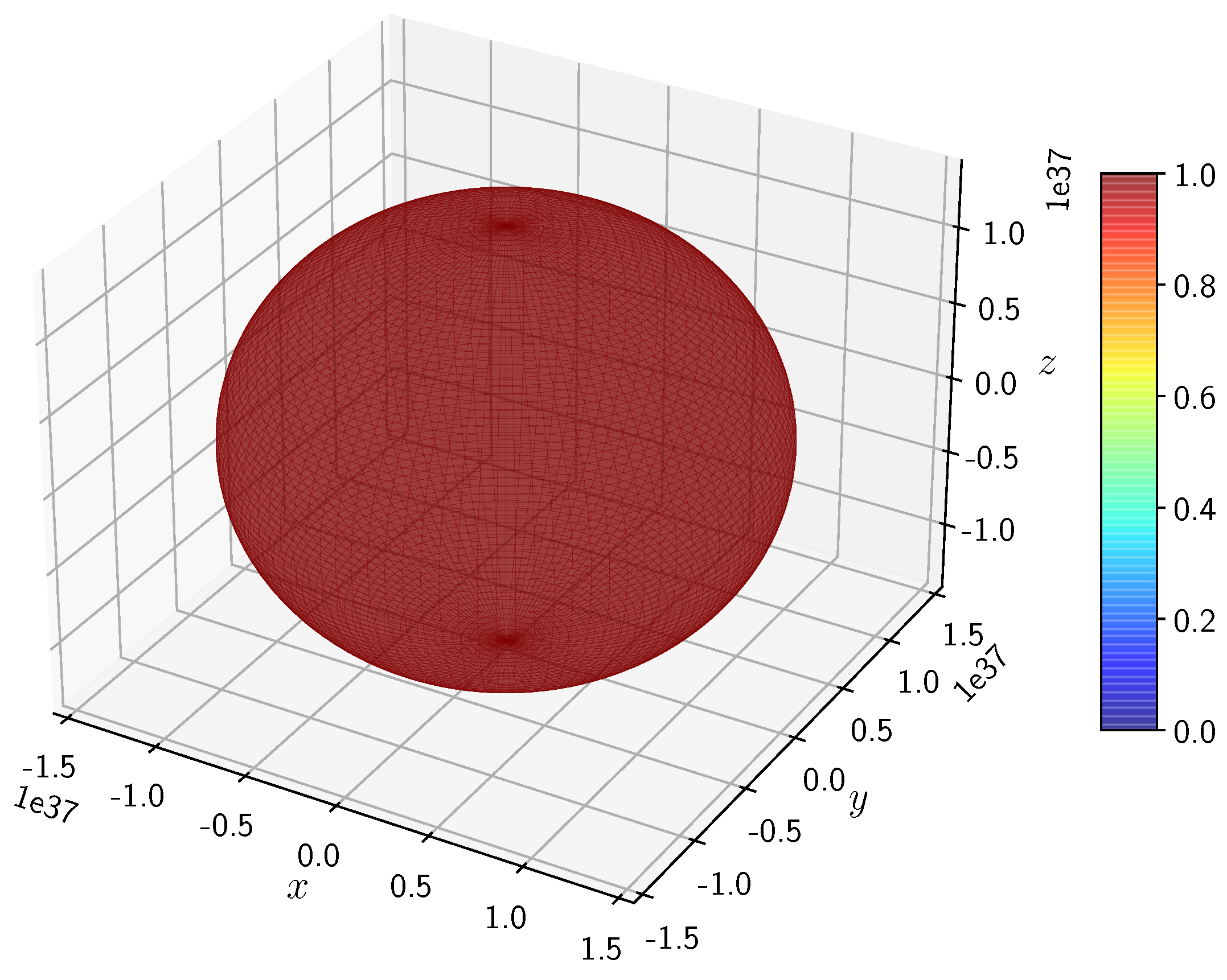
Figure 5.
Plot of for H.
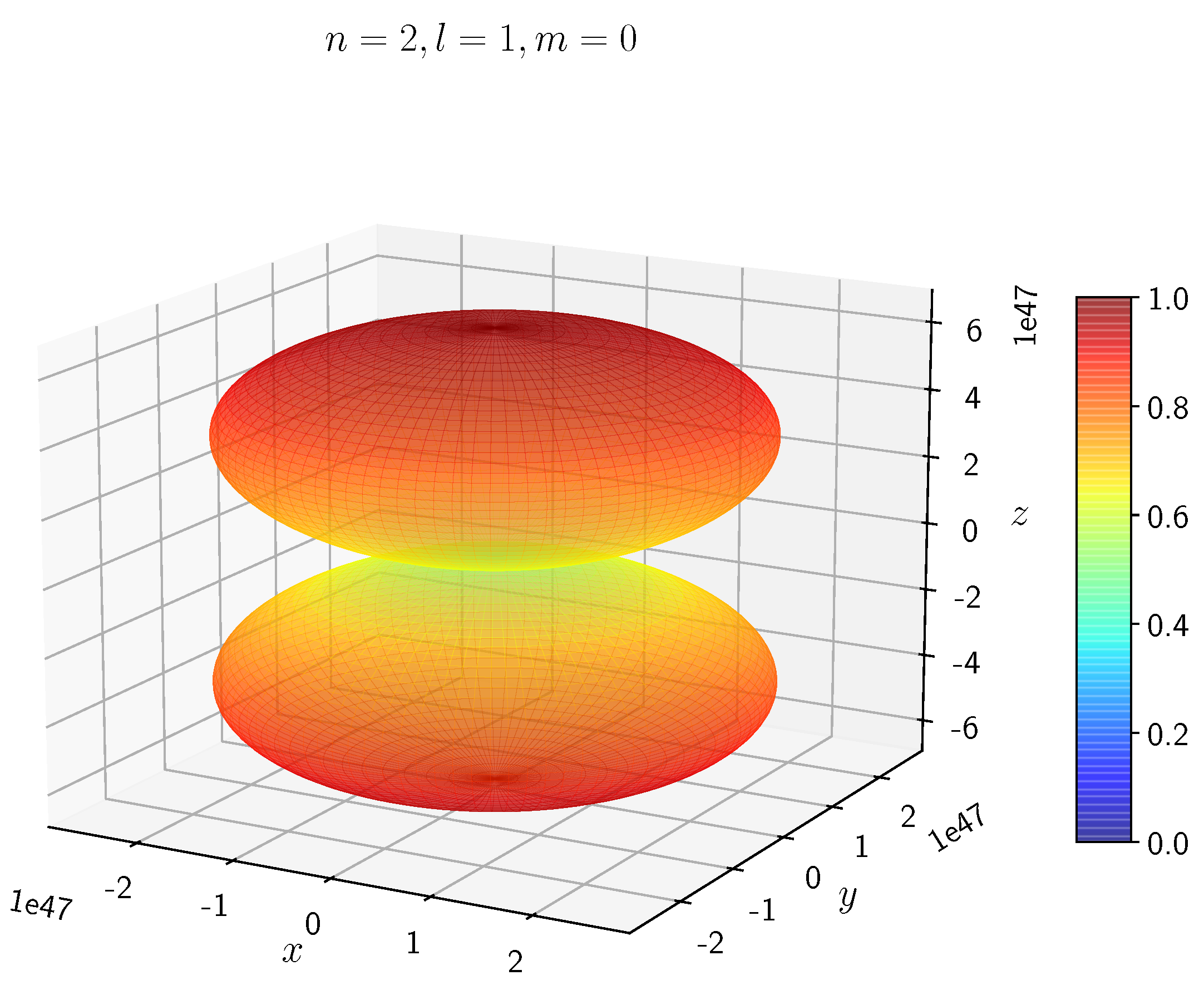
Figure 6.
Plot of for H.
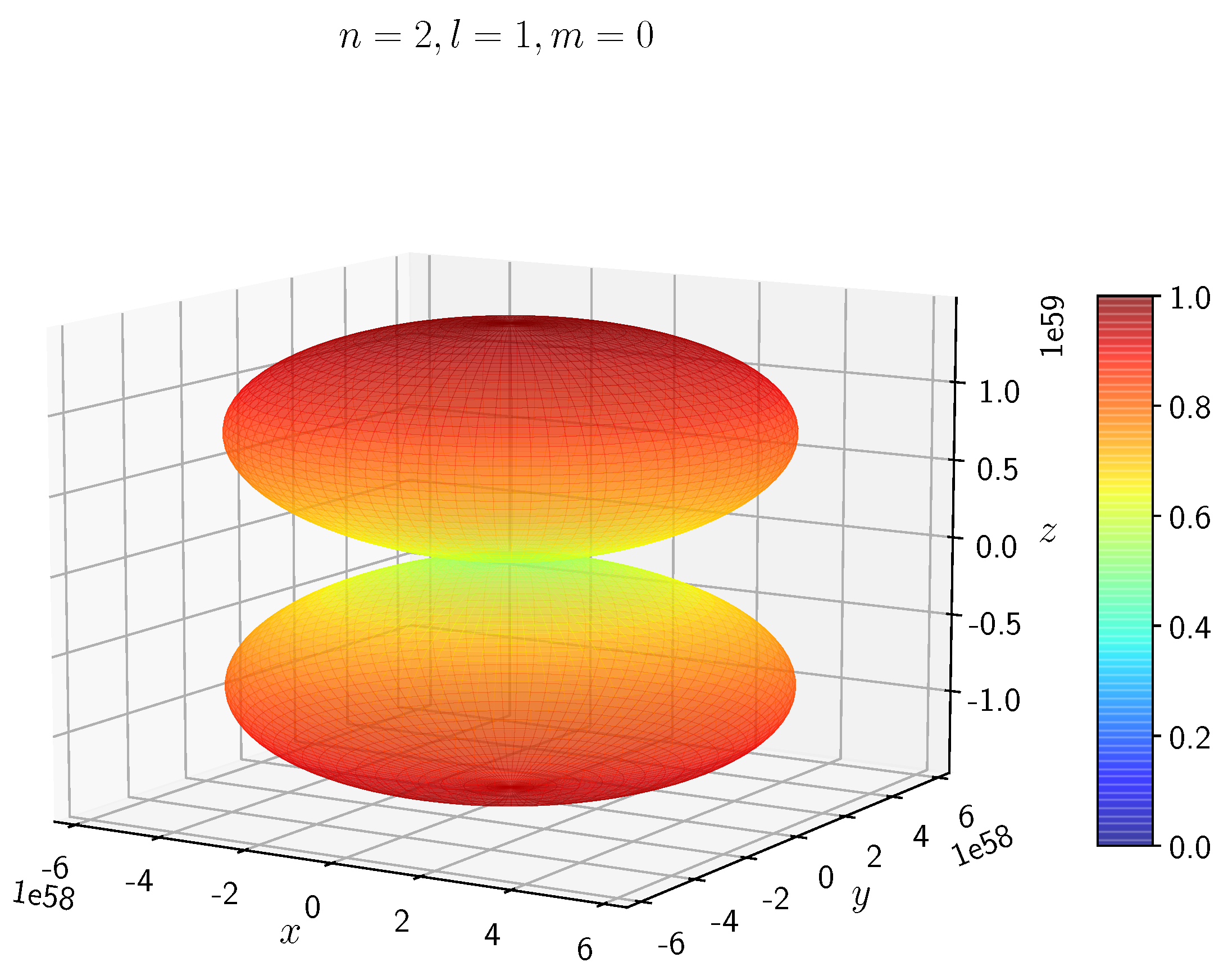
Figure 7.
Plot of for H.
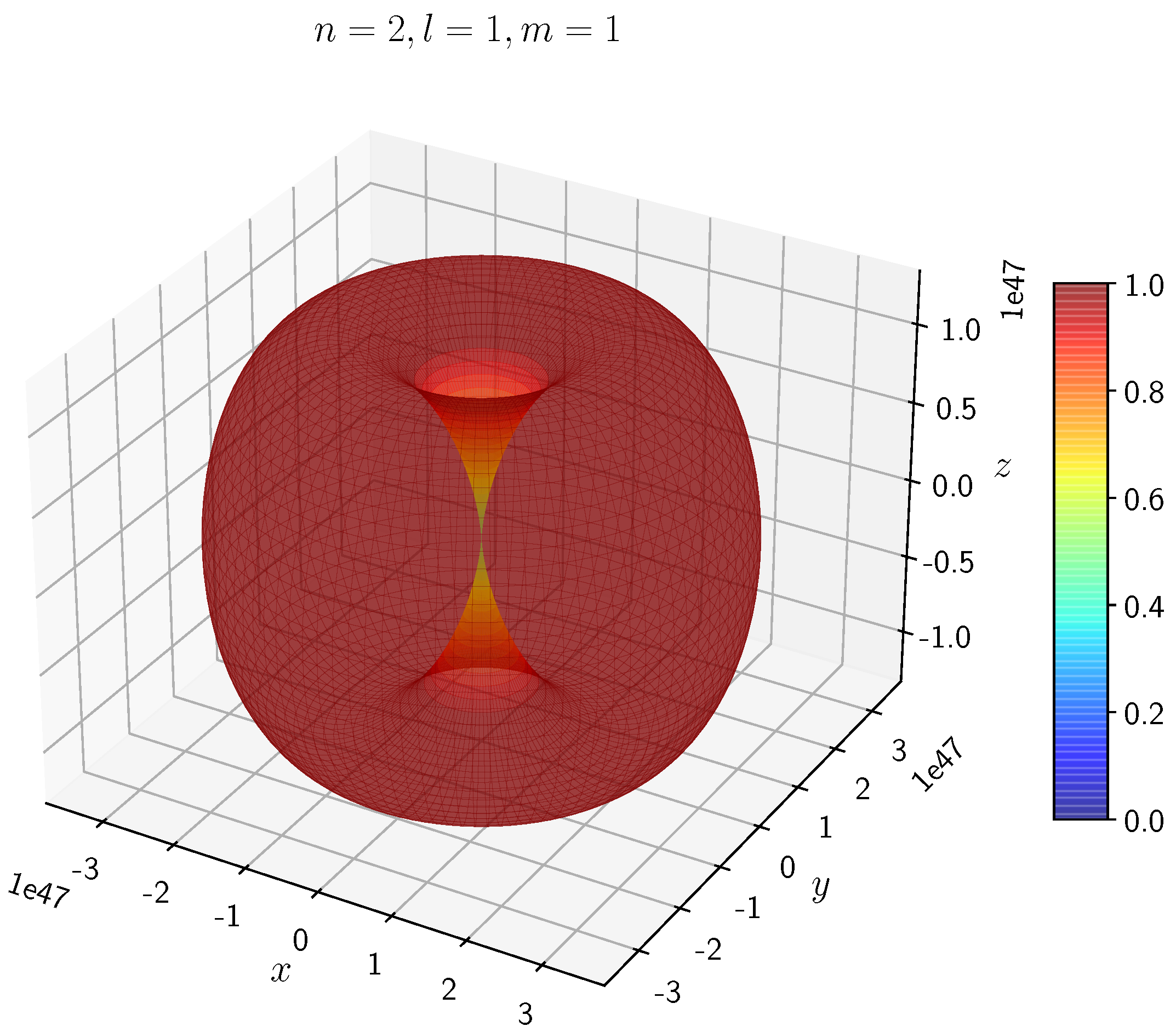
Figure 8.
Plot of for H.
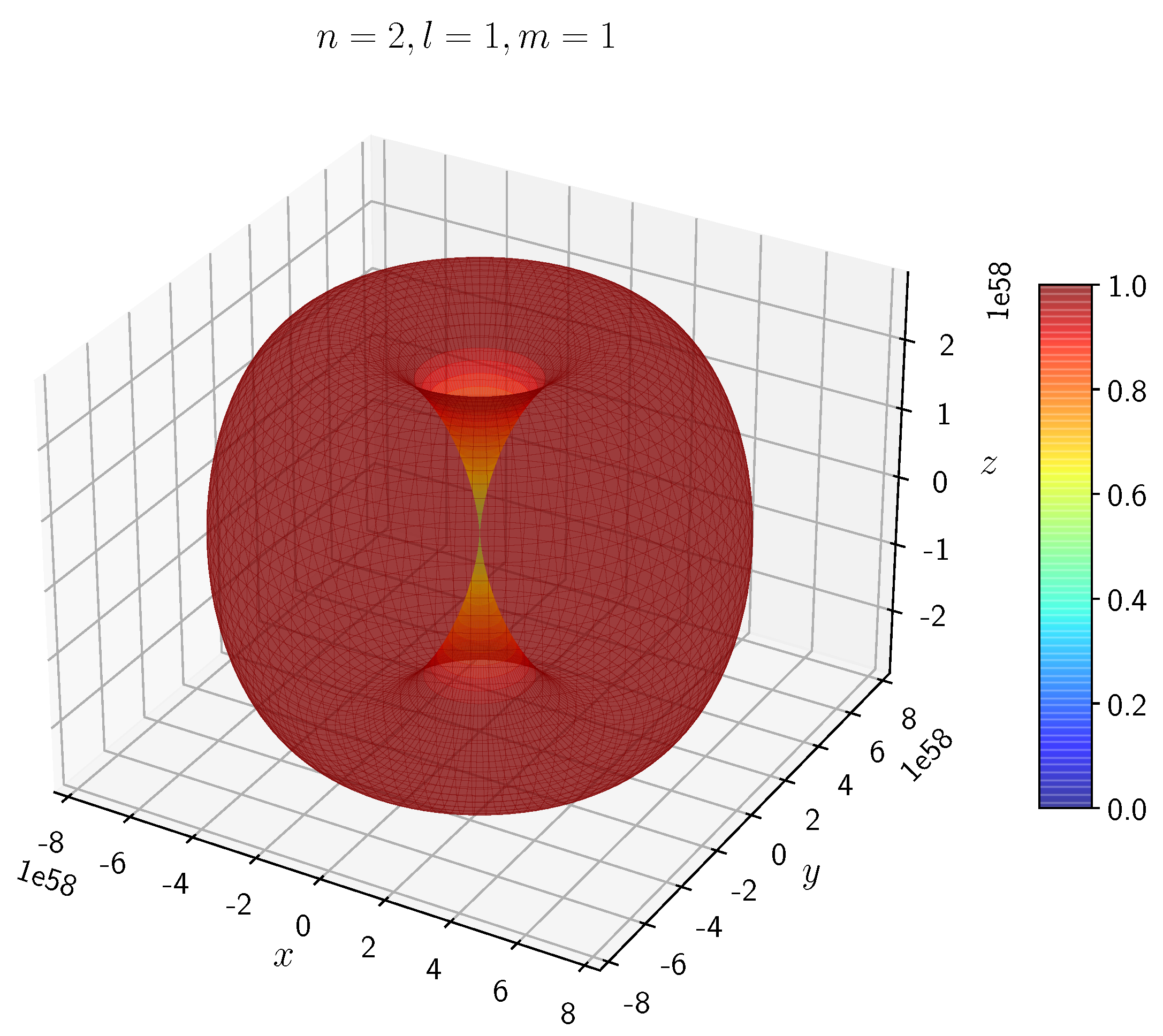
Figure 9.
Plot of for H.
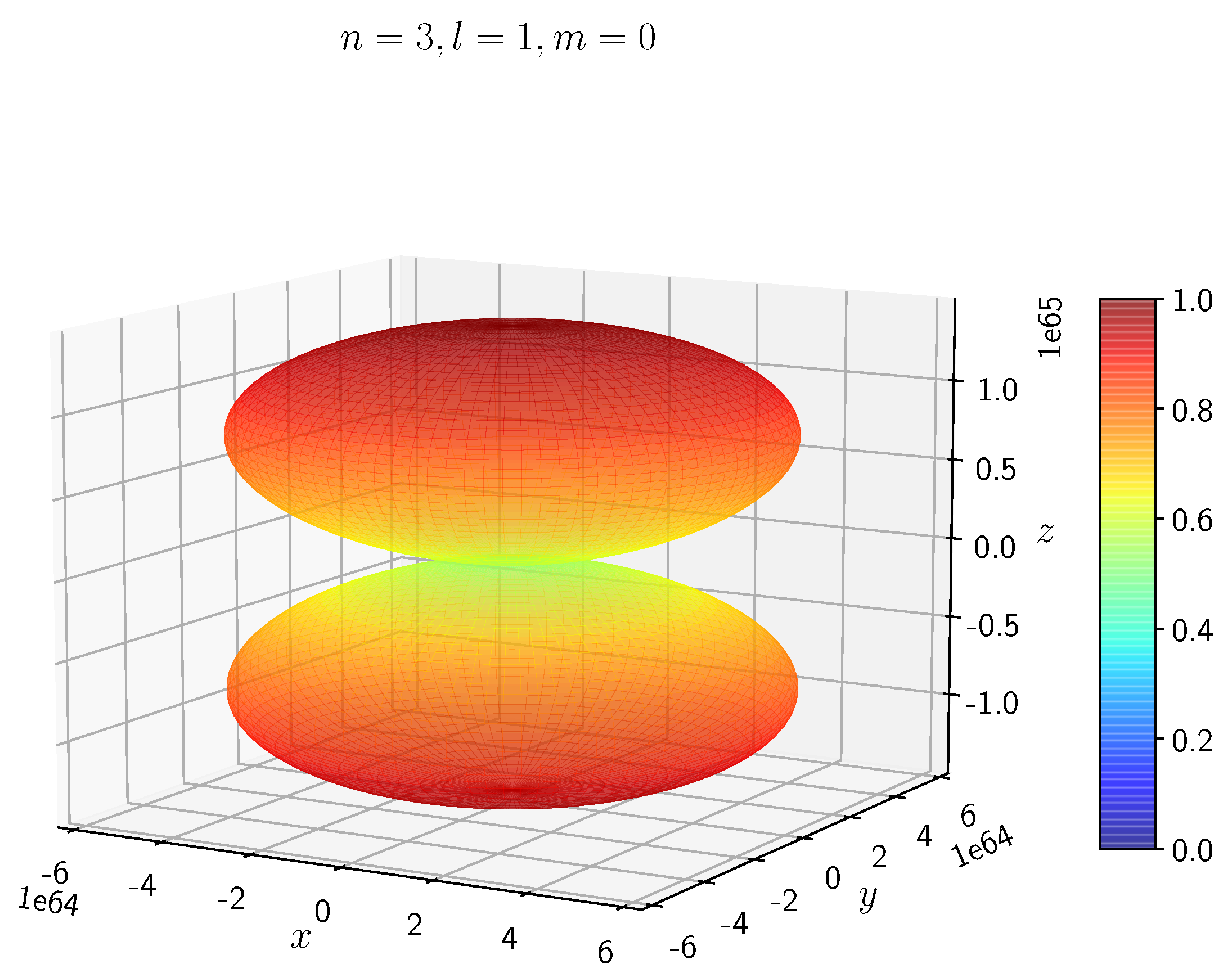
Figure 10.
Plot of for H.
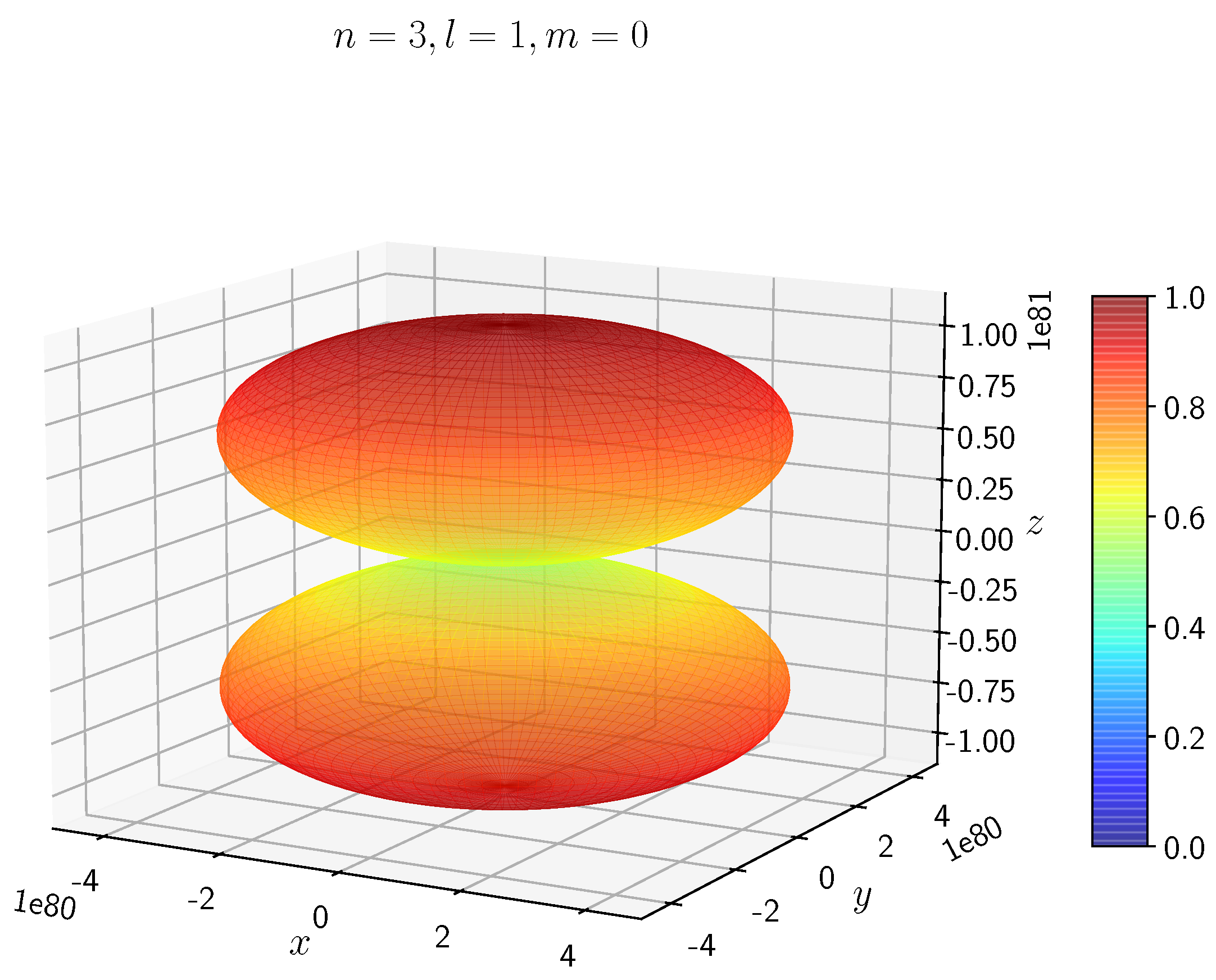
Figure 11.
Plot of for H.
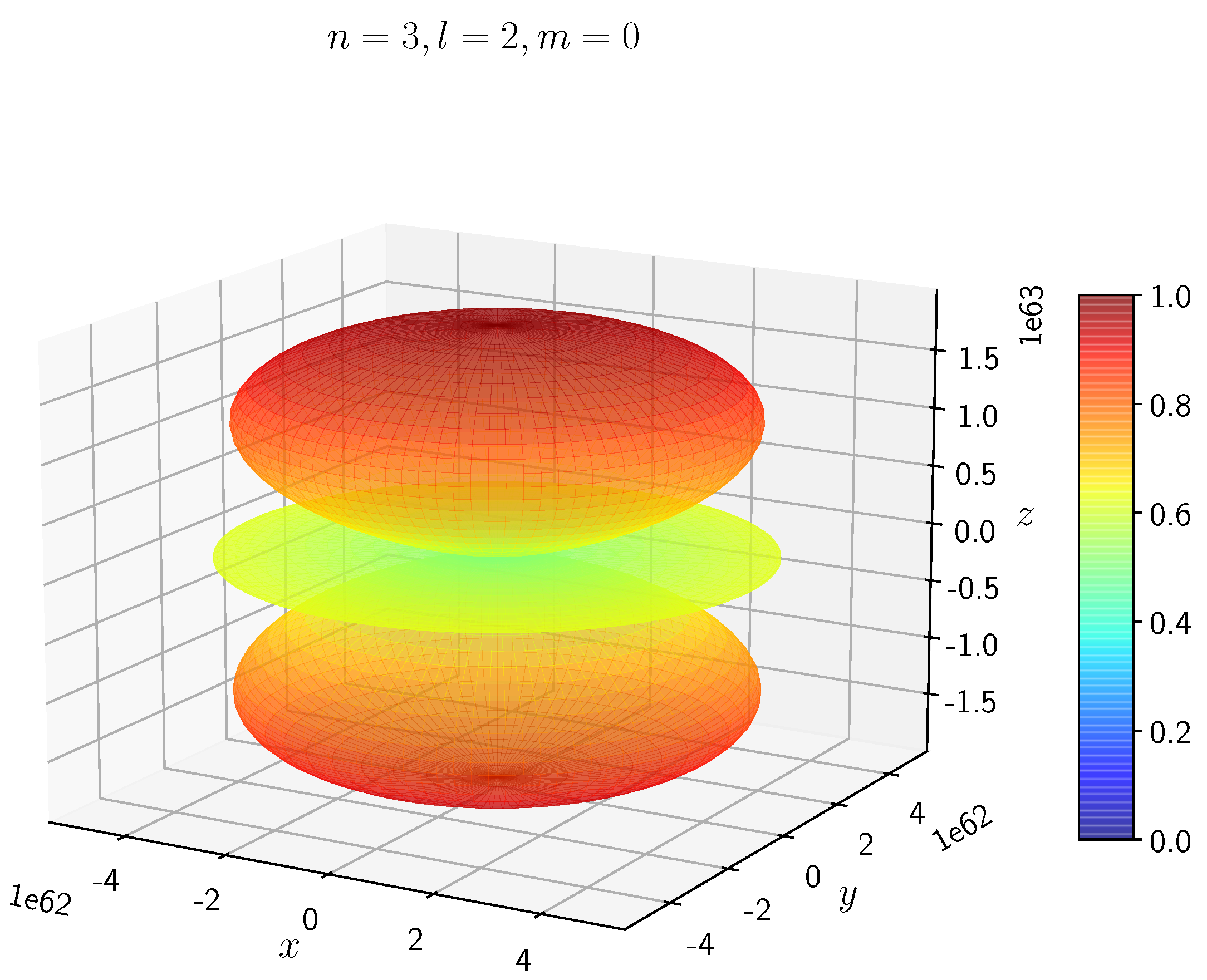
Figure 12.
Plot of for H.
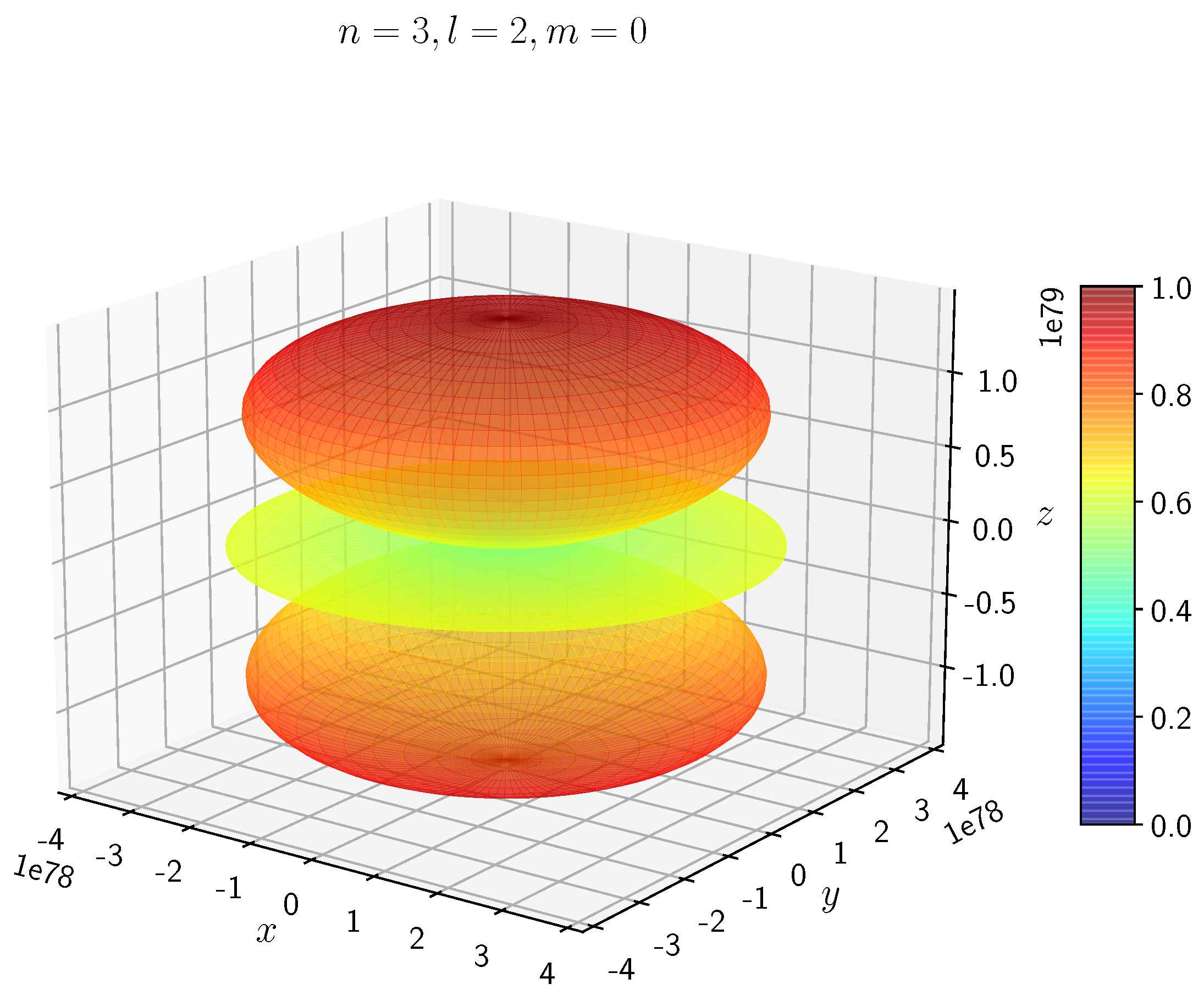
Figure 13.
Plot of for H.
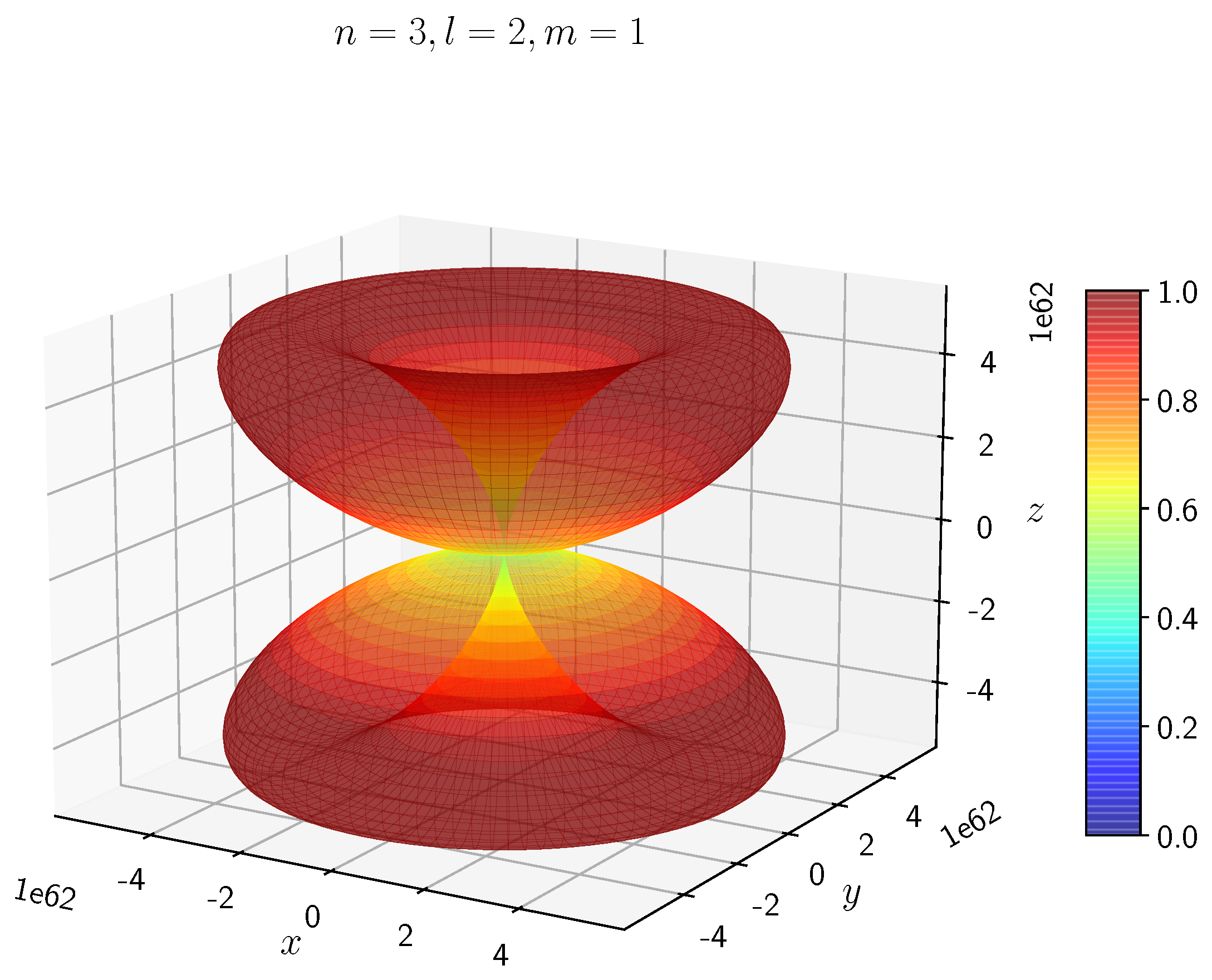
Figure 14.
Plot of for H.
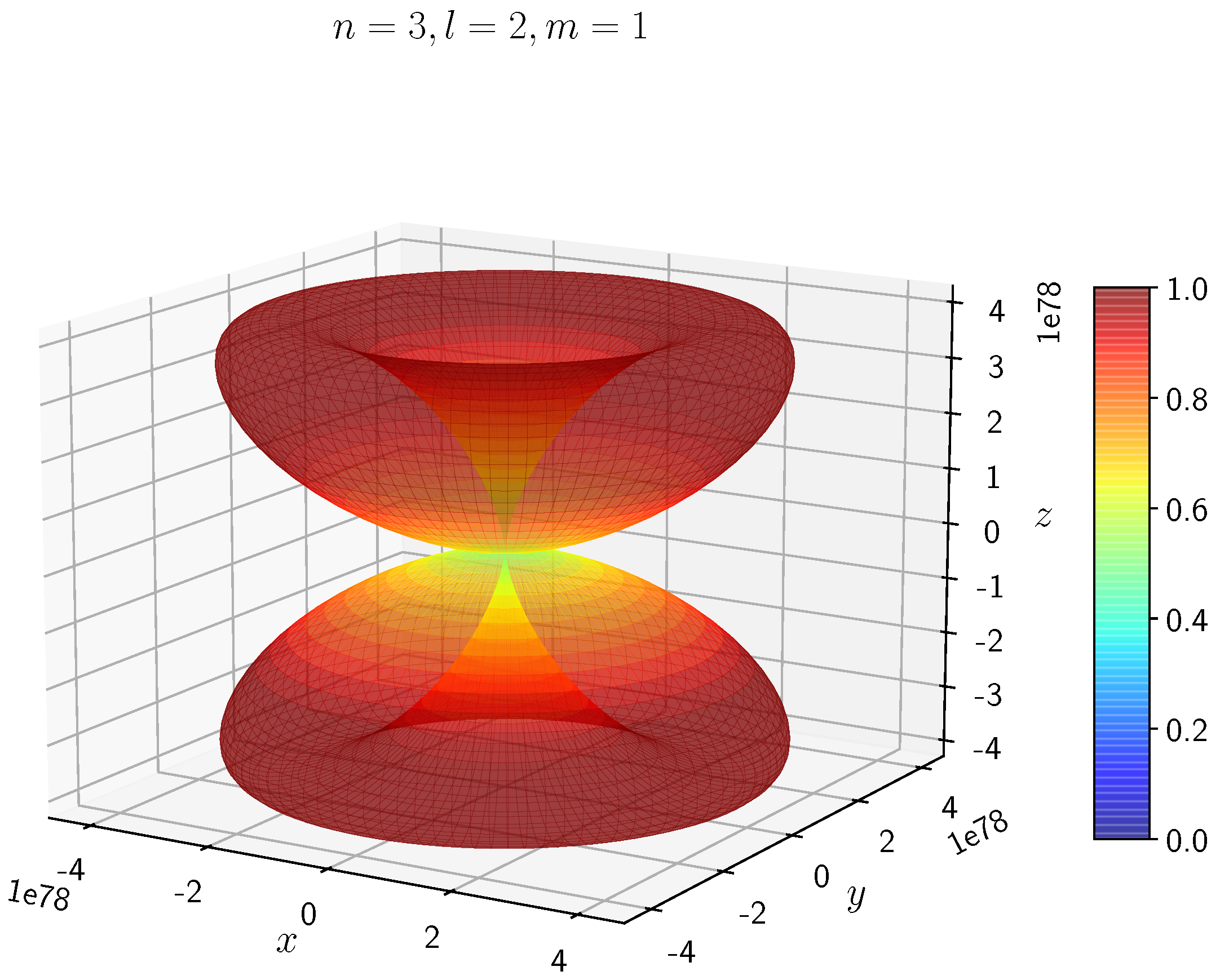
Figure 15.
Plot of for H.
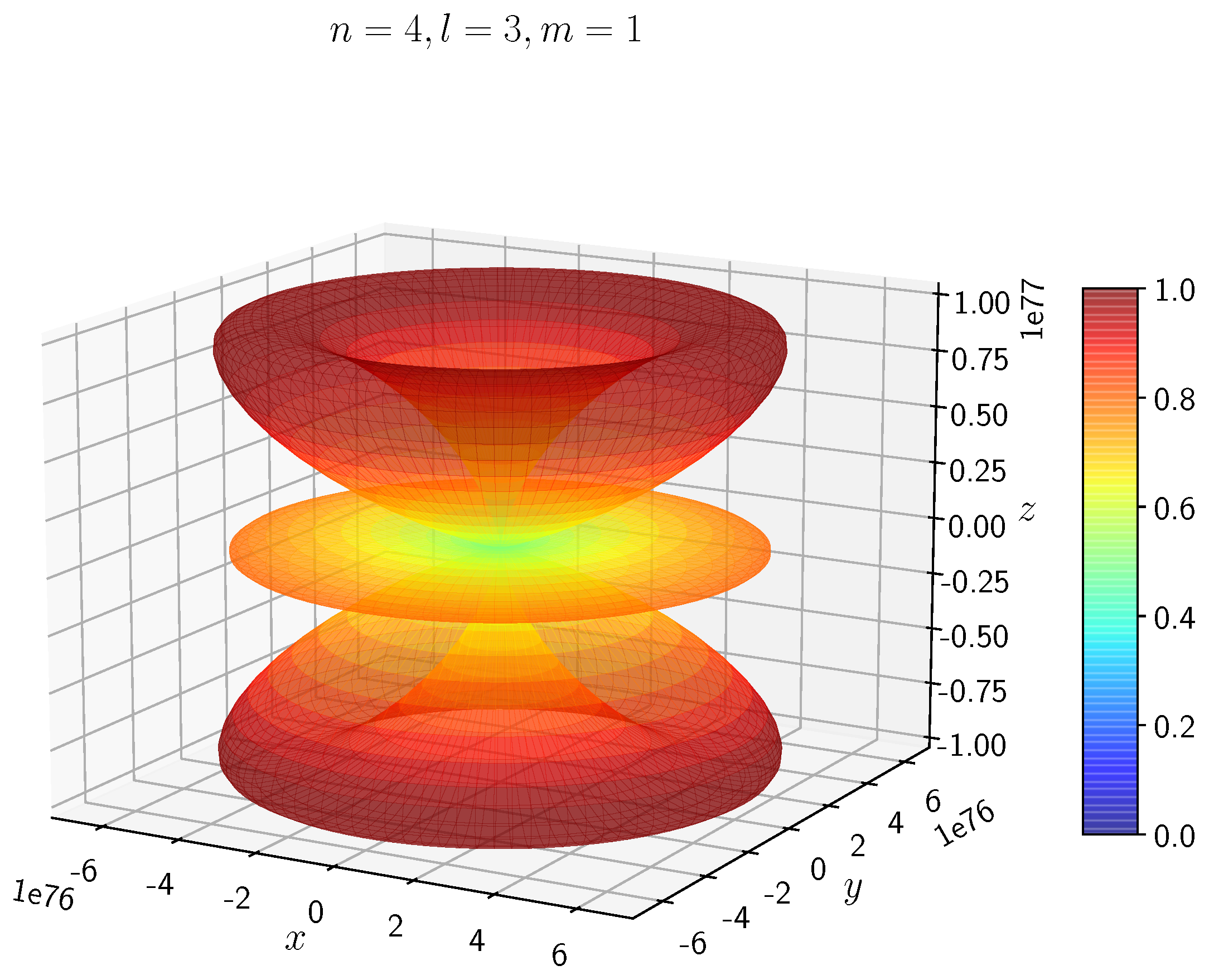
Figure 16.
Plot of for H.
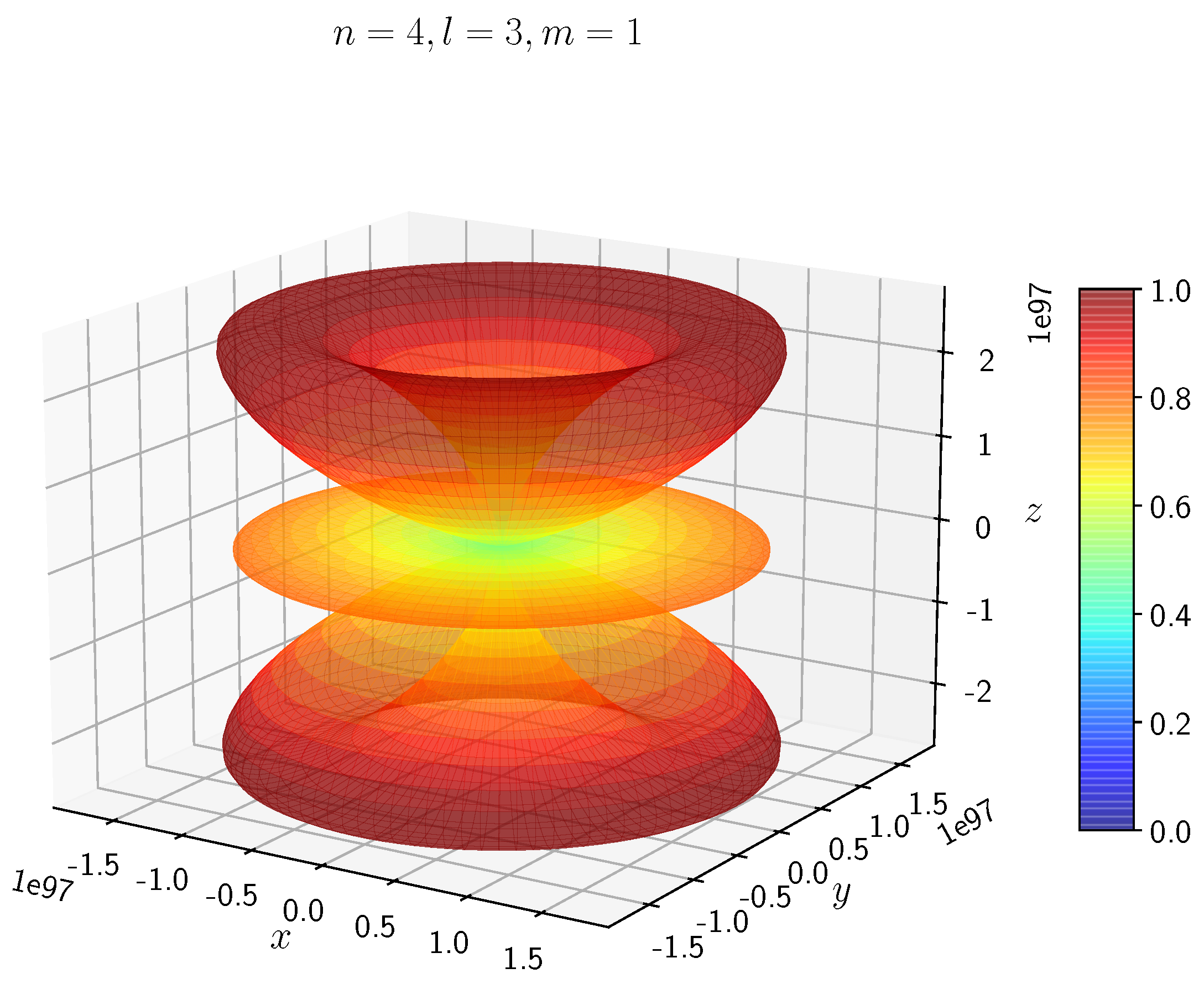
Table 1.
Orbit size of electronic and muonic hydrogen atoms.
| H | H | |
| n | () | () |
| 1 | 0.052 | 0.0002 |
| 2 | 0.211 | 0.0011 |
| 3 | 0.476 | 0.0025 |
| 4 | 0.846 | 0.0045 |
| 5 | 1.322 | 0.0071 |
| 6 | 1.904 | 0.0102 |
| 7 | 2.592 | 0.0139 |
| 8 | 3.386 | 0.0182 |
| 9 | 4.286 | 0.0230 |
| 10 | 5.291 | 0.0284 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





