Hypergraph Regularized Lp Smooth Nonnegative Matrix Factorization for Data Representation

Nonnegative matrix factorization (NMF) has been shown to be a strong data representation technique, with applications in text mining, pattern recognition, image processing, clustering and other fields. In this paper, we propose a hypergraph regularized Lp smooth nonnegative matrix factorization (HGSNMF), by incorporating hypergraph regularization and Lp smoothing constraint terms into the standard NMF. The hypergraph regularization term can capture the intrinsic geometry structure of the high dimension space data more comprehensively than simple graph, the Lp smoothing constraint may yield a smooth and more accurate solution to the optimization problem. The updating rules are given using multiplicative update techniques, and the convergence of HGSNMF is theoretically investigated. The experimental results on four different data sets show that the proposed method has better clustering effect than the related state-of-the-art methods in the vast majority of cases.

Keywords:

Subject: Computer Science and Mathematics - Mathematics

MSC: 68U10; 62H30; 15A69

1. Introduction

Data representation plays an important role in information retrieval [1], computer vision [2], pattern recognition [3], and other applied fields [4,5]. The dimensions of data matrices are extremely high in these practical applications. The high-dimensional data can cause not only storage difficulties but also possible dimensional curse. Therefore, it is necessary to find an effective and low-dimensional representation of the original high-dimensional data matrix. Matrix factorization is one of the important data representation techniques, and the typical matrix decomposition methods mainly includes: principal component analysis (PCA) [6], linear discriminant analysis (LDA) [8], singular value decomposition (SVD) [7], nonnegative matrix factorization (NMF) [9,10], and so on.

NMF has been gained popularity through the works of Lee and Seung published in Nature [9] and NIPS [10]. It has been widely applied in clustering [11,12,13], face recognition [14,15], text mining [16,17], image processing [18,19,20], hyperspectral unmixing (HU) [21,22], and other fields [23,24,25,26]. Several NMF versions are presented in order to improve data representation capabilities, by introducing with different regularization terms or constraints into the NMF model. For example, by considering the orthogonality of the factor matrices, Ding et al. [12] presented orthogonal nonnegative matrix tri-factorizators (ONMF) approach. By incorporating the graph regularization term into NMF, Cai et al. [2] presented the graph regularized nonnegative matrix factorization (GNMF) , where a simple nearest neighborhood graph is constructed by considering the pairwise geometric relationships between two sample points. However, the models did not take into account the high-order relationships among multiple sample points. Shang et al. [27] presented a graph dual regularization nonnegative matrix factorization (DNMF) approach, which simultaneously considers the intrinsic geometry matrix structures of both the data manifold and the feature manifold. But, DNMF neglects the high-order relationships among multiple sample points or multiple features. To solve the problem of DNMF, Zeng et al. [28] presented the hypergraph regularized nonnegative matrix factorization (HNMF), which incorporates the hypergraph regularization term into NMF and constructs a hypergraph by considering high-order relationships among multiple sample points. But, HNMF is unable to produce a smooth and precise solution because it does not take into account the smoothness of the basis matrix. Recently, Leng et al. [29] proposed the graph regularized

L_{p}

smooth nonnegative matrix factorization (GSNMF) by incorporating the graph regularization term and

L_{p}

smoothing term into NMF, which considers the intrinsic geometric structures of the sample data and may produce a smooth and more accurate solution of the optimization problem with the addition of graph regularization term and the

L_{p}

smoothing constraint. However, in GSNMF, only the pairwise relationships between two sample points are considered, and the high-order relationships among multiple sample points are ignored.

In this paper, by incorporating hypergraph regularization and

L_{p}

smoothing constraint terms into the standard NMF, we propose first a hypergraph regularized

L_{p}

smooth nonnegative matrix factorization (HGSNMF). The hypergraph regularization term considers the high-order relationships among multiple samples. The

L_{p}

smoothing constraint term takes into account the smoothness of the basis matrix, which has been proven it is significant in data representation [30,31,32]. To solve the optimization problem of the HGSNMF model, we offer an effective optimization algorithm using multiplicative update technique and theoretically prove the convergence of the HGSNMF algorithm. Finally, we conduct comprehensive experiments on four data sets to demonstrate the effectiveness of the proposed method.

The main contributions of this work can be summarized as follows:

1) Considering the complex relationships into pairwise ones in simple graph will inevitably lead to loss of the important information. Therefore, we construct the hypergraph regularization term to better discover the hidden semantics and simultaneously capture the underlying intrinsic geometric structure of high-dimensional spacial data samples. In the construction of a hypergraph, each vertex of the hypergraph represents a data sample, and each vertex with its k nearest neighboring samples forms a hyperedge. Each hyperedge represents the similarity relation among a group of samples with higher similarity.

2) We consider the

L_{p}

smoothing constraint of the basis matrix, which not only removes the noise of the basis matrix to make it smooth, but also obtains a smooth and more accurate solution to the optimization problem by combining the advantages of isotropic and diffusion anisotropic smoothing.

3) We solve the optimization problem using an efficient iterative technique and conduct comprehensive experiments to empirically analyze our approach on four data sets, the experimental results validate the effectiveness of our proposed method.

The rest of the paper is organized as follows. In Section 2, we introduce some related works including NMF and hypergraph learning. In Section 3, we propose the novel HGSNMF model in details, as well as its updating rules and prove the convergence of the HGSNMF method. In addition, we analysis the complexity of the proposed method. In Section 4, we conduct extensive experiments to validate the proposed method. At last, we conclude this paper in Section 5.

2. Related work

2.1. Nonnegative matrix factorization

Given a nonnegative matrix

X = [x_{1}, x_{2}, \dots, x_{n}] \in R_{+}^{m \times n}

, each column

x_{i} \in R_{+}^{m} (i = 1, 2, \dots, n)

X

represents a data point. The purpose of NMF is to decompose a nonnegative matrix into two low-rank nonnegative factor matrices

B \in R_{+}^{m \times r}

and

C \in R_{+}^{r \times n}

, the product of which is an approximation of the original matrix. Specifically, the objective function of NMF is

\begin{matrix} \begin{matrix} {\min ∥ X - BC ∥}_{F}^{2}, \\ s . t . B \geq 0, C \geq 0 \end{matrix} \end{matrix}

(1)

where

{∥ \cdot ∥}_{F}

is the Frobenius norm of a matrix,

B

is the basis matrix, and

C

is the coefficient matrix (also called encoding matrix). Obviously, the objective function is convex for

B

C

, but nonconvex for both

B

and

C

. Therefore, it is difficult to find the global minimum. To get a local optimal minimum, Lee et al. [10] proposed iterative multiplicative updating technique to solve the problem (1) as follows:

\begin{matrix} B_{i k} \leftarrow B_{i k} \frac{{({XC}^{⊤})}_{i k}}{{({BCC}^{⊤})}_{i k}}, \\ C_{k j} \leftarrow C_{k j} \frac{{(B^{⊤} X)}_{k j}}{{(B^{⊤} BC)}_{k j}}, \end{matrix}

where

B^{⊤}

is the transpose of

B

2.2. Hypergraph Learning

Simple graph only considers the pairwise geometric relationship between data samples, the complex internal structure of the data samples could not be efficiently used. To remedy this defect, the hypergraph takes into account the high-order geometric relationships among multiple samples, which can better capture potential geometric information of the data [33]. Thus, hypergraph learning [34,35,36,37,38] is an extension of simple graph learning theory.

The hypergraph

G = (V, E)

consider the high-order relationships among multiple vertices and is made up of a non-empty vertex set

V = {v_{1}, v_{2}, \dots, v_{n}}

and a non-empty hypergraph set

E = {e_{1}, e_{2}, \dots, e_{m}}

. Each element

v_{i} \in V

is called a vertex, and each element

e_{j} \in E

is a subset of V, which is known as a hyperedge of G. G is a hypergraph defined on V if

e_{j} \neq

, for

j = 1, 2, \dots, M

, and

e_{1} \cup e_{2} \cup \dots \cup e_{M} = V

When constructing a hypergraph, we generate the hyperedge by calculating the Euclidean distance between the k nearest neighbors of each vertex. The parameter k is manually set. An incidence matrix

H \in R_{+}^{| V | \times | E |}

is used to describe the incidence relationship between a vertex and a hyperedge, which is formalized as

H (v, e) = 1

v \in e

, and

H (v, e) = 0

otherwise.

Figure 1 gives an illustration the simple graph, the hypergraph

\bar{G} = (\bar{V}, \bar{E})

and an incidence matrix. In the undirected simple graph, if a vertex is in the k nearest neighbors of another vertex, the two vertices are joined together by an edge. The hypergraph

\bar{G} = (\bar{V}, \bar{E})

considers the high-order relationships among multiple vertices and is made up of a non-empty vertex set

\bar{V} = {v_{1}, v_{2}, v_{3}, v_{4}, v_{5}, v_{6}, v_{7}, v_{8}}

and a non-empty hypergraph set

\bar{E} = {e_{1} = {v_{1}, v_{2}, v_{4}}, e_{2} = {v_{3}, v_{4}, v_{5}, v_{6}}, e_{3} = {v_{6}, v_{7}, v_{8}}}

. In Figure 1, the solid nodes stand for the vertices, the node sets marked by the solid line segment and the node sets marked by the ellipses denote the hyperedges. Furthermore, each vertex is connected with at least one hypheredge in hypergraph, which is associated with a weight, and each hyperedge can have multiple vertices.

Each hyperedge e can be assigned with a positive number

ω (e)

that presents the weight of the hyperedges. The degree of a vertex v and the degree of a hyperedge can be expressed as

d (v) = \sum_{e \in E} ω (e) H (v, e)

and

δ (e) = \sum_{v \in V} H (v, e)

, respectively. According to [34], the unnormalized hypergraph Laplacian matrix can be expressed as

\begin{matrix} L_{H y p e r} = D_{v} - S \end{matrix}

(2)

where

S = {HWD}_{e}^{- 1} H^{⊤}

H

is an incidence matrix,

W

is a diagonal weight matrix composed of

ω (e)

D_{v}

and

D_{e}

denote the diagonal matrices composed of

d (v)

and

δ (e)

, respectively.

Recently, Wang et al. [21] presented hypergraph-regularized sparse NMF (HGLNMF) for hyperspectral unmixing with incorporates the sparse term into HNMF. HGLNMF considers the sparse of the coefficient matrix, and the hypergraph can simulate the higher-order relationship between multiple pixels by multiple vertices in its hyperedges. Wu et al. [39] presented nonnegative matrix factorization with mixed hypergraph regularization (MHGNMF), by considering higher-order information among the nodes into consideration. Some scholars apply nonnegative matrix factorization to multiple perspectives, Zhang et al. [40] presented semi-supervised multi-view clustering with dual hypergraph regularized partially shared nonnegative matrix factorization(DHPS-NMF). Huang et al. [41] presented diverse deep matrix factorization with hypergraph regularization for multi-view data representation. To some extent, these approaches focus more on the multiple vertices hypergraph, which reflects the higher-order relationships between the multiple vertices, but they ignore the base matrix or its smoothness. To overcome this deficiency, by fully considering the higher-order relationships of multiple vertices and the smoothness of the basis matrix, we propose the following hypergraph regularized

L_{p}

smooth nonnegative matrix factorization.

3. Hypergraph Regularized $L_{p}$ Smooth Nonnegative Matrix Factorization

In this section, we will describe the proposed HGSNMF approach in detail and the iterative updating rules of two factor matrices. Then the convergence of the proposed iterative updating rules is proved. Finally, the calculation cost of this method is given.

We first give the construction of the hypergraph regularization term. Given a nonnegative data matrix

X = [x_{1}, x_{2}, \dots, x_{n}] \in R_{+}^{m \times n}

, we expect that if two data samples

x_{i}

and

x_{j}

are close, the corresponding encoding vectors

c_{i}

and

c_{j}

in the low-dimensional space are also close to each other. Constructing the hypergraph for the coefficient matrix, we encode geometrical information by linking each data sample with its k nearest neighbors and denoting their hypergraph connections with heat kernel weight

\begin{matrix} ω (e_{i}) = \sum_{x_{j} \in e_{i}} exp (- \frac{| | x_{i} - x_{j} {| |}^{2}}{δ^{2}}), \end{matrix}

(3)

where

δ = \frac{1}{k n} \sum_{i = 1}^{n} \sum_{x_{j} \in e_{i}} | | x_{i} - x_{j} | |

denotes the average distance among all the vertices.

With the above defined weight matrix

ω (e)

, the hypergraph regularization of the matrix

C

can be caculated by the following optimization problem:

\begin{matrix} \begin{matrix} R & = \frac{1}{2} \sum_{e \in E} \sum_{i, j \in e} \frac{ω (e)}{δ (e)} | | c_{i} - c_{j} {| |}^{2} \\ = Tr (C (D_{v} - S) C^{⊤}) \\ = Tr ({CL}_{H y p e r} C^{⊤}), \end{matrix} \end{matrix}

where

Tr (\cdot)

denotes the trace of a matrix,

L_{H y p e r}

is the hypergraph Laplacian matrix of the hyergraph G and defined by (2).

3.1. The Objective Function

To discover the intrinsic geometric structure information of a data set and produce a smooth and more accurate solution, we propose the HGSNMF method by incorporating hypergraph regularization and the

L_{p}

smoothing constraint into NMF. The objective function of our HGSNMF is defined as follows:

\begin{matrix} \begin{matrix} min O = min_{B, C} | | X - {BC | |}_{F}^{2} + α Tr (C L_{H y p e r} C^{⊤}) + {2 μ | | B | |}_{p}^{p}, \\ s . t . B \geq 0, C \geq 0, \end{matrix} \end{matrix}

(4)

where

B

is the basis matrix,

{| | B | |}_{p} = {(\sum_{i = 1, j = 1}^{m, r} {(B_{i j})}^{p})}^{\frac{1}{p}},

0 < p \leq 2

and

p \neq 1

B_{i j}

is the ith row and jth column entry of matrix

B

, and

C

is the coefficient matrix,

α

and

μ

are the positive regularization parameters for balancing the reconstruction error in (4). Hypergraph regularization term and

L_{p}

smoothing regularization term are presented in the second term and the third term, respectively. The hypergraph regularization term can more effectively discover the hidden semantics and simultaneously capture the underlying intrinsic geometric structure of the high-dimensional space data. The

L_{p}

smoothing constraint of the basis matrix not only removes the noise of the basis matrix to make it smooth, but also obtains a smooth and more accurate solution to the optimization problem by combining the advantages of isotropic and diffusion anisotropic smoothing. Then, we will give the detailed derivation of the updating rules, the theoretical proof of convergence and the analysis of the computational complexity of the HGSNMF method, and provide more comparative experiments.

3.2. Optimization method

The objective function

O

in (4) is not convex in both

B

and

C

, so it is unrealistic to find the global optimal solution. Thus, we can only obtain the local optimal solution by using iterative method. There are multiplicative update, projective gradient, alternating direction multiplier and dictionary learning algorithm for solving optimization problems. Because the multiplicative update algorithm has the advantages of convergence, and simple operation and small computation, we use multiplicative update algorithm to solve optimization problems. We can turn the objective function into the following unconstrained objective function by using the Lagrange multiplier:

\begin{matrix} \begin{matrix} L = & | | X - {BC | |}_{F}^{2} + α Tr (C L_{H y p e r} C^{⊤}) + {2 μ | | B | |}^{p} - Tr (Υ B^{⊤}) - Tr (Λ C^{⊤}), \end{matrix} \end{matrix}

where

Υ = [Υ_{i k}]

Λ = [Λ_{k j}]

Υ_{i k}

and

Λ_{k j}

are the Lagrange multiplier for the constrains

B_{i k} \geq 0

and

C_{k j} \geq 0

, respectively.

Taking the partial derivatives of L with respect to

B

and

C

, respectively, we have that

\begin{matrix} \frac{\partial L}{\partial B} = 2 {BCC}^{⊤} - 2 {XC}^{⊤} + 2 μ p B^{p - 1} - Υ, \end{matrix}

\begin{matrix} \frac{\partial L}{\partial C} = 2 B^{⊤} BC - 2 B^{⊤} X + 2 α C L_{H y p e r} - Λ . \end{matrix}

By using the Karush-Kuhn-Tucker (KKT) conditions

\frac{\partial L}{\partial B} = 0

\frac{\partial L}{\partial C} = 0

Υ_{i k} \cdot B_{i k} = 0

and

Λ_{k j} \cdot C_{k j} = 0

, we obtain that

\begin{matrix} {({BCC}^{⊤})}_{i k} B_{i k} + μ p B_{i k}^{p - 1} B_{i k} - {({XC}^{⊤})}_{i k} B_{i k} = 0, \end{matrix}

(5)

\begin{matrix} \begin{matrix} {(B^{⊤} BC)}_{k j} C_{k j} + α {(C L_{H y p e r})}_{k j} C_{k j} - {(B^{⊤} X)}_{k j} C_{k j} = 0 . \end{matrix} \end{matrix}

(6)

According to (5) and (6), we can obtain the following updating rules for

B

and

C

\begin{matrix} B_{i k} \leftarrow B_{i k} \frac{{({XC}^{⊤})}_{i k}}{{({BCC}^{⊤})}_{i k} + μ p B_{i k}^{p - 1}} \end{matrix}

(7)

and

\begin{matrix} C_{k j} \leftarrow C_{k j} \frac{{(B^{⊤} X)}_{k j} + α {(CS)}_{k j}}{{(B^{⊤} BC)}_{k j} + α {(C D_{v})}_{k j}}, \end{matrix}

(8)

respectively.

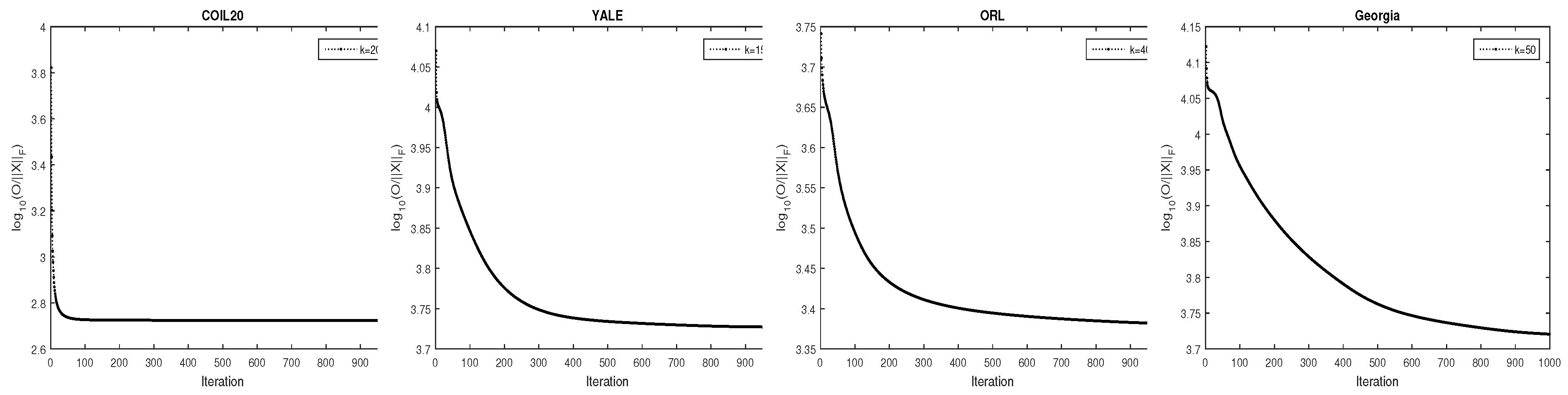
3.3. Convergence Analysis

In this subsection, we give the convergence proof of our proposed HGSNMF in (4) using the updating rules (7) and (8). First of all, we introduce some related Definitions and Lemmas.

Definition 1.

[10]

G (x, x^{'})

is an auxiliary function of

F (x)

, if

G (x, x^{'})

satisfies the condition

G (x, x^{'}) \geq F (x), G (x, x) = F (x) .

The auxiliary function plays an important role due to the following Lemma.

Lemma 1.

[10] If G is an auxiliary function of F, then F is nonincreasing under the updating rule

\begin{matrix} x^{t + 1} = arg min_{x} G (x, x^{t}) . \end{matrix}

(9)

To prove the convergence of HGSNMF under the updating step for

B

in (7), we fix the matrix

C

. For any element

B_{i k}

B

, we use

{\tilde{F}}_{i k}

to denote the part of the objective function

O

, which is only relevant to

B_{i k}

. The first and second derivatives of

\tilde{F} (B_{i k})

are given as follows

\begin{matrix} {\tilde{F}}_{i k}^{'} = {(\frac{\partial O}{\partial B})}_{i k} = 2 {({BCC}^{⊤} - {XC}^{⊤})}_{i k} + 2 μ p {(B_{i k})}^{p - 1} \end{matrix}

and

\begin{matrix} {\tilde{F}}_{i k}^{''} = {(\frac{\partial^{2} O}{\partial B^{2}})}_{i k} = 2 {({CC}^{⊤})}_{k k} + 2 μ p (p - 1) {(B_{i k})}^{p - 2}, \end{matrix}

respectively.

Lemma 2.

The function

\begin{matrix} \begin{matrix} \tilde{G} (x, B_{i k}^{t}) = \tilde{F} (B_{i k}^{t}) + {\tilde{F}}^{'} (B_{i k}^{t}) (x - B_{i k}^{t}) + \frac{{({BCC}^{⊤})}_{i k} + μ p {(B_{i k}^{t})}^{p - 1}}{B_{i k}^{t}} {(x - B_{i k}^{t})}^{2} \end{matrix} \end{matrix}

(10)

is an auxiliary function of

{\tilde{F}}_{i k} (x)

, which is only relevant to

B_{i k}

Proof.

Since from Taylor series expansion, we have that

\begin{matrix} \begin{matrix} {\tilde{F}}_{i k} (x) = & \tilde{F} (B_{i k}^{t}) + {\tilde{F}}^{'} (B_{i k}^{t}) (x - B_{i k}^{t}) + {({CC}^{⊤})}_{k k} {(x - B_{i k}^{t})}^{2} \\ + μ p (p - 1) {(B_{i k}^{t})}^{p - 2}) {(x - B_{i k}^{t})}^{2} . \end{matrix} \end{matrix}

(11)

Clearly,

\tilde{G} (x, x) = {\tilde{F}}_{i k} (x)

. By Definition 1, we just need to prove that

\tilde{G} (x, B_{i k}^{t}) \geq {\tilde{F}}_{i k} (x) .

By comparing (10) with (11), we can find that

\tilde{G} (x, B_{i k}^{t}) \geq {\tilde{F}}_{i k} (x)

is equivalent to

\begin{matrix} \begin{matrix} \frac{{(B {CC}^{⊤})}_{i k} + μ p {(B_{i k}^{t})}^{p - 1}}{B_{i k}^{t}} \geq {({CC}^{⊤})}_{k k} + μ p (p - 1) {(B_{i k}^{t})}^{p - 2} . \end{matrix} \end{matrix}

(12)

Since

B \geq 0, C \geq 0, 0 < p \leq 2

, and

p \neq 1

, we have

\begin{matrix} \begin{matrix} {(B {CC}^{⊤})}_{i k} = \sum_{l = 1, l \neq k}^{r} B_{i l}^{t} {({CC}^{⊤})}_{l k} + B_{i k}^{t} {({CC}^{⊤})}_{k k} \geq B_{i k}^{t} {({CC}^{⊤})}_{k k} \end{matrix} \end{matrix}

and

p {(B_{i k}^{t})}^{p - 1} \geq p (p - 1) {(B_{i k}^{t})}^{p - 1} .

So (12) holds, which implies

\tilde{G} (x, B_{i k}^{t}) \geq {\tilde{F}}_{i k} (x)

.□

Theorem 1.

The objective function

O

in (4) is nonincreasing under the updating rule of (7).

Proof.

Replacing

G (x, x^{t})

in (9) by (10), we can obtain the updating rule

\begin{matrix} \begin{matrix} B_{i k}^{t + 1} & = B_{i k}^{t} - B_{i k}^{t} \frac{{\tilde{F}}^{'} (B_{i k}^{t})}{2 {(B {CC}^{⊤})}_{i k} + 2 μ p {(B_{i k}^{t})}^{p - 1}} \\ = B_{i k}^{t} \frac{{({XC}^{⊤})}_{i k}}{{(B {CC}^{⊤})}_{i k} + μ p {(B_{i k}^{t})}^{p - 1}} . \end{matrix} \end{matrix}

(13)

Since (10) is an auxiliary function of

{\tilde{F}}_{i k}

{\tilde{F}}_{i k}

is nonincreasing under the updating rule of (7). □

Next, we fix the matrix

B

. For any element

C_{k j}

C

, we use

{\bar{F}}_{k j}

to denote the part of the objective function

O

, which is only relevant to

C_{k j}

. By calculation

\begin{matrix} {\bar{F}}_{k j}^{'} = {(\frac{\partial O}{\partial C})}_{k j} = 2 {(B^{⊤} BC - B^{⊤} X + α {CL}_{H y p e r})}_{k j} \end{matrix}

and

\begin{matrix} {\bar{F}}_{k j}^{''} = {(\frac{\partial^{2} O}{\partial C^{2}})}_{k j} = 2 {(B^{⊤} B)}_{k k} + 2 α {(L_{H y p e r})}_{j j} . \end{matrix}

Lemma 3.

The function

\begin{matrix} \begin{matrix} \bar{G} (x, C_{k j}^{t}) = \bar{F} (C_{k j}^{t}) + {\bar{F}}^{'} (C_{k j}^{t}) (x - C_{k j}^{t}) + \frac{{(B^{T} BC + α C D_{v})}_{k j}}{C_{k j}^{t}} {(x - C_{k j}^{t})}^{2} \end{matrix} \end{matrix}

(14)

is an auxiliary function of

{\bar{F}}_{k j} (x)

, which is only relevant to

C_{k j}

Proof.

Since from Taylor series expansion, we have that

\begin{matrix} \begin{matrix} {\bar{F}}_{k j} (x) = \bar{F} (C_{k j}^{t}) + {\bar{F}}^{'} (C_{k j}^{t}) (x - C_{k j}^{t}) + ({(B^{⊤} B)}_{k k} + α {(L_{H y p e r})}_{j j})(x - C_{k j}^{t})^{2} . \end{matrix} \end{matrix}

(15)

Clearly,

\bar{G} (x, x) = {\bar{F}}_{k j} (x)

. According to Definition 1, we only need to prove that

\bar{G} (x, C_{k j}^{t}) \geq {\bar{F}}_{k j} (x) .

By comparing (14) with (15), we see that

\bar{G} (x, C_{k j}^{t}) \geq {\bar{F}}_{k j} (x)

is equivalent to

\begin{matrix} \frac{{(B^{⊤} BC + α C D_{v})}_{k j}}{C_{k j}^{t}} \geq {(B^{⊤} B)}_{k k} + α {(L_{H y p e r})}_{j j} . \end{matrix}

(16)

Since

B \geq 0, C \geq 0

, we have

\begin{matrix} \begin{matrix} {(B^{⊤} BC)}_{k j} = \sum_{l = 1, l \neq j}^{n} C_{k l}^{t} {(B^{⊤} B)}_{k k} + C_{k j}^{t} {(B^{⊤} B)}_{k k} \geq C_{k j}^{t} {(B^{⊤} B)}_{k k} \end{matrix} \end{matrix}

and

\begin{matrix} \begin{matrix} {(C D_{v})}_{k j} = \sum_{l = 1, l \neq j}^{n} C_{k l}^{t} {(D_{v})}_{l j} + C_{k j}^{t} {(D_{v})}_{j j} \geq C_{k j}^{t} {(D_{v} - S)}_{j j} = C_{k j}^{t} {(L_{H y p e r})}_{j j} . \end{matrix} \end{matrix}

So (16) holds, which implies

\bar{G} (x, C_{k j}^{t}) \geq {\bar{F}}_{k j} (x)

.□

Theorem 2.

The objective function

O

in (4)is nonincreasing under the updating rule of (8).

Proof.

Replacing

G (x, x^{t})

in (9) by (14), we can obtain the updating rule

\begin{matrix} \begin{matrix} C_{k j}^{t + 1} & = C_{k j}^{t} - C_{k j}^{t} \frac{{\bar{F}}^{'} (C_{k j}^{t})}{2 {(B^{⊤} BC + α C D_{v})}_{k j}} \\ = C_{k j}^{t} \frac{{(B^{⊤} X + α C B)}_{k j}}{{(B^{⊤} BC + α C D_{v})}_{k j}} . \end{matrix} \end{matrix}

(17)

Since (14) is an auxiliary function of

{\bar{F}}_{k j}

{\bar{F}}_{k j}

is nonincreasing under the updating rule of (8). □

Similar to NMF, it is known from Theorem 1 and Theorem 2 that the convergence of the model (4) can be guaranteed under the updating rules of (7) and (8).

Now the specific procedure for finding the local optimal

B

and

C

of HGSNMF is summarized in Algorithm 1.

Algorithm 1 HGSNMF algorithm.

Input: Data matrix

X = [x_{1}, x_{2}, \dots, x_{n}] \in R_{+}^{m \times n}

. The number of neighbors k. The algorithm

parameters r, p and regularization parameters

α

μ

. The stopping criterion

ϵ

, and the maximum

number of iterations maxiter. Let

Δ_{0} = 1 e - 5

Output: Factors

B

and

C

;

1: Initialize

B

and

C

;

2: Construct the weight matrix

W

using (3), and calculate the

matrix

D_{v}

S

;

3: for

t = 1, 2, \dots,

maxiter do

4: Update

B^{t}

and Update

C^{t}

according to (7), (8), respectively.

5: Compute the objective function value

O

of (4) to denote

Δ_{t}

6: if

\frac{| Δ_{t} - Δ_{t - 1} |}{Δ_{t - 1}} < ϵ,

Break and return

B, C

7: end if

8: endfor

3.4. Computational Complexity Analysis

In this section, we analyze the computational complexity of the proposed HGSNMF method in comparison to other methods. The fladd, flmlt and fldiv denote a floating-point addition, multiplication and division, respectively. The “O” notation denotes the computational cost. The parameters n, m, r and k denote the number of sample points, features, factors and nearest neighbors to construct an edge or hyperedge, respectively.

According to the updating rules, we calculate the arithmetic operations of each iteration in HGSNMF and summarized the results of the proposed HGSNMF. From Table 1, it shows that the overall costs of our proposed HGSNMF are

O (m n r)

4. Numerical Experimental

In this section, we compare the results of data clustering on four popular data sets to estimate the performance of the proposed HGSNMF method with the related state-of-the-art methods, such as K-means, NMF [9], GNMF [2], HNMF [28], GSNMF [29], HGLNMF [21]. All tests will be done on the computer with a 2-Ghz Intel(R) Core(TM) i5-2500U CPU and 8-GB memory 64-bit MATLAB R2015a in Windows 10. The stopping criterion shows in with

ϵ = 10^{- 5}

, and the maximum number of iterations is set to

10^{4}

4.1. Data Sets

The clustering performance is evaluated on four widely used data sets, including COIL20 (https://www.cs.columbia.edu/CAVE/software/softlib/coil-20.php), YALE and ORL (https://www.cad.zju.edu.cn/home/dengcai.Data/data.html), and Georgia (https://www.anefian.com/research/face-reco.htm). The important statistical information of the four data sets is listed in Table 2, with more details given as follow. 1) COIL20. The data set contains

32 \times 32

gray scale images of 20 objects viewed at varying angles, and each object has 72 images.

2) ORL. The data set contains

32 \times 32

gray face images of the 40 human subjects taken at different times, different light conditions, different facial expressions, and different facial details, and each object has 10 images.

3) YALE. The data set contains

32 \times 32

gray scale images of the 15 individuals viewed at different facial expression or configuration, and each object has 11 images.

4) Georgia. The data set contains

32 \times 32

gray face images of the 50 people with cluttered background for each object, and each object has 15 colors JPEG images.

4.2. Evaluation Metrics

Two popular evaluation metrics are used to evaluate: the clustering accuracy (ACC) and the normalized mutual information (NMI) [42], which evaluate the clustering performance by comparing the obtained cluster label of each sample with the label provided by the data set. ACC is defined as follows

\begin{matrix} A C C = \frac{\sum_{i = 1}^{n} δ (r_{i}, m a p (q_{i}))}{n}, \end{matrix}

where

r_{i}

is the correct label provided by the real data set, and

q_{i}

is the clustering label obtained by the clustering result, n is the total number of documents,

δ (x, y)

is the delta function that equals one if

x = y

and equals to zero otherwise, and

m a p (\cdot)

is a mapping function that maps each cluster label

q_{i}

to a given equivalent label from the data set. The Kuhn-Munkers algorithm [43] is used to find the best mapping.

Suppose two clusters C and

C^{'}

are given, then the mutual information metric

M I (C, C^{'})

can be defined as follows

\begin{matrix} M I (C, C^{'}) = \sum_{c_{i} \in C, c_{j}^{'} \in C^{'}} p (c_{i}, c_{j}^{'}) log \frac{p (c_{i}, c_{j}^{'})}{p (c_{i}) \cdot p (c_{j}^{'})}, \end{matrix}

where

p (c_{i})

and

p (c_{j}^{'})

denote the probabilities that a sample arbitrarily selected from the data set belongs to the clusters

c_{i}

and

c_{j}^{'}

, respectively, and

p (c_{i}, c_{j}^{'})

denotes the joint possibility that this arbitrarily selected image belongs to the cluster

c_{i}

as well as

c_{j}^{'}

at the same time. The Normalized Mutual Information (NMI) is as defined follows

\begin{matrix} N M I (C, C^{'}) = \frac{M I (C, C^{'})}{m a x (H (C), H (C^{'}))}, \end{matrix}

where C is a set of the true labels, and

C^{'}

is a set of clusters obtained from the clustering algorithms.

H (C)

and

H (C^{'})

are the entropies of C and

C^{'}

, respectively.

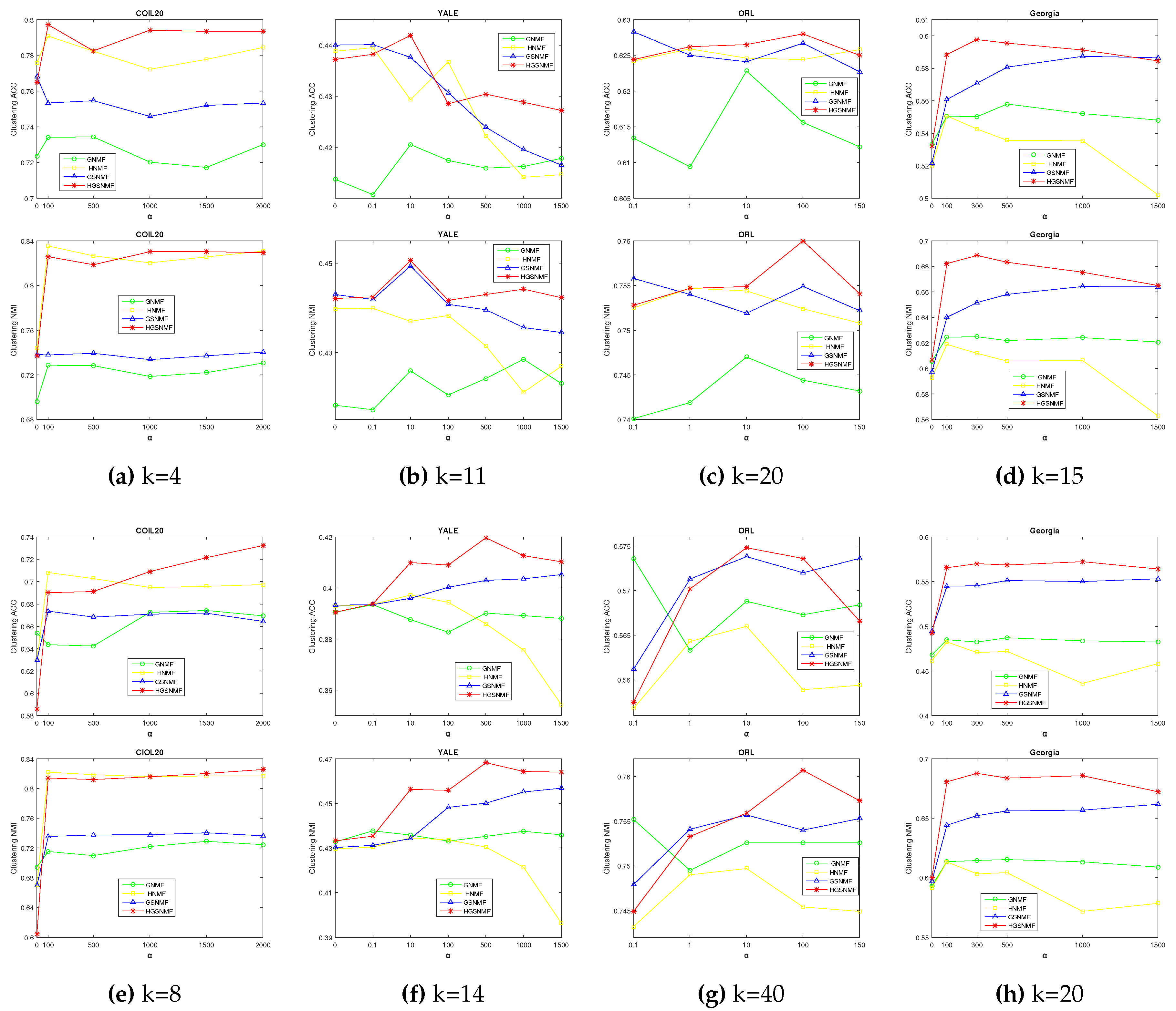
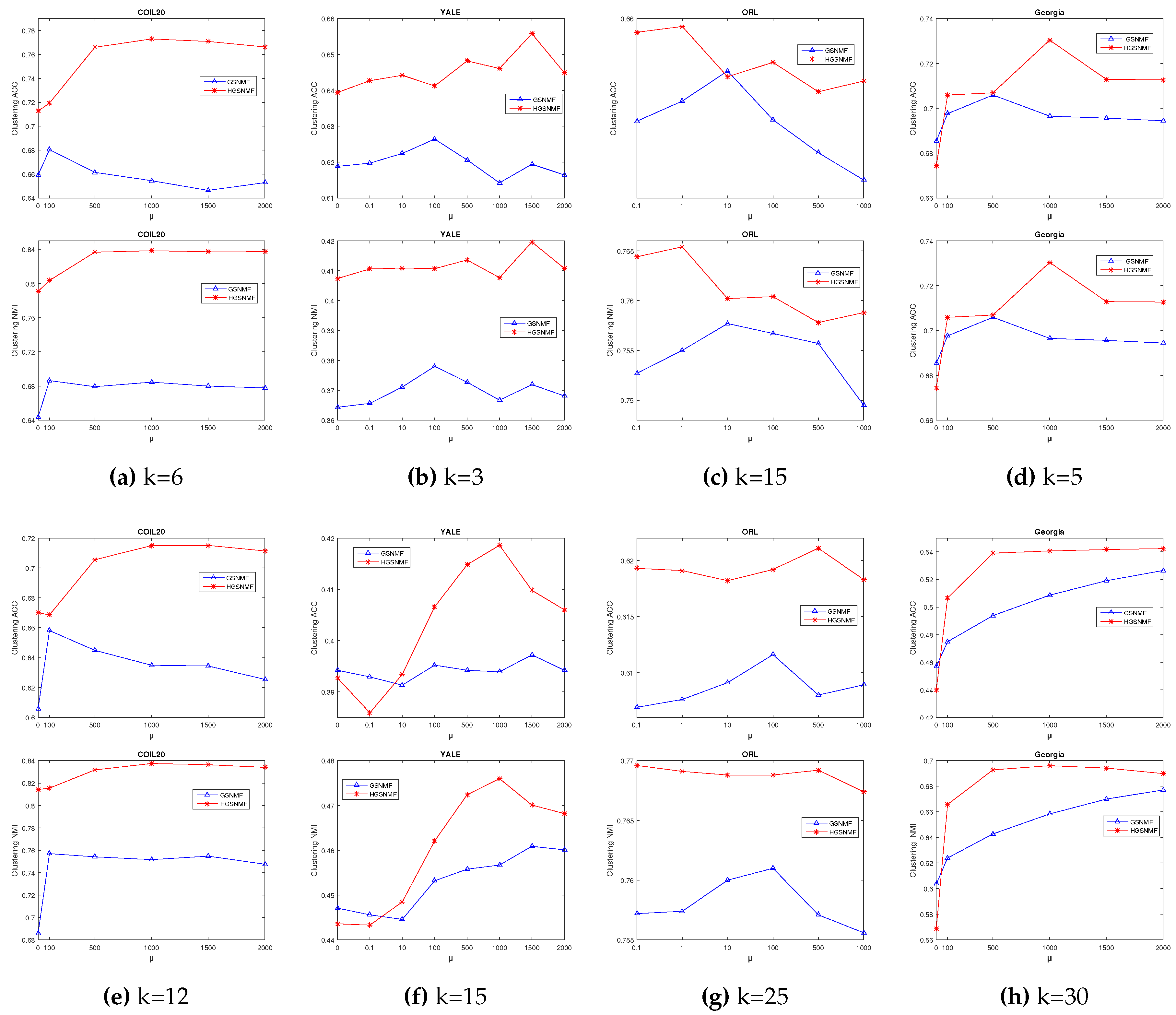
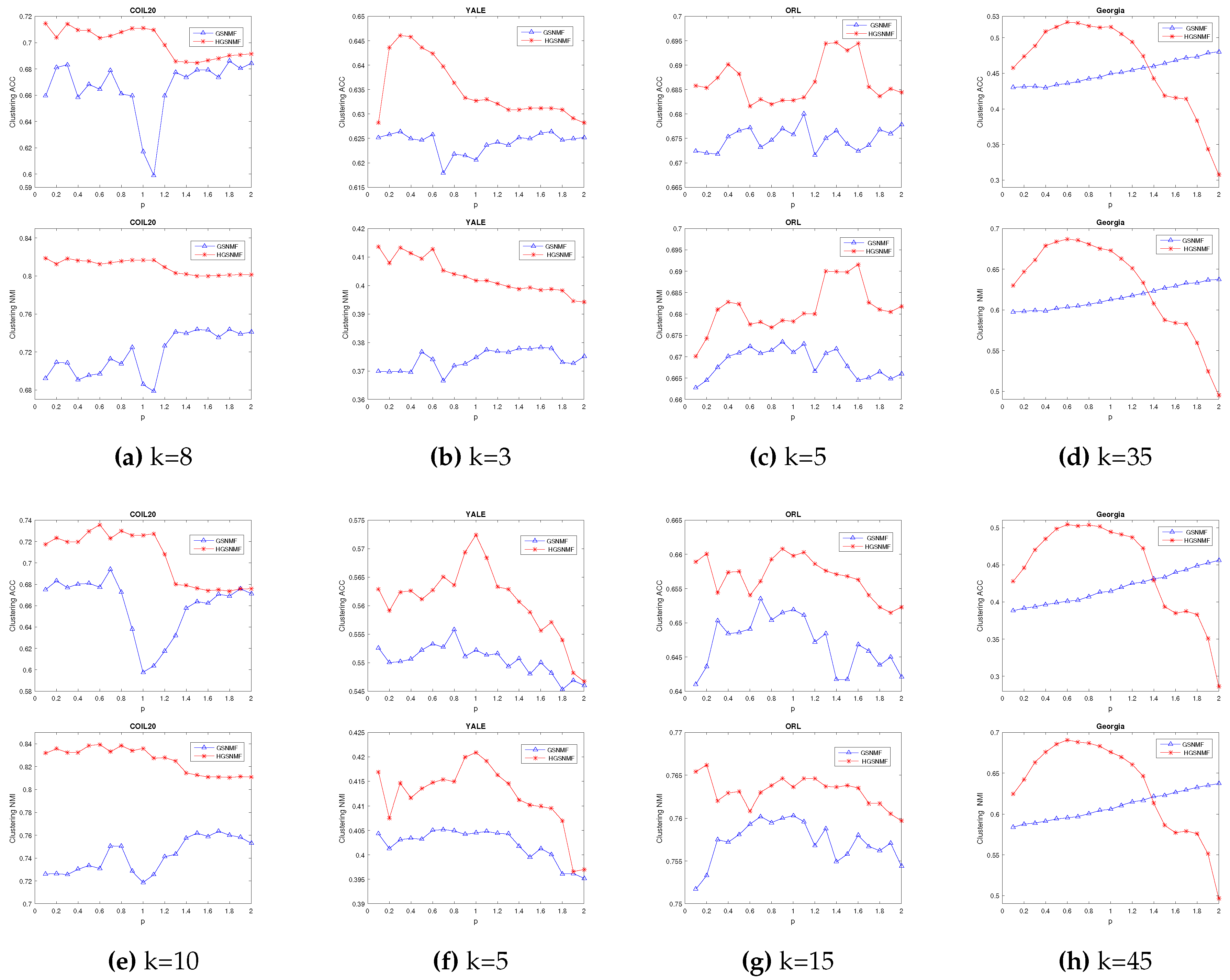
4.3. Performance Evaluations and Comparisons

To evaluate the performance of our proposed method, we choose K-means, NMF, GNMF, HNMF, and GSNMF as the comparison clustering algorithms.

1) K-means: The K-means performs clustering in the original data, we want to know whether low-dimension data can improve clustering performance on high-dimension data.

2) NMF [9]: The original NMF represented the data by imposing nonnegative constraints on the factor matrices.

3) GNMF [2]: Based on NMF, it constructs local geometric structure of original data space as regularization term.

4) HNMF [28]: It incorporates the hypergraph regularization term into NMF.

5) GSNMF [29]: It incorporates both graph regularization and

L_{p}

smoothing constraint into NMF.

6) HGLNMF [21]: It incorporates both hypergraph regularization and

L_{\frac{1}{2}}

sparse constraint into NMF.

7) HGSNMF: We proposed the hypergraph regularized

L_{p}

smooth nonnegative matrix factorization by incorporating hypergraph regularization term and

L_{p}

smoothing constraint into NMF.

The general clustering number k is fixed, and we described the experiment as follows.

In NMF, GNMF, HNMF, GSNMF, HGLNMF, and HGSNMF, we initialize two low-rank nonnegative matrix factors using a random strategy in experiments. Next, we set the dimensionality of the low-dimensional space to the number of clusters, and use the classical K-means method to cluster the samples in the new data representation space.

For NMF, GNMF, HNMF, GSNMF, HGLNMF, and HGSNMF, we use the Frobenius norm as the reconstruction error of the objective function. In GNMF and GSNMF, the heat kernel weighting scheme is used to generate the 5 nearest neighbors graph for constructing the weight matrix. In HNMF, HGLNMF, and HGSNMF, the heat kernel weighting scheme is used to generate the 5 nearest neighbors graph for constructing the weight matrix in hypergraph. In GNMF and GSNMF, the graph regularization parameter are all set to 100, in HNMF and HGLNMF, the hypergraph regularization parameter are all set to 100, and in GSNMF, set the parameter

p = 1.7

. In HGSNMF, the parameter

α

and

β

tune from

{100, 500, 1000}

for COIL20,

{0.1, 10, 500, 1000}

for YALE,

{1, 10, 100}

for ORL,

{500, 1000}

for Georgia; the parameter p tune from

{0.3, 0.5, 1.1}

for COIL20,

{0.1, 0.5, 1.1, 1.3}

for YALE,

{0.1, 1.2, 1.5}

for ORL,

{0.5, 0.6}

for Georgia, and the best results are reported.

For K-means, we repeat K-means clustering 10 times on original data. For NMF, GNMF, HNMF, GSNMF, HGLNMF, and HGSNMF, we first repeat NMF, GNMF, HNMF, GSNMF, HGLNMF, and HGSNMF 10 times on original data and then repeat K-means clustering 10 times on this low-dimensional reduced data, respectively. We reported the average clustering performance and standard deviation in Table 4, Table 5, Table 6, Table 7, Table 8, Table 9, Table 10 and Table 11, where the best results are by bold numbers.

From these experimental results in Table 4, Table 5, Table 6, Table 7, Table 8, Table 9, Table 10 and Table 11, we have the following conclusions.

1) The clustering performance of the proposed HGSNMF method on all of the data is better than that of the other algorithms in most cases, which show that the HGSNMF method can find more discriminative information for data. For COIL20, YALE, ORL, and Georgia, the average clustering ACC of the HGSNMF method is more than 1.99%, 1.89%, 0.54%, and 3.37% higher than the second-best method, respectively, and the average clustering NMI of the HGSNMF method is more than 1.84%, 2.26%, 0.6%, and 2.21% higher than the second-best method, respectively,

2)The HGSNMF method is better than the HNMF method in most cases, because the

L_{p}

smoothing constraint can combine the merits of isotropic and anisotropic diffusion smooth and more accurate solution.

3)The HGSNMF method is also better than the GSNMF method in most cases, which indicate that the hypergraph regularization term can better discover the underlying geometric information than simple graph regularization term.

For the different cluster numbers on YALE and Geogria data sets, we examine the calculation time based on NMF, GNMF, HNMF, GSNMF, and HGSNMF. In these experiments, we choose the aforementioned identical conditions including parameters and iteration times. From Table 12 and Table 3, NMF has the smallest calculation time since it does not have regularization term. HNMF, GSNMF, and HGSNMF extend GNMF by adding hypergraph regularization,

L_{p}

smoothing constraint, and the above two terms respectively, the computation time of HNMF, GSNMF, and HGSNMF is more than GNMF. However, the computation time of HGSNMF is less than HNMF in most cases, which shows the computational advantage of HGSNMF under the

L_{p}

smoothing constraint. On the YALE data set, the computation time of HGSNMF is smaller than GSNMF, which indicates that the hypergraph regularization term speeds up the convergence of the proposed HGSNMF method.

4.4. Parameters Selection

There are three parameters in our proposed HGSNMF algorithm: regularization parameters

α, μ,

and p. When

α, μ

and p are 0, the proposed HGSNMF method reduces to the NMF [9]; when

μ

and p are 0, the proposed HGSNMF method reduces to the HNMF [10]. In the experiments, we set

k = 5

for all graph-based and hypergraph-based methods on all data sets. In order to test the effect of each varying parameter, we fix the other varying parameters as subsection 4.3.

Firstly, we adjust the parameter

α

for GNMF, GSNMF, HNMF, and HGSNMF methods. In HGSNMF, for

k = 4

, we set

μ = 100

and

p = 1.1

in HGSNMF, for

k = 8

, we set

μ = 1000

and

p = 0.3

on COIL20 data set; for

k = 11

and

k = 14

, we set

μ = 1000

and

p = 0.5

on YALE data set; for

k = 20

, we set

μ = 1

and

p = 1.5

, for

k = 40

, we set

μ = 100

and

p = 1.5

on ORL data set; for

k = 15

, we set

μ = 500

and

p = 0.6

, for

k = 20

, we set

μ = 1000

and

p = 0.5

on Geogria data set. Figure 2 demonstrate the accuracy and the normalized mutual information varying with respect to

α

on four data sets. As can be seen from the Figure 2, HGSNMF performs better than other algorithms in most cases. We can see that the performance of HGSNMF is relatively stable with respect to the parameter

α

on some data sets.

Next, we adjust the parameter

μ

, for GSNMF and HGSNMF on four data sets, and set

α = 100

and

p = 1.7

in GSNMF. In HGSNMF, for

k = 6

, we set

α = 1000

and

p = 1.1

, for

k = 12

, we set

α = 1000

and

0.5

on COIL20 data set; for

k = 3

, we set

α = 500

and

p = 0.1

, for

k = 15

, we set

α = 500

α = 1000

and

p = 0.5

on YALE data set; for

k = 15

, we set

α = 10

p = 0.1

, for

k = 25

, we set

μ = 1

and

p = 1.2

on ORL data set; for

k = 5

and

k = 30

, we set

μ = 1000

and

p = 0.6

on Georgia data set. As can be seen from Figure. Figure 3, HGSNMF performs better than GSNMF in most cases on four data sets, and the performance of HGSNMF is stable with respect to the parameter

μ

on some data sets.

Finally, we consider the variation of parameter p. In HGSNMF, for

k = 8

, we set

α = μ = 1000

, for

k = 10

, we set

α = 1000

and

μ = 500

on COIL20 data set; for

k = 3

, we set

α = 0.1

and

μ = 500

; for

k = 5

, we set

α = 0.1

and

μ = 1000

on YALE data set; for

k = 5

, we set

α = μ = 10

, for

k = 15

, we set

α = 10

and

μ = 1

on ORL data set; for

k = 35

, and

k = 45

, we set

α = 500

and

μ = 1000

on Georgia data set. As show in Figure 4, the performance of HGSNMF is relatively stable and very good with respect to the parameter p varying from 0.1 to 2 on some data sets.

4.5. The Converage Analysis

As described in Section 3, the converge of the proposed HGSNMF method is theoretically proved. In this section, we analyze the convergence of the proposed method through experiments. Figure 5 shows the convergence curves of our HGSNMF method on all four data sets. As can be seen from Figure 5, the objective function is monotonically decreasing and tends to converge after 300 iterations.

5. Conclusion

In this paper, we proposed a hypergraph regularized

L_{p}

smooth constrain NMF method for data representation, by incorporating hypergraph regularization term and

L_{p}

smoothing constraint into NMF. The hypergraph regularization term can better capture the intrinsic geometry structure of the high dimension space data more comprehensively than simple graph, the

L_{p}

smoothing constraint may produce a smooth and more accurate solution to the optimization problem. We present the updating rulers and prove the convergence of our HGSNMF method. Experimental results on four real-world data sets show that our proposed method can achieve better clustering effect than other state-of-the-art methods in most cases.

Author Contributions

Conceptualization, Y.X. and Q.L.; methodology, Y.X. and L.L.; software, Q.L. and Z.C.; writing—original draft preparation, Y.X.; writing—review and editing, Q.L. All authors have read and agreed to the published version of the manuscript.

Funding

This research was partially funded by the National Natural Science Foundation of China under Grants 12061025 and 12161020; and partially funded by the Natural Science Foundation of the Educational Commission of Guizhou Province under Grant Qian-Jiao-He KY Zi [2019]186,[2019] and [2021]298, and Guizhou Provincial Science and Technology Projects (QKHJC[2020]1Z002 and QKHJC-ZK[2023]YB245).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this study are available on request from the corresponding author.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

PCA	Principal component analysis
LDA	Linear discriminant analysis
SVD	Singular value decomposition
NMF	Nonnegative matrix factorization
HU	Hyperspectral unmixing
ONMF	Orthogonal nonnegative matrix tri-factorizators
GNMF	Graph regularized nonnegative matrix factorization
DNMF	Graph dual regularization nonnegative matrix factorization
HNMF	Hypergraph regularized nonnegative matrix factorization
GSNMF	Graph regularized $L_{p}$ smooth nonnegative matrix factorization
HGLNMF	Hypergraph regularized sparse nonnegative matrix factorization
MHGNMF	nonnegative matrix factorization with mixed hypergraph regularization
DHPS-NMF	Dual hypergraph regularized partially shared nonnegative matrix factorization
HGSNMF	Hypergraph regularized $L_{p}$ smooth nonnegative matrix factorization
the ACC	Accuracy
NMI	Normalized mutual information
MI	Mutual information

References

Pham, N.; Pham, L.; Nguyen, T. A new cluster tendency assessment method for fuzzy co-clustering in hyperspectral image analysis. Neucom. 2018, 307, 213–226. [Google Scholar] [CrossRef]
Cai, D.; He, X.; Han, J.; Huang, T. Graph regularized nonnegative matrix factorization for data representation. IEEE Trans. Pattern Anal. Match. Intell. 2011, 33, 1548–1560. [Google Scholar]
Li, S.; Hou, X.; Zhang, H.; Cheng, Q. Learning spatially localized, parts-based representation. IEEE Conf. Comput. Vis. Pattern Recognit(CVPR). 2011, 1, 207–212. [Google Scholar]
He, X.; Yan, S.; Hu, Y.; Niyogi, P.; Zhang, H. ; Face recognition using laplacian faces. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27(3), 328–340. [Google Scholar]
Liu, H.; Wu, Z.; Li, X.; Cai, D.; Huang, T. Constrained nonnegative matrix factorization for image representation. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 34(7), 1299–1311. [Google Scholar] [CrossRef] [PubMed]
Kirby, M.; Sirovich, L. Application of the karhunen loeve procedure for the characterization of human faces. IEEE Trans. Pattern Anal. Mach. Intell. 1990, 12(1), 103–108. [Google Scholar] [CrossRef]
Martinez, A.; Kak, A. Pca versus lda. IEEE Trans. Pattern Anal. Mach. Intell. 2001, 23(2), 228–233. [Google Scholar] [CrossRef]
Strang, G. Introduction to Linear Algebra, USA:Wellesley, 2009.
Lee, D.; Seung, H. Learning of the parts of objects by non-negative matrix factorization. Nature. 1999, 401(4), 788–791. [Google Scholar] [CrossRef]
Lee, D.; Seung, H. Algorithms for nonnegative matrix factorization. in Proc. 13th Adv. Neural Inf. Process. Sys. 20001, 13, 556–562. [Google Scholar]
He, X.; Ding, C. ; Simon,H. On the equivalence of nonnegative matrix factorization and spectral clustering, SIAM. Int. Conf. Data Min.(SDM05) 606–610.
Ding, C.; Li, T.; Peng, W.; Park, H. Orthogonal nonnegative matrix tri-factorizations for clustering. in Proc. 12th ACM SIGKDD Int. Conf. Knowl.Disc. Data Min. 2006, 126–135. [Google Scholar]
Pan, J.; Ng, M. Orthogonal nonnegative matrix factorization by sparsity and nuclear norm optimization. SIAM. J. Matrix Anal. Appl. 2018, 39(2), 856–875. [Google Scholar] [CrossRef]
Guillamet, D.; Vitria, J.; Schiele, B. Introducing a weighted nonnegative matrix factorization for image classification. Pattern Recognit. Lett. 2003, 24, 2447–2454. [Google Scholar] [CrossRef]
Tan, X.; Triggs, B. Enhanced local texture feature sets for face recognition under difficult lighting conditions. IEEE Trans. Image Process. 2010, 19(6), 1635–1650. [Google Scholar]
Pauca, V.; Shahnaz, F.; Berry, M.; Plemmons, R. Text mining using nonnegative matrix factorizations. SIAM. Int. Conf. Data Min. 2004, 4, 452–456. [Google Scholar]
Li, T.; Ding, C. The relationships among various nonnegative matrix factorization methods for clustering. IEEE. Comput. Soci. 2006, 4, 362–371. [Google Scholar]
Liu, Y.; Jing, L.; Ng, M. Robust and non-negative collective matrix factorization for text-to-image transfer learning. IEEE Trans. Image Process. 2015, 24, 4701–4714. [Google Scholar]
Gillis, N. Sparse and unique nonnegative matrix factorization through data preprocessing. J. Mach. Learn. Res. 2012, 1, 3349–3386. [Google Scholar]
Gillis, N. Nonnegative matrix factorization,SIAM. Philadelphia. PA. USA, 2020.
Wang, W.; Qian,Y. ; Tan, Y. Hypergraph-regularized spares NMF for hyperspectral unmixing. IEEE J. Sel. Topi. APPL. Earth. Obser. Remot Sens. 2016, 9(2), 681–694. [Google Scholar] [CrossRef]
Ma, Y.; Li, C.; Mei, X.; Liu, C.; Ma, J. Robust sparse hyperspectral unmixing withL_2,1 norm. IEEE Trans. Geos. Remot Sens. 2017, 55(3), 55–1239. [Google Scholar] [CrossRef]
Li, Z.; Liu, J.; Lu, H. Structure preserving non-negative matrix factorization for dimensionality reduction. Comput. Vis. Image Underst. 2013, 117(9), 1175–1189. [Google Scholar] [CrossRef]
Luo, X.; Zhou, M.; Leung, H.; Xia, Y.; Zhu, Q.; You, Z.; Li, S. An incremental-and-static-combined scheme for matrix-factorization- based collaborative filtering. IEEE Trans. Auto. Sci. Engin. 2014, 13(1), 333–343. [Google Scholar] [CrossRef]
Zhou, G.; Yang, Z.; Xie, S.; Yang, J. Online blind source separation using incremental nonnegative matrix factorization with volume constraint. IEEE Trans. Neur Netw. 2011, 22(4), 550–560. [Google Scholar] [CrossRef] [PubMed]
Pan, J.; Gillis, N. Generalized separable nonnegative matrix factorization. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43(5), 1546–1561. [Google Scholar] [CrossRef] [PubMed]
Shang, F.; Jiao, L.; Wang, F. Graph dual regularization nonnegative matrix factorization for co-clustering. Pattern Recognit. 2012, 45, 2237–2250. [Google Scholar] [CrossRef]
Zeng, K.; Jun, Y.; Wang, C.; You, J.; Jin, T. Image clustering by hypergraph regularized nonnegatve matrix factorization. Neurocomputing. 2014, 138, 209–217. [Google Scholar] [CrossRef]
Leng, C.; Zhang, H.; Cai, G.; Cheng, I.; Basu, A. Graph regularized L_p smooth nonnegative matrix factorization for data representation. IEEE/CAA J. Auto. 2019, 6, 584–595. [Google Scholar] [CrossRef]
Wood, G.; Jennings, L. On the use of spline functions for data smoothing. J. Biomech. 1979, 12(6), 477–479. [Google Scholar] [CrossRef]
Lyons, J. Differentiation of solutions of nonlocal boundary value problems with respect to boundary data. Electron. J. Qual. Theory Differ. Equ. 2001, 51, 1–11. [Google Scholar] [CrossRef]
Xu, L. Data smoothing regularization, multi-sets-learning, and problem solving strategies. Neural Netw. 2003, 16(5), 817–825. [Google Scholar] [CrossRef]
Wang, W.; Qian,Y. ; Tan, Y. Hypergraph-regularized spares NMF for hyperspectral unmixing. IEEE J. Sel. Topi. APPL. Earth. Obser. Remot Sens. 2016, 9(2), 681–694. [Google Scholar] [CrossRef]
Zhou, D.; Huang, J.; Scholkopf, B. Learning with hypergraphs:clustering, classification,and embdding. MIT Press, Cambridge, MA. 2006, 19, 1601–1608. [Google Scholar]
Huan, Y.; Liu, Q.; Lv, F.; Gong, Y.; Metaxax, D. Unsupervised image categorization by hypergraph partition. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33(6), 17–24. [Google Scholar]
Yu, J.; Tao, D.; Wang, M. Adaptive hypergraph learning and its application in image classification. IEEE Trans. Image Process. 2012, 21(7), 3262–3272. [Google Scholar] [PubMed]
Hong, C.; Yu, J.; Li, J.; Chen, X. Multi-view hypergraph learning by patch alignment framework. Neurocomputing. 118, 79–86. [CrossRef]
Wang, C.; Yu, J.; Tao, D. High-level attributes modeling for indoor scenes classifiation. Neurocomputing. 2013, 121, 337–343. [Google Scholar] [CrossRef]
Wu, W.; Kwong, S.; Zhou, Y. Nonnegative matrix factorization with mixed hypergraph regularization for community detection. Information Sciences. 2018, 435, 263–281. [Google Scholar] [CrossRef]
Zhang, D. Semi-supervised multi-view clustering with dual hypergraph regularized partially shared nonnegative matrix factorization. Science China Technological Sciences. 2022, 65(6), 1349–1365. [Google Scholar] [CrossRef]
Huang, H; Zhou, G.; Liang, N.; Zhao, Q.; Xie, S. Diverse deep matrix factorization with hypergraph regularization for multiview data representation. IEEE/CAA Journal of Automatica Sinica. 2022.
Cai, D.; He, X.; Han, J. Documen clustering using locality preserving indexing. IEEE Trans. Knowl. Data Engi. 2005, 17(12), 1624–1637. [Google Scholar] [CrossRef]
Lovasz, L.; Plummer, M. Matching theory. American Mathematical Soc. 2009, 367. [Google Scholar]

Figure 1. An illustration the simple graph, the hypergraph

\bar{G}

and an indication matrix.

Figure 1. An illustration the simple graph, the hypergraph

\bar{G}

and an indication matrix.

	$e_{1}$	$e_{2}$	$e_{3}$
$v_{1}$	1	0	0
$v_{2}$	1	0	0
$v_{3}$	0	1	0
$v_{4}$	1	1	0
$v_{5}$	0	1	0
$v_{6}$	0	1	1
$v_{7}$	0	0	1
$v_{8}$	0	0	1

Figure 2. Performance comparison of GNMF, HNMF, GSNMF, and HGSNMF for varying parameter

α

on COIL20, YALE, ORL, and Georgia data sets.

Figure 2. Performance comparison of GNMF, HNMF, GSNMF, and HGSNMF for varying parameter

α

on COIL20, YALE, ORL, and Georgia data sets.

Figure 3. Performance comparison of GSNMF and HGSNMF for varying parameter

μ

on COIL20, YALE, ORL, and Georgia data sets.

Figure 3. Performance comparison of GSNMF and HGSNMF for varying parameter

μ

on COIL20, YALE, ORL, and Georgia data sets.

Figure 4. Performance comparison of GSNMF, and HGSNMF for varying parameter p on COIL20, YALE, ORL, and Georgia data sets.

Figure 5. The relative residuals versus the number of iterations for HGSNMF on four data sets.

Table 1. Computational operation counts for each iteration in NMF, GNMF, HNMF, GSNMF, HGLNMF, and HGSNMF

	fladd	flmlt	fidiv	overall
NMF	$2 n m r + 2 (m + n) r^{2}$	2 $n m r$ +2 $(m + n) r^{2} + m r + n r$	$m r + n r$	$O (m n r)$
GNMF	2 $n m r$ +2 $(m + n) r^{2} + n r + 3 n$	2 $n m r$ +2 $(m + n) r^{2} + (m + 2 n + n k) r$	$m r + n r$	$O (m n r)$
HNMF	2 $n m r$ +2 $(m + n) r^{2} + n r + 3 n$	2 $n m r$ +2 $(m + n) r^{2} + (m + 2 n + n k) r$	$m r + n r$	$O (m n r)$
GSNMF	2 $n m r$ +2 $(m + n) r^{2} + n k + 3 n + m r$	2 $n m r$ +2 $(m + n) r^{2} + (m + 2 n + n k) r$	$m r + n r$	$O (m n r)$
HGLNMF	2 $n m r$ +2 $(m + n) r^{2} + n k + 3 n + m r$	2 $n m r$ +2 $(m + n) r^{2} + (m + 2 n + n k) r$	$m r + n r$	$O (m n r)$
HGSNMF	2 $n m r$ +2 $(m + n) r^{2} + n k + 3 n + m r$	2 $n m r$ +2 $(m + n) r^{2} + (m + 2 n + n k) r$	$m r + n r$	$O (m n r)$

Table 2. Statistics of the four data sets

Data sets	Samples	Features	Classes
COIL20	1440	1024	20
YALE	165	1024	15
ORL	400	1024	40
Georgia	750	1024	50

Table 3. Normalized mutual information (NMI) on COIL20 data set.

k	K-means	NMF	GNMF	HNMF	GSNMF	HGLNMF	HGSNMF
4	65.13±16.60	69.63±15.76	72.86±14.86	79.53±13.65	73.79±13.51	79.52±13.64	$84.45 \pm 15.24$
6	67.70±9.79	69.65±11.27	72.79±10.70	80.72±10.58	68.63±10.00	80.76±10.54	$83.84 \pm 8.37$
8	70.56±5.89	69.44±8.78	71.53±8.60	80.94± 7.35	73.55±7.28	81.08±7.38	$81.85 \pm 8.11$
10	76.02±7.12	70.13±6.95	76.01±5.48	82.99± 5.84	76.36±5.92	83.00±5.75	$83.83 \pm 5.41$
12	73.21±4.82	70.91±5.50	77.12±5.68	82.16± 5.03	75.70±5.33	82.31±5.08	$83.75 \pm 5.31$
14	74.10±4.31	70.41±4.66	77.06±4.75	82.20±4.24	76.88±4.63	82.21±4.19	$83.69 \pm 4.78$
16	74.85±3.65	72.70±4.04	79.38±4.52	84.05± 3.95	79.04±4.27	83.99±3.97	$85.83 \pm 4.28$
18	73.28±3.08	71.49±3.00	78.03±3.65	84.61± 3.15	79.36±3.47	84.70±3.16	$85.74 \pm 3.30$
20	73.83±2.52	71.95±2.76	79.20±3.05	84.08± 2.79	78.84±2.76	84.05±2.71	$85.15 \pm 3.52$
Avg.	72.0	71.70	76.00	82.36	75.80	82.40	$84.24$

Table 4. Clustering accuracy (ACC) on COIL20 data set.

k	K-means	NMF	GNMF	HNMF	GSNMF	HGLNMF	HGSNMF
4	71.45±14.82	72.35±16.50	73.41±14.85	75.78±17.88	75.33±15.74	75.77±17.88	$81.31 \pm 19.19$
6	67.05±10.72	68.87±11.80	69.65±12.61	74.42±13.78	68.04±10.78	74.44±13.78	$77.30 \pm 11.89$
8	64.56±64.56	65.39±9.95	64.35±10.93	71.06±11.77	67.36±9.73	70.71±11.75	$71.43 \pm 11.74$
10	67.38±9.76	63.27±7.96	66.76±7.47	70.73±10.04	67.07±8.44	70.61±5.75	$73.39 \pm 8.96$
12	63.73±7.09	63.19±7.02	66.81±8.30	68.63± 8.43	65.81±8.43	69.00±5.08	$71.50 \pm 8.22$
14	62.48±6.42	60.01±6.16	65.18±7.57	68.04±8.33	64.21±7.77	68.03±8.18	$83.69 \pm 7.88$
16	61.78±5.69	62.18±6.43	65.47±7.25	69.09±7.62	66.03±7.50	68.85±7.66	$70.31 \pm 8.24$
18	59.15±6.18	59.68± 5.44	63.39±6.86	69.29±6.51	65.84±6.70	69.65±6.59	$70.85 \pm 6.35$
20	58.18±5.43	59.11±4.60	63.86±6.24	$68.68 \pm 6.52$	63.95±6.00	68.56±6.34	68.19±6.83
Avg.	63.97	63.78	66.54	70.64	67.07	70.63	$72.63$

Table 5. Normalized mutual information (NMI) on YALE data set.

k	K-means	NMF	GNMF	HNMF	GSNMF	HGLNMF	HGSNMF
3	40.18±23.03	28.96±11.71	28.81±12.06	36.08±12.82	37.80±16.40	36.12±12.89	$41.36 \pm 13.07$
5	35.72±12.87	38.23±10.25	38.48±10.02	39.37±8.83	40.01±10.61	39.35±8.85	$41.91 \pm 10.34$
7	$43.18 \pm 6.55$	38.38±6.51	38.17±7.57	39.07±6.84	39.33±6.46	39.38±5.23	42.32±7.39
9	$42.22 \pm 7.98$	41.80±3.87	40.56±5.00	38.93±5.05	38.85±4.88	39.18±5.23	40.21±4.35
11	39.80±4.40	41.82±4.45	42.05±4.25	43.88± 4.30	44.08±4.62	44.04±4.61	$45.06 \pm 4.70$
13	44.13±4.63	44.17±3.03	44.59±3.43	44.24±3.12	44.53±2.80	44.29±3.07	$47.54 \pm 3.84$
14	44.34±3.84	43.27±2.92	43.31±3.10	44.21± 3.39	44.82±3.02	44.21±3.32	$46.82 \pm 3.85$
15	44.48±2.92	43.91±2.90	44.36±2.72	45.37± 2.38	45.32±2.62	45.47±2.35	$47.60 \pm 3.06$
Avg.	41.76	40.07	40.04	41.40	41.84	41.51	$44.10$

Table 6. Clustering accuracy (ACC) on YALE data set.

k	K-means	NMF	GNMF	HNMF	GSNMF	HGLNMF	HGSNMF
3	62.24±14.91	59.30±8.16	59.12±8.11	61.49±8.20	62.64±11.14	61.91±8.61	$64.82 \pm 10.06$
5	50.24±10.66	54.15 ±8.92	53.78±8.27	54.95±7.83	54.82±9.04	54.84±7.82	$56.84 \pm 8.79$
7	49.43±6.26	47.40±6.33	46.92±6.90	47.21±6.81	46.65±6.14	47.44±6.62	$49.87 \pm 7.32$
9	44.40±7.02	$44.87 \pm 4.30$	43.12±4.87	42.48±5.45	42.15±4.74	42.81±5.49	43.68±4.98
11	39.12±4.80	41.37±5.06	41.74±4.65	43.43±5.00	43.07±5.29	43.50±5.12	$44.19 \pm 5.20$
13	40.41±4.81	41.18±3.73	41.11±4.10	40.76±3.83	41.05±3.61	40.78±3.91	$43.57 \pm 4.17$
14	39.46±4.26	39.05±4.21	38.27±3.72	39.92±4.21	40.03±3.75	39.94±4.22	$41.97 \pm 4.33$
15	38.52±3.30	38.72±3.51	38.67±3.21	40.25±3.39	39.52±3.14	40.44±3.24	$41.86 \pm 3.37$
Avg.	45.41	45.76	45.34	46.31	46.24	46.46	$48.35$

Table 7. Normalized mutual information (NMI) on ORL data set.

k	K-means	NMF	GNMF	HNMF	GSNMF	HGLNMF	HGSNMF
5	66.24±12.00	67.18±12.07	68.81±11.16	68.58±12.77	66.51±13.18	68.97±13.01	$68.98 \pm 12.29$
10	70.22±6.63	73.59±5.90	$73.72 \pm 7.10$	72.11±6.70	71.95±5.92	72.39±6.59	73.29±6.55
15	68.46±4.21	75.23±5.01	76.14±5.18	75.26±5.62	75.67±5.27	75.26±5.62	$76.54 \pm 5.42$
20	69.87±4.75	74.21±4.34	74.44±4.78	75.24±4.25	75.49±3.76	75.46±4.19	$76.00 \pm 4.08$
25	71.13±3.48	75.51±2.69	75.88±3.13	76.03±3.29	76.10±3.17	76.06±3.12	$76.91 \pm 3.22$
30	71.03±2.81	75.34±3.12	75.55±2.81	74.60±2.67	$75.89 \pm 2.78$	74.69±2.65	75.88±2.80
35	71.07±1.82	75.07±2.23	74.96±2.06	74.46±1.87	75.85±2.18	74.52±1.91	$75.96 \pm 2.35$
40	71.45±2.06	75.05±1.90	75.26±1.82	74.54±1.87	75.40±1.91	74.54±1.91	$76.07 \pm 1.77$
Avg.	69.93	73.90	74.35	73.85	74.11	73.99	$74.95$

Table 8. Clustering accuracy (ACC) on ORL data set.

k	K-means	NMF	GNMF	HNMF	GSNMF	HGLNMF	HGSNMF
5	67.32±14.91	68.12±12.11	68.76±12.31	68.70±12.27	67.36±12.72	68.97±13.01	$69.30 \pm 12.15$
10	62.72±10.66	$66.11 \pm 8.02$	65.85±9.86	64.05±7.87	64.59±7.22	64.46±7.82	65.42±7.50
15	56.19±5.80	63.55±6.85	64.84±6.96	63.99±7.44	64.59±7.32	63.99±7.44	$65.89 \pm 7.38$
20	55.29±6.25	61.21±5.83	61.56±6.21	62.44±5.87	62.67±5.30	62.52±5.57	$62.80 \pm 5.73$
25	54.15±4.50	60.58±3.98	61.01±4.84	61.31±4.66	61.16±4.96	61.32±4.80	$61.91 \pm 5.22$
30	52.52±4.29	58.57±4.67	58.88±4.52	58.07±4.42	$59.91 \pm 4.08$	58.38±4.28	59.50±4.20
35	51.30±3.20	57.83±3.62	57.22±3.46	56.95±3.28	$58.79 \pm 3.58$	57.05±3.21	58.35±4.06
40	50.68±3.43	56.57±3.39	56.73±3.15	55.88±3.32	57.20±3.46	55.88±3.37	$57.36 \pm 3.38$
Avg.	56.27	61.57	61.86	61.42	62.03	61.57	$62.57$

Table 9. Normalized mutual information (NMI) on Georgia data set.

k	K-means	NMF	GNMF	HNMF	GSNMF	HGLNMF	HGSNMF
5	67.05±11.33	59.40±11.79	63.00±12.27	60.93±11.93	64.46±10.83	60.99±11.94	$68.18 \pm 9.19$
10	$67.82 \pm 7.48$	60.25±8.93	61.24±8.51	57.48±10.50	61.59±10.12	57.63±10.67	65.91±9.15
15	64.64±5.32	60.57±4.39	62.46±4.85	61.89±5.12	64.02±5.72	61.99±5.02	$68.55 \pm 5.08$
20	67.12±4.30	60.60±3.71	62.58±3.91	60.98±3.81	64.44±3.18	61.08±3.82	$68.91 \pm 2.93$
25	66.30±3.31	59.31±2.73	61.35±2.62	61.33±3.22	64.83±2.98	61.32±3.68	$69.44 \pm 2.87$
30	66.01±3.13	60.26±2.56	63.20±2.25	60.52±3.04	64.61±2.97	60.47±2.99	$69.61 \pm 2.87$
35	65.10±2.13	59.93±2.33	63.3±1.80	59.21±2.21	63.27±2.37	59.20±2.22	$68.70 \pm 1.95$
40	66.06±2.20	59.58±2.34	62.84±1.82	58.61±2.38	63.57±1.98	58.62±2.48	$69.18 \pm 1.69$
45	66.17±1.35	59.99±1.75	62.92±1.55	58.22±1.90	62.92±1.66	58.25±1.99	$69.07 \pm 1.41$
50	66.36±1.32	59.05±1.56	62.11±1.51	58.19±1.33	63.18±1.24	58.19±1.25	$69.18 \pm 1.13$
Avg.	66.26	59.90	62.50	59.74	63.69	59.77	$68.47$

Table 10. Clustering accuracy (ACC) on Georgia data set.

k	K-means	NMF	GNMF	HNMF	GSNMF	HGLNMF	HGSNMF
5	68.73±11.50	66.68±10.96	69.52±11.15	68.00±10.33	69.76±10.50	67.68±10.47	$73.12 \pm 10.04$
10	61.71±8.56	57.79±8.48	59.25±8.44	55.73±9.09	59.07±8.94	55.83±9.23	$61.97 \pm 9.39$
15	55.38±6.27	53.33±4.41	55.05±5.38	55.07±5.41	56.08±6.15	55.21±5.38	$59.40 \pm 6.31$
20	55.14±5.07	50.55±4.58	52.30±4.60	50.22±4.45	54.93±4.36	50.37±4.40	$57.50 \pm 4.29$
25	51.82±4.40	46.8¡¤±3.59	48.50±3.42	48.25±4.38	52.10±4.09	48.311±4.30	$55.52 \pm 4.06$
30	49.67±4.12	45.20±3.49	48.31±3.13	45.82±3.48	50.17±3.82	45.68±3.33	$54.18 \pm 3.67$
35	47.80±3.28	43.78±3.12	47.09±2.92	42.57±3.03	47.19±3.31	42.53±3.02	$52.17 \pm 2.96$
40	47.88±3.28	41.93±2.95	45.35±2.81	40.47±3.26	46.27±3.02	40.41±3.45	$51.52 \pm 2.90$
45	47.39±2.26	41.07±2.52	43.93±2.44	38.53±2.49	44.34±2.50	38.58±2.59	$50.40 \pm 2.50$
50	46.18±2.19	38.94±2.22	42.14±2.40	37.24±1.92	43.78±2.32	37.26±1.90	$49.62 \pm 2.45$
Avg.	53.17	48.61	51.14	48.19	52.37	48.19	$56.54$

Table 11. Comparisons of computation time on the YALE.

k	NMF	GNMF	HNMF	GSNMF	HGLNMF	HGSNMF
3	$0.88$	1.15	2.51	3.14	4.08	3.15
11	$5.22$	9.21	20.75	21.31	35.62	14.77
13	$10.29$	17.63	41.12	42.18	67.89	28.70
14	$12.13$	20.64	49.80	46.75	80.06	35.45
15	$13.39$	22.52	55.35	54.18	96.94	43.62

Table 12. Comparisons of computation time on the Georgia.

k	NMF	GNMF	HNMF	GSNMF	HGLNMF	HGSNMF
10	$9.19$	25.39	47.79	35.77	69.7	45.07
15	$16.94$	40.36	94.57	67.58	134.67	88.01
20	$24.57$	56.96	123.30	89.73	183.88	120.07
25	$40.84$	90.97	233.04	151.94	312.03	201.96
30	$55.86$	114.43	343.62	196.97	429.94	214.84

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Hypergraph Regularized Lp Smooth Nonnegative Matrix Factorization for Data Representation

Abstract

1. Introduction

2. Related work

2.1. Nonnegative matrix factorization

2.2. Hypergraph Learning

3. Hypergraph Regularized L p Smooth Nonnegative Matrix Factorization

3.1. The Objective Function

3.2. Optimization method

3.3. Convergence Analysis

3.4. Computational Complexity Analysis

4. Numerical Experimental

4.1. Data Sets

4.2. Evaluation Metrics

4.3. Performance Evaluations and Comparisons

4.4. Parameters Selection

4.5. The Converage Analysis

5. Conclusion

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Conflicts of Interest

Abbreviations

References

MDPI Initiatives

Important Links

Subscribe

3. Hypergraph Regularized $L_{p}$ Smooth Nonnegative Matrix Factorization