Preprint
Article
Spatial Overlay Analysis of Geochemical Singularity Index α-Value of Porphyry Cu Deposit in Gangdese Metallogenic Belt, Tibet, Western China
Altmetrics
Downloads
158
Views
39
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
22 May 2023
Posted:
22 May 2023
You are already at the latest version
Alerts
Abstract
It is found in this paper that ILR-RPCA-back CLR has two problems when dealing with the closure effect of geochemical data. (1) After ilr transformation, RPCA is used for processing. It can be seen from the double-plot diagram that the first principal component and the second principal component transform with the element sequence transformation, and the unique principal component cannot be calculated; (2) the score and the load are transformed into the CLR space through the U matrix. According to the formula CLR=ALR·U, the score result can correspond to the original order of elements. However, the load result obtained by the use of this formula cannot correspond to the original order of elements, and the result can only be obtained through the formula” CLR=UT·ALR”. In order to obtain the best element assemblage of porphyry copper deposit, this paper adopted the mineral assemblage of discovered deposits in Gangdese metallogenic belt for statistical analysis, and obtained that the element assemblage of porphyry copper deposit was Cu, Mo, Au, Ag, W, Bi. Then, by analyzing the singularities of the composite elements, the spatial overlay of the combined element is carried out, and C-A fractal filtering is applied to identify the anomaly and background. In order to facilitate comparison, the different minerals and ore deposit types have been analyzed, the results show that (1) in view of the porphyry copper deposits, recognition effect of combination elements are better than which single element, (2) skarn type copper deposit that it has nothing to do with the porphyry had a high degree of difference, but skarn type copper deposit related to the porphyry had a low degree of difference, (3) This method has a certain advantage over the single element method in porphyry gold deposits, and it can reduce the level of anomalies. Such an advantage is that in the aspect of anomaly evaluation of porphyry copper deposits, the level is reduced at the initial stage of evaluation to reduce the investment in such anomalies, (4) This method has limited ability to distinguish porphyry copper deposit from porphyry molybdenum deposit.
Keywords:
Subject: Environmental and Earth Sciences - Geochemistry and Petrology
1. Introduction
Porphyry deposits are the most important sources of copper, molybdenum and gold in the world, of which porphyry copper deposits account for about 55% of the global copper reserves, porphyry molybdenum deposits account for 90% of molybdenum reserves, porphyry gold deposits accounting for 20% of gold reserves, and the proportion of considerable in China [1,2,3,4]. Over the past decade, with a series of large porphyry copper mine like the Qulong, Jiama, Xiongcun,Duolong, Tiegelongnan explored and studied, the Qinghai-Tibet Plateau leapt to most important and most promising of the province of copper in China [5].
Mineralization can lead to the enrichment and accumulation of useful materials in a relatively small space and time range. Compared with the normal regional geological processes, the temporal and spatial range of mineralization is limited [6]. The complexity of metallogenic process lies in the complex dynamics of the multi-component and multi-geologic interaction coupled Overlay and the complex dynamics process [7]. Only by means of geochemical exploration of single elements is not competent for this work. Therefore, the identification of combination elements plays an important role in geochemical data processin and at present,the methods of combination element identification are PCA, RPCA, FA and RFA and so on [8,9,10,11,12,13].They need to use logarithmic transformations (alr, clr, ilr, etc.) to eliminate the effect of component data closure as much as possible, but they have some problems in the analysis process (eg, explain difficulties , Singularity effects, etc.), it is difficult to solve. Moreover, the combination elements extracted during the analysis of the above method, especially in small scale geochemical data, are largely related to environmental (background) elements rather than to ore-forming elements. In the Gangdese metallogenic belt, the porphyry copper deposit has a specific combination of mineralization elements. Therefore, it is more favorable for the discovery of porphyry copper deposits by using the spatial overlay analysis related to the genesis of deposits.
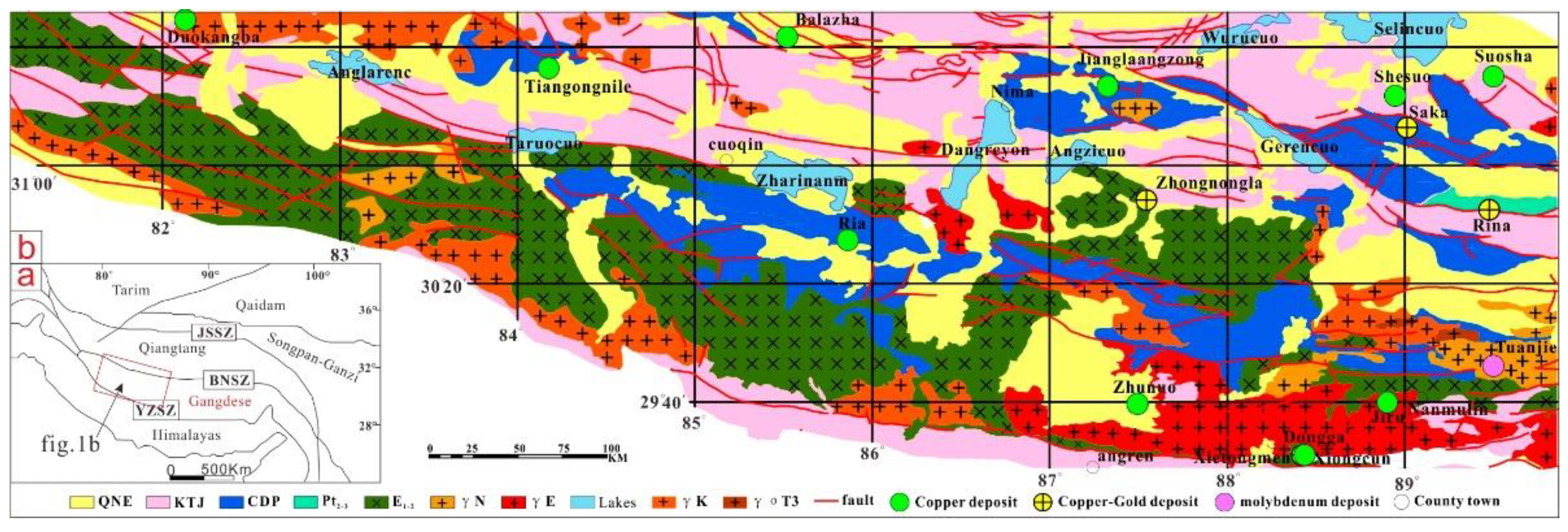
The Gangdese metallogenic belt, as the largest porphyry copper deposits ore dense district, has found a large number of large-super large porphyry deposits such as the Qulong, the Tinggong, the Chongjiang, the Jiama, and the Bairong in the eastern section, while the deposits are found in the western are relatively few. Because of the shortcomings of traditional methods in identifying complex anomalies and low-delay anomalies, it is necessary to use advanced theories and techniques to guide the prospecting work of porphyry copper deposits in the western section of Gangdese metallogenic belt. Local singularity analysis is not only a powerful multifractal tool to identify weak anomalies, but also a type of local neighborhood statistical analysis that can reduce the effects of regional background and provide useful statistical information by involving the data within a small singularity around a specific spatial location [14,15,16,17,18,19,20,21]. Therefore, local singularity analysis is widely used. Based on the shortcomings of ilr-RPCA-back-clr model, this paper takes the porphyry copper deposit in the western Gangdese metallogenic belt as the object of study, using the overlay analysis of the local singular elements of geochemical combination elements, to study geochemical spatial distribution pattern of porphyry copper deposit and to extract the real anomalies associated with porphyry copper deposits.
2. Geological Setting and Geochemical Data
2.1. Regional Geological Background
The western part of the Gangdese belt is located in the south-central part of the Tibet Autonomous Region. The tectonic structure belongs to the Gangdese-Nyainqentanglha landmass in the Gangdese-Himalayan tectonic area, which is between the Yarlung Zangbo River and the Bangong Lake-Nujiang Belt [22]. The basement is composed of the Nyainqentanglha group of presinian. On the crystalline basement of presinian, the Cambrian and low-middle Triassic strata are generally absent, since the Ordovician stratigra development more complete. The Ordovician-Permian strata are mainly distributed in the northern part of the study area, and the Upper Triassic-Jurassic strata are distributed in the northern part of the study area, while the Cretaceous-Neogene strata are distributed in the whole area. The magmatic rocks with large times, large exposing areas, wide distribution range, complicated causes and diverse types in the area are very developed. The intrusive rocks since the Triassic and the volcanic rocks since the Triassic have been extensively developed and mainly formed in Cretaceous-Paleogene, the latest volcanic magma activities to the Miocene. Pan, et al., [23] divided the tectonic unit of the Gangdese orogenic belt. By comparing the tectonic units, the study area is divided into four magmatic belts consisting of inetrmediate-acidic magmatic rocks including South Gangdese, Longgeer-Nyainqentanglha, Ze long and Ban-Bengcuo. The four magmatic belts is closely related to the distribution of the porphyry copper-molybdenum-gold deposits. The porphyry copper polymetallic deposits in the study area are mainly distributed in the volcanomagmatic arc of the South Gangdes including Zhunuo, Jiru, Xiongcun, Dongga etc, the uplift of Longgeer-Nanmulin arc-back belt containing Ria in Coqen and the Island arc belt of Coqen-Xainza consisting of Balazha, Gaerqiong ect. The detailed chronology and tectonic setting of the typical porphyry deposits mentioned above have been studied by many authors. It shows that the formation environment and metallogenic characteristics of the porphyry deposits in this area are formed in 3 tectonic settings-Island arcs, syn collisional and post collisional extensional environments and 4 metallogenic periods-Early Middle Jurassic, Late Cretaceous, Eocene and Miocen. The porphyry deposits in island arc such as Dongga and Xiongcun only distributed in the south of the southern margin of the Gangdese volcano magmatic arc zone. The porphyry deposits in syncollisional postcollisional extensional environment such as Zhunuo and Jiru are mainly distributed in the southern Gangdese volcanomagmatic arc. Secondly there are a few porphyry deposits such as Balazha and Gaerqiong distributed in the northern part of Cuoqin-Xainza Island arc, Bangor magmatic arc belt. All these insights greatly extend the prospecting of porphyry copper polymetallic ore in the western Gangdese.
2.2. Geochemical Data
The datasets used in this study were a digital 1:500,000 geological map and a regional stream sediment geochemical dataset. The regional stream sediment geochemical dataset is based on collected of 9546 stream sediment samples and analyzed for 39 major, minor, trace and subtrace elements at a density of one sample per 20km2 during the Chinese National Geochemical Mapping (CNGM) project as part of the “Regional Geochemistry National Reconnaissance (RGNR) Project”. These 39 elements in stream sediments are determined based on inductively coupled plasma-mass spectrometry (ICP-MS), X-ray fluorescence (XRF), and inductively coupled plasma-atomic emission spectrometry (ICP-AES) as the backbone combined with other methods. The concentration values of Bi, Cd, Co, Cu, La, Mo, Nb, Pb, Th, U, and W are determined by ICP-MS. The concentration values of Al, Cr, Fe, K, P, Si, Ti, Y, and Zr were determined by XRF. The concentration values of Ba, Be, Ca, Li, Mg, Mn, Na, Ni, Sr, V, and Zn were determined by ICP-AES. The concentration values of Ag, B, and Sn were determined by emission spectrometry(ES). The concentration values of As and Sb were determined by hydride generation-atomic fluorescence spectrometry (HG-AFS). The concentration values of Au, Hg, and F are determined by graphite furnace-atomic absorption spectrometry (GF-AAS), coldvapor-atomic fluore scence spectrometry (CV-AFS), andion selective electrode [27], respectively. The detection limit for each of the 39 elements is given in Table 1 [28].
3. Methods
3.1. Multifractal Inverse Distance Weighted (MIDW)
Kriging and inverse distance weighting(IDW) are two frequently used methods to construct contours and surfaces to determine spatial variations and anomalies. However, as Kriging is based on a moving weighted average calculated from variograms constructed from the assessed data, use of the Kriging interpolation method will invariably smoothen the data [30],which therefore cannot effectively reproduce any outlying data during the interpolation. A common drawback of moving average interpolation techniques is the nonconsideration of the local properties of the data. In contrast, the MIDW method incorporates a local singularity into the basic model of moving average interpolation, considering spatial correlations such as Kriging [31]. Compared to the traditional interpolation methods, the MIDW method has two significant advantages: (1) It improves the accuracy of interpolation results, and (2) it retains the local structure of interpolation surface. The MIDW method has been proven as an effective method in both exploration and environmental geochemistry [28,31,32].
3.2. Local Singularity Spatial Overlay Analysis (α-value)
The local singularity analysis is another important progress for fractal/multifractal modeling of geochemical data [33]. It is defined as the characterization of the anomalous behaviors of singular physical processes that often result in anomalous amounts of energy release or material accumulation within a narrow spatial–temporal interval [14]. The singularity can be estimated from observed element concentration within small neighborhoods based on the following equation:
where X represents element concentrations, c is a constant value, α is the singularity, E is a normalized distance measure, such as block cell edge, and E is the Euclidian dimension [17]. The window-based method can be used to estimate the singularity index a [14] based on either raw point geochemical data or raster maps using the following steps: (1) defining a set of sliding squares (or other shapes) windows A(r) with variable window sizes, rmin =<r1<r2<…<rn = rmax, and calculating the average concentration C[A(ri)] for each window size for a given location on the map, where C[A(ri)] is equal to the sum of all the cell concentrations divided by the total number of cells within the window;(2) to plot the pair data set of C[A(ri)] (i = 1,...,n) and ri in a log–log graph, the following linear relationship can be obtained
The value of α-2 can be estimated from the slope of the fitted straight line; and in step (3) repeating the similar procedure to all other locations on the geochemical map. For a geochemical map, most of the areas are linked with a singularity value a close to 2, representing a normal distribution, whereas the areas with α<2 or α>2 represent enrichment and depletion of element concentrations, respectively [14].
The method of spatial overlay local singularity analysis proposed in this paper is as follows: First step, to determine the effective combination of geochemical elements, and to do the local singularity analysis of geochemical combined elements, and make a grid diagram; The second step, using the local singularity raster of the appropriate selected elements , we use the formula (3) to carry out the Overlay analysis.
where i denotes proportionality element(such as Au, Ag and so on), n denotes types of geochemical combination elements, [αi] denotes the local singular raster datasets of the i element, [O] denotes geochemical composition element local singular value space overlay raster dataset, whose significance represents the anomaly map of the deposit type.
According to geological basis and geochemical prospecting mark, a geochemical combined element model is established. According to the model of geochemical combined element of porphyry copper mine, the geological significance of local singularity map is given.
3.3. Concentration–Area Model(C-A)
The C–A model, originally developed by [34], represents the first important step in fractal/multifractal modeling of geochemical data and has been “a fundamental technique for modeling of geochemical anomalies” [35]. The C–A fractal model gives
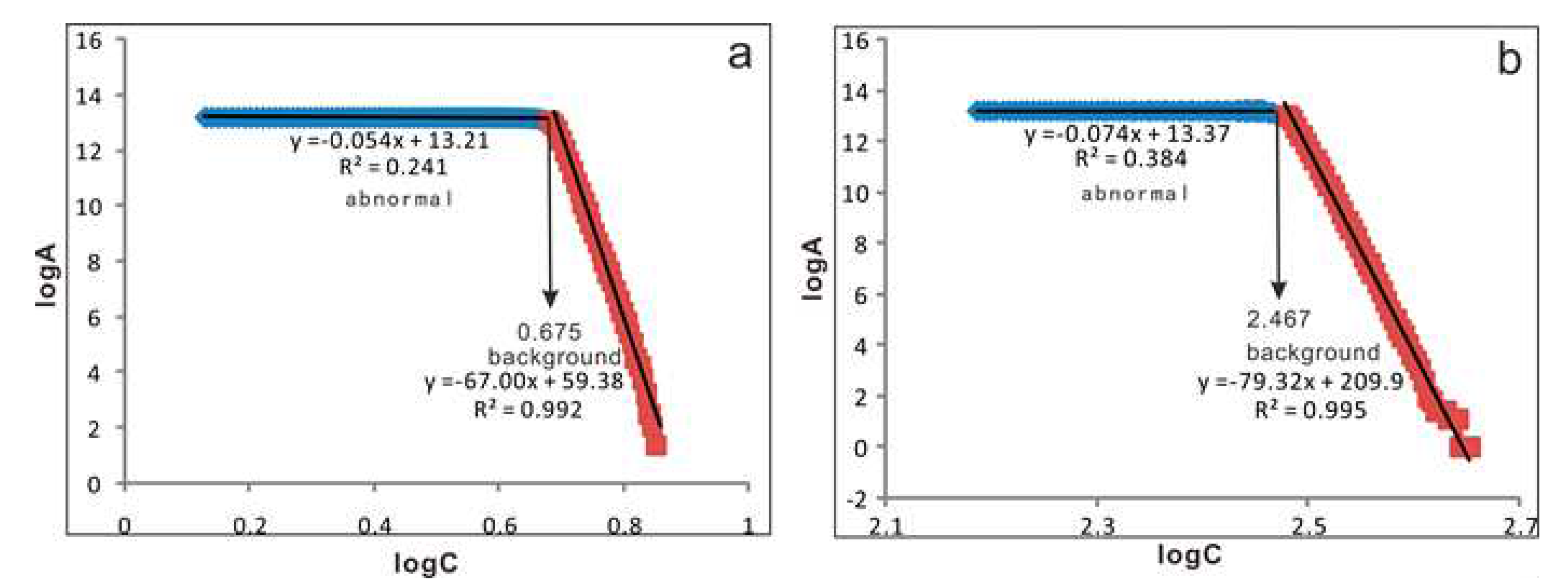
where A( ) represents the area with concentrations greater than or equal to the contour value ρ , v is the threshold, a1 and a2 are fractal dimensions, which are greater than zero. These two fractal parameters can be estimated from the slopes of the best-fitting straight lines in the log–log plot of A( ) versus . ∝ denotes proportionality (is the mathematical symbol for “proportional to”). The C–A model can be used for raw point geochemical data, contour maps or raster maps of elements. Two approaches can be used to calculate the enclosed area. One is based on the contour map created by interpolation procedures, and the other is based on superimposing a grid with cells on the study area and calculating the area by means of a box counting method. Distinct patterns, each corresponding to a set of similarly shaped contours, can be separated by different straight segments fitted to the values of the contours and enclosed areas on the log–log plot. The slopes of these straight lines can be taken as an estimation of the exponents of the power-law relation in Eq. (4). The optimum threshold for separating geochemical anomalies from background is the concentration value common to both linear relationships on the log–log plot [20] [33]. Based on the deposit type diagram, the optimal threshold is determined quantitatively by C-A method.
4. Results and Discussion
4.1. The Question of ilr-RPCA-Back clr
The extraction of geochemical combined elements has attracted much attention in geochemical prospecting, and there are many related methods. At present, the methods of combination element identification are mainly PCA, RPCA, FA, RFA and so on. These methods require the use of logarithmic transformations or logarithmic ratio transformations (alr, clr, ilr, and so on) to eliminate or attenuate the effect of component data closure as much as possible, here on the widely used ilr-RPCA-back clr method is discussed.
Question 1: The influence of elemental interchange on the composition of geochemical elements?
The ilr transform method itself belongs to the asymmetric transformation, and the correspondence between the variables before and after the transformation is disrupted. In essence, because the order changes, the elements corresponding to the xi+1 in the ilr formula change, so for the data of stream sediment, when the element positions are transformed, different element combinations can be obtained by the same method. Based on the experiments of the six elements related to the original data of porphyry copper deposit, the influence of the order change of different elements on ilr transformation is discussed. As shown in the figure, the Ag, Mo and W elements in Figure 2a represent the first principal component and are closely related and have good correlation, and the Ag, Mo and W elements in Figure 2b are poor representation and bad correlation, and the Ag-Mo-W and Au-Cu elements in Figure 2c represent respectively the first principal component negative load and position load, and the Ag, Mo and W elements in Figure 2d represent the first principal component and Ag, Mo have good correlation. It can be concluded that the application of this method to the determination of geochemical elements should be further studied.
Question 2: Score and load transform to clr space, whether the element correspondence has changed?
Figure 2.
biplots of different elements in sequence.
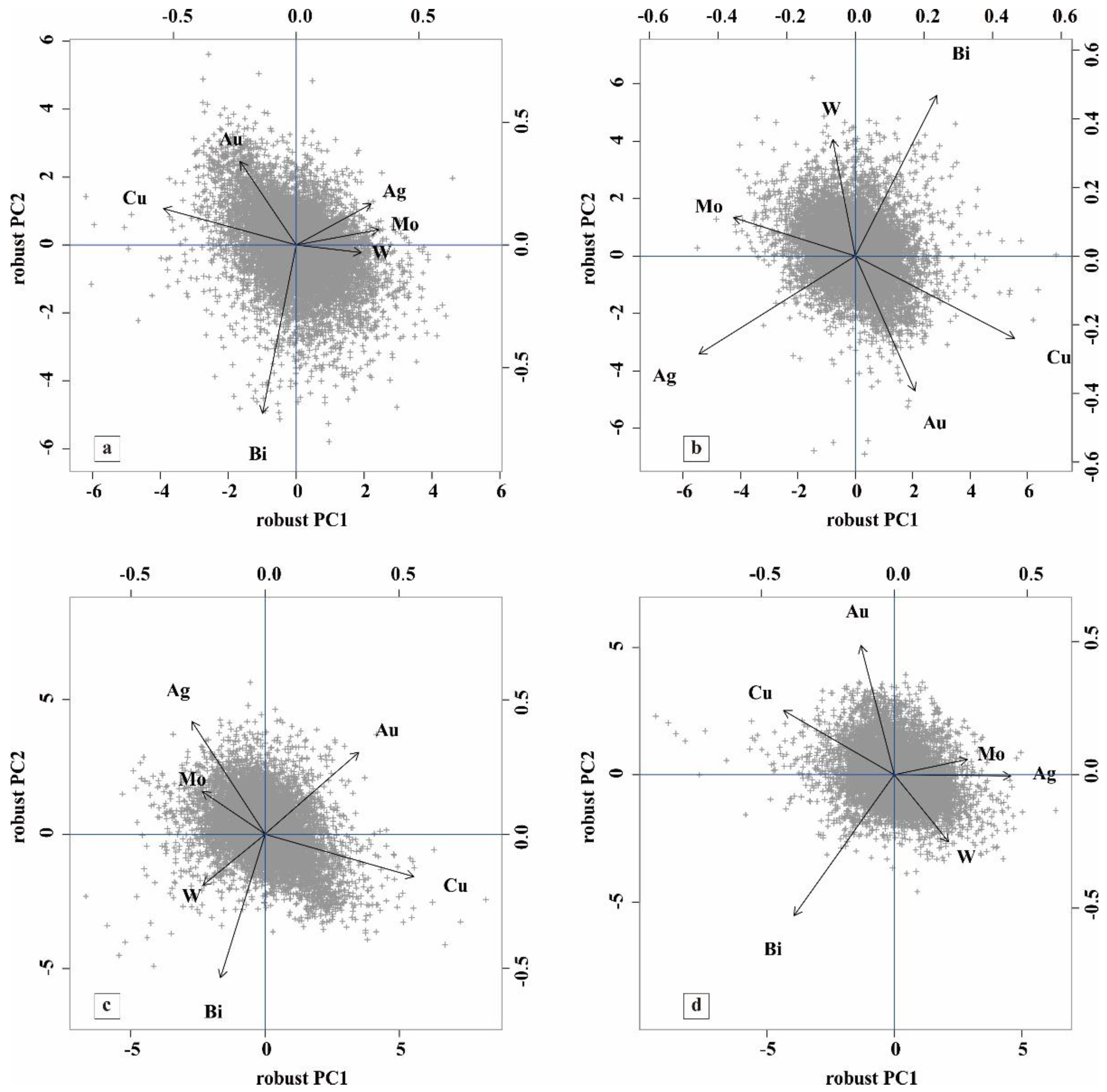
Based on the above problems, this paper analyzes the reason from the basic formula. Although the score and load can be projected into the clr space after the transformation between clr and ilr, the following problem can be seen according to the calculation steps of ilr-RPCA-back clr:
Step1: The original data matrix A(R × D), after the ILR transformation, finds that the last element has not been given the value of the ILR transform, so that the matrix B (R × (D-1)) of an element is reduced.
Step2: The RPCA transformation of data matrix B (R × (D-1)) after ilr can only obtain D-1 principal components, at this time the elements represented are only the first D-1 elements, the score is matrix C (R × (D-1)), and the load is matrix D ((D-1) × (D-1)).
Step3: U transformation of matrix C and D transform to CLR space, ·U score matrix (R×(D-1))·((D-1)×D)to get a new score matrix E (R·D), namely UT·matrix(D×(D-1))·((D-1)×(D-1)) get the new matrix F(D×(D-1)), and set up a corresponding contact element.
We can see that the last element does not participate in the principal component analysis, and finally the result of transforming the load with the transformation formula does not actually have the information of the corresponding element. And the corresponding elements of the load after the transformation is not the original relationship between the elements, but a comprehensive relationship. Moreover, the relationship between clr and ilr is ·U instead of UT·, so the correspondence between the elements in the new load matrix needs to be treated rationally. Since ilr is not a matrix, clr= ilr·U can not be converted to “clr = UT·ilr”. So the final clr space inverse transformation, the only problem is the corresponding elements of the relationship.
This paper argues that the CLR, ILR and RPCA does not have any problems, but the combination of the three should be considered carefully for the identification of geochemical combined elements and types of deposits. For this issue, this paper does not propose a good solution, but would like to take this opportunity to throw out the question and hope that the mathematical geologists will study deeply and solve this problem.
4.2. Selection of Element Association Associated with Porphyry Copper Mineralization
Since stream sediment data belong to compositional data, it is not suitable to do relevant combinatorial analysis in the data without elimination of the closure effect.
Based on the original geochemical data, this paper is under the guidance of the study of geological laws, the establishment of geochemical markers and the exploration of geochemical models (supergene). According to the porphyry deposits in Gangdese metallogenic belt in part has been found for the geochemical elements combined statistical, that elements of porphyry copper deposit in combination with Cu, Mo, Au, Ag, W, Bi, which is convenient to distinguish with other types of ore deposits.
Table 2.
Composite element statistics table.
| Deposits and Metallogenic Belts | Geochemical Anomaly Element Combination | Sampling Mode | References |
|---|---|---|---|
| Xiong Cun | ` | regional geochemical anomalies | [36] |
| Xiong Cun | Cu, Au, Ag, Pb, Zn | soil anomaly | [37] |
| Ji Ru | Cu, Mo, W, Bi | regional geochemical anomalies | [36] |
| Zhu Nuo | Au, Cu, Mo, W | regional geochemical anomalies | [36] |
| Zhu Nuo | Cu, Mo, W, Au, Pb, Zn, Ag | stream sediment | [38] |
| Chong Jiang | Cu, Mo, Au, Ag, Pb, Zn, Hg, Sb | stream sediment | [38] |
| Chong Jiang | Cu, Mo, W, Bi, Pb, Ag | regional geochemical anomalies | [38] |
| Qu Long | Cu, Mo, W, Bi, Pb, Ag | stream sediment | [39] |
| Qu Long | Cu, Mo, W, Bi, Sn | regional geochemical anomalies | [5] |
| Jia Ma | Cu, Bi, Au, Ag, Pb, Zn | stream sediment | [40] |
| Jia Ma | Cu, Mo, Au, Ag, Bi, Sn | soil geochemistry | [40] |
| Gangdese polymetallic metallogenic belt | Cu, Mo, W, Au, Ag , Bi | geochemical anomaly | [41] |
| Gangdese polymetallic metallogenic belt | Cu-Mo, Au-Ag, Cu-Mo-Au, Cu-Au-Ag | combination geochemical anomaly | [41] |
| Gangdese porphyry copper deposit | Cu, Mo, Pb, Zn, Ag | [42] | |
| Gangdese copper polymetallic metallogenic belt | Cu, Au, Ag, W, Mo, Bi | geochemical anomaly | [43] |
| Gangdese copper polymetallic metallogenic belt | Cu-Mo, Cu, Cu-Mo-Au, Cu-Au | geochemical anomaly | [43] |
| statistical results | Cu(21), Mo(16), Au(14), Ag(12), W(8), Bi(8), Pb(7), Zn(5), Hg(1), Sb(1), Sn(1) | final choice | Cu(21), Mo(16), Au(14), Ag(12), W(8), Bi(8) |
4.3. Spatial Overlay Analysis of Geochemical Singularity Index α-Value of Porphyry Copper Deposit
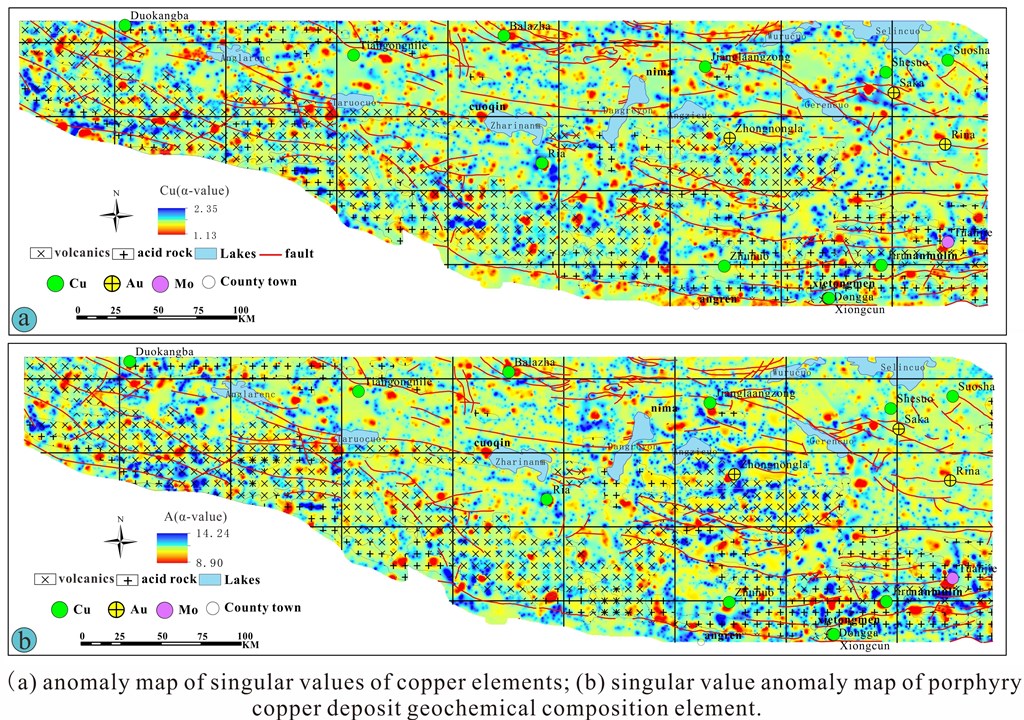
Recent advances in the identification of weak geochemical anomalies refer to the singularity mapping technique proposed by Cheng [14], and it has been demonstrated as a powerful multifractal tool to identify the weak geochemical anomalies in complex geological settings or in overburden covered areas [18,20,21,44]. The window-based method was used to calculate the local singularity index based on GeoDAS. Considering that the formation of porphyry copper deposits in the western Gangdese metallogenic belt is closely related to the specific geochemical composition elements, only the local singularity analysis of single elements can not be used to meet the objective of recognizing the weak anomalies of porphyry copper deposits. Therefore, according to the geochemical composition elements of porphyry copper deposits, singularity analysis of each element has been carried out, and the local singular maps of porphyry copper deposits have been obtained by spatial overlay analysis. The spatial distribution map of α-A (Figure 3b) highlights the weak anomalies relative to α-Cu raster contour maps (Figure 3a). It is also shown that the spatial overlay singular values (α-A) are apparently enriched in the acid intrusive rocks and volcanic rocksand spread in the NW-trending according to the regional faults. The anomaly threshold values of α-A, α-Cu were obtained by method of C-A model. Furthermore, the log–log plots of the concentration (α) versus the number of samples with concentration values greater than or equal to α are constructed to examine whether or not the distribution of A and Cu follows a fractal. It can be observed that two straight lines can be fitted (Figure 4), suggesting they may satisfy a multifractal distribution.
Figure 3.
(a) anomaly map of singular values of copper elements; (b) singular value anomaly map of porphyry copper deposit geochemical composition element.
Figure 3.
(a) anomaly map of singular values of copper elements; (b) singular value anomaly map of porphyry copper deposit geochemical composition element.
Figure 4.
(a) log-log plot of C-A fractal model of Copper element; (b) log-log plot of C-A fractal model of porphyry copper mineral combination elements.
Figure 4.
(a) log-log plot of C-A fractal model of Copper element; (b) log-log plot of C-A fractal model of porphyry copper mineral combination elements.
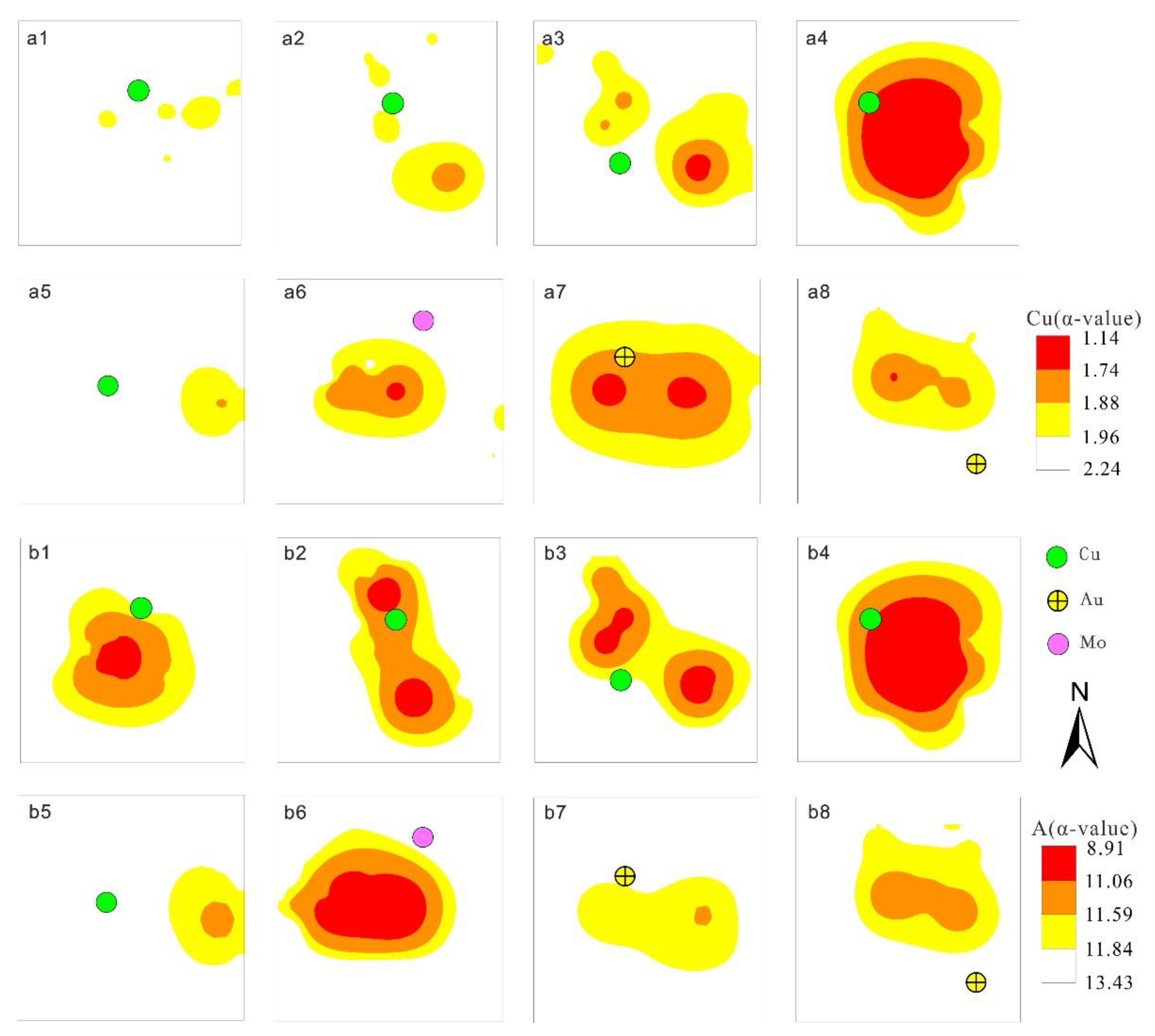
In order to facilitate the analysis of the advantages and disadvantages of the two methods, this paper based on the known deposit and abnormal range of the degree of fit, a typical deposit analysis map (Figure 5) is made. It can be shown from the analysis diagram that the recognition degree of porphyry copper is obviously improved compared with single element method(Figure 5a1-5a3 and Figure 5 b1-5b3). In the case of skarn-type copper deposits, there is a large area anomaly in the Ri a deposit. The reason is that the copper ore bodies in the Ri a deposit are produced in the porphyry bodies. Therefore, this method is difficult to identify or distinguish such deposits and porphyry copper mine. However, skarn-type deposits unrelated to porphyry, the method has a certain degree of distinction, especially the Shesuo deposit(Figure 5 b5). This method distinguishes porphyry molybdenum ore from single element method, but both of them have abnormalities, which indicates that these two methods have very limited ability to distinguish porphyry copper and porphyry molybdenum. This method is worse than the single element method in distinguishing the porphyry type molybdenum ore, but both of them have abnormalities, which indicates that these two methods have extremely limited ability to distinguish porphyry copper from porphyry molybdenum. In the case of porphyry gold, this method has the advantage of reducing the abnormal level compared with the single element method. Such as Sa ka(Figure 5 a5-b5) and Ri na(Figure 5 a6-b6) deposits, the use of single element method is divided into three abnormal zones, but the use of this method only two levels of zoning. This advantage can be reduced in the early stage of abnormal evaluation of porphyry copper, reducing the input of such abnormal identification.
Figure 5.
This is a figure. profile chart. a1-a8 Singular anomalies of copper elements of Zhu nuo, Jianglaang-zong, Balazha,Ri a, She suo, Tuan jie, Sa ka, Ri na;b1-b8 Singular anomalies of associa-tion elements of Zhu nuo, Jianglaangzong ,Balazha ,Ri a ,She suo, Tuan jie,Sa ka,Ri na; porphyry Cu deposit: Zhu nuo, Jianglaangzong,Balazha;skarn Cu deposit: Ri a,She suo;porphyry Mo deposit: Tuan jie;porphyry Au deposit: Sa ka,Ri na.
Figure 5.
This is a figure. profile chart. a1-a8 Singular anomalies of copper elements of Zhu nuo, Jianglaang-zong, Balazha,Ri a, She suo, Tuan jie, Sa ka, Ri na;b1-b8 Singular anomalies of associa-tion elements of Zhu nuo, Jianglaangzong ,Balazha ,Ri a ,She suo, Tuan jie,Sa ka,Ri na; porphyry Cu deposit: Zhu nuo, Jianglaangzong,Balazha;skarn Cu deposit: Ri a,She suo;porphyry Mo deposit: Tuan jie;porphyry Au deposit: Sa ka,Ri na.
5. Conclusions
The results of this study led to the following conclusions.
1. The ilr-RPCA-back CLR model has two problems (1) after the change of element position, the relationship between geochemical elements has been seriously affected. (2) score and load transformation to clr space, the corresponding relationship between the elements were disrupted. It is therefore important to use this model for the geochemical combination of element identification carefully.
2. The method of singular value overlay analysis proposed in this paper has obvious advantages in the identification of porphyry copper deposit, but it is difficult to distinguish skarn-type copper related to porphyry and porphyry molybdenum. And the porphyry skarn type copper deposits are not well differentiated, at the same time although it is difficult to distinguish porphyry gold deposits, the anomaly grade can be reduced.
3. Based on the geological basis, this paper studies the geochemical laws, the geochemical markers and the geochemical model (geochemistry), and gives the geochemical data to identify and evaluate the anomalies with objective geological connotations, that is also about to identify and evaluate anomalies. Which can better overcome the traditional technical methods and single element analysis method due to elemental chemical properties, redox environment, weathering erosion and many other factors on the impact of abnormal screenin. These advantages of these methods can greatly reduce the multi solution and subjectivity, so that the anomaly regularity has the abnormal value of prospecting value can clearly highlighted.
Author Contributions
Writing–original draft, S.L.; writing–review & editing, X.J., S.B., Z.Z.; visualization, S.L., L.; investigation, S.B.; methodology, X.J., S.L.;
Funding
This research was funded by Metallogenic Regularity and Prediction of Nongla-Dongzhongla Mining Area in Tibet Xinhu Mining Co., Ltd. (Project No.: 0121-ZB20575).
Acknowledgments
In this section, you can acknowledge any support given which is not covered by the author contribution or funding sections. This may include administrative and technical support, or donations in kind (e.g., materials used for experiments).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rui, Z., Huang, C., Qi, G., Xu, J., Zhang, H. Porphyry copper (molybdenum) deposits of China. Bejing: Geological Phblishing House, 1984, 350.
- Wang, Z., Qin, K., Zhang, S. Geology and exploration of large copper deposits [Z]. Beijing: Metallurgical Industry Press. 1994.
- Qin, K., Sun, S., Li, J., Fang, T., Wang, S., Liu, W. Paleozoic epithermal Au and porphyry Cu deposits in North Xinjiang, China: epochs, features, tectonic linkage and exploration significance. Resource Geology, 2002, 52(4): 291-300. [CrossRef]
- Cooke, D.R. Giant Porphyry Deposits: Characteristics, Distribution, and Tectonic Controls. Economic Geology, 2005, 100(5): 801-18.
- Zheng Y., Xue Y., Cheng L., Fan Z., Gao S. Finding, Characteristics and Significances of Qulong Superlarge Porphyry Copper (Molybdenum)Deposit. Earth Sciences: Journal of China University of Geosciences, 2004, 29(1). (In Chinese).
- Cheng Q. Singularity Modeling of Geo-Anomalies and Recognition of Anomalies Caused by Buried Sources. Earth Science-Journal of University of Geosciences, 2011, 36(2). (In Chinese).
- Xie, Y. The study of the complexity of tectonic©\fluid©\mineralization system and its dynamic mechanism: A case study of Shuikoushan Pb©\Zn©\Au polymetallic ore field in Hunan province, China [Z]. Guangzhou: Guangzhou Institute of Geochemistry Chinese Academy of Science. 2004.
- Filzmoser, P., Hron, K., Reimann, C., Garrett, R. Robust factor analysis for compositional data. Computers & Geosciences, 2009, 35(9): 1854-61. [CrossRef]
- Grunsky, E.C., Mueller, U.A., Corrigan, D. A study of the lake sediment geochemistry of the Melville Peninsula using multivariate methods: Applications for predictive geological mapping. Journal of Geochemical Exploration, 2014, 141: 15-41. [CrossRef]
- Sadeghi, M., Billay, A., Carranza, E. Analysis and mapping of soil geochemical anomalies: Implications for bedrock mapping and gold exploration in Giyani area, South Africa. Journal of Geochemical Exploration, 2015, 154: 180-93. [CrossRef]
- Wang, H., Zuo, R. A comparative study of trend surface analysis and spectrum–area multifractal model to identify geochemical anomalies. Journal of Geochemical Exploration, 2015, 155: 84-90. [CrossRef]
- Zuo, R.G., Wang, J. Fractal/multifractal modeling of geochemical data: A review. Journal of Geochemical Exploration, 2016, 164: 33-41. [CrossRef]
- Chen, X., Xu, R.K., Zheng, Y.Y., Jiang, X.J., Du, W.Y. Identifying potential Au-Pb-Ag mineralization in SE Shuangkoushan, North Qaidam, Western China: Combined log-ratio approach and singularity mapping. Journal of Geochemical Exploration, 2018, 189: 109-21.
- Cheng, Q.M. Mapping singularities with stream sediment geochemical data for prediction of undiscovered mineral deposits in Gejiu, Yunnan Province, China - ScienceDirect. Ore Geology Reviews, 2007, 32(1–2): 314-24. [CrossRef]
- Bai, J., Porwal, A., Hart, C., Ford, A., Yu, L. Mapping geochemical singularity using multifractal analysis: application to anomaly definition on stream sediments data from Funin Sheet, Yunnan, China. Journal of Geochemical Exploration, 2010, 104(1-2): 1-11. [CrossRef]
- Sun, X., Gong, Q., Wang, Q., Yang, L., Wang, C., Wang, Z. Application of local singularity model to delineate geochemical anomalies in Xiong'ershan gold and molybdenum ore district, Western Henan province, China. Journal of Geochemical Exploration, 2010, 107(1): 21-9. [CrossRef]
- Agterberg, F.P. Multifractals and geostatistics. Journal of Geochemical Exploration, 2012, 122(none): 113-22.
- Cheng, Q.M. Singularity theory and methods for mapping geochemical anomalies caused by buried sources and for predicting undiscovered mineral deposits in covered areas. Journal of Geochemical Exploration, 2012, 122(none): 55-70. [CrossRef]
- Liu, Y., Cheng, Q., Xia, Q., Wang, X. Application of singularity analysis for mineral potential identification using geochemical data¡ªA case study: Nanling W¨CSn¨CMo polymetallic metallogenic belt, South China. Journal of Geochemical Exploration, 2013, 134: 61-72.
- Zuo, R., Wang, J., Chen, G., Yang, M. Identification of weak anomalies: A multifractal perspective. Journal of Geochemical Exploration, 2015, 148: 12-24. [CrossRef]
- Zuo, R.G., Carranza, E.J.M., Wang, J. Spatial analysis and visualization of exploration geochemical data. Earth-Science Reviews, 2016, 158: 9-18. [CrossRef]
- Gao S.B. Copper-Iron Polymetal Metallogenesis and Exploration Direction in the Western of Gangdese Metallogenic Belt, Tibet, China University of Geosciences, 2015. (In Chinese).
- Pan G., Mo X., Hou Z., Zhu D., Wang L., Li G., Zhao Z., Geng Q., Liao Z. Spatial-temporal framework of the Gangdese Orogenic Belt and its evolution. 2006, (03): 521-33. (In Chinese).
- Hou, Z., Duan, L., Yang, Z., pei, Y., Lu, Y., McCuaig, C.T., Zheng, Y., Zhu, D., Zhao, Z., Yang, Z., Wang, B. Lithospheric Architecture of the Lhasa Terrane and It's Control on Deposits in the Himalayan-Tibetan Orogen [Z]//Andre-Mayer A.S., Cathelineau M., Muchez P., Pirard E., Sindern S. Mineral Resources in a Sustainable World, Vols 1-5. ASGA-ASSOC SCIENTIFIQUE GEOLOGIE \& APPLICATIONS. 2015: 113-6.
- Wu, S., Zheng, Y., Wang, D., Chang, H., Tan, M. Variation of copper isotopes in chalcopyrite from Dabu porphyry Cu-Mo deposit in Tibet and implications for mineral exploration. Ore Geology Reviews, 2017, 90: 14-24. [CrossRef]
- Zheng, S., Wu, S., Zheng, Y., Chen, L., Wei, C., Huang, P., Jing, X., Yu, Z., He, C., Ren, H. Identifying potential porphyry copper mineralization at the Zhu’nuo ore-cluster district in western Gangdese, southern Tibet: Insights from shortwave infrared (SWIR) spectrometry and geochemical anomalies. Ore Geology Reviews, 2022, 151.
- Kaiser, H.F. The varimax criterion for analytic rotation in factor analysis. Educational and Psychological Measurement, 1958, 23: 770-3. doi:10.1007/bf02289233.
- Zuo, R.G. Decomposing of mixed pattern of arsenic using fractal model in Gangdese belt, Tibet, China. Applied Geochemistry, 2011, 26(supp-S): S271-S3. [CrossRef]
- Wang, X., Xie, X., Zhang, B., Hou, Q. Geochemical probe into China's continental crust. 2011.
- Cheng Q. Multifractal and geostatistic methods forcharacterizing local structure and singularityproperties of exploration geochemical anomalies. Earth Science (Journal of China University of Geosciences), 2001, 26(2): 161-6. (In Chinese).
- Cheng, Q.M. Spatial and scaling modelling for geochemical anomaly separation. Journal of Geochemical Exploration, 1999, 65(3): 175-94. [CrossRef]
- Zuo, R.G. Identifying geochemical anomalies associated with Cu and Pb-Zn skarn mineralization using principal component analysis and spectrum-area fractal modeling in the Gangdese Belt, Tibet (China). Journal of Geochemical Exploration, 2011, 111(1-2): 13-22. [CrossRef]
- Zuo, R.G., Xia, Q.L., Wang, H.C. Compositional data analysis in the study of integrated geochemical anomalies associated with mineralization. Applied Geochemistry, 2013, 28(Complete): 202-11. [CrossRef]
- Cheng, Q.M., Agterberg, F.P., Ballantyne, S.B. The Separation of Geochemical Anomalies from Background by Fractal Methods. Journal of Geochemical Exploration, 1994, 51(2): 109-30. [CrossRef]
- Carranza, E.J.M. Geochemical anomaly and mineral prospectivity mapping in GIS. Elsevier, 2008;
- Gao, Y., Zhang, Z.J., Xiong, Y.H., Zuo, R.G. Mapping mineral prospectivity for Cu polymetallic mineralization in southwest Fujian Province, China. Ore Geology Reviews, 2016, 75: 16-28. [CrossRef]
- Lang, X., Tang, J., Li, Z., Dong, S., Ding, F., Wang, Z., Zhang, L., Huang, Y. Geochemical evaluation of exploration prospect in the Xiongcun copper-gold district and peripheral areas, Xietongmen County, Tibet. Geology and Exploration, 2012, 48(1): 12-23.
- Sun, X., Zheng, Y., Li, M., Ouyang, H., Liu, Q., Jing, X., Sun, G., Song, Q. Genesis of Luobuzhen Pb–Zn veins: Implications for porphyry Cu systems and exploration targeting at Luobuzhen-Dongshibu in western Gangdese belt, southern Tibet. Ore Geology Reviews, 2017, 82: 252-67. [CrossRef]
- Yang, S.P., Zhang, H., Liu, Y.H., Kong, M., Liu, H.Z., Dong, G.F., Luo, Y.P. Geochemical Evaluation of Potential Ore in the Qulong Copper Deposit and Its Peripheral Region in Tibet. Acta Geologica Sinica, 2006, 10(1558-1565).
- Zheng W.B. The Study on Metallogenic Model and Prospecting Pattern for Jiama Polymetallic Copper Deposit, Tibet, Chengdu University of Technology, 2012. (In Chinese).
- She, H., Li, G., Dong, Y., Pan, G., Li, J., Zhang, D., Feng, C. Regional metallogenic prognosis and mineral reserves estimation for porphyry copper deposits in Gangdese polymetallic ore belt, Tibet. Mineral deposits, 2009, 28(6): 803-14.
- Zuo, R. Synthetic information prediction of porphyry copper in Tibet. Cent South Univ Technol, 2007, 38: 368-73.
- Guang-ming, L., Hong-quan, S., Li, Z., Bo, L., Yin-jun, D. Based on mineral resource assessment system (MRAS) for the metallogenic prognosis in Gangdese metallogenic belt, Tibet. Geology and Exploration, 2009, 45(6): 645-52.
- Sun, X., Zheng, Y., Wang, C., Zhao, Z., Geng, X. Identifying geochemical anomalies associated with Sb–Au–Pb–Zn–Ag mineralization in North Himalaya, southern Tibet. Ore Geology Reviews, 2016, 73: 1-12.
Table 1.
The detection limits of 39 elements [29].
Table 1.
The detection limits of 39 elements [29].
| No. | elements | Detection limit | No. | elements | Detection limit | No. | elements | Detection limit |
|---|---|---|---|---|---|---|---|---|
| 1 | Ag | 0.02 | 14 | La | 30 | 27 | U | 0.5 |
| 2 | As | 1 | 15 | Li | 5 | 28 | V | 20 |
| 3 | Au | 0.0003 | 16 | Mn | 30 | 29 | W | 0.5 |
| 4 | B | 5 | 17 | Mo | 0.4 | 30 | Y | 5 |
| 5 | Ba | 50 | 18 | Nb | 5 | 31 | Zn | 10 |
| 6 | Be | 0.5 | 19 | Ni | 2 | 32 | Zr | 10 |
| 7 | Bi | 0.1 | 20 | P | 100 | 33 | SiO2 | 0.10% |
| 8 | Cd | 0.05 | 21 | Pb | 2 | 34 | Al2O3 | 0.10% |
| 9 | Co | 1 | 22 | Sb | 0.1 | 35 | TFe2O3 | 0.05% |
| 10 | Cr | 15 | 23 | Sn | 1 | 36 | MgO | 0.05% |
| 11 | Cu | 1 | 24 | Sr | 5 | 37 | CaO | 0.05% |
| 12 | F | 100 | 25 | Th | 4 | 38 | Na2O | 0.05% |
| 13 | Hg | 0.0005 | 26 | Ti | 100 | 39 | K2O | 0.05% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated