Prerpints.org logo
Preprint
Article

Modeling Investigation of Groove Effect on the Multipactor of Dielectric-loaded Coaxial Low-pass Filters

Altmetrics

Downloads

87

Views

38

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

19 May 2023

Posted:

22 May 2023

You are already at the latest version

Alerts
Abstract
Multipactor is a common discharge phenomenon occurred in space microwave systems. The surface microstructure has been verified to be effective to mitigate multipactor. In this work, we design a square coaxial low-pass filter (SCLPF) with dielectric sheets loaded to check the multipactor dependence on the structure parameters of the loaded dielectric sheets, and further model groove structures on the sensitive area surface to lower the risk of multipactor. Simulation results indicate that the SCLPF loaded with alumina and PTFE exhibits good operational characteristics, and the multipactor threshold is significantly improved after introducing the surface grooves. Then we investigate the effects of three typical groove parameters, groove depth, groove number, and aspect ratio, on the multipactor threshold of the SCLPF device. The results show that the multipactor threshold raise at first as the groove number and groove depth increase, and then the threshold reaches a saturation status. For a deeper analysis of multipactor, we discuss how the grooves shelter the secondary electrons, and further mitigate the electron avalanche. Furthermore, the mechanisms of threshold saturation under the effect of groove parameters are analyzed in detail, and a contour map for the multipactor threshold of PTFE-loaded SCLPFs is given, which makes significant sense for predicting the multipactor threshold of the devices with its sensitive surface being grooved. The regularity of modulating the multipactor threshold by the groove structures obtained in this study is of engineering significance for suppressing multipactor in microwave devices in practical applications.
Keywords: 
Subject: Physical Sciences  -   Applied Physics

1. Introduction

Microwave devices operating in the space environment are constantly influenced by cosmic radiation and particle irradiation. The phenomenon of secondary electron emission can be induced when space particles or rays irradiate the material surface. The excited secondary electrons may undergo resonance avalanche multiplication under the action of high-power radio frequency (RF) fields, further inducing the secondary electron multiplication discharge effect, that is, multipactor[1]. The large number of electrons generated inside the device in a short duration will severely interfere with the operation of the high-power microwave(HPM) systems, and may even cause discharge breakdown[1,2,3,4]. Nowadays, multipactor becomes one of the severe bottleneck problems that hinder the power increase of microwave components[4]. Hence the ability to suppress multipactor is a key factor in evaluating the reliability of space HPM systems. There are three requirements for the occurrence of multipactor, namely, the secondary electron emission yield (SEY) bigger than 1, the existence of RF fields, and the resonation between secondary electrons and the RF field[1]. Usually, destroying the resonation condition between electrons and the RF field can be considered an effective method to mitigate multipactor[5], besides, lowering the SEY of the multipactor sensitive surface can also decrease the risk of multipactor since secondary electron avalanche is the direct reason for the multipactor discharge[6,7,8,9]. Currently, the common methods for lowering SEY include coating low-SEY films like TiN, TiZrV, and graphene[10,11,12,13,14,15,16], as well as designing surface microstructures to trap the secondary electrons[17,18,19,20].
Alumina and polytetrafluoroethylene (PTFE) have been widely used in high-power microwave systems in space. The multipactor phenomenon for these two dielectric materials has been paid more attention to nowadays since many HPM devices have been developed with dielectric-loaded[21,22,23]. Besides, the dielectric materials possess a relatively higher SEY[24,25,26], so the multipactor may be easier to be triggered. In recent years, the construction of periodic microstructures on the surface of dielectric materials has received widespread attention and discussion[5,27,28]. These surface microstructures are capable of blocking the movement of secondary electrons while not affecting the normal function of the device, allowing fewer electrons to participate in the multiplication process.
The current studies involve the multipactor of microstructured surfaces including grooves[29,30], columnar arrays[31,32,33], and porous structures[17,18,19]. Typically, researchers use feature size parameters to quantify these microstructures for discussion. However, scholars are more concerned with a detailed discussion of the secondary electron emission process under microstructures and choose to apply the SEY to predict the ability of the material to suppress multipactor. The relationship between feature size parameters of the microstructure and multipactor threshold is not adequately studied, and the relevant mechanisms still require further discussion. Traditionally, the multipactor threshold relied on charts obtained through experimental studies. However, with the development of particle simulators, accurate predictions can be quickly and conveniently provided.
In this paper, we focus on the groove structure and design a coaxial low-pass filter with dielectric sheets loaded as a test device for multipactor. The filter has an ideal flat gap and perpendicular RF electric field to the surfaces. By simulating the multipactor threshold of alumina and PTFE with different groove sizes, we further obtain the influence regulation of groove depth, groove number, and aspect ratio on the multipactor threshold, and discuss the deep mechanism of how the groove feature sizes affect the multipactor. The obtained discharge data and their underlying regulations will have significant implications for practical engineering applications.

2. Modeling and Simulation Methods

2.1 Design of the Verification Device

Here we present the design of a square coaxial low-pass filter (SCLPF) that can operate in the L-band. For low-frequency circuits, low-pass or high-pass filters are composed of lumped parameter reactive components (inductors and capacitors). For high-frequency devices, we use microwave structures to simulate lumped parameter elements. This microwave structure can be called a "quasi-lumped element." The specific design process uses the insertion loss method. First, select the appropriate order (i.e., the number of lumped elements) according to the prototype of the equal-ripple low-pass filter to match the requirements of the filtering performance. Next, according to the normalized element values obtained from the Chebyshev polynomial solution, solve the actual values of the elements using the target cutoff frequency, and obtain the lumped circuit topology. Finally, use the appropriate microwave structure to approximately correspond to the lumped element values one by one to complete the design of the microwave SCLPF.
For the SCLPF, the method of approximating the lumped element values of the microwave structure is shown in Figure 1. Note that the value of the equivalent lumped element is related to the transmission line length and impedance. The microwave structure belongs to a distributed parameter circuit, and the length should be controlled to be less than 1/8 of the wavelength to approximate the lumped element better. Select the appropriate impedance and length according to the formula in the figure to form a low-pass filter. In the actual design process, compromises have to be made sometimes, which depends heavily on the engineer's practical engineering experience. Here, we use the optimized function of CST software to achieve the preferable size parameters for each part.
By researching the characteristic impedance of various microwave structures, the square coaxial structure is considered to be more suitable for verifying multipactor. The SCLPF designed in this article is shown in Figure 2. It is a 13th-order filter with an inner conductor being arranged alternately with rectangular blocks of different side lengths. In the central low-impedance area, there is the narrowest distance between the inner and outer conductors. Extra dielectric sheets are placed in this area to create a gap of 1 mm for checking the multipactor property of the device. According to the transmission characteristics of the TEM mode for square coaxial, a microwave electric field perpendicular to the upper and lower planes will be generated in this gap. In other low-impedance areas, the gaps are filled with PTFE to "block" them, ensuring that multipactor can only occur in the narrowest central section.
Alumina and PTFE are chosen as the dielectric sheets for checking the multipactor threshold in this work. The adoption of different materials will cause slight differences in the device transmission performance, therefore, it is necessary to make brief adjustments to optimize the final size parameters. We designed two sizes of SCLPFs equipped with alumina and PTFE sheets respectively. They have consistent performance parameters, with only slight differences in the size of the internal conductor segments. In the central low-impedance region, a pair of dielectric sheets are placed on the top surface of the inner conductor and the bottom surface of the outer conductor, separately. The size of the alumina sheets is 8×5×0.25 mm3, and the size of PTFE is 8×6.5×0.5 mm3. The frequency response in Figure 3 shows that two SCLPFs loaded with different dielectrics can achieve good transmission performance, thereinto, the insertion loss is less than 0.1 dB, and the return loss is generally greater than 20 dB from 1.5 to 5 GHz. The simulation results also indicate that the electric field between the dielectric sheets can reach nearly 6000 V/m. Therefore, the gap will experience multipactor first with the increase of input power since the region possesses the largest electric field and the narrowest gap.

2.2 Multipactor Simulation for the SCLPF with Flat Dielectric Loaded

We use SPARK3D to achieve the simulation of multipactor. SPARK3D is a module in CST that simulates the secondary electron multiplication discharge characteristics of passive devices like waveguides, microstrips, and antennas. The SPARK3D module employs the Monte Carlo method and 3D electron tracking model to solve for the electron number in the device-defined region. Hence, SPARK3D can calculate the maximum operating power of the device without multipactor, which is defined as the multipactor threshold.
The simulation process of multipactor is as follows. Firstly, determine the geometric structure of the device. Next, simulate the electric and magnetic field distribution of the device at one specific frequency, and import the necessary information into SPARK3D. Define the simulation area, and set parameters such as material SEY data, input power, seed electron number, and solution accuracy. When the above settings are completed, the variation of the electron number over time under different powers is obtained by implementing the simulation. It should be noted that SPARK3D uses a bisection search method to solve the breakdown power. In each round of calculation, when the input power causes electrons to multiply in the area and cause a breakdown, the software will reduce the input power to half and restart the simulation. On the contrary, if the input power does not cause a breakdown, the power and the nearest breakdown power are averaged and recalculated until the final result gradually approaches the actual multipactor threshold.
We employ the SEY data of the flat alumina[34] and PTFE[35] sheets into SPARK3D. The SEY peak values of alumina and PTFE are 3.60 and 2.04, respectively. The simulation region was set to the central region and the two adjacent high-impedance regions. 1500 electrons are randomly placed in the region, the simulation results are shown in Figure 4. As we can conclude from Figure 4 that the multipactor threshold values of the SCLPFs with flat alumina loaded and PTFE loaded are 137.69 W and 347.63 W, respectively.

3. Simulation Verification

3.1 The Groove Effect on the Multipactor Threshold

Then we investigate the suppression of multipactor by constructing groove structures on the dielectric sheets. Along the transmission direction of the microwave, the alumina sheets are divided into several cells by every 0.5 mm, a rectangular groove with sizes of 0.25 mm width and 0.2 mm depth is created in each cell, as shown in Figure 5(a). Here, we define the ratio of the groove projected area to the total cell area as the groove ratio, which can be expressed as d/w in Figure 5(c). According to this definition, the groove ratio in Figure 5(a) is 50%. Similarly, grooves are also created on PTFE sheets. Via the CST simulation, we discover that the groove structure is able to increase the electric field since the grooves provide several right-angle structures, and further cause local enhancement of the electric field due to the complex non-uniform structure. To make the process of multipactor less affected by the variation of the electric field, here, we shorten the groove length to 7.6 mm and left a 0.2 mm margin on two sides. Figure 5(b) and (d) show the shape of the grooves after modification, and we see the groove ratio becomes 47.5%.
Figure 6 shows the simulation results of the electron number evolution when the grooved dielectric (alumina and PTFE) sheets are loaded in the SCLPFs. By analyzing the results, we get the multipactor threshold of 240.23 W for the SCLPF with grooved alumina loaded, and 727 W for the SCLPF with grooved PTFE loaded. Compared to the results in Figure 5, we conclude that the grooved sheets are able to improve the multipactor threshold remarkably in spite of the material type.

3.2 The Effect of Groove Number on the Multipactor Threshold

In this section, we employ the SCLPFs loaded with the alumina sheets to check how the groove number affects the multipactor threshold. As shown in Figure 7, we set various groove numbers, n, on the loaded alumina sheets. The length of the grooves is 7.6 mm, the depth is 0.2 mm, and the groove ratio in each cell is 47.5%.
The multipactor simulation results are shown in Figure 8. From Figure 8, we know that the multipactor threshold values of all the SCLPFs with grooved alumina sheets loaded show an obvious improvement compared to the SCLPFs with flat alumina sheets loaded. Moreover, the multipactor threshold increases as the groove number increases. Merely, when the groove number is greater than 10, the raised magnitude of the multipactor threshold declines as the groove number increases, showing a quasi-saturation status. The threshold stays at around 250 W when the groove number reaches 20, in this case, further increasing the groove number no longer improves the multipactor threshold.

3.3 The Effect of Groove Depth on the Multipactor Threshold

In this section, we employ the SCLPFs loaded with the PTFE sheets to check how the groove depth affects the multipactor threshold. As mentioned above, we construct groove structures on the surface of PTFE sheets, the groove number is 13, the groove length is 7.6 mm, and the groove width is 0.25 mm. Under the circumstances, we simulate the multipactor threshold of the PTFE-loaded SCLPFs as the groove depth increases from 0.02 to 0.48 mm, the simulation results are shown in Figure 9. From Figure 9, we see that the multipactor threshold increases linearly as the groove depth increases linearly when the groove depth is smaller than 0.45 mm. However, the threshold shows a decline as the groove depth extends beyond 0.45 mm. In this case, the maximum of the multipactor threshold is about 1150 W when the groove depth is 0.45 mm.
The simulation results of this section and the previous section indicate that the multipactor threshold will be remarkably improved as the groove number or depth increases. Moreover, the multipactor threshold may reach a saturation status when the groove number or depth increases to a certain value. The phenomenon can be explained as follows. For the SCLPFs loaded with flat dielectric sheets, there are plenty of secondary electrons emitted from the surface after one incident event during the process of multipactor. Whereas the emission of secondary electrons is changed after introducing the groove structure on the dielectric surface, the groove plays the role of shelter to increase the collision probability of the secondary electrons, and further prevent the emission of secondary electrons, which weakens the risk of multipactor from the root.
To be specific, as shown in Figure 10, we discuss the circumstances of electrons impactor the central position of the bottom of a 2D groove. In Figure 10, e#1, e#2 and e#3 are three secondary electrons produced by the incident electron, and they are probable to be captured by the sidewall and have less chance to participate in the process of multipactor discharge. In Figure 10, e#1 and e#2 are captured by the sidewall, only e#3 can escape from the groove because its emission polar angle is smaller than θ, which depends on the size ratio of d/2h. When the groove number or the groove depth increase, d/2h will decrease and θ will decrease accordingly. In this process, more electrons will impact the sidewall, and the multipactor process can be weakened. As for the reason for saturation, we can see that when the groove narrows linearly or the depth increases linearly, θ will decrease and the rate of decrease gradually slows down. Although the number of electrons captured by the sidewall will also increase, the increase is very slow, and the suppression of multipactor tends to be saturated.

3.4 The Effect of Multiple Factors on the Multipactor Threshold

Via the analysis in Section 3.1~3.3, it is obvious that the groove aspect ratio, the groove number, and the groove depth do not affect the multipactor threshold independently. Therefore, we need to focus on the combined effect of these factors on the multipactor threshold. Here, we arrange the simulations for the SCLPFs with the grooved PTFE sheets loaded. The simulation results are shown in Table 1, with different groove numbers and aspect ratios, Figure 11 shows the contour map that describes the relationship among multipactor threshold, groove number, and aspect ratio. The groove depth is 0.5 mm, and the groove number is set as 3, 7, 13, 20, and 26, as well as the aspect ratios vary from 0.1 to 3.9. It ought to be mentioned here that a smaller groove number cannot achieve a large aspect ratio since the small groove number implies a larger groove width, and it is also limited by the groove depth of 0.5 mm. High aspect ratio grooves can only be achieved when the groove is narrow.
From Table 1 and Figure 11, we can obtain three conclusions. First, as the aspect ratio increases, the multipactor threshold exceeds 1100 W except for the condition that the groove number equals 3. Second, when the aspect ratio is constant, as the groove number increases, the multipactor threshold decreases. Third, different aspect ratios and groove numbers may achieve similar effects in multipactor mitigation. For example, the SCLPF possessing 7 grooves and 0.5 aspect ratio, has a similar multipactor threshold to the SCLPF possessing 20 grooves with 1 aspect ratio.
Figure 11 reflects the influence of depth on the multipactor threshold and its saturation status. According to Table 1, the SCLPF with 26 grooves, which can achieve a larger aspect ratio at the depth of 0.5 mm, benefits more from a narrower groove compared with the SCLPF with 7 grooves. However, a larger aspect ratio did not significantly improve the saturation value. To be specific, keeping the depth being 0.5 mm, then the saturation multipactor threshold of the SCLPF with 7 grooves and 1 aspect ratio is 1133 W, and that of the SCLPF with 26 grooves and 3.9 aspect ratio is 1137 W. The former device achieves the same multipactor suppression effect as the latter one with fewer grooves and a smaller aspect ratio. Furthermore, from Figure 11, it can be observed that the threshold saturation appears when the groove aspect ratio exceeds 1.5, thereafter, the rise of the aspect ratio will not result in a further increase for multipactor threshold.
Then we discuss the influence of groove number achieved for the loaded dielectric sheets on the multipactor threshold of the SCLPFs. During the analysis, if we keep the aspect ratio constant, the groove depth becomes shallower as the groove number increases. Figure 12 shows the two groove structure with the same aspect ratio but different groove numbers. In this case, the electron number colliding with the sidewall above the critical angle θ (the triangular area below the dashed line) is the same regardless of the number of grooves.
Theoretically speaking, the same aspect ratio should have a consistent multipactor suppression effect, but the simulation results shown in Table 1 do not support this prediction. Therefore, we need to reconsider the significance of groove depth when we analyze the multipactor threshold. The details of the grooved dielectric sheets filled in the SCLPFs are shown in Figure 13. As detailed drawing in Figure 13, the gap of REGION #2 remains at 1 mm, while the gap between the grooves in REGION #1, which is determined by the groove depth, increases greatly. The increase in the average gap cannot be ignored. According to the Hatch-Williams constant k model[36], it can be known that an increase in the gap means there will be more orders, which refers to the number of half cycles that the electron moves from one plane to another. At the same time, the threshold voltage will be higher, and the process of doubling is more difficult to establish, that is, the multipactor threshold is increased. It also ought to be mentioned here that, in addition to suppressing discharge by blocking electron path through the grooves, the passive increase in the gap between 47.5% of the areas is also an important reason for mitigating multipactor. Taking the aspect ratio of 0.5 as an example, when the groove number increases from 7 to 26, the multipactor threshold decreases from 710 W to 480 W. Correspondingly, the groove depth decreases from 0.23 mm to 0.0625 mm, that is, the gap distance at the groove decreases from 1.46 mm to 1.125 mm. However, for situations with fewer grooves, this rule may not apply. For example, the multipactor threshold of 3 grooves with an aspect ratio of 0.2 is 441.39 W, which is lower than that of 7 grooves, even though the former has a deeper depth. This indicates that the effect of depth on multipactor is also regulated by the number of grooves under the same aspect ratio.
Referring to the contour map shown in Figure 11, we know that the selection of the groove number and the aspect ratio is partly free to achieve the same effect on the multipactor threshold increase. This gives us the freedom to choose different parameters for realizing the mitigation of multipactor. For the multipactor induced by the electron avalanche between two metallic boundaries, the skin effect at high-frequency microwaves concentrates the current on the metal surface, in this case, constructing deeper grooves to suppress the discharge induced by secondary electron avalanche will affect the transmission performance of the devices. Under the circumstances, increasing the groove number and reducing the groove depth is a better solution. There are similar selection problems for the multipactor induced by the electron avalanche between two dielectric boundaries. On the other hand, for microwave devices loaded with dielectrics, constructing grooves on the dielectric is a subtractive processing method. The volume of the dielectric is reduced after subtractive processing, and the dielectric loss is correspondingly reduced, resulting in a slight reduction in the insertion loss of the device. Under the circumstances, intentionally increasing the subtractive volume within a suitable range can bring benefits to the improvement of transmission performance, which is a good choice. Therefore, suppressing multipactor through microstructures is a system engineering. Combining the saturation status discussed in sections 3.2 and 3.3, the research on the saturation pattern has strong engineering significance. This means that we should quickly estimate better cost-effectiveness of the groove preparation scheme based on the saturation pattern and contour maps.

4. Conclusions

In this paper, we have designed an L-band SCLPF with dielectric sheets loaded for checking the influence of surface microstructure on the multipactor threshold. The device possesses a 1 mm gap at the middlemost position, in which the vertical RF electric field reaches the maximum, serving as the multipactor sensitive region. Alumina and PTFE have been chosen as the loaded dielectric sheets for partly filling the narrow gap, and a surface groove structure has been constructed to verify the effect of microstructure on electron avalanche. The simulation work indicates that the transmission characteristics of the SCLPFs are little affected by introducing groove structures on the dielectric surface. The influence of groove depth, groove number, and aspect ratio on the multipactor threshold has been discussed. The results show that constructing grooves is an effective method to improve the multipactor threshold, and it is found that there is a saturation effect for the multipactor threshold as the groove depth and aspect ratio increase. By analyzing the mechanism of the phenomenon, we find that the three feature parameters of the groove, namely, groove depth, groove number, and aspect ratio, have a combined modulation effect on the multipactor threshold, and we summarize several rules that further explain the saturation effect. The contour map we obtained has practical significance for developing the surface microstructure to raise the multipactor threshold for microwave devices, and the work makes engineering sense for improving the reliability of space microwave systems.

Author Contributions

Conceptualization, J.S. and W.Z.; methodology, J.S. and Y.Z.; software, W.Z. and B.S.; validation, J.S. and D.W.; investigation, B.S., Y.L. and T.S.; data curation, J.S. and J.Z.; writing—original draft preparation, J.S. and W.Z.; writing—review and editing, Y.Z. and W.Z.; visualization, Y.Z. and Y.L.; supervision, W.Z.; project administration, T.S. and X.Z.; funding acquisition, W.T. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

All data included in this study are available upon request by contact with the corresponding author.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Vaughan, J.R.M. Multipactor. IEEE Trans Electron Dev 1988, 35, 1172-1180. [CrossRef]
  2. Lara, J.; Perez, F.; Alfonseca, M.; Galan, L.; Montero, I.; Roman, E.; Garcia-Baquero, D.R. Multipactor prediction for on-board spacecraft RF equipment with the MEST software tool. IEEE T Plasma Sci 2006, 34, 476-484. [CrossRef]
  3. Dong, Y.; Liu, Q.X.; Pang, J.; Zhou, H.J.; Dong, Z.W. Influence of secondary electron yield of material on two-sided multipactor discharge in cavity. Acta Phys Sin 2018, 67, 037901. [CrossRef]
  4. Raboso, D. Multipactor breakdown: Present status and where are we heading in 6th International Workshop on Multipactor Corona and Passive Intermodulation, Valencia, Spain, 2008.
  5. Chang, C.; Liu, Y.S.; Verboncoeur, J.; Chen, C.H.; Guo, L.T.; Li, S.; Wu, X.L. The effect of periodic wavy profile on suppressing window multipactor under arbitrary electromagnetic mode. Appl Phys Lett 2015, 106, 014102. [CrossRef]
  6. Fil, N.; Belhaj, M.; Hillairet, J.; Puech, J. Multipactor threshold sensitivity to total electron emission yield in small gap waveguide structure and TEEY models accuracy. Phys Plasmas 2016, 23, 123118. [CrossRef]
  7. Geng, G.L.; Padamsee, H.; Shemelin, V. Multipactor in a Rectangular Waveguide, in Proceedings of PAC, Chicago, USA, 2001, 1228-1230. [CrossRef]
  8. Riyopoulos, S. Multipactor with electric field retarding secondary emission. Phys Plasmas 1998, 5 305-311. [CrossRef]
  9. Hueso, J,; Vicente, C.; Gimeno, B.; Boria, V.E.; Marini S.; Taroncher, M. Multipactor Effect Analysis and Design Rules for Wedge-Shaped Hollow Waveguides. IEEE Trans Electron Devices 2010, 57, 3508-3517. [CrossRef]
  10. Wang, D.; He, Y.N.; Cui, W.Z. Secondary electron emission characteristics of TiN coatings produced by RF magnetron sputtering. J Appl Phys 2018, 124, 053301. [CrossRef]
  11. Pimpec, F.L.; Kirby, R.E.; King, F.; Pivi, M. Properties of TiN and TiZrV thin film as a remedy against electron cloud. Nucl Instrum Meth A 2005, 551, 187-199. [CrossRef]
  12. Henrist,B.; Hilleret, N.; Scheuerlein, C.; Taborelli, M. The secondary electron yield of TiZr and TiZrV non-evaporable getter thin film coatings. Appl Surf Sci 2001, 172, 95-102. [CrossRef]
  13. Le Pimpec, F.; Kirby, R.E.; King, F.K.; Pivi, M. The effect of gas ion bombardment on the secondary electron yield of TiN, TiCN and TiZrV coatings for suppressing collective electron effects in storage rings. Nucl Instrum Meth A 2006, 564, 44-50. [CrossRef]
  14. Pinto, P.; Costa. Calatroni, S,; Neupert, H.; Letant-Delrieux, D.; Edwards, P.; Chiggiato, P.; Taborelli, M.; Vollenberg, W.; Yin-Vallgren, C.; Colaux, J.L.; Lucas, S. Carbon coatings with low secondary electron yield. Vacuum 2013, 98, 29-36. [CrossRef]
  15. Wang, J.; Wang, Y.; Xu, Y.H.; Zhang, Y.X.; Zhang, B.; Wei, W. Secondary electron emission characteristics of graphene films with copper substrate. Chinese Phys C 2016, 40, 117003. [CrossRef]
  16. Cao, M.; Zhang, X.S.; Liu, W.H.; Wang, H.G.; Li, Y.D. Secondary electron emission of graphene-coated copper. Diam Relat Mater 2017, 73, 199-203. [CrossRef]
  17. Ye, M.; He, Y.N.; Wang, R.; Hu, T.C.; Zhang, N.; Yang, J.; Cui, W.Z.; Zhang, Z.B. Suppression of secondary electron emission by micro-trapping structure surface. Acta Phys Sin 2014, 63, 147901. [CrossRef]
  18. Wang, D.; Ye, M.; Feng, P.; He, Y.N.; Cui, W.Z.; An effective reduction on secondary electron emission yield of gold coated surfaces by laser etching. Acta Phys Sin 2019, 68, 067901. [CrossRef]
  19. Nistor, V.; González, L.A.; Aguilera, L.; Montero, I.; Galan, L.; Wochner, U.; Raboso, D. Multipactor suppression by micro-structured gold/silver coatings for space applications. Appl Surf Sci 2014, 315, 445-453. [CrossRef]
  20. Valizadeh, R.; Malyshev, O.B.; Wang, S.; Zolotovskaya, S.A.; Gillespie, W.A.; Abdolvand, A. Low secondary electron yield engineered surface for electron cloud mitigation. Appl Phys Lett 2014, 105, 231605. [CrossRef]
  21. Cummings, K.A.; Risbud, S.H. Dielectric materials for window applications. J Phys Chem Solids 2000, 61, 551-560. [CrossRef]
  22. Vague, J.; Melgarejo, J.C.; Guglielmi, M.; Boria, V.E.; Anza, S.; Vicente, C.; Rocio, M.M.; Maria, M.; Benito, G.M.; Raboso, D. Multipactor Effect Characterization of Dielectric Materials for Space Applications. IEEE Trans Microw Theory Techn 2018, 66, 3644-3655. [CrossRef]
  23. Li, Y.; Wang, D.; Yu, M.; He, Y.N.; Cui, W.Z. Experimental Verification of Multipactor Discharge Dynamics Between Ferrite Dielectric and Metal. IEEE Trans Electron Dev 2018, 65, 4592-4599. [CrossRef]
  24. Zhu, X.; Guo, J.J.; Li, X.X.; Zhou, R.D.; Wang, D.; Zhao, W. Evolvement Investigation of Secondary Electron Emission for Ultrathin MgO Coatings Prepared by Atomic Layer Deposition. Appl Sci 2021, 11, 4801. [CrossRef]
  25. Cao, W.W.; Wang, B.; Yang, Y.; Zhu, B.L.; Guo, J.J.; Xu, P.; Bai, X.H.; Qin, J.J.; Wang, C.; Zhu, J.P.; Bai, Y.L. Secondary electron emission characteristics of the Al2O3/MgO double-layer structure prepared by atomic layer deposition. Ceram Int 2021, 47: 9866-9872. [CrossRef]
  26. Suharyanto, Y.; Yamano, S.; Kobayashi, S.; Michizono, S.; Saito, Y. Secondary electron emission and surface charging evaluation of alumina ceramics and sapphire. IEEE Trans Dielect El In 2006, 13, 72-78. [CrossRef]
  27. Wang, D.; Mao, Z.S.; Ye, Z.; Cai, Y.H.; Li, Y.; He, Y.N.; Qi, K.C.; Xu, Y.N.; Jia, Q.Q. Ultralow electron emission yield achieved on alumina ceramic surfaces and the application in multipactor suppression. J Phys D-Appl Phys 2022, 55, 455301. [CrossRef]
  28. Meng, X.C.; Wang, D.; Cai, Y.H.; Ye, Z.; He, Y.N.; Xu, Y.N. Secondary electron emission suppression on alumina surface and its application in multipactor suppression. Acta Phys Sin 2023, 72, 107901. [CrossRef]
  29. Pivi, M.; King, F.K.; Kirby, R.E.; Raubenheimer, T.O.; Stupakov, G.; Le Pimpec, F. Sharp reduction of the secondary electron emission yield from grooved surfaces. J Appl Phys 2008, 104, 104904. [CrossRef]
  30. Vague, J.J.; Asensio, I.; Coves, A.; San Blas, A.A.; Reglero, M.; Pantaleoni, A.V.; Raboso, D. Baquero-Escudero, M. Boria, V.E. Study of the Multipactor Effect in Groove Gap Waveguide Technology. IEEE Trans Microw Theory Techn 2022, 70, 2566-2578. [CrossRef]
  31. Swanson, C.; Kaganovich, I.D. Modeling of reduced effective secondary electron emission yield from a velvet surface. J Appl Phys 2016, 120, 213302. [CrossRef]
  32. Swanson, C.; Kaganovich I.D. “Feathered” fractal surfaces to minimize secondary electron emission for a wide range of incident angles. J Appl Phys 2017, 122, 043301. [CrossRef]
  33. Swanson, C.; Kaganovich I.D. Modeling of reduced secondary electron emission yield from a foam or fuzz surface. J Appl Phys 2018, 123, 023302. [CrossRef]
  34. Guo, J.J.; Wang, D.; Xu, Y.T.; Zhu, X.P.; Wen, K.L.; Miao, G.H.; Cao, W.W.; Si, J.H.; Lu, M.; Guo, H.T. Secondary electron emission characteristics of Al2O3 coatings prepared by atomic layer deposition. AIP Adv 2019, 9, 095303. [CrossRef]
  35. Cai, Y.H.; Wang, D.; Zhang, W.; He, Y.N. Seesaw-type modulation of secondary electron emission characteristics of polytetrafluoroethylene-MgO composite coating. J Vac Sci Technol B 2022, 40, 044001. [CrossRef]
  36. Hatch, A.J.; Williams, H.B. The secondary electron resonance mechanism of low-pressure high-frequency gas breakdown. J Appl Phys 1958, 25, 417-423. [CrossRef]
Preprints 74130 g001
Figure 1. (a) An approximate lumped element circuit of the coaxial line, (b) and (c) are the two equivalent circuits with corresponding formulas.
Figure 1. (a) An approximate lumped element circuit of the coaxial line, (b) and (c) are the two equivalent circuits with corresponding formulas.
Preprints 74130 g001
Preprints 74130 g002
Figure 2. (a) The 3D model of the designed SCLPF, (b) the cross-section image of the SCLPF.
Figure 2. (a) The 3D model of the designed SCLPF, (b) the cross-section image of the SCLPF.
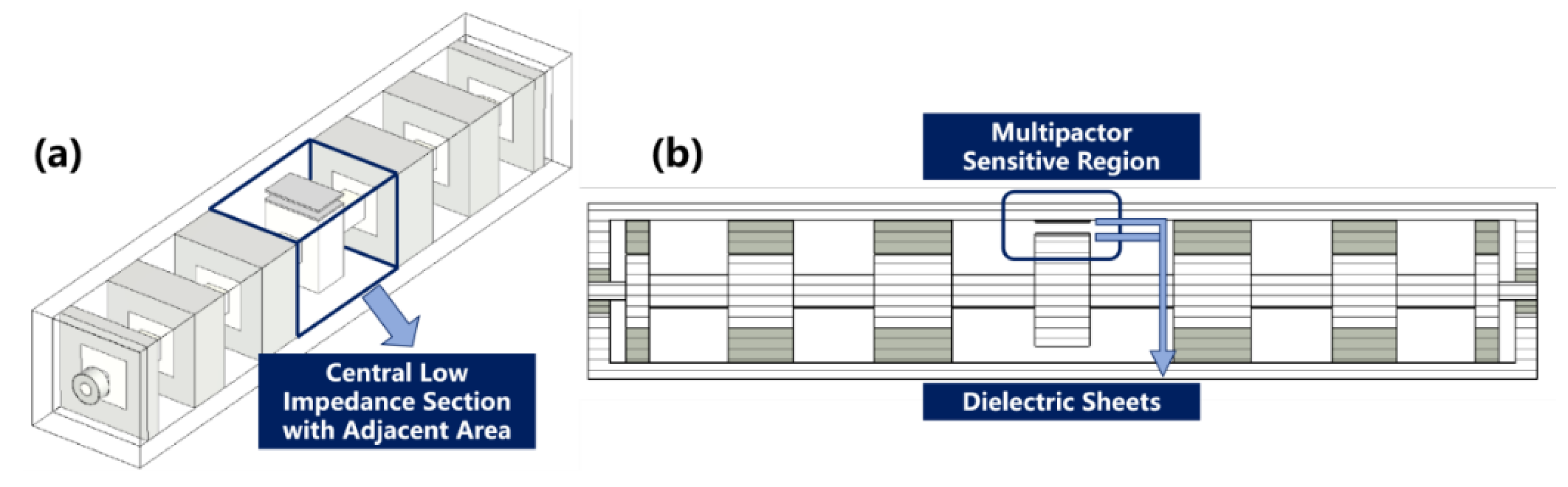
Preprints 74130 g002
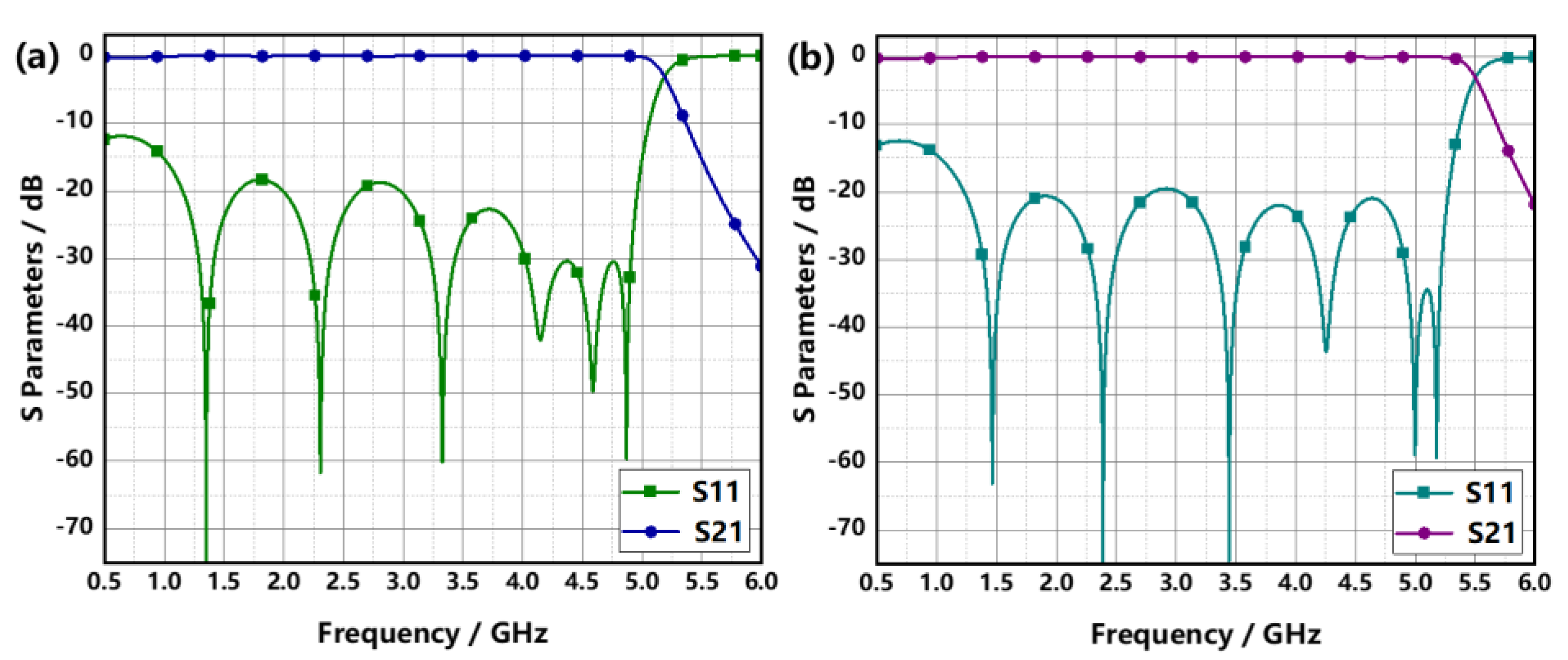
Preprints 74130 g003
Figure 3. Simulated frequency responses of SCLPFs with (a) alumina loaded and (b) PTFE loaded.
Figure 3. Simulated frequency responses of SCLPFs with (a) alumina loaded and (b) PTFE loaded.
Preprints 74130 g003
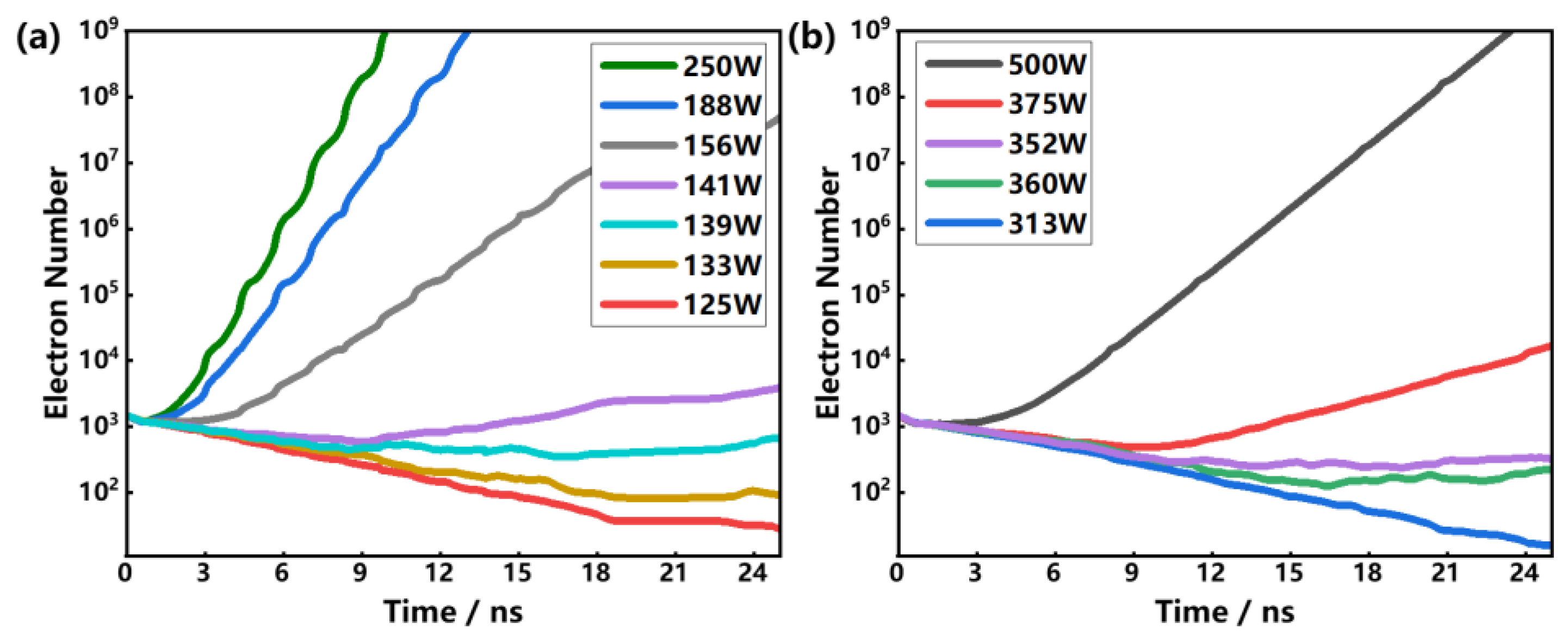
Preprints 74130 g004
Figure 4. The simulated evolution of electron number for the SCLPFs with (a) flat alumina loaded and (b) flat PTFE loaded.
Figure 4. The simulated evolution of electron number for the SCLPFs with (a) flat alumina loaded and (b) flat PTFE loaded.
Preprints 74130 g004
Preprints 74130 g005
Figure 5. The groove structures (a)with and (b)without margins on alumina substrates. Schematic models of grooves (c)with and (d)without margins on dielectric substrates.
Figure 5. The groove structures (a)with and (b)without margins on alumina substrates. Schematic models of grooves (c)with and (d)without margins on dielectric substrates.
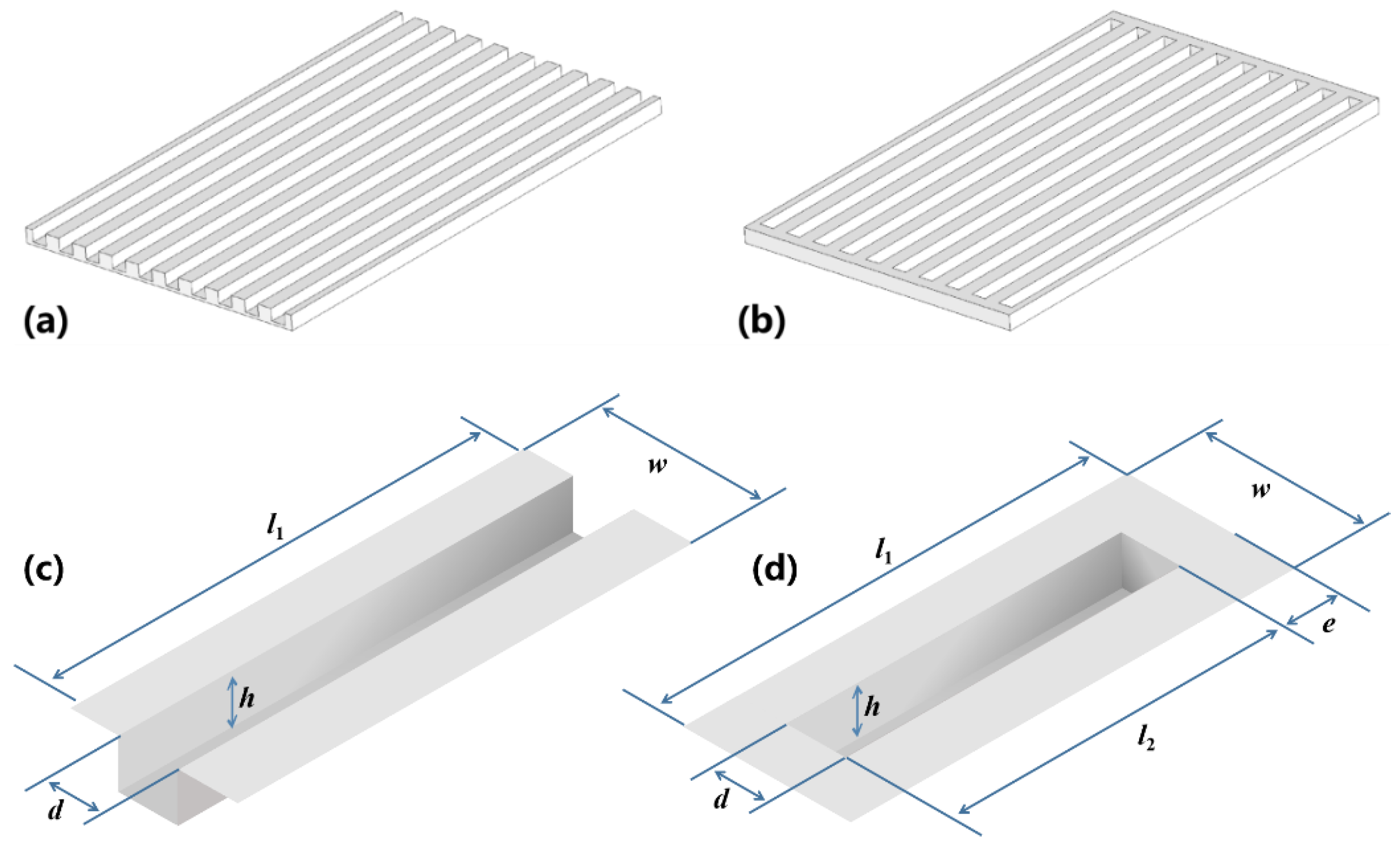
Preprints 74130 g005
Preprints 74130 g006
Figure 6. The simulated evolution of electron number for the SCLPFs with (a) grooved alumina loaded and (b) grooved PTFE loaded.
Figure 6. The simulated evolution of electron number for the SCLPFs with (a) grooved alumina loaded and (b) grooved PTFE loaded.
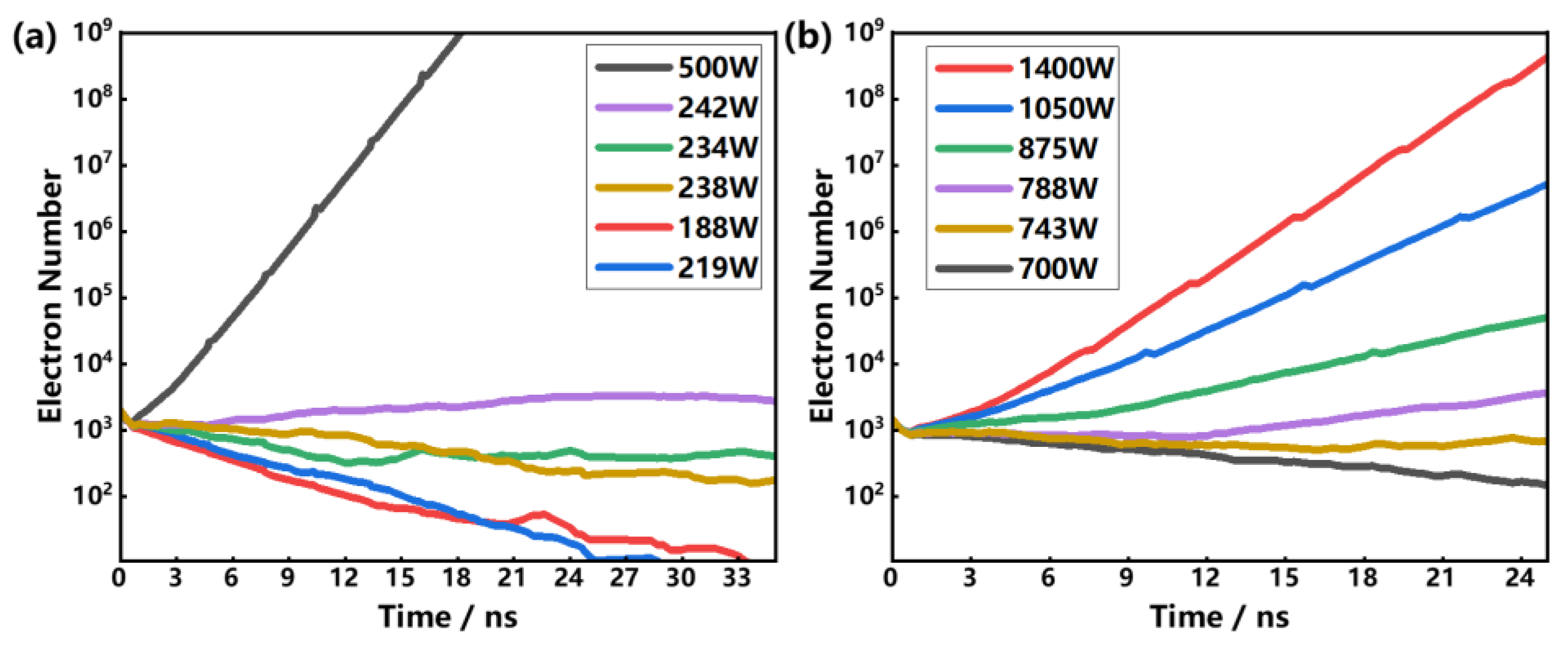
Preprints 74130 g006
Preprints 74130 g007
Figure 7. A series of grooves with different sizes on the alumina sheet, with the same groove depth and groove density but different groove numbers.
Figure 7. A series of grooves with different sizes on the alumina sheet, with the same groove depth and groove density but different groove numbers.
Preprints 74130 g007
Preprints 74130 g008
Figure 8. The effect of groove number on the multipactor threshold of the alumina-loaded SCLPFs.
Figure 8. The effect of groove number on the multipactor threshold of the alumina-loaded SCLPFs.
Preprints 74130 g008
Preprints 74130 g009
Figure 9. The effect of groove depth on the multipactor threshold of the PTFE-loaded SCLPFs.
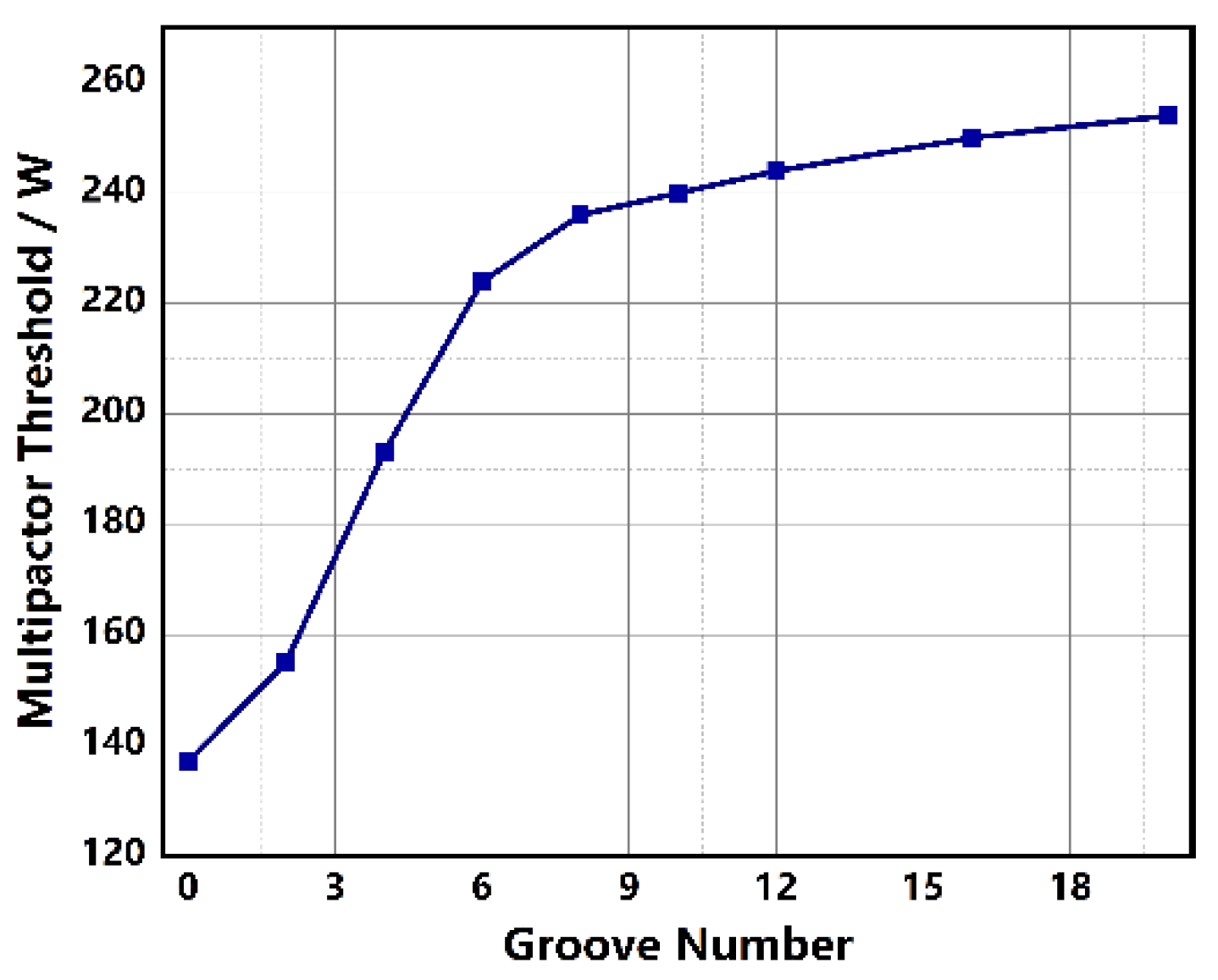
Figure 9. The effect of groove depth on the multipactor threshold of the PTFE-loaded SCLPFs.
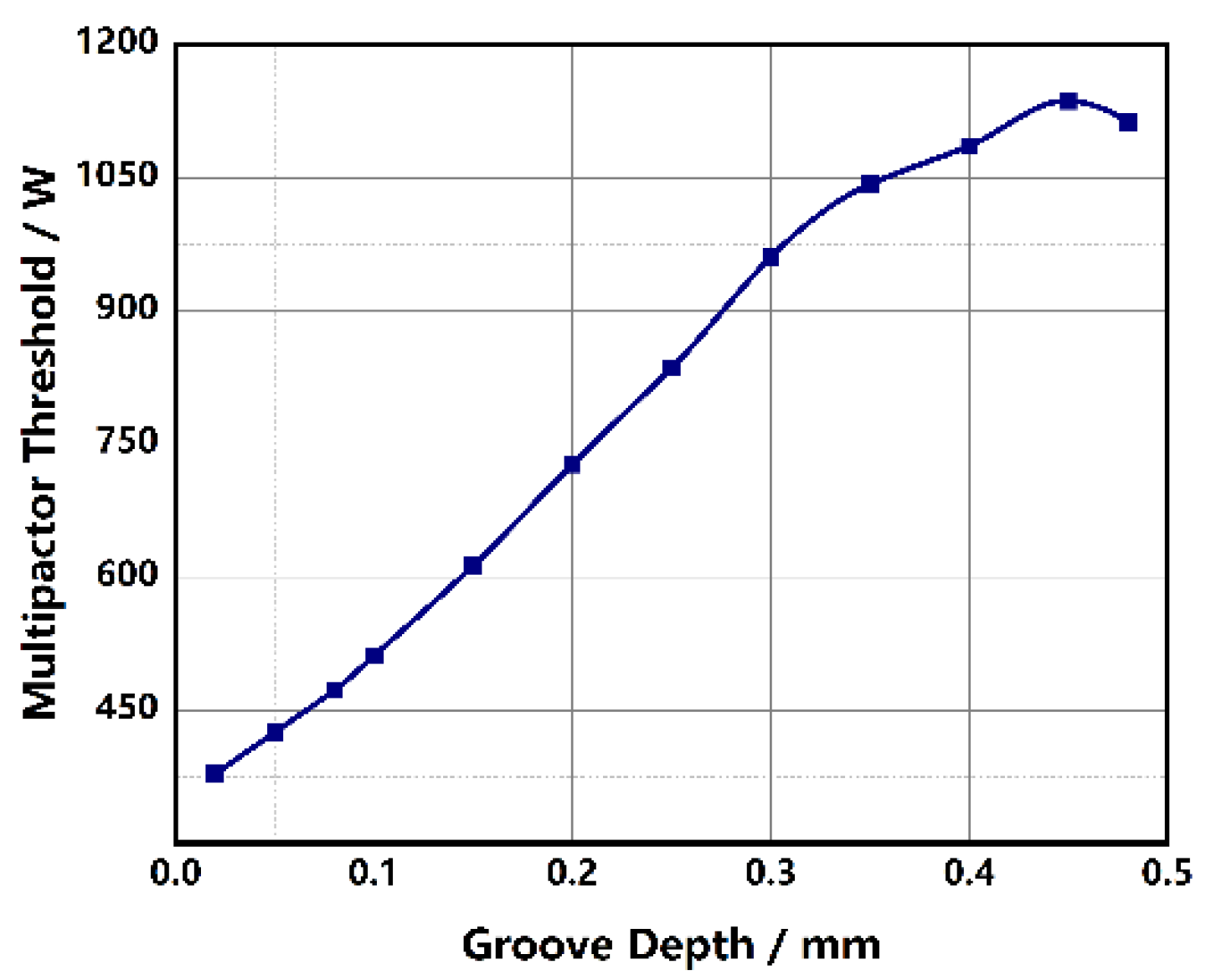
Preprints 74130 g009
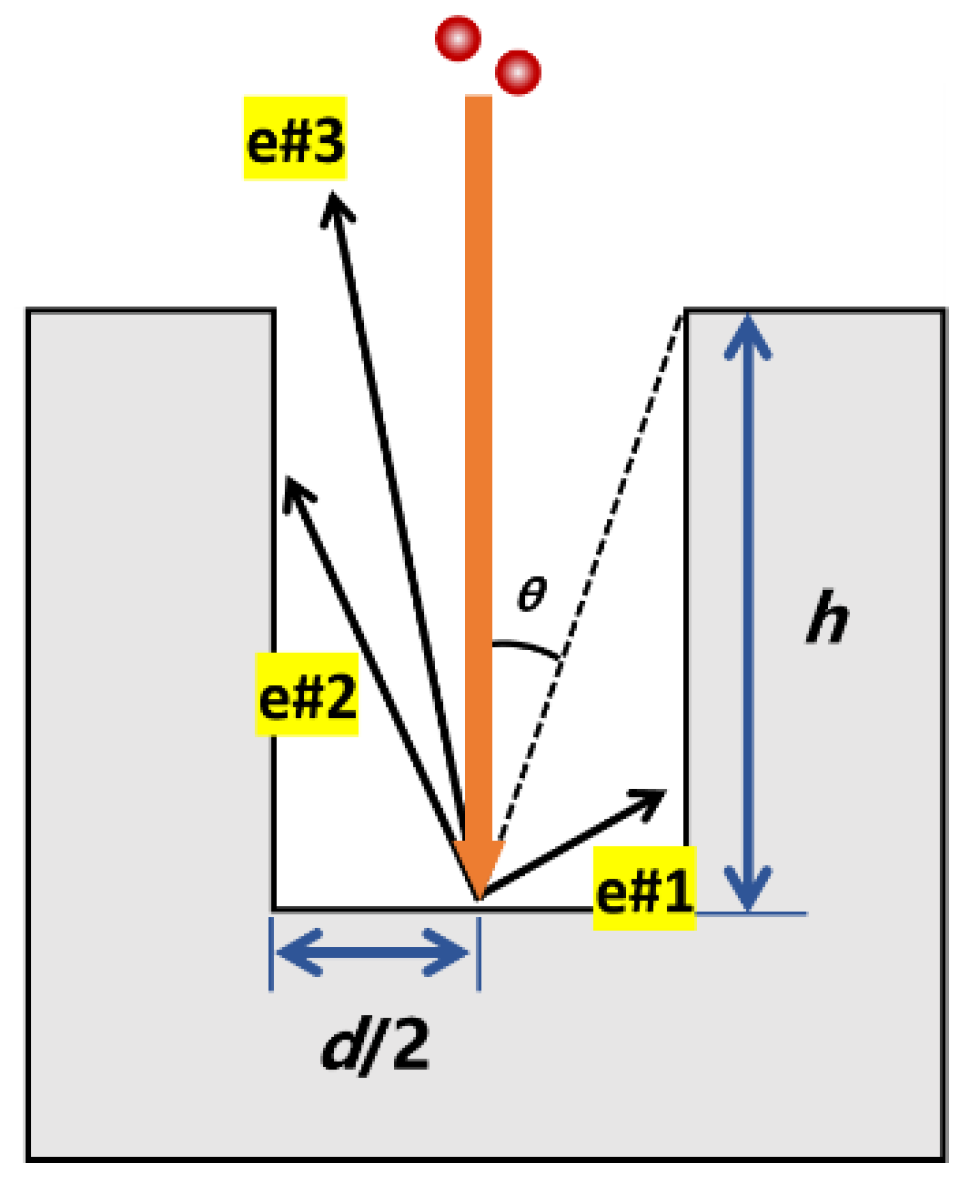
Preprints 74130 g010
Figure 10. Schematic model of the motion of secondary electrons excited by electrons incident on the center in a 2D groove.
Figure 10. Schematic model of the motion of secondary electrons excited by electrons incident on the center in a 2D groove.
Preprints 74130 g010
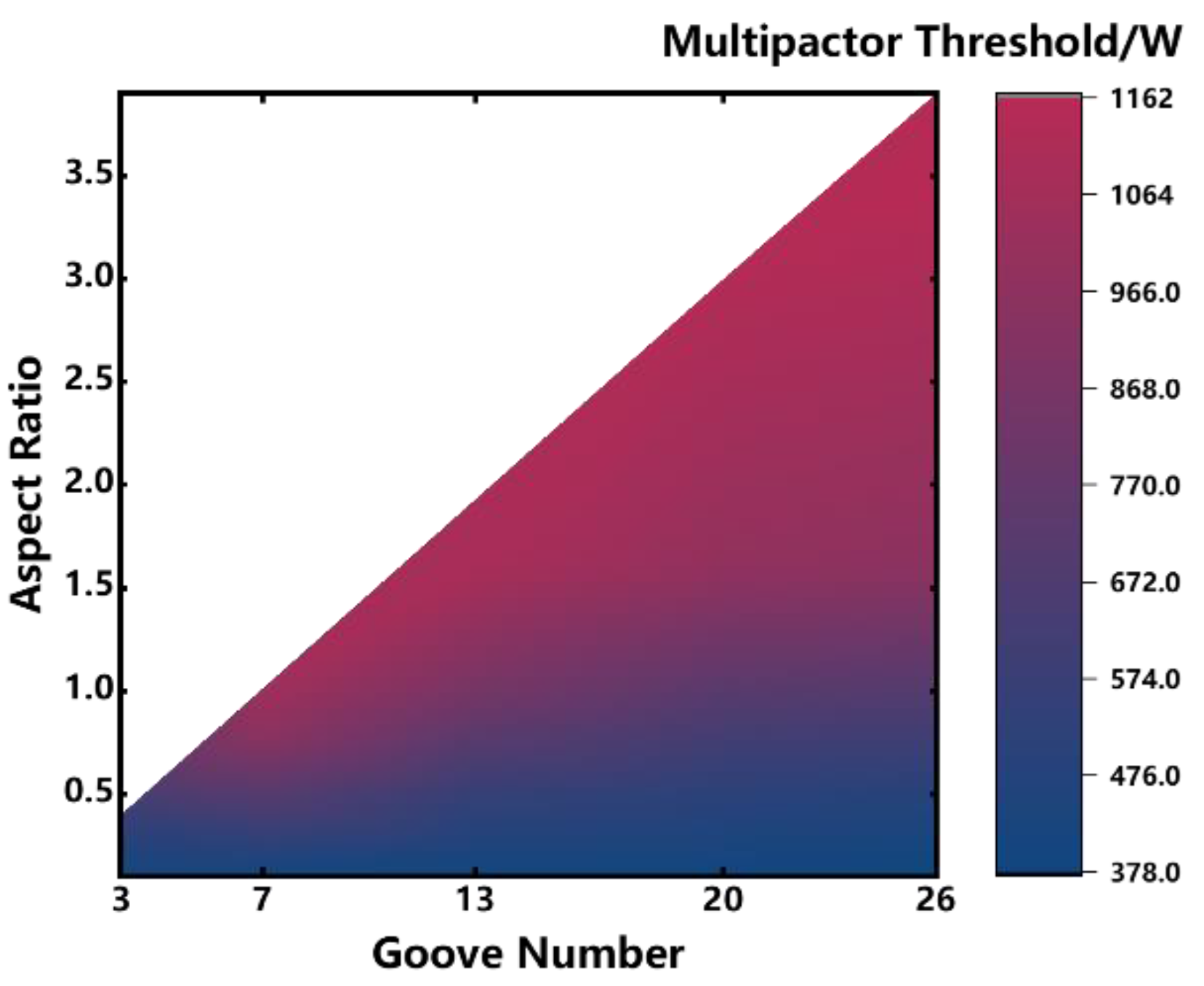
Preprints 74130 g011
Figure 11. Contour map of the PTFE-loaded SCLPFs multipactor threshold, with aspect ratio and groove number as coordinate axes.
Figure 11. Contour map of the PTFE-loaded SCLPFs multipactor threshold, with aspect ratio and groove number as coordinate axes.
Preprints 74130 g011
Preprints 74130 g012
Figure 12. Microstructures with the same aspect ratio and groove ratio but different numbers of grooves.
Figure 12. Microstructures with the same aspect ratio and groove ratio but different numbers of grooves.
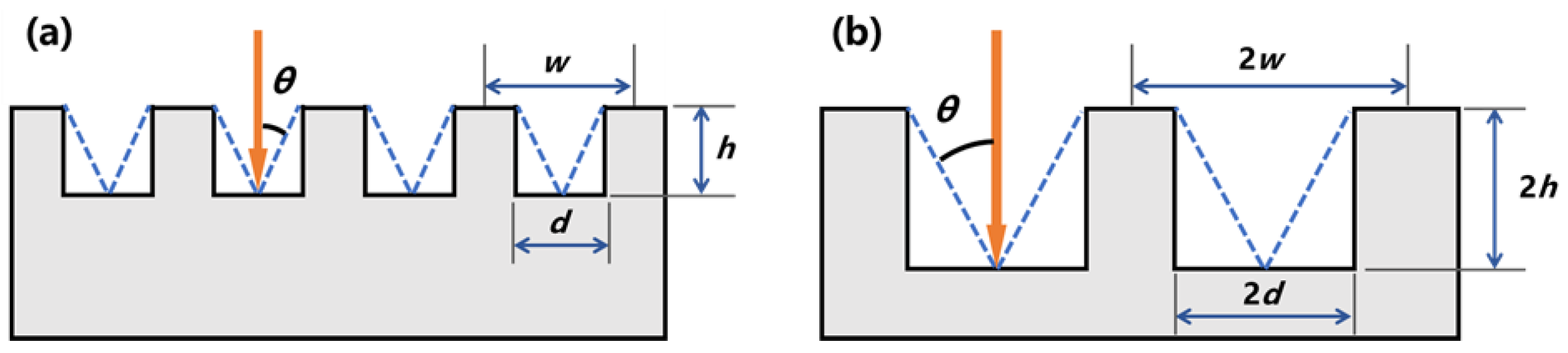
Preprints 74130 g012
Preprints 74130 g013
Figure 13. The symmetrical groove structure leads to an increase in the average spacing of the gap. REGION #2 achieves a larger multipactor threshold compared to REGION #1.
Figure 13. The symmetrical groove structure leads to an increase in the average spacing of the gap. REGION #2 achieves a larger multipactor threshold compared to REGION #1.
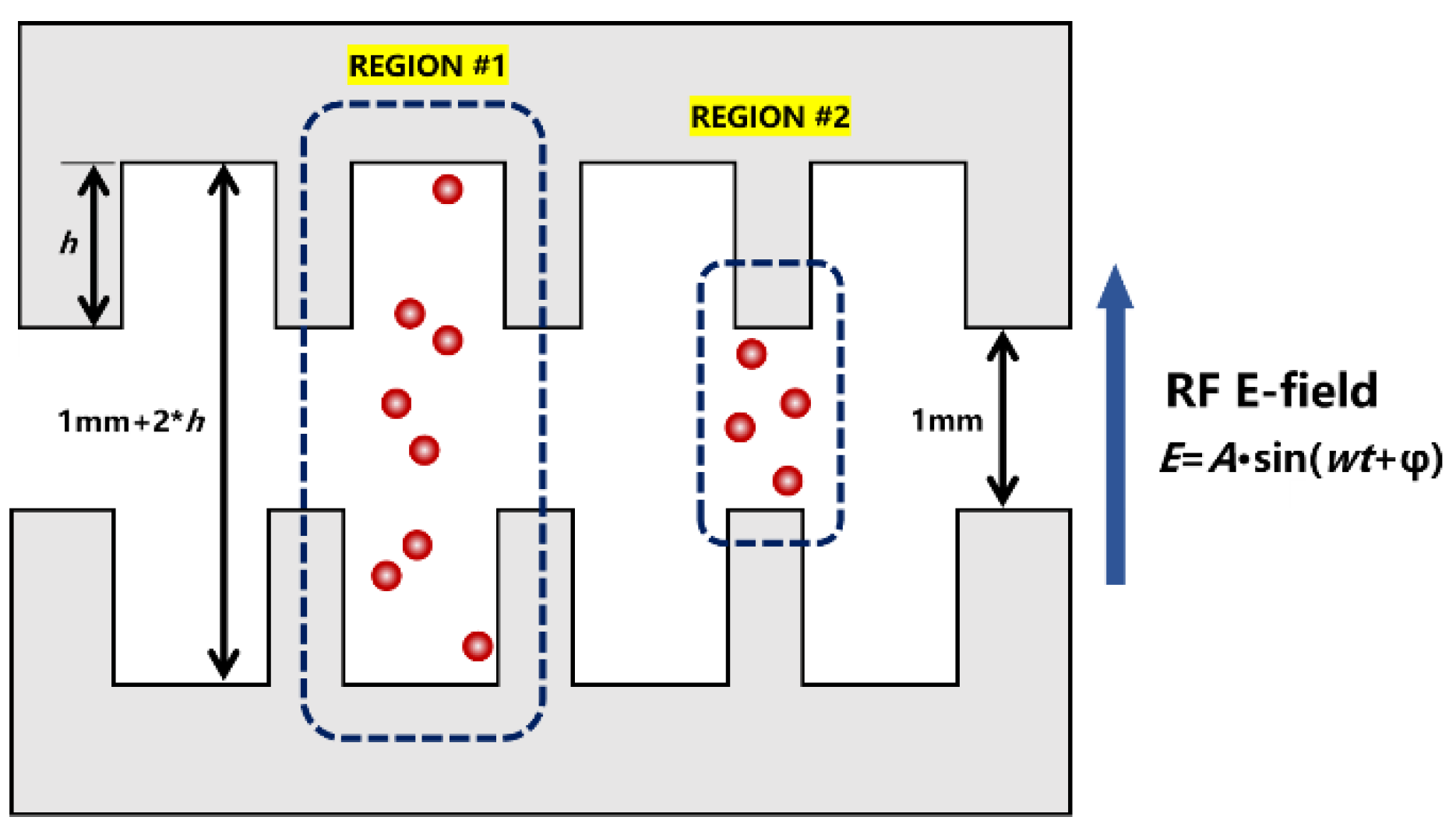
Preprints 74130 g013
Table 1. Simulated multipactor threshold (W) of the PTFE-loaded SCLPFs with various aspect ratios and groove number.
Table 1. Simulated multipactor threshold (W) of the PTFE-loaded SCLPFs with various aspect ratios and groove number.
Aspect Ratio→
Grooves Number↓		 0.1 0.2 0.4 0.5 0.8 1 1.6 3 3.5 3.9
3 417.95 441.39 568.33
7 / 472.64 / 710.89 960.91 1132.79
13 / 425.76 / 558.58 738.25 851.53 1095.24
20 / 415.61 / 509.37 628.88 718.72 984.30 1164.04
26 378.89 400.77 / 484.36 / / 955.06 / 1160.10 1136.66
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated