Preprint

Article

Dynamic Analysis and Control of Neural Networks: Stability, Oscillation, and Weight-Based Modulation

Altmetrics

Downloads

145

Views

Comments

Lei Zhang^*

This version is not peer-reviewed

Submitted:

21 May 2023

Posted:

23 May 2023

You are already at the latest version

Alerts

Abstract

This paper investigates the dynamic properties of artificial neural networks using differential equations and explores the influence of parameters on stability and neural oscillations. By analyzing the equilibrium point of the differential equations, we identify conditions for asymptotic stability and criteria for oscillation in artificial neural networks. Furthermore, we demonstrate how adjusting synaptic weights between neurons can effectively control stability and oscillation. The proposed model offers potential insights into the malfunctioning mechanisms of biological neural networks implicated in neurological disorders like Parkinson's disease tremors and epilepsy seizures, which are characterized by abnormal oscillations.

Keywords:

Subject: Engineering - Control and Systems Engineering

1. Introduction

Biological neural dynamics refer to the dynamic neural activities that underlie brain functions. Neural oscillations are well-defined physiological processes. This paper focuses on the dynamic analysis of artificial neural networks using differential equations and highlights the controllability of stability and neural oscillations through parameter adjustments. Through stability analysis of the equilibrium point in the differential equations, the conditions for asymptotic stability in artificial neural networks and the criteria for oscillation occurrence are identified. The study also reveals how synaptic weights between neurons can be utilized to regulate the stability and oscillation of artificial neural networks. Notably, neurological disorders such as tremors in Parkinson’s disease and seizures in epilepsy are characterized by abnormal oscillations in biological neural networks. Hence, the developed model has the potential to offer insights into the mechanisms underlying the malfunctioning of biological neural networks associated with these diseases.

The observation of oscillation and unstable chaotic patterns in biological brain waves captured using EEG supports the findings of this model[1,2]. The model highlights the critical role of synaptic delay in forming different patterns and stability states. This finding could potentially provide insights into the clinical experimental results of using external stimulation to suppress abnormal neural oscillation in brain disorders such as epilepsy seizures[3,4,5] and Parkinson’s Disease tremors[6,7,8,9].

Nature is rich with examples of oscillatory patterns. The oscillatory frequency is a fundamental parameter for quantifying the intrinsic characteristics individual biological neurons [10], and analyzing the collective behaviours of artificial neural networks[11,12]. A single neuron possesses the ability to generate periodic spiking output and modify its pattern by adjusting its oscillatory frequency. Nevertheless, the range of oscillation patterns exhibited by individual neurons is inherently limited. In contrast, the interaction among multiple neurons exhibiting periodic oscillations gives rise to a significantly broader spectrum of oscillatory patterns. Various mathematical models have been established to effectively simulate the dynamic behaviours of individual biological neurons [13,14,15,16] as well as neural networks [17]. The Hodgkin-Huxley model [13], employing differential equations to describe neuronal action potentials, successfully reproduces oscillatory patterns that closely resemble empirical observations of neuronal spiking. However, the model is accurate but too complex for constructing large scale artificial neural network (ANN).

The allure of simplicity holds undeniable appeal in engineering, particularly in terms of speed and power efficiency in hardware implementation. Research in neuroscience has unveiled the phenomenon of synchronized oscillations among interconnected biological neurons[18][19]. Synchronous behaviour in neural networks arises when a cluster of interconnected neurons oscillates in a phase-locked manner. Such synchronized groups of neurons can exhibit collective behaviour and interact with other synchronized clusters. To facilitate modelling and simulation, a synchronized group of neurons can be represented by a single neuron, forming a simplified neural network for dynamic analysis[20].

2. Materials and Methods

2.1. Neuronal Oscillation Vs. Neural Network Oscillation

Neuronal oscillation refers to the microscopic-scale oscillatory activity exhibited by an individual neuron. Depending on the neuron’s initial state and input stimulation, it can generate spiking outputs characterized by oscillatory patterns. The behaviours of single spiking neurons have been investigated using a combination of differential equation models and analytical approaches[21]. At the macroscopic scale, neural oscillation refers to the collective behaviour exhibited by synchronized neural networks[22]. Brainwaves serve as a biological example of neural oscillation and can be measured using Electroencephalography (EEG). When clusters of locally interconnected neurons form neural networks and engage in synchronized oscillatory activity, they produce synchronized firing patterns and local field potentials (brainwaves). While individual neurons in the brain experience continuous synaptic stimulation and exhibit seemingly random firing patterns, rhythmic firing patterns emerge when they are subjected to specific external stimuli, with positive stimuli often inducing oscillatory activity. Conversely, neural networks can exhibit oscillatory behaviour even in the absence of external input. Importantly, the oscillation frequency of synchronized neural networks can differ from the firing frequency of individual neurons. The conditions for oscillation can be analyzed by examining the interactions among neurons using the Routh-Hurwitz method[23].

2.2. Synchronized Neural Oscillation and Deep Brain Stimulation

When the brain is in a resting state, biological neurons remain active and exhibit random oscillations, collectively resembling white noise. The emergence of meaningful brain activities stems from the synchronization of groups of neurons. Neural synchronization occurs when two or more neurons oscillate in phase. If two neurons oscillate in phase at the same angular frequency (

ω

), they are considered phase-locked. Neurons oscillating at different frequencies can also synchronize and fire together at the least common multiple of their oscillation periods.

This study builds upon the insights gained from synchronized neural oscillation behaviours and their relevance to deep brain stimulation. While brain stimulation has been utilized clinically to treat neurological disorders like Parkinson’s disease tremors [7,24,25] and epilepsy seizures [4,5], the effectiveness of such treatments still relies on trial and error. Although several hypotheses have been proposed, the fundamental theory remains to be established. It has been observed that impaired movement results from abnormal oscillatory synchronization in the motor system [8]. Neural oscillation models have been employed to simulate the onset of epilepsy seizures[26]. Artificial Neural Networks (ANNs) have been utilized to model dynamic systems, allowing for the simulation of chaotic brainwave patterns [27], and have also been employed for brain stimulation control in previous studies [28]. However, ANNs require training with available data and function as black boxes without providing insight into the transfer function from inputs to outputs, making them unsuitable for direct parameter control. In this research, a bio-inspired neural network model based on differential equations is designed to simulate the synchronized oscillation of neural networks. Classical mathematical approaches are employed to analyze dynamic systems, evaluating the effects of different parameters and determining the oscillation conditions of the neural network.

2.3. Dynamic Analysis of Neural Network Model

Differential equations can be used to represent dynamical systems, inlcuding various dynamic properties such as character equations, equilibria, eigenvalues, stability of equilibrium, bifurcation (qualitative behavioural changes), and phase space. The analytical method employed in this paper is detailed in Appendix A.1. Considering a neural network model comprised of interconnected neurons, it can be treated as a dynamical system and analyzed using the same techniques employed for nonlinear systems. By utilizing differential equations, the states of neural networks can be manipulated through adjustable parameters[29]. In the context of predicting COVID-19 transmission cases, a bio-inspired neural model is developed based on nonlinear differential equations to forecast time series data [30]. In this research, the dynamical analysis approach is employed to model the nonlinear behaviours of neural networks, as elaborated in [31].

3. Complex Exponential Neuron Model

A spiking neuron exhibits periodic oscillations that can be mathematically represented by a complex exponential function of time t, denoted as

E (t) = A e^{i ω t}

, where A represents the peak amplitude of the oscillation. To simplify computations, we can express A consistently in exponential form as

A = e^{θ}

. The parameter

θ

indirectly scales the peak oscillation amplitude, with

θ = 0

corresponding to a peak amplitude of

A = e^{0} = 1

. The angular frequency

ω

is related to the oscillatory frequency f and the period T as

ω = 2 π f = \frac{2 π}{T}

. Since

ω

is a real number, the complex exponential

e^{i ω t}

can be written as

c o s (ω t) + i s i n (ω t)

, where i represents the imaginary unit defined as

i = \sqrt{- 1}

. Thus, a periodically oscillating neuron

E (t)

is defined by the complex exponential model specified in Equation (1).

E (t) = e^{i ω t + θ} = e^{θ} e^{i ω t} = e^{θ} (cos ω t + i sin ω t)

(1)

The variable

E (t)

represents the membrane voltage potential of a biological neuron, incorporating two intrinsic properties: the peak oscillatory amplitude and the oscillation frequency. The real component of the complex exponential function,

e^{θ} cos ω t

, corresponds to the sinusoidal function scaled by the peak amplitude

A = e^{θ}

. Similarly, the imaginary component,

e^{θ} sin ω t

, represents another sinusoidal function multiplied by the same peak amplitude. In this context, the peak amplitude of the sinusoid is denoted as

A = e^{θ}

, while the oscillation frequency is given by

f = \frac{ω}{2 π}

. It is worth noted that

θ

is not the initial phase.

3.1. Derivatives of Complex Exponential Neuron Model

The derivative of an oscillatory neuron function with respect to time is described by a differential equation, which captures the rate of change of one variable with respect to another. For the complex exponential neuron model

E (t)

, the first and second order derivatives with respect to the time variable t are provided in Equation (2). The first order derivative represents the change in membrane potential

Δ E (t)

over a time interval

d t

, indicating the speed of the change. On the other hand, the second order derivative characterizes the rate of change of the speed, representing the acceleration of

Δ E (t)

The first-order derivative of the original neuron model is obtained by multiplying the model by a factor of

i ω

, which is equivalent to multiplying the angular speed

ω

and adding a phase shift of

\frac{π}{2}

. This equivalence arises from the fact that multiplying by i produces a phase shift of

\frac{π}{2}

. Similarly, the second-order derivative is computed by multiplying the first-order derivative by

i ω

. This operation also results in multiplying the original neuron function by

{(i ω)}^{2} = - ω^{2}

, where the negative sign corresponds to a total phase shift of

π

. This property is unique to the complex exponential neuron model

E (t)

, as it simplifies the computation of differentiation by applying a factor. Furthermore, the time integral of

E (t)

can be obtained by dividing by the same factor:

\frac{1}{i ω} = \frac{- i}{ω} = \frac{e^{- i π / 2}}{ω}

\begin{matrix} E (t) = e^{i ω t + θ} \\ \frac{d E}{d t} = i ω e^{i ω t + θ} = ω e^{i (ω t + π / 2) + θ} = i ω E \\ \frac{d^{2} E}{d t^{2}} = {(i ω)}^{2} e^{i ω t + θ} = - ω^{2} e^{i ω t + θ} = - ω^{2} E \end{matrix}

(2)

3.2. Weighted Input of Complex Exponential Neurons

Biological neurons are cells in the nervous system that communicate with each other through synapses. These synapses serve as connections between neurons and facilitate the transmission of nerve impulses from the pre-synaptic neuron to the post-synaptic neuron. The length of a synapse plays a crucial role in controlling the delay and attenuation of the transmitted signal. In ANNs, the synaptic weight refers to a scaling factor associated with the strength of the connection between two connected neurons. It determines the positive or negative impact of the input neuron on the output neuron. Each input neuron in a network is multiplied by its corresponding synaptic weight, which is associated with the connection to an output neuron in the subsequent layer. The input of a neuron is calculated as the sum of the weighted outputs from all neurons in the preceding layer. In the context of the complex exponential neuron model, the synaptic weight of interconnections between neurons can be expressed either in exponential form or complex exponential form, depending on the specific representation chosen.

3.2.1. Exponential weight $W = e^{ϕ}$

In a biological neural network, the transmission of signals between neurons is subject to delays and attenuations as they traverse the synaptic connections. The amount of these delays and attenuations depends on the length of the synaptic connection. Longer connections result in increased delays and greater attenuation of the excitatory spiking signal. To capture this relationship, it is intuitive to represent the synaptic weight using the natural exponential function:

W = e^{ϕ}

, where

ϕ

represents the delay associated with the length of the synaptic connection. By expressing the synaptic weight as

W = e^{ϕ}

, the weighted input of a neuron can be calculated as the product of the neuron’s activity and its corresponding synaptic weight, as indicated in Equation (3).

E (t) W = e^{i ω t + θ} e^{ϕ} = e^{θ + ϕ} e^{i ω t}

(3)

3.2.2. Complex Exponential weight $W = e^{i ϕ}$

With the synaptic weight represented in the complex exponential form as

W = e^{i ϕ}

, the weighted input of a neuron can be computed as the product of the neuron’s activity and its corresponding synaptic weight, as shown in Equation (4).

E (t) W = e^{i ω t + θ} e^{i ϕ} = e^{θ} e^{i (ω t + ϕ)}

(4)

The chosen representation of synaptic weight as

W = e^{i ϕ}

is biologically plausible, as it introduces a time or phase delay to the signal originating from the pre-synaptic neuron. In biological neurons, myelin—a membranous structure—facilitates rapid impulse transmission along axons and enhances the speed of action potential propagation [32]. Consequently, it is assumed that signal attenuation over infinitesimal distances is negligible. Furthermore, the magnitude of the weight is constant, i.e.,

| W | = 1

. This characteristic eliminates the need for weight normalization typically required in conventional ANNs. With the weighted input, the oscillatory amplitude of the input neuron (

A = e^{θ}

) remains unaltered, while the unit oscillating spike is modulated by the phase (

ϕ

) of the weight. This representation is well-suited for modelling Spiking Neural Networks (SNNs) when information is encoded using temporal spike delays instead of absolute weight values.

The complex exponential function described in (5) exhibits periodic behaviour with a period of a full

2 π

cycle in the polar coordinate system. This complex exponential neuron model can be visualized as a vector circling around the origin in the polar plane at an angular frequency of

ω

(radians per second). By multiplying the weight, the phase (angle) of the vector can be altered. The range of

ϕ

is defined as

π \leq ϕ < π

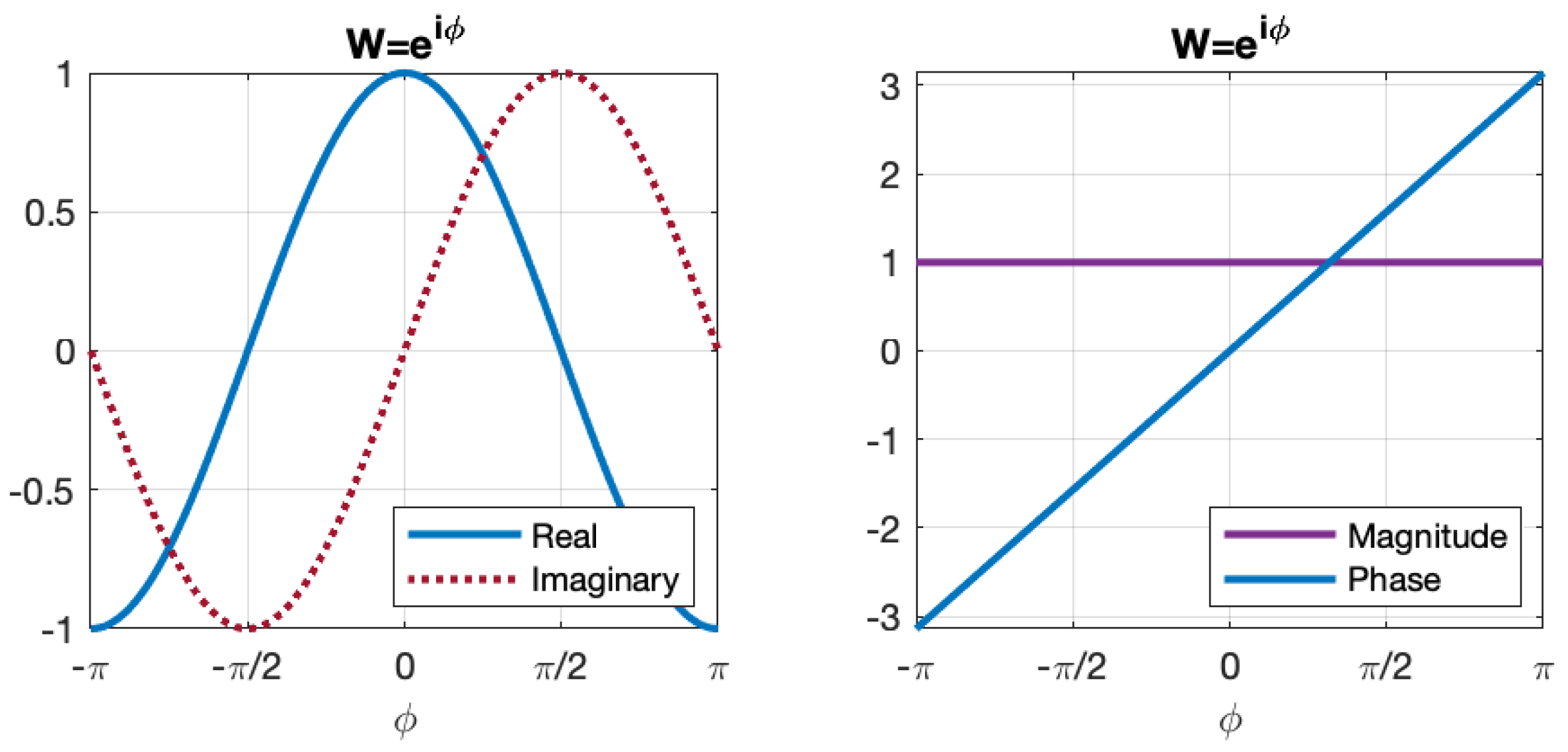
. Figure 1 illustrates the real and imaginary components, as well as the magnitude and phase of the complex exponential weight values relative to the variable

ϕ

\begin{matrix} e^{i ϕ} = e^{i (ϕ + 2 π * k)}, & k = 0, 1, 2 . . . \\ W = e^{i ϕ}, & - π \leq ϕ < π \end{matrix}

(5)

The interconnections within a neural network can be represented by a transformation matrix that includes weights corresponding to all input neurons. In a conventional ANN architecture, a nonlinear activation function (such as sigmoid or hyperbolic tangent) is typically applied to the sum of the weighted inputs in order to generate the output of a neuron. The nonlinearity of the activation function is crucial for ANNs to effectively represent nonlinear dynamic systems. However, with the complex exponential weights used in our neural network model, the weighted sum of complex exponential inputs already incorporates nonlinear properties. Therefore, the need for an additional nonlinear activation function is eliminated.

The complex exponential weight plays a key role in constructing the neural network model, and specifically, the real component of the complex weight value is used in the Routh-Hurwitz method, which is further explained in Appendix A.2.

3.3. Weighted Sum of Complex Exponential Neurons

In a neural network, a post-synaptic neuron receives multiple weighted inputs from pre-synaptic neurons. The aggregation of these inputs is represented by summing all the pre-synaptic neuron outputs multiplied by their corresponding weights (phase delays). Assuming that the neurons in the network are synchronized, the activity of the post-synaptic neuron can be represented as the sum of these weighted inputs, as shown in Equation (6).

\begin{matrix} S & = E_{1} W_{1} + E_{2} W_{2} + . . . + E_{n} W_{n} \\ = e^{i ω_{1} t + θ_{1}} e^{i ϕ_{1}} + e^{i ω_{2} t + θ_{2}} e^{i ϕ_{2}} + . . . +^{i ω_{n} t + θ_{n}} e^{i ϕ_{n}} \\ = e^{θ_{1}} e^{i (ω_{1} t + ϕ_{1})} + e^{θ_{2}} e^{i (ω_{2} t + ϕ_{2})} + . . . + e^{θ_{n}} e^{i (ω_{n} t + ϕ_{n})} \end{matrix}

(6)

4. Two-Neuron Neural Network Model

The interaction between two neurons can be described by a general two-neuron neural network model, as depicted in Figure 2. In this model, each neuron both excites and receives excitation from the other neuron. The synaptic weight

W_{12}

indicates the direction of the connection, with the subscript indicating that it is from neuron

E_{2}

to neuron

E_{1}

. Additionally, each neuron has a feedback connection to itself, represented by the synaptic weight

W_{x x}

The network dynamics can be represented by a system of two coupled linear equations, which can be written in matrix form as shown in Equation (7).

\begin{matrix} \{\begin{matrix} \begin{matrix} \frac{d E_{1}}{d t} = W_{11} E_{1} + W_{12} E_{2} \\ \frac{d E_{2}}{d t} = W_{21} E_{1} + W_{22} E_{2} \end{matrix} \end{matrix} \Rightarrow \frac{d}{d t} (\begin{matrix} E_{1} \\ E_{2} \end{matrix}) = (\begin{matrix} W_{11} & W_{12} \\ W_{21} & W_{22} \end{matrix}) (\begin{matrix} E_{1} \\ E_{2} \end{matrix}) \\ \frac{d}{d t} (\begin{matrix} E_{1} \\ E_{2} \end{matrix}) = \frac{d}{d t} (\begin{matrix} e^{i ω_{1} t + θ_{1}} \\ e^{i ω_{2} t + θ_{2}} \end{matrix}) = \frac{d}{d t} (\begin{matrix} e^{θ_{1}} e^{i ω_{1} t} \\ e^{θ_{2}} e^{i ω_{2} t} \end{matrix}) = (\begin{matrix} i ω_{1} E_{1} \\ i ω_{2} E_{2} \end{matrix}) \\ (\begin{matrix} W_{11} & W_{12} \\ W_{21} & W_{22} \end{matrix}) (\begin{matrix} E_{1} \\ E_{2} \end{matrix}) = (\begin{matrix} e^{i ϕ_{11}} & e^{i ϕ_{12}} \\ e^{i ϕ_{21}} & e^{i ϕ_{22}} \end{matrix}) (\begin{matrix} e^{θ_{1}} e^{i ω_{1} t} \\ e^{θ_{2}} e^{i ω_{2} t} \end{matrix}) = (\begin{matrix} e^{θ_{1}} e^{i (ω_{1} t + ϕ_{11})} + e^{θ_{2}} e^{i (ω_{2} t + ϕ_{12})} \\ e^{θ_{1}} e^{i (ω_{1} t + ϕ_{21})} + e^{θ_{2}} e^{i (ω_{2} t + ϕ_{22})} \end{matrix}) \\ \Rightarrow \{\begin{matrix} \begin{matrix} i ω_{1} e^{θ_{1}} e^{i ω_{1} t} = e^{θ_{1}} e^{i (ω_{1} t + ϕ_{11})} + e^{θ_{2}} e^{i (ω_{2} t + ϕ_{12})} \\ i ω_{2} e^{θ_{2}} e^{i ω_{2} t} = e^{θ_{1}} e^{i (ω_{1} t + ϕ_{21})} + e^{θ_{2}} e^{i (ω_{2} t + ϕ_{22})} \end{matrix} \end{matrix} \end{matrix}

(7)

4.1. Stability and Oscillation Conditions for Two-Neuron Network

The stability at the equilibrium and the conditions for oscillation in the two-neuron network are analyzed using the Routh-Hurwitz method, as shown in Equation (8).

\begin{matrix} Characteristic equation : d e t (A) = |(\begin{matrix} W_{11} & W_{12} \\ W_{21} & W_{22} \end{matrix})| = 0 \\ \Rightarrow λ^{2} - (W_{11} + W_{22}) λ + (W_{11} W_{22} - W_{12} W_{21}) = 0 \\ Routh - Hurwitz Coefficients : \\ a_{1} = - W_{11} - W_{22}, a_{2} = W_{11} W_{22} - W_{12} W_{21}, a_{3} = 0 \\ Eigenvalues : \\ λ = \frac{1}{2} [W_{11} + W_{22} \pm \sqrt{{(W_{11} - W_{22})}^{2} + 4 W_{12} W_{21}}] \\ Asymptotically stable condition : \\ Δ_{1} = a_{1} = W_{11} + W_{22} > 0, \\ Δ_{2} = a_{1} a_{2} = (- W_{11} - W_{22}) (W_{11} W_{22} - W_{12} W_{21}) > 0, \\ (λ = 0 is an eigenvalue if Δ_{2} = 0) \\ Oscillation condition : \\ Δ_{1} = a_{1} = W_{11} + W_{22} = 0 \\ Solution : \\ E_{k} = C_{1} e^{λ_{1} t} + C_{2} e^{λ_{2} t}, k = 1, 2 \end{matrix}

(8)

There are two types of interactions between neurons: excitatory and inhibitory. In an excitatory connection, the synaptic weight from neuron

E 1

to neuron

E 2

is positive, leading to an increase in the oscillatory frequency of

E 2

when excited by

E 1

. Conversely, in an inhibitory connection, the synaptic weight is negative, resulting in a decrease in the oscillatory frequency of

E 2

when inhibited by

E 1

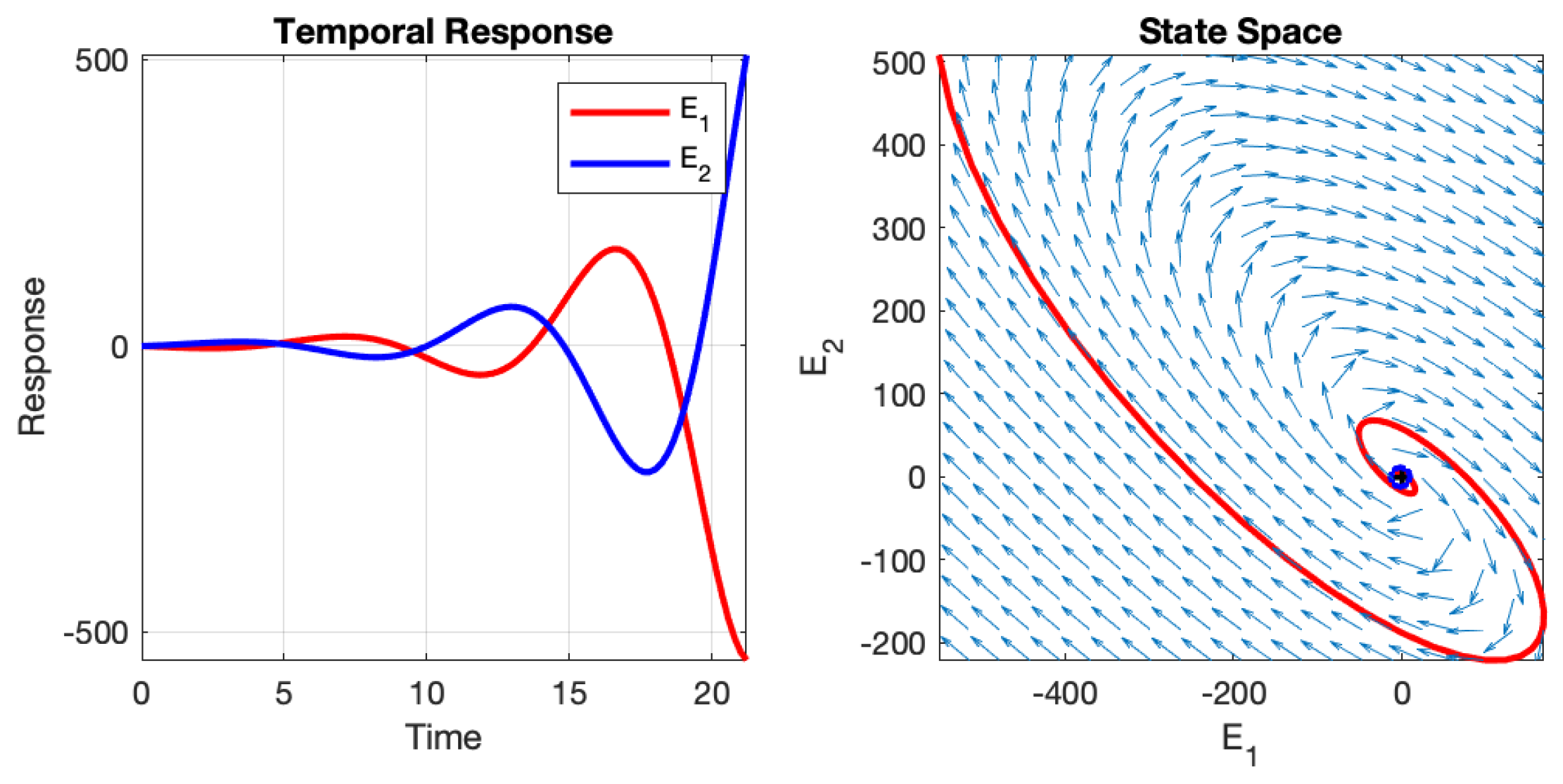
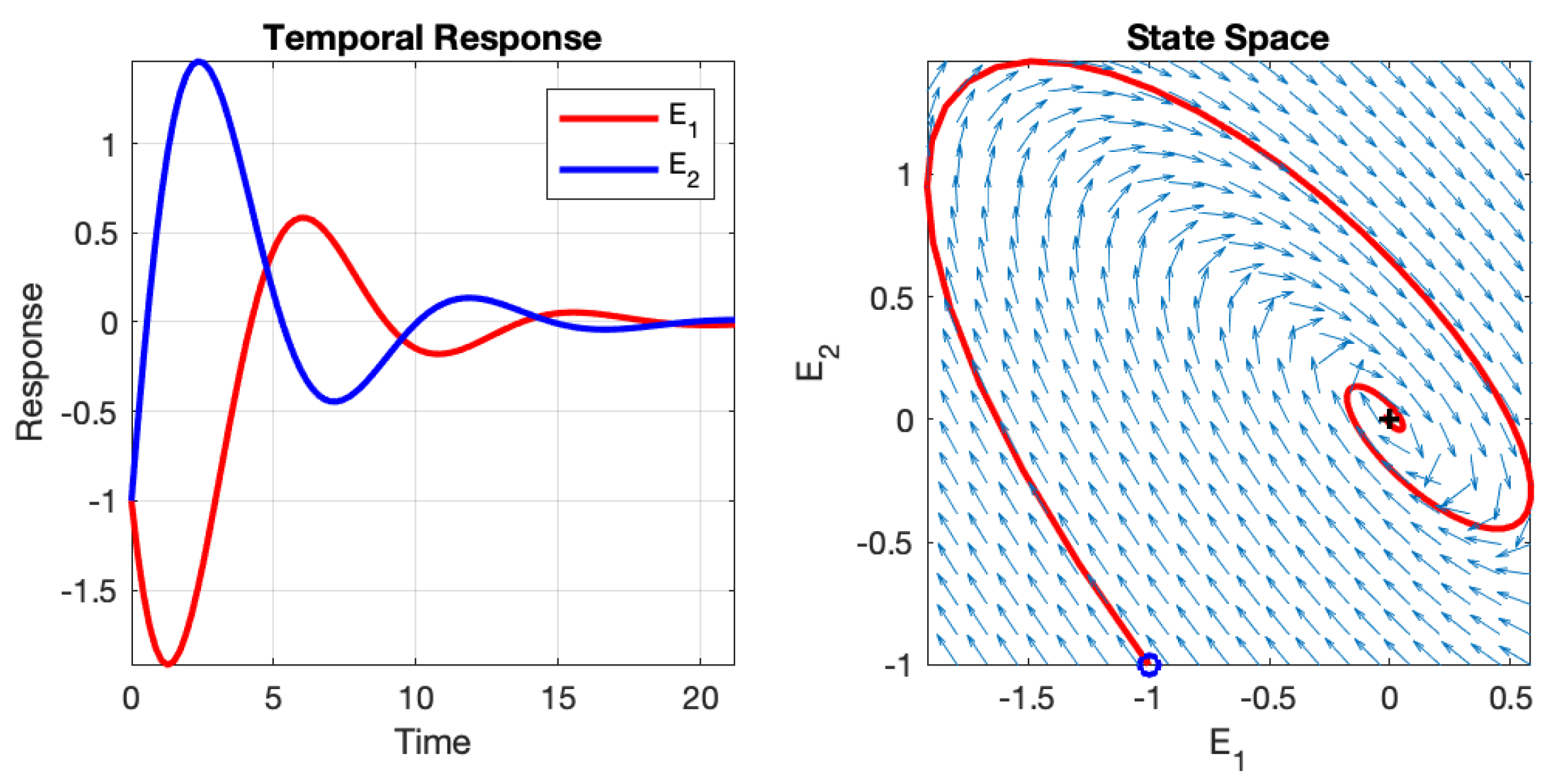
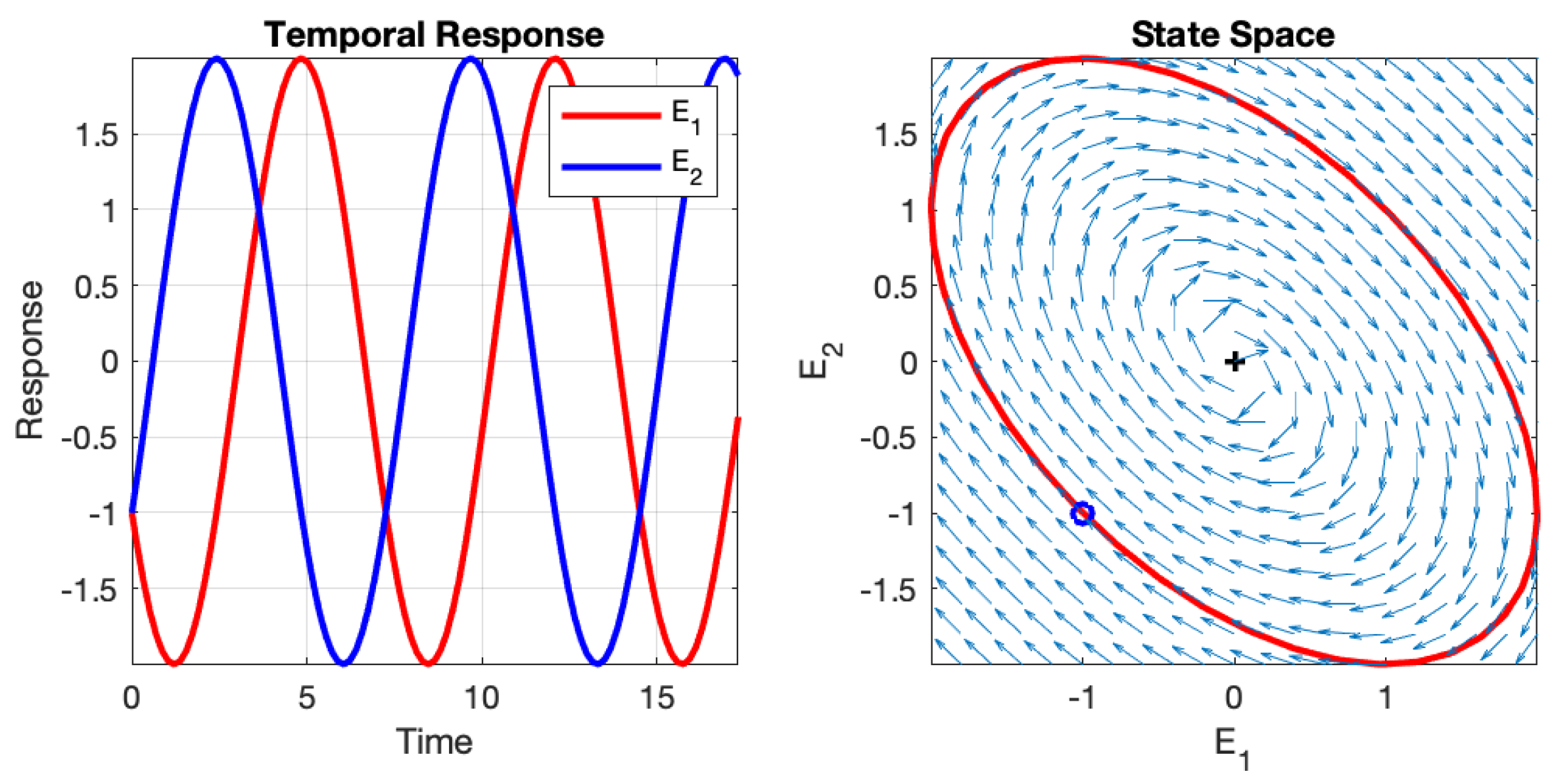
Depending on the initial values of the two neurons and the values of the four weights, the neural network can exhibit different behaviours: instability, asymptotic stability, or oscillation. These behaviours are illustrated in Figure 3, Figure 4, and Figure 5, respectively. The figures depict the temporal responses of the two neurons and their phase states during interaction. The parameters used in these examples are listed in Table 1, and the initial values are set as

E_{1} (0) = - 1

and

E_{2} (0) = - 1

4.2. Complex Exponential Model and the Eigenvalue $λ$

The complex exponential representation of the solution

e^{λ t}

provides insight into relating the eigenvalue

λ

to the complex exponential neuron model

e^{i ω t + θ}

. Considering that eigenvalues are complex numbers,

λ = x + i y

in a complex plane with Cartesian coordinates, and

e^{λ t} = e^{(x + i y) t} = e^{x t} e^{i y t}

. The real component x describes exponential decay (

x < 0

) or exponential growth (

x > 0

), while the imaginary component y describes sinusoidal oscillations. When

y = 0

λ

is a real number. When

x = 0

, the eigenvalues are pure imaginary numbers, indicating the condition for oscillation. In this case,

λ = \pm i y = \pm i ω

, where

ω_{1} = - ω_{2} = ω

. Since

θ

is a real value and

e^{θ}

is time-invariant, it can be separated to represent a constant

C_{p}

, so that

e^{i ω t + θ} = e^{θ} e^{i ω t} = C_{p} e^{i ω t}

. The solutions represented with

λ

in the complex plane and with

ω

in the polar plane are compared in (9).

\begin{matrix} Complex plane : E (t) = C_{1} e^{λ_{1} t} + C_{2} e^{λ_{2} t} = C_{1} e^{(x_{1} + i y_{1}) t} + C_{2} e^{(x_{2} + i y_{2}) t} \\ Polar plane : E (t) = e^{θ_{1}} e^{i ω_{1} t} + e^{θ_{2}} e^{i ω_{2} t} = C_{p 1} e^{i ω_{1} t} + C_{p 2} e^{i ω_{2} t} \\ \{\begin{matrix} \begin{matrix} C e^{λ t} = C e^{(x + i y) t} = C e^{x t} [cos (y t) + i sin (y t)] \\ e^{θ} e^{i ω t} = C_{p} e^{i ω t} = C_{p} [cos (ω t) + i sin (ω t)] \end{matrix} \end{matrix} \Rightarrow \{\begin{matrix} \begin{matrix} C e^{x t} cos (y t) = C_{p} cos (ω t) \\ C e^{x t} sin (y t) = C_{p} sin (ω t) \end{matrix} \end{matrix} \end{matrix}

(9)

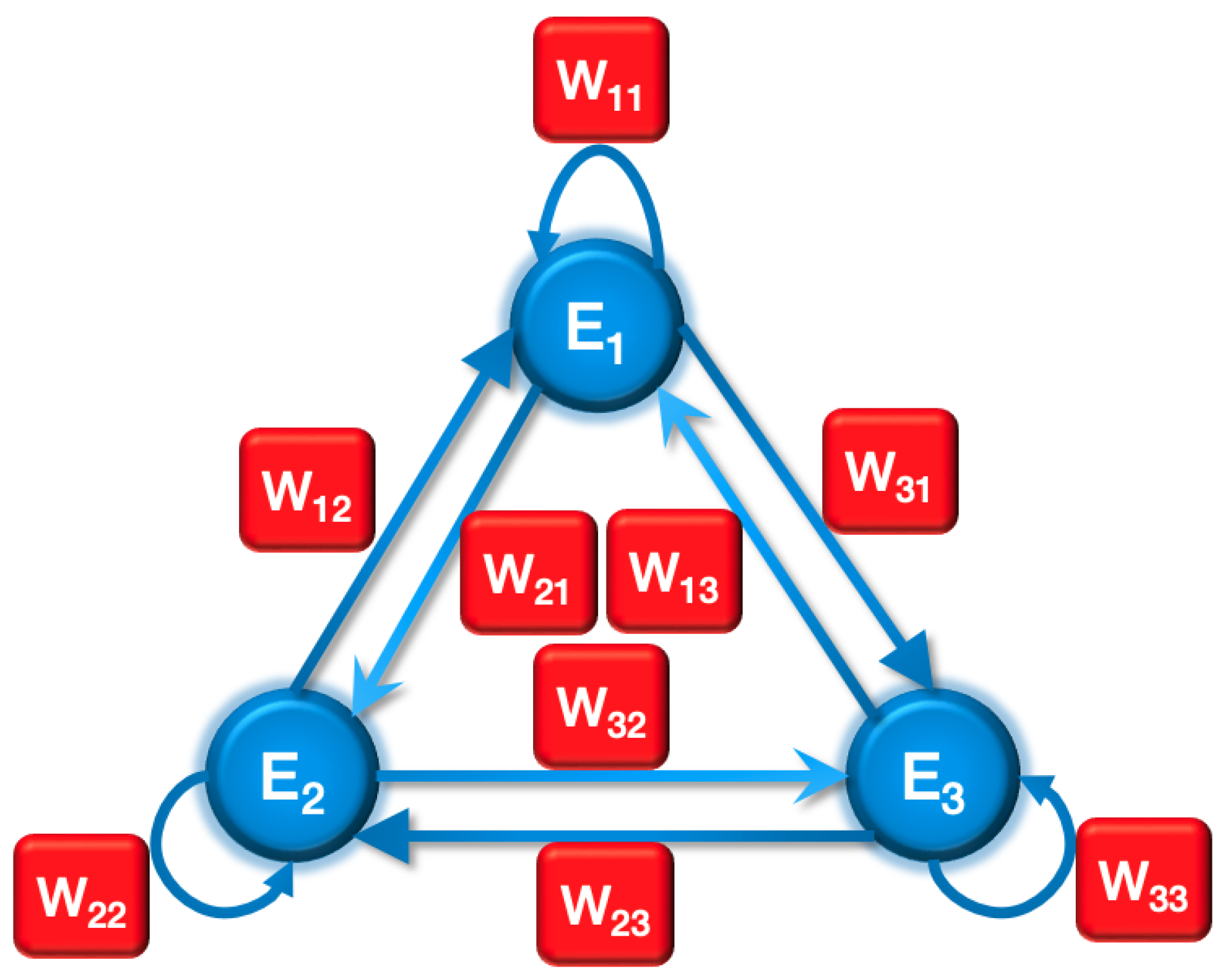
5. Three-Neuron Neuron Network Model

The three-neuron network, depicted in Figure 6, consists of three neurons interconnected in a specific pattern. Each neuron excites one neuron and inhibits another neuron, while also receiving excitation from one neuron and inhibition from another neuron. The synaptic connections between neurons are represented by the weight matrix

A

, which contains the weights of all neural connections. The system dynamics of this network can be described by three coupled linear equations, as shown in (10). These equations capture the interactions between the neurons and how their membrane potentials evolve over time. The solution to these equations is given in (11), which provides the temporal behaviour of each neuron’s membrane potential. By solving the equations, we can determine the evolution of the network dynamics and the behaviour of the individual neurons.

\frac{d}{d t} (\begin{matrix} E_{1} \\ E_{2} \\ E_{3} \end{matrix}) = [\begin{matrix} W_{11} & W_{12} & W_{13} \\ W_{21} & W_{22} & W_{23} \\ W_{31} & W_{32} & W_{33} \end{matrix}] (\begin{matrix} E_{1} \\ E_{2} \\ E_{3} \end{matrix})

(10)

E_{k} = C_{1} e^{λ_{1} t} + C_{2} e^{λ_{2} t} + C_{3} e^{λ_{3} t}, k = 1, 2, 3

(11)

The constants

C_{1}

C_{2}

, and

C_{3}

can be determined by substituting the solution into the differential equations and solving for the eigenvectors with the initial conditions. The derivation of these constants is provided in (12). The solution is represented as a column vector

E = {[E_{1}, E_{2}, E_{3}]}^{T}

, where T indicates a transpose operation, converting a row vector to a column vector. The initial condition

E_{0} = {[E_{1_{0}}, E_{2_{0}}, E_{3_{0}}]}^{T}

is also a column vector. The eigenvectors

v_{1}

v_{2}

, and

v_{3}

are column vectors with three elements. These eigenvectors are combined into a matrix

v = [v_{1}, v_{2}, v_{3}]

. To calculate the constants, it is important to note that the exponential of

A t

, denoted as

e^{A t}

, is equal to the product of three matrices:

e^{A t} = v e^{Λ t} v^{- 1}

, where

e^{Λ t}

is a diagonal matrix. By applying these calculations, we can determine the constants

C_{1}

C_{2}

, and

C_{3}

and obtain the complete solution for the network dynamics.

\begin{matrix} Eigenvectors : v = [v_{1}, v_{2}, v_{3}] = [\begin{matrix} v_{1} (1) & v_{2} (1) & v_{3} (1) \\ v_{1} (2) & v_{2} (2) & v_{3} (2) \\ v_{1} (3) & v_{2} (3) & v_{3} (3) \end{matrix}] \\ e^{Λ t} = [\begin{matrix} e^{λ_{1} t} & 0 & 0 \\ 0 & e^{λ_{2} t} & 0 \\ 0 & 0 & e^{λ_{3} t} \end{matrix}], A = [\begin{matrix} W_{11} & W_{12} & W_{13} \\ W_{21} & W_{22} & W_{23} \\ W_{31} & W_{32} & W_{33} \end{matrix}] \\ e^{A t} = v e^{Λ t} v^{- 1} = [\begin{matrix} e^{λ_{1} t} v_{1} & e^{λ_{2} t} v_{2} & e^{λ_{3} t} v_{3} \end{matrix}] v^{- 1} \\ {CC}_{3 \times 1} = {[v]}^{- 1} * E_{0} \\ \begin{matrix} E_{1} = C C (1) v_{1} (1) e^{λ_{1} t} + C C (2) v_{2} (1) e^{λ_{2} t} + C C (3) v_{3} (1) e^{λ_{3} t} \\ E_{2} = C C (1) v_{1} (2) e^{λ_{1} t} + C C (2) v_{2} (2) e^{λ_{2} t} + C C (3) v_{3} (2) e^{λ_{3} t} \\ E_{3} = C C (1) v_{1} (3) e^{λ_{1} t} + C C (2) v_{2} (3) e^{λ_{2} t} + C C (3) v_{3} (3) e^{λ_{3} t} \end{matrix} \end{matrix}

(12)

5.1. Stability and Oscillation Conditions for Three-Neuron Network

A symmetrical network geometry is adopted to simplify the dynamic analysis of stability and oscillation conditions in the three-neuron network. In this configuration, the same weight value

W_{e}

is assigned to all excitatory connections,

W_{i}

to all inhibitory connections, and

W_{d}

to all feedback connections. The general analysis for the stability and oscillation conditions of the three-neuron network is presented in (13). This analysis provides a mathematical expression using the Routh-Hurwitz method to determine the stability of the network without substituting specific parameter values. It allows for a comprehensive understanding of the network dynamics and stability properties based on the weight values assigned to the different connections.

\begin{matrix} A = (\begin{matrix} W_{d} & W_{i} & W_{e} \\ W_{e} & W_{d} & W_{i} \\ W_{i} & W_{e} & W_{d} \end{matrix}) \\ Routh - Hurwitz Coefficients : \\ a_{1} = - 3 W_{d} \\ a_{2} = - 3 W_{e} W_{i} + 3 W_{d}^{2} \\ a_{3} = - W_{i}^{3} - W_{e}^{3} + 3 W_{d} W_{e} W_{i} - W_{d}^{3} \\ Eigenvalues : \\ λ = (\begin{matrix} W_{i} + W_{e} + W_{d} \\ - \frac{W_{i}}{2} - \frac{W_{e}}{2} + W_{d} - \frac{\sqrt{3} W_{e} i}{2} + \frac{\sqrt{3} W_{i} i}{2} \\ - \frac{W_{i}}{2} - \frac{W_{e}}{2} + W_{d} + \frac{\sqrt{3} W_{e} i}{2} - \frac{\sqrt{3} W_{i} i}{2} \end{matrix}) \\ Stable condition : \\ W_{i} + W_{e} + W_{d} < 0, - \frac{W_{i}}{2} - \frac{W_{e}}{2} + W_{d} < 0 \\ Asymptotically stable condition : \\ Δ_{1} > 0, Δ_{2} > 0, Δ_{3} > 0 \\ Oscillation condition : \\ Δ_{2} = W_{i}^{3} + W_{e}^{3} + 6 W_{d} W_{e} W_{i} - 8 W_{d}^{3} = 0 \\ \Rightarrow W_{d} = (\begin{matrix} \frac{1}{2} (W_{i} + W_{e}) \\ \frac{1}{4} (- W_{e} - W_{i} - \sqrt{3} W_{e} i + \sqrt{3} W_{i} i) \\ \frac{1}{4} (- W_{e} - W_{i} + \sqrt{3} W_{e} i - \sqrt{3} W_{i} i) \end{matrix}) \end{matrix}

(13)

When the feedback weight

W_{d}

is set to

(W_{i} + W_{e}) / 2

, the solution of the three-neuron network exhibits center oscillations, where the neurons oscillate sinusoidally around the equilibrium point. The stability of the equilibrium point can be determined based on the relationship between

W_{d}

and

(W_{i} + W_{e}) / 2

. Specifically, if

W_{d} < (W_{i} + W_{e}) / 2

, the equilibrium point is asymptotically stable, whereas if

W_{d} > (W_{i} + W_{e}) / 2

, the equilibrium point is unstable. For example, consider the case where

W_{e} = 2 / 3

W_{i} = - 1

, and

W_{d} = - 1 / 3

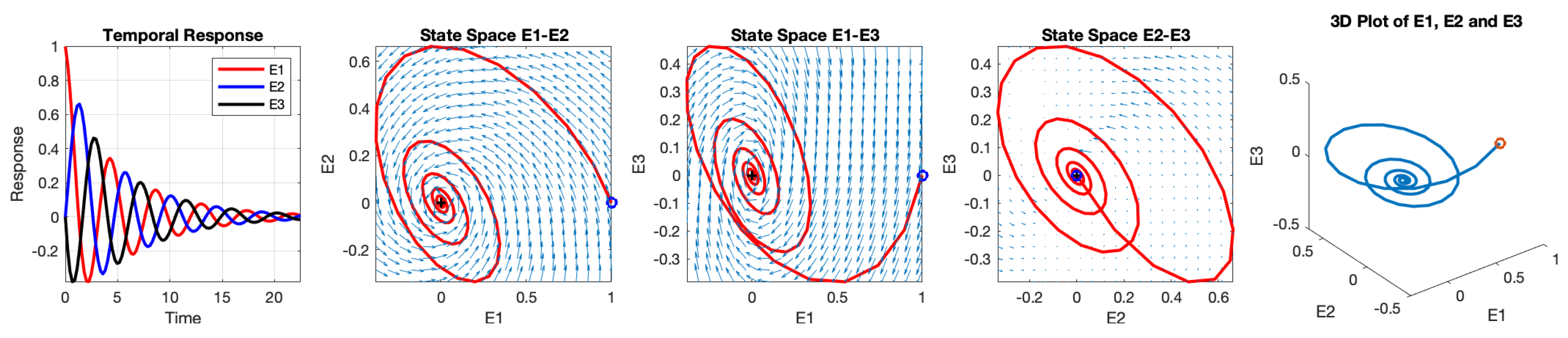
. The eigenvalues and the corresponding solutions of the equations are provided in (14). Even without explicitly obtaining the solutions, the eigenvalues alone can provide sufficient information about the equilibrium point. In this case, the equilibrium point is identified as an asymptotically stable spiral point.

The temporal responses of the three neurons and their interacting phase states are illustrated in Figure 7. The initial values are set to

E 1_{0} = 1

E 2_{0} = 0

, and

E 3_{0} = 0

, indicated by the blue dot. The phase delays between the three neurons are symmetrical. Specifically, the phase of

E 2

lags

2 π / 3

behind

E 1

, and the phase of

E 3

lags

2 π / 3

behind

E 2

. This symmetrical phase delay is a result of the symmetrical setting of the synaptic weight values. When the three-neuron network oscillates, the phase delay between two adjacent neurons that subsequently fire is

π / 3

\begin{matrix} A = (\begin{matrix} - 1 / 3 & - 1 & 2 / 3 \\ 2 / 3 & - 1 / 3 & - 1 \\ - 1 & 2 / 3 & - 1 / 3 \end{matrix}) \\ Eigenvalues : λ = e i g (A) = - 0.667, - 0.167 \pm 1.443 i \\ Solution : E_{k} = C_{1} e^{λ_{1} t} + C_{2} e^{λ_{2} t} + C_{3} e^{λ_{3} t} \\ = C_{1} e^{- 0.667 t} + C_{2} e^{- 0.167 t} s i n (1.443 t) + C_{3} e^{- 0.5 t} c o s (1.443 t), k = 1, 2, 3 \end{matrix}

(14)

5.2. Control Network Stability Using Weight Parameter $W_{i}$

In the three-neuron network, any synaptic weight can serve as a control parameter for network stability. Let’s consider a scenario where the inhibitory weight

W_{i}

is used as the control parameter, while keeping other weights fixed at

W_{e} = \frac{1}{4}

and

W_{d} = - \frac{1}{8}

. To satisfy the oscillation condition (

Δ_{2} = 0

) and ensure stability, the lower-order determinants of the Routh-Hurwitz matrix need to be greater than zero. By solving the inequalities derived in (15), it is found that oscillation is generated when

W_{i} = - \frac{1}{2}

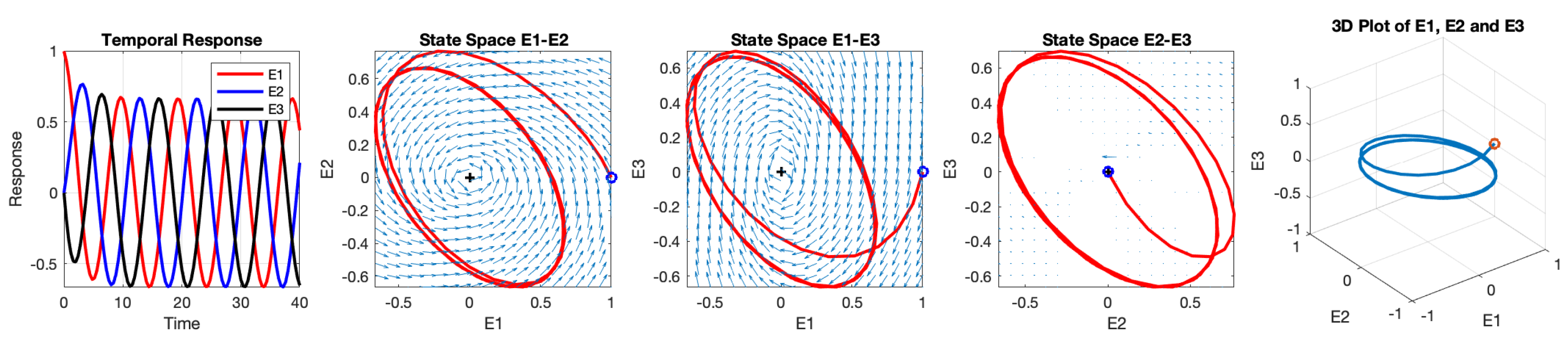
The temporal responses of the three neurons and their interactions in three-dimensional space are depicted in Figure 8. The initial values are set as

E 1_{0} = 1

E 2_{0} = 0

, and

E 3_{0} = 0

. The 3D plot illustrates that the solutions oscillate in a circular pattern around a central equilibrium. The oscillation starts in a three-dimensional state space and eventually converges to a two-dimensional plane within the 3D space. This behavior occurs because the initial point is not located on the stable circle. The frequency of this oscillation is

\frac{3 \sqrt{3}}{8}

radians per second, approximately equivalent to 0.103 Hz. It is worth noting that the equilibrium is asymptotically stable when

W_{i} > - \frac{1}{2}

and becomes unstable when

W_{i} < - \frac{1}{2}

\begin{matrix} A = (\begin{matrix} - \frac{1}{8} & W_{i} & \frac{1}{4} \\ \frac{1}{4} & - \frac{1}{8} & W_{i} \\ W_{i} & \frac{1}{4} & - \frac{1}{8} \end{matrix}) \\ Routh - Hurwitz Coefficients : \\ a_{1} = \frac{3}{8}, a_{2} = \frac{3}{64} - \frac{3 W_{i}}{4}, a_{3} = - \frac{7}{512} - \frac{3 W_{i}}{32} - W_{i}^{3} \\ Oscillation condition : \\ Δ_{1} = \frac{3}{8} > 0, \\ Δ_{2} = |\begin{matrix} a_{1} & 1 \\ a_{3} & a_{2} \end{matrix}| = a_{1} a_{2} - a_{3} = W_{i}^{3} - 3 W_{i} / 16 + 1 / 32 = 0 \\ \Rightarrow W_{i} = - \frac{1}{2}, \frac{1}{4}, \frac{1}{4} \\ Eigenvalues (W_{i} = - \frac{1}{2}) : \\ λ = (\begin{matrix} \frac{1}{8} + W_{i} \\ - \frac{W_{i}}{2} - \frac{1}{4} + \frac{\sqrt{3} W_{i} i}{2} - \frac{\sqrt{3} i}{8} \\ - \frac{W_{i}}{2} - \frac{1}{4} - \frac{\sqrt{3} W_{i} i}{2} + \frac{\sqrt{3} i}{8} \end{matrix}) = (\begin{matrix} - \frac{3}{8} \\ \frac{3 \sqrt{3} i}{8} \\ - \frac{3 \sqrt{3} i}{8} \end{matrix}) \\ Solution : \\ E_{k} = C_{1} e^{- \frac{3}{8} t} + C_{2} e^{\frac{3 \sqrt{3} i}{8} t} + C_{3} e^{\frac{3 \sqrt{3} i}{8} t}, k = 1, 2, 3 \end{matrix}

(15)

6. Discussion and Conclusions

This paper focuses on the dynamic analysis of neural networks, particularly regarding the stability and oscillation conditions in networks with symmetrical geometry. It is demonstrated that the weights of neural connections play a crucial role in controlling the stability of the network. Importantly, these weights can be adjusted to generate neural oscillation as well as stable and unstable output patterns. Individual neurons are described by differential equations with interactive weights connected to other neurons, as well as a feedback weight connected to the neuron itself. Analytical approaches are employed to determine the dynamic states of the neurons and the network. A symmetrical neural network geometry, where synaptic weights have the same values, gives rise to temporally symmetrical oscillation patterns. Notably, a three-neuron network can be represented by an equilateral triangle shape, and a four-neuron network by an equilateral triangular pyramid shape (regular tetrahedron). These geometries are of great interest as they serve as fundamental building blocks for some of the most stable structures found in nature.

When a two-neuron network oscillates, there is a phase shift of

π / 2

between the two neurons. Similarly, in a three-neuron network, the phase delay between two adjacent and subsequently firing neurons is

π / 3

. These observed oscillation patterns in the presented spiking neural network (SNN) exhibit similarities to the behaviors observed in biological neuron networks. However, further validation through clinical experimental results is necessary, and more complex SNN models are required to accurately capture real-world biological neural network behaviour. It is important to note that current clinical experimental results are limited, and the presented model can serve as a foundation for targeted data collection in clinical experiments. The insights gained from these experiments can then be utilized to design more sophisticated SNN models that better capture the behaviour of biological neural networks.

Funding

This research received no external funding.

Data Availability Statement

Not applicable

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A. Analitical Methods

Appendix A.1. Eigenvalues and the Stability of Equilibrium

An eigenvector (v) of a square matrix represents a nonzero vector that only changes by a scalar factor when the matrix is applied to it as a linear transformation. The scalar factor is the corresponding eigenvalue (

λ

) associated with the eigenvector. The characteristic equation is derived from the equation

A v = λ v

, where A is the matrix, v is the eigenvector, and

λ

is the eigenvalue. This equation can be rearranged as

(A - λ I) v = 0

, where I is the identity matrix. The characteristic equation is obtained by calculating the determinant of the matrix

(A - λ I)

and setting it equal to zero.

To find the eigenvalues of a given matrix A, we solve the characteristic equation

| (A - λ I) | = 0

, where

| (. . .) |

denotes the determinant. Each eigenvalue is substituted into the equation

(A - λ_{k} I) v_{k} = 0

to find the corresponding eigenvector

v_{k}

The stability of the equilibrium is determined by the eigenvalues

λ

, which are the roots of the characteristic equation. The characteristic equation is typically expressed as a polynomial, as shown in (A1). If all the real parts of the eigenvalues are negative, i.e.,

a_{k} > 0

for

1 \leq k \leq N

, the equilibrium of the system is asymptotically stable.

λ^{N} + a_{1} λ^{N - 1} + a_{2} λ^{N - 2} + . . . + a_{N - 1} λ + a_{N} = 0

(A1)

In the two-dimensional Hénon map chaotic system, equilibria can be classified into different types based on the system’s parameters. The stability of these equilibria can be analyzed using eigenvalues. The types of equilibria and their stability characteristics are described as follows:

Spiral point: An equilibrium is classified as a spiral point when the eigenvalues form a complex conjugate pair. The spiral point is asymptotically stable if the real part of the eigenvalues is negative.
Centre: A centre equilibrium occurs when both eigenvalues are pure imaginary. All trajectories around a centre exhibit periodic oscillations.
Node: The equilibrium is classified as a node when the eigenvalues are both real and have the same sign. If the eigenvalues are negative, the node is asymptotically stable.
Saddle point: A saddle point is characterized by a pair of eigenvalues that are both real and have opposite signs. A saddle point is always unstable.
Critical damping: Critical damping is a special case where the two eigenvalues of the characteristic equation are identical. It represents the boundary between an asymptotically stable node and an asymptotically stable spiral point. In the case of critical damping, the system reaches equilibrium quickly and exhibits the fastest exponential decay. Physiologically, critical damping can be associated with muscle contraction.

The classification of equilibria and their stability properties provides insights into the behavior of the two-dimensional Hénon map chaotic system and helps understand its dynamic characteristics.

Appendix A.2. The Routh-Hurwitz Method

The Routh-Hurwitz method[23], proposed by Edward John Routh and Adolf Hurwitz, is a mathematical technique used to analyze the dynamics and stability of systems, including neural networks. It involves calculating the coefficients of the characteristic equation and using them to construct a Routh array. The Routh array is then used to determine the stability and oscillation conditions of the system based on the signs of the coefficients.

In the case of a two-neuron system, the series of determinants, derived using the Routh-Hurwitz method, can be found in (A2). These determinants are used to evaluate the stability and oscillation conditions of the system. Similarly, for a three-neuron system, the series of determinants derived using the Routh-Hurwitz method are listed in (A3). These determinants provide information about the stability and oscillation properties of the system based on the coefficients of the characteristic equation. By analyzing the determinants and their signs, one can determine whether the system is stable, oscillatory, or unstable, and make further conclusions about its dynamic behaviour. It is mentioned that the calculations and evaluations for stability and oscillation conditions are programmed using MATLAB, a widely used numerical computing software that provides convenient tools for such analyses.

Δ_{1} = a_{1}, Δ_{2} = |\begin{matrix} a_{1} & 1 \\ a_{3} & a_{2} \end{matrix}| Δ_{3} = a_{3} Δ_{2}

(A2)

\begin{matrix} Δ_{1} = a_{1}, Δ_{2} = |\begin{matrix} a_{1} & 1 \\ a_{3} & a_{2} \end{matrix}|, Δ_{3} = |\begin{matrix} a_{1} & 1 & 0 \\ a_{3} & a_{2} & a_{1} \\ 0 & a_{4} & a_{3} \end{matrix}|, Δ_{4} = a_{4} Δ_{3} \end{matrix}

(A3)

The general form of the Routh-Hurwitz determinants for an N-dimension system is listed in (A4) [33].

Δ_{k} = |\begin{matrix} a_{1} & 1 & 0 & 0 & 0 & \dots \\ a_{3} & a_{2} & a_{1} & 1 & 0 & \dots \\ a_{5} & a_{4} & a_{3} & a_{2} & a_{1} & \dots \\ a_{7} & a_{6} & a_{5} & a_{4} & a_{3} & \dots \\ ⋮ & ⋮ & ⋮ & ⋮ & ⋮ & ⋮ \\ a_{2 k - 1} & a_{2 k - 2} & a_{2 k - 3} & \dots & \dots & a_{k} \end{matrix}|

(A4)

The coefficient of the highest order

λ^{N}

is made implicit, i.e,

a_{0} = 1

. When

k > N

a_{k} = 0

Asymptotically stable:The condition for the system to be asymptotically stable is

Δ_{k} > 0

for

1 \leq k \leq N

. In addition,

λ = 0

is an eigenvalue if

Δ_{N} = 0

Oscillation:The condition for an N-dimension system to oscillate is that one pair of eigenvalues must be purely imaginary:

Δ_{k} > 0

and

Δ_{N - 1} = 0

for

1 \leq k \leq N - 2

References

Freeman, W.J. Simulation of chaotic EEG patterns with a dynamic model of the olfactory system. Biological Cybernetics 1987, 56, 139–150. [CrossRef]
Yao, Y.; Freeman, W.J. Model of biological pattern recognition with spatially chaotic dynamics. Neural Networks 1990, 3, 153–170. [CrossRef]
Alfaro-Ponce, M.; Argüelles, A.; Chairez, I. Pattern recognition for electroencephalographic signals based on continuous neural networks. Neural Networks 2016, 79, 88 – 96. [CrossRef]
Terra, V.C.; Amorim, R.; Silvado, C.; de Oliveira, A.J.; Jorge, C.L.; Faveret, E.; Ragazzo, P.; Paola, L.D. Vagus Nerve Stimulator in Patients with Epilepsy: Indications and Recommendations for Use. Arquivos de Neuro-Psiquiatria 2013, 71, 902–906. [CrossRef]
DeGiorgio, C.M.; Krahl, S.E. Neurostimulation for Drug-Resistant Epilepsy. CONTINUUM: Lifelong Learning in Neurology 2013, 19, 743–755. [CrossRef]
Grafton, S.T.; Turner, R.S.; Desmurget, M.; Bakay, R.; Delong, M.; Vitek, J.; Crutcher, M. Normalizing motor-related brain activity: Subthalamic nucleus stimulation in Parkinson disease. Neurology 2006, 66, 1192–1199. [CrossRef]
Deuschl, G.; Schade-Brittinger, C.; Krack, P.; Volkmann, J.; Schäfer, H.; Bötzel, K.; Daniels, C.; Deutschländer, A.; Dillmann, U.; Eisner, W.; Gruber, D.; Hamel, W.; Herzog, J.; Hilker, R.; Klebe, S.; Kloß, M.; Koy, J.; Krause, M.; Kupsch, A.; Lorenz, D.; Lorenzl, S.; Mehdorn, H.M.; Moringlane, J.R.; Oertel, W.; Pinsker, M.O.; Reichmann, H.; Reuß, A.; Schneider, G.H.; Schnitzler, A.; Steude, U.; Sturm, V.; Timmermann, L.; Tronnier, V.; Trottenberg, T.; Wojtecki, L.; Wolf, E.; Poewe, W.; Voges, J. A Randomized Trial of Deep-Brain Stimulation for Parkinson’s Disease. New England Journal of Medicine 2006, 355, 896–908. [CrossRef]
Brown, P. Abnormal oscillatory synchronisation in the motor system leads to impaired movement. Current Opinion in Neurobiology 2007, 17, 656–664. [CrossRef]
Shah, S.A.A.; Zhang, L.; Bais, A. Dynamical system based compact deep hybrid network for classification of Parkinson disease related EEG signals. Neural Networks 2020, 130, 75–84. [CrossRef]
Buzsaki, G. Neuronal Oscillations in Cortical Networks. Science 2004, 304, 1926–1929. [CrossRef]
Cohen, M.X. Fluctuations in Oscillation Frequency Control Spike Timing and Coordinate Neural Networks. Journal of Neuroscience 2014, 34, 8988–8998, [http://www.jneurosci.org/content/34/27/8988.full.pdf]. [CrossRef]
L, Z. Oscillation Patterns of A Complex Exponential Neural Network. 2022 IEEE/WIC/ACM International Joint Conference on Web Intelligence and Intelligent Agent Technology (WI-IAT) 2022, pp. 423–430. [CrossRef]
Hodgkin, A.L.; Huxley, A.F. A quantitative description of membrane current and its application to conduction and excitation in nerve. The Journal of Physiology 1952, 117, 500–544. [CrossRef]
Izhikevich, E. Simple model of spiking neurons. IEEE Transactions on Neural Networks 2003, 14, 1569–1572. [CrossRef]
Wulfram Gerstner, W.K. Spiking Neuron Models; Cambridge University Press, 2002.
Borgers, C. An Introduction to Modeling Neuronal Dynamics; Springer International Publishing, 2017.
Maass, W. Networks of spiking neurons: The third generation of neural network models. Neural Networks 1997, 10, 1659–1671. [CrossRef]
Freeman, W.J. Societies of Brains: A Study in the Neuroscience of Love and Hate (INNS Series of Texts, Monographs, and Proceedings Series); Psychology Press, 1995.
Freeman, W. How Brains Make Up Their Minds; COLUMBIA UNIV PR, 2001.
Zhang, L. Neural Dynamics Analysis for A Novel Bio-inspired Logistic Spiking Neuron Model. 2023 IEEE International Conference on Consumer Electronics (ICCE), 2023, pp. 1–6. [CrossRef]
Zhang, L. Building Logistic Spiking Neuron Models Using Analytical Approach. IEEE Access 2019, pp. 1–10. [CrossRef]
Freeman, W.J., Mass Action In The Nervous System - Examination of the Neurophysiological Basis of Adaptive Behavior through the EEG; ACADEMIC PRESS, 1975; chapter 1.
Routh, E.J. A Treatise on the Stability of a Given State of Motion: Particularly Steady Motion; Macmillan, 1877.
Rodriguez-Oroz, M.C. Bilateral deep brain stimulation in Parkinson’s disease: a multicentre study with 4 years follow-up. Brain 2005, 128, 2240–2249. [CrossRef]
The Deep-Brain Stimulation for Parkinson’s Disease Study Group. Deep-Brain Stimulation of the Subthalamic Nucleus or the Pars Interna of the Globus Pallidus in Parkinson’s Disease. New England Journal of Medicine 2001, 345, 956–963. [CrossRef]
Wendling, F.; Bellanger, J.J.; Bartolomei, F.; Chauvel, P. Relevance of nonlinear lumped-parameter models in the analysis of depth-EEG epileptic signals. Biological Cybernetics 2000, 83, 367–378. [CrossRef]
Zhang, L. Artificial Neural Networks Model Design of Lorenz Chaotic System for EEG Pattern Recognition and Prediction. The first IEEE Life Sciences Conference (LSC); IEEE: Sydney, Australia, 2017; pp. 39–42. [CrossRef]
Zhang, L. Design and Implementation of Neural Network Based Chaotic System Model for the Dynamical Control of Brain Stimulation. The Second International Conference on Neuroscience and Cognitive Brain Information (BRAININFO 2017); , 2017; pp. 14–21.
Wilson, H.R. Spikes, Decisions, and Actions: The Dynamical Foundations of Neuroscience; Oxford University Press, 1999.
Zhang, L. A Bio-Inspired Neural Network for Modelling COVID-19 Transmission in Canada. 2022 IEEE Canadian Conference on Electrical and Computer Engineering (CCECE), 2022, pp. 281–287. [CrossRef]
Zhang, L. Dynamic Analysis of Neural Network Oscillation Using Routh-Hurwitz Method. Proceedings of the 32nd Annual International Conference on Computer Science and Software Engineering; IBM Corp.: USA, 2022; CASCON ’22, pp. 157–162.
Susuki, K. Myelin: A Specialized Membrane for Cell Communication. Nature Education 2010, 3(9):59.
Wilson, H.R., Spikes, Decisions, and Actions: The Dynamical Foundations of Neuroscience; Oxford University Press, 1999; chapter 4. Higher dimensional systems, p. 51.

Figure 1. Complex Exponential weight

W = e^{i ϕ}

Figure 1. Complex Exponential weight

W = e^{i ϕ}

Figure 2. Interconnection of Two-Neuron Network Model.

Figure 3. Two-neuron Network Unstable

Figure 4. Two-neuron Network Stable

Figure 5. Two-neuron Network Oscillation

Figure 6. Interconnection of 3 Neurons Network Model

Figure 7. Three-neuron Network (Asymptotically Stable)

Figure 8. Three-neuron Network (Oscillation)

Table 1. Parameter Control of Two-neuron Network

Parameter	$W_{11}$	$W_{12}$	$W_{21}$	$W_{22}$	$a_{1}$	$a_{2}$	$Δ_{1}$	$Δ_{2}$
Unstable	1	1	-1	-0.5	-0.5	0.5	-0.5	-0.25
Stable	0.5	1	-1	-1	0.5	0.5	0.5	0.25
Oscillation	0.5	1	-1	-0.5	0	0.75	0	0

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Dynamic Analysis and Control of Neural Networks: Stability, Oscillation, and Weight-Based Modulation

Abstract

1. Introduction

2. Materials and Methods

2.1. Neuronal Oscillation Vs. Neural Network Oscillation

2.2. Synchronized Neural Oscillation and Deep Brain Stimulation

2.3. Dynamic Analysis of Neural Network Model

3. Complex Exponential Neuron Model

3.1. Derivatives of Complex Exponential Neuron Model

3.2. Weighted Input of Complex Exponential Neurons

3.2.1. Exponential weight W = e ϕ

3.2.2. Complex Exponential weight W = e i ϕ

3.3. Weighted Sum of Complex Exponential Neurons

4. Two-Neuron Neural Network Model

4.1. Stability and Oscillation Conditions for Two-Neuron Network

4.2. Complex Exponential Model and the Eigenvalue λ

5. Three-Neuron Neuron Network Model

5.1. Stability and Oscillation Conditions for Three-Neuron Network

5.2. Control Network Stability Using Weight Parameter W i

6. Discussion and Conclusions

Funding

Data Availability Statement

Conflicts of Interest

Appendix A. Analitical Methods

Appendix A.1. Eigenvalues and the Stability of Equilibrium

Appendix A.2. The Routh-Hurwitz Method

References

MDPI Initiatives

Important Links

Subscribe

3.2.1. Exponential weight $W = e^{ϕ}$

3.2.2. Complex Exponential weight $W = e^{i ϕ}$

4.2. Complex Exponential Model and the Eigenvalue $λ$

5.2. Control Network Stability Using Weight Parameter $W_{i}$