Prerpints.org logo
Preprint
Article

Novel Multivariable Evolutionary Algorithm-Based Method for Modal Reconstruction of the Corneal Surface from Sparse and Incomplete Point Clouds

Altmetrics

Downloads

105

Views

43

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

22 May 2023

Posted:

23 May 2023

You are already at the latest version

Alerts
Abstract
Three-Dimensional reconstruction of the corneal surface provides a powerful tool for managing corneal diseases. This study proposes a novel method for reconstructing the corneal surface from elevation point clouds, using modal schemes capable of reproducing corneal shapes using surface polynomial functions. The multivariable polynomial fitting was performed using a non-dominated sorting multivariable genetic algorithm (NS-MVGA). Standard reconstruction methods using least-squares discrete fitting (LSQ) and sequential quadratic programming (SQP) were compared with the evolutionary algorithm-based approach. The study included 49 eyes of 49 patients (ages 11-63) sorted in two groups: control (33 eyes) and keratoconus (KC) (16 eyes). Tomographic information (Sirius, Costruzione Strumenti Oftalmici, Italy) was processed using Matlab. The goodness of fit for each method was evaluated using mean squared error (MSE), measured at the same nodes where the elevation data were collected. Polynomial fitting based on NS-MVGA improves MSE values by 86% compared to LSQ-based methods in healthy patients. Moreover, this new method improves aberrated surface reconstruction by 43% for Amsler-Krumeich (AK) Grade 1 keratoconus patients. Finally, significant improvements were also found in morpho-geometric parameters, such as asphericity and corneal curvature radii.
Keywords: 
Subject: Engineering  -   Bioengineering

1. Introduction

In ophthalmological clinical practice, the morpho-geometric analysis of corneal structure allows obtaining indices to evaluate corneal irregularities that affect patients’ visual quality [1,2,3]. These irregularities are generally present in corneal ectasias, and more specifically in keratoconus pathology, that is one of the most studied diseases of the human eye’s anterior segment [1,4,5,6]. In scientific literature, several studies have used different morphological characterization techniques of the cornea [7,8,9,10,11]. However, a geometric reconstruction that aspires to be integral, patient-specific, and more deterministic than stochastic, could only be feasible through using a computationally viable approach that reaches high accuracy and sensitivity in its reconstruction, even in the presence of complex corneal surface data dispersion and/or the absence of some geometrical information.
This data dispersion or absence can occur during the tomographer’s measurement acquisition process due to errors, which can be of a double nature: the so-called extrinsic errors, such as those caused by instability in the tear film [12], or the intrinsic errors, such as those due to noise present during the measurement acquisition process [12].
Regarding corneal reconstruction methods, there are two well-established paths: modal and zonal methods. Modal methods are based on the approximation of the surface through a combination of basic functions (modes) defined globally throughout the data domain, which may depend on a certain number of parameters and the necessary amount of them to recover the relevant information of the surface, trying to avoid over-fitting their measurement error [13]. Zonal methods are based on dividing the data domain into more elementary subdomains and approximating the surface in each defined subdomain independently of the rest [13,14].
In clinical practice, modal methods used are based on Zernike polynomials, which have shown high accuracy in slightly deformed corneas and good robustness against noise present in equipment during the measurement acquisition process [3], which gives them a lower dependence on measurement acquisition errors [14]. However, these polynomials have some problems due to their global nature, that is, in corneas that present significant surface irregularities, such as in the case of advanced keratoconus, these polynomials require high orders to perform a reliable reconstruction of corneal geometry, for which they use fitting tools such as least squares (LSQ) [15], or sequential quadratic programming (SQP) [16], but both generate instabilities against local minima caused by the discontinuities as mentioned above [17,18,19]. Therefore, it would be of interest to develop a modal reconstruction procedure that is not only accurate when irregular surfaces are present but also computationally viable in clinical practice.
Genetic Algorithms (GA) are modal reconstruction methods not affected by local minimum fitting, which are characterize for using a search space consisting of complete solutions. Genetic Algorithms have been successfully used in different fields to reconstruct complex geometric surfaces [20,21,22].
This study establishes a new modal method for corneal surface reconstruction using Genetic Algorithm fitting. Specifically, this research aims to analyze and compare the results of this fitting method to other methods by evaluating corneal morpho-geometric parameters, such as curvature radius or asphericity, in different clinical scenarios.

2. Materials and Methods

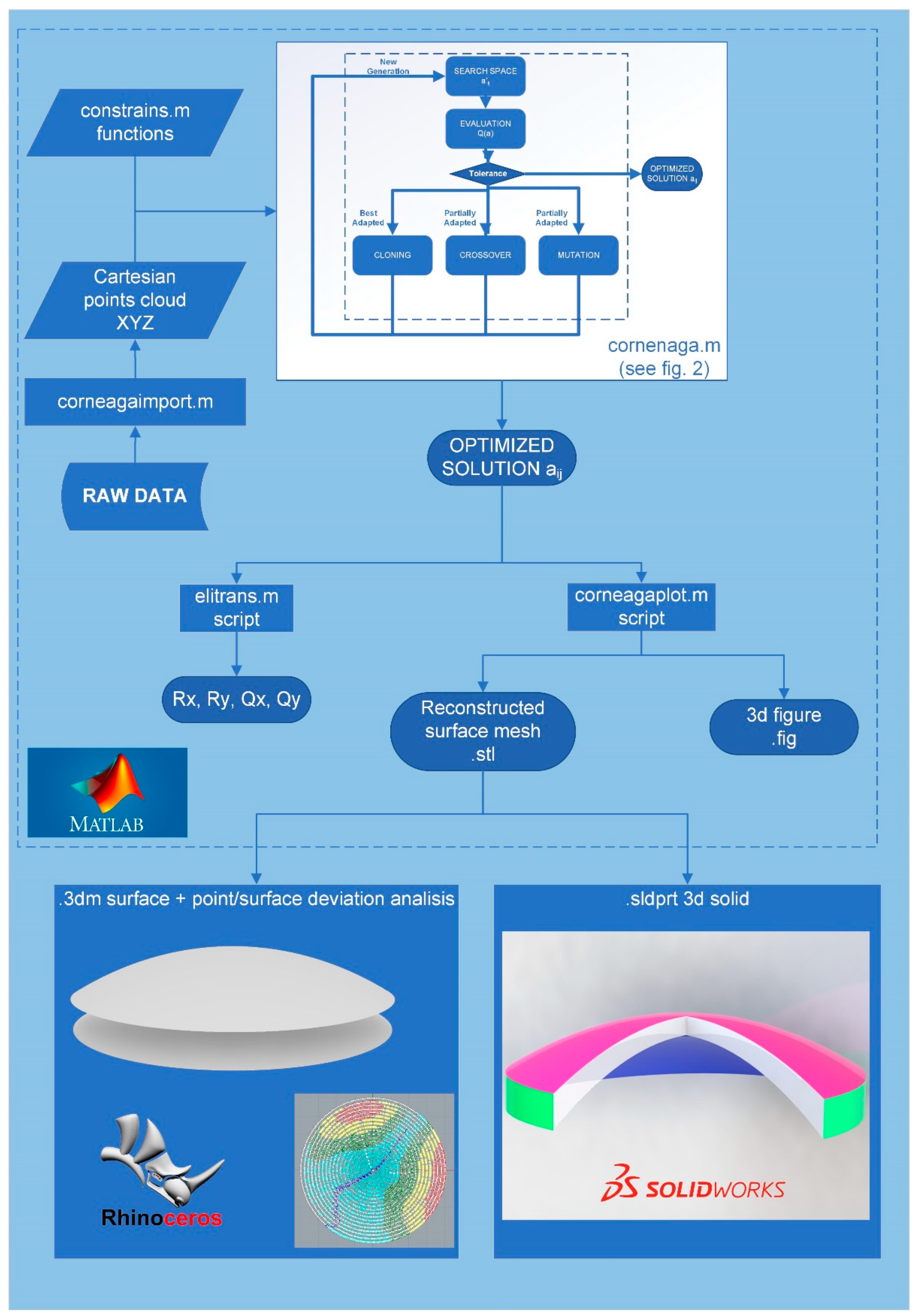
The corneal model reconstruction method proposed in this work is shown in Figure 1. Briefly, its procedure can be explained as follows: source data from the optical tomography are entered, after data conversion, into a script called “corneaga.m” run under Matlab software. The script uses ga() function of the Genetic Algorithm to obtain the optimal parameters of the modal fit of the corneal surface to an implicit equation. Once the reconstruction parameters are obtained, the surface is graphically represented within the Matlab environment and can then be exported as a mesh. Additionally, the morpho-geometric parameters of the reconstructed cornea and the goodness of fit are obtained using their Mean Squared Error (MSE). The obtained surface can be graphically represented and analyzed using CAD software such as Rhinoceros (version 7.0; McNeil Inc., NJ, USA) or Solidworks (version 2022; Dassault Systèmes, Vélizy-Villacoublay, France). In Figure 1 below, all the executed phases are shown in detail.

2.1. Data source

This experimental study included ophthalmological data from 49 patients aged between 7 and 63. Only one eye of each subject was selected to avoid correlation between each pair of eyes. In addition, to test the method on cases of keratoconus, the sample was divided into four groups according to the Amsler-Krumeich (AK) keratoconus scale [23]: 33 healthy eyes (control group), 5 eyes Grade 1, 6 eyes Grade 2, and 5 eyes of Grade 3 or higher. All data used in the study was obtained from the IBERIA BIOBANK database (Universidad Miguel Hernández de Elche, OFTARED-ISCIII), and the study was approved by the UPCT ethics committee (CEI21_001), following the ethical standards of the Helsinki Declaration (7th revision, October 2013, Fortaleza, Brazil). For each group of eyes, the inclusion criteria were: for the control group, healthy patients with no prior history of ocular pathologies; and, for the pathological groups, patients with diagnosed keratoconus classified according to the Amsler-Krumeich scale [24,25].

2.2. Data acquisition

In order to collect the experimental data, each eye underwent a clinical examination with Scheimpflug Tomography (OT) using the Sirius system (Costruzione Strumenti Oftalmici, Italy). A single experienced doctor performed all tests. A minimum of three corneal tomographies were performed for each eye, and the best one was selected according to the quality of instrument acquisition. After that, each corneal tomography data was exported in a .csv data file to be processed by the modal reconstruction algorithm, studied through morpho-geometric characterization, and validated by our research group [26].

2.3. NS-MVGA based modal-reconstruction

The surface reconstruction of the cornea proposed in this research is based on the following phases:

2.3.1. Discretization

The tomographic data file, obtained from the Sirius tomographer, comprises elevation data expressed as spatial points. Data are obtained as discrete points Ps, s = 1, …, 6144, in polar coordinates (phi, theta), distributed in radii phii = i/24, i = 1, …, 24, and semi meridians tetaj, j = 1, …, 256 between 0 and 2 pi. Using modal functions in Cartesian form requires input data in three-dimensional Cartesian point format XYZ [27]. The spatial points in polar format were transformed into Cartesian format through a script programmed in Matlab. The script, called “corneagaimport.m”, performs two processes: i) it obtains the Cartesian coordinates of the points that are in a polar format in the source data file by transforming each polar point [i, j] into its corresponding triangulation [i0.2, j360/256u] in radius and angle taking radii every 0.2 mm. and 256 points per radius, and, subsequently, ii) it eliminates invalid data in the experimental acquisition process (value = -1000).

2.3.2. Fitting of the modal surface function

In the next step, a modal fitting algorithm of the surface function, z = S(x,y), was constructed from the point cloud. Modal reconstruction was chosen due to the high number of failed reconstructions caused by noise in the data input when using zonal methods such as B-splines [7]. In modal reconstruction, the corneal surface is reconstructed by linear expansion, aj, of basic polynomial functions (modes), fj (eq. 1):
z = S (x, y) = ∑ aj fj (x, y),
A widely used criterion in the ophthalmological community to approximate the shape of the corneal surface is to use a model that approximates it to a conical or biconical surface, as proposed by Navarro et al. in 2006 [27]. This biconical surface is expressed as the implicit polynomial equation of a quadric (eq. 2):
Q(x, y, z) = a11 x2 + a12 x y + a13 x z + a10 x + a22 y2 + a23 y z + a20 y + a33 z2 + a30 z + a00 = 0
It is possible to reconstruct the corneal surface by fitting the coefficients of the polynomial equation, aij, to the input point cloud. Thus, this fitting can be assimilated into a mathematical optimization problem in the following form (eq. 3):
min Q (a),
This approximation has been successfully used numerous times in biomedical engineering to reconstruct biological surfaces [28,29].

2.3.3. Reconstruction of the corneal surface using NS-MVGA algorithm - CORNEAGA

For solving the optimization problem (eq. 3) of corneal surface reconstruction, various mathematical programming methods have been used so far, such as matrix methods like the use of the Moore-Penrose pseudoinverse matrix [30] based on the singular value decomposition of the system matrix, or weighted least squares fitting [31] where the weighting function adjusts to the points in the cloud with higher uncertainty. However, these methods can suffer from instability issues caused by input data or the presence of local minima. A previous study by our research group [32] allowed to propose, as future work, the use of a metaheuristic search optimization method supported by artificial intelligence. In this study, the application of a solution method through the implementation of a genetic algorithm for mathematical programming has been proposed.
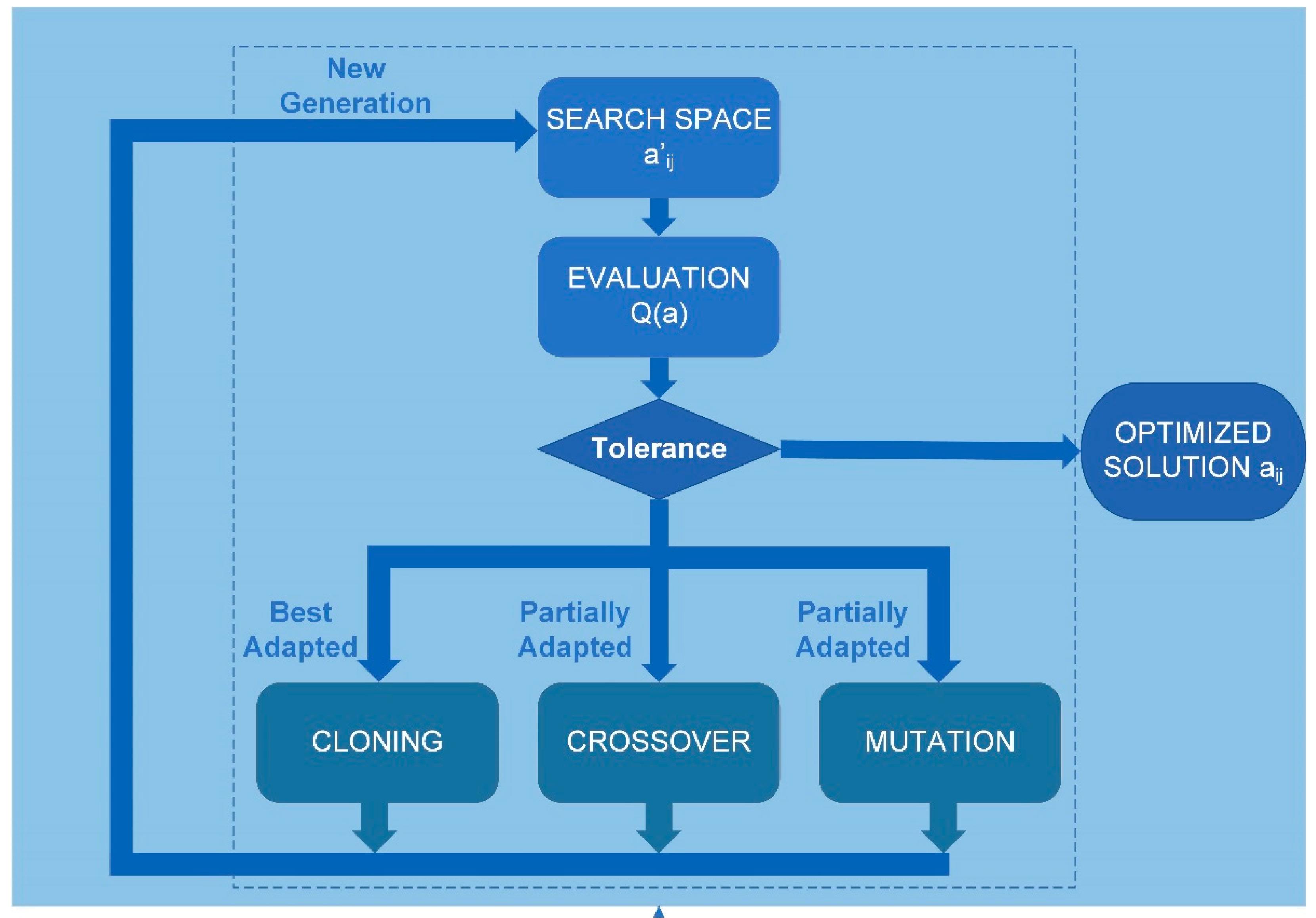
The solution to the problem of Equation 3 involves obtaining a solution vector consisting of the parameters aij. Therefore, the genetic algorithm used must have a deterministic multivariable (MVGA) configuration. The genetic algorithm was implemented using Matlab programming, following the scheme in Figure 2, with the script called “corneaga.m”. The MVGA was used to minimize the fitness function Q(aij) to obtain the ten adjustment coefficients of the implicit function of the corneal biconical surface (eq. 2).
The Genetic Algorithm receives the point cloud data in XYZ cartesian format after discretization carried out by the “corneagaimport.m” script, and the free surface of the cornea determines the problem constraints and are explicitly introduced through the “constrains.m” script (see Figure 2). The constraints are greatly influenced by the input data in other methods [30]. One proposed solution is to introduce a constraint on one of the parameters of equation 2 (eq. 2), such as a11 = 1, which provides excellent stability to the solution [27,33]. However, when working with a space of complete solutions, the Genetic Algorithm is unaffected by such discontinuities as gaps in the input data or other discontinuities. Therefore, the optimal configuration, in this case, is a non-dominant, multi-variable genetic algorithm not constrained by adjustment parameters. It is, therefore, a non-dominated sorting, multi-variable genetic algorithm (NS-MVGA).
A previous study on the application of Genetic Algorithms in clinical settings [34] allowed us to establish which were the most commonly used parameters in the literature. Then, optimal parameters were selected according to those commonly used in similar studies [35,36], and the genetic algorithm operators used in this study were: i) a population of 100 individuals for each variable, which implies a global population in each generation of 1000 individuals; ii) a crossover rate set at 0.8; iii) a cloning (survival) rate set at 0.2; and iv) mutation rate set at 0. Additionally, to configure the tolerance parameters of the genetic algorithm, experimentation was carried out with various tests varying these parameters (see Table 1). The optimal result for the tolerance parameters was a value of 10-30 for both the objective function and the constraints. With these parameters, optimal values of error and processing time can be obtained for obtaining the aij coefficients.

2.3.4. Getting the reconstructed surface, morpho-geometric parameters and graphical representation

Once the parameters aij are obtained, the expression (eq. 2) is transformed into the classic equation of an ellipsoid (eq. 4) by means of rotation and orientation using the Matlab function rot2eul(), with the script called “elitrans.m”.
x2/ a2 + y2/ b2 + z2/c2 = 1,
Here, a, b, and c are the values of the semi-axes of the ellipsoid in the ‘x’, ‘y’, and ‘z’ axes, respectively. This transformation aims to obtain the morpho-geometric parameters used in clinical practice [27]. These parameters are the radii of curvature of the surface in the ‘x’ and ‘y’ axes:
Rx = a2/c, Ry = b2/c,
And the sphericity in the ‘x’ and ‘y’ axes:
Qx = a2/c2-1, Qy = b2/c2-1,
Subsequently, the reconstructed corneal surface is graphically represented using the “corneagaplot.m” script with the fimplicit3() Matlab function along with the point cloud using the scatter3() Matlab function. In this script, the surface can be exported in a three-dimensional mesh using three-dimensional Delaunay triangulation [37,38]. The mesh is exported in a stereolithographic format in a .stl file using Matlab’s stlwrite() function.

2.3.5. Method validation and error calculation

The goodness-of-fit is evaluated within “corneaga.m” by calculating each case’s MSE. This is the most commonly used indicator in the literature [30,36]. After obtaining the vector’s ‘a’ from equation 3, the surface is reconstructed using the formula in equation 2 and then evaluated at the same nodes where the heights were collected. This gives the vector of adjusted elevations ‘Ẑ’. The MSE is calculated as the average of the squared differences between the adjusted elevations ‘Ẑ’ and the original elevations ‘Z’ (eq. 7).
MSE = (1/ N) ∑ (Ẑ − Z)2,
where N is the total number of points.
In Equation 2, some polynomial coefficients may turn null values if there is great uncertainty in the points or a significant lack of data. This implies that some polynomial terms (eq. 2) can disappear, causing the resulting quadric to not be in the correct order to fit the corneal surface. In other words, a mathematically valid solution is found. However, it is incompatible with the accepted quadric for its approximation to the corneal surface, which, according to a well-known study [27], must be a second-order quadric. This way, a failure quadric number, FQN, can be adopted in the surface reconstruction, which represents the number of times the reconstruction fails out of the total reconstructions performed in the study, a total of 82 corneal surfaces. Therefore, it can be expressed as the following equation (eq. 8):
FQN = ∑m fqj,
where fq = 1 if there is a failure in the order number of the quadratic in the reconstruction, and fq = 0 if there is no failure, and m is the counter of reconstructions carried out.

3. Results

The complete reconstruction described in Figure 2 was implemented for the experimental input data of each corneal surface described in the “data source” section. Additionally, for each of the reconstructions, the implementation of weighted least-squares modal methods, LSQ, and sequential quadratic programming, SQP, was carried out. For each of the reconstructed surfaces, the following were obtained: the coefficients aij of the adjusted geometric expression of equation 2; the corneal morpho-geometric parameters R and Q; the mean square error, MSE; the failure rate, FQN; and the graphical representations and reconstructed surface meshes.
Table 2 shows the results of comparing the reconstruction using CORNEAGA and the reconstruction using traditional fitting methods. The average MSE values are shown for each of the studied groups: the control group of healthy patients and the groups of grades according to the Amsler-Krumeich (AK) scale. The traditional methods include two methods previously used: LSQ, least squares method, and SQP, sequential quadratic programming method.
Table 3 shows the number of reconstruction failures (FQN) for the different methods applied and experimental groups.
Additionally, the corneal morpho-geometric parameter of asphericity (eq. 6) related to spherical aberration and refractive index (Q) was calculated, as studied in Navarro et al.’s work [27]. This parameter was not calculated for the SQP method due to its low accuracy. The mean values were calculated for the LSQ and CORNEAGA methods for the different groups. The results are shown in Table 4:
Another morpho-geometric parameter obtained in the results is the corneal curvature radius of the anterior and posterior corneal surface (ARC/PRC) (eq. 5) and its relationship with keratoconus pathology, according to a study conducted by Belin et al. [39]. Table 5 shows the values of the curvature radii obtained in the reconstruction of different AK grades using the LSQ and CORNEAGA methods. This parameter was calculated for the groups with keratoconus, but it was also not calculated for the SQP method due to its low accuracy:
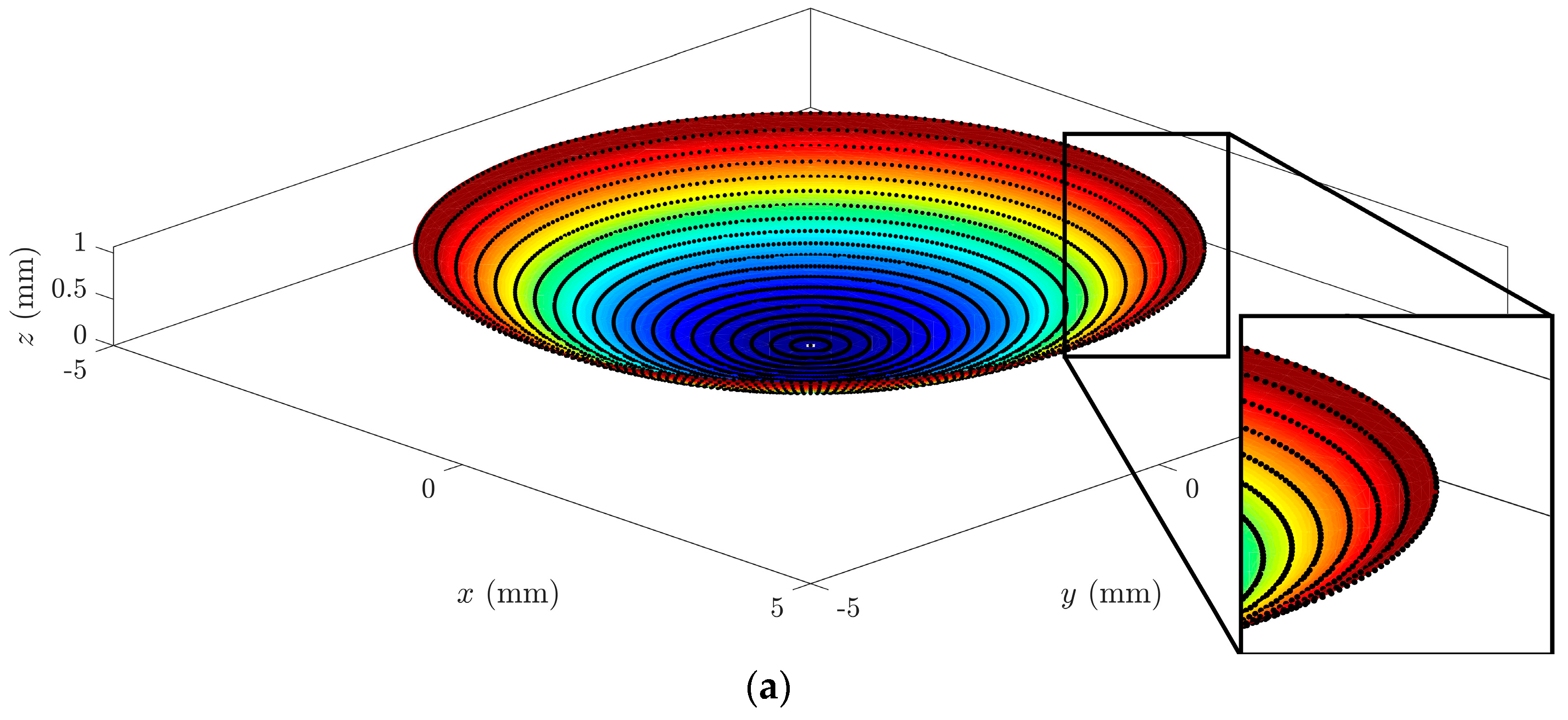
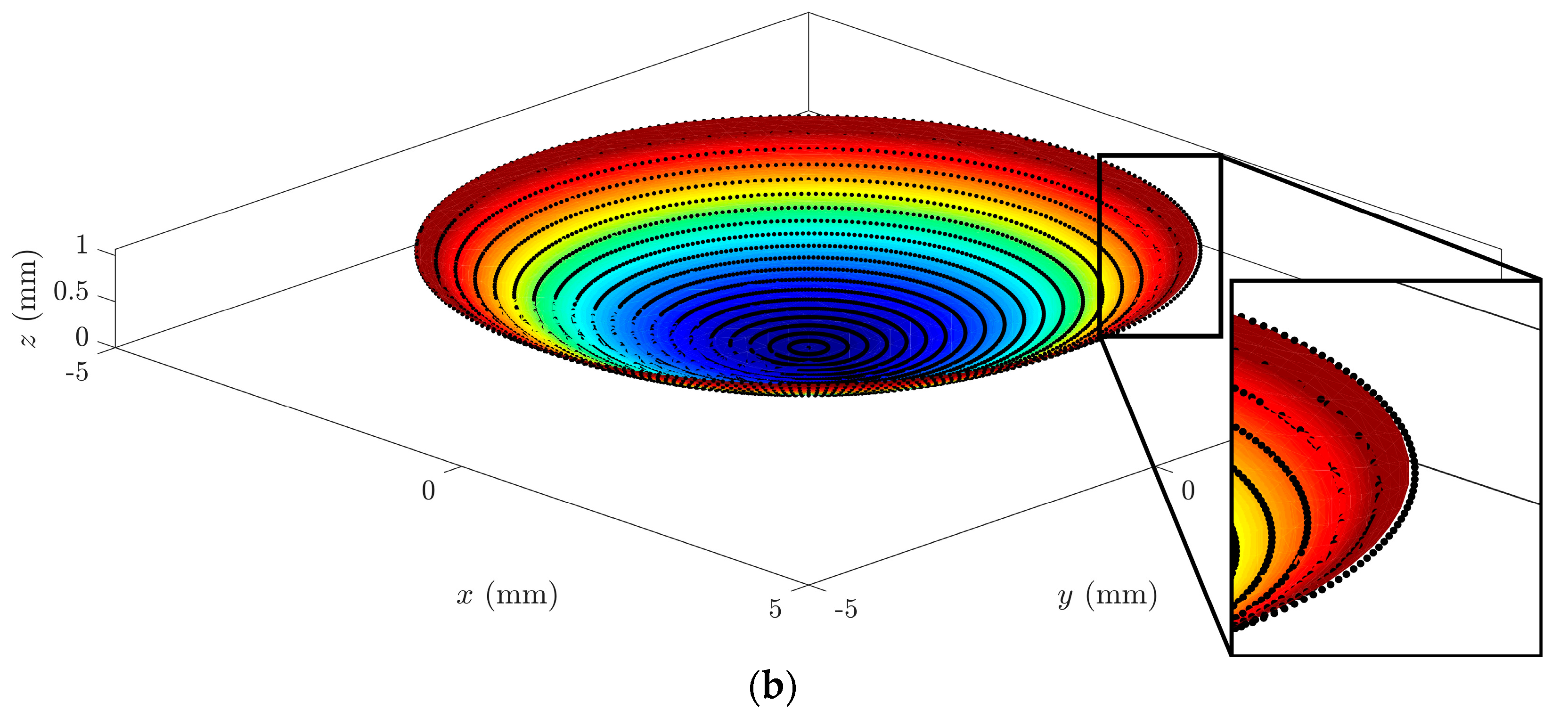
In a graphical analysis, the representation of corneal surfaces for the CORNEAGA and LSQ methods was obtained, where the surface is represented in a colored gradient scale according to the z-axis, along with original tomographic data in the form of black dots. In the following figure (Figure 3), we can see a representation and detail of an example of a corneal surface using both methods:
Additionally, a surface mesh is imported and analyzed using CAD software Rhinoceros, where the deviation in the z-axis (elevation) of points to the original data cloud and their distance to the reconstructed surface can be analyzed (Figure 4):
Finally, using SolidWorks software, the reconstructed anterior and posterior surfaces are imported and the complete cornea is converted into a closed solid by joining both surfaces. In the following figure (Figure 5), we can see the result of the reconstruction, using CORNEAGA and LSQ methods, compared to the reconstruction using the NURBS zonal method of a complete and sectioned cornea:

4. Discussion

Several studies have discussed the morpho-geometric characterization of the human cornea using novel analysis techniques. Modal reconstruction of the corneal surface is part of these fields of study. Considering the limitations of zonal methods, modal methods are a valuable tool for characterizing pathologies such as keratoconus. In present study, the point cloud data of topographic measurements from a Sirius tomographer were used as experimental data, whose use have been previously validated for the characterization of repeatable corneal geometric parameters in healthy eyes [40,41] and those with keratoconus [42,43]. Once the surfaces were reconstructed by the proposed CORNEAGA method and other modal methods, a comparative analysis was performed at the level of goodness of fit by mean squared error, MSE (eq. 7); failure rate, FQN (eq. 8), morpho-geometric parameters: curvature radii R (eq. 5) and asphericity Q (eq. 6); and, finally, a comparative graphical analysis of the obtained surfaces.
Regarding the mean squared error, MSE, as shown in Table 2, and considering the control group composed of healthy patients, the reconstruction improves up to a 86% using the genetic algorithm CORNEAGA, compared to the least squares method, LSQ. It is observed that as the deformation of the surfaces due to an increasing disease grading rises, this improvement percentage decreases. However, in the Amsler-Krumeich Grade 1 keratoconus group, the improvement percentage reaches 43%. This group is essential for the early detection of this pathology [44].
As for the failure rate, FQN, it can be observed in Table 3 that the new method has a zero-failure reconstruction rate. This is because the new method works with a population of complete solutions, so it always finds a valid solution for the reconstruction. Only a few isolated failures of quadrics have occurred during tests, when the population size in each generation was chosen to be lower than what was established in the “Reconstruction of the Corneal Surface Using NS-MVGA Algorithm - CORNEAGA” section.
Analyzing the corneal asphericity, as shown in Table 4, for the control group consisting of healthy patients, the average asphericity values increase from -0.3114 to -0.3348, which is a significantly higher value than the previous range obtained and indicates a better approximation to the optimal conic constant Qopt = -0.528 obtained by the authors Navarro et al. in previous publications [27]. As for the pathological groups, it is also observed that asphericity is better approximated to the actual pathological states, whose values are determined to be close to -1 or -2 for advanced pathological states [45]. This does not occur in the AK 2+3 group since, as seen in the MSE analysis in Table 2, the approximation is similar.
Table 5 shows the relationship between the radii of curvature and the scientific criteria established by Belin et al. [39]. This study suggests a direct relationship between the radii of curvature of the corneal surfaces and the grades of the AK scale (AK1, ARC / PRC: >7.05 / >5.7; AK2, ARC / PRC: >6.35 / >5.15; and AK3+4, ARC / PRC: ~6.15 / ~4.95). It can be verified that the new CORNEAGA method generates values farther from the limits than the LSQ method, improving the screening of cases. This result is due to the improved precision of the method achieved for this group, which can be observed in Table 2. Similar results are obtained in both methods for the AK2 grade, and the worst results are shown in both methods for the AK3 and AK4 grades.
At a graphical level, Figure 4 shows how the new method fits better to the points in the outer edge zone of the dataset. This border zone represents a discontinuity in the input data. The traditional modal method adapts worse to such discontinuity, as previously confirmed in works by other authors, such as Martinez-Finkelshtein et al. [30]. In Figure 5, it can be seen in the solid section of the entire cornea how the new genetic algorithm-based method fits much better than the LSQ method to the B-spline NURBS zonal method [1,25], which achieves an MSE of the order of 10-6 for this cornea [1] while CORNEAGA achieves an order of 10-5 and LSQ only order of 10-3. This makes it closer to the most effective zonal method.

5. Conclusions

This study aimed to establish a new modal method for corneal surface reconstruction using genetic algorithm fitting. Existing modal methods in the literature have certain limitations that can affect the accuracy of corneal surface reconstruction, especially in cases of discontinuities or incomplete data. Therefore, the objective of this study was to develop a more efficient method that could overcome these limitations.
The obtained results demonstrate that the new method of corneal surface reconstruction is reliable and highly effective. Additionally, it was found that this method significantly improves the usual modal methods used previously in the literature. The collected data show that the new method improves the reconstruction performed by the existing ones, especially for patients with KC AK1, which may allow earlier detection of the disease and, therefore, a better prognosis of its progression.
While it does not improve zonal methods in highly deformed surfaces, it does represent a significant advancement in modal approximation for cases with incomplete data. The new method has a zero-failure rate in reconstruction due to the inherent goodness of the population with which the algorithm operates.
One potential direction for future research could involve reducing the tolerance of the genetic algorithm’s adjustment and enhancing the algorithm’s intergenerational processing capacity through the use of a more advanced computer system. This approach may lead to even greater improvements in the accuracy of the fitting.
In summary, the study has shown that the new method of corneal surface reconstruction is highly effective and significantly improves reconstruction accuracy compared to previous modal methods used in the literature. The new method represents an important advance in modal approximation in cases with incomplete data and has excellent potential for further improvement in the future through the optimization of genetic algorithm adjustments.

Author Contributions

Conceptualization, F.L.S-G, J.S.V. and F.C.; methodology, J.S.V. and F.C.; software, F.L.S-G; validation, J.S.V. and F.C.; formal analysis, F.C., J.AdB. and J.L.A.; investigation, F.L.S-G and J.AdB.; resources, F.C. and J.L.A.; data curation, F.L.S-G and J.AdB.; writing—original draft preparation, F.L.S-G, J.S.V., J.AdB., J.L.A. and F.C.; writing—review and editing, F.L.S-G, J.S.V., J.AdB., J.L.A. and F.C.; visualization, F.L.S-G; supervision, F.C., J.S.V. and J.L.A.; project administration, F.C. and J.L.A.; funding acquisition, F.C. All authors have read and agreed to the published version of the manuscript.

Funding

This publication was carried out within the framework of the project “Desarrollo y validación de un nuevo concepto de caracterización biomecánica-morfofuncional de la córnea” reference number DTS21/00103. This Project has been funded by Instituto de Salud Carlos III (ISCIII) and cofunded by the European Union.

Institutional Review Board Statement

The study was conducted in accordance with the Declaration of Helsinki, and approved by the Institutional Ethics Committee of Technical University of Cartagena (UPCT) (protocol code CEI21_001).

Informed Consent Statement

Informed consent was obtained from all subjects involved in the study.

Data Availability Statement

The data presented in this study are available on request from the corresponding author. The data are not publicly available due to privacy reasons.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Cavas-Martínez, F.; Fernández-Pacheco, D.G.; De La Cruz-Sánchez, E.; Nieto Martínez, J.; Fernández Cañavate, F.J.; Vega-Estrada, A.; Plaza-Puche, A.B.; Alió, J.L. Geometrical custom modeling of human cornea in vivo and its use for the diagnosis of corneal ectasia. PLoS ONE 2014, 9. [Google Scholar] [CrossRef] [PubMed]
  2. Ribeiro, F.J.; Castanheira-Dinis, A.; Dias, J.M. Personalized Pseudophakic Model for Refractive Assessment. PLoS ONE 2012, 7. [Google Scholar] [CrossRef]
  3. Zhou, D.; Abass, A.; Eliasy, A.; Studer, H.P.; Movchan, A.; Movchan, N.; Elsheikh, A. Microstructure-based numerical simulation of the mechanical behaviour of ocular tissue. J. R. Soc. Interface 2019, 16. [Google Scholar] [CrossRef] [PubMed]
  4. De Sanctis, U.; Aragno, V.; Dalmasso, P.; Brusasco, L.; Grignolo, F. Diagnosis of subclinical keratoconus using posterior elevation measured with 2 different methods. Cornea 2013, 32, 911–915. [Google Scholar] [CrossRef]
  5. Martínez-Abad, A.; Piñero, D.P.; Ruiz-Fortes, P.; Artola, A. Evaluation of the diagnostic ability of vector parameters characterizing the corneal astigmatism and regularity in clinical and subclinical keratoconus. Contact Lens Anterior Eye 2017, 40, 88–96. [Google Scholar] [CrossRef]
  6. Shiga, S.; Kojima, T.; Nishida, T.; Nakamura, T.; Ichikawa, K. Evaluation of CorvisST biomechanical parameters and anterior segment optical coherence tomography for diagnosing forme fruste keratoconus. Acta Ophthalmol. 2021, 99, 644–651. [Google Scholar] [CrossRef] [PubMed]
  7. Ares, M.; Royo, S. Comparison of cubic B-spline and Zernike-fitting techniques in complex wavefront reconstruction. Appl. Opt. 2006, 45, 6954–6964. [Google Scholar] [CrossRef]
  8. Hall, R.C.; Mohamed, F.K.; Htoon, H.M.; Tan, D.T.; Mehta, J.S. Laser in situ keratomileusis flap measurements: Comparison between observers and between spectral-domain and time-domain anterior segment optical coherence tomography. J. Cataract Refractive Surg. 2011, 37, 544–551. [Google Scholar] [CrossRef]
  9. Kosaki, R.; Maeda, N.; Bessho, K.; Hori, Y.; Nishida, K.; Suzaki, A.; Hirohara, Y.; Mihashi, T.; Fujikado, T.; Tano, Y. Magnitude and orientation of Zernike terms in patients with keratoconus. Invest. Ophthalmol. Vis. Sci. 2007, 48, 3062–3068. [Google Scholar] [CrossRef]
  10. Trevino, J.P.; Gómez-Correa, J.E.; Iskander, D.R.; Chávez-Cerda, S. Zernike vs. Bessel circular functions in visual optics. Ophthalmic Physiol. Opt. 2013, 33, 394–402. [Google Scholar] [CrossRef]
  11. Williams, D.; Zheng, Y.; Bao, F.; Elsheikh, A. Automatic segmentation of anterior segment optical coherence tomography images. J Biomed Opt 2013, 18. [Google Scholar] [CrossRef] [PubMed]
  12. Cavas-Martínez, F.; De la Cruz Sánchez, E.; Nieto Martínez, J.; Fernández Cañavate, F.J.; Fernández-Pacheco, D.G. Corneal topography in keratoconus: state of the art. Eye and Vis 2016, 3. [Google Scholar] [CrossRef] [PubMed]
  13. Ramos-López, D.; Martínez-Finkelshtein, A.; Castro-Luna, G.M.; Piñero, D.; Alió, J.L. Placido-based indices of corneal irregularity. Optom. Vis. Sci. 2011, 88, 1220–1231. [Google Scholar] [CrossRef]
  14. Martínez-Finkelshtein, A.; López, D.R.; Castro, G.M.; Alió, J.L. Adaptive cornea modeling from keratometric data. Invest. Ophthalmol. Vis. Sci. 2011, 52, 4963–4970. [Google Scholar] [CrossRef]
  15. Kim, S.J.; Koh, K.; Lustig, M.; Boyd, S.; Gorinevsky, D. An interior-point method for large-scale ℓ1-regularized least squares. IEEE J. Sel. Top. Sign. Proces. 2007, 1, 606–617. [Google Scholar] [CrossRef]
  16. Johansen, T.A.; Fossen, T.I.; Berge, S.P. Constrained Nonlinear Control Allocation With Singularity Avoidance Using Sequential Quadratic Programming. IEEE Trans Control Syst Technol 2004, 12, 211–216. [Google Scholar] [CrossRef]
  17. Carvalho, L.A. Accuracy of Zernike polynomials in characterizing optical aberrations and the corneal surface of the eye. Invest. Ophthalmol. Vis. Sci. 2005, 46, 1915–1926. [Google Scholar] [CrossRef] [PubMed]
  18. Smolek, M.K.; Klyce, S.D. Zernike Polynomial Fitting Fails to Represent All Visually Significant Corneal Aberrations. Invest. Ophthalmol. Vis. Sci. 2003, 44, 4676–4681. [Google Scholar] [CrossRef]
  19. Vicent, L.E.; Wolf, B. Unitary transformation between Cartesian- and polar-pixellated screens. J Opt Soc Am A 2008, 25, 1875–1884. [Google Scholar] [CrossRef]
  20. Da, D.C.; Cui, X.Y.; Long, K.; Li, G.Y. Concurrent topological design of composite structures and the underlying multi-phase materials. Comput Struct 2017, 179, 1–14. [Google Scholar] [CrossRef]
  21. Gunpinar, E.; Gunpinar, S. A shape sampling technique via particle tracing for CAD models. Graphical Models 2018, 96, 11–29. [Google Scholar] [CrossRef]
  22. Zou, X.; Cheng, P.; An, B.; Song, J. Sectorization and Configuration Transition in Airspace Design. Math. Probl. Eng. 2016, 2016. [Google Scholar] [CrossRef]
  23. Alió, J.L.; Piñero, D.P.; Alesón, A.; Teus, M.A.; Barraquer, R.I.; Murta, J.; Maldonado, M.J.; Castro De Luna, G.; Gutiérrez, R.; Villa, C.; et al. Keratoconus-integrated characterization considering anterior corneal aberrations, internal astigmatism, and corneal biomechanics. J. Cataract Refractive Surg. 2011, 37, 552–568. [Google Scholar] [CrossRef]
  24. Piñero, D.P.; Nieto, J.C.; Lopez-Miguel, A. Characterization of corneal structure in keratoconus. J. Cataract Refractive Surg. 2012, 38, 2167–2183. [Google Scholar] [CrossRef]
  25. Rabinowitz, Y.S. Keratoconus. Surv. Ophthalmol. 1998, 42, 297–319. [Google Scholar] [CrossRef] [PubMed]
  26. Cavas-Martínez, F.; Bataille, L.; Fernández-Pacheco, D.G.; Cañavate, F.J.F.; Alió, J.L. A new approach to keratoconus detection based on corneal morphogeometric analysis. PLoS ONE 2017, 12. [Google Scholar] [CrossRef] [PubMed]
  27. Navarro, R.; González, L.; Hernández, J.L. Optics of the average normal cornea from general and canonical representations of its surface topography. J Opt Soc Am A 2006, 23, 219–232. [Google Scholar] [CrossRef]
  28. Ding, S.; Ye, Y.; Tu, J.; Subic, A. Region-based geometric modelling of human airways and arterial vessels. Comput. Med. Imaging Graph. 2010, 34, 114–121. [Google Scholar] [CrossRef]
  29. Duan, C.Y.; Lü, H.B.; Hu, J.Z. In vivo study on three-dimensional structure of lumbar facet joints based on computer-assisted medical image processing method. Yiyong Shengwu Lixue 2012, 27, 159–165. [Google Scholar]
  30. Martinez-Finkelshtein, A.; Delgado, A.M.; Castro, G.M.; Zarzo, A.; Alio, J.L. Comparative analysis of some modal reconstruction methods of the shape of the cornea from corneal elevation data. Invest. Ophthalmol. Vis. Sci. 2009, 50, 5639–5645. [Google Scholar] [CrossRef]
  31. Alonso-Caneiro, D.; Iskander, D.R.; Collins, M.J. Estimating corneal surface topography in videokeratoscopy in the presence of strong signal interference. IEEE Trans. Biomed. Eng. 2008, 55, 2381–2387. [Google Scholar] [CrossRef]
  32. Sáez-Gutiérrez, F.L.; Velázquez, J.S.; Mira, J.; Gómez, C.; Alió, J.; Cavas, F. Geometric Reconstruction of a Biological Structure by Explicit Modal Methods. A Case-Study in Human Corneal Surface. In Proceedings of the Lecture Notes in Mechanical Engineering; 2023; pp. 531–538. [Google Scholar]
  33. Bao, F.; Chen, H.; Yu, Y.; Yu, J.; Zhou, S.; Wang, J.; Wang, Q.; Elsheikh, A. Evaluation of the Shape Symmetry of Bilateral Normal Corneas in a Chinese Population. PLoS ONE 2013, 8. [Google Scholar] [CrossRef] [PubMed]
  34. Sáez-Gutiérrez, F.L.; Velázquez, J.S.; del Barrio, J.L.A.; Alió, J.L.; Cavas, F. Analysis of the Use of Genetic Algorithms in the Design of Models and Graphical Techniques for Early Detection, Diagnosis, and Characterization of Clinical Pathologies. In Proceedings of the Lecture Notes in Mechanical Engineering; 2022; pp. 201–207. [Google Scholar]
  35. Bevilacqua, V.; Simeone, S.; Brunetti, A.; Loconsole, C.; Trotta, G.F.; Tramacere, S.; Argentieri, A.; Ragni, F.; Criscenti, G.; Fornaro, A.; et al. A computer aided ophthalmic diagnosis system based on tomographic features. In Proceedings of the Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); 2017; pp. 598–609. [Google Scholar]
  36. Williams, D.; Zheng, Y.; Davey, P.G.; Bao, F.; Shen, M.; Elsheikh, A. Reconstruction of 3D surface maps from anterior segment optical coherence tomography images using graph theory and genetic algorithms. Biomed. Signal Process. Control 2016, 25, 91–98. [Google Scholar] [CrossRef]
  37. Edelsbrunner, H.; Mücke, E.P. Three-Dimensional Alpha Shapes. ACM Trans. Graph. 1994, 13, 43–72. [Google Scholar] [CrossRef]
  38. Shewchuk, J.R. Triangle: Engineering a 2D quality mesh generator and delaunay triangulator. In Proceedings of the Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); 1996; pp. 203–222. [Google Scholar]
  39. Belin, M.W.; Duncan, J.K. Keratoconus: The ABCD Grading System. Klin. Monatsbl. Augenheilkd. 2016, 233, 701–707. [Google Scholar] [CrossRef] [PubMed]
  40. Bao, F.; Savini, G.; Shu, B.; Zhu, S.; Gao, R.; Dang, G.; Yu, A.; Wang, Q.; Huang, J. Repeatability, reproducibility, and agreement of two scheimpflug-placido anterior corneal analyzers for posterior corneal surface measurement. J. Refractive Surg. 2017, 33, 524–530. [Google Scholar] [CrossRef]
  41. Montalbán, R.; Piñero, D.P.; Javaloy, J.; Alió, J.L. Intrasubject repeatability of corneal morphology measurements obtained with a new Scheimpflug photography-based system. J. Cataract Refractive Surg. 2012, 38, 971–977. [Google Scholar] [CrossRef]
  42. Savini, G.; Schiano-Lomoriello, D.; Hoffer, K.J. Repeatability of automatic measurements by a new anterior segment optical coherence tomographer combined with Placido topography and agreement with 2 Scheimpflug cameras. J. Cataract Refractive Surg. 2018, 44, 471–478. [Google Scholar] [CrossRef]
  43. Montalbán, R.; Alió, J.L.; Javaloy, J.; Piñero, D.P. Intrasubject repeatability in keratoconus-eye measurements obtained with a new Scheimpflug photography-based system. J. Cataract Refractive Surg. 2013, 39, 211–218. [Google Scholar] [CrossRef]
  44. Kanellopoulos, A.J.; Asimellis, G. Revisiting keratoconus diagnosis and progression classification based on evaluation of corneal asymmetry indices, derived from scheimpflug imaging in keratoconic and suspect cases. Clin. Ophthalmol. 2013, 7, 1539–1548. [Google Scholar] [CrossRef]
  45. Holladay, J.T. Corneal topography using the Holladay diagnostic summary. J. Cataract Refractive Surg. 1997, 23, 209–221. [Google Scholar] [CrossRef] [PubMed]
Preprints 74305 g001
Figure 1. Global flowchart of the method. Rx, Ry: Radii of curvature of the corneal surface in x and y axes. Qx, Qy: asphericity of the corneal surface in x and y axes.
Figure 1. Global flowchart of the method. Rx, Ry: Radii of curvature of the corneal surface in x and y axes. Qx, Qy: asphericity of the corneal surface in x and y axes.
Preprints 74305 g001
Preprints 74305 g002
Figure 2. Genetic algorithm flowchart. aij: coefficients of the polynomial of the geometry of a quadric (eq. 2). Q(a): adaptation function.
Figure 2. Genetic algorithm flowchart. aij: coefficients of the polynomial of the geometry of a quadric (eq. 2). Q(a): adaptation function.
Preprints 74305 g002
Preprints 74305 g003aPreprints 74305 g003b
Figure 3. Example of graphical representation of reconstructed corneal surface with enlarged detail for: (a) CORNEAGA (top) and (b) LSQ (bottom) methods along with the original point cloud in black. (Patient’s characteristics: Healthy, Age = 29, Sex = Male, Eye = Right, Central Thickness = 512 μm).
Figure 3. Example of graphical representation of reconstructed corneal surface with enlarged detail for: (a) CORNEAGA (top) and (b) LSQ (bottom) methods along with the original point cloud in black. (Patient’s characteristics: Healthy, Age = 29, Sex = Male, Eye = Right, Central Thickness = 512 μm).
Preprints 74305 g003aPreprints 74305 g003b
Preprints 74305 g004
Figure 4. Example of point deviation analysis in Rhinoceros©, where the deviation in elevation between the experimental point cloud and the reconstructed surface is represented using a color scale for: (a) the CORNEAGA method (top) and (b) LSQ method (bottom). (Patient’s characteristics: Healthy, Age = 35, Sex = Male, Eye = Left, Central Thickness = 521 μm).
Figure 4. Example of point deviation analysis in Rhinoceros©, where the deviation in elevation between the experimental point cloud and the reconstructed surface is represented using a color scale for: (a) the CORNEAGA method (top) and (b) LSQ method (bottom). (Patient’s characteristics: Healthy, Age = 35, Sex = Male, Eye = Left, Central Thickness = 521 μm).
Preprints 74305 g004
Preprints 74305 g005
Figure 5. Example of reconstructed cornea in solid, using Solidworks©, using NURBS [1] method (left), CORNEAGA method (center), and LSQ method (right). (Patient’s characteristics: Keratoconus, Age = 31, Sex = Female, Eye = Right, Central Thickness = 329 μm).
Figure 5. Example of reconstructed cornea in solid, using Solidworks©, using NURBS [1] method (left), CORNEAGA method (center), and LSQ method (right). (Patient’s characteristics: Keratoconus, Age = 31, Sex = Female, Eye = Right, Central Thickness = 329 μm).
Preprints 74305 g005
Table 1. Genetic algorithm parameters adjustment.
Table 1. Genetic algorithm parameters adjustment.
Function tolerance exponent Constrain tolerance exponent MSE (10-3) Processing time (s) 1
-2 -2 5,256 32
-10 -10 4,6522 65
-30 -30 0,0804 299
-50 -50 0,0117 299
-100 -1000 0,0804 1972
1 Carried out using a Win10 PC with Intel Core i5-7500 CPU @ 3.40GHz and 16.00 GB RAM.
Table 2. MSE compared to different methods. AK: Amsler-Krumeich scale. LSQ: Weighted least squares fitting method. SQP: Sequential quadratic programming fitting method.
Table 2. MSE compared to different methods. AK: Amsler-Krumeich scale. LSQ: Weighted least squares fitting method. SQP: Sequential quadratic programming fitting method.
Method Control 1 AK grade 1 2 AK grade 2 3 AK grade 3+4 2
LSQ 8,96 × 10-3 5,03 × 10-2 2,93 × 10-2 3,14 × 10-2
SQP 10,08 × 10-3 10,48 × 10-2 10,30 × 10-2 10,02 × 10-2
CORNEAGA 1,24 × 10-3 2,86 × 10-2 2,86 × 10-2 3,03 × 10-2
Table 3. Corneal surface reconstruction failure rate (FQN). AK: Amsler-Krumeich scale. LSQ: Least Squares Fitting method. SQP: Sequential Quadratic Programming fitting method.
Table 3. Corneal surface reconstruction failure rate (FQN). AK: Amsler-Krumeich scale. LSQ: Least Squares Fitting method. SQP: Sequential Quadratic Programming fitting method.
Method Control 1 AK grade 1 2 AK grade 2 3 AK grade 3+4 2
LSQ 5 2 3 7
SQP 25 5 0 4
CORNEAGA 0 0 0 0
Table 4. Average values of corneal asphericity parameter Q for the reconstructed surfaces. AK: Amsler-Krumeich scale. LSQ: least-squares fitting method.
Table 4. Average values of corneal asphericity parameter Q for the reconstructed surfaces. AK: Amsler-Krumeich scale. LSQ: least-squares fitting method.
Method 1 Control AK grade 1 AK grade 2 AK grade 3+4
LSQ -0,3114 -0,6358 -0,6349 -1,0679
CORNEAGA -0,3348 -0,6960 -0,7339 -0,9716
Table 5. Comparison of ARC (anterior radii of curvature) and PRC (posterior radii of curvature). AK: Amsler-Krumeich scale. LSQ: least squares fitting method.
Table 5. Comparison of ARC (anterior radii of curvature) and PRC (posterior radii of curvature). AK: Amsler-Krumeich scale. LSQ: least squares fitting method.
Method AK grade 1 AK grade 2 AK grade 3+4
LSQ 6,0628 / 5,7370 6,7444 / 5,4495 5,9808 / 5,0034
CORNEAGA 7,1709 / 6,0628 6,9100 / 5,5633 6,6203 / 5,4443
AK criteria [belin2016] 1 >7,05 / >5,7 >6,35 / >5,15 ~6,15 / ~4,95
1 Not a method. Comparison criterion.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated