Effect of Diffusion and Laser Pulse on a Poro-Thermoelastic Medium via Three-Phase-Lag Model

Preprint

Article

Effect of Diffusion and Laser Pulse on a Poro-Thermoelastic Medium via Three-Phase-Lag Model

Altmetrics

Downloads

147

Views

Comments

Mohamed Abdelsabour Fahmy^*,

Mohamed I. A. Othman,

Elsayed M. Abd-Elaziz

Mohamed Abdelsabour Fahmy^*,

Mohamed I. A. Othman,

Elsayed M. Abd-Elaziz

This version is not peer-reviewed

Submitted:

22 May 2023

Posted:

24 May 2023

You are already at the latest version

Alerts

Abstract

The purpose of this paper is to study the influence of diffusion and thermal loading due to pulsed laser heating on a thermoelastic solid with voids in the context of the model of three-phase-lag. The non-dimensional governing equations are formulated and then the exact expressions for the temperature field, the displacement components, the stress components, the concentration field and the change in the volume fraction field are obtained using the normal mode technique. The material is an isotropic, homogeneous elastic half-space and heated by a non-Gaussian laser beam with pulse duration of ps. The magnesium crystal element is used as an application to compare the predictions induced by diffusion and laser pulse on poro-thermoelastic medium of the model of three-phase-lag with those for the theory of Green–Naghdi of type III. The results obtained for thermal changes are verified by comparison with two theories of thermoelasticity, namely the model of three-phase lag (3PHL) and the Green and Nagdi type III theory. Plot the expressions to examine the effect of the laser pulse at two different values of time and the effect void parameter. This study also yields some interesting special cases.

Keywords:

Subject: Engineering - Mechanical Engineering

1. Introduction

The classical theory of elasticity is insufficient to describe the behavior of such materials. Analysis of such material needs to incorporate a theory-oriented medium. In the classical theory of thermoelasticity, Fourier's theory of heat conduction assumes that thermal disturbances propagate at infinite speed, which is unrealistic from a physical point of view. The generalized thermoelastic theory is one of the modified versions of the classical uncoupled and coupled thermoelastic theories. It aims to eliminate the paradox of the physically impossible phenomenon of infinite velocity of heat signals in classical coupled thermoelasticity. The first generalizations can be traced back to Lord and Shulman [1], who formulated a general theory of thermoelasticity in terms of thermal relaxation times. Green and Lindsay [2] developed a temperature-rate-dependent thermo-elasticity involving two thermal relaxation times.

A third extension of the coupled thermoelastic theory was developed by Hetnarski and Ignaczak [3] and is called low temperature thermoelasticity. The fourth generalization of the coupled thermoelastic theory introduced by Green and Naghdi [4], which involves the theory of thermoelasticity without energy dissipation. A fifth generalization of the coupled thermoelastic theory was developed by Tzou [5] and is called two-phase hysteresis thermoelasticity. He introduced the two-phase lags of the heat flow vector, temperature gradient, and considered the constitutive equation to describe the lagging behavior of heat conduction in solids. Choudhuri [6] recently introduced the heat equation with three-phase lag. In doing so, Fourier's law of heat conduction is replaced by a modified approximation of Fourier's law, which introduces three different phase lags of the heat flux vector, the temperature gradient and the thermal displacement gradient. Quintanilla and Racke [7] discuss the stability of the heat equation with three-phase lags. You have investigated the spatial behavior of the solution to the three-phase hysteresis heat equation. The general model of the formula equation in the context of the 3PHL model has been applied by many researchers in the literature. See (Mukhopadhyay and Kumar [8], Othman and Eraki [9]). The theory of void elastomers is the simplest generalization of classical elastic theory; however, it is worth remembering that porous materials have applications in many engineering fields such as the petroleum industry, materials science, biology, etc. The theory of linear elastic materials with voids deals with materials with small (porous) or a small distribution of voids. Void volume is one of the kinematic variables studied in different types of geological and biological materials, because the classical theory of elasticity is not enough.

The theory of void thermoelasticity is an important progress of classical elastic theory. When the void volume tends to zero, the theory reduces to the classical theory. Nunziato and Cowin [10] developed a nonlinear theory of elastic materials with voids. Cowin and Nunziato [11] developed a theory of linear elastic materials with voids to study the mechanical behavior of porous solids in mathematical models. Puri and Cowin [12] studied the behavior of plane waves in linear elastic materials with voids. Iesan [13] extended Cowin and Nunziato's theory of elastic solids with voids to include thermal effects. In recent years, different authors [14,15,16,17,18,19,20,21,22] have discussed different types of void thermoelasticity problems. Diffusion is the spontaneous movement of particles from a region of high concentration to a region of low concentration. It occurs in response to a concentration gradient, expressed as a concentration change due to change in position. Thermal diffusion uses the transfer of heat across a thin fluid or gas to accomplish isotope separation. Today, thermal diffusion remains a practical process to separate isotopes of noble gases (e.g. xexon) and other light isotopes (e.g. carbon) for research purposes. In most of the applications, the concentration is calculated using what is known as Fick’s law. This is a simple law that does not take into consideration the mutual interaction between the introduced substance and the medium into which it is introduced or the effect of temperature on this interaction. However, there is a certain degree of coupling with temperature and temperature gradients as temperature speeds up the diffusion process. The thermo-diffusion in elastic solids is due to the coupling of fields of temperature, mass diffusion and that of strain in addition to heat and mass exchange with the environment. Nowacki [23,24,25] developed the theory of thermo-elastic diffusion by using a coupled thermoelastic model. Sharma [26] studied the deformation in homogeneous and isotropic thermo-diffusion elastic half-space with normal and tangential loads. Said and Othman [27] studied the effects of diffusion and internal heat source on a two-temperature thermoelastic medium with the three-phase-lag model. Many authors discussed different types of problems in thermoelastic diffusion, see [28,29,30,31,32,33].

The excitement of thermoelastic waves by a pulsed laser in solid is of great interest due to extensive applications of pulsed laser technologies in material processing and non-destructive detecting and characterization. When a solid is illuminated with a laser pulse, absorption of the laser pulse results in a localized temperature increase, which in turn causes thermal expansion and generates a thermoelastic wave in the solid. In ultra-short pulsed laser heating, two effects become important. One is the non-Fourier’s effect in heat conduction, which is a modified of the Fourier heat conduction theory to account for the effect of mean free time (thermal relaxation time) in the energy carrier’s collision process. There was a great number of studies [34,35,36,37,38,39,40] dealing with the theories of thermo-elasticity under the effect of different fields.

The goal of this article is to study the effect of thermal loading due to laser pulse on the behavior of solutions in thermoelasticity with diffusion and voids in the context of the three-phase-lag model. The material is a homogeneous isotropic elastic half-space and heated by a non-Gaussian laser beam with pulse duration of

0.002

ps. The normal mode analysis is applied to derive the expressions for the considered variables for three-phase-lag theory with voids and diffusion. The variations of the considered variables are represented graphically. Some particular cases of interest are also deduced from this investigation.

2. Derivation of Field Equations

According to Cowin and Nunziato [11], Nowacki [23] and Choudhuri [6], the governing relations for a homogeneous, isotropic, generalized thermoelastic half-space with diffusion and voids can be written as:

2.1. The Constitutive Relations2.2. The Generalized Fourier’s Law 2.3. The Strain-Displacement Relation2.4. The Equation of Motion 2.5. Balance of Equilibrated Stress2.6. The Balance Energy in the Presence of Heat Source2.7. The Equation of Mass Diffusion

σ_{i j} = 2 μ e_{i j} + (λ e_{r r} + γ ϕ - β_{1} T - β_{2} C) δ_{i j},

(1)

h_{i} = a_{1} ϕ_{, i},

(2)

g = - γ e_{k k} - d_{0} ϕ + a_{2} T + a_{1} C,

(3)

ρ T_{0} η = β_{1} T_{0} e_{k k} + a_{2} T_{0} ϕ + ρ c_{E} T + a_{3} T_{0} C,

(4)

P = - β_{2} e_{k k} - a_{1} ϕ - a_{3} T + a_{4} C,

(5)

S_{i} = - a_{5} P_{, i} .

(6)

q_{i} (X, t + τ_{q}) = - [K T_{, i} (X, t + τ_{T}) + K^{*} υ_{, i} (X, t + τ_{ν})] .

(7)

e_{i j} = \frac{1}{2} (u_{i, j} + u_{j, i}), i, j, r = 1, 2, 3

(8)

σ_{j i, j} = ρ u_{i, t t},

(9)

ρ ψ ϕ_{, t t} = h_{i, i} + g,

(10)

ρ T_{0} η_{, t} = - q_{i, i} + ρ Q .

(11)

C_{, t} = - S_{i, i} .

(12)

Here, the comma represents derivative with respect to space variable.

Substituting Eqs. (1)-(3) into Eqs. (9) and (10), the equations of motion are

μ u_{i, j j} + (μ + λ) u_{j, j i} + γ ϕ_{, i} - β_{1} T_{, i} - β_{2} C_{, i} = ρ u_{i, t t},

(13)

a_{1} ϕ_{, j j} - γ u_{i, i} - d_{0} ϕ + a_{2} T + a_{1} C = ρ ψ ϕ_{, t t},

(14)

Substituting Eq. (1) into Eq. (12), the equation of mass diffusion is

a_{4} C_{, t} + a_{5} [β_{2} e_{k k, i i} + a_{1} ϕ_{, i i} + a_{3} T_{, i i} - a_{4} C_{, i i}] = 0,

(15)

Substituting Eqs. (1) and (2) into Eq. (6), the heat conduction equation with the model of three phase lag is

[K^{*} + (K + K^{*} τ_{υ}) \frac{\partial}{\partial t} + K τ_{T} \frac{\partial^{2}}{\partial t^{2}}] T_{, i i} = (1 + τ_{q} \frac{\partial}{\partial t} + \frac{1}{2} τ_{q}^{2} \frac{\partial^{2}}{\partial t^{2}}) (ρ C_{E} T_{, t t} + T_{0} β_{1} u_{i, i t t} + a_{2} T_{0} ϕ_{, t t} + a_{3} T_{0} C_{, t t} - ρ Q_{, t}),

(16)

where

0 \leq τ_{v} < τ_{T} < τ_{q}

, the superposed dot indicates derivative with respect to time.

3. Formulation of Problem

We consider a homogeneous, isotropic, thermoelastic diffusion half-space

(z \geq 0)

with voids, also all the field quantities are depend on the Cartesian coordinates

x, z

and the time

t

and independent of Figure 1

y

We assume the dynamic displacement vector as

u_{i} = (u, 0, w),

and the plate surface is illuminated by laser pulse given by Al-Qahtani and Datta [34]

Q (x, z, t) = \frac{I_{0} γ^{*} t}{2 π r^{2} t_{0}^{2}} \exp (- \frac{x^{2}}{r^{2}} - \frac{t}{t_{0}}) \exp (- γ^{*} z) .

(17)

Under the above assumptions, the Eqs. (13) - (16) take the following form

μ \nabla^{2} u + (λ + μ) \frac{\partial e}{\partial x} + γ \frac{\partial ϕ}{\partial x} - β_{1} \frac{\partial T}{\partial x} - β_{2} \frac{\partial C}{\partial x} = ρ \frac{\partial^{2} u}{\partial t^{2}},

(18)

μ \nabla^{2} w + (λ + μ) \frac{\partial e}{\partial z} + γ \frac{\partial ϕ}{\partial z} - β_{1} \frac{\partial T}{\partial z} - β_{2} \frac{\partial C}{\partial z} = ρ \frac{\partial^{2} w}{\partial t^{2}},

(19)

a_{3} a_{5} \nabla^{2} T - (a_{4} a_{5} \nabla^{2} - \frac{\partial}{\partial t}) C + a_{1} a_{5} \nabla^{2} ϕ + a_{5} β_{2} \nabla^{2} e = 0,

(20)

(a_{1} \nabla^{2} - ρ ψ \frac{\partial^{2}}{\partial t^{2}} - d_{0}) ϕ - γ e + a_{2} T + a_{1} C = 0,

(21)

[K^{*} + (K + K^{*} τ_{υ}) \frac{\partial}{\partial t} + K τ_{T} \frac{\partial^{2}}{\partial t^{2}}] T_{, i i} = (1 + τ_{q} \frac{\partial}{\partial t} + \frac{1}{2} τ_{q}^{2} \frac{\partial^{2}}{\partial t^{2}}) [ρ C_{E} T_{, t t} + T_{0} β_{1} u_{i, i t t} + a_{2} T_{0} ϕ_{, t t} + a_{3} T_{0} C_{, t t} - ρ (\frac{1}{t} - \frac{1}{t_{0}}) Q] .

(22)

The constitutive equations can be written as

σ_{x x} = λ e + 2 μ \frac{\partial u}{\partial x} + γ ϕ - β_{1} T - β_{2} C,

(23)

σ_{y y} = λ e + γ ϕ - β_{1} T - β_{2} C,

(24)

σ_{z z} = λ e + 2 μ \frac{\partial w}{\partial z} + γ ϕ - β_{1} T - β_{2} C,

(25)

σ_{x z} = μ (\frac{\partial u}{\partial z} + \frac{\partial w}{\partial x}) .

(26)

4. Solution of the Problem

For convenience, the non-dimensional variables listed below are utilized

({x^{'}}_{i}, {u^{'}}_{i}) = \frac{η_{0}}{c_{1}} (x_{i}, u_{i}), ϕ^{'} = \frac{ψ η_{0}^{2}}{c_{1}^{2}} ϕ, {σ^{'}}_{i j} = \frac{σ_{i j}}{β T_{0}}, (t^{'}, {t^{'}}_{0}, {τ^{'}}_{ν}, {τ^{'}}_{q}, {τ^{'}}_{T}) = η_{0} (t, t_{0}, τ_{ν}, τ_{q}, τ_{T}), θ^{'} = \frac{β_{1}}{ρ c_{1}^{2}} θ, C^{'} = \frac{β_{2}}{ρ c_{1}^{2}} C, {I^{'}}_{0} = \frac{η_{0}}{β_{1} T_{0} c_{1}} I_{0}, γ^{*}^{'} = \frac{c_{1}}{η_{0}} γ^{*}, r^{'} = \frac{η_{0}}{c_{1}} r, η_{0} = \frac{ρ C_{E} c_{1}^{2}}{K}, c_{1}^{2} = \frac{λ + 2 μ}{ρ} .

(27)

By applying Helmholtz decomposition, the relations between the displacement components and the potential function

N_{1} (x, z, t), N_{2} (x, z, t)

are

u = \frac{\partial N_{1}}{\partial x} - \frac{\partial N_{2}}{\partial z}, w = \frac{\partial N_{1}}{\partial z} + \frac{\partial N_{2}}{\partial x} .

(28)

The solution of the physical quantities can be introduced in terms of normal modes in the following form

[N_{1}, N_{2}, ϕ, T, C, σ_{i j}] (x, z, t) = [{\bar{N}}_{1}, {\bar{N}}_{2}, \bar{ϕ}, \bar{T}, \bar{C}, {\bar{σ}}_{i j}] (z) \exp (i a x + b t),

(29)

where

b

is the complex time constant (frequency),

i

is the imaginary unit,

a

is the wave number in the

x -

direction and

{\bar{N}}_{1}, {\bar{N}}_{2}, \bar{ϕ}, \bar{T}, \bar{C}, {\bar{σ}}_{i j}

are the amplitudes of the functions

N_{1},

N_{2},

ϕ,

T,

C,

σ_{i j},

respectively.

Using Eqs. (27) - (29), the Eqs. (18) - (22) become

(D^{2} - s_{1}) {\bar{N}}_{1} + s_{2} \bar{ϕ} - \bar{θ} - \bar{C} = 0,

(30)

(D^{2} - s_{3}) {\bar{N}}_{2} = 0,

(31)

(D^{2} - s_{4}) \bar{ϕ} - s_{5} (D^{2} - a^{2}) {\bar{N}}_{1} + s_{6} \bar{θ} + s_{7} \bar{C} = 0,

(32)

s_{8} {(D^{2} - a^{2})}^{2} {\bar{N}}_{1} + s_{9} (D^{2} - a^{2}) \bar{θ} + s_{10} (D^{2} - a^{2}) \bar{ϕ} - (s_{11} D^{2} - s_{12}) \bar{C} = 0,

(33)

(s_{13} D^{2} - s_{14}) \bar{θ} + s_{15} (D^{2} - a^{2}) {\bar{N}}_{1} + s_{16} \bar{ϕ} + s_{17} \bar{C} = Q_{0} f (x, t) \exp (- γ^{*} z),

(34)

where

s_{i} (i = 1, 2, 3, ..., 17),

Q_{0}

and

f (x, t)

are defined in Appendix A.

Eliminating

{\bar{N}}_{1}, \bar{ϕ}, \bar{θ}

and

\bar{C}

between Eqs. (30), (32), (33) and (34) we get the following non-homogeneous ordinary differential equations

(D^{8} - A_{1} D^{6} + A_{2} D^{4} - A_{3} D^{2} + A_{4}) {\bar{N}}_{1} = Q_{0} f (x, t) L_{1} \exp (- γ^{*} z),

(35)

(D^{8} - A_{1} D^{6} + A_{2} D^{4} - A_{3} D^{2} + A_{4}) \bar{ϕ} = Q_{0} f (x, t) L_{2} \exp (- γ^{*} z),

(36)

(D^{8} - A_{1} D^{6} + A_{2} D^{4} - A_{3} D^{2} + A_{4}) \bar{θ} = Q_{0} f (x, t) L_{3} \exp (- γ^{*} z),

(37)

(D^{8} - A_{1} D^{6} + A_{2} D^{4} - A_{3} D^{2} + A_{4}) \bar{C} = Q_{0} f (x, t) L_{4} \exp (- γ^{*} z) .

(38)

Here

A_{j} (j = 1, 2, 3, 4)

and

L_{j} (j = 1, 2, 3, 4)

are defined in Appendix B.

Eq. (35) can be factorized as

\prod_{m = 1}^{4} (D^{2} - k_{m}^{2}) {{\bar{N}}_{1} (z)} = Q_{0} f (x, t) L_{1} \exp (- γ^{*} z),

(39)

where

k_{m}^{2} (m = 1, 2, 3, 4)

are the roots of characteristic equation of Eq. (35).

The general solutions of Eqs. (35) - (38), bound at

z \to \infty,

are given by

N_{1} (x, z, t) = \sum_{n = 1}^{4} M_{n} \exp (- k_{n} z + i a x + b t) + Q_{0} L L_{1} g \exp (- γ^{*} z),

(40)

ϕ (x, z, t) = \sum_{n = 1}^{4} H_{1 n} M_{n} \exp (- k_{n} z + i a x + b t) + Q_{0} L L_{2} g \exp (- γ^{*} z),

(41)

θ (x, z, t) = \sum_{n = 1}^{4} H_{2 n} M_{n} \exp (- k_{n} z + i a x + b t) + Q_{0} L L_{3} g \exp (- γ^{*} z),

(42)

C (x, z, t) = \sum_{n = 1}^{4} H_{3 n} M_{n} \exp (- k_{n} z + i a x + b t) + Q_{0} L L_{4} g \exp (- γ^{*} z),

(43)

The solution of Eq. (32), bound at

z \to \infty,

is given by

N_{2} (x, z, t) = M_{5} \exp (- k_{5} z + i a x + b t),

(44)

where

k_{5}^{2} = s_{3}

are the roots.

In order to obtain the displacement components

u, w

by substituting Eqs. (40) and (44) into Eq. (28), respectively, we get

u (x, z, t) = [\sum_{n = 1}^{4} i a M_{n} \exp (- k_{n} z) + k_{5} M_{5} \exp (- k_{5} z)] \exp (i a x + b t) + Q_{0} L L_{1} g (\frac{- 2 x}{r^{2}}) \exp (- γ^{*} z),

(45)

w (x, z, t) = [\sum_{n = 1}^{4} - k_{n} M_{n} \exp (- k_{n} z) + i a M_{5} \exp (- k_{5} z)] \exp (i a x + b t) + Q_{0} L L_{1} g (- γ^{*}) \exp (- γ^{*} z) .

(46)

With the aid of (45), (46) and (28), the strain is

e (x, z, t) = \sum_{n = 1}^{4} H_{4 n} M_{n} \exp (- k_{n} z + i a x + b t) + Q_{0} L L_{5} g \exp (- γ^{*} z) .

(47)

Introducing Eqs. (27), (29), (45) and (46) in Eqs. (22) - (26), the stresses are

σ_{x x} (x, z, t) = [\sum_{n = 1}^{4} H_{5 n} M_{n} \exp (- k_{n} z) + i a k_{5} r_{4} M_{5} \exp (- k_{5} z)] \exp (i a x + b t) + Q_{0} L L_{6} g \exp (- γ^{*} z),

(48)

σ_{y y} (x, z, t) = \sum_{n = 1}^{4} H_{6 n} M_{n} \exp (- k_{n} z + i a x + b t) + Q_{0} L L_{7} g \exp (- γ^{*} z),

(49)

σ_{z z} (x, z, t) = [\sum_{n = 1}^{4} H_{7 n} M_{n} \exp (- k_{n} z) - i a k_{5} r_{4} M_{5} \exp (- k_{5} z)] \exp (i a x + b t) + Q_{0} L L_{8} g \exp (- γ^{*} z),

(50)

σ_{x z} (x, z, t) = [\sum_{n = 1}^{4} H_{8 n} M_{n} \exp (- k_{n} z) - k_{5}^{2} r_{4} M_{5} \exp (- k_{5} z)] \exp (i a x + b t) - Q_{0} L L_{9} g \exp (- γ^{*} z),

(51)

where

H_{j n} (j = 1, 2, ..., 8)

L_{m} (m = 5, 6, 7, 8, 9)

and

g

are defined in Appendix C.

5. Boundary Conditions

The boundary conditions of a diffusion thermoelastic medium with voids in the context of the three-phase-lag model of thermoelasticity that fills in the region

ℜ

defined as:

ℜ = {(x, y, z) : - \infty \leq x < \infty, - \infty \leq y < \infty, 0 \leq z < \infty}

. We now consider the boundary conditions at surface

z = 0

are

5.1. The Mechanical Boundary Condition

The mechanical boundary condition that the bounding plane to the surface

z = 0

has zero stresses, so we have

σ_{x x} (0, x, t) = σ_{x z} (0, x, t) = 0,

(52)

5.2. The Boundary Restriction of Heat

We assume that the boundary surface of the body is subject to a thermal shock described by the function

\frac{\partial θ}{\partial z} = p_{1} \exp (i a x + b t),

(53)

where

p_{1}

is constant.

5.3. Voids Conditions

\frac{\partial ϕ}{\partial z} = 0.

(54)

5.4. The Boundary Restriction of Concentration

\frac{\partial C}{\partial z} = p_{2} \exp (i a x + b t),

(55)

where

p_{2}

is constant.

In order to obtain the constants

M_{1}, M_{2}, M_{3}, M_{4}

and

M_{5},

we will use the dimensionless size

{p^{'}}_{1} = \frac{β_{1}}{ρ c_{1}^{2}} p_{1},

{p^{'}}_{2} = \frac{β_{2}}{ρ c_{1}^{2}} p_{2}

and the expressions of the variables into the boundary restrictions imposed above. Additionally, we will use the normal mode analysis in order to obtain the system of equations

\sum_{n = 1}^{4} H_{5 n} M_{n} + a r_{4} k_{5} M_{5} = 0,

(56)

\sum_{n = 1}^{4} H_{8 n} M_{n} - r_{4} k_{5}^{2} M_{5} = 0,

(57)

\sum_{n = 1}^{4} - k_{n} H_{2 n} M_{n} = p_{1},

(58)

\sum_{n = 1}^{4} k_{n} H_{1 n} M_{n} = 0,

(59)

\sum_{n = 1}^{4} - k_{n} H_{3 n} M_{n} = p_{2} .

(60)

When applying the inverse method matrix to the above equations, one can determined the constants

M_{n} (n = 1, 2, 3, 4, 5),

hence; the expressions of the field quantities for generalized thermoelastic medium with voids and diffusion in the presence of laser pulse in the context of three-phase-lag theory of thermoelasticity can be obtained.

6. Special and Particular Cases

6.1. Equations of the model of 3PHL when $K^{}, K > 0,$ $τ_{q} > τ_{T} > τ_{ν} > 0,$ and the solutions are always (exponentially) stable if $\frac{2 K τ_{T}}{τ_{q}} > τ_{ν}^{} > K^{*} τ_{q}$ as Quintanilla and Racke [7]

6.2. If we take, $(τ_{v} = τ_{T} = τ_{q} = 0,$ $K^{*}, K > 0)$ in Eqs. (40) - (51), then we obtain the corresponding results for the generalized thermoelastic medium with voids and diffusion in the context of Green and Naghdi's theory of type III.

6.3. In the absence of void effect, if we take $a_{1} = a_{2} = γ = d_{0} = ψ = 0$ in the Eqs. (30)-(34), we get:

(D^{2} - s_{1}) {\bar{N}}_{1} - \bar{θ} - \bar{C} = 0,

(61)

(D^{2} - s_{3}) {\bar{N}}_{2} = 0,

(62)

s_{8} {(D^{2} - a^{2})}^{2} {\bar{N}}_{1} + s_{9} (D^{2} - a^{2}) \bar{θ} - (s_{11} D^{2} - s_{12}) \bar{C} = 0,

(63)

(s_{13} D^{2} - s_{14}) \bar{θ} + s_{15} (D^{2} - a^{2}) {\bar{N}}_{1} + s_{17} \bar{C} = Q_{0} f (x, t) \exp (- γ^{*} z) .

(64)

Eliminating

\bar{C},

{\bar{N}}_{1}

and

\bar{θ}

between Eqs. (61), (63) and (64), one can obtain the following non-homogenous ordinary differential equations

(D^{6} - F_{1} D^{4} + F_{2} D^{2} - F_{3}) {\bar{N}}_{1} (z) = Q_{0} f (x, t) λ_{1} \exp (- γ^{*} z),

(65)

(D^{6} - F_{1} D^{4} + F_{2} D^{2} - F_{3}) \bar{θ} (z) = Q_{0} f (x, t) λ_{2} \exp (- γ^{*} z),

(66)

(D^{6} - F_{1} D^{4} + F_{2} D^{2} - F_{3}) \bar{C} (z) = Q_{0} f (x, t) λ_{3} \exp (- γ^{*} z) .

(67)

Eqs. (65)-(67) can be factorized as

\prod_{n = 1}^{3} (D^{2} - {\bar{k}}_{n}^{2}) {{\bar{N}}_{1} (z), \bar{θ} (z), \bar{C} (z)} = Q_{0} f (x, t) [λ_{1}, λ_{2}, λ_{3}] \exp (- γ^{*} z) .

(68)

Where

{\bar{k}}_{n}^{2} (n = 1, 2, 3)

are the roots leading to the solution of the Eq. (68) which is bound as

z \to \infty,

N_{1} (x, z, t) = \sum_{n = 1}^{3} {\bar{M}}_{n} \exp (- {\bar{k}}_{n} z + i a x + b t) + Q_{0} N^{*} λ_{1} g \exp (- γ^{*} z),

(69)

θ (x, z, t) = \sum_{n = 1}^{3} {\bar{H}}_{1 n} {\bar{M}}_{n} \exp (- {\bar{k}}_{n} z + i a x + b t) + Q_{0} N^{*} λ_{2} g \exp (- γ^{*} z),

(70)

C (x, z, t) = \sum_{n = 1}^{3} {\bar{H}}_{2 n} {\bar{M}}_{n} \exp (- {\bar{k}}_{n} z + i a x + b t) + Q_{0} N^{*} λ_{3} g \exp (- γ^{*} z) .

(71)

The solution of the Eq. (62), bound as

z \to \infty,

is given by

N_{2} (x, z, t) = {\bar{M}}_{4} \exp (- {\bar{k}}_{4} z + i a x + b t),

(72)

where

{\bar{k}}_{4}^{2} = s_{3}

is the root of the characteristic equation of Eq. (62).

The components of displacement, strain and stresses are

u (x, z, t) = [\sum_{n = 1}^{3} i a {\bar{M}}_{n} \exp (- {\bar{k}}_{n} z) + {\bar{k}}_{4} {\bar{M}}_{4} \exp (- {\bar{k}}_{4} z)] \exp (i a x + b t) + Q_{0} N^{*} λ_{1} g (\frac{- 2 x}{r^{2}}) \exp (- γ^{*} z),

(73)

w (x, z, t) = [\sum_{n = 1}^{3} - {\bar{k}}_{n} {\bar{M}}_{n} \exp (- {\bar{k}}_{n} z) + i a {\bar{M}}_{4} \exp (- {\bar{k}}_{4} z)] \exp (i a x + b t) - Q_{0} N^{*} λ_{1} g γ^{*} \exp (- γ^{*} z),

(74)

e (x, z, t) = \sum_{n = 1}^{3} {\bar{H}}_{3 n} {\bar{M}}_{n} \exp (- {\bar{k}}_{n} z + i a x + b t) + Q_{0} N^{*} λ_{4} g \exp (- γ^{*} z),

(75)

σ_{x x} (x, z, t) = [\sum_{n = 1}^{3} {\bar{H}}_{4 n} {\bar{M}}_{n} \exp (- {\bar{k}}_{n} z) + a r_{4} {\bar{k}}_{4} {\bar{M}}_{4} \exp (- {\bar{k}}_{4} z)] \exp (i a x + b t) + Q_{0} N^{*} λ_{5} g \exp (- γ^{*} z),

(76)

σ_{y y} (x, z, t) = \sum_{n = 1}^{3} {\bar{H}}_{5 n} {\bar{M}}_{n} \exp (- {\bar{k}}_{n} z + i a x + b t) + Q_{0} N^{*} λ_{6} g \exp (- γ^{*} z),

(77)

σ_{z z} (x, z, t) = [\sum_{n = 1}^{3} {\bar{H}}_{6 n} {\bar{M}}_{n} \exp (- {\bar{k}}_{n} z) - i a r_{4} {\bar{k}}_{4} {\bar{M}}_{4} \exp (- {\bar{k}}_{4} z)] \exp (i a x + b t) + Q_{0} N^{*} λ_{7} g \exp (- γ^{*} z),

(78)

σ_{x z} (x, z, t) = [\sum_{n = 1}^{3} {\bar{H}}_{7 n} {\bar{M}}_{n} \exp (- {\bar{k}}_{n} z) - r_{4} {\bar{k}}_{4}^{2} {\bar{M}}_{4} \exp (- {\bar{k}}_{4} z)] \exp (i a x + b t) - Q_{0} N^{*} λ_{8} g \exp (- γ^{*} z),

(79)

The boundary conditions are

σ_{x x} (0, x, t) = σ_{x z} (0, x, t) = 0, \frac{\partial θ}{\partial z} = p_{1} \exp (i a x + b t), \frac{\partial C}{\partial z} = p_{2} \exp (i a x + b t),

(80)

where

F_{1}, F_{2}, F_{3},

λ_{i} (i = 1, 2, ..., 8)

and

{\bar{H}}_{m n} (m = 1, 2, ..., 7 a n d n = 1, 2, 3)

are defined in Appendix D.

6.4. Neglecting the diffusion effect, i.e., $a_{3}, a_{4}, a_{5}$ and $β_{2}$ tend to zero. Then, the boundary conditions for a generalized thermoelastic medium with voids under laser pulse influence in the context of the 3PHL model are given by

σ_{x x} (0, x, t) = σ_{x z} (0, x, t) = 0, \frac{\partial ϕ}{\partial z} = 0. \frac{\partial θ}{\partial z} = p_{1} \exp (i a x + b t),

(81)

Follow a similar procedure with this modification, one can obtain the following ordinary differential equations

(D^{6} - B_{1} D^{4} + B_{2} D^{2} - B_{3}) {\bar{N}}_{1} (z) = Q_{0} f (x, t) N_{1}^{*} \exp (- γ^{*} z),

(82)

(D^{6} - B_{1} D^{4} + B_{2} D^{2} - B_{3}) \bar{ϕ} (z) = Q_{0} f (x, t) N_{2}^{*} \exp (- γ^{*} z),

(83)

(D^{6} - B_{1} D^{4} + B_{2} D^{2} - B_{3}) \bar{θ} (z) = Q_{0} f (x, t) N_{3}^{*} \exp (- γ^{*} z),

(84)

(D^{2} - s_{3}) {\bar{N}}_{2} (z) = 0,

(85)

and the corresponding solutions are given by

N_{1} (x, z, t) = \sum_{n = 1}^{3} R_{n} \exp (- α_{n} z + i a x + b t) + Q_{0} L^{*} N_{1}^{*} g \exp (- γ^{*} z),

(86)

ϕ (x, z, t) = \sum_{n = 1}^{3} {\tilde{H}}_{1 n} R_{n} \exp (- α_{n} z + i a x + b t) + Q_{0} L^{*} N_{2}^{*} g \exp (- γ^{*} z),

(87)

θ (x, z, t) = \sum_{n = 1}^{3} {\tilde{H}}_{2 n} R_{n} \exp (- α_{n} z + i a x + b t) + Q_{0} L^{*} N_{3}^{*} g \exp (- γ^{*} z),

(88)

N_{2} (x, z, t) = R_{4} \exp (- α_{4} z + i a x + b t),

(89)

u (x, z, t) = [\sum_{n = 1}^{3} i a R_{n} \exp (- α_{n} z) + α_{4} R_{4} \exp (- α_{4} z)] \exp (i a x + b t) + Q_{0} L^{*} N_{4}^{*} g \exp (- γ^{*} z),

(90)

w (x, z, t) = [\sum_{n = 1}^{3} - α_{n} R_{n} \exp (- α_{n} z) + i a R_{4} \exp (- α_{4} z)] \exp (i a x + b t) - Q_{0} L^{*} N_{5}^{*} g \exp (- γ^{*} z),

(91)

e (x, z, t) = \sum_{n = 1}^{3} {\tilde{H}}_{3 n} R_{n} \exp (- α_{n} z + i a x + b t) + Q_{0} L^{*} N_{6}^{*} g \exp (- γ^{*} z),

(92)

σ_{x x} (x, z, t) = [\sum_{n = 1}^{3} {\tilde{H}}_{4 n} R_{n} \exp (- α_{n} z) + i a r_{4} α_{4} R_{4} \exp (- α_{4} z)] \exp (i a x + b t) + Q_{0} L^{*} N_{7}^{*} g \exp (- γ^{*} z),

(93)

σ_{y y} (x, z, t) = \sum_{n = 1}^{3} {\tilde{H}}_{5 n} R_{n} \exp (- α_{n} z + i a x + b t) + Q_{0} L^{*} N_{8}^{*} g \exp (- γ^{*} z),

(94)

σ_{z z} (x, z, t) = [\sum_{n = 1}^{3} {\tilde{H}}_{6 n} R_{n} \exp (- α_{n} z) - i a r_{4} α_{4} R_{4} \exp (- α_{4} z)] \exp (i a x + b t) + Q_{0} L^{*} N_{9}^{*} g \exp (- γ^{*} z),

(95)

σ_{x z} (x, z, t) = [\sum_{n = 1}^{3} {\tilde{H}}_{7 n} R_{n} \exp (- α_{n} z) - r_{4} α_{4}^{2} R_{4} \exp (- α_{4} z)] \exp (i a x + b t) - Q_{0} L^{*} N_{10}^{*} g \exp (- γ^{*} z) .

(96)

Here,

α_{1}^{2}, α_{2}^{2}, α_{3}^{2}

are the roots of characteristic equations of Eqs. (82)-(84),

α_{4}^{2} = s_{3}

is the root of characteristic equation of Eq. (85),

B_{1}, B_{2}, B_{3},

N_{i}^{*} (i = 1, 2, ..., 10),

L^{*}

and

{\tilde{H}}_{m n} (m = 1, 2, ..., 7; n = 1, 2, 3)

are defined in Appendix E.

7. Numerical Results and Discussion

In view of illustrating theoretical results obtained in the preceding sections and comparing these in the context of two different theories of thermoelastic diffusion. Some of numerical results for magnesium material represent as (Said and Othman [27]), the physical data for which is given below (all the units of the used parameters are given in SI units):

λ = 9.4 \times 10^{10} N / m^{2}, μ = 4 \times 10^{10} N / m^{2}, ρ = 1.74 \times 10^{3} k g / m^{3}, T_{0} = 298 K, K = 1.7 \times 10^{2} N / s \cdot K, α_{t} = 1.78 \times 10^{- 5} K^{- 1}, α_{c} = 1.98 \times 10^{- 4} K g^{- 1} m^{3}, a = 0.001 m, C_{E} = 1.04 \times 10^{3} J / k g \cdot K, p_{1} = 0.1 K, β = 7.779 \times 10^{- 8} N / m^{2} K, p_{2} = 0.1 K g^{- 1} m^{3},

The voids parameters are:

ψ = 1.753 \times 10^{- 15} m^{2}, a_{1} = 3.688 \times 10^{- 5} N, d_{0} = 1.475 \times 10^{10} N / m^{2}, a_{2} = 2 \times 10^{6} N / m^{2}, γ = 1.13849 \times 10^{10} N / m^{2} .

The diffusion parameters are:

a_{3} = 1.2 \times 10^{4} m^{2} / K s^{2}, a_{4} = 32 \times 10^{5} m^{5} K g^{- 1} s^{- 2}, a_{5} = 0.85 \times 10^{- 8} K g / m^{3} .

The laser pulse parameters are,

I_{0} = 10^{6} J / m^{2}, t_{0} = 10^{- 6} p s, r = 100 μ m, γ^{*} = 10 m^{- 1} .

Since,

b = b_{0} + i b_{1},

e^{b t} = e^{b_{0} t} [\cos (b_{1} t) + i \sin (b_{1} t)]

and for small values of time one can take

b = b_{0}

(real). The software MALAB 7.0.4 has been used to make the calculations. The computations are performed for

a = 2.9 m,

x = 0.8 m,

b_{0} = - 1.2 r a d / s,

b_{1} = - 0.01 r a d / s

and

0 \leq z \leq 3.

The above comparisons have been made in the context of the theory of (G-N III) and model of 3PHL, in two cases:

(i): The effect of laser pulse at two different values of time [ $t = 0.11$ and $t = 0.33$ ].
(ii): Whether we have some void parameters or not.

The variations of the thermal temperature

θ,

the strain

e,

the displacement

w,

the mass concentration

C,

the change in the volume fraction field

ϕ

and the stress components

σ_{x x}, σ_{x z}

with

z,

substituted in performing the computation. The results are shown in Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16 and Figure 17. Here, all the variables are taken in non-dimensional forms and all curves reaching to zero with the increasing of

z .

7.1. The Effect of Time Parameter

Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8 presented to show comparisons between the displacement

w,

the strain

e,

the temperature

θ,

the mass concentration

C,

the change in the volume fraction field

ϕ

and the stress components

σ_{z z}, σ_{x z}

at two various values of time

t = 0.11, 0.33

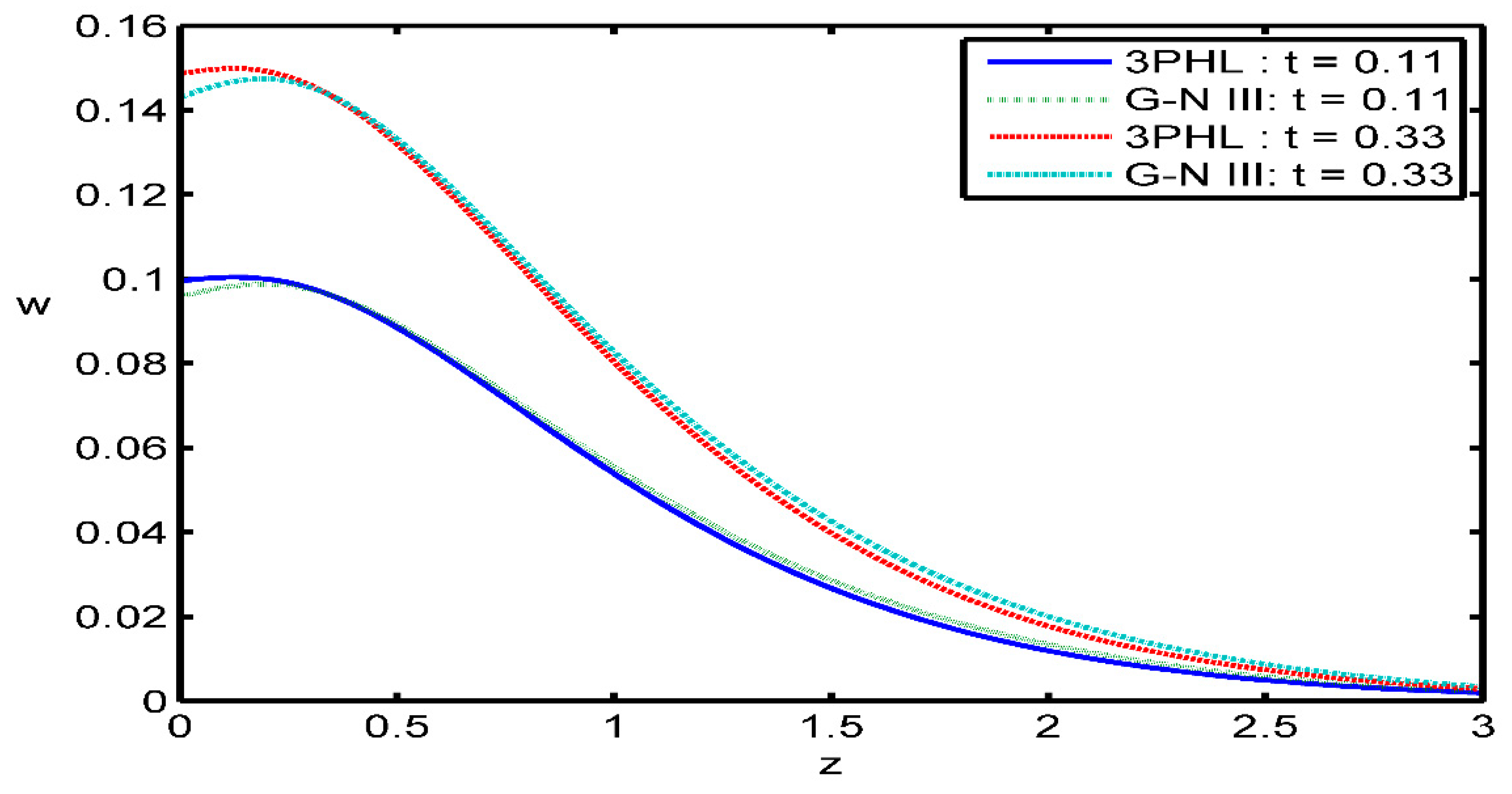
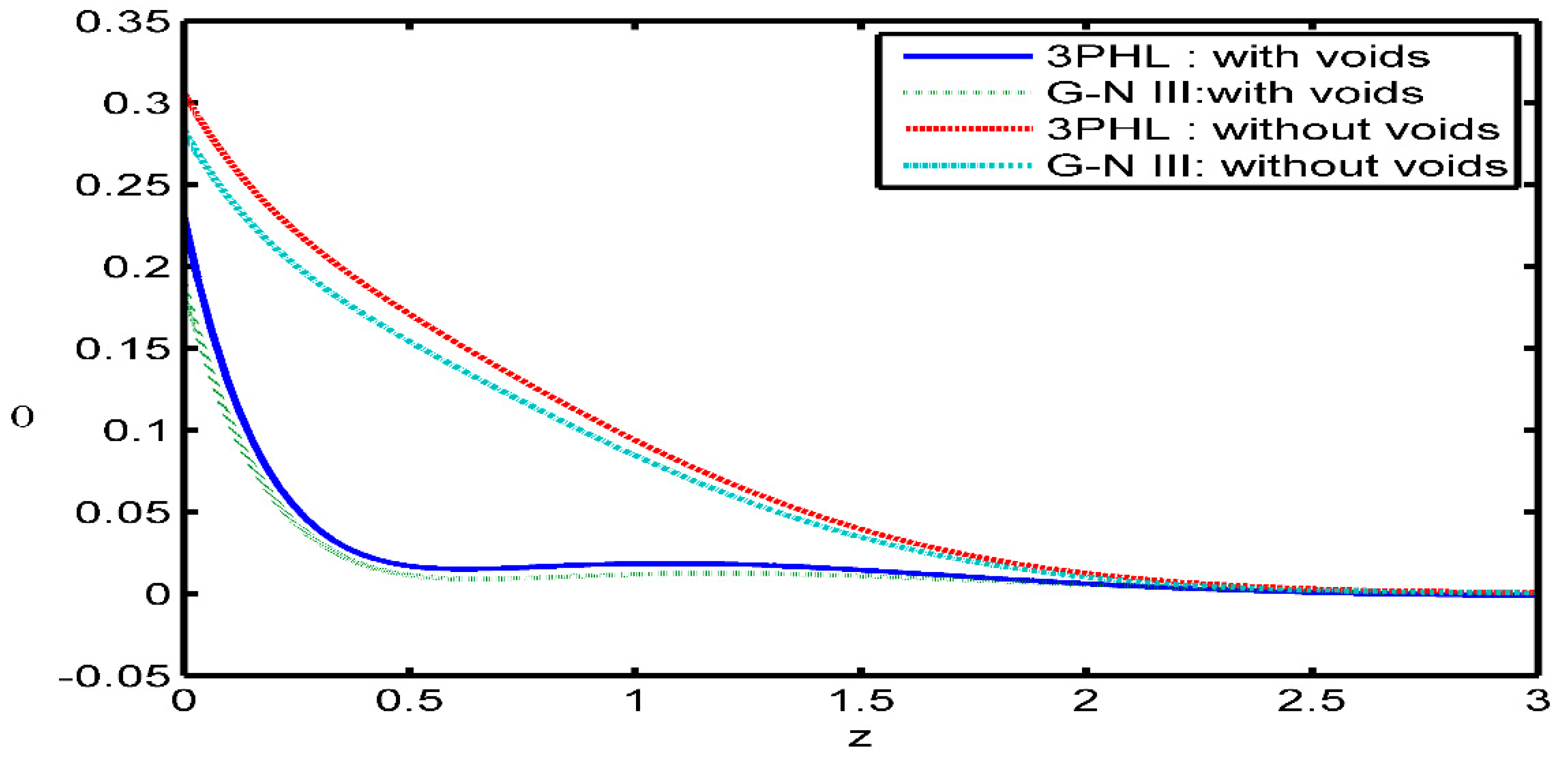
. Figure 2 investigates the variation of the displacement

w

versus

z .

The magnitude of displacement is found to be large for the theory of G-N (type III). It evident that the time parameter has an increasing effect on the magnitude of displacement

w .

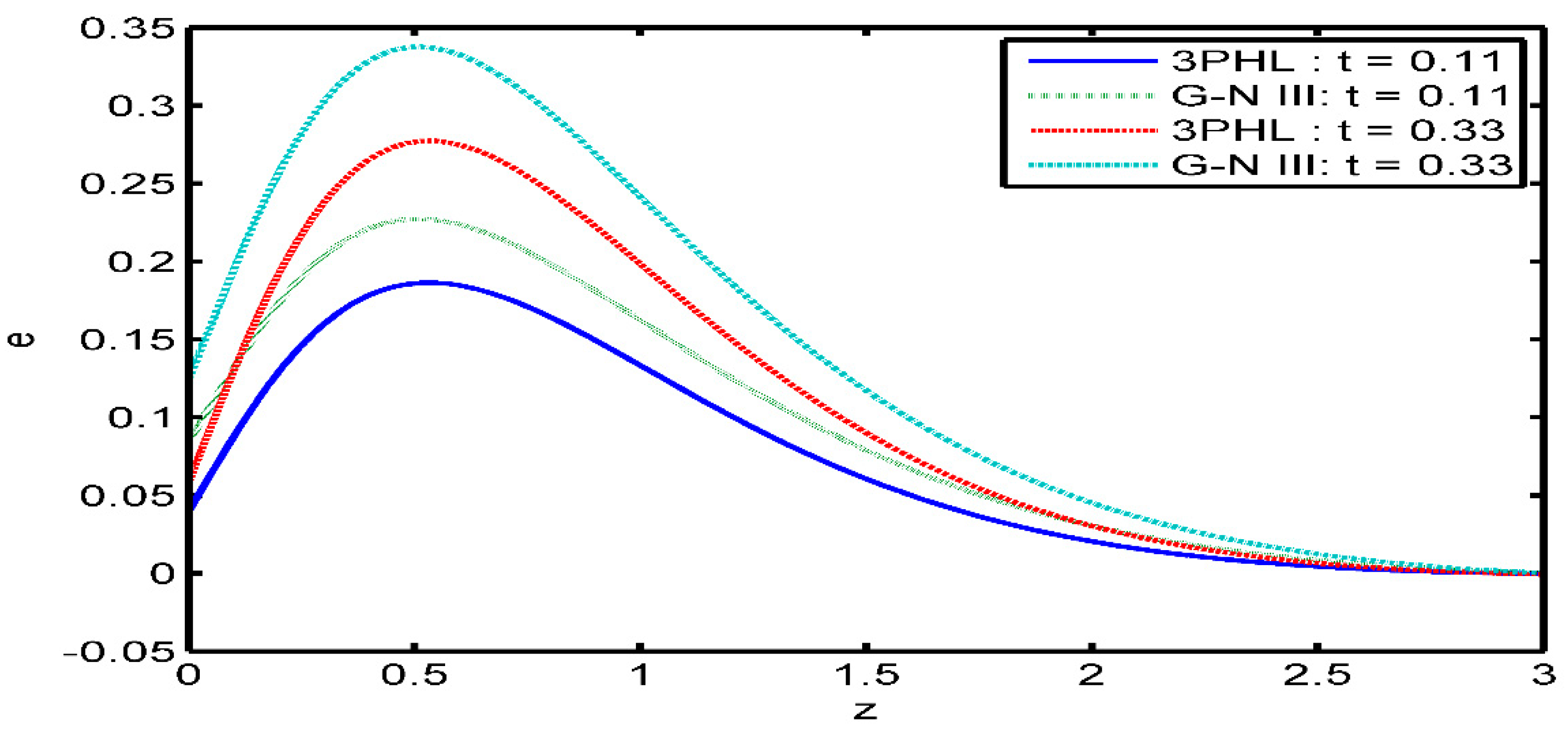
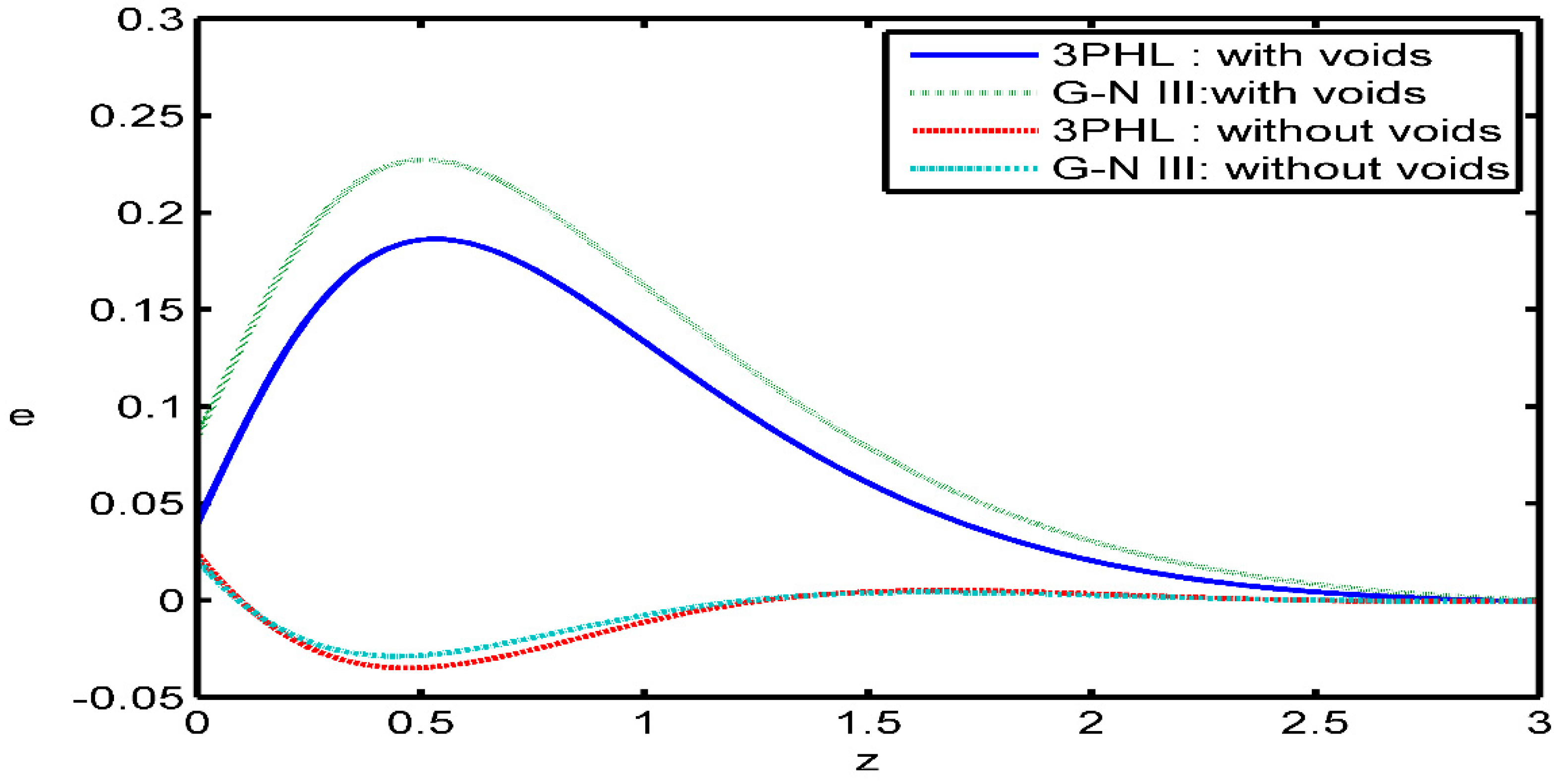
Figure 3 shows the variation of the strain

e

versus

z .

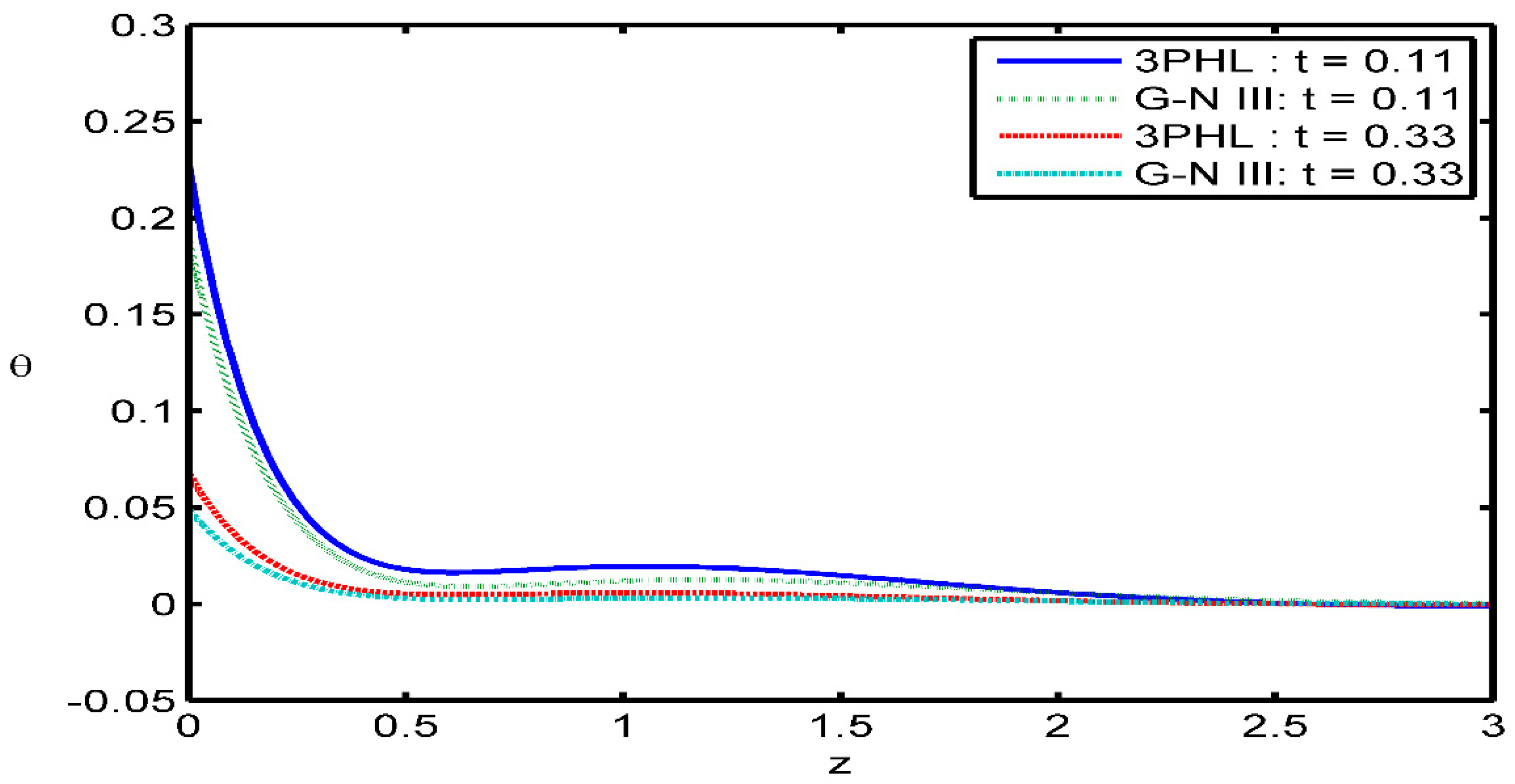
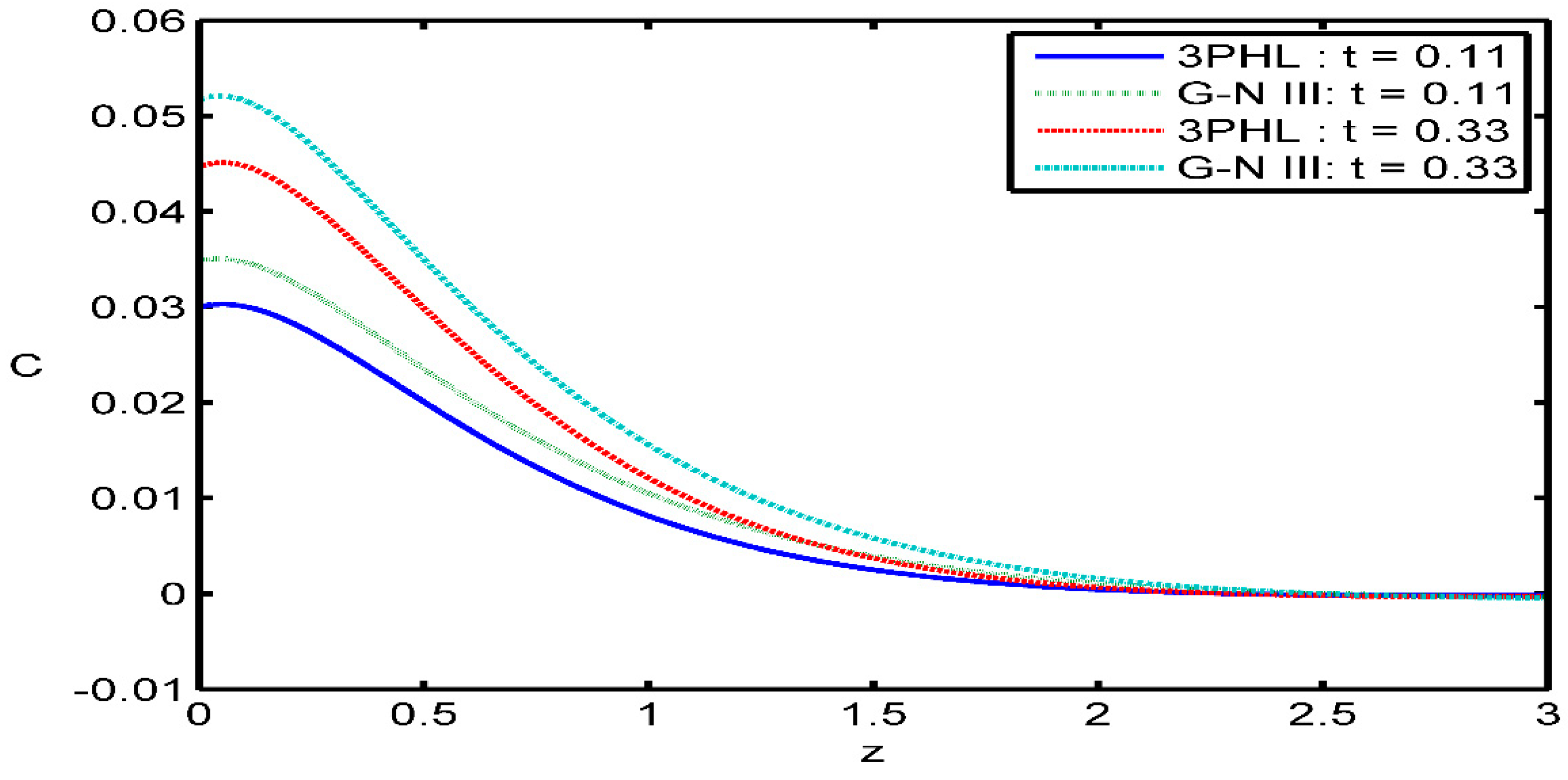
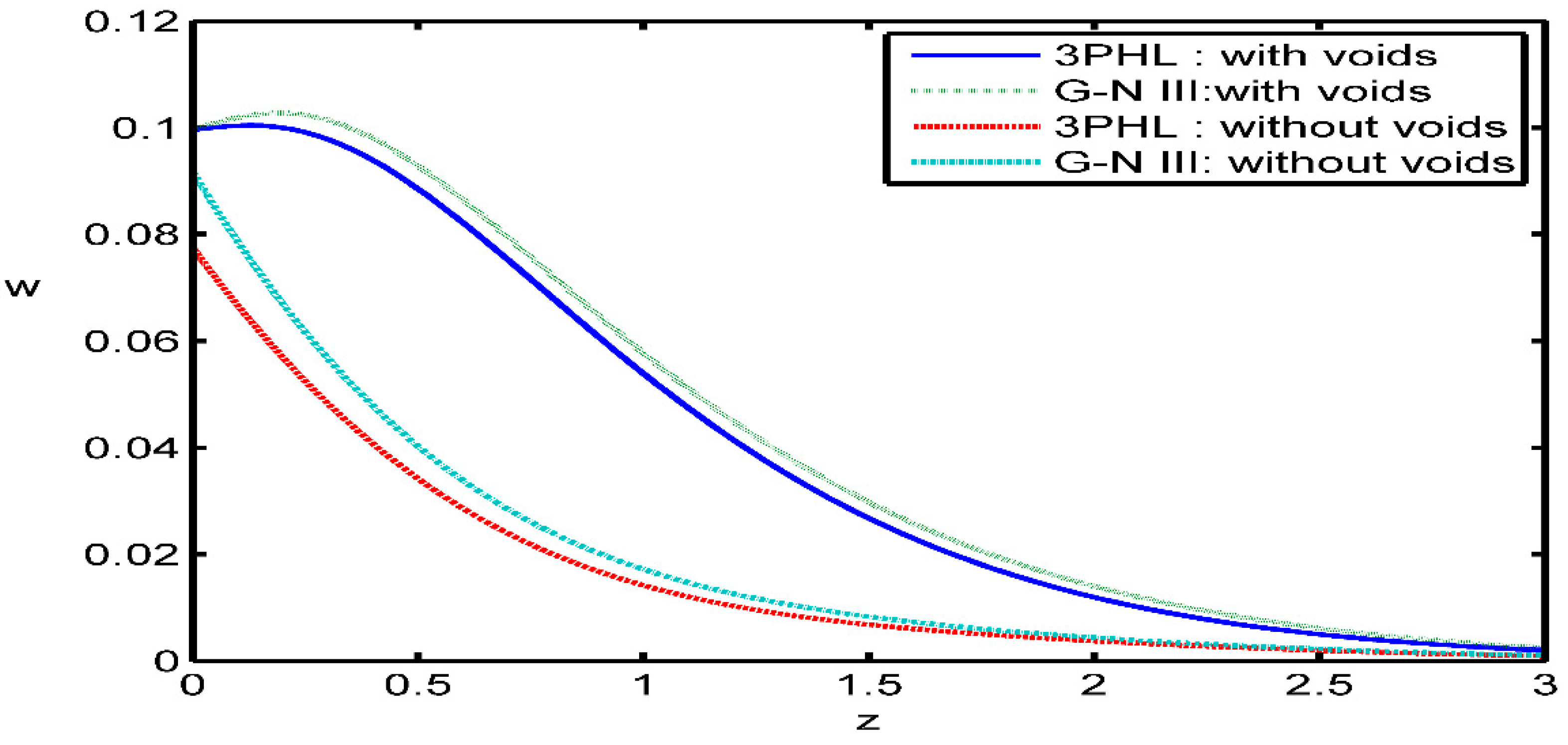
The magnitude of strain is found to be large for G-N (type III) theory. It can be seen that the time parameter has an increasing effect on the magnitude of strain. Figure 4 depicts that variation of the temperature

θ

with respect to the

z -

axis. It can be seen that: the time parameter has a decreasing effect on the magnitude of temperature

θ .

Figure 5 shows the variation of the concentration of diffusion

C

with respect to the

z -

axis. The concentration has a decreasing behavior for thermo-elastic in the interval

0 \leq z \leq 2.9

and it coincides in the interval in the range

z \geq 2.5.

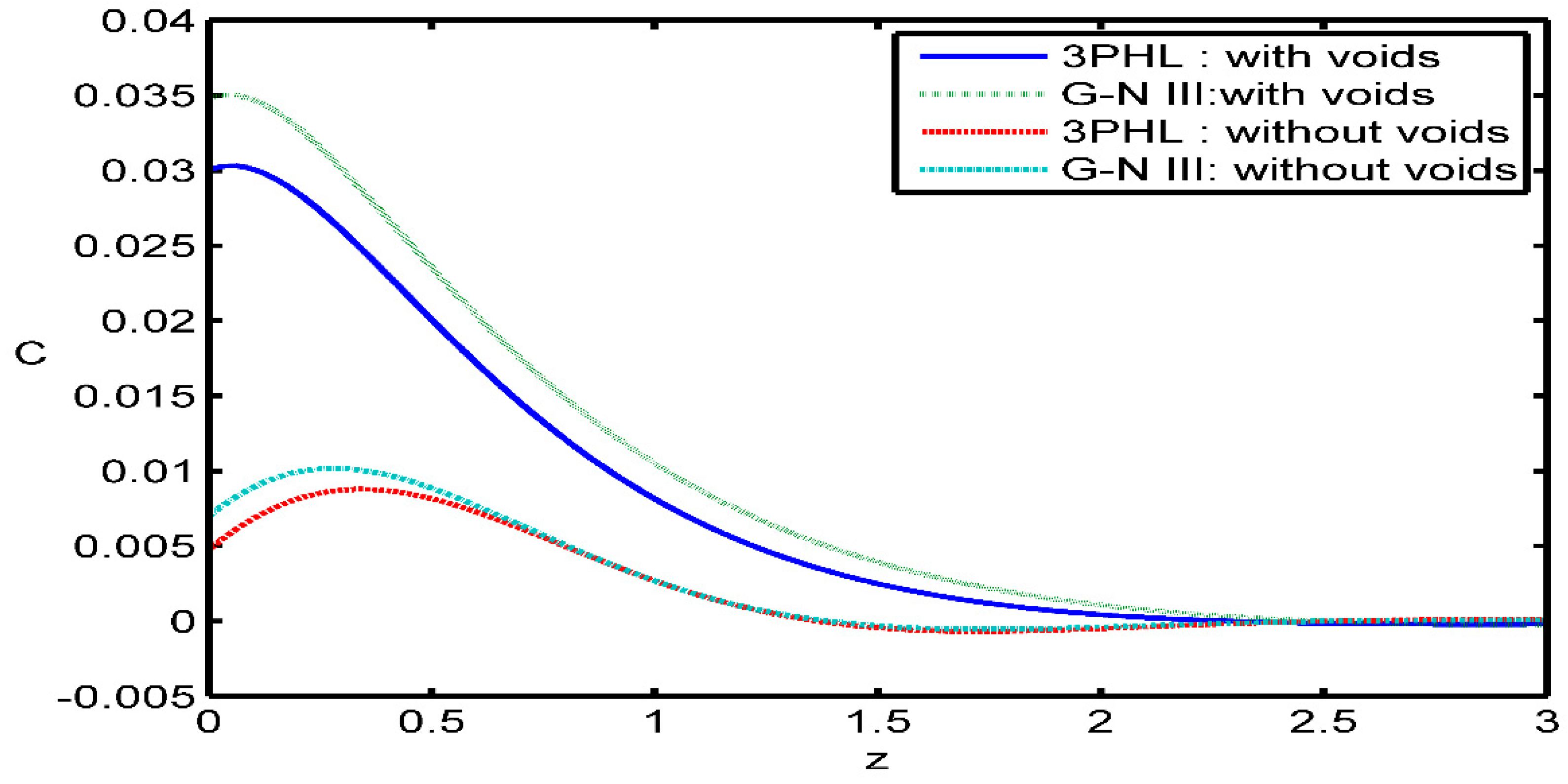
It can be seen that the magnitude of concentration is found to be large for G-N (type III) theory. Figure 6 expresses the distribution of the change in the volume fraction field

ϕ

versus

z .

It was observed that the time parameter has a great effect on the distribution of

ϕ .

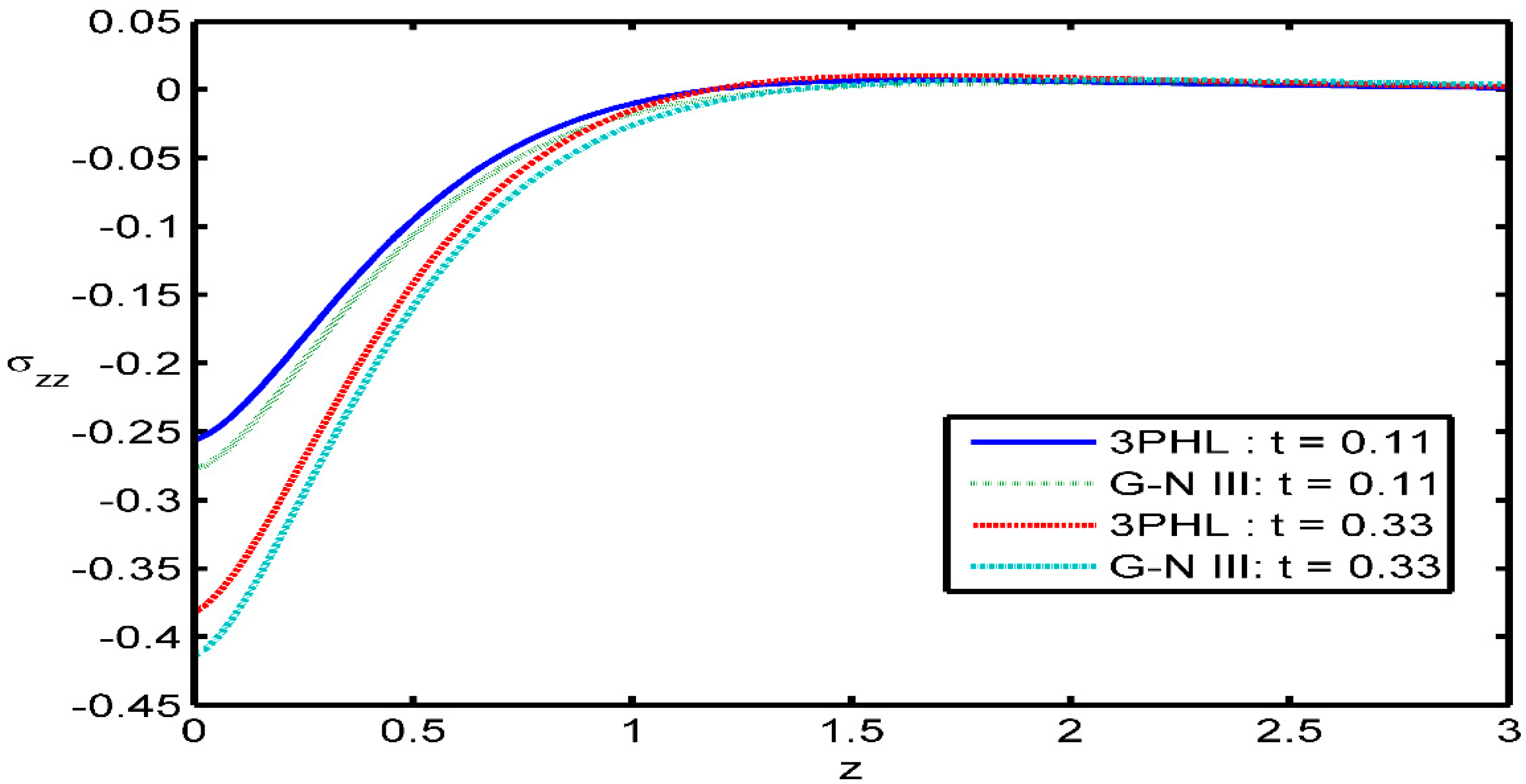
Figure 7 depicts the distribution of the normal stress component

σ_{z z}

with respect to the axial

z .

It is observed that: the values of

σ_{z z}

start from a negative value and time parameter has an increasing effect on the magnitude of

σ_{z z} .

The magnitude of

σ_{z z}

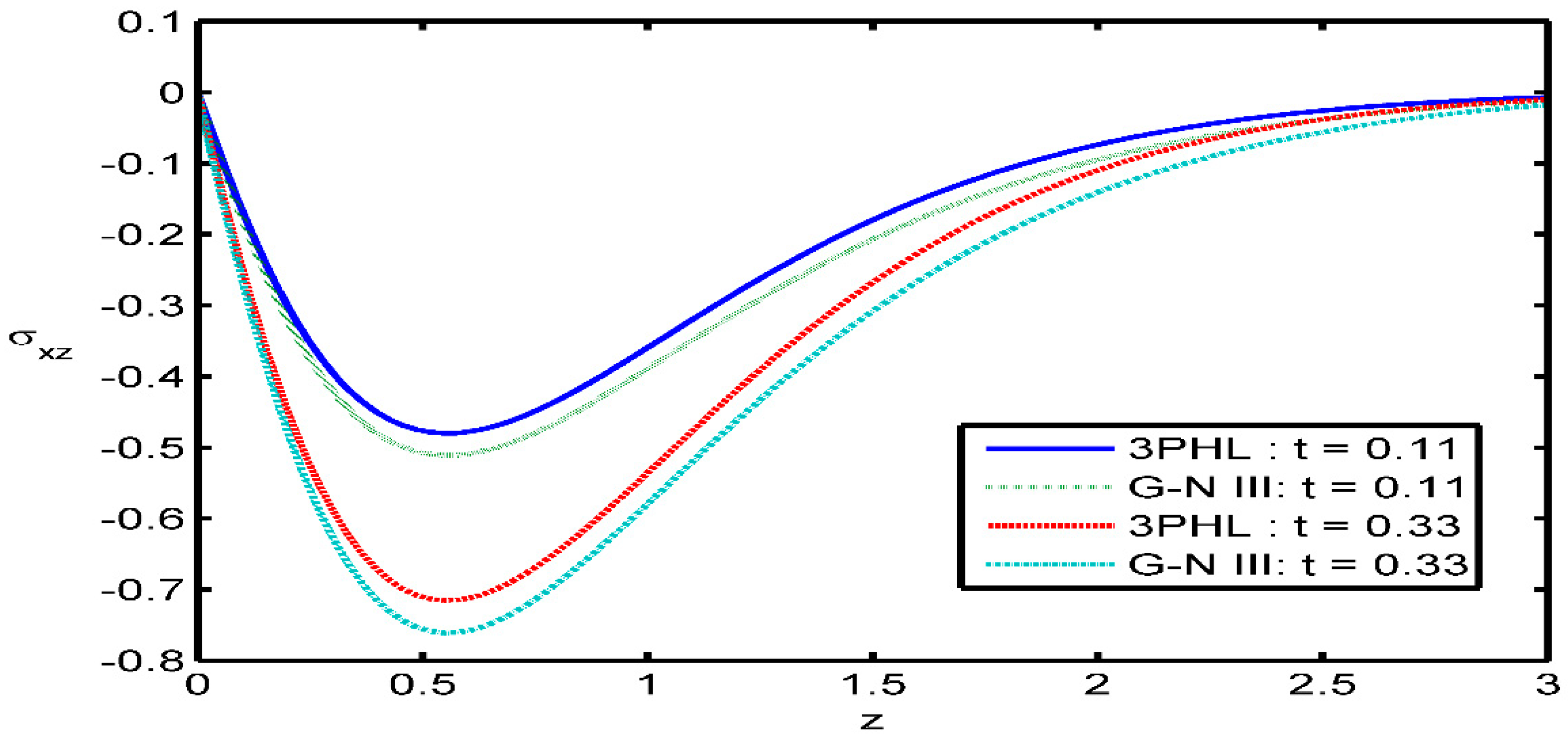
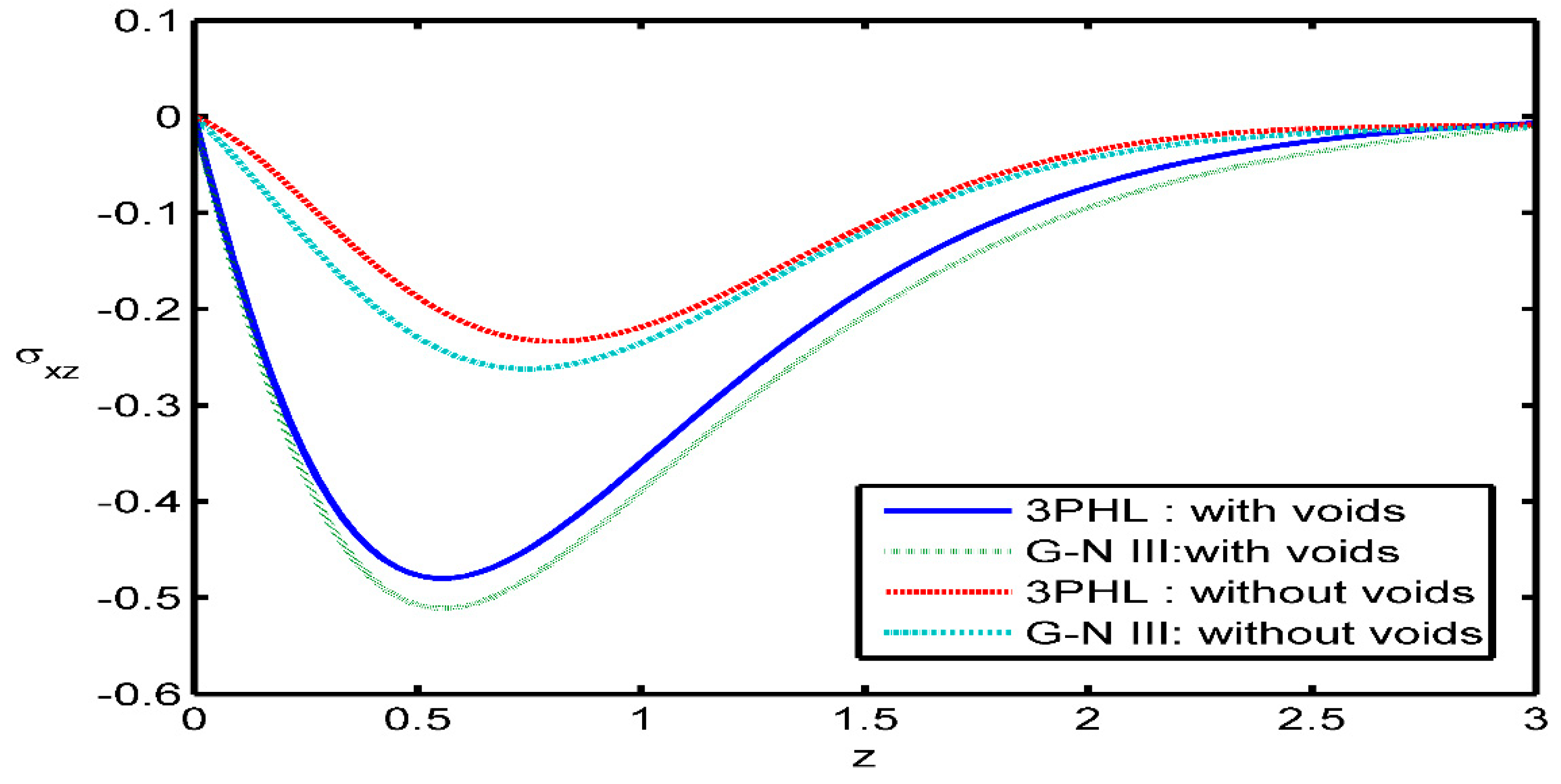
is found to be small for 3PHL model. Figure 8 appears variation of the distribution of tangential stress component

σ_{x z}

as function of the distance

z

at two various values of time parameter. It is observed that: in the context of the two theories, the values of

σ_{x z}

start from a zero, which satisfy the boundary conditions. In this figure, time parameter shows a decreasing effect on the magnitude of

σ_{x z} .

7.2. The Effect of Void Parameters

Figure 9, Figure 10, Figure 11, Figure 12, Figure 13 and Figure 14 presented to show the behavior of the field quantities as function of the distance

z

in 2D during

t = 0.11

with and without voids effect. The void has a significant role in the distribution of all field quantities of the problem. Figure 9 indicates the variation of the displacement component

w,

the values of

w

in the presence of voids are large compared to those for the absence of voids in the range

0 \leq z \leq 3;

while the values are the same for two cases at

z \geq 3.

Figure 10 shows the distribution of the strain

e

via the distance

z .

The values of

e

in the presence of voids are large compared to those for the absence of voids in the range

0 \leq z \leq 2.7,

while have the same values at

z \geq 2.7.

Figure 11 clarifies the distribution of the temperature

θ

is decreasing in the two cases (with and without voids) in the range

0 \leq z \leq 2.5

and the values of

θ

for presence voids are small compared to those for absence voids in the range

0 \leq z \leq 2.5,

while have the same values for two cases at

z \geq 2.5.

Figure 12 displays the variation of the concentration

C

with respect to

z -

axis. The values of the concentration

C

for presence voids are large compared to those for absence voids in the range

0 \leq z \leq 2.4,

while the values are the same for two cases at

z \geq 2.4.

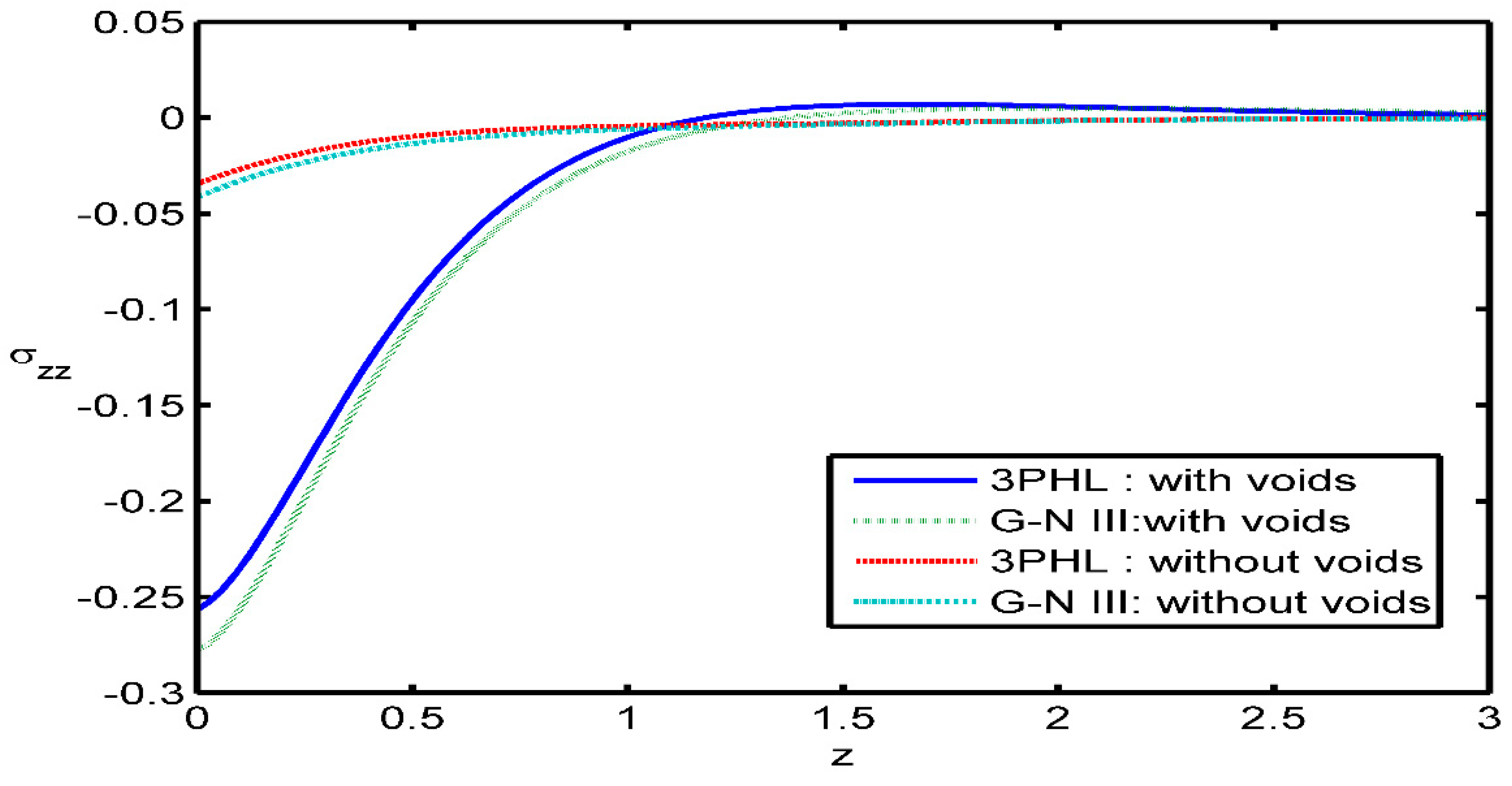
Figure 13 shows the distribution of the normal stress component

σ_{z z}

versus the distance

z .

It can be seen that the magnitude of

σ_{z z}

is found to be small for the presence voids in the range

0 \leq z \leq 1.3;

large in the range

1.3 \leq z \leq 2.8,

while the values are the same for two cases at

z \geq 2.8.

Figure 14 explains that the variation of the tangential stress

σ_{x z}

as a function of the distance

z .

The values of the stress component

σ_{x z}

for presence voids are small compared to those for absence voids in the range

0 \leq z \leq 2.8,

while the values are the same for two cases at

z \geq 2.8.

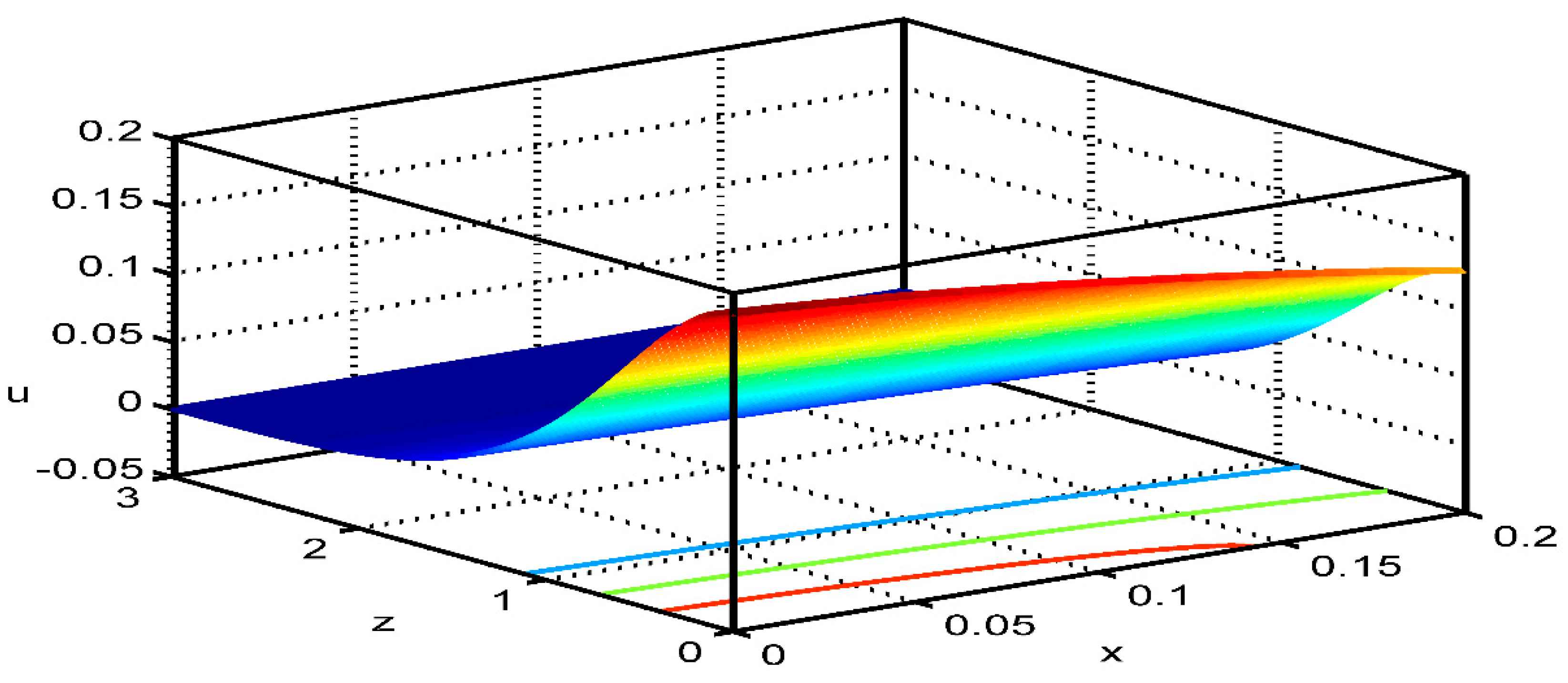
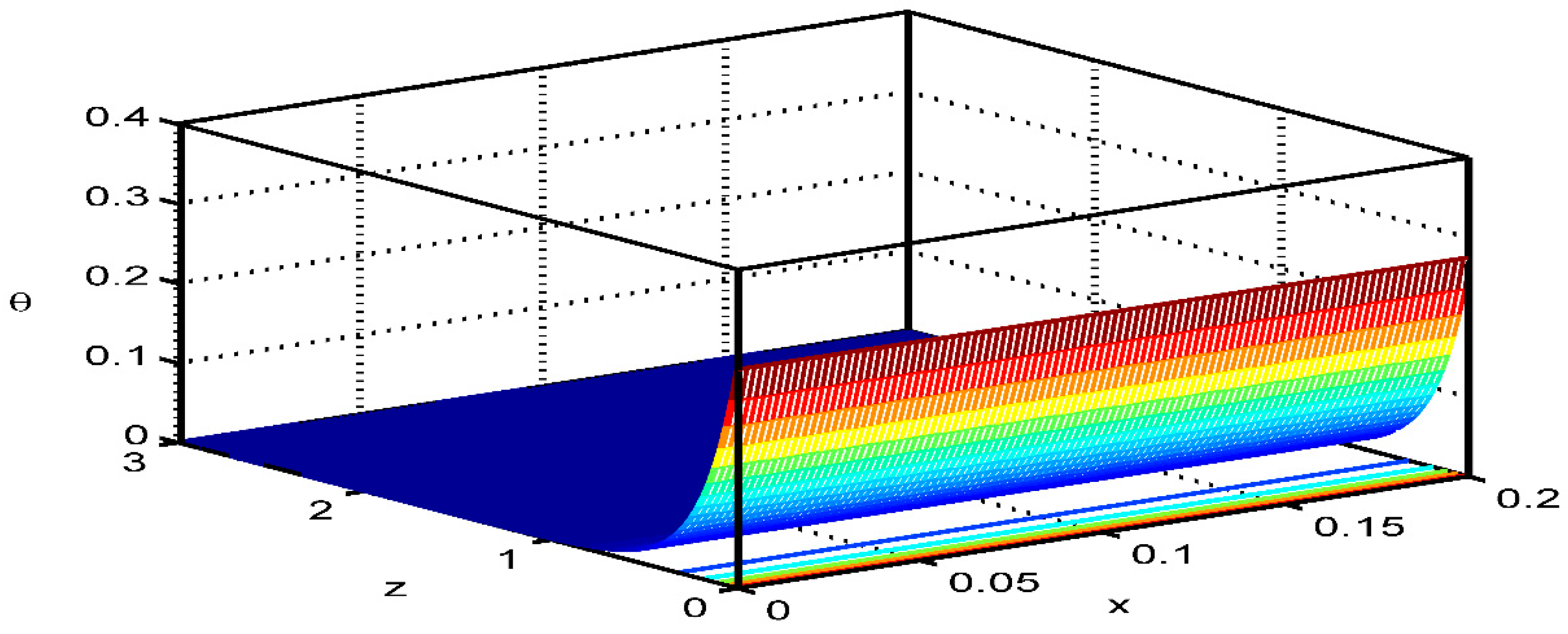
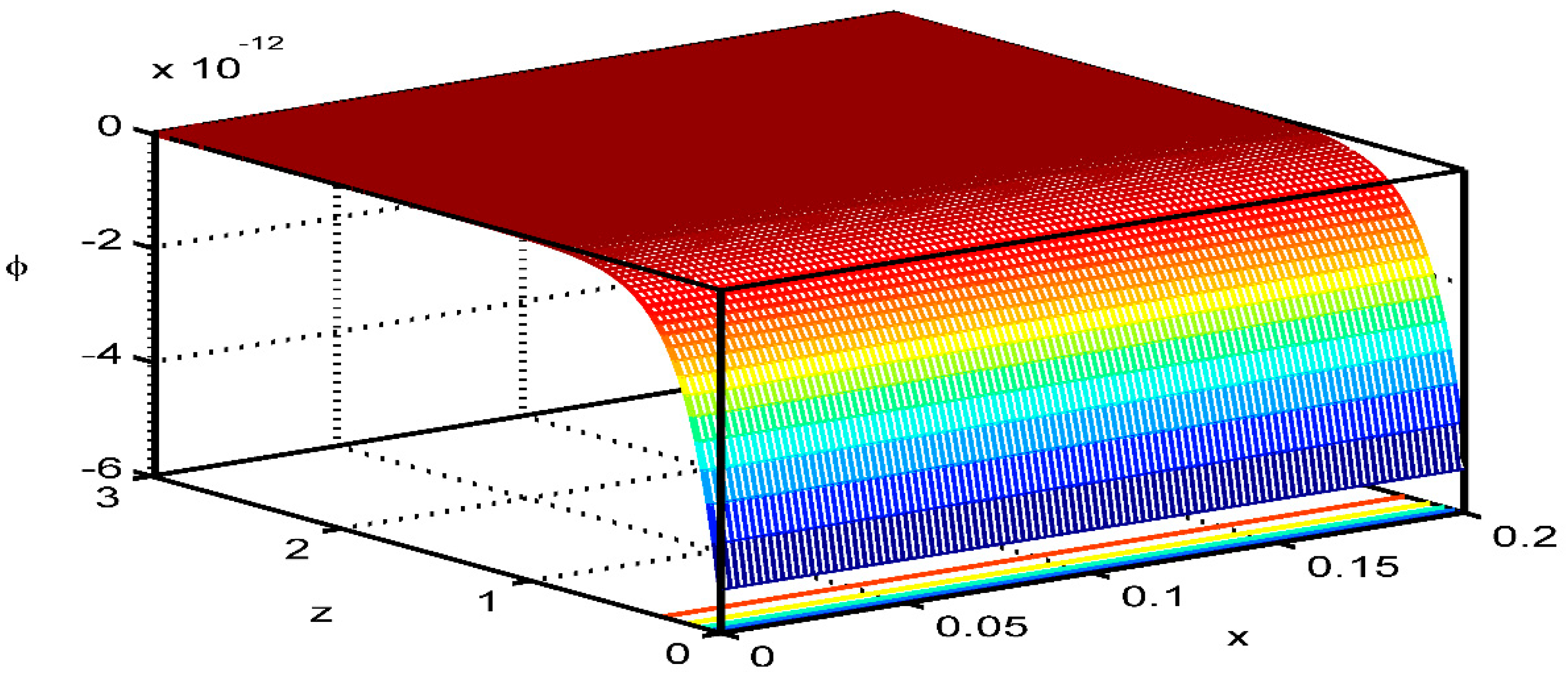
7.3. The 3D Surface Curves

Figure 15, Figure 16 and Figure 17 are giving 3D surface curves for the field quantities i.e., the displacement component

u,

temperature

θ

and the change in the volume fraction field

ϕ

for the effect of the laser pulse on a thermoelastic medium with diffusion and voids. These figures are very important to study the dependence of these field quantities on the distance

z .

8. Conclusions

Due to the complicated nature of the governing equations of the generalized thermo-elasticity theory with voids and diffusion, the done works in this field are unfortunately limited. The method used in this study provides a quite successful in dealing with such problems. The method gives exact solutions in the elastic medium without any restrictions on the actual physical quantities that paper in the governing equations of the considered problem. The important findings emerged in this study are:

According to the results of the work, we can see the presence of diffusion and voids can play a virtual role in increasing or decreasing of the displacements, strain, temperature, mass concentration, change in the volume fraction field and stresses of all field through the thermoelastic medium.
There are significant differences in the field quantities between the G-N theory and the 3PHL model due to the phase-lag of thermal displacement gradient, the phase-lag of heat flux and the phase-lag of the temperature gradient.
The deformation of a body depends on the nature of the applied forces and the type of boundary conditions.
The different values of time in the current model have significant effects on all the fields.
Analytical solutions based upon normal mode method for the thermoelastic problem in solids have been developed and used.
The deformation of a body depends on the nature of the applied forces and thermal loading due to laser pulse as well as the type of boundary conditions.

Funding

This research was funded by the Deanship of Scientific Research at Umm Al-Qura University, grant number 22UQU4340548DSR17. The APC was funded by the Deanship of Scientific Research at Umm Al-Qura University.

Data Availability Statement

All data generated or analyzed during this study are included in this published article.

Acknowledgments

The author would like to thank the Deanship of Scientific Research at Umm Al-Qura University for supporting this work, grant code 22UQU4340548DSR17.

Conflicts of Interest

The author declares no conflict of interest.

Nomenclature

$C_{E}$	Specific heat at constant strain	$T$	Absolute temperature
$T_{0}$	Reference temperature so that $\|(T - T_{0}) / T_{0}\| < < 1$	$e_{i j}$	Components of strain tensor
$u_{i}$	Components of displacement vector	t	Time
$K^{*}$	Material characteristic of the theory	$C$	Concentration distribution
$e = e_{k k}$	Cubical dilatation	$e_{i j}$	Components of strain tensor
$K$	Coefficient of thermal conductivity	$I_{0}$	The energy absorbed
$r$	The beam radius	$t_{0}$	The pulse rise time
$γ^{*}$	The absorption depth of heating energy	$ρ$	The density
$σ_{i j}$	Components of stress tensor	$λ, μ$	Lame's constants
$ϕ$	The change in volume fraction field	$δ_{i j}$	Kronecker delta function
$τ_{v}$	Phase lag of thermal displacement gradient	$τ_{q}$	Phase lag of heat flux
$τ_{T}$	Phase lag of temperature gradient	$c_{1}$	Speed of light, $c_{1}^{2} = \frac{λ + 2 μ}{ρ},$
$η_{0} = \frac{ρ C_{E} c_{1}^{2}}{K},$	Thermal viscosity
$a_{1}, a_{2}, γ, d_{0}, ψ$	The material constants due to presence of voids	$a_{3}, a_{4}, a_{5}$	Constants
$β_{1} = (3 λ + 2 μ) α_{t},$ $α_{t}$	Coefficient of linear thermal expansion
$β_{2} = (3 λ + 2 μ) α_{c},$ $α_{c},$	Coefficient of linear diffusion expansion

Appendix A

s_{1} = a^{2} - b^{2}, s_{2} = \frac{γ}{ρ ψ η_{0}^{2}}, s_{3} = a^{2} - \frac{b^{2} ρ c_{1}^{2}}{μ}, s_{4} = a^{2} - \frac{b^{2} ψ ρ c_{1}^{2}}{a_{1}} + \frac{i b c_{1}^{2} d_{0}}{a_{1} η_{0}}, s_{5} = \frac{γ ψ}{a_{1}}, s_{6} = \frac{a_{2} ψ ρ c_{1}^{2}}{a_{1} β_{1}}, s_{7} = \frac{ψ ρ c_{1}^{2}}{β_{2}}, s_{8} = a_{5} β_{2}, s_{9} = \frac{a_{3} a_{5} ρ c_{1}^{2}}{β_{1}}, s_{10} = \frac{a_{1} a_{5} c_{1}^{2}}{ψ η_{0}^{2}}, s_{11} = \frac{a_{4} a_{5} ρ c_{1}^{2}}{β_{2}}, s_{12} = s_{11} a^{2} + \frac{i b a_{4} ρ c_{1}^{2}}{β_{2} η_{0}}, s_{13} = \frac{ρ η_{0}^{2}}{β_{1}} [K^{*} + i b (K η_{0} + K^{*} τ_{υ}) - K η_{0} b^{2} τ_{T}], s_{0} = 1 + i b τ_{q} - \frac{1}{2} b^{2} τ_{q}^{2},

s_{14} = s_{13} a^{2} - \frac{s_{0} ρ^{2} c_{1}^{2} C_{E} b^{2} η_{0}^{2}}{β_{1}}, s_{15} = s_{0} T_{0} β_{1} b^{2} η_{0}^{2}, s_{16} = \frac{s_{0} a_{2} T_{0} c_{1}^{2} b^{2}}{ψ}, s_{17} = \frac{s_{0} a_{3} T_{0} c_{1}^{2} η_{0}^{2} b^{2} ρ}{β_{2}}, Q_{0} = \frac{ρ β_{1} I_{0} T_{0} γ^{*} η_{0}^{4}}{2 π r^{2} t_{0}^{2} c_{1}^{2}}, f (x, t) = s_{0} (\frac{η_{0}}{t} - \frac{η_{0}}{t_{0}}) \exp (\frac{- x^{2}}{r^{2}} - \frac{t}{t_{0}}) \exp (- a x - i b t) .

Appendix B

s_{18} = s_{4} + s_{7} s_{2}, s_{19} = s_{6} + s_{7}, s_{20} = s_{5} + s_{7}, s_{21} = s_{7} s_{1} + s_{5} a^{2}, s_{22} = s_{10} + s_{2} s_{11}, s_{23} = s_{10} a^{2} + s_{2} s_{12}, s_{24} = s_{9} - s_{11}, s_{25} = s_{12} s_{11} + s_{9} a^{2}, s_{26} = s_{8} + s_{11}, s_{27} = s_{1} s_{11} + s_{11} + 2 s_{28} a^{2}, s_{28} = s_{12} s_{1} + s_{8} a^{4}, s_{29} = s_{16} - s_{2} s_{17}, s_{30} = s_{14} - s_{17}, s_{31} = s_{15} - s_{17}, s_{32} = s_{15} a^{2} - s_{1} s_{17}, s_{33} = s_{18} s_{24} + s_{22} s_{19} + s_{25}, s_{34} = s_{18} s_{25} + s_{23} s_{19}, s_{35} = s_{19} s_{26} + s_{20} s_{24}, s_{36} = s_{19} s_{27} + s_{21} s_{24} + s_{20} s_{25}, s_{37} = s_{28} s_{19} + s_{21} s_{25}, s_{38} = s_{18} s_{13} + s_{30}, s_{39} = s_{18} s_{30} + s_{29} s_{19}, s_{40} = s_{20} s_{13}, s_{41} = s_{20} s_{30} + s_{21} s_{13} - s_{30} s_{19}, s_{42} = s_{21} s_{30} - s_{32} s_{19}, A_{0} = \frac{1}{s_{24} s_{40} - s_{13} s_{35}}, L_{3} = \frac{A_{0} L_{1} (s_{20} γ^{* 2} - s_{21}) - A_{0} L_{2} (γ^{* 2} - s_{18})}{s_{19}},

A_{1} = A_{0} (s_{24} s_{41} + s_{33} s_{40} - s_{13} s_{36} - s_{35} s_{38}), A_{3} = A_{0} (s_{33} s_{42} + s_{43} s_{41} - s_{38} s_{37} - s_{36} s_{39}), A_{2} = A_{0} (s_{24} s_{42} + s_{33} s_{41} + s_{43} s_{40} - s_{13} s_{37} - s_{36} s_{38} - s_{35} s_{39}), A_{4} = A_{0} (s_{34} s_{42} - s_{37} s_{39}), L_{1} = A_{0} s_{19} (s_{24} γ^{* 4} - s_{33} γ^{* 2} + s_{34}), L_{2} = A_{0} s_{19} (s_{35} γ^{* 4} - s_{36} γ^{* 2} + s_{37}), L_{4} = A_{0} [L_{3} - s_{2} L_{2} - L_{1} (γ^{* 2} - s_{1})] .

Appendix C

r_{1} = \frac{λ}{β_{1} T_{0}}, r_{2} = \frac{γ c_{1}^{2}}{β_{1} T_{0} ψ η_{0}^{2}}, r_{3} = \frac{ρ c_{1}^{2}}{β_{1} T_{0}}, r_{4} = \frac{2 μ}{β_{1} T_{0}}, L = \frac{1}{γ^{* 8} - A_{1} γ^{* 6} + A_{2} γ^{* 4} - A_{3} γ^{* 2} + A_{4}}, L_{5} = L_{1} (\frac{4 x^{2}}{r^{4}} - \frac{2}{r^{2}} + γ^{* 2}), L_{6} = r_{1} L_{5} + r_{2} L_{2} - r_{3} L_{3} - r_{3} L_{4} + r_{4} L_{1} (\frac{4 x^{2}}{r^{4}} - \frac{2}{r^{2}}), L_{7} = r_{1} L_{5} + r_{2} L_{2} - r_{3} L_{3} - r_{3} L_{4}, L_{8} = r_{1} L_{5} + r_{2} L_{2} - r_{3} L_{3} - r_{3} L_{4} - r_{4} L_{1} γ^{* 2}, L_{9} = r_{4} L_{1} γ^{*} (- \frac{2 x}{r^{2}}),

H_{1 n} = \frac{s_{35} k_{n}^{4} - s_{36} k_{n}^{2} + s_{37}}{s_{24} k_{n}^{4} - s_{33} k_{n}^{2} + s_{34}}, H_{2 n} = \frac{s_{20} k_{n}^{2} - s_{21} - H_{1 n} (k_{n}^{2} - s_{18})}{s_{19}}, H_{3 n} = H_{2 n} - s_{2} H_{1 n} - k_{n}^{2} + s_{1}, H_{4 n} = a + k_{n}^{2}, H_{5 n} = r_{1} H_{4 n} + r_{2} H_{1 n} - r_{3} H_{2 n} - r_{3} H_{3 n} + r_{4} a^{2}, H_{6 n} = r_{1} H_{4 n} + r_{2} H_{1 n} - r_{3} H_{2 n} - r_{3} H_{3 n}, H_{7 n} = r_{1} H_{4 n} + r_{2} H_{1 n} - r_{3} H_{2 n} - r_{3} H_{3 n} + r_{4} k_{n}^{2}, H_{8 n} = - r_{4} a k_{n}, g = s_{0} (\frac{η_{0}}{t} - \frac{η_{0}}{t_{0}}) \exp (\frac{- x^{2}}{r^{2}} - \frac{t}{t_{0}}), n = 1, 2, 3, 4.

Appendix D

χ_{1} = s_{8} - s_{11}, χ_{2} = 2 a^{2} s_{8} + s_{12} - s_{1} s_{11}, χ_{3} = a^{2} s_{8} - s_{1} s_{12}, χ_{4} = s_{9} + s_{11}, χ_{5} = a^{2} s_{9} + s_{12}, χ_{6} = s_{14} + s_{17}, χ_{7} = s_{15} + s_{17}, χ_{8} = a^{2} s_{15} + s_{1} s_{17}, χ_{0} = \frac{1}{χ_{1} s_{15}}, F_{1} = χ_{0} (χ_{1} χ_{6} + χ_{2} s_{13} + χ_{4} χ_{7}), F_{2} = χ_{0} (χ_{2} χ_{6} + χ_{3} s_{13} + χ_{4} χ_{8} + χ_{5} χ_{7}), F_{3} = χ_{0} (χ_{3} χ_{6} + χ_{5} χ_{8}), λ_{1} = χ_{0} (- χ_{4} γ^{* 2} + χ_{5}), λ_{2} = - χ_{0} (χ_{1} γ^{* 4} - χ_{2} γ^{* 2} + χ_{3}), λ_{3} = χ_{0} [λ_{1} (γ^{* 2} - s_{1}) - λ_{2}], λ_{4} = λ_{1} (\frac{4 x^{2}}{r^{4}} + γ^{* 2}), λ_{5} = r_{1} λ_{4} - r_{3} λ_{2} + r_{4} λ_{1} (\frac{4 x^{2}}{r^{4}}), λ_{6} = r_{1} λ_{4} - r_{3} λ_{2}, λ_{7} = r_{1} λ_{4} - r_{3} λ_{2} + r_{4} λ_{1} γ^{* 2}, λ_{8} = r_{4} λ_{1} γ^{*} (\frac{- 2 x}{r^{2}}), N^{*} = \frac{1}{γ^{* 6} - F_{1} γ^{* 4} + F_{2} γ^{* 2} - F_{3}},

{\bar{H}}_{1 n} = \frac{- (χ_{1} {\bar{k}}_{n}^{4} - χ_{2} {\bar{k}}_{n}^{2} + χ_{3})}{χ_{4} {\bar{k}}_{n}^{2} - χ_{5}}, {\bar{H}}_{2 n} = {\bar{k}}_{n}^{2} - s_{1} - {\bar{H}}_{1 n}, {\bar{H}}_{3 n} = a^{2} + {\bar{k}}_{n}^{2}, {\bar{H}}_{4 n} = r_{1} {\bar{H}}_{3 n} - r_{3} {\bar{H}}_{1 n} + r_{4} a^{2}, {\bar{H}}_{5 n} = r_{1} {\bar{H}}_{3 n} - r_{3} {\bar{H}}_{1 n}, {\bar{H}}_{6 n} = r_{1} {\bar{H}}_{3 n} - r_{3} {\bar{H}}_{1 n} + r_{4} {\bar{k}}_{n}^{2}, {\bar{H}}_{7 n} = - r_{4} a {\bar{k}}_{n}, n = 1, 2, 3.

Appendix E

ε_{1} = s_{4} - s_{2} s_{6}, ε_{2} = s_{5} - s_{6}, ε_{3} = a^{2} s_{5} - s_{1} s_{6}, ε_{4} = s_{13} + s_{14} - s_{15}, ε_{5} = s_{1} s_{14} - s_{15} a^{2}, ε_{6} = s_{1} s_{2} - s_{16}, ε_{0} = \frac{1}{s_{13}}, B_{1} = ε_{0} (ε_{1} s_{13} + ε_{4} - ε_{2} s_{2}), B_{2} = ε_{0} (ε_{5} + ε_{1} ε_{4} - ε_{6} ε_{2} - ε_{3} s_{2}), B_{3} = ε_{0} (ε_{5} ε_{1} - ε_{6} ε_{3}), N_{1}^{*} = ε_{0} (γ^{* 2} - ε_{1}), N_{2}^{*} = ε_{0} (ε_{21} γ^{* 2} - ε_{3}), N_{3}^{*} = N_{1}^{*} (γ^{* 2} - s_{1}), N_{4}^{*} = N_{1}^{*} (\frac{- 2 x}{r^{2}}), N_{5}^{*} = N_{1}^{*} γ^{*}, N_{6}^{*} = (N_{5}^{*} γ^{*} - \frac{2 x N_{4}^{*}}{r^{2}}), N_{7}^{*} = r_{1} N_{6}^{*} + r_{2} N_{2}^{*} - r_{3} N_{3}^{*} + r_{4} N_{4}^{*} (- \frac{2 x}{r^{2}}), N_{8}^{*} = r_{1} N_{6}^{*} + r_{2} N_{2}^{*} - r_{3} N_{3}^{*}, N_{9}^{*} = r_{1} N_{6}^{*} + r_{2} N_{2}^{*} - r_{3} N_{3}^{*} + r_{4} N_{4}^{*} γ^{*}, N_{10}^{*} = γ^{*} N_{4}^{*}, L^{*} = \frac{1}{γ^{* 6} - B_{1} γ^{* 4} + B_{2} γ^{* 2} - B_{3}}, {\tilde{H}}_{1 n} = \frac{- (ε_{2} α_{n}^{2} - ε_{3})}{α_{n}^{2} - ε_{1}}, {\tilde{H}}_{2 n} = α_{n}^{2} - s_{1} + s_{2} {\tilde{H}}_{1 n}, {\tilde{H}}_{3 n} = a^{2} + α_{n}^{2}, {\tilde{H}}_{4 n} = r_{1} {\tilde{H}}_{3 n} + r_{2} {\tilde{H}}_{1 n} - r_{3} {\tilde{H}}_{2 n} + r_{4} a^{2},

{\tilde{H}}_{5 n} = r_{1} {\tilde{H}}_{3 n} + r_{2} {\tilde{H}}_{1 n} - r_{3} {\tilde{H}}_{2 n}, {\tilde{H}}_{6 n} = r_{1} {\tilde{H}}_{3 n} + r_{2} {\tilde{H}}_{1 n} - r_{3} {\tilde{H}}_{2 n} + r_{4} α_{n}^{2}, {\bar{H}}_{7 n} = - r_{4} a α_{n}, n = 1, 2, 3.

References

Lord, H.W., Shulman, Y. A generalized dynamical theory of thermoelasticity, J. Mech. and Phys. Sol., 15, 299-309 (1967). [CrossRef]
Green, A.E., Lindsay, K.A. Thermoelasticity, J. Elast., 2, 1-7 (1972).
Hetnarski, R.B., Ignaczak, J. Generalized thermoelasticity, J. Therm. Stress., 22, 451-476 (1999).
Green, A.E., Naghdi, P.M. A re-examination of the basic postulates of thermo-mechanics, Proceedings of the Royal Society of London A, 432, 171-194 (1991).
Tzou, D.Y. A unified field approach for heat conduction from macro-to micro scales, J. Heat Transfer, 117, 8-16 (1995). [CrossRef]
Choudhuri, S.K.R. On thermoelastic three phase lag model, J. Therm. Stress., 30,231-238 (2007). [CrossRef]
Quintanilla, R., Racke, R. A note on stability in three-phase-lag heat conduction, Int. J. Heat Mass Transfer, 51, 24-29 (2008). [CrossRef]
Mukhopadhyay, S., Kumar, R. Analysis of phase-lag effects on wave propagation in a thick plate under axisymmetric temperature distribution, Acta Mech., 210, 331-341 (2010). [CrossRef]
Othman, M.I.A., Eraki, E.E.M. Generalized magneto-thermoelastic half-space with diffusion under initial stress using three-phase-lag model, Mech. Based Design of Struct. and Mach., 45(2), 145-159 (2017). [CrossRef]
Nunziato, J.W., Cowin, S.C. A non-linear theory of elastic materials with voids, Arch. for Rational Mech. and Anal., 72(2), 175-201 (1979).
Cowin, S.C., Nunziato, J.W. Linear theory of elastic materials with voids, J. Elast., 13, 125-147 (1983).
Puri, P., Cowin, S.C. Plane waves in linear elastic materials with voids, J. Elast., 15, 167-183 (1985). [CrossRef]
Iesan, D. A theory of thermoelastic materials with voids, Acta Mech., 60, 67-89 (1986). [CrossRef]
Othman, M.I.A, Abd-Elaziz, E.M. Effect of initial stress and Hall current on a magneto-thermoelastic porous medium with microtemperatures, Ind. J. Phys., 93(4), 475-485 (2019). [CrossRef]
Othman, M.I.A., Abd-Elaziz, E.M. 2-D Problem of generalized thermoelastic porous media under the effect of initial stress and microtemperatures, J. Porous Media, 24(5), 63-76 (2021).
Abd-Elaziz, E.M., Marin, M., Othman, M.I.A. On the effect of Thomson and initial stress in a thermo-porous elastic solid under G-N electromagnetic theory, Symmetry, in Appl. Cont. Mech., 11(3), 413-430 (2019). [CrossRef]
M.A. Fahmy, Boundary element algorithm for modeling and simulation of dual-phase lag bioheat transfer and biomechanics of anisotropic soft tissues, Int. J. Appl. Mech. 10(10) (2018) 1850108. [CrossRef]
M.A. Fahmy, A new LRBFCM-GBEM modeling algorithm for general solution of time fractional-order dual phase lag bioheat transfer problems in functionally graded tissues, Numer. Heat Trans., part A: Appl. 75(9) (2019) 616-626. [CrossRef]
M.A. Fahmy, A new boundary element algorithm for a general solution of nonlinear space-time fractional dual-phase-lag bio-heat transfer problems during electro-magnetic radiation, Case Stud. in Therm. Eng. 25(6) (2021), 100918.
Alharbi, A.M., Abd-Elaziz, E.M., Othman, M.I.A. Effect of temperature-dependent and internal heat source on a micropolar thermoelastic medium with voids under 3PHL model, ZAMM, 101(6), 1-24. (2021). [CrossRef]
Abd-Elaziz, E.M., Othman, M.I.A. Effect of Thomson and thermal loading due to laser pulse in a magneto-thermoelastic porous medium with energy dissipation, ZAMM 99(8), 1-18 (2019) e201900079.
Othman, M.I.A., Eraki, E.E.M. Effect of gravity on generalized thermoelastic diffusion due to laser pulse using dual-phase-lag model, Multi. Model. Mater. and Struct., 14(3), 457-481 (2018). [CrossRef]
Nowacki, W. Dynamical problems of thermodiffusion in solids-I, Bulletin of Polish Academy of Sciences Series, Science and Technology, 22, 55-64 (1974).
Nowacki, W. Dynamical problems of thermodiffusion in solids-II, Bulletin of Polish Academy of Sciences Series, Science and Technology, 22, 205-211 (1974).
Nowacki, W. Dynamical problems of thermodiffusion in solids-III, Bulletin of Polish Academy of Sciences Series, Science and Technology, 22, 257-266 (1974).
Sharma, K. Analysis of deformation due to inclined load in generalized thermo-diffusive elastic medium”, Int. J. Eng. Sci. Tech., 3, 117-129 (2011).
Said, S.M., Othman, M.I.A. Effects of diffusion and internal heat source on a two-temperature thermoelastic medium with three-phase-lag model, Arch. Thermody., 39 (2), 15-39 (2018).
Singh B. Reflection of P and SV waves from free surface of an elastic solid with generalized thermodiffusion, J. Earth and System and Sci., 114(2), 159-168 (2005). [CrossRef]
Othman, M.I.A., Atwa, S.Y., Farouk, R.M. The effect of diffusion on two-dimensional problem of generalized thermoelasticity with Green-Naghdi theory, Int. Commun. Heat and Mass Transfer, 36(8), 857-864 (2009). [CrossRef]
Marin, M. Weak solutions in elasticity of dipolar porous materials, Math. Probl. Eng., 2008, 1-8, ID 158908 (2008). [CrossRef]
Said, S.M., Abd-Elaziz, E.M., Othman, M.I.A. Modeling of memory-dependent derivative in a rotating magneto-thermoelastic diffusive medium with variable thermal conductivity, Steel and Comp. Struct., An Int. J., 36(6), 617-629 (2020).
McDonald, F.A. On the precursor in laser-generated ultrasound waveforms in metals, Appl. Phys. Letters, 56(3), 230-232 (1990). [CrossRef]
Wang, X., Xu, X. Thermoelastic wave induced by pulsed laser heating, Appl. Phys. A: Mater. Sci. and Proc., 73(1), 107-114 (2001). [CrossRef]
Al-Qahtani, H.M., Datta, S.K. Laser-generalized thermoelastic waves in an anisotropic infinite blate: exact analysis, J. Therm. Stress., 31, 569-583 (2008).
Marin, M. Harmonic vibrations in thermoelasticity of microstretch materials, J. Vib. and Acoust., ASME, 132(4), 044501-1_044501-6 (2010). [CrossRef]
Youssef, H.M., Al-Felali, A.S. Generalized thermoelasticity problem of material subjected to thermal loading due to laser pulse, Appl. Math., 3, 142-146 (2012). [CrossRef]
Othman, M.I.A., Hasona, W.M., Abd-Elaziz, E.M. The influence of thermal loading due to laser pulse on generalized micropolar thermoelastic solid with comparison of different theories, Multi. Model. Mater. and Struct., 10(3), 328-345 (2014). [CrossRef]
Zenkour, A.M., Abouelregal, A.E., The effect of two temperatures on a FG nanobeam induced by a sinusoidal pulse heating, Int. J. Struct. Eng. and Mech., 51(2), 199-214 (2014). [CrossRef]
Abouelregal, A.E., Mohammad-Sedighi, H., Shirazi, A.H., Malikan, M., Eremeyev, V.A. Computational analysis of an infinite magneto-thermoelastic solid periodically dispersed with varying heat flow based on non-local Moore–Gibson–Thompson approach, Contin. Mech. and Thermody., 34(4), 1067-1085 (2022). [CrossRef]
Marin, M., Öchsner, A. An initial boundary value problem for modeling a piezo-electric dipolar body. Contin. Mech. Thermody. 30, 267–278 (2018).

Figure 1. The mechanical force and thermal load over a thermoelastic medium with voids and diffusion.

Figure 2. The distribution of the displacement component

w

against

z

Figure 2. The distribution of the displacement component

w

against

z

Figure 3. The distribution of the strain

e

against

z

Figure 3. The distribution of the strain

e

against

z

Figure 4. The distribution of the temperature

θ

against

z

Figure 4. The distribution of the temperature

θ

against

z

Figure 5. The distribution of the concentration

C

against

z

Figure 5. The distribution of the concentration

C

against

z

Figure 6. The distribution of the change in the volume fraction field

ϕ

against

z

Figure 6. The distribution of the change in the volume fraction field

ϕ

against

z

Figure 7. The distribution of the stress component

σ_{z z}

against

z

Figure 7. The distribution of the stress component

σ_{z z}

against

z

Figure 8. The distribution of the stress component

σ_{x z}

against

z

Figure 8. The distribution of the stress component

σ_{x z}

against

z

Figure 9. The distribution of the displacement component

w

against

z

Figure 9. The distribution of the displacement component

w

against

z

Figure 10. The distribution of the strain

e

against

z

Figure 10. The distribution of the strain

e

against

z

Figure 11. The distribution of the temperature

θ

against

z

Figure 11. The distribution of the temperature

θ

against

z

Figure 12. The distribution of the concentration

C

against

z

Figure 12. The distribution of the concentration

C

against

z

Figure 13. The distribution of the stress component

σ_{z z}

against

z

Figure 13. The distribution of the stress component

σ_{z z}

against

z

Figure 14. The distribution of the stress component

σ_{x z}

against

z

Figure 14. The distribution of the stress component

σ_{x z}

against

z

Figure 15. Three-dimensional curve distribution of the displacement component

u

versus the distances.

Figure 15. Three-dimensional curve distribution of the displacement component

u

versus the distances.

Figure 16. Three-dimensional curve distribution of the temperature

θ

versus the distances.

Figure 16. Three-dimensional curve distribution of the temperature

θ

versus the distances.

Figure 17. Three-dimensional curve distribution of the change in the volume fraction field

ϕ

versus the distances.

Figure 17. Three-dimensional curve distribution of the change in the volume fraction field

ϕ

versus the distances.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Effect of Diffusion and Laser Pulse on a Poro-Thermoelastic Medium via Three-Phase-Lag Model

Abstract

1. Introduction

2. Derivation of Field Equations

2.1. The Constitutive Relations2.2. The Generalized Fourier’s Law 2.3. The Strain-Displacement Relation2.4. The Equation of Motion 2.5. Balance of Equilibrated Stress2.6. The Balance Energy in the Presence of Heat Source2.7. The Equation of Mass Diffusion

3. Formulation of Problem

4. Solution of the Problem

5. Boundary Conditions

5.1. The Mechanical Boundary Condition

5.2. The Boundary Restriction of Heat

5.3. Voids Conditions

5.4. The Boundary Restriction of Concentration

6. Special and Particular Cases

6.1. Equations of the model of 3PHL when K ∗ , K > 0 , τ q > τ T > τ ν > 0 , and the solutions are always (exponentially) stable if 2 K τ T τ q > τ ν ∗ > K ∗ τ q as Quintanilla and Racke [7]

6.2. If we take, ( τ v = τ T = τ q = 0 , K ∗ , K > 0 ) in Eqs. (40) - (51), then we obtain the corresponding results for the generalized thermoelastic medium with voids and diffusion in the context of Green and Naghdi's theory of type III.

6.3. In the absence of void effect, if we take a 1 = a 2 = γ = d 0 = ψ = 0 in the Eqs. (30)-(34), we get:

6.4. Neglecting the diffusion effect, i.e., a 3 , a 4 , a 5 and β 2 tend to zero. Then, the boundary conditions for a generalized thermoelastic medium with voids under laser pulse influence in the context of the 3PHL model are given by

7. Numerical Results and Discussion

7.1. The Effect of Time Parameter

7.2. The Effect of Void Parameters

7.3. The 3D Surface Curves

8. Conclusions

Funding

Data Availability Statement

Acknowledgments

Conflicts of Interest

Nomenclature

Appendix A

Appendix B

Appendix C

Appendix D

Appendix E

References

MDPI Initiatives

Important Links

Subscribe

6.1. Equations of the model of 3PHL when $K^{}, K > 0,$ $τ_{q} > τ_{T} > τ_{ν} > 0,$ and the solutions are always (exponentially) stable if $\frac{2 K τ_{T}}{τ_{q}} > τ_{ν}^{} > K^{*} τ_{q}$ as Quintanilla and Racke [7]

6.2. If we take, $(τ_{v} = τ_{T} = τ_{q} = 0,$ $K^{*}, K > 0)$ in Eqs. (40) - (51), then we obtain the corresponding results for the generalized thermoelastic medium with voids and diffusion in the context of Green and Naghdi's theory of type III.

6.3. In the absence of void effect, if we take $a_{1} = a_{2} = γ = d_{0} = ψ = 0$ in the Eqs. (30)-(34), we get:

6.4. Neglecting the diffusion effect, i.e., $a_{3}, a_{4}, a_{5}$ and $β_{2}$ tend to zero. Then, the boundary conditions for a generalized thermoelastic medium with voids under laser pulse influence in the context of the 3PHL model are given by