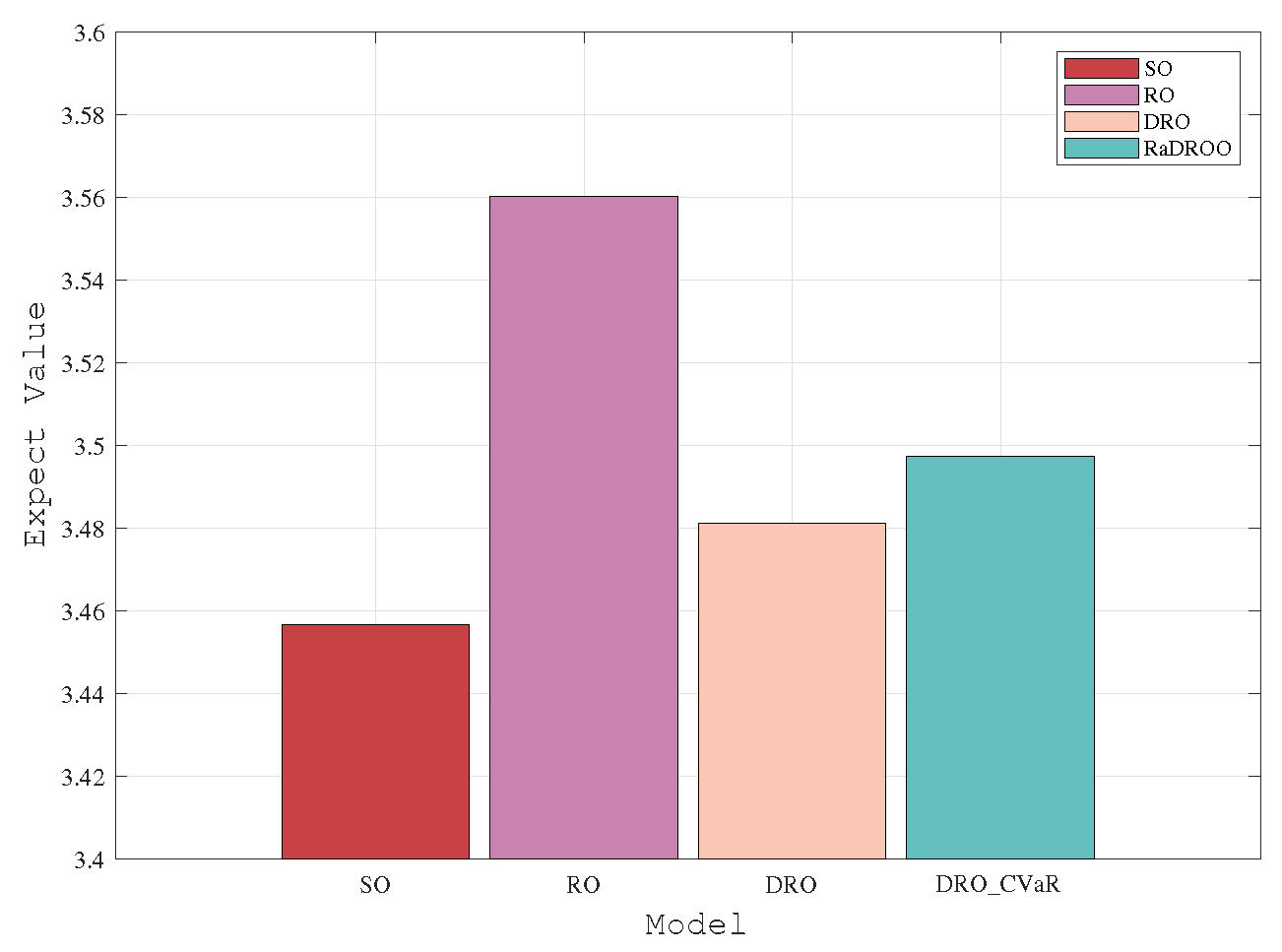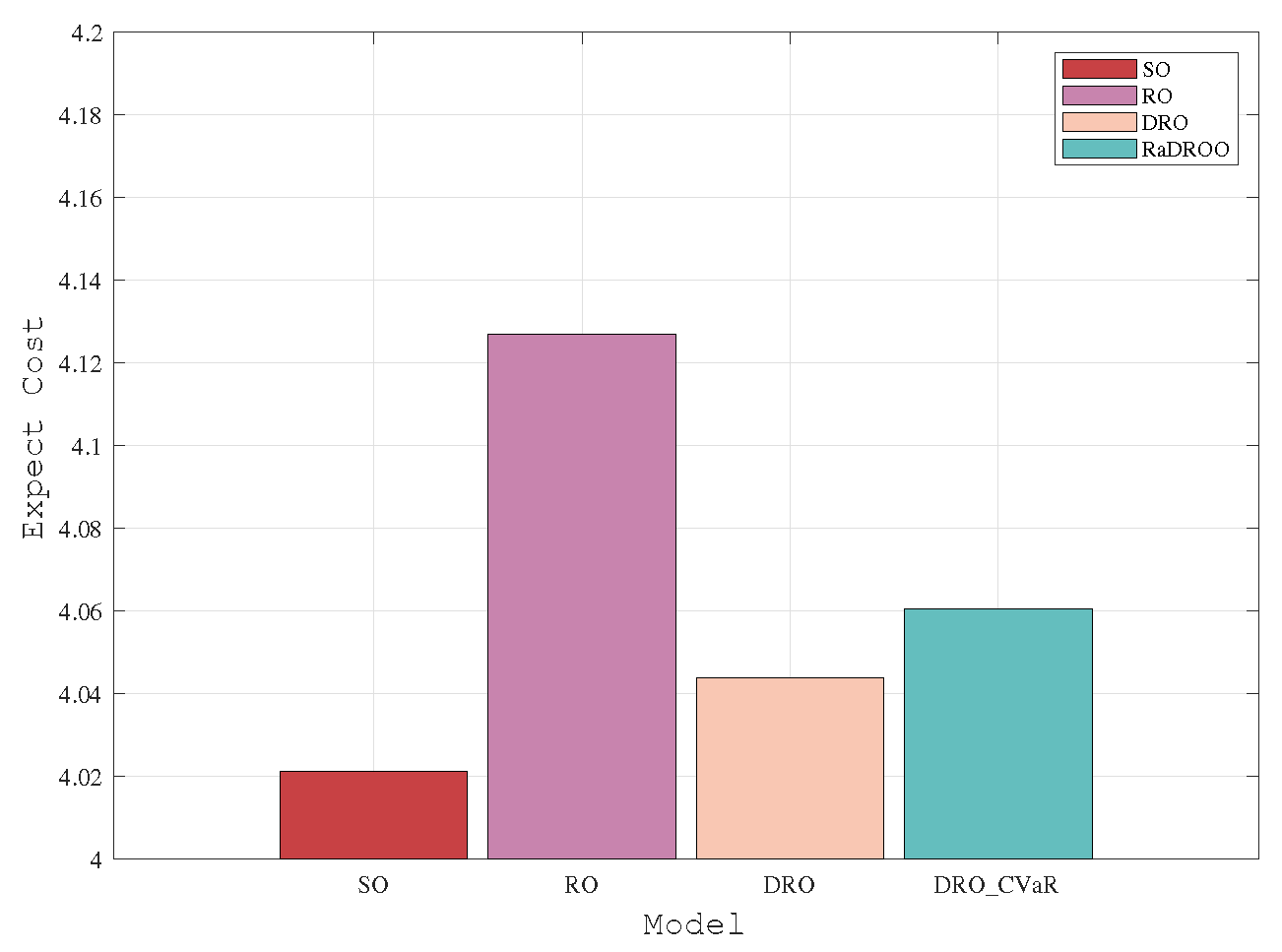Preprint

Article

Risk-aware Distributionally Robust Optimization for Mobile Edge Computation Task Offloading in Space–Air–Ground Integrated Networks

Altmetrics

Downloads

123

Views

Comments

A peer-reviewed article of this preprint also exists.

Zhiyuan Li^*,

Pinrun Chen

Zhiyuan Li^*,

Pinrun Chen

This version is not peer-reviewed

Submitted:

23 May 2023

Posted:

24 May 2023

You are already at the latest version

Alerts

Abstract

As an emerging network paradigm, Space-Air-Ground integrated networks (SAGIN) has attracted the attentions from academia and industry. That is because SAGIN can implement seamless global coverage and connections among electronic devices in space, air, and ground spaces. Additionally, the shortages of computing and storage resources in mobile devices greatly affect the quality of experiences for intelligent applications. Hence, we devise to integrate SAGIN as an abundant resource pool into mobile edge computing environments (MEC). To facilitate efficient processing, we need to solve the optimal task offloading decisions. Different from the existing MEC task offloading solutions, we have to face some new challenges, such as the fluctuation of processing capability for an edge computing node, the uncertainty of the transmission latency caused by the heterogeneous network protocols, the uncertain amount of uploaded tasks during a period, and so on. In this paper, we firstly describe a task offloading decision problem in new challenge environments. But, we cannot use the standard robust optimization and stochastic optimization methods to obtain the optimal result under the uncertain network environments. In this paper, we propose the condition value at risk-aware distributionally robust optimization algorithm, named as CVAR-DRO, to solve the task offloading decision problem. The proposed CVAR-DRO method combines the distributionally robust optimization and the condition value at risk model for solving the optimal result. And then, We have evaluated our approach in simulation SAGIN environments with the confidence interval, the number of mobile task-offloading and the various parameters. We compare our proposed CVAR-DRO algorithm with the state-of-the-art algorithms, such as the standard robust optimization algorithm, the stochastic optimization algorithm, the DRO algorithm, and the brute algorithm. The experimental results show that CVAR-DRO can get a sub-optimal mobile task-offloading decision. Overall, CVAR-DRO is more robust than others to the new challenges mentioned above in SAGIN.

Keywords:

Subject: Computer Science and Mathematics - Computer Networks and Communications

1. Introduction

With the booming development of the Internet of Things (IoT) ecosystem, users expect to obtain higher quality experiences (QoE) for various IoT applications. After the official deployment and operation of the fifth generation (5G) mobile system, the sixth generation (6G) mobile system is gradually coming into the limelight. The high-speed communication technologies can provide higher quality of service (QoS) for the IoT applications, such as intelligent transportation, intelligent agriculture, maritime surveillance, smart cities, natural disaster relief, and so on. However, the existing terrestrial communication networks cannot effectively provide the QoS and QoE guarantee for the intelligent and low-latency IoT applications. In recent years, the Space-Air-Ground integrated network (SAGIN) architecture has attracted the attention from academia and industry. SAGIN is an integration of space layer, aerial layer, and ground layer. As a multidimensional network, SAGIN adopts different communication protocols in each segment or the integration of different segments to achieve high throughput and high-reliability data delivery [1].

However, we have to face some new challenges in SAGIN, such as the mobile edge computationally intensive tasks offloading and resources allocation in uncertain and heterogeneous network environments. The uncertain network parameters, such as the uncertain latency, the uncertain amount of arrival tasks, and the uncertain computation resources, may seriously impact the efficiency of edge task execution. Nowadays, the stochastic optimization (SO) [2] and the robust optimization (RO) [3,4,5] methods are proposed to solve the uncertainty problems. The SO method can use the probability distribution of measuring parameters to predict the potential uncertainty and obtain the mathematical expectation of objective function. The RO method can directly solve the target value under the worst-case conditions, and it doesn’t need to obtain the probability distributions of measuring parameters. Distributionally robust optimization (DRO) can be viewed as a unifying framework for the SO and RO methods. The DRO method can replace the probability distribution of uncertain measuring parameters with a fuzzy set [6]. And then it can choose the worst case in the fuzzy set to get better robustness. Additionally, literature [7] proposed the conditional value at risk (CVaR) aware DRO method, which can reflect the potential risk and improve its stability.

There are two main technical challenges in solving the risk-aware two-stage DRO problem. Firstly, it is difficult to solve the DRO problem due to the fuzzy sets. Secondly, the first-stage offloading decision is the zero-one integer programming. And, the second-stage is a resources allocation procedure for latency insensitivity and computation-intensive tasks. But, in this paper, we have to solve the risk-aware two-stage DRO problem, which brings new challenge. If we can solve the risk-aware two-stage DRO problem, we can get the better revenue under the uncertainty and the quality of service(QoS) in SAGIN network architecture.

Our contributions are summarized as follows:

•: Investigate the task offloading decision model in the SAGIN environment. The task offloading model consists of two stages: the first stage is task offloading decision, and the second stage is edge-cloud collaboration and cloud resource allocation.
•: Building upon the work in (1), a fuzzy set of computational resources for edge computing nodes is constructed, and consideration for CVaR is introduced. Then, based on the theory of Lagrange duality, the model is transformed into a semidefinite programming form, and the Conditional Value at Risk (CVaR)-aware Distributionally Robust Optimization for Task Offloading (RaDROO) algorithm is proposed to solve the task offloading problem with distributional robustness under risk awareness.
•: We conducted simulation experiments from two aspects. On the one hand, we adjust some parameters of the proposed model to get the optimal parameter values. On the other hand, we fix the parameters and compare with the the state of the art algorithms in different computation and network environments. The experimental results demonstrate that our proposed model and algorithm have better results than the state of the art methods in terms of usability, robustness and risk.

The remainder of this paper is organized as follows. Section II gives a brief introduction to SAGIN before reviewing the computation task offloading. Section III describes the network architecture and proposes a computation task offloading model under uncertain computation environments. Section IV gives the risk-aware DRO algorithm to obtain the optimal task offloading decision and resource allocation strategy. Section V shows the performance evaluation and analysis. Section VI concludes our work and presents the future work.

2. Related Work

In this section, we firstly introduce the SAGIN architecture. And then, we review the traditional computation task offloading, the computation task offloading under the uncertain network and computation environments, and the risk-aware computation offloading, respectively.

2.1. SAGIN Architecture

The SAGIN refers to the integration and synergy of systems from multiple domains-space, air, ground-to form a wide area coverage and high speed network for more efficient communication and data exchange. It is a proposed solution to address the growing need for enhanced communication and information sharing capabilities. SAGIN requires the use of various technical means, such as satellite communications, unmanned aerial vehicles and ground sensors, to enable collaborative operations and data sharing between different platforms. By sharing data and information in real time, situational awareness can be improved, decision making can be optimised, and mission effectiveness can be enhanced.

Over time, the SAGIN architecture has evolved rapidly and various projects like Global Information Grid (GIG) have been proposed and widely deployed [8]. liu et al. [1] describe the communication network design and resource allocation algorithm of SAGIN in a high-dimensional network environment. Likewise, SAGIN can be invoked in MEC environments and has excellent performance in unique environments, i.e. desert, disaster scenarios. Yuet al. [9] considered the fine-grained offloading problem and caching problem and proposed the SAGIN framework which supports edge computing.

The impact of SAGIN on computating tasks offloading is multifaceted and can be summarized as follows:

−: Cross-platform efficiency: Through the integration and collaborative operations achieved by SAGIN, different tasks can be offloaded and migrated between different platforms, thereby improving the efficiency of task execution.
−: Increased Flexibility through Edge-Cloud Collaboration: In the SAGIN network, tasks can be dynamically allocated and scheduled, allowing them to be offloaded to the most suitable platforms based on their computational requirements. This improves resource utilization.

Overall, the impact of SAGIN on the field of task offloading is positive, as it can improve task execution efficiency, safety, flexibility, and coverage. An ECN built on the SAGIN framework will be able to more fully exploit its capabilities. Consolidate all available resources to provide computing resources for the computing tasks in this network environment.

2.2. Traditional Computation Offloading

First of all, a class of existing tasks offloading optimization algorithms in practice applications is on task dependency. Yuan et al. [10] paid an attention to a dependent task assignment problem over multiple mobile terminal devices (MTDs). In [11], an efficient partitioned search method was implemented for obtaining optimal solutions for task offloading policies and resource allocation under task-dependent models. Besides, without considering task dependency, whether to offload to edge computing nodes(ECN) for tasks and how much computing resources are allocated by ECNs according to the performance requirements for computing offloads is a hot topic of current researchers. The mainstream research directions under this scope are the following three. The first one is to explore task offloading decision schemes that minimize task execution delay[12,13]. Xiao et al. [14] designed a heat prediction method to analyze the dynamics of urban heat zones, aided by the design of a non-cooperative game-theoretic strategy selection based on regret matching to achieve minimum time delay. Dai, Y. et al. [15] proposed a JSCO algorithm to search for the solution to the optimization problem in a distributed manner with less overhead, using the integrated task processing delay as the performance metric. In [16], Farhangi, E.et al. proposed a novel offload approach OAMC, which takes into account the dynamic changes of mobile applications and reduces the number of migrations and overall data movement while minimizing the turnaround time of mobile applications. Secondly, plenty of studies[17,18,19,20] focus on obtaining task offloading decisions in edge computing networks that minimize energy consumption, which is affected by the amount of offloading computations, MTD-MECs distance, channel conditions, application type, compression efficiency, and etc.. Hmimz et al. [19] jointly considered both the priority of certain MTDs and minimizing overall power consumption. Third, [21,22] assumes that the system can gain a certain amount of revenue by completing the task, and the goal is to find the offloading decision that maximizes the revenue. Samantaet al. [23] synthetically explores delay-sensitive and delay-tolerant edge services and guaranteed Quality of Experience(QoE) to be maximized over a long period using the Lyapunov method. Chenget al. [24] applied gaming offloading algorithms to maximize mobile network operator revenue.

In addition to the common is solved by traditional optimization methods, Some researchers[25] have also chosen to apply intelligent optimization algorithms to pick the optimal unloading decision.In [20], it developed a new adaptive inertia weight-based particle swarm optimization (NAIWPSO) algorithm to minimize the energy consumption of MTDs while considering the channel constraint condition during task offloading. Li et al. [26] proposed an algorithm, named EIPSO, based on an developed particle swarm optimization. Tout et al. [27] designed a multi-objective intelligent optimization algorithm based on genetic algorithm.

Machine learning and deep learning algorithms are now extraordinary prevalent in the research field in droves. Maleki, E. F.et al. [16] applied a Machine Learning(ML) algorithm called matrix complementation to design two fresh offloading methods, S-OAMC and G-OAMC, that enhance scalability and find low turnaround time offloading decisions. In [28], various machine learning techniques for the communication, network and security components of the future 6G environment in vehicular networks were profiled, and methods and directions for implementing artificial intelligence in future 6G vehicular networks are envisioned. However, machine learning algorithms typically require a significant amount of training data and cannot be directly computed. They rely on training on large datasets to learn patterns and make predictions. Additionally, machine learning algorithms are sensitive to changes in the environment and may require retraining or adaptation to maintain their performance.

Table 1. Content in the relevant literature.

Previous Work	Game	ML	RO	SO	DRO	mean risk-aware	SAGIN
[29]	✓
[3,30]			✓
[16]		✓
[7]					✓
[2]				✓
[31,32]						✓
[33]					✓		✓
Our Algorithm					✓	✓	✓

2.3. Uncertain-aware Computation Offloading

The above research scenarios whole assume that controllers has access to accurate computing resource and channel information either statically or dynamically. Nevertheless, in application environments, MECN are transient which can considerably impact resource utilization and user QoE. [30][3] investigates robust task offloading that is tolerant to failures in offloading scenarios and can effectively overcome this. In [4], robust tasks with tolerant server failures offloaded were contemplated to achieve higher application responsiveness. To counter the inaccuracy of channel measurements, [5] design a robust offloading strategy for channel information estimation errors. Facing the connection instability between MTDs and small clouds, [3] proposed a robust computation offloading strategy with failure recovery. [34] introduced a mobility model and a trade-off fault tolerance mechanism for the offload system, taking into account the dependencies between services.

In contrast to the robust optimization described above, which sacrifices a lot of device performance to ensure its robustness during application, stochastic optimization is used. The investigations of Stochastic Optimization (SO) in MEC gives the probability distribution of channel resources, computational resources of ECNs varying randomly[2]. proposed a two-stage SO to tackle the challenge of uncertain dynamic environments.

2.4. Risk-aware Computation Offloading

Unlike the uncertain or undefined parameter scenarios described above, risk considerations refer to unexpected conditions that occur during system operation. Bai et al. [29] solve risk-aware computation offloading (RCO) problem by considering the use of Bayesian Stackelberg Game to rationally disperse the nodes for task offloading when the server is attacked by outside miscreants. Apostolopoulos et al. [35] take account of the uncertainty in MEC server computational resources as well as storage space under heterogeneous networks. Schultz, R.et al. [32] explain the risk consideration in stochastic programming, i.e., mean-risk, and also give the expression formula for CVaR. With CVaR, Pan et al. [36] considered the availability of the MEC system in case of possible link failure. Mean-CVaR is commonly deployed in finance, where Zhang et al. [31] have studied portfolio selection under return fuzzy set conditions, considering a downside risk measure to reduce investment risk.

3. Network Architecture and System Model

In this section, we elaborate on the SAGIN architecture and channel models. Based on the compute, caching and communication (3C) requirements, We developed an optimization model for making computing offload decisions, aiming to minimize cost.

3.1. SAGIN Architecture and Channel Models

SAGIN is a novel network structure integrating multiple dimensions. It adopts different protocols and occupies different frequency bands for establishing communications between the different dimensions[1]. We select the rational frequency band for communications by taking into account the distance between ECNs, the influence of current environmental factors on the link, the free-space path loss, tropospheric attenuation, and other factors.

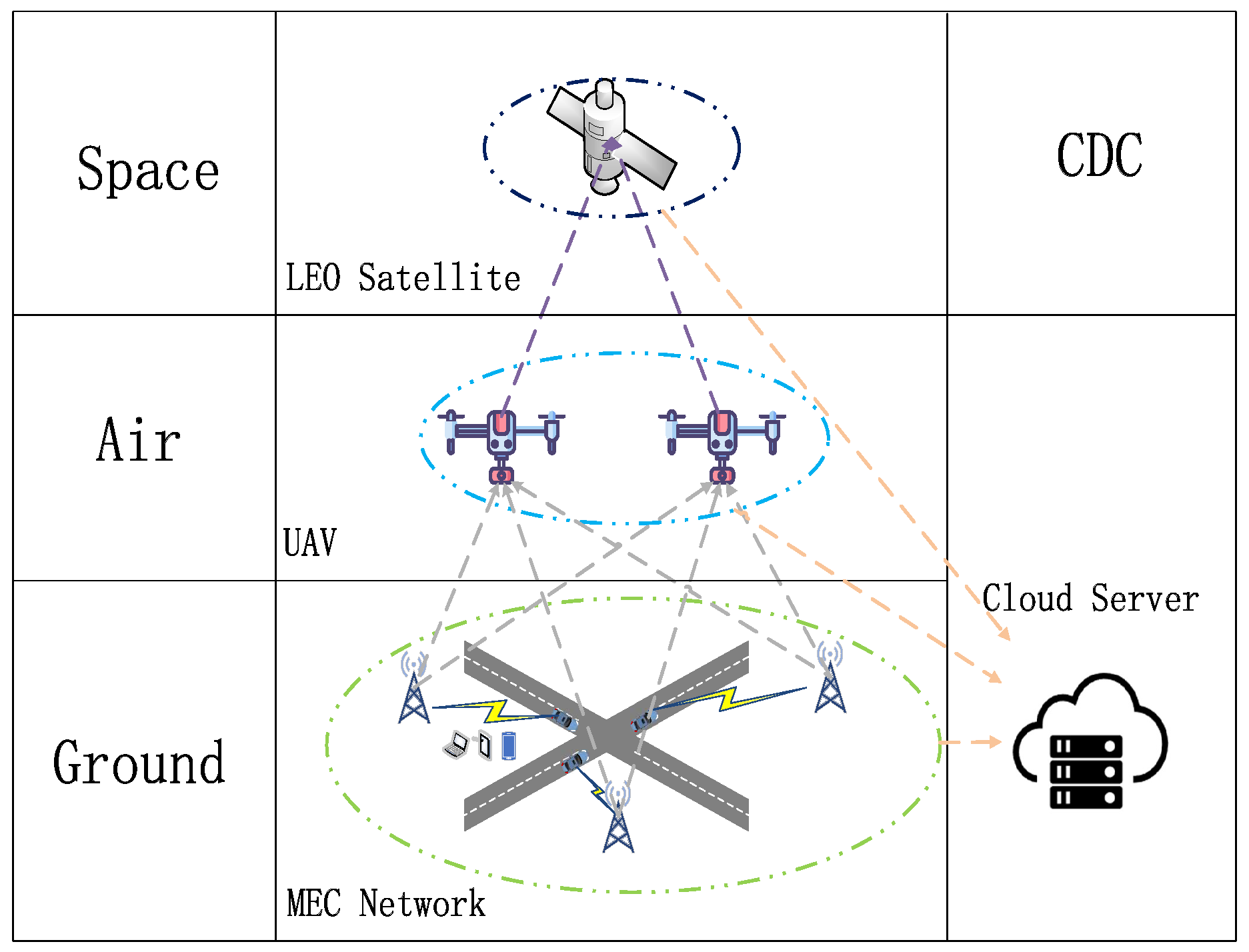
In the study, tasks are uploaded to the nearest BSs from MTDs by default. As shown in Figure 1, the SAGIN architecture consists of five components: the MTD segment, ground segment, satellite segment, aerial segment, and cloud data centre (CDC) segment. Let

B = {1, 2, \dots, B}

be used as the set of BSs . Furthermore, as a representative of the aerial segment, UAVs are despatched as the extension of the ground BS process. The set of the UAVs are denoted by

U = {1, 2, \dots, U}

. The satellite segment consists of LEO satellites. Due to the utilization of higher communication frequency bands, satellites possess lower propagation delay and free space attenuation [37].

The SAGIN system offers three tasks offload strategies, depending on the task information uploaded by MTDs: firstly, selecting a BS that possess sufficient computing resources to calculate the task; secondly, applying for a UAV offload and compute the task; thirdly, selecting for a UAV as an intermediary and applying an LEO satellite to offload and compute the task. As a multi-dimensional 6G network, SAGIN integrates several network segments and uses communication protocols to achieve high reliability and high throughput data transmission [38].

The maximum achievable transmission rate K[bits/s] for the tasks in the channel can be expressed as follows.

\{\begin{matrix} K = B {log}_{2} (1 + \frac{P \times 10^{- [L_{P} / 10]}}{N o i s e}), \\ L_{p} = 32.45 + 20 lg d (k m) + 20 lg f (M H z) . \end{matrix}

(1)

Within the above equation,

B (H Z)

, P and

N o i s e

represent channel bandwidth, average signal power and noise power;

L_{p}

, d, f represent propagation loss in free space, and the distance between ECNs and signal frequency, respectively.

3.2. Computation Tasks Offloading Model

We suppose that there are n latency sensitivity and computation-intensive tasks offloaded to nearby BSs, where the set of tasks is denoted as

N = {1, 2, \dots, N}

. And, each of tasks is charactered by any parameters,

(n_{i}^{u p}, n_{i}^{c o m p}, n_{i}^{d o w n}), i \in N

, in which

n^{u p}

denotes the input and uploaded data size;

n^{c o m p}

denotes the number of CPU cycles required to process data;

n^{d o w n}

denotes the processed and downloaded data size. In this research, the study’s objective is 3C and the total cost of tasks, thus keeping the atomicity of the tasks, i.e. each task can only be served by one processing ECN.

In our proposed SAGIN system, there are four offload destinations: BSs, UAVs, LEO satellites ,and CDC. We assume that

x^{B S}

x^{U A V}

, and

x^{L E O}

are three binary parameters, where

x_{i b}^{B S}

denotes whether task i selects BS b as the offload target,

x_{i u}^{U A V}

denotes whether task i selects UAV u as the offload target and

x_{i s}^{L E O}

denotes whether task i selects LEO satellite s as the offload target.

\sum_{b = 1}^{B} x_{i b}^{B S} + \sum_{u = 1}^{U} x_{i u}^{U A V} + \sum_{s = 1}^{S} x_{i s}^{L E O} = 1, \forall i \in N

(2)

x_{i b}^{B S}, x_{i u}^{U A V}, x_{i s}^{L E O} \in {0, 1}, b \in B, u \in U, s \in S

(3)

The above equation indicates that each task would be offloaded to one ECN in the SAGIN architecture.

x_{i b}^{B S} = 1

if task

n_{i}

is offloaded to BS b and

x_{i b}^{B S} = 0

otherwise;

x_{i u}^{U A V} = 1

if task

n_{i}

is offloaded to UAV u and

x_{i u}^{U A V} = 0

otherwise;

x_{i s}^{L E O} = 1

if task

n_{i}

is offloaded to LEO satellite s and

x_{i s}^{L E O} = 0

otherwise. These three different computing units own different computing power and storage resources.

f_{i b}^{B S}

f_{i u}^{U A V}

, and

f_{i s}^{S A T}

denote the number of computing resources in per second requested by task i from BSs, UAVs, or LEO satellites, respectively.

We assume that tasks are uploaded to the nearest base station first and then propagate them from the base station to the target computing nodes. And since the propagation delay of tasks directly to edge computing nodes is much greater than uploading tasks to the nearest base station, we will ignore the upload delay of tasks.

The time taken by a task to be uploaded and downloaded between ECNs and the latency taken to calculate the task can be expressed as

\begin{matrix} T^{u p} & = \frac{n^{u p}}{k^{u p}} = \frac{n^{u p}}{B {log}_{2} (1 + \frac{P \times 10^{- [L_{P} / 10]}}{N})} \end{matrix}

(4)

\begin{matrix} T^{d o w n} & = \frac{n^{d o w n}}{k^{d o w n}} = \frac{n^{d o w n}}{B {log}_{2} (1 + \frac{P \times 10^{- [L_{P} / 10]}}{N})} \end{matrix}

(5)

\begin{matrix} T^{c o m p} & = L^{t i m e} - T^{u p} - T^{d o w n} \end{matrix}

(6)

where

T^{c o m p}

is the time to execute the task,

T^{u p}

and

T^{d o w n}

represent the time of uploading and downloading the task message.

The overall latency of the tasks offloaded to the BSs spent by the task related to the transfer delay to the target BS, the computation delay of the BS, and the transfer delay of the result download.

T_{i b}^{B S} = T_{i b}^{u p} + T_{i b}^{c o m p} + T_{i b}^{d o w n}, i \in N

(7)

It is one of the options to upload tasks to the UAVs when the computing resources on the ground are insufficient to cope with the large influx of tasks.

T_{i u}^{U A V} = T_{i u}^{u p} + T_{i u}^{c o m p} + T_{i u}^{d o w n}, i \in N

(8)

The tasks process changes with the calculations of offloading tasks to LEO satellites. Tasks information must be uploaded to the nearest UAV, before spreading to satellites. After the task processing is completed, the data is returned in the original path. The total latency taken to offload the tasks to an LEO satellite can be expressed as

T_{i s}^{L E O} = T_{i u}^{u p} + T_{i s}^{u p} + T_{s}^{c o m p} + T_{i u}^{d o w n} + T_{i b}^{d o w n}

(9)

where

T_{i b u}^{u p}

T_{i u s}^{u p}

T_{i s u}^{d o w n}

T_{i u b}^{d o w n}

and

T_{i s}^{c o m p}

represent uploading latency of task i from BSs to UAVs, and from UAVs to LEO satellites, downloading latency from LEO satellites to UAVs and from UAVs to BSs, and the computation delay of the task i, respectively.

For this paper, we have chosen to ensure that the task is completed within the time delay constraints. Therefore, in order to allocating of computing resources rationally, the node only provides the lowest possible computational resources,

f_{i} = n_{i}^{c o m p} /

LiT - Ttrans

, w h e r e

Ttransi

r e p r e s e n t t h e t i m e t a k e n f o r t a s k

t o b e t r a n s m i t t e d o v e r t h e l i n k .

There is an upper bound on the total amount of computing resources an ECN can have. As a result, the combined computational resources required for the tasks assigned to a node should not exceed the upper limit.

\begin{matrix} \sum_{i = 1}^{n} f_{i} x_{i b}^{B S} & \leq L_{b}^{B c o m p}, \forall b \in B, \end{matrix}

(10a)

\begin{matrix} \sum_{i = 1}^{n} f_{i} x_{i u}^{U A V} & \leq L_{u}^{U c o m p}, \forall u \in U, \end{matrix}

(10b)

\begin{matrix} \sum_{i = 1}^{n} f_{i} x_{i s}^{L E O} & \leq L_{s}^{L c o m p}, \forall s \in S, \end{matrix}

(10c)

Consider the caching in 3C, where each ECN has its own storage limit.

\begin{matrix} \sum_{i = 1}^{N} x_{i b}^{B S} n_{i}^{u p} & \leq L_{b}^{B c a c h e}, \forall b \in B \end{matrix}

(11a)

\begin{matrix} \sum_{i = 1}^{N} x_{i u}^{U A V} n_{i}^{u p} & \leq L_{u}^{U c a c h e}, \forall u \in U \end{matrix}

(11b)

\begin{matrix} \sum_{i = 1}^{N} x_{i s}^{L E O} n_{i}^{u p} & \leq L_{s}^{L c a c h e}, \forall s \in S \end{matrix}

(11c)

L_{b}^{B c a c h e}

L_{b}^{U c a c h e}

, and

L_{b}^{L c a c h e}

represent the cache upper bound of BS b, UAV u, and LEO satellite s, separately.

The cost for tasks offloading is closely related to the server type, the number of computing resources needed. In this paper, we focus on solving computational intensive and time delayed sensitive tasks. Therefore it is the key to minimize the offload cost by picking a reasonable offloading target. Hence

\begin{matrix} C_{i} = & \sum_{b = 1}^{B} (δ_{b}^{B S} \times n_{i}^{c o m p} \times x_{i b}^{B S}) \\ + \sum_{u = 1}^{U} (δ_{u}^{U A V} \times n_{i}^{c o m p} \times x_{i u}^{U A V}) \\ + \sum_{s = 1}^{S} (δ_{s}^{L E O} \times n_{i}^{c o m p} \times x_{i s}^{L E O}), i \in N \end{matrix}

(12)

C^{a l l} = \sum_{n = 1}^{N} C_{n}

(13)

In the above equation,

C_{i}

denotes the final cost of task i;

C^{A L L}

denotes the cost for accomplishing whole tasks;

δ_{b}^{B S}

δ_{b}^{U A V}

and

δ_{b}^{L E O}

represent the ratio between the fees and the data size that will be processed by BSs, UAVs, and LEO satellites, respectively.

\begin{matrix} min_{x_{i b}^{B S}, x_{i u}^{U A V}, x_{i s}^{L E O}} C^{a l l} \\ s . t . & (2), (3), (10 a), (10 b), (10 c), (11 a), (11 b), (11 c) \end{matrix}

(14)

3.3. Computing Resources Fussy Set Model

Realistically, the computational resources of each node can be greatly influenced by external factors, and the Qu et al. [30] then considered the resource uncertainty of MECN in a traditional environment. In this paper, for the computing resource uncertainty of ECNs, we propose a realistic scenario-based set of definite probability distribution to represent the possible range of uncertain resources.

Based on a fuzzy set of random parameters

ξ

, we will make the one-stage offloading decision and the two-stage cloud resource request.

Delage, E. et al. [39] considered a general bounded moments uncertainty set, based on realistic data, with exact moment uncertainty, i.e.,

\begin{matrix} D (ξ, \sum, μ_{0}, γ_{1}, γ_{2}) \\ = \{P \subseteq F : \begin{matrix} P \{ξ \in M\} = 1 \\ {(E [ξ] - μ_{0})}^{T} \sum^{- 1} (E [ξ] - μ_{0}) ⩽ γ_{1} \\ E [(ξ - μ_{0}) {(ξ - μ_{0})}^{T}] ⩽ γ_{2} \sum \end{matrix}\} \end{matrix}

(15)

where paraments

γ_{1}

and

γ_{2}

, based on historical data, are utilised to control the size of the ambiguity set and the conservatism of optimal solutions.

M

is the closed convex set of the support of the currently known random

ξ

, and ∑ and

μ_{0}

are, respectively, its corresponding first-order and second-order moments. In contrast,

F

is the set of all probability measures on the measurable space (

R^{m}

B

), with

B

the Borel

β

-algebra on

R^{m}

The first constraint indicates that the probability density sum of

ξ

is 1 over

M^{ξ}

; the second constraint assumes that the mean of

ξ

lies on an ellipsoid of size

γ_{1}

centred at

μ_{0}

; the third constraint forces that the covariance matrix lies in a positive semi-positive definite cone bounded by matrix inequalities.

4. Risk-aware Distributionally Robust Optimization Tasks Offloading Algorithm Design

In this section, we consider fuzzy sets and CVaR to address the uncertainty of computational resources in edge computing nodes. We reconstruct the original problem with the uncertainty of the computational resources, due to the challenging nature of dealing directly with the DRO problem. We use Lagrangian duals to transform it into a semi-definite programming (SDP) problem to solve it.

In fact, we know that the offloading decision is an integer programming problem, and the additional computational resources requested from CDC are linear programming, which makes our problem

(19)

a MILP problem. Hence, we use branching implicit enumeration method to obtain the optimal offloading decision based on the uncertainty of computational resources and the minimum average cost.

4.1. Network Architecture and System Model

In this section, We consider the transformation of the original problem into a two-stage DRO programming model with a mean-CVaR recourse function, namely a risk-aware DRO model.

Above all, we represent (14) in terms of matrix form variables and parameters. We consider the set

D = B \cup U \cup S

and

M = B + U + S

. Then, the formulated problem is written as follow:

\begin{matrix} min_{X} {N^{c o m p}}^{T} \times X \times δ \end{matrix}

(16)

\begin{matrix} s . t . X \times O_{m} = O_{n}, \end{matrix}

(16a)

\begin{matrix} X^{T} \times N^{u p} \leq L^{c a c h e}, \end{matrix}

(16b)

\begin{matrix} X^{T} \times F \leq L^{c o m p}, \\ X \in R^{N \times M}, δ \in R^{N}, N^{c o m p} \in R^{M}, N^{u p} \in R^{N}, \end{matrix}

(16c)

\begin{matrix} f \in R^{N}, L^{c a c h e} \in R^{M}, L^{c o m p} \in R^{M} \end{matrix}

(16d)

where the offloading strategy matrix variable

X : = {\{x_{n m}\}}_{n \in N, m \in D}

, the upper bound of computing resource vector parameter

L^{c o m p} : = {\{L_{m}^{c o m p}\}}_{m \in D}

, the upper bound of cache ceiling vector parameter

L^{c a c h e} : = {\{L_{m}^{c a c h e}\}}_{m \in D}

, computing resource vector parameter

F : = {\{f_{i}\}}_{i \in N}

, the ratio between the cost and the data size vector parameter

δ : = {\{δ_{i}\}}_{i \in N}

, and the all ones vector parameter O.

Thus, given the uncertainty of the parameter

L^{c o m p}

, a two-stage offloading strategy model is created using the distribution set proposed above. We constructed a fuzzy set based on the historical data of the computing resources of the offload node. Expressed as:

ξ = {\tilde{L}}^{c o m p}

\begin{matrix} min_{X} & {N^{c o m p}}^{T} \times X \times δ + E_{ξ} [ϑ (X, ξ)], \\ s . t . & ((16 a) - (16 d)), \end{matrix}

(17)

\begin{matrix} \{P \subseteq F^{ξ} : \begin{matrix} P \{ξ \in M^{ξ}\} = 1 \\ {(E [ξ] - μ_{0})}^{T} \sum^{- 1} (E [ξ] - μ_{0}) \leq γ_{1} \\ E [(ξ - μ_{0}) {(ξ - μ_{0})}^{T}] \leq γ_{2} \sum \end{matrix}\} \end{matrix}

(17a)

\begin{matrix} w i t h & ϑ (X, ξ) = \{\begin{matrix} min_{Y} φ^{T} \times Y, \\ {(X \otimes F^{r e q})}^{T} \times O_{n} ⩽ ξ + Y, \\ 0 \leq Y, \end{matrix} \end{matrix}

(17b)

ϑ (X, ξ)

represent the additional cost of uploading tasks to the cloud when the real-time computing resources change in a phase of decision task offloading and are insufficient to meet demand. Vector

φ

indicates the ratio of additional costs to required computational power.

Instead, we further consider the mean-CVaR (Conditional Value at Risk) criterion in the model, which can be expressed in the following form:

\begin{matrix} V a R_{α} (ζ) & = inf \{v \in R : F (v) \geq α\} \\ C V a R_{α} (ζ) & = E {ζ | ζ \geq V a R_{α} (ζ)} \end{matrix}

(18a)

\begin{matrix} = min_{v \in R} {v + \frac{1}{1 - α} E [{(ζ - v)}_{+}]} \end{matrix}

(18b)

where

F

is the cumulative distribution function of the function used to solve for the random variable

ζ

, and a is the given confidence level.

{(a)}_{+}

means

max (a, 0)

This model gives the set of possible distributions

M^{ξ}

for the unknown stochastic parameter

ξ

while ensuring its robustness using a mean-CVaR with two-stage minimization of fees. The following formulation will be made using min-max theory:

\begin{matrix} min_{X} h (x) + sup_{ξ} \{(1 - λ) E [ϑ (x, ξ)] + λ C V a R (ϑ (x, ξ))\} \\ w i t h h (x) = {N^{c o m p}}^{T} \times X \times δ, \\ s . t . (16 a), (16 b), (16 c), (16 d), (17 a), (17 b)), \end{matrix}

(19)

which

λ

indicates the trade-off coefficient of conditional risk considered in the objective function and

1 \geq λ \geq 0

4.2. Transform from DRO to SDP

Problem (19) has presented a DRO problem, below We further analyze the target formula and convert it to more explicit form.

\begin{matrix} sup_{ξ} \{(1 - λ) E [ϑ (x, ξ)] + λ C V a R (ϑ (x, ξ))\} \\ = & sup_{ξ} {min_{v \in R} {λ v + (1 - λ) E [ϑ (x, ξ)] + \frac{λ}{1 - α} E [{(ϑ (x, ξ) - v)}_{+}]}} \\ = & min_{v \in R} {λ v + sup_{ξ} {E [(1 - λ) ϑ (x, ξ) + \frac{λ}{1 - α} {(ϑ (x, ξ) - v)}_{+}]}} \end{matrix}

(20)

The ambiguous distribution set of the random parameter cannot be used directly for the solution, and we need to convert it into the common inequality form. Consider only the latter half of finding the optimal value in relation to the random parameter

ξ

. Instead of the original distribution set form, turn to the following semi-infinite conic linear problem form expressed as:

\begin{matrix} sup_{ξ} & \int_{M} [(1 - λ) ϑ (x, ξ) + \frac{λ}{1 - α} {(ϑ (x, ξ) - v)}_{+}] d f (ξ) \end{matrix}

(21)

\begin{matrix} s . t . & \int_{M} d f (ξ) = 1, \end{matrix}

(21a)

\begin{matrix} \int_{M} (ξ - μ_{0}) {(ξ - μ_{0})}^{T} d f (ξ) ≼ γ_{2} \sum, \end{matrix}

(21b)

\begin{matrix} \int_{M} [\begin{matrix} \sum & ξ - μ_{0} \\ {(ξ - μ_{0})}^{T} & γ_{1} \end{matrix}] d f (ξ) ≽ 0, \end{matrix}

(21c)

\begin{matrix} ξ \in M^{ξ}, \end{matrix}

(21d)

Secondly, we utilize the duality theory to convert it into a SDP problem. Consider the dual of problem (21):

\begin{matrix} (D u a l) : \end{matrix}

\begin{matrix} inf_{r, H, [\begin{matrix} Z & z \\ z^{T} & \hat{z} \end{matrix}]} r + 〈H, γ_{2} \sum - μ_{0} μ_{0}^{T}〉 + 〈Z, \sum〉 + \hat{z} γ_{1} - 2 z^{T} μ_{0} \end{matrix}

(22)

\begin{matrix} s . t . u (x, ξ) - r - ξ H ξ^{T} + 2 ξ^{T} H μ_{0} + 2 z^{T} ξ \leq 0, ξ \in M^{ξ}, \end{matrix}

(22a)

\begin{matrix} r \in R, \end{matrix}

(22b)

\begin{matrix} H ≽ 0, \end{matrix}

(22c)

\begin{matrix} [\begin{matrix} Z & z \\ z^{T} & \hat{z} \end{matrix}] ≽ 0, \\ w i t h u (x, ξ) = (1 - λ) ϑ (x, ξ) + \frac{λ}{1 - α} {(ϑ (x, ξ) - v)}_{+} \end{matrix}

(22d)

where r, H, and

[\begin{matrix} Z & z \\ z^{T} & \hat{z} \end{matrix}]

are correspondingly the dual variables of constraints (21a), (21b), and (21c).

〈a, b〉

represent

T r a c e (A B)

Due to the inclusion of ()₊, the inequality constraint (22a) has to be processed as follow:

\begin{matrix} r + ξ H ξ^{T} - 2 ξ^{T} H μ_{0} - 2 z^{T} ξ \\ ⩾ & (1 - λ) ϑ (x, ξ) + \frac{λ}{1 - α} {(ϑ (x, ξ) - v)}_{+} \end{matrix}

When the random parameter

ξ

appears in the constraint, it cannot be directly substituted into constraint (22a). Therefore, it is necessary to consider the dual of problem

ϑ (x, ξ)

such that the random parameters are transferred into the objective function. Another problem ensues, the coupling of variables the dual variable q and the variable Y. The constraint on the dual variable q confines it to a boxed region, as indicated by the constraint.

\begin{matrix} (D u a l) : \end{matrix}

\begin{matrix} ϑ^{'} (x, ξ) = max_{q, p} q^{T} ({(X \otimes F^{r e q})}^{T} O_{N} - ξ), \end{matrix}

(23)

\begin{matrix} s . t . φ - p ⩾ q ⩾ 0, \end{matrix}

(23a)

\begin{matrix} p ⩾ 0, \end{matrix}

(23b)

Responding to constraint (22a), taking its extreme value points, each point corresponds to two corresponding semi-definite matrix constraints. We transformed (22a) into a clearer and more concise form.

\begin{matrix} \{\begin{matrix} r + ξ H ξ^{T} - 2 ξ^{T} H μ_{0} - 2 z^{T} ξ \\ ⩾ (1 - λ) ϑ^{'} (x, ξ) + \frac{λ}{1 - α} (ϑ^{'} (x, ξ) - v) \\ = (1 + \frac{λ α}{1 - α}) ϑ^{'} (x, ξ) - \frac{λ v}{1 - α} \\ r + ξ H ξ^{T} - 2 ξ^{T} H μ_{0} - 2 z^{T} ξ ⩾ (1 - λ) ϑ^{'} (x, ξ) \end{matrix} \end{matrix}

In the above constraints, we represent

(1 + \frac{λ α}{1 - α})

ϕ

and transform them into the following two Semi-definite matrix constraint.

\begin{matrix} \{\begin{matrix} [\begin{matrix} H & \frac{1}{2} ϕ q^{T} - H μ_{0} - z \\ {(\frac{1}{2} ϕ q - H μ_{0} - z)}^{T} & r - ϕ q^{T} {(X \otimes F^{r e q})}^{T} O_{N} + \frac{λ v}{1 - α} \end{matrix}] ≽ 0 \\ [\begin{matrix} H & \frac{1 - λ}{2} q - H μ_{0} - z \\ {(\frac{1 - λ}{2} q - H μ_{0} - z)}^{T} & r - (1 - λ) q^{T} {(X \otimes F^{r e q})}^{T} O_{N} \end{matrix}] ≽ 0 \end{matrix} \end{matrix}

Then, dual problem (22) can be rewritten as following:

\begin{matrix} min_{X, v, r, H, [\begin{matrix} Z & z \\ z^{T} & \hat{z} \end{matrix}]} h (x) + λ v + r + 〈H, γ_{2} \sum - μ_{0} μ_{0}^{T}〉 \\ + 〈Z, \sum〉 + \hat{z} γ_{1} - 2 z^{T} μ_{0} \end{matrix}

(24)

\begin{matrix} s . t . X \times O_{M} = O_{N}, \end{matrix}

(24a)

\begin{matrix} X^{T} \times N^{u p} ⩽ L^{c a c h e}, \end{matrix}

(24b)

\begin{matrix} [\begin{matrix} H & \frac{1}{2} ϕ q^{T} - H μ_{0} - z \\ {(\frac{1}{2} ϕ q - H μ_{0} - z)}^{T} & r - ϕ q^{T} {(X \otimes F^{r e q})}^{T} O_{N} + \frac{λ v}{1 - α} \end{matrix}] ≽ 0 \end{matrix}

(24c)

\begin{matrix} [\begin{matrix} H & \frac{1 - λ}{2} q - H μ_{0} - z \\ {(\frac{1 - λ}{2} q - H μ_{0} - z)}^{T} & r - (1 - λ) q^{T} {(X \otimes F^{r e q})}^{T} O_{N} \end{matrix}] ≽ 0 \end{matrix}

(24d)

\begin{matrix} [\begin{matrix} Z & z \\ z^{T} & \hat{z} \end{matrix}] ≽ 0, H ≽ 0, r \in R, \end{matrix}

(24e)

\begin{matrix} x_{i j} = {0, 1}, v \in R, \end{matrix}

(24e)

4.3. DRO-MILP Algorithm

In the above SDP problem, the X-matrix variables, 0-1 integer variables, and the Y-vector variables, continuous variables, are included. This makes the original problem a mixed-integer linear formulation, but he is not able to solve it directly. We relax the problem to a linear problem - simplifying the discrete variable X to a continuous variable from 0 to 1, i.e.,

0 ⩽ x_{i j} ⩽ 1, \forall x_{i j} \in X

In fact, the above SDP problem can be solved by using the SDPT3 solver through the CVX package in MATLAB. Then, the original problem MILP problem needs to be solved, and here we choose to use the branching implicit enumeration method to solve it, which a special branch and bound method for 0-1 integer problems, using the feature that the variables can only take two values of 0 or 1, to branch delimitation for the purpose of hidden enumeration. Where, for each task is divided into m sub-nodes, i.e., each task can only be offloaded and completely offloaded to one node.

Algorithm 1 present the progress of the calculation of the minimize cost of computation offloading. First of all, tasks should be sorted according to the number of CPU cycles they require, which determines the cost spent to a large degree. Then the solution of the relaxed LP problem is obtained, based on which the implicit enumeration method is performed to solve the solution of the branching subproblem. During the process of branch and bound, the two nodes with the highest values in the

X_{i}

vector, representing the most probable nodes for offloading the current task, are selected at each iteration. Constantly branching, updating the gradually increasing lower bound; constantly in delimitation, updating the gradually decreasing upper bound.

Algorithm 1:Cost-based MILP algorithms for DRO task offloading problem.

4.4. Complexity Analysis

In Algorithm 1, a solver is used to solve the optimization problem. Here, the time complexity for solving the optimization problem is set to T, the number of unloading tasks is set to N, and the branch and bound method is used to traverse all unloading tasks. In the unloading target section, it is simplified to select only the optimal two node locations with a cycle number of. The time complexity of the proposed algorithm is

O (T N)

5. Performance Evaluation

In this section, we try the performance and effectiveness under different parameters; analyze the results of the above proposed algorithm under different risk confidence conditions; and compare it with the traditional algorithm to give its superiority.

5.1. Simulation Setup

We accomplished the simulation on a laptop with an AMD Ryzen 7 4800H with Radeon Graphics 2.90 GHz, 16G RAM, and a Windows 10 OS. We envision a SAGIN-Cloud system where the coverage of the space layer contains the air layer and the coverage of the air layer contains the whole MECN. (The following parameters are all randomly within a certain range, given that the mean values are generated according to a normal distribution)

1) Channel State Information (CSI)

For information transportation within ECNs, different frequency bands are borrowed between the different layers, resulting in different bandwidths and transmission speeds. Currently, the C-band is one of the most commonly used frequency bands for satellite operations, with the Ka-band being a latecomer. This paper assumes that data transmission between BSs and UAVs occupies the C-band, while the Ka-band is occupied between UAVs and LEO satellites. The bandwidth of C-band is 20MHz, while the available bandwidth of Ka-band can reach 3500MHz. As for signal frequency range, C-band and Ka-band are 3.4GHz-8GHz and 26.5-36GHz, respectively.

2) ECNs Information

The horizontal and vertical coordinates of the BSs on the ground and the UAVs in the air are within

(- 1, 1)

km, respectively, while vertically, they are all 0. In contrast, the UAVs are located at an altitude of (0.075,0.15) km. LEO satellites are located in space and they are at a distance of (780, 800) km from the earth’s surface. LEO satellites are located in space and they are (780, 800) km away from the surface. they are not too space constrained, so are deployed in a square area with four points as vertices, (-200, -200), (-200, 200), (200, -200), (200, 200).

BSs, UAVs and LEO satellites possess CPU process speed of

2 * 10^{9}

cycles/s,

3 * 10^{8}

cycles/s, and

5 * 10^{9}

cycles/s, respectively.

3) Comparison Algorithm

First, we propose to use the most basic comparison algorithm, namely the Brute-Force algorithm.

•: In Brute-Force algorithm, It does not take into account any uncertainty and possible overflow of computation of task to the extent that it may eventually lead to an inability to obtain an optimal solution.

Secondly, we compare two traditional algorithms that take parameter uncertainty into account: robust optimization(RO) algorithm and stochastic optimization(SO) algorithm.

•: In RO, only the uncertainty of computational resources of ECNs is considered and their possible worst-case scenarios are experimentally selected to ensure their robustness.
•: In SO, the fuzzy set is constructed based on the historical data of the computational resources of the given ECNs, thus obtaining their means and variances.

Thirdly, there is another algorithm closest to our proposed one, which is the DRO algorithm for obtaining the optimal solution.

•: In DRO [33], the mean value in the range of uncertainty set is obtained and its optimal robust result is obtained by minmax theory, which guarantees both robustness and practicality. However, there is also a drawback, namely that it is an uncertainty set constructed from historical data, which does not guarantee the stability of its uncertainty set and does not consider its risk.

Lastly, we proposed CVaR-aware DRO algorithm on the basis of the traditional DRO algorithm.

•: In CVaR-aware DRO, in addition to what the DRO considers, it also complements certain defects that it has. It considers CVaR, choosing only the $α - t a i l$ part as the benchmark, while using $λ$ as a weight with the original part. That is to say, he selectively aggravates the proportion of the worse part of the results within the final result in order to guarantee its risk resistance.

5.2. Experiments

5.2.1. RaDROO algorithm

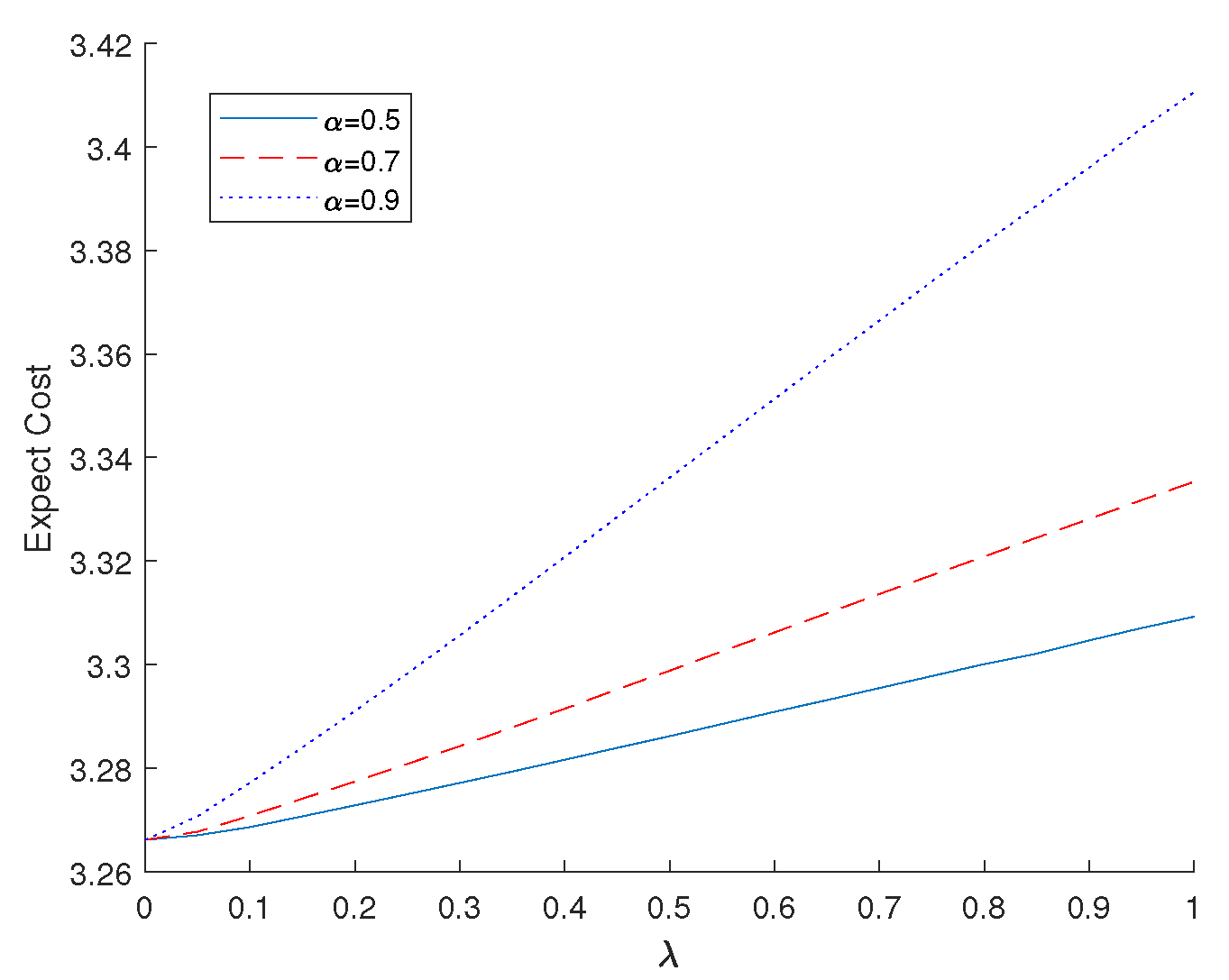
First observe the practical results of our proposed RaDROO algorithm under the practical problem of solving the optimization of offloading cost of edge network tasks. The optimal values of lambda in the range of (0,1) are given as

α

of 0.5, 0.7, and 0.9, respectively. As illustrated in Figure 2, when lambda is 0, it means that CVaR is not considered and weakened to a classical distribution robust problem, and the obtained results converge to a point. However as the

λ

increases, the consideration of risk is reinforced step by step, further constraining the range of values provided within the uncertainty set. This results in a progressive increase in the amount to be spent, but at the same time, a more superior and stable optimal choice is obtained. At the same time, the larger the lambda, i.e., the larger the weight considering the CVaR value, the worse the optimal value of the required spend.

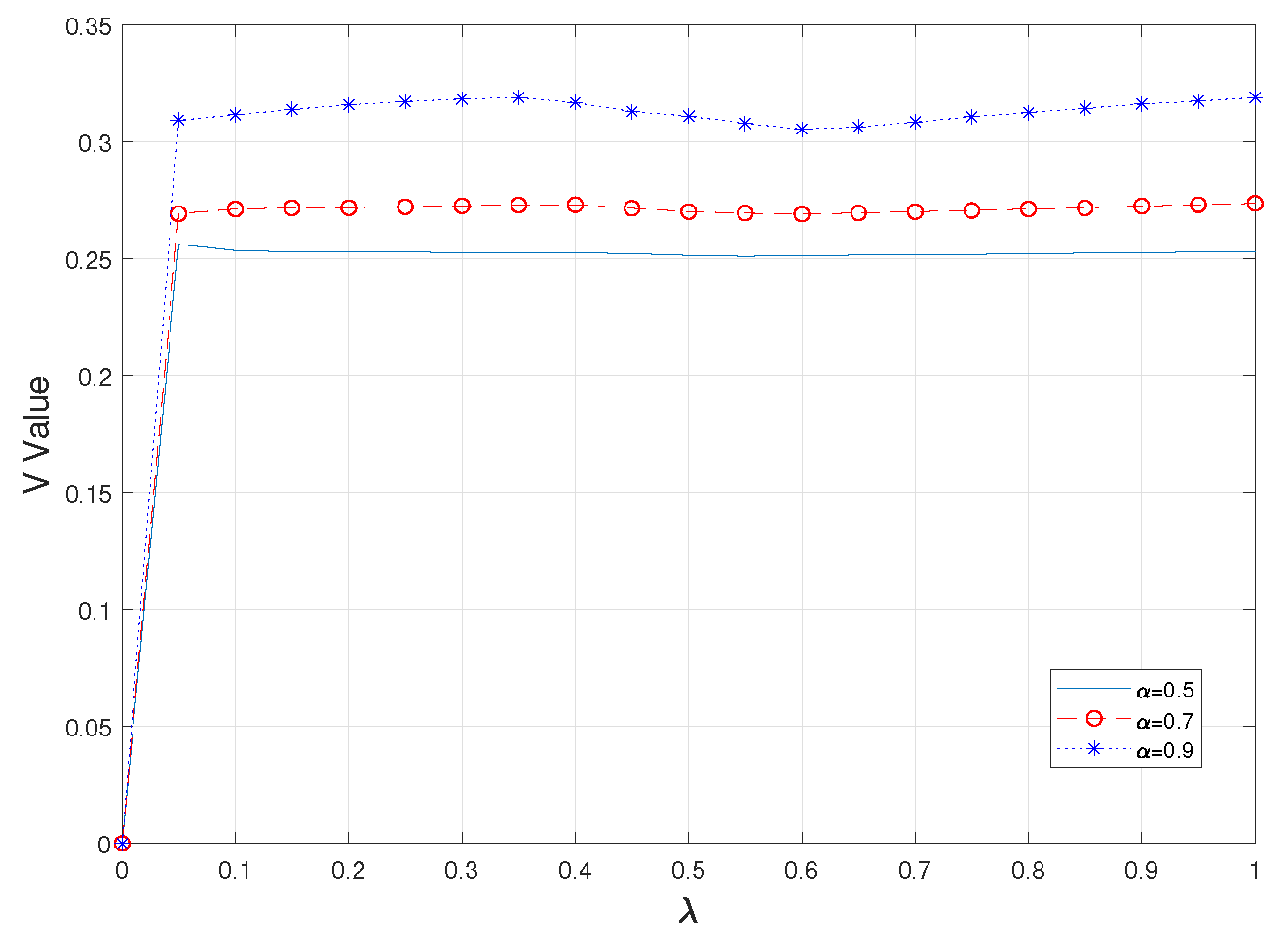
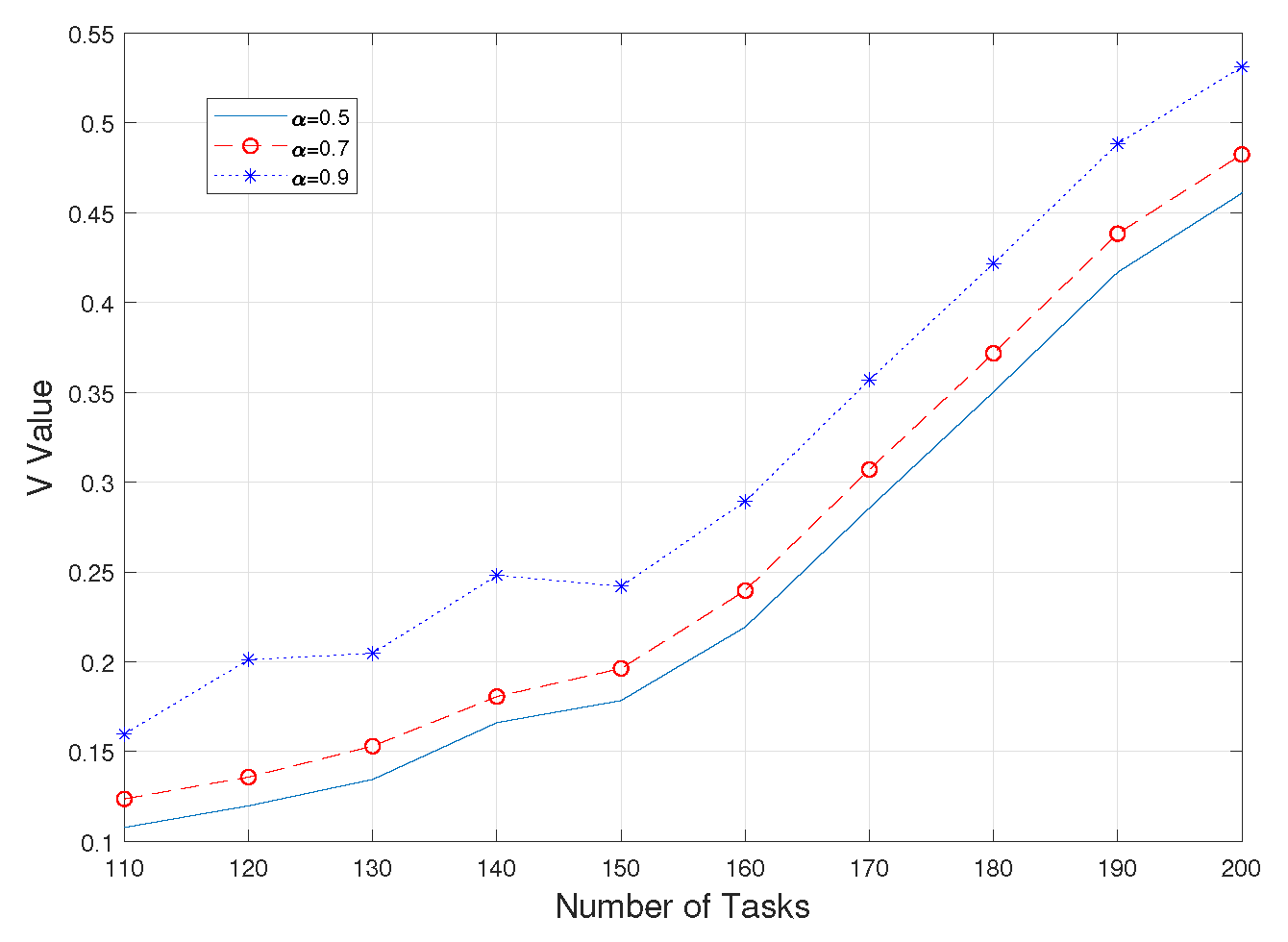
Second, observing the value of V gives a more intuitive view of the degree of consideration of risk in CVaR. As shown in Figure 3 and Figure 4, it is obvious that the value of V is larger when a higher alpha value is taken, i.e., when the worse part of the fuzzy set is used as a criterion, and at the same time, this value is almost unaffected by the value of

λ

taken; however, with a fixed value of

α

, as the simultaneous upload of amount of tasks increases, the value of V for each experiment also increases gradually and steadily, which means that the value of CVaR also increases, that is, the risk is further considered as a way to ensure the authenticity and practicality of the whole system.

5.2.2. Comparing with other algorithms

For comparison with other algorithms, some of the parameters of RaDROO are

λ = 0.5, α = 0.5, γ_{1} = 0, γ_{2} = 1

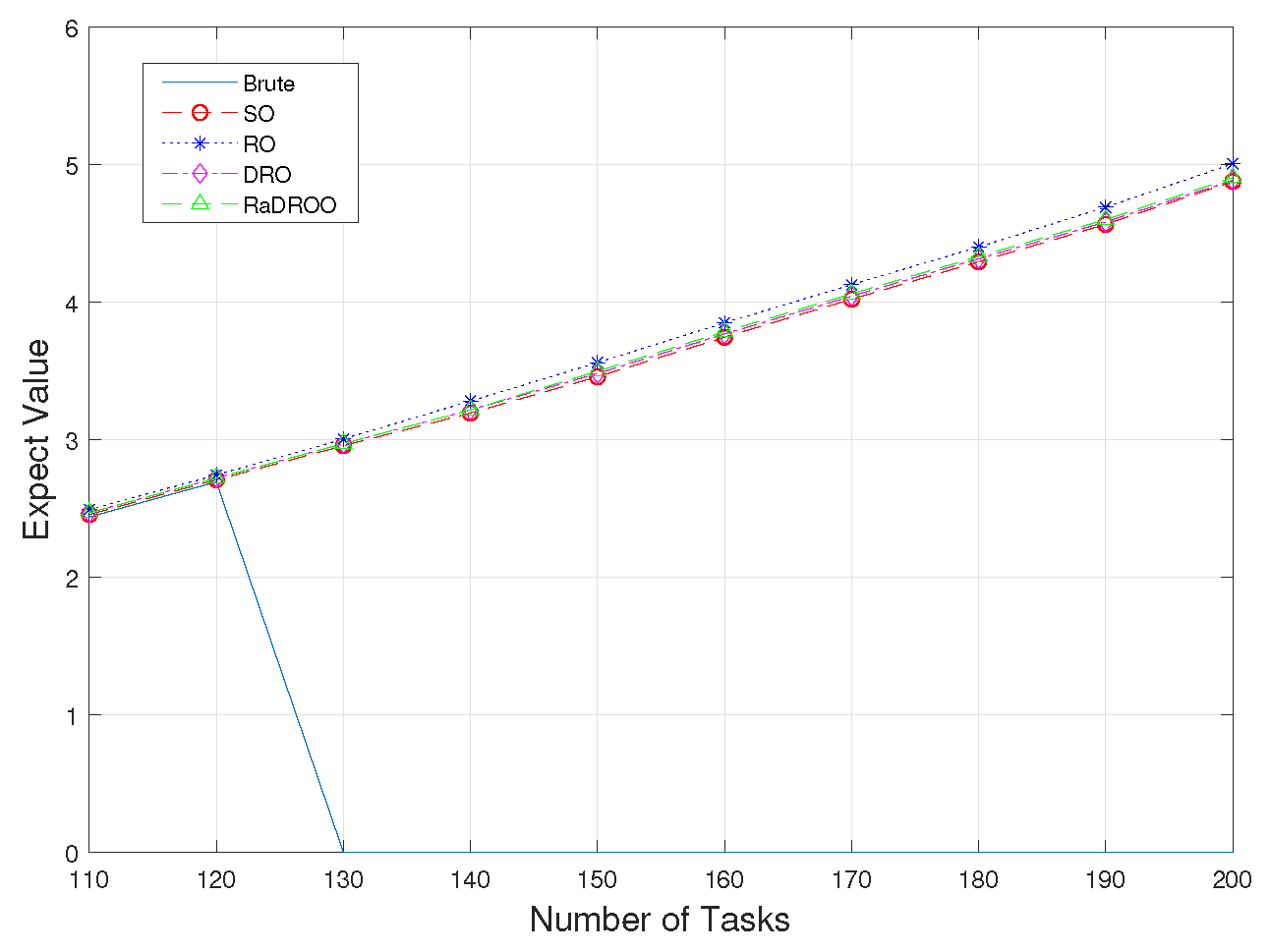
The comparison between algorithms takes the obtained target value as the evaluation criterion. Figure 5 shows the optimal cost results obtained by different algorithms at the same time as the amount of tasks received increases. Figure 6 and Figure 7 show the comparison of the results of the four algorithms at task volumes of 150 and 170. When the number of tasks is small, considering only known allocatable resources all algorithms give better results. As the total number of tasks that may be uploaded simultaneously rises, the Brute-Force algorithm fails to obtain an optimal solution because it does not take into account the lack of computational resources. In contrast, RO, SO, DRO and RaDROO can obtain their optimal solutions and the optimal cost obtained increases with the increasing number of tasks.

In the two observations with the number of tasks 150 and 170, we can clearly get from Figure 6 and Figure 7 that the results obtained by the RaDROO are closer to those obtained by the traditional DRO algorithm. Therefore, it can be concluded that RaDROO ensures its robustness while considering CVaR to obtain higher risk resistance and better results under the uncertainty of computational resources.

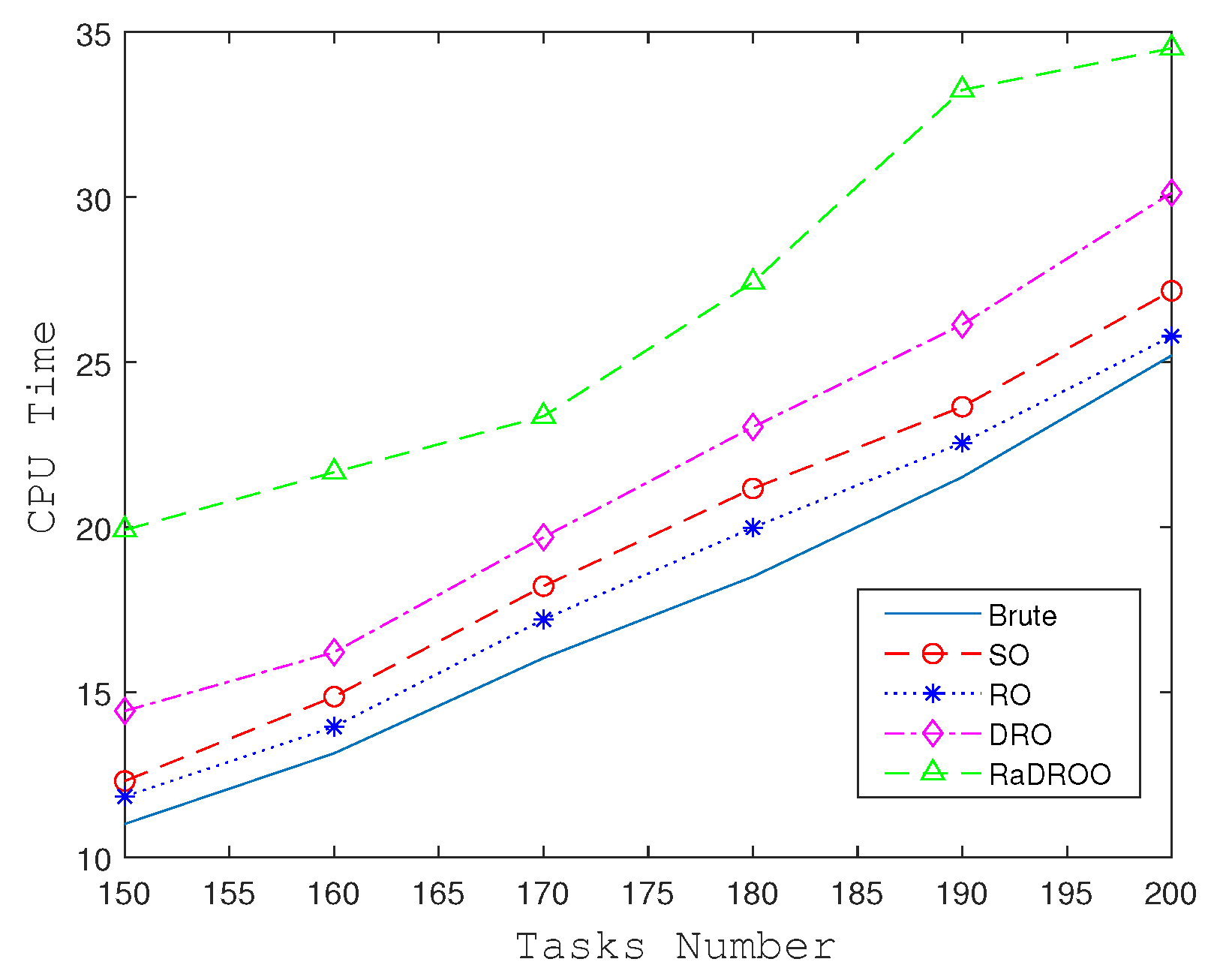
The RaDROO algorithm obtains better results also pays a price in terms of computational time, as shown in Figure 8. the time taken to solve the RO, SO, Brute algorithm is close and lower. the DRO algorithm obtains the optimal two-stage mean based on fuzzy sets in the minmax theory of robust algorithms. The RaDROO algorithm considers CVaR on top of this, which further increases the complexity of the algorithm and takes more time to solve problem.

Overall, although RaDROO incurs a certain time cost, it strikes a balance between computational time and risk consideration by incorporating CVaR into the decision-making process. It achieves improved robustness compared to traditional methods while maintaining competitive performance. By considering CVaR, RaDROO is able to effectively manage the risk associated with uncertain factors and make more informed task offloading decisions in the SAGIN environment.

6. Conclusions

This paper focuses on the offloading decision problem of tasks in the SAGIN framework, considering the instability of computational resources of each node and the limited channel resources and storage resources of ECNs. Based on this problem, we propose the RaDROO algorithm, which considers while CVaR to improve its risk resistance on the basis of the traditional DRO algorithm. In addition, we conducted simulation experiments in a simulation environment, and the algorithm obtained better results than the traditional robust algorithm and close to the traditional DRO algorithm, and proved the effectiveness of the algorithm.

There are several directions in which we can extend this work in the future. First, the execution time of the RaDROO algorithm is a major problem that needs to be solved, which may be solved by optimizing the algorithm architecture and using a better model solving method; second, the task upload is transient, and we can consider the real-time task unloading decision problem within the SAGIN framework; third, the value of lambda is freely variable and it is a problem to choose a rational value; Finally, this experiment only considers the uncertainty of computational resources, in the actual environment, the storage space of ECNs and CSI also have uncertainty, and the impact of these uncertainties on the offloading decision is also worth considering.

Acknowledgments

This work was supported by Natural Science Foundation of Jiangsu Province under Grant BK20201415.

References

J. Liu, Y. Shi, Z. M. Fadlullah, and N. Kato. Space-air-ground integrated network: A survey. IEEE Communications Surveys & Tutorials 2018, 20, 2714–2741. [Google Scholar]
W. Ma and L. Mashayekhy, “Quality-aware video offloading in mobile edge computing: A data-driven two-stage stochastic optimization,” in 2021 IEEE 14th International Conference on Cloud Computing (CLOUD). IEEE, 2021, pp. 594–599.
M. Chen, S. Guo, K. Liu, X. Liao, and B. Xiao. Robust computation offloading and resource scheduling in cloudlet-based mobile cloud computing. IEEE Transactions on Mobile Computing 2020, 20, 2025–2040. [Google Scholar]
H. Wang, H. Xu, H. Huang, M. Chen, and S. Chen. Robust task offloading in dynamic edge computing. IEEE Transactions on Mobile Computing 2021. [Google Scholar]
Z. Wu, B. Li, Z. Fei, Z. Zheng, and Z. Han. Energy-efficient robust computation offloading for fog-iot systems. IEEE Transactions on Vehicular Technology 2020, 69, 4417–4425. [Google Scholar] [CrossRef]
H. Rahimian and S. Mehrotra, “Distributionally robust optimization: A review,” arXiv preprint arXiv:1908.05659, 2019.
Ling, J. Sun, N. Xiu, and X. Yang. Robust two-stage stochastic linear optimization with risk aversion. European Journal of Operational Research 2017, 256, 215–229. [Google Scholar] [CrossRef]
M. Albuquerque, A. Ayyagari, M. A. Dorsett, and M. S. Foster, “Global information grid (gig) edge network interface architecture,” in MILCOM 2007-IEEE Military Communications Conference. IEEE, 2007, pp. 1–7.
S. Yu, X. Gong, Q. Shi, X. Wang, and X. Chen. Ec-sagins: Edge-computing-enhanced space–air–ground-integrated networks for internet of vehicles. IEEE Internet of Things Journal 2021, 9, 5742–5754. [Google Scholar]
Y. Yuan, X. Xu, M. Sun, and P. Zhang. Terminal cooperative interdependent computing task offloading for 6g. IEEE Transactions on Network Science and Engineering 2022. [Google Scholar]
J. Yan, S. Bi, Y. J. Zhang, and M. Tao. Optimal task offloading and resource allocation in mobile-edge computing with inter-user task dependency. IEEE Transactions on Wireless Communications 2019, 19, 235–250. [Google Scholar]
Y. Yang, X. Chang, Z. Jia, Z. Han, and Z. Han, “Towards 6g joint haps-mec-cloud 3c resource allocation for delay-aware computation offloading,” in 2020 IEEE Intl Conf on Parallel & Distributed Processing with Applications, Big Data & Cloud Computing, Sustainable Computing & Communications, Social Computing & Networking (ISPA/BDCloud/SocialCom/SustainCom). IEEE, 2020, pp. 175–182.
Li, Zhiyuan and Peng, Ershuai. Software-defined optimal computation task scheduling in vehicular edge networking. Sensors 2021, 21, 955. [Google Scholar] [CrossRef]
Z. Xiao, X. Dai, H. Jiang, D. Wang, H. Chen, L. Yang, and F. Zeng. Vehicular task offloading via heat-aware mec cooperation using game-theoretic method. IEEE Internet of Things Journal 2019, 7, 2038–2052. [Google Scholar]
Y. Dai, D. Xu, S. Maharjan, and Y. Zhang. Joint load balancing and offloading in vehicular edge computing and networks. IEEE Internet of Things Journal 2018, 6, 4377–4387. [Google Scholar]
E. F. Maleki, L. Mashayekhy, and S. M. Nabavinejad. Mobility-aware computation offloading in edge computing using machine learning. IEEE Transactions on Mobile Computing 2021. [Google Scholar]
S. Chouhan, “Energy optimal partial computation offloading framework for mobile devices in multi-access edge computing,” in 2019 International Conference on Software, Telecommunications and Computer Networks (SoftCOM). IEEE, 2019, pp. 1–6.
F. Wang, J. Xu, and S. Cui. Optimal energy allocation and task offloading policy for wireless powered mobile edge computing systems. IEEE Transactions on Wireless Communications 2020, 19, 2443–2459. [Google Scholar] [CrossRef]
Y. Hmimz, T. Chanyour, M. El Ghmary, and M. O. C. Malik, “Energy efficient and devices priority aware computation offloading to a mobile edge computing server,” in 2019 5th International Conference on Optimization and Applications (ICOA). IEEE, 2019, pp. 1–6.
Y. Wang, L. Wu, X. Yuan, X. Liu, and X. Li. An energy-efficient and deadline-aware task offloading strategy based on channel constraint for mobile cloud workflows. IEEE access pp. 69 858–69 872. 2019, 7. [Google Scholar]
Z. Ma, S. Zhang, Z. Chen, T. Han, Z. Qian, M. Xiao, N. Chen, J. Wu, and S. Lu. Towards revenue-driven multi-user online task offloading in edge computing. IEEE Transactions on Parallel and Distributed Systems 2021, 33, 1185–1198. [Google Scholar]
D. Wang, X. Tian, H. Cui, and Z. Liu. Reinforcement learning-based joint task offloading and migration schemes optimization in mobility-aware mec network. China Communications 2020, 17, 31–44. [Google Scholar]
A. Samanta and Z. Chang. Adaptive service offloading for revenue maximization in mobile edge computing with delay-constraint. IEEE Internet of Things Journal 2019, 6, 3864–3872. [Google Scholar] [CrossRef]
N. Cheng, N. Lu, N. Zhang, X. Zhang, X. S. Shen, and J. W. Mark. Opportunistic wifi offloading in vehicular environment: A game-theory approach. IEEE Transactions on Intelligent Transportation Systems 2016, 17, 1944–1955. [Google Scholar] [CrossRef]
J. Bi, K. Zhang, H. Yuan, and Q. Hu, “Energy-aware task offloading with genetic particle swarm optimization in hybrid edge computing,” in 2021 IEEE International Conference on Systems, Man, and Cybernetics (SMC). IEEE, 2021, pp. 3194–3199.
S. Li, H. Ge, X. Chen, L. Liu, H. Gong, and R. Tang, “Computation offloading strategy for improved particle swarm optimization in mobile edge computing,” in 2021 IEEE 6th International Conference on Cloud Computing and Big Data Analytics (ICCCBDA). IEEE, 2021, pp. 375–381.
H. Tout, A. Mourad, N. Kara, and C. Talhi. Multi-persona mobility: joint cost-effective and resource-aware mobile-edge computation offloading. IEEE/ACM Transactions on Networking 2021, 29, 1408–1421. [Google Scholar] [CrossRef]
F. Tang, Y. Kawamoto, N. Kato, and J. Liu. Future intelligent and secure vehicular network toward 6g: Machine-learning approaches. Proceedings of the IEEE 2019, 108, 292–307. [Google Scholar]
Y. Bai, L. Chen, L. Song, and J. Xu. Risk-aware edge computation offloading using bayesian stackelberg game. IEEE Transactions on Network and Service Management 2020, 17, 1000–1012. [Google Scholar] [CrossRef]
Y. Qu, H. Dai, F. Wu, D. Lu, C. Dong, S. Tang, and G. Chen, “Robust offloading scheduling for mobile edge computing,” IEEE Transactions on Mobile Computing, 2020.
X. Zhang and W. Sun, “Mean-cvar models for fuzzy portfolio selection,” in 2010 International Conference on Intelligent System Design and Engineering Application, vol. 1. IEEE, 2010, pp. 928–930.
R. Schultz and F. Neise, “Algorithms for mean-risk stochastic integer programs in energy,” in 2006 IEEE Power Engineering Society General Meeting. IEEE, 2006, pp. 8–pp.
Y. Chen, B. Ai, Y. Niu, H. Zhang, and Z. Han. Energy-constrained computation offloading in space-air-ground integrated networks using distributionally robust optimization. IEEE Transactions on Vehicular Technology pp. 12 113–12 125. 2021, 70. [Google Scholar]
Deng, L. Huang, J. Taheri, and A. Y. Zomaya. Computation offloading for service workflow in mobile cloud computing. IEEE transactions on parallel and distributed systems 2014, 26, 3317–3329. [Google Scholar]
. A. Apostolopoulos, E. E. Tsiropoulou, and S. Papavassiliou. Risk-aware data offloading in multi-server multi-access edge computing environment. IEEE/ACM Transactions on Networking 2020, 28, 1405–1418. [Google Scholar] [CrossRef]
S. Pan, Z. Zhang, T. Xue, and G. Hu, “Enhancing availability for the mec service: Cvar-based computation offloading,” in 2020 IEEE 26th International Conference on Parallel and Distributed Systems (ICPADS). IEEE, 2020, pp. 342–347.
F. Vatalaro, G. E. Corazza, C. Caini, and C. Ferrarelli. Analysis of leo, meo, and geo global mobile satellite systems in the presence of interference and fading. IEEE Journal on selected areas in communications 1995, 13, 291–300. [Google Scholar] [CrossRef]
F. Qi, G. Mang, S. Zhang, and L. Liu, “A multi-layer architecture for space-air-ground network and iot services,” in 2021 International Wireless Communications and Mobile Computing (IWCMC). IEEE, 2021, pp. 1809–1813.
E. Delage and Y. Ye. Distributionally robust optimization under moment uncertainty with application to data-driven problems. Operations research 2010, 58, 595–612. [Google Scholar] [CrossRef]

Figure 1. SAGIN model.

Figure 2. Expect cost under different

α

Figure 2. Expect cost under different

α

Figure 3. V value under different

α

Figure 3. V value under different

α

Figure 4. V value between 110 and 200 tasks.

Figure 5. optimal cost of compared algorithms between 110 tasks to 200 tasks

Figure 6. optimal cost under 150 tasks

Figure 7. optimal cost under 170 tasks

Figure 8. Execution time of each algorithm.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Risk-aware Distributionally Robust Optimization for Mobile Edge Computation Task Offloading in Space–Air–Ground Integrated Networks

Abstract

1. Introduction

2. Related Work

2.1. SAGIN Architecture

2.2. Traditional Computation Offloading

2.3. Uncertain-aware Computation Offloading

2.4. Risk-aware Computation Offloading

3. Network Architecture and System Model

3.1. SAGIN Architecture and Channel Models

3.2. Computation Tasks Offloading Model

3.3. Computing Resources Fussy Set Model

4. Risk-aware Distributionally Robust Optimization Tasks Offloading Algorithm Design

4.1. Network Architecture and System Model

4.2. Transform from DRO to SDP

4.3. DRO-MILP Algorithm

4.4. Complexity Analysis

5. Performance Evaluation

5.1. Simulation Setup

5.2. Experiments

5.2.1. RaDROO algorithm

5.2.2. Comparing with other algorithms

6. Conclusions

Acknowledgments

References

MDPI Initiatives

Important Links

Subscribe