Prerpints.org logo
Preprint
Article

Effect of Bending Load and Sulfate Erosion on the Properties of Cementitious Materials

This version is not peer-reviewed.

Submitted:

23 May 2023

Posted:

24 May 2023

You are already at the latest version

Abstract
The goal of this lab is to look at how the characteristics of cementitious materials are affected by bending loads combined with dry and wet cycles of sulfate. In this paper, three sets of specimens with different water–cement ratios were designed. This study applied 20% and 40% of the ultimate bending load as a continuous bending load to the cementitious material specimens for a sulfate erosion test. It was discovered that the specimens' porosity, flexural strength, and compressive strength all tended to improve initially before declining as the cementitious material was degraded in the sulfate solution aged. The flexural strength of the cementitious materials declined as the bending load increased, and their internal sulfate ion concentration rose. A transport model of sulfate ions in cementitious materials under the coupling effect of bending load and sulfate erosion was created by combining the improved version of Fick’s second law and chemical reaction kinetics. The simulation results show that the ion transport properties of sulfate ions in cementitious materials are in accordance with the experimental laws. These research results formed the basis of the unified standards for the coupling of load dry and wet cycle systems, as well as evaluating the durability of cementitious materials under corrosive environments.
Keywords: 
Subject: 
Engineering  -   Civil Engineering

1. Introduction

With the implementation of national initiatives such as “peak carbon/carbon neutrality [1]” and “One Belt, One Road [2],” basic buildings are being gradually developed in salt areas where there is an alpine climate or dry heat. Cement-based materials can be applied in foundations for construction because of their convenience and low cost [3,4]. In practical engineering, cementitious materials’ damage is inevitably caused by sulfate corrosion, and also by various forms of loading [5,6,7]. The flexural strength of the cementitious materials declined as the bending load increased, and their internal sulfate ion concentration rose.The above effects can reduce the strength, elastic modulus and other properties of cementitious materials, ultimately leading to a reduction in their durability and expected service life [8,9]. Extending the service life of cementitious materials in salt environments is therefore a critical issue that needs to be addressed as soon as possible[10].
Researchers from China and other nations have recently done a variety of tests and numerical simulations to investigate the cementitious materials' endurance in salt environments. Qi et al. [11] shows how, as the erosion time increases under the combined effect of sulphate and the dry and wet cycles, visible microcracks would first form in the interface transition zone in concrete specimens. Ikumi et al[12] investigated the effect of porosity on sulfate attack and concluded that the durability of cementitious materials depends on the porosity in the early stages of sulfate attack and the porosity in the later stages of attack. Wang et al [13] investigated the effect of the ratio of dry to wet content on the migration behaviour and the reaction mechanism of sulfate in concrete. The results show that the sulphate ion migration process involves chemical reaction and physical crystallisation, with the chemical reaction of the sulphate dominating and the proportion of physical attack of the sulphate gradually increasing. The most suitable ratio to promote the inward transport of sulphate ions is a dry to wet ratio of 7:1.
Loading accelerates sulphate erosion. Researchers have also investigated the effects of sulphate erosion on concrete under static and fatigue bending loading conditions. SEM, MIP, XRD, and other techniques were used by Gao et al. [14] to investigate the concrete damage process under flexural loads and the dry-wet cycle of sulphate.The findings demonstrate that the deterioration process of concrete under sulfate assault can be sped up by bending force as well as wetting and drying cycles. The impact of sulphate attack on concrete exposed to bending fatigue and dry-wet cycling was examined by Liu et al[15]. Both fatigue loading and dry-wet cycling can hasten sulfate ion migration within concrete and result in concrete deterioration under sulfate attack. Zhang et al. [16] studied the impact of the volume of sulfate erosion cycles on the residual deformation and elastic modulus of concrete during the dry-wet cycle and load. The results show that the elastic modulus changes within a defined range and that initial stage and stable stage residual deformation and damage variables of concrete can be distinguished.
Simulation versus test increases the credibility of the test.He et al [17] described the transport properties of sulfate ions in concrete and proposed a coupled chemical-mechanical approach to evaluate the transportation of sulfate ions in concrete under stress. It was concluded that volume strain-induced crack damage is crucial in the diffusion of sulfate ions. By performing four-point bending tests on reinforced concrete beams, Zhang et al. [18] investigated the coupling effect of sulfate erosion and external load conditions and compared the outcomes to those predicted by the model. According to the findings, external loads cause the concrete matrix to experience tensile strain, which quickens the process by which concrete deteriorates when subjected to sulfate attack. In order to develop a diffusion model for sulphate ions in cement mortar that takes into account variations in surface concentration, Zhuang et al [19] studied the pore changes caused by sulphate damage to cement mortar. The results indicate that the corrosion depth increases with increasing coarse aggregate content. The concentration of sulphate ions and the depth of corrosion in concrete both increase as the water/cement ratio and the concentration of the sulphate solution increase.
In summary, the sulfate erosion of cementitious materials leads to performance deterioration, especially with the addition of bending load, which is mainly caused by disrupting the cementitious microstructure. There are currently few studies on the microscopic transport of sulphate in cement-based materials under the coupled effect of flexural loading and the environment. It is necessary to analyse the transport law of sulphate ions in cement-based materials due to the coupling effect of bending force and sulphate.
With this in mind, a series of tests on the effect of continuous flexural loading with different flexural stress ratios under the action of dry and wet cycles coupled with sulphate erosion on the deterioration of cementitious materials are designed and carried out in this study. A sulphate ion transport model is also established to assist in the evaluation for durability design of cementitious materials in a long-term saline environment.

2. Experiments

2.1. Raw Materials

The cement used was of the P-O42.5 grade produced by the Tian Shan cement works, with the chemical composition shown in Table 1. The mixing water comes from the tap water in Kashgar City, and the high-performance water reducing agent in liquid form was polycarboxylic acid. The fine aggregate was washed river sand from Kashi with a fineness modulus of 2.86, an apparent density of 2460 kg/m3 and a silt content of 0.5%.The coarse aggregate was crushed gravel with a particle of size 5–10 mm, mud content of 0.7%, and apparent density of 2680 kg/m3.

2.2. Matching ratio

The tests were designed with three groups of mortar ratio, i.e., M1, M2, and M3, and three groups of concrete ratio, i.e., C1, C2, and C3. Table 2 shows the detailed ratios.

2.3. Test method

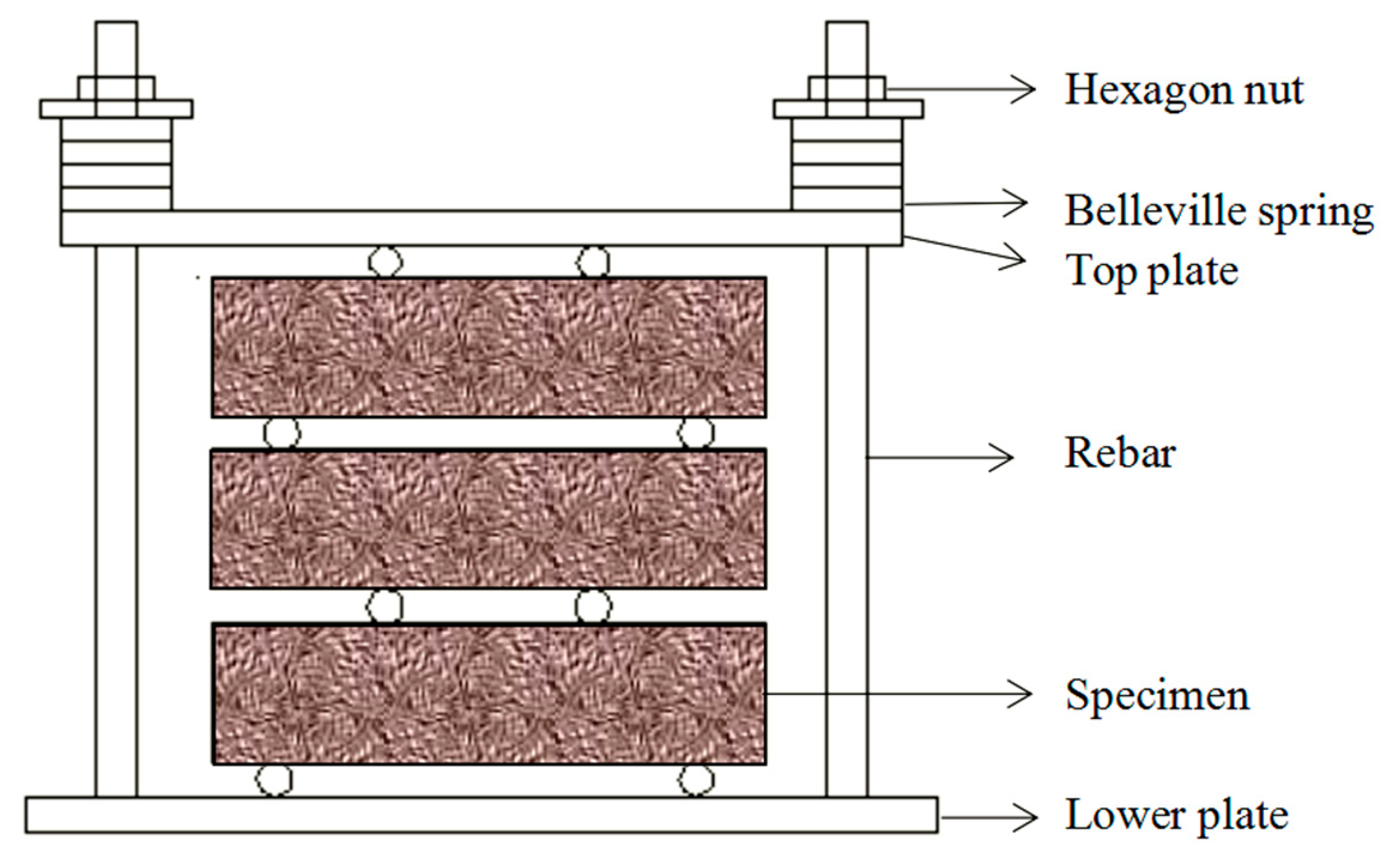
2.3.1. Sulfate wet and dry cycle

The specimen was sealed on five sides with epoxy resin glue, leaving one side open to erosion, and the specimen size was 40 mm × 40 mm × 160 mm.The dry and wet cycle system refers to the Chinese standard GB/T50082-2009 “Standard for long-term performance and durability test methods of ordinary concrete[20]”. These include the subsequent actions: The specimen was dried for 48 hours in an oven set at 80°C once curing was complete. The specimen was cooled, submerged in a 5% sodium sulfate solution for 16 hours, removed, and left in the natural environment for 9 hours. A whole cycle lasts for 24 hours, totaling 150 cycles.For each group, three specimens were repeated, and the findings were averaged.
In this paper, based on the research of Zhao et al. [21], a loading device was designed, which can simultaneously perform stress loading and wet and dry cycles of sulfate, and was also used as the loading device of the test. Meanwhile, the surface without epoxy resin adhesive was used as the bending and tension surface of the specimen. In this study, 0%, 20%, 40% of the bending stress was selected as the loading stress, such as, M1-0%, 20%, 40% for M1 group ratios were applied 0%, 20%, 40% of the bending stress. The loader's schematic is depicted in Figure 1.

2.3.2. Mechanical analysis

The ETM305F-2 microcomputer-controlled electronic compression and folding integrated testing machine was used to test the flexural and compressive strength of specimens before and after wet-dry cycles in accordance with GB/T 50081-2002 "Standard of Test Methods for Mechanical Properties of Ordinary Concrete [22]".

2.3.3. Microstructure

For the scanning electron microscopy (SEM) test, after a certain number of wet and dry cycles, a flat sheet with a diameter of less than 5mm and a thickness of 2–3mm was first taken out from the specimen, placed in anhydrous ethanol for 24h, and then put in an oven at 40℃ for 24h. The erosion products and microstructure morphology were analysed using Phenom Prox, a FERNER automatic tabletop electron microscope and spectroscope, after the gold spray treatment of the sample surface.
For X-ray diffraction (XRD), the samples were placed in anhydrous ethanol to complete hydration. They were then baked in an oven at 40℃ for 48 h and finally ground to powder. The product composition was characterised using a TD-3500 X-ray diffractometer with a scanning range of 10-80°.
For the mercury intrusion porosimetry (MIP ) test, a 5mm depth range inside the specimen was selected, and the sample was cut into a size of about 3~5mm in diameter using a cutter. The samples were then placed in anhydrous ethanol for 5 to 7 days to complete hydration and then placed in an oven at 50°C for 2 to 3 days to dry. MIP testing was performed using the Micrometrics AutoPore IV9510 automated porosity testing system.
In the drill core sampling procedure, cement materials were selected at five depth classes of 0 to 5 mm, 5 to 10 mm, 10 to 15 mm, 15 to 20 mm and 20 to 25 mm for sampling using a drill core sampler. The EDTA complex titration method was then used to determine the concentration of sulphate ions at different depths. The principle of detection is: BaCl2 reacts with sulfate ions in the sample to produce an insoluble BaSO4 white precipitate, and the excess barium ions are titrated with EDTA standard solution to obtain the sulfate ion content.

3. Results and analysis

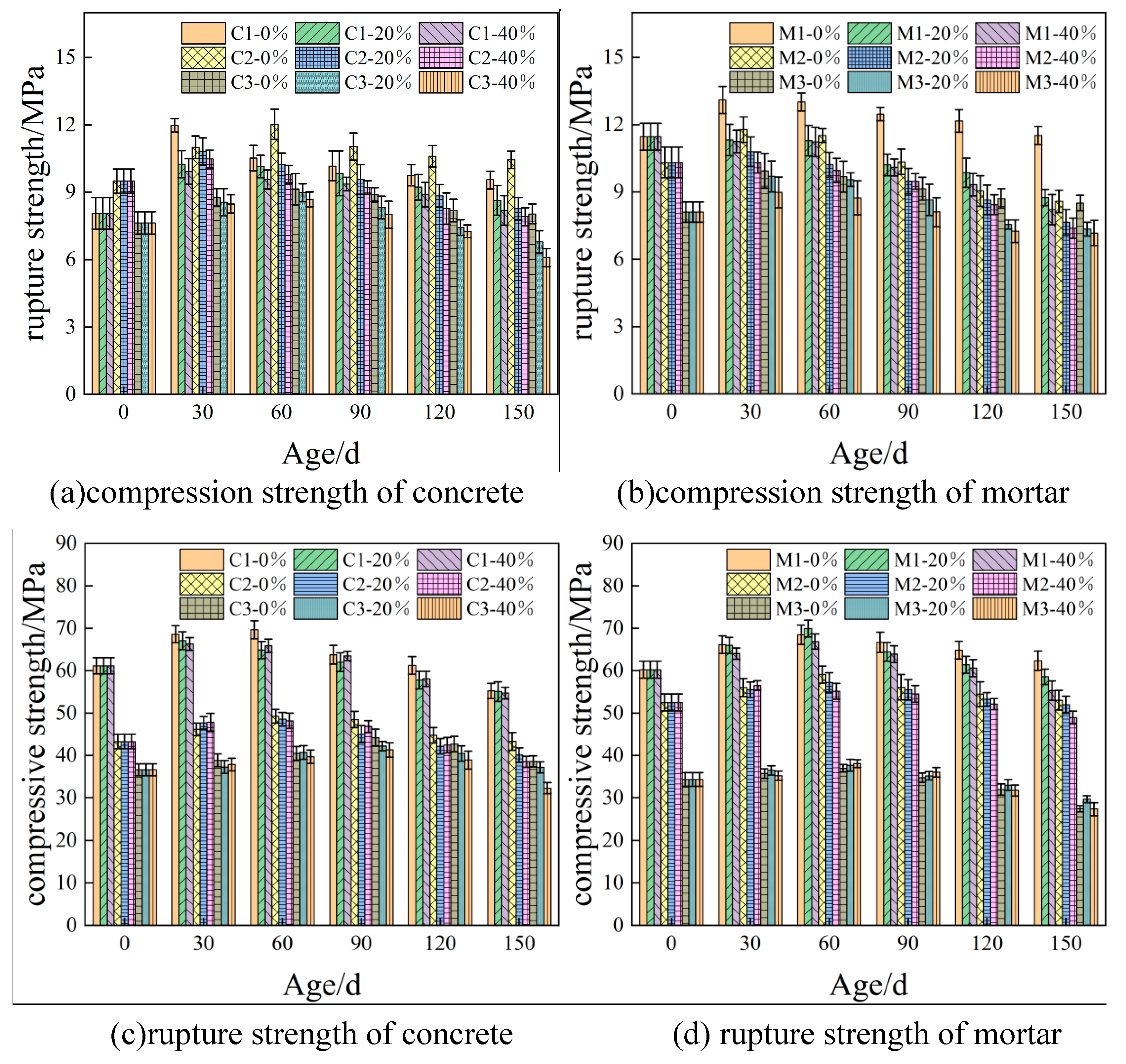
3.1. Effect of coupling of load and sulfate on the mechanical properties of cementitious materials

Figure 2 shows the effect of load and sulphate coupling on the mechanical properties of cementitious materials. From Figure 2 it can be seen that the compressive and flexural strengths of mortar and concrete under different flexural loads showed an overall tendency to increase and then decrease. The flexural strength was lower as the flexural load increased. The flexural and compressive strength reached their maximum values when the wet and dry cycles reached 60 d. On the one hand, this is due to the evaporation of water inside the specimen during the dry cycle, which resulted in the formation of sulfate crystals as shown in Equation (1), while the wet cycle accelerated the entry of sulfate ions inside the specimen. On the other hand, Once in the sample, the sulfate reacts with the cementitious material to form plaster, and as the erosive age increases, the plaster reacts with the calciumaluminate and calciumhydroxide in the cementitious material to form calciumalumina, as shown in Eqs.2-6
Na2SO4+10H2O→Na2SO4·10H2O
CH+Na2SO4+H2O→CS̅H2+2NaOH
C-S-H+Na2SO4+H2O→CS̅H2+2𝑁𝑎+
C4AS̅H12+2CS̅H2+16H2O→C6AS̅3H32
C3A+3CS̅H2+26H2O→C6AS̅3H32
C4AH13+3CS̅H2+14H2O→C6AS̅3H32+CH
where CH is calcium hydroxide, C-S-H is calcium silicate hydrate, CS̅H2 is gypsum; C4AS̅H12, C6AS̅3H32 is natural gas hydrates calcium sulfoaluminate (AFt), C3A is tricalcium aluminate hydrate, C is calcium oxide, A is aluminum oxide, S is silicon dioxide, and S̅ is sulfur trioxide.
The effect of bending load on sulfate erosion is reflected in the increase in the number of cracks on the specimen surface and the width of microcracks inside the specimen, which makes it easier for sulfate to enter the specimen through the cracks.Secondly, after 28 d of maintenance, the cement is not fully hydrated, and the load accelerates the sulfate into the cementitious material and promotes the hydration of some cementitious materials, which makes the flexural and compressive strength increase. After the peak, the flexural and compressive strengths of the specimens showed a slow decline influenced by the expansion force generated by the large accumulation of the product, which made the specimens crack. In the process of cracking, some small particles and even some of the corners fell off, resulting in a decline in flexural and compressive strength.

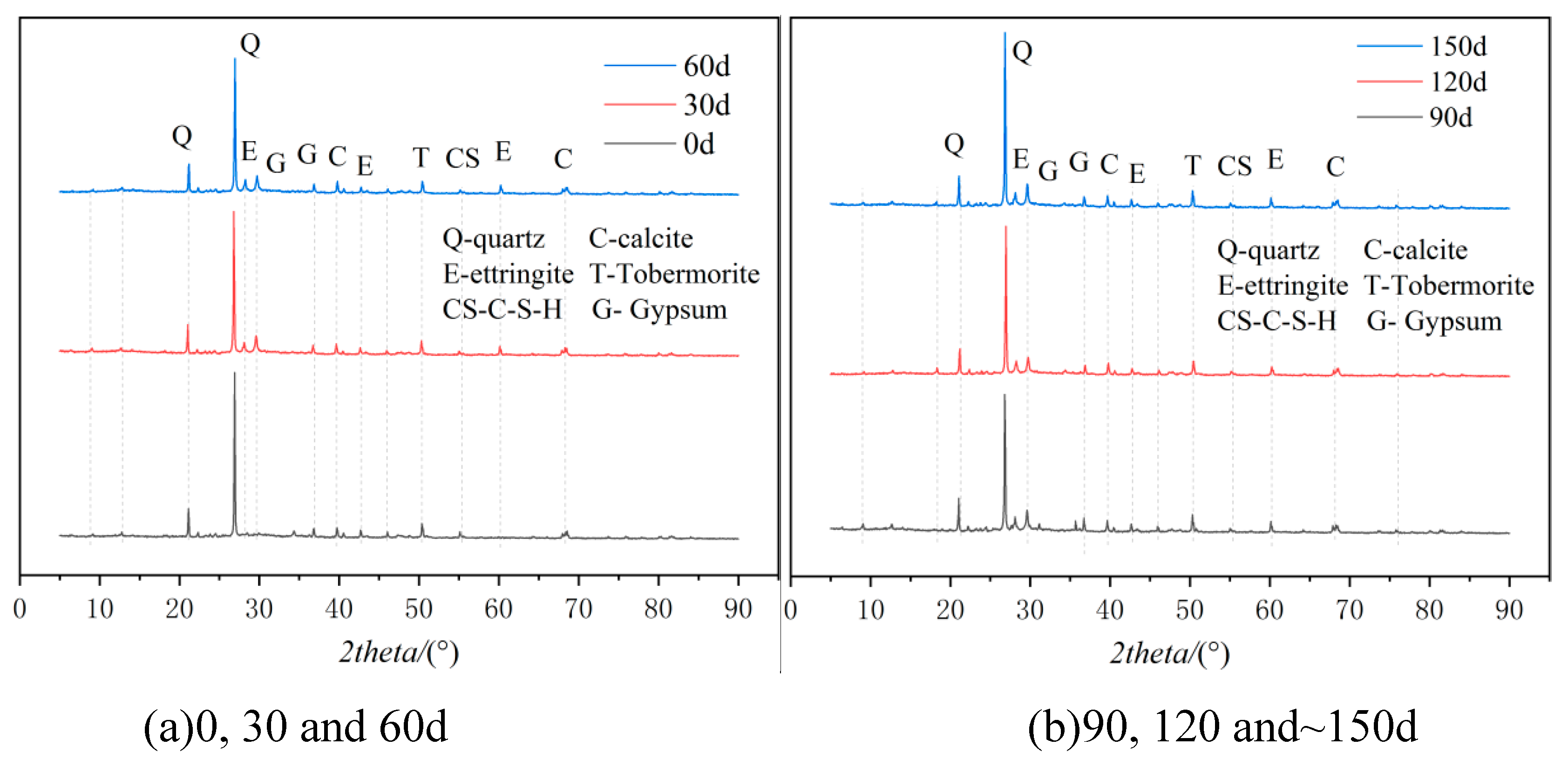
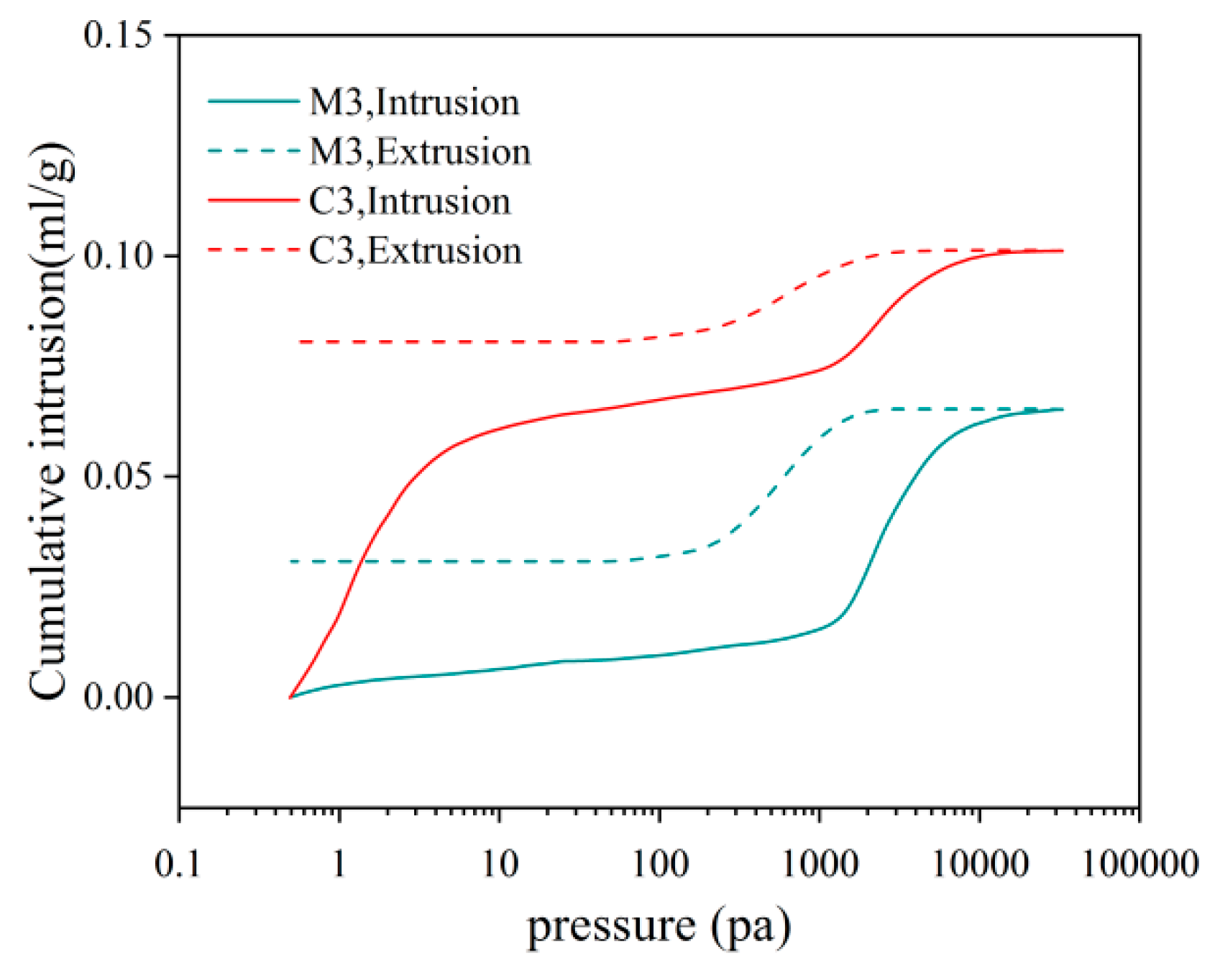
3.2. Microscopic Analysis

The XRD pattern of the cementitious material after sulphate attack is shown in Figure 3.It can be noticed that the main phases are hydrated calcium silicate, quartz, calcium alumite, calcite, gypsum, and C-S-H gel. In the absence of erosion, gypsum and calcite do not appear in the peak XRD diffraction peaks. With the increase of erosion, the diffraction peaks of gypsum and calcium alumina increased with the growth of erosion age, indicating that the cementitious material produced a large amount of gypsum and calcium alumina as erosion products. The diffraction peaks of calcium alumina increase with the age of erosion. This indicates that the content of calcium alum and gypsum is increasing, and calcium alum and gypsum will first fill the internal pores of the specimen. When the content of calcium alum and gypsum increases to a certain degree, it will lead to the expansion of the cementitious material, and when the expansion force is larger than the tensile force of the specimen itself, the specimen will be cracked. Macroscopically, the flexural and compressive strengths of cementitious material specimens rose up initially and then fell down.
Figure 4 shows a SEM image of the cementitious material after sulfate erosion. It can be concluded from Figure 4, when the specimen is not eroded, the interior of the specimen is relatively flat, but there are a small number of pores, which indicates that the cement hydration is not complete. When the erosion age reaches 30d, a small amount of columnar or plate-like erosion products appear inside the specimen. When the erosion age reaches 60d, the erosion products inside the specimen increase and the internal pores decrease, which is due to the full hydration of the cement on the one hand and the generation of erosion products filling the pores on the other hand. When the erosion age reaches 90d, a large number of columnar or plate-like erosion products appear inside the specimen and begin to accumulate. When the erosion age reaches 120d, a large amount of erosion products accumulate inside the specimen and generate a large amount of swelling force, which makes micro-cracks appear inside the specimen. When the erosion age reached 150d, the erosion products of the specimen continued to increase, and a large amount of needle-like calcarenite appeared. With the further growth of erosion age, the internal microstructure of the specimen shows a large difference. The longer the age of erosion, and the more crystallization and swelling products inside the cementitious material, the smaller the pore space.
Figure 5 shows the graphs of incoming and outgoing tribute pressure for C3 and M3. It can be seen from the graph that the amount of incoming mercury is greater than the amount of outgoing mercury due to the ink bottle hole effect regarding to the water-cement ratio in the same conditions. With the incorporation of fine aggregates, the amount of incoming mercury of the material decreases, and the amount of incoming mercury of the material increases after the incorporation of coarse aggregates but is smaller than the amount of incoming mercury of the net slurry, and the total porosity and effective porosity show an upward trend followed by downward trend. In the mercury pressure test, liquid mercury enters inside the pores of the material under pressure, and after the end of pressure application, part of the liquid mercury remains inside the pores, so the amount of incoming mercury is larger than the amount of outgoing mercury, and the residual part is the ink bottle hole [23]. The pores that can flow out freely after unloading are the effective pores. The effective pore is the main channel for the transport of moisture and erosion medium, which is the key to determine the durability of the material.
Figure 6 and Figure 7 show the pore size distribution curves for C3 and M3 with the cumulative suction curves. In Figure 6, since the pore diameter is 100nm~10000nm, the pore size distribution of mortar and concrete is basically the same. If the pore diameter is less than 100nm or more than 10000nm, the intrusion volume of concrete is larger than that of mortar.
Regardless of the pore size, Figure 7 shows that the contribution of concrete is greater than that of mortar. The tribution of concrete is about 3~5 times that of mortar when the pore size is in the range of 100nm~100000nm.Under the same conditions of water-cement ratio, the pore size and the amount of mercury intake changes for concrete > mortar. This is due to the fact that, as the coarse aggregate is incorporated, the non-homogeneity of the material is enhanced, the porosity increases significantly, and the harmful pores increase significantly.
Figure 8 and Figure 9 show pore size distribution curves and cumulative contribution curves for different erosion ages of M3. From Fig. 8, it can be seen that when the pore diameter is less than 100nm, the cumulative tribution is greater than that of sulphate erosion 60d than that of erosion 120d than that of no erosion. When the pore diameter is from 100nm to 1000nm, the cumulative tribution presents: un-erosion is greater than sulfate erosion 60d than erosion 120d. When the pore diameter is from 1000nm to 100000nm, the cumulative tribution presents: sulfate erosion for 120d is greater than un-erosion 0d and erosion for 60d.
In Figure 9, the volume of non-erosion is greater than the volume of erosion 120 days is greater than the volume of erosion 60 days when the pore size is in 10nm~100nm. When the pore size is in 100nm~1000nm, the volume of eroded 60 days is larger than the volume of uneroded than the volume of eroded 120. When the pore size is in the range of 1000nm~100000nm, the volume of erosion 120 days is greater than the volume of uneroded than the volume of eroded 60.
In the early stages of erosion, sulphate ions enter the cementitious material by diffusion and other means. Then chemical reaction occurs with hydrated calcium silicate and calcium hydroxide etc. within the cementitious material to produce gypsum, calcium alumina etc. The pores inside the specimen are filled and the porosity is reduced. In the mid - to late stages of erosion, after the internal pores of cementitious materials are filled with the generated products, the erosion products are still continuously generated. If the expansion force of the synthesised compounds is greater than the tensile strength of the cementitious material, the cementitious material will crack and spall, etc., resulting in an increase in the porosity of the cementitious material.
Figure 10 shows the pore size variation pile diagram for M3 versus C3 without erosion. Figure 11 shows that the pores in mortar and concrete with the same water-cement ratio differ greatly. For pores larger than 1000 nm, C3 pores are larger than M3; for pores between 100 nm and 1000 nm, M3 and C3 pores are basically equal. The pore volume of M3 is greater than that of C3 when the pore diameter is less than 100nm.
Figure 11 shows the pore volume changes of M3 group mortar specimens subjected to sulfate erosion after 0d, 60d and 120d. The number of different pore sizes varies with the age of erosion. After 60 d of erosion and then with increasing erosion age, the 10-100 nm pores, which make up the largest proportion of the total pore volume, decrease. The total pore volume decreases at 60 days compared to the uneroded specimens, and increases with the age of erosion after 120 d of erosion, exceeding the total pore volume of the cementitious material when it is not eroded.
At different erosion ages, the pore volume of 10-100 nm accounted for the largest proportion, and its trend was consistent with the change of total pore volume with the erosion age. The pore volume of 10-100 nm decreased by 20% after 60 d of erosion and increased by 0.6% after 120 d of erosion. The pore size of the zone is largely responsible for the permeability of the cementitious material. As a result, the water absorbency of cementitious materials in tests usually decreases and then increases with the age of the eroded material, and this is inextricably linked to the trend in the volume of pores between 10 and 100nm. The pore volume of 100-1000nm diameter increased after 60 days of erosion and increased by 84%, and increased by 29% after 120 d of erosion compared with the pore volume of 100-1000nm diameter, this tends to increase and then decrease as erosive ages increase.
The pore volume of diameter 1000-10000nm with the prolongation of the erosion age is increasing trend, more than 10000nm pore change for the first decrease and then increase. Pore change over the pore size of 10-100nm pore volume without erosion, the phenomenon corresponds to the first increase and then decrease in capillary pressure in the process of water transfer, which directly affects the capillary water absorption characteristics. The unit pore volume of pore size less than 10 nm continues to increase with the age of erosion, which is due to the formation of CSH gel dissolution.
Table 3. shows porosity characteristics, with a tendency for porosity to decrease and then increase with eroding. After 60 d of erosion, the porosity decreased by 1.01%. At 120 d of erosion, the porosity increased by 1.6%. For the same water-cement ratio, concrete porosity is 6.48% higher than that of cement mortar.The table shows that the porosity of concrete is about 4-6 times that of mortar when the pore diameter is greater than 10000nm.

4. Simulation

In order to compare the effects of different bending stresses on cementitious materials, the transport of sulphate ions in cementitious materials was simulated numerically and the bending stress F was set to 0%, 20% and 40% in the numerical model. To investigate the sulphate ion concentrations at different depths at different ages of erosion, the sulphate ion concentrations at different ages of erosion were simulated in the numerical model.

4.1. Theoretical basis of sulfate ion diffusion model

Sulfate ions in solution enter the cementitious material and undergo free diffusion, physical crystallization, and chemical reactions. Based on Fick's second law and chemical kinetics, the diffusion equation for sulphate ions in the cementitious material is established. [24,25].
∂ C ∂ t = ∂ ∂ x ( D ∂ C ∂ x ) + ∂ U ∂ t
∂ U ∂ t = K C c a C 1
In the above equation, ∂ U ∂ t is the amount of sulphate ions that are consumed in the chemical reaction in the cement-based material.; C1 is the sulphate ion content of cement-based materials.; t is the eroding time; x is the eroding depth; C𝑐𝑎 is the concentration of calcium ions; K is the chemical reaction rate and D is the sulphate ion diffusion coefficient.

4.1.1. Diffusion coefficient of sulfate ions in cement mortar

The volume fraction of the cement mortar (V𝑠) is closely related to the diffusion coefficient of sulphate ions in the mortar., the degree of hydration (α), the maintenance time (T), and the porosity (φ). In this paper, we adopted the method of Powers et al. [26] to calculate the following:
φ 1 = 0.19 α w / c + 0.32
φ 2 = w / c − 0.36 α w / c + 0.32
  φ s = φ 1 + φ 2 = w / c − 0.17 α w / c + 0.32
In the above equations, 𝜑1 is the capillary space, 𝜑2 is the gel pore, and 𝜑s is the initial porosity of cement mortar.
The degree of hydration（α）was obtained by Sun et al. [27] as follows:
α = 0.716 T 0.0901 exp [ − 0.103 T 0.0719 ( w / c ) ]
According to the theories of Sarkar et al [28] and Zuo et al [29], the diffusion coefficient of sulphate ions in cement mortar (DS) can be deduced, and the calculation model can be obtained as shown in Equations (13) and (14):
D s = φ s D e τ
τ = w h α β s β s a ( 1 + 0.35 V s ) ( 1 − 1 − φ s ) 2 + 0.25 1 − 1 − φ s
In the above equations, D𝑒 is the coefficient of diffusion of the sulphate ions in the pore solution, and the value is 1.7 × 10−11 𝑚2⁄𝑠 [30]. w is the adjustment coefficient, for which the value is 1.28; βs is a parameter with value 1.77; β𝑠𝑎 is the sand shape coefficient, for which the value is 1.08; and 𝑉𝑠 is the sand volume fraction [29].

4.1.2. Coefficient of diffusion of the sulphate ion in the interface transition zone

The durability and flexural and compressive strength of cementitious materials are greatly influenced by the interfacial transition zone.For example, Therefore, this paper adopts the viewpoint of Cao and He et al. [31,32] that these do not affect the transport of sulphate ions, although the strength at the interface is much lower than that of the mortar and the porosity is much higher than that of the cement mortar, and simplifies the interfacial transition zone into a homogeneous phase. The diffusion coefficient (𝐷𝐼) of sulfate ions in the interfacial transition zone (ITZ) was obtained as shown in Equation (15):
D I = D 0 [ 0.001 + 0.07 φ i 2 + H ( φ i − 0.18 ) × 0.18 × ( φ i − 0.18 ) 2 ]
In the above equation, D0 is 1.06×10−9 𝑚2/𝑠; 𝜑i is the porosity of the interfacial transition zone; and H(x) is the Heaviside function, where, if x > 0, the value is 1 and otherwise, the value is 0.

4.1.3. Coefficient of diffusion of sulphate ions in concrete

Concrete consists of cement mortar, coarse aggregate and a transition zone between them. Since sulfate ions cannot enter into the coarse aggregate, the diffusion coefficient of sulfate ions of coarse aggregate is considered to be zero in this paper. The diffusion coefficient Dx of concrete is obtained by theoretical derivation based on a model in the literature [33].
D x = 6 D s ( 1 − V a ) ( V a + V I ) + 2 V I ( D I − D s ) ( 1 + 2 V a + V I ) 3 D s ( 2 + V a ) ( V a + V I ) + 2 V I ( 1 − V a − V I ) ( D I − D s )
Here, 𝑉𝑎 refers to the volume fraction of concrete coarse aggregate and 𝑉𝐼 refers to the volume fraction of the interfacial transition zone.
The effect of loading on the diffusion coefficient is not considered, as the diffusion coefficient (𝐷𝑥) only takes into account the transfer coefficient of sulphate ions in the cement mortar, interfacial transition zone and coarse aggregate, respectively. Therefore, In this paper, the diffusion coefficient of sulphate ions in concrete under bending load (D) is derived by considering the load action and introducing the load influence factor λ as follows:
D = λ 6 D s ( 1 − V a ) ( V a + V I ) + 2 V I ( D I − D s ) ( 1 + 2 V a + V I ) 3 D s ( 2 + V a ) ( V a + V I ) + 2 V I ( 1 − V a − V I ) ( D I − D s )

4.1.4. Effect of loading action on the diffusion coefficient of sulfate ions

The diffusion coefficient and the chemical reaction coefficient of the sulphate ions will be changed to a certain extent under the bending load. The diffusion coefficient of sulphate ions in cementitious materials can be calculated according to the above, and the load deterioration coefficient K of bending load on the diffusion coefficient of sulphate ions in cementitious materials can be obtained on the basis of the test results in Section 4. In view of the effect of the load action on the diffusion coefficient, this paper uses the modified Fick's second law in the form of equation (18), the diffusion coefficient of sulphate ions in cement mortar (equation 19) and the diffusion coefficient of sulphate ions in concrete (equation 20).
∂ C ∂ t = k [ ∂ ∂ x ( D e f f ∂ C ∂ x ) + ∂ U ∂ t ]
D s = k φ s D e τ
D c = k D x 1.38 + 0.483 V a

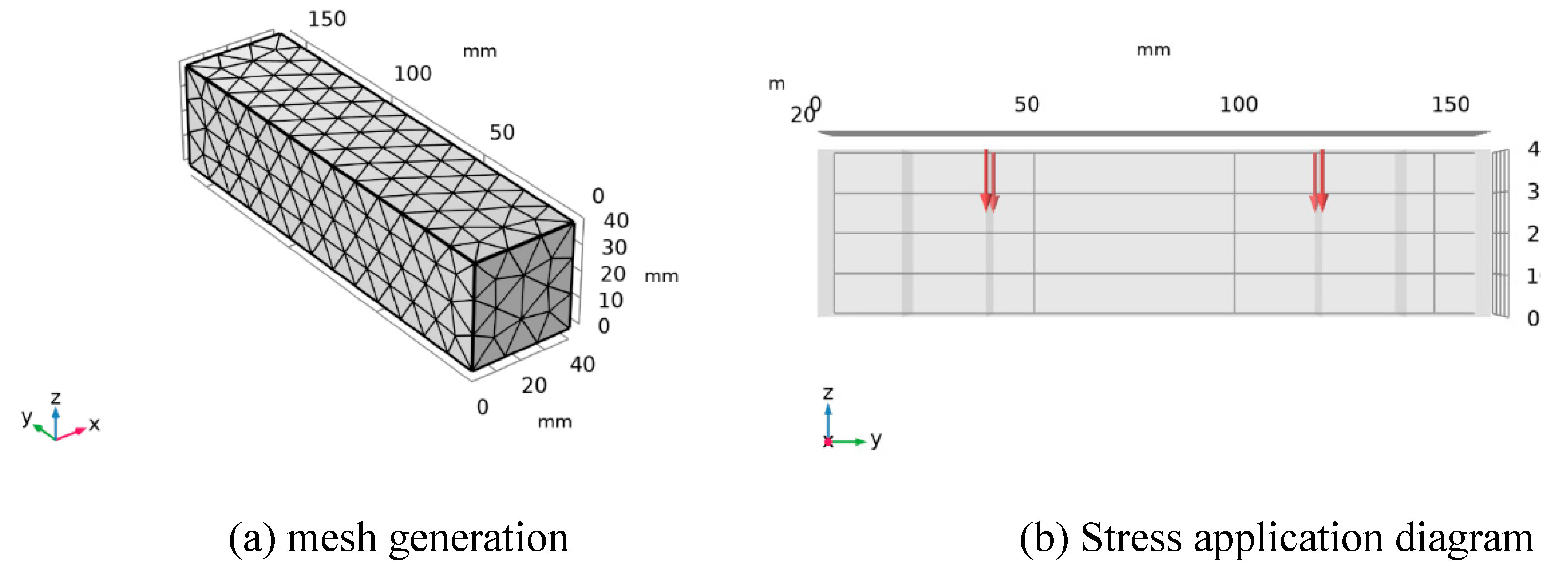
4.2. Numerical Simulation

The specimen size is 40㎜ × 40㎜ × 160㎜, and the sulfate ion diffuses from the eroded surface of the cementitious material in one dimension. The boundary concentration is C(0,t) = 5% Na2SO4, bending load F1=0, F2=0.2f, F3=0.4f (f is the ultimate flexural strength of the specimen). The ratio coefficients are R1=0.6, R2=0.5, R3=0.35. temperature T=298.15 K, density of cement ρc=3100 kg/m3. density of mortar ρs=2300 kg/m3, density of concrete ρc=2 600 kg/m3, diffusion coefficient of sulfate ion D.
In this study, a conditional statement command is used to automatically switch between the wet and dry cycle conditions by entering commands into the COMSOL Multiphysics finite element software physical field boundary conditions input box.
Figure 12 shows the numerical simulations, (a) for the mesh division, (b) for the stress application, and Figure 13 shows the numerical simulations of sulfate ion concentrations, with (a)–(f) showing different erosion ages.

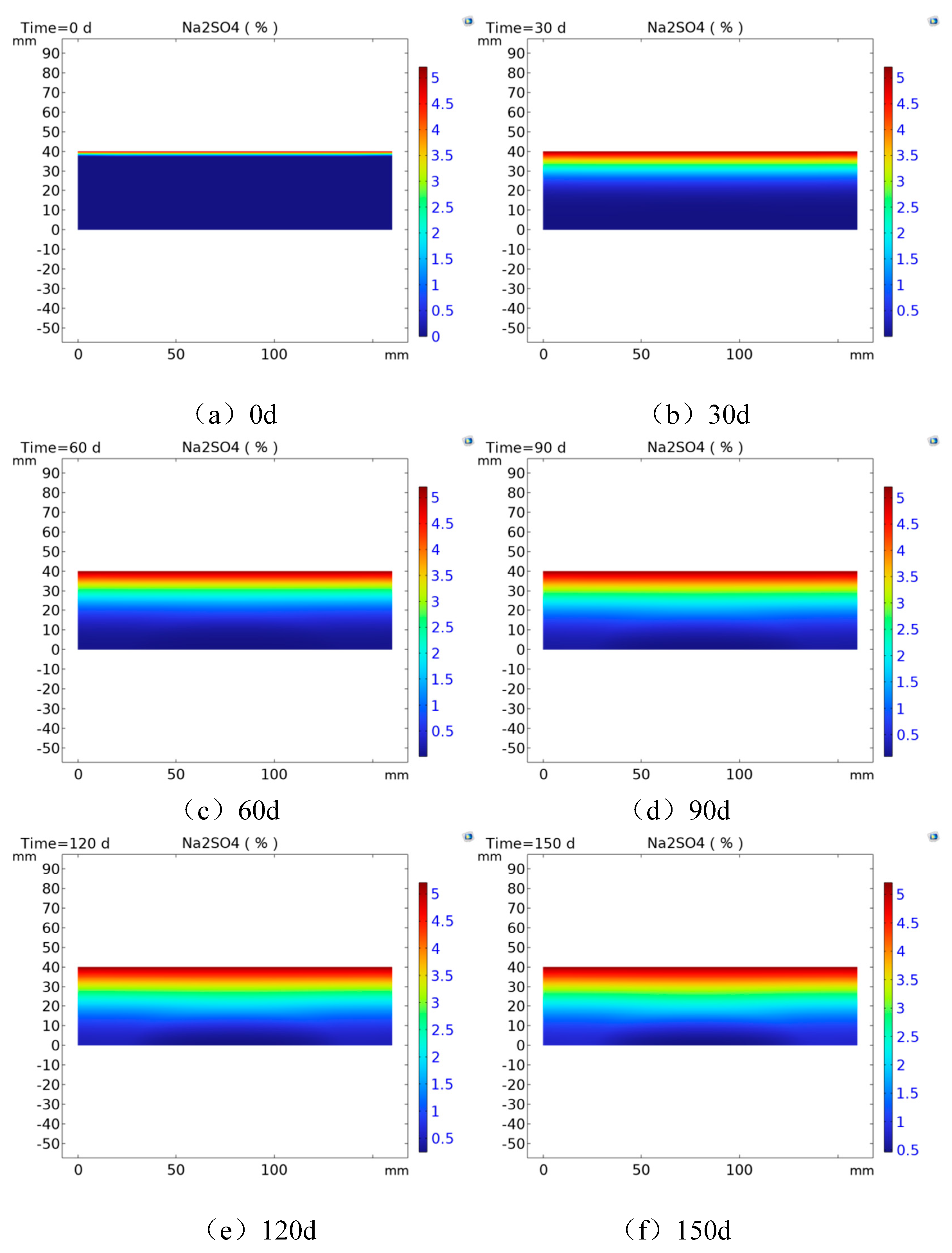
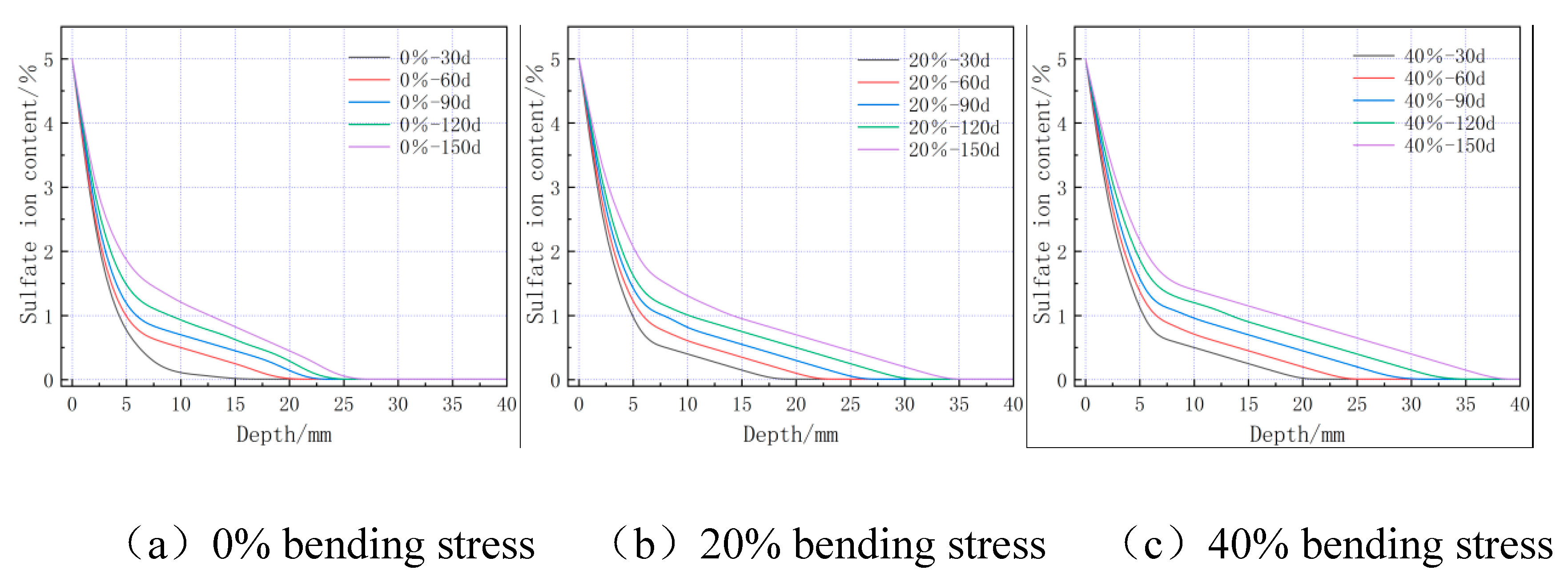
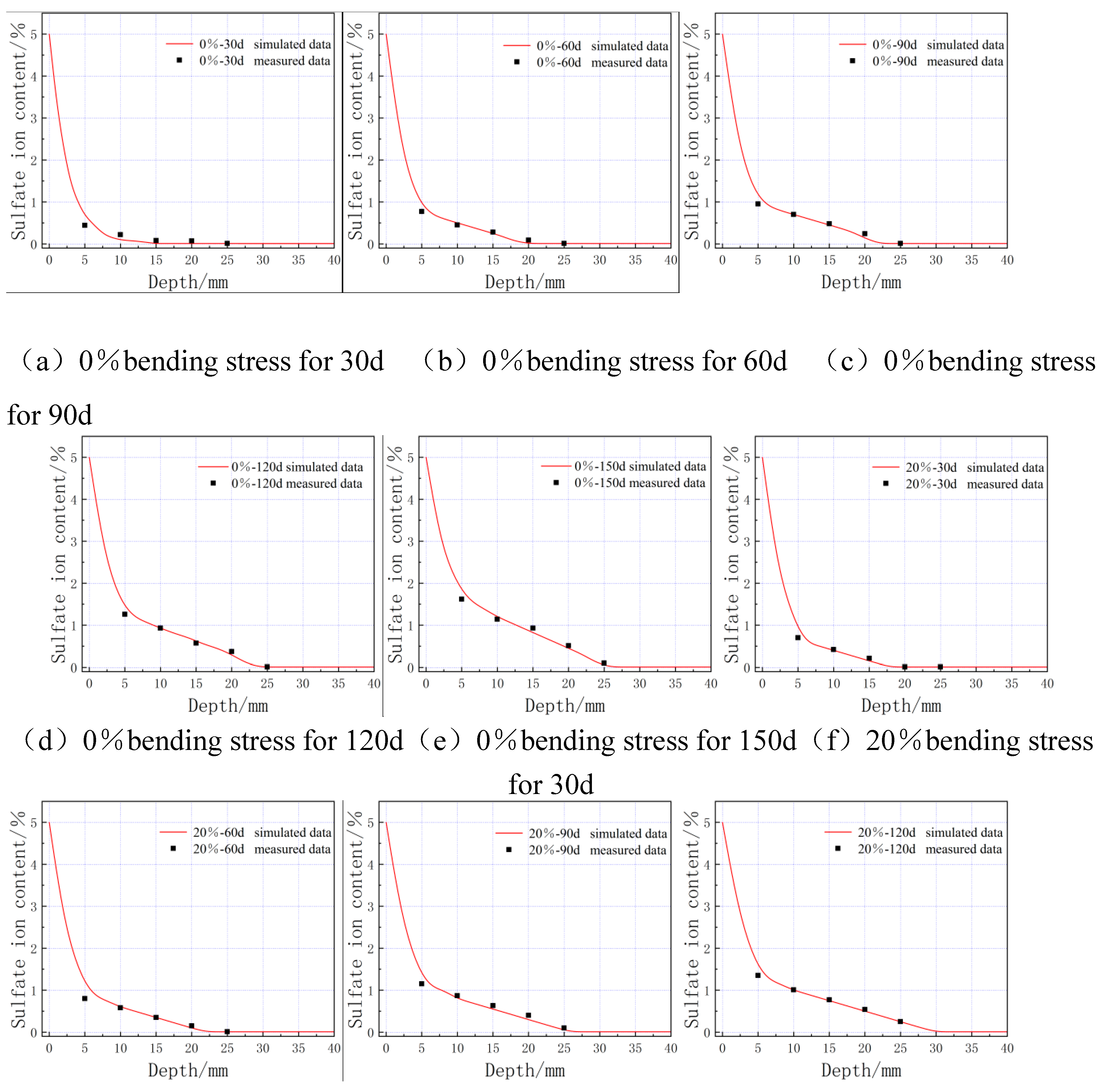
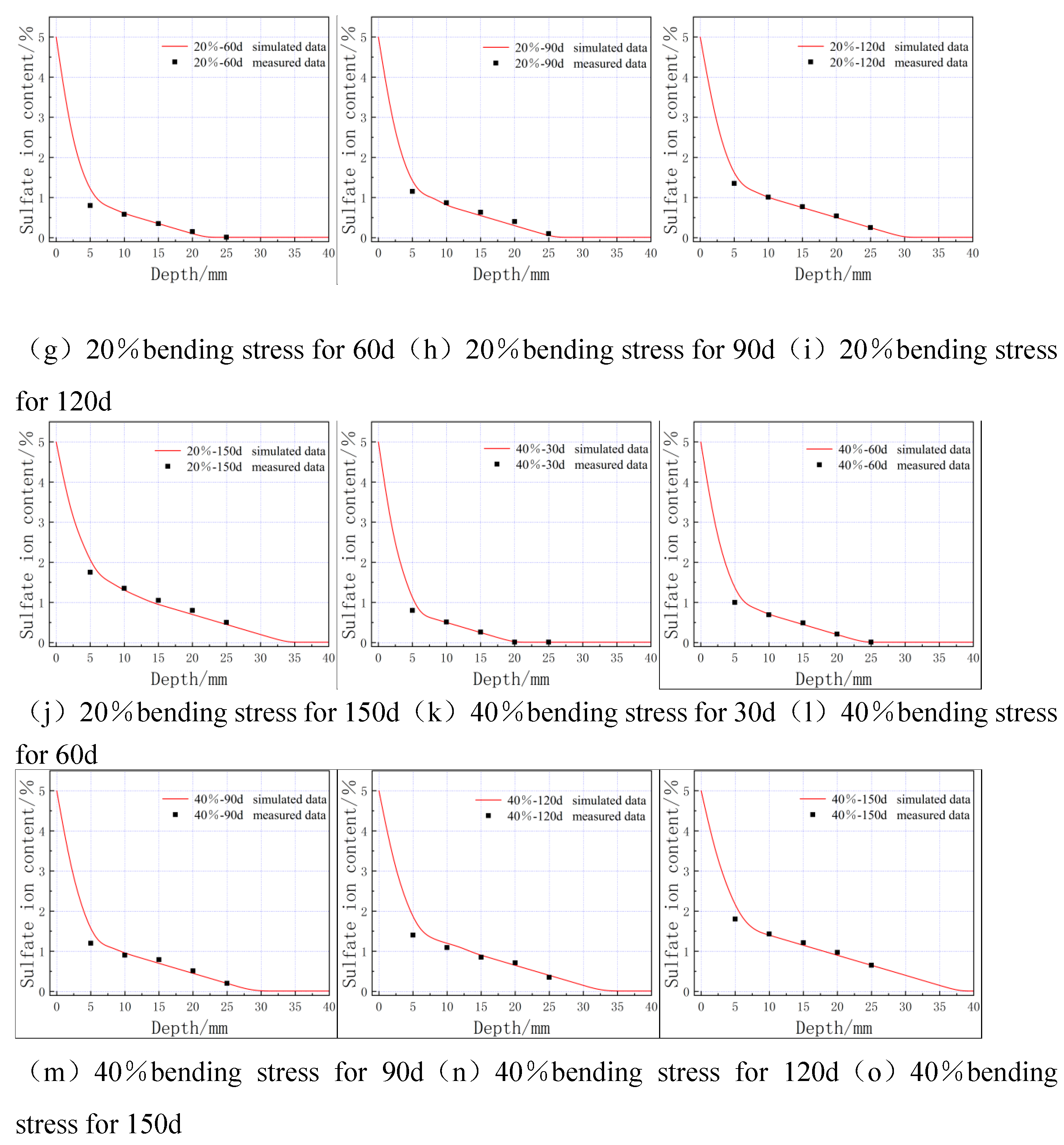
4.3. Numerical simulation results and analysis

The graph of sulphate ion concentration at different depths under different bending stresses is shown in Figure 13. The graph shows that the sulphate content in the interior of the cement rises with increasing age; the bending stress promotes the penetration of the sulphate into the interior of the cement. For the same depth of the cementitious material specimens ion concentration presents: 0% bending stress ion concentration
Figure 14 shows the simulated and measured results of sulfate ion concentration at different erosion ages and depths under different magnitudes of bending stresses (tested by EDTA complex titration method). It can be seen from the figure that there is only an error of about 5% at a depth of 5㎜, and that the measured results are basically in agreement with the simulated results.This is due to the fact that cementitious materials are porous media with more internal pores. The applied stress will change the internal pore structure and increase the microcracks. This leads to a certain error between the test results and simulation results. However, the error is within the controllable range, and the error between this test and the simulation is about 5%.

5. Conclusions

The following conclusions have been drawn from the study of cementitious materials and the effects of flexural loading and sulphate coupling on the properties of cementitious materials.
  • Sulfate erosion of cementitious materials is caused by sulfate ions entering cementitious materials by diffusion and other means, and then chemically reacting with hydrated calcium silicate, etc., in cement-based materials, swell products like plaster and calcium aluminate can form and cause rusting.
  • The compressive and flexural strength of the cementitious material increases with the age of sulphate erosion and then decreases, reaching a maximum value at 60 d. The flexural strength of the cementitious material decreases with increasing flexural stress, which to some extent promotes sulphate erosion.
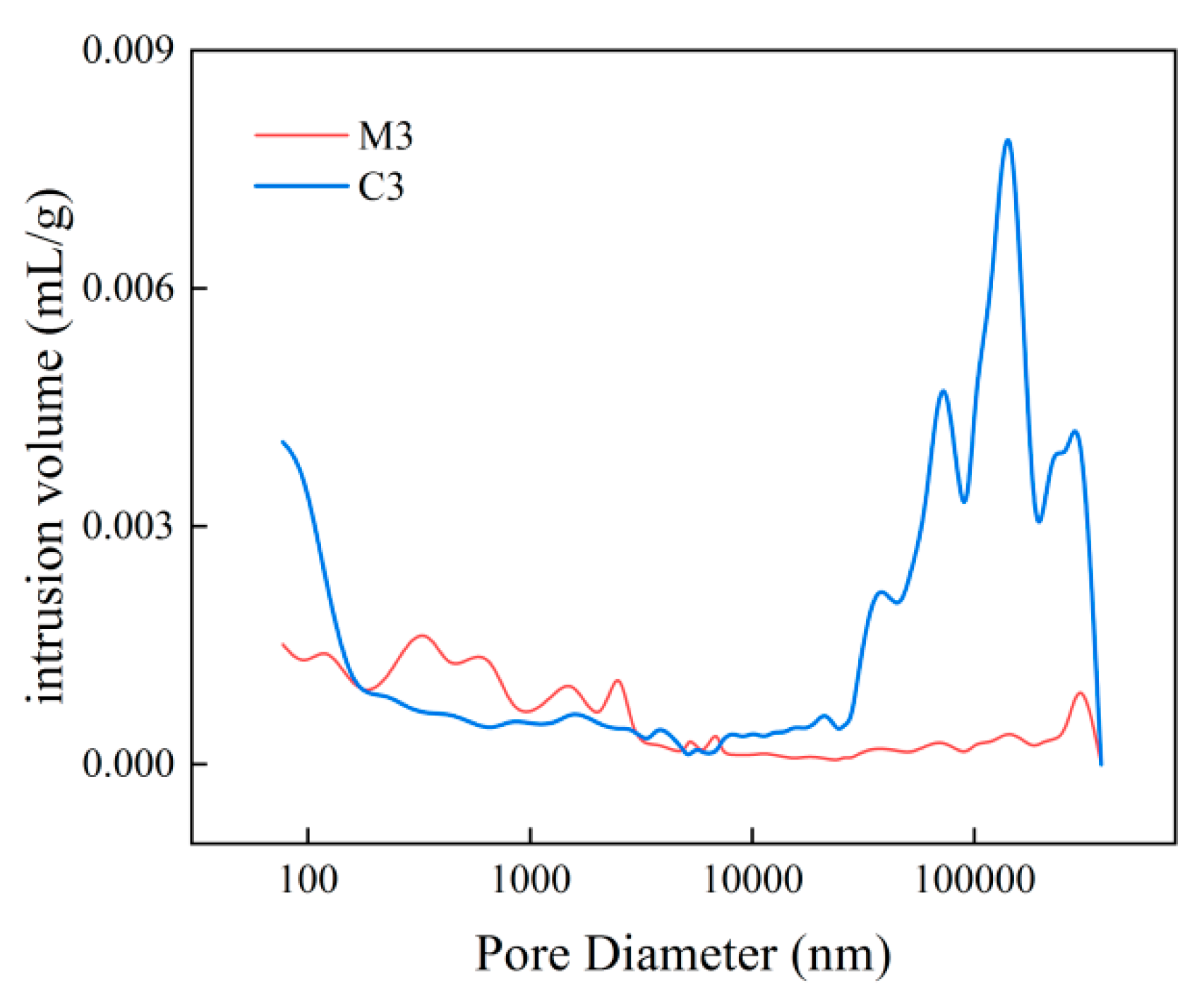
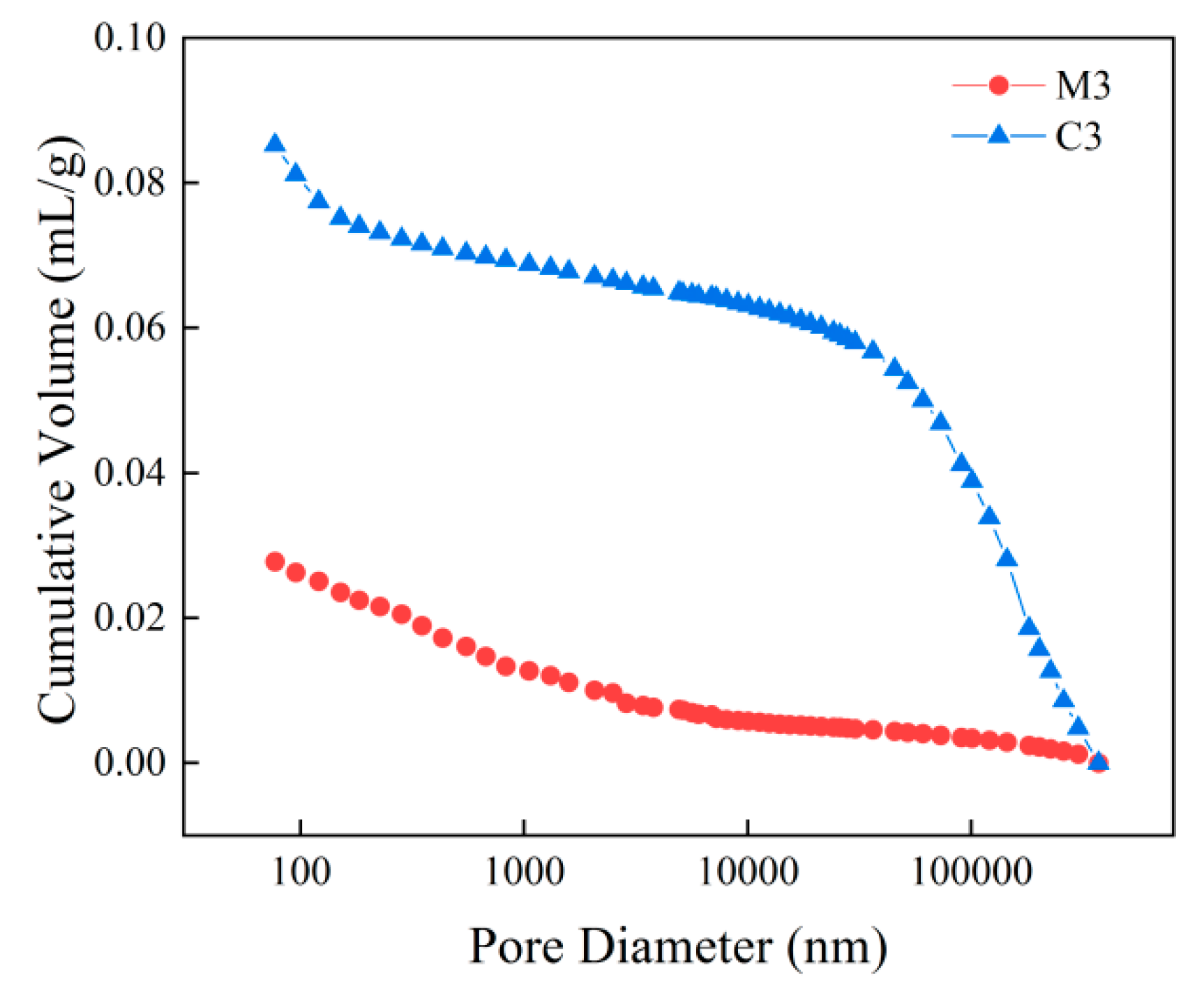
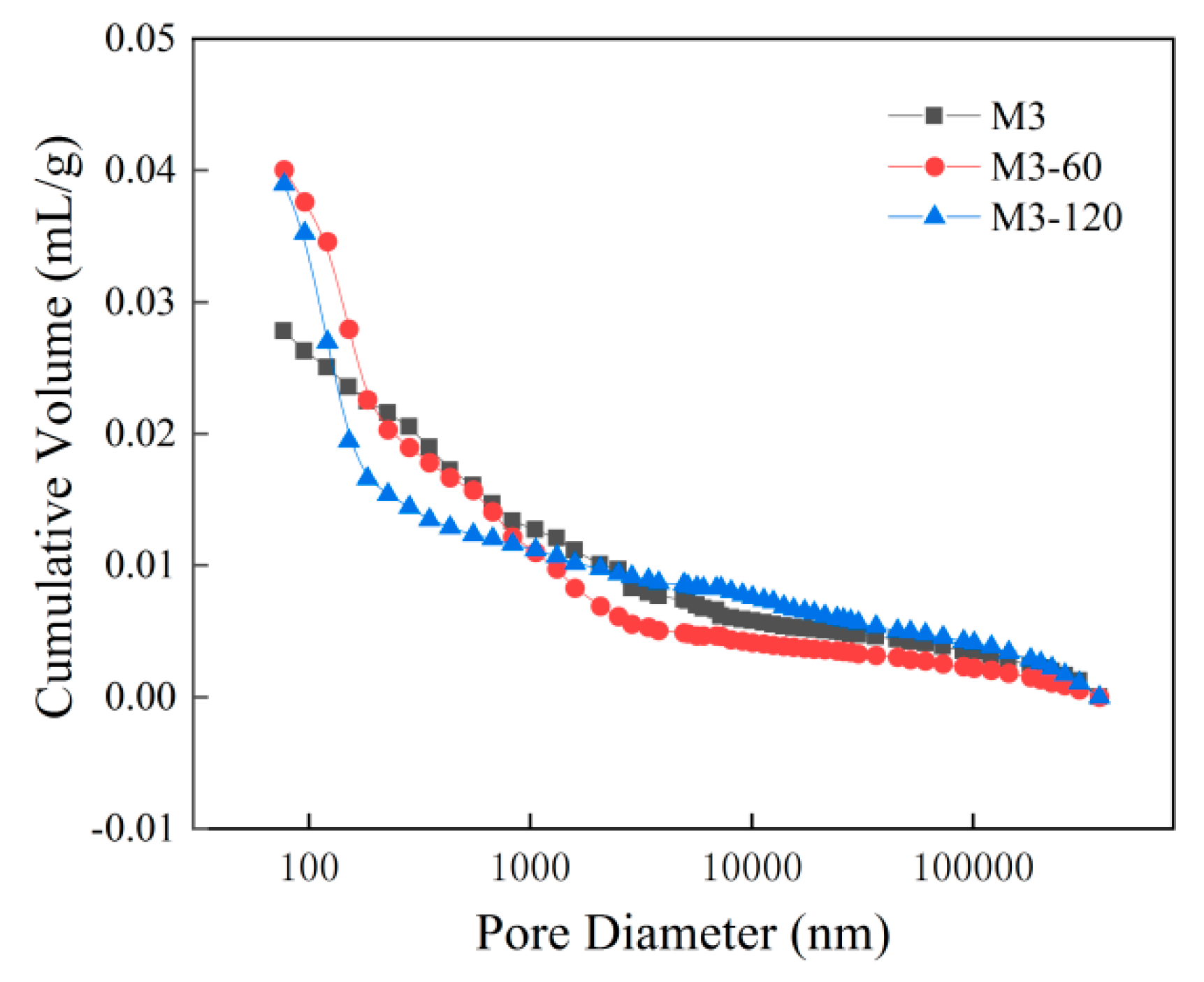
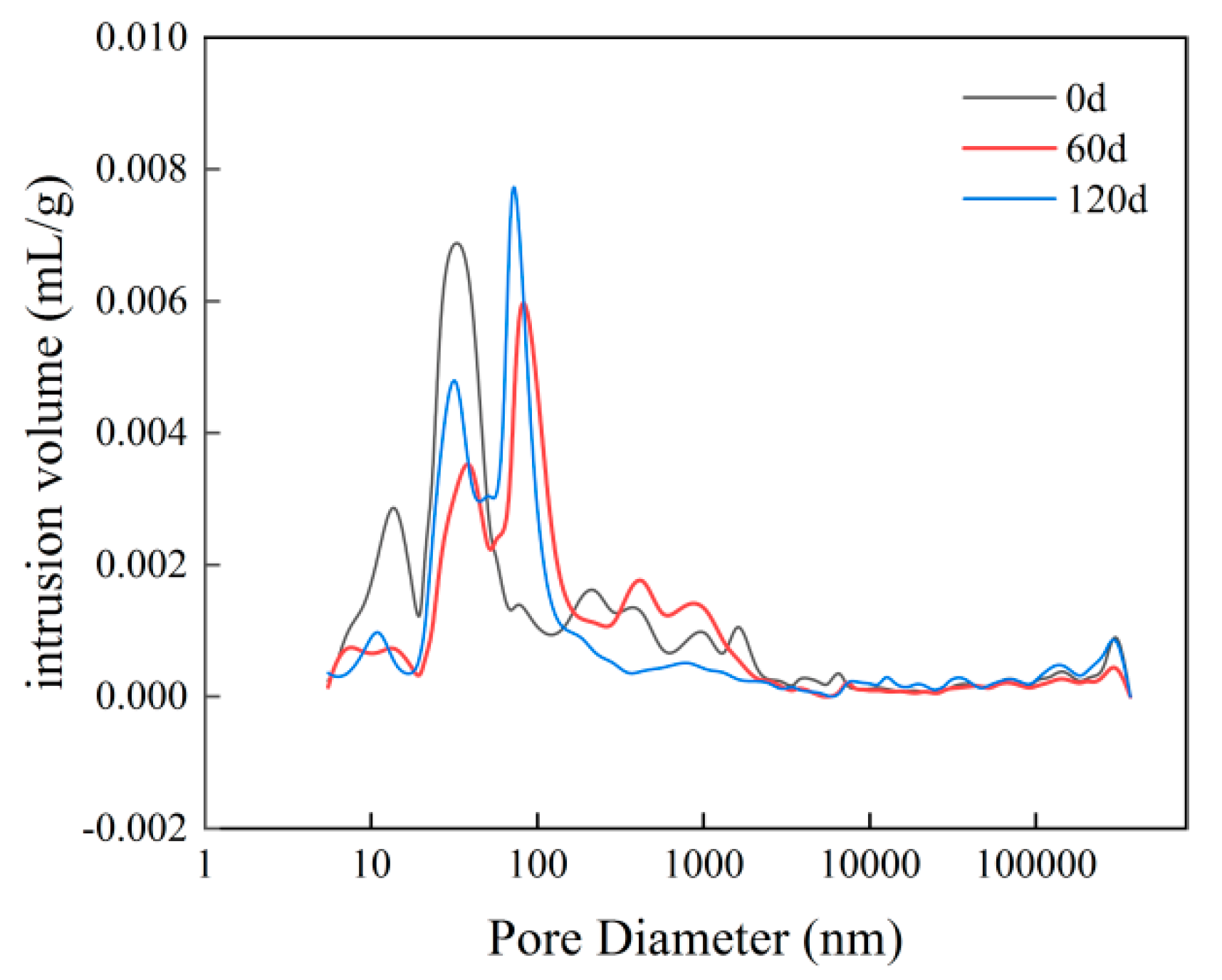
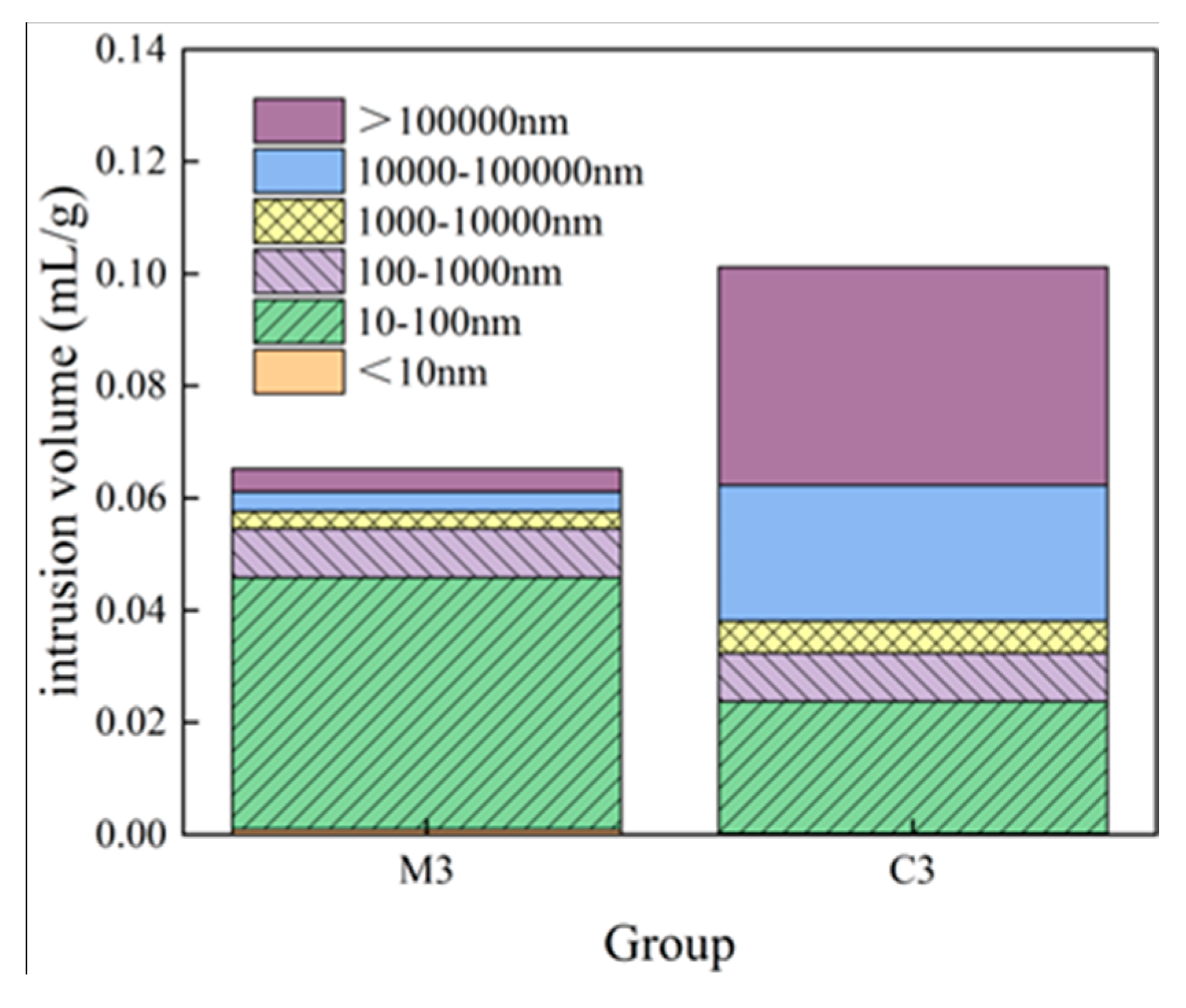
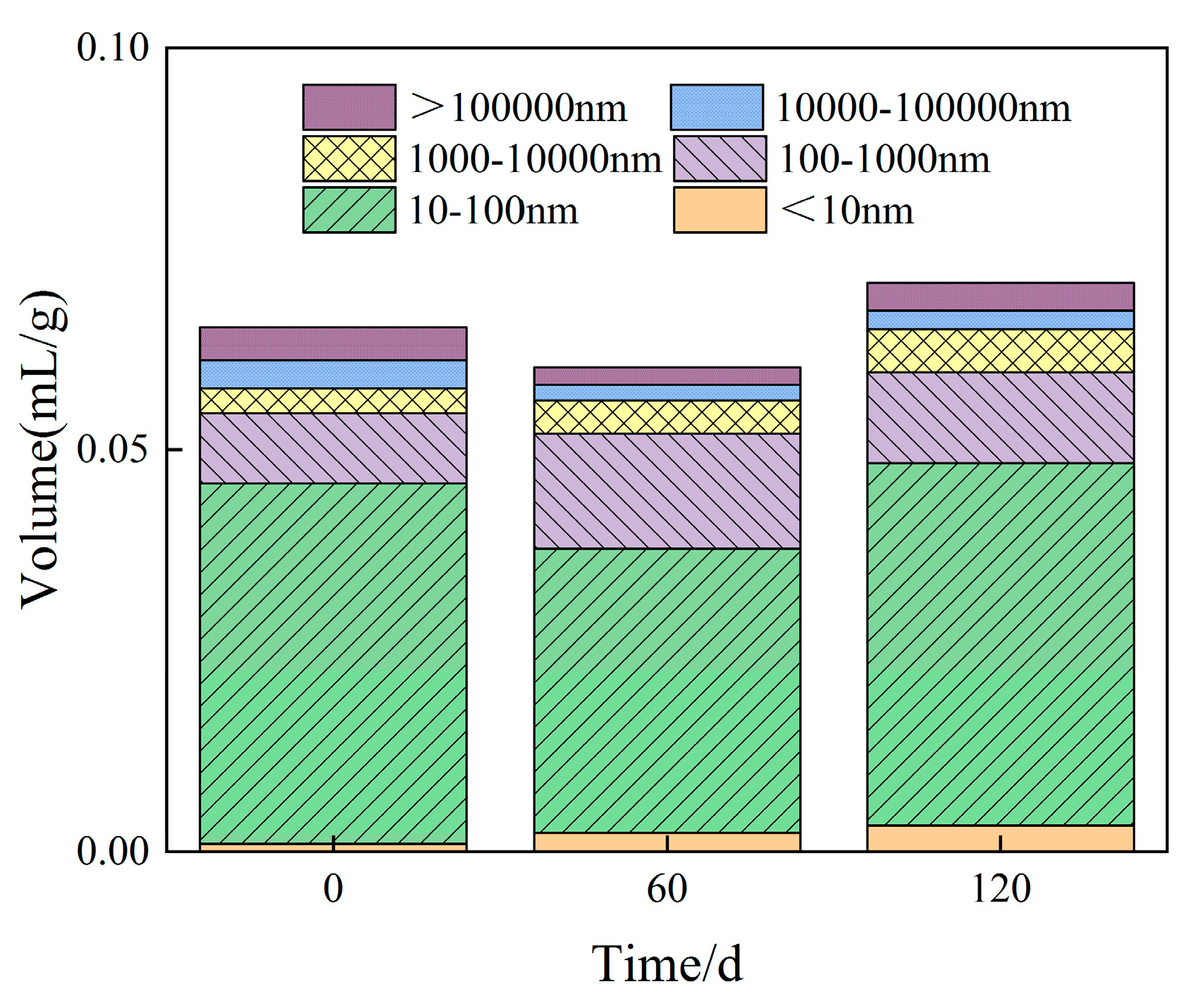
  • With increasing sulphate erosion age, the porosity of cementitious materials tends to decrease and then increase. With the incorporation of coarse aggregates, the porosity in cementitious materials increases, and the porosity of concrete is about 4-6 times that of mortar when the pore diameter is greater than 10,000 nm.
  • Through refinement of Fick's second law and chemical reaction kinetics, the diffusion coefficient of sulphate ions within the cementitious material was derived and a three-dimensional COMSOL finite element model was created. The simulation results were compared with the measured data to ensure the validity and accuracy of the theoretical model, which serves as a reference for the design of anti-erosion measures in the field of sulphate erosion.

Author Contributions

Yong Wen: Writing–review & editing, Conceptualization, Methodology, Supervision, Data curation, Project administration, Funding acquisition; Yuhang Li: Writing–original draft, Conceptualization, Methodology, Data curation, Software, Validation; Guoqi Han: Writing–review & editing, Supervision, Conceptualization, Formal analysis, Validation; Lang Liu: Writing–review & editing, Supervision, Project administration, Validation; Chao Zhang: Conceptualization, Software, Formal analysis; Yanyu Feng: Resources, Validation, Writing–review & editing.

Acknowledgments

This work was financially supported by the National Natural Science Foundation of China (52168036), the Research and Application of Key Technologies of Green and Low-Carbon Building Materials (2022B03035–2).

Conflicts of interest

The authors declare no conflict of interest.

References

  1. Lippiatt N, Ling T C, Pan S Y. Towards carbon-neutral construction materials: Carbonation of cement-based materials and the future perspective[J]. Journal of Building Engineering 2020, 28, 101062. [Google Scholar] [CrossRef]
  2. Ascensão F, Fahrig L, Clevenger A P, et al. Environmental challenges for the Belt and Road Initiative[J]. Nature Sustainability 2018, 1, 206–209. [Google Scholar] [CrossRef]
  3. Delong Xu, Yuansheng Cui, Hui Li, et al. On the future of Chinese cement industry [J]. Cement and Concrete Research 2015, 78, 2–13. [Google Scholar] [CrossRef]
  4. Zhao L, Guo X, Song L, et al. An intensive review on the role of graphene oxide in cement-based materials[J]. Construction and Building Materials 2020, 241, 117939. [Google Scholar] [CrossRef]
  5. Yang L, Fulin Y, Gaozhan Z. Synergistic effects of sustained loading and sulfate attack on the damage of UHPC based on lightweight aggregate[J]. Construction and Building Materials 2023, 374, 130929. [Google Scholar] [CrossRef]
  6. Yu D, Guan B, He R, et al. Sulfate attack of Portland cement concrete under dynamic flexural loading: A coupling function[J]. Construction and Building Materials 2016, 115, 478–485. [Google Scholar] [CrossRef]
  7. Yu D, Feng C, Fu T, et al. Effect of Sulfate Concentration on Chloride Diffusion of Concrete under Cyclic Load[J]. Materials 2022, 15, 2036. [Google Scholar] [CrossRef]
  8. Chen F , Gao J , Qi B , et al. Degradation progress of concrete subject to combined sulfate-chloride attack under drying-wetting cycles and flexural loading[J]. Construction & Building Materials 2017, 151, 164–171. [Google Scholar]
  9. Cheng H, Liu T, Zou D, et al. Compressive strength assessment of sulfate-attacked concrete by using sulfate ions distributions[J]. Construction and Building Materials 2021, 293, 123550. [Google Scholar] [CrossRef]
  10. Wang F , Zhang Y , Jiang J , et al. Effect of temperature on the capillary transport of sodium sulfate solution in calcium silicate hydrate nanopore: A molecular dynamics study[J]. Construction and Building Materials 2020, 231, 117111. [Google Scholar] [CrossRef]
  11. Qi B , Gao J , Chen F , et al. Evaluation of the damage process of recycled aggregate concrete under sulfate attack and wetting-drying cycles[J]. Construction and Building Materials 2017, 138, 254–262. [Google Scholar] [CrossRef]
  12. Ikumi T, Cavalaro S H P, Segura I. The role of porosity in external sulphate attack[J]. Cement and Concrete Composites 2019, 97, 1–12. [Google Scholar] [CrossRef]
  13. Wang K, Guo J, Yang L. Effect of dry–wet ratio on sulfate transport-reaction mechanism in concrete[J]. Construction and Building Materials 2021, 302, 124418. [Google Scholar] [CrossRef]
  14. Gao J, Yu Z, Song L, et al. Durability of concrete exposed to sulfate attack under flexural loading and drying–wetting cycles[J]. Construction and Building Materials 2013, 39, 33–38. [Google Scholar] [CrossRef]
  15. Liu F, You Z, Diab A, et al. External sulfate attack on concrete under combined effects of flexural fatigue loading and drying-wetting cycles[J]. Construction and Building Materials 2020, 249, 118224. [Google Scholar] [CrossRef]
  16. Zhang P, Ren S, Zhao Y, et al. Combined effects of sulfate attack under drying–wetting cycles and loading on the fatigue behavior of concrete[J]. Advances in Structural Engineering 2021, 24, 3825–3836. [Google Scholar] [CrossRef]
  17. He W. Numerical Simulation of the Ion Transport Behavior in Concrete under Coupled Axial Loading and Sulfate Attack[J]. Tehnički vjesnik Tehnički vjesnik, Tehnički vjesnik, 1791–1799. [Google Scholar]
  18. Zhang J, Sun M, Hou D, et al. External sulfate attack to reinforced concrete under drying-wetting cycles and loading condition: Numerical simulation and experimental validation by ultrasonic array method[J]. Construction and Building Materials 2017, 139, 365–373. [Google Scholar] [CrossRef]
  19. Zhuang Y, Liu X, Zhou X, et al. Diffusion model of sulfate ions in concrete based on pore change of cement mortar and its application in mesoscopic numerical simulation[J]. Structural Concrete 2022. [Google Scholar]
  20. GB/T 50082-2009, Standard for long-term performance and durability test methods for ordinary concrete[S]. （in Chinese）.
  21. Zhao Y, Gao J, Qi B, et al. Effect of flexural loading on degradation progress of recycled aggregate concrete subjected to sulfate attack and wetting-drying cycles[J]. J. Southeast Univ. Engl. Ed 2019, 35, 85–90. [Google Scholar]
  22. GB/T 50080-2002, Standard of Test Methods for Mechanical Properties of ordinary concrete [S]. （in Chinese）.
  23. Ma Y, Hu J, Ye G. The pore structure and permeability of alkali activated fly ash[J]. Fuel 2013, 104, 771–780. [Google Scholar] [CrossRef]
  24. Yin G J, Zuo X B, Tang Y J, et al. Numerical simulation on time-dependent mechanical behavior of concrete under coupled axial loading and sulfate attack[J]. Ocean Engineering 2017, 142, 115–124. [Google Scholar] [CrossRef]
  25. Li J, Xie F, Zhao G, et al. Experimental and numerical investigation of cast-in-situ concrete under external sulfate attack and drying-wetting cycles[J]. Construction and Building Materials 2020, 249, 118789. [Google Scholar] [CrossRef]
  26. POWERS T, C. Structure and physical properties of hardened Portland cement paste[J]. Journal of the american ceramic society 1958, 41, 1–6. [Google Scholar] [CrossRef]
  27. SUN Y, LIANG M, CHANG T. Time/depth dependent diffusion and chemical reaction model of chloride transportation in concrete[J]. Applied Mathematical Modelling 2012, 36, 1114–1122. [Google Scholar] [CrossRef]
  28. SARKAR S, MAHADEVAN S, MEEUSSEN J, et al. Numerical simulation of cementitious materials degradation under external sulfate attack[J]. Cement and Concrete Composites 2010, 32, 241–252. [Google Scholar] [CrossRef]
  29. ZUO X, SUN W, YU C. Numerical investigation on expansive volume strain in concrete subjected to sulfate attack[J]. Construction and Building Materials 2012, 36, 404–410. [Google Scholar] [CrossRef]
  30. MALTAIS Y, SAMSON E, MARCHAND J. Predicting the durability of Portland cement systems in aggressive environments—Laboratory validation[J]. Cement and concrete research 2004, 34, 1579–1589. [Google Scholar] [CrossRef]
  31. CAO C, CHEUNG M M, CHAN B Y. Modelling of interaction between corrosion-induced concrete cover crack and steel corrosion rate[J]. Corrosion Science 2013, 69, 97–100. [Google Scholar] [CrossRef]
  32. He R, Zheng S, Gan V J L, et al. Damage mechanism and interfacial transition zone characteristics of concrete under sulfate erosion and Dry-Wet cycles[J]. Construction and Building Materials 2020, 255, 119340. [Google Scholar] [CrossRef]
  33. JIN L, ZHANG R, DU X, et al. Multi-scale analytical theory of the diffusivity of concrete subjected to mechanical stress[J]. Construction and Building Materials 2015, 95, 171–185. [Google Scholar] [CrossRef]
Preprints 74414 g001
Figure 1. Bending stress loading device.
Figure 1. Bending stress loading device.
Preprints 74414 g001
Preprints 74414 g002
Figure 2. Mechanical properties of cement-based materials influenced by load and sulphate coupling.
Figure 2. Mechanical properties of cement-based materials influenced by load and sulphate coupling.
Preprints 74414 g002
Preprints 74414 g003
Figure 3. XRD images of M3 specimen at different erosion ages.
Figure 3. XRD images of M3 specimen at different erosion ages.
Preprints 74414 g003
Preprints 74414 g004aPreprints 74414 g004b
Figure 4. SEM images of M3 specimen at different erosion ages.
Figure 4. SEM images of M3 specimen at different erosion ages.
Preprints 74414 g004aPreprints 74414 g004b
Preprints 74414 g005
Figure 5. M3 and C3 incoming and outgoing tribute pressure variation.
Figure 5. M3 and C3 incoming and outgoing tribute pressure variation.
Preprints 74414 g005
Preprints 74414 g006
Figure 6. M3 and C3 pore size distribution curve.
Figure 6. M3 and C3 pore size distribution curve.
Preprints 74414 g006
Preprints 74414 g007
Figure 7. M3 and C3 cumulative tribute intake curve.
Figure 7. M3 and C3 cumulative tribute intake curve.
Preprints 74414 g007
Preprints 74414 g008
Figure 8. Cumulative feed curves for different erosion ages of M3.
Figure 8. Cumulative feed curves for different erosion ages of M3.
Preprints 74414 g008
Preprints 74414 g009
Figure 9. Pore size distribution curves for different erosion ages of M3.
Figure 9. Pore size distribution curves for different erosion ages of M3.
Preprints 74414 g009
Preprints 74414 g010
Figure 10. Pore change stacking diagram of M3 and C3.
Figure 10. Pore change stacking diagram of M3 and C3.
Preprints 74414 g010
Preprints 74414 g011
Figure 11. Pore change stacking diagram of M3 after sulfate erosion degradation.
Figure 11. Pore change stacking diagram of M3 after sulfate erosion degradation.
Preprints 74414 g011
Preprints 74414 g012
Figure 12. Numerical simulation diagram.
Figure 12. Numerical simulation diagram.
Preprints 74414 g012
Preprints 74414 g013
Figure 13. Numerical simulation of sulfate ion concentration.
Figure 13. Numerical simulation of sulfate ion concentration.
Preprints 74414 g013
Preprints 74414 g014
Figure 14. Sulfate ion concentrations at different depths under different bending stresses.
Figure 14. Sulfate ion concentrations at different depths under different bending stresses.
Preprints 74414 g014
Preprints 74414 g015aPreprints 74414 g015b
Figure 15. Graph of sulfate ion concentration of M3 specimen at different depths under different bending stresses for different erosion ages.
Figure 15. Graph of sulfate ion concentration of M3 specimen at different depths under different bending stresses for different erosion ages.
Preprints 74414 g015aPreprints 74414 g015b
Table 1. Chemical composition of cement from XRF (X-ray fluorescence) test.
Table 1. Chemical composition of cement from XRF (X-ray fluorescence) test.
Ingredient. SiO2 Al2O3 Fe2O3 CaO MgO SO3 K2O Na2O LiO
Cement(mass fraction, %） 20.12 5.75 3.26 63.44 0.98 2.71 0.49 0.73 2.13
Table 2. Mixture ratios.
Table 2. Mixture ratios.
Scheme W/C Amount of each material in concrete (kg·m-3)
Water Cement Sand Gravel Superplasticizer
M1 0.60 242.3 403.8 872.3 0 1.00
M2 0.50 262.0 523.0 1413.0 0 1.00
M3 0.35 219.4 626.8 1253.7 0 3.10
C1 0.60 218.2 363.6 1090.8 727.2 0.91
C2 0.50 210.0 386.0 1044.0 774.0 0.96
C3 0.35 173.0 494.0 741.0 988.0 2.40
Table 3. Aperture characteristics parameters.
Table 3. Aperture characteristics parameters.
Specimen Porosity/％ Average pore diameter/nm ＜10nm 10nm~100nm 100nm~1000nm 1000nm~10000nm 10000nm~1000000nm ＞1000000nm
M3-0 13.58 58.87 1.48％ 68.41％ 13.4％ 4.76％ 5.33％ 6.62％
M3-60 12.57 55.26 3.78％ 58.75％ 23.73％ 6.87％ 3.2％ 3.67％
M3-120 14.17 36.09 4.52％ 63.77％ 15.97％ 7.57％ 3.3％ 4.87％
C3 20.06 177.56 0.19％ 23.27％ 8.53％ 5.62％ 23.96％ 38.44％
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated