Coordinated Obstacle Avoidance of Multi-AUV Based on Improved Artificial Potential Field Method and Consistency Protocol

Preprint

Article

Coordinated Obstacle Avoidance of Multi-AUV Based on Improved Artificial Potential Field Method and Consistency Protocol

Altmetrics

Downloads

103

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

23 May 2023

Posted:

24 May 2023

You are already at the latest version

Alerts

Abstract

Formation avoidance is one of the critical technologies for autonomous underwater vehicle (AUV) formations. To this end, a cooperative obstacle avoidance algorithm based on an improved artificial potential field and a consistency protocol is proposed in this paper. A cooperative obstacle avoidance algorithm based on the improved artificial potential field method and consistency protocol is proposed for the local obstacle avoidance problem of AUV formation. Firstly, for the disadvantage that the traditional artificial potential field method is easy to fall into local minima, an auxiliary potential field perpendicular to the AUV moving direction is designed to solve the problem that AUVs are easy to have zero combined force in the potential field and local minima. Secondly, the control law of AUV formation that keeps the speed and position consistent is designed for the problem that the formation will change during the local obstacle avoidance of the formation system. The control conflict problem of the combined algorithm of the artificial potential field law and the consistency protocol is solved by adjusting the desired formation of the consistency protocol through the potential field force. Finally, the bounded energy function demonstrates system convergence's stability. The simulation verification confirmed that the AUV formation could achieve the convergence of the formation state under local obstacle avoidance.

Keywords:

Subject: Engineering - Marine Engineering

1. Introduction

Autonomous Underwater Vehicle (AUV) has recently become a new marine development tool for marine resource exploitation and environmental exploration operations [1]. It has the advantages of autonomy, independence, a tiny target, and high applicability. However, it is difficult for a single underwater autonomous vehicle to meet the increasing mission requirements in the complex and broad ocean environment. Single unmanned underwater autonomous vehicles have limited energy load, small range, low task performance efficiency, and instability. With the Multi Autonomous Underwater Vehicles (MAUVs) system [2] coming into operation, the mutual coordination between single AUVs [3] more rationally compensates for the shortcomings of single AUVs.

In recent years, many researchers have investigated formation avoidance algorithms in complex environments [4]. Obstacle avoidance can be divided into path planning for global obstacle avoidance and path planning for local obstacle avoidance. If the global environment information is known, international path planning can be seen as a nonlinear optimization problem to find the optimal solution for global variables. Many scholars have proposed many standard global path-planning algorithms at home and abroad. For example, the A* algorithm（Dechter, R and Pearl，1985）[5], the genetic algorithm（Cobb and Grefenstette, 1993）[6], fast extended random tree (Cui, RX and Li, Y, 2016)[7], particle swarm algorithm （Eberhart and Kennedy，1995）[8], ant colony algorithm [9] and so on. And the local obstacle avoidance aspects are more applied such as the artificial potential field method [10], fuzzy decision making (Smith, SM and Ganesan, K, 1998)[11], neural network[12] and reinforcement learning methods[13], etc.

Due to the rapid change of the ocean environment and many uncertainties, although global path planning can plan a better path, the path cannot be used as the actual reference path of the AUV. Cheng, Chun Lei et al. [14] considered the ocean current’s force. They synthesized the current’s velocity with the AUV’s velocity, combined with the artificial potential field method to overcome the influence of the ocean current on path planning. Song [15] proposed an improved artificial potential field method by improving the parameters such as angle limit to solve the problem that the artificial potential field algorithm can easily fall into particular terrain and improve the algorithm’s stability. Zhao, ZY [16] proposed a hybrid adaptive preference method based on the improved artificial potential field (HAP-IAPF). Adaptive weight control units are used to adjust the preference strategy. Cooperative multi-AUV hunting in dynamic underwater obstacle environments is achieved under weakly connected conditions. Wang SM et al. [17] combined the H-infinity controller with the artificial potential field method (APFM) for the subsea navigation of autonomous underwater vehicles (AUVs). Depth control and altitude control prevent AUVs from colliding with the seafloor or obstacles, and simulations and laboratory tests of various seafloor profiles show that the combination of the H infinity controller and APFM is feasible and effective. Zhen, QZ [18] confronted with the attitude adjustment problem in AUV deployment and the detection of seafloor topographic undulations, proposed a finite-time position and attitude tracking control method combining artificial potential fields and virtual structures. This control method ensures that the AUVs avoid colliding with each other during the dive and form and change formations after reaching a set depth. Orozco-Rosas et al.[19] proposed a membrane-evolutionary artificial potential field method for solving the path planning problem of mobile robots, which combines membrane computation with genetic algorithms (membrane-inspired evolutionary algorithms with a first-class membrane structure) and artificial potential field methods to find the parameters that generate feasible and safe paths.

The rest of this paper is organised as follows. Section 2 gives the AUV dynamic and kinetics model and the problem description. Section 3 presents the improved artificial potential field method and the consistency protocol. The flow and stability proof of the cooperative obstacle avoidance algorithm are given in Section 4. Subsequently, the simulation experiments are given in Section 5. Finally, the conclusions are obtained in Section 6.

2. Problem Statement and Model Description

2.1. Problem Description

In unknown underwater environments, AUVs may encounter complex terrains such as reefs, islands, trenches and valleys, and the obstacles they encounter vary in shape, complexity and number. To ensure the AUV’s safety and the mission’s successful completion, the AUV must be capable of avoiding these complex obstacles [20].

1. Movement limitation: In the actual motion state, AUVs are limited by the performance of their equipment and so on. Therefore, it is necessary to consider the impact of the actual model of AUV in the motion limitation function on the track planning during the AUV navigation.

2. Obstacle types: When AUVs perform missions in unknown underwater environments, they will encounter multiple obstacle types. In this paper, the threat values of each point of the obstacles to AUVs are represented uniformly for modelling the probabilistic threat environment. Grouping different types of obstacles under the same map is helpful in improving the speed and stability of the algorithm.

2.2. AUV Movement Model

Based on the characteristics of AUVs, the dynamics and dynamics of AUVs are usually modelled by a six-degree-of-freedom (DOF) model. However, since the AUV needs an actuator for roll control, the roll motion is usually not considered. In the inertial coordinate system and its own fixed coordinate system. According to (Fossen, 2011), the kinematic and dynamical model of the AUV kinematic and dynamical model of the AUV can be represented by five degrees of freedom as follows [22].

\{\begin{cases} \dot{η} = R (ψ) v \\ M \dot{v} + C (v) v + D (v) v + g (η) = T \end{cases}

(1)

where,

η = {[x, y, z, θ, ψ]}^{T}, v = {[u, v, w, q, r]}^{T}

R (ψ)

is the rotational transformation matrix from the body-fixed coordinate frame to the inertial coordinate frame

M

is the inertia matrix,

C (v)

is the hydrodynamic Coriolis and centripetal force matrix,

D (v)

is the nonlinear fluid hydrodynamic damping matrix,

g (η)

is the restoring force (moment) vector, and

T

is the external force and external moment vector applied to the vehicle.

The navigator system itself is strongly coupled and vulnerable to the influence of external waves and currents. The nonlinear characteristics of the navigator cause some difficulties in engineering processing, so this paper linearizes the model of the navigator with feedback.

First, the AUV dynamics can be expressed as a general nonlinear system.

\begin{array}{l} \dot{x} (t) = f (x (t)) + g (x (t)) u (t) \\ y (t) = h (x (t)) \end{array}

(2)

where

x \in ℝ^{m}

is the system state vector,

u \in ℝ^{p}

is the system control input vector, and

y \in ℝ^{q}

is the system output vector.

f (x)

g (x)

and

h (x)

are the corresponding vector coefficients.

Define the matrix

M_{c}

and Damping matrix

M_{x}

M_{c} = [\begin{matrix} m - \frac{1}{2} ρ L^{3} X_{\dot{u}}^{'} & 0 & 0 & 0 & 0 \\ 0 & m - \frac{1}{2} ρ L^{3} Y_{\dot{v}}^{'} & 0 & 0 & - \frac{1}{2} ρ L^{4} Y_{\dot{r}}^{'} \\ 0 & 0 & m - \frac{1}{2} ρ L^{3} Z_{\dot{w}}^{'} & - \frac{1}{2} ρ L^{4} Z_{\dot{q}}^{'} & 0 \\ 0 & 0 & - \frac{1}{2} ρ L^{4} M_{\dot{w}}^{'} & I_{y} - \frac{1}{2} ρ L^{5} M_{\dot{q}}^{'} & 0 \\ 0 & - \frac{1}{2} ρ L^{4} N_{\dot{v}}^{'} & 0 & 0 & I_{z} - \frac{1}{2} ρ L^{5} N_{\dot{r}}^{'} \end{matrix}]

(3)

M_{x} = [\begin{matrix} I & 0 \\ 0 & M_{c} \end{matrix}]

(4)

M_{x}

must be a non-singular matrix and the system function

f (x)

and

g (x)

can be expressed as:

\{\begin{cases} f (x) = M_{x}^{- 1} f^{'} (x) \\ g (x) = M_{x}^{- 1} g^{'} (x) \end{cases}

(5)

Define the output equation of the system:

h (x) = {[\begin{array}{l} x & y & z & θ & ψ \end{array}]}^{T}

(6)

Based on the nonlinear model of AUV and the principle of feedback linearization, the feedback control rate and the set of coordinate transformations are found to obtain the feedback linearization model of the unmanned aerial vehicle.

The system function vector

f (x)

h (x)

g (x)

can be obtained from the previous presentation.

f (x) = M_{x}^{- 1} f^{'} (x) = [\begin{matrix} I & 0 \\ 0 & M_{c}^{- 1} \end{matrix}] [\begin{matrix} R (η) v \\ N (η, v) \end{matrix}]

(7)

h (x) = {[h_{1} (x), h_{2} (x), h_{3} (x), h_{4} (x), h_{5} (x)]}^{T} = {[x, y, z, θ, ψ]}^{T}

(8)

g (x) = [g_{1} (x), g_{2} (x), \dots, g_{5} (x)] = [\begin{matrix} 0 \\ M^{- 1} g^{'} (x) \end{matrix}]

(9)

where, 0 is a

5 \times 5

zero matrix.

Based on the Lee derivative [23] and the definition of

g (x)

, for any

1 \leq i \leq 10

1 \leq j \leq 10

, it follows that:

L_{g_{i}} h_{j} (x) = 0

(10)

By calculating the above equation we can obtain the matrix

Γ (x) = [Γ_{i j} (x)]

Γ_{i j} (x) = L_{g_{j}} L_{f} h_{i} (x)

1 \leq i \leq p, 1 \leq j \leq p

Γ (x) = [\begin{matrix} {\tilde{g}}_{11} \cos ψ \cos θ & - {\tilde{g}}_{22} \sin ψ & {\tilde{g}}_{33} \cos ψ \sin θ & {\tilde{g}}_{34} \cos ψ \sin θ & - {\tilde{g}}_{25} \sin ψ \\ {\tilde{g}}_{11} \sin ψ \cos θ & {\tilde{g}}_{22} \cos ψ & {\tilde{g}}_{33} \sin ψ \sin θ & {\tilde{g}}_{34} \sin ψ \sin θ & {\tilde{g}}_{25} \cos ψ \\ - {\tilde{g}}_{11} \sin θ & 0 & {\tilde{g}}_{33} \cos θ & {\tilde{g}}_{34} \cos θ & 0 \\ 0 & 0 & {\tilde{g}}_{43} & {\tilde{g}}_{44} & 0 \\ 0 & \frac{{\tilde{g}}_{52}}{\cos θ} & 0 & 0 & \frac{{\tilde{g}}_{55}}{\cos θ} \end{matrix}]

(11)

where matrix

Γ (x)

a is a non-singular matrix, and

ρ_{1} + ρ_{2} + ρ_{3} + ρ_{4} + ρ_{5} = 10

. The relative order is the same as the system order, i.e., the nonlinear model of the navigator can be linearized by feedback. By transforming

z = φ (x)

by coordinates, it follows that:

\begin{array}{l} z_{1} = {[\begin{array}{l} h_{1} (x) & h_{2} (x) & h_{3} (x) & h_{4} (x) & h_{5} (x) \end{array}]}^{T} \\ z_{2} = {[\begin{array}{l} L_{f} h_{1} (x) & L_{f} h_{2} (x) & L_{f} h_{3} (x) & L_{f} h_{4} (x) & L_{f} h_{5} (x) \end{array}]}^{T} \end{array}

(12)

Based on the definition of the Lee derivative:

\begin{array}{l} {\dot{z}}_{1} = z_{2} \\ {\dot{z}}_{2} = L_{f}^{2} h (x) + L_{g} L_{f} h (x) u \end{array}

(13)

Control inputs in the new coordinate system:

\tilde{u} = B (x) + Γ (x) u = L_{f}^{2} h (x) + L_{g} L_{f} h (x) u

(14)

In the presence of a transformed coordinate system and feedback control inputs:

u = Γ^{- 1} (x) (u - B (x))

(15)

The model feedback linearization of the navigator can be expressed as:

\begin{array}{l} {\dot{z}}_{1}^{i} = z_{2}^{i} \\ {\dot{z}}_{2}^{l} = u_{i} \end{array}

(16)

where,

{\dot{z}}_{1}^{i} \in ℝ^{5}

z_{2}^{i} \in ℝ^{5}

u_{i} \in ℝ^{5}

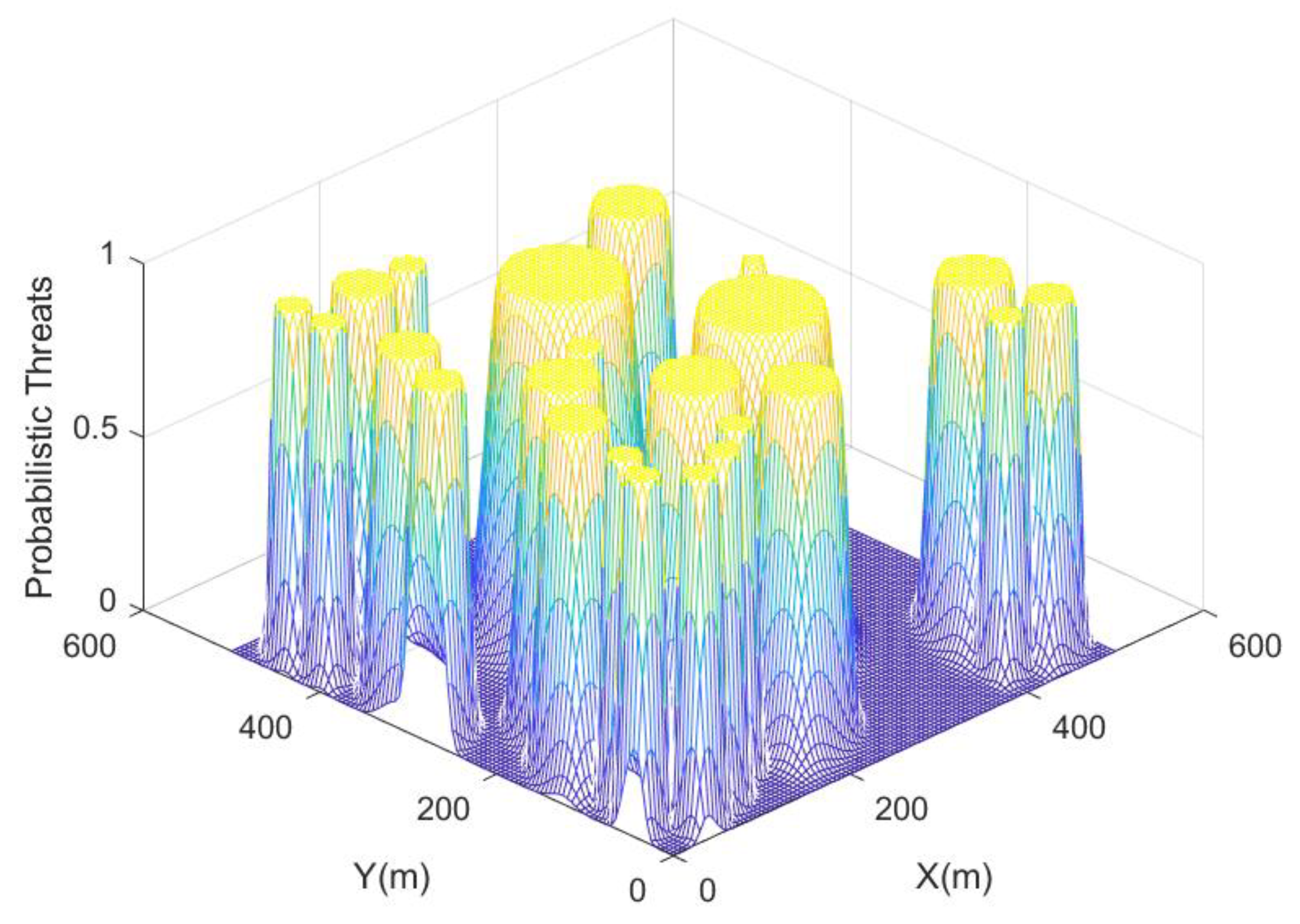
2.3. Probabilistic Threat Environment Map

To represent the threats to AUVs in complex subsea environments, probabilistic threat environment maps are defined in this paper to model them. The probabilistic threat map is a function of location and describes the threat probability of the threat sources at different locations to which the AUV is exposed [24]. It is an environment that shows the distribution of threats in the environment in a probabilistic form. Each location coordinate corresponds to a probability density value as an indication of the risk of AUV exposure to a threat source at that coordinate point.

Suppose there are

m

suspicious locations in the region, the threat probability for any location

r

in the region can be expressed as a multidimensional Gaussian probability function:

t h r e a t (r) = \sum_{i = 1}^{m} \frac{1}{2 π} \exp [- \frac{1}{2} {(r - r_{i})}^{T} K_{i} (r - r_{i})]

(17)

Since this paper conducts the study of local obstacle avoidance problem of AUV formation, only local threat environment modeling is performed when designing the environment.

Figure 1. Probabilistic Threat Environment Map.

3. Improvement of artificial potential field method

3.1. Auxiliary potential field repulsion field design for obstacles

The artificial potential field method is widely used in the scenario of local obstacle avoidance, which has the advantages of good real-time and does not rely on global information [25]. But it is prone to disadvantages such as zero combined force falling into local minima and overlapping potential fields of neighboring obstacles that prevent the optimal path from being obtained. In the actual AUV control process, it also generates insufficient time to complete the obstacle avoidance operation command due to the longitudinal speed of the AUV. Based on the shortcomings of the traditional artificial potential field method, this chapter introduces an obstacle-assisted potential field on the traditional artificial potential field method to avoid falling into local minima due to zero combined forces.

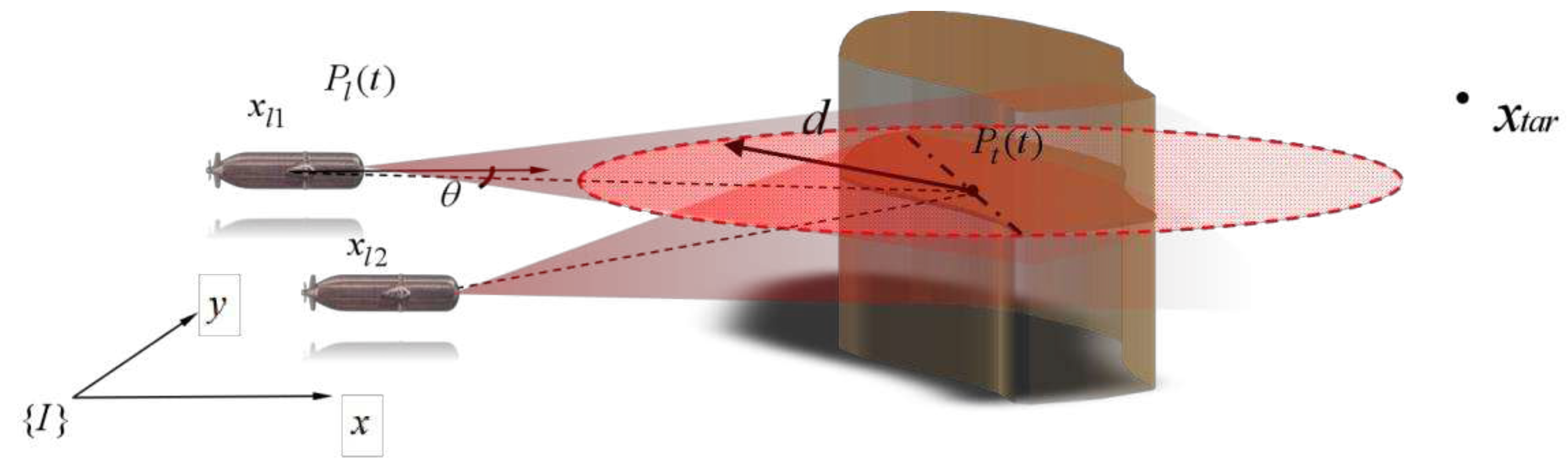
Figure 2. AUV formation obstacle recognition.

Suppose

p_{t} (t) = (x (t), y (t), z (t))

is an obstacle reference point in the same plane as the AUV.

x_{t a r} (x_{t a r}, y_{t a r}, z_{t a r})

is the coordinate of the target point. The target point and the obstacle reference point exert gravitational force

F_{t} (t)

and repulsive force

F_{o} (t)

on the AUV, respectively. The repulsive force generated between the other internal AUVs is

F_{i n} (t)

. The current AUV position A is denoted as

p_{l} (t) = [x_{l} (t), y_{l} (t), z_{l} (t)]

In the probabilistic threat environment, the probabilistic threat value of the obstacle also affects the potential energy function of the AUV. The potential energy function varies with the transformation of the probabilistic threat value at the current location. Suppose the distance vector between the AUV and the boundary barrier reference point is

△ l = p_{l} (t) - p_{t} (t)

. With a time-varying distance vector, the potential energy function at the current position of AUV at time can be expressed as:

U = t h r e a t (r) = \sum_{i = 1}^{m} \frac{1}{2 π} \exp [- \frac{1}{2} {(r_{i})}^{T} K_{i} (r_{i})]

(18)

Potential energy function with reference to the barrier point.

U_{r e q} (p_{t} (t)) = \{\begin{matrix} γ^{2} \exp \{- \frac{1}{2} {(p_{l} (t) - p_{t} (t))}^{T} K_{i} (p_{l} (t) - p_{t} {(t)}_{i})\} & △ l \leq d \\ 0 & △ l > d \end{matrix}

(19)

where

γ

denotes the potential energy function coefficient,

K_{i}

is the diagonal matrix indicating the threat intensity at the obstacle reference point, and

d

is the radius of the potential field action.

The potential energy function based on the reference barrier point yields the gradient function:

\nabla U_{r e q 1} (p_{l} (t)) = \{\begin{matrix} [\begin{matrix} \frac{\partial U_{r e q} (p_{l} (t))}{\partial △ x} & \frac{\partial U_{r e q} (p_{l} (t))}{\partial △ y} \end{matrix}] & △ l \leq d \\ 0 & △ l > d \end{matrix}

(20)

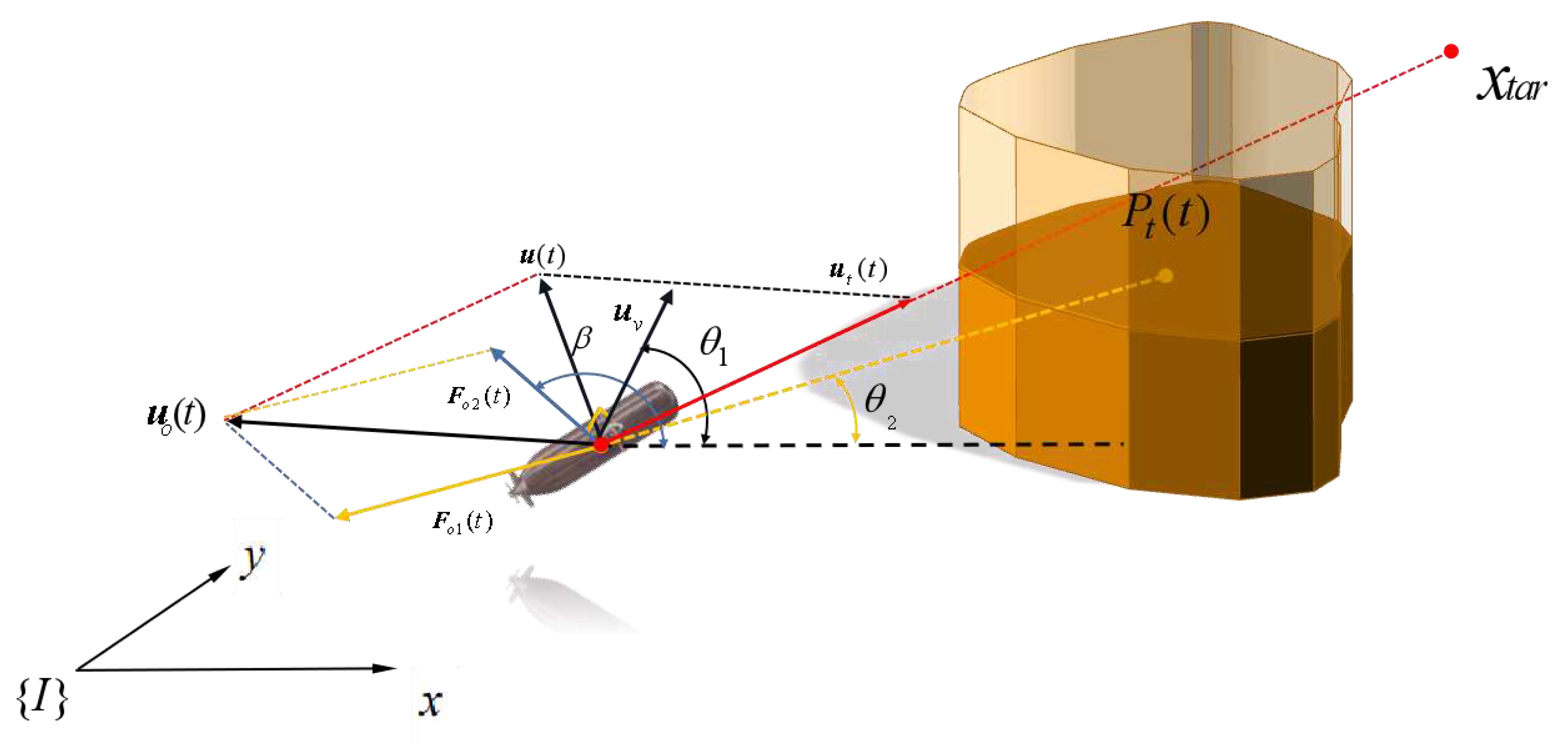
In order to avoid the AUV from falling into a local optimal solution, the artificial potential field method is improved here by constructing an obstacle-assisted potential field [26]. As shown in Figure 3: the direction of the potential field force of the auxiliary obstacle is perpendicular to the direction of travel of the AUV. The angle formed with the AUV is

θ_{1}

Obstacle-assisted potential energy function

U_{r e q 2} (p_{t} (t))

is designed as:

U_{r e q 2} (p_{t} (t)) = \frac{1}{2} g_{v} {(1 + v)}^{2} R_{r e q 2}^{v} (β)

(21)

where,

g_{v} = k_{o}^{2} (1 + r_{n})

is the random adjustment gain of the auxiliary potential field function.

k_{o}^{2}

is the gain adjustment factor.

0 \leq r_{n} \leq 1

r_{n}

indicates a random number between 0 and 1.

R_{r e q 2}^{v} (β) = {[\begin{matrix} R_{1} & R_{2} \end{matrix}]}^{T}

is expressed as the potential field transformation angle matrix. where,

R_{1} = {[\begin{matrix} \cos (β) & \sin (β) \end{matrix}]}^{T}

R_{2} = {[- \sin \begin{matrix} (β) & \cos (β) \end{matrix}]}^{T}

β

indicates the rotation angle, which is related to the speed of the AUV itself and the relative angle of the obstacle. As shown in Figure 3, at this point

0 < θ_{1} - θ_{2} < π / 2

. The direction of the potential field force is

π / 2

clockwise rotation of the current bow of AUV in the direction of velocity.

β = \{\begin{matrix} θ_{1} + π / 2 & 0 < θ_{1} - θ_{2} \leq π / 2 \\ θ_{1} - π / 2 & - π / 2 < θ_{1} - θ_{2} \leq 0 \\ 0 & else \end{matrix}

(22)

The potential energy function based on the auxiliary potential field yields the gradient function:

\nabla U_{r e q 2} (p_{t} (t)) = - g_{v} {(1 + v)}^{2} R_{r e q 2}^{v} (β) {\vec{n}}_{v}

(23)

where the unit vector of the current velocity direction of the navigator is denoted as

{\vec{n}}_{v}

The repulsion control input B

u_{o} (t)

is denoted as:

u_{o} (t) = - \nabla U_{r e q 1} (p_{l} (t)) - \nabla U_{r e q 2} (p_{t} (t))

(24)

3.2. Gravitational field design for target points.

Based on the artificial potential field method, it is known that the target point will exert a gravitational effect on the AUV formation, and the potential energy function of the target point on the current AUV is denoted as:

U_{a t t} (p_{l} (t)) = \frac{κ}{λ^{2}} ρ (p_{l} (t), x_{t a r}) + \frac{κ}{ρ (p_{l} (t), x_{t a r}) + λ}

(25)

where,

λ, κ

denotes the positive coefficient of the potential energy function.

Gradient of the potential energy function based on the target point:

\nabla U_{a t t} (p_{l} (t)) = \frac{\partial U_{a t t} (p_{l} (t))}{\partial ρ} {\vec{n}}_{a t t}

(26)

where，

{\vec{n}}_{a t t}

is the unit vector from the navigator to the target point

\frac{\partial U_{a t t} (p_{l} (t))}{\partial ρ} = \frac{κ}{λ^{2}} - \frac{κ}{{(ρ (p_{l} (t), x_{t a r}) + λ)}^{2}}

(27)

{\vec{n}}_{a t t} = \frac{p_{l} (t) - x_{t a r}}{‖p_{l} (t) - x_{t a r}‖}

(28)

Gravity control input

u_{t} (t)

is denoted as:

u_{t} (t) = - \nabla U_{a t t} (p_{l} (t))

(29)

The potential energy gradient function of the target point can be regarded as a constant value because the target point is at a location far from the AUV, and the potential energy gradient function of the target point remains essentially constant.

3.3. Coordination and control within the formation

In order to ensure the overall robustness of the formation, make it less likely to have obvious formation changes due to the disturbance of external environment and obstacle avoidance behavior, reduce the risk of AUVs colliding with each other within the formation, and ensure the AUVs can converge stably, based on the communication structure in the formation AUVs, design the coordination control force within the formation based on the position and velocity state information of each AUV [27].

u_{i n} (t) = - ω x_{i} (t) + K_{i n} [K_{p} \sum_{j \in N_{i}^{x}} a_{i j} (t) (x_{j} - x_{i}) + K_{v} \sum_{j \in N_{i}^{v}} b_{i j} (t) (v_{j} - v_{i})]

(30)

where,

K_{i n}

and

ω

denote the control gain of the formation coordination control input.

a_{i j} (t)

and

b_{i j} (t)

are the communication weights within the system.

K_{p}

and

K_{v}

denote the control gains in the position and velocity communication topologies, respectively.

Based on the forces on the AUV in the potential field, the control input to the AUV can be expressed as:

u (t) = u_{t} (t) + u_{o} (t) + u_{i n} (t)

(31)

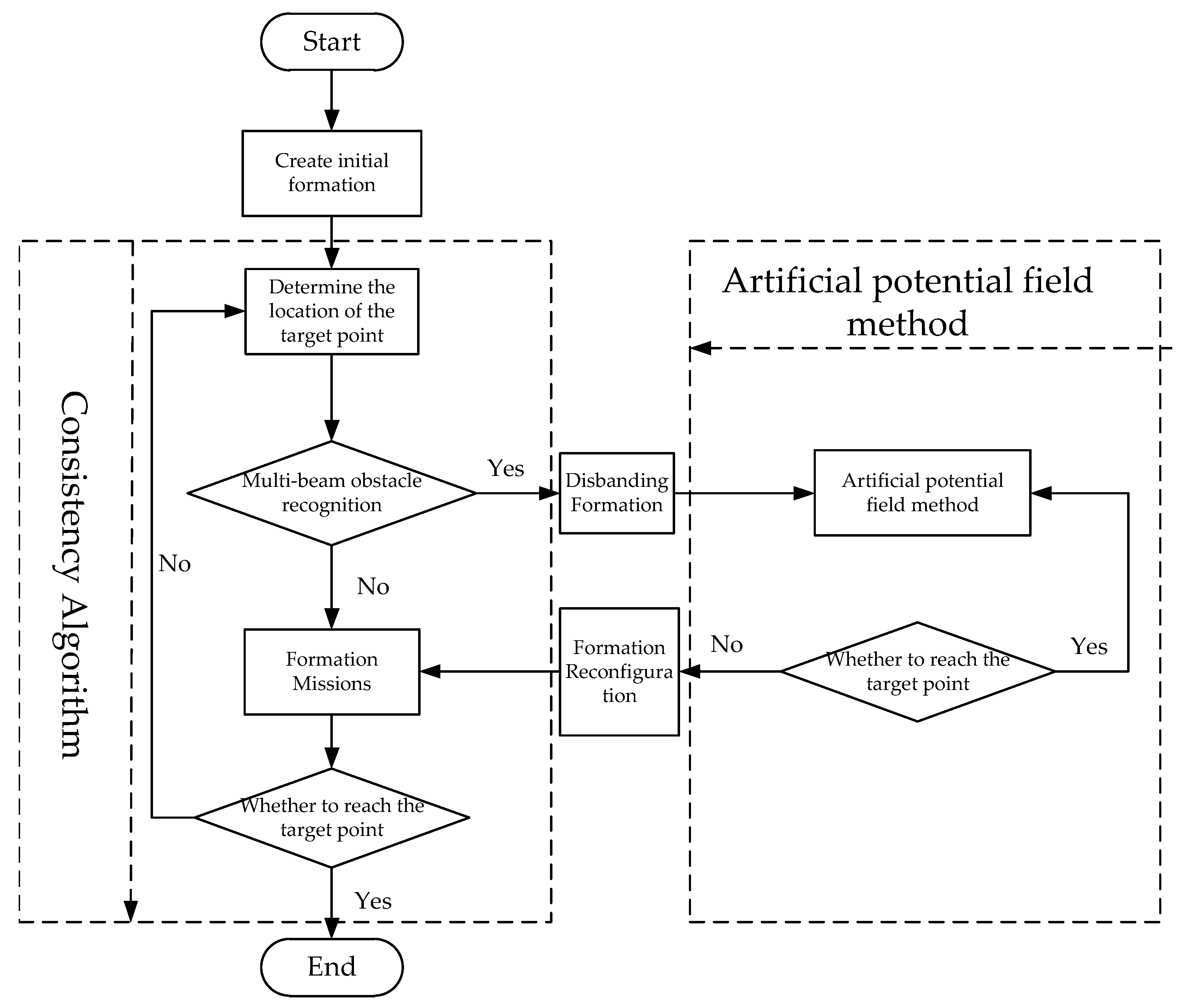
3.3. Algorithm flow of cooperative obstacle avoidance

The AUV formation is controlled by the formation clustering algorithm to complete the overall movement of the formation before the threat is perceived [28]. When a threatening obstacle is encountered, the above-mentioned obstacle avoidance algorithm is used to successfully avoid the high-threatening obstacle by the multi-beam sonar sensing obstacle and the improved artificial potential field algorithm to return to the cluster formation control after getting rid of the obstacle.

The second-order integral model of AUV after feedback linearization can be expressed as:

\begin{array}{l} {\dot{x}}_{i} (t) = v_{i} (t) \\ {\dot{v}}_{i} (t) = {\tilde{u}}_{i} (t) \end{array}

(32)

The actual position and velocity state information during the AUV voyage can be expressed as

D_{i} (x) = {[x_{i} (t), v_{i} (t)]}^{T}

. The desired time-varying formation state is expressed as

{\bar{D}}_{i} (x) = {[{\bar{x}}_{i} (t), {\bar{v}}_{i} (t)]}^{T}

.There exists a vector

C (t)

is called the central function, such that

\lim_{t \to \infty} (D_{i} (x) - {\bar{D}}_{i} (x) - C (t)) = 0

The pre-command generates the initial desired formation, and the desired formation is modified by the modified artificial potential field method above when the AUV cluster system senses an obstacle. The corrected desired formation is denoted as

\bar{H} (x) = \bar{D} (x) + F (x) .

where,

F (x) = - \nabla U_{r e q} (x_{i} (t)) - \nabla U_{a t t} (x_{i} (t))

The consistency protocol at this point is denoted as:

{\tilde{u}}_{i} (t) = F (x) + K_{1} (D_{i} (x) - {\bar{H}}_{i} (t)) + K_{2} \sum_{j \in N_{i}} w_{i j} ((D_{j} (x) - {\bar{H}}_{j} (t)) - (D_{i} (x) - {\bar{H}}_{i} (t))

(33)

where,

K_{1} = K_{i n} K_{p}

K_{2} = K_{i n} K_{v}

w

indicates the coefficient of the effect of the current position on its motion state.

At this point, the AUV formation cooperative obstacle avoidance algorithm flow can be shown in Figure 4.

4. Stability analysis

The different potential field effects due to the obstacle space produce different directional forces in the formation system. It causes the AUV to produce obstacle avoidance routes in different directions [29]. In this paper, the AUV formation system will form two small subsystems. The total number of AUVs in the two subsystems is

m

，The number of AUVs in the two subsystems are

m_{1}

and

m_{2}

respectively, and

m_{1} + m_{2} = m

The stability of the system can be proved by constructing an energy function. The energy functions of the two systems are defined as

W_{1} (V (t), X (t))

and

W_{2} (V (t), X (t))

respectively.

V (t)

is denoted as the velocity energy function,

X (t)

is denoted as the position energy primary function, and

η (V (t))

is denoted as the sum of the energies of the subsystem potential fields.

W_{1} (V_{i} (t), X_{i} (t)) = V_{i} (t) + X_{i} (t) + 2 η_{1} (V_{i} (t))

(34)

W_{2} (V_{j} (t), X_{j} (t)) = V_{j} (t) + X_{j} (t) + 2 η_{2} (V_{j} (t))

(35)

where,

V_{i} (t) = \sum_{i = 1}^{m_{1}} v_{i}^{T} v_{i} (t)

X_{i} (t) = ω \sum_{i = 1}^{m_{1}} x_{i}^{T} x_{i} (t)

η_{1} (V_{i} (t)) = \sum_{i = 1}^{m_{1}} (U_{r e q}^{i} (x (t)) + U_{a t t}^{i} (x (t)))

V_{j} (t) = \sum_{j = 1}^{m_{2}} v_{j}^{T} v_{j} (t)

X_{j} (t) = ω \sum_{j = 1}^{m_{2}} x_{i}^{T} x_{i} (t)

η_{2} (V_{j} (t)) = \sum_{j = 1}^{m_{2}} (U_{r e q}^{j} (x (t)) + U_{a t t}^{j} (x (t)))

The two subsystems are similar in the formation process and the stability proof process. In this section, only one subsystem stability proof is carried out and the conclusion is given.

Theorem 4.1: The initial energy function of the system includes the velocity energy function, the position energy function, and the sum of the energy of the potential field. Then, the initial energy function A of the system is bounded, then the formation can be transformed by autonomous formation and the following conclusion holds: in the process of formation avoidance, the splitting transformation of the formation is generated and the subsystem always keeps converging.

{\dot{W}}_{1} (V (t), X (t)) < 0, {\dot{W}}_{2} (V (t), X (t)) < 0

(36)

PROOF: Derive the subsystem energy function as follows:

{\dot{W}}_{1} (V (t), X (t)) = 2 \sum_{i = 1}^{m_{1}} v_{i}^{T} (t) {\dot{v}}_{i} (t) + 2 ω \sum_{i = 1}^{m_{1}} x_{i}^{T} (t) {\dot{x}}_{i} (t) + 2 {\dot{η}}_{1} (ζ (t))

(37)

Substitute equation (17) into (21):

\begin{array}{l} {\dot{W}}_{1} (V (t), X (t)) = & 2 \sum_{i = 1}^{m_{1}} v_{i}^{T} (t) (- \nabla_{l} ψ_{t} - \nabla_{l} ψ_{o} - ω x_{i} (t)) \\ + 2 \sum_{i = 1}^{m_{1}} v_{i}^{T} (t) (K_{i n}^{p} \sum_{j \in N_{i}^{x}} a_{i j} (t) (x_{j} - x_{i}) + K_{i n}^{v} \sum_{j \in N_{i}^{x}} b_{i j} (t) (v_{j} - v_{i})) \\ + 2 {\dot{η}}_{1} (V (t)) + 2 ω \sum_{i = 1}^{m_{1}} x_{i}^{T} (t) v_{i} (t) \end{array}

(38)

Since

v_{i} (t)

and

x_{i} (t)

are column vectors of the same dimension, there exists

x_{i}^{T} (t) v_{i} (t) = v_{i}^{T} (t) x_{i} (t)

\begin{array}{l} {\dot{W}}_{1} (V (t), X (t)) = & - 2 \sum_{i = 1}^{m_{1}} v_{i}^{T} (t) (\nabla_{l} ψ_{t} + \nabla_{l} ψ_{o}) \\ + 2 \sum_{i = 1}^{m_{1}} v_{i}^{T} (t) K_{i n}^{p} \sum_{j \in N_{i}^{x}} a_{i j} (t) (x_{j} - x_{i}) \\ + 2 \sum_{i = 1}^{m_{1}} K_{i n}^{v} \sum_{j \in N_{i}^{x}} b_{i j} (t) (v_{j} - v_{i}) + 2 {\dot{η}}_{1} (x (t)) \end{array}

(39)

The derivative of the total potential energy function of the subsystem can be obtained from its definition.

{\dot{η}}_{1} (V (t)) = {(\sum_{i = 1}^{m_{1}} (ψ_{o}^{i} (△ l) + ψ_{t}^{i} (△ l)))}^{'} = X (t) \sum_{i = 1}^{m_{1}} (\nabla_{l} ψ_{o}^{i}) + X (t) \sum_{i = 1}^{m_{1}} (\nabla_{l} ψ_{t}^{i} (△ l))

(40)

Substitute equation (25) into (22):

{\dot{W}}_{1} (V (t), X (t)) = - 2 X^{T} (t) (L_{p} \otimes K_{i n}^{p}) V (t) - - 2 X^{T} (t) (L_{p} \otimes K_{i n}^{v}) X (t)

(41)

Lemma 4.1: When

x \in ℝ^{n}

y \in ℝ^{n}

β > 0

, there exists the following inequality that holds.

x^{T} y + y^{T} x \leq β x^{T} x + β^{- 1} y^{T} y

(42)

Based on the above lemma, the following inequalities exist

- 2 X^{T} (t) (L_{p} \otimes K_{i n}^{p}) V (t) \leq - δ X^{T} (t) - V^{T} (t) {(L_{p} \otimes K_{i n}^{p})}^{T} (L_{p} \otimes K_{i n}^{p}) V (t)

(43)

Substitute equation (26) into (28):

{\dot{W}}_{1} (V (t), V (t)) \leq - δ X^{T} (t) X (t) - V^{T} (t) Θ V (t)

(44)

where,

Θ = {(L_{p} \otimes K_{i n}^{p})}^{T} (L_{p} \otimes K_{i n}^{p}) + 2 (L_{p} \otimes K_{i n}^{v})

According to the properties of the Laplacian matrix, it must be a vivacious semi definite matrix. From this, it can be deduced that the formation must be able to converge stably.

5. Simulation verification and analysis

The following simulation example verifies the effectiveness of the research on the multi-AUV coordinated obstacle avoidance method based on the improved artificial potential field method and the consistency protocol algorithm.

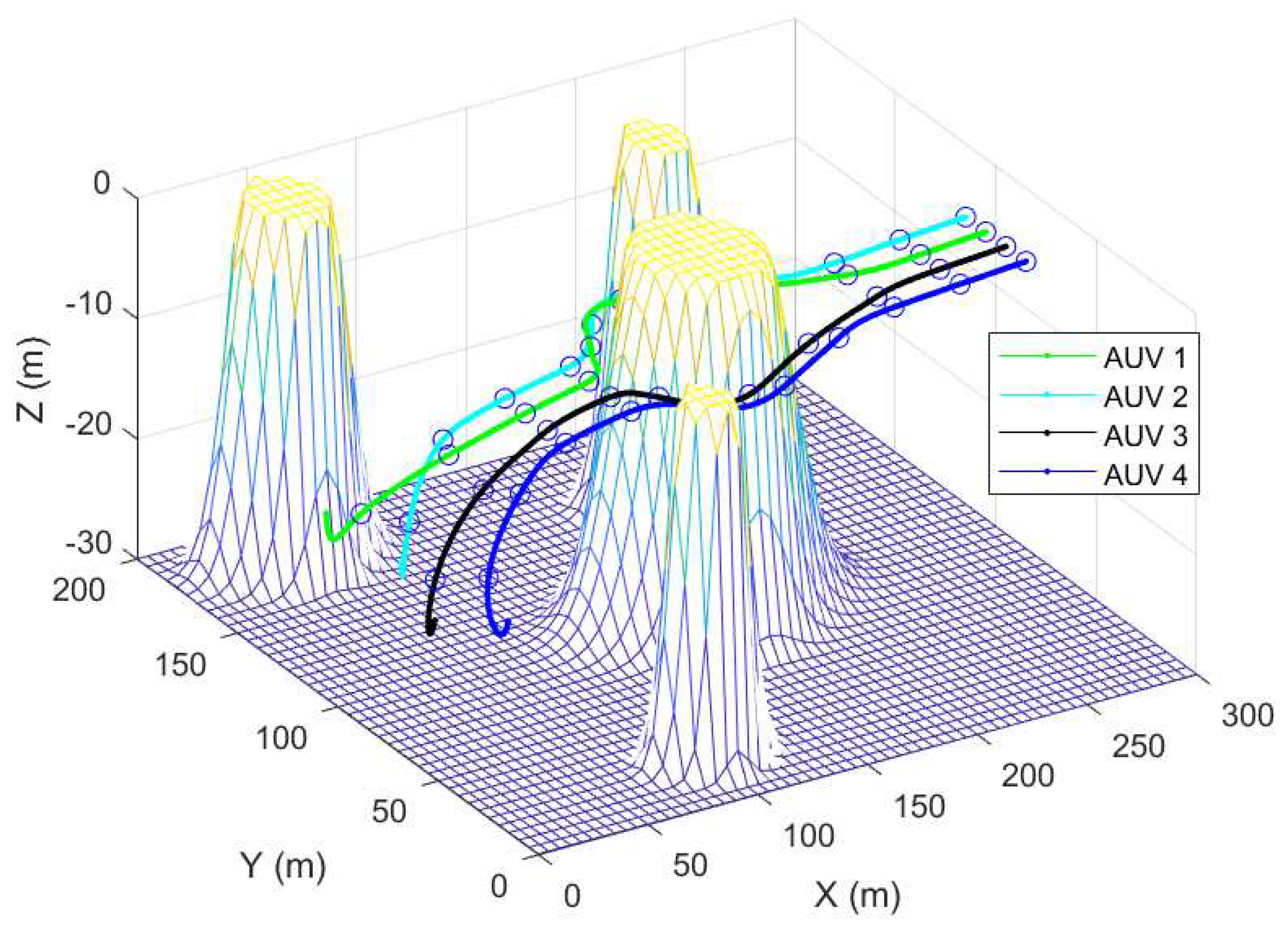
The number of AUVs in the formation is 4. The initial position status information of each AUV are

x_{i} \in [0, 50]

、

y_{i} \in [0, 140]

、

i \in \{1, 2, 3, 4\}

.The initial velocity of AUV are 0. Probabilistic Threat Intensity Diagonal Matrix

K_{i}

0.002 I_{3 \times 3}

. Potential field coefficient

γ = 1, κ = 0.1, λ = 1

. Obstacles are randomly distributed in the map. The target points for the cooperative operation of the AUV formation are

[300, y_{i}, - 5]

.After reaching consistency, the distance between the formation AUVs is maintained at 10m.

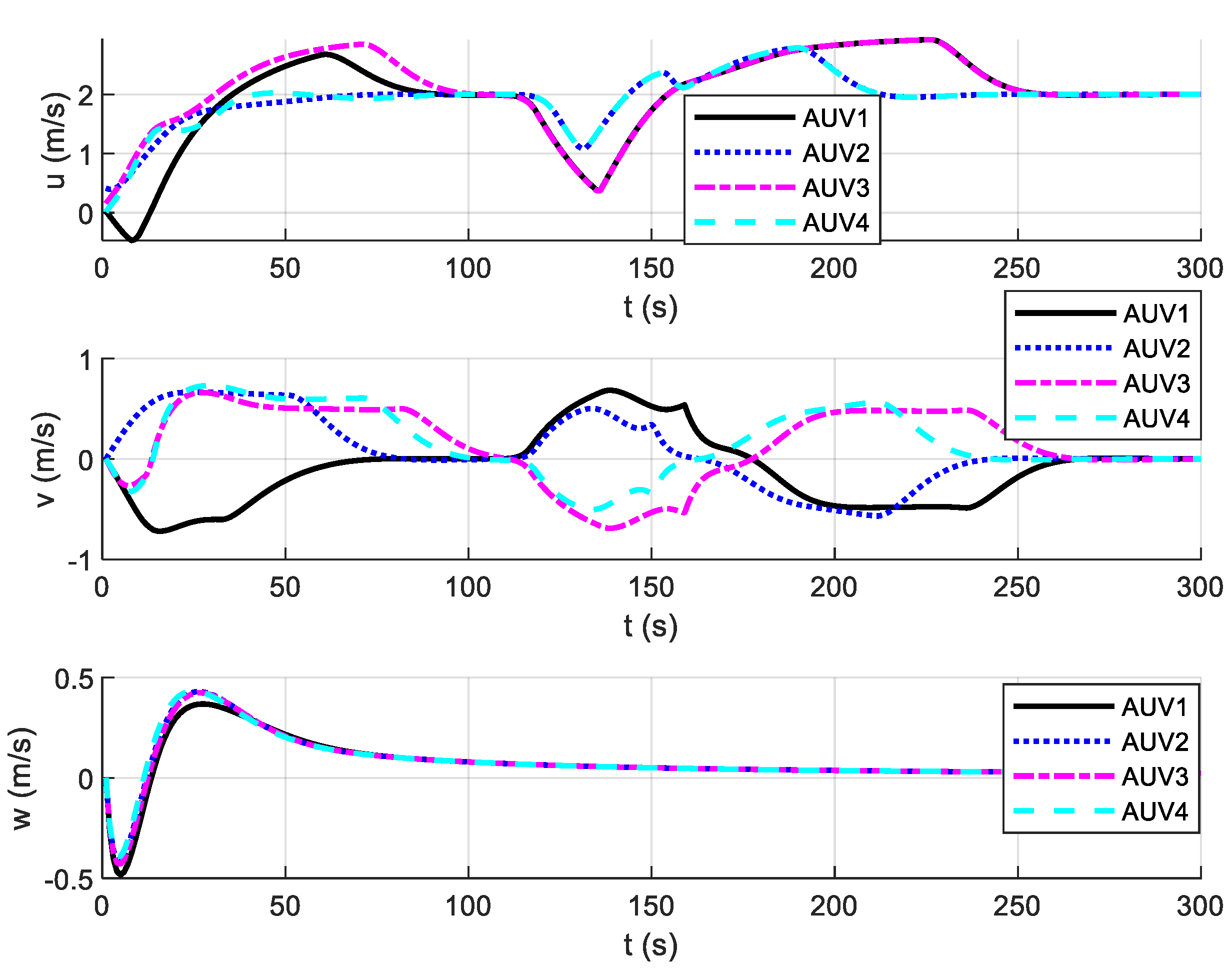
Figure 5 gives the paths of the formation AUVs in the process of coordinated obstacle avoidance. The formation AUVs feel different threat levels and decelerate differently after entering the potential field area, but each keeps relative distance between the formations and no collision behavior occurs, and finally the formation finally achieves consistency according to the consistency protocol.

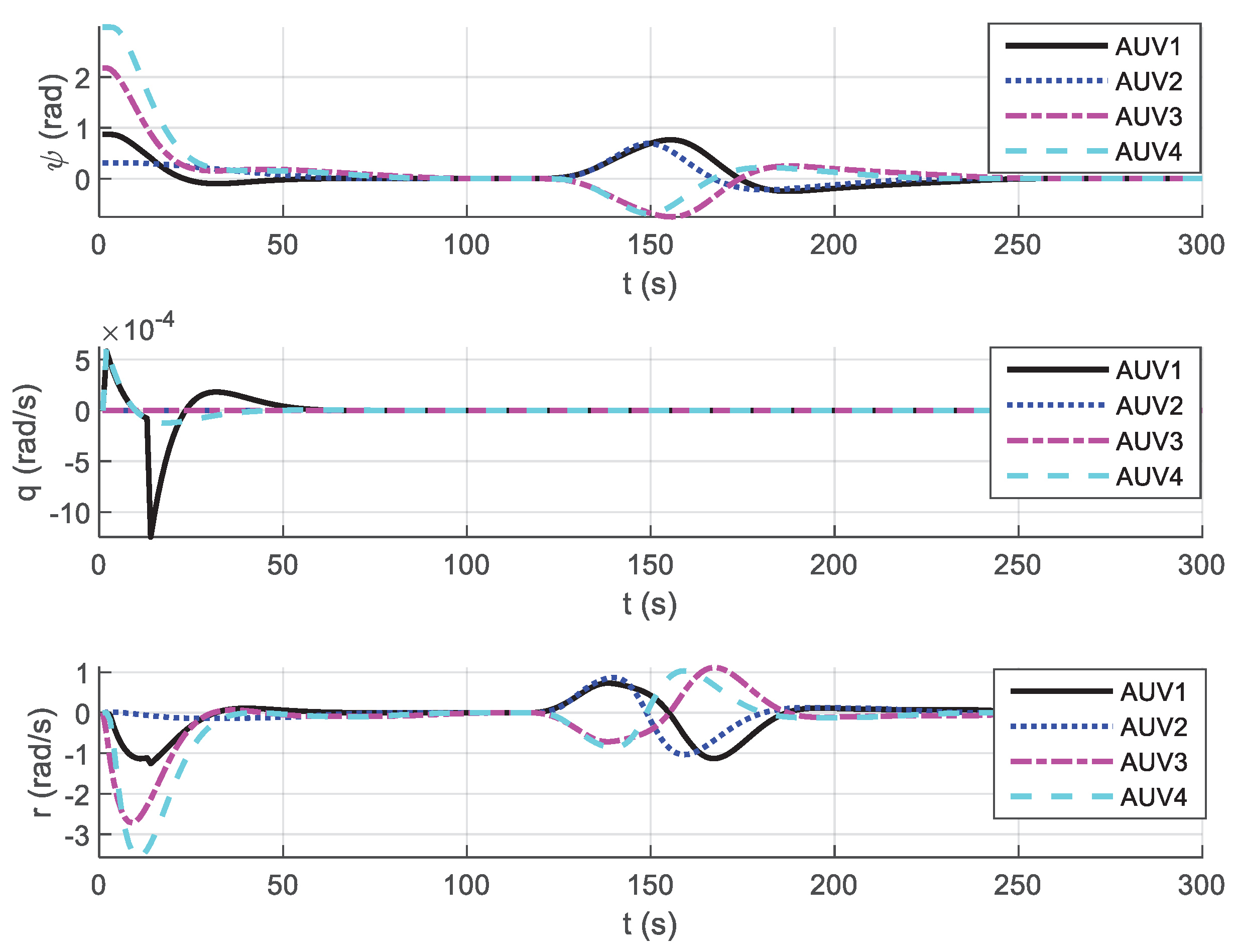
Figure 6, Figure 7 and Figure 8 show the changes of position attitude and each velocity state during the formation dissolution, formation coordinated obstacle avoidance process and formation reconfiguration process of multi-AUV in the face of obstacles, respectively. From Figure 6, it can be seen that the spatial position relationship of the AUV formation in the formation system can still converge after passing through the potential field region and generating the separation of obstacle avoidance actions. In Figure 7 and Figure 8, the motion states of each AUV similarly converge-separate-converge as the potential field appears.

Comprehensive simulation results above can be judged that the algorithm based on the improved artificial potential field method and consistency protocol proposed in this chapter can effectively solve the problem of multi-AUV coordinated obstacle avoidance, and ensure the convergence and stability of the formation while ensuring the formation avoidance of obstacles and formation change.

6. Conclusions

This paper focuses on the local obstacle avoidance problem of AUV formation and proposes a cooperative obstacle avoidance algorithm based on an improved artificial potential field method and a consistency protocol. Firstly, for the disadvantage that the traditional artificial potential field method is easy to fall into local minima, an auxiliary potential field perpendicular to the AUV moving direction is designed to solve the problem that AUVs are easy to have zero combined force in the potential field and local minima. Secondly, the control law of AUV formation that keeps the speed and position consistent is designed for the problem that the formation will change during the local obstacle avoidance of the formation system. The control conflict problem of the combined algorithm of the artificial potential field law and the consistency protocol is solved by adjusting the desired formation of the consistency protocol through the potential field force. Finally, the stability of system convergence is demonstrated by bounded energy function. Through simulation verification, it is confirmed that the AUV formation can achieve convergence of the formation state under local obstacle avoidance. The effectiveness of the proposed algorithm is confirmed.

Author Contributions

H.Y.: Conceptualization, Writing—Review & Editing, Supervision, Project administration. L.N.: Conceptualization, Software, Writing—Original Draft, Writing—Review &Editing, Visualization. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported in part by the National Natural Science Foundation of China under Grant 51809028, in part by the China Postdoctoral Science Foundation under Grant 2020M670733, and in part by the Doctoral Start-up Foundation of Liaoning Province under Grant2019-BS-022.

Data Availability Statement

Not applicable.

Acknowledgments

Not applicable.

Conflicts of Interest

Not applicable.

References

Antonelli G. Underwater Robots, Springer: Berlin, Germany 2014; pp. 20–23.
Sahu B K; Subudhi B. Flocking control of multiple AUVs based on fuzzy potential functions. IEEE Transactions on Fuzzy Systems. 2018, 26(5): 2539-2551. [CrossRef]
Xin L; Zhu D. An adaptive SOM neural network method to distributed formation control of a group of AUVs. IEEE Transactions on Industrial Electronics. 2018, PP (99):1-1. [CrossRef]
J Fu, G. Sun. Trajectory Homotopy to Explore and Penetrate Dynamically of Multi-UAV. IEEE Trans. Intell. Transp. Syst. 2022, 23(12), pp. 24008-24019. [CrossRef]
Dechter, R; Pearl. Generalized best-first search strategies and the optimalityof A*. Assoc. Comput. Mach. 1985, 32 (3), 505–536. [CrossRef]
Cobb, H.G; Grefenstette, J. Genetic algorithms for tracking changing environments. Proceedings of International Genetic Algorithms Conference. 1993, pp. 1–8.
Cui, RX; Li, Y and Yan, WS. Mutual information-based multi-AUV path planning for scalar field sampling using multidimensional RRT*. IEEE Transactions on systems man cybernetics-systems. 2016. 46(7), pp.993-1004. [CrossRef]
Eberhart, R; Kennedy. A new optimizer using particle Swarm Theory. IEEE, Proceedings of the Sixth International Symposium on Micro Machine and Human Science. 1995, pp. 39–43.
Ma, Y.N; Gong, Y.J; Xiao, C.F; Gao, Y; Zhang, J. Path planning for autonomous underwater vehicles: An ant colony algorithm incorporating alarm pheromone. IEEE Trans. Veh. Technol. 2018, 68 (1), 141–154. [CrossRef]
Noguchi, Y; Maki, T. Path planning method based on artificial potential field and reinforcement learning for intervention AUVs. IEEE Underwater Technology 2019, 1–6.
Smith, S M; Ganesan, K; An, PE; Dunn, SE. Strategies for simultaneous multiple autonomous underwater vehicle operation and control. International Journal of systems science. 1998, 29(10), pp.1045-1063. [CrossRef]
Sun, B; Zhu, D.Q; Tian, C.; Luo, C.M. Complete coverage autonomous underwater vehicles path planning based on glasius bio-inspired neural network algorithm for discrete and centralized programming. IEEE Transactions on cognitive and developmental systems. 2018, 11 (1), 73–84. [CrossRef]
Yan, C; Xiang, X.J; Wang, C. Towards real-time path planning through deep reinforcement learning for a UAV in dynamic environments. Journal of intelligent and robotic systems. 2020, 98 (2), pp.297-309. [CrossRef]
Cheng, C.L; Zhu, D.Q., Sun, B., Chu, Z.Z., Nie, J.D., Zhang, S. Path planning for autonomous underwater vehicle based on artificial potential field and velocity synthesis. IEEE 28th Canadian Conference on Electrical and Computer Engineering . 2015, pp. 717–721.
Song, J; Hao, C and Su, JC. Path planning for unmanned surface vehicle based on predictive artificial potential field. International journal of advanced robotic systems. 2020, 17 (2). [CrossRef]
Zhao, ZY;Hu, Q. A cooperative hunting method for multi-AUV swarm in un-dewater weak in formation environment with Obstacles. Journal of marine science and engineering. 2020, 10 (9). [CrossRef]
Wang, SM; Fang, MC and Hwang. Vertical obstacle avoidance and navigation of autonomous underwater vehicles with H infinity controller and the artificial potential field method. Journal of navigation. 2019, 72 (1), 207-228. [CrossRef]
Zhen, QZ; Wan, L; Li, YL; Jiang, DP. Formation control of a multi-AUVs system based on virtual structure and artificial potential field on SE(3). Ocean Engineering. 2022, 253. [CrossRef]
Orozco-Rosas, U; Montiel, O and Sepulveda, R. Mobile robot path planning using membrane evolutionary artificial potential field. Applied soft computing. 2021, 77, 236-251. [CrossRef]
Li J, Zhang JX, Zhang HH, Yan ZP. A predictive guidance obstacle avoidance algorithm for AUV in unknown environments. [CrossRef]
Sensors. 2019, 19(13), 2862.
Fossen T I. Handbook of marine craft hydrodynamics and motion control. Chichester: John Wiley and Son, 2011.
Li, J, Zhang, HD, Chen, T, Wang, JQ. AUV Formation Coordination Control Based on Transformed Topology under Time-Varying Delay and Communication Interruption. Journal of Marine Science and Engineering.2022, 10(7), 950. [CrossRef]
Zhang, BT, Liu, Y, Liu, Y, Wang, J. A path planning strategy for searching the most reliable path in uncertain environments. International Journal of Advanced Robotic Systems. 2017, 13 (5), 23–32. [CrossRef]
Khatib, O. Real-time obstacle avoidance for manipulators and mobile robots. Int. J. Robot. Res. 1986, 5, 90–98. [CrossRef]
Zhang, W, Wei, SL, Zeng, J, Wang, NX, Multi-UUV path planning based on improved artificial potential field method. International Journal of Robotics and Automation. 2021, 36 (4), 231-239. [CrossRef]
Chen YL, Ma XW, Bai GQ, Sha YB, Liu, J. Multi-autonomous underwater vehicle formation control and cluster search using a fusion control strategy at complex underwater environment. Ocean Engineering, 2021, 216, 108048. [CrossRef]
Liang, D, Liu, ZY, Bhamra, R. Collaborative Multi-Robot Formation Control and Global Path Optimization. Applied Sciences-Basel. 2022, 12(14), 7046. [CrossRef]
Civelek, C. Stability analysis of engineering/physical dynamic systems using residual energy function. Archives of Control Sciences. 2019, 28(2), 201-222. [CrossRef]

Figure 3. Based on obstacle-assisted potential field artificial potential field method..

Figure 4. Formation cooperative obstacle avoidance algorithm flow.

Figure 5. Multi-AUV formation obstacle avoidance path.

Figure 6. Position state curve of multi-AUV.

Figure 7. Linear velocity profile of multi-AUV.

Figure 8. Attitude and angular velocity profile of multi-AUV.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Coordinated Obstacle Avoidance of Multi-AUV Based on Improved Artificial Potential Field Method and Consistency Protocol

Abstract

1. Introduction

2. Problem Statement and Model Description

2.1. Problem Description

2.2. AUV Movement Model

2.3. Probabilistic Threat Environment Map

3. Improvement of artificial potential field method

3.1. Auxiliary potential field repulsion field design for obstacles

3.2. Gravitational field design for target points.

3.3. Coordination and control within the formation

3.3. Algorithm flow of cooperative obstacle avoidance

4. Stability analysis

5. Simulation verification and analysis

6. Conclusions

Author Contributions

Funding

Data Availability Statement

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe