Prerpints.org logo
Preprint
Article

Quantum Beam Scattering --- Beam's Coherence Length, Which-path Information, and Weak Values

Altmetrics

Downloads

123

Views

30

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

23 May 2023

Posted:

24 May 2023

You are already at the latest version

Alerts
Abstract
The conventional theory of neutron beams interacting with many-body systems treats the beam as a classical system, i.e. with its dynamical variables appearing in the quantum dynamics of the scattering process not as operators but only as c-numbers. Moreover, neutrons are described with plane waves, i.e. the concept of neutron's (finite) coherence length is here irrelevant. The same holds for electron, atom or X-ray scattering. This simplification results in the full decoupling of the probe particle's dynamics from the quantum dynamics of the scatterer---a well-known fact also reflected in the standard formalism of time-correlation functions (see textbooks). Making contact with modern quantum theoretical approaches (e.g., quantum entanglement, 'which-path detection' versus interference, von Neumann measurement, Week Values, etc.) new observable effects may be exposed and/or predicted, for instance, a momentum-transfer deficit and an intensity deficit in neutron scattering from protons of hydrogen-containing samples. 7
Keywords: 
Subject: Physical Sciences  -   Quantum Science and Technology

1. Introduction

The well-known particle-wave dual nature of a quantum object, known as complementarity, allows for various (often strange appearing) quantum correlation and interference phenomena, like e.g. the delocalization and self-interference of very large organic molecules [1], and the “bomb detection” method in a Mach-Zehnder interferometer (MZI) with the aid of the so-called interaction-free measurement (IFM) method discovered by Elitzur and Vaidman [2]. The most striking of these non-classical phenomena is quantum entanglement (QE), which has been the most debated element of quantum mechanics ever since the theory was formulated about 100 years ago. QE (see e.g. [3]) is the phenomenon that two or more particles can exist in a shared quantum state, regardless of how far apart they are. Einstein criticized QE a “spooky action at a distance” and Schrödinger said it was quantum mechanics’ most important trait. “The Nobel prize in physics 2022” statement of grounds refers to QE as quantum mechanics’ most important resource, which also pioneered quantum information science and the associated emerging new quantum technologies [4,5,6,7].
In this paper, all the considerations and results are specifically focused on the non-relativistic scattering of particles from many-body (or condensed) systems, with a particular emphasis on incoherent neutron scattering (INS). When we say "incoherent," we mean that a neutron (or any other particle such as a photon, electron, or atom) collides and scatters from a single particle, such as a nucleus, atom, or molecule. When neutrons scatter from protons (commonly referred to as H-atoms), the scattering is predominantly incoherent due to the neutron-proton spin-flip mechanism involved in the collision process. Details to this spin-flip mechanism can be found in textbooks such as [8,9].
Essentially, this means that the scattering process provides "which-path information," as e.g. described in the texbook [10], allowing us to identify and isolate the scattering proton from all other potential scatterers. Consequently, this destroys any possible interferences between different paths that the neutron could take during the scattering process.
A clear first-principles explanation of this effect, and of coherent versus incoherent scattering, may be found in the Feynman Lectures [11], in particular Sec. 3.3. Here is considered neutron scattering from a crystal consisting of atoms with nuclear spin 1/2 (as the neutron, too). Now consider the case that the neutron has spin-up and the crystal nuclei have spin-down (before scattering), in which case spin-exchange (or -flip) can happen. This causes the incoherent part of the scattering process which produces no sharp interference peaks in the scattered neutron beam (the latter being characteristic of coherent scattering). This spin-flip corresponds to “which-path knowledge”—the specific spin-flip scattering nucleus (now having spin-up) is singled out, i.e. which-path information concerning the neutron does exist. This constitutes a generally valid quantum-mechanical feature that suppresses quantum interference phenomena. Moreover, Feynman emphasizes this phenomenon as follows:
  • “You may argue, “I don’t care which atom is up.” Perhaps you don’t, but nature knows; and the probability is, in fact, what we gave above—there isn’t any interference.”; [11], page 3-9.
This quotation is strongly related to the intrinsic physical connections between the basic quantum-mechanical concepts of wave-particle duality, complementarity, uncertainty principle, and which-path-knowledge versus interference. These have attracted great interest and are still under vivid theoretical and experimental investigations, see Refs. [10,12,13,14,15,16,17,18,19] and references cited therein.
The presentation below is organized as follows. Section 2 considers in some detail the fact that conventional (neutron) scattering theory treats the neutron beam as a classical system, and even as a plane wave. In the light of modern quantum mechanics, this has certain severe theoretical and experimental consequences, which are examined in the following Sections. The introductory Section 3 about the “neutron beam as a quantum object” gives an introduction to the specific topics of impulsive (von Neumann, or strong) measurement and creation of QE caused by the scattering. Section introduces (very) shortly the basic concepts of Weak Value (WV) and Two-State Vector Formalism (TSCF).
Contact with real neutron scattering experiments is done in the next two sections. In Section 5 the theory is further developed with respect to the experimental field of incoherent and inelastic neutron scattering (INS) with thermal neutrons [20]. Section 6 extends the theoretical investigation towards the field of epithermal neutron scattering (i.e., in the energy transfer range 1-100 eV) which is known as neutron Compton scattering (NCS) [21,22,23]. Both sections 5 and 6 contain subsections dealing explicitly with concrete experiments and their theoretical interpretations, which also includes examples of effects that have no interpretation within conventional theory.
The last Section 7 provides some additional discussion of the main aspects and succinct features of scattering of a quantum beam from a quantum scattering system. Here, as well as in appropriate places during the preceding presentations, is stressed the theoretical connection of our investigations with modern quantum theoretical approaches and concepts (e.g., quantum entanglement, `which path detection’ versus quantum interference, complementarity, and Weak Values).

2. Conventional Theory: Neutron Beam as a Classical Object

In the conventional non-relativistic neutron scattering theory, the concept of quantum entanglement (QE) is not explicitly mentioned, leaving uncertainty about its role in the theory [8,9,20] Although a neutron is a quantum object and would generally be expected to become entangled with a colliding nucleus or atom (see Setion 3), this process is not considered in this theory. Specifically, the neutron’s quantum degrees-of-freedom are not properly incorporated into the fundamental scattering formulas of the theory, such as the equation for the partial differential cross-section or the van Hove correlation functions. Instead, these formulas only involve classical values (c-numbers) associated with the neutron.
To illustrate this point, let’s examine the basic formulas of the theory, including the expression for the partial differential cross-section.
d 2 σ A d Ω d ω = k f k i σ A S ( K , ω )
( E = ℏ ω , d Ω : solid angle measured/covered by the detector. k i and k f initial and final wavevectors of the scattered neutron. K : momentum transfer from the neutron to the system due to the collision, K = k i − k f . σ A : scattering cross-section of scattering system A.)
S ( K , ω ) is the dynamic structure factor of the scattering system A (also known as scattering function of A), which contains dynamical variables of A only. (In simpler terms, the wavefunction of the complete neutron-A system contains dynamical variables referring to the scatterer only, but not to the neutron.) Thus the neutron is “downgraded” to a classical object. I.e., no operator quantity, but only c-numbers referring to the neutron appear here: the scattering cross-section σ A of the neutron-A collision process, and the initial ( k i ) and final ( k i ) wavevectors of the impinging and scattered neutron.
This is related with properties of the first Born approximation and the so-called Fermi’s Golden Rule which the conventional theory is based on [8,9,21,22]. as a consequence, the complete dynamics of the two systems (neutron and scattering system) become decoupled—the neutron dynamics do not appear in Eq. 1, since it contains only c-numbers of neutron quantities, i.e. only the quantum dynamics of the system A captured with the dynamical structure factor S ( K , ω ) .
This imposed classicality for the neutron has as a consequence that the typical quantum concept of the particle’s (or beam’s) coherence length, l c o h is also absent in the frame of conventional neutron scattering theory. As a matter of fact, the main Eq. 1 contains the values of the initial and final wavevectors only, which are considered as plane waves—another basic element of conventional theory.
In other terms, the scattering process describes the scattering probability from a infinitely well defined state k i to an accordingly precise final state k f . Of course, the actually observed quantity is the (double) average over the finite distributions of k i and k f associated with a real experimental setup.
Now the following crucial point made by conventional theory should be considered: According to standard quantum mechanics, there are no quantum interference effects between incoming particles (or photons) with different wavenumbers. Thus it seems natural to argue that there is no experimentally detectable difference between
(a) a wave packet with a given finite coherence length (i.e., a coherent superposition of waves with different wavenumbers) and
(b) an incoherent classical ensemble of plane waves, i.e. waves with infinitely well defined wavenumbers (which means that their coherence lengths are infinite), and with no definite phase relations between them.
This is because every observable scattering quantity is expected to only depend on the square | a ( k ) | 2 of the k -component of the incoming beam, and not on products | a ( k 1 ) a * ( k 2 ) | of components with different wavenumbers ( k 1 ≠ k 2 ), where the asterisk indicates complex conjugation. This is consistent with Dirac’s famous remark in his textbook: ``...Each photon then interferes only with itself. Interference between two different photons never occurs.”; see [24], p. 9.
Summarizing, in the frame of standard scattering theory holds that an experimental problem is completely characterized by the classical wavenumber distributions of the incoming and outgoing particle (or photon) beams; structural details of the wavefunctions of the beam-particles are irrelevant, and thus also the coherence properties of these wavefunctions. Impinging and scattered neutrons are described by plane waves.

2.1. FurtherExplanatory Remarks on the Basic Formula Eq.(1)

Some additional remarks on the validity of Eq. 1 are in order. In conventional theory, it holds
S ( K , ω ) = 1 2 π ℏ ∫ − ∞ ∞ exp ( − i ω t ) F ( K , t ) d t
where F ( K , t ) is the intermediate correlation function
F ( K , t ) = 1 N ∑ j , k N 〈 exp ( − i K · r j ( 0 ) ) exp ( i K · r k ( t ) ) 〉
The operators r j ( t ) , with j = 1 , … N , represent the spatial positions (in the Heisenberg representation) of the particles of the N-body scattering system A with Hamiltonian H A , A being assumed to be isolated. 〈 … 〉 represents an appropriate average over all N particles.
However, note that the complete neutron-system Hamiltonian is
H = H A + H n + H n A
The unitary time evolution operator
U A ( t ) = exp ( − i ℏ H A t )
which defines the Heisenberg operators
r j ( t ) = U A † ( t ) r j U A ( t )
( j = 1 , … N ) refers to the complete N-body system A, but not to the neutron. [8,9]. That is, the neutron-system interaction Hamiltonian H n A and the Hamiltonian of the free neutron H n play no role here.
The Heisenberg operators r j ( t ) in Eqs. (3) and (5), if “interpreted” in classical terms, represent particles’ positions. Obviously this is a crude oversimplification, because the unitary operator U A ( t ) is an N-body operator depending on the N-body Hamiltonian H A of the scattering system—and so any operator r j ( t ) is (for t ≠ t 0 ) an N-body quantity, too. (The pathological limiting case of A consisting on N non-interacting atoms is irrelevant for the present paper.)

3. Neutron Beam as a Quantum Object—Introductory Considerations

As already pointed out, the above considerations refer to conventional neutron scattering theory, and the situation in neutron interferometry theory is totally different. Here, wavepackets with finite coherence length for the initial and final neutron states represent the standard situation in real experiments.
Perhaps the most important fact to be stress from the beginning is the following. After scattering of a neutron n from a particle (say, H, as in the experiments considered below), the neutron and the particle are in an entangled state, in general. This always happens if the scattering interaction is strong enough, so that an initial not entangled two-body product state evolves into a linear superposition of final two-body states
| ψ n 〉 ⊗ | ϕ H 〉 ⟶ ∑ j c j ψ n , j 〉 ⊗ | ϕ H , j 〉
with amplitudes c j ( j = 1 , 2 , . . . ) and ∑ | c j | 2 = 1 . In general, this final state is entangled. Trivially, this plain quantum-theoretical fact is not captured within conventional theory since there is no QE of a quantum with a classical (here: neutron) object. (Parenthetically, QE between particles belonging to a many-particle scattering system may exist, in principle, also within conventional theory; see e.g.[25].)
Let us emphasize here again that the QE shown in Eq.(6) is impossible within the frame of conventional neutron scattering theory.
An important feature in the following investigations is that here the scattering is mainly incoherent; cf. the Introduction. Moreover, Feynman’s citation given in the Introduction appears to play a decisive role in the theoretical analysis and interpretation of the neutron scattering experimental results considered below. Interestingly, the fundamental point stressed by Feynman is intimately related with several basic concepts of quantum theory, e.g. which-path information versus interference, complementarity, and uncertainty principle.
The neutron (and more generally, the incoming beam of particles or photons) is assumed to be a quantum system, and so, in this respect, it has to be treated on an equal footing with the quantum scatterer. That is, the dynamical variables of the neutron (or at least some of them) have to be represented by operators (instead of c-numbers) and should appear explicitly in the theoretical derivations and results. Obviously, when the above requirements become fulfilled, then the obtained results may expected to be beyond the reach of conventional theory.
The simplest and best known theoretical model of the interaction between two quantum systems is given by the von Neumann Hamiltonian [26]
H i n t = g ( t ) A ^ ⊗ M ^
which also plays a central role in the theoretical derivations below. Operator A ^ refers to the first system, and M ^ the second one. g ( t ) is a real function describing the interaction strength, and it is assumed to be nonzero only for a very short time interval. As an example, M ^ may correspond to a neutron (electron, atom, etc), i.e. it is associated with the quantum beam of a scattering process as considered below; A ^ represents an observable of the (many-body) scattering system. In the case of neutron scattering, g ( t ) is proportional to the delta-like Fermi pseudo-potential; see textbooks, e.g. [8,9].
Parenthetically, the following investigations will appear to have a strong similarity with well established theoretical approaches in the field of so-called quantum optics, quantum circuits theory, and quantum information theory; e.g. see [4,5,10].

4. On Weak Values, Two-State-Vector-Formalism and Impulsive Weak Measurements

Some introductory remarks about the theory of WV and TSVF (in short also denoted as TV-TSVF) [27,28] are ir order. Consider the standard expression of the expectation value
〈 A 〉 = 〈 ψ i | A ^ | ψ i 〉
A ^ is the operator representing an observable A and | ψ i 〉 is the state of the system just before the measurement interaction, which is assumed to by of short duration. A ^ is hermitian and 〈 A 〉 is a real number.
Now one defines
A w ≡ 〈 ψ f | A ^ | ψ i 〉 〈 ψ f | ψ i 〉
in which appears the final state | ψ f 〉 of the system, i.e. the system’s state after the interaction is turned off. Note that this number, A w , is a complex in general. A w is called the weak value (WV) of A ^ . | ψ i 〉 is called the initial, or pre-selected, state and | ψ f 〉 is called the final, or post-selected state. Note that these two states are assumed to be experimentally accessible [27]. Hence. the real and the imaginary parts of A w are experimentally accessible quantities; For some examples, see the review article [29].
Obviously it holds
if | ψ i 〉 = | ψ f 〉 then 〈 A 〉 = A w
Hence Eq. (9) represents a generalization of the common expectation value, Eq. (8). Note that, for sufficiently weak measurements, the denominator in Eq. (9) does not vanish, 〈 ψ f | ψ i 〉 ≠ 0 ,27].
Now we consider once more the expectation value of A ^ , Eq. (8), and presume the expansion | ψ i 〉 = ∑ j c j | j 〉 . The set of kets { | j 〉 } denote an orthogonal basis of the Hilbert space associated with the considered system. Now we may assume that we carry out a measurement of the observable A ^ with respect to this basis and, additionally, make also a post-selection of the results associated withj the final state | j 〉 . In other terms, we envisage a strong (called projective, or von Neumann) measurement associated with the projector | j 〉 〈 j | . Hence, in the case we are interested to determine the average of the measuring results, we obtain:
〈 A 〉 = 〈 ψ i | A ^ | ψ i 〉 = ∑ j c j * 〈 j | A ^ | ψ i 〉 = ∑ j | c j | 2 〈 j | A ^ | ψ i 〉 〈 j | ψ i 〉 ≡ ∑ j | c j | 2 A j , ψ i w
As defined above, A j , ψ i w is the WV of A ^ with respect to the pre- and post-selected states | ψ i 〉 and | j 〉 , respectively. | c j | 2 is the probability for the appearance of | j 〉 ; cf. [27,30,31]. Thus we see that possibly existing experimental features associated with the experimentally accessible quantity A j , ψ i w become "smeared out” in the common expectation value 〈 ψ i | A ^ | ψ i 〉 .
Indeed, Aharonov and collaborators have demonstrated the basic physical significance of Eq. (9). Namely, in well-defined and properly designed experimental setups, WVs become measurable quantities [27]. As WVs are unknown in standard quantum mechanics (see textbooks), their existence and experimental accessibility should be considered to represent a novelty and/or discovery.
Further physical insight to the basic quantum nature of the concept of WV may be provided by the following consideration by Pati and Wu [32].
To start with, one notices the formula
A ^ | ψ i 〉 = 〈 A ^ 〉 | ψ i 〉 + Δ A ^ | ψ ¯ i 〉
which may be found in the textbook [27], p. 39, or in Ref. [32]. | ψ ¯ i 〉 is a state orthogonal to | ψ i 〉 , A ^ represents an observable, 〈 A ^ 〉 = 〈 ψ i | A ^ | ψ i 〉 . Further, Δ A ^ denotes the uncertainty of the observable A when the system is in the state | ψ i 〉 , that is, ( Δ A ^ ) 2 = 〈 ψ i | ( A ^ − 〈 A ^ 〉 ) 2 | ψ i 〉 . Taking the scalar product of 〈 ψ f | with both sides of Eq. (12) we gwet
A w = 〈 A ^ 〉 + Δ A ^ 〈 ψ f | ψ ¯ i 〉 〈 ψ f | ψ i 〉 ≡ 〈 A ^ 〉 + δ A w
Hence we may say that δ A w is the WV-correction to the conventional-theoretical expectation value 〈 A ^ 〉 .
This simple derivation shows the crucial reason for the term δ A w , which represents the difference between the common quantity 〈 A ^ 〉 and the WV A w . This difference is caused (1) by a non-vanishing uncertainty Δ A ^ > 0 , and (b) by an accompanying non-vanishing scalar product 〈 ψ f | ψ ¯ i 〉 ≠ 0 . Obviously, the latter relation means that the two states | ψ f 〉 and | ψ ¯ i 〉 are capable of producing quantum interferences.
It should be emphasized that the aforementioned condition 〈 ψ f | ψ ¯ i 〉 ≠ 0 is fully unknown in conventional quantum dynamics (exact and/or perturbative). Or, in simpler terms, this condition appears nowhere in conventional-theoretical treatments and/or interpretations of experimental observations or results. This also demonstrates the novelty of the two-state vector formalism (TSVF) which is an indispensable part of the general WV-theory [27,28].
In summary, this remarkably short derivation, Eqs. (12) and (13), shows that the new effects being interpretable within WV-TSVF are caused by the quantum interference of the post-selected state with a quantum state being orthogonal to the pre-selected state of the system [32].

4.1. Impulsive von Neumann Measurement and WV-TSVF Theory

In WV-TSVF theory, the measurement process is characterized by an impulsive von Neumann interaction Hamiltonian [26], see below. This incorporates an observable for a pointer or measuring apparatus, whose wavefunction is denoted by by | Φ 〉 . That is, the pointer itself is also a quantum object.
The implementation of the von Neumann model, which describes an ideal, is modeled by the two-body interaction Hamiltonian
H i n t = g ( t ) A ^ ⊗ M ^ with g ( t ) = g δ ( t − t 0 )
where M ^ is a dynamical variable of the pointer and A ^ is the system’s operator representing the physical quantity to be measured. g ( t ) is a (small and real) coupling function, and t 0 specifies the time of the impulsive two-body collision. In an ideal measurement, g ( t ) is nonzero only during a very short time interval—formally captured with the delta function— and thus the free Hamiltonians of the participating systems during this time period can be neglected.
The von Neumann measurement, also known as a strong measurement, provides the eigenvalues of the measured observable. However, it simultaneously disturbs the measured system, resulting in a change of its initial state. The final state corresponds to an eigenstate of the operator representing the observable. Alternatively, by weakly coupling a measuring device to the system, a technique known as Weak Measurement (WM), it becomes possible to extract specific information while limiting the disturbance induced by the measurement on the system. As initially proposed by Aharonov and collaborators [33,34], additional physical insights are unveiled when one selectively post-selects a specfic outcome of the experiment.
Let the initial system-apparatus state, i.e. for t < t 0 be ψ i ⊗ Φ i . Due to the interaction, this evolves as follows:
ψ i ⊗ Φ i → e − i g A ^ ⊗ M ^ ψ i ⊗ Φ i
For convenience, and as often done in theoretical papers, in the following derivations we temporarily put ℏ = 1 . We also may write g instead of g ( t ) .
Then one post-selects (with a strong measurement) a specific final state of the system, say ψ f . The experimental result is associated with the corresponding apparatus’ final state, Φ f , from which the measurement’s result is determined. Φ f is obtained by tracing out the dynamical variables of the system, i.e.,
Φ f = 〈 ψ f | e − i g A ^ ⊗ M ^ | ψ i 〉 Φ i
In the following one considers the weak interaction limit (i.e., small g) and obtains through power expansion of the xponent:
Φ f ≈ 〈 ψ f | 1 − i g A ^ ⊗ M ^ | ψ i 〉 Φ i = 〈 ψ f | ψ i 〉 ( 1 − i g A w M ^ ) Φ i ≈ 〈 ψ f | ψ i 〉 e − i g A w M ^ Φ i
A w is the WV of the system’s observable A ^ . It is assumed that 〈 ψ f | ψ i 〉 ≠ 0 . Thus the state of the measuring device evolves with an effective one-body Hamiltonian H ^ M = g A w M ^ , i.e.,
Φ i → e − i g A w M ^ Φ i
Thus the following interesting result is obtained: The pointer’s dynamics displays information about the system only through the single complex number A w .
For the following theoretical derivations we will make the specific choice
M ^ = p ^ ,
In other words, the pointer’s variable in the interation Hamiltonian will be its momentum. We will also need the variance of p ^ in its initial pointer state
V a r p = 〈 Φ i | p ^ 2 | Φ i 〉 − 〈 Φ i | p ^ | Φ i 〉 2
In the theoretical treatment of the experimental neutron scattering results presented below, it will be shown that the imaginary part I m [ A w ] of A w is of particular interest. According to the general WV-TSVF theory, the pointer momentum after the interaction changes from 〈 p 〉 i (its initial value) to
〈 p 〉 f = 〈 p 〉 i + 2 g I m [ A w ] V a r p
(its final value) Note that V a r p refers to the scattering system only and not to the apparatus (opointer). Moreover, the real part of the weak value, R e [ A w ] , is determined by the shifted position (x shift of the pointer, i.e.
〈 x 〉 f = 〈 x 〉 i + g R e [ A w ]
For full derivations and further explanations see e.g. [30,35]. It will be shown that, in our investigations, the relevant WV entering the scattering process is purely imaginary. The physical significance of an imaginary WV was analyzed by Dressel and Jordan [36].

5. Momentum Transfer Deficit in the INS Scattering in the Frame of WV Theory

Let us point out already here, for clarity, that the following derivations refer to a possible correction to a conventionally expected measurement outcome, as predicted by Weak Values (WM) and Two-State Vector Formalism (TSVF); see e.g. Eqs.(29) below.
For simplicity of notation, we take the direction of momentum-transfer vector, K A due to scattering of a neutron with initial momentum p n , to be parallel to the x-axis of the laboratory system. Now we consider the von Neumann-type interaction Hamiltonian
H i n t = g p ^ ⊗ X ^
(g: small coupling constant, as discussed above), with the understanding that H i n t should theoretically describe a (possibly existing) deviation from the conventional momentum transfer due to the neutron-system collision. X ^ is the position operator of the system (or a system’s part, e.g. a nucleus) being hit by the neutron, which has the momentum operator p ^ . The sign of g is not specified yet.
Now one has to calculate the WV of the system variable x ^ c r y s t a l ≡ X ^ , according to Eq. (9)
X w ≡ 〈 ψ f | X ^ | ψ i 〉 〈 ψ f | ψ i 〉
Clearly, the explicit forms of the state vectors in configuration space are very complicated (and time dependent even over a short time interval around the time t 0 of collision). So we may be able to perform a part of the calculation in the momentum space—as done in our earlier works [37,38]. To do so, one has the replacement
X ^ → − 1 i ∂ ∂ P ^
(recall the aforementioned convention ℏ = 1 ) where P ^ is the associated momentum variable of the quantum system. (Note that the fundamental commutation relation [ P ^ , X ^ ] = 1 / i is fulfilled.)
Let us now calculate X w in the momentum representation, making the usual assumption of the wavefunctions of initial and final states to be approximated by Gaussians (i.e of the form G ( P ) = exp ( − P 2 / 2 σ P 2 ) . This gives for the nominator
〈 ψ f | X ^ | ψ i 〉 = ( − 1 / i ) 〈 ψ f | ∂ ∂ P ^ | ψ i 〉 = ( − 1 / i ) 〈 G ( P − K A ) | ∂ ∂ P ^ | G ( P ) 〉 = ( − 1 / i ) ( − 1 / σ P 2 ) 〈 G ( P − K A ) | P ^ | G ( P ) 〉 = − i 1 / σ P 2 〈 ψ f | P ^ | ψ i 〉
The integral 〈 ψ f | P ^ | ψ i 〉 is exactly the same as the one that appeared in the calculation of the WV of momentum P in the treatment of INS [37,38]. Those calculations showed that P w is real and positive. Thus we immediately arrive at the interesting result that X w is purely imaginary.
It is in order to repeat the short calculation of P w here, see [37,38]:
P w = 〈 G f | P ^ | G i 〉 〈 G f | G i 〉 = ∫ d P G ( P − K A ) f P G ( P ) i ∫ d P G ( P − K A ) f G ( P ) i = + K A 2 ≡ + K 2
Here holds K A ≡ K by definition. The value of the integral in the numerator follows immediately from the following facts: ( a ) the two functions G are positioned symmetrically around the middle point P ¯ = K A / 2 —one function is centered at 0, the other at K A ; and ( b ) in this integral P is a linear factor. Note also that this result is independent of the width of the Gaussian G.
Of course, this integral, and thus P w , should change with variations of the assumed shape (and width) of the final state G f . See the discussion of this issue given in [37].
Thus we obtain from Eqs. (26) and (27)
X w = − i g 1 / σ P 2 K 2
which is a negative imaginary number, (if the smallness parameter g is positive). It may be noted that an imaginary WV is associated with the backaction of one system on the second, due to the interaction [36].
We apply now the main result (21) of the WV-TSVF theory [30,35]. By re-introducing explicitly the factor ℏ in the expression for momentum transfer, K → ℏ K , we obtain for the WV-correction to the conventionally expected pointer momentum,
〈 p ^ 〉 f − 〈 p ^ 〉 i WV-correction = = − 2 g / σ P 2 ℏ K 2 V a r p = − g ℏ K V a r p V a r P
using the definition V a r P = σ P 2 . Note that K > 0 since the neutron impinges on the system (initially at rest) along the x-axis “from the left” and thus the momentum transfer ℏ K on the scatterer is positive, ℏ K > 0 . This result contains the variances of both quantum participants (i.e. neutron and scatterer) in the collisional process. Moreover, Eq. (29) constitutes the main result of our derivation.

5.1. Physical Significance of the Main result Eq. (29)

We make now the following crucial observations:
(I) This concise theoretical result predicts the vanishing of the correction term caused by the WV-TSVF theory when considering the limiting case of a perfect plane wave neutron beam, where the variance of momentum ( V a r p ) equals zero. This outcome is highly satisfactory as it accurately reproduces the conventional results found in textbooks [8,9].
(II) Additionally, if the scatterer is composed of quantum objects with well-defined positions, the uncertainty principle dictates that the variance of their momenta becomes infinite, denoted as 1 / V a r P → 0 . Consequently, the correction term (29) disappears. Thus, also this limit aligns with the expected outcomes according to conventional theory [8,9].
Moreover, these observations yield the following noteworthy conclusions:
(III) Specifically for the mentioned hydrogenous materials, which exhibit an unusual deficiency in momentum transfer from the neutron to the impacted hydrogen atom, the coupling factor g in the model Hamiltonian (23) must be positive ( g > 0 ). It is important to note that there is no inherent restriction on g being negative ( g < 0 ) beforehand. This finding introduces a novel quantum characteristic associated with the overall dynamics of neutron-matter interactions, as uncovered by the WV-TSVF theory.
(IV) The preceding effect of momentum transfer deficit, and the intensity deficit effect presented below, both are absent in the above limiting, or idealized, cases Iand II which are crucial for validity of conventional theory [8,9].
Summarizing, the above results provide new insights into the consequences following from the nature of quantum beams (here: neutron beam), and also further evidence of the novel character of WV-TSVF theory. The new experimental field of applicability of WV-TSVF (i.e. neutron scattering) may be pointed out.

5.2. Momentum Transfer Deficit in INS from H 2 Molecules in C-Nanotubes

In this subsection, we examine an incoherent (and inelastic) neutron scattering (INS) experiment to illustrate the preceding theoretical findings. The theoretical basis and experimental method of INS are thoroughly explained in the textbook [20].
The experiment of Olsen et al. [39] focuses on INS involving individual hydrogen molecules adsorbed in carbon nanotubes. The measurements were conducted at the Oak Ridge National Laboratory’s new generation spallation neutron source (SNS) in the United States. Detailed information about the experiment and a comprehensive data analysis can be found in the original publication [39]. The primary outcomes of this INS experiment are depicted in Figure 1.
Figure 1 illustrates the primary outcomes of the INS experiment. In the realm of WV-TSVF theory, it is crucial to emphasize that achieving the post-selected state of H (or H 2 ) is easily accomplished by orienting the axis of the C-nanotube in relation to the momentum transfer. This can be observed in the following two extreme scenarios: (1) When the C-nanotube axis is perpendicular to K , the trapped H (or H 2 ) experiences a strong potential due to the repulsive nature of the C-nanotube wall.
(2) When the C-nanotube axis is parallel to K , the trapped H (or H 2 ) encounters a weak potential since it is only lightly adsorbed on the C-nanotube wall. As a result, it can undergo translational motion.
Evidently, the INS experimental results in scenario (2), specifically regarding the roto-translation motion of H 2 , exhibit a significant WV-correction. This correction deviates from the conventionally expected momentum transfer value and is even apparent upon visual examination.
To our knowledge, there exists no first-principles conventional (quantum or classical) theoretical explanation of this effect until now.

6. Intensity Deficit in Neutron Compton Scattering from H-Containing Materials

In this section we consider exclusively the experimental method of neutron Compton scattering (NCS), and in particular an effect known as intensity deficit in the scattering from protons of H containing materials. Here it will be of crucial importance to take into account the value of some NCS characteristic parameters, i.e. the collisional time window, and the energy and momentum transfers involved.

6.1. Characteristic Parameters of NCS

In the context of NCS, which applies so-called epithermal neutrons, the achieved momentum and energy transfers are large, i.e.
Δ E ≈ 1 − 100 eV and | K | ∼ 20 − 200 Å − 1
As a consequence, here the so-called Impulse Approximation (IA) applies [21,22]. Moreover, the time scale — often called “scattering time”, τ s c — characterizing the neutron-proton scattering dynamics is very short [21], i.e. about
τ s c ∼ 100 − 1000 as
(as: attosecond, 10 − 18 s). These physical parameters are provided at the eVS-Vesuvio instrument of the ISIS facility, Rutherford Appleton Laboratory, UK. These parameters are related as described by the theoretical result of IA [21,22]
τ s c | K | 〈 v 0 〉 ≈ 1
〈 v 0 〉 is the root-mean-square velocity of the nucleus (here: proton) before collision, which of course depends on the system (material) under investigation. ℏ K is the momentum transfer as already defined in the previous sections. Furthermore, it holds that τ s c equals the t-width of the intermediate correlation function F ( K , t ) (see section 2) [21,22].
In the IA, the scattering is assumed to be essentially incoherent, essentially meaning that each neutron scatters from a single nucleus—a single proton, in our case. Indeed, experimental determination of the energy transfer associated with the measured H-recoil peak shows that the struck object of the benzene-sample has mass equal to 1 a.m.u.—i.e., the neutron collides with a single proton.
For these reasons, the NCS method is applied to explore single-particle properties, and especially the momentum distribution of an atom in its initial state. Furthermore, this is supposed to reflect the (width shape of the) Born-Oppenheimer potential of the struck atom before collision [21].
The original motivation to establish the NCS experimental method was the possibility to measure the momentum distributions n ( p ) of He atom in the normal liquid state of helium and in its superfluid state [21,22]; see the original proposal by Hohenberg and Platzman [23].

6.2. WV-TSVF Interpretation of the Intensity Deficit Effect

A surprisingly straightforward consequence based on the preceding theoretical derivations predicts, from first principles, the so-called intensity deficit effect for hydrogen, earlier observed in several neutron Compton scattering (NCS) experiments from various H-containing materials; see [40,41,42,43] and papers cited therein.
To show this, it suffices to refer to the preceding general WV-theoretical result, Eq. (18), stated here again for convenience:
Φ i → Φ f = e − i g A w M ^ Φ i
Namely, for the case of an imaginary and negative, A w = − i | I m [ A w ] | , we get
Φ i → Φ f = e − g | I m [ A w ] | M ^ Φ i
And so the exponential factor, which now is a real negative number, reduces the norm of the pointer-state wavefunction,
| | Φ f | | < | | Φ i | |
In other terms, here the time evolution is non-unitary.
Now, in our case (see below) we are interested in the scattering intensity from protons (or H). On physical ground, it is obvious that 〈 Φ f | Φ f 〉 is proportional to the scattering intensity ( I H ) as measured by the pointer:
〈 Φ f | Φ f 〉 ∝ I H
Finding (35) is sometimes criticized as being an artifact of the post-selection and not a true quantum dynamical effect, due to the fact that here the pointer operator p ^ commutes with the interaction Hamiltonian H i n t . However, it must be emphasized that there is no arbitrariness, or any “improper approximation” involved in the preceding derivation of the imaginary weak value X w and the associated non-unitary evolution Eq. (34). In this context, note also that the choice of the final state of the system (i.e. a displaced Gaussian in momentum space) is common in theoretical investigations. Moreover, the fact that here X w has a vanishing real part implies that the associated pointer’s position remains invariant, i.e.
〈 x ^ 〉 f = 〈 x ^ 〉 i
Furthermore, this is fully consistent with the impulsive, δ -like, nature of H i n t . In simple terms, the hit system has no time to change its position just after the interaction is turned off.

6.3. Experiment: H-Intensity Deficit in NCS from Liquid Benzene

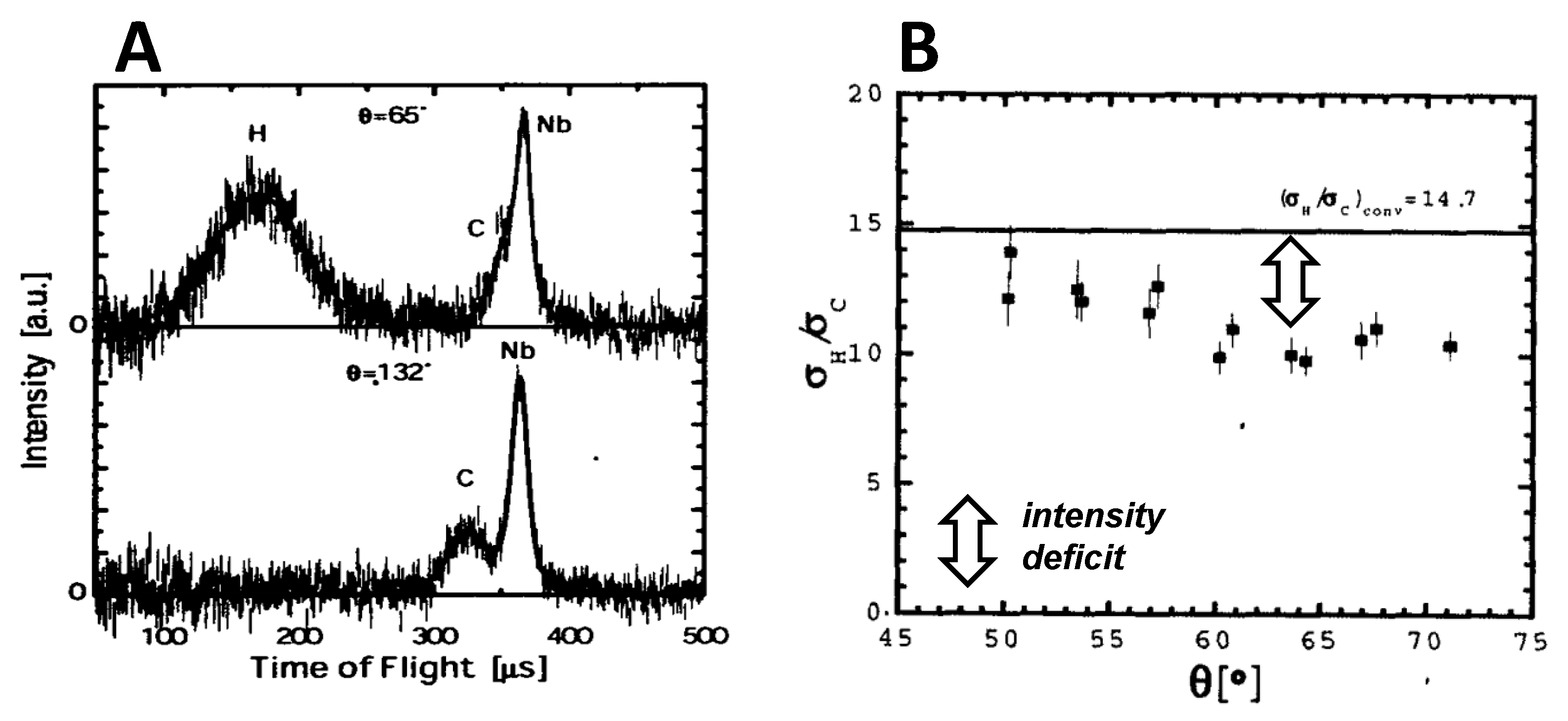
In short, the experimental NCS procedure is as follows. From a measured TOF spectrum with an individual detector, the data analysis routine determines the relevant peak areas A X , or intensities I X , (with X=H, C, Nb) from the measured partial differential cross-section d 2 σ / d ω d Ω ; see Section 2. Thus one determines by standard numerical analysis the ratio
R e x p ≡ I H / I X .
Standard NCS theory [21] predicts that the expected value R c o n v of this ratio is
R c o n v = N H σ H N X σ X .
N X is the number density of atom X and σ X the (bound) cross-section of the nucleus.
Here we are interested in the ratio I H / I C for benzene—which is achieved by the data analysis after subtraction of the “overlapping” Nb-peak of the metallic nyobium container (see Figure 2A). Surprisingly, the experimental results presented below (and many others, too) exhibit a striking intensity deviation, i.e.,
( I H / I C ) e x p ≈ 0.75 ( I H / I C ) c o n v
This effect has found no conventional interpretation thus far.
Assuming approximately that the heavier C-atoms behave “conventionally”, we may attribute this effect to the H atoms (i.e. the protons) and speak of the H-intensity deficit effect.
Parenthetically, some accompanying NCS measurements on deuterated benzene (C 6 D 6 ) were done, which showed a considerably smaller (although discernible) D-intensity deficit relative to the C-intensity (results not shown). Moreover, similar electron Coptmon-like scattering (ECS) experiments from H 2 and D 2 in the gas phase reveals a intensiti deficit effect, too [42].

6.4. Which-Path Information and Impossibility of Neutron Beam Interferences Due to Scattering from Different Protons

A theoretical interpretation of this NCS intensity deficit effect has been proposed, which is based on the premise that a few protons in the characteristic coherence volume of the neutron beam—a few Å 3 —are quantum entangled. This QE is furthermore assumed to affect positional and spin degrees-of-freedom of the involved protons (H atoms). It was theoretically derived that this QE reduces the scattering intensity of the system—say, two entangled protons— as compared to the conventionally expected NCS-scattering intensity from the same system without QE.
However, this interpretation becomes highly questionable in the light of modern quantum mechanics, where the aforementioned phenomenon of impossibility of interference in the case of (full) which-path information plays a central role. Indeed, the high energy transfer (say, e.g. 10-30 eV) on a scattering proton clearly singles it out from the other, not struck H atoms of the scattering system, independently of QE effects being present or not. In other terms, this huge energy transfer is equivalent to a full which-path information which rules out the aforementioned proposed interpretation of the intensity deficit effect: Namely, the path of the scattered neutron is here fully known because the scattering proton is well distinguishable from the non-hit protons in the aforementioned coherence volume.
To put it differently, the NCS intensity-deficit effect can be described as a singular impact of a single hydrogen atom, unrelated to the quantum interference arising from different paths taken by a neutron originating from various protons in the scattering material.
The comparison to the widely known two-slit experiment is apparent. When we have information about which path an atom (such as a neutron or photon) takes, this disrupts the interference pattern on the screen (or the measurement device). Moreover, having partial knowledge about the path reduces the visibility of the interference fringes accordingly; see [10,12,13,14,15,16,17,18,19].
These remarks are fully in line with Feynman’s statement stressed in the Introduction, which may be rephrased in the present case as follows:
You may argue, “I don’t care which specific proton has scattered the neutron” Perhaps you don’t, but nature knows; and neutron’s scattering amplitude behaves, in fact, as we just discussed—there isn’t any interference.

7. Discussion

In order to facilitate a bit more the understanding of the preceding results, here we may provide some additional remarks and explanations.
In some cases, the quantum character of the beam-particles (i.e., neutrons in the cases considered above) enforces the need to go “beyond” the conventional scattering theory. E.g., the neutrons have to be considered as quantum objects with finite coherence length; the duration of the neutron-nucleus collision has to be specified; the neutron-nucleus colliding system is a open quantum system, which in general may have a non-unitary time evolution. These remarks are in clear contrast to conventional theory, where (1) the neutrons are plane waves, (2) the concept of duration of the collision plays no role in the interpretation of experimental scattering results, and (3) the quantum dynamics of the scattering system (being asumed as being isolated) is unitary and (4) where the neutron is described by c-numbers (and not by operators).
The novel theory of weak values (WV) and two-state vector formalism (TSVF) introduces a fresh perspective by explicitly considering the quantum nature of the probe beam. This approach uncovers various counter-intuitive effects that might appear "strange" or even "wrong" when compared to conventional theory. For example, the momentum transfer deficit effect may seem to violate the fundamental laws of energy and momentum conservation. However, these objections stem from the incorrect (often tacit) assumption that the scatterer A is an isolated quantum system. In other words, the quantum dynamics of the "environment" of A actively participate in the neutron-A scattering process, and thus play an indispensable role in understanding the new WV-TSVF effects mentioned earlier. Therefore, it is beneficial to highlight the accurate conservation relations in the following manner:
Δ E H + e n v = − Δ E n and Δ ℏ K H + e n v = − Δ ℏ K n
Δ X Y represents the change of quantity X Y due to the collision. The participating environmental degrees-of-freedom are indicated by the subscript env, n refers to the neutron, and H refers to the system—here, the (proton of) the struck H atom.
Here, a note of caution should be made. In most experimental situations, the environment of a quantum system A disturbs its dynamics. Hence the environment referred to here could be alternatively called ancilla—as done in the theory of quantum computing [4]—because it plays a constructive role in the dynamics, i.e. preserves the unitarity of the whole “A + ancilla” system. Note that ancillas are present in the overwhelming majority of quantum circuits designed to carry out specific algorithms in quantum computers.
Additionally, considering these comments, a straightforward corollary arises that is highly perplexing for conventional theory: The time evolution of any elementary neutron-H scattering process involving INS or NCS, where H is a component of a hydrogenous condensed material (or molecule), is non-unitary.
In conventional NCS theory, an approximation is made where the complete Hamiltonian is replaced "by hand" using intuitive justifications, such as the extremely short scattering time τ s c . Instead of the complete Hamiltonian, a one-particle Hamiltonian, like that of a proton or hydrogen atom, is used in an effective Born-Oppenheimer potential; see e.g. [21]. This theoretical framework suggests that any non-unitary process, such as decoherence, is seemingly impossible. Additionally, the validity of various experimental investigations claiming to "directly measure the ab initio BO potential" should be critically reconsidered.
In our theoretical models concerning neutron scattering (INS and NCS), the interaction Hamiltonian in Equation (14) involves two distinct quantum systems, namely a neutron and a proton. The operators p ^ and X ^ within this Hamiltonian pertain to these individual systems. Consequently, as noted by Vaidman [44], the concept of WV emerges in this context due to the interference of an entangled quantum wave, and thus it lacks an equivalent counterpart in classical wave interference or classical physics. This highlights that WV is a fundamentally quantum concept rather than an approximation. It is important to recognize that there is no quantum entanglement between a classical system and a quantum system.
All the preceding derivations and consideration are related to (or based on) the concept of weak measurement, which should not correspond to the usual situations “in real experiments”. However, it has been shown that weak measurements are universal [45]. In essence, this holds because any projective (strong) measurement can be decomposed into a sequence of weak measurements, which cause only small changes to the system’s state. Futher analysis showed that this result holds even in the broader case of so-called generalized measurements [45].
The theoretical results we derived showed that the WV of the coupling system variable X ^ is purely imaginary, Eq. (26). The physical significance of imaginary WVs has been analyzed in detail in Ref.[36]. It was argued that the imaginary WV provides direct information about how the initial state would be unitarily disturbed by the observable operator. Furthermore, as the imaginary part constitutes a shift in the pointer momentum, this latter effect is a reflection of the back-action of a measurement on the particle (scatterer).
Moreover, our analysis of the intensity deficit effect provides a new insight into, or a new aspect of, the physical meaning of an imaginary WV. Furthermore note that a positive imaginary WV, together with a positive coupling g, would theoretically predict an intensity surplus (instead of deficit). However, until now we are not aware of a related experimental observation in some other quantum beam scattering context.
Here let us mention some additional references which provide further evidence for the predictive power of (and newer physical insights in) the theory of WV and TSVF [46,47,48,49].
It should be helpful to emphasize the connection of the above NCS and INS investigations with the vivid scientific debate about complementarity, which-path experiments, and the uncertainty principle. This is a topic of considerable activity (and controversy), during the past three decades. In short, the intensity deficit NCS effect is a “single H-atom effect”, and it has nothing to do with quantum interference of all possible paths of a neutron originating from many protons of the scattering material. This is due to the fact that the struck proton (which receives several tens of eVs by the collision) is distinguishable from the adjacent non-struck protons. E.g. in the case of the measured H-intensity in NCS from benzene, one proton is struck and the remaining 5 protons are not. (This is proven by the H-peak position in the measured time-of-flight spectra). That is, the struck proton is the scattering “system” A, and the remaining 5 protons, 6 C-nuclei, and all the electrons of the molecule constitute the environment or ancilla.
Concluding these considerations, and in the spirit of Feynman’s quotation (see the Introduction), let us notice: ....nature knows; and therefore there isn’t any interference between the amplitudes of the six potential n-H scattering trajectories from C 6 H 6 to the H-recoil peak shown in Figure 2(A). Hence the above considered surprising NCS effect appears to have a true quantum dynamical origin based on in the open-system quantum dynamics of specific few-body interactions. These involve the struck system (proton, or H), which is coupled with its quantum environment (or ancilla) and the impinging quantum particle, i.e. the neutron.

Conflicts of Interest

The author declares no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:
a.m.u. Atomic Mass Unit
eV electron Volt
IA Impulse Approximation
INS Inelastic Incoherent Neutron Scattering, also known as IINS
meV Milli-Electron Volt
NCS Neutron Compton Scattering, also known as DINS
QE Quantum Entanglement
TSVF Two-State Vector Formalism
WV Weak Value

References

  1. Fein, Y.Y., Geyer, P., Zwick, P.; Kiałka, F.; Pedalino, S.; Mayor, M.; Gerlich, S.; Arndt, M. Quantum superposition of molecules beyond 25 kDa. Nat. Phys. 2019, 2019 15, 1242–1245. [CrossRef]
  2. Elitzur, A.C.; Vaidman, L. Quantum mechanical interaction-free measurements. Found. Phys. 1993, 23, 987–997. [Google Scholar] [CrossRef]
  3. Horodecki, R.; Horodecki, P.; Horodecki, M.; Horodecki, K. Quantum entanglement. Rev. Mod. Phys. 2009, 81, 865–942. [Google Scholar] [CrossRef]
  4. Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, 2010. [Google Scholar]
  5. Preskill, J. Quantum computing and the entanglement frontier. arXiv 2012, arXiv:1203.5813. [Google Scholar]
  6. Arute, F., et al. Quantum supremacy using a programmable superconducting processor. Nature 2019, 574, 505–510. [CrossRef]
  7. Wang, H., et al., Boson sampling with 20 input photons and a 60-Mode interferometer in a 1014-dimensional Hilbert space. Phys. Rev. Lett. 2019, 123, 250503. [CrossRef]
  8. Squires, G.L. Introduction to the Theory, of Thermal Neutron Scattering, 2nd ed.; Cambridge University Press: Cambridge, 2012. [Google Scholar]
  9. Lovesey, S.W. Theory of Neutron Scattering form Condensed Matter; Oxford University Press: Oxford, 1984. [Google Scholar]
  10. Scully, M.O.; Zubairy, M.S. Quantum Optics; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
  11. Feynman, R.P.; Leighton, R.B.; Sands, M. The Feynman Lectures on Physics, Vol. III, Quantum Mechanics; Addison-Wesley: Reading, MA, USA, 1965; Available online: http://www.feynmanlectures.caltech.edu/.
  12. Scully, M.O.; Englert, R.-G.; Walther, H. Quantum optical tests of complementarity. Nature 1991, 351, 111–116. [Google Scholar] [CrossRef]
  13. Storey, P.; Tan, S.; Collett, M.; Walls, D. Path detection and the uncertainty principle. Nature 1994, 367, 626–628. [Google Scholar] [CrossRef]
  14. Wiseman, H.; Harrison, F. Uncertainty over complementarity? Nature 1995, 377, 584. [Google Scholar] [CrossRef]
  15. Bertet, P.; Osnaghi, S.; Rauschenbeutel, A.; Nogues, G.; Auffeves, A.; Brune, M.; Raimond, J.M.; Haroche, S. A complementarity experiment with an interferometer at the quantum– classical boundary. Nature 2001, 411, 166–170. [Google Scholar] [CrossRef]
  16. Greenberger, D.M.; Yasin, A. Simultaneous wave and particle knowledge in a neuron interferometer. Phys. Lett. A 1988, 128, 391–394. [Google Scholar] [CrossRef]
  17. Drezet, A.; Hohenau, A.; Krenn, J.R. Momentum transfer for momentum transfer-free which-path experiments. Phys. Rev. A 2006, 73, 062112. [Google Scholar] [CrossRef]
  18. Qureshi, T.; Vathsan, R. Einstein’s recoiling slit experiment, complementarity and Uncertainty. Quanta 2013, 2, 58–64. [Google Scholar] [CrossRef]
  19. Tanimura, S. Complementarity and the nature of uncertainty relations in Einstein–Bohr recoiling slit experiment. Quanta 2015, 4, 1–9. [Google Scholar] [CrossRef]
  20. Mitchell, P.C.H.; Parker, S.F.; Ramirez-Cuesta, A.J.; Tomkinson, J. Vibrational Spectroscopy with Neutrons; World Scientific: Singapore, 2005. [Google Scholar]
  21. Watson, G.I. Neutron Compton scattering. J. Phys. Condens. Matter. 1996, 8, 5955–5975. [Google Scholar] [CrossRef]
  22. Sears, V.F. Scaling and final-state interactions in deep-inelastic neutron scattering. Phys. Rev. B, 1984, 30, 44–51. [Google Scholar] [CrossRef]
  23. Hohenberg, P.C.; Platzman, P.M. High-energy neutron scattering from liquid He4. Phys. Rev. 1966, 1966 152, 198–200. [Google Scholar] [CrossRef]
  24. Dirac, P.A.M. The Principles of Quantum Mechanics, 4th ed.; Clarendon Press: Oxford, 1957. [Google Scholar]
  25. Karlsson, E.B.; Lovesey, S.W. Neutron Compton scattering by proton and deuteron systems with entangled spatial and spin degrees of freedom. Phys. Rev A 2000, 61, 062714. [Google Scholar] [CrossRef]
  26. von Neumann, J. Mathematical Foundations of Quantum Mechanics; Princeton: Princeton University Press; 1955.
  27. Aharonov, Y.; Rohrlich, D. Quantum Paradoxes: Quantum Theory for the Perplexed; WILEY-VCH: Weinheim, 2005. [Google Scholar]
  28. Y. Aharonov; A.; Vaidman,L. The two-state vector formalism: An updated review. Lect. Notes Phys. 2008, 734, 399–447.
  29. Dressel, J.; Malik, M.; Miatto F., M.; Jordan A., N.; Boyd R., W. Colloquium: Understanding quantum weak values: Basics and applications. Rev. Mod. Phys. 2014, 86, 307–316. [Google Scholar] [CrossRef]
  30. Tamir, B.; Cohen, E. Introduction to weak measurements and weak values. Quanta 2013, 2, 7–17. [Google Scholar] [CrossRef]
  31. Qin, L.; Feng, W.; Li, X.-Q. Simple understanding of quantum weak values. Sci. Rep. 2016, 6, 20286. [Google Scholar] [CrossRef] [PubMed]
  32. Pati, A. K.; Wu, J. Conditions for anomalous weak value. ArXiv arXiv:1410.5221v1, 2014.
  33. Aharonov, Y.; Bergmann, P.G.; Lebowitz, J.L. Time symmetry in the quantum process of measurement. Phys. Rev. B 1964, 134, 1410–1416. [Google Scholar] [CrossRef]
  34. Aharonov, Y.; Albert, D.Z.; Vaidman, L. How the result of a measurement of a component of a spin 1/2 particle can turn out to be 100? Phys. Rev. Lett. 1988, 60, 1351–1354. [Google Scholar] [CrossRef] [PubMed]
  35. Josza, R. Complex weak values in quantum measurement. Phys. Rev. A 2007, 76, 044103. [Google Scholar]
  36. Dressel, J.; Jordan, A.N. Significance of the imaginary part of the weak value. Phys. Rev. A 2012, 85, 012107. [Google Scholar] [CrossRef]
  37. Chatzidimitriou-Dreismann, C.A. Weak measurement and Two-State-Vector formalism: Deficit of momentum transfer in scattering processes. Quanta 2016, 5, 61–84. [Google Scholar] [CrossRef]
  38. Chatzidimitriou-Dreismann, C.A. Weak values and two-state-vector formalism in elementary scattering and reflectivity – A new effect. Universe 2019, 5, 58. [Google Scholar] [CrossRef]
  39. Olsen, R.J.; Beckner, M.; Stone, M.B.; Pfeifer, P.; Wexler, C.; Taub, H. Quantum excitation spectrum of hydrogen adsorbed in nanoporous carbons observed by inelastic neutron scattering. Carbon 2013, 58, 46–58. [Google Scholar] [CrossRef]
  40. Abdul-Redah, T.; Chatzidimitriou-Dreismann, C.A.; Karlsson, E. Neutron Compton Scattering Unveils Short-Lived Quantum Entanglement of Hydrogen in Condensed Matter. Neutron News 2004, 15, 12–17. [Google Scholar] [CrossRef]
  41. Chatzidimitriou-Dreismann, C.A.; Abdul-Redah, T.; Kolari, B. Entanglement of protons in organicmolecules: and attosecond neutron scattering study of C-H bond breaking. J. Am. Chem. Soc. 2001, 123, 11945–11951. [Google Scholar] [CrossRef]
  42. Cooper, G.; Hitchcock, A.P.; Chatzidimitriou-Dreismann, C.A. Anomalous quasielastic electron scattering from single H2, D2, and HD molecules at large momentum transfer. Phys. Rev. Lett. 2008, 2008 100, 043204. [Google Scholar] [CrossRef]
  43. Chatzidimitriou-Dreismann, C.A.; Gray, E. Chatzidimitriou-Dreismann, C.A.; Gray, E.MacA; Blach, T.P. Distinguishing new science from calibration effects in the electron-volt neutron spectrometer eVS-Vesuvio at ISIS. Nucl. Instr. Meth. A 2012, 676, 120–125. [Google Scholar] [CrossRef]
  44. Vaidman, L. Comment on "How the result of a single coin toss can turn out to be 100 heads". ArXiv arXiv:1409.5386, 2014.
  45. Oreshkov, O.; Brun T., A. Weak measurements are universal. Phys. Rev. Lett. 2005, 95, 110409. [Google Scholar] [CrossRef] [PubMed]
  46. Vaidman, L.; Ben-Israel, A.; Dziewior, J.; Knips, L.; Weissl, M.; Meinecke, J.; Schwemmer, C.; Ber, R.; Weinfurter, H. Weak value beyond conditional expectation value of the pointer readings. Phys. Rev. A 2017, 96, 032114. [Google Scholar] [CrossRef]
  47. Cohen, E.; Pollak, E. Determination of weak values of quantum operators using only strong measurements. Phys. Rev. A 2018, 98, 042112. [Google Scholar] [CrossRef]
  48. Aharonov, Y.; Popescu, S.; Rohrlich, D. On conservation laws in quantum mechanics. Proc. Natl. Acad. Sci. USA 2021, 2021 118, e1921529118. [Google Scholar] [CrossRef]
  49. Chatzidimitriou-Dreismann, C.A. Evidence of predictive power and experimental relevance of Weak-Values theory. Quantum Rep. 2021, 3, 286–315. [Google Scholar] [CrossRef]
Preprints 74497 g001
Figure 1. INS results from H 2 in carbon (C-)nanotubes, adapted from Figure 1 of Ref. [39] at T = 23 Kelvin (schematic). The broad intensity band—also called "roto-recoil" (white-blue ribbon)—is due to the translational motion of the recoiling H 2 molecules This starts at the first rotational excitation of H 2 , centered at E r o t ≈ 14.7 meV and K r o t ≈ 2.7 Å − 1 (blue ellipsoid)., in agreement with conventional theory. In clear contrast, the data analysis of [39] provides a fit (red parabola; full thick line) to the roto-recoil data, which exhibits a striking momentum transfer deficit of the recoiling H 2 molecule along the C-nanotube axis, schematically shown with the large double-arrow The experimental data are consistent with a fictitious (or: effective) mass of a translating H 2 being only 0.64 a.m.u. This is in contrast to conventional theory which predicts the red thin dashed parabola, i.e. the recoil parabola of H 2 having mass equal to 2 a.m.u. See [39] for full details of data analysis and further experimental data.
Figure 1. INS results from H 2 in carbon (C-)nanotubes, adapted from Figure 1 of Ref. [39] at T = 23 Kelvin (schematic). The broad intensity band—also called "roto-recoil" (white-blue ribbon)—is due to the translational motion of the recoiling H 2 molecules This starts at the first rotational excitation of H 2 , centered at E r o t ≈ 14.7 meV and K r o t ≈ 2.7 Å − 1 (blue ellipsoid)., in agreement with conventional theory. In clear contrast, the data analysis of [39] provides a fit (red parabola; full thick line) to the roto-recoil data, which exhibits a striking momentum transfer deficit of the recoiling H 2 molecule along the C-nanotube axis, schematically shown with the large double-arrow The experimental data are consistent with a fictitious (or: effective) mass of a translating H 2 being only 0.64 a.m.u. This is in contrast to conventional theory which predicts the red thin dashed parabola, i.e. the recoil parabola of H 2 having mass equal to 2 a.m.u. See [39] for full details of data analysis and further experimental data.
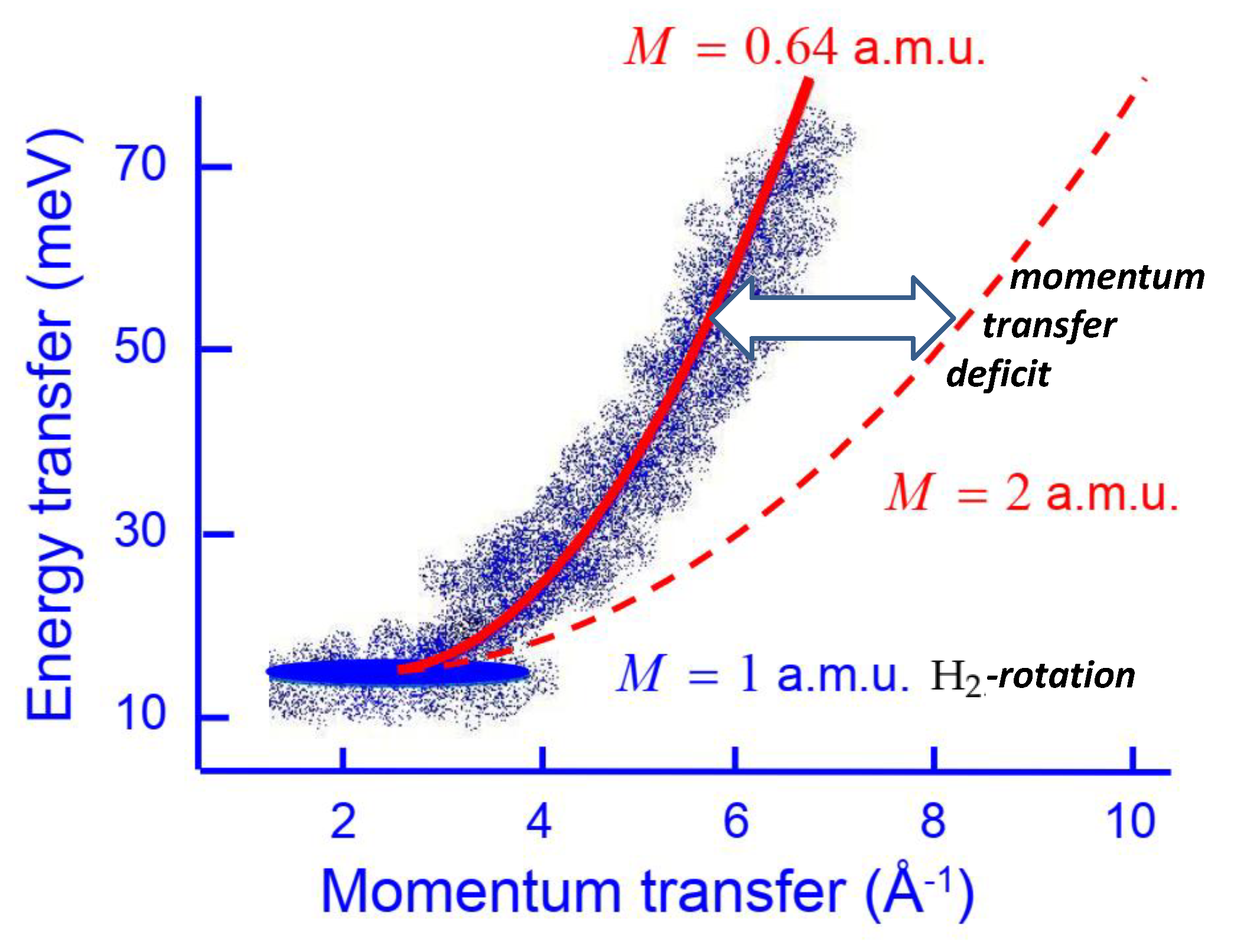
Preprints 74497 g001
Preprints 74497 g002
Figure 2. Experimental NCS results obtained from liquid benzene (C 6 H 6 ). (A) Two time-of-flight (TOF) spectra measured on a liquid sample of C 6 H 6 within an Nb container, at a temperature of 295 K. The solid lines depict the fitted TOF spectra. The peaks’ positions are calculated based on conventional theory. The C- and Nb-recoil peaks overlap at a scattering angle of θ = 65 o . However, at θ = 132 o , the maxima of these two peaks are clearly distinguishable, enabling accurate determination of their intensities. (B) Ratios of neutron cross-sections (equivalent to intensities’ ratios) for H and C obtained experimentally at various scattering angles (detector positions). The error bars solely represent counting statistics. The vertical line at 14.7 signifies the ratio σ H / σ C derived from the tabulated cross-section values for H and C. In clear contrast, the experimentally observed values of I H / I C are approximately 20-30% smaller than the anticipated values based on conventional theory.
Figure 2. Experimental NCS results obtained from liquid benzene (C 6 H 6 ). (A) Two time-of-flight (TOF) spectra measured on a liquid sample of C 6 H 6 within an Nb container, at a temperature of 295 K. The solid lines depict the fitted TOF spectra. The peaks’ positions are calculated based on conventional theory. The C- and Nb-recoil peaks overlap at a scattering angle of θ = 65 o . However, at θ = 132 o , the maxima of these two peaks are clearly distinguishable, enabling accurate determination of their intensities. (B) Ratios of neutron cross-sections (equivalent to intensities’ ratios) for H and C obtained experimentally at various scattering angles (detector positions). The error bars solely represent counting statistics. The vertical line at 14.7 signifies the ratio σ H / σ C derived from the tabulated cross-section values for H and C. In clear contrast, the experimentally observed values of I H / I C are approximately 20-30% smaller than the anticipated values based on conventional theory.
Preprints 74497 g002
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated