Preprint
Article
Attention Mechanism Combined Lstm for Grain Yield Prediction in China Using Multi-Source Satellite Imagery
Altmetrics
Downloads
111
Views
23
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
23 May 2023
Posted:
25 May 2023
You are already at the latest version
Alerts
Abstract
Grain yield prediction affects policy making in various aspects such as agricultural production planning, food security assurance, and adjustment of foreign trade. Accurately predicting grain yield is of great significance in ensuring global food security. This paper is based on the MODIS remote sensing image data products from 2010 to 2020, and adds band information such as vegetation index and temperature to form composite remote sensing data as a data set. Aiming at the lack of models for large-scale forecasting and the need for human intervention in traditional models, this paper proposes a grain production estimation model based on deep learning. First, image cropping and yield mapping techniques are used to process the data to generate training samples. Then the channel and spatial attention mechanism (Convolutional Block Attention Module, CBAM) is added for extracting spatial information in different remote sensing bands to improve the efficiency of the model. Long Short-Term Memory (LSTM) neural networks is also added to obtain feature information in the time dimension. Finally, a national-scale grain yield prediction model is constructed. The proposed model was tested on data from 2018 to 2020 showing an average R2 of 0.940 and an average RMSE of 80,020 tons, indicating that it can predict Chinese grain yield better. The model proposed in this paper extracts grain yield information directly from the composite remote sensing data, and solves the problem of small-scale research and imprecise yield prediction in an end-to-end manner.
Keywords:
Subject: Environmental and Earth Sciences - Sustainable Science and Technology
1. Introduction
In recent years, floods, wind and hail, geological and other natural disasters have occurred many times around the world, and droughts, earthquakes and low-temperature freezes have also occurred to varying degrees. Various natural disasters have caused certain impacts on agricultural production in some areas, resulting in reduced food crop production, and the issue of food security has become a hot topic of concern. At the same time, global environmental climate change and international conflicts can threaten food security [1,2]. To address food security issues, FAO promotes global food security and improved food supply by promoting efficient agricultural technologies, providing knowledge on food nutrition, supporting rural economic development and raising farmers’ incomes. In addition, FAO is committed to promoting fairness and transparency in global food trade to ensure the stability and sustainability of global food markets.
Agriculture plays a crucial role in modern society, and the growing global population further highlights the importance of food security [3]. The primary solution to the food security issue is to accurately predict grain yield. Accurately predicting grain yield in advance to obtain first-hand quantitative data will not only effectively improve our grain production process and trade, but also inform policy makers of potential food shortages, price volatility and trade imbalances. Investors use yield predictions to determine the profitability of agricultural investments, which can affect the overall economic growth of a region or country. Farmers rely on yield predictions to effectively plan their planting and harvest schedules, as well as manage their crop inputs and resources.
Current grain yield prediction methods have several limitations that limit prediction accuracy. First, yield prediction models are usually based on a single piece of historical data. Most studies assess the impact of climate change on agricultural production based on specific regions and do not consider the impact of human economic behavior [4]. Second, the accuracy of yield prediction models may be affected by data quality and availability, and different data may produce different predictions. Third, yield prediction models usually do not take into account the complex interactions between certain factors and crop growth, including soil conditions, rainfall, temperature, solar radiation, and human activities.
Traditional models often use statistical models and plant growth models for yield prediction, which can be effective in predicting grain yield to a certain extent. However, grain yield is often affected by the spatial distribution and temporal variation of the growing environment, and traditional models lack spatial and temporal information of plant growth, which leads to poor prediction accuracy and lack of robustness [5]. At the same time, traditional methods require field surveys, resulting in high time and material costs [6], and can lead to problems of small yield estimation areas and poor timeliness. In contrast, with the development of technology, remote sensing technology is widely used for grain yield prediction due to its advantages of good timeliness and low cost, and its ability to effectively cope with the problems of complex terrain, scattered cultivated land and diverse crops [7]. Therefore, some researchers have combined remote sensing data and meteorological data to establish grain yield prediction models [8], and some studies have combined remote sensing data with plant growth models for yield prediction [9,10], and these studies have demonstrated that models using remote sensing technology can be a good solution to the previous problems of difficult data statistics, high labor consumption and low accuracy. Also, since remote sensing images have spatial information, the use of these data can be effective in making more accurate predictions using spatiotemporal information [11], and it has been shown [12] that the use of traditional models is laborious, error-prone, costly, and inefficient in the study of maize yield prediction in Africa. Tuvdendorj et al. [13] chose to use NDWI, VSDI, and NDVI to develop regression prediction yield models for spring wheat yields in Selenge and Darkhan Provinces of Mongolia. As a comparison, using remote sensing images to predict grain yield is a more cost effective option.
With the development of computer technology, a large number of studies have started to use machine learning methods to build models due to its advantage of being able to handle complex agricultural data. Some researchers have used machine learning to build a low-cost grain yield prediction model [14] and found that it can effectively improve the prediction efficiency. Yang et al. [15] used multispectral remote sensing data collected by an unmanned aerial vehicle (UAV) in a major rice growing region in southern China and applied a neural network model to predict rice yield, achieving superior results compared to traditional regression models. Meroni et al. [16] used small data samples to train neural networks to predict grain yield, and Paudel et al. [17] combined agronomic principles with machine learning to build a large-scale grain yield prediction model using a modular approach so that the model could be used for different crop yield prediction in different countries, and demonstrated experimentally that the performance of the machine learning model would be better with the addition of new data sources. Using science, technology and knowledge and experience to achieve rational use and planning of resources can meet people’s survival needs and reduce the waste of resources to achieve sustainable development of resources.
However, most of the existing data are used for single crop yield prediction at the county or municipal scale using Normalized Difference Vegetation Index (NDVI), Enhanced Vegetation Index (EVI), etc. [18], lacking multiple sources of data and holistic prediction of multiple crops. And we also note that the existing machine learning methods usually process the relevant indices (e.g. NDVI, EVI, etc.) of a region after averaging [19] or sampling [20] (selecting the maximum or minimum values) and then use them as input data for the model, neglecting the study of subtle features. Therefore, in order to improve the prediction of grain yield, this paper proposes the use of hybrid neural networks for prediction of composite data. The contribution of this paper is as follows.
- A multi-source dataset was created containing grain yield and remote sensing images, temperature and vegetation index with spatial and temporal information.
- Using the cropping and mapping method, the remote sensing image of each province is cropped into size image blocks, and the yield weights of each block are calculated and mapped through the land use classification mask, effectively combining multiple information for large scale prediction.
- The incorporation of spatial and channel attention mechanisms with long short-term memory neural networks is proposed for learning the trend characteristics of different categories of plant indices and indices in crop growth in composite data as a way to improve the accuracy of model predictions.
2. Materials
2.1. Study area and Data acquisition
The study area selected for this paper is the People’s Republic of China, and the data collection comes from 31 provincial administrative regions. The acquired remote sensing image data were obtained from NASA’s Earth Science Data and Information System (ESDIS), among which the data products used were MOD11A2, MOD13A1 and MOD15A2H, and the detailed information is shown in Table 1. The data are chosen to span the period from 2010 to 2020, a total of 11 years.
Among them, the land use classification information of China is selected from the Resource Environment Science and Data Center, Institute of Geographical Sciences and Resources, Chinese Academy of Sciences.
In addition, the grain crop production data for the study area are obtained from the China Statistical Yearbook for 2011-2021. The grain crop production data include three cereal crops: rice, wheat, and maize, in addition to beans and potatoes. These crops have different growth cycles and harvesting times are scattered among different months, so our training sample contains monthly data in order to improve predictive model performance.
2.2. Data Processing
Depending on the study area and time, we selected data from the Sinusoidal tile grid of the MODIS product (Figure 1). Because the data provided by MODIS is not uniform in resolution in time and spatial, we used the GDAL library for batch processing while using ArcGIS software. First, we extracted the data layers we needed from the downloaded raw files in HDF format and saved them as raster files in TIF format. The scattered rasters that have undergone the mosaic operation are also put together, and the MOD11A2 data are individually resampled to a spatial resolution of 500 m so that all data have the same resolution. Then all images were uniformly reprojected to China Geodetic Coordinate System 2000 to facilitate subsequent experiments. Next we processed the data according to the Valid Range and Scale Factor provided by ESDIS. Finally, all data are cropped according to the provincial administrative divisions of China, and all data are synthesized on a monthly basis at a temporal resolution (Figure 2) to make the time series consistent. In order to reduce useless information interference and increase effective data density, we used land use classification masks to extract data on the location of farmland distribution. Note that all data are normalized by Min-Max Normalization.
2.3. GYP Dataset
China’s provincial administrative regions are divided according to geographical conditions, ethnic distribution, historical customs and other factors, and the area as well as the shape varies greatly among provinces. In order to enable the model to better learn the relational features among them, we use the image cropping method to ensure the resolution of each map is of the same size. We cropped the remote sensing image of each province into size image blocks, and used the fill 0 value for the image boundary that cannot be completely cropped.
The total grain production of each province in each year was queried from the China Statistical Yearbook, and we used a case-by-case calculation method to map the total production to each image block. First, the land use classification masks were used as the total area of farmland. The percentage of farmland area in each plot relative to the total farmland area in the corresponding province is then calculated as the production weight of the current image block. Finally, the production of the corresponding image block is calculated based on the calculated weights:
where represents the yield corresponding to each image block, S represents the total farmland area, represents the area of farmland in each image block, and O represents the total yield.
We cropped all the remote sensing images of different bands to the same size, and then fused the six bands of data together, with each band as an image channel. In the time dimension, since the remote sensing images have been previously synthesized to a monthly resolution, we synthesized the remote sensing images together for every 12 months. Finally, a matrix was combined as one of the samples, the shape of which is .
Since cropping the images produces many pure black images (all values are 0), after removing these images, a total of 22,303 valid images are obtained. Among them, 16219 images from 2010-2017 were used as the training set and 6084 from 2018 to 2020 were used as the test set. The final grain yield dataset was generated and named as GYP.
3. Methods
3.1. Overall flow of the model
Prediction has been a more complex matter due to the number of factors that affect grain yield. Therefore, this paper uses a model of deep learning to perform grain prediction. The model uses Convolutional Neural Networks (CNN) as the basic structure, and then incorporates spatial and channel attention mechanisms to extract features effectively and autonomously. Also, we incorporate a Long Short-Term Memory network to enhance the sensitivity of the model to the temporal features of grain yield. Finally, we use the composite remote sensing data from 2010 to 2017 as the training sample to generate the grain yield prediction model (Figure 3).
3.2. CNN-LSTM model with attention mechanism module embedded
The proposed model in this paper is based on Convolutional Neural Networks, while introducing attention mechanism and combining with Recurrent neural network (RNN) to form a hybrid neural network model, and the overall network structure is shown in Figure 4. Our neural network input layer is designed as a matrix of based on our samples, where B represents the batch size, 12 represents the time series, 6 represents the band, and 128 is the height and width, respectively. Before going through the convolutional neural network layers, we reshape the matrix to the shape of . After that by three layers of convolution operation and average pooling operation. The number of convolutional kernels in the convolutional layer is 12, 8 and 4, respectively, and the convolutional kernel size is with a step size of 1. Each convolutional layer is followed by an average pooling layer with a kernel size of and a step size of 2. A LeakyReLU function activation operation is also performed after each convolutional layer. We add Convolutional Block Attention Module (CBAM) after the first and third convolutional layers respectively. Then comes the LSTM layer with 128 hidden nodes in each layer. Finally, a fully connected layer and an additional Dropout layer is used in the fully connected layer.
3.2.1. Attention mechanism module
The attention mechanism is a technique used in artificial neural networks to allow the model to selectively focus on certain input features or patterns while processing data. This can be useful in situations where the input data is complex or large, and the model needs to identify important patterns or features that are relevant to the task at hand.
In recent years, in order to further expand the differences between features, research scholars have introduced attention mechanisms in some deep learning models [21,22]. The attention mechanism highlights more representative features by assigning different weighting coefficients, similar to the brain signal processing mechanism specific to human vision, and can be used to obtain target areas that need to be focused on by quickly scanning the entire image [23,24,25,26]. Therefore, to effectively acquire data in composite images, we use CBAM proposed by Woo et al. [27], which combines channel attention and spatial attention in a lightweight way to embed into the model for feature extraction. The CBAM embedding method is shown in the Figure 5.
The overall structure of channel attention is shown in Figure 6. The input data are processed by Max Pooling and Average Pooling, and then sent to Multilayer Perceptron (MLP) for calculation to obtain the transformation results. Then the two sets of channel features obtained after the transformation are performed element-wise addition operation, and finally the is obtained by activation with Sigmod, and its formula is shown in Equation 2. When is calculated using channel attention, the obtained from channel attention is performed element-wise multiplication operation with the original input feature map F before sending it to spatial attention to obtain , and the calculation formula is shown in Equation 3.
where denotes the Sigmoid function, , and . Note that the MLP weights, and , are shared for both inputs and the ReLU activation function is followed by .
After the channel attention is calculated, the spatial attention mechanism (Figure 7) will first perform Max Pooling and Average Pooling operations on the input according to the channel, and then the obtained feature map will be subjected to the concatenation operation on the channel. After completing the channel concatenation, a convolution is performed to reduce the dimensionality. Finally, is obtained by using the Sigmoid activation function, and the calculation formula is shown in Equation 4.
where ⊗ denotes element-wise multiplication.
where denotes the Sigmoid function and represents a convolution operation with the filter size of .
Finally, use Equations 3 and 4 to obtain the final feature map :
where ⊗ denotes element-wise multiplication.
In the grain yield prediction model, the attention mechanism is used to extract spatial information from different remote sensing bands in order to make more accurate predictions. The attention mechanism is implemented by adding additional layers to the neural network model, which is trained to learn to focus on relevant features in the input data. The attention mechanism can improve the performance of the model by helping it to better capture and utilize relevant patterns or features in the data, leading to more accurate predictions.
3.2.2. Long Short-Term Memory
LSTM network is a recurrent neural network (RNN) first proposed in 1997 by Hochreiter et al. [28]. RNN cannot learn relevant information about the input data when the input gap is large and cannot handle very long input sequences, while LSTM can deal well with long-term dependencies by introducing gate functions in the cell structure [29,30], such as the effect of changing processes of grain crops on yield throughout the growth cycle. So, to better obtain the features in the temporal dimension, the LSTM network is introduced..
The cell structure of LSTM network is shown in Figure 8. Compared with the previous recurrent neural network, LSTM adds the concept of Cell state, while LSTM mainly consists of three gates, namely Forget Gate, Input Gate and Output Gate.
Among them, the Forget Gate is calculated as shown in Equation 6, which is mainly used to decide the retention or forgetting of information. The hidden information of the previous layer and the input information of the current layer will be sent into the Sigmoid function for processing at the same time. The processing result will be between . The closer it is to 1, the more it should be retained, and vice versa, it will be forgotten.
And the equation of Input Gate is shown in Equations 7 and 8, which is mainly used to update the information of the current layer. The hidden information of the previous layer and the input information of the current layer will be sent into the Sigmoid function for processing at the same time. The processing result will be between . The closer it is to 1, the more important it will be. Next, the information from the hidden state of the previous layer and the current input is also passed into the tanh function to create a new candidate vector. Finally, the output value of Sigmoid is multiplied by the output value of tanh. The output value of Sigmoid will determine which information in the output value of tanh is important and needs to be retained.
The Output Gate, shown in Equations 9, 10 and 11, is used to determine the value of the next hidden state, which contains the previously inputted information. The hidden information from the previous layer and the information from the current layer input are simultaneously sent to the Sigmoid function for processing. Then the newly obtained cell state is sent to the tanh function. Finally, the output of tanh is multiplied with the output of Sigmoid to determine the information that the hidden state should contain. The hidden state is then used as the output of the current cell, and the new cell state and the new hidden state are sent to the next time step.
3.2.3. Leaky ReLU
Choosing the right activation function can significantly improve the performance of neural networks. Deep learning uses gradient descent algorithms to train models, but the training results can often fall into local minima rather than global optimal solutions [31,32,33]. To avoid this problem, this paper has chosen to use the Leaky ReLU proposed by Mass et al. [34], which is defined as:
The advantage of using Leaky ReLU is that a gradient is also obtained for the part of the input that is less than zero, so that the problem of inactive units is avoided.
3.2.4. Loss Funtion
In regression prediction problems, we often use Mean Absolute Error (MAE, Equation 13) to measure the closeness between the model prediction and the true value, and MAE trains the neural network to converge quickly.
where represents the actual yield corresponding to the sample, represents the predicted yield of the model, and n is the number of samples.
3.3. Model accuracy evaluation metrics
In this study we used Root Mean Square Error (RMSE, Equation 14) and Coefficient of determination (denoted as , Equation 15) to evaluate the effectiveness of the model in predicting yield.
where represents the actual yield of the corresponding sample, is the actual average yield, represents the yield predicted by the model, and n is the total number of samples.
4. Results
4.1. Experimental setting and result analysis
The model is built using the PyTorch deep learning framework and trained on an RTX A5000 24G graphics card. The optimizer used for the experiments is Adam, and the initial learning rate is set to 0.01, and when the epoch reaches 5 and 10, the learning rate is dynamically adjusted, and the multiplicative factor of learning rate decay is set to 0.1. Also, our experiments use Dropout and set the Dropout probability to 0.5.
The results of the tests conducted after training shows that our model could simulate the grain yield of most provinces well with high overall accuracy (=0.942, RMSE=80,020 tons), as shown in Table 2. As shown in Figure 9, this is a scatter plot of the actual grain yield versus the predicted yield for the test years.
Although our model performs well in most provinces, its performance is relatively poor in some provinces including Bejing, Guangxi, Tianjin and Shanghai. In these four regions, our model is unable to simulate the grain yield well, and it does not fit well during the training process, so the statistics of these four provinces are excluded from all the results of the experiment. Overall, the model can obtain effective yield features directly from remote sensing images in an end-to-end form and predict grain yield at a large scale.
The convergence of the model is shown in Figure 10. From the figure, we can see that the curves eventually all tend to be smooth, but Yunnan, Qinghai, Ningxia and other regions show abnormal fluctuations in the loss curves during the model training. Through observation and analysis, we found that the fluctuation of the learning rate may result in these fluctuations. The learning rate is a parameter that controls the update rate of the model parameters, and when the learning rate changes, the update rate of the model parameters will also change, and this change may lead to a turning point in the training of the model. Because our learning rate automatically declines through adjustment after a period of training epoch, some fluctuations occur during the training process, and eventually the loss values all tend to converge. Dynamically adjusting the learning rate can adjust the learning rate in real time according to the performance of the model, which enables the model to obtain better gradients during training, thus improving the accuracy of the model, accelerating the convergence of the model, and enabling the model to obtain better generalization on both training and test data.
4.2. Projected results for different provinces
China is a vast country with great differences in topography and climate among provinces, and water resources are unevenly distributed [35]. In order to take full advantage of the favorable conditions in each region to increase the total amount of grain yield. In different regions and different seasons, farmers choose to grow different grain crops. These include summer grain, early rice and autumn grain, cereals, legumes and potatoes.
To verify the robustness of our proposed neural network model for predicting multiple grain crops in different regions, we calculated the yield prediction accuracy of different provinces separately (Figure 11). The results in the figure show that in some provinces the yield estimation accuracy is low, but in most cases the accuracy is satisfactory. For example, Guangdong has the highest accuracy with of 0.989 and RMSE of 18,040 tons, and the lowest is in Chongqing with of 0.815 and RMSE of 132,370 tons. This proves that our proposed neural network model has good robustness.
The predicted and actual yields for 2018-2020 are shown in Figure 12, Table 3, from which it can be visualized that in some provinces with large grain production, such as Heilongjiang, Henan and Shandong, the model correctly predicts the yield trend, but there is a gap between the predicted and actual yields. There are many potential factors that could influence the accuracy of a grain yield prediction model in different provinces, including variations in local climate, soil conditions, and agricultural practices. The model’s ability to capture these differences and accurately predict grain yield may depend on the quality and quantity of data available for training and testing, as well as the specific techniques and algorithms used in the model. It is also possible that the model’s performance may be influenced by other factors, such as the availability and accuracy of ground real data for validation, or the specific crops and varieties grown in different provinces.
During the 2018-2020 period, our prediction model also shows some fluctuations in predicted values, in addition to provinces with relatively high or low actual grain yields. This may be due to the structural reform of the supply-side of Chinese agriculture, which aims to improve the quality and efficiency of grain production by adjusting the cropping structure. Different provinces can adjust the acreage of different crops according to their local geographical and climatic factors. However, the land classification masks used in our model are fixed and may not be able to fully take into account these variations, leading to errors in the processed remote sensing images and eventually the fluctuations in the prediction results.
4.3. Ablation experiment
To verify the validity of each module in this model, ablation experiments are conducted. Tests are also conducted separately for each year to accurately test the predictive ability of the present model. As can be seen from Table 4, our average is 0.940 and the average RMSE is 80,020 tons on the test data from 2018 to 2020. Compared to the CNN network, our model predicts an improved of 0.089 and a reduced RMSE of 39,020 tons, which is a significant improvement in the metrics. Meanwhile, the inclusion of LSTM is better compared to the inclusion of CBAM, but the difference between them is not significant.
5. Discussion
In recent years, the concept of sustainable development has been widely accepted and implemented in many fields. In particular, many countries are actively addressing food security, climate change, environmental protection and resource use. However, the challenges to the development of sustainable agriculture are also significant. Global food security has deteriorated in the past few years. Climate change, natural disasters, market volatility, and policy instability have all contributed to high food prices and increased food insecurity. In addition, global population growth and urbanization have exacerbated food security issues. Despite the enormous challenges, many countries and organizations are taking steps to address these issues. Only global cooperation and joint efforts can ensure globally sustainable development and food security.
Because different food crops have different growth cycles, some regions often grow crops that span two years. For example, in the North China Plain, winter wheat is planted from October to December of each year and only matures for harvest in the middle of the fol-lowing year. However, our data samples are constructed based on each calendar year rather than on the crop growth cycle. Still, the model shows good accuracy for yield prediction, which we attribute to the fact that the actual yield data in the Statistical Yearbook are also based on calendar years. In subsequent research work, we could change the time series of the data sample to two or even three years instead of the currently used one year. This includes data for the complete cycle of each crop from sowing to harvest and may give us more accurate results. In addition, some of the remote sensing data variables selected in our study (Table 1) are selected empirically and based on the summaries of previous studies by some scholars, and their relevance to grain yield is not explored in depth, but this highlights the effectiveness of neural networks in end-to-end problem studies.
The attention mechanism in a neural network model allows it to selectively focus on certain input features or patterns, which can be particularly useful in situations where the input data are complex or large. In the context of a grain yield estimation model, the attention mechanism can be used to improve the model’s performance by helping it to better capture and utilize relevant patterns or features in the data, such as vegetation index and temperature, that are known to influence grain yield. For example, the vegetation index, which is a measure of the density and health of vegetation, is an important factor in grain yield prediction. By using the attention mechanism to focus on this feature, the model can more accurately capture the relationship between vegetation index and grain yield, leading to more accurate predictions. Similarly, temperature is also known to affect grain yield, and the attention mechanism can be used to focus on temperature data to improve the model’s ability to predict grain yield based on temperature. Overall, the attention mechanism can improve the performance of a grain yield estimation model by allowing it to more accurately capture and utilize relevant patterns or features in the data.
The fluctuations in prediction values that we observed may be due to the use of an inappropriate land classification mask for the corresponding year. Initially, we planned to use the land classification mask from the Moderate Resolution Imaging Spectroradiometer (MODIS) MCD12Q1 product, but this product has relatively large errors in the distribution of grain crops in China. In comparison, the land use mask from the Institute of Geographic Sciences and Natural Resources Research of the Chinese Academy of Sciences has been manually verified and is more representative of actual conditions, but may not be available annually due to the large workload involved in its production.
In our study, the attention mechanism shows strong performance in learning crop yield features, and we could potentially apply the attention mechanism to the learning of farmland distribution features and further reduction of the errors. By focusing on relevant features, the attention mechanism can help the model to more accurately capture and utilize the patterns or characteristics that influence the prediction task. In this case, applying the attention mechanism to the learning of farmland distribution features could potentially help the model to better capture the changes in planting structures and land use that may have contributed to the observed fluctuations in prediction values.
6. Conclusions
In order to make grain yield prediction less costly and improve the accuracy of grain yield prediction at the same time, a hybrid neural network grain yield prediction model is proposed in this paper. The underlying data used in the model are from MODIS satellite products, and we combine information from different bands into composite remote sensing image data to provide as many training features as possible for the model. Then, based on the convolutional network as the base structure, we use the attention of channel and spatial mixing to enhance the extraction of vegetation index and temperature associated features. Finally, we use LSTM to process the data of each month to obtain as much information as possible in the temporal dimension. Through experiments, we find that the proposed model in this paper has an of 0.940 and an RMSE of 80,020 tons for grain yield prediction in China, which is a large improvement in yield prediction compared with the traditional convolutional network. We also calculate the accuracy of grain yield prediction for different provinces one by one, and Guangdong province has the most accurate grain yield prediction with of 0.989 and RMSE of 18,040 tons, while Chongqing city has the worst prediction accuracy with of 0.815 and RMSE of 132,370 tons. Overall, the model is more accurate in predicting Chinese grain yield in an end-to-end manner on a large scale, providing an effective technical method for agricultural testing and grain yield estimation.
Author Contributions
Conceptualization, X.J.; Methodology, F.L. and X.J.; Data curation, F.L.; writing—original draft preparation, F.L.; writing—review and editing, X.J. and Z.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key R&D Program of China, grant numbers: 2022YFD2200505 and 2018YFB0703900.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Raw remote sensing data can be found at https://earthdata.nasa.gov/esdis. The Chinese land use classification masks can be found at https://www.resdc.cn/Datalist1.aspx?FieldTyepID=1,3.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hendriks, S.L.; Montgomery, H.; Benton, T.; Badiane, O.; de la Mata, G.C.; Fanzo, J.; Guinto, R.R.; Soussana, J.F. Global Environmental Climate Change, Covid-19, and Conflict Threaten Food Security and Nutrition. BMJ 2022, 378, e071534. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Zhang, Z.; Liu, Y. Spatial Shifts in Grain Production Increases in China and Implications for Food Security. Land Use Policy 2018, 74, 204–213. [Google Scholar] [CrossRef]
- Khan, H.R.; Gillani, Z.; Jamal, M.H.; Athar, A.; Chaudhry, M.T.; Chao, H.; He, Y.; Chen, M. Early Identification of Crop Type for Smallholder Farming Systems Using Deep Learning on Time-Series Sentinel-2 Imagery. Sensors 2023, 23, 1779. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Liu, H.; Ma, R. Assessment and Prediction of Grain Production Considering Climate Change and Air Pollution in China. Sustainability 2022, 14, 9088. [Google Scholar] [CrossRef]
- Jaynes, D.B.; Kaspar, T.C.; Colvin, T.S.; James, D.E. Cluster Analysis of Spatiotemporal Corn Yield Patterns in an Iowa Field. Agronomy Journal 2003, 95, 574–586. [Google Scholar] [CrossRef]
- Espinosa-Herrera, J.M.; Macedo-Cruz, A.; Fernández-Reynoso, D.S.; Flores-Magdaleno, H.; Fernández-Ordoñez, Y.M.; Soria-Ruíz, J. Monitoring and Identification of Agricultural Crops through Multitemporal Analysis of Optical Images and Machine Learning Algorithms. Sensors 2022, 22, 6106. [Google Scholar] [CrossRef]
- Hara, P.; Piekutowska, M.; Niedbała, G. Selection of Independent Variables for Crop Yield Prediction Using Artificial Neural Network Models with Remote Sensing Data. Land 2021, 10, 609. [Google Scholar] [CrossRef]
- Kern, A.; Barcza, Z.; Marjanović, H.; Árendás, T.; Fodor, N.; Bónis, P.; Bognár, P.; Lichtenberger, J. Statistical Modelling of Crop Yield in Central Europe Using Climate Data and Remote Sensing Vegetation Indices. Agricultural and Forest Meteorology 2018, 260–261, 300–320. [Google Scholar] [CrossRef]
- Zhuo, W.; Huang, J.; Li, L.; Zhang, X.; Ma, H.; Gao, X.; Huang, H.; Xu, B.; Xiao, X. Assimilating Soil Moisture Retrieved from Sentinel-1 and Sentinel-2 Data into WOFOST Model to Improve Winter Wheat Yield Estimation. Remote Sensing 2019, 11, 1618. [Google Scholar] [CrossRef]
- Delécolle, R.; Maas, S.J.; Guérif, M.; Baret, F. Remote Sensing and Crop Production Models: Present Trends. ISPRS Journal of Photogrammetry and Remote Sensing 1992, 47, 145–161. [Google Scholar] [CrossRef]
- Moriondo, M.; Maselli, F.; Bindi, M. A Simple Model of Regional Wheat Yield Based on NDVI Data. European Journal of Agronomy 2007, 26, 266–274. [Google Scholar] [CrossRef]
- Chivasa, W.; Mutanga, O.; Biradar, C. Application of Remote Sensing in Estimating Maize Grain Yield in Heterogeneous African Agricultural Landscapes: A Review. International Journal of Remote Sensing 2017, 38, 6816–6845. [Google Scholar] [CrossRef]
- Tuvdendorj, B.; Wu, B.; Zeng, H.; Batdelger, G.; Nanzad, L. Determination of Appropriate Remote Sensing Indices for Spring Wheat Yield Estimation in Mongolia. Remote Sensing 2019, 11. [Google Scholar] [CrossRef]
- You, J.; Li, X.; Low, M.; Lobell, D.; Ermon, S. Deep Gaussian Process for Crop Yield Prediction Based on Remote Sensing Data. Proceedings of the AAAI Conference on Artificial Intelligence 2017, 31. [Google Scholar] [CrossRef]
- Yang, Q.; Shi, L.; Han, J.; Zha, Y.; Zhu, P. Deep Convolutional Neural Networks for Rice Grain Yield Estimation at the Ripening Stage Using UAV-based Remotely Sensed Images. Field Crops Research 2019, 235, 142–153. [Google Scholar] [CrossRef]
- Meroni, M.; Waldner, F.; Seguini, L.; Kerdiles, H.; Rembold, F. Yield Forecasting with Machine Learning and Small Data: What Gains for Grains? Agricultural and Forest Meteorology 2021, 308–309, 108555. [Google Scholar] [CrossRef]
- Paudel, D.; Boogaard, H.; de Wit, A.; Janssen, S.; Osinga, S.; Pylianidis, C.; Athanasiadis, I.N. Machine Learning for Large-Scale Crop Yield Forecasting. Agricultural Systems 2021, 187, 103016. [Google Scholar] [CrossRef]
- Kouadio, L.; Newlands, N.K.; Davidson, A.; Zhang, Y.; Chipanshi, A. Assessing the Performance of MODIS NDVI and EVI for Seasonal Crop Yield Forecasting at the Ecodistrict Scale. Remote Sensing 2014, 6, 10193–10214. [Google Scholar] [CrossRef]
- Leroux, L.; Castets, M.; Baron, C.; Escorihuela, M.J.; Bégué, A.; Lo Seen, D. Maize Yield Estimation in West Africa from Crop Process-Induced Combinations of Multi-Domain Remote Sensing Indices. European Journal of Agronomy 2019, 108, 11–26. [Google Scholar] [CrossRef]
- Tian, H.; Wang, P.; Tansey, K.; Zhang, S.; Zhang, J.; Li, H. An IPSO-BP Neural Network for Estimating Wheat Yield Using Two Remotely Sensed Variables in the Guanzhong Plain, PR China. Computers and Electronics in Agriculture 2020, 169, 105180. [Google Scholar] [CrossRef]
- Ji, J.; Zhang, T.; Jiang, L.; Zhong, W.; Xiong, H. Combining Multilevel Features for Remote Sensing Image Scene Classification With Attention Model. IEEE Geoscience and Remote Sensing Letters 2020, 17, 1647–1651. [Google Scholar] [CrossRef]
- Cai, W.; Wei, Z. Remote Sensing Image Classification Based on a Cross-Attention Mechanism and Graph Convolution. IEEE Geoscience and Remote Sensing Letters 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Fukushima, K. Neocognitron: A Self-Organizing Neural Network Model for a Mechanism of Pattern Recognition Unaffected by Shift in Position. Biological Cybernetics 1980, 36, 193–202. [Google Scholar] [CrossRef]
- Mou, L.; Bruzzone, L.; Zhu, X.X. Learning Spectral-Spatial-Temporal Features via a Recurrent Convolutional Neural Network for Change Detection in Multispectral Imagery. IEEE Transactions on Geoscience and Remote Sensing 2019, 57, 924–935. [Google Scholar] [CrossRef]
- Kattenborn, T.; Leitloff, J.; Schiefer, F.; Hinz, S. Review on Convolutional Neural Networks (CNN) in Vegetation Remote Sensing. ISPRS Journal of Photogrammetry and Remote Sensing 2021, 173, 24–49. [Google Scholar] [CrossRef]
- Niu, Z.; Zhong, G.; Yu, H. A Review on the Attention Mechanism of Deep Learning. Neurocomputing 2021, 452, 48–62. [Google Scholar] [CrossRef]
- Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. CBAM: Convolutional Block Attention Module. Proceedings of the European Conference on Computer Vision (ECCV), 2018, pp. 3–19.
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Computation 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Yu, Y.; Si, X.; Hu, C.; Zhang, J. A Review of Recurrent Neural Networks: LSTM Cells and Network Architectures. Neural Computation 2019, 31, 1235–1270. [Google Scholar] [CrossRef]
- Smagulova, K.; James, A.P. A Survey on LSTM Memristive Neural Network Architectures and Applications. The European Physical Journal Special Topics 2019, 228, 2313–2324. [Google Scholar] [CrossRef]
- Hara, K.; Saito, D.; Shouno, H. Analysis of Function of Rectified Linear Unit Used in Deep Learning. 2015 International Joint Conference on Neural Networks (IJCNN), 2015, pp. 1–8. [CrossRef]
- Zeiler, M.; Ranzato, M.; Monga, R.; Mao, M.; Yang, K.; Le, Q.; Nguyen, P.; Senior, A.; Vanhoucke, V.; Dean, J.; Hinton, G. On Rectified Linear Units for Speech Processing. 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, 2013, pp. 3517–3521. [CrossRef]
- Gu, J.; Wang, Z.; Kuen, J.; Ma, L.; Shahroudy, A.; Shuai, B.; Liu, T.; Wang, X.; Wang, G.; Cai, J.; Chen, T. Recent Advances in Convolutional Neural Networks. Pattern Recognition 2018, 77, 354–377. [Google Scholar] [CrossRef]
- Maas, A.L.; Hannun, A.Y.; Ng, A.Y. Rectifier Nonlinearities Improve Neural Network Acoustic Models. Proc. Icml. Atlanta, Georgia, USA, 2013, Vol. 30, p. 3.
- Yu, A.; Cai, E.; Yang, M.; Li, Z. An Analysis of Water Use Efficiency of Staple Grain Productions in China: Based on the Crop Water Footprints at Provincial Level. Sustainability 2022, 14, 6682. [Google Scholar] [CrossRef]
Figure 1.
MODIS Sinusoidal tile grid corresponding to the study area.
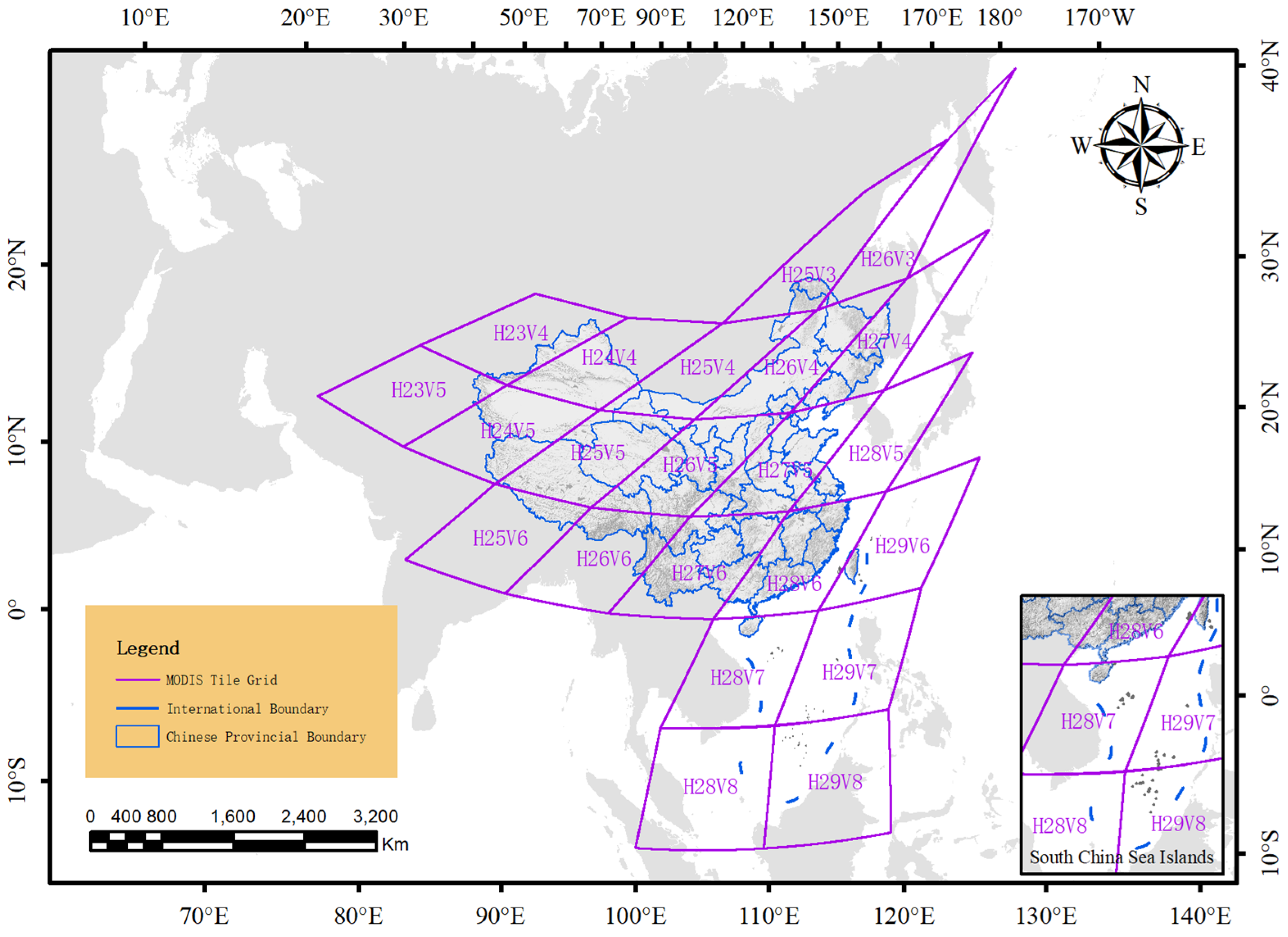
Figure 2.
Remote sensing data processing flow. Where T represents the time, C represents the channel, H represents the height of the remote sensing image, and W represents the width of the remote sensing image.
Figure 2.
Remote sensing data processing flow. Where T represents the time, C represents the channel, H represents the height of the remote sensing image, and W represents the width of the remote sensing image.
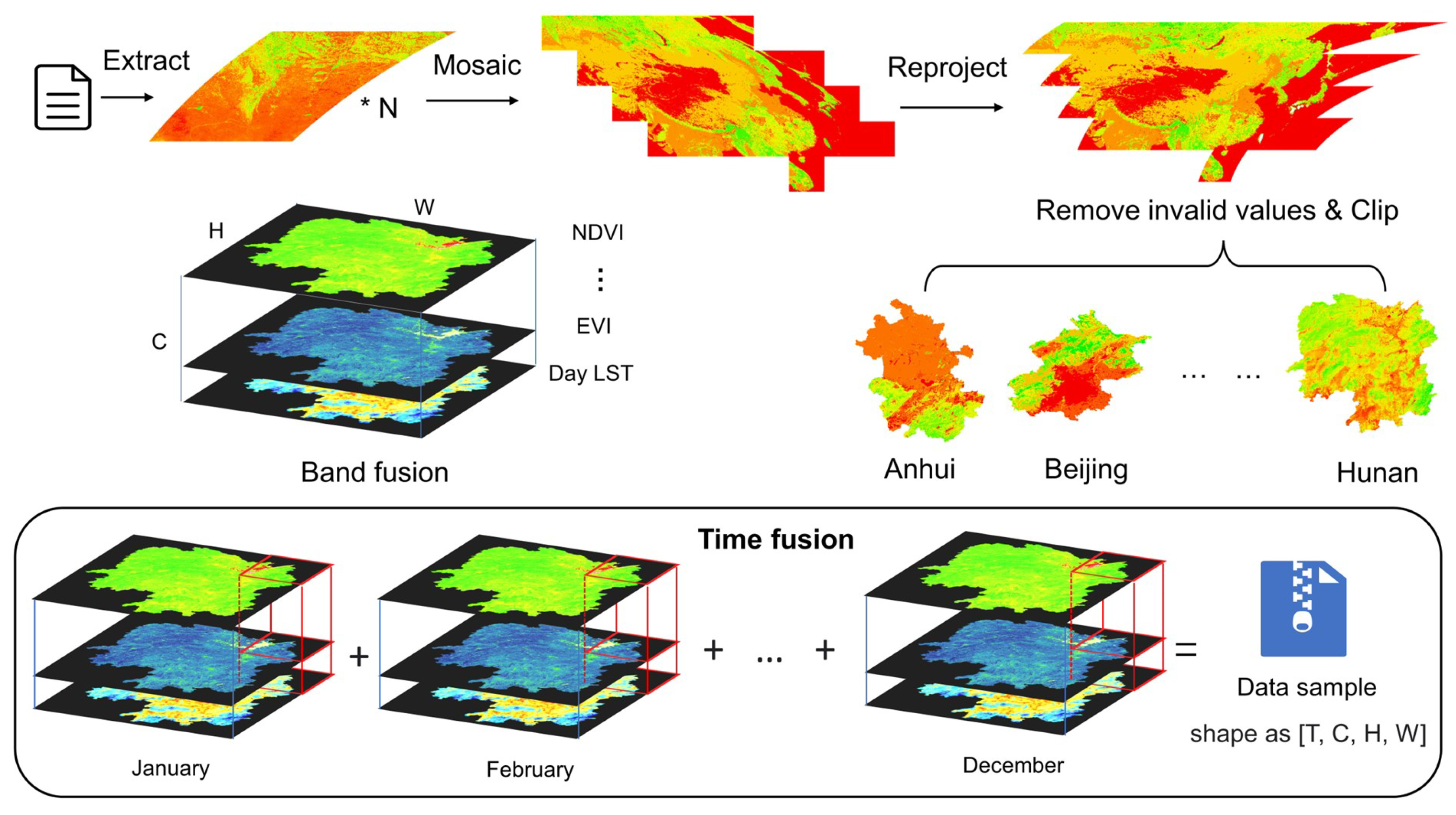
Figure 3.
Remote sensing data processing flow.
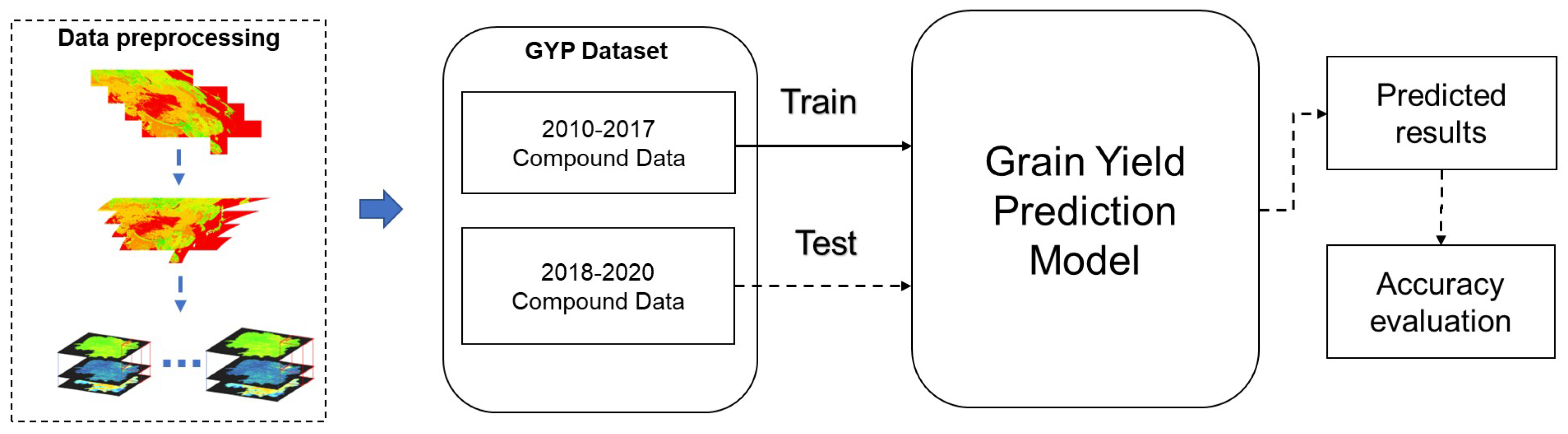
Figure 4.
Channel Attention Module Structure.
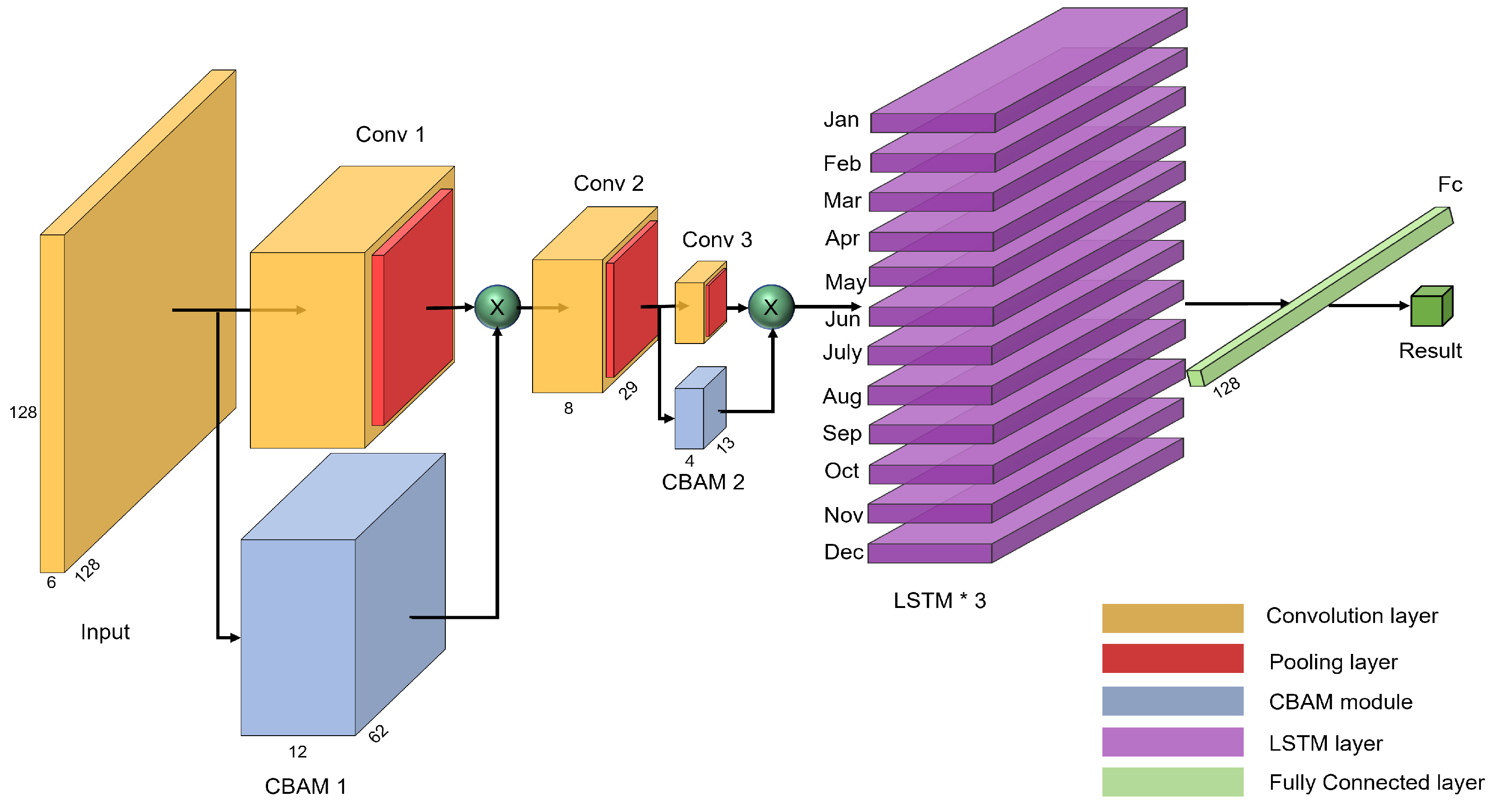
Figure 5.
Schematic diagram of CBAM.
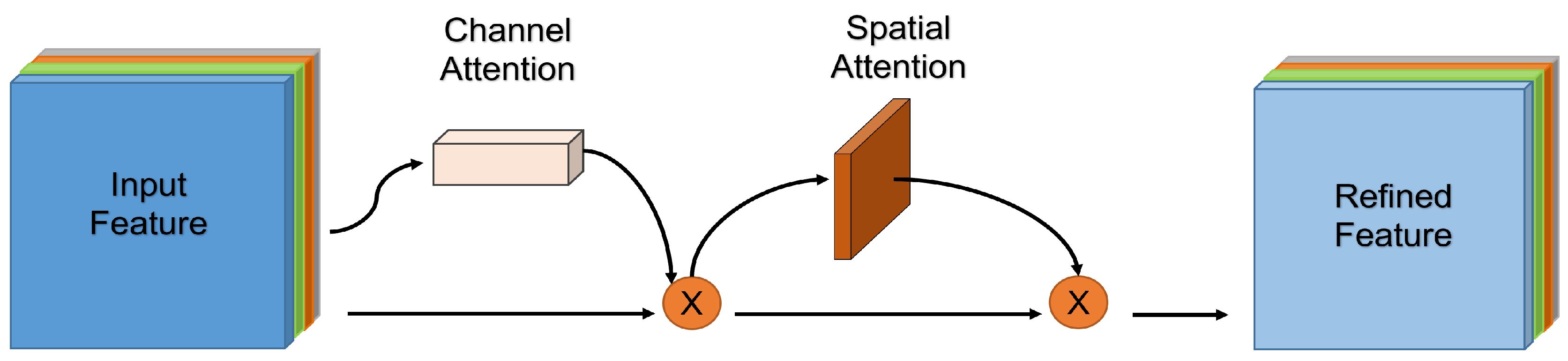
Figure 6.
Channel Attention Module Structure.
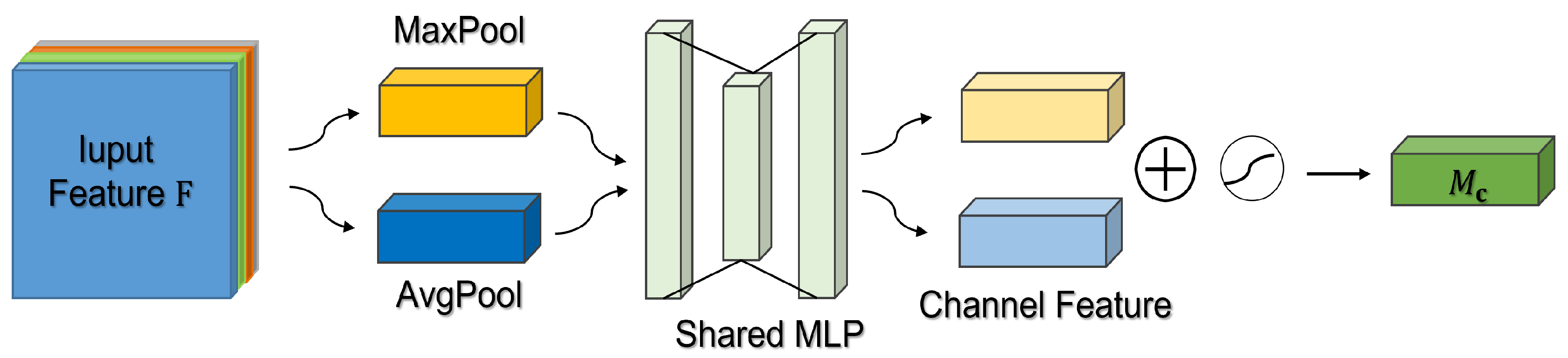
Figure 7.
Spatial Attention Module Structure.
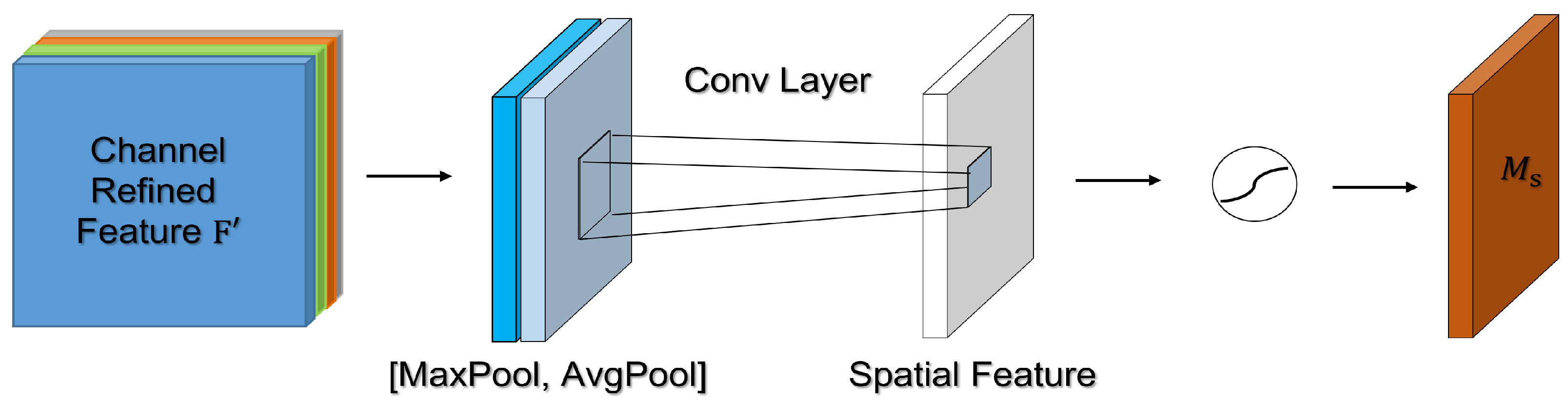
Figure 8.
Cell structure of LSTM.
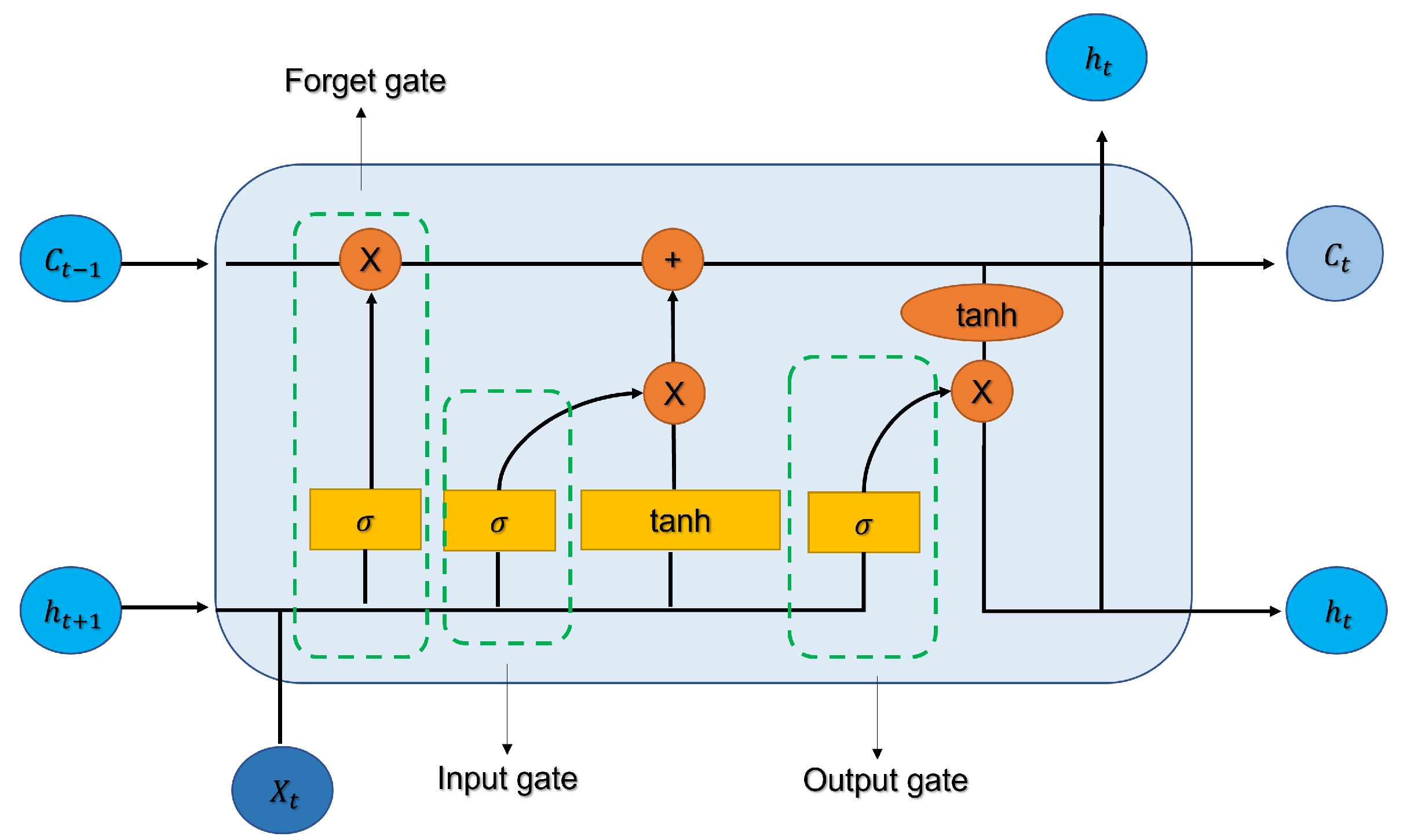
Figure 9.
Scatter plot of actual versus predicted grain production.
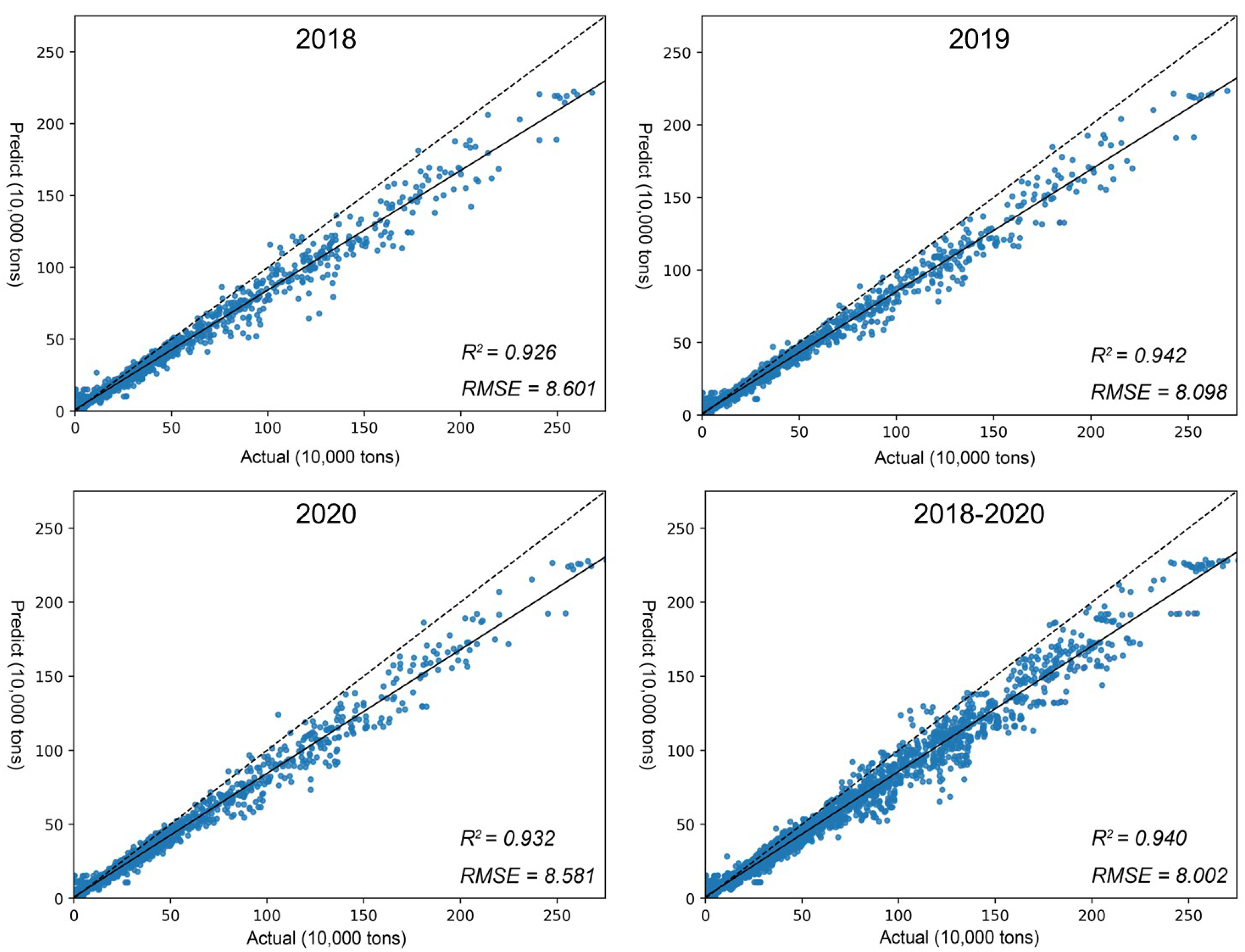
Figure 10.
Model training convergence by province.
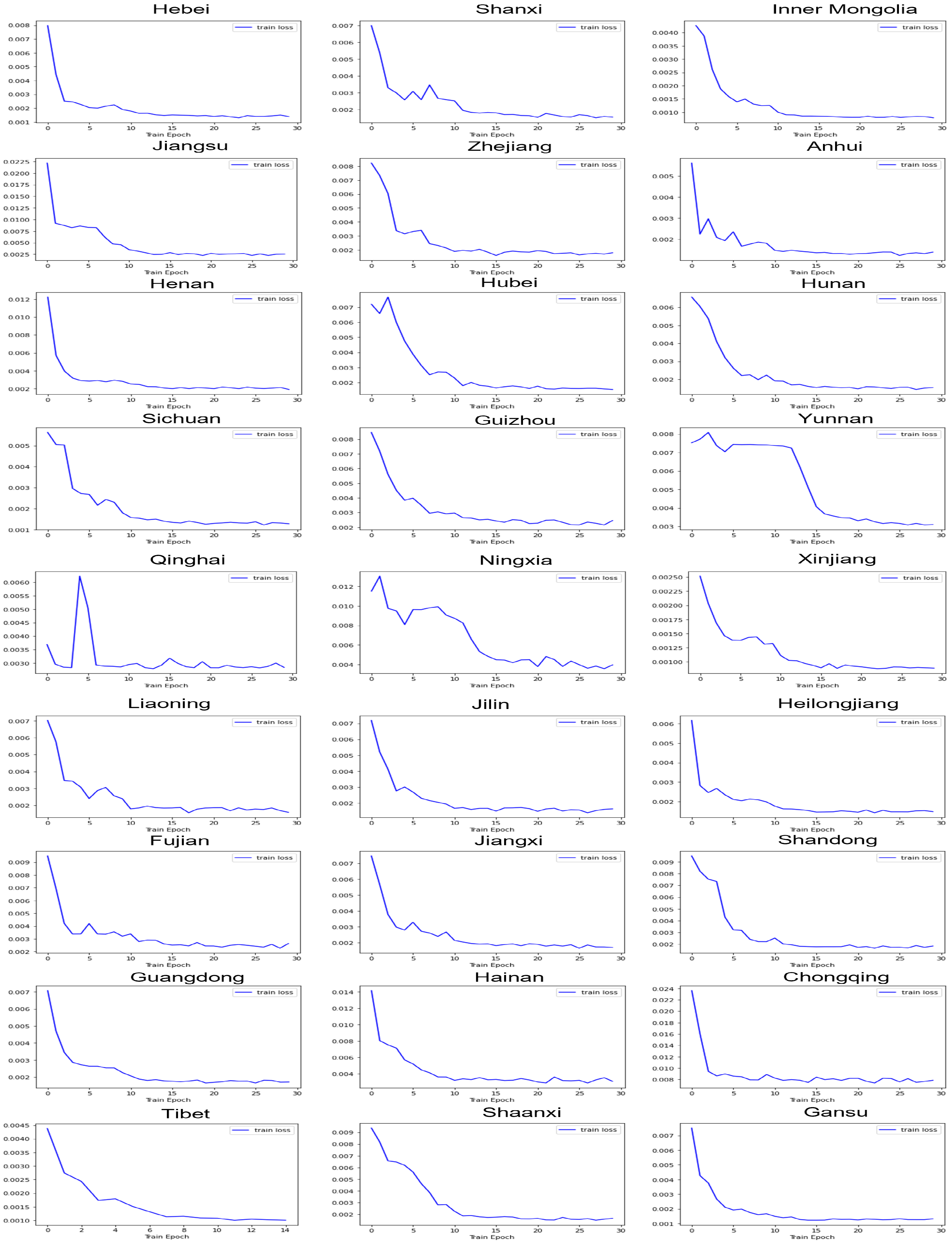
Figure 11.
Model performance in different provinces..
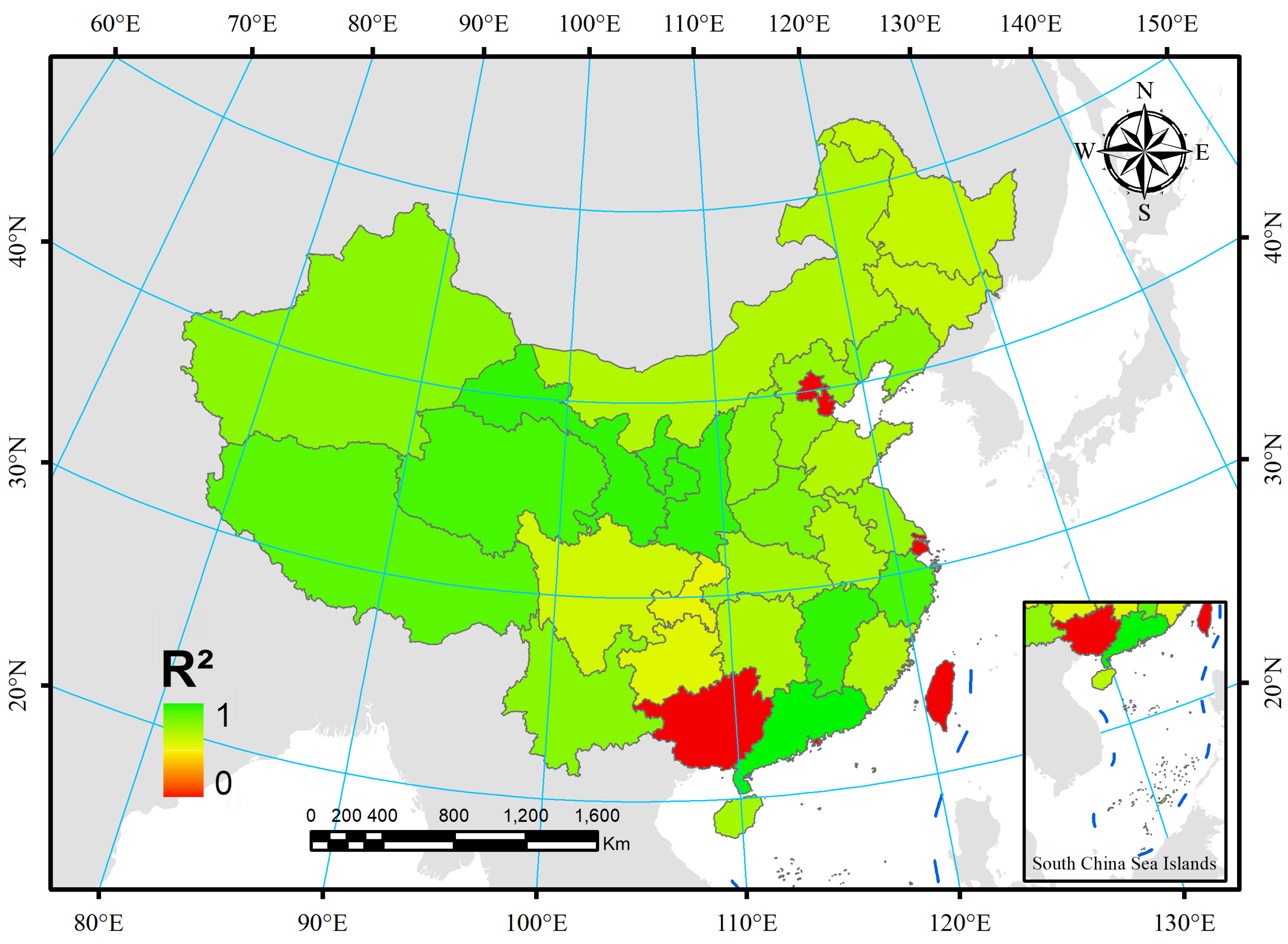
Figure 12.
Predicted and actual production in 2018-2020.
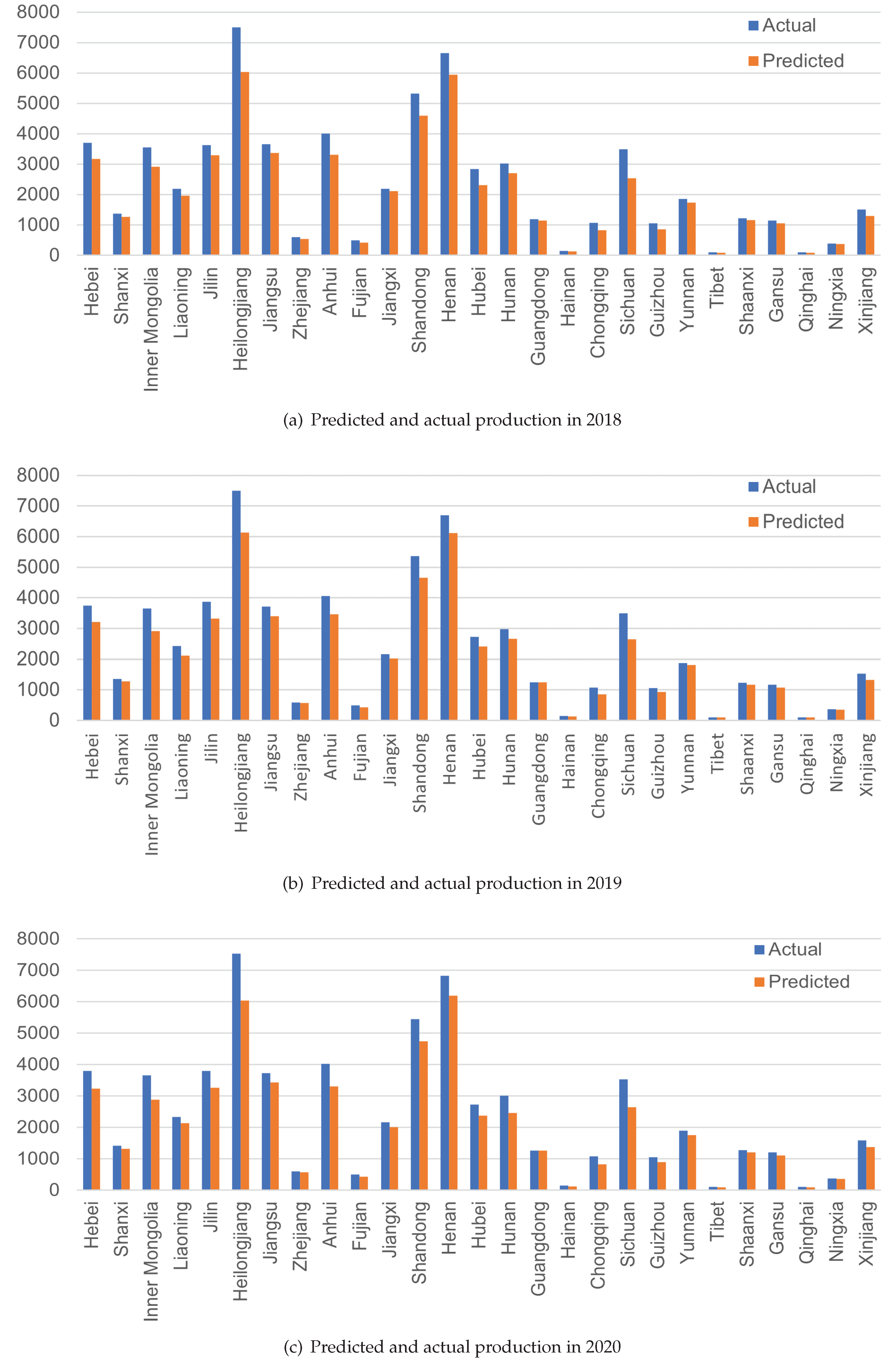
Table 1.
MODIS data products and band information.
| Product Name | Band | Time Resolution | Spatial Resolution | Valid Range |
|---|---|---|---|---|
| MOD11A2 | Daytime Land Surface Temperature Nighttime Land Surface Temperature |
8 Days | 1 km | 7500–65535 |
| MOD13A1 | Normalized Difference Vegetation Index Enhanced Vegetation Index |
16 Days | 0.5 km | -2000–10000 |
| MOD15A2H | Leaf Area Index Fraction of Photosynthetically Active Radiation |
8 Days | 0.5 km | 0–100 |
Table 2.
Test Results.
| Item | 2018 | 2019 | 2020 | Average | ||||
|---|---|---|---|---|---|---|---|---|
| RMSE | RMSE | RMSE | RMSE | |||||
| Ours Models | 0.926 | 8.601 | 0.942 | 8.098 | 0.932 | 8.581 | 0.940 | 8.002 |
Table 3.
2018-2020 model prediction accuracy by province.
| Country | 2018 | 2019 | 2020 | |||
|---|---|---|---|---|---|---|
| RMSE | RMSE | RMSE | ||||
| Hebei | 0.942 | 11.708 | 0.944 | 11.644 | 0.940 | 12.272 |
| Shanxi | 0.941 | 4.469 | 0.953 | 3.915 | 0.944 | 4.476 |
| Inner Mongolia | 0.938 | 4.606 | 0.927 | 5.117 | 0.917 | 5.462 |
| Liaoning | 0.946 | 7.933 | 0.922 | 10.605 | 0.955 | 7.772 |
| Jilin | 0.915 | 14.782 | 0.901 | 17.027 | 0.892 | 17.413 |
| Heilongjiang | 0.910 | 15.215 | 0.920 | 14.381 | 0.908 | 15.427 |
| Jiangsu | 0.943 | 18.020 | 0.941 | 18.612 | 0.944 | 18.238 |
| Zhejiang | 0.962 | 2.933 | 0.983 | 1.954 | 0.977 | 2.285 |
| Anhui | 0.891 | 24.045 | 0.923 | 20.500 | 0.903 | 22.727 |
| Fujian | 0.892 | 3.087 | 0.937 | 2.331 | 0.916 | 2.745 |
| Jiangxi | 0.985 | 4.725 | 0.972 | 6.322 | 0.970 | 6.473 |
| Shandong | 0.919 | 19.449 | 0.924 | 19.001 | 0.924 | 19.313 |
| Henan | 0.947 | 20.401 | 0.957 | 18.650 | 0.955 | 19.334 |
| Hubei | 0.894 | 16.741 | 0.941 | 11.987 | 0.941 | 12.056 |
| Hunan | 0.9486 | 8.954 | 0.935 | 10.097 | 0.875 | 13.957 |
| Guangdong | 0.9809 | 2.2982 | 0.9893 | 1.7854 | 0.9879 | 1.9398 |
| Hainan | 0.919 | 2.567 | 0.956 | 1.876 | 0.901 | 2.814 |
| Chongqing | 0.792 | 13.909 | 0.824 | 12.756 | 0.812 | 13.617 |
| Sichuan | 0.847 | 16.122 | 0.887 | 13.904 | 0.873 | 14.818 |
| Guizhou | 0.697 | 7.686 | 0.903 | 4.351 | 0.830 | 5.606 |
| Yunnan | 0.961 | 2.767 | 0.975 | 2.216 | 0.961 | 2.846 |
| Tibet | 0.967 | 0.270 | 0.971 | 0.255 | 0.975 | 0.231 |
| Shaanxi | 0.973 | 2.573 | 0.974 | 2.535 | 0.973 | 2.649 |
| Gansu | 0.976 | 1.918 | 0.977 | 1.896 | 0.976 | 2.010 |
| Qinghai | 0.970 | 0.562 | 0.973 | 0.544 | 0.974 | 0.549 |
| Ningxia | 0.974 | 2.461 | 0.973 | 2.377 | 0.970 | 2.573 |
| Xinjiang | 0.958 | 2.018 | 0.959 | 2.011 | 0.959 | 2.094 |
Table 4.
Results of ablation experiments.
| Item | 2018 | 2019 | 2020 | Average | ||||
|---|---|---|---|---|---|---|---|---|
| RMSE | RMSE | RMSE | RMSE | |||||
| CNN | 0.834 | 12.589 | 0.848 | 12.240 | 0.840 | 12.157 | 0.851 | 11.905 |
| CNN+CBAM | 0.883 | 10.155 | 0.900 | 9.441 | 0.889 | 9.738 | 0.899 | 9.362 |
| CNN+LSTM | 0.896 | 9.836 | 0.918 | 9.288 | 0.897 | 10.393 | 0.910 | 9.548 |
| CNN+CBAM+LSTM(Ours) | 0.926 | 8.601 | 0.942 | 8.098 | 0.932 | 8.581 | 0.940 | 8.002 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





