Prerpints.org logo
Preprint
Article

Efficient D---A Type Dye-Sensitizer Based on the Benzothiadiazole Moiety: A Computational Study

Altmetrics

Downloads

129

Views

65

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

23 May 2023

Posted:

25 May 2023

You are already at the latest version

Alerts
Abstract
The design of highly efficient sensitizers is one of the most significant areas in dye-sensitized solar cell (DSSC) research. We have studied a series of benzothiadiazole-based D-π-π-A organic dyes, putting emphasis on the influence of the donor moiety on the DSSC’s efficiency. Using linear response time-dependent density functional theory (TDDFT) with the CAM-B3LYP functional different donor groups were characterized in terms of electronic absorption spectra and key photovoltaic parameters. As a reference a dye has been considered which has a benzothiadiazole fragment linked via thiophene rings to a diphenylamine donor and a cyanoacrylic acid acceptor. The different systems are first studied in terms of individual performance parameters, which are eventually aggregated into the power conversion efficiency. Here only the amino-substituted species shows a modest increase, whereas the dimethylamino case even shows a decrease.
Keywords: 
Subject: Chemistry and Materials Science  -   Theoretical Chemistry

1. Introduction

Solar cells are among the most promising devices for clean energy generation. Considering the various design strategies, dye-sensitized solar cells (DSSCs) have attracted substantial attention over the past decades due to their inexpensive materials, simple fabrication process, and high-power conversion efficiency in comparison with conventional high-cost silicon solar cells [1,2]. Generally, DSSCs consist of the following components: the dye-sensitized semiconductor electrode (the working electrode or photoanode), the redox electrolyte, the counter electrode, and a photosensitizer or a monolayer of dye molecules. The monolayer of dye molecules adsorbed on the semiconductor surface is responsible for light absorption in the device and consists of three basic parts, an electron-donating group (D), π-spacer (π), and an electron acceptor (A). In DSSCs light is absorbed by the sensitizing dye, which is anchored to a semiconducting mesoporous TiO2 film. Electrons are injected from the excited state of the sensitizer into the conduction band of the TiO2 electrode, eventually leading to an electric current. Furthermore, the redox electrolyte (typically I3−/I−) regenerates the oxidized sensitizer to provide efficient charge separation. Generally, dye sensitizers bind covalently to the surface of the TiO2, which leads to an electronic connection between them which facilitates an efficient electron injection process [3]. To enhance the DSSCs’ effectiveness significant attention has been given to the modification of the photosensitizer. It should meet specific requirements regarding its optoelectronic properties, including the region of the electromagnetic spectrum, absorption coefficient, and band alignment [1].
Generally, organic photosensitizers (metal-free dyes) have attracted a lot of attention due to their ability to harvest a considerable portion of the solar spectrum with high molar absorption coefficients, from the ultraviolet to near-IR regions, which results in an increase in power conversion efficiency (PCE) values. In addition, metal-free organic dyes are a promising DSSC material due to their non-toxicity, high flexibility regarding the molecular structure, tunable absorption properties, and high molar extinction coefficient compared with metal (Ru and Zn) based dyes [4]. It was reported that PCE for metal-based DSSCs reached up to 13% for Zn porphyrin [5] and 11.5% for a polypyridyl ruthenium complex [6]. The reported PCE for metal-free organic dyes of donor-π-acceptor (D-π-A) framework bounded to the surface of TiO2 reached up to 13% [7].
In D-π-A systems the π-bridges facilitate the charge separation between donor and acceptor and inhibit competing charge recombination. The performance of photovoltaic cells based on organic dyes can be enhanced by choosing suitable groups within the D–π–A molecular architecture [8,9]. For instance, increasing the electron donating strength of the donor or the electron-withdrawing strength of the acceptor can improve the performance of DSSCs [10]. Typical organic dyes with relatively high performance include those with triphenylamine [9], carbazole [11,12], indoline [13], quinoline [14], and coumarin [15] as electron-donating groups. On the other hand, 2-cyanoacrylic acid is the most commonly used electron acceptor. Phenyl, thiophene, furan, and their derivatives are the moieties most often used as π-bridges [16].
In this work using Computational Chemistry we investigate the effect of the donor group on the optoelectronic properties of organic dyes with a D-π-π-A structure. As a reference structure (D0) we consider a dye synthesized and characterized in Ref. [17]. It has a benzothiadiazole fragment placed between two thiophene rings as a bridge that connects the diphenylamine donor and cyanoacrylic acid acceptor, see Figure 1. Phenylamine donors are common in DSSCs (see, e.g., the studies of the influence of the type of π-spacer in Ref. [9,18,19] or of donor properties in Ref. [20]) and we consider five substitutions (D1-D5) as given in Figure 1b. While the modifications are modest, it will be shown that the effect on DSSC relevant parameters are substantial.
In what follows we start in Section 2.1 with a discussion of the electrostatic potential map obtained using DFT. In Section 2.2 a frontier orbital analysis is presented. Section 2.3 optical properties are discussed and in Section 2.4 electron transfer is characterized. Section 3 presents a discussion of our findings and computational methods are summarized in Section 4.

2. Results

2.1. Electrostatic Potentials

The electrostatic potential maps (EPMs) of all studied dyes at the optimized geometries in the electronic ground state are shown in Figure 2. The appearance of negative electrostatic potentials (red) around the oxygen and nitrogen atoms of the anchoring acceptor group evidences its negative partial charge. These sites are potentially relevant for electrophilic attack of the electrolyte, a finding that is in accord with previous studies on D0 in Refs. [18,19]. Positive electrostatic potentials (blue) are found at the donor moieties, in particular for the NH2 group in D3. Notice that upon photoexcitation and oxidation, electron density is removed from the donor site making it even more attractive for the reduced redox couple such as to facilitate dye regeneration (for instance, Ref. [20]). Overall, the change of the donor moiety doesn’t have a noticeable influence on the geometry and EPM of the remaining dye.

2.2. Frontier Molecular Orbitals and Chemical Reactivity

The HOMO and LUMO of a dye sensitizer must show suitable energetic positions to match the redox potential of the electrolyte and the conduction-band of TiO2. In other words, the dye’s ELUMO must be above the semiconductor’s conduction band edge, indicating that electrons can be easily injected from the excited dyes into the conduction band. At the same time, EHOMO of the dye must be below the redox potential of the electrolyte (I3−/I−) couple to facilitate regeneration of the dyes [1]. Figure 3 shows the HOMO and LUMO of all studied dyes. The electron distribution in the HOMO is mostly located on the electron donor and π-spacer, while the LUMO is mostly located on the π-conjugated moiety and the electron acceptor group in the anchoring unit. Especially the latter behavior represents an ideal spatial arrangement of the molecular orbitals for DSSCs applications. Ionization potential (IP=- EHOMO), electron affinity (EA=- ELUMO), chemical potential (µ), global hardness (η), electrophilicity (ω), electroaccepting power (ω+), and electrodonating power (ω-) of all studied dyes are summarized in Table 1 (for definitions, see Section 4).
It is obvious that the modification of the donor units significantly affects the HOMO energy levels of the dyes, while the energy of the LUMO, having only little amplitude at the donor moiety, is less affected. The energies EHOMO of all studies dyes are below the redox potential of the electrolyte (I3−/I−) couple (-4.80 eV), this favors charge regeneration, with D5 being the most effective case. In other words, the electron donating power of the different donor groups increases from D0 to D5. Moreover, the energies, ELUMO, of all dyes are above the semiconductor’s conduction band edge (-4.0 eV), a precondition for electron injection from the excited dye to the conduction band of TiO2. The energy levels are sketched in Figure 4.
Inspecting the other quantities in Table 1 we observe the following trends: The studied dyes D1-D5 show a lower band gap compared to the reference dye (D0), this may enhance light harvesting efficiency [20]. It is shown that D5 had the smallest values for IP and EA in our calculations, thus according to Ref. [20] it should give the best balance between electron and hole transfer among the considered dyes. Further chemical hardness and chemical potential decrease from D0 to D5, leading to an increase of the electrophilicity and thus to a potential improvement of charge separation capability. This in turn is also reflected in the electron accepting/donating powers.

2.3. Optical Absorption

The experimental spectrum is available for the parent compound D0 only. It shows peaks at 541 nm, 398 nm, and 312 nm with an intensity ratio of 1.16/0.96/1.00 [34]. CAM-B3LYP predicts the lowest transition at 534 nm (f=1.31). Further transitions with appreciable oscillator strength (f) are located at 382 nm (f=0.37) and 310 nm (f=0.26). Although the ratio of oscillator strengths doesn’t match the experiment, the agreement of spectral positions is excellent, justifying the use of the computational setup for the following analysis. This is justified since according to Eq. (8) only the properties of a single transition will be compared for the different dyes.
The absorption spectra of all considered dyes are shown in Figure 5. The calculated values of the vertical excitation energy (Emax) and absorption wavelength (λmax) for the transition with the largest oscillator strength (f) are given in Table 2 together with the light harvesting efficiency (LHE). When designing dye sensitizers, one of the essential aims is to establish a system having an optical absorption that overlaps with the sun’s emission spectrum. For the considered organic dyes this implies to increase the absorption toward the UV–Vis and IR ranges with a high molar extinction coefficient. Overall, all studied dye modifications (D1-D5) have a strong absorption at longer wavelengths as compared with the reference dye D0 (bathochromic shift). Interestingly, for D4 and D5 this shift is large enough to move the main peak of the spectrum into the infrared range. In all cases the lowest and strongest band is dominated by a HOMO to LUMO transition and thus has ICT character, see Figure 3. The oscillator strength increases when going from D0 to D5 and so does the LHE. Hence, in terms of this property the designed dyes should yield an improved PCE.

2.4. Electron injection, dye regeneration and open-circuit voltage

The complete cycle occurs, when electrons after photoexcitation are spontaneously injected from the LUMO into the conduction band of TiO2 semiconductor, and the dyes are regenerated by the redox couple into their ground state. The driving force for electron injection ΔGinj is negative for all dyes as outlined in Table 3. Thus, conditions for electron injection are favorable for all dyes. The ΔGinj values of the investigated dyes follows the order: D3 < D0 < D1 < D2 < D4 < D5, although one observes that, apart from D4 and D5, the values are rather similar.
The dye regeneration is determined by the potential difference between the electrolyte and the oxidized dye. This should be large enough to provide a driving force for the regeneration of the ground state dyes. At the same time its value also influences the recombination rate between the oxidized dye and conduction band of the TiO2 semiconductor. Efficient dye regeneration requires ΔGreg values in the range 0.1 to 0.3 eV [20]. Inspecting Table 3 we notice that only D3 falls into that range, whereas D0-D2 are larger and D4 and D5 approximately have zero driving force.
The open circuit voltage, VOC, provides an idea about mobility and the number of charge carriers across the interface, a high-value VOC results in a smaller loss due to charge recombination, so that a higher value improves the cell efficiency. The calculated values of VOC for the studied dyes are ranging from 1.55 eV to 1.77 eV, Table 3. D2 and D3 have the highest VOC values. However, again, only D4 and D5 have substantially different values.
The overall performance of the different dyes can be quantified by the PCE value defined in Eq. (6) and given in Table 3. Since we are interested in the effect of the donor modification, PCE values are given relative to D0. Inspecting Table 3 it is clear that only D3 gives an improvement of the PCE, whereas for D4 and D5 PCE values are considerably smaller than for D0.

3. Discussion

We performed a (TD)DFT investigation of a series of novel organic sensitizers based on the D–π-π–A structure for potential application in DSSCs. These dyes derived from a parent compound with a diphenylamine donor, linked via a thiophene and a thiophene-fused benzothiadiazole bridge to a cyanoacrylic acid acceptor (D0). The donor was modified at the para-position yielding D1-D5 as shown in Figure 1. First, the ground state and frontier molecular orbitals were analyzed. Electrostatic potential maps showed not much influence by the substitution. The IP is decreasing from D0 to D5, whereas the EA increases accordingly. This, taking also into account the derived quantities (cf. Eqs. (1-5)) suggest D5 as the best candidate among the studied dyes for DSSC applications. D5 as well as D4 also stand out when it comes to optical absorption insofar as the bathochromic is rather considerable. The LHE values, however, are mostly comparable among the different systems. Inspecting electron transfer related properties, injection in terms of ΔGinj is favored for all dyes, whereas only D3 is in the range of reasonable regeneration as far as ΔGreg is concerned. Judging the performance based on PCE, only D3, i.e., substitution with an amino group, gives an improvement compared with D0. This is interesting insofar as some of the individual characteristics would have suggested D5 to outperform D0.
There is a large body of literature on (TD)DFT studies of D–π–A systems, even if one focusses only on those systems with a cyanoacrylic acid acceptor (e.g., [8,9,10,12,14,18,19,20,21,22,23,24,25,26,27,28,29,30]). Most of these studies lack experimental verification and, therefore, should be viewed as an in silico screening of potential sensitizer materials. The present investigation adds to this endeavor as it set the focus on modification of the donor moiety starting from a simple diphenylamine. Here we find that, for the considered systems, in terms of the PCE there is little room for improvement (up to 11%), but the performance can get worse (-25 %). Closest to our work is the study of Hailu et al. [20], although they have used a different spacer. In fact, the present dye D4 correspond to their dye1. Apart from this dimethylamino case they considered methylphenylamino, diphenylamino, diindoline, and dicarbazole substitution. Interestingly, they considered the first three dyes as potentially good performers (a direct comparison is not possible because Voc has not been reported). This is at variance with the poor PCE performance of D4 in the present case, although one should notice that in terms of IP and EA D4 was superior to D0-D3. A major bottleneck for the direct comparison of reported quantum chemical results is the use of different computational protocols. For instance, in Ref. [20] the ωB97XD functional has been used, whereas in the present case it was CAM-B3LYP. In passing we note that both functionals contain all-purpose parameters for the range separation. More accurate results would be obtained applying optimal tuning of these parameters for the specific type of systems [31].
In summary in order to advance the field of computational screening of dyes for application as sensitizers in DSSCs it will be necessary to identify and benchmark a computational protocol to be used to establish a data base of these materials.

4. Materials and Methods

4.1. Characterization of Dye Molecules

The ionization potential (IP) and electron affinity (EA) of the sensitizer describe the electronic energy barrier for creating holes and electrons, respectively. A lower IP should promote the hole-creating ability, whereas a higher EA should enhance the electron-accepting ability of the dye. Based on these two parameters, the chemical reactivity of the model dyes can be characterized by the electronic chemical potential (μ), chemical hardness (η), electrophilicity index (ω). The electronic chemical potential is the negative of the electronegativity, which quantifies the ability of the system to attract and retain electrons. The chemical hardness describes the resistance of a dyes to a change its electronic state, e.g., by means of intra-molecular charge transfer (ICT) in a multicomponent system as the present D-π- π-A.
The electrophilicity index ω encompasses both, the propensity of the electrophile to acquire additional electronic charge (μ) and the resistance of the system to exchange electronic charge with the environment (η), simultaneously. Thus, electrophilicity represents the stabilization energy of the dyes upon acquiring additional charge. Consequently, dyes suitable for DSSCs should have low chemical hardness and high chemical potential to increase charge separation.
Following Parr and Yang, electronic chemical potential, chemical hardness, electrophilicity index are commonly expressed by the following equations [32]
μ = − I P + E A 2 = 1 2 E H O M O + E L U M O ,
= I P − E A 2 = 1 2 E L U M O − E H O M O ,
ω = μ 2 η .
Further we define the electron-accepting (ω+) and electron-donating (ω-) power
ω + = I P + 3 E A 2 16 I P − E A     ,
ω − = 3 I P + 3 E A 2 16 ( I P − E A ) .
The parameters ω– and ω+ are quantifying the ability of these dyes to withdraw or gain electron charges, for good performance large values are desirable.
The overall power conversion efficiency (PCE) of DSSCs is given by the photocurrent density measured at short-circuit (Jsc), the open-circuit photo-voltage (Voc), the fill factor of the cell (FF), and the intensity of the incident light (Pin) as summarized in the following expression [25]:
P C E = F F   J s c V o c P i n × 100 %   ,
where Jsc can be determined using the following equation [29,30,33]:
J s c = L H E   Φ i n j e c t   η c o l l e c t
Here LHE is the light-harvesting efficiency at maximum wavelength, Фinject is the electron injection efficiency and ηcollect is the charge collection efficiency. In systems where the only difference is in the sensitizer, ηcollect is assumed constant. According to equation (7), to obtain a high Jsc, LHE and Фinject should be as large as possible. The LHE can be expressed by the following equation:
L H E = 1 − 10 f
where f is the oscillator strength of dye related to the maximum absorption wavelength λmax.
The open-circuit-voltage Voc in equation (6) is related to electron injection from the excited dye to the conduction band of the semiconductor and determined by the following equation (neglecting occupation effects as well as conduction band shift in the semiconductor):
V o c = E L U M O − E C B T i O 2 ,
where ELUMO is LUMO energy of the dye and E C B T i O 2 is the conduction band energy of the semiconductor (here TiO2). It is difficult to accurately determine E C B T i O 2 because it is highly sensitive to operating conditions such as the pH of the solution. In the present study we have used E C B T i O 2 = -4.0 eV, which is the experimental value corresponding to conditions where the semiconductor is in contact with aqueous redox electrolytes of fixed pH 7.0 [25]. Фinject is closely related to the thermodynamic driving force ΔGinject of electron injection from the excited states of dye to the conduction band of TiO2 according to the following relation [29]
Φ i n j e c t ∝ Δ G i n j e c t = E d y e * − E C B T i O 2 .
Here E d y e * is the oxidation potential of the excited dye at the ground state geometry (neglecting vibrational relaxation upon excitation) following from   E d y e * = E d y e − ∆ E with E d y e being the oxidation potential energy of the dye in the ground-state, while ∆ E is the vertical electronic excitation energy, corresponding to λmax. In order to obtain more reliable results for the oxidation potential we have used the ∆ S C F method instead of Koopmans theorem, that is, E d y e = E G S − E G S + with GS referring to the ground state and vibrational relaxation effects have been neglected. The dye regeneration energy ( ∆ G r e g e n ) can be calculated by the equation [18]:
∆ G r e g e n = E r e d o x − E d y e .
E r e d o x is the ground state oxidation potential of the triiodide/iodide redox couple electrolyte redox potential (-4.80 eV) [18].

4.2. Computational Chemistry

Density functional theory (DFT) calculations were performed for the determination of optimized structures of the molecules D0-D5 at the CAM-B3LYP/6-31G(d) level of theory [34] using the Gaussian09 program [35]. In fact, these molecules show multiple conformations and we have taken the one previously reported for the diphenylamine donor [20]. Optimization was followed by frequency calculations to confirm the minimum structure on the potential energy surface. Linear response time-dependent TDDFT computations have been carried out to calculate the electronic absorption spectra for the 25 lowest singlet vertical excitations. The solvent environment (tetrahydrofuran) was treated implicitly using the self-consistent reaction field-polarizable continuum model [36]. In passing we note that we have also calculated the absorption spectrum using the B3LYP functional. B3LYP predicts the lowest and strongest transition for D0 at 758 nm which is at variance with the experiment and with the CAM-B3LYP results reported in Section 2.3. In passing we note that, in view of results reported in Ref. [20] (although with a different spacer), we have repeated the calculation of the absorption spectrum of D5 using a 6-311+G(d) basis set. Here we observed no noticeable change as far as the low energy absorption peak is concerned. The HOMO, LUMO energies, HOMO-LUMO energy gap, and other parameters defined in Section 4.1 were calculated at the optimized geometry.

Author Contributions

Conceptualization, Mahmoud K. Abdel-Latif (MA) and Fatma M. Mustafa (FM); methodology, MA and FM; validation, Oliver Kühn (OK) and FM; formal analysis, MA and FM; investigation, FM; writing—original draft preparation, FM; writing—review and editing, OK and MA; supervision, MA, A.A. Abdel-Khalek, and OK.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Acknowledgments

We are grateful to Dr. Mahmoud A. A. Ibrahim (Computational Chemistry Laboratory, Chemistry Department, Faculty of Science, Minia University, Minia 61519, Egypt) for his assistance in performing our calculations.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Muñoz-García, A.B.; Benesperi, I.; Boschloo, G.; Concepcion, J.J.; Delcamp, J.H.; Gibson, E.A.; Meyer, G.J.; Pavone, M.; Pettersson, H.; Hagfeldt, A.; et al. Dye-Sensitized Solar Cells Strike Back. Chem. Soc. Rev. 2021, 50, 12450–12550. [Google Scholar] [CrossRef]
  2. Kokkonen, M.; Talebi, P.; Zhou, J.; Asgari, S.; Soomro, S.A.; Elsehrawy, F.; Halme, J.; Ahmad, S.; Hagfeldt, A.; Hashmi, S.G. Advanced Research Trends in Dye-Sensitized Solar Cells. J. Mater. Chem. A 2021, 9, 10527–10545. [Google Scholar] [CrossRef]
  3. Park, H.; Bae, E.; Lee, J.-J.; Park, J.; Choi, W. Effect of the Anchoring Group in Ru−Bipyridyl Sensitizers on the Photoelectrochemical Behavior of Dye-Sensitized TiO2 Electrodes:  Carboxylate versus Phosphonate Linkages. J. Phys. Chem. B 2006, 110, 8740–8749. [Google Scholar] [CrossRef] [PubMed]
  4. Lee, C.-P.; Lin, R.Y.-Y.; Lin, L.-Y.; Li, C.-T.; Chu, T.-C.; Sun, S.-S.; Lin, J.T.; Ho, K.-C. Recent Progress in Organic Sensitizers for Dye-Sensitized Solar Cells. RSC Adv. 2015, 5, 23810–23825. [Google Scholar] [CrossRef]
  5. Mathew, S.; Yella, A.; Gao, P.; Humphry-Baker, R.; Curchod, B.F.E.; Ashari-Astani, N.; Tavernelli, I.; Rothlisberger, U.; Nazeeruddin, M.K.; Grätzel, M. Dye-Sensitized Solar Cells with 13% Efficiency Achieved through the Molecular Engineering of Porphyrin Sensitizers. Nature Chem 2014, 6, 242–247. [Google Scholar] [CrossRef] [PubMed]
  6. Chen, C.-Y.; Wang, M.; Li, J.-Y.; Pootrakulchote, N.; Alibabaei, L.; Ngoc-le, C.; Decoppet, J.-D.; Tsai, J.-H.; Grätzel, C.; Wu, C.-G.; et al. Highly Efficient Light-Harvesting Ruthenium Sensitizer for Thin-Film Dye-Sensitized Solar Cells. ACS Nano 2009, 3, 3103–3109. [Google Scholar] [CrossRef]
  7. Ahmad, S.; Guillén, E.; Kavan, L.; Grätzel, M.; Nazeeruddin, M.K. Metal Free Sensitizer and Catalyst for Dye Sensitized Solar Cells. Energy Environ. Sci. 2013, 6, 3439–3466. [Google Scholar] [CrossRef]
  8. Liu, B.; Wang, R.; Mi, W.; Li, X.; Yu, H. Novel Branched Coumarin Dyes for Dye-Sensitized Solar Cells: Significant Improvement in Photovoltaic Performance by Simple Structure Modification. J. Mater. Chem. 2012, 22, 15379–15387. [Google Scholar] [CrossRef]
  9. Teng, C.; Yang, X.; Yang, C.; Tian, H.; Li, S.; Wang, X.; Hagfeldt, A.; Sun, L. Influence of Triple Bonds as π-Spacer Units in Metal-Free Organic Dyes for Dye-Sensitized Solar Cells. J. Phys. Chem. C 2010, 114, 11305–11313. [Google Scholar] [CrossRef]
  10. Lee, D.H.; Lee, M.J.; Song, H.M.; Song, B.J.; Seo, K.D.; Pastore, M.; Anselmi, C.; Fantacci, S.; De Angelis, F.; Nazeeruddin, M.K.; et al. Organic Dyes Incorporating Low-Band-Gap Chromophores Based on π-Extended Benzothiadiazole for Dye-Sensitized Solar Cells. Dyes and Pigments 2011, 91, 192–198. [Google Scholar] [CrossRef]
  11. Wang, Z.-S.; Koumura, N.; Cui, Y.; Takahashi, M.; Sekiguchi, H.; Mori, A.; Kubo, T.; Furube, A.; Hara, K. Hexylthiophene-Functionalized Carbazole Dyes for Efficient Molecular Photovoltaics: Tuning of Solar-Cell Performance by Structural Modification. Chem. Mater. 2008, 20, 3993–4003. [Google Scholar] [CrossRef]
  12. Janjua, M.R.S.A.; Khan, M.U.; Khalid, M.; Ullah, N.; Kalgaonkar, R.; Alnoaimi, K.; Baqader, N.; Jamil, S. Theoretical and Conceptual Framework to Design Efficient Dye-Sensitized Solar Cells (DSSCs): Molecular Engineering by DFT Method. J Clust Sci 2021, 32, 243–253. [Google Scholar] [CrossRef]
  13. Wu, Y.; Zhang, X.; Li, W.; Wang, Z.-S.; Tian, H.; Zhu, W. Hexylthiophene-Featured D–A–π–A Structural Indoline Chromophores for Coadsorbent-Free and Panchromatic Dye-Sensitized Solar Cells. Advanced Energy Materials 2012, 2, 149–156. [Google Scholar] [CrossRef]
  14. Pounraj, P.; Mohankumar, V.; Pandian, M.S.; Ramasamy, P. Donor Functionalized Quinoline Based Organic Sensitizers for Dye Sensitized Solar Cell (DSSC) Applications: DFT and TD-DFT Investigations. J Mol Model 2018, 24, 343. [Google Scholar] [CrossRef]
  15. Hara, K.; Kurashige, M.; Dan-oh, Y.; Kasada, C.; Shinpo, A.; Suga, S.; Sayama, K.; Arakawa, H. Design of New Coumarin Dyes Having Thiophene Moieties for Highly Efficient Organic-Dye-Sensitized Solar Cells. New J. Chem. 2003, 27, 783–785. [Google Scholar] [CrossRef]
  16. Liang, M.; Chen, J. Arylamine Organic Dyes for Dye-Sensitized Solar Cells. Chem. Soc. Rev. 2013, 42, 3453–3488. [Google Scholar] [CrossRef] [PubMed]
  17. Velusamy, M.; Justin Thomas, K.R.; Lin, J.T.; Hsu, Y.-C.; Ho, K.-C. Organic Dyes Incorporating Low-Band-Gap Chromophores for Dye-Sensitized Solar Cells. Org. Lett. 2005, 7, 1899–1902. [Google Scholar] [CrossRef]
  18. Tripathi, A.; Ganjoo, A.; Chetti, P. Influence of Internal Acceptor and Thiophene Based π-Spacer in D-A-π-A System on Photophysical and Charge Transport Properties for Efficient DSSCs: A DFT Insight. Solar Energy 2020, 209, 194–205. [Google Scholar] [CrossRef]
  19. Li, Y.; Liu, J.; Liu, D.; Li, X.; Xu, Y. D-A-π-A Based Organic Dyes for Efficient DSSCs: A Theoretical Study on the Role of π-Spacer. Computational Materials Science 2019, 161, 163–176. [Google Scholar] [CrossRef]
  20. Hailu, Y.M.; Nguyen, M.T.; Jiang, J.-C. Effects of the Terminal Donor Unit in Dyes with D–D–π–A Architecture on the Regeneration Mechanism in DSSCs: A Computational Study. Phys. Chem. Chem. Phys. 2018, 20, 23564–23577. [Google Scholar] [CrossRef]
  21. Wazzan, N.A. A DFT/TDDFT Investigation on the Efficiency of Novel Dyes with Ortho-Fluorophenyl Units (A1) and Incorporating Benzotriazole/Benzothiadiazole/Phthalimide Units (A2) as Organic Photosensitizers with D–A2–π–A1 Configuration for Solar Cell Applications. J Comput Electron 2019, 18, 375–395. [Google Scholar] [CrossRef]
  22. Zhang, J.; Li, H.-B.; Sun, S.-L.; Geng, Y.; Wu, Y.; Su, Z.-M. Density Functional Theory Characterization and Design of High-Performance Diarylamine-Fluorene Dyes with Different π Spacers for Dye-Sensitized Solar Cells. J. Mater. Chem. 2011, 22, 568–576. [Google Scholar] [CrossRef]
  23. Fan, W.; Tan, D.; Deng, W.-Q. Acene-Modified Triphenylamine Dyes for Dye-Sensitized Solar Cells: A Computational Study. ChemPhysChem 2012, 13, 2051–2060. [Google Scholar] [CrossRef] [PubMed]
  24. Haid, S.; Marszalek, M.; Mishra, A.; Wielopolski, M.; Teuscher, J.; Moser, J.-E.; Humphry-Baker, R.; Zakeeruddin, S.M.; Grätzel, M.; Bäuerle, P. Significant Improvement of Dye-Sensitized Solar Cell Performance by Small Structural Modification in π-Conjugated Donor–Acceptor Dyes. Advanced Functional Materials 2012, 22, 1291–1302. [Google Scholar] [CrossRef]
  25. Feng, J.; Jiao, Y.; Ma, W.; Nazeeruddin, Md.K.; Grätzel, M.; Meng, S. First Principles Design of Dye Molecules with Ullazine Donor for Dye Sensitized Solar Cells. J. Phys. Chem. C 2013, 117, 3772–3778. [Google Scholar] [CrossRef]
  26. Ma, W.; Jiao, Y.; Meng, S. Modeling Charge Recombination in Dye-Sensitized Solar Cells Using First-Principles Electron Dynamics: Effects of Structural Modification. Phys. Chem. Chem. Phys. 2013, 15, 17187–17194. [Google Scholar] [CrossRef]
  27. Kar, S.; Roy, J.K.; Leszczynski, J. In Silico Designing of Power Conversion Efficient Organic Lead Dyes for Solar Cells Using Todays Innovative Approaches to Assure Renewable Energy for Future. npj Comput Mater 2017, 3, 1–12. [Google Scholar] [CrossRef]
  28. Li, Y.; Xu, B.; Song, P.; Ma, F.; Sun, M. D–A−π–A System: Light Harvesting, Charge Transfer, and Molecular Designing. J. Phys. Chem. C 2017, 121, 12546–12561. [Google Scholar] [CrossRef]
  29. Manzoor, T.; Pandith, A.H. Theoretical Studies on the Structure, Optoelectronic and Photosensitizer Applications of NKX Class of Coumarin Dye Molecules. ChemistrySelect 2018, 3, 2376–2385. [Google Scholar] [CrossRef]
  30. Manzoor, T.; Niaz, S.; Pandith, A.H. Exploring the Effect of Different Coumarin Donors on the Optical and Photovoltaic Properties of Azo-Bridged Push-Pull Systems: A Theoretical Approach. International Journal of Quantum Chemistry 2019, 119, e25979. [Google Scholar] [CrossRef]
  31. Bokareva, O.S.; Grell, G.; Bokarev, S.I.; Kühn, O. Tuning Range-Separated Density Functional Theory for Photocatalytic Water Splitting Systems. J. Chem. Theory Comput. 2015, 11, 1700–1709. [Google Scholar] [CrossRef] [PubMed]
  32. Domingo, L.R.; Ríos-Gutiérrez, M.; Pérez, P. Applications of the Conceptual Density Functional Theory Indices to Organic Chemistry Reactivity. Molecules 2016, 21, 748. [Google Scholar] [CrossRef] [PubMed]
  33. Nazeeruddin, M.K.; Kay, A.; Rodicio, I.; Humphry-Baker, R.; Mueller, E.; Liska, P.; Vlachopoulos, N.; Graetzel, M. Conversion of Light to Electricity by Cis-X2bis(2,2′-Bipyridyl-4,4′-Dicarboxylate)Ruthenium(II) Charge-Transfer Sensitizers (X = Cl-, Br-, I-, CN-, and SCN-) on Nanocrystalline Titanium Dioxide Electrodes. J. Am. Chem. Soc. 1993, 115, 6382–6390. [Google Scholar] [CrossRef]
  34. Yanai, T.; Tew, D.P.; Handy, N.C. A New Hybrid Exchange–Correlation Functional Using the Coulomb-Attenuating Method (CAM-B3LYP). Chemical Physics Letters 2004, 393, 51–57. [Google Scholar] [CrossRef]
  35. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision D.01; Gaussian Inc.: Wallingfort, CT, 2009. [Google Scholar]
  36. Tomasi, J.; Mennucci, B.; Cammi, R. Quantum Mechanical Continuum Solvation Models. Chem. Rev. 2005, 105, 2999–3093. [Google Scholar] [CrossRef]
Preprints 74425 g001
Figure 1. Structures of the series of dyes D0 to D5 with different donor moieties studied in this work. The dyes are composed of a (modified) diphenylamine donor (D), a π- π bridge (B) consisting of a thiophene and a thiophene-fused benzothiadiazole group, and a cyanoacrylic acid acceptor (A). Note that D4 corresponds to dye1 of Ref. [20], which contained, however, a different π-spacer.
Figure 1. Structures of the series of dyes D0 to D5 with different donor moieties studied in this work. The dyes are composed of a (modified) diphenylamine donor (D), a π- π bridge (B) consisting of a thiophene and a thiophene-fused benzothiadiazole group, and a cyanoacrylic acid acceptor (A). Note that D4 corresponds to dye1 of Ref. [20], which contained, however, a different π-spacer.
Preprints 74425 g001
Preprints 74425 g002
Figure 2. EPMs of the studied dyes (in atomic units, a.u.); D0 (colors from −0.80 (red) to 0.80 (blue) a.u), D1 (−0.81 to 0.81a.u), D2 (−0.81 to 0.81a.u), D3 (−0.80 to 0.80 a.u), D4 (−0.86 to 0.86 a.u), and D5 (−0.88 to 0.88 a.u).
Figure 2. EPMs of the studied dyes (in atomic units, a.u.); D0 (colors from −0.80 (red) to 0.80 (blue) a.u), D1 (−0.81 to 0.81a.u), D2 (−0.81 to 0.81a.u), D3 (−0.80 to 0.80 a.u), D4 (−0.86 to 0.86 a.u), and D5 (−0.88 to 0.88 a.u).
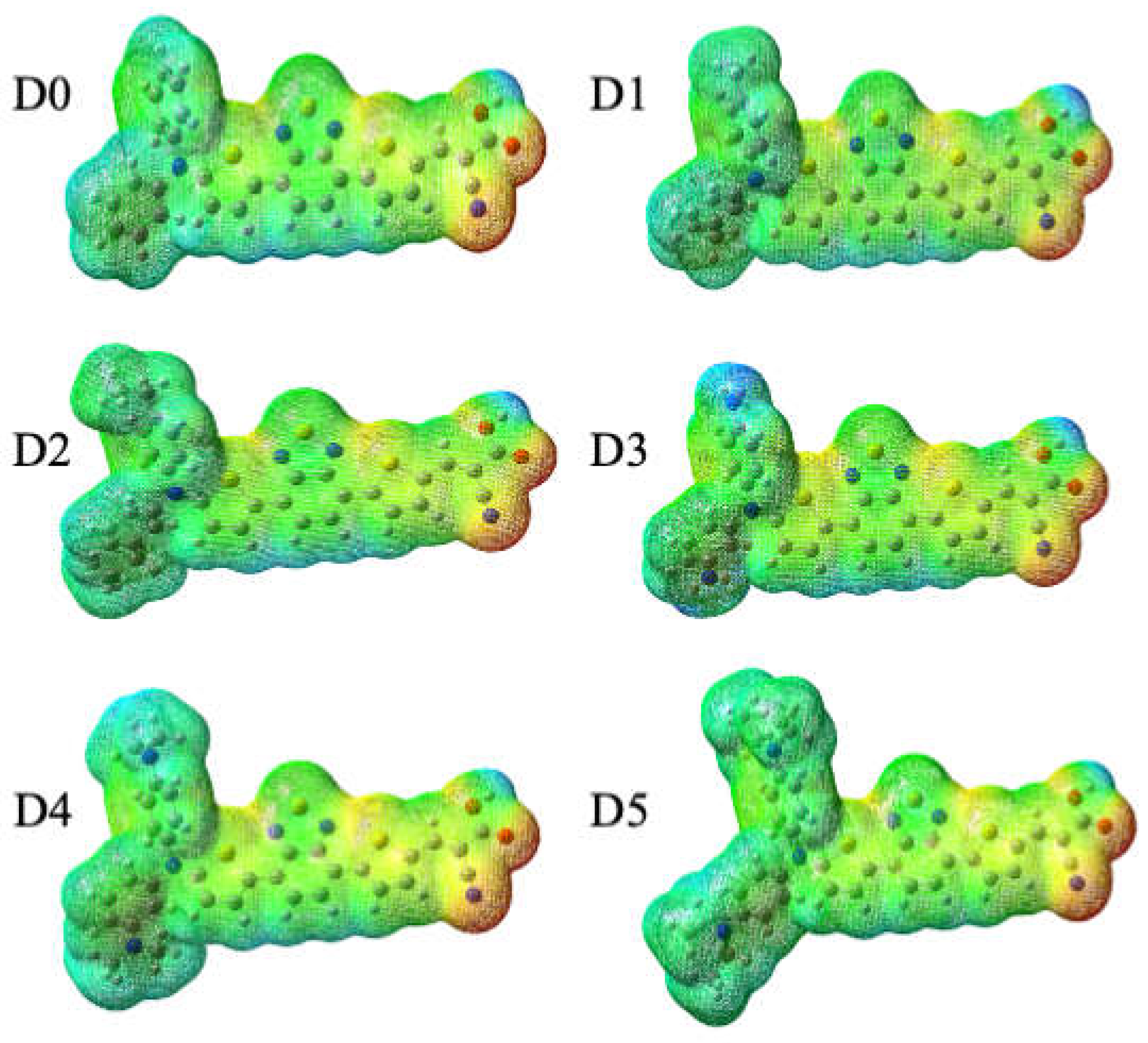
Preprints 74425 g002
Preprints 74425 g003
Figure 3. Selected frontier molecular orbitals of the considered dyes.
Figure 3. Selected frontier molecular orbitals of the considered dyes.
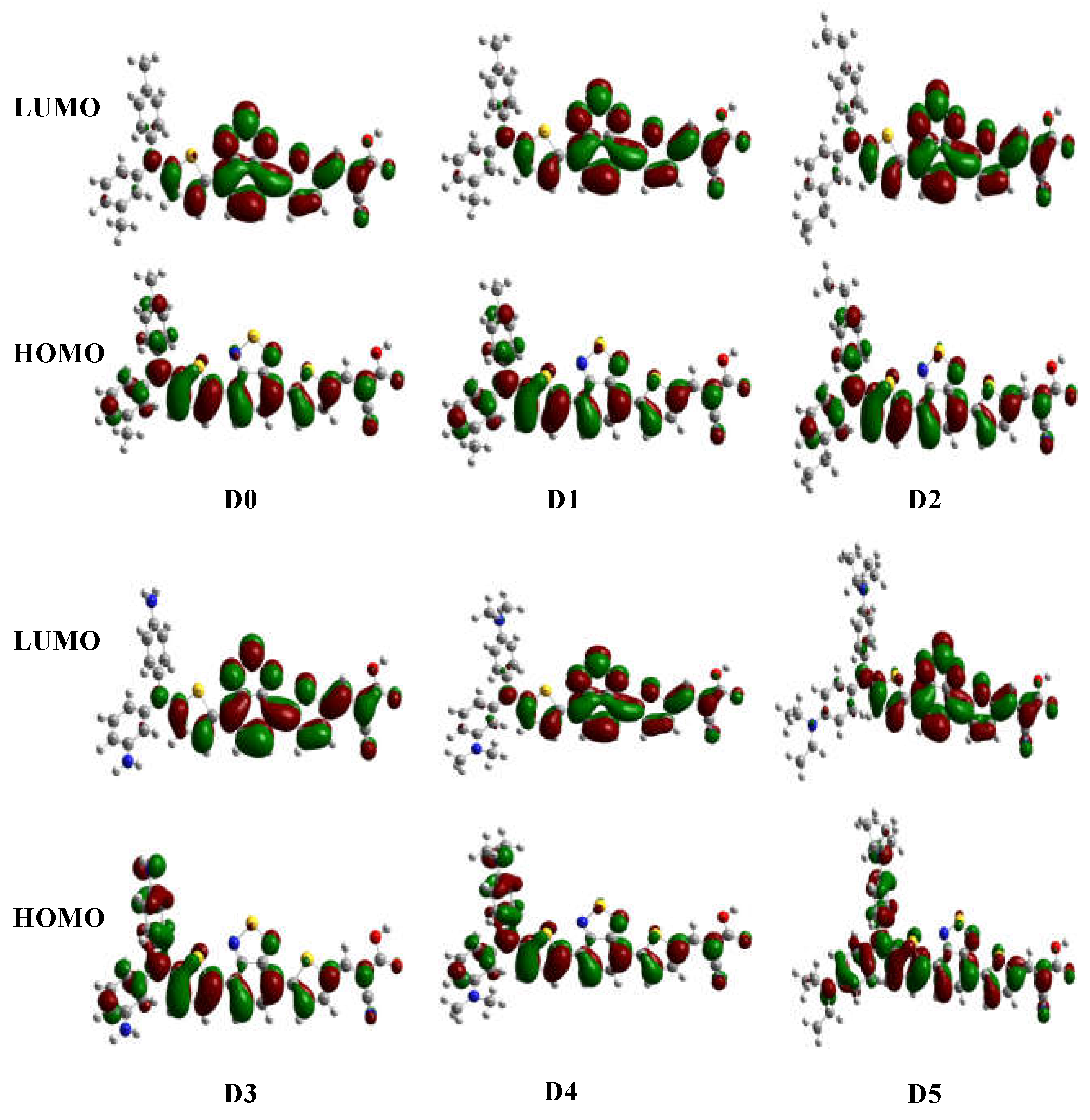
Preprints 74425 g003
Preprints 74425 g004
Figure 4. Energy level diagrams of the studied dyes including the conduction band of TiO2 and the redox potential of the (I-∕ I3-) redox couple, values of conduction and valence bands of TiO2, and electrolyte are taken from Ref. [21].
Figure 4. Energy level diagrams of the studied dyes including the conduction band of TiO2 and the redox potential of the (I-∕ I3-) redox couple, values of conduction and valence bands of TiO2, and electrolyte are taken from Ref. [21].
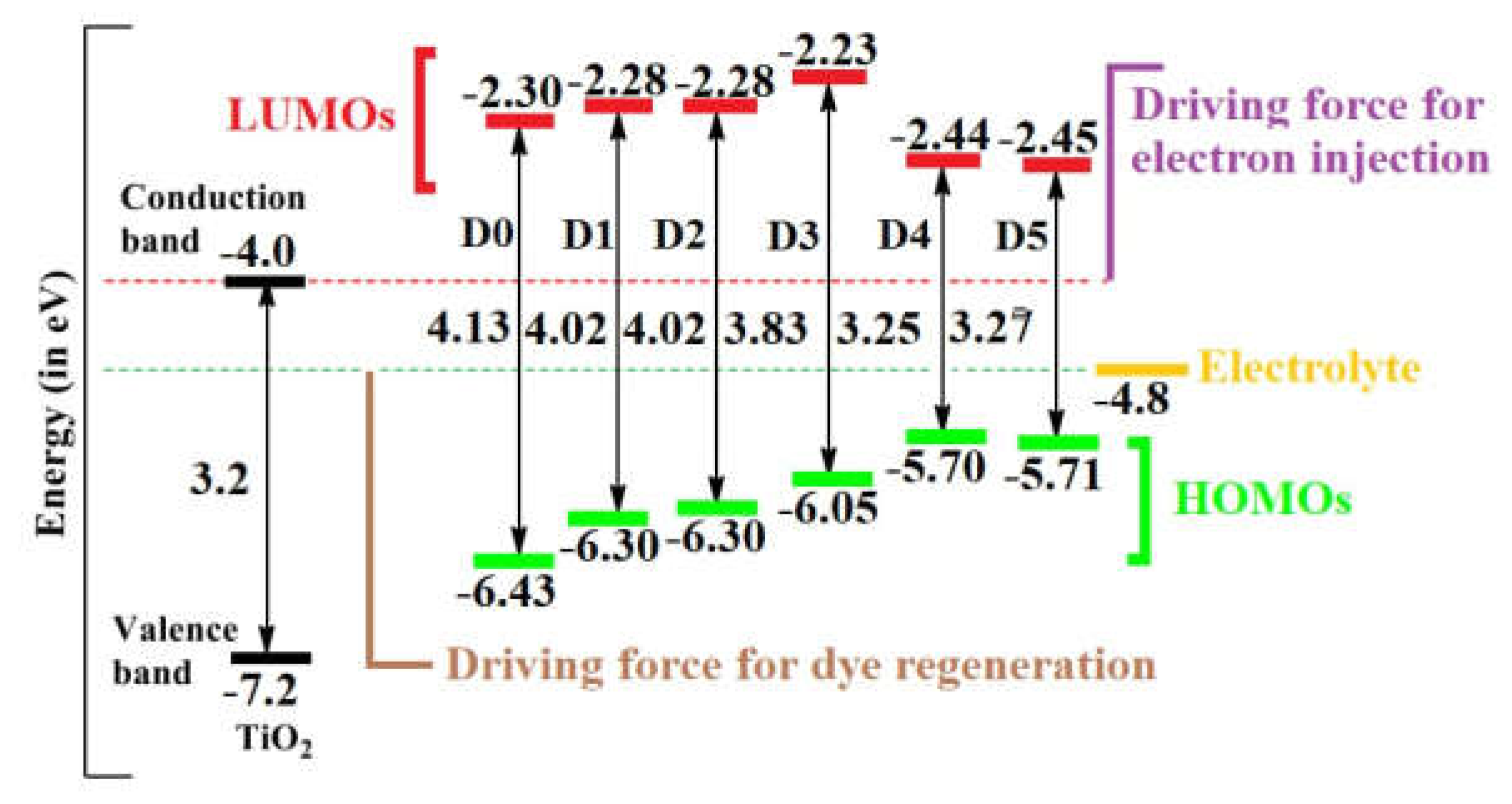
Preprints 74425 g004
Preprints 74425 g005
Figure 5. Calculated absorption spectra of the studied dyes in THF solution. Note that the spectra of D1 and D2 and of D4 and D5 are rather similar and only D1 and D4 are shown. A Gaussian-type broadening of 0.1 eV has been used to mimic environmental effects.
Figure 5. Calculated absorption spectra of the studied dyes in THF solution. Note that the spectra of D1 and D2 and of D4 and D5 are rather similar and only D1 and D4 are shown. A Gaussian-type broadening of 0.1 eV has been used to mimic environmental effects.
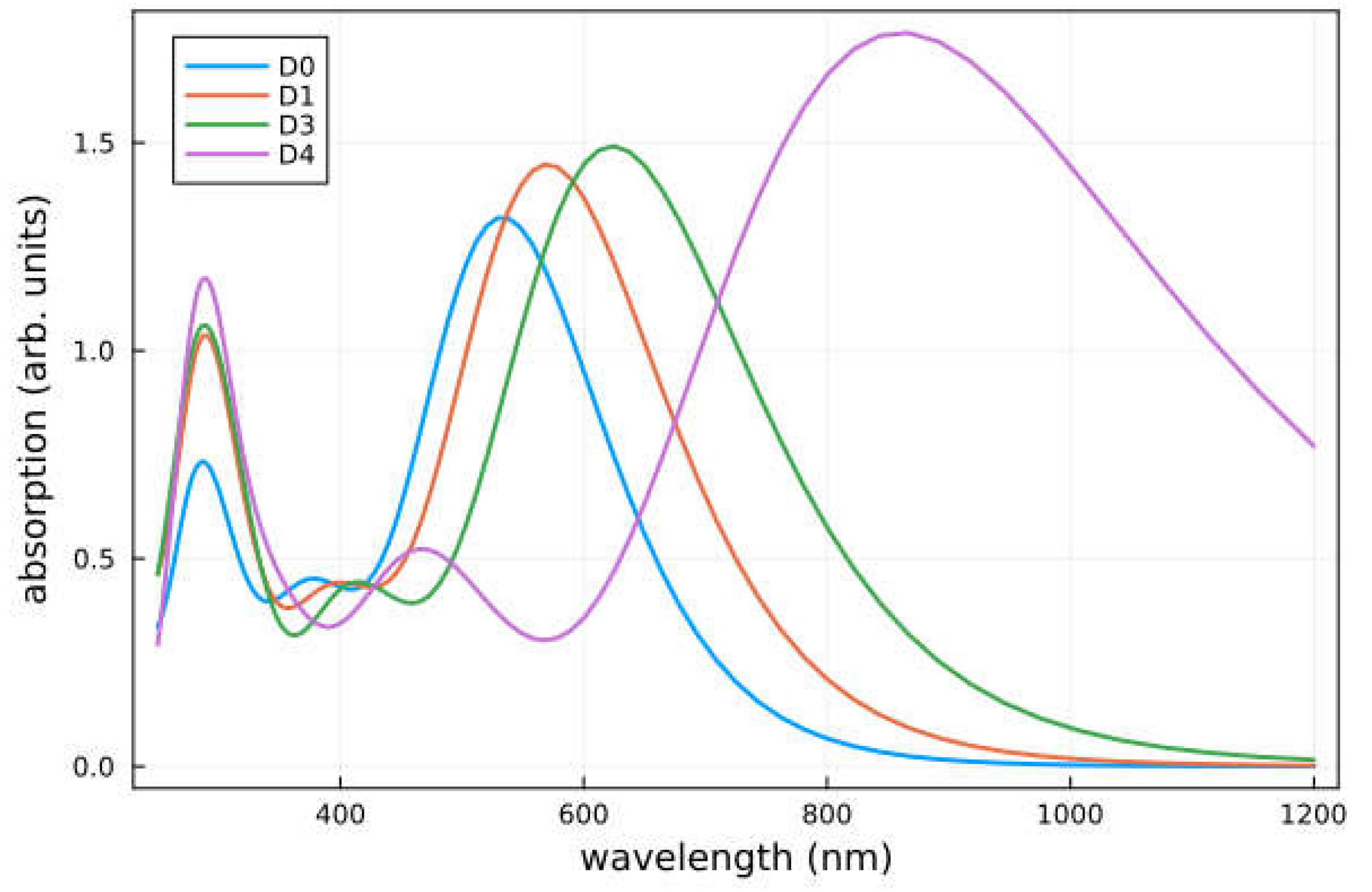
Preprints 74425 g005
Table 1. Ionization potential (IP=-EHOMO, in parentheses the ∆ S C F values which includes electronic relaxation effects), electron affinity (EA=-ELUMO), chemical potential (µ), global hardness (η), electrophilicity (ω), electron accepting power (ω+), and electron donating power (ω-) (all in eV).
Table 1. Ionization potential (IP=-EHOMO, in parentheses the ∆ S C F values which includes electronic relaxation effects), electron affinity (EA=-ELUMO), chemical potential (µ), global hardness (η), electrophilicity (ω), electron accepting power (ω+), and electron donating power (ω-) (all in eV).
Dye IP EA η μ ω ω+ ω-
D0 6.43 (5.45) 2.31 2.06 -4.37 9.26 2.70 10.41
D1 6.31(5.31) 2.28 2.01 -4.30 9.17 2.69 10.32
D2 6.30 (5,.31) 2.28 2.01 -4.29 9.18 2.69 10.32
D3 6.06 (5.07) 2.23 1.91 -4.14 8.98 2.66 10.10
D4 5.70 (4.75) 2.45 1.63 -4.07 10.20 3.27 11.48
D5 5.72 (4.76) 2.45 1.63 -4.09 10.23 3.28 11.51
Table 2. Vertical transition energy, wavelength, and oscillator strength of maximum absorption peak according to CAM-B3LYP TDDFT calculation. All transitions are dominated by HOMO to LUMO configurations. For D0-D3 there is some admixture of HOMO-1 to LUMO and HOMO to LUMO+1, whereas for D4 and D5 it is only HOMO-1 to LUMO. In the last column the LHE, Eq. (8), is given.
Table 2. Vertical transition energy, wavelength, and oscillator strength of maximum absorption peak according to CAM-B3LYP TDDFT calculation. All transitions are dominated by HOMO to LUMO configurations. For D0-D3 there is some admixture of HOMO-1 to LUMO and HOMO to LUMO+1, whereas for D4 and D5 it is only HOMO-1 to LUMO. In the last column the LHE, Eq. (8), is given.
Dye Emax (eV) λmax (nm) f LHE
D0 2.32 534.2 1.31 0.95
D1 2.17 570.7 1.43 0.96
D2 2.16 571.2 1.44 0.96
D3 1.98 624.3 1.48 0.97
D4 1.44 860.8 1.76 0.98
D5 1.44 857.1 1.75 0.98
Table 3. Free energies of charge injection (ΔGinj), dye regeneration (ΔGreg), and the open-circuit voltage (Voc), all values in eV. Also give is the PCE relative to D0 under the assumption that FF, ηcollect, and Pin are the same for all dyes. The factor Voc L H E   Φ i n j e c t   amounts to 1.4 for D0.
Table 3. Free energies of charge injection (ΔGinj), dye regeneration (ΔGreg), and the open-circuit voltage (Voc), all values in eV. Also give is the PCE relative to D0 under the assumption that FF, ηcollect, and Pin are the same for all dyes. The factor Voc L H E   Φ i n j e c t   amounts to 1.4 for D0.
Dye ΔGinj ΔGreg Voc PCE
D0 -0.87 0.65 1.69 100
D1 -0.86 0.51 1.72 101
D2 -0.85 0.51 1.77 100
D3 -0.91 0.27 1.77 111
D4 -0.69 -0.05 1.55 75
D5 -0.68 -0.04 1.55 73
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated